Porting the Meso-NH atmospheric model on different GPU architectures for the next generation of supercomputers (version MESONH-v55-OpenACC)

The advent of heterogeneous supercomputers with multi-core central processing units (CPUs) and graphics processing units (GPUs) requires geoscientific codes to be adapted to these new architectures. Here, we describe the porting of Meso-NH version 5.5 community weather research code to GPUs named MESONH-v55-OpenACC with guaranteed bit reproducibility thanks to its own MPPDB_CHECK library. This porting includes the use of OpenACC directives, specific memory management, communications optimization, development of a geometric multigrid (MG) solver and creation of an in-house preprocessor. Performance on the AMD MI250X GPU Adastra platform shows up to 6.0× speedup (4.6× on the NVIDIA A100 Leonardo platform), and achieves a gain of a factor of 2.3 in energy efficiency compared to AMD Genoa CPU Adastra platform using the same configuration with 64 nodes. The code is even 17.8× faster by halving the precision and quadrupling the nodes with a gain in energy efficiency of a factor of 1.3. First scientific simulations of three representative storms using 128 GPUs nodes of Adastra show successful cascade of scales for horizontal grid spacing down to 100 m and grid size up to 2.1 billion points. For one of these storms, Meso-NH is also successfully coupled to the WAVEWATCH III wave model via the OASIS3-MCT coupler without any extra computational cost. This GPU porting paves the way for Meso-NH to be used on future European exascale machines.

1 Introduction

Numerical simulation of the atmosphere plays a crucial role in understanding and anticipating extreme weather phenomena. The skill of numerical weather prediction (NWP) has continuously improved over the last few decades thanks to a steady accumulation of scientific knowledge and technological advances (Bauer et al., 2015). Increased computing power has enabled numerical simulation to represent even greater complexity on a wider range of scales. Current operational NWP codes typically achieve horizontal resolutions of 𝒪(10 km) on a global scale and 𝒪(1 km) on a regional scale, which represent deep convection in parameterized and explicit ways, respectively. Global storm-resolving models used in research can simulate the atmosphere globally with convection-permitting resolutions of 𝒪(1 km) to seamlessly represent scales from local storms to planetary waves (e.g., Tomita et al., 2005; Fuhrer et al., 2018; Stevens et al., 2019; Giorgetta et al., 2022; Donahue et al., 2024).

The Meso-NH community weather research code (Lac et al., 2018) takes advantage of an efficient parallelization and from increases in computing power to run large-eddy simulations (LESs; horizontal resolution of 𝒪(10–100 m)) on very large computational grids of the order of a billion grid points. These so-called giga-LESs (Khairoutdinov et al., 2009) resolve most of the turbulent kinetic energy over the full extent of weather systems (𝒪(100 km)). Such giga-LES runs with Meso-NH make it possible to show, for example, the effect of small-scale surface heterogeneities and buildings on the radiation fog over an airport (Bergot et al., 2015), turbulent mixing leading to stratospheric hydration by overshooting convection (Dauhut et al., 2018), the multiscale modeling of coupled radiative and heat transfer in complex urban geometry (Villefranque et al., 2022), and the downward transport of strong winds by roll vortices in a Mediterranean windstorm (Lfarh et al., 2023). Designed for studies of scale interactions between processes, these giga-LESs provide a unique research base for statistical or climate studies in a scientific community beyond that of Meso-NH.

To benefit from technological advances, numerical codes of the atmosphere need to be adapted to current and future supercomputers based on hybrid architectures with both central processing units (CPUs) and graphical processing units (GPUs). For instance, the most powerful system today is Frontier in the USA, a nearly 2 exaFLOPS machine (i.e., exceeding 2×10¹⁸ floating-point operations per second) based on AMD MI250X GPUs. In Europe, while the most powerful systems are below the exascale level (i.e., below 1 exaFLOPS), they are also built with GPUs, such as Leonardo in Italy with NVIDIA A100 GPUs (0.3 exaFLOPS) and Adastra in France with AMD MI250X GPUs (0.06 exaFLOPS). Running a model like Meso-NH on these new supercomputers is a big challenge because the code must be ported to GPU. An abundant literature documents the efforts made by the various modeling communities. For example, Fuhrer et al. (2018) completely rewrote the dynamical core of the COSMO model using a domain-specific language. Giorgetta et al. (2022) ported the ICON atmosphere model to GPUs by introducing OpenACC directives. After 5 years of model development, Donahue et al. (2024) have fully rewritten the Energy Exascale Earth System Model atmosphere model in C++ using the Kokkos library.

Here, we describe the porting of Meso-NH version 5.5 to GPU named MESONH-v55-OpenACC and illustrate applications with giga-LES runs in the framework of a grand challenge pilot project on the Adastra supercomputer, ranked 10th in the June 2022 TOP500 (TOP500.org, 2022b) and 3rd in the November 2022 GREEN500 (TOP500.org, 2022a). We choose the directive-based method using OpenACC for the porting. First, this method of manually adding GPU directives has less of an impact on the code structure, thus limiting the human effort involved in porting the code. Second, it preserves the readability of the original code. This point is of particular importance for a research code developed and used by many different people and for many different applications in the fields of meteorology, air quality and surface coupling. Third, this method allows the same source code to run on either CPU or GPU. This is another crucial point for Meso-NH, which runs on different computing architectures from personal computers to supercomputers in regional, national and international facilities. Fourth, this method enables step-by-step verification of the addition of GPU modifications and thus allows for the detection of any mistake in implementation or compiler bug. This is of increased importance for the quality of Meso-NH, which is bit-reproducible on CPU. Indeed, Meso-NH provides the same results whatever the number of CPUs, which is verified using our own MPPDB_CHECK library. This bit reproducibility of Meso-NH has been extended here to the OpenACC GPU version, providing bit reproducibility from CPU execution to GPU execution and even more so to multi-GPU execution. To our knowledge, Meso-NH is the only atmospheric (or oceanic) model offering bit-level reproducibility. This outstanding capability guarantees that Meso-NH is parallelization bug-free, i.e., there are no bugs in its implementation for parallel executions on CPUs and GPUs.

The remainder of the paper is organized as follows. Section 2 details the methodology with a brief overview of Meso-NH (Sect. 2.1), inclusion of OpenACC directives (Sect. 2.2), checking bit reproducibility between CPU and GPU (Sect. 2.3), memory management replacing the use of automatic or allocatable arrays to reduce overhead (Sect. 2.4), optimization of communications with a GPU-aware MPI (message passing interface) library (Sect. 2.5), development of a geometric multigrid (MG) solver (Sect. 2.6), and the creation of an in-house preprocessor to facilitate the support and optimization of Meso-NH on different architectures (Sect. 2.7). Section 3 presents performance achieved on a single node and the scaling up to multiple nodes across multiple platforms. Section 4 describes several large-grid weather applications running on the Adastra supercomputer. Section 5 concludes the paper.

2 Methodology

2.1 The Meso-NH community weather research code

Meso-NH is a community weather research code (Lac et al., 2018), initially developed by the Centre National de Recherches Météorologiques (CNRS and Météo-France) and the Laboratoire d'Aérologie (LAERO; UT3 and CNRS). It is a grid-point limited-area model based on a non-hydrostatic system of equations to handle a wide range of atmospheric phenomena, from synoptic to turbulent scales. The code includes fourth-order centered and odd-order WENO advection schemes for momentum and monotonic advection schemes for scalar transport (Lunet et al., 2017). It has a complete set of physical parameterizations, including clouds, turbulence and radiation. Meso-NH is coupled with the SURFEX surface model (Masson et al., 2013) and can be coupled with any ocean or wave model that includes OASIS code instructions (Voldoire et al., 2017). Since Meso-NH is based on an anelastic continuity equation (Lafore et al., 1998), an elliptic equation must be solved with great precision to determine the pressure perturbation. The current pressure solver is an iterative method consisting of a conjugate residual algorithm (Skamarock et al., 1997) accelerated by a flat fast Fourier transform (FFT) preconditioner (Bernardet, 1995). The horizontal part of the operator to invert in the elliptic pressure problem is processed with FFT, while its vertical part leads to the classical tridiagonal matrix. For a detailed description, the reader is referred to Chap. 9, Part I of the scientific documentation available on the Meso-NH website (http://mesonh.aero.obs-mip.fr, last access: 16 December 2024).

Meso-NH is written mainly in Fortran 95 with the use of some more recent functionalities from Fortran 2003 and 2008. It is fully vectorized; i.e., it uses array syntax with almost no loops. Since 1999, most of the code is parallel (Jabouille et al., 1999). The 3-dimensional domain is split into horizontal subdomains in the x and y directions. Each subdomain is then assigned to one process on the parallel computer, and an interface package based on the standard MPI library ensures communications between the processes. The initial parallel implementation of the FFT pressure solver takes into account two other types of partitioning on each horizontal direction called x slice and y slice. Communication routines have been implemented to move a field between these different decompositions. It is then possible to perform the FFT for each horizontal direction (Giraud et al., 1999). In 2011, parallel capability was extended to petaFLOPS computers (i.e., exceeding 10¹⁵ floating-point operations per second) by allowing the grid to be sliced during input/output (I/O) into horizontal planes and parallelizing the FFT preconditioner vertically and horizontally (Pantillon et al., 2011). In the case of FFT, moving data from a vertical pencil decomposition to x and y slices limit the number of processes to the smallest horizontal dimension. For example, a model on a $\mathrm{512}\times \mathrm{512}\times \mathrm{128}$ grid can only be run with 512 processes. Instead, a 3-dimensional decomposition of the pencil was implemented and optimized. For a run using p_x×p_y processes, the global domain of size $N_x\times N_y\times N_z$ is divided into z pencils of size $(N_x/p_x)\times (N_y/p_y)\times N_z$. The FFT is first performed on each x pencil of size $N_x\times (N_y/p_y)\times (N_z/p_x)$ in the x direction and then on each y pencil of size $(N_x/p_y)\times N_y\times (N_z/p_x)$ in the y direction. Next, the tridiagonal system is solved in the Fourier space for each z pencil. Finally, inverse FFTs are calculated on each y pencil and then on each x pencil. As a result, the above example can now be run with up to $\mathrm{512}\times \mathrm{128}=\mathrm{65}$ 536 processes.

The standard Meso-NH benchmark is Hector The Convector, a case of very deep convection that occurs over the Tiwi Islands, north of Darwin, Australia (Dauhut et al., 2015). This test case is easy to run on any supercomputer because it is initialized in temperature, humidity and wind with a single sounding and applies open boundary conditions. In this paper, the weather applications use initial and lateral boundary conditions provided by either the operational analyses of the European Centre for Medium-Range Weather Forecasts (ECMWF) Integrated Forecasting System (IFS) or the Météo-France Applications de la Recherche à l'Opérationnel à Méso-Echelle (AROME) code. The benchmark and weather application runs on Adastra AMD MI250X GPUs nodes include the most commonly used transport schemes and physical parameterizations in Meso-NH. Momentum variables are advected with a centered fourth-order scheme, while scalar variables are advected with the piecewise parabolic method (PPM) advection scheme (Colella and Woodward, 1984). The physical parameterizations are a 1.5-order closure scheme for turbulence (Cuxart et al., 2000) and a one-moment bulk microphysics scheme named ICE3 (Pinty and Jabouille, 1998) which includes five water species (cloud droplets, raindrops, pristine ice crystals, snow/aggregates and graupel). The simulations also involve a radiation scheme (Gregory et al., 2000), usually called every 30 or 60 time steps. The latter coming from the ECMWF, no attempt of porting to GPU has been done.

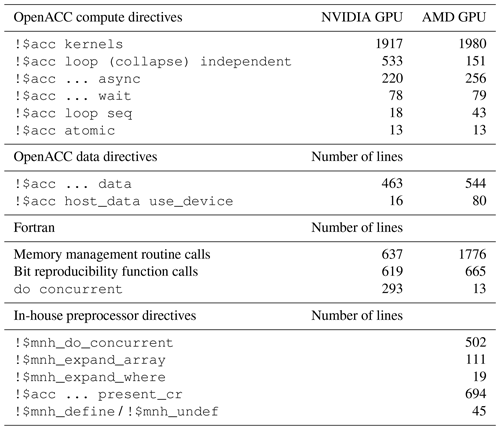
Porting the complete code to GPU is a huge task as Meso-NH contains several thousand source files totaling about a million lines of code. However, the Pareto principle holds for Meso-NH, so 90 % of the computation time comes from 10 % of the code. Thus, the porting work mainly concerns the most computationally intensive parts of Meso-NH, that is, the advection, turbulence, cloud microphysics and pressure solver. This porting work is the result of a development initiated in the early 2010s on an NVIDIA GPU using OpenACC directives with the PGI compiler (since then acquired by NVIDIA). More recently, from late 2021, it has continued with the start of implementation on AMD GPUs using the Cray compiler. In the following, the changes made to port Meso-NH to NVIDIA and AMD GPUs are detailed. The overall impact that leads to the MESONH-v55-OpenACC version is summarized in Table 1. The left column shows the changes made in Meso-NH before the port to AMD GPUs (i.e., for the initial port to NVIDIA GPUs) and the right column the state after it (i.e., for the port to both GPU types). This results in the inclusion of thousands of OpenACC directives. Memory management routines are frequently used, among other things, to reduce the performance impact of allocations and deallocations. Calls to bit-reproducible mathematical functions appear wherever they are necessary. Moreover, loops in array syntax are replaced, in some cases, by do concurrent constructs. For AMD GPUs, an in-house preprocessor was developed, leading to its use in more than 1 000 occurrences and a reduction in the number of do concurrent loops.

Table 1 Number of modified Meso-NH lines for the initial GPU porting on NVIDIA GPUs and after the porting on AMD GPUs. Other changes – multigrid solver, memory manager (except calls to it), algorithmic modifications, code transformations and optimizations – are not accounted for.

2.2 Inclusion of OpenACC directives

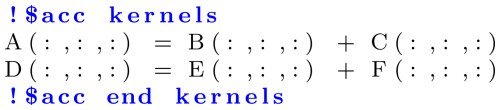
The OpenACC paradigm offers a promising approach for Meso-NH. The developer only has to add directives (seen as comments) in the code to port it to GPUs. Moreover, since the Meso-NH code is mostly written in array syntax, supported by OpenACC, this syntax, free of loops, is well suited to auto-parallelization and auto-vectorization. To limit the impact on the source code and facilitate the porting work, the use of the auto-parallelization kernels directives is preferred. The code largely resembles the one shown in Listing 1.

Listing 1 OpenACC kernels directives with array syntax.

The drawback of the OpenACC paradigm is the data location. Since the memory of the CPU and the GPU is usually separate, the developer must carefully manage data location and transfers between them by adding appropriate OpenACC directives. It is easy to make mistakes and to introduce bugs or have poor performance if unnecessary transfers are coded. Adding OpenACC directives is not always sufficient because for optimization or to work around compiler bugs, some loops need to be explicitly written, which results in losing the compact array syntax. Array-returning functions are not parallelized on GPU (at least in our early developments). They are replaced by subroutines and the use of temporary arrays to store intermediate results (Listing 2).

Listing 2 Example of replacing an array-returning function by a subroutine using temporary arrays to store intermediate results. Note that the original version is preserved and compiled if the preprocessor key MNH_OPENACC is not set.

2.3 Verification of bit reproducibility between CPUs and GPUs

The original CPU-only Meso-NH code, running in parallel on CPU clusters using the MPI library, is already bit-reproducible when the number of MPI tasks varies. This guarantees that no parallelization bugs have been introduced in the CPU coding. This is achieved using our own MPPDB_CHECK library (Fig. 1). The principle is to run two similar simulations concurrently. The primary simulation launches the replica one with a call to mpi_comm_spawn. At certain points, the MPPDB_CHECK library checks on the fly that array values are exactly the same down to the bit. These two executions can have any number of MPI processes.

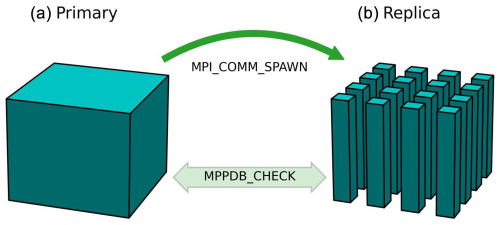
Figure 1 Schematic of bit-reproducible verification between primary and replica simulations using the MPPDB_CHECK library. On the left, the primary simulation is a computation performed on the entire domain, i.e., without any domain decomposition on CPU. On the right, the replica simulation is a parallel computation performed on CPU or GPU on the domain broken down into 4×4 pencils.

The internal MPPDB_CHECK library has been ported to GPU, with the ability to compare values stored in CPU or GPU memory. For NVIDIA GPUs, the Meso-NH code is compiled with the NVIDIA compiler by setting the -acc=host,gpu flag. In this way, the same executable can run on both CPUs and GPUs. The primary simulation runs on CPUs with ACC_DEVICE_TYPE=HOST, while the replica runs on GPUs with ACC_DEVICE_TYPE=NVIDIA. Validation of code changes in Meso-NH for GPU porting is a step-by-step process. To validate the port, the results must be exactly the same on both sides. For AMD GPUs, it is not possible to compile a single executable that can run indifferently on CPU or GPU with the Cray compiler. Therefore, two different executables are generated, one for CPU only and one that supports GPU offloading. To ensure bit reproducibility, options "-Kieee -Mnofma -gpu=nofm" are passed to the NVIDIA compiler to enforce compliance with the IEEE 754 standard (IEEE, 2019) and to disable FMA (fused multiply–add) instructions. For the Cray compiler, options "-Ofp0 -hnofma" are provided.

Some operations are optional (recommended but not required) in the IEEE 754 standard, such as sqrt, exp and log. Several rounding modes are also possible. The sqrt standard implementation is available with NVIDIA and Cray compilers and architectures (if certain compiler options mentioned above are enabled) and gives exactly the same result on both CPU and GPU. This is not true for other mathematical operations provided by the compiler-linked mathematical libraries that are not bit-reproducible between CPU and GPU. It is therefore necessary to replace the intrinsic functions log, pow, sin, cos, atan and atan2. They have all been replaced with equivalent operations based on reproducible standard operations. This is achieved using the bitrep library (Spiros, 2014) written in C++. The performance of these functions tends to be lower, but in practice, the impact on runtime is very limited (less than a few percent). As they are only used to check the correct implementation of the port, their use could be disabled to restore performance. However, the bit-reproducible version is kept even for the run tests presented in this paper.

The bitrep C++ functions have been ported to GPU (Listing 3). This is done by adding OpenACC directives for the NVIDIA compiler. Since the Cray C++ compiler does not support OpenACC directives natively, OpenMP directives are used as an alternative. This implementation seamlessly integrates the OpenACC and OpenMP paradigms, allowing for efficient execution on either NVIDIA or Cray environments. This hybrid approach enables us to leverage the strengths of each programming model while ensuring compatibility with the targeted hardware.

Listing 3 Extract of the porting of the log function of the bitrep library. OpenMP and OpenACC directives are used.

To call these C/C++ functions from Meso-NH, a C–Fortran interface has been written (Listing 4). All the new bit-reproducible math functions are prefixed by BR_. An example of using the logarithm function is shown in Listing 5.

Listing 4 Extract of the C–Fortran interface for the br_log function.

Listing 5 An example of using the logarithm function. The MNH_BITREP preprocessor key is used to choose between the original and bit-reproducible versions.

2.4 Memory management

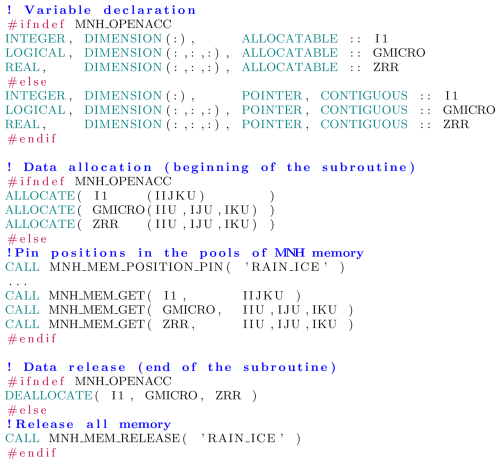
In Meso-NH, memory management for arrays consists mainly of automatic or allocatable arrays. Due to various compiler bugs and the very poor performance of memory allocation on GPUs, this management has been redesigned for use on the GPU. A relatively simple approach is adopted. In the initialization phase, a large 1-dimensional array is allocated once in both CPU and GPU memory spaces. This operation is done for each main intrinsic data type (real, integer and logical). These arrays are used as a memory pool in which the different variable arrays are stored. Therefore, no more array allocation is needed during calculations. The size of these arrays must be carefully chosen to be large enough to contain all the required data but not so large as to waste memory. Their dimensions can be selected using a parameter read from a standard Meso-NH namelist at the simulation start without the need to recompile the model.

When necessary, usually at the beginning of a subroutine (Listing 6), and instead of relying on automatic or dynamic allocation, allocations are replaced by calls that provide pointers to unique portions of the memory pool with MNH_MEM_GET. To keep memory management as simple as possible, before a series of allocations, the positions of the pointers within the pools are stored using MNH_MEM_POSITION_PIN. When the memory is no longer needed (usually at the end of the subroutine), the pointers are reset to these values with MNH_MEM_RELEASE. This is a LIFO (last in–first out) approach, which is ensured by providing the same dummy argument before the block of allocations and the release of the corresponding data. In this way, no deallocation or clean-up is required and no memory fragmentation is possible.

Listing 6 Example of code structure for memory management.

To reduce the number of memory pools to just one per intrinsic data type, pointer bounds remapping (a Fortran 2003 functionality) is used to map multidimensional arrays onto 1-dimensional pools. A possible optimization is to align the memory addresses of the beginning of each returned pointer to GPU memory segments, but tests on NVIDIA and AMD GPUs show no performance improvement. The use of pointers instead of automatic or allocated arrays may prevent the compiler from doing some optimizations because it must assume that aliasing is possible between different pointers. This behavior has a significant impact on the performance with the Cray compiler used for the porting to AMD GPUs. To restore good performance, it is necessary to pass the "-halias=none" option to this compiler.

2.5 Communications with a GPU-aware MPI library

When run on a supercomputer with multiple CPUs and GPUs, Meso-NH uses the MPI library and domain decomposition with additional halo points at grid boundaries in horizontal directions to maintain computational consistency. For halo exchange communications on the GPU, the data are already in GPU memory as they are computed there. It is therefore more efficient to transfer data directly between GPUs or within a given GPU if the processes run on the same GPU. Otherwise, the data are copied to CPU memory, transferred between CPUs and finally copied to the memory of the target GPU. On some architectures, such as Adastra, network cards are physically connected to GPUs rather than CPUs, and the available MPI library is GPU-aware, allowing direct transfer between GPUs. On other architectures, even if the network is not directly connected to the GPUs, direct transfers between processes running on GPUs inside a machine node are possible if the MPI library supports them. For OpenACC coding, this is implemented by the directive !$acc host_data use_device. An extract from the GET_HALO_START_D and GET_HALO_STOP_D subroutines is shown in Listing 7. It details how this GPU-aware capability is combined with MPI non-blocking communications and OpenACC asynchronous kernels.

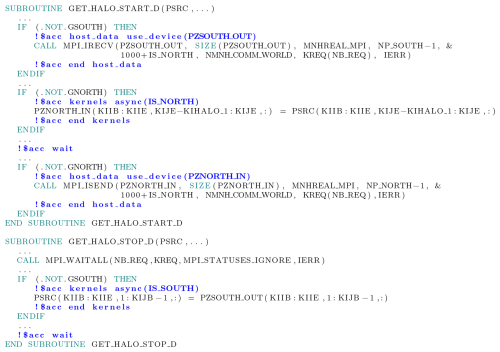
Listing 7 Extract of MPI GPU-aware usage for north–south halo exchange (west–east removed) with MPI non-blocking communications and OpenACC asynchronous kernels.

In the GET_HALO_START_D routine, halo communication is initiated. First, a non-blocking receive (MPI_IRECV) is posted in advance for the output halo buffer (PZSOUTH_OUT), indicating that the data are stored in GPU memory (!$acc host_data use_device(PZSOUTH_OUT) directive). Then, in an asynchronous OpenACC kernel (!$acc kernels async(IS_NORTH)), the input halo buffer (PZNORTH_IN) is filled from the boundary of the field PSRC. The same operation (not shown) is done for the south, east and west boundaries. To ensure completion of the four kernels filling the north, south, east and west buffers, an OpenACC synchronization is performed with !$acc wait. At the end of the routine, the input halo buffer PZNORTH_IN is sent with a non-blocking MPI_ISEND call, encapsulated by the OpenACC directive indicating again that the data are on the GPU with !$acc host_data use_device(PZNORTH_IN). In the GET_HALO_STOP_D routine, halo communication is finalized. First, the completion of the previous non-blocking MPI communication is ensured with a MPI_WAITALL call. Next, the output halo buffer PZSOUTH_OUT is copied to the southern boundary of the field PSRC in an asynchronous OpenACC kernel (!$acc kernels async(IS_SOUTH)). The same operation is repeated for the three other boundaries in three other asynchronous kernels (not shown). Finally, the subroutine ends by waiting for the completion of these kernels (!$acc wait). Between calls to the GET_HALO_START_D and GET_HALO_STOP_D routines, operations not dependent on the field involved in the halo exchange can be interspersed. This allows calculations to overlap with communications.

2.6 Development of a multigrid pressure solver

A critical point for GPU porting is the pressure solver needed for the elliptic equation inversion. In the original version of Meso-NH, this solver consists of an FFT preconditioner associated with the conjugate residual algorithm. The FFT preconditioner requires all-to-all communications between MPI processes and therefore between GPUs when several GPUs are used. These data transfers are very bandwidth-intensive, and their cost increases rapidly with the number of GPUs. As the local FFT calculations run faster on GPU than on CPU, the fraction of time consumed by these communications is not negligible and can become very high, especially when multiple GPUs distributed across multiple nodes are used. Such a negative impact of all-to-all communications in the FFT preconditioner has been seen with Meso-NH running on MIRA, a Blue Gene/Q system at Argonne National Laboratory by showing sub-optimal scalability when using 2 billion threads (Lac et al., 2018, see their Fig. 1). Verma et al. (2023) performed a scaling analysis of their GPU-FFT library for grid sizes of 1024³, 2048³ and 4096³, utilizing up to 512 A100 GPUs. They reported a ratio of communication time to total time of 50 % when using 8 GPUs and over 90 % when using more than 128 GPUs. Ibeid et al. (2020) showed in exascale projections for grid size of 65 536³ that the FFT total time is solely due to the FFT communication time, which is dominated by the network access cost.

As the FFT solver tends to be inefficient as the number of GPUs increases, a more efficient algorithm is required. The most promising alternative for solving this type of elliptic equation is the use of a geometric multigrid solver for regular structured grids (Fig. 2). In particular, Müller et al. (2015) ported a C CUDA version of a geometric multigrid algorithm that scaled up to 16 384 GPUs. To our knowledge, there is no Fortran numerical library ported with OpenACC that provides such a tool. Consequently, the Fortran version of the TensorProductMultigrid solver developed by Müller and Scheichl (2014) was selected. This multigrid (MG) solver developed for the UK Met Office is well suited for NWP models with a highly vertically stretched grid. The original code is a standalone benchmark version (Müller, 2014), and many modifications have been made to integrate it into Meso-NH.

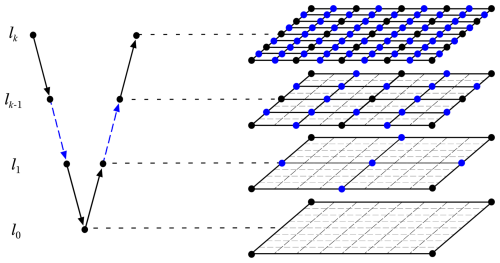
Figure 2 Schematic of the V cycle of the geometric multigrid pressure solver on the horizontal grid. Starting from the finest grid at level k with 2^k cells in the x and y directions, the restriction phase is performed on the coarse grid at level k−1, which is obtained by halving the number of cells in each direction. The process proceeds from top to bottom until the grid contains only one cell. Then, in the prolongation phase, the grids are refined in the reverse process upward, multiplying the grid cells in each direction by 2 (blue points figuring edges added/removed in this process).

The MG code was first adapted for the CPU version of Meso-NH. On the Meso-NH part, interface routines were introduced. On the MG part, the tensor-product coefficients were fitted to meet the needs of Meso-NH; new Neumann boundary conditions specific to Meso-NH were added. For debugging and bit reproducibility purposes, calls to our MPPDB_CHECK library were incorporated into the MG code. This revealed a bug in the original parallel code (a missing MPI halo exchange). After fixing, a version of Meso-NH fully bit-reproducible on multiple CPUs with this new solver was obtained. Extensive performance and scalability tests were performed to set optimal parameters for the solver, such as the iterative method, the convergence rate, the smoother, the number of grid levels, the restriction and prolongation phases, and the coarsest-grid solver.

Due to the characteristics and the original implementation of the MG solver, its use imposes some constraints. First, the grid size must be of the form 2^N for both horizontal axes, as shown in Fig. 2. At each level of coarsening, from k to k−1, the number of cells is halved in each direction until the last level, which contains only one cell. Second, the grid size on the vertical axis is free since no downsizing is done in this direction due to strong stretching that makes it unfit. In this direction, since the matrix to be inverted has a tridiagonal form, a Thomas algorithm (simplified form of Gaussian elimination) is used instead. Finally, as the original solver does not allow for load imbalance, the number of MPI processes must be 2^(2×P) because the size of the solver grids must be halved in each direction at each coarsening. This limitation has been relaxed somewhat. The number of MPI processes can be of the form 2^P, but the MG must use one fewer grid level. In that case, the last coarse level can have 2×2 or 2×1 cells, and two iterations are needed in this last level.

To port this multigrid pressure solver on GPUs, the MG code has been refactored to change the original layout of the arrays from KJI to IJK indexing (as in Meso-NH) to optimize memory accesses on GPUs, and OpenACC kernels directives have been added. The same recipes as for Meso-NH have been applied: memory management with a preallocated memory pool, replacement of array syntax with do concurrent constructs where necessary, and MPI communications with GPU-aware OpenACC directives to avoid unnecessary data transfers between CPUs and GPUs. A new optimization is also introduced specifically for the MG solver for hybrid executions on CPUs and GPUs: a new parameter, configurable at runtime, is added to select the coarse grid level at which the MG solver switches calculations from GPUs to CPUs. This parameter is useful when the local sub-grid is too small to provide performance gains on GPUs. Bit reproducibility is again ensured between CPU and GPU executions.

Despite the limitations of the FFT solver, it is also ported on GPUs for comparison with the new MG solver. The FFT solver also has the advantage of fewer restrictions on grid dimensions and the number of MPI processes. Test results (Sect. 3) show that it remains a good choice for simulations with a limited number of GPUs. It should be noted that the comparison between FFT and MG pressure solvers is presented only in terms of computational performance. No reproducibility of pressure between solvers is expected. Similar accuracy, i.e., the same threshold in the residual divergence of the pressure value, is, however, demanded by both solvers.

2.7 Creation of an in-house preprocessor

Loop performance optimizations for AMD or NVIDIA GPUs are often incompatible and cannot be mixed. To avoid having two different versions of the Meso-NH code and to avoid degrading readability by multiplying preprocessing keys (i.e., #ifdef keywords), a small preprocessor named mnh_expand has been developed. It uses filepp (Miller, 2008), an enhanced programmable preprocessor, compatible and similar to cpp, with powerful user-defined macros, all written in Perl. With this tool, different transformations can be applied on different architectures, allowing for customized optimizations on different CPUs, GPUs and compilers.

For NVIDIA GPUs, it is necessary to rewrite some loops originally in array syntax as nested loops or with do concurrent constructs. This approach works very well and generates parallel and collapsed loops that are optimal for the GPU. For AMD GPUs, the do concurrent syntax is not managed efficiently by the Cray compiler, which generates poor parallel uncollapsed loops. In addition, inclusion of the OpenACC directives, which collapses and parallelizes loops (!$acc loop collapse(X) independent directive) generates compiler errors or serializes kernels. However, this directive leads to good parallelization if used in conjunction with nested loops instead of a do concurrent construct. The exception is when our bit-reproducible mathematical functions are present in the loop. In the latter case, it is necessary to inhibit the transformation of array syntax into nested loops and not to supply the collapse OpenACC directive (Listing 8).

Listing 8 Example of using the !$mnh_expand_array macro for the not-bit-reproducible math functions exp and power. For the Cray compiler, expansion to nested loops and the addition of OpenACC directives are first inhibited around bit-reproducible procedures and then reactivated for the remaining of the code with the mnh_undef and mnh_define macros.

Optimization choices are made via preprocessor keys. For example, the MNH_EXPAND_OPENACC key generates loop collapse and independent OpenACC directives and the MNH_EXPAND_LOOP transforms the code into nested loops. If the latter is omitted, the do concurrent instructions are added instead. To manage all these different and contradictory situations, three different macros are introduced (Listing 9). At the preprocessing stage, they generate the most efficient form of expression according to the architecture and compiler targeted.

Listing 9 Synthetic example of the three main in-house preprocessing directives.

Loops in Fortran array syntax requiring transformation are enclosed by the !$mnh_expand_array and !$mnh_end_expand_array directives (Listing 10). They allow for automatic rewriting of the loop index in array expressions and generate the appropriate nested loops or do concurrent constructs depending on the activated keys (Listings 11 and 12). For expressions already transformed into the do concurrent form, the macro !$mnh_do_concurrent is used. For where constructs in array syntax, the !$mnh_expand_where directive is implemented.

Listing 10 Example of the use of the !$mnh_expand_array and present_cr macros.

Listing 11 Example of transformed sources after preprocessing the !$mnh_expand_array and present_cr macros for the NVIDIA compiler. Note that the present_cr clause has vanished; otherwise, the NVIDIA compiler issues an error for the double present declaration of ZWORK arrays.

Listing 12 Example of transformed sources after preprocessing the !$mnh_expand_array and present_cr macros for the Cray compiler. In this case, the second present clause is needed for parallelization and to avoid false recurrence detection by the Cray compiler.

Another preprocessor directive is necessary to circumvent the frequent erroneous detection of recurrences between loop iterations by the Cray compiler. These recurrences prevent the parallelization of these loops and lead to the generation of serial code. The bypass found is to add extra OpenACC present clauses with loop or kernels directives for certain variables even if they are already in a block where they have been declared as present. Since, in some cases, the NVIDIA compiler reports errors if a variable is declared as present twice, different behaviors are necessary for these two compilers. The present_cr macro (Listing 10) generates the OpenACC present clause only by activating the MNH_COMPILER_CCE preprocessor key (set for the Cray compiler).

3 Computational performance

The computational performance is estimated for the Hector The Convector test case, the standard Meso-NH benchmark. The test case uses advection, turbulence, cloud microphysics, pressure solver (see Sect. 2.1 for more details) and other components. These other components include elements not covered by the abovementioned processes, such as gravity and Coriolis terms (executed on GPUs), radiation (called every 900 s only, executed on CPUs), time advancement of all variables, and I/O operations (which are largely disabled in our simulations). The vertical grid has 128 levels. The horizontal grid covers a square with a 204.8 km side centered over the Tiwi islands. Results are shown here for two grids, $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ with an horizontal grid spacing of 800 m and $\mathrm{4096}\times \mathrm{4096}\times \mathrm{128}$ with an horizontal grid spacing of 50 m. It is run during 100 time steps using a time step of 10 s for the small grid and 4 s for the large one. For this benchmark, I/O is disabled (except for reading the initial state). Executions start from a situation in which convection has already been initiated and clouds cover a significant portion of the domain. Running times are given without the initialization phase, unless otherwise stated, and are per model time step.

3.1 Computer systems

The software versions of essential packages for building and running the Meso-NH executable are listed in Table 2. Computer systems on which the computational performance is measured are detailed in Table 3.

Table 2 Software used for compiling Meso-NH.

Table 3 Main characteristics of the supercomputer nodes used for the porting and performance tests. Note that each AMD MI250X contains two GCDs (graphics compute dice), seen as two GPUs by the system.

3.2 Performance on a single node

All results for a single node are for the $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ grid. The domain decomposition is performed by dividing the domain into blocks of the closest possible dimensions in both horizontal directions and distributing the subdomains on the different MPI processes (one subdomain per process). Then, each MPI process is associated (bound) with a GPU on which it will offload part of its calculations (those that have been ported to GPU). It is then possible to associate several MPI processes with the same GPU, which will then share its resources (in a way quite similar to sharing cores on a CPU). Binding on CPU cores and GPUs is carefully chosen to take into account the fact that Meso-NH is memory-bound (i.e., its runtime is dominated by memory access rather than computation), the interconnection between cores on different NUMA (non-uniform memory access) zones, between cores, between CPUs and GPUs, and between GPUs and also the way the domain is distributed onto the MPI processes. If several binding configurations have been tested, only the one giving the fastest results is kept. For example, the best run on an Adastra node with 16 MPI processes uses a 4×4 subdomain grid. To optimize MPI communications, processes with neighboring subdomains are mapped to nearby GPUs, prioritizing proximity and direct network links. To optimize memory bandwidth, each process is pinned to a separate CPU core, evenly distributed across the eight L3 caches (two processes per cache) and four NUMA nodes. Finally, MPI processes are paired with their closest GPU for optimal host–device memory transfers. On NVIDIA GPUs, if several MPI processes are started on each one, the NVIDIA Multi-Process Service (MPS) is launched. If this is not the case, performance is severely impacted.

The performance is first detailed on a routine-by-routine basis for a single Adastra node (see its characteristics in Table 3). The best performance obtained for the $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ configuration using the FFT solver is shown, that is, using 64 MPI processes for the CPU-only version of Meso-NH and eight GPUs multiplied by two MPI processes for the GPU version (Fig. 3).

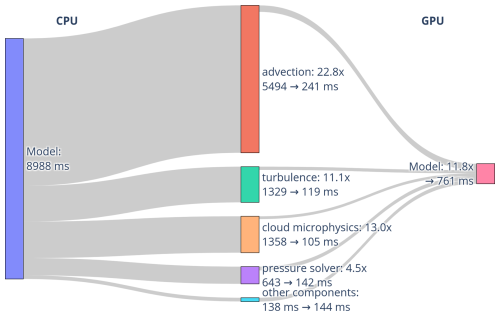
Figure 3 Sankey diagram showing the mean runtime per time step achieved on a single Adastra node for the code running on CPU on the left and running on GPU on the right. Results are shown for the $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ configuration using the FFT pressure solver.

Overall, Meso-NH is $\sim \mathrm{12}\times$ faster on GPUs than when using only the CPUs of the same node on Adastra. This reduces the mean time per time step from 8988 to 761 ms. This speedup is mainly due to the advection running $\sim \mathrm{23}\times$ faster on GPUs. The result is a time reduction from 5494 to 241 ms. The second- and third-biggest time reductions concern cloud microphysics (from 1358 to 105 ms, $\sim \mathrm{13}\times$ faster) and turbulence (from 1329 to 119 ms, $\sim \mathrm{11}\times$ faster). Time is also reduced from 643 to 142 ms for the pressure solver. This $\sim \mathrm{4}\times$ acceleration is, however, lower than for the previous subroutines. This could be due to the numerous MPI inter-process communications required for global pressure solving. No reduction is achieved for the other subroutines. These mainly consist of subroutines not ported to GPU. As the number of processes is 16 for the fastest GPU run versus 64 for the fastest CPU one, and a small fraction of subroutines are ported to GPU, two opposing effects compete and no gain is expected on this side.

Results on Jean-Zay (see its characteristics in Table 3) show similar performance for the GPU run (553 ms instead of 761 ms per time step; Sankey diagram not shown). As Meso-NH is a memory-bound code, and the memory bandwidths on the NVIDIA A100 and AMD MI250X are relatively similar, this result is expected. The GPU speedup on Jean-Zay compared to the fastest results on the CPUs of the same node is only a factor of 6.2. This difference with an Adastra node (speedup of 11.8) can be attributed to the fact that the memory bandwidth available to the CPU is higher on Jean-Zay nodes compared to Adastra nodes, leading to a performance increase of around 2 between the two different node types.

GPU performance depends on the number of MPI processes per GPU. Overload performance results are shown using one, two, four and eight GPUs of a single node of Adastra and Jean-Zay (Fig. 4). Runtimes for the $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ configuration using the FFT pressure solver are presented for up to 4 processes per GPU for Adastra and 16 for Jean-Zay. Overloading the Adastra GPU with more than four processes leads to very deteriorated performance and is therefore not shown. On Jean-Zay, due to constraints imposed by the supercomputing center, it is not possible to run jobs with more than 32 processes per node.

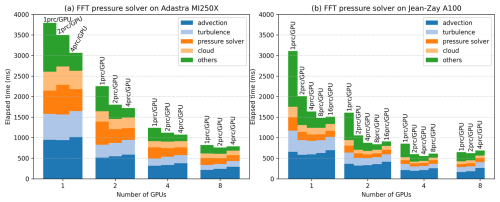
Figure 4 Mean runtime per model time step of Meso-NH as function of the number of GPUs for (a) Adastra and (b) Jean-Zay. The abbreviation prc stands for MPI process. Results are shown for the $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ configuration using the FFT pressure solver.

The more GPUs, the faster the code. An exception is the similar elapsed time obtained for four and eight GPUs on Jean-Zay, particularly as the number of MPI processes per GPU increases. Two possible explanations should be investigated: the interconnection between GPUs and/or between CPUs and GPUs is saturated, or the workload by process becomes too low due to the decreasing size of the MPI subdomains. Increasing the number of MPI processes while maintaining the same number of GPUs generally reduces the total elapsed time. The greatest time reduction is achieved by doubling the number of processes from one to two for one, two and four GPUs. This reduction is most dramatic for the other components, i.e., those parts of the code that are very partially ported to GPU. By increasing the number of processes, the workload of the other components can be distributed over a greater number of CPU cores, reducing the total elapsed time. This reduction with MPI overloading is also found for the pressure solver, and only on Jean-Zay for cloud and turbulence. Advection is also accelerated when using two processes per GPU instead of one on Jean-Zay for one, two or four GPUs and only for one GPU on Adastra. Otherwise, the cost is higher. Using four or more processes per GPU does not significantly reduce elapsed time. It even increases it by doubling their number on Jean-Zay from 8 to 16 for 1 and 2 GPUs, from 4 to 8 for 4 GPUs and from 2 to 4 for 8 GPUs. On Adastra (not shown in Fig. 4), using eight processes per GPU multiplies running time several times. In summary, this result suggests recommending an overload of two MPI processes per GPU when running on a full node.

GPUs of Adastra have 2.5 times the peak computing power of those of Jean-Zay, but their memory bandwidth is very close (see Table 3). As Meso-NH is memory-bound, similar results are expected. For a relatively low number of GPUs, performance without the other components (and therefore with only the GPU part of the code) shows runs on Adastra 2 times slower than on Jean-Zay. But as the number of processes and GPUs increases, elapsed times on the two systems come closer together. These differences likely come from the different architectures, GPUs and software environments.

The dependence of GPU performance on the number of MPI processes per GPU is examined in more details for the results of the FFT and MG pressure solvers (Fig. 5). As expected, the results for the FFT pressure solver are similar to those obtained above: (i) the more GPUs, the faster the FFT pressure solver (with the exception of four and eight GPUs on Jean-Zay); (ii) doubling the number of processes from one to two for one, two and four GPUs significantly reduces elapsed time (with the exception of one GPU on Adastra). In other words, overloading GPUs with at least two MPI processes makes the FFT pressure solver faster.

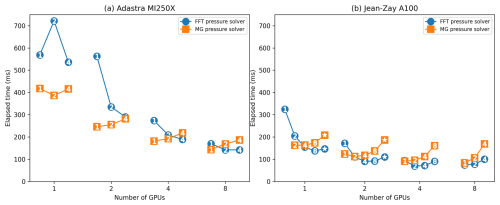
Figure 5 Mean runtime per time step of the FFT and MG pressure solvers as a function of the number of GPUs for (a) Adastra and (b) Jean-Zay. Numbers indicate the numbers of MPI processes per GPU, and the star symbol represents 16 MPI processes per GPU. Results are shown for the $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ configuration.

Alternatively, overloading GPUs with two MPI processes does not greatly affect the speed of the MG pressure solver. Elapsed time increases slightly using up to 4 MPI processes per GPU (with the exception of 8 GPUs on Jean-Zay) and becomes much longer with 8 or 16 MPI processes per GPU (not shown but also true and much worse with 8 GPUs on Adastra). It is therefore not recommended to overload GPUs with MPI processes for the MG pressure solver, especially as the number of GPUs increases. The MG pressure solver is faster than the FFT solver when the number of MPI processes is low. The scalability of the MG solver seems lower. As the number of MPI processes increases, the performance of the FFT solver improves faster than the MG one until it overtakes it. Note that this conclusion is different for the $\mathrm{4096}\times \mathrm{4096}\times \mathrm{128}$ configuration run over a large number of nodes (see Sect. 3.3). Finally, the performance on eight GPUs of Jean-Zay is, as seen for the model as a whole, not better than on four GPUs.

The energy efficiency of the GPU port is also examined (Fig. 6). The results are shown for the $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ configuration using the FFT solver on one Adastra node. The energy consumption measurement is returned by the job scheduling software, here, the Simple Linux Utility for Resource Management (SLURM), and corresponds to the aggregated node consumption. It does not include network and storage energy consumption. These can be neglected here as the runs are done on a single computer node, and I/O is limited to reading data in the initialization phase. The results compare the CPU and GPU versions of Meso-NH. They are detailed according to the number of MPI processes. The results for the GPU version use all the eight GPUs available on the node. Results for the GPU version running with 64 MPI processes are not shown, as overloading AMD MI250X GPUs with 8 MPI processes reduces performance by significantly increasing execution time, nor are they shown for the CPU version run with 16 MPI processes (or even less), as this configuration partially loads the computing node, leading to almost equivalent power use for double the run time compared with the CPU version running with 32 MPI processes. To obtain a fair comparison between CPU and GPU energy use, all running on the same node configurations, the CPU measurements have to be corrected to remove GPU energy use in idle mode. This is estimated by taking the power usage reported by the rocm-smi command when the GPUs are idle. An average power usage of 90 W is found for each graphics compute die (GCD; a GCD contains two GPUs). Note that, unlike the results presented elsewhere, the initialization phase is included in the measurements.

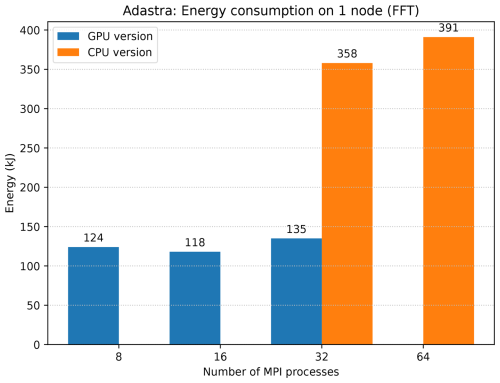
Figure 6 Energy use of Meso-NH on a single Adastra node for the CPU and GPU versions. Results are shown for the $\mathrm{256}\times \mathrm{256}\times \mathrm{128}$ configuration using the FFT pressure solver.

Overall, the GPU version is 3 times more energy-efficient than the CPU-only version. Although GPUs need more power than CPUs and significantly increase the energy requirements of compute nodes, running on GPUs leads to very important gains in terms of energy use. Here, the instantaneous power is around 4 times higher with GPUs, but running time is 12 times shorter. This perfectly illustrates the benefits of using GPUs: shorter running times combined with greater energy efficiency. The number of MPI processes per GPU has an impact on energy consumption. As it increases, so does power draw (power is energy divided by the running time). However, as seen before, the optimum situation in terms of running time is to put two MPI processes per GPU for this test case on Adastra. Here, the fastest GPU run is also the most energy-efficient. If the MG pressure solver is used instead of the FFT solver, the fastest run also corresponds to two MPI processes per GPU, but the run with a single process per GPU is slightly more energy-efficient (needing 110 kJ instead of 116 kJ). For CPU-only runs, using all node cores (64 cores per node) is the fastest but not necessarily the most energy-efficient. For runs with the FFT pressure solver, energy use increases by 9 % compared to a depopulated run with just 32 processes. However, the opposite is found when the MG pressure solver is used (reduction of 11 % in energy need).

3.3 Scaling

The results of the scaling study on Adastra and Leonardo (see their characteristics in Table 3) are shown for the $\mathrm{4096}\times \mathrm{4096}\times \mathrm{128}$ configuration (Fig. 7). The x axis corresponds to the number of nodes used by the model. Four curves are shown for the two computer systems: one using the FFT pressure solver (OpenACC R8I4 FFT) and three using the MG pressure solver. The managed memory version (Managed R8I4 MG) enables the system to implicitly manage data transfers between CPUs and GPUs. The OpenACC R4I4 MG version is compiled with single precision for floating-point numbers. The OpenACC R8I4 MG version corresponds to double precision floating-point numbers. In addition, performance on the CPU AMD Genoa partition of Adastra is shown, and its run time with 64 nodes is used as a reference for speedup calculation. Tables 4 and 5 list the data corresponding to the OpenACC R8I4 MG and Managed R8I4 MG curves, respectively, and detail the speedup routine by routine.

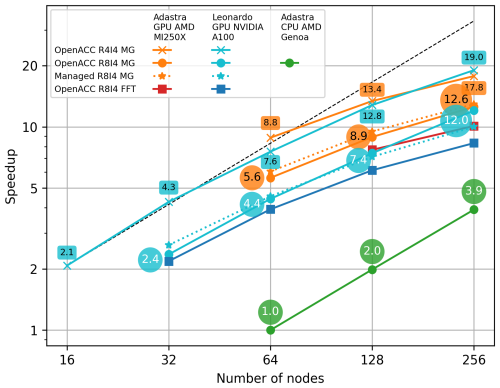
Figure 7 Results for the $\mathrm{4096}\times \mathrm{4096}\times \mathrm{128}$ configuration run on Adastra GPU AMD MI250X, Leonardo GPU NVIDIA A100 and Adastra CPU AMD Genoa. The dashed black line is the reference for the perfect scaling. The speedup is calculated with respect to the elapsed time for the Adastra CPU AMD Genoa partition using 64 nodes.

Table 4 Data, in speedup, corresponding to the OpenACC R8I4 MG curve in Fig. 7.

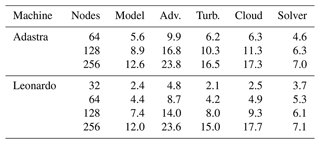
Table 5 Data, in speedup, corresponding to the Managed R8I4 MG curve in Fig. 7.

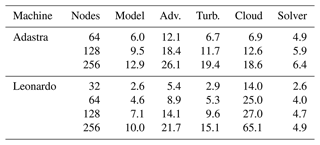
The speedup of GPUs compared to CPUs using 64 nodes is between 2.1 and 19.0, depending on the number of nodes and compiled versions of Meso-NH. This demonstrates the benefits of porting. With the same OpenACC R8I4 MG version, the code is 5.6× faster on Adastra using 64 nodes, with 9.9× faster advection. Performance is a little lower on Leonardo, with a speedup of 4.4 for the model and 8.7 for advection. This is not completely unexpected, as Leonardo nodes have four GPUs instead of eight for Adastra. The Managed R8I4 MG version mainly shows a higher speedup than the OpenACC R8I4 MG version, with the exception of Leonardo with 128 and 256 nodes. Although transfers are better optimized by manual management and have less overhead than managed memory, current developments still incorporate some unnecessary transfers. This explains why Managed R8I4 MG tends to be better. The Meso-NH OpenACC R8I4 FFT version is slower than the OpenACC R8I4 MG version. The difference in speedup is greatest for 256 nodes, where it increases by 50 % on Leonardo (12.0 versus 8.3). The speedup in the pressure solver is indeed 7.0 for MG and 3.2 for FFT. This clearly shows the benefit of introducing a MG pressure solver for GPU porting when the number of GPUs is high.

The OpenACC R4I4 MG version offers greater acceleration than other versions for a given number of nodes. This results in the highest speedup with 256 nodes, 17.8 and 19.0 for Leonardo and Adastra, respectively. This is expected because Meso-NH is memory bound. Reducing the size of floating-point numbers by a factor of 2 also reduces the amount of data that have to be read from or written to memory by almost 2. This also has the benefit of reducing the memory footprint. The benefit of a reduced precision is higher on Leonardo probably because NVIDIA A100s have twice the computing performance with 32-bit floats than with 64-bit floats unlike AMD MI250Xs, which have the same computing power for 32 and 64-bit floats. This reduction in precision does not significantly reduce the convergence time of the pressure solver for this test case.

Scaling is almost perfect with CPUs: doubling the number of nodes doubles the speed. The same applies to GPUs up to 64 nodes only. Using more nodes, the code still runs faster but at a lower rate than expected, i.e., 13.4 against 16 expected with 128 nodes and 19.0 against 32 expected with 256 nodes with the OpenACC R4I4 MG version on Adastra.

The energy gain factor of Meso-NH on Adastra using the GPU AMD MI250X and CPU AMD Genoa partitions is shown for the $\mathrm{4096}\times \mathrm{4096}\times \mathrm{128}$ configuration run (Fig. 8). Four curves are shown for the GPU partition: one using the FFT pressure solver (OpenACC R8I4 FFT) and three using the MG pressure solver, compiled with managed memory (Managed R8I4 MG) or using OpenACC directives with single or double precision (OpenACC R4I4 MG and OpenACC R8I4 MG, respectively). The value for the CPU AMD Genoa partition using 64 nodes is taken as reference.

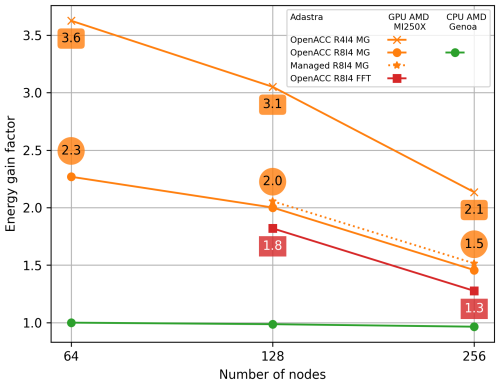
Figure 8 Energy gain factor of Meso-NH on Adastra, using the GPU AMD MI250X and CPU AMD Genoa partitions, for the $\mathrm{4096}\times \mathrm{4096}\times \mathrm{128}$ configuration run. The energy gain factor is calculated with respect to the value for the CPU AMD Genoa partition using 64 nodes.

Table 6 Summary of the simulations undertaken for the grand challenge Adastra. Gpts: 10⁹ grid points.

When using the CPU partition, the energy gain is around 1 regardless of the number of nodes used. In other words, energy cost with CPUs remains the same. This illustrates the perfect scaling of Meso-NH on CPUs seen above. This contrasts with energy gain obtained using GPUs by a factor of 1.3 to 3.6 compared with the CPU reference whatever the Meso-NH version and number of nodes (up to the limit of 256 here). With the OpenACC R8I4 MG version, using GPUs gains energy use to a factor of 2.3, 2.0 and 1.5 for 64, 128 and 256 nodes, respectively. As expected, the use of single precision instead of double precision offers an even greater reduction, with gain factor of 3.6, 3.1 and 2.1 for 64, 128 and 256 nodes, respectively. Gain in energy consumption is increased by up to 0.1 with automatic managed memory from the standard version values. Finally, using the FFT pressure solver results in higher energy use compared to the version with the MG pressure solver. This results in the lowest gain factor with respect to the CPU reference, that is, 1.8 and 1.3 for 128 and 256 nodes, respectively.

4 Weather applications

As part of a grand challenge pilot project on the GPU partition of Adastra, simulations at hectometric resolution are carried out for recent storms leading to extreme wind gusts. Wind gusts are responsible for major damage but remain poorly understood due to their local and intermittent nature (∼1 s), which is inaccessible to standard atmospheric simulations. The numerical efficiency of the Meso-NH code ported to GPU allows for explicit representation of the broad range of mechanisms involved in the formation of small-scale wind gusts in storms. Specifically, the hectometric resolution combined with large grid size makes it possible to describe the scale cascade from the core of the storms (> 100 km) to the deep and shallow convective circulations at the origin of the gusts (< 1 km). Table 6 summarizes the setup of the simulations, which all use the same transport schemes and physical parameterizations as those used in the benchmark.

Two weather events representative of the major types of storms that hit Europe are first simulated (Fig. 9): a North Atlantic storm associated with the midlatitude cyclone Alex, more typical of the winter season (windstorm; a–b), and a Mediterranean storm associated with intense convection and characterized as a derecho, which is more typical of the summer season (thunderstorm; c–d). In both cases, the weather event extends over several hundred kilometers and quickly propagates eastward at a pace of nearly 100 km h⁻¹, which requires a large simulation domain to capture the life cycle of several hours (a, c). However, the formation of gusts occurs at scales of a few kilometers at most, which requires high resolution to be accurately represented (b, d). The wind acceleration involves both deep and shallow convection but contrasts between the two storms, as exemplified by the clear spatial separation between strong winds and rain in the Atlantic cyclonic storm (panel b) and their close proximity in the Mediterranean convective storm (panel d).

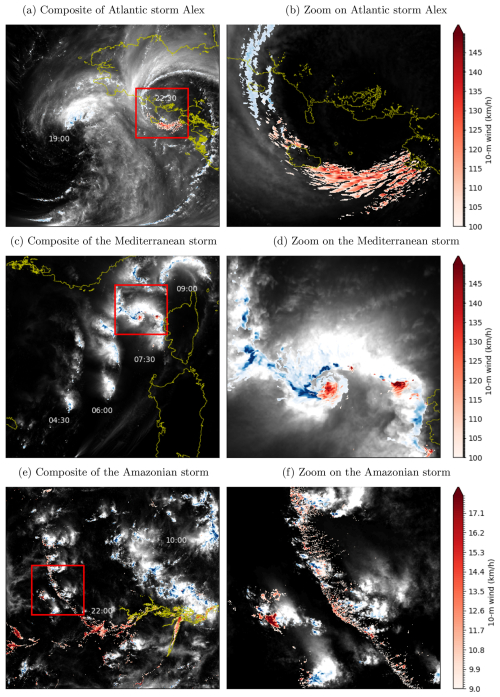
Figure 9 Illustrations of Meso-NH simulations for (a–b) the Atlantic storm Alex on 1 October 2020, (c–d) a Mediterranean storm on 18 August 2022 and (e–f) the Amazon storms on 18 January 2023. Light shadings show the integrated content of hydrometeors, blue shadings show the precipitation rate above 20 mm h⁻¹, and red shadings show the 10 m wind speed. Panels (a, c, e) illustrate composites of different times (in UTC) on the whole domain, while panels (b, d, f) illustrate zooms at specific times in the red boxes.

To complement the study of midlatitude storms, a third event representative of tropical weather is also simulated: a convective storm that spreads over the Amazon forest during the recent field campaign CAFE-Brazil (Fig. 9e–f). In this case, the event extends again over several hundred kilometers (the domain is 800 km large) but propagates much more slowly and westward due to the weak easterly ambient wind in the tropics compared to the strong westerlies in the midlatitudes. Also, the surface wind is much weaker and does not lead to severe gusts or related damages. However, the moderate gusts play a crucial role in continuously triggering new convective cells and ensuring the organization and maintenance of the convective storm as a whole. This upscale effect starts at scales of a few kilometers at most – contrarily to the downscale effect of gust formation in midlatitude storms described above – but also requires high resolution to be accurately represented.

In order to better represent ocean–atmosphere exchanges, which can be crucial for the formation of wind gusts, Meso-NH can be coupled to a wave and/or an oceanic model thanks to the OASIS3-MCT coupler (Craig et al., 2017; Voldoire et al., 2017; Pianezze et al., 2018). This kind of coupled system has been widely used on the CPU partitions of various supercomputers. For the first time and thanks to the grand challenge, coupled simulations between Meso-NH and version 7.02 of the WAVEWATCH III (WW3) spectral wave model (WW3DG, 2019) have been successfully performed on the Adastra GPU partition for the example of the Atlantic storm Alex (Table 6). Since WW3 runs faster than Meso-NH for the same horizontal resolution, parallel exchanges between models via OASIS are very efficient, and WW3 uses CPUs not used by Meso-NH, the computational cost of the coupled simulation is equal to the computational cost of the Meso-NH simulation. No additional cost is found for the coupling component.

While the detailed processes involved are investigated in separate studies, the results illustrate how the simulation of different types of storms may benefit from the combination of large domain and high resolution. Focusing on the Atlantic storm Alex prior to landfall over Brittany (Fig. 9b), Fig. 10 shows the scale cascade as spectrum of kinetic energy in the middle of the boundary layer. The Meso-NH simulation (blue curve) exhibits three distinct ranges: the mesoscale for λ>10 km, the inertial subrange approaching the theoretical slope of the Kolmogorov spectrum (grey line) for λ<1 km, and an energy accumulation range in between for $\mathrm{10}>\mathit{\lambda }>\mathrm{1}$ km. Specifically, the energy accumulation range includes the fine-scale wind structures at the origin of gusts illustrated in Fig. 9b. At smaller scales, the drop in energy for λ<400 m in Fig. 10 indicates that the effective resolution of the simulation reaches 4Δx. In contrast, the AROME operational analysis that provides the initial and lateral boundary conditions for the simulation (orange curve) diverges from Meso-NH for λ<10 km: it captures only the mesoscale only and misses the energy accumulation and inertial subrange.

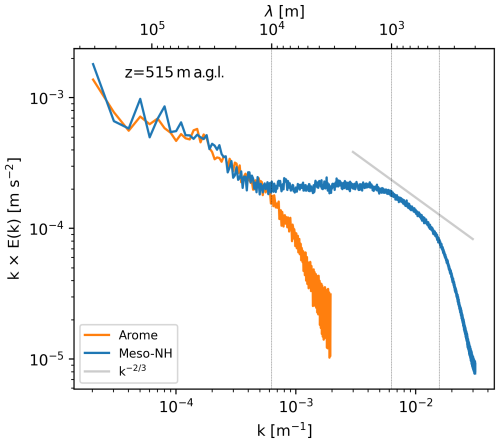
Figure 10 Energy spectrum for the Atlantic storm Alex at 515 m a.g.l. in the Meso-NH simulation (blue curve) and the AROME operational analysis (orange curve). The grey line shows the theoretical slope of the inertial range, while the vertical lines indicate the approximate wavelengths of the lower limit of the mesoscale (λ≈10 km) and the upper limit of the inertial subrange (λ≈1 km), as well as the effective resolution of the simulation (λ≈400 m).

5 Conclusions

Porting Meso-NH to GPUs is achieved by including OpenACC directives to the most computationally expensive parts of the code: advection, turbulence, cloud microphysics and pressure solver. This approach allows for the same code to be run on CPUs and on hybrid CPU-GPU architectures. Using our own MPPDB_CHECK library, the bit reproducibility of Meso-NH has already been ensured on CPUs. This property is extended to GPUs, thus guaranteeing accuracy of the porting and the absence of bugs. A critical point lies in the atmospheric pressure solver, which requires the inversion of an elliptic equation. A multigrid pressure solver is integrated because the fast Fourier transform approach used in the original version of the code becomes expensive with a high number of GPUs. Currently, the code runs on different NVIDIA GPU and AMD GPU platforms and scales efficiently up to at least 1024 GPUs (256 nodes on Adastra and Leonardo). Using the same configuration with 64 nodes on Adastra, Meso-NH is 5.6× faster on GPUs, with 9.9× faster advection, and achieves a 2.3× energy efficiency gain compared to CPUs only.

Porting of other functionalities of the code to GPU is in progress. This includes grid nesting capabilities, ability to use other grid configurations than those imposed by the multigrid pressure solver and other components such as the two-moment cloud microphysics scheme. Moreover, the current porting concerns version 5.5, while the latest version of Meso-NH is version 5.7. An update of the latest version with MESONH-V55-OpenACC is therefore necessary. In particular, in version 5.7, the physical parameterizations have been externalized to create PHYEX (PHYsique EXternalisée). This library shared with the operational NWP code AROME of Météo-France aims to provide greater modularity, enable coherent management of developments in physics and facilitate adaptation to different computing architectures. This also opens up possibilities for use in other models. Thus, the next version of PHYEX will include the GPU modifications from MESONH-V55-OpenACC as well as domain-specific language development in order to integrate the operational constraints inherent to AROME. A physical parameterization not included in PHYEX is the ECMWF radiation scheme (neither the version by Gregory et al., 2000, nor ecRad by Hogan and Bozzo, 2018). The most recent scheme, ecRad, is a method for efficiently handling the 3-dimensional radiative effects associated with clouds, a property essential for fine resolution. It is currently being ported to GPUs at ECMWF and will be included, when available, in a future version of Meso-NH. Finally, it is expected that the MESONH-V55-OpenACC version will work as such on the new machines equipped with an accelerated processing unit (APU), with the advantages of automatic data transfer for memory and I/O (Tandon et al., 2024; Fusco et al., 2024).

First scientific applications focus on the simulation of extreme weather events across scales as part of a grand challenge pilot project on the GPU-based Adastra supercomputer, ranked third in the November 2022 GREEN500 (TOP500.org, 2022a). Three representative storms are simulated: a North Atlantic windstorm associated with a midlatitude cyclone, a Mediterranean convective storm characterized as a derecho and a mesoscale convective system over the Amazon rainforest. Representation of the North Atlantic storm requires downscaling from the synoptic cyclone scale (>100 km) down to local wind gust formation (<1 km). Inversely, the representation of the Amazon storm requires upscaling from the local triggering of convective cells (<1 km), which organize and maintain the system at the mesoscale (>100 km). Finally, the Mediterranean storm involves both up- and downscaling. We show that Meso-NH successfully represents the cascade of scales for the three representative storms for horizontal grid spacing down to 100 m and grid size up to $\mathrm{4096}\times \mathrm{4096}\times \mathrm{128}$ points (2.1 Gpts). On the Adastra GPU partition and for one of the three storms, coupled simulations between Meso-NH and the WW3 spectral wave model are successfully carried out using the OASIS3-MCT coupler. It should be noted that the additional cost of the coupling is negligible compared with the cost of Meso-NH since WW3 and OASIS use the free CPUs of the GPU nodes.

Porting Meso-NH to GPUs opens up new opportunities for simulating extreme weather events across scales. These opportunities are all the greater in a context where artificial intelligence (AI) is experiencing rapid development in meteorology. Meso-NH simulations, on a fine scale, over very large domains and integrating various couplings, constitute a unique source of data for the development of AI emulators. A strong need for giga-LESs (large-eddy simulations on a billion grid points) already exists for variables that are very rarely measured, such as the vertical speed of the cloud envelope or in storms that the C3IEL (Cluster for Cloud Evolution, ClImatE and Lightning) and C2OMODO (Convective Core Observations trOugh Microwave Derivatives in the trOpics) satellite projects aim to retrieve (Auguste and Chaboureau, 2022; Brogniez et al., 2022; Dandini et al., 2022). This need is also expressed for near-real-time simulations of natural hazards for urgent decision-making (Flatken et al., 2023). Finally, this GPU porting paves the way for future European exascale supercomputers. The upcoming arrival of such machines will enable the creation of tera-LES (over a trillion grid points) and a better understanding of the upscaling and downscaling processes occurring during extreme weather events.