the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A three-stage model pipeline predicting regional avalanche danger in Switzerland (RAvaFcast v1.0.0): a decision-support tool for operational avalanche forecasting
Alessandro Maissen
Frank Techel
Michele Volpi
Despite the increasing use of physical snow cover simulations in regional avalanche forecasting, avalanche forecasting is still an expert-based decision-making process. However, recently, it has become possible to obtain fully automated avalanche danger level predictions with satisfying accuracy by combining physically based snow cover models with machine learning approaches. These predictions are made at the location of automated weather stations close to avalanche starting zones. To bridge the gap between these local predictions and fully data- and model-driven regional avalanche danger maps, we developed and evaluated a three-stage model pipeline (RAvaFcast v1.0.0), involving the steps classification, interpolation, and aggregation. More specifically, we evaluated the impact of various terrain features on the performance of a Gaussian-process-based model for interpolation of local predictions to unobserved locations on a dense grid. Aggregating these predictions using an elevation-based strategy, we estimated the regional danger level and the corresponding elevation range for predefined warning regions, resulting in a forecast similar to the human-made public avalanche forecast in Switzerland. The best-performing model matched the human-made forecasts with a mean day accuracy of approximately 66 % for the entire forecast domain and 70 % specifically for the Alps. However, the performance depended strongly on the classifier's accuracy (i.e., a mean day accuracy of 68 %) and the density of local predictions available for the interpolation task. Despite these limitations, we believe that the proposed three-stage model pipeline has the potential to improve the interpretability of machine-made danger level predictions and has, thus, the potential to assist avalanche forecasters during forecast preparation, for instance, by being integrated in the forecast process in the form of an independent virtual forecaster.
- Article
(9446 KB) - Full-text XML
-
Supplement
(35911 KB) - BibTeX
- EndNote
Snow avalanches rank among the deadliest natural hazards in snow-covered, mountainous regions (Nadim et al., 2008; Badoux et al., 2016). Consequently, public avalanche forecasts are issued in many countries, informing and warning public and professional decision-makers about the snow and avalanche conditions in a region. Over the last decades, winter sport activities in terrain not secured from avalanches have become very popular (e.g., in Switzerland as in Winkler et al., 2016, and in the United States as in Birkeland et al., 2017). Nowadays, in Europe and North America, the majority of avalanche accidents are related to recreational winter sport activities (e.g., Techel and Zweifel, 2013; Birkeland et al., 2017), emphasizing the importance of timely and accurate avalanche forecasts to support the decision-making process, particularly during the planning phase. Despite recent advances in physical snowpack modeling, coupled with machine learning approaches (e.g., Mayer et al., 2022; Herla et al., 2024), avalanche forecasting is still an expert-based process, involving the evaluation and interpretation of a variety of data describing weather and snowpack conditions, from which expected avalanche conditions are inferred (e.g., SLF, 2023). One of the key pieces of information communicated in avalanche forecasts is an avalanche danger level summarizing avalanche conditions in a given region according to a five-level avalanche danger scale (e.g., in Europe according to EAWS, 2022). The five levels describe avalanche situations ranging from “generally favorable” avalanche conditions (danger level: 1 – low) to “extraordinary avalanche conditions” (5 – very high; EAWS, 2022).
It is our objective to design a fully automated, data- and model-driven pipeline producing a forecast similar to the current human-made regional avalanche forecast in Switzerland by building upon a recently developed classifier predicting the avalanche danger level (Pérez-Guillén et al., 2022a). This random forest (RF) model relies on data from physical simulations of snowpack stratigraphy and snowpack stability, driven with inputs from automated weather stations (described in detail in Pérez-Guillén et al., 2022a). Inspired by the ideas of Brabec and Meister (2001) for regional avalanche forecasting, we develop and validate a three-stage model pipeline for regional avalanche danger forecasting (RAvaFcast v1.0.0), comprising the stages classification, interpolation, and aggregation. Concretely, we propose an interpolation algorithm allowing the prediction of high-resolution danger level maps for the Swiss Alps based on point predictions at the locations of the automated weather stations, where the RF classifier from Pérez-Guillén et al. (2022a) infers danger levels. Then, a novel elevation-based aggregation strategy infers an avalanche danger level for predefined warning regions to ultimately produce a regional avalanche forecast that mimics human forecasts. Lastly, we compare the model's predictive performance to the point-based approach used by Pérez-Guillén et al. (2022a) and importantly to the published avalanche forecast bulletins.
2.1 Models in support of avalanche forecasting
To support avalanche forecasting, various statistical approaches have been explored during the past 5 decades. One of the early works on tool-assisted avalanche forecasting was done by Buser (1983, 1989) in Switzerland. By leveraging historical information on recorded avalanches and meteorological conditions, Buser (1983) developed a nearest-neighbor (NN) classifier identifying past days with similar avalanche conditions. Kristensen and Larsson (1994), also using an NN classifier, estimated the probability of avalanche occurrence through a weighted sum of the frequency and magnitude of avalanche activity among the nearest neighbors. Due to its success, NN classifiers were used as part of several operational assisting tools for avalanche forecasting in Switzerland (Bolognesi, 1998; Brabec and Meister, 2001), Scotland (Purves et al., 2003), and Austria (Kleemayr and Moser, 1998). Since then, other various statistical methods have been applied, for instance support vector machines (Pozdnoukhov et al., 2008, 2011), classification trees (e.g., Baggi and Schweizer, 2009; Hendrikx et al., 2014), and random forests (e.g., Mitterer and Schweizer, 2013; Mayer et al., 2023), providing predictions of avalanche activity at a local or regional scale. More recently developed models use a combination of meteorological data and simulated snow stratigraphy (e.g., Schirmer et al., 2010; Mayer et al., 2022; Hendrick et al., 2023).
In addition to predictions of avalanche activity and snowpack instability, attempts have been made to predict the avalanche danger level directly. Early approaches relied on (hybrid) expert-based systems (Schweizer et al., 1994; Schweizer and Föhn, 1996) simulating the forecasters' decision-making process to estimate the danger level in the region of Davos (Switzerland). Later on, Brabec and Meister (2001) adopted the NN classifier originally developed by Buser (1983) to predict the avalanche danger level based on meteorological variables measured at a local measuring site. Furthermore, Brabec and Meister (2001) proposed a strategy for predictions of the danger level at a regional scale by applying this model to 60 manual measurement sites in Switzerland, followed by interpolating the resulting danger level predictions using inverse distance weighting on a 1 km resolution grid, to obtain predictions for all regions in the Swiss Alps. The model reached a cross-validated overall accuracy of about 52 %, which was attributed to insufficient information on snow stability. In Switzerland, over time, a comparably dense network of automated weather stations (AWSs) was built (SLF, 2022), known as the Intercantonal Measurement and Information System (IMIS). At each of these AWSs the physics-based, one-dimensional snow cover model SNOWPACK (Lehning et al., 1999, 2002a, b) is running, providing simulations of the snow stratigraphy and stability (Morin et al., 2019). Schirmer et al. (2009) showed that incorporating features describing the snowpack structure improved the accuracy of danger level predictions. An NN classifier with the danger level of the previous day as an input feature performed best, achieving a cross-validated accuracy of 73 %. More recently, Pérez-Guillén et al. (2022a) proposed a random forest (RF) classifier for avalanche danger level prediction. In contrast to Brabec and Meister (2001) and Schirmer et al. (2009), Pérez-Guillén et al. (2022a) trained a model not only using data from a single station describing meteorological variables but also including snow stratigraphy information simulated with SNOWPACK on more than 120 AWSs located at the elevation of avalanche-prone areas in all regions of the Swiss Alps. Their standard version of the classifier exhibited an accuracy of 74 %, which is remarkably good considering that the accuracy of human-made avalanche forecasts in Switzerland is estimated to be in the range between 75 % and 81 % (Techel and Schweizer, 2017; Techel et al., 2020). Since the winter season 2021/2022, several machine learning models have been operationally tested by avalanche forecasters in Switzerland, including the model by Pérez-Guillén et al. (2022a), with generally positive feedback from the forecasters regarding model performance and usefulness (van Herwijnen et al., 2023).
2.2 Public avalanche forecasting in Switzerland
In Switzerland, the country-wide public avalanche forecast or avalanche bulletin (SLF, 2023) is published by the WSL Institute for Snow and Avalanche Research SLF in Davos. An example of a forecast is shown in Fig. 1a. Typically, the avalanche bulletin is issued twice a day during the winter season: in the evening at 17:00 LT (local time), with an update in the morning at 8:00 LT. The morning and evening editions are valid until 17:00 LT of the same day or the next day, respectively. The start and end of the forecasting season depend on the snowfall in autumn and the snow melting in spring, but it typically starts in late November and ends in May. In early winter (November to early December) and late spring (late April to May), the avalanche bulletin is only published in the evening.
In Switzerland, a team of forecasters produces the avalanche bulletin. The primary data used for forecasting are observations provided by about 200 specifically trained observers, measurements from a network of more than 120 automated weather stations (AWSs) located at the elevation of potential avalanche starting zones (SLF, 2022; Lehning et al., 1999) (Fig. 1b), physics-based simulations of snowpack stratigraphy and stability driven with measurements from AWSs, and numerical weather prediction models. When preparing the bulletin, forecasters assess expected avalanche conditions for the following 24 h. In the forecast product, expected conditions are summarized with a danger level according to the five-level European avalanche danger scale (1 – low, 2 – moderate, 3 – considerable, 4 – high, 5 – very high) (EAWS, 2022). Moreover, slope aspects and elevation are indicated, highlighting where the danger level applies. In addition, a sub-level qualifier assigned to these danger levels provides an indication of whether danger is low, in the middle, or high within the level (Techel et al., 2022; Lucas et al., 2023), and one or several avalanche problems describe the typical situations of snow instability (SLF, 2023). To communicate spatial variations in expected avalanche conditions, the territory of Switzerland is divided into 149 warning regions (as of 2023) of approximately equal size, except for some larger warning regions in non-mountainous zones (SLF, 2023). These warning regions, represented by the small polygons in Fig. 1a, are the smallest spatial units used in the forecast. During bulletin production, warning regions having the same expected avalanche conditions are grouped into larger regions (bold polygon boundaries in Fig. 1a).
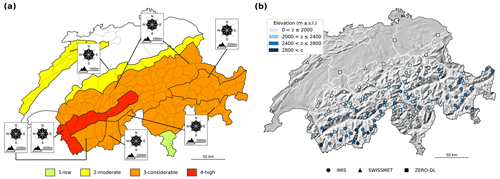
Figure 1Maps of Switzerland showing (a) an example of the avalanche bulletin (published on 24 December 2019 at 08:00 LT) and (b) the distribution of the automated weather stations used in this study. In (a), the forecast danger level (colors) and the critical slope aspects and elevations (insert) are shown. The polygons (black in a and white in b) show the warning regions, which are the spatial units used for forecast production in Switzerland. In (a), polygon lines marked in bold summarize warning regions aggregated in the forecast product.
For this work, we rely extensively on the previous work by Pérez-Guillén et al. (2022a), also in terms of data. The data we use are very similar to the publicly available dataset (Pérez-Guillén et al., 2022b). In the following, we describe the data briefly. For a more thorough description, the reader is referred to the detailed description in Pérez-Guillén et al. (2022a).
-
As in Pérez-Guillén et al. (2022a), we used the pre-processed meteorological data and snowpack simulations at the locations of the AWSs. In addition to the data used by Pérez-Guillén et al. (2022a), we also used stations operated by MeteoSwiss (FOMC, 2023), at which SNOWPACK simulations (flat field) are run for the purpose of avalanche forecasting (marked with SWISSMET in Fig. 1b). Moreover, we used more recent snowpack simulations, which stem from operational SNOWPACK v3.6.0. Following Pérez-Guillén et al. (2022a), we extracted avalanche-related features from the meteorological time series, resampled to 24 h resolution, and centered at 18:00 LT, which is closest to the valid time of the forecast. In addition, snow cover data were extracted from the simulated stratigraphy at 12:00 LT. This results in 67 available meteorological and snowpack features, described in detail in Pérez-Guillén et al. (2022a).
-
The forecast danger level is extracted from the avalanche forecast valid at 12:00 LT on the day in question. When available, we use the forecast update published at 08:00 LT or the forecast published at 17:00 LT the day before. Similar to Pérez-Guillén et al. (2022a), we focus on dry-snow avalanches, and thus we disregard forecasts relating to wet-snow avalanche conditions.
The forecast danger level is assigned to each station-specific set of meteorological and snowpack features by date and location. If there is no forecast or if the elevation of the station is lower than the elevation threshold mentioned in the forecast (see also the example of the forecast in Fig. 1b and Sect. 2), we still keep the extracted features as an unlabeled sample. Although unlabeled samples are excluded from the training process, they are preserved for prediction purposes. As in Pérez-Guillén et al. (2022a), the few cases of danger level 5 (very high) are merged with level 4 (high). The dataset encompasses the winter periods from 1997/1998 to 2020/2021. To conduct model optimization (Sect. 5) and evaluation (Sect. 6), we adhere to the standard method of dividing the data into three sets: training, validation, and test. Specifically, the training set covers winter seasons from 1997/1998 to 2017/2018, consisting of 242 751 labeled station/danger level samples out of a total of 304 019 samples spread across 3482 d. The validation set includes the winter seasons of 2018/2019 and 2019/2020 with 35 354 labeled station/danger level samples out of a total of 44 781 samples over 359 d. Lastly, the test set encompasses the winter season 2020/2021, including 17 396 labeled station/danger level samples out of a total of 22 262 samples spread across 165 d.
For spatial interpolation, we rely on the digital surface model (DSM) EU-DEM v1.1 (EEA, 2016), which has complete coverage of the whole of Europe. The advantage of EU-DEM v1.1 over Swiss national DSM products (e.g., swissALTI3D) is that it extends beyond the political boundaries of our study area. Hence, no special care has to be taken when extracting terrain features from spatial windows at the border of Switzerland. This DSM raster uses the ETRS89-LAEA coordinate reference system (epsg:3035) with a spatial resolution of 25 m. However, since the avalanche danger level in the training data was typically assessed on a scale of warning regions, adopting finer-resolution interpolation grids would unnecessarily increase computational complexity. Therefore, the DSM is downsampled to 1 km × 1 km raster cells by simple averaging.
On a smaller scale, within distances of tens or hundreds of meters, topographical properties like the steepness of the slope, the shape of the terrain, and the slope's orientation relate to locations where humans can potentially trigger avalanches (e.g., Schweizer and Lütschg, 2001; Vontobel et al., 2013) but also to where natural avalanches may release (e.g., Veitinger et al., 2016), and, hence, automated approaches to classify avalanche terrain make use of a variety of topographical parameters (Schmudlach and Köhler, 2016; Harvey et al., 2018; Sykes et al., 2024). It is less clear whether such properties, derived for larger scales, correlate with regional avalanche conditions. We therefore extracted different terrain features from the resampled 1 km resolution DSM for a range of spatial scales (i.e., 1, 2, …, 32 km2). At 1 km resolution, topographical properties coarsely describe valleys and mountain ridges, while at 32 km resolution primarily high-level patterns are characterized.
Specifically, we extract elevation, slope angle, profile curvature, and aspect from the resampled 1 km resolution DSM. Then, the technique of Gaussian pyramids (Adelson et al., 1984) is applied for the feature elevation, slope angle, and profile curvature to capture patterns at lower resolution (2–32 km2) at the scale of long mountain ridges, mountain groups, plateaus, and valleys. Gaussian pyramids are built by constructing a sequence of images in which the resolution of the image at the next pyramid stage is half of the resolution of the previous one, while a Gaussian filter is applied before the downsampling operation.
Finally, these features are complemented by extracting directional derivatives and differences of Gaussians (DoGs) (Gonzalez and Woods, 2006). Both techniques are commonly used for detecting and enhancing edges and corners in given orientations, aiding capturing valleys and ridges, as well as their concavity and convexity, exhaustively. Directional derivatives are extracted by applying a Sobel operator (Sobel and Feldman, 1973) to a blurred DSM (i.e., Gaussian filter), focusing on the north–south and east–west directions. On the other hand, DoGs are computed by subtracting two blurred versions of the DSM. Different degrees of blurring are taken into account for both of these features.
Inspired by the ideas of Brabec and Meister (2001), we propose a three-stage model pipeline for regional avalanche forecasting (RAvaFcast v1.0.0) consisting of classification, interpolation, and aggregation. A graphical overview of the pipeline is given in Fig. 2.
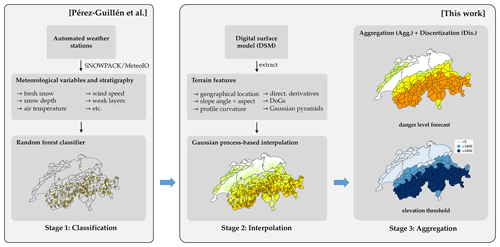
Figure 2An overview of the three-stage model pipeline (RAvaFcast v1.0.0). In the classification stage avalanche danger level is assessed at weather stations based on meteorological variables and stratigraphy. Secondly, predictions are interpolated to unobserved locations, forming a high-resolution danger level map. In the final step of the pipeline, the danger levels in warning regions are estimated by aggregation.
In the classification stage (Sect. 4.1), we predict the avalanche danger level at the location of automated weather stations (AWSs) for a given day with the random forest (RF) classifier designed by Pérez-Guillén et al. (2022a). Secondly, in the interpolation step (Sect. 4.2), we spatially interpolate danger level predictions to unobserved locations of the study area. In particular, we model the interpolation problem as Gaussian process regression, in which different terrain attributes are explored. The interpolation model is then used to predict the avalanche danger level at every location of a grid with 1 km resolution covering the study area. Finally, in the third step (Sect. 4.3), we consider several strategies to aggregate the gridded predictions to danger level assessments for the predefined warning regions used in the avalanche forecast in Switzerland.
In the following subsections, we describe the theoretical concepts and methods; the actual model optimization related to these three stages is described in Sect. 5.
4.1 Stage 1: classification
In the classification stage, we follow the strategy presented by Pérez-Guillén et al. (2022a) to predict the danger level at locations of AWSs for the current day using as input meteorological data recorded on the current and on previous days, as well as snow cover simulations using SNOWPACK (Lehning et al., 1999, 2002a, b).
Let be a dataset with extracted d-dimensional avalanche-related features xi∈ℝd and the danger level as targets (i.e., classes). We can reduce this ordinal regression problem into a standard supervised multi-class classification problem. Pérez-Guillén et al. (2022a) considered several state-of-the-art machine learning models for classification and found that a random forest (RF) classifier (Breiman, 2001) works well for this kind of problem. An RF classifier uses both bagging and feature bagging to train a number of weak estimators in the form of decision tree classifiers. Let fi(c | x) be such a weak estimator that models the probability of class c given a sample feature x. Then, an RF classifier with Q∈ℕ estimators models the posterior class probability as
where [⋅] is the Iverson bracket, returning 1 if the condition is true and 0 otherwise. Consequently, the posterior class probability equals the fraction of individual estimators predicting the class c, also known as majority voting.
The optimal danger level prediction dpred(x) is given by the class with the highest posterior class probability (see Eq. 2) and minimizes the probability of misclassification. Furthermore, we can determine the expected danger level davg(x) by applying Eq. (3).
It is important to emphasize that avalanche danger (or the severity of avalanche conditions) increases exponentially with the avalanche danger level (e.g., SLF, 2023). However, the expected danger level (see Eq. 3) is determined based on the levels rather than the danger, thereby maintaining the nonlinear relationship.
4.2 Stage 2: interpolation
A trained RF classifier, as introduced in the classification stage, is used to predict the danger level for a day of interest at each AWS. For the spatial interpolation, we model the expected danger level instead of the discrete danger level, as it better captures the underlying continuous nature of the avalanche danger. Consequently, we end up with N samples distributed across the study area for a given day that can be summarized as , where is the expected danger level for station i computed according to Eq. (3) and xi∈ℝd represents the features of station i; e.g., if the features correspond to the spatial location (latitude, longitude, elevation), d=3. For a more compact notation, input features are aggregated to the matrix and target variables collected in the column vector d∈ℝN so that . We further augment the data by adding samples with a danger level of zero (i.e., expected danger level di=0.5) at manually chosen avalanche-free locations (i.e., Bern, Zurich, St. Gallen, and Luzern, depicted as the ZERO-DL network in Fig. 1b) in the Swiss plateau to model the notion of no forecast (no danger) as in the avalanche bulletin.
The problem of generating dense spatial maps from sparsely sampled data is known as spatial interpolation and is widely applied across the domain of geosciences. Most popular spatial interpolation techniques include inverse distance weighting or variants of kriging, while the latter additionally provides a notion to estimate uncertainty (e.g., Dale and Fortin, 2014). Kriging is a geostatistical terminology and its formulation is identical to Gaussian process regression, although geostatistical literature has focused primarily on two- and three-dimensional input spaces (Rasmussen and Williams, 2006). As we plan to enrich the input space defined by the geographical location (i.e., latitude, longitude, elevation) with descriptive terrain features (e.g., slope angle, profile curvature) we rely on the more modern notion of Gaussian processes (GPs) (Rasmussen and Williams, 2006).
A GP is completely defined by a mean function and a covariance (or kernel) function , so we refer to it as . The mean function and covariance function are parameterized and optimized during the training procedure. To account for the noise in the danger level assessments, we model the avalanche danger level with homoscedastic additive noise (i.e., the level of noise is independent of the location). In particular, we have
with and trainable variance σ2. Accordingly, for the dataset the joint data distribution is defined by means of a multivariate Gaussian distribution:
where is the mean vector and the covariance matrix with elements . Then, assume a test location x* (not contained in the training dataset), for which we are interested in the unknown noise-free avalanche danger level . The joint distribution between the training data and f* is given by
where is the vector of pairwise covariance between the sample locations and the test location. Note that location refers to the geographical location (latitude, longitude, elevation) and may be augmented by several terrain attributes. As our joint distribution is Gaussian, conditioning on the observed samples is straightforward. Thus, the posterior (or predictive) distribution is Gaussian as well and given by
where the posterior (or predictive) mean is determined as
and the posterior (or predictive) variance is given by
The optimal prediction of the expected danger level at location x* is given by the posterior mean . On the other hand, we use the posterior standard deviation σp(x*) as a measure of uncertainty. Finally, computing the optimal predictor and its uncertainty for every location of a 1 km × 1 km grid covering Switzerland results in spatially continuous expected danger level and uncertainty maps as shown in Fig. 3.
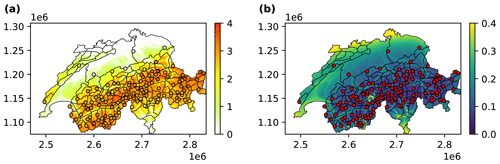
Figure 3Maps of Switzerland showing (a) the interpolation and (b) the corresponding standard deviation as a measure of uncertainty at a resolution of 1 km × 1 km. The circles on the map show the location of the AWSs, while in (a), they are colored according to the predicted danger level by the RF classifier.
Equations (8) and (9) again demonstrate that interpolation by means of GP regression is exclusively defined by a mean function and covariance function. The mean function is commonly considered to be either zero or constant, and we favor the latter option by setting m(x)=θc with parameter θc∈ℝ that can be learned. This approach offers the advantage of not requiring standardization of the target variable (i.e., the expected danger level), which is typically necessary when using a zero mean function. In contrast, choosing a suitable covariance function is more crucial as it captures the spatial correlations effectively.
We choose the popular and widely used squared exponential kernel, which is also known as the radial basis function (RBF) kernel (Rasmussen and Williams, 2006). It is defined as
with a learnable length scale . The length scale parameter controls the degree of similarity between two samples x and x′. When increasing the length scale, the covariance between the samples also increases, and vice versa. Additionally, the RBF kernel has the property of being infinitely differentiable so that the resulting Gaussian process is characterized by a high level of smoothness.
To increase complexity and flexibility of the model we construct expressive and interpretable kernels by allowing the model to learn compositions of base kernels (Plate, 1999; Duvenaud et al., 2011, 2013). Consequently, let be an input feature vector, where represents one feature or one group of features (it does not necessarily have to be a scalar). Then we can form a linear combination of m kernels as
where the weighting coefficients αl≥0 are learned and represents independently parameterized RBF kernel functions (this combination can be extended to kernels of different types, but we stick to RBF kernels). When considering different terrain features (e.g., slope angle, profile curvature) the kernel is able to adapt to the daily avalanche danger situation by learning the appropriate weighting coefficient. Notably, the significance of a specific feature is reflected in the corresponding weighting coefficient, meaning that more important features lead to higher coefficients, while less important ones have lower coefficients.
4.3 Stage 3: aggregation
The first two stages of the three-stage pipeline for automated avalanche forecasting were concerned with local avalanche prediction at weather stations and the interpolation of these on the 1 km × 1 km grid. Human-made avalanche forecasts assess avalanche danger levels at a regional scale (Fig. 1a). On that account, this section presents a method of deriving a bulletin-like avalanche danger forecast by spatially aggregating a high-resolution danger map (i.e., 𝒟grid) into assessments for a set of fixed warning regions.
Let be this grid comprising Ng danger level assessments, where si∈ℝ3 specifies the geographical location (latitude, longitude, elevation) of the ith grid cell and di∈ℝ>=0 its avalanche danger level. For Nw warning regions, we first partition 𝒟grid into disjoint sets according to the spatial boundaries of the warning regions. Each set contains the cells belonging to each region. Secondly, an aggregation function fagg(⋅) determines the danger level of each warning region. Besides exploring standard aggregation functions such as simple averaging (i.e., the mean method), as proposed by Brabec and Meister (2001), we considered aggregating only a fraction of the highest danger level predictions, a strategy that we denote as top-α. Since we deal with complex topography, the simple averaging might result in underestimation of the danger level, particularly when regions contain many low-elevation cells.
Avalanche danger is often elevation-dependent, with generally higher danger in higher-elevation zones. This is reflected in the human-made forecasts in Switzerland, where an elevation threshold is generally indicated. More specifically, for dry-snow avalanches, an elevation threshold of telev indicates that particularly affected altitudes are above telev m a.s.l. In Switzerland, these thresholds are normally described in increments of 200 m, between 1000 and 3000 m a.s.l. If no elevation threshold is indicated in the forecast, no particularly affected altitudes exist (SLF, 2023), which is most often the case at danger level 1 (low). Consequently, we propose an elevation-based aggregation strategy that considers thresholds similar to those used in the human-made avalanche bulletin. The key idea is to estimate, for each region, the danger level at several chosen elevation ranges and consider the maximum over the elevation intervals to be the final danger level estimate. This has the additional advantage that particularly affected altitudes are revealed, as reported in human-made forecasts.
Consider an ordered set of elevations containing Ne elements, where ei≤ej for i≤j. Then, for a fixed bandwidth b and a warning region i, danger level assessments in the elevation band , which we denote as , are averaged with the ordinary mean method to estimate the danger level at elevation ej. The danger level for dry-snow avalanches (as opposed to wet-snow avalanches) typically increases with increasing elevation; determining the maximum danger level iteratively from the bottom to top provides an elevation threshold for a particularly affected altitude range as in human-made forecasts. For this work we choose similar elevation thresholds as in the avalanche bulletins but restrict ourselves to the most commonly used thresholds between 1400 and 2600 (Pérez-Guillén et al., 2022a), while the bandwidth b is fine-tuned on the validation set (see Sect. 5.3).
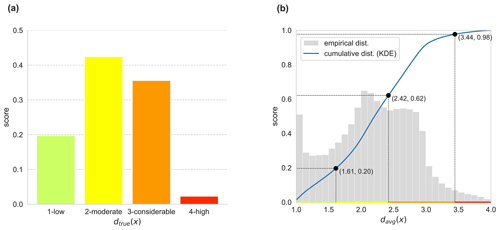
Figure 4(a) Empirical true danger level distribution of the training data. (b) Cumulative distribution (blue) and empirical distribution (gray) of the expected danger level for the out-of-bag predictions of the training data; the former is computed by Gaussian kernel density estimation. Points (black) fulfill Eq. (13) and hence define the refined thresholds for discretization.
The three proposed aggregation strategies above (i.e., mean, top-α, elevation-based) estimate the danger level as a real number instead of a discrete value in the range of 0 to 4. Consequently, we perform a discretization as a last step in the aggregation. More specifically, we consider a discretization function that defines the decision boundaries as follows:
where the thresholds specify the range of the intervals. A possible greedy discretization strategy is rounding, which ensures that values are clamped to integers from 0 to 4, and is expressed as . However, it is important to note that the target variable used for interpolation represents the expected danger level, which arises from the class probabilities predicted by the RF classifier. Hence, the discretization strategy should ideally map the expected danger level back to the most probable level. As stated by Niculescu-Mizil and Caruana (2005), RF classifiers suffer from one-sided errors due to the variance of their base estimators. For instance, predicting a class probability of p=1 requires that all base estimators predict the same class. Consequently, as the RF classifier predicts danger levels 1 (low) to 4 (high), the expected danger level typically falls within the range of for both ϵ1>0 and ϵ2>0.
To refine the discretization, we derive the thresholds using a cumulative sum approach similar to Brabec and Meister (2001), which preserves the a priori danger level distributions of the training data. In particular, we first estimate the cumulative distribution of the expected danger level through kernel density estimation with Gaussian kernels (Scott, 1992). The estimation is performed by utilizing the out-of-bag predictions from the RF classifier to avoid any data leakage to the validation and test set, which can be used for model selection and hyperparameter tuning, and estimation of the generalization error. Let be the empirical cumulative distribution function of the true danger levels from the bulletins of the training data (see Fig. 4a). Then, the thresholds are chosen so that
Figure 4b visualizes the outcomes of this approach, with the black points in the figure fulfilling Eq. (13) and ultimately leading to threshold values of . This particular strategy is denoted as the refined rounding method and is the preferred discretization strategy for all our configurations of the three-stage pipeline.
The proposed three-stage model pipeline (RAvaFcast v1.0.0) consists of several independent models, in particular an RF classifier for danger level prediction, a Gaussian process regression for interpolation, and an aggregation step to estimate a regional avalanche forecast. Consequently, model selection and hyperparameter tuning occur at several points throughout the pipeline. We will utilize the training set for fitting and hyperparameter tuning of the RF classifier and the validation set for selecting the combination of the best interpolation model and aggregation strategy, while the best pipeline configuration is evaluated in Sect. 6 on the (holdout) test set.
5.1 Hyperparameter tuning for the RF classifier
We employ the same pre-processing and training strategy as presented in Pérez-Guillén et al. (2022a). In particular, stations lying outside the indicated elevation threshold and noisy data samples (i.e., danger level 4 (high) samples recording less than 30 cm of 24 h fresh snow) are dropped from the training data. Hyperparameters, such as the number of estimators (i.e., decision trees), the maximum depth of the bagged trees, and parameters related to the splitting strategy, are optimized via a grid search cross-validation. Splitting the training data into folds is performed group-wise, ensuring that samples belonging to the same winter season end up in the same fold. More specifically, the folds are Fold 1 (1997/98 to 2002/03), Fold 2 (2003/04 to 2006/07), Fold 3 (2007/08 to 2010/11), Fold 4 (2010/11 to 2013/14), and Fold 5 (2014/15 to 2017/18). For a more detailed overview of the training strategy we refer to Pérez-Guillén et al. (2022a).
5.2 Terrain feature selection
Recall that we proposed an adaptive composable kernel function (see Eq. 11) for the interpolation covariance. More specifically, the kernel function is a linear combination of RBF kernels, each covering a feature group (e.g., 2D spatial location, elevation, slope angle). To investigate the effect of these features, we compare different variants of the adaptive kernel function, including or excluding several features and feature groups. These include GPall (i.e., all the terrain features described in Sect. 3), GPno-aspect (i.e., all the features except the aspect), GPxyz (i.e., 2D spatial location and elevation), and GPslope (i.e., 2D spatial location, elevation, and slope angle). We append “-Δ” to the identifier of models (e.g., GPxyz-Δ for GPxyz) to denote that features are computed with five-level Gaussian pyramids, hence incorporating multiscale information.
Table 1Statistics of daily LOOCV errors (ME, MAE, RMSE) for different variations of the adaptive kernel function and a simple nearest-neighbor (NN) interpolation. Errors are computed for the validation set (in fact a training set for the interpolation stage), which includes winter seasons 2018/2019 and 2019/2020. The best scores are marked in bold.
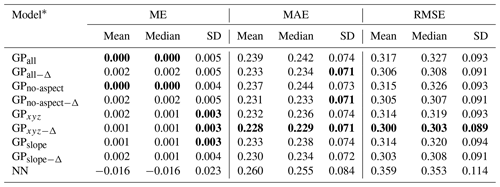
* These include GPall (i.e., all the terrain features described in Sect. 3), GPno-aspect (i.e., all the features except the aspect), GPxyz (i.e., 2D spatial location and elevation), and GPslope (i.e., 2D spatial location, elevation, and slope angle). We append “−Δ” to the identifier of models (e.g., GPxyz−Δ for GPxyz) to denote that features are computed with five-level Gaussian pyramids, hence incorporating multiscale information.
One of the most common ways of evaluating the performance of a spatial interpolation algorithm relies on cross-validation, especially on leave-one-out cross-validation (LOOCV) since the number of samples per day is rather small (e.g., Agou et al., 2022; Wu and Hung, 2016). Given N samples, LOOCV trains the spatial interpolation model on N−1 samples and predicts the value for the remaining sample. This is repeated for all possible N splits. Recall that the validation set – which was used as a holdout test set in Pérez-Guillén et al. (2022a) for final evaluation of the RF classifier – is now used as a training set for the spatial interpolation and LOOCV is used to perform model selection of the GP regression. Finally, performance is evaluated using standard error measures, which include the mean error (ME), the mean absolute error (MAE), and the root mean square error (RMSE). The smaller the measures, the better the model's performance. Formal definitions of the error measures are given in the Appendix (Sect. A2). However, since the validation set covers a period of two winter seasons, we compute the LOOCV errors per day and consider several statistics, especially the mean and the median, including confidence intervals.
The results of the LOOCV are shown in Table 1. Gaussian-process-based interpolation models clearly outperform the simple nearest-neighbor (NN) interpolator, but there are only small differences in terms of performance gain between variations of the adaptive kernel function. Nevertheless, it is possible to discern certain emerging trends within these variations, such as the slightly improved LOOCV errors for variations utilizing features extracted from Gaussian pyramids (i.e., models with a Δ in the name). Furthermore, models with a reduced terrain feature set (e.g., GPxyz, GPslope) perform better than models with the complete set of features, such as GPall−Δ. Finally, it can be affirmed that the GPxyz−Δ model stands out as the most effective choice for interpolating avalanche danger, as it consistently exhibits the lowest errors across the majority of the evaluated metrics.
Table 2Statistics of the adaptive kernel function's weighting coefficients, defined in Eq. (11), for GPall evaluated on the validation set. The higher the value of the weighting coefficient, the more important the corresponding feature group. The best metrics are marked in bold.
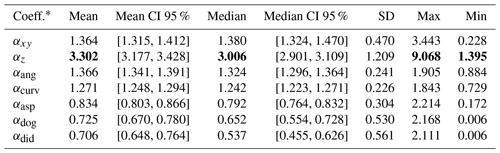
* Learnable coefficients within the adaptive kernel function (see Eq. 11): αxy (spatial location), αz (elevation), αang (slope angle), αcurv (profile curvature), αasp (aspect), αdog (DoGs), and αdid (directional derivatives).
An alternative method for assessing the importance of various terrain features involves examining the learned coefficients denoted as αl within the adaptive kernel function (see Eq. 11). In particular, for every day in the validation set, the interpolation model is fitted to record learned coefficients, which then serve as a means to gauge the importance of different terrain characteristics. The statistical properties (i.e., mean, median, etc.) of these coefficients (see Table 2) align with the LOOCV errors, as they show that the elevation coefficient αz stands out with substantially higher mean and median values. In contrast, coefficients associated with feature categories such as the aspect αasp, difference of Gaussians αdog, and directional derivatives αdid are less significant compared to elevation. Nevertheless, certain feature groups demonstrate a moderate level of importance, as evidenced by the mean and median values of their respective coefficients (i.e., αang and αcurv).
5.3 Aggregation strategy selection
In Sect. 4.3 we propose novel aggregation strategies, in particular the top-α and the elevation-based strategy. Both of them have free parameters (i.e., the fraction α, the bandwidth b, or the elevation thresholds) that can be tuned. To compare different aggregation strategies, we determine the expected daily performance by considering several statistics (e.g., mean and median) for the daily accuracy of the pipeline-predicted avalanche bulletin and the true avalanche bulletin.
For the elevation-based aggregation strategy we fix two sets of elevation thresholds that are in line with those used in the bulletin from the forecasters. The first strategy, denoted as elev-simple, operates with a reduced set of coarser-grained elevation thresholds (or bands). This choice is motivated by the desire for simplicity and the primary objective of accurately predicting the avalanche danger level within each warning region. In contrast, the elev-full strategy takes into account finer-grained thresholds. Specifically, we have the following.
-
elev-simple:
-
elev-full: , 2600}
Figure 5a and b clearly show that, regardless of the chosen interpolation model, the elevation-based aggregation and the top-α aggregation outperform the mean method by a considerable margin. Furthermore, combinations involving an interpolation model utilizing solely elevation and slope as additional terrain features (e.g., GPxyz, GPslope) tend to yield superior performance, which is in accordance with the outcomes of the LOOCV (see Sect. 5.2). Nevertheless, it is noteworthy that interpolation models employing Gaussian pyramids seem to have a negative effect on the accuracy of the predicted avalanche bulletin, which stands in contrast to the reduced errors observed during the LOOCV evaluation. This discrepancy could potentially be attributed to the smoothing that occurs in both low- and high-elevation zones when using Gaussian pyramids.
The top-α strategy is a simple modification of the mean aggregation that already shows a large improvement, at least in combination with GP regression models. Fine-tuning the fraction to α=0.3 (see Fig. 5c) in combination with GPxyz gives a mean day accuracy of 0.685 and a median day accuracy of 0.700 for the validation set. Nevertheless, elevation-based aggregation strategies elev-simple and elev-full perform even better. Figure 5d shows the mean day accuracy and the median day accuracy when varying the bandwidth b. We observe that scores exhibit a substantial increase until the bandwidth reaches a point where the elevation bands start to overlap. In the case of elev-full, this transition occurs at b=200, and for elev-simple, it happens at b=400. Slightly overlapping elevation bands can marginally enhance the accuracy scores, but the actual improvement gained is quite low. Elevation-based aggregation strategies with large bandwidths will eventually be equal to the mean aggregation strategy.
To sum up, the best accuracy score for the validation set is attained by combining the interpolation model GPxyz with the elev-simple aggregation strategy, a bandwidth parameter set to b=400, and a refined rounding strategy. We denote this configuration of the pipeline as .
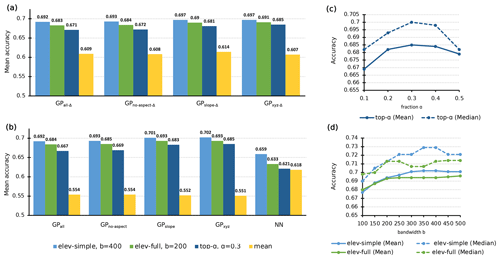
Figure 5(a, b) Mean day accuracy for combinations of interpolation models and aggregation strategy. (c) Mean and median day accuracy of GPxyz with top-α for different values of α. (d) Mean and median day accuracy of GPxyz combined with elevation-based aggregation strategies for varying bandwidth b values. All scores are computed on the validation set.
This section assesses the performance of the optimal pipeline configuration as determined through the model selection conducted in Sect. 5. To prevent any potential data leakage, we evaluate the model on a dedicated holdout test set that was neither utilized for training nor employed in the model selection process. This test set covers the winter season 2020/2021. Additionally, we provide scores computed on the validation set to examine the generalization gap.
For evaluation purposes, we split the territory of Switzerland into five geographical regions, shown in Fig. 6. These are the Jura Mountains in the northwest, the Swiss plateau with few hills reaching elevations higher than 1000 , and the Swiss Alps, with the Alps surrounded by the Pre-Alps in the north and the Southern Alps in the south. This particular subdivision takes into account the fact that the Swiss plateau normally has no avalanche danger and where no forecast is thus issued. This region is excluded from the analysis. Moreover, the remaining parts are grouped according to the number of weather stations above the tree line, with the bulk of the stations in the Alps and very few, if any, stations in the Jura, Pre-Alps, and Southern Alps (see also Fig. 1b). We perform the evaluation for all regions combined (All), combining the three regions of the Swiss Alps excluding the Jura (No Jura), and for the four regions separately.
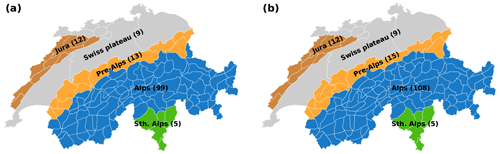
Figure 6Maps of Switzerland showing the boundaries of the warning regions within the time span encompassed by the validation set (a) and the test set (b), as well as their aggregation into larger geographic regions. The number of warning regions is indicated in parentheses.
6.1 Performance of the RF classifier
We employed the same pre-processing, splitting, and training strategy as outlined in Pérez-Guillén et al. (2022a). However, our results yielded a lower overall accuracy of 0.699 for the validation set and 0.707 for the test set, in contrast to the 0.74 overall accuracy reported in Pérez-Guillén et al. (2022; Table 1a) for their standard RF classifier. Similar trends were observed for the macro F1 score, where our RF classifier achieved macro F1 scores of 0.686 for the validation set and 0.656 for the test set, marking a reduction of up to 0.044 compared to the RF classifier of Pérez-Guillén et al..
Possible explanations for this may be related to our RF classifier being trained on a slightly different dataset compared to Pérez-Guillén et al. (2022a) (see Sect. 5.1) and relying on snow stratigraphy simulations using a more recent SNOWPACK version (i.e., v.3.6.0). Still, these differences in performance are minor and do not affect our analysis and extension of the model.
6.2 Performance of the three-stage pipeline
One of the performance measures we consider for the evaluation of the proposed three-stage pipeline is the daily agreement between the avalanche bulletin predicted by the pipeline and the forecast danger level in the true avalanche bulletin. We refer to this agreement as accuracy. Calculating statistics such as the mean and median of the daily accuracy across the entire test set provides valuable insights into the pipeline's overall performance. Figure 7 shows box plots of the daily accuracy for the test set and the validation set for the best pipeline configuration , but also for the point predictions of the RF classifier used as input for the pipeline. Considering all regions (All in Fig. 7a), the pipeline achieves a mean accuracy of 0.662 and a median accuracy of 0.700 for the test set and is thus comparable to the RF classifier's accuracy values.
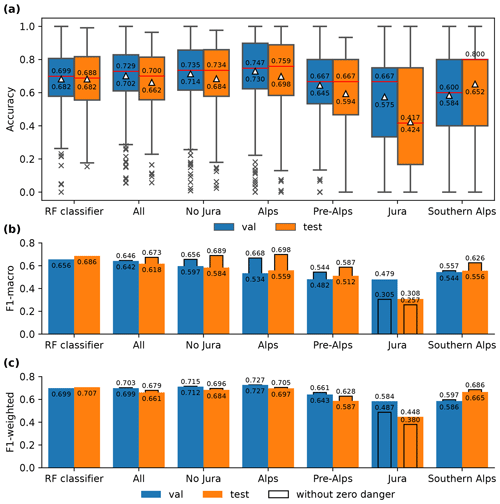
Figure 7Evaluation of the RF classifier and the three-stage pipeline-predicted bulletin for different groups of warning regions, as defined in Fig. 6. (a) Box plots summarizing the daily accuracy scores shown in the time series in Fig. 8. The median is marked by a horizontal line, and the mean is denoted by a triangle-shaped marker. The respective values are shown either above (median) or below (mean). (b, c) Overall per-class F1 scores (F1 macro and F1 weighted). The narrow bars featuring a black edge highlight the corresponding F1 score calculated by excluding the class 0 (i.e., the class for no danger).
As already identified by Pérez-Guillén et al. (2022a), the RF classifier's agreement with the forecast danger levels varies from day to day, with several days exhibiting a particularly strong mismatch between the pipeline-predicted and the human-forecast bulletin, resulting in remarkably low accuracy values (Fig. 8). As can be seen, the patterns in the RF classifier's daily scores propagate to the accuracy scores of the pipeline, resulting in high Pearson correlations across the validation and test set. The comparably few days with very poor agreement between the forecast and pipeline, represented as outliers in Fig. 7a, influence the overall mean daily accuracy. As a result, both the pipeline and the RF classifier show negatively skewed patterns of accuracy values, with the median accuracy consistently surpassing the mean accuracy. When contrasting the pipeline's mean and median accuracy for the test set with those calculated for the validation set, we observe a decline between 0.03 and 0.04 and a generally wider spread in the interquartile range (IQR) and whiskers shown in the box plot (Fig. 7a).
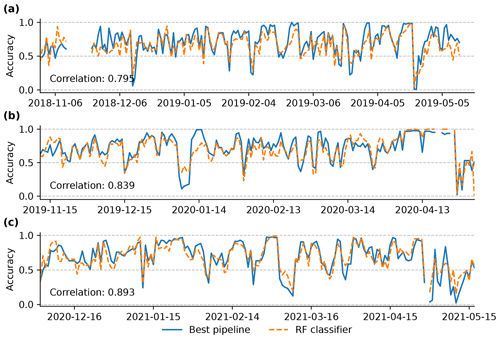
Figure 8Per day comparison of the accuracy of the RF classifier (dashed orange) and the pipeline predictions (solid blue) for (a, b) the validation set and (c) the test set for the region No Jura. The Pearson correlation between these two scores is displayed in the lower left corner.
Given the imbalanced distribution of avalanche danger levels, we incorporate the F1 score as a supplementary performance metric for the evaluation (Fig. 7b, c). Specifically, we consider two F1 scores, one which is simply averaged over the classes (F1 macro) and one that is a weighted average according to the class size (F1 weighted) (see definitions for these in Appendix A). These metrics address the class imbalance and offer deeper insights into the individual class (or danger level) performance, as opposed to accuracy. We calculate the F1 scores on a global scale across the entire test set (or validation set), thereby disregarding any temporal dependencies in the predictions, as opposed to the previously considered accuracy score that is computed per day. To ensure a fair comparison between the RF classifier and the overall pipeline, we analyze F1 scores excluding class 0 (i.e., danger level zero), as the RF classifier exclusively predicts danger levels 1 (low) through 4 (high). Considering all regions, the pipeline achieves a macro F1 score of 0.673 and an F1 weighted score of 0.679 for the test set, which is slightly lower than the corresponding scores for the RF classifier. Having a look at the F1 scores considering the zero danger level, we recognize that scores are lower, particularly with a significant decrease of up to 0.1 in the macro F1 score. This is expected, since the only notion of danger level zero is induced by the data augmentation that adds samples of danger level zero at locations with no avalanche forecast. We will further investigate the per-class performance in Sect. 6.4.
6.3 Regional performance
When interpreting the findings in the previous section, we want to emphasize that performance scores for the RF classifier were only computed for predictions at weather stations which have a ground truth available. Thus, the RF classifier is primarily compared to the forecast in the Alps due to the high density of weather stations in this particular region, while the pipeline was compared to the entire forecast domain. As can be seen in Fig. 7 for No Jura, excluding Jura improves the scores to a level that they match and sometimes even outperform the RF classifier's scores. The best accuracy values are achieved for the Alps, with all scores surpassing the RF classifier's performance. In the regions adjacent to the Alps, Pre-Alps, and Southern Alps), performance is lower, while particularly poor performance was observed for Jura. For instance, in Jura, the mean daily accuracy was a mere 0.424 for the test set. Higher scores for the regions of the Alps are not surprising as nearly all available weather stations in Switzerland are located in this region, and only a few warning regions have no weather stations. This result also emphasizes that a low density of weather stations, as is the case in Jura, proves insufficient to reliably interpolate across space and elevations, which is not surprising given the variable nature of avalanche conditions across space and different elevations.
6.4 Per-class performance
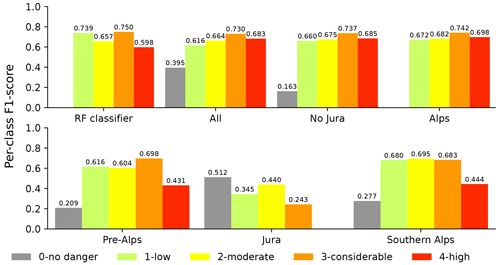
Figure 9 displays the per-class F1 scores attained for the test set for different regions, offering a comprehensive insight into the individual class performance. It can be recognized that the distribution of the F1 score across the classes is more uniform in comparison to the RF classifier, at least for regions with an overall macro F1 score ≥0.67 (i.e., regions All, No Jura, and Alps). For instance, for the Alps the class-wise performance of the pipeline ranges between 0.672 and 0.742 compared to 0.598 and 0.75 for the RF classifier. The most notable improvement compared to the point predictions of the RF classifier is shown for danger level 4 (high), with the F1 score reaching 0.698 in the region of the Alps. This is interesting considering that the interpolation model only uses the geographical location (latitude, longitude, elevation) as additional information, combined with a slight re-adjustment of the thresholds used to distinguish between danger levels 3 (considerable) and 4 (high) (3.44 vs. 3.5; see Sect. 4.3 and Fig. 4b). Additionally, there are reasonable increases in the F1 score for 2 (moderate) for all regions except Pre-Alps and Jura, which, however, come at the cost of slightly lower scores for 3 (considerable). The other notable difference relates to the F1 score for danger level 1 (low), which is substantially lower compared to the RF classifier. Nevertheless, regions that basically never have zero avalanche danger, such as the Alps and the Southern Alps, exhibit a less deficient F1 score for danger level 1 (low) compared to the Pre-Alps. We suppose, but have not empirically verified, that the notion of danger level zero has increased the complexity of the classification task, making it challenging to distinguish between danger levels 1 (low) and zero in some settings. Furthermore, the F1 score for danger level zero is consistently poor across all regions; thus, we suggest not using this approach to differentiate between regions with a low danger (1 – low) and no avalanche danger (zero).
We have demonstrated that our three-stage pipeline for regional avalanche danger forecasting (RAvaFcast v1.0.0), producing output similar to human-made avalanche bulletins, achieves a comparable performance as the RF classifier, which predicts danger levels at weather stations. However, when excluding warning regions with very few or no weather stations (i.e., Jura), our pipeline surpasses the RF classifier's performance. In other words, given a reasonable density of weather stations, a combination of interpolation and elevation-based aggregation shows proficient capabilities of extrapolating point estimates of avalanche danger to a regional context. In contrast, in regions where station density is low, performance depends strongly on how well conditions are represented by the few, and often far-away points, for which predictions are available. This is a serious limitation for the applicability of the pipeline for the Jura, which is not only far away from the Alps compared to the Pre-Alps and Southern Alps but in addition has a different topography compared to Alpine regions. This also explains why extrapolation is more likely to succeed in the Southern Alps than in the Jura.
To aid the interpretation of the spatial predictions, uncertainty maps provided by the GP-based interpolation model enable quantifying and distinguishing between regions with low and high uncertainty in the spatial predictions (see example in Fig. 3b). Notably, areas and elevations with low station coverage exhibit higher uncertainty, while regions with denser station networks show lower uncertainty. This is in line with the observed performance values for these regions. In addition to using uncertainty maps when interpreting predicted conditions on a specific day, long-term summaries of these data may be a way to identify locations where new weather stations would provide the greatest benefit when consistent performance of spatial interpolations is required.
We have further shown that the pipeline's performance is substantially impacted by the performance of the initial classification model; for instance, on days when the accuracy of the RF classifier predictions was high, the accuracy of the resulting predictions of the pipeline tended to be high as well, and vice versa. Thus, we conclude that the classifier's performance is another potential bottleneck in the proposed three-stage pipeline. Moreover, if the conditions captured by the AWSs and SNOWPACK differ significantly from those on the nearby slopes, it is expected that the RF classifier may generate more inaccurate predictions. We explored the performance of the classifier and the pipeline at the resolution of the danger levels, similar to the evaluation performed by Pérez-Guillén et al. (2022a). However, based on the analysis by Techel et al. (2022), who showed that the expected danger level davg(x) (Eq. 3) correlates with the recently introduced sub-levels in the Swiss avalanche forecast, which indicate whether expected danger is high (+), in the middle (=), or low (−) within the level (see also Lucas et al., 2023), we surmise that errors in the predictions provided by the RF classifier, and therefore the pipeline, may actually often be less than a full danger level. Moreover, some observed errors may be due to erroneous avalanche forecasts, which we used as ground truth for evaluation of the classifier and pipeline, rather than wrong model predictions (e.g., Pérez-Guillén et al., 2022a). Even though additional work will be required, we believe that it should be possible to train a regression or ordinal classification model using the sub-levels as input and to adapt the aggregation strategy in a way to provide predictions incorporating sub-level information.
Although we explored several combinations of terrain features derived at various scales, the most successful interpolation model relied solely on the geographical location (coordinates) and elevation. Maybe this is not too surprising as we derived terrain characteristics using a comparably coarse scale (kilometer to several kilometers), while models classifying avalanche terrain normally use a much higher resolution (a few meters; e.g., Harvey et al., 2018). Moreover, aggregating predictions over an area of 200 km2, the average size of the warning regions in Switzerland, means that a wide range of terrain properties will be included in a single spatial unit.
In this study, we focused on the development and validation of the interpolation algorithm and aggregation strategy, optimizing their performance with regard to predicting the regional danger level. However, in the human-made avalanche bulletin, the regional danger level is directly linked to the respective most critical elevation and slope aspects. Avalanche danger, and hence the risk to be caught in a potentially life-threatening avalanche, often changes considerably with elevation (Winkler et al., 2021). As we did not evaluate the pipeline's predicted elevation threshold, we can only assume that the elevational threshold provides a reasonably good correlation with forecast conditions. This assumption is based on the studies by Pérez-Guillén et al. (2022a, for elevation threshold) and Techel et al. (2022, for aspect and elevation), who showed that the RF classifier's point predictions capture variations in forecast avalanche conditions as a function of aspect and elevation.
Recent advances in grid-based predictions of snow cover properties like new-snow height and total snow height, coupling numerical weather prediction models and snow cover simulations and assimilating ground-based measurements (e.g., Mott et al., 2023), and snow coverage products derived from satellite images offer the potential to be used as supplementary features in the interpolation model. Moreover, physical snowpack simulations are increasingly being driven by gridded weather and snow data directly rather than exclusively at the locations of weather stations (e.g., Bellaire et al., 2011; Sharma et al., 2023; Mott et al., 2023; Herla et al., 2024). While this development reduces the need to obtain spatial predictions through interpolation from a small number of points, the complex and spatially highly resolved data must be provided in an accessible way to allow efficient interpretation by humans (e.g., Herla et al., 2022). The proposed aggregation strategy may be one suitable approach to summarize and smooth in spatially consistent ways such information, regardless whether this is done for fixed regions, as in this study, or at other spatial scales.
We developed and evaluated a three-stage pipeline for regional avalanche forecasting in Switzerland (RAvaFcast v1.0.0) with the stages comprising the following.
-
Classification. Avalanche danger is predicted at the location of automated weather stations using weather data and physical snow cover simulations as input.
-
Interpolation. Point predictions are interpolated on a 1 km × 1 km resolution DSM grid using latitude, longitude, and elevation as input features.
-
Aggregation. Gridded predictions are aggregated to infer a regional avalanche danger level for predefined warning regions, similar to human-made avalanche forecasts in Switzerland.
While relying on the Pérez-Guillén et al. (2022a) RF classifier for avalanche danger level prediction, we introduced data-driven classification thresholds, optimizing the classification task and leading to a more balanced performance across danger levels. We investigated the performance of Gaussian-process-based interpolation models using a variety of terrain features (e.g., elevation, slope) as predictors extracted from a digital surface model; however, interpolation using a relatively simple set of features (location and elevation) proved to be the best approach. And lastly, we proposed a novel elevation-based aggregation strategy providing regional danger level predictions, which additionally indicates the elevation band where the respective danger level is reached.
The performance of the regional danger level predictions provided by the three-stage pipeline strongly depends on the RF classifier's performance. In the Alps, where station density is high, the pipeline exceeded the classifier performance on most days, achieving a mean day accuracy of about 70 %. However, on days when the RF classifier performed poorly or in regions where station density is low, the pipeline's predictions were of particularly poor quality (i.e., Jura). This causes a lower mean day accuracy of 66 % for the entire forecast domain, closely aligning with the RF classifier's mean day accuracy of 68 %. Thus, we conclude that both the number of stations, distributed over a range of elevations, and the accuracy of the input model are the key bottlenecks hindering a fully automated regional danger level prediction using a station-based approach.
Swiss avalanche forecasters operationally use the RF classifier's point predictions to support their danger level assessments (van Herwijnen et al., 2023). The proposed pipeline can further aid avalanche forecasting by providing a second opinion regarding the critical elevation threshold. However, the poor performances of the classifier and pipeline on some days, and in general in the Jura, emphasize that such fully automated danger level forecasts can assist avalanche forecasters but cannot yet fully replace human-made forecasts.
In this section of the Appendix, we define scores and error metrics used for model selection and evaluation.
A1 Classification metrics
Accuracy is defined as follows.
where TP is true positive, FP is false positive, TN is true negative, and FN is false negative.
Precision quantifies the accuracy of the positive predictions and is formally defined as follows.
On the other hand, the recall is defined as the proportion of the actual positives that were identified correctly by the classifier. It assesses the classifier's ability to identify all the positives.
Finally, the F1 score balances precision and recall; more specifically, it is defined as the harmonic mean.
In multi-class classification, the above scores are computed per class and averaged. Concretely, macro-averaging is a simple average, and weighted averaging considers the support of each class. We refer to Sokolova and Lapalme (2009) for a complete discussion of classification metrics.
A2 Interpolation error metrics
Let be a dataset and the predicted value by the interpolation model. Then, the following common error metrics for quantitative model assessment can be defined.
Mean error (ME)
Mean absolute error (MAE)
Root mean squared error (RMSE)
For leave-one-out cross-validation, , while the model fi(⋅) is trained on all samples except xi.
-
12 December 2020 (Fig. B1, left column). The RF classifier's accuracy is 0.753, while 85 out of 97 AWSs lie above the forecast elevation threshold in the published bulletin. The interpolation algorithm interpolates well to unobserved locations, leading to a predicted avalanche bulletin exhibiting an accuracy of 0.743. Under the circumstances of only having one active station in the region of Jura the pipeline's predictions show an accuracy of about 0.5 for this particular region. Furthermore, it is noteworthy that the predicted danger level 3 (considerable) was reached for an elevation threshold of 1600 , which would put only three isolated Jura summits into this class.
-
23 December 2020 (Fig. B1, right column). With 0.667, the RF classifier's accuracy is below its mean accuracy for the test set. A total of 69 out of 93 AWSs lie above the elevation threshold indicated in the published bulletin. Nonetheless, the interpolation model and elevation-based strategy successfully smooth out erroneous predictions, leading to an accuracy of 0.783 for the predicted avalanche bulletin, which is higher than the corresponding mean accuracy. Considering that the pipeline exhibits a nearly complete failure to predict the correct danger level in Jura due to the missing local danger level assessments, the overall accuracy is still relatively high. Excluding the Jura gives an accuracy of 0.813.
-
27 February 2021 (Fig. B2, left column). The RF classifier's accuracy stands at a remarkable 0.906, while nearly all AWSs lie above the forecast elevation threshold in the published bulletin. Consequently, the pipeline-predicted bulletin has an exceptional accuracy of 0.943.
-
19 January 2021 (Fig. B2, right column). The RF classifier achieved an accuracy of 0.802, with 111 out of 123 AWSs lying above the indicated elevation threshold. The accuracy of the pipeline-predicted bulletin is 0.893. On this day, four stations in Jura provided predictions, leading to a more reasonable interpolation and aggregation in this particular region. However, despite having comparably many stations providing predictions in Jura, only about half of the warning regions align with the published bulletin's danger level. Similar as on 12 December 2020 (Fig. B1, left column), the predicted danger level 3 (considerable) in Jura applies for elevations higher than 1600
-
28 January 2021 (Fig. B3, left column). The accuracy of the RF classifier stands at 0.706, while 107 out of 121 AWSs lie above the forecast elevation threshold in the true bulletin. The distribution of the RF classifier predictions (samples used for the interpolation) is such that 52 % of them predict 4 (high) and 39 % 3 (considerable). This makes interpolation and aggregation easier, resulting in an accuracy of 0.793 for the pipeline-predicted bulletin and an accuracy of 0.844 when disregarding regions in Jura.
-
30 January 2021 (Fig. B3, right column). The RF classifier yields an accuracy of 0.654, while 109 out of 121 AWSs lie above the elevation threshold that indicates particularly avalanche-prone locations. A total of 77 % of the RF classifier predictions are classified as 3 (considerable), while only 13 % belong to danger level 4 (high). Consequently, the pipeline mostly fails to predict a danger level of 4 (high), leading to an accuracy of 0.629.
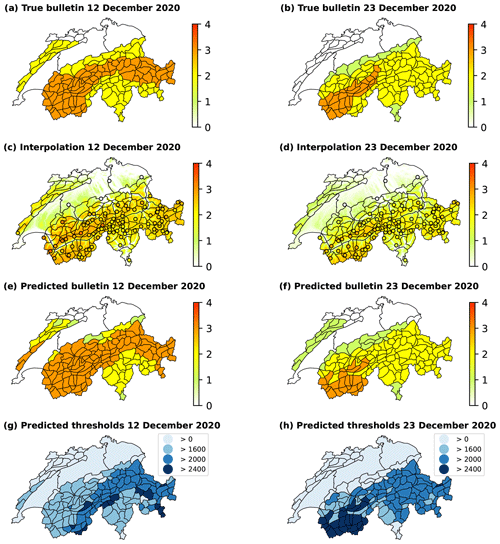
Figure B1The true avalanche bulletin (a, b) and danger level predictions of the three-stage pipeline (c–h) for 12 December 2020 and 23 December 2020. Maps (c) and (d) illustrate the interpolation of the RF classifier's predictions of the local danger level at AWSs, represented by circular markers. Maps (e) and (f) depict the predictions at the scale of warning regions resulting in an avalanche bulletin, with corresponding elevation thresholds in maps (g) and (h).
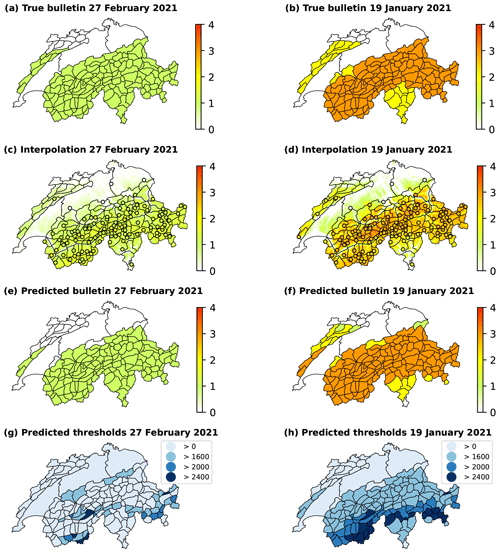
Figure B2The true avalanche bulletin (a, b) and danger level predictions of the three-stage pipeline (c–h) for 27 February 2021 and 19 January 2021. Maps (c) and (d) illustrate the interpolation of the RF classifier's predictions of the local danger level at AWSs, represented by circular markers. Maps (e) and (f) depict the predictions at the scale of warning regions resulting in an avalanche bulletin, with corresponding elevation thresholds in maps (g) and (h).
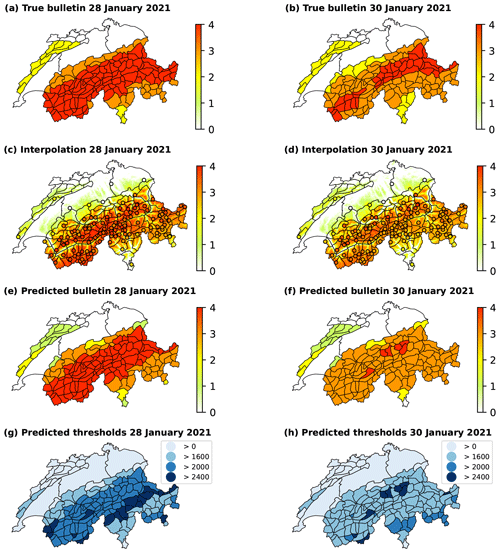
Figure B3The true avalanche bulletin (a, b) and danger level predictions of the three-stage pipeline (c–h) for 28 January 2021 and 30 January 2021. Maps (c) and (d) illustrate the interpolation of the RF classifier's predictions of the local danger level at AWSs, represented by circular markers. Maps (e) and (f) depict the predictions at the scale of warning regions resulting in an avalanche bulletin, with corresponding elevation thresholds in maps (g) and (h).
The code and software developed for this project are available via Zenodo at https://doi.org/10.5281/zenodo.10521973 (Maissen et al., 2023) or via Renku at https://renkulab.io/projects/deapsnow/three-stage-pipeline (last access: 9 August 2024). The repository contains all the necessary datasets, scripts, modules, and data processing files required to reproduce the results and plots of this paper. Additionally, detailed instructions on setting up the environment and running the code are provided in the repository's README file.
We provide the evolution of the three-stage pipeline's predictions (b–d) for the winter season 2018/2019 until the winter season 2020/2021 in comparison to the true avalanche bulletin (a). Map (b) illustrates the interpolation of the RF classifier's predictions of the local danger level at AWSs, represented by circular markers. Map (c) depicts the predictions at the scale of warning regions resulting in an avalanche bulletin, with corresponding elevation thresholds in map (d). The supplement related to this article is available online at: https://doi.org/10.5194/gmd-17-7569-2024-supplement.
AM prepared the data, implemented the models, analyzed the results, and prepared the draft manuscript with the contributions of all co-authors. FT brought domain expertise to the project, contributing to both result analysis and manuscript development. MV developed the research idea and provided the expertise for model choice and implementation. FT and MV reviewed and edited the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Cristina Pérez Guillén provided access to the most recent dataset, which encompasses an additional winter season and incorporates simulations using SNOWPACK v3.6.0.
This project was funded by the Swiss Data Science Center (grant no. C18-05 “DEAPSnow”).
This paper was edited by Fabien Maussion and reviewed by Simon Horton and one anonymous referee.
Adelson, E., Anderson, C., Bergen, J., Burt, P., and Ogden, J.: Pyramid Methods in Image Processing, RCA Engineer, 29, 33–41, 1984. a
Agou, V. D., Pavlides, A., and Hristopulos, D. T.: Spatial Modeling of Precipitation Based on Data-Driven Warping of Gaussian Processes, Entropy, 24, 321, https://doi.org/10.3390/e24030321, 2022. a
Badoux, A., Andres, N., Techel, F., and Hegg, C.: Natural hazard fatalities in Switzerland from 1946 to 2015, Nat. Hazards Earth Syst. Sci., 16, 2747–2768, https://doi.org/10.5194/nhess-16-2747-2016, 2016. a
Baggi, S. and Schweizer, J.: Characteristics of wet-snow avalanche activity: 20 years of observations from a high alpine valley (Dischma, Switzerland), Nat. Hazards, 50, 97–108, https://doi.org/10.1007/s11069-008-9322-7, 2009. a
Bellaire, S., Jamieson, J. B., and Fierz, C.: Forcing the snow-cover model SNOWPACK with forecasted weather data, The Cryosphere, 5, 1115–1125, https://doi.org/10.5194/tc-5-1115-2011, 2011. a
Birkeland, K. W., Greene, E. M., and Logan, S.: In Response to Avalanche Fatalities in the United States by Jekich et al, Wild. Environ. Med., 28, 380–382, https://doi.org/10.1016/j.wem.2017.06.009, 2017. a, b
Bolognesi, R.: NivoLog: An Avalanche Forecasting Support System, in: International Snow Science Workshop Proceedings 1998, Sunriver, Oregon, USA, https://arc.lib.montana.edu/snow-science/objects/issw-1998-412-418.pdf (last access: 25 October 2024), 1998. a
Brabec, B. and Meister, R.: A nearest-neighbor model for regional avalanche forecasting, Ann. Glaciol., 32, 130–134, https://doi.org/10.3189/172756401781819247, 2001. a, b, c, d, e, f, g, h
Breiman, L.: Random Forests, Machine Learning, 45, 5–32, https://doi.org/10.1023/A:1010933404324, 2001. a
Buser, O.: Avalanche forecast with the method of nearest neighbours: An interactive approach, Cold Reg. Sci. Technol., 8, 155–163, https://doi.org/10.1016/0165-232X(83)90006-X, 1983. a, b, c
Buser, O.: Two Years Experience of Operational Avalanche Forecasting using the Nearest Neighbours Method, Ann. Glaciol., 13, 31–34, https://doi.org/10.3189/S026030550000759X, 1989. a
Dale, M. and Fortin, M.-J.: Spatial analysis: a guide for ecologists, Cambridge University Press, 2 edn., ISBN 978-0-521-14350-9, 2014. a
Duvenaud, D., Lloyd, J. R., Grosse, R., Tenenbaum, J. B., and Ghahramani, Z.: Structure Discovery in Nonparametric Regression through Compositional Kernel Search, in: Proceedings of the 30th International Conference on International Conference on Machine Learning – Volume 28, 17–19 June 2013, Atlanta, Georgia, USA, http://proceedings.mlr.press/v28/duvenaud13.pdf (last access: 25 October 2024), 1166–1174, 2013. a
Duvenaud, D. K., Nickisch, H., and Rasmussen, C.: Additive Gaussian Processes, in: Advances in Neural Information Processing Systems, edited by: Shawe-Taylor, J., Zemel, R., Bartlett, P., Pereira, F., and Weinberger, K., vol. 24, Curran Associates, Inc., https://proceedings.neurips.cc/paper/2011/file/4c5bde74a8f110656874902f07378009-Paper.pdf (last access: 25 October 2024), 2011. a
EAWS: Avalanche Danger Scale, https://www.avalanches.org/standards/avalanche-danger-scale/ (last access: 4 October 2023), 2022. a, b, c
EEA: EU-DEM v1.1, https://land.copernicus.eu/imagery-in-situ/eu-dem/eu-dem-v1.1 (last access: 4 October 2023), 2016. a
FOMC: Automatic monitoring network, https://www.meteoswiss.admin.ch/home/measurement-and-forecasting-systems/land-based-stations/automatisches-messnetz.html (last access: 4 October 2023), 2023. a
Gonzalez, R. C. and Woods, R. E.: Digital Image Processing, 3rd edn., Prentice-Hall, Inc., USA, ISBN 013168728X, 2006. a
Harvey, S., Schmudlach, G., Bühler, Y., Dürr, L., Stoffel, A., and Christen, M.: Avalanche terrain maps for backcountry skiing in Switzerland, in: Proceedings ISSW 2018, International Snow Science Workshop Innsbruck, Austria, 7–12 October 2018, Innsbruck, Austria, https://arc.lib.montana.edu/snow-science/objects/ISSW2018_O19.1.pdf (last access: 25 October 2024), 1625–1631, 2018. a, b
Hendrick, M., Techel, F., Volpi, M., Olevski, T., Pérez-Guillén, C., van Herwijnen, A., and Schweizer, J.: Automated prediction of wet-snow avalanche activity in the Swiss Alps, J. Glaciol., 69, 1365–1378, https://doi.org/10.1017/jog.2023.24, 2023. a
Hendrikx, J., Murphy, M., and Onslow, T.: Classification trees as a tool for operational avalanche forecasting on the Seward Highway, Alaska, Cold Reg. Sci. Technol., 97, 113–120, https://doi.org/10.1016/j.coldregions.2013.08.009, 2014. a
Herla, F., Haegeli, P., and Mair, P.: A data exploration tool for averaging and accessing large data sets of snow stratigraphy profiles useful for avalanche forecasting, The Cryosphere, 16, 3149–3162, https://doi.org/10.5194/tc-16-3149-2022, 2022. a
Herla, F., Haegeli, P., Horton, S., and Mair, P.: A large-scale validation of snowpack simulations in support of avalanche forecasting focusing on critical layers, Nat. Hazards Earth Syst. Sci., 24, 2727–2756, https://doi.org/10.5194/nhess-24-2727-2024, 2024. a, b
Kleemayr, K. and Moser, A.: NAFT – New Avalanche Forecasting Technologies (Neue Lawinenprognosemodelle), Schriftenreihe der Forschung im Verbund, 1998. a
Kristensen, K. and Larsson, C.: An avalanche forecasting program based on a modified nearest neighbour method, in: Proceedings International Snow Science Workshop Proceedings ISSW,Snowbird, Utah, USA, https://arc.lib.montana.edu/snow-science/objects/issw-1994-022-030.pdf (last access: 25 October 2024), 1994. a
Lehning, M., Bartelt, P., Brown, B., Russi, T., Stöckli, U., and Zimmerli, M.: SNOWPACK model calculations for avalanche warning based upon a new network of weather and snow stations, Cold Reg. Sci. Technol., 30, 145–157, https://doi.org/10.1016/S0165-232X(99)00022-1, 1999. a, b, c
Lehning, M., Bartelt, P., Brown, B., and Fierz, C.: A physical SNOWPACK model for the Swiss avalanche warning: Part III: meteorological forcing, thin layer formation and evaluation, Cold Reg. Sci. Technol., 35, 169–184, https://doi.org/10.1016/S0165-232X(02)00072-1, 2002a. a, b
Lehning, M., Bartelt, P., Brown, B., Fierz, C., and Satyawali, P.: A physical SNOWPACK model for the Swiss avalanche warning: Part II. Snow microstructure, Cold Reg. Sci. Technol., 35, 147–167, https://doi.org/10.1016/S0165-232X(02)00073-3, 2002b. a, b
Lucas, C., Trachsel, J., Eberli, M., Grüter, S., Winkler, K., and Techel, F.: Introducing sublevels in the Swiss avalanche forecast, in: International Snow Science Workshop ISSW 2023, Bend, Oregon, USA, https://arc.lib.montana.edu/snow-science/objects/ISSW2023_P1.19.pdf (last acess: 25 October 2024), 2023. a, b
Maissen, A., Techel, F., and Volpi, M.: RAvaFcast v1.0.0, Zenodo [code and data set], https://doi.org/10.5281/zenodo.10521973, 2023. a
Mayer, S., van Herwijnen, A., Techel, F., and Schweizer, J.: A random forest model to assess snow instability from simulated snow stratigraphy, The Cryosphere, 16, 4593–4615, https://doi.org/10.5194/tc-16-4593-2022, 2022. a, b
Mayer, S., Techel, F., Schweizer, J., and van Herwijnen, A.: Prediction of natural dry-snow avalanche activity using physics-based snowpack simulations, Nat. Hazards Earth Syst. Sci., 23, 3445–3465, https://doi.org/10.5194/nhess-23-3445-2023, 2023. a
Mitterer, C. and Schweizer, J.: Analysis of the snow-atmosphere energy balance during wet-snow instabilities and implications for avalanche prediction, The Cryosphere, 7, 205–216, https://doi.org/10.5194/tc-7-205-2013, 2013. a
Morin, S., Horton, S., Techel, F., Bavay, M., Coléou, C., Fierz, C., Gobiet, A., Hagenmuller, P., Lafaysse, M., Ližar, M., Mitterer, C., Monti, F., Müller, K., Olefs, M., Snook, J. S., van Herwijnen, A., and Vionnet, V.: Application of physical snowpack models in support of operational avalanche hazard forecasting: A status report on current implementations and prospects for the future, Cold Reg. Sci. Technol., 170, 102910, https://doi.org/10.1016/j.coldregions.2019.102910, 2019. a
Mott, R., Winstral, A., Cluzet, B., Helbig, N., Magnusson, J., Mazzotti, G., Quéno, L., Schirmer, M., Webster, C., and Jonas, T.: Operational snow-hydrological modeling for Switzerland, Frontiers in Earth Science, 11, https://doi.org/10.3389/feart.2023.1228158, 2023. a, b
Nadim, F., Pedersen, S. A. S., Schmidt-Thomé, P., Sigmundsson, F., and Engdahl, M.: Natural hazards in Nordic Countries, International Union of Geological Sciences, 31, 176–184, http://episodes.org/journal/view.html?doi=10.18814/epiiugs/2008/v31i1/024 (last access: 25 October 2024), 2008. a
Niculescu-Mizil, A. and Caruana, R.: Predicting Good Probabilities with Supervised Learning, in: Proceedings of the 22nd International Conference on Machine Learning, ICML '05, Association for Computing Machinery, New York, NY, USA, ISBN 1595931805, 625–632, https://doi.org/10.1145/1102351.1102430, 2005. a
Pérez-Guillén, C., Techel, F., Hendrick, M., Volpi, M., van Herwijnen, A., Olevski, T., Obozinski, G., Pérez-Cruz, F., and Schweizer, J.: Data-driven automated predictions of the avalanche danger level for dry-snow conditions in Switzerland, Nat. Hazards Earth Syst. Sci., 22, 2031–2056, https://doi.org/10.5194/nhess-22-2031-2022, 2022a. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac, ad, ae
Pérez-Guillén, C., Techel, F., Hendrick, M., Volpi, M., van Herwijnen, A., Olevski, T., Obozinski, G., Pérez-Cruz, F., and Schweizer, J.: Weather, snowpack and danger ratings data for automated avalanche danger level predictions, EnviDat [data set], https://doi.org/10.16904/envidat.330, 2022b. a
Plate, T. A.: Accuracy Versus Interpretability in Flexible Modeling: Implementing a Tradeoff Using Gaussian Process Models, Behaviormetrika, 26, 29–50, https://doi.org/10.2333/bhmk.26.29, 1999. a
Pozdnoukhov, A., Purves, R., and Kanevski, M.: Applying machine learning methods to avalanche forecasting, Ann. Glaciol., 49, 107–113, https://doi.org/10.3189/172756408787814870, 2008. a
Pozdnoukhov, A., Matasci, G., Kanevski, M., and Purves, R. S.: Spatio-temporal avalanche forecasting with Support Vector Machines, Nat. Hazards Earth Syst. Sci., 11, 367–382, https://doi.org/10.5194/nhess-11-367-2011, 2011. a
Purves, R. S., Morrison, K. W., Moss, G., and Wright, D. S. B.: Nearest neighbours for avalanche forecasting in Scotland–development, verification and optimisation of a model, Cold Reg. Sci. Technol., 37, 343–355, https://doi.org/10.1016/S0165-232X(03)00075-2, 2003. a
Rasmussen, C. E. and Williams, C. K. I.: Gaussian Processes for Machine Learning, The MIT Press, ISBN 9780262256834, https://doi.org/10.7551/mitpress/3206.001.0001, 2006. a, b, c
Schirmer, M., Lehning, M., and Schweizer, J.: Statistical forecasting of regional avalanche danger using simulated snow-cover data, J. Glaciol., 55, 761–768, https://doi.org/10.3189/002214309790152429, 2009. a, b
Schirmer, M., Schweizer, J., and Lehning, M.: Statistical evaluation of local to regional snowpack stability using simulated snow-cover data, Cold Reg. Sci. Technol., 64, 110–118, https://doi.org/10.1016/j.coldregions.2010.04.012, 2010. a
Schmudlach, G. and Köhler, J.: Method for an automatized avalanche terrain classification, in: Proceedings, International Snow Science Workshop, Breckenridge, Colorado, 2016, 729–736, https://arc.lib.montana.edu/snow-science/objects/ISSW16_P2.04.pdf (last access: 25 October 2024), 2016. a
Schweizer, J. and Föhn, P. M. B.: Avalanche forecasting – an expert system approach, J. Glaciol., 42, 318–332, https://doi.org/10.3189/S0022143000004172, 1996. a
Schweizer, J. and Lütschg, M.: Characteristics of human-triggered avalanches, Cold Reg. Sci. Technol., 33, 147–162, https://doi.org/10.1016/S0165-232X(01)00037-4, 2001. a
Schweizer, M., Föhn, P. M. B., Schweizer, J., and Ultsch, A.: A Hybrid Expert System for Avalanche Forecasting, in: Information and Communications Technologies in Tourism, edited by: Schertler, W., Schmid, B., Tjoa, A. M., and Werthner, H., Springer Vienna, 148–153, ISBN 978-3-7091-9343-3, https://doi.org/10.1007/978-3-7091-9343-3_23, 1994. a
Scott, D. W.: Multivariate Density Estimation: Theory, Practice, and Visualization, Wiley Series in Probability and Statistics, John Wiley & Sons, Inc., ISBN 9780471547709, https://doi.org/10.1002/9780470316849, 1992. a
Sharma, V., Gerber, F., and Lehning, M.: Introducing CRYOWRF v1.0: multiscale atmospheric flow simulations with advanced snow cover modelling, Geosci. Model Dev., 16, 719–749, https://doi.org/10.5194/gmd-16-719-2023, 2023. a
SLF: Description automated stations, https://www.slf.ch/en/avalanche-bulletin-and-snow-situation/measured-values/description-of-automated-stations.html (last access: 4 October 2023), 2022. a, b
SLF: Avalanche Bulletin Interpretation Guide: Edition November 2023, WSL Institute for Snow and Avalanche Research SLF, https://www.slf.ch/fileadmin/user_upload/SLF/Lawinenbulletin_Schneesituation/Wissen_zum_Lawinenbulletin/Interpretationshilfe/Interpretationshilfe_EN.pdf (last access: 25 October 2024), 2023. a, b, c, d, e, f
Sobel, I. and Feldman, G.: A 3×3 Isotropic Gradient Operator for Image Processing, Pattern Classification and Scene Analysis, 271–272, ISBN 9780471223610, 1973. a
Sokolova, M. and Lapalme, G.: A systematic analysis of performance measures for classification tasks, Information Processing and Management, 45, 427–437, https://doi.org/10.1016/j.ipm.2009.03.002, 2009. a
Sykes, J., Toft, H., Haegeli, P., and Statham, G.: Automated Avalanche Terrain Exposure Scale (ATES) mapping – local validation and optimization in western Canada, Nat. Hazards Earth Syst. Sci., 24, 947–971, https://doi.org/10.5194/nhess-24-947-2024, 2024. a
Techel, F. and Schweizer, J.: On using local avalanche danger level estimates for regional forecast verification, Cold Reg. Sci. Technol., 144, 52–62, https://doi.org/10.1016/j.coldregions.2017.07.012, 2017. a
Techel, F. and Zweifel, B.: Recreational avalanche accidents in Switzerland: Trends and patterns with an emphasis on burial, rescue methods and avalanche danger, in: International Snow Science Workshop Proceedings 2013, 7–11 October 2013, Grenoble, France, 1106–1112, https://arc.lib.montana.edu/snow-science/objects/ISSW13_paper_P1-08.pdf (last access: 25 October 2024), 2013. a
Techel, F., Pielmeier, C., and Winkler, K.: Refined dry-snow avalanche danger ratings in regional avalanche forecasts: Consistent? And better than random?, Cold Reg. Sci. Technol., 180, 103162, https://doi.org/10.1016/j.coldregions.2020.103162, 2020. a
Techel, F., Mayer, S., Pérez-Guillén, C., Schmudlach, G., and Winkler, K.: On the correlation between a sub-level qualifier refining the danger level with observations and models relating to the contributing factors of avalanche danger, Nat. Hazards Earth Syst. Sci., 22, 1911–1930, https://doi.org/10.5194/nhess-22-1911-2022, 2022. a, b, c
van Herwijnen, A., Mayer, S., Pérez-Guillén, C., Techel, F., Hendrick, M., and Schweizer, J.: Data-driven models used in operational avalanche forecasting in Switzerland, in: International Snow Science Workshop ISSW 2023, 8–13 October 2023, Bend, Oregon, USA, https://arc.lib.montana.edu/snow-science/objects/ISSW2023_P1.33.pdf (last access: 25 October 2024), 2023. a, b
Veitinger, J., Purves, R. S., and Sovilla, B.: Potential slab avalanche release area identification from estimated winter terrain: a multi-scale, fuzzy logic approach, Nat. Hazards Earth Syst. Sci., 16, 2211–2225, https://doi.org/10.5194/nhess-16-2211-2016, 2016. a
Vontobel, I., Harvey, S., and Purves, R.: Terrain analysis of skier-triggered avalanche starting zones, in: International Snow Science Workshop Proceedings 2013, 7–11 October 2013, 371–375, https://arc.lib.montana.edu/snow-science/objects/ISSW13_paper_O5-05.pdf (last access: 25 Ocotober 2024), 2013. a
Winkler, K., Fischer, A., and Techel, F.: Avalanche risk in winter backcountry touring: status and recent trends in Switzerland, in: Proceedings ISSW 2016. International Snow Science Workshop, 2–7 October 2016, Breckenridge, Co., 270–276, https://arc.lib.montana.edu/snow-science/item.php?id=2277 (last access: 25 October 2024), 2016. a
Winkler, K., Schmudlach, G., Degraeuwe, B., and Techel, F.: On the correlation between the forecast avalanche danger and avalanche risk taken by backcountry skiers in Switzerland, Cold Reg. Sci. Technol., 188, 103299, https://doi.org/10.1016/j.coldregions.2021.103299, 2021. a
Wu, Y.-H. E. and Hung, M.-C.: Comparison of Spatial Interpolation Techniques Using Visualization and Quantitative Assessment, in: Applications of Spatial Statistics, edited by: Hung, M.-C., 17–34, IntechOpen, Rijeka, https://doi.org/10.5772/65996, 2016. a
- Abstract
- Introduction
- Background
- Data
- Method
- Model optimization and selection
- Evaluation
- Discussion and outlook
- Conclusions
- Appendix A: Scores and error metrics
- Appendix B: Case study
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Background
- Data
- Method
- Model optimization and selection
- Evaluation
- Discussion and outlook
- Conclusions
- Appendix A: Scores and error metrics
- Appendix B: Case study
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement