the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
The dynamical core of the Aeolus 1.0 statistical–dynamical atmosphere model: validation and parameter optimization
Alexey V. Eliseev
Stefan Petri
Michael Flechsig
Levke Caesar
Vladimir Petoukhov
Dim Coumou
We present and validate a set of equations for representing the atmosphere's large-scale general circulation in an Earth system model of intermediate complexity (EMIC). These dynamical equations have been implemented in Aeolus 1.0, which is a statistical–dynamical atmosphere model (SDAM) and includes radiative transfer and cloud modules (Coumou et al., 2011; Eliseev et al., 2013). The statistical dynamical approach is computationally efficient and thus enables us to perform climate simulations at multimillennia timescales, which is a prime aim of our model development. Further, this computational efficiency enables us to scan large and high-dimensional parameter space to tune the model parameters, e.g., for sensitivity studies.
Here, we present novel equations for the large-scale zonal-mean wind as well as those for planetary waves. Together with synoptic parameterization (as presented by Coumou et al., 2011), these form the mathematical description of the dynamical core of Aeolus 1.0.
We optimize the dynamical core parameter values by tuning all relevant dynamical fields to ERA-Interim reanalysis data (1983–2009) forcing the dynamical core with prescribed surface temperature, surface humidity and cumulus cloud fraction. We test the model's performance in reproducing the seasonal cycle and the influence of the El Niño–Southern Oscillation (ENSO). We use a simulated annealing optimization algorithm, which approximates the global minimum of a high-dimensional function.
With non-tuned parameter values, the model performs reasonably in terms of its representation of zonal-mean circulation, planetary waves and storm tracks. The simulated annealing optimization improves in particular the model's representation of the Northern Hemisphere jet stream and storm tracks as well as the Hadley circulation.
The regions of high azonal wind velocities (planetary waves) are accurately captured for all validation experiments. The zonal-mean zonal wind and the integrated lower troposphere mass flux show good results in particular in the Northern Hemisphere. In the Southern Hemisphere, the model tends to produce too-weak zonal-mean zonal winds and a too-narrow Hadley circulation. We discuss possible reasons for these model biases as well as planned future model improvements and applications.
- Article
(12363 KB) - Full-text XML
-
Supplement
(232 KB) - BibTeX
- EndNote
Numerical models of the Earth system play a key role in our understanding of physical processes in Earth and atmosphere and can be used to simulate past and future climate changes. General circulation models (GCMs) are physically the most realistic tools for studying and modelling climate variability and climate change in the Earth system. However, due to their relatively high resolution, they are costly in terms of CPU runtime, limiting their applicability to study climate variability over long (∼ millennia) timescales.
On the other hand, highly idealized and computational efficient models for the climate system are able to simulate long time periods, but those are often box or one- or two-dimensional models describing only a limited number of processes or feedbacks of the real world. Hence, their application is limited, but they have been applied to study paleoclimate (Berger et al., 1992; Harvey, 1989) and future global change (Xiao et al., 1997).
A third class of models are so-called Earth system models of intermediate complexity (EMICs) which form a compromise between the computationally expensive (but more realistic) GCMs and the highly simplified models (Claussen et al., 2002). The number of processes and feedbacks are comparable to GCMs; however, due to a reduction in resolution and/or complexity of some model components, it is possible to study climate simulations up to multimillennia timescales (Eliseev et al., 2014a, b; Ganopolski et al., 2001; Montoya et al., 2005). Other applications include determining quick assessments of climate change impacts or running thousands of parameter sensitivity experiments (Knutti et al., 2002; Schmittner and Stocker, 1999).
EMICs are thus particularly useful for understanding the roles of different Earth components on very long timescales (multimillennia and longer) and consequently form useful tools complementary to GCMs. Internal climate processes on such very long timescales are primarily driven by ocean and ice dynamics (Holland et al., 2001; Latif, 1998; Polyakov et al., 2003), with the atmosphere's role being likely limited to globally distributing any perturbations to the system. In GCMs, it is however often the atmosphere which takes most of the computational load due to the need to resolve synoptic weather systems, which requires a high-resolution discretization in space and time. For these reasons, a key step in the development of EMICs intended for studying ocean and ice dynamics on multimillennial timescales is the derivation and validation of statistical–dynamical equations which accurately represent atmosphere dynamics (Coumou et al., 2011).
EMICs have been used in many climate studies and several different types of simplified atmospheric components that form part of an EMIC exist including two-dimensional, zonally averaged atmosphere models, 2.5-D atmosphere models (the vertical dimension is reconstructed using two-dimensional fields) with simple energy balance or statistical–dynamical atmosphere models (SDAMs) (Claussen et al., 2002; McGuffie and Henderson-Sellers, 2005). Most EMIC studies focus on climate variability on very long timescales (e.g., glacial cycles), and therefore fast processes are normally parameterized. In particular, SDAMs parameterize smaller-scale (and more short-lived) processes like synoptic eddy activity in terms of the large-scale, long-term fields. The assumption of those models is thus that atmospheric variables can be expressed in separate terms of a large-scale, long-term component, with characteristic spatial and temporal scales of L>1000 km and T>10 days, and a small-scale component-like ensemble of synoptic-scale eddies and waves. The latter are then parameterized by their averaged statistical characteristics (their total kinetic energy and heat, their moist and momentum fluxes, etc.). This means that transport effects of the fast-moving weather systems on the large-scale, long-term atmospheric motion are averaged (Ehlers and Krafft, 2001).
The essential difference compared to GCMs is the point of truncation in the frequency spectrum of atmospheric motion (Saltzman, 1978). GCMs solve all phenomena of frequencies lower than and including synoptic cyclones (and sometimes even mesoscale systems), whereas statistical–dynamical (SD) models parameterize all scales smaller than and equal to synoptic. Much of the difficulty in SD models is to define physically reasonable parameterizations occurring in the equations (Saltzman, 1978). For Aeolus, the synoptic parameterization has been described in detail in Coumou et al. (2011).
As written above, SD models are also spatially averaged since, for long-term climate simulations, we are typically interested in the large spatial aspects of the climate. It is further practical to split the large-scale, long-term field into two components: the zonally averaged mean field and the asymmetric departure of the field from the zonally averaged fields characterizing the east–west variations. The azonal variables can be, for example, resolved by one-dimensional Fourier components around latitude circles or into spherical harmonics (Saltzman, 1978).
Here, we present the Aeolus 1.0 dynamical core, developed at the Potsdam Institute for Climate Impact Research (PIK), a new SD model for the atmosphere. It uses some aspects of the atmosphere module of the EMIC CLIMBER-2 developed by Petoukhov et al. (2000). The dynamical core is completely new with novel equations for the large-scale meridional wind speed as well as quasi-stationary planetary waves. Together with the synoptic parameterizations presented in Coumou et al. (2011), these equations form the new dynamical core of Aeolus 1.0. The model is coupled with the cloud module consisting of a three-layer stratiform plus convective cloud scheme as presented and validated in Eliseev et al. (2013).
Further, we present the equations of the model and validate the dynamical core using a parameter optimization experiment. Aeolus 1.0 is forced with prescribed surface temperature, surface humidity and cumulus cloud fraction to test the model's performance. In particular, we examine the reproduction of the seasonal cycle and the influence of El Niño–Southern Oscillation (ENSO) and compare relevant dynamical fields of the model output against seasonal means of ERA-Interim reanalysis data (climatology 1983–2009). The effects of parameter tuning are evaluated to improve the performance of the model.
In Sect. 2, we present the novel equations of the Aeolus 1.0 dynamical core with the derivation of these equations presented in the Supplement (Sects. S1–S2). The dynamical core is coupled with a convective plus three-layer stratiform cloud scheme (which includes low-level, mid-level and upper-level stratiform clouds) developed by Eliseev et al. (2013). In Sect. 3, we describe the experiment setup and the used reanalysis data sets. In Sect. 4, we explain the model discretization, and in Sect. 5 we introduce our specific calibration method. For parameter optimization of the wind velocities, we use simulated annealing, which approximates the global minimum of a high-dimensional function (Flechsig et al., 2013). In Sect. 6, we present Aeolus' dynamical fields with pre-optimized and optimized parameters and compare them with observations and output from models of the Coupled Model Intercomparison Project phase 5 (CMIP5). We conclude by discussing performance and limitations of the model in Sect. 7.
2.1 General structure of the atmosphere
Aeolus 1.0 is a 2.5-D SD model, with the vertical dimension being largely parameterized and only coarsely resolved, and it therefore belongs to the class of intermediate complexity atmosphere models. Water and energy conservation is achieved via a set of two-dimensional, vertically averaged prognostic equations for temperature and specific humidity (Petoukhov et al., 2000).
The three-dimensional structure is described by these two-dimensional surface fields with the vertical dimensions reconstructed using an equation for the lapse rate and assuming an exponential profile for specific humidity (Petoukhov et al., 2000).
For given temperature and specific humidity fields, the three-dimensional wind field is calculated using a set of diagnostic equations. These statistical–dynamical equations for the wind fields are coupled and thus need several time steps or iterations to equilibrate.
The equations of the dynamical core of Aeolus 1.0 are separated into equations for the (1) synoptic-scale transient waves (or storm tracks), (2) quasi-stationary planetary waves and (3) the zonal-mean wind. Thus, following classical statistical–dynamical approaches (Dobrovolski, 2000; Imkeller and von Storch, 2012), the key assumption is that the wind velocity field V can be split into a synoptic-scale component V′ (2- to 6-day period) and a large-scale, long-term component 〈V〉 (Fraedrich and Böttger, 1978) such that
The variables u, v and w describe the wind velocity in zonal, meridional and vertical directions. The brackets (〈…〉) symbolize time-averaged quantities and the prime (…′) indicates deviations from this time-averaged field. The large-scale long-term component 〈V〉 is subdivided into a zonal-mean and an azonal component 〈V∗〉 :
The large-scale, zonal-mean zonal wind velocity with height above surface z and latitude ϕ is assumed to be geostrophic (resulting in the thermal wind balance):
where the sea level pressure gradient is calculated by with ageostrophic velocity parameter Cα=5 and the Earth radius a (derived and explained by Pethoukov et al. 2000; Eq. 13) and α is the cross-isobar angle defined as in Coumou et al. (2011; their Eq. A31). The variable v∗ is the azonal meridional wind velocity, ρ is the air density with the reference air density ρ0, f is the Coriolis parameter, ϕ is the latitude, T0 is the reference temperature and g is the gravitational acceleration (see Petoukhov et al., 2000).
As derived in the Supplement in Sect. S2, the large-scale, zonal-mean meridional wind velocity is given by
where and n3 are tunable parameters and A represents the convection-related term:
The atmospheric-scale height H0, the exchange for the momentums Kz, the Earth's angular velocity Ω as well as the dry adiabatic lapse rate Γa, latent heat of evaporation L and model parameters are explained in Table 1. Ta is a temperature which would occur near the surface if the lapse rate did not change within the planetary boundary layer (PBL), qs is the surface air specific humidity and nc is the cumulus cloud amount. The latter variable is either computed by the cloud module or, as in this experiment, observational data are used. The variable Pco is the convective precipitation rate and is calculated by the cloud model (Eliseev et al., 2013). The variable usf is the zonal surface wind; see Eq. (S10) in the Supplement.
The azonal component of the large-scale wind field describes quasi-stationary planetary waves and depends on latitude, longitude and height. At the equivalent barotropic level (EBL), azonal geostrophic components of horizontal velocities are computed by employing the definition of the stream function ψ depending on latitude ϕ and longitude λ:
whereby the stream function can be subdivided into contributions from thermally and orographically induced waves depicted by subscripts “th” and “or”, respectively. They are considered to be additive due to linearity of the barotropic vorticity equations such that
The parameter Ψ0 is a tuning parameter which is necessary since smoothing is applied to dampen local moisture feedbacks in the model. This smoothing however reduces spatial gradients in and therefore and themselves. The equation for the orographically induced waves is introduced in Sect. S1.2 in the Supplement.
The zeroth-order solution of the thermally induced waves of the barotropic vorticity equation is given by (see Sect. S1.3 in the Supplement)
It is solved at two beta planes, for the Northern Hemisphere and Southern Hemisphere, respectively:
The beta plane is an approximation in which the Coriolis parameter is linearized to reference latitudes βNH and βSH for the Northern Hemisphere and Southern Hemisphere, respectively. In the tropical belt, the variable is interpolated linearly between the two beta planes.
The standardized integrated heat content in Eq. (8) is calculated analytically by assuming a lapse rate such that . One obtains
In addition, Iv is smoothed by five points in latitude to avoid numerical artifacts which may arise due to spatial differentiating.
To remove possible singularities near the poles, at high latitudes, the stream function is dampened by a fourth-order interpolation function. Planetary waves at other tropospheric levels are directly calculated from those at the EBL (see Sect. S1.1 in the Supplement).
Finally, the time-averaged kinetic energy of transient eddies is determined using the statistical–dynamical equations as described in Coumou et al. (2011). Since detailed derivations are provided in Coumou et al. (2011), we only briefly discuss the diagnostic equations for transient eddy activity here. The equations are derived starting from the equation of the kinetic energy of transient eddies:
By assuming that the vertical (baroclinic) flux term is equipartitioned between the zonal and the meridional kinetic energy components, we can split Eq. (11) into three separate equations for , and :
Here, Kfh and Kfz are internal atmospheric small-/mesoscale friction coefficients in the horizontal and vertical directions, respectively; Kfs is the surface friction coefficient; f is the Coriolis parameter; and the subscript “ag” denotes ageostrophic terms.
The terms for Ksyn, the vertical macro-turbulent diffusion coefficient and , need to be parameterized, which is derived in Coumou et al. (2011). This way, a set of diagnostic equations for synoptic transient eddies is derived which, as also seen in Eqs. (12)–(14), are all coupled to the large-scale wind field.
This provides us with a coupled set of equations for and , which can be solved. Cross terms like can be determined by multiplying 〈u∗〉 with 〈v∗〉 and taking the zonal mean of that quantity. All derivatives are determined numerically. The values of the parameters are listed in Table 1.
The simulations were forced by multiyear averages of monthly mean climatological, El Niño and La Niña month data (surface temperature, surface specific humidity, temperature at 500 mb, geopotential height at 500 and 1000 mb) using ERA-Interim reanalysis data (Dee et al., 2011) for 1983–2009, as our aim is to show that Aeolus captures year-to-year variability associated with the ENSO cycle. We identified 87 El Niño (74 La Niña) months using 3-month running means of Extended Reconstructed Sea Surface Temperature (ERSST) v4 anomalies (Huang et al., 2016) using the definition that at least five consecutive overlapping seasons of sea surface temperature (SST) anomalies are greater than 0.5 K (less than −0.5 K) for El Niño (La Niña) events.
Multiyear averages of monthly mean, El Niño and La Niña month cumulative cloud fractions are taken from ISSCP (Rossow and Schiffer, 1999). The spatial resolution is 2.5×2.5∘ (lat × long) and the time range is 1983–2009.
We chose this time period, because the cumulative cloud fraction data, which are needed to calculate the lapse rate, are only available for this time period.
To avoid strong temperature gradients in the specified boundary conditions for the numerical experiments, we use the lapse rate equation to calculate temperatures at 1000 mb from those at 500 mb. We first calculate the lapse rate using the temperature field and specific humidity utilizing the equation as given in Petoukhov et al. (2000) at 1000 mb. Then, we recalculate the temperature field at 1000 mb by employing the temperature field at 500 mb and the linear lapse rate equation. This way, we ensure that the temperature at 500 mb is close to observations, and at the same time we have a vertical temperature realistic profile for a model like Aeolus. Since the ERA-Interim 500 mb temperatures contain an orographic component, we exclude in Eq. (7) in order not to incorporate orographic forcing of planetary waves twice.
We optimized the parameters for the numerical solutions of the wind velocities u∗, v∗ and as well as eddy kinetic energy at 500 mb. To compare the strength and position of the Hadley and Ferrell cells between observation and model, we calculate a zonal-mean mass flux in the lower troposphere using the zonal-mean meridional wind velocity at levels between 1000 and 500 mb, assuming exponential decay of air density with height (Petoukhov et al., 2000).
Before use with Aeolus, all data sets are interpolated to 3.75×3.75∘ (lat × long) spatial resolution.
Aeolus operates on a reduced grid to overcome the restriction of small time steps near the poles due to the Courant–Friedrichs–Lewy (CFL) criteria (Jablonowski et al., 2009). In the grid generation, longitudinally adjacent cells are merged if their zonal width in meters would be less than half of the cell width at the Equator.
This way the reduced grid has the same resolution as a regular grid at the Equator, but at nominal resolution (3.75×3.75∘) around the poles only six cells are defined. On the regular grid, the maximum permissible time step due to the CFL criteria would be approximately 5 min, while the limit for the reduced grid is approximately 2 h.
Equations (1)–(14) are implemented in Aeolus and numerically solved on a 3.75×3.75∘ reduced grid with four tropospheric height levels (1000, 3000, 5000 and 9000 m).
The calibration of the winds is divided into two parts. First, we optimize the dynamical variables primarily driven by the thermal state of the atmosphere: the azonal velocities in zonal and meridional directions 〈u∗〉 and 〈v∗〉 as well as the zonal-mean zonal wind velocity . In the second step, we tune the zonal-mean synoptic kinetic energy and the lower troposphere integrated mass flux , which solely depend on the zonal-mean meridional wind .
A common approach for parameter tuning is simulated annealing (Ingber, 1996; Kirkpatrick, 1984). It is one experiment type in the multirun simulation environment SimEnv for sensitivity and uncertainty analysis of model output (Flechsig et al., 2013) which we use for all calibration experiments. A schematic plot of the optimization process is shown in Sect. S3 in the Supplement.
For each model run, the thermal state of the atmosphere is kept constant (and initialized as described above) and the dynamical core is equilibrated to this thermal state. This typically requires only a few time steps. Since we tune only the parameters of the dynamical core, Aeolus first calculates the clouds using its cloud scheme (Eliseev et al., 2013) to determine the lapse rate and initialize the three-dimensional thermal state. After that, only the state of the dynamical core is updated each time step.
5.1 Dynamical core tuning – step 1
For a good starting point, the parameters are first tuned manually, providing “pre-optimized” values. Next, we define physically realistic parameter ranges for automatic tuning as listed in Table 2.
For the azonal wind velocities, we use a weighting function which excludes the tropics (from 10∘ S to 10∘ N) and polar regions (poleward of 60∘ S for the Southern Hemisphere to exclude influences of Antarctica and poleward of 70∘ N for the Northern Hemisphere) such that the midlatitudes, where planetary waves are important, are optimized.
The non-excluded grid as well as the zonal-mean zonal wind are weighted by w(ϕ)=|cos (ϕ)|.
The total skill score for the scheme in step 1 is calculated by multiplying the individual skills for the azonal velocities in zonal and meridional directions and the skill for the zonal-mean zonal wind velocity:
The goal of the optimization procedure is to maximize the skill S.
Skill score functions for individual variables are computed as in Taylor (2001):
In Eq. (15), rX is the coefficient of the spatial correlation between the area-weighted modeled and observed fields of X; AX is the so-called relative spatial variation calculated according to
Here, the variable AX,M is the spatial average of and XM,g is a globally averaged value of the modeled field XM. The observed field is similarly defined by AX,O.
5.2 Dynamical core tuning – step 2
For tuning the zonal-mean meridional wind velocity , and in particular the strength and width of the Hadley cell, we use the vertical integral of the lower tropospheric integrated mass flux . In addition, we tune the zonal-mean area-weighted synoptic kinetic energy . Both variables strongly depend on the dynamic fields tuned in step 1, which is the reason for tuning them in a separate second step.
Total skill score for the scheme in step 2 is calculated by multiplying the individual skills for the vertical integral of lower troposphere mass flux as well as the eddy kinetic energy :
The goal of the optimization procedure is again to maximize skill S.
The skill score function for the eddy kinetic energy is given by the Taylor skill score function (Eq. 15).
The skill score is then calculated by
Here, rX is the coefficient of the spatial correlation between area-weighted modeled and observed fields (as in Eq. 15), meanHadley_Model and meanHadley_Obs are the mean values of the area-weighted modeled and observed mean mass flux. We use this more elaborate skill function to promote a proper Hadley circulation in the model.
The weights of the lower troposphere mass flux are calculated according to
For calculating the mean intensity of the Hadley cell, we determine the roots of the mass flux in observation data close to 0 and 30∘ which determine the Hadley cell latitudinal boundaries. This way, we have 36 values for the boundaries of the northern Hadley cell. Between these latitudinal borders, we calculate the mean strength of the Hadley cell.
In Table 3, the manually tuned (or pre-optimized) parameters and their ranges are listed.
6.1 Results of calibration – step 1
We compared the numerical solutions using the optimized parameters for the wind fields 〈u∗〉, 〈v∗〉 and of climatological monthly averages, El Niño and La Niña months from ERA-Interim reanalysis (Dee et al., 2011) for 1983–2009.
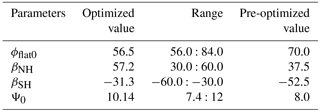
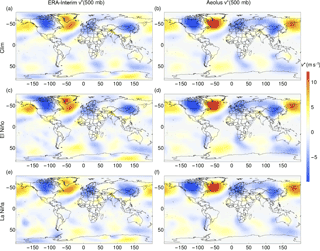
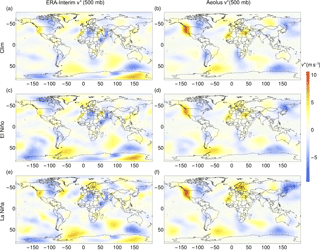
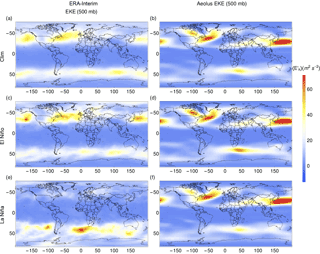
The figures for azonal wind velocities are divided into six subplots. The left column shows observational data and the right column model data. The top row shows climatological monthly averages, the middle row multiyear averages of El Niño months and the bottom row multiyear averages of La Niña months.
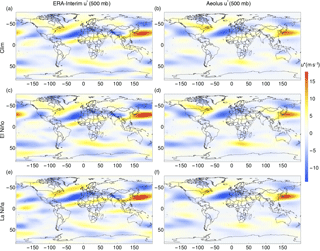
Figure 1Azonal large-scale zonal wind u* at 500 mb for all February months/El Niño February months/La Niña February months. The left column shows the results from reanalysis data and the right column shows the results from Aeolus received by optimized parameters. The model is forced by surface temperature, humidity and cumulus cloud fraction.
In Figs. 1 and 2, the azonal components of the zonal wind velocities (〈u∗〉) for February and August at 500 mb are displayed, respectively. The figures show that with optimized parameters the model reasonably reproduces the main observed features both in terms of spatial position and magnitude. In particular, the extratropical planetary waves are well captured with some minor discrepancies in the tropics. Both the seasonal cycle and the response to the ENSO cycle are well captured by the model.
Figures 3 and 4 show the same type of plots for the azonal meridional wind velocity (〈v∗〉). Also, for the meridional wind velocity, the most important features of the reanalysis data are well represented in the model. The model results coincide well in wind strength and spatial pattern with the reanalysis data. The wind strength in winter, for both climatological and El Niño months, is stronger than for La Niña months. In summer, the opposite is seen for both model and reanalysis data.
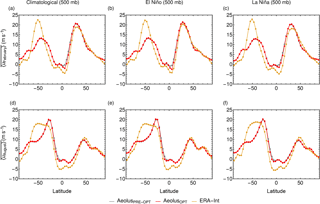
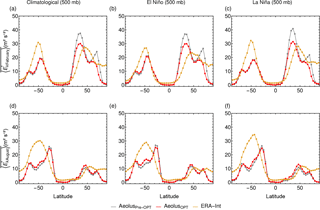
Figure 5Zonal-mean large-scale zonal wind velocity at 500 mb. Panel (a) shows the climatological monthly mean zonal-mean zonal velocity in February, (b) the monthly mean zonal-mean velocity of El Niño February months and (c) the monthly mean zonal-mean velocity of La Niña February months. Panel (d) displays the monthly mean climatological zonal-mean zonal velocity in August, (e) the monthly mean zonal-mean velocity in El Niño August months and (f) the monthly mean zonal-mean velocity in La Niña August months. The yellow line represents zonal-mean large-scale zonal wind obtained by reanalysis data, the gray line is zonal-mean large-scale zonal wind velocity from Aeolus using pre-optimized parameters and the red line represents zonal-mean large-scale zonal wind velocity from Aeolus using optimized parameters.
In Fig. 5, the zonal-mean zonal wind velocity at 500 mb is shown with the orange line representing reanalysis data, red representing model data with optimized parameters and gray representing model data with pre-optimized parameters. The figure is subdivided into six subplots. The top row depicts in February and the bottom row shows in August, while the columns show climatological data, El Niño data and La Niña data, respectively. It is noticeable that the results obtained with pre-optimized parameters are already reasonable. Apparently, the initial choice of tuning parameter values was already near the optimum, and hence the optimized parameters led only to small improvements of the model results. The Northern Hemisphere profile is well resolved in both seasons for both El Niño and La Niña months. Parameter optimization slightly improves the results in the tropics. The modeled amplitude of in the Southern Hemisphere is too small in February for all plots and too high in August.
The optimized parameters are listed in Table 2. The βNH in the Northern Hemisphere has a higher value, whereas the βSH in the Southern Hemisphere has a lower value than the pre-optimized parameter values.
The last parameter is Ψ0 and is changed to a higher value in order to strengthen speeds in 〈v∗〉 and 〈u∗〉.
6.2 Results of calibration – step 2
We compared the numerical solutions using the optimized parameters for the zonal-mean lower troposphere integrated mass flux and eddy kinetic energy
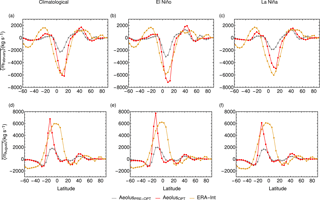
Figure 6Zonal-mean large-scale mass flux . Panel (a) shows the climatological monthly mean zonal-mean mass flux in February, (b) the monthly mean zonal-mean mass flux of El Niño February months and (c) the monthly mean zonal-mean mass flux of La Niña February months. Panel (d) displays the monthly mean climatological zonal-mean mass flux in August, (e) the monthly mean zonal-mean mass flux in El Niño August months and (f) the monthly mean zonal-mean mass flux in La Niña August months. The yellow line represents zonal-mean large-scale mass flux obtained by reanalysis data, the gray line is the zonal-mean large-scale mass flux from Aeolus using pre-optimized parameters and the red line represents the zonal-mean large-scale mass flux from Aeolus using optimized parameters.
The plots in Fig. 6 show that in general the monthly mean zonal-mean mass flux calculated with optimized parameters matches better with observational data. Here, the gain of the parameter optimization is clearly better than we saw with calibration step 1. The ENSO cycle is clearly visible. However, the width of the Hadley cell (especially in August) is still too small compared to the width of the Hadley cell obtained by reanalysis data. The figure shows only plots with a latitudinal range from 60∘ S to 90∘ N as reanalysis data are spiky over Antarctica.
Figure 7 shows the zonal-mean eddy kinetic energy . We show the same color code as in Fig. 6. Northern Hemisphere modeled profile is again well resolved in both seasons and for El Niño and La Niña months with the parameter optimization. Smaller spikes vanish such that the modeled better matches the observed data. The parameter optimization gained more improvement in the Northern Hemisphere (NH) than in the Southern Hemisphere (SH).
In Figs. 8 and 9, the eddy kinetic energies for February and August are displayed. The left column shows observational data and the right column model data. The top row presents climatological monthly averages, the middle row El Niño months and the bottom row La Niña months.
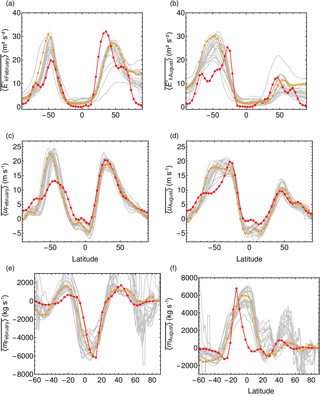
Figure 10Comparison to CMIP5 models. The orange line represents ERA-Interim data, the red line results from Aeolus and gray lines CMIP5 models (annual mean zonal-mean data).
The spatial position and the magnitude are well captured; seasons and the ENSO cycles are also well resolved, with some discrepancies in the tropics (i.e., the region over the Atlantic and Pacific oceans) and the Southern Hemisphere. In February and August, is stronger in the Northern Hemisphere than in the Southern Hemisphere for both the climatology and in El Niño months. Only in La Niña months, is weaker in the Northern Hemisphere.
The optimized parameters are listed in Table 3. The parameters U0 and m for optimizing the eddy kinetic energy are greater than the manually tuned values.
The parameters d3 and n3 are close to 1, whereas the parameters d2, d4 and n1 are close to 2 and have a strong impact on the amplitude of the Hadley cell and the Ferrell cell. The parameter with the smallest influence is d1.
6.3 Comparison to CMIP5 models
Figure 10 shows the comparison of February and August and between CMIP5 models (gray lines), Aeolus (red) and ERA-Interim data (orange). In general, CMIP5 models represent the and very well in both hemispheres. However, in the Southern Hemisphere, the storm tracks, i.e., , of all models are too weak compared to observations with Aeolus on the lower end of the CMIP5 range. Further, some individual CMIP5 models can have too-low or too-high and compared to ERA-Interim, similar to Aeolus.
The CMIP5 multimodel mean of appears to be close to the reanalysis and most models reproduce this well. Still, some CMIP5 models can differ strongly from in ERA-Interim with some spiky behavior. Nevertheless, the width and strength of the Hadley cell is in most models well presented, but the Ferrell cell is often too strong. Aeolus' results give reasonable strength and width of the Ferrell cell, but the width of the Southern Hemisphere Hadley cell in August is too small compared to both reanalysis and CMIP5 models.
In this paper, we presented the atmosphere model Aeolus, which is a statistical–dynamical atmosphere model and belongs to the class of intermediate complexity models. The equations of Aeolus are time averaged and the model has a spatial resolution of (lat × long). The three-dimensional structure of Aeolus is reconstructed using a set of two-dimensional, vertically averaged prognostic equations for temperature and water vapor (Petoukhov et al., 2000). The advantage of such types of models is the fast computation time and for that reason the possibility to study and simulate long time periods as well as conduct sensitivity experiments.
We performed parameter optimization of the dynamical core consisting of a large multidimensional parameter space and can be searched due to its fast computation time. For this approach, we used the simulated annealing optimization algorithm, which approximates the global minimum of a high-dimensional function. We divided the calibration into two parts. First, the azonal velocities in zonal and meridional directions as well as the zonal-mean zonal wind velocity were optimized, because they are primarily driven by the thermal state of the atmosphere. In the second step, we optimized the zonal-mean synoptic kinetic energy and the lower troposphere integrated mass flux, and hence the zonal-mean meridional velocity, since those variables depend strongly on variables of step 1.
The results of the winds and eddy kinetic energy are in reasonable agreement with the reanalysis data and showed that our model is able to reproduce the dynamic response from the seasonal cycle as well as the ENSO cycle which is a prime goal of our model development efforts. Parameter optimization in particular improves representation of the Hadley cell in terms of strength and width.
In the Southern Hemisphere, the dynamical fields tend to be too weak. This model bias might be related to the missing Antarctic ice sheet, upper tropospheric ozone, the constant lapse rate assumption or fundamental limitations of the equations. These possibilities will be analyzed in future work using the Potsdam Earth Model (POEM) to which Aeolus has been coupled.
Compared to CMIP5 models, Aeolus captures reasonably well the dynamical state of the atmosphere in the Northern Hemisphere, particularly for monthly mean eddy kinetic energy , zonal-mean wind velocity and mass flux . Especially the mass flux of the Ferrell cell is better captured than in other models, whereas the Southern Hemisphere Hadley cell width of Aeolus in August is too small compared to CMIP5 models.
Code and data are stored in PIK's long-term archive and are made available to interested parties on request.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-665-2018-supplement.
The authors declare that they have no conflict of interest.
We thank ECMWF for making the ERA-Interim data available.
The work was supported by the German Federal Ministry of Education and Research, grant no. 01LN1304A, (S.T., D.C.).
Alexey V. Eliseev's contribution was partly supported by supported by the Government of the Russian Federation (agreement no. 14.Z50.31.0033).
The authors gratefully acknowledge the European Regional Development Fund
(ERDF), the German Federal Ministry of Education and Research and the Land
Brandenburg for supporting this project by providing resources on the
high-performance computer system at the Potsdam Institute for Climate Impact
Research.
Edited by: Didier Roche
Reviewed by: two anonymous referees
Berger, A., Fichefet, T., Gallée, H., Tricot, C., and van Ypersele, J. P.: Entering the glaciation with a 2-D coupled climate model, Quaternary Sci. Rev., 11, 481–493, https://doi.org/10.1016/0277-3791(92)90028-7, 1992.
Claussen, M., Mysak, L., Weaver, A., Crucifix, M., Fichefet, T., Loutre, M. F., Weber, S., Alcamo, J., Alexeev, V., Berger, A., Calov, R., Ganopolski, A., Goosse, H., Lohmann, G., Lunkeit, F., Mokhov, I., Petoukhov, V., Stone, P., and Wang, Z.: Earth system models of intermediate complexity: Closing the gap in the spectrum of climate system models, Clim. Dynam., 18, 579–586, https://doi.org/10.1007/s00382-001-0200-1, 2002.
Coumou, D., Petoukhov, V., and Eliseev, A. V.: Three-dimensional parameterizations of the synoptic scale kinetic energy and momentum flux in the Earth's atmosphere, Nonlin. Processes Geophys., 18, 807–827, https://doi.org/10.5194/npg-18-807-2011, 2011.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., Mcnally, A. P., Monge-Sanz, B. M., Morcrette, J. J., Park, B. K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Dobrovolski, S. G.: Stochastic Climate Theory, Springer-Verlag Berlin Heidelberg, 2000.
Ehlers, E. and Krafft, T.: Understanding the Earth System: Compartments, Processes and Interactions, Springer-Verlag, Berlin, Heidelberg, 2001.
Eliseev, A. V., Coumou, D., Chernokulsky, A. V., Petoukhov, V., and Petri, S.: Scheme for calculation of multi-layer cloudiness and precipitation for climate models of intermediate complexity, Geosci. Model Dev., 6, 1745–1765, https://doi.org/10.5194/gmd-6-1745-2013, 2013.
Eliseev, A. V., Mokhov, I. I., and Chernokulsky, A. V.: An ensemble approach to simulate CO2 emissions from natural fires, Biogeosciences, 11, 3205–3223, https://doi.org/10.5194/bg-11-3205-2014, 2014a.
Eliseev, A. V., Demchenko, P. F., Arzhanov, M. M., and Mokhov, I. I.: Transient hysteresis of near-surface permafrost response to external forcing, Clim. Dynam., 42, 1203–1215, https://doi.org/10.1007/s00382-013-1672-5, 2014b.
Flechsig, M., Böhm, U., Nocke, T., and Rachimow, C.: The Multi-Run Simulation Environment SimEnv, available at: https://www.pik-potsdam.de/research/transdisciplinary-concepts-and-methods/tools/simenv/ (last access: 26 January 2018), 2013.
Fraedrich, K. and Böttger, H.: A Wavenumber-Frequency Analysis of the 500 mb Geopotential at 50∘ N, J. Atmos. Sci., 35, 745–750, https://doi.org/10.1175/1520-0469(1978)035<0745:AWFAOT>2.0.CO;2, 1978.
Ganopolski, A., Petoukhov, V., Rahmstorf, S., Brovkin, V., Claussen, M., Eliseev, A. V., and Kubatzki, C.: Climber-2: A climate system model of intermediate complexity. Part II: Model sensitivity, Clim. Dynam., 17, 735–751, https://doi.org/10.1007/s003820000144, 2001.
Harvey, L. D. D.: Milankovitch Forcing, Vegetation Feedback, and North Atlantic Deep-Water Formation, J. Climate, 2, 800–815, 1989.
Holland, M., Bitz, C., Eby, M., and Weaver, A.: The Role of Ice – Ocean Interactions in the Variability of the North Atlantic Thermohaline Circulation, J. Climate, 14, 656–675, https://doi.org/10.1175/1520-0442(2001)014<0656:TROIOI>2.0.CO;2, 2001.
Huang, B., Thorne, P. W., Smith, T. M., Liu, W., Lawrimore, J., Banzon, V. F., Zhang, H.-M., Peterson, T. C., and Menne, M.: Further Exploring and Quantifying Uncertainties for Extended Reconstructed Sea Surface Temperature (ERSST) Version 4 (v4), J. Climate, 29, 3119–3142, https://doi.org/10.1175/JCLI-D-15-0430.1, 2016.
Imkeller, P. and von Storch, J.-S.: Stochastic Climate Models, Birkhäuser, 2012.
Ingber, L.: Adaptive simulated annealing (ASA): Lessons learned, Control Cybern., 25, 32–54, 1996.
Jablonowski, C., Oehmke, R. C., and Stout, Q. F.: Block-structured adaptive meshes and reduced grids for atmospheric general circulation models, Philos. T. Roy. Soc. A, 367, 4497–522, https://doi.org/10.1098/rsta.2009.0150, 2009.
Kirkpatrick, S.: Optimization by simulated annealing: Quantitative studies, J. Stat. Phys., 34, 975–986, https://doi.org/10.1007/BF01009452, 1984.
Knutti, R., Stocker, T. F., Joos, F., and Plattner, G.-K.: Constraints on radiative forcing and future climate change from observations and climate model ensembles, Nature, 416, 719–723, https://doi.org/10.1038/416719a, 2002.
Latif, M.: Dynamics of interdecadal variability in coupled ocean-atmosphere models, J. Climate, 11, 602–624, https://doi.org/10.1175/1520-0442(1998)011<0602:DOIVIC>2.0.CO;2, 1998.
McGuffie, K. and Henderson-Sellers, A.: A Climate Modelling Primer, 3rd Edn., J. Wiley and Sons, 2005.
Montoya, M., Griesel, A., Levermann, A., Mignot, J., Hofmann, M., Ganopolski, A., and Rahmstorf, S.: The earth system model of intermediate complexity CLIMBER-3alpha. Part I: Description and performance for present-day conditions, Clim. Dynam., 25, 237–263, https://doi.org/10.1007/s00382-005-0044-1, 2005.
Petoukhov, V., Ganopolski, A., Brovkin, V., Claussen, M., Eliseev, A. V., Kubatzki, C., and Rahmstorf, S.: CLIMBER 2: a climate system model of intermediate complexity. Part I: model description and performance for present climate, Clim. Dynam., 16, 1–17, https://doi.org/10.1007/PL00007919, 2000.
Polyakov, I. V., Alekseev, G. V., Bekryaev, R. V., Bhatt, U. S., Colony, R., Johnson, M. A., Karklin, V. P., Walsh, D., and Yulin, A. V.: Long-term ice variability in Arctic marginal seas, J. Climate, 16, 2078–2085, https://doi.org/10.1175/1520-0442(2003)016<2078:LIVIAM>2.0.CO;2, 2003.
Rossow, W. B. and Schiffer, R. A.: Advances in Understandig Clouds from ISCCP, B. Am. Meteorol. Soc., 80, 2261–2287, https://doi.org/10.1175/1520-0477(1999)080<2261:AIUCFI>2.0.CO;2, 1999.
Saltzman, B.: A Survey of Statistical-Dynamical Models of the Terrestrial Climate, Adv. Geophys., 20, 183–304, https://doi.org/10.1016/S0065-2687(08)60324-6, 1978.
Schmittner, A. and Stocker, T. F.: The stability of the thermohaline circulation in global warming experiments, J. Climate, 12, 1117–1133, https://doi.org/10.1175/1520-0442(1999)012<1117:TSOTTC>2.0.CO;2, 1999.
Taylor, K. E.: Summarizing multiple aspects of model performance in a Single Diagram, J. Geophys. Res., 106, 7183–7192, https://doi.org/10.1029/2000JD900719, 2001.
Xiao, X., Kicklighter, D. W., Melilo, J. M., McGuire, A. D., Stone, P. H., and Sokolov, A. P.: Linking a global terrestrial biogeochemcal model and a 2-dimensional climate model: implications for the global carbon budget, Tellus, 49B, 18–37, 1997.