the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Supporting hierarchical soil biogeochemical modeling: version 2 of the Biogeochemical Transport and Reaction model (BeTR-v2)
Jinyun Tang
William J. Riley
Qing Zhu
Reliable soil biogeochemical modeling is a prerequisite for credible projections of climate change and associated ecosystem feedbacks. This recognition has called for frameworks that can support flexible and efficient development and application of new or alternative soil biogeochemical modules in Earth system models (ESMs). The the Biogeochemical Transport and Reaction model version 1 (BeTR-v1) code (i.e., CLM4-BeTR) is one such framework designed to accelerate the development and integration of new soil biogeochemistry formulations into ESMs and to analyze structural uncertainty in ESM simulations. With a generic reactive transport capability, BeTR-v1 can represent multiphase (e.g., gaseous, aqueous, and solid), multi-tracer (e.g., nitrate and organic carbon), and multi-organism (e.g., plants, bacteria, and fungi) dynamics. Here, we describe the new version, Biogeochemical Transport and Reaction model version 2 (BeTR-v2), which adopts more robust numerical solvers for multiphase diffusion and advection and coupling between biogeochemical reactions and improves code modularization over BeTR-v1. BeTR-v2 better supports different mathematical formulations in a hierarchical manner by allowing the resultant model be run for a single topsoil layer or a vertically resolved soil column, and it allows the model to be fully coupled with the land component of the Energy Exascale Earth System Model (E3SM). We demonstrate the capability of BeTR-v2 with benchmark cases and example soil biogeochemical (BGC) implementations. By taking advantage of BeTR-v2's generic structure integrated in E3SM, we then found that calibration could not resolve biases introduced by different numerical coupling strategies of plant–soil biogeochemistry. These results highlight the importance of numerically robust implementation of soil biogeochemistry and coupling with hydrology, thermal dynamics, and plants – capabilities that the open-source BeTR-v2 provides. We contend that Earth system models should strive to minimize this uncertainty by applying better numerical solvers.
- Article
(3668 KB) - Full-text XML
- BibTeX
- EndNote
Soil biogeochemical (BGC) modeling is essential for predicting terrestrial ecosystem dynamics in natural and managed lands and is an important component of Earth system models (ESMs) that perform projections and hindcasts of ecosystem–climate feedbacks (e.g., Golaz et al., 2019, Hurrell et al., 2013). Over the years, many soil BGC models have been developed, each of which has its merits and deficiencies (e.g., Zaehle et al., 2014). Nonetheless, when the carbon dynamics simulated by many different ecosystem models (including those integrated within ESMs) are synthesized, large uncertainties prevail (e.g., Davies-Barnard et al., 2020; Todd-Brown et al., 2014). Several sources, including parametric, structural, numerical, and boundary conditions (e.g., forcing and initial conditions), have been cited to explain the large modeling uncertainty (Ahlstrom et al., 2013; Huntzinger et al., 2017; Tang and Riley, 2018). Accordingly, various strategies have been proposed to alleviate or constrain these types of uncertainty (Luo et al., 2012; Riley et al., 2021; Wieder et al., 2015; Zhu et al., 2019).
From the many uncertainty quantification studies, one urgent need identified is for a software platform to support systematic comparisons of how different soil BGC formulations influence simulated soil BGC feedbacks within a single ecosystem model, thereby facilitating more process-specific hypotheses testing. To address this infrastructural gap, the Biogeochemical Transport and Reaction model version 1 (BeTR-v1) was developed as a submodule of the Community Land Model version 4 (CLM4; Tang et al., 2013). The design philosophy of BeTR is that, assuming all other factors are equal, one can investigate (1) the various levels of mechanistic complexity and model formulations even for the same number of biogeochemical processes being represented, (2) the same mathematical formulation implemented with different numerical methods (e.g., Tang and Riley, 2018), and (3) the sharing of common process representations across diverse ecosystem types. For point (1), some researchers have argued that more explicit representation of processes are needed to resolve complex soil BGC dynamics (Berardi et al., 2020; Riley et al., 2021; Tang and Riley, 2020; Wieder et al., 2015). For instance, active transport of various substrates in soils is needed if microbial dynamics are to be explicitly considered (e.g., Ahrens et al., 2015; Dwivedi et al., 2017; Grant, 2013; Riley et al., 2021). Point (2) is less discussed in land BGC modeling but has been clearly called out in computational biology and computational geophysical fluids (e.g., Gross et al., 2018; Petrovskii and Petrovskaya, 2012). Specifically, when the differential equations of a model are approximated with inappropriate numerical solvers, the model may obtain answers that better match observations for wrong reasons because calibration may inappropriately make up for deficiencies in the model's governing equations (i.e., a type I error that gets the right answers with poor model formulations). This problem can result in incorrect inference of causality and interactions between processes. For instance, Tang et al. (2015) found that the simulated evapotranspiration agreed better with observations when the coupled equations for soil and root water exchange were purposely solved incorrectly in a sequential manner than when they were solved correctly as tightly coupled. Alternatively, if calibration cannot make up the deficiency caused by the inappropriate numerical method, one may assert that a right model formulation is wrong (i.e., a type II error that gets the wrong answers with good model formulations). For example, when the 1-D diffusion equation is solved with central difference in both time and space, the numerical solution actually approximates a wave equation instead, and this deficiency cannot be fixed by calibration. Both types of inference error will contribute to the uncertainty of climate–biogeochemistry feedback simulated by ESMs. For point (3), aqueous environments, such as wetlands, groundwater, rivers, lakes, and oceans, share many biogeochemical processes with soils, but different representations are often used (e.g., early diagenesis in marine sediments vs. terrestrial soil organic matter decomposition; Koven et al., 2013; Munhoven, 2021). Therefore, developing a generic modeling infrastructure could benefit the mechanistic consistency in integrated Earth system BGC modeling (e.g., Fisher and Koven, 2020).
Since the publication of BeTR-v1, we made a number of new developments in numerical algorithms for transport and BGC process coupling (Tang and Riley, 2016, 2014). We also made better use of the object-oriented programming feature of Fortran 2003 to enable more efficient code sharing among the Fortran modules. All of these are integrated into the Biogeochemical Transport and Reaction model version 2 (BeTR-v2): a platform to accelerate soil BGC model development and enable efficient code and knowledge sharing among ESM BGC components. Below, we describe the improvements that have brought into BeTR-v2 since BeTR-v1 in detail, give some examples based on its integration with the land module of the Energy Exascale Earth System Model (ELM; Burrows et al., 2020), and apply the model to evaluate whether parameter calibration can resolve the uncertainty associated with different numerical implementations.
BeTR-v2 adopts the same governing equations as in BeTR-v1 but implements improved numerical algorithms (developed after the development of BeTR-v1) for both tracer transport and biogeochemical reaction coupling (to be described in Sect. 2.1). Compared to BeTR-v1, BeTR-v2 is also better modularized and structured software-wise. Importantly, BeTR-v2 is a standalone capability to support more efficient model development and soil BGC coupling to alternative host models (E3SM in this case), while BeTR-v1 is embedded within CLM4.5 and cannot be run independently. It is noted that since significant code rewriting and data restructuring have occurred after ELM branched out from CLM4.5, a comparison between BeTR-v1 and BeTR-v2 is not feasible.
2.1 Governing equations and numerical implementation
The same as BeTR-v1, BeTR-v2 solves the following one-dimensional reactive-transport equation:
where θw is volumetric water content (m3 m−3), Cw is aqueous concentration (mol m−3), εg is air-filled porosity (m3 m−3), Cg is gaseous concentration (mol m−3), Cs is adsorbed concentration (mol m−3), τw is aqueous tortuosity (unitless), τg is gaseous tortuosity (unitless), Dw is aqueous diffusivity (m2 s−1), and Dg is gaseous diffusivity (m2 s−1). Ds is solid-phase diffusivity (m2 s−1), as an approximation for processes like bioturbation (Jarvis et al., 2010) and cryoturbation (Koven et al., 2009), which do not have mechanistically based formulations. qw is aqueous advection (m s−1), Ebub is ebullition flux (mol m−3 s−1), Tr is transport via transpiration flux (mol m−3 s−1; including aerenchyma-enabled gas transport), and Rbgc is biogeochemical reaction rate (mol m−3 s−1).
Depending on how z (m) is interpreted, the transport can be regarded as either vertical or horizontal, provided that the advection velocity qw is defined accordingly.
Besides the one-dimensional solution, BeTR-v2 also solves standalone single-layer models (a new feature that BeTR-v1 does not have), whose governing equation is as follows:
where gas is the conductance (m s−1) for the gaseous exchange of the tracer between soil and air, Catm is the atmospheric gas concentration (mol m−3), and Δz (m) is the single-layer thickness (taken as 10 cm in the examples below). Simulations from Eq. (2) can be used for comparisons with incubation experiments.
To achieve numerically robust solutions and to adapt to the hydrological dynamics in ELM (which solves surface runoff, variably saturated flow, and subsurface drainage sequentially), Eq. (1) is solved with the operator splitting approach (Simpson and Landman, 2007). Specifically, tracer loss through surface runoff is solved first, then biogeochemical reactions are solved, followed by advection, diffusion, ebullition (using the hydrostatic approximation from Tang et al., 2010), and subsurface drainage. Gaseous and aqueous diffusion are solved together using the dual-phase algorithm (that assumes equilibrium between gaseous and aqueous phases) with the implicit time-stepping method (Tang and Riley, 2014), which is equally accurate but simpler than the treatment in BeTR-v1, which requires calculating locations of wetting fronts in the soil. Solid-phase diffusion is also solved implicitly. Aqueous advection is solved using the mass-conserving semi-Lagrangian approach (Manson and Wallis, 2000), which is more accurate (by reducing numerical dispersion) than the upstream scheme used in BeTR-v1. Biogeochemical reactions are solved using the multiple-flux co-limiting algorithm (Tang and Riley, 2016), which considers the production and consumption fluxes concurrently so that there is no delay between nutrient mineralization and its competition by consumption fluxes within a time step, a critical feature to resolve the nutrient limitation dynamics (Tang and Riley, 2018). To ensure numerical accuracy, within each modeling time step of ELM (which is 30 min) each solver uses the adaptive time stepping that exits when either the relative difference between solutions based on the coarse time step and halved time step is less than 0.1 % or when the minimum time step (30 s) is reached.
2.2 Code structure
The open-source code BeTR-v2 can be found at https://github.com/BeTR-biogeochemistry-modeling/sbetr/tree/jinyuntang/ELM-BeTR-ECA.r (last access: 21 February 2022) (and it is also archived at https://doi.org/10.5281/zenodo.5526854), where each folder has a readme.md file explaining the purpose of each sub-directory or each source code file. For interested users, the major code to look into is under the directories “sbetr/src/betr” (core betr code), “sbetr/src/Applications” (customized BGC modules), “sbetr/src/driver/” (driver files for 1-D models and APIs to couple BeTR with land models like ELM), and “sbetr/src/jarmodel/” (driver files for single-layer models). In the directory “src/Applications/soil-farm/”, each folder (except “bgcfarm_util”) is a soil BGC implementation. For this paper, the BGC implementation ELMv1-BeTR-ECA under the directory “sbetr/src/Applications/soil-farm/v1eca/” is used to test the global simulation capability of BeTR, while “ecacnp” under “sbetr/src/Applications/soil-farm/ecacnp/” is used to demonstrate the standalone simulation capability. More details about why two implementations are used for different purposes will be explained in Sect. 2.4. Instructions on how to build and run BeTR on typical platforms can be found at https://github.com/BeTR-biogeochemistry-modeling/sbetr (last access: 21 February 2022).
2.3 Model benchmark and verification
As was done for BeTR-v1, two analytical solutions with different boundary conditions are employed to benchmark the numerical accuracy of the BeTR-v2 reactive transport solver that solves the following equation:
where D (m2 s−1) and u (m s−1) are diffusivity and advection velocity, respectively.
The two analytical solutions are as follows:
for a pulse tracer imposed at the top of a 1-D soil column of length L (Kumar et al., 2009), where erfc(x) is the complementary error function of x, and
for a wave-like tracer imposed at the top of a 1-D soil column, where mol of tracer per cubic meter, mol of tracer per cubic meter, mol of tracer per cubic meter, d−1, and ω2=2π d−1. For both cases, m s−1, m2 s−1, and L=35.17 m, and the lower boundary condition is as follows:
These two tests have been integrated as part of the standard test suite for BeTR-v2. After doing “make test” by following the instructions, their output can be found under “regression-tests/tests/standalone/” as analytical-adr-b1 and analytical-adr-b2, respectively.
2.4 Example soil BGC implementation
We re-implemented the soil BGC from ELMv1-ECA (Zhu et al., 2019) to illustrate the capability of BeTR-v2. By re-implementation we mean to solve the ELMv1-ECA soil BGC in the form of Eq. (1) in BeTR-v2 based on input fluxes of organic matter and nutrients from ELM and return fluxes of carbon and nutrient fluxes to ELM (after calculations in BeTR-v2). The ELMv1-ECA soil BGC model consists of a century-like soil carbon decomposition cascade based on Koven et al. (2013), but competition of inorganic nitrogen (ammonium and nitrate) and phosphorus between plants and (the implicitly represented) microbial organisms is calculated using equilibrium chemistry approximation kinetics (Tang and Riley, 2013; Zhu et al., 2016). Differing from other nutrient competition paradigms, particularly the popular relative demand approach that is implemented in many existing BGC models (Riley et al., 2018), the ECA approach explicitly considers the kinetic traits of the involved plants, microbes, and soil sorption surfaces and is more capable of resolving the diverse dynamical processes involved in plant–soil nutrient competition (Medvigy et al., 2019; Tang and Riley, 2021; Zhu et al., 2017). ELMv1-ECA also allows plant organs to vary their carbon to nutrient ratios to fluctuate within empirically inferred ranges. The performance of ELMv1-ECA was evaluated comprehensively by using the International Land Model Benchmarking (ILAMB) system (Collier et al., 2018; Zhu et al., 2019).
In BeTR-v2, a soil BGC formulation is implemented in two-steps: (1) a single-layer implementation of the given soil BGC process, which is then populated through BeTR-v2's reactive transport code to form (2) a 1-D vertically resolved implementation of the soil BGC process. Take ecacnp for example, the single-layer implementation is in the folder “ecacnp/ecacnp1layer/”, which is extended to 1-D soil column using codes in the folder “ecacnp/ecacnpNlayer/”, and corresponding model parameters are set using codes in the folder “ecacnp/ecacnpPara/”. The single-layer code is called by the driver file in “sbetr/src/jarmodel/driver” to conduct single-layer simulations. In contrast, BeTR-v1 did not separate the single-layer models from the vertically resolved models. The soil BGC formulations in the folder “src/Applications/soil-farm/ecacnp” adopt the mathematical formulation of the soil BGC module from ELMv1-ECA but concurrently solve the incoming litter input, soil carbon decomposition, nitrification–denitrification, plant–soil nutrient competition, etc., when updating the soil BGC state variables. The treatment in ecacnp enables us to cleanly separate vegetation and soil BGC in ELM but requires a significant amount of reordering of the subroutines and two additional parameters for plant BGC; i.e., besides the introduction of two parameters on the turnover of plant nitrogen and phosphorus storage pools, ecacnp has to compute soil BGC and plant–soil nutrient competition after all the phenological updates (including plant carbon and nutrient allocation for growth and vegetation mortality induced by fire and other natural factors), whereas ELMv1-ECA computes plant–soil nutrient competition before updating the phenological variables. When using the same parameters, the reordering required by ecacnp caused significant differences in the simulated carbon and nutrient cycling compared to ELMv1-ECA (which confirms our previous findings in Tang and Riley, 2018), and such differences were inferred to be not correctable by calibration. Therefore, we did another implementation of the soil BGC of ELMv1-ECA in BeTR-v2 by following the exact subroutine execution order of ELMv1-ECA and named it ECAv1-BeTR-ECA0 (the corresponding code is in src/Applications/soil-farm/v1eca). ELM-BeTR-ECA0 can run with the same parameters as those in ELMv1-ECA, thus minimizing the need to change parameters to obtain acceptable simulations. Since we found that ELM-BeTR-ECA0 performed significantly differently to ELMv1-ECA, we include ELMv1-BeTR-ECA by calibrating ELM-BeTR-ECA0 against ELMv1-ECA to evaluate to what extent the structural difference can be reduced by adjusting model parameters.
Overall, ELMv1-BeTR-ECA0 differs from ELMv1-ECA in the following two aspects: (1) in belowground BGC, ELMv1-BeTR-ECA0 solves the plant–soil nutrient competition using the multiple-flux co-limiting solver such that nutrient mineralization and immobilization are concurrently coupled (Tang and Riley, 2016), whereas ELMv1-ECA solves nutrient mineralization and uptake asynchronously using the explicit Euler scheme, where newly mineralized nutrients at the current time step become available only in the next time step. (2) For aboveground BGC, ELMv1-BeTR-ECA0 solves plant carbon and nutrient allocation for growth using the multiple-flux co-limiting solver to avoid sporadic negative litter flux inputs to the soil BGC, whereas ELMv1-ECA updates these state variable sequentially using the explicit Euler scheme and only corrects negative variables (which occur sporadically) at the end of each simulation step. ELMv1-BeTR-ECA differs from ELMv1-BeTR-ECA0 with values of the model parameters. Besides these three configurations, we also included ELMv1-ECA-V that differs from ELMv1-ECA by using the multiple-flux co-limiting solver for plant carbon and nutrient allocation. A brief description of the four model configurations is given in Table 1.
All in all, by using ecacnp soil BGC for standalone simulations (which can be created by following the instructions in the front page of the sbetr Git repository), we show how BeTR-v2 can support an easy extension from a single-layer model to a 1-D vertically resolved model. By comparing ELMv1-ECA-V and ELMv1-ECA, we verify the correct implementation of the multiple-flux co-limiting solver. Using ELMv1-BeTR-ECA0 for ELM-coupled simulations, we demonstrate that different numerical implementations for the same BGC formulation results in significantly different model behavior. More importantly, by using ELMv1-BeTR-ECA we then show that such model behavior differences cannot be resolved by recalibrating model parameters.
We drove the standalone 1-D model simulation with 365 d half-hourly time step output from an earlier ELM simulation Zhu et al. (2019). Model input variables include vertically resolved litter fluxes (of carbon, nitrogen, and phosphorus), soil temperature and moisture, infiltration flux, and atmospheric pressure and temperature. The example simulations are from the CA-Gro Ameriflux site: Groundhog River, Ontario, with boreal mixed-wood forest (see https://ameriflux.lbl.gov/sites/siteinfo/CA-Gro for more descriptions of the site, last access: 21 February 2022). The single-layer simulation used inputs for the first soil layer. For all global simulations, we used 200 year accelerated spinup, 600 year regular spinup (Koven et al., 2013; Zhu et al., 2019), and a transient simulation from 1850–2010. All forcing data are the same from Zhu et al. (2019), and all simulations are 1.9 latitude by 2.5∘ longitude spatial resolution.
3.1 Benchmark of the BeTR-v2 transport code
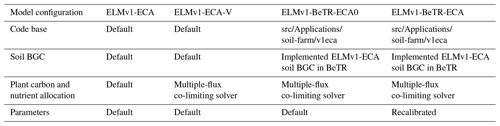
We found that the BeTR-v2 advection–diffusion solver solutions agreed well with the analytical solutions for both benchmarking cases (Fig. 1). For the pulse tracer solution (left column in Fig. 1), the depth-averaged root-mean-square error (RMSE) and R2 of linear fitting are 0.013 mol m−3 and 0.999, respectively, and for the wave-like solution (right column in Fig. 1), these two metrics are 0.0050 mol m−3 and 0.999, respectively. As time increases, we observed some increase in the RMSE for both benchmark cases. However, the overall magnitudes are still small (Fig. 1e, f). Overall, we infer that using the exponential spatial discretization from the ELM (which is similar to that in the CLM, Oleson et al., 2013) for the BeTR-v2 solver led to very accurate reproduction of the analytical solutions.
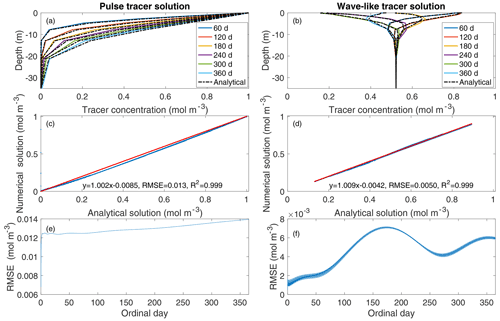
Figure 1Comparison of the analytical solutions with the numerical solutions derived from BeTR-v2. Panels (a) and (b) are comparisons of simulated and analytical tracer concentrations sampled at the end of 6 different days. In panels (c) and (d), blue dots are plotted using analytical solutions on the x axis and numerical solutions on the y axis; red lines are linear regressions of these data. Panels (e) and (f) are the depth-averaged root-mean-square error (RMSE) through time.
3.2 Single-layer and 1-D column model simulations
In the example standalone simulations using the ecacnp soil BGC, the single-layer and the vertically resolved 10-layer models demonstrate very similar temporal patterns for heterotrophic CO2 production (Fig. 2a and b). For the 1-D vertically resolved model simulation, surface CO2 flux is smaller than the heterotrophic CO2 respiration plus infiltration CO2 flux throughout the 30 year period. Accordingly, the soil CO2 concentration builds up continuously, with a seasonal cycle that has its maximum in July and minimum in March (Fig. 2c). We did not run the 1-D model to equilibrium because the example case here is only used for demonstration and to check if the model behavior agrees with our physical intuition. Additionally, this example does not account for root respiration. Therefore, we do not expect the soil CO2 to be as high as 10 000 ppm as it is often observed (Hirano et al., 2003); however, in global simulations, we do find soil CO2 below 30 cm could reach as high as a few percent. In a previous study with BeTR-v1 (Tang et al., 2013), we showed that some water-dissolved soil CO2 can be lost through the hydrological outflow. However, this hydrological loss is small in the above simulation because the forcing data does not include lateral runoff (i.e., lateral runoff is set to zero for standalone simulations for simplicity) and the leaching is negligible. Overall, we conclude that BeTR-v2 consistently represents vertically resolved soil BGC reactions and transport.
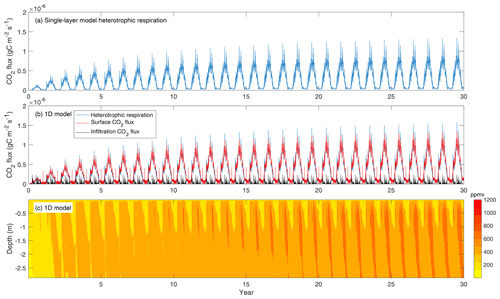
Figure 2(a) Heterotrophic CO2 flux simulated by the 10 cm thick single-layer model. (b) Column-integrated heterotrophic flux (by summing up contributions from all layers in the soil column), soil surface CO2 flux (from capillary exchange and diffusion considering equilibrium between gaseous and aqueous phases), and CO2 infiltration flux. (c) Evolution of soil CO2 concentration corresponding to panel (b). The single-layer model used the forcing data for the first layer of the 10-layer model.
3.3 Global simulations
We first ran three global model configurations for a 200 year accelerated spinup using the same parameters (see Koven et al., 2013, for information on how the accelerated spinup is designed). Because there was very little competition among the plant organs for carbon and nutrients, the spinup simulations led to almost identical model outputs between ELMv1-ECA and ELMv1-ECA-V (Fig. 3), suggesting that resolved plant carbon and nutrient allocation using the multiple-flux co-limiting solver has negligible influence and that this solver is properly implemented. ELMv1-BeTR-ECA0 (cyan lines) and ELMv1-ECA (blue lines) produced very different latitudinal patterns of primary flux variables, such as GPP (gross primary productivity; Fig. 3a), ER (ecosystem respiration; Fig. 3c), and therefore NBP (net biome productivity; Fig. 3e), particularly in the tropics. Noticeable differences among fluxes are also found in the middle to high latitudes. Accordingly, the vegetation, soil, and total ecosystem carbon pools differ substantially between ELMv1-ECA and ELM-BeTR-ECA0 (Fig. 3b, d, f) in the tropics and northern middle to high latitudes. We found that the differences are caused by different nutrient uptake rates simulated by the two models. In particular, with the multiple-flux co-limiting solver, both plants and soil carbon processes in ELM-BeTR-ECA0 are overall less nitrogen limited given the same nutrient uptake parameters, but as the simulation proceeds in time, less soil carbon is accumulated and soils become less fertile, consistent with our previous findings (Tang and Riley, 2018).
Figure 3Comparison of simulated flux and state variables at the end of the 200th year during the accelerated spinup for four model configurations (see Table 1). ELMv1-ECA-V differs from ELMv1-ECA as it uses the multiple-flux co-limiting solver for allocating carbon and nutrients for plant growth. ELMv1-BeTR-ECA0 differs from ELMv1-ECA-V by further solving belowground nutrient competition using the multiple-flux co-limiting solver. ELMv1-BeTR-ECA differs from ELMv1-BeTR-ECA0 by using re-calibrated parameters for two tropical plant functional types: broadleaf evergreen tropical trees and broadleaf deciduous tropical trees. We note that the soil carbon here is smaller than vegetation carbon because factors of accelerated decomposition have not been applied.
Since the simulated differences between ELMv1-BeTR-ECA0 and ELMv1-ECA are caused by different numerical implementations and are greatest in the tropics, we calibrated ELMv1-BeTR-ECA0 with respect to ELMv1-ECA for plant parameters important for plant–soil coupling for two tropical plant functional types (Table 2) and to analyze to what extent these differences can be minimized. We did not use the other plant function types because including them in the calibration is unlikely to change the conclusion of our analysis, as we will see later, while this decision significantly reduced the carbon footprint of this computationally intensive study. We conducted the parameter calibration using predicted total column soil C, vegetation C, GPP, ER, and leaf area index from ELMv1-ECA as constraints. We applied the grid-search approach (e.g., Bergstra and Bengio, 2012) to iteratively minimize model differences until no significant further improvement could be obtained. We ended up with 10 iterations wherein each iteration consists of 50 simulations.
Table 2Comparison of calibrated (ELMv1-BeTR-ECA) and default (ELMv1-ECA) parameters. PFT-4 is a broadleaf evergreen tropical tree and PFT-6 is a broadleaf deciduous tropical tree.
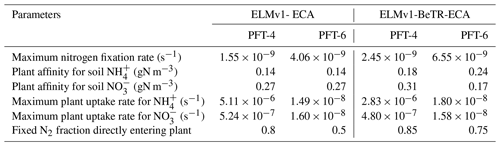
We found significant differences between default and calibrated model parameter values (Table 2). For ELMv1-BeTR-ECA, the calibrated substrate affinity parameters for and are of the same magnitudes as their default counterparts. The maximum uptake rates for and and the maximum nitrogen fixation rates are of the same order as their default values. For both PFT-4 (broadleaf evergreen tropical trees) and PFT-6 (broadleaf deciduous tropical trees), a higher amount of fixed nitrogen is directly acquired by plants in ELMv1-BeTR-ECA. When these new parameters were accordingly applied to tropical grid cells, we found smaller differences between ELMv1-ECA and ELMv1-BeTR-ECA for GPP and ER in the tropics (Fig. 3a and c), while differences in other variables (NBP, vegetation carbon, soil carbon, and total ecosystem carbon) remain quite significant (Fig. 3). Therefore, we assert that different numerical implementations result in different model predictions, and such different model predictions are likely not to be rectified by parameter calibration.
To further quantify the modeling uncertainty induced by different numerical implementations, we evaluated the four global simulations using the ILAMB benchmark software (Collier et al., 2018; version 2.5). Consistent with the results shown in Fig. 3, ELMv1-ECA and ELMv1-ECA-V have almost identical performance (Table 3). ELMv1-BeTR-ECA0 performed similarly or worse than ELMv1-ECA, but significantly better for the metric of Global Net Ecosystem Carbon Balance (or Net Biome Production, NBP; see also Fig. 4). Out of eight carbon metrics, ELMv1-BeTR-ECA performed slightly worse than ELMv1-ECA in net ecosystem exchange and significantly worse in vegetation biomass. For the remaining four hydrological cycle metrics, five radiation and energy metrics, and four climate forcing metrics, their performances are almost the same. ELMv1-BeTR-ECA performed slightly better for the metric of Global Net Ecosystem Carbon Balance (also see Fig. 4). For functional relationship benchmarks, ELMv1-BeTR-ECA0, ELMv1-BeTR-ECA, and ELMv1-ECA performed quite similarly (Fig. 5). Notably, ELMv1-BeTR-ECA was able to simulate higher evapotranspiration, resulting in better performance for the functional relationship between GPP and evapotranspiration (red line in Fig. 5a). ELMv1-BeTR-ECA also performed slightly better in some cases, e.g., GPP vs. precipitation (Fig. 5b), evapotranspiration vs. precipitation (Fig. 5d), and leaf area index vs. precipitation (Fig. 5e). This better agreement between ELMv1-BeTR-ECA and some benchmarks suggests that the numerical difference can significantly influence the performance of a supposedly good mathematical representations of ecosystem biogeochemistry.
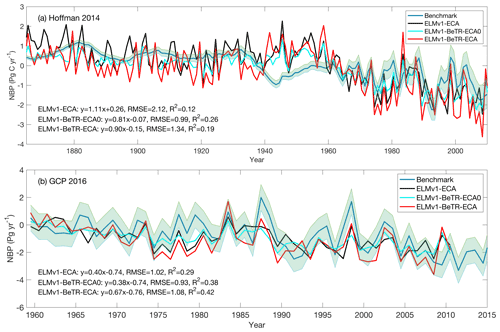
Figure 4Benchmark of simulated NBP with two global syntheses (a) compared with data from Hoffman et al. (2014) and (b) compared with data from Le Quere et al. (2016). In the linear regression, x is the benchmark and y is the model output.

Figure 5Benchmark of simulated vs. empirical data-derived variable relationships. The empirical benchmarks are derived from FluxCom output for the period from January 1980 through December 2013 (Jung et al., 2017; Tramontana et al., 2016) and used in ILAMB.
Table 3Comparison of ILAMB scores for 23 simulated variables by three different model versions. The three entries in bold for ELMv1-BeTR-ECA (and ELMv1-BeTR-ECA0) differ by greater than 5 % from ELMv1-ECA. All metrics are normalized to the range from 0 to 1, where greater values indicate better performance.
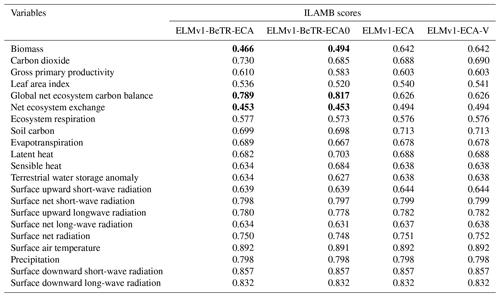
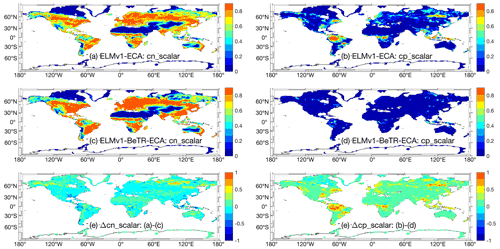
Figure 6Comparison of simulated plant nutrient stresses (on a scale from zero to one) at year 2010. Panels (a), (c), and (e) are for nitrogen stress, and panels (b), (d), and (e) are for phosphorus stress. Greater values indicate stronger limitation for the corresponding nutrient.
Nevertheless, there are significant differences in the simulated nutrient dynamics (as reflected in the fast variables that have a significant seasonal cycle), which over a longer time period can affect the cumulative carbon state variables (e.g., right column in Fig. 3). For instance, for the simulation year 2010, the hydrological nitrogen loss estimated by ELMv1-ECA is 56.8 TgN yr−1, while that estimated by ELMv1-BeTR-ECA is ∼10 times smaller (4.2; the value estimated by ELMv1-BeTR-ECA0 is 4.5 TgN yr−1). The global N2O emission estimated by ELMv1-ECA is 13.2, whereas ELMv1-BeTR-ECA estimated 14.3 (and the value by ELMv1-BeTR-ECA0 is 12.5 TgN yr−1).
Further, ELMv1-ECA and ELMv1-BeTR-ECA predicted different spatial distributions of plant nutrient limitations. For example, ELMv1-ECA predicted higher nitrogen limitation to plant productivity in northern high-latitude regions and some regions in northwestern Australia (Fig. 6e) for the simulation year 2010, even though the general patterns of plant nitrogen limitation are very similar (Fig. 6a, b). However, compared to ELMv1-BeTR-ECA, ELMv1-ECA predicted much more widespread plant phosphorus limitation (Fig. 6f). Therefore, a model calibration using C cycle variables led to very different estimates of N cycle parameters and thereby different nitrogen dynamics and phosphorus dynamics (through N and P co-modulated biogeochemical feedbacks). This type of discrepancy indicates that simulations under a future climate with these two seemingly similar models may very well diverge.
In summary, adopting different numerical coupling strategies resulted in different model behavior, even with many similar C cycle metrics. In particular, we found important differences in N and P dynamics that could impact 21st century simulations when atmospheric CO2 increases are expected to cause progressive nutrient limitations.
In this study, we present BeTR-v2, a reactive transport module for flexible implementation of soil biogeochemistry in ecosystem models. We benchmarked the numerical solver with two analytical solutions and demonstrated that BeTR-v2 can support soil biogeochemical modeling in single-layer, 1-D vertically resolved single column and global simulation modes. We implemented the soil biogeochemistry formulation from ELMv1-ECA into ELMv1-BeTR-ECA and explored the role of numerical solver robustness and calibration on carbon and nutrient cycling. We found that because the multiple-flux co-limiting numerical solver more tightly couples plant and soil processes during nutrient competition (so that it is numerically more robust than the solver used by default ELMv1-ECA model; Tang and Riley, 2018, 2016), ELMv1-BeTR-ECA has to use different model parameters to produce similar model behavior (as compared to ELMv1-ECA) for carbon and water cycling. However, the calibration was not able to correct the important differences in predicted N and P cycling, indicating that inappropriate numerical coupling will potentially result in incorrect model parameters that may affect predictions of carbon cycling variables under a changing climate and increasing atmospheric CO2 concentrations.
For this study, BeTR-v2 can be accessed at https://github.com/BeTR-biogeochemistry-modeling/sbetr/tree/jinyuntang/ELM-BeTR-ECA.r (last access: 21 February 2022) and is archived at https://doi.org/10.5281/zenodo.5526854. ELM can be accessed at https://github.com/E3SM-Project/E3SM/tree/jinyuntang/lnd/betr_v2eca_qz_fix, or https://doi.org/10.5281/zenodo.6233165 (Edwards et al., 2022). ILAMB can be accessed at https://github.com/rubisco-sfa/ILAMB (rubisco-sfa, 2021). Model simulation data are available upon request to the first author and can also be reproduced with the above code and the parameters in Table 2.
JT developed the model, analyzed the results, and wrote the paper. WJR and QZ discussed the results and contributed to the manuscript writing.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was supported by the Reducing Uncertainties in Biogeochemical Interactions through Synthesis and Computation (RUBISCO) Scientific Focus Area and the Energy Exascale Earth System Modeling Project, which are sponsored by the Earth and Environmental Systems Modeling (EESM) Program under the Office of Biological and Environmental Research of the U.S. Department of Energy Office of Science. Lawrence Berkeley National Laboratory (LBNL) is managed by the University of California for the U.S. Department of Energy under contract no. DE-AC02-05CH11231.
This research has been supported by the U.S. Department of Energy Office of Science (contract no. DE-AC02-05CH11231).
This paper was edited by Christoph Müller and reviewed by two anonymous referees.
Ahlström, A., Smith, B., Lindström, J., Rummukainen, M., and Uvo, C. B.: GCM characteristics explain the majority of uncertainty in projected 21st century terrestrial ecosystem carbon balance, Biogeosciences, 10, 1517–1528, https://doi.org/10.5194/bg-10-1517-2013, 2013.
Ahrens, B., Braakhekke, M. C., Guggenberger, G., Schrumpf, M., and Reichstein, M.: Contribution of sorption, DOC transport and microbial interactions to the C-14 age of a soil organic carbon profile: Insights from a calibrated process model, Soil. Biol. Biochem., 88, 390–402, 2015.
Berardi, D., Brzostek, E., Blanc-Betes, E., Davison, B., DeLucia, E. H., Hartman, M. D., Kent, J., Parton, W. J., Saha, D., and Hudiburg, T. W.: 21st-century biogeochemical modeling: Challenges for Century-based models and where do we go from here?, GCB Bioenergy, 1–15, https://doi.org/10.1111/gcbb.12730, 2020.
Bergstra, J. and Bengio, Y.: Random Search for Hyper-Parameter Optimization, J. Mach. Learn. Res., 13, 281–305, 2012.
Burrows, S. M., Maltrud, M., Yang, X., Zhu, Q., Jeffery, N., Shi, X., Ricciuto, D., Wang, S., Bisht, G., Tang, J., Wolfe, J., Harrop, B. E., Singh, B., Brent, L., Baldwin, S., Zhou, T., Cameron-Smith, P., Keen, N., Collier, N., Xu, M., Hunke, E. C., Elliott, S. M., Turner, A. K., Li, H., Wang, H., Golaz, J. C., Bond-Lamberty, B., Hoffman, F. M., Riley, W. J., Thornton, P. E., Calvin, K., and Leung, L. R.: The DOE E3SM v1.1 Biogeochemistry Configuration: Description and Simulated Ecosystem-Climate Responses to Historical Changes in Forcing, J. Adv. Model. Earth. Sy., 12, e2019MS001766, https://doi.org/10.1029/2019MS001766, 2020.
Collier, N., Hoffman, F. M., Lawrence, D. M., Keppel-Aleks, G., Koven, C. D., Riley, W. J., Mu, M. Q., and Randerson, J. T.: The International Land Model Benchmarking (ILAMB) System: Design, Theory, and Implementation, J. Adv. Model. Earth. Sy., 10, 2731–2754, 2018.
Davies-Barnard, T., Meyerholt, J., Zaehle, S., Friedlingstein, P., Brovkin, V., Fan, Y., Fisher, R. A., Jones, C. D., Lee, H., Peano, D., Smith, B., Wårlind, D., and Wiltshire, A. J.: Nitrogen cycling in CMIP6 land surface models: progress and limitations, Biogeosciences, 17, 5129–5148, https://doi.org/10.5194/bg-17-5129-2020, 2020.
Dwivedi, D., Riley, W. J., Torn, M. S., Spycher, N., Maggi, F., and Tang, J. Y.: Mineral properties, microbes, transport, and plant-input profiles control vertical distribution and age of soil carbon stocks, Soil. Biol. Biochem., 107, 244–259, 2017.
Fisher, R. A. and Koven, C. D.: Perspectives on the Future of Land Surface Models and the Challenges of Representing Complex Terrestrial Systems, J. Adv. Model. Earth. Sy., 12, e2018MS001453, https://doi.org/10.1029/2018MS001453, 2020.
Golaz, J. C., Caldwell, P. M., Van Roekel, L. P., Petersen, M. R., Tang, Q., Wolfe, J. D., Abeshu, G., Anantharaj, V., Asay-Davis, X. S., Bader, D. C., Baldwin, S. A., Bisht, G., Bogenschutz, P. A., Branstetter, M., Brunke, M. A., Brus, S. R., Burrows, S. M., Cameron-Smith, P. J., Donahue, A. S., Deakin, M., Easter, R. C., Evans, K. J., Feng, Y., Flanner, M., Foucar, J. G., Fyke, J. G., Griffin, B. M., Hannay, C., Harrop, B. E., Hoffman, M. J., Hunke, E. C., Jacob, R. L., Jacobsen, D. W., Jeffery, N., Jones, P. W., Keen, N. D., Klein, S. A., Larson, V. E., Leung, L. R., Li, H. Y., Lin, W. Y., Lipscomb, W. H., Ma, P. L., Mahajan, S., Maltrud, M. E., Mametjanov, A., McClean, J. L., McCoy, R. B., Neale, R. B., Price, S. F., Qian, Y., Rasch, P. J., Eyre, J. E. J. R., Riley, W. J., Ringler, T. D., Roberts, A. F., Roesler, E. L., Salinger, A. G., Shaheen, Z., Shi, X. Y., Singh, B., Tang, J. Y., Taylor, M. A., Thornton, P. E., Turner, A. K., Veneziani, M., Wan, H., Wang, H. L., Wang, S. L., Williams, D. N., Wolfram, P. J., Worley, P. H., Xie, S. C., Yang, Y., Yoon, J. H., Zelinka, M. D., Zender, C. S., Zeng, X. B., Zhang, C. Z., Zhang, K., Zhang, Y., Zheng, X., Zhou, T., and Zhu, Q.: The DOE E3SM Coupled Model Version 1: Overview and Evaluation at Standard Resolution, J. Adv. Model. Earth. Sy., 11, 2089–2129, 2019.
Grant, R. F.: Modelling changes in nitrogen cycling to sustain increases in forest productivity under elevated atmospheric CO2 and contrasting site conditions, Biogeosciences, 10, 7703–7721, https://doi.org/10.5194/bg-10-7703-2013, 2013.
Gross, M., Wan, H., Rasch, P. J., Caldwell, P. M., Williamson, D. L., Klocke, D., Jablonowski, C., Thatcher, D. R., Wood, N., Cullen, M., Beare, B., Willett, M., Lemarie, F., Blayo, E., Malardel, S., Termonia, P., Gassmann, A., Lauritzen, P. H., Johansen, H., Zarzycki, C. M., Sakaguchi, K., and Leung, R.: Physics-Dynamics Coupling in Weather, Climate, and Earth System Models: Challenges and Recent Progress, Mon. Weather Rev., 146, 3505–3544, 2018.
Hirano, T., Kim, H., and Tanaka, Y.: Long-term half-hourly measurement of soil CO2 concentration and soil respiration in a temperate deciduous forest, J. Geophys. Res.-Atmos., 108, 4631, https://doi.org/10.1029/2003JD003766, 2003.
Hoffman, F. M., Randerson, J. T., Arora, V. K., Bao, Q., Cadule, P., Ji, D., Jones, C. D., Kawamiya, M., Khatiwala, S., Lindsay, K., Obata, A., Shevliakova, E., Six, K. D., Tjiputra, J. F., Volodin, E. M., and Wu, T.: Causes and implications of persistent atmospheric carbon dioxide biases in Earth System Models, J. Geophys. Res.-Biogeo., 119, 141–162, 2014.
Huntzinger, D. N., Michalak, A. M., Schwalm, C., Ciais, P., King, A. W., Fang, Y., Schaefer, K., Wei, Y., Cook, R. B., Fisher, J. B., Hayes, D., Huang, M., Ito, A., Jain, A. K., Lei, H., Lu, C., Maignan, F., Mao, J., Parazoo, N., Peng, S., Poulter, B., Ricciuto, D., Shi, X., Tian, H., Wang, W., Zeng, N., and Zhao, F.: Uncertainty in the response of terrestrial carbon sink to environmental drivers undermines carbon-climate feedback predictions, Sci. Rep.-UK, 7, 4765, https://doi.org/10.1038/s41598-017-03818-2, 2017.
Hurrell, J. W., Holland, M. M., Gent, P. R., Ghan, S., Kay, J. E., Kushner, P. J., Lamarque, J. F., Large, W. G., Lawrence, D., Lindsay, K., Lipscomb, W. H., Long, M. C., Mahowald, N., Marsh, D. R., Neale, R. B., Rasch, P., Vavrus, S., Vertenstein, M., Bader, D., Collins, W. D., Hack, J. J., Kiehl, J., and Marshall, S.: The Community Earth System Model A Framework for Collaborative Research, B. Am. Meteorol. Soc., 94, 1339–1360, 2013.
Jarvis, N. J., Taylor, A., Larsbo, M., Etana, A., and Rosen, K.: Modelling the effects of bioturbation on the re-distribution of 137Cs in an undisturbed grassland soil, Eur. J. Soil. Sci., 61, 24–34, 2010.
Jung, M., Reichstein, M., Schwalm, C. R., Huntingford, C., Sitch, S., Ahlstrom, A., Arneth, A., Camps-Valls, G., Ciais, P., Friedlingstein, P., Gans, F., Ichii, K., Ain, A. K. J., Kato, E., Papale, D., Poulter, B., Raduly, B., Rodenbeck, C., Tramontana, G., Viovy, N., Wang, Y. P., Weber, U., Zaehle, S., and Zeng, N.: Compensatory water effects link yearly global land CO2 sink changes to temperature, Nature, 541, 516–520, 2017.
Koven, C., Friedlingstein, P., Ciais, P., Khvorostyanov, D., Krinner, G., and Tarnocai, C.: On the formation of high-latitude soil carbon stocks: Effects of cryoturbation and insulation by organic matter in a land surface model, Geophys. Res. Lett., 36, L21501, https://doi.org/10.1029/2009GL040150, 2009.
Koven, C. D., Riley, W. J., Subin, Z. M., Tang, J. Y., Torn, M. S., Collins, W. D., Bonan, G. B., Lawrence, D. M., and Swenson, S. C.: The effect of vertically resolved soil biogeochemistry and alternate soil C and N models on C dynamics of CLM4, Biogeosciences, 10, 7109–7131, https://doi.org/10.5194/bg-10-7109-2013, 2013.
Kumar, A., Jaiswal, D. K., and Kumar, N.: Analytical solutions of one-dimensional advection-diffusion equation with variable coefficients in a finite domain, J. Earth. Syst. Sci., 118, 539–549, 2009.
Le Quéré, C., Andrew, R. M., Canadell, J. G., Sitch, S., Korsbakken, J. I., Peters, G. P., Manning, A. C., Boden, T. A., Tans, P. P., Houghton, R. A., Keeling, R. F., Alin, S., Andrews, O. D., Anthoni, P., Barbero, L., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Currie, K., Delire, C., Doney, S. C., Friedlingstein, P., Gkritzalis, T., Harris, I., Hauck, J., Haverd, V., Hoppema, M., Klein Goldewijk, K., Jain, A. K., Kato, E., Körtzinger, A., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Lombardozzi, D., Melton, J. R., Metzl, N., Millero, F., Monteiro, P. M. S., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S., O'Brien, K., Olsen, A., Omar, A. M., Ono, T., Pierrot, D., Poulter, B., Rödenbeck, C., Salisbury, J., Schuster, U., Schwinger, J., Séférian, R., Skjelvan, I., Stocker, B. D., Sutton, A. J., Takahashi, T., Tian, H., Tilbrook, B., van der Laan-Luijkx, I. T., van der Werf, G. R., Viovy, N., Walker, A. P., Wiltshire, A. J., and Zaehle, S.: Global Carbon Budget 2016, Earth Syst. Sci. Data, 8, 605–649, https://doi.org/10.5194/essd-8-605-2016, 2016.
Luo, Y. Q., Randerson, J. T., Abramowitz, G., Bacour, C., Blyth, E., Carvalhais, N., Ciais, P., Dalmonech, D., Fisher, J. B., Fisher, R., Friedlingstein, P., Hibbard, K., Hoffman, F., Huntzinger, D., Jones, C. D., Koven, C., Lawrence, D., Li, D. J., Mahecha, M., Niu, S. L., Norby, R., Piao, S. L., Qi, X., Peylin, P., Prentice, I. C., Riley, W., Reichstein, M., Schwalm, C., Wang, Y. P., Xia, J. Y., Zaehle, S., and Zhou, X. H.: A framework for benchmarking land models, Biogeosciences, 9, 3857–3874, https://doi.org/10.5194/bg-9-3857-2012, 2012.
Manson, J. R. and Wallis, S. G.: A conservative, semi-Lagrangian fate and transport model for fluvial systems – I. Theoretical development, Water Res., 34, 3769–3777, 2000.
Medvigy, D., Wang, G. S., Zhu, Q., Riley, W. J., Trierweiler, A. M., Waring, B. G., Xu, X. T., and Powers, J. S.: Observed variation in soil properties can drive large variation in modelled forest functioning and composition during tropical forest secondary succession, New Phytol., 223, 1820–1833, 2019.
Munhoven, G.: Model of Early Diagenesis in the Upper Sediment with Adaptable complexity – MEDUSA (v. 2): a time-dependent biogeochemical sediment module for Earth system models, process analysis and teaching, Geosci. Model Dev., 14, 3603–3631, https://doi.org/10.5194/gmd-14-3603-2021, 2021.
Oleson, K. W., Lawrence, D. M., Bonan, G. B., Drewniak, B., Huang, M., Koven, C. D., Levis, S., Li, F., Riley, W. J., Subin, Z. M., Swenson, S. C., Thornton, P. E., Bozbiyik, A., Fisher, R., Heald, C. L., Kluzek, E., Lamarque, J. F., Lawrence, P. J., Leung, L. R., Lipscomb, W. H., Muszala, S., Ricciuto, D. M., Sacks, W., Sun, Y., Tang, J. Y., and Yang, Z.: Technical Description of version 4.5 of the Community Land Model (CLM), National Center for Atmospheric Research, Boulder, Colorado, NCAR/TN-503+STR, https://doi.org/10.5065/D6RR1W7M, 2013.
Petrovskii, S. and Petrovskaya, N.: Computational ecology as an emerging science, Interface Focus, 2, 241–254, 2012.
Riley, W. J., Zhu, Q., and Tang, J. Y.: Weaker land-climate feedbacks from nutrient uptake during photosynthesis-inactive periods, Nat. Clim. Change., 8, 1002–1006, 2018.
Riley, W. J., Sierra, C., Tang, J. Y., Bouskill, N. J., Zhu, Q., and Abramoff, R.: Next generation soil biogeochemistry model representations: A proposed community open source model farm (BeTR-S), in: Multi-scale Biogeochemical Processes in Soil Ecosystems: Critical Reactions and Resilience to Climate Changes, edited by: Yang, Y., Keiluweit, M., Senesi, N., and Xing, B., John Wiley & Sons, Inc, 233–257, ISBN 9781119480433, 2022.
rubisco-sfa: ILAMB, GitHub [code], https://github.com/rubisco-sfa/ILAMB (last access: 23 February 2022), 2021.
Simpson, M. J. and Landman, K. A.: Analysis of split operator methods applied to reactive transport with Monod kinetics, Adv. Water Resour., 30, 2026–2033, 2007.
Tang, J. Y.: BeTR-biogeochemistry-modeling/sbetr: New release after bgc update with elm, Zenodo [data set], https://doi.org/10.5281/zenodo.5526854, 2021.
Tang, J. Y.: v1.0.0 jinyuntang/E3SM: ELMv1-BeTR-ECA for BeTR-v2 paper, Zenodo [data set], https://doi.org/10.5281/zenodo.6233165, 2022.
Tang, J. Y. and Riley, W. J.: A total quasi-steady-state formulation of substrate uptake kinetics in complex networks and an example application to microbial litter decomposition, Biogeosciences, 10, 8329–8351, https://doi.org/10.5194/bg-10-8329-2013, 2013.
Tang, J. Y. and Riley, W. J.: Technical Note: Simple formulations and solutions of the dual-phase diffusive transport for biogeochemical modeling, Biogeosciences, 11, 3721–3728, https://doi.org/10.5194/bg-11-3721-2014, 2014.
Tang, J. Y. and Riley, W. J.: Technical Note: A generic law-of-the-minimum flux limiter for simulating substrate limitation in biogeochemical models, Biogeosciences, 13, 723–735, https://doi.org/10.5194/bg-13-723-2016, 2016.
Tang, J. Y. and Riley, W. J.: Predicted Land Carbon Dynamics Are Strongly Dependent on the Numerical Coupling of Nitrogen Mobilizing and Immobilizing Processes: A Demonstration with the E3SM Land Model, Earth Interact., 22, 11, https://doi.org/10.1175/EI-D-17-0023.1, 2018.
Tang, J. Y. and Riley, W. J.: Linear two-pool models are insufficient to infer soil organic matter decomposition temperature sensitivity from incubations, Biogeochemistry, 149, 251–261, 2020.
Tang, J. Y. and Riley, W. J.: On the modeling paradigm of plant root nutrient acquisition, Plant Soil, 459, 441–451, 2021.
Tang, J., Zhuang, Q., Shannon, R. D., and White, J. R.: Quantifying wetland methane emissions with process-based models of different complexities, Biogeosciences, 7, 3817–3837, https://doi.org/10.5194/bg-7-3817-2010, 2010.
Tang, J. Y., Riley, W. J., Koven, C. D., and Subin, Z. M.: CLM4-BeTR, a generic biogeochemical transport and reaction module for CLM4: model development, evaluation, and application, Geosci. Model Dev., 6, 127–140, https://doi.org/10.5194/gmd-6-127-2013, 2013.
Tang, J. Y., Riley, W. J., and Niu, J.: Incorporating root hydraulic redistribution in CLM4.5: Effects on predicted site and global evapotranspiration, soil moisture, and water storage, J. Adv. Model. Earth. Sy., 7, 1828–1848, 2015.
Todd-Brown, K. E. O., Randerson, J. T., Hopkins, F., Arora, V., Hajima, T., Jones, C., Shevliakova, E., Tjiputra, J., Volodin, E., Wu, T., Zhang, Q., and Allison, S. D.: Changes in soil organic carbon storage predicted by Earth system models during the 21st century, Biogeosciences, 11, 2341–2356, https://doi.org/10.5194/bg-11-2341-2014, 2014.
Tramontana, G., Jung, M., Schwalm, C. R., Ichii, K., Camps-Valls, G., Ráduly, B., Reichstein, M., Arain, M. A., Cescatti, A., Kiely, G., Merbold, L., Serrano-Ortiz, P., Sickert, S., Wolf, S., and Papale, D.: Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms, Biogeosciences, 13, 4291–4313, https://doi.org/10.5194/bg-13-4291-2016, 2016.
Wieder, W. R., Allison, S. D., Davidson, E. A., Georgiou, K., Hararuk, O., He, Y. J., Hopkins, F., Luo, Y. Q., Smith, M. J., Sulman, B., Todd-Brown, K., Wang, Y. P., Xia, J. Y., and Xu, X. F.: Explicitly representing soil microbial processes in Earth system models, Global Biogeochem. Cy., 29, 1782–1800, 2015.
Zaehle, S., Medlyn, B. E., De Kauwe, M. G., Walker, A. P., Dietze, M. C., Hickler, T., Luo, Y. Q., Wang, Y. P., El-Masri, B., Thornton, P., Jain, A., Wang, S. S., Warlind, D., Weng, E. S., Parton, W., Iversen, C. M., Gallet-Budynek, A., McCarthy, H., Finzi, A. C., Hanson, P. J., Prentice, I. C., Oren, R., and Norby, R. J.: Evaluation of 11 terrestrial carbon-nitrogen cycle models against observations from two temperate Free-Air CO2 Enrichment studies, New Phytol., 202, 803–822, 2014.
Zhu, Q., Riley, W. J., Tang, J., and Koven, C. D.: Multiple soil nutrient competition between plants, microbes, and mineral surfaces: model development, parameterization, and example applications in several tropical forests, Biogeosciences, 13, 341–363, https://doi.org/10.5194/bg-13-341-2016, 2016.
Zhu, Q., Riley, W. J., and Tang, J. Y.: A new theory of plant-microbe nutrient competition resolves inconsistencies between observations and model predictions, Ecol. Appl., 27, 875–886, 2017.
Zhu, Q., Riley, W. J., Tang, J. Y., Collier, N., Hoffman, F. M., Yang, X. J., and Bisht, G.: Representing nitrogen, phosphorus, and carbon interactions in the E3SM land model: development and dlobal benchmarking, J. Adv. Model. Earth. Sy., 11, 2238–2258, 2019.