R²D² v2.0: accounting for temporal dependences in multivariate bias correction via analogue rank resampling

Over the last few years, multivariate bias correction methods have been developed to adjust spatial and/or inter-variable dependence properties of climate simulations. Most of them do not correct – and sometimes even degrade – the associated temporal features. Here, we propose a multivariate method to adjust the spatial and/or inter-variable properties while also accounting for the temporal dependence, such as autocorrelations. Our method consists of an extension of a previously developed approach that relies on an analogue-based method applied to the ranks of the time series to be corrected rather than to their “raw” values. Several configurations are tested and compared on daily temperature and precipitation simulations over Europe from one Earth system model. Those differ by the conditioning information used to compute the analogues and can include multiple variables at each given time, a univariate variable lagged over several time steps or both – multiple variables lagged over time steps. Compared to the initial approach, results of the multivariate corrections show that, while the spatial and inter-variable correlations are still satisfactorily corrected even when increasing the dimension of the conditioning, the temporal autocorrelations are improved with some of the tested configurations of this extension. A major result is also that the choice of the information to condition the analogues is key since it partially drives the capability of the proposed method to reconstruct proper multivariate dependences.

1 Introduction

Climate model simulations are and will remain the main source of numerical projections to understand and anticipate climate change consequences. Those projections are performed under various greenhouse gas emission scenarios, prescribed for instance within the fifth international Coupled Model Intercomparison Project (CMIP5; IPCC, 2013) or the ongoing CMIP6 (Eyring et al., 2016) and are widely used by the scientific community investigating climate changes and their manifold impacts. Indeed, climate changes have been anticipated to affect multiple domains: hydrology and water resources (e.g., Gleick, 1989; Christensen et al., 2004; Piao et al., 2010), agronomy and crops (e.g., Ciais et al., 2005; Ben-Ari et al., 2018), ecology and biodiversity (e.g., Brown et al., 2011; Bellard et al., 2012), economy (e.g., OCDE, 2015; Tol, 2018) or human migrations (e.g., Defrance et al., 2017) are examples of domains where expected impacts of climate evolution can be high and therefore quite problematic for society.

To get robust impact estimations, the climate projections have thus to be as precise and informative as possible. However, even simulations of the current climate often present statistical biases: their mean, variance or more generally their distributions can more or less largely differ from observational reference datasets (see, e.g., Christensen et al., 2008; Teutschbein and Seibert, 2012; François et al., 2020, among many other studies). This also means that climate projections for future periods are also expected to have biases, potentially similar. That is why many impact studies, for current or future climate, have to rely on “adjusted” climate simulations obtained via bias correction (BC) methods. Over the last decades, many statistical and data-science BC techniques have been progressively devised for this specific purpose. The objective of such techniques is to transform (i.e., “correct” or “adjust”) the climate model simulations such that, for a calibration time period, the obtained corrections are equivalent to a reference dataset in terms of one or several targeted statistical features (e.g., means, variances or distributions). Simple methods can be used in the event that the target is only the mean (as the so-called “delta” or “anomaly” methods, e.g., Xu, 1999) or the variance (e.g., “simple scaling” Eden et al., 2012; Schmidli et al., 2006). Nevertheless, in general, the most employed methods are based on the “quantile-mapping” approach (e.g., Déqué, 2007; Gudmundsson et al., 2012) and its many variants (e.g., Kallache et al., 2011; Vrac et al., 2012; Cannon et al., 2015), whose target is the whole univariate distribution (i.e., not only the mean and variance but all moments of higher order, as well as any percentile) of a given climate variable.

However, if many statistical aspects can be adjusted with such methods, all are only univariate, i.e., related to only one physical variable at a single location. If multiple variables and/or at multiple locations have to be corrected, the independent applications of several one-dimensional bias correction (1d-BC) methods will not modify the intrinsic dependence structure of the simulations to be corrected (Vrac, 2018). Therefore, if the climate model simulations have biases in their inter-variable and/or inter-site dependences (e.g., in their correlations), most of the quantile-mapping and univariate BC techniques will not correct these features and will basically preserve their biases. This obviously has consequences for the impact models requiring multiple climate variables as input: if the physical relationships (i.e., the statistical dependences) of those input variables are not realistic enough, the biases in the multivariate situations can quickly propagate to the simulated impacts themselves, even if the simulations are adjusted by 1d-BC methods (e.g., Boé et al., 2007). More generally in climate sciences, the accurate modeling of dependences is a key aspect for proper assessments and projections of compound events and their associated risks (e.g., Leonard et al., 2014; Zscheischler et al., 2018; Bevacqua et al., 2019).

Consequently, some multivariate bias correction (MBC) methods have been recently designed to tackle the issues of the biases in multivariate dependences. The goal is basically the same as for univariate corrections: find a transformation that makes climate model simulations have the same targeted statistical features as a reference in the calibration period. In this case, the target statistical features include not only univariate features but also multivariate statistical features such as correlations or the empirical copula. The various MBCs developed so far can be categorized into three main families (Vrac, 2018; Robin et al., 2019; François et al., 2020):

• the “marginal/dependence” approaches, correcting separately univariate distributions and dependences before joining them to provide multivariate corrections (e.g., Vrac, 2018; Cannon, 2017);

• the “conditional successive” methods, adjusting one variable at a time but conditionally on the previously corrected variables to ensure proper multidimensional relationships (e.g., Piani and Haerter, 2012; Dekens et al., 2017);

• the “all-in-one” models, which do not separate the multivariate distribution, neither in marginal/dependence, nor in conditional distributions, but directly transform one multidimensional distribution into another multidimensional distribution (e.g., Robin et al., 2019).

A first intercomparison and critical review of MBC methods has been carried out by François et al. (2020). One major finding was that, although most of the MBC techniques (depending on their hypotheses and configurations) are more or less able to provide adjusted multidimensional properties, none of them explicitly account for temporal dependence properties. This implies that, although multivariate properties can be correctly adjusted (and sometimes, spatial properties as well, depending on the method), the temporal structure of the data generated by MBC methods is different from that of the model data to be corrected but not necessarily closer to that of the reference data. Therefore, there is a need to improve temporal properties resulting from MBC outputs. Of course, this specific need should not be filled at the expense of the other (marginal, inter-variable or inter-site) properties.

In the present study, we rely on a recently developed MBC method named R²D² to propose an extension allowing us to improve the autocorrelation of the multivariate adjusted data. This R²D² extension takes advantage of an analogue-based technique to reconstruct the multidimensional dependence conditionally on a temporal sequences of ranks.

The rest of this article is organized as follows: Sect. 2 describes the reference and model data on which the proposed R²D² extension is evaluated. Section 3 provides a short reminder about the initial R²D² approach and the detailed description of its new extension, as well as the experimental design set up for evaluation. Then, results are given and analyzed in Sect. 4, under the following underlying focus question: can the suggested method improve the temporal dependences without degrading the other (marginal, spatial and inter-variable) properties? Finally, the main findings are summarized and discussed in Sect. 5.

2 Reference and model data

To perform tests and analyses of the proposed correction method, we will rely on daily temperature at 2 m (T2) and precipitation (PR) from one run of a global climate model to be corrected on one hand and from an observation-based reference dataset on the other hand.

The latter corresponds to WFDEI data, which are the WATCH Forcing Data (WFD; Weedon et al., 2011) methodology applied to ERA-Interim data for the period from 1 January 1979 to 31 December 2016 on a 0.5^∘ × 0.5^∘ spatial grid (Weedon et al., 2014) over the land-only European region (30^∘ N, −10^∘ E – 70^∘ N, 30^∘ E), corresponding to 4167 grid points.

The climate model data to be corrected are extracted – for the same region – from simulations performed by the IPSL-CM5A-MR Earth system model (Marti et al., 2010; Dufresne et al., 2013). Historical simulations from the ensemble member “r1i1p1” are used for 1979–2005. This is concatenated with simulations under RCP8.5 scenario made from the same ensemble member for 2006–2016, hence providing a 1979–2016 time period. Those simulations have an initial 1.25^∘ × 2.5^∘ spatial resolution. To allow comparisons and applications of BC methods, they are then regridded to the WFDEI spatial resolution with a bi-cubic interpolation for temperature and a conservative interpolation for precipitation.

Note that only one climate model is used for application and evaluation purposes in the present study. Of course, other models will have other biases that must be corrected differently. However, our goal is not to test the proposed approach on many climate models but rather to establish a proof of concept of the R²D² extensions on an illustrative simulations run. We hypothesize that the main general findings obtained on this single model will still be valid for other models and simulations.

3 Methods and design of experiments

3.1 A short reminder about the R²D² method

The proposed methodology relies on – or can be seen as an extension of – the Rank Resampling for Distributions and Dependences (R²D²) bias correction method (Vrac, 2018). R²D² consists of two steps: first, a univariate BC is performed to adjust the marginal distributions, and then the empirical copula function (i.e., the dependence structure between the variables of interest, rid of their marginal distribution) is adjusted. Thus, R²D² belongs to the “marginal/dependence” family of multivariate bias corrections (see François et al., 2020, for a description of the other families: “successive conditional” and “all in one”).

For the first step, any 1d-BC method can be employed. In Vrac (2018) and in the following details of the present study, the cumulative distribution function – transform (CDF-t) approach, e.g., Vrac et al. (2012), is used to adjust the marginal properties for temperature. A specific version of CDF-t is used to correct precipitation data. This version relies on a stochastic singularity removal (SSR; Vrac et al., 2016) approach to manage dry time steps: first, zeros (from both references and simulations) are randomly transformed to positive but very small values (< 10⁻⁶); then CDF-t is applied onto the whole set of data (i.e., transformed data and initially positive values altogether), and the correction results are thresholded such that values < 10⁻⁶ are set to 0.

For the second step, R²D² uses a “conditioning dimension” (called “reference variable” in Vrac, 2018) from the 1d-BC results. This univariate 1d-BC time series – and more precisely its ranks – serves as a conditioning to find, within the other 1d-BC variables, the values that have the same rank associations as those in the training reference dataset (details and examples on R²D² can be found in Vrac, 2018). Hence, this method relies on a univariate conditioning dimension to generate rank associations, in the same way as an analogue technique (initially developed by Lorenz, 1969) relies on its predictors to generate values. By doing so, this MBC approach allows us to reproduce observed multivariate (spatial and multi-variable) dependence structures, while preserving some temporal properties of the initial simulations via the conditioning dimension.

However, if the temporal features of the conditioning dimension (i.e., one physical variable at one given location) is preserved by construction, this is not necessarily the case for the other variables (i.e., different physical variables and/or spatial locations) and even not the case at all for variables having a weak rank correlations with the conditioning dimension. Therefore, taking advantage of the analogue-based philosophy of R²D², several extensions are here proposed to improve the temporal properties of the corrections brought by the initial R²D².

3.2 Accounting for temporal structures via multivariate rank conditioning

The main idea of the proposed extensions consists of seeing the R²D² approach as an analogue-based method. Indeed, in Sect. 3.1, it is clear that the resampling of the multivariate ranks is conditional to a single rank value of the conditioning dimension. In analogue techniques used in the climate literature (e.g., Zorita and von Storch, 1999; Yiou, 2014; Jézéquel et al., 2018, among others), the conditioning (i.e., predictor) variable can be multivariate. In our case, since the purpose of R²D² is to correct the dependence structure, we want the notion of analogue situations to only account for the dependence structure and not for the marginal distribution. Hence, the distance between two situations is not computed based on the raw values of the conditioning dimensions but based on their ranks. The best analogue is thus defined as the situation (e.g., day) having the association of ranks the closest to that of the conditioning dimension in terms of Euclidean distance. Here, an extension of R²D² is proposed and allows different configurations, all relying on R²D² applied conditionally on a multidimensional conditioning dimension:

• R²D² conditional on a multivariate information at a given time t. The conditioning dimensions in R²D² can be chosen freely. They can belong to the set of variables to be corrected, provided as exogenous variables or be a combination of both. There is no restriction either on the spatial scales of the conditioning dimensions. For instance, as a bivariate conditioning dimension, one could combine a daily North Atlantic Oscillation (NAO) index, to provide large-scale information, with the temperature at one grid point as a source of small-scale information. Other choices could be the temperature at two given locations, the temperature and the precipitation at one location, etc.

• R²D² conditional on a rank sequence at times ($t-n,t-n+\mathrm{1},\mathrm{\dots },t$) of a univariate conditioning dimension. The idea here is about the same as in the previous suggestion but instead of conditioning the rank resampling on a multivariate conditioning dimension at time t, it is on a univariate one (e.g., temperature at a given location, or NAO index) but at several (e.g., n) lagged time steps ($t-n,t-n+\mathrm{1},\mathrm{\dots },t$).

• R²D² conditional on a rank sequence of a multivariate conditioning dimension. This is a logical combination of the two previous configurations to condition R²D² on information characterizing a temporal sequence of multiple variables.

Whatever the configuration, the choice of the conditioning dimension is however not trivial, as it conditions the temporal properties of the model that will be conserved after correction. In the case of a configuration accounting for the rank sequence, the length of the sequence to search the analogues has to be chosen. This length will be referred to as “Block-A” (for “block analogue”) hereafter. Moreover, in order to avoid discontinuities in the reconstructed final sequence of ranks, the whole sequence of the best analogue is not fully kept but only a subsequence corresponding to a given number of elements at the end of the complete sequence. This kept subsequence is referred to as “Block-K” (for “block kept”) hereafter, and its length also has to be chosen as shorter than or equal to Block-A. Searching for the best analogue with a length Block-A and then keeping only a length Block-K – shorter than Block-A – allows us to not only avoid discontinuities in the (rank and correction) time series but also give flexibility to the proposed BC method to adapt to the temporal dynamics of the climate model to correct. Preliminary tests (not shown) indicate that Block-A = 9 and Block-K = 7 are reasonable choices and that the results are only weakly influenced by a slight change of those values.

In the case of ties for the choice of best analogues, the proposed R²D² algorithm selects the first time step having the minimal Euclidean distance. Hence, the order in which the dataset is searched to find the analogue ranks will influence the selected time step and may thus potentially also influence the results. For example, ties might occur when including daily precipitation as a conditioning variable, particularly when precipitation at a single location is the only conditioning dimension. Indeed, there are potentially many time steps where it did not rain at the conditioning location. All of these time steps would all have the same rank (in this case, 1). This means that some rank combinations that are also compatible with the rank of the conditioning dimension (in this example, no rain at the conditioning location) will not be present in the corrected dataset. Hence, some rank associations can be either under-represented or over-represented in the corrected dataset compared to the reference dataset because of ties in the conditioning dimensions. However, when using multiple conditioning dimensions (i.e., multiple conditioning locations and/or variables), the number of candidates for the best analogue with the same exact minimal Euclidean distance decreases, hence reducing the effect of the ties in the time series of the conditioning dimensions. Other choices could be made to deal with tied ranks: last or median time step (instead of first) could be selected or even a randomly drawn time step (among those with a common minimal distance to the condition information). Nevertheless, this is not investigated in the present paper and left for future work.

In the following, 20 different R²D² configurations are applied and compared to the reference WFDEI dataset, the plain simulations and the univariate BC results obtained from CDF-t. Those 20 configurations and their notations are given in Table 1. For the versions including five grid points in the conditioning, the locations are chosen to characterize five cities – Paris, Madrid, Stockholm, Rome and Warsaw – spread out over the region. In the same manner – but more automatically – the N grid points (N= 100 or 400) in the other versions are chosen to uniformly cover the region of interest.

Table 1 Summary of the 20 R²D² configurations tested. The identification name is organized in the following way. The first number indicates the number of grid points used for the conditioning dimension of R²D²; the second one corresponds to the number of variables considered at each grid point for the conditioning dimension (here, “1” indicates “only temperature”; “2” indicates “temperature and precipitation”); and the third number indicates if some lagged (i.e., temporal) information is used by R²D² (“0” means “no lag used”; “1” means “lags used”). “Block-A” corresponds to the block size (i.e., lag length) used for the analogue search and “Block-K” to the block size that is kept from the selected analogues of size Block-A.

Note that the configuration using a conditioning with only one physical variable at a single location without accounting for lags (i.e., R.1.1.0) exactly corresponds to the initial R²D² method.

Moreover, in practice, the R²D² configurations with 400 grid points or with 4167 (i.e., all) grid points for the conditioning dimension provided results equivalent to those from the same configurations but with only 100 grid points (not shown). This emphasizes a preliminary result: taking a large number of spatial information is not necessarily needed once a sufficient information is provided. Hence, in the following, experiments R.400.1.0, R.400.2.0, R.400.1.1 and R.400.2.1 will not be presented, nor will experiments R.4167.1.0, R.4167.2.0, R.4167.1.1 and R.4167.2.1, as they provide results similar to R.100.1.0, R.100.2.0, R.100.1.1 and R.100.2.1, respectively.

3.3 Experimental design of the correction schemes

The different configurations of the R²D² extensions, as well as the CDF-t univariate BC (referred to as BC1D in the following), are applied and evaluated according to the following 2-fold cross-validation approach. First, the methods are calibrated over the 1979–1997 period and applied to correct the 1998–2016 climate projections for evaluation. Then, they are also applied the other way around, i.e., calibrated on 1998–2016 and applied for evaluation on 1979–1997. Finally, the two 19-year evaluation periods are gathered to dispose of the whole 38-year time period for evaluation.

Every method is applied on daily values but on a monthly basis, i.e., for each month separately that are joined afterwards. However, evaluations are performed on a seasonal basis – i.e., for each season (DJF, MAM, JJA, SON) separately – to reduce the number of figures and to group similar behaviors.

4 Results

In this section, we examine the effects of R²D² on the temporal, spatial, inter-variable and marginal properties of the dataset to be corrected. In the rest of the paper, most results are presented for winter only, but analyses for the other seasons are given in the Supplement when meaningful. Figure “X” of the Supplement will be referred to as Fig. S“X” in the following.

4.1 Temporal correlations: are they improved?

Here, we first look at the ability of R²D² to reproduce the short-term temporal dependences of the conditioning dimensions, through the first-order autocorrelation ρ, corresponding to the coefficient of a first-order auto-regressive model (AR1).

4.1.1 Temperature temporal correlation

For winter temperature (Fig. 1), the reference dataset shows high AR1 coefficients for the whole region of interest (ρ(AR1) > 0.7). The IPSL (Institut Pierre Simon Laplace) dataset and the BC1D dataset also exhibit this characteristic, indicating that the initial model simulations are consistent with the reference. The root mean square error (RMSE) between the AR1 coefficients of the reference dataset, the IPSL dataset or the BC1D dataset is around 0.04. Slight differences can be observed, for instance, in Italy and Spain where the ρ values are slightly lower than those from the reference dataset.

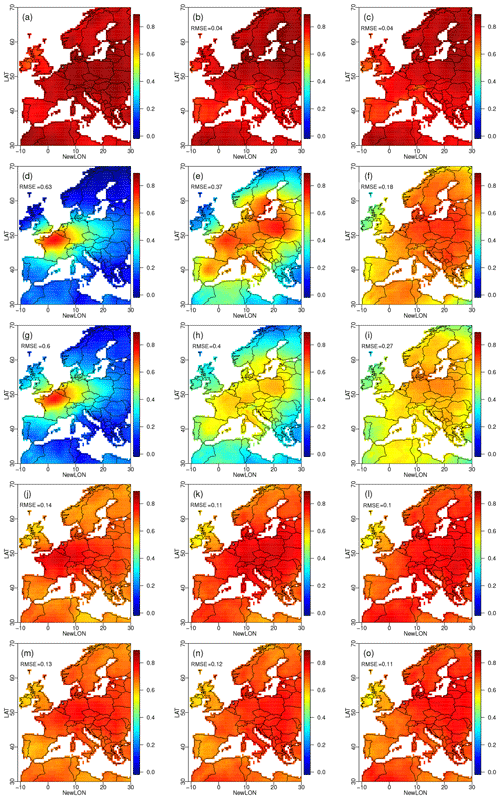
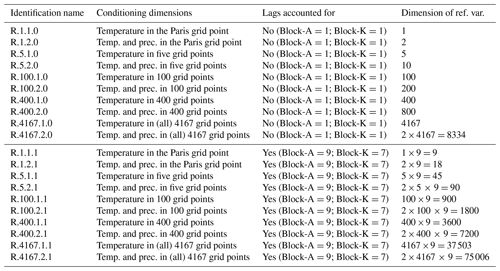
Figure 1 Maps of temperature autocorrelations of the order of 1 d for winter over the 1979–2016 period, for (a) WFDEI, (b) IPSL raw simulations, (c) 1d-BC (CDF-t), (d) R.1.1.0, (e) R.5.1.0, (f) R.100.1.0, (g) R.1.2.0, (h) R.5.2.0, (i) R.100.2.0, (j) R.1.1.1, (k) R.5.1.1, (l) R.100.1.1, (m) R.1.2.1, (n) R.5.2.1 and (o) R.100.2.1. In other words, the second row shows the results for temperature as a conditioning dimension (for different numbers of locations) and without accounting for lags; the third row is the same but for temperature and precipitation together as a conditioning dimension; the fourth and fifth rows are the same as the second and third rows but with lags accounted for. For panels (b–o), the RMSE value, computed over the whole domain between WFDEI autocorrelations and those from the model or corrected data, is indicated.

For R.1.1.0 (conditioning dimension is temperature in Paris; Fig. 1d), the AR1 coefficient of the conditioning dimension from the univariate correction is close to that from the reference data. After the R.1.1.0 correction, the sites whose temperature autocorrelations are similar to those in the reference are located around Paris. The further the points are from Paris, the less the R²D² correction is able to reproduce the AR1 coefficients observed in the reference. This is explained by two factors. First, the conditioning dimensions in the reference and in BC1D are similar in terms of AR1 coefficients. Second, in the reference dataset, there is a strong correlation between the conditioning dimension (the temperature in Paris) and the temperature at sites that are geographically close. Indeed, in R²D², at each time step we copy the rank association observed in the reference dataset, given the rank of the conditioning variable in the BC1D dataset. Hence, for a site close to Paris, the multivariate correction will alter the temperature rank sequence of the reference dataset to make it consistent with the rank sequence of the conditioning dimension in the BC1D dataset. In this case, since temperature in Paris in the BC1D dataset possesses temporal properties similar to the references and because of a strong spatial dependence around Paris, the temporal properties of temperature at a site close to Paris will be, after correction, consistent with the temporal properties of the temperature in Paris in the BC1D dataset and, thus, by transitivity, consistent with the temporal properties of the temperature in Paris in the reference dataset. In the following, we will refer to this phenomenon as the “transitivity effect”. Note that variables that are independent from (or only weakly correlated to) the conditioning dimension in the reference dataset have their ranks altered as well but not necessarily in a meaningful way. Indeed, for independent or weakly correlated variables, the rearrangement of the rank sequence is equivalent to a random permutation. Hence, to maximize the transitivity effect, it is needed to select conditioning variables (i) that have similar temporal properties in the reference and in the simulations to be corrected and (ii) that, in the reference dataset, show strong dependences with the other variables (i.e., the climate variables at the different sites) that we want to correct. Based on Fig. 1d, it is clear that it is not the case for the temperature in Paris, as already found by Vrac (2018).

However, when increasing the number of sites (R.5.1.0 and R.100.1.0; Fig. 1e and f, respectively) in the conditioning dimension, an amplification of the transitivity effect is visible: the areas where the AR1 coefficients are well reproduced have expanded and are located close to the conditioning sites. Indeed, the mean daily temperature is a relatively smooth signal over this large region and the AR1 coefficients are well represented by the simulations.

Adding precipitation in the conditioning dimension (R.1.2.0, R.5.2.0 and R.100.2.0, respectively, Fig. 1g to i) degrades the AR1 properties compared to having only temperature as a conditioning dimension. It may come from the fact that temperature and precipitation may not be strongly dependent and that conditioning on precipitation to find the value of temperatures for points in the neighborhood of conditioning sites introduces more noise than signal.

When using lags in the conditioning dimensions, all configurations with lags give similar results in terms of RMSE computed on the AR1 coefficient (RMSE = 0.11) and perform generally better than the configurations without lags. This could be expected since, in this case, short sequences of ranks in the reference dataset are resampled in the R²D² corrected dataset. Hence, it mechanically improves the agreement between the reference dataset and the R²D² corrected dataset in terms of short-term temporal dependence. This mechanism is the essence of the R²D² philosophy, where we copy, in the multivariate corrected dataset, the rank association that is given by the conditioning dimensions.

Moreover, the configurations using more sites (R.100.1.1 and R.100.2.1) give slightly better results. The spatial variations of the AR1 coefficients are qualitatively better respected, with lower values of autocorrelation in Spain, the UK and Libya compared to the rest of the map. Quantitatively, however, there is a negative bias of about −0.1 on average in terms of AR1 coefficients compared to the reference dataset.

In the end, as the initial temperature simulations have AR1 coefficients similar to those from the references, the IPSL and BC1D simulations show the best temporal properties (best R²D² RMSE = 0.1, BC1D RMSE = 0.04). In terms of temporal correlation, R.1.1.0 (i.e., initial R²D² method) and R.2.1.0 give the worst results with only sensible values of the AR1 coefficient around the Paris area. However, the use of a multivariate conditioning dimension and overall the use of a rank sequence into the conditioning dimensions strongly improve the capability of R²D² to account for temporal dependence features of the temperature variable. Indeed, the best R²D² results are clearly obtained for configurations accounting for lags.

4.1.2 Precipitation temporal correlation

For winter precipitation (Fig. 2), the reference dataset exhibits AR1 coefficients with spatial structures smaller than those for temperature. Globally, the model roughly reproduces the spatial distribution of the AR1 coefficients (IPSL RMSE = 0.09) but clearly lacks spatial resolution. The BC1D results exhibit finer spatial structures, for instance in the northern coastline of Scandinavia. However, the BC1D AR1 coefficients are not as good as those from the IPSL dataset (BC1D RMSE = 0.12). For both IPSL and BC1D, the AR1 coefficients are higher than those for the references in Spain, on the coasts of northern Africa and on the northern coasts of Scandinavia. The agreement between the reference data and the raw simulations in terms of AR1 coefficients is not as good for precipitation as for temperature.

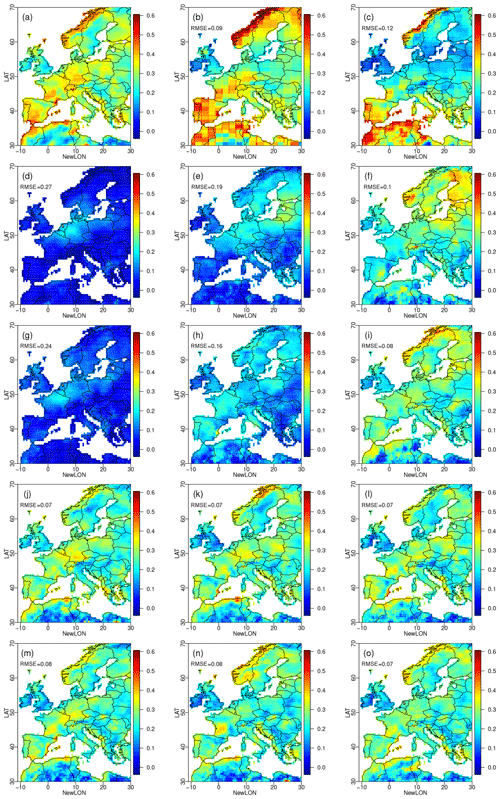
Figure 2 Same as Fig. 1 but for winter precipitation autocorrelations. Note that here precipitation is never used alone as a conditioning dimension.

When applying R.1.1.0 – the configuration of R²D² with the temperature in Paris as a univariate conditioning dimension without lag – the AR1 coefficient is not correctly reconstructed. In most areas, the AR1 coefficient is close to zero, except in Belgium, the Netherlands and northwestern Germany where the AR1 coefficient is positive but still negatively biased. This probably reveals a rather weak correlation between the temperature in Paris and the precipitation in the surrounding area. With R.5.1.0, which adds Madrid, Stockholm, Rome and Warsaw as conditioning sites, the precipitation autocorrelation is better reconstructed around the added conditioning sites. The effect is notably stronger around Warsaw and Stockholm, where the correlation between temperature and precipitation is stronger than in Rome and in Madrid (in general, stronger correlations are observed in northeastern Europe in winter; not shown). With R.100.1.0, using 100 conditioning sites, the AR1 coefficient reconstruction is improved over all Europe but is still relatively far from the reference.

Adding precipitation in the conditioning dimensions helps to improve the precipitation AR1 coefficient since it is likely that the correlation between precipitation in two close sites is stronger than the correlation between temperature in one site and precipitation in the other site. With 100 conditioning sites, geographical features present in the reference dataset start to be visible, for instance, higher AR1 coefficients on the coasts of northern Africa and on the northern coasts of Scandinavia. Nevertheless, the first-order autocorrelations are still biased negatively with respect to the reference dataset. In terms of RMSE, R.1.100.0 performs slightly better than the BC1D dataset (RMSE(BC1D) = 0.12; RMSE(R.1.100.0) = 0.1) and is on the same level as the raw IPSL simulations (RMSE = 0.09), although spatial structures are quite different. The transitivity effect is also limited by the fact that temporal properties of the references and of the BC1D dataset are not so similar. For instance, the AR1 coefficients tend to be lower in the BC1D dataset, both for temperature and precipitation. Such differences necessarily minimize the transitivity effect.

As for the temperature, the configurations of R²D² using lags in the conditioning dimensions perform better (RMSE = 0.07), with performance relatively independent from the number of conditioning sites or the type of climate conditioning dimensions. In this case, those configurations of R²D² provide an improvement in terms of RMSE compared to the raw IPSL simulations. Still, the AR1 coefficients are biased negatively compared to the reference dataset: the first-order autocorrelations are globally not as high as in the WFDEI reanalyses. This is also the case for the other seasons, as shown in the Supplement in Figs. S1–S3 for temperature and in Figs. S4–S6 for precipitation.

Hence, depending on the choice of the conditioning dimensions, R²D² can partially recover temporal properties of the reference dataset, especially when conditioning by lagged information via rank sequences. It is however hard for R²D² to reconstruct the temporal properties perfectly or even do better than the raw IPSL dataset or the BC1D dataset for temperature, a variable whose temporality is already well represented in the model simulations. The improvement brought by R²D² is more pronounced for precipitation temporal properties: including precipitation itself, more conditioning sites or lagged ranks into the conditioning dimension provides autocorrelation values and structures that are more similar to the reference ones than the other datasets are (e.g., raw or BC1D simulations, initial R²D² configuration R.1.1.0).

Generally, as seen in this section, although the proposed extensions clearly improve the initial R²D² method in terms of temporal correlations, the latter can present some underestimation of the temporal properties of the reference dataset, both for temperature and precipitation. This could be linked to an inhomogeneous sampling of the rank associations that are taken from the reference dataset. This is thus investigated in the next section (Sect. 4.2).

4.2 Reference time sampling and model chronology agreement

When the conditioning dimension is univariate and continuous, with unique ranks (i.e., no repetitions of values) and belongs to the variables to be corrected, it is the only variable (from the BC1D dataset) that the R²D² resampling scheme does not modify. Therefore, in this case, if the number of days is the same in the reference and model dataset, each time step is sampled exactly once and they are uniformly selected. Hence, in this specific case, R²D² reproduces exactly the inter-site and inter-variable empirical copula of the reference but not the temporal dependences of the data.

However, when the conditioning has a dimension equal to or greater than 2, there is no guarantee that the exact same rank associations exist in the reference dataset. Indeed, the higher the dimension of the conditioning, the less probable it is to find the exact rank association in the reference and in the BC1D dataset. This can come from either (i) a sampling issue: the higher the dimension, the more points are needed to uniformly sample the space or (ii) from biases in the dependence structure (biases in the rank associations) of the conditioning dimension in the dataset to be corrected. In this case, R²D² uses the rank associations of the reference dataset that is the closest in terms of Euclidean distance. Hence, the rank association of the conditioning dimension in the resulting R²D² dataset can be different from that of the BC1D dataset. One consequence is that some time steps (i.e., days in our case) can be resampled several times, while others might not be sampled at all. This can obviously have consequences on the properties (marginal, inter-site, spatial, temporal) of the multivariate corrections.

Therefore, we now analyze the distributions of the time steps that have been selected, since it is an indicator of potential biases introduced by the analogue-resampling scheme in R²D².

To reproduce exactly the empirical copula of the reference dataset, each time has to be selected only once. The more uneven the distribution of selected time steps, the more likely it is that the correction has modified the frequency of some situations with respect to the reference dataset. However, there is not a direct relationship between the unevenness of the distributions and the biases introduced in the correction. For instance, if some rank associations do not appear in the correction, they could have been substituted by a very similar association. In this case, the bias introduced would be very small.

The distributions of time steps selected in the reference dataset in January by the different configurations of R²D² are shown in Fig. 3 (the distributions for April, July and October are provided in Figs. S7–S9). As expected, R.1.1.0 presents a uniform histogram, since it uses a univariate conditioning that permits the sampling of the whole reference time steps. However, this is not the case for the other configurations of R²D², which all have dimensions of the conditioning equal to or greater than 2 (see Table 1). For the configurations of R²D² with only temperature as the conditioning dimension and without time lags (R.5.1.0, R.100.1.0), the sampling is quite uniform. This suggests that the spatial properties of the temperature are quite similar between the reference dataset and the BC1D dataset. When adding the precipitation as the conditioning dimension without time lags (R.2.1.0, R.2.5.0, R.2.100.0), the histograms are slightly less uniform. This indicates that there can be discrepancies between the references and the BC1D dataset for the spatial dependence of precipitation or the dependence between temperature and precipitation. Finally, when adding time lags in the conditioning dimensions, both for temperature and precipitation (R.1.1.1, R.1.2.1, R.1.100.1, R.5.1.1, R.5.2.1, R.5.100.1), the distributions of selected times also appear to be less uniform. This is especially true for R.5.2.1, where we observe a trough in the distribution between days 600 and 700. It indicates that the modeled rank sequences in this period rarely appear in the BC1D dataset.

Figure 3 Distributions of time steps selected in the reference dataset in January by the different R²D² configurations. The equivalent histograms for April, July and October are provided in the Supplement in Figs. S7–S9.

Those elements can help us to interpret the performance of the different configurations of R²D² with respect to the reconstruction of temporal, spatial and marginal properties of the temperature and precipitation fields.

Moreover, in order to see how much the different R²D² configurations change the temporal structures of the original raw simulations, for all sites and climate variables, we have computed the correlation between the ranks of the initial raw simulations and the ranks of the multivariate corrected time series. The closer the correlation is to 1, the less R²D² has modified the temporal structures of the raw simulations. The correlation coefficients for the different sites in winter are shown in Figs. 4 for temperature and 5 for precipitation. The other seasons are shown in Figs. S10–S15 in the Supplement. By construction, the CDF-t BC1D mostly conserves the ranks of the raw simulations.

For temperature (Fig. 4), we see that the time series of ranks have been modified substantially by R.1.1.0 (Fig. 4b). When the number of geographical sites increases (R.5.1.0 and R.100.1.0; Fig. 4c and d), we observe the transitive effect and the rank time series are more correlated to those from raw simulations. It is made possible because the variations of temperature are spatially smooth and because the references and BC1D data seem to have similar temperature temporal properties.

Figure 4 Maps of Spearman (rank) correlations calculated for each grid point in winter over 1979–2016 between the initial climate model temperature simulations and their corrections by (a) 1d-BC, (b) R.1.1.0, (c) R.5.1.0, (d) R.100.1.0, (e) R.1.2.0, (f) R.5.2.0, (g) R.100.2.0, (h) R.1.1.1, (i) R.5.1.1, (j) R.100.1.1, (k) R.1.2.1, (l) R.5.2.1 and (m) R.100.2.1. The results for the other seasons are provided in the Supplement.

The transitivity effect is also seen when precipitation is added as a conditioning dimension (R.1.2.0, R.5.2.0, R.100.2.0; Fig. 4e–g) or when time lags are added (R.1.1.1, R.5.1.1, R.100.1.1, R.1.2.1, R.5.2.1, R.100.2.1; Fig. 4h–m). However, fewer changes are made in the rank time series when the number of conditioning sites increases. However, for those versions of R²D² with a high number of conditioning sites, the resulting rank time series are slightly more modified (i.e., rank correlation further away from 1) than with just the temperature as the conditioning dimension. It may come from the fact that the higher the dimension of the conditioning, the more likely the rank sequence of the conditioning dimension has to be modified.

For precipitation (Fig. 5), similar observations can be made. However, the changes in the rank time series are larger than for temperature. It can be partially explained by the fact that the transitivity effect is weaker for precipitation. Indeed, precipitation events occur at local scale and with a spatial correlation radius smaller than for temperature.

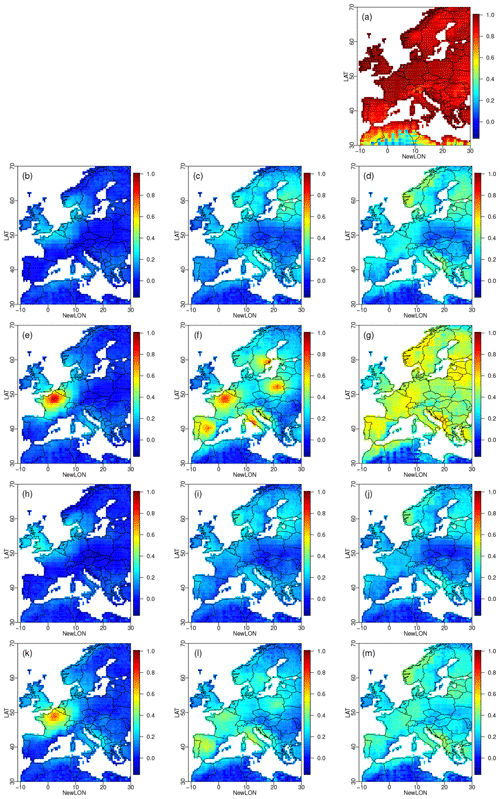
Figure 5 Same as Fig. 4 but for precipitation.

Globally, due to the transitivity effect, sites strongly correlated with the conditioning dimension in the reference dataset have their rank sequences mostly conserved after the correction if the conditioning dimension has similar temporal properties in the reference and the model. As a consequence, adding more sites in the conditioning dimension generally leads to more regions that mostly preserve the rank sequences of the model. However, to some extent, this effect can be counteracted by the fact that, as the dimension of the conditioning grows (e.g., adding rank lags in the conditioning), it becomes harder to find the exact rank associations in the reference data. It leads to alterations in the rank sequences for the conditioning dimension and for the sites that are correlated with it, and finally to a potential decrease of the rank correlation between the raw simulations and their corrections.

4.3 Marginal, spatial and inter-variable evaluations

As seen previously, some of the proposed R²D² extensions allow us to adjust temporal dependence structure. However, as the initial R²D² method was designed to bias correct multi-site and inter-variable dependences in addition to marginal distribution, one can wonder how the temporal structure improvements – as well as the time-sampling features – made by the R²D² extensions impact the corrections performed on the other dependences, i.e., whether or not they degrade the marginal, spatial and inter-variable properties. This is the purpose of Sect. 4.3.1 (marginal), 4.3.2 (inter-variable) and 4.3.3 (spatial).

4.3.1 Marginal properties

We first check whether the R²D² correction schemes are able to reconstruct the marginal properties of the reference dataset through two statistics: the mean and the standard deviation.

For each season and each grid point, biases in mean temperatures have been computed and are shown in Fig. 6 as boxplots. The associated maps are given in Figs. S16–S19. For all seasons, there are clear differences between the reference and the IPSL simulations (1.58 < RMSE < 1.84 ^∘C). The best performance is achieved by BC1D (0.08 < RMSE < 0.2 ^∘C), although some light positive or negative biases may appear on some regions, depending on the season (see Figs. S16–S19). This strong improvement of CDF-t over the raw simulations was expected as the univariate BC focuses on reconstructing the marginal distribution of the reference.

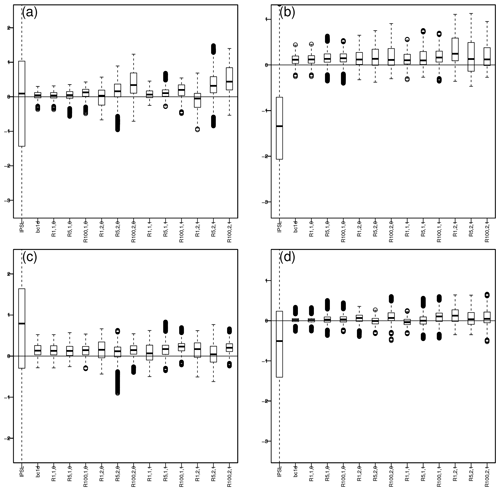
Figure 6 Boxplots of differences in mean temperature per grid point with respect to WFDEI, i.e., mean(model or BC) minus mean(WFDEI): (a) winter, (b) spring, (c) summer and (d) fall. The associated maps are given in Figs. S16–S19.

R.1.1.0 provides similar performance. Since the conditioning dimension is univariate, R²D² only performs a permutation of the ranks in time. It then only corresponds to a time reordering of the BC1D correction and does not affect the marginal distributions.

On average, going from one conditioning site to five, with R.5.1.0, increases the biases in mean (0.13 < RMSE < 0.24 ^∘C). However, using 100 sites (R.100.1.0) is equivalent to five in terms of mean (0.13 < RMSE < 0.22 ^∘C). Yet, the degradation is more visible when adding precipitation into the conditioning dimensions and when increasing the number of conditioning sites to 100. For R.100.2.0, the RMSE is between 0.19 and 0.54 ^∘C depending on the season, and biases can locally exceed 0.5 or even 1 ^∘C in winter over eastern Europe, for instance (Fig. S16i). It can be linked to the fact that for R.100.2.0, the distribution of time steps selected is less uniform (Fig. 3), hence, modifying the marginal mean values provided by CDF-t.

Similar observations can be made when looking at R²D² corrections accounting for lags in the conditioning dimension. Configurations including precipitation have less uniform distributions of selected time steps and have thus higher biases.

Somehow similar patterns of biases also occur when looking at the standard deviation of the temperatures (Fig. S20).

For precipitation, univariate biases are investigated in separating occurrences of rainfall and conditional intensities given rainfall occurrences. Hence, Fig. 7 displays, for the four seasons, boxplots of the relative differences of the probabilities of rainfall occurrence with respect to that of the reference data (Fig. 7a–d), as well as the boxplots of relative differences of the mean conditional intensities given rainfall occurrences, with regard to that of the reference data (Fig. 7e–h). The associated maps are given in the Supplement (Figs. S21–S24 for occurrence probabilities and S25–28 for mean conditional intensities). Rainfall occurrences are defined as precipitation values > 0.1 mm d⁻¹ to get rid of the drizzle effect present in many climate model simulations (e.g., Dai, 2006; Kjellström et al., 2010; Teutschbein and Seibert, 2012). Generally speaking, the effects of R²D² on the occurrence and conditional mean precipitation biases are similar to those observed on the mean temperature: (i) the R.1.1.0 configuration provides similar performance to BC1D, (ii) with or without time lags and with or without adding precipitation in the conditioning, increasing the number of conditioning sites may lead to relatively higher biases, both for occurrence probability and intensity. However, including precipitation itself in the conditioning does not amplify the precipitation biases and can even reduce them depending on the season.

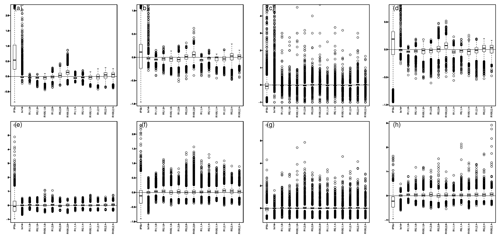
Figure 7 (a–d) Boxplots of relative differences of the probabilities of rainfall occurrence with respect to that of the reference data; (e–h) boxplots of relative differences of the mean conditional intensities given rainfall occurrences, with regard to that of the reference data. The results are given for winter (a, e), spring (b, f), summer (c, g) and fall (d, h). To get rid of the drizzle effect, the threshold for precipitation occurrence is set to 0.1 mm d⁻¹. Associated maps are given in Figs. S21–S24 for occurrence probabilities and Figs. S25–S28 for mean conditional precipitation.

Biases in standard deviations for conditional precipitation values are also given for information (Fig. S29) and coincide with results for means.

Generally, for both temperature and precipitation marginal properties, the biases tend to be stronger for R²D² configurations that exhibit non-uniform sampling of the time steps selected.

4.3.2 Inter-variable correlations

We now evaluate the capability of the different R²D² configurations to adjust inter-variable dependences. We first compute the Pearson correlation between temperature and precipitation for each grid point in the corrected dataset. We then compare these correlation values with those from the references. The results are summarized as boxplots of differences in correlation (Fig. 8). The associated maps are given for each season in Figs. S30–S33 in the Supplement. Note that the Spearman rank correlation analysis provides similar conclusions, although they are perturbed by the rare rainfall occurrences, especially over northern Africa (not shown), which complicates the analysis of the boxplots. Indeed, daily precipitation data contain many zeros and therefore many tied first ranks. In a case with, for example, 100 values whose 80 % are zeros, 80 ranks are ties and equal to 1, while the first rank not equal to 1 is the 81st, creating a “jump” in the rank distribution. A relatively small error in the rainfall occurrence frequency can then lead to a high bias in the Spearman (rank) correlation, while the Pearson correlation is less sensitive since it is based on “real” values and not ranks. Hence, the Pearson correlation has been preferred.

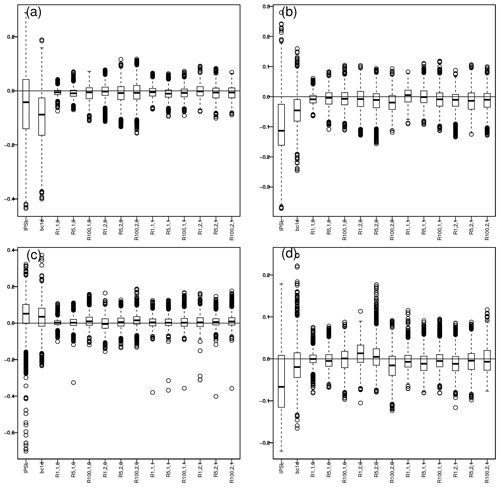
Figure 8 Boxplots of differences in temperature vs. precipitation Pearson correlations between WFDEI and the different datasets (IPSL, 1d-BC IPSL and the R²D² configurations) over 1979–2016 in (a) winter, (b) spring, (c) summer and (d) fall. The associated maps are given for each season in the Supplement.

In the IPSL model and in the BC1D correction, the correlation between temperature and precipitation is weaker than in the reference dataset. We expect R.1.1.0 to have the best performance with regards to inter-variable rank correlation. Indeed, it has a univariate conditioning dimension, implying that the empirical copula between temperature and precipitation of the reference data observed during the calibration periods is reproduced almost exactly. In practice, in Fig. 8, the boxplots for R.1.1.0 are not exactly 0. It indicates that in the references, the empirical copula between temperature and precipitation is not exactly the same during the two time periods used alternatively for calibration and validation. However, R.1.1.0 (i.e., the initial R²D² method) is the main benchmark of the inter-variable evaluation. Indeed, it was designed to adjust the temperature–precipitation dependence of the raw simulations, which is the case since it strongly improves IPSL and BC1D dataset properties. Then, the similar behaviors of the different R²D² configurations indicate that their T2 vs. PR correlations are also improved and in a similar way. In other words, for all R²D² extensions, including those improving the temporal dependence structures (see Sect. 4.1), the inter-variable correlation is not degraded with respect R.1.1.0 and therefore satisfyingly corrected.

4.3.3 Spatial correlations

Finally, we evaluate the spatial correlation by computing the loading values of the first empirical orthogonal function (EOF) obtained from a principal component analysis (PCA) applied on temperature and precipitation separately. For each dataset, we compare the associated loading values with those obtained for the references. The results for winter and summer are summarized in Fig. 9 as boxplots drawn from differences of loading values between the R²D² corrections and the WFDEI references. The associated maps are given in Figs. S34–S37 in the Supplement.

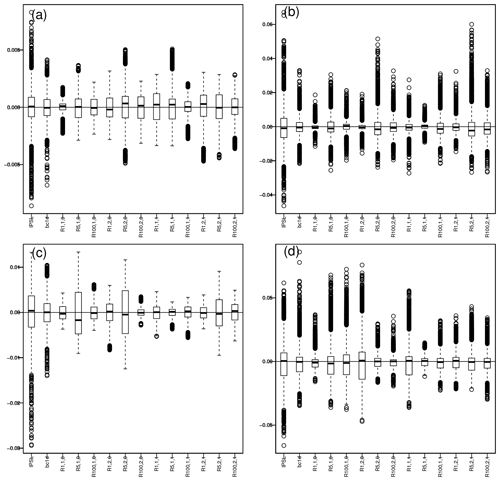
Figure 9 Boxplots of differences in loading values for the first EOF (EOF1) between model or corrected data and WFDEI (i.e., EOF1(model or BC) minus EOF1(WFDEI)). Panels (a) and (c) are for temperature, (b) and (d) for precipitation, for winter (a, b) and summer (c, d). The associated maps are given in the Supplement.

For both temperature and precipitation, and for all seasons, the raw IPSL simulations have loading values well centered around those of WFDEI since the median of the differences is close to 0.

Simply by correcting the marginal distribution, BC1D improves the agreement with the reference dataset. Indeed, EOFs are computed from the variance–covariance matrix, which is sensitive to the change in the marginal distributions.

In the R²D² configurations, as already explained, the ranks of the non-conditioning variables are shuffled to match those in the reference dataset during the calibration period. If the inter-site copula is similar during the calibration and validation periods, the R²D² configurations should improve the spatial correlations compared to BC1D. This is the case for R.1.1.0, as well as for other configurations, where the median of the difference is close to 0 and where an interquartile range of the differences is narrower than that for BC1D. Interestingly, the configurations with the largest interquartile range are those for which the sampling of the time steps is less uniform (Fig. 3), illustrating again the potential impacts of an uneven sampling. However, many R²D² configurations are able to reconstruct spatial properties correctly, at least as well as the initial R²D² method (i.e., with a univariate conditioning dimension) that was explicitly designed for it. This is even more visible when looking at the maps of loading values (Figs. S34–S37). Hence, the introduction of additional conditioning information into R²D² – needed to improve temporal properties as seen in Sect. 4.1 – does not degrade much the capability of R²D² to adjust the spatial dependence structures of the climate simulations.

Spatial correlograms are not shown but clearly indicate similar results.

5 Conclusions and discussion

5.1 Conclusions

To fill some needs of the climate change impact community, an MBC method has been proposed in this study. In addition to marginal properties, this MBC is designed to adjust both the inter-site and inter-variable dependence structures of climate simulations and at the same time to improve the temporal properties of the corrections. Our approach is based on the previously existing R²D² method (Vrac, 2018) that relied on a univariate “conditioning dimension” to sample ranks from a reference dataset and therefore reconstruct the copula-based spatial and inter-variable dependences. The suggested R²D² extensions allow resampling ranks given a multivariate conditioning dimension, which could be ranks of multiple physical variables at a time step t, ranks from a single physical variable but over a sequence of N time steps ($t-(N-\mathrm{1}),\mathrm{\dots },t$) or ranks of multiple physical variables over a sequence of N time steps.

Several configurations (i.e., different conditioning dimensions including different sites and climate variables, with or without lagged information) have been applied to correct daily precipitation and temperature simulations over Europe from a single climate model run, the IPSL-CM5 Earth system model (Marti et al., 2010; Dufresne et al., 2013), with respect to the WFDEI data (Weedon et al., 2014) as references. As the initial R²D² approach by Vrac (2018) was able to properly adjust spatial and inter-variable structure but not the temporal properties of the simulations, the underlying question of the present study was to understand (i) if the proposed multidimensional conditioning in R²D² improves the temporal aspects of the corrections and (ii) the impact of this conditional resampling on the adjustment quality of the other (i.e., marginal, spatial, inter-variable) properties. Hence, the various R²D² configurations have been evaluated and compared to the raw simulations as well as to corrections from the univariate BC method CDF-t (e.g., Vrac et al., 2012), first in terms of autocorrelation to characterize the main temporal aspects and then in terms of marginal properties, spatial dependences and temperature vs. precipitation correlations.

For temporal properties, although the R²D² variants strongly improve the initial R²D² approach, they do not reach the rather good level obtained for temperature with the tested 1d-BC (due to the correct auto-correlations from the raw temperature simulations), while the results are more debatable for precipitation. In general, the main conclusions were that including more information (sites and/or lagged ranks) in the conditioning dimension generally improves the reconstruction of the autocorrelation coefficients, both for temperature and precipitation. However, when the dimension of the conditioning (i.e., the number of variables, sites and lags to condition the resampling) increases, the distribution of the sampled time steps can be quite different from the uniform one. This has then consequences mostly on the marginals (i.e., univariate properties), where the mean and standard deviation can have stronger biases for non-uniform sampling. For the other evaluations (spatial and inter-variable properties), although variations in the results are visible depending on the conditioning dimension used, the main conclusion is that the proposed R²D² configurations are relatively stable. Thus, in general, the introduction of additional conditioning information into R²D² allows improving temporal properties with a good preservation of the capability of the initial R²D² to adjust both the spatial and inter-variable dependences of the raw simulations. Hence, in practice, we recommend a “compromise setting” in the choice of the conditioning dimension, with not too few and not too many sites. Such a choice would prevent both from missing transitivity effects and from having an uneven time step distribution.

5.2 Discussion and perspectives

The method suggested in this study is of course upgradable along different axes.

First, as our goal was not to test the various R²D² configurations on several climate models but rather to establish a proof of concept of the R²D² extension on an illustrative simulation run, only one climate model has been used for application and evaluation in the present study. Although we hypothesize that the main general findings obtained on this single model application will still be valid for other models and simulations, this will need to be confirmed to generalize and refine our results to more model simulations.

Moreover, the fundamental assumption of R²D² is that the spatial and inter-variable copulas (i.e., rank association) is stationary in time, even for future climate projections. This assumption – considering that rank associations act as proxies of physics (Vrac, 2018) and that physics does not change in time – is nevertheless debatable since it needs to be verified in further works. However, it highlights the fact that the conditioning dimension has to be carefully chosen to be relevant, both to drive (i.e., condition) the correction of the properties of interest and to translate the potential changes that may happen in future climate and that would impact the corrections. Hence, the potential non-stationarity of the dependences between climate variables (i.e., rank association) may be worth exploring further. This could be done via several questions; e.g., how stable is the rank association with time? How long does the considered period have to be in order to faithfully estimate the association? How can climate change alter it? Those questions, however, are not specific to our suggested method. They concern many methods and studies relying on dependences of climate variables in climate change contexts. Such fundamental questions deserve to be investigated on their own and are thus left for future works.

More generally, the choice of the conditioning dimension is a key element of the R²D² method. Indeed, as seen in this study, what is corrected or not by R²D² is partially driven by the chosen conditioning information. Thus, testing alternative conditioning dimensions could also be of interest for future work, to bring additional physical/geographical information, valuable to generate proper multivariate corrections. This alternative conditioning – e.g., including NAO or other indices, characterization of the circulation or other covariates – nevertheless has to be determined according to the specific region of interest, the climate variables to be corrected, etc. This adaptation of the conditioning to the application is a requirement to inject the relevant and suited physical information into R²D².

Of course, if a “good” conditioning must optimize the R²D² correction of some statistical properties, it mainly has to optimize the properties that are the most useful for the users of the corrections. In other words, the choice of the R²D² configuration has to be tailored for the end users of the simulations. It is thus very important for the end users to know which properties are essential to be corrected in order to design the R²D² configuration that is most appropriate for their specific application. Indeed, if many statistical features of the simulations are to be corrected, it is not clear that a single configuration will be able to correct all properties. For some regions and sets of climate variables, this can happen, but in other cases it might be needed to prioritize the most essential ones and then choose the associated R²D² configuration.

Finally, trying to correct multiple statistical properties at the same time remains a difficult challenge, as adjusting one often modifies another one. Additionally, one can wonder what is kept from the raw climate simulations if a correction is performed to adjust many statistical aspects. Hence, when applying a multivariate bias correction method with a configuration allowing us to modify (explicitly or implicitly) several properties, a compromise has to always be searched in order to balance, on the one hand, the level of correction needed to make the simulations useful for the application of interest and, on the other hand, the climate model signal preserved by the applied correction method. This is the only way to make the (M)BC useful in practice and physically reliable.