A new method (M³Fusion v1) for combining observations and multiple model output for an improved estimate of the global surface ozone distribution

We have developed a new statistical approach (M³Fusion) for combining surface ozone observations from thousands of monitoring sites around the world with the output from multiple atmospheric chemistry models to produce a global surface ozone distribution with greater accuracy than can be provided by any individual model. The ozone observations from 4766 monitoring sites were provided by the Tropospheric Ozone Assessment Report (TOAR) surface ozone database, which contains the world's largest collection of surface ozone metrics. Output from six models was provided by the participants of the Chemistry-Climate Model Initiative (CCMI) and NASA's Global Modeling and Assimilation Office (GMAO). We analyze the 6-month maximum of the maximum daily 8 h average ozone value (DMA8) for relevance to ozone health impacts. We interpolate the irregularly spaced observations onto a fine-resolution grid by using integrated nested Laplace approximations and compare the ozone field to each model in each world region. This method allows us to produce a global surface ozone field based on TOAR observations, which we then use to select the combination of global models with the greatest skill in each of eight world regions; models with greater skill in a particular region are given higher weight. This blended model product is bias corrected within 2^∘ of observation locations to produce the final fused surface ozone product. We show that our fused product has an improved mean squared error compared to the simple multi-model ensemble mean, which is biased high in most regions of the world.

1 Introduction

Tropospheric ozone is a pollutant detrimental to human health and has been associated with a range of adverse cardiovascular and respiratory health effects due to short-term and long-term exposure (World Health Organization, 2005; Jerrett et al., 2009; US Environmental Protection Agency, 2013; GBD, 2015; Turner et al., 2016; Cohen et al., 2017). Assessing the human health impacts of ozone on the global scale requires accurate exposure estimates at any given inhabited location (Shaddick et al., 2018). Due to the limited availability of surface ozone observations in many regions of the world (Fleming et al., 2018), global atmospheric chemistry models are required to calculate surface ozone exposure. Despite continual development and improvement, global models struggle in their ability to accurately simulate ozone in all regions of the world (Young et al., 2018). The ability to accurately simulate observed ozone at a particular location also varies between models, as demonstrated by several multi-model comparisons (Stevenson et al., 2006; Young et al., 2013; Cooper et al., 2014).

A useful endeavor for producing an accurate representation of the global surface ozone distribution is to combine the output from many models in a way that takes advantage of the strengths of each model and minimizes the weaknesses. Such efforts have already been made for both climate and chemistry–climate models. For example, multi-model output has been combined using a parametric approach, either by assigning an equal or optimum weight to each model (Stevenson et al., 2006; He and Xiu, 2016; Braverman et al., 2017) or by tuning the initial conditions under different scenarios or parameterizations (Cariolle and Teyssèdre, 2007; Wu et al., 2008; Young et al., 2013). These approaches often assume that individual model biases will at least partly cancel by averaging or weighting, according to certain measures of predictive performance. Thus, the combined model product is likely to be more accurate than a single model prediction, as has been shown for multi-model combinations of past or present-day climate (Buser et al., 2009; Knutti et al., 2010; Weigel et al., 2010; Chandler, 2013).

For the case of simply averaging the output from multiple climate models, most studies either explicitly or implicitly assume that every model is independent and is a random sample from a distribution, with the true climate as its unbiased mean. This implies that the average of a set of models converges to the true climate as more and more models are added. This multi-model ensemble often outperforms any single model in terms of the predictive capability. Undeniably, when one has several dozen or hundreds of possible ensemble members, the most straightforward and efficient approach is to simply take the ensemble average, ignoring the impact of potentially erroneous outlier ensemble members. From a statistical point of view, one might argue that ruling out potentially erroneous ensemble members prior to conducting the ensemble mean would yield an even better result, especially if the overall number of ensemble members is small.

Combining model ensembles using a method more sophisticated than the simple average is a challenge because a meaningful model evaluation can rarely be condensed into a single metric, and there is no technique that can explicitly quantify the degree of similarity (i.e., both accuracy and precision) between two different spatial fields (Hyde et al., 2018). Indeed, Stainforth et al. (2007) concluded that any attempt to assign weights is, in principle, inappropriate. With a lack of appropriate criteria, the model weighting approach has not become a standard alternative to the ensemble average. Accordingly, there is presently no objective criterion for combining surface ozone estimates from a model ensemble to produce a surface ozone product with improved accuracy beyond that of any ensemble member or the simple ensemble mean. The absence of such a methodology is the motivation for this paper.

This paper presents a new statistical approach (M³Fusion) for combining surface ozone output from multiple atmospheric chemistry models with all available surface ozone observations to produce a global surface ozone distribution with greater accuracy than the multi-model ensemble mean. As described in greater detail below, this fused surface ozone product is constructed in three steps: (1) ozone observations from all available surface ozone monitoring sites around the world are spatially interpolated to a smooth global field; (2) for each of eight continental regions of the world, six global atmospheric chemistry models are evaluated against the interpolated observed ozone field by a quadratic programming optimization, with the most accurate models receiving the highest weight; a locally confined spline interpolation is used at the regional boundaries to avoid unphysical step changes; (3) finally, the global ozone field derived from the polynomial equation is bias corrected but only within a limited distance from available observations. The final product is based on the annual maximum of the 6-month running mean of the monthly average daily maximum 8 h average mixing ratios (DMA8), a metric that can be used to estimate human mortality due to long-term ozone exposure (Turner et al., 2016; Malley et al., 2017; Seltzer et al., 2018; Shindell et al., 2018).

Past estimates of global mortality due to long-term ozone exposure have relied on surface ozone fields produced by global atmospheric chemistry models due to the limited coverage of the global ozone monitoring network (Anenberg et al., 2010; Brauer et al., 2012, 2015; Malley et al., 2017). The fused surface ozone product is a blend of global surface ozone observations and model output that has been adjusted according to the observations. This particular product will be available for future estimates of global human mortality due to long-term ozone exposure (e.g., Global Burden of Disease, Brauer et al., 2012, 2015). Furthermore, the methodology can be applied to a range of ozone metrics for quantifying the impacts of ozone on human health, or vegetation, and it can also be applied to PM_2.5, CO₂ or any other trace gas.

Section 2 provides details of the data sources and fusion process, including the techniques to register all data sources onto a common grid and the statistical model used to minimize the difference between interpolated observations and the multi-model combination. In Sect. 3, the results of employing these techniques are presented, including the mapping accuracy, evaluation of regional model performance and the final multi-model bias correction. The paper concludes with a summary and discussion in Sect. 4.

2 Data and method

2.1 Observations and model output

1. Tropospheric Ozone Assessment Report (TOAR) surface ozone database. In this analysis, surface ozone observations are used to evaluate the performance of six global atmospheric chemistry models and to also bias correct the multi-model surface ozone product. TOAR has produced the world's largest database of surface ozone metrics based on hourly observations at over 9000 sites around the globe (Schultz et al., 2017, ozone metrics available for download at https://doi.org/10.1594/PANGAEA.876108). Spatial coverage is high in North America, Europe, South Korea and Japan, but much lower across the rest of the world with very low data availability across Africa, the Middle East, Russia and India. In addition to data sparseness, other challenges, such as data inhomogeneity in time and the irregular spatial distribution of stations (Chang et al., 2017), make the comparison between model output and observations difficult without serious statistical modeling. While satellite retrievals have been utilized by previous works for quantifying the health impacts of PM_2.5 (Brauer et al., 2012, 2015), satellite retrievals of tropospheric ozone have limited sensitivity near the surface and are inadequate for this analysis (Gaudel et al., 2018).

   TOAR has gathered ozone observations through 2014 at most sites and has chosen 2008–2014 as a “present-day” window for more rigorous analysis. The purposes of the multi-year average are to reduce the effects of ozone interannual variability, which is largely driven by changes in meteorological conditions (Strode et al., 2015), and to increase the number of available sites than if we used a single year. In this analysis, we focus on the annual maximum of the 6-month running mean of the maximum daily 8 h average (DMA8) at every site in the TOAR database. Specifically, the metric was calculated from the 6-month running mean of the monthly mean DMA8 ozone values at a given site. This metric was selected because it aligns with the ozone metric used by Turner et al. (2016) to quantify the impact of long-term ozone exposure on human mortality. Hereinafter, this quantity is simply referred to as “the ozone metric”.

2. Atmospheric chemistry model simulations. We use output from models from phase 1 of the Chemistry-Climate Model Initiative (CCMI), downloaded from the Centre for Environmental Data Analysis (CEDA) database (http://archive.ceda.ac.uk, CEDA, 2019). We chose four models (CHASER, GEOSCCM, MOCAGE and MRI-ESM1r1) because they report hourly ozone output (Table 1). These particular simulations were part of CCMI's REF-C2 experiment (Morgenstern et al., 2017), which follows the World Meteorological Organization (2011) A1 scenario for ozone depleting substances, and RCP6.0 for tropospheric ozone precursors, and aerosol and aerosol precursor emissions (Morgenstern et al., 2010) for the period 1960–2100. Even though the most appropriate experiment would have been the REF-C1SD, in which the models are nudged to the reanalysis meteorology and thus best represent the past in the observations, we use output from the REF-C2 simulation in this study, as the last year of the REF-C1SD was 2010 and would therefore not cover the most recent period where observations are available. However, the NOAA Geophysical Fluid Dynamics Laboratory (GFDL) AM3 model continued the simulation over the entire study period and was therefore selected for this analysis. In addition, we obtained output from the GEOS-5 nature run with chemistry (G5NR-Chem), provided by the NASA Global Modeling and Assimilation Office (GMAO), which we included in our analysis because of the model's very fine horizontal resolution (Hu et al., 2018), but the output was only available for July 2013 to June 2014.

   The output from each individual model is shown in Fig. S1 in the Supplement. Note that NASA G5NR-Chem has the finest resolution of these models; accordingly, we aim to produce our final product on the same $\mathrm{0.125}{}^{\circ }\times \mathrm{0.125}{}^{\circ }$ grid. However, even at this resolution, the output is not street resolving and thus will not capture urban-scale variability in the regions with the highest population density.

Sudo et al. (2002a, b)Watanabe et al. (2011)Oman et al. (2011)Lin et al. (2012, 2014, 2017)Hu et al. (2018)Josse et al. (2004)Teyssèdre et al. (2007)Adachi et al. (2013)

Table 1 List of the ensemble members used in this paper.

^a Meteorological forcing includes coupled ocean–atmosphere (C2) and nudged to observed reanalysis meteorology (C1SD) in CCMI reference simulations (Morgenstern et al., 2017). ^b The specification of forcing scenario for this special run is described by Hu et al. (2018).

In order to compare model output to observations, we need to register model output and observations to a common grid. This registration enables us to quantify the differences between the models and observations. Previous attempts have usually relied on a variant from a general statistical interpolation framework to combine incompatible spatial data (Gotway and Young, 2002; Fuentes and Raftery, 2005; Gelfand and Sahu, 2010; Berrocal et al., 2012; Nguyen et al., 2012). Due to the highly irregular locations of ozone monitors around the globe, we use a kriging technique to build a statistical model, interpolate the ozone distribution based on the surrogate and then project the global surface onto a common grid.

2.2 Fusion of observations and models

Following is a description of our method for fusing observations and output from multiple global atmospheric chemistry models to produce a surface ozone product with maximized accuracy. This method is known as Measurement and Multi-Model Fusion (version 1), or M³Fusion (v1), and the code accompanies this paper in the Supplement. We consider a general framework of uncertainty quantification consisting of the following components (Kennedy and O'Hagan, 2001; Chang and Guillas, 2019):

$$\begin{array}{ll}{\displaystyle }\text{observation}& {\displaystyle }=\text{reality}+\text{random error};\\ {\displaystyle }\text{reality}& {\displaystyle }=\text{model}+\text{structured bias}.\end{array}$$

Since this equation requires matching components (observations and model output) on a common grid, we use the interpolated observations to estimate an optimized weight for each model by a L² norm (details are given later), which means that we expect the multi-model combination to capture the general pattern of the surface ozone distribution in terms of their joint predictive capability, and the model bias is considered as a model correction term. The difference between observation error and model bias is that the former term is assumed to be a normal noise with zero mean and constant variance, and the latter term is considered as a systematic and structured discrepancy (Williamson et al., 2015), which will be revealed as a spatial cluster across a poorly simulated region.

Due to this study's human health focus, we do not consider ozone above the data-sparse oceans. Above land, large observational gaps are present across Africa, the Middle East, South America, and south and southeast Asia, where the spatial interpolation is generally too uncertain to yield a reliable surface ozone approximation. The ozone estimates in these regions must come from either models or distant observations, neither of which is ideal to solve this issue. As a compromise strategy, we fill these gaps with a weighted model product evaluated by the interpolated ozone observations. We propose the following procedure to combine model output and observations for data integration:

1. Interpolating irregularly located monitoring observations to the model output grid. Kriging is a procedure used to statistically interpolate irregularly spaced and/or sparse observed data onto a regular and dense grid, based on a weighted average of the fitted surrogate model in the neighborhood of the grid. We assume that the global ozone distribution can be approximated by a Gaussian spatial process (GP) with a constant mean and Matérn covariance function (Stein, 2012). The GP fitting typically involves a cubic complexity and thus is computationally expensive for large spatial data sets. Therefore, several alternatives have been developed to address the large n issue by using a reduced set of data (Cressie and Johannesson, 2008; Banerjee et al., 2012; Liang et al., 2013), tapering the covariance between two grid points to zero if their distance is beyond a certain range (Furrer and Sain, 2009; Sang and Huang, 2012) and/or evaluating the covariance only through the specification of a neighborhood system (also known as the Gaussian Markov random field) (Rue et al., 2009; Lindgren et al., 2011).

   In this study, we carry out the spatial interpolation by using the combination of the integrated nested Laplacian approximation (INLA) framework (Rue et al., 2009) and the stochastic partial differential equation (SPDE) technique (Lindgren et al., 2011), available as an R package (http://www.r-inla.org/) (Lindgren and Rue, 2015). The details of this technique are rather complex and the reader is referred to the original paper (Lindgren et al., 2011); however, we describe the key component of this INLA-SPDE technique in Appendix A. INLA-SPDE spatial modeling has proven to be effective in a wide range of applications (Cameletti et al., 2013; Shaddick and Zidek, 2015; Heath et al., 2016; Liu and Guillas, 2017; Rue et al., 2017). We chose this technique because it manages a fairly large and complex spatial field in a relatively efficient way (Rue and Held, 2005) and allows an extension for nonstationarity on the sphere (Bolin and Lindgren, 2011; Chang et al., 2015). Notably, a recent study elaborately compared dozens of spatial modeling approaches, and the results suggest that almost all of these approaches can achieve a similar performance in terms of their predictive accuracy, albeit with very different computation times (Heaton et al., 2018). Therefore, we expect that the choice of spatial modeling approach is not the most crucial component in our data fusion process as long as the analysis is carried out in a rigorous way (i.e., through the statistical model selection and diagnostics). To differentiate this result from the actual observations in the TOAR database, we refer to this interpolated surface as the “spatially interpolated ozone”.

   We carry out the statistical interpolation via the following steps: (1) calculate the ozone metric at each TOAR site and for every year in 2008–2014; (2) perform the statistical interpolation using all available sites with their exact coordinates and project the surface onto a $\mathrm{0.125}{}^{\circ }\times \mathrm{0.125}{}^{\circ }$ spherical grid for every year; (3) average these surfaces over the 7 years to yield an observation-based present-day ozone distribution. We expect that this aggregation will smooth out at least some of the potential uncertainties. The kriging can be seen as a nonparametric regression problem; therefore, a statistical assessment of fitted quality must be considered to select the best representation to the data (Hoeting et al., 2006). Further details on the statistical model selection procedure are provided in Appendix A.

   We use a bilinear interpolation to smooth model output from coarser resolution to a $\mathrm{0.125}{}^{\circ }\times \mathrm{0.125}{}^{\circ }$ grid (Jun et al., 2008). The ozone metric for each model was calculated for each single grid in each year, then averaged over 2008–2014 (except for NASA G5NR-Chem, which was already in fine resolution, but only available for 1 year).

2. Weighting model output against spatially interpolated ozone by region. The next step is to create an intermediate “multi-model composite”. We divide the global land surface into eight regions (see Fig. 1), roughly matching the continental outlines or major population regions. We adopt this regional approach because global models vary in their ability to simulate ozone in different regions of the world. Next, we regress the observations on multi-model output by a constrained least square approach within each of the eight regions. Let s_g be the grid cell at resolution $\mathrm{0.125}{}^{\circ }\times \mathrm{0.125}{}^{\circ }$, $\widehat{y}\left(s_{\mathrm{g}}\right)$ be the interpolated observations and $\mathit{\left\{}{\mathit{\eta }}_k\right(s_{\mathrm{g}});k=\mathrm{1},\mathrm{\dots },\mathrm{6}\mathit{\}}$ be the model output registered onto the same grid from the six models considered in this paper (Table 1). The optimization equation is based on a constrained least squares approach:

   $$\begin{array}{ll}\text{(1)}& {\displaystyle }& {\displaystyle }\underset{\mathit{\{}{\mathit{\alpha }}_{\mathrm{r}},{\mathit{\beta }}_{rk};k=\mathrm{1},\mathrm{\dots },\mathrm{6}\mathit{\}}}{\text{minimize}}\sum _{s_{\mathrm{g}}\in \text{Region}r}{\left(\widehat{y}\left(s_{\mathrm{g}}\right)-{\mathit{\alpha }}_{\mathrm{r}}-\sum _{k=\mathrm{1}}^{\mathrm{6}}{\mathit{\beta }}_{rk}{\mathit{\eta }}_k\left(s_{\mathrm{g}}\right)\right)}^{\mathrm{2}},{\displaystyle }& {\displaystyle }\text{subject to}\sum _{k=\mathrm{1}}^{\mathrm{6}}{\mathit{\beta }}_{rk}=\mathrm{1}\text{and}{\mathit{\beta }}_{rk}\ge \mathrm{0}.,\end{array}$$

   where α_r is a constant that allows adjustment to the overall (regional) underestimation or overestimation; β_r k is an optimal weight for the kth model in region r. Note that since the interpolated observations and models use the same ozone metric with the same units, we constrain the weights to be positive and sum to 1 for a better physical interpretability, such that the most accurate models receive the higher weight. The offset term α_r is aimed to adjust the overall residuals between the observation field and the multi-model composite into zero mean in each region (regardless of the spatial pattern); therefore, if two spatial fields share a great similarity in terms of their spatial curvatures, but the overall means are different, this term can fill the gap of the overall mean difference between the two fields. The weights are optimized in terms of the squared distance between the interpolated ozone and multi-model output. A different criterion of optimization, such as mean absolute error, can be established accordingly.

   Due to the sparsity of stations in many regions, we use a predefined geometric boundary to differentiate regions. A more meaningful physical boundary (i.e., regions with similar chemical regimes or major features such as deserts, mountain ranges or water bodies) might be determined using a cluster analysis technique (Hyde et al., 2018), but such a step is beyond the scope of this paper.

   Since we partition the global land surface into eight regions and evaluate the models individually, inevitably there will be disjointed boundaries between regions. The boundaries between North and South America, or between east Asia and Oceania, fall mostly in the oceans, so we do not need to adjust these regions. However, we should make an adjustment to disjointed boundaries that fall across inhabited areas (see Fig. S2 for the illustration). As an example of our method, consider the boundary between east Asia and Russia near 50^∘ N. We increase the northern boundary of east Asia to 55^∘ N and decrease the southern boundary of Russia to 45^∘ N, to create an overlapping intersection, and then fit cubic splines (performed for each grid cell) with knots placed at every 2^∘ grid cell (Wood et al., 2008). This smoothing is carried out using a low-rank Gaussian process by the default penalized least square from the function “gam” in the R package mgcv (Kammann and Wand, 2003; Wood, 2017), following the examples of Wood and Augustin (2002). The purpose is to merely avoid a sharp and unrealistic (geometric) transition between three regions and to efficiently smooth out the discontinuity, performed in a regular spaced grid only around the geometric boundary. Any region away from the geometric boundary will not be affected by this smoothing, which should be considered as a blending of multiple models without any attempt of bias correction. It should be noted that the INLA-SPDE technique in step 1 is applied to the observations, while the smoothing spline is only applied to the boundaries between regions of the model composite, not directly involving any observations.

   We adopted a regression weighting approach that only accounts for the mean spatial fields of the interpolated ozone and model output, rather than the underlying associated uncertainty. We take this approach due to the prohibitive size of high-resolution output (over 1 million output points for each model) but also due to the lack of a thorough investigation regarding the ideal method for combining models based on different sources of uncertainty. For example, the interpolation uncertainty can be quantified easily through the posterior distribution and considered to be related to measurement error (small scale) or sparse sampling across a region (large scale); however, model uncertainty is a different concept altogether that could result from input uncertainty (e.g., air pollution emissions inventories) or limitations of the transport and chemistry mechanisms within the model (Brynjarsdóttir and O'Hagan, 2014). The current interest of this study focuses on a better estimate of mean ozone exposure. Explicit quantification of different sources of model uncertainty and incorporation of this information into the data fusion process presents another level of complexity that cannot be tackled until model uncertainties are better characterized. Young et al. (2018) provide a current overview of chemistry–climate modeling and discuss the challenges of improving models in light of so many uncertainties.

3. Correcting multi-model bias in areas close to observations. A common practice of studying the model discrepancy in the spatial fields is to fit a statistical model for their differences from observations on the whole spatial domain, to see whether or not these residuals reveal any structured spatial pattern (Jun and Stein, 2004; Sang et al., 2011). If the model adequately simulates the ozone distribution (up to a level shift and a scale factor), then there is no relevant information in these residuals. On the other hand, if the model does not properly represent the local structure, then the residuals should exhibit a signal of the discrepancy in that region (Guillas et al., 2006; Williamson et al., 2015). However, in our case, the regular grid observation field is obtained from spatial kriging, such that in many data-sparse regions we do not actually have observed ozone, which prevents us from correcting the model in these regions. Instead, we conduct a limited model bias correction based on the distance to the nearest monitoring station, but we ignore the differences between the multi-model composite and the interpolated observations in the sparsely monitored regions. In our approach, we only correct the output grid where there is at least one observational station within a 2^∘ radial distance of the grid cell in question (i.e., the distance to the nearest station is less than 2^∘). We then end up using

   $${\displaystyle }\left\{\begin{array}{l}\widehat{y}\left(s_{\mathrm{g}}\right),\text{if a grid cell}{s}_{\mathrm{g}}\text{is within a}\mathrm{2}{}^{\circ }\text{radial distance}\\ \text{of the station};\\ {\mathit{\alpha }}_{\mathrm{r}}+\sum _{k=\mathrm{1}}^{\mathrm{6}}{\mathit{\beta }}_{rk}{\mathit{\eta }}_k\left(s_{\mathrm{g}}\right),\text{otherwise},\end{array}\right.$$

   to generate our high-resolution global surface ozone estimate. Given the limited availability of observations worldwide, we were only able to apply this final bias correction to 14.4 % of the globe's land area. We refer to the final outcome as the “fused surface ozone product”.

3 Results

3.1 Mapping and uncertainty

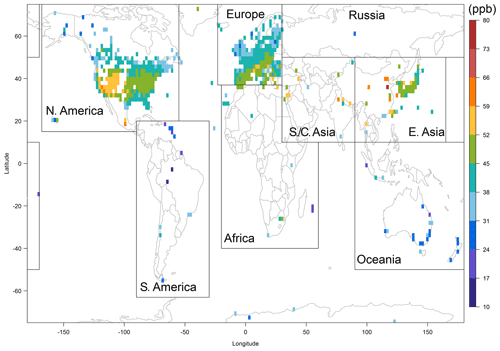
Ground-based measurements were available from 4766 stations reported in the TOAR database (Schultz et al., 2017). To illustrate the spatial coverage of the database, Fig. 1 shows the ozone metric discretized to a $\mathrm{2}{}^{\circ }\times \mathrm{2}{}^{\circ }$ grid (a finer resolution will be too obscure for illustrative purposes), averaged over the period 2008–2014. This figure also shows our regionalized classification, including Africa, North America, South America, east Asia, southeast and central Asia, Europe, Oceania and Russia. Note that dense station networks are found in North America, Europe and east Asia (mostly in Japan and South Korea), while monitoring sites are more widely scattered across the remaining regions. The highest average ozone levels are found at sites in China, South Korea, Japan, Taiwan, India, Greece, California and Mexico City.

Figure 1 TOAR observations where the monitoring locations are discretized to a $\mathrm{2}{}^{\circ }\times \mathrm{2}{}^{\circ }$ grid in 2008–2014.

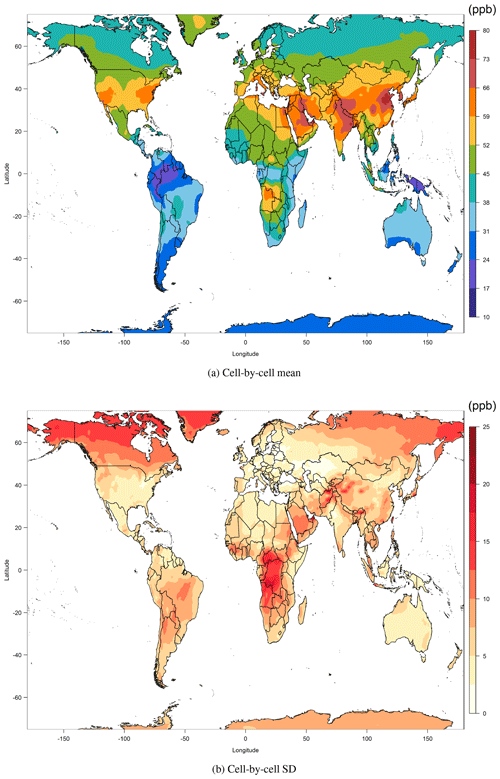
Figure 2a shows the spatially interpolated surface in each cell. For each grid cell, there is an underlying (posterior) probability distribution which incorporates information about the interpolation uncertainty. Figure 2b shows the half width of the 95 % posterior credible interval in each cell (Shaddick et al., 2018). From the spatial pattern of uncertainty, we can see that relatively higher uncertainties are expected in Africa, the Middle East, south Asia and Russia, regions with very limited observations; lower uncertainty is associated with regions with a dense station network, such as North America and Europe. Due to the limitations of spatial kriging in a sparsely monitored region, the observations are often interpolated across very great distances, such as in South America, Africa and central Asia. This method is not ideal, and instead information from models can be used to fill in the blanks.

Figure 2 Estimates of spatially interpolated surface ozone distribution and associated uncertainty (half width of the 95 % credible interval from each cell).

The ozone metric for each model was calculated for each individual grid cell in each year, then averaged over 2008–2014 and registered to the common $\mathrm{0.125}{}^{\circ }\times \mathrm{0.125}{}^{\circ }$ grid (except for NASA G5NR-Chem, which was already in fine resolution, but only available for 1 year). Figure 3a shows the surface ozone metric which results from the simple ensemble average of the six models. It was generated from bilinear interpolation of the ozone metric on the standard output grid, by calculating the same metric for each grid cell in each year, averaging over 2008–2014 and then averaging over the six models. We refer to this product as the “multi-model mean”, and we use it to validate our final product, which should outperform not only each individual model but also the multi-model mean.

Figure 3 Multi-model mean and standard deviation (SD) in each grid cell from six ensemble members.

Averaging all six models captures the large-scale variations of the ozone distribution; however, many regions in northern midlatitudes and low latitudes are biased high compared to the observations in the TOAR database. A simple approach to address the uncertainty in the multi-model mean is to calculate the standard deviation for each grid cell from the different models, as shown in Fig. 3b. Higher model uncertainties across south Africa and the Middle East match the pattern of the interpolation uncertainty in Fig. 2b, and lower model uncertainties occur in regions with dense station networks. These findings suggest that the multi-model mean uncertainty can also reflect the current limited understanding of surface ozone in regions with limited or no observations.

It should be noted that the spatially interpolated observations are smoother in regions with fewer sites and reveal a more detailed structure in regions with a dense station network. In contrast, the multi-model mean is more noisy. Even though we average across multiple years and multiple models, the resulting ozone metric can still be noisy because it is calculated at each grid cell independently. In order to make maximum use of the skill of each model, we restrict the model evaluation to the regional scale in the next section.

3.2 Regional model evaluation and multi-model composite

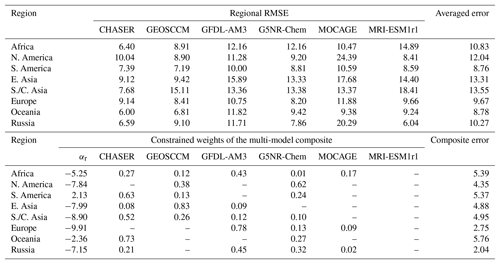
To evaluate the performance of each model in a given region, we calculate the mean differences over all grid cells within the region and summarize them with the root mean square error (RMSE). Let $\widehat{y}\left(s_{\mathrm{g}}\right)$ be the spatially interpolated observations and $\mathit{\left\{}{\mathit{\eta }}_k\right(s_{\mathrm{g}});k=\mathrm{1},\mathrm{\dots },\mathrm{6}\mathit{\}}$ be the output corresponding to the six ensemble models considered in this paper; then, the (normalized) RMSE is given by

$${\displaystyle }{\text{RMSE}}_{rk}=\sqrt{{\displaystyle \frac{{\sum }_{s_{\mathrm{g}}\in \text{Region}r}{\left({\mathit{\eta }}_k\left(s_{\mathrm{g}}\right)-\widehat{y}\left(s_{\mathrm{g}}\right)\right)}^{\mathrm{2}}}{n}}},$$

where n is the number of grid cells in a given region r. The first part of Table 2 shows the RMSE statistics for each model by region. The reliability of such an evaluation is limited by the station density in a given region, with greater reliability in a dense network (e.g., USA) and less reliability in a sparse network (e.g., Africa, South America or Australia). On average, CHASER, GEOSCCM and G5NR-Chem have the lowest biases in multiple regions; GFDL-AM3 and MRI-ESM1r1 also show low mean biases in certain regions, such as America and Europe. However, larger model biases can be found in Africa, and east and south Asia.

Next, we select three regions with extensive monitoring: North America, Europe and east Asia. Figure 4 shows the differences between the spatially interpolated observations and model output in North America. A consistent underestimation can be found in the Mexico City region for all models. A clear overestimation is also found across much of the eastern US, as well as the western US and Canada, except for CHASER, which shows a mild underestimation in these regions; in Europe (Fig. 5), the models show mild levels of overestimation across most of the region, especially for Italy. In east Asia (Fig. 6), the models show a major bias across east China and a similar bias pattern across the entire region, although the bias amplitude is smaller for GEOSCCM. However, since the observations are relatively sparse in mainland China, the large scale of these estimated biases might be an interpolation artifact.

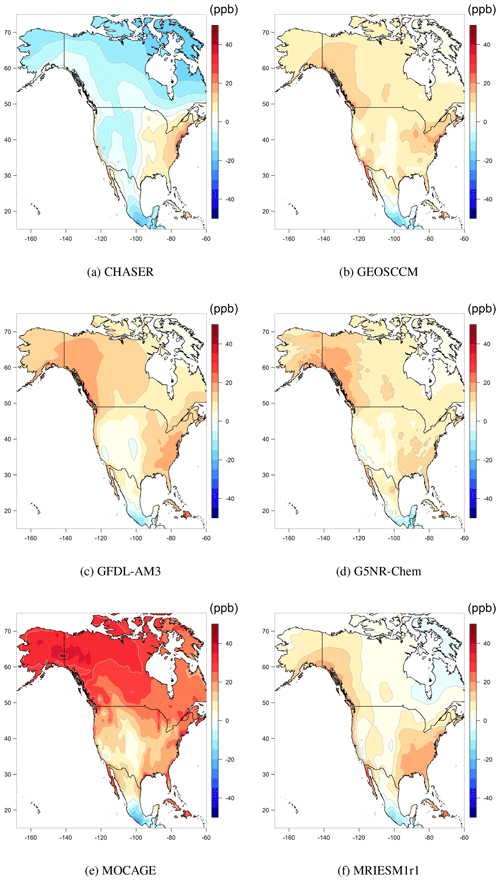
Figure 4 Spatial distributions of the ozone metric in North America from each model minus spatially interpolated observations.

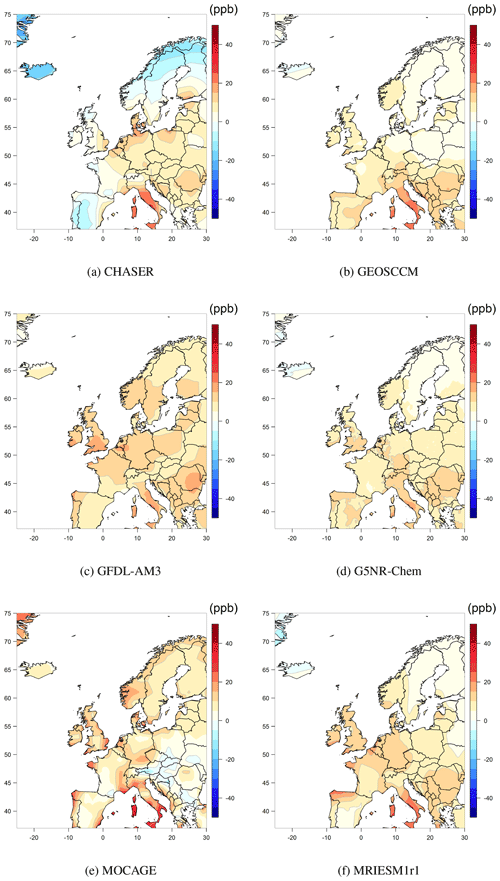
Figure 5 Spatial distributions of the ozone metric in Europe from each model minus spatially interpolated observations.

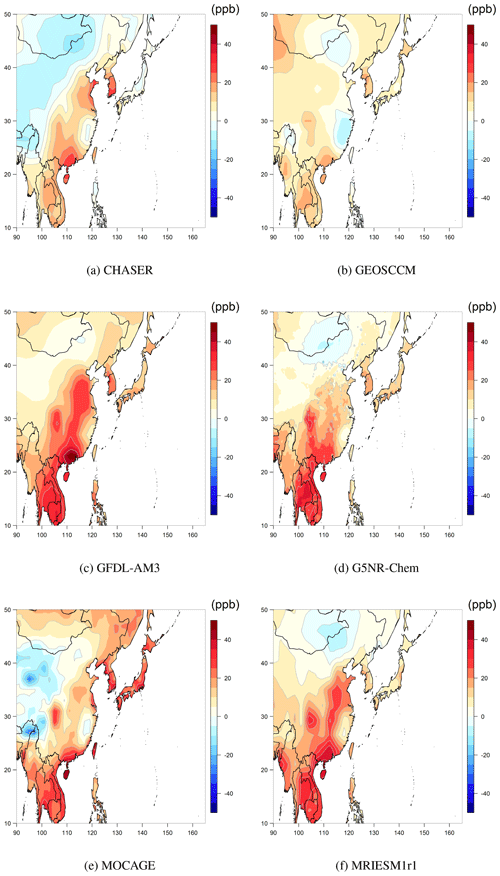
Figure 6 Spatial distributions of the ozone metric in east Asia from each model minus spatially interpolated observations.

We argue that the credibility of the model is not entirely decided by the RMSE (i.e., the mean difference): the smoother the difference plots, the easier it is to carry out the model bias correction. Indeed, the observations and model output are not expected to match point by point. We should also expect the model to capture the general pattern of the spatial distribution, rather than a pointwise agreement.

The estimated weights from the constrained least squares (Eq. 1) are given in the second part of Table 2. Due to fixed underlying spatial structures, this approach tends to give greater weight to a single model (i.e., ≥50 %); the one which provides the best match between its spatial structure and the observational field (e.g., G5NR-Chem in North America). Note that this approach disfavors noisy spatial structure; therefore, the algorithm gives low weights to MOCAGE, for several reasons. First, the MOCAGE ozone field has not been smoothed by interpolation since it is already produced on the MOCAGE model grid, whereas all other models are interpolated. Secondly, MOCAGE uses a more complete tropospheric chemical scheme with a larger range of species (77 tropospheric species) and has generally a higher reactivity compared to most chemistry–climate models (CCMs) (Voulgarakis et al., 2013). Thus, it tends to provide more temporal and spatial variability. Note that our optimization algorithm estimates the weights according to the similarity of the spatial structures between the interpolated surface and each model. In regions with sparse monitoring, the kriged surface can be greatly affected by a few scattered stations; therefore, we cannot use the resulting weights to evaluate the actual model performance in these regions.

The last column of Table 2 shows the averaged and combined RMSEs from the equal weights and the constrained weights. A reduced overall bias can be generally achieved from the constrained weights. This approach suggests that even if a model has a large mean error (e.g., GFDL-AM3), it can still be a good simulation if it produces a spatial pattern and curvature similar to the observation field. A constant offset α_r in the optimization Eq. (1) is included to remove the overall bias over each region, such that the residuals from the optimization have a zero mean. On the other hand, if we do not include α_r in the equation, GFDL-AM3 will have a smaller weight in the optimization, and CHASER, GEOSCCM and G5NR-Chem will dominate most of these regions (not shown).

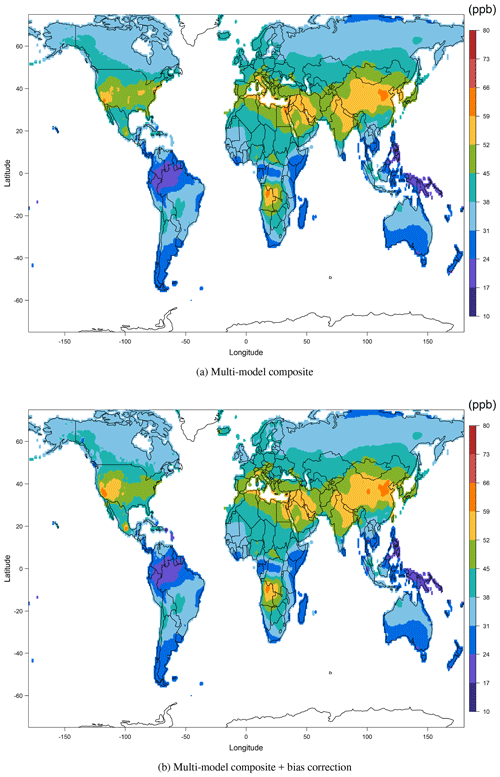
We combine all models according to the optimum weights from each region for each model. Figure 7a shows a map of the multi-model composite, a weighted blend of the six models, with the weighting calculated separately for each continent. Models with greater simulation skill receive higher weighting. The result reveals a systematic adjustment to the large-scale overestimation from the ensemble mean in Fig. 3a. This demonstration of a general high bias among the models argues against using the simple ensemble model mean for estimating surface ozone. However, when compared to the TOAR observations, the multi-model composite still has clear local biases.

Table 2 RMSEs (averaged errors in a given region) between spatially interpolated observations and each model, along with regionally optimized weights {β_rk: for kth model in region r} (zero weights are not displayed). Last column shows the RMSEs from equal weighted averages or constrained weights from the multi-model composite. All the numbers are reported in units of ppb (i.e., parts per billion by volume).

Figure 7 Multi-model composite and bias-corrected surface.

3.3 Local bias correction

The last step of producing the final fused surface ozone product is to apply a bias correction to our multi-model composite, limited to just those areas in close proximity to ozone observations. Ideally, we would like to apply a bias correction according to raw observations, but most stations are not exactly located on the model grid coordinates (even at $\mathrm{0.125}{}^{\circ }\times \mathrm{0.125}{}^{\circ }$ resolution). Therefore, to carry out a statistical bias correction on a particular grid, we need to consider the number of nearby stations and the distance to each station. All these considerations aim to deduce a single correction value on a single grid, and thus we are still faced with implementing statistical interpolation. To avoid adding another level of complexity, we set the final fused product to be exactly equal to the spatially interpolated ozone field within 2^∘ of an observation, as the spatially interpolated ozone field has already accounted for all observations. Due to the global sparseness of observations, about 85 % of model grid cells over land were not affected by this bias correction. After bias correcting the multi-model composite grid cells within 2^∘ of a TOAR observation site, an immediate benefit is seen for the US, Mexico City, Italy and South Korea (see Fig. 7b).

The choice of the correction range, in this case 2^∘, is a ad hoc decision; we also present results with different correction ranges in Figs. S3 and S4. When the radius of influence of the TOAR observations is increased to 5^∘ or more, the greatest impact is seen for the Mexico City region and eastern China. An increase of correction range is not ideal because it extrapolates the Mexico City ozone values into the less populated regions of Mexico. Increasing the radius to 5^∘ or more does not improve upon the RMSE associated with 2^∘. Therefore, accepting the 2^∘ bias correction over other ranges is subjective.

The fused product can be evaluated in terms of spatial correlation using the variogram which assumes that spatial correlation is not a function of absolute location but only a function of distance (i.e., stationarity). Since spatial variability and continuity from the models are the result of geophysical processes represented by mathematical equations, the variogram must be customized for each field. In addition, the extremely large size of the model output prohibits us from carrying out a standard empirical variogram analysis, which requires calculating the variance of the difference between all pairwise grid cells.

Nevertheless, we provide examples of omnidirectional variograms for the spatial field in North America from each model and product in Fig. S5. The standard variogram analysis focuses on the following three parameters: (1) the nugget (variance at zero distance, which represents a subgrid variation), which is similar for all cases; (2) the sill (total variance of a field), where the variogram value reaches a maximum and levels off; (3) the range (a distance where the sill is reached, and beyond that there is no longer spatial correlation). Note that a continuously increasing variogram indicates the evidence of nonstationarity in the field, which is the case for SPDE, an issue that we have accounted for. The variogram peak is about 35–40^∘ for the models. The result is very similar for G5NR-Chem, GEOSCCM and GFDL-AM3, while CHASER and MRI-ESM show a larger variance in the spatial field. The reason is that the latter two models produce low ozone in the high-latitude region over Canada (see Fig. S1), but the former three models simulate relatively higher ozone in the same region, and this difference is reflected by the total variance. Even though North America has one of the most extensive monitoring networks in the world, some of the remote areas (mostly in Canada) are mainly described by the model output in the final fused product. Therefore, the variogram of the fused product is likely adjusted toward the remote areas of Canada as simulated by G5NR-Chem, which provided the largest weighting in North America).

3.4 Validation of the results

Since the raw observations are the only reliable source for validating our results, we align each model grid to observed locations for evaluating the predictive performance. The RMSEs of the residuals from all observations in 2008–2014 are displayed in Table 3. Note that, since the global network of monitoring stations is heavily weighted by North America, Europe, South Korea and Japan, these numbers are not representative of the sparsely monitored regions. We compare the fused surface ozone results to the simple multi-model mean from all six models. Our interim product, i.e., the multi-model composite, is also compared in Table 3.

Table 3 RMSE against TOAR observations (i.e., not interpolated ozone) from the multi-model mean (MMM), multi-model composite (from fusion step 2) and the final fused product (from fusion step 3).

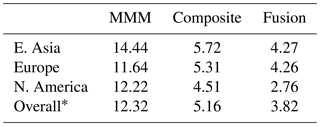
^* Overall category includes all available sites around the world.

Our multi-model composite outperforms the multi-model mean in terms of lowest mean predicted error. Based on the spatially interpolated observations, the resulting multi-model composite takes advantage of the strengths of each model and achieves a better accuracy. This result proves that our approach is effective, since our interim product has already improved upon the simple multi-model mean. The bias correction further reduces the residuals: this is expected because the spatial kriging algorithm is designed to minimize the difference to observations; thus, it has the lowest RMSE (this value is the same for the kriging result and the fused product since we apply the correction based on observed locations). The RMSE of approximately 5 ppb may represent the interannually varying meteorological influence during the years 2008–2014. If this is the case, then 5 ppb may approximate the minimal RMSE that can be achieved in a multi-year analysis.

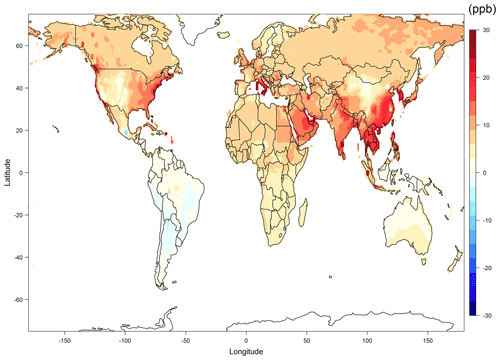
In summary, the simple multi-model mean method may perform fairly well at the continental or regional scale but does not provide an accurate representation of the subregional structure; this is of course a limitation on the use of coarse model resolutions. The weighting applied during the construction of the multi-model composite improved the accuracy but the effect could be limited, because many small-scale processes are not (yet) resolved by the models. To alleviate the discrepancy further, a statistical method based on local observations is applied to correct the bias. The advantage of our fused surface ozone product over the simple multi-model mean can be clearly seen in Fig. 8. When interpreting the fused product, the reader should consider the following: (1) for a region with an extensive monitoring network, such as the US, a detailed bias correction can be achieved. We can utilize the observations to accurately reflect many local features (i.e., subgrid variations) as shown in the ozone pollution hotspots of southern California and Mexico City. However, it should be noted that this improvement is due to local bias correction instead of model weighting. (2) For regions with large observational gaps, such as South America, Africa or Russia, the spatial difference between the fused product and the multi-model mean is rather featureless, because the model weighting can only adjust the overall regional mean according to a few monitoring sites and cannot address the local variations. Filling large data gaps with the intermediate multi-model composite can indeed avoid the influence of preferential sampling (Diggle et al., 2010; Shaddick and Zidek, 2014), but it is still subject to a high uncertainty due to lack of data.

Figure 8 Map showing result for multi-model mean minus the fused surface ozone.

4 Discussion and conclusions

In this article, we present a flexible framework to incorporate observations and multiple models for providing an improved estimate of the global surface ozone distribution. Combining multivariate spatial fields in the estimation of ozone distribution is an extension of both the conventional multi-model ensemble approach (i.e., simple average) and a statistical bias correction approach, and was found to improve the prediction of surface ozone. In summary, our approach has the following properties:

1. The multi-year average enables us to reduce the meteorological influence on surface ozone. An extension of this method to time-resolved multi-annual fields can be expected to capture the interannual variability (Shaddick and Zidek, 2015); however, such an endeavor would be highly computationally demanding in such a fine-resolution setting.

2. The INLA-SPDE interpolation framework allows for modeling of potential nonstationarity in the spatial processes.

3. Regional model evaluation facilitates a feature selection for multiple competing atmospheric models.

4. Local bias correction of the multi-model composite only at a limited range of grid cells avoids using the spatially interpolated ozone field in regions associated with higher levels of uncertainty.

5. For the regions with dense monitoring networks (such as North American, Europe, South Korea and Japan), the final fused product was obtained mainly from the interpolation of observations; elsewhere, the final product relied on the multi-model composite through an optimized weight from each model.

Human health studies typically adopt a fine grid resolution, such as a $\mathrm{0.1}{}^{\circ }\times \mathrm{0.1}{}^{\circ }$ grid product, for matching to the gridded world population database. Even though the spatial kriging surrogate can produce the predicted value at any resolution, the accuracy of the fused surface ozone product is still limited by the density of observations around that point and by the resolution of the global model output. Regarding future improvements, two key developments can be expected to yield a better estimation of the global surface ozone distribution: firstly, we can include more simulators for increased leverage. Another way to increase the estimation accuracy is to expand ozone monitoring networks across sparsely sampled regions (Sofen et al., 2016; Schultz et al., 2017; Weatherhead et al., 2017).

The application of our methodology focuses on, but is not limited to, a particular ozone metric relevant for quantifying the impact of long-term ozone exposure on human health. We expect that this framework could also be applied to other ozone metrics relevant to crop production or natural vegetation (Lefohn et al., 2018; Mills et al., 2018), or any other trace gas, provided adequate in situ observations are available for model evaluation.

In general, atmospheric chemistry model estimates of surface ozone levels are biased high, as demonstrated by a comparison of the annual mean surface ozone produced by the ACCMIP (Atmospheric Chemistry and Climate Model Intercomparison Project) multi-model ensemble to the TOAR surface ozone database (see Fig. 6 of Young et al., 2018). This analysis has shown that the high bias is also prevalent among models when employing an ozone metric that focuses on the high end of the ozone distribution (Fig. 8). Similarly, Shindell et al. (2018) compared the NASA GISS-E2 model to observed values of annual mean DMA8 and concluded that the model was biased high by 25 %. Given the common tendency for models to overestimate surface ozone, the methodology developed by this paper can be used to improve the accuracy of model output, either for individual models or for multi-model ensembles.

Appendix A: Spatial modeling using the INLA-SPDE approach

In this paper, the aim of spatial interpolation is to use (discretized) monitoring observations to build a statistical surrogate model for estimating the ozone distribution over the whole domain on a sphere. We assume that this ozone distribution follows a Gaussian process (GP). A GP is a collection of random variables such that any subset of the observations has a joint Gaussian distribution. It has been widely used in many applications as a machine learning algorithm (Rasmussen and Williams, 2006). In this section, we briefly introduce the GP model with a focus on spatial kriging. The GP is a popular choice in spatial statistics because it allows modeling of fairly complicated functional forms, and it also provides a prediction and associated uncertainty at any new location. A common limitation of this interpolation is that the resulting distribution of estimated uncertainty will be lower around individual stations or within dense monitoring networks, and higher in sparsely monitored regions.

Let Y denote an n vector of ozone observations measured at monitoring sites s; then a statistical model for the spatial field can be expressed as $Y=f\left(\mathit{s}\right)+\mathit{\epsilon }$; i.e., the model comprises a smooth GP spatial process f(s), capturing spatial association, and an independent normal error ε, which follows a normal error N(0,σ²). This error term can accommodate potential measurement error; on the other hand, kriging without measurement error is usually used for the surrogate of a deterministic model (i.e., the same input always produces the same output), also known as an emulator (e.g., Conti and O'Hagan, 2010).

The specification of a GP is through its mean function and covariance function, denoted by $f\left(\mathit{s}\right)\sim \text{GP}\left(m\left(\mathit{s}\right),c(\mathit{s},{\mathit{s}}^{\prime })\right)$. To reduce computational intensity, the mean function can be assumed to be a constant m(s)=μ; thus, the resulting spatial distribution is completely defined by the covariance function. A covariance function characterizes correlations between different locations in the spatial process; it is the crucial component in a GP, as it represents our assumptions about the latent field from which we wish to build a surrogate. Specifically, we use the Matérn covariance function, which is a flexible covariance structure and widely used in spatial statistics (Hoeting et al., 2006; Jun and Stein, 2007, 2008). With the shape parameter ν>0, the scale parameter κ>0 and the marginal precision τ²>0, the covariance structure can be written as

$${\displaystyle }c\left(\mathit{h}\right)={\displaystyle \frac{{\mathrm{2}}^{\mathrm{1}-\mathit{\nu }}}{\mathrm{4}\mathit{\pi }{\mathit{\kappa }}^{\mathrm{2}\mathit{\nu }}{\mathit{\tau }}^{\mathrm{2}}\mathrm{\Gamma }(\mathit{\nu }+\mathrm{1})}}(\mathit{\kappa }\Vert \mathit{h}\Vert {)}^{\mathit{\nu }}{K}_{\mathit{\nu }}(\mathit{\kappa }\Vert \mathit{h}\Vert ),\mathit{h}\in {\mathbb{S}}^{\mathrm{2}},$$

where h denotes the distance between any two locations: $\mathit{h}=\mathit{s}-{\mathit{s}}^{\prime }$, Γ is a gamma function, and K_ν is the modified Bessel function of the second kind of order ν>0. The scale parameter κ controls the rate of decay of the correlation between two locations as distance increases. Smaller values of κ allow for longer ranges over which two sites can be correlated. The smoothness parameter ν can be seen as the determining behavior of the autocorrelation for observations that are separated by a small distance.

The major disadvantage of using a GP is the computational complexity, which typically involves a cubic complexity in the number of data points, usually denoted as O(n³). Several attempts have been made to reduce the computational burden: e.g., Cressie and Johannesson (2008), Rue et al. (2009), Banerjee et al. (2012) and Gramacy and Apley (2015). Lindgren et al. (2011) introduced a popular approach in which the Matérn covariance can be approximated by the solution of certain stochastic partial differential equations (SPDEs). According to Lindgren et al. (2011), a GP process f(s) with Matérn covariance on a sphere is the solution of the following stationary SPDE:

$${\displaystyle }({\mathit{\kappa }}^{\mathrm{2}}-\mathrm{\Delta }{)}^{(\mathit{\nu }+\mathrm{1})/\mathrm{2}}\mathit{\tau }f(\mathit{s})=\mathcal{W}(\mathit{s}),$$

where Δ is the Laplace operator and 𝒲 is the Gaussian white noise. The core implication of this mathematical relationship is that an efficient algorithm for solving this SPDE can be applied to approximate the GP (Lindgren et al., 2011).

This INLA-SPDE technique also enables us to quantify the level of nonstationarity in a spatial field by employing basis function representations for both κ and τ (i.e., these quantities are constants in a stationary field). To obtain basic identifiability, κ(s) and τ(s) are taken to be positive, and their logarithm can be represented as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\log \mathit{\kappa }\left(\mathit{s}\right)=\sum _{k=\mathrm{1}}^p{\mathit{\theta }}_k^{\mathit{\kappa }}{\mathit{\psi }}_k\left(\mathit{s}\right)\text{and}\\ \text{(A1)}& {\displaystyle }& {\displaystyle }\log \mathit{\tau }\left(\mathit{s}\right)=\sum _{k=\mathrm{1}}^p{\mathit{\theta }}_k^{\mathit{\tau }}{\mathit{\psi }}_k\left(\mathit{s}\right),\end{array}$$

where {ψ_k(s)} is a set of spherical harmonics. The coefficients $\mathit{\left\{}{\mathit{\theta }}_k^{\mathit{\kappa }}\mathit{\right\}}$ and $\mathit{\left\{}{\mathit{\theta }}_k^{\mathit{\tau }}\mathit{\right\}}$ represent local variances and correlation ranges (Bolin and Lindgren, 2011; Lindgren et al., 2011). A larger number of basis functions permits the representation of smaller local features.

We now illustrate a series of statistical model fits to select the best predictive ability of the SPDE model. To choose the maximum number of basis functions for the parameters κ and τ in Eq. (A1), model selection techniques must be used. We perform the model selection based on the following criteria:

• RMSE is the measure of the overall mean difference between predicted values and the observed values.

• DIC (deviance information criterion) is a measure to compare performance of statistical models by using a criterion based on a trade-off between the goodness of fit and the corresponding complexity of the model. Smaller values of the DIC indicate a better balance between complexity and a good fit.

• GCV (generalized cross validation) calculates the mean residuals in a leave-one-out test. The model that minimizes the average predicted residuals over all the data is selected as the best model (Schneider, 2001).

We estimate nine statistical models with different numbers of basis functions, presented in Table A1. The simplest model is a stationary Matérn model (we use basis number 0 to represent κ and τ as constants). The best fit of all criteria occurs when the orders of the basis functions are increased from four to five. We therefore conclude that a model with five spatially varying basis functions is most appropriate for the TOAR observations.

Table A1 Summary of results from fitting nine candidate statistical models (annual average over 2008–2014).