Climate projections of a multivariate heat stress index: the role of downscaling and bias correction

Along with the higher demand for bias-corrected data for climate impact studies, the number of available data sets has largely increased in recent years. For instance, the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP) constitutes a framework for consistently projecting the impacts of climate change across affected sectors and spatial scales. These data are very attractive for any impact application since they offer worldwide bias-corrected data based on global climate models (GCMs). In a complementary way, the CORDEX initiative has incorporated experiments based on regionally downscaled bias-corrected data by means of debiasing and quantile mapping (QM) methods. In light of this situation, it is challenging to distil the most accurate and useful information for climate services, but at the same time it creates a perfect framework for intercomparison and sensitivity analyses.

In the present study, the trend-preserving ISIMIP method and empirical QM are applied to climate model simulations that were carried out at different spatial resolutions (CMIP5 GCM and EURO-CORDEX regional climate models (RCMs), at approximately 150, 50 and 12 km horizontal resolution) in order to assess the role of downscaling and bias correction in a multivariate framework. The analysis is carried out for the wet-bulb globe temperature (WBGT), a heat stress index that is commonly used in the context of working people and labour productivity. WBGT for shaded conditions depends on air temperature and dew-point temperature, which in this work are individually bias corrected prior to the index calculation. Our results show that the added value of RCMs with respect to the driving GCM is limited after bias correction. The two bias correction methods are able to adjust the central part of the WBGT distribution, but some added value of QM is found in WBGT percentiles and in the inter-variable relationships. The evaluation in present climate of such multivariate indices should be performed with caution since biases in the individual variables might compensate, thus leading to better performance for the wrong reason. Climate change projections of WBGT reveal a larger increase in summer mean heat stress for the GCM than for the RCMs, related to the well-known reduced summer warming of the EURO-CORDEX RCMs. These differences are lowered after QM, since this bias correction method modifies the change signals and brings the results for the GCM and RCMs closer to each other. We also highlight the need for large ensembles of simulations to assess the feasibility of the derived projections.

1 Introduction

In the last years the amount of available climate projection data has largely increased thanks to the development of intercomparison projects (Coupled Model Intercomparison Project – CMIP, Taylor et al., 2011; Inter-Sectoral Impact Model Intercomparison Project – ISIMIP, Warszawski et al., 2014) and other initiatives (CORDEX; Giorgi et al., 2009; Jones et al., 2011; CORDEX-Adjust). Due to this, there have been many efforts towards the distillation of climate data into usable climate information (Hewitson et al., 2014; Fernández et al., 2018). This is largely hampered by the large envelope of uncertainty, which grows in the subsequent steps in the production of climate information, the so-called “uncertainty cascade” (Wilby and Dessai, 2010). In this work we assess the role of downscaling and bias correction as key elements in the development of climate information. For this purpose, we intercompare climate change projections of heat stress in Europe coming from different data sources, at different spatial resolution and corrected with two different bias correction methods, in order to identify the major sources of uncertainty in terms of present and future climate.

Global climate models (GCMs) are able to reproduce the main features of the climate system and are commonly used to examine changes in climate on a global scale (Taylor et al., 2011). Despite recent improvements, systematic biases remain and the model resolution is still too coarse to adequately describe mesoscale processes (Giorgi and Mearns, 1991). Regional climate models (RCMs) are frequently used to bridge the gap between the GCM and the regional to local scales (Giorgi, 2006; Feser et al., 2011). They solve the governing equations of the climate system in a limited spatial domain using initial and boundary conditions from GCMs (reanalysis for model evaluation experiments). Despite the increased horizontal resolution, RCMs, similar to GCMs, include physical parameterisations for subgrid processes which occur at spatial scales smaller than the model grid spacing (microphysics, convection, radiation, etc.). RCMs add valuable information with respect to their driving GCM due to more detailed spatial patterns and the better representation of local processes, e.g. high precipitation frequencies (see e.g. Maraun et al., 2010; Warrach-Sagi et al., 2013). However, both GCMs and RCMs are prone to systematic biases and some sort of bias adjustment or correction is typically needed before they are used in impact modelling (Christensen et al., 2008; Hagemann et al., 2011). Bias correction (BC) methods typically adjust some features of the model distribution (e.g. the mean or percentiles) towards the observed counterparts, partly removing systematic errors in the model output. However, the added value of bias-corrected RCM simulations with respect to the bias-corrected GCM counterparts remains unclear. The same question applies for the difference between bias-corrected high-resolution RCM simulations (at approximately 12 km) and the coarser counterparts (at approximately 50 km). For the latter, Casanueva et al. (2016) showed that the added value (in terms of mean, percentiles and precipitation frequency) is not statistically significant after applying simple (scaling) bias correction methods.

Many BC methods with different characteristics have been described in the literature (Maraun et al., 2010; Piani et al., 2010; Gutiérrez et al., 2019): empirical or parametric methods, variable-specific (e.g. assuming a certain distribution) or nonspecific methods, multivariate or univariate methods, and seamless or for specific time horizons (e.g. the correction of ensemble spread in monthly–seasonal forecasts). All of them consist of a training phase (in which the correction function is calibrated) and an application phase under different conditions. Note that the correction functions (calibrated in present climate) are assumed to be invariant on time (stationarity assumption). Moreover, in a climate change context, the way the correction is applied in future climate might affect the climate change signal.

A specific bias correction method was developed in the framework of the ISIMIP initiative (Warszawski et al., 2014). This project attempted to offer a consistent framework for cross-sectoral, cross-scale modelling of the impacts of climate change in order to ease the application of climate model data and meet user-specific needs. The ISIMIP method (Hempel et al., 2013; ISIMIP2b, Frieler et al., 2017) was applied to several GCMs from CMIP5 (the Coupled Model Intercomparison Project Phase 5; Taylor et al., 2011). The ready-to-use, bias-corrected data have been used to produce impact model simulations for different sectors such as agriculture, biomes, forests and fisheries permafrost, as well as to derive climate impact indices, including heat stress (Kjellstrom et al., 2018).

Among other BC methods, empirical quantile mapping stands out as one of the most widely used methods. Despite its limitations and shortcomings (Maraun et al., 2017; Lanzante et al., 2018), it is one of the best-performing bias correction and statistical downscaling methods in evaluation experiments (Gutiérrez et al., 2019; Hertig et al., 2019). One reason for this might be that it is often favoured by the evaluation metrics – commonly based on moments of the probability density function – considered in intercomparison experiments. Quantile mapping is, by construction, able to correct for intensity-dependent biases (i.e. biases that change throughout the distribution; Gobiet et al., 2015). As a consequence, it can modify the raw model climate change signal, which might be debatable (Gobiet et al., 2015; Casanueva et al., 2018; Ivanov et al., 2018). In contrast, the main objective of the ISIMIP correction is to preserve the trend of the raw data in the calibration period.

In the present work, we consider CMIP5 and EURO-CORDEX (European branch of CORDEX) simulations, the latter at the two available spatial resolutions (approximately 12 and 50 km), and the ISIMIP correction and empirical quantile mapping as bias correction methods for the following purposes:

• to assess the added value of a more complex (in terms of the number of parameters calibrated) bias correction method (empirical quantile mapping) with respect to the ISIMIP correction;

• to assess the added value of RCMs compared to their driving GCM after bias correction; and

• to assess the impact of downscaling and bias correction in the climate change signal.

The added value is examined by evaluating several statistics under present climate conditions and exploring the feasibility of climate change projections. All analyses are applied in the context of climate change projections of heat stress in Europe. Heat stress depends mainly on temperature and humidity (low wind speed and high solar radiation also contribute to heat stress but are not considered in this work). Whereas empirical quantile mapping is a univariate bias correction method (typically with the same core implementation for all variables when it is applied in a multivariate context), the ISIMIP correction includes dependencies between some variables (e.g. mean temperature is needed to correct maximum–minimum temperatures) in order to preserve the physical consistency among them. Hence, the ability of the methods to reproduce multivariate structures is implicitly investigated.

2 Data and methods

2.1 Heat stress index

Under very hot and humid conditions, the ability of the human body to regulate the core temperature and dissipate heat via sweat evaporation is reduced, provoking heat stress (Koppe et al., 2004; Parsons, 2014). Other meteorological variables such as strong radiation or low wind speed can exacerbate heat stress. Such conditions directly affect human well-being and can develop into heat-related illnesses such as fatigue, muscle cramps and heat stroke. In the context of working people, several studies have revealed the negative impact of heat stress on workers' health (Pogačar et al., 2018) and labour productivity (Kjellstrom et al., 2009; Ioannou et al., 2017). International organisations such as the International Standards Organization (ISO) and the US National Institute for Occupational Safety and Health (NIOSH) have developed guidelines to protect working people against heat stress (ISO, 1989, 2017; NIOSH, 2016). The recommendations comprise work–rest cycles and water intake under specific heat conditions. A combination of technical, regulatory and behavioural measures is needed to adapt workers to increasing temperatures at an individual, sectoral and governmental level (Vivid Economics, 2017). In the context of global warming, the development and dissemination of heat-health planning and warning systems is now among the priorities of the World Meteorological Organization (WMO) and the World Health Organization (WHO; WMO, 2015), as well as the International Labour Organization (UNDP/ILO, 2016) and the International Organization for Migration (IOM, 2016). Within this framework, the Horizon 2020 HEAT-SHIELD project (https://www.heat-shield.eu/, last access: 2 August 2019) aims to address the effects of climate change on the European working population within an inter-sectoral framework (Nybo et al., 2017). In particular, one of the specific objectives of the project is to generate climate change projections of heat stress (Casanueva et al., 2019).

There are many indices based on meteorological variables which have been often used to assess occupational heat stress conditions in the literature (de Freitas and Grigorieva, 2015; Coccolo et al., 2016). The wet-bulb globe temperature (WBGT) has been chosen in the HEAT-SHIELD project as the primary heat stress index since it can be computed from standard meteorological variables available in both observations and climate models, it can be interpreted by occupational scientists and physicians by means of the corresponding international (ISO) and national (e.g. NIOSH, 2016) standards regulations, and it can be adjusted according to the workers' clothing.

In this study we focus on the WBGT in the shade (Bernard and Pourmoghani, 1999; Lemke and Kjellstrom, 2012), which assumes that there are no strong radiation sources (the globe temperature equals the air temperature) and wind speed of 1 m s⁻¹, which corresponds to the movement of arms or legs during work. Bearing this in mind, the input variables for the calculation of the WBGT in the shade are air temperature and dew-point temperature. The latter accounts for the humidity conditions and can be obtained from daily mean temperature and relative humidity (or specific humidity and air pressure) in models and observational data sets. In order to account for the highest daily heat stress, we used daily maximum temperature and daily mean dew-point temperature (unlike relative humidity, it usually only slightly varies along the day) to approximate the daily maximum WBGT (Casanueva et al., 2019). WBGT is calculated through the R package HeatStress (see the “Code availability” section).

2.2 Observational data

The observational reference used to validate the climate models and perform the bias correction is the WFDEI (WATCH forcing data methodology applied to ERA-Interim; Weedon et al., 2014) data set, which is based on the ERA-Interim reanalysis (Dee et al., 2011) corrected by the Climate Research Unit (CRU) observational data set (or Global Precipitation Climatology Centre – GPCC – for precipitation). It is developed on a 50 km regular grid and provides 3-hourly and daily values of temperature, precipitation, humidity, wind and radiation, among others. Its predecessor, WFD, was used as an observational reference in the ISIMIP 2a experiment (Hempel et al., 2013) and its successor (EWEMBI; Frieler et al., 2017) in the newer ISIMIP2b. Note that the WFDEI data are identical to the EWEMBI over land and for the considered variables (daily maximum and mean temperature, specific humidity, and surface air pressure). In the present work we use the WFDEI data set over Europe for the period 1981–2010. Daily maximum temperature is obtained as the maximum of the 3-hourly values.

2.3 Global and regional climate model data

The GCM considered in the present analysis is HadGEM2-ES_r1i1p1 (Collins et al., 2011; denoted as HadGEM along the paper) from CMIP5, which is one of the GCMs used in the ISIMIP experiments. Data covering the EURO-CORDEX domain were extracted considering only land grid boxes (land area fraction larger than 50 %).

Table 1 EURO-CORDEX RCMs driven by HadGEM for two spatial resolutions (EUR-11 for approximately 12 km spatial resolution and EUR-44 for approximately 50 km resolution) and three RCPs (RCP2.6, RCP4.5 and RCP8.5).

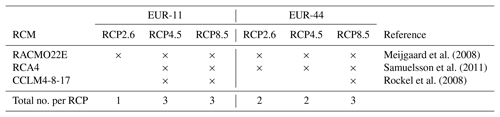
We additionally use the EURO-CORDEX RCM simulations (Jacob et al., 2014; Kotlarski et al., 2014) driven by HadGEM2-ES accessible via the Earth System Grid Federation (ESGF archive; https://esgf.llnl.gov, last access: 2 August 2019) as of May 2017. These are the same HadGEM-driven RCM simulations as used by Casanueva et al. (2019) in a comprehensive study about climate projections of heat stress in Europe. The RCM simulations were conducted at two different spatial resolutions which correspond to approximately 12 (EUR-11) and 50 km (EUR-44) grid spacing. The final set of regional models consists of RACMO, CCLM and RCA run by the KNMI (Royal Netherlands Meteorological Institute), CLMcom (Climate Limited-area Modelling Community) and SMHI (Swedish Meteorological and Hydrological Institute), respectively. The historical simulations cover the common historical period 1981–2005 (the 5 years 2006–2010 from the scenario simulations are added in this work to complete the observational period) and future projections cover the period up to 2099. The available RCPs (Representative Concentration Pathways) vary for each GCM–RCM combination (Table 1).

We retrieved GCM and GCM–RCM data for daily maximum temperature, as well as daily mean temperature and relative humidity (or specific humidity and sea level or surface air pressure, depending on the model), which were used to calculate daily mean dew-point temperature. Note that HadGEM and the HadGEM-driven RCMs present a 360 d calendar, so to harmonise this with the observations, five (or six in a leap year) missing values were included randomly along each year but keeping the same position for all variables (to avoid inter-variable modifications), RCPs and models. All analyses were carried out at the spatial resolution of the observational grid (regular 50 × 50 km). For this reason, all model simulations (GCM and GCM–RCMs) were conservatively remapped into the WFDEI grid (first-order conservative remapping, as in the ISIMIP experiments). As a consequence, there will be aspects of the added value of the high-resolution EUR-11 experiments (related to better-resolved, fine-scale processes; Prein et al., 2016) that can be smoothed out, but they may still be present after remapping them onto a coarse resolution (Casanueva et al., 2016).

2.4 Bias correction methods

2.4.1 ISIMIP bias correction

The ISIMIP bias correction was developed in the framework of ISIMIP (Hempel et al., 2013). It consists of a correction of the monthly mean biases followed by the correction of the daily variability around the monthly mean. For temperature the monthly correction is additive, whereas it is multiplicative for precipitation, radiation and wind. The daily variability correction consists of a parametric quantile mapping adjusting a normal distribution for temperature and a gamma distribution for precipitation. After ISIMIP (see light green dashed line in Fig. 1a, b), the mean of the historical data is adjusted towards the observations (black lines), but the variance and shape of the raw distribution are mostly retained. The monthly means and monthly variability are adjusted using only a constant correction (either an offset or a multiplicative factor) in the historical and future periods (see green lines in Fig. 1a, b for an example for temperature; light and dark green lines represent the historical and future bias-corrected data through ISIMIP, respectively). Therefore, the corrections cancel out when calculating the mean (additive or relative) climate change signal, and the long-term trend of the raw simulated variables (red arrow in Fig. 1b) is preserved.

Figure 1 (a–d) Illustrative example of the effect of the two bias correction methods on the empirical cumulative distribution function (a, c) and the probability density function (b, d) for either RCM or GCM data. Observations are depicted in black and historical (HIST) and future (FUT) model simulations in light and dark colours, respectively. Raw data are depicted in red, ISIMIP-corrected data in green (a, b) and QM-corrected data in purple (c, d). The magnitude of the mean change signal is shown with the arrows. This example corresponds to daily maximum temperature as represented by HadGEM for an exemplary grid box (HIST: 1981–2010, FUT: 2070–2099 for RCP8.5). (e) Conceptual scheme of the present study.

The ISIMIP correction includes dependencies between some variables (e.g. mean temperature and wind speed are needed to correct maximum–minimum temperatures and eastward–northward wind components, respectively) in order to preserve the physical consistency among them. However, there are no implemented dependencies between temperature and relative humidity yet. This BC method is implemented for several variables as part of the R package downscaleR (Bedia et al., 2017), included in the R bundle climate4R (Cofiño et al., 2018; Iturbide et al., 2019). We correct dew-point temperature following the same procedure as for daily mean temperature; thus, dependencies with other variables are not considered. As mentioned before, daily mean temperature is used in the correction of the daily maximum temperature in order to maintain the physical consistency between variables. Although the ISIMIP initiative provides bias-corrected GCM data, for the sake of consistency we apply the corrections to the raw GCM as well as RCM data.

2.4.2 Empirical quantile mapping (QM)

In this work we use the implementation from Déqué (2007) and Rajczak et al. (2016), included in the R package qmCH2018 (see the “Code availability” section), which consists of the correction of the 99 percentiles of the empirical distribution of the model towards their observational counterparts. The corrections between two consecutive percentiles are linearly interpolated and constant extrapolation is considered for the values beyond the calibration range; i.e. the correction of the 99th (1st) percentile is applied to values above (below) the calibration range (Themeßl et al., 2012). The correction is calibrated for each day of the year with a 91 d moving window. It is a univariate BC method and in this work it was applied independently to daily maximum temperature and daily mean dew-point temperature.

For a historical simulation (see e.g. light purple dashed lines in Fig. 1c, d) the corrected data largely resemble the distribution of the observations. During the application of QM to a future climate simulation, the model data are mapped into the percentiles of the training data and the corresponding correction function is applied (dark purple lines in Fig. 1c, d); thus, QM would differently correct the future and the historical distributions if the relative frequencies in the future differ from the training counterparts (Casanueva et al., 2018). Therefore, QM is able to correct for intensity-dependent biases, and subsequently modifications of the raw model climate change signal may occur. In the example for temperature in Fig. 1d, QM narrows the distribution of the future simulated data, thus leading to a smaller mean change signal than the raw counterpart (see purple and red arrows).

2.4.3 Application of the bias correction methods

For both bias correction methods, the corrections are applied independently to each grid box of each GCM and RCM, resolution (if applicable), and RCP. These corrections are calibrated in the period 1981–2010 and are applied (1) to the same period to evaluate the performance in present climate and (2) to a future period at the end of the 21st century (2070–2099) to produce bias-corrected climate projections. Due to the multivariate nature of the WBGT, we separately correct daily maximum temperature and daily mean dew-point temperature prior to the WBGT calculation (i.e. the component-wise approach; Casanueva et al., 2018). Although the BC methods are applied to the full time series (monthly mean correction for ISIMIP, 91 d moving window centred on each day of the year for QM), all results shown refer to the summer season (June, July, August), since it is the time when extreme heat stress conditions occur.

As shown in Fig. 1e, the ISIMIP bias correction is applied to the GCM and the RCMs to assess the added value of the RCMs after bias correction. We additionally correct the climate models using quantile mapping to assess the added value of a more complex (in terms of the number of parameters calibrated) bias correction method.

2.5 Evaluation metrics

The performance of the raw and bias-corrected data is firstly evaluated by using the mean bias (model minus observations) of several parameters of the distribution, such as the mean and 95th and 99th percentiles of the WBGT.

Pearson correlation coefficients (Pearson, 1895) between the daily series of maximum temperature and dew-point temperature are obtained to show the linear dependency between the two input variables in the modelled and observed data. In order to further assess the inter-variable relationships, two-dimensional kernel densities are constructed combining the distribution of the two input variables. The representation of the two-dimensional densities shows the probability of having different combinations of daily maximum and dew-point temperatures. Density plots are obtained for the raw and bias-corrected data and compared to the observation counterparts. Perkins et al. (2007) introduced a skill score which determines the similarity between two probability density functions (PDFs). It is a very useful metric since it allows for a comparison across the entire distribution. It measures the common area between two PDFs by calculating the cumulative minimum value of two distributions of each binned value (skill scores of 1 mean perfect performance). Here a two-dimensional extension of the Perkins skill score is used, obtained from two-dimensional kernel densities instead of univariate PDFs. Therefore the cumulative minimum value is calculated in a two-dimensional field and the score shows the similarity (overlap) between the modelled joint distribution of daily maximum and dew-point temperatures and the observed counterpart.

3 Results

3.1 Evaluation of mean biases of WGBT

The two BC methods (ISIMIP and QM) are applied to the two primary variables of the heat stress index, namely daily maximum air temperature and daily mean dew-point temperature, prior to the WBGT calculation. Under no cross-validation (i.e. the methods are calibrated and validated in the same period) both BC methods adjust, by construction, the central part of the distribution (mean for ISIMIP, median for QM; see Fig. 1a–d). ISIMIP further adjusts the variability around the mean, whereas QM additionally adjusts the 99 empirical percentiles. The performance in terms of mean biases of the two BC methods for individual variables is good and differences related to the parametric (ISIMIP) or empirical (QM) nature of the method may arise on the tails of the distribution, for which QM outperforms ISIMIP (not shown).

The suitability of the component-wise BC approach of the WBGT prior to its application in a climate change context is assessed by evaluating the corrected WBGT with the observed counterpart for the period 1981–2010. Although the calibration and validation periods are the same, our approach can be considered independent since the evaluated aspect (i.e. multivariate consistency and WBGT statistics) is not directly tackled by the BC methods. An additional split-sample cross-validation (cold vs. warm years; not shown) indicates that WBGT biases are of the same order of magnitude as in the non-cross-validated analysis.

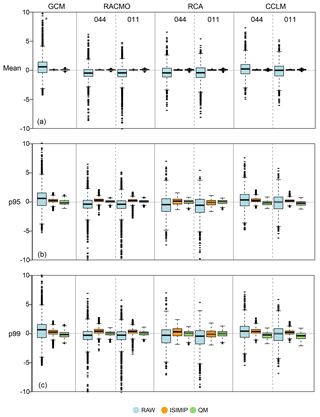
Figure 2 Biases of mean (a), 95th percentile (b) and 99th percentile (c) summer WBGT for the GCM and RCMs at EUR-44 and EUR-11. Biases are calculated as model minus observations. Each box represents the biases across all grid boxes for raw (blue), ISIMIP corrected (orange) and QM corrected (green). Due to the different land–sea masks in the observations, the GCM and RCMs (EUR-44 and EUR-11), all box plots consider the grid boxes common to all data sets.

Mean biases of summer mean WBGT (Fig. 2a) are evident for the raw GCM and RCMs (blue boxes; note that no height correction has been applied to the raw data, which might be mainly responsible for the skewed distribution of the raw biases). These are largely reduced after both BC methods, equally well for GCM and RCM data. The evaluation of the 95th and 99th percentiles reveals better performance for ISIMIP or QM depending on the model (Fig. 2b, c). QM improves on mean biases and reduces their variability in higher percentiles for the GCM, RACMO and RCA, whereas a cold bias emerges for CCLM. There is no evident added value of the RCMs with respect to the GCM after bias correction (see also the spatial pattern of the differences between bias-corrected GCM and RCMs in Fig. S1 in the Supplement). This is in agreement with the findings for coarser vs. the higher resolution of RCM simulations by Casanueva et al. (2016).

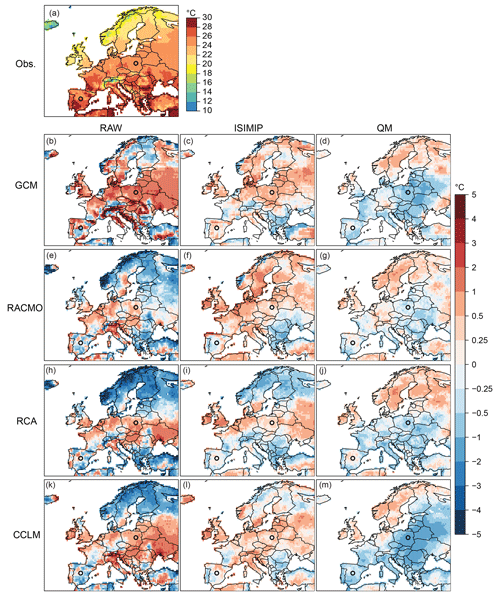
Figure 3 Spatial distribution of the observed 99th percentile of summer WBGT (WBGTp99, a) and model biases for the GCM (b–d) and RCMs at EUR-11 (e–m) for raw (first column), ISIMIP corrected (second column) and QM corrected (third column). The grid boxes over Warsaw and Madrid are marked as a reference for subsequent analyses.

The spatial pattern of biases in the 99th percentile of the WBGT (WBGTp99) is shown in Fig. 3. In general, the bias correction methods alleviate the biases of the raw models over Europe (in particular, large biases due to complex orography), although there are cases in which, in some regions, the biases after bias correction remain as high as or even higher than for the raw output. For the GCM, biases of similar magnitude remain after ISIMIP and QM, with completely different spatial structures. For the RCMs RACMO and RCA, slightly better results are found for QM compared to ISIMIP, with biases up to ±1 ^∘C. The added value of the two BC methods with respect to the raw simulations is also shown in Fig. S2, being larger in areas with complex orography and slightly better for QM. The above-mentioned cold bias for the CCLM after QM is present, especially in eastern Europe (Figs. 3m and S2h). The causes for that are analysed in more detail in the next section.

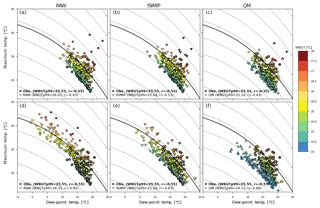
Figure 4 Inter-variable relationship for the observations and (raw and bias corrected) model data for RACMO-011 (a–c) and CCLM-011 (d–f) for the grid box over Warsaw. Each scatter plot represents pairs of values of daily dew-point temperature (x axis) and maximum temperature (y axis) which produce summer WBGT values above WBGTp95 (Pearson correlation coefficient between the represented pairs of dew-point and maximum temperatures, r, is included in the legend). The three coloured markers correspond to WBGT values for the observations (circles in all panels), raw RCMs (squares in panels a, d), RCM–ISIMIP (downward triangles in panels b, e) and RCM QM (upward triangles in panels c, f). Isolines also represent WBGT values, and the thicker line depicts the observed WBGTp99.

3.2 Evaluation of inter-variable relationships

The component-wise correction of the WBGT is able to correct for large biases in some WBGT statistics, but some biases remain for specific locations and models. We focus on the eastern European region and select the closest grid box to the city of Warsaw (Poland), where the original positive bias of WBGTp99 (0.7 ^∘C) turns into a negative bias (−1.4 ^∘C) after QM for CCLM-011 (Fig. 3m). The application of QM to the input variables of WBGT reduces their raw biases to less than ±0.3 ^∘C for all analysed statistics in that grid box. QM corrects for distributional biases of each variable, but the temporal sequence (i.e. day-to-day variability) of the raw data is not altered and the ranks are preserved. Given that maximum temperature and dew-point temperature are combined non-linearly to produce the daily sequence of WBGT, deficient inter-variable relationships may lead to an inaccurate representation of pairs of input variables and consequently to biases in the WBGT distribution. We assess pairs of values of maximum temperature and dew-point temperature that produce the highest values of WBGT (in particular those above the 95th percentile, WBGTp95) for the observations and model (raw and bias corrected) data (Fig. 4). According to the observations, the 5 % of days with the highest heat stress is produced by high maximum temperatures (28–36 ^∘C) and high dew-point temperature (13–21 ^∘C), and both input variables present a negative linear relation (Pearson correlation coefficient of −0.55). Within these ranges, WBGT can reach values of 23–27 ^∘C (see circles in Fig. 4). The raw models (squares in Fig. 4a, d) present some biases on the upper tail of the distribution of the two input variables, which translates into positive biases of the WBGTp99 in the two models. Raw RACMO (Fig. 4a) overestimates maximum and dew-point temperatures but captures the inter-variable relationships rather well ($r=-\mathrm{0.43}$), whereas raw CCLM (Fig. 4d) presents more deficiencies in representing the inter-variable structure ($r=-\mathrm{0.82}$); in particular, it shows large positive biases for maximum temperature and negative biases for dew-point temperature. Overall, the remaining biases after the ISIMIP correction (downward triangles in Fig. 4b, e) approximately resemble the original counterparts for RACMO and improve on the raw data for CCLM, whereas QM (upward triangles in Fig. 4c, f) overcorrects the original biases. For CCLM QM the highest 5 % WBGT values are produced by lower values of both input variables compared to the observed pairs, especially dew-point temperature (down to 5 ^∘C), leading to an underestimation of WBGTp99. The stronger negative correlation between the input variables for QM than for the observations might also contribute to the negative biases in extreme WBGT, since high values of maximum temperature would then be linked to rather low dew-point temperatures (or vice versa), which may imply lower WBGT. Low dew-point temperatures are also found for CCLM–ISIMIP, but they are combined with positively biased maximum temperatures, and thus the biases (maximum temperatures that are too high – above 38 ^∘C – and dew-point temperatures that are too low – below 12 ^∘C; see top left corner in Fig. 4e) compensate, leading to a small bias in WBGTp99. Therefore, the evaluation of WBGT statistics should be done with caution since the results can be right for the wrong reason, highlighting the need for multivariable model evaluations (García-Díez et al., 2015).

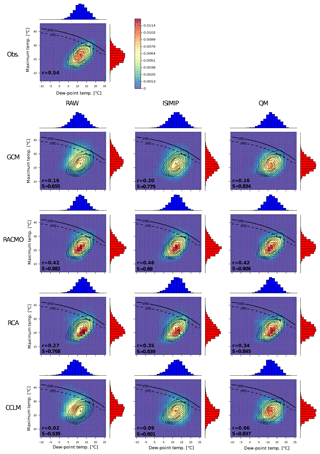
Figure 5 Two-dimensional kernel density plots for the grid box over Warsaw. Blue histograms (and x axis) refer to dew-point temperature and red histograms (and y axis) refer to maximum temperature. The isolines for the observed WBGTp95 and WBGTp99 are also shown as the thick dashed and solid black lines, respectively. Shadings represent the 2-D density distribution for the observations (first row), the GCM (second row) and RCMs at EUR-11 (third to fifth rows). Very similar results are found for EUR-44 (not shown). Contour lines represent the observed probabilities, which are overlaid on the model probabilities for the sake of comparison. r depicts the Pearson correlation coefficient between all pairs of daily dew-point and maximum temperatures, and S represents the two-dimensional Perkins skill score of distributional similarity (the closer to 1 the better; see Sect. 2.5).

To investigate the effects of the downscaling methods on the full joint probability distribution of the maximum temperature and dew-point temperature in more detail, consider Fig. 5. It shows the two-dimensional kernel density distribution (see Sect. 2.5) together with marginal histograms for the same grid box (Warsaw) as in Fig. 4. Higher values of the observed joint probability (Fig. 5, top panel) are associated with more likely values of maximum temperature and dew-point temperatures around the mean of the distribution (approximately 23 and 10 ^∘C, respectively). For the GCM, the distributions of the WBGT input variables are wider than the observed ones, leading to a more diffuse and displaced distribution of joint probabilities (Fig. 5, second row). In agreement with the previous results, after ISIMIP the joint probabilities are centred, but neither the shape nor the maximum values are well represented. QM systematically narrows the distributions and slightly improves the results, which is consistent with the higher values of the Perkins score (see Sect. 2.5). The raw RACMO and RCA outputs tend to better represent the shape of the joint distribution than the GCM, although the maximum probabilities are biased towards somewhat lower maximum temperatures for RACMO as well as towards lower maximum temperature and higher dew-point temperature for RCA. The ISIMIP correction largely preserves the original structure in the raw data, whereas QM often narrows the original skewed distributions towards the observed counterpart. There is, however, an overestimation of the maximum probabilities after QM. The CCLM raw simulations (EUR-44 and EUR-11) for this grid box present more deficiencies in representing the inter-variable structure in terms of the magnitudes and location of the joint probabilities. The ISIMIP correction brings the CCLM maximum closer to the observational counterpart, but the joint probabilities are too wide. For instance, unlike the observations, there is some probability of high values of WBGT (see isoline denoting observed WBGTp99) associated with rather low dew-point temperatures and high maximum temperatures (as also shown in Fig. 4). This problem is very likely inherited from the raw data and is slightly improved by QM. The remaining underestimation of WBGTp99 after QM is also visible from this plot, since the probability above the observed WBGTp99 isoline is negligible. In terms of the general structure, the joint distributions of the RCM QM data are better than those with the ISIMIP correction, although the performance greatly depends on the quality of the raw data.

RACMO (especially EUR-44; not shown) is the best-performing model in terms of joint probabilities for this specific grid box, with slightly improved results after QM. The improvement of QM on the joint probabilities is more noticeable in RCA, CCLM and the GCM, for which QM is able to adjust important deficiencies in the inter-variable dependencies. An example for Madrid (Fig. S3) shows that all RCMs perform equally well after QM.

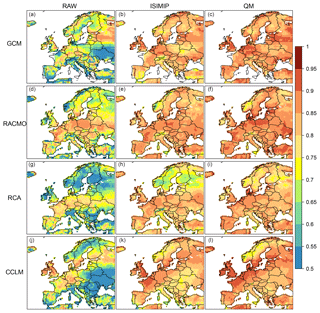
Figure 6 Spatial distribution of Perkins skill scores calculated from the two-dimensional distribution of summer values of daily maximum temperature and daily mean dew-point temperature for the GCM (a–c) and the RCMs at EUR-11 (d–l) for raw (first column), ISIMIP corrected (second column) and QM corrected (third column).

An overall conclusion about better performance is not evident since the results depend on each grid box and GCM–RCM combination, and they might be affected by compensations for biases in the individual variables. A summary for the evaluation of the inter-variable relationships across Europe is presented through the Perkins score (Fig. 6). Lower scores are apparent in the raw GCM and RCM data, especially in areas with complex orography and southeastern Europe. The two BC methods are able to improve the representation of the inter-variable relationships on the whole continent just by centring the distributions. High Perkins scores are found, especially along the Atlantic coast. QM improves on ISIMIP in large areas, although low scores are found in Scandinavia (0.7–0.8) for the RCMs. The spatial distribution of the scores qualitatively agrees with biases in the temporal variability of maximum and dew-point temperatures (Figs. S4–S5). This is a first-order indication that the misrepresentation of the temporal variability of the individual variables might be responsible for most of the deficiencies in the inter-variable relationships. Raw model data overestimate the temporal variability, especially in eastern Europe, leading to Perkins scores lower than 0.6. In other areas, such as Scandinavia, the models underestimate the temporal variability of the two input variables and thus present the lowest scores even after QM. The best results are obtained for GCM QM, with large scores also in northern Europe (Fig. 6c).

3.3 Future changes of heat stress

For all the models considered (GCM, RCMs and BC methods) summer mean WBGT and WBGTp99 are projected to increase by the end of the 21st century under RCP8.5 (Figs. 7 and S4). For a given RCP, the major source of uncertainty in the magnitude of this change comes from the choice of GCM or RCM, with a systematically lower change signal in the RCMs. The differences in the climate change signal between the GCM and the RCMs may range between 0.5 and 1 ^∘C, depending on the RCM and RCP, for the European averaged values. It is related to the reduced summer warming in many EURO-CORDEX RCMs with respect to their driving GCMs that was noted already in previous works, which pointed to different circulation patterns, surface energy fluxes and feedback mechanisms as possible causes for this (Keuler et al., 2016; Sørland et al., 2018). The raw GCM projects changes in summer mean WBGT above 4.5 ^∘C over most parts of the continent, with the highest values in the Alpine area (more than 6 ^∘C), whereas RCMs project increases between 3 and 5 ^∘C on most of the continent (Fig. 7; shown are RCMs at 0.11^∘ but similar results are found for 0.44^∘). The Alps and north of Scandinavia stand out with larger positive signals. By construction, ISIMIP approximately preserves the climate change signals of the input variables (Hempel et al., 2013), whereas QM can potentially modify them (e.g. Gobiet et al., 2015; Ivanov et al., 2018; see also Sect. 2.4). Our results show that little changes become apparent for the mean WBGT after ISIMIP (up to half a degree). The effect of the QM on the WBGT signal is especially noticeable for the case of the GCM, for which QM reduces the signal by up to 1.5 ^∘C and brings it closer to the RCM counterpart. The large positive signal over the Alpine area is retained and stands out (although with smaller magnitude) for the RCM QM. Similar conclusions can be drawn for the change in WBGTp99, with a slightly patchier spatial pattern (Fig. S4).

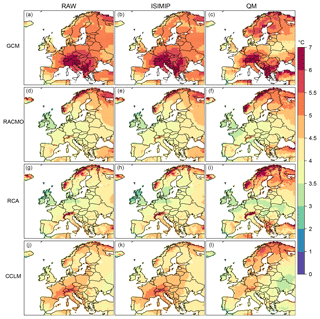
Figure 7 Spatial distribution of changes in summer mean WBGT under RCP8.5 for the GCM (a–c) and RCMs at EUR-11 (d–l) for raw (first column), ISIMIP corrected (second column) and QM corrected (third column). The climate change signals are calculated for the period 2070–2099 with respect to 1981–2010.

Figure 8 Climate change signals for summer mean WBGT (a), daily maximum temperature (Tx, b) and daily mean dew-point temperature (Td, c) for the period 2070–2099 with respect to 1981–2010 and RCP2.6, 4.5 and 8.5. Each box represents the changes across all grid boxes in Europe for raw (blue), ISIMIP corrected (orange) and QM corrected (green) for the GCM and the RCMs (EUR-11 and EUR-44). Due to the different land–sea masks in the observations, the GCM and RCMs (EUR-44 and EUR-11), all box plots consider the grid boxes common to all data sets.

The main conclusions qualitatively hold for the other RCPs, with quite consistent signals among RCMs and BC methods (Fig. 8a). Differences between the GCM and RCM projected signals are also evident for the input variables (Fig. 8b, c). These differences increase with the RCP and are larger for maximum temperature than for dew-point temperature. Whereas the RCMs tend to lower the signal of the GCM for maximum temperature, they increase the signal for dew-point temperature. That is explained by the opposite behaviour of temperature and relative humidity, as well as the fact that models showing hotter temperatures tend to simulate lower relative humidity (Fischer and Knutti, 2013). In general, QM tends to expand the range of the raw RCM climate change signals and slightly lower the median for the two CCLM simulations.

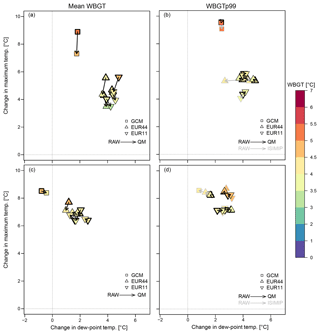
Figure 9 Scatter plots showing the effect of BC on the climate change signal for dew-point temperature (x axis), maximum temperature (y axis) and WBGT (coloured markers) for the grid box over Warsaw (a, b) and Madrid (c, d) for RCP8.5 and the period 2070–2099 with respect to 1981–2010. Panels (a, c) show results for the change signal of the mean variables and panels (b, d) for the 99th percentiles. Each marker depicts results for a different data set (squares for the GCM, upwards triangles for RCMs at EUR-44 and downwards triangles for RCMs at EUR-11). The black arrows point from the value in the raw data (thicker markers) to the change in the QM-corrected data, whereas the grey arrows point from the raw to the ISIMIP-corrected data (only discernible for the change signal of the 99th percentiles).

The modification of the climate change signal by BC is further analysed for the grid boxes over Warsaw (Fig. 9a, b) and Madrid (Fig. 9c, d), considering the change signals in the mean variables (Fig. 9a, c) and in the 99th percentile (Fig. 9b, d). In Warsaw, QM tends to reduce the signal of the GCM and RCMs towards lower maximum temperatures (Fig. 9a). These changes in the signal are larger for the GCM than the RCMs. In this grid box, the effect of QM on mean dew-point temperature is negligible. As a consequence, the modification of the signal in mean WBGT is less than 0.5 ^∘C for the RCMs and 1 ^∘C for the GCM. Given that the projected change for mean WBGT is 3.5–5 ^∘C for the RCMs (∼5.5 ^∘C for the GCM), the impact of the QM can amount to a maximum of 15 % (18 %) of the raw signal. Modifications in the climate change signal of the WBGTp99 by QM are smaller than for the mean, along with smaller changes in the signal of the 99th percentile of the input variables (Fig. 9b; note that WBGTp99 is not necessarily linked to the 99th percentile of maximum temperature and dew-point temperature but to some percentile in the upper tail of the distribution). In this example, however, it is evident that the preservation of trends by ISIMIP depends on the parameter under consideration, since e.g. the signal in the 99th percentile of dew-point temperature for CCLM-044 is reduced by 1.3 ^∘C after the application of ISIMIP (see grey lines in Fig. 9b). Again the modifications of the climate change signal are grid box specific, and negligible changes are found after QM and ISIMIP for the grid box closest to Madrid (Fig. 9c, d).

4 Summary and discussion

In the present work we compared global and regional climate model data at different spatial resolutions and bias corrected by two bias correction methods (namely, the ISIMIP method and empirical quantile mapping, QM) in order to assess the added value of (1) a more complex BC method, as well as (2) bias-corrected RCM simulations versus bias-corrected GCM simulations, and (3) the role of downscaling and BC on the climate change signal of a multivariate index. For this purpose, we used GCM data from the CMIP5 HadGEM2-ES and the HadGEM-driven EURO-CORDEX simulations at approximately 12 and 50 km horizontal resolution, respectively. The study was performed for the case of heat stress in Europe, considering as a heat stress index the wet-bulb globe temperature (WBGT) in shaded conditions. It depends on air temperature and dew-point temperature, which were separately corrected prior to the index calculation. The performance of the models and methods in such a multivariate framework was analysed. The results were examined considering present climate simulations (reference period 1981–2010) and future climate projections (2070–2099).

Regarding the performance of the two bias correction methods, the evaluation results show that both methods are able to correct for biases in the multivariate WBGT as represented by the GCM and RCMs, with smaller biases for ISIMIP or QM depending on the GCM–RCM model chain. ISIMIP mostly retains the distributional features of the raw data, whereas QM narrows the two original distributions, producing some improvement of the joint probability distribution with respect to ISIMIP. The added value of higher climate model resolution (from GCM to RCM and from EUR-44 to EUR-11) is not evident in the evaluation of the bias-corrected WBGT statistics, since the biases of both the GCM and RCMs become indistinguishable after bias correction. The joint probabilities are, however, better reproduced by the RCMs after the two bias corrections, especially due to a more accurate representation of these relationships in the raw data. For cases (i.e. grid boxes) for which the raw models do not represent the inter-variable relationships well (e.g. CCLM for the grid box closest to Warsaw), some biases in the joint distribution may remain after bias correction. Large biases of the raw GCM in the inter-variable dependencies might be related to biases in large-scale processes and feedbacks. Further research is needed to understand the causes for these biases, while the application of BC for those cases in a multivariate context is then debatable (Piani et al., 2010; Ehret et al., 2012; Muerth et al., 2013). Other methods and approaches (i.e. perfect prognosis approach, high-resolution regional models) are viable alternatives to bias correction in those cases (Maraun, 2016; Maraun et al., 2017).

Regarding climate change projections of WBGT, the largest differences for a given RCP come from the use of GCM versus RCM data, with systematically lower signals for the RCMs. The GCM–RCM differences amount to 0.5–1 ^∘C for the European averaged signal and increase with the emission scenario, regardless of the bias correction method and RCM resolution. QM tends to reduce the signal in both the GCM and RCMs, bringing the GCM-based and RCM-based results closer to each other. Some modifications of the raw RCM signal are visible after QM (up to 20 % of the raw signal); however, the original signal of the GCM is qualitatively retained by the RCM QM, with larger increments in the Alpine ridge and northern Scandinavia. Although the ISIMIP method is by construction a trend-preserving BC method, due to the non-linearities in the WBGT calculation some modifications of the signal in WBGT statistics may become apparent after the correction. The modifications of the climate change signals due to bias correction are generally smaller than the model uncertainty (spread over the GCM and RCMs at two resolutions) by the end of the century. The magnitude of these changes should also be analysed in the context of natural variability (Räisänen, 2001), since the latter can mask or enhance long-term trends.

Summarising, there is some added value of QM with respect to ISIMIP in the representation of the inter-variable structures, whereas the present climate evaluation shows limited added value of bias-corrected RCM versus bias-corrected GCM data. Future works including convection-permitting simulations could help to assess the robustness of these results. More distinct results between RCMs and the GCM are obtained regarding climate projections, with systematically smaller change signals in the RCMs. The bias-corrected data qualitatively retain the change signal of the raw counterparts, although QM tends to decrease the signal of the WBGT and the input variables.

Some limitations and points for discussion remain. The use of a single GCM (even downscaled with several RCMs and bias corrected) for the production of climate projections does not sample the full uncertainty range, and the use of large ensembles of simulations is strongly recommended. GCMs typically produce larger estimates for the change signal of temperature than RCMs due to different circulation patterns, surface energy fluxes and feedback mechanisms (Keuler et al., 2016; Sørland et al., 2018). HadGEM in particular projects an increase in summer mean WBGT of 5 ^∘C (European average, end of 21st century, RCP8.5) and HadGEM-driven RCM simulations of about 4–4.5 ^∘C. These results are at the upper limit of the uncertainty range when compared to a large ensemble of GCM–RCM simulations (Casanueva et al., 2019). Therefore, relying only on this GCM could lead to misleading conclusions when combined with other factors in impact assessments. This example highlights even further the need for ensembles of simulations.

The differences between the two RCM resolutions were negligible in our study, mainly due to the experimental design (both resolutions are remapped onto the 50 × 50 km observational grid). The higher-resolution RCMs could show some potential added value if the evaluation was carried out at their original resolution. However, there is no pan-European, high-resolution, observational grid for air temperature or for dew-point temperature (or relative humidity) to bias correct and evaluate these simulations. While high-resolution grids for temperature are available at a national level, the lack of a gridded product for relative humidity remains a limitation. Furthermore, model evaluation can depend on the reference data set employed and observations play a fundamental role in bias correction, especially in QM for which the whole distribution is adjusted. Previous studies have shown that model uncertainty dominates over observational uncertainty for the case of mean temperature (Kotlarski et al., 2019a), but dew-point temperature (or relative humidity) has not been broadly investigated so far. In the present work, we do not account for observational uncertainty but acknowledge that the reliability and spatial representativeness of the reference data set might quantitatively modify the results. Future works also including a comparison of different observational data products might shed light on the robustness of the current results.