Progress towards a probabilistic Earth system model: examining the impact of stochasticity in the atmosphere and land component of EC-Earth v3.2

We introduce and study the impact of three stochastic schemes in the EC-Earth climate model: two atmospheric schemes and one stochastic land scheme. These form the basis for a probabilistic Earth system model in atmosphere-only mode. Stochastic parametrization have become standard in several operational weather-forecasting models, in particular due to their beneficial impact on model spread. In recent years, stochastic schemes in the atmospheric component of a model have been shown to improve aspects important for the models long-term climate, such as El Niño–Southern Oscillation (ENSO), North Atlantic weather regimes, and the Indian monsoon. Stochasticity in the land component has been shown to improve the variability of soil processes and improve the representation of heatwaves over Europe. However, the raw impact of such schemes on the model mean is less well studied. It is shown that the inclusion of all three schemes notably changes the model mean state. While many of the impacts are beneficial, some are too large in amplitude, leading to significant changes in the model's energy budget and atmospheric circulation. This implies that in order to maintain the benefits of stochastic physics without shifting the mean state too far from observations, a full re-tuning of the model will typically be required.

1 Introduction

One of the key guiding principles of the scientific method is the need to assess and quantify uncertainty. The truncation of the true climate system to a finite grid necessarily introduces a large source of uncertainty from unresolved sub-grid-scale processes. While parameterizations are usually developed to account for these unresolved processes (Bauer et al., 2015), the parametrization process relies on introducing a number of simplifications and assumptions that are not always valid, effectively introducing an additional layer of uncertainty in any model prediction (Palmer et al., 2005). Some of these assumptions are resolution-dependent: for example, convection parameterizations typically assume that the size of a grid box is large enough for the grid box to contain a large sample of clouds, such that the average influence of the clouds is well constrained by the resolved flow (Arakawa and Schubert, 1974; Lord et al., 1982). As the model resolution continues to increase, such assumptions can become increasingly tentative, even while the resolution is still far from being explicitly cloud resolving. Hence, the need to represent the uncertainty of the sub-grid contribution to the flow becomes increasingly important.

In medium-range and seasonal forecasts using numerical weather prediction models, the use of stochastic schemes has become widespread as a means to sample this uncertainty. Studies have shown that when properly calibrated, such schemes have a beneficial impact on both the spread and mean state of these forecasts (Weisheimer et al., 2011; Berner et al., 2017; Leutbecher et al., 2017). In recent years, there has also been increasing interest in understanding the impact of these schemes on the long-term climate of models. In Palmer (2012), it was argued that introducing stochasticity into climate models may be a key step towards eliminating persistent model biases and reducing uncertainty in climate projections. Since then, the insertion of a stochastic component into a climate model has been demonstrated to improve several key processes, including El Niño–Southern Oscillation (ENSO) (Christensen et al., 2017a; Yang et al., 2019; Berner et al., 2018), the Madden–Julian Oscillation (MJO) (Wang and Zhang, 2016), and the representation of the Indian monsoon (Strømmen et al., 2017). Improvements were also found on regime behaviour, northern hemispheric blocking patterns, and tropical precipitation (Dawson and Palmer, 2015; Davini et al., 2017; Watson et al., 2017). Most of these studies focused on a particular, multiplicative noise scheme called the “stochastically perturbed parametrization tendencies” scheme (SPPT). A more flexible variant of this scheme (dubbed “ISPPT”) was developed and found to substantially improve the skill of weather forecasts in areas with significant convective activity, although only a limited evaluation of its impact over longer timescales was reported (Christensen et al., 2017b). Most modern climate models also incorporate a full land system and are coupled to an ocean model, both of which carry their own sources of uncertainties. In MacLeod et al. (2016), stochasticity was added to the land scheme in the Integrated Forecast System (IFS) used by the European Centre for Medium-Range Weather Forecasts (ECMWF) and was found to have a positive impact on seasonal predictability, as well as the 2003 European heatwave. In the ocean, a number of schemes have been considered, including perturbations of ocean mixing processes and sea ice (Juricke et al., 2013; Juricke and Jung, 2014; Juricke et al., 2017, 2018). Both variability and mean states of key quantities were found to improve. More recently, there have also been some studies focusing on the impact of stochastic schemes on the atmosphere–ocean coupling (Williams, 2012; Rackow and Juricke, 2019).

The idea behind the “Probabilistic Earth-System”, as put forward in Palmer (2012), is to incorporate stochastic representations of model uncertainty not only into the atmosphere, but also into the land, sea ice, and ocean components of the EC-Earth model, thus obtaining a state-of-the-art Earth system model with stochasticity in each major component. Such a fully probabilistic coupled climate model will be tested in the PRIMAVERA project (Haarsma et al., 2016). In this paper, we will present the schemes used in the land and atmosphere components, and perform initial tests in an atmosphere-only configuration. This allows us to test the raw impact of the atmosphere and land schemes on the mean climate with no ocean coupling. In this sense, the study conducted here is a first test of the configurations to be used in the PRIMAVERA simulations. A key motivating question is whether the benefits of such schemes can be achieved without any additional model tuning.

As will be seen, the two atmosphere schemes and one land scheme have a notable impact on the energy budget of the model, implying that in coupled mode, the inclusion of different combinations of these schemes can be expected to shift the model climate to a potentially quite different stable state. In fact, even in these atmosphere-only simulations, we demonstrate significant changes in the mean state of several variables on the large scale, such as atmospheric water vapour content, cloud liquid water, cloud cover, soil temperature, and soil moisture. This highlights that the non-linear impacts of random model error, as represented through a zero-mean stochastic perturbation, cannot be neglected in climate models. While some of the changes are positive compared with reanalysis data, not all are. In particular, key global quantities such as net surface energy that models are frequently tuned for, can be strongly altered. This implies that while adding stochasticity can be beneficial, additional model tuning may be required to keep the mean state close to observations.

In Sect. 2, we describe the model used and the stochastic schemes under consideration. In Sect. 3, we describe the experiments carried out, the reference data, and the statistical methods. Sections 4–7 contain the actual analysis. We choose to focus our evaluation on the impact of these stochastic schemes on the mean climate. In Sects. 4–6, we examine, for each scheme in turn, changes in the global mean of key variables relative to a set of deterministic simulations. These changes provide insight into the impact of the schemes on the energy budget and the hydrological budget. In Sect. 7 we compare changes in the modelled circulation as represented by the Hadley cell and the quasi-biennial oscillation (QBO) across all three schemes (SPPT, ISPPT, and stochastic land). Finally, Sect. 8 contains a discussion on the cause of the observed changes as well as our conclusions.

We note that while we do not test the stochastic ocean schemes here, basic tests of the impact of these on the ocean component NEMO (the Nucleus for European Modelling of the Ocean model) of EC-Earth can be found in Juricke et al. (2017, 2018).

2 Model description

2.1 About EC-Earth

EC-Earth is an Earth system model developed by the international EC-Earth consortium (Hazeleger et al., 2012). The atmospheric component utilizes a modified version of the Integrated Forecast System used by ECMWF. Land surface processes are simulated using the Hydrology Tiled ECMWF Scheme of Surface Exchanges over Land (H-TESSEL) (Balsamo et al., 2009). More details are given in Sect. 2.3. Dynamic ocean coupling is available using the NEMO model version 3.6; as we will consider atmosphere only simulations, we omit further details on the ocean component. The tests in this paper were performed using EC-Earth version 3.2.1, a stable version for atmosphere-only simulations, based on cycle 36r4 of the IFS (released in 2010). The IFS solves the resolved processes in spectral space, with advection and physics parameterizations computed on a reduced Gaussian grid. The parameterizations used are described extensively in Beljaars (2004). Modifications to the IFS are carried out to improve the model performance on climate timescales. In particular, various parameters controlling the physics parameterizations were tuned by the consortium to obtain a realistic energy budget for the period from 1990 to 2010, as compared to observational estimates (Trenberth et al., 2009).

In all experiments carried out, we used the default resolution of the current EC-Earth version, which uses 91 vertical levels and a spectral resolution of T255, corresponding to a horizontal resolution of around 80 km.

2.2 Description of the SPPT and ISPPT schemes

The SPPT scheme has been included in the operational model of the IFS since 1998. The scheme is designed to represent forecast uncertainty that arises from the simplifications and approximations involved in the parametrization of unresolved atmospheric processes. It does this by perturbing, at each time step, the total net tendency from the physics parameterizations using a multiplicative noise term r:

$$\begin{array}{}\text{(1)}& \widehat{{\mathit{P}}_k}=\left(\mathrm{1}+{\mathit{\mu }}_{k}r\right)\sum _{i=\mathrm{1}}^{\mathrm{6}}{\mathit{P}}_{i,k},\end{array}$$

where P_i,k is the vector made up of the tendencies of the prognostic model variables (winds, temperature, and humidity) from the ith physics parametrization scheme, and k indicates the vertical model level. The physics schemes are as follows: 1st is radiation (RDTN); 2nd is turbulence, vertical mixing, and orographic drag (TGWD); 3rd is convection (CONV); 4th is large-scale water (cloud) processes (LSWP); 5th is non-orographic drag (NOGW); and 6th is methane oxidation (MOXI). The perturbation, r, is constant in the vertical, but is tapered through ${\mathit{\mu }}_k\in \left[\mathrm{0},\mathrm{1}\right]$ to smoothly reduce the perturbation to zero in the boundary layer and stratosphere; this is done to avoid introducing numerical instabilities. The perturbation r, which evolves in time, follows a Gaussian distribution with mean zero, and is smoothly correlated in space and time. The implementation in EC-Earth follows that in the Integrated Forecasting System as described in Palmer et al. (2009). The perturbation r is generated by summing over three independent spectral patterns with standard deviations (0.52, 0.18, and 0.06), spatial correlation lengths (500, 1000, and 2000 km), and temporal decorrelation scales (6 h, 3 d, and 30 d) respectively: the different patterns are meant to capture model error at different scales which may, in principle, be independent of each other. The perturbation r is limited between −1 and 1 to ensure that $\widehat{\mathit{P}}$ has the same sign as $\mathit{P}=\sum {\mathit{P}}_i$.

The SPPT scheme described above assumes that the different physics parameterizations have the same model error characteristics. If the net tendency is small, SPPT represents the associated model uncertainty as small, even if the associated individual tendencies were large. Christensen et al. (2017b) proposed a generalization to the SPPT approach in which each physics process is perturbed independently using multiplicative noise:

$$\begin{array}{}\text{(2)}& \widehat{\mathit{P}}=\sum _{i=\mathrm{1}}^{\mathrm{6}}\left(\mathrm{1}+{\mathit{\mu }}_k{r}_i\right){\mathit{P}}_{i,k}.\end{array}$$

The random patterns, r_i, are independently generated and evolved. The statistical properties of the r_i (standard deviation, and spatial and temporal correlations) can be individually specified to account for differences in the uncertainty characteristics arising from each physics scheme. This generalization, “Independent SPPT” (ISPPT), was shown to significantly improve the reliability of ensemble forecasts in the tropics, and in areas with significant convective activity (Christensen et al., 2017b). This indicates that ISPPT is likely a better representation of the uncertainty associated with convection than SPPT. Further justification for the use of ISPPT over SPPT has been provided by considering coarse-graining experiments (Christensen, 2019).

Note that in these standard implementations of SPPT and ISPPT, the fluxes in precipitation and evaporation are not perturbed using a random pattern. Implementing such a change would improve consistency in the transport of moisture in the model, and is of interest for future investigation.

Finally, it has been found, in Davini et al. (2017), that the SPPT scheme does not conserve water, leading to an unphysical drying of the atmosphere. A “humidity fix” was introduced in ibid, which we also use for our SPPT and ISPPT experiments. At each tim step, the “fix” computes, global mean precipitation, and evaporation, and reinserts the amount of humidity required to bring these into balance. This humidity is reinserted with spatial weighting favouring regions where the imbalance is large.

2.3 Description of the stochastic land scheme

The land surface model used here is H-TESSEL, the Tiled ECMWF Scheme for Surface Exchanges over Land (TESSEL) with revised land surface hydrology, comprising a surface tiling scheme and vertically discretized soil. The surface tiling scheme allows each grid box a time-varying fractional cover of up to six tiles over land (bare ground, low and high vegetation, intercepted water, and shaded and exposed snow) and two over water (open and frozen water). Each tile has a separate energy and water balance, which is solved and then combined to give a total tendency for the grid box, weighted by the fractional cover. Full details of the model may be found in Balsamo et al. (2009).

Stochasticity is induced in the land-scheme via the hydraulic conductivity, which is calculated in H-TESSEL using the van Genuchten formulation (van Genuchten, 1980). This formulation is favoured by soil scientists as it has shown good agreement with observations in intercomparison studies (Shao and Irannejad, 1999). The hydraulic conductivity is in this formulation given by

$$\begin{array}{}\text{(3)}& \mathit{\gamma }={\mathit{\gamma }}_{\mathrm{sat}}{\displaystyle \frac{\left[\right(\mathrm{1}+\mathit{\alpha }{h}^n{)}^{\mathrm{1}-\mathrm{1}/n})-\mathit{\alpha }{h}^{n-\mathrm{1}}){]}^{\mathrm{2}}}{(\mathrm{1}+\mathit{\alpha }{h}^n{)}^{(\mathrm{1}-\mathrm{1}/n)(l+\mathrm{2})}}},\end{array}$$

where α, l, and n are soil texture parameters that are dependent on the soil type, h is soil water potential (the potential energy of soil water due to hydrostatic pressure), and γ_sat is the hydraulic conductivity at saturation. The two key soil parameters α and γ_sat of Eq. (3) are stochastically perturbed. These particular parameters have been chosen as previous studies found them to be particularly sensitive (Cloke et al., 2008; MacLeod et al., 2016). Each parameter is perturbed with its own integration of the spectral pattern generator. As with SPPT and ISPPT, the spectral pattern is obtained as a sum of three patterns, each with the same spatial and temporal decorrelation scales as for those schemes. In this case, the weightings for each scale are set to 0.33. Estimates of these parameters based on observational data suggest that the two parameters are correlated (Cosby et al., 1984), and so a third pattern is used as a base for each pattern in order to introduce a correlation between them. The correlation coefficient between the two parameters is prescribed to be 0.6 on average. The perturbation is multiplicative, as with SPPT. That is, each parameter p is multiplied by (1+r), where r is the randomly generated spectral pattern described above.

Previous work has investigated the impact of representing uncertainty in these particular hydrology parameters. Perturbing coupled atmosphere–ocean seasonal hindcast experiments (MacLeod et al., 2016) resulted in an improved representation of soil-moisture driven processes active during the 2003 heatwave, leading to an improved signal in the seasonal forecast of surface air temperature. In a set of atmosphere-only experiments, MacLeod et al. (2016) showed a strong sensitivity of soil moisture memory to uncertainty in these parameters. Using the same atmosphere-only model, Orth et al. (2016) also demonstrate an improvement in subseasonal forecast skill via the incorporation of land surface parameter uncertainty.

3 Data and methods

3.1 Experimental set-up and reference data

We performed four ensemble experiments, which we will, for brevity, introduce as CTRL, SPPT, ISPPT, and LAND, referring to the scheme being used in each (in the CTRL experiments no stochastic schemes were used). The ensemble members were run for 20 years each, starting from 1 February of the following years: 1960, 1965, 1970, 1975, and 1980. Thus, the total period covered by all the experiments is 1960–2000. The motivation for spacing out the members in this way was to account for the possibility that the impact of the schemes may be sensitive to the initial ocean state. The creation of an ensemble, as opposed to e.g. a single, longer run, was motivated by the experience from ensemble forecasting using stochastic schemes, where multiple ensemble members are typically needed to estimate changes robustly. While spin-up issues may have been a complicating factor in these shorter experiments (especially for the LAND simulations, given the slow variations in soil moisture), initial testing suggested that the model adjustment was rapid, further justifying the use of an ensemble of shorter runs.

Atmospheric initial conditions for these dates were provided by the Climate Prediction group at the Barcelona Supercomputing Center. These initial condition files are obtained by interpolation of reanalysis data using the FULL-POS post-processing software for the IFS: this carries out the interpolation using the model executable to ensure minimal model drift (Bellprat et al., 2016). The sea surface temperatures and sea ice are then specified using the CMIP6 forcing datasets to match observations. Radiative forcings such as those from anthropogenic or volcanic sources were provided by the same source.

For the SPPT scheme, we used the default settings for the magnitudes and time/length-scales of the perturbations as in Leutbecher et al. (2017), described in Sect. 2.2.

For ISPPT, we used the same settings for the three fields as for SPPT. We set the convection and large-scale water process tendencies to share the same perturbation, and let the remaining four tendencies (radiation, turbulence and gravity wave-drag, and non-orographic gravity wave drag) have separate, independent perturbations. We chose to use the same perturbation because of the feedbacks between the convection and large-scale water processes schemes in the IFS, whereby detrained moisture from the convection scheme acts as an input to the large-scale water processes scheme. Thus, perturbing the two schemes together improves consistency of moisture transport in the model. Following the naming convention introduced in Christensen et al. (2017a), this corresponds to ISPPT $\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{3},\mathrm{4},\mathrm{5}$, where the number indicates which random seed was used to generate a pattern and the ordering of the numbers indicates which of the six physics parametrization schemes are perturbed with that pattern (see Sect. 2.2).

For the LAND scheme, the parameter perturbations r were restricted to be strictly between 1 and −1, as numbers greater than or equal to 1 were found to produce unphysical runoff behaviour. For this reason, the standard deviation of the noise perturbations were set to 0.33, allowing 3 standard deviations to explore the full available range.

To allow for a single reanalysis dataset to be used across all of the experiments, ERA40 (Uppala et al., 2005) was chosen as our reference point. When evaluating the QBO, we use the more recent reanalysis dataset ERA-Interim (Dee et al., 2011). A disclaimer here is that these reanalysis datasets are both created via data assimilation using previous versions of the IFS; therefore, they are related to EC-Earth in some ways. For variables that are less strongly constrained by the assimilation of existing observations (such as total cloud cover), this may imply that the model bias may not be independent of any existing biases within the reanalysis data themselves.

Finally, we note that additional simulations were also performed with both SPPT+LAND and ISPPT+LAND configurations, to test the combined impact of schemes. However, it was found that the impact of SPPT/ISPPT dominates the impact of LAND when it comes to the large-scale changes considered in this paper. Therefore, we have omitted these configurations in the present paper.

3.2 Methodology

3.3 Statistical techniques

All fields considered were filtered by taking monthly means. To compute the mean impact of the scheme, each simulation is paired with the corresponding CTRL simulation covering the same time period. The difference of each individual pair is computed, and the mean across the five ensemble pairs gives the mean impact of the scheme. When comparing the CTRL simulations with the reanalysis, each CTRL simulation is paired with the reanalysis data for the corresponding time period, and again the mean across all five pairs defines the CTRL bias. The standard deviation across the five ensemble members is used to estimate the statistical significance of the mean differences between model simulations. Twice the standard deviations is used as an error bound (displayed either with shading in time-series plots or explicitly written as a number in percentage change plots). Because there are only five samples, it is hard to claim that differences are definitively significant even if the zero-line is further than 2 standard deviations away from the mean. However, in the cases where this does happen, we have observed that all five individual differences have the same sign, suggesting that in these cases the difference is likely significant.

To assess differences in spatial patterns, the five ensemble members are concatenated to produce a time series spanning 1200 months at each grid point for each simulation, with the ensemble members ordered according to their start date. A two-tailed t test is applied to assess the significance of the difference in the mean. Spatial plots then indicate the mean difference across all the five simulations. Grid points where the difference lies outside the 95 % confidence interval are marked with dots. A cruder test was also used which simply tested if four of the five differences had the same sign. The results were almost identical.

Finally, to assess whether a reduction in the mean-square error (MSE), relative to the reanalysis, was significant, we computed the MSE for all five simulations of the scheme in question, as well as the five MSEs of the CTRL simulations. If the difference between the mean CTRL MSE and the mean MSE of the scheme was greater than 2 standard deviations of the spread in the MSEs across the five scheme simulations, the difference was deemed significant.

3.4 Energy budget

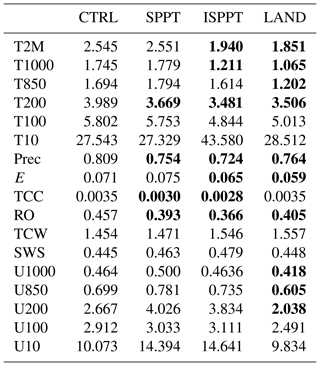
As the simulations were performed with historical forcings, the energy budgets of the five CTRL simulations are not comparable with each other. However, as the EC-Earth consortium tuned the deterministic model to have a realistic energy budget over the period from 1991 to 2010, the surface fluxes of the CTRL simulation covering the period from 1991 to 2000 are shown in Table 1. The table has been split into two parts, as the Pinatubo eruption in 1991 has a strong influence on the first half of the period. For reference, the estimates of these quantities from Trenberth et al. (2009), covering 2000–2004, are also shown.

Table 1 Globally averaged surface energy fluxes for the CTRL simulation. The values in the “Observed” row are the estimates from Trenberth et al. (2009) for the period from 2000 to 2004. STR represents net surface thermal radiation, SSR represents net surface solar radiation, SLHF represents surface latent heat flux, SSHF represents surface sensible heat flux, and SRF represents net surface energy. Units are in watts per square metre (W m⁻²) in all cases.

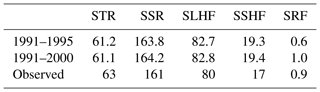
It can be seen that the CTRL simulation achieves a reasonable energy balance, with the net surface energy close to the observational estimate. As will be seen, the adjustment to this budget by the introduction of the different stochastic schemes is very fast and approximately constant in time. Therefore, it is possible to assess whether the stochastic schemes lead to an improved or degraded energy budget overall, although it should be kept in mind that variations in the budget between years is often large. Focusing the comparison against observations during this particular time period ignores possible changes in the evolution of the surface energy fluxes over time, i.e. possible changes in the climate sensitivity of the model. As this is the topic of the forthcoming study Strommen et al. (2019), we do not consider this in the present paper.

4 The impact of SPPT

4.1 Impact on the mean state

Figure 1a shows the percentage changes in global mean quantities due to SPPT, relative to the CTRL simulation. Evaporation has notably increased by about 1 %. Figure 2b shows the spatial distribution of these changes¹ averaged across all seasons, to be compared against the bias of the CTRL simulations to the reanalysis (Fig. 2a). The increase can be seen to be concentrated in the western Pacific Ocean in particular, with a notable decrease in the eastern Pacific. We note that the spatial changes due to SPPT are not well correlated with the CTRL bias, reducing the bias in places and exacerbating it elsewhere. As the overall mean CTRL bias is close to zero, the net increase in evaporation due to SPPT represents a small degradation. This is also reflected in the mean-square error (MSE) between the spatial means of SPPT and the reanalysis, as found in Table 2, where it can be seen that the MSE has increased with SPPT.

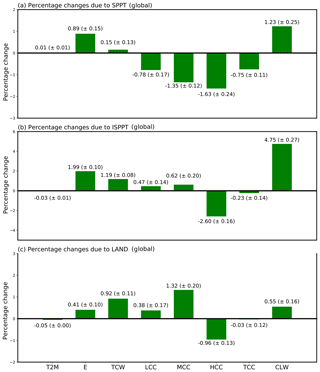
Figure 1 Average percentage change, relative to the CTRL, in the global mean of (a) SPPT, (b) ISPPT, and (c) LAND simulations. Variables shown (see the x axis of (c)) are as follows: 2 m temperature (T2M), evaporation (E), total column water (TCW), low cloud cover (LCC), mid-level cloud cover (MCC), high-level cloud cover (HCC), total cloud cover (TCC), and cloud liquid water (CLW). Uncertainty estimates are twice the standard deviation of the five individual differences. Note that, due to conservation of water, the change in precipitation (not shown) is almost exactly equal to the change in evaporation.

By contrast, precipitation, as seen in Fig. 3b, has generally improved. This can be seen both in terms of the mean bias, which has approximately halved, and the MSE (Table 2). While the precipitation biases of the CTRL model (Fig. 3a) are targeted well in key areas, such as the Pacific and Indian oceans, the scheme exacerbates the biases elsewhere, such as over the Maritime Continent and in sub-Saharan Africa.

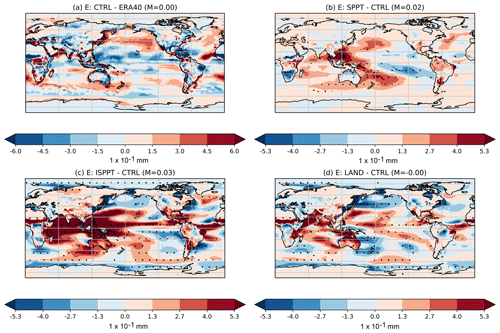
Figure 2 Mean differences in evaporation between the (a) CTRL and ERA40, (b) SPPT and CTRL, (c) ISPPT and CTRL, and (d) LAND and CTRL. Stippling indicates regions where the difference is statistically significant to the 95 % confidence interval, as measured by a two-tailed t test. In each panel, M denotes the mean of the difference. Note the difference in the scales between (a) and (b, c, d).

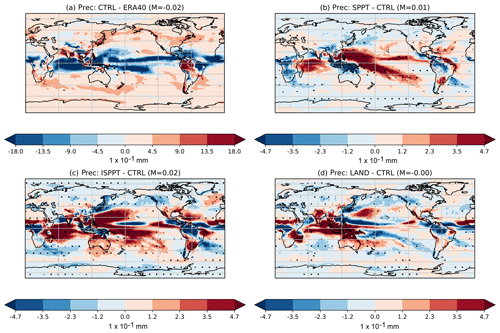
Figure 3 Mean differences in precipitation between the (a) CTRL and ERA40, (b) SPPT and CTRL, (c) ISPPT and CTRL, and (d) LAND and CTRL. Stippling indicates regions where the difference is statistically significant to the 95 % confidence interval, as measured by a two-tailed t test. In each panel, M denotes the mean of the difference. Note the difference in the scales between (a) and (b, c, d).

Table 2 Mean-square errors between the spatial means of the reanalysis (ERA40) and each EC-Earth configuration (CTRL, SPPT, ISPPT, and LAND) for T2M (2 m temperature), T (temperature) at various levels (hPa), Prec (precipitation), E (evaporation), TCC (total cloud cover), RO (total runoff), TCW (total column water), SWS (10 m wind speeds), and U (zonal winds) at different pressure levels (hPa). Values where a stochastic scheme significantly reduced the error (see Sect. 3.2) are displayed in bold.

The scheme has also notably affected clouds, with cloud cover decreasing at all levels and cloud liquid water (the vertical integral of liquid water contained within clouds in a grid-point column) robustly increasing. Figure 4b shows the spatial distribution of total cloud cover changes. The spatial pattern of cloud liquid water changes (not shown) are well correlated with these cloud cover changes, suggesting that while cloud cover has decreased overall, the remaining clouds are more optically thick. Note that because cloud cover has decreased, the actual increase in cloud water due to SPPT is likely proportionally larger than the ∼1.2 % measured. Comparing Fig. 4a and b also shows that the net impact of SPPT on total cloud cover is to significantly reduce the CTRL bias. Indeed, SPPT has almost uniformly reduced the bias everywhere, bringing the mean bias down to nearly zero. The MSE has also gone down by about 15 %.

Figure 4 Mean differences in total cloud cover between the (a) CTRL and ERA40, (b) SPPT and CTRL, (c) ISPPT and CTRL, and (d) LAND and CTRL. Stippling indicates regions where the difference is statistically significant to the 95 % confidence interval, as measured by a two-tailed t test. In each panel, M denotes the mean of the difference. Note the difference in the scales between (a) and (b, c, d). The percentage (%) units indicate the proportion of the column occupied by clouds.

The impact on the spatial biases of the 2 m temperature across all seasons are also shown in Fig. 5b. The cold bias in the CTRL simulations (Fig. 5a) across the Equator can be seen to be robustly decreased by SPPT. Conversely, the statistically significant increase in temperatures over sub-Saharan Africa introduces a bias that was not present in the CTRL model. No notable impact is made on the warm bias in the Arctic and Antarctic regions, and there is no notable change in the MSE overall, nor in the total mean bias.

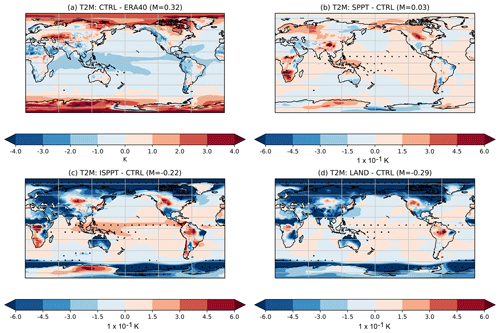
Figure 5 Mean differences in 2 m temperature between (a) CTRL and ERA40, (b) SPPT and CTRL, (c) ISPPT and CTRL, and (d) LAND and CTRL. Stippling indicates regions where the difference is statistically significant to the 95 % confidence interval, as measured by a two-tailed t test. In each panel, M denotes the mean of the difference. Note the difference in the scales between (a) and (b, c, d).

4.2 Impact on the energy budget

Figure 6a shows the mean difference between each SPPT simulation with the corresponding CTRL simulation for the globally averaged surface energy fluxes shown in Table 1. Note that the standard EC-Earth convention has been used, whereby downward fluxes are positive. Hence, a positive difference for a given flux indicates that the scheme increased the flux in the downward direction on average, whereas a negative difference indicates an increase in the upward direction on average. The benefit of adhering to this convention is that the net surface energy, always in black, can be obtained by summing all of the other flux quantities in the plots. In this way, it is easy to assess which quantity has the strongest influence on altering the net budget. The time series have also been smoothed by a 12-month running mean both to remove the seasonal cycle and to highlight the overall trends.

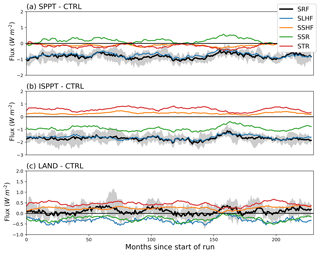
Figure 6 Global mean time series of energy fluxes for (a) SPPT minus CTRL, (b) ISPPT minus CTRL, and (c) LAND minus CTRL. Fluxes shown are latent heat flux (SLHF, blue), sensible heat flux (SSHF, orange), surface thermal radiation (STR, red), surface solar radiation (SSR, green), and net surface energy (SRF, black). Note the IFS convention that downward fluxes are positive and upward fluxes (such as sensible and latent heat flux) are negative. SRF is the sum of the other fluxes. The black shading captures 2 standard deviations around the SRF mean as sampled from the five individual differences. Time series have been smoothed with a 12-month running mean to remove the seasonal cycle.

It can be seen that the dominant impact of SPPT is a large increase in latent heat flux consistent with the strongly increased evaporation identified in the previous section. This, in turn, is the main contribution to the reduced net surface energy, with the total mean difference being −0.8 W m⁻². Compared with the baseline budget from Table 1, this clearly represents an unrealistic reduction in surface energy.

There is also a notable increase in surface solar radiation (SSR). The previous section indicated that, while cloud liquid water increased by around 1.2 %, the total cloud cover decreased at all levels through the atmosphere. Thus, it appears that while the clouds are more optically thick, which would tend to decrease SSR, the reduction in cloud cover leads to an overall increase in shortwave radiation reaching the surface.

Finally, note that because the difference is essentially constant in time, we can infer two important points. Firstly, the impact of the scheme on the energy budget is independent of the initial ocean state, and secondly, the scheme does not lead to any systematic drift: the model fully adjusts to the scheme within ∼1 month.

4.3 Impact on the hydrological budget

Figure 7a shows the percentage changes in the total column soil water content (SWVLTOT) along with the three quantities responsible for modulating this quantity: precipitation, evaporation, and total runoff. Note that precipitation and evaporation here have been restricted to land-points only, explaining why the numbers do not exactly match those in Fig. 1a. There is a small but significant decrease in the total soil water of around 1 %. As the SPPT scheme only directly interacts with atmospheric processes, this change will be driven by the observed changes in precipitation and evaporation. Over land, precipitation decreases by around 1.7 % and evaporation increases by about 1 %, both of which contribute to the decrease in soil water. The notable decrease in runoff is likely a consequence of the reduction in water in the soil column. By reference to Table 2, the runoff changes, seen in Fig. 8b are beneficial overall, reducing the MSE.

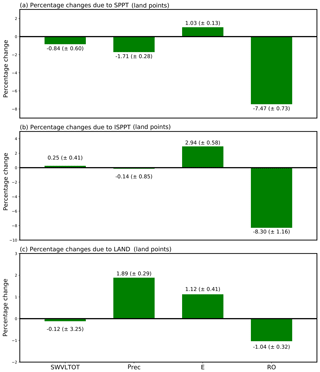
Figure 7 Average percentage change, relative to CTRL, in the global mean of (a) SPPT simulations, (b) ISPPT, and (c) LAND. All data were restricted to land-points only. For LAND, Antarctica was also excluded. Variables shown are total soil water content (SWVLTOT), precipitation (Prec), evaporation (E), and runoff (RO). Uncertainty estimates are twice the standard deviation of the five individual differences.

5 The impact of ISPPT

5.1 Impact on the mean state

Figure 1b shows the percentage changes in global means induced by the ISPPT scheme. The signal of increased evaporation and cloud liquid water seen with SPPT is greatly amplified. Figure 2c shows the spatial distribution of evaporation changes, which as with SPPT are strongest over the tropical oceans. The total increase in evaporation is even greater than that from SPPT, and again represents an overall increase in the global mean bias. However, there is an enhanced spatial coherence between the local changes from ISPPT and the CTRL bias (Figure 2a). It can be seen that the sign of the ISPPT changes are generally the opposite of the sign of the CTRL bias, indicating that the scheme is effectively targeting the local biases, with a notable exception being the ocean region south of Australia. This is reflected in the fact that while the global mean bias has increased, the MSE (Table 2) has decreased.

Figure 3c shows the changes in precipitation. Again, local biases are well targeted, with the MSE decreasing even more than with SPPT. The mean bias relative to reanalysis has been reduced to near zero.

Unlike SPPT, total cloud cover has only decreased by a very small amount, due entirely to a decrease in the high-level clouds which dominates a small increase in low and mid-level clouds. Figure 4c shows the change in total cloud cover, where areas of overall decrease indicate decreases in high-level cloud cover. As with SPPT, the changes serve to decrease the CTRL bias, both in total and locally, as can be seen by a notable decrease in the MSE (Table 2). Interestingly, there is great spatial coherence between these changes and those seen for SPPT in Fig. 4b. Indeed, an examination of these and other variables generally suggests that a first-order approximation of the mean impact of ISPPT is a stronger amplitude version of the impact of SPPT, but with the changes being even more closely correlated with the local biases, as seen with evaporation and precipitation above. The added freedom of non-correlated perturbations with ISPPT allows for a stronger influence on non-linear climate processes, most notably those associated with convective processes (Christensen et al., 2017b).

Figure 5c shows the local changes in 2 m temperature. As with SPPT, the cold bias along the Equator is reduced, but unlike SPPT, the warm biases in the Arctic and Antarctic regions are also reduced. The globally averaged mean bias has been reduced by nearly 70 %, and the MSE has decreased by nearly 25 %.

5.2 Impact on the energy budget

Figure 6b shows the flux impact of ISPPT. As with SPPT, the dominant effect is from the substantial increase in evaporation, as seen in Fig. 2c. In contrast to SPPT, ISPPT also results in a substantial reduction in SSR of almost 1 W m⁻². Figure 1b shows that while there was a small decrease in total cloud cover, low-level cloud cover (the layer reflecting the most solar radiation), has increased by around 0.5 %. Even more notably, the cloud liquid water content has increased by nearly 5 %, increasing the albedo of these clouds significantly. These factors combine to explain the decreased SSR. A mild increase in sensible heat flux and thermal radiation cannot compensate for this, such that the net result is a large decrease in surface energy of around 1.7 W m⁻² relative to CTRL. By reference to Table 1, this represents a large divergence from observed values.

As with SPPT, the impact of the scheme is effectively constant in time, and therefore independent of the underlying initial ocean state.

5.3 Impact on the hydrological budget

Figure 7b shows percentage changes for the hydrological budget for the ISPPT scheme. There is no notable change in precipitation over land, but evaporation has increased by around 3 %. This will have a drying effect on the top soil layer. Despite this, no meaningful change is seen in the total column soil water. One possible explanation for this is to first note that in general, if the top soil layer holds more water, heavy rainfall events will more frequently saturate the surface, triggering the land scheme to expel a lot of this water as runoff at the top soil layer. This will tend to inhibit moisture from sinking down to the lower soil layers. Conversely, if the top layer is drier, as seen with ISPPT (due to e.g. the increased evaporation), runoff at the top soil layer will not be triggered as easily during rainfall, allowing more water to reach the lower layers. In this way, increased evaporation can be balanced by reduced runoff to produce no overall change in total soil water. Noting the reduced runoff in Fig. 7b, presented visually in Fig. 8c, we speculate that this is the reason that there is no change in soil water due to ISPPT. Of relevance to this is the fact that more frequent heavy rainfall events may be expected with ISPPT, as this is the case with SPPT (Watson et al., 2017), and this could easily trigger the above mechanism.

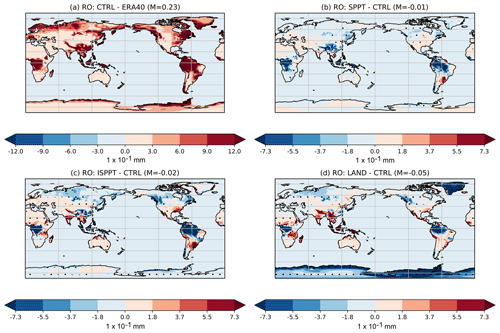
Figure 8 Mean differences in runoff between the (a) CTRL and ERA40, (b) SPPT and CTRL, (c) ISPPT and CTRL, and (d) LAND and CTRL. Stippling indicates regions where the difference is statistically significant to the 95 % confidence interval, as measured by a two-tailed t test. In each panel, M denotes the mean of the difference. Note the difference in the scales between (a) and (b, c, d).

We finally note from Table 2 that the runoff changes are broadly beneficial, reducing the MSE even more than SPPT does.

6 The impact of stochastic land on the mean state

6.1 Impact on the basic mean state

Figure 1c shows the percentage changes in global means induced by LAND. As with both SPPT and ISPPT, evaporation increases. Spatial changes here are displayed in Fig. 2d, where visual inspection shows that the changes mostly serve to reduce the CTRL bias (Fig. 2a). This is confirmed by a reduction in the MSE, as seen in Table 2. As we will see in the section on hydrology, the changes in evaporation over land are strongly correlated with changes in runoff. As evaporation changes over land can have knock-on effects on the global circulation more broadly, this already suggests a mechanism whereby the LAND scheme, which only directly interacts with soil processes, can still lead to global mean state changes.

For precipitation, seen in Fig. 3d and Table 2, while the MSE has decreased compared with the CTRL runs, the mean bias remains unchanged. While the precipitation bias over the Indian ocean and Maritime Continent are lower, biases over India are higher and the changes over the Pacific ocean are fairly ambiguous in their merit.

Unlike SPPT and ISPPT, the LAND scheme has a more notable impact on total column water, increasing it by nearly 1 %. The cloud cover changes are similar in characteristic to those of ISPPT, with low and mid-level cloud cover increasing, and high-level cloud cover decreasing: Fig. 4d shows the spatial distribution of these changes. It can be seen that while the LAND scheme has reduced biases over all the major continents (with the exception of Australia), as well as over the Indian Ocean, it has had only a limited impact over the Pacific and Atlantic oceans. Consequently, the MSE, recorded in Table 2, has not changed relative to CTRL.

Figure 5d shows the spatial changes in the 2 m temperature, where the major, statistically robust change is a big reduction in the warm bias in the Arctic and Antarctic regions. This has reduced the overall mean bias relative to the reanalysis by around 90 %, as well as notably reducing the MSE.

6.2 Impact on the energy budget

Turning on the LAND scheme only has a small impact on the energy budget (Fig. 6c), increasing net surface energy by about 0.1 W m⁻² relative to the CTRL. The primary culprit appears to be a decrease in outgoing longwave radiation. Figure 1c shows that atmospheric water vapour has increased by about 1 %, which would (by strengthening the greenhouse effect) serve to trap more thermal radiation in the atmosphere. While the same figure shows that high-level cloud cover has decreased, which would tend to negate that effect, the increase in mid-level cloud cover may counteract the change in high-level cloud to a large degree, such that the water vapour increase ends up being the dominant driver of energy budget changes.

As with SPPT and ISPPT, the impact of the scheme is effectively constant in time, and therefore independent of the underlying initial ocean state.

6.3 Impact on the hydrological budget

Figure 7c shows the percentage changes observed upon including the LAND scheme, restricted to land-points only. The scheme has a big impact on both runoff and soil moisture over Antarctica. However, the runoff scheme typically does not behave realistically here, where the soil is trapped under thick layers of ice. To avoid the quantified impacts being dramatically skewed from this contribution, we excluded Antarctica from the data prior to computing percentage changes².

Firstly, it can be seen that there is no statistically robust change to the overall soil water content. This is puzzling at first glance, as it can also be seen that there is an increase in precipitation over land which is not cancelled out by an equal amount of evaporation; runoff has also decreased robustly by around 1 %. These changes would be expected to lead to an increase in soil water. Indeed, examining the spatial distribution of soil water changes (not shown), one finds that areas of increased precipitation (Fig. 3d) mostly correspond to areas of increased soil water content, and vice versa. The two main exceptions are over Greenland and Siberia, where a behaviour similar to that seen in Antarctica is observed (strongly decreased soil water and runoff) even with no meaningful change in precipitation. Figure 8d shows the spatial distribution of runoff changes. The areas of increased runoff correlate well with areas of increased precipitation/soil water content, with runoff triggered more frequently the wetter the soil. The exceptions of Greenland and Siberia are clearly visible.

This suggests that in regions not dominated by ice and snow, long-term changes in runoff and soil water are driven by the long-term circulation changes induced when stochastically perturbing hydraulic conductivity. However, in regions such as Siberia and Greenland, there is a sharp decrease in soil water content within the first month of each LAND simulation, with no associated change in surface evaporation. This extra decrease in soil water, independent of precipitation and evaporation changes, explains why the total soil water mean has not changed overall.

Comparing the runoff impacts with the CTRL bias (Fig. 8a, d), we see that the local biases have mostly been improved, with the MSE (Table 2) decreasing by about 10 %, suggesting the increased variability in the LAND scheme is serving to reduce the model bias.

7 Impact on the atmospheric circulation

We now assess the impact of all three schemes on two key components of the atmospheric circulation: the Hadley cell and the quasi-biennial oscillation (QBO). Our examination of the former is motivated by the fact that, as we have seen in the above sections, the schemes tend to have a large impact on tropical convection, hinting at possible changes in the Hadley cell circulation. The motivation for examining the latter comes from an earlier study, Leutbecher et al. (2017), on the impact of the SPPT scheme on the IFS in shorter-range forecasts. It was found in ibid that the most notable degradation of the scheme on the model was in the upper level winds, where the QBO dominates variability. This was noted as a potential source of concern, as literature suggests that the QBO influences the extratropical winter climate. Table 2 shows the MSE of zonal winds at various levels: in agreement with ibid, we see a large increase in the bias at the 10 hPa level. Therefore, we explicitly examine the performance of the QBO in our experiments to assess the possible changes.

7.1 Impact on the Hadley cell

The impact of the stochastic perturbations on the atmospheric circulation is considered through analysis of the Hadley circulation. The Hadley cell varies with the seasonal cycle, and is stronger and wider in the winter hemisphere: we consider the characteristics of the dominant Hadley cell separately for the key seasons December–January–February (DJF) and June–July–August (JJA). We characterize the zonally averaged overturning circulation using a stream function, ψ, defined as a function of latitude and height, following Waliser et al. (1999). The procedure is performed separately for each simulation.

To consider the effect of stochastic physics, we calculate three summary diagnostics for the cell. Firstly, the strength of the overturning is characterized using the maximum of the stream function. The width of the overturning cell is indicated by estimating the latitude of the upwelling and downwelling branches of the cell respectively. This is defined as the latitude at which the stream function changes sign at the 700 hPa level. The 700 hPa level was chosen as this corresponds to the approximate level at which the stream-function maximum is found. These results are shown for each ensemble member in Fig. 9 using the five scattered points. The diagnostics are also shown for ERA40 for the five time periods corresponding to the five ensemble members.

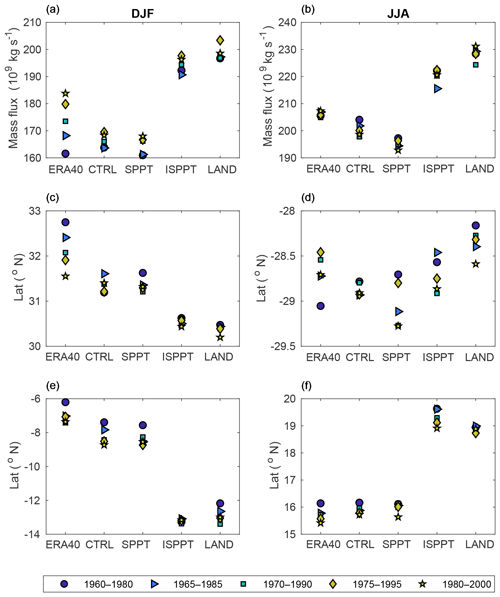
Figure 9 Impact of stochastic parameterizations on the Hadley circulation. The magnitude of the overturning circulation indicated by the maximum of the stream function of the dominant cell in (a) DJF and (b) JJA for each scheme. The latitude of the downwelling branch of the dominant (winter hemisphere) cell in (c) DJF and (d) JJA. The latitude of the upwelling branch of the dominant (winter hemisphere) cell in (e) DJF and (f) JJA. The data diagnostic is shown for each of the five AMIP simulations in turn, the darker colours indicate earlier years, ranging from dark blue (1960–1980) to yellow (1980–2000).

Figure 9a and b show the strength of the overturning circulation for each simulation and both seasons. The SPPT scheme shows no significant impact on the strength of the overturning in DJF, and a slight (although not significant) weakening in JJA. In contrast, both the ISPPT and LAND approaches show a significant strengthening of the overturning cell in both DJF and JJA. For all simulations, the JJA cell is stronger than the DJF cell. While the CTRL and SPPT simulations have an overly weak Hadley cell, the Hadley cell in the ISPPT and LAND experiments is too strong.

Figure 9c and d show the latitude of the downwelling branch of the dominant cell for each season. As for the strength of the circulation, SPPT has no significant impact on this diagnostic. Both the ISPPT and LAND schemes lead to a significant equatorward shift of the downwelling latitude in DJF, in contrast to what is seen in reanalysis. In JJA all simulations are in agreement with ERA40, and only the LAND scheme leads to a slight equatorward shift.

Figure 9e and f show the latitude of the upwelling branch of the circulation. SPPT leads to no significant change in this diagnostic, whereas the ISPPT and LAND schemes lead to a large poleward shift. This introduces a substantial bias when compared with ERA40, which needs to be understood. The net effect of this is to increase the width of the Hadley circulation in the ISPPT and LAND simulations.

The Hadley circulation is changing in response to climate change. There is evidence that it has widened over recent decades (Hu and Fu, 2007; Seidel and Randel, 2007), and some evidence that it has also strengthened (Seager et al., 2007), although GCMs struggle to reproduce the observational signal (Mitas and Clement, 2005; Johanson and Fu, 2009). To compare the climate change impact on the Hadley circulation for each stochastic model, we indicate the years covered by each simulation in Fig. 9.

The deterministic simulations show a general strengthening of the DJF Hadley circulation, although a weakening of the JJA Hadley circulation is seen. This trend is also observed in DJF for the three stochastic models, although the signal in JJA is more mixed. While there is no climate change signal observed in the latitude of the downwelling branch for any simulation, the simulations generally agree that the DJF upwelling branch has shifted poleward. The exception is the ISPPT simulation, which does not show a strong sensitivity in this diagnostic.

7.2 Impact on the quasi-biennial oscillation

The QBO is a periodic downward propagation of easterly and westerly wind regimes which accounts for the majority of variability in the equatorial stratosphere (Baldwin et al., 2001), also exerting a notable influence on the extratropical atmosphere through modulating extratropical waves. Its period is typically estimated to be around 28 months.

Figure 10 shows the average QBO period across each simulation for each of the four experimental set-ups, as well as that for ERA-Interim. For each scheme, the period marked with a cross in the figure is the average period across the five ensemble members; the error bar shows 2 standard errors of this mean estimate. The period was diagnosed here using zonal equatorial (10^∘ S–10^∘ N) winds at 50 hPa, which were zonally averaged. This produces a periodic time series from which we can readily estimate the average spacing between zero-crossings to determine the average period. When applied to the ERA-Interim reanalysis dataset, this produces a period of almost exactly 28 months, suggesting that this method captures the expected period well. It can be seen that the deterministic model itself cannot achieve nearly as long a period, falling just below 21 months. Both SPPT and ISPPT have reduced the period by a small amount, but compared with the initial bias of the deterministic model itself these changes are small. While the mean period of LAND is slightly smaller than CTRL, the error bars are large enough to imply that this decrease is not statistically robust.

Figure 10 Estimates of the QBO period, as measured using equatorial zonal winds at 50 hPa. The red crosses show the mean across the five estimates (computed from the five ensemble members) for each scheme, and the error bars capture twice the standard error of this mean estimate. The ERA-Interim reanalysis product is shown in black for comparison.

Figure 11 shows a time–pressure level section of monthly averaged zonal wind, restricted to the equatorial region 10^∘ S–10^∘ N with the seasonal mean removed. This gives the usual visual representation of the QBO for the ensemble members covering the 1980–2000 period, with ERA-Interim over the same period also shown; the behaviour of these members are representative of the full ensemble, where there is little year to year variability in the degradation of the QBO. It can be seen that EC-Earth indeed struggles to attain both a strength, period, and extent of downwelling comparable to ERA-Interim. None of the stochastic schemes notably change this; in particular, there is no notable additional degradation compared to the CTRL simulation.

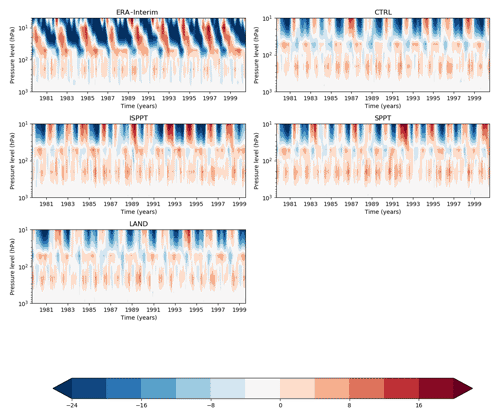
Figure 11 Visualization of the QBO (time–pressure level section of zonal winds between 10^∘ S and 10^∘ N with the seasonal mean removed) for the ensemble member covering 1980–2000, the period overlapping the most with ERA-Interim. Pressure levels are plotted according to a logarithmic scale for ease of interpretation. Units are in metres per second (m s⁻¹).

8 Discussion and conclusions

8.1 Discussion

Because the impact of the schemes appears to be firmly in place within the first month of each experiment, a comprehensive study pinning down the cause of the observed changes would require a more process-based investigation of the rapid response. As the experiments considered in this paper were constructed to examine long-term rather than rapid changes, such an investigation will be left to future work. However, for completeness, we include some discussion here on what the key processes at play may be. We note that an examination of the rapid response of EC-Earth to SPPT was carried out in Strommen et al. (2019). Analysis in that paper shows that the most robust, rapid change when turning SPPT on is an increase in cloud liquid water and evaporation, thereby largely supporting the arguments presented in what follows.

With both SPPT and ISPPT, the dominant impact on the energy budget is increased evaporation. In the IFS, the amount of evaporation at a grid point depends primarily on the surface wind speeds and the extent to which the specific humidity at the surface grid point differs from the saturation humidity (a function of surface temperature). While wind speeds do increase by about 1.4 % on average with ISPPT, the mean wind speeds are unchanged with SPPT, with a tiny increase of only 0.06 %. Given that the increase in evaporation of both SPPT and ISPPT are of the same order of magnitude, this suggests that changes in humidity are a key factor. Because sea surface temperatures are held fixed, such changes will be, to first order, driven by changes in the water content of the atmosphere as opposed to temperature changes at the surface. One possibility is that the increase in cloud liquid water is depleting the near-surface humidity, causing more favourable conditions for evaporation. The fact that both cloud liquid water and surface wind speeds increase more with ISPPT could then explain why this impact is amplified in those experiments. Another possibility is that the first-order impact is on convection in the tropics, which may be activated more frequently with SPPT/ISPPT. This could lead to a drying of the boundary layer, promoting more evaporation in response.³

Furthermore, the increase in cloud liquid water with both SPPT and ISPPT could be due to an asymmetric response to stochastic perturbations in the convection schemes. Given a parcel of air close to saturation, whether the model actually triggers condensation depends sensitively on the humidity and temperature tendencies, both of which are perturbed by the stochastic schemes. A perturbation in one direction may result in condensation, and thereby an increase in the cloud liquid water, whereas a perturbation in the other direction leaves the parcel stable and the total cloud liquid water unchanged. As the stochastic perturbations are zero mean, it is expected that these two scenarios will occur at the same rate, such that the net impact of the perturbations is to increase the total amount of cloud liquid water, as observed. An important point here is that the SPPT/ISPPT scheme has a “supersaturation limiter” in place (Palmer, 2012). This limiter essentially ensures that any perturbations which would result in a parcel of air being pushed into a supersaturated state are ignored. Therefore, the mechanism described above cannot take place within a single time step. Nevertheless, a perturbation may still push a parcel of air closer to saturation, whereby the model dynamics themselves may bring the parcel towards condensation in the subsequent time step. In this way, SPPT/ISPPT, by generally broadening the distribution of temperature/humidity tendencies, may lead to increased condensation on average.

We suggest that the changes in evaporation/convection and cloud liquid water are the main sources of large-scale changes to the mean climate caused by SPPT and ISPPT. These variables strongly control cloud formation, cloud albedo and latent heat release, which are the dominant sources of changes to the energy budget.

In addition, changes to evaporation (and thereby precipitation) dominate the hydrological budget. As the atmospheric circulation is also coupled to thermodynamic processes, especially in the tropics, it is likely that the observed impact on the Hadley cell can also be traced to these changes in the hydrological cycle. This is supported by Numaguti (1993), who showed that the strength and meridional structure of the Hadley cell is closely linked to the distribution of evaporation. With both ISPPT and LAND, the change in the Hadley cell is largely detrimental compared to the reanalysis, implying that some of the positive impacts seen on the mean state may be due to a compensation of errors. This would need to be studied more carefully in future work.

For the LAND scheme, the first-order impact appears to be regional changes in average runoff. That such changes should be expected to occur can be understood by reference to Eq. (3), which defines hydraulic conductivity. Because runoff is triggered when the soil becomes saturated, its triggering is intimately linked to the γ∕γ_sat ratio, which reaches its maximum of one precisely at saturation. This ratio, as seen in Eq. (3), is highly non-linear in the perturbed parameter α, implying that even mean-zero perturbations can be expected to alter the mean state. This will lead to regional changes in the moisture content of the soil layer, which, in turn, influences evaporation over land. The net impact is a decrease in runoff and therefore an increase in evaporation. This change permeates through to influence the rest of the climate system, including an increase in total column water and large changes in the vertical distribution of cloud coverage.

8.2 Conclusions

Three stochastic schemes are introduced into the atmosphere and land components of the EC-Earth climate model. The stochastic schemes incorporate zero-mean perturbations into the model physics to represent uncertainty associated with unresolved, sub-grid-scale variability. The interaction of these perturbations with the non-linear Earth system results in systematic changes to the mean state of the model in a way that is not obvious a priori. Schemes that are fairly similar (SPPT and ISPPT) may have very different impacts, and schemes that only directly affect a relatively small component of the model (LAND) may still notably change the global circulation. This highlights the importance of representing random model error in climate models, as well as in initialized simulations, where stochastic schemes have long been used to improve the reliability of forecasts (Palmer et al., 2009; Berner et al., 2017).

Our experiments showed that the inclusion of all three stochastic schemes, particularly ISPPT and LAND, led to notable reductions in model biases compared with the deterministic model. This is seen perhaps most strikingly for 2 m temperature, precipitation, and total cloud cover, three important quantities where both the mean bias and the MSE were reduced. The distribution of runoff, a key driver of land–atmosphere interaction in EC-Earth, was also improved by all three schemes. This demonstrates that the inclusion of stochastic schemes can have a beneficial impact on a model's long-term climate mean state.

Conversely, none of the schemes are able to improve the representation of the QBO, and the Hadley cell becomes too strong and widens too far polewards with ISPPT and LAND. This latter point is likely related to changes in evaporation: while the spatial changes are targeting model biases, leading to a reduced MSE, the overall amplitude of the change is too large. Changes in evaporation may be due to increased tropical convection. The impact of this change in evaporation is seen most clearly in the energy budget, where both schemes significantly reduced the net surface energy from the relatively realistic levels attained in the deterministic model. However, it is critical to recall that these schemes have not been tuned, whereas the deterministic version of EC-Earth used as a reference has been extensively tuned, specifically when it comes to having a realistic energy budget. Tuning parameters for EC-Earth include constants that regulate processes such as entrainment and convection in the atmospheric case, and runoff in the LAND scheme case. In particular, the intensity and frequency of convection/runoff is modulated by these parameters, and tuned in a way to achieve realistic mean states. Non-linear impacts of stochastic schemes can strongly alter both the intensity and frequency of these processes, as our experiments have shown, and this significantly alters the mean state of the model.

Therefore, it is clear that the inclusion of a stochastic scheme must be treated in the same way as the inclusion of any other new parametrization scheme, in that it will typically require a full re-calibration of the model parameters. By doing so, one may be able to obtain all the benefits to second-order diagnostics in the climate model in question (ENSO, the Asian monsoon, the MJO, European blocking, etc.) while still maintaining a realistic mean state and energy budget. In fact, given the improvements seen in key regional biases in our experiments, such a tuning procedure could potentially lead to a notably improved mean state compared to a deterministic model. This will be examined further as part of the PRIMAVERA project, where these schemes will be tested in a fully coupled atmosphere–ocean framework. This work, presented in a future paper, will also include the stochastic ocean and sea ice schemes and thereby examine the impact of adding stochasticity in every component.