the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
CompLaB v1.0: a scalable pore-scale model for flow, biogeochemistry, microbial metabolism, and biofilm dynamics
Heewon Jung
Hyun-Seob Song
Microbial activity and chemical reactions in porous media depend on the local conditions at the pore scale and can involve complex feedback with fluid flow and mass transport. We present a modeling framework that quantitatively accounts for the interactions between the bio(geo)chemical and physical processes and that can integrate genome-scale microbial metabolic information into a dynamically changing, spatially explicit representation of environmental conditions. The model couples a lattice Boltzmann implementation of Navier–Stokes (flow) and advection–diffusion-reaction (mass conservation) equations. Reaction formulations can include both kinetic rate expressions and flux balance analysis, thereby integrating reactive transport modeling and systems biology. We also show that the use of surrogate models such as neural network representations of in silico cell models can speed up computations significantly, facilitating applications to complex environmental systems. Parallelization enables simulations that resolve heterogeneity at multiple scales, and a cellular automaton module provides additional capabilities to simulate biofilm dynamics. The code thus constitutes a platform suitable for a range of environmental, engineering and – potentially – medical applications, in particular ones that involve the simulation of microbial dynamics.
- Article
(2222 KB) - Full-text XML
- BibTeX
- EndNote
Biogeochemical turnover in Earth's near-surface environments is governed by the activity of microbes adapted to their surroundings to catalyze reactions and gain energy. In turn, these activities shape the environmental composition, which feeds back on metabolic activities and creates ecological niches. Such feedbacks can be captured by reactive transport models that compute the evolution of geochemical conditions as a function of time and space and simulate microbial activities in porous media (Meile and Scheibe, 2019). Commonly used macroscopic reactive transport models simplify small-scale features of natural porous media. For example, heterogeneous pore geometry and transport phenomena are represented by only a few macroscopic parameters such as porosity, permeability, and dispersivity (Steefel et al., 2015). However, such simplifications can lead to a disparity between model estimations and actual observations because these models do not resolve the physical and geochemical conditions at the scale that is relevant for microbial activity (e.g., Molins, 2015; Oostrom et al., 2016). Furthermore, microbial reaction rates are often formulated using Monod expressions, which describe a dependency of metabolic rates on nutrient availability but substantially simplify the complex metabolic adaptation of microbes in changing environments. This recognition has prompted the development of constraint-based models including, for example, COMETS (Harcombe et al., 2014), BacArena (Bauer et al., 2017), and IndiMeSH (Borer et al., 2019), which have enabled detailed descriptions of complex microbial metabolisms and metabolic interactions (Dukovski et al., 2021). However, most constraint-based models are not designed to capture combined diffusive and advective transport of metabolites in heterogeneous subsurface environments and are not optimized to handle such settings in a computationally efficient way. Notably, computational efficiency and the integration of adequate formulations of microbial function have been identified as critical aspects in pore-scale models of microbial activity (Golparvar et al., 2021).
To account for the feedback between environmental conditions, chemical processes, microbial metabolism, and structural changes in the porous medium caused by these activities, we introduce a novel pore-scale reactive transport modeling framework with spatially explicit descriptions of hydrological and biogeochemical processes. Our work complements existing efforts, encompassing both individual- and population-based spatially explicit microbial models reviewed by König et al. (2020), some of which take into consideration the structure of the porous medium. Our modular framework is developed to account for various chemical reactions and/or genome-scale metabolic models with advective and diffusive transports in porous media at the pore scale. The lattice Boltzmann (LB) method is used to compute fluid flow and solute transport in complex porous media, capable of simulating both advection- and diffusion-dominated settings. Microbial metabolism and chemical reactions are incorporated as source or sink terms in the LB method solving mass conservation equations. These sources or sinks can be described classically using approximations such as Monod kinetics (Tang et al., 2013) or can be derived from cell-scale growth and metabolic fluxes simulated with flux balance analysis (Orth et al., 2010). Biomass dynamics can be described by keeping track of cell densities (similar to chemical concentration fields) of different organisms or populations, with cell movement either based on an advection–diffusion formulation or using a cellular automaton approach. In addition, we incorporate a surrogate modeling approach to make larger-scale simulations possible. Thus, the framework provides options either to maximize computational efficiency via the use of surrogate models or to directly utilize well-established metabolic modeling environments without losing the inherent parallel scalability of the LB method. The model is validated by comparing model simulations to published simulation results. We demonstrate the flexibility of the new microbial reactive transport framework, its scalability, and the benefits of using surrogate models to circumvent computational bottlenecks posed by flux balance analysis. Our work therefore facilitates cross-disciplinary efforts that integrate bioinformatic approaches underlying cell models with descriptions suitable to resolving the dynamic nature of natural environments. This allows for the representation of microbial interactions, which is a major challenge to our current quantitative understanding of microbially mediated elemental cycling (Sudhakar et al., 2021).
To establish a modeling framework that builds on the existing and future knowledge and know-how from multiple disciplines, our approach uses the open-source software Palabos (Parallel Lattice Boltzmann Solver) and integrates it with the open-source linear programming solver GLPK (GNU Linear Programming Kit) and the COBRApy (CPY) Python package for genome-scale metabolic modeling. Palabos is a modeling platform that has established itself as a powerful approach in the field of computational fluid dynamics based on the lattice Boltzmann (LB) method. The Palabos software is designed to be highly extensible to couple complex physics and other advanced algorithms without losing its inherent capability of massive parallelization (Latt et al., 2021). Palabos has been parallelized using the Message Passing Interface, where computational domains are subdivided while minimizing the inter-process communication. It has been used for building modeling platforms to simulate deformable cell suspensions in relation to blood flows (Kotsalos et al., 2019) and complex subsurface biogeochemical processes at the pore scale (Jung and Meile, 2019, 2021). It is highly scalable and hence was chosen as a high-performance modeling framework to be integrated with our representations of chemical and microbial dynamics. GLPK is an open-source library designed for solving linear programming (LP), mixed integer programming and other related problems (GLPK, 2022). It contains the simplex method, a well-known efficient numerical approach to solve LP problems, and the interior-point method, which solves large-scale LP problems faster than the simplex method. GLPK provides an application programming interface (API) written in C language to interact with a client program. COBRApy is an object-oriented Python implementation of constraints-based reconstruction and analysis (COBRA) methods (Ebrahim et al., 2013), which is suitable to be integrated with other libraries without requiring commercial software. Through a simple Python API, the fast evolving and expanding biological modeling capacity of COBRApy, which includes features such as flux balance analysis (FBA), flux variability analysis (FVA), metabolic models (M models), and metabolism and expression models (ME models), can be employed.
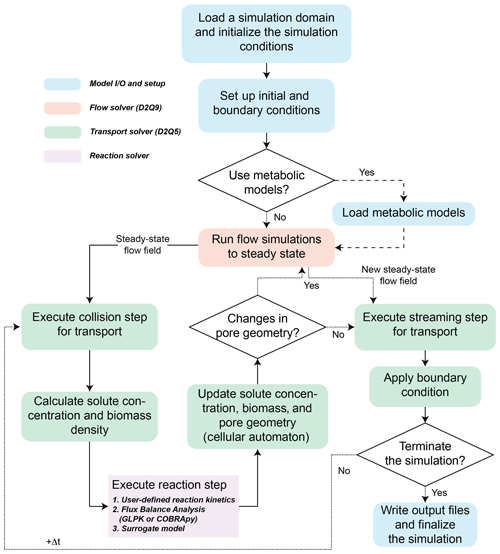
CompLaB simulates a fully saturated 2D fluid flow and solute transport at the pore scale based on the LB method implemented in Jung and Meile (2019, 2021). These earlier efforts established some of the underlying model developments, such as the simulation of the flow field, mass transport, and biochemical processes including kinetic rate expressions and cellular automaton implementation of biofilm growth. This study expands on the previously established models to offer a much broader applicability by building the modular structure that makes the use of flux balance and surrogate models possible. The LB method is particularly useful for simulating subsurface processes because boundaries between solid and fluid can be handled by a simple bounce-back algorithm (Ziegler, 1993) in addition to its massive parallelization efficiency (Latt et al., 2021). For these reasons, the LB method has been applied to simulate a broad range of pore-scale reactive transport processes (e.g., Huber et al., 2014; Kang et al., 2007; Tang et al., 2013). The simulations are guided by an input file, CompLaB.xml, that sets the scope of the simulation and capabilities utilized through command blocks that define the model domain, chemical state variables, microorganisms, and model input and output (Fig. 1). Below, the features of the model are presented, and we refer to the manual in the code repository for examples of the implementation.
3.1 The lattice Boltzmann flow and mass transport solvers
The LB method retrieves the numerical solutions of the Navier–Stokes (NS) for fluid flow and advection–diffusion-reaction equations (ADREs) for solute transport by solving the mesoscopic Boltzmann equation across a defined set of particles (Krüger et al., 2017). CompLaB obtains a steady-state flow field by running a flow solver with a D2Q9 lattice BGK (Bhatnagar–Gross–Krook; Bhatnagar et al., 1954) model defined as
where fi(r,t) is the ith discrete set of particles streamed from a position r to a new position r+ci after a time step with lattice velocities ci(c0 = [0,0], c1 = [1,0], c2 = [0,1], c3 = [−1,0], c4 = [0,−1], c5 = [1,1], c6 = [−1,1], c7 = [−1,−1], c8 = [1,−1]). τf is the relaxation time related to the fluid viscosity νf (; cs is a lattice-dependent constant; here, = ). The equilibrium distribution function for fluid flow () is given by
where ωi is the lattice weights (ω0 = , ω1−4 = , ω5−8 = ), ρ is the macroscopic density (ρ=Σfi), ρ0 is the rest state constant, and u is the macroscopic velocity calculated from the momentum (ρu = Σcifi). The steady-state flow field is then imposed on a transport solver defined as
where gi(r,t) represents the discrete particle set i of a transported entity j at position r and time t. is the relaxation time for solute transport related to the diffusivity (Dj = ). The equilibrium distribution function for transport () using a D2Q5 lattice for numerical efficiency, which, satisfying the isotropy requirement for a LB transport solver, is given by
with the lattice weights ω0 = and ω1−4 = , lattice velocities c0−4, and the solute concentration Cj (). In solving an advection–diffusion problem, CompLaB adjusts the value of , which controls the length of a time step, to obtain a user-provided Péclet number (Pej = ) for a given average flow velocity U and a user-provided characteristic length L. With a steady-state flow field obtained from the solution of Eq. (1) and a reaction step , the LB transport solver recovers an ADRE with the following form:
Here, the transported entity j includes solute concentrations (C) and planktonic biomass densities, and R is a reaction term computed by the reaction solver of CompLaB as described below.
3.2 Reactions
The reaction step () computation is separated from a transport computation via the sequential non-iterative approach (Alemani et al., 2005). A unique feature of CompLaB is that its reaction solver can compute biochemical reaction rates R through (1) kinetic rate expressions, (2) flux balance analysis, and (3) a surrogate model such as a pre-trained artificial neural network or combinations thereof, by summing their contributions to the net reaction rates of individual state variables.
3.2.1 Kinetic rate expressions
CompLaB provides a C template that users can adapt to formulate kinetic rate expressions using metabolite concentrations and biomass densities (defineReactions.hh). This is designed to accommodate user-specific needs and to enable simulating various microbial dynamics including Monod kinetics, microbial attachment and detachment, and arbitrary rate expressions defined by the user. Reactions can be restricted to particular locations using material numbers (mask) differentiating fluid, biomass, and grain surfaces.
Local biomass densities and concentrations calculated after the collision step of transport solvers are transferred to the function as vectors B and C, where the vector elements follow the order defined in the user interface (CompLaB.xml). The biomass density and metabolite concentrations are updated according to
where γt values are the cell-specific biomass growth rates, Rt values are the microbially mediated reaction rates, expressed as the product of metabolite uptake/release rates per cell (Ft) and the cell density Bt (i.e., Rt=FtBt), calculated every time step for every pore and biomass grid cell.
3.2.2 Flux balance analysis
For genome-enabled metabolic modeling, CompLaB loads metabolic networks and calculates microbial growth rates as well as metabolite uptake/release rates through an FBA method (Orth et al., 2010). FBA investigates the metabolic capabilities by imposing several constraints on the metabolic flux distributions. Assuming that metabolic systems are at steady state, the system dynamics for a metabolic network are described by the mass balance equation Sv = 0. Here, S is a m × n matrix with m compounds and n reactions, where the entries in each column are the stoichiometric coefficients of the metabolites composing a reaction and v is a n × 1 flux vector representing metabolic reactions and uptake/release of chemicals by the cell. Most metabolic models have more reactions than compounds (n > m), meaning that there are more unknowns than equations. To solve such underdetermined systems, FBA confines the solutions to a feasible set by imposing constraints on metabolic fluxes lb (lower bounds) ≤ v ≤ ub (upper bounds) and applies an objective function f(v) = cTv, where c is the vector of weights for the objective function to identify an optimal solution. Commonly used objective functions include maximization of biomass yield, maximization of ATP production, and minimization of nutrient uptake (Nikdel et al., 2018). CompLaB utilizes the stoichiometric matrix S from standard metabolic databases such as BiGG and KEGG, which are widely used in FBA simulation environments (e.g., COBRA toolbox, Heirendt et al., 2019; COBRApy, Ebrahim et al., 2013; KBase, Arkin et al., 2018). Therefore, CompLaB can integrate many existing in silico cell models.
CompLaB computes the solution of the metabolic models at each point in space and time for each organism or microbial community (if the model represents multiple microorganisms) and updates biomass density and metabolite concentrations according to Eqs. (6) and (7). The metabolic uptake fluxes are set through imposing constraints by defining the lower bound (lb) of a chemical (uptake fluxes are negative) through one of the following approaches. The first is the parameter-based method employed by Harcombe et al. (2014), setting the metabolic fluxes in analogy with Michaelis–Menten kinetics using a maximum uptake rate (Vmax; e.g., , where gDW is gram dry weight):
where C is a local metabolite concentration (e.g., mM) and Ks is a half-saturation constant (e.g., mM). The second is the semi-linear approach employed by Borer et al. (2019). This method replaces Vmax with C(BΔt)−1, where B is a local biomass density (e.g., gDW L−1) and Δt is the length of a time step (e.g., h):
If Ks is set to 0, then the uptake flux estimation becomes a linear function to local concentrations. Note that the units in the fluid flow and mass conservations model simulation must match those of the FBA bounds, which in our case were . With lower bounds defined, the solution of an FBA problem outputs biomass growth rate (γ; e.g., h−1) and uptake/release rates of metabolites (F; e.g., ).
3.2.3 Surrogate model
CompLaB also provides a C template (surrogateModel.hh) where users can incorporate a pre-trained surrogate model for calculating biogeochemical reactions, including artificial neural networks (ANNs). This functionality can be used to replace FBA, which requires solving many computationally expensive linear optimization problems (Sect. 3.2.2). In the example shown in Sect. 5, CompLaB provides local metabolite concentrations and biomass densities as inputs and the surrogate model outputs microbial growth rate (γ) and uptake/production rates of metabolites (F). While our demonstration is based on ANN models, any pre-trained statistical surrogate model (e.g., De Lucia and Kühn, 2021) that describes the sources and sinks – or their parameterization – can be used to enhance computational efficiency and accommodate various user-specific needs.
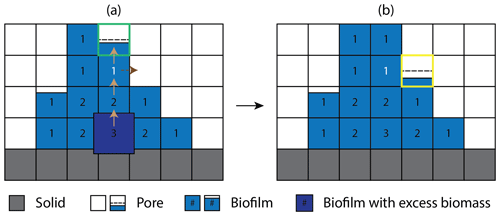
Figure 2Schematic representation of the cellular automaton method for biomass spreading (a) before and (b) after biomass redistribution. The solid, pore, and biomass are color-coded gray, white, and blue, respectively. Brown solid arrows indicate the randomly chosen path which excess biomass travels. The numbers in the biofilm grid cells are the Manhattan distances to the nearest pore grid cell. Because all the neighbors of the dark-blue grid cell are saturated with biomass, the excess biomass is first moved to a neighboring cell randomly chosen amongst those with the shorter Manhattan distance. This allocation process is repeated until the excess biomass is moved to the grid cell with the Manhattan distance of 1 (color-coded white) where the excess biomass first encounters unsaturated neighbor cells. The biomass holding capacity () of the randomly selected neighboring grid cell (outlined green) is first evaluated. If the excess biomass exceeds the holding capacity, the excess biomass is redistributed to the first chosen neighbor up to the maximum holding capacity and the remaining excess biomass is placed to the next available neighbor grid cell (outlined yellow), finalizing the cellular automaton algorithm. The dashed black horizontal lines indicate the minimum biomass level required for a grid cell to be designated as biofilm.
3.3 Biomass redistribution
To explicitly model the spatial biomass expansion, CompLaB utilizes a cellular automaton (CA) with a predefined maximum biomass density (Bmax) based on the CA algorithm developed by Jung and Meile (2021). After updating local biomass densities, the CA algorithm checks at every time step if there is any grid cell exceeding Bmax and redistributes the excess biomass () to a randomly selected neighboring grid cell. If the selected grid cell cannot hold the excess biomass, the first chosen grid cell is filled up to the maximum holding capacity (Bmax, a value defined by the user), and then the remaining excess biomass is allocated to a randomly chosen second neighbor cell. If all the neighboring grid cells are saturated with biomass () and hence the excess biomass cannot be placed, the Manhattan distances of biomass grid cells to the closest pore cells are evaluated. The remaining excess biomass is then placed in a neighboring grid cell that is closer to pores. and this biomass allocation process is repeated until all the excess biomass is redistributed. Figure 2 shows an example of the cellular automaton process for biomass redistribution. Note that this biomass redistribution method is a simple approximation for biomass density conservation with room for improvement (e.g., Tang and Valocchi, 2013).
When the sessile biomass reaches a threshold density (, where ψ is a user-defined threshold biomass fraction; ), the pore grid cell is designated as biomass; if the biomass density falls below the threshold due to microbial decay or detachment (B < ψBmax), then a biomass grid cell is converted back to a pore. Pore grid cells allow for both advective and diffusive transport, but in the biofilm, sessile biomass hinders (i.e., permeable biofilm) or prevents (i.e., impermeable biofilm) flow, and the feedback between biomass growth/decay and advective flow conditions is accounted for by rerunning the flow solver to steady state after updating biomass distribution and corresponding pore geometry (Jung and Meile, 2021). The reduced advective transport efficiency in permeable biomass grid cells is implemented by modifying local fluid viscosity in the biofilm (νbf) with , where X is a user-defined viscosity ratio (), while for impermeable biomass, a bounce-back condition is imposed (Pintelon et al., 2012). After imposing the new steady-state flow field, a streaming step of the transport solver is executed (Fig. 1).
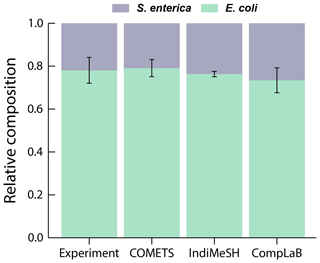
To verify the CompLaB implementation, the engineered metabolic interaction between two co-dependent mutant strains (Escherichia coli K12 and Salmonella enterica LT2) originally established by Harcombe (2010) and implemented in COMETS (Harcombe et al., 2014) and IndiMeSH (Borer et al., 2019) was chosen as a test case. E. coli K12 is deficient in producing methionine and relies on the release of methionine by the mutant S. enterica LT2. In turn, S. enterica LT2 requires acetate released by E. coli K12 because of its inability to metabolize lactose. As a result, these genetically engineered strains are obliged to engage in mutual interaction where neither species can grow in isolation. The ratio of the two strains converges to a stable relative composition after 48 h in all the in vitro and in silico experiments at both initial ratios of 1:99 and 99:1.
Both COMETS (Harcombe et al., 2014) and IndiMeSH (Borer et al., 2019) integrate flux balance cell models of these two microorganisms into a two-dimensional environment in which metabolites are exchanged via diffusion. The initial and boundary conditions of these simulations were mirrored in CompLaB, with 100 grid cells containing 3 × 10−7 g biomass each (total = 3 × 10−5 g biomass) distributed randomly across a two-dimensional domain of 25 × 25 grid squares. The grid length was set to 500 µm, and the initial distributions of the two species were allowed to overlap. Three replicate simulations were carried out for each initial microbial ratio of E. coli and S. enterica (1:99 and 99:1). For the exchange metabolites acetate and methionine, fixed boundary concentrations of 0 mM were imposed on the left and right side of the domain, respectively, with no flux conditions at the top and bottom boundaries. The concentrations of lactose (2.92 mM) and oxygen (0.25 mM) were imposed at all domain boundaries. Solute and biomass diffusion coefficients were fixed at 5 × 10−10 and 3 × 10−13 m2 s−1, respectively. Consistent with the IndiMeSH model implementation, the simulation was carried out using Eq. (9), a finite-difference method for biomass diffusion, and reduced metabolic models of E. coli K12 and S. enterica LT2 in which the number of metabolites and reactions of the original metabolic models was systematically reduced by 1 order of magnitude (Borer et al., 2019).
Figure 3 illustrates the average ratio of E. coli and S. enterica of all six simulations (triplicates for each initial composition ratios of 1:99 and 99:1) after 48 h of simulation time. CompLaB simulation results agree with both the observations and the model results of COMETS and IndiMeSH, demonstrating the metabolic inter-dependence of two strains, and the convergence to a stable composition ratio (Appendix A, Fig. A1).
A major issue in fully coupling genome-scale metabolic networks to reactive transport models is the large computational demand due to the repeated calculation of the LP problems at every biomass grid cell and every time step. Previous studies have alleviated this issue by interpolating the solutions of LP problems from a lookup table generated in advance to a reactive transport simulation (Scheibe et al., 2009), dynamically creating a solution pool of the LP problems during the reactive transport process (Fang et al., 2011), or systematically reducing the size of the matrix encoding the metabolic network (Ataman et al., 2017; Ataman and Hatzimanikatis, 2017). Here, we introduce a statistical surrogate modeling approach using a pre-trained artificial neural network (ANN) following the approach presented in Song et al. (2023). A trained ANN model directly relates input parameters (i.e., uptake rates of substrates) to outputs (i.e., biomass and metabolite production rates) through a set of nonlinear algebraic equations. As computing such input–output relationships from a pre-trained ANN model is several orders of magnitude faster than running FBA using a fully fledged metabolic model, the use of such surrogate models to achieve a significant speed-up has attracted much attention recently (e.g., De Lucia and Kühn, 2021; Prasianakis et al., 2020).
Here, we use the metabolic network of Geobacter metallireducens GS-15 (iAF987; Lovley et al., 1993; http://bigg.ucsd.edu/models/iAF987, last access: September 2022), a strict anaerobe capable of coupling the oxidation of organic compounds to the reduction of metals such as iron and manganese, using ammonium as its nitrogen source to train an ANN model. The dataset used for training a surrogate ANN model was obtained by collecting FBA solutions of the base model obtained using the IBM ILOG cplex optimizer with the objective function chosen to maximize biomass production. The solution set was prepared by randomly sampling 5000 combinations of two growth-limiting metabolites – acetate (CAc) and ammonium () – within the concentration ranges of 0.5 mM and 0.05 mM via Monte Carlo simulations. Substrate concentrations were converted to uptake fluxes via the parameter-based approach (Eq. 7) using the parameters from Fang et al. (2011) (Vmax = 10 and 0.5 ; Ks = 0.01 mM acetate and 0.1 mM ammonium). These fluxes were used as lower bounds, and Fe3+ was allowed to be consumed without limitation. The collected FBA solution dataset was split and used to train (70 %), validate (15 %), and test (15 %), and we developed an ANN model using MATLAB's neural network toolbox. As key hyperparameters, the number of layers and the number of nodes in the ANN model were, respectively, determined to be 4 and 10 through grid search. Ensuring the accuracy of a surrogate model is of critical importance in reactive transport models because even small errors accumulating over successive time steps can lead to a substantial error. In this simple example, the trained ANN estimates the biomass growth rate of the full FBA model almost perfectly (R > 0.999) against training, validation, and test datasets. This shows that the fully fledged metabolic model can be replaced by the surrogate ANN model without substantial loss of accuracy, boosting the simulation speed as shown next.
CompLaB inherits the massive scalability of Palabos which decomposes a simulation domain into multiple subdomains and assigns them to individual computational nodes. In the following, the scalability of various components of CompLaB is assessed for a simplified microbial dynamics problem.
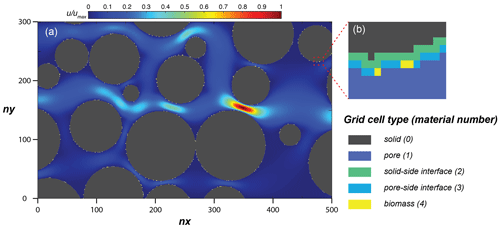
Figure 4(a) Simulation domain of the model performance simulation, with the steady-state flow velocity distribution and (b) an enlarged subsection showing the distribution of material numbers around a solid.
6.1 Test case
The simulation domain (Fig. 4) was prepared by taking a subsection of 500 × 300 square elements from the porous medium of Souzy et al. (2020). The length of each element was 16.81 µm, and material numbers were assigned to solid (0), pore (1), and solid–pore interfaces (solid side of interface: 2; pore side of interface: 3). In total, 10 % of the interface grid cells (pore side) were randomly assigned as sessile biomass grid cells (4) initially. Flow was induced from left to right by imposing a fixed pressure gradient between left- and right-side boundaries, and no flow conditions were set at the top and bottom boundaries as well as on the grain surfaces. The steady-state flow field was then provided to the CompLaB transport solver for mass transport and reaction simulations (Péclet number is 1 for a characteristic length scale of 2 mm). Two growth-limiting metabolites – acetate (CH3COO−) and ammonium () – were considered for the mass transport simulations. Acetate was injected at the inlet (left) boundary with the fixed concentration of 0.45 mM to the simulation domain initially filled with the same concentration. Ammonium concentration in the inflowing fluid and initially in the domain was 0 mM, but it was produced at solid surfaces assuming a zeroth-order mineralization rate (Table 1). For both metabolites, no gradient conditions were imposed at the outlet, top, bottom, and grain boundaries. No external source and initial planktonic biomass were assumed, so that all planktonic biomass is detached sessile biomass.
The biogeochemical problem is described by the following set of ADREs:
CAc and are the concentrations of acetate and ammonium, respectively; BP is the planktonic biomass density; BS is the sessile biomass density; u denotes the flow field; δ indicates the presence (δ = 1) or absence (δ = 0) of a grain surface (δS) and a biomass grid cell (δB); and DAc, , and DB are the diffusion coefficients of acetate, ammonium, and planktonic biomass, respectively, which differ between pore, biomass, and solids. For simplicity, the diffusivities of all the metabolites and planktonic biomass were set to 10−9 m2 s−1 in the pores, 8 × 10−10 m2 s−1 in biomass grid cells, and 0 in the solid. Biomass attachment and detachment (katt and kdet), biomass decay (μB), and organic matter mineralization () were simulated using the reaction kinetics solver, with the corresponding rate constants summarized in Table 1. The simulation assumed that G. metallireducens grows only on solid surfaces and planktonic biomass attaches only to existing surface-attached aggregates (Grinberg et al., 2019).
The computational efficiency and parallel performance of CompLaB was tested by executing four independent simulations utilizing each reaction solver. The cell-specific metabolic fluxes (F, Eq. 9) and biomass growth rates (γ, Eq. 12) were calculated either through FBA (CPY or GLPK), ANN, and/or reaction kinetics (KNS). The KNS solver was combined with other solvers (CPY, GLPK, and ANN) or used as a stand-alone reaction solver with the cellular automaton algorithm invoked (CA) and Bmax set to 100 gDW L−1. The model performance simulations with the FBA solvers (CPY and GLPK) were prepared with the same conditions used for training the ANN model (Sect. 5). The pre-trained ANN model from Sect. 5 was used for the separate simulation ANN. For the CA simulation, we create a situation similar to the above examples but in which substantial biofilm growth over a short simulation time is artificially induced. To that end, F and γ were computed as
where F denotes the metabolic fluxes (for simplicity assuming FAc = ), γ is the biomass growth rate, kkns = 2.5 × 10−6 mM s−1 (Marozava et al., 2014) is the maximum uptake rate, and KAc = 0.1 mM and = 0.01 mM are the half-saturation constants for acetate and ammonium, respectively. The growth yield Y is set to 40 000 , an arbitrarily large number used only to invoke the CA algorithm within 10 000 time steps (440 s). The flow field was updated every 10 time steps when the CA algorithm was invoked (as, e.g., Thullner and Baveye, 2008; Jung and Meile, 2021).
The performance tests were carried out on the computing nodes of the Georgia Advanced Computing Resources Center. Each node has an AMD EPYC 7702P 64-core processor with a 2.0 GHz clock cycle (AMD Rome), with 128 GB of RAM. The nodes are interconnected via an EDR InfiniBand network with 100 GB s−1 effective throughput and run a 64-bit Linux operating system (CentOS 7.9 distribution). The elapsed (wall-clock) time for 10 000 time steps was recorded.
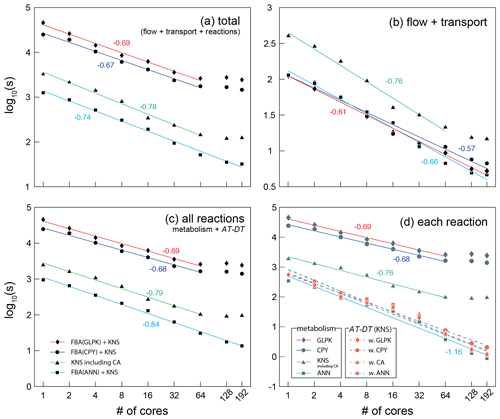
Figure 5The wall-clock time recorded in seconds for (a) the total, (b) flow and transport, (c) all reactions, and (d) each reaction part of the CompLaB algorithm. Four different simulations were carried out deploying each reaction solver: three simulations used COBRApy (CPY), GLPK, artificial neural network (ANN) solvers for microbial metabolism calculation, and a kinetic solver (KNS) for the attachment/detachment of biomass (AT-DT). One simulation used only a kinetic solver for both microbial metabolism and AT-DT with the cellular automaton algorithm invoked (CA). The simulation time for CA only can be inferred by subtracting the time for AT-DT with CA (dashed green line with orange triangle symbols) from the time for KNS including CA (solid green line with gray triangle symbols) in (d). Each symbol represents the average of two simulations. The simulations exhibiting no or limited speed-up with 128 and 192 cores except the ANN simulation were excluded when drawing the regression lines. The negative numbers are the slopes of the solid regression lines. The average slope of all the dashed regression lines in panel (d) is −1.14.
6.2 Performance
A comparison of simulation times for flow, transport, and reaction shows that most compute time is used for simulating the reactions, in particular when integrating in silico cell models into a reactive transport framework (Fig. 5). This highlights the benefit of using efficient surrogate models. The surrogate ANN model substantially improves computational efficiency compared to CPY and GLPK (about 2 orders of magnitude in total elapsed time; Fig. 5a) because calculating the pre-trained ANN is much faster than solving the linear programming problem every time step in FBA (Fig. 5c). For reaction calculations (Fig. 5d), the ANN simulation (solid sky-blue line with gray square symbols) even exhibits comparable but slightly shorter simulation times than the traditional reaction kinetics calculation (KNS; dashed lines with orange symbols) because the ANN implementation only operates on biomass grid cells while KNS operates on both biomass and pore grid cells.
In addition to the computational efficiency, negligible errors introduced by the surrogate ANN model assure the use of a surrogate ANN model (Fig. B1). Although the error in biomass calculation accumulates over simulation time steps, it is kept to very low values throughout the simulation (the relative error is on the order of 10−9; Appendix B) and has practically no influence on metabolite concentration calculations. This observation illustrates that CompLaB can calculate microbial metabolic reactions in porous media with a heterogeneous distribution of pore, biomass, organic matter, and minerals, based on the genome-scale metabolic model with the superior computational efficiency of a surrogate model without losing accuracy. Applying Monte Carlo simulations to generate FBA data to train a neural network model required solving the linear programming problem 5000 times with a set of randomly chosen uptake rates of acetate and ammonium, which does not add a significant computational burden. In our application, we determined the number of layers and nodes in the neural network to be 4 and 10, respectively, because no further improvement in model performance was observed beyond those values.
The computational efficiency of ANN also works in favor of scalability. The reaction processes of CompLaB are inherently an embarrassing parallel task because calculating biogeochemical sub-processes is completely independent of the neighbors (except CA) and all model performance simulations show the reasonable scalability up to 64 cores (Fig. 5). However, the scaling behaviors of all simulations except ANN illustrate suboptimal scalability with no or limited speed-up when using more compute resources. The loss of efficiency originates mostly from the calculation of reaction processes (Fig. 5c) because the domain decomposition applied to the heterogeneous simulation domain (Fig. 4) resulted in an uneven distribution of biofilm grid cells per subdomain and hence a variable size of the problem to be solved on each core. In fact, in our simple example problem (a total of 500 × 300 computational grid cells, constant random seeds), a domain decomposition when using 64, 128, and 192 cores produced 6, 38, and 76 subdomains, respectively, that have no initial biomass grid cells. Such subdomains do not contribute to computing microbial metabolisms (FBA) and biomass redistribution (CA) that consumes most of the computational cost (e.g., GLPK calculation consumes ∼ 99 % of the total computational cost), preventing ideal parallel performance (Fig. 5d). While this is also true for ANN, computational efficiency of ANN reduces the time wasted by such subdomains. As a result, the suboptimality is not readily apparent in ANN (Fig. 5c).
The CA algorithm implemented in CompLaB is a nonlocal process requiring information from neighboring grid cells, but the result still exhibits a good scalability when using up to 64 cores and suboptimal scalability when more cores are used. The CA simulation required less time than FBA simulations because the metabolic reactions were calculated using KNS. But CA spent extra time on updating the flow field (Fig. 5b) and redistributing excess biomass (Fig. 5c and d). This illustrates that the actual time required for the CA algorithm depends on the nature of the biomass expansion. For example, more time will be required for a system with rapid biofilm growth excess because excess biomass has to travel a longer distance through a thick biofilm. Furthermore, flow fields will need to be updated more often to reflect the influence of rapid biofilm growth on flow.
The numerical modeling platform CompLaB for simulating 2D pore-scale reactive transport processes is capable of utilizing the quantitative implementation of the microbial metabolism through the coupling of genome-scale metabolic models. The integration of in silico cell models with reactive transport simulations makes this framework broadly applicable and enables the integration of knowledge gained from the “omics”-based characterization of microbial systems. For example, the successful reproduction of experimentally observed convergences to a stable composition of a two-species consortium (S. enterica and E. coli) demonstrates the capability of CompLaB to investigate metabolic interactions between multiple microbial species.
Our novel numerical framework based on the lattice Boltzmann method allows simulating advection as well as diffusion of metabolites in complex porous media. A wide range of simulation domains can be used to represent soil structure and fractured rock images directly obtained from various imaging techniques (e.g., μ-CT, FIB-SEM) or numerically generated porous media with material numbers assigned to pore, solid, and source/sink grid cells for biogeochemical reactions which include but are not limited to biofilms. The inherent parallel efficiency of CompLaB facilitates simulating dynamic flux balance analysis capturing the microbial feedback on flow and transport in porous media, as done previously using Monod-type representations of microbial activity (Jung and Meile, 2021). Furthermore, the versatile simulation environment of CompLaB allows utilizing surrogate models, such as an artificial neural network. The resulting speed-up enables the investigation of complex biogeochemical processes in natural environments.
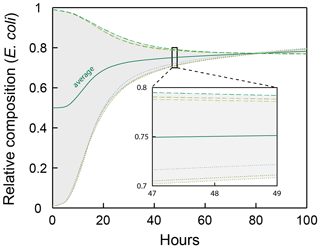
The six simulation cases used in Sect. 4 for model verification were run for 100 h of simulation time to further evaluate whether the observed convergence to an average composition ratio is stable (Fig. A1). The composition ratio observed after 48 h (0.75) is largely maintained through the extended simulation period (increases only to 0.78 after 100 h).
The surrogate modeling approach inevitably introduces errors in model estimations. The errors should be maintained sufficiently low throughout the surrogate simulation otherwise errors can propagate in successive iterations and result in unphysical results. To quantify the errors in surrogate model estimations, the solutions of our artificial neural network (ANN) were compared to the reference simulation COBRApy (CPY) by calculating the arithmetic mean of the root mean squared errors:
where j is the variable type (BS, BP, CAc, and ), m is the number of variables j used in calculating the error, nj is the number of grid cells for each variable j, and t is the time step where the error is evaluated. The differences between the FBA simulations using GLPK and CPY solvers are negligible, so only the CPY solution was chosen as the reference (Fig. B1).
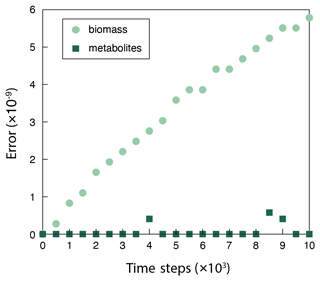
Figure B1The discrepancy (relative error) between the surrogate ANN and the fully fledged physical model simulation using COBRApy calculated via Eq. (A1). The surrogate model overestimates biomass (BS+BP), and the errors accumulate over time. But the errors are kept low and negligible throughout the simulation, as evidenced by no influence on metabolite concentrations ().
The model code, input files used for this study, and a manual are available at https://doi.org/10.5281/zenodo.7095756 (Jung et al., 2022). Developments after the publication of this article will continue to be hosted at https://bitbucket.org/MeileLab/complab/ (Jung and Meile, 2022).
The neural network model was established from flux balance model simulations. That model (the genome-scale metabolic network of Geobacter metallireducens GS-15 (iAF987)) was obtained from the BiGG database (King et al., 2016). The artificial neural network model along with iAF987 are publicly available through the Zenodo code repository (Jung et al., 2022).
HJ developed the research, performed the overall programming and simulations, analyzed and interpreted the data, wrote the initial draft, and revised the paper, HS trained the ANN model and reviewed the paper, CM conceived the research, carried out the performance measures, and revised the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors thank Shan-Ho Tsai for help with the simulations, Benjamin Borer for constructive discussions and feedback on IndiMeSH, and Maria De La Fuente Ruiz and an anonymous reviewer for their comments, which helped improve the paper. This study was also supported by resources and technical expertise from the Georgia Advanced Computing Resource Center, a partnership between the University of Georgia's Office of the Vice President for Research and the Office of the Vice President for Information Technology.
This work was supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research, Genomic Sciences Program under award number DE-SC0016469 and DE-SC0020373 to Christof Meile and by the Ministry of Science and ICT, South Korea, Institute for Korea Spent Nuclear Fuel (iKSNF) and the National Research Foundation of Korea (NRF) under award number 2021M2E1A1085202 to Heewon Jung.
This paper was edited by Sandra Arndt and reviewed by Maria De La Fuente Ruiz and one anonymous referee.
Alemani, D., Chopard, B., Galceran, J., and Buffle, J.: LBGK method coupled to time splitting technique for solving reaction-diffusion processes in complex systems, Phys. Chem. Chem. Phys., 7, 3331–3341, https://doi.org/10.1039/b505890b, 2005.
Arkin, A. P., Cottingham, R. W., Henry, C. S., Harris, N. L., Stevens, R. L., Maslov, S., Dehal, P., Ware, D., Perez, F., Canon, S., Sneddon, M. W., Henderson, M. L., Riehl, W. J., Murphy-Olson, D., Chan, S. Y., Kamimura, R. T., Kumari, S., Drake, M. M., Brettin, T. S., Glass, E. M., Chivian, D., Gunter, D., Weston, D. J., Allen, B. H., Baumohl, J., Best, A. A., Bowen, B., Brenner, S. E., Bun, C. C., Chandonia, J. M., Chia, J. M., Colasanti, R., Conrad, N., Davis, J. J., Davison, B. H., Dejongh, M., Devoid, S., Dietrich, E., Dubchak, I., Edirisinghe, J. N., Fang, G., Faria, J. P., Frybarger, P. M., Gerlach, W., Gerstein, M., Greiner, A., Gurtowski, J., Haun, H. L., He, F., Jain, R., Joachimiak, M. P., Keegan, K. P., Kondo, S., Kumar, V., Land, M. L., Meyer, F., Mills, M., Novichkov, P. S., Oh, T., Olsen, G. J., Olson, R., Parrello, B., Pasternak, S., Pearson, E., Poon, S. S., Price, G. A., Ramakrishnan, S., Ranjan, P., Ronald, P. C., Schatz, M. C., Seaver, S. M. D., Shukla, M., Sutormin, R. A., Syed, M. H., Thomason, J., Tintle, N. L., Wang, D., Xia, F., Yoo, H., Yoo, S., and Yu, D.: KBase: The United States Department of Energy Systems Biology Knowledgebase, Nat. Biotechnol., 36, 566–569, https://doi.org/10.1038/nbt.4163, 2018.
Ataman, M. and Hatzimanikatis, V.: lumpGEM: Systematic generation of subnetworks and elementally balanced lumped reactions for the biosynthesis of target metabolites, PLOS Comput. Biol., 13, 1–21, https://doi.org/10.1371/journal.pcbi.1005513, 2017.
Ataman, M., Hernandez Gardiol, D. F., Fengos, G., and Hatzimanikatis, V.: redGEM: Systematic reduction and analysis of genome-scale metabolic reconstructions for development of consistent core metabolic models, PLOS Comput. Biol., 13, 1–22, https://doi.org/10.1371/journal.pcbi.1005444, 2017.
Bauer, E., Zimmermann, J., Baldini, F., Thiele, I., and Kaleta, C.: BacArena: Individual-based metabolic modeling of heterogeneous microbes in complex communities, PLOS Comput. Biol., 13, 1–22, https://doi.org/10.1371/journal.pcbi.1005544, 2017.
Bhatnagar, P. L., Gross, E. P., and Krook, M.: A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems, Phys. Rev., 94, 511–525, https://doi.org/10.1103/PhysRev.94.511, 1954.
Borer, B., Ataman, M., Hatzimanikatis, V., and Or, D.: Modeling metabolic networks of individual bacterial agents in heterogeneous and dynamic soil habitats (IndiMeSH), Plos Comput. Biol., 15, 1–21, https://doi.org/10.1371/journal.pcbi.1007127, 2019.
De Lucia, M. and Kühn, M.: DecTree v1.0 – chemistry speedup in reactive transport simulations: purely data-driven and physics-based surrogates, Geosci. Model Dev., 14, 4713–4730, https://doi.org/10.5194/gmd-14-4713-2021, 2021.
Dukovski, I., Bajić, D., Chacón, J. M., Quintin, M., Vila, J. C. C., Sulheim, S., Pacheco, A. R., Bernstein, D. B., Riehl, W. J., Korolev, K. S., Sanchez, A., Harcombe, W. R., and Segrè, D.: A metabolic modeling platform for the computation of microbial ecosystems in time and space (COMETS), Nat. Protoc., 16, 5030–5082, https://doi.org/10.1038/s41596-021-00593-3, 2021.
Ebrahim, A., Lerman, J. A., Palsson, B. O., and Hyduke, D. R.: COBRApy: COnstraints-Based Reconstruction and Analysis for Python, BMC Syst. Biol., 7, 74, https://doi.org/10.1186/1752-0509-7-74, 2013.
Fang, Y., Scheibe, T. D., Mahadevan, R., Garg, S., Long, P. E., and Lovley, D. R.: Direct coupling of a genome-scale microbial in silico model and a groundwater reactive transport model, J. Contam. Hydrol., 122, 96–103, https://doi.org/10.1016/j.jconhyd.2010.11.007, 2011.
Fang, Y., Wilkins, M. J., Yabusaki, S. B., Lipton, M. S., and Long, P. E.: Evaluation of a genome-scale in silico metabolic model for Geobacter metallireducens by using proteomic data from a field biostimulation experiment, Appl. Environ. Microbiol., 78, 8735–8742, https://doi.org/10.1128/AEM.01795-12, 2012.
GLPK (GNU Linear Programming Kit): GLPK – GNU Project – Free Software Foundation (FSF), https://www.gnu.org/software/glpk/glpk.html, last access: July 2022.
Golparvar, A., Kästner, M., and Thullner, M.: Pore-scale modeling of microbial activity: What we have and what we need, Vadose Zone J., 20, 1–17, https://doi.org/10.1002/vzj2.20087, 2021.
Grinberg, M., Orevi, T., and Kashtan, N.: Bacterial surface colonization, preferential attachment and fitness under periodic stress, PLOS Comput Biol, 15, e1006815, https://doi.org/10.1371/journal.pcbi.1006815, 2019.
Harcombe, W.: Novel cooperation experimentally evolved between species, Evolution (N.Y)., 64, 2166–2172, https://doi.org/10.1111/j.1558-5646.2010.00959.x, 2010.
Harcombe, W. R., Riehl, W. J., Dukovski, I., Granger, B. R., Betts, A., Lang, A. H., Bonilla, G., Kar, A., Leiby, N., Mehta, P., Marx, C. J., and Segrè, D.: Metabolic resource allocation in individual microbes determines ecosystem interactions and spatial dynamics, Cell Rep., 7, 1104–1115, https://doi.org/10.1016/j.celrep.2014.03.070, 2014.
Heirendt, L., Arreckx, S., Pfau, T., Mendoza, S. N., Richelle, A., Heinken, A., Haraldsdóttir, H. S., Wachowiak, J., Keating, S. M., Vlasov, V., Magnusdóttir, S., Ng, C. Y., Preciat, G., Žagare, A., Chan, S. H. J., Aurich, M. K., Clancy, C. M., Modamio, J., Sauls, J. T., Noronha, A., Bordbar, A., Cousins, B., El Assal, D. C., Valcarcel, L. V., Apaolaza, I., Ghaderi, S., Ahookhosh, M., Ben Guebila, M., Kostromins, A., Sompairac, N., Le, H. M., Ma, D., Sun, Y., Wang, L., Yurkovich, J. T., Oliveira, M. A. P., Vuong, P. T., El Assal, L. P., Kuperstein, I., Zinovyev, A., Hinton, H. S., Bryant, W. A., Aragón Artacho, F. J., Planes, F. J., Stalidzans, E., Maass, A., Vempala, S., Hucka, M., Saunders, M. A., Maranas, C. D., Lewis, N. E., Sauter, T., Palsson, B. Ø., Thiele, I., and Fleming, R. M. T.: Creation and analysis of biochemical constraint-based models using the COBRA Toolbox v.3.0, Nat. Protoc., 14, 639–702, https://doi.org/10.1038/s41596-018-0098-2, 2019.
Huber, C., Shafei, B., and Parmigiani, A.: A new pore-scale model for linear and non-linear heterogeneous dissolution and precipitation, Geochim. Cosmochim. Ac., 124, 109–130, https://doi.org/10.1016/j.gca.2013.09.003, 2014.
Jung, H. and Meile, C.: Upscaling of microbially driven first-order reactions in heterogeneous porous media, J. Contam. Hydrol., 224, 103483, https://doi.org/10.1016/j.jconhyd.2019.04.006, 2019.
Jung, H. and Meile, C.: Pore-Scale Numerical Investigation of Evolving Porosity and Permeability Driven by Biofilm Growth, Transport Porous Med., 139, 203–221, https://doi.org/10.1007/s11242-021-01654-7, 2021.
Jung, H. and Meile, C.: Complab bitbucket repository [code], https://bitbucket.org/MeileLab/complab/, last access: September 2022.
Jung, H., Song, H.-S., and Meile, C.: CompLaB: a scalable pore-scale model for flow, biogeochemistry, microbial metabolism, and biofilm dynamics, Zenodo [code], https://doi.org/10.5281/zenodo.7095756, 2022.
Kang, Q., Lichtner, P. C., and Zhang, D.: An improved lattice Boltzmann model for multicomponent reactive transport in porous media at the pore scale, Water Resour. Res., 43, 1–12, https://doi.org/10.1029/2006WR005551, 2007.
King, E. L., Tuncay, K., Ortoleva, P., and Meile, C.: Modeling biogeochemical dynamics in porous media: Practical considerations of pore scale variability, reaction networks, and microbial population dynamics in a sandy aquifer, J. Contam. Hydrol., 112, 130–140, https://doi.org/10.1016/j.jconhyd.2009.12.002, 2010.
King, Z. A., Lu, J. S., Dräger, A., Miller, P. C., Federowicz, S., Lerman, J. A., Ebrahim, A., Palsson, B. O., and Lewis, N. E.: BiGG Models: A platform for integrating, standardizing, and sharing genome-scale models, Nucleic Acids Res., 44, D515–D522, doi:10.1093/nar/gkv1049, 2016.
König, S., Vogel, H. J., Harms, H., and Worrich, A.: Physical, Chemical and Biological Effects on Soil Bacterial Dynamics in Microscale Models, Front. Ecol. Evol., 8, 1–10, https://doi.org/10.3389/fevo.2020.00053, 2020.
Kotsalos, C., Latt, J., and Chopard, B.: Bridging the computational gap between mesoscopic and continuum modeling of red blood cells for fully resolved blood flow, J. Comput. Phys., 398, 108905, https://doi.org/10.1016/j.jcp.2019.108905, 2019.
Krüger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O., Silva, G., and Viggen, E. M.: The Lattice Boltzmann Method, Springer International Publishing, Cham, https://doi.org/10.1007/978-3-319-44649-3, 2017.
Latt, J., Malaspinas, O., Kontaxakis, D., Parmigiani, A., Lagrava, D., Brogi, F., Belgacem, M. Ben, Thorimbert, Y., Leclaire, S., Li, S., Marson, F., Lemus, J., Kotsalos, C., Conradin, R., Coreixas, C., Petkantchin, R., Raynaud, F., Beny, J., and Chopard, B.: Palabos: Parallel Lattice Boltzmann Solver, Comput. Math. Appl., 81, 334–350, https://doi.org/10.1016/j.camwa.2020.03.022, 2021.
Lovley, D. R., Giovannoni, S. J., White, D. C., Champine, J. E., Phillips, E. J., Gorby, Y. A., and Goodwin, S.: Geobacter metallireducens gen. nov. sp. nov., a microorganism capable of coupling the complete oxidation of organic compounds to the reduction of iron and other metals, Arch Microbiol., 159, 336–344, https://doi.org/10.1007/BF00290916, 1993.
Marozava, S., Röling, W. F. M., Seifert, J., Küffner, R., Von Bergen, M., and Meckenstock, R. U.: Physiology of Geobacter metallireducens under excess and limitation of electron donors. Part I. Batch cultivation with excess of carbon sources, Syst. Appl. Microbiol., 37, 277–286, https://doi.org/10.1016/j.syapm.2014.02.004, 2014.
Meile, C. and Scheibe, T. D.: Reactive Transport Modeling of Microbial Dynamics, Elements, 15, 111–116, https://doi.org/10.2138/gselements.15.2.111, 2019.
Molins, S.: Reactive Interfaces in Direct Numerical Simulation of Pore-Scale Processes, Rev. Mineral. Geochem., 80, 461–481, https://doi.org/10.2138/rmg.2015.80.14, 2015.
Nikdel, A., Braatz, R. D., and Budman, H. M.: A systematic approach for finding the objective function and active constraints for dynamic flux balance analysis, Biopro. Biosyst. Eng., 41, 641–655, https://doi.org/10.1007/s00449-018-1899-y, 2018.
Oostrom, M., Mehmani, Y., Romero-Gomez, P., Tang, Y., Liu, H., Yoon, H., Kang, Q., Joekar-Niasar, V., Balhoff, M. T., Dewers, T., Tartakovsky, G. D., Leist, E. A., Hess, N. J., Perkins, W. A., Rakowski, C. L., Richmond, M. C., Serkowski, J. A., Werth, C. J., Valocchi, A. J., Wietsma, T. W., and Zhang, C.: Pore-scale and continuum simulations of solute transport micromodel benchmark experiments, Comput. Geosci., 20, 857–879, https://doi.org/10.1007/s10596-014-9424-0, 2016.
Orth, J. D., Thiele, I., and Palsson, B. O.: What is flux balance analysis?, Nat. Biotechnol., 28, 245–248, https://doi.org/10.1038/nbt.1614, 2010.
Pintelon, T. R. R., Picioreanu, C., van Loosdrecht, M. C. M., and Johns, M. L.: The effect of biofilm permeability on bio-clogging of porous media, Biotechnol. Bioeng., 109, 1031–1042, https://doi.org/10.1002/bit.24381, 2012.
Prasianakis, N. I., Haller, R., Mahrous, M., Poonoosamy, J., Pfingsten, W., and Churakov, S. V.: Neural network based process coupling and parameter upscaling in reactive transport simulations, Geochim. Cosmochim. Ac., 291, 126–143, https://doi.org/10.1016/j.gca.2020.07.019, 2020.
Scheibe, T. D., Mahadevan, R., Fang, Y., Garg, S., Long, P. E., and Lovley, D. R.: Coupling a genome-scale metabolic model with a reactive transport model to describe in situ uranium bioremediation, Microb. Biotechnol., 2, 274–286, https://doi.org/10.1111/j.1751-7915.2009.00087.x, 2009.
Song, H.-S., Ahamed, F., Lee, J.-Y., Henry, C. C., Edirisinghe, J. N., Nelson, W. C., Chen, X., Moulton, J. D., and Scheibe, T. D.: Coupling flux balance analysis with reactive transport modelling through machine learning for rapid and stable simulation of microbial metabolic switching, bioRxiv, 2023.02.06.527371, https://doi.org/10.1101/2023.02.06.527371, 2023.
Souzy, M., Lhuissier, H., Méheust, Y., Le Borgne, T., and Metzger, B.: Velocity distributions, dispersion and stretching in three-dimensional porous media, J. Fluid Mech., 891, A16, https://doi.org/10.1017/jfm.2020.113, 2020.
Steefel, C. I., Appelo, C. A. J., Arora, B., Jacques, D., Kalbacher, T., Kolditz, O., Lagneau, V., Lichtner, P. C., Mayer, K. U., Meeussen, J. C. L., Molins, S., Moulton, D., Shao, H., Šimůnek, J., Spycher, N., Yabusaki, S. B., and Yeh, G. T.: Reactive transport codes for subsurface environmental simulation, Comput. Geosci., 19, 445–478, https://doi.org/10.1007/s10596-014-9443-x, 2015.
Sudhakar, P., Machiels, K., Verstockt, B., Korcsmaros, T., and Vermeire, S.: Computational Biology and Machine Learning Approaches to Understand Mechanistic Microbiome-Host Interactions, Front. Microbiol., 12, 1–19, https://doi.org/10.3389/fmicb.2021.618856, 2021.
Tang, Y. and Valocchi, A. J.: An improved cellular automaton method to model multispecies biofilms, Water Res., 47, 5729–5742, https://doi.org/10.1016/j.watres.2013.06.055, 2013.
Tang, Y., Valocchi, A. J., Werth, C. J., and Liu, H.: An improved pore-scale biofilm model and comparison with a microfluidic flow cell experiment, Water Resour. Res., 49, 8370–8382, https://doi.org/10.1002/2013WR013843, 2013.
Thullner, M. and Baveye, P.: Computational pore network modeling of the influence of biofilm permeability on bioclogging in porous media, Biotechnol. Bioeng., 99, 1337–1351, https://doi.org/10.1002/bit.21708, 2008.
Trinsoutrot, I., Recous, S., Bentz, B., Linères, M., Chèneby, D., and Nicolardot, B.: Biochemical Quality of Crop Residues and Carbon and Nitrogen Mineralization Kinetics under Nonlimiting Nitrogen Conditions, Soil Sci. Soc. Am. J., 64, 918–926, https://doi.org/10.2136/sssaj2000.643918x, 2000.
Ziegler, D. P.: Boundary conditions for lattice Boltzmann simulations, J. Stat. Phys., 71, 1171–1177, https://doi.org/10.1007/BF01049965, 1993.
- Abstract
- Introduction
- Use of open-source codes
- Model description
- Model verification
- Surrogate model integration
- Model performance
- Conclusions
- Appendix A: Convergence of the verification model to a stable ratio after 100 h
- Appendix B: Surrogate model accuracy
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Use of open-source codes
- Model description
- Model verification
- Surrogate model integration
- Model performance
- Conclusions
- Appendix A: Convergence of the verification model to a stable ratio after 100 h
- Appendix B: Surrogate model accuracy
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References