Transfer learning for landslide susceptibility modeling using domain adaptation and case-based reasoning

Transferability of knowledge from well-investigated areas to a new study region is gaining importance in landslide hazard research. Considering the time-consuming compilation of landslide inventories as a prerequisite for landslide susceptibility mapping, model transferability can be key to making hazard-related information available to stakeholders in a timely manner. In this paper, we compare and combine two important transfer-learning strategies for landslide susceptibility modeling: case-based reasoning (CBR) and domain adaptation (DA). Care-based reasoning gathers knowledge from previous similar situations (source areas) and applies it to solve a new problem (target area). Domain adaptation, which is widely used in computer vision, selects data from a source area that has a similar distribution to the target area. We assess the performances of single- and multiple-source CBR, DA, and CBR–DA strategies to train and combine landslide susceptibility models using generalized additive models (GAMs) for 10 study areas with various resolutions (1, 10, and 25 m) located in Austria, Ecuador, and Italy. The performance evaluation shows that CBR and combined CBR–DA based on our proposed similarity criterion were able to achieve performances comparable to benchmark models trained in the target area itself. Particularly the CBR strategies yielded favorable results in both single- and multi-source strategies. Although DA tended to have overall lower performances than CBR, it had promising results in scenarios where the source–target similarity was low. We recommend that future transfer-learning research for landslide susceptibility modeling can build on the similarity criterion we used, as it successfully helped to transfer landslide susceptibility models by identifying suitable source regions for model training.

1 Introduction

Landslides are among the most common and severe natural hazards in mountain areas. Globally, the destruction caused by landslides continues to have severe impacts on human activity and life (Froude and Petley, 2018; Haque et al., 2019). Landslide susceptibility mapping, the modeling of areas prone to landslide occurrence, is an effective method to assist land managers in decision-making aimed at minimizing landslide risk. These models are typically data-driven and rely heavily on terrain characteristics to capture conditions that can lead to landslide occurrence (Goetz et al., 2015; Reichenbach et al., 2018). One of the most challenging aspects of building data-driven landslide susceptibility models is establishing the landslide inventory data for model training and testing (Lin et al., 2021). Landslide inventories from different areas and time periods can provide relevant knowledge for predictive landslide susceptibility modeling (Petschko et al., 2016). In the case where a region has insufficient landslide data to produce a susceptibility model, previous studies in ecology and on landslides have demonstrated that model transfers can aid the prediction of susceptibility in adjacent regions (i.e., regional susceptibility modeling), and allow us to improve process understanding (Wenger and Olden, 2012; Sequeira et al., 2016; Rudy et al., 2016).

Machine learning is currently the most applied method for solving the problem of landslide prediction (Goetz et al., 2015; Kavzoglu et al., 2019; Merghadi et al., 2020). Traditional machine learning operates on the condition that the training and test data are taken from the same input feature space and data distribution (Pan, 2014). In the case of spatial and temporal predictions, this means that most fitted machine-learning models are limited to the spatial and temporal bounds of the input data. Thus, when extrapolating or transferring traditional machine-learning models to new spatial and temporal domains, model performance can be degraded due to differences in feature space and/or data distributions (Shimodaira, 2000; Pan and Yang, 2010; Yates et al., 2018).

A successful model transfer does not necessarily rely solely on the extent of geographic or temporal separation, but rather on the similarity of the environmental conditions between the source and target areas (Yates et al., 2018). The field of transfer learning offers various techniques to exploit this observation, which have yet to be fully utilized by the geospatial modeling communities – including landslide susceptibility modeling. For example, Wang et al. (2022) combined deep learning and transfer learning for landslide assessments in Hong Kong and obtained good prediction results. Xu et al. (2022) demonstrated landslide model transfers for regions with earthquake-induced landslides. Qin et al. (2021) applied distant domain transfer learning for landslide detection in the city of Shenzhen, Guangdong province, China. However, these studies required training samples from the target region, which may lead to problems, such as the timing of sample acquisition, and whether the selected sample can correctly characterize the entire region. Thus, unsupervised transfer learning is highly attractive in landslide assessments. Zhu et al. (2020) proposed unsupervised feature learning and improved landslide susceptibility model transfer performance in Chongqing, China. These studies were based on landslide data and predictors from the same or adjacent areas with the same spatial resolution as the target area: i.e., their environmental characteristics and data distributions were highly similar, which may not always be the case. It is therefore necessary to find more suitable landslide transfer-learning methods without the limitation of scale and spatial resolution. Transfer-learning techniques such as domain adaptation (DA) and case-based reasoning (CBR) are emerging techniques to tackle the challenge of model transfer. In general, they have been developed to select the most suitable data and corresponding models from source areas with similar data characteristics for predicting a distinct target area in space and time.

The general concept of transfer learning is to solve new problems by applying knowledge gained from previous experiences in which similar problems were solved. That is, transfer learning has the potential to allow us to take existing knowledge of landslide occurrence from previous modeling experiences and apply it to new locations that lack any landslide data. Thus, this approach has great potential to minimize the considerable time and effort needed for building landslide inventories for susceptibility modeling in new areas, especially in large and geographically remote areas where landslide mapping and detection is particularly challenging.

In CBR, we consider multiple landslide inventories from various source areas, each of which contains a large amount of information. The problem is that not all inventories (so-called “cases”) are suitable for training a model that can be applied to the new target task. Furthermore, processing the large amount of information for each case is time-consuming. Therefore, it is desirable to compare the overall characteristics of each case to transfer the appropriate knowledge. Case-based reasoning is a method to solve these problems by identifying similar cases and applying them to a new target area. This CBR similarity analysis can be performed by considering various attributes, such as data structure and topographic characteristics (Shi et al., 2004; Qin et al., 2016; Liang et al., 2020a, b, 2021). In contrast, instead of finding best cases using the overall similarity of source areas to a target, which is done by CBR, DA transfer-learning techniques can be applied to select the observations within a source area that match the data distribution of the target area. Previous applications of CBR in the geosciences have focused on selecting one source area to transfer to a target area (Qin et al., 2016; Liang et al., 2021). Yet, there is also potential for using CBR and DA to combine cases from multiple source areas to generate transferable models.

The objective of this study is to assess the potential of transfer learning using CBR and DA techniques for enhancing model transferability of machine-learning landslide susceptibility models. We evaluate the performance of transferred susceptibility models using DA, CBR and a combined CBR–DA technique, as well as the sensitivity of these methods to spatial resolution. We consider two scenarios for training landslide susceptibility models: only one source area available (single-source area) and multiple source areas available for model training (multi-source area). We examine both scenarios and compare them to benchmark situations, where susceptibility models are applied to a new target area without using transfer-learning techniques.

2 Methods and data

In transfer learning, the general goal is to train a model f on data from a single or multiple source areas $S=\left\{S_{\mathrm{1}},S_{\mathrm{2}},\mathrm{\dots },S_N\right\}$ to make predictions in an unseen target area T with N_t observations, regardless of spatial and temporal differences. A source area S_i consists of $N_{S_i}$ observations of a set of predictors, x_j, and the corresponding labels y_j (e.g., landslide or non-landslide), $j=\mathrm{1},\mathrm{\dots },N_{S_i}$.

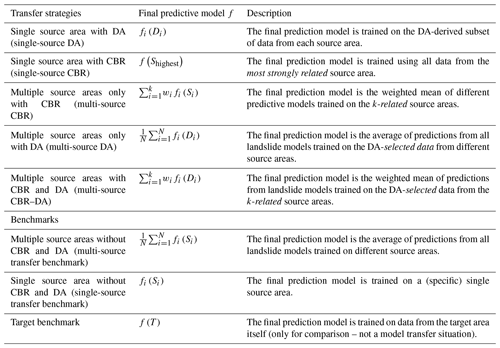
Altogether, we evaluate five different transfer-learning strategies for landslide susceptibility modeling that consider the use of data from a single or multiple source areas, which are applied to CBR, DA, and both combined (CBR–DA) (Fig. 1). To assess the relative performance of the transfer-learning strategies, we include benchmark landslide susceptibility models that are simply trained using data from a single source area (single-source transfer benchmark), multiple source areas (multi-source transfer benchmark), and the target area (target benchmark), and then applied to the target area. In the case where multiple source areas were used, the benchmark transfer model was calculated by averaging the model predictions of multiple source areas without weighting (Table 2). The target benchmark, which is trained and tested with all target data, is meant to represent an overoptimistic yet potentially obtainable performance for a given target area.

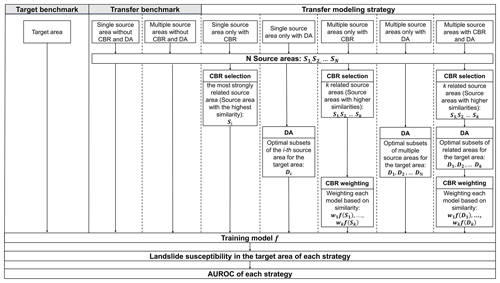
Figure 1 Flow chart of transfer-modeling strategies and benchmarks for landslide susceptibility mapping in a target area. Case-based reasoning (CBR) involves selection and weighting steps. In the single-source situation, weighting does not apply. Domain adaptation (DA) can be used by itself or combined with CBR to select source areas.

In this section, we first introduce the general CBR and DA methods separately (Sect. 2.1 and 2.2). We then explain how CBR and DA models as well as the combined CBR–DA approach are trained and tested in this work (Sect. 2.3). The data used for demonstrating the proposed approaches is then briefly presented, referring the readers to the relevant literature for more details (Sect. 2.4).

2.1 Case-based reasoning method

In machine learning, case-based reasoning (CBR) is one of the most well-known methods for solving a new problem by referring to similar cases, which can translate the knowledge from geographical space to parameter space (Shi et al., 2004, 2009; Hammond, 2012). It finds cases in a data collection that are similar to the current case in terms of metadata and/or data distribution, and then adopts those similar cases for training models (Liang et al., 2020a). This method has been reported to reduce the users' modeling efforts while achieving good performances in use cases involving terrain attributes (Qin et al., 2016; Liang et al., 2020b).

The CBR strategies are designed to find source areas $S=\mathit{\{}{S}_{\mathrm{1}},S_{\mathrm{2}},\mathrm{\dots },S_k\mathit{\}}$ that are most similar to the target area based on statistical summary information and metadata; these selected areas are referred to as related areas. In generating a CBR model, the individual models trained on the selected source areas are combined as a weighted sum:

$$\begin{array}{}\text{(1)}& f\left(x\right)={\sum }_{i=\mathrm{1}}^k{w}_i{f}_i\left(x\right),\end{array}$$

where w_i are weights that correspond to similarity scores and are normalized to sum up to 1. The individual models f_i may be trained using conventional sampling strategies as well as DA strategies, both of which are described in detail below.

Generally, CBR consists of the case problem and the corresponding case solution parts (Qin et al., 2016; Liang et al., 2020b). In our study, the challenge of formalizing the similarity of areas in landslide susceptibility modeling is to contrive a way to adequately describe the data and areas' contextual information, such as how a study area's spatial data can describe the pattern of landslide occurrence.

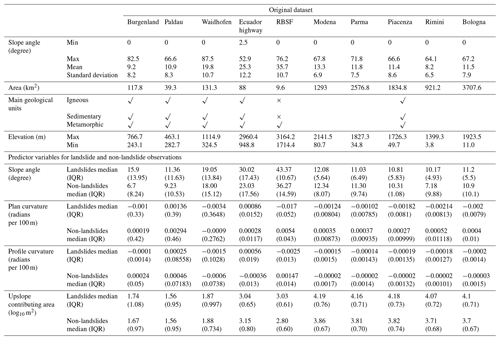
In applying CBR, it is first necessary to define and calculate similarity measures for relevant attributes that describe the data distributions of the source and target areas. In this study, we chose geological characteristics, spatial resolution, and topographic characteristics. Similarities in each attribute were estimated based on a similarity function (Table 1).

Table 1 Similarity functions for the attributes used in CBR to identify related source areas: geological characteristics, data characteristics, and topographic characteristics of the study area.

Note: Sim is the similarity of each individual attribute between the target area t and a source area S, which is in [0,1]. The following constants were used for normalization: 8848 m is the elevation of Mount Everest. For mean slope, 40^∘ can properly cover the mean slope in all study areas.

The geological characteristics of a region are an essential factor that influences multiple landslide conditioning factors such as the geomechanical and hydrological properties of hillslopes (Segoni et al., 2020). Considering the difficulties in matching geological descriptors such as heterogeneous chronostratigraphic units in different areas, we chose a simplified approach as a first-order approximation. Specifically, we used an indicator method that is based on whether the main rock types (igneous, sedimentary, and volcanic rocks) coincide in source and target areas.

Topographic conditions were described by measures of total relief, standard deviation of slope angle, and mean slope angle (Wang et al., 2019). Total relief describes the overall terrain situation of a study area by subtracting the minimum elevation from the maximum elevation within the study area. The relief, which reflects the macroscopic characteristics of surface topography in a large area, has been found to describe well landslide susceptibility (Wang et al., 2010). The standard deviation of the slope is used to describe the topographic complexity of a study area. It is one of the most influential topographic variables in landslide susceptibility studies (e.g., Van Den Eeckhaut et al., 2012).

The similarity values obtained for each factor were combined into a single indicator by taking their minimum value (Zhu and Band, 1994; Qin et al., 2009, 2016). In this study, for a given target area, we referred to source areas that have an overall (i.e., minimum) similarity score ≥ 0.65 as related source areas.

2.2 Domain adaptation

The general machine-learning approach of domain adaptation (DA) aims to solve a learning problem in the target area by utilizing data from different source areas to construct a learning sample (Wang and Deng, 2018). At first, a latent feature space is defined in which the source and target areas have the same distribution; as a consequence, classifiers trained on labeled data from source areas are likely to perform well in the corresponding target area (Baktashmotlagh et al., 2013; Patel et al., 2015; Wilson and Cook, 2020). There are supervised DA techniques that require labeled data from the target area, and unsupervised methods that do not require such data (Ben-David et al., 2010; Courty et al., 2017). We adopt unsupervised DA in our study because its smaller data requirements seem more appealing for practical applications.

Domain adaptation used in our study is a strategy for selecting instances D_i⊂S_i (i.e., sample locations or grid cells for training) from a source area S_i in such a way that their distribution is more similar to the target area's data distribution. In situations with multiple source areas, DA is applied to each of them independently to obtain instance sets $D=\left\{D_{\mathrm{1}},D_{\mathrm{2}},\mathrm{\dots },D_k\right\}$ on which k models are trained. The predictions from these models are either averaged (referred to as “plain” DA), or a weighted average is calculated when combined with source-area selection from CBR. The DA is conventionally used as a single-source strategy, which is also included in this study for comparison, although multi-source strategies may seem more appealing in real-world applications.

Many DA strategies for transferring or weighting features can result in models that are difficult to interpret in terms of the physical process's modeled influence on the response. Moreover, not all instances from different source areas may be suitable for transfer to a target area (Jiang and Zhai, 2007; Gong et al., 2013; Long et al., 2013). Thus, the landmark-based domain adaptation (LBDA) approach (Gong et al., 2013) was applied in our study. This method selects the instances (or landmarks) from source areas with the same or similar distribution as the target area without creating new predictors. It aims at minimizing the difference in sample means in latent feature space.

In our study, considering computational constraints, a randomly selected set of 50 000 unlabeled (landslide and non-landslide) points x_n from the target area were used as reference points, and were compared to a randomly selected set of 30 000 labeled $\left(x_{S,m},y_{S,m}\right)$ (landslide and non-landslide) points from the source area S as reference points from which to select a subset with similar data distribution as the target area. In the case of some of the smaller source areas in our study, all observations were used for subset selection.

The DA selects training data by formally solving the optimization problem:

$$\begin{array}{}\text{(2)}& \min {∥{\displaystyle \frac{\mathrm{1}}{\sum _{m=\mathrm{1}}^{N_S}{\mathit{\alpha }}_{S,m}}}\sum _{m=\mathrm{1}}^{N_S}{\mathit{\alpha }}_{S,m}\mathit{\varphi }\left(x_{S,m}\right)-{\displaystyle \frac{\mathrm{1}}{N_t}}\sum _{n=\mathrm{1}}^{N_t}\mathit{\varphi }\left(x_{t,n}\right)∥}_H^{\mathrm{2}},\end{array}$$

subject to

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{1}}{\sum _{m=\mathrm{1}}^C{\mathit{\alpha }}_{S,m}}}{\sum }_{m=\mathrm{1}}^C{\mathit{\alpha }}_{S,m}{y}_{S,m}={\displaystyle \frac{\mathrm{1}}{N_S}}{\sum }_{m=\mathrm{1}}^C{y}_{S,m},\end{array}$$

where indicator variables $\mathit{\alpha }=\mathit{\{}{\mathit{\alpha }}_m\in \mathit{\{}\mathrm{0},\mathrm{1}\mathit{\}},m=\mathrm{1},\mathrm{\dots },N_S\mathit{\}}$ are used to judge whether a landslide/non-landslide point in the source area is a landmark for minimizing the difference between source and target areas in the latent feature space. When α_m is 1, $(x_{S,m},y_{S,m})$ is regarded as a landmark, i.e., a landslide/non-landslide point that can provide valuable information for the landslide susceptibility model of the target area. In order to determine an optimal α, it is necessary to apply a selection threshold (for a quantity β in Gong et al., 2013); we chose $\mathrm{1}/N_S$ as this would allow us to select all source points as landmarks in the ideal situation where the source and target areas have identical latent feature space distributions. Furthermore, ϕ is a nonlinear feature function to map x to a reproducing kernel Hilbert space (Gretton et al., 2006). Following Gong et al. (2013, 2017), Gaussian RBF kernels are used for ϕ in our study; C is the number of landslide or non-landslide points. The collection α is chosen so that the quantity in Eq. (2) is minimized, i.e., the difference is minimized. Equation (3) is the constraint that considers the distribution of labels in the selected landmarks. This problem can be solved efficiently with convex optimization.

2.3 Susceptibility model training and testing

The transfer-learning strategies were applied using generalized additive models (GAMs) for susceptibility modeling. The logistic GAM, which performs a binomial classification of the absence or presence of landslides, has been well established as a method suitable for landslide susceptibility (Goetz et al., 2011; Petschko, 2014; Conrad et al., 2015; Bordoni et al., 2020). In fitting our model, we assumed that the feature space is the same for source and target areas. We therefore only used common predictors of landslide susceptibility (Goetz et al., 2015) that are available in all source and target areas, which include local slope angle, plan and profile curvature, catchment slope angle, and upslope contributing area. These terrain attributes are intended to act as proxies for destabilizing forces (slope, catchment slope angle), water availability (logarithm of upslope contributing area and concave curvatures), and exposure to wind (convex curvatures), as well as general variability in characteristics of soil and vegetation (Muenchow et al., 2012).

We used the mgcv package (Wood, 2006) for GAM modeling. We set the dimension of the basis used to represent the smooth term k as 4. Since it can be difficult to separate landslide scarp and body from medium to low-resolution data (Dou et al., 2020), landslide presence points were randomly sampled from the entire landslide polygon and non-landslide points were randomly sampled from the area where the mapped landslides were excluded. At the same time, landslides that are smaller than one grid cell were excluded from our study.

In turn, each study area was used as a target area. The landslide label data from the target area were not involved in the training process of all strategies embedded in CBR, DA, or CBR–DA. Model performance was assessed using test data only within a target area. The training dataset was composed of an equal number of landslide and non-landslide observations. These landslide and non-landslide grid cells were obtained from the whole study area, or a subset of the study area based on DA.

Altogether, we explored five CBR and DA strategies for susceptibility modeling based on single and multiple source areas, which are summarized in Table 2. In our implementation of CBR, only source areas related to the target area were used for modeling, where we defined related areas as source areas that had a (minimum) similarity score ≥ 0.65. In the case of DA (without CBR), multi-source models were created for all N source areas, excluding the target area. The final susceptibility models for multi-source CBR, DA, and CBR–DA strategies were based on combining model predictions from multiple source areas (described in Table 2).

Table 2 Transfer strategies and benchmarks adopted in our study.

The area under the receiver operating characteristic (ROC) curve (AUROC) (Hosmer et al., 2013) was used to assess the predictive performance of the transferred models based on their predictions in the target area. In choosing the AUROC, we treated model predictions as relative scores instead of actual probability estimates, which is common practice in landslide susceptibility modeling.

2.4 Case study transfer source and target areas

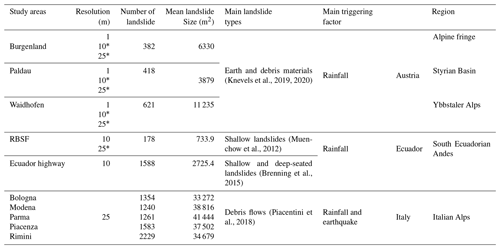
We demonstrated the application of CBR and DA for transfer learning using 10 case study areas for source and target areas from three distinct geographic regions (Fig. 2): the Andes of southern Ecuador (the Reserva Biológica San Francisco (RBSF) area, and a highway corridor; Muenchow et al., 2012; Brenning et al., 2015), the Emilia Romagna Region in northern Italy (Bologna, Modena, Parma, Piacenza, and Rimini areas; Rossi et al., 2010; Segoni et al., 2018; Piacentini et al., 2018; Ciccarese et al., 2021), and eastern Austria (Burgenland, Waidhofen and Paldau areas; Gasser et al., 2009; Petschko et al., 2012; Knevels et al., 2019, 2020). Rainfall is considered the main trigger of landslides in all study areas.

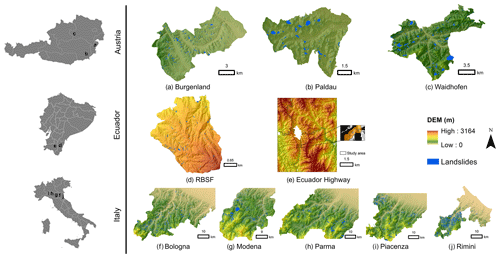
Figure 2 Overview of study areas for landslide susceptibility mapping in our study. The study areas are shown as DEM map in the same scale. Landslide inventories of study areas are shown as blue polygons. From top to bottom, study areas are from Austria, Ecuador, and Italy. Map extents correspond to study areas, with the exception of the Ecuador highway area, where the study area is limited to a 300 m buffer on both sides of the highway and outside urban areas.

All study areas have similar types of igneous rocks (e.g., basalt), sedimentary rocks (e.g., sandstone), and metamorphic rocks (e.g., schist), except that the RBSF area has no igneous and sedimentary rocks. The above references provide additional detailed information on the study areas. We also summarized the geological information of all study areas in Table A1 in the Appendix.

In our study, DEMs with different resolutions were available for the Austrian, Italian, and Ecuadorian study areas. For Ecuador, the 10 m × 10 m DEMs were produced by Ekkehard Jordan and Lars Ungerechts (Düsseldorf); for Italy, an EU-DEM with a 25 m × 25 m resolution was used; and an airborne lidar-derived digital terrain model (DTM) with a 1 m × 1 m resolution was available for the Austrian areas from the governments of Styria and Burgenland. Landslide inventories in our study were provided by Jannes Muenchow (Erlangen) for Ecuador, who also did a more detailed study in Muenchow et al. (2012). Additional information can furthermore be found in SGSS (2019) for the Emilia-Romagna region, Knevels et al. (2019) for Burgenland, and Knevels et al. (2020) for Waidhofen and Paldau. For the Emilia-Romagna region, we chose the subset of landslides labeled as active.

We furthermore resampled the DEMs with 1 m resolution to 10 and 25 m, and the data with 10 m resolution to 25 m in order to use up to three dataset versions to mimic various mismatches in target and source resolution. Resampling was based on B-spline interpolation in SAGA (System for Automated Geoscientific Analysis) GIS 7.4.0 (Conrad et al., 2015). Overall, we therefore had 17 datasets (Table 3). For brevity, we combined the place name with the resolution, e.g., Waidhofen 10 for Waidhofen with a 10 m resolution.

Table 3 Summary of the landslide datasets used in this study.

^* resolution of resampled data

3 Results

3.1 CBR similarity analysis

For the majority of the areas, mean slope angle and spatial resolution were the most limiting and therefore the most influential similarity attributes in determining which source areas were related to the target area. For some target areas, multiple similarity attributes contributed to differentiating candidate source areas, while for others, a single attribute (mean slope or resolution) dominated the exclusion of unrelated source areas (Fig. 3). For high-resolution datasets, the resolution attribute was primarily responsible for the overall similarity. The combination of spatial resolution and the standard deviation of slope or mean slope affected the overall similarity as the resolutions of the source and target areas got closer. In general, as the spatial resolution of the target and source areas became coarser, the number of related source areas tended to increase. Mean slope, standard deviation of slope, and geological units had more influence on the overall similarity assessment when resolutions were similar. Topographic characteristics and resolution were generally the main attributes that determined the overall similarity.

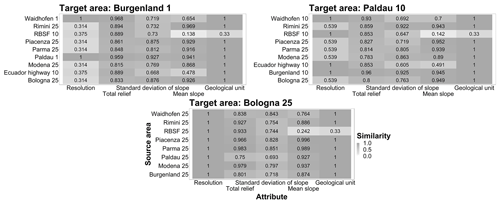
Figure 3 Similarity scores for three selected representative target areas (Burgenland 1, Paldau 10, and Bologna 25). Light colors represent smaller similarities. The overall similarity value of each source area is marked with a black box.

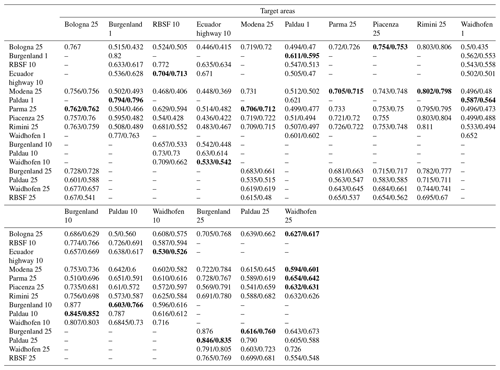
Most of the target areas (14 out of 17) had one or more related source areas. There were only 3 cases where the target had no related source areas (RBSF 10, 25, and Waidhofen 1), 2 cases with only one source area, and 12 with multiple related source areas (Fig. 4). Target areas with a resolution of 25 m tended to have a larger number of related source areas. Some target areas had related source areas in different geographic regions (e.g., Italian Alps and Burgenland).

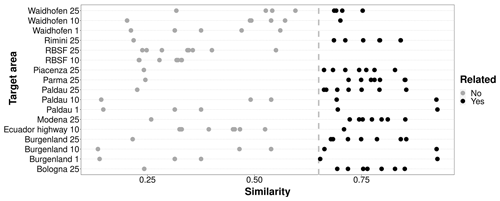
Figure 4 Distribution of related (black points) and unrelated (gray points) source areas for different target areas in the CBR transfer-learning strategies. Related source areas are defined as having a minimum similarity score ≥ 0.65 (vertical line).

Three representative target areas were selected to show the contribution of each attribute to the overall similarity because similar patterns were observed elsewhere (Fig. 3; complete results in the Supplement).

3.2 Single-source learning

In single-source transfer learning, CBR achieved the highest model performance overall. The DA resulted in stronger predictive performances only when source and target areas were substantially dissimilar (Figs. 5, 6). The AUROCs obtained by single-source CBR were always distributed between the median and maximum values of transfer benchmark models and close to the AUROCs obtained by the model trained using only target data (Fig. 5 and Table A2 in Appendix). For example, when Bologna 25 was the target data, the AUROCs of a model trained in the most related source area Piacenza 25 was 0.762 and that of the model trained with Bologna 25 data as source was also 0.762. Moreover, the majority of median AUROC performances obtained with single-source DA were greater than the median AUROC performance of single-source transfer benchmark models (Fig. 5). This distribution trend implied to some extent that single-source DA improved performances, which was consistent with the results shown in Fig. 6. Specifically, for similarities below 0.27, AUROCs achieved with DA were up to 0.14 higher than without it. When the overall similarity of the source area for the target area gradually increased up to ∼ 0.60–0.65, the difference values were centered at around +0.03. As the overall similarity was greater than 0.65, the AUROCs obtained by single-source DA were close to the ones achieved by the single-source transfer benchmark.

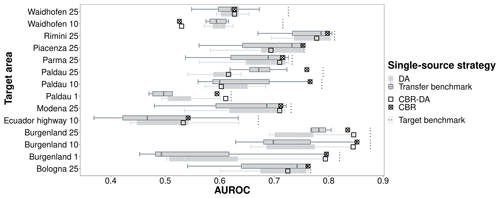
Figure 5 Comparison of single-source strategies: AUROCs obtained by models trained on individual source areas with case-based reasoning (CBR), domain adaptation (DA), combined CBR–DA, and in the single-source transfer benchmark.

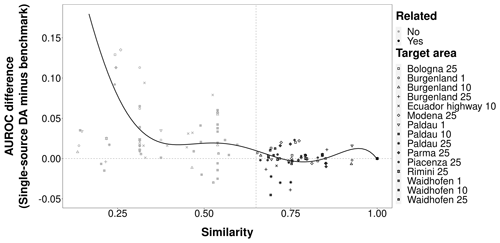
Figure 6 Similarity scores vs. AUROC differences between models trained on individual source areas with DA and models without DA (“single-source DA” minus “single-source transfer benchmark”).

CBR–DA also showed good performances. Its results were located in the upper part of transfer benchmark results (Fig. 5). This may be due to the contribution of CBR rather than DA. Throughout all the results, single-source CBR demonstrated more stable prediction performances compared to the results obtained by the strategies involving DA.

From this perspective, it can be concluded that by selecting the related areas, CBR was effective in identifying a suitable source area that resulted in favorable performances regardless of the use of DA.

3.3 Multi-source learning

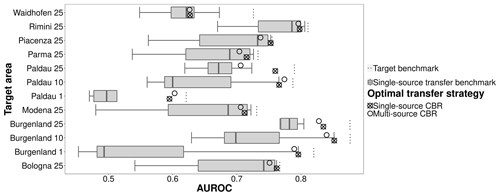
The strategies that involved CBR had better prediction performances in multi-source transfer learning compared to the multi-source transfer benchmark and multi-source DA (Fig. 7). Multi-source CBR obtained good performances regardless of the number of related source areas and whether the related source areas were from the same region (Figs. 4 and 7). However, multi-source CBR–DA underperformed in general, usually having predictive performances lower than the multi-source transfer benchmark. When comparing the average of AUROCs of different strategies for all target areas in multi-source transfer learning, CBR was the best multi-source strategy followed by the transfer benchmark and CBR–DA, while DA had the worst multi-source performance. Furthermore, with respect to the stability of the results, multi-source CBR performed best since the performances it obtained were always in the top two of all performances obtained by different multi-source transfer-learning strategies. In contrast, the results obtained for strategies involving DA were highly variable and always inferior to the results of the corresponding multi-source transfer benchmark.

Figure 7 AUROCs of models trained on multiple source areas with case-based reasoning (CBR), domain adaptation (DA), combined CBR–DA, and the multi-source transfer benchmark (averaged across all source areas) and target benchmark.

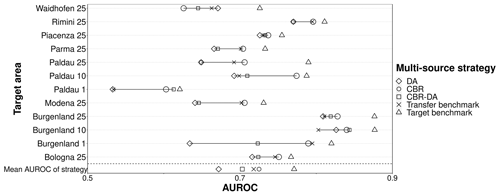
3.4 Comparing single- and multi-source learning

For the majority of target areas, single-source CBR was the best-performing transfer-learning strategy, closely followed by multi-source CBR (Fig. 8). Both were located between the median and the maximum of single-source transfer benchmark and tended to be closer to the maximum, which meant that CBR-based source selection was highly effective at identifying the most suitable sources of training data. On average, the single-source and multi-source CBR AUROCs were below the overoptimistic target benchmark (training and testing in target area) by only ∼ 0.05. The strong performance of CBR in both single- and multi-source strategies indicated that the most effective transfer-learning methods were to train the predictive model using the most related source area or performing a weighted combination based on the similarity scores of the predictive models trained on the most strongly related source areas.

Figure 8 Comparison of single- and multi-source CBR strategies and the single-source target benchmark.

3.5 Comparing susceptibility map appearances

The best-performing transfer-learning strategies (single-source and multi-source CBR and CBR–DA) had spatial patterns of landslide-prone areas that most resembled the target benchmark (Fig. 9). Strategies with CBR, which considers target–source similarity, were able to better avoid falsely detecting landslide-prone areas. Using classified landslide susceptibility maps for Burgenland 10 as an example, the lower-performing, multi-source DA (Fig. 9h) and the multi-source benchmark (Fig. 9e) appeared to overpredict susceptibility in some areas (e.g., on alluvial fans) compared to the target benchmark (Fig. 9a) and the better-performing CBR-based transfer-learning strategies (Fig. 9c, f, and g). The susceptibly maps also showed that if a single source area had a high similarity (e.g., Paldau 10 and Burgenland 10) to the target area, DA strategies (Fig. 9d) can also properly detect landslide-prone areas. The difference in landslide-prone areas of single- and multi-source benchmarks compared to the target benchmark also indicates that not all source areas were suitable for predicting landslides for unseen areas.

Figure 9 An example of classified landslide susceptibility maps for each benchmark and transfer-learning strategy for the Burgenland 10 target area. Predicted probabilities were classified into five susceptible levels (very high, high, moderate, low, very low) using the top 5th, 10th, 25th, and 50th percentile of each strategy's predictions. The results of single-source CBR and single-source DA are illustrated using models trained on Paldau 10 data. The single-source benchmark result is illustrated using a model trained with Waidhofen 10 data.

4 Discussion

4.1 Case-based reasoning in landslide assessment studies

By calculating the similarities between source and target areas to find the most transferable source area(s), CBR is able to transfer the knowledge from source areas to the target area. In our study, we considered data from a variety of regions, and our results provided a comprehensive understanding of the potential of CBR in single- and multi-source transfer learning. Consistent with the literature for digital soil mapping and digital terrain analysis (Qin et al., 2016; Liang et al., 2020a, 2021), our results further support the adoption of CBR and provide useful methodological information for landslide assessment studies.

Case-based reasoning may give fresh insight into improving the understanding of knowledge transfer in landslide susceptibility modeling. It is an effective method to capture past experiences to improve the predictive capabilities of models (Wang et al., 2020; Bannour et al., 2021). In particular, it only needs to consider the basic characteristics of the data and the region to quickly match historical scenarios to the current study area and thus solve the task at hand. Additionally, the use of CBR to compare similarities between datasets makes it possible to reuse existing predictive models. These attractive abilities may benefit landslide mapping for emergency response as well as landslide susceptibility modeling for hazard mitigation. Moreover, we determined that by using similarity as the basis for the weight of each related source area and the strategies involved, CBR in multiple source areas displayed good and robust performance in our study (Fig. 7).

Until now, model transfer in landslide modeling have usually relied on a homogeneous availability of data and a strong model generalization to avoid local overfitting and allow the application of a model in an adjacent target region (Goetz et al., 2011; Wenger and Olden, 2012; Petschko et al., 2014; Bordoni et al., 2020). Although this approach has been identified as a robust method for regional susceptibility modeling, its model transferability is often limited to nearby locations that have the same feature space and a nearly identical data distribution. However, when the data distribution is different, the above approach may not be effective, even though the training data are from adjacent regions. Yates et al. (2018) have pointed out that the spatial and temporal separation may have little impact on model transfers, while environmental dissimilarity and data resolution are critical factors for successful model transfer. These factors could be considered as the spatial and temporal limits to extrapolation in model transfers, as well as for landslide susceptibility model transfers; CBR may be able to handle these limits by calculating the overall similarity, indicating the suitability of landslide susceptibility model transfers between different study areas. In Figs. 3 and 7, we found that combining data from multiple related source areas with CBR yielded excellent results, even though some of the related source areas are from different regions than the target area.

After selecting related source areas, the predictors designed for training the model need to be examined. In our study, we assumed that the source and target areas used the same predictors and focused on topographic predictors. However, when the source and target areas have different predictors, one of the problems is that topographic predictors are not the only factors that play a key role in landslide prediction. Thus, a method should be implemented to select suitable predictors for model transfer since not all predictors can be used in the training process. Liang et al. (2021) selected suitable predictors for a new task by using each model trained by individual predictors of the source area to predict in the target area; they concluded that this method was effective. However, since they only focused on terrain attributes, it is unclear how this approach would work on other predictors such as antecedent rainfall intensity, which, in addition to regional rainfall pattern variations, can strongly differ from one region to another. From this perspective, we would suggest that future research using CBR transfer learning could focus on the selection of features that are more likely transferable.

4.2 CBR similarity criteria

The proposed similarity scores in this study based on geologic, topographic, and data characteristics (i.e., spatial resolution) worked quite well in supporting CBR strategies for identifying the most similar and thus transferable source areas. These similarity attributes do not explicitly account for landslide type, which is an important factor to consider when modeling landslide susceptibility (Huang and Zhao, 2018). However, geologic attributes and terrain attributes such as slope angle, may work together as a suitable surrogate to anticipate the most likely landslide types given little to no landslide data in the target area. Landslide type information is also difficult to collect and often lacking in landslide inventories (Mezaal and Pradhan, 2018). Prior information on unseen areas or integrating expert experience may be helpful in formulating landslide types for transfer learning.

In general, the use of similarity indices can be somewhat arbitrary since there are currently no clear criteria for how to select suitable similarity indices. For example, Liang et al. (2020a) analyzed the importance of each attribute for digital soil mapping based on previous studies to select the similarity index. Qin et al. (2016) indicated that the similarity indices should be structured to effectively represent the contextual information relevant to digital terrain analysis applications, hence the similarity indices used were based on knowledge and experience. Wang et al. (2020) selected similarity indices based on their importance for disaster situations.

For CBR applied to landslide susceptibility modeling, more elaborate criteria that could be indirectly used to account for differences in landslide type could focus on preparatory and triggering conditions such as land use (Steger et al., 2017; Knevels et al., 2021) and the density of paved and unpaved road networks (Brenning et al., 2015). Adding more process-related similarity indices may lead to improved CBR transfer learning, but this may not be easy to implement across different study regions in different countries with different mapping agencies and standards. Therefore, similar to selecting individual features for landslide susceptibility modeling (without model transfer), we recommend the use of expert knowledge to help guide the selection of similarity attributes.

In terms of choosing related source areas, the minimum operator method worked well in our study and avoided selecting a “falsely” related source. However, we did observe a scenario where one area was considered to be related but the reciprocal area not (Paldau and Waidhofen; Fig. 4). As pointed out by Humphreys et al. (2003), when using CBR for similarity evaluation, the evaluation criterion used may be different in different categories and situations. By analogy, we can assume that the threshold settings for similarity may also differ for different attributes in different study areas in landslide assessment studies. Additionally, there are other methods to obtain the related area, such as Manhattan distance, gray relational analysis, or k-nearest neighbors (Dou et al., 2015).

4.3 Utility of domain adaptation in geospatial learning and other limitations

Our study showed that DA did not generally improve transfer-learning performance in landslide susceptibility modeling. This holds true for single-source as well as multi-source DA with and without CBR-based source selection. Nevertheless, DA increased the AUROC performance when the source area was rather dissimilar to the target area (Fig. 6), which is less relevant in landslide studies that have access to a large and geographically diverse case base.

It is impressive that models trained on multiple related source areas with CBR and DA showed good performances. For instance, when Paldau with a 1 m × 1 m, and Burgenland with a 10 m × 10 m resolution were the target areas, AUROCs obtained by multi-source CBR–DA were nearly equal to those achieved by the best single-source transfer benchmark and higher than the other strategies (Fig. 7). The reason may lie in the improvement of DA through the weighting of source areas.

A further consideration is to use labeled data from the target area. Fang et al. (2021) proposed a new domain adaptation for landslide inventory mapping by considering pre-landslide and post-landslide conditions and concluded that the proposed method was successful. This new method could be considered as supervised DA in landslide susceptibility mapping. In other geospatial learning fields, such as land cover mapping, Mboga et al. (2021) compared two unsupervised DA strategies (the correlation alignment domain adaptation network and the domain adversarial neural network) and found that classification performance was improved by adding labeled data from the target area. We suggest that active-learning strategies (Wang and Brenning, 2021) could be useful in efficiently generating limited amounts of labeled data for transfer learning, which should therefore be investigated in a next step.

Although the study areas cover a wide range of climates with different land cover types and landslide process types, our set of source areas is by no means complete and the results may therefore not be fully representative for the performances that might be achieved at a global scale. Future work should therefore broaden the database of source areas.

4.4 The potential of the novel methods for landslide assessment

Deep learning is getting more and more popular in the study of landslide model transfer. For example, Ai et al. (2022) proposed a supervised method by combining deep learning and transfer learning for landslide susceptibility modeling. Liu et al. (2021) performed landslide classification using VGG-19 and transfer learning based on limited data from the unseen area. Lu et al. (2020) mapped landslides based on deep learning and transfer learning. These studies show that deep learning is a potential method in landslide model transfer studies, although they are limited to a regional scale or require training data from the target area.

Combining CBR with deep learning could be a worthy unsupervised method in landslide assessments. By calculating similarities between the target area and source areas and selecting related source areas, deep learning can directly use them to train landslide models for the target area, which might avoid the need for tuning hyperparameters.

5 Conclusions

The aim of our study was to examine the performances of geographically informed case-based reasoning (CBR) and unsupervised domain adaptation (DA) in geographically transferring knowledge for landslide susceptibility modeling in “new” target areas without landslide inventory data. We extended the study of landslide model transfers to a larger global scale and considered the effect of different spatial resolutions on landslide model transfer. In addition, different scenarios (single source area and multiple source areas) were considered, which made methods and results much closer to practical applications in the real world. Moreover, in the multi-source scenario, we proposed a method to combine multiple landslide models based on environmental similarity. Our comparative study revealed that CBR strategies with a single source area and multiple related source areas were robust and effective in developing highly transferable landslide susceptibility models without requiring prior knowledge of landslides in the target area. In particular, single-source CBR was the most effective method for performing model transfer to the target area in most situations. Its performance was also very close to that obtained by models trained with data from the target area itself. The CBR similarity criteria in our study are still preliminary, and datasets used in our study might not be enough for an application at a global scale, which should therefore be considered in future research.

Overall, the findings of this paper demonstrated that the proposed transfer-leaning approaches can alleviate the burden of collecting and labeling data, resulting in a more expedited preparation of landslide susceptibility maps for large and data-scarce regions. By calculating the similarity between data and region characteristics, trained models can directly be used for the new task, especially in situations that require rapid model development, such as emergency situations. Furthermore, we suggest that novel methods such as deep learning may also benefit greatly for landslide model transfer studies.

Appendix A

Table A1 Information of all study areas.

Table A2 AUROCs of models trained on individual source areas with domain adaptation (DA) versus without domain adaptation. The results are shown as DA/target benchmark. The bold font indicates that the source area corresponding to this AUROC was the most related for the current target area.