Impacts of the ice-particle size distribution shape parameter on climate simulations with the Community Atmosphere Model Version 6 (CAM6)

The impacts of the ice-crystal size distribution shape parameter (μ_i) were considered in the two-moment bulk cloud microphysics scheme of the Community Atmosphere Model Version 6 (CAM6). The μ_i's impact on the statistical mean radii of ice crystals can be analyzed based on their calculating formulas. Under the same mass (q_i) and number (N_i), the ratios of the mass-weighted radius ($R_{q_{\mathrm{i}}}$, not related to μ_i) to other statistical mean radii (e.g., effective radiative radius) are completely determined by μ_i. Offline tests show that μ_i has a significant impact on the cloud microphysical processes owing to the μ_i-induced changes in ice-crystal size distribution and statistical mean radii (excluding $R_{q_{\mathrm{i}}}$). Climate simulations show that increasing μ_i would lead to higher q_i and lower N_i in most regions, and these impacts can be explained by the changes in cloud microphysical processes. After increasing μ_i from 0 to 5, the longwave cloud radiative effect increases (stronger warming effect) by 5.58 W m⁻² (25.11 %), and the convective precipitation rate decreases by −0.12 mm d⁻¹ (7.64 %). In short, the impacts of μ_i on climate simulations are significant, and the main influence mechanisms are also clear. This suggests that the μ_i-related processes deserve to be parameterized in a more realistic manner.

1 Introduction

Clouds are an integral part of the Earth's radiation budget and global water cycle (Liou, 1986; Luo and Rossow, 2004; Bony et al., 2015; Zhou et al., 2016). Since cloud microphysical processes occur at scales that are much smaller than the resolution of commonly used atmospheric models, it remains a significant challenge for atmospheric models to represent cloud-related processes, especially ice-phase cloud microphysical processes (Mitchell et al., 2008; Spichtinger and Gierens, 2009; Wang and Penner, 2010; Erfani and Mitchell, 2016; Paukert et al., 2019; Morrison et al., 2020; Proske et al., 2022). Because it is impossible for commonly used atmospheric models (excluding the ideal model with the recently developed Lagrangian-particle-based scheme) to individually describe cloud particles (e.g., cloud droplets or ice crystals), only the macrostatistical features of cloud particles are represented in cloud microphysics schemes. From the outset, the development of cloud microphysics schemes has resulted in two distinct categories: bulk microphysics parameterization and spectral (bin) microphysics (Milbrandt and Yau, 2005; Khain et al., 2015). The spectral (bin) approach explicitly represents the cloud particle size distributions (PSDs) using tens to hundreds of bins. The computational cost of this approach is very high because of the massive interactions among different bins. The bulk microphysics scheme represents the PSDs by a semiempirical distribution function. Compared to the spectral (bin) scheme, the bulk microphysics scheme has high computational efficiency and has been widely used in climate models (Morrison et al., 2005; Lohmann et al., 2007; Salzmann et al., 2010; Gettelman and Morrison, 2015).

In the bulk cloud microphysics schemes used for climate models, the PSD is usually described by the gamma distribution function with three parameters, namely, the intercept parameter (N₀), the slope parameter (λ), and the spectral shape parameter (μ) (Khain et al., 2015; Morrison et al., 2020). Note that the commonly used two-moment bulk microphysics scheme predicts only the mass and number of cloud particles, which cannot constrain these three parameters (i.e., N₀, λ, and μ). Therefore, one of these three parameters (typically μ) must be determined from an empirical formula or set to a given value (e.g., Morrison and Gettelman, 2008; Barahona et al., 2014; Eidhammer et al., 2017). For instance, the μ(μ_i) of ice crystals (ICs; only represent cloud ice in this study) in the two-moment bulk stratiform cloud microphysics scheme developed by Morrison and Gettelman (2008) (hereafter “MG scheme”) is set to zero (i.e., the μ_i is ignored). In recent years, offline tests and short-term simulations (a few days or less) with high-resolution atmospheric models (e.g., cloud-resolving models and mesoscale models) have shown that μ_i has a significant impact on cloud microphysical processes and synoptic systems (Milbrandt and Yau, 2005; Milbrandt and McTaggart-Cowan, 2010; Loftus et al., 2014; Khain et al., 2015; Milbrandt et al., 2021). Unlike short-term simulations, climate simulations pay more attention to the equilibrium states or quasi-equilibrium states because the feedback processes become important (Sherwood et al., 2015; King et al., 2020). However, in terms of climate simulations, few studies have focused on the influence of μ_i.

In this study, in order to investigate the impacts of μ_i on climate simulations with the Community Atmosphere Model version 6 (CAM6) model, the impacts of μ_i were considered in the MG scheme by a tunable parameter. There were two major motivations behind this work. First, are the impacts of μ_i notable? If yes, it is necessary for climate models to represent the μ_i and μ_i-related processes in a more realistic manner. And second, what are the main mechanisms for these impacts? These would be helpful to understand the climate simulations with the impacts of μ_i. This paper is organized as follows: the modified MG scheme and experimental setup are described in Sect. 2; cloud microphysical process offline tests and CAM6 model simulation results are analyzed in Sect. 3; and finally, the summary and conclusions are provided in Sect. 4.

2 Model and experiments

2.1 The modified MG scheme

The CAM6 model, which is the atmospheric component of the Community Earth System Model Version 2.1.3 (CAM6; Bogenschutz et al., 2018; CESM2, Danabasoglu et al., 2020), was used in this study. It is noteworthy that the treatments of clouds in climate models are usually divided into two categories: convective cloud schemes with simplified cloud microphysics and larger-scale stratiform cloud schemes with relatively detailed cloud microphysics. In the CAM6 model, the convective cloud scheme does not consider the PSD of ICs (Zhang and McFarlane, 1995; Zhang et al., 1998; Bogenschutz et al., 2013; Larson, 2017). The stratiform cloud microphysics was represented by the updated MG scheme with prognostic precipitation (Gettelman and Morrison, 2015). In both versions of the MG scheme, the ICs are assumed to be spherical, and the PSD of ICs is described by the gamma distribution function:

$$\begin{array}{}\text{(1)}& {N^{\prime }}_{\mathrm{i}}\left(D\right)=N_{\mathrm{0}\mathrm{i}}{D}^{{\mathit{\mu }}_{\mathrm{i}}}{e}^{-{\mathit{\lambda }}_{\mathrm{i}}D},\end{array}$$

where $N_{\mathrm{i}}^{\prime }\left(D\right)$ is the number density (i.e., $\mathit{\delta }{N}_{\mathrm{i}}/\mathit{\delta }D)$ of the ICs with diameter D. N_0i, λ_i, and μ_i (nonnegative values) are the intercept parameter, the slope parameter, and the spectral shape parameter, respectively. Given that μ_i is known, N_0i and λ_i can be determined by the local in-cloud IC mass and number mixing ratio (q_i and N_i, prognostic variables in units of kg kg⁻¹ and kg⁻¹, respectively).

$$\begin{array}{}\text{(2)}& {\displaystyle }{\mathit{\lambda }}_{\mathrm{i}}& {\displaystyle }={\left[{\displaystyle \frac{\mathit{\pi }{\mathit{\rho }}_{\mathrm{i}}}{\mathrm{6}}}{\displaystyle \frac{N_{\mathrm{i}}}{q_{\mathrm{i}}}}{\displaystyle \frac{\mathrm{\Gamma }\left(\mathrm{4}+{\mathit{\mu }}_{\mathrm{i}}\right)}{\mathrm{\Gamma }\left(\mathrm{1}+{\mathit{\mu }}_{\mathrm{i}}\right)}}\right]}^{\mathrm{1}/\mathrm{3}}\text{(3)}& {\displaystyle }{N}_{\mathrm{0}\mathrm{i}}& {\displaystyle }={\displaystyle \frac{N_{\mathrm{i}}{\mathit{\lambda }}_{\mathrm{i}}^{\left(\mathrm{1}+{\mathit{\mu }}_{\mathrm{i}}\right)}}{\mathrm{\Gamma }\left(\mathrm{1}+{\mathit{\mu }}_{\mathrm{i}}\right)}},\end{array}$$

where the IC bulk density (ρ_i) is 500 kg m⁻³, and μ_i is zero in the default MG scheme. $\mathrm{\Gamma }\left(x\right)={\int }_{\mathrm{0}}^{\mathrm{\infty }}{t}^{x-\mathrm{1}}{e}^{-t}\mathrm{d}t$ is the gamma function. It is noteworthy that the kth moment of this size distribution (M_k) is found by integrating the distribution in this form: $M_k={\int }_{\mathrm{0}}^{\mathrm{\infty }}{N}_{\mathrm{0}\mathrm{i}}{D}^{{\mathit{\mu }}_{\mathrm{i}}+k}{e}^{-{\mathit{\lambda }}_{\mathrm{i}}D}\mathrm{d}D=N_{\mathrm{0}\mathrm{i}}\mathrm{\Gamma }(k+{\mathit{\mu }}_{\mathrm{i}}+\mathrm{1})/{\mathit{\lambda }}_{\mathrm{i}}^{(k+{\mathit{\mu }}_{\mathrm{i}}+\mathrm{1})}$ (Eidhammer et al., 2014). Furthermore, the recursive property of the gamma function (i.e., $\mathrm{\Gamma }\left(x+\mathrm{1}\right)=x\mathrm{\Gamma }\left(x\right)$ ) is also used for the following formula derivation.

Equations (2) and (3) also indicate that, under the same q_i and N_i, changes in μ_i could impact the other two parameters regarding the PSD of ICs (i.e., N_0i and λ_i). Meanwhile, the number-weighted radius ($R_{{\mathrm{n}}_{\mathrm{i}}}$) related to the IC deposition/sublimation process, the effective radiative radius ($R_{{\mathrm{e}}_{\mathrm{i}}}$) used for the radiative transfer scheme, and other statistical mean radii might be influenced. To better understand the influence of μ_i on the ice-phase cloud microphysical processes, the equations for calculating the statistical mean radii are introduced first. The mass-weighted radius ($R_{q_{\mathrm{i}}}$) is calculated from Eq. (4). The number-weighted radius ($R_{{\mathrm{n}}_{\mathrm{i}}}$), which is the so-called mathematical mean value, is calculated from Eq. (5). The area-weighted radius ($R_{{\mathrm{a}}_{\mathrm{i}}}$) is calculated from Eq. (6). $R_{{\mathrm{e}}_{\mathrm{i}}}$, which is defined as the cross-section-weighted radius (Schumann et al., 2011; Wyser, 1998), is calculated from $R_{q_{\mathrm{i}}}^{\mathrm{3}}/R_{{\mathrm{a}}_{\mathrm{i}}}^{\mathrm{2}}$ (Eq. 7). Note that $R_{q_{\mathrm{i}}}$ can be calculated by q_i and N_i (the last term of Eq. 4, without μ_i), and the other statistical mean radii (e.g., $R_{{\mathrm{n}}_{\mathrm{i}}}$, $R_{{\mathrm{a}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$) can be calculated by $R_{q_{\mathrm{i}}}$ and μ_i (Eqs. 5–7). In other words, the ratios of the other statistical mean radii (e.g., $R_{{\mathrm{n}}_{\mathrm{i}}}$, $R_{{\mathrm{a}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$) to $R_{q_{\mathrm{i}}}$ are functions of μ_i. For nonnegative μ_i values, Eqs. (5) and (6) indicate that $R_{{\mathrm{n}}_{\mathrm{i}}}$ and $R_{{\mathrm{a}}_{\mathrm{i}}}$ are always less than $R_{q_{\mathrm{i}}}$. This can be explained by the physical reason that larger ICs contribute more to $R_{q_{\mathrm{i}}}$ than to $R_{{\mathrm{n}}_{\mathrm{i}}}$ and $R_{{\mathrm{a}}_{\mathrm{i}}}$. Similarly, $R_{{\mathrm{e}}_{\mathrm{i}}}$ is always greater than $R_{q_{\mathrm{i}}}$ (Eq. 7). Furthermore, Eqs. (5), (6), and (7) also indicate that with increasing μ_i, $R_{{\mathrm{n}}_{\mathrm{i}}}$, $R_{{\mathrm{a}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$ approach $R_{q_{\mathrm{i}}}$. In Sect. 3.1, more analyses are provided by offline tests.

$$\begin{array}{ll}{\displaystyle }{R}_{q_{\mathrm{i}}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left[{\displaystyle \frac{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{D}^{\mathrm{3}}{N}_{\mathrm{i}}\left(D\right)\mathrm{d}D}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{N}_{\mathrm{i}}\left(D\right)\mathrm{d}D}}\right]}^{\mathrm{1}/\mathrm{3}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\lambda }}_{\mathrm{i}}}}{\left[{\displaystyle \frac{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{4}\right)}{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right)}}\right]}^{\mathrm{1}/\mathrm{3}}\\ \text{(4)}& {\displaystyle }& {\displaystyle }={\left({\displaystyle \frac{\mathrm{3}}{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{i}}}}{\displaystyle \frac{q_{\mathrm{i}}}{N_{\mathrm{i}}}}\right)}^{\mathrm{1}/\mathrm{3}}{\displaystyle }{R}_{{\mathrm{n}}_{\mathrm{i}}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\int }_{\mathrm{0}}^{\mathrm{\infty }}D{N}_{\mathrm{i}}\left(D\right)\mathrm{d}D}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{N}_{\mathrm{i}}\left(D\right)\mathrm{d}D}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\lambda }}_{\mathrm{i}}}}{\displaystyle \frac{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{2}\right)}{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right)}}\\ {\displaystyle }& {\displaystyle }=R_{q_{\mathrm{i}}}{\left[{\displaystyle \frac{\mathrm{\Gamma }\left(\mathrm{1}+{\mathit{\mu }}_{\mathrm{i}}\right)}{\mathrm{\Gamma }\left(\mathrm{4}+{\mathit{\mu }}_{\mathrm{i}}\right)}}\right]}^{\frac{\mathrm{1}}{\mathrm{3}}}{\displaystyle \frac{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{2}\right)}{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right)}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }=R_{q_{\mathrm{i}}}{\displaystyle \frac{\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right)}{{\left[\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{3}\right)\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{2}\right)\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right)\right]}^{\frac{\mathrm{1}}{\mathrm{3}}}}}{\displaystyle }{R}_{{\mathrm{a}}_{\mathrm{i}}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left[{\displaystyle \frac{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{D}^{\mathrm{2}}{N}_{\mathrm{i}}\left(D\right)\mathrm{d}D}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{N}_{\mathrm{i}}\left(D\right)\mathrm{d}D}}\right]}^{\mathrm{1}/\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\lambda }}_{\mathrm{i}}}}{\left[{\displaystyle \frac{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{3}\right)}{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right)}}\right]}^{\mathrm{1}/\mathrm{2}}\\ {\displaystyle }& {\displaystyle }=R_{q_{\mathrm{i}}}{\left[{\displaystyle \frac{\mathrm{\Gamma }\left(\mathrm{1}+{\mathit{\mu }}_{\mathrm{i}}\right)}{\mathrm{\Gamma }\left(\mathrm{4}+{\mathit{\mu }}_{\mathrm{i}}\right)}}\right]}^{\mathrm{1}/\mathrm{3}}{\left[{\displaystyle \frac{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{3}\right)}{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right)}}\right]}^{\mathrm{1}/\mathrm{2}}\\ \text{(6)}& {\displaystyle }& {\displaystyle }=R_{q_{\mathrm{i}}}{\displaystyle \frac{{\left[\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{2}\right)\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right)\right]}^{\frac{\mathrm{1}}{\mathrm{2}}}}{[\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{3}\right)\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{2}\right)\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right){]}^{\frac{\mathrm{1}}{\mathrm{3}}}}}{\displaystyle }{R}_{{\mathrm{e}}_{\mathrm{i}}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{D}^{\mathrm{3}}{N}_{\mathrm{i}}\left(D\right)\mathrm{d}D}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{D}^{\mathrm{2}}{N}_{\mathrm{i}}\left(D\right)\mathrm{d}D}}={\displaystyle \frac{(R_{q_{\mathrm{i}}}{)}^{\mathrm{3}}}{(R_{{\mathrm{a}}_{\mathrm{i}}}{)}^{\mathrm{2}}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\lambda }}_{\mathrm{i}}}}{\displaystyle \frac{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{4}\right)}{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{3}\right)}}\\ {\displaystyle }& {\displaystyle }=R_{q_{\mathrm{i}}}{\left[{\displaystyle \frac{\mathrm{\Gamma }\left(\mathrm{1}+{\mathit{\mu }}_{\mathrm{i}}\right)}{\mathrm{\Gamma }\left(\mathrm{4}+{\mathit{\mu }}_{\mathrm{i}}\right)}}\right]}^{\mathrm{1}/\mathrm{3}}{\displaystyle \frac{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{4}\right)}{\mathrm{\Gamma }\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{3}\right)}}\\ \text{(7)}& {\displaystyle }& {\displaystyle }=R_{q_{\mathrm{i}}}{\displaystyle \frac{\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{3}\right)}{[\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{3}\right)\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{2}\right)\left({\mathit{\mu }}_{\mathrm{i}}+\mathrm{1}\right){]}^{\frac{\mathrm{1}}{\mathrm{3}}}}}\end{array}$$

Because μ_i is zero in the default MG scheme, the equations for the cloud microphysical processes are simplified by omitting μ_i (Morrison and Gettelman, 2008; Gettelman and Morrison, 2015). In this study, these equations are modified to consider the impact of μ_i (i.e., nonzero μ_i). In the default MG scheme, there are three cloud microphysical processes, which are related to the PSD of ICs. They consist of the deposition/sublimation of ICs, the autoconversion of IC to snow, and the mass-weighted and number-weighted IC fall velocities ($V_{q_{\mathrm{i}}}$ and $V_{{\mathrm{n}}_{\mathrm{i}}}$), respectively. Table 1 shows the original and modified equations for these cloud microphysical processes. The d$q_{\mathrm{i}}/\mathrm{d}t$ (i.e., the time derivative of q_i) caused by the deposition/sublimation process (including the Wegener-Bergeron process in mixed-phase clouds) is calculated from d$q_{\mathrm{i}}/\mathrm{d}t=S_{\mathrm{i}}/(T_{\mathrm{p}}{\mathit{\tau }}_{\mathrm{i}}$), where S_i, T_p, and τ_i are the ice supersaturation, a psychrometric correction to account for the release of latent heat, and the supersaturation relaxation timescale, respectively (Morrison and Gettelman, 2008). Among them, τ_i is related to μ_i. In the original equation of τ_i (Table 1, left column), N_0i=λ_iN_i (Eq. 3) and ${\mathit{\lambda }}_{\mathrm{i}}^{-\mathrm{1}}=\mathrm{2}{R}_{{\mathrm{n}}_{\mathrm{i}}}$ at μ_i=0 (Eq. 5). Therefore, the original equation for τ_i can be rewritten as the modified equation (Table 1, right column). The modified equation indicates that τ_i is inversely proportional to $N_{\mathrm{i}}{R}_{{\mathrm{n}}_{\mathrm{i}}}$, which is consistent with the equation obtained by Korolev and Mazin (2003). This modified equation also indicates that, under the same q_i and N_i ($R_{q_{\mathrm{i}}}$ is also fixed), μ_i can affect τ_i (i.e., the IC deposition/sublimation process) via the influence on $R_{{\mathrm{n}}_{\mathrm{i}}}$. In the MG scheme, ICs with radii greater than the threshold (R_cs) are considered to be snow. Correspondingly, the mass and number of ICs converted to snow (q_iauto and N_iauto) are represented by the integration of those ICs with radii greater than R_cs. Therefore, the incomplete gamma function, ($\mathrm{\Gamma }\left(s,x\right)={\int }_x^{\mathrm{\infty }}{t}^{s-\mathrm{1}}{e}^{-t}\mathrm{d}t)$, is used to calculate q_iauto and N_iauto (right column). It is necessary to note that, at μ_i=0, the modified equations for q_iauto and N_iauto can be rewritten as the original equations (i.e., omitting μ_i, left column) based on a property of the incomplete gamma function (i.e., $\mathrm{\Gamma }\left(s,x\right)=\left(s-\mathrm{1}\right)\mathrm{!}{e}^{-x}\sum _{k=\mathrm{0}}^{s-\mathrm{1}}\frac{x^k}{k\mathrm{!}}$, where s is a positive integer). Based on the diameter–fall speed relationship, V=aD^b (a and b are empirical coefficients), and the properties of the gamma function, μ_i is considered in the equations for mass-weighted and number-weighted terminal fall speeds ($V_{q_{\mathrm{i}}}$ and $V_{{\mathrm{n}}_{\mathrm{i}}}$, Table 1).

Table 1 Equations for calculating the μ_i-related cloud microphysical processes^*.

^* where D_v is the diffusivity of water vapor in air (D_v is calculated as a function of temperature and pressure, D_v=8.794 × 10${}^{-\mathrm{5}}\times T^{\mathrm{1.81}}/P$), R_cs is the threshold radius for the autoconversion of IC to snow (R_cs=100 µm), ρ_a is the air density, ρ_a850 is the reference air density at 850 hPa, and a and b are empirical coefficients (a=700 m^1−b s⁻¹, b=1).

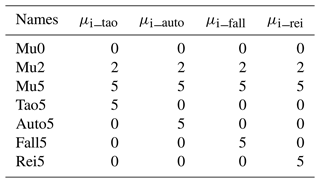
2.2 CAM6 experimental design

Observational studies have shown that μ_i is less than 5 under most conditions (Heymsfield, 2003; McFarquhar et al., 2015). This study focuses only on investigating the influence of μ_i. There are four μ_i-related processes (i.e., the radiative transfer process and three cloud microphysical processes) in the modified CAM6 model. Note that μ_i can be set to different values for different processes with the advantage of model simulations. Seven experiments were conducted in this study (Table 2). The Mu0 experiment is considered to be the reference experiment because μ_i is set to zero for all of the μ_i-related processes. The μ_i is set to 2 for all of the μ_i-related processes in the Mu2 experiment, and the μ_i is set to 5 for all of the μ_i-related processes in the Mu5 experiment. The comparison between the Mu2 (or Mu5) and Mu0 experiments shows the influence of μ_i on climate simulations. Furthermore, to investigate the influence of each μ_i-related process, an additional four experiments, namely, Tao5, Auto5, Fall5, and Rei5, were conducted. It is also necessary to investigate negative μ_i because negative μ_i has also been reported by observational studies. However, the bulk cloud microphysics schemes usually constrain μ_i to be nonnegative (see Appendix A). Therefore, only nonnegative μ_i was investigated. In this study, for ease of expression, “Δ” is used to denote the difference from the Mu0 experiment (e.g., ΔTao5 = Tao5 − Mu0). Without specification, the comparisons between model simulations are relative to the Mu0 experiment. When analyzing a cloud property variable (e.g., q_i), it is necessary to know which experiment the variable comes from. To show this information, the experiment name is added as a superscript. For example, the q_i from the Mu5 experiment is denoted as $q_{\mathrm{i}}^{\mathrm{Mu}\mathrm{5}}$, the difference in q_i between the Mu5 and Mu0 experiments is denoted as $q_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$, and the relative change of q_i from the Mu5 experiment is denoted as $q_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$.

In this study, all experiments were atmosphere-only simulations (i.e., sea surface temperature and sea ice are prescribed) with a horizontal resolution of 1.9^∘ latitude × 2.5^∘ longitude and 32 vertical layers. All experiments ran for 11 model years, and the last 10 years was used for the analyses. In addition, the standard deviation calculated from the averages of each year (i.e., 10 averages) was used to check the statistical significance of the multiyear average (i.e., 10-year average).

Table 2 The values of μ_i in all experiments conducted in this study. μ_i__tao, μ_i__auto, μ_i__fall, and μ_i__rei indicate the μ_i used for calculating the IC deposition/sublimation (tao), autoconversion of IC to snow (auto), IC fall velocity (fall), and the $R_{{\mathrm{e}}_{\mathrm{i}}}$ used for the radiation scheme (rei), respectively.

3 Results and analysis

3.1 Offline tests

To better understand the impact of μ_i on climate simulations, the impacts of μ_i on the IC PSD and μ_i-related cloud microphysical processes are first illustrated by offline tests. In these offline tests, the impact of μ_i was analyzed at a given $R_{q_{\mathrm{i}}}$ (i.e., the ratio of q_i to N_i is fixed).

Equations (1), (2), and (3) indicate that the normalized IC size distribution (i.e., the relative contributions of each bin) can be calculated from $R_{q_{\mathrm{i}}}$ and μ_i. Figure 1 shows the impact of μ_i on the normalized PSDs of ICs. Under the same μ_i, the shapes of the PSDs (i.e., the relative number or mass contributions of each bin) with $R_{q_{\mathrm{i}}}=\mathrm{20}$ µm (small IC scenario) are the same as those with $R_{q_{\mathrm{i}}}=\mathrm{60}$ µm (large IC scenario). In other words, the shape of the PSD is completely determined by μ_i (i.e., spectral shape parameter). As expected, the PSDs move toward larger radii with increasing $R_{q_{\mathrm{i}}}$. As introduced in the study of Milbrandt et al. (2021), the PSD becomes narrow with increasing μ_i. Note that, in terms of number, the contributions of the smaller size bins significantly decrease with increasing μ_i. Unlike the number contributions, the mass contributions of the larger size bins significantly decrease with increasing μ_i because the mass contribution is more sensitive to the IC radius. Under the large IC scenario (i.e., $R_{q_{\mathrm{i}}}=\mathrm{60}$ µm), the mass contribution of the ICs with radii greater than R_cs is significantly decreased with increasing μ_i. The above analyses suggest that the cloud microphysical processes that depend on the PSD of ICs (e.g., autoconversion of IC to snow) might be significantly influenced by μ_i.

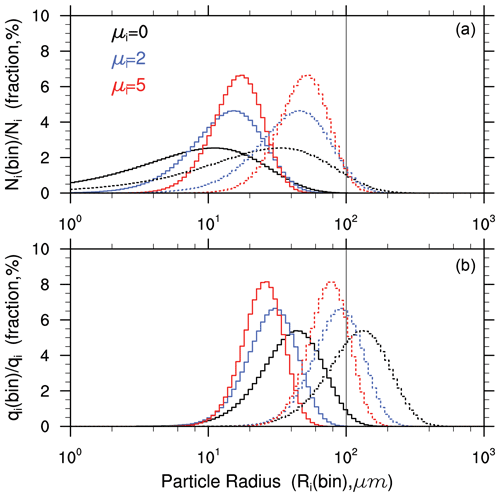
Figure 1 The relative number (a) and mass (b) contributions from each radius bin of ICs. Each bin width is the same based on the logarithm of the particle radius. N_i and q_i are the total number and mass of ICs, respectively. A total of 100 bins were used here. The solid lines indicate the normal IC scenario (i.e., $R_{q_{\mathrm{i}}}=\mathrm{20}$ µm), and the dotted lines indicate the large IC scenario (i.e., $R_{q_{\mathrm{i}}}=\mathrm{60}$ µm). The vertical black line indicates the R_cs that was used for the autoconversion of IC to snow (R_cs=100 µm).

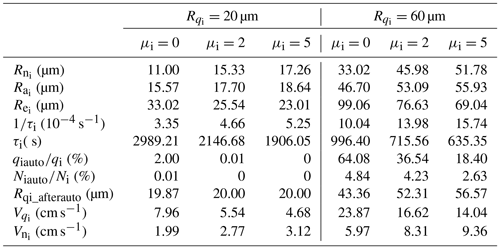
The offline tests were performed for the μ_i-related cloud microphysical processes and statistical mean radii (Table 3). As introduced in Sect. 2.1, $R_{{\mathrm{n}}_{\mathrm{i}}}$, $R_{{\mathrm{a}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$ can be calculated from $R_{q_{\mathrm{i}}}$ and μ_i. Both $R_{{\mathrm{n}}_{\mathrm{i}}}$ and $R_{{\mathrm{a}}_{\mathrm{i}}}$ significantly increase with increasing μ_i (Table 3). This is in agreement with their calculation equations (Eqs. 5, 6). $R_{{\mathrm{n}}_{\mathrm{i}}}$ is approximately half of $R_{q_{\mathrm{i}}}$ at μ_i=0 (i.e., $\mathrm{11.00}/\mathrm{20}$ and $\mathrm{33.02}/\mathrm{60}$), while $R_{{\mathrm{n}}_{\mathrm{i}}}$ is close to $R_{q_{\mathrm{i}}}$ at μ_i=5 (i.e., $\mathrm{17.26}/\mathrm{20}$ and $\mathrm{51.78}/\mathrm{60}$). According to the calculation equation of $R_{{\mathrm{e}}_{\mathrm{i}}}$ (Eq. 7), $R_{{\mathrm{e}}_{\mathrm{i}}}$ decreases with increasing μ_i. The ratios of $R_{{\mathrm{e}}_{\mathrm{i}}}$ to $R_{q_{\mathrm{i}}}$ at μ_i=0, 2, and 5 are 1.65 (i.e., $\mathrm{33.02}/\mathrm{20}$ and $\mathrm{99.06}/\mathrm{60}$), 1.28 (i.e., $\mathrm{25.54}/\mathrm{20}$ and $\mathrm{76.63}/\mathrm{60}$), and 1.15 (i.e., $\mathrm{23.01}/\mathrm{20}$ and $\mathrm{69.04}/\mathrm{60}$), respectively. It is necessary to point out that with increasing μ_i, $R_{{\mathrm{n}}_{\mathrm{i}}}$, $R_{{\mathrm{a}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$ approach $R_{q_{\mathrm{i}}}$ (Table 3) because the PSD of ICs becomes narrow (Fig. 1). As expected, τ_i decreases with increasing μ_i (Table 3) because τ_i is inversely proportional to $R_{{\mathrm{n}}_{\mathrm{i}}}$ (Table 2). The decrease in τ_i suggests that the d$q_{\mathrm{i}}/\mathrm{d}t$ caused by the deposition/sublimation process is accelerated (Morrison and Gettelman, 2008). Compared to the $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ with μ_i=0 (i.e., $\mathrm{3.35}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹ and 10.$\mathrm{04}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹), the $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ with μ_i=2 ($\mathrm{4.66}\times {\mathrm{10}}^{-\mathrm{4}}$ and $\mathrm{13.98}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹) and μ_i=5 ($\mathrm{5.25}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹ and $\mathrm{15.74}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹) increase by 39.10 % and 56.72 %, respectively. This is consistent with the previous finding (ICs vapor deposition process is obviously accelerated by increasing μ_i) reported by Mitchell (1991). In Table 3, $N_{\mathrm{iauto}}/N_{\mathrm{i}}$ and $q_{\mathrm{iauto}}/q_{\mathrm{i}}$ indicate the portion of ICs that convert to snow in terms of number and mass, respectively. Under the small IC scenario (i.e., $R_{q_{\mathrm{i}}}=\mathrm{20}$ µm), regardless of the value of μ_i, both $N_{\mathrm{iauto}}/N_{\mathrm{i}}$ and $q_{\mathrm{iauto}}/q_{\mathrm{i}}$ are very small (< 2 %, Table 3) because there are few ICs with radii greater than R_cs (Fig. 1). Under the large IC scenario (i.e., $R_{q_{\mathrm{i}}}=\mathrm{60}$ µm), there is a considerable portion of ICs with radii greater than R_cs, especially the mass contribution (Fig. 1). The $q_{\mathrm{iauto}}/q_{\mathrm{i}}$ at μ_i=0, 2, and 5 is 64.08 %, 36.54 %, and 18.40 %, respectively (Table 3). This suggests that the autoconversion of IC to snow becomes difficult with increasing μ_i. Compared with the considerable values for $q_{\mathrm{iauto}}/q_{\mathrm{i}}$, the $N_{\mathrm{iauto}}/N_{\mathrm{i}}$ is relatively small (i.e., 4.84 % at μ_i=0, 4.23 % at μ_i=2, and 2.63 % at μ_i=5). Therefore, the $R_{q_{\mathrm{i}}}$ of the residual ICs (R_{qi_afterauto}; 43.36 µm at μ_i=0, 52.31 µm at μ_i=2, and 56.57 µm at μ_i=5) is obviously lower than the original $R_{q_{\mathrm{i}}}$ (60 µm). During the falling process, it is inevitable that $V_{q_{\mathrm{i}}}$ is greater than $V_{{\mathrm{n}}_{\mathrm{i}}}$ because larger ICs with faster falling contribute more in the $V_{q_{\mathrm{i}}}$. Thus, larger ICs appear preferentially in the lower model layers. This is called the size-sorting mechanism (Milbrandt and Yau, 2005). $V_{q_{\mathrm{i}}}$ decreases with increasing μ_i, while $V_{{\mathrm{n}}_{\mathrm{i}}}$ increases with increasing μ_i (Table 3). This could also be explained by their calculation equations (the corresponding derivations are similar to those for $R_{{\mathrm{n}}_{\mathrm{i}}}$, $R_{{\mathrm{a}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$, not shown). With increasing μ_i, the difference between $V_{q_{\mathrm{i}}}$ and $V_{{\mathrm{n}}_{\mathrm{i}}}$ decreases (Table 3) because the PSD of ICs becomes narrow (Fig. 1). As a result, the size-sorting process becomes slow. For instance, there are many ICs with $R_{q_{\mathrm{i}}}=\mathrm{60}$ µm in a model layer. The height of each model layer is 200 m. After one model time step (10 min), some ICs fall into the lower layer. For μ_i=0, the $R_{q_{\mathrm{i}}}$ of the ICs that are still in the model layer (R_{qi_leftover}) is 42.11 µm, and the $R_{q_{\mathrm{i}}}$ of the ICs in the lower layer ($R_{{\mathrm{qi}}_{\mathrm{l}}\mathrm{owlayer}}$) is 95.24 µm. For μ_i=2, R_{qi_leftover} is 52.45 µm, and R_{qi_lowerlayer} is 75.60 µm. For μ_i= 5, R_{qi_leftover} is 55.81 µm, and R_{qi_lowerlayer} is 68.68 µm. It is clear that the difference in $R_{q_{\mathrm{i}}}$ between these two adjacent layers that is caused by the sedimentation process (i.e., the difference between R_{qi_leftover} and R_{qi_lowerlayer}) becomes small with increasing μ_i. In short, the above analyses clearly suggest that μ_i has a significant impact on the cloud microphysical processes and statistical mean radii of ICs.

Table 3 Offline tests^* for the cloud microphysical processes and statistical mean radii at $R_{q_{\mathrm{i}}}=\mathrm{20}$ µm (left) and $R_{q_{\mathrm{i}}}=\mathrm{60}$ µm (right).

^* Note τ_i is calculated at T=220 K, P=330 hPa, and N_i=10⁵ kg⁻¹ (∼ 50 L⁻¹). $V_{{\mathrm{n}}_{\mathrm{i}}}$ and $V_{q_{\mathrm{i}}}$ are calculated at T=220 K and P=330 hPa.

3.2 CAM6 simulations

During the evolution of stratiform clouds, the properties of ice clouds (e.g., q_i, N_i, and $R_{{\mathrm{n}}_{\mathrm{i}}}$, including mixed-phase clouds) largely determine the ice-phase cloud microphysical processes. Meanwhile, these cloud microphysical processes in turn change the cloud properties. They interact as both cause and effect and finally reach equilibrium climate states. To facilitate the subsequent analyses, the cloud properties and μ_i-related cloud microphysical processes are shown together in one figure. For ease of expression, “δ” is used to denote the changes in cloud properties that are caused by the cloud microphysical process during one model time step (tendency × one time step). For example, the changes in q_i and N_i that are caused by the sedimentation process during one model time step are denoted as δq_ised and δN_ised, respectively.

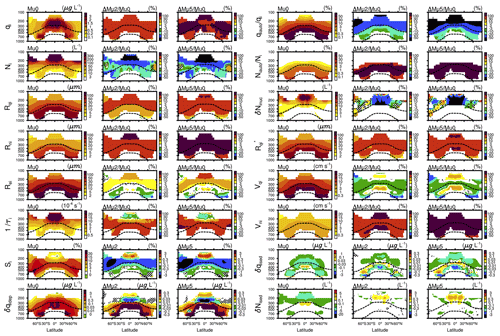
Figure 2 Annual zonal mean in-cloud variables from the Mu0 (first and fourth columns), ΔMu2 (second and fifth columns), and ΔMu5 (third and sixth columns) experiments. Shown are the ICs' mass mixing ratio (q_i) and number density (N_i), mass-weighted and number-weighted radii ($R_{q_{\mathrm{i}}}$ and $R_{{\mathrm{n}}_{\mathrm{i}}}$), effective radius ($R_{{\mathrm{e}}_{\mathrm{i}}}$), reciprocal of the supersaturation relaxation timescale ($\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$), ice supersaturation (S_i), change in q_i caused by deposition/sublimation process (δq_idep), portion of ICs that are converted to snow in terms of mass and number ($q_{\mathrm{iauto}}/q_{\mathrm{i}}$ and $N_{\mathrm{iauto}}/N_{\mathrm{i}}$), newly formed IC number density from the nucleation process (δN_inuc), the updated mass-weighted radius ($R_{q_{\mathrm{i}}}^{\ast }$) used for calculating the sedimentation process, mass-weighted and number-weighted fall velocities ($V_{q_{\mathrm{i}}}$and $V_{{\mathrm{n}}_{\mathrm{i}}}$), and changes in q_i and N_i that are caused by the sedimentation process (δq_ised and δN_ised). Except for δq_idep, δq_ised, δN_inuc, and δN_ised, the other variables are shown as their relative changes (i.e., ΔMu2$/$Mu0 and ΔMu5$/$Mu0). The y axis indicates the atmospheric pressure (unit: hPa). The two dashed black curves are the 0 and −37^∘ isotherms. All results are sampled from model grids where the ice cloud fraction is greater than 1 %. The shading indicates that the differences between two experiments are not significant at the 95 % level based on Student's t test.

Figure 2 shows the model results from the Mu0, Mu2, and Mu5 experiments. The $q_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ is larger in the upper tropical troposphere (> 3 µg L⁻¹) and relatively larger in the lower troposphere over middle latitudes in both hemispheres (> 1 µg L⁻¹). The spatial pattern of $q_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ is generally in agreement with the satellite retrieval data (Li et al., 2012). Higher $N_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ (> 200 L⁻¹) can be found in the tropopause region, where homogeneous freezing produces a large number of ICs (not shown) due to sufficient soluble aerosol particles, higher subgrid vertical velocity, and lower temperature (Shi et al., 2015). All statistical mean radii (i.e., $R_{q_{\mathrm{i}}}$, $R_{{\mathrm{n}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$) decrease with an altitude increase. One possible reason is that it is hard for ICs to grow big in the upper troposphere because there the water vapor density is very low (lower temperature). Furthermore, the size-sorting effect (i.e., sedimentation process) could also be a contributor to this phenomenon (Milbrandt and Yau, 2005; Khain et al., 2015). As expected, $R_{{\mathrm{n}}_{\mathrm{i}}}$ is less than $R_{q_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$ is larger than $R_{q_{\mathrm{i}}}$. After considering the impact of μ_i (i.e., μ_i=2 or 5), the ΔMu2 and ΔMu5 experiments show that q_i is significantly increased, while N_i is significantly decreased. The $q_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ is 30 %–100 % in nearly all regions, and the $q_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ reaches even higher levels (> 100 %) in most regions. Both $N_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $N_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ are $<-$20 % above the −37^∘ isotherm and even reach −50 % in the upper tropical troposphere. Consistent with the increase in q_i and the decrease in N_i, the $R_{q_{\mathrm{i}}}$ significantly increases. The $R_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ is 30 %–100 % above the −37^∘ isotherm, and the $R_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ is 30 %–100 % in most regions and even reaches 100 % in a few regions of the upper tropical troposphere. Because $R_{{\mathrm{n}}_{\mathrm{i}}}$ increases with increasing μ_i at a fixed $R_{q_{\mathrm{i}}}$ value (Sect. 3.1), the relative increases in $R_{{\mathrm{n}}_{\mathrm{i}}}$ from the ΔMu2 and ΔMu5 experiments (i.e., $R_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $R_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$) are obviously higher than the relative increases in $R_{q_{\mathrm{i}}}$ (i.e., $R_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $R_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$). The $R_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ is > 100 % in some regions, and the $R_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ is > 100 % in most regions. Compared with the relative increases in $R_{q_{\mathrm{i}}}$, the relative increases in $R_{{\mathrm{e}}_{\mathrm{i}}}$ from the ΔMu2 and ΔMu5 experiments are obviously reduced or even negative because $R_{{\mathrm{e}}_{\mathrm{i}}}$ decreases with increasing μ_i at a fixed $R_{q_{\mathrm{i}}}$ value (Sect. 3.1). Overall, the impacts of μ_i on q_i and N_i are notable. The changes in the statistical mean radii (i.e., $R_{q_{\mathrm{i}}}$, $R_{{\mathrm{n}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$) can be explained by the changes in q_i, N_i, and μ_i.

This paragraph analyzes the interaction between the ice cloud properties (q_i, N_i, and$R_{{\mathrm{n}}_{\mathrm{i}}}$) and the IC deposition/sublimation process and the influence of μ_i on this interaction. Since $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ is proportional to $N_{\mathrm{i}}{R}_{{\mathrm{n}}_{\mathrm{i}}}$ (Table 1), the $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ is larger in the upper tropical troposphere (> $\mathrm{20}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹) due to the high $N_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ (> 200 L⁻¹). Both the ΔMu2 and ΔMu5 experiments show that the $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ increases in most regions because the relative increase in $R_{{\mathrm{n}}_{\mathrm{i}}}$ (i.e., $R_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $R_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$) is stronger than the relative decrease in N_i (i.e., $N_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $N_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$). However, the $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ is slightly decreased in some regions of the upper tropical troposphere because the relative decrease in N_i is remarkable ($<-$50 %) in these regions. The δq_idep which indicates the change in q_i caused by the deposition/sublimation process is mainly determined by the $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ and in-cloud ice supersaturation (S_i) (Morrison and Gettelman, 2008). Except for a very small region, the annual zonal mean $S_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ is positive. This is consistent with the deposition events being much more frequent than sublimation events (not shown). When S_i>0, ice supersaturation (i.e., S_i>0) towards ice saturation (i.e., S_i=0) occurs because the water vapor is consumed by δq_idep (Korolev and Mazin, 2003; Krämer et al., 2009). The $S_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ is lower (< 3 %) in the upper tropical troposphere due to the high $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ (> $\mathrm{20}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹). Both the ΔMu2 and ΔMu5 experiments show that S_i is increased in the upper tropical troposphere due to the decreasing $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$, and S_i is decreased in the other regions due to the increasing $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$. It is noteworthy that the $S_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}}$ and $S_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$ in the mixed-phase cloud layers are obviously weaker than those in the pure ice cloud layers (i.e., above the −37^∘ isotherm). This is consistent with the fact that the S_i is relatively stable in mixed-phase clouds because liquid droplets are often present. The $\mathit{\delta }{q}_{\mathrm{idep}}^{\mathrm{Mu}\mathrm{0}}$ is generally decreased with the altitude because the saturated vapor pressure significantly decreases with decreasing air temperature. The comparison between δq_idep and q_i suggests that δq_idep is an important source of q_i. The $\mathit{\delta }{q}_{\mathrm{idep}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}}$ and $\mathit{\delta }{q}_{\mathrm{idep}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$ are greater than 0.1 µg L⁻¹ in most mixed-phase cloud layers due to the strongly increasing $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ and relatively stable S_i values. This suggests that the increasing μ_i could lead to a higher equilibrium state of q_i in the mixed-phase cloud layers via the deposition process. The $\mathit{\delta }{q}_{\mathrm{idep}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}}$ and $\mathit{\delta }{q}_{\mathrm{idep}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$ are negative between 200 and 300 hPa, mainly because the $S_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}}$ and $S_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$ are negative, and the $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ are relatively small. The $\mathit{\delta }{q}_{\mathrm{idep}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}}$ and $\mathit{\delta }{q}_{\mathrm{idep}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$ are positive above 100 hPa, mainly because the $S_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}}$ and $S_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$ are positive. These results indicate that the impact of μ_i on δq_idep becomes complex above the −37^∘ isotherm, where S_i is more susceptible to $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ and δq_idep. Meanwhile, the impact of μ_i on δq_idep also becomes weak above the −37^∘ isotherm because the feedback processes (i.e., the interaction between S_i and δq_idep) become important. In short, the μ_i-induced changes in the deposition/sublimation process (i.e., $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ and δq_idep) can be largely explained by the changes in N_i and $R_{{\mathrm{n}}_{\mathrm{i}}}$. One reason for the higher q_i in the mixed-phase cloud layers from the Mu2 and Mu5 experiments is that δq_idep increases with increasing μ_i.

This paragraph analyzes the interaction between the ice cloud properties (q_i, N_i, and $R_{q_{\mathrm{i}}}$) and the autoconversion process of IC to snow (hereafter “the autoconversion process”) and the influence of μ_i on this interaction. Both $q_{\mathrm{iauto}}/q_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ and $N_{\mathrm{iauto}}/N_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ are decreased with the altitude because the $R_{q_{\mathrm{i}}}^{\mathrm{Mu}\mathrm{0}}$ is decreased with the altitude. As expected, the $q_{\mathrm{iauto}}/q_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$ is considerable and much larger than the $N_{\mathrm{iauto}}/N_{\mathrm{i}}^{\mathrm{Mu}\mathrm{0}}$. It is clear that the autoconversion process is an important sink of q_i. However, the autoconversion process is not an important sink of N_i because the $N_{\mathrm{iauto}}/N_{\mathrm{i}}$ is very small. Both the ΔMu2 and ΔMu5 experiments show that the $q_{\mathrm{iauto}}/q_{\mathrm{i}}$ is significantly decreased because the autoconversion process obviously becomes difficult at higher μ_i values (offline tests, Sect. 3.1). The difficult autoconversion process leads to an equilibrium state with higher q_i and larger $R_{q_{\mathrm{i}}}$. Because of the larger $R_{q_{\mathrm{i}}}$, the $N_{\mathrm{iauto}}/N_{\mathrm{i}}$ from the Mu2 and Mu5 experiments is significantly increased. The increasing $N_{\mathrm{iauto}}/N_{\mathrm{i}}$ from the Mu2 and Mu5 experiments might be a main reason for the decrease in N_i in the mixed-phase cloud layers. However, the remarkable decrease in N_i (mostly in the pure ice cloud layers) from the Mu2 and Mu5 experiments is mainly due to the ice nucleation process. In the MG scheme, the newly formed IC number density (excluding the ICs in mixed-phase clouds) is calculated by a physically based ice nucleation parameterization (Liu and Penner, 2005). Because the autoconversion process becomes difficult in the Mu2 and Mu5 experiments, the in-cloud ICs should have longer lifetimes and larger radii. As a result, δN_inuc, which denotes the newly formed IC number density from the nucleation process, significantly decreases in the Mu2 and Mu5 experiments (Fig. 2). The main reason is that the preexisting ICs would hinder the subsequent ice nucleation process (especially for homogeneous freezing), owing to the depletion of water vapor via deposition growth (Barahona et al., 2014; Shi et al., 2015). δN_inuc is the main source of N_i. Therefore, both the ΔMu2 and ΔMu5 experiments show that N_i is significantly decreased. In short, the increase in μ_i causes the autoconversion process to be difficult and then leads to a higher equilibrium state of q_i and $R_{q_{\mathrm{i}}}$. Meanwhile, N_i is significantly decreased due to the higher equilibrium state of q_i and $R_{q_{\mathrm{i}}}$ (i.e., the stronger suppression effect of the preexisting ICs on the ice nucleation process).

This paragraph analyzes the interaction between the ice cloud properties and the IC sedimentation process and the influence of μ_i on this interaction. The sedimentation process is the last cloud microphysical process in the MG scheme. The IC fall velocity is calculated based on the updated cloud properties (i.e., the other cloud microphysical processes at this model time step have been considered). Here, $R_{q_{\mathrm{i}}}^{\ast }$ denotes the updated $R_{q_{\mathrm{i}}}$, which includes the changes caused by the deposition/sublimation and autoconversion processes at this model time step. In the mixed-phase cloud layers, the $R_{q_{\mathrm{i}}}^{\ast ,\mathrm{Mu}\mathrm{0}}$ is slightly less than the $R_{q_{\mathrm{i}}}^{\mathrm{Mu}\mathrm{0}}$ because the sedimentation process has not occurred. After considering the impacts of μ_i on the cloud microphysical processes introduced above, the relative increases in $R_{q_{\mathrm{i}}}^{\ast }$ from the ΔMu2 and ΔMu5 experiments (i.e., $R_{q_{\mathrm{i}}}^{\ast ,\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $R_{q_{\mathrm{i}}}^{\ast ,\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$) are higher than the relative increase in $R_{q_{\mathrm{i}}}$. As expected, both $V_{q_{\mathrm{i}}}^{\mathrm{Mu}\mathrm{0}}$ and $V_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{Mu}\mathrm{0}}$ decrease with an altitude increase, and the $V_{q_{\mathrm{i}}}^{\mathrm{Mu}\mathrm{0}}$ is obviously larger than the $V_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{Mu}\mathrm{0}}$. Although the $R_{q_{\mathrm{i}}}^{\ast ,\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $R_{q_{\mathrm{i}}}^{\ast ,\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ are positive, the $V_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $V_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ are negative in most regions because $V_{q_{\mathrm{i}}}$ decreases with increasing μ_i (offline tests, Sect. 3.1). However, both $V_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $V_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ are positive in some layers over the tropics and subtropics, where the $R_{q_{\mathrm{i}}}^{\ast ,\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ and $R_{q_{\mathrm{i}}}^{\ast ,\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ are relatively higher. Because $V_{{\mathrm{n}}_{\mathrm{i}}}$ increases with increasing μ_i at a fixed $R_{q_{\mathrm{i}}}$ value (offline tests, Table 3) and the $R_{q_{\mathrm{i}}}^{\ast }$ from the Mu2 and Mu5 experiments are increased, the relative increases in $V_{{\mathrm{n}}_{\mathrm{i}}}$ from the ΔMu2 and ΔMu5 experiments are remarkable. The $V_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}/\mathrm{Mu}\mathrm{0}}$ is > 100 % in some regions, and the $V_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ is > 100 % in most regions. δq_ised is mainly determined by the gradient of $V_{q_{\mathrm{i}}}{q}_{\mathrm{i}}$ in the vertical direction. Actually, the newly updated q_i between the substeps of the sedimentation process is used for calculating δq_ised. Similarly, δN_ised is mainly determined by the gradient of $V_{{\mathrm{n}}_{\mathrm{i}}}{N}_{\mathrm{i}}$ in the vertical direction. Furthermore, the ICs that fall into the clear portions of the lower model layer sublimate instantly. Therefore, both $\mathit{\delta }{q}_{\mathrm{ised}}^{\mathrm{Mu}\mathrm{0}}$ and $\mathit{\delta }{N}_{\mathrm{ised}}^{\mathrm{Mu}\mathrm{0}}$ are negative in most regions. This is consistent with sedimentation being a sink of clouds. The δq_ised from the Mu2 and Mu5 experiments (i.e., $\mathit{\delta }{q}_{\mathrm{ised}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}}$ and $\mathit{\delta }{q}_{\mathrm{ised}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$) decreases (negative, stronger sink) in most regions, mainly because of the increasing $V_{q_{\mathrm{i}}}$ and higher q_i. The δN_ised from the Mu2 and Mu5 experiments (i.e., $\mathit{\delta }{N}_{\mathrm{ised}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{2}}$ and $\mathit{\delta }{N}_{\mathrm{ised}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$) increases (positive, weaker sink) in a few layers over the tropics. This is mainly due to the changes in the vertical gradient of N_i. Both the ΔMu2 and ΔMu5 experiments show that the changes in δq_ised and δN_ised are generally weaker than the changes in δq_idep, δq_iatuo (i.e., $q_{\mathrm{i}}\times q_{\mathrm{iauto}}/q_{\mathrm{i}}$), and δN_inuc. In short, the fall velocities (i.e., $V_{q_{\mathrm{i}}}$ and $V_{{\mathrm{n}}_{\mathrm{i}}}$) and their impacts on ice clouds (i.e., δq_ised and δN_ised) are mainly determined by the cloud properties (i.e., q_i, N_i, $R_{q_{\mathrm{i}}}$, and $R_{q_{\mathrm{i}}}^{\ast }$). Although the sedimentation process is also a main factor that determines the cloud properties, the changes in the sedimentation process that are caused by the increasing μ_i are not as strong as those in the deposition/sublimation, autoconversion, and nucleation processes.

Based on the analyses presented above, it can be concluded that increasing μ_i would lead to a climate equilibrium state with higher q_i and lower N_i in most regions. The changes in the statistical mean radii (i.e., $R_{q_{\mathrm{i}}}$, $R_{{\mathrm{n}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$) and ice-phase cloud microphysical processes (i.e., δq_idep, $q_{\mathrm{iauto}}/q_{\mathrm{i}}$, $N_{\mathrm{iauto}}/N_{\mathrm{i}}$, δN_inuc, δq_ised, and δN_ised) are mainly determined by the higher q_i, lower N_i, and increasing μ_i. On the other hand, the higher q_i and lower N_i can largely be explained by the changes in the ice-phase cloud microphysical processes (i.e., δq_idep, $q_{\mathrm{iauto}}/q_{\mathrm{i}}$, and δN_inuc) that are caused by the increasing μ_i. Furthermore, the ΔMu2 and ΔMu5 experiments show very similar spatial patterns for the μ_i-induced changes. This suggests that the impact of μ_i on the simulated climate equilibrium state is stable.

Figure 3 Similar to Fig. 2 but for the ΔTao5, ΔAuto5, ΔFall5, and ΔRei5 experiments. Except for the $R_{{\mathrm{e}}_{\mathrm{i}}}^{\mathrm{Rei}\mathrm{5}}$, all statistical mean radii are calculated with μ_i=0.

Figure 3 shows the changes in the simulated climate equilibrium states that are caused by each individual μ_i-related process. The $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ from the Tao5 experiment is significantly increased ($\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Tao}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$). Similar to the ΔMu2 and ΔMu5 experiments, this increasing $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ could lead to a higher equilibrium state of q_i in the mixed-phase cloud layers ($q_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Tao}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$) via the deposition/sublimation process ($\mathit{\delta }{q}_{\mathrm{idep}}^{\mathrm{\Delta }\mathrm{Tao}\mathrm{5}}$). However, this increasing $\mathrm{1}/{\mathit{\tau }}_{\mathrm{i}}$ leads to lower q_i and lower N_i in most of the pure ice cloud layers. The main reason might be that the ICs grow faster and their lifetimes become shorter (Mitchell, 1991; DeMott et al., 2010; Storelvmo et al., 2013). The $q_{\mathrm{iauto}}/q_{\mathrm{i}}$ from the Auto5 experiment is significantly decreased ($q_{\mathrm{iauto}}/q_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Tao}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$). This could lead to a higher q_i in nearly all regions ($q_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Auto}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$) and a lower N_i in the pure ice cloud layers ($N_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Auto}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$). The mechanism is the same as that introduced based on the ΔMu2 and ΔMu5 experiments. It is noteworthy that the N_i from the Auto5 experiment is slightly increased in some mixed-phase cloud layers. The main reason might be that the accretion of N_i by snow is significantly decreased in the mixed-phase cloud layers (not shown) due to the difficult autoconversion process. The$V_{q_{\mathrm{i}}}$ from the Fall5 experiment is significantly decreased ($V_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Fall}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$), and the sink term of q_i due to sedimentation becomes weaker (i.e., positive $\mathit{\delta }{q}_{\mathrm{ised}}^{\mathrm{\Delta }\mathrm{Fall}\mathrm{5}}$) in most regions. Unlike the $V_{q_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Fall}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$, the $V_{{\mathrm{n}}_{\mathrm{i}}}$ from the Fall5 experiment obviously increases ($V_{{\mathrm{n}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Fall}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$), and the sink term of N_i due to sedimentation becomes stronger (i.e., negative $\mathit{\delta }{N}_{\mathrm{ised}}^{\mathrm{\Delta }\mathrm{Fall}\mathrm{5}}$) in the pure ice cloud layers. These might be the main reasons for the increase in q_i and the decrease in N_i in the pure ice cloud layers over the tropics ($q_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Fall}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$ and $N_{\mathrm{i}}^{\mathrm{\Delta }\mathrm{Fall}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$). It is interesting to note that the $R_{q_{\mathrm{i}}}$, $R_{{\mathrm{n}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$ from the Fall5 experiment all increase in pure ice cloud layers (i.e., upper layers) and decrease in mixed-phase cloud layers (i.e., lower layers). This can be explained by the μ_i-induced weaker size-sorting mechanism (Sect. 3.1). The $R_{{\mathrm{e}}_{\mathrm{i}}}$ from the Rei5 experiment ($R_{{\mathrm{e}}_{\mathrm{i}}}^{\mathrm{\Delta }\mathrm{Rei}\mathrm{5}/\mathrm{Mu}\mathrm{0}}$) is significantly decreased. Because the change of $R_{{\mathrm{e}}_{\mathrm{i}}}$ does not directly affect the cloud microphysical processes, the changes in cloud properties from the ΔRei5 experiment are not statistically significant in most regions. Taken overall, the above analyses clarify the mechanism of μ_i's impacts. Increasing μ_i in autoconversion impacts pure ice clouds the most (i.e., significantly increased q_i and significantly decreased N_i in the pure ice cloud layers). Furthermore, increasing μ_i in autoconversion also leads to a much higher q_i in the mixed-phase cloud layers. Increasing μ_i in deposition/sublimation can also lead to a higher q_i in the mixed-phase cloud layers. Increasing μ_i in sedimentation can lead to a higher IC radius in the upper layers and lower IC radius in the lower layers. The impacts from sedimentation and deposition/sublimation are obviously weaker than those from autoconversion. The changes caused by increasing μ_i in the radiative process (i.e., $R_{{\mathrm{e}}_{\mathrm{i}}}$) are relatively chaotic.

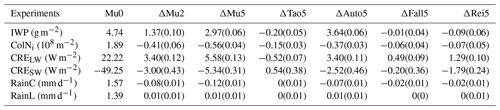
The above analyses focus on cloud properties and cloud microphysical processes (i.e., in-cloud variables). This paragraph discusses the impacts of μ_i on radiation and precipitation. The annual zonal mean distributions of the ice water path (IWP), column N_i (ColN_i), longwave (CRE_LW) and shortwave (CRE_SW) cloud radiative effects, and convective (RainC) and large-scale (RainL) precipitation rates are shown in Fig. 4, and the corresponding global annual mean values are listed in Table 4. The comparison of the Mu0, Mu2, and Mu5 experiments shows that the zonal mean IWPs over all latitudes clearly increase with increasing μ_i. This is consistent with the changes in in-cloud q_i (Fig. 2). The comparison of the ΔMu5, ΔTao5, ΔAuto5, ΔFall5, and ΔRei5 experiments shows that the μ_i-induced increases in IWP are mainly provided by the autoconversion process. Compared to the Mu0 experiment, the ColN_i from the Mu2 and Mu5 experiments obviously decreases over tropical regions. It is clear that the autoconversion process is also the main contributor to the decreases in ColN_i (Fig. 4, right column). Compared to the Mu0 experiment, both CRE_LW and CRE_SW from the Mu2 and Mu5 experiments are obviously enhanced, mainly because of the increasing IWPs. It is clear that the enhancements of CRE_LW and CRE_SW are also mainly contributed to by the autoconversion process (Fig. 4). Both the CRE_LW and CRE_SW from the Rei5 experiment are also obviously enhanced in terms of their zonal mean values (Fig. 4) and global mean values (Table 4, CRE${}_{\mathrm{LW}}^{\mathrm{\Delta }\mathrm{Rei}\mathrm{5}}=\mathrm{1}$.29 W m⁻² and CRE${}_{\mathrm{SW}}^{\mathrm{\Delta }\mathrm{Rei}\mathrm{5}}=-$1.79 W m⁻²). This suggests that the impact of μ_i on $R_{{\mathrm{e}}_{\mathrm{i}}}$ could lead to considerable changes in the Earth's radiation budget. Compared to the impacts of μ_i on radiation, the impact on large-scale precipitation (i.e., RainL) is not statistically significant (Fig. 4, left column). However, the convective precipitation from the ΔMu5 experiment (i.e., RainC^ΔMu5) is significantly reduced over the tropics and subtropics (Fig. 4, right column). The reason is that the increase in ice clouds (i.e., q_i) increases atmospheric stability via the radiative budget and then leads to weaker convective precipitation (Andrews et al., 2010; Wang et al., 2014). Overall, the impacts of μ_i on radiation and precipitation are considerable. The global mean CRE${}_{\mathrm{LW}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$, CRE${}_{\mathrm{SW}}^{\mathrm{\Delta }\mathrm{Mu}\mathrm{5}}$, and RainC^ΔMu5 are 5.58 W m⁻², −5.34 W m⁻², and −0.12 mm d⁻¹, respectively. These changes are mainly contributed to by the autoconversion process. Furthermore, the comparisons between the ΔMu2 and ΔMu5 experiments (Fig. 4 and Table 4) show that, in most cases, the μ_i-induced changes are enhanced with increasing Δμ_i. This suggests that, in terms of the zonal mean and global mean values, the impacts of μ_i are relatively stable.

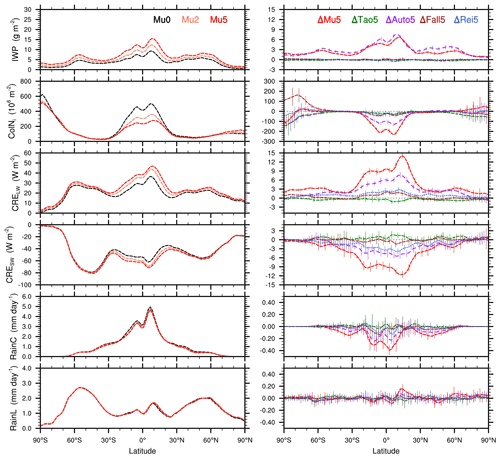
Figure 4 Annual zonal mean distributions of the ice water path (IWP), column N_i (ColN_i), longwave and shortwave cloud radiative effects (CRE_LW and CRE_SW), and convective and large-scale precipitation rates (RainC and RainL). In the right panel (i.e., Δ), the vertical bars overlying these lines indicate the ranges of 2 standard deviations from the difference of each of 10 years at different latitudes.

Table 4 The global annual mean variables are shown in Fig. 4. The corresponding standard deviations calculated from the difference of each year for 10 years are shown in brackets.

4 Summary and conclusions

This paper investigates the impacts of μ_i on climate simulations with the CAM6 model. To achieve this, the two-moment bulk cloud microphysics scheme used in CAM6 was modified to consider the μ_i's impacts by a tunable parameter. After that, the impacts of μ_i on the IC size distribution and μ_i-related cloud microphysical processes are illustrated first by calculation equations and offline tests, and the impacts of μ_i on the climate simulations are then analyzed with the CAM6 model.

The impacts of μ_i on the IC size distribution and various statistical mean radii are clearly explained by the calculation equations. $R_{q_{\mathrm{i}}}$ can be calculated from q_i and N_i, and the normalized IC size distribution (i.e., the relative contributions from each bin) can be calculated from $R_{q_{\mathrm{i}}}$ and μ_i. The impact of μ_i on mass-weighted size distribution is obviously different from that on the commonly used number-weighted size distribution (Fig.1). Unlike the number contributions, the mass contributions of the larger size bins significantly decrease with increasing μ_i because the mass contribution is more sensitive to the IC radius. In the bulk cloud microphysics scheme, the physical processes are calculated based on various statistical mean radii. The ratios of the other statistical mean radii (i.e., $R_{{\mathrm{n}}_{\mathrm{i}}}$, $R_{{\mathrm{a}}_{\mathrm{i}}}$, and $R_{{\mathrm{e}}_{\mathrm{i}}}$) to $R_{q_{\mathrm{i}}}$ are functions of μ_i. At μ_i≥0, $R_{{\mathrm{n}}_{\mathrm{i}}}$ and $R_{{\mathrm{a}}_{\mathrm{i}}}$ are always less than $R_{q_{\mathrm{i}}}$, whereas $R_{{\mathrm{e}}_{\mathrm{i}}}$ is always greater than $R_{q_{\mathrm{i}}}$. The differences among these statistical mean radii become small with increasing μ_i, which is consistent with the narrower size distribution determined by higher μ_i values.

The impacts of μ_i on the μ_i-related cloud microphysical processes are clearly illustrated by the offline tests. Under the same q_i and N_i ($R_{q_{\mathrm{i}}}$ is also fixed), the IC deposition/sublimation process is considerably accelerated with increasing μ_i because the $R_{{\mathrm{n}}_{\mathrm{i}}}$ used for calculating deposition/sublimation is increasing with increasing μ_i. Under the same $R_{q_{\mathrm{i}}}(R_{q_{\mathrm{i}}}$ is much less than the snow radius), the autoconversion of IC to snow obviously becomes difficult with increasing μ_i because the portion of ICs with radii greater than the threshold (> R_cs) decreases under the narrow size distribution. A major effect of IC sedimentation is size-sorting because $V_{q_{\mathrm{i}}}$ is greater than $V_{{\mathrm{n}}_{\mathrm{i}}}$, and μ_i plays an important role in determining the rate of size-sorting (Milbrandt and Yau, 2005). In this study, the offline tests clearly show that the difference in IC radius between two adjacent model layers caused by sedimentation becomes small with increasing μ_i because the difference between $V_{q_{\mathrm{i}}}$ and $V_{{\mathrm{n}}_{\mathrm{i}}}$ becomes small (i.e., the size-sorting rate becomes slow).

The climate simulations show that the impacts of μ_i on the ice cloud properties are notable, and the main corresponding mechanisms are clear. After increasing μ_i from 0 to 2 and 5, q_i significantly increases, while N_i significantly decreases. The accelerated deposition process contributes to the higher q_i in the mixed-phase cloud layers where the ice supersaturation (S_i>0) is relatively stable. The difficult autoconversion process leads to longer IC lifetime and higher q_i. Meanwhile, N_i significantly decreases because the newly formed IC number density is significantly decreased, owing to the longer IC lifetime and higher q_i. The experiments with only one modified μ_i-related process make the mechanisms of μ_i's impacts more clear. Autoconversion contributes the most. The μ_i also has considerable impacts on radiation and precipitation. After increasing μ_i from 0 to 5, the global mean CRE_LW is increased (stronger warming effect) by 5.58 W m⁻² (25.11 %). Meanwhile, the CRE_SW is decreased (less cooling effect) by −5.34 W m⁻² (10.84 %). The enhancement of the cloud radiative effects is largely provided by the higher equilibrium state of q_i. The considerably stronger CRE_LW could increase the atmospheric stability and then lead to weaker convective precipitation (Andrews et al., 2010; Wang et al., 2014). As expected, after increasing μ_i from 0 to 5, the global mean RainC is decreased by −0.12 mm d⁻¹ (7.64 %). In short, the impacts of μ_i on climate simulations are significant. This suggests that the μ_i (i.e., the PSD of ICs) and μ_i-related cloud microphysical processes deserve a more realistic representation in climate models, especially for cloud schemes with autoconversion. Fortunately, there have been some studies that can help to address this issue. For example, μ_i is described by an empirical formula (Eidhammer et al., 2017), μ_i is predicted in a three-moment cloud scheme (Milbrandt et al., 2021), and single-ice-category cloud schemes could obviate the need for autoconversion process (e.g., Morrison and Milbrandt, 2015; Eidhammer et al., 2017; Zhao et al., 2017).

This study only focuses on the impacts of μ_i; the default tunable parameters (except for μ_i) are used in all the simulations. After improving the representation of μ_i-related processes, further model tuning and analyses are required based on the updated cloud scheme. Therefore, this study does not estimate which value of μ_i could lead to a better simulation. Finally, it is necessary to point out that the main mechanism for μ_i's impacts introduced in this study (i.e., autoconversion becomes difficult with increasing μ_i) is not applicable to climate simulations with the single-ice-category cloud scheme. However, similar to the μ_i's impact on autoconversion, the interaction between small ICs and large ICs (e.g., the accretion of small ICs by large ICs) should become weaker with increasing μ_i (i.e., narrower size distribution). Therefore, we can speculate that the impacts of μ_i on climate simulations with the single-ice-category cloud scheme may still be worth noting.

Appendix A: The limitation in the use of gamma functions for representing ice-phase PSDs in bulk cloud microphysics schemes

Here, we show the PSDs represented by gamma functions of the form $N^{\prime }\left(D\right)=$ N₀D^μe^−λD firstly and then discuss the reason why bulk cloud microphysics schemes usually constrain μ to be nonnegative.

Figure A1 shows that the PSDs are relatively wide with negative μ. Under negative μ, the particle number densities (N^′) are increased with decreasing D and become very large at D<1 µm (Fig. A1 left). In the real world, the cloud particles are usually not less than 1 µm. It is necessary to point out that the contribution from small particles (e.g., D<50 µm) is usually neglected for getting the gamma-fitted PSD from observations (Heymsfield, 2003). For instance, when only considering the particles over sizes (D) from as small as 10 µm to as large as 2000 µm (measured particle size), the uncertainty from the extrapolation below 50 µm is negligible in the linear space of particle size (Fig. A1 right). Therefore, some gamma-fitted PSDs from observations might show negative μ values (e.g., Heymsfield, 2003; Heymsfield et al., 2013; Schmitt and Heymsfield, 2009).

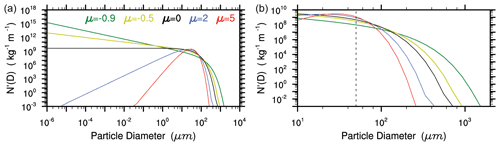
Figure A1 The particle number densities (N^′, which is a function of D) calculated from the gamma distributions with various μ values. Here, the total particle number and mass-weighted diameter are set to 10⁵ kg⁻¹ (∼50 L⁻¹) and 40 µm, respectively. Note different markers in the y axis and x axis between the left column and right column. The vertical black line indicates D=50 µm.

Unlike the gamma-fitted PSDs from observations (small particles might be neglected), the gamma functions used in bulk cloud microphysics schemes represent the particles with diameter from 0 to ∞ (hereafter “mathematical size range”). For instance, the other two gamma distribution parameters (N₀ and λ) used in the bulk cloud scheme are calculated by the particle's mass (q) and number (N) and some gamma functions of μ ($\mathit{\lambda }=[\frac{\mathit{\pi }\mathit{\rho }}{\mathrm{6}}\frac{N}{q}\frac{\mathrm{\Gamma }\left(\mathrm{4}+\mathit{\mu }\right)}{\mathrm{\Gamma }\left(\mathrm{1}+\mathit{\mu }\right)}{]}^{\mathrm{1}/\mathrm{3}}$, $N_{\mathrm{0}}=\frac{N{\mathit{\lambda }}^{\left(\mathrm{1}+\mathit{\mu }\right)}}{\mathrm{\Gamma }\left(\mathrm{1}+\mathit{\mu }\right)}$). Because the gamma function, $\mathrm{\Gamma }\left(x\right)={\int }_{\mathrm{0}}^{\mathrm{\infty }}{t}^{x-\mathrm{1}}{e}^{-t}\mathrm{d}t$, is used for deriving these calculation formulas, the q and N in these calculation formulas indicate the mass and number of particles from the mathematical size range (i.e., 0 to ∞). Furthermore, the μ must be greater than −1 in these two calculation formulas because the negative integer and zero are the singularity of the gamma function. Under negative μ ($-\mathrm{1}<\mathit{\mu }<\mathrm{0}$; the N^′ is very large at D<1 µm, Fig. A1 left), more attention should be paid to using the gamma function because it integrates from 0 to ∞. Figure A2 shows the relative number contributions from each radius bin of ICs under different $R_{q_{\mathrm{i}}}$. Table A1 lists the contributions of ICs with a radius from 1 to 1000 µm (hereafter “realistic size range”) to the total number (i.e., the N_i from the mathematical size range). At μ_i≥0 (i.e., μ_i=0, 2, and 5), the number contributions are mostly from the realistic size range except for one case (μ_i=0 and $R_{q_{\mathrm{i}}}=\mathrm{5}$ µm). Under the small IC scenario (i.e., $R_{q_{\mathrm{i}}}=\mathrm{5}$ µm) and ${\mathit{\mu }}_{\mathrm{i}}=-$0.5, the number of ICs from the realistic size range only contributes $\sim \mathrm{1}/\mathrm{2}$ to the total number. At ${\mathit{\mu }}_{\mathrm{i}}=-$0.9, the contributions of ICs from the realistic size range cannot reach $\mathrm{1}/\mathrm{2}$, even for the large IC scenario (i.e., $R_{q_{\mathrm{i}}}=\mathrm{60}$ µm). In other words, under negative μ_i, the gamma distribution functions (mathematical size range) used in the bulk cloud schemes might be not suited for representing realistic ICs (realistic size range). Therefore, our study only evaluates the impacts of changing μ_i from 0 to 2 and 5.

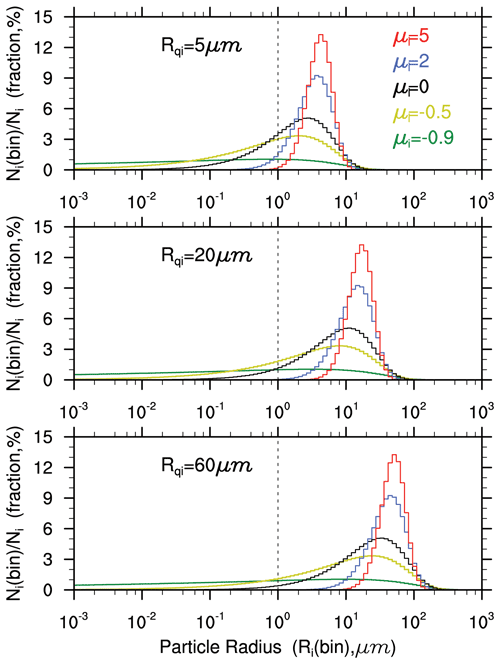
Figure A2 The relative number contributions from each radius bin of ICs under different $R_{q_{\mathrm{i}}}$. A total of 100 bins were used here. Each bin width is the same based on the logarithm of the particle radius.

Table A1 The contributions of ICs from the realistic size range (i.e., 1–1000 µm) to the total number.

^* The PSDs of ICs are represented by gamma functions with a range from 0 to ∞. The contributions given are only approximate because the value of the incomplete gamma function is not very accurate.