Prediction error growth in a more realistic atmospheric toy model with three spatiotemporal scales

This article studies the growth of the prediction error over lead time in a schematic model of atmospheric transport. Inspired by the Lorenz (2005) system, we mimic an atmospheric variable in one dimension, which can be decomposed into three spatiotemporal scales. We identify parameter values that provide spatiotemporal scaling and chaotic behavior. Instead of exponential growth of the forecast error over time, we observe a more complex behavior. We test a power law and the quadratic hypothesis for the scale-dependent error growth. The power law is valid for the first days of the growth, and with an included saturation effect, we extend its validity to the entire period of growth. The theory explaining the parameters of the power law is confirmed. Although the quadratic hypothesis cannot be completely rejected and could serve as a first guess, the hypothesis's parameters are not theoretically justifiable in the model. In addition, we study the initial error growth for the ECMWF forecast system (500 hPa geopotential height) over the 1986 to 2011 period. For these data, it is impossible to assess which of the error growth descriptions is more appropriate, but the extended power law, which is theoretically substantiated and valid for the Lorenz system, provides an excellent fit to the average initial error growth of the ECMWF forecast system. Fitting the parameters, we conclude that there is an intrinsic limit of predictability after 22 d.

1 Introduction

The improvement of the numerical weather prediction systems raised the question of the intrinsic atmospheric prediction limit, i.e., for the maximal lead time into the future, after which every forecast will be useless. While the notion of seamless prediction (Shukla, 2009) and seasonal prediction implies that it will be only a matter of technology to make forecasts far into the future, in recent years, there have been several publications whose authors assume a strict upper bound in time for making useful predictions (Palmer et al., 2014; Brisch and Kantz, 2019; Zhang et al., 2019). Even if the numerical model were perfect, the uncertainty of the initial condition would give rise to prediction errors which grow over time. In the setting of classical low-dimensional chaos, one would observe an exponential error growth whose exponent is given by the largest Lyapunov exponent of the system, with some saturation when the error reaches the magnitude of the standard deviation of the quantity to be predicted. Although exponential error growth has been associated with the fact that a detailed forecast is meaningful only up to lead times of a few multiples of the Lyapunov time, which is the inverse of the Lyapunov exponent, in principle, with absolutely perfect knowledge of the initial condition, one could compute meaningful predictions up to arbitrary times.

In contrast to this, it has been observed by several authors in the past (Toth and Kalnay, 1993; Lorenz, 1996; Aurell et al., 1996, 1997; Boffetta et al., 1998) that the proper Lyapunov exponent of a dynamical system might not be relevant for the issue of predictability, in two ways. First, the Lyapunov exponent of, for example, atmospheric dynamics is so large that no useful weather prediction was possible. On the other hand, and this is the issue of the present paper, if the proper Lyapunov exponent is much larger than the error growth rate of large-scale errors, it might render every gain in resolution and in better precision of the knowledge of the initial condition useless and thereby impose a strict limit to the time into the future where prediction is meaningful. Brisch and Kantz (2019) and Zhang et al. (2019) predicted a strictly finite prediction horizon associated with a scale-dependent error growth, where tiny errors grow much faster than larger ones. In an idealized model, this could even mean that the proper Lyapunov exponent of the system was infinite, and that finite size approximations of the Lyapunov exponent (Aurell et al., 1996, 1997) were the larger, the smaller the scale of this finite size. In real physical systems, one would certainly expect some cut-off of such divergent small-scale instability, e.g., in turbulence at the Kolmogorov length, the lower end of the inertial range, but the Lyapunov exponent of the system then would still be so large that it could never be compensated by more precise measurements.

Palmer et al. (2014), referring to Lorenz (1969), call this growth the “real butterfly effect,” and it is not an exponential error growth defined by the largest positive Lyapunov exponent, but growth where the exponent is replaced by a scale-dependent quantity (scale-dependent error growth rate).

The atmosphere exhibits multi-scale dynamics both in space and time, and observations show a close linkage between spatial and temporal scales: the smaller some structure, the shorter its lifetime and the faster its time evolution. Planetary-scale structures (e.g., semi-permanent pressure centers or the westerlies and trade winds) have sizes on the order of 10⁴ km and live on timescales of weeks and longer. Synoptic-scale structures (e.g., high and low pressure systems) have sizes of several thousands of kilometers and live on timescales of several days. Mesoscale structures (e.g., thunderstorms and weather fronts) have sizes from a few kilometers to several hundred kilometers and live on a timescale of a day or less. Microscale structures (e.g., turbulence) have sizes smaller than 1 km and live on a timescale of minutes. In addition to different spatiotemporal scales, structures also have different error growth rates and predictability. Error growth is faster, and predictability is lesser for smaller-scale structures.

Lorenz (1996) gave a sketch of error growth in such a system: a typical quantity to be predicted is a superposition of the dynamics on different scales. After a fast growth of the small-scale errors with saturation at these very same small scales, the large-scale errors continue to grow at a slower rate until even these saturate. Therefore, Lyapunov exponents of structures of various spatiotemporal scales are taken as the previously mentioned scale-dependent quantity, and they determine the error growth on their respective scales.

Zhang et al. (2019) take a very different starting point and suggest the quadratic hypothesis to describe the scale-dependent error growth. It was originally designed to describe initial and model error growth (Savijarvi, 1995; Dalcher and Kalnay, 1987). Zhang et al. (2019) recently used a parameter previously specifying the model error to describe upscale error propagation from small-scale processes and showed the validity of this hypothesis on data of the numerical weather prediction systems of the European Centre for Medium Range Weather Forecasts (ECMWF) and the US Next Generation Global Prediction System.

A scale-dependent error growth in the spirit of Lorenz (1996) was described by Brisch and Kantz (2019) using a power law, which successfully approximated the data of the National Centers for Environmental Prediction Global Forecast System (Harlim et al., 2005). Brisch and Kantz (2019) also introduced a theory connecting the power law exponent with the Lyapunov exponents and limit errors of the different scales, and its validity was demonstrated by a low-dimensional atmospheric system (Lorenz, 1996) extended to five spatiotemporal levels. However, the different scales in this model cannot be superimposed in order to gain a general signal in the real space, but the different scales were living in different subspaces of phase space. This lack of realism may limit the general acceptance of this theory and stimulated the present study.

This article expands Lorenz's (2005) system from two spatiotemporal levels to three and discusses the setting of parameters and its advantage over other systems. In this system, the scale-dependent growth of the initial error is calculated and is approximated by the power law and the quadratic hypothesis. The results are discussed, the power law is modified, and the theoretical justifications of the approximations' parameter values are sought and verified. The findings are then applied to the initial error growth of the ECMWF numerical weather prediction system over the 1986 to 2011 period (500 hPa geopotential height).

This article is divided into five sections. The second describes the system with three spatiotemporal scales based on Lorenz (2005). In Sect. 3, we present the numerical error growth behavior and fit it with previously suggested laws such as a power law growth and the so-called quadratic law, where we also introduce extensions into the saturation regime where there are large errors. In Sect. 4, we trace back the empirically found parameters of the power law error growth to properties of the system and show that we can explain these findings self-consistently with the different error growth rates at different scales. In the fifth section, we perform a similar analysis for the ECMWF forecast system data. Conclusions and discussions are then presented in the final section.

2 Multi-hierarchical system L05-3

The designed system with three spatiotemporal levels (L05-3) is based on systems created by Lorenz (2005). The first and simplest of this type is the low-dimensional atmospheric system (L96) presented by Lorenz (1996). It is a nonlinear model, with N variables connected by governing equations:

$$\begin{array}{}\text{(1)}& \mathrm{d}{X}_n/\mathrm{d}t=-X_{n-\mathrm{2}}{X}_{n-\mathrm{1}}+X_{n+\mathrm{1}}{X}_{n-\mathrm{1}}-X_n+F,\end{array}$$

where $n=\mathrm{1},\mathrm{\dots },N$. $X_{n-\mathrm{2}},X_{n-\mathrm{1}},X_n,X_{n+\mathrm{1}}$ are unspecified (i.e., unrelated to actual physical variables) scalar meteorological quantities (units), F is a constant representing external forcing, and t is time. The index is cyclic so that $X_{n-N}=X_{n+N}=X_n$ and variables can be viewed as existing around a latitude circle. Nonlinear terms of Eq. (1) simulate advection. Linear terms represent mechanical and thermal dissipation. The model quantitatively, to a certain extent, describes weather systems, but, unlike the well-known Lorenz model of atmospheric convection (Lorenz, 1963), it cannot be derived from any atmospheric dynamic equations. The motivation was to formulate the simplest possible set of dissipative chaotically behaving differential equations that share some properties with the “real” atmosphere. One of the model's properties is to have 5 to 7 main highs and lows that correspond to planetary waves (Rossby waves) and several smaller waves corresponding to synoptic-scale waves. For Eq. (1), this is only valid for N=30. Lorenz (2005), therefore, introduced spatial continuity modification (L05). Equation (1) is then rewritten to the following form:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{d}{X}_n}{\mathrm{d}t}}=[X,X{]}_{L,n}-X_n+F,\end{array}$$

where

$$\begin{array}{rl}[X,X{]}_{L,n}=\sum _{j=-J}^J{}^{\prime }\sum _{i=-J}^J{}^{\prime }(& -X_{n-\mathrm{2}L-i}{X}_{n-L-j}\\ & +X_{n-L+j-i}{X}_{n+L+j})/L^{\mathrm{2}}.\end{array}$$

If L is even, ${\sum }^{\prime }$ denotes a modified summation, in which the first and last terms are to be divided by 2. If L is odd, ${\sum }^{\prime }$ denotes an ordinary summation. Generally, L is much smaller than N, $J=L/\mathrm{2}$ if K is even, and $J=(L-\mathrm{1})/\mathrm{2}$ if L is odd. To keep a desirable number of main highs and lows, Lorenz (2005) suggested a ratio $N/L=\mathrm{30}$ and F=15. The choice of parameters F, and the setting of time unit as 5 d, is also made to obtain a similar value of the largest Lyapunov exponent to the ECMWF forecasting system (Lorenz, 2005).

A two-level (scales) system (L96-2) was introduced by Lorenz (1996) by coupling two such systems, each of which, aside from the coupling, obeys a suitably scaled variant of Eq. (1). There are N variables X_n plus J⋅N variables Y_j,n defined for $n=\mathrm{1},\mathrm{\dots },N$ and $j=\mathrm{1},\mathrm{\dots },J$. Governing equations are as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle }\begin{array}{rl}\mathrm{d}{X}_n/\mathrm{d}t=& -X_{n-\mathrm{2}}{X}_{n-\mathrm{1}}+X_{n+\mathrm{1}}{X}_{n-\mathrm{1}}-X_n\\ & +F-(c/b)\sum _{j=\mathrm{1}}^J{Y}_{j,n},\end{array}\text{(4)}& {\displaystyle }\begin{array}{rl}\mathrm{d}{Y}_{j,n}/\mathrm{d}t=& -cb{Y}_{j-\mathrm{2},n}{Y}_{j-\mathrm{1},n}+cb{Y}_{j+\mathrm{1},n}{Y}_{j-\mathrm{1},n}\\ & -c{Y}_{j,n}+(c/b)X_n,\end{array}\end{array}$$

where c sets the rapidness of small scale compared to large scale, and b sets the small-scale amplitude size compared to large scale. $Y_{j,n-N}=Y_{j,n+N}=Y_{j,n}$ while $Y_{j+J,n}=Y_{j,n+\mathrm{1}}$, and $Y_{j-J,n}=Y_{j,n-\mathrm{1}}$. X_n represent the values of some quantity in N sectors of latitude circle, while the variables Y_j,n ($Y_{\mathrm{1},\mathrm{1}},Y_{\mathrm{2},\mathrm{1}},\mathrm{\dots },Y_{J,\mathrm{1}},Y_{\mathrm{1},\mathrm{2}},Y_{\mathrm{2},\mathrm{2}},\mathrm{\dots },Y_{J,\mathrm{2}},Y_{\mathrm{3},\mathrm{1}},\mathrm{\dots }$) can represent some other quantity in JN sectors. In this system, one could construct a more general variable defined on all JN sectors, namely $Z_{j,k}=X_j+Y_{j,k}$.

Similarly to the L96-2 systems, Brisch and Kantz (2019) created L-level systems (L96-H). Their model, however, lacks an essential property of atmospheric variables: the different levels of their hierarchy are different variables, occupying different subspaces of the phase space, as if it were different Fourier modes of some system but were defined in real space. Therefore, we introduce here a model which is closer to reality.

We start from a system L05-2 like L96-2 (Lorenz, 2005):

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{d}{X}_n/\mathrm{d}t=[X,X{]}_{L,n}-X_n-c{Y}_n+F,\text{(6)}& {\displaystyle }& {\displaystyle }\mathrm{d}{Y}_n/\mathrm{d}t=b^{\mathrm{2}}[Y,Y{]}_{\mathrm{1},n}-b{Y}_n+c{X}_n.\end{array}$$

Equation (6) is analogue to Eq. (1) (if we substitute F for X_n), and Eq. (5) is analogue to Eq. (2) (aside from the coupling where c is the coupling coefficient, and that Y_n fluctuates b times as rapidly, and their amplitude is reduced by the factor b). L05-2 or L96-2 systems, however, have an unrealistic property compared to the numerical weather prediction systems. The large-scale and small-scale features are represented by separate sets of variables X and Y instead of appearing as superimposed features of a single set Z. Lorenz (2005) wanted to keep the system as simple as possible, so instead of, for example, Fourier analysis, a procedure for expressing variables Z_n as sums of X_n and Y_n was introduced:

$$\begin{array}{}\text{(7)}& {\displaystyle }& {\displaystyle }{X}_n=\sum _{i=-I}^I{}^{\prime }(\mathit{\alpha }-\mathit{\beta }\mathrm{|}i\mathrm{|}|)Z_{n+i},\text{(8)}& {\displaystyle }& {\displaystyle }{Y}_n=Z_n-X_n.\end{array}$$

Parameters α, β, and I are chosen so that X is a low-pass filtered version of Z, and Y represents the difference between the full signal Z and the filtered signal. By this procedure, Y has a much smaller amplitude than X, and also its time evolution should be faster since the temporal derivative is related to the spatial derivative via the difference ($X_{n+\mathrm{1}}-X_{n-\mathrm{2}}$), which for the low-pass-filtered signal X is typically smaller than for the signal Y.

More precisely, Lorenz's (2005) idea is that the parameters α, β are chosen so that X equals Z whenever Z changes quadratically over the longitudes (variables) n−I through n+I. It is when ${\sum }_{i=-I}^I{}^{\prime }(\mathit{\alpha }-\mathit{\beta }\mathrm{|}i\mathrm{|})=\mathrm{1}$ and ${\sum }_{i=-I}^I{}^{\prime }{i}^{\mathrm{2}}(\mathit{\alpha }-\mathit{\beta }\mathrm{|}i\mathrm{|}t)=\mathrm{0}$. By solving these equations, we get the following:

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }\mathit{\alpha }=(\mathrm{3}{I}^{\mathrm{2}}+\mathrm{3})/(\mathrm{2}{I}^{\mathrm{3}}+\mathrm{4}I),\text{(10)}& {\displaystyle }& {\displaystyle }\mathit{\beta }=(\mathrm{2}{I}^{\mathrm{2}}+\mathrm{1})/(I^{\mathrm{4}}+\mathrm{2}{I}^{\mathrm{2}}).\end{array}$$

The procedures (Eqs. 7 and 8) are functions of the length of the interval $[-I,I]$. When creating a system $\mathrm{d}Z/\mathrm{d}t$ as the sum of $\mathrm{d}X/\mathrm{d}t$ and $\mathrm{d}Y/\mathrm{d}t$ (sum of Eqs. 5 and 6), the coupling term cX_n in Eq. (6), which enables short waves to develop, is combined with the dissipation term −X_n in Eq. (6). Therefore the coupling term can be completely canceled, or it can appear in X rather than Y when Z is analyzed, and there might be nothing to enable the short waves in Y to grow. Lorenz (2005) reformulated the coupling process by adding a small fraction of X to Y, so small waves in Y can amplify, and proved that this is done by replacing $b^{\mathrm{2}}[Y,Y{]}_{\mathrm{1},n}+c{X}_n$ by $[Y,Y+c^{\prime }X{]}_{\mathrm{1},n}$ in Eq. (6), and a new form of L05-2 system would be as follows:

$$\begin{array}{}\text{(11)}& \begin{array}{rl}\mathrm{d}{Z}_n/\mathrm{d}t& =[X,X{]}_{L,n}+b^{\mathrm{2}}[Y,Y{]}_{\mathrm{1},n}+c[Y,X{]}_{\mathrm{1},n}\\ & -X_n-b{Y}_n+F,\end{array}\end{array}$$

where $c=c^{\prime }\cdot b^{\mathrm{2}}$.

Based on the L05-2 system (Eqs. 7–11), we designed a three-level (three-scale) system (L05-3):

$$\begin{array}{}\text{(12)}& \begin{array}{rl}\mathrm{d}{X}_{\text{tot},n}/\mathrm{d}t=& [X_{\mathrm{1}},X_{\mathrm{1}}{]}_{L,n}+b_{\mathrm{1}}^{\mathrm{2}}[X_{\mathrm{2}},X_{\mathrm{2}}{]}_{\mathrm{1},n}+b_{\mathrm{2}}^{\mathrm{2}}[X_{\mathrm{3}},X_{\mathrm{3}}{]}_{\mathrm{1},n}\\ & +c_{\mathrm{1}}[X_{\mathrm{2}},X_{\mathrm{1}}{]}_{\mathrm{1},n}+c_{\mathrm{2}}[X_{\mathrm{3}},X_{\mathrm{2}}{]}_{\mathrm{1},n}-X_{\mathrm{1},n}\\ & -b_{\mathrm{1}}{X}_{\mathrm{2},n}-b_{\mathrm{2}}{X}_{\mathrm{3},n}+F,\end{array}\end{array}$$

where c₁, c₂, b₁, and b₂ are parameters and the procedure for expressing the variables:

$$\begin{array}{}\text{(13)}& {\displaystyle }\begin{array}{rl}{X}_{\mathrm{1},n}=\sum _{i=-I_{\mathrm{1}}}^{I_{\mathrm{1}}}{}^{\prime }& (\left(\left(\mathrm{3}{I}_{\mathrm{1}}^{\mathrm{2}}+\mathrm{3}\right)/\left(\mathrm{2}{I}_{\mathrm{1}}^{\mathrm{3}}+\mathrm{4}{I}_{\mathrm{1}}\right)\right)\\ & -(\left(\mathrm{2}{I}_{\mathrm{1}}^{\mathrm{2}}+\mathrm{1}\right)/\left(I_{\mathrm{1}}^{\mathrm{4}}+\mathrm{2}{I}_{\mathrm{1}}^{\mathrm{2}}\right))\mathrm{|}i\mathrm{|})X_{\text{tot},n+i},\end{array}\text{(14)}& {\displaystyle }\begin{array}{rl}{X}_{\mathrm{2},n}=\sum _{j=-I_{\mathrm{2}}}^{I_{\mathrm{2}}}{}^{\prime }& (\left(\left(\mathrm{3}{I}_{\mathrm{2}}^{\mathrm{2}}+\mathrm{3}\right)/\left(\mathrm{2}{I}_{\mathrm{2}}^{\mathrm{3}}+\mathrm{4}{I}_{\mathrm{2}}\right)\right)\\ & -(\left(\mathrm{2}{I}_{\mathrm{2}}^{\mathrm{2}}+\mathrm{1}\right)/\left(I_{\mathrm{2}}^{\mathrm{4}}+\mathrm{2}{I}_{\mathrm{2}}^{\mathrm{2}}\right))\mathrm{|}j\mathrm{|})\\ & \cdot (X_{\text{tot},n+j}-X_{\mathrm{1},n+j}),\end{array}\text{(15)}& {\displaystyle }{X}_{\mathrm{3},n}=X_{\text{tot},n}-X_{\mathrm{2},n}-X_{\mathrm{1},n},\end{array}$$

where I₁ and I₂ set the length of the intervals $[-I,I]$.

The parameters of any multi-level Lorenz's system (L96-2, L96-H, L05-2, L05-3) should be set so that all levels behave chaotically (the largest Lyapunov exponent of each level is positive) and that all levels have a significant difference in amplitudes and fluctuation rates. For the L-96 system (Eq. 1), the chaotic behavior is determined by the value of F, and the number of variables N. Lorenz (2005) states that for N≥12 chaos is found when F>5 (for N=4 it is when F>12 and for N>6 when F>8). In cases such as the L96-2 system (Eqs. 3 and 4), where the forcing F acts only on the largest scale, the chaotic behavior of smaller scales is created by coupling. The size of the coupling is cascaded from the largest scale to the smaller ones. Because the values of the largest-scale variables are determined by the forcing F, the F value indirectly affects the smaller scales' chaotic behavior and must be chosen large enough to ensure chaotic behavior through coupling for all scales (levels). For the L05-2 system (Eq. 11), variables are superposed features of a single set calculated by Eqs. (7) and (8). In addition to those mentioned above, this procedure affects the chaotic behavior, amplitude, and fluctuation rate of the levels, and the choice of I between 10 and 20 may be optimal (Lorenz, 2005). In order to maintain the required properties of the two-scale L05-2 system, Lorenz (2005) chose N = 960, L = 32, I = 12, F = 15, b = 10, and c = 2.5 (note that for L05-2 and L05-3 systems it is not possible to directly determine the amplitude and fluctuation rate of smaller scales using spatiotemporal scaling factors b, because these values are mainly determined by the procedure for expressing variables and the length of the intervals $[-I,I])$.

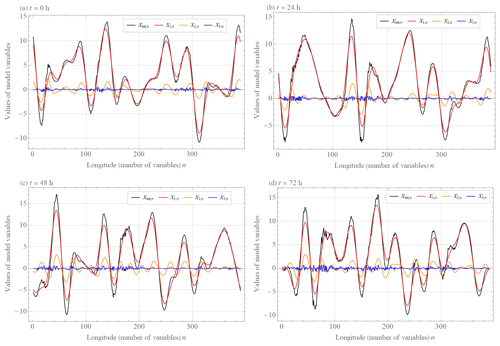
Figure 1 (a) Initial conditions (after discarding a transient of 10 years) and values of variables ($X_{\text{tot}},X_{\mathrm{1}},X_{\mathrm{2}},X_{\mathrm{3}}$) at days (b) one, (c) two, and (d) three of the L05-3 system (Eqs. 13–15) with the parameters N = 390, L = 13, J = 6, F = 15, b₁ = 1, b₂ = 10, c₁ = 1, c₂ = 1, I₁ = 20, I₂ = 10 calculated by a fourth-order Runge–Kutta method with a time step Δt = $\mathrm{1}/\mathrm{240}$ or 0.5 h.

For the L05-3 system (Eqs. 12–15), it is necessary to specify eight parameters. We tested that the values of coupling coefficients c₁ and c₂ do not affect the L05-3 system compared to the values of other parameters, and therefore for simplification c₁ = 1 and c₂ = 1. The parameter F=15 is set the same as for other L05 systems. For the medium-scale amplitude to be approximately 10 times smaller than the large-scale amplitude and the small-scale amplitude to be approximately 10 times smaller than the medium-scale amplitude and for the scales to have different oscillation rates (Fig. 1), the spatiotemporal scale factors are chosen as b₁ = 1 and b₂ = 10 and interval lengths I₁ = 20 and I₂ = 10. N = 390 turned out to be most suitable for the chaotic behavior of all three levels. In the following, we will present numerical results of the L05-3 system (Eqs. 12–15) with the parameters N = 390, L = 13, J = 6, F = 15, b₁ = 1, b₂ = 10, c₁ = 1, c₂ = 1, I₁ = 20, and I₂ = 10, calculated by a fourth-order Runge–Kutta method with a time step Δt = $\mathrm{1}/\mathrm{240}$ or 0.5 h. Initial conditions ($X_{\text{tot},\mathrm{0},n}$, $X_{\mathrm{1},\mathrm{0},n}$, $X_{\mathrm{2},\mathrm{0},n}$, $X_{\mathrm{3},\mathrm{0},n}$), which should be free of transient effect, are chosen as final values of arbitrary values integrated for 175 200 steps or 10 years. Initial conditions and values of variables at days one, two, and three can be seen in Fig. 1.

3 Error growth in the L05-3 system

3.1 Concepts to characterize scale-dependent error growth

In the pioneering papers of Aurell et al. (1996, 1997), a mathematical concept and a numerical scheme for the calculation of scale-dependent error growth was introduced, called the “finite size Lyapunov exponent”. Actually, Aruell et al. (1996) have already referred to the atmospheric predictability problem and named this as one motivation for their work. These papers triggered a set of follow-up publications where it was studied how scale-dependent error growth manifests itself in different models with intrinsic hierarchies such as models for fully developed turbulence like the shell model (Aurell et al., 1996) or how they can be used to study the issue of predictability (Boffetta et al., 1998; for a review see Cencili and Vulpiani, 2013). In brief, a finite size Lyapunov exponent can be defined as the ergodic average over phase space of the growth rate of perturbations of a given magnitude, where the growth rate is defined as the inverse of the time needed for the error magnitude to increase by a pre-defined factor.

In order to be able to investigate the data from the ECMWF forecasts as well, we use here a less rigorous approach: we measure the error amplitude after fixed time intervals. We then calculate the mean error amplitudes after fixed times, calculate the average growth rates during the last time interval, and can report the mean growth rates versus mean error magnitudes. Due to the fact that the conditioning is different, this is not the same as the calculation of the finite size Lyapunov exponent, but it reports similar properties of the system. However, our quantity is more appropriate for the forecast problem: the initial condition of a forecast has some small error compared to the unknown truth, and assuming a perfect model, we therefore calculate the average forecast error after a finite time.

3.2 Numerical scheme for scale-dependent error growth rates

In the following, we describe in more detail our numerical approach. By “error growth”, we denote the growth of errors in the initial conditions, which limit predictability if a system is chaotic. A numerical error growth experiment in a model system, therefore, consists of repeatedly generating a reference trajectory, which is considered to be the “truth” or verification, and a perturbed trajectory which is the numerical solution of the system for a perturbed initial condition (perfect model assumption). The time evolution of the difference vector between these two trajectories averaged over many repetitions then gives insight into the growth of prediction errors. In order for this scheme to be meaningful, we have to ensure that the reference trajectory is on the attractor of the system, that the repetition of this scheme samples the whole attractor with correct weights (the invariant measure), and that initial perturbations point already into the locally most unstable direction, since otherwise errors might even shrink on short timescales (this is also a relevant issue in ensemble forecasts and there its solutions are found in using bred vectors; Toth and Kalnay, 1997). We solve these issues in the following way: we first integrate the system over 10 years, starting from arbitrary initial conditions, and assume that after discarding this transient, the trajectory is on the attractor. We continue to integrate this single trajectory and consider segments of it as reference trajectories for error growth, i.e., the many reference trajectories are simply segments of one very long trajectory, which ensures not only that all these segments are located on the attractor, but that in addition, they sample the attractor according to the invariant measure. For the perturbed trajectories, we start with a random perturbation of the reference trajectory of very small amplitude and let this trajectory evolve over time before we start to determine its distance towards the reference trajectory. In other words, we discard some initial time interval of error growth from our study since this is affected by some complicated transient behavior before it starts to grow with the maximum Lyapunov exponent. However, due to the hierarchical nature of our model, the error growth with the maximal Lyapunov exponent will saturate already for rather small error amplitudes and will be replaced by slower error growth on larger scales, an effect which we will study in detail. The above-described scheme was originally introduced by Lorenz (1996).

In our system, the three spatial scales X₁, X₂, and X₃ cannot be separated in terms of a coordinate transform but are intrinsically coupled and superimposed in the variables X_tot of the system. The initial conditions of the “reality” are called $X_{\text{tot},\mathrm{0},n}$, from which one finds $X_{\mathrm{1},\mathrm{0},n}$, $X_{\mathrm{2},\mathrm{0},n}$, and $X_{\mathrm{3},\mathrm{0},n}$ through Eqs. (13)–(15). The initial values of the “prediction” are then $X_{\text{tot},\mathrm{0},n}^{\prime }=X_{\mathrm{1},\mathrm{0},n}+X_{\mathrm{2},\mathrm{0},n}+X_{\mathrm{3},\mathrm{0},n}+e_{\mathrm{3},n}=X_{\text{tot},\mathrm{0},n}+e_{\mathrm{3},n}$, where e_3,n(0) denotes the initial errors randomly selected from the normal distribution $\text{ND}(\mathit{\mu }=\mathrm{0};\mathit{\sigma }=\mathrm{0.01})$. Hence, these initial conditions differ only by the small perturbation e_3,n(0). Since the state of the model X_tot is the sum over the three components, any arbitrary but small error with spatially uncorrelated components affects only $X_{\mathrm{3},\mathrm{0},n}$. Only a spatially correlated initial error would appear in another component, but since this error would immediately propagate into the small-scale variables and then grow fastest in these, a perturbation with initial errors in $X_{\mathrm{3},\mathrm{0},n}$ is the only practical choice. From $X_{\text{tot},\mathrm{0},n}$ and $X_{\text{tot},\mathrm{0},n}^{\prime }$ Eq. (12) is integrated forward for 41.7 d (K = 2000 steps). In each time step k of the numerical integration, $X_{\mathit{\tau },k,n}$, and $X_{\mathit{\tau },k,n}^{\prime }$ is obtained. The size of the error at a given time kΔt is $e_{\mathit{\tau },n}(k\cdot \mathrm{\Delta }t)=X_{\mathit{\tau },k,n}^{\prime }-X_{\mathit{\tau },k,n}$, where $k=\mathrm{1},\mathrm{\dots },K$, $n=\mathrm{1},\mathrm{\dots },N$ and $\mathit{\tau }=\text{tot},\mathrm{1},\mathrm{2},\mathrm{3}$. We perform M = 400 runs in order to calculate the average error growth. In each new run, the initial values $X_{\mathit{\tau },\mathrm{0},n}$ are the last values $X_{\mathit{\tau },K,n}$ of the previous run. The average initial error growth E(t) is defined as the geometric mean of the runs of the Euclidean distances between “reality” and “prediction”:

$$\begin{array}{}\text{(16)}& E_{\mathit{\tau }}(k\cdot \mathrm{\Delta }t)=\sqrt[\mathrm{2}M]{\prod _{m=\mathrm{1}}^M\left({\displaystyle \frac{\mathrm{1}}{N}}\sum _{n=\mathrm{1}}^N{e}_{\mathit{\tau },n,m}^{\mathrm{2}}(k\cdot \mathrm{\Delta }t)\right)},\end{array}$$

where $\mathit{\tau }=\text{tot},\mathrm{1},\mathrm{2},\mathrm{3}$. The initial transient behavior (0.7 d) of the average error growth E(t) is discarded. We do this since the random initial errors perturb the initial state off the attractor. On very short timescales, the perturbed trajectory relaxes back to the attractor (Brisch and Kantz, 2019; Bednář et al., 2014) so that the error does not grow. Only after this transient does one observe the characteristic error growth of the system. In real weather forecasts, the data assimilation scheme 4D-Var usually ensures that the (error-prone) analysis which is used as the initial condition of the forecast is on the attractor, and also in ensemble forecasts, the perturbations to the analysis are, for example, by the usage of bred vectors, done in a way that all ensemble members start on (or at least very close to) the attractor. As a result, we have numerical averages for the error growth as a function of time steps after perturbing the reference trajectories in the full phase space and for $\mathit{\tau }=\mathrm{1},\mathrm{2},\mathrm{3}$. We can convert these results into the error growth rate as a function of time, and into the error growth rate as a function of the error magnitude. Inspired by Anonymous Referee #1 (2021), we also performed for our model system an analysis in terms of the finite size Lyapunov exponent (Aurell et al. 1996). The results are qualitatively the same as found by our analysis, with small quantitative differences in the magnitude of the error growth rates (not shown here). As we discussed before, the ECMWF data can be only analyzed using our approach, and our approach is also more consistent with the performance of forecasts.

3.3 Functional forms for error growth rates

Let us first consider a classical low-dimensional chaotic system. If the initial errors were infinitesimal, one could follow their growth for infinite times and define the maximal Lyapunov exponent of the system as ${\mathrm{\Lambda }}_{max}={lim}_{t\to \mathrm{\infty }}{lim}_{\mathit{ϵ}\to \mathrm{0}}\frac{\mathrm{1}}{t}\ln \left(\mathrm{|}{X}_{\mathit{\tau }}^{\prime }\right(t)-X_{\mathit{\tau }}(t)\mathrm{|}/\mathit{ϵ})$, with a time- and error-independent growth rate Λ. This exponential growth is associated with single scale systems, infinitesimal initial error, and the early part of the error growth (Bednář et al., 2014). In reality, since the initial perturbation is non-infinitesimal, the exponential error growth will cross over to a constant: the distance between the “true” and the perturbed trajectories cannot become larger than the largest distance on the attractor. Hence, for large times. the average “error” is then the average distance of two arbitrary points on the attractor, averaged over the invariant measure. In order to take this saturation effect into account, we use the extended exponential law for the error growth rate: $\mathit{\lambda }\left(E\right)=\mathrm{\Lambda }(\mathrm{1}-E/E_{\mathrm{\infty }})$, where E_∞ is the saturation value of the respective error. Notice that this extension does not involve any free parameter other than the measurable saturation value E_∞.

We calculate the error growth rate in our L05-3 system using the method of Sprott (2006) ($e_{\mathit{\tau },n}\left(\mathrm{0}\right)={\mathrm{10}}^{-\mathrm{10}}$, k=10 and k=100, M=10⁵). In the following, E_τ(t) denotes mean over many initial conditions of the Euclidian distances between the “true” and the perturbed trajectories at a time t after initializing the perturbation, measured in the subspace of the coordinates τ, where $\mathit{\tau }\in \mathit{\{}\text{tot},\mathrm{1},\mathrm{2},\mathrm{3}\mathit{\}}$. Numerically, we find $E_{\text{tot},\mathrm{\infty }}=\mathrm{7.4}$, $E_{\mathrm{1},\mathrm{\infty }}=\mathrm{6.6}$, $E_{\mathrm{2},\mathrm{\infty }}=\mathrm{1.4}$, and $E_{\mathrm{3},\mathrm{\infty }}=\mathrm{0.3}$ (units). We determine the maximal Lyapunov exponents in all four cases and find the values ${\mathrm{\Lambda }}_{\text{theor}}={\mathrm{\Lambda }}_{\text{tot},\text{theor}}={\mathrm{\Lambda }}_{\mathrm{3},\text{theor}}$ ≈ 2.5 (d)⁻¹ and ${\mathrm{\Lambda }}_{\mathrm{1},\text{theor}}={\mathrm{\Lambda }}_{\mathrm{2},\text{theor}}$ ≈ 2 (d)⁻¹. The similarity of the values Λ_tau,theor for all levels $\mathit{\tau }=\mathrm{1},\mathrm{2},\mathrm{3}$ indicates that they are coupled, so that the maximal Lyapunov exponent when calculated in the double limit E₀→0 and t→∞ shows up in arbitrary subsystems. These values must not be confused with the Lyapunov exponents characterizing the different levels which we will calculate later: the evolution of the errors E_τ can always be studied in a way to see the largest exponent of the system (done here), but also in a way to see a value which would be the exponent of the corresponding sub-system if one were able to isolate this. In the context of the coupled system, these sub-system exponents are just some other positive exponents of the full system, since Eq. (12) in total has, as every dynamical system, as many Lyapunov exponents as it has degrees of freedom (here N = 390), where several of these can be positive.

The L05-3 system is designed with three spatial and temporal scales, so the error growth rate $\mathit{\lambda }\left(E\right)\approx \frac{\mathrm{1}}{\mathrm{\Delta }t}\ln \left(E\right(t+\mathrm{\Delta }t)/E(t\left)\right)$ is expected to be a function of the error magnitude E: after the small-scale errors are no longer growing, the large-scale errors continue to grow at a lower rate. Brisch and Kantz (2019) described this dependence by a power law:

$$\begin{array}{}\text{(17)}& {\mathit{\lambda }}_{\mathrm{p}}\left(E\right):={\displaystyle \frac{\mathrm{d}\ln \left(E\right)}{\mathrm{d}t}}={\displaystyle \frac{\dot{E}}{E}}=a{E}^{-\mathit{\sigma }},\end{array}$$

with an exponent σ and a coefficient a>0. By integrating Eq. (17) over time, the power law dependence of the error growth rate on the error magnitude translates into a power law growth of errors over time:

$$\begin{array}{}\text{(18)}& E_{\mathrm{p}}\left(t\right)={\left(E_{\mathrm{0}}^{\mathit{\sigma }}+a\mathit{\sigma }t\right)}^{\mathrm{1}/\mathit{\sigma }}.\end{array}$$

Similar to the exponential law, this power law does not take the saturation of errors at their largest scale into account. We, therefore, multiply the right hand side by $(\mathrm{1}-E/E_{\mathrm{\infty }})$ and arrive at the extended power law:

$$\begin{array}{}\text{(19)}& {\mathit{\lambda }}_{\mathrm{w}}\left(e\right):={\displaystyle \frac{\mathrm{d}\ln E}{\mathrm{d}E}}={\displaystyle \frac{\dot{E}}{E}}=a{E}^{-\mathit{\sigma }}\left(\mathrm{1}-{\displaystyle \frac{E}{E_{\mathrm{\infty }}}}\right).\end{array}$$

Unfortunately, the time integration in order to arrive at an expression of E_w(t) cannot be done analytically but numerically once the parameters are fixed.

A different description of scale-dependent error growth rate was proposed by Zhang et al. (2019), namely a quadratic model which we write down directly in its extended form containing the saturation effect:

$$\begin{array}{}\text{(20)}& {\mathit{\lambda }}_{\mathrm{q}}\left(E\right):={\displaystyle \frac{\mathrm{d}\ln E}{\mathrm{d}t}}={\displaystyle \frac{\dot{E}}{E}}=(\mathit{\alpha }+\mathit{\beta }{E}^{-\mathrm{1}})\left(\mathrm{1}-{\displaystyle \frac{E}{E_{\mathrm{\infty }}}}\right),\end{array}$$

where α is a synoptic-scale error growth rate and β is an upscale error growth rate from small-scale processes, which was originally designed to describe model error (Savijarvi, 1995; Dalcher and Kalnay, 1987). By integrating Eq. (20) over time, we find

$$\begin{array}{}\text{(21)}& \begin{array}{rl}& E_{\mathrm{q}}\left(t\right)=E_{\mathrm{\infty }}\\ & -{\displaystyle \frac{(E_{\mathrm{\infty }}-\mathit{\beta }/\mathit{\alpha })}{\mathrm{1}-(E_{\mathrm{0}}+\mathit{\beta }/\mathit{\alpha })\exp \left[\right(\mathit{\alpha }+\mathit{\beta }/E_{\mathrm{\infty }}\left)t\right]/(E_{\mathrm{0}}-E_{\mathrm{\infty }})}}.\end{array}\end{array}$$

When removing the saturation factor $(\mathrm{1}-E/E_{\mathrm{\infty }})$ in Eq. (21), then it is what was called the quadratic model,

$$\begin{array}{}\text{(22)}& {\mathit{\lambda }}_{\mathrm{r}}\left(E\right):={\displaystyle \frac{\mathrm{d}\ln E}{\mathrm{d}t}}={\displaystyle \frac{\dot{E}}{E}}=\mathit{\alpha }+\mathit{\beta }{E}^{-\mathrm{1}},\end{array}$$

with the time evolution of the error

$$\begin{array}{}\text{(23)}& E_{\mathrm{r}}\left(t\right)=E_{\mathrm{0}}+\left(E_{\mathrm{0}}+{\displaystyle \frac{\mathit{\beta }}{\mathit{\alpha }}}\right)\left(\exp \right[\mathit{\alpha }t]-\mathrm{1}),\end{array}$$

which is suitable for the first few days of the error growth.

To summarize, we can test the validity of the following laws for scale-dependent error growth rates and for the error growth over time: a constant Lyapunov exponent and hence an exponential error growth, as is expected for the initial time of very small initial errors in a low-dimensional chaotic system; the extension of this behavior with a saturation factor $(\mathrm{1}-E/E_{\mathrm{\infty }})$ expected to be valid for all times in a low-dimensional chaotic system; the (extended) quadratic law proposed in Zhang et al. (2019); and the (extended) power law growth proposed in Brisch and Kantz (2019).

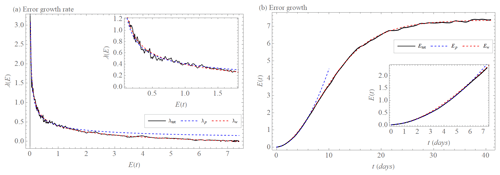
Figure 2 (a) Error growth rate λ_tot(E)of the L05-3 system (black). Power law λ_p(E) (Eq. 19) with the exponent σ=0.5 and the coefficient a=0.41 (units^0.5 d⁻¹) (λ_tot,p(E), blue, dashed) and extended power law λ_w(E) (Eq. 26) with the exponent σ=0.47, the coefficient a=0.46 (units^0.47 d⁻¹), and E_∞=7.36 (units) (λ_tot,w(E), red, dashed) that approximate λ_tot(E). (b) Error growth E_tot(t) (Eq. 17) (black), solution E_tot,p(t) (blue, dashed) of λ_tot,p(E) (Eq. 19), and numerical solution of λ_tot,w(E) (red, dashed).

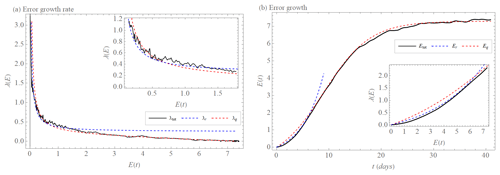
Figure 3 (a) Error growth rate λ_tot(E) of the L05-3 system (black). Quadratic model λ_r(E) (Eq. 22) with α=0.25 (d⁻¹) and β=0.13 (units per day) (λ_tot,p(E), blue, dashed) and extended quadratic model λ_q(E) (Eq. 20) with α=0.2 (d⁻¹), the coefficient β=0.19 (units per day), and E_∞=7.3 (units) (λ_q,w(E), red, dashed) that approximate λ_tot(E). (b) Error growth E_tot(t) (Eq. 17) (black), solution E_tot,r(t) (blue, dashed) of λ_tot,r(E) (Eq. 22), and solution E_tot,q(t) (blue, dashed) of λ_tot,q(E) (Eq. 21) (red, dashed).

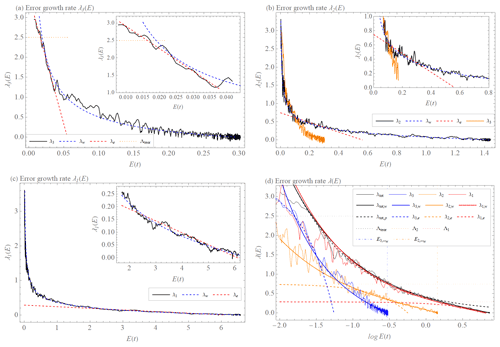
Figure 4 (a) Error growth rate λ₃(E)of the L05-3 system's X₃ scale (black). Extended exponential growth λ_e(E) (Eq. 24) with Λ₃ = 3.6 (d⁻¹) and $E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{e}}}$ = 0.06 (units) (λ_3,e(E), red, dashed) and extended power law λ_w(E) (Eq. 26) with the exponent σ=0.75, the coefficient a=0.13 (units^0.75 d⁻¹), and $E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{w}}}$ = 0.3 (units) (λ_3,w(E), blue, dashed) and ${\mathrm{\Lambda }}_{\text{teor}}={\mathrm{\Lambda }}_{\text{tot},\text{teor}}={\mathrm{\Lambda }}_{\mathrm{3},\text{teor}}$ ≈ 2.5 (d⁻¹) (Sprott's, 2006, method, orange, dotted). (b) Error growth rate λ₂(E) of the L05-3 system's X₂ scale (black). Extended exponential growth λ_e(E) (Eq. 24) with Λ₂ = 0.8 (d⁻¹) and $E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{e}}}$ = 0.55 (units) (λ_2,e(E), red, dashed) and extended power law λ_w(E) (Eq. 26) with the exponent σ=0.44, the coefficient a = 0.25 (units^0.44 d⁻¹), and $E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{w}}}$ = 1.4 (units) (λ_2,w(E), blue, dashed) and error growth rate λ₃(E) of the L05-3 system's X₃ scale (orange). (c) Error growth rate λ₁(E)of the L05-3 system's X₁ scale (black). Extended exponential growth λ_e(E) (Eq. 24) with Λ₁ = 0.28 (d⁻¹) and $E_{\mathrm{1},{\mathrm{\infty }}_{\mathrm{e}}}$ = 6.1 (units) (λ_1,e(E), red, dashed) and extended power law λ_w(E) (Eq. 26) with the exponent σ = 0.5, the coefficient a = 0.43 (units^0.5 d⁻¹), and $E_{\mathrm{1},{\mathrm{\infty }}_{\mathrm{w}}}$ = 6.6 (units) (λ_1,w(E), blue, dashed). (d) Error growth rate λ_τ(E) where τ = tot (black, thin), τ = 1 (red, thin), τ = 2 (orange, thin), τ = 3 (blue, thin). Extended power law λ_τ,w(E) where τ = tot (black), τ = 1 (red), τ = 2 (orange) with $E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{w}}}$ (orange, dashed–dotted), τ = 3 (blue) with $E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{w}}}$ (blue, dashed–dotted). Power law λ_tot,p(E) (black, dashed). Extended exponential growth λ_τ,e(E) where τ = 1 (red, dashed) with Λ₁ (red, dotted), τ = 2 (orange, dashed) with Λ₂ (orange, dotted), τ = 3 (blue, dashed) and Λ_teor (black, dotted).

In Figs. 2–4, we present the numerical results of the error growth over time of the errors E_τ(t) for $\mathit{\tau }\in \mathit{\{}\text{tot},\mathrm{1},\mathrm{2},\mathrm{3}\mathit{\}}$, and the corresponding error growth rates as a function of the error magnitude.

The power law λ_p(E) (Eq. 17) approximates the L05-3 system error growth rate λ_tot(E) in the interval $E_{\text{tot}}\left(t\right)\in [E_{\text{tot},\mathrm{0}},\mathrm{1.5}]$ (Fig. 2a). For larger errors, there is no “next level” of the hierarchy any more, so that the power law evidently cannot be valid. For $E_{\text{tot}}\left(t\right)\in [\mathrm{1.5},E_{\text{tot},\mathrm{\infty }}]$, the empirical error growth rate λ_tot(E) (Fig. 2a) decreases much faster than the power λ_p(E), due to saturation of the errors at E_∞. Hence, the power law E_p(t) (Eq. 18) yields a good approximation of L05-3 system error growth E_tot(t) only in the early part of the growth within 6 d (Fig. 2b), where we find the numerical values σ=0.5 and a=0.41 (units^0.5 d⁻¹). This power law needs to be corrected on times beyond 6 d in order to be able to model the saturation of errors, called the extended power law above. Inserting the numerically observed saturation value E_∞=7.4, a fit of λ_w(E) Eq. (19) yields σ=0.47, a=0.46 (units^0.47 d⁻¹). With this extension, we are able to suitably approximate the L05-3 system error growth $E_{\text{tot}}\left(t\right)\in [E_{\text{tot},\mathrm{0}},E_{\text{tot},\mathrm{\infty }}]$ (Fig. 2a) on the entire range of errors. The numerical time integration of Eq. (19) approximates correspondingly well the L05-3 system error growth E_tot(t) from the initial conditions E₀ to the limit (saturated) value E_tot,∞ (Fig. 2b).

We also fit the quadratic model λ_r(E), Eq. (22), to the numerically obtained L05-3 system error growth rate λ_tot(E). It can reproduce the error growth rate in the interval $E_{\text{tot}}\left(t\right)\in [E_{\mathrm{0}},\mathrm{1.5}]$ as well, but not as accurately as the power law (Fig. 3a). For larger errors in the interval $E_{\text{tot}}\left(t\right)\in [\mathrm{1.5},E_{\text{tot},\mathrm{\infty }}]$, the quadratic model λ_r(E) decreases more slowly than the L05-3 system error growth rate λ_tot(E) and the power law λ_p(E) (Figs. 3a and 2a). The solution of the quadratic model for the time evolution of the error, E_r(t) (Eq. 23), with α=0.25 (d⁻¹) and β=0.13 (units per day) determined from the approximation is similar to E_p(t) with a given coefficient and exponent, but it does not approximate the data as accurately (Fig. 3b). The factor (1−E_∞) with E_∞=7.3 in the extended quadratic model, Eq. (20), yields a much better approximation along the entire time interval, $E_{\text{tot}}\left(t\right)\in [E_{\text{tot},\mathrm{0}},E_{\text{tot},\mathrm{\infty }}]$ (Fig. 3a), but it is slightly less accurate than the extended power law in the interval $E_{\text{tot}}\left(t\right)\in [E_{\text{tot},\mathrm{0}},\mathrm{1.5}]$. This inaccuracy is significant for the solution of the extended quadratic model E_q(t) (Eq. 21) with α=0.2 (d⁻¹) and β=0.19 (units per day) determined from the approximation, where the early part of growth is the least similar to error growth E_tot(t) (Fig. 3b).

3.3.1 Self-consistent explanation of the observed approximate power law

Brisch and Kantz (2019) derived the value of the exponent σ of the power law Eq. (17) from other system properties. They argue that the power law is a result of the superposition of the error growth on different spatial scales with different growth rates. Translated into our L05-3 system it should work as follows: the small-scale error growth E₃(t) should follow the (extended) exponential growth (solution of $\dot{E}/E=\mathrm{\Lambda }(\mathrm{1}-E/E_{\mathrm{\infty }})$, with Λ₃ and a saturation scale E_3,∞. After its saturation, the medium-scale error continues to grow, but with a lower rate Λ₂, and will saturate at a larger scale E_2,∞. Beyond that, the total error growth can only be driven by the growth of the large-scale errors with an even slower growth rate Λ₁ and saturation scale E_1,∞. If the model is designed such that Λ₂=cΛ₁ and Λ₃=c²Λ₁, while $E_{\mathrm{2},\mathrm{\infty }}=E_{\mathrm{1},\mathrm{\infty }}/b$ and $E_{\mathrm{3},\mathrm{\infty }}=E_{\mathrm{1},\mathrm{\infty }}/b^{\mathrm{2}}$, then it was argued that the exponent of the power law should be $\mathit{\sigma }=\ln c/\ln b$.

The model of Brisch and Kantz (2019) was constructed of weakly coupled identical sub-systems, with additional scaling parameters for the amplitude and time of the different subsystems. Therefore, there were rather well defined error growth rates Λ_τ, $\mathit{\tau }=\mathrm{1},\mathrm{2},\mathrm{3}$, and it was easily possible to tune these so that $c^{\mathrm{2}}{\mathrm{\Lambda }}_{\mathrm{1}}=c{\mathrm{\Lambda }}_{\mathrm{2}}={\mathrm{\Lambda }}_{\mathrm{3}}$ and $E_{\mathrm{3},\mathrm{\infty }}=E_{\mathrm{2},\mathrm{\infty }}/b=E_{\mathrm{1},\mathrm{\infty }}/b^{\mathrm{2}}$. In our L05-3 model, all this is not the case. The advantage of our model, however, is that it is much closer to the phenomenology of an atmospheric model: in a single field X_tot, we observe both large-scale and small-scale structures, and we observe both fast and slow motion.

In the L05-3 model, we have determined the error growth of a given level by the study of the distance between reference trajectories and perturbed trajectories in the corresponding coordinates X_τ, $\mathit{\tau }=\mathrm{1},\mathrm{2},\mathrm{3}$; see Fig. 4. It is straightforward to identify the saturation values E_τ,∞. We describe here how we find approximate values for the growth rates Λ_τ in the extended exponential law ($\mathit{\lambda }\left(E\right)=\mathrm{\Lambda }(\mathrm{1}-E/E_{\mathrm{\infty }})$ from our numerics. We can then determine c and b and hence a theoretical value for σ, which we will compare to the numerical fit.

By Sprott's method (Sprott, 2006) we calculate the error growth rates of the three levels separately and the total error growth rate. As one can see in Fig. 4, λ_τ(E) can be well described by the extended power law λ_w(E) on the whole range of E for all τ. The individual contributions of the levels (scales) X_τ, $\mathit{\tau }=\mathrm{1},\mathrm{2},\mathrm{3}$ to the error growth rates λ_τ(E) are then identified as parts that fulfill the extended exponential growth λ_e(E). Numerically, we identify the following values: the extended growth rates are Λ₃=3.6 (d⁻¹), Λ₂=0.8 (d⁻¹), and Λ₁=0.28 (d⁻¹). The corresponding saturation scales are determined as $E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{e}}}=\mathrm{0.06}$ (units), $E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{e}}}=\mathrm{0.55}$ (units), and $E_{\mathrm{1},{\mathrm{\infty }}_{\mathrm{e}}}=\mathrm{6.1}$ (units). The values for levels τ=2 are extracted from the range where the effect of λ₃(E) is no longer present (Fig. 4b), while for τ=1 we consider the late stage of the error growth rate λ₁(E) (Fig. 4c). Following the arguments from above, we derive σ as $\mathit{\sigma }=\ln b_{\mathrm{1}}/\ln c_{\mathrm{1}}=\mathrm{0.47}$ where $b_{\mathrm{1}}=E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{e}}}/E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{e}}}$ and $c_{\mathrm{1}}={\mathrm{\Lambda }}_{\mathrm{2},\mathrm{e}}/{\mathrm{\Lambda }}_{\mathrm{1},\mathrm{e}}$. We get the same value of $\mathit{\sigma }=\ln b_{\mathrm{2}}/\ln c_{\mathrm{2}}=\mathrm{0.47}$ where $b_{\mathrm{2}}=E_{\mathrm{1},{\mathrm{\infty }}_{\mathrm{e}}}/E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{e}}}$, and $c_{\mathrm{2}}={\mathrm{\Lambda }}_{\mathrm{3},\text{teor}}/{\mathrm{\Lambda }}_{\mathrm{2},\mathrm{e}}$, even though b₁≠b₂ and c₁≠c₂. Note that c₂ uses Λ_3,teor instead of Λ₃. This is because Λ₃ should be computed from the ranges where E and t are small/short but which include some transient behavior (Fig. 4a), and therefore Λ_3,teor is a more appropriate value.

These derived values for σ are in perfect agreement with the empirical fit of the extended power law λ_w(E), which yields σ=0.47, and it is close to the value σ=0.50 of the power law λ_p(E) without the saturation effect.

The coupling of the levels has the consequence that one cannot define the Lyapunov exponents for the individual levels in a mathematically rigorous way. We calculated them as ${\mathrm{\Lambda }}_{\mathrm{1}}\left(E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{e}}}\right)=\mathrm{0.28}=\text{const.}$ (d⁻¹) at $E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{e}}}=\mathrm{0.55}$ and ${\mathrm{\Lambda }}_{\mathrm{2}}\left(E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{e}}}\right)=\mathrm{0.8}=\text{const.}$ (d⁻¹) at $E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{e}}}=\mathrm{0.06}$ using the extended exponential law. It is well justified to use these to determine the exponent σ. However, they do not fit the error growth rate ${\mathit{\lambda }}_{\text{tot}}\left(E\right)\left({\mathit{\lambda }}_{\text{tot}}\right(E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{e}}})\ne {\mathrm{\Lambda }}_{\mathrm{1}}$, ${\mathit{\lambda }}_{\text{tot}}\left(E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{e}}}\right)\ne {\mathrm{\Lambda }}_{\mathrm{2}}$, Fig. 4d). Instead, a fit to λ_tot(E) yields ${\mathit{\lambda }}_{\text{tot}}\left(E_{\mathrm{2},\mathrm{\infty }}\right)={\mathrm{\Lambda }}_{\mathrm{1}}=\mathrm{0.28}$ (d⁻¹) in the limit value of medium-scale error growth $E_{\mathrm{2},\mathrm{\infty }}=\mathrm{1.4}$ and ${\mathit{\lambda }}_{\text{tot}}\left(E_{\mathrm{3},\mathrm{\infty }}\right)={\mathrm{\Lambda }}_{\mathrm{2}}=\mathrm{0.8}$ (d⁻¹) in the limit value of small-scale error growth $E_{\mathrm{3},\mathrm{\infty }}=\mathrm{0.3}$ (Fig. 4d). If we approximate the values ${\mathrm{\Lambda }}_{\mathrm{1}}\left(E_{\mathrm{2},{\mathrm{\infty }}_{\mathrm{e}}}\right)$ and ${\mathrm{\Lambda }}_{\mathrm{2}}\left(E_{\mathrm{3},{\mathrm{\infty }}_{\mathrm{e}}}\right)$ by the power law λ_p(E) with the exponent σ=0.5, we get the coefficient a=0.2 (units^0.5 d⁻¹), and by the power law λ_p(E) with the exponent σ=0.47, we get a=0.21 (units^0.47 d⁻¹). These power laws should describe the error growth of the system without coupling (the extended power law was not used because $(\mathrm{1}-E/E_{\mathrm{\infty }})$ is negligible in this area), and if we compare these values with the values of the power laws (λ_tot,p(E): σ=0.5, a=0.41 (units^0.5 d⁻¹), λ_tot,w(E): σ=0.47, a=0.46 (units^0.46 d⁻¹)) that approximate the error growth rate of the L05-3 system λ_tot(E) (the system with coupling), we find that the value of the coefficient a changed. We, therefore, conclude that the coefficient a is subject to the degree of coupling of the system.

Values α=0.25 (d⁻¹) for the quadratic model λ_r(E) (Eq. 22) and α=0.2 (d⁻¹) for the extended quadratic model λ_q(E) (Eq. 20) should describe the synoptic-scale error growth rate (Zhang et al., 2019; Zhang and Sun, 2020). For the L05-3 system, it is Λ₁=0.28(d⁻¹) obtained from the approximation by the extended exponential growth ($\mathit{\lambda }\left(E\right)=\mathrm{\Lambda }(\mathrm{1}-E/E_{\mathrm{\infty }})$) for X₁. We can see that Λ₁ is closer to α from the quadratic model λ_r(E), but none of α describes Λ₁ exactly. Values β=0.13 (units per day) and β=0.19 (units per day) that according to Zhang et al. (2019) and Zhang and Sun (2020) should describe upscale error growth rate from small-scale processes could not be identified or described in the L05-3 system.

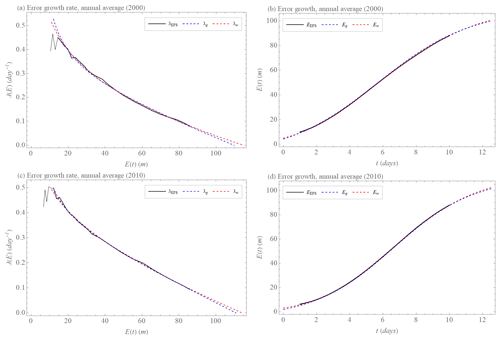
Figure 5 The error growth rate λ_EFS(E) and error growth E_EFS(t) of the ECMWF forecasting system's 500 hPa geopotential height values (Northern Hemisphere, 20–90^∘) calculated as differences between two operational forecasts issued with 1 d lag but valid on the same day (black), approximation by the extended power law λ_w(E) (Eq. 26) and E_w(t) (Eq. 27) (red, dashed), and approximation by the extended quadratic model λ_q(E) (Eq. 20) and E_q(t) (Eq. 21) (blue, dashed). (a, b) Annual average of 2000, λ_EFS,w(E) and E_EFS,w(t) with σ = 0.28, a = 1.1 (m^0.28 d⁻¹), and E_∞ = 115 (m), λ_EFS,p(E) and E_EFS,p(t) with α = 0.32 (d⁻¹) and β = 3.2 (m d⁻¹) and E_∞ = 110 (m). (c, d) Annual average of 2010, λ_EFS,w(E) and E_EFS,w(t) with σ = 0.17, a = 0.8 (m^0.17 d⁻¹), and E_∞ = 114 (m), λ_EFS,p(E) and E_EFS,p(t) with α = 0.4 (d⁻¹) and β = 2 (m d⁻¹) and E_∞ = 111 (m).

4 Error growth in the ECMWF forecast system

The error growth E_EFS(t) of the ECMWF forecasting system's 500 hPa geopotential height values (Magnusson, 2013) is calculated (Magnusson and Kallen, 2013) as annual averages over the Northern Hemisphere (20–90^∘) obtained daily from 1 January 1986 to 31 December 2011. As “errors” one uses the differences between two operational forecasts issued with 1 d lag for the same day, in order to eliminate the effects of model errors. Specifically, we evaluate these for 27 different lead times and used the following time intervals in hours: 0–24, 6–30, 12–36, 18–42, 24–48, 30–54, 36–60, 42–66, 48–72, 54–78, 60–84, 66–90, 72–96, 78–102, 84–108, 90–114, 96–120, 108–132, 120–144, 132–156, 144–168, 156–180, 168–192, 180–204, 192–216, 204–228, 216–240. Detailed information about calculating the error growth of the ECMWF forecasting system can be found in Lorenz (1982). The error growth rate ${\mathit{\lambda }}_{\text{EFS}}\left(E\right):=d\ln E/\mathrm{d}t\approx \ln \left(E\right(t+\mathrm{\Delta }t)/E(t\left)\right)/\mathrm{\Delta }t$ with Δt=6 h for the first 17 time steps and Δt = 12 h for the remaining 10 time steps and the error growth E_EFS(t) are calculated between the first and tenth day. The differences 0–24, 6–30, 12–36 are discarded because λ_EFS(E) for these differences is either increasing or constant due to transient behavior; see Fig. 5.

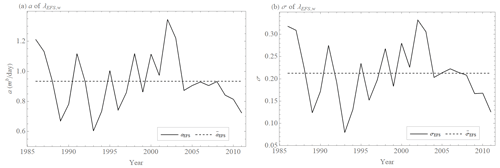
Figure 6 Values of coefficients a (a) and exponents σ (b) of the extended power law λ_w(E) (Eq. 26) approximated from annual averages of the error growth rate λ_EFS(E) of the ECMWF forecasting system's 500 hPa geopotential height values (Northern Hemisphere, 20–90^∘) calculated as differences between two operational forecasts issued with 1 d lag but valid on the same day (black) and the average value of coefficients ${\stackrel{\mathrm{‾}}{a}}_{\text{EFS}}$ = 0.93 ± 0.18 m^σ d⁻¹ and exponents ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{\text{EFS}}$ = 0.21 ± 0.07 over all years (black, dashed).

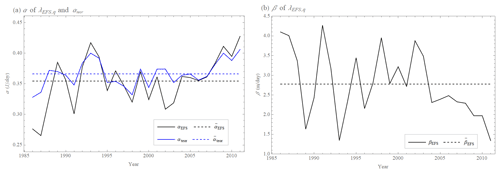
Figure 7 Values of parameters α (a) and β (b) of the extended quadratic model λ_q(E) approximated from annual averages of the error growth rate λ_EFS(E) of the ECMWF forecasting system's 500 hPa geopotential height values (Northern Hemisphere, 20–90^∘) calculated as differences between two operational forecasts issued with 1 d lag but valid on the same day (black), the average value of parameters ${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\text{EFS}}$ = 0.35 ± 0.04 d⁻¹ and ${\stackrel{\mathrm{‾}}{\mathit{\beta }}}_{\text{EFS}}$ = 2.8 ± 0.9 m d⁻¹ over all years (black, dashed) and theoretical value of α_teor (blue) and its average value ${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\text{teor}}$ = 0.37 ± 0.02 d⁻¹ (blue, dashed) over all years determined by Bednář et al. (2021).

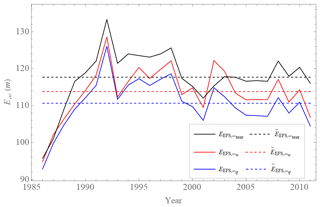
Figure 8 Values of limit (saturated) values $E_{\text{EFS},{\mathrm{\infty }}_{\mathrm{w}}}$ of the extended power law λ_w(E) (red), $E_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ of the extended quadratic model λ_q(E) (blue), and theoretical value $E_{\text{EFS},{\mathrm{\infty }}_{\text{teor}}}$ determined by Bednář et al. (2021) (black) approximated from annual averages of the error growth rate λ_EFS(E) of the ECMWF forecasting system's 500 hPa geopotential height values (Northern Hemisphere, 20–90^∘) calculated as differences between two operational forecasts issued with 1 d lag but valid on the same day. The average value of ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{w}}}$ = 114 ± 7 m (red, dashed), ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ = 111 ± 7 m (blue, dashed), and ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\text{teor}}}$ = 118 ± 7 m (black, dashed).

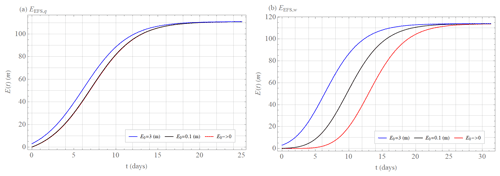
Figure 9 (a) The solution of the extended quadratic model E_q(t) with parameters ${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\text{EFS}}$ = 0.35 d⁻¹ and ${\stackrel{\mathrm{‾}}{\mathit{\beta }}}_{\text{EFS}}$ = 2.8 m d⁻¹, limit (saturated) value ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ = 111 m and with initial errors E₀ = 3 m (blue), E₀ = 0.1 m (black), and E₀→0 (red). (b) The solution of the extended power law E_w(t) with the coefficient ${\stackrel{\mathrm{‾}}{a}}_{\text{EFS}}$ = 0.93 m^σ d⁻¹, exponent ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{\text{EFS}}$ = 0.21, limit (saturated) value ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ = 114 m and with initial errors E₀ = 3 m (blue), E₀ = 0.1 m (black), and E₀→0 (red). Bar above parameters and limit value means averages over approximations of λ_q(E) and λ_w(E) from annual averages of the error growth rate λ_EFS(E) of the ECMWF forecasting system's 500 hPa geopotential height values (Northern Hemisphere, 20–90^∘) calculated as differences between two operational forecasts issued with 1 d lag but valid on the same day.

Despite these missing parts of the error growth E_EFS(t), Bednář et al. (2021) showed that the extended quadratic model E_q(t) Eq. (21) is more accurate than the extended exponential growth (solution of $\dot{E}/E=\mathrm{\Lambda }(\mathrm{1}-E/E_{\mathrm{\infty }})$). Because E_EFS(t) calculated in the abovementioned way should be insensitive to any model error which therefore can not affect the error growth, the extended quadratic model parameter β describes the effect of small-scale processes, which justifies considering the error growth rate λ_EFS(E) for all annual averages as scale-dependent and also approximating it by the extended power law λ_w(E) Eq. (19). The quadratic model λ_r(E) (Eq. 22) and the power law λ_p(E) (Eq. 17) cannot be used due to the lack of an early part of the error growth E_EFS(t). The extended power law λ_w(E) (Eq. 19) matches well with the annual averages of the error growth rate λ_EFS(E) of the ECMWF forecasting system (Fig. 5) with the values of the exponent σ_EFS displayed in Fig. 6b (${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{\text{EFS}}$ = 0.21 ± 0.07), the value of the coefficient a_EFS shown in Fig. 6a (${\stackrel{\mathrm{‾}}{a}}_{\text{EFS}}$ = 0.93 ± 0.18 m^0.21 d⁻¹), and with the limit (saturated) values $E_{\text{EFS},{\mathrm{\infty }}_{\mathrm{w}}}$ displayed in Fig. 8 (${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{w}}}$ = 114 ± 7 m). Exponents σ_EFS, coefficients a_EFS, and limit values $E_{\text{EFS},{\mathrm{\infty }}_{\mathrm{w}}}$ do not have significant trends over the years (Figs. 6 and 8). The extended quadratic model λ_q(E) Eq. (20) approximates annual averages of the error growth rate λ_EFS(E) of the ECMWF forecasting system (Fig. 5) with the values of the parameter α_EFS shown in Fig. 7a (${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\text{EFS}}$ = 0.35 ± 0.04 d⁻¹), the value of the parameter β_EFS displayed in Fig. 7b (${\stackrel{\mathrm{‾}}{\mathit{\beta }}}_{\text{EFS}}$ = 2.8 ± 0.9 m d⁻¹), and with the limit (saturated) values $E_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ displayed in Fig. 8 (${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ = 111 ± 7 m). Again, parameters α_EFS and β_EFS and limit values $E_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ do not have significant trends over the years (Figs. 7 and 8). The approximations by the extended quadratic model λ_q(E) and the extended power law λ_w(E) differ in parts where data are not available (Fig. 5). The limit values $E_{\text{EFS},{\mathrm{\infty }}_{\mathrm{w}}}$ and initial errors $E_{\text{EFS},{\mathrm{0}}_{\mathrm{w}}}$ of the extended power law are greater than the limit values $E_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ and initial errors $E_{\text{EFS},{\mathrm{0}}_{\mathrm{q}}}$ of the extended quadratic model (Figs. 5 and 8). If we set the initial errors of both approximations to the same value, the error growth of the extended quadratic model E_EFS,q(t) approximation would grow faster and would reach the limit value E_EFS,∞ earlier than the error growth of the power law E_EFS,w(t). This difference is more significant when E₀→0. Of particular interest is the limit of predictability. We, therefore, study the time when the error E(t) reaches 95 % of the limit error E_∞ for the size of the initial error E₀ ≈ 3 m, which is an accepted value for current global operational numerical weather prediction (NWP) models (Zhang et al., 2019). The limit time is 14 d for the extended quadratic model ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},\mathrm{q}}\left(t\right)$ when using the abovementioned parameter values for ${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\text{EFS}}$, ${\stackrel{\mathrm{‾}}{\mathit{\beta }}}_{\text{EFS}}$, and ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ (Fig. 9a). For the extended power law ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},\mathrm{w}}\left(t\right)$, using the above listed values for the exponent ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{\text{EFS}}$, coefficient ${\stackrel{\mathrm{‾}}{a}}_{\text{EFS}}$, and limit values ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{w}}}$, it is 15 d (Fig. 9b). When the size of the initial error E₀ is reduced to E₀ ≈ 0.1 m, which is realistic for the current global experimental NWP models (Zhang et al., 2019), this limit time is 15 d for the extended quadratic model ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},\mathrm{q}}\left(t\right)$ (Fig. 9a), and 18 d for the extended power law ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},\mathrm{w}}\left(t\right)$ (Fig. 9b). Both models have an intrinsic predictability limit even if the size of the initial error E₀→0, which is 15 d for the extended quadratic model (Fig. 9a) and 22 d for the extended power law ${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},\mathrm{w}}\left(t\right)$ (Fig. 9b).

5 Conclusion and discussion

We designed a three-level (three-scale) system (L05-3; Eqs. 12–15) with the parameters N=390, L=13, J=6, F=15, b₁=1, b₂=10, c₁=1, c₂=1, I₁=20, I₂=10. These parameters were chosen in such a way that all levels behave chaotically, i.e., the largest Lyapunov exponents of each level is positive, and that all levels have a significant difference in amplitudes and fluctuation rates (Fig. 1). In this system, the error growth rates λ_τ(E) and the error growths as a function of time E_τ(t) were calculated for the system as a whole (τ=tot) and for the different levels ($\mathit{\tau }=\mathrm{1},\mathrm{2},\mathrm{3})$. We fitted the numerically obtained results by the power law λ_p(E) (Eq. 17), the extended power law λ_w(E) (Eq. 19), the quadratic hypothesis λ_r(E) (Eq. 22), the extended quadratic hypothesis λ_q(E) (Eq. 20), and their corresponding time integrations E(t). Without the saturation terms $(\mathrm{1}-E/E_{\mathrm{\infty }})$ both the power law and the quadratic hypothesis fail to provide good fits for larger errors or longer times (Figs. 2 and 3) but are reasonable for the early parts of error growth when the initial error is small. Indeed, with our type of numerical analysis, we are unable to reach the very small scales where the error growth rate saturates at the proper Lyapunov exponent of the system which we estimate to be about 2.5 d⁻¹ but instead are faced by an overshooting of the initial error growth.

The quadratic hypothesis does not provide an as good a fit as the extended power law does. Its parameter β that according to Zhang et al. (2019) and Zhang and Sun (2020) should describe the upscale error growth rate from small-scale processes could not be identified or described in the L05-3 system. In contrast, the extended power law λ_w(E) and E_w(t) with the exponent σ=0.47, the coefficient a=0.46 (units^0.47 d⁻¹), and E_∞=7.36 best describes the error growth rate λ_tot(E) and the error growth E_tot(t) of the L05-3 system on the whole range of times and error magnitudes. The Brisch and Kantz (2019) definition of the exponent σ was confirmed and extended to cases when c₁≠c₂ (c is the ratio of the rapidness of a smaller scale compared to the rapidness of a larger scale) and b₁≠b₂ (b is the ratio of a smaller-scale amplitude compared to a larger-scale amplitude) for $\mathit{\sigma }=\ln c_{\mathrm{1}}/\ln b_{\mathrm{1}}=\ln c_{\mathrm{2}}/\ln b_{\mathrm{2}}$. It was shown that the coefficient a determines the degree of the system's coupling because the same value of the exponent σ is valid for the same system with and without coupling.

We also checked the appropriateness of the extended quadratic hypothesis and the extended power law to describe the error growth rate λ_EFS(E) and the error growth over time E_EFS(t) of the ECMWF forecasting system's 500 hPa geopotential height values over the 1986 to 2011 period. Their behaviors differ in parts where data are not available (Fig. 5), while they agree quite well and both describe the numerical observations on the main part of the data. Therefore, it is not possible to assess which approximation is the more appropriate one for the description of the entire length of λ_EFS(E) and E_EFS(t) from the initial to the limit (saturated) error. One might argue, however, that because we can observe the similarities of the differences between the data and the approximations in both systems (${\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\text{teor}}}>{\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{w}}}>{\stackrel{\mathrm{‾}}{E}}_{\text{EFS},{\mathrm{\infty }}_{\mathrm{q}}}$ (Fig. 8) and $E_{\text{tot},\mathrm{\infty }}>E_{\text{tot},{\mathrm{\infty }}_{\mathrm{w}}}>E_{\text{tot},{\mathrm{\infty }}_{\mathrm{q}}}$; ${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\text{teor},\mathrm{w}}>{\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\text{EFS},\mathrm{w}}$ (Fig. 7) and ${\mathrm{\Lambda }}_{\mathrm{1}}>{\mathit{\alpha }}_{\text{tot},\mathrm{w}}$), the extended power law λ_w(E) is also a valid description of the ECMWF forecasting system. From the average of the fit parameters over many years we calculate that the intrinsic limit to predictability is 22 d in the idealized case of perfect initial conditions, which is in nice agreement with Krishnamurthy (2019).