the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Surface Urban Energy and Water Balance Scheme (v2020a) in vegetated areas: parameter derivation and performance evaluation using FLUXNET2015 dataset
Hamidreza Omidvar
Dave Bilesbach
Andrew Black
Jiquan Chen
Zexia Duan
Zhiqiu Gao
Hiroki Iwata
Joseph P. McFadden
To compare the impact of surface–atmosphere exchanges from rural and urban areas, fully vegetated areas (e.g. deciduous trees, evergreen trees and grass) commonly found adjacent to cities need to be modelled. Here we provide a general workflow to derive parameters for SUEWS (Surface Urban Energy and Water Balance Scheme), including those associated with vegetation phenology (via leaf area index, LAI), heat storage and surface conductance. As expected, attribution analysis of bias in SUEWS-modelled QE finds that surface conductance (gs) plays the dominant role; hence there is a need for more estimates of surface conductance parameters. The workflow is applied at 38 FLUXNET sites. The derived parameters vary between sites with the same plant functional type (PFT), demonstrating the challenge of using a single set of parameters for a PFT. SUEWS skill at simulating monthly and hourly latent heat flux (QE) is examined using the site-specific derived parameters, with the default NOAH surface conductance parameters (Chen et al., 1996). Overall evaluation for 2 years has similar metrics for both configurations: median hit rate between 0.6 and 0.7, median mean absolute error less than 25 W m−2, and median mean bias error ∼ 5 W m−2. Performance differences are more evident at monthly and hourly scales, with larger mean bias error (monthly: ∼ 40 W m−2; hourly ∼ 30 W m−2) results using the NOAH-surface conductance parameters, suggesting that they should be used with caution. Assessment of sites with contrasting QE performance demonstrates how critical capturing the LAI dynamics is to the SUEWS prediction skills of gs and QE. Generally gs is poorest in cooler periods (more pronounced at night, when underestimated by ∼ 3 mm s−1). Given the global LAI data availability and the workflow provided in this study, any site to be simulated should benefit.
- Article
(14911 KB) - Full-text XML
- BibTeX
- EndNote
The Surface Urban Energy and Water Balance Scheme (SUEWS, Grimmond et al., 1986, 1991; Grimmond and Oke, 1991; Järvi et al., 2011) is widely used to simulate urban surface energy and hydrological fluxes, with heat and water released by anthropogenic activities accounted for (Grimmond et al., 1986; Grimmond, 1992). SUEWS characterises the heterogeneity of urban surfaces allowing an integrated mix of seven land covers within a grid cell (neighbourhood scale: O(0.1–10 km)) of impervious (buildings, paved) and pervious (evergreen trees/shrubs, deciduous trees/shrubs, grass, soil, water) types. Although SUEWS has been evaluated in cities around the globe (e.g. Karsisto et al., 2016; Ward et al., 2016; Ao et al., 2018; Kokkonen et al., 2018; Harshan et al., 2018) with varying mixes of integrated impervious–pervious land covers, its performance has not been comprehensively examined in fully vegetated areas that commonly occur adjacent to cities.
One common and demanding application of urban climate models, including SUEWS, is to examine the very well-known canopy-layer urban heat island effects – parts of cities are often warmer than their surroundings at night – and to understand the causes (Oke, 1973, 1982). This requires both the “rural” context – usually characterised by pervious land cover – and the urban area of focus to be simulated appropriately ideally using the same modelling framework. As SUEWS v2020a (Tang et al., 2021) can diagnose near-surface meteorology in the roughness sub-layer and canopy layer (e.g. air temperature and humidity at 2 (above ground level), wind speed at 10 ), it is essential to ensure that any urban–rural comparison in these diagnostics has the proper rural skill and parameters (i.e. coefficient values used in parameterisations).
For meso-scale numerical weather prediction (NWP) of an urban region, both rural and urban areas need to be simulated. With plans to couple SUEWS to a meso-scale model (e.g. Weather Research and Forecasting (WRF); Skamarock and Klemp, 2008), most regions have extensive areas that have completely pervious grid cells. As these need to be simulated using a consistent surface scheme, it is essential to have appropriate parameters for these areas.
Central to the SUEWS biophysics is the Penman–Monteith approach (Penman, 1948; Monteith, 1965) with a Jarvis-type (Jarvis, 1976) surface moisture conductance (Grimmond and Oke, 1991). Parameters for different types of urban areas (e.g. land cover differences) and regions (e.g. high latitude or mid-latitude) have been derived. However, both limited observations and lack of a standard workflow for deriving parameters remain a constraint. This is evident in the availability of conductance- and storage-heat-flux-related parameters (e.g. Järvi et al., 2011, 2014; Ward et al., 2016). Other land surface schemes have parameters for a wide range of plant functional types (PFTs) (e.g. NOAH within WRF,r Chen et al., 1996; Chen and Dudhia, 2001) but are often derived from a small number of observational sites, and their widespread applicability is unexamined. For example, NOAH largely adopted values from the HAPEX-MOBILHY observational program (Andre et al., 1986) following Noilhan and Planton (1989).
FLUXNET (Baldocchi et al., 2001) is a global network of sites that monitor surface–atmosphere exchanges (e.g. carbon, water, and energy turbulent fluxes using the eddy covariance technique). These data provide unprecedented possibilities to advance process-based land surface modelling, through both development (e.g. Stöckli et al., 2008) and evaluation (e.g. Zhang et al., 2017). Extensive analysis of FLUXNET datasets for the variety of terrestrial PFTs have considered various surface atmosphere controls (e.g. albedo: Cescatti et al., 2012; latent heat flux: Ershadi et al., 2014; spatiotemporal representativeness: Chu et al., 2017; Villarreal and Vargas, 2021; energy balance closure: Franssen et al., 2010; landscape heterogeneity: Göckede et al., 2008; Stoy et al., 2013) to enhance understanding of land–atmosphere interactions. As such, this is an ideal data source for deriving widely applicable parameters and assessing performance of SUEWS over different land cover types.
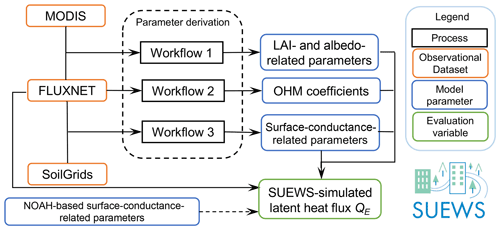
Figure 1Overview of workflows to derive parameters and to undertake and to evaluate simulations. Acronyms are defined in Sects. 2 and 3. More details are provided in Figs. 3, 5 and 6.
In this work, we develop general workflows (Fig. 1) to derive vegetation-related parameters associated with phenology, the storage heat flux and surface moisture conductance and comprehensively examine model skill in modelling latent heat fluxes. We briefly review the key vegetation biophysics schemes in SUEWS (Sect. 2), describe the FLUXNET2015 (Pastorello et al., 2020) and auxiliary datasets used (Sect. 3), and outline the workflows for deriving parameters (Sect. 4). To assess the quality of the derived parameters the SUEWS-modelled latent heat flux is evaluated (Sect. 5). Model parameters related to surface conductance are derived for NOAH at the PFT level (Appendix A) as well as those related to surface roughness based on the FLUXNET2015 dataset at the site level (Appendix B). Other model parameters derived following workflows (Sect. 4) are also provided (Appendix C). The source code, input data and model simulations analysed are provided in Sun et al. (2021).
2.1 Overview of SUEWS physics for vegetated areas
The Surface Urban Energy and Water Balance Scheme (SUEWS) is a local-scale land surface model for simulating the surface energy and hydrological fluxes (Grimmond and Oke, 1986, 1991; Järvi et al., 2011, 2014; Offerle et al., 2003; Ward et al., 2016) without requiring specialised computing facilities. It has been extensively evaluated and applied in many cities (Lindberg et al., 2018, their Table 3; Sun and Grimmond, 2019, their Table 1). Other details of how SUEWS computes the surface energy, water and carbon fluxes are given in recent model description papers (Järvi et al., 2011, 2019; Ward et al., 2016).
The surface energy and water balances are directly linked by the turbulent latent heat flux (QE) or its mass equivalent evaporation (E) (Grimmond and Oke, 1986, 1991):
where Q∗ is the net all-wave radiation flux; QF is the anthropogenic heat flux; QH is the turbulent sensible heat flux; ΔQS the net storage heat flux; and P, Ie, ΔS and R are precipitation, external water use, net change in the water storage (e.g. canopy, soil moisture, water bodies) and runoff, respectively. The sites selected in this work are assumed to have no irrigation, so Ie is assumed to be 0 mm s−1.
In SUEWS, a modified Penman–Monteith equation (Penman, 1948; Monteith, 1965) is used to compute QE with an expectation in cities that the anthropogenic heat flux (QF) is greater than zero (Grimmond and Oke, 1991):
However, with our current focus on extensive (non-urban) pervious areas QF is assumed to be 0 W m−2. The atmospheric state is obtained from the slope of saturation water vapour pressure curve with respect to air temperature (s, Pa K−1), density of air (ρ, kg m−3), specific heat of air at constant pressure (cp, ), vapour pressure deficit (VPD, Pa), psychrometric “constant” (γ, Pa K−1) and the aerodynamic resistance for water vapour (ra, s m−1).
Table 1Parameters and the first process they are used in by SUEWS (i.e. most impact multiple variables). Sources (S) include this study (∗), Ward et al. (2016) (W16) and FLUXNET2015 (F15, Pastorello et al., 2020) where values are given or used in individual equations (Eq.). Two key phenology periods are related to growing and senescence degree days (GDD, SDD).
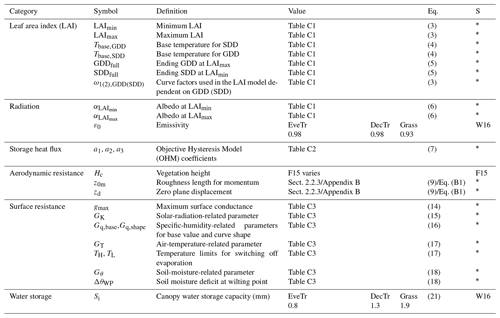
Under given ambient meteorological conditions (e.g. incoming solar radiation K↓, air temperature Ta, humidity) at an extensive vegetated site, QE from this method is sensitive to the estimation of available energy (i.e. ), aerodynamic resistance ra and surface resistance rs. Hence, the critical vegetation-related parameters (Table 1) are addressed with these caveats and/or assumptions:
-
Surface emissivity ε0 and canopy water storage capacity Si are assumed to be the same as reported in Ward et al. (2016).
-
Aerodynamic resistance ra is highly dependent on aerodynamic parameters that vary with canopy height (Hc) and leaf area index (LAI) (Kent et al., 2017a, b; Appendix B). The temporally varying Hc is obtained from FLUXNET2015 (Sect. 2.2.3). LAI varies with phenology (Sect. 2.2.1).
2.2 QE-related sub-schemes in SUEWS
2.2.1 Leaf area index (LAI) and radiation
In SUEWS, leaf growth is triggered by reaching a critical growing-degree-day (GDD) threshold ), and similarly for leaf fall by senescence degree days (SDDs, ) using daily (d) mean air temperatures (Td) based on the previous day (d−1) for each vegetation type i (one of evergreen trees, deciduous trees and grass). For forests and grass we use the following (Järvi et al., 2011):
with curve factors needing to be derived. Td−1 is derived from the daily maximum () and minimum () air temperature of the previous day:
For each site and vegetation type i, the maximum and minimum LAI values (, ) and Tbase,GDD and Tbase,SDD are determined for each site (Sect. 4.1). For sites at higher latitude (e.g. > 60∘), other characteristics – such as day length and photo period – are helpful to account for corresponding LAI controls (Bauerle et al., 2012; Gill et al., 2015).
LAI influences several processes in SUEWS – such as dynamics of surface conductance (later in Sect. 2.2.4) and albedo – the latter varies with daily LAI between a minimum () and maximum () by vegetation type:
We note the SUEWS urban snow module (Järvi et al., 2014) is not used in this work, so we focus on snow-free conditions. This may bias some modelled α and subsequent fluxes, but evaluating the snow module is a large task in its own right.
Within SUEWS the albedo is used with the observed incoming shortwave radiation and longwave radiation to obtain Q∗. In the current analyses, the observed incoming longwave (L↓) and modelled outgoing longwave radiation (, where ε0 is the surface emissivity; σ is the Stefan Boltzmann constant, ; and Ts is the surface temperature, K) are used. Table 1 gives the emissivity values used.
2.2.2 Storage heat flux
Storage heat flux ΔQS is simulated with the objective hysteresis model (OHM, Grimmond et al., 1991):
where fi is the plan area (or three-dimensional fraction area, Grimmond et al., 1991; Grimmond and Oke, 1999) fraction of surface i, a1−3 are the OHM coefficients (Sect. 4.2), and t is time.
2.2.3 Aerodynamic resistance
Aerodynamic resistance ra is obtained from Järvi et al. (2011) and van Ulden and Holtslag (1985):
where zm is the measurement height for mean wind speed (u) and κ the von Kármán constant (0.4 assumed); the aerodynamic parameters zd (zero plane displacement height) and z0m (roughness length for the momentum) are estimated as a function of canopy height Hc (Garratt, 1992; Grimmond and Oke, 1999):
with f0 and fd being vegetation-based coefficients (see Appendix B for derivation details). The stability parameter ζ () depends on the Obukhov length L. The atmospheric stability functions of momentum (ψm) and water vapour (ψv) for unstable conditions are (Campbell and Norman, 1998)
and for stable conditions (Campbell and Norman, 1998; Högström, 1988)
2.2.4 Surface resistance (rs) or conductance (gs)
For completely wet surfaces, the surface resistance rs is assumed to be 0 s m−1 (i.e. potential evaporation is calculated from Eq. 3). Otherwise rs, or its inverse, surface conductance gs, is parameterised with a Jarvis-type formulation (Jarvis, 1976) in SUEWS (Grimmond and Oke, 1991; Järvi et al., 2011; Ward et al., 2016):
where gs is determined from the ith land cover areally weighted maximum surface conductance () (with fi=1 for a “homogeneous” site) and environmental (x) rescaling functions (g(x)) ranging between [0, 1], including the following:
-
Leaf area index (LAI) (Ward et al., 2016).
which is relative to the maximum LAI of land cover i (). For bare soil surfaces (i.e. no vegetation), when LAI is irrelevant g(LAIi)=1.
-
Incoming shortwave radiation (K↓) (Stewart, 1988).
where the GK parameter modifies the K↓ response, relative to the maximum observed incoming shortwave radiation (= 1200 W m−2): when K↓ approaches GK, g(K↓) reaches 50 % of (i.e. normalised by ). At night g(K↓) goes to 1.
-
Specific humidity deficit (Δq) (Ogink-Hendriks, 1995).
where the specific-humidity-related parameters are for the “base” Gq,base and curve shape Gq,shape: the former indicates the limit of g(Δq) when Δq approaches extremely large values, while the latter determines the curvature of the g(Δq) (e.g. Fig. 9c).
-
Air temperature (Ta) (Stewart, 1988).
where is a function of the lower (TL) and upper (TH) limits when the evaporation occurs, and GT the optimal temperature for evaporation to reach its potential maximum.
-
Soil moisture deficit (Δθsoil, difference between soil water capacity and soil moisture content) (Ward et al., 2016).
Both the wilting point (ΔθWP) and a soil-type-dependent parameter (Gθ) vary with soil and plant type.
Appendix A gives the equivalent form used in the NOAH model for Eq. (13).
SUEWS has a running water balance that accounts for the multiple surface types. The amount of water on the canopy of each surface (Ci) (Grimmond and Oke, 1991) is used to vary the surface resistance between dry and wet (rs = 0 s m−1) by replacing rs with rss (Shuttleworth, 1978):
where W is a function of the relative amount of water present on each surface to its water storage capacity (Si, Table 1):
K depends on the aerodynamic and surface resistances:
where rb, the boundary layer resistance, is a function of friction velocity u∗ (Shuttleworth, 1983):
Equations (19)–(22) ensure that the surface resistance rss has a smooth transition from 0 (a completely wet surface) to rs (a dry surface).
We use three global datasets FLUXNET2015 (Pastorello et al., 2020), MODIS (Myneni et al., 2015) and SoilGrids (Hengl et al., 2014) to derive the parameters. The FLUXNET2015 surface energy fluxes and other meteorology observations are used for three purposes: to derive parameter values, force simulations and evaluate simulations. The remotely sensed (MODIS) derived LAI products are used for the LAI-related parameters. To derive soil-moisture-related parameters the SoilGrids data are used. Unlike the FLUXNET2015 data, the latter two datasets are spatially continuous.
3.1 FLUXNET2015
The FLUXNET2015 dataset (Pastorello et al., 2020) is the newest version of the FLUXNET data products. The gap-filled dataset includes 212 flux sites from around the world. Although the FLUXNET focus is on local-scale ecosystem CO2 eddy covariance (EC) fluxes, it also includes water and energy EC fluxes plus other meteorological and biological data. The biosphere–atmosphere exchange dataset contains more than 1500 site years for the period to the end of 2014. The open-source package ONEFlux (Open Network-Enabled Flux processing pipeline; https://github.com/fluxnet/ONEFlux, last access: 4 November 2021) is used to produce FLUXNET2015 (Pastorello et al., 2020).
Table 2FLUXNET2015 (Pastorello et al., 2020) variables used in this work to derive parameters (P), to force (F) model simulations and to evaluate (E) models.
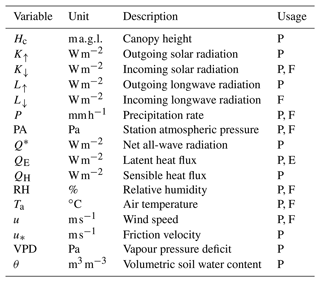
Table 3Key information about the FLUXNET2015 sites (Pastorello et al., 2020, and their DOI reference used in this work; site name, country name, with altitude above sea level, ) or anemometer sensor height above ground level (). More details about the simulation and analyses given in Sect. 5.1. The land cover type as defined based on IGBP (International Geosphere–Biosphere Programme) by the FLUXNET curators (https://fluxnet.org/data/badm-data-templates/igbp-classification/, last access: 4 November 2021) with the crops (CRO) being as follows: 1 – rotation: cereal, potato, sugar beet (Moureaux et al., 2006); 2 – rotation: winter barley, rapeseed, winter wheat, maize and spring barley at DE-Kli (Prescher et al., 2010); 3 – continuous maize (https://doi.org/10.18140/FLX/1440084); 4 – rotation: maize and soybean (https://doi.org/10.18140/FLX/1440085); 5 – rotation: maize and soybean (https://doi.org/10.18140/FLX/1440086). The SUEWS recommended vegetation or PFT class (informed by IGBP) data as used in this paper are given in Sun et al. (2021).
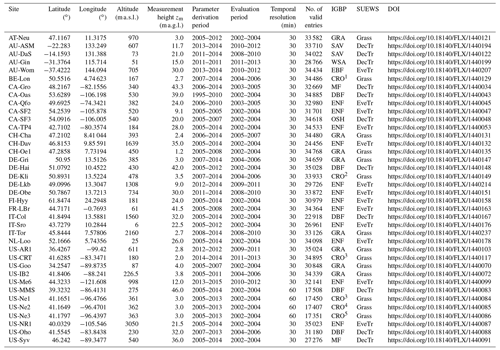
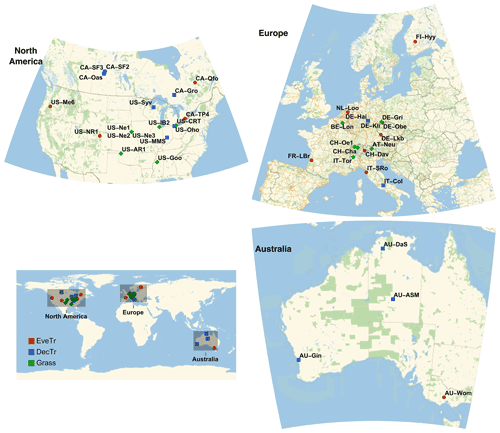
Figure 2Location of FLUXNET sites (Table 3) coded by into three land cover types: deciduous trees (DecTr), evergreen trees (EveTr) and grass (Grass). Source of base map: © OpenStreetMap contributors, 2021. Distributed under the Open Data Commons Open Database License (ODbL) v1.0.
Half-hourly observations (Table 2) are used from 38 sites (Table 3) in three regions (Fig. 2). These sites are selected to meet the following criteria (number of remaining sites that met the criteria):
-
Sites with CC-BY 4.0 license (206/212).
-
Data availability (56/206). This requires both MODIS LAI data (available from 2002, Sect. 3.2) and long-term continuity (defined here as ≥ 3 years for the multiple needs).
-
Model capacity (38/56). The SUEWS v2020a LAI scheme is forced with only air temperature and not other variables (e.g. rainfall), which may strongly influence phenology at some sites (Appendix D). Hence, these sites are excluded.
Unfortunately, no datasets are left after selection based on the above criteria for some regions (Fig. 2), including Africa, Asia and South America.
As SUEWS allows any grid cell to have three vegetation or plant functional types (PFTs), with the sub-type or properties varying between grids, we subdivide the 38 sites into three classes using IGBP (Table 3) (code, number of sites):
- a.
Evergreen trees/shrubs (EveTr, 13). Evergreen needleleaf forests (ENF, 12), evergreen broadleaf forests (EBF, 1).
- b.
Deciduous trees/shrubs (DecTr, 11). Mixed forests (MF, 2), deciduous broadleaf forests (DBF, 5), open shrublands (OSH, 1), woody savannas (WSA, 1), savannas (SAV, 2).
- c.
Grass (14). Grasslands (GRA, 8), croplands (CRO, 6).
The landscape heterogeneity of many FLUXNET EC flux measurements sites have been systematically examined by Stoy et al. (2013) using satellite imagery. Of the sites they examined, they found them to be located within homogeneous parts of the targeted PFT, but the larger landscape (∼ 20 km) may have considerable variability. As a FLUXNET site is typically assigned to one PFT for land surface model development and evaluation (e.g. Stöckli et al., 2008; Zhang et al., 2017; Chu et al., 2021), we configure each as a homogeneous grid cell and assume fi=1.
3.2 MODIS LAI
The NASA Moderate Resolution Imaging Spectroradiometer (MODIS; Nishihama et al., 1997) four-day composite product MCD15A3H (Myneni et al., 2015) with 500 m resolution is treated as “observed” LAI. Product data are available from 2002. We use the Fixed Sites Subsetting and Visualization Tool (ORNL DAAC, 2018) for the FLUXNET dataset to extract the MCD15A3H time series. To obtain a daily time series we linearly interpolate between values, for parameter derivation (Sect. 4.1).
3.3 Soil information
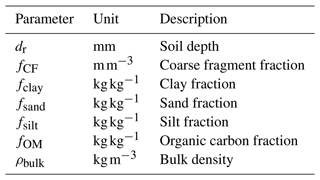
The SoilGrids (Hengl et al., 2014) database provides soil properties (i.e. organic carbon, bulk density, cation exchange capacity (CEC), pH, soil texture fractions and coarse fragments) at seven depths (0, 0.05, 0.15, 0.30, 0.60, 1.00 and 2.00 m), as well as a bedrock depth prediction, World Reference Base (WRB) and USDA soil classes. We use the SoilGrids250m (Hengl et al., 2017) version, with its ∼ 280 raster layers, to obtain the parameters (Table 4) to derive soil moisture deficit at wilting point (ΔθWP in mm) for soil-moisture-related calculations (e.g. Eq. 18).
Table 4Soil-related parameters obtained from the SoilGrids (Hengl et al., 2014) database for each site (Table 3) at 250 m resolution for seven depths (Sect. 3.3). Values for each site (Table 3) are given in Sun et al. (2021).
The difference in soil moisture between field capacity (θFC in mm) and wilting point (θWP in mm) are used with parameters defined as follows (Saxon and Rawls, 2006):
with
using the weight fractions of sand fsand, clay fclay and organic matter fOM:
and
where
4.1 Leaf area index (LAI) and albedo-related parameters
LAI is a key phenology parameter in SUEWS; it moderates albedo (α) and therefore surface radiative exchanges. LAI changes also modify both aerodynamic roughness parameters (roughness length z0, zero plane displacement height zd) (e.g. Kent et al., 2017a, b) impacting aerodynamic resistance (ra) and surface resistance (rs). LAI directly moderates QE and canopy interception capacity, which modifies when potential evaporation occurs and aspects of the water balance.
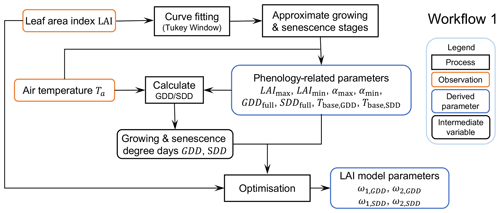
Figure 3Workflow 1 (Fig. 1) for deriving LAI- and albedo-related parameters. Related Jupyter notebooks are provided in Sun et al. (2021).
As the SUEWS LAI equation (Eq. 4) makes global optimisation techniques numerically challenging to derive all the required parameters, we take a two-step approach (Fig. 3).
4.1.1 Approximating growing stages using an asymmetric Tukey window function
The Tukey or cosine-tapered window (TW) is used in signal processing applications when data need to be processed in short segments. It is defined as follows (Bloomfield, 2000):
where x is the independent variable and a is the curve shape factor. We propose an asymmetric form of the Tukey window (aTW) to approximate the intra-annual LAI dynamics:
where b is a curve shape factor for different segments, x0 the segment parameter and l the rescaling factor.
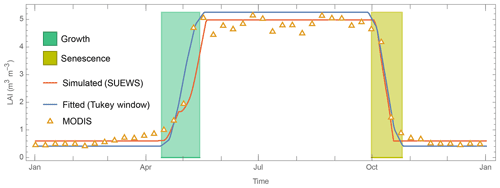
Figure 4Intra-annual LAI dynamics at US-MMS multi-year (2002–2014) ensemble median derived from MODIS observations (open triangle, Sect. 3.2) and simulated by SUEWS temperature-based LAI scheme (Eq. 4) (orange line) with Tukey window fit (blue line, Sect. 4.1) using to derive the leaf-on or growth period (green shading) and senescence (yellow shading) periods.
To demonstrate this we use the US-MMS site (Table 3), to fit the intra-annual LAI dynamics using an aTW curve (blue line, Fig. 4) to determine different phenological stages (shading, Fig. 4) and subsequently derive several related parameters:
-
LAImin. 5th percentile of LAI values before the growth and after the senescence.
-
LAImax. 75th percentile of LAI values after the growth and before the senescence.
-
Tbase,GDD. 99th percentile of air temperatures before the growth.
-
Tbase,SDD. 10th percentile of air temperature after the growth and before the senescence.
-
GDDfull. GDD at the end of growth based on Tbase,GDD.
-
SDDfull. SDD at the end of senescence based on Tbase,SDD.
-
αmin/αmax. 10th/90th percentile of daily albedo values after the growth and before the senescence. A daily albedo is calculated from 30 or 60 min FLUXNET observations of incoming and outgoing shortwave radiation for the period 10:00 to 14:00 LST (local standard time). To remove outliers a clustering method is applied (ClusterClassify of Mathematica v12.3.1, Wolfram Research, 2020). For example, at some high-latitude sites (e.g. CA-Oas) snow occurs, the winter values are based on data from shortly after senescence to shortly before growth (next spring) and the clustering approach removes the snow period albedo values.
For evergreen and deciduous trees, () in Eq. (6) typically corresponds to αmin (αmax), while for grassland a reverse relation holds (i.e. corresponds to αmax and vice versa; see Cescatti et al., 2012, for a detailed analysis of albedo dynamics at FLUXNET sites).
4.1.2 Deriving curve factors used in SUEWS LAI scheme
With the parameters derived in step 1, we can determine the curve factors by minimising the bias between MODIS observed (open triangle, Fig. 4) and SUEWS-simulated (red line, Fig. 4) LAI values.
Table 5Inter-site variability within the three vegetation classes of LAI- and albedo-related parameters (Eq. 4, Sect. 4.1) shown by mean and standard deviation. For individual site and PFT parameters see Appendix C (for digital version see Sun et al., 2021). Median and interquartile range (IQR) see Fig. 5.
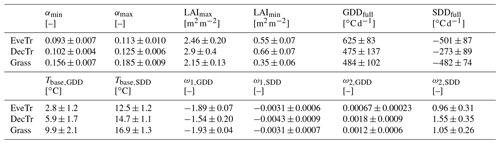
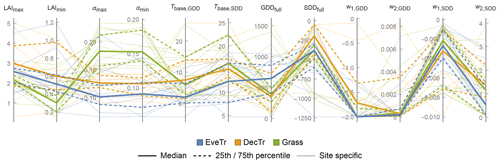
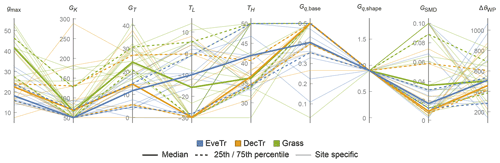
Figure 5Variation in LAI-related parameters (12 labelled vertical lines, Sect. 2.2.1) within three land cover classes (colour) showing median (thick line), interquartile range (IQR, 25th and 75th percentiles, dashed lines) and site-specific values (thin lines).
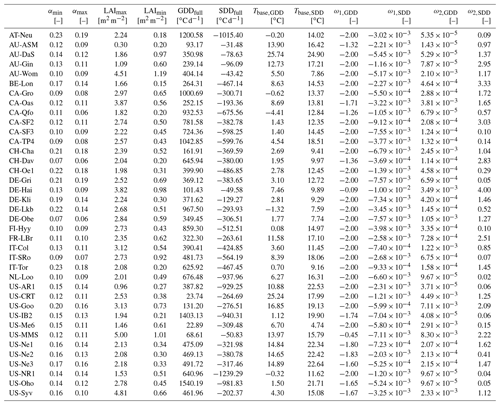
The derived LAI-related parameters for the 38 FLUXNET sites vary between different land cover groups (Table 5, Fig. 5). The derived results are consistent with those reported in the literature (Asaadi et al., 2018). For EveTr sites, the large contrast between LAImax and LAImin in the ENF sites analysed here is consistent with MODIS derived LAI for ENF, which has larger seasonal variability than EBF (Heiskanen et al., 2012), but some of this is caused by a known issue of particularly low winter values (Garrigues et al., 2008).
Given the global availability of MODIS LAI and reanalysis-based air temperature datasets, we suggest the LAI-related parameters be derived following this workflow (Fig. 3) to set parameters for SUEWS simulations. This can be done independent of the availability of flux tower observations.
4.2 Storage heat flux coefficients
To calculate the storage heat flux ΔQS, the required OHM coefficients (Eq. 7) can be determined from observed net all-wave radiation and observed storage heat flux, using ordinary linear regression. As the FLUXNET sites chosen are considered to be homogeneous, we derive coefficients for each site.
Ideally the storage heat flux measurements would include each of the components that are heating and cooling down on a daily basis, such as the soil, trunk, branches, leaves and air volume in a forest (e.g. McCaughey et al., 1985; Oliphant et al., 2004). However, these measurements are unavailable in the FLUXNET2015 dataset. Hence, we calculate a residual flux by assuming energy balance closure. This has the problem of accumulating the net measurement errors in this term (Grimmond et al., 1991; Grimmond and Oke, 1999).
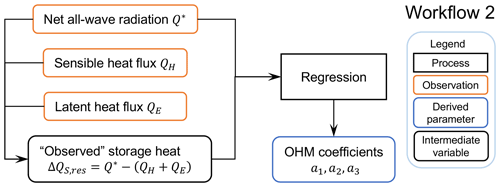
Figure 6Workflow 2 (Fig. 1) to derive OHM coefficients. Related notebooks are provided in Sun et al. (2021).
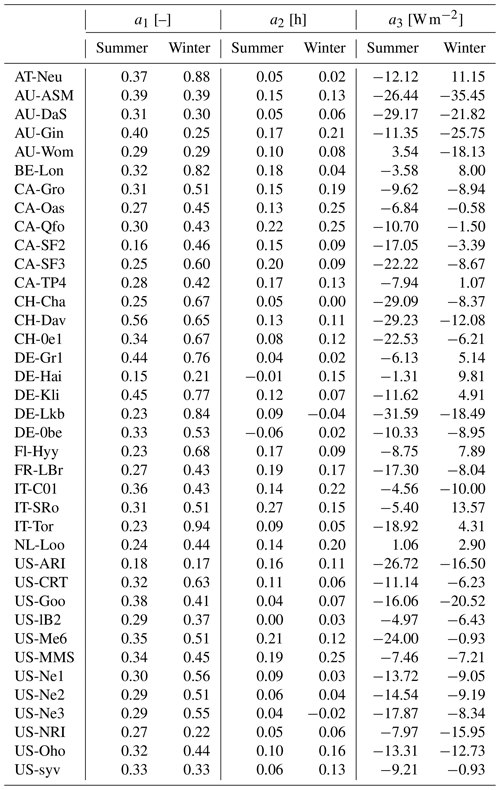
The derived OHM coefficients (Fig. 6) can be determined by season (Anandakumar, 1999; Ward et al., 2016; Sun et al., 2017). We distinguish warm (“summer”) and cold (“winter”) seasons using months (summer: Northern Hemisphere JJA; Southern Hemisphere: DJF; winter: DJF (JJA), respectively). For simplicity, we omit periods when LAI may be changing rapidly. If the daily mean air temperature is warmer (cooler) than the annual mean of daily median temperature, then summer (winter) OHM coefficients are used in the simulations.
Table 6As Table 5, but for OHM-related parameters (Sect. 4.2). See Fig. 7 for comparison and Table C2 for site-specific values.
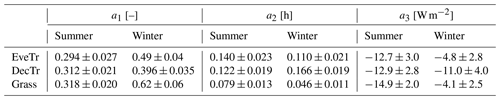
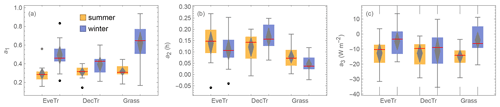
Figure 7Boxplots showing variability of OHM coefficients between land covers (EveTr, DecTr and Grass) and seasons (summer and winter): (a) a1 (b) a2 and (c) a3. Boxes (25th and 75th percentiles) and whiskers (5th and 95th percentiles), with median (red line) and mean (middle grey diamond, with 95 % confidence level (top and bottom) values, and outliers (dots).
The OHM coefficients derived for the 38 FLUXNET sites (Table 6, Fig. 7) vary between land cover types and seasons. For each land cover type, a1 and a3 are notably larger in winter than in summer while the seasonal difference in a2 is relatively small. Thus the overall fraction of heat stored does not vary much, but the diurnal hysteresis effect is weaker in winter. These results are consistent with previous analytical results (Sun et al., 2017). Within each PFT, there is larger variability in a2 and a3 (cf. a1), notably for evergreen and deciduous trees, suggesting using the most appropriate site values (e.g. medians) may improve predictions of the storage heat flux. In addition to the values derived here, we note that more detailed ΔQS observations are available for vegetated sites to derive such OHM coefficients (e.g. McCaughey, 1985; Oliphant et al., 2004).
4.3 Surface-conductance-related parameters
As the Jarvis-type formulation of stomatal and surface conductance is widely used for many land cover types, many parameter sets exist (e.g. Stewart, 1988; Grimmond and Oke, 1991; Ogink-Hendriks, 1995; Wright et al., 1995; Bosveld and Bouten, 2001; Järvi et al., 2011). Hoshika et al.'s (2018) comprehensive meta-analysis of published Jarvis-type stomatal conductance parameter values includes major woody and crop plants broadly similar to PFTs examined here.
Conventionally, the surface conductance parameters are derived by minimising the bias between the parameterised (Eq. 14) and so-called “observed” values derived from an inverse form of the Penman–Monteith equation (Eq. 3):
This requires the surface be dry (Sect. 2.2.4) which we define as being without recorded rainfall in 24 h.
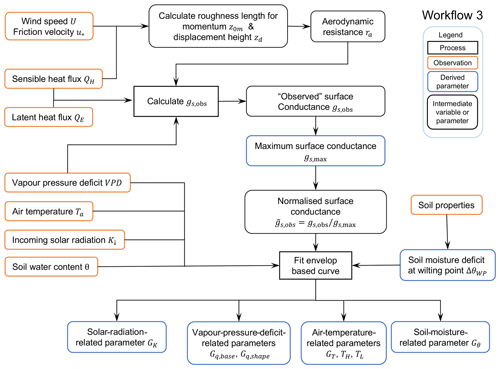
Figure 8Workflow 3 (Fig. 1) for deriving surface-conductance-related parameters. Related notebooks are provided in Sun et al. (2021).
However, as the optimisation may not return values because of the complexity in Eq. (13) and the challenge of interpreting the derived parameter values, we adopt Matsumoto et al.'s (2008) approach to derive these parameters. Rather than using all the data combinations for gs, the upper boundary of each forcing variable component (e.g. g(K↓)) is considered as the response for unconstrained conditions. Specifically, the workflow is as follows (Fig. 8):
-
Calculate aerodynamic resistance ra (Eq. 8) with roughness length z0m and displacement height zd derived from observed wind speed under neutral conditions (Appendix B).
-
Calculate “observed” surface conductance gs,obs (Eq. 30).
-
Remove outliers from gs,obs data (step 2) iteratively (i.e. values larger than the 98th percentile until difference between 98th and 99th percentiles is < 1 mm s−1). The remainder are used for deriving parameters.
-
Determine the upper boundaries of gs curves with each component variable. To demonstrate this we use the US-MMS site (Fig. 9). First, original data are binned (sizes: 50 W m−2 for K↓, 2 ∘C for Ta, 2 kg kg−1 for Δq and 10 mm for Δθ), the 95th percentiles of these bins are sampled 100 times (bootstrapped) to determine anchor points (red dots, Fig. 9). Second, the parameters are fit to the gs related curves (Eqs. 14–17) using the anchor points using NonlinearModelFit of Mathematica v12.3.1 (Wolfram Research, 2008).
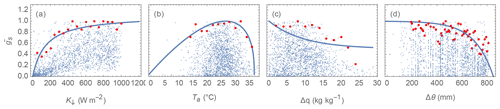
Figure 9Derived relations (blue lines) between normalised surface conductance and (a) incoming solar radiation K↓, (b) air temperature Ta, (c) specific humidity deficit Δq, and (d) soil moisture deficit Δθ based on anchor data points (red dots) after bootstrapping of observations (blue dots) for an example site (US-MMS).
Table 7As Table 5, but for surface-conductance-related parameters (Sect. 4.3). See Fig. 10 and Appendix C.

The derived surface conductance parameters for the 38 FLUXNET sites (Tables 7 and C3) have different intra-PFT variability based on the IQR (dotted lines, Fig. 10) and demonstrates the benefit of the observations and of deriving site values when possible. It may help in selecting appropriate PFTs from other sources (e.g. NOAH values in Appendix A). The gmax results are consistent with Hoshika et al. (2018) in terms of inter-PFT ordering (Grass > EveTr and DecTr). The grass and crop values are comparable (Table C3) to Hoshika et al. (2018); however, our derived deciduous trees values are smaller (22 vs. 31 mm s−1) and evergreen trees values larger (20 vs. 12 mm s−1).
A consistent Gq,shape (Eq. 16) value (0.9 units) is obtained for all sites, implying potential for improvements to the g(Δq) relation between gs and Δq (e.g. other formulations gs(Δq) in Matsumoto et al., 2008) in future SUEWS development. This would be beneficial as there is a clear “plateau” observed for low Δq (Fig. 9c). Similar issues are found in g(Δθ) for soil-moisture-related parameters. Although the parameters derived here are the “best” fit to the gs forms in SUEWS v2020a, for each component variable multiple gs formulations exist with a range of variable fitting performance (e.g. Fig. A1 in Ward et al., 2016). Here, we focus on deriving the parameters rather than proposing new or more appropriate formulations.
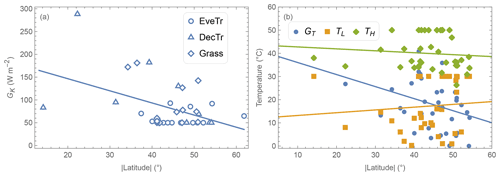
Figure 11Relations between absolute latitude and derived parameters: (a) solar-radiation-related GK by PFT (symbol) and (b) temperature-related GT, TL and TH. Lines are derived by ordinary linear regression. See text for notation definitions.
The solar-radiation-related GK parameter is linked to the level of incoming solar radiation needed for evapotranspiration to occur. Given incoming solar radiation intensity varies with latitude, we see GK generally decreases polewards (Fig. 11a), suggesting geographical location could be used as a proxy for deriving GK.
The air-temperature-related GT parameter indicates the optimal temperature for evapotranspiration to reach its probable maxima. GT appears to have a negative relation with latitude, but the two other temperature parameters (TL and TH) have a very weak (or no) relation with latitude (Fig. 11b). This suggests a universal temperature range between TL and TH might be applicable across different sites while GT should be determined on a site-by-site basis.
5.1 SUEWS configuration and evaluation
SUEWS v2020a (Tang et al., 2021) is evaluated using its Python wrapper SuPy v2021.3.18 (Sun and Grimmond, 2019) with parameters (Table 1) and gap-filled 30 or 60 min meteorological forcing data (Table 2) based on FLUXNET2015 dataset. Simulations are conducted, with forcing data interpolated to a 5 min time step (Ward et al., 2016), for 3 years (Table 3, Evaluation period) starting in mid-winter. The first year is discarded to allow for model spin-up. The two subsequent years are evaluated when observed latent heat flux data are available. In these model runs, the z0m and zdm values used are derived (Appendix B) by LAI state using observations for each LAI season (approximately nine values per site; see Sun et al. (2021) for values). All other parameters (Table 1) are determined for the parameter derivation period indicated in Table 3. At one site (AU-Gin), there are insufficient data for independent evaluation period from the parameter derivation period.
For the periods with 30 or 60 min QE EC observations (Yobs) available, the 5 min simulated values (Ymod) are averaged to 30 or 60 min to evaluate the j cases between 1 and the number of data points (N). The following metrics are used:
-
Hit rate (HR).
with Heaviside step function H defined by
and the threshold δY,jbeing a value dependent on evaluation variable Y.
In particular, δY,j for QE is determined as a function of net all-wave radiation Q∗ following Hollinger and Richardson (2005) to be (in W m−2) based on measurement uncertainties.
-
Mean absolute error (MAE).
-
Mean bias error (MBE).
Both the MAE and MBE would ideally be 0 (with units of parameter and variable assessed), whereas if the HR = 1 it indicates all model predictions fall within the acceptable threshold set, while HR = 0 would suggest none are within the acceptance threshold.
A performance score PS as a function for each metric (x; i.e. HR, MAE, |MBE|) is used to rank the sites:
where is the rescaled ranking score of a given metric after being ranked from poorest to best, and wx is a weight associated with the temporal analysis type k which varies from 1 to N (number of component periods; e.g. N = 24 for hourly results). Equal weights () are used in the PS calculations for HR, MAE and |MBE|.
5.2 Impacts of model parameters on model performance
Given the many parameters in SUEWS, first we assess the relative importance of the parameters. We assume in this analysis our derived parameters (Sect. 4) are “perfect”, so we can undertake a sensitivity analysis (McCuen, 1974; Beven, 1979) of the Penman–Monteith equation (i.e. Eq. 3, denoted by PM hereafter):
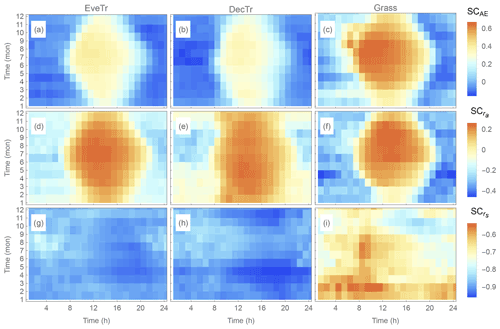
Figure 12Temporal variation in median (colour) sensitivity coefficient (SC, Eq. 38) of (a–c) available energy (AE, Sect. 5.1), (d–f) aerodynamic resistance (ra) and (g–i) surface resistance (rs) for (a, d and g) evergreen trees (EveTr), (b, e and h) deciduous trees (DecTr), and (c, f and i) grassland and crops (Grass).
where is the available energy, incorporating parameter influences related to LAI, albedo and OHM. Similarly, multiple parameters influence the resistance terms. In Eq. (36) the prefix Δ indicates bias terms. For simplicity, we consider the direct impacts only (i.e. secondary impacts from parameters inter-dependence are ignored). Expanding Eq. (36) in Taylor series, gives the following:
where PM′(x), the first-order derivative of x, indicates the sensitivity of modelled QE. Note “≈” implies the approximation of ΔQE as the sum of bias from the chosen parameters. To examine the influences of different parameters in model performance, we use two non-dimensional metrics derived from Eq. (37):
-
Sensitivity coefficient (SC) (McCuen, 1974).
gives the fractional change in x causing a change in QE, indicating a relative sensitivity of PM to x. For instance, SC = 0.5 suggests a 20 % increase in x may increase QE by 10 % (= 20 % × 0.5).
-
Attribution fraction (AF). quantifies the fraction of model bias derived from a given parameter x:
Ideally, the sum of all AF contributors would equal 1, but as we omit inter-dependence of impacts of parameters, this may not occur. However, comparing the different contributors is indicative of their relative importance in modelled QE.
Both SCAE and generally show a similar type of pattern (Fig. 12a–f) with seasonal and diurnal variations for the three PFTs. During warm periods (summer and noon), with an increase in ΔAE and Δra it is found to lead to larger positive bias in modelled QE, whereas in cooler periods (winter and night-time) the ΔAE and Δra is found to increase the negative bias.
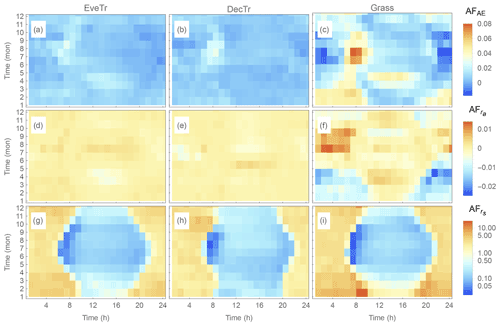
Figure 13As Fig.12, but the attribution fraction (AF, Eq. 39). Note AFrs scale is logarithmic.
However, the temporal patterns in differ (Fig. 13g–i) from those in SCAE (Fig. 13a–c) and (Fig. 13d–f): the values are always negative, and consistently larger in magnitude (cf. SCAE and ), implying a particularly strong sensitivity of QE to rs. This is consistent with Beven (1979), who found it to dominate the modelled summertime QE sensitivity in the PM framework.
The relative (cf. total) bias from the parameters is assessed in modelled QE at monthly and hourly temporal scales using the median AF (Fig. 13). is larger than both AFAE and ; i.e. rs imposes a dominant influence in modelled QE bias. There is more temporal variability in (cf. AFAEand ) with cooler periods (morning and evening, whole winter) generally having values greater than 1, indicating the bias in rs dominates modelled QE. As is still generally larger than ∼ 0.3 (except for transitional periods in summer, 08:00–09:00 LST, when ), rs remains an important control on modelled QE. These results together indicate that it is critical to assign accurate rs to obtain accurate estimates of QE.
5.3 Evaluation of SUEWS-simulated QE with two different sources of gs parameters
Given the critical importance of surface resistance to model performance in QE (Sect. 5.2), we assess the impact of two different sources of gs parameters (keeping all other site parameters the same, with the values as indicated in Sect. 5.1): (i) site-specific values derived from FLUXNET2015 data (Sect. 4) and (ii) PFT-specific NOAH values modified for SUEWS (Appendix A). Errors in the other derived parameters (e.g. LAI-related parameters, storage heat flux coefficients via available energy) will impact both sets of results, but they are assumed to be equal, allowing the impacts of using site- and PFT-specific gs parameters on SUEWS-simulated QE to be assessed. Given NOAH is extensively used in NWP systems (e.g. WRF, Skamarock and Klemp, 2008), the result also allows the applicability of NOAH-based gs parameters at FLUXNET sites to be assessed.
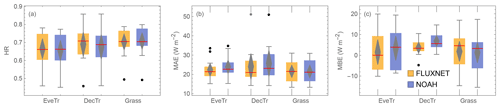
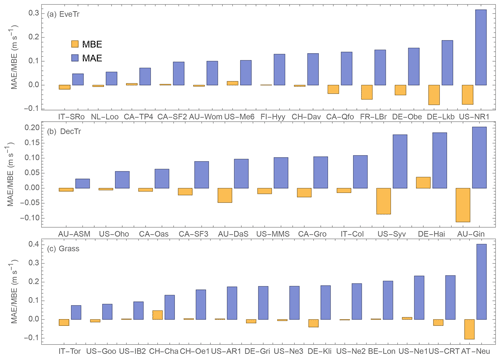
Figure 14Simulated QE using two sets of parameters (colour, FLUXNET – Table C3, NOAH – Table A1 assigned based on Table 3 PFT class) at 38 sites (boxplots, as Fig. 9, subdivided into three land cover classes: EveTr, DecTr and Grass) evaluated for 2 years with observed 30 or 60 min fluxes using three metrics (Sect. 5.1): (a) HR, (b) MAE and (c) MBE.
Analysis using 2 years of QE EC flux data (after a 1-year spin-up) uses three metrics (Sect. 5.1). The overall median results are similar between the two sets of parameters across the 38 sites split into the three PFTs (Fig. 14, red lines). The median HRs are between 0.6 and 0.7, median MAEs are less than 25 W m−2, and median MBEs are ∼ 5 W m−2. At the Grass site, HR and MAE (Fig. 14a and b) performance is very similar, suggesting the NOAH-based parameters could be used for these sites at annual scales as a first-order proxy.
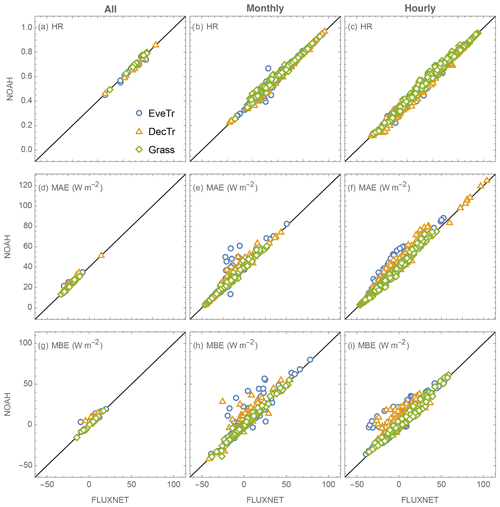
Figure 15Relation between NOAH and FLUXNET of (rows) three evaluation metrics for (columns) three temporal scales (all, n=38 sites but different number of samples per site, Table 3; monthly, n = 456 = 38 sites × 12 months; and hourly, n = 912 = 38 sites × 24 h). Data points are colour coded by land cover class.
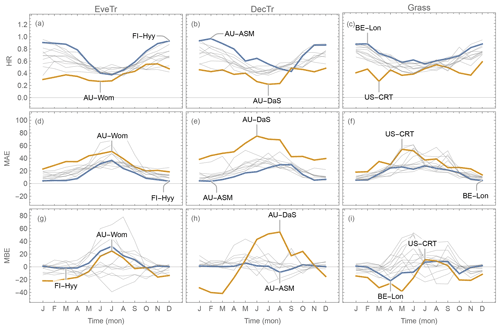
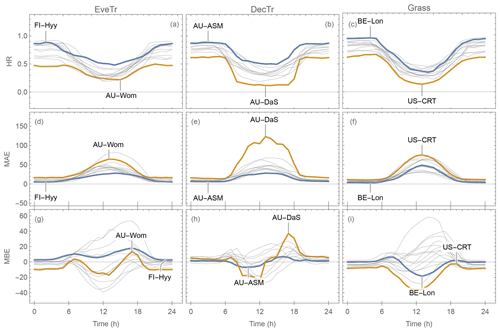
Figure 16Variation in evaluation metrics (Sect. 5.2) based on 30 or 60 min QE data by month using the derived parameters based on FLUXNET2015 dataset (Tables C1–C3): (a–c) HR, (d–f) MAE, (g–i) MBE by sites grouped into three PFTs, (a, d and g) EveTr, (b, e and h) DecTr and (c, f and i) Grass with sites of best (blue) and poorest (orange) performance highlighted and others in grey (indicated by PS: see text and Eq. 35 for details). Note Southern Hemisphere sites are offset by 6 months (Sect. 5.1), so “general” seasons are consistent across sites.
Evaluation using three different time periods (annual, monthly and hourly) shows differences in performance between using the FLUXNET2015 and NOAH-based parameters (Fig. 15). The HR is similar for all three temporal scales (Fig. 15a–c) for the three site types (colour). Both the MAE (Fig. 15d–f) and MBE (Fig. 15g–i) indicate better model performance can be obtained using the FLUXNET2015-based parameters (i.e. not above the 1:1 line). When using the NOAH parameters (Fig. 15h and i), some monthly MBEs are ∼ 40 W m−2 larger at EveTr sites for 8 of 156 cases and 5 of 312 for DecTr sites. Similarly, at the hourly scale the NOAH MBEs are on occasions ∼ 30 W m−2 larger (4 of 132 EveTr cases and 6 of 264 DecTr cases). However, the NOAH results have similar metrics at Grass sites. This suggests at the EveTr and DecTr sites, the NOAH-based gs parameters may on occasion be less appropriate, suggesting that the individual sites' values may be better.
5.4 Evaluation of SUEWS-simulated QE and key parameters at sites with contrasting model performance
Given the results in Sect. 5.3, the performance of individual sites using the FLUXNET2015-derived parameters (Sect. 4) at monthly (Fig. 16) and hourly (Fig. 17) timescales are investigated.
As expected (Sect. 5.2), the HR values are consistently better at all sites during cooler (winter) than warmer (summer) seasons (Fig. 16a–c), and similarly for night rather midday time periods (Fig. 17a–c). Given the consistency in MAE and HR (Figs. 16 and 17d–f) patterns, the sites identified to be simulated the “best” (blue) and “poorest” (orange) are the same (Sect. 5.1).
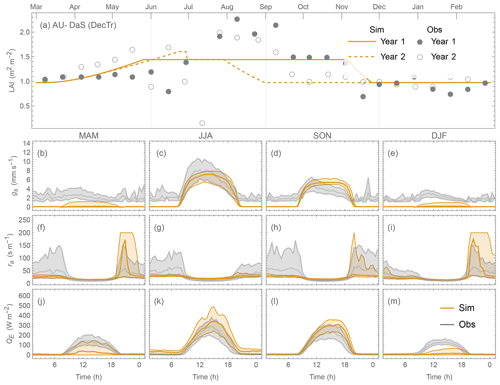
However, using the MBE different sites are selected. For example, monthly MBE at AU-ASM stays close to zero throughout the year while at AU-Das it varies between −40 and 60 W m−2 (Fig. 16h). The largest intra-month MBE range for an EveTr site is 87.1 W m−2, which occurs at FR-LBr. The equivalent range for DecTr sites is larger (96.1 W m−2 at AU-DaS) but smaller at Grass sites (69.6 W m−2; US-Ne3). The intra-hourly MBE ranges are smaller than intra-monthly values, with a DecTr and a Grass site having a larger range than the largest EveTr site (AU-DaS (61.9 W m−2), US-Goo (60.0 W m−2), FR-LBr (53.1 W m−2), respectively).
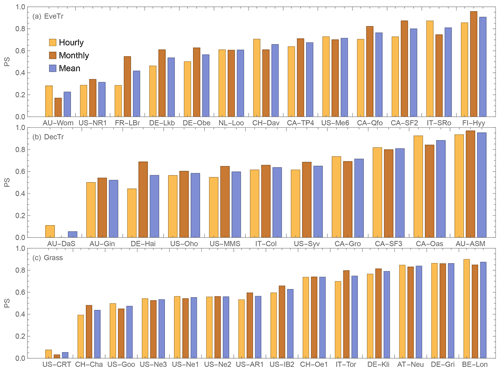
Figure 18Performance score (PS, Eq. 35, higher value better) using FLUXNET2015 derived parameters for sites (Table 3) from three PFT: (a) EveTr, (b) DecTr and (c) Grass.
To investigate QE performance relative to key parameters (LAI, ra and gs) we select the sites with contrasting results from each PFT to understand the drivers. The hourly and monthly ranked performances (Eq. 35) are broadly consistent within each PFT (Fig. 18). Sites with higher hourly scores generally have better monthly scores, except for IT-SRo within the EveTr cohort. It has the highest hourly PS (0.86) but is ranked fourth based on PSmonthly (0.64), whereas the highest PSmonthly (0.91) is for FI-Hyy which also has the second rank PShourly (0.83). To select sites for further analysis we rank based on the mean of monthly and hourly PS results. The six sites chosen are the best and poorest sites for the three PFTs (i.e. extremes in Fig. 18, highlighted in Figs. 16 and 17).
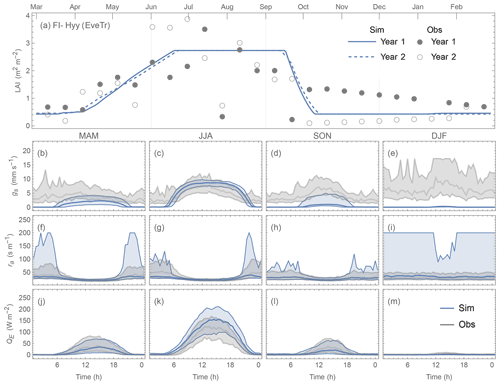
Figure 19FI-Hyy (EveTr, PS = 0.92) performance: (a) annual LAI, (b–e) gs (in seasonal ensemble of diurnal cycles: median values in bold lines, while interquartile ranges in shadings), (f–i) ra and (j–m) QE. Note the same colouring of simulations for sites with best and poorest model performance and 6-month offset in annual cycles are applied for consistency with Figs. 16 and 17.
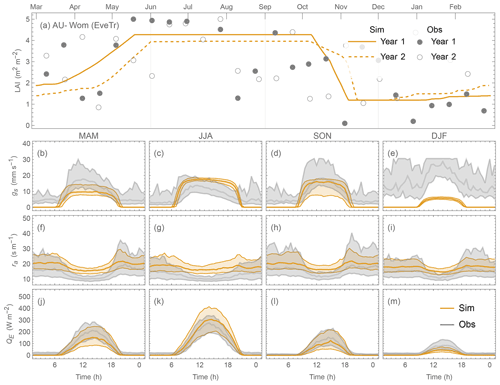
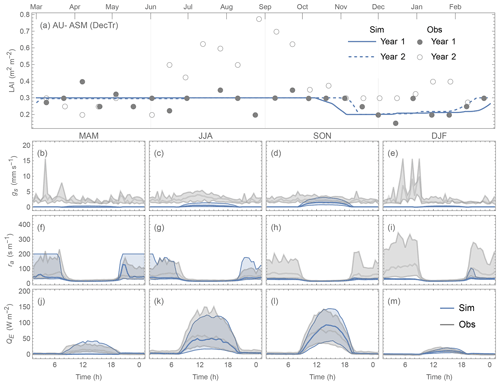
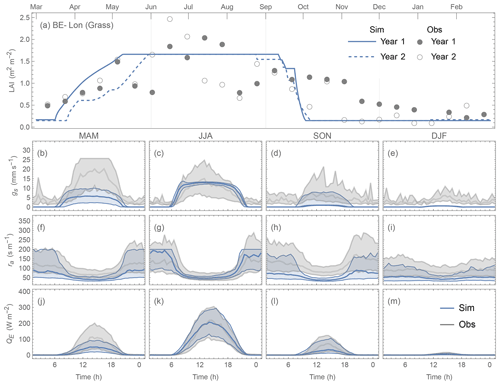
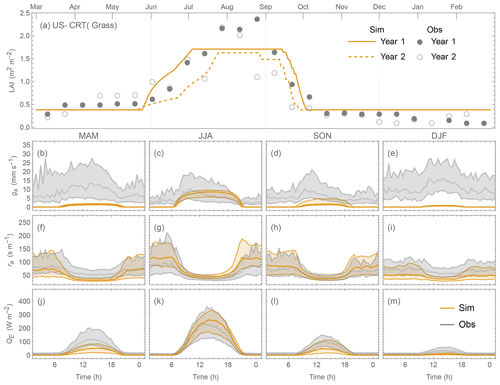
Comparing the contrasting site QE performance (best vs. poorest) for the three PFTs (Figs. 19 vs. 20; 21 vs. 22; 23 vs. 24), we identify the skill of capturing the annual LAI dynamics is crucial to seasonal model performance (Figs. 19–24a). At the “best” sites (except for BE-Lona, a Grass site whose performance is more controlled by surface conductance gs skill and shall be discussed later) the phenology generally has the correct timing, while at the poorest onsets of some stages are missed (e.g. Fig. 22a). Timing appears to be more critical than magnitude, as although the LAI magnitude at AU-ASM has a large bias in year 2 (0.5 m2 m−2, Fig. 21a) the phenology timing is well captured. This result for a first rank site (i.e. best performance) implies the rescaling nature of LAI in parameterisation of albedo (Eq. 6) and surface conductance (Eq. 14) plays an important role. This indicates the importance of assigning appropriate LAI parameters, notably those influencing the timing (i.e. temperature thresholds Tbase,GDD and Tbase,SDD in Eq. 4), in SUEWS modelling QE at vegetated sites.
As expected (Sect 5.2), SUEWS performance is critically impacted by surface conductance gs skill (Figs. 19–24b–e vs. j–m): sites and seasons with better model gs skill (i.e. simulations and observations closer) show overall better performance (e.g. for Grass sites, BE-Lon vs. US-CRT, cf. Figs. 23c and 24c). gs is better modelled in warmer (JJA and SON) than cooler seasons (MAM and DJF). At night, gs is generally underestimated, by a similar order of magnitude to that in cooler seasons (∼ 3 mm s−1). These results, consistent with SUEWS results for two UK urban sites (Ward et al., 2016), suggest improvements are needed in the Jarvis-type gs parameterisation during cooler periods. Given the method adopted here of using summertime observations, as used by many other land surface models (e.g. NOAH – Chen and Dudhia, 2001; HTESSEL – Balsamo et al., 2009), it is implied that the widely adopted Jarvis-type gs parameterisations and/or related parameter values (see Sect. 4.3) may be biased towards vegetation canopies in warmer periods. The “cool” bias in modelled gs found here, and in earlier SUEWS work (e.g. Ward et al., 2016), should be considered a more common issue beyond the SUEWS model. Given the needs in long-term climate modelling, systematic biases should be removed, suggesting other land surface models that adopt the Jarvis-type gs parameterisation might need revisions as well.
The aerodynamic resistance ra is modelled well at all sites (Figs. 19–24f–i), with nocturnal biases larger (e.g. underestimate of ∼ 50 s m−1 at AT-Neu, Fig. 23f–i). This good performance may be largely attributed to the use of local growth-stage-derived aerodynamic roughness parameters (Appendix B) rather than estimated using a morphometric model (e.g. based on canopy height). To estimate z0m and zd using Eqs. (9) and (10) the f0 and fd parameters can be derived using Sun et al. (2021) for different growing stages with the FLUXNET2015 data when canopy heights are available. The largest intra-PFT variability occurs for “Grass” sites (Fig. B1).
In this work, we derive parameters for SUEWS for fully vegetated land covers that are commonly found in background (“rural”) contexts of cities, where SUEWS has been widely used to model urban climates. To facilitate derivation of SUEWS parameters we provide workflows in Jupyter notebooks (Sun et al., 2021) for leaf area index (LAI), albedo, Objective Hysteresis Model (OHM) coefficients, aerodynamic roughness parameters and surface conductance (gs). We use these to determine parameters at 38 vegetated FLUXNET sites in North America, Europe and Australia. Using the derived parameters, we assess the performance of SUEWS in predicting latent heat flux (QE) at different temporal scales (monthly and hourly).
The following conclusions were made:
-
Where observations are available, we recommend determining local parameters, as derived parameters vary within PFT (Appendix C). The tools provided here are designed to facilitate this (Sect. 4).
-
Given the global availability of MODIS LAI and reanalysis-based air temperature datasets (e.g. ERA5), it is feasible to derive site-by-site LAI parameters for SUEWS (Sect. 4.1).
-
OHM coefficients for modelling storage heat flux derived here show clear seasonality: summertime (i.e. days warmer than annual median air temperature) a1 and a3 are smaller than their wintertime counterparts, while the seasonal contrast in a2 is smaller, suggesting seasonally varying values should be used for long-term (i.e. > 1 year) simulations.
-
Surface-conductance-related parameters derived using a summertime upper-boundary-based approach (Matsumoto et al., 2008) produce parameters related to solar radiation (GK) and optimal air temperature (GT) with some dependence on geographical locations, which could be used as a proxy to derive these two parameters.
-
SUEWS-modelled QE is particularly sensitive to surface conductance as informed by the attribution analysis using an analytical framework by McCuen (1974) and consistent with results of Beven (1979) that surface conductance plays a dominant role in moderating the bias in modelled QE.
-
SUEWS configured with NOAH-based parameters has comparable prediction skill in QE compared to site-specific parameters when assessed by hit rate (HR) with medians being ∼ 0.65. However, site-specific parameters improve SUEWS performance as shown by the mean absolute error (MAE) and mean bias error (MBE) metrics, becoming increasingly evident at finer temporal scales (monthly and hourly).
-
SUEWS with site-specific parameters outperforms in cooler periods (i.e. winter and night) compared to warmer periods (i.e. summer and day): HR is consistently higher in the former periods than the latter (0.71 vs. 0.52 in median) while MAE shows an opposite pattern (cooler vs. warmer seasons median: ∼ 12 vs. ∼ 31 W m−2).
-
Correctly predicting LAI timing dynamics has a crucial influence on overall QE model performance, followed by surface conductance gs that is generally underestimated during cooler periods (more pronounced at night by ∼ 3 mm s−1).
As the first comprehensive study of SUEWS at multiple vegetated sites, we also identify future development and application needs:
-
None of the simple LAI schemes in SUEWS account for hydrological impacts on LAI. Vegetation with shallow roots (e.g. US-SRG in Arizona, US, categorised as GRA according to IGBP, Fig. D2) are not well modelled when air temperature is the only phenology forcing variable. Hydrological feedback should be considered in future development of the LAI scheme in SUEWS.
-
The specific humidity deficit surface conductance parameter relation needs improvement as a plateau-like trend is observed near the lower end (e.g. Fig. 9c).
-
A potential source of parameter values for PFT beyond those studied here (i.e. values provided Appendix C, Sun et al., 2021) could be NOAH-based parameters (Appendix A) but these should be used with caution, as demonstrated (Sect. 5).
-
More careful treatment of snow cover should be incorporated to enhance SUEWS capacity in high-latitude regions.
The NOAH land surface scheme (Chen et al., 1996) uses a similar Jarvis-type parameterisation of surface conductance gs to that in SUEWS (i.e. Eq. 13) but with different formulation of gs sub-components from SUEWS (Eqs. A1–A4 vs. Eqs. 15–18). The NOAH equations using our notation are as follows:
-
Incoming solar radiation (K↓).
where with Rgl an adjustable parameter for K↓.
-
Air specific humidity (q).
where hs is the adjustable parameter for specific humidity q and qs the saturation specific humidity.
-
Air temperature (Ta).
where Tref is the adjustable parameter for air temperature Ta.
-
Soil moisture (θsoil).
where θFC and θWP are field capacity and wilting point (see Table A2 for values of different soil types).
To use the NOAH parameters (as given in Tables 1 and 2 of Chen and Duhdia, 2001), we convert the NOAH parameters (Eqs. A1–A4) to the SUEWS required parameters (i.e. for Eqs. 15–18). The resulting SUEWS parameters (Table A1) are used (Sect. 5) to produce results in Figs. 14 and 15 denoted by NOAH.
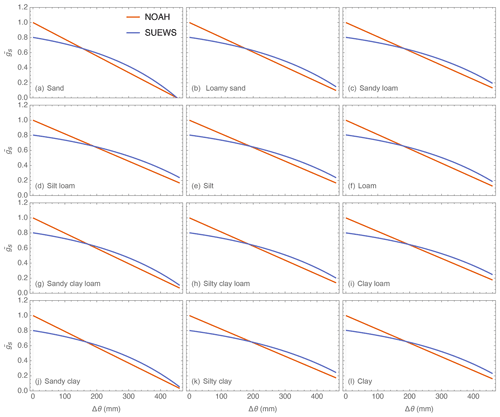
Except for the gs function for air temperature – SUEWS and NOAH adopt the effectively same formulation – other gs functions may produce different results even using the converted parameter values (Table A1). In particular, for the shortwave radiation and specific humidity (Fig. A1), the SUEWS values (blue) are higher than NOAH values (red) for all PFTs. The role of soil type (Table A2) on the soil moisture deficit function (Fig. A2) results in larger differences at dry and mid-wet extremes.
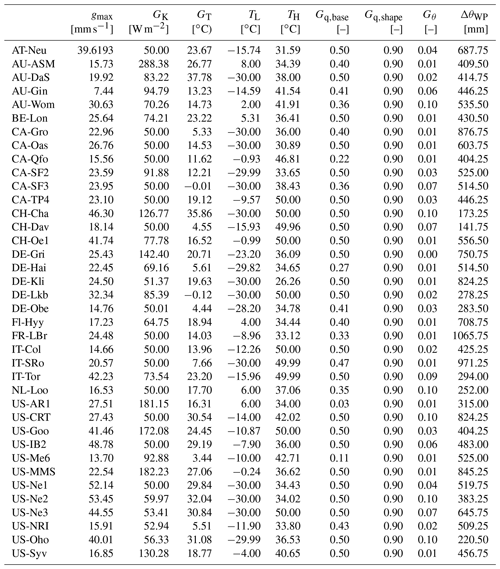
Table A1NOAH-derived (data: based on Tables 1 and 2 of Chen and Duhdia, 2001) surface-conductance-related parameters for SUEWS.
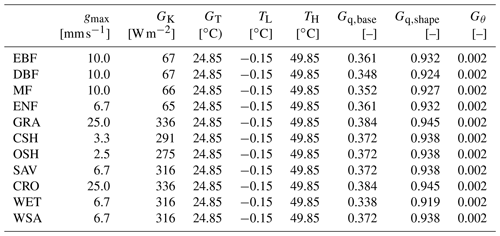
Table A2Soil field capacity (θFC) and wilting point (θWP) used in NOAH (data: based on Table 2 of Chen and Duhdia, 2001).
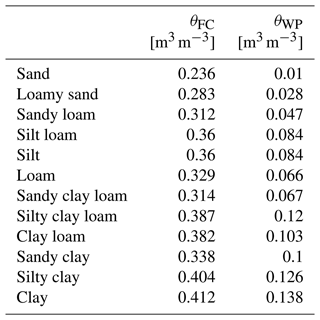
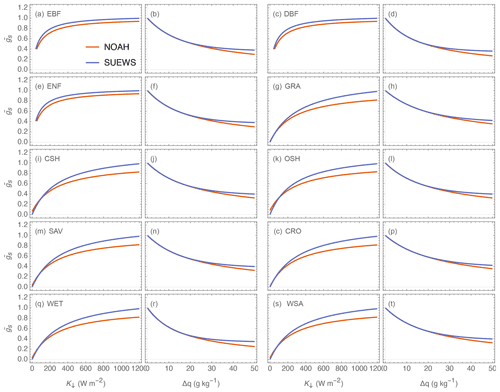
Figure A1NOAH (red) and SUEWS (blue) surface conductance functions for incoming solar radiation (K↓) and specific humidity deficit (Δq) for different IGBP PFTs.
The aerodynamic roughness parameters for momentum (roughness length z0m and zero-plane displacement height zd) are derived using observed u∗ and u under neutral conditions (i.e. with an initial estimate of zd=0.7Hc) of different vegetation stages based on LAI (see Sect. 4.1 for classification details) by the least-square method for the following relation (Monin and Obukhov, 1954):
where κ is the von Kármán constant (0.4 is used here). In particular, for sites with varying canopy height Hc, z0m and zd are derived for each of the periods when Hc stayed unchanged and more than 20 observational pairs of u∗ and u are available.
Using the derived z0m and zd, f0 and fd parameters can be obtained (Eqs. 9 and 10). These is considerable intra-PFT variability of both f0 and fd (Fig. B1). There are also intra-site variations associated with varying Hc. Given the large variability in both f0 and fd, the rule-of-thumb approach would incur a large bias in estimated aerodynamic and surface resistances and subsequently the modelled QE. To reduce such a bias, in the evaluation of the other sub-models and parameter determinations in this paper, we use the derive z0m and zd determined for each vegetation stage and site.
Modelled wind speed under neutral conditions matches well with observations at 38 study sites with MAE < 0.3 m s−1 and MBE close to zero (Fig. B2). Of the three SUEWS PFTs, “Grass” sites have the poorer performance. This is probably because this PFT includes crops which will change frequently because of crop rotations: cereal, potato, sugar beet at BE-Lon (Moureaux et al., 2006); winter barley, rapeseed, winter wheat, maize and spring barley at DE-Kli (Prescher et al., 2010); and maize and soybean at US-Ne2 and US-Ne3.
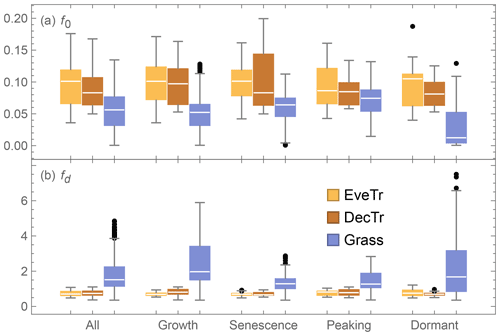
Figure B1Relations between canopy height (Hc) and (a) roughness length for momentum (z0m, Eq. B2) and (b) displacement height (zd, Eq. B3) for different vegetation stages based on LAI (see Sect. 4.1 for classification details).
Given sufficient CO2, vegetation phenology indicated by LAI dynamics is predominantly controlled by input energy and water (Fang et al., 2019). Two variables that capture this seasonal variability are air temperature and precipitation. Different intra-annual LAI dynamics are evident between sites, with contrasting meteorological controls:
- (a)
Thermally dominant (US-MMS; Fig. D1). Intra-annual cumulative precipitation at US-MMS steadily increases throughout the year (Fig. D1a), implying a fairly even distribution of water supply, while air temperature gradually increases from the mid-winter (beginning of a year), peaks in August and decreases with the start of the next winter (Fig. D1b). The LAI pattern at US-MMS responds to the air temperature, notably the growing degree days (GDDs) and then autumn senescence (SDD). This inverse “U”-shape typifies sites with thermally dominant LAI dynamics. These types of sites are well parameterised by the current LAI scheme in SUEWS (Sect. 2.2.1).
- (b)
Rainfall and thermal controls (US-SRG; Fig. D2). At this grassland site in Arizona, USA, the intra-annual precipitation has clear dry and wet seasons. The monsoon wet season after the peak air temperature in July through September (Fig. D2a), which has warmest air temperatures, unlike US-MMS (Fig. D2b), the peak air temperature is more distinct (for a shorter period). A clear relation between the onset of rainfall and LAI enhancement can be seen but the GDD and SDD relation differs from US-MMS, and it not captured by the current models in SUEWS. The rainfall and enhanced LAI and QE are associated with cooler daily air temperatures. Sites where the LAI dynamics are not captured are not explored further in this paper.
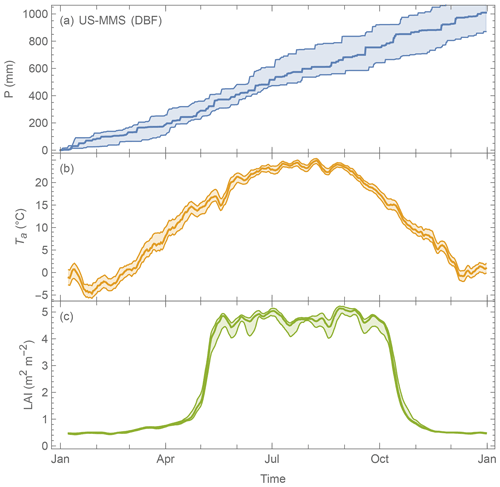
Figure D1Median (line) and interquartile range (shading) daily variation at US-MMS a DBF site during the period 2002–2015 of (a) precipitation (cumulative), (b) air temperature (7 d moving average) and (c) LAI (7 d moving average).
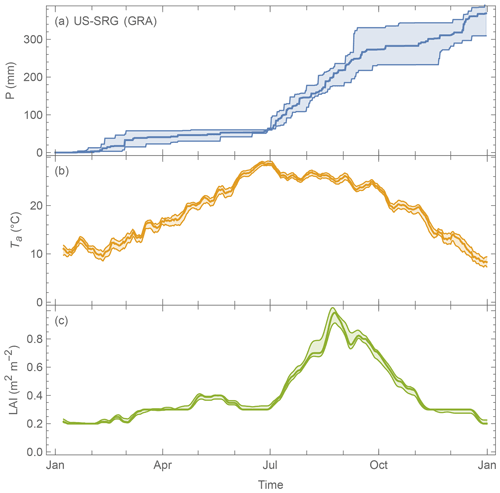
Figure D2As Fig. D1, but for US-SRG (GRA according to IGBP; time span: 2008–2015; https://doi.org/10.18140/FLX/1440114).
All source codes, input and output data are archived at Zenodo in Sun et al. (2021) which can be accessed at: https://doi.org/10.5281/zenodo.5519919.
HO, TS and SG contributed to data preparation, parameter derivation, running simulations and writing the paper. HO led the initial and TS the revised versions of this work. All other authors (DB, AB, JC, ZD, ZG, HI and JPM) provided data for analysis of this work at different stages (some not used in this paper), interpreted the results, and reviewed the paper.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the editor Jeffery Neal and two anonymous reviewers for their constructive comments that led to remarkable improvements in this paper.
This research has been supported by the Natural Environment Research Council (grant no. NE/S005889/1), the Met Office (grant no. CSSP-China), the Natural Environment Research Council (grant no. NE/P018637/1), and the National Natural Science Foundation of China (grant no. 41875013).
This paper was edited by Jeffrey Neal and reviewed by two anonymous referees.
Anandakumar, K.: A study on the partition of net radiation into heat fluxes on a dry asphalt surface, Atmos. Environ., 33, 3911 3918, https://doi.org/10.1016/s1352-2310(99)00133-8, 1999.
André, J.-C., Goutorbe, J.-P., and Perrier, A.: HAPEX–MOBLIHY: A Hydrologic Atmospheric Experiment for the Study of Water Budget and Evaporation Flux at the Climatic Scale, B. Am. Meteorol. Soc., 67, 138–144, https://doi.org/10.1175/1520-0477(1986)067<0138:hahaef>2.0.co;2, 1986.
Ao, X., Grimmond, C. S. B., Ward, H. C., Gabey, A. M., Tan, J., Yang, X.-Q., Liu, D., Zhi, X., Liu, H., and Zhang, N.: Evaluation of the Surface Urban Energy and Water Balance Scheme (SUEWS) at a Dense Urban Site in Shanghai: Sensitivity to Anthropogenic Heat and Irrigation, J. Hydrometeorol., 19, 1983–2005, https://doi.org/10.1175/JHM-D-18-0057.1, 2018.
Asaadi, A., Arora, V. K., Melton, J. R., and Bartlett, P.: An improved parameterization of leaf area index (LAI) seasonality in the Canadian Land Surface Scheme (CLASS) and Canadian Terrestrial Ecosystem Model (CTEM) modelling framework, Biogeosciences, 15, 6885–6907, https://doi.org/10.5194/bg-15-6885-2018, 2018.
Baldocchi, D., Falge, E., Gu, L., Olson, R., Hollinger, D., Running, S., Anthoni, P., Bernhofer, C., Davis, K., Evans, R., Fuentes, J., Goldstein, A., Katul, G., Law, B., Lee, X., Malhi, Y., Meyers, T., Munger, W., Oechel, W., Paw, U. K. T., Pilegaard, K., Schmid, H. P., Valentini, R., Verma, S., Vesala, T., Wilson, K., and Wofsy, S.: FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem-Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities, B. Am. Meteorol. Soc., 82, 2415–2434, https://doi.org/10.1175/1520-0477(2001)082<2415:FANTTS>2.3.CO;2, 2001.
Balsamo, G., Beljaars, A., Scipal, K., Viterbo, P., van den Hurk, B., Hirschi, M., and Betts, A. K.: A Revised Hydrology for the ECMWF Model: Verification from Field Site to Terrestrial Water Storage and Impact in the Integrated Forecast System, J. Hydrometeorol., 10, 623–643, https://doi.org/10.1175/2008jhm1068.1, 2009.
Bauerle, W. L., Oren, R., Way, D. A., Qian, S. S., Stoy, P. C., Thornton, P. E., Bowden, J. D., Hoffman, F. M., and Reynolds, R. F.: Photoperiodic regulation of the seasonal pattern of photosynthetic capacity and the implications for carbon cycling, P. Natl. Acad. Sci. USA, 109, 8612–8617, https://doi.org/10.1073/pnas.1119131109, 2012.
Beven, K.: A sensitivity analysis of the Penman–Monteith actual evapotranspiration estimates, J. Hydrol., 44, 169–190, https://doi.org/10.1016/0022-1694(79)90130-6, 1979.
Bloomfield, P.: Fourier Analysis of Time Series: An Introduction, Wiley-Interscience, New York, 2000.
Bosveld, F. C. and Bouten, W.: Evaluation of transpiration models with observations over a Douglas-fir forest, Agr. Forest Meteorol., 108, 247–264, https://doi.org/10.1016/s0168-1923(01)00251-9, 2001.
Campbell, G. S. and Norman, J. M.: An Introduction to Environmental Biophysics, in: An Introduction to Environmental Biophysics, Springer New York, New York, NY, pp. 1–13, 1998.
Cescatti, A., Marcolla, B., Vannan, S. K. S., Pan, J. Y., Román, M. O., Yang, X., Ciais, P., Cook, R. B., Law, B. E., Matteucci, G., Migliavacca, M., Moors, E., Richardson, A. D., Seufert, G., and Schaaf, C. B.: Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network, Remote Sens. Environ., 121, 323–334, https://doi.org/10.1016/j.rse.2012.02.019, 2012.
Chen, F. and Dudhia, J.: Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity, Mon. Weather Rev., 129, 569 585, https://doi.org/10.1175/1520-0493(2001)129<0569:caalsh>2.0.co;2, 2001.
Chen, F., Mitchell, K., Schaake, J., Xue, Y., Pan, H., Koren, V., Duan, Q. Y., Ek, M., and Betts, A.: Modeling of land surface evaporation by four schemes and comparison with FIFE observations, J. Geophys. Res.-Atmos., 101, 7251–7268, https://doi.org/10.1029/95jd02165, 1996.
Chu, H., Baldocchi, D. D., John, R., Wolf, S., and Reichstein, M.: Fluxes all of the time? A primer on the temporal representativeness of FLUXNET, J. Geophys. Res.-Biogeo., 122, 289–307, https://doi.org/10.1002/2016jg003576, 2017.
Chu, H., Luo, X., Ouyang, Z., Chan, W. S., Dengel, S., Biraud, S. C., Torn, M. S., Metzger, S., Kumar, J., Arain, M. A., Arkebauer, T. J., Baldocchi, D., Bernacchi, C., Billesbach, D., Black, T. A., Blanken, P. D., Bohrer, G., Bracho, R., Brown, S., Brunsell, N. A., Chen, J., Chen, X., Clark, K., Desai, A. R., Duman, T., Durden, D., Fares, S., Forbrich, I., Gamon, J. A., Gough, C. M., Griffis, T., Helbig, M., Hollinger, D., Humphreys, E., Ikawa, H., Iwata, H., Ju, Y., Knowles, J. F., Knox, S. H., Kobayashi, H., Kolb, T., Law, B., Lee, X., Litvak, M., Liu, H., Munger, J. W., Noormets, A., Novick, K., Oberbauer, S. F., Oechel, W., Oikawa, P., Papuga, S. A., Pendall, E., Prajapati, P., Prueger, J., Quinton, W. L., Richardson, A. D., Russell, E. S., Scott, R. L., Starr, G., Staebler, R., Stoy, P. C., Stuart-Haëntjens, E., Sonnentag, O., Sullivan, R. C., Suyker, A., Ueyama, M., Vargas, R., Wood, J. D., and Zona, D.: Representativeness of Eddy-Covariance flux footprints for areas surrounding AmeriFlux sites, Agr. Forest Meteorol., 301–302, 108350, https://doi.org/10.1016/j.agrformet.2021.108350, 2021.
Ershadi, A., McCabe, M. F., Evans, J. P., Chaney, N. W., and Wood, E. F.: Multi-site evaluation of terrestrial evaporation models using FLUXNET data, Agr. Forest Meteorol., 187, 46–61, https://doi.org/10.1016/j.agrformet.2013.11.008, 2014.
Fang, H., Baret, F., Plummer, S., and Schaepman-Strub, G.: An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications, Rev. Geophys., 57, 739–799, https://doi.org/10.1029/2018RG000608, 2019.
Franssen, H. J. H., Stöckli, R., Lehner, I., Rotenberg, E., and Seneviratne, S. I.: Energy balance closure of eddy-covariance data: A multisite analysis for European FLUXNET stations, Agr. Forest. Meteorol., 150, 1553–1567, https://doi.org/10.1016/j.agrformet.2010.08.005, 2010.
Garratt, J. R.: The atmospheric boundary layer, 1st edn., Cambridge University Press, 316 pp., ISBN 978-0-521-46745-2, 1992.
Garrigues, S., Lacaze, R., Baret, F., Morisette, J. T., Weiss, M., Nickeson, J. E., Fernandes, R., Plummer, S., Shabanov, N. V., Myneni, R. B., Knyazikhin, Y., and Yang, W.: Validation and intercomparison of global Leaf Area Index products derived from remote sensing data, J. Geophys. Res.-Biogeo., 113, G02028, https://doi.org/10.1029/2007jg000635, 2008.
Gill, A. L., Gallinat, A. S., Sanders-DeMott, R., Rigden, A. J., Short Gianotti, D. J., Mantooth, J. A., and Templer, P. H.: Changes in autumn senescence in Northern Hemisphere deciduous trees: a meta-analysis of autumn phenology studies, Ann. Bot., 116, 875–888, https://doi.org/10.1093/aob/mcv055, 2015.
Göckede, M., Foken, T., Aubinet, M., Aurela, M., Banza, J., Bernhofer, C., Bonnefond, J. M., Brunet, Y., Carrara, A., Clement, R., Dellwik, E., Elbers, J., Eugster, W., Fuhrer, J., Granier, A., Grünwald, T., Heinesch, B., Janssens, I. A., Knohl, A., Koeble, R., Laurila, T., Longdoz, B., Manca, G., Marek, M., Markkanen, T., Mateus, J., Matteucci, G., Mauder, M., Migliavacca, M., Minerbi, S., Moncrieff, J., Montagnani, L., Moors, E., Ourcival, J.-M., Papale, D., Pereira, J., Pilegaard, K., Pita, G., Rambal, S., Rebmann, C., Rodrigues, A., Rotenberg, E., Sanz, M. J., Sedlak, P., Seufert, G., Siebicke, L., Soussana, J. F., Valentini, R., Vesala, T., Verbeeck, H., and Yakir, D.: Quality control of CarboEurope flux data – Part 1: Coupling footprint analyses with flux data quality assessment to evaluate sites in forest ecosystems, Biogeosciences, 5, 433–450, https://doi.org/10.5194/bg-5-433-2008, 2008.
Grimmond, C. S. B.: The suburban energy balance: Methodological considerations and results for a mid-latitude west coast city under winter and spring conditions, Int. J. Climatol., 12, 481–497, https://doi.org/10.1002/joc.3370120506, 1992.
Grimmond, C. S. B. and Oke, T. R.: An evapotranspiration-interception model for urban areas, Water Resour. Res., 27, 1739–1755, https://doi.org/10.1029/91WR00557, 1991.
Grimmond, C. S. B. and Oke, T. R.: Aerodynamic Properties of Urban Areas Derived from Analysis of Surface Form, J. Appl. Meteorol., 38, 1262–1292, https://doi.org/10.1175/1520-0450(1999)038<1262:APOUAD>2.0.CO;2, 1999.
Grimmond, C. S. B., Oke, T. R., and Steyn, D. G.: Urban Water Balance: 1. A Model for Daily Totals, Water Resour. Res., 22, 1397–1403, https://doi.org/10.1029/WR022i010p01397, 1986.
Grimmond, C. S. B., Cleugh, H. A., and Oke, T. R.: An objective urban heat storage model and its comparison with other schemes, Atmos. Environ. B-Urb., 25, 311–326, https://doi.org/10.1016/0957-1272(91)90003-W, 1991.
Harshan, S., Roth, M., Velasco, E., and Demuzere, M.: Evaluation of an urban land surface scheme over a tropical suburban neighborhood, Theor. Appl. Climatol., 133, 867–886, https://doi.org/10.1007/s00704-017-2221-7, 2018.
Heiskanen, J., Rautiainen, M., Stenberg, P., Mõttus, M., Vesanto, V.-H., Korhonen, L., and Majasalmi, T.: Seasonal variation in MODIS LAI for a boreal forest area in Finland, Remote Sens. Environ., 126, 104–115, https://doi.org/10.1016/j.rse.2012.08.001, 2012.
Hengl, T., de Jesus, J. M., MacMillan, R. A., Batjes, N. H., Heuvelink, G. B. M., Ribeiro, E., Samuel-Rosa, A., Kempen, B., Leenaars, J. G. B., Walsh, M. G., and Gonzalez, M. R.: SoilGrids1km – Global Soil Information Based on Automated Mapping, Plos One, 9, e105992, https://doi.org/10.1371/journal.pone.0105992, 2014.
Hengl, T., de Jesus, J. M., Heuvelink, G. B. M., Gonzalez, M. R., Kilibarda, M., Blagotić, A., Shangguan, W., Wright, M. N., Geng, X., Bauer-Marschallinger, B., Guevara, M. A., Vargas, R., MacMillan, R. A., Batjes, N. H., Leenaars, J. G. B., Ribeiro, E., Wheeler, I., Mantel, S., and Kempen, B.: SoilGrids250m: Global gridded soil information based on machine learning, Plos One, 12, e0169748, https://doi.org/10.1371/journal.pone.0169748, 2017.
Högström, U.: Non-dimensional wind and temperature profiles in the atmospheric surface layer: A re-evaluation, Bound.-Lay. Meteorol., 42, 55–78, https://doi.org/10.1007/BF00119875, 1988.
Hollinger, D. Y. and Richardson, A. D.: Uncertainty in eddy covariance measurements and its application to physiological models, Tree Physiol., 25, 873–885, https://doi.org/10.1093/treephys/25.7.873, 2005.
Hoshika, Y., Osada, Y., Marco, A. de, Peñuelas, J., and Paoletti, E.: Global diurnal and nocturnal parameters of stomatal conductance in woody plants and major crops, Global Ecol. Biogeogr., 27, 257–275, https://doi.org/10.1111/geb.12681, 2018.
Järvi, L., Grimmond, C. S. B., and Christen, A.: The Surface Urban Energy and Water Balance Scheme (SUEWS): Evaluation in Los Angeles and Vancouver, J. Hydrol., 411, 219–237, https://doi.org/10.1016/j.jhydrol.2011.10.001, 2011.
Järvi, L., Grimmond, C. S. B., Taka, M., Nordbo, A., Setälä, H., and Strachan, I. B.: Development of the Surface Urban Energy and Water Balance Scheme (SUEWS) for cold climate cities, Geosci. Model Dev., 7, 1691–1711, https://doi.org/10.5194/gmd-7-1691-2014, 2014.
Järvi, L., Havu, M., Ward, H. C., Bellucco, V., McFadden, J. P., Toivonen, T., Heikinheimo, V., Kolari, P., Riikonen, A., and Grimmond, C. S. B.: Spatial Modeling of Local-Scale Biogenic and Anthropogenic Carbon Dioxide Emissions in Helsinki, J. Geophys. Res.-Atmos., 124, 2018JD029576, https://doi.org/10.1029/2018JD029576, 2019.
Jarvis, P. G.: The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field, Philos. T. R. Soc. B, 273, 593–610, https://doi.org/10.1098/rstb.1976.0035, 1976.
Karsisto, P., Fortelius, C., Demuzere, M., Grimmond, C. S. B., Oleson, K. W., Kouznetsov, R., Masson, V., and Järvi, L.: Seasonal surface urban energy balance and wintertime stability simulated using three land-surface models in the high-latitude city Helsinki, Q. J. Roy. Meteor. Soc., 142, 401–417, https://doi.org/10.1002/qj.2659, 2016.
Kent, C. W., Grimmond, S., and Gatey, D.: Aerodynamic roughness parameters in cities: Inclusion of vegetation, J. Wind Eng. Ind. Aerod., 169, 168–176, https://doi.org/10.1016/j.jweia.2017.07.016, 2017a.
Kent, C. W., Lee, K., Ward, H. C., Hong, J.-W., Hong, J., Gatey, D., and Grimmond, S.: Aerodynamic roughness variation with vegetation: analysis in a suburban neighbourhood and a city park, Urban Ecosyst., 21, 227–243, https://doi.org/10.1007/s11252-017-0710-1, 2017b.
Kokkonen, T. V., Grimmond, C. S. B., Räty, O., Ward, H. C., Christen, A., Oke, T. R., Kotthaus, S., and Järvi, L.: Sensitivity of Surface Urban Energy and Water Balance Scheme (SUEWS) to downscaling of reanalysis forcing data, Urban Clim., 23, 36–52, https://doi.org/10.1016/j.uclim.2017.05.001, 2018.
Lindberg, F., Grimmond, C. S. B., Gabey, A., Huang, B., Kent, C. W., Sun, T., Theeuwes, N. E., Järvi, L., Ward, H. C., Capel-Timms, I., Chang, Y., Jonsson, P., Krave, N., Liu, D., Meyer, D., Olofson, K. F. G., Tan, J., Wästberg, D., Xue, L., and Zhang, Z.: Urban Multi-scale Environmental Predictor (UMEP): An integrated tool for city-based climate services, Environ. Modell. Softw., 99, 70–87, https://doi.org/10.1016/j.envsoft.2017.09.020, 2018.
Matsumoto, K., Ohta, T., Nakai, T., Kuwada, T., Daikoku, K., Iida, S., Yabuki, H., Kononov, A. V., van der Molen, M. K., Kodama, Y., Maximov, T. C., Dolman, A. J., and Hattori, S.: Responses of surface conductance to forest environments in the Far East, Agr. Forest Meteorol., 148, 1926–1940, https://doi.org/10.1016/j.agrformet.2008.09.009, 2008.
McCaughey, J. H.: Energy balance storage terms in a mature mixed forest at Petawawa, Ontario – A case study, Bound.-Lay. Meteorol., 31, 89–101, https://doi.org/10.1007/BF00120036, 1985.
McCuen, R. H.: A Sensitivity and Error Analysis of Procedures Used for Estimating Evaporation, J. Am. Water Resour. As., 10, 486–497, https://doi.org/10.1111/j.1752-1688.1974.tb00590.x, 1974.
Monin, A. S. and Obukhov, A. M.: Basic laws of turbulent mixing in the surface layer of the atmosphere, Contrib. Geophys. Inst. Acad. Sci. USSR, 24, 163–187, 1954.
Moureaux, C., Debacq, A., Bodson, B., Heinesch, B., and Aubinet, M.: Annual net ecosystem carbon exchange by a sugar beet crop, Agr. Forest Meteorol., 139, 25–39, https://doi.org/10.1016/j.agrformet.2006.05.009, 2006.
Monteith, J. L.: Evaporation and environment, Sym. Soc. Exp. Biol., 19, 205–34, 1965.
Myneni, R., Knyazikhin, Y., and Park, T.: MCD15A3H MODIS/Terra+Aqua Leaf Area Index/FPAR 4-day L4 Global 500m SIN Grid V006, NASA EOSDIS Land Processes DAAC [data set], 2015.
Nishihama, M., Wolfe, R., Solomon, D., Patt, F., Blanchette, J., Fleig, A., and Masuoka, E.: MODIS Level 1A Earth Location: Algorithm Theoretical Basis Document By the MODIS Science Data Support Team, Greenbelt, Md., 1997.
Noilhan, J. and Planton, S.: A Simple Parameterization of Land Surface Processes for Meteorological Models, Mon. Weather Rev., 117, 536–549, https://doi.org/10.1175/1520-0493(1989)117<0536:aspols>2.0.co;2, 1989.
Offerle, B., Grimmond, C. S. B., and Oke, T. R.: Parameterization of Net All-Wave Radiation for Urban Areas, J. Appl. Meteorol., 42, 1157–1173, https://doi.org/10.1175/1520-0450(2003)042<1157:PONARF>2.0.CO;2, 2003.
Ogink-Hendriks, M. J.: Modelling surface conductance and transpiration of an oak forest in the Netherlands, Agr. Forest Meteorol., 74, 99–118, https://doi.org/10.1016/0168-1923(94)02180-r, 1995.
Oke, T. R.: City size and the urban heat island, Atmos. Environ., 7, 769–779, https://doi.org/10.1016/0004-6981(73)90140-6, 1973.
Oke, T. R.: The energetic basis of the urban heat island, Q. J. Roy. Meteor. Soc., 108, 1–24, https://doi.org/10.1002/qj.49710845502, 1982.
Oliphant, A. J., Grimmond, C. S. B., Zutter, H. N., Schmid, H. P., Su, H. B., Scott, S. L., Offerle, B. D., Randolph, J. C., and Ehman, J.: Heat storage and energy balance fluxes for a temperate deciduous forest, Agr. Forest Meteorol., 126, 185–201, https://doi.org/10.1016/j.agrformet.2004.07.003, 2004.
OpenStreetMap contributors: OpenStreetMap database, OpenStreetMap Foundation, Cambridge, https://www.openstreetmap.org (last access: 30 July 2021), 2021.
Pastorello, G., Trotta, C., Canfora, E., Chu, H., Christianson, D., Cheah, Y.-W., Poindexter, C., Chen, J., Elbashandy, A., Humphrey, M., Isaac, P., Polidori, D., Reichstein, M., Ribeca, A., van Ingen, C., Vuichard, N., Zhang, L., Amiro, B., Ammann, C., Arain, M. A., Ardö, J., Arkebauer, T., Arndt, S. K., Arriga, N., Aubinet, M., Aurela, M., Baldocchi, D., Barr, A., Beamesderfer, E., Marchesini, L. B., Bergeron, O., Beringer, J., Bernhofer, C., Berveiller, D., Billesbach, D., Black, T. A., Blanken, P. D., Bohrer, G., Boike, J., Bolstad, P. V., Bonal, D., Bonnefond, J.-M., Bowling, D. R., Bracho, R., Brodeur, J., Brümmer, C., Buchmann, N., Burban, B., Burns, S. P., Buysse, P., Cale, P., Cavagna, M., Cellier, P., Chen, S., Chini, I., Christensen, T. R., Cleverly, J., Collalti, A., Consalvo, C., Cook, B. D., Cook, D., Coursolle, C., Cremonese, E., Curtis, P. S., D'Andrea, E., Rocha, H. da, Dai, X., Davis, K. J., Cinti, B. D., de Grandcourt, A., Ligne, A. D., Oliveira, R. C. D., Delpierre, N., Desai, A. R., Bella, C. M. D., di Tommasi, P., Dolman, H., Domingo, F., Dong, G., Dore, S., Duce, P., Dufrêne, E., Dunn, A., Dušek, J., Eamus, D., Eichelmann, U., ElKhidir, H. A. M., Eugster, W., Ewenz, C. M., Ewers, B., Famulari, D., Fares, S., Feigenwinter, I., Feitz, A., Fensholt, R., Filippa, G., Fischer, M., Frank, J., Galvagno, M., et al.: The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data, Sci. Data, 7, 225, https://doi.org/10.1038/s41597-020-0534-3, 2020.
Penman, H. L.: Natural evaporation from open water, hare soil and grass, P. Roy. Soc. Lond. A Math., 193, 120–145, https://doi.org/10.1098/rspa.1948.0037, 1948.
Prescher, A.-K., Grünwald, T., and Bernhofer, C.: Land use regulates carbon budgets in eastern Germany: From NEE to NBP, Agr. Forest Meteorol., 150, 1016–1025, https://doi.org/10.1016/j.agrformet.2010.03.008, 2010.
Saxton, K. E. and Rawls, W. J.: Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions, Soil Sci. Soc. Am. J., 70, 1569–1578, 2006.
Shuttleworth, W. J.: A simplified one-dimensional theoretical description of the vegetation–atmosphere interaction, Bound.-Lay. Meteorol., 14, 3–27, https://doi.org/10.1007/BF00123986, 1978.
Shuttleworth, W. J.: Evaporation models in the global water budget, in: Variations in the Global Water Budget, edited by: Street-Perrott, A., Beran, M., and Ratcliffe, R., Springer, Dordrecht, 147–171, https://doi.org/10.1007/978-94-009-6954-4_11, 1983.
Skamarock, W. C. and Klemp, J. B.: A time-split nonhydrostatic atmospheric model for weather research and forecasting applications, J. Comput. Phys., 227, 3465–3485, https://doi.org/10.1016/j.jcp.2007.01.037, 2008.
Stewart, J. B.: Modelling surface conductance of pine forest, Agr. Forest Meteorol., 43, 19–35, https://doi.org/10.1016/0168-1923(88)90003-2, 1988.
Stoy, P. C., Mauder, M., Foken, T., Marcolla, B., Boegh, E., Ibrom, A., Arain, M. A., Arneth, A., Aurela, M., Bernhofer, C., Cescatti, A., Dellwik, E., Duce, P., Gianelle, D., van Gorsel, E., Kiely, G., Knohl, A., Margolis, H., McCaughey, H., Merbold, L., Montagnani, L., Papale, D., Reichstein, M., Saunders, M., Serrano-Ortiz, P., Sottocornola, M., Spano, D., Vaccari, F., and Varlagin, A.: A data-driven analysis of energy balance closure across FLUXNET research sites: The role of landscape scale heterogeneity, Agr. Forest Meteorol., 171, 137–152, https://doi.org/10.1016/j.agrformet.2012.11.004, 2013.
Stöckli, R., Lawrence, D. M., Niu, G.-Y., Oleson, K. W., Thornton, P. E., Yang, Z.-L., Bonan, G. B., Denning, A. S., and Running, S. W.: Use of FLUXNET in the Community Land Model development, J. Geophys. Res.-Biogeo., 113, G01025, https://doi.org/10.1029/2007jg000562, 2008.
Sun, T., Wang, Z.-H., Oechel, W. C., and Grimmond, S.: The Analytical Objective Hysteresis Model (AnOHM v1.0): methodology to determine bulk storage heat flux coefficients, Geosci. Model Dev., 10, 2875–2890, https://doi.org/10.5194/gmd-10-2875-2017, 2017.
Sun, T. and Grimmond, S.: A Python-enhanced urban land surface model SuPy (SUEWS in Python, v2019.2): development, deployment and demonstration, Geosci. Model Dev., 12, 2781–2795, https://doi.org/10.5194/gmd-12-2781-2019, 2019.
Sun, T., Omidvar, H., and Grimmond, S.: Workflow notebooks and FLUXNET2015 data for deriving parameter of SUEWS v2020 based FLUXNET2015 dataset, Zenodo [data set], https://doi.org/10.5281/zenodo.5519919, 2021.
Tang, Y., Sun, T., Luo, Z., Omidvar, H., Theeuwes, N., Xie, X., Xiong, J., Yao, R., and Grimmond, S.: Urban meteorological forcing data for building energy simulations, Build. Environ., 204, 108088, https://doi.org/10.1016/j.buildenv.2021.108088, 2021.
Villarreal, S. and Vargas, R.: Representativeness of FLUXNET Sites Across Latin America, J. Geophys. Res.-Biogeo., 126, e2020JG006090, https://doi.org/10.1029/2020jg006090, 2021.
Ward, H. C., Kotthaus, S., Järvi, L., and Grimmond, C. S. B.: Surface Urban Energy and Water Balance Scheme (SUEWS): Development and evaluation at two UK sites, Urban Clim., 18, 1–32, https://doi.org/10.1016/j.uclim.2016.05.001, 2016.
Wolfram Research: NonlinearModelFit, Wolfram Language function, Wolfram Research, https://reference.wolfram.com/language/ref/NonlinearModelFit.html (last access: 3 August 2021), 2008.
Wolfram Research: ClusterClassify, Wolfram Language function, Wolfram Research, https://reference.wolfram.com/language/ref/ClusterClassify.html (last access: 3 August 2021), 2020.
Wright, I. R., Manzi, A. O., and da Rocha, H. R.: Surface conductance of Amazonian pasture: model application and calibration for canopy climate, Agr. Forest Meteorol., 75, 51–70, https://doi.org/10.1016/0168-1923(94)02203-v, 1995.
Zhang, X., Dai, Y., Cui, H., Dickinson, R. E., Zhu, S., Wei, N., Yan, B., Yuan, H., Shangguan, W., Wang, L., and Fu, W.: Evaluating common land model energy fluxes using FLUXNET data, Adv. Atmos. Sci., 34, 1035–1046, https://doi.org/10.1007/s00376-017-6251-y, 2017.
- Abstract
- Introduction
- SUEWS model
- Global observational datasets used
- Parameter derivation for vegetated land covers: workflows and results
- SUEWS performance in vegetated areas
- Concluding remarks
- Appendix A: NOAH-based equivalent values for surface-conductance-related parameters for SUEWS
- Appendix B: Derivation of roughness length and zero-plane displacement height for momentum
- Appendix C: SUEWS parameters derived at selected FLUXNET sites
- Appendix D: Typical intra-annual LAI dynamics under contrasting meteorological controls
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- SUEWS model
- Global observational datasets used
- Parameter derivation for vegetated land covers: workflows and results
- SUEWS performance in vegetated areas
- Concluding remarks
- Appendix A: NOAH-based equivalent values for surface-conductance-related parameters for SUEWS
- Appendix B: Derivation of roughness length and zero-plane displacement height for momentum
- Appendix C: SUEWS parameters derived at selected FLUXNET sites
- Appendix D: Typical intra-annual LAI dynamics under contrasting meteorological controls
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References