the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
RADIv1: a non-steady-state early diagenetic model for ocean sediments in Julia and MATLAB/GNU Octave
Matthew P. Humphreys
Monica M. Wilhelmus
Dustin Carroll
William M. Berelson
Dimitris Menemenlis
Jack J. Middelburg
Jess F. Adkins
We introduce a time-dependent, one-dimensional model of early diagenesis that we term RADI, an acronym accounting for the main processes included in the model: chemical reactions, advection, molecular and bio-diffusion, and bio-irrigation. RADI is targeted for study of deep-sea sediments, in particular those containing calcium carbonates (CaCO3). RADI combines CaCO3 dissolution driven by organic matter degradation with a diffusive boundary layer and integrates state-of-the-art parameterizations of CaCO3 dissolution kinetics in seawater, thus serving as a link between mechanistic surface reaction modeling and global-scale biogeochemical models. RADI also includes CaCO3 precipitation, providing a continuum between CaCO3 dissolution and precipitation. RADI integrates components rather than individual chemical species for accessibility and is straightforward to compare against measurements. RADI is the first diagenetic model implemented in Julia, a high-performance programming language that is free and open source, and it is also available in MATLAB/GNU Octave. Here, we first describe the scientific background behind RADI and its implementations. Following this, we evaluate its performance in three selected locations and explore other potential applications, such as the influence of tides and seasonality on early diagenesis in the deep ocean. RADI is a powerful tool to study the time-transient and steady-state response of the sedimentary system to environmental perturbation, such as deep-sea mining, deoxygenation, or acidification events.
- Article
(3155 KB) - Full-text XML
-
Supplement
(569 KB) - BibTeX
- EndNote
The seafloor, which covers ∼70 % of the surface of the planet and modulates the transfer of materials and energy from the biosphere to the geosphere, remains for the vast majority unexplored. Today, this rich, poorly understood ecosystem is threatened locally by deep-sea mining activities (e.g., plowing of the seabed) because it contains abundant valuable minerals and metals essential for the energy transition (Thompson et al., 2018). The deep ocean is also being perturbed globally by climate change, including seawater acidification caused by the uptake of t of anthropogenic carbon dioxide (CO2) into the ocean each year (Perez et al., 2018; Gruber et al., 2019), roughly a quarter of our total annual emissions (Friedlingstein et al., 2020). In this context, it is important to improve our understanding of the seafloor's response to environmental change.
Accumulation of sinking biogenic aggregates and lithogenic particles at the seafloor provides reactive material that regulates the chemical composition of sediment porewaters. Whereas biogenic particles typically sink through the water column at rates from a few meters to hundreds of meters per day (Riley et al., 2012), the same particles accumulate in sediments much more slowly, typically a few centimeters per thousand years (Jahnke, 1996). The residence time of solid particles in the top centimeter of sediments is therefore very long (a few hundred or thousand years) compared to their residence time in the water column (a few weeks). Additionally, while solutes are dispersed by advection in the water column, molecular diffusion dominates in porewaters, which is slower. The long residence time of reactive solid material in surface sediments, coupled with the slow diffusive transport of dissolved species, can lead to large gradients in chemical composition between sediment porewaters and the overlying seawater, inducing solute fluxes between the two (Hammond et al., 1996). Thus, the top few millimeters of the seafloor play a significant role in many major marine biogeochemical cycles.
The overall rate of biogeochemical reactions is determined by the slowest, “rate-limiting” step, which can be (i) transport to or from the reaction site or (ii) the reaction kinetics of the particle at the mineral–water interface. At the seafloor, the rate-limiting step for many biogeochemical reactions is solute transport via molecular diffusion through the sediment porewaters or through the diffusive boundary layer (DBL). The DBL is a thin film of water extending up to a few millimeters above the sediment–water interface in which molecular diffusion is the dominant mode of solute transport. The presence of a DBL above the sediment–water interface (Fig. 1) has been reported by several investigators (Morse, 1974; Archer et al., 1989b; Gundersen and Jørgensen, 1990; Santschi et al., 1991; Glud et al., 1994) and its thickness depends on the composition and roughness of the substrate, as well as on the flow speed of the overlying seawater (Chriss and Caldwell, 1982; Dade, 1993; Røy et al., 2002; Han et al., 2018). Diffusive fluxes of solutes across the sediment–water interface are driven by concentration gradients between the overlying seawater and the sediment column being considered. If most of the concentration gradient for a given solute occurs within the porewaters, rather than within the DBL, then the diffusive flux of this solute is termed “internal” or “sediment-side controlled” (Boudreau and Guinasso, 1982). Conversely, if the majority of the concentration gradient for a given solute is within the DBL, the chemical flux across the sediment–water interface is termed “external” or “water-side transport-controlled”. In practice, the chemical exchange of most solutes is controlled by a combination of both regimes termed “mixed-control”, such as dissolved oxygen (Jørgensen and Revsbech, 1985; Hondzo, 1998), radon (Homoky et al., 2016; Cook et al., 2018), and the products of calcium carbonate dissolution (Sulpis et al., 2018; Boudreau et al., 2020), which have concentration gradients on both sides of the sediment–water interface. Despite the importance of the DBL in controlling diffusive fluxes across the sediment–water interface, DBLs are not explicitly included in most models that simulate early diagenesis in the deep ocean.
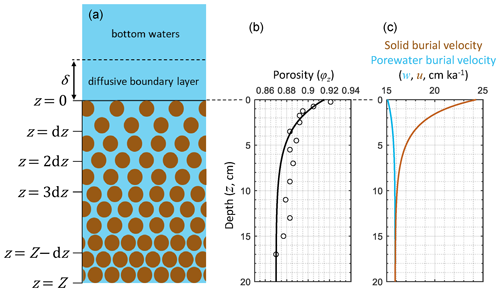
Figure 1Schematic of RADI's vertical structure alongside steady-state depth profiles of porosity φz (see Eqs. 3 and 4), porewater (u, solid light blue line) and solid (w, solid brown line) burial velocities at in situ conditions taken at station 7 of Sayles et al. (2001). Burial velocity varies with depth due to porosity, as described in Sect. 2.3. The open circles in the porosity profile are porosity measurements from Sayles et al. (2001).
Multiple numerical models simulating early diagenesis have previously been published (Burdige and Gieskes, 1983; Rabouille and Gaillard, 1991; Boudreau, 1996b; Van Cappellen and Wang, 1996; Soetaert et al., 1996b; Archer et al., 2002; Munhoven, 2007, 2021; Couture et al., 2010; Yakushev et al., 2017; Hülse et al., 2018), each with its own assumptions and best area of application (Paraska et al., 2014). For instance, most existing models are limited to a steady state and are thus unable to predict the transient sediment response to time-dependent phenomena such as tides, seasonal change, ocean deoxygenation, or acidification. Moreover, most of these models do not take the presence of a DBL into account, even though diffusion through the DBL may control the overall rate of many biogeochemical reactions. Finally, as the landscape of computing software and programming languages evolves and improves computing efficiency and code accessibility, it is important to leverage emerging developments to implement new biogeochemical models. Here, we describe a new sediment porewater model built upon earlier work termed RADI, an acronym accounting for the main processes included in the model that control the vertical distribution of solutes and solids: chemical reactions, advection, molecular and bio-diffusion, and bio-irrigation. The novelty of RADI is that it combines degradation-driven organic matter CaCO3 dissolution (Archer et al., 2002) with a diffusive boundary layer (Boudreau, 1996b) and integrates the state-of-the art parameterization of CaCO3 dissolution kinetics in seawater (Dong et al., 2019; Naviaux et al., 2019a). RADI thus links mechanistic surface reaction modeling to global-scale biogeochemical models (Carroll et al., 2020). By integrating components (e.g., total alkalinity) rather than individual chemical species (e.g., carbonate and bicarbonate ions), RADI is easy to compare to observations. RADI is implemented in two popular scientific programming languages: Julia and MATLAB/GNU Octave. To our knowledge, this is the first diagenetic model implemented in Julia (https://julialang.org, last access: 28 January 2022), a high-level, high-performance, and cross-platform programming language that is free and open source (Bezanson et al., 2017). Here, we first describe the scientific background behind RADI and its implementations. Following this, we evaluate its performance in three selected locations and explore other potential applications, such as the influence of tides and seasonality on early diagenesis in the deep ocean.
In the following section, we describe how reactions, advection, diffusion, and irrigation are implemented in RADIv1. Model variables are italicized and their names as coded in the model are shown in monospaced font. Tables 1 and 2 include an inventory of model variables and parameters and a list of nomenclature for chemical species, respectively.
Table 2Nomenclature of modeled chemical species. All variables are concentrations, expressed in mol per cubic meter of solid for solid species and mol per cubic meter of water for solute species.
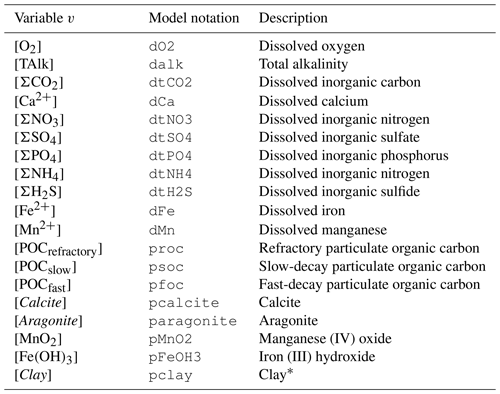
* We consider all clay minerals to be montmorillonite (Al2H2O12Si4; molar mass is equal to 360.31 g mol−1).
2.1 Model structure and fundamental equation
RADI uses the same set of reactive-transport partial differential equations as implemented in CANDI (Boudreau, 1996b), i.e., for each solute component,
and for each solid component,
where v is the concentration of a given component, t is time, φ is sediment porosity, φs is the solid–volume fraction, d is the effective molecular diffusion coefficient, b is the bioturbation coefficient, z is depth, u is the porewater burial velocity, w is the solid burial velocity, α is the irrigation coefficient, vw is the concentration of a solute in the bottom waters, and ΣR is the net production rate from all biogeochemical reactions for a given component. Each of these terms will be described in detail later in this section. These partial differential equations are solved numerically using the method of lines described in Boudreau (1996b). Instead of searching for steady-state solutions directly, RADI computes the concentrations of a set of solids and solutes at each depth and time step following a time vector set by the user. The user determines the simulation time depending on the objectives, e.g., multimillennial to predict a steady state, or a few days to study the response of the sedimentary system to high-frequency cyclic phenomena such as tides. For initial conditions, the user can choose between predefined uniform values (e.g., set all concentrations to zero) or a set of saved concentrations (e.g., from a previous simulation that has reached steady state). T is the total simulation time, dt is the temporal resolution, i.e., the interval between each time step, and t refers to the array of modeled time points. All time units are in years (a). The interface between the surface sediment and overlying seawater, conventionally set at a sediment depth z=0, represents the top layer of RADI's vertical axis (Fig. 1). The bottom layer of the model is at a sediment depth Z. Between these limits, n layers are present, each being separated by a constant vertical gap dz. Depth units are in meters. The values assigned to dz and dt depend on the nature of the problem and on the kinetics of the chemical reactions. In the present study, all cases use dz=2 mm and a, i.e., ∼4 min. If a lower dz is used, dt needs to be lowered as well to preserve numerical stability. In general, the ratio should be kept below a value of 256 m a−1. If dz is divided by two, dt needs to be divided by two as well, and the speed at which RADI runs will be reduced by a factor of four.
RADI operates on a static, user-defined porosity profile. Sediment porosity, φz in Fig. 1, refers to the porewater volume fraction in the sediment (dimensionless) and typically decreases exponentially with sediment depth due to steady-state compaction. The sediment porosity profile is parameterized following Boudreau (1996b) as follows:
where φ∞ is the porosity at great depth, φ0 is the porosity at the sediment–water interface, and β is an attenuation coefficient (in m−1). A typical deep-sea sediment porosity profile is shown in Fig. 1. Here the measured porosity profile at station 7 of cruise NBP98-2 (Sayles et al., 2001) is fit using φ∞=0.87, φ0=0.915, and β=33 m−1. The solid volume fraction (φs, dimensionless) is defined as follows:
and increases with sediment depth (as compaction forces squeeze porewaters out).
Within this grid and for each time step, RADI computes the concentrations of 11 solute variables (TAlk, ΣCO2, O2, Ca2+, ΣNO3, ΣSO4, ΣPO4, ΣNH4, ΣH2S, Fe2+, and Mn2+) and 8 solid variables (Calcite, Aragonite, Fe(OH)3, MnO2, Clay, and three kinds of particulate organic carbon, collectively termed POC). Note that clay is simply modeled as a non-reactive solid that is included because the clay accumulation flux to the sediment–water interface participates in the calculation of the solid burial velocity; see Sect. 2.3. Concentration units are in mol per square meter of water for solutes and in mol per square meter of solid for solid species. For each modeled solute or solid concentration v at time t and sediment depth z, the following equation applies:
where R(vt,z) quantifies the rate of change of vt,z due to chemical reactions, A(vt,z) quantifies the rate of change of vt,z due to advection, D(vt,z) quantifies the rate of change of vt,z due to molecular and bio-diffusion, and I(vt,z) quantifies the rate of change of vt,z due to bio-irrigation. In general, only the subscript z variables are explicitly written out in this paper for variables and parameters that vary with depth. The t variables are implicit but excluded for clarity.
2.2 Reactions
In RADI, biogeochemical reactions operate on solutes and solids throughout the entire sediment column, including the very top and bottom layers. R(vz) is the net rate at which vz is being consumed (negative R) or produced (positive R) by these reactions. Biogeochemical reactions in RADI (Table 3) are grouped into three categories: (i) organic matter degradation, (ii) oxidation of reduced metabolites (organic matter degradation byproducts), and (iii) dissolution or precipitation of calcium carbonate minerals. RADI has been designed for early diagenesis in deep-sea sediments, and thus formation and re-oxidation of metal sulfide minerals are not considered.
2.2.1 Organic matter degradation
Organic carbon deposited on the seafloor originates mainly from primary
production in the upper ocean or on land and (to a lesser extent) from the
ocean interior via chemoautotrophy. Despite the differences in origin,
detrital organic matter found in marine sediments typically has the same
composition: ∼60 % proteins, ∼20 % lipids,
∼20 % carbohydrates, and a fraction of other compounds
(Hedges et al., 2002; Burdige, 2007; Middelburg, 2019). Here, the
stoichiometry of organic matter is represented by the coefficients c (for
carbon), n (for nitrogen), and p (for phosphorus). By default, the c:p ratio is
set to 106:1 and the n:p ratio set to 16:1, following the Redfield ratio that
describes the average composition of phytoplankton biomass (Redfield, 1958),
but these values can easily be adjusted. In RADI, is denoted RC, is
denoted RN, and is denoted RP, which is unity. Organic matter is also
simplified here as an elementary carbohydrate (CH2O). In reality, loss
of H and O during biosynthesis of proteins, lipids, and polysaccharides
occurs (Anderson, 1995; Hedges et al., 2002; Middelburg, 2019), which
results in an effective molar ratio of O2 consumed to C degraded of
∼1.2 during aerobic respiration (Anderson and Sarmiento,
1994) instead of 1 as assumed here (Table 3).
Observations show that some organic compounds are preferentially degraded and become selectively depleted (Cowie and Hedges, 1994; Lee et al., 2000). As a result, the bulk reactivity of organic matter decreases with increasing age (Middelburg, 1989). Degradation of organic matter deposited at the seafloor typically follows a sequential utilization of available oxidants, O2, , MnO2, Fe(OH)3, and , followed by methanogenesis (Froelich et al., 1979; Berner, 1980; Arndt et al., 2013). All organic matter degradation reactions implemented in RADI are shown in Table 3.
To account for the decrease in organic matter degradation rate with sediment depth, we separate organic matter into fractions of different reactivity, and we assign a rate constant to each of the degradable fractions. Following Jørgensen (1978), Westrich and Berner (1984), and Soetaert et al. (1996b), three different classes of organic matter are considered: refractory, slow-decay, and fast-decay organic matter. The refractory organic matter class is not reactive during the timescales considered here. The fast- and slow-decay organic matter fractions each have a depth-dependent, oxidant-independent reactivity. The overall organic matter degradation rate decreases with depth because the quantity of organic matter and the relative proportions of fast- and slow-decay materials decline with depth. Organic matter is degraded following the sequential utilization of available oxidants. The oxidant limitation is represented by a Michaelis–Menten-type (also termed “Monod”) function, in which each oxidant has an associated half-saturation constant (Koxidant in mol m−3) that symbolizes the oxidant concentration at which the process proceeds at half its maximal speed (Soetaert et al., 1996b). The presence of some oxidants may also inhibit other metabolic pathways; this is represented by an inhibition constant ( in mol m−3) that is specific to each oxidant. These limiting and inhibitory functions have been widely used (Boudreau, 1996b; Van Cappellen and Wang, 1996; Soetaert et al., 1996b; Couture et al., 2010), they allow a single equation to be used for each component across the entire model depth range, and they also permit some overlap between the different pathways, as observed in nature (Froelich et al., 1979). In RADI, the overall degradation of fast- or slow-decay organic carbon occurs at the following rate:
where kPOC is the rate constant for the degradation of a given type of organic carbon (fast- or slow-decay types, expressed in a−1), [POCfast or slow] is the concentration of organic carbon (fast- or slow-decay) in sediments, and fOx. is the sum of the fractions of organic carbon degraded by each oxidant (dimensionless, always equal to one), given by
where
Half-saturation and inhibition constants for each oxidant used in RADI are given in Table 4. The degradation rate constant of organic carbon, , is computed as a function of the flux of organic carbon reaching the seafloor and is sediment depth dependent (Archer et al., 2002):
where FPOC is the total flux of organic carbon reaching the seafloor (i.e., fast, slow, and refractory, in ). The numbers and have been tuned to best fit observations of both a Southern Ocean station and a North Atlantic station; see Sect. 3.
2.2.2 Oxidation of organic matter degradation by-products
Organic matter degradation reactions primarily change oxidants (e.g., O2, , MnO2, Fe(OH)3, ) into their reduced forms (e.g., H2O, N2, Mn2+, Fe2+, H2S; Table 3). If oxygen is introduced into the system or the reduced metabolites diffuse upwards in oxic porewaters, then these reduced byproducts are converted back into their oxidized form and the energy contained in them becomes available to the microbial community, though these energetics are not considered in RADI.
Here, four redox reactions involving organic matter degradation byproducts are implemented (Table 3): oxidation of Fe2+, Mn2+, ΣH2S, and ΣNH3, respectively. These four reactions consume porewater total alkalinity (TAlk) but do not alter porewater ΣCO2 (Table 3), thus locally acidifying porewaters. Here, we use the TAlk definition of Dickson (1981), in which TAlk is defined as “the number of moles of hydrogen ion equivalent to the excess of proton acceptors (bases formed from weak acids with a dissociation constant and zero ionic strength) over proton donors (acids with ) in one kilogram of sample.” This scheme should be sufficient for all open-ocean applications but may not be suitable for coastal and anoxic environments with extensive metal sulfide mineral turnover, which require a more complete set of redox reactions such as that from the CANDI model of Boudreau (1996b). Additional components and reactions can easily be implemented in future versions (see Sect. 5). The rate constants for these four redox reactions are taken from Boudreau (1996b) and reported in Table 4.
2.2.3 CaCO3 dissolution and precipitation
RADI includes two CaCO3 polymorphs: low Mg calcite and aragonite, but more could be added in future versions, e.g., high Mg calcite and/or vaterite. Calcite and aragonite both have different dissolution kinetics, in which their dissolution rates increase as the undersaturation state of seawater with respect to calcite () or aragonite () increases (Keir, 1980; Walter and Morse, 1985; Sulpis et al., 2017; Dong et al., 2019; Naviaux et al., 2019b). Here, Ωz is the sediment-depth-dependent saturation state of seawater with respect to calcite or aragonite, computed as , where is the stoichiometric solubility constant of calcite or aragonite at in situ temperature, pressure, and salinity, as given in Mucci (1983) and Millero (1995). At each time step, Ωz is computed using porewater [Ca2+]z and from the previous time step, the latter being calculated as a function of TAlk and the proton concentration [H+]. At each model time step, the total hydrogen ion concentration [H+] is computed from TAlk and ∑CO2 using a single Newton–Raphson iteration from the previous time step (Humphreys et al., 2022):
where [H+]t is the new [H+] value and is the [H+] from the previous time step. TAlk(, ∑CO2) is the total alkalinity computed from user-specified total dissolved silicate, [∑PO4] and total borate calculated from salinity (Uppström, 1974), plus equilibrium constants for silicic acid (Sillén et al., 1964) and phosphoric acid (Yao and Millero, 1995). Its derivative is computed following the approach of CO2SYS; see Humphreys et al. (2022). The carbonate ion concentration is then computed as follows:
where and are the first and second dissociation constants for carbonic acid, respectively, taken from Lueker et al. (2000).
The dissolution rates (Rdiss, in ) of calcite (solid blue line in Fig. 2a) and of aragonite (solid red line in Fig. 2a) as a function of (1−Ωca) are empirically defined as follows:
In these expressions, the dissolution rate constant (kdiss, in a−1) and the reaction order (ηdiss, unitless) are mineral specific. The dissolution rate constants implicitly account for each mineral's specific surface area. Similar formulations have previously been implemented to describe calcite dissolution rates (e.g., Archer et al., 2002) but in most cases used a high reaction order and a tuned rate constant independent of solution chemistry (Fig. 2). Such discretizations are convenient but lack a mechanistic description of the controls on calcite dissolution in seawater (Adkins et al., 2021).
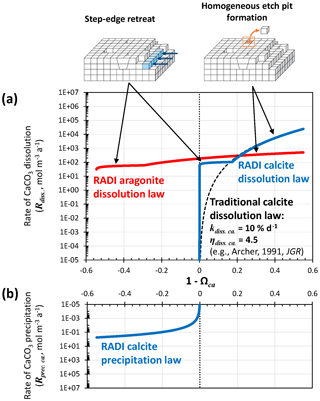
Figure 2(a) Dissolution rate of calcite as computed using Eq. (12) and [Calcite]=104 mol m−3 (solid blue line), and dissolution rate of aragonite as computed using Eq. (13) and [Aragonite]=104 mol m−3 (solid red line). Note that for each dissolution rate profile, two different rate constants (kdiss) and reaction orders (ηdiss) are used, depending on the seawater saturation state, with each accounting for a separate dissolution mechanism, i.e., step-edge retreat or homogeneous-edge pit formation. The dashed black line stands for a “traditional” dissolution rate profile obtained using [Calcite]=104 mol m−3, a single dissolution rate constant for the entire (1−Ωca) range kdiss=10 % d−1, and a reaction order ηdiss of 4.5. (b) Precipitation rate of calcite as computed from Eq. (14). Note that dissolution rates are normalized here per total solid sediment volume and not per CaCO3 surface area as in traditional kinetics studies.
The latest advances using isotope-labeling approaches to study carbonate dissolution kinetics show abrupt changes in dissolution mechanism depending on solution saturation state with either calcite or aragonite (Subhas et al., 2017; Dong et al., 2019; Naviaux et al., 2019a, b). Close to equilibrium, dissolution occurs primarily at sites on the crystal surfaces that are most exposed to the solution, e.g., steps and kinks. Further away from equilibrium, dissolution etch pits are activated at surface sites associated with defects and impurity atoms. Far away from equilibrium, there is enough free energy for dissolution etch pits to occur anywhere on the mineral surface, without the aid of crystal defects (Adkins et al., 2021). However, at temperatures most relevant to the deep oceans, ∼5 ∘C or less, the defect-assisted dissolution mechanism is skipped (Naviaux et al., 2019b) and only the step-edge retreat (close to equilibrium) and homogeneous etch-pit formation (far away from equilibrium) dissolution regimes remain (Naviaux et al., 2019b) (Fig. 2). For both aragonite and calcite, while homogeneous etch-pit formation is indeed associated with a high-order dependency on the solution saturation state, step-edge retreat dissolution rates dominating near equilibrium show very little dependence on seawater saturation (Dong et al., 2019; Naviaux et al., 2019a). This could have significant consequences for the predicted carbonate dissolution rate near equilibrium: saturation-state-independent step-edge retreat dissolution will always be predicted to be faster close to equilibrium than dissolution associated with a high reaction order because a high reaction order forces the dissolution rate to converge to zero as the solution gets closer to equilibrium (Fig. 2).
Naviaux et al. (2019a) derived reaction orders for two separate regions of the (1−Ωca) spectrum: the Ωca threshold value dividing these two regions was Ωca. critical≈0.8. Here, based on the results of Naviaux et al. (2019a), we set ηdiss. ca.=0.11 for and ηdiss. ca.=4.7 for Ωca≤0.828. The Ωca critical value used here is slightly higher than the ∼0.8 value given in Naviaux et al. (2019a) in order to have a smooth transition between defect-assisted and homogeneous dissolution. For aragonite, based on the results of Dong et al. (2019), we set ηdiss. ar.=0.13 for and ηdiss. ar.=1.46 for Ωar≤0.835. The rate constants are tuned to best fit the observations in the two stations presented in Sect. 3. We use a−1 for , kdiss. ca.=20 a−1 for Ωca≤0.828, a−1 for , and a−1 for Ωar≤0.835. Both calcite and aragonite dissolution rate constants are lower than the values reported in the original publications. We suspect that (i) the reactive surface area of grains in sediments is much smaller than their specific surface area measured using adsorption isotherms via the Brunauer–Emmett–Teller (BET) method and (ii) unaccounted dissolution inhibitors are present in sediments, such as dissolved organic carbon (Naviaux et al., 2019a). A comparison of the steady-state [] and [Calcite] porewater profiles predicted by RADI using the tuned rate constants implemented in RADIv1 and the original rate constants is shown in Fig. S1 in the Supplement.
Calcite precipitation is also included in the model and its rate (solid blue line in Fig. 2b) is parameterized with the following function:
where kprec. ca is the precipitation rate constant set to 0.4 and η is equal to 1.76. The precipitation reaction order is taken from Zuddas and Mucci (1998), corrected for a seawater-like ionic strength of 0.7 mol kg−1. The precipitation and dissolution rate continuum implemented in RADI (see Fig. 2) is very different from what a classic model with only calcite dissolution following high reaction order kinetics would display. For comparison, the dissolution rate of calcite using a dissolution rate constant kdiss of 10 % d−1 and a reaction order η of 4.5, as implemented in most diagenetic models, including Archer (1991), is shown in Fig. 2a. The value of 10 % d−1 for the rate constant was chosen because it makes the “traditional” calcite dissolution law overlap with the RADI dissolution law so that any differences between the two can be attributed to enhanced dissolution caused by step-edge retreat close to equilibrium. Mechanistic interpretations of the “kinks” in the dissolution rate profiles and of a non-zero dissolution rate near equilibrium still require more research, but the implications of these features for our understanding of marine CaCO3 cycles can be explored with the present model.
2.3 Advection
The solid burial velocity at the sediment–water interface, w0 in m a−1, is given by
where Fv is the flux of a solid species at the sediment–water interface (), Mv is the molar mass of that solid (g mol−1), and ρv is its solid density (g m−3). The solid and porewater burial velocity at greater depth are assumed to be equal and are computed as follows:
Thus, the porewater burial velocity, u, at all depths is
and the solid burial velocity, w, is
Depth profiles of u and w are shown in Fig. 1, computed from the solid fluxes at station 7 of cruise NBP98-2 (Sayles et al., 2001); see Sect. 3.2. In Fig. 1, the sharp porosity decline in the top centimeters of the sediments causes the solid fraction at ∼5 cm depth to be roughly 50 % higher than just below the interface. This leads to a solid burial velocity decrease of about the same magnitude (Fig. 1).
Advection is implemented following Boudreau (1996b), where the advection rate (Az, in ) for solutes is given by
where dz is the effective diffusion coefficient for a given solute at a given depth (in m2 a−1), d∘ is the “free-solution” molecular diffusion coefficient for a given solute (in m2 a−1), and θz is the depth-dependent tortuosity (unitless) defined in Sect. 2.4. For solids, a more sophisticated weighted-difference scheme is employed (Fiadeiro and Veronis, 1977; Boudreau, 1996b):
where bz is the depth-dependent bioturbation coefficient (m2 a−1) and
where
The parameter Peh is half of the cell Péclet number, which expresses the influence of advection relative to bioturbation across a distance separating two points of the grid, centered at the depth z. If bioturbation dominates (Peh≪1), e.g., near the sediment–water interface, σz tends toward zero and a centered-difference discretization is implemented. If advection dominates (Peh≫1), e.g., deeper in sediments, σz tends toward unity and backward-difference discretization prevails; see Eq. (20). This differencing scheme, originally developed by Fiadeiro and Veronis (1977), maintains stability in the entire sediment column (Boudreau, 1996b).
2.4 Diffusion
The diffusion flux of any species depends on its effective diffusion coefficient, dz(v), which varies with depth within the sediment.
For each solute, free-solution diffusion coefficients, denoted dz∘(v), were computed at in situ temperatures (Li and Gregory, 1974; Boudreau, 1997; Schulz, 2006). For solute variables representing several individual species (e.g., ΣPO4, ΣCO2), the diffusion coefficient of the dominant species was considered. Given the high proportion of relative to and CO2 (aq) in seawater and porewaters (see Fig. S2 in the Supplement), the diffusion coefficient of was adopted for both TAlk and ΣCO2. However, this approach may not be suited for sedimentary environments in which pH is lower than 7 because a greater proportion of dissolved inorganic species would then be under the form of carbonic acid, i.e., CO2 (aq), which has a higher diffusion coefficient than (Fig. S2). Free-solution diffusion coefficients, their temperature dependencies, and their sources are reported in Table 5. The diffusion of solutes in the porewaters is slower than in an equivalent volume of water as a result of the physical barriers caused by the presence of solid grains in a sediment. To correct for this effect, we follow Boudreau (1996b) and compute the effective diffusion coefficient for a given solute as follows:
where so-called tortuosity (θ) is defined as follows (Boudreau, 1996a):
Table 5Temperature-dependent molecular diffusion coefficients (m2 a−1).
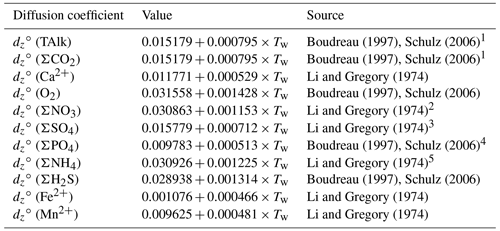
1 value for ion, 2 Value for ion. 3 Value for ion. 4 Value for ion. 5 Value for ion.
For each solid, effective diffusion occurs through the mixing action of burrowing microorganisms, quantified using a bioturbation coefficient that decreases with depth. Archer et al. (2002) used a dataset including 53 sediment sites ranging in depth from 47 to 5668 m to derive an optimal bioturbation rate profile, in which the rate of bioturbation increases with increasing flux of total organic carbon reaching the seafloor (FPOC) and attenuates in low-oxygen conditions. This pattern was also observed by Smith et al. (1997) and Smith and Rabouille (2002). As in Archer et al. (2002), we couple both bioturbation and irrigation to the incoming carbon deposition flux (Fig. 3) rather than water depth or sediment accumulation rate (Boudreau, 1994; Middelburg et al., 1997; Soetaert et al., 1996c), although all these quantities are related to each other. From an ecological perspective, more carbon to the seafloor represents more food available to benthic communities, hence more biological transport. Linking bioturbation activity to carbon deposition flux also allows for a direct coupling with Earth system models simulating carbon sinking fluxes in the ocean. Following Archer et al. (2002), we express the surficial bioturbation mixing rate (b0, in m2 a−1) as follows:
where FPOC is expressed in . The bioturbation mixing rate at all depths (bz, in m2 a−1) is
where the characteristic depth λb=8 cm, following Archer et al. (2002), and [O2]w is the oxygen concentration in the bottom waters. This depth-dependent bioturbation mixing rate is common to all solids, and its depth distribution is shown in Fig. 3 as a function of in situ [O2]w and FPOC. The effective diffusion coefficient for solids is then set as follows:
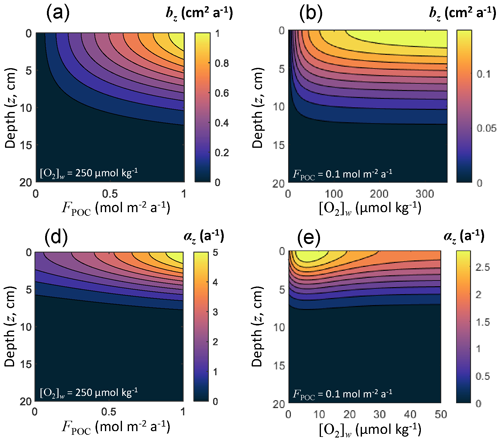
Figure 3Bioturbation mixing rate bz and irrigation coefficients αz as a function of sediment depth z, organic carbon deposition flux FPOC, and dissolved oxygen concentration in the bottom waters [O2]w.
The (bio)diffusion is implemented in RADI following the centered difference discretization scheme from Boudreau (1996b). At sediment depth z, where , for both solutes and solids:
where dz(v) is the relevant effective diffusion coefficient.
2.5 Irrigation
The mixing of solutes caused by burrow flushing or ventilation occurs through an ensemble of processes collectively termed irrigation. Macroscopic burrows are often present in the seafloor sediment, with a complex three-dimensional structure and filled with oxygenated water that is ventilated for aerobic respiration. In a one-dimensional framework, this causes apparent internal sources or sinks of porewater solutes at particular depths (Boudreau, 1984; Emerson et al., 1984; Aller, 2001). Mathematically, this is parameterized as a non-local exchange function, i.e., a first-order kinetic reaction:
where αz is an irrigation coefficient common to all solutes (expressed in a−1). Following Archer et al. (2002), who used a dataset of 53 sediment sites comprised of microelectrode oxygen profiles and chamber oxygen fluxes across the sediment–water interface to derive an irrigation rate profile, we express the surficial irrigation coefficient as a function of the organic carbon deposition flux and the oxygen concentration of the overlaying waters:
and the irrigation coefficient at all depths as follows:
where the characteristic depth λi is 5 cm (Archer et al., 2002). The depth distribution of the irrigation coefficient is shown in Fig. 3 as a function of in situ [O2]w and FPOC.
2.6 Boundary conditions
Modeling of advection and diffusion processes requires appropriate boundary conditions in the layers above and below (z−dz and z+dz, respectively). Effective values of each variable immediately adjacent to the modeled depth domain are calculated following Boudreau (1996b) and used to compute the effects of advection and diffusion in the top and bottom layers using the same equations as within the sediment itself.
At the sediment–water interface, RADI enables prescribed solid fluxes and a diffusive boundary layer control for solutes. Following Boudreau (1996b), we calculate advection and diffusion at z=0 for solutes and solids as follows:
and
respectively. Here, θ is the tortuosity, δ is the boundary layer thickness (expressed in m; see Fig. 1), and vw is the solute concentration above the diffusive boundary layer, i.e., in the bottom waters. At the sediment depth z=Z, v(Z+dz) falls outside the depth range of the model. The bottom boundary condition demands that concentration gradient disappear, which can be translated by the following for both solutes and solids:
This “no-flux” bottom boundary condition should be appropriate here because we set Z so that all action occurs at shallower depth. However, if anaerobic methane oxidation or subsurface weathering are included in future versions, a “constant” flux boundary condition might need to be included.
2.7 Julia and MATLAB/GNU Octave implementations
We have implemented RADI both in Julia (Humphreys and Sulpis, 2021) and in MATLAB/GNU Octave (Sulpis et al., 2021). Both implementations use similar nomenclature and provide identical results. Documentation for both is available from https://radi-model.github.io (last access: March 2022). The Julia implementation is available from https://github.com/RADI-model/Radi.jl (last access: March 2022), and the MATLAB/GNU Octave implementation is available from https://github.com/RADI-model/Radi.m (last access: March 2022).
Julia (https://julialang.org, last access: March 2022) is a high-level,
high-performance, and cross-platform programming language that is free and
open source (Bezanson et al., 2017). Its high performance stems primarily
from just-in-time (JIT) compilation of code before execution, which has been
built-in since its origin. RADI uses Julia's multiple-dispatch paradigm, a
core feature of the language, which improves the readability of the code and
reduces the scope for errors. Specifically, each modeled component of the
sediment column is either a porewater solute or a solid. These components
are initialized in the model as variables either of Solute or Solid type.
Advection and diffusion are governed by different equations for porewater
solutes than for solids, but the same top-level functions (advect! and
diffuse!) can be used within RADI to calculate the effects of these
processes for both component types; the multiple-dispatch paradigm ensures
that the correct equations are automatically used on the basis of the type
of the input variable. While the model has been designed to solve a single
profile at a time, Julia's support for parallelized computation (across
multiple processors) would also support efficient computations across a
series or grid of vertical profiles.
As of version R2015b, MATLAB also features JIT compilation with a corresponding execution speed-up. However, MATLAB is an expensive, proprietary software, which limits how widely it can be used. The MATLAB implementation also runs in GNU Octave (https://www.gnu.org/software/octave/, last access: March 2022), which is a free and open-source clone of MATLAB. However, GNU Octave executes more slowly than MATLAB for a variety of reasons, including a lack of JIT compilation.
For a model that necessarily includes long simulations with relatively short time steps, computational speed is an important consideration. Our testing indicates that the Julia implementation runs ∼3 times faster than the MATLAB (R2020a) implementation and ∼70 times faster than the GNU-Octave implementation.
Simultaneously developing the model in two languages allowed us to quickly identify and remedy bugs and typographical errors in both implementations. Each was coded independently, with equations and parameterizations written out from the original sources, thus avoiding code copy-and-paste errors. Frequent comparisons were made throughout this process to ensure that the results were consistent. For a typographical error to survive to the final models would therefore require an identical mistake to have been made independently in both implementations. The risk of such errors is thus substantially reduced by our dual-language approach. Where errors were identified, in some cases they were subtle enough that they may otherwise not have been noticed, while still causing meaningful errors in final model results.
To evaluate the performance of RADI, we used in situ data obtained at three different locations and compared our predictions to the measured porewater and sediment solid-phase composition profiles. We used these comparisons to tune the CaCO3 dissolution and POC degradation rate constants; all other parameters were assigned a priori using values from the literature. Thus, we did not aim to reproduce observations as accurately as possible by tuning a wide selection of parameters. Instead, we evaluated whether a generic approach using measured deposition fluxes and bottom-water conditions could explain observations while tuning only the inorganic and organic reactivity constants.
3.1 Northwestern Atlantic Ocean
First, RADI was compared to the porewater and sediment composition measurements of station no. 9 described in Hales et al. (1994), located in the northwestern Atlantic Ocean (24.33∘ N, 70.35∘ W) at a 5210 m depth. The bottom-water TAlk and ΣCO2 were 2342 and 2186 µmol kg−1, respectively, bottom-water in situ temperature was 2.2 ∘C, salinity was 34.9, and oxygen concentration was 266.6 µmol kg−1 (Hales et al., 1994). The computed bottom-water saturation state with respect to calcite was 0.88. The only CaCO3 polymorph reaching the seafloor was assumed to be calcite. The calcite flux to the seafloor was set to 0.20 (20.02 ) and the POC flux to 0.18 , which correspond to the low end of fluxes measured by sediment traps on the continental slope (Hales et al., 1994). The clay flux was set to a value of 26 to fit the calcite sediment surface concentration measured by Hales et al. (1994). The porosity at the sediment–water interface was set to that measured by Sayles et al. (2001) in the Southern Pacific Ocean station; see Fig. 1. Following the diffusive boundary layer distribution from Sulpis et al. (2018), δ at the station location was set to 938 µm. This value represents an annual-mean estimate derived using a number of assumptions, e.g., considering the sediment–water interface to be a horizontal surface and neglecting sediment roughness. A complete description of the environmental parameters for this North Atlantic station, along with their sources, is available in Table S1 in the Supplement.
RADI was run using the environmental conditions described above and the steady-state concentration profiles of O2, ΣNO3, calcite, and POC were compared with observations. Complete methods for solute and solids measurements are described in Hales et al. (1994). Briefly, porewater O2 concentration was measured both in situ using microelectrodes and on board (along with ΣNO3) from the retrieved box core (Hales et al., 1994). The steady-state calcite, TAlk and ΣCO2 profiles were compared to those obtained from a RADI simulation with “traditional”, 4.5-order calcite dissolution kinetics (see Fig. 2) with all other variables being unchanged.
RADI predicts a porewater O2 concentration decreasing from the bottom-water value to zero at ∼20 cm depth (Fig. 4). In the top 2 cm, the RADI porewater O2 predictions near the surface are in good agreement with the in situ microelectrode measurements. The RADI-predicted [O2] is lower than that measured on board, but [ΣNO3] is well reproduced by RADI. RADI predicts that organic matter respiration is mainly aerobic (see Table 3a) until about 20 cm depth. Between 20 and 35 cm depth, ΣNO3 is the preferred oxidant for organic matter degradation (see Table 3b), which leads to a decrease in porewater [ΣNO3] in both RADI predictions and observations, followed by ΣSO4 deeper than 35 cm depth. The calcite profile is relatively well reproduced by RADI in the top 20 cm, but the measured calcite concentration drop below 20 cm depth is not well reproduced. When “traditional” 4.5-order calcite dissolution kinetics are implemented, calcite concentrations are similar to those predicted by RADI, but the predicted [TAlk] and [∑CO2] are slightly different, being lower (≲10 µmol kg−1) than RADI's in the top 15 cm, and higher in the deeper part of the sediment column. The observed lower calcite concentrations below 20 cm depth may be attributed to a lower calcite accumulation rate to the seafloor in the past, whereas the model considers accumulation of solids to be unchanged through time. Calcite concentration predicted by RADI does increase again below 25 cm depth due to porewater supersaturation (Ωca at 40 cm depth is about 1.05), but this increase is too small to be noticed in the figure.
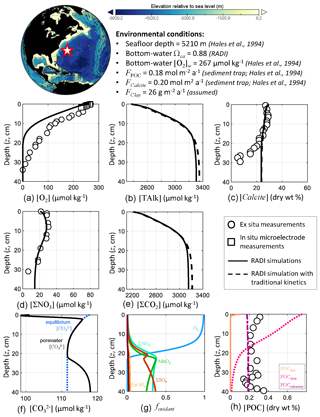
Figure 4Comparison of RADI with measurements from the northwestern Atlantic station no. 9 described in Hales et al. (1994). The lower panels represent (f) the computed concentrations in porewaters (solid black line) and at equilibrium with respect to calcite (dashed blue line) and (g) the fractions of organic matter degraded by a given oxidant.
3.2 Southern Pacific Ocean
RADI was also compared with data collected at the station no. 7 mooring no. 3 described in Sayles et al. (2001), located in the southern Pacific Ocean (60.15∘ S, 170.11∘ W), where the seafloor lies at a 3860 m depth. This dataset (http://usjgofs.whoi.edu/jg/dir/jgofs/southern/nbp98_2/, last access: 28 January 2022) constrains the sedimentary system well: sediment trap CaCO3 and POC fluxes, CaCO3, and POC sediment composition, sediment porosity, and porewater solute depth profiles are all available from the same cruise and location.
The bottom-water chemical composition was taken from the GLODAPv2 climatologies (Lauvset et al., 2016), linearly interpolated over depth, latitude, and longitude to match the station location and seafloor depth. The bottom-water in situ temperature was 0.84 ∘C, salinity was 34.696, oxygen concentration was 215.7 µmol kg−1, and calculated saturation state with respect to calcite was 0.85. Solid fluxes at this station were measured by Sayles et al. (2001) using sediment traps collecting sinking particles between the months of November and December 1997. Their deepest sediment trap available was at a depth of 3257 m, i.e., 600 m a.s.f., which we assume to be representative of sinking fluxes to the seafloor, although the loss of material after collection usually causes sediment traps to underestimate the real sinking fluxes (Buesseler et al., 2007). The only CaCO3 polymorph reaching the seafloor was assumed to be calcite, and its flux was set to 0.25 (25.02 ), rather than using the sediment trap value, in order to fit the calcite sediment surface concentration measured by Sayles et al. (2001). This CaCO3 flux to the seafloor is slightly higher than the measured CaCO3 flux at 600 m above the seafloor in mid-January 1997 (0.19 ; Sayles et al., 2001). The POC flux was set to 0.14 (4.62 ), which is also slightly higher than the measured POC flux averaged between the months of November and December 600 m above the seafloor (0.11 ). The clay flux, which we considered to be the total measured sediment flux minus the assumed POC and calcite fluxes, was 32 . The porosity profile was tuned to best fit the porosity measurements at this station (Sayles et al., 2001, see Fig. 1). Finally, using the diffusive boundary layer world map computed in Sulpis et al. (2018) based on bottom current speeds at in situ temperature and pressure measurements, the diffusive boundary layer thickness (δ) at the station location was set to 715 µm. A complete description of the environmental parameters for this station, along with their sources, is available in Table S2 in the Supplement.
RADI was run using the environmental conditions described above to compare the steady-state concentration profiles of TAlk, ΣCO2, O2, ΣNO3, calcite, and POC to in-situ measurements. Methods for solutes and solids concentration analyses are described in Sayles et al. (2001). Briefly, TAlk, ΣCO2, and ΣNO3 were sampled in situ using the Woods Hole Interstitial Marine Probe (Sayles, 1979), while O2 was sampled at a higher depth resolution but in the ship laboratory using whole-core squeezing (Bender et al., 1987). We also compare the RADI steady-state concentration profiles with those obtained from a simulation with “traditional” 4.5-order calcite dissolution kinetics, all other variables being the same.
RADI predicts porewater O2 concentrations that are slightly higher than observed (Fig. 5). Because RADI does not predict porewater O2 to go to zero until about the 30 cm depth, the dominant organic matter degradation pathway switches from mainly aerobic to ΣNO3 at about the 30 cm depth. Nevertheless, the RADI-predicted ΣNO3 profile is lower than observed values, particularly toward the bottom of the resolved depth. The TAlk and ΣCO2 porewater profiles predicted by a RADI simulation using 4.5-order calcite dissolution kinetics are slightly lower (≲40 µmol kg−1) than those using the new calcite dissolution kinetics scheme, and the predicted calcite concentrations are slightly higher (≲2 %).
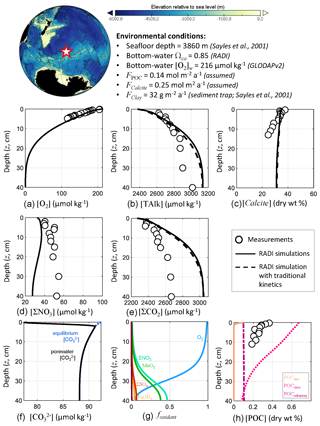
Figure 5Comparison of RADI with measurements from the station no. 7 mooring no. 3 MC-1 described in Sayles et al. (2001). The lower panels represent (f) the computed concentrations in porewaters (solid black line) and at equilibrium with respect to calcite (dashed blue line) and (g) the fractions of organic matter degraded by a given oxidant.
3.3 Central equatorial Pacific Ocean
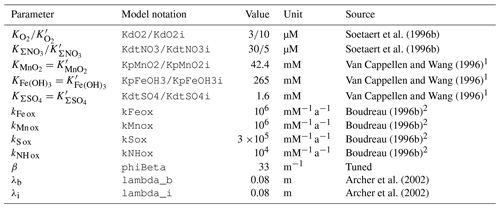
As a third case study to evaluate the performance of RADI, solute fluxes through the sediment–water interface computed from model steady-state runs were compared to fluxes measured using benthic chambers. The comparison took place at station no. W-2 described in Berelson et al. (1994) and Hammond et al. (1996), located in the central equatorial Pacific Ocean (0∘ N, 139.9∘ W) at a depth of 4370 m. Bottom-water in situ temperature was set to 1.40 ∘C and salinity was set to 34.69 (Lauvset et al., 2016). Bottom-water oxygen concentration was set to 159.7 µmol kg−1 and the bottom-water saturation state with respect to calcite computed using the carbonate system solver within RADI was 0.78. For the purposes of this evaluation, the CaCO3 flux to the seafloor was assumed to be entirely calcite. The calcite flux was set to 0.22 , which represents 22.02 g of calcite m−2 a−1, the POC flux was 0.20 , that is, 6.6 g of organic matter m−2 a−1, and the clay flux was set to 2.0 . The steady-state calcite content within the top centimeter was 61 dry wt %, in line with CaCO3 contents observed in this area (Archer, 1996; Hammond et al., 1996). The porosity profile was built using an attenuation coefficient β=33 m−1, φ0=0.85, which is the measured surface porosity (Hammond et al., 1996), and φ∞=0.74, which is the measured porosity at depth (Berelson et al., 1994); see Eq. (3). The DBL thickness, δ, was fixed to a value of 1 mm. A complete description of the environmental parameters for this station, along with their sources, is available in Table S3 in the Supplement.
The diffusive fluxes for a given solute (Jv) between the sediment–water interface and the bottom waters occur as a response to the concentration gradient within the DBL and can be expressed by
where v0 and vw are solute concentrations at the sediment–water interface and in bottom waters, respectively. In this definition, a positive Jv indicates a solute release from the sediment porewaters to the bottom waters, while a negative Jv represents a solute flux towards the sediment.
The predicted TAlk, ΣCO2, ΣPO4, and O2 fluxes (0.30 , 0.32 , 1.9 , and −0.23 , respectively) are all within the uncertainty bounds of the fluxes measured by benthic chambers at the same location (0.28±0.09 , 0.24±0.09 , 1.4±0.5 , and , respectively; see Fig. 6). Nevertheless, the predicted ΣNO3 flux (9.0 ) is lower than its measured value (18±5 ).
3.4 Discussion of model performance
These three model evaluation examples allowed us to determine a set of organic carbon degradation rate constants, CaCO3 dissolution rate constants and organic carbon flux composition (fast-decay, slow-decay, or refractory) that can best reproduce sediment and porewater measurements in all stations while keeping all other model parameters to values from the literature. In each station, bottom-water composition was fixed from observations. Due to a lack of adequate data, solid deposition fluxes were tuned to best fit observed CaCO3 and POC contents in sediments, except in the northwestern Atlantic station, where the CaCO3 and POC fluxes were taken from measurements, and in the southern Pacific station, where the clay flux was inferred from observations. The POC composition that allows to best fit porewater and sediment data in the three stations was as follows: 70 % of fast-decay POC, 27 % of slow-decay POC, and 3 % of refractory POC. The tuned fast- and slow-decay POC degradation rate constants are reported in Sect. 2.2.1 and are of similar orders of magnitude as in most other models (Arndt et al., 2013). The tuned CaCO3 dissolution rate constants are reported in Sect. 2.2.3 and are 2 orders of magnitude lower than their laboratory-based values (Fig. S1), which we attribute to the presence of dissolution inhibitors (e.g., dissolved organic carbon, Naviaux et al., 2019a) or to the reactive surface area of natural grains in situ being lower than in laboratory experimental settings. Thus, with its current settings, RADI should be able to accurately predict porewater chemistry and sediment composition in deep-sea environments, provided that the POC and CaCO3 deposition fluxes are known.
In the central equatorial Pacific, all RADI diffusive fluxes are within the uncertainty range of observations except the ΣNO3 flux, which is underestimated by RADI. The low ΣNO3 flux could be attributed, for example, to the presence of organic matter with a stoichiometry different than the Redfield ratio used in the current version of RADI or to errors in the nitrification parameters.
In addition, we note that the choice of calcite dissolution kinetics implemented in RADI does not seem to have a large impact on TAlk and ΣCO2 porewater profiles or on the predicted calcite concentrations. RADI's step-edge retreat dissolution regime and its low reaction order induce calcite dissolution rates near equilibrium that are orders of magnitude higher than what is predicted in a high-order rate law (Fig. 2), but if the rate constant of a high-order rate law is tuned so that it overlaps the homogeneous dissolution rate law far from equilibrium, differences are limited (Fig. 2). Thus, we conclude that using a 4.5-order rate law with a 10 % d−1 rate constant or using the new, mechanistic calcite dissolution rate scheme implemented in RADI should lead to similar predictions.
In the following section, we continue to analyze the results obtained using the environmental conditions of the equatorial Pacific station no. W-2 and present a few examples of relevant model applications. RADI can be used to study both steady-state and transient conditions, but in the following subsections we focus on time-dependent problems, since transient diagenetic models are underrepresented in the literature.
4.1 Seasonal variability
At the seafloor, the fluxes of sinking material regulating the chemical composition of sediment porewaters are patchy in both space and time. Seafloor microbes and macrofauna respond quickly to pulses of organic matter delivery to the seafloor (Smith et al., 1992), causing short-term variability of sediment oxygen consumption (Smith and Baldwin, 1984; Smith et al., 1994). In addition, both the POC and CaCO3 fluxes to the deep seafloor are strongly affected by seasonal flux variability (Billett et al., 1983; Smith and Baldwin, 1984; Lampitt, 1985; Lampitt et al., 1993, 2010). In the northeastern Atlantic Ocean at 3000 m depth, Lampitt et al. (2010) have shown that the summer POC and CaCO3 fluxes can be ∼10 and ∼4 times higher, respectively, than the wintertime minima. The seasonal coupling between organic matter and CaCO3 fluxes to the seafloor and the state of upper-ocean ecosystem is the result of rapid vertical transport of these materials (Sayles et al., 1994). If the fluxes of reactive material reaching the seafloor are affected by seasons, early diagenesis could display a seasonal signal, and this should be taken into account when interpreting sedimentary data (Martin and Bender, 1988; Sayles et al., 1994; Soetaert et al., 1996a). Here we use RADI to assess how the porewater chemistry and solid composition of deep-sea sediments may be impacted by seasonally varying fluxes.
Seasonally time-varying solid fluxes to the seafloor (F, in ) can be represented with the following sinusoidal function:
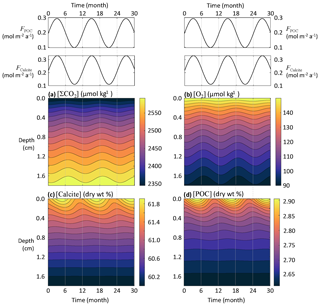
where t is time in years, Δt is the time period separating two maxima (here set to 1 year), and ΔF is the amplitude. We assume that all CaCO3 settling at the seafloor is calcite and set the mean FCalcite to 0.22 , its amplitude change ΔFCalcite to 0.11 , the mean FPOC to 0.20 , and its amplitude change ΔFPOC to 0.10 . All other parameters correspond to values from the central equatorial Pacific stations described in Sect. 3.3.
Seasonal variations in the calcite and POC fluxes reaching the seafloor are visible in sediment profiles of both solids and solutes (Fig. 7). Nonetheless, the amplitude of concentration changes separating an annual minimum from an annual maximum is very small, barely if (at all) detectable by observations. The annual amplitude is about 0.5 wt % for calcite, 0.07 wt % for POC, 2 µmol kg−1 for [O2], and 7 µmol kg−1 for [ΣCO2]. While concentrations at the sediment–water interface respond quickly to seasonal flux changes, there is a phase lag that increases with depth between the concentrations of solids and porewater solutes and the seasonally changing fluxes to the seafloor. Thus, it is possible that porewaters and solid particles at the top millimeter-thick sediment layers are never really at a steady state but always lagging behind seasonal changes, even if these are minimal. This is in agreement with earlier modeling (Martin and Bender, 1988) and observational (Sayles et al., 1994) studies, indicating that biogeochemical reactions and bioturbation at the deep seafloor are too slow to show a discernible seasonal signal. However, this might not be the case for sites receiving more reactive organic matter (Soetaert et al., 1996a).
4.2 Tidal cycles
This section explores the applicability of RADI for studying the response of sediments to higher-frequency phenomena such as tides. The DBL thickness is dependent on the overlying current speed (Levich, 1962; Santschi et al., 1983; Lorke et al., 2003): slower currents generate thicker DBLs, whereas faster currents cause the DBL to thin (Larkum et al., 2003; Lorke et al., 2003; Higashino and Stefan, 2004). In the deep sea, tidal forces are an important contributor to benthic current speeds, which means that tidal currents are a potentially important contributor to biogeochemical exchanges across the sediment–water interface (Egbert and Erofeeva, 2002; Sulpis et al., 2019). If tidal current speed fluctuations induce DBL thickness fluctuations, they may induce solute concentration fluctuations at the sediment–water interface, thus affecting early diagenesis. The strongest tidal currents occur during the transition from high to low tides. For semidiurnal tides, the time period separating a low from a high tide is ∼6 h (Pugh, 1987). Setting the average DBL thickness to δ=1 mm and assuming that tides generate δ fluctuations with an amplitude Δδ=0.5 mm, the time-dependent δ can be expressed as follows:
where t is time in years and Δt is set to a (∼6 h). RADIv1 was run using the steady-state solutes and solids depth profiles from the equatorial Pacific station no. W-2 as initial conditions, with a DBL thickness fluctuating in response to tidal currents computed using Eq. (37).
While none of the solids seem to respond to tidal velocity fluctuation due to their slow accumulation rate, solutes show a clear response (Fig. 8). At the sediment–water interface, the simulated porewater [ΣCO2] variation amplitude within a single tidal cycle is about 25 µmol kg−1, while [O2] oscillates with an amplitude of about 8 µmol kg−1. Deeper than a few millimeters below the sediment–water interface, the amplitude of both [ΣCO2] and [O2] changes become very small and tidal cycles are not measurable in the concentration profiles.
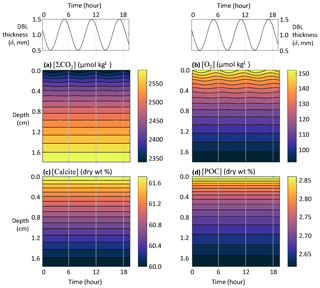
Figure 8Response of porewater O2, ΣCO2, calcite, and POC concentrations to fluctuations in DBL thickness (δ) driven by tidal currents.
The implications are potentially important for our interpretation of porewater microprofiles. Profiles of pH (Archer et al., 1989b; Cai and Reimers, 1993; Zhao and Cai, 1999; Cai et al., 2000); pCO2 (Cai et al., 2000; Zhao and Cai, 1997); (de Beer et al., 2008; Han et al., 2014; Cai et al., 2016); O2 (Revsbech et al., 1980; Reimers, 1987; Archer et al., 1989a; Sosna et al., 2007); and even dissolved Fe, Mn, or S(-II) (Brendel and Luther, 1995) microelectrodes have been developed during the past decades. According to the results presented here, microprofiles, which capture instantaneous snapshots of porewater chemistry, should show appreciable differences depending on when they are carried out during a tidal cycle. That organic matter degradation rates inferred from oxygen microprofiles span a wide range (Archer et al., 1989a; Arndt et al., 2013; Wenzhöfer et al., 2016) may be, among other factors, due to the dependency on tidal and other ocean bottom current fluctuations. To adequately capture O2 consumption rate in sediments, O2 fluxes should be measured and integrated over a period of time longer than a tidal cycle (Berg et al., 2022).
4.3 Benthic chambers
RADI can also be used in the calibration of sensors and the optimization of sampling protocols and experimental designs. In the DBL, molecular diffusion is the dominant mode of solute transport, and laboratory experiments of CaCO3 dissolution in seawater suggest that diffusion through the DBL is the rate-limiting step for CaCO3 dissolution at the seafloor in the absence of organic matter respiration (Sulpis et al., 2017; Boudreau et al., 2020). Nevertheless, earlier assessments of in situ CaCO3 dissolution at the sediment–water interface in the central equatorial Pacific indicated that DBL thickness does not impact overall dissolution rates (Berelson et al., 1994).
In their study, Berelson et al. (1994) deployed a set of free-sinking benthic chambers onto the seafloor. In each chamber, the portion of the chamber exposed above the sediment–water interface was sealed and isolated from external bottom waters, and water samples were drawn during the incubation period. Each incubation lasted between 80 and 120 h. Chambers were stirred with a paddle at various rates to quantify the dependency of the measured diffusive fluxes across the sediment–water interface on the DBL thickness, which were calibrated via anhydrite dissolution to the 300–600 µm range. Seeing no influence of the stirring rate on the measured diffusive fluxes, Berelson et al. (1994) discarded the hypothesis of fast, surficial carbonate dissolution and instead argued for slow, high reaction order calcite dissolution kinetics at the seafloor, as subsequently implemented in most models. To better interpret the results from a benthic-chamber study such as that of Berelson et al. (1994), RADI can be used to predict the time response of diffusive fluxes across the DBL following an instantaneous change of DBL thickness due to, for instance, a change in paddle stirring rate within a chamber.
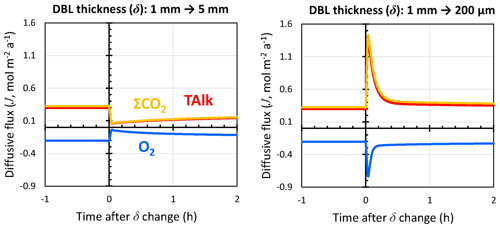
Figure 9Response of TAlk, ΣCO2, and O2 diffusive fluxes through the DBL to instantaneous changes in the DBL thickness (δ) as caused by, for instance, a stirred benthic chamber. Positive values represent solute fluxes toward the bottom waters, while negative values represent solute fluxes toward the sediments.
RADI was run using the steady-state solutes and solids depth profiles from the equatorial Pacific station no. W-2 as initial conditions. In the initial run, the DBL thickness was set to 1 mm. We simulated the response of this sediment to an instantaneous change in the DBL thickness, with one model run representing a situation where δ increases from 1 to 5 mm (e.g., a slow stirring rate) and one model run representing a δ drop from 1 mm to 200 µm (e.g., a fast stirring rate). Following a 5-fold increase in δ, diffusive fluxes of TAlk, ΣCO2, and O2 initially decrease by a factor ∼5 but then increase back as the solute concentrations at the interface adapt to the new DBL (Fig. 9). A total of 2 h after the δ increase, diffusive fluxes converge toward a new steady state. Following a 5-fold decrease in δ, diffusive fluxes immediately increase by the same magnitude but go back to close to their initial value within an hour as the interfacial porewater concentrations adjust to the new DBL. These results suggest that the incubation periods of the Berelson et al. (1994) benthic-chamber experiments were long enough to let porewaters adjust to the changes caused by the paddle stirrers and confirm that, in sediment rich in organic matter and CaCO3 such as that of the Equatorial Pacific, the influence of a DBL on diffusive fluxes across the sediment–water interface should indeed be limited. Additionally, these results confirm the observation by Berelson et al. (1994) that changing the stirring rate in a benthic chamber does not alter steady-state diffusive fluxes by much under the CaCO3 and POC deposition fluxes encountered in the equatorial Pacific. Part of the reason may be the quick adjustment of porewater concentrations to the new diffusive boundary layer (see Fig. S3 in the Supplement).
4.4 Additional applications
The time-dependent problems presented above focus on relatively short timescales (from minutes to months). A non-steady-state model such as RADI can also be used to project the sediment response to perturbations over longer periods of time. Examples include estimating the effect of negative emission technologies, such as coastal enhanced weathering with olivine on early diagenesis (Meysman and Montserrat, 2017; Montserrat et al., 2017), deep-sea mining (Haffert et al., 2020), or bottom trawling (Trimmer et al., 2005; van de Velde et al., 2018; De Borger et al., 2021); the impacts of a decadal bottom-water deoxygenation event such as in the Saint Lawrence estuary (Jutras et al., 2020); or the present anthropogenic CO2 transient. However, the current version of RADI cannot deal with long-term major dissolution (erosion) events because the burial velocity calculation scheme currently implemented does not account for solid mass gain or loss within the sediment. To study the response of sediments to a global-scale, long-duration ocean acidification event such as the Paleocene–Eocene Thermal Maximum (Zachos et al., 2005; Cui et al., 2011), a different burial velocity calculation scheme would have to be implemented, such as that adopted by Munhoven (2021).
One advantage of RADI is that it is easily tunable by the user: adding new components is straightforward as long as the chemical reactions are known. In future releases, we plan to add oxygen, carbon, and calcium isotopes as individual components in order to predict the diagenetic response of isotopic signals. Additionally, adsorption and desorption reactions on clay surfaces could be a critically important advance, especially regarding the prediction of sedimentary pH profiles (Meysman et al., 2003), as RADI currently treats clay minerals as non-reactive.
The representation of organic matter in the current version of the model is oversimplified. All reactive organic matter in RADI is associated with a Redfield stoichiometry, but marine organic matter can considerably deviate from this ideal (Martiny et al., 2013; Teng et al., 2014).
Finally, a model is only as good as its assumptions. RADI is targeted to study deep-sea, carbonate sediments. To be used in coastal environments, additional biogeochemical reactions would be necessary, particularly those involving methane and iron sulfide. Close to the shore, sediments become more permeable, and the assumption of molecular diffusion as the dominant mode of solute transport in porewaters does not hold. In very shallow environments that are subject to high wave energy, pressure-induced advection in the sediment porewaters also needs to be included (Huettel et al., 2014). Moreover, coastal sediments typically have lower pH than open-ocean sediments, which may render our assumption of both ΣCO2 and TAlk diffusing with a fixed diffusion coefficient set to that of the ion inaccurate; see Fig. S2. Other chemical species (e.g., dissolved sulfide, ammonium) that also contribute to the measured pore water alkalinity may also invalidate this assumption.
The current versions of RADI in both Julia and MATLAB/GNU Octave are freely available from GitHub (https://github.com/RADI-model, last access: March 2022) under the GNU General Public License v3. The exact version of the model used to produce the results used in this paper is archived on Zenodo (RADI.jl v0.3; https://doi.org/10.5281/zenodo.5005650 (Humphreys and Sulpis, 2021); v1 will be released after review), along with input data and scripts to run the model for all the simulations presented in this paper. RADI users should cite both this publication and the relevant Zenodo reference (https://doi.org/10.5281/zenodo.5005650, Humphreys and Sulpis, 2021; https://doi.org/10.5281/zenodo.4739205, Sulpis et al., 2021).
Sediment and porewater composition, porosity, and solid fluxes data for the southern Pacific Ocean station described in Sayles et al. (2001) are available at http://usjgofs.whoi.edu/jg/dir/jgofs/southern/nbp98_2/. Sediment and porewater composition for the northwestern Atlantic Ocean station described in Hales et al. (1994) are available at https://doi.pangaea.de/10.1594/PANGAEA.730420. The GLODAPv2 dataset used in this study is available at https://www.glodap.info/index.php/mapped-data-product/ (last access: March 2022, https://doi.org/10.5194/essd-8-325-2016, Lauvset el al., 2016).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-15-2105-2022-supplement.
OS was responsible for conceptualization, methodology, software, validation, formal analysis, investigation, writing of the original draft, and visualization. MPH was responsible for conceptualization, methodology, software, formal analysis, investigation, and writing of the original draft. MMW was responsible for conceptualization, methodology, software, formal analysis, and reviewing and editing the manuscript. DC was responsible for the methodology, software, formal analysis, and reviewing and editing the manuscript. WMB was responsible for validation and reviewing and editing the manuscript. DM was responsible for reviewing and editing the manuscript and supervision of the project. JJM was responsible for the methodology, validation, reviewing and editing the manuscript, and supervision of the project. JFA was responsible for conceptualization, methodology, validation, resources, reviewing and editing the manuscript, and supervision of the project.
The contact author has declared that neither they nor their co-authors have any competing interests
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Thanks are due to Bernard P. Boudreau, whose CANDI model (Boudreau, 1996b) was a large source of inspiration during the creation of the present RADI model, and to Daniel L. Johnson for fruitful discussions. We thank David Burdige and one anonymous reviewer for their constructive feedback. We also thank Lukas van de Wiel for assistance with the Utrecht Geoscience computer cluster. Olivier Sulpis also acknowledges the Department of Earth and Planetary Sciences at McGill University for financial support during his residency in the graduate program and the Faculty of Science at McGill University for a graduate mobility award. Monica M. Wilhelmus, Dustin Carroll, and Dimitris Menemenlis carried out research at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA, with support from the Biological Diversity, Carbon Cycle, Physical Oceanography, and Modeling, Analysis, and Prediction Programs.
This research has been supported by the Netherlands Earth System Science Centre (grant no. 024.002.001), the Department of Earth and Planetary Sciences at McGill University, and NASA.
This paper was edited by Andrew Yool and reviewed by David Burdige and one anonymous referee.
Adkins, J. F., Naviaux, J. D., Subhas, A. V., Dong, S., and Berelson, W. M.: The Dissolution Rate of CaCO3 in the Ocean, Annu. Rev. Mar. Sci., 13, 57–80, https://doi.org/10.1146/annurev-marine-041720-092514, 2021.
Aller, R. C.: Transport and reactions in the bioirrigated zone, in: The benthic boundary layer: transport processes and biogeochemistry, edited by: Boudreau, B. P. and Jørgensen, B. B., Oxford University Press, New York, 269–301, ISBN-13 978-0195118810, 2001.
Anderson, L. A.: On the hydrogen and oxygen content of marine phytoplankton, Deep-Sea Res. Pt. I, 42, 1675–1680, https://doi.org/10.1016/0967-0637(95)00072-E, 1995.
Anderson, L. A. and Sarmiento, J. L.: Redfield ratios of remineralization determined by nutrient data analysis, Global Biogeochem. Cy., 8, 65–80, https://doi.org/10.1029/93GB03318, 1994.
Archer, D.: Modeling the calcite lysocline, J. Geophys. Res., 96, 17037–17050, https://doi.org/10.1029/91JC01812, 1991.
Archer, D. E.: An atlas of the distribution of calcium carbonate in sediments of the deep sea, Global Biogeochem. Cy., 10, 159–174, https://doi.org/10.1029/95GB03016, 1996.
Archer, D., Emerson, S., and Reimers, C.: Dissolution of calcite in deep-sea sediments: pH and O2 microelectrode results, Geochim. Cosmochim. Ac., 53, 2831–2845, https://doi.org/10.1016/0016-7037(89)90161-0, 1989a.
Archer, D., Emerson, S., and Smith, C. R.: Direct measurement of the diffusive sublayer at the deep sea floor using oxygen microelectrodes, Nature, 340, 623–626, https://doi.org/10.1038/340623a0, 1989b.
Archer, D. E., Morford, J. L., and Emerson, S. R.: A model of suboxic sedimentary diagenesis suitable for automatic tuning and gridded global domains, Global Biogeochem. Cy., 16, 171–1721, https://doi.org/10.1029/2000GB001288, 2002.
Arndt, S., Jørgensen, B. B., LaRowe, D. E., Middelburg, J. J., Pancost, R. D., and Regnier, P.: Quantifying the degradation of organic matter in marine sediments: A review and synthesis, Earth-Sci. Rev., 123, 53–86, https://doi.org/10.1016/j.earscirev.2013.02.008, 2013.
Bender, M., Martin, W., Hess, J., Sayles, F., Ball, L., and Lambert, C.: A whole-core squeezer for interfacial pore-water sampling, Limnol. Oceanogr., 32, 1214–1225, https://doi.org/10.4319/lo.1987.32.6.1214, 1987.
Berelson, W. M., Hammond, D. E., McManus, J., and Kilgore, T. E.: Dissolution kinetics of calcium carbonate in equatorial Pacific sediments, Global Biogeochem. Cy., 8, 219–235, https://doi.org/10.1029/93GB03394, 1994.
Berg, P., Huettel, M., Glud, R. N., Reimers, C. E., and Attard, K. M.: Aquatic Eddy Covariance: The Method and Its Contributions to Defining Oxygen and Carbon Fluxes in Marine Environments, 14, 431–455, Annu. Rev. Mar. Sci., https://doi.org/10.1146/annurev-marine-042121-012329, 2022.
Berner, R. A.: Early diagenesis: A theoretical approach, Princeton University Press, 256 pp., ISBN 13 9780691082585, 1980.
Bezanson, J., Edelman, A., Karpinski, S., and Shah, V. B.: Julia: A Fresh Approach to Numerical Computing, SIAM Rev., 59, 65–98, https://doi.org/10.1137/141000671, 2017.
Billett, D. S. M., Lampitt, R. S., Rice, A. L., and Mantoura, R. F. C.: Seasonal sedimentation of phytoplankton to the deep-sea benthos, Nature, 302, 520–522, https://doi.org/10.1038/302520a0, 1983.
Boudreau, B. P.: On the equivalence of nonlocal and radial-diffusion models for porewater irrigation, J. Mar. Res., 42, 731–735, https://doi.org/10.1357/002224084788505924, 1984.
Boudreau, B. P.: Is burial velocity a master parameter for bioturbation?, Geochim. Cosmochim. Ac., 58, 1243–1249, https://doi.org/10.1016/0016-7037(94)90378-6, 1994.
Boudreau, B. P.: The diffusive tortuosity of fine-grained unlithified sediments, Geochim. Cosmochim. Ac., 60, 3139–3142, https://doi.org/10.1016/0016-7037(96)00158-5, 1996a.
Boudreau, B. P.: A method-of-lines code for carbon and nutrient diagenesis in aquatic sediments, Comput. Geosci., 22, 479–496, https://doi.org/10.1016/0098-3004(95)00115-8, 1996b.
Boudreau, B. P.: Diagenetic Models and Their Implementation, Springer-Verlag, Berlin, 414 pp., ISBN-13 978-0387611259, 1997.
Boudreau, B. P. and Guinasso Jr., N. L.: The influence of a diffusive boundary layer on accretion, dissolution, and diagenesis at the sea floor, in: The Dynamic Environment of the Ocean Floor, edited by: Fanning, K. A., Manheim, F. T., Lexington Books, Lexington, 115–145, ISBN 13 9780669028096, 1982.
Boudreau, B. P., Sulpis, O., and Mucci, A.: Control of CaCO3 dissolution at the deep seafloor and its consequences, Geochim. Cosmochim. Ac., 268, 90–106, https://doi.org/10.1016/j.gca.2019.09.037, 2020.
Brendel, P. J. and Luther, G. W. I.: Development of a Gold Amalgam Voltammetric Microelectrode for the Determination of Dissolved Fe, Mn, O2, and S(-II) in Porewaters of Marine and Freshwater Sediments, Environ. Sci. Technol., 29, 751–761, https://doi.org/10.1021/es00003a024, 1995.
Buesseler, K. O., Antia, A. N., Chen, M., Fowler, S. W., Gardner, W. D., Gustafsson, O., Harada, K., Michaels, A. F., van der Loeff, M. R., Sarin, M., Steinberg, D. K., and Trull, T.: An assessment of the use of sediment traps for estimating upper ocean particle fluxes, J. Mar. Res., 65, 345–416, 2007.
Burdige, D. J.: Preservation of Organic Matter in Marine Sediments: Controls, Mechanisms, and an Imbalance in Sediment Organic Carbon Budgets?, Chem. Rev., 107, 467–485, https://doi.org/10.1021/cr050347q, 2007.
Burdige, D. J. and Gieskes, J. M.: A pore water/solid phase diagenetic model for manganese in marine sediments, Am. J. Sci., 283, 29–47, https://doi.org/10.2475/ajs.283.1.29, 1983.
Cai, W.-J. and Reimers, C. E.: The development of pH and pCO2 microelectrodes for studying the carbonate chemistry of pore waters near the sediment-water interface, Limnol. Oceanogr., 38, 1762–1773, https://doi.org/10.4319/lo.1993.38.8.1762, 1993.
Cai, W.-J., Zhao, P., and Wang, Y.: pH and pCO2 microelectrode measurements and the diffusive behavior of carbon dioxide species in coastal marine sediments, Mar. Chem., 70, 133–148, https://doi.org/10.1016/S0304-4203(00)00017-7, 2000.
Cai, W.-J., Ma, Y., Hopkinson, B. M., Grottoli, A. G., Warner, M. E., Ding, Q., Hu, X., Yuan, X., Schoepf, V., Xu, H., Han, C., Melman, T. F., Hoadley, K. D., Pettay, D. T., Matsui, Y., Baumann, J. H., Levas, S., Ying, Y., and Wang, Y.: Microelectrode characterization of coral daytime interior pH and carbonate chemistry, Nat. Commun., 7, 11144, https://doi.org/10.1038/ncomms11144, 2016.
Carroll, D., Menemenlis, D., Adkins, J. F., Bowman, K. W., Brix, H., Dutkiewicz, S., Fenty, I., Gierach, M. M., Hill, C., Jahn, O., Landschützer, P., Lauderdale, J. M., Liu, J., Manizza, M., Naviaux, J. D., Rödenbeck, C., Schimel, D. S., Van der Stocken, T., and Zhang, H.: The ECCO-Darwin Data-Assimilative Global Ocean Biogeochemistry Model: Estimates of Seasonal to Multidecadal Surface Ocean pCO2 and Air-Sea CO2 Flux, J. Adv. Model. Earth Sy., 12, e2019MS001888, https://doi.org/10.1029/2019MS001888, 2020.
Chriss, T. M. and Caldwell, D. R.: Evidence for the influence of form drag on bottom boundary layer flow, J. Geophys. Res., 87, 4148–4154, https://doi.org/10.1029/JC087iC06p04148, 1982.
Cook, P. G., Rodellas, V., Andrisoa, A., and Stieglitz, T. C.: Exchange across the sediment-water interface quantified from porewater radon profiles, J. Hydrol., 559, 873–883, https://doi.org/10.1016/j.jhydrol.2018.02.070, 2018.
Couture, R.-M., Sfafei, B., Van Cappellen, P., Tessier, A., and Gobeil, C.: Non-Steady State Modeling of Arsenic Diagenesis in Lake Sediments, Environ. Sci. Technol., 44, 197–203, https://doi.org/10.1021/es902077q, 2010.
Cowie, G. L. and Hedges, J. I.: Biochemical indicators of diagenetic alteration in natural organic matter mixtures, Nature, 369, 304–307, https://doi.org/10.1038/369304a0, 1994.
Cui, Y., Kump, L. R., Ridgwell, A. J., Charles, A. J., Junium, C. K., Diefendorf, A. F., Freeman, K. H., Urban, N. M., and Harding, I. C.: Slow release of fossil carbon during the Palaeocene–Eocene Thermal Maximum, Nat. Geosci., 4, 481–485, https://doi.org/10.1038/ngeo1179, 2011.
Dade, W. B.: Near-bed turbulence and hydrodynamic control of diffusional mass transfer at the sea floor, Limnol. Oceanogr., 38, 52–69, https://doi.org/10.4319/lo.1993.38.1.0052, 1993.
de Beer, D., Bissett, A., de Wit, R., Jonkers, H., Köhler-Rink, S., Nam, H., Kim, B. H., Eickert, G., and Grinstain, M.: A microsensor for carbonate ions suitable for microprofiling in freshwater and saline environments, Limnol. Oceanogr.-Meth., 6, 532–541, https://doi.org/10.4319/lom.2008.6.532, 2008.
De Borger, E., Tiano, J., Braeckman, U., Rijnsdorp, A. D., and Soetaert, K.: Impact of bottom trawling on sediment biogeochemistry: a modelling approach, Biogeosciences, 18, 2539–2557, https://doi.org/10.5194/bg-18-2539-2021, 2021.
Dickson, A. G.: An exact definition of total alkalinity and a procedure for the estimation of alkalinity and total inorganic carbon from titration data, Deep-Sea Res., 28, 609–623, https://doi.org/10.1016/0198-0149(81)90121-7, 1981.
Dong, S., Berelson, W. M., Rollins, N. E., Subhas, A. V., Naviaux, J. D., Celestian, A. J., Liu, X., Turaga, N., Kemnitz, N. J., Byrne, R. H., and Adkins, J. F.: Aragonite dissolution kinetics and calcite/aragonite ratios in sinking and suspended particles in the North Pacific, Earth Planet. Sc. Lett., 515, 1–12, https://doi.org/10.1016/j.epsl.2019.03.016, 2019.
Egbert, G. D. and Erofeeva, S. Y.: Efficient Inverse Modeling of Barotropic Ocean Tides, J. Atmos. Ocean. Tech., 19, 183–204, https://doi.org/10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2, 2002.
Emerson, S., Jahnke, R., and Heggie, D.: Sediment-water exchange in shallow water estuarine sediments, J. Mar. Res., 42, 709–730, https://doi.org/10.1357/002224084788505942, 1984.
Fiadeiro, M. E. and Veronis, G.: On weighted-mean schemes for the finite-difference approximation to the advection-diffusion equation, Tellus, 29, 512–522, https://doi.org/10.3402/tellusa.v29i6.11385, 1977.
Friedlingstein, P., O'Sullivan, M., Jones, M. W., Andrew, R. M., Hauck, J., Olsen, A., Peters, G. P., Peters, W., Pongratz, J., Sitch, S., Le Quéré, C., Canadell, J. G., Ciais, P., Jackson, R. B., Alin, S., Aragão, L. E. O. C., Arneth, A., Arora, V., Bates, N. R., Becker, M., Benoit-Cattin, A., Bittig, H. C., Bopp, L., Bultan, S., Chandra, N., Chevallier, F., Chini, L. P., Evans, W., Florentie, L., Forster, P. M., Gasser, T., Gehlen, M., Gilfillan, D., Gkritzalis, T., Gregor, L., Gruber, N., Harris, I., Hartung, K., Haverd, V., Houghton, R. A., Ilyina, T., Jain, A. K., Joetzjer, E., Kadono, K., Kato, E., Kitidis, V., Korsbakken, J. I., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Liu, Z., Lombardozzi, D., Marland, G., Metzl, N., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., Niwa, Y., O'Brien, K., Ono, T., Palmer, P. I., Pierrot, D., Poulter, B., Resplandy, L., Robertson, E., Rödenbeck, C., Schwinger, J., Séférian, R., Skjelvan, I., Smith, A. J. P., Sutton, A. J., Tanhua, T., Tans, P. P., Tian, H., Tilbrook, B., van der Werf, G., Vuichard, N., Walker, A. P., Wanninkhof, R., Watson, A. J., Willis, D., Wiltshire, A. J., Yuan, W., Yue, X., and Zaehle, S.: Global Carbon Budget 2020, Earth Syst. Sci. Data, 12, 3269–3340, https://doi.org/10.5194/essd-12-3269-2020, 2020.
Froelich, P. N., Klinkhammer, G. P., Bender, M. L., Luedtke, N. A., Heath, G. R., Cullen, D., Dauphin, P., Hammond, D., Hartman, B., and Maynard, V.: Early oxidation of organic matter in pelagic sediments of the eastern equatorial Atlantic: suboxic diagenesis, Geochim. Cosmochim. Ac., 43, 1075–1090, https://doi.org/10.1016/0016-7037(79)90095-4, 1979.
Glud, R. N., Gundersen, J. K., Revsbech, N. P., and Jørgensen, B. B.: Effects on the benthic diffusive boundary layer imposed by microelectrodes, Limnol. Oceanogr., 39, 462–467, https://doi.org/10.4319/lo.1994.39.2.0462, 1994.
Gruber, N., Clement, D., Carter, B. R., Feely, R. A., van Heuven, S., Hoppema, M., Ishii, M., Key, R. M., Kozyr, A., Lauvset, S. K., Monaco, C. L., Mathis, J. T., Murata, A., Olsen, A., Perez, F. F., Sabine, C. L., Tanhua, T., and Wanninkhof, R.: The oceanic sink for anthropogenic CO2 from 1994 to 2007, Science, 363, 1193–1199, https://doi.org/10.1126/science.aau5153, 2019.
Gundersen, J. K. and Jørgensen, B. B.: Microstructure of diffusive boundary layers and the oxygen uptake of the sea floor, Nature, 345, 604–607, https://doi.org/10.1038/345604a0, 1990.
Haffert, L., Haeckel, M., de Stigter, H., and Janssen, F.: Assessing the temporal scale of deep-sea mining impacts on sediment biogeochemistry, Biogeosciences, 17, 2767–2789, https://doi.org/10.5194/bg-17-2767-2020, 2020.
Hales, B., Emerson, S., and Archer, D.: Respiration and dissolution in the sediments of the western North Atlantic: estimates from models of in situ microelectrode measurements of porewater oxygen and pH, Deep-Sea Res. Pt. I, 41, 695–719, https://doi.org/10.1016/0967-0637(94)90050-7, 1994 (data available at: https://doi.org/10.1594/PANGAEA.730420).
Hammond, D. E., McManus, J., Berelson, W. M., Kilgore, T. E., and Pope, R. H.: Early diagenesis of organic material in equatorial Pacific sediments: stpichiometry and kinetics, Deep-Sea Res. Pt. II, 43, 1365–1412, https://doi.org/10.1016/0967-0645(96)00027-6, 1996.
Han, C., Cai, W.-J., Wang, Y., and Ye, Y.: Calibration and evaluation of a carbonate microsensor for studies of the marine inorganic carbon system, J. Oceanogr., 70, 425–433, https://doi.org/10.1007/s10872-014-0243-7, 2014.
Han, X., Fang, H., He, G., and Reible, D.: Effects of roughness and permeability on solute transfer at the sediment water interface, Water Res., 129, 39–50, https://doi.org/10.1016/j.watres.2017.10.049, 2018.
Hedges, J. I., Baldock, J. A., Gélinas, Y., Lee, C., Peterson, M. L., and Wakeham, S. G.: The biochemical and elemental compositions of marine plankton: A NMR perspective, Mar. Chem., 78, 47–63, https://doi.org/10.1016/S0304-4203(02)00009-9, 2002.
Higashino, M. and Stefan, H. G.: Diffusive boundary layer development above a sediment – water interface, Water Environ. Res., 76, 292–300, https://doi.org/10.2175/106143004X141870, 2004.
Homoky, W. B., Weber, T., Berelson, W. M., Conway, T. M., Henderson, G. M., van Hulten, M., Jeandel, C., Severmann, S., and Tagliabue, A.: Quantifying trace element and isotope fluxes at the ocean–sediment boundary: a review, Philos. T. Roy. Soc., 374, 20160246, https://doi.org/10.1098/rsta.2016.0246, 2016.
Hondzo, M.: Dissolved oxygen transfer at the sediment-water interface in a turbulent flow, Water Resour. Res., 34, 3525–3533, https://doi.org/10.1029/1998WR900009, 1998.
Huettel, M., Berg, P., and Kostka, J. E.: Benthic exchange and biogeochemical cycling in permeable sediments, Annu. Rev. Mar. Sci., 6, 23–51, https://doi.org/10.1146/annurev-marine-051413-012706, 2014.
Hülse, D., Arndt, S., Daines, S., Regnier, P., and Ridgwell, A.: OMEN-SED 1.0: a novel, numerically efficient organic matter sediment diagenesis module for coupling to Earth system models, Geosci. Model Dev., 11, 2649–2689, https://doi.org/10.5194/gmd-11-2649-2018, 2018.
Humphreys, M. P. and Sulpis, O.: Radi.jl: the reactive-advective-diffusive-irrigative diagenetic sediment module in Julia, Zenodo [code], https://doi.org/10.5281/zenodo.5005650, 2021.
Humphreys, M. P., Lewis, E. R., Sharp, J. D., and Pierrot, D.: PyCO2SYS v1.8: marine carbonate system calculations in Python, Geosci. Model Dev., 15, 15–43, https://doi.org/10.5194/gmd-15-15-2022, 2022.
Jahnke, R. A.: The global ocean flux of particulate organic carbon: Areal distribution and magnitude, Global Biogeochem. Cy., 10, 71–88, https://doi.org/10.1029/95GB03525, 1996.
Jørgensen, B. B.: A comparison of methods for the quantification of bacterial sulfate reduction in coastal marine sediments, Geomicrobiol. J., 1, 29–47, https://doi.org/10.1080/01490457809377722, 1978.
Jørgensen, B. B. and Revsbech, N. P.: Diffusive boundary layers and the oxygen uptake of sediments and detritus, Limnol. Oceanogr., 30, 111–122, https://doi.org/10.4319/lo.1985.30.1.0111, 1985.
Jutras, M., Dufour, C. O., Mucci, A., Cyr, F., and Gilbert, D.: Temporal Changes in the Causes of the Observed Oxygen Decline in the St. Lawrence Estuary, J. Geophys. Res.-Oceans, 125, e2020JC016577, https://doi.org/10.1029/2020JC016577, 2020.
Keir, R. S.: The dissolution kinetics of biogenic calcium carbonates in seawater, Geochim. Cosmochim. Ac., 44, 241–252, https://doi.org/10.1016/0016-7037(80)90135-0, 1980.
Lampitt, R. S.: Evidence for the seasonal deposition of detritus to the deep-sea floor and its subsequent resuspension, Deep-Sea Res., 32, 885–897, https://doi.org/10.1016/0198-0149(85)90034-2, 1985.
Lampitt, R. S., Hillier, W. R., and Challenor, P. G.: Seasonal and diel variation in the open ocean concentration of marine snow aggregates, Nature 362, 737–739, https://doi.org/10.1038/362737a0, 1993.
Lampitt, R. S., Salter, I., de Cuevas, B. A., Hartman, S., Larkin, K. E., and Pebody, C. A.: Long-term variability of downward particle flux in the deep northeast Atlantic: Causes and trends, Deep-Sea Res. Pt. II, 57, 1346–1361, https://doi.org/10.1016/j.dsr2.2010.01.011, 2010.
Larkum, A. W. D., Koch, E. M. W., and Kühl, M.: Diffusive boundary layers and photosynthesis of the epilithic algal community of coral reefs, Mar. Biol., 142, 1073–1082, https://doi.org/10.1007/s00227-003-1022-y, 2003.
Lauvset, S. K., Key, R. M., Olsen, A., van Heuven, S., Velo, A., Lin, X., Schirnick, C., Kozyr, A., Tanhua, T., Hoppema, M., Jutterström, S., Steinfeldt, R., Jeansson, E., Ishii, M., Perez, F. F., Suzuki, T., and Watelet, S.: A new global interior ocean mapped climatology: the GLODAP version 2, Earth Syst. Sci. Data, 8, 325–340, https://doi.org/10.5194/essd-8-325-2016, 2016 (data available at: https://www.glodap.info/index.php/mapped-data-product/, last access: March 2022).
Lee, C., Wakeham, S. G., and Hedges, J. I.: Composition and flux of particulate amino acids and chloropigments in equatorial Pacific seawater and sediments, Deep-Sea Res. Pt. I, 47, 1535–1568, https://doi.org/10.1016/S0967-0637(99)00116-8, 2000.
Levich, V. G.: Physicochemical Hydrodynamics, Prentice-Hall Inc., Englewood Cliffs, 1962.
Li, Y.-H. and Gregory, S.: Diffusion of ions in sea water and in deep-sea sediments, Geochim. Cosmochim. Ac., 38, 703–714, https://doi.org/10.1016/0016-7037(74)90145-8, 1974.
Lorke, A., Müller, B., Maerki, M., and Wüest, A.: Breathing sediments: The control of diffusive transport across the sediment – water interface by periodic boundary-layer turbulence, Limnol. Oceanogr., 48, 2077–2085, https://doi.org/10.4319/lo.2003.48.6.2077, 2003.
Lueker, T. J., Dickson, A. G., and Keeling, C. D.: Ocean pCO2 calculated from dissolved inorganic carbon, alkalinity, and equations for K1 and K2: validation based on laboratory measurements of CO2 in gas and seawater at equilibrium, Mar. Chem., 70, 105–119, https://doi.org/10.1016/S0304-4203(00)00022-0, 2000.
Martin, W. R. and Bender, M. L.: The variability of benthic fluxes and sedimentary remineralization rates in response to seasonally variable organic carbon rain rates in the deep sea; a modeling study, Am. J. Sci., 288, 561–574, https://doi.org/10.2475/ajs.288.6.561, 1988.
Martiny, A. C., Pham, C. T. A., Primeau, F. W., Vrugt, J. A., Moore, J. K., Levin, S. A., and Lomas, M. W.: Strong latitudinal patterns in the elemental ratios of marine plankton and organic matter, Nat. Geosci., 6, 279–283, https://doi.org/10.1038/ngeo1757, 2013.
Meysman, F. J. and Montserrat, F.: Negative CO2 emissions via enhanced silicate weathering in coastal environments, Biol. Lett.-UK, 13, 20160905, https://doi.org/10.1098/rsbl.2016.0905, 2017.
Meysman, F. J. R., Middelburg, J. J., Herman, P. M. J., and Heip, C. H. R.: Reactive transport in surface sediments. II. Media: an object-oriented problem-solving environment for early diagenesis, Comput. Geosci., 29, 301–318, https://doi.org/10.1016/S0098-3004(03)00007-4, 2003.
Middelburg, J. J.: A simple rate model for organic matter decomposition in marine sediments, Geochim. Cosmochim. Ac., 53, 1577–1581, https://doi.org/10.1016/0016-7037(89)90239-1, 1989.
Middelburg, J. J.: Marine Carbon Biogeochemistry: A Primer for Earth System Scientists, Springer International Publishing, 118 pp., https://doi.org/10.1007/978-3-030-10822-9, 2019.
Middelburg, J. J., Soetaert, K., and Herman, P. M. J.: Empirical relationships for use in global diagenetic models, Deep-Sea Res. Pt. I, 44, 327–344, https://doi.org/10.1016/S0967-0637(96)00101-X, 1997.
Millero, F. J.: Thermodynamics of the carbon dioxide system in the oceans, Geochim. Cosmochim. Ac., 59, 661–677, https://doi.org/10.1016/0016-7037(94)00354-O, 1995.
Montserrat, F., Renforth, P., Hartmann, J., Leermakers, M., Knops, P., and Meysman, F. J.: Olivine Dissolution in Seawater: Implications for CO2 Sequestration through Enhanced Weathering in Coastal Environments, Environ. Sci. Technol., 51, 3960–3972, https://doi.org/10.1021/acs.est.6b05942, 2017.
Morse, J. W.: Calculation of diffusive fluxes across the sediment-water interface, J. Geophys. Res., 79, 5045–5048, https://doi.org/10.1029/JC079i033p05045, 1974.
Mucci, A.: The solubility of calcite and aragonite in seawater at various salinities, temperatures and one atmosphere total pressure, Am. J. Sci., 283, 780–799, https://doi.org/10.2475/ajs.283.7.780, 1983.
Munhoven, G.: Glacial–interglacial rain ratio changes: Implications for atmospheric and ocean–sediment interaction, Deep-Sea Res. Pt. II, 54, 722–746, https://doi.org/10.1016/j.dsr2.2007.01.008, 2007.
Munhoven, G.: Model of Early Diagenesis in the Upper Sediment with Adaptable complexity – MEDUSA (v. 2): a time-dependent biogeochemical sediment module for Earth system models, process analysis and teaching, Geosci. Model Dev., 14, 3603–3631, https://doi.org/10.5194/gmd-14-3603-2021, 2021.
Naviaux, J. D., Subhas, A. V., Dong, S., Rollins, N. E., Liu, X., Byrne, R. H., Berelson, W. M., and Adkins, J. F.: Calcite dissolution rates in seawater: Lab vs. in-situ measurements and inhibition by organic matter, Mar. Chem., 215, 103684, https://doi.org/10.1016/j.marchem.2019.103684, 2019a.
Naviaux, J. D., Subhas, A. V., Rollins, N. E., Dong, S., Berelson, W. M., and Adkins, J. F.: Temperature dependence of calcite dissolution kinetics in seawater, Geochim. Cosmochim. Ac., 246, 363–384, https://doi.org/10.1016/0016-7037(84)90276-X, 2019b.
Paraska, D. W., Hipsey, M. R., and Salmon, S. U.: Sediment diagenesis models: Review of approaches, challenges and opportunities, Environ. Modell. Softw., 61, 297–325, https://doi.org/10.1016/j.envsoft.2014.05.011, 2014.
Perez, F. F., Fontela, M., García-Ibáñez, M., Mercier, H., Velo, A., Lherminier, P., Zunino, P., de la Paz, M., Alonso-Pérez, F., Guallart, E. F., and Padin, X. A.: Meridional overturning circulation conveys fast acidification to the deep Atlantic Ocean, Nature, 554, 515–518, https://doi.org/10.1038/nature25493, 2018.
Pugh, D. T.: Tides, surges and mean sea level, John Wiley & Sons Ltd., 472 pp., ISBN 13 9780471915058, 1987.
Rabouille, C. and Gaillard, J.-F.: Towards the EDGE: Early diagenetic global explanation. A model depicting the early diagenesis of organic matter, O2, NO3, Mn, and PO4, Geochim. Cosmochim. Ac., 55, 2511–2525, https://doi.org/10.1016/0016-7037(91)90369-G, 1991.
Redfield, A. C.: The biological control of chemical factors in the environment, Am. Sci., 46, 205–221, 1958.
Reimers, C. E.: An in situ microprofiling instrument for measuring interfacial pore water gradients: methods and oxygen profiles from the North Pacific Ocean, Deep-Sea Res., 34, 2023–2035, https://doi.org/10.1016/0198-0149(87)90096-3, 1987.
Revsbech, N. P., Jørgensen, B. B., and Blackburn, T. H.: Oxygen in the Sea Bottom Measured with a Microelectrode, Science, 207, 1355–1356, https://doi.org/10.1126/science.207.4437.1355, 1980.
Riley, J. S., Sanders, R., Marsay, C., Le Moigne, F. A. C., Achterberg, E. P., and Poulton, A. J.: The relative contribution of fast and slow sinking particles to ocean carbon export, Global Biogeochem. Cy., 26, GB1026, https://doi.org/10.1029/2011GB004085, 2012.
Røy, H., Hüttel, M., and Jørgensen, B. B.: The role of small-scale sediment topography for oxygen flux across the diffusive boundary layer, Limnol. Oceanogr., 47, 837–847, https://doi.org/10.4319/lo.2002.47.3.0837, 2002.
Santschi, P. H., Bower, P., Nyffeler, U. P., Azevedo, A., and Broecker, W. S.: Estimates of the resistance to chemical transport posed by the deep-sea boundary layer, Limnol. Oceanogr., 28, 899–912, https://doi.org/10.4319/lo.1983.28.5.0899, 1983.
Santschi, P. H., Anderson, R. F., Fleisher, M. Q., and Bowles, W.: Measurements of diffusive sublayer thicknesses in the ocean by alabaster dissolution, and their implications for the measurements of benthic fluxes, J. Geophys. Res.-Oceans, 96, 10641–10657, https://doi.org/10.1029/91JC00488, 1991.
Sayles, F. L.: The composition and diagenesis of interstitial solutions – I. Fluxes across the seawater-sediment interface in the Atlantic Ocean, Geochim. Cosmochim. Ac., 43, 527–454, https://doi.org/10.1016/0016-7037(79)90163-7, 1979.
Sayles, F. L., Martin, W. R., and Deuser, W. G.: Response of benthic oxygen demand to particulate organic carbon supply in the deep sea near Bermuda, Nature, 371, 686–689, https://doi.org/10.1038/371686a0, 1994.
Sayles, F. L., Martin, W. R., Chase, Z., and Anderson, R. F.: Benthic remineralization and burial of biogenic SiO2, CaCO3, organic carbon, and detrital material in the Southern Ocean along a transect at 170∘ West, Deep-Sea Res. Pt. II, 48, 4323–4383, https://doi.org/10.1016/S0967-0645(01)00091-1, 2001 (data available at: http://usjgofs.whoi.edu/jg/dir/jgofs/southern/nbp98_2/, last access: March 2022).
Schulz, H. D.: Quantification of Early Diagenesis: Dissolved Constituents in Pore Water and Signals in the Solid Phase, in: Marine Geochemistry, edited by: Schulz, H. D. and Zabel, M., Springer, Berlin, Heidelberg, ISBN 13 9783540321439, 2006.
Sillén, L. G., Martell, A. E., and Bjerrum, J.: Stability constants of metal-ion complexes, Special publication, 17 edn., Chemical Society, London, UK, https://doi.org/10.1021/ed042p521.1, 1964.
Smith, C. R. and Rabouille, C.: What controls the mixed-layer depth in deep-sea sediments? The importance of POC flux, Limnol. Oceanogr., 47, 418–426, https://doi.org/10.4319/lo.2002.47.2.0418, 2002.
Smith, C. R., Berelson, W., Demaster, D. J., Dobbs, F. C., Hammond, D., Hoover, D. J., Pope, R. H., and Stephens, M.: Latitudinal variations in benthic processes in the abyssal equatorial Pacific: control by biogenic particle flux, Deep-Sea Res. Pt. II, 44, 2295–2317, https://doi.org/10.1016/S0967-0645(97)00022-2, 1997.
Smith Jr., K. L. and Baldwin, R. J.: Seasonal fluctuations in deep-sea sediment community oxygen consumption: central and eastern North Pacific, Nature, 307, 624–626, https://doi.org/10.1038/307624a0, 1984.
Smith, K. L., Baldwin, R. J., and Williams, P. M.: Reconciling particulate organic carbon flux and sediment community oxygen consumption in the deep North Pacific, Nature, 359, 313–316, https://doi.org/10.1038/359313a0, 1992.
Smith, K. L., Kaufmann, R. S., and Baldwin, R. J.: Coupling of near-bottom pelagic and benthic processes at abyssal depths in the eastern North Pacific Ocean, Limnol. Oceanogr., 39, 1101–1118, https://doi.org/10.4319/lo.1994.39.5.1101, 1994.
Soetaert, K., Herman, P. M. J., and Middelburg, J. J.: Dynamic response of deep-sea sediments to seasonal variations: A model, Limnol. Oceanogr., 41, 1651–1668, https://doi.org/10.4319/lo.1996.41.8.1651, 1996a.
Soetaert, K., Herman, P. M. J., and Middelburg, J. J.: A model of early diagenetic processes from the shelf to abyssal depths, Geochim. Cosmochim. Ac., 60, 1019–1040, https://doi.org/10.1016/0016-7037(96)00013-0, 1996b.
Soetaert, K., Herman, P. M. J., Middelburg, J. J., Heip, C., deStigter, H. S., van Weering, T. C. E., Epping, E., and Helder, W.: Modeling 210Pb-derived mixing activity in ocean margin sediments: Diffusive versus nonlocal mixing, J. Mar. Res., 54, 1207–1227, https://doi.org/10.1357/0022240963213808, 1996c.
Sosna, M., Denuault, G., Pascal, R. W., Prien, R. D., and Mowlem, M.: Development of a reliable microelectrode dissolved oxygen sensor, Sensor. Actuat. B-Chem., 123, 344–351, https://doi.org/10.1016/j.snb.2006.08.033, 2007.
Subhas, A. V., Adkins, J. F., Rollins, N. E., Naviaux, J., Erez, J., and Berelson, W. M.: Catalysis and chemical mechanisms of calcite dissolution in seawater, P. Natl. Acad. Sci. USA, 114, 8175–8180, https://doi.org/10.1073/pnas.1703604114, 2017.
Sulpis, O., Lix, C., Mucci, A., and Boudreau, B. P.: Calcite dissolution kinetics at the sediment-water interface in natural seawater, Mar. Chem., 195, 70–83, https://doi.org/10.1016/j.marchem.2017.06.005, 2017.
Sulpis, O., Boudreau, B. P., Mucci, A., Jenkins, C. J., Trossman, D. S., Arbic, B. K., and Key, R. M.: Current CaCO3 dissolution at the seafloor caused by anthropogenic CO2, P. Natl. Acad. Sci. USA, 115, 11700–11705, https://doi.org/10.1073/pnas.1804250115, 2018.
Sulpis, O., Dufour, C. O., Trossman, D. S., Fassbender, A. J., Arbic, B. K., Boudreau, B. P., Dunne, J. P., and Mucci, A.: Reduced CaCO3 Flux to the Seafloor and Weaker Bottom Current Speeds Curtail Benthic CaCO3 Dissolution Over the 21st Century, Global Biogeochem. Cy., 33, 1654–1673, https://doi.org/10.1029/2019GB006230, 2019.
Sulpis, O., Humphreys, M. P., Wilhelmus, M. M., and Carroll, D.: Radi.m: the reactive-advective-diffusive-irrigative diagenetic sediment module in MATLAB/ GNU Octave, Zenodo [code], https://doi.org/10.5281/zenodo.4739205, 2021.
Teng, Y.-C., Primeau, F. W., Moore, J. K., Lomas, M. W., and Martiny, A. C.: Global-scale variations of the ratios of carbon to phosphorus in exported marine organic matter, Nat. Geosci., 7, 895–898, https://doi.org/10.1038/ngeo2303, 2014.
Thompson, K. F., Miller, K. A., Currie, D., Johnston, P., and Santillo, D.: Seabed Mining and Approaches to Governance of the Deep Seabed, Frontiers in Marine Science, 5, 480, https://doi.org/10.3389/fmars.2018.00480, 2018.
Trimmer, M., Petersen, J., Sivyer, D. B., Mills, C., Young, E., and Parker, E. R.: Impact of long-term benthic trawl disturbance on sediment sorting and biogeochemistry in the southern North Sea, Mar. Ecol. Prog. Ser., 298, 79–94, https://doi.org/10.3354/meps298079, 2005.
Uppström, L. R.: The boron/chlorinity ratio of deep-sea water from the Pacific Ocean, Deep-Sea Res., 21, 161–162, https://doi.org/10.1016/0011-7471(74)90074-6, 1974.
Van Cappellen, P. and Wang, Y.: Cycling of iron and manganese in surface sediments; a general theory for the coupled transport and reaction of carbon, oxygen, nitrogen, sulfur, iron, and manganese, Am. J. Sci., 296, 197–243, https://doi.org/10.2475/ajs.296.3.197, 1996.
van de Velde, S., Van Lancker, V., Hidalgo-Martinez, S., Berelson, W. M., and Meysman, F. J. R.: Anthropogenic disturbance keeps the coastal seafloor biogeochemistry in a transient state, Sci. Rep., 8, 5582, https://doi.org/10.1038/s41598-018-23925-y, 2018.
Walter, L. M. and Morse, J. W.: The dissolution kinetics of shallow marine carbonates in seawater: A laboratory study, Geochim. Cosmochim. Ac., 49, 1503–1513, https://doi.org/10.1016/0016-7037(85)90255-8, 1985.
Wenzhöfer, F., Oguri, K., Middelboe, M., Turnewitsch, R., Toyofuku, T., Kitazato, H., and Glud, R. N.: Benthic carbon mineralization in hadal trenches: Assessment by in situ O2 microprofile measurements, Deep-Sea Res. Pt. I, 116, 276–286, https://doi.org/10.1016/j.dsr.2016.08.013, 2016.
Westrich, J. T. and Berner, R. A.: The role of sedimentary organic matter in bacterial sulfate reduction: The G model tested, Limnol. Oceanogr., 29, 236–249, https://doi.org/10.4319/lo.1984.29.2.0236, 1984.
Yakushev, E. V., Protsenko, E. A., Bruggeman, J., Wallhead, P., Pakhomova, S. V., Yakubov, S. Kh., Bellerby, R. G. J., and Couture, R.-M.: Bottom RedOx Model (BROM v.1.1): a coupled benthic–pelagic model for simulation of water and sediment biogeochemistry, Geosci. Model Dev., 10, 453–482, https://doi.org/10.5194/gmd-10-453-2017, 2017.
Yao, W. and Millero, F. J.: The chemistry of the anoxic waters in the Framvaren Fjord, Norway, Aquat. Geochem., 1, 53–88, https://doi.org/10.1007/BF01025231, 1995.
Zachos, J. C., Röhl, U., Schellenberg, S. A., Sluijs, A., Hodell, D. A., Kelly, D. C., Thomas, E., Nicolo, M., Raffi, I., Lourens, L. J., McCarren, H., and Kroon, D.: Rapid Acidification of the Ocean During the Paleocene-Eocene Thermal Maximum, Science, 308, 1611–1615, https://doi.org/10.1126/science.1109004, 2005.
Zhao, P. and Cai, W.-J.: An Improved Potentiometric pCO2 Microelectrode, Anal. Chem., 69, 2052–5058, https://doi.org/10.1021/ac970747g, 1997.
Zhao, P. and Cai, W.-J.: pH polymeric membrane microelectrodes based on neutral carriers and their application in aquatic environments, Anal. Chim. Acta, 395, 285–291, https://doi.org/10.1016/S0003-2670(99)00359-1, 1999.
Zuddas, P. and Mucci, A.: Kinetics of calcite precipitation from seawater: II. The influence of the ionic strength, Geochim. Cosmochim. Ac., 62, 757–766, https://doi.org/10.1016/S0016-7037(98)00026-X, 1998.