Comparing an exponential respiration model to alternative models for soil respiration components in a Canadian wildfire chronosequence (FireResp v1.0)

Forest fires modify soil organic carbon and suppress soil respiration for many decades after the initial disturbance. The associated changes in soil autotrophic and heterotrophic respiration from the time of the forest fire, however, are less well characterized. The FireResp model predicts soil autotrophic and heterotrophic respiration parameterized with a novel dataset across a fire chronosequence in the Yukon and Northwest Territories of Canada. The dataset consisted of soil incubation experiments and field measurements of soil respiration and soil carbon stocks. The FireResp model contains submodels that consider a Q₁₀ (exponential) model of respiration compared to models of heterotrophic respiration using Michaelis–Menten kinetics parameterized with soil microbial carbon. For model evaluation we applied the Akaike information criterion and compared predicted patterns in components of soil respiration across the chronosequence. Parameters estimated with data from the 5 cm soil depth had better model–data comparisons than parameters estimated with data from the 10 cm soil depth. The model–data fit was improved by including parameters estimated from soil incubation experiments. Models that incorporated microbial carbon with Michaelis–Menten kinetics reproduced patterns in autotrophic and heterotrophic soil respiration components across the chronosequence. Autotrophic respiration was associated with aboveground tree biomass at more recently burned sites, but this association was less robust at older sites in the chronosequence. Our results provide support for more structured soil respiration models than standard Q₁₀ exponential models.

1 Introduction

While containing 15 % of the total global soil area, high-latitude permafrost soils contain a significant proportion of global organic matter and global soil carbon content (Schuur et al., 2008; McGuire et al., 2009). These high-latitude regions are warming faster than the rest of the world, consequentially leading to (1) drier soils during the spring and summer (Masrur et al., 2018), (2) increases in the intensity and frequency of forest fires (Walsh et al., 2020), and (3) destabilization of the permafrost extent (Schuur et al., 2008; McGuire et al., 2009). For these regions, the combination of the above factors may lead to increased release of soil CO₂ into the atmosphere from soil organic matter (Abbott et al., 2016). Soil respiration (denoted here as R_S) represents the product of several semi-independent processes: autotrophic (root) respiration (denoted here as R_A), heterotrophic respiration (denoted here as R_H), and to some extent fungal respiration (Anderson and Domsch, 1973). Heterotrophic respiration consists of microbial respiration of labile carbon and microbial respiration associated with the breakdown of dead organic matter and other by-products (Bosatta and Ågren, 2002; Harmon et al., 2011). Autotrophic and heterotrophic respiration will also be affected by permafrost warming: while R_A is strongly associated with primary productivity (Vargas et al., 2010; Pumpanen et al., 2015), R_H may increase due to priming by newly accessible soil substrate (Fan et al., 2013; Karhu et al., 2016).

In high-latitude forests, soil respiration fluxes and soil carbon stocks exhibit variation depending on the time since the last wildfire (Bond-Lamberty et al., 2004; O'Donnell et al., 2011). Fire modifies soil organic carbon quality, making it harder for microbes to access carbon (Holden et al., 2016; Song et al., 2019; Zhao et al., 2021). A recent meta-analysis by Ribeiro-Kumara et al. (2020b) of 32 studies measuring soil respiration following wildfires indicates two emergent patterns. First, overall soil respiration stabilizes 10–30 years following a fire. Second, for components of soil respiration, R_A will increase and ultimately approach a steady-state value associated with forest succession and vegetation regrowth. On the other hand, R_H may decrease by association with post-fire changes in soil organic matter quality, temperature, or moisture (Aaltonen et al., 2019a, b; Wei et al., 2010). For a sense of the magnitude of these changes, Bond-Lamberty et al. (2004) found the proportion of annual soil respiration: that is, R_A changes from 5 % (following disturbance) to 40 % (21 years post-disturbance), returning to 15 % (150 years post-disturbance). The robustness of any patterns in R_A and R_H is highly uncertain given known soil heterogeneity in these high-latitude soils (e.g., permafrost versus non-permafrost soils, microbial versus fungal species composition).

Observations of overall soil respiration can be linked with process-based soil models to estimate (and perhaps benchmark) R_A and R_H. Models can span a range from empirical models (Köster et al., 2017) to highly structured models of interacting soil microbes (Allison, 2014; Allison et al., 2018). There is agreement that a more detailed structural representation of microbial processes is needed in ecosystem models (Shao et al., 2013; Wieder et al., 2013, 2015; Luo et al., 2016; Vereecken et al., 2016). Improving the structural representation of microbial respiration in Earth system models (e.g., accounting for microbial acclimation to non-equilibrium temperature changes; Zobitz et al., 2008; Wieder et al., 2013; Wang et al., 2021), when appropriately benchmarked with data, may reduce uncertainties in the turnover and stabilization of soil carbon (Wieder et al., 2013; Sihi et al., 2016). However, there are two main challenges to developing and evaluating more complicated soil process models. First, soil incubation studies may lead to underestimation of soil respiration components at larger scales (Reichstein and Beer, 2008; Hamdi et al., 2013; Chakrawal et al., 2020; Jian et al., 2020). Second, more complex models may lead to model equifinality – or when different models yield similar results (Tang and Zhuang, 2008; Famiglietti et al., 2021). The combination of these multiple factors poses challenges for both systematically developing and evaluating different soil respiration models. The objective of many modeling activities (especially for the remote sites studied here) is to strike a balance between modeling complex processes (Burnham and Anderson, 2002; Shiklomanov et al., 2020) while also parameterizing a model with available site measurements.

We have previously measured soil biogeochemical properties (stocks and associated respiration rates) across an established fire chronosequence in the Yukon and Northwest Territories in Canada (Köster et al., 2017; Aaltonen et al., 2019a, b; Zhou et al., 2019). Our previous work focused on empirical associations between respiration and biogeochemical and environmental measurements (e.g., soil organic matter, microbial content, and temperature) across the fire chronosequence. These results included both field measurements and soil incubation studies. For this study we synthesize both types of measurements across the chronosequence to parameterize a process model of R_A and R_H (German et al., 2012; Todd-Brown et al., 2012; Sihi et al., 2016), which we call the FireResp model. The FireResp model contains submodels that represent a continuum of complexity in modeling soil carbon. We investigate two specific hypotheses in this study.

1. Autotrophic respiration is positively associated with the time since disturbance. This positive association is caused by an underlying positive association of R_A with foliage biomass.

2. When tested against observational data, soil models that incorporate microbial carbon will better replicate the observed dynamics and associated fluxes (R_A, R_H, and the ratio $R_{\mathrm{A}}/R_{\mathrm{S}}$) across the fire chronosequence.

To evaluate our hypotheses we combine data from soil incubation experiments (Aaltonen et al., 2019b) with field data (Köster et al., 2017) at chronosequence sites. For both incubation and field data, measurements were collected at the same time from similar plots to minimize any spatial and temporal biases in the data. Submodels are evaluated based on their ability to replicate measured soil respiration (both from incubation and field measurements). To reduce any biases with model fitting or model equifinality (Christiansen, 2018; Marschmann et al., 2019) we evaluate a range of parameter estimation approaches and data types.

2 Methods

2.1 Study sites

In 2015 we established a transect of sites in the northern boreal forests of Canada (Fig. 1). All of these sites are located near Eagle Plains, Yukon (66^∘220^′ N, 136^∘430^′ W), and Tsiigehtchic, Northwest Territories (67^∘260^′ N, 133^∘450^′ W). The mean annual air temperature at these sites is −8.8 ^∘C. The sites are evergreen needle forests dominated by Picea mariana (Mill.) BSP and Picea glauca (Moench) Voss species. Site selection and physical characteristics of the sites are also described in Köster et al. (2017) and Aaltonen et al. (2019b).

Chronosequence sites were selected from the time since the last fire (in 1968, 1990, and 2012) that burned all aboveground vegetation. We also included a control site, where the last fire was more than 100 years ago. The date and boundaries of the fires were determined from geographic data from the Canadian Wildfire Information System (Natural Resources Canada, 2021). We visually corroborated the geographic location of our sites with reported fire boundaries. Previous studies with these data (Köster et al., 2017; Aaltonen et al., 2019b, a; Zhou et al., 2019) classified the 1968 site as 1969, which we attribute to this site being classified by fire season rather than the year of burn. For this paper we will refer to a site as a categorical variable by the year it was burned (2012, 1990, 1968) or the control site, as “control”. sites will be ordered by the fire year (2012, 1990, 1968, or control).

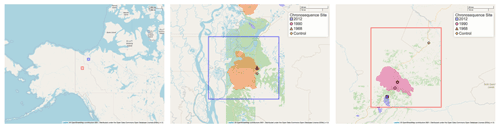
Figure 1 Map of chronosequence site locations in the Yukon and the Northwest Territories of Canada. In the two inset maps the boundaries of the fire areas are shown along with the location of the sampling sites (color-coded the same as the fire areas). Fire boundary areas are determined from geographic data from the Canadian Wildfire Information System (Natural Resources Canada, 2021). The middle inset map also shows additional fire areas burned in 1968 and 2012. Maps provided by OpenStreetMap; © OpenStreetMap contributors 2021. Distributed under the Open Data Commons Open Database License (ODbL) v1.0.

At each site we measured soil temperature, fluxes of CO₂, microbial biomass assays, soil carbon, tree biomass (foliage, branches, and stems), and other auxiliary measurements by establishing three different lines at each site and, within each line, three replicate plots (Köster et al., 2017). Additionally, at each plot, soil samples were collected for further analysis in soil temperature incubation experiments. Roots were excluded from incubation soils; we assume the measured respiration from these samples is R_H. The soil samples were incubated at 1, 7, 13, and 19 ^∘C for 24 h, and the respiration was measured from syringe samples taken at the end of each 24 h period. The method is described in more detail in Aaltonen et al. (2019b).

The field data measured total soil carbon in the top 30 cm, whereas the incubation data included measurements of soil carbon to a given depth (which extended to 50 cm). To determine the total soil carbon to a given depth in the field data we applied a multistep process. This process assumes that the soil carbon profiles in the incubation and field data are similar. First, for the soil carbon in each of the incubation samples (for each replicate line and plot described above) we computed the cumulative proportion of soil carbon (g C m⁻²) to 50 cm (dots in Fig. 2). We acknowledge that soil carbon is present in deeper layers (estimated to be 59 100 g C m⁻² in the top 100 cm at our sites; see Hugelius et al., 2013, and https://bolin.su.se/data/ncscd/, last access: 26 September 2021). However, the objective of this process is a representative empirical estimate of soil carbon for the field data. Second, at each incubation sample we fit a saturating function to the cumulative proportion of soil carbon. The function we fit had the form $y_i=\mathrm{1}-e^{-k{D}_i}$, where y_i is the cumulative proportion of soil carbon at depth D_i in incubation sample i. Third, we computed the median ensemble average and 95 % confidence interval from the saturating functions grouped by chronosequence site (2012, 1990, 1968, and the control sites, Fig. 2). The median ensemble average allowed estimation of the proportion of soil carbon up to a given depth (5 or 10 cm) at each field site (Table 1). These proportions were then used for determining the amount of soil carbon at 5 or 10 cm for the field data.

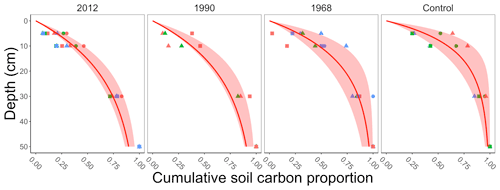
Figure 2 Summary plot of the cumulative proportion of soil carbon collected by depth determined from the incubation data. Each facet represents when a different site in the chronosequence experienced a stand-replacing fire (2012, 1990, 1968, control). The control site was where the last fire was more than 100 years ago. The points in each plot represent a measurement from an incubation sample determined from three different lines (represented by different shapes) at each chronosequence site and, within each line, three replicate plots (represented by different colors; Köster et al., 2017). At each incubation sample we then fit a saturating function for each plot (not shown) and computed the ensemble average for each chronosequence site (median with 95 % confidence interval, red shading) from the fitted results.

The incubation data included measurements of the available soil organic carbon extracted from incubation soils, denoted here as C_A, as described in Zhou et al. (2019). Briefly, soil dissolved organic C content was measured using a total organic C analyzer (Shimadzu TOC-V CPH, Shimadzu Corp., Kyoto, Japan) from soil extracts extracted with 0.5 M K₂SO₄. Microbial carbon used in the FireResp model was extracted using the chloroform fumigation extraction method (Beck et al., 1997). Briefly, 3 g dry weight equivalent of soil was fumigated at 25 ^∘C with ethanol-free chloroform for 24 h and extracted with 0.5 M K₂SO₄. The conversion factor, also known as the extraction efficiency, for estimating the microbial carbon is 0.45 (Beck et al., 1997). For the field data, we approximated C_A as linearly associated with total soil carbon C_S at a given depth, extrapolated from linear regression in the incubation data (results not shown).

For the field samples an estimate of root carbon C_R was assumed to be proportional to total tree biomass collected at each plot (Härkönen et al., 2011; Neumann et al., 2020). A summary of all input variables is reported in Table 1.

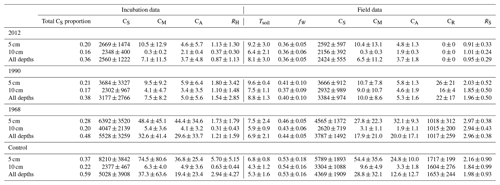
Table 1 Summary of soil measurements for this study organized by site in the chronosequence (2012, 1990, 1968, control) and depth of measurement. The row “All depths” refers to the combination of 5 and 10 cm measurements together. Reported values are averages ± standard deviation of plots from three sample lines. T_soil: soil temperature ^∘C); f_W: volumetric soil moisture (%); C_S: soil carbon (g C m⁻²); C_M: microbial carbon (g C m⁻²); C_A: available soil organic carbon (g C m⁻²); C_R: root carbon (g C m⁻²); R_H: soil heterotrophic respiration from incubation studies (g C m⁻² d⁻¹); R_S: total soil respiration (g C m⁻² d⁻¹).

2.2 Description of FireResp model

The FireResp model predicts plot-level soil respiration (R_S) and its components: autotrophic respiration (R_A), microbial maintenance respiration (R_M), and microbial growth respiration (R_G). All respiration units are reported as g C m⁻² d⁻¹. The FireResp model expresses respiration components with two primary functions; the different combinations of these functions yield different submodels (described in detail below). First, we assume that R_A and R_M both follow an exponential Q₁₀ relationship (Eq. 1) parameterized by soil temperature (T_soil; ^∘C):

$$\begin{array}{}\text{(1)}& R_X=k_X{\mathrm{C}}_X\cdot r\left(f_W\right)\cdot Q_{\mathrm{10},X}^{(T_{\mathrm{soil}}-\mathrm{10})/\mathrm{10}}.\end{array}$$

Equation (1) is a commonly applied (empirical) paradigm for respiration, motivated by temperature dependencies of enzymatic reactions (van't Hoff and Lehfeldt, 1898). This exponential temperature model is applied for R_A and R_M, similar to process models for these components at the ecosystem scale (Aber et al., 1997; Zobitz et al., 2008). The function r(f_W) is an empirical function developed by Moyano et al. (2013) to represent the response of respiration across a range of soil moisture conditions, where f_W represents volumetric soil moisture ( %) and r(f_W)=3.11f_W–$\mathrm{2.42}{f}_W^{\mathrm{2}}$. The variable C_X represents a soil carbon pool (g C m⁻²). For R_A this C_X equals root carbon (C_R); for R_M this C_X equals soil carbon (C_S) or microbial carbon (C_M) depending on the type of submodel considered (e.g., Null, Microbe, Quality, Microbe-mult, or Quality-mult; all described below). Equation (1) has two parameters: k_X, the base rate of respiration (d⁻¹) for pool C_X, and Q_10,X, the temperature response of respiration (Q₁₀ value) (no units) for pool X. To aid the representation of model equations, we will write Eq. (1) as R_X=g_XC_X, where $g_X=k_X{\mathrm{C}}_{X}r\left(f_W\right)Q_{\mathrm{10},X}^{(T_{\mathrm{soil}}-\mathrm{10})/\mathrm{10}}$. As an example, autotrophic respiration R_A would be written as R_A=g_RC_R.

Second, we model microbial growth respiration (R_G) via Michaelis–Menten kinetics (Michaelis and Menten, 1913; Davidson et al., 2006; German et al., 2012):

$$\begin{array}{}\text{(2)}& R_{\mathrm{G}}=\mathit{ϵ}{\displaystyle \frac{\mathit{\mu }{\mathrm{C}}_X{\mathrm{C}}_{\mathrm{M}}}{k_A+{\mathrm{C}}_X}}.\end{array}$$

Equation (2) arises from first-order microbial enzyme kinetics (Allison et al., 2010) under quasi-steady-state assumptions (Keener et al., 2009). In Eq. (2), ϵ is the efficiency converting substrate to microbial biomass (no units), μ is the maximum microbial uptake rate (h⁻¹), k_A (g C m⁻²) represents the half-saturation rate, and C_X represents the substrate for respiration. Depending on the model variant, C_X may be total soil carbon (C_S) or available soil organic carbon (C_A), which represents more labile carbon for ingestion by microbes.

The FireResp model has five different submodels which arise through different combinations of these functional representations of respiration. These submodels are slightly modified from a similar approach in Zobitz et al. (2008).

• Null submodel. The Null submodel assumes soil carbon consists of a single pool (Davidson et al., 1998; Reichstein and Beer, 2008). Here, soil maintenance respiration depends on soil carbon (so R_M=g_SC_S). Microbial carbon is not considered in the Null submodel, so total soil respiration (R_S) is the sum of autotrophic and maintenance respiration (Eq. 3).

  $$\begin{array}{}\text{(3)}& R_{\mathrm{S}}=R_{\mathrm{A}}+R_{\mathrm{M}}=g_{\mathrm{R}}{\mathrm{C}}_{\mathrm{R}}+g_{\mathrm{S}}{\mathrm{C}}_{\mathrm{S}}\end{array}$$

• Microbe submodel. Here, maintenance respiration is proportional to microbial carbon, so R_M=g_MC_M. For growth respiration (R_G) total soil carbon (C_S) is the input for pool C_X in Eq. (2). With these considerations total soil respiration is expressed in Eq. (4).

  $$\begin{array}{}\text{(4)}& R_{\mathrm{S}}=R_{\mathrm{A}}+R_{\mathrm{M}}+R_{\mathrm{G}}=g_{\mathrm{R}}{\mathrm{C}}_{\mathrm{R}}+g_{\mathrm{M}}{\mathrm{C}}_{\mathrm{M}}+\mathit{ϵ}{\displaystyle \frac{\mathit{\mu }{\mathrm{C}}_{\mathrm{S}}{\mathrm{C}}_{\mathrm{M}}}{k_A+{\mathrm{C}}_{\mathrm{S}}}}\end{array}$$

  The Microbe submodel is based on a two-pool soil-microbe model described in Sihi et al. (2016).

• Microbe-mult submodel. This submodel is structured similarly to the Microbe model but with two modifications. First, growth respiration is not considered. Second, maintenance respiration is multiplied by a Michaelis–Menten factor.

  $$\begin{array}{}\text{(5)}& R_{\mathrm{S}}=R_{\mathrm{A}}+R_{\mathrm{M}}=g_{\mathrm{R}}{\mathrm{C}}_{\mathrm{R}}+g_{\mathrm{M}}{\mathrm{C}}_{\mathrm{M}}\cdot {\displaystyle \frac{{\mathrm{C}}_{\mathrm{S}}}{k_{\mathrm{A}}+{\mathrm{C}}_{\mathrm{S}}}}\end{array}$$

  The Microbe-mult model is designed to be an intermediate model between the Null model and the Microbe model. The additional multiplicative factor is a heuristic designed to represent maintenance respiration as substrate limited by C_S.

• Quality submodel.. This submodel is structured similarly to the Microbe model, but for growth respiration (R_G) available soil organic carbon (C_A) is the input for pool C_X in Eq. (2). Total soil respiration is expressed in Eq. (6).

  $$\begin{array}{}\text{(6)}& R_{\mathrm{S}}=R_{\mathrm{A}}+R_{\mathrm{M}}+R_{\mathrm{G}}=g_{\mathrm{R}}{\mathrm{C}}_{\mathrm{R}}+g_{\mathrm{M}}{\mathrm{C}}_{\mathrm{M}}+\mathit{ϵ}{\displaystyle \frac{\mathit{\mu }{\mathrm{C}}_{\mathrm{A}}{\mathrm{C}}_{\mathrm{M}}}{k_{\mathrm{A}}+{\mathrm{C}}_{\mathrm{A}}}}\end{array}$$

  The Quality submodel is based on a multi-pool soil model that structures the soil into different pools based on the recalcitrance and turnover time of the soil parent material, similar to models by Bosatta and Ågren (1985). Inputs from litterfall, enzymatic degradation, root turnover, or root exudation create a pool of available soil organic carbon (C_A) that can be incorporated into microbial biomass. While in this case R_G is represented with Eq. (2), a dynamic model of soil would additionally include expressions for the transformation of each soil pool through enzymatic degradation and mineralization to a more recalcitrant pool (both under first-order kinetics).

• Quality-mult submodel. This submodel is structured similarly to the Quality model with two modifications (similar to the modifications made in the Microbe-mult model). First, growth respiration is not considered. Second, maintenance respiration is multiplied by a Michaelis–Menten factor.

  $$\begin{array}{}\text{(7)}& R_{\mathrm{S}}=R_{\mathrm{A}}+R_{\mathrm{M}}=g_{\mathrm{R}}{\mathrm{C}}_{\mathrm{R}}+g_{\mathrm{M}}{\mathrm{C}}_{\mathrm{M}}\cdot {\displaystyle \frac{{\mathrm{C}}_{\mathrm{A}}}{k_{\mathrm{A}}+{\mathrm{C}}_{\mathrm{A}}}}\end{array}$$

  Like the Microbe-mult model, Quality-mult is a heuristic model designed to represent maintenance respiration as substrate limited by C_A.

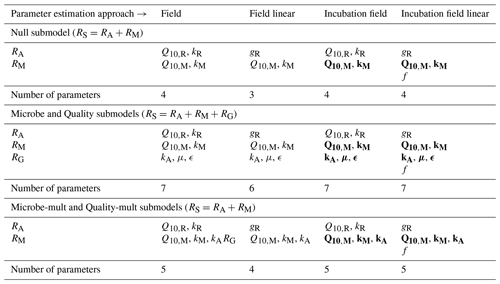
Table 2 summarizes the different parameters for each model and their allowed ranges when estimating parameters.

Table 2 Description of parameters used for the FireResp model along with the allowed range.

^a Denotes a parameter for the incubation field linear parameter estimation approach. ^b Denotes a parameter for the field linear parameter estimation approach.

2.3 Parameter estimation routine

The different submodels (Null, Microbe, Quality, Microbe-mult, and Quality-mult) may be nonlinear with respect to the parameters. For parameter estimation we applied the Levenberg–Marquardt algorithm (Elzhov et al., 2016). The Levenberg–Marquardt algorithm optimizes an objective function, which in this case is the residual sum of squares between measured and modeled soil respiration R_S. The algorithm also requires (1) the Jacobian of the model to accelerate convergence to the optimum value, (2) an initial guess for parameters, (3) and bounds for all parameters.

The Levenberg–Marquardt algorithm may converge to a local (rather than global) optimum, or the estimated parameter values may be at the boundaries of the allowed range. To ensure that parameter estimates converged to a global (rather than local) optimum, initial parameter guesses for the method were drawn from a uniform distribution with reasonable bounds on parameters (Table 2). The Levenberg–Marquardt algorithm is implemented in R with the package nlsr (Nash, 2014; Nash and Murdoch, 2019).

For parameter estimation, we applied a quasi-factorial design with the field and incubation data. This design allowed us to investigate how predictions for autotrophic (R_A) and heterotrophic (R_H) respiration varied when different data are incorporated into the parameter estimation routine. Four different data combinations were used for parameter estimation.

1. Field. All model parameters (e.g., Q_10,M, k_M, k_A, μ, ϵ, k_S, Q_10,R, and k_R, depending on the type of model) were estimated with the field data only.

2. Field linear. Model parameters for R_H (e.g., Q_10,M, k_M, k_A, μ, ϵ, and k_S, depending on the type of model) are estimated with the field data. Rather than a Q₁₀ function for R_A (Eq. 1), for this approach R_A equals g_RC_R, where C_R is provided by the field data. We then estimated g_R from the field data.

3. Incubation field. Two separate parameter estimations were applied. First, model parameters for R_H (e.g., Q_10,M, k_M, k_A, μ, ϵ, and k_S, depending on the type of model) were estimated with the incubation data. Next, autotrophic respiration parameters (Q_10,R and k_R) were estimated from field data.

4. Incubation field linear. Similar to the incubation field approach, parameters relating to R_H were first estimated with incubation data. Next, using these parameter estimates, heterotrophic respiration was computed from the corresponding field measurements (denoted here as R_H,field). Total soil respiration then equals $R_{\mathrm{S}}=g_{\mathrm{R}}{\mathrm{C}}_{\mathrm{R}}+f\cdot R_{\mathrm{H},\mathrm{field}}$, with R_A=g_RC_R and $R_{\mathrm{H}}=f\cdot R_{\mathrm{H},\mathrm{field}}$. We then estimated f and g_R from the field data.

Table 3 shows the relationship between the different parameter estimation approaches studied.

Table 3 Relationship between the different parameter estimation approaches utilized for this study.

Table 4 lists the parameters estimated for each submodel and parameter estimation approach. Data used for parameter estimation consisted of combinations from five different categories of sites (2012, 1990, 1968, control, or all sites together) and three different depths (5 cm, 10 cm, or both depths together). Additionally, with the four different parameter estimation approaches (field, field linear, incubation field, and incubation field linear) and five different submodels (Null, Microbe, Microbe-mult, Quality, and Quality-mult), 300 separate parameter estimations were computed.

When parameters were estimated using (1) the incubation data, (2) field parameter estimation approach, and (3) field linear parameter estimation approach, we applied 1000 iterations of the Levenberg–Marquardt algorithm. Following these iterations we reduced post-processing computational time in two ways. First, duplicated parameter sets were reduced to a single instance. Second, we excluded parameter sets for which the residual sum of squares was outside the 50 % centered confidence interval. For the incubation field and incubation field linear approaches, we used these filtered parameter sets for subsequent estimation of the remaining parameters with field data.

Table 4 Listing of parameters estimated with each submodel and parameter estimation approach. Parameters in bold-face font (incubation and incubation field linear approaches) were estimated from the incubation data first, followed by all remaining parameters with the field data.

2.4 Model evaluation

We applied two different approaches to evaluate the reasonableness of a model–data fit. The first approach relied on Taylor diagrams (Taylor, 2001), which facilitates intercomparison between models when compared to measured values (in this case R_S). The Taylor diagram is structured as a polar coordinate plot; here, the radius ν is the normalized ratio between modeled and measured standard deviation ${\mathit{\sigma }}_{\mathrm{model}}/{\mathit{\sigma }}_{\mathrm{measured}}$ and the angle θ corresponding to the correlation coefficient r for measured and modeled R_S. Two comparisons can be visually inferred from the Taylor diagram. First, the point located at $(\mathit{\nu },\mathit{\theta })=(\mathrm{1},\mathrm{0})$ represents a set of modeled values of R_S that perfectly match measured R_S. Values of ν less than unity indicate that modeled R_S has less variability. Second, the distance from a point on the diagram to $(\mathit{\nu },\mathit{\theta })=(\mathrm{1},\mathrm{0})$ is the centered-pattern root mean square distance. Concentric circles from the point $(\mathit{\nu },\mathit{\theta })=(\mathrm{1},\mathrm{0})$ help assess the centered-pattern root mean square distance for modeled results.

A second approach relies on Akaike's information criterion (AIC) (Akaike, 1974). The AIC is defined as $-\mathrm{2}\cdot \mathrm{LL}+\mathrm{2}\cdot p$, where LL is the log-likelihood and p the number of parameters in the model. The submodel with the lowest AIC is defined as the best approximating model for the data. We apply the AIC to compare across submodels for a parameter estimation approach to control for sample size effects in the AIC.

3 Results

With the different combinations of measurements (incubation or field measurements), FireResp submodels (Sect. 2.2), and parameter estimation approaches (Sect. 2.3) we have over 300 different estimates of the parameters. Parameter estimates were evaluated based on the summary distributions of modeled R_A, R_H, and R_S. Results were evaluated for their reasonableness to produce estimates of R_A and R_H as well as the comparisons between measured and modeled R_S for incubation and field data (Taylor diagrams).

Figure 3 shows the Taylor diagram comparing measured and modeled R_S for the incubation data for each FireResp submodel, faceted by the depth of soil data used for parameter estimation (5 cm, 10 cm, or both). We combined data from all sites in the chronosequence to make these comparisons. In general, most models had high correlation coefficients (≈0.7–0.9); combining all the sites together did not improve the model–data comparisons. Figure 4 is structured similarly to Fig. 3 and compares measured and modeled R_S for each FireResp submodel and parameter estimation approach.

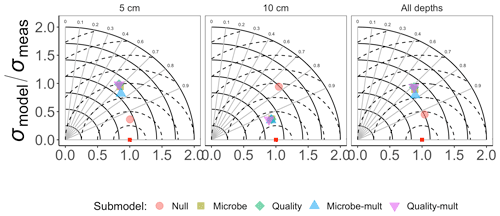
Figure 3 Taylor diagram for comparing measured and modeled R_S for the incubation data for each of the FireResp submodels. Columns in the facetted plot represent the depth of the data used for parameterization (5 cm, 10 cm, or all depths). Radii represent the normalized standard deviation between a FireResp submodel value of R_S and measured R_S; angles represent the correlation coefficient r (labeled). The dashed concentric circles represent contours (increments 0.25) for the normalized centered-pattern root mean square distance.

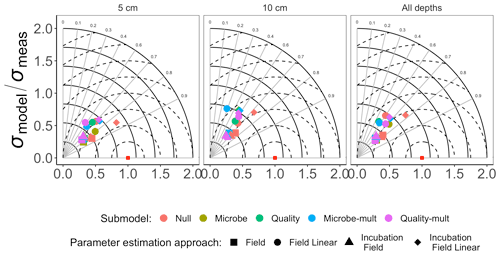
Figure 4 Taylor diagram for comparing measured and modeled R_S for field data for each of the FireResp submodels (colors) and parameter estimation approaches (symbols). Columns in the facetted plot represent the depth of the data used for parameterization (5 cm, 10 cm, or all depths). Radii represent the normalized standard deviation between a FireResp submodel value of R_S and measured R_S; angles represent the correlation coefficient r (labeled). The dashed concentric circles represent contours (increments 0.25) for the normalized centered-pattern root mean square distance.

We used sparkline tables to summarize and compare the panoply of parameter statistics (Fig. 5) and model statistics (adjusted R² and AIC, Fig. 6). In a particular column (parameter) in Fig. 5, the vertical axis is scaled to the ranges of the parameters in Table 2; the horizontal axis is ordered by the time since disturbance (2012, 1990, 1968, or control sites). For ease of presentation, Fig. 5 displays results from the incubation field linear approach at 5 cm; all the model results are presented in the Supplement. Figure 5 also denotes edge-hitting parameters (defined here as within 1 $/$ 10 of a percent of the allowed parameter range) as separate colors. In contrast, Fig. 6 structures each sparkline plot by the submodel studied (Null, Microbe, Quality, Microbe-mult, and Quality-mult), facilitating comparisons between models for a given parameter estimation and depth of data used in the parameter estimation. In Fig. 6, sparkline plots for adjusted R² or AIC values are all respectively scaled the same for each statistic. The models with the largest adjusted R² or lowest AIC value are denoted as separate colors.

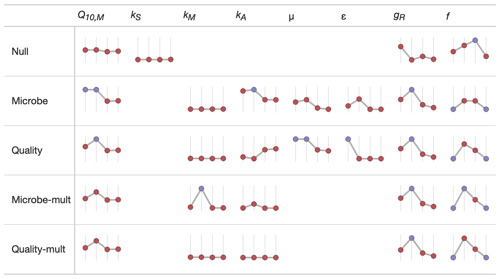
Figure 5 Median values of parameter estimates for different FireResp submodels using the incubation field linear approach at 5 cm of depth. The horizontal axis on each sparkline plot is arranged by the year since the burn in the chronosequence (2012, 1990, 1968, or control). In each column the vertical axis scale is the same. Edge-hitting parameters (defined here as within 1 $/$ 10 of a percent of the allowed parameter range) are denoted with the blue coloring.

Figure 6 Median values of the adjusted R² and AIC from different parameter estimation approaches (field, field linear, incubation field, and incubation field linear) using measurements made at a given depth. The horizontal axis on each sparkline plot is arranged by FireResp submodels (Null, Microbe, Quality, Microbe-mult, and Quality-mult). For the adjusted R² sparkline plot, the vertical axis ranges between 0 and 1, with gridlines every 0.25 units. The submodel with the highest adjusted R² value is denoted with red coloring. For the AIC plots, the vertical axis ranges from 50 to 250, with gridlines every 50 units. The submodel with the lowest AIC is denoted with red coloring.

We computed R_A, R_H, and the proportion of soil respiration due to autotrophic respiration ($p_{\mathrm{A}}=R_{\mathrm{A}}/(R_{\mathrm{A}}+R_{\mathrm{H}})$) for each parameter set generated through the parameter estimation routine (Sect. 2.3). We then computed summary statistics from the distribution of R_A, R_H, and p_A for each parameter estimation approach. Summary results for the median of these distributions for R_A and R_H are shown in Fig. 7, organized by the parameter estimation approach. Additionally, the red shading in Fig. 7 shows the minimum and maximum ranges of measured R_S (lines), first or third quarters (boxes), and median R_S for comparison. Figure 7 visually displays no significant difference in patterns of R_A and R_H by the depth of the soil data used for parameter estimation (5 cm, 10 cm, or both depths together).

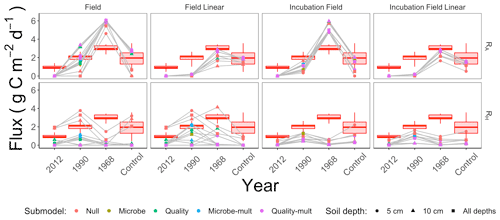
Figure 7 Median modeled fluxes of R_A and R_H from different parameter estimation approaches (field, field linear, incubation field, incubation field linear), soil depth data used for parameter optimization (5 cm, 10 cm, or both depths together), and submodels (Null, Microbe, Quality, Microbe-mult, and Quality-mult). The grey lines are used as a guide to show the chronosequence trend for a particular parameter estimation approach and soil depth. The box plot shows measured ranges of R_S at each site in the chronosequence.

Figure 8 is structured similarly to Fig. 7 but shows $p_{\mathrm{A}}=R_{\mathrm{A}}/(R_{\mathrm{A}}+R_{\mathrm{H}})$, which facilitates better comparison across the different types of approaches to estimate parameters. For comparison, the green boxes show the predicted values of p_A based on R_A and R_H data reported in Fig. 1 of Ribeiro-Kumara et al. (2020b) (available through Mendeley; Ribeiro-Kumara et al., 2020a). We computed the predicted values of p_A from a loess fit using years since disturbance and p_A as variables.

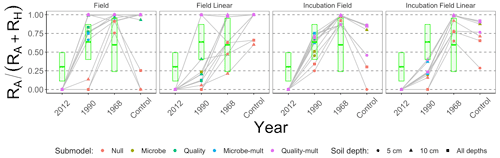
Figure 8 Median contribution of the proportion of autotrophic respiration ($p_{\mathrm{A}}=R_{\mathrm{A}}/R_{\mathrm{S}}$) from different parameter estimation approaches (field, field linear, incubation field, and incubation field linear), soil depth data used for parameter optimization (5 cm, 10 cm, or both depths together), and models (Null, Microbe, Quality, Microbe-mult, and Quality-mult). The crossbar plot shows predicted values of p_A with twice the standard error from data reported in Fig. 1 in Ribeiro-Kumara et al. (2020b).

4 Discussion

Soil models that directly incorporated microbial carbon produced patterns of R_A and R_H that increased from the time since the fire (Fig. 7). As these patterns also conform to changes in root carbon (which was proportional to tree biomass, Table 1), we have initial support for our two primary hypotheses: (1) autotrophic respiration should be positively associated with the time since disturbance because of changes in aboveground foliar vegetation from forest succession, and (2) when tested against observational data, soil models that include soil microbial carbon will better replicate expected patterns for soil respiration components across the chronosequence. We will further evaluate the two hypotheses through subsequent analysis of the data used for parameter estimation, parameter estimation approaches, and the soil respiration models.

4.1 Evaluation of datasets for parameter estimation

We had two categories of datasets for this study: the type of data (incubation or field data) or the depth at which measurements were made (5 cm, 10 cm, or both depths together). This controlled experimental design is also represented in the Taylor diagrams (Fig. 3), which comparatively shows a centered-pattern root mean square distance (distance between a point on the Taylor diagram and $(\mathit{\nu },\mathit{\theta })=(\mathrm{1},\mathrm{0})$) ranging from 0.25–1 and r ranging 0.7–0.9. For the field data (Fig. 4), the centered-pattern root mean square distance ranged from 0.5–1 and r 0.3–0.9. We attributed the differences between Figs. 3 and 4 to the soil temperatures from the incubation experiments spanning 1–19 ^∘C, allowing for a wider temperature range to characterize any exponential temperature profile. In contrast, field measurements ranged from 4–9 ^∘C (Table 1). For both Figs. 3 and 4, the 5 cm depth had higher values for r and a smaller centered-pattern root mean square distance compared to the 10 cm depth.

We did not find any noticeable site differences in submodel outputs depending on the depth of the soil used for data assimilation (5 cm, 10 cm, or both depths together; Figs. 3, 4, 6). While soil model parameters (such as Q₁₀) are expected to vary with soil depth (Pavelka et al., 2007; Graf et al., 2008; Pumpanen et al., 2008) we did not observe any significant depth-dependent differences in parameter estimates (see the figures in the Supplement). The primary reason for this result is that the inter-site variability is larger than the variability by depth at a given site (Table 1 and Fig. 2). We also did not find any improvements in our results when all data from sites were pooled together (Figs. 7 and 8). From these conclusions, we will limit the discussion to evaluating model results generated from data at the 5 cm depth.

4.2 Evaluation of parameter estimation approaches

We cannot eliminate a parameter estimation approach (field, field linear, incubation field, or incubation field linear) simply by the magnitude of the estimated fluxes R_A (Fig. 7). Measured autotrophic respiration in actively growing high-latitude boreal forests (Bond-Lamberty et al., 2004; Vogel et al., 2005, 2014; Pumpanen et al., 2015) or inferred from synthesis studies (Ribeiro-Kumara et al., 2020b; Morgan et al., 2021) can range from 0.5–4 g C m⁻² d⁻¹. Most of the modeled values of R_A for all the parameter estimation approaches are within that range. The incubation field and field parameter estimation approaches predicted higher R_S values outside this range at the 1968 site.

While there is no universal pattern to R_H following forest fire disturbances (Ribeiro-Kumara et al., 2020b), we have reason to believe that the near-zero modeled values for R_H for the 1968 site in Fig. 7 may be an underestimate. For our sites we expect modest, and perhaps decreasing (but not zero), changes in R_H from the time of disturbance for three reasons. First, factors influencing recovery of R_H are burn severity or intensity (Meigs et al., 2009; Hu et al., 2017) and decomposition of pyrogenic litter (Kulmala et al., 2014; Muñoz-Rojas et al., 2016). The fires at our sites combusted a significant amount of soil organic matter (Köster et al., 2017) resistant to decomposition (Knicker, 2007; Aaltonen et al., 2019a), thereby minimizing any increases in R_H from the decomposition of labile litter. Additionally, from this chronosequence, Aaltonen et al. (2019b) reported increased temperature sensitivity (Q_10,M) in recently burned sites, but this was tempered by decreases in soil organic matter quality (Aaltonen et al., 2019a). Second, as succession occurs, the increase in aboveground vegetation insulates the soil, decreasing the active layer and thereby decreasing R_H (Köster et al., 2017). Third, at the same chronosequence sites Zhou et al. (2019) found constant $\mathrm{C}:\mathrm{N}:\mathrm{P}$ and fungal-to-bacterial ratios for microbes, indicating homeostatic regulation of the microbial community. The cumulative effect of these confounding factors may translate into R_H remaining constant across the chronosequence.

Our models implicitly assumed an increasing exponential relationship between temperature and respiration. The temperature sensitivity of respiration (Q₁₀) across ecosystems can vary (usually around 2-5) (Chen and Tian, 2005; Wang et al., 2006; Bond-Lamberty and Thomson, 2010) and is generally expected to be greater than 1, but the Q₁₀ value may decrease as soils warm (Niu et al., 2021). Some degree of additional variability is expected when considering the biochemical or thermodynamic foundations of respiration (Lloyd and Taylor, 1994; Ito et al., 2015), the methodological approach used to measure soil respiration (Ribeiro-Kumara et al., 2020b), or variation in the soil organic matter supply (Davidson et al., 2006).

However, an increasing exponential relationship between temperature and respiration may not be robustly supported by observed data at the chronosequence sites. The forest fires at each site burned a large portion of soil organic matter and killed the roots. Immediately following a fire, R_S will be lower even if there are higher soil temperatures. In late-successional forests, the soil is colder and the active layer depth is shallower, even though there may be more soil respiration due to higher quantities of roots and soil organic matter; we observed such patterns across the chronosequence. The 2012 and 1990 sites had the highest values of T_soil (Table 1) but the lowest overall respiration (Fig. 7). Across the chronosequence, scatterplots of respiration with temperature had a null or negative relationship (results not shown). Empirically the negative association of respiration with temperature would imply a Q₁₀ value less than unity. As a result, to compensate for these opposing tendencies the R_H parameters tend to be edge-hitting (Fig. 5 and the Supplement).

We recommend either the incubation field or incubation field linear parameter estimation approach for two reasons. First, values of the proportion of the respiration that is autotrophic ($p_{\mathrm{A}}=R_{\mathrm{A}}/(R_{\mathrm{A}}+R_{\mathrm{H}})$, Fig. 8) for the field or field linear approaches are unexpectedly and unrealistically large, attributed to the variation in R_H (Fig. 7). As a baseline, Hanson et al. (2000) reported values of $R_{\mathrm{A}}/(R_{\mathrm{A}}+R_{\mathrm{H}})$ to be approximately 0.50, which has also been supported in meta-analyses (Soil Respiration Database, Bond-Lamberty and Thomson, 2010). Second, the incubation field and incubation field linear approaches in Fig. 8 show a temporal pattern in p_A similar to patterns reported in Bond-Lamberty et al. (2004) and the predicted p_A inferred from Ribeiro-Kumara et al. (2020b). The modeled values of p_A are larger at late-successional sites (0.75–1), which may be an effect of the timing of field collection (August) when R_A is at a seasonal peak (Bond-Lamberty et al., 2004; Pumpanen et al., 2015).

4.3 Evaluation of hypotheses

Our first hypothesis concerned the dependence of R_A on tree biomass. We developed this hypothesis from our previous studies, which concluded that tree biomass was a key factor explaining patterns of soil respiration across the chronosequence (Köster et al., 2017; Aaltonen et al., 2019a, b). For all submodels and the field linear or incubation field linear parameter estimation approaches, R_A is proportional to C_R, which is proportional to tree biomass. Values of C_R increase across the chronosequence (Table 1). However, even with this proportional association, the results in Fig. 7 indicate less support for our first hypothesis for two reasons. First, some modeled values R_A at the 1990 site are higher than expected, especially given the association with R_A to C_R. Since C_R is still comparatively low at this site, we might expect R_A (and by association p_A) to be near zero as well. Additionally, the near-zero values of R_A are not a consequence of parameters relating to R_A (k_R, Q_10,R, or g_R) being estimated as zero. (Otherwise, the values for these aforementioned parameters in Fig. 5 or the Supplement for all the different models and approaches would be edge-hitting and indicated with blue-colored dots.) Second, and perhaps more importantly, all parameter estimation approaches in Fig. 7 predict R_A to decrease between the 1968 and control sites. The modeled decreases in R_A are a result of observed decreases in R_S (Fig. 7) as C_S increases. To compensate, estimated parameters k_R or g_R decrease across the chronosequence sites (Fig. 5 or the Supplement). The patterns of k_R or g_R may be due to the parameter estimation routine compensating for the confounding effects of increasing C_R with decreasing R_S. In summary, even though there is evidence for association between R_A and tree biomass in earlier chronosequence sites (2012 and 1990 sites), additional work is needed to explain the reasons for the decline in R_A for later chronosequence sites (1968 and control sites). Future work could quantify field estimates of root mass, production, and turnover (Kalyn and Van Rees, 2006; Steele et al., 1997) to corroborate the values of C_R used here and with the estimated decreases in k_R across the chronosequence.

Our second hypothesis concerns the structural representation of soil respiration for soil models. Our submodels are arranged on a continuum of complexity (Null, Microbe, Quality, Microbe-mult, or Quality-mult). When parameterizing more complex models, parameters may be non-informative and/or edge-hitting (Zobitz et al., 2011). Reducing parameter dimensionality is a key consideration for model–data assimilation in the carbon cycle (Tang and Zhuang, 2008; Luo et al., 2009; Kraemer et al., 2020). Considering the incubation field linear approach only, across the range of submodels the Microbe submodel had the smallest percentage of edge-hitting parameters (10 %), ranging from 30 %–50 % for the other models.

While the AIC suggests a preference towards the Null submodel, we do not believe it is a sufficient criterion to choose it over the Microbe and Quality submodels. There was no noticeable improvement with the Null submodel in the Taylor diagrams for the field data (in both the values of r and the centered-pattern root mean square difference; Fig. 4) or with the adjusted R² or AIC values (Fig. 6). While all models could not account for a majority of the variance in observed soil respiration (the adjusted R² values in Fig. 6 ranged from 0.25–0.61), no submodel significantly improved the adjusted R² or AIC. In other words, the model statistics indicated that the parameter estimation approaches all performed similarly. This model result similarity conforms to a study by Sulman et al. (2018), which synthesized a range of experimental data with different types of process-based models to predict long-term soil organic carbon storage.

A design constraint was to construct models with the greatest potential to be fully parameterized from the collected data. For the Quality-mult and Microbe-mult submodels, k_A was estimated at the lower end of its range (Fig. 5), essentially reducing these models to the Quality and Microbe submodels, respectively. Even though we cannot definitively conclude which of the two submodels (Quality or Microbe) is the better approximating model, we recommend that some consideration of microbial growth and maintenance respiration be considered using Michaelis–Menten kinetics as a starting point (Davidson et al., 2006). Several frameworks already exist for incorporating Michaelis–Menten kinetics (Todd-Brown et al., 2012) or substrate quality degradation (Bosatta and Ågren, 1991, 2002). Continuous (daily or sub-daily) soil respiration measurements could better support more complex soil models (Rayment and Jarvis, 2000; Subke et al., 2006; Subke and Bahn, 2010; Phillips et al., 2011; Pumpanen et al., 2015; Zhang et al., 2015). Each of the models could be incorporated into a dynamic model of ecosystem carbon cycling (Zobitz et al., 2008) that also includes temporal changes in permafrost active layer depth (Zhu et al., 2019).

5 Conclusions

We examined the ability to parameterize a range of soil respiration models using data collected from a fire chronosequence. Importantly, we found support for parameterizing a more complex submodel to replicate patterns in soil respiration and its components across a fire chronosequence. Separate analysis of soils with incubation experiments reduces the number of parameters to be estimated; however, care must be taken in scaling incubation studies to field measurements.

For these high-latitude sites, future work could couple the models here to more continuous measurements of soil temperature along with a dynamic active layer depth model (Zhu et al., 2019). These modeling approaches could examine the effects of gross primary productivity on soil respiration components (Zhuang et al., 2002; Pumpanen et al., 2003; Vargas et al., 2010; Pumpanen et al., 2015; Phillips et al., 2017). For sites that cannot be instrumented continuously (such as the ones studied here), this model–data integration could be supported with periodic surveys of aboveground biomass and other remote sensing data (Neumann et al., 2020).