the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Comparing an exponential respiration model to alternative models for soil respiration components in a Canadian wildfire chronosequence (FireResp v1.0)
John Zobitz
Heidi Aaltonen
Xuan Zhou
Frank Berninger
Jukka Pumpanen
Forest fires modify soil organic carbon and suppress soil respiration for many decades after the initial disturbance. The associated changes in soil autotrophic and heterotrophic respiration from the time of the forest fire, however, are less well characterized. The FireResp model predicts soil autotrophic and heterotrophic respiration parameterized with a novel dataset across a fire chronosequence in the Yukon and Northwest Territories of Canada. The dataset consisted of soil incubation experiments and field measurements of soil respiration and soil carbon stocks. The FireResp model contains submodels that consider a Q10 (exponential) model of respiration compared to models of heterotrophic respiration using Michaelis–Menten kinetics parameterized with soil microbial carbon. For model evaluation we applied the Akaike information criterion and compared predicted patterns in components of soil respiration across the chronosequence. Parameters estimated with data from the 5 cm soil depth had better model–data comparisons than parameters estimated with data from the 10 cm soil depth. The model–data fit was improved by including parameters estimated from soil incubation experiments. Models that incorporated microbial carbon with Michaelis–Menten kinetics reproduced patterns in autotrophic and heterotrophic soil respiration components across the chronosequence. Autotrophic respiration was associated with aboveground tree biomass at more recently burned sites, but this association was less robust at older sites in the chronosequence. Our results provide support for more structured soil respiration models than standard Q10 exponential models.
- Article
(2218 KB) - Full-text XML
-
Supplement
(1164 KB) - BibTeX
- EndNote
While containing 15 % of the total global soil area, high-latitude permafrost soils contain a significant proportion of global organic matter and global soil carbon content (Schuur et al., 2008; McGuire et al., 2009). These high-latitude regions are warming faster than the rest of the world, consequentially leading to (1) drier soils during the spring and summer (Masrur et al., 2018), (2) increases in the intensity and frequency of forest fires (Walsh et al., 2020), and (3) destabilization of the permafrost extent (Schuur et al., 2008; McGuire et al., 2009). For these regions, the combination of the above factors may lead to increased release of soil CO2 into the atmosphere from soil organic matter (Abbott et al., 2016). Soil respiration (denoted here as RS) represents the product of several semi-independent processes: autotrophic (root) respiration (denoted here as RA), heterotrophic respiration (denoted here as RH), and to some extent fungal respiration (Anderson and Domsch, 1973). Heterotrophic respiration consists of microbial respiration of labile carbon and microbial respiration associated with the breakdown of dead organic matter and other by-products (Bosatta and Ågren, 2002; Harmon et al., 2011). Autotrophic and heterotrophic respiration will also be affected by permafrost warming: while RA is strongly associated with primary productivity (Vargas et al., 2010; Pumpanen et al., 2015), RH may increase due to priming by newly accessible soil substrate (Fan et al., 2013; Karhu et al., 2016).
In high-latitude forests, soil respiration fluxes and soil carbon stocks exhibit variation depending on the time since the last wildfire (Bond-Lamberty et al., 2004; O'Donnell et al., 2011). Fire modifies soil organic carbon quality, making it harder for microbes to access carbon (Holden et al., 2016; Song et al., 2019; Zhao et al., 2021). A recent meta-analysis by Ribeiro-Kumara et al. (2020b) of 32 studies measuring soil respiration following wildfires indicates two emergent patterns. First, overall soil respiration stabilizes 10–30 years following a fire. Second, for components of soil respiration, RA will increase and ultimately approach a steady-state value associated with forest succession and vegetation regrowth. On the other hand, RH may decrease by association with post-fire changes in soil organic matter quality, temperature, or moisture (Aaltonen et al., 2019a, b; Wei et al., 2010). For a sense of the magnitude of these changes, Bond-Lamberty et al. (2004) found the proportion of annual soil respiration: that is, RA changes from 5 % (following disturbance) to 40 % (21 years post-disturbance), returning to 15 % (150 years post-disturbance). The robustness of any patterns in RA and RH is highly uncertain given known soil heterogeneity in these high-latitude soils (e.g., permafrost versus non-permafrost soils, microbial versus fungal species composition).
Observations of overall soil respiration can be linked with process-based soil models to estimate (and perhaps benchmark) RA and RH. Models can span a range from empirical models (Köster et al., 2017) to highly structured models of interacting soil microbes (Allison, 2014; Allison et al., 2018). There is agreement that a more detailed structural representation of microbial processes is needed in ecosystem models (Shao et al., 2013; Wieder et al., 2013, 2015; Luo et al., 2016; Vereecken et al., 2016). Improving the structural representation of microbial respiration in Earth system models (e.g., accounting for microbial acclimation to non-equilibrium temperature changes; Zobitz et al., 2008; Wieder et al., 2013; Wang et al., 2021), when appropriately benchmarked with data, may reduce uncertainties in the turnover and stabilization of soil carbon (Wieder et al., 2013; Sihi et al., 2016). However, there are two main challenges to developing and evaluating more complicated soil process models. First, soil incubation studies may lead to underestimation of soil respiration components at larger scales (Reichstein and Beer, 2008; Hamdi et al., 2013; Chakrawal et al., 2020; Jian et al., 2020). Second, more complex models may lead to model equifinality – or when different models yield similar results (Tang and Zhuang, 2008; Famiglietti et al., 2021). The combination of these multiple factors poses challenges for both systematically developing and evaluating different soil respiration models. The objective of many modeling activities (especially for the remote sites studied here) is to strike a balance between modeling complex processes (Burnham and Anderson, 2002; Shiklomanov et al., 2020) while also parameterizing a model with available site measurements.
We have previously measured soil biogeochemical properties (stocks and associated respiration rates) across an established fire chronosequence in the Yukon and Northwest Territories in Canada (Köster et al., 2017; Aaltonen et al., 2019a, b; Zhou et al., 2019). Our previous work focused on empirical associations between respiration and biogeochemical and environmental measurements (e.g., soil organic matter, microbial content, and temperature) across the fire chronosequence. These results included both field measurements and soil incubation studies. For this study we synthesize both types of measurements across the chronosequence to parameterize a process model of RA and RH (German et al., 2012; Todd-Brown et al., 2012; Sihi et al., 2016), which we call the FireResp model. The FireResp model contains submodels that represent a continuum of complexity in modeling soil carbon. We investigate two specific hypotheses in this study.
-
Autotrophic respiration is positively associated with the time since disturbance. This positive association is caused by an underlying positive association of RA with foliage biomass.
-
When tested against observational data, soil models that incorporate microbial carbon will better replicate the observed dynamics and associated fluxes (RA, RH, and the ratio ) across the fire chronosequence.
To evaluate our hypotheses we combine data from soil incubation experiments (Aaltonen et al., 2019b) with field data (Köster et al., 2017) at chronosequence sites. For both incubation and field data, measurements were collected at the same time from similar plots to minimize any spatial and temporal biases in the data. Submodels are evaluated based on their ability to replicate measured soil respiration (both from incubation and field measurements). To reduce any biases with model fitting or model equifinality (Christiansen, 2018; Marschmann et al., 2019) we evaluate a range of parameter estimation approaches and data types.
2.1 Study sites
In 2015 we established a transect of sites in the northern boreal forests of Canada (Fig. 1). All of these sites are located near Eagle Plains, Yukon (66∘220′ N, 136∘430′ W), and Tsiigehtchic, Northwest Territories (67∘260′ N, 133∘450′ W). The mean annual air temperature at these sites is −8.8 ∘C. The sites are evergreen needle forests dominated by Picea mariana (Mill.) BSP and Picea glauca (Moench) Voss species. Site selection and physical characteristics of the sites are also described in Köster et al. (2017) and Aaltonen et al. (2019b).
Chronosequence sites were selected from the time since the last fire (in 1968, 1990, and 2012) that burned all aboveground vegetation. We also included a control site, where the last fire was more than 100 years ago. The date and boundaries of the fires were determined from geographic data from the Canadian Wildfire Information System (Natural Resources Canada, 2021). We visually corroborated the geographic location of our sites with reported fire boundaries. Previous studies with these data (Köster et al., 2017; Aaltonen et al., 2019b, a; Zhou et al., 2019) classified the 1968 site as 1969, which we attribute to this site being classified by fire season rather than the year of burn. For this paper we will refer to a site as a categorical variable by the year it was burned (2012, 1990, 1968) or the control site, as “control”. sites will be ordered by the fire year (2012, 1990, 1968, or control).
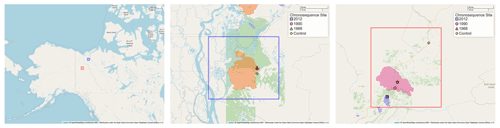
Figure 1Map of chronosequence site locations in the Yukon and the Northwest Territories of Canada. In the two inset maps the boundaries of the fire areas are shown along with the location of the sampling sites (color-coded the same as the fire areas). Fire boundary areas are determined from geographic data from the Canadian Wildfire Information System (Natural Resources Canada, 2021). The middle inset map also shows additional fire areas burned in 1968 and 2012. Maps provided by OpenStreetMap; © OpenStreetMap contributors 2021. Distributed under the Open Data Commons Open Database License (ODbL) v1.0.
At each site we measured soil temperature, fluxes of CO2, microbial biomass assays, soil carbon, tree biomass (foliage, branches, and stems), and other auxiliary measurements by establishing three different lines at each site and, within each line, three replicate plots (Köster et al., 2017). Additionally, at each plot, soil samples were collected for further analysis in soil temperature incubation experiments. Roots were excluded from incubation soils; we assume the measured respiration from these samples is RH. The soil samples were incubated at 1, 7, 13, and 19 ∘C for 24 h, and the respiration was measured from syringe samples taken at the end of each 24 h period. The method is described in more detail in Aaltonen et al. (2019b).
The field data measured total soil carbon in the top 30 cm, whereas the incubation data included measurements of soil carbon to a given depth (which extended to 50 cm). To determine the total soil carbon to a given depth in the field data we applied a multistep process. This process assumes that the soil carbon profiles in the incubation and field data are similar. First, for the soil carbon in each of the incubation samples (for each replicate line and plot described above) we computed the cumulative proportion of soil carbon (g C m−2) to 50 cm (dots in Fig. 2). We acknowledge that soil carbon is present in deeper layers (estimated to be 59 100 g C m−2 in the top 100 cm at our sites; see Hugelius et al., 2013, and https://bolin.su.se/data/ncscd/, last access: 26 September 2021). However, the objective of this process is a representative empirical estimate of soil carbon for the field data. Second, at each incubation sample we fit a saturating function to the cumulative proportion of soil carbon. The function we fit had the form , where yi is the cumulative proportion of soil carbon at depth Di in incubation sample i. Third, we computed the median ensemble average and 95 % confidence interval from the saturating functions grouped by chronosequence site (2012, 1990, 1968, and the control sites, Fig. 2). The median ensemble average allowed estimation of the proportion of soil carbon up to a given depth (5 or 10 cm) at each field site (Table 1). These proportions were then used for determining the amount of soil carbon at 5 or 10 cm for the field data.
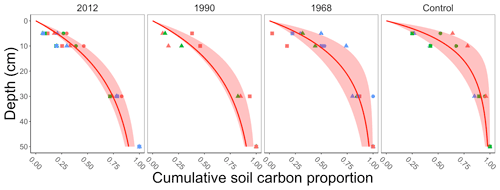
Figure 2Summary plot of the cumulative proportion of soil carbon collected by depth determined from the incubation data. Each facet represents when a different site in the chronosequence experienced a stand-replacing fire (2012, 1990, 1968, control). The control site was where the last fire was more than 100 years ago. The points in each plot represent a measurement from an incubation sample determined from three different lines (represented by different shapes) at each chronosequence site and, within each line, three replicate plots (represented by different colors; Köster et al., 2017). At each incubation sample we then fit a saturating function for each plot (not shown) and computed the ensemble average for each chronosequence site (median with 95 % confidence interval, red shading) from the fitted results.
The incubation data included measurements of the available soil organic carbon extracted from incubation soils, denoted here as CA, as described in Zhou et al. (2019). Briefly, soil dissolved organic C content was measured using a total organic C analyzer (Shimadzu TOC-V CPH, Shimadzu Corp., Kyoto, Japan) from soil extracts extracted with 0.5 M K2SO4. Microbial carbon used in the FireResp model was extracted using the chloroform fumigation extraction method (Beck et al., 1997). Briefly, 3 g dry weight equivalent of soil was fumigated at 25 ∘C with ethanol-free chloroform for 24 h and extracted with 0.5 M K2SO4. The conversion factor, also known as the extraction efficiency, for estimating the microbial carbon is 0.45 (Beck et al., 1997). For the field data, we approximated CA as linearly associated with total soil carbon CS at a given depth, extrapolated from linear regression in the incubation data (results not shown).
For the field samples an estimate of root carbon CR was assumed to be proportional to total tree biomass collected at each plot (Härkönen et al., 2011; Neumann et al., 2020). A summary of all input variables is reported in Table 1.
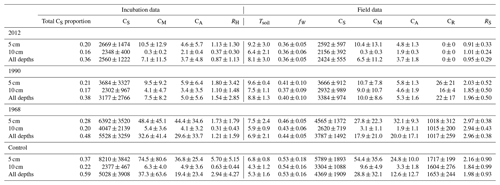
Table 1Summary of soil measurements for this study organized by site in the chronosequence (2012, 1990, 1968, control) and depth of measurement. The row “All depths” refers to the combination of 5 and 10 cm measurements together. Reported values are averages ± standard deviation of plots from three sample lines. Tsoil: soil temperature ∘C); fW: volumetric soil moisture (%); CS: soil carbon (g C m−2); CM: microbial carbon (g C m−2); CA: available soil organic carbon (g C m−2); CR: root carbon (g C m−2); RH: soil heterotrophic respiration from incubation studies (g C m−2 d−1); RS: total soil respiration (g C m−2 d−1).
2.2 Description of FireResp model
The FireResp model predicts plot-level soil respiration (RS) and its components: autotrophic respiration (RA), microbial maintenance respiration (RM), and microbial growth respiration (RG). All respiration units are reported as g C m−2 d−1. The FireResp model expresses respiration components with two primary functions; the different combinations of these functions yield different submodels (described in detail below). First, we assume that RA and RM both follow an exponential Q10 relationship (Eq. 1) parameterized by soil temperature (Tsoil; ∘C):
Equation (1) is a commonly applied (empirical) paradigm for respiration, motivated by temperature dependencies of enzymatic reactions (van't Hoff and Lehfeldt, 1898). This exponential temperature model is applied for RA and RM, similar to process models for these components at the ecosystem scale (Aber et al., 1997; Zobitz et al., 2008). The function r(fW) is an empirical function developed by Moyano et al. (2013) to represent the response of respiration across a range of soil moisture conditions, where fW represents volumetric soil moisture ( %) and r(fW)=3.11fW–. The variable CX represents a soil carbon pool (g C m−2). For RA this CX equals root carbon (CR); for RM this CX equals soil carbon (CS) or microbial carbon (CM) depending on the type of submodel considered (e.g., Null, Microbe, Quality, Microbe-mult, or Quality-mult; all described below). Equation (1) has two parameters: kX, the base rate of respiration (d−1) for pool CX, and Q10,X, the temperature response of respiration (Q10 value) (no units) for pool X. To aid the representation of model equations, we will write Eq. (1) as RX=gXCX, where . As an example, autotrophic respiration RA would be written as RA=gRCR.
Second, we model microbial growth respiration (RG) via Michaelis–Menten kinetics (Michaelis and Menten, 1913; Davidson et al., 2006; German et al., 2012):
Equation (2) arises from first-order microbial enzyme kinetics (Allison et al., 2010) under quasi-steady-state assumptions (Keener et al., 2009). In Eq. (2), ϵ is the efficiency converting substrate to microbial biomass (no units), μ is the maximum microbial uptake rate (h−1), kA (g C m−2) represents the half-saturation rate, and CX represents the substrate for respiration. Depending on the model variant, CX may be total soil carbon (CS) or available soil organic carbon (CA), which represents more labile carbon for ingestion by microbes.
The FireResp model has five different submodels which arise through different combinations of these functional representations of respiration. These submodels are slightly modified from a similar approach in Zobitz et al. (2008).
-
Null submodel. The Null submodel assumes soil carbon consists of a single pool (Davidson et al., 1998; Reichstein and Beer, 2008). Here, soil maintenance respiration depends on soil carbon (so RM=gSCS). Microbial carbon is not considered in the Null submodel, so total soil respiration (RS) is the sum of autotrophic and maintenance respiration (Eq. 3).
-
Microbe submodel. Here, maintenance respiration is proportional to microbial carbon, so RM=gMCM. For growth respiration (RG) total soil carbon (CS) is the input for pool CX in Eq. (2). With these considerations total soil respiration is expressed in Eq. (4).
The Microbe submodel is based on a two-pool soil-microbe model described in Sihi et al. (2016).
-
Microbe-mult submodel. This submodel is structured similarly to the Microbe model but with two modifications. First, growth respiration is not considered. Second, maintenance respiration is multiplied by a Michaelis–Menten factor.
The Microbe-mult model is designed to be an intermediate model between the Null model and the Microbe model. The additional multiplicative factor is a heuristic designed to represent maintenance respiration as substrate limited by CS.
-
Quality submodel.. This submodel is structured similarly to the Microbe model, but for growth respiration (RG) available soil organic carbon (CA) is the input for pool CX in Eq. (2). Total soil respiration is expressed in Eq. (6).
The Quality submodel is based on a multi-pool soil model that structures the soil into different pools based on the recalcitrance and turnover time of the soil parent material, similar to models by Bosatta and Ågren (1985). Inputs from litterfall, enzymatic degradation, root turnover, or root exudation create a pool of available soil organic carbon (CA) that can be incorporated into microbial biomass. While in this case RG is represented with Eq. (2), a dynamic model of soil would additionally include expressions for the transformation of each soil pool through enzymatic degradation and mineralization to a more recalcitrant pool (both under first-order kinetics).
-
Quality-mult submodel. This submodel is structured similarly to the Quality model with two modifications (similar to the modifications made in the Microbe-mult model). First, growth respiration is not considered. Second, maintenance respiration is multiplied by a Michaelis–Menten factor.
Like the Microbe-mult model, Quality-mult is a heuristic model designed to represent maintenance respiration as substrate limited by CA.
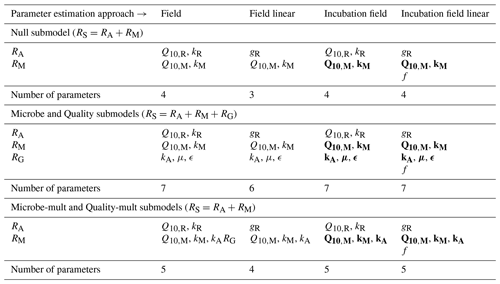
Table 2 summarizes the different parameters for each model and their allowed ranges when estimating parameters.
2.3 Parameter estimation routine
The different submodels (Null, Microbe, Quality, Microbe-mult, and Quality-mult) may be nonlinear with respect to the parameters. For parameter estimation we applied the Levenberg–Marquardt algorithm (Elzhov et al., 2016). The Levenberg–Marquardt algorithm optimizes an objective function, which in this case is the residual sum of squares between measured and modeled soil respiration RS. The algorithm also requires (1) the Jacobian of the model to accelerate convergence to the optimum value, (2) an initial guess for parameters, (3) and bounds for all parameters.
The Levenberg–Marquardt algorithm may converge to a local (rather than global) optimum, or the estimated parameter values may be at the boundaries of the allowed range. To ensure that parameter estimates converged to a global (rather than local) optimum, initial parameter guesses for the method were drawn from a uniform distribution with reasonable bounds on parameters (Table 2). The Levenberg–Marquardt algorithm is implemented in R with the package nlsr (Nash, 2014; Nash and Murdoch, 2019).
For parameter estimation, we applied a quasi-factorial design with the field and incubation data. This design allowed us to investigate how predictions for autotrophic (RA) and heterotrophic (RH) respiration varied when different data are incorporated into the parameter estimation routine. Four different data combinations were used for parameter estimation.
-
Field. All model parameters (e.g., Q10,M, kM, kA, μ, ϵ, kS, Q10,R, and kR, depending on the type of model) were estimated with the field data only.
-
Field linear. Model parameters for RH (e.g., Q10,M, kM, kA, μ, ϵ, and kS, depending on the type of model) are estimated with the field data. Rather than a Q10 function for RA (Eq. 1), for this approach RA equals gRCR, where CR is provided by the field data. We then estimated gR from the field data.
-
Incubation field. Two separate parameter estimations were applied. First, model parameters for RH (e.g., Q10,M, kM, kA, μ, ϵ, and kS, depending on the type of model) were estimated with the incubation data. Next, autotrophic respiration parameters (Q10,R and kR) were estimated from field data.
-
Incubation field linear. Similar to the incubation field approach, parameters relating to RH were first estimated with incubation data. Next, using these parameter estimates, heterotrophic respiration was computed from the corresponding field measurements (denoted here as RH,field). Total soil respiration then equals , with RA=gRCR and . We then estimated f and gR from the field data.
Table 3 shows the relationship between the different parameter estimation approaches studied.
Table 4 lists the parameters estimated for each submodel and parameter estimation approach. Data used for parameter estimation consisted of combinations from five different categories of sites (2012, 1990, 1968, control, or all sites together) and three different depths (5 cm, 10 cm, or both depths together). Additionally, with the four different parameter estimation approaches (field, field linear, incubation field, and incubation field linear) and five different submodels (Null, Microbe, Microbe-mult, Quality, and Quality-mult), 300 separate parameter estimations were computed.
When parameters were estimated using (1) the incubation data, (2) field parameter estimation approach, and (3) field linear parameter estimation approach, we applied 1000 iterations of the Levenberg–Marquardt algorithm. Following these iterations we reduced post-processing computational time in two ways. First, duplicated parameter sets were reduced to a single instance. Second, we excluded parameter sets for which the residual sum of squares was outside the 50 % centered confidence interval. For the incubation field and incubation field linear approaches, we used these filtered parameter sets for subsequent estimation of the remaining parameters with field data.
2.4 Model evaluation
We applied two different approaches to evaluate the reasonableness of a model–data fit. The first approach relied on Taylor diagrams (Taylor, 2001), which facilitates intercomparison between models when compared to measured values (in this case RS). The Taylor diagram is structured as a polar coordinate plot; here, the radius ν is the normalized ratio between modeled and measured standard deviation and the angle θ corresponding to the correlation coefficient r for measured and modeled RS. Two comparisons can be visually inferred from the Taylor diagram. First, the point located at represents a set of modeled values of RS that perfectly match measured RS. Values of ν less than unity indicate that modeled RS has less variability. Second, the distance from a point on the diagram to is the centered-pattern root mean square distance. Concentric circles from the point help assess the centered-pattern root mean square distance for modeled results.
A second approach relies on Akaike's information criterion (AIC) (Akaike, 1974). The AIC is defined as , where LL is the log-likelihood and p the number of parameters in the model. The submodel with the lowest AIC is defined as the best approximating model for the data. We apply the AIC to compare across submodels for a parameter estimation approach to control for sample size effects in the AIC.
With the different combinations of measurements (incubation or field measurements), FireResp submodels (Sect. 2.2), and parameter estimation approaches (Sect. 2.3) we have over 300 different estimates of the parameters. Parameter estimates were evaluated based on the summary distributions of modeled RA, RH, and RS. Results were evaluated for their reasonableness to produce estimates of RA and RH as well as the comparisons between measured and modeled RS for incubation and field data (Taylor diagrams).
Figure 3 shows the Taylor diagram comparing measured and modeled RS for the incubation data for each FireResp submodel, faceted by the depth of soil data used for parameter estimation (5 cm, 10 cm, or both). We combined data from all sites in the chronosequence to make these comparisons. In general, most models had high correlation coefficients (≈0.7–0.9); combining all the sites together did not improve the model–data comparisons. Figure 4 is structured similarly to Fig. 3 and compares measured and modeled RS for each FireResp submodel and parameter estimation approach.
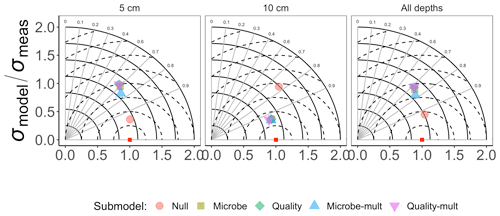
Figure 3Taylor diagram for comparing measured and modeled RS for the incubation data for each of the FireResp submodels. Columns in the facetted plot represent the depth of the data used for parameterization (5 cm, 10 cm, or all depths). Radii represent the normalized standard deviation between a FireResp submodel value of RS and measured RS; angles represent the correlation coefficient r (labeled). The dashed concentric circles represent contours (increments 0.25) for the normalized centered-pattern root mean square distance.
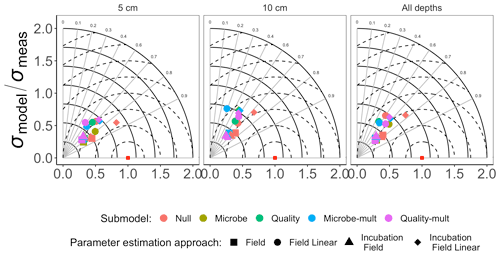
Figure 4Taylor diagram for comparing measured and modeled RS for field data for each of the FireResp submodels (colors) and parameter estimation approaches (symbols). Columns in the facetted plot represent the depth of the data used for parameterization (5 cm, 10 cm, or all depths). Radii represent the normalized standard deviation between a FireResp submodel value of RS and measured RS; angles represent the correlation coefficient r (labeled). The dashed concentric circles represent contours (increments 0.25) for the normalized centered-pattern root mean square distance.
We used sparkline tables to summarize and compare the panoply of parameter statistics (Fig. 5) and model statistics (adjusted R2 and AIC, Fig. 6). In a particular column (parameter) in Fig. 5, the vertical axis is scaled to the ranges of the parameters in Table 2; the horizontal axis is ordered by the time since disturbance (2012, 1990, 1968, or control sites). For ease of presentation, Fig. 5 displays results from the incubation field linear approach at 5 cm; all the model results are presented in the Supplement. Figure 5 also denotes edge-hitting parameters (defined here as within 1 10 of a percent of the allowed parameter range) as separate colors. In contrast, Fig. 6 structures each sparkline plot by the submodel studied (Null, Microbe, Quality, Microbe-mult, and Quality-mult), facilitating comparisons between models for a given parameter estimation and depth of data used in the parameter estimation. In Fig. 6, sparkline plots for adjusted R2 or AIC values are all respectively scaled the same for each statistic. The models with the largest adjusted R2 or lowest AIC value are denoted as separate colors.
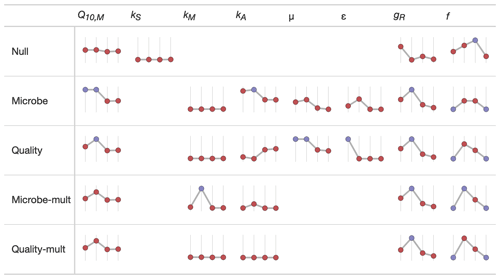
Figure 5Median values of parameter estimates for different FireResp submodels using the incubation field linear approach at 5 cm of depth. The horizontal axis on each sparkline plot is arranged by the year since the burn in the chronosequence (2012, 1990, 1968, or control). In each column the vertical axis scale is the same. Edge-hitting parameters (defined here as within 1 10 of a percent of the allowed parameter range) are denoted with the blue coloring.

Figure 6Median values of the adjusted R2 and AIC from different parameter estimation approaches (field, field linear, incubation field, and incubation field linear) using measurements made at a given depth. The horizontal axis on each sparkline plot is arranged by FireResp submodels (Null, Microbe, Quality, Microbe-mult, and Quality-mult). For the adjusted R2 sparkline plot, the vertical axis ranges between 0 and 1, with gridlines every 0.25 units. The submodel with the highest adjusted R2 value is denoted with red coloring. For the AIC plots, the vertical axis ranges from 50 to 250, with gridlines every 50 units. The submodel with the lowest AIC is denoted with red coloring.
We computed RA, RH, and the proportion of soil respiration due to autotrophic respiration () for each parameter set generated through the parameter estimation routine (Sect. 2.3). We then computed summary statistics from the distribution of RA, RH, and pA for each parameter estimation approach. Summary results for the median of these distributions for RA and RH are shown in Fig. 7, organized by the parameter estimation approach. Additionally, the red shading in Fig. 7 shows the minimum and maximum ranges of measured RS (lines), first or third quarters (boxes), and median RS for comparison. Figure 7 visually displays no significant difference in patterns of RA and RH by the depth of the soil data used for parameter estimation (5 cm, 10 cm, or both depths together).
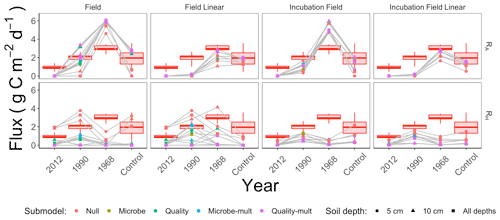
Figure 7Median modeled fluxes of RA and RH from different parameter estimation approaches (field, field linear, incubation field, incubation field linear), soil depth data used for parameter optimization (5 cm, 10 cm, or both depths together), and submodels (Null, Microbe, Quality, Microbe-mult, and Quality-mult). The grey lines are used as a guide to show the chronosequence trend for a particular parameter estimation approach and soil depth. The box plot shows measured ranges of RS at each site in the chronosequence.
Figure 8 is structured similarly to Fig. 7 but shows , which facilitates better comparison across the different types of approaches to estimate parameters. For comparison, the green boxes show the predicted values of pA based on RA and RH data reported in Fig. 1 of Ribeiro-Kumara et al. (2020b) (available through Mendeley; Ribeiro-Kumara et al., 2020a). We computed the predicted values of pA from a loess fit using years since disturbance and pA as variables.
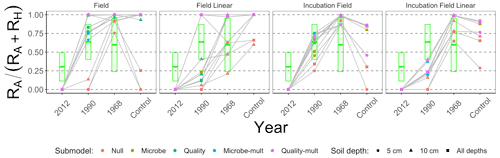
Figure 8Median contribution of the proportion of autotrophic respiration () from different parameter estimation approaches (field, field linear, incubation field, and incubation field linear), soil depth data used for parameter optimization (5 cm, 10 cm, or both depths together), and models (Null, Microbe, Quality, Microbe-mult, and Quality-mult). The crossbar plot shows predicted values of pA with twice the standard error from data reported in Fig. 1 in Ribeiro-Kumara et al. (2020b).
Soil models that directly incorporated microbial carbon produced patterns of RA and RH that increased from the time since the fire (Fig. 7). As these patterns also conform to changes in root carbon (which was proportional to tree biomass, Table 1), we have initial support for our two primary hypotheses: (1) autotrophic respiration should be positively associated with the time since disturbance because of changes in aboveground foliar vegetation from forest succession, and (2) when tested against observational data, soil models that include soil microbial carbon will better replicate expected patterns for soil respiration components across the chronosequence. We will further evaluate the two hypotheses through subsequent analysis of the data used for parameter estimation, parameter estimation approaches, and the soil respiration models.
4.1 Evaluation of datasets for parameter estimation
We had two categories of datasets for this study: the type of data (incubation or field data) or the depth at which measurements were made (5 cm, 10 cm, or both depths together). This controlled experimental design is also represented in the Taylor diagrams (Fig. 3), which comparatively shows a centered-pattern root mean square distance (distance between a point on the Taylor diagram and ) ranging from 0.25–1 and r ranging 0.7–0.9. For the field data (Fig. 4), the centered-pattern root mean square distance ranged from 0.5–1 and r 0.3–0.9. We attributed the differences between Figs. 3 and 4 to the soil temperatures from the incubation experiments spanning 1–19 ∘C, allowing for a wider temperature range to characterize any exponential temperature profile. In contrast, field measurements ranged from 4–9 ∘C (Table 1). For both Figs. 3 and 4, the 5 cm depth had higher values for r and a smaller centered-pattern root mean square distance compared to the 10 cm depth.
We did not find any noticeable site differences in submodel outputs depending on the depth of the soil used for data assimilation (5 cm, 10 cm, or both depths together; Figs. 3, 4, 6). While soil model parameters (such as Q10) are expected to vary with soil depth (Pavelka et al., 2007; Graf et al., 2008; Pumpanen et al., 2008) we did not observe any significant depth-dependent differences in parameter estimates (see the figures in the Supplement). The primary reason for this result is that the inter-site variability is larger than the variability by depth at a given site (Table 1 and Fig. 2). We also did not find any improvements in our results when all data from sites were pooled together (Figs. 7 and 8). From these conclusions, we will limit the discussion to evaluating model results generated from data at the 5 cm depth.
4.2 Evaluation of parameter estimation approaches
We cannot eliminate a parameter estimation approach (field, field linear, incubation field, or incubation field linear) simply by the magnitude of the estimated fluxes RA (Fig. 7). Measured autotrophic respiration in actively growing high-latitude boreal forests (Bond-Lamberty et al., 2004; Vogel et al., 2005, 2014; Pumpanen et al., 2015) or inferred from synthesis studies (Ribeiro-Kumara et al., 2020b; Morgan et al., 2021) can range from 0.5–4 g C m−2 d−1. Most of the modeled values of RA for all the parameter estimation approaches are within that range. The incubation field and field parameter estimation approaches predicted higher RS values outside this range at the 1968 site.
While there is no universal pattern to RH following forest fire disturbances (Ribeiro-Kumara et al., 2020b), we have reason to believe that the near-zero modeled values for RH for the 1968 site in Fig. 7 may be an underestimate. For our sites we expect modest, and perhaps decreasing (but not zero), changes in RH from the time of disturbance for three reasons. First, factors influencing recovery of RH are burn severity or intensity (Meigs et al., 2009; Hu et al., 2017) and decomposition of pyrogenic litter (Kulmala et al., 2014; Muñoz-Rojas et al., 2016). The fires at our sites combusted a significant amount of soil organic matter (Köster et al., 2017) resistant to decomposition (Knicker, 2007; Aaltonen et al., 2019a), thereby minimizing any increases in RH from the decomposition of labile litter. Additionally, from this chronosequence, Aaltonen et al. (2019b) reported increased temperature sensitivity (Q10,M) in recently burned sites, but this was tempered by decreases in soil organic matter quality (Aaltonen et al., 2019a). Second, as succession occurs, the increase in aboveground vegetation insulates the soil, decreasing the active layer and thereby decreasing RH (Köster et al., 2017). Third, at the same chronosequence sites Zhou et al. (2019) found constant and fungal-to-bacterial ratios for microbes, indicating homeostatic regulation of the microbial community. The cumulative effect of these confounding factors may translate into RH remaining constant across the chronosequence.
Our models implicitly assumed an increasing exponential relationship between temperature and respiration. The temperature sensitivity of respiration (Q10) across ecosystems can vary (usually around 2-5) (Chen and Tian, 2005; Wang et al., 2006; Bond-Lamberty and Thomson, 2010) and is generally expected to be greater than 1, but the Q10 value may decrease as soils warm (Niu et al., 2021). Some degree of additional variability is expected when considering the biochemical or thermodynamic foundations of respiration (Lloyd and Taylor, 1994; Ito et al., 2015), the methodological approach used to measure soil respiration (Ribeiro-Kumara et al., 2020b), or variation in the soil organic matter supply (Davidson et al., 2006).
However, an increasing exponential relationship between temperature and respiration may not be robustly supported by observed data at the chronosequence sites. The forest fires at each site burned a large portion of soil organic matter and killed the roots. Immediately following a fire, RS will be lower even if there are higher soil temperatures. In late-successional forests, the soil is colder and the active layer depth is shallower, even though there may be more soil respiration due to higher quantities of roots and soil organic matter; we observed such patterns across the chronosequence. The 2012 and 1990 sites had the highest values of Tsoil (Table 1) but the lowest overall respiration (Fig. 7). Across the chronosequence, scatterplots of respiration with temperature had a null or negative relationship (results not shown). Empirically the negative association of respiration with temperature would imply a Q10 value less than unity. As a result, to compensate for these opposing tendencies the RH parameters tend to be edge-hitting (Fig. 5 and the Supplement).
We recommend either the incubation field or incubation field linear parameter estimation approach for two reasons. First, values of the proportion of the respiration that is autotrophic (, Fig. 8) for the field or field linear approaches are unexpectedly and unrealistically large, attributed to the variation in RH (Fig. 7). As a baseline, Hanson et al. (2000) reported values of to be approximately 0.50, which has also been supported in meta-analyses (Soil Respiration Database, Bond-Lamberty and Thomson, 2010). Second, the incubation field and incubation field linear approaches in Fig. 8 show a temporal pattern in pA similar to patterns reported in Bond-Lamberty et al. (2004) and the predicted pA inferred from Ribeiro-Kumara et al. (2020b). The modeled values of pA are larger at late-successional sites (0.75–1), which may be an effect of the timing of field collection (August) when RA is at a seasonal peak (Bond-Lamberty et al., 2004; Pumpanen et al., 2015).
4.3 Evaluation of hypotheses
Our first hypothesis concerned the dependence of RA on tree biomass. We developed this hypothesis from our previous studies, which concluded that tree biomass was a key factor explaining patterns of soil respiration across the chronosequence (Köster et al., 2017; Aaltonen et al., 2019a, b). For all submodels and the field linear or incubation field linear parameter estimation approaches, RA is proportional to CR, which is proportional to tree biomass. Values of CR increase across the chronosequence (Table 1). However, even with this proportional association, the results in Fig. 7 indicate less support for our first hypothesis for two reasons. First, some modeled values RA at the 1990 site are higher than expected, especially given the association with RA to CR. Since CR is still comparatively low at this site, we might expect RA (and by association pA) to be near zero as well. Additionally, the near-zero values of RA are not a consequence of parameters relating to RA (kR, Q10,R, or gR) being estimated as zero. (Otherwise, the values for these aforementioned parameters in Fig. 5 or the Supplement for all the different models and approaches would be edge-hitting and indicated with blue-colored dots.) Second, and perhaps more importantly, all parameter estimation approaches in Fig. 7 predict RA to decrease between the 1968 and control sites. The modeled decreases in RA are a result of observed decreases in RS (Fig. 7) as CS increases. To compensate, estimated parameters kR or gR decrease across the chronosequence sites (Fig. 5 or the Supplement). The patterns of kR or gR may be due to the parameter estimation routine compensating for the confounding effects of increasing CR with decreasing RS. In summary, even though there is evidence for association between RA and tree biomass in earlier chronosequence sites (2012 and 1990 sites), additional work is needed to explain the reasons for the decline in RA for later chronosequence sites (1968 and control sites). Future work could quantify field estimates of root mass, production, and turnover (Kalyn and Van Rees, 2006; Steele et al., 1997) to corroborate the values of CR used here and with the estimated decreases in kR across the chronosequence.
Our second hypothesis concerns the structural representation of soil respiration for soil models. Our submodels are arranged on a continuum of complexity (Null, Microbe, Quality, Microbe-mult, or Quality-mult). When parameterizing more complex models, parameters may be non-informative and/or edge-hitting (Zobitz et al., 2011). Reducing parameter dimensionality is a key consideration for model–data assimilation in the carbon cycle (Tang and Zhuang, 2008; Luo et al., 2009; Kraemer et al., 2020). Considering the incubation field linear approach only, across the range of submodels the Microbe submodel had the smallest percentage of edge-hitting parameters (10 %), ranging from 30 %–50 % for the other models.
While the AIC suggests a preference towards the Null submodel, we do not believe it is a sufficient criterion to choose it over the Microbe and Quality submodels. There was no noticeable improvement with the Null submodel in the Taylor diagrams for the field data (in both the values of r and the centered-pattern root mean square difference; Fig. 4) or with the adjusted R2 or AIC values (Fig. 6). While all models could not account for a majority of the variance in observed soil respiration (the adjusted R2 values in Fig. 6 ranged from 0.25–0.61), no submodel significantly improved the adjusted R2 or AIC. In other words, the model statistics indicated that the parameter estimation approaches all performed similarly. This model result similarity conforms to a study by Sulman et al. (2018), which synthesized a range of experimental data with different types of process-based models to predict long-term soil organic carbon storage.
A design constraint was to construct models with the greatest potential to be fully parameterized from the collected data. For the Quality-mult and Microbe-mult submodels, kA was estimated at the lower end of its range (Fig. 5), essentially reducing these models to the Quality and Microbe submodels, respectively. Even though we cannot definitively conclude which of the two submodels (Quality or Microbe) is the better approximating model, we recommend that some consideration of microbial growth and maintenance respiration be considered using Michaelis–Menten kinetics as a starting point (Davidson et al., 2006). Several frameworks already exist for incorporating Michaelis–Menten kinetics (Todd-Brown et al., 2012) or substrate quality degradation (Bosatta and Ågren, 1991, 2002). Continuous (daily or sub-daily) soil respiration measurements could better support more complex soil models (Rayment and Jarvis, 2000; Subke et al., 2006; Subke and Bahn, 2010; Phillips et al., 2011; Pumpanen et al., 2015; Zhang et al., 2015). Each of the models could be incorporated into a dynamic model of ecosystem carbon cycling (Zobitz et al., 2008) that also includes temporal changes in permafrost active layer depth (Zhu et al., 2019).
We examined the ability to parameterize a range of soil respiration models using data collected from a fire chronosequence. Importantly, we found support for parameterizing a more complex submodel to replicate patterns in soil respiration and its components across a fire chronosequence. Separate analysis of soils with incubation experiments reduces the number of parameters to be estimated; however, care must be taken in scaling incubation studies to field measurements.
For these high-latitude sites, future work could couple the models here to more continuous measurements of soil temperature along with a dynamic active layer depth model (Zhu et al., 2019). These modeling approaches could examine the effects of gross primary productivity on soil respiration components (Zhuang et al., 2002; Pumpanen et al., 2003; Vargas et al., 2010; Pumpanen et al., 2015; Phillips et al., 2017). For sites that cannot be instrumented continuously (such as the ones studied here), this model–data integration could be supported with periodic surveys of aboveground biomass and other remote sensing data (Neumann et al., 2020).
Code and data necessary to reproduce all results are available through GitHub at https://github.com/jmzobitz/FireResp and archived on Zenodo (Zobitz et al., 2021).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-14-6605-2021-supplement.
Co-authors JZ and JP conceived the ideas for the research project; co-authors JP, KK, and FB collected the field data. Co-authors HA and XZ analyzed the incubation data. All authors contributed to evaluating the results and the writing of the paper.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “The role of fire in the Earth system: understanding interactions with the land, atmosphere, and society (ESD/ACP/BG/GMD/NHESS inter-journal SI)”. It is a result of the EGU General Assembly 2020, 3–8 May 2020.
Co-author Zobitz was funded by the Fulbright Finland Foundation and Saastamoinen Foundation Grant in Health and Environmental Sciences. This work was funded by the Academy of Finland. Co-author John Zobitz acknowledges Ben S. Chelton for helpful discussions on this paper.
This research has been supported by the Academy of Finland (grant nos. 286685, 294600, 307222, 327198, and 337550) and the European Commission, Horizon 2020 Framework Programme (grant no. INTERACT (730938)).
Open-access funding was provided by the Helsinki University Library.
This paper was edited by Christoph Müller and reviewed by two anonymous referees.
Aaltonen, H., Köster, K., Köster, E., Berninger, F., Zhou, X., Karhu, K., Biasi, C., Bruckman, V., Palviainen, M., and Pumpanen, J.: Forest Fires in Canadian Permafrost Region: The Combined Effects of Fire and Permafrost Dynamics on Soil Organic Matter Quality, Biogeochemistry, 143, 257–274, https://doi.org/10.1007/s10533-019-00560-x, 2019a. a, b, c, d, e, f
Aaltonen, H., Palviainen, M., Zhou, X., Köster, E., Berninger, F., Pumpanen, J., and Köster, K.: Temperature Sensitivity of Soil Organic Matter Decomposition after Forest Fire in Canadian Permafrost Region, J. Environ. Manag., 241, 637–644, https://doi.org/10.1016/j.jenvman.2019.02.130, 2019b. a, b, c, d, e, f, g, h
Abbott, B. W., Jones, J. B., Schuur, E. A. G., Chapin III, F. S., Bowden, W. B., Bret-Harte, M. S., Epstein, H. E., Flannigan, M. D., Harms, T. K., Hollingsworth, T. N., Mack, M. C., McGuire, A. D., Natali, S. M., Rocha, A. V., Tank, S. E., Turetsky, M. R., Vonk, J. E., Wickland, K. P., Aiken, G. R., Alexander, H. D., Amon, R. M. W., Benscoter, B. W., Bergeron, Y., Bishop, K., Blarquez, O., Ben Bond-Lamberty, Breen, A. L., Buffam, I., Cai, Y., Carcaillet, C., Carey, S. K., Chen, J. M., Chen, H. Y. H., Christensen, T. R., Cooper, L. W., Cornelissen, J. H. C., de Groot, W. J., DeLuca, T. H., Dorrepaal, E., Fetcher, N., Finlay, J. C., Forbes, B. C., French, N. H. F., Gauthier, S., Girardin, M. P., Goetz, S. J., Goldammer, J. G., Gough, L., Grogan, P., Guo, L., Higuera, P. E., Hinzman, L., Hu, F. S., Hugelius, G., Jafarov, E. E., Jandt, R., Johnstone, J. F., Jan Karlsson, Kasischke, E. S., Kattner, G., Kelly, R., Keuper, F., Kling, G. W., Kortelainen, P., Kouki, J., Kuhry, P., Laudon, H., Laurion, I., Macdonald, R. W., Mann, P. J., Martikainen, P. J., McClelland, J. W., Molau, U., Oberbauer, S. F., Olefeldt, D., Paré, D., Parisien, M.-A., Payette, S., Peng, C., Pokrovsky, O. S., Rastetter, E. B., Raymond, P. A., Raynolds, M. K., Rein, G., Reynolds, J. F., Robards, M., Rogers, B. M., Schädel, C., Schaefer, K., Schmidt, I. K., Shvidenko, A., Sky, J., Spencer, R. G. M., Starr, G., Striegl, R. G., Teisserenc, R., Tranvik, L. J., Virtanen, T., Welker, J. M., and Zimov, S.: Biomass Offsets Little or None of Permafrost Carbon Release from Soils, Streams, and Wildfire: An Expert Assessment, Environmental Research Letters, 11, 034 014, https://doi.org/10.1088/1748-9326/11/3/034014, 2016. a
Aber, J. D., Ollinger, S. V., and Driscoll, C. T.: Modeling Nitrogen Saturation in Forest Ecosystems in Response to Land Use and Atmospheric Deposition, Ecol. Model., 101, 61–78, https://doi.org/10.1016/S0304-3800(97)01953-4, 1997. a
Akaike, H.: A New Look at the Statistical Model Identification, IEEE T. Automat. Contr., 19, 716–723, https://doi.org/10.1109/TAC.1974.1100705, 1974. a
Allison, S. D.: Modeling Adaptation of Carbon Use Efficiency in Microbial Communities, Front. Microbiol., 5, 571, https://doi.org/10.3389/fmicb.2014.00571, 2014. a
Allison, S. D., Wallenstein, M. D., and Bradford, M. A.: Soil-Carbon Response to Warming Dependent on Microbial Physiology, Nat. Geosci., 3, 336–340, https://doi.org/10.1038/ngeo846, 2010. a
Allison, S. D., Romero-Olivares, A. L., Lu, Y., Taylor, J. W., and Treseder, K. K.: Temperature Sensitivities of Extracellular Enzyme Vmax and Km across Thermal Environments, Glob. Change Biol., 24, 2884–2897, https://doi.org/10.1111/gcb.14045, 2018. a
Anderson, J. P. E. and Domsch, K. H.: Quantification of Bacterial and Fungal Contributions to Soil Respiration, Arch. Mikrobiol., 93, 113–127, https://doi.org/10.1007/BF00424942, 1973. a
Beck, T., Joergensen, R. G., Kandeler, E., Makeschin, F., Nuss, E., Oberholzer, H. R., and Scheu, S.: An Inter-Laboratory Comparison of Ten Different Ways of Measuring Soil Microbial Biomass C, Soil Biol. Biochem., 29, 1023–1032, https://doi.org/10.1016/S0038-0717(97)00030-8, 1997. a, b
Bond-Lamberty, B. and Thomson, A.: A Global Database of Soil Respiration Data, Biogeosciences, 7, 1915–1926, https://doi.org/10.5194/bg-7-1915-2010, 2010. a, b
Bond-Lamberty, B., Wang, C., and Gower, S. T.: Contribution of Root Respiration to Soil Surface CO2 Flux in a Boreal Black Spruce Chronosequence, Tree Physiol., 24, 1387–1395, https://doi.org/10.1093/treephys/24.12.1387, 2004. a, b, c, d, e
Bosatta, E. and Ågren, G. I.: Theoretical Analysis of Decomposition of Heterogeneous Substrates, Soil Biol. Biochem., 17, 601–610, 1985. a
Bosatta, E. and Ågren, G. I.: Dynamics of Carbon and Nitrogen in the Organic Matter of the Soil: A Generic Theory, Am. Nat., 138, 227–245, 1991. a
Bosatta, E. and Ågren, G. I.: Quality and Irreversibility: Constraints on Ecosystem Development, Proc. R. Soc. Lond. B, 269, 203–210, https://doi.org/10.1098/rspb.2001.1865, 2002. a, b
Burnham, K. P. and Anderson, D. R., (Eds.): Model Selection and Multimodel Inference, Springer New York, New York, NY, 2002. a
Chakrawal, A., Herrmann, A. M., Koestel, J., Jarsjö, J., Nunan, N., Kätterer, T., and Manzoni, S.: Dynamic Upscaling of Decomposition Kinetics for Carbon Cycling Models, Geosci. Model Dev., 13, 1399–1429, https://doi.org/10.5194/gmd-13-1399-2020, 2020. a
Chen, H. and Tian, H.-Q.: Does a General Temperature-Dependent Q10 Model of Soil Respiration Exist at Biome and Global Scale?, J. Integr. Plant Biol., 47, 1288–1302, https://doi.org/10.1111/j.1744-7909.2005.00211.x, 2005. a
Christiansen, B.: Ensemble Averaging and the Curse of Dimensionality, J. Clim., 31, 1587–1596, https://doi.org/10.1175/JCLI-D-17-0197.1, 2018. a
Davidson, E. A., Belk, E., and Boone, R. D.: Soil Water Content and Temperature as Independent or Confounded Factors Controlling Soil Respiration in a Temperate Mixed Hardwood Forest, Glob. Change Biol., 4, 217–227, https://doi.org/10.1046/j.1365-2486.1998.00128.x, 1998. a
Davidson, E. A., Janssens, I. A., and Luo, Y.: On the Variability of Respiration in Terrestrial Ecosystems: Moving beyond Q10, Glob. Change Biol., 12, 154–164, https://doi.org/10.1111/j.1365-2486.2005.01065.x, 2006. a, b, c
Elzhov, T. V., Mullen, K. M., Spiess, A.-N., and Bolker, B.: Minpack.Lm: R Interface to the Levenberg-Marquardt Nonlinear Least-Squares Algorithm Found in MINPACK, Plus Support for Bounds, R package version 1.2-1, available at: https://CRAN.R-project.org/package=minpack.lm (last access: 1 April 2021), 2016. a
Famiglietti, C. A., Smallman, T. L., Levine, P. A., Flack-Prain, S., Quetin, G. R., Meyer, V., Parazoo, N. C., Stettz, S. G., Yang, Y., Bonal, D., Bloom, A. A., Williams, M., and Konings, A. G.: Optimal Model Complexity for Terrestrial Carbon Cycle Prediction, Biogeosciences, 18, 2727–2754, https://doi.org/10.5194/bg-18-2727-2021, 2021. a
Fan, Z., Jastrow, J. D., Liang, C., Matamala, R., and Miller, R. M.: Priming Effects in Boreal Black Spruce Forest Soils: Quantitative Evaluation and Sensitivity Analysis, PLOS ONE, 8, e77880, https://doi.org/10.1371/journal.pone.0077880, 2013. a
German, D. P., Marcelo, K. R. B., Stone, M. M., and Allison, S. D.: The Michaelis–Menten Kinetics of Soil Extracellular Enzymes in Response to Temperature: A Cross-Latitudinal Study, Glob. Change Biol., 18, 1468–1479, https://doi.org/10.1111/j.1365-2486.2011.02615.x, 2012. a, b
Graf, A., Weihermüller, L., Huisman, J. A., Herbst, M., Bauer, J., and Vereecken, H.: Measurement Depth Effects on the Apparent Temperature Sensitivity of Soil Respiration in Field Studies, Biogeosciences, 5, 1175–1188, https://doi.org/10.5194/bg-5-1175-2008, 2008. a
Hamdi, S., Moyano, F., Sall, S., Bernoux, M., and Chevallier, T.: Synthesis Analysis of the Temperature Sensitivity of Soil Respiration from Laboratory Studies in Relation to Incubation Methods and Soil Conditions, Soil Biol. Biochem., 58, 115–126, https://doi.org/10.1016/j.soilbio.2012.11.012, 2013. a
Hanson, P., Edwards, N., Garten, C., and Andrews, J.: Separating Root and Soil Microbial Contributions to Soil Respiration: A Review of Methods and Observations, Biogeochemistry, 48, 115–146, https://doi.org/10.1023/A:1006244819642, 2000. a
Härkönen, S., Lehtonen, A., Eerikäinen, K., Peltoniemi, M., and Mäkelä, A.: Estimating Forest Carbon Fluxes for Large Regions Based on Process-Based Modelling, NFI Data and Landsat Satellite Images, Forest Ecol. Manag., 262, 2364–2377, https://doi.org/10.1016/j.foreco.2011.08.035, 2011. a
Harmon, M. E., Bond-Lamberty, B., Tang, J., and Vargas, R.: Heterotrophic Respiration in Disturbed Forests: A Review with Examples from North America, J. Geophys. Res., 116, G00K04, https://doi.org/10.1029/2010JG001495, 2011. a
Holden, S. R., Rogers, B. M., Treseder, K. K., and Randerson, J. T.: Fire Severity Influences the Response of Soil Microbes to a Boreal Forest Fire, Environ. Res. Lett., 11, 035004, https://doi.org/10.1088/1748-9326/11/3/035004, 2016. a
Hu, T., Sun, L., Hu, H., Weise, D. R., and Guo, F.: Soil Respiration of the Dahurian Larch (Larix Gmelinii) Forest and the Response to Fire Disturbance in Da Xing'an Mountains, China, Sci. Rep., 7, 2967, https://doi.org/10.1038/s41598-017-03325-4, 2017. a
Hugelius, G., Tarnocai, C., Broll, G., Canadell, J. G., Kuhry, P., and Swanson, D. K.: The Northern Circumpolar Soil Carbon Database: Spatially Distributed Datasets of Soil Coverage and Soil Carbon Storage in the Northern Permafrost Regions, Earth Syst. Sci. Data, 5, 3–13, https://doi.org/10.5194/essd-5-3-2013, 2013. a
Ito, E., Ikemoto, Y., and Yoshioka, T.: Thermodynamic Implications of High Q10 of thermoTRP Channels in Living Cells, Biophysics, 11, 33–38, https://doi.org/10.2142/biophysics.11.33, 2015. a
Jian, S., Li, J., Wang, G., Kluber, L. A., Schadt, C. W., Liang, J., and Mayes, M. A.: Multi-Year Incubation Experiments Boost Confidence in Model Projections of Long-Term Soil Carbon Dynamics, Nat. Commun., 11, 5864, https://doi.org/10.1038/s41467-020-19428-y, 2020. a
Kalyn, A. L. and Van Rees, K. C. J.: Contribution of Fine Roots to Ecosystem Biomass and Net Primary Production in Black Spruce, Aspen, and Jack Pine Forests in Saskatchewan, Agr. Forest Meteorol., 140, 236–243, https://doi.org/10.1016/j.agrformet.2005.08.019, 2006. a
Karhu, K., Hilasvuori, E., Fritze, H., Biasi, C., Nykänen, H., Liski, J., Vanhala, P., Heinonsalo, J., and Pumpanen, J.: Priming Effect Increases with Depth in a Boreal Forest Soil, Soil Biol. Biochem., 99, 104–107, https://doi.org/10.1016/j.soilbio.2016.05.001, 2016. a
Keener, J., Sneyd, J., Antman, S., Marsden, J., and Sirovich, L., eds.: Mathematical Physiology, Vol. 8/1, Interdisciplinary Applied Mathematics, Springer New York, New York, NY, https://doi.org/10.1007/978-0-387-75847-3, 2009. a
Knicker, H.: How Does Fire Affect the Nature and Stability of Soil Organic Nitrogen and Carbon? A Review, Biogeochemistry, 85, 91–118, https://doi.org/10.1007/s10533-007-9104-4, 2007. a
Köster, E., Köster, K., Berninger, F., Aaltonen, H., Zhou, X., and Pumpanen, J.: Carbon Dioxide, Methane and Nitrous Oxide Fluxes from a Fire Chronosequence in Subarctic Boreal Forests of Canada, Sci. Total Environ., 601/602, 895–905, https://doi.org/10.1016/j.scitotenv.2017.05.246, 2017. a, b, c, d, e, f, g, h, i, j
Kraemer, G., Camps-Valls, G., Reichstein, M., and Mahecha, M. D.: Summarizing the State of the Terrestrial Biosphere in Few Dimensions, Biogeosciences, 17, 2397–2424, https://doi.org/10.5194/bg-17-2397-2020, 2020. a
Kulmala, L., Aaltonen, H., Berninger, F., Kieloaho, A.-J., Levula, J., Bäck, J., Hari, P., Kolari, P., Korhonen, J. F. J., Kulmala, M., Nikinmaa, E., Pihlatie, M., Vesala, T., and Pumpanen, J.: Changes in Biogeochemistry and Carbon Fluxes in a Boreal Forest after the Clear-Cutting and Partial Burning of Slash, Agr. Forest Meteorol., 188, 33–44, https://doi.org/10.1016/j.agrformet.2013.12.003, 2014. a
Lloyd, J. and Taylor, J. A.: On the Temperature Dependence of Soil Respiration, Funct. Ecol., 8, 315–323, https://doi.org/10.2307/2389824, 1994. a
Luo, Y., Weng, E., Wu, X., Gao, C., Zhou, X., and Zhang, L.: Parameter Identifiability, Constraint, and Equifinality in Data Assimilation with Ecosystem Models, Ecol. Appl., 19, 571–574, https://doi.org/10.1890/08-0561.1, 2009. a
Luo, Y., Ahlström, A., Allison, S. D., Batjes, N. H., Brovkin, V., Carvalhais, N., Chappell, A., Ciais, P., Davidson, E. A., Finzi, A., Georgiou, K., Guenet, B., Hararuk, O., Harden, J. W., He, Y., Hopkins, F., Jiang, L., Koven, C., Jackson, R. B., Jones, C. D., Lara, M. J., Liang, J., McGuire, A. D., Parton, W., Peng, C., Randerson, J. T., Salazar, A., Sierra, C. A., Smith, M. J., Tian, H., Todd-Brown, K. E. O., Torn, M., van Groenigen, K. J., Wang, Y. P., West, T. O., Wei, Y., Wieder, W. R., Xia, J., Xu, X., Xu, X., and Zhou, T.: Toward More Realistic Projections of Soil Carbon Dynamics by Earth System Models, Global Biogeochem. Cy., 30, 40–56, https://doi.org/10.1002/2015GB005239, 2016. a
Marschmann, G. L., Pagel, H., Kügler, P., and Streck, T.: Equifinality, Sloppiness, and Emergent Structures of Mechanistic Soil Biogeochemical Models, Environ. Model. Softw., 122, 104518, https://doi.org/10.1016/j.envsoft.2019.104518, 2019. a
Masrur, A., Petrov, A. N., and DeGroote, J.: Circumpolar Spatio-Temporal Patterns and Contributing Climatic Factors of Wildfire Activity in the Arctic Tundra from 2001–2015, Environ. Res. Lett., 13, 014019, https://doi.org/10.1088/1748-9326/aa9a76, 2018. a
McGuire, A. D., Anderson, L. G., Christensen, T. R., Dallimore, S., Guo, L., Hayes, D. J., Heimann, M., Lorenson, T. D., Macdonald, R. W., and Roulet, N.: Sensitivity of the Carbon Cycle in the Arctic to Climate Change, Ecol. Monogr., 79, 523–555, https://doi.org/10.1890/08-2025.1, 2009. a, b
Meigs, G. W., Donato, D. C., Campbell, J. L., Martin, J. G., and Law, B. E.: Forest Fire Impacts on Carbon Uptake, Storage, and Emission: The Role of Burn Severity in the Eastern Cascades, Oregon, Ecosystems, 12, 1246–1267, https://doi.org/10.1007/s10021-009-9285-x, 2009. a
Michaelis, L. and Menten, M.: Die Kinetik Der Invertin Wirkung, Biochem. Z., 49, 334–336, 1913. a
Morgan, R. B., Herrmann, V., Kunert, N., Bond-Lamberty, B., Muller-Landau, H. C., and Anderson-Teixeira, K. J.: Global Patterns of Forest Autotrophic Carbon Fluxes, Glob. Change Biol., 27, 2840–2855, https://doi.org/10.1111/gcb.15574, 2021. a
Moyano, F. E., Manzoni, S., and Chenu, C.: Responses of Soil Heterotrophic Respiration to Moisture Availability: An Exploration of Processes and Models, Soil Biol. Biochem., 59, 72–85, https://doi.org/10.1016/j.soilbio.2013.01.002, 2013. a
Muñoz-Rojas, M., Lewandrowski, W., Erickson, T. E., Dixon, K. W., and Merritt, D. J.: Soil Respiration Dynamics in Fire Affected Semi-Arid Ecosystems: Effects of Vegetation Type and Environmental Factors, Sci. Total Environ., 572, 1385–1394, https://doi.org/10.1016/j.scitotenv.2016.02.086, 2016. a
Nash, J. C.: Nonlinear Parameter Optimization Using R Tools, Chichester, West Sussex, 1st Edn., Wiley, Chichester, West Sussex, 2014. a
Nash, J. C. and Murdoch, D.: Nlsr: Functions for Nonlinear Least Squares Solutions, R package version 2021.8.19, available at: https://CRAN.R-project.org/package=nlsr (last access: 9 May 2021), 2019. a
Natural Resources Canada: Canadian Wildland Fire Information System, available at: https://cwfis.cfs.nrcan.gc.ca/home, last access: 29 March 2021. a, b
Neumann, M., Godbold, D. L., Hirano, Y., and Finér, L.: Improving Models of Fine Root Carbon Stocks and Fluxes in European Forests, J. Ecol., 108, 496–514, https://doi.org/10.1111/1365-2745.13328, 2020. a, b
Niu, B., Zhang, X., Piao, S., Janssens, I. A., Fu, G., He, Y., Zhang, Y., Shi, P., Dai, E., Yu, C., Zhang, J., Yu, G., Xu, M., Wu, J., Zhu, L., Desai, A. R., Chen, J., Bohrer, G., Gough, C. M., Mammarella, I., Varlagin, A., Fares, S., Zhao, X., Li, Y., Wang, H., and Ouyang, Z.: Warming Homogenizes Apparent Temperature Sensitivity of Ecosystem Respiration, Sci. Adv., 7, eabc7358, https://doi.org/10.1126/sciadv.abc7358, 2021. a
O'Donnell, J. A., Harden, J. W., McGuire, A. D., and Romanovsky, V. E.: Exploring the Sensitivity of Soil Carbon Dynamics to Climate Change, Fire Disturbance and Permafrost Thaw in a Black Spruce Ecosystem, Biogeosciences, 8, 1367–1382, https://doi.org/10.5194/bg-8-1367-2011, 2011. a
Pavelka, M., Acosta, M., Marek, M. V., Kutsch, W., and Janous, D.: Dependence of the Q10 Values on the Depth of the Soil Temperature Measuring Point, Plant Soil, 292, 171–179, https://doi.org/10.1007/s11104-007-9213-9, 2007. a
Phillips, C. L., Nickerson, N., Risk, D., and Bond, B. J.: Interpreting Diel Hysteresis between Soil Respiration and Temperature, Glob. Change Biol., 17, 515–527, https://doi.org/10.1111/j.1365-2486.2010.02250.x, 2011. a
Phillips, C. L., Bond-Lamberty, B., Desai, A. R., Lavoie, M., Risk, D., Tang, J., Todd-Brown, K., and Vargas, R.: The Value of Soil Respiration Measurements for Interpreting and Modeling Terrestrial Carbon Cycling, Plant Soil, 413, 1–25, https://doi.org/10.1007/s11104-016-3084-x, 2017. a
Pumpanen, J., Ilvesniemi, H., and Hari, P.: A Process-Based Model for Predicting Soil Carbon Dioxide Efflux and Concentration, Soil Sci. Soc. Am. J., 67, 402–413, https://doi.org/10.2136/sssaj2003.4020, 2003. a
Pumpanen, J., Ilvesniemi, H., Kulmala, L., Siivola, E., Laakso, H., Kolari, P., Helenelund, C., Laakso, M., Uusimaa, M., and Hari, P.: Respiration in Boreal Forest Soil as Determined from Carbon Dioxide Concentration Profile, Soil Sci. Soc. Am. J., 72, 1187–1196, https://doi.org/10.2136/sssaj2007.0199, 2008. a
Pumpanen, J., Kulmala, L., Lindén, A., Kolari, P., Nikinmaa, E., and Hari, P.: Seasonal Dynamics of Autotrophic Respiration in Boreal Forest Soil Estimated by Continuous Chamber Measurements, Boreal Environ. Res., 20, 637–650, 2015. a, b, c, d, e
Rayment, M. B. and Jarvis, P. G.: Temporal and Spatial Variation of Soil CO2 Efflux in a Canadian Boreal Forest, Soil Biol. Biochem., 32, 35–45, https://doi.org/10.1016/S0038-0717(99)00110-8, 2000. a
Reichstein, M. and Beer, C.: Soil Respiration across Scales: The Importance of a Model – Data Integration Framework for Data Interpretation, J. Plant Nutr. Soil Sci., 171, 344–354, https://doi.org/10.1002/jpln.200700075, 2008. a, b
Ribeiro-Kumara, C., Köster, E., Aaltonen, H., and Köster, K.: Forest-fires-GHG: A dataset derived from a literature review on soil greenhouse gas emissions after forest fires in upland boreal forests, Mendeley dataset, V1, https://doi.org/10.17632/v7gxtvv9z3.1, 2020a. a
Ribeiro-Kumara, C., Köster, E., Aaltonen, H., and Köster, K.: How Do Forest Fires Affect Soil Greenhouse Gas Emissions in Upland Boreal Forests? A Review, Environ. Res., 184, 109328, https://doi.org/10.1016/j.envres.2020.109328, 2020b. a, b, c, d, e, f, g
Schuur, E. A. G., Bockheim, J., Canadell, J. G., Euskirchen, E., Field, C. B., Goryachkin, S. V., Hagemann, S., Kuhry, P., Lafleur, P. M., Lee, H., Mazhitova, G., Nelson, F. E., Rinke, A., Romanovsky, V. E., Shiklomanov, N., Tarnocai, C., Venevsky, S., Vogel, J. G., and Zimov, S. A.: Vulnerability of Permafrost Carbon to Climate Change: Implications for the Glob. Carbon Cy., BioScience, 58, 701–714, https://doi.org/10.1641/B580807, 2008. a, b
Shao, P., Zeng, X., Moore, D. J. P., and Zeng, X.: Soil Microbial Respiration from Observations and Earth System Models, Environ. Res. Lett., 8, 034034, https://doi.org/10.1088/1748-9326/8/3/034034, 2013. a
Shiklomanov, A. N., Bond-Lamberty, B., Atkins, J. W., and Gough, C. M.: Structure and Parameter Uncertainty in Centennial Projections of Forest Community Structure and Carbon Cycling, Glob. Change Biol., 26, 6080–6096, https://doi.org/10.1111/gcb.15164, 2020. a
Sihi, D., Gerber, S., Inglett, P. W., and Inglett, K. S.: Comparing Models of Microbial – Substrate Interactions and Their Response to Warming, Biogeosciences, 13, 1733–1752, https://doi.org/10.5194/bg-13-1733-2016, 2016. a, b, c
Song, J., Liu, Z., Zhang, Y., Yan, T., Shen, Z., and Piao, S.: Effects of Wildfire on Soil Respiration and Its Heterotrophic and Autotrophic Components in a Montane Coniferous Forest, J. Plant Ecol., 12, 336–345, https://doi.org/10.1093/jpe/rty031, 2019. a
Steele, S. J., Gower, S. T., Vogel, J. G., and Norman, J. M.: Root Mass, Net Primary Production and Turnover in Aspen, Jack Pine and Black Spruce Forests in Saskatchewan and Manitoba, Canada, Tree Physiol., 17, 577–587, https://doi.org/10.1093/treephys/17.8-9.577, 1997. a
Subke, J.-A. and Bahn, M.: On the “Temperature Sensitivity” of Soil Respiration: Can We Use the Immeasurable to Predict the Unknown?, Soil Biol. Biochem., 42, 1653–1656, https://doi.org/10.1016/j.soilbio.2010.05.026, 2010. a
Subke, J.-A., Inglima, I., and Cotrufo, M. F.: Trends and Methodological Impacts in Soil CO2 Efflux Partitioning: A Metaanalytical Review, Glob. Change Biol., 12, 921–943, https://doi.org/10.1111/j.1365-2486.2006.01117.x, 2006. a
Sulman, B. N., Moore, J. A. M., Abramoff, R., Averill, C., Kivlin, S., Georgiou, K., Sridhar, B., Hartman, M. D., Wang, G., Wieder, W. R., Bradford, M. A., Luo, Y., Mayes, M. A., Morrison, E., Riley, W. J., Salazar, A., Schimel, J. P., Tang, J., and Classen, A. T.: Multiple Models and Experiments Underscore Large Uncertainty in Soil Carbon Dynamics, Biogeochemistry, 141, 109–123, https://doi.org/10.1007/s10533-018-0509-z, 2018. a
Tang, J. and Zhuang, Q.: Equifinality in Parameterization of Process-Based Biogeochemistry Models: A Significant Uncertainty Source to the Estimation of Regional Carbon Dynamics, J. Geophys. Res., 113, G04010, https://doi.org/10.1029/2008JG000757, 2008. a, b
Taylor, K. E.: Summarizing Multiple Aspects of Model Performance in a Single Diagram, J. Geophys. Res.-Atmos., 106, 7183–7192, https://doi.org/10.1029/2000JD900719, 2001. a
Todd-Brown, K. E. O., Hopkins, F. M., Kivlin, S. N., Talbot, J. M., and Allison, S. D.: A Framework for Representing Microbial Decomposition in Coupled Climate Models, Biogeochemistry, 109, 19–33, https://doi.org/10.1007/s10533-011-9635-6, 2012. a, b
van't Hoff, J. H. and Lehfeldt, R. A.: Lectures in Theoretical and Physical Chemistry: Part I : Chemical Dynamics, Edward Arnold, London, 1898. a
Vargas, R., Baldocchi, D. D., Allen, M. F., Bahn, M., Black, T. A., Collins, S. L., Yuste, J. C., Hirano, T., Jassal, R. S., Pumpanen, J., and Tang, J.: Looking Deeper into the Soil: Biophysical Controls and Seasonal Lags of Soil CO2 Production and Efflux, Ecol. Appl., 20, 1569–1582, https://doi.org/10.1890/09-0693.1, 2010. a, b
Vereecken, H., Schnepf, A., Hopmans, J. W., Javaux, M., Or, D., Roose, T., Vanderborght, J., Young, M. H., Amelung, W., Aitkenhead, M., Allison, S. D., Assouline, S., Baveye, P., Berli, M., Brüggemann, N., Finke, P., Flury, M., Gaiser, T., Govers, G., Ghezzehei, T., Hallett, P., Franssen, H. J. H., Heppell, J., Horn, R., Huisman, J. A., Jacques, D., Jonard, F., Kollet, S., Lafolie, F., Lamorski, K., Leitner, D., McBratney, A., Minasny, B., Montzka, C., Nowak, W., Pachepsky, Y., Padarian, J., Romano, N., Roth, K., Rothfuss, Y., Rowe, E. C., Schwen, A., Šimůnek, J., Tiktak, A., Dam, J. V., van der Zee, S. E. A. T. M., Vogel, H. J., Vrugt, J. A., Wöhling, T., and Young, I. M.: Modeling Soil Processes: Review, Key Challenges, and New Perspectives, Vadose Zone J., 15, 1–57, https://doi.org/10.2136/vzj2015.09.0131, 2016. a
Vogel, J., Valentine, D., and Ruess, R.: Soil and Root Respiration in Mature Alaskan Black Spruce Forests That Vary in Soil Organic Matter Decomposition Rates, Canadian Journal of Forest Research-revue Canadienne De Recherche Forestiere, Can. J. Forest Res., 35, 161–174, https://doi.org/10.1139/x04-159, 2005. a
Vogel, J. G., Bronson, D., Gower, S. T., and Schuur, E. A.: The Response of Root and Microbial Respiration to the Experimental Warming of a Boreal Black Spruce Forest, Can. J. Forest Res., 44, 986–993, https://doi.org/10.1139/cjfr-2014-0056, 2014. a
Walsh, J. E., Ballinger, T. J., Euskirchen, E. S., Hanna, E., Mård, J., Overland, J. E., Tangen, H., and Vihma, T.: Extreme Weather and Climate Events in Northern Areas: A Review, Earth-Sci. Rev., 209, 103324, https://doi.org/10.1016/j.earscirev.2020.103324, 2020. a
Wang, W., Wang, H., Zu, Y., Li, X., and Koike, T.: Characteristics of the Temperature Coefficient, Q10, for the Respiration of Non-Photosynthetic Organs and Soils of Forest Ecosystems, Front. Forestr. China, 1, 125–135, https://doi.org/10.1007/s11461-006-0018-4, 2006. a
Wang, Y.-P., Zhang, H., Ciais, P., Goll, D., Huang, Y., Wood, J. D., Ollinger, S. V., Tang, X., and Prescher, A.-K.: Microbial Activity and Root Carbon Inputs Are More Important than Soil Carbon Diffusion in Simulating Soil Carbon Profiles, J. Geophys. Res.-Biogeo., 126, e2020JG006205, https://doi.org/10.1029/2020JG006205, 2021. a
Wei, W., Weile, C., and Shaopeng, W.: Forest Soil Respiration and Its Heterotrophic and Autotrophic Components: Global Patterns and Responses to Temperature and Precipitation, Soil Biol. Biochem., 42, 1236–1244, https://doi.org/10.1016/j.soilbio.2010.04.013, 2010. a
Wieder, W. R., Bonan, G. B., and Allison, S. D.: Global Soil Carbon Projections Are Improved by Modelling Microbial Processes, Nat. Clim. Change, 3, 909–912, https://doi.org/10.1038/nclimate1951, 2013. a, b, c
Wieder, W. R., Allison, S. D., Davidson, E. A., Georgiou, K., Hararuk, O., He, Y., Hopkins, F., Luo, Y., Smith, M. J., Sulman, B., Todd-Brown, K., Wang, Y.-P., Xia, J., and Xu, X.: Explicitly Representing Soil Microbial Processes in Earth System Models, Global Biogeochem. Cy., 29, 1782–1800, https://doi.org/10.1002/2015GB005188, 2015. a
Zhang, Q., Katul, G. G., Oren, R., Daly, E., Manzoni, S., and Yang, D.: The Hysteresis Response of Soil CO2 Concentration and Soil Respiration to Soil Temperature, J. Geophys. Res.-Biogeo., 120, 1605–1618, https://doi.org/10.1002/2015JG003047, 2015. a
Zhao, B., Zhuang, Q., Shurpali, N., Köster, K., Berninger, F., and Pumpanen, J.: North American Boreal Forests Are a Large Carbon Source Due to Wildfires from 1986 to 2016, Sci. Rep., 11, 7723, https://doi.org/10.1038/s41598-021-87343-3, 2021. a
Zhou, X., Sun, H., Pumpanen, J., Sietiö, O.-M., Heinonsalo, J., Köster, K., and Berninger, F.: The Impact of Wildfire on Microbial Stoichiometry and the Fungal-to-Bacterial Ratio in Permafrost Soil, Biogeochemistry, 142, 1–17, https://doi.org/10.1007/s10533-018-0510-6, 2019. a, b, c, d
Zhu, D., Ciais, P., Krinner, G., Maignan, F., Jornet Puig, A., and Hugelius, G.: Controls of Soil Organic Matter on Soil Thermal Dynamics in the Northern High Latitudes, Nat. Commun., 10, 3172, https://doi.org/10.1038/s41467-019-11103-1, 2019. a, b
Zhuang, Q., A. D. McGuire, K. P. O’Neill, J. W. Harden, V. E. Romanovsky, and J. Yarie, Modeling soil thermal and carbon dynamics of a fire chronosequence in interior Alaska, J. Geophys. Res., 107, 8147, https://doi.org/10.1029/2001JD001244, 2002. a
Zobitz, J., Desai, A., Moore, D., and Chadwick, M.: A Primer for Data Assimilation with Ecological Models Using Markov Chain Monte Carlo (MCMC), Oecologia, 167, 599–611, https://doi.org/10.1007/s00442-011-2107-9, 2011. a
Zobitz, J., Aaltonen, H., Zhou, X., Berninger, F., Pumpanen, J., and Köster, K.: FireResp (v1.0.2), Zenodo [code], https://doi.org/10.5281/zenodo.5542011, 2021. a
Zobitz, J. M., Moore, D. J. P., Sacks, W. J., Monson, R. K., Bowling, D. R., and Schimel, D. S.: Integration of Process-Based Soil Respiration Models with Whole-Ecosystem CO2 Measurements, Ecosystems, 11, 250–269, https://doi.org/10.1007/s10021-007-9120-1, 2008. a, b, c, d