A spatially explicit approach to simulate urban heat mitigation with InVEST (v3.8.0)

Mitigating urban heat islands has become an important objective for many cities experiencing heat waves. Despite notable progress, the spatial relationship between land use and/or land cover patterns and the distribution of air temperature remains poorly understood. This article presents a reusable computational workflow to simulate the spatial distribution of air temperature in urban areas from their land use and/or land cover data. The approach employs the InVEST urban cooling model, which estimates the cooling capacity of the urban fabric based on three biophysical mechanisms: tree shade, evapotranspiration and albedo. An automated procedure is proposed to calibrate the parameters of the model to best fit air temperature observations from monitoring stations. In a case study in Lausanne, Switzerland, spatial estimates of air temperature obtained with the calibrated model show that the urban cooling model outperforms spatial regressions based on satellite data. This represents two major advances in urban heat island modeling. First, unlike in black-box approaches, the calibrated parameters of the urban cooling model can be interpreted in terms of the physical mechanisms that they represent; therefore, they can help promote an understanding of how urban heat islands emerge in a particular context. Second, the urban cooling model requires only land use and/or land cover and reference temperature data and can, therefore, be used to evaluate synthetic scenarios such as master plans, urbanization prospects and climate scenarios. The proposed approach provides valuable insights into the emergence of urban heat islands which can serve to inform urban planning and assist the design of heat mitigation policies.

1 Introduction

Since the industrial revolution, the Earth has seen a global increase in temperature which has been especially prominent in urban areas (Oke, 1973; Arnfield, 2003; Clinton and Gong, 2013). Such a trend concurs with the unprecedented growth of urban areas, making contemporary cities a major source of landscape changes and greenhouse gas emissions (Angel et al., 2005; Grimm et al., 2008; United Nations, 2015). By modifying the energy and water balance processes and influencing the movement of air, urban surfaces alter local climatic characteristics, often resulting in warmer temperatures than their rural surroundings (Oke, 1982). This phenomenon is known as the “urban heat island” (UHI) effect.

The quantification of UHIs can be broadly divided into two main approaches (Schwarz et al., 2011), namely the canopy-layer UHI, measured by the air temperature, usually at 2 m height (Stewart, 2011), and the surface UHI, measured by land surface temperatures (LSTs) derived from remote sensing data (Voogt and Oke, 2003). The increasing availability of satellite raster datasets has fostered a large body of research on the spatial distribution of LSTs and their relationship with the spatial composition and configuration of urban landscapes (Voogt and Oke, 2003; Zhou et al., 2019), which contrasts with the spatial sparsity of meteorological stations that measure air temperature. Despite exhibiting some correlations, air temperature and LST are essentially different physical quantities. Air temperature is closer to thermal comfort felt by humans and can therefore be employed to evaluate the influence of UHIs on key matters such as the energy demand for air conditioning or human health. Additionally, depending on the satellite overpass time, the differences between air temperature and LST can range from a few degrees (^∘C) up to tens of degrees (Jin and Dickinson, 2010; Sobrino et al., 2012), which calls for special caution when employing satellite-derived LST data for the study of UHIs.

Although notable studies have explored the relationship between satellite-derived LST raster data and air temperature measurements to provide high-resolution insights into the canopy-layer UHI (Fabrizi et al., 2010; Schwarz et al., 2012; Anniballe et al., 2014; Sheng et al., 2017; Shiflett et al., 2017), they have mostly focused on finding statistical relationships between UHIs and the spatial distribution of terrain features such as vegetation indices, without exploring how the observed patterns relate to the biophysical mechanisms that explain the canopy-layer UHI. Such a limitation is important when models are used in simulations – for example, to examine the effect of urban planning scenarios on air temperatures. As part of the Integrated Valuation of Ecosystem Services and Tradeoffs (InVEST) software, a suite of spatial models to quantify and value the goods and services from nature that sustain and fulfill human life (Sharp et al., 2020), an urban cooling model has been developed following recent research on the effects of surface materials and vegetation cover on UHIs (Phelan et al., 2015; Zardo et al., 2017). The aim of the urban cooling model is to simulate the spatial distribution of UHIs based on three key mechanisms, namely the shade provided by trees, the evapotranspiration of urban vegetation and the albedo of the urban surface. In a preliminary application of the model, Hamel et al. (2020) showed its capability to represent the spatial pattern of nighttime air temperature of the 2003 heat waves in the Île-de-France region.

The main objective of this study is to extend such preliminary experiments by proposing a reusable computational workflow to apply the InVEST urban cooling model to predict the spatial distribution of air temperature in a given study area. The validity of the simulated results is optimized by calibrating some key parameters to best fit a set of air temperature measurements from monitoring stations. Additionally, the simulated spatial pattern of air temperature is compared with one obtained using an alternative approach, namely a spatial regression over features extracted from satellite data.

2 Materials and methods

2.1 Study area

Situated at the western end of the Swiss Plateau and on the shores of Lake Geneva, Lausanne is the fourth largest Swiss urban agglomeration with 420 757 inhabitants as of January 2019 (Swiss Federal Statistical Office, 2018). As the second most important student and research center in Switzerland (after Zurich), the urban agglomeration of Lausanne has experienced substantial growth during recent decades, which has mostly occurred in the form of suburbanization (Bosch et al., 2020).

A notable geographic feature of Lausanne is its elevation difference of about 500 m between the lake shore at 372 m a.s.l. and the northeastern part of the agglomeration (see Fig. 1). The area is characterized by a continental temperate climate with mean annual temperatures of 10.9 ^∘C and mean annual precipitation of 1100 mm, and a dominating vegetation of mixed broadleaf forest.

Spatial extent of the study

In line with urban economics and regional sciences, many works rely on administrative boundaries to define the spatial extent of the study. However, the way in which boundaries are constructed overlooks the characteristic scales at which landscape changes and environmental processes unfold, and might thus lead to equivocal results (Liu et al., 2014; Oliveira et al., 2014). Considering such issues, the spatial extent for this study was determined quantitatively by following the method employed in the Atlas of Urban Expansion (Angel et al., 2012). The core idea is that a pixel is considered part of the spatial extent depending on the proportion of built-up pixels that surround it. In this study, a pixel is considered part of the spatial extent when more than 15 % of the pixels that lay within a 500 m radius are built-up. Additionally, in order to evaluate how temperatures change across the urban–rural gradient, the spatial extent has been extended by a 1000 m buffer. The above procedure has been applied to the rasterized land use and/or land cover (LULC) map by means of the Urban footprinter (Bosch, 2020b) Python library. The obtained spatial extent, displayed in Fig. 1, has a surface of 112.46 km².

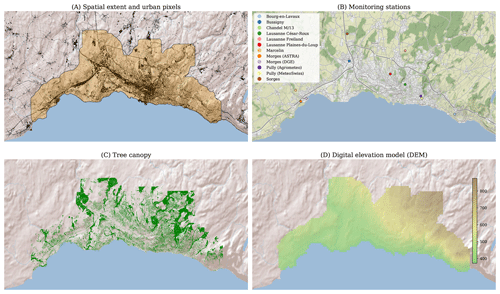
Figure 1 Study area. The upper left plot (A) shows the computed spatial extent (in orange) over the repartition of urban pixels (in black) derived from the rasterized cadastral survey (Association pour le Système d'information du Territoire Vaudois, 2018). The upper right plot (B) shows the locations of the air temperature measurement stations (see Appendix A2). The bottom row shows, for the computed spatial extent of the study, (C) the tree canopy map derived from the SWISSIMAGE orthomosaic (Federal Office of Topography, 2019) and (D) the altitude map derived from the free version of the digital height model of Switzerland (Federal Office of Topography, 2004). The basemap of plots (A), (C) and (D) is based on the World Shaded Relief (© 2009 Esri). The basemap tiles of plot (B) have been provided by Stamen Design (https://stamen.com, last access: 28 July 2020), under a Creative Commons BY 3.0 License (http://creativecommons.org/licenses/by/3.0, last access: 28 July 2020), with data from OpenStreetMap (https://openstreetmap.org, last access: 28 July 2020, © OpenStreetMap contributors 2021, distributed under a Creative Commons BY-SA License).

2.2 Data

2.2.1 Land use and/or land cover data

The LULC maps were obtained by rasterizing the vector geometries of the official cadastral survey of August 2019 to a 10 m resolution. Such a dataset is provided and maintained (i.e., updated weekly) by the cantonal administration of Vaud, and it features the whole spatial extent of the canton of Vaud (Association pour le Système d'information du Territoire Vaudois, 2018). The classification distinguishes 25 LULC classes that are relevant to the urban, rural and wild landscapes encountered in Switzerland (Conference des Services Cantonaux du Cadastre, 2011). Moreover, a 1 m binary tree canopy mask was derived from the SWISSIMAGE orthomosaic (Federal Office of Topography, 2019), by means of the DetecTree (Bosch, 2020a) Python library, which implements the methods proposed by Yang et al. (2009). The tree canopy mask of the spatial extent of the study is shown in Fig. 1.

2.2.2 Elevation data

The elevation map for the study area, which is displayed in Fig. 1, is extracted from the free version of the digital height model of Switzerland (Federal Office of Topography, 2004), provided at a 200 m resolution by the Federal Office of Topography.

2.2.3 Satellite data

The satellite dataset consists of the eight Landsat 8 images in 2018 and 2019 that do not feature clouds over the study area and comprise days on which the maximum observed air temperature was over 25 ^∘C (see the list of selected image tiles in Appendix A1). Data from Landsat 7 were excluded because of the scan line corrector malfunction.

2.2.4 Air temperature data

A dataset of consistent air temperature measurements in the study area was assembled by combining data from 11 stations operated by various governmental and research sources, which are shown in Fig. 1. The temporal resolution of the stations ranges from 10 to 30 min. Given that the UHI effect in Switzerland reaches its maximal intensity around 21:00 CET (Burgstall, 2019), the remainder of this study evaluates it based on the air temperature observations at the abovementioned time.

2.3 Simulation with the InVEST urban cooling model

The simulation of the spatial distribution of UHIs employs the InVEST urban cooling model, version 3.8.0 (Sharp et al., 2020), which is based on the heat mitigation provided by shade, evapotranspiration and albedo. The main inputs are a LULC raster map, a reference evapotranspiration raster and a biophysical table containing model information of each LULC class of the map. Each row of the biophysical table represents a LULC class and features the following columns:

• lucode – the LULC class code as represented in the LULC raster map;

• Shade – a value between zero and one representing the proportion of tree cover in such a LULC class;

• Kc – the evapotranspiration coefficient;

• Albedo – a value between zero and one representing the proportion of solar radiation directly reflected by the LULC class;

• Green_area – whether the LULC class should be considered a green area or not;

• Building_intensity – a value between zero and one representing the ratio between floor area and land area (for nighttime simulations).

2.3.1 Model description

The data inputs described above are used to compute the cooling capacity index, which is based on the physical mechanisms that contribute to cooling urban temperatures. More precisely, the cooling capacity index used in the InVEST urban cooling model builds upon the indices proposed by Zardo et al. (2017), which are based on shading and evapotranspiration, and extends them by adding a factor to account for the albedo. For each pixel i of the LULC raster map, the cooling capacity index is computed as follows:

$$\begin{array}{}\text{(1)}& {\text{CC}}_i=w_{\mathrm{S}}\cdot S_i+w_{\mathrm{AL}}\cdot {\text{AL}}_i+w_{\mathrm{ET}}\cdot {\text{ETI}}_i,\end{array}$$

where S_i, AL_i and ETI_i represent the respective tree shading, albedo and evapotranspiration values of pixel i as defined in the biophysical table, and w_S, w_AL and w_ET represent the weights attributed to each respective component. The values of S_i and AL_i are retrieved from the biophysical table according to the LULC class k of the pixel i (see Appendix A3). The tree shading is computed by overlaying the binary tree canopy mask with the rasterized LULC map so that for each LULC class k, the shade coefficient S_k corresponds to the average proportion of tree cover over all the LULC pixels of class k, as follows:

$$\begin{array}{}\text{(2)}& S_k={\displaystyle \frac{\mathrm{1}}{\left|{\mathrm{\Omega }}_k\right|}}\sum _{j\in {\mathrm{\Omega }}_k}{x}_j.\end{array}$$

Here, Ω_k is the set of pixels of the tree canopy mask whose location corresponds to class k in the LULC raster, and x_j is the value of pixel j of the tree canopy mask, i.e., one if j corresponds to a tree and zero otherwise. The albedo coefficients are based on the local climate zone classification by Stewart and Oke (2012).

The evapotranspiration index ETI is computed as a normalized value of the potential evapotranspiration as follows:

$$\begin{array}{}\text{(3)}& \text{ETI}={\displaystyle \frac{K_{\mathrm{c}}\cdot {\mathrm{ET}}_{\mathrm{ref}}}{{\mathrm{ET}}_{\max }}},\end{array}$$

where K_c is the evapotranspiration coefficient, ET_ref is the reference evapotranspiration raster for the period and area of interest, and ET_max is the maximum evapotranspiration value observed in the area of interest.

In line with the studies of Nistor and Porumb (2015), Nistor et al. (2016) and Nistor (2016), the evapotranspiration coefficients are attributed to each LULC class by distinguishing four cases, namely the crop coefficient for single crops for vegetation LULC classes, the water evaporation coefficient for surface water, the rock and soil evaporation coefficient for bare soils and rocks, and evaporation coefficients for artificial LULC classes (e.g., urban areas). The evapotranspiration coefficients attributed to the LULC classes of the Swiss cadastral survey are listed in Table A3.

Following the recommendations of Allen et al. (1998), the daily evapotranspiration ET_ref (in mm/d) was estimated for each pixel using the Hargreaves equation (Hargreaves and Samani, 1985) as follows:

$$\begin{array}{}\text{(4)}& {\mathrm{ET}}_{\mathrm{ref}}=\mathrm{0.0023}\cdot (T_{\mathrm{avg}}+\mathrm{17.8})\cdot (T_{\max }-T_{\min }{)}^{\mathrm{0.5}}\cdot R_{\mathrm{a}},\end{array}$$

where T_avg, T_max and T_min correspond to the average, maximum and minimum T_air (in ^∘C) of each day, respectively, and R_a is the extraterrestrial radiation (in mm/d), which is estimated for the latitude of Lausanne (i.e., 46.519833^∘) for each date following the methods of Allen et al. (1998, Eq. 21). The temperature values of each day have been extracted from the inventory of gridded datasets provided by the Federal Office of Meteorology and Climatology (MeteoSwiss), which feature the minimum, average and maximum daily T_air for the extent of the whole country at a resolution of 1 km. Such a dataset is obtained by interpolating 100 T_air stations across Switzerland (including the MeteoSwiss Pully station in Fig. 1) based on nonlinear thermal profiles of major basins and non-Euclidean distance weighting that accounts for terrain effects (Frei, 2014).

In order to account for the cooling effect of large green spaces, the computed cooling capacity index of pixels that are part of large green areas (>2 ha) is adjusted as follows:

$$\begin{array}{}\text{(5)}& {\text{CC}}_i^{\mathrm{green}}=\sum _{j\in {\mathrm{\Omega }}_i}{g}_i\cdot {\text{CC}}_j\cdot e^{-\frac{d(i,j)}{d_{\mathrm{cool}}}},\end{array}$$

where g_i is one when the pixel i is a green area and zero otherwise (as defined in the biophysical table), d(i,j) is the distance between pixels i and j, d_cool is a parameter that defines the distance over which a green space has a cooling effect, and Ω_i is the set of pixels whose distance to i is lower than d_cool.

A heat mitigation (HM) index is then computed as follows:

$$\begin{array}{}\text{(6)}& {\text{HM}}_i=\left\{\begin{array}{ll}{\text{CC}}_i& \text{ if }i\text{ is part of a large green area}\\ & \text{ or }{\text{CC}}_i>{\text{CC}}_i^{\mathrm{green}}\\ {\text{CC}}_i^{\mathrm{green}}& \text{ otherwise}.\end{array}\right.\end{array}$$

In order to simulate the spatial distribution of T_air, the model requires two additional inputs. The first is the rural reference temperature T_ref, where the UHI effect is not observed, e.g., in the rural surroundings of the city. The second is the magnitude of the UHI effect UHI_max, namely the difference between the rural reference temperature and the maximum T_air observed in the city center. The two parameters are combined with HM_i to compute the T_i for each pixel i of the study area as follows:

$$\begin{array}{}\text{(7)}& T_i^{\mathrm{no}\mathrm{mix}}=T_{\mathrm{ref}}+(\mathrm{1}-{\text{HM}}_i)\cdot {\mathrm{UHI}}_{\max }.\end{array}$$

Finally, the T_air values of each pixel $T_i^{\mathrm{no}\mathrm{mix}}$ are spatially averaged using a Gaussian function with a kernel radius r defined by the user.

2.3.2 Calibration and evaluation of the model

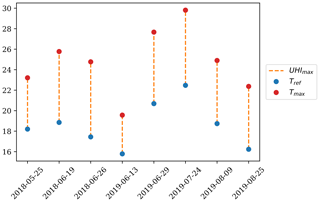
To compare the InVEST urban cooling model with the spatial regression based on satellite features, the urban cooling model is used to simulate the spatial distribution of T_air for the same eight dates used to train the spatial regression model, i.e., the dates of the selected Landsat images. It is implicitly assumed that no significant LULC changes have occurred throughout study period (i.e., from May 2018 to August 2019); therefore, all simulations depart from the same LULC raster, i.e., the rasterized cadastral survey of the canton of Vaud as described above. Given the rugged terrain of the study area, the T_ref was set as the minimum average T_air observed among the monitoring stations, while UHI_max was set as the difference between the maximum average T_air observed among the monitoring stations and T_ref. The values of T_ref and UHI_max for the 8 d considered in this study are displayed in Fig. A1.

Although the documentation of the InVEST urban cooling model (Sharp et al., 2020) provides some suggested values for several parameters of the model, their suitability depends strongly on the local geographic conditions of the study area. Therefore, calibration of the parameters is required in order to better understand how the physical mechanisms beyond the emergence of UHIs take place in the context of Lausanne. Following the manual calibration approach drafted by Hamel et al. (2020), the target parameters are the weights attributed to the tree shading (w_S), albedo (w_A) and evapotranspiration (w_ET), the distance over which green spaces have a cooling effect (d_cool) and the T_air mixing radius (r). As an additional contribution, this article implements an automated calibrated procedure based on simulated annealing optimization (Kirkpatrick et al., 1983) that aims at the minimization of the R² between the T_air values observed in the monitoring stations and those predicted by the model¹. The parameter values suggested in the documentation of the model are set as the initial state of the simulation annealing procedure, which corresponds to a T_air mixing radius of r=500 m, a green area cooling distance of d_cool=100 m, and weights attributed to tree shading, albedo and evapotranspiration of w_S=0.6, w_A=0.2 and w_ET=0.2, respectively. The number of calibration iterations is set to 100.

Given that the T_ref and UHI_max parameters in this study were obtained from observations from each simulated day, metrics such as the mean absolute error (MAE) and the root mean squared error (RMSE) are effectively constrained to the [0, UHI_max] range, which affects the interpretation of these metrics. Therefore, in order to evaluate the ability of the InVEST urban cooling model to spatially simulate UHIs, the coefficient of adjustment R², MAE and RMSE of the calibrated model are compared with those computed in two additional experiments. The first experiment consisted of randomly sampling the T_air values from a uniform distribution over the [T_ref, UHI_max] range of each date. In the second experiment, the T_air values of each date were randomly sampled from a normal distribution with the mean and standard deviation of the T_air measurements of the monitoring stations. For both experiments, the three evaluation metrics are reported as their average over 10 runs.

2.4 Spatial regression of air temperature based on satellite data

The spatial regression to predict T_air from features derived from satellite data is performed over a raster dataset on a per-pixel basis. A regression model is then trained to fit the observed T_air measurements by minimizing the error at the pixels that correspond to the locations of the monitoring stations.

The regression operates in each pixel with the T_air as the target variable, and the elevation, the LST and the normalized difference water index (NDWI) (Gao, 1996) as independent variables. Additionally, to account for the influence of the temperature and moisture surface conditions of each pixel, the LST and NDWI are spatially averaged over a series of circular neighborhoods with radii of 200, 400, 600 and 800 m, thereby reckoning eight supplementary features. Based on previous research on the sensitivity of the landscape pattern–UHI relationships to the spatial resolution (Weng et al., 2004; Song et al., 2014), the target resolution was set to 200 m.

2.4.1 Computation of satellite-derived features

The estimation of the LST from Landsat 8 images followed the methods of Avdan and Jovanovska (2016). On the one hand, the data from the near-infrared (NIR) and red bands of Landsat 8 (i.e., bands 4 and 5, respectively) were used to compute the normalized difference vegetation index (NDVI), which was then used to estimate the ground emissivity (ε_λ). On the other hand, following the Landsat 8 Data Users Handbook (Zanter, 2015), the data from the thermal band of Landsat 8 (i.e., band 10) were first converted to top-of-atmosphere spectral radiance (L_λ), from which brightness temperature (BT) was estimated (in ^∘C) as follows:

$$\begin{array}{}\text{(8)}& \text{BT}={\displaystyle \frac{K_{\mathrm{2}}}{\ln \left(\right(K_{\mathrm{1}}/L_{\mathit{\lambda }})+\mathrm{1})}}-\mathrm{273.15}.\end{array}$$

Here, K₁ and K₂ are band-specific thermal conversion constants embedded in the Landsat image metadata. Finally, the ground emissivity (ε_λ) and the brightness temperature (BT) were used to compute the LST by inversion of Planck's Law:

$$\begin{array}{}\text{(9)}& \text{LST}={\displaystyle \frac{\text{BT}}{\mathrm{1}+\mathit{\lambda }\cdot (\text{BT}/\mathit{\rho })\cdot \ln \left({\mathit{\epsilon }}_{\mathit{\lambda }}\right)}},\end{array}$$

where $\mathit{\rho }=\mathrm{1.438}\times {\mathrm{10}}^{-\mathrm{2}}$ m K is a constant computed as a product of the Boltzmann constant and Planck's constants divided by the velocity of the light, and $\mathit{\lambda }=\mathrm{10.895}\times {\mathrm{10}}^{-\mathrm{9}}$ is the average of the limiting wavelengths of the thermal band.

The NDWI is computed from the green and near-infrared (NIR) bands of Landsat 8 (i.e., bands 3 and 5, respectively) as follows:

$$\begin{array}{}\text{(10)}& \text{NDWI}={\displaystyle \frac{X_{\mathrm{green}}-X_{\mathrm{NIR}}}{X_{\mathrm{green}}+X_{\mathrm{NIR}}}}.\end{array}$$

2.4.2 Model selection and evaluation

Based on the work of Ho et al. (2014), three regression models have been considered, namely a multiple linear regression model, a support-vector machine (SVM) model and a random forest model. The accuracy of each regression model is assessed by means of a k-fold cross-validation procedure, where the regression samples are first shuffled and partitioned into three folds. For each fold k, a regression model is then trained using the other two folds, and it is validated using the samples of the k fold. Finally, the model that shows the best validation score (i.e., the R² averaged over 10 repetitions of the k-fold procedure) is selected. Additionally, the MAE and RMSE are computed in order to evaluate the deviations between the observed T_air and the predictions of each model.

The importance of each feature is also evaluated by computing its permutation importance (Breiman, 2001), namely the average decrease in the regression accuracy when a feature is randomly shuffled. The training of the regression models, the cross-validation and the permutation feature importance described above have been implemented by means of the Scikit-learn library (Pedregosa et al., 2011).

3 Results

3.1 Spatial regression of air temperature based on satellite data

When including all of the samples, the R² for the linear regression, SVM and random forest are 0.832, 0.014 and 0.960, respectively, with a respective MAE of 1.198, 2.671 and 0.580 ^∘C, and a respective RMSE of 1.508, 3.652 and 0.738 ^∘C. The coefficients suggest that SVM is not well suited for such a regression in this study area, whereas the linear regression and random forest models obtain a very strong fit – with the latter achieving the best performance. Nevertheless, the average cross-validation scores suggest that the linear regression (average score R²=0.733) is more robust to missing data and also less likely to over-fit the observations than the random forest regressor (average score R²=0.658). Thus, the remainder of the article only considers the results obtained with a linear regression model trained with all of the samples.

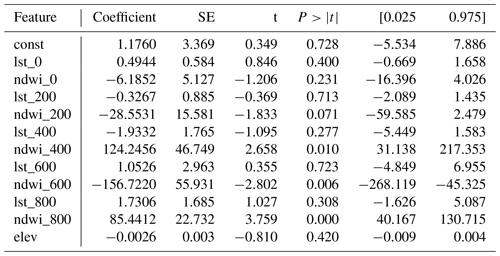
The importance of features of the chosen linear regression model can be evaluated by means of an F test, as implemented in the statsmodels (Seabold and Perktold, 2010) Python library (see Table B1). With a significance level of p=0.05, the results of the F test suggest that the most significant variable for the linear regression is the NDWI spatially averaged over a 800, 600 and 400 m radius (in decreasing order of significance). The following most significant variable is the NDWI spatially averaged over a 200 m radius (p=0.071) and without spatial averaging (p=0.231), and the LST spatially averaged over a 400 m radius (p=0.277). With a significance level of p=0.420, the elevation does not appear to be significant in this particular regression. The low significance obtained for the LST features in this study might be attributable to the large time lag between the acquisition time of the Landsat images (which ranges from 11:15 to 11:23 CET) and the time of the T_air measurements (i.e. 21:00 CET).

The relationship between the predicted and the observed values is displayed in Fig. B1. The respective MAE and RMSE values of 1.198 and 1.508 ^∘C demonstrate a stronger fit than the values of 1.82 and 2.31 ^∘C obtained in the study of Ho et al. (2014) in Vancouver. The two plots in Fig. 2 show the relationship between the elevation and T_obs of each sample and the regression errors. While there is no discernable relationship regarding the elevation of the samples (i.e., the elevation of the monitoring stations), the regression errors seem to be negatively correlated with T_obs. This pattern, which was also noted by Ho et al. (2014), indicates that high-temperature samples are systematically underestimated by the regression model, whereas low-temperature samples are consistently overestimated.

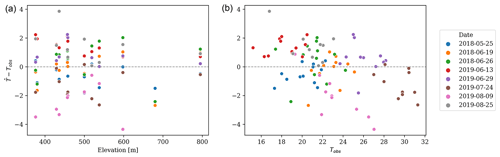
Figure 2 Scatterplot of the spatial regression residuals (y axis) against the elevation of the monitoring station (x axis of panel a) and the observed T_air (x axis of panel b), colored by the sample date. See Appendix B.

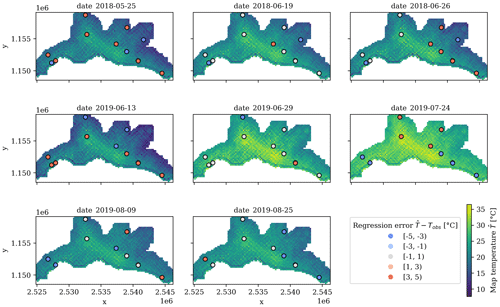
The series of predicted T_air maps for the eight dates as well as the prediction errors at the locations of the monitoring stations are displayed in Fig. 3. While the range of temperatures exhibits important differences throughout the dates, the spatial distribution of T_air is seemingly consistent. The highest temperatures persistently occur in the most urbanized areas, whereas the lowest temperatures take place at higher elevations located in the east and northeast of the map. Finally, there seems to be no discernable pattern in space nor time regarding the prediction errors at the monitoring stations.

Figure 3 Maps of the T_air predicted by the spatial regression for the eight dates. The points in the map correspond to the location of the monitoring stations and are colored according to the regression errors.

3.2 Simulation with the InVEST urban cooling model

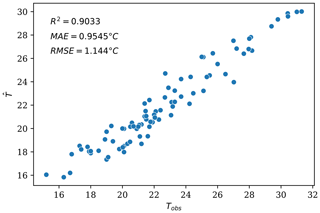
The parameters of the model that result in the best fit of the station measurements are a T_air mixing radius of r=236.02 m, a green area cooling distance of d_cool=89.21 m, and weights attributed to tree shading, albedo and evapotranspiration of w_S=0.59, w_A=0.24 and w_ET=0.17, respectively (see Appendix B). The R², MAE and RMSE of the calibrated model are 0.903, 0.955 and 1.144 ^∘C, respectively; these values suggest better model performance than randomly sampling from the station measurements. Random sampling from the station measurements yields a respective R², MAE and RMSE of 0.573, 1.947 and 2.405 ^∘C when sampling from a uniform distribution and 0.550, 1.952 and 2.468 ^∘C when sampling from a normal distribution. Furthermore, the values of R², MAE and RMSE obtained with the calibrated parameters reveal a stronger fit than the spatial regression reported above.

The relationship between the T_air values at the monitoring stations simulated with the calibrated parameters and the actual observed measurements is shown in Fig. B2. The differences between T_air simulated at the monitoring stations and the observed values are plotted against the elevation and the observed temperatures (T_obs) in Fig. 4. The pattern of such relationships is very similar to that observed in the spatial regression. Conversely, there is no clear relationship between the prediction error of the urban cooling model and elevation. Moreover, the prediction errors exhibit a negative correlation with the observed temperature, denoting a systematic tendency to both underestimate high temperatures and overestimate low temperatures – with the former being more prominent in this case, as is noticeable from the asymmetry of the y axis in Fig. 4.

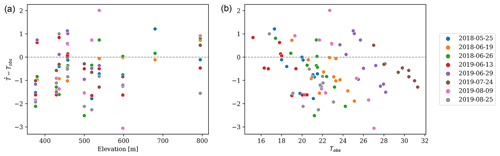
Figure 4 Scatterplot of the differences between the T_air simulated by the InVEST urban cooling model and the values observed at the monitoring stations (y axis) against the elevation of the monitoring station (x axis of panel a) and the observed T_obs (x axis of panel b), colored by the sample date.

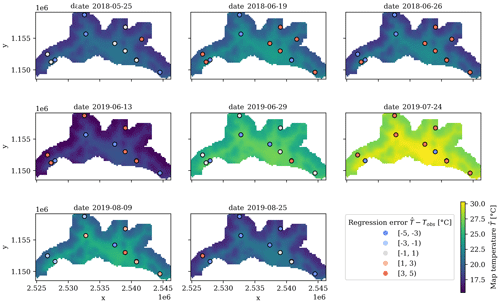
Figure 5 Maps of the T_air simulated by the InVEST urban cooling model for the eight dates. The points on the map correspond to the location of the monitoring stations and are colored according to the simulation errors.

The simulated T_air maps for the eight dates and the prediction errors at the monitoring stations are shown in Fig. 5. As in the spatial regression, the temperature ranges show important differences across dates, yet the same spatial pattern of T_air persists. The simulated distribution of T_air shows its highest values in the center of Lausanne and along the most urbanized (and hence less forested) zones along the main transportation axes, whereas the lowest temperatures are found in the forested areas located in the eastern and western extremes of the upper half of the study area.

3.3 Model comparison

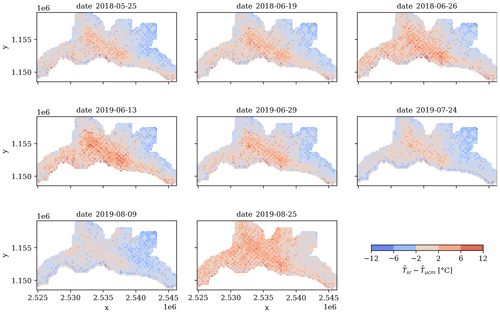
A comparison of the maps predicted by the spatial regression and the urban cooling model is displayed in Fig. 6. In line with the temporal consistency of the spatial patterns predicted by the respective two approaches, the comparison maps also show a spatial distribution of T_air that persists throughout the dates. Such a spatial pattern is strongly reminiscent of the elevation maps (see Fig. 1 above) and reflects the fact that elevation is explicitly considered in the spatial regression but not in the urban cooling model. The overall distribution of the T_air pixel differences between the two approaches follows a normal distribution that ranges from −9.620 to 11.929 ^∘C (reflecting the lower and higher temperatures predicted in the spatial regression, respectively), which is a considerably large range when compared with the small overall MAE and RMSE of both approaches. Nonetheless, the way in which the histogram is centered around 0 ^∘C suggests that the differences between the two approaches follow no particular correlation other than the spatial regression predicting more extreme T_air values, which is not surprising considering that the range of T_air is systematically bounded in the urban cooling model by the T_ref and UHI_max parameters.

Figure 6 Maps comparing the difference between the T_air predicted by the spatial regression ${\widehat{T}}_{\mathrm{sr}}$ and the InVEST urban cooling model ${\widehat{T}}_{\mathrm{ucm}}$ for the eight dates (see Appendix B).

4 Discussion

The results obtained in this study suggest that both the spatial regression based on satellite data and the InVEST urban cooling model are capable of predicting the spatial distribution of air temperature with a large degree of statistical determination. Furthermore, the fact that a similar spatial pattern is predicted by both models suggests that the biophysical mechanisms embedded in the urban cooling model are well represented. If that is the case, the urban cooling model presents two central advantages with respect to the spatial regression.

The first advantage is that, in contrast to regressions and black-box approaches, the biophysical mechanisms that drive the emergence of UHIs are represented explicitly; this allows for a physical interpretation of the parameters of the model. For example, in a comparative study of the relationship between the LST and the spatial configuration of trees in Baltimore and Sacramento, Zhou et al. (2017) suggested that the distinctive results observed in each city might be related to how the shading of trees and evapotranspiration contribute differently to urban cooling in the climatic context of each city. More precisely, the abovementioned study suggested that in the dry climate of Sacramento, large patches of trees ameliorate the efficiency of the evapotranspiration, whereas the gains from the tree shading are likely more important in the humid climate of Baltimore. The urban cooling model provides a suitable means to quantitatively address such matters – i.e., by calibrating the model in the two cities, we can explore the weights obtained for each factor to support such a hypothesis. In the case study of Lausanne reported above, the weight attributed to the tree shading (w_S=0.59) is higher than that attributed to the evapotranspiration (w_ET=0.17). This is consistent with the local climatic conditions being more similar in Lausanne and Baltimore than in Sacramento; however, the weights obtained in this study might be partly determined by the initial solution provided. Nonetheless, to further understand this issue, validation and calibration of the InVEST urban cooling model in a broader variety of cities is required. Overall, the way in which the calibrated parameters differ from the recommendations in the documentation of the model are in consonance with the particular characteristics of Lausanne. More precisely, the smaller mixing radius and cooling distances are consistent with the uneven relief of the study area.

The second major advantage of the urban cooling model is that once the model is calibrated for a given city, it can be used to evaluate synthetic scenarios, such as those stemming from master plans, urbanization prospects or the like, and to spatially design solutions. This kind of spatially explicit evaluation of the impacts of alternative scenarios on ecosystem services is in fact one of the central purposes of the InVEST suite of models (Tallis and Polasky, 2009). Statistical models like the spatial regression are not well suited to such a purpose, as they rely on features, such as the LST, that are hard to obtain other than empirically.

The approach proposed in this article is nevertheless subject to some limitations that merit thoughtful consideration. On the one hand, as acknowledged in its user guide (Sharp et al., 2020), the design of the InVEST urban cooling model presents a number of limitations, the most relevant to this study being the simplified and homogeneous way in which the air is mixed and the cooling effects of large green spaces. In complex terrains such as the Lausanne agglomeration, models with uniform weighting of space show considerable deviations from the observed distribution of air temperature (Frei, 2014). On the other hand, the relationship between the calibration parameters and the resulting R² is likely to define a complex optimization landscape with multiple local optima. As a metaheuristic that strongly depends on random decisions, the simulated annealing procedure is susceptible to convergence to local optima, arbitrarily leading to different solutions in each run. A sensitivity analysis of the parameters of the urban cooling model as undertaken preliminarily by Hamel et al. (2020) for the Île-de-France region could serve as a basis to improve the simulated annealing procedure by careful design of an appropriate neighborhood search and annealing schedule. Finally, the approach of the present study is based on observations at the moment of maximal UHI intensity (i.e., 21:00 CET in Switzerland); however, the factors that influence UHIs are likely to operate differently across the diurnal UHI cycle. In fact, several studies point to distinct relationships between the spatial patterns of vegetation and daytime and nighttime UHIs (Anniballe et al., 2014; Sheng et al., 2017; Shiflett et al., 2017; Hamel et al., 2020). Considering the nature of the implications of UHIs, e.g., energy consumption, work productivity or human health (Koppe et al., 2004; Santamouris et al., 2015; Zander et al., 2015), a sound understanding of the full diurnal UHI cycle becomes crucial towards the design of robust solutions.

Nevertheless, the limitations on how the urban cooling model represents the spatial air mixing and the cooling effects of green spaces seem hard to overcome with the current spatial sparsity of monitoring stations. Such a major shortcoming, which contrasts with the growing availability of high-resolution LST datasets, is one of the main reasons why most UHI studies have focused on the latter (Jin and Dickinson, 2010; Zhou et al., 2019). As illustrated in this article, spatial regressions based on remote sensing features such as the LST and NDWI do not necessarily replicate the air temperature measurements better than biophysical models such as the InVEST urban cooling model. Therefore, improving the spatial density of the monitoring network becomes imperative for further enlightenment with respect to the UHI phenomena.

5 Conclusions

The present article presents a spatially explicit approach to simulate UHIs with the InVEST urban cooling model, which is based on three biophysical mechanisms, namely tree shade, evapotranspiration and albedo. The proposed approach shows how LULC and air temperature data can be combined to calibrate the parameters of the model to best fit measurements from monitoring stations by means of an automated procedure. The simulations performed for the urban agglomeration of Lausanne show that the InVEST urban cooling model can outperform spatial regressions based on satellite-derived features such as LST, NDWI and elevation. The way in which both approaches consistently predict the highest temperatures in the most urbanized parts of the agglomeration suggests that the enhancement of green infrastructure can be an effective heat mitigation strategy; however, further exploration in other climatic contexts is required to fully understand this issue. To that end, the reusability of the computational workflow paves the way for further application of the urban cooling model to a broad variety of cities, which can serve to improve the understanding of the UHI phenomena and support the design of heat mitigation strategies.

Appendix A: Data

A1 Landsat tiles

The list of product identifiers for the Landsat image tiles are available as a comma-separated value (CSV) file at https://zenodo.org/record/4384675/files/landsat-tiles.csv (last access: 13 July 2020).

A2 Monitoring stations

The list of monitoring stations with their operator and their elevation in meters above sea level is available as a CSV file at https://zenodo.org/record/4384675/files/station-tair.csv (last access: 13 July 2020). The operators are Agrometeo, the Federal Roads Office (ASTRA), the Federal Office for the Environment (BAFU), the general directorate for the environment of the canton of Vaud (DGE), and the Federal Institute of Forest, Snow and Landscape Research (WSL) (Rebetez et al., 2018).

A3 Biophysical table

The biophysical table used in the computational workflow is available as a CSV file at https://zenodo.org/record/4384675/files/biophysical-table.csv (last access 13 July 2020). The crop and water coefficients are based on Allen et al. (1998), whereas rock, soil and urban coefficients are derived from the results of Grimmond and Oke (1999) in the city of Chicago. Given that the evapotranspiration of the vegetation and crops is subject to seasonal changes in temperate zones such as Switzerland (Allen et al., 1998), the values correspond to the mid-season estimation (June to August) in Nistor (2016). The albedo values are based on the work of Stewart and Oke (2012). The shade column, which represents the proportion of tree cover of each LULC class, has been computed with a high-resolution tree canopy map of Lausanne and is, therefore, specific to the study area. Rows with a dash (–) in the shade column denote that the corresponding LULC class is not present in the study area.

A4 Reference temperatures and UHI magnitude

Figure A1 Reference temperatures T_ref (i.e., minimum T_air at 21:00 CET among the monitoring stations) and magnitude of the UHI UHI_max (i.e., difference between T_ref and the maximum T_air at 21:00 CET among the monitoring stations) for the eight dates considered in this study.

Appendix B: Results

B1 Tables

Table B1 F test of variable significance of the linear regression.

B2 Figures

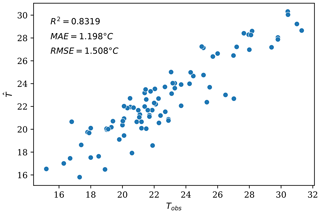
Figure B1 Scatterplot of the T_air predicted by the linear regression model trained with all of the samples (y axis) versus the observed measurements (x axis).

Figure B2 Scatterplot of the T_air values simulated with the InVEST urban cooling model (y axis) versus the observed measurements (x axis).