Simulating stable carbon isotopes in the ocean component of the FAMOUS general circulation model with MOSES1 (XOAVI)

Ocean circulation and the marine carbon cycle can be indirectly inferred from stable and radiogenic carbon isotope ratios (δ¹³C and Δ¹⁴C, respectively), measured directly in the water column, or recorded in geological archives such as sedimentary microfossils and corals. However, interpreting these records is non-trivial because they reflect a complex interplay between physical and biogeochemical processes. By directly simulating multiple isotopic tracer fields within numerical models, we can improve our understanding of the processes that control large-scale isotope distributions and interpolate the spatiotemporal gaps in both modern and palaeo datasets. We have added the stable isotope ¹³C to the ocean component of the FAMOUS coupled atmosphere–ocean general circulation model, which is a valuable tool for simulating complex feedbacks between different Earth system processes on decadal to multi-millennial timescales. We tested three different biological fractionation parameterisations to account for the uncertainty associated with equilibrium fractionation during photosynthesis and used sensitivity experiments to quantify the effects of fractionation during air–sea gas exchange and primary productivity on the simulated δ¹³C_DIC distributions. Following a 10 000-year pre-industrial spin-up, we simulated the Suess effect (the isotopic imprint of anthropogenic fossil fuel burning) to assess the performance of the model in replicating modern observations. Our implementation captures the large-scale structure and range of δ¹³C_DIC observations in the surface ocean, but the simulated values are too high at all depths, which we infer is due to biases in the biological pump. In the first instance, the new ¹³C tracer will therefore be useful for recalibrating both the physical and biogeochemical components of FAMOUS.

1 Introduction

Carbon isotopes are often used as proxies for ocean circulation and the marine carbon cycle. There are three naturally occurring carbon isotopes: the stable isotopes ¹²C (98.9 %) and ¹³C (1.1 %), and the radioactive isotope ¹⁴C ($\mathrm{1.2}\times {\mathrm{10}}^{-\mathrm{10}}$ %), which is also known as radiocarbon (Key, 2001). In this study, we focus on the stable isotopes, with ¹⁴C being discussed in detail elsewhere (Dentith et al., 2019a). The relative proportions of ¹²C and ¹³C in a given oceanic pool (e.g. dissolved inorganic carbon, DIC, or particulate organic carbon, POC) are controlled by ocean circulation and mixing, and mass-dependent fractionation during biogeochemical processes such as air–sea gas exchange (Lynch-Stieglitz et al., 1995; Zhang et al., 1995), photosynthesis (e.g. Sackett et al., 1965; Rau et al., 1989; Hollander and McKenzie, 1991; Keller and Morel, 1999), and calcium carbonate formation (Emrich et al., 1970; Turner, 1982; Ziveri et al., 2003). This is typically reported in delta (δ) notation, which is the heavy to light isotope ratio (R) of a sample relative to a standard in per mille (‰) units:

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=\left({\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}{\mathrm{C}}_{\mathrm{sample}}}{{}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}{\mathrm{C}}_{\mathrm{standard}}}}-\mathrm{1}\right)\times \mathrm{1000}.\end{array}$$

Oceanic δ¹³C is primarily used to track individual water masses (Curry and Oppo, 2005), study past changes in the carbon cycle (e.g. de la Fuente et al., 2017), and investigate changes in ocean circulation on glacial–interglacial timescales (e.g. Spero and Lea, 2002; Campos et al., 2017). It has also been used to constrain air–sea gas exchange rates (Gruber and Keeling, 2001) and to estimate the uptake of anthropogenic carbon by the global oceans (Quay et al., 1992, 2003).

Oceanographic surveys conducted since the 1970s, such as the World Ocean Circulation Experiment (WOCE; Orsi and Whitworth, 2005; Talley, 2007, 2013; Koltermann et al., 2011), and synthesis projects such as Carbon dioxide in the Atlantic Ocean (CARINA; Key et al., 2010), Pacific Ocean Interior Carbon (PACIFICA; Suzuki et al., 2013), and the Global Ocean Data Analysis Project (GLODAP; Key et al., 2004, 2015; Olsen et al., 2016), provide an indication of large-scale carbon isotope distributions in the modern oceans. The two main drawbacks of these surveys are that they include relatively few measurements from the subsurface ocean and that there were only a limited number of repeat measurements at fixed locations, which were often taken decades apart. These datasets are therefore insufficient for studying transient changes in carbon isotope distributions at subdecadal resolution.

Geological archives such as corals (e.g. Guilderson et al., 2013) and sediment cores (e.g. Oliver et al., 2010) are used to extend the record further back in time. However, interpreting isotopic ratios in geological archives is non-trivial because they result from a complex interplay between physical processes and biogeochemical processes, both in the water column itself and during biomineralisation, which can be difficult to disentangle.

Table 1 Overview of existing ¹³C-enabled models.

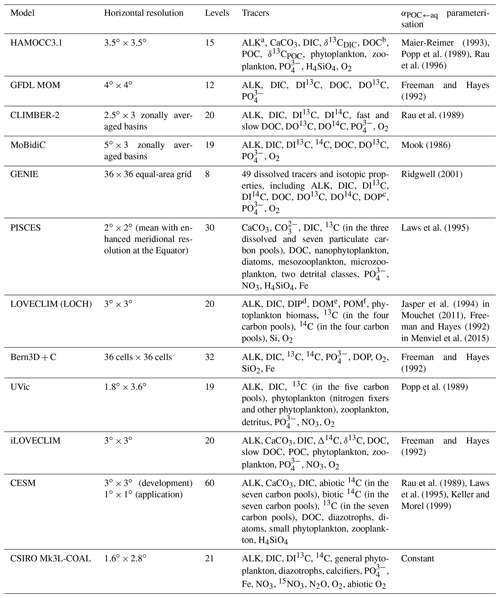
^a ALK: alkalinity; ^b DOC: dissolved organic carbon; ^c DOP: dissolved organic phosphorus; ^d DIP: dissolved inorganic phosphorus; ^e DOM: dissolved organic matter; ^f POM: particulate organic matter

By including carbon isotopes in climate models, we can fill in the spatiotemporal gaps in both modern and palaeo datasets, and improve our understanding of the processes that control their large-scale distributions (Tagliabue and Bopp, 2008; Schmittner et al., 2013; Menviel et al., 2017). The Ocean Carbon-Cycle Modelling Intercomparison Project (OCMIP) was initiated in 1995 with the aim of evaluating the major differences between global ocean carbon cycle models and advancing our understanding of the ocean as a long-term CO₂ reservoir (Orr, 1999). Carbon isotopes are not routinely incorporated into climate models because of the computational expense associated with the long equilibration between the deep ocean and the atmosphere (Bardin et al., 2014). However, since OCMIP produced a legacy of standard input fields (Orr, 1999; Orr et al., 2000, 2017), carbon isotopes have increasingly been implemented into models of varying complexities to validate physical and biogeochemical schemes, to investigate the spatiotemporal variability in isotope distributions, and to reconcile the interpretation of ocean proxy data. As outlined in Table 1, the community of ¹³C-enabled models currently includes HAMOCC3.1 (Hofmann et al., 2000), the Geophysical Fluid Dynamics Laboratory (GFDL) Modular Ocean Model (MOM; Murnane and Sarmiento, 2000), CLIMBER-2 (Brovkin et al., 2002), MoBidiC (Crucifix, 2005), GENIE (Ridgwell et al., 2007), Pelagic Interactions Scheme for Carbon and Ecosystem Studies (PISCES) (Tagliabue and Bopp, 2008), LOVECLIM (Mouchet, 2011; Menviel et al., 2015), Bern3D+C (Tschumi et al., 2011), the University of Victoria (UVic) Earth system model (ESM) (Schmittner et al., 2013), iLOVECLIM (Bouttes et al., 2015), the Community Earth System Model (CESM) (Jahn et al., 2015), and the Commonwealth Scientific and Industrial Research Organisation Mark 3L climate system model with the Carbon of the Ocean, Atmosphere and Land (CSIRO Mk3L-COAL) biogeochemical model (Buchanan et al., 2019). Most of these are low-resolution (3 to 5^∘), intermediate-complexity models that are valuable tools for studying changes in ocean biogeochemistry on multi-millennial timescales. The more complex models (e.g. PISCES and CESM) provide a more sophisticated representation of physical and biogeochemical processes because of increased spatial resolution and/or the inclusion of more carbon pools. However, the higher-complexity models are computationally expensive; for example, at the time of their study, a 6010-year spin-up simulation with CESM took over 7 months to run (Jahn et al., 2015). Without employing offline or accelerated spin-up techniques (e.g. Lindsay, 2017), these models are therefore less practical for running the long simulations required to fully spin up the components of the Earth system that evolve on millennial timescales, such as deep ocean circulation (England, 1995) and ocean biogeochemical cycles (Falkowski et al., 2000; Key et al., 2004).

Here, we describe the implementation of ¹³C in the ocean component of the FAMOUS general circulation model (GCM). FAMOUS is well suited to studying complex interactions between different components of the Earth system on decadal to multi-millennial timescales, due to its reduced spatial resolution and increased time step relative to the latest generation of state-of-the-art GCMs (Sect. 2.1). We use sensitivity experiments to quantify the effects of isotopic fractionation during air–sea gas exchange and primary productivity on the simulated δ¹³C_DIC distributions (Sects. 2.3.3 and 3.1) and test three different parameterisations for photosynthetic fractionation to account for the uncertainty associated with the relative influence of ambient conditions, physiological effects and transport mechanism on the fractionation of carbon isotopes during photosynthetic CO₂ fixation (Sects. 2.2.2 and 3.3). We evaluate the overall performance of the model in simulating large-scale δ¹³C_DIC distributions by comparing to modern observations (Sect. 3.2) and discuss the potential of the new ¹³C tracer as a tuning target for future recalibration work (Sect. 3.4).

2 Methods

2.1 Model description

FAMOUS is a coupled atmosphere–ocean GCM (Jones et al., 2005; Smith et al., 2008; Smith, 2012; Williams et al., 2013) based on HadCM3 (Gordon et al., 2000; Pope et al., 2000). Both are configurations of the UK Met Office Unified Model (UM) version 4.5 (Valdes et al., 2017). The quasi-hydrostatic primitive equation atmospheric model is 5^∘ in latitude by 7.5^∘ in longitude, with 11 vertical levels on a hybrid sigma-pressure coordinate system. The rigid-lid ocean model has a horizontal resolution of 2.5^∘ × 3.75^∘ and 20 unevenly spaced vertical levels, which are approximately 10 m thick in the near-surface ocean and 600 m thick in the deep ocean. The atmosphere and ocean operate on 1 and 12 h time steps, respectively, and are coupled once per model day. The model currently includes oxygen (Williams et al., 2014) and chlorofluorocarbons (Pope et al., 2000) as optional tracers. At the time of this study, FAMOUS is capable of simulating 400 to 500 model years per wall-clock day on tier 2 (regional) and tier 3 (local) high-performance computers at the University of Leeds, which is more than 5 times the run speed of HadCM3. This makes FAMOUS ideal for running long (multi-millennial) simulations (Smith and Gregory, 2012; Gregoire et al., 2012, 2015) or large (hundred-member) ensembles (Gregoire et al., 2011; Sagoo et al., 2013). Further technical documentation can be found in an ongoing special issue in Geoscientific Model Development (http://www.geosci-model-dev.net/special_issue15.html, last access: 23 December 2019).

We added ¹³C as an optional passive tracer into the ocean component of FAMOUS, using the Met Office Surface Exchange Scheme (MOSES) version 1 (Cox et al., 1999) generation of the model to evaluate our scheme. Although a newer version of the land surface model exists, which includes the terrestrial carbon cycle and interactive vegetation (MOSES2.2; Essery et al., 2001, 2003; Williams et al., 2013; Valdes et al., 2017), problems have been identified with its representation of meridional overturning circulation (MOC) in multi-millennial simulations with constant pre-industrial boundary conditions (Dentith et al., 2019b). Specifically, FAMOUS-MOSES2.2 simulates a collapsed Atlantic MOC (AMOC) and a strong, deep Pacific MOC when the run length exceeds 6000 years, resulting in spurious ocean tracer distributions. However, our code is directly transferable between the different generations of the model, meaning that the isotope system can be extended into the terrestrial carbon cycle following additional tuning to improve the physical ocean circulation in FAMOUS-MOSES2.2.

2.1.1 Hadley Centre Ocean Carbon Cycle Model (HadOCC)

The marine carbon cycle in FAMOUS is modelled by HadOCC, a coupled physical–biogeochemical model that simulates air–sea gas exchange, the circulation of DIC, and the cycling of carbon by marine biota (Palmer, 1998; Palmer and Totterdell, 2001). The ecosystem model provides a simplified representation of the ocean biological system, with a single (nitrogenous) nutrient, a single class of phytoplankton, a single class of (non-migrating) zooplankton, and detritus. Changes in the size of these pools are calculated through a series of coupled differential equations that describe primary production, respiration, mortality, grazing, excretion, and the sinking and remineralisation of detritus. The system is nitrogen limited and carbon flows are coupled to the nitrogen flows by stoichiometric ratios that are fixed for each pool of organic matter. In addition to the four biological components, HadOCC also explicitly simulates DIC and alkalinity. Modelled DIC concentrations depend upon phytoplankton growth and biological breakdown. Alkalinity is similarly affected by biological processes and is used to calculate the proportion of DIC that is in the form of CO₂ in the surface waters and consequently the air–sea CO₂ flux. All six tracers are advected, diffused, and mixed across all levels, although phytoplankton and zooplankton concentrations are negligible below the euphotic zone (approximately the uppermost 100 m of the ocean). Detritus is the only biological tracer that is subject to sinking, which is parameterised at a constant rate of 10 m d⁻¹. However, there is no representation of sediments: any detrital material that reaches the ocean floor is therefore immediately refluxed back to the top layer of the ocean to conserve carbon and nitrogen. Calcium carbonate (CaCO₃) production is represented as an instantaneous redistribution of DIC and alkalinity below the lysocline, the depth of which is spatially and temporally constant (approximately 2500 m below sea level).

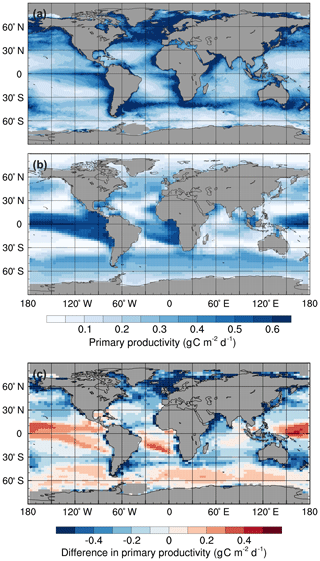
Figure 1 Mean annual surface primary productivity: (a) observations estimated from surface chlorophyll concentrations using the Vertically Generalised Production Model (Behrenfeld and Falkowski, 1997), (b) the std simulation in the 1990s, and (c) simulated minus observed. Monthly mean primary productivity data were obtained from the Oregon State University Ocean Productivity website (http://www.science.oregonstate.edu/ocean.productivity, last access: 23 December 2019).

HadOCC accurately simulates low primary production in the subtropical gyres and high production in the regions with the greatest nutrient supply: the subpolar North Pacific and North Atlantic oceans, and around the Antarctic Convergence Zone (Fig. 1). However, primary production is higher than observed in the equatorial Pacific, which is attributed to excessive upwelling in the eastern equatorial Pacific (Palmer and Totterdell, 2001). Production is lower than observed northwards of 50^∘ N in the Atlantic and Pacific basins because sea ice formation and melt do not affect salinity distributions (an area for future development), although the model does include an iceberg meltwater flux (Smith et al., 2008). Consequently, stably stratified, low-salinity layers of meltwater, which promote phytoplankton growth, are not represented in the model (Palmer and Totterdell, 2001). Furthermore, the simulated production in coastal regions is lower than observed. There are three main reasons for this: (1) HadOCC does not simulate riverine input of nutrients, which are a significant source of coastal nutrients; (2) most of the coastlines in FAMOUS are directly adjacent to ocean grid cells that are more than 1 km deep, which dilutes near-surface nutrient concentrations; and (3) upwelling is spread out over several grid points, which causes production to be more diffuse than observed (Palmer and Totterdell, 2001).

The level of representation of ecosystem processes in HadOCC is of intermediate complexity, making it computationally faster than more sophisticated ecosystem models that include additional POC species and/or multiple nutrients (e.g. PISCES). Previous studies have found that errors in biogeochemical simulations are largely driven by biases in the physical ocean circulation (i.e. inaccuracies in the climate or ocean model to which the ecosystem model has been coupled; Doney, 1999; Doney et al., 2004; Najjar et al., 2007). Thus, simulating carbon isotopes in a more complex ecosystem model would not necessarily yield substantially better results.

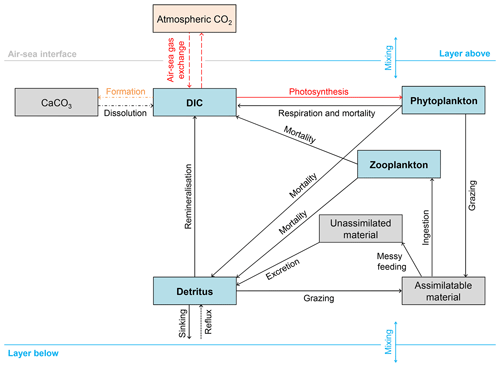
Figure 2 Schematic overview of the ¹³C implementation in FAMOUS. Blue boxes represent permanent carbon pools. Grey boxes represent temporary carbon pools (note that CaCO₃ is a temporary carbon pool because the export of CaCO₃ in FAMOUS is represented as an instantaneous redistribution of alkalinity and carbon at depth). The orange box represents the prescribed atmospheric carbon pool. The dashed lines represent fluxes of ¹³C∕¹²C. However, note that the outgassed ¹³C∕¹²C has no effect on δ¹³C_atm because FAMOUS does not currently have a fully interactive carbon cycle. Solid lines represent fluxes of ¹³C. Dot-dashed lines represent processes that occur below the lysocline (≈2500 m below sea level). The dotted line represents the reflux of detrital material from the seafloor to the surface layer. Red lines represent fractionation effects. The orange line represents isotopic fractionation during calcium carbonate formation (${\mathit{\alpha }}_{{\mathrm{CaCO}}_{\mathrm{3}}}$), which is included in the code as a user-specified constant. Note that all simulations presented in this study were run without fractionation during calcium carbonate formation (i.e. ${\mathit{\alpha }}_{{\mathrm{CaCO}}_{\mathrm{3}}}=\mathrm{1.0}$, which is equivalent to a fractionation effect of 0 ‰).

2.2 Carbon isotope implementation

We added ¹³C to the four carbon pools in HadOCC: DIC, phytoplankton, zooplankton, and detritus (Fig. 2). We assume that modelled DIC is ¹²C and carry ¹³C as a ratio (DI¹³C∕DI¹²C); therefore, virtual fluxes are not required to account for the dilution or concentration effects of surface freshwater fluxes (Appendix A). We also use model units to minimise the error associated with carrying small numbers:

$$\begin{array}{}\text{(2)}& \text{Model units}={\displaystyle \frac{{\mathrm{DI}}^{\mathrm{13}}\mathrm{C}}{{\mathrm{DI}}^{\mathrm{12}}\mathrm{C}}}\times {\displaystyle \frac{\mathrm{100}}{{}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}{\mathrm{C}}_{\mathrm{std}}}},\end{array}$$

where ${}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}{\mathrm{C}}_{\mathrm{std}}=\mathrm{1.12372}\times {\mathrm{10}}^{-\mathrm{2}}$ (Craig, 1957). We account for isotopic fractionation during air–sea gas exchange (Sect. 2.2.1 and Appendix B) and photosynthesis (Sect. 2.2.2 and Appendix C). Observational estimates suggest that isotopic fractionation during CaCO₃ formation is between +3 ‰ and −2 ‰ (Ziveri et al., 2003), which is small compared to the other fractionation effects (Turner, 1982). Previous ¹³C isotope implementation studies have therefore assumed either no isotopic fractionation during CaCO₃ production (Schmittner et al., 2013) or prescribed constant values, for example, +1 ‰ (Tagliabue and Bopp, 2008) or +2 ‰ (Jahn et al., 2015). We conducted sensitivity tests where fractionation during CaCO₃ formation was included at constant rates of −2 ‰, 0 ‰, and +2 ‰, respectively. After 10 000 years, there was 0.001 ‰ difference in both the mean surface ocean δ¹³C_DIC values and the surface standard deviations between all three simulations, and 0.02 ‰ difference between the three global volume-weighted integrals. Since these differences are small, we proceeded with the equivalent of no fractionation during CaCO₃ production (${\mathit{\alpha }}_{{\mathrm{CaCO}}_{\mathrm{3}}}=\mathrm{1.0}$).

2.2.1 Air–sea gas exchange

The air–sea gas flux of DI¹²C (F) is calculated as

$$\begin{array}{}\text{(3)}& F=\text{PV}\times (C_{\mathrm{sat}}-C_{\mathrm{surf}}),\end{array}$$

where C_sat is the saturation concentration of atmospheric CO₂ (in mol m⁻³), C_surf is the surface aqueous concentration of CO₂ (in mol m⁻³), and PV is the piston velocity (in cm h⁻¹), which is calculated as

$$\begin{array}{}\text{(4)}& \text{PV}=a\times u^{\mathrm{2}}\times (\mathrm{1}-a_{\mathrm{ice}})\times {\left({\displaystyle \frac{\mathit{Sc}}{\mathrm{660}}}\right)}^{-\mathrm{0.5}},\end{array}$$

where a is a tuneable coefficient, u is the wind speed (in m s⁻¹), a_ice is the fractional ice cover, and Sc is the Schmidt number for CO₂, calculated as a function of sea surface temperature (SST, in ^∘C):

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\mathit{Sc}& =\mathrm{2073.1}-\mathrm{125.62}\times \text{SST}+\mathrm{3.6276}\times {\text{SST}}^{\mathrm{2}}\\ & -\mathrm{0.043219}\times {\text{SST}}^{\mathrm{3}}.\end{array}\end{array}$$

The air–sea gas flux of DI¹³C∕DI¹²C $\left(F_{\frac{\mathrm{13}}{\mathrm{12}}}\right)$ is calculated as

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{F}_{\frac{\mathrm{13}}{\mathrm{12}}}& ={\displaystyle \frac{\mathrm{1}}{{}^{\mathrm{12}}\mathrm{C}}}\times \text{PV}\times [{\mathit{\alpha }}_{\mathrm{k}}\times {\mathit{\alpha }}_{\mathrm{aq}\leftarrow \mathrm{g}}\\ & \times \left(C_{\mathrm{sat}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{A}}{{}^{\mathrm{12}}\mathrm{A}}}-{\displaystyle \frac{C_{\mathrm{surf}}\times \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}{{\mathit{\alpha }}_{\mathrm{DIC}\leftarrow \mathrm{g}}}}\right)\\ & -\left({\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}\times \left[C_{\mathrm{sat}}-C_{\mathrm{surf}}\right]\right)],\end{array}\end{array}$$

where ¹³A∕¹²A and ¹³C∕¹²C are the ¹³C∕¹²C ratios of the atmosphere and DIC, respectively, α_k is the constant kinetic fractionation factor (0.99919), α_aq←g is the temperature-dependent fractionation during gas dissolution:

$$\begin{array}{}\text{(7)}& {\mathit{\alpha }}_{\mathrm{aq}\leftarrow \mathrm{g}}=\mathrm{0.9986}-(\mathrm{4.9}\times {\mathrm{10}}^{-\mathrm{6}})\times \text{SST},\end{array}$$

and α_DIC←g is the temperature-dependent fractionation between aqueous CO₂ and DIC:

$$\begin{array}{}\text{(8)}& {\mathit{\alpha }}_{\mathrm{DIC}\leftarrow \mathrm{g}}=\mathrm{1.01051}-(\mathrm{1.05}\times {\mathrm{10}}^{-\mathrm{4}})\times \text{SST}.\end{array}$$

All three fractionation factors are based on the equations of Zhang et al. (1995). However, following Schmittner et al. (2013), we neglect the effect that the carbonate fraction (fCO₃) has on α_DIC←g because this is much smaller (0.05 ‰) than the temperature effect (3 ‰). Currently, atmospheric CO₂ and δ¹³C concentrations can either be held constant or prescribed from a file that contains a single global weighted-average value per year.

2.2.2 Photosynthesis

Isotopic fractionation during photosynthesis (α_POC←DIC, herein α_p) is calculated as

$$\begin{array}{}\text{(9)}& {\mathit{\alpha }}_{\mathrm{p}}={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{aq}\leftarrow \mathrm{g}}}{{\mathit{\alpha }}_{\mathrm{DIC}\leftarrow \mathrm{g}}}}\times {\mathit{\alpha }}_{\mathrm{POC}\leftarrow \mathrm{aq}},\end{array}$$

where α_POC←aq is the equilibrium fractionation factor between aqueous CO₂ and POC.

Empirical relationships for the different biogeochemical fractionation effects (α_aq←g, α_DIC←g, and α_POC←aq) have been established from laboratory experiments, modern oceans and lakes, and the sedimentary record. However, there are still uncertainties associated with the parameterisation of α_POC←aq. Early studies investigated a potential temperature dependence of the carbon isotope composition of marine phytoplankton. For example, Sackett et al. (1965) proposed that photosynthetic fractionation is higher at lower temperatures (0.23 ‰ per ^∘C) after observing that phytoplankton in the Drake Passage had more negative δ¹³C values than those in the tropics. Wong and Sackett (1978) also recorded small temperature effects (−0.13 ‰ to +0.36 ‰ per ^∘C) in 17 species of marine phytoplankton; however, the authors concluded that the 15 ‰ range observed in their samples was primarily related to different metabolic pathways within the organisms. Numerous studies have suggested that the fractionation of carbon isotopes during photosynthetic CO₂ fixation relates to aqueous CO₂ concentrations (${\mathrm{CO}}_{\mathrm{2}}^{\ast }$) in the ambient environment (Popp et al., 1989; Rau et al., 1989; Jasper and Hayes, 1990; Hollander and McKenzie, 1991; Freeman and Hayes, 1992). However, these studies assumed that CO₂ only enters the phytoplankton by passive diffusion and neglected physiological effects, such as phytoplankton growth rate, cell size and geometry, and cell membrane permeability. Taking into consideration that physiological factors may modify, weaken, or eliminate the relationship between ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$ and photosynthetic fractionation, Rau et al. (1996) proposed a model that accounted for the isotopic composition of the ambient aqueous CO₂, isotopic fractionation associated with diffusive transport into the cell, and isotopic fractionation associated with enzymatic, intracellular fixation. Laws et al. (1995) identified a linear relationship between phytoplankton growth rate, ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$, and isotopic fractionation during photosynthesis under the assumption that the growth rate is proportional to the net transport of CO₂ into the cell. A later study by Laws et al. (1997), which analysed the same species of marine diatom over a larger range of ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$, revised this to a non-linear relationship. Burkhardt et al. (1999) and Keller and Morel (1999) additionally included active bicarbonate transport in their calculations, recognising that aqueous CO₂ is not the only substrate for photosynthetic fixation and that processes other than diffusion can contribute to inorganic carbon acquisition. This has been a relatively inactive research area in the last 20 years, but there remains no single accepted model for fractionation during photosynthesis.

Consequently, previous carbon isotope implementation studies have used a number of different parameterisations for biological fractionation (Table 1), with the choice of scheme largely reflecting the complexity of the simulated biogeochemical and ecosystem processes. It is difficult to compare the success of the different parameterisations used by individual modelling groups because inter-model differences in the simulated isotopic distributions predominantly relate to resolution, complexity, and biases in the physical ocean circulation and ocean biogeochemistry, as opposed to the choice of fractionation scheme. However, Hofmann et al. (2000) tested three different fractionation schemes within a single model. In their study, the oversimplified assumption of constant biological fractionation, taken from Maier-Reimer (1993), failed to reproduce the observed latitudinal gradients in δ¹³C_POC. Calculating the fractionation as a function of ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$, as per Popp et al. (1989), successfully replicated the interhemispheric asymmetry in δ¹³C_POC, but a growth-rate-dependent fractionation (e.g. Rau et al., 1996) was required to additionally capture the seasonal variations. Jahn et al. (2015) also demonstrated differences between three different fractionation schemes within a single model. In their study, the simple scheme of Rau et al. (1989) produced lower δ¹³C_DIC values in the surface ocean and higher δ¹³C_DIC values below 150 m compared to the more complex parameterisations of Laws et al. (1995) and Keller and Morel (1999). The differences between the intermediate-complexity formulation (Laws et al., 1995) and the most complex formulation (Keller and Morel, 1999) were small, and the Laws et al. (1995) equation was chosen as the default scheme.

To account for the uncertainty associated with biological fractionation in FAMOUS, we tested three different parameterisations for α_POC←aq. In the standard simulation (std), we calculated α_POC←aq according to Popp et al. (1989):

$$\begin{array}{}\text{(10)}& {\mathit{\alpha }}_{\mathrm{POC}\leftarrow \mathrm{aq}}=-\mathrm{0.017}\log \left({\mathrm{CO}}_{\mathrm{2}}^{\ast }\right)+\mathrm{1.0034},\end{array}$$

where ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$ is the aqueous CO₂ concentration (in µmol L⁻¹).

Both of the alternative parameterisations calculated α_POC←aq as a function of the phytoplankton-specific growth rate (μ) and ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$, representing an increase in complexity relative to the standard scheme. The first was a linear relationship derived from the experimental results of Laws et al. (1995):

$$\begin{array}{}\text{(11)}& {\mathit{\alpha }}_{\mathrm{POC}\leftarrow \mathrm{aq}}={\displaystyle \frac{-\mathrm{15}}{\left(\mathit{\mu }/{\mathrm{CO}}_{\mathrm{2}}^{\ast }\right)-\mathrm{15.371}}}.\end{array}$$

The second was a non-linear relationship derived from the experimental results of Laws et al. (1997):

$$\begin{array}{}\text{(12)}& {\mathit{\alpha }}_{\mathrm{POC}\leftarrow \mathrm{aq}}={\displaystyle \frac{\mathrm{1}+\left(\mathit{\mu }/\mathrm{0.225}{\mathrm{CO}}_{\mathrm{2}}^{\ast }\right)}{\mathrm{1.0268}+\mathrm{1.0055}\left(\mathit{\mu }/\mathrm{0.225}{\mathrm{CO}}_{\mathrm{2}}^{\ast }\right)}}.\end{array}$$

Because HadOCC is a relatively simple ecological model, with only a single representation of phytoplankton, we did not test more complex schemes, such as those that use phytoplankton-type-specific cell parameters (e.g. Burkhardt et al., 1999; Keller and Morel, 1999).

2.2.3 Advection

The default advection scheme in FAMOUS is Quadratic Upstream Interpolation for Convective Kinematics (QUICK) with flux limiter (Leonard et al., 1993). This scheme is used to compute the transport of tracers such as temperature, salinity, nutrients, and DIC throughout the ocean. For consistency, we use the same advection scheme to calculate ¹³C concentrations in the ocean interior. For greater numerical stability, δ¹³C_DIC is fixed at 0 ‰ in the Hudson Bay and Baltic Sea. With the model's standard pre-industrial land–sea mask, these inland bodies of water are isolated from the global oceans; therefore, their isotope concentrations will not affect large-scale tracer distributions.

2.3 Simulations

2.3.1 Spin-up simulation

Carbon isotope simulations must be spun up over multiple millennia (5000 to 15 000 years; Orr et al., 2000) to reach steady state because of the long timescale of deep ocean ventilation (Bardin et al., 2014). We therefore ran our spin-up simulation for 10 000 years with constant pre-industrial boundary conditions, where δ¹³C_atm was fixed at −6.5 ‰ (Francey et al., 1999) and δ¹³C_ocn was initialised at a globally uniform value of 0 ‰. The global volume-weighted integral of δ¹³C_DIC started to stabilise after 7000 years, and at the end of the spin-up simulation, the drift was less than 0.001 ‰ yr⁻¹ (Fig. S1 in the Supplement).

Figure 3 Prescribed atmospheric δ¹³C values (solid) from the Law Dome and South Pole ice core records (Rubino et al., 2013) and prescribed atmospheric CO₂ values (dashed) from the OCMIP-2 files (Orr et al., 2000).

2.3.2 Historical simulation

A transient simulation for the period 1765 to 2000 CE was initialised from the end of the spin-up simulation to generate model output that is directly comparable to modern observations (Fig. 3). Atmospheric CO₂ concentrations were prescribed from the OCMIP-2 files (Orr et al., 2000) and δ¹³C_atm was prescribed from the Law Dome and South Pole ice core records (Rubino et al., 2013). The decrease in δ¹³C_atm from −6.5 ‰ in 1750 to approximately −8.0 ‰ in 2000 is due to the Suess effect. First observed in tree ring records of atmospheric composition, the Suess effect refers to the dilution of ¹³C in any carbon pool due to fossil fuel burning (Suess, 1955; Keeling, 1979). Fossil fuels formed millions of years ago from organic matter, which is relatively ¹³C depleted due to isotopic fractionation during photosynthesis. Their isotopic signature is therefore approximately 20 ‰ lower than that of the ambient atmosphere (Andres et al., 1994, 1996). To act as a control, the spin-up simulation was continued for an additional 235 years with constant CO₂ and δ¹³C_atm.

2.3.3 Sensitivity experiments

Five further simulations were conducted to quantify the effects of fractionation during air–sea gas exchange and primary productivity on the simulated δ¹³C_DIC distributions. All five simulations were run for 10 000 years with constant pre-industrial boundary conditions. In each of the simulations, δ¹³C_atm was fixed at −6.5 ‰ and δ¹³C_ocn was initialised at 0 ‰. At the end of each of the spin-up simulations, the global volume-weighted δ¹³C_DIC integral was drifting by less than 0.001 ‰ yr⁻¹.

Table 2 Overview of the fractionation factors used in the sensitivity experiments.

^a 0.99919; ^b Calculated as per Eqs. (7)–(8)

Three of the simulations were designed to quantify the effects of the individual processes outlined in Sect. 2.2 (Table 2). In the ki-fract-only simulation, α_aq←g, α_DIC←g, and α_p were all set to 1; therefore, only kinetic fractionation effects were calculated. In the no-asgx-fract simulation, α_k, α_aq←g, and α_DIC←g were all set to 1 to eliminate the effect of fractionation during air–sea gas exchange. Fractionation during photosynthesis continued to be calculated using the std biological fractionation scheme, as per Eqs. (9)–(10). In the no-bio-fract simulation, α_p was set to 1 to remove the effect of fractionation during photosynthesis, but fractionation during air–sea gas exchange continued to be calculated as per Eqs. (6)–(8).

The other two simulations were designed to assess the sensitivity of the simulated δ¹³C_DIC distributions to the choice of biological fractionation scheme (Sect. 2.2.2). In the L95 simulation, α_POC←aq was calculated using Eq. (11), whilst in the L97 simulation, α_POC←aq was calculated using Eq. (12). As with the std simulation, we initialised a 235-year transient simulation (with the ¹³C-Suess effect) from the end of both of these spin-ups to allow the output from all three photosynthetic fractionation schemes to be compared directly to observations.

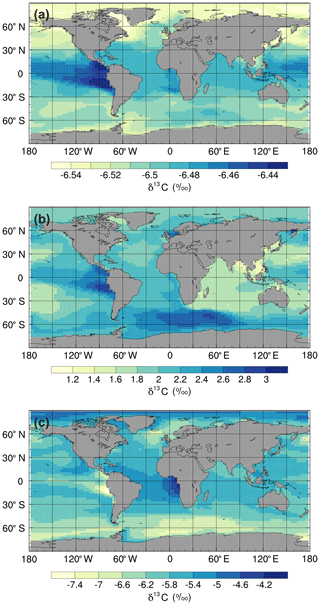
Figure 4 Mean annual surface δ¹³C_DIC values at the end of the sensitivity experiment spin-up simulations (years 9900 to 10 000): (a) ki-fract-only, (b) no-bio-fract, and (c) no asgx-fract.

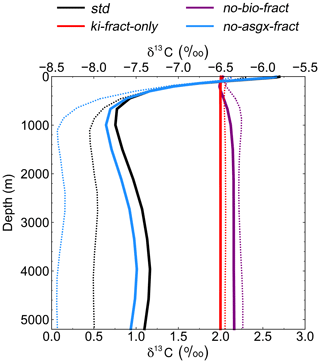
Figure 5 Depth profiles of globally averaged δ¹³C_DIC at the end of the sensitivity experiment spin-up simulations (years 9900 to 10 000). The std (black) and no-bio-fract (purple) simulations use the bottom axis, whilst the ki-fract-only (red) and no-asgx-fract (blue) simulations use the top axis. The dotted lines are the equivalent simulations conducted by Schmittner et al. (2013) with the UVic ESM: std (black) and no-bio (purple) on the bottom axis; ki-only (red) and const-gasx (blue) on the top axis.

3 Results and discussion

3.1 Validating the isotope scheme

Isolating the different fractionation effects allows us to assess the relative contribution of air–sea gas exchange and biology to the simulated δ¹³C_DIC distributions, and validate that the new isotope scheme is responding to physical and biogeochemical processes as expected. If there is no fractionation during either air–sea gas exchange or photosynthesis, the ocean equilibrates at a uniform value of −6.5 ‰, in line with the atmosphere (simulation not shown). Kinetic fractionation has only a minor effect on surface ocean δ¹³C_DIC distributions, with simulated δ¹³C_DIC values in the ki-fract-only simulation ranging between −6.57 ‰ in the Labrador Sea and −6.42 ‰ in the eastern equatorial Pacific (Fig. 4a). This represents a −0.07 ‰ to +0.08 ‰ shift relative to no isotopic fractionation. Specifically, there is ¹³C depletion (low δ¹³C_DIC) in areas of net CO₂ invasion, such as the extratropics and high latitudes, and ¹³C enrichment (high δ¹³C_DIC) in the equatorial upwelling zones and the deep water formation regions where CO₂ is being outgassed. Kinetic fractionation has a negligible effect on the δ¹³C_DIC depth profile, with globally averaged δ¹³C_DIC values of −6.4955 ‰ in the surface ocean and −6.5011 ‰ in the abyssal ocean (Fig. 5).

When both the equilibrium and kinetic fractionation effects are included during air–sea gas exchange (no-bio-fract), the large-scale δ¹³C_DIC distributions are closely related to the SST patterns because of the temperature dependence of α_aq←g and α_DIC←g (Fig. 4b). In the absence of biological fractionation, relatively high δ¹³C_DIC values ($>+\mathrm{2.5}$ ‰) are simulated in the Southern Ocean due to the combined effect of CO₂ outgassing and low SSTs, both of which cause ¹³C enrichment. The δ¹³C_DIC values in the Arctic Ocean are comparably low because the model has more extensive sea ice in the Northern Hemisphere than in the Southern Hemisphere, which inhibits air–sea gas exchange. The highest values (+3.00 ‰) are simulated in the eastern equatorial Pacific where there are high rates of net CO₂ outgassing, and southern-sourced waters, which have a high δ¹³C_DIC signature in this simulation because there is no biological fractionation, are upwelled. Low δ¹³C_DIC values are simulated in the Indian Ocean, with the lowest values (+1.1 ‰) in southeast Asia, because the sea surface is warmer than at the equivalent latitudes in the Atlantic and Pacific oceans. The globally averaged δ¹³C_DIC values in this simulation range between +2.03 ‰ in the surface ocean and +2.16 ‰ in the deep ocean, with a minimum value of +2.00 ‰ at a depth of approximately 200 m (Fig. 5). Below approximately 1500 m, the globally averaged δ¹³C_DIC is near constant with depth, matching the simulated temperature profile.

When only biological fractionation effects are included (no-asgx-fract), δ¹³C_DIC values in the surface ocean range between −7.65 ‰ in the eastern equatorial Pacific and −3.89 ‰ in the eastern equatorial Atlantic (Fig. 4c), representing a shift of −1.15 ‰ to +2.61 ‰ relative to no isotopic fractionation. The asymmetry between these two upwelling zones occurs because the waters that are being upwelled from the deep Pacific Ocean are approximately 600 years older than the equivalent waters in the Atlantic Ocean. They therefore contain a higher percentage of remineralised organic matter, which is enriched in ¹²C. Relatively low δ¹³C_DIC values are also simulated in the Southern Ocean and northeast North Atlantic Ocean where older water is mixed upwards from the abyssal ocean to the surface ocean at sites of deep water formation. The globally averaged δ¹³C_DIC values in this simulation range between −5.85 ‰ in the productive surface ocean and −7.56 ‰ in the abyssal ocean, with a minimum value of −7.86 ‰ at a depth of approximately 1000 m, which corresponds to the depth of maximum remineralisation in the model (Fig. 5). The values change from greater than −6.5 ‰ (enriched in ¹³C relative to no fractionation) to less than −6.5 ‰ (depleted in ¹³C relative to no fractionation) at a depth of approximately 100 m, which corresponds to the photic zone.

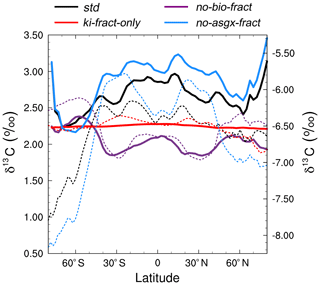
Figure 6 Zonally averaged mean annual surface δ¹³C_DIC at the end of the sensitivity experiment spin-up simulations (years 9900 to 10 000). The std (black) and no-bio-fract (purple) simulations use the left-hand axis, whilst the ki-fract-only (red) and no-asgx-fract (blue) simulations use the right-hand axis. The dotted lines are the equivalent simulations conducted by Schmittner et al. (2013) with the UVic ESM: std (black) and no-bio (purple) on the left-hand axis; ki-only (red) and const-gasx (blue) on the right-hand axis.

The spatial patterns in the std simulation and the no-asgx-fract simulation are closely matched, both in the surface ocean (Fig. 6) and at depth (Fig. 5), demonstrating the importance of biology to the large-scale δ¹³C_DIC distributions. However, in the surface layer, air–sea gas exchange partly compensates for the biological effects in the Southern Ocean, the Northern Hemisphere deep water formation region, and the equatorial upwelling zones, as inferred from the peak surface zonal mean δ¹³C_DIC values at 60^∘ S, 55^∘ N and 0^∘ in the no-bio-fract simulation, which correspond with reduced amplitude troughs in the std simulation relative to the no-asgx-fract simulation. Similar results pertaining to the relative influence of air–sea gas exchange and biology were presented by Schmittner et al. (2013), who concluded that air–sea gas exchange and temperature-dependent fractionation reduce the spatial δ¹³C_DIC gradients that are created by biology. Earlier work by Murnane and Sarmiento (2000) and Schmittner et al. (2013) also supports the notion that biology is the dominant factor controlling δ¹³C_DIC distributions in the interior ocean. Overall, the sensitivity experiments demonstrate that the new carbon isotope scheme is accurately responding to physical and biogeochemical processes in the model, such as temperature, air–sea gas exchange, and the biological pump.

3.2 Comparison to observations

To assess the model performance in representing modern large-scale ¹³C distributions, we compare the simulated mean δ¹³C_DIC values for the 1990s with observations from GLODAP version 2 (v2; Key et al., 2015; Olsen et al., 2016) and the gridded global ocean climatology of Eide et al. (2017). The δ¹³C_DIC values in the std simulation are, on average, 0.97 ‰ higher than the GLODAPv2 observations in the surface ocean (Fig. 7) and 0.64 ‰ higher globally, with root mean square error (RMSE) values of 1.03 ‰ and 0.91 ‰, respectively. However, the simulated range in the surface ocean (3.2 ‰) is in excellent agreement with the observed range (3.3 ‰). Specifically, the simulated surface δ¹³C_DIC values are between +1.4 ‰ and +4.6 ‰, with a mean value of +2.6 ‰, whilst the observed surface δ¹³C_DIC values range between −0.3 ‰ and +3.0 ‰, with a mean value of +1.5 ‰.

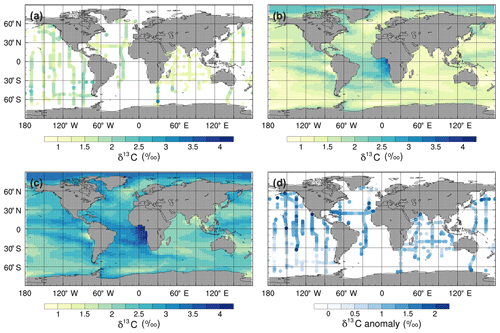
Figure 7 Mean annual surface δ¹³C_DIC during the 1990s: (a) observations from GLODAPv2 (Key et al., 2015; Olsen et al., 2016), (b) the std simulation corrected for the mean surface bias (0.97 ‰), which is calculated as ∑(simulated-observed)/number of observations, (c) the std simulation, and (d) std minus GLODAPv2.

Re-examining the results of the sensitivity experiments allows us to ascertain the underlying causes of the model–data discrepancy. Schmittner et al. (2013; herein S13) conducted a similar set of simulations with the UVic ESM to elucidate the relative influence of biology and air–sea gas exchange on the distribution of oceanic δ¹³C_DIC (see Table 1 in S13). Overall, there is good agreement between our ki-fract-only and no-bio-fract simulations and the equivalent simulations in S13 (ki-fract and no-bio, respectively), both in the surface ocean (Fig. 6) and at depth (Fig. 5). However, there is a clear difference between the results of our no-asgx-fract simulation and the equivalent simulation in S13 (const-gasx). Specifically, the surface ocean zonal mean δ¹³C_DIC values in our no-asgx-fract simulation range between −6.6 ‰ at 60^∘ S and −5.5 ‰ in the subtropics, with a local minimum of −5.8 ‰ at the Equator (solid blue line in Fig. 6). For comparison, the surface ocean zonal mean values in const-gasx range between −8.0 ‰ in the Southern Ocean and −5.75 ‰ in the Southern Hemisphere subtropics, with a localised minimum of −6.25 ‰ at the Equator (dotted blue line in Fig. 6). Similarly, whilst the globally averaged deep ocean δ¹³C_DIC values in our no-asgx-fract simulation have a comparable range (2.01 ‰) to the deep ocean values in const-gasx, there is an offset of approximately 1 ‰, with S13 simulating δ¹³C_DIC values of −6.4 ‰ in the surface ocean, −8.4 ‰ in the deep ocean, and near constant values below 1000 m (blue lines in Fig. 5). Overall, the δ¹³C_DIC values in the standard simulation with the UVic ESM are in good agreement with observations, with a global linear regression r² value of 0.91 and a global RMSE of 0.33 ‰ (Schmittner et al., 2013; Buchanan et al., 2019). We therefore postulate that the offset in the simulated δ¹³C_DIC values in FAMOUS relates to biases in the biological carbon cycle.

Elucidating the exact cause of δ¹³C_DIC model–data discrepancy is difficult. There are a number of fluxes going into and out of the DI¹³C pool (Fig. 2), each of which could have biases that are compounding or reducing the overall δ¹³C_DIC bias. For example, if any of the rates of phytoplankton respiration, phytoplankton mortality, or zooplankton mortality are too low, the input of ¹²C-enriched material back into the DIC pool would be insufficient. Similarly, if the model is not simulating enough remineralisation, either as a direct consequence of the parameterised remineralisation rate or as a result of insufficient POC export, the input of ¹²C-enriched material back into the DIC pool would again be too low.

Primary producers preferentially take up ¹²C during photosynthesis; therefore, higher-than-observed rates of net primary production in the photic zone would increase δ¹³C_DIC. However, if the δ¹³C_DIC discrepancy in FAMOUS was a simple function of the biases in net primary production, δ¹³C_DIC would be lower than observed in the subtropical gyres, the Indian Ocean, and the northern North Atlantic and North Pacific oceans, and higher than observed in the equatorial upwelling zones and the Southern Ocean (Fig. 1). Thus, whilst the differences in net primary production could be contributing towards the δ¹³C_DIC bias, particularly in the equatorial upwelling zones, they alone cannot explain the unidirectional offset.

Alternatively, the fractionation during photosynthesis could be too strong as a result of imbalances in the carbonate chemistry (Fig. S2). The global mean alkalinity in FAMOUS is 81 µmol kg⁻¹ higher than observed and the mean alkalinity in the uppermost 50 m of the ocean is 107 µmol kg⁻¹ too high (Key et al., 2004; Sarmiento and Gruber, 2006). In addition, the simulated global mean DIC concentration is 54 µmol kg⁻¹ higher than observed and the mean DIC concentration in the uppermost 50 m of the ocean is 96 µmol kg⁻¹ too high (Key et al., 2004; Sarmiento and Gruber, 2006). Furthermore, the mean ocean temperatures in FAMOUS are warmer than observed, both globally (2.2 ^∘C) and in the uppermost 50 m of the ocean (1 ^∘C; Sarmiento and Gruber, 2006; Locarnini et al., 2013). Increasing alkalinity increases ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$, whilst increasing the temperature and DIC concentrations decreases ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$. Hence, the overall effect of the carbonate chemistry biases in FAMOUS result in the global mean ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$ being 3.03 µmol L⁻¹ too low and the mean ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$ in the uppermost 50 m of the ocean being 0.58 µmol L⁻¹ too high. In the photic zone, this translates to a simulated α_p of 0.97378 compared to an observed α_p of 0.97415 using the std fractionation parameterisation. Thus, we postulate that imbalances in the carbonate chemistry, and the consequent differences in α_p, are contributing towards the δ¹³C_DIC bias, but the overall effect is small.

The smallest model–data discrepancies in the surface layer are in the Southern Ocean and the northeast North Atlantic Ocean where deep convection mixes ¹²C-enriched waters upwards (Fig. 7). In contrast, in the equatorial upwelling zones, the effect of higher than observed primary productivity (increasing δ¹³C_DIC) outweighs the effect of vertical mixing (reducing δ¹³C_DIC); therefore, the overall model–data biases are higher in these regions. Despite the global offset, the model correctly simulates lower δ¹³C_DIC values in the Indian Ocean compared to the Atlantic and Pacific oceans, because the Indian Ocean is relatively nutrient poor, both in the model and reality (Fig. S3), which limits primary productivity (Fig. 1). Similar to previous ¹³C modelling studies (e.g. Hofmann et al., 2000; Tagliabue and Bopp, 2008; Schmittner et al., 2013), FAMOUS also accurately simulates the observed latitudinal gradient in mixed layer δ¹³C_POC, with relatively high values ($\approx -\mathrm{20}$ ‰) in the low latitudes and relatively low values ($\approx -\mathrm{27}$ ‰) at high latitudes (Fig. 8).

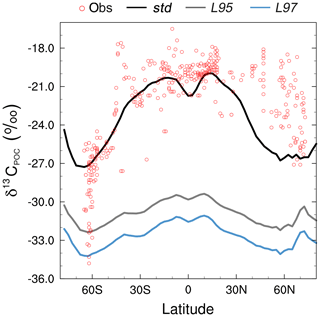
Figure 8 Zonally averaged mean annual mixed layer δ¹³C_POC during the 1990s: observations (Goericke and Fry, 1994; red), the std simulation (black), the L95 simulation (grey), and the L97 simulation (blue).

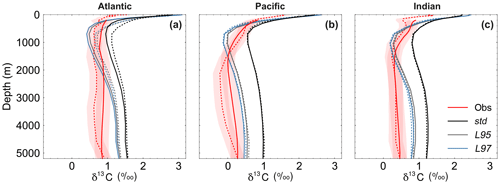
Figure 9 Depth profiles of δ¹³C_DIC during the 1990s: (a) Atlantic Ocean, (b) Pacific Ocean, and (c) Indian Ocean. The δ¹³C_DIC values in the std (black), L95 (grey) and L97 (blue) simulations are compared to observations (red). Solid lines are used for the global dataset, with observations from the gridded climatology produced by Eide et al. (2017). The simulated values have also been subsampled at the locations where there is a corresponding observation in the GLODAPv2 dataset (Key et al., 2015; Olsen et al., 2016; dashed). The red shading shows the estimated uncertainty in δ¹³C_DIC observations due to unresolved intercalibration between different laboratories (±0.2 ‰; Schmittner et al., 2013; Eide et al., 2017).

Figure 10 Zonal mean δ¹³C_DIC during the 1990s in the Atlantic Ocean (left), Pacific Ocean (centre), and Indian Ocean (right): (a–c) gridded observations (Eide et al., 2017), (d–f) the std simulation, (g–i) the L95 simulation, and (j–l) the L97 simulation.

As observed, δ¹³C_DIC decreases with depth in all basins due to the remineralisation of isotopically light organic matter (Fig. 9). The maximum remineralisation depth in the model is approximately 1000 m, which is 200 to 500 m shallower than observed. In the deep ocean, the highest δ¹³C_DIC values are in the Atlantic basin, with intermediate values in the Indian basin, and the lowest values in the Pacific basin, where the waters are older and therefore contain more remineralised organic material (enriched in ¹²C). However, there are notable structural differences in the zonal means (Fig. 10), which arise due to inaccuracies in the physical ocean circulation in FAMOUS. Specifically, FAMOUS does not capture the observed structure in the Atlantic basin because, in this generation of the model, the AMOC is characterised by an overdeep North Atlantic Deep Water (NADW) cell and insufficient Antarctic Bottom Water formation (Dentith et al., 2019b). FAMOUS also simulates weak (less than 3 Sv) ventilation to depths of 2000 m in the North Pacific Ocean (Dentith et al., 2019b), which prevents the accumulation of old, ¹²C-enriched (low δ¹³C_DIC) waters at intermediate depths in the Northern Hemisphere. Instead, the oldest carbon in the model is in the eastern equatorial Pacific. In addition, the surface winds in the model are weaker than observed (Kalnay et al., 1996), resulting in a relatively shallow mixed layer. This promotes the excessive accumulation of high δ¹³C_DIC values in the surface ocean, which is particularly notable in the Southern Hemisphere subtropical gyres. These physical model biases are also clearly visible in the zonal mean profiles of other tracers, such as nutrients (Fig. S4) and DIC (Fig. S5). The overall shape of the simulated depth profile reaffirms the notion that there are inaccuracies in both the physical and biogeochemical components of the model (Fig. 9). Below approximately 1000 m, the simulated δ¹³C_DIC values increase with depth in each ocean basin, whilst the observed basin averages are near constant with depth. The offset between the simulated and observed values is greatest in the deep Atlantic Ocean, where too much ¹³C-enriched water from the shallow ocean is being circulated into the abyssal ocean. However, the trend towards increasing δ¹³C_DIC with depth could also be in part explained by insufficient remineralisation in the model. This is supported by lower-than-observed nutrient concentrations in the deep ocean (Fig. S4). HadOCC's global export ratio at 2000 m is within the observed range, but a lack of spatial variation means that the geographic distributions are partially incorrect (Palmer and Totterdell, 2001). Hence, we postulate that localised inaccuracies in the export ratio, together with deficiencies in the parameterisation of the remineralisation rate, are contributing towards the δ¹³C_DIC offset. The basin-averaged δ¹³C_DIC bias is smallest in the Pacific Ocean, where the waters are old and therefore have had more time to remineralise, thereby partially compensating for the biogeochemical biases. Indeed, the shape of the simulated and observed basin-averaged depth profiles are in good agreement below approximately 2000 m in the Pacific Ocean, despite the structural differences in the zonal mean.

As outlined in Sect. 3.1, our carbon isotope implementation is sensitive to physical and biogeochemical processes in the model. Thus, whilst biases in the overturning circulation and the biological pump are currently limiting the model's ability to accurately represent modern large-scale ¹³C distributions, the model–data agreement could be improved if the physical and ecological components of FAMOUS were recalibrated. This will be discussed further in Sect. 3.4.

Figure 11 Mean annual isotopic fractionation during photosynthesis (α_p) in the surface ocean at the end of the spin-up simulations (years 9900 to 10 000): (a) the std simulation, (b) the L95 simulation, and (c) the L97 simulation.

3.3 Biological fractionation parameterisations

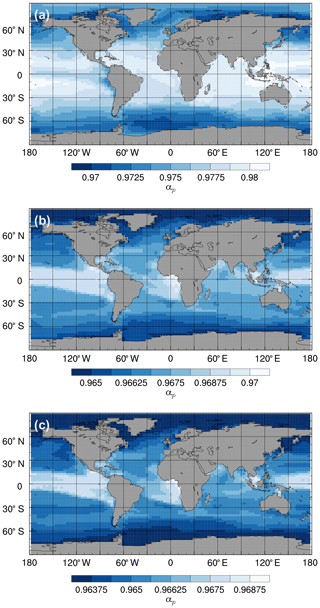
Given the uncertainty associated with biological fractionation (Sect. 2.2.2), we tested three different parameterisations for equilibrium fractionation during photosynthesis. For all three parameterisations, the total fractionation during photosynthesis is greatest in the high latitudes (where SSTs are relatively low and ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$ is relatively high) and lowest in the equatorial regions (where SSTs are relatively high and ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$ is relatively low; Fig. 11). The std parameterisation produces the largest range of α_p values (between approximately 0.97 and 0.98), whilst the L95 parameterisation produces the smallest range (between approximately 0.964 and 0.970). The total fractionation during photosynthesis increases with the complexity of the parameterisation, with L97 producing the largest overall effect (with a minimum α_p of 0.9635). For all three parameterisations, α_p decreases (i.e. the strength of fractionation increases) with depth in the photic zone, with the largest gradient produced by the std parameterisation (Fig. S6).

The large-scale δ¹³C_DIC patterns are very similar for all three photosynthetic fractionation schemes, but the parameterisations that take the phytoplankton growth rate in account simulate higher surface ocean δ¹³C_DIC values everywhere except in the Southern Ocean, the Nordic Seas, and the eastern equatorial regions, where older ¹³C-depleted waters are mixed upwards from the abyssal ocean during deep water formation and upwelling (Fig. S7). The differences are amplified when using the L97 parameterisation (RMSE=1.24 ‰, bias =1.15 ‰), which specifies a non-linear relationship between μ and ${\mathrm{CO}}_{\mathrm{2}}^{\ast }$, compared to the L95 parameterisation (RMSE=1.21 ‰, bias=1.13 ‰), which specifies a linear relationship (Fig. S8). Conversely, the alternative parameterisations decrease δ¹³C_DIC at depth compared to the std simulation, bringing the simulated values closer to the observations (Fig. 9). Below approximately 500 m depth, the δ¹³C_DIC values are consistently lower when using the L97 parameterisation compared to the L95 parameterisation. This is due to the preconditioning of δ¹³C_DIC and δ¹³C_POC as a result of fractionation during photosynthesis in the photic zone. In the L95 and L97 simulations, δ¹³C_POC is lower than in the std simulation due to increased uptake of ¹²C during primary production (lower α_p). The latitudinal δ¹³C_POC gradients in the mixed layer in these simulations are lower than observed, with zonal mean values ranging between approximately −30 ‰ at the Equator and −33 ‰ at 60^∘ N/S (Fig. 8). When the POC is remineralised, a relatively low δ¹³C signal is therefore being released back into the DIC pool, which causes the δ¹³C_DIC in the deep ocean to be lower than in the std simulation. Thus, although the rates of biological exchange and overturning circulation are the same in all three simulations, the preconditioning of δ¹³C_DIC and δ¹³C_POC in the photic zone creates differences between the three simulations at depth. Whilst the global RMSE compared to the GLODAPv2 dataset is lower in the L95 and L97 simulations (0.86 ‰ and 0.87 ‰, respectively), it is still almost double the RMSE in other models (Buchanan et al., 2019). Overall, increasing the complexity of the fractionation scheme does not significantly improve the model–data agreement because of the aforementioned physical and biogeochemical biases.

3.4 A new tuning target

In contrast with earlier studies, we have demonstrated that the new carbon isotope scheme in FAMOUS is sensitive to both physical and biogeochemical processes. The simulated δ¹³C_DIC distributions reflect known physical inaccuracies (such as overdeep NADW and weak convection in the subpolar North Pacific Ocean) and have allowed us to identify previously undisclosed biogeochemical biases (e.g. in the representation of remineralisation). The new tracer therefore offers excellent potential as a holistic tuning target for recalibrating FAMOUS in the future.

FAMOUS has previously been tuned both systematically (Jones et al., 2005; Gregoire et al., 2011; Williams et al., 2013) and manually (Smith et al., 2008). Most recently, Williams et al. (2013) tuned the 20 structural parameters in HadOCC (coupled to FAMOUS-MOSES2.2) using an objective hypercube technique. Specifically, the parameter set included the C:N ratios for the different carbon pools, phytoplankton-specific parameters (e.g. maximum rate of photosynthesis), zooplankton-specific parameters (e.g. linear and quadratic zooplankton mortality rates), detritus-specific parameters (e.g. shallow and deep remineralisation rates), and carbonate-specific parameters (e.g. calcite export ratio). The main diagnostics used to evaluate the performance of the ensemble members were December–January–February and June–July–August surface air temperatures, annual mean total precipitation rate, annual mean nitrate concentrations, and primary productivity. Crucially, this study only ran each perturbed parameter simulation for 200 years and neglected to evaluate the strength and structure of the AMOC. The optimal parameter set therefore had small but important imbalances in the surface climate, which caused the AMOC to collapse over longer (multi-millennial) timescales (Dentith et al., 2019b).

HadOCC has not yet been tuned for the configuration of the model used in our study (FAMOUS-MOSES1). Simultaneously recalibrating HadOCC and the physical ocean circulation in FAMOUS-MOSES1 could therefore improve the simulated δ¹³C_DIC distributions. In the first instance, further sensitivity studies would provide more insight into the extent to which our results could be improved by small adjustments to the model's biogeochemistry (e.g. modifying the remineralisation rate and/or the export ratio). Longer term, we propose that the addition of carbon isotope ratios as tuning targets (both the δ¹³C presented here and the new Δ¹⁴C tracer for FAMOUS discussed by Dentith et al., 2019a) would improve the work of Williams et al. (2013) because they provide an objective and straightforward way of assessing whether the balance between all of the ecological processes in the model is correct.

4 Summary

We have added the stable isotope ¹³C to the ocean component of the FAMOUS GCM, using the MOSES1 generation of the model to validate our scheme. We account for fractionation during air–sea gas exchange and photosynthesis, and have tested three different parameterisations for the latter. The model captures the range of observed δ¹³C_DIC values in the surface ocean, but the simulated values are approximately 1 ‰ too high at all depths. The differences between the three fractionation schemes are relatively minor, but when fractionation during photosynthesis accounts for phytoplankton growth rates as opposed to just aqueous CO₂ concentrations the discrepancies between the model and observations are further increased in the surface ocean and reduced at depth. The sensitivity experiments suggest that the simulated values are too high because of underlying biases in the biological carbon cycle; therefore, retuning HadOCC could improve the model–data agreement. Biases in the large-scale ocean circulation also inhibit the model's ability to accurately simulate the large-scale distribution of tracers in the deep ocean. Retuning the ocean circulation to improve the representation of the AMOC, in particular, would further reduce the model–data discrepancies. Thus, our results emphasise the utility of implementing carbon isotopes in GCMs; the simulated isotope distributions provide an additional measure against which the physical and biogeochemical model performance can be evaluated and offer an extra tuning metric for prospective development work. In the future, we intend to use the isotope-enabled model to study ocean circulation and the marine carbon cycle in both a modern and palaeo context, for example, at the Last Glacial Maximum (21 000 years ago) and during the last deglaciation (21 000 to 11 000 years ago).

Appendix A: Virtual fluxes

The standard equation for calculating the virtual flux to account for the dilution or concentration effect of surface freshwater fluxes is

$$\begin{array}{}\text{(A1)}& {\displaystyle \frac{\mathrm{d}{}^{\mathrm{12}}\mathrm{C}}{\mathrm{d}t}}={}^{\mathrm{12}}\mathrm{C}\times {\displaystyle \frac{(E-P)}{\mathrm{dz}}},\end{array}$$

where E is evaporation, P is precipitation, and dz is layer depth.

As we carry ¹³C as a ratio (¹³C∕¹²C), virtual fluxes are not required:

$$\begin{array}{}\text{(A2)}& {\displaystyle \frac{\mathrm{d}\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}{\mathrm{d}t}}={\displaystyle \frac{{}^{\mathrm{12}}\mathrm{C}\times \frac{\mathrm{d}{}^{\mathrm{13}}\mathrm{C}}{\mathrm{d}t}-{}^{\mathrm{13}}\mathrm{C}\times \frac{\mathrm{d}{}^{\mathrm{12}}\mathrm{C}}{\mathrm{d}t}}{{\left({}^{\mathrm{12}}\mathrm{C}\right)}^{\mathrm{2}}}}\text{(A3)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{1}}{{}^{\mathrm{12}}\mathrm{C}}}\times \left[{}^{\mathrm{13}}\mathrm{C}\times {\displaystyle \frac{(E-P)}{\mathrm{dz}}}\right]\\ & -{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{\left({}^{\mathrm{12}}\mathrm{C}\right)}^{\mathrm{2}}}}\times \left[{}^{\mathrm{12}}\mathrm{C}\times {\displaystyle \frac{(E-P)}{\mathrm{dz}}}\right]\end{array}\text{(A4)}& {\displaystyle \frac{\mathrm{d}\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}{\mathrm{d}t}}=\mathrm{0}.\end{array}$$

Appendix B: Air–sea gas exchange equations

The standard equation for calculating the change in DI¹³C due to air–sea gas exchange is

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{}^{\mathrm{13}}\mathrm{C}}{\mathrm{d}t}}=& {\mathit{\alpha }}_{\mathrm{k}}\times {\mathit{\alpha }}_{\mathrm{aq}\leftarrow \mathrm{g}}\times \text{PV}\\ & \times \left(C_{\mathrm{sat}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{A}}{{}^{\mathrm{12}}\mathrm{A}}}-{\displaystyle \frac{C_{\mathrm{surf}}\times \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}{{\mathit{\alpha }}_{\mathrm{DIC}\leftarrow \mathrm{g}}}}\right),\end{array}\end{array}$$

where PV is the piston velocity (Eq. 4), C_sat is the saturation concentration of atmospheric CO₂ (in mol m⁻³), C_surf is the surface aqueous concentration of CO₂ (in mol m⁻³), α_k is the constant kinetic fractionation factor, α_aq←g is the temperature-dependent fractionation during gas dissolution (Eq. 7), α_DIC←g is the temperature-dependent fractionation between aqueous CO₂ and DIC (Eq. 8), and ¹³A∕¹²A and ¹³C∕¹²C are the ¹³C∕¹²C ratios of the atmosphere and DIC, respectively.

The equation for calculating the change in DI¹³C∕DI¹²C due to air–sea gas exchange is

$$\begin{array}{}\text{(B2)}& {\displaystyle \frac{\mathrm{d}\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}{\mathrm{d}t}}={\displaystyle \frac{{}^{\mathrm{12}}\mathrm{C}\times \frac{\mathrm{d}{}^{\mathrm{13}}\mathrm{C}}{\mathrm{d}t}-{}^{\mathrm{13}}\mathrm{C}\times \frac{{\mathrm{d}}^{\mathrm{12}}\mathrm{C}}{\mathrm{d}t}}{{\left({}^{\mathrm{12}}\mathrm{C}\right)}^{\mathrm{2}}}}\text{(B3)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{1}}{{}^{\mathrm{12}}\mathrm{C}}}\times \left[{\mathit{\alpha }}_{\mathrm{k}}\times {\mathit{\alpha }}_{\mathrm{aq}\leftarrow \mathrm{g}}\times \text{PV}\right.\\ & \left.\times \left(C_{\mathrm{sat}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{A}}{{}^{\mathrm{12}}\mathrm{A}}}-{\displaystyle \frac{C_{\mathrm{surf}}\times \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}{{\mathit{\alpha }}_{\mathrm{DIC}\leftarrow \mathrm{g}}}}\right)\right]\\ & -{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{\left({}^{\mathrm{12}}\mathrm{C}\right)}^{\mathrm{2}}}}\times \left[\text{PV}\times (C_{\mathrm{sat}}-C_{\mathrm{surf}})\right]\end{array}\text{(B4)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}\left(\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}\right)}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{1}}{{}^{\mathrm{12}}\mathrm{C}}}\times \text{PV}\times [{\mathit{\alpha }}_{\mathrm{k}}\times {\mathit{\alpha }}_{\mathrm{aq}\leftarrow \mathrm{g}}\\ & \times \left(C_{\mathrm{sat}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{A}}{{}^{\mathrm{12}}\mathrm{A}}}-{\displaystyle \frac{C_{\mathrm{surf}}\times \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}{{\mathit{\alpha }}_{\mathrm{DIC}\leftarrow \mathrm{g}}}}\right)\\ & -\left({\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}\times \left[C_{\mathrm{sat}}-C_{\mathrm{surf}}\right]\right)].\end{array}\end{array}$$

Appendix C: Biological equations

For consistency with the standard biological tracers, the ¹³C contents of phytoplankton (¹³P), zooplankton (¹³Z), and detritus (¹³D) are carried in mmol N m⁻³, with the carbon concentrations and fluxes calculated using fixed stoichiometric ratios. The DI¹³C∕DI¹²C values are therefore converted from a ratio in model units (Eq. 2) to normalised DI¹³C concentrations before entering the soft tissue pump. The conversion is reversed at the end of each time step.

C1 Phytoplankton (P)

The standard equation for calculating the change in phytoplankton (¹²P) is

$$\begin{array}{}\text{(C1)}& {\displaystyle \frac{\mathrm{d}P}{\mathrm{d}t}}=R_{\mathrm{P}}-G_{\mathrm{P}}-m_{\mathrm{P}}-{\mathit{\eta }}_{\mathrm{P}},\end{array}$$

where R_P is the specific growth rate of phytoplankton, G_P represents grazing by zooplankton, m_P represents phytoplankton mortality due to overpopulation, and η_P represents phytoplankton respiration.

The equation for calculating the change in ¹³P is

$$\begin{array}{}\text{(C2)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{}^{\mathrm{13}}P}{\mathrm{d}t}}=& R_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}\times {\mathit{\alpha }}_{\mathrm{p}}-G_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}-m_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}\\ & -n_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}},\end{array}\end{array}$$

where α_p is the isotopic fractionation that occurs during photosynthesis (Eq. 9), ¹³C∕¹²C is the ¹³C∕¹²C ratio of DIC, and ¹³P∕¹²P is the ¹³C∕¹²C ratio of phytoplankton. The ¹³P tracer is updated using the forward Euler method:

$$\begin{array}{}\text{(C3)}& \begin{array}{rl}{}^{\mathrm{13}}{P}_{(t+\mathrm{\Delta }t)}& ={}^{\mathrm{13}}{P}_{\left(t\right)}+\mathrm{\Delta }t\times \left(R_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}}_{\left(t\right)}\times {\mathit{\alpha }}_{{\mathrm{p}}_{\left(t\right)}}\right.\\ & -G_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}}_{\left(t\right)}-m_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}}_{\left(t\right)}\\ & \left.-n_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}}_{\left(t\right)}\right).\end{array}\end{array}$$

C2 Zooplankton (Z)

The standard equation for calculating the change in zooplankton (¹²Z) is

$$\begin{array}{}\text{(C4)}& {\displaystyle \frac{\mathrm{d}Z}{\mathrm{d}t}}={\mathit{\beta }}_{\mathrm{P}}\times G_{\mathrm{P}}+{\mathit{\beta }}_{\mathrm{D}}\times G_{\mathrm{D}}-m_{\mathrm{Z}},\end{array}$$

where β_P and β_D are the assimilation efficiencies associated with zooplankton grazing on phytoplankton (G_P) and detritus (G_D), respectively, and m_Z represents zooplankton mortality due to predation and natural causes.

The equation for calculating the change in ¹³Z is

$$\begin{array}{}\text{(C5)}& {\displaystyle \frac{{\mathrm{d}}^{\mathrm{13}}Z}{\mathrm{d}t}}={\mathit{\beta }}_{\mathrm{P}}\times G_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}+{\mathit{\beta }}_{\mathrm{D}}\times G_{\mathrm{D}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}}-m_{\mathrm{Z}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{Z}}{{}^{\mathrm{12}}\mathrm{Z}}},\end{array}$$

where ¹³P∕¹²P, ¹³D∕¹²D, and ¹³Z∕¹²Z are the isotopic ratios of phytoplankton, detritus and zooplankton, respectively.

The ¹³Z tracer is updated using the forward Euler method:

$$\begin{array}{}\text{(C6)}& \begin{array}{rl}{}^{\mathrm{13}}{Z}_{(t+\mathrm{\Delta }t)}& ={}^{\mathrm{13}}{Z}_{\left(t\right)}+\mathrm{\Delta }t\times \left({\mathit{\beta }}_{{\mathrm{P}}_{\left(t\right)}}\times G_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}}_{\left(t\right)}+{\mathit{\beta }}_{{\mathrm{D}}_{\left(t\right)}}\right.\\ & \left.\times G_{{\mathrm{D}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}}}_{\left(t\right)}-m_{{\mathrm{Z}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{Z}}{{}^{\mathrm{12}}\mathrm{Z}}}}_{\left(t\right)}\right).\end{array}\end{array}$$

C3 Dissolved inorganic carbon (DIC, C)

The standard equation for calculating the change in DI¹²C is

$$\begin{array}{}\text{(C7)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}C}{\mathrm{d}t}}& =-R_{\mathrm{P}}+{\mathit{\lambda }}_{\mathrm{D}}+\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{P}}\right)\times G_{\mathrm{P}}+\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{D}}\right)\times G_{\mathrm{D}}\\ & +m_{\mathrm{Z}}+m_{\mathrm{P}}+{\mathit{\eta }}_{\mathrm{P}},\end{array}\end{array}$$

where R_P is the specific growth rate of phytoplankton, λ_D is detrital remineralisation, which is specified at a constant rate (0.1 d⁻¹ in the uppermost 250 m of the ocean and 0.02 d⁻¹ at all other depths), β_P and β_D are the assimilation efficiencies associated with zooplankton grazing on phytoplankton (G_P) and detritus (G_D), respectively, m_Z represents zooplankton mortality due to predation and natural causes, m_P represents phytoplankton mortality due to overpopulation, and η_P represents phytoplankton respiration.

The equation for calculating the change in DI¹³C is

$$\begin{array}{}\text{(C8)}& \begin{array}{rl}{\displaystyle \frac{{\mathrm{d}}^{\mathrm{13}}C}{\mathrm{d}t}}& =-R_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}\times {\mathit{\alpha }}_{\mathrm{p}}+{\mathit{\lambda }}_{\mathrm{D}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}}+\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{P}}\right)\\ & \times G_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}+\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{D}}\right)\times G_{\mathrm{D}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}}\\ & +m_{\mathrm{Z}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{Z}}{{}^{\mathrm{12}}\mathrm{Z}}}+m_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}+{\mathit{\eta }}_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}},\end{array}\end{array}$$

where α_p is the isotopic fractionation that occurs during photosynthesis (Eq. 9), and ¹³C∕¹²C, ¹³D∕¹²D, ¹³P∕¹²P, and ¹³Z∕¹²Z are the isotopic ratios of DIC, detritus, phytoplankton, and zooplankton, respectively.

The DI¹³C tracer is updated using the forward Euler method:

$$\begin{array}{}\text{(C9)}& \begin{array}{rl}{}^{\mathrm{13}}{C}_{(t+\mathrm{\Delta }t)}& ={}^{\mathrm{13}}{C}_{\left(t\right)}+\mathrm{\Delta }t\times \left(-R_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}}}_{\left(t\right)}\times {\mathit{\alpha }}_{{\mathrm{p}}_{\left(t\right)}}+{\mathit{\lambda }}_{{\mathrm{D}}_{\left(t\right)}}\right.\\ & \times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}}}_{\left(t\right)}+\left(\mathrm{1}-{\mathit{\beta }}_{{\mathrm{P}}_{\left(t\right)}}\right)\times G_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}}_{\left(t\right)}\\ & +\left(\mathrm{1}-{\mathit{\beta }}_{{\mathrm{D}}_{\left(t\right)}}\right)\times G_{{\mathrm{D}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}}}_{\left(t\right)}+m_{{\mathrm{Z}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{Z}}{{}^{\mathrm{12}}\mathrm{Z}}}}_{\left(t\right)}\\ & \left.+m_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}}_{\left(t\right)}+{\mathit{\eta }}_{{\mathrm{P}}_{\left(t\right)}}\times {{\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}}_{\left(t\right)}\right).\end{array}\end{array}$$

C4 Detritus (D)

Unlike the other biological tracers, the standard detritus tracer (¹²D) is updated using a semi-implicit scheme:

$$\begin{array}{}\text{(C10)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{D_{\left(t+\mathrm{\Delta }t,k\right)}-D_{(t,k)}}{\mathrm{\Delta }t}}& ={{\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}}_{{\mathrm{bio}}_{(t,k)}}+{{\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}}_{\mathrm{sink}\mathrm{\_}{\mathrm{in}}_{(t+\mathrm{\Delta }t,k-\mathrm{1})}}\\ & -{{\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}}_{\mathrm{sink}\mathrm{\_}{\mathrm{out}}_{(t+\mathrm{\Delta }t,k)}}\end{array}\text{(C11)}& {\displaystyle }\begin{array}{rl}{D}_{\left(t+\mathrm{\Delta }t,k\right)}& -D_{(t,k)}=\mathrm{\Delta }t\times D_{{\mathrm{bio}}_{(t,k)}}+\mathrm{\Delta }t\times {\displaystyle \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}\\ & \times D_{(t+\mathrm{\Delta }t,k-\mathrm{1})}-\mathrm{\Delta }t\times {\displaystyle \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}\times D_{(t+\mathrm{\Delta }t,k)}\end{array}\text{(C12)}& {\displaystyle }\begin{array}{rl}{D}_{\left(t+\mathrm{\Delta }t,k\right)}& +\mathrm{\Delta }t\times {\displaystyle \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}\times D_{(t+\mathrm{\Delta }t,k)}\\ & =D_{\left(t,k\right)}+\mathrm{\Delta }t\times D_{{\mathrm{bio}}_{(t,k)}}+\mathrm{\Delta }t\\ & \times {\displaystyle \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}\times D_{(t+\mathrm{\Delta }t,k-\mathrm{1})}\end{array}\text{(C13)}& {\displaystyle }\begin{array}{rl}{D}_{\left(t+\mathrm{\Delta }t,k\right)}& \times \left(\mathrm{1}+\mathrm{\Delta }t\times {\displaystyle \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}\right)=D_{\left(t,k\right)}+\mathrm{\Delta }t\\ & \times D_{{\mathrm{bio}}_{(t,k)}}+\mathrm{\Delta }t\times {\displaystyle \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}\times D_{(t+\mathrm{\Delta }t,k-\mathrm{1})}\end{array}\text{(C14)}& {\displaystyle }\begin{array}{rl}& D_{\left(t+\mathrm{\Delta }t,k\right)}\\ & ={\displaystyle \frac{D_{\left(t,k\right)}+\mathrm{\Delta }t\times D_{{\mathrm{bio}}_{(t,k)}}+\mathrm{\Delta }t\times \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}\times D_{(t+\mathrm{\Delta }t,k-\mathrm{1})}}{\mathrm{1}+\mathrm{\Delta }t\times \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}}\end{array}\text{(C15)}& {\displaystyle }{D}_{\left(t+\mathrm{\Delta }t,k\right)}=D_{(t,k)}+{{\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}}_{(t,k)}\text{(C16)}& {{\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}}_{(t,k)}=D_{\left(t+\mathrm{\Delta }t,k\right)}-D_{(t,k)}\text{(C17)}& {\displaystyle }\begin{array}{rl}& {{\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}}_{\left(t,k\right)}\\ & ={\displaystyle \frac{D_{\left(t,k\right)}+\mathrm{\Delta }t\times D_{{\mathrm{bio}}_{\left(t,k\right)}}+\mathrm{\Delta }t\times \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}\times D_{\left(t+\mathrm{\Delta }t,k-\mathrm{1}\right)}}{\mathrm{1}+\mathrm{\Delta }t\times \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}}\\ & -D_{\left(t,k\right)},\end{array}\end{array}$$

where t is the current time step, k is the model level, dD∕dt_bio is the change in detritus due to biological effects (Eq. C19), γ is the sinking rate, which is parameterised at 10 m d⁻¹, dz is the depth of the layer (in cm), and D is the detritus concentration.

Following the same principles, the ¹³D tracer is updated using

$$\begin{array}{}\text{(C18)}& \begin{array}{rl}& {{\displaystyle \frac{{\mathrm{d}}^{\mathrm{13}}D}{\mathrm{d}t}}}_{\left(t,k\right)}\\ & ={\displaystyle \frac{{}^{\mathrm{13}}{D}_{\left(t,k\right)}+\mathrm{\Delta }t\times {}^{\mathrm{13}}{D}_{{\mathrm{bio}}_{\left(t,k\right)}}+\mathrm{\Delta }t\times \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}\times {}^{\mathrm{13}}{D}_{\left(t+\mathrm{\Delta }t,k-\mathrm{1}\right)}}{\mathrm{1}+\mathrm{\Delta }t\times \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}}\\ & -{}^{\mathrm{13}}{D}_{\left(t,k\right)}.\end{array}\end{array}$$

C4.1 Biological effects

The standard equation for calculating the change in detritus (¹²D) due to biology is

$$\begin{array}{}\text{(C19)}& \begin{array}{rl}{{\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}}_{\mathrm{bio}}& =m_{\mathrm{Z}}+m_{\mathrm{P}}-{\mathit{\lambda }}_{\mathrm{D}}-G_{\mathrm{D}}-\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{P}}\right)\times G_{\mathrm{P}}\\ & -\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{D}}\right)\times G_{\mathrm{D}},\end{array}\end{array}$$

where m_Z represents zooplankton mortality due to predation and natural causes, m_P represents phytoplankton mortality due to overpopulation, λ_D is detrital remineralisation, which is specified at a constant rate (0.1 d⁻¹ in the uppermost 250 m of the ocean and 0.02 d⁻¹ at all other depths), and β_P and β_D are the assimilation efficiencies associated with zooplankton grazing on phytoplankton (G_P) and detritus (G_D), respectively.

The equation for calculating the change in ¹³D due to biology is

$$\begin{array}{}\text{(C20)}& \begin{array}{rl}{{\displaystyle \frac{{\mathrm{d}}^{\mathrm{13}}D}{\mathrm{d}t}}}_{\mathrm{bio}}& =m_{\mathrm{Z}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{Z}}{{}^{\mathrm{12}}\mathrm{Z}}}+m_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}-{\mathit{\lambda }}_{\mathrm{D}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}}-G_{\mathrm{D}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}}\\ & -\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{P}}\right)\times G_{\mathrm{P}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{P}}{{}^{\mathrm{12}}\mathrm{P}}}-\left(\mathrm{1}-{\mathit{\beta }}_{\mathrm{D}}\right)\times G_{\mathrm{D}}\times {\displaystyle \frac{{}^{\mathrm{13}}\mathrm{D}}{{}^{\mathrm{12}}\mathrm{D}}},\end{array}\end{array}$$

where ¹³Z∕¹²Z, ¹³P∕¹²P, and ¹³D∕¹²D are the isotopic ratios of zooplankton, phytoplankton, and detritus, respectively.

C4.2 Reflux

The small amount of detritus that reaches the ocean floor is immediately refluxed back to the surface layer to conserve nitrogen and carbon.

$$\begin{array}{}\text{(C21)}& {{\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}}_{\mathrm{sink}\mathrm{\_}{\mathrm{in}}_{(k=\mathrm{1})}}={\displaystyle \frac{\mathit{\gamma }}{\mathrm{dz}/\mathrm{100}}}\times D_{\left(k=\text{KMT}\right)},\end{array}$$

where k is the model level, γ is the sinking rate, which is parameterised at 10 m d⁻¹, dz is the depth of the layer (in cm), D is the detritus concentration, and KMT is the maximum depth of the ocean. The same equation applies for ¹³D.