DCMIP2016: the splitting supercell test case

This paper describes the splitting supercell idealized test case used in the 2016 Dynamical Core Model Intercomparison Project (DCMIP2016). These storms are useful test beds for global atmospheric models because the horizontal scale of convective plumes is O(1 km), emphasizing non-hydrostatic dynamics. The test case simulates a supercell on a reduced-radius sphere with nominal resolutions ranging from 4 to 0.5 km and is based on the work of Klemp et al. (2015). Models are initialized with an atmospheric environment conducive to supercell formation and forced with a small thermal perturbation. A simplified Kessler microphysics scheme is coupled to the dynamical core to represent moist processes. Reference solutions for DCMIP2016 models are presented. Storm evolution is broadly similar between models, although differences in the final solution exist. These differences are hypothesized to result from different numerical discretizations, physics–dynamics coupling, and numerical diffusion. Intramodel solutions generally converge as models approach 0.5 km resolution, although exploratory simulations at 0.25 km imply some dynamical cores require more refinement to fully converge. These results can be used as a reference for future dynamical core evaluation, particularly with the development of non-hydrostatic global models intended to be used in convective-permitting regimes.

1 Introduction

Supercells are strong, long-lived convective cells containing deep, persistent rotating updrafts that operate on spatial scales O(10 km). They can persist for many hours and frequently produce large hail, tornados, damaging straight-line winds, cloud-to-ground lightning, and heavy rain (Browning, 1964; Lemon and Doswell, 1979; Doswell and Burgess, 1993). Therefore, accurate simulation of these features is of great societal interest and critical for atmospheric models.

The supercell test applied in the 2016 Dynamical Core Model Intercomparison Project (DCMIP2016) (Ullrich et al., 2017) permits the study of a non-hydrostatic moist flow field with strong vertical velocities and associated precipitation. This test is based on the work of Klemp and Wilhelmson (1978) and Klemp et al. (2015), and assesses the performance of global numerical models at extremely high spatial resolution. It has recently been used in the evaluation of next-generation weather prediction systems (Ji and Toepfer, 2016).

Previous work regarding the role of model numerics in simulating extreme weather features has generally focused on limited area domains (e.g., Gallus and Bresch, 2006; Guimond et al., 2016). While some recent work has targeted global frameworks and extremes – primarily tropical cyclones (e.g., Zhao et al., 2012; Reed et al., 2015) – these studies have almost exclusively employed hydrostatic dynamical cores at grid spacings approximately 0.25^∘ and coarser.

The supercell test here emphasizes resolved, non-hydrostatic dynamics. In this regime, the effective grid spacing is very similar to the horizontal scale of convective plumes. Further, the addition of simplified moist physics injects energy near the grid scale in a conditionally unstable atmosphere, which imposes significant stress on model numerics. The supercell test case therefore sheds light on the interplay of the dynamical core and subgrid parameterizations and highlights the impact of both implicit and explicit numerical diffusion on model solutions. It also demonstrates credibility of a global modeling framework to simulate extreme phenomena, essential for future weather and climate simulations.

2 Description of test

Table 1 List of constants used for the supercell test.

The test case is defined as follows. The setup employs a non-rotating reduced-radius sphere with scaling factor X=120. Reducing the model's planetary radius allows for fine horizontal grid spacing and non-hydrostatic motions to be resolved at relatively low computational cost compared to a configuration using the actual size of the Earth (Kuang et al., 2005). Wedi and Smolarkiewicz (2009) provide a detailed overview of the reduced-radius framework for testing global models. For a 1^∘ mesh, the grid spacing of the reduced-radius sphere is approximately $\mathrm{1}{}^{\circ }/X\sim \mathrm{111}\mathrm{km}/X\sim \mathrm{111}\mathrm{km}/\mathrm{120}\sim \mathrm{1}\mathrm{km}$ near the Equator. Klemp et al. (2015) demonstrated excellent agreement between simulations using this value of X and those completed on a flat, Cartesian plane with equivalent resolution. The model top (z_t) is placed at 20 km with uniform vertical grid spacing (Δz) equal to 500 m, resulting in 40 full vertical levels. No surface drag is imposed at the lower boundary (free slip condition). Water vapor (q_v), cloud water (q_c), and rainwater (q_r) are handled by a simple Kessler microphysics routine (Kessler, 1969). In particular, the Kessler microphysics used here is outlined in detail in Appendix C of Klemp et al. (2015) and code for reproducing this configuration is available via the DCMIP2016 repository (https://doi.org/10.5281/zenodo.1298671, Ullrich et al., 2018).

All simulations are integrated for 120 min. Outputs of the full three-dimensional prognostic fields as well as all variables pertaining to the microphysical routines were stored for post-processing at least every 15 min. Four different horizontal resolutions were specified: 4, 2, 1, and 0.5^∘. For the reduced-radius framework, this results in approximate grid spacings of 4, 2, 1, and 0.5 km, respectively. Note that here we use “(nominal) resolution” and “grid spacing” interchangeably to refer to the horizontal length of a single grid cell or distance between grid points. All relevant constants mentioned here and in the following section are defined in Table 1.

2.1 Mean atmospheric background

The mean atmospheric state is designed such that it consists of large instability (convective available potential energy (CAPE) of approximately 2200 m² s⁻¹) and strong low-level wind shear, both of which are strong precursors of supercell formation (Weisman and Klemp, 1982).

The definition of this test case relies on hydrostatic and cyclostrophic wind balance, written in terms of Exner pressure π and virtual potential temperature θ_v as

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial \mathit{\pi }}{\partial z}}=-{\displaystyle \frac{g}{c_{\text{p}}{\mathit{\theta }}_{\text{v}}}},\text{and}{u}^{\mathrm{2}}\tan \mathit{\phi }=-c_{\text{p}}{\mathit{\theta }}_{\text{v}}{\displaystyle \frac{\partial \mathit{\pi }}{\partial \mathit{\phi }}}.\end{array}$$

Defining u=u_eqcos φ to maintain solid body rotation, where u_eq is the equatorial wind velocity, these equations can be combined to eliminate π, leading to

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\text{v}}}{\partial \mathit{\phi }}}={\displaystyle \frac{\sin \left(\mathrm{2}\mathit{\phi }\right)}{\mathrm{2}g}}\left(u_{\text{eq}}^{\mathrm{2}}{\displaystyle \frac{\partial {\mathit{\theta }}_{\text{v}}}{\partial z}}-{\mathit{\theta }}_{\text{v}}{\displaystyle \frac{\partial u_{\text{eq}}^{\mathrm{2}}}{\partial z}}\right).\end{array}$$

The wind velocity is analytically defined throughout the domain. Meridional and vertical wind is initially set to zero. The zonal wind is obtained from

$$\begin{array}{ll}\text{(3)}& {\displaystyle }& {\displaystyle }u(\mathit{\phi },z)={\displaystyle }& {\displaystyle }\left\{\begin{array}{ll}\left(U_{\text{s}}{\displaystyle \frac{z}{z_{\text{s}}}}-U_{\text{c}}\right)\cos \left(\mathit{\phi }\right)& \text{for}z<z_{\text{s}}-\mathrm{\Delta }{z}_u,\\ \left[\left(-{\displaystyle \frac{\mathrm{4}}{\mathrm{5}}}+\mathrm{3}{\displaystyle \frac{z}{z_{\text{s}}}}-{\displaystyle \frac{\mathrm{5}}{\mathrm{4}}}{\displaystyle \frac{z^{\mathrm{2}}}{z_{\text{s}}^{\mathrm{2}}}}\right)U_{\text{s}}-U_{\text{c}}\right]\cos \left(\mathit{\phi }\right)& \text{for}\mathrm{|}z-z_{\text{s}}\mathrm{|}\le \mathrm{\Delta }{z}_u\\ \left(U_{\text{s}}-U_{\text{c}}\right)\cos \left(\mathit{\phi }\right)& \text{for}z>z_{\text{s}}+\mathrm{\Delta }{z}_u\end{array}\right..\end{array}$$

The equatorial profile is determined through numerical iteration. Potential temperature at the Equator is specified via

$$\begin{array}{}\text{(4)}& {\mathit{\theta }}_{\text{eq}}\left(z\right)=\left\{\begin{array}{ll}{\mathit{\theta }}_{\mathrm{0}}+({\mathit{\theta }}_{\text{tr}}-{\mathit{\theta }}_{\mathrm{0}}){\left({\displaystyle \frac{z}{z_{\text{tr}}}}\right)}^{\frac{\mathrm{5}}{\mathrm{4}}}& \text{for}\mathrm{0}\le z\le z_{\text{tr}},\\ {\displaystyle }{\mathit{\theta }}_{\text{tr}}\exp \left({\displaystyle \frac{g(z-z_{\text{tr}})}{c_p{T}_{\text{tr}}}}\right)& \text{for}{z}_{\text{tr}}\le z\end{array}\right.,\end{array}$$

and relative humidity is given by

$$\begin{array}{}\text{(5)}& H\left(z\right)=\left\{\begin{array}{ll}\mathrm{1}-{\displaystyle \frac{\mathrm{3}}{\mathrm{4}}}{\left({\displaystyle \frac{z}{z_{\text{tr}}}}\right)}^{\mathrm{5}/\mathrm{4}}& \text{for}\mathrm{0}\le z\le z_{\text{tr}},\\ {\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}& \text{for}{z}_{\text{tr}}\le z.\end{array}\right.\end{array}$$

It is assumed that the saturation mixing ratio is given by

$$\begin{array}{}\text{(6)}& q_{\text{vs}}(p,T)=\left({\displaystyle \frac{\mathrm{380.0}}{p}}\right)\exp \left(\mathrm{17.27}\times {\displaystyle \frac{T-\mathrm{273.0}}{T-\mathrm{36.0}}}\right).\end{array}$$

Pressure and temperature at the Equator are obtained by iterating on hydrostatic balance with initial state

$$\begin{array}{}\text{(7)}& {\mathit{\theta }}_{\text{v,eq}}^{\left(\mathrm{0}\right)}\left(z\right)={\mathit{\theta }}_{\text{eq}}\left(z\right),\end{array}$$

and iteration procedure

$$\begin{array}{}\text{(8)}& {\displaystyle }& {\displaystyle }{\mathit{\pi }}_{\text{eq}}^{\left(i\right)}=\mathrm{1}-\underset{\mathrm{0}}{\overset{z}{\int }}{\displaystyle \frac{g}{c_{\text{p}}{\mathit{\theta }}_{\text{v,eq}}^{\left(i\right)}}}\text{d}z\text{(9)}& {\displaystyle }& {\displaystyle }{p}_{\text{eq}}^{\left(i\right)}=p_{\mathrm{0}}{\left({\mathit{\pi }}_{\text{eq}}^{\left(i\right)}\right)}^{c_{\text{p}}/R_{\text{d}}}\text{(10)}& {\displaystyle }& {\displaystyle }{T}_{\text{eq}}^{\left(i\right)}={\mathit{\theta }}_{\text{eq}}\left(z\right){\mathit{\pi }}_{\text{eq}}^{\left(i\right)}\text{(11)}& {\displaystyle }& {\displaystyle }{q}_{\text{eq}}^{\left(i\right)}=H\left(z\right)q_{\text{vs}}\left(p_{\text{eq}}^{\left(i\right)},T_{\text{eq}}^{\left(i\right)}\right)\text{(12)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\text{v,eq}}^{(i+\mathrm{1})}={\mathit{\theta }}_{\text{eq}}\left(z\right)\left(\mathrm{1}+M_{\text{v}}{q}_{\text{eq}}^{\left(i\right)}\right).\end{array}$$

This iteration procedure generally converges to machine epsilon after approximately 10 iterations. The equatorial moisture profile is then extended through the entire domain:

$$\begin{array}{}\text{(13)}& q(z,\mathit{\phi })=q_{\text{eq}}\left(z\right).\end{array}$$

Once the equatorial profile has been constructed, the virtual potential temperature through the remainder of the domain can be computed by iterating on Eq. (2):

$$\begin{array}{ll}\text{(14)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\text{v}}^{(i+\mathrm{1})}(z,\mathit{\phi })={\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\text{v,eq}}\left(z\right)+\underset{\mathrm{0}}{\overset{\mathit{\phi }}{\int }}{\displaystyle \frac{\sin \left(\mathrm{2}\mathit{\varphi }\right)}{\mathrm{2}g}}\left(u_{\text{eq}}^{\mathrm{2}}{\displaystyle \frac{\partial {\mathit{\theta }}_{\text{v}}^{\left(i\right)}}{\partial z}}-{\mathit{\theta }}_{\text{v}}^{\left(i\right)}{\displaystyle \frac{\partial u_{\text{eq}}^{\mathrm{2}}}{\partial z}}\right)\text{d}\mathit{\phi }.\end{array}$$

Table 2 Participating modeling centers and associated dynamical cores that submitted results for the splitting supercell test.

Again, approximately 10 iterations are needed for convergence to machine epsilon. Once virtual potential temperature has been computed throughout the domain, Exner pressure throughout the domain can be obtained from Eq. (1):

$$\begin{array}{}\text{(15)}& \mathit{\pi }(z,\mathit{\phi })={\mathit{\pi }}_{\text{eq}}\left(z\right)-\underset{\mathrm{0}}{\overset{\mathit{\phi }}{\int }}{\displaystyle \frac{u^{\mathrm{2}}\tan \mathit{\phi }}{c_{\text{p}}{\mathit{\theta }}_{\text{v}}}}\text{d}\mathit{\phi },\end{array}$$

and so

$$\begin{array}{}\text{(16)}& {\displaystyle }& {\displaystyle }p(z,\mathit{\phi })=p_{\mathrm{0}}\mathit{\pi }(z,\mathit{\phi }{)}^{c_{\text{p}}/R_{\text{d}}},\text{(17)}& {\displaystyle }& {\displaystyle }{T}_{\text{v}}(z,\mathit{\phi })={\mathit{\theta }}_{\text{v}}(z,\mathit{\phi })(p/p_{\mathrm{0}}{)}^{R_{\text{d}}/c_{\text{p}}}.\end{array}$$

Note that, for Eqs. (13)–(14), Smolarkiewicz et al. (2017) also derived an analytic solution for the meridional variation of the initial background state for shallow atmospheres.

2.2 Potential temperature perturbation

To initiate convection, a thermal perturbation is introduced into the initial potential temperature field:

$$\begin{array}{ll}\text{(18)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}^{\prime }(\mathit{\lambda },\mathit{\varphi },z)={\displaystyle }& {\displaystyle }\left\{\begin{array}{ll}\mathrm{\Delta }\mathit{\theta }{\cos }^{\mathrm{2}}\left({\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}{R}_{\mathit{\theta }}(\mathit{\lambda },\mathit{\phi },z)\right)& \text{for}{R}_{\mathit{\theta }}(\mathit{\lambda },\mathit{\phi },z)<\mathrm{1},\\ \mathrm{0}& \text{for}{R}_{\mathit{\theta }}(\mathit{\lambda },\mathit{\phi },z)\ge \mathrm{1},\end{array}\right.\end{array}$$

where

$$\begin{array}{}\text{(19)}& R_{\mathit{\theta }}(\mathit{\lambda },\mathit{\phi },z)={\left[{\left({\displaystyle \frac{R_{\text{c}}(\mathit{\lambda },\mathit{\phi };{\mathit{\lambda }}_{\text{p}},{\mathit{\phi }}_{\text{p}})}{r_{\text{p}}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{z-z_{\text{c}}}{z_{\text{p}}}}\right)}^{\mathrm{2}}\right]}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

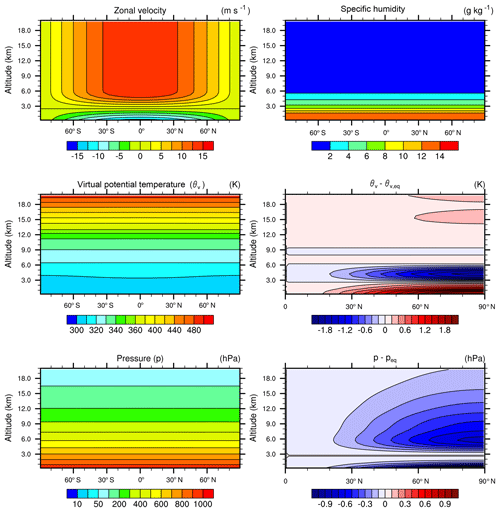
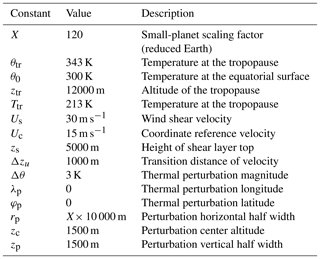
Figure 1 Initial state for the supercell test. All plots are latitude–height slices at 0^∘ longitude. Deviations from equatorial values are shown for virtual potential temperature and pressure.

Figure 2 Same as Fig. 1 for temperature and potential temperature.

An additional iterative step is then required to bring the potential temperature perturbation into hydrostatic balance. Without this additional iteration, large vertical velocities will be generated as the flow rapidly adjusts to hydrostatic balance since the test does not possess strong non-hydrostatic characteristics at initialization. Plots showing the initial state of the supercell are shown in Figs. 1 and 2 for reference. Code used by modeling centers during DCMIP2016 for initialization of the supercell test case is archived via Zenodo (https://doi.org/10.5281/zenodo.1298671, Ullrich et al., 2018).

The test case is designed such that the thermal perturbation will induce a convective updraft immediately after initialization. As rainwater is generated by the microphysics, reduced buoyancy and a subsequent downdraft at the Equator in combination with favorable vertical pressure gradients near the peripheral flanks of the storm will cause it to split into two counter-rotating cells that propagate transversely away from the Equator until the end of the test (Rotunno and Klemp, 1982, 1985; Rotunno, 1993; Klemp et al., 2015).

2.3 Physical and numerical diffusion

As noted in Klemp et al. (2015), dissipation is an important process near the grid scale, particularly in simulations investigating convection in unstable environments such as this. To represent this process and facilitate solution convergence as resolution is increased for a given model, a second-order diffusion operator with a constant viscosity (value) is applied to all momentum equations (ν=500 m² s⁻¹) and scalar equations (ν=1500 m² s⁻¹). In the vertical, this diffusion is applied to the perturbation from the background state only in order to prevent the initial perturbation from mixing out.

Models that contributed supercell test results during DCMIP2016 are listed in Table 2. They are formally described in Ullrich et al. (2017) and the references therein. Further, specific versions of the code used in DCMIP2016 and access instructions are also listed in Ullrich et al. (2017). Note that not all DCMIP2016 participating groups submitted results for this particular test.

Due to the multitude of differing implicit and explicit diffusion in the participating models, some groups chose to apply variations in how either horizontal or vertical diffusion were treated in this test case. Deviations from the above-specified diffusion are as follows. CSU applied uniform three-dimensional second-order diffusion with coefficients of ν=1500 m² s⁻¹ for q_v and θ_v, ν=1000 m² s⁻¹ for q_c and q_r, and ν=500 m² s⁻¹ for divergence and relative vorticity. FV³ applied divergence and vorticity damping separately to the velocity fields along the floating Lagrangian surface. A Smagorinsky diffusion is also applied to the horizontal wind. ICON applied constant horizontal second-order diffusion to the horizontal and vertical velocity components (ν=500 m² s⁻¹) as well as the scalar variables θ_v and q_v,c,r (ν=1500 m² s⁻¹). No explicit diffusion was applied in the vertical. NICAM applied a dynamically defined fourth-order diffusion to all variables in the horizontal with vertical dissipation being implicitly handled by the model's vertical discretization.

3 Results

The following section describes the results of the supercell test case during DCMIP2016, both from a intermodel time evolution perspective and intramodel sensitivity to model resolution and ensuing convergence. Note that there is no analytic solution for the test case, but features specific to supercells should be observed and are subsequently discussed. It is not the intent of this paper to formally explore the precise mechanisms for model spread or define particular solutions as superior but rather to publish an overview set of results from a diverse group of global, non-hydrostatic models to be used for future development endeavors. Future work employing this test case in a more narrow sense can isolate some of the model design choices that impact supercell simulations.

3.1 Time evolution of supercell at control resolution

Figure 3 shows the temporal evolution (every 30 min, out to 120 min test termination) of the supercell for contributing models at the control resolution of 1 km. The top four panels for each model highlight a cross-section at 5 km elevation through vertical velocity (w), while the bottom four show a cross-section (at the same elevation) through the rainwater (q_r) field produced by the Kessler microphysics. For w, red contours represent rising motion, while blue contours denote sinking air. Note that the longitudes plotted vary slightly in each of the four time panes to account for zonal movement. This analysis framework closely follows that originally outlined in Klemp et al. (2015).

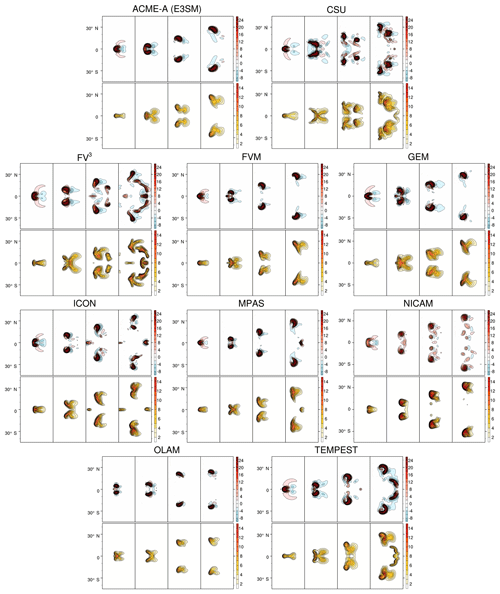
Figure 3 Time evolution of cross-sections of 5 km vertical velocity (m s⁻¹, top) and 5 km rainwater (g kg⁻¹, bottom) for each model with the r100 configuration of the test case. From left to right, fields are plotted at 30, 60, 90, and 120 min.

All model solutions show bulk similarities. With respect to vertical velocity, a single, horseshoe-shaped updraft is noted at 30 min in all models, although the degree to which the maximum updraft velocities are centered on the Equator vary. A corresponding downdraft is located immediately to the east of the region of maximum positive vertical velocity. This downdraft is single-lobed (e.g., ACME-A) or double-lobed (e.g., GEM) in all simulations. Separation of the initial updraft occurs by 60 min across all models, although variance begins to develop in the meridional deviation from the Equator of the splitting supercell. Models such as NICAM, FV³, OLAM, and ICON all have larger and more distinct north–south spatial separation, while FVM, GEM, ACME-A, and TEMPEST show only a few degrees of latitude between updraft cores.

Structural differences also begin to emerge at 60 min. For example, FVM, GEM, ACME-A, and TEMPEST all exhibit three local maxima in vertical velocity: two large updrafts mirrored about the Equator with one small maximum still located over Equator centered near the initial perturbation. Similar behavior is noted in the q_r fields. This is in contrast with other models which lack a third updraft on the equatorial plane. Generally speaking, q_r maxima are collocated with the locations of maximum updraft velocities and thereby conversion from q_v and q_c to q_r in the Kessler microphysics.

While the aggregate response of a single updraft eventually splitting into poleward-propagating symmetric storms about the Equator is well matched between the configurations, notable differences exist, particularly towards the end of the runs. At 120 min, FVM, GEM, ACME-A, OLAM, and MPAS all show two discrete supercells approximately 30^∘ from the Equator. FV³ and TEMPEST both produce longitudinally transverse storms that stretch towards the Equator in addition to the two main cells. Each of the splitting supercells splits a second time in ICON, forming, in conjunction with a local maximum at the Equator, five maxima of vertical velocity (and correspondingly rainwater). NICAM produces two core supercells (as more clearly evident in the q_r field at 120 min) but has noticeable alternating weak updrafts and downdrafts in the north–south space between the two storm cores.

The relative smoothness of the storms as measured by the vertical velocity and rainwater fields also varies between models, particularly at later times. ACME-A, FVM, GEM, OLAM, and MPAS produce updrafts that are relatively free of additional, small-scale local extrema in the vicinity of the core of the splitting supercell. Conversely, CSU, FV³, ICON, NICAM, and TEMPEST all exhibit solutions with additional convective structures, with multiple updraft maxima versus two coherent cells. This spread is somewhat minimized when looking at rainwater, implying that the overall dynamical character of the cells as noted by precipitation generation is more similar, with all models showing cohesive rainwater maxima O(10 g kg⁻¹).

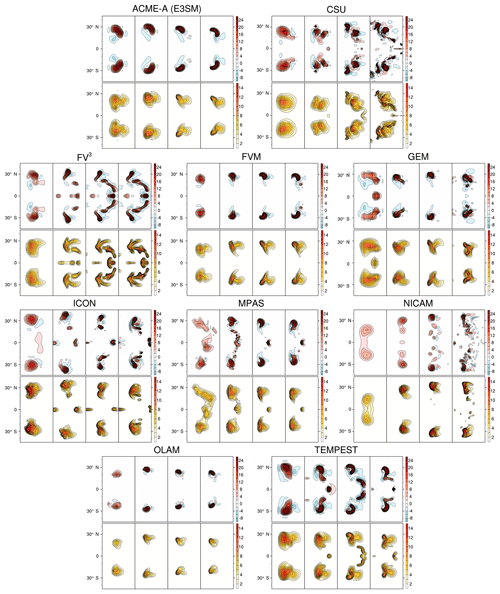
Figure 4 Resolution sensitivity of cross-sections of 5 km vertical velocity (m s⁻¹, top) and 5 km rainwater (g kg⁻¹, bottom) plotted at 120 min for each model. From left to right, nominal model resolutions are 4, 2, 1, and 0.5 km.

Figure 5 Maximum domain updraft velocity (m s⁻¹) as a function of time (seconds from initialization) for each model at each of the four specified resolutions. Note that the dark grey line is the finest grid spacing (0.5 km) in this test.

3.2 Resolution sensitivity of the supercell

Figure 4 shows the same cross-section variables as Fig. 3 except across the four specified test resolutions (nominally 4, 2, 1, and 0.5 km, from left to right) at test termination of 120 min. Therefore, the third panel from the left for each model (1 km) should match the fourth panel from the left for each model in Fig. 3.

As resolution increases (left to right), models show increasing horizontal structure in both the vertical velocity and rainwater fields. Updraft velocity generally increases with resolution, particularly going from 4 to 2 km, implying that the supercell is underresolved at 4 km resolution. This is supported by previous mesoscale simulations investigating supercells in other frameworks (Potvin and Flora, 2015; Schwartz et al., 2017), although it should be emphasized that this response is also subject to each numerical scheme's effective resolution (Skamarock, 2004) and that the resolvability of real-world supercells can depend on the size of individual storms.

At the highest resolutions, there is a distinct group of models that exhibit more small-scale structure, particularly in vertical velocity, at +120 min at higher resolutions. CSU, GEM, and NICAM appear to have the largest vertical velocity variability at 0.5 km, while ACME-A, FVM, MPAS, and TEMPEST appear to produce the smoothest solutions. This result is likely due to the differences in explicit diffusion treatment as noted before, as well as differences in the numerical schemes' implicit diffusion, particularly given the large impact of dissipation on kinetic energy near the grid scale (Skamarock, 2004; Jablonowski and Williamson, 2011; Guimond et al., 2016; Kühnlein et al., 2019). Additional focused sensitivity runs varying explicit diffusion operators and magnitude may be insightful for developers to explore. It is also hypothesized that differences in the coupling between the dynamical core and subgrid parameterizations may lead to some of these behaviors (e.g., Staniforth et al., 2002; Gallus and Bresch, 2006; Malardel, 2010; Thatcher and Jablonowski, 2016; Gross et al., 2018), although more constrained simulations isolating physics–dynamics coupling in particular modeling frameworks is a target for future work. As before, rainwater cross-sections tend to be less spatially variable at 0.5 km than vertical velocity, although CSU and NICAM both show some additional local maxima in the field associated with some of the aforementioned w maxima.

Figure 6 Same as Fig. 5 except showing area-integrated instantaneous precipitation rate (×10⁵ kg s⁻¹).

3.3 Convergence of global supercell quantities with resolution

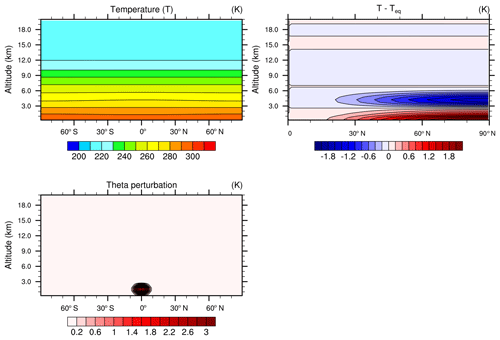
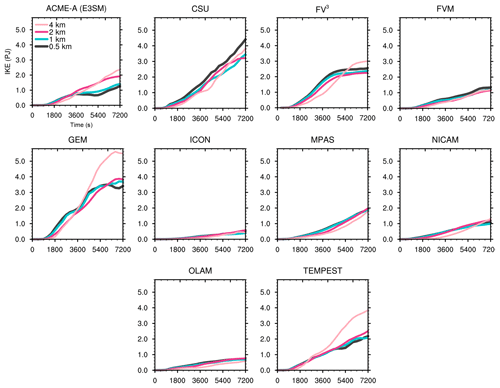
While Fig. 4 highlights the structural convergence with resolution, more storm-wide measures of supercell intensity are also of interest. Figure 5 shows the maximum resolved updraft velocity over the global domain as a function of time for each dynamical core and each resolution (finer model resolution is denoted by progressively darker lines). Maximum updraft velocity is chosen as a metric of interest due to its common use in both observational and modeling studies of supercells. All models show increasing updraft velocity as a function of resolution, further confirming that, at 4 km, the supercell is underresolved dynamically. For the majority of models and integration times, the gap between 4 and 2 km grid spacing is the largest in magnitude, with subsequent increases in updraft velocity being smaller as models further decrease horizontal grid spacing. At 0.5 km, the majority of models are relatively converged, with FV³, ICON, and MPAS showing curves nearly on top of one another at these resolutions. Other models show larger differences between 0.5 and 1 km curves, implying that these configurations may not yet be converged in this bulk sense. Further grid refinement or modifications to the dissipation schemes are necessary to achieve convergence; this is left to the individual modeling groups to verify (see Sect. 3.4 for an example).

The maximum updraft velocity as a function of resolution for particular model configurations varies quite widely. NICAM produces the weakest supercell, with velocities around 30 m s⁻¹ at 0.5 km, while ACME-A, TEMPEST, GEM, and CSU all produce supercells that surpass 55 m s⁻¹ at some point during the supercell evolution. Models that have weaker supercells at 0.5 km tend to also have weaker supercells at 4 km (e.g., NICAM), while the same is true for stronger supercells (e.g., TEMPEST), likely due to configuration sensitivity. This agrees with the already discussed structural plots (Fig. 4) which demonstrated model solutions were generally converging with resolution on an intramodel basis but not necessarily across models.

Figure 7 Same as Fig. 5 except showing storm-integrated kinetic energy (PJ) as defined in Eq. (20).

Figure 8 As in Fig. 4 except showing the subset of models that completed a 0.25 km test. From left to right, nominal model resolutions are 2, 1, 0.5, and 0.25 km.

Figure 9 As in Fig. 7 except showing the subset of models that completed a 0.25 km test.

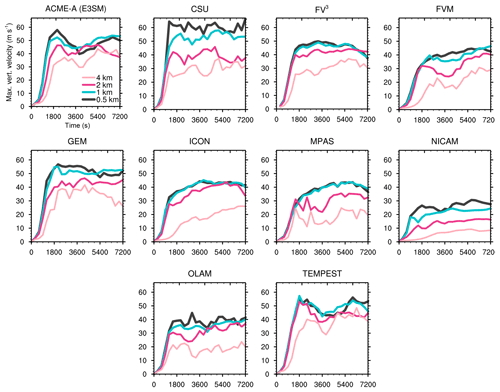
Figure 6 shows the same analysis except for area-integrated precipitation rate for each model and each resolution. Similar results are noted as above – with most models showing large spread at the coarsest resolutions but general convergence in precipitation by 0.5 km. All models produce the most precipitation at 120 min with the 4 km simulation. This is consistent with Klemp et al. (2015), who postulated this behavior is due to increased spatial extent of available q_r to fall out of the column at these grid spacings, even though updraft velocities are weaker at coarser resolutions. Unlike maximum vertical velocity, the integrated precipitation rate does not monotonically increase with resolution for most models. At 120 min, integrated rates at 0.5 km range by approximately a factor of 3 or 4, from a low of 50–70 ×10⁵ kg s⁻¹ (ACME-A, FVM, OLAM) to a high of 170–200 ×10⁵ kg s⁻¹ (CSU, FV³), highlighting the sensitivity of final results that have been already been discussed.

In addition to Figs. 5 and 6, which directly correspond to analysis in Klemp et al. (2015), we also define a storm-integrated kinetic energy (IKE) metric as follows:

$$\begin{array}{}\text{(20)}& \text{IKE}\left(t\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{\mathrm{0}}{\overset{z_{\text{t}}}{\int }}\underset{\mathrm{0}}{\overset{A_e}{\int }}\mathit{\rho }\left({u^{\prime }}^{\mathrm{2}}+{v^{\prime }}^{\mathrm{2}}+{w^{\prime }}^{\mathrm{2}}\right)\text{d}A\text{d}z,\end{array}$$

where z_t is the model top, A_e is the area of the sphere, and winds (u^′, v^′, w^′) are calculated as perturbations from the initial model state at the corresponding spatial location (e.g., $u^{\prime }=u^{\prime }(t,\mathit{\varphi },\mathit{\psi },z)=u(t,\mathit{\varphi },\mathit{\psi },z)-u(\mathrm{0},\mathit{\varphi },\mathit{\psi },z)$). Here, local air density, $\mathit{\rho }(t,\mathit{\varphi },\mathit{\psi },z)$, is computed using a standard atmosphere due to limitations in available data from some groups.

As a metric, IKE is less sensitive to grid-scale velocities and is also a more holistic measure of storm-integrated intensity. This is shown in Fig. 7. Results are generally analogous to those in Fig. 6. This should be expected since total precipitation within a supercell is tied to the spatial extent and magnitude of the upward velocities that dominate the IKE term. Convergence behavior between 1 and 0.5 km appears similar for each model as noted earlier. The total spread across models at the end of the simulation for the 0.5 km simulations is also similar to that seen in Fig. 6, demonstrating the large range in “converged” solutions across models due to the various design choices discussed earlier.

3.4 Sample experiments at 0.25 km grid spacing

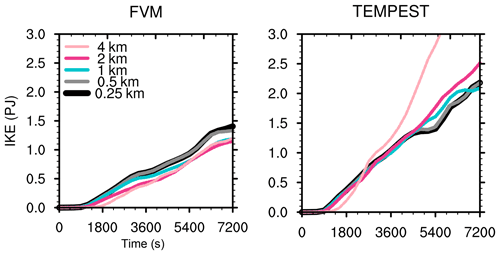
While the formal supercell test case definition during DCMIP2016 specified 0.5 km grid spacing as the finest resolution for groups to submit, it is clear that full convergence has not been reached for some of the modeling groups (e.g., Sect. 3.3). To confirm that the solution still converges further, two groups (FVM and TEMPEST) completed an exploratory set of simulations at 0.25 km resolution. Figure 8 shows the structural grid spacing convergence at 120 min for the two models from 2 to 0.25 km. Note that the left three panels for each model in Fig. 8 should match the corresponding three rightmost panels in Fig. 4. Figure 9 shows FVM and TEMPEST IKE results, including the 0.25 km simulations.

For TEMPEST and FVM, results indicate solution differences are markedly smaller between 0.5 and 0.25 km than between 1 and 0.5 km, implying the test is not fully converged at 0.5 km for these models. Therefore, 0.25 km may be a better target for a reference grid spacing going forward.

It is worth noting that the reference solution in Klemp et al. (2015) is indeed converged at 0.5 km, as are some of the models in DCMIP2016. Given this, it is unclear whether the need to go beyond DCMIP2016 protocols for “full” convergence is due to the test case definition itself or, rather, the implementation of the test case in particular models. This is left for subsequent analyses. However, given this result, it is recommended that groups applying this test case in the future continue to push beyond the four resolutions specified here if convergence is not readily apparent in either storm structure or bulk quantities at 0.5 km.

4 Conclusions

Non-hydrostatic dynamics are required for accurate representation of supercells. The results from this test case show that clear differences and uncertainties exist in storm evolution when comparing identically initialized dynamical cores at similar nominal grid resolutions. Intramodel convergence in bulk, integrated quantities appears to generally occur at approximately 0.5 km grid spacing. However, intermodel differences are quite large even at these resolutions. For example, maximum updraft velocity within a storm between two models may vary by almost a factor of 2 even at the highest resolutions assessed at DCMIP2016.

Structural convergence is weaker than bulk-integrated metrics. Two-dimensional horizontal cross-sections through the supercells at various times show that some models are well converged between 1 and 0.5 km, while results from other models imply that finer resolutions are needed to assess whether convergence will occur with a particular test case formulation and model configuration. Interestingly, in some cases, maximum bulk quantities converge faster than snapshots of cross-sections.

We postulate that these differences and uncertainties likely stem from not only the numerical discretization and grid differences outlined in Ullrich et al. (2017) but also from the form and implementation of filtering mechanisms (either implicit or explicit) specific to each modeling center. The simulation of supercells at these resolutions are particularly sensitive to numerical diffusion since damping of prognostic variables in global models is occurring at or near the scales required for resolvability of the storm. This is different from other DCMIP2016 tests (baroclinic wave and tropical cyclone), which produced dynamics that were less non-hydrostatic in nature and required resolvable scales much coarser than the grid cell level. Further, since DCMIP2016 did not formally specify a particular physics–dynamics coupling strategy, it would not be surprising for particular design choices regarding how the dynamical core is coupled to subgrid parameterizations to also impact results.

Given the lack of an analytic solution, we emphasize that the goal of this paper is not to define particular supercells as optimal answers. Rather, the main intention of this test at DCMIP2016 was to produce a verifiable database for models to use as an initial comparison point when evaluating non-hydrostatic numerics in dynamical cores. Pushing grid spacings to 0.25 km and beyond to formalize convergence would be a useful endeavor in future application of this test, either at the modeling center level or as part of future iterations of DCMIP. Variable-resolution or regionally refined dynamical cores may reduce the burden of such simulations, making them more palatable for researchers with limited computing resources.

We acknowledge that, as groups continue to develop non-hydrostatic modeling techniques, small changes in the treatment of diffusion in the dynamical core will likely lead to changes in their results from DCMIP2016. We recommend modeling centers developing or optimizing non-hydrostatic dynamical cores to perform this test and compare their solutions to the baselines contained in this paper as a check of sanity relative to a large and diverse group of next-generation dynamical cores actively being developed within the atmospheric modeling community.