the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The probabilistic hydrological MARCSHYDRO (the MARkov Chain System) model: its structure and core version 0.2
Andrey Silaev
The question of the environmental risks of social and economic infrastructure has recently become apparent due to an increase in the number of extreme weather events. Extreme runoff events include floods and droughts. In water engineering, extreme runoff is described in terms of probability and uses methods of frequency analysis to evaluate an exceedance probability curve (EPC) for runoff. It is assumed that historical observations of runoff are representative of the future; however, trends in the observed time series show doubt in this assumption. The paper describes a probabilistic hydrological MARCSHYDRO (the MARkov Chain System) model that can be applied to predict future runoff extremes. The MARCSHYDRO model simulates statistical estimators of multi-year runoff in order to perform future projections in a probabilistic form. Projected statistics of the meteorological variables available in climate scenarios force the model. This study introduces the new model's core version and provides a user guide together with an example of the model set-up in a single case study. In this case study, the model simulates the projected EPCs of annual runoff under three climate scenarios. The scope of applicability and limitations of the model's core version 0.2 are discussed.
- Article
(1719 KB) - Full-text XML
- BibTeX
- EndNote
Streamflow runoff serves as a water resource for humans, food production and energy generation, while the risks of water-sensitive economics are usually connected to runoff extremes. In fact, runoff extremes are always connected to human activity since they do not exist in a natural water cycle. Engineering science considers runoff extremes as critical values of runoff that lead to the damage of infrastructure or water shortages, and it introduces the extremes in terms of probability. In particular, in water engineering runoff extremes are evaluated from the tails of exceedance probability curves (EPCs) that are used in risk assessment for water infrastructure and decision-making in cost–loss situations (Mylne, 2002; Murphy, 1977, 1976). The EPC of multi-year runoff allows the estimation of the runoff extremes and supports the designing of building construction, bridges, dams and withdrawal systems, etc.
Modern hydrology uses two approaches to evaluate runoff extremes with their exceedance probability: conceptual modelling (Lamb, 2006) and frequency analysis (Kite, 1977; Benson, 1968; Kritsky and Menkel, 1946). In the conceptual modelling approach, synthetic runoff series are simulated from meteorological series in order to calculate the runoff values of a chosen exceedance probability (Arheimer and Lindström, 2015; Veijalainen et al., 2012; Seibert, 1999). In the frequency-analysis approach, historical yearly time series of runoff are used to evaluate statistical estimators, that is, the mean value, the coefficient of variation (CV) and the coefficient of skewness (CS) (van Gelder, 2006). These estimators are applied to calculate runoff values with their exceedance probability (Guidelines SP 33-101-2003, 2004; Guidelines, 1984; Bulletin 17–B, 1982) needed to support the designing of roads, dams, bridges or water-withdrawal stations. The basic assumption of this approach is that the future risks during an infrastructure's operational period are equal to the risks estimated from the past observations. The runoff extremes are simply extrapolated for the next 20–30 years on the assumption that past observations are representative of the future: the “stationarity” assumption (Madsen et al., 2013).
The number of weather extremes – including hurricanes, wind, rain- and snowstorms, floods and droughts – has increased (Vihma, 2014; Wang and Zhou, 2005; Manton et al., 2001). Historical time series of many climate variables show evident trends which are statistically significant, among which are the series of streamflow runoff (Wagner et al., 2011; Dai et al., 2009; Milly et al., 2005). Rosmann et al. (2016) applied the Mann–Kendall test to analyse a time series of daily, monthly and yearly river discharges for the last four decades. The highest number of trends was detected for the yearly time series of annual runoff. The statistically significant trends are founded on historical time series; thus the water engineers and managers are motivated to revise the basic stationarity assumption that lies behind infrastructures' risk assessment since past observations are not representative of the future (Madsen et al., 2013; Kovalenko, 2009; Milly at al., 2008).
In this paper, we described a method that combines conceptual modelling and frequency analysis in order to estimate runoff extremes in a changing climate. The method adapts the theory of stochastic systems to water engineering practice, and it was further named as advance of frequency analysis (AFA). It was introduced by Kovalenko (1993) and relied on the theory of stochastic systems (Pugachev et al., 1974). The basic idea behind the method is to simulate the statistical estimators of multi-year runoff (annual, minimal and maximal runoff) from the statistical estimators of precipitation and air temperature on a climate scale (Budyko and Izrael, 1991). The simulated statistical estimators of runoff are used to construct EPCs with distributions from the Pearson system (Pearson, 1895). Kovalenko (1993) suggested modelling the EPCs within a Pearson type III distribution based on traditional practice in water engineering (Rogdestvenskiy and Chebotarev, 1974; Matalas and Wallis, 1973; Sokolovskiy, 1968). However, the distribution can also be chosen by fitting (Laio et al., 2009), defined in accordance with local hydrological guidelines (Bulletin 17-B, 1982), or somehow more advanced (Andreev et al., 2005).
A linear “black box” (or a “linear filter model”) with stochastic components is suggested as a catchment-scale hydrological model (Kovalenko, 1993). For this linear model, the theory of stochastic systems provides methods to direct the simulation of probability distributions for a random process (Pugachev et al., 1974). The theory of stochastic systems is applied to analyse and predict runoff extremes on various timescales, ranging from days (Rosmann and Domínguez, 2017) to seasons (Domínguez and Rivera, 2010; Shevnina, 2001), and on various climate scales (Shevnina et al., 2017; Kovalenko, 2014; Viktorova and Gromova, 2008). The AFA approach is a simplification of the theory of stochastic systems on a climate scale. Kovalenko et al. (2010) gave guidelines for water engineers to estimate runoff extremes in a changing climate.
AFA was suggested about 30 years ago; however, a full description of this approach has still not been published in English. Moreover, previous publications in Russian contain many typewriting mistakes in the formulas (Kovalenko, 1993; Kovalenko et al., 2006), and this makes understanding them troublesome, even for native Russians. In this paper, the theory and assumptions of the AFA approach were formulated step by step (see Appendix 1), and the formulas behind the core of the probabilistic hydrological model MARCSHYDRO (the MARkov Chain System) were accepted for the new version, version 0.2 (see Sect. 1). This model core allows the prediction of a skewness parameter of a Pearson type III distribution. An example of the model set-up, forcing and output for a case study of the Iijoki River is given in Sect. 2. The main features of the model and the limitations of the AFA method are formulated in the Discussions section in order to better place the MARCSHYDRO model among other hydrological models.
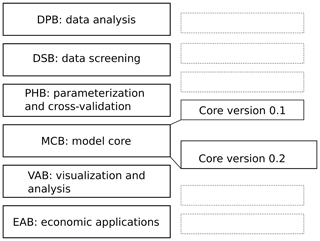
The probabilistic hydrological MARCSHYDRO model consists of six blocks (Shevnina, 2015). Figure 1 shows the tools for data analysis grouped into blocks: two blocks for the analysis and screening of observed data (DPB and DSB); a block with the model parametrization, cross-validation and hindcasts (“forecasts in the past”; PHP); a block to visualize the model's results (VAB); and a block with socio-economic applications (EAB). Shevnina and Gaidukova (2017) provided details about the algorithms already implemented in each block in the model. In this paper, only version 0.2, for the model's core, is introduced. The formulas behind the model's core version 0.1 are published in the Appendix of the work of Shevnina et al. (2017).
The MARCSHYDRO model simulates three non-central statistical moments of multi-year runoff based on the means of precipitation calculated over a period of 20–30 years. Now, the model's application is only limited by a prediction on the climate scale. The development of a socio-economic infrastructure also needs the climate-scale prediction of river runoff (Milly et al., 2008) because water extremes, such as floods and droughts, lead to economical losses. The AFA approach has found practical applications in building construction (Shevnina et al., 2017; Kovalenko, 2009). The MARCSHYDRO model allows a quick analysis of the runoff extremes under different climate scenarios. The model needs fewer computational resources because it simulates the parameters of the distribution, while conceptual hydrological models simulate the runoff time series.
The MARCSHYDRO model parametrization, cross-validation and hindcasts need observations of the river water discharges of a hydrological network for a period in the past (Kovalenko, 1993). For the cross-validation, the yearly time series of river runoff are split into two sub-periods, namely the training period and the control period (Shevnina et al., 2017). The splitting year corresponds to the year when the statistically significant difference in observations within two periods is detected by the Student and Kolmogorov–Smirnov tests (Kovalenko, 1993; Kovalenko et al., 2006). The description of the analysis and screening of the observed river runoff time series, as well as the model cross-validation procedure, fell outside the topics of this paper. We focused on the equations behind the model's core version 0.2 and its limitations.
2.1 Model input
Two blocks of the MARCSHYDRO model are needed to analyse and screen the observations. The time series of river runoff and precipitation are required for a period as long as possible. However, the length of yearly time series on water discharges does not usually exceed 80–90 years. Hydrological yearbooks or runoff data sets provide observations at sites of national hydrological networks, and the river runoff is expressed as a volumetric flow rate (water discharge, m3 s−1). In the data preparation block of the model, the volumetric flow rate (m3 s−1) is converted to a specific water discharge (ARR, mm yr−1):
where Q is the yearly average water discharge (m3 s−1), T is the number of seconds in a year and A is the catchment area (m2). In the data screening block of the model, the yearly time series of ARR are used in the analysis of homogeneity and trends (Dahmen and Hall, 1990) and to define a period for the model parametrization (called the “reference period” by Shevnina et al., 2017). Then, the reference three non-central moments for k=1, 2, 3) are estimated from time series of ARR using the method of moments (van Gelder et al., 2006).
The observations on precipitation are collected from meteorological sites, and they may be interpolated into grids in order to better estimate a precipitation rate over a river basin area. In the data preparation block of the model, the mean annual precipitation rate (mm yr−1) is calculated from the observed yearly time series for the reference period. The mean annual precipitation rate for the future period can be calculated from an output of any global/regional climate model or even a set of models. In a study on the catchment scale, the time series of water discharges can be extracted from the Global Runoff Data Centre (GRDC), while the precipitation rate can be estimated from gridded data sets (Willmott and Robeson, 1995). These two data sets were used to perform an example of the model application on the Iijoki River basin.
2.2 Model cross-validation
The MARCSHYDRO model allows the simulation of the non-central moments of runoff that can be used for the construction of probability distribution (or an EPC); in other words, it provides a probabilistic form of prediction. The end product of the model is the probability density function (PDF) (or the EPC), and there are no simulated time series of runoff to compare with the observations. Kovalenko (1993) suggested comparing the simulated PDF with an empirical PDF by using known statistical tests such as the Kolmogorov–Smirnov test (Smirnov, 1948). In the PHP block of the MARCSHYDRO model, a specific cross-validation procedure allows conclusions to be drawn about the model's validation and the quality of hindcasts. For the model's cross-validation, the observed time series of river runoff is divided into two sub-periods, namely the training period and the control period. The splitting year corresponds to the year when a statistically significant difference in mean values is estimated over two periods. In this study, we did not pay much attention to the cross-validation procedure since it is described in detail in Shevnina et al. (2019) for the model version 0.2.
2.3 The MARCSHYDRO model core
In our study, the core version 0.2 of the probabilistic MARCSHYDRO model was suggested instead of version 0.1 (Shevnina et al., 2017). Version 0.2 allows the evaluation of the skewness parameter of the Pearson type III distribution. In the new core, the non-central statistical moments of the ARR were calculated as follows:
where m1, m2 and m3 are the moment estimates of the non-central statistical moments of the ARR; and a, b0, b1 and b2 are the parameters of the distributions of the Pearson equation (Andreev et al., 2005).
To set up the MARCSHYDRO model, observations of water discharges are needed. For the reference period (denoted by low index r) the moments' estimates for the non-central moments (m1r, m2r, m3r) were first calculated from observed times series of runoff (mm yr−1); then the non-central moments were used to evaluate the parameters of the Pearson equation a, b0 and b1:
Then, the parameters of the linear filter model (see Appendix 1 for details), , and , denoted with a low index r, were calculated:
where is the mean annual precipitation rate (mm yr−1) estimated from the observed time series as an average over any chosen reference period.
To force the MARCSHYDRO model, the outputs from global-/regional-scale climate models are needed. The Coupled Model Intercomparison Project 5 (CMIP5; Taylor et al., 2012) is one collection of data sets that is available for climate-scale hydrological studies. At present, the model only needs to be forced by mean precipitation (mm yr−1), evaluated for a future period of 20–30 years. A low index pr indicated that the values were estimated for the future, and is estimated from climate scenarios. Following the assumption that , and are constant for both periods, , and (a “basic parametrization scheme” according to Kovalenko, 1993); new parameters of the Pearson equation are calculated from :
Finally, the non-central moments of runoff are calculated for the projected period (denoted by a low index pr):
It should be noted that in core version 0.2 the linear filter model includes the multiplicative stochastic component (see Appendix 1 for details). It may lead to unstable solutions for the Fokker–Planck–Kolmogorov equation (mk→∞) for statistical moments of high orders. Two methods for getting stable solutions for the Fokker–Planck–Kolmogorov equation are suggested by Kovalenko (2004), and one of them is already implemented in core version 0.1 (Shevnina et al., 2017).
2.4 Model output
In our study, the EPC of runoff was modelled within a Pearson type III distribution. This distribution is commonly used by water engineers to estimate water extremes (Koutrouvelis and Canavos, 1999; Rogdestvenskiy and Chebotarev, 1974; Matalas and Wallis, 1973). The water engineering guidelines provide the ordinates of EPCs from lookup tables (Guidelines, 1984) depending on the CV and CS. These coefficients are calculated from non-central moments' estimates (Rogdestvenskiy and Chebotarev, 1974):
The MARCSHYDRO model output includes the estimates of the mean values of CV and CS, calculated for the reference period from observations, as well as these estimates simulated from mean precipitation for the projected period. The ordinates of the EPC available from lookup tables then allow the calculation of the runoff values together with their exceedance probability.
In our study, we chose the basin of the Iijoki River at the Raasakka gauge (lat 25.4∘, long. 65.3∘) in order to give an example of the application of the MARCSHYDRO model on the catchment scale. The Iijoki River is located in north-west Finland, and the Raasakka gauge outlines a watershed area of over 14 191 km2. The catchment has a small population, and there are no hydropower plants of multi-year regulation to affect the natural regime of the annual cycle. Thus, one can expect that historical yearly time series of the annual runoff rate do not contain trends connected to artificial regulation. This case study shows an example of the set-up and output of the probabilistic MARCSHYDRO model.
3.1 The MARCSHYDRO model set-up: the reference period
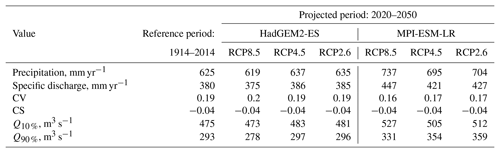
The yearly time series of volumetric water discharge of the Iijoki River were extracted from a data set of the GRDC (GRDC 56068 Koblenz, Germany). The observations at the Raasakka gauge (ID = 6 854 600) cover the period 1911–2014, and they do not contain gaps. This period was considered as the reference period. The annual specific water discharge (ARR, mm yr−1) was calculated from the average volumetric water discharge for each year in the reference period. Then, the non-central moments were calculated from the yearly time series of the ARR with the method of moments (see Table 1). The reference climatology (the means of precipitation and air temperature) was evaluated from the data set of NOAA (NOAA/OAR/ESRL PSD, Boulder, Colorado, USA) at a grid node nearest to the watershed centroid (this technique will be discussed in a separate paper, as will the methods of a forcing pre-analysis).
Table 1The MARCSHYDRO model set-up: the Iijoki River at Raasakka as a case study.

The values of m1r, m2r and m3r, the moments of runoff, and the mean of precipitation ( were evaluated from observations. The mean air temperature ( was not used in the model set-up in the case of the Iijoki River; however this value allows advancement of the model parametrization (Shevnina et al., 2017).
3.2 The MARCSHYDRO model forcing: the projected period
Climate scenarios provide a range of projections for temperature and moisture regimes in the future. This range is produced by different assumptions about climate scenarios as well as specific climate models. However, the climate projections include precipitation and air temperature, and they give a forcing to hydrological models in order to simulate projections of runoff. In the case study of the Iijoki River, the data from CMIP5 (Taylor et al., 2012) for three representative concentration pathways (RCPs) were used to force the MARCSHYDRO model. For each RCP scenario, the projections of annual precipitation rate were applied to test how the MARCSHYDRO model simulates the EPC under different forcing trajectories. For the period of 2020–2050 (considered the projected period), the mean values of the precipitation rate (mm yr−1) were calculated based on four world-leading global climate models. We used the outputs from the global models CaESM2 (Chylek et al., 2011), HadGEM2-ES (Collins et al., 2011), INM-CM4 (Volodin et al., 2010) and MPI-ESM-LR (Giorgetta et al., 2013) (see Table 2). The mean values of the precipitation rate varied by 2–5 % of the model's average over the RCP scenarios; however, these values alter substantially between the climate models. Among the outputs considered, the MPI-ESM-LR model projects the highest changes in the mean values of the precipitation rate compared to the reference period (see Tables 1 and 2). The HadGEM2-ES model gives the lowest values for the mean values of the precipitation rate. The projected means of the precipitation rate varied slightly between the scenarios. At the same time, they exhibited a significant range of changes among the climate models (the mean values of the precipitation rate ranges from 619 to 737 mm yr−1) for the case of the Iijoki River at Raasakka.
Table 2The forcing of the MARCSHYDRO model for the case study of the Iijoki River at Raasakka.
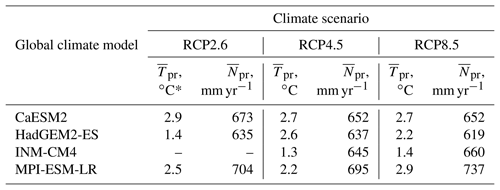
Projected mean air temperature ( is needed for a regional parametrization scheme (see details in Shevnina, 2011), and these values were not used in the model forcing in the case of the Iijoki River at Raasakka. is the projected mean annual precipitation amount.
3.3 The MARCSHYDRO model output: the projected period
The projected non-central moments' estimates were simulated for the scenarios and models listed in Table 2. These estimates were used to calculate the mean values of CV and CS (see Eqs. 16–17) that were included in the output of the MARCSHYDRO model. Table 3 shows the modelling results for the HadGEM2-ES and MPI-ESM-LR global models, for which the water discharges with 10 % and 90 % exceedance probabilities are given. The ordinates of the Pearson type III distribution were extracted from the lookup tables used in hydrological engineering (Druzhinin and Sikan, 2001), and they allow runoff to be expressed as water discharge (m3 s−1). For the Iijoki River at Raasakka, the mean values of ARR and CV vary under the RCP scenarios by over 7 % and 5 % correspondingly. The maximum alteration in the projected mean values of ARR was obtained under RCP8.5 (619 to 737 mm yr−1). Under the projections of the MPI-ESM-LR model, the mean ARR increases by over 17 %.
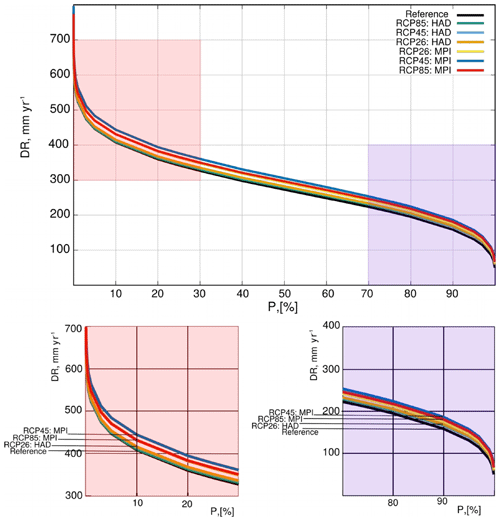
In the case of the Iijoki River at Raasakka gauge, the 10 % water discharge exceedance probability will increase in the future under the scenarios and models considered (see Table 3). It may lead to risks of energy spills at hydropower stations located within the catchment of the Iijoki River in the period 2020–2050. At the same time, risks connected with water shortages may be fewer since they are connected to a 90 % water discharge exceedance probability, which is predicted to increase. Figure 2 shows another way in which the model performs the EPC of the annual runoff rate for the Kyrönjoki River at Skatila gauge (GRDC ID: 6854900). The set of EPCs was simulated under three RCP scenarios using a similar set-up to the MARCSHYDRO model (Shevnina et al., 2019). In the further development of the visualization block, it would be important to involve water managers and decision makers in order to better outline practical applications for the probabilistic hydrological model.
Nowadays, the future vision of the climate is changing continuously. Climate projections are updated almost every 5–6 years, and many climate models generate meteorological projections for variables such as precipitation and air temperature. Hydrological models are needed to perform an express analysis of future changes in water resources and water extremes (floods and droughts) on a climate scale. The climate scale means that the express analysis is provided for a period of 20–30 years. Lumped or semi-distributed physically based hydrological models are traditionally used on a short-term or seasonal scale to simulate a runoff time series from a time series of meteorological variables (Seibert, 1999). In many catchment-scale hydrological studies, these models are driven by the outputs of climate models or their ensembles in order to evaluate water resources and extremes in the near future (Arheimer and Lindström, 2015; Veijalainen et al., 2012; Yip et al., 2012). The simulation of the runoff time series from a time series of meteorological variables (see Fig. 2 in Veijalainen et al., 2012) leads to high computational costs for such estimations that need to be provided in terms of probability in economical applications (Murphy, 1976). The probabilistic MARCSHYDRO model is computationally cheaper when compared to lumped or semi-distributed physically based hydrological models. It can easily be coupled with global and regional climate models, and it can provide the express analysis of water resources under a modern version of the future climate.
In this paper we described the structure for the probabilistic hydrological MARCSHYDRO model, together with the AFA method that lies behind the new model's core version 0.2. The AFA method has a more than 25-year-long history; however, most of the studies are published in Russian (Kovalenko, 1993, 2004, 2009; Kovalenko et al., 2010). The AFA method is based on the statistical theory of automatic systems (Pugachev et al., 1974), which is an outsider among the classical hydrological disciplines. The AFA method is one simplification of the Fokker–Planck–Kolmogorov equation approach that has been developed in the Russian State Hydrometeorological University. It has been tested in many case studies on river basins located in Russia, Colombia, Bolivia and Mali, etc. There are also a number of publications in English (Rosmann and Domínguez, 2017; Shevnina et al., 2017; Kovalenko, 2014; Domínguez and Rivera, 2010; Viktorova and Gromova, 2008). In this paper we formulated the theory logically in an attempt to provide the equations for the new core 0.2 of the MARCSHYDRO model; however, it also needs to describe the AFA method that lies behind it.
The probabilistic hydrological MARCSHYDRO model includes the core versions 0.1 and 0.2. In both cores, only three non-central moments are evaluated to construct the EPC within the theoretical distribution the Pearson III type, which is among the traditional distributions of the frequency and risk analysis in hydrology (Kite, 1977; Rogdestvenskiy and Chebotarev, 1974; Sokolovskiy, 1968; Elderton, 1969; Benson, 1968). The model simulates three estimates of non-central moments of runoff instead of a runoff time series, and this circumstance makes the computations by the MARCSHYDRO model low-cost compared to conceptual hydrological models (Arheimer and Lindström, 2015; Veijalainen et al., 2012). The MARCSHYDRO model allows the projections of runoff to be put in terms of probability; that is, they appear as runoff values together with their exceedance probability.
The MARCSHYDRO model includes six modules, and each module allows improvements by including new methods. In this paper, the new model – core version 0.2, extended to simulate the third statistical estimator (skewness) – is presented. The applicability of core version 0.2 is limited by the assumptions behind the AFA approach. Among others, there is the “quasi-stationarity” assumption for the expected climate change. In this case, the climate is described by the statistical estimators (i.e. mean value, variability, etc.) of precipitation, air temperature, evapotranspiration and river runoff, etc., for the period of 20–30 years. It is assumed to consider two time period periods with statistically different climates, namely the reference period and the projected period. Another limitation is connected to the linear filter stochastic model (for details, see Appendix 1) used in core version 0.2. It should be noted that there is a multiplicative component in the model core, and it may lead to unstable solutions of the Fokker–Planck–Kolmogorov equation. Kovalenko (2004) suggests two solutions that result in stable solutions of the Fokker–Planck–Kolmogorov equation. One of the solutions was given by Kovalenko et al. (2010) and is coded in the model core version 0.1 (Shevnina et al., 2017). However, a checking procedure needs to be applied before using this core version. In the checking procedure we plan to use the “beta criterion” method suggested by Kovalenko (2004) to further develop the MARCSHYDRO model.
Further improvements of the MARCSHYDRO model are going to be implemented in the block of parametrization and hindcasts. Recently, only the basic parametrization scheme (Kovalenko, 1993) has been included. This basic scheme gives over 70 %–80 % successful hindcasts (forecasts in the past) in the model cross-validation (Shevnina et al., 2017), and the implementation of a regionally oriented parametrization scheme (Shevnina, 2011) is the next step. It needs to include a mean value of the air temperature of the parameter, connected to “noised” watershed physiography in Eq. (A4), the inverse of the runoff coefficient in the work of Kovalenko (1993). It is also important to study the role of the spatial resolution of meteorological forcing in affecting the modelling uncertainties for the simulated mean values of the CV and CS of runoff.
To place the probabilistic MARCSHYDRO model among other hydrological models, its practical applications need to be better outlined. The model serves as a probabilistic form of long-term hydrological projections, and they require adaptation to the needs of water engineers and water managers as a tool for risk analysis under the expected climate change. The projected EPCs of multi-year river runoff can be applied in designing bridges, pipes and dams, etc., in order to minimize the future risks connected to extreme floods (Shevnina et al., 2017; Kovalenko et al., 2014; Kovalenko, 2009) and to water shortage due to droughts (Viktorova and Gromova, 2008). It is important to define informative forms for the outputs of the MARCSHYDRO model that can be adapted to the needs of practice, and the development of the block of economic application is among the others studies that are to be continued in close cooperation with water managers and decision makers.
The paper describes the theory and assumptions of the AFA approach, as well as the probabilistic hydrological MARCSHYDRO model's structure and core version 0.2. The features of the model are the close connection to water engineering due to providing the runoff projection in terms of probability, cheapness in terms of computational cost and a wide range of techniques allowing model improvement. In the new core, the third moment linked to the location parameter of the Pearson type III distribution (or asymmetry) was implemented for simulation. In the previous version of the model core, a constant CS∕CV ratio is used to calculate the location parameter of the distribution.
To give a practical example of how to set up the MARCSHYDRO model, the case of the Iijoki River at Raasakka located in Finland was considered. The model simulated the tailed values of 10 % and 90 % of annual water discharge from the outputs of global climate models. We showed two forms of the probabilistic projections of runoff: an EPC and the runoff values with their exceedance probability. This case study of the Iijoki River at Raasakka shows that the MARCSHYDRO model gives reasonable results for the meteorological projections considered. The practical applications in water management and decision-making should be clarified in further studies in close co-operation with water engineers.
Currently, the MARCSHYDRO model code is hosted at https://github.com/ElenaShe000/MARCS (last access: 2 July 2019; Shevnina, 2015), with details of its applications for catchment-scale case studies. The model source code for core version 0.2 is distributed under the Creative Commons Attribution 4.0 License and can be downloaded from https://zenodo.org/record/1220096/\#.XSLG1qLRaUl (last access: 4 May 2019; Shevnina and Krasikov, 2018) and used freely in scientific research with reference to this publication. We hope that this type of licence provides the best way to create a community of motivated people to further develop the model. Then, the source code will be distributed under the terms of a user agreement.
The following data sets can be used to set up and force the MARCSHYDRO model: the GRDC (GRDC, 56068 Koblenz, Germany), the NOAA/OAR/ESRL PSD (Boulder, Colorado, USA) and CMIP5 (Taylor et al., 2012).
The sample data set for the case study of the Iijoki River at Raasakka is given by Shevnina and Krasikov (2018).
A1 The assumptions behind advance of frequency analysis
Advance of frequency analysis (AFA) is based on the theory of stochastic systems, specifically, the Fokker–Planck–Kolmogorov equation, which is simplified into a system for three non-central statistical moments (Pugachev et al., 1974). The time series of annual runoff is considered as a realization of a random-process Markov chain type that is assumed to be “stationary”. It means that the statistical estimators (mean, variance and skewness) do not change over the period considered. The statistical estimators are used to model an exceedance probability curve (EPC) of the annual runoff with a Pearson type III distribution. The AFA approach is developed with an assumption of quasi-stationarity (Kovalenko et al., 2010; Kovalenko, 1993). The quasi-stationarity assumption suggests that the statistical estimators of multi-year runoff are different for two periods (the reference period and the projected period). For the reference period, the statistical estimators are evaluated from historical yearly time series of runoff. For the projected period, the statistical estimators of runoff are simulated based on the outputs of global- or regional-scale climate models under any climate scenario.
A2 The linear filter stochastic model
In this context, models replace a complicated hydrological system using maths abstractions and aim to reveal the spatial and temporal river runoff features which are important depending on the goals of study. Among other models, black box hydrological models consider a river basin as a dynamic system with lumped parameters. These models are “based on analysis of concurrent inputs and temporal output series” (WMO-No. 168, 2009) and transform series of meteorological variables (precipitation, air temperature) into series of river runoff. Both input and output series are functions of time (WMO-No. 168, 2009):
where Q is the runoff in volumetric flow rate, P is the precipitation in volumetric flow rate (rain, snowmelt), and the coefficients ai and bi are the empirical parameters of a translating system. These coefficients are the lumped parameters of the black box model. The solution to Eq. (A1) for zero initial conditions gives
where the function h(t,τ) represents the response of a river basin at time t to a single portion of precipitation P(τ) at time (τ). In the AFA approach, a river basin is considered as a linear system, transforming the annual precipitation into the annual runoff:
On the other hand, a river basin can be considered as a linear system with stochastic components in the input function and the model parameter (Kovalenko, 1993):
where is the stochastic parameter of the system (a noised watershed physiography, the inverse of runoff coefficient), is the stochastic input for the system (a noised precipitation) and a1=1. The stochastic components of and are the Gaussian “white noise” with zero means, and their intensities are and . The intensities are mutually correlated as . It should be noted that the multiplicative parameter in Eq. (A4) is the sum of the constant and Gaussian white noise , and it may lead to unstable solutions of the Fokker–Planck–Kolmogorov equation (i.e. it may lead to infinite statistical moments of high orders). It limits the application of the AFA method (Kovalenko, 1993). Kovalenko (2004) suggests two solutions, and we will introduce them in a further paper.
A3 The Fokker–Planck–Kolmogorov equation and simplifications
The Fokker–Planck–Kolmogorov equation can be applied to simulate the probability density function (PDF) for the stochastic Q(t) in Eq. (A4) (Kovalenko, 1993; Pugachev et al., 1974):
where p(Q,t) is the PDF of Q at time t; and the drift coefficient (A(Q)) and diffusion coefficients (B(Q)) are calculated as follows (Kovalenko, 1993; Pugachev, 1974):
The analytical solution of Eq. (A5) is difficult and not always needed for practical applications in water engineering since the PDFs of runoff are modelled from a set of statistical estimators, and the moments are from, among others, van Gelder et al. (2006). The PDFs are described with the set of moments (where k is the number of the moment, k→∞). To obtain the equations for mk, both sides of Eq. (A5) were multiplied by a differentiable function ψ(Y) and then integrated within limits from −∞ to +∞ by Q (however, it is supposed that Q>0):
Then, ψ(Q) was replaced with ψ(Q)=Qk, and Eq. (A8) was written as
For a stationary random process, , and the drift and diffusion coefficients are constant. Thus, Eq. (A9) was simplified as follows:
For k=1,
For k≥2,
Further, the summands in Eqs. (A10)–(A11) were divided by , and new notation was introduced as suggested in the work of Kovalenko (1993) and Pugachev et al. (1974):
Then, for k= 1, 2, 3, 4 the system of Eqs. (A10)–(A11) includes
The set of four moments (m1, m2, m3, m4) is sufficient to model distributions from the Pearson equation (Andreev et al., 2005; Elderton and Johnson, 1969). However, in water engineering we usually only use three-parameter probability distributions fitted to observations (Guidelines, 2004, 1984; Bulletin 17-B, 1982). In this case, is assumed; thus it leads to and , , . To model the PDFs (or EPCs) of annual river runoff within the Pearson type III distribution, the system of Eqs. (A12)–(A15) is simplified as follows:
Denoting , and , the parameters a, b0 and b1 are calculated as , where D is the determinant of matrix A, and Di is the determinant of the matrix obtained by replacing of the column i (1, 2, 3) in matrix A by the vector lk. Finally, the parameters a, b0 and b1 are calculated as follows:
A4 Notation
There is too much notation used to describe the model's core version 0.2; thus the secondary parameters of equations were grouped by the model behind it. Table A1 shows the notation and description of the secondary parameters for the linear filter stochastic model. Equation (A3) is a simplification of Eq. (A1) that limits the first-order ordinal differential equation. It includes three parameters, a0, a1 and b0, and two of them are assumed to be noised. These noised parameters include a constant component (indicated with a bar) and a Gaussian white noise component (indicated with a tilde) with their own intensities.
Table A2 gives a description of the parameters of the Fokker–Planck–Kolmogorov equation and the Pearson system. It should be noted that we do not solve the Fokker–Planck–Kolmogorov equation, and only its simplification for the system of three non-central moments is applied. These non-central moments are estimated from runoff observations for the reference period. For the projected period the moments are calculated from the mean of precipitation.
To set up the model for a single river catchment, the non-central moments should be calculated from historical time series of the annual river runoff rate as well as from a mean value of annual precipitation rate. These values should be placed manually (lines 45–48 in model_core.py, located at https://zenodo.org/record/1220096\#.WyTXxxxRVhw, last access: 4 May 2019) as should the ID number of the catchment (line 51 of model_core.py). To force the model, the projected mean value of the annual precipitation rate should be evaluated from an output of a climate model, and then the model_core.py can be run in the Unix command line: ./model_core.py XXX (where XXX is the mean of the annual precipitation rate for the projected period). The output of model_core.py is stored in the output file model_GPSCH.txt and included in line with the following format: the ID of the catchment, the first non-central moment estimate of the annual runoff rate (mm yr−1) for a reference period, the mean value of the annual precipitation rate (mm yr−1) for a reference period, the coefficient of variation for a reference period, the coefficient of skewness for a reference period, the model parameters , and , the first non-central moment estimate of annual runoff rate (mm yr−1) for a projected period, the mean value of the annual precipitation rate (mm yr−1) for a projected period, the coefficient of variation for a projected period and the coefficient of skewness for a projected period.
ES contributed to the MARCSHYDRO model coding and to the Russian–English translation of some parts from Kovalenko (1993), Kovalenko (2004) and Pugachev et al. (1974). She is responsible for writing the text. AS supported the theoretical part of the AFA method (Pugachev et al., 1974; Kovalenko, 1993) and formulated the equations step by step. Both authors took care of the terms used in the paper, which we tried to write in “a language in common” between water engineering and radiophysics.
The authors declare that they have no conflict of interest.
The authors would like to thank two anonymous referees, the editor and Anatoly Frolov for their comments. Our special thanks are given to Alexander Krasikov, who supported the model coding.
This research has been supported by the Academy of Finland (contract no. 283101).
This paper was edited by Wolfgang Kurtz and reviewed by two anonymous referees.
Andreev, A., Kanto, A., and Malo, P.: Simple approach for distribution selection in the Pearson system, Working papers of Helsingin kauppakorkeakoulu, Helsinki, Finland, 25 pp., 2005.
Arheimer, B. and Lindström, G.: Climate impact on floods: changes in high flows in Sweden in the past and the future (1911–2100), Hydrol. Earth Syst. Sci., 19, 771–784, https://doi.org/10.5194/hess-19-771-2015, 2015.
Benson, M. A.: Uniform flood frequency estimating methods for federal agencies, Water Resour. Res., 4, 891–908, https://doi.org/10.1029/WR004i005p00891, 1968.
Budyko, M. I. and Izrael, Y. A. (Eds): Anthropogenic Climatic Change, University of Arizona Press, Tucson, USA, 1991.
Bulletin 17–B: Guideline for Determining Flood Flow Frequency, U.S. Geological Survey, Virginia, USA, 1982.
Chylek, P., Li, J., Dubey, M. K., Wang, M., and Lesins, G.: Observed and model simulated 20th century Arctic temperature variability: Canadian Earth System Model CanESM2, Atmos. Chem. Phys. Discuss., 11, 22893–22907, https://doi.org/10.5194/acpd-11-22893-2011, 2011.
Collins, W. J., Bellouin, N., Doutriaux-Boucher, M., Gedney, N., Halloran, P., Hinton, T., Hughes, J., Jones, C. D., Joshi, M., Liddicoat, S., Martin, G., O'Connor, F., Rae, J., Senior, C., Sitch, S., Totterdell, I., Wiltshire, A., and Woodward, S.: Development and evaluation of an Earth-System model – HadGEM2, Geosci. Model Dev., 4, 1051–1075, https://doi.org/10.5194/gmd-4-1051-2011, 2011.
Dahmen, E. R. and Hall, M. J.: Screening of Hydrological Data: Tests for Stationarity and Relative Consistence, International Institute for Land Reclamation and Improvement, the Netherlands, 1990.
Dai, A., Qian, T., Trenberth, K. E., and Milliman, J. D.: Changes in continental freshwater discharge from 1948 to 2004, J. Climate, 22, 2773–2792, https://doi.org/10.1175/2008JCLI2592.1, 2009.
Domínguez, E. and Rivera, H.: A Fokker–Planck–Kolmogorov equation approach for the monthly affluence forecast of Betania hydropower reservoir, J. Hydroinform., 12, 486–501, https://doi.org/10.2166/hydro.2010.083, 2010.
Druzhinin, V. S. and Sikan A. V.: Methods of Statistical Processing of Hydrometeorological Information, Russian State Hydrometeorological University Press, St. Petersburg, 2001 (in Russian).
Elderton, S. W. P. and Johnson, N. L.: Systems of Frequency Curves, Cambridge University Press, London, 1969.
Giorgetta, M., Jungclaus, J., Reick, C., Legutke, S., Bader, J., Böttinger, M., Brovkin, V., Crueger, T., Esch, M., Fieg, K., Glushak, K., Gayler, V., Haak, H., Hollweg, H.-D., Ilyina, T., Kinne, S., Kornblueh, L., Matei, D., Mauritsen, T., Mikolajewicz, U., Mueller, W., Notz, D., Pithan, F., Raddatz, T., Rast, S., Redler, R., Roeckner, E., Schmidt, H., Schnur, R., Segschneider, J., Six, K., Stockhause, M., Timmreck, C., Wegner, J., Widmann, H., Wieners, K., Claussen, M., Marotzke, J., and Stevens, B.: Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5, J. Adv. Model Earth Syst., 5, 572–597, https://doi.org/10.1002/jame.20038, 2013.
Guidelines to Estimate Basic Hydrological Characteristics, Gidrometeoizdat, Leningrad, USSR, 1984 (in Russian).
Guidelines SP 33-101-2003: to Estimate Basic Hydrological Characteristics, Gosstroy, Moscow, Russia, 2004 (in Russian).
Kite, G. W.: Frequency and Risk Analysis in Hydrology, Fort Collins, Colorado, 1977.
Koutrouvelis, I. A. and Canavos, G. C.: Estimation in the Pearson type 3 distribution, Water Resour. Res., 35, 2693–2704, https://doi.org/10.1029/1999WR900174, 1999.
Kovalenko, V. V.: Modelling of Hydrological Processes, Gidrometeizdat, St. Petersburg, Russia, 1993 (in Russian).
Kovalenko, V. V.: Partial Infinite Modelling and Forecasting of the Process of River-Runoff Formation, St. Petersburg: RSHU Publishers, available at: http://elib.rshu.ru/files_books/pdf/img-417153826.pdf (last access: 2 July 2019), 2004.
Kovalenko, V. V.: Hydrological Security of Building Projects with Climate Change, Russian State Hydrometeorological University Press, St. Petersburg, Russia, 2009 (in Russian).
Kovalenko, V. V.: Using a probability model for steady long-term estimation of modal values of long-term river runoff characteristics, Russ. Meteorol. Hydrol., 39, 57–62, https://doi.org/10.3103/S1068373914010099, 2014.
Kovalenko, V. V., Victorova, N. V., and Gaydukova, E. V.: Modelling of Hydrological Processes, the Russian State Hydrometeorological University Press, St. Petersburg, Russia, 2006 (in Russian).
Kovalenko, V. V., Victorova, N. V., Gaydukova, E. V., Gromova, M. A., Khaustov, V. A., and Shevnina, E. V.: Guideline to Estimate a Multi-Year Runoff Regime Under Non-Steady Climate to Design Hydraulic Contractions, Russian State Hydrometeorological University Press, St. Petersburg, 2010 (in Russian).
Kritsky, S. N. and Menkel, M. F.: On the Methods of Studying the Random Variations of River Flow, Gidrometeoizdat, Leningrad, USSR, 1946 (in Russian).
Laio, F., Baldassarre, G. D., and Montanari, A.: Model selection techniques for the frequency analysis of hydrological extremes, Water Resour. Res., 45, W07416, https://doi.org/10.1029/2007WR006666, 2009.
Lamb, R.: Rainfall-runoff modeling for flood frequency estimation, in: Encyclopedia of Hydrological Sciences, edited by: Anderson, M. G. and McDonnell, J. J., 125, 11–125, https://doi.org/10.1002/0470848944.hsa133, 2006.
Madsen, H., Lawrence, D., Lang, M., Martinkova, M., and Kjeldsen, T. R.: A Review of Applied Methods in Europe for Flood-Frequency Analysis in a Changing Environment, NERC/Centre for Ecology & Hydrology on behalf of COST, available at: http://nora.nerc.ac.uk/501751/ (last access: 2 November 2017), 2013.
Manton, M. J., Della-Marta, P. M., Haylock, M. R., Hennessy, K. J., Nicholls, N., Chambers, L. E., Collins, D. A., Daw, G., Finet, A., Gunawan, D., Inape, K., Isobe, H., Kestin, T. S., Lefale, P., Leyu, C. H., Lwin, T., Maitrepierre, L., Ouprasitwong, N., Page, C. M., Pahalad, J., Plummer, N., Salinger, M. J., Suppiah, R., Tran, V. L., Trewin, B., Tibig, I., and Yee, D.: Trends in extreme daily rainfall and temperature in Southeast Asia and the South Pacific: 1961–1998, Int. J. Climatol., 21, 269–284, https://doi.org/10.1002/joc.610, 2001.
Matalas, N. C. and Wallis, J. R.: Eureka! It fits a Pearson type 3 distribution, Water Resour. Res., 9, 281–289, https://doi.org/10.1029/WR009i002p00281, 1973.
Milly, P. C. D., Dunne, K. A., and Vecchia, A. V.: Global pattern of trends in streamflow and water availability in a changing climate, Nature, 438, 347–350, https://doi.org/10.1038/nature04312, 2005.
Milly, P., Betancourt, J., Falkenmark, M., Hirsch, R. M., Kundzewicz, Z. W., Lettenmaier, D. P., and Stouffer, R. J.: Stationarity is dead: whither water management, Science, 319, 573–574, https://doi.org/10.1126/science.1151915, 2008.
Murphy, A. H.: Decision-making models in the cost-loss ratio situation and measures of the value of probability forecasts, Mon. Weather Rev., 104, 1058–1065, https://doi.org/10.1175/1520-0493(1976)104<1058:DMMITC>2.0.CO;2, 1976.
Murphy, A. H.: The value of climatological, categorical and probabilistic forecasts in the cost-loss situation, Mon. Weather Rev., 105, 803–816, https://doi.org/10.1175/1520-0493(1977)105<0803:TVOCCA>2.0.CO;2, 1977.
Mylne, K. R.: Decision-making from probability forecasts based on forecast value, Met. Apps., 9, 307–315, https://doi.org/10.1017/S1350482702003043, 2002.
Pearson, K.: Contributions to the mathematical theory of evolution, II: Skew variation in homogeneous material, Phil. Trans. Roy. Soc., 186, 343–414, https://doi.org/10.1098/rsta.1895.0010, 1895.
Pugachev, V. S., Kazakov, I. E., and Evlanov, L. G.: Basics of Statistical Theory of Automatic System, Mashinostroenie, Moscow, USSR, 1974 (in Russian).
Rogdestvenskiy, A. V. and Chebotarev, A. I.: Statistical methods in hydrology, Gidrometeizdat, Leningrad, USSR, 1974 (in Russian).
Rosmann, T. and Domínguez, E.: A Fokker–Planck–Kolmogorov equation-based inverse modelling approach for hydrological systems applied to extreme value analysis, J. Hydroinfo., 20, 1296–1309, https://doi.org/10.2166/hydro.2017.079, 2017.
Rosmann, T., Domínguez, E., and Chavarro, J.: Comparing trends in hydrometeorological average and extreme data sets around the world at different time scales, J. Hydrol.: Reg. Stud., 5, 200–212, https://doi.org/10.1016/j.ejrh.2015.12.061, 2016.
Seibert, J.: Conceptual runoff models – fiction or representation of reality?, comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology, 436, Sweden, 52 pp., 1999.
Shevnina, E.: Deterministic and stochastic models for seasonal forecasting of inflow to reservoirs of hydropower stations, PhD thesis, Russian State Hydrometeorological University, Russia, 188 pp., 2001 (in Russian).
Shevnina, E.: The regional parametrization of the probabilistic model to represent a spring runoff regime in the Russian Arctic, scientific notes of the Russian State Hydrometeorological University, 21, 38–46, 2011 (in Russian).
Shevnina, E.: Long-term assessment of the multi-year statistical characteristics of the maximal runoff under the climate change over the Russian Arctic, doctor of science thesis, Russian State Hydrometeorological University, Russia, 355 pp., 2015 (in Russian).
Shevnina, E. and Gaidukova E. V.: Hydrological probabilistic model MARCS and its application to simulate the probability density functions of multi-year maximal runoff: the Russian Arctic as a case of study, in: The Interconnected Arctic, Springer International Publishing, 77–87, https://doi.org/10.1007/978-3-319-57532-2_8, 2017.
Shevnina, E. and Krasikov A.: The probabilistic hydrological model MARCS (MARkov Chain System): the core code, Zenodo, https://doi.org/10.5281/zenodo.1220096, 2018.
Shevnina, E., Kourzeneva, E., Kovalenko, V., and Vihma, T.: Assessment of extreme flood events in a changing climate for a long-term planning of socio-economic infrastructure in the Russian Arctic, Hydrol. Earth Syst. Sci., 21, 2559–2578, https://doi.org/10.5194/hess-21-2559-2017, 2017.
Shevnina, E., Silaev, A., and Vihma, T.: Probabilistic Projections of Annual Runoff and Potential Hydropower Production in Finland, Univ. J. Geosci., 7.2, 43–55, 2019.
Smirnov, N.: Table for estimating the goodness of fit of empirical distributions, Ann. Math. Statist., 19, 279–281, https://doi.org/10.1214/aoms/1177730256, 1948.
Sokolovskiy D. L.: River Runoff (Based on a Theory and Methods of Calculations). Leningrad, Hydrometeoidat, 540 p., 1968 (in Russian).
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An overview of CMIP5 and the experiment design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2012.
van Gelder, P., Wang, W., and Vrijling, J. K.: Statistical estimation methods for extreme hydrological events, in: New Concepts for Security, NATO Science Series, 78, Springer, Dordrecht, 2006.
Veijalainen, N., Korhonen, J., Vehviläinen, B., and Koivusalo, H. L.: Modelling and statistical analysis of catchment water balance and discharge in Finland in 1951–2099 using transient climate scenarios, J. Water Clim. Change, 3, 55–78, 2012.
Vihma, T.: Effects of Arctic sea ice decline on weather and climate: a review, Surv. Geophys., 35, 1175–1214, https://doi.org/10.1007/s10712-014-9284-0, 2014.
Viktorova, N. V. and Gromova, M. N.: Long-term forecasting of characteristics of minimal river runoff discharges in Russia in case of possible climate change, Russ. Meteorol. Hydrol., 33, 388–393, 2008.
Volodin, E. M., Dianskii, N. A., and Gusev, A. V.: Simulating present-day climate with the INMCM4.0 coupled model of the atmospheric and oceanic general circulations, Izvestiya Atmos. Ocean. Phys., 46, 448–466, https://doi.org/10.1134/S000143381004002X, 2010.
Wagner, A., Lohmann, G., and Prange, M.: Results of modelled Arctic river discharge trends since 7 ka BP, Global Planet Change, 79, 48–60, https://doi.org/10.1016/j.gloplacha.2011.07.006, 2011.
Wang, Y. and Zhou, L.: Observed trends in extreme precipitation events in China during 1961–2001 and the associated changes in large-scale circulation, Geophys. Res. Lett., 32, L09707, https://doi.org/10.1029/2005GL022574, 2005.
Willmott, C. J. and Robeson S. M.: Climatologically aided interpolation (CAI) of terrestrial air temperature, Int. J. Climatol., 15, 221–229, 1995.
WMO-No. 168: Guide to Hydrological Practices. Vol. II: Management of Water Resources and Application of Hydrological Practices, World Meteorological Organization (WMO), Geneva, Switzerland, 302 pp., 2009.
Yip, Q. K. Y., Burn, D. H., Seglenieks, F., Pietroniro, A., and Soulis, E. D.: Climate impacts on hydrological variables in the Mackenzie River basin, Can. Water Resou. J., 37, 209–230, 2012.
- Abstract
- Introduction
- Model description
- Model application: a case study
- Discussions
- Conclusions
- Code availability
- Data availability
- Sample availability
- Appendix A: The theoretical basis for core version 0.2
- Appendix B: A short user guide for the MARCS model
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Model description
- Model application: a case study
- Discussions
- Conclusions
- Code availability
- Data availability
- Sample availability
- Appendix A: The theoretical basis for core version 0.2
- Appendix B: A short user guide for the MARCS model
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References