the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A Lagrangian approach towards extracting signals of urban CO2 emissions from satellite observations of atmospheric column CO2 (XCO2): X-Stochastic Time-Inverted Lagrangian Transport model (“X-STILT v1”)
John C. Lin
Benjamin Fasoli
Tomohiro Oda
Xinxin Ye
Thomas Lauvaux
Emily G. Yang
Eric A. Kort
Urban regions are responsible for emitting significant amounts of fossil fuel carbon dioxide (FFCO2), and emissions at the finer, city scales are more uncertain than those aggregated at the global scale. Carbon-observing satellites may provide independent top-down emission evaluations and compensate for the sparseness of surface CO2 observing networks in urban areas. Although some previous studies have attempted to derive urban CO2 signals from satellite column-averaged CO2 data (XCO2) using simple statistical measures, less work has been carried out to link upwind emission sources to downwind atmospheric columns using atmospheric models. In addition to Eulerian atmospheric models that have been customized for emission estimates over specific cities, the Lagrangian modeling approach – in particular, the Lagrangian particle dispersion model (LPDM) approach – has the potential to efficiently determine the sensitivity of downwind concentration changes to upwind sources. However, when applying LPDMs to interpret satellite XCO2, several issues have yet to be addressed, including quantifying uncertainties in urban XCO2 signals due to receptor configurations and errors in atmospheric transport and background XCO2.
In this study, we present a modified version of the Stochastic Time-Inverted Lagrangian Transport (STILT) model, “X-STILT”, for extracting urban XCO2 signals from NASA's Orbiting Carbon Observatory 2 (OCO-2) XCO2 data. X-STILT incorporates satellite profiles and provides comprehensive uncertainty estimates of urban XCO2 enhancements on a per sounding basis. Several methods to initialize receptor/particle setups and determine background XCO2 are presented and discussed via sensitivity analyses and comparisons. To illustrate X-STILT's utilities and applications, we examined five OCO-2 overpasses over Riyadh, Saudi Arabia, during a 2-year time period and performed a simple scaling factor-based inverse analysis. As a result, the model is able to reproduce most observed XCO2 enhancements. Error estimates show that the 68 % confidence limit of XCO2 uncertainties due to transport (horizontal wind plus vertical mixing) and emission uncertainties contribute to ∼33 % and ∼20 % of the mean latitudinally integrated urban signals, respectively, over the five overpasses, using meteorological fields from the Global Data Assimilation System (GDAS). In addition, a sizeable mean difference of −0.55 ppm in background derived from a previous study employing simple statistics (regional daily median) leads to a ∼39 % higher mean observed urban signal and a larger posterior scaling factor. Based on our signal estimates and associated error impacts, we foresee X-STILT serving as a tool for interpreting column measurements, estimating urban enhancement signals, and carrying out inverse modeling to improve quantification of urban emissions.
- Article
(8120 KB) - Full-text XML
-
Supplement
(5571 KB) - BibTeX
- EndNote
Carbon dioxide (CO2) is a major atmospheric greenhouse gas in terms of radiative forcing, with its concentration having increased significantly over the past century (Dlugokencky and Tans, 2015). The largest contemporary net source of CO2 to the atmosphere over decadal timescales is anthropogenic emissions, namely fossil fuel burning and net land-use change (Ciais et al., 2013). Urban areas play significant roles in the global carbon cycle and are responsible for over 70 % of the global energy-related CO2 emissions (Rosenzweig et al., 2010). Global fossil fuel CO2 (FFCO2) emission uncertainty (8.4 %, 2σ, Andres et al., 2014) may be smaller than other less-constrained emissions such as emissions from wildfire (Brasseur and Jacob, 2017). Still, uncertainties associated with national FFCO2 emissions derived from bottom-up inventories typically range from 5 % to 20 % per year (Andres et al., 2014). These estimated emission uncertainties primarily result from differences in emission inventories, such as the emission factors and energy consumptions data used. Moreover, heightened interests in regional- and urban-scale emissions require modelers to investigate FFCO2 emissions at finer spatiotemporal resolutions (Lauvaux et al., 2016; Mitchell et al., 2018) as well as uncertainties in gridded emissions (Andres et al., 2016; Gately and Hutyra, 2017; Hogue et al., 2016; Oda et al., 2018). Dramatic increases in emission uncertainties are associated with finer scales, with these uncertainties being biases due to different methods disaggregating national-level emissions (Marland, 2008; Oda and Maksyutov, 2011). For instance, emission uncertainties of 20 % at regional scales increased to 50 %–250 % at city scales even for the northeastern United States (Gately and Hutyra, 2017), an area that is considered relatively “data-rich”.
Given the large differences/discrepancies in emission inventories at urban scales, the use of atmospheric top-down constraints could be helpful for quantifying urban emissions and possibly providing monitoring support (Pacala et al., 2010). Observed concentrations used in the top-down approach can often be obtained from ground-based instruments (Kim et al., 2013; Mallia et al., 2015; Wunch et al., 2011) and aircraft observations (Gerbig et al., 2003; Lin et al., 2006). Each type of measurement offers valuable information and has both advantages and disadvantages. Most ground-based measurements provide reliable, continuous CO2 concentrations from fixed locations/heights. Unfortunately, current ground-based observing sites are too sparse to constrain urban emissions around the globe. Most sites as part of the National Oceanic and Atmospheric Administration (NOAA) network are designed to measure background concentrations relatively unaffected by urban emissions. Other than a few notable examples (Feng et al., 2016; Lauvaux et al., 2016; Mitchell et al., 2018; Verhulst et al., 2017; Wong et al., 2015; Wunch et al., 2009), near-surface CO2 measurements may not be available over many cities around the world. Alternatively, airborne measurements from field campaigns provide vertical and regional coverage (Cambaliza et al., 2014); however, continuous airborne operations over months to years are often impractical due to limited resources, which restricts researchers' capability to track the temporal variability of anthropogenic carbon emissions (Sweeney et al., 2015).
The carbon cycle community has entered a new era with advanced carbon-observing satellites routinely in orbit to measure variations in the atmospheric column-averaged CO2 mole fraction (XCO2), such as the Greenhouse gases Observing SATellite (GOSAT; Yokota et al., 2009), TanSat (Liu et al., 2013), and the Orbiting Carbon Observatory (OCO-2) satellite (Crisp et al., 2012). Although most carbon-observing satellites have revisit times of multiple days (e.g., 3 days for GOSAT and 16 days for OCO-2), their global coverage, large number of retrievals, and multi-year observations may further complement the current surface observing networks. Space-borne CO2 measurements, in combination with surface CO2 networks, may help reduce emission uncertainties and benefit urban emissions analysis, especially over regions with no surface observations (Duren and Miller, 2012; Houweling et al., 2004; Rayner and O'Brien, 2001).
Previous studies have demonstrated the potential for detecting and deriving urban CO2 emission signals from satellite CO2 observations, in the form of XCO2 enhancements above the background, without making use of much atmospheric transport information (Hakkarainen et al., 2016; Kort et al., 2012; Schneising et al., 2013; Silva and Arellano, 2017; Silva et al., 2013). However, due to this simplification, the linkage between derived urban CO2 emission signals and upstream sources is tenuous, as downwind XCO2 can be enhanced not only by near-field upwind urban activities (e.g., traffic, houses, and power plants/industries), but also by regional-scale advection of upwind sources/sinks. Simulations using transport models are able to isolate the portion of satellite observations influenced by urban regions from the portion affected by natural fluxes or long-range transport (e.g., Ye et al., 2017). Therefore, accurate knowledge of atmospheric transport is essential in top-down assessment. As importantly, transport modeling is a necessary step within inverse modeling, which can help improve fossil fuel emission estimates and shed light on CO2 emission monitoring networks (Kort et al., 2013; Lauvaux et al., 2009). Uncertainties in transport modeling have been identified as a significant error source that affects inferred surface fluxes (Peylin et al., 2011; Stephens et al., 2007; Ye et al., 2017). However, by analyzing an increased number of satellite overpasses, uncertainties from atmospheric inversions due to non-systematic transport errors in emission estimates can be reduced (Ye et al., 2017).
Two main approaches can be considered for atmospheric transport modeling. Eulerian models, in which fixed grid cells are adopted and CO2 concentrations within the grid cells are calculated by forward numerical integrations, have been widely utilized and customized to understand urban emissions and quantify model uncertainties over specific metropolitan regions worldwide (Deng et al., 2017; Lauvaux et al., 2013; Palmer, 2008; Ye et al., 2017). The Lagrangian approach, especially the time-reversed approach in which atmospheric transport is represented by air parcels moving backward in time from the measurement location (“receptor”), is efficient in locating upwind sources and facilitating the construction and calculation of the “footprint” (e.g., Lin et al., 2003) or “source–receptor matrix” (Seibert and Frank, 2004) – i.e., the sensitivity of downwind CO2 variations to upwind fluxes.
In particular, the receptor-oriented Stochastic Time-Inverted Lagrangian Transport (STILT) model, a Lagrangian particle dispersion model (LPDM), has the ability to more realistically resolve the sub-grid scale transport and near-field influences (Lin et al., 2003). STILT has been used to interpret CO2 observations within the planetary boundary layer (PBL) (Gerbig et al., 2006; Kim et al., 2013; Lin et al., 2017) and, in recent years, to analyze column observations, i.e., XCO2 (Fischer et al., 2017; Heymann et al., 2017; Macatangay et al., 2008; Reuter et al., 2014). Among STILT-based XCO2 studies, most aim at either natural CO2 sources and sinks like wildfire emissions and biospheric fluxes, or anthropogenic emissions at regional or state scales. Very few studies have focused on city-scale FFCO2 using column data and LPDMs. Moreover, when applying LPDMs to interpret column CO2 data, three key issues have yet to be carefully examined and will be addressed in this paper:
-
Uncertainty of modeled XCO2 enhancements due to model configurations. Very few studies have examined model uncertainties resulting from model configurations, i.e., receptors and particles in LPDMs. A negligible amount to ∼20 % of the modeled enhancements are reported as the error impact due to the STILT particle number (released from a fixed level), depending on adopted particle numbers, examined species, and their components/sources (Zhao et al., 2009; Gerbig et al., 2003; Mallia et al., 2015). When it comes to representing an atmospheric column using particle ensembles, many studies describe their setups for receptors/particles without detailed explanations of why the setups were chosen or the error impact on modeling XCO2 due to model configurations. Although this error impact may be small, we still perform a set of sensitivity tests to provide more guidance regarding placing column receptors.
-
Horizontal and vertical transport error impact on XCO2 simulations. Flux inversions, e.g., Bayesian inversion (Rodgers, 2000) involving LPDMs have been widely adopted to constrain emissions. Approaches to quantify errors in horizontal wind fields and vertical mixing have been proposed followed by comprehensive error characterizations on atmospheric simulations (Gerbig et al., 2008; Jeong et al., 2013; Lauvaux et al., 2016; Lin and Gerbig, 2005; Zhao et al., 2009). Recent efforts (e.g., Lauvaux and Davis, 2014; Ye et al., 2017) have been made to rigorously examine the column transport errors. The uncertainties in horizontal wind fields and vertical mixing within X-STILT will be propagated into column CO2 space in this study.
-
Determining background XCO2 and characterizing its uncertainties. We define the background value as the CO2 “uncontaminated” by fossil fuel emissions from the city of interest. As urban emission signals are defined as the enhancements of XCO2 over the background, errors in the background value introduce first-order errors into the derived urban XCO2 signal from total XCO2, with such errors propagating directly into fluxes calculated from atmospheric inversions (e.g., Göckede et al., 2010). Consequently, background determination is another critical task.
One commonly used method to determine model boundary conditions of various species in LPDMs is the “trajectory-endpoint” method that establishes the background based on CO2 extracted at endpoints of back trajectories from modeled regional/global concentration fields (Lin et al., 2017; Macatangay et al., 2008; Mallia et al., 2015). The aforementioned studies (adopting the trajectory-endpoint method) aim at extracting relatively large CO2 anomalies (e.g., at a fixed level within the PBL or due to large emissions such as of wildfire) from the total measured CO2. However, for studying XCO2 that is less variable than near-surface CO2 (Olsen and Randerson, 2004), potential errors in modeled concentration fields and atmospheric transport may pose a more significant adverse impact on derived urban signals. Other ways of defining the background include geographic definitions (Kort et al., 2012; Schneising et al., 2013) and simple statistical estimates (Hakkarainen et al., 2016; Silva and Arellano, 2017). These simple statistical methods often neglect atmospheric transport and may use a less accurate upwind region to select measurements for deriving background values. Lastly, but more importantly, recent column studies (Nassar et al., 2017; Fischer et al., 2017) have examined the impact of potential errors/biases in the background values on their emission or fluxes estimates. In this work, we introduce a new background determination that combines OCO-2 observations and the STILT-based atmospheric transport, and we account for errors in our background estimates.
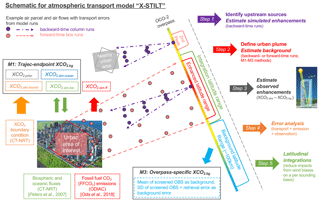
Figure 1A schematic of X-STILT in five steps (represented by the arrows on the right of the figure). Pink and purple dots and arrows represent the air parcels and overall air flows based on forward-time box runs and backward-time column runs with the wind error component accounted for. The “rainbow band” (running diagonally through the figure) is an example of one OCO-2 overpass with warmer colors indicating higher observed XCO2 values. M1 includes modeled-derived biospheric, oceanic XCO2 changes, CO2 boundary conditions, and the prior CO2 portion from OCO-2. M3 requires an enhanced latitude range based on either backward-time XCO2 enhancements or the forward-time urban plume.
In general, we attempt to address the aforementioned issues by extending STILT with column features and comprehensive error analyses, referred to as the column-enabled STILT, “X-STILT”. We illustrate the model's application regarding extracting urban XCO2 signals from OCO-2 retrievals (Fig. 1) and evaluate model performance via a case study focused on Riyadh, Saudi Arabia. Riyadh, which had a population of over 6 million people in 2014 (WUP, 2014), is chosen as the city of interest because of its low cloud interference, limited vegetation coverage, and isolated, barren location; these factors lead to higher data recovery rates and facilitate the background determination. Saudi Arabia has the highest CO2 emissions among Middle Eastern countries and ranked eighth globally in 2016 (Boden et al., 2017; BP, 2017; UNFCCC, 2017). We examine several satellite overpasses and focus on a small spatial domain adjacent to Riyadh for each overpass.
Before demonstrating the model details, Fig. 1 highlights several X-STILT characteristics, e.g., column transport error quantifications, background XCO2 approximations, and the identification of upwind emitters using backward-time runs from column receptors. Our goal is to evaluate the model by comparing both the latitude-dependent model–data XCO2 urban enhancements (Sect. 3.4) and the overall latitude-integrated urban signals within a small latitudinal range (Sect. 3.5). We selected and examined five OCO-2 overpasses during the time period from September 2014 to December 2016, based on four stringent criteria (Appendix A).
2.1 STILT-based approach for XCO2 simulation (“X-STILT”)
The OCO-2 column averaging kernel is the product of normalized averaging kernel (AKnorm) and the pressure weighing (PW) function and represents the sensitivity of the change in retrieved XCO2 due to the CO2 anomaly at each retrieved grid. Column AKnorm peaks near the surface and exhibits values near unity throughout most of the troposphere (Boesch et al., 2011). Lower AKnorm values are mainly found aloft, which means that more information is required in the a priori CO2 profiles (CO2,prior; Fig. 2a). For direct comparisons against OCO-2 retrieved XCO2, CO2 anomalies at model grids should be properly weighted using the satellite's column averaging kernels (Basu et al., 2013; Lin et al., 2004). Thus, the final AK-weighted simulated XCO2 () are weighted between model-derived CO2 profiles and OCO-2 a priori profiles (O'Dell et al., 2012):
In the abovementioned equation, n stands for the combined vertical levels of STILT plus OCO-2. Specifically, we replaced OCO-2 levels with denser model release levels for the lower part of the troposphere (red circles from the surface in Fig. 2), while we kept OCO-2 levels for upper part of the troposphere (blue circles in Fig. 2). To reduce computational cost, the air column is only simulated up to the maximum release height (MAXAGL, in meters above ground level – m a.g.l.; Fig. 2).
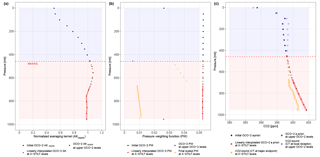
Figure 2Demonstrations of interpolations on the (a) normalized averaging kernel (AKnorm) profile, (b) pressure weighing (PW) function, and (c) the CO2 boundary conditions (derived from CarbonTracker – CT-NRT) and OCO-2 a priori profile, given one sounding (with the same lat/long coordinates as column receptors). The red and blue shading denotes the X-STILT release levels from the surface up to MAXAGL and upper OCO-2 levels, respectively.
Interpolations are further needed to resolve the mismatch between prescribed OCO-2 retrieval grids and model levels for the lower part of the troposphere. Our intention is to preserve the finer modeled CO2 variations by performing interpolations of satellite profiles from retrieval grids to model levels. Vertical profiles of AKnorm, PW and CO2,prior are treated as continuous functions and interpolated linearly to model grids (red circles in Fig. 2). Note that the initial OCO-2 PW functions have a steady value of ∼0.052 (except for the very bottom and top levels; black dots in Fig. 2b), which results from constant pressure spacings (dp_oco2) between two adjacent OCO-2 levels. However, X-STILT levels are much denser with smaller pressure spacings (dp_stilt) or less air mass between their two adjacent levels. Therefore, the linearly interpolated PW (red circles in Fig. 2b) needs additional scaling via a set of “scaling factors” representing the ratios of pressure spacings in STILT versus OCO-2 retrieval (dp_stilt/dp_oco2), to arrive at the correct PW for each finer model grid (orange circles in Fig. 2b).
Equation (1) can further be rewritten as Eq. (2), as the simulated CO2 profile in Eq. (1) is comprised of a CO2 boundary condition plus CO2 anomalies due to sources/sinks (FFCO2, biospheric, and oceanic fluxes):
Given our focus, we defined the background value as the XCO2 portion not “contaminated” by urban emissions. Thus, is the sum of the XCO2 enhancement due to FFCO2 () and the estimated background value (XCO2.bg). Estimates of XCO2 anomalies are further explained in Sect. 2.1.2, and four ways to estimate background values (XCO2.bg) are proposed in Sect. 2.3.
2.1.1 X-STILT setup (“column receptors”)
The linkage between the observed XCO2 concentration from a given OCO-2 sounding and upwind CO2 sources and sinks is determined by atmospheric transport. We adopt the STILT model to describe this connection. Fictitious particles, representing air parcels, are released from a “receptor” (location of interest) and are dispersed backward in time. The Lagrangian air parcels within STILT are transported along with the mean wind (), turbulent wind component (u′), and other meteorological variables, which are derived from Eulerian meteorological fields. In this study, we used meteorological fields simulated by the Weather Research and Forecasting (WRF; Skamarock and Klemp, 2008) model and the Global Data Assimilation System (GDAS; Rolph et al., 2017; Stein et al., 2015). Hourly WRF fields contain 51 vertical levels with boundary conditions from 6 h NCEP FNL (final) operational global analysis data (Ye et al., 2017) and are customized and utilized for the first two of the five total overpasses over Riyadh. We note that the primary focus is on assessing the resulting errors given the choice of a particular wind field (i.e., GDAS 0.5∘), rather than on carrying out detailed analyses of differences between WRF and GDAS.
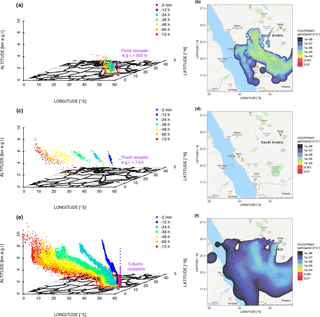
Figure 3A 3-D scatterplot of STILT ensembles that are initially released from a fixed receptor of 500 m(a), 3 km(c), and column receptors(e) for Riyadh at 10:00 UTC on 29 December 2014. The different colors represent the number of minutes/hours backwards (−2 min, −12, −24, −36, −48, −60, and −72 h) for each trajectory. Column receptors (e) are placed every 100 m within 3 km and every 500 m from 3 to 6 km. (b, d, f) Modeled fixed footprints versus column footprints are plotted using a blue to red gradient. Column footprints are weighted by pressure weighing functions. Only footprint values > 1E-8 ppm ∕ (µmol m−2 s−1) are displayed.
To represent the air arriving at the atmospheric column of each OCO-2 sounding, we release air parcels from multiple vertical levels, “column receptors” (Fig. 3e), using the same lat/long coordinates as the satellite sounding at the same time and allow those parcels to disperse backward for 72 h (see Appendix D2 for model impact from backward durations). About 10–20 satellite soundings are selected for simulations over every 0.5∘ latitude with data filtering using the criteria explained in Sect. 2.2. Sensitivity tests are conducted regarding different configurations – the maximum release level (MAXAGL), the vertical spacing of release levels (dh), and the particle number per level (dpar) – when placing column receptors (Sect. 2.5).
2.1.2 Modeling XCO2 anomalies
Air parcels traveling back in time provide valuable information about how upwind sources and sinks impact the air arriving at a receptor. However, since particles within the ensemble are subject to stochastic motion, the surface fluxes observed by any single particle caries limited information. The influence of upstream surface fluxes on a receptor is given by summing the sensitivities of all particles in the ensemble over a surface grid , which is referred to as the “footprint” (Lin et al., 2003; Fasoli et al., 2018) or the “source–receptor matrix” (Seibert and Frank, 2004). Formally, the sensitivity of the receptor located at xr at time tr to surface fluxes originating from xi,yj is given by summing , the time spent by particle p over grid position ij within the surface layer of height h for each discrete time step m:
where Ntot is the total number of particles in the ensemble, mair is the molar mass of dry air, and is the average air density below h. The dilution of surface fluxes to half of the PBL height h=0.5zpbl is often used. In general, f increases if particles travel at heights z≤h and if h is low, concentrating surface fluxes within a shallower atmospheric column.
To reduce grid noise caused by the aggregation of a finite number of dispersed particles, a kernel density estimator is used to variably smooth f as a function of elapsed time and particle location uncertainty. The reader is referred to Fasoli et al. (2018) for additional details pertaining to the formulation of f.
We introduce the weighted column footprint fw that describes the sensitivity of changes in column concentration due to potential upstream sources/sinks and incorporates satellite profiles. The formulation of fw is similar to Eq. (3) but scales the sensitivity with AKnorm(n,r) and PW(n,r):
where denotes a column receptor. Multiplying fw by gridded flux estimates yields a change in CO2 at the downwind column receptor. Thus, surface fluxes cause a change in column integrated mole fraction ΔXCO2 as follows:
For this study, modeled XCO2 enhancements due to FFCO2 emissions are derived from the convolution of spatially varying fw and ODIAC emissions (Sect. 2.4.1). Also, we account for modeled uncertainties that include errors in prior FFCO2 emissions (Sect. 2.4.1), receptor configurations (Sect. 2.5), and atmospheric transport (Sect. 2.6).
2.2 OCO-2 retrieved XCO2 and data preprocessing
The OCO-2 algorithm for retrieving XCO2 from radiances employs an optimal estimation approach (Rodgers, 2000) involving a forward model, an inverse model, and prior information regarding the vertical CO2 profiles (O'Dell et al., 2012). We used the bias-corrected XCO2 values from OCO-2 lite files (version 7R; OCO-2 Science Team/Michael Gunson, Annmarie Eldering, 2015). The impacts of different versions of the OCO-2 datasets on our results are briefly discussed in Sect. 5. Satellite measurements over Riyadh were carried out in “land nadir” and “glint” modes. Soundings with quality flags equal zero (QF = 0) were selected; this implied that the selected observations had passed the cloud and aerosol screening (with removal of albedo >0.4) and that their retrievals had converged (Mandrake et al., 2013; Patra et al., 2017). For smoothing noisy observations, we binned the screened XCO2 data according to the lat/long coordinates of model receptors (that served as the midpoints of each bin) and calculated the mean and standard deviation of screened measurements within each bin. Next, background values were defined (Sect. 2.3) and subtracted from the bin-averaged observed XCO2 to estimate the increase in observed XCO2 (step 3 in Fig. 1). The impacts of different bin-widths on the bin-averaged observed signals are shown in Appendix E1. Total observed errors contain the spatial and natural variation of observed XCO2 in each bin, the background uncertainties (Sect. 2.3.3), and the retrieval errors provided by lite files. Retrieval error variances per sounding are then averaged within each observed bin to obtain the bin-averaged retrieval error variances.
2.3 Estimates of background XCO2
Definitions of “background” vary among studies with different applications. Here, we define the background values as atmospheric XCO2 that is not “contaminated” by the urban emissions around our study site. The determination of background XCO2 is crucial, as it can significantly affect the magnitude of inferred observed anthropogenic signals. If the background is underestimated, then the detected signal may be overestimated, and vice versa. In this study, we seek to develop the best-estimated background values given five tracks, where three methods are proposed and investigated as follows:
-
M1. a “trajectory-endpoint” method is investigated by assigning CO2 values extracted from global models to trajectory endpoints including simulating biospheric, oceanic, and prior components (Sect. 2.3.1);
-
M2. statistical methods estimate the background values solely from XCO2 observations based on two previous studies (Sect. 2.3.2);
-
M3. an “overpass-specific” background that requires a model-defined urban plume and measurements outside the plume is examined (Sect. 2.3.3).
We compare the aforementioned three methods (Sect. 3.3) and investigate the background impact on model–data comparisons and emission estimates (Sect. 4.2). We choose the M3-based background for the following analysis as it is specifically designed for examining a particular city and specific overpasses downwind of the city.
2.3.1 Trajectory-endpoint method (M1)
Modeled background XCO2 comprises a simulated boundary condition confined by 4-D CO2 fields from a global model (CT-NRT; see Sect. 2.4.2) and contributions from biospheric fluxes, oceanic fluxes, and OCO-2 prior profiles (M1 in Fig. 1 and Eq. 2). Specific for modeling CO2 boundary conditions, CO2 values for upper levels, above MAXAGL, are estimated based on CT CO2 at those OCO-2 pressure levels (purple circles in Fig. 2c). Averaged CO2 values from the global model extracted at trajectory endpoints are used for boundary conditions at model release levels (orange circles in Fig. 2c). Then, modeled boundary conditions at vertical levels are weighted accordingly via OCO-2's column averaging kernel (red and blue circles in Fig. 2c). Model trajectories are properly subsetted according to the boundary of the footprint domain (i.e., ) used for simulating the XCO2 anomalies.
We note that for the trajectory-endpoint method, potential uncertainties in transport may strongly influence the distribution of Lagrangian parcels as backward duration time increases and may lead to potential spatial mismatch of the background region. Furthermore, potential biases and the relatively coarse resolution of the adopted global product may add inaccuracies to CO2 values at trajectory-endpoints.
2.3.2 Statistical method (M2)
Hakkarainen et al. (2016) (referred to as M2H) extracted local XCO2 anomalies from the daily median of screened, measured XCO2 within a relatively broad region (0–60∘ N, 15∘ W–60∘ E over the Middle East; Fig. S7 in the Supplement). Their detected anomalies vary from 1 to 2 ppm over grid cells near Riyadh. Silva and Arellano (2017) (referred to as M2S) used measurements within a combustion region centered around “urban and dense settlements” inferred from the anthropogenic biomes dataset (“anthromes”; Ellis and Ramankutty, 2008). Then, they derived the background as the mean minus 1 standard deviation of the available observations within their studied urban extents.
While both statistical methods are highly efficient in estimating background values, they can be limited to certain applications. For instance, M2H may be not suitable for determining background values when zooming into specific cities. Measurements within their broad spatial domain are lumped together, regardless of their locations (whether over rural or urban areas) and atmospheric transport. Silva and Arellano (2017) have also pointed out that their defined combustion region is suitable for studying the “bulk” characteristics and may be too coarse for studying urban emissions. Furthermore, the Gaussian statistics assumed in M2S may be less applicable when multiple observed peaks are merged due to close proximity between clusters of multiple cities. Therefore, without incorporating much atmospheric transport information, it may be difficult for either statistical method to locate the exact XCO2 peak elevated by target city or background region. These difficulties motivate us to introduce a new approach in the next subsection.
2.3.3 Overpass-specific background (M3)
A few space-based studies have defined the background values as the averaged observed XCO2 values over a “clean” upwind region. For instance, Kort et al. (2012) and Schneising et al. (2013) defined the “clean” region based on geographic information (e.g., rural area to the north of the Los Angeles basin). Although OCO-2 has relatively narrow swaths, transport models can be used to differentiate the enhanced versus background portions along an overpass. For example, Janardanan et al. (2016) calculated background XCO2 as the averaged GOSAT observations among grid cells with modeled anthropogenic signals <0.1 ppm. This 0.1 ppm threshold is determined from the average simulated fossil fuel abundance over desert areas worldwide using the FLEXible PARTicle dispersion model (FLEXPART; Stohl et al., 2005), a model similar to STILT in that both are time-reversed LPDMs. Nassar et al. (2017) derived the overpass-dependent background and its uncertainty based on the averaged OCO-2 observations within four different tested background latitudinal ranges.
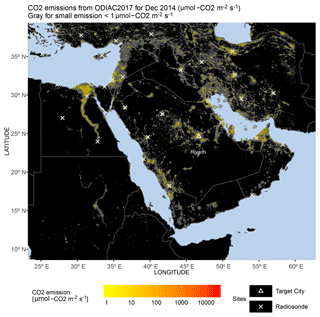
Figure 4Monthly ODIAC emissions (yellow to orange) in log-scale at 1 km×1 km grid spacing for December 2014. White crosses and the triangle denote the radiosonde networks used to provide the wind error statistics and our study site of Riyadh, respectively. Small emissions (<1 µmol m−2 s−1) are shaded in gray.
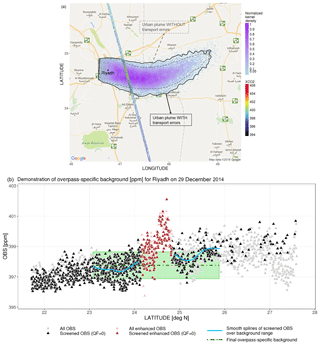
Figure 5Demonstration of the overpass-specific background using the 29 December 2014 overpass for Riyadh as an example. (a) Forward particle distributions with random transport error included (blue and purple dots) and their derived normalized kernel density (solid purple contours) during the OCO-2 overpass time (∼3 mins) with observed XCO2 (blue to red dots). Urban plumes are defined based on 5 % of the max 2-D kernel density estimated from parcels' distributions without (gray dashed line) and with (black solid line) transport errors. (b) Latitude-series of observed XCO2 with the demonstration of background estimates. Smooth splines (solid blue lines) are drawn to visually reveal the variation of observed XCO2 over the background latitudinal band. The background uncertainty (green shaded area) includes both the spatial uncertainty and the retrieval uncertainty of observations over the background latitude range.
We present an alternative method using a forward-time run from an urban box to reveal the urban influence on satellite soundings, which are more straightforward and efficient than relying solely on backward-time runs. Fictitious particles are released from a box around the city center (pink dots in Fig. 1) as a feature implemented with STILT (Thomas Nehrkorn, personal communication, 2017) to track air parcels over a city and the transport of the urban plume. Specifically, the model continuously releases air parcels over a 30 min window from a box around the city center, with multiple 30 min releases of 1000-particle ensembles over the 10 h before the satellite overpass hour (00:00–10:00 UTC). An urban plume can then be derived from the parcels' distribution during the ∼3 min OCO-2 passing window (purple dots in Fig. 5a). Note that air parcels are tracked forward in time for 12 h, allowing for equal contributions from parcels that were initially released from different time intervals (every 30 min) into the defined urban plume. We are aware of potential model errors and their adverse impacts on the defined urban plume. Therefore, a wind error component (Sect. 2.6) is also added in the forward run to broaden the polluted range (solid black line in Fig. 5a). Next, 2-D kernel density estimation (Venables and Ripley, 2002) is applied to determine the boundary of the city plume based on the air parcels' distributions. We normalized the 2-D kernel density by its maximum value and sketched the boundary of the city plume based on a threshold kernel density value of 0.05, which is sufficient to include most air parcels. No dramatic change in the shape/size of the resultant urban plume was found when testing other thresholds <0.05. The urban-influenced latitude range is defined as the intersection of the urban plume and the OCO-2 overpass (Fig. 5a). Overall, the urban-influenced latitudinal band represented by 5 % of the maximum kernel density covers the area from 23.5 to 26∘ N, given multiple overpasses for Riyadh (Fig. S2). The background latitudinal range unaffected by Riyadh's urban plume for the estimating background then extends ∼100 km from the northernmost and/or southernmost limits of the derived urban plume (Fig. 5b). We neglect observations with latitudes >26 and N, because these retrievals are too scattered (black triangles in Fig. 5b) and may indicate a second peak during other overpasses. If the near-field wind vectors point more toward the north, screened measurements over the southern background latitudinal range are utilized, and vice versa. Eventually, the background value is calculated as the mean value of the screened observations over the background region (dashed green line in Fig. 5b). Two error sources are incorporated into the background error: the measured (standard deviation, SD) and the retrieval errors of background observations.
In addition to random errors accounted for by the inclusion of the aforementioned wind error component and broadening of the city plume, potential large biases in near-field wind direction may lead to a mismatch in the modeled and observed background regions and may bring relatively higher XCO2 values into background XCO2. However, we do not explicitly account for the potential impact of near-field wind biases on the forward-trajectories defined urban plume due to the following considerations. Firstly, we attempted to propagate a near-field wind bias into the modeled plume by rotating the forward trajectories, whereas the robustness of this near-field bias can be affected by the rare wind measurements near Riyadh (further explained in Sect. 2.6.1). Secondly, the background latitude range defined by M3 with the broadening effect (blue curves in Fig. 5b) generally matches well with that observed from OCO-2 for most overpasses, which implies that the overall wind bias around our study site is not significant. Lastly, even if the potential wind bias may result in a less accurate background range and could potentially bring elevated XCO2 into the background, the background uncertainty implicitly contains information about the spatial variation in background measurements (green shaded region in Fig. 5b). Furthermore, the M3-derived background is generally the mean value of hundreds of background observations (numbers of observations shown in Fig. 6e), which may not be greatly affected by a few potential urban-enhanced measurements.
2.4 Sources of information for CO2 fluxes
2.4.1 Fossil fuel emission (ODIAC) and prior emission uncertainties
To calculate modeled XCO2 enhancements, we used the latest (2017) version of the Open-Data Inventory for Anthropogenic Carbon dioxide (ODIAC2017 dataset, Oda et al., 2018; Oda and Maksyutov, 2011, 2015) with monthly fossil fuel CO2 emissions at a 1×1 km resolution (Fig. 4). ODIAC starts with annual national emission estimates, separated by fuel type, from the Carbon Dioxide Information Analysis Center (CDIAC, Andres et al., 2011), which are then recategorized into specific ODIAC emission categories on a monthly basis, i.e., point source, non-point source, cement production, international aviation, and marine bunker (Oda et al., 2018). Because CDIAC only covers the years up to 2013, ODIAC extrapolates emissions in 2013 for emissions in 2014 and 2015 based on BP (i.e., the British Petroleum Company) global fuel statistical data (BP, 2017). ODIAC also estimates point source emissions according to a global power plants database – the Carbon Monitoring and Action (CARMA) database (Wheeler and Ummel, 2008), and collects and distributes non-point source emissions using an advanced nighttime lights dataset from the Defense Meteorological Satellite Program Operational Line Scanner (DMSP/OLS). The use of the nightlight dataset allows ODIAC to characterize the spatial patterns of the anthropogenic sources such as point sources, line sources, and diffuse sources.
To estimate emission uncertainties, we followed a method similar to those reported in Oda et al. (2015) and Fischer et al. (2017). Three emission inventories derived from different methods are intercompared: ODIAC, the Fossil Fuel Data Assimilation System (FFDASv2; Asefi-Najafabad et al., 2014; Rayner et al., 2010) and the Emission Database for Global Atmospheric Research (EDGARv4.2; http://edgar.jrc.ec.europa.eu, last access: 10 December 2013; Janssens-Maenhout et al., 2017). To resolve different spatial grid spacing among the three inventories, we aggregated ODIAC emissions from 1 km to 0.1∘ grid cells. The fractional uncertainty for gridded emissions is characterized by the emission spread (1σ, among three inventories) and mean values (μ) of estimated emissions for each grid cell within a given region (10–40∘ N, 25–60∘ E; Fig. S3). In general, fractional uncertainties in gridded emissions mostly range from 60 % to 130 % (Fig. S3) around Riyadh. Ultimately, these fractional emission uncertainties and ODIAC emissions are convolved with X-STILT's weighted column footprints to provide the XCO2 uncertainties due to prior emission uncertainties.
2.4.2 Natural fluxes (CarbonTracker)
The trajectory-endpoint method (M1 in Sect. 2.3.1) requires the oceanic and terrestrial biospheric fluxes from the 3 h product – CarbonTracker Near-Real Time (CT-NRT.v2016 and CT-NRT.v2017, http://carbontracker.noaa.gov, last access: 27 July 2017). CT-NRT, an extension of the standard CarbonTracker (Peters et al., 2007), is designed for the OCO-2 program and uses different prior flux models and “real-time” ERA-Interim reanalysis in its transport model than regular CT, which allows for more timely model results. To calculate oceanic and biospheric XCO2 changes, we multiplied these natural fluxes by the column weighted footprint according to Eq. (5). Although wildfire emissions can greatly modify atmospheric XCO2 (e.g., Heymann et al., 2017), we expected relatively small XCO2 contributions from wildfire; hence, we excluded wildfire-elevated XCO2 estimations, considering the periods studied (wintertime overpasses) and the study region (the Middle East). Note that the horizontal grid spacing of oceanic and biospheric fluxes provided by CT-NRT is ; while the grid spacing of the CT-NRT 4-D CO2 fields previously mentioned in Sect. 2.3.1 is over the Middle East.
2.5 Sensitivity analyses for X-STILT column receptors
The goal of carrying out sensitivity tests is to understand any systematic/random errors of STILT simulations caused by receptor configurations. Under the premise of limited computational resources, proper column receptors are set up with allowable random errors. The total number of particles (NUMPAR) released from column receptors are decomposed into three parameters: the maximum release level (MAXAGL), the vertical spacing of release levels (dh), and the particle number per level (dpar).
Instead of regenerating model trajectories (Jeong et al., 2013; Mallia et al., 2015), we adopted the bootstrap method to resample model ensembles. The bootstrap approach helps construct hypothesis tests and infer error statistics (Efron and Tibshirani, 1986). The initial sample size before the bootstrap should be large enough to ensure the performance of the bootstrap method and its related statistics. Thus, a “base run” of trajectories starting from the surface to 10 km with a vertical spacing of 25 m and 200 particles per level is generated and stored. For testing each parameter (MAXAGL, dh, or dpar), we fixed the other two parameters and randomly selected/resampled model particles from the base run 100 times allowing for repetitions. A hundred urban enhancements are calculated from 100 new sets of trajectories for each test. Basic statistics – i.e., mean values and standard deviations (or fractional uncertainty, i.e., SD∕mean) among these 100 enhancements – are used to infer systematic and random uncertainties in each test, respectively (the results are displayed in Sect. 3.1).
2.6 X-STILT column transport errors
Uncertainty in atmospheric transport modeling has been identified to significantly affect emission constraints (Cui et al., 2017; Lauvaux et al., 2016; Stephens et al., 2007). Here we quantify uncertainties in modeled XCO2 due to transport errors caused by uncertainties in both horizontal wind fields (Sect. 2.6.1) and vertical mixing (Sect. 2.6.2).
2.6.1 Horizontal transport errors
Previous studies (Lin and Gerbig, 2005; Mallia et al., 2017) have aimed at estimating transport error at one particular level, whereas for XCO2 we account for transport error in a column sense (i.e., column transport error). Macatangay et al. (2008) briefly explained the column transport error as the weighting of transport error variances with respect to pressures. Similarly, we treat each model level separately and calculate one CO2 transport error per level, denoted as , following Lin and Gerbig (2005). In short, an additional wind error component (uε) is added to the mean wind () and turbulent wind component (u′) that are embedded in normal STILT runs (Lin et al., 2003), to randomly perturb air parcels for each level. RMS errors of the u- and v-component modeled wind, error correlation timescales and length scales describe the uε in space and time. Details about the wind error calculations are given in Appendix B.
For each model level (n), we obtained two sets of parcel distributions: one without and one with the wind error component (uε). Then, the difference in the spread of these two distributions, or mathematically the difference in the variances of derived CO2 distributions among air parcels (Lin and Gerbig, 2005), serve as the XCO2 uncertainty (in ppm) due to transport error. We tested both the normal and log-normal statistics for describing this XCO2 transport uncertainty. Since transport error using log-normal statistics did not show very distinct improvement from that using normal statistics, we ended up adopting normal statistics for the consideration of benefiting inverse modeling. Because the parcel distribution with uε (orange dots in Fig. S4) is more dispersed than the parcel distribution without uε (blue dots in Fig. S4), the increase in CO2 variance with uε compared to that without uε describes the transport error for each level. However, negative values of transport error can occasionally occur due to statistical sampling from insufficient model parcel trajectories. To resolve this technical issue, we modified Lin and Gerbig (2005) using a regression-based approach. A weighted linear regression slope is used to describe the increase in CO2 variances and then estimate transport error. More information about this regression-based method is given in Appendix B. Overall, transport errors at levels within the PBL are expected to be larger than those at higher levels that approach zero.
Lastly, vertical profiles of transport errors were weighted against OCO-2's weighting functions. Following the definition of modeled AK-weighted XCO2 in Eq. (1), the weighted column transport error follows Eq. (6):
where wn denotes the product of AKnorm and PW at level n, and covε represents the correlation of transport errors between every two levels n and m (). To calculate a typical vertical error correlation length scale, we fit an exponential variogram according to transport errors and their separation distances between levels. Results of the transport error at each sounding and its latitudinal integration for each track are shown in Sect. 3.4 and 3.5.
In addition to the random error component mentioned above, we are aware of potential systematic wind errors in certain areas, e.g., positive wind speed bias reported over Los Angeles (Ye et al., 2017), and their impacts on both the forward- and backward- time simulations. As an attempt to resolve these obstacles, X-STILT can incorporate a near-field wind bias correction (to both backward- and forward-time simulations). By rotating model trajectories, this bias correction aims at “correcting” air parcel distributions and the resultant footprints, given the knowledge that the near-field wind bias can be properly interpolated. Details about this wind bias correction are described in Appendix C. Unfortunately, only two radiosonde stations around Riyadh with three vertical pressure levels within the PBL (and sometimes with missing data) may be insufficient to correctly interpolate the near-field vertical wind biases. However, cities with meteorological profiles sampling more levels within the PBL and a higher temporal frequency in reporting observed vertical winds (such as Los Angeles) may be more suitable sites for retrieving the near-field wind errors. Other methods include the rotation and stretching of urban plumes derived from WRF-Chem (Ye et al., 2017), similar to the rotation of X-STILT air parcels, to quantify errors in wind directions and speeds. Deng et al. (2017) sought the correction of wind biases in a sophisticated manner via data assimilation. However, the near-field correction within X-STILT can potentially be utilized in the future as a quick bias correction for the near-field wind in LPDMs, given denser wind observations and relatively flat terrains. Therefore, we decided to reduce the potential impact of wind bias on model–data comparisons using a latitudinal integration (further information in Sect. 3.5).
2.6.2 Vertical transport errors
Vertical turbulent mixing dominates the vertical transport of air parcels and controls the dilution of surface emissions within the PBL (e.g., Gerbig et al., 2008). Uncertainties in the vertical mixing or PBL height can affect both the footprint magnitude and the its spatial distribution via different horizontal advections at each altitude. Although column-integrated measurements may be less sensitive to the vertical distribution of air particles than in situ measurements, vertical transport errors can nonetheless have some impacts on column simulations, due to wind shear and its interaction with vertical redistribution of air parcels (Lauvaux and Davis, 2014). Comprehensive quantifications of the vertical transport errors in a column sense are performed in Lauvaux and Davis (2014) using an ensemble of surface and planetary boundary layer (SBL-PBL) parameterizations involving a regional inverse modeling framework.
Here, we made use of the stochastic nature of STILT and propagated typical PBL height errors in the model. Changes in STILT-modeled mixed layer height modify the vertical profiles of turbulent statistics that directly control the stochastic motions of the Lagrangian air parcels (Lin et al., 2003). Thus, we obtained different air parcel trajectories with rescaled PBL heights. The resultant vertical transport error in XCO2 space is calculated as the root-mean-squared errors (RMSEs) between two sets of XCO2 enhancements among different receptors for each overpass. Due to this calculation, vertical transport errors are only provided at the overpass level (results in Sect. 3.5). Gerbig et al. (2008) reported typical relative PBL errors in the range of ±20 %. Thus, we rescaled the PBL heights higher and lower by 20 % and evaluated the scaling's impact on XCO2 enhancements. Due to our focus on the urban emissions and potential small XCO2 enhancement contributions beyond 1 day backward in time, we only rescaled the PBL within the first 24 h of transport before arrival of the air parcels at the column receptors.
3.1 X-STILT sensitivity tests with column receptors
Figure 6 shows test results from a sounding on 29 December 2014 around Riyadh. In general, urban enhancements increase as MAXAGL increases from 1 to 2 km and then stabilize (Fig. 6a). When MAXAGL is small (<2 km), the model fails to fully capture the CO2 enhancements within the mixing height and causes underestimations of the elevated XCO2. Random errors reflect the stochastic nature of the model particles leading to small fluctuations in parcel distributions and resultant signals. In this experiment, dpar and dh are fixed to 100 particles and 100 m. For testing particle number per level (dpar), MAXAGL is set to 6 km (well above the top of the PBL; see Appendix D for the choice of 6 km). No obvious bias is associated with mean XCO2 enhancements. The random error reduces as particle numbers increases (error bars in Fig. 6b). We ended up placing 100 particles for each level, as random errors do not change dramatically from 100 to 200 particles.
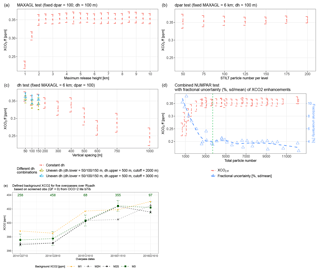
Figure 6Results of sensitivity tests for one sounding (a–d) and background comparisons for five tracks (e) over Riyadh. The random error for each simulation is indicated using dashed red error bars (a–d); potential biases are shown as the trend of the mean XCO2 enhancements (red dots; a–d) derived from 100 bootstraps. (c) Vertical spacing tests include several tests with constant dh (red dots and error bars) and two tests with uneven dh above/below the cutoff level. The two uneven dh tests both use three different lower dh (50, 100, and 150 m) and a fixed upper dh of 500 m, but with two different cutoff levels, i.e., 2 km (yellow-green triangles and error bars) and 3 km (blue triangles and error bars). (d) A summary plot of the mean and SD of the XCO2 enhancements (red dots and dashed red error bars) and fractional uncertainties (%; blue triangles and dashed line) as functions of total particle number (NUMPAR). The green dashed vertical line denotes the configuration used in this study. (e) Background comparisons using different methods (M1, M2H, M2S, and M3) for five tracks. The number of screened observations used for M3 background is noted in dark green. M3 background errors (including spatial variation and retrieval errors over the background region) are indicated as dashed green error bars.
In addition, we conducted two experiments using constant and uneven vertical spacings with a fixed MAXAGL of 6 km and a dpar of 100. Vertical spacing in the constant dh experiment ranges from 50 m to 1 km. Mean enhancements generally decrease as the vertical spacing increases (red dots in Fig. 6c), likely because fewer release levels are insufficient to represent air parcels in a column and their interactions with surface emissions, especially under strong wind shear. We further performed two cases with uneven vertical spacing below and above a “cutoff level”. Both cases tested three different lower spacings (of 50, 100, or 150 m) with a fixed upper spacing of 500 m. The two cases differ only in their cutoff levels (2 or 3 km). The comparison of the uneven dh with the constant dh experiment shows that their XCO2 enhancement results are fairly similar; this suggests that the lower spacing below the cutoff level matters most with respect to the model results, because most anthropogenic XCO2 enhancements are confined within the PBL. Furthermore, results for the uneven dh case with the cutoff level of 3 km (blue triangles in Fig. 6c) are more closed to the “truth” implied by the constant dh case (red dots in Fig. 6c). To be safe, column receptors are placed from 0 to 3 km with a spacing of 100 m and from 3 to 6 km with a spacing of 500 m. See Appendix D for the derivation of the cutoff level.
To summarize, the fractional uncertainties in modeled XCO2 enhancements reduce rapidly as total particle number increases (blue triangles in Fig. 6d). Our choice of column receptors and particle numbers has no noticeable bias and a fractional uncertainty of ∼4 % per simulation (dashed green line in Fig. 6d). Overall changes in X-STILT column receptors have a fairly small impact on the modeled anthropogenic signals, which is consistent with the finding (for biospheric signals) in Reuter et al. (2014).
3.2 X-STILT column footprints and upwind emission contributions
Upstream source regions and their contributions to the downwind air column can be identified as the “footprint” using backward-time simulations. Here we illustrate the differences in parcel distributions and footprint patterns derived from 500 m, 3 km, and multiple levels, for one sounding at 24.4961∘ N on 29 December 2014 (when southwestern winds dominated). Air parcels released at 500 m are associated with large footprints in the adjacent area of Riyadh (Fig. 3b). While parcels released from a higher level of 3 km travel backwards much faster to upwind regions, most parcels hardly get entrained back into the PBL (Fig. 3c) and make minimal contact with the surface (implied from the zero footprint values in Fig. 3d). When air parcels are released from multiple levels, the column footprints (Fig. 3f) cover a broader spatial domain with relatively smaller values than footprints derived from 500 m (Fig. 3b). Thus Fig. 3 highlights the difference in upwind influences from a PBL-based, tower-like measurement versus a column-integrated measurement. As expected, surface influence arriving at an air column can be 1 or a few orders of magnitude smaller than that arriving at a given location. Consequently, CO2 changes within the PBL are expected to be larger than column changes.
3.3 Comparisons between methods used to calculate background XCO2
As Silva and Arellano (2017) have pointed out, their urban extent may be too coarse for studying urban emissions. Thus, we adopted their statistical method (μ−σ) and used a smaller domain instead for computing the background of M2S. M2S and M3 calculate background values from local observations. Therefore, M2S may agree better with M3 in their derived background regarding both the temporal variations and their magnitudes (black diamonds and green squares in Fig. 6e). The M1 modeled background differs significantly from the other three and exhibits positive biases spanning roughly from 0.5 to 1.5 ppm (orange dots in Fig. 6e). Reasons for this large bias may be the accumulated transport errors as the backward duration increases in combination with potential errors in the global concentration fields, due to its coarse resolution.
We now focus on the comparison between M3 and M2H. On average, the M2H-derived background is lower than our localized “overpass-specific” background by 0.55 ppm (Fig. 6e), which can primarily be attributed to different defined background regions. M3 defined the background region from the same track as the one over Riyadh; thus, the M3-defined background air contains variations due to long-term atmospheric transport, natural sources/sinks, and FFCO2 emissions except for local urban emissions. Therefore, the subtraction of the M3-defined background from the enhanced air correctly represent the XCO2 portion enhanced by the local emissions. On the contrary, M2H use a fairly broad background region (0–60∘ N, 15∘ W–60∘ E in Fig. S7) to estimate gridded anomalies over all locations in Europe, the Middle East, and North Africa. Although the broad spatial region may yield more data, it may also misrepresent the correct upwind region because the wind regime can be quite different between different overpass dates or seasons.
The M3-defined background can be affected by potential large wind biases over cities other than Riyadh, where atmospheric transport may be more difficult to simulate. However, the impact is implicitly considered in the background uncertainty (Sect. 2.3.3). In contrast, all regional OCO-2 measurements are lumped into the M2H background calculation. For example, some measurements on the easternmost overpass in Fig. S7 are affected by Riyadh's emissions, whereas atmospheric columns at soundings along the two westernmost overpasses in Fig. S7 may not necessarily be the background air that eventually arrives at region around Riyadh. Thus, the regional median of XCO2 may not physically indicate the accurate background that is supposed to isolate local-scale fluxes. Therefore, the localized overpass-specific background (M3) is designed specifically for extracting local-scale XCO2 anomalies. Given relatively small urban enhancements around our study site, this 0.55 ppm difference between M3 and M2H leads to large differences in estimated observed urban signals and emission evaluations (Sect. 4.2).
3.4 Latitude-dependent urban enhancements and associated uncertainties
We compare the modeled and observed anthropogenic enhancements along the satellite track. Models using GDAS and WRF report fairly similar XCO2 peaks as bin-averaged observations for the 29 December 2014 overpass (Fig. 8). Although XCO2 contributions using GDAS and WRF can differ in their spatial distributions for some receptors (Fig. 7b versus Fig. 7f), the overall XCO2 contributions integrated from all receptors along the overpass (Fig. 7d versus Fig. 7h) share fairly similar spatial distributions and magnitudes and indicate large contributions due to urban emissions from Riyadh and small contributions from regions to the south of Riyadh. Regarding the shape of latitude-dependent XCO2 enhancements, large enhancements inferred from bin-averaged observations (solid black line in Fig. 8) cover a wider range compared to narrower modeled enhancements (dashed blue or purple lines in Fig. 8). Furthermore, modeled versus observed enhancements exhibit a 0.1∘ latitudinal shift for the event on 29 December 2014 (Fig. 8) and vary from 0.1 to 0.4∘ for other events (Fig. S8). Column simulations with strong near-field influences can be sensitive to potential errors in the near-field wind speeds and directions along with errors in the gridded emissions. The limited wind observations within the near-field land surface around Riyadh render difficult estimation of representative wind statistics that can be directly linked with model–data mismatches in XCO2. All of these challenges led us to perform a latitude integration on the urban XCO2 enhancements over a certain latitudinal band to reduce near-field sensitivity on model–data comparisons and emission evaluations (further discussed in Sect. 3.5).
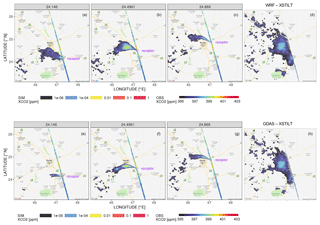
Figure 7Spatial maps of 1 km×1 km modeled XCO2 contributions (ppm; log-scale) from three selected soundings along with screened observations (QF = 0) at 10:00 UTC on 29 December 2014 over Riyadh, with meteorological fields driven by WRF (a–d) and GDAS (e–h). Panel (d) and (h) denote the latitude-integrated XCO2.ff contributions (with weights of receptor spacings, e.g., 0.02∘) using WRF and GDAS, derived from spatial XCO2 enhancements for over 60 column receptors along each overpass. The sum of the latitude-weighted spatial XCO2 enhancements over all grid cells (in panel d or h) equals to the latitude-integrated XCO2.ff signal (ppm-degree of latitude) reported in Sect. 3.5. Only large enhancements ppm are plotted.
Based on available radiosonde sites over the Middle East with relatively flat terrain (white crosses in Fig. 4), regional RMS errors associated with the GDAS u- and v-component winds are predominantly <2 m s−1 (Fig. S1) and generally smaller than those from previous studies over regions with relatively more complex terrains (Henderson et al., 2015; Lin et al., 2017). Even though positive/negative biases may exist per overpass, the averaged wind bias over a dozen tracks is fairly small, with absolute values close to zero. In other words, no obvious systematic error over times is found in the GDAS wind field around Riyadh. Similarly, Ye et al. (2017) also reported no bias in the transport for Riyadh using WRF-Chem. Due to the spatial inhomogeneity in urban emissions, wider parcel distributions after randomization may have a higher possibility of making contact with more emission sources than those before randomization. The 29 December 2014 track is a prime example of this. Small transport errors can often be found over less polluted latitudinal ranges (<24.3 and >24.9∘ N in Fig. 8). Transport errors then start to increase as a few randomized parcels intersect with some emission sources, even though simulated enhancements are still small (24–24.5 and 24.7–24.8∘ N in Fig. 8). Although air parcels at higher altitudes are also under perturbations, the change in the parcel distribution barely affects the column transport errors due to the minimal contact of those parcels with surface emissions. As a result, the transport error per sounding for this overpass ranges from 0.07 to 2.87 ppm (Fig. 8). For the other tracks with more intense urban enhancements, the maximum transport error per sounding can reach >5 ppm, e.g., 2016011510 in Fig. S8. In addition, XCO2 errors due to the vertical mixing error are not provided at the sounding level given our method described in Sect. 2.6.2; however, these values are reported on a per overpass basis in Sect. 3.5.
Spatial fractional uncertainties in gridded emissions over the Middle East from this work (Fig. S3) are comparable to values reported from prior studies. For instance, several commonly used emission inventories differ by >100 % over half of the examined 0.1∘ grid cells (Gately and Hutyra, 2017) in the northeastern US. Our resultant XCO2 uncertainties due to prior emission errors range from 0.1 to 1.48 ppm per sounding for the overpass on 29 December 2014 (Fig. 8) and from 0.04 to 2.82 ppm for all five overpasses (orange shaded region in Fig. S8).
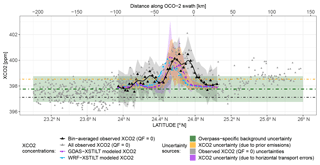
Figure 8Latitude-series of sounding-level signal comparisons and error estimates for Riyadh. Screened observations with QF = 0 and bin-averaged observed XCO2 are shown using gray and black triangles. GDAS- and WRF- derived XCO2 are displayed using purple and light blue dots, with smooth splines applied to visually reveal the main variations (purple and blue dashed lines). XCO2 errors due to errors in emissions, transport and observation are displayed using yellow, purple, and light gray shading. Overpass-specific (M3) background XCO2 is represented using a dark green dot-dashed line with its background uncertainty displayed using light green shading. Background values using M1, M2H, and M2S are shown as orange, gray, and black dot-dashed lines, respectively. The latitudinal range for integrating XCO2 enhancements and associated various uncertainties is ∼ 24–25∘ N in this case. The top x axis is the distance (in km) along the OCO-2 swath from a “minimum distance sounding” that has the smallest distance from the city center.
Retrieval errors are reported for each sounding from the OCO-2 lite files and exhibit a Gaussian-like distribution with the most frequent values of ∼0.5 ppm. Background uncertainty calculated from the variation of background measurements and their retrieval errors varies from 0.77 to 1.00 ppm among tracks (error bars in Fig. 6e). The overall observed uncertainty per sounding varies from 0.8 to 1.27 ppm (gray shading in Fig. 8). Worden et al. (2017) performed a comprehensive error analysis of version 7 OCO-2 XCO2 data within small regions (100 km×10.5 km). Two observed error sources they focused on included the natural variation in XCO2 and the calculated measurement uncertainty due to noise and interferences in the OCO-2 product. Their reported precision of a typical land measurement (WL < 10) is ∼0.75 ppm. Our larger observed uncertainties per sounding may be attributed to the lack of WL filtering applied to observations and the specific region examined here.
On a per sounding basis, XCO2 resulting from horizontal wind errors is comparable to or higher than XCO2 emission errors. Both errors are higher than observed uncertainties. Yet, uncertainty reductions are expected as sounding-level uncertainties are aggregated along the track (Sect. 3.5).
3.5 Latitudinally integrated urban signals and uncertainties
Because the shapes and the locations of XCO2 peaks between models and observations did not line up perfectly (Sect. 3.4; Fig. 8), direct model–data comparison may lead to significant deviations for each sounding. Thus, we compare urban signals and their associated errors integrated over a latitude band for each overpass.
Firstly, we integrated bin-averaged observed or modeled anthropogenic enhancements (i.e., differences between total XCO2 and overpass-specific background) along their latitudes. While multiple degrees of freedom are sacrificed by the integration, this calculation gains the larger benefit of potentially reducing the impact of the near-field wind bias on emission evaluations, as long as the latitude band for aggregation is representative. Secondly, a representative latitudinal range for integration (e.g., ∼ 24–25.2∘ N in Fig. 8) is required. Note that negative observed urban enhancements may occur when the bin-averaged total observed XCO2 is slightly lower than the background value. The occurrence of these negative values is partially caused by the natural variations in measured XCO2 and have been included as the background uncertainty. To minimize the inclusion of those negative values, we start with the widened latitudinal range (e.g., 24.2–24.9∘ N in Fig. 5b) and further account for latitudinal mismatch in model–data XCO2 peaks. To further include urban enhancements over the “tails” outside the distinct XCO2 peaks, we then extend the previous latitudinal range by 20 % on both sides. We tested percentages other than 20 % and found no dramatic changes in estimated signals due to small enhancements outside the plume (Appendix E).
Overall, the latitude-integrated modeled XCO2 signals range from 0.64 to 3.04 ppm-degree with a mean signal of 1.57 ppm-degree, whereas the observed signals detected by OCO-2 vary from 1.09 to 2.92 ppm-degree with a mean value of 1.65 ppm-degree (Table 1, Fig. 9a). The magnitudes of observed signals can be slightly affected by how observations are selected and binned up (Appendix E1).
Table 1Results of signal and error calculations for the five overpasses examined, including latitude-integrated observed versus modeled XCO2 enhancements and errors (ppm-degree of latitude), regional wind RMSE (m s−1), and the standard deviation of the mean (SDOM) for various errors and posterior scaling factors (unitless) of the mean modeled XCO2 signal. The GDAS and WRF regional wind speed RMSEs from 0 to 3 km or from 3 to 6 km are shown within or outside the parentheses, respectively.
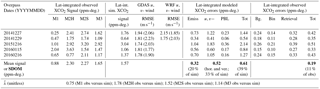
Emiss. – modeled XCO2 errors due to emission errors; u, v – modeled XCO2 errors due to horizontal wind errors; PBL – modeled XCO2 errors due to vertical mixing errors; Bg. – observed XCO2 errors due to background errors; Bin – observed XCO2 errors due to binning errors (spatial variations); and Retrieval – observed XCO2 errors due to retrieval errors.
To arrive at integrated errors per overpass, error variance–covariance matrices can be built. For example, diagonal elements comprise transport error variance per sounding/receptor with off-diagonal elements filled with error covariance between each two soundings/receptors (Fig. S9a). A correlation length scale of transport errors (∼25 km) among receptor locations is estimated by fitting exponential variograms (Fig. S9b), given the transport errors (further driven by plume structures) and our choice of grid spacing between receptors. Furthermore, similar calculations are performed to integrate sounding-level errors to overpass-level errors due to various error sources. Then, assuming errors are independent given the multiple days to months between overpasses, overpass-level XCO2 errors (Table 1) are further aggregated to arrive at an overall error for all five overpasses.

Figure 9Correlation between observed and simulated anthropogenic XCO2 signals for five overpasses. Colors differentiate different satellite overpass dates. Model–data comparisons using GDAS-derived XCO2 signals and observed signals based on different background methods. Error bars along the x axis and y axis represent the overall observed uncertainty (represented as 1σ, including the XCO2 spatial variability, background uncertainty, and retrieval errors) associated with observed signals and the overall modeled uncertainty (1σ, including emission uncertainty and transport uncertainty) around modeled signals. The dashed line represents the 1:1 line. Monte Carlo experiments are performed to fit linear regression lines based on sampled model–data signals and the associated errors. Regression lines with positive slopes are shaded in light gray. Median values of the slopes and y intercepts from the multiple regression lines (with positive slopes) are used to draw a linear regression (black solid line).
XCO2 errors solely resulting from vertical mixing errors are generally <15 % of the modeled signal for each overpass, whereas XCO2 errors due to horizontal wind errors dominate the overall XCO2 transport error (Table 1). The random uncertainties due to the choices of column receptors/parcels are negligible: <1 % of the latitude-integrated modeled XCO2 signal per track. The 68 % (1σ) confidence limits of the XCO2 uncertainties due to errors in prior emission and transport (i.e., horizontal wind fields and vertical mixing) are 0.32 and 0.52 ppm-degree, which is ∼20 % and 33 % of the mean modeled urban signal over five tracks, respectively (Table 1). The integrated XCO2 transport error per track reflects the aggregate effect of several factors which interact, given how we propagate wind errors into XCO2 space (Sect. 2.6):
-
The magnitude of the modeled urban XCO2 enhancements. In general, air parcels that are very far away from potential upstream emitters may barely “hit” the emission sources or gain their enhancements, even after wind perturbation. If the estimated signal is large (e.g., 3.04 ppm-deg. on 20151216 in Table 1), its resultant integrated transport error can also be fairly large (1.83 ppm-deg. in Table 1).
-
The RMSE of the u- and v-component winds. In general, larger wind errors will lead to larger changes in model trajectories and a higher possibility that perturbed trajectories will intersect an emission source.
-
How air parcels interact with surface emissions, i.e., the geometry/angle between the model footprint (or the wind direction) and satellite swaths. Changes in this angle may fluctuate the width of the enhanced latitudinal band along with the final integration latitudinal ranges (i.e., 1.10–2.25∘). If the back-trajectory or backward wind direction is more parallel to the OCO-2 swath (events on 20141227, 20151216, and 20160216 in Fig. S10), the integration range and error covariance among soundings are usually larger, which yields larger integrated XCO2 errors (e.g., 1.22, 1.83, and 1.05 ppm-degree in Table 1). The averaged latitudinal range for integration is about 1.66∘ (∼189 km) over the five tracks.
Retrieval errors between OCO-2 soundings are found to be correlated, in both space and time, with correlation coefficients (for land nadir) of 0.45 and 0.31 as a function of the satellite footprint and time, respectively (Worden et al., 2017). Uncertainties of bin-averaged observed XCO2 share a similar source to the background uncertainties, both of which rely on spatial variation in noisy observations (in each bin or over background region). Different types of observed uncertainties are assumed to be uncorrelated. Because observations along with their uncertainties have been binned up, we only account for the temporal correlation of retrieval errors between soundings. As a result, the total observed uncertainty per track varies from 0.33 to 0.50 ppm-degree and the observed error is 0.19 ppm-degree (1σ confidence limit), i.e., ∼11 % of the mean observed signals (1.65 ppm-deg.) over the five overpasses.
4.1 Model capabilities and performances
In this study, we demonstrate the application of LPDM simulations within X-STILT regarding locating the urban plume, determining background XCO2, identifying upwind sources, and estimating enhanced XCO2 caused by sources/sinks (Fig. 1). Specifically, backward-time simulations over an atmospheric column connect upwind emission sources with downwind atmospheric columns and generate spatial maps of this connection with additional information from satellite retrieval profiles. Although forward-time simulations from an urban box are an alternative and optional portion of X-STILT, these simulations effectively reveal information regarding the location and size of the time-varying urban plume (Fig. 5a) and locate the downwind polluted range on a satellite overpass.
Model sensitivity tests suggest two implications on simulating urban XCO2 enhancements using LPDMs: (1) receptor levels need to reach levels exceeding a typical mean PBL height to fully capture influences from surface emissions. (2) The model may capture a larger urban signal as the number of levels increases. However, to minimize computational costs, researchers may adopt sparser levels above and denser levels within a representative mean PBL height (the cutoff level) over upwind regions. Users can adopt their own setup of receptors in X-STILT according to combined results from sensitivity tests (Fig. 6d).
Additionally, X-STILT offers alternative solutions for dealing with errors in the meteorological fields, including regional random wind error perturbations and potential near-site wind bias corrections on model trajectories (Appendix C). For several satellite overpasses over Riyadh, meteorological models such as WRF and GDAS are capable of capturing XCO2 enhancements due to urban emissions, even though small mismatches in the locations of model–data XCO2 peaks remain. Model-to-model discrepancies between GDAS and WRF in latitudinally integrated urban signals are not substantial, likely due to the models benefiting from the relatively flat terrain around Riyadh. No noticeable difference in overall RMSE in the u- and v- component winds derived from radiosonde comparisons with WRF versus GDAS is reported in this case. Thus, global meteorological fields such as 0.5∘ GDAS can be used for studying “flat cities” like Riyadh.
When dealing with enhancements in the column concentration with a low signal-to-noise ratio, careful attention needs to be paid to the background XCO2 value. While one could possibly “eyeball” the city plume from the observed XCO2 (especially when a signal XCO2 peak is visually distinctive), forward-time simulations with additional information on transport errors implemented in X-STILT may provide a more objective and efficient method (in that valuable human time is unnecessary) for determining the urban-enhanced section along track and for extrapolating the overpass-specific background. These advantages of an overpass-specific background will become more important as more satellite tracks are incorporated within the analyses in addition to future flux inversions.
4.2 Implications regarding error analysis and future inversion using LPDMs
Column transport uncertainties have hitherto not been rigorously examined for studies employing LPDMs such as STILT and column measurements like OCO-2. In this work, we conducted comprehensive analyses of observed errors incorporating natural and spatial XCO2 variabilities and background and retrieval uncertainties; the simulated errors included errors resulting from model configurations, horizontal and vertical atmospheric transport, and prior anthropogenic emissions. On average, column transport errors contribute to 33 % (1σ confidence limit) of the mean modeled urban signal over five overpasses, whereas the horizontal transport errors on a per track basis are still substantial. We also accounted for horizontal correlations in transport errors between X-STILT release levels and between multiple soundings. For instance, the inclusion of horizontal covariance in transport errors between soundings generally leads to an increase of ∼67 % in the latitude integrated transport errors for each overpass, which emphasizes the importance of considering error covariance in model evaluations (e.g., Lin and Gerbig, 2005).
Estimated background uncertainty is represented by the spatial variation and retrieval errors of background observations. To further demonstrate X-STILT's potential role in inverse modeling and the potential background “bias” via different background methods on inversed results, we conducted a simple scaling factor inversion (Rodgers, 2000), based on five pairs of model–data latitudinally integrated urban signals. Even though our sampling may seem to be small and the gridded urban source emissions are adjusted as a lumped total (i.e., no adjustments for emissions at grid cell level), these integrated signals and errors are chosen to reduce the impact of potential near-field wind bias on model evaluations. Also, we are partially limited by the overpasses over Riyadh (black bars in Fig. S1). The prior emissions from ODIAC are assumed to be “unbiased”, which yields a prior scaling factor of unity (λa=1). The prior error (Sa) represents the overall uncertainties of the sum and spatial spread of ODIAC emissions around Riyadh (further calculated from the intercomparisons against FFDAS and EDGAR). The observational error covariance matrix (Sλ) contains error variances related to observation, horizontal and vertical transport errors (Table 1). Errors between every two overpasses separated in time by at least multiple weeks are assumed to be independent.
Our conservative results based on GDAS suggest that the posterior scaling factor (; of the mean XCO2 signal) and its posterior uncertainty (of the scaling factor) is 1.14±0.31 using the M3 background. However, potential errors in the background XCO2 defined by other methods may affect the resultant observed signals and posterior scaling factors. Since the M2H- and M1-derived background values are generally lower and higher than the M3 background, respectively, M2H- and M1-derived background values result in a higher and lower mean observed signal (2.30 and 0.88 ppm-degree in Table 1) than that based on M3 (1.65 ppm-degree). Furthermore, based on M2H is about 2.30, 40 % larger than based on M3. The derived from the M3 background (1.14) is more comparable to the WRF-Chem-based emission estimate in Ye et al. (2017). These results again emphasize the significant role that background definitions played in the estimated observed signals and emission estimates. In particular, simple statistical approaches without considering the atmospheric transport may lead to erroneous conclusions (as previously discussed in Sect. 3.3).
4.3 X-STILT's potential for broader applications
In theory, X-STILT can be applied to other column measurements and other species. The underlying Lagrangian atmospheric model (STILT) has been applied to simulate other atmospheric species, such as CO, CH4, and N2O (Mallia et al., 2015; Kort et al., 2008). One of the key modifications to X-STILT from STILT is the column weighting of STILT footprint values (Sect. 2.1.2). Specifically, X-STILT interpolates the OCO-2 AK and PW onto each modeled level and then applies weighting of the trajectory-level footprints before generating a horizontal footprint map. In a similar fashion, the X-STILT code can be easily modified to apply sensor-specific vertical profiles of AK and PW from other satellites or ground-based column measurements.
However, the background may need to be derived differently according to different applications, e.g., local urban emissions versus regional fluxes. The overpass specific background (M3) aims at isolating the citywide emissions; therefore, M3 makes use of the measurements outside the city, although these measurements are still quite close to the city – within a few degrees of latitude. If the study focus is on emissions over a much broader region (e.g., statewide emissions), the background region should be defined farther from the target region, e.g., the study may take advantage of measurements from available upstream overpasses.
Robust constraints on urban emission can be hampered due to their alternating-sign nature and signals potentially comparable to anthropogenic emissions (Shiga et al., 2014; Ye et al., 2017), which are also inferred from tracks we modeled over Cairo with non-negligible biomass (results not shown in this paper). When examining summertime tracks or tracks over certain other cities, potential local gradients in biospheric fluxes should be considered as these gradients can affect our overpass-specific background. Although biospheric fluxes or their resultant changes in XCO2 concentrations are beyond the scope of this work, many studies have been working to address this challenge. Ye et al. (2017) incorporated biospheric fluxes from the North American Carbon Program (NACP) Multi-scale Synthesis and Terrestrial Model Intercomparison Project (MsTMIP; Fisher et al., 2016; Huntzinger et al., 2013) and performed downscaling on biospheric fluxes using the MODIS-derived green vegetation fraction, to provide high-resolution biospheric flux fields and estimated background XCO2 using modeling. In addition, radiocarbon and terrestrial solar-induced chlorophyll fluorescence (SIF) data are helpful to isolate fossil fuel CO2 and biospheric CO2 (Fischer et al., 2017; Levin et al., 2003; Sun et al., 2017). In particular, recent studies have identified SIF as a better indicator/proxy of gross or net primary production than some other greenness indices over several different vegetation types (Shiga et al., 2018; Sun et al., 2017; Zuromski et al., 2018), which then improves biospheric flux estimation in ecosystem models and improves the interpretation of OCO-2/OCO-3 retrievals (Luus et al., 2017).
X-STILT extends previous LPDM methods to account for transport errors, background uncertainties, and particle statistics in a column sense within LPDMs. Admittedly, the transport error analysis and near-field correction may work better with the assistance of denser meteorological observing networks to characterize the error structures of transport errors. Increasing the density of surface networks may modify the wind error statistics including the wind error variances and horizontal correlated length-scale, and further impact the model transport uncertainties and inversed fluxes. However, this shortcoming is not inherent to X-STILT and also applies to other means of quantifying the transport errors based on real data. The trade-off of choosing a city in the Middle East, like Riyadh, to minimize cloud and vegetation influences is the relatively sparse observations from the surface meteorological network or aircraft. The recent OCO-2 b8 lite files include retrieved surface winds for each sounding. Unfortunately, most of those surface wind retrievals are not available over Riyadh, although the retrieved surface winds for other urban areas, if available, may be used for assimilation and to assist X-STILT error analysis.
Emission evaluations for different regions can be different and affected by different observational constraints. Even changes in different versions of the retrieval (lite b7 versus b8) may slightly affect the model–data comparisons and simple inversion results in this work. Modeled XCO2 enhancements using the newer b8 differ slightly from those using b7 (purple dots in Fig. S8 versus in Fig. S13) due to changes in the locations of the receptors, column averaging kernels, and data filtering (QF) for measurements around Riyadh. Specifically, observations from b8 may yield more overpasses with sufficient screened soundings than those from b7 (black and red bars in Fig. S1). However, much larger differences in observed enhancements are found; these differences are caused by the changes in total observed XCO2 and estimated background values. Specifically, background uncertainty decreases by up to 0.1 ppm which is primarily attributed to smaller spread (smaller SD) of the observed XCO2. Positive shifts in the total observed XCO2 for b8 from b7 are found over most overpasses (Fig. S11). The M3-derived observed enhancements may be less affected by positive shifts in total observations, given cancellation of this effect from a similar positive shift in the overpass-specific background near the target urban region (dark green dashed lines in Fig. 6e versus Fig. S12).
OCO-2 observations have been utilized in several recent studies including this work with a particular focus on relatively small areas, e.g., individual power plants (Nassar et al., 2017) and megacities (Ye et al., 2017). Even though the XCO2 urban signal over Riyadh may generally be smaller than those over other large cities, both the model and observations successfully detect the urban signal. Still, no summertime XCO2 signal has been derived, due to the lack of screened observations (QF = 0) reported in the OCO-2 lite b7 file over most summertime tracks (black bars in Fig. S1). No diurnal variation, a revisit time of 16 days, and a relatively narrow swath of OCO-2 may still pose challenges to urban emission estimates. We expect the inclusion of more column observations in stationary (target) modes, e.g., by scanning over megacities by OCO-3 (Eldering et al., 2016), which may offer more concrete spatial and diurnal variabilities that then benefit urban flux inversions. Many nations are devoting considerable resources to launching carbon-observing satellites that can potentially be coordinated into a larger monitoring system (Tollefson, 2016). Given that X-STILT can potentially work with most satellites (given their sensor-specific vertical profiles), we expect enhanced capability in emission constraints of urban emissions by combining column measurements with X-STILT.
X-STILT is built on STILT (Lin et al., 2003) and STILT-R version 2 (Fasoli et al., 2018), which can be downloaded from the GitHub repository (https://github.com/uataq/X-STILT, last access: 1 November 2018). The version of the X-STILT code coinciding with the work described in this paper is on Zenodo https://doi.org/10.5281/zenodo.1241514 (Wu et al., 2018).
We accounted for four factors, including (1) the prevailing wind directions and downwind regions, (2) the portion of soundings with QF = 0, (3) the distance between the satellite track and the city center, and (4) regional wind errors in modeled meteorological fields. In the end, we selected five overpasses via manual check.
-
First, we defined a spatial domain (2∘ latitude by 3∘ longitude) centered around Riyadh (i.e., 24.71∘ N, 46.74∘ E) and counted the total sounding numbers that fell into this domain for each overpass. This spatial domain can be determined by examining prevailing wind directions and locating downwind regions based on wind rose plots from radiosonde stations at the city center and at the Riyadh airport (with four-character international ID of OERK and OERY) during each overpass date. Alternatively, forward-time model runs starting from a box around the center of Riyadh allowed us to determine polluted latitudinal ranges on satellite overpasses (Fig. 5). Detailed demonstrations of the forward-time runs are in Sect. 2.3.3. A total of 43 overpasses with at least one measurement fell into this allocated spatial domain for Riyadh (gray bars in Fig. S1).
-
Next, we ensured the amount of screened observed data using warn levels/quality flags (QF). Because a high warn level is associated with a high total aerosol optical depth inferred from soundings (lite b7) near Riyadh, we only used quality flags to control data quality in this study. After selecting overpasses with >100 soundings with QF = 0, 11 overpasses remained. Most spring- and summer-time tracks (from March to August) failed to satisfy this criterion (black bars in Fig. S1). Furthermore, we ensured that enough screened observations fell within a prescribed urban domain ( area) around the city center (red bars in Fig. S1). Only eight overpasses had >50 screened soundings (red dashed line in Fig. S1).
-
Overpasses with distinct enhancements in retrieved XCO2 due to urban emissions were preferred. The near-field domain affected by PBL processes may extend from 100 to 1000 km based on the globally averaged ventilation time for the PBL (Lin et al., 2003). We made a conservative assumption that the impacted near-field domain was a circle with a radius of 50 km around the city center. Thus, we calculated the smallest distance between the soundings and the city center (orange dots in Fig. S1) and most soundings passed this filter given our examined spatial domain.
-
As a final step, since model results can potentially be affected by meteorological fields, regional u- and v- wind RMS errors below 3 km (derived from comparison with radiosonde stations – white crosses in Fig. 4) were calculated (numbers in brown in Fig. S1). Details regarding the wind error calculation are given in Appendix B.
In terms of the wind error component (uε) mentioned in Sect. 2.6, two sets of parameters are used to describe, (1) σuverr, the standard deviation of horizontal wind errors (RMSE) that describes the extent to which we should randomly perturb air parcels, and (2) the horizontal and vertical length-scales and timescales (Lx, Lz, and Lt) that determine how wind errors are correlated and decay in space and time. We calculated different sets of wind error statistics over three vertical bins, i.e., 0–3, 3–6, and 6–10 km, for randomizing air parcels. To obtain σuverr, observed winds at mandatory levels (i.e., 925, 850, 700, 500, 400, and 300 mb) from surrounding radiosonde sites (Fig. 4) were compared against WRF- or GDAS-interpolated winds. Then, we averaged wind errors at different mandatory levels over the aforementioned three vertical bins. In addition, wind errors are considered to be spatiotemporally correlated. To determine error correlation scales, differences in the wind errors are calculated and wind errors at different radiosonde stations or different reported hours (00:00 or 12:00 UTC) are paired up based on their separation length-scales or timescales. An exponential variogram is then applied to estimate the horizontal, vertical, and temporal correlation scales, which are the separation scales when errors become statistically uncorrelated.
Solution of negative transport errors The CO2 variance derived from model trajectories after the randomizations () can occasionally be smaller than the variance before the randomization () for a few levels, due to insufficient parcel numbers (green dots in Fig. S5). Instead of abandoning these data, we developed a regression-based method to deal with the reduction in CO2 variances. Specifically, we applied linear regression lines to the two sets of CO2 variances before and after the randomizations, with weights of . This meant that larger variances were weighted less. Several other methods (without the weights) to apply linear regression were also tried, but extremely large regression slopes and negative y intercept occurred, which could potentially lead to unreasonably large transport errors (in ppm) at lower levels within the PBL and negative transport errors aloft. Next, we scaled and recalculated based on the weighted regression slope SWLR and . The regression line indicates the overall increase in CO2 variance that serves as transport error in ppm:
where the weighted linear regression is fitted for variances with versus variances without the wind error component (dashed blue line in Fig. S5). An extremely large anthropogenic enhancement (e.g., >1000 ppm) for a given parcel may exist in a few cases. Thus, outliers (i.e., the upper 1st percentile of both parcel distributions before and after the randomizations) are removed for each level, before variances in both CO2 distributions are calculated.
While we did not apply the wind bias correction for the overpasses analyzed in this paper due to the biases being generally small (as previously explained in Sect. 2.3.3), X-STILT has the capability to account for biases, if necessary. The basic idea is to correct the near-field wind biases in both forward- and backward-time trajectories. As wind error at each observed pressure level can be quite different, vertically weighted u- and v- wind biases were calculated by fitting logarithmic mean wind profiles based on the available near-field observed and simulated wind speeds and directions. We then calculated the deviations in latitudinal and longitudinal directions (dx, dy, with conversion from distance to degrees) given estimated u- and v- wind biases. These deviations accumulate as air parcels travel further backward or forward in time and are used to correct the location of each particle. After fixing the particle locations, Fig. S6b shows that the general distribution of backward trajectory is rotated clockwise compared with the initial trajectory distribution in Fig. S6b. Air parcels in Fig. S6b appear to be “noisier” than those in Fig. S6a, due to inclusion of the random wind error component. The new bias-corrected set of column trajectory is then used to generate a spatial footprint. This correction can also be performed to the forward-time trajectory to reduce the wind bias impact on the best-estimated background value using the M3 method.
MAXAGL and a cutoff level (below which more model levels are placed) are the most important factors in determining modeled urban signals; these values can be determined based on a few model trajectories starting from a few satellite soundings for each overpass. Modeled mixing height h reported for an individual air parcel at a timestamp, h(p,tm), can be very high over the upwind desert region near Riyadh. We determine MAXAGL to be the maximum mixing height for each individual air parcel. To determine a cutoff level, we calculate the averaged h over all parcels as a function of backward time as follows:
where tm represents the backward timestamp, ranging from 0 to 72 h back in time. The mean modeled mixing heights among air parcels at each timestamp h(tm) exhibited a diurnal cycle, where expected high values were present during the daytime. Furthermore, typically displayed relatively high values where parcels were more concentrated within a day backward, and low values as parcels dispersed outwards a few days back. We ended up using the maximum value of the mean mixing heights over parcels and over time as a representative cutoff level.
The maximum h(p,tm) and maximum are 5816 and 2420 m, respectively, for the specific sounding shown in this paper (Sect. 3.1, Fig. 6). Considering potential uncertainties in the modeled PBL or mixing heights, these two numbers are rounded to 6 and 3 km for a respective representative MAXAGL and cutoff level. In addition, we generalize the rules for placing column receptors to other seasons, based on the aforementioned calculations. Maximum h(p,tm) and maximum over the upwind region vary slightly between different soundings during different seasons. Typically, maximum h(p,tm) are mostly under 6 km for wintertime soundings (December, January, and February), but can reach ∼7 and 10 km for soundings in spring/fall and summer, respectively. Maximum are <3 km for wintertime tracks and ∼4 and 6 km for tracks in spring/fall and summer. Therefore, column receptors are placed from the surface to 3 km with 100 m spacing and from 3 to 6 km with 500 m spacing for wintertime overpasses with 100 parcels per level (Fig. 3e). For other seasons such as the summertime, additional receptors are placed from 6 to 10 km with a spacing of 1 km, to ensure that the model captures all contributions from surface emissions. Although we expect relatively similar MAXAGLs and cutoff levels for most soundings over the Middle East, due to overlaps in upwind regions, these values should be recalculated when other cities are examined (Eq. D1).
In Sect. 3.5, we integrated XCO2 enhancements along latitudes to estimate modeled and observed signals within a certain latitudinal band for each overpass. This latitudinal band starts with an enhanced latitudinal range, is then corrected based on the model–data latitudinal shift in XCO2 peaks, and finally extends by 20 % of its length. Furthermore, we tested the impact of percentages other than 20 % on the latitudinally integrated signals. Because of relatively small XCO2 enhancements over the background range, the impact due to different percentages (i.e., 10 %, 15 %, 20 % and 25 %) is relatively small – e.g., changes of 0.03 and 0.06 ppm in the averaged modeled and observed signals, respectively. These small changes show that our latitude integration band is representative as it does not include a second peak or miss large XCO2 enhancements.
E1 Influences on observed signals (bin-widths, warn levels)
These modeled and observed signals reported in Sect. 3.5 are calculated based on the uneven sampling choice for the model receptor lat/long, i.e., with smaller bin widths of 0.025∘ and larger bin widths of 0.05∘ over which urban influences are stronger and weaker, respectively. In addition, we tested the impact on observed signals resulting from different bin widths with constant values starting from 0.01 to 0.5∘. Both the latitudinal variation and the overall observed signal for an overpass generally decreased as the bin widths increased, as bin-averaged observed XCO2 enhancements get smoothed out, especially over latitudes with strong urban influences. Some information is lost in latitude-integrated observed signals based on our sampling choices when comparing them against the signals calculated using constant bin widths such as 0.02∘. However, binning observations based on the lat/long of model receptors ensures a fair comparison with the model and our uneven sampling choices may better resolve XCO2 enhancements within much finer grid spacing (particularly under urban influences) on the premise of limited computational resources. In addition, warn levels (WLs) may impact the filtering of observed data, the bin-averaged observed XCO2, the defined background, and the conclusion regarding the model–data comparisons. Based on three simple tests involving selecting measurements with QF = 0 and additional WL filters (WL < 10, 12, and 15), observed signals slightly increase as more conservative WL filtering is applied. Changes in linear regression slopes and correlation between best-estimated modeled and observed signals due to sample choices and WL filtering are small.
E2 Influences on modeled signals (hourly versus monthly emissions, nhrs, averaging kernel)
An additional set of hourly scaling factors (Nassar et al., 2013) can be applied to ODIAC to downscale the monthly mean emissions to hourly values. In this study, we used monthly mean FFCO2 emissions from ODIAC and applied TIMES to only one of the five total overpasses. Simulations including TIMES are slightly larger than simulations without the hourly scaling factors. Also, the number of hours may impact the modeled enhancements at each sounding/receptor. We also conducted another simulation for the 27 December 2014 event using model trajectories with only 24 h backward runs (different from the 72 h backward runs used in main text). The decrease in the anthropogenic enhancements is <0.05 ppm per sounding, which is small due to the very small surface influence from distant emission sources. Lastly, we report the overall discrepancy in the modeled anthropogenic enhancements with or without weighting by OCO-2 prior profiles to be small. The difference is about 1 %–2 % of the weighted modeled anthropogenic enhancements, which is much smaller than the impact caused by uncertainties in transport, emissions, or different setups. Note that XCO2 portion of OCO-2's prior profile is zero and the averaging kernel is simply unity everywhere for non-AK weighted simulations.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-4843-2018-supplement.
DW and JCL designed the study. DW, JCL, and BF contributed to the X-STILT model codes. TO provided the ODIAC anthropogenic emissions inventory used for this analysis. XY and TL provided the customized WRF meteorological fields over the study area. EGY and EAK helped with the analysis of OCO-2 XCO2 data and city selections. All authors gave valuable input to the final paper.
The authors declare that they have no conflict of interest.
This study is based upon work supported by the National Aeronautics and Space
Administration funding under grant no. NNX15AI41G and the National Science
Foundation Graduate Research Fellowship under grant no. DGE 1256260 to Emily
G. Yang. We gratefully acknowledge Thomas Nehrkorn for providing code
modifications to facilitate the forward-time box runs, and we thank Derek
Mallia, Feng Deng, Arlyn Andrews, and Andy Jacobson for their valuable advice
on STILT-based modeling. The OCO-2 data were produced by the OCO-2 project at
the Jet Propulsion Laboratory, California Institute of Technology, and
obtained from the OCO-2 data archive maintained at the NASA Goddard Earth
Science Data and Information Services Center. The authors acknowledge the
NOAA Air Resources Laboratory (ARL) for the provision of the GDAS
meteorological files used in this publication, which were downloaded from the
READY website (http://www.ready.noaa.gov, last access: 1 May 2018).
CarbonTracker CT-NRT.v2017 results are provided by NOAA ESRL, Boulder,
Colorado, USA from http://carbontracker.noaa.gov (last access:
27 July 2017). The support and resources from the Center for High Performance
Computing (CHPC) at the University of Utah are gratefully
acknowledged.
Edited by: Christoph
Knote
Reviewed by: two anonymous referees
Andres, R. J., Gregg, J. S., Losey, L., Marland, G. and Boden, T. A.: Monthly, global emissions of carbon dioxide from fossil fuel consumption, Tellus, Ser. B Chem. Phys. Meteorol., 63, 309–327, https://doi.org/10.1111/j.1600-0889.2011.00530.x, 2011.
Andres, R. J., Boden, T. A., and Higdon, D.: A new evaluation of the uncertainty associated with CDIAC estimates of fossil fuel carbon dioxide emission, Tellus B, 66, 23616, https://doi.org/10.3402/tellusb.v66.23616, 2014.
Andres, R. J., Boden, T. A., and Higdon, D. M.: Gridded uncertainty in fossil fuel carbon dioxide emission maps, a CDIAC example, Atmos. Chem. Phys., 16, 14979–14995, https://doi.org/10.5194/acp-16-14979-2016, 2016.
Asefi-Najafabad, S., Rayner, P. J., Gurney, K. R., Mcrobert, A., Song, Y., Coltin, K., Huang, J., Elvidge, C. and Baugh, K.: A multiyear, global gridded fossil fuel emission data product: Evaluation and analysis of results, J. Geophys. Res.-Atmos., 119, 10213–10231, https://doi.org/10.1002/2013JD021296, 2014.
Basu, S., Guerlet, S., Butz, A., Houweling, S., Hasekamp, O., Aben, I., Krummel, P., Steele, P., Langenfelds, R., Torn, M., Biraud, S., Stephens, B., Andrews, A., and Worthy, D.: Global CO2 fluxes estimated from GOSAT retrievals of total column CO2, Atmos. Chem. Phys., 13, 8695–8717, https://doi.org/10.5194/acp-13-8695-2013, 2013.
Brasseur, G. P. and Jacob, D. J.: Modeling of Atmospheric Chemistry, Cambridge University Press, Cambridge, 2017.
Boden, T. A., Marland, G., and Andres, R. J.: Global, Regional, and National Fossil-Fuel CO2 Emissions, Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge, Tenn., USA, https://doi.org/10.3334/CDIAC/00001_V2017, 2017.
Boesch, H., Baker, D., Connor, B., Crisp, D., and Miller, C.: Global characterization of CO2 column retrievals from shortwave-infrared satellite observations of the Orbiting Carbon Observatory-2 mission, Remote Sens., 3, 270–304, https://doi.org/10.3390/rs3020270, 2011.
BP: Statistical Review of World Energy, available at: http://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html (last access: 6 June 2017), 2017.
Cambaliza, M. O. L., Shepson, P. B., Caulton, D. R., Stirm, B., Samarov, D., Gurney, K. R., Turnbull, J., Davis, K. J., Possolo, A., Karion, A., Sweeney, C., Moser, B., Hendricks, A., Lauvaux, T., Mays, K., Whetstone, J., Huang, J., Razlivanov, I., Miles, N. L., and Richardson, S. J.: Assessment of uncertainties of an aircraft-based mass balance approach for quantifying urban greenhouse gas emissions, Atmos. Chem. Phys., 14, 9029–9050, https://doi.org/10.5194/acp-14-9029-2014, 2014.
Ciais, P., Sabine, C., Govindasamy, B., Bopp, L., Brovkin, V., Canadell, J., Chhabra, A., DeFries, R., Galloway, J., Heimann, M., Jones, C., Le Quéré, C., Myneni, R., Piao, S., and Thornton, P.: Chapter 6: Carbon and Other Biogeochemical Cycles, in: Climate Change 2013 The Physical Science Basis, Cambridge University Press, Cambridge, 2013.
Crisp, D., Fisher, B. M., O'Dell, C., Frankenberg, C., Basilio, R., Bösch, H., Brown, L. R., Castano, R., Connor, B., Deutscher, N. M., Eldering, A., Griffith, D., Gunson, M., Kuze, A., Mandrake, L., McDuffie, J., Messerschmidt, J., Miller, C. E., Morino, I., Natraj, V., Notholt, J., O'Brien, D. M., Oyafuso, F., Polonsky, I., Robinson, J., Salawitch, R., Sherlock, V., Smyth, M., Suto, H., Taylor, T. E., Thompson, D. R., Wennberg, P. O., Wunch, D., and Yung, Y. L.: The ACOS CO2 retrieval algorithm – Part II: Global XCO2 data characterization, Atmos. Meas. Tech., 5, 687–707, https://doi.org/10.5194/amt-5-687-2012, 2012.
Cui, Y. Y., Brioude, J., Angevine, W. M., Peischl, J., McKeen, S. A., Kim, S. W., Neuman, J. A., Henze, D. K., Bousserez, N., Fischer, M. L., Jeong, S., Michelsen, H. A., Bambha, R. P., Liu, Z., Santoni, G. W., Daube, B. C., Kort, E. A., Frost, G. J., Ryerson, T. B., Wofsy, S. C., and Trainer, M.: Top-down estimate of methane emissions in California using a mesoscale inverse modeling technique: The San Joaquin Valley, J. Geophys. Res.-Atmos., 122, 3686–3699, https://doi.org/10.1002/2016JD026398, 2017.
Deng, A., Lauvaux, T., Davis, K. J., Gaudet, B. J., Miles, N., Richardson, S. J., Wu, K., Sarmiento, D. P., Hardesty, R. M., Bonin, T. A., Brewer, W. A., and Gurney, K. R.: Toward reduced transport errors in a high resolution urban CO2 inversion system, Elem. Sci. Anth., 5, 20, https://doi.org/10.1525/elementa.133, 2017.
Dlugokencky, E. and Tans, P.: Trends in atmospheric carbon dioxide, National Oceanic & Atmospheric Administration, Earth System Research Laboratory (NOAA/ESRL), available at: http://www.esrl.noaa.gov/gmd/ccgg/trends (last access: 27 July 2017), 2015.
Duren, R. M. and Miller, C. E.: Measuring the carbon emissions of megacities, Nat. Clim. Chang., 2, 560–562, https://doi.org/10.1038/nclimate1629, 2012.
Efron, B. and Tibshirani, R.: Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy, Stat. Sci., 1, 54–75, 1986.
Eldering, A., Bennett, M., and Basilio, R.: The OCO-3 Mission: overview of science objectives and status, in: EGU General Assembly Conference Abstracts, 18, 5189, 2016.
Ellis, E. C. and Ramankutty, N.: Putting people in the map: anthropogenic biomes of the world, Front. Ecol. Environ., 6, 439–447, 2008.
Fasoli, B., Lin, J. C., Bowling, D. R., Mitchell, L., and Mendoza, D.: Simulating atmospheric tracer concentrations for spatially distributed receptors: updates to the Stochastic Time-Inverted Lagrangian Transport model's R interface (STILT-R version 2), Geosci. Model Dev., 11, 2813–2824, https://doi.org/10.5194/gmd-11-2813-2018, 2018.
Feng, S., Lauvaux, T., Newman, S., Rao, P., Ahmadov, R., Deng, A., Díaz-Isaac, L. I., Duren, R. M., Fischer, M. L., Gerbig, C., Gurney, K. R., Huang, J., Jeong, S., Li, Z., Miller, C. E., O'Keeffe, D., Patarasuk, R., Sander, S. P., Song, Y., Wong, K. W., and Yung, Y. L.: Los Angeles megacity: a high-resolution land-atmosphere modelling system for urban CO2 emissions, Atmos. Chem. Phys., 16, 9019–9045, https://doi.org/10.5194/acp-16-9019-2016, 2016.
Fischer, M. L., Parazoo, N., Brophy, K., Cui, X., Jeong, S., Liu, J., Keeling, R., Taylor, T. E., Gurney, K., Oda, T., and Graven, H.: Simulating estimation of California fossil fuel and biosphere carbon dioxide exchanges combining in situ tower and satellite column observations, J. Geophys. Res.-Atmos., 122, 3653–3671, https://doi.org/10.1002/2016JD025617, 2017.
Fisher, J. B., Sikka, M., Huntzinger, D. N., Schwalm, C., and Liu, J.: Technical note: 3-hourly temporal downscaling of monthly global terrestrial biosphere model net ecosystem exchange, Biogeosciences, 13, 4271–4277, https://doi.org/10.5194/bg-13-4271-2016, 2016.
Gately, C. K. and Hutyra, L. R.: Large Uncertainties in Urban-Scale Carbon Emissions, J. Geophys. Res.-Atmos., 122, 242–260, https://doi.org/10.1002/2017JD027359, 2017.
Gerbig, C., Lin, J. C., Wofsy, S. C., Daube, B. C., Andrews, A. E., Stephens, B. B., Bakwin, P. S., and Grainger, C. A.: Toward constraining regional-scale fluxes of CO2 with atmospheric observations over a continent: 2. Analysis of COBRA data using a receptor-oriented framework, J. Geophys. Res.-Atmos., 108, 4757, https://doi.org/10.1029/2003JD003770, 2003.
Gerbig, C., Lin, J. C., Munger, J. W., and Wofsy, S. C.: What can tracer observations in the continental boundary layer tell us about surface-atmosphere fluxes?, Atmos. Chem. Phys., 6, 539–554, https://doi.org/10.5194/acp-6-539-2006, 2006.
Gerbig, C., Körner, S., and Lin, J. C.: Vertical mixing in atmospheric tracer transport models: error characterization and propagation, Atmos. Chem. Phys., 8, 591–602, https://doi.org/10.5194/acp-8-591-2008, 2008.
Göckede, M., Turner, D. P., Michalak, A. M., Vickers, D., and Law, B. E.: Sensitivity of a subregional scale atmospheric inverse CO2 modeling framework to boundary conditions, J. Geophys. Res.-Atmos., 115, 2010.
Hakkarainen, J., Ialongo, I., and Tamminen, J.: Direct space-based observations of anthropogenic CO2 emission areas from OCO-2, Geophys. Res. Lett., 43, 11400–11406, https://doi.org/10.1002/2016GL070885, 2016.
Henderson, J. M., Eluszkiewicz, J., Mountain, M. E., Nehrkorn, T., Chang, R. Y.-W., Karion, A., Miller, J. B., Sweeney, C., Steiner, N., Wofsy, S. C., and Miller, C. E.: Atmospheric transport simulations in support of the Carbon in Arctic Reservoirs Vulnerability Experiment (CARVE), Atmos. Chem. Phys., 15, 4093–4116, https://doi.org/10.5194/acp-15-4093-2015, 2015.
Heymann, J., Reuter, M., Buchwitz, M., Schneising, O., Bovensmann, H., Burrows, J. P., Massart, S., Kaiser, J. W., and Crisp, D.: CO2 emission of Indonesian fires in 2015 estimated from satellite-derived atmospheric CO2 concentrations, Geophys. Res. Lett., 44, 1537–1544, https://doi.org/10.1002/2016GL072042, 2017.
Hogue, S., Marland, E., Andres, R. J., Marland, G., and Woodard, D.: Uncertainty in gridded CO2 emissions estimates, Earths Future, 4, 225–239, https://doi.org/10.1002/2015EF000343, 2016.
Houweling, S., Breon, F.-M., Aben, I., Rödenbeck, C., Gloor, M., Heimann, M., and Ciais, P.: Inverse modeling of CO2 sources and sinks using satellite data: a synthetic inter-comparison of measurement techniques and their performance as a function of space and time, Atmos. Chem. Phys., 4, 523–538, https://doi.org/10.5194/acp-4-523-2004, 2004.
Huntzinger, D. N., Schwalm, C., Michalak, A. M., Schaefer, K., King, A. W., Wei, Y., Jacobson, A., Liu, S., Cook, R. B., Post, W. M., Berthier, G., Hayes, D., Huang, M., Ito, A., Lei, H., Lu, C., Mao, J., Peng, C. H., Peng, S., Poulter, B., Riccuito, D., Shi, X., Tian, H., Wang, W., Zeng, N., Zhao, F., and Zhu, Q.: The North American Carbon Program Multi-Scale Synthesis and Terrestrial Model Intercomparison Project – Part 1: Overview and experimental design, Geosci. Model Dev., 6, 2121–2133, https://doi.org/10.5194/gmd-6-2121-2013, 2013.
Janardanan, R., Maksyutov, S., Oda, T., Saito, M., Kaiser, J. W., Ganshin, A., Stohl, A., Matsunaga, T., Yoshida, Y., and Yokota, T.: Comparing GOSAT observations of localized CO2 enhancements by large emitters with inventory-based estimates, Geophys. Res. Lett., 43, 3486–3493, https://doi.org/10.1002/2016GL067843, 2016.
Janssens-Maenhout, G., Crippa, M., Guizzardi, D., Muntean, M., Schaaf, E., Dentener, F., Bergamaschi, P., Pagliari, V., Olivier, J. G. J., Peters, J. A. H. W., van Aardenne, J. A., Monni, S., Doering, U., and Petrescu, A. M. R.: EDGAR v4.3.2 Global Atlas of the three major Greenhouse Gas Emissions for the period 1970–2012, Earth Syst. Sci. Data Discuss., https://doi.org/10.5194/essd-2017-79, 2017.
Jeong, S., Hsu, Y. K., Andrews, A. E., Bianco, L., Vaca, P., Wilczak, J. M., and Fischer, M. L.: A multitower measurement network estimate of California's methane emissions, J. Geophys. Res.-Atmos., 118, 11339–11351, https://doi.org/10.1002/jgrd.50854, 2013.
Kim, S. Y., Millet, D. B., Hu, L., Mohr, M. J., Griffis, T. J., Wen, D., Lin, J. C., Miller, S. M., and Longo, M.: Constraints on carbon monoxide emissions based on tall tower measurements in the US Upper Midwest, Environ. Sci. Technol., 47, 8316–8324, 2013.
Kort, E. A., Eluszkiewicz, J., Stephens, B. B., Miller, J. B., Gerbig, C., Nehrkorn, T., Daube, B. C., Kaplan, J. O., Houweling, S., and Wofsy, S. C.: Emissions of CH4 and N2O over the United States and Canada based on a receptor-oriented modeling framework and COBRA-NA atmospheric observations, Geophys. Res. Lett., 35, L18808, https://doi.org/10.1029/2008GL034031, 2008.
Kort, E. A., Frankenberg, C., Miller, C. E., and Oda, T.: Space-based observations of megacity carbon dioxide, Geophys. Res. Lett., 39, 1–5, https://doi.org/10.1029/2012GL052738, 2012.
Kort, E. A., Angevine, W. M., Duren, R., and Miller, C. E.: Surface observations for monitoring urban fossil fuel CO2 emissions: Minimum site location requirements for the Los Angeles megacity, J. Geophys. Res.-Atmos., 118, 1–8, https://doi.org/10.1002/jgrd.50135, 2013.
Lauvaux, T., Pannekoucke, O., Sarrat, C., Chevallier, F., Ciais, P., Noilhan, J., and Rayner, P. J.: Structure of the transport uncertainty in mesoscale inversions of CO2 sources and sinks using ensemble model simulations, Biogeosciences, 6, 1089–1102, https://doi.org/10.5194/bg-6-1089-2009, 2009.
Lauvaux, T. and Davis, K. J.: Planetary boundary layer errors in mesoscale inversions of column-integrated CO2 measurements, J. Geophys. Res.-Atmos., 119, 490–508, 2014.
Lauvaux, T., Miles, N. L., Richardson, S. J., Deng, A., Stauffer, D. R., Davis, K. J., Jacobson, G., Rella, C., Calonder, G. P., and DeCola, P. L.: Urban emissions of CO2 from Davos, Switzerland: The first real-time monitoring system using an atmospheric inversion technique, J. Appl. Meteorol. Climatol., 52, 2654–2668, 2013.
Lauvaux, T., Miles, N. L., Deng, A., Richardson, S. J., Cambaliza, M. O., Davis, K. J., Gaudet, B., Gurney, K. R., Huang, J., O'Keefe, D., Song, Y., Karion, A., Oda, T., Patarasuk, R., Razlivanov, I., Sarmiento, D., Shepson, P., Sweeney, C., Turnbull, J., and Wu, K.: High-resolution atmospheric inversion of urban CO2 emissions during the dormant season of the Indianapolis Flux Experiment (INFLUX), J. Geophys. Res.-Atmos., 121, 5213–5236, https://doi.org/10.1002/2015JD024473, 2016.
Levin, I., Kromer, B., Schmidt, M., and Sartorius, H.: A novel approach for independent budgeting of fossil fuel CO2 over Europe by 14CO2 observations, Geophys. Res. Lett., 30, 2194, https://doi.org/10.1029/2003GL018477, 2003.
Lin, J. C. and Gerbig, C.: Accounting for the effect of transport errors on tracer inversions, Geophys. Res. Lett., 32, L01802, https://doi.org/10.1029/2004GL021127, 2005.
Lin, J. C., Gerbig, C., Wofsy, S. C., Andrews, A. E., Daube, B. C., Davis, K. J., and Grainger, C. A.: A near-field tool for simulating the upstream influence of atmospheric observations: The Stochastic Time-Inverted Lagrangian Transport (STILT) model, J. Geophys. Res.-Atmos., 108, 4493, https://doi.org/10.1029/2002JD003161, 2003.
Lin, J. C., Gerbig, C., Daube, B. C., Wofsy, S. C., Andrews, A. E., Vay, S. A., and Anderson, B. E.: An empirical analysis of the spatial variability of atmospheric CO2: Implications for inverse analyses and space-borne sensors, Geophys. Res. Lett., 31, 1–5, https://doi.org/10.1029/2004GL020957, 2004.
Lin, J. C., Gerbig, C., Wofsy, S. C., Daube, B. C., Matross, D. M., Chow, V. Y., Gottlieb, E., Andrews, A. E., Pathmathevan, M., and Munger, J. W.: What have we learned from intensive atmospheric sampling field programmes of CO2?, Tellus B, 58, 331–343, https://doi.org/10.1111/j.1600-0889.2006.00202.x, 2006.
Lin, J. C., Mallia, D. V., Wu, D., and Stephens, B. B.: How can mountaintop CO2 observations be used to constrain regional carbon fluxes?, Atmos. Chem. Phys., 17, 5561–5581, https://doi.org/10.5194/acp-17-5561-2017, 2017.
Liu, Y., Yang, D., and Cai, Z.: A retrieval algorithm for TanSat XCO2 observation: Retrieval experiments using GOSAT data, Chin. Sci. Bull., 58, 1520–1523, https://doi.org/10.1007/s11434-013-5680-y, 2013.
Luus, K. A., Commane, R., Parazoo, N. C., Benmergui, J., Euskirchen, E. S., Frankenberg, C., Joiner, J., Lindaas, J., Miller, C. E., Oechel, W. C., Zona, D., Wofsy, S., and Lin, J. C.: Tundra photosynthesis captured by satellite-observed solar-induced chlorophyll fluorescence, Geophys. Res. Lett., 44, 1564–1573, https://doi.org/10.1002/2016GL070842, 2017.
Macatangay, R., Warneke, T., Gerbig, C., Körner, S., Ahmadov, R., Heimann, M., and Notholt, J.: A framework for comparing remotely sensed and in-situ CO2 concentrations, Atmos. Chem. Phys., 8, 2555–2568, https://doi.org/10.5194/acp-8-2555-2008, 2008.
Mallia, D. V, Lin, J. C., Urbanski, S., Ehleringer, J., and Nehrkorn, T.: Impacts of upwind wildfire emissions on CO, CO2, and PM2.5 concentrations in Salt Lake City, Utah, J. Geophys. Res.-Atmos., 120, 147–166, 2015.
Mallia, D. V., Kochanski, A., Wu, D., Pennell, C., Oswald, W., and Lin, J. C.: Wind-blown dust modeling using a backward-Lagrangian particle dispersion model, J. Appl. Meteorol. Climatol., 56, 2845–2867, https://doi.org/10.1175/JAMC-D-16-0351.1, 2017.
Mandrake, L., Frankenberg, C., O'Dell, C. W., Osterman, G., Wennberg, P., and Wunch, D.: Semi-autonomous sounding selection for OCO-2, Atmos. Meas. Tech., 6, 2851–2864, https://doi.org/10.5194/amt-6-2851-2013, 2013.
Marland, G.: Uncertainties in accounting for CO2 from fossil fuels, J. Ind. Ecol., 12, 136–139, https://doi.org/10.1111/j.1530-9290.2008.00014.x, 2008.
Mitchell, L., Lin, J. C., Bowling, D. R., Pataki, D. E., Strong, C., Schauer, A. J., Bares, R., Bush, S., Stephens, B. B., Mendoza, D., Mallia, D. V, Holland, L., Gurney, K. R., and Ehleringer, J. R.: Long-term urban carbon dioxide observations reveal spatial and temporal dynamics related to urban characteristics and growth, P. Natl. Acad. Sci. USA, 115, 2912–2917, https://doi.org/10.1073/pnas.1702393115, 2018.
Nassar, R., Napier-Linton, L., Gurney, K. R., Andres, R. J., Oda, T., Vogel, F. R., and Deng, F.: Improving the temporal and spatial distribution of CO2 emissions from global fossil fuel emission data sets, J. Geophys. Res.-Atmos., 118, 917–933, https://doi.org/10.1029/2012JD018196, 2013.
Nassar, R., Hill, T. G., McLinden, C. A., Wunch, D., Jones, D. B. A., and Crisp, D.: Quantifying CO2 emissions from individual power plants from space, Geophys. Res. Lett., 44, 10045–10053, https://doi.org/10.1002/2017GL074702, 2017.
OCO-2 Science Team/Michael Gunson, Annmarie Eldering: OCO-2 Level 2 bias-corrected solar-induced fluorescence and other select fields from the IMAP-DOAS algorithm aggregated as daily files, Retrospective processing V7r, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), updated data available at: https://doi.org/10.5067/XR7ZWYSKP7D0, 2015.
O'Dell, C. W., Connor, B., Bösch, H., O'Brien, D., Frankenberg, C., Castano, R., Christi, M., Eldering, D., Fisher, B., Gunson, M., McDuffie, J., Miller, C. E., Natraj, V., Oyafuso, F., Polonsky, I., Smyth, M., Taylor, T., Toon, G. C., Wennberg, P. O., and Wunch, D.: The ACOS CO2 retrieval algorithm – Part 1: Description and validation against synthetic observations, Atmos. Meas. Tech., 5, 99–121, https://doi.org/10.5194/amt-5-99-2012, 2012.
Oda, T. and Maksyutov, S.: A very high-resolution (1 km×1 km) global fossil fuel CO2 emission inventory derived using a point source database and satellite observations of nighttime lights, Atmos. Chem. Phys., 11, 543–556, https://doi.org/10.5194/acp-11-543-2011, 2011.
Oda, T. and Maksyutov, S.: ODIAC Fossil Fuel CO2 Emissions Dataset (Version name: ODIAC2017), Center for Global Environmental Research, National Institute for Environmental Studies, https://doi.org/10.17595/20170411.001 (last access: 18 October 2017), 2015.
Oda, T., Ott, L., Topylko, P., Halushchak, M., Bun, R., Lesiv, M., Danylo, O., and Horabik-Pyzel, J.: Uncertainty associated with fossil fuel carbon dioxide (CO2) gridded emission datasets, 2015.
Oda, T., Maksyutov, S., and Andres, R. J.: The Open-source Data Inventory for Anthropogenic CO2, version 2016 (ODIAC2016): a global monthly fossil fuel CO2 gridded emissions data product for tracer transport simulations and surface flux inversions, Earth Syst. Sci. Data, 10, 87–107, https://doi.org/10.5194/essd-10-87-2018, 2018.
Olsen, S. C. and Randerson, J. T.: Differences between surface and column atmospheric CO2 and implications for carbon cycle research, J. Geophys. Res., 109, D02301, https://doi.org/10.1029/2003JD003968, 2004.
Pacala, S. W., Breidenich, C., Brewer, P. G., Fung, I., Gunson, M. R., Heddle, G., Marland, G., Paustian, K., Prather, M., Randerson, J. T., Tans, P., and Wofsy, S. C.: Verifying Greenhouse Gas Emissions: Methods to Support International Climate Agreements, Tech. rep., Committee on Methods for Estimating Greenhouse Gas Emissions, Washington, DC, 2010.
Palmer, P. I.: Quantifying sources and sinks of trace gases using space-borne measurements: current and future science, Philos. T. R. Soc. A, 366, 4509–4528, https://doi.org/10.1098/rsta.2008.0176, 2008.
Patra, P. K., Crisp, D., Kaiser, J. W., Wunch, D., Saeki, T., Ichii, K., Sekiya, T., Wennberg, P. O., Feist, D. G., Pollard, D. F., Griffith, D. W. T., Velazco, V. A., De Maziere, M., Sha, M. K., Roehl, C., Chatterjee, A., and Ishijima, K.: The Orbiting Carbon Observatory (OCO-2) tracks 2–3 peta-gram increase in carbon release to the atmosphere during the 2014–2016 El Niño, Sci. Rep., 7, 13567, https://doi.org/10.1038/s41598-017-13459-0, 2017.
Peters, W., Jacobson, A. R., Sweeney, C., Andrews, A. E., Conway, T. J., Masarie, K., Miller, J. B., Bruhwiler, L. M. P., Petron, G., Hirsch, A. I., Worthy, D. E. J., van der Werf, G. R., Randerson, J. T., Wennberg, P. O., Krol, M. C., and Tans, P. P.: An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker, P. Natl. Acad. Sci. USA, 104, 18925–18930, https://doi.org/10.1073/pnas.0708986104, 2007.
Peylin, P., Houweling, S., Krol, M. C., Karstens, U., Rödenbeck, C., Geels, C., Vermeulen, A., Badawy, B., Aulagnier, C., Pregger, T., Delage, F., Pieterse, G., Ciais, P., and Heimann, M.: Importance of fossil fuel emission uncertainties over Europe for CO2 modeling: model intercomparison, Atmos. Chem. Phys., 11, 6607–6622, https://doi.org/10.5194/acp-11-6607-2011, 2011.
Rayner, P. J. and O'Brien, D. M.: The utility of remotely sensed CO2 concentration data in surface source inversions, Geophys. Res. Lett., 28, 175–178, https://doi.org/10.1029/2000GL011912, 2001.
Rayner, P. J., Raupach, M. R., Paget, M., Peylin, P., and Koffi, E.: A new global gridded data set of CO2 emissions from fossil fuel combustion: Methodology and evaluation, J. Geophys. Res., 115, D19306, https://doi.org/10.1029/2009JD013439, 2010.
Reuter, M., Buchwitz, M., Hilker, M., Heymann, J., Schneising, O., Pillai, D., Bovensmann, H., Burrows, J. P., Bösch, H., Parker, R., Butz, A., Hasekamp, O., O'Dell, C. W., Yoshida, Y., Gerbig, C., Nehrkorn, T., Deutscher, N. M., Warneke, T., Notholt, J., Hase, F., Kivi, R., Sussmann, R., Machida, T., Matsueda, H., and Sawa, Y.: Satellite-inferred European carbon sink larger than expected, Atmos. Chem. Phys., 14, 13739–13753, https://doi.org/10.5194/acp-14-13739-2014, 2014.
Rodgers, C. D.: Inverse methods for atmospheric sounding: theory and practice, World scientific, Singapore, 2000.
Rolph, G., Stein, A., and Stunder, B.: Real-time Environmental Applications and Display sYstem: READY, Environ. Model. Softw., 95, 210–228, https://doi.org/10.1016/j.envsoft.2017.06.025, 2017.
Rosenzweig, C., Solecki, W., Hammer, S. A., and Mehrotra, S.: Cities lead the way in climate-change action, Nature, 467, 909–911, https://doi.org/10.1038/467909a, 2010.
Schneising, O., Heymann, J., Buchwitz, M., Reuter, M., Bovensmann, H., and Burrows, J. P.: Anthropogenic carbon dioxide source areas observed from space: assessment of regional enhancements and trends, Atmos. Chem. Phys., 13, 2445–2454, https://doi.org/10.5194/acp-13-2445-2013, 2013.
Seibert, P. and Frank, A.: Source-receptor matrix calculation with a Lagrangian particle dispersion model in backward mode, Atmos. Chem. Phys., 4, 51–63, https://doi.org/10.5194/acp-4-51-2004, 2004.
Shiga, Y. P., Michalak, A. M., Gourdji, S. M., Mueller, K. L., and Yadav, V.: Detecting fossil fuel emissions patterns from subcontinental regions using North American in situ CO2 measurements, Geophys. Res. Lett., 41, 4381–4388, https://doi.org/10.1002/2014GL059684, 2014.
Shiga, Y. P., Tadić, J. M., Qiu, X., Yadav, V., Andrews, A. E., Berry, J. A., and Michalak, A. M.: Atmospheric CO2 Observations Reveal Strong Correlation Between Regional Net Biospheric Carbon Uptake and Solar-Induced Chlorophyll Fluorescence, Geophys. Res. Lett., 45, 1122–1132, https://doi.org/10.1002/2017GL076630, 2018.
Silva, S. and Arellano, A.: Characterizing Regional-Scale Combustion Using Satellite Retrievals of CO, NO2 and CO2, Remote Sens., 9, 744, https://doi.org/10.3390/rs9070744, 2017.
Silva, S. J., Arellano, A. F., and Worden, H. M.: Toward anthropogenic combustion emission constraints from space-based analysis of urban CO2∕CO sensitivity, Geophys. Res. Lett., 40, 4971–4976, https://doi.org/10.1002/grl.50954, 2013.
Skamarock, W. C. and Klemp, J. B.: A time-split nonhydrostatic atmospheric model for weather research and forecasting applications, J. Comput. Phys., 227, 3465–3485, 2008.
Stein, A. F., Draxler, R. R., Rolph, G. D., Stunder, B. J. B., Cohen, M. D., and Ngan, F.: Noaa's hysplit atmospheric transport and dispersion modeling system, B. Am. Meteorol. Soc., 96, 2059–2077, https://doi.org/10.1175/BAMS-D-14-00110.1, 2015.
Stephens, B. B., Gurney, K. R., Tans, P. P., Sweeney, C., Peters, W., Bruhwiler, L., Ciais, P., Ramonet, M., Bousquet, P., Nakazawa, T., Aoki, S., Machida, T., Inoue, G., Vinnichenko, N., Lloyd, J., Jordan, A., Heimann, M., Shibistova, O., Langenfelds, R. L., Steele, L. P., Francey, R. J., and Denning, A. S.: Weak Northern and Strong Tropical Land Carbon Uptake from Vertical Profiles of Atmospheric CO2, Science, 316, 1732–1736, https://doi.org/10.1126/science.1137004, 2007.
Stohl, A., Forster, C., Frank, A., Seibert, P., and Wotawa, G.: Technical note: The Lagrangian particle dispersion model FLEXPART version 6.2, Atmos. Chem. Phys., 5, 2461–2474, https://doi.org/10.5194/acp-5-2461-2005, 2005.
Sun, Y., Frankenberg, C., Wood, J. D., Schimel, D. S., Jung, M., Guanter, L., Drewry, D. T., Verma, M., Porcar-Castell, A., Griffis, T. J., Gu, L., Magney, T. S., Kohler, P., Evans, B., and Yuen, K.: OCO-2 advances photosynthesis observation from space via solar-induced chlorophyll fluorescence, Science, 358, eaam5747, https://doi.org/10.1126/science.aam5747, 2017.
Sweeney, C., Karion, A., Wolter, S, Newberger, T, Guenther, D, Higgs, J. A., Andrews, A. E., Lang, P. M., Neff, D., Dlugokencky, E., and Miller, J. B.: Seasonal climatology of CO2 across North America from aircraft measurements in the NOAA/ESRL Global Greenhouse Gas Reference Network, J. Geophys. Res.-Atmos., 120, 5155–5190, 2015.
Tollefson, J.: Carbon-sensing satellite system faces high hurdles, Nature, 533, 446–447, 2016.
UNFCCC: National Inventory Submissions 2017, United Nations Framework Convention on Climate Change, available at: http://unfccc.int/national_reports/annex_i_ghg_inventories/national_inventories_submissions/items/9492.php, last access: June 2017.
Venables, W. N. and Ripley, B. D.: Random and mixed effects, in: Modern applied statistics with S, Springer, New York, NY, 271–300, 2002.
Verhulst, K. R., Karion, A., Kim, J., Salameh, P. K., Keeling, R. F., Newman, S., Miller, J., Sloop, C., Pongetti, T., Rao, P., Wong, C., Hopkins, F. M., Yadav, V., Weiss, R. F., Duren, R. M., and Miller, C. E.: Carbon dioxide and methane measurements from the Los Angeles Megacity Carbon Project – Part 1: calibration, urban enhancements, and uncertainty estimates, Atmos. Chem. Phys., 17, 8313–8341, https://doi.org/10.5194/acp-17-8313-2017, 2017.
Wheeler, D. and Ummel, K.: Calculating CARMA: Global Estimation of CO2 Emissions from the Power Sector, Work. Pap., 145, 37, available at: https://www.cgdev.org/publication/calculating-carma-global-estimation-co2-emissions-power-sector-working-paper-145 (last acess: 18 October 2017), 2008.
Wong, K. W., Fu, D., Pongetti, T. J., Newman, S., Kort, E. A., Duren, R., Hsu, Y.-K., Miller, C. E., Yung, Y. L., and Sander, S. P.: Mapping CH4: CO2 ratios in Los Angeles with CLARS-FTS from Mount Wilson, California, Atmos. Chem. Phys., 15, 241–252, https://doi.org/10.5194/acp-15-241-2015, 2015.
Worden, J. R., Doran, G., Kulawik, S., Eldering, A., Crisp, D., Frankenberg, C., O'Dell, C., and Bowman, K.: Evaluation and attribution of OCO-2 XCO2 uncertainties, Atmos. Meas. Tech., 10, 2759–2771, https://doi.org/10.5194/amt-10-2759-2017, 2017.
Wu, D., Lin, J., and Fasoli, B.: X-Stochastic Time-Inverted Lagrangian Transport model (“X-STILT” v1), available at: https://doi.org/10.5281/zenodo.1241514, 2018.
Wunch, D., Wennberg, P. O., Toon, G. C., Keppel-Aleks, G., and Yavin, Y. G.: Emissions of greenhouse gases from a North American megacity, Geophys. Res. Lett., 36, 1–5, https://doi.org/10.1029/2009GL039825, 2009.
Wunch, D., Wennberg, P. O., Toon, G. C., Connor, B. J., Fisher, B., Osterman, G. B., Frankenberg, C., Mandrake, L., O'Dell, C., Ahonen, P., Biraud, S. C., Castano, R., Cressie, N., Crisp, D., Deutscher, N. M., Eldering, A., Fisher, M. L., Griffith, D. W. T., Gunson, M., Heikkinen, P., Keppel-Aleks, G., Kyrö, E., Lindenmaier, R., Macatangay, R., Mendonca, J., Messerschmidt, J., Miller, C. E., Morino, I., Notholt, J., Oyafuso, F. A., Rettinger, M., Robinson, J., Roehl, C. M., Salawitch, R. J., Sherlock, V., Strong, K., Sussmann, R., Tanaka, T., Thompson, D. R., Uchino, O., Warneke, T., and Wofsy, S. C.: A method for evaluating bias in global measurements of CO2 total columns from space, Atmos. Chem. Phys., 11, 12317–12337, https://doi.org/10.5194/acp-11-12317-2011, 2011.
World Urbanization Prospects: The 2014 Revision (WUP 2014), United Nations, Department of Economic and Social Affairs, Population Division, CD-ROM Edition, 2014.
Ye, X., Lauvaux, T., Kort, E. A., Oda, T., Feng, S., Lin, J. C., Yang, E., and Wu, D.: Constraining fossil fuel CO2 emissions from urban area using OCO-2 observations of total column CO2, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2017-1022, in review, 2017.
Yokota, T., Yoshida, Y., Eguchi, N., Ota, Y., Tanaka, T., Watanabe, H., and Maksyutov, S.: Global Concentrations of CO2 and CH4 Retrieved from GOSAT: First Preliminary Results, Sola, 5, 160–163, https://doi.org/10.2151/sola.2009-041, 2009.
Zhao, C., Andrews, A. E., Bianco, L., Eluszkiewicz, J., Hirsch, A., MacDonald, C., Nehrkorn, T., and Fischer, M. L.: Atmospheric inverse estimates of methane emissions from Central California, J. Geophys. Res.-Atmos., 114, 1–13, https://doi.org/10.1029/2008JD011671, 2009.
Zuromski, L. M., Bowling, D. R., Köhler, P., Frankenberg, C., Goulden, M. L., Blanken, P. D., and Lin, J. C.: Solar-Induced Fluorescence Detects Interannual Variation in Gross Primary Production of Coniferous Forests in the Western United States, Geophys. Res. Lett., 45, 7184–7193, https://doi.org/10.1029/2018GL077906, 2018.
- Abstract
- Introduction
- Data and methodology
- Results
- Discussions
- Limitations and future plans
- Code availability
- Appendix A: Four conservative criteria to select overpasses over Riyadh
- Appendix B: Wind error calculation and regression-based transport error method in X-STILT
- Appendix C: Correcting for wind biases within X-STILT
- Appendix D: The determinations of MAXAGL and the cutoff level
- Appendix E: Factors that may influence observed or modeled enhancements/signals
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement
- Abstract
- Introduction
- Data and methodology
- Results
- Discussions
- Limitations and future plans
- Code availability
- Appendix A: Four conservative criteria to select overpasses over Riyadh
- Appendix B: Wind error calculation and regression-based transport error method in X-STILT
- Appendix C: Correcting for wind biases within X-STILT
- Appendix D: The determinations of MAXAGL and the cutoff level
- Appendix E: Factors that may influence observed or modeled enhancements/signals
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement





