the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluation of Monte Carlo tools for high-energy atmospheric physics II: relativistic runaway electron avalanches
Casper Rutjes
Gabriel Diniz
Alejandro Luque
Kevin M. A. Ihaddadene
Joseph R. Dwyer
Nikolai Østgaard
Alexander B. Skeltved
Ivan S. Ferreira
Ute Ebert
The emerging field of high-energy atmospheric physics studies how high-energy particles are produced in thunderstorms, in the form of terrestrial γ-ray flashes and γ-ray glows (also referred to as thunderstorm ground enhancements). Understanding these phenomena requires appropriate models of the interaction of electrons, positrons and photons with air molecules and electric fields. We investigated the results of three codes used in the community – Geant4, GRanada Relativistic Runaway simulator (GRRR) and Runaway Electron Avalanche Model (REAM) – to simulate relativistic runaway electron avalanches (RREAs). This work continues the study of Rutjes et al. (2016), now also including the effects of uniform electric fields, up to the classical breakdown field, which is about 3.0 MV m−1 at standard temperature and pressure.
We first present our theoretical description of the RREA process, which is based on and incremented over previous published works. This analysis confirmed that the avalanche is mainly driven by electric fields and the ionisation and scattering processes determining the minimum energy of electrons that can run away, which was found to be above ≈10 keV for any fields up to the classical breakdown field.
To investigate this point further, we then evaluated the probability to produce a RREA as a function of the initial electron energy and of the magnitude of the electric field. We found that the stepping methodology in the particle simulation has to be set up very carefully in Geant4. For example, a too-large step size can lead to an avalanche probability reduced by a factor of 10 or to a 40 % overestimation of the average electron energy. When properly set up, both Geant4 models show an overall good agreement (within ≈10 %) with REAM and GRRR. Furthermore, the probability that particles below 10 keV accelerate and participate in the high-energy radiation is found to be negligible for electric fields below the classical breakdown value. The added value of accurately tracking low-energy particles (<10 keV) is minor and mainly visible for fields above 2 MV m−1.
In a second simulation set-up, we compared the physical characteristics of the avalanches produced by the four models: avalanche (time and length) scales, convergence time to a self-similar state and energy spectra of photons and electrons. The two Geant4 models and REAM showed good agreement on all parameters we tested. GRRR was also found to be consistent with the other codes, except for the electron energy spectra. That is probably because GRRR does not include straggling for the radiative and ionisation energy losses; hence, implementing these two processes is of primary importance to produce accurate RREA spectra. Including precise modelling of the interactions of particles below 10 keV (e.g. by taking into account molecular binding energy of secondary electrons for impact ionisation) also produced only small differences in the recorded spectra.
- Article
(2507 KB) - Full-text XML
-
Supplement
(10296 KB) - BibTeX
- EndNote
1.1 Phenomena and observations in high-energy atmospheric physics
In 1925, Charles T. R. Wilson proposed that thunderstorms could emit a “measurable amount of extremely penetrating radiation of β or γ type” (Wilson, 1925), about 60 years before such radiation was observed from the atmosphere and from space (Fishman et al., 1994; Parks et al., 1981; Williams, 2010). This and subsequent observations and modelling are now being investigated within the field of high-energy atmospheric physics (HEAP). A review is provided by Dwyer et al. (2012).
Observationally different types of high-energy emissions have been identified coming from thunderclouds, naturally categorised by duration. Microsecond-long bursts of photons, which were first observed from space (Fishman et al., 1994; Grefenstette et al., 2009; Marisaldi et al., 2014; Roberts et al., 2018), are known as terrestrial γ-ray flashes (TGFs). TGFs also produce bursts of electron and positrons (Briggs et al., 2011; Dwyer et al., 2008; Sarria et al., 2016) that follow the geomagnetic field lines into space and show longer durations. Two space missions specifically designed to study TGFs and related phenomena will provide new observations in the near future: ASIM (Atmosphere-Space Interaction Monitor) (Neubert et al., 2006), successfully launched in April 2018, and TARANIS (Tool for the Analysis of Radiation from lightning and Sprites) (Lefeuvre et al., 2009; Sarria et al., 2017), which is to be launched at the end of 2019.
Seconds to minutes or even hours long X and γ radiation has been observed on the ground, from balloons and from aircraft (Adachi et al., 2008; Chilingarian et al., 2010, 2011; Dwyer et al., 2015; Eack et al., 1996; Kelley et al., 2015; Kochkin et al., 2017, 2018; McCarthy and Parks, 1985; Torii et al., 2002; Tsuchiya et al., 2007); these are called γ-ray glows or thunderstorm ground enhancements. Some modelling attempts of both γ-ray and electron observations are also presented in Chilingarian et al. (2012).
TGFs were predicted to create a neutron emission on the millisecond duration, with associated isotope production (Babich, 2006). Such emission was observed from the ground (Bowers et al., 2017; Teruaki et al., 2017). A similar phenomenon was modelled at higher altitudes by Rutjes et al. (2017), who also proposed to call it “TGF afterglow”.
Following the idea of Wilson (1925), high-energy X and γ radiation is created by runaway electrons, which may further grow by the effect of Møller scattering in the form of so-called relativistic runaway electron avalanches (RREAs) (Gurevich et al., 1992). For the multiplication to occur, a threshold electric field of Eth=0.28 MV m−1 (at standard temperature and pressure; STP) is required (Babich et al., 2004a; Dwyer, 2003).
The difference in duration between TGFs and γ-ray glows can be explained by two possible scenarios to create runaway electrons, which is traditionally illustrated using the average energy loss or friction curve (see, e.g. Fig. 1 of Dwyer et al., 2012). In this curve, there is a maximum at around ε≈123 eV, illustrating the scenario that for electric fields higher than a critical electric field, of Ec≈26 MV m−1 at STP, thermal electrons can be accelerated into runaway regime, described in the so-called cold runaway theory (Gurevich, 1961). The effective value of Ec may be significantly lower, as electrons could overcome the friction barrier due to their intrinsic random interactions (Chanrion et al., 2016; Lehtinen et al., 1999; Li et al., 2009; Liu et al., 2016). Cold runaway could happen in the streamer phase (Chanrion and Neubert, 2010; Li et al., 2009; Moss et al., 2006) or leader phase (Celestin and Pasko, 2011; Celestin et al., 2012; Chanrion et al., 2014; Köhn and Ebert, 2015; Köhn et al., 2014, 2017) of a transient discharge, explaining the high-energy electron seeding that will evolve to RREAs and produce γ rays by bremsstrahlung emission from the accelerated electrons. The cold runaway mechanism may be further investigated with laboratory experiments, in high-voltage and pulsed plasma technology, and may be linked to the not fully understood X-ray emissions that have been observed during nanosecond pulsed discharge and the formation of long sparks (Dwyer et al., 2008; Kochkin et al., 2016; Rahman et al., 2008; Shao et al., 2011, and references therein), with different possible production mechanisms that were proposed and tested using analytical modelling (Cooray et al., 2009) and computer simulations (Ihaddadene and Celestin, 2015; Lehtinen and Østgaard, 2018; Luque, 2017). Alternatively, the relativistic feedback discharge model is also proposed to explain TGF production using large-scale and high-potential electric fields (Dwyer, 2012), where the RREA initial seeding may be provided by cosmic-ray secondaries, background radiation or cold runaway (Dwyer, 2008).
For fields significantly below the thermal runaway critical electric field Ec≈26 MV m−1 but above the RREA threshold electric field of Eth=0.28 MV m−1 (at STP), runaway behaviour is still observed in detailed Monte Carlo studies (see Dwyer et al., 2012, and references therein). At thundercloud altitudes, cosmic particles create energetic electrons that could run away in patches of the thundercloud where the electric field satisfies this criterion. RREAs are then formed if space permits and could be sustained with feedback of photons and positrons creating new avalanches (Babich et al., 2005; Dwyer, 2007, 2012). The γ-ray glows could be explained by this mechanism, as they are observed irrespectively of lightning or observed to be terminated by lightning (Chilingarian et al., 2015; Kelley et al., 2015; Kochkin et al., 2017; McCarthy and Parks, 1985). The fact that γ-ray glows are not (necessarily) accompanied by classical discharge results in the conclusion that the electric fields causing them are usually also below the conventional breakdown. The conventional (or classical) breakdown field of Ek≈3.0 MV m−1 (at STP) is where low-energy electrons (<123 eV) exponentially grow in number as ionisation overcomes attachment. This exponential growth of charged particles will affect the electric field, which requires a self-consistent simulation to be properly taken into account. That is not something we want to test in this study, since Geant4 is not capable of simulating it. Therefore, we will focus on electric fields below the breakdown field (Ek≈3.0 MV m−1) and above the RREA threshold (Eth≈0.28 MV m−1).
As a note, one can find in the literature that Ek can be given between 2.36 and 3.2 MV m−1 (Raizer, 1997), the theoretical lowest breakdown field being between 2.36 and 2.6 MV m−1 (Raizer, 1997). The value of ≈3.2 MV m−1 is the measured breakdown field in centimetre gaps in laboratory spark experiments (Raizer, 1997), which can be lower for longer gaps.
1.2 Theoretical understanding of RREAs
In the energy regime of a kilo-electronvolt (keV) to a hundred mega-electronvolts (MeV), the evolution of electrons is mostly driven by electron impact ionisation (Landau et al., 2013), as this energy loss channel is much larger than the radiative (bremsstrahlung) energy loss. However, the bremsstrahlung process does impact the shape of the electron energy spectrum that can be understood by the straggling effect, which is discussed in the next section. When the electric field is below the classical breakdown Ek≈3.0 MV m−1 (at STP), the system can be simplified, because the effect of the electrons below a certain energy can be neglected, in particular the population that would otherwise (if E>Ek) multiply exponentially and have an important effect on the electric field. The part of the electron population that decelerates, and eventually attaches, cannot contribute to the production of the high-energy radiation. Let be the minimum energy for a secondary electron to have a chance to run away and thus participate in the production of high-energy radiation. The subscript index i=2 indicates a secondary electron. A precise value of will be evaluated in Sect. 3 with the help of simulations, but, by looking at the friction curve, one can guess it is located in the keV to tens of keV energy regime (Dwyer et al., 2012). As almost all energy loss of ionisation is going into producing secondary electrons of lower energy (ϵ2 ≲ 200 eV), it is reasonable to approximate that channel as continuous energy loss or friction.
In the case of electric fields above the RREA threshold (Eth=0.28 MV m−1 at STP), the electrons, when considered as a population, will undergo avalanche multiplication. Some individual electrons do not survive (because there can be hard bremsstrahlung or ionisation collisions that will remove enough energy to get below ), but the ensemble grows exponentially as new electrons keep being generated from the ionisation collisions on air molecules, including a fraction with energy larger than . The production of secondaries with energies much larger than the ionisation threshold (a few kilo-electronvolts being a reasonable value) can be described using the Møller cross-section, which is the exact solution for a free–free electron–electron interaction (see, e.g. Landau et al., 2013, p. 321):
where Z is the number of electrons in the molecule, the index i=1 indicates the primary electron, i=2 the secondary, γi is the Lorentz factor, is the kinetic energy divided by the electron rest energy (with rest mass me) and m is the classical electron radius. In the case of and δ2≪1, we observe that the term is dominating. Thus, we can write Eq. (1) as
with the velocity of the primary particle. Integrating Eq. (2) from δ2 to the maximum energy (ϵ1∕2) yields the production rate
using again ϵ2≪ϵ1. The remaining sensitivity of σprod in units of area to the primary particle is given by the factor , which converges strongly to 1 as the mean energy of the primary electrons exceeds 1 MeV. In other words, as the mean energy of the electrons grows towards even more relativistic energies, the production rate σprod becomes independent of the energy spectrum.
For illustrative purposes, we now consider the one-dimensional deterministic case, which results in an analytical solution of the electron energy spectrum. We make the system deterministic by assuming that the differential cross-section is a delta function at (the minimum energy at which a secondary electron can run away) and use as the constant collision length, with N the air number density. In other words, every length Λprod a secondary electron of energy is produced. The derivation below is close to what was presented by Celestin and Pasko (2010), Dwyer et al. (2012), Skeltved et al. (2014) and references therein.
Consider a population of electrons in one dimension with space coordinate z, a homogeneous and constant electric field E above the RREA threshold and a friction force F(ϵ). The minimum energy at which an electron can run away is given by the requirement (where q is the elementary charge); that is to say, is constant. Assuming that the mean energy of the ensemble is relativistic results in a constant production rate Λprod=Λprod(ϵmin). Thus, in space, the distribution fe grows exponentially as
While in energy, the differential equation is given by the net force:
Solving for steady state means
and using Eqs. (4) and (5) results in
For the largest part of the energy spectrum, specifically above 0.511 MeV and below 100 MeV, F(ϵ) is not sensitive to ϵ (e.g. see Rutjes et al., 2016). Only at around ϵ≈100 MeV electron energy F(ϵ) starts increasing again because of the bremsstrahlung process. Thus, one may assume F(ϵ)≈F constant, which yields that the RREA energy spectrum f(ϵ) at steady state is given by
with the exponential shape parameter and approximated average energy given by
Equivalently, in terms of collision frequency , Eq. (9) can be written as
with β the velocity v∕c of the RREA avalanche front. For the 1-D case, there is no momentum loss or diffusion, so β≈1. Note that Λprod depends on (the minimum energy at which a secondary electron can run away), which depends on the electric field E as that determines the minimum electron energy that can go into a runaway regime. In this analysis, we illustrate with Eqs. (8) and (9) that the full RREA characteristics, such as the mean energy or the collision length Λprod (directly related to the avalanche length scale λ discussed in Sect. 4.1), are driven by processes determining .
In reality, there are important differences compared to the one-dimensional deterministic case described previously, which we propose to discuss qualitatively for understanding the Monte Carlo simulations evaluated in this study. During collisions, electrons deviate from the path parallel to E. Therefore, in general, electrons experience a reduced net electric field as the cosine function of the opening angle θ, which reduces the net force to qEcos(θ)−F and thereby the mean energy of Eq. (9). In reality, the 3-D scattering (with angle parameter θ) changes of the path of the particle. Although the velocity remains still close to c (as the mean energy is still larger than several MeV), the RREA front velocity parallel to the electric field (E) is reduced again because of the opening angle as function of its cosine:
which also reduces the mean energy . Note that θ is not a constant and may change with each collision. Equivalently, the avalanche scale length Λprod in 3-D changes to . However, most importantly, the momentum-loss of the lower energetic electrons results in a significant increase of , as it is much harder for electrons to run away. The increase of significantly increases Λprod and thereby increases the characteristic mean energy . On the other hand, the stochasticity creates an interval of possible energies () that can run away with a certain probability and for thin targets a straggling effect (Rutjes et al., 2016). A recent article discussed the influence of the angular scattering of electrons on the runaway threshold in air (Chanrion et al., 2016).
The effects discussed above prevent a straightforward analytical derivation of the RREA characteristics in three dimensions, but what remains is the important notion that the physics is completely driven by the intermediate energy electron production. “Intermediate” means they are far above ionisation threshold (≫123 eV) but much below relativistic energies (≪1 MeV). The parameterisation of the electron energy spectrum, given by Eq. (9), turns out to be an accurate empirical fit, as it was already shown in Celestin and Pasko (2010), Dwyer et al. (2012), Skeltved et al. (2014) and references therein. Nevertheless, in these works, λmin(E), or equivalently the velocity over collision frequency (βc∕νprod), is fitted by numerical Monte Carlo studies, and the final direct relation to is not executed. Celestin and Pasko (2010) calculated that νprod(E)∝E and thus explains why must saturate to constant value. Celestin and Pasko (2010) argue that is given by the deterministic friction curve F for which they use the Bethe formula and an integration of a more sophisticated electron impact ionisation cross-section (RBEB) including molecular effects, but that is only true in one dimension without stochastic fluctuations. Other attempts to simulate RREA by solving the kinetic equation instead of using Monte Carlo methods are presented in Roussel-Dupre et al. (1994), Gurevich and Zybin (1998), Babich et al. (2001) and references therein. An analytical approach is provided by Cramer et al. (2014).
1.3 Model reductions and previous study
Apart from analytical calculations, the physics behind TGFs, TGF afterglows and γ-ray glows are also studied with the help of experimental data, computer simulations and often a combination of both. Simulations necessarily involve model reduction and assumptions. As we argued previously, in scenarios where the electric field is below the classical breakdown field (Ek≈3.0 MV m−1 at STP), electrons below a certain energy can be neglected, because they will decelerate and eventually attach, thus not contributing to the production of the hard radiation. In Monte Carlo simulations, it is therefore common to apply a so-called “low-energy cutoff” (or threshold), noted as εc, which is a threshold where particles with lower energy can be discarded (or not produced) to improve code performance. It is different from (the minimum energy at which a secondary electron can run away) as one is a simulation parameter and the other is a physical value. Ideally, εc should be set as close as possible to . A second simplification can be made for the energetic enough particles that stay in the ensemble by treating collisions that would produce particles below the low-energy cutoff as friction.
Both simplifications can be implemented in different ways, leading to different efficiencies and accuracies. Rutjes et al. (2016) benchmarked the performance of the Monte Carlo codes Geant4 (Agostinelli et al., 2003), EGS5 (Hirayama et al., 2005) and FLUKA (Ferrari et al., 2005) developed in other fields of physics, and of the custom-made GRanada Relativistic Runaway simulator (GRRR) (Luque, 2014) and MC-PEPTITA (Sarria et al., 2015) codes within the parameter regime relevant for HEAP, in the absence of electric and magnetic fields. In that study, they focused on basic tests of electrons, positrons and photons with kinetic energies between 100 keV and 40 MeV through homogeneous air using a low-energy cutoff of 50 keV and found several differences between the codes and invited other researchers to test their codes on the provided test configurations. We found that the usage of average friction fails in the high-energy regime (≳100 keV), as the energy loss is averaged too much, resulting in an incorrect energy distribution (Rutjes et al., 2016).
As we indicated in Sect. 1.2, the ionisation energy loss channel is much larger than the radiative (bremsstrahlung) energy loss, by a few orders of magnitude. However, this is only true for the average, and bremsstrahlung does have a significant effect on the electron spectrum because of straggling (Rutjes et al., 2016). This straggling effect was first studied by Bethe and Heitler (1934). If it is not taken into account in the implementation of the low-energy cutoff, the primary particle suffers a uniform (and deterministic) energy loss. This means that only the energy of the primary particle is altered, but not its direction. The accuracy of the assumed uniform energy loss is a matter of length scale: on a small length scale, the real energy loss distribution (if all interactions are considered explicitly) among the population would have a large spread. One way to obtain an accurate energy distribution is by implementing stochastic friction mimicking the straggling effect.
Rutjes et al. (2016) also indicated that including electric fields in the simulations would potentially enhance the differences found by introducing new errors, the simulation results being supposedly sensitive to the low-energy cutoff. This effect is believed to be responsible of the observed differences between the two Geant4 physics lists tested in Skeltved et al. (2014): for all fields between 0.4 and 2.5 MV m−1 (at STP), they found that the energy the spectrum and the mean energy of runaway electrons depended on the low-energy cutoff, even when it was chosen between 250 eV and 1 keV. In the following, this interpretation is challenged.
1.4 Content and order of the present study
In the context of high-energy atmospheric physics, the computer codes that were used are either general purpose codes developed by large collaborations or custom-made codes programmed by smaller groups or individuals. Examples of general purpose codes that were used are Geant4 (Bowers et al., 2017; Carlson et al., 2010; Sarria et al., 2015, 2017; Skeltved et al., 2014; Østgaard et al., 2008) and FLUKA (Dubinova et al., 2015; Rutjes et al., 2017). Custom-made codes were used in Roussel-Dupre et al. (1994), Lehtinen et al. (1999), Dwyer (2003), Babich et al. (2004b), Østgaard et al. (2008), Celestin and Pasko (2011), Luque (2014), Köhn et al. (2014), Chanrion et al. (2014) and Sarria et al. (2015), among others. Rutjes et al. (2016) presented in their Sect. 1.3 the reasons why different results between codes (or models) can be obtained and why defining a comparison standard (based on the physical outputs produced by the codes) is the easiest way (if not the only) to compare and verify the codes. Here, we continue the work of Rutjes et al. (2016), now with electric fields up to the classical breakdown field (Ek≈3.0 MV m−1). As mentioned previously, we chose not to use larger electric fields because that would produce an exponential growth of low-energy electrons (<123 eV) which would affect the electric field and therefore require a self-consistent simulation that Geant4 is not capable of. We aim to provide a comparison standard for the particle codes able to simulate relativistic runaway electron avalanches, as simply and informatively as possible, by only considering their physical outputs. These comparison standards are described in the Supplement (Sects. S1 and S2).
In Sect. 1.2, we illustrated that the full RREA characteristics, such as the mean energy or the collision length Λprod, are driven by processes determining (the minimum energy at which a secondary electron can run away). To prove this insight, and to benchmark codes capable of computing RREA characteristics for further use, we calculated the probability for an electron to accelerate into the runaway regime (see Sect. 3), which is closely related to the quantity . From this probability study, it is directly clear that it is safe to choose the low-energy cutoff εc higher than previously expected by Skeltved et al. (2014) and Rutjes et al. (2016), given an electric field E<Ek. In Sect. 3, we will demonstrate that the probability for particles below 10 keV to accelerate and participate in the penetrating radiation is actually negligible. Thus, in practice, an energy threshold value of εc≈10 keV can be used for any electric field below Ek. However, in Sect. 2.4, we will show that step-length restrictions are of major importance (e.g. it can lead to an underestimation of a factor of 10 of the probability to produce a RREA, in some cases). The results of the comparison of several parameters of the RREAs produced by the four tested codes is then presented in Sect. 4. We conclude in Sect. 5.
The test set-ups of the two types of simulations (RREA probability and RREA characteristics) are described in the Supplement, together with the data we generated and figures in the Supplement comparing several characteristics of the showers. The Geant4 source codes used in this study are also provided (see Sects. 6 and 7).
The data we discuss in the next sections were produced by the general purpose code Geant4 (with several set-ups) and two custom-made codes – GRRR and Runaway Electron Avalanche Model (REAM) – which we describe below. However, we do not describe comprehensively all the processes, models or cross-sections used by the different codes, but provide, in Sect. S13 in the Supplement, a table mentioning all implemented processes and models, including all references.
2.1 Geant4
Geant4 is a software toolkit developed by the European Organization for Nuclear Research (CERN) and a worldwide collaboration (Agostinelli et al., 2003; Allison et al., 2006, 2016). We use version 10.2.3. The electromagnetic models can simulate the propagation of photons, electrons and positrons including all the relevant processes and the effect of electric and magnetic fields. Geant4 uses steps in distance, whereas REAM and GRRR use time steps. In the context of this study, three main different electromagnetic cross-section sets' implementations are included: one based on analytical of semi-analytical models (e.g. using the Møller cross-section for ionisation and Klein–Nishina cross-section for Compton scattering), one based on the Livermore data set (Perkins et al., 1991) and one based on the Penelope models (Salvat et al., 2011). Each of them can be implemented with a large number of different electromagnetic parameters (binning of the cross-section tables, energy thresholds, production cuts, maximum energies, multiple scattering factors and accuracy of the electromagnetic field stepper, among others), and some processes have multiple models in addition to the main three, e.g. the Monash University model for Compton scattering (Brown et al., 2014). Skeltved et al. (2014) used two different physics lists: low- and high-energy physics (LHEP) and low background experiments (LBE). The first one, based on parameterisation of measurement data and optimised for speed, was deprecated since the 10.0 version of the toolkit. The LBE physics list is based on the Livermore data, but it is not considered as the most accurate electromagnetic physics list in the Geant4 documentation, which is given by the Option 4 physics list (O4). This last uses a mix of different models and in particular the Penelope model for the impact ionisation of electrons. For this study, we will use two GEANT4 physics list options: Option 4 (referred to as simply O4 hereafter), which is the most accurate one according to the documentation, and Option 1 (referred to as simply O1 hereafter), which is less accurate but runs faster. In practice, O1 and O4 give very similar results for simulations without electric field and energies above 50 keV, as produced in our previous code comparison study (Rutjes et al., 2016).
By default, Geant4 follows all primary particles down to zero energy. A primary particle is defined as a particle with more energy than a threshold energy (which is different from εc described before). By default, is set to 990 eV and was not changed to obtain the results presented in the next sections. The LBE physics list used by Skeltved et al. (2014) uses a threshold down to 250 eV (i.e. more accurate than using 990 eV, in principle) and this parameter was thought to be responsible for a major change in the accuracy of the obtained RREA energy spectra. In Sect. 3, we will argue that the most important factor able to effect the spectra obtained from Geant4 simulations is the accuracy of the stepping method for the tracking of the electrons and not the low-energy threshold. Actually, we found that the stepping accuracy of the simulation is indirectly improved by reducing , which explains why Skeltved et al. (2014) could make this interpretation.
2.2 GRRR
The GRRR is a time-oriented code for the simulation of energetic electrons propagating in air and can handle self-consistent electric fields. It is described in detail in the Supplement of Luque (2014) and its source code is fully available in a public repository (see the “Code and data availability” section). In the scope of this work, we want to point out three important features. (1) Electron ionisation and scattering processes are simulated discretely, and the friction is uniform and without a way to mimic the straggling effect. (2) Bremsstrahlung collisions are not explicit and are simulated as continuous radiative losses, without straggling. (3) GRRR uses a constant time step Δt both for the integration of the continuous interactions using a fourth-order Runge–Kutta scheme and for determining the collision probability of each discrete process k as νkΔt, where νk is the collision rate of process k. This expression assumes that νkΔt≪1 and therefore that the probability of a particle experiencing two collisions within Δt is negligibly small. The collisions are sampled at the beginning of each time step, and therefore the rate νk is calculated using the energy at that instant. In this work, we used Δt=0.25 ps for the avalanche probability simulations and Δt=1 ps for the simulations used to characterise the RREA. For both cases, the time steps are small enough to guarantee a very accurate integration.
2.3 REAM
REAM is a three-dimensional Monte Carlo simulation of the relativistic runaway electron avalanche (also referred to as runaway breakdown), including electric and magnetic fields (Cramer et al., 2016; Dwyer, 2003, 2007). This code is inspired by earlier work by Lehtinen et al. (1999) and takes accurately into account all the important interactions involving runaway electrons, including energy losses through ionisation, atomic excitation and Møller scattering. A shielded-Coulomb potential is implemented in order to fully model elastic scattering, and it also includes the production of X/γ rays from radiation energy loss (bremsstrahlung) and the propagation of the photons, by including photoelectric absorption, Compton scattering and electron–positron pair production. The positron propagation is also simulated, including the generation of energetic seed electrons through Bhabha scattering. The bremsstrahlung photon emissions from the newly produced electrons and positron are also included.
In the scope of this study, it is important to point out that REAM limits the time step size of the particles so that the energy change within one time step cannot be more than 10 %. The effect of reducing this factor down to 1 % was tested and did not make any noticeable difference in the resulting spectra. The comparative curves are presented in Sect. S10 in the Supplement.
2.4 Stepping methodology
2.4.1 General method
In Monte Carlo simulations, particles propagate in steps, collide and interact with surrounding media by means of cross-sections (and their derivatives). A step is defined by the displacement of a particle between two collisions. As it is presented in Sects. 3 and 4, the stepping methodology is responsible for most of the differences we observed between the codes we tested. Simulations can be either space-oriented or time-oriented, if the stepping is done in space or in time. By construction, space-oriented simulations are thus not synchronous in time. Usually, a single particle is simulated until it goes below the low-energy threshold (εc) chosen by the user. However, there are exceptions, like Geant4, that by default follow all primary particles down to zero energy. The advantage of asynchronous simulations is the ability to easily include boundaries to have particles step as far as possible in the same material (minimising the overhead due to null collisions) and smaller memory usage since there is no need to store all the particles alive at a given time (which may be a million or more). However, asynchronous simulations make it impossible to incorporate particle-to-particle interactions, such as a space charge electric field, or self-consistent electric fields.
During steps, charged particles can lose energy (and momentum) by collisions and also change in energy (and momentum) when an electric fields is present. To guarantee accuracy, energies should be updated frequently enough. An accurate method would be to exponentially sample step lengths with
in space-oriented perspective or
in time-oriented perspective, with v the velocity, σt the total cross-section and N the number density of the medium. Then, at each updated location (and energy), the type of collision must be sampled from probability distributions. The probability of having a collision of the given process (“pr”) can be calculated with
where the index i refers to the beginning of the step and f to its end, ℓ is the step length variable along the trajectory, and dℓ is an infinitesimal step length. For time-oriented simulations, we have equivalently
Using these probabilities along a given step length or duration, there is a chance that no interactions happen, but the energy of the particle is guaranteed to be updated correctly.
2.4.2 The case of Geant4
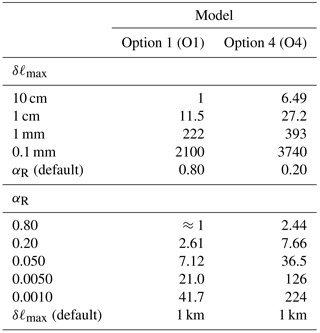
In the Geant4 documentation, the stepping method presented in the previous section is referred to as the “the integral approach to particle transport”. This method is set up by default in Geant4 for impact ionisation and bremsstrahlung. However, the way it is implemented does not exactly follow what was described in the previous section. The description of the exact implementation is out of the scope of this article but is presented in detail in Ivanchenko et al. (1991) and Apostolakis et al. (2009). The method relies on determining the maximum of the cross-section over the step (σmax) using a parameter αR (called “dR over range” in the Geant4 documentation) that is also used to determine the step lengths. Another related parameter is the maximum range parameter (ρmax), set to the default values of 1 and 0.1 mm for O1 and O4, respectively, and was never changed in the scope of this study. The exact definition of these parameters is given in Allison et al. (2016) and in the online Geant4 documentation (available at https://geant4.web.cern.ch/support/user_documentation, last access: 31 October 2018). The default value of αR is set to 0.80 for O1 and to 0.20 for O4. We found that both values are not low enough to be able to produce accurate results for the RREA probability simulations presented in the next section. To make Geant4 able to produce accurate RREA simulations using the multiple scattering algorithm, two methods are possible.
The first method is to tweak the value of the αR parameter. Its value is set to 0.80 by default for O1 and to 0.20 by default for O4. We found that these default values are way too high to be able to produce accurate RREA simulations, and values of should be used, as presented in the next section.
The second method is to implement a step limiter process (or maximum acceptable step). By default, this max step (δℓmax) is set to 1 km, and such a large value has no effect in practice, since the mean free path of energetic electrons in STP air is orders of magnitude smaller. Acceptable values of δℓmax depend on the electric field, and we found that it should be set to 1 mm or less to produce accurate RREA simulations, as presented in the next section. However, using this method results in relatively long simulation time required to achieve an acceptable accuracy, as the step is not adapted to the energy of the electrons. For information, the relative impact on performance (in terms of requirements of computation time) of tweaking the δℓmax and αR parameters is presented in Appendix A.
As a first comparison test, we estimated the probability for an electron to accelerate into the runaway regime and produce a RREA, given its initial energy ϵ and some electric field magnitude E. Note that the momentum of the initial electrons is aligned along the opposite direction of the electric field, so that it gets accelerated. That gives maximum RREA probabilities, as other alignments reduce the chance to produce a shower (see, e.g. Lehtinen et al., 1999, Fig. 2.6). We defined this probability as the fraction of initial (seed) electrons that created an avalanche of at least 20 electrons above 1 MeV. Once this state is reached, there is no doubt the RREA is triggered and can go on forever if no limits are set. The number 20 is arbitrary to be well above 1 but small enough for computational reasons. For some initial conditions, we also tested requirements of 30 and 50 electrons above 1 MeV, which resulted in very similar probabilities. This study is somewhat similar to the works presented in Lehtinen et al. (1999), Li et al. (2009), Liu et al. (2016) and Chanrion et al. (2016), but they all looked at the probability to have only a single runaway electron, whereas we used the criterion of N=20 electrons above 1 MeV, which is a stricter constraint. The difference between the two criteria is mainly noticeable for low electric field (<0.4 MV m−1) and high seed energies (>700 keV). A figure illustrating how the probability can change with N is presented in Sect. S5.3 in the Supplement.
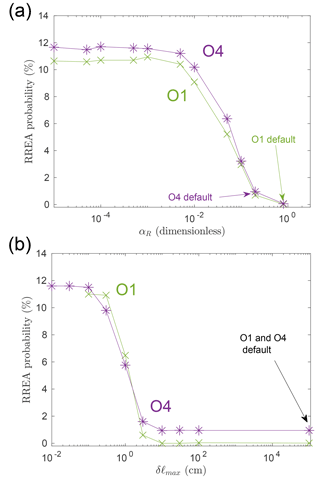
Figure 1Relativistic avalanches probabilities calculated from Geant4 simulations for a specific point (illustrated by a cross in Fig. 2) and for two stepping settings. (a) Avalanche probability versus αR setting for Geant4 O4 and Geant4 O1. δℓmax is set to the default value of 1 km. (b) Avalanche probability versus maximum step setting (δℓmax) for Geant4 O4 and Geant4 O1. The parameter αR is set to the default value of the models, which is 0.8 for O1 and 0.2 for O4.
As a test case, we calculated the probability to produce RREAs as a function of αR and δℓmax (these parameters are presented in the previous section) for the configuration ϵ=75 keV, E=0.80 MV m−1. This case was chosen because it showed a particularly large sensitivity to the stepping methodology, as discussed later. The results are presented in Fig. 1. Although this configuration has a very low RREA probability for O1 and O4 by default (where αR, respectively, is equal to 0.80 and 0.20, and δℓmax is 1 km for both), the probability increases as αR decreases and converges to a value between 10 % and 12 % for both models when . The same effect is observed when reducing δℓmax. In this case, the user should not set δℓmax below the maximum range parameter, which is set to 1 mm for O1 and 0.1 mm for O4 by default (and never changed in the scope of this article). When reducing the αR parameter to arbitrarily small values, both Geant4 models converge to slightly different probabilities: 10.7 % for O1 and 11.7 % for O4. We think this small difference is not due to the stepping method, as reducing ρmax or αR further does not produce a significant difference. It is a probability due to other factors, in particular the difference in the physical models and cross-section sets used. We encourage other researchers to check if their simulations produce a RREA probability for this {ϵ, E} setting that is consistent with our result.

Figure 2(a) Relativistic avalanche probability comparison between GRRR, REAM, O4 and O1. It shows three contour lines at 10 %, 50 % and 90 % as functions of seed (primary) energy ϵ and electric field magnitude E. These contours are derived from the full probability scans that are presented in the Supplement (Sect. S5). The cross at highlights the point where we studied the effect of the simulation stepping parameters (for O4 and O1) on the probability; see Fig. 1. (b) Five contour lines indicating the 0 %, 10 %, 50 %, 90 % and 100 % probabilities to generate a RREA as function of ϵ and E for the Geant4 O4 model for which we could run a very large number of initial electrons (> 50 000) to obtain curves with a very low noise level.
As explained in Sect. 1.2, the final electron spectrum is essentially driven by the minimum energy of electrons that can create a RREA. Here, we can clearly see this probability is strongly affected by the choice of the αR and δℓmax simulation parameters, affecting the accuracy of the stepping method, and that the values set by default for these parameters are not precise enough to obtain correct RREA probabilities. In order to help future researchers, we provide example Geant4 source codes where the αR and δℓmax parameters can be changed and their effect to be tested (see Sect. 6 and the “Code and data availability” section).
In Fig. 2a, we compare the contour lines of the 10 %, 50 % and 90 % probability of triggering a RREA as function ϵ and E for the four models: Geant4 O4 (), Geant4 O1 (), GRRR and REAM. The full RREA probability results in the ϵ, E domain for each model are presented in Sect. S5 in the Supplement.
The most important difference between Geant4 and GRRR is present for energies >200 keV and E fields <0.5 MV m−1. At 1 MeV, the level curves are significantly different between the Geant4 models and GRRR: the 50 % probability to trigger RREA for GRRR is approximately located at the 10 % probability for O4 and at the 90 % probability for GRRR is located at the 50 % probability for O1. The reason is probably similar to a point we raised in our previous study (Rutjes et al., 2016): GRRR does not include a way to simulate the straggling effect for the ionisation process. By looking at Fig. 2 of Rutjes et al. (2016), we can see that 200 keV is roughly the energy from where the difference in the spectrum of GRRR, compared to codes that simulate straggling, starts to become significant.
For low electron energy (<40 keV) and high electric field (>2 MV m−1), GRRR and O4 present good agreement; however, O1 deviates significantly from O4. We investigated the effects of the stepping parameters (αR, δℓmax and ρmax) and it is clear that they were not involved in this case. We think the Møller differential cross-section (with respect to the energy of the secondary electron) used by O1 and extrapolated down to low energies leads to the production of secondary electrons with average energies lower than the Penelope model (used by O4), which includes the effects of the atomic electron shells, and hence is probably more accurate. This hypothesis is confirmed by looking at the shape of the differential cross-sections of impact ionisation, whose plots are presented in Sect. S11.4 in the Supplement.
The RREA probability data for REAM are also displayed in Fig. 2a as the red curves. The three REAM level curves show significantly higher noise than the Geant4 data, mainly because the latter used 1000 electron seeds, whereas the former used only 100. The algorithms used to calculate the level curves were also found to impact the noise level. Nevertheless, the noise level is low enough to be able to evaluate the consistency between the codes. REAM shows a consistency with Geant4 (O1 and O4) within less than 12 % in the full parameter range and less than 5 % in some part of it. The most apparent deviations between REAM and Geant4 O1/O4 can be noticed for a seed electron energy range between 50 and 300 keV, for the 50 % and 90 % level curves, where there is a systematic, statistically significant difference in the probability for REAM compared to Geant4 (REAM requiring about a 10 % larger electric field or primary electron energy to reach the 90 % or 50 % contour levels). However, we do not expect such a small difference to significantly affect the characteristics of the RREA showers, such as the multiplication factors or the mean energies of the RREA electrons. To test this quantitatively, a detailed comparison of the most important characteristics of the RREA showers obtained with the four models is presented in the following section.
In Fig. 2b, we show the 0 %, 10 %, 50 %, 90 % and 100 % probability contour lines for the Geant4 O4 model where we could run a very large number of initial electrons (“seeds”) to obtain curves with a very low noise level. These are the most accurate probabilities we could obtain. From this figure, it is clear that the RREA probability for an electron of less than ≈10 keV is null for any electric field below Ek≈3.0 MV m−1. Therefore, 10 keV is a reasonable a lower boundary of (the minimum energy at which a secondary electron can run away), and any simulation with an electric field below Ek≈3.0 MV m−1 could use an energy threshold (εc) of this value while keeping accurate results. If electric fields with lower magnitude are used, it is also reasonable to increase this energy threshold by following the 0 % level curve showed in Fig. 2b.
We compared the output of the four models over 12 different electric field magnitudes from E=0.60 to E=3.0 MV m−1. Two types of simulations were set: record in time and record in distance (or space). This last choice was made because the resulting spectra can change significantly depending on the record method, as presented in Fig. 10 of Skeltved et al. (2014). All the curves presenting the simulation results are presented in the Supplement, as well as the complete details on how the simulation should be set up. In the following section, we discuss only the most important differences we found between the four codes. We show the comparison of avalanche scales in space and time in Sect. 4.1 and in Sect. 4.2 the evolution to self-similar state. Finally, in Sect. 4.3, we show the comparison of the self-similar energy spectra of electrons and photons of the RREA.
4.1 Avalanche timescales and length scales
Figures 3 and 4 show the avalanche length scales and timescales as a function of electric fields, for the four models, together with their relative difference with respect to REAM. Note that we could not compute any values for electric fields below 0.60 MV m−1, as we only used 200 initial electron seeds of 100 keV, which could not produced enough showers. The choice of 200 initial electrons is purely due to computational limitations. The avalanches' length and times of the different models agree within ±10 %. There is also a systematic shift of about 7 % between the two Geant4 models for both timescales and length scales. The Geant4 O4 model is in principle more accurate than the O1 model, since it includes more advanced models. For most of the electric fields, O1 tends to be closer to REAM and O4 tends to be closer to GRRR. Following Coleman and Dwyer (2006), the avalanche length and time can be fitted by the empirical models
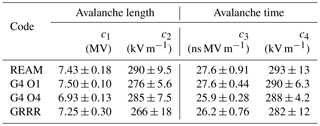
where c1 is in V, c2 and c4 in V m−1 and c3 in s V m−1. The c2 and c4 parameters can be seen as two estimates of the magnitude of the electric field of the minimum of ionisation for electrons along the avalanche direction and also of the electric field magnitude of the RREA threshold; both values are close. However, we note that these fits neglect the sensitivity of the mean energy and velocity to the electric field. These empirical fits are motivated from the relations presented in Eqs. (9) and (10), derived for the one-dimensional case. First results of such fits were presented in Babich et al. (2004b) and Coleman and Dwyer (2006), and they obtained consistent results. Here, we will compare our results against Coleman and Dwyer.
The best fit values of the two models to the simulation data are given in Table 1. The c1 parameter is directly linked to the average energy of the RREA spectrum, though the definition of this average energy can be ambiguous as energy spectra change significantly if recorded in time or in space. The values given by all the codes are located between 6.8 and 7.61 MV, and are all consistent with each other within a 95 % confidence interval, with the exception of O4, which slightly deviates from O1. Combining the four values gives
By “combining”, we mean that the four values are averaged and the rule is used to “combine” the four uncertainty ranges. The value is consistent with the value of 7.3±0.06 MV given in Coleman and Dwyer (2006). Also, all the estimated values of the c2 and c4 are consistent with each other within a 95 % confidence interval. Combining all the values of c2 and c4 gives
In addition, both values are also consistent with each other, leading to the final value of kV m−1. These values slightly deviate from the value of 276.5±2.24 obtained from Coleman and Dwyer (2006), if the values they obtained for the fits of λ and τ are combined. The work of Coleman and Dwyer (2006) used the REAM model too, in a version that should not have significantly changed compared to the one used here. Thus, we think this difference is purely attributed to differences in the methodology that was used to make these estimates from the output data of the code. Concerning the c3 parameter, combining all the estimates gives ns MV m−1, which is slightly lower than the value of 27.3±0.1 ns MV m−1 of Coleman and Dwyer (2006), but none of the values are consistent within the 95 % confidence interval. For this case, we also think the slight difference can be attributed to differences in methodology. Furthermore, the ratio can also be used to determine an average speed of the avalanche along the direction of the electric field (which also corresponds to the z direction), and we can estimate , which is very close to what was found in previous studies.
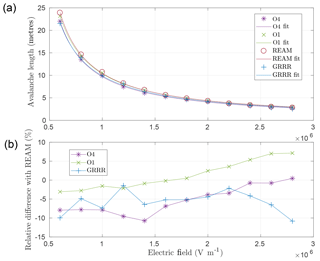
Figure 3(a) Avalanche multiplication length as function of ambient electric field for each of the codes included in this study. (b) The relative difference of all other models with respect to REAM. Table 1 indicates the values of the fit parameters.

Figure 4(a) Avalanche multiplication time as function of ambient electric field for each of the codes included in this study. (b) The relative difference of all other models with respect to REAM. Table 1 indicates the values of the fit parameters.
4.2 Evolution to self-similar state
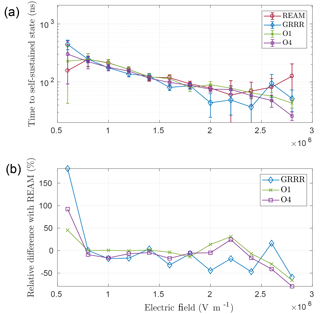
The photon and electron energy spectra of a RREA is known to converge in time to a self-similar solution, where its shape is not evolving anymore, even if the number of particles continues growing exponentially. It may also be referred to as the “self-sustained state” or the “steady state” in the literature. At least five avalanche lengths (or avalanche times) are required to be able to assert that this state is reached. We propose to estimate this time by looking at the mean electron energy evolution as a function of time. Notice that, as already mentioned in the beginning of Sect. 4, this mean energy recorded in time is different from the one recorded in distance, which is used in the next section. We arbitrarily choose to evaluate this mean by averaging all the energies of each individually recorded electron from 10 keV and above. This choice of a 10 keV energy threshold (instead of a higher value, like 511 keV or 1 MeV) does not affect significantly the final estimate of this time to self-similar state.We started with a mono-energetic beam of 100 keV electrons, which is considered low enough compared to the self-similar state mean energy of 6 to 9 MeV. To define the time to self-similar state (Ts), we fitted the time evolution of the mean electron energy with the model
where b1 and b2 have a dimension of energy and b3 has a dimension of time, and we define Ts=5 b3, which is five e-folding times, i.e. converged to 99.3 %. The evolution of electron spectra to self-similar state is illustrated for the Geant4 O4 model in the Supplement (Sect. S12.4). The values of Ts we estimated for the different models are presented in Fig. 5, together with relative differences of the models with respect to REAM. The relatively high uncertainty (within 95 % confidence intervals) that can be seen in the estimate of Ts is due to a combination of the confidence interval from the exponential fit from the statistics of the number of seed electrons that could produce a RREA and from the statistics of the particle counts. For most cases, 200 initial seed were used, but for REAM, only 16 seeds were simulated for E≥2.2 MV m−1, and for GRRR, only 20 seeds were simulated above E≥2.0 MV m−1 because of computation time limitations.
In Fig. 5, Geant4 O1, O4, GRRR and REAM show consistent times to reach the self-similar state for all the E fields. Notice that, for them, is close to the avalanche time value τ given in the top panel of Fig. 4. For the low electric field of 0.60 MV m−1, it seems to take about 5 times longer to reach self-similar state. For this field, there were only three electron seeds that could produce a RREA, giving a large uncertainty on the estimate of Ts, making it impossible to conclude on an inconsistency. From 0.60 to 1.8 MV m−1, where all data from codes have good statistics, the times to self-similar state are consistent. From 2.0 to 2.4 MV m−1, the two Geant4 models and REAM are consistent, but GRRR presents lower times by about −20 % to −50 %, but it is impossible to conclude an inconsistency given the large confidence intervals. For E-field magnitudes of 2.6 to 2.8 MV m−1, O1 and O4 present times to self-similar state lower than REAM by about 50 %, which is significant given the uncertainty intervals, whereas GRRR and REAM are consistent. We could not find a clear explanation for it.
4.3 RREA spectra
The Supplement (Sect. S6) presents all the comparison spectra we obtained for photons, electrons and positrons for the electric field between 0.60 and 3.0 MV m−1. In this section, we discuss the most important differences we could find between the four models.
4.3.1 Electrons
After the RREA electron spectra have reached self-similar state (which requires at least five avalanche lengths or times), we recorded the energy spectrum in a plane at a given distance (which is different for each electric field). Then, we fitted it with an exponential spectrum model (see also Eq. 8). Note that, for an exponential distribution, the mean of the energy distribution is an estimator of its parameter , justifying the bar notation. We chose to evaluate the mean energy for record at distances because, contrary to time records, it produces spectra that can be perfectly fit with an exponential distribution over the whole energy range (0 to 100 MeV). Therefore, in this case, only the mean RREA electron energy is uniquely defined and does not depend on an arbitrarily chosen energy threshold or fitting method. The mean energy of the exponential spectrum is calculated for the several codes as a function of electric field E, as presented in Fig. 6. For Geant4 O1, the entire simulation and analysis were done twice for maximum allowed step length settings of δℓmax=1 cm and δℓmax=1 mm, to show that the first case generates totally incorrect spectra, which is consistent with having incorrect RREA probabilities (presented in Sect. 3). In addition, values of the mean energy for O1 with and δℓmax=1 cm are presented in Sect. 7 in the Supplement. The data of Fig. 6 were fit following the model,
motivated by the facts that is roughly a power law of E (see Fig. 2) and λ is a power law of (see Eq. 3). It has three adjustable parameters: a1, a2 and a3. We set F=0.28 MeV m−1, which is approximately the RREA threshold. The speed β is set constant, equal to 0.90, because the RREA velocity does not change more than 5 % over the range of electric fields we tested. This model is in general agreement with the calculations of Celestin et al. (2012), where λ(E) presents an approximately linear relation with the electric field. Table 2 gives the parameters' best fits (with confidence intervals) for the different models, and Fig. 6 shows the corresponding curves.
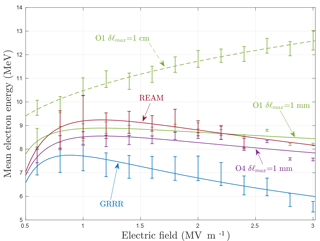
Figure 6Mean electron energies at self-similar state (for distance record) for different electric field magnitudes. The data points are fitted with the model presented in Sect. 4.3.1 (Eq. 20). The values of the fitted parameters are presented in Table 2. To highlight the importance of including step limitations, Geant4 O1 values are presented for two different max step (δℓmax) settings: one that is not acceptable (1 cm) and one that is acceptable (1 mm). The parameter αR is set to its default value of 0.8 for O1 and 0.2 for O4.
Table 2Values of the parameters of the fits (with 95 % confidence intervals) for the electron mean energies using Eq. (20). F is set to 0.28 Me Vm−1. The corresponding curves are shown in Fig. 6.

In Fig. 6, it is clear that the Geant4 O1 model with δℓmax=1 cm presents a significantly higher than the other codes, with values ranging from 9.5 to 12.5 MeV. From the previous RREA probability simulations (see Sect. 3), we know that this δℓmax parameter is not low enough, and so the results of this model can be disqualified. However, when δℓmax is reduced to 1 mm, the results of both Geant4 models are close. There seems to be a consensus between Geant4 (O1 and O4) and REAM, which gives mean energy that is between 8 and 9 MeV and can vary up to 10 % depending on the electric field. For all electric field magnitudes, GRRR shows a smaller average energy from about 10 % less at 1 MV m−1 to about 20 % less at 2.8 MV m−1. The reason is certainly because GRRR only includes radiative energy losses as continuous friction. This is actually a similar difference to what has been observed and discussed in Rutjes et al. (2016) concerning the high-energy electron beams, and one can read the discussion therein for more details.
Figure 7 compares the electron spectra recorded at z=128 m (the electric field has a non-null component only in the z direction, so that electrons are accelerated towards positive z) for an electric field magnitude E=0.80 MV m−1, for a RREA generated from 200 initial (“seed”) electrons with ϵ=100 keV. This record distance was chosen because it corresponds to about 8.5 avalanche lengths, giving a maximum multiplication factor of about 5000 for which there is no doubt the RREA is fully developed and has reached self-similar state. This electric field of E=0.80 MV m−1 was chosen because it is where we could observe the most interesting differences between the models, and it also happens to be the lowest for which we could build spectra with enough statistics on all the models to be able to present a precise comparison. The choice of 200 initial electrons is purely due to computational limitations.
In Fig. 7b, the error bars represent the uncertainty due to the Poisson statistics inherent when counting particles. The four models are consistent within 10 % between 20 keV and 7 MeV. Below 20 keV, we think the discrepancy is not physical and can be attributed to the recording methods set up for the different codes, which are not perfect and have a more or less important uncertainty range (which is not included in the display errors bars and only based on Poisson statistics). Above 7 MeV, O1 remains consistent with REAM overall, but O4 and O1 deviate significantly: up to 50 % for O4 and up to 90 % for GRRR. For the last bin between 58 and 74 MeV, O4 and GRRR are inconsistent, which is explained by the fact that GRRR does not include straggling for bremsstrahlung (i.e. either explicit bremsstrahlung collision or some stochastic fluctuations mimicking straggling). The deviations for the high-energy part (>7 MeV) in the electron spectrum are significant for this particular field (E=0.80 MV m−1); however, this is not true for all electric fields, where the codes are overall roughly consistent, as seen in the Supplement (Sect. S6). In principle, O4 should be more precise than O1 (Allison et al., 2006), as it includes more advanced models, yet we cannot argue that O4 is more accurate than REAM. One way of deciding which model is the most accurate might be to compare these results with experimental measurements. However, in the context of TGFs and γ-ray glows, it is complicated to get a proper measurement of electron spectra produced by RREA. However, photons have much longer attenuation lengths than electrons and can be more easily detected, e.g. from mountains, planes, balloons or satellites. In the next section, we present and discuss the corresponding photon spectra.
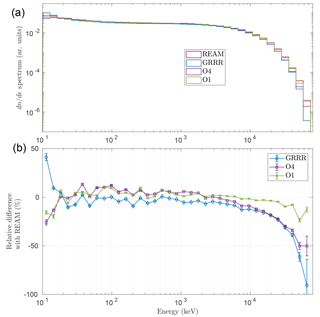
Figure 7(a) Electron (kinetic) energy spectra of Geant4 (O4 and O1), REAM and GRRR for E=0.80 MV m−1, recorded at z=128 m. The RREA is generated from 200 seed electrons of ϵ=100 keV. (b) Relative difference between REAM and the three other models. The error bars are calculated from the Poisson statistics.
4.3.2 Photons
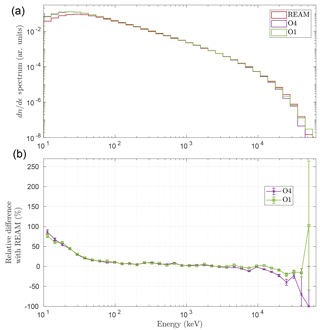
In Fig. 8, the photon spectra recorded at z=128 m (the electric field has a non-null component only in the z direction) for a magnitude E=0.80 MV m−1 are given for Geant4 O1/O4 and REAM, together with the relative difference with respect to REAM. The reasons why these z and E values were chosen are given in the previous section.
The error bars in the relative differences represent the uncertainty due to the inherent Poisson statistics when evaluating particle counts. The Geant4 O1 and O4 models are consistent for the full energy range, except a small discrepancy below 20 keV, which can be attributed to different physical models, with O4 being more accurate in principle. In this case, it cannot be attributed to recording methods, since they are exactly the same for both Geant4 models. At 10 keV, the two Geant4 spectra are about 80 % larger than REAM. With increasing energy, the discrepancy reduces and reaches 0 % at 100 keV. Above 100 keV, the three models show consistent spectra. There may be some discrepancy above 30 MeV, but it is hard to conclude since the uncertainty interval is relatively large.
As just presented, the main noticeable discrepancy between O1/O4 and REAM is present below 100 keV. As far as we know, there is no reason to argue that Geant4 gives a better result than REAM in this range, or vice versa. One way to find out which model is the most accurate could be to compare these results with real measurements. Are such measurement possible to obtain? Any photon that an instrument could detect has to travel in a significant amount of air before reaching detectors. The average path travelled in the atmosphere by a 100 keV photon in 12 km altitude air is 1540±806 m. It decreases for lower energies and is 671±484 m at 50 keV and 63.0±61.5 m at 20 keV. Note that these lengths have been evaluated from precise Geant4 simulations and are smaller than the attenuation lengths at the same energies, because photons gradually lose energy due to stochastic collisions. These average travelled paths are too small for the photons to have a reasonable chance to escape the atmosphere and to be detected by a satellite. However, we cannot exclude that they may reach an airborne detector located inside or close to a thunderstorm. As a side note, we want to indicate that the vast majority (if not all) of the photons observed from space with energies below a few hundred kilo-electronvolts (e.g. by the Fermi space telescope; see Mailyan et al., 2016) had very likely more than 1 MeV when they were emitted. They lost some part of their energy by collisions (with air molecules in the atmosphere and/or with some part of the satellite) before being detected by the satellite. For information, a figure presenting the probability of a photon to escape the atmosphere as function of its primary energy for a typical TGF is presented in Sect. S14 in the Supplement.
4.4 Other differences
In addition to what is presented so far in this article, the following points should also be mentioned when comparing the results of the codes. The corresponding plots are available in the Supplement.
-
The mean parallel (to the E-field direction) velocity β∥ of the avalanche is shown in Sect. S4.2 of the Supplement (labelled “mean Z velocity”). We observe that GRRR is giving β∥ faster than all the other codes, and O4 is systematically slower than REAM and O1, though the differences are less than 2 %. The variation of β∥ towards the electric field E is small, about 10 % for all codes. For increasing E fields, electrons are less scattered and more focused in the field direction, hence slightly increasing β∥.
-
The electron to (bremsstrahlung) photon ratio re∕p was also calculated and compared for different distance record in the RREA shower, and the corresponding plots are presented in Sect. S3 in the Supplement. GRRR is excluded because it does not include photons. For any electric field, the same discrepancy is observed. At the beginning of the shower (<4 avalanche lengths), re∕p appears to be about 20 % larger for REAM compared to O1 and O4; then, the three models are consistent at a given distance, and finally for more than about four avalanche lengths, the tendency is inverted and REAM presents a re∕p about 20 % smaller than Geant4. The magnitude of this discrepancy is largely reduced for increasing electric fields. We did not fully understand the reasons of these differences, and it may be due to the bremsstrahlung models used. More investigations are required.
-
The positron spectra have relatively low statistics (on the order of a few hundred particles recorded) and are all quite consistent within the relatively large uncertainties.
-
In the photon spectra obtained from particle records at fixed times, REAM seems to show significantly less (at least a factor of 10) photon counts than the two Geant4 models for most of the electric field magnitudes. For some fields, it even shows a lack of high-energy photons, with a sharp cut at about 30 MeV. It seems to point to a problem in the record method, explaining why we chose not to discuss these spectra in the main article. The spectra produced by the Geant4 O1 and O4 models for this case are consistent with one another for all the E fields.
We have investigated the results of three Monte Carlo codes able to simulate RREAs, including the effects of electric fields up to the classical breakdown field, which is Ek≈3 MV m−1 at STP. The Monte Carlo codes REAM, GRRR and Geant4 (two models: O1 and O4) were compared. The main difference between the Geant4 O4 and O1 models is the inclusion of more precise cross-sections for low-energy interactions (<10 keV) for O4.
We first proposed a theoretical description of the RREA process that is based on and incremented over previous published works. Our analysis confirmed that the relativistic avalanche is mainly driven by electric fields and the ionisation and scattering processes determining , the minimum energy of electrons that can run away. This is different from some of the previous works that speculated that the low-energy threshold (εc), when changed from 1 keV to 250 eV, was the most important factor affecting the electron energy spectra (Rutjes et al., 2016; Skeltved et al., 2014).
Then, we estimated the probability to produce a RREA from a given electron energy (ϵ) and a given electric field magnitude (E). We found that the stepping methodology is of major importance, and the stepping parameters are not set up satisfactorily in Geant4 by default. We pointed out which settings should be adjusted and provided example codes to the community (see Sect. 6 and the “Code and data availability” section). When properly set up, the two Geant4 models showed good overall agreement (within ≈10 %) with REAM and GRRR. From the Geant4, GRRR and REAM simulations, we found that the probability for the particles below ≈10 keV to accelerate and participate in the penetrating radiation is actually negligible for the full range of electric field we tested (E<3 MV m−1). It results that a reasonable lower boundary of the low-energy threshold (εc) can be set to ≈10 keV for any electric field below Ek≈3 MV m−1 (at STP), making it possible to have relatively fast simulations. For lower electric fields, it is possible to use larger εc, following a curve we provided (Fig. 2b).
The advantage of using more sophisticated cross-sections able to accurately take into account low-energy particles could be probed by comparing directly the O1 and O4 models. They showed minor differences that are mainly visible only for high E fields (E>2 MV m−1), where low-energy particles have more chances to run away.
In a second part, we produced RREA simulations from the four models and compared the physical characteristics of the produced showers. The two Geant4 models and REAM showed good agreement on all the parameters we tested. GRRR also showed overall good agreement with the other codes, except for the electron energy spectra. That is probably because GRRR does not include straggling for the radiative and ionisation energy losses, hence implementing these two processes is of primary importance to produce accurate RREA spectra. By comparing O1 and O4, we also pointed out that including precise modelling of the interactions of particles below ≈10 keV provided only small differences; the most important being a 5 % change in the avalanche multiplication times and lengths. We also pointed out a discrepancy from Geant4 (O1 and O4) compared to REAM, which is a 10 % to 100 % relative difference in the low-energy part (<100 keV) of the photon energy spectrum for an electric field of E=0.80 MV m−1. However, we argued that it is unlikely to have an impact on spectra detected from satellites.
From the experience of this study, we give the following general recommendations concerning RREA simulations:
-
Codes should be checked/tested/benchmarked using standard test set-ups. In the Supplement, we provide a precise description of such tests. In Sect. 7 of this article, we provide links to download the full data set we obtained for the codes we tested (Geant4 with two set-ups, REAM and GRRR), as well as processing scripts. We also provide the source code of the Geant4 codes.
-
Custom-made codes should be make available to other researchers or at least the results they give for standard tests.
-
In order to make it possible to compare results from different studies, the methodology used to derive a given quantity should be rigorously chosen and presented clearly somewhere.
-
Extending the recommendations of Rutjes et al. (2016), we concluded that to get an accurate RREA electron spectra above 10 MeV, radiative loss (bremsstrahlung) should not be implemented with uniform friction only: straggling should be included. Straggling should also be included for ionisation energy loses below the energy threshold.
Concerning the usage of Geant4 for simulating RREA:
-
Default settings are not able to simulate RREA accurately. To get accurate RREA results, one of the following tweaks is possible:
-
Changing the αR (“dR over range”) parameter of the electron/positron ionisation process to or less gives the best ratio between accuracy and computation time. Leave the “final range” parameter at 1 mm (default value) or less.
-
Setting up a step limitation process (or a maximum acceptable step) to 1 mm or less will significantly increase the required computation time.
-
Using the single (Coulomb) scattering model instead of multiple scattering (the two previous tweaks relying on the multiple scattering algorithm) will substantially increase the necessary computation time. This is because multiple scattering algorithms were invented to make the simulation run faster by permitting to use substantially larger (usually >10 times) step lengths compared to a pure single scattering strategy, while keeping a similar accuracy.
-
-
In the “Code and data availability” section, we provide a link to Geant4 example source codes implementing these three methods.
-
Compared to using the default Møller/Bhabha scattering models for ionisation, the usage of more accurate cross-sections, e.g. taking into account the electrons' molecular binding energies (as done for the Livermore or Penelope models), only leads to minor differences.
The full simulation output data of the four models are available through the following link: https://filesender.uninett.no/?s=download&token=738a8663-a457-403a-991e-ae8d3fca3dc3 (Sarria, 2018a).
The scripts used to process these data to make the figures of the Supplement are available in the following repository: https://gitlab.com/dsarria/HEAP2_matlab_codes.git (Sarria, 2018b).
The full GRRR source code is available in the following repository: https://github.com/aluque/grrr/tree/avalanches (last access: 30 October 2018; Luque, 2014).
The Geant4 source code for the RREA probability simulations is available in the following repository: https://gitlab.com/dsarria/av_prob.git (Sarria, 2018c).
The Geant4 source code for the RREA characterisation simulations is available in the following repository: https://gitlab.com/dsarria/RREA_characteristics.git (Sarria, 2018d).
Table A1 presents the relative computation times it takes to complete the simulation with an electric field magnitude of 1.2 MV m−1, 100 initial (“seed”) electrons with initial energy ϵ=100 keV and a stop time (physical) of 233 ns. The fastest simulation uses Geant4 with the O1 physics list and δℓmax=10 cm and took 4.53 s to complete on one thread with the microprocessor we used. The simulations with the O4 physics list with δℓmax=1 mm require about 400 times more computation time. Setting up δℓmax=1 mm or lower is necessary to achieve correct simulation of the RREA process, as argued in Sect. 3. To achieve it for the full range of electric fields we tested (in a reasonable amount of time), it required the use of the Norwegian Fram computer cluster. The simulations with δℓmax=0.1 mm for all electric fields could not be achieved in a reasonable amount of time, even by using the computer cluster.
On the other hand, if δℓmax is left at its default value (1 km) and the αR parameter is tweaked instead, accurate simulations can be achieved with a value of or lower. It requires almost an order of magnitude less computation time compared to using δℓmax=1 mm.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-4515-2018-supplement.
DS, CR and GD designed the tests. DS, CR and GD wrote most of the manuscript. DS, GD and CR conducted the data analysis and made the figures and tables. DS carried out the Geant4 simulations and provided the data. AL carried out the GRRR simulations and provided the data. JRD and KMAI carried out the REAM simulations and provided the data. NO, KMAI, JRD, UE, ABS and ISF provided important feedback on and review of the text.
The authors declare that they have no conflict of interest.
This work was supported by the European Research Council under the European Union's Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement no. 320839 and the Research Council of Norway under contracts 208028/F50 and 223252/F50 (CoE). For part of the results of this work, it was necessary to use the Fram computer cluster of the UNINETT Sigma2 AS, under project no. NN9526K.
Gabriel Diniz is supported by the Brazilian agency CAPES. Casper Rutjes acknowledges funding by FOM project no. 12PR3041, which also supported Gabriel Diniz's 12-month stay in the Netherlands. Ivan S. Ferreira thanks CNPqs grant PDE(234529/2014-08) and also FAPDF grant no. 0193.000868/2015, 03/2015.
This material is based in part upon work supported by the Air Force Office of
Scientific Research under award no. FA9550-16-1-0396. The authors
would like to thank the two referees, Ashot Chilingarian and an anonymous referee, for their valuable
comments and suggestions that helped to improve the quality of this work.
Edited by: Josef Koller
Reviewed by: Ashot Chilingarian and one anonymous referee
Adachi, T., Takahashi, Y., Ohya, H., Tsuchiya, F., Yamashita, K., Yamamoto, M., and Hashiguchi, H.: Monitoring of Lightning Activity in Southeast Asia: Scientific Objectives and Strategies, Kyoto Working Papers on Area Studies, G-COE Series, 2008. a
Agostinelli, S., Allison, J., Amakon, K., et al.: GEANT4: A simulation toolkit, Nucl. Instrum. Meth., 506, 250–303, https://doi.org/10.1016/S0168-9002(03)01368-8, 2003. a, b
Allison, J., Amako, K., Apostolakis, J., Araujo, H., Dubois, P. A., Asai, M., Barrand, G., Capra, R., Chauvie, S., Chytracek, R., Cirrone, G. A. P., Cooperman, G., Cosmo, G., Cuttone, G., Daquino, G. G., Donszelmann, M., Dressel, M., Folger, G., Foppiano, F., Generowicz, J., Grichine, V., Guatelli, S., Gumplinger, P., Heikkinen, A., Hrivnacova, I., Howard, A., Incerti, S., Ivanchenko, V., Johnson, T., Jones, F., Koi, T., Kokoulin, R., Kossov, M., Kurashige, H., Lara, V., Larsson, S., Lei, F., Link, O., Longo, F., Maire, M., Mantero, A., Mascialino, B., McLaren, I., Lorenzo, P. M., Minamimoto, K., Murakami, K., Nieminen, P., Pandola, L., Parlati, S., Peralta, L., Perl, J., Pfeiffer, A., Pia, M. G., Ribon, A., Rodrigues, P., Russo, G., Sadilov, S., Santin, G., Sasaki, T., Smith, D., Starkov, N., Tanaka, S., Tcherniaev, E., Tome, B., Trindade, A., Truscott, P., Urban, L., Verderi, M., Walkden, A., Wellisch, J. P., Williams, D. C., Wright, D., and Yoshida, H.: Geant4 developments and applications, IEEE T. Nucl. Sci., 53, 270–278, https://doi.org/10.1109/TNS.2006.869826, 2006. a, b
Allison, J., Amako, K., Apostolakis, J., et al.: Recent developments in Geant4, Nucl. Instrum. Meth., 835, 186–225, https://doi.org/10.1016/j.nima.2016.06.125, 2016. a, b
Apostolakis, J., Asai, M., Bogdanov, A., Burkhardt, H., Cosmo, G., Elles, S., Folger, G., Grichine, V., Gumplinger, P., Heikkinen, A., Hrivnacova, I., Ivanchenko, V., Jacquemier, J., Koi, T., Kokoulin, R., Kossov, M., Kurashige, H., McLaren, I., Link, O., Maire, M., Pokorski, W., Sasaki, T., Starkov, N., Urban, L., and Wright, D.: Geometry and physics of the Geant4 toolkit for high and medium energy applications, Radiat. Phys. Chem., 78, 859–873, https://doi.org/10.1016/j.radphyschem.2009.04.026, 2009. a
Babich, L., Donskoy, E., Kutsyk, I., and Roussel-Dupré, R.: The feedback mechanism of runaway air breakdown, Geophys. Res. Lett., 32, L09809, https://doi.org/10.1029/2004GL021744, 2005. a
Babich, L. P.: Generation of neutrons in giant upward atmospheric discharges, JETP letters, 84, 285–288, 2006. a
Babich, L. P., Donskoy, E. N., Kutsyk, I. M., Kudryavtsev, A. Y., Roussel-Dupre, R. A., Shamraev, B. N., and Symbalisty, E. M.: Comparison of relativistic runaway electron avalanche rates obtained from Monte Carlo simulations and kinetic equation solution, IEEE T. Plasma Sci., 29, 430–438, 2001. a
Babich, L. P., Bakhov, K. I., Balakin, V. A., Donskoi, E. N., Zavada, N. I., Zelenskii, K. F., Il'kaev, R. I., Kutsyk, I. M., Loiko, T. V., Nedoikash, Y. M., Pavlovskaya, N. G., Roussel-Dupre, R. A., Symbalisty, E. M. D., and Shamraev, B. N.: An Experimental Investigation of an Avalanche of Relativistic Runaway Electrons under Normal Conditions, High Temperature, 42, 1–11, https://doi.org/10.1023/B:HITE.0000020085.61526.40, 2004a. a
Babich, L. P., Donskoy, E. N., Il'kaev, R. I., Kutsyk, I. M., and Roussel-Dupre, R. A.: Fundamental parameters of a relativistic runaway electron avalanche in air, Plasma Phys. Rep., 30, 616–624, https://doi.org/10.1134/1.1778437, 2004b. a, b
Bethe, H. and Heitler, W.: On the stopping of fast particles and on the creation of positive electrons, P. Roy. Soc. A-Math. Phy., 146, 83–112, 1934. a
Bowers, G. S., Smith, D. M., Martinez-McKinney, G., Kamogawa, M., Cummer, S., Dwyer, J., Wang, D., Stock, M., and Kawasaki, Z.: Gamma Ray Signatures of Neutrons From a Terrestrial Gamma Ray Flash, Geophys. Res. Lett., 44, 10063–10070, 2017. a, b
Briggs, M. S., Connaughton, V., Wilson-Hodge, C., Preece, R. D., Fishman, G. J., Kippen, R. M., Bhat, P., Paciesas, W. S., Chaplin, V. L., Meegan, C. A., von Kienlin, A., Greiner, J., Dwyer, J. R., and Smith, D. M.: Electron-positron beams from terrestrial lightning observed with Fermi GBM, Geophys. Res. Lett., 38, L02808, https://doi.org/10.1029/2010GL046259, 2011. a
Brown, J. M. C., Dimmock, M. R., Gillam, J. E., and Paganin, D. M.: A low energy bound atomic electron Compton scattering model for Geant4, Nucl. Instrum. Meth. B, 338, 77–88, https://doi.org/10.1016/j.nimb.2014.07.042, 2014. a
Carlson, B., Lehtinen, N. G., and Inan, U. S.: Neutron production in terrestrial gamma ray flashes, J. Geophys. Res.-Space, 115, A00E19, https://doi.org/10.1029/2009JA014696, 2010. a
Celestin, S. and Pasko, V. P.: Soft collisions in relativistic runaway electron avalanches, J. Phys. D, 43, 315206, https://doi.org/10.1088/0022-3727/43/31/315206, 2010. a, b, c, d
Celestin, S. and Pasko, V. P.: Energy and fluxes of thermal runaway electrons produced by exponential growth of streamers during the stepping of lightning leaders and in transient luminous events, J. Geophys. Res.-Space, 116, A03315, https://doi.org/10.1029/2010JA016260, 2011. a, b
Celestin, S., Xu, W., and Pasko, V. P.: Terrestrial gamma ray flashes with energies up to 100 MeV produced by nonequilibrium acceleration of electrons in lightning, J. Geophys. Res.-Space, 117, A05315, https://doi.org/10.1029/2012JA017535, 2012. a, b
Chanrion, O. and Neubert, T.: Production of runaway electrons by negative streamer discharges, J. Geophys. Res.-Space, 115, A00E32, https://doi.org/10.1029/2009JA014774, 2010. a
Chanrion, O., Bonaventura, Z., Çinar, D., Bourdon, A., and Neubert, T.: Runaway electrons from a “beam-bulk” model of streamer: application to TGFs, Environ. Res. Lett., 9, 055003, https://doi.org/10.1088/1748-9326/9/5/055003, 2014. a, b
Chanrion, O., Bonaventura, Z., Bourdon, A., and Neubert, T.: Influence of the angular scattering of electrons on the runaway threshold in air, Plasma Phys. Contr. F., 58, 044001, https://doi.org/10.1088/0741-3335/58/4/044001, 2016. a, b, c
Chilingarian, A., Daryan, A., Arakelyan, K., Hovhannisyan, A., Mailyan, B., Melkumyan, L., Hovsepyan, G., Chilingaryan, S., Reymers, A., and Vanyan, L.: Ground-based observations of thunderstorm-correlated fluxes of high-energy electrons, gamma rays, and neutrons, Phys. Rev. D, 82, 043009, https://doi.org/10.1103/PhysRevD.82.043009, 2010. a
Chilingarian, A., Hovsepyan, G., and Hovhannisyan, A.: Particle bursts from thunderclouds: Natural particle accelerators above our heads, Phys. Rev. D, 83, 062001, https://doi.org/10.1103/PhysRevD.83.062001, 2011. a
Chilingarian, A., Mailyan, B., and Vanyan, L.: Recovering of the energy spectra of electrons and gamma rays coming from the thunderclouds, Atmos. Res., 114, 1–16, https://doi.org/10.1016/j.atmosres.2012.05.008, 2012. a
Chilingarian, A., Hovsepyan, G., Khanikyanc, G., Reymers, A., and Soghomonyan, S.: Lightning origination and thunderstorm ground enhancements terminated by the lightning flash, EPL (Europhysics Letters), 110, 49001, https://doi.org/10.1209/0295-5075/110/49001, 2015. a
Coleman, L. M. and Dwyer, J. R.: Propagation speed of runaway electron avalanches, Geophys. Res. Lett., 33, L11810, https://doi.org/10.1029/2006GL025863, 2006. a, b, c, d, e, f
Cooray, V., Arevalo, L., Rahman, M., Dwyer, J., and Rassoul, H.: On the possible origin of X-rays in long laboratory sparks, J. Atmos. Sol.-Terr. Phy., 71, 1890, https://doi.org/10.1016/j.jastp.2009.07.010, 2009. a
Cramer, E. S., Dwyer, J. R., Arabshahi, S., Vodopiyanov, I., Liu, N., and Rassoul, H.: An analytical approach for calculating energy spectra of relativistic runaway electron avalanches in air, J. Geophys. Res.-Space, 119, 7794–7823, 2014. a
Cramer, E. S., Dwyer, J. R., and Rassoul, H. K.: Magnetic field modification to the relativistic runaway electron avalanche length, J. Geophys. Res.-Space, 121, 11261–11270, https://doi.org/10.1002/2016JA022891, 2016. a
Dubinova, A., Rutjes, C., Ebert, U., Buitink, S., Scholten, O., and Trinh, G. T. N.: Prediction of Lightning Inception by Large Ice Particles and Extensive Air Showers, Phys. Rev. Lett., 115, 015002, https://doi.org/10.1103/PhysRevLett.115.015002, 2015. a
Dwyer, J., Saleh, Z., Rassoul, H., Concha, D., Rahman, M., Cooray, V., Jerauld, J., Uman, M., and Rakov, V.: A study of X-ray emission from laboratory sparks in air at atmospheric pressure, J. Geophys. Res.-Atmos., 113, D23207, https://doi.org/10.1029/2008JD010315, 2008. a
Dwyer, J. R.: A fundamental limit on electric fields in air, Geophys. Res. Lett., 30, 2055, https://doi.org/10.1029/2003GL017781, 2003. a, b, c
Dwyer, J. R.: Relativistic breakdown in planetary atmospheres, Phys. Plasmas, 14, 042901, https://doi.org/10.1063/1.2709652, 2007. a, b
Dwyer, J. R.: Source mechanisms of terrestrial gamma-ray flashes, J. Geophys. Res.-Atmos., 113, D10103, https://doi.org/10.1029/2007JD009248, 2008. a
Dwyer, J. R.: The relativistic feedback discharge model of terrestrial gamma ray flashes, J. Geophys. Res.-Space, 117, A02308, https://doi.org/10.1029/2011JA017160, 2012. a, b
Dwyer, J. R., Grefenstette, B. W., and Smith, D. M.: High-energy electron beams launched into space by thunderstorms, Geophys. Res. Lett., 35, L02815, https://doi.org/10.1029/2007GL032430, 2008. a
Dwyer, J. R., Smith, D. M., and Cummer, S. A.: High-Energy Atmospheric Physics: Terrestrial Gamma-Ray Flashes and Related Phenomena, Space Sci. Rev., 173, 133–196, https://doi.org/10.1007/s11214-012-9894-0, 2012. a, b, c, d, e, f
Dwyer, J. R., Smith, D. M., Hazelton, B. J., Grefenstette, B. W., Kelley, N. A., Lowell, A. W., Schaal, M. M., and Rassoul, H. K.: Positron clouds within thunderstorms, J. Plasma Phys., 81, 475810405, https://doi.org/10.1017/S0022377815000549, 2015. a
Eack, K. B., Beasley, W. H., Rust, W. D., Marshall, T. C., and Stolzenburg, M.: Initial results from simultaneous observation of X-rays and electric fields in a thunderstorm, J. Geophys. Res.-Atmos., 101, 29637–29640, https://doi.org/10.1029/96JD01705, 1996. a
Ferrari, A., Sala, P. R., Fasso, A., and Ranft, J.: FLUKA: A multi-particle transport code (Program version 2005), Tech. rep., 2005. a
Fishman, G. J., Bhat, P. N., Mallozzi, R., Horack, J. M., Koshut, T., Kouveliotou, C., Pendleton, G. N., Meegan, C. A., Wilson, R. B., Paciesas, W. S., Goodman, S. J., and Christian, H. J.: Discovery of Intense Gamma-Ray Flashes of Atmospheric Origin, Science, 264, 1313–1316, https://doi.org/10.1126/science.264.5163.1313, 1994. a, b
Grefenstette, B. W., Smith, D. M., Hazelton, B. J., and Lopez, L. I.: First RHESSI terrestrial gamma ray flash catalog, J. Geophys. Res.-Space, 114, A02314, https://doi.org/10.1029/2008JA013721, 2009. a
Gurevich, A.: On the theory of runaway electrons, Sov. Phys. JETP, 12, 904–912, 1961. a
Gurevich, A. and Zybin, K.: Kinetic equation for high energy electrons in gases, Phys. Lett. A, 237, 240–246, 1998. a
Gurevich, A., Milikh, G., and Roussel-Dupre, R.: Runaway electron mechanism of air breakdown and preconditioning during a thunderstorm, Phys. Lett. A, 165, 463–468, https://doi.org/10.1016/0375-9601(92)90348-P, 1992. a
Hirayama, H., Namito, Y., Nelson, W. R., Bielajew, A. F., Wilderman, S. J., and Michigan, U.: The EGS5 code system, Tech. rep., Department of Energy, United States, 2005. a
Ihaddadene, M. A. and Celestin, S.: Increase of the electric field in head-on collisions between negative and positive streamers, Geophys. Res. Lett., 42, 5644–5651, https://doi.org/10.1002/2015GL064623, 2015. a
Ivanchenko, V. N., Bukin, A. D., Dubrovin, M. S., Eidelman, S. I., Grozina, N. A., and Tayursky, V. A.: UNIMOD2: Universal Monte Carlo code for simulation of e+ e- experiments, in: MC 91: Detector and event simulation in high-energy physics, Proceedings, Workshop, Amsterdam, the Netherlands, 8–12 April, 1991, 79–85, 1991. a
Kelley, N. A., Smith, D. M., Dwyer, J. R., Splitt, M., Lazarus, S., Martinez-McKinney, F., Hazelton, B., Grefenstette, B., Lowell, A., and Rassoul, H. K.: Relativistic electron avalanches as a thunderstorm discharge competing with lightning, Nat. Commun., 6, 7845, https://doi.org/10.1038/ncomms8845, 2015. a, b
Kochkin, P., Köhn, C., Ebert, U., and van Deursen, L.: Analyzing x-ray emissions from meter-scale negative discharges in ambient air, Plasma Sources Sci. T., 25, 044002, https://doi.org/10.1088/0963-0252/25/4/044002, 2016. a
Kochkin, P., van Deursen, A. P. J., Marisaldi, M., Ursi, A., de Boer, A. I., Bardet, M., Allasia, C., Boissin, J.-F., Flourens, F., and Østgaard, N.: In-flight observation of gamma-ray glows by ILDAS, J. Geophys. Res.-Atmos., 122, 12801–12811,https://doi.org/10.1002/2017JD027405, 2017. a, b
Kochkin, P., Sarria, D., Skeie, C., Deursen, A. P. J., Boer, A. I., Bardet, M., Allasia, C., Flourens, F., and Østgaard, N.: In-Flight Observation of Positron Annihilation by ILDAS, J. Geophys. Res.-Atmos., 123, 8074–8090, https://doi.org/10.1029/2018JD028337, 2018. a
Köhn, C. and Ebert, U.: Calculation of beams of positrons, neutrons, and protons associated with terrestrial gamma ray flashes, J. Geophys. Res.-Atmos., 120, 1620–1635, 2015. a
Köhn, C., Ebert, U., and Mangiarotti, A.: The importance of electron–electron bremsstrahlung for terrestrial gamma-ray flashes, electron beams and electron–positron beams, J. Phys. D, 47, 252001, https://doi.org/10.1088/0022-3727/47/25/252001, 2014. a, b
Köhn, C., Diniz, G., and Harakeh, M. N.: Production mechanisms of leptons, photons, and hadrons and their possible feedback close to lightning leaders, J. Geophys. Res.-Atmos., 122, 1365–1383, 2017. a
Landau, L. D., Bell, J., Kearsley, M., Pitaevskii, L., Lifshitz, E., and Sykes, J.: Electrodynamics of continuous media, vol. 8, elsevier, 2013. a, b
Lefeuvre, F., Blanc, E., and Pinçon, J. L.: TARANIS-a Satellite Project Dedicated to the Physics of TLEs and TGFs, American Institute of Physics Conference Series, 1118, 3–7, https://doi.org/10.1063/1.3137711, 2009. a
Lehtinen, N. G. and Østgaard, N.: X-ray Emissions in a Multiscale Fluid Model of a Streamer Discharge, J. Geophys. Res.-Atmos., 123, 6935–6953, https://doi.org/10.1029/2018JD028646, 2018. a
Lehtinen, N. G., Bell, T. F., and Inan, U. S.: Monte Carlo simulation of runaway MeV electron breakdown with application to red sprites and terrestrial gamma ray flashes, J. Geophys. Res., 104, 24699–24712, https://doi.org/10.1029/1999JA900335, 1999. a, b, c, d, e
Li, C., Ebert, U., and Hundsdorfer, W.: 3D hybrid computations for streamer discharges and production of runaway electrons, J. Phys. D, 42, 202003, https://doi.org/10.1088/0022-3727/42/20/202003, 2009. a, b, c
Liu, C., Brennan, D. P., Bhattacharjee, A., and Boozer, A. H.: Adjoint Fokker-Planck equation and runaway electron dynamics, Phys. Plasmas, 23, 010702, https://doi.org/10.1063/1.4938510, 2016. a, b
Luque, A.: Relativistic Runaway Ionization Fronts, Phys. Rev. Lett., 112, 045003, https://doi.org/10.1103/PhysRevLett.112.045003, 2014. a, b, c
Luque, A.: Radio Frequency Electromagnetic Radiation From Streamer Collisions, J. Geophys. Res.-Atmos., 122, 10497–10509, https://doi.org/10.1002/2017JD027157, 2017. a
Mailyan, B. G., Briggs, M. S., Cramer, E. S., Fitzpatrick, G., Roberts, O. J., Stanbro, M., Connaughton, V., McBreen, S., Bhat, P. N., and Dwyer, J. R.: The spectroscopy of individual terrestrial gamma-ray flashes: Constraining the source properties, J. Geophys. Res.-Space, 121, 11346–11363, https://doi.org/10.1002/2016JA022702, 2016. a
Marisaldi, M., Fuschino, F., Tavani, M., Dietrich, S., Price, C., Galli, M., Pittori, C., Verrecchia, F., Mereghetti, S., Cattaneo, P. W., Colafrancesco, S., Argan, A., Labanti, C., Longo, F., Del Monte, E., Barbiellini, G., Giuliani, A., Bulgarelli, A., Campana, R., Chen, A., Gianotti, F., Giommi, P., Lazzarotto, F., Morselli, A., Rapisarda, M., Rappoldi, A., Trifoglio, M., Trois, A., and Vercellone, S.: Properties of terrestrial gamma ray flashes detected by AGILE MCAL below 30 MeV, J. Geophys. Res.-Space, 119, 1337–1355, https://doi.org/10.1002/2013JA019301, 2014. a
McCarthy, M. and Parks, G.: Further observations of X-rays inside thunderstorms, Geophys. Res. Lett., 12, 393–396, https://doi.org/10.1029/GL012i006p00393, 1985. a, b
Moss, G. D., Pasko, V. P., Liu, N., and Veronis, G.: Monte Carlo model for analysis of thermal runaway electrons in streamer tips in transient luminous events and streamer zones of lightning leaders, J. Geophys. Res.-Space, 111, A02307, https://doi.org/10.1029/2005JA011350, 2006. a
Neubert, T., Kuvvetli, I., Budtz-Jørgensen, C., Østgaard, N., Reglero, V., and Arnold, N.: The atmosphere-space interactions monitor (ASIM) for the international space station, in: Proceedings of the ILWS Workshop, edited by: Gopalswamy, N. and Bhattacharyya, A., p. 448, 2006. a
Østgaard, N., Gjesteland, T., Stadsnes, J., Connell, P., and Carlson, B.: Production altitude and time delays of the terrestrial gamma flashes: Revisiting the Burst and Transient Source Experiment spectra, J. Geophys. Res.-Space, 113, A02307, https://doi.org/10.1029/2007JA012618, 2008. a, b
Parks, G. K., Mauk, B. H., Spiger, R., and Chin, J.: X-ray enhancements detected during thunderstorm and lightning activities, Geophys. Res. Lett., 8, 1176–1179, https://doi.org/10.1029/GL008i011p01176, 1981. a
Perkins, S., Cullen, D., and Seltzer, S.: Tables and graphs of electron-interaction cross sections from 10 eV to 100 GeV derived from the LLNL Evaluated Electron Data Library (EEDL), Z=1–100, Tech. rep., https://doi.org/10.2172/5691165,1991. a
Rahman, M., Cooray, V., Azlinda Ahmad, N., Nyberg, J., Rakov, V. A., and Sharma, S.: X rays from 80-cm long sparks in air, Geophys. Res. Lett., 35, L06805, https://doi.org/10.1029/2007GL032678, 2008. a
Raizer, Y. P.: Gas discharge physics, vol. 2, Springer Berlin, 1997. a, b, c
Roberts, O. J., Fitzpatrick, G., Stanbro, M., McBreen, S., Briggs, M. S., Holzworth, R. H., Grove, J. E., Chekhtman, A., Cramer, E. S., and Mailyan, B. G.: The First Fermi-GBM Terrestrial Gamma Ray Flash Catalog, J. Geophys. Res.-Space, 123, 4381–4401, https://doi.org/10.1029/2017JA024837, 2018. a
Roussel-Dupre, R. A., Gurevich, A. V., Tunnell, T., and Milikh, G. M.: Kinetic theory of runaway air breakdown, Phys. Rev. E, 49, 2257–2271, https://doi.org/10.1103/PhysRevE.49.2257, 1994. a, b
Rutjes, C., Sarria, D., Skeltved, A. B., Luque, A., Diniz, G., Østgaard, N., and Ebert, U.: Evaluation of Monte Carlo tools for high energy atmospheric physics, Geosci. Model Dev., 9, 3961–3974, https://doi.org/10.5194/gmd-9-3961-2016, 2016. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Rutjes, C., Diniz, G., Ferreira, I. S., and Ebert, U.: TGF afterglows: a new radiation mechanism from thunderstorms, Geophys. Res. Lett., 44, 10702–10712, https://doi.org/10.1002/2017GL075552, 2017. a, b
Salvat, F., Fernández-Varea, J. M., and Sempau, J.: PENELOPE-2011: A Code System for Monte Carlo Simulation of Electron and Photon Transport, 2011. a
Sarria, D.: Dataset used in the Article “Evaluation of Monte Carlo tools for high-energy atmospheric physics II: relativistic runaway electron avalanches” (Version 1) [Data set], https://doi.org/10.5281/zenodo.1475209, 2018a.
Sarria, D.: MATLAB scripts for processing the dataset “Full RREA Dataset” (Version 1), Zenodo, https://doi.org/10.5281/zenodo.1475245, 2018b.
Sarria, D.: Probability Evaluation of Relativistic Runaway Electron Avalanches (RREA) (GEANT4 based source code), Zenodo, https://doi.org/10.5281/zenodo.1475231, 2018c.
Sarria, D.: Characterization of Relativistic Runaway Electron Avalanches (RREA) (GEANT4 based source code) (Version 1), Zenodo, https://doi.org/10.5281/zenodo.1475220, 2018d.
Sarria, D., Blelly, P.-L., and Forme, F.: MC-PEPTITA: a Monte Carlo model for Photon, Electron and Positron Tracking In Terrestrial Atmosphere. Application for a Terrestrial Gamma-ray Flash, J. Geophys. Res.-Space, 120, 3970–3986, https://doi.org/10.1002/2014JA020695, 2015. a, b, c
Sarria, D., Blelly, P.-L., Briggs, M. S., and Forme, F.: Studying the time histogram of a terrestrial electron beam detected from the opposite hemisphere of its associated TGF, J. Geophys. Res.-Space, 121, 4698–4704, https://doi.org/10.1002/2015JA021881, 2016. a
Sarria, D., Lebrun, F., Blelly, P.-L., Chipaux, R., Laurent, P., Sauvaud, J.-A., Prech, L., Devoto, P., Pailot, D., Baronick, J.-P., and Lindsey-Clark, M.: TARANIS XGRE and IDEE detection capability of terrestrial gamma-ray flashes and associated electron beams, Geosci. Instrum. Method. Data Syst., 6, 239–256, https://doi.org/10.5194/gi-6-239-2017, 2017. a, b
Shao, T., Zhang, C., Niu, Z., Yan, P., Tarasenko, V. F., Baksht, E. K., Burahenko, A. G., and Shut'ko, Y. V.: Diffuse discharge, runaway electron, and x-ray in atmospheric pressure air in an inhomogeneous electrical field in repetitive pulsed modes, Appl. Phys. Lett., 98, 021503, https://doi.org/10.1063/1.3540504, 2011. a
Skeltved, A. B., Østgaard, N., Carlson, B., Gjesteland, T., and Celestin, S.: Modeling the relativistic runaway electron avalanche and the feedback mechanism with GEANT4, J. Geophys. Res.-Space, 119, 9174–9191, https://doi.org/10.1002/2014ja020504, 2014. a, b, c, d, e, f, g, h, i, j
Teruaki, E., Wada, Y., Furuta, Y., Nakazawa, K., Yuasa, T., Okuda, K., Makishima, K., Sato, M., Sato, Y., Nakano, T., Umemoto, D., and Tsuchiya, H.: Photonuclear reactions triggered by lightning discharge, Nature, 551, 481–484, https://doi.org/10.1038/nature24630, 2017. a
Torii, T., Takeishi, M., and Hosono, T.: Observation of gamma-ray dose increase associated with winter thunderstorm and lightning activity, J. Geophys. Res.-Atmos., 107, 4324, https://doi.org/10.1029/2001JD000938, 2002. a
Tsuchiya, H., Enoto, T., Yamada, S., Yuasa, T., Kawaharada, M., Kitaguchi, T., Kokubun, M., Kato, H., Okano, M., Nakamura, S., and Makishima, K.: Detection of high-energy gamma rays from winter thunderclouds, Phys. Rev. Lett., 99, 165002, https://doi.org/10.1103/PhysRevLett.99.165002, 2007. a
Williams, E. R.: Origin and context of C. T. R. Wilson's ideas on electron runaway in thunderclouds, J. Geophys. Res.-Space, 115, A00E50, https://doi.org/10.1029/2009JA014581, 2010. a
Wilson, C. T. R.: The Acceleration of β-particles in Strong Electric Fields such as those of Thunderclouds, PCPS-P. Camb. Philol. S., 22, 534, https://doi.org/10.1017/S0305004100003236, 1925. a, b