the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Veros v0.1 – a fast and versatile ocean simulator in pure Python
Dion Häfner
René Løwe Jacobsen
Carsten Eden
Mads R. B. Kristensen
Markus Jochum
Roman Nuterman
Brian Vinter
A general circulation ocean model is translated from Fortran to Python. Its code structure is optimized to exploit available Python utilities, remove simulation bottlenecks, and comply with modern best practices. Furthermore, support for Bohrium is added, a framework that provides a just-in-time compiler for array operations and that supports parallel execution on both CPU and GPU targets.
For applications containing more than a million grid elements, such as a typical horizontal resolution global ocean model, Veros is approximately half as fast as the MPI-parallelized Fortran base code on 24 CPUs and as fast as the Fortran reference when running on a high-end GPU. By replacing the original conjugate gradient stream function solver with a solver from the pyAMG Python package, this particular subroutine outperforms the corresponding Fortran version by up to 1 order of magnitude.
The study is concluded with a simple application in which the North Atlantic wave response to a Southern Ocean wind perturbation is investigated. It is found that even in a realistic setting the phase speeds of boundary waves matched the expectations based on theory and idealized models.
- Article
(4660 KB) - Full-text XML
- BibTeX
- EndNote
Numerical simulations have been used to advance our understanding of the ocean circulation for more than 50 years now (e.g., Bryan, 2006), and in particular for regimes that are difficult to treat analytically, they have become irreplaceable. However, numerical representations of the ocean have their own pitfalls, and it is paramount to build trust in the numerical representation of each and every process that is thought to be relevant for the ocean circulation (e.g., Hsieh et al., 1983). The last 20 years have seen a massive increase in computing resources available to oceanographers, in contrast to human resources, which appear to be fixed. Arguably, this leads to a shift from process studies to analysis of climate model output (or from “Little Science” to “Big Science”; Price de Solla, 1963). This is not necessarily a bad development; it may simply be an indication that the field has matured. However, there are still basic questions about ocean dynamics that remain unanswered (e.g., Marshall and Johnson, 2013), and to tackle these questions, the scientific community requires flexible tools that are approachable, powerful, and easy to adapt. We therefore decided to build Veros (the versatile ocean simulator).
The ocean interior is mostly adiabatic and has a long memory, easily exceeding 1000 years (e.g., Gebbie and Huybers, 2006). This requires long integration times for numerical models; experiments can take several months in real time to complete. Thus, ocean models are typically written to optimize the use of computing rather than human resources using low-level programming languages such as Fortran or C. These languages' core design, lack of abstraction, and established coding patterns often make it a daunting challenge to, for example, keep track of indices or global variables. Even for experienced scientists this is more than just a nuisance. As the model code becomes increasingly complex, it jeopardizes a core principle of science: reproducibility. Especially inexperienced programmers cannot ascertain beyond all doubt if the impact of a recently implemented physical component is caused by new physics or simply a bug.
High-level programming languages like Python, MATLAB, Scala, or Julia, on the other hand, are usually designed with the explicit goal of improving code structure and thus readability. While this in itself cannot eliminate coding mistakes, a more concise, better structured code makes it easier to spot and avoid bugs altogether. In the case of Python, additional abstraction, a powerful standard library, and its immense popularity in the scientific community1, which has in turn created a wide range of learning resources and a large third-party package ecosystem, lower the bar of entry for inexperienced programmers.
In fact, this is one of our main motivations behind developing Veros: in our experience, a substantial amount of the duration of MSc and PhD projects is devoted to understanding, writing, and debugging legacy Fortran code. This leads to frustration and anxieties, even for lecturers. With Veros, we anticipate that students can translate their physical insights rapidly into numerical experiments, thereby maintaining the high level of enthusiasm with which they entered the field. At the same time, it allows more seasoned researchers to quickly spin up experiments that dramatically change the ocean dynamics, which would be impractical or infeasible using traditional ocean models (for one such application, see Sect. 4).
The price to pay for these advantages is often a significantly reduced integration speed due to less aggressive compiler optimizations, additional overhead, and lack of direct memory access. Thus, while there are some modeling projects that implement a Python front end (CliMT, Monteiro and Caballero, 2016; OOFε, Marta-Almeida et al., 2011; PyOM, Eden, 2016), all of those projects rely on a Fortran back end for performance reasons. However, in Veros, the performance impact of using Python turns out to be much less severe than expected, as all expensive computations are deferred to a well-performing numerical back end (NumPy or Bohrium; see Sect. 3.2 for performance comparisons), making Veros the (to our knowledge) first global-scale ocean simulator in pure Python.
The next section describes the challenges overcome during the translation and resulting changes in the code structure. Section 3 presents model validation and benchmarks, and Sect. 4 evaluates the properties of coastally trapped waves in Veros.
At its numerical core, the present version of Veros (v0.1) is a direct translation of pyOM2 (v2.1.0), a primitive equation finite-difference ocean model with a special emphasis on energetic consistency (Eden and Olbers, 2014; Eden, 2016). PyOM2 consists of a back end written in Fortran 90 and front ends for both Fortran and Python (via f2py, Peterson, 2009). Most of the core features of pyOM2 are available in Veros, too; they include the following:
-
a staggered, three-dimensional numerical grid (Arakawa C grid, after Arakawa and Lamb, 1977) discretizing the primitive equations in either Cartesian or pseudo-spherical coordinates (e.g., Olbers et al., 2012) (the grid is staggered in all dimensions, placing quantities on so-called T, U, V, W, and ζ cells);
-
free-slip boundary conditions for momentum and no-normal-flow boundary conditions for tracers;
-
several different friction, advection, and diffusion schemes to choose from, such as harmonic or biharmonic lateral friction, linear or quadratic bottom friction, explicit or implicit vertical mixing, and central difference or Superbee flux-limiting advection schemes;
-
either the full 48-term TEOS equation of state (McDougall and Barker, 2011) or various linear and nonlinear model equations from Vallis (2006);
-
closures for mesoscale eddies (after Gent et al., 1995; Eden and Greatbatch, 2008), turbulence (Gaspar et al., 1990), and internal wave breaking (IDEMIX; Olbers and Eden, 2013); and
-
support for writing output in the widely used NetCDF4 binary format (Rew and Davis, 1990) and writing restart data to pick up from a previous integration.
Veros, like pyOM2, aims to support a wide range of problem sizes and architectures. It is meant to be usable on anything between a personal laptop and a computing cluster, which calls for a flexible design and which makes a dynamical programming language like Python a great fit for this task. Unlike pyOM2, which explicitly decomposes and distributes the model domain across multiple processes via MPI (message passing interface; e.g., Gropp et al., 1999), Veros is not parallelized directly. Instead, all hardware-level optimizations are deferred to a numerical back end, currently either NumPy (Walt et al., 2011) or Bohrium (Kristensen et al., 2013). While NumPy is commonly used, easy to install, and highly compatible, Bohrium provides a powerful runtime environment that handles high-performance array operations on parallel architectures.
The following section describes which procedures we used when translating the pyOM2 Fortran code to a first, naive Python implementation. Section 2.2 then outlines the necessary steps to obtain a vectorized NumPy implementation that is well-performing and idiomatic. Section 2.3 gives an overview of some additional features that we implemented in Veros, and Sect. 2.4 finally gives an introduction to the internal workings of Bohrium.
2.1 From Fortran to naive Python
When using NumPy, array operations in Fortran can be translated to Python with relative ease, as long as a couple of pitfalls are avoided (such as 0-based indexing in Python vs. arbitrary index ranges in Fortran). As an example, consider the following Fortran code from pyOM2.
do j=js_pe,je_pe
do i=is_pe-1,ie_pe
flux_east(i,j,:) = &
0.25*(u(i,j,:,tau)+u(i+1,j,:,tau)) &
*(utr(i+1,j,:)+utr(i,j,:))
enddo
enddoHere, is_pe, js_pe, ie_pe, je_pe denote the start and end indices of the current process. Translating this snippet verbatim to Python, the resulting code looks very similar.
for j in range(js_pe,je_pe):
for i in range(is_pe-1,ie_pe):
flux_east[i,j,:] = (
0.25*(u[i,j,:,tau]
+u[i+1,j,:,tau])
*(utr[i+1,j,:]+utr[i,j,:])
)In fact, we transformed large parts of the Fortran code base into valid Python by replacing all built-in Fortran constructs (such as if statements and do loops) with the corresponding Python syntax. We automated much of the initial translation process through simple tools like regular expressions to pre-parse the Fortran code base, e.g., the regular expression
do (\w)=((\w|[\+\-])+,(\w|[\+\-])+)
would find all Fortran do loops, while the expression
for \1 in range(\2):
replaces them with the equivalent for loops in Python2. This semiautomatic preprocessing allowed for a first working Python implementation of the pyOM2 code base after only a few weeks of coding that could be used as a basis to iterate towards a more performant (and idiomatic) implementation.
2.2 Vectorization
After obtaining a first working translation of the pyOM2 code, we refactored and optimized all routines for performance and readability, while ensuring consistency by continuously monitoring results. This mostly involves using vector operations instead of explicit Fortran-style loops over indices (that typically carry a substantial overhead in high-level programming languages). Since most of the operations in a finite-difference discretization consist of basic array arithmetic, a large fraction of the core routines were trivial to vectorize, such as the above example, which becomes
flux_east[1:-2,2:-2,:] = (
0.25*(u[1:-2,2:-2,:,tau]
+u[2:-1,2:-2,:,tau])
*(utr[2:-1,2:-2,:]+utr[1:-2,2:-2,:])
)Note that we replaced all explicit indices (i,j) with basic slices (index ranges). The first and last two elements of the horizontal dimensions are ghost cells, which makes it possible to shift arrays by up to two cells in each dimension without introducing additional padding. Since all parallelism is handled in the back end, there is no need to retain the special indices is_pe, js_pe, ie_pe, je_pe, and we replaced them with hard-coded values (2, 2, −2, and −2, respectively).
Apart from those trivially vectorizable loops, there were several cases that required special treatment.
-
Boolean masks are either cast to floating point arrays and multiplied to the to-be-masked array or applied using NumPy's where function. We decided to avoid “fancy indexing” due to poor parallel performance.
-
Operations in which, e.g., a three-dimensional array is to be multiplied with a two-dimensional array slice-by-slice can be written concisely thanks to NumPy's powerful array broadcasting functionalities (e.g., by using newaxis as an index).
-
We vectorized loops representing (cumulative) sums or products using NumPy's sum (cumsum) and prod (cumprod) functions, respectively.
-
Oftentimes, recursive loops can be reformulated analytically into a form that can be vectorized. A simple example is
which arises when calculating the positions xt of the T grid cells and is equivalent to
which can easily be expressed through a cumulative sum operation (cumsum).
On top of this, there were two loops in the entire pyOM2 code base that were only partially vectorizable using NumPy's current tool set3 (such that an explicit loop over one axis remains). Since they did not have a measurable impact on overall performance, they were left in this semi-vectorized form; however, it is certainly possible that those loops (or similar future code) could become a performance bottleneck on certain architectures. In this case, an extension system could be added to Veros in which such instructions are implemented using a low-level API and compiled upon installing Veros. Conveniently, Bohrium offers zero-copy interoperability for this use case via Cython (Behnel et al., 2011) on CPUs and PyOpenCL and PyCUDA (Klöckner et al., 2012) on GPUs.
2.3 Further modifications
Since there is an active community of researchers developing Python packages, many sophisticated tools are just one import statement away, and the dynamic nature of Python allows for some elegant implementations that would be infeasible or outright impossible in Fortran 90. Moving the entire code base to Python thus allowed us to implement a number of modifications that comply with modern best practices without too much effort, some of which are described in the upcoming sections.
2.3.1 Dynamic back-end handling
Through a simple function decorator, a pointer to the back end currently used for computations is automatically injected as a variable np into each numerical routine. This allows for using the same code for every back end, provided their interface is compatible to NumPy's. Currently, the only included back ends are NumPy and Bohrium, but in principle, one could build their own NumPy-compatible back end, e.g., by replacing some critical functions with a better-performing implementation.
Since Veros is largely agnostic of the back end that is being used for vector operations, Veros code is especially easy to write. Everything concerning, e.g., the parallelization of array operations is handled by the back end, so developers can focus on writing clear, readable code.
2.3.2 Generic stream function solvers
The two-dimensional barotropic stream function Ψ of the vertically integrated flow is calculated in every iteration of the solver to account for effects of the surface pressure. It can be obtained by solving a two-dimensional Poisson equation of the form
with coordinates , total water depth h, vorticity ζ, and Laplacian Δ. The discrete version of this Laplacian in pseudo-spherical coordinates as solved by pyOM2 and Veros reads (Eden, 2014a)
with
-
the discrete stream function Ψi,j at the ζ cell with indices (i,j),
-
latitude x and longitude y, each defined at T cells (, ) and U/V cells (, ), and
-
grid spacings of T (, ) and U/V cells (, ) in each horizontal direction.
By reordering all discrete quantities xi,j to a one-dimensional object xi+Nj (with , , and ) and writing them as column vectors x, Eq. (3) results in the equation
where Z represents the right-hand side of Eq. (3), and A is a banded matrix with nonzero values on five or seven diagonals4 that reduces to the classical discrete Poisson problem for equidistant Cartesian coordinates, but is generally nonsymmetric.
In pyOM2, the system Eq. (5) is solved through a conjugate gradient solver with a Jacobi preconditioner in a matrix-free formulation taken from the Modular Ocean Model (MOM; Pacanowski et al., 1991). Since both the matrix-free formulation and the fixed preconditioner lead to a quite specific solver routine, our first step was to transform this into a generic problem by incorporating all boundary conditions into the actual Poisson matrix and to use scipy.sparse from the SciPy library (Jones et al., 2001) to store the resulting banded matrix. At this stage, any sufficiently powerful sparse linear algebra library can be used to solve the system. This is especially important for Veros as it is targeting a wide range of architectures: a small, idealized model running with NumPy does not require a sophisticated algorithm (and can stick with, e.g., the readily available solvers provided by scipy.sparse.linalg),intermediate problem sizes might require a strong, sequential algorithm, and for large setups, highly parallel solvers from a high-performance library are usually most adequate (e.g., PETSc, Balay et al., 1997, on CPUs; e.g., CUSP, Dalton et al., 2014, on GPUs).
In fact, substantial speedups could be achieved by using an AMG (algebraic multigrid; Vaněk et al., 1996) preconditioner provided by the Python package pyAMG (Bell et al., 2013). As shown in the performance comparisons in Sect. 3.2.2, our AMG-based stream function solver is up to 20 times faster than pyOM2's Fortran equivalent. Even though the AMG algorithms are mathematically highly sophisticated, pyAMG is simple to install (e.g., via the PyPI package manager pip), and implementing the preconditioner into Veros required merely a few lines of code, making this process a prime example for the huge benefits one can expect from developing in a programming language as popular in the scientific community as Python. And thanks to the modular structure of the new Poisson solver routines, it will be easy to switch (possibly dynamically) to even more powerful libraries as it becomes necessary.
2.3.3 Multi-threaded I–O with compression
In geophysical models, writing model output or restart data to disk often comes with its own challenges. When output is written frequently, significant amounts of CPU time may be wasted waiting for disk operations to finish. Additionally, data sets tend to grow massive in terms of file size, usually ranging from gigabytes to petabytes. To address this, we took the following measures in Veros.
-
Since I–O operations usually block the current thread from continuing while barely consuming any CPU resources, all disk output is written in a separate thread (using Python's
threadingmodule). This enables computations to continue without waiting for flushes to disk to finish. To prevent race conditions, all output data are copied in-memory to the output thread before continuing. -
By default, Veros makes use of the lossless compression abilities built into NetCDF4 and HDF5. Simply by passing the desired compression level as a flag to the respective library, the resulting file sizes were reduced by about two-thirds, with little computational overhead. Since the zlib (NetCDF4) and gzip (HDF5) compression is built into the respective format specification, most standard post-processing tools are able to read and decompress data on the fly, without any explicit user interaction.
2.3.4 Back-end-specific tridiagonal matrix solvers
Many dissipation schemes contain implicit contribution terms, which usually requires the solution of some linear system Ax=b with a tridiagonal matrix A for every horizontal grid point (e.g., Gaspar et al., 1990; Olbers and Eden, 2013).
In pyOM2, those systems are solved using a naive Thomas algorithm (simplified Gaussian elimination for tridiagonal systems). This algorithm cannot be fully vectorized with NumPy's tool kit, and explicit iteration turned out to be a major bottleneck for simulations. One possible solution was to rewrite all tridiagonal systems for each horizontal grid cell into one large, padded tridiagonal system that could be solved in a single pass. This proved to be feasible for NumPy, since it exposes bindings to LAPACK's dgtsv solver (Anderson et al., 1999), but performance was not sufficient when using Bohrium. We therefore made use of Bohrium's interoperability functionalities, which allowed us to implement the Thomas algorithm directly in the OpenCL language for high-performance computing on GPUs via PyOpenCL (Klöckner et al., 2012); on CPUs, Bohrium provides a parallelized C implementation of the Thomas algorithm as an “extension method”.
When encountering such a tridiagonal system, Veros automatically chooses the best available algorithm for the current runtime system (back end and hardware target) without manual user interaction. This way, overall performance increased substantially to the levels reported in Sect. 3.2.
2.3.5 Modular diagnostic interface
All model diagnostics, such as snapshot output, vertical (overturning) stream functions, energy flux tracking, and temporal mean output, are implemented as subclasses of a diagnostics base class, and instances of these subclasses are added to a Veros instance dynamically. This makes it possible to add, remove, and modify diagnostics on the fly.
def set_diagnostics(self): diag = veros.diagnostics.Average() diag.name = "annual-mean" diag.output_frequency = 360 * 86400 self.diagnostics["annual-mean"] = diag
This code creates a new averaging diagnostic that outputs annual means and can be repeated, e.g., for also writing monthly means.
Besides enforcing a common interface, creating all diagnostics as subclass of a “virtual” base class also has the benefit that common operations like data output are defined as methods of said base class, providing a complete and easy-to-use tool kit to implement additional diagnostics.
2.3.6 Metadata handling
About 2000 of the approximately 11 000 SLOC (source lines of code) in pyOM2 were dedicated to specifying variable metadata (often multiple times) for each output variable, leaving little flexibility to add additional variables and risking inconsistencies. In Veros, all variable metadata are contained in a single, central dictionary; subroutines may then look up metadata from this dictionary on demand (e.g., when allocating arrays or preparing output for a diagnostic). Additionally, a “cheat sheet” containing a description of all model variables is compiled automatically and added to the online user manual.
This approach maximizes maintainability by eliminating inconsistencies and allows users to add custom variables that are treated no differently from the ones already built in.
2.3.7 Quality assurance
To ensure consistency with pyOM2, we developed a testing suite that runs automatically for each commit to the master branch of the Veros repository. The testing suite is comprised of both unit tests and system tests.
- Unit tests
-
are implemented for each numerical core routine; they call a single routine with random data and make sure that all output arrays match between Veros and pyOM2 within a certain absolute tolerance chosen by the author of the test (usually 10−8 or 10−7).
- System tests
-
integrate entire model setups for a small number of time steps and compare the results to pyOM2.
These automated tests allow developers to detect breaking changes early and ensure consistency for all numerical routines and core features apart from deliberately breaking changes. To achieve strict compliance with pyOM2 during testing, we introduced a compatibility mode to Veros that forces all subroutines to comply with their pyOM2 counterpart, even if the original implementation contains errors that we corrected when porting them to Veros.
Using this compatibility mode, the results of most of the Veros core routines match those of pyOM2 within a global, absolute tolerance of 10−8, while in a few cases an accuracy of just 10−7 is achieved (presumably due to a higher sensitivity to round-off errors of certain products). The longer-running system tests achieve global accuracies between 10−6 and 10−4 for all model variables. All arrays are normalized to unit scale by dividing by their global maximum before comparing.
2.4 About Bohrium
Since Veros relies heavily on the capabilities of Bohrium for large problems on parallel architectures, this section gives a short introduction to the underlying concepts and implementation of Bohrium.
Bohrium is a software framework for efficiently mapping array operations from a range of front-end languages (currently C, C++, and Python) to various hardware architectures, including multi-core CPUs and GPGPUs (Kristensen et al., 2013). The components of Bohrium are outlined in Larsen et al. (2016). All array operations called by the front-end programming languages are passed to the respective bridge, which translates all instructions into Bohrium bytecode. After applying several bytecode optimizations, it is compiled into numerical kernels that are then executed at the back end. Parallelization is handled by so-called vector engines, currently using OpenMP (Dagum and Menon, 1998) on CPUs and either OpenCL (Stone et al., 2010) or CUDA (Nickolls et al., 2008) on GPUs.
Since Bohrium uses lazy evaluation, successive operations on the same array views can be optimized substantially. On the one hand, operations can be reordered or simplified analytically to reduce total operation counts. On the other hand, a sophisticated fusion algorithm is applied, which “is a program transformation that combines (fuses) multiple array operations into a kernel of operations. When it is applicable, the technique can drastically improve cache utilization through temporal data locality and enables other program transformations, such as streaming and array contraction (Gao et al., 1993)” (Larsen et al., 2016). In fact, this fusion algorithm alone may increase performance significantly in many applications (Kristensen et al., 2016).
Bohrium's Python bridge is designed to be a drop-in replacement for NumPy, supplying a multi-array class bohrium.ndarray that derives from NumPy's numpy.ndarray. All array metadata are handled by the original NumPy, and only actual computations are passed to Bohrium, e.g., when calling one of NumPy's “ufuncs” (universal functions). This way, most of NumPy's functionality is readily available in Bohrium5, which allows developers to use Bohrium as a high-performance numerical back end while writing hardware-agnostic code (and leaving all optimizations to Bohrium). These properties make Bohrium an ideal fit for Veros.
3.1 Consistency check
Since all Veros core routines are direct translations of their pyOM2 counterparts, an obvious consistency check is to compare the output of both models. On a small scale, this is already done in the Veros testing suite, which ensures consistency for most numerical routines in isolation and for a few time steps of the model as a whole (see Sect. 2.3.7). However, real-world simulations often run for anything between thousands and millions of iterations, possibly allowing numerical roundoff or minor coding errors to accumulate to significant deviations.
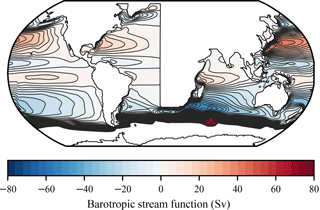
In order to check whether this is a concern in our case, we integrated a global model setup with coarse resolution (approx. , grid elements) for a total of 50 model years (18 000 iterations) using Veros with NumPy, Veros with Bohrium, and pyOM2. Neither the long-term average, zonally averaged temperature nor long-term average barotropic stream function show a physically significant deviation between either of the simulations. Maximum relative errors amount to about 10−4 (Veros, between NumPy and Bohrium) and 10−6 (between Veros with NumPy and pyOM2 when using the compatibility mode).
3.2 Benchmarks
As high-performance computing resources are still expensive and slow model execution is detrimental to a researcher's workflow, performance is of course a critical measure for any geophysical model (and usually the biggest counterargument against using high-level programming languages in modeling). It is thus essential to try and measure the performance of Veros through benchmarking, and since we are in the lucky position to have a well-performing reference implementation available, an obvious test is to compare the Veros throughput to that of pyOM2.
To this end, we developed a benchmarking suite that is part of the Veros code repository so that benchmarks can easily be executed and verified on various architectures. These benchmarks consist of either complete model runs or single subroutines that are executed with varying problem sizes for each of the available numerical back ends (NumPy, Bohrium, and pyOM2's Fortran library with and without MPI support).6
Since we do not (yet) reach scales on which memory consumption, rather than compute power, becomes a limiting factor, we did not study the memory demands in Veros compared to those of pyOM2 in detail. However, especially when using Bohrium, the memory demands of Veros seem to be similar (within 10 % of each other), as Bohrium's JIT compiler is often able to eliminate temporary array allocations. All tested model configurations could thus comfortably run within the same memory bounds for all back ends.
The benchmarks were executed on two different architectures: a typical desktop PC and a cluster node, marked as architecture I and II, respectively (Table 1). Note that since Bohrium does not yet support distributed memory architectures, comparisons have to stay confined to a single computational node. Bohrium v0.8.9 was compiled from source with GCC and BUILD_TYPE=Release flags, and pyOM2 with GFortran using -O3 optimization flags and OpenMPI support.
3.2.1 Overall performance
In order to benchmark the overall performance of Veros against that of pyOM2, an idealized model setup consisting of an enclosed basin representing the North Atlantic with a zonal channel in the south is integrated for a fixed number of 100 iterations, but with varying problem sizes, for each numerical back end.
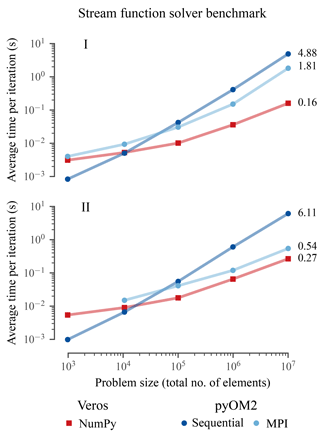
The results (Fig. 1) show the following.
-
For large problems with a number of total elements exceeding 107 (which is about the number of elements in a global setup with horizontal resolution), the Bohrium back end is at its peak efficiency and about 2.3 times slower than parallel pyOM2 regardless of the number of CPU cores. Running on architecture II's high-end GPU, the Veros throughput is comparable to that of pyOM2 running on 24 CPUs.
-
The Veros NumPy back end is about 3 times slower than pyOM2 running serially, largely independent of the problem size.
-
For small problems containing less than 2×104 elements, parallelism is inefficient, so NumPy performs relatively well.
-
Using Bohrium carries a high overhead, and it only surpasses NumPy in terms of speed for problems larger than about 105 elements.
-
Veros is least efficient for intermediate problem sizes of about 105 elements (up to 50 times slower than parallel pyOM2 on 24 CPUs).
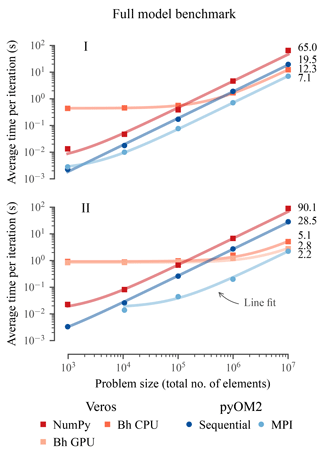
Figure 1In terms of overall performance, Veros using Bohrium (Bh) is slower than pyOM by a factor of about 1.3 to 2.3 for large problems, depending on the hardware architecture (I and II; see Table 1). Solid lines are line fits, suggesting a linear scaling with constant overheads for all components.
We believe that these performance metrics show that Veros is indeed usable as the versatile ocean simulator it is trying to be. Even students without much HPC experience can use Veros to run small- to intermediate-sized, idealized models through NumPy and seamlessly switch to Bohrium later on to run realistic, full-size setups while experiencing performance comparable to traditional ocean models. And given that Bohrium is still undergoing heavy development, we expect that many of the current limitations will be alleviated in future versions, causing Veros to perform even better than today.
3.2.2 Stream function solver
To illustrate the speedups that could be achieved for the stream function solver alone (Sect. 2.3), we conducted similar benchmarks calling only the corresponding solvers in pyOM2 and Veros using pseudo-spherical coordinates, uniform grid spacings, cyclic boundary conditions, and a solver tolerance of 10−12 for a total of 100 times with different, random right-hand-side vectors.
The results show that the Veros stream function solver easily beats pyOM2's for most relevant problem sizes (Fig. 2), even though the underlying BiCGstab solver scipy.sparse.linalg.bicgstab is not parallelized (apart from internal calls to the multi-threaded OpenBLAS library for matrix–vector products). The credit for this speedup belongs entirely to pyAMG, as the AMG preconditioner causes much faster convergence of the iterative solver.
When running on an even higher number (possibly hundreds) of CPU cores, pyOM2's parallel conjugate gradient solver can be expected to eventually outperform the Veros serial AMG solver. However, thanks to the new, generalized structure of the stream function routines (Sect. 2.3), the SciPy BiCGstab solver could easily be switched with a different parallel library implementation.
In the current literature we see a gap between theory and very idealized models on the one hand, and primitive equation models with realistic forcing and topography on the other hand. Here, we will apply Veros to an aspect of the Southern Ocean (SO) hypothesis by Toggweiler and Samuels (1995).
They propose that a strengthening of SO winds leads to a strengthening of the Atlantic Meridional Overturning Circulation (AMOC). Their main argument is based on geostrophy and mass conservation, and it states that mass pushed north by the Atlantic Ocean Ekman layer has to be replaced by upwelled water from depths below the Drake Passage sill. This basic idea is largely accepted, and much of the discussion in the literature is now quantitative, i.e., how much of the wind-driven Eulerian transport in the SO is compensated for by mesoscale eddy-driven transport of opposite sign (Munday et al., 2013). However, Jochum and Eden (2015) show that in at least one general circulation model (GCM) the AMOC does not respond to changes in SO winds. Thus, testing the Southern Ocean hypothesis requires us not only to test if ocean models represent mesoscale eddies appropriately, but also if the propagation of SO anomalies into the Northern Hemisphere is simulated realistically.
The main propagation mechanism is planetary waves; changes to SO Ekman divergence and convergence set up buoyancy anomalies that are radiated as Kelvin and Rossby waves and set up changes to the global abyssal circulation (McDermott, 1996). Because they are so important there is a large literature devoted to the fidelity of planetary waves in ocean models. For example, Hsieh et al. (1983) and Huang et al. (2000) show that even coarse-resolution ocean models can support meridionally propagating waves similar to Kelvin waves, and Marshall and Johnson (2013) quantify exactly how numerical details will affect wave propagation. We wish to bridge the gap between these idealized studies and GCMs by investigating the dependence of Kelvin wave phase speed on resolution in Veros. While this is in principle a minor exercise suitable for undergraduate students, the presence of internal variability and irregular coastlines makes this a major challenge (Getzlaff et al., 2005).
To remove many of these effects, we decided to replace the eastern boundary of the Atlantic with a straight meridional line. This enables a direct comparison with theory since one does not have to worry about the flow's effective path length or artificial viscosity introduced by the staggered grid representation of curved coastlines. Veros allows even nonexpert users to make profound modifications to the default model setups and simplifies this problem in several ways (the exact process of modifying the coastline is outlined in the upcoming section).
-
All post-processing tools from the scientific Python ecosystem that many users are already familiar with are readily available in Veros setups. It is thus possible to use scipy.interpolate's routines, for example, to interpolate the initial condition to the model grid simply by importing them instead of having to reinvent the wheel.
-
Veros setups (as inherited from pyOM2) allow the user to modify all internal arrays, giving users the freedom to make invasive changes if necessary.
-
Veros users do not have to care about an explicit domain decomposition or communication across processors, as all parallelism is handled by Bohrium. All model variables look and feel like a single array.
Accordingly, we use this setup for 3-month BSc projects.
4.1 Modified geometry with flexible resolution
Modifying the geometry of a realistic geophysical model is no trivial task, especially when allowing for a flexible number of grid elements. Any solution that converts cells from water to land or vice versa has to infer reasonable values for initial conditions and external forcing at these cells since, e.g., atmospheric conditions tend to differ fundamentally between water and land.
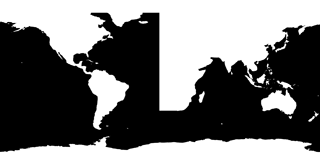
To automate this process, we created a downsampled version of the ETOPO1 global relief model (Amante and Eakins, 2009), which we exported as a binary mask indicating either water or land. We then manually edited this mask using common image processing software by removing lakes and inland seas, thickening Central America, and converting the eastern boundary of the Atlantic to a straight meridional line running from the southern tip of Africa to the Arctic (Fig. 3).
This binary mask is read by Veros during model setup and interpolated to the chosen grid (the number of grid cells in each dimension is defined by the user; grid steps are chosen to minimize discretization error according to Vinokur, 1983). The ocean bathymetry is read from the same downsampled version of ETOPO1, and cells are converted between water and land according to the interpolated mask.
Since all cells that were converted from land to water lie in the North Atlantic, it is sufficient to modify initial conditions and atmospheric forcing in this region only. Initial conditions are read from a reference file with horizontal resolution and interpolated bilinearly to the modified grid. The bathymetry in the Atlantic is replaced by a constant depth of 4000 m. Optionally, a different constant depth and/or linear slope for some distance from each coast can be added to model a continental shelf. All atmospheric forcing is replaced by its zonal mean value in the Atlantic basin.
This leaves us with a modified setup that is smooth enough to be stably integrated and that allows us to track Kelvin waves in a more isolated environment. As a first sanity check, the resulting ocean circulation looks largely as expected (Fig. 4).
4.2 The experiment
If coarse-resolution ocean models can support Kelvin-wave-like features, the question of phase speed becomes paramount: a wave that is too slow will be damped away too early and inhibit oceanic teleconnections, which may cause different observed climate sensitivities in different climate models (Greatbatch and Lu, 2003). Hsieh et al. (1983) discuss in great detail how choices in the numerical setup modify the phase speed of Kelvin waves: resolution, friction, discretization (Arakawa B or C grid; Arakawa and Lamb, 1977), and boundary conditions all affect the phase speed. However, Marshall and Johnson (2013) point out that for an adjustment timescale on the order of years or longer (relevant for the Toggweiler and Samuels SO hypothesis), the corresponding waves have the properties of Rossby waves, albeit with a phase speed of , where c is the Kelvin wave phase speed, Ld is the Rossby radius of deformation, and the Munk boundary layer width. Here we test their analytical result, particularly whether the phase speed really depends only on friction but not resolution.
The global setup of Veros is used in two configurations: 2∘ (2DEG) and 1∘ zonal resolution. Both have 180 meridional grid cells with a spacing of approximately 0.5∘ at the Equator and 1.5∘ at the poles. The 1∘ setup is used with two different viscosities: 5×104 m2 s−1 (same as 2DEG) and 5×103 m2 s−1, called 1DEG and 1DEGL, respectively. Each of these three setups is initialized with data from Levitus (1994) and integrated for 60 years (these are our three control integrations). All setups use daily atmospheric forcings from Uppala et al. (2005) interpolated as described in Sect. 4.1.
After 50 years, one new integration is branched off from each, with the maximum winds over the SO increased by 50 % (sine envelope between 27 and 69∘ S). The velocity fields are sampled as daily means. By comparing the solution during the first 150 days to the first 150 days of year 51 of the control integrations at 200 m of depth, we arrive at an estimate of the speed with which the information on the SO wind stress anomaly travels north along the eastern boundary of the Atlantic Ocean.
As a first step we confirm that the anomaly signal is well resolved along the Equator. Indeed, for all three setups we find the same phase speed of 2.7 ms−1 (Fig. 5a, only 1DEG is shown), slightly less than the 2.8 ms−1 that is expected from theory and observations (Chelton et al., 1998). Along the African coast we find a similar speed in 1DEGL, but slower in 1DEG and 2DEG (Fig. 5b–d). Using the approximate slope of the propagating signal's contours as a metric for the average phase speed between the Equator and 40∘ N, we arrive at about 2.1 ms−1 for 1DEGL and 1.0 ms−1 for 2DEG and 1DEG.
The Rossby radius of deformation Ld along the western coast of North Africa changes from approximately 100 km at 5∘ N to 40 km at 30∘ N (Chelton et al., 1998). The Munk boundary layer width δM for our two different viscosities is 130 and 60 km. The large range of Ld along the coast makes it difficult to determine the exact theoretically expected phase speed, but based on Marshall and Johnson (2013) one can expect that the anomalies generated by an SO wind perturbation travel slower by a factor of less than 3 in 2DEG and 1DEG and twice as fast as that in 1DEGL. This is exactly what is found here.
This minor initial application demonstrates how Veros can be used to bridge the gap between theory and full ocean GCMs. Future studies will investigate in more detail the interaction between the anomalies traveling along the coast and high-latitude stratification and topography.
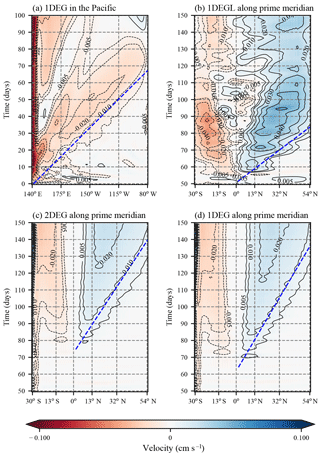
Figure 5The Kelvin wave phase speed in Veros approximately only depends on viscosity, not resolution, as predicted by Marshall and Johnson (2013). (a) Zonal velocity in 1DEG at the Equator and (b–d) meridional velocity in 1DEGL, 2DEG, and 1DEG, respectively, along 0∘ longitude in the Atlantic at 200 m of depth. The slopes of the blue dashed lines are used to estimate phase speeds. Note that the signal arrives at different times at the African coast due to the location of the maximum wind field perturbation, which is not at the South American coast. Thus, the buoyancy perturbation that eventually arrives in the North Atlantic has to be advected to the South American coast before it can travel north as a fast coastal wave.
By translating pyOM2's core routines from Fortran 90 to vectorized Python code using the NumPy API (Sect. 2.1 and 2.2) and adding integration with the Bohrium framework (Sect. 2.4), we were able to build a Python ocean model (Veros) that is both consistent with pyOM2 to a high degree (Sect. 3.1) and does not perform significantly worse, even on highly parallel architectures (Sect. 3.2). Additional modifications (Sect. 2.3) include a powerful algebraic multigrid (AMG) Poisson solver, compressed NetCDF4 output, a modular interface for diagnostics, self-documentation, and automated testing.
A simple experiment investigating planetary wave propagation in the Atlantic showed that boundary waves in GCMs travel with phase speeds consistent with theoretical expectations.
While creating Veros did require a deep understanding of the workings of NumPy and Bohrium to avoid performance bottlenecks and to write concise, idiomatic, vectorized code, the presented version of Veros took less than a year to develop by a single full-time researcher. Nevertheless, Veros is still at an early stage of development. In future releases, we plan to address the following issues.
- More abstraction.
-
Most of the Veros core routines are currently direct vectorized translations of pyOM2's Fortran code, which manipulate array objects through basic arithmetic and provide little exposition of the underlying numerical concepts. In order to create a truly approachable experience, it is crucial to deviate from this approach and introduce more abstraction by grouping common patterns into higher-order operations (like transpositions between grid cell types or the calculation of gradients).
- Parallelized stream function solvers.
-
A parallel Poisson solver is a missing key ingredient to scale Veros efficiently to even larger architectures. Solvers could either be provided through Bohrium or by binding to another third-party library such as PETSc (Balay et al., 1997), ViennaCL (Rupp et al., 2010), or CUSP (Dalton et al., 2014).
- Distributed memory support.
-
High-resolution representations of the ocean (such as eddy-permitting or eddy-resolving models) are infeasible to be simulated on a single machine, since the required integration times may well take decades to compute. In order for Veros to become a true all-purpose tool, it is crucial that work can be distributed across a whole computing cluster (which could either consist of CPU or GPU nodes). Therefore, providing distributed memory support either through Bohrium or another numerical back end is a top priority for ongoing development.
However, we think that Veros has proven that it is indeed possible to implement high-performance geophysical models entirely in high-level programming languages.
The entire Veros source code is available under a GPL license on GitHub (https://github.com/dionhaefner/veros, Häfner and Jacobsen, 2016). All comparisons and benchmarks presented in this study are based on the Veros v0.1.0 release, which is available under the DOI 10.5281/zenodo.1133130 (Häfner and Jacobsen, 2017). The model configuration used in Sect. 4 is included as a default configuration (“wave propagation”).
The Veros user manual is hosted on ReadTheDocs (https://veros.readthedocs.io, last access: 1 August 2018). An archived version of the Veros v0.1.0 manual, along with the user manual of pyOM2 describing the numerics behind Veros, is found under the DOI 10.5281/zenodo.1174390 (Häfner et al., 2017).
Recent versions of pyOM2 are available at https://wiki.cen.uni-hamburg.de/ifm/TO/pyOM2 (Eden, 2014b). A snapshot of the pyOM2 version Veros is based on, and that is used in this study, can be found in the Veros repository.
MJ, BV, and RLJ conceived the idea for Veros. CE contributed the PyOM2 source code and supported its translation into Python. RLJ contributed a first prototype of a Python ocean model, which was then extended and improved by DH into what is now Veros. BV and MRBK provided critical help to integrate support for Bohrium. MJ designed the numerical experiments and RN carried them out. DH prepared the paper with contributions from all coauthors.
The authors declare that they have no conflict of interest.
Dion Häfner was supported through PREFACE (EU FP7/2007-2013) under grant
agreement no. 603521; all others were supported through the Niels Bohr
Institute. Computational resources were provided by DC3, the Danish Center
for Climate Computing. We kindly thank everyone involved in the development
of Veros and the scientific Python community for providing the necessary
tools.
Edited by: Claire Levy
Reviewed by: two anonymous referees
Amante, C. and Eakins, B. W.: ETOPO1 1 arc-minute global relief model: procedures, data sources and analysis, US Department of Commerce, National Oceanic and Atmospheric Administration, National Environmental Satellite, Data, and Information Service, National Geophysical Data Center, Marine Geology and Geophysics Division Colorado, 2009. a
Anderson, E., Bai, Z., Bischof, C., Blackford, L. S., Demmel, J., Dongarra, J., Du Croz, J., Greenbaum, A., Hammarling, S., McKenney, A., and Sorensen, D.: LAPACK Users' guide, SIAM, https://doi.org/10.1137/1.9780898719604, 1999. a
Arakawa, A. and Lamb, V. R.: Computational design of the basic dynamical processes of the UCLA general circulation model, Methods in Computational Physics, 17, 173–265, 1977. a, b
Balay, S., Gropp, W. D., McInnes, L. C., and Smith, B. F.: Efficient Management of Parallelism in Object Oriented Numerical Software Libraries, in: Modern Software Tools in Scientific Computing, edited by: Arge, E., Bruaset, A. M., and Langtangen, H. P., 163–202, Birkhäuser Press, 1997. a, b
Behnel, S., Bradshaw, R., Citro, C., Dalcin, L., Seljebotn, D., and Smith, K.: Cython: The Best of Both Worlds, Comput. Sci. Eng., 13, 31–39, https://doi.org/10.1109/MCSE.2010.118, 2011. a
Bell, W. N., Olson, L. N., and Schroder, J.: PyAMG: Algebraic Multigrid Solvers in Python, available at: http://www.pyamg.org (last access: 1 August 2018), version 2.1, 2013. a
Bryan, K.: Modeling Ocean Circulation: 1960–1990, the Weather Bureau, and Princeton, in: Physical oceanography: Developments since 1950, edited by: Jochum, M. and Murtugudde, R., 250 pp., Springer Science & Business Media, 2006. a
Chelton, D. B., deSzoeke, R. A., Schlax, M. G., El Naggar, K., and Siwertz, N.: Geographical variability of the first baroclinc Rossby radius of deformation, J. Phys. Oceanogr., 28, 433–460, 1998. a, b
Dagum, L. and Menon, R.: OpenMP: an industry standard API for shared-memory programming, IEEE Comput. Sci. Eng., 5, 46–55, 1998. a
Dalton, S., Bell, N., Olson, L., and Garland, M.: Cusp: Generic Parallel Algorithms for Sparse Matrix and Graph Computations, available at: http://cusplibrary.github.io/ (last access: 1 August 2018), version 0.5.0, 2014. a, b
Eden, C.: pyOM2.0 Documentation, available at: https://wiki.cen.uni-hamburg.de/ifm/TO/pyOM2 (last access: 1 May 2017), 2014a. a
Eden, C.: Python Ocean Model 2 (pyOM2), available at: https://wiki.cen.uni-hamburg.de/ifm/TO/pyOM2 (last acces: 1 August 2018), 2014b. a
Eden, C.: Closing the energy cycle in an ocean model, Ocean Model., 101, 30–42, https://doi.org/10.1016/j.ocemod.2016.02.005, 2016. a, b
Eden, C. and Greatbatch, R. J.: Towards a mesoscale eddy closure, Ocean Model., 20, 223–239, 2008. a
Eden, C. and Olbers, D.: An energy compartment model for propagation, nonlinear interaction, and dissipation of internal gravity waves, J. Phys. Oceanogr., 44, 2093–2106, 2014. a
Gao, G., Olsen, R., Sarkar, V., and Thekkath, R.: Collective loop fusion for array contraction, in: Languages and Compilers for Parallel Computing, Springer Berlin Heidelberg, 281–295, 1993. a
Gaspar, P., Grégoris, Y., and Lefevre, J.-M.: A simple eddy kinetic energy model for simulations of the oceanic vertical mixing: Tests at station Papa and Long-Term Upper Ocean Study site, J. Geophys. Res.-Oceans, 95, 16179–16193, 1990. a, b, c
Gebbie, J. and Huybers, P.: Meridional circulation during the Last Glacial Maximum explored through a combination of South Atlantic d18O observations and a geostrophic inverse model, Geochem. Geophy. Geosy., 7, 394–407, 2006. a
Gent, P. R., Willebrand, J., McDougall, T. J., and McWilliams, J. C.: Parameterizing eddy-induced tracer transports in ocean circulation models, J. Phys. Oceanogr., 25, 463–474, 1995. a
Getzlaff, J., Boening, C., Eden, C., and Biastoch, A.: Signal propagation related to the North Atlantic overturning, Geophys. Res. Lett., 32, L09602, https://doi.org/10.1029/2004GL021002, 2005. a
Häfner, D. and Jacobsen, R. L.: Veros, the versatile ocean simulator, in pure Python, powered by Bohrium, GitHub, available at: https://github.com/dionhaefner/veros (last access: 1 August 2018), 2016. a
Greatbatch, R. J. and Lu, J.: Reconciling the Stommel box model with the Stommel-Arons model: A possible role for Southern Hemisphere wind forcing?, J. Phys. Oceanogr., 31, 1618–1632, 2003. a
Griffies, S. M.: The Gent–McWilliams skew flux, J. Phys. Oceanogr., 28, 831–841, 1998. a
Gropp, W., Lusk, E., and Skjellum, A.: Using MPI: portable parallel programming with the message-passing interface, vol. 1, MIT press, 1999. a
Häfner, D. and Jacobsen, R.: Veros v0.1.0, Zenodo, https://doi.org/10.5281/zenodo.1133130, 2017. a
Häfner, D., Jacobsen, R., and Eden, C.: Veros v0.1.0 User Manual (Version v0.1.0), Zenodo, https://doi.org/10.5281/zenodo.1174390, 2017. a
Hsieh, W. W., Davey, M. K., and Wajsowicz, R. C.: The free Kelvin wave in finite-difference numerical models, J. Phys. Oceanogr., 13, 1383–1397, 1983. a, b, c
Huang, R. X., Cane, M. A., Naik, N., and Goodman, P.: Global adjustment of the thermocline in the response to deepwater formation, Geophys. Res. Lett., 27, 759–762, 2000. a
IEEE Spectrum: The 2017 Top Programming Languages, available at: http://spectrum.ieee.org/computing/software/the-2017-top-programming-languages, last access: 25 July 2017. a
Jochum, E. and Eden, C.: The connection between Southern Ocean winds, the Atlantic Meridional Overturning Circulation and Pacific upwelling, J. Climate, 28, 9250–9256, 2015. a
Jones, E., Oliphant, T., and Peterson, P.: SciPy: Open source scientific tools for Python, available at: http://www.scipy.org/ (last access: 1 August 2018), 2001. a
Klöckner, A., Pinto, N., Lee, Y., Catanzaro, B., Ivanov, P., and Fasih, A.: PyCUDA and PyOpenCL: A scripting-based approach to GPU run-time code generation, Parallel Comput., 38, 157–174, 2012. a, b
Kristensen, M. R., Lund, S. A., Blum, T., Skovhede, K., and Vinter, B.: Bohrium: unmodified NumPy code on CPU, GPU, and cluster, Python for High Performance and Scientific Computing (PyHPC 2013), available at: http://dlr.de/Portaldata/15/Resources/dokumente/PyHPC2013/submissions/pyhpc2013_submission_1.pdf (last access: 1 August 2018), 2013. a, b
Kristensen, M. R., Lund, S. A., Blum, T., and Avery, J.: Fusion of parallel array operations, in: Parallel Architecture and Compilation Techniques (PACT), 2016 International Conference on IEEE, 71–85, 2016. a
Larsen, M. O., Skovhede, K., Kristensen, M. R., and Vinter, B.: Current Status and Directions for the Bohrium Runtime System, Compilers for Parallel Computing, available at: https://cpc2016.infor.uva.es/preliminary-program/ (last access: 1 August 2018), 2016. a, b
Levitus, S.: Climatological Atlas of the World Ocean, NOAA Prof. Paper 13, 1994. a
Marshall, D. P. and Johnson, H. L.: Propagation of meridional circulation anomalies along western and eastern boundaries, J. Phys. Oceanogr., 43, 2699–2717, 2013. a, b, c, d, e
Marta-Almeida, M., Ruiz-Villarreal, M., Otero, P., Cobas, M., Peliz, A., Nolasco, R., Cirano, M., and Pereira, J.: OOFϵ: a python engine for automating regional and coastal ocean forecasts, Environ. Modell. Softw., 26, 680–682, 2011. a
McDermott, D. A.: The regulation of northern overturning by southern hemisphere winds, J. Phys. Oceanogr., 26, 1234–1254, 1996. a
McDougall, T. J. and Barker, P. M.: Getting started with TEOS-10 and the Gibbs Seawater (GSW) oceanographic toolbox, SCOR/IAPSO WG, 127, 1–28, 2011. a
Monteiro, J. M. and Caballero, R.: The climate modelling toolkit, in: Proceedings of the 15th Python in Science Conference, 69–74, 2016. a
Munday, D., Johnson, H., and Marshall, D.: Eddy Saturation of Equilibrated Circumpolar Curremts, J. Phys. Oceanogr., 43, 507–523, 2013. a
Nickolls, J., Buck, I., Garland, M., and Skadron, K.: Scalable parallel programming with CUDA, Queue, 6, 40–53, 2008. a
Olbers, D. and Eden, C.: A global model for the diapycnal diffusivity induced by internal gravity waves, J. Phys. Oceanogr., 43, 1759–1779, 2013. a, b
Olbers, D., Willebrand, J., and Eden, C.: Ocean dynamics, Springer Science & Business Media, 2012. a
Pacanowski, R. C., Dixon, K., and Rosati, A.: The GFDL modular ocean model users guide, GFDL Ocean Group Tech. Rep., 2, p. 142, 1991. a
Peterson, P.: F2PY: a tool for connecting Fortran and Python programs, International Journal of Computational Science and Engineering, 4, 296–305, 2009. a
Price de Solla, D.: Little science, big science, New York, Columbia Uni, 119 pp., 1963. a
PYPL: PYPL PopularitY of Programming Language index, available at: http://pypl.github.io, last access: 25 July 2017. a
Rew, R. and Davis, G.: NetCDF: an interface for scientific data access, IEEE Comput. Graph., 10, 76–82, 1990. a
Rupp, K., Rudolf, F., and Weinbub, J.: ViennaCL – a high level linear algebra library for GPUs and multi-core CPUs, in: Intl. Workshop on GPUs and Scientific Applications, 51–56, 2010. a
Stack Overflow: Stack Overflow Developer Survey, available at: https://insights.stackoverflow.com/survey/2017, last access: 25 July 2017. a
Stone, J. E., Gohara, D., and Shi, G.: OpenCL: A parallel programming standard for heterogeneous computing systems, Comput. Sci. Eng., 12, 66–73, 2010. a
TIOBE Group: TIOBE Programming Community Index, available at: https://www.tiobe.com/tiobe-index, last access: 25 July 2017. a
Toggweiler, J. and Samuels, B.: Effect of the Drake Passage on the global thermohaline circulation, Deep-Sea Res., 42, 477–500, 1995. a, b
Uppala, S. M., Kållberg, P., Simmons, A., Andrae, U., Bechtold, V. D. C., Fiorino, M., Gibson, J., Haseler, J., Hernandez, A., Kelly, G.,, Li, X., Onogi, K., Saarinen, S., Sokka, N., Allan, R. P., Andersson, E., Arpe, K., Balmaseda, M. A., Beljaars, A. C. M., Berg, L. Van De, Bidlot, J., Bormann, N., Caires, S., Chevallier, F., Dethof, A., Dragosavac, M., Fisher, M., Fuentes, M., Hagemann, S., Hólm, E., Hoskins, B. J., Isaksen, L., Janssen, P. A. E. M., Jenne, R., Mcnally, A. P., Mahfouf, J.-F., Morcrette, J.-J., Rayner, N. A., Saunders, R. W., Simon, P., Sterl, A., Trenberth, K. E., Untch, A., Vasiljevic, D., Viterbo, P., Woollen, J.: The ERA-40 re-analysis, Q. J. Roy. Meteor. Soc., 131, 2961–3012, 2005. a
Vallis, G. K.: Atmospheric and oceanic fluid dynamics: fundamentals and large-scale circulation, Cambridge University Press, 2006. a
Vaněk, P., Mandel, J., and Brezina, M.: Algebraic multigrid by smoothed aggregation for second and fourth order elliptic problems, Computing, 56, 179–196, 1996. a
Vinokur, M.: On one-dimensional stretching functions for finite-difference calculations, J. Comput. Phys., 50, 215–234, 1983. a
Walt, S. V. D., Colbert, S. C., and Varoquaux, G.: The NumPy array: a structure for efficient numerical computation, Comput. Sci. Eng., 13, 22–30, 2011. a
There are many attempts to rank programming languages by popularity, and Python is usually placed in the top 10 of such rankings; see, e.g., IEEE Spectrum (2017), Stack Overflow (2017), TIOBE Group (2017), or PYPL (2017).
For example,
through the GNU command line tool sed, which is readily available on
most Linux distributions.
One that arises when calculating mixing lengths as in Gaspar et al. (1990) that involves updating values dynamically based on the value of the previous cell, and one inside the overturning diagnostic for which a vectorization would require temporarily storing elements in memory (where Nx,Ny, and Nz denote the number of grid elements in the x,y, and z direction, respectively).
Two additional diagonals are introduced when using cyclic boundary conditions to enforce .
Except NumPy functions implemented in C, which have to be re-implemented inside Bohrium to be available.
Since pyOM2 offers Python bindings through f2py for all of its core routines, it can actually be used as a Veros back end. This way, we can ensure that all components solve the exact same problem.