the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Implementing the nitrogen cycle into the dynamic global vegetation, hydrology, and crop growth model LPJmL (version 5.0)
Werner von Bloh
Sibyll Schaphoff
Christoph Müller
Susanne Rolinski
Katharina Waha
Sönke Zaehle
The well-established dynamical global vegetation, hydrology, and crop growth model LPJmL is extended with a terrestrial nitrogen cycle to account for nutrient limitations. In particular, processes of soil nitrogen dynamics, plant uptake, nitrogen allocation, response of photosynthesis and maintenance respiration to varying nitrogen concentrations in plant organs, and agricultural nitrogen management are included in the model. All new model features are described in full detail and the results of a global simulation of the historic past (1901–2009) are presented for evaluation of the model performance. We find that the implementation of nitrogen limitation significantly improves the simulation of global patterns of crop productivity. Regional differences in crop productivity, which had to be calibrated via a scaling of the maximum leaf area index, can now largely be reproduced by the model, except for regions where fertilizer inputs and climate conditions are not the yield-limiting factors. Furthermore, it can be shown that land use has a strong influence on nitrogen losses, increasing leaching by 93 %.
- Article
(2661 KB) - Full-text XML
-
Supplement
(13539 KB) - BibTeX
- EndNote
The dynamics of the terrestrial biosphere and the associated terrestrial carbon cycle are of central importance for Earth system science. Climate–carbon cycle feedbacks have become integral parts of Earth system models (ESMs) for climate change projections. However, the terrestrial carbon cycle dynamic are not only driven by climate and carbon dioxide (CO2) fertilization (Schimel et al., 2015; Norby et al., 2005), but also by land use change (Müller et al., 2006, 2016; Arneth et al., 2017; Le Quéré et al., 2016) and vegetation dynamics (Müller et al., 2016, and references therein). Nutrient limitations, especially from nitrogen, are also important constraints on vegetation growth and the terrestrial carbon cycle. Smith et al. (2016) and Zaehle et al. (2015) suggested that Earth system models contributing to the CMIP5 data archive overestimate the response of net primary productivity to elevated CO2 because the models largely miss the constraints from nutrient limitation. Also Wieder et al. (2015) find that nitrogen limitation may substantially reduce projected increases in net primary productivity (NPP) under climate change and elevated atmospheric CO2 concentrations ([CO2]), possibly even converting the terrestrial biosphere into a net carbon source by the end of the 21st century. Over the last decade, nitrogen limitation has been increasingly accounted for in dynamic global vegetation models (DGVMs) and ESMs (Thornton et al., 2007; Gerber et al., 2010; Zaehle et al., 2010b; Smith et al., 2014). The Lund Potsdam Jena managed Land (LPJmL) dynamic global vegetation, hydrology, and crop growth model has been widely applied to research questions on the terrestrial carbon cycle, hydrology, and agricultural production (Schaphoff et al., 2018b, and references therein) and performed similarly to other dynamic vegetation models (Friend et al., 2014; Warszawski et al., 2013; Chang et al., 2017), hydrology models (Schewe et al., 2014), and crop models (Müller et al., 2017). However, LPJmL so far has not explicitly accounted for nutrient limitations. We extend the LPJmL model to cover the terrestrial nitrogen cycle by explicitly adding processes of soil nitrogen dynamics, plant uptake, nitrogen allocation, response of photosynthesis, transpiration, and maintenance respiration to variable nitrogen concentrations in plant organs, and agricultural nitrogen management. Our implementation is based on previous model implementations (Parton et al., 2001; Gerber et al., 2010; Smith et al., 2014), but some soil processes, e.g., for denitrification and volatilization, are more complex than in Smith et al. (2014), while plant N cycling is similarly parameterized. All implemented processes and the corresponding references are described in full detail in the following sections. LPJmL is the only dynamic global vegetation model that explicitly covers natural vegetation, managed croplands and grasslands, and the full terrestrial hydrology in one consistent modeling framework (Schaphoff et al., 2018b, a). We describe all new model features in full detail and present the results of a global simulation of the historic past (1901–2009) that we use to evaluate model performance.
The model description focuses on the nitrogen-dependent (N-dependent) part of the model. A general description of the LPJmL model is supplied by Sitch et al. (2003), Bondeau et al. (2007), and Schaphoff et al. (2018b, a). Note that Schaphoff et al. (2018b, a) provide the most comprehensive model description available, which includes a few model features added to the model after the development of the N modules had begun and which are thus not part of the LPJmL5.0 version described here. These include several minor amendments of the code, the updated grass allocation scheme (Rolinski et al., 2018), and the updated phenology scheme for natural vegetation (Forkel et al., 2014).
In the LPJmL model vegetation is represented by different plant functional types (PFTs) that can establish concurrently within a cell. These established PFTs share the same soil stand and compete for light, water, and nitrogen resources, while crop functional types (CFTs) are established exclusively at sowing on their own soil stand.
In the predecessor version LPJmL3.5, all organic matter pools (vegetation, soil) were represented as carbon pools. We now also implemented a corresponding N pool for each of these carbon pools and pools for inorganic reactive N forms (, ) in the soil (Fig. 1). Nitrogen dynamics have been incorporated in other dynamical vegetation models, e.g., in LPJ-GUESS (Smith et al., 2014). In addition to LPJ-GUESS our model considers not only natural vegetation but also takes into account managed crops. Furthermore, nitrogen transformation in soils is simulated in a more sophisticated way incorporating the immobilization of nitrogen. In the following sections we describe the implementation of the plant N demand, uptake, allocation, the effects of N limitation, photosynthesis, maintenance respiration, and N inputs, and transformations and losses in and/or from soils. All processes are computed at a daily time step, except for fire events (annual) and the allocation of carbon and N in plants, which is computed daily only for crops but annually for natural vegetation and before each harvest event for managed grasslands. Soil processes are vertically resolved in six soil layers including one bedrock layer.
2.1 Nitrogen demand
Daily photosynthesis and maximum carboxylation capacity (Vmax) are computed based on absorbed photosynthetically active radiation (APAR) and canopy conductance reflecting the level of water stress (Sitch et al., 2003). This water-stressed carboxylation capacity Vmax determines the demand for N of trees, grasses, and crops in the leaves. Depending on PFT-specific requirements for Vmax, the N demand of leaf, Nleaf (g N m−2), is calculated according to Smith et al. (2014) based on Haxeltine and Prentice (1996) as
where Cleaf is the actual leaf carbon content (g C m−2) and daylength is the duration of daylight (h). The function fLAI(LAI) is a modifier dependent on current leaf area index (LAI) accounting for a stronger leaf N content decline with canopy depth compared to incoming sunlight.
The pre-factor 0.12 in the exponential term of Smith et al. (2014) has been replaced by 0.08 for two reasons. First, we find that canopy C : N ratios are too low for the original value. Second, the computed values for the average leaf C : N ratio of the canopy should monotonically increase with LAI, whereas they decline again at higher LAI. This unwanted decline is not completely prevented with our pre-factor of 0.08 but much weaker and occurs only at much higher LAI values than in the original implementation (see Fig. S1 in the Supplement). We choose a maximum of LAI=7 and for LAI<1 a linear decrease to avoid too-high respiration rates at low LAI levels, where C : N ratios would become very small otherwise. Daily gross photosynthesis Agd depends on the light-limited photosynthesis rate JE and Rubisco-limited photosynthesis rate JC:
where θ is the shape parameter describing the co-limitation of light and Rubisco activity. The value of θ of LPJmL3.5 has been changed from 0.7 to 0.9, which is in better agreement with Collatz et al. (1990) and results in lower Rubisco demand to reach the light-limited photosynthesis rate (see Fig. S2). The factor αa determining the fraction of photosynthetic active radiation (PAR) assimilated at ecosystem level relative to leaf level has been changed from 0.5 to 0.6 to counterbalance the reduction of GPP due to additional nitrogen limitations.
Because the allocation of carbon and nitrogen for grass and tree PFTs is done on a yearly time interval, the actual carbon stored in leaves Cleaf,t at time t of the current year is calculated from the carbon stored in leaves at the end of the previous year Cleaf:
where is the accumulated biomass increment and fleaf is the fraction of biomass that was allocated to leaves at the end of the previous year. Then the total N demand is determined by the actual (t) carboxylation-based demand for N in leaves Nleaf,t (see Eq. 1), the current N content of the other organs (roots Nroot and sapwood Nsapwood for trees), and the approximated N demand for the newly accumulated NPP (Eq. 5). For this approximation, we use the allocation shares of the previous year (froot, fsapwood):
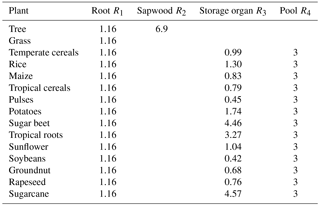
where R1 and R2 are the prescribed PFT-specific C : N ratios of roots and sapwood relative to the C : N ratio of leaves (Table 1).
The daily allocation scheme of crops enables the calculation of nitrogen demand by using the carbon compartment itself. Plants maintain a store of labile N, Nstore (g N m−2), to buffer fluctuations between N demand and supply from the soil mineral N pool (Smith et al., 2014). N demand is therefore increased by a factor of kstore=1.15 for trees and kstore=1.3 for grass and crops. Thus, the optimum N uptake fulfilling the demand Nuptake,opt can be calculated from the demand increment.
2.2 Nitrogen uptake
The mechanism for the uptake of N (Nuptake in g N m−2 d−1) is the same for trees, crops, and grasses. Following Smith et al. (2014), plant Nuptake is determined by soil mineral N concentrations, fine root mass, soil temperature and porosity, and plant demand for N. This is computed for all soil layers individually and summed up to compute overall N uptake:
where Nup,root is the maximum N uptake rate per unit of fine root mass in each layer, fN(Navail) parameterizes the dependence on available N, fT(Tsoil) parameterizes the temperature dependence, fNC parameterizes the dependence on plant N : C ratio, Croot is the carbon stored in the roots, nsoillayer is the number of soil layers (nsoillayer=6), and rootdistl determines the fraction of roots in each layer. Nup,root is g N g C−1 d−1 for trees and g N g C−1 d−1 for crops and grasses (Smith et al., 2014). The available N is the sum of and in the soil layer l.
The function fN can be parameterized by Michaelis–Menten kinetics:
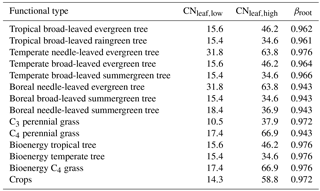
where dsoil,l is the soil column depth (m), θmax is the soil-type-specific fractional pore space (dimensionless), is 1.48 g N m−3 for woody and 1.19 for grassy PFTs (half-saturation concentration of fine root N uptake), and (dimensionless) is 0.05, which is the basal rate of N uptake that is not associated with Michaelis–Menten kinetics. The function fNC(NCplant) is from Zaehle et al. (2010b):
where NCleaf,low and NCleaf,high are the lower and upper limits of N : C ratios and NCplant is the actual plant N : C ratio. The lower and upper limits NCleaf,low and NCleaf,high are derived from the TRY database (Kattge et al., 2011). Their reciprocal C : N values for each PFT are shown in Table 2. The actual plant N : C ratio is calculated according to
The temperature function fT for N uptake is given by Thornley (1991):
where . For the chosen Tm=15 ∘C, Tr=15 ∘C, and ∘C, the maximum of 1 is reached at 15∘ and the function is positive above −25 ∘C.
The root distribution rootdistl can be calculated from the proportion of roots from the surface to soil depth z, rootdistz, as in Jackson RB et al. (1996):
where βroot is a PFT-specific parameter (for parameter values, see Table 2); rootdistl is then given by the difference . If the soil depth of the layer l is greater than the thawing depth then rootdistl is reduced accordingly. The nonzero rootdistl values are rescaled so that their sum is normalized to 1, accounting for the modified root distribution under freezing conditions. Soil and soil pools are reduced accordingly every simulation day t.
Table 2PFT-specific βroot based on Schaphoff et al. (2018b) and minimum and maximum leaf C : N ratios based on the TRY database (Kattge et al., 2011) with data from Kurokawa and Nakashizuka (2008), Garnier et al. (2007), Penuelas et al. (2010a, b), Fyllas et al. (2009), Loveys et al. (2003), Han et al. (2005), Ordonez et al. (2010), Atkin et al. (1999), White et al. (2000), Xu and Baldocchi (2003), Freschet et al. (2010a, b), Laughlin et al. (2010), Niinemets (2001, 1999), Willis et al. (2010), Baker et al. (2009), Patiño et al. (2009), Pakeman et al. (2009, 2008), Fortunel et al. (2009), Cornelissen et al. (1996, 1997, 2004), Quested et al. (2003), Sardans et al. (2008b, a), and Ogaya and Penuelas (2003, 2006, 2007, 2008). The C : N ratios for C3 and C4 grasses and crops are based on White et al. (2000).
2.3 Determination of the N limitation scalar
For trees, grass, and crops, the N limitation scalar vscal is calculated as the ratio of N demand Nuptake,opt to actual N uptake:
The scalar vscal is used to account for N limitation in the allocation of N to different plant organs (Sect. 2.5) and is computed as the growing season mean, which is re-initialized to zero every year for natural vegetation and at sowing for crops.
2.4 Photosynthesis and gross and net primary production under N limitation
To calculate the limitation by N availability, N stress is calculated after determining water stress on photosynthesis. If N demand from the water-limited photosynthesis rate cannot be fulfilled by N uptake, carboxylation capacity Vmax has to be reduced. The reduced Vmax is determined by solving Eq. (1) for Vmax. Water demand is then recalculated using the reduced Vmax. From this reduced Vmax, the actual photosynthesis rate and canopy conductance can be calculated (Fig. 2). For the determination of the canopy conductance we assume higher PFT-specific minimum canopy conductances gmin (see Table S1 in the Supplement) than Schaphoff et al. (2018b), which are in the range of values reported by Barnard and Bauerle (2013). Furthermore, we have adjusted some additional parameters (Tables S1, S2) to meet global and local evapotranspiration fluxes under nitrogen limitation effects on transpiration.
The gross primary production (GPP) derived from the actual photosynthesis rate is reduced by leaf, root, and sapwood (for tree PFTs) respiration Rleaf, Rroot, and Rsapwood in order to get the net primary production (NPP). Respiration rates of roots and sapwood are assumed to be linearly dependent on the N : C ratio of the corresponding pool, whereas the respiration rate of leaves (Rleaf) is a fraction (1.5 % for C3 plants, 3.5 % for C4 plants) of Vmax (Sitch et al., 2003):
where kresp(T) is a temperature-dependent respiration rate (g C g N−1 d−1) (as in Sitch et al., 2003). Therefore, higher N : C ratios lead to a reduction in net primary production (NPP), which is computed as
where Rgrowth is 25 % of GPP and Rsapwood is zero for all non-woody plants.
2.5 Nitrogen allocation and turnover in plants
Carbon allocation to plant compartments follows functional and allometric rules as described by Sitch et al. (2003) and is computed annually for natural vegetation and daily for crops (Bondeau et al., 2007). The allocation rules account for the functional relationships that leaf area needs to be supported by sufficient sapwood (in trees) and fine root biomass. Fine root biomass increases relative to leaf biomass under water stress and also under nitrogen limitation. The allometric rules specify the relationship of stem diameter to plant height and crown diameter (Sitch et al., 2003). Plants require N in varying amounts to satisfy organ-specific C : N ratios. Leaf N content is determined by photosynthetic potential and structural requirements and can vary within PFT-specific limits of C : N ratios. The PFT-specific range of possible C : N ratios is based on the TRY database (Kattge et al., 2011, Table 2).
The allocation of N (Ninc) to plant compartments follows the allocation rules for carbon and ensures distribution between plant compartments as established with the relative ratios given for the C : N ratio of, e.g., roots in comparison to leaves (CNroot / CNleaf). These relative ratios for natural vegetation are taken from Friend et al. (1997, Table 4).
For crops the C : N ratios for the storage organ are derived from Bodirsky et al. (2012). Therefore, average crop-functional-type-specific leaf C : N ratios as simulated by LPJmL5.0 were used to estimate the factors R3 that relate leaf C : N ratios to storage organ C : N ratios (Table 1).
The allocation scheme follows the algebraic solution of the following set of equations when there are n plant compartments.
, N1, N2, …, Nn are the C and N pools of plant compartments , and are the relative C : N ratios in comparison to leaves. The system is solved for so that the relative ratios are ensured. Thus, the model has to solve the equation system for n=2 pools for grass, n=3 pools for trees, and n=4 pools for crops. If the N : C ratio for a pool is below the PFT-specific minimum N : C ratio allowed, then the excess carbon is put into the litter pools. To avoid overly large C fluxes from excess carbon to the litter pools in N-limited environments, we have introduced a sink limitation for the photosynthesis of trees. For this, the excess carbon from the sapwood pool is stored in an additional carbon pool Cexcess. If this excess pool is filled and if there is a minimum Csapwood pool of at least 1 kg m−2, photosynthesis is downregulated by a scaling factor s in the following year (Eq. 21). At the end of the year, the newly acquired carbon (NPP) and the Cexcess are allocated to the plant organs according to the usual allocation rules. If all carbon can be allocated within allowed compartment-specific C : N ratios, the Cexcess pool is empty afterwards and photosynthesis is no longer downregulated.
where KM=0.1 is the Michaelis constant of the Michaelis–Menten kinetics and R2 is the relative C : N ratio of sapwood with respect to leaves.
Similar to water stress, we assume that plants allocate more biomass to roots under N limitation. For this, the leaf to root mass ratio (lmtorm) is modified by the minimum of the N limitation factor vscal and the water limitation factor wscal. Both factors are computed as growing season means with daily updates, i.e., for the entire calendar year for natural vegetation, between harvest events for managed grasslands, and since sowing for crops.
LPJmL employs PFT-specific turnover rates for living leaves and fine roots. At turnover the corresponding amount of carbon is moved into the litter pools, whereas not all of the associated N is disposed of but remains in the plant. We assume that grasses and deciduous trees recover kturn=70 % of their N upon biomass turnover, whereas evergreen trees only recover kturn=20 %. At turnover sapwood carbon is transformed into heartwood carbon. Not all nitrogen from sapwood turnover goes into heartwood, and only a fraction fheartwood=0.7 of nitrogen is transformed.
2.6 Nitrogen transformation in soils
Nitrogen occurs in soils in different reactive forms, mainly the organic forms nitrate () and ammonium (), which are represented by different pools in LPJmL5.0. Transformations between different forms of N in the soil are represented by mineralization, immobilization, nitrification, and denitrification and are simulated in sequential order. Each soil and litter pool consists of carbon and nitrogen stocks and the resulting C : N ratios are flexible. Losses from the soil are represented by the implemented nitrification, leaching, denitrification, and volatilization processes. The corresponding pools and fluxes are depicted in Fig. 3 and described, including their parameterization (see Table S2), in this section.

Figure 3Nitrogen transformations and losses in soils. Pools and fluxes are denoted by boxes and arrows, respectively.
2.6.1 Mineralization of nitrogen
The mineralization of N from soil organic matter and the decomposition of litter pools follow that of carbon as described by Schaphoff et al. (2013). First, for each soil layer the fluxes of carbon from the soil into the atmosphere are calculated and the respective fluxes of N, reflecting the actual C : N ratios of the material, are transferred to the soil pool of the corresponding soil layer.
Fluxes (F) of carbon and nitrogen for slow (s) and fast (f) pools (P) depend on parameters , (per year), and R(T,M) as a function of temperature (T) and soil moisture (M) per soil layer (l).
where
The mineralization of soil N, N, in soil layer l is given by
Whereas the mineralization fluxes of carbon go completely to the atmosphere as CO2, mineralized N goes to the mineral pools, where it is subject to further transformation (Parton et al., 2001).
The decomposition of N in soil organic material (Ndecom) consists of a mineralization part (Af=0.6, dimensionless) that forms and a humification part (1−Af), in which organic N from the litter pool is transferred to the soil pools. The humification flux is divided into fluxes to slow (s) and fast (f) N soil pools (P) for which the parameter Ff=0.98 (dimensionless) specifies the portion that goes to the fast soil pool.
where the annual shift rates N describe the organic matter input from the different PFTs into the respective layer due to cryoturbation and bioturbation (Schaphoff et al., 2013).
Net mineralized material N is
which adds N to an intermediate N mineralization pool
In contrast to Parton et al. (2001) in which 20 % of this pool is directly nitrified to , we follow Schimel and Bennett (2004) and transfer all mineralized N to the pool.
2.6.2 Nitrogen immobilization
Immobilization, i.e., the transformation of mineral N to organic N in soils, is determined per soil layer directly after soil and litter mineralization, following the LM3V land model described by Gerber et al. (2010). If available mineral soil N is constraining immobilization, mineral N is first immobilized into the fast soil pool and then into the slow soil pool. The immobilized N, Nimmo,l, is calculated according to
where CNsoil is the desired soil C : N ratio of 15 (dimensionless) for all soil types, dsoil,l is the soil depth of layer l in meters, (g N m−3) is the half-saturation concentration for immobilization in soils (Gerber et al., 2010), and N is the parameter that determines the distribution of the humified organic matter in the topsoil to the different soil layers l (Schaphoff et al., 2013). The available mineral N in the soil layer l (Nsum,l in g N m−2) is the sum of and .
The immobilized N (Nimmo,l) is added to the fast soil N pool of layer l and subtracted from the and pools.
The immobilization into the slow soil N pool () is computed accordingly as in Eq. (30) but with (1−Ff) instead of Ff.
2.6.3 Nitrification
Nitrogen fluxes from nitrification in the soil are modeled modified after Parton et al. (2001) with the schematic representation of a series of pipes for the main flow from over to N2 from which N2O leaks in between. As suggested by Parton et al. (2001, Eq. 2), nitrification is computed as a fixed fraction of the mineralization flux (see Sect. 2.6.1) and an explicit transformation flux from ammonium to nitrate in g N m−2 d−1, which is described here.
where is the model-derived soil ammonium concentration (g N m−2), Kmax is the maximum nitrification rate of ( d−1), F1(Tsoil,l) is the limiting function for temperature, and F1(Wsat,l) the corresponding limiting function for water saturation Wsat,l. Parton et al. (2001) show nitrification rates after data from Malhi and McGill (1982) in Table 3 without a formula. Using these data from three different sites in the US, Canada, and Australia, we fitted a bell-shaped function for the temperature dependence:
where a=18.79 ∘C and b=5.26 give the best fist to the data (see Fig. S3). The function is also applicable for negative values.
The soil water response function F1(Wsat) is parameterized according to Doran et al. (1988) as described in Parton et al. (1996):
where Wsat,l is the water-filled pore space of soil layer l, and parameters anit to dnit are given for sandy and medium soil (Table S2).
This soil pH function is based on Parton et al. (1996).
Soil pH values are taken from the WISE data set (Batjes, 2000). Part of the N during nitrification is lost to the atmosphere as nitrous oxide (N2O). Parton et al. (2001) assume that the N2O flux (in g N m−2 d−1) is proportional to the nitrification rate with
where K2 is the fraction of nitrified N lost as N2O flux (K2=0.02). Finally, soil and are updated accordingly.
2.6.4 Denitrification
The reduction of to NO2 and N2 is determined for each soil layer using the implementation in SWIM (Krysanova and Wechsung, 2000).
where F2(Wsat,l) is the water response function and F2(T,C) the soil temperature and carbon reaction function. The water response function depends on the water-filled pore space Wsat,l in the following way.
The water response function shows a qualitatively similar behavior to Eq. (151) from SWIM while ensuring continuity (see Fig. S4). Parameters are fitted and adjusted so that for full soil water saturation, the value is not greater than 1. The soil temperature and carbon reaction function is parameterized according to
where CDN=1.4 is the shape coefficient (Arnold et al., 2012), Corg,l is the sum of the fast and slow C pools, and F2(Tsoil,l) is the soil temperature reaction function. F2(Tsoil,l) is replaced by Eq. (C5) from Smith et al. (2014), which is only valid for positive Tsoil,l. The original function from the soil and water assessment tool (SWAT) approaches 1 for high temperatures, whereas the function from Smith declines, which seems more sensible. Equation (C5) of Smith et al. (2014) is taken from Comins and McMurtrie (1993).
Bessou et al. (2010) assume that the N2O flux from , (in g N m−2 d−1), is proportional to the denitrification rate with
where rmx=0.11 is the fraction of denitrified N lost as N2O flux. The N2 flux is then derived by
The soil pools have to be reduced by the denitrification flux.
2.6.5 Nitrogen leaching and movement
Nitrate movement with water fluxes is simulated as in SWAT (Neitsch et al., 2002, 2005). Nitrate is assumed to be fully dissolved in water and moves with surface runoff, lateral runoff, and percolation water. To compute the amount of nitrate transported with the water from a soil layer, we first calculate the concentration of nitrate in the mobile water. This concentration is then multiplied by the volume of surface runoff, lateral runoff, or percolation water between soil layers or into the aquifer. The amount of nitrate leached depends on the climatic and soil conditions and on the type and intensity of soil management (e.g., plant cover, soil treatment, fertilization).
The concentration of nitrate in the mobile water in layer l (kg N m−3) is
where is the content of nitrate in layer l (g N m−2), wmobile is the amount of mobile water in the layer (mm), θ=0.4 is the fraction of porosity from which anions are excluded (0.5 in Neitsch et al., 2002), and SATl is the saturated water content of the soil layer (mm).
The mobile water wmobile,l in the layer l is the amount of water lost by surface runoff, lateral flow, and percolation:
where Qsurf is the surface runoff (only in the topsoil layer; mm), Qlat,l is the water discharged from the layer by lateral flow (mm), and wperc,l is the amount of water percolating to the underlying soil layer on a given day.
Finally, the amount of nitrate that is removed with surface runoff and lateral flow is calculated as
for the top layer and
for the lower soil layers, where is the nitrate percolation coefficient. It controls the amount of removed from the surface layer in runoff relative to the amount removed via percolation (Neitsch et al., 2002). The value for can range from 0.01 to 1.0. For , the concentration of nitrate in the runoff approaches 0. For , surface runoff has the same concentration of nitrate as the percolating water. We choose for a value of 0.4.
Nitrate moved to the lower soil layer with percolation is calculated as
is subtracted from the current in the soil layer and added to the pool of the following soil layer.
2.6.6 Nitrogen volatilization
The volatilization of is parameterized according to Montes et al. (2009). A convective mass transfer model is applied in which the flux varies with air temperature, air velocity over the surface, and the NH3 concentration gradient between the ammonium () in solution and in the air:
where is the NH3 volatilization flux (g NH3-N m−2 s−1), hm is the convective mass transfer coefficient (m s−1), [NH3]gas is the concentration of gaseous NH3 in equilibrium with dissolved NH3 in solution (g NH3 − N m−3 air), and [NH3]air is the concentration of NH3 in ambient air (g NH3 − N m−3 air), which is usually very small and can be neglected. The convective mass transfer coefficient hm is a function of temperature T (in K), air velocity U (in m s−1), and characteristic length L (m) of the emitting surface.
The concentration of gaseous NH3 in equilibrium with the dissolved NH3 is determined using Henry's law. The Henry's law Kh constant relates the concentration of dissolved NH3 in water to an equilibrium concentration of NH3 in the air.
The Henry's law constant Kh can be parameterized as a function of air temperature Tair (K).
The fraction of total ammoniacal N present as NH3 can be estimated using equilibrium thermodynamic principles:
where Ka is the dissociation constant, [H+] is the proton concentration in solution, and pH . The dissociation constant Ka is parameterized as a function of temperature T (K).
Then the volatilization flux Fvol (in g N m−2 d−1) is calculated according to
and soil is reduced in the top layer l=1 accordingly:
2.7 Nitrogen and fire
Fire creates emissions of N2O and NOx and leaves nutrient-rich ashes as well as charcoal. Following Gerber et al. (2010), the flux of N due to fire is divided between atmospheric emissions and ash introduction to the nitrate pool of the upper soil layer NO.
Above, qash=0.45 is the fraction of N going into the topsoil layer .
2.8 Biological N fixation
The biological fixation of N occurs at all stands with an exception for agricultural stands. There, it is applied only for the nodulating leguminous crops pulses and soybean. For these two crops, biological N fixation (BNF) is simply the difference between N demand and N uptake, basically first using the easily plant-available N from the soils and then fixing extra N at no extra cost. For natural vegetation and grasslands, the function from Cleveland et al. (1999) is applied depending on the 20-year average annual evapotranspiration (etp; in mm yr−1). BNF (in g N m−2 d−1) is assumed to only occur if there is a minimum root biomass of 20 g C m−2. All N fixed by BNF is assumed to enter the system as ammonium in the upper soil layer (l=1).
The function gives linearly increasing values that are positive for etp>7.35 and are set to zero otherwise. Note that in Zaehle et al. (2010a) this function is also cited in the Supplement but with a positive intercept that is not the original equation from Cleveland et al. (1999).
2.9 Nitrogen fertilization of crops
Fertilizer is applied at sowing and when the amount of fertilizer is larger than 5 g N m−2, only half of the fertilizer is applied at sowing. The second application occurs when the phenological stage of the crop development (fphu) exceeds 0.4 to avoid large loss fluxes (leaching, volatilization, nitrification, denitrification) when fertilizing large amounts of N at the beginning of the season.
Nitrogen fertilizer is assumed to be ammonium nitrate (NH4NO3), so half of the applied rate is put into the topsoil layer nitrate pool () and the other half into the topsoil layer ammonium pool ().
For the assessment of model performance, we focus on the historic period 1901–2009. The spatial longitudinal–latitudinal resolution is . We conduct six different sets of simulations, two simulations with the carbon-only predecessor model version LPJmL3.5 and four with the newly implemented nitrogen version LPJmL5.0. Both model versions are used for a standard historic simulation with dynamic land use change, referred to as LPJmL35 and LPJmL5, respectively, and for a simulation without human land use in which potential natural vegetation (PNV) is simulated on the entire land surface. These runs are referred to as LPJmL35-PNV and LPJmL5-PNV. For analyzing the current N limitation, we also conduct a simulation with dynamic land use but with unlimited N supply (LPJmL5-nL) and one with no fertilizer application (LPJmL5-nF). Unlimited N supply has been modeled by a deposition rate of 1 Kg N m−2 d−1 on every LPJ cell.
3.1 Model input
Model simulations are driven with observational monthly input data on monthly precipitation from the Global Precipitation Climatology Centre (GPCC Full Data Reanalysis version 7.0; Becker et al., 2013) and daily mean temperatures from the Climatic Research Unit (CRU TS version 3.23; University of East Anglia Climatic Research Unit and Harris, 2015; Harris et al., 2014). Radiation data, shortwave downward and net downward longwave, are provided by reanalysis data from ERA-Interim (Dee et al., 2011). Monthly precipitation is allocated to individual days of the corresponding month by deriving the number of wet days per month synthetically as suggested by New et al. (2000).
Land use input is derived from MIRCA2000 (Portmann et al., 2010) using the maximum monthly growing areas per crop and grid cell combined with the extent of areas equipped for irrigation (Siebert et al., 2015). HYDE3 (Klein Goldewijk and van Drecht, 2006) gives the relative changes in cropland and pasture extent backward to 1700. Further information is given by Fader et al. (2010).
The global data set “Simulated Topological Network” (STN-30) drainage direction map (Vorosmarty and Fekete, 2011) gives the transport directions of the river-routing scheme. We use the GRanD database (Lehner et al., 2011), which provides detailed information on water reservoirs that includes information on storage capacity, total area, and main purpose. Furthermore, information on natural lakes is obtained from Lehner and Döll (2004).
Nitrogen deposition is based on the ACCMIP database (Lamarque et al., 2013) for and separately, which is applied daily to the corresponding mineral N pools of the topsoil layer. Dry and wet deposition are not distinguished. Soil pH data are taken from the WISE data set (Batjes, 2000). Fertilizer data are crop specific, but static in time. We use the data supplied by the Global Gridded Crop Model Intercomparison (GGCMI phase 1; Elliott et al., 2015), which is based on gridded mineral fertilizer data (Mueller et al., 2012) and manure data (Potter et al., 2010) from which 60 % are assumed to be plant available and thus included, whereas the remainder are ignored and not included in Elliott et al. (2015).
3.2 Model initialization, spin-up, and equilibration of soil
All carbon and water pools are initialized to zero except soil water, soil carbon, and soil temperatures, which are computed from a 30-year averaged climate. Then a spin-up simulation of 5000 years is performed to bring permafrost extent, vegetation patterns, and carbon stocks into dynamic equilibrium. The long spin-up time is necessary for reaching these equilibrium states in the permafrost regions (Schaphoff et al., 2013).
Soil N pools (organic and mineral) are initialized with assumptions to allow for initial vegetation growth. Organic N pools (slow, fast) and mineral N pools ( and ) are set to 104 g N m−2. After 1320 simulation years, vegetation composition is assumed to have reached an equilibrium (Schaphoff et al., 2013) and litterfall is tracked for another 3680 years to allow for estimating soil carbon and soil N stocks. Based on these estimates for carbon and N fluxes under equilibrium conditions, nitrogen and carbon pools are re-initialized following Sitch et al. (2003). Hence, all N from the initialization is removed that is not supporting plant growth because of other constraints such as water shortage (e.g., in deserts).
A second spin-up phase of 390 years is conducted for all versions, including land use change (except in the PNV runs LPJmL35-PNV and LPJmL5-PNV) by using the land use input of Fader et al. (2010) to capture the influence of historic land use change on the carbon and nitrogen pools in soil and vegetation.
Table 3Global carbon pools (soil and vegetation carbon) and fluxes (net biome productivity NBP, net primary productivity NPP, and gross primary productivity GPP) for the six different experiments (averages over the period 2000 to 2009). The suffix -PNV denotes experiments with potential natural vegetation, -nL with unlimited N supply, and -nF without fertilizer input.
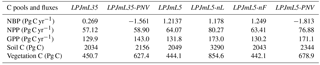
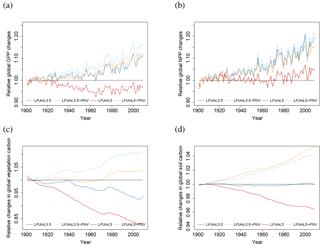
Figure 4Relative global changes in GPP (a), NPP (b), vegetation carbon (c), and soil carbon (d). Relative changes are calculated by dividing the values by their 1901–1910 average to make the different model versions and settings comparable. The blue lines denote values for LPJmL3.5 with land use (LPJmL3.5), the light blue lines for LPJmL3.5 with natural vegetation only (LPJmL3.5-PNV), the red lines for LPJmL5.0 with land use (LPJML5), and the orange lines for LPJmL5.0 with natural vegetation only (LPJmL5-PNV).
4.1 Carbon pools and fluxes
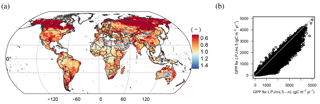
Simulations with LPJmL5.0 result in carbon pools, NPP, and GPP fluxes comparable to the carbon-only LPJmL3.5 version (Table 3) and show a similar temporal dynamic (Fig. 4). Net biome productivity (NBP) shows in both versions a carbon source driven by productivity on managed grassland. The residual sink is at the lower end of global estimations from Le Quéré et al. (2016), but land use and land use change emissions are too high for the LPJmL5.0 simulation. The actual vegetation carbon pool is strongly limited by current N levels and increases substantially across all ecosystems, when N limitations are lifted (LPJmL5-nL). Under actual N limitations and static current fertilizer levels (Elliott et al., 2015), global GPP is relatively stable throughout the simulation period (1901–2009; red line in Fig. 4a) as the expansion of cropland into increasingly low-input areas compensates for the increase in GPP in natural vegetation (orange line in Fig. 4a). NPP increases in the standard simulation with dynamic land use (LPJmL5), but not as strongly as for natural vegetation (compare red and orange lines in Fig. 4b). The difference in global annual NPP between simulations with natural vegetation only and dynamic land use increases significantly from 3 % (LPJmL35-PNV-LPJmL35) to 19 % (LPJmL5-PNV-LPJmL5). This indicates that agricultural land is increasingly N limited so that the C : N-ratio-dependent maintenance respiration declines and NPP increases, whereas GPP does not. This is in part because simulations are conducted with static fertilizer inputs and because land use change predominantly causes cropland expansion in countries with low fertilizer use so that the global average fertilizer use declines, causing higher N limitation on agricultural land. Land-use-driven declines in vegetation carbon over the 20th century are similar between the carbon-only LPJmL35 and the simulation with nitrogen LPJmL5 (Fig. 4c), but soil carbon stocks decline with nitrogen, whereas increases in the natural vegetation balance the land-use-change-induced losses in the carbon-only version (Fig. 4d).
When N limitations are lifted through unlimited N supply (LPJmL5-nL), GPP is mostly increased, except in very dry environments. Most limitation occurs in the boreal zone and in the tundra (Fig. 5a). The scatter plot (Fig. 5b) shows that the GPP increase mainly occurs in low to moderately productive areas. Decreases in GPP under unlimited N supply are possible where other factors are strongly limiting (e.g., water) and the higher N supply leads to higher maintenance respiration under lower tissue C : N ratios so that less biomass is available for leaves and thus less light can be intercepted.
4.2 Nitrogen pools and fluxes
The comparison of global N values to literature estimates is divided between values including natural vegetation only and those considering land use dynamics (Table 4). Whereas several estimates exist for global N pools and fluxes under natural vegetation, those including land use dynamics are rather rare and given mostly for emissions from the soil (e.g., denitrification or N2O). Lifting N limitation (LPJmL5-nL) results in similar responses for all global nitrogen pools (Table 4). Vegetation N and plant uptake increase substantially by a factor of 2.87 and 2.89, respectively, whereas soil N pools increase by a factor of 1.81. The omission of N fertilizers has little effect on N pools, which are dominated by natural ecosystems, but strongly affect nitrogen losses, especially leaching and volatilization fluxes (Table 4). A comparison to literature estimates is discussed further in Sect. 4.4.1.
4.3 Land use and nitrogen dynamics
The role of human land use for the limitation of plant growth by nitrogen availability is apparent when comparing simulations with land use (LPJmL5, red lines in Fig. 6) and natural vegetation only (LPJmL5-PNV, orange lines in Fig. 6). The nitrogen pool in the natural vegetation is stable during the 20th century (Fig. 6a) with some minor fluctuations and the global C : N ratio increases slightly by 3.5 % (Fig. 6b), whereas vegetation nitrogen with the inclusion of historical land use declines by more than 26 %. The predominant difference between the two simulations is the 22 % increase in losses of N by leaching under land use (Fig. 6c), which is caused by the additional fertilizer and irrigation water inputs under land use.
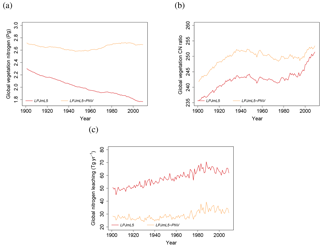
Figure 6Simulated global time series of vegetation nitrogen (a), vegetation C : N ratios (b), and leaching (c) with land use (LPJmL5, red line) and potential natural vegetation (LPJmL5-PNV, orange line).
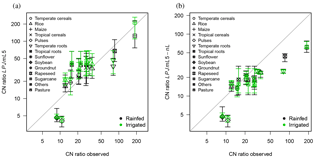
Figure 7Observed C : N ratios of harvested crops versus simulated mean ratios for the crop PFTs (a) with N limitation (LPJmL5) and (b) without N limitation (LPJmL5-nL). The vertical error bars denote the 95 % percentile.
Table 4Global nitrogen pools and fluxes for the four different experiments with LPJmL5 and literature estimates (averages over the period 2000 to 2009). The suffix -PNV denotes experiments with potential natural vegetation, -nL with unlimited N supply, and -nF without fertilizer input.

1 Smith et al. (2014), 2 Zaehle et al. (2010a), 3 Xu-Ri and Prentice (2008), 4 Lin et al. (2000), 5 Post et al. (1985), 6 Bouwman et al. (2013), 7 Sutton et al. (2013), 8 Galloway et al. (2013), 9 Galloway et al. (2004), 10 Vitousek et al. (2013).
The approximated relationships between leaf C : N ratios and storage organ C : N ratios based on Bodirsky et al. (2012) lead to consistent but variable C : N ratios in harvested crop organs, reflecting differences between crop types (Fig. 7). The leguminous crops (soybean, pulses) are not limited by N, as they can acquire the necessary N via biological N fixation. For these, the C : N ratios of harvested organs are typically underestimated. Under unlimited N supply, C : N ratios are typically reduced (Fig. 7b).
We find that agricultural land use and the associated fertilizer application greatly increases nitrogen pollution. Leaching (+93 %) and ammonia volatilization (+33 %) increase strongly, which is almost entirely driven by fertilizer inputs, not by land use change (compare LPJmL5 with LPJmL5-PNV and LPJmL5-nF in Table 4). In contrast, N2O emissions only change slightly when agricultural land use is accounted for as increases in denitrification are partially compensated for by decreases in nitrification under reduced net mineralization (mineralization minus immobilization flux) of soil organic matter (Table 4). The effect of agricultural land use and fertilizer application is also clearly detectable in the spatial patterns of leaching. The ratio of LPJmL5-PNV to LPJmL5 (Fig. 8a) is mostly below 1, indicating higher leaching in agricultural areas. In natural vegetation under dry conditions ratios above 1 can also occur (Fig. 8b).
4.4 Model evaluation
To evaluate model performance, we focus here on carbon and nitrogen pools and fluxes at global and specific sites. Many estimates are also model based so that these cannot be used for model evaluation but only for putting our simulation results into context.
4.4.1 N pools and fluxes
Typically, simulated N pools and fluxes are within literature estimates (Table 4), although literature estimates are often broad, reflecting substantial uncertainty in these values. Values from other model simulations are generally not suitable for an evaluation of model results as they may be wrong (Kelley et al., 2013), and we only include them here for pools and fluxes for which no independent data are available. These model-based reference points include the vegetation N pool, soil mineral N pools, plant uptake rates, mineralization rates, and most global values assessed for potential natural vegetation (PNV). The vegetation N of the potential natural vegetation simulation, LPJmL5-PNV, is slightly below the other model-based estimates (Table 4), whereas other fluxes (e.g., plant uptake of N or mineralization) and pools (soil organic N) are within the range of reported values. For simulations with land use history, LPJmL5, a comparison with independent data is possible for most of the emissions from the soil. Our values for leaching and N2 emissions are slightly below other estimates. For the complementary flux, N2O emissions from denitrification, there is no other estimate, but total N2O emissions from denitrification and nitrification are within the range of other estimates again (Table 4). Xu-Ri and Prentice (2008) provide the only study reporting global soil pools of mineral N forms, but for potential natural vegetation only and for the upper 1.5 m soil layer, and this estimate is based on their model application, not on independent data. Our values for and are the inventory of 3 m soil. In comparison to Xu-Ri and Prentice (2008) we overestimate values by a factor of 5 and underestimate values by a factor of 2 in the soil. The accumulation of in lower soil layers is a phenomenon also reported by Walvoord et al. (2003) and Ascott et al. (2017). In any case, this nitrogen pool is largely inaccessible to plants, as they have very little root access to these layers in our model. Also, higher than concentrations are common in soils as reported by, e.g., Kabala et al. (2017).
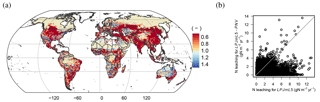
Figure 8Ratio of leaching flux under potential natural vegetation (LPJmL5-PNV) to the leaching flux under actual land use patterns (LPJmL5) (a); values less than 1 indicate higher leaching under actual land use patterns. The scatter plot in (b) shows that leaching is increased strongly mostly in regions where leaching is low under potential natural vegetation.

Figure 9Observed GPP (a), NPP (b), and vegetation carbon (c) data (Luyssaert et al., 2007) versus simulated data for natural vegetation (LPJmL5-PNV). The horizontal error bars denote the minima and maxima of observed site data belonging to the same LPJmL grid cell and the open dot is the mean. The thin black line denotes the 1 : 1 line. RMSE: root mean square error, NMSE: normalized mean square error, NME: normalized mean error, s: slope, p: significance.
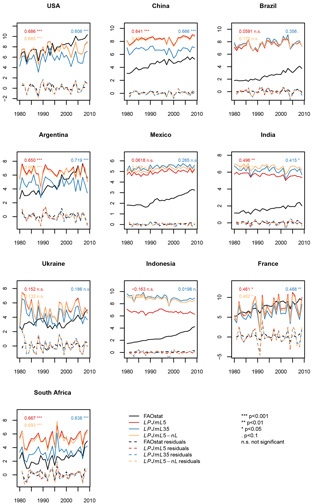
Figure 10Maize yield simulations (in tons of fresh matter (FM) ha−1) for the 10 top-producing countries for the carbon-only LPJmL3.5 version (LPJmL35), the version with N limitation (LPJmL5), and with unlimited N supply (LPJmL5-nL). The residuals plotted are the detrended observed and simulated yields.
4.4.2 Carbon cycle dynamics
Carbon dynamics are mostly unchanged from the predecessor version LPJmL3.5 (Table 3 and Fig. 4). In comparison to measured site-level GPP, NPP, and vegetation carbon (Luyssaert et al., 2007), LPJmL5.0 performs well, especially for GPP and NPP, but with a tendency to underestimate vegetation carbon (Fig. 9). The correlation of observed and simulated GPP and NPP values is statistically significant, and the values of vegetation carbon are less correlated owing to the often broad spread of observations within one grid cell (error bars) and general difficulties to exactly reproduce disturbances, mortality, and age class distributions (Schaphoff et al., 2018a). Still, the comparison shows that simulated values are of the right order of magnitude and are also often within the range of observations (error bar crosses 1 : 1 line in Fig. 9). The best correlation with observational data can be found for GPP. We also provide comparisons to eddy flux tower measurements (ORNL DAAC, 2011) in the Supplement. Figures S5–S11 show the modeled versus observed net ecosystem exchange (NEE) rate defined as
where Rh is the heterotrophic respiration. For some sites a time lag (e.g., site Renon–Ritten) between modeled and observed is visible. Because LPJmL5.0 uses the phenology scheme of LPJmL3.5 incorporating the new phenology of LPJmL4 might reduce these deviations (for a comparison, see the Supplement of Schaphoff et al., 2018a). The overall agreement between modeled and observed NEE is satisfying. While LPJmL4 has an averaged Willmott coefficient of agreement (Willmott, 1982) of , LPJmL5.0 results in . The simulated evapotranspiration fluxes shown in Figs. S12–S20 also agree very well with the observations (). The study by Schlesinger and Jasechko (2014), which partitions evapotranspiration into transpiration and evaporation, reports that transpiration accounts for 61 % of global evapotranspiration. In the LPJmL5.0 simulations, transpiration accounts for 59 % on average for the years 2000 to 2009.
4.4.3 Crop yields
The implementation of nitrogen limitation also substantially helps to improve the simulation of global patterns of crop productivity. Regional differences in crop productivity had to be calibrated via a scaling of the maximum leaf area index (LAImax), the harvest index, and the factor for scaling leaf-level photosynthesis to stand level (αa), as described in Fader et al. (2010), because the LPJmL3.5 version could only distinguish irrigated from rainfed production but not other inputs such as fertilizers. The difference in crop productivity between low- and high-input regions can now largely be reproduced by the model (compare yellow asterisk for uncalibrated with blue asterisk for calibrated LPJmL3.5 simulations with red circle and cross for LPJmL5 in Figs. S21–S24), which are based on the evaluation procedure as described by Müller et al. (2017). In regions where fertilizer inputs and climate conditions are not the only yield-limiting factors, e.g., in regions with poor pest management, an additional calibration of yield levels could be performed as described by Fader et al. (2010), but is not performed here. The temporal variance of simulated crop yields is often not affected much by accounting for N limitation and sometimes improves or worsens the time series correlation with FAO yield statistics (FAOSTAT, 2018) (Figs. 10 and S25–S27 in the Supplement).
We also use the online tool as supplied by Müller et al. (2017) for comparing the crop yield simulations against the Global Gridded Crop Model Intercomparison (GGCMI) ensemble. Also here, results show that LPJmL5.0 improves with respect to reproducing absolute yield levels across different countries, but there is little effect on the simulated interannual variability of crop yields. As with the calibrated LPJmL3.5 version (Fader et al., 2010), the uncalibrated LPJmL5.0 simulations perform well in comparison to the other GGCMI models. We supply the output of that online model evaluation tool in the Supplement.
The current implementation of nitrogen dynamics into LPJmL3.5, forming LPJmL5.0, introduces a missing feature into a unique modeling framework of the terrestrial biosphere. LPJmL5.0 combines natural vegetation dynamics, the full terrestrial hydrology, and managed grasslands and croplands in one consistent framework with the associated carbon, water, and now also nitrogen pools and fluxes. Owing to parallel model development efforts, LPJmL5.0 does not yet include all model features of the first open source version of LPJmL, LPJmL4 (Schaphoff et al., 2018b, a), such as the updated allocation scheme for managed grasslands (Rolinski et al., 2018) and the updated phenology scheme for natural vegetation (Forkel et al., 2014).
With the implementation of nitrogen dynamics, the model simulations require new inputs, especially on atmospheric deposition, but also on fertilizer applications for which we currently use a static crop- and irrigation-specific data set developed for the harmonization of crop models in the Agricultural Model Intercomparison and Improvement Project (AgMIP) (Elliott et al., 2015). This static fertilizer set also affects the simulation of historic carbon cycle dynamics, as high-input regions such as large parts of Europe and northern America receive current high N inputs in the early 20th century, whereas historic land expansion mostly moves into regions with currently lower input systems. As a consequence, land use change leads to increasing nitrogen limitation and increasing C : N ratios, which may be an artifact from the static fertilizer input data set used.
As historic land use development and fertilizer application are important for simulated current biogeochemical cycles, historic time series of crop-specific fertilizer application would be desirable. Also, global data sets on crop rotations (Kollas et al., 2015), the timing of field operations (Hutchings et al., 2012), and crop residue management, as well as livestock management systems (Rolinski et al., 2018) would be an asset, as the interaction of different cropping systems and natural vegetation is now further increased via the nitrogen cycle.
This first implementation of nitrogen dynamics into LPJmL constitutes an operational modeling framework with many detailed processes resolved explicitly. Specific processes are currently implemented in a simplified manner, even though more detailed approaches are available, such as for biological N fixation (Fisher et al., 2010). As such, some process may have to be revised upon further testing against new reference data. Additional reference data would greatly help to evaluate model performance, which currently is largely constrained to comparisons against other modeling results.
LPJmL5.0 constitutes a unique modeling framework that can now simulate global terrestrial carbon, water, and nitrogen dynamics, consistently accounting for natural vegetation dynamics, agricultural cropland and grassland management, and water management.
The source code is publicly available under the GNU AGPL version 3 license. An exact version of the code described here is archived under https://doi.org/10.5880/pik.2018.011 and should be referenced as von Bloh et al. (2018). Data from the simulations conducted here are available upon request from the main author.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-2789-2018-supplement.
WvB, SS, CM, and SR contributed equally to the paper, KW contributed to the model development and SZ contributed to paper writing and discussions.
The authors declare that they have no conflict of interest.
We thank the two anonymous reviewers for their helpful comments that significantly
improved the paper. This study was supported by the German Federal Ministry
of Education and Research (BMBF) project “PalMod 2.3 Methankreislauf,
Teilprojekt 2 Modellierung der Methanemissionen von Feucht- und
Permafrostgebieten mit Hilfe von LPJmL” (FKZ 01LP1507C). Christoph
Müller and Susanne Rolinski acknowledge financial support from the MACMIT
project (01LN1317A) funded through the German Federal Ministry of Education
and Research (BMBF). Sönke Zaehle was supported by the European Research
Council (ERC) under the European Union's Horizon 2020 research and innovation
program (QUINCY; grant no. 647204).
The
article processing charges for this open-access
publication
were covered by the Potsdam Institute
for Climate Impact
Research (PIK).
Edited by: Julia
Hargreaves
Reviewed by: two anonymous referees
Arneth, A., Sitch, S., Pongratz, J., Stocker, B. D., Ciais, P., Poulter, B., Bayer, A. D., Bondeau, A., Calle, L., Chini, L. P., Gasser, T., Fader, M., Friedlingstein, P., Kato, E., Li, W., Lindeskog, M., Nabel, J. E. M. S., Pugh, T. A. M., Robertson, E., Viovy, N., Yue, C., and Zaehle, S.: Historical carbon dioxide emissions caused by land-use changes are possibly larger than assumed, Nat. Geosci., 10, 79–84, https://doi.org/10.1038/ngeo2882, 2017. a
Arnold, J. G., Kiniry, J. R., Williams, J. R., Haney, E. B., and Neitsch, S. L.: Soil and water assessment tool input/output documentation version 2012, Texas Water Resources Institute, College Station, Texas, 2012. a
Ascott, M. J., Gooddy, D. C., Wang, L., Stuart, M. E., Lewis, M. A., Ward, R. S., and Binley, A. M.: Global patterns of nitrate storage in the vadose zone, Nat. Comm., 8, 1416, https://doi.org/10.1038/s41467-017-01321-w, 2017. a
Atkin, O., Schortemeyer, M., McFarlane, N., and Evans, J.: The response of fast- and slow-growing Acacia species to elevated atmospheric CO2: an analysis of the underlying components of relative growth rate, Oecologica, 120, 544–554, https://doi.org/10.1007/s004420050889, 1999. a
Baker, T. R., Phillips, O. L., Laurance, W. F., Pitman, N. C. A., Almeida, S., Arroyo, L., DiFiore, A., Erwin, T., Higuchi, N., Killeen, T. J., Laurance, S. G., Nascimento, H., Monteagudo, A., Neill, D. A., Silva, J. N. M., Malhi, Y., López Gonzalez, G., Peacock, J., Quesada, C. A., Lewis, S. L., and Lloyd, J.: Do species traits determine patterns of wood production in Amazonian forests?, Biogeosciences, 6, 297–307, https://doi.org/10.5194/bg-6-297-2009, 2009. a
Barnard, D. M. and Bauerle, W. L.: The implications of minimum stomatal conductance on modeling water flux in forest canopies, J. Geophys. Res.-Biogeo., 118, 1322–1333, https://doi.org/10.1002/jgrg.20112, 2013. a
Batjes, N. H. (Ed.): Global Data Set of Derived Soil Properties, 0.5-Degree Grid (ISRIC-WISE), Oak Ridge National Laboratory Distributed Active Archive Center, Oak Ridge, Tennessee, USA, https://doi.org/10.3334/ORNLDAAC/546., 2000. a, b
Becker, A., Finger, P., Meyer-Christoffer, A., Rudolf, B., Schamm, K., Schneider, U., and Ziese, M.: A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present, Earth Syst. Sci. Data, 5, 71–99, https://doi.org/10.5194/essd-5-71-2013, 2013. a
Bessou, C., Mary, B., Léonard, J., Roussel, M., Gréhan, E., and Gabrielle, B.: Modelling soil compaction impacts on nitrous oxide emissions in arable fields, Eur. J. Soil Sci., 61, 348–363, https://doi.org/10.1111/j.1365-2389.2010.01243.x, 2010. a
Bodirsky, B. L., Popp, A., Weindl, I., Dietrich, J. P., Rolinski, S., Scheiffele, L., Schmitz, C., and Lotze-Campen, H.: N2O emissions from the global agricultural nitrogen cycle – current state and future scenarios, Biogeosciences, 9, 4169–4197, https://doi.org/10.5194/bg-9-4169-2012, 2012. a, b
Bondeau, A., Smith, P. C., Zaehle, S., Schaphoff, S., Lucht, W., Cramer, W., and Gerten, D.: Modelling the role of agriculture for the 20th century global terrestrial carbon balance, Glob. Change Biol., 13, 679–706, 2007. a, b
Bouwman, A. F., Beusen, A. H. W., Griffioen, J., Van Groenigen, J. W., Hefting, M. M., Oenema, O., Van Puijenbroek, P. J. T. M., Seitzinger, S., Slomp, C. P., and Stehfest, E.: Global trends and uncertainties in terrestrial denitrification and N2O emissions, Philos. T. Roy. Soc. B, 368, 20130112, https://doi.org/10.1098/rstb.2013.0112, 2013. a
Chang, J., Ciais, P., Wang, X., Piao, S., Asrar, G., Betts, R., Chevallier, F., Dury, M., François, L., Frieler, K., Ros, A. G. C., Henrot, A.-J., Hickler, T., Ito, A., Morfopoulos, C., Munhoven, G., Nishina, K., Ostberg, S., Pan, S., Peng, S., Rafique, R., Reyer, C., Rödenbeck, C., Schaphoff, S., Steinkamp, J., Tian, H., Viovy, N., Yang, J., Zeng, N., and Zhao, F.: Benchmarking carbon fluxes of the ISIMIP2a biome models, Environ. Res. Lett. 12, 045002, https://doi.org/10.1088/1748-9326/aa63fa, 2017. a
Cleveland, C. C., Townsend, A. R., Schimel, D. S., Fisher, H., Howarth, R. W., Hedin, L. O., Perakis, S. S., Latty, E. F., Von Fischer, J. C., Elseroad, A., and Wasson, M. F.: Global patterns of terrestrial biological nitrogen (N2) fixation in natural ecosystems, Global Biogeochem. Cy., 13, 623–645, https://doi.org/10.1029/1999GB900014, 1999. a, b
Collatz, G. J., Berry, J. A., Farquhar, G. D., and Pierce, J.: The relationship between the Rubisco reaction mechanism and models of photosynthesis, Plant Cell Environ., 13, 219–225, 1990. a
Comins, H. N. and McMurtrie, R. E.: Long-Term Response of Nutrient-Limited Forests to CO2 Enrichment; Equilibrium Behavior of Plant-Soil Models, Ecol. Appl., 3, 666–681, https://doi.org/10.2307/1942099, 1993. a
Cornelissen, J., Diez, P., and Hunt, R.: Seedling growth, allocation and leaf attributes in a wide range of woody plant species and types, J. Ecol., 84, 755–765, https://doi.org/10.2307/2261337, 1996. a
Cornelissen, J., Werger, M., CastroDiez, P., vanRheenen, J., and Rowland, A.: Foliar nutrients in relation to growth, allocation and leaf traits in seedlings of a wide range of woody plant species and types, Oecologia, 111, 460–469, https://doi.org/10.1007/s004420050259, 1997. a
Cornelissen, J., Quested, H., Gwynn-Jones, D., Van Logtestijn, R., De Beus, M., Kondratchuk, A., Callaghan, T., and Aerts, R.: Leaf digestibility and litter decomposability are related in a wide range of subarctic plant species and types, Funct. Ecol., 18, 779–786, https://doi.org/10.1111/j.0269-8463.2004.00900.x, 2004. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, I., Biblot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Greer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Holm, E. V., Isaksen, L., Kallberg, P., Kohler, M., Matricardi, M., McNally, A. P., Mong-Sanz, B. M., Morcette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thepaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Doran, J. W., Mielke, L. N., and Stamatiadis, S.: Microbial activity and N cycling as regulated by soil water-filled pore space, in: 11th International Conference, Int. Soil Tillage Res. Orgo (ISTRO), Edinburgh, Scotland, 1988. a
Elliott, J., Müller, C., Deryng, D., Chryssanthacopoulos, J., Boote, K. J., Büchner, M., Foster, I., Glotter, M., Heinke, J., Iizumi, T., Izaurralde, R. C., Mueller, N. D., Ray, D. K., Rosenzweig, C., Ruane, A. C., and Sheffield, J.: The Global Gridded Crop Model Intercomparison: data and modeling protocols for Phase 1 (v1.0), Geosci. Model Dev., 8, 261–277, https://doi.org/10.5194/gmd-8-261-2015, 2015. a, b, c, d
Fader, M., Rost, S., Müller, C., Bondeau, A., and Gerten, D.: Virtual water content of temperate cereals and maize: Present and potential future patterns, J. Hydrol., 384, 218–231, https://doi.org/10.1016/j.jhydrol.2009.12.011, 2010. a, b, c, d, e
FAOSTAT: FAOSTAT, Food and Agriculture Organization of the United Nations, available at: http://www.fao.org/faostat/en/#data/QC, last access: 3 June 2017. a
Fisher, J. B., Sitch, S., Malhi, Y., Fisher, R. A., Huntingford, C., and Tan, S.-Y.: Carbon cost of plant nitrogen acquisition: A mechanistic, globally applicable model of plant nitrogen uptake, retranslocation, and fixation, Global Biogeochem. Cy., 24, GB1014, https://doi.org/10.1029/2009GB003621, 2010. a
Forkel, M., Carvalhais, N., Schaphoff, S., v. Bloh, W., Migliavacca, M., Thurner, M., and Thonicke, K.: Identifying environmental controls on vegetation greenness phenology through model–data integration, Biogeosciences, 11, 7025–7050, https://doi.org/10.5194/bg-11-7025-2014, 2014. a, b
Fortunel, C., Garnier, E., Joffre, R., Kazakou, E., Quested, H., Grigulis, K., Lavorel, S., Ansquer, P., Castro, H., Cruz, P., Dolezal, J., Eriksson, O., Freitas, H., Golodets, C., Jouany, C., Kigel, J., Kleyer, M., Lehsten, V., Leps, J., Meier, T., Pakeman, R., Papadimitriou, M., Papanastasis, V. P., Quetier, F., Robson, M., Sternberg, M., Theau, J.-P., Thebault, A., and Zarovali, M.: Leaf traits capture the effects of land use changes and climate on litter decomposability of grasslands across Europe, Ecology, 90, 598–611, https://doi.org/10.1890/08-0418.1, 2009. a
Freschet, G. T., Cornelissen, J. H. C., van Logtestijn, R. S. P., and Aerts, R.: Evidence of the “plant economics spectrum” in a subarctic flora, J. Ecol., 98, 362–373, https://doi.org/10.1111/j.1365-2745.2009.01615.x, 2010a. a
Freschet, G. T., Cornelissen, J. H. C., van Logtestijn, R. S. P., and Aerts, R.: Substantial nutrient resorption from leaves, stems and roots in a subarctic flora: what is the link with other resource economics traits?, New Phytol., 186, 879–889, https://doi.org/10.1111/j.1469-8137.2010.03228.x, 2010b. a
Friend, A. D., Stevens, A. K., Knox, R. G., and Cannell, M. G. R.: A process-based, terrestrial biosphere model of ecosystem dynamics (Hybrid v3.0), Ecol. Model., 95, 249–287, https://doi.org/10.1016/S0304-3800(96)00034-8, 1997. a
Friend, A. D., Lucht, W., Rademacher, T. T., Keribin, R., Betts, R., Cadule, P., Ciais, P., Clark, D. B., Dankers, R., Falloon, P. D., Ito, A., Kahana, R., Kleidon, A., Lomas, M. R., Nishina, K., Ostberg, S., Pavlick, R., Peylin, P., Schaphoff, S., Vuichard, N., Warszawski, L., Wiltshire, A., and Woodward, F. I.: Carbon residence time dominates uncertainty in terrestrial vegetation responses to future climate and atmospheric CO2, P. Natl. Acad. Sci. USA, 111, 3280–3285, https://doi.org/10.1073/pnas.1222477110, 2014. a
Fyllas, N. M., Patiño, S., Baker, T. R., Bielefeld Nardoto, G., Martinelli, L. A., Quesada, C. A., Paiva, R., Schwarz, M., Horna, V., Mercado, L. M., Santos, A., Arroyo, L., Jiménez, E. M., Luizão, F. J., Neill, D. A., Silva, N., Prieto, A., Rudas, A., Silviera, M., Vieira, I. C. G., Lopez-Gonzalez, G., Malhi, Y., Phillips, O. L., and Lloyd, J.: Basin-wide variations in foliar properties of Amazonian forest: phylogeny, soils and climate, Biogeosciences, 6, 2677–2708, https://doi.org/10.5194/bg-6-2677-2009, 2009. a
Galloway, J. N., Dentener, F. J., Capone, D. G., Boyer, E. W., Howarth, R. W., Seitzinger, S. P., Asner, G. P., Cleveland, C. C., Green, P. A., Holland, E. A., Karl, D. M., Michaels, A. F., Porter, J. H., Townsend, A. R., and Vöosmarty, C. J.: Nitrogen Cycles: Past, Present, and Future, Biogeochemistry, 70, 153–226, https://doi.org/10.1007/s10533-004-0370-0, 2004. a
Galloway, J. N., Leach, A. M., Bleeker, A., and Erisman, J. W.: A chronology of human understanding of the nitrogen cycle, Philos. T. Roy. Soc. B, 368, https://doi.org/10.1098/rstb.2013.0120, 2013. a
Garnier, E., Lavorel, S., Ansquer, P., Castro, H., Cruz, P., Dolezal, J., Eriksson, O., Fortunel, C., Freitas, H., Golodets, C., Grigulis, K., Jouany, C., Kazakou, E., Kigel, J., Kleyer, M., Lehsten, V., Leps, J., Meier, T., Pakeman, R., Papadimitriou, M., Papanastasis, V. P., Quested, H., Quetier, F., Robson, M., Roumet, C., Rusch, G., Skarpe, C., Sternberg, M., Theau, J.-P., Thebault, A., Vile, D., and Zarovali, M. P.: Assessing the effects of land-use change on plant traits, communities and ecosystem functioning in grasslands: A standardized methodology and lessons from an application to 11 European sites, Ann. Bot., 99, 967–985, https://doi.org/10.1093/aob/mcm215, 2007. a
Gerber, S., Hedin, L. O., Oppenheimer, M., Pacala, S. W., and Shevliakova, E.: Nitrogen cycling and feedbacks in a global dynamic land model, Global Biogeochem. Cy., 24, https://doi.org/10.1029/2008GB003336, 2010. a, b, c, d, e
Han, W., Fang, J., Guo, D., and Zhang, Y.: Leaf nitrogen and phosphorus stoichiometry across 753 terrestrial plant species in China, New Phytol., 168, 377–385, https://doi.org/10.1111/j.1469-8137.2005.01530.x, 2005. a
Harris, I., Jones, P., Osborn, T., and Lister, D.: Updated high-resolution grids of monthly climatic observations – the CRU TS3.10 Dataset, Int. J. Climatol., 34, 623–642, https://doi.org/10.1002/joc.3711, 2014. a
Haxeltine, A. and Prentice, I. C.: A General Model for the Light-Use Efficiency of Primary Production, Funct. Ecol., 10, 551–561, https://doi.org/10.2307/2390165, 1996. a
Hutchings, N. J., Reinds, G. J., Leip, A., Wattenbach, M., Bienkowski, J. F., Dalgaard, T., Dragosits, U., Drouet, J. L., Durand, P., Maury, O., and de Vries, W.: A model for simulating the timelines of field operations at a European scale for use in complex dynamic models, Biogeosciences, 9, 4487–4496, https://doi.org/10.5194/bg-9-4487-2012, 2012. a
Jackson, R. B., Canadell, J., Ehleringer, J. R., Mooney, H. A., Sala, O.E., and Schulze, E. D.: A global analysis of root distributions for terrestrial biomes, Oecologia, 108, 389–411, https://doi.org/10.1007/BF00333714, 1996. a
Kabala, C., Karczewska, A., Gałka, B., Cuske, M., and Sowiński, J.: Seasonal dynamics of nitrate and ammonium ion concentrations in soil solutions collected using MacroRhizon suction cups, Environ. Monit. Assess., 189, 304, https://doi.org/10.1007/s10661-017-6022-3, 2017. a
Kattge, J., Díaz, S., Lavorel, S., Prentice, I. C., Leadley, P., Bönisch, G., Garnier, E., Westoby, M., Reich, P. B., Wright, I. J., Cornelissen, J. H. C., Violle, C., Harrison, S. P., Van Bodegom, P. M., Reichstein, M., Enquist, B. J., Soudzilovskaia, N. A., Ackerly, D. D., Anand, M., Atkin, O., Bahn, M., Baker, T. R., Baldocchi, D., Bekker, R., Blanco, C. C., Blonder, B., Bond, W. J., Bradstock, R., Bunker, D. E., Casanoves, F., Cavender-Bares, J., Chambers, J. Q., Chapin Iii, F. S., Chave, J., Coomes, D., Cornwell, W. K., Craine, J. M., Dobrin, B. H., Duarte, L., Durka, W., Elser, J., Esser, G., Estiarte, M., Fagan, W. F., Fang, J., Fernández-Méndez, F., Fidelis, A., Finegan, B., Flores, O., Ford, H., Frank, D., Freschet, G. T., Fyllas, N. M., Gallagher, R. V., Green, W. A., Gutierrez, A. G., Hickler, T., Higgins, S. I., Hodgson, J. G., Jalili, A., Jansen, S., Joly, C. A., Kerkhoff, A. J., Kirkup, D., Kitajima, K., Kleyer, M., Klotz, S., Knops, J. M. H., Kramer, K., Kühn, I., Kurokawa, H., Laughlin, D., Lee, T. D., Leishman, M., Lens, F., Lenz, T., Lewis, S. L., Lloyd, J., Llusià, J., Louault, F., Ma, S., Mahecha, M. D., Manning, P., Massad, T., Medlyn, B. E., Messier, J., Moles, A. T., Müller, S. C., Nadrowski, K., Naeem, S., Niinemets, Ü., Nöllert, S., Nüske, A., Ogaya, R., Oleksyn, J., Onipchenko, V. G., Onoda, Y., Ordoñez, J., Overbeck, G., Ozinga, W. A., Patiño, S., Paula, S., Pausas, J. G., Peñuelas, J., Phillips, O. L., Pillar, V., Poorter, H., Poorter, L., Poschlod, P., Prinzing, A., Proulx, R., Rammig, A., Reinsch, S., Reu, B., Sack, L., Salgado-Negret, B., Sardans, J., Shiodera, S., Shipley, B., Siefert, A., Sosinski, E., Soussana, J.-F., Swaine, E., Swenson, N., Thompson, K., Thornton, P., Waldram, M., Weiher, E., White, M., White, S., Wright, S. J., Yguel, B., Zaehle, S., Zanne, A. E., and Wirth, C.: TRY – a global database of plant traits, Glob. Change Biol., 17, 2905–2935, https://doi.org/10.1111/j.1365-2486.2011.02451.x, 2011. a, b, c
Kelley, D. I., Prentice, I. C., Harrison, S. P., Wang, H., Simard, M., Fisher, J. B., and Willis, K. O.: A comprehensive benchmarking system for evaluating global vegetation models, Biogeosciences, 10, 3313–3340, https://doi.org/10.5194/bg-10-3313-2013, 2013. a
Klein Goldewijk, K. and van Drecht, G. (Eds.): HYDE 3: Current and historical population and land cover, in: Integrated modelling of global environmental change, An overview of IMAGE 2.4., Netherlands Environmental Assessment Agency (MNP), Bilthoven, the Netherlands, 93–111, 2006. a
Kollas, C., Kersebaum, K. C., Nendel, C., Manevski, K., Müller, C., Palosuo, T., Armas-Herrera, C. M., Beaudoin, N., Bindi, M., Charfeddine, M., Conradt, T., Constantin, J., Eitzinger, J., Ewert, F., Ferrise, R., Gaiser, T., Cortazar-Atauri, I. G. d., Giglio, L., Hlavinka, P., Hoffmann, H., Hoffmann, M. P., Launay, M., Manderscheid, R., Mary, B., Mirschel, W., Moriondo, M., Olesen, J. E., Öztürk, I., Pacholski, A., Ripoche-Wachter, D., Roggero, P. P., Roncossek, S., Rötter, R. P., Ruget, F., Sharif, B., Trnka, M., Ventrella, D., Waha, K., Wegehenkel, M., Weigel, H.-J., and Wu, L.: Crop rotation modelling – A European model intercomparison, Eur. J. Agron., 70, 98–111, https://doi.org/10.1016/j.eja.2015.06.007, 2015. a
Krysanova, V. and Wechsung, F.: SWIM (Soil and Water Integrated Model) User Manual, available at: https://www.pik-potsdam.de/members/valen/swim (last access: 31 July 2014), 2000. a
Kurokawa, H. and Nakashizuka, T.: Leaf herbivory and decomposability in a Malaysian tropical rain forest, Ecology, 89, 2645–2656, https://doi.org/10.1890/07-1352.1, 2008. a
Lamarque, J.-F., Dentener, F., McConnell, J., Ro, C.-U., Shaw, M., Vet, R., Bergmann, D., Cameron-Smith, P., Dalsoren, S., Doherty, R., Faluvegi, G., Ghan, S. J., Josse, B., Lee, Y. H., MacKenzie, I. A., Plummer, D., Shindell, D. T., Skeie, R. B., Stevenson, D. S., Strode, S., Zeng, G., Curran, M., Dahl-Jensen, D., Das, S., Fritzsche, D., and Nolan, M.: Multi-model mean nitrogen and sulfur deposition from the Atmospheric Chemistry and Climate Model Intercomparison Project (ACCMIP): evaluation of historical and projected future changes, Atmos. Chem. Phys., 13, 7997–8018, https://doi.org/10.5194/acp-13-7997-2013, 2013. a
Laughlin, D. C., Leppert, J. J., Moore, M. M., and Sieg, C. H.: A multi-trait test of the leaf-height-seed plant strategy scheme with 133 species from a pine forest flora, Funct. Ecol., 24, 493–501, https://doi.org/10.1111/j.1365-2435.2009.01672.x, 2010. a
Le Quéré, C., Andrew, R. M., Canadell, J. G., Sitch, S., Korsbakken, J. I., Peters, G. P., Manning, A. C., Boden, T. A., Tans, P. P., Houghton, R. A., Keeling, R. F., Alin, S., Andrews, O. D., Anthoni, P., Barbero, L., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Currie, K., Delire, C., Doney, S. C., Friedlingstein, P., Gkritzalis, T., Harris, I., Hauck, J., Haverd, V., Hoppema, M., Klein Goldewijk, K., Jain, A. K., Kato, E., Körtzinger, A., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Lombardozzi, D., Melton, J. R., Metzl, N., Millero, F., Monteiro, P. M. S., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., O'Brien, K., Olsen, A., Omar, A. M., Ono, T., Pierrot, D., Poulter, B., Rödenbeck, C., Salisbury, J., Schuster, U., Schwinger, J., Séférian, R., Skjelvan, I., Stocker, B. D., Sutton, A. J., Takahashi, T., Tian, H., Tilbrook, B., van der Laan-Luijkx, I. T., van der Werf, G. R., Viovy, N., Walker, A. P., Wiltshire, A. J., and Zaehle, S.: Global Carbon Budget 2016, Earth Syst. Sci. Data, 8, 605–649, https://doi.org/10.5194/essd-8-605-2016, 2016. a, b
Lehner, B. and Döll, P.: Development and validation of a global database of lakes, reservoirs and wetlands, J. Hydrol., 296, 1–22, https://doi.org/10.1016/j.jhydrol.2004.03.028, 2004. a
Lehner, B., Liermann, C. R., Revenga, C., Vörösmarty, C., Fekete, B., Crouzet, P., Döll, P., Endejan, M., Frenken, K., and Magome, J.: High-resolution mapping of the world's reservoirs and dams for sustainable river-flow management, Front. Ecol. Environ., 9, 494–502, https://doi.org/10.1890/100125, 2011. a
Lin, B.-L., Sakoda, A., Shibasaki, R., Goto, N., and Suzuki, M.: Modelling a global biogeochemical nitrogen cycle in terrestrial ecosystems, Ecol. Model., 135, 89–110, https://doi.org/10.1016/S0304-3800(00)00372-0, 2000. a
Loveys, B., Atkinson, L., Sherlock, D., Roberts, R., Fitter, A., and Atkin, O.: Thermal acclimation of leaf and root respiration: an investigation comparing inherently fast- and slow-growing plant species, Glob. Change Biol., 9, 895–910, https://doi.org/10.1046/j.1365-2486.2003.00611.x, 2003. a
Luyssaert, S., Inglima, I., Jung, M., Richardson, A. D., Reichstein, M., Papale, D., Piao, S. L., Schulze, E. D., Wingate, L., Matteucci, G., Aragao, L., Aubinet, M., Beer, C., Bernhofer, C., Black, K. G., Bonal, D., Bonnefond, J. M., Chambers, J., Ciais, P., Cook, B., Davis, K. J., Dolman, A. J., Gielen, B., Goulden, M., Grace, J., Granier, A., Grelle, A., Griffis, T., Grünwald, T., Guidolotti, G., Hanson, P. J., Harding, R., Hollinger, D. Y., Hutyra, L. R., Kolari, P., Kruijt, B., Kutsch, W., Lagergren, F., Laurila, T., Law, B. E., Le Maire, G., Lindroth, A., Loustau, D., Malhi, Y., Mateus, J., Migliavacca, M., Misson, L., Montagnani, L., Moncrieff, J., Moors, E., Munger, J. W., Nikinmaa, E., Ollinger, S. V., Pita, G., Rebmann, C., Roupsard, O., Saigusa, N., Sanz, M. J., Seufert, G., Sierra, C., Smith, M. L., Tang, J., Valentini, R., Vesala, T., and Janssens, I. A.: CO2 balance of boreal, temperate, and tropical forests derived from a global database, Glob. Change Biol., 13, 2509–2537, https://doi.org/10.1111/j.1365-2486.2007.01439.x, 2007. a, b
Malhi, S. S. and McGill, W. B.: Nitrification in three Alberta soils: Effect of temperature, moisture and substrate concentration, Soil Biol. Biochem., 14, 393–399, https://doi.org/10.1016/0038-0717(82)90011-6, 1982. a
Montes, F., Rotz, C. A., and Chaoui, H.: Process Modeling of Ammonia Volatilization from Ammonium Solution and Manure Surfaces: A Review with Recommended Models, T. ASABE, 52, 1707–1720, https://doi.org/10.13031/2013.29133, 2009. a
Mueller, N. D., Gerber, J. S., Johnston, M., Ray, D. K., Ramankutty, N., and Foley, J. A.: Closing yield gaps through nutrient and water management, Nature, 490, 254–257, https://doi.org/10.1038/nature11420, 2012. a
Müller, C., Bondeau, A., Lotze-Campen, H., Cramer, W., and Lucht, W.: Comparative impact of climatic and nonclimatic factors on global terrestrial carbon and water cycles, Global Biogeochem. Cy., 20, GB4015, https://doi.org/10.1029/2006GB002742, 2006. a
Müller, C., Stehfest, E., van Minnen, J. G., Strengers, B., von Bloh, W., Beusen, A. H., Schaphoff, S., Kram, T., and Lucht, W.: Drivers and patterns of land biosphere carbon balance reversal, Environ. Res. Lett., 11, 044002, https://doi.org/10.1088/1748-9326/11/4/044002, 2016. a, b
Müller, C., Elliott, J., Chryssanthacopoulos, J., Arneth, A., Balkovic, J., Ciais, P., Deryng, D., Folberth, C., Glotter, M., Hoek, S., Iizumi, T., Izaurralde, R. C., Jones, C., Khabarov, N., Lawrence, P., Liu, W., Olin, S., Pugh, T. A. M., Ray, D. K., Reddy, A., Rosenzweig, C., Ruane, A. C., Sakurai, G., Schmid, E., Skalsky, R., Song, C. X., Wang, X., de Wit, A., and Yang, H.: Global gridded crop model evaluation: benchmarking, skills, deficiencies and implications, Geosci. Model Dev., 10, 1403–1422, https://doi.org/10.5194/gmd-10-1403-2017, 2017. a, b, c
Neitsch, S. L., Arnold, J. G., Kiniry, J. R., Srinivasan, R., and Williams, J. R.: Soil and water assessment tool user's manual version 2000, GSWRL report, 202 pp., 2002. a, b, c
Neitsch, S. L., Arnold, J. G., Kiniry, J. R., and Williams, J. R.: Soil and water assessment tool theoretical documentation, Texas Water Resources Institute, College Station, Texas, 2005. a
New, M., Hulme, M., and Jones, P.: Representing Twentieth-Century Space–Time Climate Variability. Part II: Development of 1901–96 Monthly Grids of Terrestrial Surface Climate, J. Climate, 13, 2217–2238, https://doi.org/10.1175/1520-0442(2000)013<2217:RTCSTC>2.0.CO;2, 2000. a
Niinemets, U.: Components of leaf dry mass per area – thickness and density – alter leaf photosynthetic capacity in reverse directions in woody plants, New Phytol., 144, 35–47, https://doi.org/10.1046/j.1469-8137.1999.00466.x, 1999. a
Niinemets, U.: Global-scale climatic controls of leaf dry mass per area, density, and thickness in trees and shrubs, Ecology, 82, 453–469, https://doi.org/10.1890/0012-9658(2001)082<0453:GSCCOL>2.0.CO;2, 2001. a
Norby, R. J., DeLucia, E. H., Gielen, B., Calfapietra, C., Giardina, C. P., King, J. S., Ledford, J., McCarthy, H. R., Moore, D. J. P., Ceulemans, R., De Angelis, P., Finzi, A. C., Karnosky, D. F., Kubiske, M. E., Lukac, M., Pregitzer, K. S., Scarascia-Mugnozza, G. E., Schlesinger, W. H., and Oren, R.: Forest response to elevated CO2 is conserved across a broad range of productivity, P. Natl. Acad. Sci. USA, 102, 18052–18056, https://doi.org/10.1073/pnas.0509478102, 2005. a
Ogaya, R. and Penuelas, J.: Comparative field study of Quercus ilex and Phillyrea latifolia: photosynthetic response to experimental drought conditions, Environ. Exp. Bot., 50, 137–148, https://doi.org/10.1016/S0098-8472(03)00019-4, 2003. a
Ogaya, R. and Penuelas, J.: Contrasting foliar responses to drought in Quercus ilex and Phillyrea latifolia, Biol. Plantarum, 50, 373–382, https://doi.org/10.1007/s10535-006-0052-y, 2006. a
Ogaya, R. and Penuelas, J.: Tree growth, mortality, and above-ground biomass accumulation in a holm oak forest under a five-year experimental field drought, Plant Ecol., 189, 291–299, https://doi.org/10.1007/s11258-006-9184-6, 2007. a
Ogaya, R. and Penuelas, J.: Changes in leaf δ13C and δ15N for three Mediterranean tree species in relation to soil water availability, Acta Oecol., 34, 331–338, https://doi.org/10.1016/j.actao.2008.06.005, 2008. a
Ordonez, J. C., van Bodegom, P. M., Witte, J.-P. M., Bartholomeus, R. P., van Hal, J. R., and Aerts, R.: Plant Strategies in Relation to Resource Supply in Mesic to Wet Environments: Does Theory Mirror Nature?, Am. Nat., 175, 225–239, https://doi.org/10.1086/649582, 2010. a
ORNL DAAC: Oak Ridge National Laboratory Distributed Active Archive Center (ORNL DAAC), available at: http://fluxnet.ornl.gov/ (last access: 19 October 2015), 2011. a
Pakeman, R. J., Garnier, E., Lavorel, S., Ansquer, P., Castro, H., Cruz, P., Dolezal, J., Eriksson, O., Freitas, H., Golodets, C., Kigel, J., Kleyer, M., Leps, J., Meier, T., Papadimitriou, M., Papanastasis, V. P., Quested, H., Quetier, F., Rusch, G., Sternberg, M., Theau, J.-P., Thebault, A., and Vile, D.: Impact of abundance weighting on the response of seed traits to climate and land use, J. Ecol., 96, 355–366, https://doi.org/10.1111/j.1365-2745.2007.01336.x, 2008. a
Pakeman, R. J., Leps, J., Kleyer, M., Lavorel, S., Garnier, E., and the VISTA consortium: Relative climatic, edaphic and management controls of plant functional trait signatures, J. Veg. Sci., 20, 148–159, https://doi.org/10.1111/j.1654-1103.2009.05548.x, 2009. a
Parton, W. J., Mosier, A. R., Ojima, D. S., Valentine, D. W., Schimel, D. S., Weier, K., and Kulmala, A. E.: Generalized model for N2 and N2O production from nitrification and denitrification, Global Biogeochem. Cy., 10, 401–412, https://doi.org/10.1029/96GB01455, 1996. a, b
Parton, W. J., Holland, E. A., Del Grosso, S. J., Hartman, M. D., Martin, R. E., Mosier, A. R., Ojima, D. S., and Schimel, D. S.: Generalized model for NO2 and N2O emissions from soils, J. Geophys. Res.-Atmos., 106, 17403–17419, https://doi.org/10.1029/2001JD900101, 2001. a, b, c, d, e, f, g
Patiño, S., Lloyd, J., Paiva, R., Baker, T. R., Quesada, C. A., Mercado, L. M., Schmerler, J., Schwarz, M., Santos, A. J. B., Aguilar, A., Czimczik, C. I., Gallo, J., Horna, V., Hoyos, E. J., Jimenez, E. M., Palomino, W., Peacock, J., Peña-Cruz, A., Sarmiento, C., Sota, A., Turriago, J. D., Villanueva, B., Vitzthum, P., Alvarez, E., Arroyo, L., Baraloto, C., Bonal, D., Chave, J., Costa, A. C. L., Herrera, R., Higuchi, N., Killeen, T., Leal, E., Luizão, F., Meir, P., Monteagudo, A., Neil, D., Núñez-Vargas, P., Peñuela, M. C., Pitman, N., Priante Filho, N., Prieto, A., Panfil, S. N., Rudas, A., Salomão, R., Silva, N., Silveira, M., Soares de Almeida, S., Torres-Lezama, A., Vásquez-Martínez, R., Vieira, I., Malhi, Y., and Phillips, O. L.: Branch xylem density variations across the Amazon Basin, Biogeosciences, 6, 545–568, https://doi.org/10.5194/bg-6-545-2009, 2009. a
Penuelas, J., Sardans, J., Llusia, J., Owen, S. M., Carnicer, J., Giambelluca, T. W., Rezende, E. L., Waite, M., and Niinemets, U.: Faster returns on “leaf economics” and different biogeochemical niche in invasive compared with native plant species, Glob. Change Biol., 16, 2171–2185, https://doi.org/10.1111/j.1365-2486.2009.02054.x, 2010a. a
Penuelas, J., Sardans, J., Llusia, J., Owen, S. M., Silva, J., and Niinemets, U.: Higher Allocation to Low Cost Chemical Defenses in Invasive Species of Hawaii, J. Chem. Ecol., 36, 1255–1270, https://doi.org/10.1007/s10886-010-9862-7, 2010b. a
Portmann, F. T., Siebert, S., and Döll, P.: MIRCA2000 – Global monthly irrigated and rainfed crop areas around the year 2000: A new high-resolution data set for agricultural and hydrological modeling, Global Biogeochem. Cy., 24, 1–24, https://doi.org/10.1029/2008GB003435, 2010. a
Post, W. M., Pastor, J., Zinke, P. J., and Stangenberger, A. G.: Global patterns of soil nitrogen storage, Nature, 317, 613–616, https://doi.org/10.1038/317613a0, 1985. a
Potter, P., Ramankutty, N., Bennett, E. M., and Donner, S. D.: Characterizing the Spatial Patterns of Global Fertilizer Application and Manure Production, Earth Interact., 14, 1–22, https://doi.org/10.1175/2009EI288.1, 2010. a
Quested, H., Cornelissen, J., Press, M., Callaghan, T., Aerts, R., Trosien, F., Riemann, P., Gwynn-Jones, D., Kondratchuk, A., and Jonasson, S.: Decomposition of sub-arctic plants with differing nitrogen economies: A functional role for hemiparasites, Ecology, 84, 3209–3221, https://doi.org/10.1890/02-0426, 2003. a
Rolinski, S., Müller, C., Heinke, J., Weindl, I., Biewald, A., Bodirsky, B. L., Bondeau, A., Boons-Prins, E. R., Bouwman, A. F., Leffelaar, P. A., te Roller, J. A., Schaphoff, S., and Thonicke, K.: Modeling vegetation and carbon dynamics of managed grasslands at the global scale with LPJmL 3.6, Geosci. Model Dev., 11, 429–451, https://doi.org/10.5194/gmd-11-429-2018, 2018. a, b, c
Sardans, J., Penuelas, J., and Ogaya, R.: Drought-induced changes in C and N stoichiometry in a Quercus ilex Mediterranean forest, Forest Sci., 54, 513–522, 2008a. a
Sardans, J., Penuelas, J., Prieto, P., and Estiarte, M.: Changes in Ca, Fe, Mg, Mo, Na, and S content in a Mediterranean shrubland under warming and drought, J. Geophys. Res.-Biogeo., 113, G03039, https://doi.org/10.1029/2008JG000795, 2008b. a
Schaphoff, S., Heyder, U., Ostberg, S., Gerten, D., Heinke, J., and Lucht, W.: Contribution of permafrost soils to the global carbon budget, Environ. Res. Lett., 8, 014026, https://doi.org/10.1088/1748-9326/8/1/014026, 2013. a, b, c, d, e
Schaphoff, S., Forkel, M., Müller, C., Knauer, J., von Bloh, W., Gerten, D., Jägermeyr, J., Lucht, W., Rammig, A., Thonicke, K., and Waha, K.: LPJmL4 – a dynamic global vegetation model with managed land – Part 2: Model evaluation, Geosci. Model Dev., 11, 1377–1403, https://doi.org/10.5194/gmd-11-1377-2018, 2018a. a, b, c, d, e, f
Schaphoff, S., von Bloh, W., Rammig, A., Thonicke, K., Biemans, H., Forkel, M., Gerten, D., Heinke, J., Jägermeyr, J., Knauer, J., Langerwisch, F., Lucht, W., Müller, C., Rolinski, S., and Waha, K.: LPJmL4 – a dynamic global vegetation model with managed land – Part 1: Model description, Geosci. Model Dev., 11, 1343–1375, https://doi.org/10.5194/gmd-11-1343-2018, 2018b. a, b, c, d, e, f, g
Schewe, J., Heinke, J., Gerten, D., Haddeland, I., Arnell, N. W., Clark, D. B., Dankers, R., Eisner, S., Fekete, B. M., Colón-González, F. J., Gosling, S. N., Kim, H., Liu, X., Masaki, Y., Portmann, F. T., Satoh, Y., Stacke, T., Tang, Q., Wada, Y., Wisser, D., Albrecht, T., Frieler, K., Piontek, F., Warszawski, L., and Kabat, P.: Multimodel assessment of water scarcity under climate change, P. Natl. Acad. Sci. USA, 111, 3245–3250, https://doi.org/10.1073/pnas.1222460110, 2014. a
Schimel, D., Stephens, B. B., and Fisher, J. B.: Effect of increasing CO2 on the terrestrial carbon cycle, P. Natl. Acad. Sci. USA, 112, 436–441, https://doi.org/10.1073/pnas.1407302112, 2015. a
Schimel, J. P. and Bennett, J.: Nitrogen mineralization: Challenges of a changing paradigm, Ecology, 85, 591–602, https://doi.org/10.1890/03-8002, 2004. a
Schlesinger, W. H. and Jasechko, S.: Transpiration in the global water cycle, Agr. Forest Meteorol., 189–190, 115–117, https://doi.org/10.1016/j.agrformet.2014.01.011, 2014. a
Siebert, S., Kummu, M., Porkka, M., Döll, P., Ramankutty, N., and Scanlon, B. R.: A global data set of the extent of irrigated land from 1900 to 2005, Hydrol. Earth Syst. Sci., 19, 1521–1545, https://doi.org/10.5194/hess-19-1521-2015, 2015. a
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J. O., Levis, S., Lucht, W., Sykes, M. T., Thonicke, K., and Venevsky, S.: Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model, Glob. Change Biol., 9, 161–185, https://doi.org/10.1046/j.1365-2486.2003.00569.x, 2003. a, b, c, d, e, f, g
Smith, B., Wårlind, D., Arneth, A., Hickler, T., Leadley, P., Siltberg, J., and Zaehle, S.: Implications of incorporating N cycling and N limitations on primary production in an individual-based dynamic vegetation model, Biogeosciences, 11, 2027–2054, https://doi.org/10.5194/bg-11-2027-2014, 2014. a, b, c, d, e, f, g, h, i, j, k, l
Smith, W., Reed, S., Cleveland, C., Ballantyne, A., Anderegg, W., Wieder, W., Liu, Y., and Running, S.: Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization, Nat. Clim. Change, 6, 306–310, https://doi.org/10.1038/nclimate2879, 2016. a
Sutton, M., Bleeker, A., Howard, C., Bekunda, M., Grizzetti, B., de Vries, W., van Grinsven, H., Abrol, Y., Adhya, T., Billen, G., Davidson, E., Datta, A., Diaz, R., Erisman, J., Liu, X., Oenema, O., Palm, C., Raghuram, N., Reis, S., Scholz, R., Sims, T., Westhoek, H., and Zhang, F.: Our nutrient world: the challenge to produce more food and energy with less pollution, NERC/Centre for Ecology & Hydrology, Edinburgh, available at: http://nora.nerc.ac.uk/500700/, 2013. a
Thornley, J. H. M.: A Transport-resistance Model of Forest Growth and Partitioning, Ann. Bot., 68, 211–216, 1991. a
Thornton, P. E., Lamarque, J.-F., Rosenbloom, N. A., and Mahowald, N. M.: Influence of carbon-nitrogen cycle coupling on land model response to CO2 fertilization and climate variability, Global Biogeochem. Cy., 21, GB4018, https://doi.org/10.1029/2006GB002868, 2007. a
University of East Anglia Climatic Research Unit and Harris, I. C.: CRU TS3.23: Climatic Research Unit (CRU) Time-Series (TS) Version 3.23 of High Resolution Gridded Data of Month-by-month Variation in Climate (Jan. 1901–Dec. 2014), Centre for Environmental Data Analysis, https://doi.org/10.5285/4c7fdfa6-f176-4c58-acee-683d5e9d2ed5, 2015. a
Vitousek, P. M., Menge, D. N. L., Reed, S. C., and Cleveland, C. C.: Biological nitrogen fixation: rates, patterns and ecological controls in terrestrial ecosystems, Philos. T. Roy. Soc. B, 368, 20130119, https://doi.org/10.1098/rstb.2013.0119, 2013. a
von Bloh, W., Schaphoff, S., Müller, C., Rolinski, S., Waha, K., and Zaehle, S.: LPJmL5 Model Code. V 5.0.001, GFZ Data sevices, https://doi.org/10.5880/pik.2018.011, 2018. a
Vorosmarty, C. and Fekete, B.: ISLSCP II River Routing Data (STN-30p), ISLSCP Initiative II Collection, data set, edited by: Hall, F. G., Collatz, G., Meeson, B., Los, S., Brown de Colstoun, E., and Landis, D., ORNL Distributed Active Archive Center, https://doi.org/10.3334/ORNLDAAC/1005, 2011. a
Walvoord, M. A., Phillips, F. M., Stonestrom, D. A., Evans, R. D., Hartsough, P. C., Newman, B. D., and Striegl, R. G.: A Reservoir of Nitrate Beneath Desert Soils, Science, 302, 1021–1024, https://doi.org/10.1126/science.1086435, 003. a
Warszawski, L., Friend, A., Ostberg, S., Frieler, K., Lucht, W., Schaphoff, S., Beerling, D., Cadule, P., Ciais, P., Clark, D. B., Kahana, R., Ito, A., Keribin, R., Kleidon, A., Lomas, M., Nishina, K., Pavlick, R., Rademacher, T. T., Buechner, M., Piontek, F., Schewe, J., Serdeczny, O., and Schellnhuber, H. J.: A multi-model analysis of risk of ecosystem shifts under climate change, Environ. Res. Lett., 8, 044018, https://doi.org/10.1088/1748-9326/8/4/044018, 2013. a
White, M. A., Thornton, P. E., Running, S. W., and Nemani, R. R.: Parameterization and Sensitivity Analysis of the BIOME–BGC Terrestrial Ecosystem Model: Net Primary Production Controls, Earth Interact., 4, 1–85, https://doi.org/10.1175/1087-3562(2000)004<0003:PASAOT>2.0.CO;2, 2000. a, b
Wieder, W. R., Cleveland, C. C., Smith, W. K., and Todd-Brown, K.: Future productivity and carbon storage limited by terrestrial nutrient availability, Nat. Geosci., 8, 441–444, https://doi.org/10.1038/ngeo2413, 2015. a
Willis, C. G., Halina, M., Lehman, C., Reich, P. B., Keen, A., McCarthy, S., and Cavender-Bares, J.: Phylogenetic community structure in Minnesota oak savanna is influenced by spatial extent and environmental variation, Ecography, 33, 565–577, https://doi.org/10.1111/j.1600-0587.2009.05975.x, 2010. a
Willmott, C. J.: Some comments on the evaluation of model performance, B. Am. Meteorol. Soc., 63, 1309–1313, https://doi.org/10.1175/1520-0477(1982)063<1309:SCOTEO>2.0.CO;2, 1982. a
Xu, L. and Baldocchi, D.: Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature, Tree Physiol., 23, 865–877, 2003. a
Xu-Ri and Prentice, I. C.: Terrestrial nitrogen cycle simulation with a dynamic global vegetation model, Glob. Change Biol., 14, 1745–1764, https://doi.org/10.1111/j.1365-2486.2008.01625.x, 2008. a, b, c
Zaehle, S. Jones, C. D., Houlton, B., Lamarque, J.-F., and Robertson, E.: Nitrogen availability reduces CMIP5 projections of twenty-first-century land carbon uptake, J. Climate, 28, 2494–2511, https://doi.org/10.1175/JCLI-D-13-00776.1, 2015. a
Zaehle, S., Friend, A. D., Friedlingstein, P., Dentener, F., Peylin, P., and Schulz, M.: Carbon and nitrogen cycle dynamics in the O-CN land surface model: 2. Role of the nitrogen cycle in the historical terrestrial carbon balance, Global Biogeochem. Cy., 24, GB1006, https://doi.org/10.1029/2009GB003522, 2010a. a, b
Zaehle, S., Sitch, S., Prentice, I. C., Liski, J., Cramer, W., Erhard, M., Hickler, T., and Smith, B.: The importance of age-related decline in forest NPP for modeling regional carbon balances, Ecol. Appl., 16, 1555–1574, https://doi.org/10.1890/1051-0761(2006)016<1555:TIOADI>2.0.CO;2, 2010b. a, b