Hybrid Lake Model (HyLake) v1.0: unifying deep learning and physical principles for simulating lake-atmosphere interactions

Lake-atmosphere interactions play a critical role in Earth systems dynamics. However, accurately modelling key indicators of these interactions remains challenging due to their oversimplified physics in traditional process-based models or the limited interpretability of purely data-driven approaches. Hybrid models, which integrate physical principles with sparse observations, offer a promising path forward.

This study introduces the Hybrid Lake Model v1.0 (HyLake v1.0), a novel framework that combines physics-based surface energy balance equations with a Bayesian Optimized Bidirectional Long Short-Term Memory-based (BO-BLSTM-based) surrogate to approximate lake surface temperature (LST) dynamics. The model was trained using data from the Meiliangwan (MLW) site in Lake Taihu. We evaluate HyLake v1.0 against the Freshwater Lake (FLake) model and other hybrid benchmarks (Baseline and TaihuScene) across multiple sites in Lake Taihu using both eddy flux covariance observations and ECMWF Reanalysis v5 (ERA5) data.

Results show that HyLake v1.0 outperformed all comparative models at the MLW site and demonstrated strong capability in simulating lake-atmosphere interactions. In experiments assessing generalization and transferability in ungauged lake sites, HyLake v1.0 consistently exhibited superior performance over FLake and TaihuScene across all Lake Taihu sites using both observation- and ERA5-based forcing. It also maintained excellent skill when applied to the ungauged Chaohu, confirming its robustness even with unlearned forcing datasets. This study underscores the potential of hybrid modeling to advance the representation land-atmosphere interaction in Earth system models.

1 Introduction

Lakes constitute a critical component of the Earth system and serve as sensitive indicators of climate-land surface interactions (O'Reilly et al., 2015; Wang et al., 2024a). Lake surface temperature (LST) is a central variable in lake-atmosphere systems, governing key hydro-biogeochemical processes such as evaporation rates, ice cover duration, mixing regimes, and thermal storage (Culpepper et al., 2024; Tong et al., 2023; Woolway et al., 2020). Globally, LST has been increasing at a rate of 0.34 °C per decade, contributing to shifts in aquatic biodiversity and alterations in ecosystem services (Wang et al., 2024a; Woolway et al., 2020). These observed trends underscore the significant threats that climate change poses to global lake ecosystems (Carpenter et al., 2011; Woolway et al., 2020).

Accurate prediction of LST is fundamental for assessing physical and biogeochemical changes in lakes, including phenomena like algal blooms, lake heatwaves and cold spells (O'Reilly et al., 2015; Wang et al., 2024b, c; Woolway et al., 2024). Existing lake thermodynamics models can be categorized into process-based, statistical, and machine learning (ML) approaches. Process-based lake models, such as the Freshwater Lake model (Flake; Mironov et al., 2010), the General Lake Model (GLM; Hipsey et al., 2019), and the lake model within the Weather Research & Forecasting Model (WRF-Lake; Gu et al., 2015), are built upon simplified assumptions derived from empirical physical principles. They typically do not incorporate data-driven information and can be challenging to apply in data-scarce regions (Piccolroaz et al., 2024; Shen et al., 2023; Xu et al., 2016; Mironov et al., 2010). In contrast, statistical models, such as the Air2Water model, establish mathematical relationships between forcing variables and LST in well-mixed lakes, relying on extensive high-quality observational data but often lacking explicit mechanistic linkages (Piccolroaz et al., 2020; Wang et al., 2024a; Huang et al., 2021). ML models, such as Artificial Neural Networks (ANNs) and Long Short-Term Memory (LSTM) networks, often viewed as a subset of statistical models, offer greater complexity and automation by leveraging large datasets (Piccolroaz et al., 2024; Wikle and Zammit-Mangion, 2023) and have demonstrated superior performance in reconstructing LST globally (Almeida et al., 2022; Willard et al., 2022). However, their dependence on substantial training datas, high computational demands, and inherent “black-box” nature can limit model transferability and explainability (Piccolroaz et al., 2024; Korbmacher and Tordeux, 2022). These limitations highlight the potential of hybrid approaches that integrate the strengths of both process-based and data-driven models.

Hybrid models integrate physical principles with data-driven techniques, often featuring a multi-output structure that enhances explainability and transferability while preserving flexibility and accuracy (Piccolroaz et al., 2024; Shen et al., 2023; Kurz et al., 2022). For example, Read et al. (2019) developed a hybrid deep learning framework that embedded an energy balance-guided loss function from GLM into a Recurrent Neural Network (RNN) to reconstruct LST, outperforming process-based models when applied to unmonitored lakes (Willard et al., 2021). Despite their promise, such hybrid models can still face challenges related to computational cost, explainability, and transferability, particularly for ungauged lakes and periods (Raissi et al., 2019; Willard et al., 2023). To mitigate these issues, Feng et al. (2022) embedded neural networks into the Hydrologiska Byråns Vattenbalansavdelning (HBV) hydrological model to predict multiple physical variables, achieving performance comparable to purely data-driven models. Similarly, Zhong et al. (2024) developed a distributed framework integrating ML and traditional river routing models for streamflow prediction. By incorporating physical constraints, these hybrid models typically outperform traditional process-based models and require less training data than purely ML-based approaches, thereby providing a powerful tool for elucidating previously unrecognized physical relationships (Shen et al., 2023). Given that lake-atmosphere interactions represent a tightly coupled system where LST modulates latent heat (LE) and sensible heat (HE) fluxes (Wang et al., 2019a; Woolway et al., 2015), hybrid modeling represents a promising way for advancing our understanding of these complex physical processes.

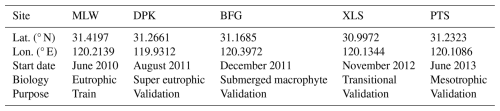
Table 1 Overview of selected lake sites in Lake Taihu, including their geographic coordinates, observation start dates, biological characteristics, and roles in model development. The MLW site was used for model training, while the remaining sites served for validation.

Predicting key indicators of lake-atmosphere interactions in Lake Taihu, a large and eutrophic lake in China, remains challenging for traditional lake models due to its significant regional heterogeneity in biological characteristics (Table 1; Zhang et al., 2020b; Yan et al., 2024). The lake benefits from extensive observational data collected through field investigations. To advance hybrid modeling techniques and improve the accuracy of simulating lake-atmosphere interactions, this study aims to: (1) develop a novel hybrid lake model, HyLake v1.0, by embedding an LSTM-based surrogate into a process-based lake model; (2) validate the performance of HyLake v1.0 in simulating LST, LE, and HE against observations from the Taihu Lake Eddy Flux Network; and (3) evaluate the transferability of HyLake v1.0 to ungauged sites with varying biological characteristics using ECMWF Reanalysis v5 (ERA5) forcing datasets. The results of this research are expected to enhance the representation of lake-atmosphere interactions by synergistically unifying physical principles with deep learning, particularly in data-sparse regions.

2 Materials and Methodology

2.1 Study area and datasets

Lake Taihu (30.12–32.22° N, 119.03–121.91° E), located in the Yangtze Delta, is the third-largest freshwater lake in China, covering an area of 2400 km² with an average depth of 1.9 m, with a rapid increasing rate of ∼ 0.37 °C per decade in LST (Yan et al., 2024; Zhang et al., 2020b, 2018). As a typical urban lake, Lake Taihu is situated in one of the most densely populated regions of China. It has experienced significant eutrophication, characterized by recurrent algae blooms that threaten local drinking water security (Yan et al., 2024). Given the pressing need to understand the challenges surrounding water quality improvement and hydro-biogeochemical processes in Lake Taihu, this study employs the lake models to assess these issues across 5 distinct sites from the Taihu Lake Eddy Flux Network (Zhang et al., 2020b): Meiliangwan (MLW), Dapukou (DPK), Bifenggang (BFG), Xiaoleishan (XLS), and Pingtaishan (PTS) (Fig. 1, Table 1). These sites span varying biological characteristics and eutrophication gradients, offering a comprehensive view on lake ecological diversity (Zhang et al., 2020b), providing a solid data base for evaluating the generalizability and transferability of lake models. Specifically, MLW (31.4197° N, 120.2139° E) as the first lake site in Lake Taihu Eddy Flux Network, located at the northern shore of the lake in MLW Bay, has a biological characteristic of eutrophication. BFG (31.1685° N, 120.3972° E) is located in the eastern shore of Lake Taihu, features a submerged macrophyte community and relatively clean water. PTS (31.2323° N, 120.1086° E), situated centrally in the lake, has experienced significant algae blooms and lacks aquatic vegetation. DPK (31.2661° N, 119.9312° E), located on the western shore of Lake Taihu, is marked by severe eutrophication and deeper water; while XLS (30.9972° N, 120.1344° E), located on the southern shore of Lake Taihu, is a vegetation-free, clean water site (Zhang et al., 2020b).

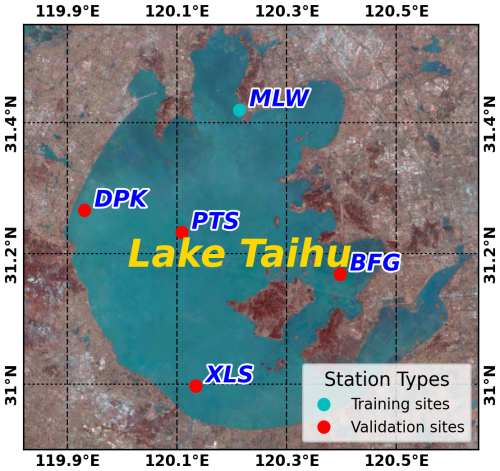
Figure 1 The locations of Lake Taihu and the five eddy covariance lake sites (MLW, DPK, BFG, XLS, and PTS) are shown in cyan and red bubbles, overlaid on a true-color image from Landsat 8. MLW as a training site was used to train BO-BLSTM-based surrogate, while the other validation sites were adapted as ungauged sites to validate the HyLake v1.0 performance.

The datasets included two parts: (1) hydrometeorological variables observed from the Taihu Lake Eddy Flux Network to force and validate the models, and (2) meteorological variables from ERA5 datasets to fill the gaps of observations and force the models. Within the network, each site is equipped with an eddy covariance system that continuously monitors LE and HE using sonic anemometers and thermometers (Model CSAT3A; Campbell Scientific, Logan, UT, USA) positioned 3.5 to 9.4 m above the lake surface. Hydrometeorological variables, including air humidity and temperature (Model HMP45D/HMP155A; Vaisala, Helsinki, Finland), wind speed (Model 03002; R.M. Young Co., Traverse City, MI, USA), and net radiation components (Model CNR4; Kipp & Zonen, Delft, the Netherlands), are also measured. These meteorological variables were used to force lake models while LE, HE and LST from observations were used to validate the results of each numerical experiment, on top of which, the inferred radiative LST, were collected at 30 min intervals that are publicly accessible via Harvard DataVerse (Lee, 2004; https://doi.org/10.7910/DVN/HEWCWM, Zhang et al., 2020b, c). The dataset spans from 2012 to 2015 and contains several data gaps across these lake sites. Specifically, 475 time steps (∼ 1.36 %) of observed surface pressure were found missing at the DPK site during 2012 and 2015; 7959 time steps (∼ 22.71 %) of all observed variables were missing at the XLS site; 12,539 time steps (∼ 35.78 %) of all observed variables were missing at the PTS site. Observations at the MLW and BFG sites were complete during the entire study periods. In the evaluation of all observations-forced experiments, the data gaps of observed variables in these lake sites were directly filled by ERA5 datasets at the corresponding time steps to predict lake-atmosphere interactions. In this study, observed meteorological variables from the MLW site, an eutrophic lake site that presents the trophic status of Lake Taihu (Table 1, Wang et al., 2019b), are used to train the Long Short-Term Memory (LSTM)-based surrogates (Sect. 2.2), while data from the remaining sites serve to evaluate the generalization of HyLake v1.0 and train the LSTM-based surrogates. To further address the generalization and transferability of HyLake v1.0 across different forcing datasets, this study utilized 8 meteorological variables that where obtained from hourly ERA5 datasets from 2012 to 2015, with a spatial resolution of 0.25° at a single level to force HyLake v1.0. These datasets, available from the Climate Data Store (Hersbach et al., 2020; https://cds.climate.copernicus.eu, last access: 25 December 2024), include variables such as air temperature, dew point temperature, surface pressure, wind speed, and surface net longwave and shortwave radiation, which has similar probability distribution to observations across Lake Taihu (Fig. S1 in the Supplement). The ERA5 datasets are also individually used to force FLake and TaihuScene for comparison and predict lake-atmosphere interactions in Lake Taihu, providing insights into the model's generalization, transferability and performance using different climatic forcing datasets.

2.2 Model architecture of HyLake v1.0

HyLake v1.0 is based on the backbone of physical principles from process-based lake models and then couple to a LSTM-based surrogate for LST approximation to further solve the untrained variables (e.g., LE, HE), as schematically shown in Fig. 2. The following sections will introduce the architecture of HyLake v1.0 from the physical principles, LSTM-based surrogates and their training strategies, respectively.

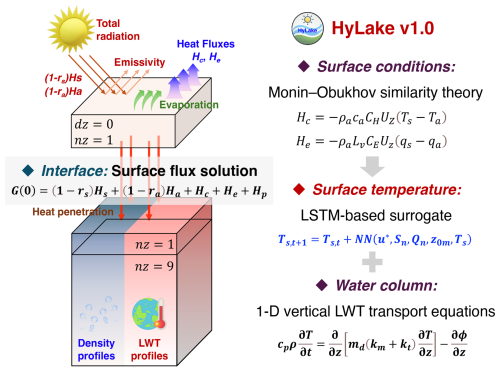
Figure 2 Conceptual model of HyLake v1.0. The LSTM-based surrogates were added to approximate the LST based on the surface conditions that calculated from Monin-Obukhov similarity theory, which further correct the LST in surface flux solution at the next time step.

2.2.1 Physical principles for lake-atmosphere modeling systems

A process-based backbone lake model (PBBM) is separately constructed to serve as the backbone of HyLake v1.0, which referred to the process-based lake models based on the governing equations and parameterization schemes of previously validated lake physical processes (Šarović et al., 2022). The conceptual model of PBBM is depicted in Fig. 2 and Table 2. Specifically, the lake-atmosphere modeling system in PBBM primarily involves energy balance equations for solving LE and HE at the lake-atmosphere interface and the 1-D vertical lake water temperature transport equations within the water column for solving LST (Piccolroaz et al., 2024).

Table 2 Specification of each model for intercomparison.

The changes in LST are primarily driven by the net heat fluxes entering the lake surface. Therefore, the net heat flux is imposed as a Neumann boundary condition at the upper boundary of the water column. Following Piccolroaz et al. (2024), the net heat flux G(0) (W m⁻²) into the lake surface can be expressed by the energy balance equation:

$$\begin{array}{}\text{(1)}& G\left(\mathrm{0}\right)=\left(\mathrm{1}-r_{\mathrm{s}}\right)H_{\mathrm{s}}+\left(\mathrm{1}-r_{\mathrm{a}}\right)H_{\mathrm{a}}+H_{\mathrm{c}}+H_{\mathrm{e}}+H_{\mathrm{p}}\end{array}$$

where H_s (W m⁻²) and H_a (W m⁻²) represent net downward shortwave and longwave radiation (also referred to the net solar and thermal radiation in ERA5), respectively; r_s and r_a account for the shortwave and longwave albedos of water; the HE and LE are denoted by H_c (W m⁻²) and H_e (W m⁻²); H_p represent the heat flux (W m⁻²) brought from precipitation, often calculated via an empirical equation to quantify (Šarović et al., 2022). All heat fluxes are considered positive in downward direction. The net shortwave and longwave radiation are derived from observation in Lake Taihu Eddy Flux Network and ERA5 reanalysis datasets.

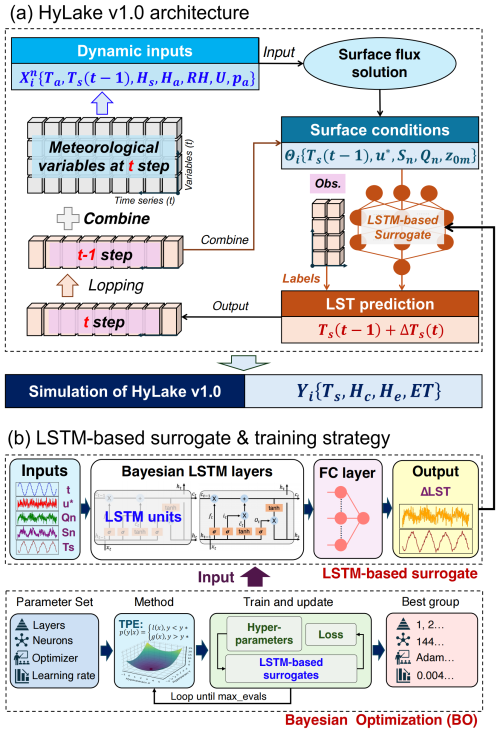
Figure 3 The general architecture of HyLake v1.0. (a) Coupling strategy of physical principles and LSTM-based surrogates and (b) training strategy of LSTM-based surrogates in HyLake v1.0. $X_i^n$, θ_i, and Y_i represent dynamic inputs for forcing surface flux solution in PBBM, surface conditions calculated from surface flux solution, and the outputs calculated from HyLake v1.0, respectively.

The sensible (HE, H_c) and latent (LE, H_e) heat fluxes follows the scheme by Verburg and Antenucci (2010) (Figs. 2–3):

$$\begin{array}{}\text{(2)}& {\displaystyle }{H}_{\mathrm{c}}=-{\mathit{\rho }}_{\mathrm{a}}{c}_{\mathrm{a}}{C}_{\mathrm{H}}{U}_Z\left(T_{\mathrm{s}}-T_{\mathrm{a}}\right)\text{(3)}& {\displaystyle }{H}_{\mathrm{e}}=-{\mathit{\rho }}_{\mathrm{a}}{L}_{\mathrm{v}}{C}_{\mathrm{E}}{U}_z\left(q_{\mathrm{s}}-q_{\mathrm{a}}\right)\end{array}$$

where ρ_a (kg m⁻³) donated air density; c_a=1005 J kg⁻¹ K⁻¹ is the specific heat of air; L_v≈2500 kJ kg⁻¹ is the LE of vaporization; C_E and C_H are transfer coefficients for HE and LE derived iteratively with the Monin–Obukhov length based on bulk flux algorithms; U_Z (m s⁻¹) is the wind speed at observed height; T_s (°C) accounts for LST solved by 1-D vertical lake water temperature (LWT) transport equation; and T_a (°C) present the air temperature. Further details on the heat flux calculations can be found in Verburg and Antenucci (2010) and Woolway et al. (2015).

At the bottom boundary of the 1-D lake model, the zero-temperature-gradient boundary and the zero-flux boundary are imposed as shown in Fig. 2, which can be expressed as:

$$\begin{array}{}\text{(4)}& {\displaystyle }\partial T_z/\partial z=\mathrm{0}\text{(5)}& {\displaystyle }G\left(z_{max}\right)=\mathrm{0}\end{array}$$

where T_z (°C) present the lake water temperature; z means the mean lake depth; G(z_max) (W m⁻²) account for the heat exchange between water column and sediment, which is set to 0 at the bottom boundary.

To simulate vertical temperature profiles in the water column (Fig. 2), PBBM solves a 1-D vertical lake water temperature transport equation within a cylindrical water column assumption of constant surface area as follows:

$$\begin{array}{}\text{(6)}& c_p\mathit{\rho }{\displaystyle \frac{\partial T}{\partial t}}={\displaystyle \frac{\partial }{\partial z}}\left[m_{\mathrm{d}}\left(k_{\mathrm{m}}+k_{\mathrm{t}}\right){\displaystyle \frac{\partial T}{\partial z}}\right]-{\displaystyle \frac{\partial \mathit{\varphi }}{\partial z}}\end{array}$$

where c_p is the specific heat capacity of water, which is set to 1006 J kg⁻¹ K⁻¹; ρ (kg m⁻³) present water density, which can be calculated from lake water temperature (T, °C) at different depths; t (s) and z (m) is simulated time and depth of water column respectively; m_d is the enlarge coefficient of thermal conductivity, which is also set to 5 in PBBM; k_m and k_t (W m⁻¹ K⁻¹) are the molecular and turbulent thermal conductivity, respectively; ϕ (W m⁻²) is defined by the heat flux that penetrate into the lake from net solar radiation. The specific parameterization of PBBM follows the lake module in CLM v5.0 (Subin et al., 2012). The PBBM provides a backbone for HyLake v1.0, which adapted a LSTM-based surrogate to solve the LST instead of solving 1-D vertical lake water temperature transport equations by the implicit Euler scheme (Fig. 3a).

2.2.2 LST approximation using LSTM-based surrogates

In PBBM, LST along with the LWT in the 1-D vertical lake water temperature transport equations (Eq. 6) are typically solved simultaneously using an implicit Euler scheme for numerical stability (Šarović et al., 2022). This can be expressed in matrix form as:

$$\begin{array}{}\text{(7)}& M{T}^{n+\mathrm{1}}=A{T}^n+B\end{array}$$

where, M, A and B jointly form the tridiagonal system of equations based on implicit Euler scheme, which can be further decomposed into Eqs. (8) to (10):

$$\begin{array}{}\text{(8)}& {\displaystyle }M=\left\{\begin{array}{ll}\frac{-k_{\mathrm{m}}-k_{\mathrm{t},j-\mathrm{1}/\mathrm{2}}}{z_j-z_{j-\mathrm{1}}},& z=j-\mathrm{1}\\ \frac{\mathrm{\Delta }{z}_j{c}_p{\mathit{\rho }}_j}{\mathrm{\Delta }t}+\frac{k_{\mathrm{m}}+k_{\mathrm{t},j+\mathrm{1}/\mathrm{2}}}{z_{j+\mathrm{1}}-z_{j-\mathrm{1}}}+\frac{k_{\mathrm{m}}+k_{\mathrm{t},j-\mathrm{1}/\mathrm{2}}}{z_j-z_{j-\mathrm{1}}},& z=j\\ \frac{-k_{\mathrm{m}}-k_{\mathrm{t},j+\mathrm{1}/\mathrm{2}}}{z_{j+\mathrm{1}}+z_j},& z=j+\mathrm{1}\end{array}\right.\text{(9)}& {\displaystyle }A={\displaystyle \frac{\mathrm{\Delta }{z}_j{c}_p{\mathit{\rho }}_j}{\mathrm{\Delta }t}}\text{(10)}& {\displaystyle }B={\mathit{\varphi }}_{j+\mathrm{1}/\mathrm{2}}^n-{\mathit{\varphi }}_{j-\mathrm{1}/\mathrm{2}}^n\end{array}$$

where j denotes the index of each water-column layer (from 1 to 10 in this study); n represents the time step. Δz_j and ρ_j are the thickness and density at jth water column, respectively. The terms $k_{\mathrm{t},j-\mathrm{1}/\mathrm{2}}$ and ${\mathit{\varphi }}_{j-\mathrm{1}/\mathrm{2}}^n$ refer to the molecular diffusivity and residual radiation at middle location between j−1th and jth at n step. All other variables in these equations follow the same notations and definitions as given previously.

It has been demonstrated that LSTM could capture historical time-step dependencies and handle variable-length input sequences using gradient optimization combined with backpropagation in hydrological applications (Liu et al., 2024a). Bayesian LSTM (as an improved LSTM) adapts probability distributed weight parameters, which reduces the model overfitting, thereby providing robust predictions in hydrology (Li et al., 2021a; Lu et al., 2019). The development of LSTM-based surrogates offers the possibility of accurate predictions in addressing the critical processes in lake-atmosphere modeling systems. HyLake v1.0 and other hybrid lake models, including Baseline and TaihuScene, employed LSTM-based surrogates rather than the implicit Euler scheme in process-based models to solve LST for each time step (Fig. 3a). Specifically, several sequence-to-one LSTM-based surrogates are adapted to be trained to approximate ΔLST (the difference of LST between two time steps) based on dynamic inputs, including time series of historical 24-step variables of LST, friction velocity (u^∗, m s⁻¹), surface roughness length (z_0 m, m), and G(0). These dynamic parameters were calculated from the outputs of surface flux solutions based on the observations. Thus, to address the numerical stability of autoregressive prediction in iterations, the LST increments can be expressed by:

$$\begin{array}{}\text{(11)}& T_{\mathrm{s},t+\mathrm{1}}=T_{\mathrm{s},t}+\mathrm{\Delta }T=T_{\mathrm{s},t}+\mathrm{NN}\left(u^{\ast },S_n,Q_n,z_{\mathrm{0}\mathrm{m}},T_{\mathrm{s}}\right)\end{array}$$

where NN(⋅) donates different LSTM-based surrogates within HyLake v1.0, Baseline and TaihuScene, which will activate to approximate the increment of lake surface temperature for each time step. Such LSTM-based surrogates have shown stable autoregressive prediction capabilities in hydrological modeling (Liu et al., 2024a) and can readily be coupled with PBBM to provide numerically robust predictions of lake surface temperature. The other untrained variables, such as LE, and HE, were derived from the module of surface flux solutions (Eqs. 1–3).

2.2.3 Training strategy of LSTM-based surrogates

The LSTM-based surrogates in HyLake v1.0 are composed by the stacked LSTM or Bayesian LSTM (BLSTM) units and fully-connected layers (Fig. 3b), including two different units to separately construct LSTM-based surrogates in HyLake v1.0 that trained on observations. LSTM units are a type of Recurrent Neural Network (RNN) designed to avoid vanishing gradients problem, making them particularly suited for time series forecasting (Sherstinsky, 2020). Here, this study constructed a LSTM surrogate for Baseline and a BLSTM surrogate for HyLake v1.0 to couple in PBBM (Table 2). Specifically, the LSTM unit comprises three gates: the forget gate, the input gate and the output gate, which controls whether information should be retained or updated (Hochreiter, 1997). The forget gate was firstly introduced by Gers et al. (2000), which can be expressed as follow:

$$\begin{array}{}\text{(12)}& {\displaystyle }{\mathit{f}}_t=\mathit{\sigma }\left(W_{\mathrm{f}}{\mathit{x}}_t+U_{\mathrm{f}}{\mathit{h}}_{t-\mathrm{1}}+{\mathit{b}}_{\mathrm{f}}\right)\text{(13)}& {\displaystyle }{\stackrel{\mathrm{̃}}{c}}_t=\tanh \left(W_{\stackrel{\mathrm{̃}}{c}}{\mathit{x}}_t+U_{\stackrel{\mathrm{̃}}{c}}{\mathit{h}}_{t-\mathrm{1}}+{\mathit{b}}_{\stackrel{\mathrm{̃}}{c}}\right)\end{array}$$

where f_t is a resulting vector of the forget gate; σ(⋅) and tanh (⋅) are the logistic sigmoid and hyperbolic tangent functions; W_f, U_f and b_f represent the trainable parameters in two weight matrices and a bias vector of the forget gate; $W_{\stackrel{\mathrm{̃}}{c}}$, $U_{\stackrel{\mathrm{̃}}{c}}$ and ${\mathit{b}}_{\stackrel{\mathrm{̃}}{c}}$ are another set of trainable parameters to calculate the next hidden state in LSTM unit. x_t and h_t−1 are the current input and last hidden state, respectively, to calculate a potential update vector ${\stackrel{\mathrm{̃}}{c}}_t$. The input gate determines which information of ${\stackrel{\mathrm{̃}}{\mathit{c}}}_t$ will be used to update the cell state in the current time step:

$$\begin{array}{}\text{(14)}& {\displaystyle }{\mathit{i}}_t=\mathit{\sigma }(W_{\mathrm{i}}{\mathit{x}}_t+U_{\mathrm{i}}{\mathit{h}}_{t-\mathrm{1}}+{\mathit{b}}_{\mathrm{i}})\text{(15)}& {\displaystyle }{\mathit{c}}_t={\mathit{f}}_t\odot {\mathit{c}}_{t-\mathrm{1}}+{\mathit{i}}_t\odot {\stackrel{\mathrm{̃}}{\mathit{c}}}_t\end{array}$$

where i_t is a resulting vector in the input gate, determining which new information will store in ${\stackrel{\mathrm{̃}}{\mathit{c}}}_t$ (Kratzert et al., 2018); W_i, U_i and b_i are trainable parameters in input gate. The output vector of the input gate c_t is updated by Eq. (15). Specifically, ⊙ represents element-wise multiplication. The last gate is the output gate controlling the information of c_t that flows into the new hidden state h_t, which can be calculated from:

$$\begin{array}{}\text{(16)}& {\displaystyle }{\mathit{O}}_t=\mathit{\sigma }(W_{\mathrm{o}}{\mathit{x}}_t+U_{\mathrm{o}}{\mathit{h}}_{t-\mathrm{1}}+{\mathit{b}}_{\mathrm{o}})\text{(17)}& {\displaystyle }{\mathit{h}}_t=\tanh \left({\mathit{c}}_t\right)\odot {\mathit{O}}_t\end{array}$$

where O_t is a resulting vector; W_o, U_o and b_o are the trainable parameters for the output gate. The new hidden state h_t is calculated by combining the results from Eqs. (14)–(15), allowing for an effective learning from long-term dependencies in historical time series (Kratzert et al., 2018). By stacking multiple LSTM layers on the top of the neural networks, LSTM-based surrogates used a fully-connected layer or Bayesian fully connected layer to connect the results from the last hidden state in LSTM to a single output neuron to acquire the final prediction. The basic formula of these layers is given by the following equation:

$$\begin{array}{}\text{(18)}& y=W_{\mathrm{d}}{\mathit{h}}_n+{\mathit{b}}_{\mathrm{d}}\end{array}$$

where y is the prediction variable, which is LST in this study; h_n is the output from the last LSTM layer. In the fully-connected layer, W_d and b_d are deterministic constants learned during training, while in the Bayesian fully-connected layer, W_d and b_d are instead modeled as random variables from Gaussian distribution to capture uncertainty of parameters.

The hyperparameters of these LSTM-based surrogates are both adjusted to be optimal. Specifically, the LSTM-based surrogate in Baseline that was trained with an Adam Optimizer consists of two layers with 256 LSTM units and 1 fully-connected layer, with a batch size of 32, and a learning rate of 0.01. This surrogate was adjusted manually to achieve the optimal performance. The BLSTM-based surrogate was composed by 4 layers with 467 LSTM units and 1 Bayesian fully-connected layer, with a batch size of 64, a learning rate of 0.00096, and an optimizer of RMSprop. The BLSTM surrogate in HyLake v1.0 was adjusted using Bayesian Optimization (BO-BLSTM), which is a powerful tool for the joint optimization of design choices using less computational power to compute better solution (Shahriari et al., 2016), with a hyperparameter space of the number of layers and units, learning rate and optimizer to search for the optimal group of hyperparameters (Fig. 3b). The BO-BLSTM-based surrogate in TaihuScene comprised 7 layers with 836 BLSTM units and 1 Bayesian fully-connected layer, with a batch size of 145, a learning rate of 0.2538, and an optimizer of AdamW using Bayesian Optimization to search for the optimize group of hypermeters. The hyperparameter space included the number of hidden layers (ranging from 1 to 8), neurons per layer (ranged from 16 to 1024), optimizer (Adam, or RMSprop), batch size (ranging from 8 to 256), and learning rate (ranging from 1 × 10⁻⁶ to 1 × 10⁻²). The hyperparameters in BO-BLSTM-based surrogates were optimized using BO with a maximum of 100 iterations, 1000 epochs for each iteration, and 50 patience in an EarlyStopping strategy. A Tree-structured Parzen Estimator (TPE) is adopted in BO, performing 20 to 100 iterations of surrogate training and updates. Training, validation, and test datasets for each lake site were divided by 80 %, 10 % and 10 % of the length of time series (2013–2015), respectively. They are divided into 1 January 2013 00:00:00 to 26 May 2015 04:00:00, 26 May 2015 04:00:00 to 12 September 2015 14:00:00, and 12 September 2015 14:00:00 to 30 December 2015 23:00:00 (UTC+ 08:00).

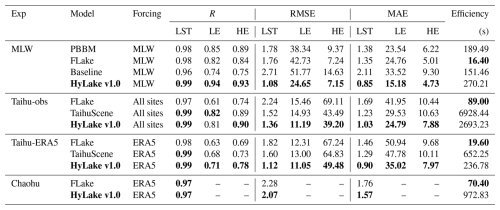
Table 3 Intercomparison of model performance across different experiments conducted in diverse regions with different forcing datasets. Observations from all lake sites (MLW, DPK, BFG, XLS, and PTS) on Lake Taihu, were used to drive models in the Taihu-obs experiment. Bold values in the table present the best-performing model with each group of experiments. Computational efficiency is reported as the runtime for a single simulation.

2.3 Numerical experiments design and evaluation metric

2.3.1 Numerical experiments for model intercomparison

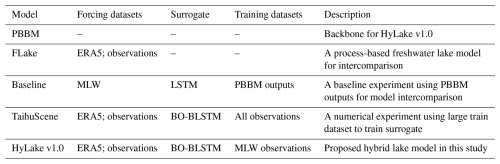
To address the generalization and transferability of HyLake v1.0 in studied (MLW) and ungauged lake sites (DPK, BFG, XLS, and PTS) (Table 1), this study further conducted three numerical experiments, including MLW experiment, Taihu-obs experiment, Taihu-ERA5 experiment, and Chaohu experiment, using distinct models and forcing datasets (Tables 2 and 3), including FLake, Baseline, and TaihuScene to intercompare. Baseline and TaihuScene serve as extended models of HyLake v1.0 that are composed of the same physical principles and distinct LSTM-based surrogates using different training strategies were used to intercompare with HyLake v1.0. The descriptions of these models are listed as follows:

• PBBM as a backbone of HyLake v1.0 is a simplified process-based lake model and was constructed based on the energy balance equations and the 1-D vertical lake water temperature transport equations.

• FLake is a bulk model based on a two-layer parametric representation of the evolving temperature profile and on the integral budgets of heat and of kinetic energy for the layers, which is widely used as a lake module for simulating lake-atmosphere interactions in Earth System Models (ESMs) (Huang et al., 2021; Mironov et al., 2010). FLake served as a well-known traditional process-based lake model and is suitable for model intercomparison.

• Baseline is a hybrid lake model that is coupled to an LSTM-based surrogate trained on outputs of PBBM, which is used to intercompare the performance with HyLake v1.0.

• TaihuScene is another hybrid lake model that is coupled to a BO-BLSTM-based surrogate trained on observations from all sites (MLW, BFG, DPK, PTS, and XLS) in Lake Taihu, which is different from the HyLake v1.0. The purpose of TaihuScene is to compare the performance of using a larger training dataset to train a surrogate model with that of using a small dataset from HyLake v1.0.

The PBBM performed like FLake in MLW site, indicating a high reliability and accuracy (Fig. S2). Except for PBBM, the LST, LE and HE calculated from models in all experiments were initially intercompared in each lake site from Lake Taihu. FLake and TaihuScene were additionally intercompared using the ERA5 datasets in Taihu-ERA5 experiment. The specification of the datasets used, surrogate, and the descriptions for each model can be found in Table 2. Furthermore, this study implemented the HyLake v1.0 into Lake Chaohu, the 5th-largest shallow freshwater lake in China, with a deeper lake depth of 3.06 m and lake area of 760 km² (Fig. S6, Jiao et al., 2018), which has experienced heavy eutrophication and harmful algal blooms (Yang et al., 2020), to assess its transferability to other lakes (Chaohu experiment). A LST dataset in Lake Chaohu was obtained from MODIS/Terra Land Surface Temperature/Emissivity Daily L3 Global 1km SIN Grid V061 imageries (MYD11A1, https://www.earthdata.nasa.gov/data/catalog/lpcloud-mod11a1-061, last access: 23 June 2025), which were used to validate the performance of LST derived from HyLake v1.0. The computational efficiency for each 1-time prediction was recorded using a 16G 10-Core Apple M4 processor based on the established HyLake v1.0 model in this study. The training of the above-mentioned surrogates was run using a 24G NVIDIA GeForce RTX 4090 GPU.

2.3.2 Metrics for model evaluation and intercomparison

To evaluate the performance of these numerical experiments, the Pearson correlation coefficient (R), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) was used in this study to compare the accuracy of LST and heat fluxes between simulations and observations. Specifically, the R is proposed to measure the linear correlation of the observed and modeled values, RMSE and MAE assess if the models over or underestimate the observations with the same data units (Piccolroaz et al., 2024). The calculation of R, RMSE, and MAE can be expressed by:

$$\begin{array}{}\text{(19)}& {\displaystyle }R={\displaystyle \frac{\sum \left(x_i-{\stackrel{\mathrm{‾}}{x}}_i\right)\left(y_i-{\stackrel{\mathrm{‾}}{y}}_i\right)}{\sqrt{\sum {\left(x_i-{\stackrel{\mathrm{‾}}{x}}_i\right)}^{\mathrm{2}}\sum {\left(y_i-{\stackrel{\mathrm{‾}}{y}}_i\right)}^{\mathrm{2}}}}}\text{(20)}& {\displaystyle }\mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n{\left(y_i-{\stackrel{\mathrm{‾}}{y}}_i\right)}^{\mathrm{2}}}\text{(21)}& {\displaystyle }\mathrm{MAE}={\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n\left|y_i-{\stackrel{\mathrm{‾}}{y}}_i\right|\end{array}$$

where x_i and ${\stackrel{\mathrm{‾}}{x}}_i$ are the observations and its average; while y_i and ${\stackrel{\mathrm{‾}}{y}}_i$ are the results of model and its average; n represents the length of time series.

3 Results

3.1 Validation of HyLake v1.0 in MLW experiment

The PBBM, a backbone of HyLake v1.0, has already been validated in Fig. S2 by comparing with FLake model and observations from MLW site, indicating a robust prediction with a R of 0.98 and RMSE of 1.78 °C in LST, a R of 0.85 and RMSE of 38.34 W m⁻² in LE and a R of 0.89 and RMSE of 9.37 W m⁻² in HE. FLake demonstrated a slightly better performance to PBBM in LST and HE while performed poorer in LE (LST: R = 0.98, RMSE = 1.76 °C; LE: R = 0.82, RMSE = 42.73 W m⁻²; HE: R = 0.84, RMSE = 7.24 W m⁻²). These results fully indicated that the backbone provided from PBBM for HyLake v1.0 is reasonable for all variables.

This study separately validated Baseline, TaihuScene, HyLake v1.0 and their adapted LSTM-based surrogates using MLW observations to address the performance of integrated models (Figs. 4–5 and S3). Firstly, the results from HyLake v1.0 and its BO-BLSTM-based surrogate was individually validated based on MLW observations. Specifically, this study separately assessed the accuracy of the BO-BLSTM-based surrogate of HyLake v1.0 in the training, validation, and test sets, aiming to evaluate their ability to describe the physical principles between climate change and LST (Fig. 4). The ΔLST obtained from observations was used to train surrogate in HyLake v1.0. For the BO-BLSTM-based surrogate in HyLake v1.0, a higher consistency between predictions and observations was observed (Fig. 4). Specifically, the ΔLST results for the BO-BLSTM-based surrogate showed RMSE values of 0.1945 °C and MAE of 0.1306 °C in the training dataset, RMSE of 0.3359 °C and MAE of 0.1925 °C in the validation dataset, and RMSE of 0.2271 °C and MAE of 0.1461 °C in the test dataset, respectively.

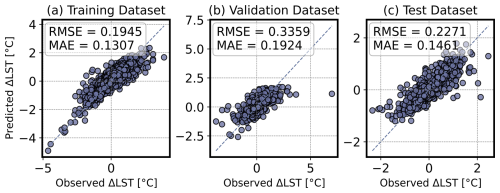
Figure 4 The validation of BO-BLSTM-based surrogate in HyLake v1.0 for (a) training, (b) validation and (c) test datasets.

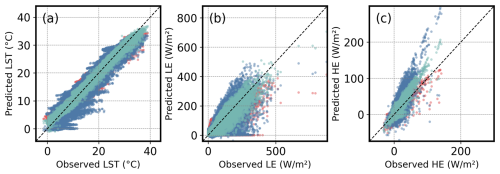
Figure 5 Comparison of predicted (a) LST, (b) LE and (c) HE by using FLake (red points), Baseline (blue points), HyLake v1.0 (green points) and observations in MLW experiments.

Considering the model intercomparison, the LSTM-based surrogate-derived ΔLST in Baseline model, which is trained from process-based simulations of PBBM, also performed superior performance, indicating a great capacity for learning physical principles (Fig. S3a–c). The results indicated a RMSE of 0.0580 °C and a MAE of 0.0112 °C in the training dataset, RMSE of 0.0079 °C and MAE of 0.0058 °C in the validation dataset, and RMSE of 0.0161 °C and MAE of 0.0094 °C in the dataset. These results suggest that the LSTM-based surrogate can capture approximately about 90 % of the physical principles even during validation and testing. When applied to Lake Taihu, another BO-BLSTM-based surrogate in TaihuScene was used to train with observations from all lake sites. It demonstrated a close match to observations, with RMSE values of 0.2363 °C and MAE of 0.1537 °C in the training dataset, RMSE of 0.3342 °C and MAE of 0.1880 °C in the validation dataset, and RMSE of 0.2281 °C and MAE of 0.1480 °C in the test dataset. These results were somewhat lower than HyLake v1.0 due to the larger dataset size in training for ΔLST. Therefore, these surrogates, improved on the basis of purely LSTM-based surrogates, ensure robust capacity for autoregressive prediction of ΔLST while maintaining numerical stability, laying a solid foundation for algorithms coupled to HyLake v1.0 backbone.

After validating the accuracy of all LSTM-based surrogates in Baseline, TaihuScene and HyLake v1.0, this study conducted MLW experiment, which forced and validated by the hydrometeorological variables in MLW observations, to predict the LST, LE and HE by using Baseline and HyLake v1.0 that integrated these surrogates, then compared with the outputs of traditional process-based FLake model using MLW observations (Fig. 5 and Table 3). Compared to FLake, Baseline which utilized the LSTM-based surrogate trained on outputs from PBBM performed slightly poorer, with an R of 0.96 and RMSE of 2.71 °C for LST, an R of 0.74 and RMSE of 51.77 W m⁻² for LE, and an R of 0.75 and RMSE of 14.63 W m⁻² for HE. The physical principles learned from these simulations is limited but enabled the surrogate to provide predictions similar to those of PBBM. For LST, HyLake v1.0 outperformed both FLake and Baseline, with an R of 0.99 and RMSE of 1.08 °C (Fig. 5a). For heat fluxes calculated from the energy balance equations of surface flux solution, HyLake v1.0 also outperformed FLake and Baseline, with an R of 0.94 and RMSE of 24.65 W m⁻² for LE and an R of 0.93 and RMSE of 7.15 W m⁻² for HE (Fig. 5b–c). These results demonstrate the HyLake v1.0 that using BO-BLSTM-based surrogate as a module of the HyLake backbone to solve LST and thereby compute LE and HE in the subsequent time step offers numerical stability and predictability. Furthermore, HyLake v1.0 proves capable of estimating lake-atmosphere interactions, surpassing FLake in the integration of deep-learning-based and process-based models, which offered a robust way for applying in ungagged locations. TaihuScene was used to intercompare with HyLake v1.0 in model generalization and transferability across all lake sites and different forcing datasets, which will be discussed in Sect. 3.3.

3.2 Intercomparisons of LST, LE and HE from 2013 to 2015

This study conducted a comprehensive intercomparison of daily and hourly trends in LST, LE and HE from MLW experiment in the MLW site during the period from 2013 to 2015, including FLake, Baseline, and HyLake v1.0 (Figs. 6–8).

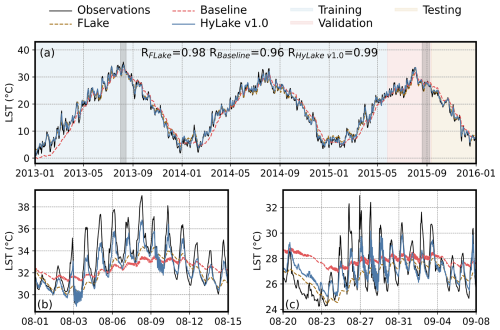
Figure 6 Comparison of observations and predictions by FLake, Baseline, and HyLake v1.0 in temporal trends of LST. Comparison of (a) the full time series and (b–c) partial time series of models derived LST and observations from 2013 to 2015. All results in panel (a) were presented at a daily-average scale by resampling. Blue, red, and yellow regions represent the period for the train, validation, and test datasets, respectively. Black solid, brown dashed, red dashed, and blue solid lines represent LST from observations, FLake, Baseline, and HyLake v1.0, respectively.

As shown in Fig. 6, the temporal changes in LST for the period of surrogates training (1 January 2013 00:00:00 to 26 May 2015 04:00:00 UTC+08:00), validation (26 May 2015 04:00:00 to 12 September 2015 14:00:00 UTC+08:00), and test datasets (12 September 2015 14:00:00 to 30 December 2015 23:00:00 UTC+08:00) were compared. For daily changes in LST, HyLake v1.0 and FLake showed a closer match to observations, whereas Baseline, trained with process-based simulations, exhibited a larger error in comparison to the observed values (R = 0.96, RMSE = 2.71 °C, Fig. 6a). HyLake v1.0 demonstrated a greater capability in capturing the daily changes in LST, particularly in mid-winter for each dataset, thus indicating long-term stability in LST modeling (R = 0.99, RMSE = 1.08 °C, Fig. 6a). Specifically, FLake provided a good match to observations at a daily-average scale, which, however, showed poorer performance in capturing diurnal variations of LST (R = 0.98, RMSE = 1.76 °C, Fig. 6a). This study randomly selected two subperiods from the training, validation, and test periods (Fig. 6b and c), where the diurnal variations of LST observations exhibited a significant bias compared to FLake, indicating that FLake is not able to accurately describe variations at the diurnal scale. Meanwhile, Baseline primarily captured the long-term trends of LST from PBBM but did not effectively represent diurnal variations due to the limitations of the datasets and physical principles provided by PBBM. In contrast, HyLake v1.0 was able to capture more information about the diurnal variations of LST from the observations, thereby outperforming both FLake and Baseline. Overall, HyLake v1.0, coupled with the BO-BLSTM-based surrogates trained on observations, offers a robust way for predicting LST trends at a finer temporal resolution.

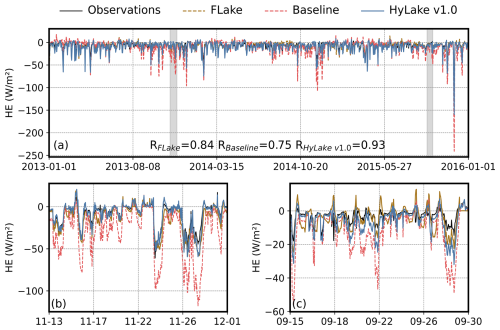
Figure 7 Comparisons of observations and predictions by FLake, Baseline, and HyLake v1.0 in temporal trends for LE. Comparison of (a) full and (b–c) partial time series of model derived LE and observations from 2013 to 2015.

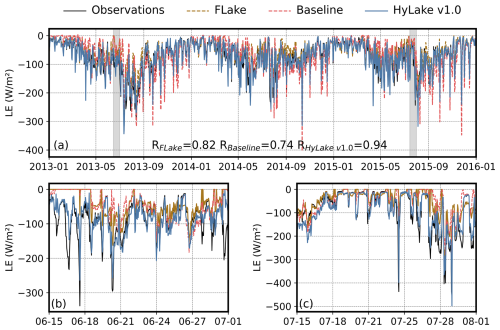
Figure 8 Comparisons of observations and predictions by FLake, Baseline, and HyLake v1.0 in temporal trends for HE. Comparison of (a) full and (b–c) partial time series of model derived HE and observations from 2013 to 2015.

The LE and HE were calculated using the energy balance equations, where the LST, updated by LSTM-based surrogates in HyLake, served as an essential input. Consequently, it is necessary to validate the variations in these heat fluxes outputted by HyLake v1.0 to assess its capacity for modeling lake-atmosphere interactions. This study validated the observed LE and HE at the MLW site on both daily and hourly scales (Figs. 7–8).

Regarding the changes in LE (Figs. 5b and 7), HyLake v1.0, which used LST calculated from the BO-BLSTM-based surrogate, demonstrated a minor bias in estimating LE (R = 0.94, RMSE = 24.65 W m⁻², Fig. 5b), outperforming both FLake (R = 0.82, RMSE = 42.73 W m⁻², Fig. 5b) and Baseline (R = 0.74, RMSE = 51.77 W m⁻², Fig. 5b). Notably, using an improved LSTM-based surrogate resulted in a slightly and significant improvement of LE compared to the FLake and Baseline. Specifically, Baseline showed more similar performance to FLake, capturing the major trends of these heat fluxes. The LE predicted by HyLake v1.0 reproduces both the peak and trough magnitudes more closely to the MLW observations than FLake and Baseline models (Fig. 7b–c), indicating its overall superior capacity for describing the diurnal variations. Still, some biases persisted in the validation and test periods. For example, HyLake v1.0 overestimated to the observations during 20 and 23 August 2015 (Fig. 7c).

For HE (Figs. 5c and 8), which exhibited relatively insignificant diurnal and seasonal variations during the studied period, HyLake v1.0 (R = 0.93, RMSE = 7.15 W m⁻², Fig. 5c) outperformed both FLake (R = 0.84, RMSE = 7.24 W m⁻², Fig. 5c) and Baseline (R = 0.75, RMSE = 14.63 W m⁻², Fig. 5c) in simulating variations of both hourly and daily trends. The results were found that Hylake v1.0 is capable of correcting some of the partial biases in HE estimation by integrating the BO-BLSTM-based surrogate (Fig. 8b–c), leading to more accurate simulations of these heat fluxes. Besides that, the HE calculated from both FLake and Baseline was difficult to accurately estimate the minor variations in hourly scale during simulations, which could accumulate bias in subsequent time steps. This issue was especially evident in the validation and test datasets (Fig. 8c), whereas HyLake v1.0 showed minimal bias due to its improved representation of LST. In summary, HyLake v1.0 that coupled PBBM to a BO-BLSTM-based surrogate provided a more robust and reasonable prediction of LST, leading to better corrections for untrained variables (LE and HE) produced by the other modules. This improvement ensures HyLake v1.0's capability in accurately describing lake-atmosphere interactions with improved performance.

3.3 Validation across observational sites in Lake Taihu

A successful hybrid model that unified physical principles and deep learning techniques requires strong generalization, evidenced by a remarkably small gap between its performance on training and test datasets (Zhang et al., 2021), and strong transferability, defined as the ability to generalize well to a novel task for domain adaptation (Long et al., 2015). The transferability and generalization of traditional deep-learning-based models remain challenging (Xu and Liang, 2021). However, integrating process-based models with deep learning-based models can mitigate these issues to some degree. To address these challenges with HyLake v1.0, this study specially developed a TaihuScene (Table 2), another hybrid lake model which enlarges the size of training datasets by incorporating data from 5 lake sites in Lake Taihu to train its BO-BLSTM-based surrogates and evaluate the potential difference from HyLake v1.0. The primary objectives of TaihuScene are to (1) offer a theoretically optimal coupled model (previous studies allocated that larger train datasets improve deep-learning-based models' performance; Halevy et al., 2009) for simulating lake-atmosphere interactions in Lake Taihu, and (2) compare with HyLake v1.0 in generalization and transferability for ungauged regions.

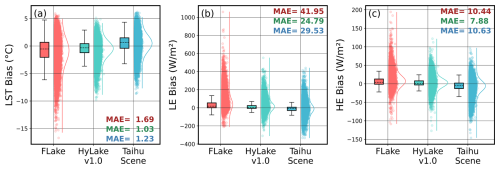
Figure 9 Comparisons of (a) LST, (b) LE, and (c) HE between observations, FLake, HyLake v1.0 and TaihuScene in five sites (MLW, BFG, DPK, PTS, and XLS) of Lake Taihu based on the Taihu-obs experiment. Dashed lines in boxplot represent median biases between observations and predictions simulated by FLake, HyLake v1.0, and TaihuScene, respectively. The scatterplots and probability distribution curves illustrate the data distribution of LST, LE and HE. The Numbers at the top or bottom right of subfigures with same color to boxes indicate the MAE of outputs for FLake, HyLake v1.0, and TaihuScene, respectively.

Given to the Taihu-obs experiment which was forced and validated by hydrometeorological observed variables from five lake sites in Lake Taihu, HyLake v1.0 still performed the best in predicting LST (MAE = 1.03 °C), HE (MAE = 24.79 W m⁻²), and LE (MAE = 7.88 W m⁻²) among FLake and TaihuScene (Fig. 9). While FLake performed the worst in each variable, with a MAE of 1.69 °C in LST, a MAE of 41.95 W m⁻² in LE and a MAE of 10.44 W m⁻² in HE, respectively. TaihuScene performed moderately, with a MAE of 1.23 °C in LST, a MAE of 29.53 W m⁻² in HE and a MAE of 10.63 W m⁻² in LE, respectively.

Involving the relative bias (the difference between simulation and observation), the median biases (the dashed lines) and distribution of outputs by TaihuScene indicated an overestimation of LST (Fig. 9a), which may contribute to the underestimation of heat fluxes derived from the common physical principles learned from large datasets during step-by-step iterative calculations (Fig. 9b–c). While HyLake v1.0 exhibited an opposite estimation, with a slightly underestimation in LST and overestimation in HE and LE. This suggests that BO-BLSTM-based surrogates trained with observations from MLW site provide more reliable results than those trained with data from all sites due to the more clearly physical principles for training. But it is worthy to note that TaihuScene still far outperformed FLake, as evidenced by a denser distribution of biases. These results challenge the assumption that larger datasets always improve the performance of deep-learning-based models (Xu and Liang, 2021; Zhong et al., 2020), with the results suggested that HyLake v1.0, trained on relatively smaller datasets, performs better than TaihuScene in Lake Taihu.

The results of intercomparison in each lake site for FLake and TaihuScene models further explain the reasons for this phenomenon (Fig. S4). HyLake v1.0 performed best at the MLW, PTS, and XLS sites but showed poorer results at the BFG and DPK sites. Specifically, HyLake v1.0 outperformed FLake and TaihuScene at the MLW site, with a MAE of 0.85 °C, 15.18 W m⁻², and 4.73 W m⁻² for LST, LE, and HE, respectively. In contrast, TaihuScene performed relatively worse, with a MAE of 1.38 °C, 23.28 W m⁻², and 8.33 W m⁻². FLake showed moderate performance, with MAE values of 1.35 °C, 24.76 W m⁻², and 5.01 W m⁻² for LST, LE, and HE, respectively (Fig. S4a–c). A similar pattern was apparent at the PTS and XLS sites. At PTS, HyLake v1.0 also showed the best performance (LST: MAE = 0.79 °C; LE: MAE = 20.12 W m⁻²; HE: MAE = 6.90 W m⁻²), while FLake performed moderately (LST: MAE = 1.22 °C; LE: MAE = 24.77 W m⁻²; HE: MAE = 6.93 W m⁻²), and TaihuScene performed the worst (LST: MAE = 1.47 °C; LE: MAE = 39.66 W m⁻²; HE: MAE = 15.11 W m⁻²) (Fig. S4j–i). Similarly, at the XLS site, HyLake v1.0 performed the best (LST: MAE = 0.86 °C; LE: MAE = 20.40 W m⁻²; HE: MAE = 6.61 W m⁻²), while FLake performed moderately (LST: MAE = 1.33 °C; LE: MAE = 30.00 W m⁻²; HE: MAE = 7.69 W m⁻²), and TaihuScene performed the worst (LST: MAE = 1.29 °C; LE: MAE = 32.20 W m⁻²; HE: MAE = 12.19 W m⁻²) (Fig. S4m–o). However, at the BFG and DPK sites, TaihuScene outperformed the other models in estimating LST, LE, and HE, with MAE values of 1.06 °C, 27.92 W m⁻², and 9.73 W m⁻² at BFG and 1.00 °C, 26.05 W m⁻², and 8.43 W m⁻² at DPK (Fig. S4d–i). Specifically, TaihuScene performed slightly better than HyLake v1.0 (BFG: LST: MAE = 1.32 °C, LE: MAE = 32.88 W m⁻², HE: MAE = 10.47 W m⁻²; DPK: LST: MAE = 1.29 °C, LE: MAE = 34.71 W m⁻², HE: MAE = 10.54 W m⁻²) but was far superior to FLake (BFG: LST: MAE = 2.32 °C, LE: MAE = 65.05 W m⁻², HE: MAE = 16.53 W m⁻²; DPK: LST: MAE = 2.16 °C, LE: MAE = 62.71 W m⁻², HE: MAE = 15.56 W m⁻²).

It is clear that HyLake v1.0 demonstrated outstanding capacity to apply for ungauged regions, surpassing traditional lake-atmosphere interaction models such as FLake in prediction accuracy for each variable, which demonstrated a strong transferability for future applications. TaihuScene, though capable of predicting changes across all sites in Lake Taihu, also exhibited a superior overall performance at specific sites when compared to HyLake v1.0. This highlights HyLake v1.0 offers promising potential for extending its application to these ungauged lakes or sites with similar characteristics by effectively learning physical principles.

3.4 Performance comparison of models in Lake Taihu based on ERA5 datasets

This study additionally conducted Taihu-ERA5 experiment that using meteorological variables from ERA5 datasets to force several lake models demonstrate transferability of HyLake v1.0, which proves its superior capability to apply for the ungauged locations based on different forcing datasets. The meteorological variables from ERA5 dataset, which are widely used as forcing datasets for process-based models (Albergel et al., 2018; Hersbach et al., 2020), were selected to force FLake, TaihuScene and HyLake v1.0 and then compared their performance on LST, LE and HE observations from the Lake Taihu Eddy Flux Network. The spatial resolution of ERA5 dataset covers 5 grid cells that encompass the studied lake sites, among the 11 grids for the entire Lake Taihu. These grids include portions of the land surface surrounding the lake, inevitably introducing uncertainty due to the scale mismatch between climatic forcing datasets and the lake model (Hersbach et al., 2020).

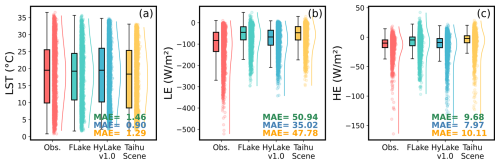
Figure 10 The statistical characteristics and spatial average of LST, LE and HE for observations, FLake, HyLake v1.0 and TaihuScene in all sites using ERA5 forcing datasets. Green, blue and yellow texts in figures represent the MAEs of LST, LE and HE for FLake, HyLake v1.0 and TaihuScene, respectively.

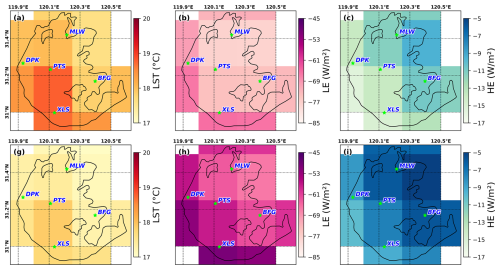
Figure 11 The statistical characteristics and spatial average of predicted LST, LE and HE for HyLake v1.0 and TaihuScene drove by ERA5 forcing datasets. Panels (a)–(c) represent LST, LE and HE for HyLake v1.0, respectively; panels (d)–(f) represent LST, LE and HE for TaihuScene, respectively. The green stars noted in all figures are lake sites in Lake Taihu.

Despite these limitations, it was surprising to find that the evaluation showed that HyLake v1.0 exhibited performance similar to or even superior to that of FLake for each lake site, with consistent spatial patterns for LST, LE, and HE (Figs. 10–11 and S5). From the statistical properties, HyLake v1.0 still exhibited an incomparable performance in overall datasets, with MAE values of 0.90 °C, 35.02 W m⁻², and 7.97 W m⁻² for LST, LE and HE, respectively, which following with TaihuScene performed with MAE values of 1.29 °C, 47.78 W m⁻², and 10.11 W m⁻² for LST, LE and HE, far outperforming FLake with MAE values of 1.46 °C, 50.94 W m⁻², and 9.68 W m⁻² for LST, LE and HE, respectively (Fig. 10). From spatial patterns observed, LST in the middle of the lake was relatively higher for all models (Fig. 11c and d), while LE was higher in the southern and western shore (Fig. 11b and e), and HE showed higher values in the northwestern shores of Lake Taihu (Fig. 11c and f). Both HyLake v1.0 and TaihuScene revealed similar patterns of average across all variables, except for a slight overestimation of LE and underestimation of HE in the southeastern and northeastern shores of Lake Taihu in HyLake v1.0, respectively (Fig. 11a–c). However, TaihuScene predicted relatively higher values in LE and HE, and lower in LST than the other models although it still followed similar spatial patterns for LST, LE, and HE (Fig. 11d–f). This indicates that HyLake v1.0, coupled with a small dataset-trained BO-BLSTM-based surrogate, can still provide robust and reasonable predictions for estimating spatial patterns of Lake Taihu.

HyLake v1.0 in Taihu-ERA5 experiments exhibited superior performance for each lake site, showing a strong transferability using ERA5 datasets (Fig. S5). At the MLW site (Fig. S5a–c), which is located on the northern shore of Lake Taihu, HyLake v1.0 outperformed both FLake (LST: MAE = 1.68 °C; LE: MAE = 33.84 W m⁻²; HE: MAE = 9.68 W m⁻²) and TaihuScene (LST: MAE = 1.30 °C; LE: MAE = 36.81 W m⁻²; HE: MAE = 8.39 W m⁻²), with MAE values of 1.05 °C, 31.46 W m⁻², and 9.12 W m⁻² for LST, LE, and HE, respectively. The training datasets used for the BO-BLSTM-based surrogate in HyLake v1.0 contributed to its powerful performance at this site, while predictions from TaihuScene performed farther from the observations. HyLake v1.0 still performed considerable well in ungauged sites by learning physical principles from MLW observations (Fig. S4d–o). TaihuScene showed robust predictions but outperformed HyLake v1.0 only at the XLS and MLW sites. For the BFG site (Fig. S5d–f), HyLake v1.0 outperformed both FLake and TaihuScene, with MAE values of 0.94 °C, 42.30 W m⁻², and 9.94 W m⁻², respectively. TaihuScene performed the worst among these models, with MAE values of 1.85 °C, 60.32 W m⁻², and 15.73 W m⁻². FLake exhibited a moderately performance with MAE values of 1.15 °C, 49.52 W m⁻², and 10.77 W m⁻² for LST, LE and HE, respectively. At the DPK site (Fig. S5g–i), HyLake v1.0 performed better than FLake for LST but performed slightly worse for LE and HE, with MAE values of 0.68 °C, 52.82 W m⁻², and 8.43 W m⁻². TaihuScene performed the worst in this site (LST: MAE = 1.49 °C; LE: MAE = 69.67 W m⁻²; HE: MAE = 12.40 W m⁻²). FLake performed the moderate in this site (LST: MAE = 1.14 °C; LE: MAE = 56.12 W m⁻²; HE: MAE = 9.11 W m⁻²). At the PTS site (Fig. S5j–l), HyLake v1.0 (LST: MAE = 0.75 °C; LE: MAE = 22.28 W m⁻²; HE: MAE = 6.43 W m⁻²) outperformed FLake for LST, LE, and HE (LST: MAE = 1.89 °C; LE: MAE = 57.12 W m⁻²; HE: MAE = 9.84 W m⁻²) and TaihuScene (LST: MAE = 0.94 °C; LE: MAE = 31.75 W m⁻²; HE: MAE = 6.74 W m⁻²). HyLake v1.0 showed a slightly better performance at the XLS site (Fig. S5m–o), with MAE values of 1.05 °C, 24.29 W m⁻², and 5.69 W m⁻², while TaihuScene performed slightly worse for LE (MAE = 37.94 W m⁻²) and HE (MAE = 6.79 W m⁻²), FLake performed the worst with MAE values of 1.49 °C, 58.78 W m⁻², and 9.01 W m⁻².

Overall, both HyLake v1.0 and TaihuScene showed reliable performance across lake sites in Lake Taihu (Fig. S5). Specifically, HyLake v1.0 performed the best in 13 of 15 variables (included LST, LE and HE for 5 lake sites) in Lake Taihu among these 3 models; TaihuScene outperformed HyLake v1.0 in 1 of 15 variables and outperformed FLake in 7 of 15 variables in Lake Taihu. HyLake v1.0 providing superior results in most cases, proving its potential for extensive application in ungauged lakes under different forcing datasets. However, the prediction accuracy of these models based on ERA5 datasets were almost reduced due to the potential uncertainty in lake-atmosphere modeling systems. The current coupling strategies of HyLake v1.0 ensured the numerical stability and superior performance in validation due to the robust capability of auto-regressive predictions by proposed LSTM-based surrogates and to avoid the numerical divergence or error accumulation in step-by-step iteration loops. The results evidenced that HyLake v1.0 coupled with BO-BLSTM-based surrogate is suitable for discovering the potential physical principles for lake-atmosphere interactions systems, indicating that the integration of deep learning-based surrogates as a module with process-based models is effective for improving predictions in ungauged lakes.

4 Discussion

4.1 Limitations of HyLake v1.0

In this study, we developed HyLake v1.0 by integrating a process-based backbone (PBBM) with an observation-trained, LSTM-based surrogate for LST approximation, forming a hard-coupled and auto-regressive hybrid structure. The model was evaluated against FLake, Baseline, and TaihuScene to assess its generalization and transferability across sites in Lake Taihu and Lake Chaohu. Results demonstrate that HyLake v1.0 maintains robust predictive accuracy when forced with ERA5 data across ungauged sites in Lake Taihu and in Lake Chaohu (Table 3; Figs. S7–S9). Despite these strengths, several limitations remain, mainly concerning data availability, computation efficiency, model architecture, explainability, and coupling strategies.

A primary limitation lies in the increasing demand for high-quality and representative data, stemming from the expanding development and application of the deep-learning-based surrogates and parameterizations (Almeida et al., 2022; Guo et al., 2021; Read et al., 2019). Long-term, high-frequency observations of radiation, energy fluxes, and temperature are scarce and costly to maintain (Erkkilä et al., 2018; Nordbo et al., 2011). While reanalysis products such as ERA5, NLDAS-2, and GLSEA offer valuable alternatives (Kayastha et al., 2023; Monteiro et al., 2022; Notaro et al., 2022; Wang et al., 2022), they may introduce systematic forcing biases. These biases can propagate through deep-learning-based surrogates into the physical base of the model, potentially hindering a ground-truth understanding of lake-atmosphere interactions. Nevertheless, our experiments demonstrate that incorporating well-trained deep-learning surrogates, calibrated with carefully curated observations and reliable coupling strategies, into process-based backbones can yield robust and transferable performance in ungauged regions. This underscores the critical value of high-quality data for enhancing model generalization at larger scales.

Another limitation stems from simplified parameterizations in two critical components of the process-based backbone: the energy balance equations and 1-D vertical lake temperature transport equations (Golub et al., 2022; Mooij et al., 2010). For instance, the bulk-aerodynamic method used to solve surface flux solutions of LE and HE, based on Monin–Obukhov similarity theory (Monin and Obukhov, 1954), remains sensitive to friction velocity (u^∗) and surface roughness length (z_0 m). Although the estimation of these variables has evolved from constant empirical values to iterative routines (Woolway et al., 2015; Hostetler et al., 1993), substantial discrepancies still exist between simulations and observations (Fig. S6). Several recent hybrid models have employed knowledge-guided loss functions to improve prediction of lake temperature profiles (He and Yang, 2025; Ladwig et al., 2024; Read et al., 2019). However, the underlying 1-D transport equations, often solved using finite difference methods (e.g., Crank-Nicholson solution, implicit Euler scheme), still struggle to accurately capture diurnal variability and long-term trends (Piccolroaz et al., 2024; Šarović et al., 2022; Subin et al., 2012). While such models may perform well on training and test datasets, their generalization and transferability require further validation, particularly given their complex coupling strategies and higher computational costs. These process simplifications introduce structural uncertainties that can only be partially compensated by the surrogate component.

A third issue involves computational efficiency and model architecture. The BO-BLSTM-based surrogate in HyLake v1.0 improves stability and performance in autoregressive forecasting but incurs computational costs compared to traditional process-based models (Table 3). We observed that the computational efficiency of HyLake v1.0 is sensitive to the number of parameters. For example, in the MLW experiment, HyLake v1.0 required ∼ 9 times longer to run than FLake, with a cost of 151.46 s. As modeling objectives shift toward long-term predictions, the inherent limitations of LSTMs in capturing long-range dependencies will become more pronounced, motivating the integration of more advanced deep-learning surrogates, such as those in the Transformer-based family (Bi et al., 2023; Chen et al., 2023). Future improvements should explore state-of-the-art architectures, including Transformers, Graph Neural Networks, Temporal Convolutional Networks, TimesNet, and Kolmogorov-Arnold Networks, which have shown exceptional capability in time series forecasting (Liu et al., 2024b; Wen et al., 2022; Wu et al., 2022; Bai et al., 2018), and are increasingly applied in hydrological modeling (Koya and Roy, 2024; Wang et al., 2024d; Sun et al., 2021). However, developing powerful surrogates such as the Fuxi and Pangunot only demands large-scale observational datasets but also substantial computational resources (Bi et al., 2023; Chen et al., 2023). This underscores a critical trade-off among model complexity, predictive accuracy, and computational efficiency, highlighting the need for more compact and efficient surrogate designs.

Although the hard-coupled structure of the HyLake v1.0 enhances interpretability compared to purely data-driven approaches, the LSTM-based surrogate still function partially as a “black box”, limiting physical transparency (De la Fuente et al., 2024; Chakraborty et al., 2021). Developing deep-learning surrogates that inherently incorporate physical knowledge is an active research area (Piccolroaz et al., 2024; Willard et al., 2023; Read et al., 2019). For example, Read et al. (2019) proposed a process-guided deep-learning model that incorporated a GLM-based energy budget loss function and evaluated it across 68 lakes. Ladwig et al. (2024) developed a modular framework integrating four deep-learning models with an eddy diffusion scheme to improve temperature predictions in Lake Mendota. However, such approaches often rely on simplified parameterizations, exhibit opaque inter-module relationships, and entail high computational costs, factors that currently constrain model generalization and transferability. Future versions of HyLake should prioritize the development of physically informed surrogates and more transparent coupling strategies to enhance explainability, numerical stability, and physical consistency.

4.2 Future improvements

HyLake v1.0 demonstrates strong generalization capability across different lake sites, establishing a promising foundation for further extensions. Subsequent improvements should focus on three key areas: investigating data scaling laws, advancing surrogate architectures, and extending the range of coupled physical modules.

Expanding the training dataset to include lakes with diverse morphometric and climatic characteristic will enhance model robustness. However, simply adding more data does not guarantee improved performance; rather, physically informative and highly representative samples from distinct lake regimes are more beneficial. This aligns with observations from other large deep-learning models, where training on heterogeneous datasets without strategic sampling can hinder performance gains (Wang et al., 2025). In this study, we hypothesized that training LSTM surrogates individually for each site would better represent localized lake–atmosphere interactions, a premise largely supported by our results. While surrogates trained on data from sites with limited observations (DPK, PTS, XLS) performed comparably in estimating ΔLST (except for XLW; Table S1), the surrogate trained at BFG, despite its relatively complete dataset, underperformed the proposed BO-BLSTM surrogate in capturing diurnal LST patterns (Fig. S10). As HyLake is scaled to more lakes or larger regions, the computational architecture must efficiently handle large training datasets, which may otherwise constrain site-specific performance. Furthermore, scaling laws for deep-learning models indicate that performance diminish with increasing model size beyond a certain point (Hestness et al., 2017). Adopting more advanced deep-learning surrogates will thus be essential to improving HyLake's representation of lake-atmosphere interactions in ungauged settings.

Although the BO-BLSTM-based surrogate improves model robustness, its complex architecture increases training costs (Peng et al., 2025; Ferianc et al., 2021). Simplified Bayesian architecture may offer comparable uncertainty quantification capabilities at a lower computational expense (Klotz et al., 2022). Notably, HyLake v1.0 holds potential for future uncertainty assessment, such as predictive variance and the probability of extreme lake events, by further developing its surrogate component (Kar et al., 2024; Gawlikowski et al., 2023). To overcome current limitations related to high computational demand and performance ceilings, future work should explore novel surrogate architectures that are both efficient and scalable, trained on larger and more diverse datasets.

The modular Python-based framework of HyLake v1.0 offers greater flexibility than traditional process-based models for coupling additional modules, such as those for lake temperature profiles, greenhouse gas exchange, oxygen dynamics, and lake-watershed interactions (Saloranta and Andersen, 2007; Stepanenko et al., 2016). Emphasizing energy-mass balance closure and parameter sharing across modules will improve physical consistency and reduce uncertainty propagation. Precedents for such integrated modeling exist: Lake 2.0 (Stepanenko et al., 2016) coupled methane and carbon dioxide modules to study gas dynamics in Kuivajärvi Lake, while MyLake (Saloranta and Andersen, 2007) has been extended to include modules for DOC degradation, DO dynamics, microbial respiration, gas exchange, sediment-water interactions, dynamic light attenuation, nitrogen uptake, and even floating solar panels (Exley et al., 2022; Salk et al., 2022; Kiuru et al., 2019; Pilla and Couture, 2021; Markelov et al., 2019; Couture et al., 2015; Holmberg et al., 2014). Many of these hydro-biogeochemical processes are currently described by simplified PDEs or empirical models, introducing structural uncertainties (Li et al., 2021b). The flexible design of HyLake v1.0 enables the integration of deep-learning surrogates to approximate complex processes such as temperature dynamics, gas flux, and oxygen variability, potentially outperforming both purely process-based and purely data-driven models.

In summary, HyLake v1.0 provides a flexible and extensible framework for advancing hybrid lake modeling. Future development should prioritize enhancing physical consistency, improving uncertainty quantification, and increasing computational efficiency to better represent complex lake–atmosphere processes across diverse settings.

5 Conclusion

This study introduced a novel hybrid lake model, HyLake v1.0, by hard-coupling a BO-BLSTM-based surrogate trained with observations from the MLW lake site in Lake Taihu. It replaced the implicit Euler scheme typically used in traditional process-based lake models with this BO-BLSTM-based surrogate, enabling the prediction of LST, LE, and HE at the lake-atmosphere interface by collectively using energy balance equations. The HyLake v1.0 was proposed to offer more accurate prediction and flexibility in development of hybrid hydrological models. Specifically, in three numerical experiments (MLW, Taihu-obs, and Taihu-ERA5), including three models (FLake, Baseline, and TaihuScene), this study intercompare the performance of HyLake v1.0 by adapting different surrogates, training strategies, and forcing datasets. Additionally, this study used different forcing datasets, including observations from 5 lake sites in Lake Taihu and the ERA5 datasets, to evaluate the transferability of HyLake v1.0 in ungauged regions and unlearned datasets. The experiments demonstrated that HyLake v1.0 effectively learns the physical principles governing lake-atmosphere interactions, highlighting its potential for application in ungauged lakes. Major conclusions are summarized as follows:

1. The BO-BLSTM-based surrogate in HyLake v1.0 performed well in representing changes in ΔLST of test dataset (RMSE = 0.2587 °C, MAE = 0.1594 °C), outperforming TaihuScene while underperforming Baseline;

2. HyLake v1.0 showed superior generalization capacity in LST (R = 0.99, RMSE = 1.08), LE (R = 0.94, RMSE = 24.65), and HE (R = 0.93, RMSE = 7.15) at both daily and hourly scales compared to observations, FLake and Baseline model, indicating that integrating physical principles with LSTM-based surrogates improves model accuracy and better captures changes in lake-atmosphere interactions;

3. HyLake v1.0 demonstrated its capability of transferability in ungauged regions of Lake Taihu and with low-resolution ERA5 forcing datasets. The results of intercomparison across lake site showed HyLake v1.0 presented the best capability in representation of LST (MAE = 1.03 °C), LE (MAE = 24.79 W m⁻²) and HE (MAE = 7.88 W m⁻²) than FLake and TaihuScene. Specifically, it performed the best in MLW, PTS, and XLS, but slightly poorer in BFG and DPK sites than TaihuScene. Regarding the capability of spatial transferability using ERA5 forcing datasets, results indicated HyLake v1.0 performed the most closely matched the observations in Lake Taihu compared to FLake and TaihuScene in 14 of 15 variables (LST, LE and HE in 5 lake sites).

These intercomparison experiments highlighted that HyLake v1.0, when coupled with a BO-BLSTM-based surrogate, offers excellent flexibility and is capable of capturing the underlying physical principles, providing more accurate predictions than traditional process-based models in ungauged regions. This also demonstrates the model's promising potential for application in ungauged lakes. Future work should focus on expanding HyLake v1.0 by exploring different architectures, utilizing larger training datasets, and incorporating additional coupled modules.