Decomposition of skill scores for conditional verification: impact of Atlantic Multidecadal Oscillation phases on the predictability of decadal temperature forecasts

As the performance of weather and climate forecasting systems and their benchmark systems are generally not homogeneous in time and space and may vary in specific situations, improvements in certain situations or subsets have different effects on overall skill. We present a decomposition of skill scores for the conditional verification of such systems. The aim is to evaluate the performance of a system individually for predefined subsets with respect to the overall performance. The overall skill score is decomposed into a weighted sum representing subset contributions, where each individual contribution is the product of the following: (1) the subset skill score, assessing the performance of a forecast system compared to a reference system for a particular subset; (2) the frequency weighting, accounting for varying subset size; and (3) the reference weighting, relating the performance of the reference system in the individual subsets to the performance of the full data set. The decomposition and its interpretation are exemplified using synthetic data. Subsequently, we use it for a practical example from the field of decadal climate prediction: an evaluation of the Atlantic European near-surface temperature forecast from the German “Mittelfristige Klimaprognosen” (MiKlip) initiative decadal prediction system that is conditional on different Atlantic Multidecadal Oscillation (AMO) phases during initialization. With respect to the chosen western European North Atlantic sector, the decadal prediction system “preop-dcpp-HR” performs better than the uninitialized simulations mostly due to contributions during the positive AMO phase driven by the subset skill score. Compared to the low-resolution system (preop-LR), no overall performance benefits are made in this region, but positive contributions are achieved for initialization in neutral AMO phases. Additionally, the decomposition reveals a strong imbalance among the subsets (defined by AMO phases) in terms of reference weighting, allowing for insightful interpretation and conclusions. This skill score decomposition framework for conditional verification is a valuable tool to analyze the effect of physical processes on forecast performance and, consequently, supports model development and the improvement of operational forecasts.

1 Introduction

The verification of forecast systems plays an important role in the field of weather and climate prediction with respect to assessing the quality of such systems and, moreover, of the entire forecast process. Furthermore, a common practice for evaluating forecast systems is comparison against another competing prediction system or a standard reference forecast, such as the persistence or climatological forecast. Basically, the relative performance, in terms of accuracy, of a prediction system with respect to a reference is expressed as forecast skill and is usually presented as a skill score (Wilks, 2011). Therefore, a variety of skill scores are widely used for verification; for example, the mean-squared error skill score (MSESS) is a common way to verify a deterministic forecast, while the Brier skill score (BSS), the ranked probability skill score (RPSS), or the continuous ranked probability skill score (CRPSS), used in applications such as decadal forecast verification (e.g., Kadow et al., 2016; Kruschke et al., 2016; Pasternack et al., 2018, 2021), could be the choice for a probabilistic forecast.

As the forecast performance is typically not homogeneous in time and space, it is of interest how variable the forecast skill is for different states of the system. Therefore, conditional verification is a common practice in weather and climate research, i.e., the evaluation of forecasts separately for different regions (e.g., Northern Hemisphere and Southern Hemisphere) or seasons (e.g., winter and summer). Additionally, the initial state and particular conditions that the system goes through during the forecast might also affect the prediction skill. In weather forecasting, the state of atmospheric flow regimes or circulation patterns can influence the forecast quality (Grönås, 1982, 1985), where a more stable regime (such as blocking) can improve the forecast quality of a model (Tibaldi and Molteni, 1990). The presence of different climate states during the initialization procedure of medium-range forecasts, which can improve the predictive ability in certain periods, is addressed in the subseasonal-to-seasonal (S2S) prediction community (Mariotti et al., 2020). Large-scale atmospheric circulation variability, such as the North Atlantic Oscillation (NAO; Jones et al., 2004; Ferranti et al., 2015; Jones et al., 2015), the Madden–Julian Oscillation (MJO; Ferranti et al., 2018), or circulation patterns (Frame et al., 2013; Richardson et al., 2021), and coupled ocean–atmosphere phenomena, like the El Niño–Southern Oscillation (ENSO; e.g., Qin and Robinson, 1995; Branković and Palmer, 2000; Goddard and Dilley, 2005; Frías et al., 2010; Kim et al., 2012; Manzanas et al., 2014; Miller and Wang, 2019), can contribute to a forecast skill improvement. In decadal climate prediction – the focus of this study – the state of the ocean has the potential to affect long-term forecasts of the following years, i.e., an enhanced subpolar ocean heat transport (OHT) linked to North Atlantic upper-ocean heat content (UOHC) and, in some way, via the Atlantic Meridional Overturning Circulation (AMOC) to the positive Atlantic Multidecadal Oscillation/Variability (AMO/AMV) phase, resulting in the potential to improve predictive ability during the initialization of a climate model (Müller et al., 2014; Zhang and Zhang, 2015; Borchert et al., 2018, 2019).

In a typical verification study, the accuracy of a given forecast is compared to a reference to evaluate the quality of the forecast. To assess the forecast quality for specific situations (e.g., states, seasons, or regions), verification can be carried out in a manner that is conditional on these situations by stratifying the full data set by situation type. Thus the forecast data set is split up and (skill) scores are obtained individually for the splits. The interpretation of these partial skill scores is not necessarily straightforward. This is particularly the case when the reference strongly varies among individual subsets compared with the overall behavior; this is commonly known as “Simpson's paradox” (Pearson et al., 1899; Yule, 1903; Simpson, 1951; Blyth, 1972). With respect to weather and climate prediction, a potential misinterpretation of the forecast performance stratified using specific conditions or samples may arise if the underlying climatology that is used as the reference forecast differs in some way among these samples (e.g., Murphy, 1996; Goeber et al., 2004; Hamill and Juras, 2006). In that case, a fair comparison should consider the varying behavior of such a climatology in the verification procedure.

While the majority of mentioned studies focus more on decomposing a skill score to measure basic aspects of forecast quality with respect to a climatological reference forecast in a fair way, we apply a decomposition framework in the context of conditional verification in the field of decadal predictions in this work. The aim is to evaluate the performance of individual subsets in relation to the performance of the entire forecast set. The decomposition provides a simple diagnostic tool to assess the contribution of certain subsets to the overall skill as well as to identify potential causes of variable skill between these subsets. The resulting information can be further used to analyze physical processes related to certain subsets and, consequently, to support model development and optimize operational forecasts. In terms of decadal forecasts, we exploit the potential source of long-term predictability forced by ocean states associated with the AMO to improve the forecast assessment.

First, the general decomposition procedure of the skill score is described in Sect. 2 and exemplified in Sect. 3 using synthetic data. In Sect. 4, the decomposition is applied to decadal predictions to evaluate the Atlantic European near-surface temperature forecast of a preoperational forecast system depending on different North Atlantic ocean states. The latter are determined by the Atlantic Meridional Oscillation (AMO). The results are summarized and discussed in Sect. 5. Section 6 concludes this study.

2 Decomposition of skill score

This section presents the decomposition of a skill score into contributions from different subsets derived from the full set of forecast–observation pairs and discusses the interpretation of individual terms.

2.1 Subset contribution

To verify a forecast f_n, we calculate a verification score $S_n=S(f_n,o_n)$, an error metric between an individual forecast f_n and the corresponding observation o_n (Wilks, 2011). Considering all forecast–observation pairs (f_n,o_n), $n=\mathit{\{}\mathrm{1},\mathrm{\dots },N\mathit{\}}$, the mean score $\stackrel{\mathrm{‾}}{S}$ of the full set can be computed by

$$\begin{array}{}\text{(1)}& \stackrel{\mathrm{‾}}{S}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{n=\mathrm{1}}^N{S}_n=\sum _{i=\mathrm{1}}^K{\displaystyle \frac{N_i}{N}}\left({\displaystyle \frac{\mathrm{1}}{N_i}}\sum _{n=\mathrm{1}}^{N_i}{S}_n\right)=\sum _{i=\mathrm{1}}^K{\displaystyle \frac{N_i}{N}}{\stackrel{\mathrm{‾}}{S}}_i\end{array}$$

with $N=N_{\mathrm{1}}+\mathrm{\dots }+N_K$, where K is the number of nonoverlapping subsets i of the data, N_i is the number of forecast–observation pairs in subset i, and N is the total number of forecast–observation pairs.

The mean-squared error (MSE) is an adequate score for a deterministic forecast of a continuous variable, while the ranked probability score (RPS) is an appropriate choice for a probabilistic forecast of a discrete forecast. To measure the performance of a forecast system “fc” compared to a reference forecast “ref”, the associated skill score SS (e.g., MSE skill score MSESS and ranked probability skill score RPSS, respectively) is used.

The forecast performance may vary for individual subsets of the data, and the resulting interpretation may depend on the different behavior of the reference system. To assess varying skill scores for specific situations (e.g., states, periods, seasons, or regions), the verification is carried out in a manner that is conditional on these situations, i.e., the full data set is stratified. Thus, we split the data into K subsets and determine the individual subset contribution of each subset i to the overall mean skill score SS.

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\text{SS}& ={\displaystyle \frac{{\stackrel{\mathrm{‾}}{S}}^{\text{fc}}-{\stackrel{\mathrm{‾}}{S}}^{\text{ref}}}{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}^{\text{ref}}}}\\ & ={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^K\frac{N_i}{N}{\stackrel{\mathrm{‾}}{S}}_i^{\text{fc}}-{\sum }_{i=\mathrm{1}}^K\frac{N_i}{N}{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}^{\text{ref}}}}\\ & =\sum _{i=\mathrm{1}}^K\underset{\text{contribution\hspace{0.17em}\hspace{0.17em}subset}i}{\underbrace{{\displaystyle \frac{N_i}{N}}\left({\displaystyle \frac{{\stackrel{\mathrm{‾}}{S}}_i^{\text{fc}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}^{\text{ref}}}}\right)}},\end{array}\end{array}$$

where ${\stackrel{\mathrm{‾}}{S}}^{\text{fc}}$ and ${\stackrel{\mathrm{‾}}{S}}^{\text{ref}}$ are the mean scores of the forecast system fc and the reference system ref, respectively, over an entire data set with N forecast–observation pairs, and S^perf is the score of a perfect forecast, which is zero for the MSE or RPS. ${\stackrel{\mathrm{‾}}{S}}_i^{\text{fc}}$ and ${\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}$ represent the mean score of the forecast system and reference system, respectively, for individual subsets.

2.2 Terms of decomposition

In order to evaluate how strongly and in which situations the skill score of the subsets affects the total skill score, we include and separate any component that influences the contribution of a subset to the overall skill score. We multiply Eq. (2) by $\mathrm{1}=\frac{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}$, yielding

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\text{SS}& =\sum _{i=\mathrm{1}}^K\underset{\begin{array}{c}\text{frequency}\\ \text{weighting}\end{array}}{\underbrace{{\displaystyle \frac{N_i}{N}}}}\cdot \underset{\begin{array}{c}\text{subset}\\ \text{skill score}\end{array}}{\underbrace{\left({\displaystyle \frac{{\stackrel{\mathrm{‾}}{S}}_i^{\text{fc}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}}\right)}}\cdot \underset{\begin{array}{c}\text{reference}\\ \text{weighting}\end{array}}{\underbrace{\left({\displaystyle \frac{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}^{\text{ref}}}}\right)}}\\ & =\sum _{i=\mathrm{1}}^K{W}_{{\text{freq}}_i}\cdot {\text{SS}}_i\cdot W_{{\text{ref}}_i}=\sum _{i=\mathrm{1}}^K{W}_i\cdot {\text{SS}}_i.\end{array}\end{array}$$

The individual subset contribution W_iSS_i to the overall skill score depends on (i) SS_i, the performance of the forecasting system compared to the reference system in that given subset, weighted by (ii) $W_{{\text{freq}}_i}$, the relative size of the subset (frequency of the stratification event occurring), and (iii) $W_{{\text{ref}}_i}$, the performance of the reference system in the subset compared to the full set of forecast–observation pairs.

In detail, SS_i is the mean subset skill score of the forecast system fc versus the reference system ref with respect to forecast–observation pairs of the given subset i. This term characterizes how well the forecast system performs in comparison to the reference system in that specific subset (e.g., during a positive AMO phase). It is commonly applied in model evaluations to find enhanced predictability during certain climate or large-scale circulation states or specific seasons.

$W_{{\text{freq}}_i}$ is the frequency weighting and considers the number of forecast–observation pairs (e.g., time steps) in subset i relative to the total number of forecast–observation pairs. For a time series, one could imagine that this part reflects the relative frequency of occurrence of the situation stratified within the total time period.

$W_{{\text{ref}}_i}$ is the reference weighting and defines the ratio of the mean score of the reference system for the subset i (numerator) and the full set of forecast–observation pairs (denominator). It adjusts the scale (or range) of the subset skill score, which was set by $S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}$, to the scale used for the overall skill score. This component can be interpreted as a weighting of the subset skill score by means of the performance of the reference system in the subset compared to its performance in the full set of forecast–observation pairs. If the performance of the reference varies strongly among subsets, the individual subset skill scores will contribute to the total skill score according to the performance of the reference.

The total subset weight W_i (product of the frequency weighting and the reference weighting) determines the influence of the subset skill score on the total skill score; i.e., for an improvement/degradation ΔSS_i of the forecast in the subset i, the total skill score for the full set of forecast–observation pairs changes accordingly by

$$\begin{array}{}\text{(4)}& \mathrm{\Delta }{\text{SS}}_{\left(\mathrm{\Delta }{\text{SS}}_i\right)}=W_i\cdot \mathrm{\Delta }{\text{SS}}_i.\end{array}$$

3 Synthetic cases

In the following, we illustrate the effect of the different reference performance using synthetic data. In the context of near-term climate prediction, one could imagine the annual mean of 2 m temperature being verified in two different forecast systems with respect to the same observation for a certain defined period.

Table 1 Cases of setup A (A0–A2) showing the mean scores ($\stackrel{\mathrm{‾}}{S}$) and skill scores (SS) of two subsets and of the total forecasts. The influence of the skill score in subset 1 on the total skill score is weak compared with that of subset 2. The skill score changes as described in A1 and A2, with both being related to the first case A0.

Table 2 Cases of setup B (B0–B2); similar to Table 1, but the influences of the skill score of subset 1 and subset 2 on the total skill score are similar.

3.1 Example cases with different skill score behavior

With respect to a time-based stratified verification, which is addressed in this study, we assume that the performance of both forecast systems varies systematically within the period considered. For this purpose, we divide the entire period – here a period of N=60 time steps representing 60 years – into two subsets of equal size (K=2, $N_{\mathrm{1}}=N_{\mathrm{2}}=\mathrm{30}$). The performance of the two forecast systems shows a systematically different behavior for the two subsets. An example from near-term climate prediction could be the state of the ocean in terms of years dominated by a negative or positive AMO phase during the initialization procedure, which might have an influence on the forecast performance in some regions via OHT (Borchert et al., 2018).

Applied to our fictive example, the mean scores of the reference systems differ between both subsets. In some situations, it is possible that the long-term performance, expressed in terms of the total skill score SS of a forecast system compared to another forecast system, is dominated by a specific subset period. With the setting described above and the decomposition approach from Sect. 2, we illustrate and discuss the individual contributions of subsets to the total skill score. For this purpose, we generate six hypothetical cases with different performance combinations of forecast fc and reference ref during the two subsets i=1 and i=2. Three cases in setup A assume very different performance of the reference system in the two subsets, whereas three cases in setup B assume almost equal performance of the reference. For simplicity, we set S^perf=0.

3.1.1 Setup A: unequal performance of the reference

In the base case of setup A (A0; see Table 1), we assume that the forecast system fc performs better than the reference in subset i=1 (subset skill score SS₁=0.15). In subset i=2, the forecast system fc performs slightly more poorly than the first subset (SS₂=0.08). Following Simpson's paradox and based on the skill scores, one might be tempted to think that the total skill score SS is an equal composition (e.g., arithmetic mean) of both subset skill scores ${\text{SS}}_{\mathrm{1}/\mathrm{2}}$. However, in this specific configuration, the total skill score of the overall data (SS=0.09) is very close to that in subset 2. The total skill of forecast system fc is mainly dominated by this subset.

The next scenario will be covered in case A1 (Table 1), where an improvement of the subset skill score is achieved for the first subset by improving the error metric, i.e., reducing the mean score of the forecast system ${\stackrel{\mathrm{‾}}{S}}_{\mathrm{1}}^{\text{fc}}$ by half, while the mean score and skill score of the second subset remain the same. Although the skill score of the forecast system fc in subset i=1 is improved (A1: SS₁=0.58), the overall skill score hardly changes (A1: SS=0.13). In contrast, in the last case (A2 in Table 1), we set a similar improvement of the skill score in subset i=2 (SS₂=0.54). Here, the total skill score (SS=0.51) increased considerably compared with A1.

Taking all three cases into account, it can be summarized that the total skill score of the forecast system fc with respect to the reference ref is mainly dominated by the subset skill score from subset i=2; this can be seen in Fig. 1a, where the overall skill score of the full set of forecast–observation pairs (gray bars) behaves very sensitively towards changes in the subset skill score from subset i=2 (orange), whereas changes in the skill score from subset i=1 (green) yield almost no effect.

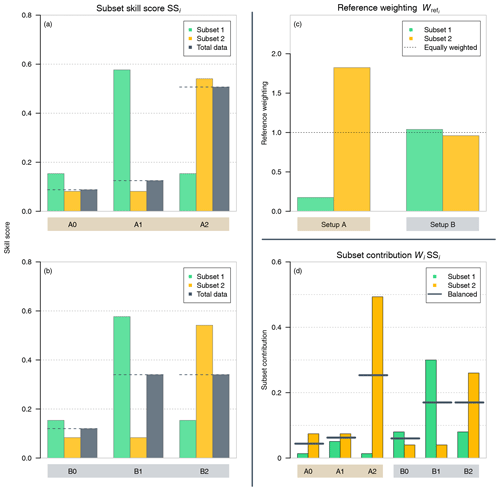
Figure 1 (a, b) Subset skill scores (green and orange bars) and their influence on the respective total skill score (gray bars and dashed lines) from synthetic example cases of (a) setup A (brown background; shown in Table 1; strong reference weighting imbalance among both subsets) and (b) setup B (gray background; shown in Table 2; nearly balanced reference weighting among both subsets). (c) Reference weighting of both subsets for setup A and B (green and orange bars, respectively). The dashed line reflects balanced behavior among both subsets. (d) Subset contributions of both subsets from cases of setup A and setup B (green and orange bars, respectively). Gray horizontal lines indicate a balanced contribution SS_bal (see Sect. 3.3) with respect to the total skill score.

3.1.2 Setup B: equal performance of the reference

In contrast to setup A, we show three related examples in setup B (B0–B2 in Table 2) in which the influence on the total skill score is nearly equally balanced between both subsets. To see the different behavior, the subset skill scores and the relative sizes of the score improvements in the forecast system fc of all cases will be the same as before. Consequently, in the base case of setup B (B0 in Table 2), the forecast system fc performs better in subset i=1 compared with the reference system ref (SS₁=0.15), while it shows a weaker performance in subset i=2 (SS₂=0.08). Unlike case A0, the total skill score now depends almost equally on both subsets (SS=0.12). The changes made to the two cases B1 and B2 follow a similar pattern to the changes in A1 and A2, as can be seen in Fig. 1b, whereas the total skill score is almost given by the arithmetic mean of both periods. With the skill score decomposition from Sect. 2, the reason for this behavior can be investigated.

3.2 Decomposition of skill scores and impact of the reference weighting

The different behaviors shown can be investigated using the decomposition terms from Eq. (3) with S^perf=0. As demonstrated there, the contribution of an individual subset to the total skill score depends on three terms: frequency weighting, reference weighting, and the subset skill score. As defined above, we varied the subset skill scores in the same way and used subsets of equal size, resulting in the same frequency weighting of $\frac{\mathrm{1}}{\mathrm{2}}$ for both subsets. Consequently, the reference weighting for the individual subsets must play a crucial role. For setup A, the mean scores (${\stackrel{\mathrm{‾}}{S}}_{\mathrm{1}/\mathrm{2}}$) between subsets differ by more than one unit. In detail, the scores are generally much higher in subset i=2 than in subset i=1. As a result, potential subset skill score changes for the forecast system fc that are just achieved during the first subset will not affect the total skill score very much. The larger scores in subset i=2 show a stronger relevance with respect to the total skill.

In contrast to setup A, setup B shows an almost balanced behavior in this respect. These difference can also be seen when we compare the reference weighting term from the skill score decomposition described before. Figure 1c visualizes this behavior, in which the cases from setup A show a different value for the reference weighting in both subsets, while the reference weighting is close to 1 in both cases in setup B.

Generally, the reference weighting lies between 0 and K (number of subsets). Values below (above) 1 reflect a lower-than-average (higher-than-average) contribution to the overall skill score. Figure 2 demonstrates the impact of individual subset skill scores on the resulting total skill score depending on their reference weighting. We compute the total skill score SS with respect to our cases (Fig. 2b) with a prescribed subset skill score in subset i=1 (SS₁) and subset i=2 (SS₂), respectively, and successively change the reference weighting term (Fig. 2a). On the left of Fig. 2, we start with behavior similar to setup A, which is dominated by subset i=2, where the reference weighting term of subset i=2 (orange bars) is larger than that of subset i=1 (green); a balanced ratio between both subsets (similar to setup B) is shown in the middle; and the right part shows a total skill score that is mainly controlled by subset i=1. Thus, the reference weighting controls the subset's contribution to the overall skill score.

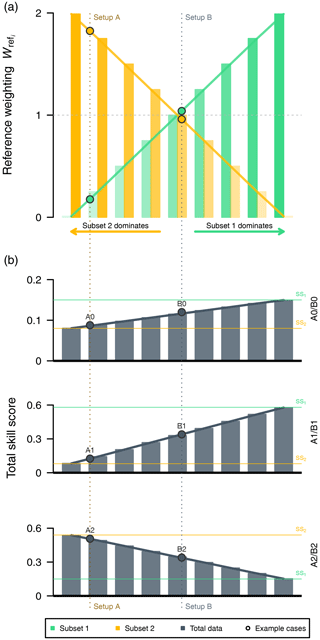
Figure 2 (a) Variations in the reference weighting term of both subsets (green and orange bars) and (b) their potential influence on the corresponding total skill score (gray bars) for given subset skill scores ${\text{SS}}_{\mathrm{1}/\mathrm{2}}$ (green and orange horizontal lines) from example cases of setup A (A0–A2; Table 1) and setup B (B0–B2; Table 2). Current values of the example cases are highlighted with a dot. A balanced (enhanced unbalanced) behavior among both subsets reflects the center bar pair (bar pairs towards left/rights edges).

According to Eq. (4), we can compute potential changes in the total skill score ΔSS depending on changes in the subset skill score ΔSS_i. For example, in setup A, a change in the subset skill score in subset i=1 of ΔSS₁=0.5 would change the total skill score by only ΔSS=0.045. On the other hand, a skill gain of 0.5 in subset i=2 would increase the total skill score by a value of 0.455. In detail, with S^perf=0, the derived weighting terms from the decomposition are shown in Table 3. In this example, it is more effective in terms of the gain in the total skill score to focus on the subset i=2 for improvement of the forecast system.

Table 3 Individual effect of a 0.5 change in the subset skill score SS_i on the total skill score SS for setup A. The weighting terms from the decomposition are also shown.

The synthetic example is focused on the reference weighting; however, the decomposition is also useful for unequal subset sizes. The contribution to the total skill score is then additionally controlled by the frequency weighting. Depending on the verification setup, both parts should be considered in weather and climate forecasts. As a consequence, complexity is reduced when each subset has the same size and the reference weighting of all subsets is 1 due to a chosen reference. This leads to equally weighted skill scores of the subsets.

3.3 Subset contributions

In Fig. 1d, we assess the subset contributions compared to a balanced contribution across the synthetic example cases. The balanced contribution (gray horizontal lines) represents a hypothetical value resulting from distributing the total skill score into equal contributions from the K subsets: ${\text{SS}}_{\text{bal}}=\frac{\text{SS}}{K}$. The sign of the subset contribution indicates a positive or negative contribution to the total skill score, while its value indicates the size of the contribution. In setup A, the values of the contribution from subset 2 (orange bars) are larger than the contributions of subset 1 (green bars), even for cases in which the subset skill score SS₁ is higher (A0 and A1; Fig. 1a). In setup B, the contributions behave in a similar manner to the subset skill scores. Strongly differing deviations from SS_bal between the subsets show the strong imbalance between the contributions of both subsets. As the frequency weighting of both subsets is identical, the observed characteristic is driven by the reference weightings.

In summary, the decomposition of the subset contribution into its three components reveals the potential impact of a subset on the overall skill score considering the combination of all three terms of the subset (i.e., size and performance of the reference), instead of only the skill score for a particular subset.

4 Conditional verification in the MiKlip decadal prediction system

4.1 Simulations from the MiKlip decadal prediction system

We investigate the influence of ocean states – given in terms of AMO phases – on the near-surface air temperature hindcast skill in the MiKlip decadal climate prediction system. The MiKlip decadal climate prediction system (Marotzke et al., 2016) generation preop-dcpp is based on the coupled atmosphere–ocean Earth system model of the Max-Planck Institute (version 1.2) simulated in the high-resolution (HR) setting (Müller et al., 2018; Mauritsen et al., 2019). The model for the atmospheric component – ECHAM6.3 – has a T127 horizontal resolution (0.9375°) and 95 vertical levels. The ocean part is simulated by the Max Planck Institute ocean model (MPIOM) with a horizontal resolution of 0.4° and 40 vertical levels.

The 10-member ensemble of the system is initialized on an annual basis from 1960 to 2012, with a period of 10 years being simulated for each run. The initialization procedure is similar to that in Pohlmann et al. (2013), who nudged the model toward atmospheric and oceanic fields obtained from reanalysis data. With respect to the atmospheric model component, a full-atmospheric-field initialization from ERA-40 (Uppala et al., 2005) and ERA-Interim (Dee et al., 2011) reanalyses is applied. For the ocean component, salinity and ocean temperature anomalies derived from an assimilation experiment forced by Ocean Reanalysis System 4 (ORAS4) ocean reanalysis data (Balmaseda et al., 2013) as well as sea ice concentrations from the National Snow and Ice Data Center (Fetterer et al., 2018) described in Bunzel et al. (2016) are taken as initial conditions. The external forcing is based on the Coupled Model Intercomparison Project (CMIP) Phase 6 forcing (see Eyring et al., 2016, and Pohlmann et al., 2019, for details). In addition to the initialized simulations, an ensemble of 10 uninitialized runs (historical simulations) is used as the competitive prediction for the skill assessment. Further details about the simulations can be found in Müller et al. (2018) and Pohlmann et al. (2019). To evaluate the probabilistic hindcast skill, both sets of predictions are verified against observations from the Hadley Centre and Climate Research Unit (HadCRUT4; Morice et al., 2012). To be on the same horizontal resolution as the observational data, the model data of the prediction system are regridded to a regular 5° × 5° grid.

4.2 Atlantic Multidecadal Oscillation time series

As the multidecadal variability in the ocean state in the North Atlantic (e.g., AMV, AMOC, and OHT) is represented in the decadal prediction system and shows predictive potential (Müller et al., 2014; Borchert et al., 2018, 2019; Höschel et al., 2019), we will apply the conditional verification of the temperature stratified along three different phases of the Atlantic Multidecadal Oscillation (AMO). We calculate the AMO index proposed by Enfield et al. (2001) in the ORAS4 ocean reanalysis data to match the current state of the Atlantic Ocean during the initialization procedure. Specifically, monthly anomalies (base period: 1960–2010) of the sea surface temperature (SST) averaged over the North Atlantic region (0–60° N, 80–0° W) are exploited to compute the North Atlantic temperature time series. Afterwards, the linear trend (base period: 1960–2010) in this time series is removed to obtain the AMO time series. With regard to the subsequent conditional evaluation of the decadal prediction system, annual averages of the AMO are used to split the entire period into three different subsets (based on 0 ± 0.5σ thresholds using the base period from 1960 to 2010) representing years of negative, neutral, and positive AMO phases.

4.3 Verification of probabilistic forecasts for three categories

We verify the decadal ensemble predictions using the ranked probability score (e.g., Wilks, 2011; Kruschke et al., 2016). The score is computed for both sets of predictions against the HadCRUT4 observation to assess the probabilistic skill of the initialized versus uninitialized simulations. For near-surface air temperature, we build time series of forecast–observation pairs depending on the lead time for all initialized decadal experiments from 1960 to 2012. Temperature data with lead times of between 2 and 5 years are averaged to compute a score for the lead-time period of 2–5 years.

In the next step, we divide the resulting data sets (separately for initialized, uninitialized, and observational data) into three equal parts along their terciles to obtain J=3 different temperature categories $j=\mathrm{1},\mathrm{\dots },J$ (below normal, normal, and above normal). For both simulation data sets, the entire ensemble is used to determine the respective terciles. With this approach, an implicit lead-time-dependent bias correction, which is commonly applied in decadal climate predictions projects, will be achieved.

The ranked probability score (RPS), defined as

$$\begin{array}{}\text{(5)}& {\text{RPS}}_t=\sum _{j=\mathrm{1}}^J(Y_{j,t}-O_{j,t}{)}^{\mathrm{2}},\end{array}$$

is calculated between both sets of predictions and the observational data, where Y_j,t is the cumulative forecast probability of class j (with J=3) derived from the forecast ensemble of initialization year t for the given forecast lead-time mean of 2–5 years by counting the ensemble members in each category and then dividing by the ensemble size. O_j,t represents the corresponding observed cumulative probability represented as the Heaviside step function, where either $O_{j,t}=\mathrm{0}$ if a higher category than j is observed or $O_{j,t}=\mathrm{1}$ otherwise. To assess the skill between the initialized (fc) and uninitialized (ref) simulations, the ranked probability skill score (RPSS) is computed:

$$\begin{array}{}\text{(6)}& \text{RPSS}=\mathrm{1}-{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\text{RPS}}}_{\text{fc}}}{{\stackrel{\mathrm{‾}}{\text{RPS}}}_{\text{ref}}}}.\end{array}$$

Here, with respect to the conditional verification using the decomposition of the skill score, we want to evaluate the probabilistic hindcast skill stratified along three phases (negative, neutral, and positive) of the AMO, instead of two (as demonstrated in Sect. 2). That means, the RPS and RPSS of the entire period contain every initialization year t from 1960 to 2012 as a time step, while the AMO-phase-specific terms only consider initialization years that are related to the associated AMO phase.

The information about the significance of the RPSS is based on a 5-year-block bootstrapping method by a 1000-fold resampling of the forecast and reference observation cases in the entire period. The RPSS value is considered statistically significant if 0 is outside of the 95 % of inner values of the bootstrap distribution.

A large part of the routines used for verification presented here is implemented via the ProblEMS verification plug-in (https://www.xces.dkrz.de/plugins/problems/detail/; via guest login; last access: 29 July 2024) in the MiKlip module and the ClimXtreme (https://www.xces.dkrz.de; last access: 29 July 2024) and Coming Decade central evaluation system (https://codes.dkrz.de; last access: 29 July 2024) – based on the Free Evaluation System Framework for Earth system modeling (Freva; Kadow et al., 2021).

4.4 Subset contributions of RPSS

Figure 3a shows the RPSS over the European region for the decadal hindcast with respect to the uninitialized simulations averaged over the entire hindcast period for lead years 2–5. Significant values (marked with a cross) are rare. Negative significant values can be found in the Barents Sea and a larger patch of the southwestern North Atlantic. The latter is presumably caused by a displacement of ocean currents in that area, as the region is especially sensitive to initializations (Kröger et al., 2018; Polkova et al., 2019). Positive significant skill can be found in the Greenland Sea. Besides individual grid points with significant values, patches with positive but nonsignificant skill are visible in the eastern Mediterranean and in the northeastern part of the North Atlantic.

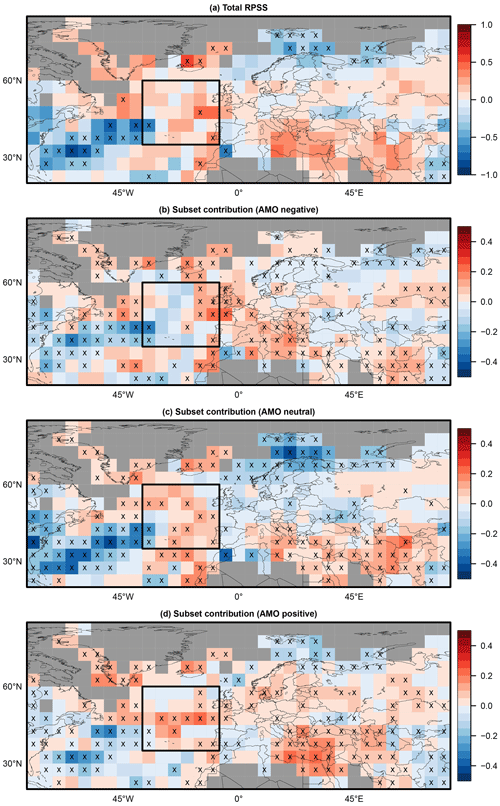
Figure 3 (a) Total ranked probability skill score (RPSS) of near-surface temperature of the initialized decadal simulations (preop-dcpp-HR) with respect to uninitialized historical simulations and HadCRUT4 observations for lead year 2–5 from 1962 to 2017. Additionally, individual subset contributions W_iSS_i are shown for the (b) negative, (c) neutral, and (d) positive AMO phase at the time of the initialization. Missing values are depicted in gray. Crosses indicate areas with significant (95 % level) values. The box highlights the W-EU NA region analyzed in Sect. 4.5.

To exemplify the stratified verification, Fig. 3b, c, and d show the subset contributions W_iSS_i to the total RPSS during the respective negative, neutral, and positive AMO phases at the time of the initialization following Eq. (3). Significance is computed as for the RPSS but with 1-year-block bootstrapping in the related subset period. The AMO neutral phase (Fig. 3c) contributes to a negative (positive) RPSS in the southwestern North Atlantic and Barents Sea (western European North Atlantic), while positive significant contributions are found in western Europe (W-EU) and central Europe (C-EU) during the negative AMO phase (Fig. 3b) as well as in the North Atlantic under positive AMO conditions during the initialization procedure (Fig. 3d).

4.5 Decomposition of the RPSS over the western European North Atlantic

Next, we focus on the western European North Atlantic (W-EU NA) region. This is motivated by (1) the different predictability associated with certain states of the ocean identified in previous studies (Zhang and Zhang, 2015; Borchert et al., 2018, 2019) and (2) the positive total skill found in that region. We investigate the subset contributions W_iSS_i and the three terms (subset skill score SS_i, frequency weighting $W_{{\text{freq}}_i}$, and reference weighting $W_{{\text{ref}}_i}$) of the decomposition for the annual field-mean value of the W-EU NA region (35–60° N, 40–10° W; the box in Fig. 3), according to Eqs. (2) and (3). The subset skill score (subset RPSS) in Fig. 4b shows no or, at most, very weak improvement of the initialized prediction system over the uninitialized simulations under negative and neutral AMO conditions during the initialization procedure. In contrast, the subset RPSS=0.3 for initialization during positive AMO years. For comparison, the total RPSS is around 0.1 (gray horizontal line). The frequency weighting (Fig. 4c) indicates that initialization years with a neutral AMO phase are more frequent (0.4) than years with the other two phases. This leads to a higher frequency weighting factor associated with the AMO neutral phase. Figure 4d shows that the reference weighting is close to 1 for all phases. As this component represents a potentially different score for the reference system along the three subsets, we do not expect large variability, as the uninitialized reference is not influenced by the AMO phases in the observations.

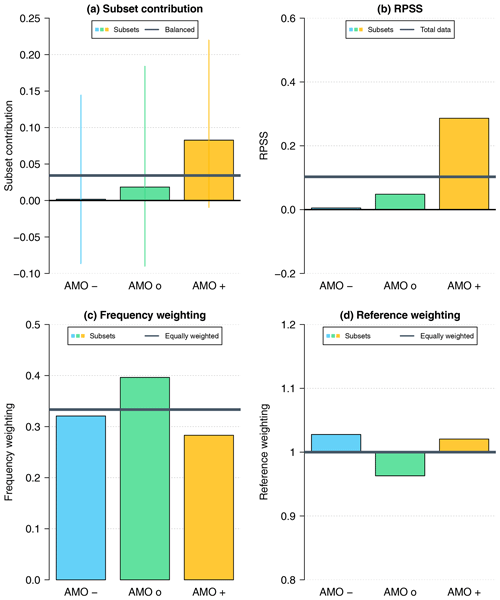
Figure 4 (a) Subset contributions (95 % confidence intervals as vertical segments) related to Eq. (2) as well as the (b) subset RPSS, (c) frequency weighting, and (d) reference weighting of subsets (defined by the AMO phase during the initialization) according to Eq. (3) for the conditional verification of near-surface temperature in the W-EU NA region between initialized decadal simulations (preop-dcpp-HR) and uninitialized historical simulations with respect to HadCRUT4 observations for lead year 2–5 from 1962 to 2017. Gray horizontal lines represent (b) total skill score, (c, d) balanced weightings, and (a) balanced contributions with respect to the total skill score.

Multiplying the three components for the individual subsets, we arrive at the subset contributions W_iSS_i (Fig. 4a). Although the contributions show large uncertainties and are not statistically significant, tendencies can be derived. The contribution is mainly determined by the subset skill score (Fig. 4b) and, to a small extent, modified by the frequency weighting (Fig. 4c). The resulting subset contributions related to the AMO phases show that the positive AMO phase contributes the most (around 0.08) to the total RPSS, followed by the neutral AMO phase with a much smaller contribution of 0.02.

As the reference weighting was not relevant in the above case, we now choose a reference system affected by the AMO phase: a lower-resolution version of the decadal prediction system. The preoperational (preop) version in a low-resolution (LR) configuration has a T63 horizontal grid (1.875°) and 47 vertical levels in the atmospheric component, while the ocean part has a horizontal resolution of 1.5° and 40 vertical levels. Being an older version, the low-resolution system is forced by CMIP5 external forcing (Giorgetta et al., 2013). The other settings (e.g., initialization and assimilation procedure) remain unchanged compared to the preop-dcpp-HR version introduced in Sect. 4.1. Figure 5b again shows the RPSS of the individual subsets (bars) and the total RPSS as a horizontal gray line. As the latter coincides with the zero-skill-score line, we see that the initialized prediction system preop-dcpp-HR does not outperform the low-resolution version preop-LR over the entire period. The subset RPSS under positive AMO conditions during the initialization procedure is strongly negative (−0.55); a similar tendency can be seen during the negative phase (−0.2). Only during the neutral AMO phase does preop-dcpp-HR show an improvement over the low-resolution version.

Figure 5 Same as Fig. 4 but with the preop-LR-initialized prediction system as a reference.

As classification of AMO phases is again based on ORA-S4, the frequency weighting terms are the same as in the previous case. Again, the weighting factor of the neutral AMO phase is slightly higher than that of the other two phases (Fig. 5c). The reference weighting exhibits huge differences among the individual phases (Fig. 5d). While the subset of the neutral AMO phase shows a weighting factor of 1.4, which is approximately 40 % higher than the balanced value (1; gray horizontal line), the reference weighting term of the subset of the positive phase is 0.5 and, thus, only half of the balanced one. The reference weighting associated with the negative AMO phase (0.9) lies in between.

The individual subset contributions (Fig. 5a) are now affected by all three terms of the skill score decomposition. In particular, the reference weighting now influences the contribution to a large extent. While the subset RPSS (Fig. 5b) suggests a strong negative contribution to the overall skill driven by a positive AMO phase alone, the subset contribution (Fig. 5a) allows a slightly different interpretation: positive (statistically significant) as well as negative AMO phases contribute negatively to the overall skill score by similar amounts, counteracting the benefits from the neutral AMO phase.

5 Summary and discussion

We present a decomposition of skill scores into contributions from subsets of the forecasts that are selected according to characteristics of processes or large-scale circulation, climate states during initialization of the forecast system, seasons, or regions. We give examples of this decomposition in the context of synthetic data designed to reveal situations in which this decomposition shows its usefulness. To achieve this, the synthetic cases show different performance characteristics of forecast and reference systems in two subsets. These subsets contribute differently to the overall skill score in an additive way according to their size, the performance of the forecast system on the subset, and the performance of the reference system on the subset compared to the full data set. Hence, the subset contribution of a specific subset to the overall skill can be decomposed into the following:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\text{subset skill score }{\text{SS}}_i={\displaystyle \frac{{\stackrel{\mathrm{‾}}{S}}_i^{\text{fc}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}},\\ {\displaystyle }& {\displaystyle }\text{frequency weighting }{W}_{{\text{freq}}_i}={\displaystyle \frac{N_i}{N}},\\ {\displaystyle }& {\displaystyle }\text{reference weighting }{W}_{{\text{ref}}_i}={\displaystyle \frac{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}_i^{\text{ref}}}{S^{\text{perf}}-{\stackrel{\mathrm{‾}}{S}}^{\text{ref}}}}.\end{array}$$

The subset skill score measures the performance of a forecast system compared to a reference system for a particular subset, a useful and popular quantity to assess the varying performance of a forecast system over different subsets; this is frequently used to detect enhanced/reduced predictability for certain climate and large-scale circulation states or specific seasons and regions (see the references mentioned in Sect. 1). The frequency weighting reflects the size of the subset with respect to the full data set. For small subsets, it reduces the subset's contribution to the overall skill and vice versa for large subsets. The reference weighting adjusts the scale (or range) of the skill score, which is set by the difference between the reference performance of the subset and the perfect forecast, to the scale relevant for the overall data set. For negatively oriented scores with S^perf=0, this is expressed by the ratio of the two differences (see Eq. 3). Reference weighting and frequency weighting are both independent of the forecast system. The product of all three terms yields the subset's contributions to the overall skill score.

We expect that this decomposition helps to avoid misinterpreting a potential performance increase in a subset resulting, for example, from a significant performance decrease in the reference system. In this context, climatological forecasts used as a reference system could also impact the interpretation of the skill, as discussed in publications such as Hamill and Juras (2006).

Subsequently, we exemplify the RPSS decomposition in the context of the MiKlip decadal prediction system stratified along characteristics of the AMO during forecast system initialization. The goal is the quantification of hindcast skill for the near-surface air temperature for lead year 2–5 over the North Atlantic and European region. The hindcasts (preop-dcpp-HR) show a weakly positive overall skill (locally significant) in the northeastern part of the North Atlantic and in the eastern Mediterranean compared with uninitialized historical simulations. Stratified verification along positive, negative, and neutral AMO phases for initialization reveals the following:

• a negative subset contribution to the total RPSS in the southwestern North Atlantic and Scandinavia for a subset associated with neutral AMO;

• a positive subset contribution for W-EU and C-EU (AMO negative) and in the North Atlantic (AMO positive) for subsets associated with negative and positive AMO.

Although not statistically significant, the decomposition for the western European North Atlantic box shows that the subset associated with a positive AMO phase at the time of the initialization contributes to the positive total RPSS, with a positive subset skill score only slightly modified by the frequency weighting. The latter findings are similar to those of Borchert et al. (2018), as the AMO/AMV phases are linked to OHT with a lag of 5–10 years. Nevertheless, a stratification along different OHT states may strengthen the distinction between each subset.

Additionally, evaluation of the decadal hindcast system versus a low-resolution (preop-LR) version shows that individual subset contributions are affected by all three terms of the decomposition, with the reference weighting playing a particular role. This leads to a slightly different conclusion: while the subset RPSS suggests that the strong negative contribution to the overall skill is mainly driven by positive AMO initialization, the decomposition reveals that both the negative and the positive AMO phases contribute negatively by the same amount, counteracting the benefits of the neutral AMO phase.

As our study does not fully account for uncertainties and the results are partly sensitive to the defined W-EU NA region and the chosen AMO index representing the ocean state (see the Supplement), further indices and sensitivity studies including the consideration of uncertainties can be applied for a more robust analysis. As this paper focuses on suggesting the framework of skill score decomposition for stratified verification, demonstrated as a potential application in decadal predictions, detailed and robust analysis of the physical processes responsible for varying skill is beyond the scope of this study.

6 Conclusions

The verification of forecast systems stratified by the characteristics of physical processes, large-scale circulation, climate states at initialization, seasons, or regions can be a helpful tool for model development, the detailed assessment of forecasts quality, and the communication of forecasts. However, interpretation and comparison of skill scores across different strata can be challenging. This is not only the case for different subset sizes (frequency weighting) but also if the performance of the reference system varies strongly across subsets (reference weighting).

Both examples, the synthetic data and the decadal forecasting case, exemplify the potential of skill score decomposition for stratified verification. For the decadal prediction system, we see the strongest degradation of performance compared with its low-resolution system if it is initialized during positive AMO phases. However, the error in the reference system compared to the observation in that subset is smaller than that of the entire time series (as can be seen by the lower reference weighting). As a consequence, the positive AMO phase negatively contributes to the overall performance by nearly the same amount as the negative AMO phase, although the subset skill score is much worse. In practice, potential model diagnostics and improvements should focus on both phases, rather than examining only the positive AMO phase suggested by the subset skill score assessment alone.

As the predictability is linked to the state of the ocean (Zhang and Zhang, 2015; Borchert et al., 2018, 2019), we can apply the interpretation to the perspective of predictability. Assuming that a reasonably skillful reference can indicate inherent predictability, we would benefit more from improvements to subsets/situations with limited predictability in terms of the overall skill, as there is more room for improvement if the reference system performs poorly. However, it can be more challenging to improve the skill in these low-predictability situations, as the factors that contribute to predictability may be less influential or absent. Accordingly, the decomposition can help to prioritize the aspects in order to support decision-making assessments. Beyond decadal predictions, the simultaneous investigation of the terms could be useful to evaluate and interpret regionally (e.g., between mountains and lowlands) or seasonally varying error behaviors with respect to the total model performance. A possible application is shown in Peter et al. (2024) using the example of the evaluation of statistical models for extreme precipitation.

The skill score decomposition into contributions from suitable chosen subsets helps to understand possible model misbehavior in a detailed and robust way, as subsets can be chosen based on the characteristics of physical processes. This yields valuable information for the refinement of the forecast system or model development. Besides the state of the ocean or other large-scale conditions, seasonal and regional aspects or other aspects can be addressed. Conditional or stratified verification can be used to investigate known or hypothetical linkages in the area of climate and weather forecasts, including the ability to simulate and represent specific feedback mechanisms. The example above examines the potential source of long-term predictability forced by certain ocean states associated with the AMO.

Finally, to support decision-making related to weather and climate, operational forecasts can be optimized by assessing and communicating their credibility in a more specific and situation-based way using stratified evaluation based on the initialization conditions and the related skill score decomposition. Depending on the initialization conditions, forecast skill can be quantified and the forecast can eventually be rated as more precise, as addressed in Borchert et al. (2019). The identification of windows of opportunity for enhanced skill on subseasonal to decadal timescales is similar (Mariotti et al., 2020). A potential application outside of the domain of decadal prediction could be the identification and analysis of such a window. In weather forecasting, the conditional verification stratified along particular flow regime conditions (e.g., blocking) or along different states of the MJO and ENSO in subseasonal to seasonal predictions could be reasonable. In the example using decadal forecasting, a better temperature forecast ability of the prediction system compared with the uninitialized one is achieved over parts of the North Atlantic for initialization during positive AMO phases.

The skill score decomposition framework suggested and exemplified in the context of conditional or stratified verification is a relatively simple tool to analyze physical processes related to certain subsets and, consequently, supports model development and the optimization of operational forecasts and their communication.