The impact of cloud microphysics and ice nucleation on Southern Ocean clouds assessed with single-column modeling and instrument simulators

Supercooled liquid clouds are common at higher latitudes (especially over the Southern Ocean) and are critical for constraining climate projections. We take advantage of the Macquarie Island Cloud and Radiation Experiment (MICRE) to perform an analysis of observed and simulated cloud processes over the Southern Ocean in a region and season dominated by supercooled liquid clouds. Using a single-column version of the European Centre for Medium-Range Weather Forecasts (ECMWF) Integrated Forecast System (IFS), we compare two different cloud microphysical schemes to ground-based observations of cloud, precipitation, and radiation over a 2.5-month period (1 January–17 March 2017). Both schemes are able to reproduce aspects of the cloud and radiation observations during MICRE to within the uncertainty of the data when the thermodynamic profile is prescribed with relaxation. There are differences in water mass and representation of reflectivity between the schemes. A sensitivity study of the cloud microphysics schemes, one a bulk one-moment scheme and the other a two-moment scheme with prediction of mass and number, indicates that several key processes create differences between the schemes. Surface radiative fluxes and total water path are highly sensitive to the formation and fall speed of precipitation. The prediction of hydrometeor number with the two-moment scheme yields a better comparison with observed reflectivity and radiative fluxes, despite predicting higher liquid water contents than observed. With the two-moment scheme, we are also able to test the sensitivity of the results to the input of liquid cloud condensation nuclei (CCN) and ice nuclei (IN). The cloud properties and resulting radiative effects are found to be sensitive to the CCN and IN concentrations. More CCN and IN increase liquid and ice water paths, respectively. Thus, both the dynamic environment and aerosols, integrated through the cloud microphysics, are important for properly representing Southern Ocean cloud radiative effects.

1 Introduction

Supercooled liquid water, defined as water below the freezing point of 0 °C (273 K), is common in colder regions of the planet (Hu et al., 2010). Freezing at temperatures between 0 and −40 °C (273 and 233 K) typically require very high ice supersaturations and/or ice-nucleating particles, also called ice nuclei (IN). IN are relatively rare (McCluskey et al., 2018), leading to the presence of supercooled liquid and an important role for secondary ice (number) production processes (Järvinen et al., 2022). Recent work has made clear that supercooled liquid is important for both weather and climate. For example, improving supercooled liquid has been shown to improve forecasts of 2 m temperatures at high latitudes over land (Forbes and Ahlgrimm, 2014) and cold-air outbreaks at high latitudes (Forbes et al., 2015), while Bodas-Salcedo et al. (2012) showed a deficiency of supercooled liquid in several climate models and demonstrated how this deficiency resulted in substantial errors in the radiative budget of the Southern Ocean. More generally, Bodas-Salcedo et al. (2019) and Gettelman et al. (2019b) illustrated in two different models how supercooled liquid clouds can impact cloud feedbacks and the climate sensitivity of the planet to an imposed forcing.

There is a long-standing bias in climate (Trenberth and Fasullo, 2010) and weather forecast (Forbes et al., 2015) models of too few Southern Ocean clouds and too much surface absorption of solar radiation. To reduce cloud model biases at middle to high latitudes, it is necessary to focus on the representation of cloud phase and precipitation, which is handled by the cloud microphysical scheme in a large-scale model. In this paper we present observational and model comparisons over a season for supercooled liquid clouds over the Southern Ocean. We attempt to reproduce the observations in a single-column version of the ECMWF IFS (Integrated Forecast System) with cloud microphysics schemes from both a weather forecast model (the ECMWF IFS) and a climate model (Community Earth System Model version 2, CESM2).

There are several unique aspects to this study. First, we compare two “operational” cloud microphysics codes in a region with complex cloud regimes within the same modeling framework. Forbes and Tompkins (2011) describe a bulk one-moment (predicted mass only) scheme designed for weather forecasting. The other scheme (Gettelman et al., 2019a) is a two-moment (predicted mass and number) scheme designed for climate simulation. We seek to understand what is similar between the schemes, what is different, and how the differences affect model biases relative to the observations. In particular, is a two-moment scheme more representative of observations than the one-moment IFS scheme? When comparing to observations, we also consider the limits of the observations in detecting clouds, as well as the assumptions for cloud cover and sub-grid representation of clouds, which add uncertainty to the comparisons. We use a constrained model setup, with a single-column model forced by observed winds and temperatures over a 75 d austral summer period. This allows a statistical representation of a series of events and regimes, while also being able to look at detailed process rates and a close comparison to observations. Finally, we focus on clouds with extensive supercooled liquid, a long-standing issue for weather and climate models.

Section 2 discusses the simulation setup, the microphysical parameterization schemes, and the observations. Section 3 presents the results, including comparisons to the observations and comparisons between the two schemes. We also present sensitivity studies of the model configurations to understand the role of different microphysical processes and why the schemes differ. A summary is in Sect. 4, and conclusions are in Sect. 5.

2 Methodology

Here we first describe the observations (Sect. 2.1), followed by the IFS single-column model, the IFS microphysical and the MG3 microphysical schemes, the model radar simulator in (Sect. 2.2), and details of the simulations (Sect. 2.3).

2.1 MICRE observations

During the Macquarie Island Cloud and Radiation Experiment (MICRE), observations were collected from March 2016 to March 2018 at Macquarie Island (54.5° S, 158.9° E), located about half-way between Aotearoa / New Zealand and Antarctica. The project is described in detail in McFarquhar et al. (2021) and included deployment of a suite of ground-based instruments including a ceilometer, surface rain disdrometer, microwave radiometer, and broadband shortwave (SW) and longwave (LW) radiometers, as well as an upward-looking W-band cloud radar and depolarization lidar. Most of the instruments had periods with significant downtime, and we focus on the 75 d period from 1 January to 17 March 2017, when upward-looking cloud radar and microwave radiometer observations are available, in addition to twice-daily radiosondes and broadband radiometer fluxes. We focus on observations of surface downward radiation, radar reflectivity, and microwave-radiometer-derived liquid water path, as well as the ancillary radiosonde temperature data. The MICRE broadband radiometer SW and LW fluxes have been evaluated and compared with the Clouds and the Earth's Radiant Energy System (CERES) satellite synoptic (SYN) product (Doelling et al., 2013; Rutan et al., 2015) and the surface energy balanced and filled (surface EBA; Kato et al., 2018) fluxes by Hinkelman and Marchand (2020). The MICRE instrument's location was on a narrow point of land and is generally representative of maritime conditions. The location is representative of the Southern Ocean, with frequent frontal passages and different cloud types.

2.2 Model description

In this study we run a version of the Integrated Forecast System (IFS) (ECMWF, 2019) in single-column mode with two different cloud microphysical schemes. Both are “bulk” schemes representing hydrometeors with a mean mass, and one is a two-moment scheme that also represents the mean number of hydrometeors. The schemes, however, often use similar bulk formulations for process rates, either solely mass-based or with an assumed size in the one-moment (mass-only) scheme. This makes for an interesting and direct set of process rate comparisons and highlights where two-moment schemes may be necessary to capture different atmospheric process sensitivities and regimes.

2.2.1 IFS single-column model

The single-column model (SCM) is a standalone vertical column version of the IFS with the same suite of physical parameterizations as the global model. Time-varying surface and advective forcings can be specified, as can relaxation towards a specified time-varying state with a given timescale. The particular version used here is IFS Cycle 46r1, used operationally at ECMWF from June 2019 to June 2020. There are 137 vertical levels, the same as the operational global model, with a layer depth increasing from 20 to 170 m in the lowest 2 km and around 300 m in the rest of the troposphere. Only an overview of the parameterizations is given here, and further details can be found in the IFS 46r1 documentation (ECMWF, 2019).

The IFS has prognostic variables for cloud fraction, specific humidity, specific cloud liquid, cloud ice, rain, and snow water contents. The sub-grid cloud parameterization is based on Tiedtke (1993), with sources and sinks from the vertical advection, radiation, and convection parameterizations. Cloud fraction and saturation adjustments are determined by the sub-grid cloud parameterization scheme and are the same for both microphysics schemes. Supersaturation with respect to ice is allowed and the assumptions are described in Tompkins et al. (2007). The cloud scheme is tightly coupled with the convection parameterization with detrainment of cloud fraction, condensate, and precipitation from sub-grid convective updrafts. Vertical advection due to convectively generated sub-grid subsidence within a convecting grid cell is represented, as is turbulent erosion of cloud fraction and condensate at sub-grid cloud edges. The cloud and precipitation microphysics are described in the next subsection.

The parameterization of shallow, mid-level and deep convection is based on the mass-flux approach (Tiedtke, 1989; Bechtold et al., 2008, 2014). The turbulent mixing scheme follows the eddy diffusivity mass flux (EDMF) framework, with a K-diffusion turbulence closure and a mass flux component to represent the nonlocal eddy fluxes in unstable boundary layers (Siebesma et al., 2007; Köhler et al., 2011). The radiation scheme (ecRad) is described in Hogan and Bozzo (2018), with the gas optics from the Rapid Radiation Transfer Model (RRTMG; Mlawer et al., 1997; Iacono et al., 2008). Cloud–radiation interactions are taken into account using the McICA (Monte Carlo independent column approximation) method (Morcrette et al., 2008). Surface exchange and gravity wave drag are also represented (Balsamo et al., 2009; Lott and Miller, 1997; Beljaars et al., 2004; Orr et al., 2010).

2.2.2 IFS microphysics

The IFS microphysics scheme is a one-moment bulk scheme with prognostic variables for the mass of four classes of hydrometeor (liquid, ice, rain, snow) as described in Forbes and Tompkins (2011) and Forbes et al. (2011), with various modifications, particularly to improve the representation of mixed-phase boundary layer clouds (Forbes and Ahlgrimm, 2014) and warm-rain processes (Ahlgrimm and Forbes, 2014). The numerical formulation of the hydrometeor sedimentation follows an implicit upstream approach with parameterized fall speed for rain (Sachidananda and Zrnic, 1986; Abel and Boutle, 2012) and fixed fall speeds for snow (1 m s⁻¹) and ice (0.13 m s⁻¹).

2.2.3 MG3 microphysics

The Morrison–Gettelman microphysics scheme version 3 (MG3) is a two-moment bulk microphysics scheme with prognostic variables for the mass and number concentration of five classes of hydrometeors (liquid, ice, rain, snow, graupel) as described by Gettelman et al. (2019a). MG3 is based on the original Morrison et al. (2005) scheme, adapted and modified extensively for climate models (Morrison and Gettelman, 2008), with extensions for ice nucleation (Gettelman et al., 2010) and prognostic precipitation (Gettelman and Morrison, 2015). The scheme without graupel is used in the Community Earth System Model version 2 (CESM2; Danabasoglu et al., 2020). The scheme compares well to mesoscale schemes by Morrison et al. (2005) and Thompson and Eidhammer (2014) for idealized shallow and convective cloud cases, as shown by Gettelman et al. (2019a).

For this study MG3 has been adapted for use in the IFS SCM as an alternative to the IFS parameterization of microphysical processes and sedimentation. The rest of the model is kept the same including the saturation adjustment, sub-grid cloud parameterization, and convection interactions.

The additional MG3 prognostic variables for the mass and number concentration of all five classes of hydrometeors have been added to the IFS SCM. The two-moment MG3 scheme can run with a fixed hydrometeor number concentration or use activated number concentration rates (# s⁻¹) for liquid drops (cloud condensation nuclei, CCN) and ice crystals (ice nuclei, IN). Since the IFS does not have an explicit representation of aerosols or an activation scheme, for this work we assume constant CCN and IN activation rates of 1 cm⁻³ s⁻¹ and 5 L⁻¹ s⁻¹, respectively, for all altitudes at every time step. These rates are just used to initialize new particles in the microphysics when the model physics condenses water or ice and we test the sensitivity of the results to the activation/nucleation rate.

2.2.4 Radar simulator

The radar simulator, described in full in Fielding and Janisková (2020), provides the model-equivalent radar reflectivity factor to compare with observations. It has been adapted to run in-line within the SCM and, wherever possible, uses assumptions consistent with the two microphysics schemes used in this study. The simulator runs in “one-moment” mode when the IFS microphysics scheme is used and “two-moment” mode when the MG3 scheme is used. When in two-moment mode, the simulator computes bulk scattering properties by combining the MG3 particle size distributions and densities (Morrison and Gettelman, 2008) with the prognostic number concentration, mass, and the same single-scattering properties as the one-moment simulator described in Fielding and Janisková (2020).

The size distribution of hydrometeors is chosen such that it is consistent with the predicted masses (and prognostic number concentrations when in two-moment mode). The radar reflectivity and attenuation are calculated by the radar simulator (primarily using Mie theory) using the double-column approach as described in Fielding and Janisková (2020), partitioning the signal into a uniform cloudy layer and a uniform clear layer. The hydrometeors are assumed to be uniformly distributed within each species' cloud or precipitation fraction. The attenuation by hydrometeors depends on the overlap of clouds and precipitation; the simulations here assume maximum random overlap. This has a large effect on the simulated reflectivity, as will be discussed later. Attenuation due to gaseous attenuation is also included based on the models of Liebe (1985) and Liebe et al. (1992). Details can be found in Fielding and Janisková (2020). Attenuation does not include a cut-off for any height-dependent minimum detectable signal (MDS), which will also affect the comparisons with observed reflectivity.

2.3 Simulation setup

The simulations are set up by generating forcing files for the location of Macquarie Island station (54.5° S, 158.9° E) from January to March 2017. The forcing comes from CESM2 simulations relaxed to the MERRA-2 reanalysis (Molod et al., 2015), similar to that used by Gettelman et al. (2020) for the Southern Ocean Clouds, Radiation, Aerosol, Transport Experimental Study (SOCRATES) project. The IFS SCM is relaxed back to the forcing profile with an 8 h relaxation time for winds, temperature, and humidity to keep the boundary layer structure from drifting too far from the radiosonde observations. Longer relaxation timescales, or no relaxation at all, caused the simulations to drift by several degrees Celsius in the upper part of the boundary layer, resulting in significant biases in clouds relative to the observations. This is a key feature: getting the boundary layer structure correct is vital for constraining cloud radiative effects. There is no relaxation of cloud variables and these are allowed to freely evolve during the simulation. The base time step for the simulations is 225 s, but we also investigate the time step sensitivity of both schemes by running at 60 s and 900 s (the time step used in the global forecast model at ECMWF depends on resolution but typically ranges from 225 s to 900 s).

Simulations are repeated with the IFS and MG3 microphysics for comparison, and a series of sensitivity tests are performed, modifying different aspects of the MG3 code (see Sect. 3.2.3). The CESM2 version of the MG3 microphysics was initially implemented in the SCM, but first comparisons highlighted significant differences in the profiles of rain that were due to differences in a few basic assumptions in the IFS. To allow a more meaningful comparison of the process rates, it was decided to implement these IFS assumptions in the MG3 scheme. Rain evaporation is modified to more closely match the IFS, with a scaling factor of 0.3 and a relative humidity threshold between 80 % and 90 % before evaporation can occur, both currently required in the IFS to reduce excessive evaporation in the operational IFS. The threshold for rain freezing is changed from −40 °C in CESM2 to the value of −5 °C in the IFS, so all precipitation below −5 °C is treated as snow. In addition, MG3 did not originally calculate a fall speed for layers with no hydrometeors, so sedimenting condensate can enter a layer of zero velocity. A fall speed correction was added to ensure that if there are hydrometeors above, the fall speed is not zero (this particularly affects rain). The sedimentation of precipitation is changed to an implicit monotonic scheme (Harris et al., 2020; Zhou et al., 2019) to reduce time step sensitivity. Finally, there is one change for the ice microphysics: mixed-phase ice nuclei are determined by the Meyers et al. (1992) empirical function of temperature as in Morrison et al. (2005) and the IFS rather than the Hoose et al. (2010) classical nucleation theory scheme used in CESM2. These changes together define the “base” version of the MG3 scheme used for the comparison with the IFS in Sect. 3, although the original CESM2 version of the MG3 scheme is also included for comparison in the sensitivity study (Sect. 3.2.3).

3 Results

First we compare the IFS and MG3 microphysics (modified from the CESM2 version as described in Sect. 2.3) to observations from MICRE. We then examine the differences between the IFS and MG3 microphysics, including their time step sensitivity, differences in the balance of process rates between the schemes, and finally sensitivity tests with the MG3 scheme.

3.1 Comparison to observations

In this subsection, we compare model simulations to surface and satellite-based observations. We begin by focusing on shortwave and longwave radiative fluxes, followed by in-cloud liquid water path (LWP) and radar reflectivity (obtained from the model via a radar simulator as described in Sect. 2).

3.1.1 Top-of-atmosphere and surface radiation

Figure 1 shows the downward surface shortwave (SW; Fig. 1a) and longwave (LW; Fig. 1b) radiative fluxes for the 75 d time series for the surface radiometer (SFC, black line), the CERES SYN product retrieved from combined geostationary and MODIS satellite data (for the SW flux, SYN, blue), and the simulation results from the MG3 (orange) and IFS (green) microphysical schemes. Although there are short periods during which the model-simulated fluxes depart noticeably from the surface and satellite data, there is generally good agreement (on average). Differences are not easy to distinguish because they are small and it is the average difference that is really important (hence the importance of the 90 d record). Hourly correlations for both simulations with the observations are ∼ 0.75 for the SW flux and ∼ 0.6 for the LW, and the mean SW flux for both simulations lies between the mean values from the surface and satellite datasets. The 1 standard deviation (1σ) sampling uncertainty in the surface and satellite daily mean SW flux is about 17 and 5 W m⁻² for the LW. The sampling uncertainty is estimated as the standard deviation divided by the square root of the number of days, effectively treating each day as equivalent to a single independent sample. The difference between the surface and satellite mean SW flux might be due to a bias in one or both datasets or due to differences in the field of view (for example, it is possible that it is slightly cloudier or clouds are less optically transparent over the island site than the nearby ocean), but we do not know for certain the source of the mean difference. In short, the small differences among all of the mean SW fluxes shown in Fig. 1a are not significant with respect to the sampling uncertainty. Sampling and systematic uncertainties in the surface and satellite fluxes are discussed in more detail by Hinkelman and Marchand (2020). Figure 1b also shows the strong correspondence between the simulated and observed surface downward longwave fluxes. Here the SYN retrievals are not shown because there is a significant bias in the CERES SYN retrievals at night (Hinkelman and Marchand, 2020). The small differences (<5 W m⁻²) between the mean model LW fluxes and the observed mean value are likewise not significant with respect to the sampling uncertainty.

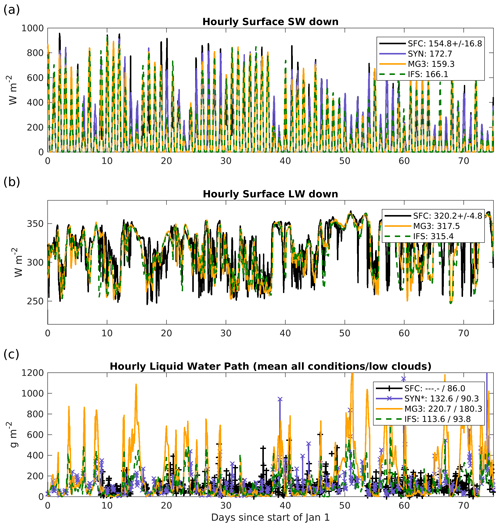
Figure 1 Time series of hourly averaged values: (a) downward surface shortwave (SW) flux, (b) downward longwave (LW) flux, and (c) liquid water path (LWP). For each dataset the legend gives the mean value, and for the SW and LW flux, the estimated 1σ uncertainty in the mean is also given. For LWP, the legend gives the mean value for all times, followed by the mean restricted to periods where only low clouds are present (see text): surface observations (solid black and ticked), MG3 microphysics (solid orange), IFS microphysics (dashed green). The CERES SYN data (solid purple and crosses) and average values are also restricted to data collected between 9:00 and 16:00 local time to avoid biases associated with low solar zenith angles (see text).

We examine the diurnal cycle of surface and top-of-atmosphere (TOA) SW and LW fluxes in Fig. 2. For both the models and the observational datasets, hours containing only low clouds occurred about 35 % of the time and completely clear hours only about 2 %, with the remainder containing some hydrometeors above 2 km (most often with hydrometer both above and below 2 km). In Fig. 2 each dataset is processed independently, and we have not restricted the low-cloud times to those hours in which only low clouds occur at the same time in both surface observations and model simulations. Doing so significantly decreases the total number of hours and increases the estimated sampling uncertainties but does not otherwise qualitatively change the results. We examine the observed and simulated radar reflectivity and associated vertical profiles of cloud occurrence in more detail later in this section.

The simulated diurnal cycle of surface downward SW (Fig. 2e, f) and LW (Fig. 2g, h) fluxes compare well with the surface and satellite data, and the good agreement holds for low-cloud periods (Fig. 2f, h). There is no discernible diurnal cycle in the observed or modeled surface LW flux (Fig. 2g, h). The mean surface SW downward flux is about 30 W m⁻² larger during low-cloud periods (Fig. 2f) compared with all times (Fig. 2e), while the LW downward flux is about 8 W m⁻² smaller (Fig. 2g, h). This demonstrates the significant role played by both shallow and deeper clouds in the radiative energy budget, and the models capture this well. The modeled outgoing TOA SW flux (Fig. 2a, b) also agrees reasonably well with the CERES SYN product. The model (daily) means are within about 15 W m⁻² of the SYN mean, with the CERES SYN product being a bit smaller (consistent with the downward CERES SYN surface SW flux being a bit larger than the model-simulated surface SW flux). For clarity, the sampling uncertainty is not shown on the model-simulated curves. If displayed, the 1σ uncertainty in the model mean diurnal cycle would just overlap with the uncertainty shown for the observations. A paired data test (not shown) indicates that the 15 W m⁻² difference between the models and SYN data is significant at the 1σ level. Nonetheless, it remains a reasonable possibility that the 15 W m⁻² difference is just a result of sampling uncertainty. The same is not true for the outgoing TOA LW flux (Fig. 2c). In the LW, while there is good agreement between the model-simulated outgoing TOA LW and the CERES SYN product during periods with low clouds for both simulations (Fig. 2d), under all-sky conditions (Fig. 2c) the IFS microphysical scheme has too little outgoing LW flux (and this is significant at the 2σ level in a paired data test). The underestimate in the IFS flux becomes even clearer when restricted to hours when only high-level hydrometeors are present (not shown). As will be shown later, an examination of radar reflectivity fields likewise reveals that the simulations with the IFS microphysics have a higher occurrence of cloud above 6 km, and we will return to this topic after an examination of the liquid water path.

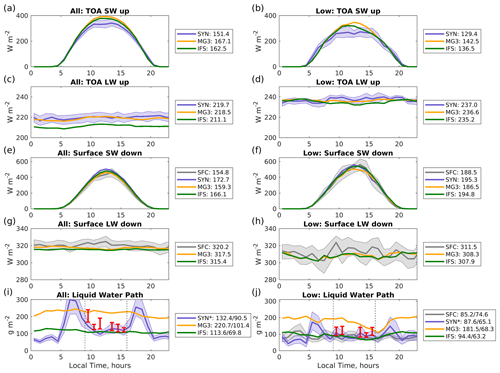
Figure 2 Mean diurnal cycles. Outgoing TOA (a, b) SW and (c, d) LW flux. Downward surface (e, f) SW and (g, h) LW flux, as well as LWP. The left column (a, c, e, g, i) shows diurnal averages for all times, and the right column (b, d, f, h, j) is for periods when only low clouds (hydrometeors <2 km) are present based on hourly average (simulated or observed) radar reflectivity. In each panel, shading that surrounds the surface or satellite values depicts the estimated 1σ sampling uncertainty for a particular hour over all days. Sampling uncertainty for all datasets is of similar magnitude. The diurnal cycle of LWP is also shown for all times (i) and just low-cloud periods (j). CERES-SYN-retrieved LWP is in purple (which combines geostationary and MODIS data). MODIS-only (red symbols) retrievals are as described in the text. The legend gives the daily mean for each dataset, and for LWP both the daily mean and median are given. CERES SYN means and medians are restricted to data collected between 9:00 and 16:00 local time (see text).

3.1.2 Liquid water path

The time series of LWP is shown in Fig. 1c, and the mean diurnal cycle for all and low-cloud conditions is shown in Fig. 2i and j. Both figures depict the mean in-cloud LWP, with the model in-cloud value taken as the grid mean value divided by the model prognostic cloud fraction. Retrievals of the LWP based on the surface microwave radiometer (MWR) are only accurate when the microwave radiometer is dry (when it has not recently rained or even drizzled heavily), so the surface (SFC) MWR data include only periods when low and non-precipitating cloud are present. The SFC LWP was derived using a physical-iterative approach (Marchand et al., 2003), with a structural uncertainty of about 15 to 30 g m⁻² (owing primarily to uncertainties in the underlying microwave spectroscopy and the treatment of supercooled liquid water absorption). Here the structural uncertainty is larger than the sampling uncertainty. As a minor note, the very small differences between the mean LWP values given in the legends in Figs. 1c and 2i arise because in Fig. 2i the data are first averaged in each hour before the overall (daily) mean is taken, and the number of samples is not constant throughout the day but depends on when low-cloud conditions occur.

The CERES SYN mean (and median) values given in the legend of Fig. 2i and j are restricted to data collected between 9:00 and 16:00 local time. The diurnal cycle plots show that there are large nonphysical “spikes” in the CERES SYN LWP before and after this time, approaching sunrise and sunset. During daylight, the CERES SYN cloud property retrieval is based on visible and near-infrared imagery and assumes that clouds (whether they are liquid- or ice-phase) are sufficiently spatially homogeneous that scattering at these wavelengths can be treated using a one-dimensional (plane-parallel) approximation. Details on the CERES retrieval methodology are given in Minnis et al. (2011, 2008) and largely follow the approach used in CERES-MODIS products. The plane-parallel approximation is widely known to work poorly at large solar zenith angles or large view angles, and we speculate that these spikes are a result of this approximation not working well. The CERES SYN product does use an infrared-only algorithm at night, and we also speculate that the lower SYN LWP values observed during nighttime are also a retrieval artifact (and may play a role in the nighttime downward LW surface bias in the SYN product noted by Hinkelman and Marchand, 2020). As a point of comparison, we have also plotted (red bars in Fig. 2i, j) the mean plus or minus 1 standard error in the operational MODIS MOD06 and MYD06 mean LWP (Platnick et al., 2003, 2017), different than the CERES-MODIS algorithm. While MODIS, on board the Terra and Aqua satellites, orbits in a sun-synchronous orbit, Macquarie Island is far enough south that it is often observed on the edges of the MODIS swath, resulting in local overpasses that can be somewhat earlier or later than the nominal 10:30 and 13:30 Equator crossing times. The mean MOD06 and MYD06 LWP values, which are processed independently of the CERES project, are in reasonable agreement with the CERES SYN data.

As is apparent in Fig. 2i and j, the MG3 microphysics scheme results in an LWP that is too large on average, even when restricted to periods of low clouds. The time series of LWP in Fig. 1c shows that the MG3 scheme results in much larger LWP during periods when the IFS scheme is relatively large (more than 300 g m⁻², e.g., near 350 and 1200 h since 1 January), while at other times it is noticeably lower than IFS and the observational data (e.g., near 250, 800, and 1000 h since 1 January). How is it that the MG3 shortwave radiative fluxes show little bias with respect to observations while there is a large bias in LWP? Part of the answer to this apparent contradiction is that the distribution of LWP is highly skewed, where a small occurrence of large-LWP events substantially increases the mean. The median values of MG3 LWP are comparable to that for the observational dataset and higher than the IFS (the mean and median values are given in the legend of Fig. 2i and j). The nonlinear relationship between albedo and LWP is also a factor. Figure 3 plots the TOA SW albedo as a function of the LWP for the low-cloud periods. The MG3 simulation clearly has more high-LWP events, but the high LWP does not substantially increase the SW albedo because the albedo begins to saturate when the LWP is above about 300 g m⁻², with little change in albedo (from 0.55–0.65) for large changes in LWP. The partially offsetting greater occurrence of low-LWP events in MG3 is also evident in Fig. 3. We note that ice condensate also has a major effect on the SW albedo in deeper clouds and likely reduces the impact of the large-LWP events on albedo, but the cloud condensate below 2 km is predominantly liquid.

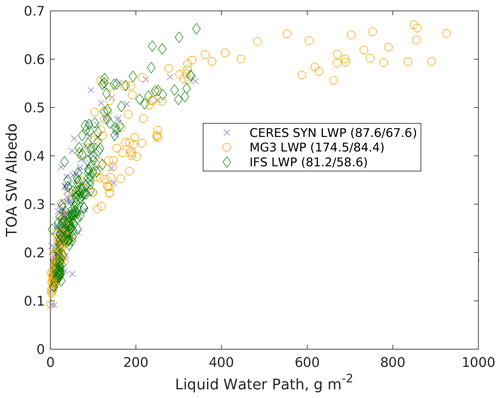
Figure 3 TOA SW albedo from CERES SYN as a function of in-cloud liquid water path (LWP) for low-cloud periods during daylight (local time from 9:00 to 16:00) from CERES observations (purple crosses), MG3 simulation (orange circles), and IFS simulation (green diamond). The legend shows the mean and median LWP.

3.1.3 Radar reflectivity

Figure 4 illustrates the observed (Fig. 4a) and simulated reflectivity from the simulations with MG3 (Fig. 4b) and IFS (Fig. 4c) microphysics. Reflectivity is estimated using a radar simulator as described in Sect. 2. Liquid, ice, rain, and snow and their attenuation are included. In this figure, the observed and simulated reflectivities are averaged over an hour (in power or Z space), with the hourly values given here as equivalent radar reflectivity (dBZe, where dBZe = 10 log₁₀(Ze)). As with the SW and LW fluxes, there is good correspondence between the simulations and observations with both depicting synoptic events with deep cloud layers that have high reflectivity and periods with persistent low cloud. However, compared to the observations the models show a greater occurrence of high reflectivity near the surface related to rain (red), especially beneath the deep clouds, and a greater occurrence of low reflectivity (light blue) in the upper troposphere related to ice cloud. Here, the radar simulator does NOT represent the effect of the ground-based radar's minimum detectable signal (MDS) such that the simulated radar reflectivity is sometimes below the reflectivity the actual radar can measure. As we will discuss in more detail below, this depends strongly on the altitude (distance from the radar). Also note that rain on the radar radome can result in attenuation of the radar signal, so with periods of significant rain, more attenuation can be expected than has been included in the radar simulator. Thus, we do not expect the observed radar reflectivity to definitively characterize high-altitude clouds. The TOA radiative fluxes (Fig. 2a, c) are a better measure of the climate effect of high clouds.

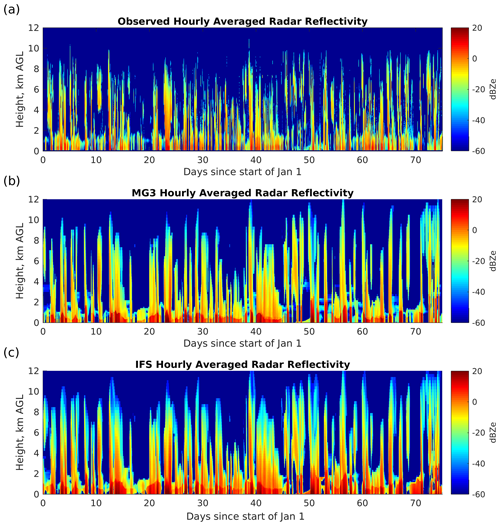
Figure 4 Hourly mean reflectivity from (a) observations and SCM simulations with (b) MG3 and (c) IFS microphysics.

To better understand these differences, we look at reflectivity–height histograms (often called a contoured frequency altitude diagram, or CFAD). Figure 5a shows the reflectivity–height histogram for the surface (vertically pointing W-band) radar, followed below by simulated histograms using the MG3 (Fig. 5c) and IFS (Fig. 5e) microphysics. The reflectivity data shown here are not hourly averages. Rather, the observational surface radar data have a temporal resolution of about 12 s (and therefore represent a horizontal grid scale less than 1 km), while the radar simulator reflectivities depend on the assumed model sub-grid distribution (more on this below). The surface radar histogram has very few detections below (to the left of) the minimum detectable signal (MDS) of the radar (violet line). For reference, the surface radar MDS is also plotted on the model-simulated histograms (Fig. 5c, e). The model simulations contain a large occurrence of hydrometeors above 5 km that the surface radar would be unable to detect due to the reduction of the MDS with height (violet line in Fig. 5a, c, e). To a degree, this detection limit explains the larger occurrence of low-reflectivity hydrometeors in the model simulations (noted in connection with the time series in Fig. 4). The IFS microphysics scheme produces more low- and high-reflectivity high-altitude cloud than the MG3 microphysics (Fig. 5c). While the surface radar does not help to evaluate the models in this regard, we note that earlier it was found that the IFS microphysics scheme produces too little outgoing LW flux (during periods with deeper clouds), while the MG3 microphysics compared well to the CERES SYN product (Fig. 2c). This suggests that the MG3 microphysics scheme is likely better representing this high-altitude cloud, likely because the MG3 two-moment scheme allows for an evolution of the size distribution of ice crystals, which better represents variable sedimentation and precipitation processes for ice.

Above (to the right of) the surface radar MDS (the violet line), both simulations (Fig. 5c, e) produce a higher occurrence of hydrometeors than observed (Fig. 5a): note the many orange and red shades in the simulated reflectivity–height histograms that are absent in the observations. This is also demonstrated in Fig. 5b, which displays the vertical profile of hydrometeor occurrence counting only detections above the radar MDS. In addition to attenuation, the occurrence of hydrometeors above the MDS is strongly affected by the model sub-grid representation. Specifically, in the model radar simulator, clouds and precipitation are assumed to be uniformly distributed in the horizontal (e.g., liquid and ice water content do not vary horizontally) and to have the same fractional coverage when both exist (meaning the precipitation fraction equals the cloud fraction). The cloud fraction is given by the largest of (i) the model prognostic cloud fraction, (ii) the stratiform precipitation fraction, or (iii) a fixed value of 10 % representing convective precipitation. So, for example, if the model prognostic cloud fraction is 78 % and convective precipitation is present (at a given vertical level) then both the cloud and precipitation are assumed to cover 78 % of the region (at the given vertical level) and the amount of “in-cloud” condensate will be equal to the grid mean amount divided by 0.78. This uniform horizontal distribution has a significant affect on the simulated radar reflectivities. An analysis by Hillman et al. (2018) found that these approximations cause the simulated radar reflectivity histograms to narrow around a “characteristic curve” where the reflectivity associated with precipitation most frequently occurs. In Fig. 5a, the characteristic curve for the observations is depicted by the solid black line. The effect of the model assumption is especially evident near the surface, below about 2 km. Here the surface radar shows two distinct modes, a low-reflectivity mode with a peak near −25 dBZe and a high-reflectivity mode with a peak near 0 dBZe. This is also clear in Fig. 5f (black line), which plots the mean observed reflectivity distribution below 2 km for both the observations and the simulations. The presence of these two modes is typical of most regions (Marchand et al., 2009) and is associated with non-precipitating (low-reflectivity) cloud (left) and precipitation (high reflectivity, right). As a minor note, these modes are much less distinct over the Southern Ocean in the spring through fall, when there is more frequent drizzle, as well as frozen (snow) and mixed-phase precipitation with intermediate reflectivity factors (not shown). The simulations (especially with the IFS microphysics) show very little low-reflectivity cloud near the surface (Fig. 5f). This is because some precipitation is almost always present in the simulations and even a small quantity of precipitation can generate a significant radar reflectivity. Thus, while the model-simulated total hydrometeor occurrence near the surface is only slightly larger than observed (Fig. 5b), the assumption that precipitation (when present) is coincident with cloud results in a large overestimate in the occurrence of reflectivity factors larger than about −20 dBZe and an underestimate below −20 dBZe.

Of course, one could make a completely different assumption about the horizontal distribution of condensate and about the co-occurrence of cloud and precipitation (i.e., not maximize the horizontal cloud and precipitation overlap) in the radar simulator and thereby obtain a simulated histogram that more closely matches the observations. But doing so only in the context of the simulator and without accounting for this sub-grid variability in a consistent way throughout the microphysics scheme is problematic. In our view, the point of using a radar simulator in the present analysis is to help evaluate the model physics rather than trying to predict what a radar might observe. While in some sense the conclusion that cloud and precipitation should not be maximally overlapped is obvious; on the positive side, the analysis shows that the radiative effect of clouds in the simulations is reasonable (Fig. 2) and also points to the potential value of these radar data in helping develop more sophisticated microphysics schemes that can represent sub-grid variability (and such schemes would nominally be able to better account for cloud–aerosol–precipitation interactions).

Returning to the topic of the characteristic curve, Hillman et al. (2018) suggest that while the distribution of reflectivities around the curve is sensitive to the sub-grid distribution, the position of the characteristic curve is not very sensitive to this representation. For comparison purposes the observed characteristic curve (shown by the solid black line) is plotted on top of the simulated histograms in Fig. 5c and e, with the simulated characteristic curves given by the solid white lines. With the IFS microphysics (Fig. 5e), there is good agreement between the simulated and observed characteristic curves between 1 and 5 km, suggesting that typical modeled precipitating ice water content (and the underlying parameterized or fixed particle size in the one-moment scheme) is quite reasonable. With the MG3 microphysics (Fig. 5c), on the other hand, the characteristic curve is shifted to smaller reflectivity between 1 and perhaps 4 km. As we will see in the next section, the mean ice water content in the MG3 and IFS experiments is similar, and the difference in the characteristic curve is likely due in some combination to the additional attenuation caused by having too much liquid water in MG3 or the particle size (which is not fixed) being too small. In both experiments, below 1 km the characteristic reflectivity is below (left of) the observations and there is a large occurrence of reflectivity values between −15 and −5 dBZe relative to the observations. This is consistent with the early discussion of precipitation being spread over too wide an area (too frequent and consequently too light). Above 5 km, the MDS is likely affecting the observed characteristic curve in the observations and should not be compared directly with the model, but as noted above, IFS clearly has a larger volume of ice and a higher occurrence of smaller reflectivity factors.

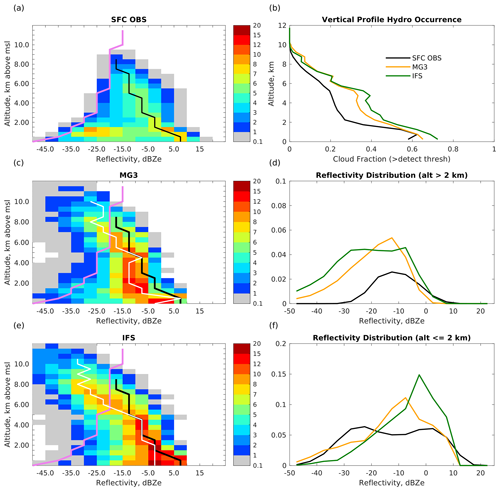
Figure 5 Radar reflectivity–height histograms from (a) surface (vertically pointing W-band) radar and from simulations using a radar simulator with the (c) MG3 and (e) IFS microphysics. Colors indicate the fraction of time that hydrometeors are detected at the specified altitude and reflectivity. Histogram bins are 0.5 km × 5 dBZe. The violet line shows the minimum detectable signal (MDS) of the surface radar. Black and white lines show the characteristic curve (see text) for observations (black, same in all panels) and simulations (white). (b) Profile of total hydrometeor occurrence, including only detections above the MDS (violet line). (d) Mean distribution of radar reflectivity for hydrometeors above 2 km altitude (note that occurrence in OBS is strongly affected by MDS below about −20 dBZe). (f) Same as (d) but includes only hydrometeors below 2 km (occurrence in OBS is unaffected by MDS above about −35 dBZe).

3.2 Model simulation differences

In this section we explore the differences between the MG3 and IFS microphysics schemes in more detail. This SCM framework provides a good platform for a detailed analysis of two very different microphysical schemes in a large-scale model. We start by examining the difference in hydrometeor profiles and time step sensitivity of the two schemes (Sect. 3.2.1). We then look at the differences between process rates in MG3 and IFS microphysics (Sect. 3.2.2). Being able to compare the processes in detail is a unique feature of the SCM-forced thermodynamics framework. Finally we look at configuration differences between the MG3 and IFS schemes that can be adjusted (Sect. 3.2.3), including some additional MG3 process sensitivity tests.

3.2.1 Mean hydrometeor profile and time step sensitivity

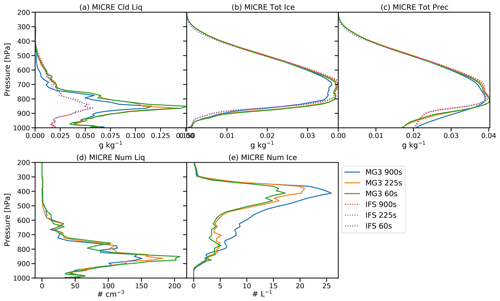
Figure 6 shows the mean profiles of key hydrometeors for the IFS and MG3 microphysical schemes. There is overall more supercooled liquid water (SLW; Fig. 6a) in the MG3 scheme than the IFS, consistent with the LWP discussion in Sect. 3.1.2, with almost a factor of 2 more at altitudes below 750 hPa but less SLW above. Sea surface temperature is about 5 °C and the average freezing level is about 900 hPa or 0.8 km. Total ice (ice, snow, and graupel; Fig. 6b) is quite similar between the two schemes, as is the total precipitation (rain, snow, and graupel; Fig. 6c). A common problem is a sensitivity of microphysical processes to the length of the time step (Gettelman et al., 2015; Santos et al., 2021), particularly for sedimentation, with various different numerical solutions proposed with different accuracy and stability. Figure 6 also shows the sensitivity of the mean profile of supercooled liquid water, total ice and precipitation, and liquid and ice number concentration (for MG3) to the time step used in the MG3 and IFS microphysics schemes. A range of time steps, specifically 60, 225, and 900 s, are shown for each microphysics scheme. The default used in the baseline simulations described above is 225 s. The IFS microphysics scheme is insensitive to time step due to the fact that it is has all the microphysical process calculations inside an implicit sedimentation loop for each model level. As the CESM2 version of the MG3 scheme has a significant time step sensitivity (not shown), a modification was made to change the sedimentation numerics from an explicit to an implicit calculation (as discussed in Sect. 3.2.3). It is the modified MG3 scheme that is used here, and Fig. 6 shows that it is quite stable with respect to time step, with some differences in peak SLW (Fig. 6a) and in ice number (Fig. 6e), particularly for the long (900 s) time step.

Figure 6 Vertical time averages of (a) supercooled liquid water, (b) total ice (ice+snow+graupel), (c) total precipitation, (d) liquid number concentration, and (e) ice number concentration for reference IFS simulations (dotted) and MG3 microphysics simulations (solid) at different time steps.

3.2.2 Microphysical process rates

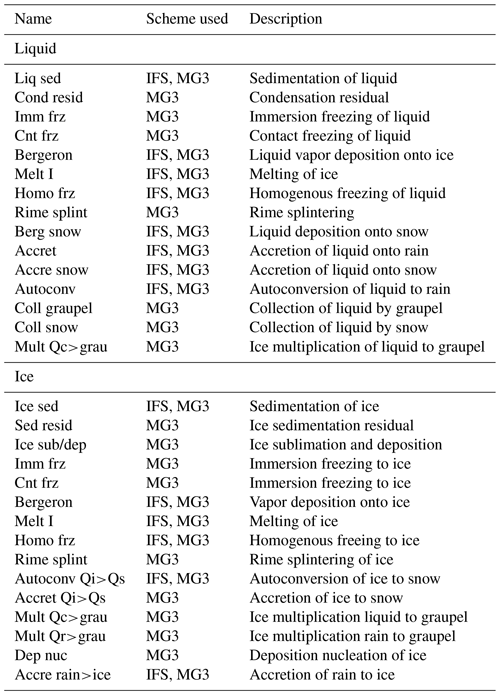
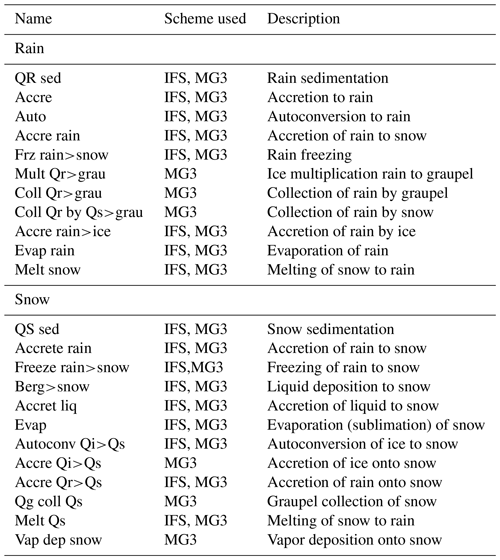
The two schemes have many similarities but also significant differences in the formulation of the microphysical process rates, and in this section we explore the balance of individual process rates for each hydrometeor (cloud liquid, ice, rain, and snow) in both schemes. We do not break this down by regime (e.g., low clouds) but look at process rates for all conditions. A longer descriptive name for each process rate (and which scheme uses it) is contained in Table A1 (liquid and ice) and Table A2 (rain and snow).

Figure 7a and b illustrate different process rates that sum to give the total sink (loss) tendency for cloud liquid water. These are the microphysical process rates after the cloud scheme has produced large-scale condensation by removing supersaturation (i.e., the source term for cloud condensate, which therefore has the same formulation for both simulations). MG3 represents more microphysical processes than the IFS due primarily to the more detailed representation of ice nucleation and the addition of graupel. The mixed-phase vapor deposition (or Wegener–Bergeron–Findeisen or “Bergeron”) process for the growth of ice particles is the most important loss process for supercooled liquid water droplets at upper levels in both schemes. At lower altitudes the collision (accretion) of snow with liquid droplets (“Accre snow”) dominates and rain collision–coalescence (“accretion”) dominates below that at warmer temperatures. The major difference for liquid water is the vapor deposition process onto snow (“Berg snow”) in MG3, a process that is not active in the IFS. The IFS accretion onto snow compensates for the missing process to some extent but still ends up being less than the sum of the accretion and the Bergeron vapor deposition onto snow in MG3 at altitudes above 750 hPa. There are several other terms that are different with relatively small magnitudes, such as the autoconversion of liquid to rain, rime splintering, and graupel collection of liquid.

Ice process rates have similar dominant processes in both microphysics schemes (Fig. 7c, d), with a source from vapor deposition (“Bergeron”) offset by a loss of ice through autoconversion to snow (“Autoconv Qi>Qs”). However, the Bergeron process is much more active at lower altitudes and in warmer temperatures for MG3 compared to the IFS (as also seen in Fig. 7a and b), with a similar difference in magnitude for ice autoconversion to snow, which compensates. The more active Bergeron process in MG3 is likely due to the larger supercooled liquid water present at these lower levels (Fig. 6a). In MG3 (Fig. 7d), there is also loss from accretion of ice onto snow (“Accret Qi>Qs”) throughout the depth of the cloud from 300 to 800 hPa and a source due to deposition onto ice (“Ice sub/dep”) at high altitudes around 400 hPa. The ice sedimentation in the IFS shows a small loss in the upper part of the cloud and gain lower down, whereas the net redistribution is much smaller in MG3, a difference likely due to the different sedimentation numerics in the two schemes.

Rain process rates are illustrated in Fig. 8a and b. Rain sedimentation (“QR sed”) is the major loss for precipitation, which is larger in the IFS, and snow melting (“Melt snow”) and accretion of liquid cloud droplets (“Accre”) are the main rain source terms. Snow melting is more active nearer the surface in the MG3 scheme. There is not much rain evaporation in the planetary boundary layer (PBL), which is consistent with large reflectivity in the lowest kilometer (Fig. 5e). This is due to the specific rain evaporation assumptions in the IFS and modified MG3 (see Sect. 2.3). There is even less rain evaporation in MG3 due to the deeper melting layer and the two-moment scheme allowing rapidly falling raindrops rather than slower-falling drizzle.

Figure 7 Profiles of (a, b) cloud liquid water and (c, d) cloud ice process rates (a, c) for the IFS microphysics and (b, d) for MG3. Process rates are described in Table A1.

Figure 8 Profiles of (a, b) rain and (c, d) snow process rates (a, b) for the IFS microphysics and (c, d) for MG3. Process rates are described in Table A2.

There are some differences in snow process rates (Fig. 8c, d). The general balance at upper levels is a sedimentation loss (“QS sed”) and an ice autoconversion (“Autoconv Qi>Qs”) source, representing aggregation of ice crystals. Snow fall speeds are fixed in the IFS and set to be the same in MG3, making the sedimentation rate similar. MG3 also has a source from the vapor deposition onto snow (“Berg>snow”) and loss from snow sublimation and evaporation (“Evap”) (larger in MG3 than IFS). At lower levels, the sedimentation source term for snow falling from above (“QS sed”) is balanced by a melting loss term to rain (“Melt Qs”), which is just the inverse of the melting source term for rain (Fig. 8a, b). The shallower melting layer in IFS is also evident.

In summary, both microphysics schemes produce a largely similar balance of process rates. Given that some of the microphysical process formulations are similar between the two schemes and that there is some convergence that has been imposed by adjusting the MG3 scheme towards the IFS (see Sect. 2.3), this is perhaps not surprising. However, there are also some differences in the formulations that result in different hydrometeor profiles, particularly for the radiatively important supercooled liquid water. As shown in Fig. 6, the mean profiles of ice and snow are very similar between the two schemes (panels b, c). There is clearly compensation between some of the processes, such as the higher Bergeron process rate for ice growth and snow accretion rates in the IFS, which compensates for the lack of a Bergeron process for snow in the IFS compared to MG3 (Fig. 7a, b). This compensation results in a similar supercooled liquid water profile at altitudes above 750 hPa, apart from for the MG3 900 s time step simulation (Fig. 6a). However, at altitudes below 750 hPa, the profile of supercooled liquid water is more than a factor of 2 different, with much higher values in MG3 compared to the IFS (Fig. 6s). The higher cloud liquid accretion rates for both snow and rain below 750 hPa in the IFS (Fig. 7a, b) likely lead to the lower SLW in the IFS, which agrees more closely with the observations (Fig. 2i, j). At lower levels below 850 hPa, there are also differences in rain in the precipitation profile (Fig. 6c). For sedimenting precipitation, differences can come from higher in the column, but given that the ice and snow hydrometeor profiles are very similar, differences in the low-level precipitation must therefore be due to the local impact of processes, particularly the melting rate of snow to rain, evaporation of rain, and differences in the rain fall speed.

3.2.3 Modifications and sensitivity

In order to further understand the impacts of the changes to the MG3 scheme and differences from the IFS, a series of sensitivity experiments are performed by changing individual aspects of the MG3 microphysics. The first set of changes (Fig. 9) investigates the impact of the initial modifications from the original CAM6 version to the base MG3 scheme used for all the simulations described so far, as described in Sect. 2.3. These changes were made for this study to remove some of the most obvious differences due to numerical implementation and basic threshold and other assumptions to allow a more meaningful comparison of the process rates between the two microphysics schemes. The second set of changes investigates the sensitivity to assumptions that affect several of the important microphysical process rates (Fig. 10).

The sensitivity experiments are summarized in Table 1 and are described in more detail below. Figures 9 and 10 show the impacts on time-averaged vertical profiles for various quantities, and the impacts on time-averaged single-level quantities are shown in Fig. 11. For reference, the figures also show the IFS, the modified MG3 used for this study (MG3 base), on which all of the sensitivity experiments are based, and the original MG3 CAM6 settings used with the MG3 microphysics in the CAM6 atmospheric component of the coupled climate model CESM2. In general, the MG3 CAM6 settings are outliers for various quantities and far away from the IFS and MG3 base results. It is therefore notable that significant differences can occur from the numerical implementation of the sedimentation and microphysical threshold assumptions.

Meyers et al. (1992)

Table 1 Sensitivity tests applied to MG3 simulations.

(i) Sensitivity to MG3 modifications from CAM6

We first assess changes to the fall speed of hydrometeors (“Fall speed”) and numerical formulation of the sedimentation of precipitation (“Explicit fall”) in MG3. The “Fall speed” sensitivity test removes a numerical fix for zero fall speed in the column when no precipitation is initialized there in MG3, and “Explicit fall” reverts the change from an implicit sedimentation of precipitation calculation, which is more stable across time steps, back to the explicit scheme in CAM6. In addition, the IFS and MG3 base have constant fall speeds for ice and snow, which are reverted to the MG3 CAM6 fall speed formulation (fall speed varies as a function of hydrometeor size) in the “Sediment” test. The “Fall speed” and “Explicit fall” tests slightly decrease the total amount of ice (Fig. 9b), and the “Sediment” change increases the (supercooled) cloud liquid water at altitudes above 700 hPa (Fig. 9a). A reversion to allow the immediate evaporation of sedimenting condensate (“Evapsed”) has a negligible impact.

A series of changes to harmonize evaporation was also conducted (“Old evap”) as the IFS uses a relative humidity threshold of 90 % before evaporation starts, and the IFS has a similar evaporation formula as MG3 but is multiplied by a factor of 0.3. The rain freezing threshold (“Rain freeze”) has small effects on total precipitation (Fig. 9c) near 850 hPa in the temperature range just below −5 °C. Finally the IFS and MG3 base do not have a threshold relative humidity (RH) for ice nucleation (RH for IN), whereas MG3 CAM6 has an RH threshold of 105 % with respect to ice for ice nucleation to occur. Reverting the RH threshold for ice nucleation (RH for IN) increases liquid mass (Fig. 9a) and number (Fig. 10d) near 600 hPa and reduces ice number (Fig. 9e) significantly between 300–600 hPa by making it harder to form ice. Each of these experiments is a single reversion experiment that removes these elements from MG3 base in IFS to get back to MG3 CAM6. However, the combination of these effects is important. The test “Old rain” combines the “Rain freeze”, “Sediment”, and “Fall speed” tests, and it is this combination that reduces the unrealistic increase in precipitation (rain) mass near the surface in MG3 CAM6 (Fig. 9c).

The implicit formulation for sedimentation as in MG3 base has lower LWP (Fig. 11a) than MG3 CAM6 and shortwave (Fig. 11e) and longwave (Fig. 11f) downward radiation more similar to the IFS, which also has an implicit formulation. The largest difference between MG3 CAM6 and the MG3 base is generally due to the different fall speed estimates (mostly affecting total ice) and rain freezing (affecting total ice and precipitation). Note that the SW downward radiation (Fig. 11e) is generally inversely proportional to the LWP (Fig. 11a) and to a lesser extent total cloud cover (Fig. 11c). The spread in the LW downward flux is relatively small (6 W m⁻², Fig. 11f) relative to the spread in SW downward flux (35 W m⁻²; Fig. 11e).

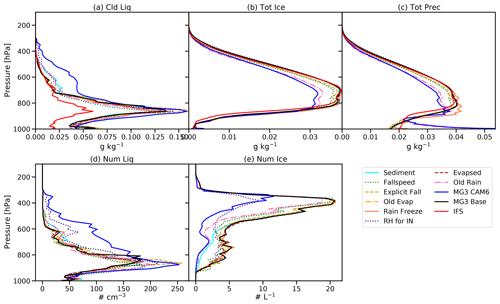
Figure 9 Vertical time averages of (a) supercooled liquid water, (b) total ice (ice+snow+graupel), (c) total precipitation, (d) liquid number concentration, and (e) ice number concentration for the MG3 base version (black solid) and various MG3 microphysics sensitivity tests as noted in the legend to differentiate MG3 and IFS microphysics. The reference IFS microphysics are included in panels (a), (b), and (c) (solid red).

Figure 10 Vertical time averages of (a) supercooled liquid water, (b) total ice (ice+snow+graupel), (c) total precipitation, (d) liquid number concentration, and (e) ice number concentration for the MG3 base version (solid black) and various MG3 microphysics sensitivity tests as noted in the legend to understand MG3 sensitivity.

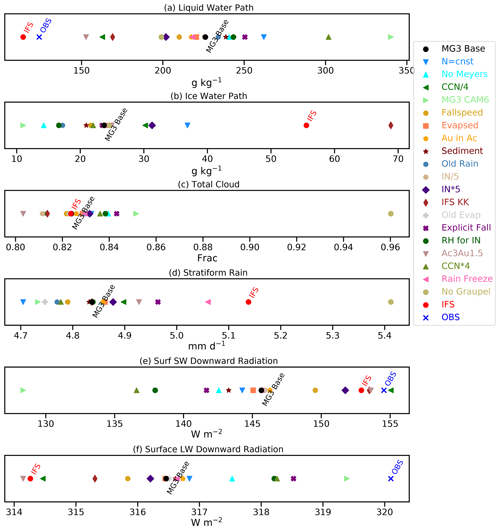
Figure 11 Time averages of (a) liquid water path, (b) ice water path, (c) cloud fraction, (d) surface stratiform rain rate, (e) surface SW down, and (f) surface LW down for MG3 microphysics sensitivity tests as noted on the plot. The MG3 base case is in black. Reference IFS is plotted in red. MICRE observations for LWP as well as SW and LW radiation are in blue.

Finally, it is worth noting that supercooled liquid water above 700 hPa is much higher in the MG3 CAM6 version (Fig. 9a). This is due to the fall speed changes (“Sediment”, which is also in the “Old rain” test) combining in a nonlinear way with the change to the relative humidity used for ice nucleation (RH for IN).

(ii) Additional MG3 process sensitivity tests

The second set of tests is performed with further modifications to the MG3 base code to understand its sensitivity relative to the IFS.

One of the most important aspects of the microphysics is the generation of precipitation. For liquid clouds, this is defined by the collision–coalescence process of interacting hydrometeors of different sizes. In bulk microphysics schemes like the IFS and MG3, this process has to be highly parameterized since the different-sized drops are not explicitly represented. The parameterizations are for autoconversion (formation of rain from cloud water) and accretion (the removal of cloud water by rain). In MG3 and IFS, these parameterizations come from Khairoutdinov and Kogan (2000), a regression fit to a bin microphysical model. In MG3, the parameters for autoconversion were adjusted to better match recent observations, with resulting reduced sensitivity to droplet number, whereas in the IFS the original Khairoutdinov and Kogan (2000) parameters are used (IFS KK). In the IFS there is also an enhancement factor of 1.5 for autoconversion and 3 for accretion (Ac3Au1.5), representing the effects of sub-grid heterogeneity of cloud and precipitation. We test the MG3 scheme with these factors. The scaling of autoconversion and accretion (Ac3Au1.5) significantly reduces cloud water, as expected (Fig. 11a), and slightly increases ice water path (Fig. 11b), with corresponding increases in the downward SW radiation (Fig. 11e). Changing MG3 to the IFS parameters for Khairoutdinov and Kogan (2000) (IFS KK) has more of an impact higher up, reducing SLW at altitudes above 800 hPa, but with the major impact seen as a large increase in ice number (Fig. 10e). This seems to result from a conversion process from liquid (possibly freezing rain) to ice at supercooled temperatures. These settings produce a simulation with LWP and surface SW downward radiation closer to observations (and IFS microphysics), largely due to lower LWP (Fig. 11a). We also test the MG3 scheme with a change that allows the autoconverted rain to be immediately used by the accretion process (“Au in Ac”), which slightly enhances accretion but has little overall effect on the simulations. The CAM6 settings result in the highest LWP (Fig. 11a), which does enhance the surface LW down (Fig. 11f) and brings it closer to the observations (but note the difference is only a few W m⁻²) but produces surface SW down that is much too small (Fig. 11e).

Two changes to the mixed phase have substantial impacts. Turning off the prognostic graupel (rimed ice particles) in the MG3 simulation results in a significant increase in ice mass (Fig. 10b) and precipitation (Fig. 10c). This is due to the removal of a loss process for rain onto graupel, which now occurs only onto snow, a less efficient process, and leads to higher snow mass. Removing the Meyers et al. (1992) mixed-phase ice nucleation significantly reduces ice number (Fig. 10e) and ice water path (IWP) (Fig. 11b), as well as supercooled liquid at higher altitudes (Fig. 10a).

Next, we examine the role of number concentrations for liquid and ice in the simulations. Because MG3 typically runs with an aerosol model, it requires the activation of liquid drops and ice crystals to set the hydrometeor number concentrations, unless they are set to a constant. In the IFS there is no explicit representation of activation of aerosol, so for the MG3 simulations a constant rate of cloud condensation nuclei (CCN) and ice nuclei (IN) production is defined. The ice and liquid mass and number concentrations are sensitive to these rates and this will naturally create differences between MG3 and IFS microphysics. Indeed, increasing the CCN production rate (CCN*4) results in many more (Fig. 10d) and hence smaller cloud water drops, increasing SLW (Fig. 10a) and averaged LWP (Fig. 11a) and reducing downward SW (Fig. 11e). The opposite effects are seen for reductions in the CCN production rate (CCN/4). CCN and IN vary by an order of magnitude over the Southern Ocean (McFarquhar et al., 2021). There are also tests performed by adjusting the constant for the rate of production of ice nuclei (IN/5 and IN*5). More IN slightly increases IWP (Fig. 11b, c), with opposite effects for reducing IN.

We also perform a simulation with fixed number concentrations for all species in the MG3 scheme (rather than fixed production rates), as specified in Table 1. A fixed number concentration ignores any drop or ice nucleation, resets the prognostic number to a set value every time step, and uses this throughout the microphysics. Fixed number concentrations (N=cnst) have a substantial effect on the simulations if they are not set to reasonable values. Here the number concentrations have been adjusted to produce similar number concentrations as the prognostic MG3 base simulation. Nonetheless, even with similar LWP, average liquid number concentrations are decreased (Fig. 10d), similar to the CCN/4 experiment. Note that the average number is lower than the fixed drop number due to averaging and number depletion.

In summary, in MG3 there is sensitivity of LWP and radiation to the fall speed. The autoconversion and accretion processes that dominate rain formation and remaining LWP are also important for surface radiation. Changes to the activation of cloud drops (CCN) also affects cloud water and rain partitioning and hence LWP and radiation. Finally, the ice phase is also important, with the inclusion of graupel changing the loss process of rain to make it less efficient, and increases the snow mass (included in IWP) significantly. Ice nucleation and mixed-phase ice nucleation (“No Meyers”) are important for ice water path and surface radiation. Note that none of the experiments reduce the MG3 LWP to the level of the observations or IFS (Fig. 11a), but with further combination of some of these tests, like the conversion and accretion scaling, fixed number concentration at low number or large size, and/or reduced CCN, the MG3 LWP could be further reduced to match the IFS more closely.

4 Summary

Simulations are performed with the IFS single-column model with two “operational” microphysics parameterizations (the one-moment IFS scheme used at the ECMWF for numerical weather prediction and the two-moment MG3 scheme used in the CAM6 climate model). Both are able to reproduce many of the characteristics as well as the evolution and time mean variability of Southern Ocean clouds observed during the MICRE campaign at Macquarie Island during the period January–March 2017 in a regime with significant amounts of supercooled liquid cloud and in a maritime location representative of the broader Southern Ocean.

Assessing the fidelity of simulated clouds with respect to observations requires dealing with uncertainty in the observations and the model. Observations have their own biases, such as the minimum detectable signal and loss of signal in precipitation for the radar (in addition to attenuation). The IFS simulation results (for both microphysical schemes) when compared to observations are sensitive to the model assumptions, such as the definition of cloud cover and the sub-grid treatment of clouds and hydrometeor size distributions. We have carefully considered these uncertainties in performing these evaluations.

Surface radiation is well represented compared to the ground-based radiometer and satellite datasets with radiative flux biases within or close to the uncertainty of the observations in both the LW and SW. In particular, in the shortwave solar spectrum, there is no “too few/too bright” problem that has previously been seen in some global models (Wall et al., 2017; Kuma et al., 2020). Hydrometeor occurrence (cloud fraction) is slightly higher than observed when radar simulator output is compared to observations.

There are large uncertainties in the observed surface (passive microwave) LWP retrievals, largely due to the presence of precipitation, but for low-level non-precipitating clouds, the surface radiometer values at Macquarie Island are consistent with satellite estimates based on geostationary (Himawari-8) and MODIS polar-orbiting satellites. Mean LWP for the IFS microphysics compares well to both surface and satellite LWP retrievals for low clouds, while mean LWP from the MG3 microphysics is too large. An analysis of the distribution of LWP shows that the MG3 microphysics scheme produces more high-LWP events than the observations and IFS simulations. Median LWP values for MG3 are comparable to the IFS and the observations. Because the radiative effects of condensed water saturate when the LWP is larger than ∼ 400 g m⁻² (cloud albedo does not change much), the large-LWP events do not translate into a large SW radiation bias in the MG3 scheme.

A comparison of radar reflectivity with the vertically pointing radar at Macquarie Island shows that the simulations capture the overall characteristic shape of the reflectivity–height distribution, although the mean frequency of occurrence of hydrometeors (with reflectivity higher than the surface radar minimum detectable signal) is too high, at least above the boundary layer. In general, the simulations contain a higher occurrence of reflectivity factors larger than −15 dBZ compared to the observations. While some of this difference is expected due to attenuation of the observed radar reflectivity that results from rain on the radar radome, the difference also occurs for periods when there is no surface rain. Rather, this difference in the distribution of reflectivity factors is largely driven by the model assumption that when precipitation is present, it occupies the same area (fraction) as that predicted for cloud. A better model sub-grid representation of cloud and precipitation could reduce biases in the radiation and address this “too frequent, too light” precipitation problem. While this problem is certainly not unique to the Southern Ocean (Stephens et al., 2010), it is perhaps especially pertinent because of the high occurrence of light precipitation in the region. This also highlights the fact that this issue of precipitation that is too light may be related to sub-grid assumptions in models, not a fundamental flaw in the cloud physical process rates.

The single-column model is a partially constrained testing environment and for long simulations requires forcing to keep the temperature, humidity, and wind profile from drifting too far from the observations. However, the cloud and microphysical response to the forcing is not constrained, and thus it is a useful platform for assessing different microphysical schemes. In a test without any relaxation of the temperature, the PBL deviates from observations, and significant SW and LW radiation biases emerge on the order of tens of W m⁻² with both the IFS and MG3 microphysics. While advective forcing of wind and temperature is included in the SCM, advection of hydrometeors is not included and could create errors. However, the timescale for microphysical processes is shorter than an advection timescale (for a 10 m s⁻¹ wind and a 50 km global model grid box, this implies a 2500 s advection timescale, but the microphysical time steps are 225 s) and means the issue should be a small one. The good reproduction of observed cloudiness (Fig. 4) and LWP (Fig. 1) indicates that this is the case.

A series of sensitivity tests modifying the numerical and physical representation of various cloud and precipitation processes in the MG3 scheme are performed to understand the differences from the IFS microphysics scheme. When MG3 is modified to use formulations similar to the IFS (the MG3 base microphysics scheme), the average ice, snow, and rain hydrometeor profiles are remarkably similar, with the main difference being double the amount of supercooled liquid water on average in MG3. The detailed process rate analysis illustrates that the schemes have a different discretization of process rates (with MG3 being more complex) and that the phase transition between liquid and ice, as well as precipitation formation and sedimentation, is the major cause of differences between the schemes, despite significant compensation between processes (e.g., the IFS has a higher vapor deposition for ice growth, which compensates for a lack of vapor deposition onto snow). The sensitivity simulations confirm that differences in the autoconversion to rain and accretion onto rain loss processes for liquid water at sub-freezing temperatures are the primary cause of the differences in LWP (which is mostly SLW), and the MG3 scheme could be adjusted to enhance the liquid loss process and reduce the LWP in deeper clouds. Finally, for cloud liquid and cloud ice formation, there are clearly large sensitivities to the specification of the CCN and IN production rates. Although tuning these in the SCM can bring closer agreement, a full comparison in the 3D model with interactive aerosol activation is required for the impact to be fully assessed.

5 Conclusions

The SCM is a good framework for testing cloud physics. Part of getting clouds and cloud radiative effects correct is getting the PBL structure right and the correct coupling of the thermodynamics to the cloud physics, as well as the microphysical processes themselves. With constrained dynamics, the cloud radiative effects stay close to observations and we do not see the large-scale biases seen in many global models in the Southern Ocean, indicating that coupled dynamics and microphysical processes are important.

The required complexity of microphysical parameterization is a key question for future development of atmospheric models and one of the motivations for the comparison here of the one-moment (mass) IFS with the higher-complexity two-moment (mass and number concentration) MG3 scheme including graupel. Representing a graupel (rimed ice) hydrometeor in MG3 has a small impact, with more precipitation and less SLW than without graupel, but there was not a significant amount of graupel present in the type of clouds at this location and a larger difference would be expected in regimes with more deep convection. Regarding the two-moment versus one-moment representation, it is difficult to disentangle the impacts on the mean fields of the two-moment representation in MG3 from the differences in microphysical process formulation between the schemes as there can be compensation between processes, and numerical formulation and different tunings of microphysical process rates can dominate. However, the representation of supercooled liquid is better in the two-moment scheme. Despite similar ice and precipitation mass profiles, there are differences in the radar reflectivity profiles, which are at least partly due to the additional degrees of freedom from the representation of particle number concentration in MG3. The two-moment scheme as a result likely produces a slightly better reproduction of observed radiative fluxes.

These results have several important implications for 3D modeling, which should be tested in future work. The correct PBL structure (the temperature and stability profile) is necessary for getting clouds and radiation right. There is little bias in the constrained SCM. The major differences between microphysics schemes lie in precipitation formation, sedimentation of hydrometeors, and freezing processes. The two-moment scheme is sensitive to the number of condensation and ice nuclei. The representation of supercooled liquid is better in the two-moment scheme. The additional degrees of freedom from the two-moment scheme representation of variable particle number concentration improve the simulation of reflectivity and likely produce a slightly better reproduction of observed radiative fluxes. Finally, the sub-grid assumptions for cloud and precipitation impact both the ability to compare to observations and the model evolution itself for both one- and two-moment schemes. One promise of higher-resolution “storm-resolving” models without fractional cloud and precipitation is to reduce the need to make these assumptions and enable more direct evaluation against observations.

Appendix A

Table A1 Microphysical process rates: liquid and ice.

Table A2 Microphysical process rates: rain and snow.