A fully coupled solid-particle microphysics scheme for stratospheric aerosol injections within the aerosol–chemistry–climate model SOCOL-AERv2

Recent studies have suggested that injection of solid particles such as alumina and calcite particles for stratospheric aerosol injection (SAI) instead of sulfur-based injections could reduce some of the adverse side effects of SAI such as ozone depletion and stratospheric heating. Here, we present a version of the global aerosol–chemistry–climate model SOCOL-AERv2 and the Earth system model (ESM) SOCOLv4 which incorporate a solid-particle microphysics scheme for assessment of SAI of solid particles. Microphysical interactions of the solid particle with the stratospheric sulfur cycle were interactively coupled to the heterogeneous chemistry scheme and the radiative transfer code (RTC) for the first time within an ESM. Therefore, the model allows simulation of heterogeneous chemistry at the particle surface as well as feedbacks between microphysics, chemistry, radiation and climate. We show that sulfur-based SAI results in a doubling of the stratospheric aerosol burden compared to the same mass injection rate of calcite and alumina particles with a radius of 240 nm. Most of the sulfuric acid aerosol mass resulting from SO₂ injection does not need to be lifted to the stratosphere but is formed after in situ oxidation and subsequent water uptake in the stratosphere. Therefore, to achieve the same radiative forcing, larger injection rates are needed for calcite and alumina particle injection than for sulfur-based SAI. The stratospheric sulfur cycle would be significantly perturbed, with a reduction in stratospheric sulfuric acid burden by 53 %, when injecting 5 Mt yr⁻¹ (megatons per year) of alumina or calcite particles of 240 nm radius. We show that alumina particles will acquire a sulfuric acid coating equivalent to about 10 nm thickness if the sulfuric acid is equally distributed over the whole available particle surface area in the lower stratosphere. However, due to the steep contact angle of sulfuric acid on alumina particles, the sulfuric acid coating would likely not cover the entire alumina surface, which would result in available surface for heterogeneous reactions other than the ones on sulfuric acid. When applying realistic uptake coefficients of 1.0, 10⁻⁵ and 10⁻⁴ for H₂SO₄, HCl and HNO₃, respectively, the same scenario with injections of calcite particles results in 94 % of the particle mass remaining in the form of CaCO₃. This likely keeps the optical properties of the calcite particles intact but could significantly alter the heterogeneous reactions occurring on the particle surfaces. The major process uncertainties of solid-particle SAI are (1) the solid-particle microphysics in the injection plume and degree of agglomeration of solid particles on the sub-ESM grid scale, (2) the scattering properties of the resulting agglomerates, (3) heterogeneous chemistry on the particle surface, and (4) aerosol–cloud interactions. These uncertainties can only be addressed with extensive, coordinated experimental and modelling research efforts. The model presented in this work offers a useful tool for sensitivity studies and incorporating new experimental results on SAI of solid particles.

1 Introduction

Even if greenhouse gas (GHG) emissions stopped today, high GHG concentrations and their effects would persist for centuries if GHG removal techniques can not be scaled up fast enough (IPCC, 2023). Stratospheric aerosol injection (SAI) has the potential to rapidly mitigate some of the adverse impacts of climate warming by increasing the Earth's albedo. SAI would be feasible at relatively low cost (Smith, 2020, i.e. about USD 18 billion per year), but it also entails considerable risks such as adverse environmental side effects and challenges such as governance of ethical considerations on global and inter-generational equity and the power of decision (e.g. Robock, 2008; Burns, 2011). For these reasons, the US National Academy of Sciences and others have proposed research that explores the risks and benefits of SAI (e.g. Shepherd, 2012; Schäfer et al., 2015; National Research Council, 2015; Field et al., 2021).

The idea of SAI evolved from the temporary cooling effect of sulfuric acid aerosols formed after stratospheric SO₂ injections of large explosive volcanic eruptions and was first proposed by Budyko (1974). In addition, solid particles as alternative materials were explored in conceptual studies and reports on various climate engineering techniques (e.g. Keith and Dowlatabadi, 1992; Teller et al., 1996; Keith, 2000). However, research on SAI was initially a taboo among researchers since it does not present an actual solution to climate change but instead at best a treatment of some of its symptoms (MacMartin et al., 2014; Keith and Macmartin, 2015). The need for research on SAI has only come more to the forefront with the growing appearance of the impacts of climate change and after the proposal to investigate the risks, benefits and the feasibility of SAI by Crutzen (2006). Potential scenarios for SAI involve reducing the current rate of climate change or in what is referred to as an “overshoot scenario”, where SAI would aim at keeping global temperature increase below 1.5 K, the target set by the Paris Agreement in 2015, until global net zero GHG emissions are achieved and until solutions are found on how to remove GHGs from the air efficiently (MacMartin et al., 2014, 2022; Keith and Macmartin, 2015; Visioni et al., 2024).

To date, research on SAI has mainly focused on injection of sulfuric acid aerosol precursor species such as SO₂. This has a number of reasons: due to the natural occurrence of sulfuric acid aerosols in the atmosphere, the stratospheric sulfur cycle is relatively well known and interactively simulated in many chemistry–climate models (e.g. Thomason and Peter, 2006; Deshler, 2008; Feinberg et al., 2019; Brodowsky et al., 2024), which makes it easier for modellers to investigate sulfur-based SAI scenarios. Furthermore, heterogeneous chemistry and optical properties of sulfuric acid aerosols in the stratosphere are also relatively well known from experimental studies (e.g. Burkholder et al., 2020; Ammann et al., 2013). In addition, observations after large explosive volcanic eruptions such as the Mt. Pinatubo eruption 1991 (e.g. Arfeuille et al., 2013; Thomason et al., 2018; Baran and Foot, 1994; Kovilakam et al., 2020) allow for model evaluation of the chemical and radiative impacts of large stratospheric sulfur emissions (e.g. Deshler et al., 2019; Quaglia et al., 2023).

However, SAI via SO₂ injections is also subject to several limitations, making sulfuric acid aerosols less attractive for a potential use in SAI. These limitations include (1) aerosol size distributions that are inefficient for backscattering solar radiation with either too many large or too many small particles (Vattioni et al., 2019); (2) ozone depletion due to chlorine activation on aerosols (Tilmes et al., 2008; Weisenstein et al., 2022); and (3) absorption of mainly outgoing terrestrial radiation reducing the net radiative forcing and resulting in stratospheric warming, which changes the large-scale atmospheric circulation and global and regional precipitation patterns (Aquila et al., 2014; Tilmes et al., 2017; Visioni et al., 2021; Jones et al., 2022; Wunderlin et al., 2024; Laakso et al., 2024).

Recent studies have shown that injection of solid particles could overcome several of these limitations (e.g. Pope et al., 2012; Weisenstein et al., 2015; Keith et al., 2016; Dykema et al., 2016). Most importantly, the absorption efficiency of longwave (LW) and shortwave (SW) radiation per resulting aerosol burden is significantly smaller for many solid materials compared to sulfuric acid aerosols, resulting in reduced stratospheric warming (Dykema et al., 2016). Furthermore, many solid-particle candidates such as alumina (Al₂O₃), calcite (CaCO₃) or diamond particles have larger backscatter efficiencies per stratospheric burden compared to sulfuric acid aerosols (Dykema et al., 2016). Other studies showed that the injection of alumina or calcite particles would result in less ozone depletion (Weisenstein et al., 2015; Dai et al., 2020) or even in ozone increase in the case of calcite particles (Keith et al., 2016).

However, contrary to sulfuric acid aerosols, the solid-particle types proposed for SAI do not occur naturally in the stratosphere. Therefore, relatively little is known about their microphysical interactions and chemical ageing processes, which could alter their scattering properties, their stratospheric residence time and the heterogeneous chemistry hosted on the particles. This makes it very difficult to have confidence in the modelled impacts of solid-particle injections on stratospheric chemistry and climate.

There have been investigations on the impact of alumina-containing solid-fuel space rocket exhaust on stratospheric ozone and radiative forcing. These studies used flow-tube experiments (Molina et al., 1997), 2D chemistry transport modelling (Jackman et al., 1998; Danilin et al., 2001) and conceptual methods (Ross and Sheaffer, 2014). However, the rocket exhaust investigated in these studies also contains other species such as water, HCl and black carbon, which makes attribution of the alumina particle effects on ozone alteration and radiative forcing difficult (Vattioni et al., 2023b). Therefore, microphysical interactions of solid particles with background aerosols, as well as their impact on stratospheric chemistry and radiative forcing, remain subject to large uncertainties.

Nevertheless, there have been several studies that investigated SAI scenarios using solid particles. Fujii (2011) and Pope et al. (2012) were among the first conceptual studies which pointed at potential benefits, such as better scattering properties, from SAI of various solid materials in their studies. At the same time Ferraro et al. (2011) and Ferraro et al. (2015) used a radiative transfer code (RTC) and a general circulation model, respectively, to quantify stratospheric heating resulting from some materials as well as the dynamical stratospheric feedbacks, while prescribing the stratospheric solid-particle number densities. Later, Jones et al. (2016) was the first study that compared tropospheric climate impacts from SAI of sulfuric acid aerosols with injections of TiO₂ and BC using a global circulation model with an interactive ocean module, while simulating injection and transport of solid particles with prescribed size distributions. However, none of these studies accounted for heterogeneous chemistry on particle surfaces, nor for microphysical processes. Impacts on stratospheric ozone from SAI of solid particles were first assessed by Kravitz et al. (2012), who investigated SAI with BC aerosols using a chemistry–climate model. In summary, the conclusion from these first studies which mainly investigated SAI of BC and TiO₂ particles is that these materials are not suitable as injection species for SAI since both TiO₂ and BC have strong UV–VIS absorption, which results in significant stratospheric heating. However, while injection of BC would result in substantial ozone depletion, experimental studies on heterogeneous chemistry on TiO₂ surfaces indicated reduced impacts on modelled stratospheric ozone (Tang et al., 2014, 2016; Moon et al., 2018) compared to sulfuric acid aerosols, providing additional motivation for exploration of other species.

Meanwhile, Dykema et al. (2016) performed detailed radiative transfer calculations of various solid particles, including feedbacks from stratospheric water vapour, and concluded that solid particles such as calcite, diamond, alumina and SiC scatter solar radiation with better mass efficiency and less stratospheric heating compared to sulfuric acid aerosols. Weisenstein et al. (2015) were the first to study the use of a 2D chemistry transport model with interactive solid-particle microphysics, as well as microphysical interactions of solid particles with condensed and gaseous sulfuric acid, to assess impacts from heterogeneous chemistry on alumina particle surfaces. The resulting zonal mean number concentrations were then fed into a RTC offline to simulate the resulting radiative forcing. Limitations of this study stem from a simplified representation of heterogeneous chemistry on alumina particles (Vattioni et al., 2023b) as well as from the 2D approach, which causes significant simplifications in atmospheric dynamics and transport of the injected particles. Keith et al. (2016) used the same model to propose substantial stratospheric ozone increase through removal of HCl from the stratosphere via uptake on calcite particle surfaces and subsequent sedimentation. Later, Cziczo et al. (2019) pointed to the over-simplified assessment used in the latter study, which applied over-simplified heterogeneous chemistry such as neglecting the formation of hydrates as well as a potential sealing effect due to the formation of reaction products at the surface. However, most importantly, this latter study showed that especially CaCO₃ and Ca(NO₃)₂, as well as their hydrates, are good ice nucleation materials, which could result in a 33 % reduction in the radiative forcing compared to Keith et al. (2016) due to increased cirrus cloud coverage. Furthermore, the interactions of aerosols with polar stratospheric clouds (PSCs) could create a feedback on polar ozone concentrations, which has not been investigated so far (Cziczo et al., 2019).

Therefore, to assess the real risks and benefits of SAI of solid particles compared to the more conventionally researched sulfur-based approach, it is important to interactively couple (1) microphysical processes such as agglomeration and sedimentation of solid particles and their microphysical interaction with condensed and gaseous sulfuric acid with (2) heterogeneous chemistry on the particle surface and the subsequent impacts on stratospheric ozone and with (3) interactive aerosol cloud interactions, as well as with (4) the resulting dynamical feedbacks from changes in ozone, stratospheric warming and cooling of tropospheric climate interactively in one model. Simulating all these effects in a self-consistent way is crucial because (1) strong agglomeration can significantly decrease the backscatter efficiency or increase the sedimentation speed compared to a compact monomer, while (2) it can lead to significant ozone alteration depending on the material, and (3) it can result in a positive or negative feedback on radiative forcing through cirrus cloud alteration (e.g. Cziczo et al., 2019). The combination of these processes ultimately determines the large-scale circulation response and surface climate response to SAI with alternate materials.

This study presents a microphysics module for solid particles within the aerosol–chemistry–climate model SOCOL-AERv2, which represents injected solid particles interactively coupled to advection and sedimentation as well as to the model's radiative transfer and heterogeneous chemistry modules (see Fig. 1). Additionally, the module calculates microphysical interactions between solid particles and background sulfuric acid in gaseous and condensed form online. This allows us to account for feedbacks between different processes, which enables us to comprehensively assess the risks and benefits of SAI of solid particles. However, it has to be kept in mind that direct aerosol–cloud interactions are not considered in this model, which could alter the resulting radiative forcing through cirrus cloud feedbacks (e.g. Cziczo et al., 2019). In this study, we focus on the injection of alumina and calcite particles since these are some of the few potential particle types for which some heterogeneous reaction rates have previously been measured (Molina et al., 1997; Huynh and McNeill, 2020, 2021; Dai et al., 2020).

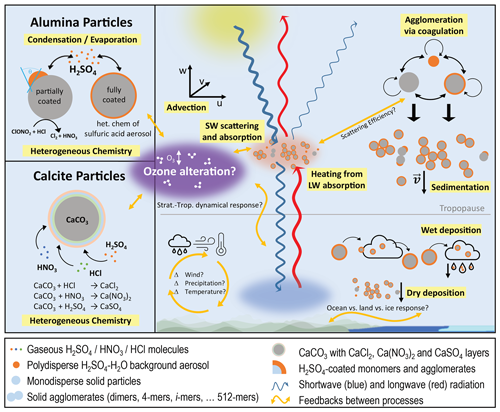
Figure 1 Schematic illustration of the different processes (yellow boxes) represented in the solid-particle microphysics model incorporated in SOCOL-AERv2 and SOCOLv4. The right side of the figure depicts processes relevant for solid particles in general (see Sect. 2.2), and the left side depicts specific processes relevant to alumina (upper part; see Sect. 2.3) and calcite (lower part; see Sect. 2.4) particles. Orange arrows represent the most important feedbacks between processes considered in the model.

2 Model description

The interactive coupling of aerosol microphysics with heterogeneous chemistry and radiation makes the SOCOL models (Feinberg et al., 2019; Sukhodolov et al., 2021) suitable to explore feedbacks between microphysics, stratospheric chemistry, radiation, and tropospheric and stratospheric climate. The SOCOL model family has been successfully used to reproduce the global sulfur cycle under volcanically active (e.g. Mt. Pinatubo 1991) and quiescent conditions (e.g. Sheng et al., 2015; Sukhodolov et al., 2018; Feinberg et al., 2019; Brodowsky et al., 2021; Quaglia et al., 2023; Brodowsky et al., 2024) as well as to evaluate impacts of sulfur-based SAI scenarios (Heckendorn et al., 2009; Vattioni et al., 2019; Weisenstein et al., 2022; Wunderlin et al., 2024), which makes them the tools of choice to evaluate SAI of solid particles. Despite the lack of in situ solid-particle measurements in the stratosphere to evaluate the solid-particle module presented here, the SOCOL models have been extensively evaluated against observations for climate (Stenke et al., 2013; Sukhodolov et al., 2021; Morgenstern et al., 2022), stratospheric chemistry (Friedel and Chiodo, 2022), background aerosol (Brodowsky et al., 2024) and volcanic aerosol (Sukhodolov et al., 2018; Clyne et al., 2021; Quaglia et al., 2023) in the past.

2.1 SOCOL-AERv2

SOCOL-AERv2 is based on the chemistry–climate model SOCOLv3 (Stenke et al., 2013), which consists of the middle atmosphere version of the spectral general circulation model ECHAM5 (Roeckner et al., 2003, 2006) and the chemistry transport model MEZON (Rozanov et al., 1999; Egorova et al., 2003). MEZON treats 89 gaseous species of the nitrogen, oxygen, carbon, chlorine, bromine and sulfur families, which are subject to ECHAM5.4 advection. The chemical solver of MEZON is based on the implicit iterative Newton–Raphson scheme (Ozolin, 1992; Stott and Harwood, 1993) and accounts for 16 heterogeneous, 58 photolysis and 160 gas-phase reactions, which represent the most relevant aspects of atmospheric chemistry. The sectional (size-resolved) aerosol-microphysics module of the chemistry transport model 2D-AER (Weisenstein et al., 1997, 2007) was then interactively integrated into the three-dimensional grid of SOCOLv3, resulting in the first version of SOCOL-AERv2 (Sheng et al., 2015, i.e. SOCOL-AERv1), which was later further updated by Feinberg et al. (2019, i.e. SOCOL-AERv2). SOCOL-AERv2 tracks sulfuric acid aerosols within 40 dry aerosol mass bins ranging from 2.8 molecules to 1.6×10¹² molecules corresponding to dry radii from 0.39 nm to 3.2 µm (assuming a density of 1.8 g cm⁻³), with the number of molecules doubling for subsequent bins. The wet aerosol properties are then calculated in every SOCOL grid box taking into account the H₂SO₄ weight percent as a function of relative humidity and temperature (Tabazadeh et al., 1997). AER calculates microphysical processes such as sulfuric acid aerosol formation from gaseous H₂SO₄ via nucleation (Vehkamäki et al., 2002) and condensation, as well as their evaporation (Ayers et al., 1980; Kulmala and Laaksonen, 1990). Coagulation of sulfuric acid aerosols is calculated using the semi-implicit method of Jacobson and Seinfeld (2004), while the coagulation kernel is calculated using the empirical formula of Fuchs (1964). Finally, sedimentation is treated based on Kasten (1968) adopting the numerical scheme of Walcek (2000), and aerosols are removed from the model via interactive calculation of wet and dry deposition (Tost et al., 2006, 2007; Kerkweg et al., 2006, 2009; Revell et al., 2018). In the stratosphere, the aerosol module is fully interactive. The aerosol number densities, the wet aerosol volume, the surface area density (SAD) and the H₂SO₄ weight percent of the aerosols resulting from AER are subsequently passed on to the heterogeneous chemistry scheme and to the RTC of SOCOL-AER, while in the troposphere, prescribed aerosol quantities are used for chemistry and radiative transfer calculations, and aerosol–cloud interactions are not accounted for.

The LW scheme of the RTC of ECHAM5.4 is based on the Rapid Radiative Transfer Model (RRTM; Mlawer et al., 1997) using the correlated-k method with a resolution of 16 bands in the spectral range from 10 to 3000 cm⁻¹. The shortwave code is based on Fouquart and Bonnel (1980) and has a spectral resolution of 6 bands ranging from 185 nm to 4 µm. While the short wave code accounts for scattering and absorption of radiation on aerosols, the RRTM only accounts for absorption and emission of radiation. Tabulated values of absorption and scattering efficiencies as well as asymmetry factors are used together with the model's aerosol number densities to calculate the scattering and absorption coefficients of the aerosol size distribution, which are then fed into the RTC of SOCOL-AERv2. The tabulated absorption and scattering efficiencies were calculated as a function of aerosol size, H₂SO₄ weight percent and spectral resolution based on Mie theory with refractive indexes from Yue et al. (1994) and Biermann et al. (1996).

The version of SOCOL-AERv2 used for this study has a vertical resolution of 39 sigma-pressure levels reaching up to 0.01 hPa (about 80 km altitude) and T42 horizontal resolution (2.8°×2.8°). The dynamical time step is 15 min, while chemistry is calculated every 2 h. The aerosol microphysics (nucleation, condensation and coagulation) is calculated with operator splitting by applying a loop of 20 iterations within the chemistry call every 2 h, making the microphysical time step 6 min. However, Vattioni et al. (2024) have shown that for enhanced H₂SO₄ supersaturations a microphysical time step of 6 min is not short enough. Therefore, we applied a microphysical time step of 2 min (60 subloops within the chemistry routine) for all SO₂ injection scenarios. Other processes relevant for aerosols such as wet and dry deposition and sedimentation, as well as calculations of aerosol quantities relevant for radiative transfer and heterogeneous chemistry such as SAD, pH and number densities are calculated and updated every 2 h.

The same solid-particle microphysics module was also incorporated in the fully coupled Earth system model (ESM) SOCOLv4 (Sukhodolov et al., 2021), a further development of SOCOL-AERv2 that is based on the CMIP6 version of MPI-ESM (Mauritsen et al., 2019). While SOCOL-AERv2 and SOCOLv4 share the chemistry and aerosol microphysics scheme, SOCOLv4 is based on ECHAM6 (Stevens et al., 2013), which incorporates an interactive ocean module (Jungclaus et al., 2013). Furthermore, it provides a finer resolution of the shortwave spectrum as well as a higher spatial resolution and a smaller dynamical time step, which makes it computationally much more expensive. This paper is based on SOCOL-AERv2, which uses prescribed sea surface temperatures and sea ice concentrations to study the effective radiative forcing as well as microphysics and impacts on heterogeneous chemistry, while SOCOLv4 will be used in the near future for studies on tropospheric climate impacts of solid-particle injections.

2.2 The interactive solid-particle microphysics module

For the representation of the solid particles, we use a similar sectional approach as for the sulfuric acid aerosols. Particles are always injected as monomers, which can grow to larger order agglomerates via coagulation (see Coagulation subsubsections). The injected monomer radius can be specified in the model via a namelist parameter and varies between 80 and 320 nm in this study to investigate trade-offs between agglomeration, sedimentation speed and backscatter efficiency of different injected monomer radii. To keep track of the monomers and their agglomerates, the solid particles are represented by different mass bins (i=1–10), with mass doubling between subsequent bins (i.e. monomers, 1-, 2-, 4-, 8-, 16-, 32-, 64-, 128-, 256- and 512-mers). Since coagulation is much more efficient for smaller particles, we only used all 10 solid-particle mass bins (up to 512-mer) for injections of particles with small monomer radii, while for radii larger than 200 nm, 5 mass bins (up to 16-mers) are sufficient due to minor agglomeration. The solid particles are fully interactive with the stratospheric sulfur cycle including sulfuric acid aerosols (see Coagulation and Condensation subsubsections). We also accounted for heterogeneous chemistry taking place on solid-particle surfaces (see “Heterogeneous chemistry” subsubsections) as well as for scattering and absorption of radiation (see Radiation subsubsection), which makes this the first fully coupled aerosol chemistry–climate model to simulate SAI of solid particles except for aerosol cloud interactions. The various processes, which are accounted for in the model, are depicted in Fig. 1 and described in detail in the following subsections. Since calcite and alumina particles differ significantly in their heterogeneous chemistry and microphysical interactions with sulfuric acid, we present two different model versions for the two particle types. While this section describes processes which apply to both calcite and alumina particles (see right part of Fig. 1), Sects. 2.3 and 2.4 present processes which only apply to alumina and calcite particles, respectively (see left part of Fig. 1).

2.2.1 Mobility radius

To represent processes such as the sedimentation and coagulation of agglomerates, the mobility radius of the agglomerates (r_m,i) is required (Spyrogianni et al., 2018). The mobility radii of alumina (ρ=3.98 g cm⁻³) and calcite (ρ=2.71 g cm⁻³) agglomerates, with primary particle radii of 5, 80 and 215 nm for alumina particles as well 5, 80 and 275 nm for calcite particles, were determined using a discrete element model (DEM) of particle motion and coagulation (Kelesidis and Kholghy, 2021). The model simulates the coagulation dynamics of nanoparticles and has been validated with experimental data from black carbon (Kelesidis et al., 2017a, b), zirconia (Eirini Goudeli and Pratsinis, 2016) and silica (Kelesidis and Goudeli, 2021) nanoparticles. Furthermore, it was recently interfaced with the discrete dipole approximation (Kelesidis and Pratsinis, 2019; Kelesidis et al., 2020, 2023) and global climate models (Kelesidis et al., 2022) to accurately estimate the direct radiative forcing from black carbon agglomerates. In brief, 1000 monodisperse alumina or calcite particles with initial number concentration of 10⁷–10¹⁴ cm⁻³ and radii of 5, 80, and 215 or 275 nm are randomly distributed in a cubic simulation box at constant pressure and temperature of 50 hPa and 240 K, respectively. Then, the particle motion and coagulation are derived using an event-driven method (Goudeli et al., 2015). That way, the evolution of the total number concentration (Sect. S1 and Fig. S1 in the Supplement) and size distribution (Fig. S2 in the Supplement) can be derived accounting for the realistic agglomerate structure. Furthermore, the agglomerate r_m,i can be obtained from its projected area, A_proj,i (Rogak et al., 1993):

$$\begin{array}{}\text{(1)}& r_{\mathrm{m},i}=\sqrt{{\displaystyle \frac{A_{\text{proj},i}}{\mathit{\pi }}}}.\end{array}$$

No significant differences in the resulting average mobility radius of the agglomerates could be observed within the modelled range of initial concentrations (see Figs. 2, S1 and S2). The mobility radii of other particle sizes (i.e. 160, 240 and 320 nm; see Sect. 3) can be linearly extrapolated from the radii resulting for 80, 215, and 275 nm particles. Further details on the DEM simulations can be found in the Supplement (Sect. S1 and Figs. S1 and S2). The representation of the particles with the mobility radius is an improvement compared to previous studies (e.g. Weisenstein et al., 2015, who used the radius of gyration assuming the same fractal dimensions of 1.6 or 2.6 for all agglomerates; see Fig. S3 in the Supplement), especially for representation of sedimentation and, thus, the resulting stratospheric aerosol burden. It should be noted that the agglomerate fractal dimension evolves during coagulation and attains its asymptotic value of 1.6–1.8 when agglomerates containing at least 15 monomers are formed (Goudeli et al., 2015). Thus, assuming constant fractal dimensions can result in an overestimation of the agglomerate number density and mobility radius (see Fig. S3, Kelesidis and Kholghy, 2021).

Figure 2 The averaged mobility radius of different agglomerates for calcite (blue) and alumina (red) particles with a primary particle radius of 80 nm as a function of initial concentrations modelled by a DEM. The averaged shape of agglomerates resulting from initial concentrations of 2×10¹² cm⁻³ is illustrated in dark blue.

However, these DEM simulations also showed that it could be challenging to reduce initial particle concentrations in an aircraft wake to levels that are small enough to avoid rapid agglomeration in an aircraft wake (see Fig. S2). Most simulations showed agglomerates size distributions peaking at agglomerates between 10¹ and 10³ primary particles per agglomerate after only 2 h, which would reduce scattering efficiencies as well as increase sedimentation speeds of the solid particles. However, these simulations neglected the effect of dilution, which could reduce number concentrations and, thus, coagulation. Nevertheless, the neglected injection plume processes at the sub-ESM grid scale remain one of the major limitations of most global models, including the one used in this study.

2.2.2 Sedimentation

The solid particles were integrated into the same sedimentation scheme as applied for sulfuric acid aerosols in SOCOL-AERv2, which is based on Kasten (1968) and Walcek (2000). Following Spyrogianni et al. (2018) we used the mobility radius for calculation of the terminal velocity. The terminal velocity of a falling particle in a fluid can be described with Stokes' law, when the Reynolds number is significantly smaller than 1 (Seinfeld and Pandis, 1997). This applies to falling submicrometre particles in the atmosphere. Assuming buoyancy is negligible, the terminal velocity is reached when the drag force (F_D, Eq. 2) and the gravitation force (F_G, Eq. 3) of a falling particle are in equilibrium (i.e. F_G=F_D).

$$\begin{array}{}\text{(2)}& {\displaystyle }{F}_{\mathrm{D}}={\displaystyle \frac{\mathrm{6}\mathit{\pi }{\mathit{\eta }}_{\text{air}}{r}_{\mathrm{m},i}}{\text{C}\left(r_{\mathrm{m},i}\right)}}{v}_{\mathrm{t},i}\text{(3)}& {\displaystyle }{F}_{\mathrm{G}}=m_{i}g={\mathit{\rho }}_{\mathrm{p}}i{\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}{r}_{\mathrm{0}}^{\mathrm{3}}g\end{array}$$

In Eqs. (3) and (2), m_i is the particle mass of mass bin i, g the gravitational constant, η_air the viscosity of air, ρ_p the density of the particle, r_m,i the mobility radius of the particle, C(r_i) the Cunningham correction of the particles in mass bin i and r₀ the monomer radius. Solving for v_t,i gives Eq. (4), which is used to calculate the sedimentation speed of the solid particles in the aerosol sedimentation scheme of SOCOL-AERv2 (Feinberg et al., 2019):

$$\begin{array}{}\text{(4)}& v_{\mathrm{t},i}={\displaystyle \frac{m_{i}g\text{C}\left(r_{\mathrm{m},i}\right)}{\mathrm{6}\mathit{\pi }{\mathit{\eta }}_{\text{air}}{r}_{\mathrm{m},i}}}.\end{array}$$

The resulting sedimentation speeds of solid particles and their agglomerates calculated in SOCOL-AERv2 are shown in Fig. S4 in the Supplement.

2.2.3 Wet and dry deposition

Solid particles are removed from the atmosphere via the same interactive wet and dry deposition schemes as used for sulfuric acid aerosols in SOCOL-AERv2, which were implemented and tested in Feinberg et al. (2019; see Sect. 2.1). Uptake of solid particles in cloud and rain droplets is calculated based on a mobility-radius-dependent calculation of nucleation and impaction scavenging. Solid particle mass released to the atmosphere after cloud evaporation is added back to the largest available solid-particle mass bin. Dry deposition velocities are calculated following the resistance approach by Wesely (1989) using the mobility radius (see Sect. 2.2.1) and the corresponding densities of the solid particles.

2.2.4 Radiation

To make the solid particles interact with the RTC, SOCOL-AERv2 requires a lookup table with the absorption and scattering efficiencies (Q_abs and Q_sca) normalized to the geometric cross section obtained from their volume equivalent radii (r_ve,i) as well as the asymmetry factor (g_asy) for all mass bins, i. The volume equivalent radius is given by

$$\begin{array}{}\text{(5)}& r_{\text{ve},i}=\sqrt[\mathrm{3}]{i{r}_{\mathrm{0}}^{\mathrm{3}}},\end{array}$$

where r₀ is the primary particle radius (i.e. monomer radius). While Q_abs, Q_sca and g_asy are required for all spectral SW bands, the LW bands only require the lookup table for Q_abs, since the RRTM (Mlawer et al., 1997) incorporated in SOCOL-AERv2 does not account for scattering in the LW spectral bands.

For the monomers these optical properties are calculated from Mie theory utilizing the solution of (Bohren and Huffman, 2008) for calcite and alumina particles, implemented with an open-source MATLAB code (Mätzler, 2002). For the aggregates the code developed by Rannou et al. (1999) was applied, which is a semi-empirical fit to a mean-field theory solution of the Maxwell equations for interaction of fractal agglomerates with electromagnetic waves. Both of these codes provide the full scattering phase function, although it is not utilized by SOCOL-AER's RTC. The required inputs for the monomer code are complex refractive index as a function of wavelength and monomer size, which were taken from Tropf and Thomas (1997) for alumina and from Ghosh (1999) and Long et al. (1993) for calcite. This is also consistent with Dykema et al. (2016). For the aggregates, the number of monomers comprising the aggregate and the fractal dimension is also required as an input. Within each SW radiative transfer model band, the optical scattering and absorption are weighted by the incident top-of-the-atmosphere (ToA) solar spectrum and averaged, whereas in the LW bands scattering is neglected and absorption is given as a simple average over each spectral band. The resulting Q_abs values for all spectral bands as well as Q_sca and g_asy for the SW bands, which were subsequently used in SOCOL-AERv2, are shown in Figs. S5 and S6 in the Supplement.

In SOCOL-AERv2 the scattering and absorption cross sections (σ_sca,i and σ_abs,i) of a particle in mass bin i is given by

$$\begin{array}{}\text{(6)}& {\mathit{\sigma }}_i=\mathit{\pi }{r}_{\text{ve},i}^{\mathrm{2}}{Q}_i.\end{array}$$

The scattering and absorption coefficients, ϵ_sca,i and ϵ_abs,i of each mass bin are then calculated via Eq. (7) by multiplying the cross sections of each mass bin by the number densities (N_i) of each mass bin. Summing up over all mass bins yields the total scattering and absorption coefficient (ϵ_sca and ϵ_abs) for each spectral SW band:

$$\begin{array}{}\text{(7)}& \mathit{ϵ}=\sum _{i=\mathrm{1}}^{\mathrm{10}}{\mathit{ϵ}}_i=\sum _{i=\mathrm{1}}^{\mathrm{10}}{N}_i{\mathit{\sigma }}_i.\end{array}$$

The extinction coefficient (ϵ_ext) and the single scattering albedo (ω_ssa) are given by Eqs. (8) and (9), respectively.

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathit{ϵ}}_{\text{ext}}={\mathit{ϵ}}_{\text{sca}}+{\mathit{ϵ}}_{\text{abs}}\text{(9)}& {\displaystyle }{\mathit{\omega }}_{\text{ssa}}={\displaystyle \frac{{\mathit{ϵ}}_{\text{sca}}}{{\mathit{ϵ}}_{\text{ext}}}}\end{array}$$

Additionally, the bulk asymmetry factor (g_asy) for the solid aerosol size distribution is calculated by the sum of each mass bin's asymmetry factor (g_asy,i) weighted by the corresponding scattering coefficient:

$$\begin{array}{}\text{(10)}& g_{\text{asy}}={\displaystyle \frac{\mathrm{1}}{{\mathit{ϵ}}_{\text{sca}}}}\sum _{i=\mathrm{1}}^{\mathrm{10}}{g}_{\text{asy},i}{\mathit{ϵ}}_{\text{sca},i}.\end{array}$$

Parameters derived from Eqs. (7) to (10) are then fed to the RTC of SOCOL-AERv2, where the absorption and the scattering due to solid particles are calculated for each spectral band.

For simplicity, the optical properties of the monomers comprising all particles were calculated assuming pure, un-aged materials (i.e. calcite or alumina) for interactions of the particles with radiation, although the model would allow optical properties to be applied as a function of particle ageing if data were available. We used the semi-empirical code of Rannou et al. (1999) to look at the change of the optical properties of alumina particles with a radius of 240 nm when assuming a 10 nm thick spherical sulfuric acid coating (a valid assumption; see Sect. 4.3) but found only very little change in scattering and absorption properties (not shown). However, for this calculation an effective medium approximation (i.e. using a volume-weighted function of the refractive indices of the constituent materials; Lesins et al., 2002) was applied to provide an effective refractive index for the alumina–sulfuric acid core–shell. This was necessary because the Rannou et al. (1999) code can only handle homogeneous spherical constituent monomers. Since composition changes of the particles resulting from the simulations in this study are only small (see Sect. 4), with only little impact on optical properties, we only accounted for the optical properties of bare calcite and alumina particles. Changes in optical properties as a result of composition changes of the solid particles through ageing processes such as uptake of HNO₃ on calcite particles resulting in formation of Ca(NO₃)₂ (see Sect. 2.4) or as a result of sulfuric acid uptake at the alumina particle surface (see Sect. 2.3) were not accounted for.

2.3 Alumina particles

Alumina particles are represented with two sets of prognostic variables, where each set represents 10 mass bins (see Sect. 2.2) for solid-particle monomers (mass bin 1) and agglomerates (mass bin 2 to 10) as well as an additional prognostic variable for the sulfuric acid coating of each alumina mass bin. One set of mass bins represents particles partially coated by sulfuric acid, while the other set represents particles fully coated by sulfuric acid. This results in a total amount of 4×10 additional prognostics variables for alumina particle representation, their agglomerates and their sulfuric acid coating. Particles are injected as spherical monomers with density ρ=3.98 g cm⁻³ and a molar weight of 101.1 g mol⁻¹ into the partially coated alumina monomer mass bin (mass bin 1). They can acquire a sulfuric acid coating via condensation of H₂SO_4(g) or via coagulation with sulfuric acid aerosols. When the coating mass per primary particle reaches a certain threshold (see Sect. 2.3.3, “Contact angle of H₂SO_4(aq) on solid particles”), they are moved to the fully coated mass bins.

2.3.1 Coagulation of alumina particles

The coagulation dynamics of solid particles and their interaction with sulfuric acid aerosols were integrated into the same semi-implicit coagulation schemes for sulfuric acid aerosols, presented in Sheng et al. (2015) and Feinberg et al. (2019; see subsection “SOCOL-AERv2”). Coagulation of solid particles and sulfuric acid aerosols are represented following the description in Weisenstein et al. (2015, see their Appendix A), with the only difference that here we do not account for pure solid particles and coated solid particles but for partially coated and fully coated particles (see Fig. 1). We account for self-coagulation of sulfuric acid aerosols, partially coated solid particles and fully coated sulfuric acid particles as well as coagulation between these three categories.

As already stated in Weisenstein et al. (2015), applying a discrete aerosol mass binning leads to an artificial broadening of the particle size distribution since coagulation would often result in agglomerates of sizes, which fall in between two mass bins. In these cases the resulting mass is split up between neighbouring mass bins by applying a statistical weighting (see Weisenstein et al., 2015, Appendix A). The resulting error depends on the coarseness of the bin spacing (Weisenstein et al., 1997, 2007), which is a mass doubling in the presented model. This is a good compromise between accuracy of representation and usage of computational resources (Weisenstein et al., 2015), since computational resources increase with every additional prognostic variable.

The coagulation kernel was calculated using the mobility radius for solid-particle agglomerates (see previous subsubsection “Mobility radius”) and the spherical radius for liquid sulfuric acid aerosols for every possible combination of collisions, i.e. self-coagulation between aerosol mass bins of every category (40 liquid sulfuric acid mass bins and 10 partially coated and 10 fully coated solid-particle mass bins), as well as coagulation between all mass bins of every aerosol particle category. The calculation of the coagulation kernel followed the same methodology as for sulfuric acid aerosols in SOCOL-AERv2 (see Sect. 2.1) and was implemented following Weisenstein et al. (2015, Appendix A). The representation used considers only Brownian coagulation with a sticking coefficient of 1, which is an upper limit but a reasonable assumption when considering the Van der Waal forces of submicrometre particles (Blackstock et al., 2009). Gravitational and convective coagulation are not considered as they are of minor importance for submicrometre particles (Weisenstein et al., 2015).

2.3.2 Condensation and evaporation of H₂SO₄

Condensation of H₂SO₄ on alumina particles and evaporation of H₂SO₄ from alumina particles were treated the same way as described in Weisenstein et al. (2015, Appendix A) following the methodology described in Jacobson and Seinfeld (2004). However, contrary to Weisenstein et al. (2015), we accounted for condensation of H₂SO₄, not only on fully coated but also on partially coated solid particles. The H₂SO₄ condensation rates on solid particles are calculated as a function of the SAD of solid particles, their number density, the molecular diffusion coefficient of H₂SO₄, the difference between the H₂SO₄ partial pressure and the H₂SO₄, equilibrium vapour pressure, and the primary particle radius of every agglomerate to account for the Kelvin effect. Evaporation of H₂SO₄ is represented with the same scheme as for condensation and occurs when the partial pressure of H₂SO₄ is smaller than the equilibrium vapour pressure of H₂SO₄, which mainly occurs above 35 km altitude.

2.3.3 Contact angle of H₂SO_4(aq) on solid particles

Vattioni et al. (2023b) measured the contact angle (θ) of H₂SO₄−H₂O on alumina surfaces as a function of weight percent and found θ to be 31 ± 7°. Therefore, in the model the sulfuric acid coating is represented by accounting for the contact angle, θ, of H₂SO₄−H₂O on alumina particles to differentiate between surface area covered by sulfuric acid and uncovered Al₂O₃ surface area on partially coated alumina particles. Figure 3a shows the basic geometry of a partial sphere from which equations were derived to calculate the share of the two types of surface area (Polyanin and Manzhirov, 2006). The volume of liquid sulfuric acid per monomer (V_liq) as well as the contact angle (θ) is known, and β can then be determined by inserting Eqs. (12)–(16) into Eq. (11; see Fig. 2c). In Eq. (11) V_p and V_l are the volumes of the partial spheres of the solid particle and the liquid sulfuric acid respectively (see Fig. 3a), while h is referring to the height of the missing part of the sphere, r to the radius of the partial spheres and c to the base radius of the partial spheres (see Fig. 3a) of liquid sulfuric acid (l) and the solid particle (p; see Fig. 3c).

$$\begin{array}{}\text{(11)}& {\displaystyle }{V}_{\text{liq}}=V_{\mathrm{l}}-V_{\mathrm{p}}={\displaystyle \frac{\mathit{\pi }}{\mathrm{6}}}{h}_{\mathrm{l}}(\mathrm{3}{c}^{\mathrm{2}}+h_{\mathrm{l}}^{\mathrm{2}})-{\displaystyle \frac{\mathit{\pi }}{\mathrm{6}}}{h}_{\mathrm{p}}(\mathrm{3}{c}^{\mathrm{2}}+h_{\mathrm{p}}^{\mathrm{2}})\text{(12)}& {\displaystyle }{h}_{\mathrm{l}}=r_{\mathrm{l}}-r_{\mathrm{l}}\left(\cos \right(\mathit{\theta }+\mathit{\beta }\left)\right)\text{(13)}& {\displaystyle }{h}_{\mathrm{p}}=r_{\mathrm{p}}-r_{\mathrm{p}}\left(\cos \right(\mathit{\beta }\left)\right)\text{(14)}& {\displaystyle }c=r_{\mathrm{p}}\sin \left(\mathit{\beta }\right)\text{(15)}& {\displaystyle }c=r_{\mathrm{l}}\sin (\mathit{\theta }+\mathit{\beta })\text{(16)}& {\displaystyle }{r}_{\mathrm{l}}={\displaystyle \frac{\sin \left(\mathit{\beta }\right)r_{\mathrm{p}}}{\sin (\mathit{\theta }+\mathit{\beta })}}\end{array}$$

The solid-particle surface area and the sulfuric acid surface area per solid-particle monomer can then be calculated with Eqs. (17) and (18).

$$\begin{array}{}\text{(17)}& {\displaystyle }{S}_{\text{liq}}=\mathit{\pi }(c^{\mathrm{2}}+h_{\mathrm{l}}^{\mathrm{2}})\text{(18)}& {\displaystyle }{S}_{\text{solid}}=\mathrm{4}\mathit{\pi }{r}_{\mathrm{p}}^{\mathrm{2}}-\mathit{\pi }(c^{\mathrm{2}}+h_{\mathrm{p}}^{\mathrm{2}})\end{array}$$

Figure 3 Schematic illustration of the representation of the contact angle of H₂SO₄ (depicted in orange) on alumina particles (depicted in grey). Panel (a) depicts the general geometry of a partial sphere with basic equations. The criterion for immersion is illustrated in panel (b). An additional molecule of H₂SO₄ acquired on this particle will lead to transfer of the particle mass to the fully coated mass bins. Panel (c) illustrates the quantities used for the equations used in the main text to determine the angle β (see Eqs. 11–16), which is then used to determine the sulfuric acid SAD and the alumina SAD (see Eqs. 17 and 18).

The liquid sulfuric acid volume of each mass bin is assumed to be equally distributed over all primary particles within one agglomerate, assuming that every primary particle hosts the same amount of sulfuric acid. The whole alumina and sulfuric acid coating mass is transferred to the fully coated mass bins as soon as β is larger than 90°, an arbitrarily but realistic criterion for immersion (see Fig. 3b). The fully coated mass bins assume the alumina particles to be equally spherical and fully covered by sulfuric acid (see Fig. 1).

2.3.4 Heterogeneous chemistry on alumina particles

The sulfuric acid SAD resulting from the partially coated alumina particles as well as the one from fully coated alumina particles is added to the total available sulfuric acid aerosol SAD, and the same heterogeneous chemistry is assumed to take place on this surface area as for sulfuric acid aerosols (Sheng et al., 2015). On alumina SAD of partially coated alumina particles, we accounted for Reactions (R1), (R2) and (R3):

$$\begin{array}{}\text{(R1)}& {\displaystyle }{\mathrm{ClONO}}_{\mathrm{2}}+\mathrm{HCl}& {\displaystyle }\to {\mathrm{Cl}}_{\mathrm{2}}+{\mathrm{HNO}}_{\mathrm{3}}\text{(R2)}& {\displaystyle }{\mathrm{ClONO}}_{\mathrm{2}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}& {\displaystyle }\to \mathrm{HClO}+{\mathrm{HNO}}_{\mathrm{3}}\text{(R3)}& {\displaystyle }{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}& {\displaystyle }\to \mathrm{2}{\mathrm{HNO}}_{\mathrm{3}}.\end{array}$$

Though Molina et al. (1997) measured uptake coefficients for Reaction (R1), their data are not representative of low stratospheric HCl partial pressures. To extrapolate the experimental data of Molina et al. (1997) to typical stratospheric values, we applied a Langmuir–Hinshelwood representation of adsorption and reaction as detailed in Vattioni et al. (2023b). For this study we used the scenario “dissociative γ, α=0.1” to calculate the uptake coefficient of ClONO₂ on alumina particles for Reaction (R1). Due to the lack of experimental data on other heterogeneous reactions we only accounted for Reactions (R2) and (R3) by assuming the same reaction rates as on sulfuric acid aerosols, which is an upper-limit estimate (Vattioni et al., 2023b).

2.4 Calcite particles

In contrast to alumina, calcite is alkaline and thus reactive towards the acids in the stratosphere. Therefore, calcite particle can change their composition by forming salts at the surface (Keith et al., 2016; Cziczo et al., 2019; Huynh and McNeill, 2020, 2021; Dai et al., 2020). This requires a different treatment than for alumina particles, which do not undergo compositional changes but only acquire a sulfuric acid coating at the surface.

2.4.1 Heterogeneous chemistry on calcite particles

For calcite particles the following heterogeneous reactions upon uptake of HCl, HNO₃ and H₂SO₄ are considered (Reactions R1–R3):

$$\begin{array}{}\text{(R4)}& {\displaystyle }{\mathrm{CaCO}}_{\mathrm{3}}+\mathrm{2}\mathrm{HCl}& {\displaystyle }\to {\mathrm{CaCl}}_{\mathrm{2}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{CO}}_{\mathrm{2}}\text{(R5)}& {\displaystyle }{\mathrm{CaCO}}_{\mathrm{3}}+\mathrm{2}{\mathrm{HNO}}_{\mathrm{3}}& {\displaystyle }\to \mathrm{Ca}({\mathrm{NO}}_{\mathrm{3}}{)}_{\mathrm{2}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{CO}}_{\mathrm{2}}\text{(R6)}& {\displaystyle }{\mathrm{CaCO}}_{\mathrm{3}}+{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}& {\displaystyle }\to {\mathrm{CaSO}}_{\mathrm{4}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{CO}}_{\mathrm{2}}.\end{array}$$

To keep track of the reaction products (Ca(NO₃)₂, CaCl₂ and CaSO₄) additional prognostic variables for all three products were implemented for every calcite mass bin, resulting in a total of 40 prognostic variables (4 species times 10 mass bins). The total number of molecules per particle is always the same, but depending on the uptake of acids they are either in the form of CaCO₃, Ca(NO₃)₂, CaCl₂ or CaSO₄. This changes the density of the particles (i.e. ${\mathit{\rho }}_{{\mathrm{CaCO}}_{\mathrm{3}}}=\mathrm{2.71}$ g cm⁻³, ${\mathit{\rho }}_{{\mathrm{CaSO}}_{\mathrm{4}}}=\mathrm{2.32}$ g cm⁻³, ${\mathit{\rho }}_{\mathrm{Ca}({\mathrm{NO}}_{\mathrm{3}}{)}_{\mathrm{2}}}=\mathrm{2.50}$ g cm⁻³, ${\mathit{\rho }}_{{\mathrm{CaCl}}_{\mathrm{2}}}=\mathrm{2.15}$ g cm⁻³) and therefore also their radius, which is accounted for in the model. As stated by Cziczo et al. (2019), this is a simplification since in reality the reaction products would form hydrates, which are less dense than their anhydrous forms, and likely also mixed salts.

Reactions (R4)–(R6) are treated as first-order reactions, resulting in the following mass balance for calcite and the reaction products:

$$\begin{array}{}\text{(19)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}\left[{\mathrm{CaCO}}_{\mathrm{3}}\right]}{\mathrm{d}t}}=& {\displaystyle }-\mathrm{0.5}\left[\mathrm{HCl}\right]k_{\mathrm{HCl}+{\mathrm{CaCO}}_{\mathrm{3}}}\\ {\displaystyle }& {\displaystyle }-\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\right]k_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}+{\mathrm{CaCO}}_{\mathrm{3}}}\\ {\displaystyle }& {\displaystyle }-\mathrm{0.5}\left[{\mathrm{HNO}}_{\mathrm{3}}\right]k_{{\mathrm{HNO}}_{\mathrm{3}}+{\mathrm{CaCO}}_{\mathrm{3}}}\end{array}\text{(20)}& {\displaystyle \frac{\mathrm{d}\left[{\mathrm{CaCl}}_{\mathrm{2}}\right]}{\mathrm{d}t}}=\mathrm{0.5}\left[\mathrm{HCl}\right]k_{\mathrm{HCl}+{\mathrm{CaCO}}_{\mathrm{3}}}\text{(21)}& {\displaystyle \frac{\mathrm{d}\left[\mathrm{Ca}({\mathrm{NO}}_{\mathrm{3}}{)}_{\mathrm{2}}\right]}{\mathrm{d}t}}=\mathrm{0.5}\left[{\mathrm{HNO}}_{\mathrm{3}}\right]k_{{\mathrm{HNO}}_{\mathrm{3}}+{\mathrm{CaCO}}_{\mathrm{3}}}\text{(22)}& {\displaystyle \frac{\mathrm{d}\left[{\mathrm{CaSO}}_{\mathrm{4}}\right]}{\mathrm{d}t}}=\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\right]k_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}+{\mathrm{CaCO}}_{\mathrm{3}}}.\end{array}$$

Values in brackets are the molecule number densities of the different species. The resulting CO₂ and H₂O from Reactions (R4) to (R6) are not tracked further since resulting quantities are very small compared to background concentrations of these species. For the calculation of heterogeneous chemistry, CaCO₃ molecules of all bins are summed up, but the resulting products are redistributed to the different size bins depending on the share of available SAD from each mass bin. The SAD is always assumed to be pure CaCO₃, which means that all reaction sites are always available for reaction. Therefore, no passivation occurs, but instead a constant uptake coefficient (γ) is applied to calculate the reaction rate (k) for Reactions (R4)–(R6) following Eq. (23), where $\stackrel{\mathrm{‾}}{v}$ is the thermal velocity of the molecule colliding with the surface (i.e. HCl, HNO₃ or H₂SO₄ in this case):

$$\begin{array}{}\text{(23)}& k={\displaystyle \frac{\mathit{\gamma }\stackrel{\mathrm{‾}}{v}\text{SAD}}{\mathrm{4}}}.\end{array}$$

For simplicity, we neglect temporal variation in the uptake coefficients. Therefore, the passivation effect of the surface must be accounted for via the uptake coefficient γ, which should be representative of the whole stratospheric lifetime of the calcite particles (about 1 year) and not only for the generally much larger initial reactive uptake on pure calcite particles such as those measured in Huynh and McNeill (2020, 2021). The setup presented here allows for sensitivity analysis of different processes such as varying the uptake coefficients and analysing the total uptake of HCl, HNO₃ and H₂SO₄ as well as the impact on stratospheric chemistry.

In this study we applied uptake coefficients of 10⁻⁴ and 10⁻⁵ for the uptake of HNO₃ (Reaction R5) and HCl (Reaction R4), respectively, following Dai et al. (2020), and an uptake coefficient of 1.0 for H₂SO₄ (Reaction R6), assuming that every collision of a H₂SO₄ molecule with a calcite particle results in immediate uptake and reaction to CaSO₄. Other heterogeneous chemistry on calcite particles is neglected.

2.4.2 Coagulation of calcite particles

Coagulation of calcite particles is calculated by the same schemes as for alumina particles. However, instead of tracking the sulfuric acid coating, the CaCO₃, Ca(NO₃)₂, CaCl₂ and CaSO₄ mass per bin is tracked. Additionally, coagulation of calcite particles with sulfuric acid aerosols is assumed to result in instantaneous and irreversible formation of CaSO₄ (same as Reaction R6).

3 Experimental setup

Each injection scenario (see Table 1) injected continuously between 30° S and 30° N at all longitudes at 54 hPa (∼20 km altitude). The baseline scenarios injected alumina and calcite particles at particle radii of 240 nm at a rate of 5 Mt yr⁻¹ (megatons per year). Additionally, we performed sensitivity analyses with respect to the injected particle radius, the injection rate and the sulfuric acid contact angle on alumina particles (see Table 1 for details). For comparison with sulfur-based SAI, different scenarios with injections of gaseous SO₂, as well as accumulation-mode aerosol of condensed H₂SO₄, assuming a log-normal distribution with a mean radius of 0.095 µm and a σ of 1.5, were also simulated (see Vattioni et al., 2019; Weisenstein et al., 2022; see Table 1 for details). The latter scenario assumes that an aerosol size distribution with a mean radius of 0.095 µm can be produced by injecting gaseous H₂SO₄ into an aircraft plume (Pierce et al., 2010; Benduhn et al., 2016; Vattioni et al., 2019; Weisenstein et al., 2022). The resulting aerosol size distribution could result in larger radiative forcing (RF), while simultaneously reducing some side effects such as ozone depletion compared to SO₂ injections. However, the underlying assumptions are subject to large uncertainty (Vattioni et al., 2019).

Table 1 Overview of the simulations performed in this study. Columns show the injected species, the injection rate, the injected primary particle radius and the contact angle where applicable. Scenarios injected continuously between 30° N and 30° S at 20 km altitude. The baseline configurations are marked in bold. n/a: not applicable.

All simulations are time slices spanning 20 years with all boundary conditions set to the year 2020. For sea surface temperatures (SSTs) and sea ice concentrations (SICs), a climatological 10-year (2010–2019) average seasonal cycle from the Hadley dataset was used (Kennedy et al., 2019), while concentrations of GHGs and ozone-depleting substances (ODSs) were taken from SSP5-8.5 (O'Neill et al., 2015) and WMO (2018), respectively. The first 5 years of each simulation served as a spin-up to equilibrate stratospheric aerosol burden. Hence, all SOCOL-AERv2 data shown in this study are 15-year averages. The boundary conditions follow the GeoMIP test-bed experiment “accumH2SO4”¹ except for injecting the absolute mass of each species and not the equivalent sulfur mass as well as for the boundary conditions following the year 2020 instead of 2040 (see also Weisenstein et al., 2022).

4 Results

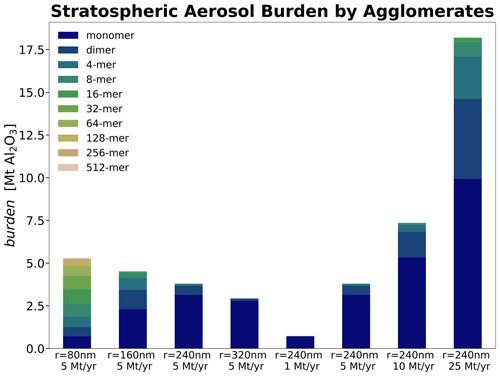
The stratospheric sulfur cycle is usually represented by sulfur equivalent burden (i.e. gigagrams of sulfur, Gg S), fluxes and injection rates (i.e. Gg S yr⁻¹) in both SAI and non-SAI studies (e.g. Feinberg et al., 2019; Weisenstein et al., 2022; Brodowsky et al., 2024). This allows easy comparison of burden and fluxes of different sulfur species. However, when comparing SAI scenarios with gaseous (e.g. SO₂), liquid (e.g. H₂SO₄−H₂O, i.e. sulfuric acid aerosols) and solid (e.g. CaCO₃ and Al₂O₃) species to each other, it is important to compare both the absolute burden and injection rates to allow for direct comparison (see Fig. 4). Thus, compared to the sulfur equivalent burden, the resulting H₂SO₄−H₂O burden is larger by a factor of about 3 when accounting for H₂SO₄ and another 40 %–50 % when accounting for the aerosol water content. Therefore, the resulting sulfuric acid aerosol burden reported in Fig. 4a is much larger compared to previous studies (e.g. Weisenstein et al., 2015), which compared the solid-particle burden and injection rates to sulfur equivalent quantities without accounting for H₂O. The comparison shown in Fig. 4a shows that, for a given injection rate, the resulting sulfuric acid burden is about a factor of ∼2 larger compared to the burden resulting from calcite and alumina particle injections. This is mainly due to the larger densities (i.e. 1.69 g cm⁻³ for 70 wt % H₂SO₄, 2.71 g cm⁻³ for CaCO₃ and 3.95 g cm⁻³ for Al₂O₃) as well as the larger particle radius for the solids, which makes them sediment much faster.

Figure 4 Resulting global stratospheric aerosol burden (a) and total net all-sky ToA RF (b) as a function of injection rate. Shown are absolute injection rates (i.e. Mt H₂SO₄ yr⁻¹ and SO₂ yr⁻¹ and not Mt S yr⁻¹) and absolute burden (i.e. the wet sulfuric acid burden in Mt H₂SO₄−H₂O and not Mt S).

The resulting globally averaged alumina particle burden for an injection of 5 Mt yr⁻¹ of 80, 160, 240 and 320 nm particles is 5.6, 4.7, 3.8 and 3.0 Mt, respectively, and therefore about one-third smaller compared to the ones found in Weisenstein et al. (2015). This is likely not a result of differences in sedimentation speeds between the models since our modelled sedimentation velocities are slightly smaller compared to the ones shown in Weisenstein et al. (2015; see Fig. S3) despite applying different representations of the agglomerate particle radius (see Sect. 2.2.1). However, compared to the original 2D-AER code used in Weisenstein et al. (2015), SOCOL-AERv2 has undergone several updates (e.g. Sheng et al., 2015; Feinberg et al., 2019; Vattioni et al., 2024). Most notably, updates include the replacement of the simple updraft sedimentation scheme by the numerical scheme of Walcek (2000) to reduce numerical diffusion, implementation of interactive wet and dry deposition schemes, and updates to the coagulation kernel. The difference in burden might also be affected by the three-dimensional representation of dynamics and transport in our model compared to the 2D-zonal mean representation in 2D-AER. The large number of differences between the two models makes it difficult to identify the specific processes which are responsible for the differences in results.

4.1 Radiative forcing efficiency

For the same injection rates we find that AM−H₂SO₄ injections result in the largest net all-sky ToA RF, slightly larger than CaCO₃ injections of 240 nm radius. Injecting SO₂ results in similar net ToA all-sky RF as for AM−H₂SO₄ for injection rates of 10 Mt yr⁻¹ and smaller. At very large injection rates of 25 Mt yr⁻¹, a non-linearity in the RF efficiency of SO₂ injections becomes apparent; SO₂ injections result in the smallest net ToA all-sky RF values compared to injections of the other species investigated in this study. This is mainly due to the unfavourable aerosol size distribution resulting from the large continuous H₂SO₄ condensation fluxes at large SO₂ injection rates, which shifts the aerosol size distribution towards larger particles, which decreases the total scattering cross section per resulting aerosol burden (Heckendorn et al., 2009; Vattioni et al., 2019; Weisenstein et al., 2022). The injection of Al₂O₃ particles of 240 nm radius results in about 25 % less net ToA all-sky RF compared to injections of AM−H₂SO₄ and CaCO₃ particles with radii of 240 nm across all the investigated injection rates. However, the injection of both Al₂O₃ and CaCO₃ particles results in larger RF per unit of stratospheric aerosol burden compared with the sulfur-based injection scenarios. Despite the larger aerosol burden in our model, the resulting net ToA all-sky RF shown in Fig. 4b is in agreement with the net clear-sky RF values found in Weisenstein et al. (2015). However, the largest net all-sky ToA RF is achieved with SAI of particles with 160 nm radius, which is in contrast with Weisenstein et al. (2015) for alumina particles, where the largest RF was obtained for injection of slightly larger particles of 240 nm radius.

4.2 Coagulation

Both the resulting stratospheric aerosol burden and the RF scale almost linearly with increasing injection rate for solid particles (see Fig. 4). This linearity is mainly due to the relatively small agglomeration found for the injected 240 nm particles even at large injection rates (see Fig. 5). This is likely different in scenarios which inject smaller particles (e.g. r=80 nm) or which apply larger injection rates and more confined injection regions. The fraction of monomers for injections of 5 Mt yr⁻¹ of 80, 160, 240 and 320 nm particles amounts to 13 %, 48 %, 82 % and 92 %, respectively, which is slightly more than what was found in Weisenstein et al. (2015). The more efficient formation of agglomerates in Weisenstein et al. (2015) could be due to the different representation of the radius of the agglomerates (see Sect. 2.2.1) or updates in the coagulation scheme (see subsection “Coagulation”). Aerosol size distributions for the scenarios injecting 5 Mt yr⁻¹ of particles with a radius of 240 nm can be found in Fig. S7 in the Supplement. For the model presented here, the only scenario resulting in significant agglomeration is the one injecting particles at 80 nm radius, where most of the particle mass is in the form of 16-mers (i.e. mass bin 5; see Fig. 5). However, these results are subject to large uncertainties due to lack of resolution of sub-ESM grid-scale plume injection processes (Blackstock et al., 2009). In the injection plume (e.g. of an aircraft), the particle concentrations would be significantly higher, which could result in effective agglomeration, whereas we only assume injections equally distributed to the grid of the climate model (i.e. about $\mathrm{325}\mathrm{km}\times \mathrm{325}\mathrm{km}\times \sim \mathrm{1.5}\mathrm{km}$ in SOCOL-AERv2 at the Equator at 50 hPa).

Figure 5 The resulting globally averaged stratospheric aerosol burden resolved for the contribution of the individual mass bins resulting from 5 Mt yr⁻¹ injection of 80, 160, 240 and 320 nm particles as well as 1, 5, 10 and 25 Mt yr⁻¹ injection of 240 nm particles.

4.3 The stratospheric sulfur cycle under conditions of SAI of alumina particles

Previous studies showed that injection of solid particles will likely result in uptake of sulfuric acid at the particle surface via coagulation with sulfuric acid aerosols and via condensation of gaseous sulfuric acid (Weisenstein et al., 2015; Keith et al., 2016). These processes are also represented in the model presented here (see Fig. 6). On the one hand, injecting 5 Mt yr⁻¹ of alumina particles will deplete the global stratospheric background sulfuric acid layer mass by 86 %, 69 %, 54 % and 45 % for injection of 80, 160, 240 and 320 nm particles, respectively (see Fig. 6). On the other hand, the mass of sulfuric acid coating on alumina particles reaches values of 78 %, 53 %, 35 % and 24 % of the unperturbed global stratospheric sulfuric acid aerosol burden, respectively (see Fig. S7 for resulting aerosol size distributions). The sum of the globally averaged stratospheric coating and sulfuric acid aerosol mass is smaller than the unperturbed stratospheric sulfuric acid aerosol burden, which is due to the faster removal via sedimentation of condensed sulfuric acid mass on heavier solid particles compared to sulfuric acid aerosols. Injection of 80 nm particles results in the largest coating mass of sulfuric acid; this is mainly due to the larger coagulation efficiency with sulfuric acid aerosols of small particles, as well as the larger surface area availability for condensation. The bigger fraction of sulfuric acid coating is acquired via direct condensation of H₂SO_4(g) in all scenarios. However, the share of acquisition via coagulation increases with decreasing alumina particle size from 18 % for 320 nm particle injection to 42 % for 80 nm particle injection. The same tendencies in the response of the stratospheric sulfur cycle to alumina injection can be observed when increasing the injection rate from 1 to 25 Mt yr⁻¹ (see Fig. S8 in the Supplement).

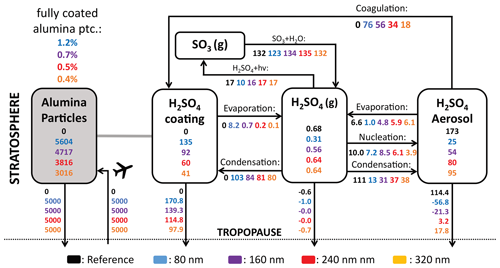
Figure 6 The global stratospheric sulfur cycle under conditions of SAI of 5 Mt yr⁻¹ alumina particles with radii of 80 (blue), 160 (violet), 240 (red) and 320 nm (orange). All sulfur species are shown in Gg S for burden (boxes) and Gg S yr⁻¹ for net fluxes (arrows). The alumina burden (grey box) is given as Gg Al₂O₃ and fluxes as Gg Al₂O₃ yr⁻¹. Cross-tropopause fluxes are calculated by balancing the mass balance of the individual species. The percentages in the upper left of the figure indicate the share of fully coated alumina particles from the global stratospheric alumina burden for each scenario.

When distributing the sulfuric acid coating (i.e. the total condensed H₂SO₄−H₂O mass on the alumina particles) equally on the alumina particles the corresponding coating thickness would reach values of maximal 6–10, 4–8, 7–14 and 8–16 nm for injections of 5 Mt yr⁻¹ of 80, 160, 240 and 320 nm particles in the lower stratosphere (see Fig. 7). Similar coating thicknesses can be found for different injection rates of particles with a radius of 240 nm (see Fig. S9 in the Supplement).

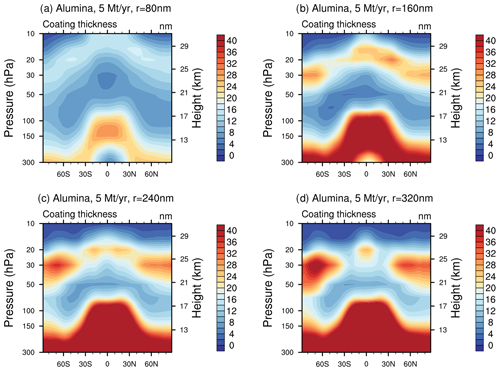
Figure 7 The resulting coating thickness when injecting 5 Mt yr⁻¹ of alumina particles with radii of 80 (a), 160 (b), 240 (c) and 320 nm (d). The values listed above correspond to the average coating thickness of the mass bin with the largest share of alumina burden (i.e. bin 5 for 80 nm particle injection and bin 1 for the others).

4.4 Contact angle sensitivity analysis

The sulfuric acid coating thickness on alumina particles shown in Fig. 7 is only representative if the sulfuric acid coating is distributed uniformly on the alumina particle surface, which is likely not true for the real system. In Vattioni et al. (2023b) we performed contact angle measurements of H₂SO₄ at different weight percentages, and we found a contact angle of about 31 ± 7° at 70 wt % H₂SO₄. This measurement is subject to large uncertainty, since the contact angle is dependent on factors such as the relative humidity and the temperature during the measurement as well as the surface characteristics (polished vs. unpolished, cleaned vs. uncleaned). However, the results show that H₂SO₄ is likely contracting on alumina surfaces, which would leave parts of the alumina surface uncovered from H₂SO₄−H₂O. Therefore, the sulfuric acid coating on alumina particles is represented by accounting for the contact angle in the model presented here (see Sect. 2.3.3). We have performed sensitivity simulations on the stratospheric ozone response from applying contact angles ranging from 15 to 60° as well as assuming the alumina particles to be fully coated by sulfuric acid (see Fig. 8).

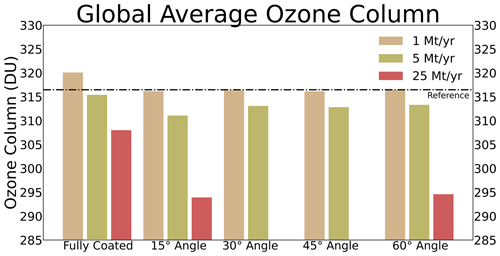
Figure 8 The resulting globally averaged total ozone column (TOC) from 1, 5, 10 and 25 M yr⁻¹ alumina injections when applying a H₂SO₄−H₂O contact angle of 15, 30, 45 and 60° as well as when assuming the alumina particles to be fully covered by sulfuric acid (coloured bars). Black line shows the TOC of the reference scenario.

This sensitivity analysis shows that particles assumed to be fully covered with sulfuric acid lead to smallest impacts on stratospheric ozone. This is mostly due to the relatively small resulting total SAD of alumina particles when injecting 5 Mt yr⁻¹ of particles with 240 nm radius (Fig. 10e). Depletion of background sulfuric acid aerosol SAD, which consists mostly of much smaller particles (size distribution peaking at r=80 nm; see Fig. S7), is compensated for by the additional alumina SAD covered by sulfuric acid. In the case of 1 Mt yr⁻¹ injections, this reduces the overall sulfuric acid SAD and thus even results in an increased global mean total ozone column (TOC). However, as discussed previously, complete coverage of alumina particles by sulfuric acid is unlikely. Therefore, it is more realistic to assume representation of sulfuric acid coating with the contact angle of H₂SO₄−H₂O on alumina surfaces. Applying a contact angle between 15 and 60° leads to higher ozone depletion, mainly due to the availability of uncoated alumina surface and the resulting chlorine activation (see subsubsection “Heterogeneous chemistry on alumina particles”). However, there are no significant differences between different contact angles (Fig. 8) since for all cases at least 50 % of the alumina surface will remain uncovered by sulfuric acid, and the sulfuric acid coating SAD does not significantly change when represented with contact angles of 15 or 60° (see Fig. 3). Therefore, we use the measured contact angle of 30° for the representation of the sulfuric acid coating on alumina particles. This is a valid assumption given the small coating thickness.

4.5 The stratospheric sulfur cycle under conditions of SAI of calcite particles

For the injection of calcite particles, the depletion of the background sulfuric acid aerosol layer, as well as condensation and coagulation fluxes on calcite particles, is very similar compared to the injection of alumina particles (Fig. 9). The only difference compared to alumina particles is that sulfuric acid on calcite particles is immediately assumed to undergo irreversible reaction with CaCO₃ to form CaSO₄. This results in depletion of the background stratospheric sulfuric acid aerosol layer of 90 %, 72 %, 53 % and 38 % for injection of particles with a radius of 80, 160, 240 and 320 nm, respectively (see Fig. 9). The resulting globally averaged CaSO₄ burden varies between 90 and 296 Gg for 80 and 320 nm particles, respectively. This corresponds to only 4.1 % and 2.3 % of the entire stratospheric calcite burden, respectively. At the same time the uptake of HCl with a uptake coefficient of 10⁻⁵ results in a CaCl₂ burden of 2 and 24 Gg for 320 and 80 nm particle injections, respectively, which is 0.05 % and 0.3 % of the resulting total globally averaged stratospheric calcite burden. The biggest fraction other than CaCO₃ comes from calcium nitrate, which results from uptake of HNO₃ at an uptake coefficient of 10⁻⁴. The Ca(NO₃)₂ burden is between 65 and 456 Gg for 80 and 320 nm particle injection, respectively, accounting for 1.6 % and 6.3 % of the resulting total globally averaged stratospheric calcite burden, respectively (see Sect. S6 and Fig. S10 in the Supplement for sensitivity to injection rate). Therefore, between 89 % and 96 % of the calcite burden will remain unchanged in the form of CaCO₃ during the entire stratospheric residence time for injection of 80 nm particles and 320 nm particles, respectively. Thus, the scattering and absorption properties of the calcite particles are unlikely to change significantly due to ageing processes. However, the ageing has significant consequences for heterogeneous chemistry on the particle surfaces, since these salts might host different heterogeneous reactions at different reaction rates. The sensitivity analysis of the role of heterogeneous chemistry of calcite particles using this model will be topic of another publication.

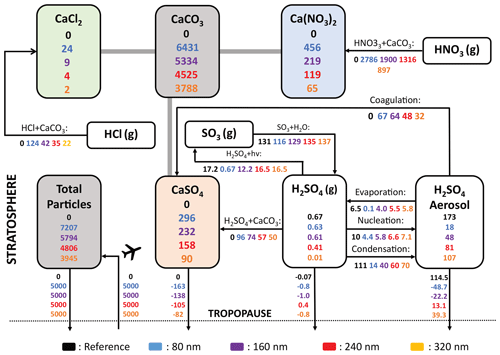
Figure 9 The stratospheric sulfur cycle under conditions of SAI of 5 Mt yr⁻¹ calcite particles with radii of 80 (blue), 160 (violet), 240 (red) and 320 nm (orange). All sulfur species (except CaSO₄) are shown in Gg S for burden (boxes) and Gg S yr⁻¹ for net fluxes (arrows). The solid species (coloured boxes) are given in Gg of the corresponding material. The HNO₃ and HCl flux to Ca(NO₃)₂ and CaCl₂ are given in Gg HNO₃ yr⁻¹ and Gg HCl yr⁻¹. Cross-tropopause fluxes are calculated by balancing the mass balance of the individual species.

4.6 Solid-particle number concentrations and surface area densities

The resulting solid-particle number concentrations reach values of up to 7 particles cm⁻³ in the lower stratosphere when injecting 5 Mt yr⁻¹ of alumina particles with a radius 240 nm (Fig. 10b). For 25 Mt yr⁻¹ of 240 nm particles or 5 Mt yr⁻¹ of particles with 80 nm radius, these number concentrations reach values of up to 30 and 80 particles cm⁻³, respectively (see Fig. 10a and c; see Fig. S11 in the Supplement for corresponding resulting number densities from calcite injections). This is a substantial perturbation to the otherwise relatively clean air in the lower stratosphere and in the upper troposphere, with background sulfuric acid aerosol number concentrations of about 10 cm⁻³ (Thomason and Peter, 2006) and ice nuclei concentration in the range of 10⁻¹ to 10⁻⁴ cm⁻³ (DeMott et al., 2010). The injected particles will likely influence cirrus and polar stratospheric cloud abundances (e.g. Cziczo et al., 2019), an effect not accounted for by the model presented here. However, we account for heterogeneous chemistry on alumina and calcite surfaces (see “Heterogeneous chemistry” subsubsections). The total sulfuric acid SAD (i.e. sum of sulfuric acid coating and sulfuric acid aerosols) for injection rates of 5 and 25 Mt yr⁻¹ alumina particles with 240 nm radius is not significantly different from the sulfuric acid aerosol SAD of the reference simulation (see Fig. 10h and i and also Sect. 4.4). This is mostly due to the small angle β for a constant contact angle (θ) when the amount of sulfuric acid volume is small compared to the solid-particle volume (i.e. for large alumina burden and large primary particle radius, see Fig. 3). When injecting 5 Mt yr⁻¹ of 80 nm particles, β gets much larger, and so does the sulfuric acid surface area per particle too (see Fig. 10g). The alumina particle number density and SAD increase linearly with injection rate when keeping the radius constant. For the same injection rate, the number density is inversely proportional to the radius with a cubic power law, while the SAD increases linearly with decreasing particle radius, as observed in Fig. 10a–f.

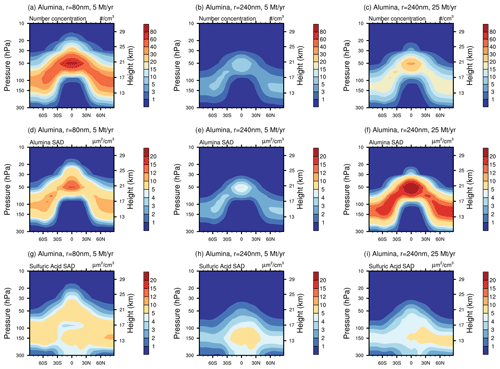
Figure 10 The resulting zonal mean number densities (a–c), alumina SAD (d–f) and total sulfuric acid SAD (sum of sulfuric acid aerosols SAD and SAD from sulfuric acid coating on alumina particles, g–i) from injection of 5 Mt yr⁻¹ of particles with 80 nm (a, d, f), 5 Mt yr⁻¹ of particles with 240 nm particles (b, e, h) and 25 Mt yr⁻¹ of particles with 240 nm radius (c, f, i). The same figure for calcite particles is shown in Fig. S11.

4.7 Ozone response to calcite and alumina particle injection

The resulting SAD presented in the previous section (see Fig. 10) results in TOC depletion, which mainly correlates with the available alumina SAD (see Fig. 11). Under present-day ODSs, injection of 5 Mt yr⁻¹ of 80 nm particles and injection of 25 Mt yr⁻¹ of 240 nm particles both result in TOC depletion of more than 4 % in the tropics and up to 16 % and 12 % in the polar regions, respectively. The baseline scenario, which injected 5 Mt yr⁻¹ of alumina particles with a radius of 240 nm, only resulted in TOC depletion of less than 2 % across all latitudes. Only the injection of 5 Mt yr⁻¹ of alumina particles of 320 and 240 nm radius results in a smaller TOC depletion compared to the sulfur-based scenarios. The resulting RF from injection of alumina particles of this size is about 25 %–33 % smaller compared to the sulfur-based scenarios at the same injection rates (see Fig. 4b). For injection of 5 Mt yr⁻¹ of alumina particles with a radius of 160 nm, the TOC depletion is only slightly enhanced compared to the sulfur-based scenarios (Fig. 11a), while resulting only in about 10 % reduced RF compared to the sulfur-based scenarios (see Fig. 4b). When injecting 25 Mt yr⁻¹ of alumina particles with a radius of 240 nm the ozone depletion is 50 % larger compared to the injection of SO₂ (see Fig. 11). However, these results are subject to large uncertainty (see Vattioni et al., 2023b) due to the lack of experimental data on heterogeneous chemistry on alumina particles.

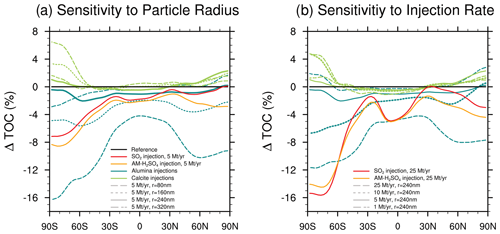
Figure 11 The simulated zonal mean total ozone column (TOC) anomaly resulting from (a) injecting 5 Mt yr⁻¹ of alumina and calcite particles with radii of 80, 160, 240 and 320 nm as well as 5 Mt yr⁻¹ injections of SO₂ and AM−H₂SO₄ and (b) injecting 1, 5, 10 and 25 Mt yr⁻¹ calcite and alumina particles at radius of 240 nm as well as 25 Mt yr⁻¹ SO₂ and AM−H₂SO₄ injections.

All calcite injection scenarios result in an increase in TOC in the polar regions of up to about 6 % but almost no change at midlatitudes under present-day ODSs. This is mostly due to the removal of HCl from the stratosphere on calcite particles in agreement with the findings of Dai et al. (2020). However, the uptake of HCl, HNO₃ and H₂SO₄ (Reactions R4–R6) is the only heterogeneous chemistry process considered on calcite particles, which is a simplification. The resulting products will likely form hydrates (Cziczo et al., 2019), which may host other heterogeneous reactions such as Reactions (R1)–(R3); our study only considers them on alumina particles. However, there are no experimental data on such reactions available for calcite surfaces, which makes the modelled response of the stratospheric ozone layer to calcite particle injections highly uncertain.

5 Conclusions

This study presents the first aerosol–chemistry–climate model incorporating an interactive solid-particle microphysics scheme to investigate the risks and benefits of SAI of solid particles. The solid particles considered in this study are fully interactive with the stratospheric sulfur cycle. The model also allows for uptake of sulfuric acid at the particle surface via coagulation with sulfuric acid aerosols and condensation of H₂SO_4(g) on the particle surfaces, as well as for the formation of agglomerates via coagulation of solid particles. The solid particles are subject to advection, sedimentation, and interactive wet and dry deposition in the troposphere. Furthermore, the model allows for representation of heterogeneous chemistry on the particle surface and, in particular, for the representation of the radiative effects of the particles, even after their microphysical interactions. The modular design of the model allows the coupling of individual processes to be switched on and off, which makes it perfectly suited to investigating the sensitivity and importance of the different processes relevant for the assessment of the risks and benefits of SAI of solid particles.

While this model was primarily developed for the evaluation of potential SAI scenarios of calcite and alumina injections, the model could also be adapted for representation of any other potential particle type or even for other applications. This could, for example, be the re-evaluation of radiative and chemical impacts of alumina particles emitted to the atmosphere from solid fuel space shuttle rocket launches, which will likely increase significantly in the future (Jackman et al., 1998; Danilin et al., 2001; Ross and Sheaffer, 2014); the evaluation of the growing impacts of microplastic nanoparticles transported in the atmosphere (Revell et al., 2021); analysis of wildfire impacts on stratospheric ozone (Solomon et al., 2023); and analysis of the role of meteoritic dust in the upper atmosphere (Biermann et al., 1996).

Using the model documented here, we show that the injection of solid particles likely results in significantly smaller stratospheric aerosol burden compared to the same injection rate of SO₂ and AM−H₂SO₄, even when injecting small particles with a radius of 80 nm. This is mainly due to more than half of the resulting sulfuric acid aerosol burden already being in the stratosphere without the need for lifting it up. The injected SO₂ is oxidized to H₂SO₄ in situ in the stratosphere, which subsequently forms sulfuric acid aerosols via nucleation and condensation with an average weight percent of about 60 % (i.e. 60 wt % H₂SO₄−H₂O). Therefore, the corresponding net all-sky ToA RF is largest for sulfur-based injection scenarios when injecting the same amount of material per year (see Fig. 4). Thus, alumina and calcite particles injected at a radius of 240 nm are only more effective in backscattering solar radiation per resulting aerosol burden but not per injection rate of material.

Furthermore, we show that injection of solid particles to the stratosphere would deplete the stratospheric background sulfuric acid aerosol layer by more than 50 % when injecting 5 Mt yr⁻¹ of particles at 240 nm radius or smaller. Alumina particles would acquire a sulfuric acid coating through condensation of gaseous sulfuric acid on the particle surface and through coagulation of sulfuric acid aerosols with solid particles. The acquired sulfuric acid coating would have the equivalent thickness of about 10 nm if equally distributed over the resulting alumina SAD when injecting particles at 5 Mt yr⁻¹ with radii of 240 nm. The resulting coating thickness would be smaller when increasing the injection rate due to a larger ratio of alumina SAD to sulfuric acid. However, a sulfuric acid coating distributed homogeneously over the alumina particles is unlikely due to a rather steep contact angle of about 30° of sulfuric acid on alumina surfaces (Vattioni et al., 2023b). Thus, it is likely that some of the alumina surface would also be available for heterogeneous chemistry.

Therefore, the response of TOC from alumina particle injections is largely dependent on the resulting alumina SAD, which is a function of the alumina injection rate and the injected particle size. While for small injection rates a large fraction of the alumina particles would be covered by sulfuric acid, for large injection rates this fraction decreases significantly when assuming injection of alumina particles with radii of 240 nm. We assumed a realistic parameterization from Vattioni et al. (2023b, dissociative, HCl only with ${\mathit{\alpha }}_{{\mathrm{ClONO}}_{\mathrm{2}}}=\mathrm{0.1}$) for the heterogeneous reaction of ClONO₂ with HCl (Reaction R1) on alumina SAD and the same heterogeneous chemistry on sulfuric acid coating as on sulfuric acid aerosols to quantify the expected TOC alteration from alumina particle injections under present-day ODS concentrations. Compared to the same injection rate of sulfuric acid aerosols, the resulting response of the zonal mean TOC from injection of alumina particles is only smaller for small injection rates or large injected particle radii (see Fig. 11).

For the injection of calcite particles we find similar perturbations to the stratospheric sulfur cycle as for alumina particles. However, the sulfuric acid taken up on calcite particles would react to CaSO₄. Assuming uptake coefficients of 10⁻⁴ for HNO₃ and 10⁻⁵ for HCl following Dai et al. (2020), 92 % of average solid-particle burden would remain in the form of CaCO₃ at injection rates of 5 Mt yr⁻¹ CaCO₃ under present-day ODSs. This would likely not change the scattering properties of calcite particles but could significantly alter heterogeneous chemistry hosted on the particle surface. Accounting for the uptake of HCl, HNO₃ and H₂SO₄ alone is not expected to alter stratospheric ozone significantly. However, heterogeneous chemistry on solid particles is not yet very well constrained due to the lack of experimental and observational data, which introduces substantial uncertainty on the ozone response of solid particles.

The two biggest limitations of the model which result in major uncertainty of the presented results are the (1) missing interactions of the solid particles with clouds, such as PSCs and cirrus clouds, and (2) the missing sub-grid-scale microphysical injection plume-scale processes. Solid particles could serve as ice condensation nuclei for cirrus clouds in the upper troposphere after re-entry to the troposphere via sedimentation. Altering the cirrus cloud thickness could result in a strong positive (cirrus cloud thickening) or a negative (cirrus cloud thinning) feedback on climate (Cziczo et al., 2019). Furthermore, the effect of solid particles on PSCs is unclear, but theoretically, the solid particles could also serve as cloud condensation nuclei for PSCs. It is only speculation whether this would result in overall fewer, but larger, or more, but smaller, PSCs. The latter case could, for example, result in less denitrification over the winter poles, which would result in less ozone depletion. This increases uncertainty of impacts on stratospheric ozone even more.

The second major limitation concerns the dispersion methods within the stratosphere (see also Blackstock et al., 2009). In contrast to a gas like SO₂, solid particles cannot easily be released to the stratosphere. They might require a carrier gas or a carrier liquid, which could add further perturbation to stratospheric composition. Furthermore, the DEM simulations presented in this study (see Sect. S1) show that it could be challenging to release solid particles to the stratosphere without immediate agglomeration. However, processes such as wind speed, turbulence, dilution and Van der Waals forces could affect coagulation efficiencies. On the one hand, this could result in rapid formation of big agglomerates, which significantly reduce the stratospheric residence time as well as the backscattering efficiencies of the particles. On the other hand, particles could spend more time as monomers if collision speeds in the turbulent plume overcome the large Van der Waals forces of small particles. This limitation poses major uncertainty to the results presented here, and it can only be addressed via injection plume modelling at the sub-grid scale or through experimental research or small-scale field experiments such as those proposed in Dykema et al. (2014).

With this study, we have shown that our model can be a useful tool to explore the risks and benefits of SAI of solid particles. However, the results are still uncertain due to a number of limitations, such as a lack of experimental data needed to refine the parameterizations of microphysical processes and heterogeneous chemistry. Despite this process uncertainty, there is potential for SAI of alumina and calcite particles to carry fewer side effects compared to sulfur-based SAI, but the environmental risks are still poorly understood. This is in agreement with Arias et al. (2021, IPCC, AR6, WG1, Chap. 4, p. 628), who state the following: “Injection of non-sulfate aerosols is likely to result in less stratospheric heating and ozone loss”. Moreover, we confirm the conclusions of the latest ozone assessment report (WMO, 2022) highlighting the existing uncertainties. We recommend conducting further experimental research, as well as the integration of solid-particle schemes into other Earth system models, to allow for more comprehensive assessment of the climate feedbacks and environmental risks.