Advances and prospects of deep learning for medium-range extreme weather forecasting

In recent years, deep learning models have rapidly emerged as a stand-alone alternative to physics-based numerical models for medium-range weather forecasting. Several independent research groups claim to have developed deep learning weather forecasts that outperform those from state-of-the-art physics-based models, and operational implementation of data-driven forecasts appears to be drawing near. However, questions remain about the capabilities of deep learning models with respect to providing robust forecasts of extreme weather. This paper provides an overview of recent developments in the field of deep learning weather forecasts and scrutinises the challenges that extreme weather events pose to leading deep learning models. Lastly, it argues for the need to tailor data-driven models to forecast extreme events and proposes a foundational workflow to develop such models.

1 Introduction

The very first deep learning models for weather applications date back to the 1990s (Schizas et al., 1991; Hall et al., 1999), and extensive research on the use of deep learning models for weather forecasting at a local scale (e.g. Zhu et al., 2017; Li et al., 2018; Haidar and Verma, 2018) and for short-term weather predictions (e.g. Klein et al., 2015; Qiu et al., 2017) has been ongoing since the mid-2010s. More recently, deep learning models have also been employed successfully as a nowcasting tool for precipitation (e.g. Ravuri et al., 2021; Espeholt et al., 2021) and as post-processing tools for numerical weather forecasts (e.g. Grönquist et al., 2021; Silini et al., 2022). However, it has only been in the last few years that deep learning models have started to become competitive as self-standing medium-range and subseasonal large-scale forecasting tools. As late as 2021, in a popular review article, Schultz et al. (2021) noted how deep learning research in the field of meteorology “is still in its infancy” and underscored that “a number of fundamental breakthroughs are needed” before deep learning applications may compete with physics-based weather forecasts.

Much has changed since then. From early 2022, at least seven different research groups (Pathak et al., 2022; Bi et al., 2023; Keisler, 2022; Lam et al., 2023; Chen et al., 2023a; Nguyen et al., 2023; Chen et al., 2023b) claim to have developed deep learning models able to forecast key atmospheric variables with greater accuracy than deterministic forecasts from the European Centre for Medium-Range Weather Forecasts (ECMWF), which are widely regarded as the leading global numerical weather predictions. In addition to technical advances, a key contextual enabler of this explosive development has been the contribution of “Big Tech” – major private actors in the field of information technology (Bauer et al., 2023). This has contributed to closing the gap between state-of-the-art deep learning, cutting-edge computational resources, and weather practitioners, and it has attracted a larger number of machine learning experts to the field. Although only one of several developments within machine learning, we argue for a crucial role of Big Tech in the advent of the latest generation of large-scale deep learning weather forecast models, which notably require larger computational resources and more specialised knowledge than previous state-of-the-art models (Bi et al., 2023; Lam et al., 2023).

Despite this astounding rise, deep learning models for weather forecasting still face a number of challenges. Some of these are well known. For example, deep learning approaches typically do not incorporate physical constraints (Ren et al., 2021), which may lead to unphysical forecasts. Furthermore, deep learning models usually produce deterministic forecasts, making it hard to compute reasonable estimates of the uncertainty around their predictions (Schultz et al., 2021). A less-studied challenge is that data-driven models have limited capabilities with respect to extrapolating at the edge of their training range or beyond (Gutzwiller and Serno, 2023). Thus, these models may not be as helpful as numerical models for investigating future climates (Scher and Messori, 2019a) and, more prominently, might struggle with forecasting extreme weather events lying in the tails of a meteorological variable's distribution (Watson, 2022). If unaddressed, the latter limitation is likely to hold back deep learning models from becoming a credible alternative to numerical, physics-driven forecasting models. Indeed, accurate predictions and early warnings of extreme weather play a key role in disaster prevention and mitigation (World Meteorological Organization, 2022; Merz et al., 2020) and are crucial for several economically prominent activities, including but not limited to the energy and insurance sectors (e.g. Kron et al., 2019). Nonetheless, the pace of development of deep learning weather prediction models continues to be rapid, and a number of promising approaches are being developed to address the above challenges (e.g. Hu et al., 2023; Bi et al., 2023; Zhang et al., 2023; Cisneros et al., 2023; Guastavino et al., 2022; Clare et al., 2021; Kashinath et al., 2021).

This article reflects on the rise of medium-range weather forecasting with deep learning, the challenges currently being faced when forecasting extreme weather, and the future perspectives opened by the latest research advances. We do not consider in detail issues related to computing forecast uncertainty estimates (Scher and Messori, 2021; Clare et al., 2021) or incorporating physical reasoning in deep learning models (Kashinath et al., 2021; Beucler et al., 2020), for which we remand the reader to some recent review articles discussing these topics (Molina et al., 2023; de Burgh-Day and Leeuwenburg, 2023). We begin with a survey of recent developments in the field of large-scale deep learning weather prediction (DLWP), with a focus on the aforementioned models claiming to outperform deterministic state-of-the-art numerical weather prediction models (Pathak et al., 2022; Keisler, 2022; Bi et al., 2023; Lam et al., 2023; Chen et al., 2023a; Nguyen et al., 2023; Chen et al., 2023b). Then, we provide a technical justification of why those models might struggle with predictions in the tails of the distribution, namely, weather extremes. Last, we outline alternative approaches that may be employed in order to design deep learning models specifically tailored to extreme weather forecasting.

2 Overview of DLWP models

2.1 Early DLWP efforts

The very first DLWP models were developed in the 1990s (Schizas et al., 1991; Hall et al., 1999) and followed a “feed-forward architecture” (Ivakhnenko and Lapa, 1965), a unidirectional, non-recurrent structure in which the input is transmitted through the network sequentially. Feed-forward neural networks (FNNs) are limited in treating spatial data, due to their inability to leverage spatial patterns and their large computational burden, which makes them unsuitable for large datasets. For these reasons, FNNs were soon replaced by convolutional neural networks (CNNs; LeCun and Bengio, 1995), which can learn spatial patterns and display better scalability. Early meteorological applications of CNNs had either a very local character (Zhu et al., 2017; Li et al., 2018; Haidar and Verma, 2018) or were aimed at producing nowcasts with lead times from a few minutes to a few hours (Klein et al., 2015; Qiu et al., 2017).

A further step in the direction of today's medium-range DLWP models was taken with the adoption of recurrent neural network (RNN) architectures (Rumelhart et al., 1986; Bengio et al., 1994; Bengio and Gingras, 1995) and, subsequently, long short-term memory (LSTM) models (Hochreiter and Schmidhuber, 1997). These follow the dynamical nature of time-series data by making current observations of the variable of interest depend on previous iterations of that same variable. Thus, they provide an effective framework for accounting for time dependencies in the data and produce predictions on multiple timescales. However, due to their sequential, recursive nature, RNNs and LSTMs are hard to parallelise, preventing an effective exploitation of modern high-resolution climate reanalysis datasets, such as ERA5 (Hersbach et al., 2020).

FNNs, CNNs, and RNNs/LSTMs are the cornerstones of deep learning and were also the dominant supervised learning architectures within DLWP at the time that the review by Schultz et al. (2021) was written. Since then, a number of new architectures have been developed that address the limitations of the classical models via a number of creative innovations, often combining different elements of pre-existing architectures. Here, we focus primarily on those deep learning applications that are most relevant to medium-range, large-scale forecasting of weather extremes. Nonetheless, we acknowledge that data-driven nowcasting and subseasonal forecasting are both thriving fields of research with many potential applications, including for extreme events (e.g. Chkeir et al., 2023; Barnes et al., 2023; Civitarese et al., 2021).

2.2 State-of-the-art DLWP

A common element of current global medium-range DLWP models is the use of a large number of input variables (“features”) at a high temporal and spatial resolution. This is in contrast to older models that, to a large extent, relied on a theoretical understanding of atmospheric dynamics and feature selection for the choice of a few atmospheric variables and pressure levels (e.g. Dueben and Bauer, 2018; Weyn et al., 2019). For example, Lam et al. (2023) include 6 input variables on 37 pressure levels, 5 inputs at single levels, and several constant masks. Similarly, Bi et al. (2023) make use of 4 atmospheric variables at 13 pressure levels, 4 surface variables, and 3 constant masks.

The fact that the latest DLWP models make use of a larger number of features than prior models may be partly ascribed to (1) computational improvements and (2) deep learning architectural developments. A key factor in this respect is the encoder–decoder architecture (Kramer, 1991; Cho et al., 2014). Encoders and decoders can be seen as two separate neural networks connected to each other through a latent encoding vector. Here, “latent” refers to quantities inferred indirectly from the input data. The aim of the first network is to identify and compress (“encode”) into the encoding vector the most important features contained in the input data. The aim of the second network is to upscale (“decode”) the information encoded in the encoding vector until it reaches the dimensionality of the desired output. The target output can then either be the same as the input, perhaps with some small variation (self-supervised problems, e.g. variational autoencoders), or different from the input in terms of timescale, spatial resolution, or even actual features.

In DLWP, the target output is usually different from the input, and encoders are mostly used to reduce the dimensionality of the input and identify the key latent features. This allows models to use very large input layers, namely, many different atmospheric variables at several pressure levels. Encoder–decoder architectures are used to this effect within cutting-edge global DLWP applications, such as Keisler (2022), Lam et al. (2023), Bi et al. (2023), and Chen et al. (2023a).

The encoder–decoder structure is also at the core of transformers (Vaswani et al., 2017), a recent architectural innovation allowing for efficient parallelisation of sequential data. Transformers use a so-called attention mechanism (Bahdanau et al., 2015), i.e. they compute a score for each element in the input sequence which determines its relevance for the associated decoding step. This removes the need for sequential data intake, thereby enabling an effective utilisation of modern GPUs and TPUs for time-series data. This represents a major improvement over classic RNNs, which instead rely on serial arrangement to learn key features and are, therefore, not easily parallelisable.

Recently, the use of transformers has been extended to computer vision tasks as an alternative, or complement, to CNNs. Dosovitskiy et al. (2020) propose the use of vision transformers, which adapt transformers to visual tasks by introducing an innovative preprocessing step: images are first divided into patches of fixed N×N size and then run through a flattening layer, so that each patch can be treated as a separate token. Next, transformers are applied just as in sequential tasks. This approach has been applied to weather forecasting, for instance, by Pathak et al. (2022) and Bi et al. (2023), who use flattened patches of 4×4 pixels to apply transformers to gridded meteorological data.

A distinct approach featured by several global DLWP models is the use of graph neural networks (GNNs; Scarselli et al., 2009). Classic CNNs implicitly assume regular grids, in which the distance between points and the importance of each point is fixed (Thuemmel et al., 2023). This assumption is problematic in the case of global forecast models, as climate variables are often provided on regular latitude–longitude or reduced-Gaussian grids. Given that the Earth is quasi-spherical, the distance between degrees of latitude is greater at the Equator than at the poles, and even the length of degrees of longitude varies slightly with latitude. GNNs, unlike CNNs, allow for complex, quasi-spherical shapes. A way to understand this is by drawing a parallel with Cartesian and spherical coordinates. CNNs, similar to Cartesian coordinates, assume a “flat” grid and, in the best case, may introduce a weighting scheme not unlike the one of the β-plane, whereas GNNs can model the relation between the nodes as a complex polygon resembling a sphere.

The bearing of the architectural change from CNNs to GNNs on forecast performance is still the object of debate, and it is likely that it plays a larger role for global rather than local-to-regional applications, given the greater variation in the size of the grid cells in the former case. However, several recent deep learning weather forecasting models have introduced the use of GNNs to good effect. For instance, Keisler (2022) and, more prominently, Lam et al. (2023) have made use of GNNs to obtain accurate medium-range forecasts of several key atmospheric variables, managing to outperform the most accurate ECMWF deterministic forecasts available at the time of their publication.

Other current approaches look at ways of accounting for Earth's quasi-spherical nature within a CNN framework, without resorting to GNNs. Examples of this include spherical convolutions (Boomsma and Frellsen, 2017) and spherical cross-correlations (Cohen et al., 2018). Recent work by Scher and Messori (2023) showcases the advantages of spherical and hemispheric convolutions over classic CNNs. The authors compare models based on different architectures using the WeatherBench dataset (Rasp et al., 2020) and show that models incorporating spherical or hemispheric convolutions produce more accurate medium-range forecasts of the 500 hPa geopotential height (Z500) and 850 hPa temperature (t850) than models featuring classic CNN architectures. However, feature-rich and high-resolution applications of this kind are still under development.

Finally, we outline how recent medium-range DLWP models treat temporal information. Instead of trying to incorporate the time aspect directly into the model in the form of extra features or channels, they account for the sequential nature of data through a dynamic approach, by using the predictions generated by a given model time step as the input for the next model time step. In other words, as clearly stated by Chen et al. (2023a), they approximate the forecast at time t, $Y^t=f(Y^{t-\mathrm{1}}+Y^{t-\mathrm{2}}+\mathrm{\dots }+Y^{\mathrm{1}})$ through an autoregressive approach of order 1 (AR 1), namely, by sequentially using the forecasts at the previous time steps: $Y^t=f\left(Y^{t-\mathrm{1}}\right),Y^{t-\mathrm{1}}=f\left(Y^{t-\mathrm{2}}\right),\mathrm{\dots },Y^{\mathrm{2}}=f\left(Y^{\mathrm{1}}\right)$. A similar approach is adopted by Lam et al. (2023), with the main difference being that the data generated by the previous two forecasts are used as input for the latest forecast (AR 2).

If the focus is on a specific lead time, it is, however, not clear whether this iterative approach always outperforms training a model to make a single prediction at the chosen lead time (Scher and Messori, 2019b). In this regard, Chen et al. (2023b) show that producing a cascade of models fine-tuned on different timescales can lead to improvements in performance compared with a single model optimised on the whole forecasting window.

An overview of the DLWP model developments over time is provided in Figs. 1 and 2. Figure 1 summarises the evolution of model architectures described in this section, while Fig. 2 outlines the continuous improvements in the spatial and temporal domains handled by DLWP models. The current leading global DLWP models are systematically presented in Table 1, where we provide information on the inputs, outputs, main architectural innovations, and performance for extreme weather forecasts of each model.

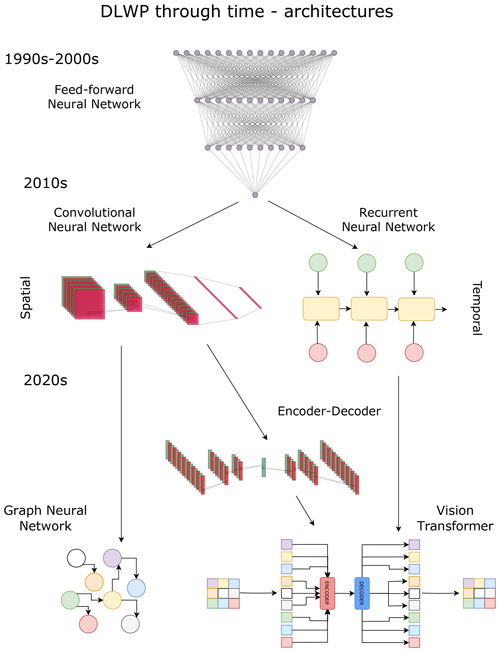
Figure 1 Evolution of deep learning weather prediction (DLWP) through time: from feed-forward neural networks to graph neural networks and vision transformers.

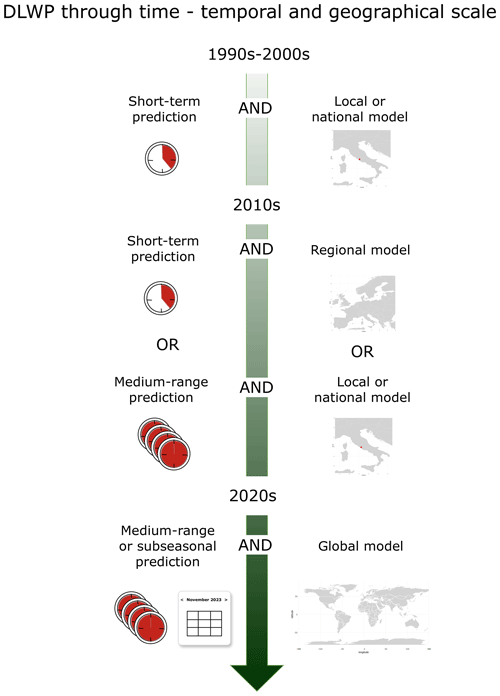
Figure 2 Evolution of the largest geographical and temporal scales of deep learning weather prediction (DLWP) models over time.

Pathak et al. (2022)(Dosovitskiy et al., 2020)Keisler (2022)(Battaglia et al., 2018)Bi et al. (2022, 2023)(Ben-Bouallegue et al., 2023)Lam et al. (2022, 2023)(Battaglia et al., 2018)Chen et al. (2023a)Nguyen et al. (2023)Chen et al. (2023b)(Zhong et al., 2023)

Table 1 Overview of recent global medium-range DLWP applications.

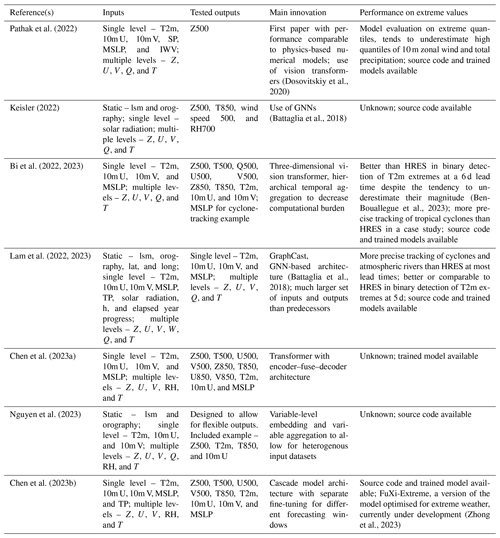
The abbreviations used in the table are as follows: 10m U and 10m V denote the u wind and v wind at 10 m, respectively; lsm – land–sea mask; MSLP – mean sea-level pressure; RH – relative humidity; Q – specific humidity; SP – surface pressure; T – temperature; IWV – integrated total column water vapour; U – u wind; V – v wind; Z – geopotential; TP – total precipitation; lat – latitude; long – longitude; h – hour of the day; 2m – 2 m height; 10m – 10 m height; 500 – 500 hPa; 850 – 850 hPa; and HRES – ECMWF high-resolution deterministic forecast.

3 Challenges and opportunities

3.1 Current challenges in DLWP

A common limitation of most large-scale DLWP applications introduced so far is that they are not targeted in any specific way at extreme weather events; rather, their focus lies on maximising the average skill of the forecasts. Typically, machine learning models struggle to make accurate predictions of extreme values, partly due to (1) the inherently limited training samples for extreme values and (2) the intrinsic inferential challenges related to extrapolation. Given the key role of accurate prediction and of early warnings for extreme weather in disaster prevention and risk mitigation (World Meteorological Organization, 2022; Merz et al., 2020), it would be desirable for current DLWP applications to dedicate greater attention to forecast skill for extreme weather (Watson, 2022).

As highlighted in Table 1, this problem is further exacerbated by the fact that many global DLWP papers provide no or very limited diagnostics on the performance of their models for extreme weather scenarios (e.g. Keisler, 2022; Chen et al., 2023a; Nguyen et al., 2023), making it hard to assess their performance in those situations. Even those that do provide extreme weather diagnostics mostly focus on selected variables and case studies, supplying no systematic overview of how the models perform in the prediction of high-impact surface extremes such as total precipitation or peak wind gusts. Indeed, some state-of-the-art DLWP models, such as Bi et al. (2023), do not even produce forecasts for those variables.

Watson (2022) suggests some simple measures that authors could adopt to help readers evaluate whether or not a machine learning model can provide robust forecasts of extreme events: for instance, that all papers should include scatterplots and quantile–quantile plots of forecasted vs. observed values and that performance metrics computed only on extreme values should complement classic metrics of average skill. A positive note since the release of Watson (2022) is that several research groups have chosen to make the code of their global models publicly available, making it possible for third-party actors with enough computational resources to implement and further test their models. For instance, ECMWF has recently launched an experimental programme running daily 10 d forecasts with 6-hourly time steps of the models introduced by Pathak et al. (2022), Bi et al. (2023), and Lam et al. (2023), whose forecasts are available to the general public (ECMWF, 2023). Similarly, WeatherBench 2 (Rasp et al., 2024) provides additional scorecards and out-of-sample predictions for several models included in Table 1.

Some key “inductive biases”, i.e. implicit assumptions of the employed estimation techniques (Battaglia et al., 2018), may also hamper the performance of current DLWP applications for extreme weather forecasting. Most global DLWP models choose to minimise the overall mean-squared error (L2) of the forecast, averaging over all grid points and time steps of interest (Pathak et al., 2022; Keisler, 2022). The minimisation thus uses the conditional mean of the dependent variable through space and time given the predictors, optimising forecasts for mean rather than extreme values. Furthermore, the use of L2 (and also L1, the mean absolute error, used, for instance, by Bi et al., 2023, and Chen et al., 2023b) implicitly assumes that, for any given variable, the distribution of the forecast error is symmetric, i.e. that it is possible to obtain both positive and negative errors of the same magnitude, and that deviations from the modelled value in the two directions are equally important. This is seldom the case in weather forecasting. Many weather variables display a high degree of autocorrelation and follow highly asymmetric truncated distributions (e.g. peak wind speed or precipitation), which in combination tend to produce non-asymmetric error distributions (Hodson, 2022). Moreover, deviations of a variable from its mean in one of the two directions can have larger impacts on human societies than deviations in the other direction (e.g. one would expect that severely underestimating the amount of rain in a flash-flood event would be more harmful than incorrectly predicting rain on a dry day).

While the suggestions in Watson (2022), if implemented, would go a long way in ensuring greater transparency and credibility for DLWP forecasts of extreme weather, the challenges related to the extrapolation issue and inductive biases still remain. The limited diagnostics provided by Pathak et al. (2022) and Bi et al. (2022) suggest that their models perform reasonably well on extremes but also that they consistently tend to underestimate their magnitude. Similarly, Ben-Bouallegue et al. (2023) find that Pangu-Weather (Bi et al., 2023) can provide high-quality binary forecasts of moderately extreme temperatures but that it also tends to oversmooth the prediction and underestimate the magnitude of the largest cold and hot extremes.

Thus, we argue for the need for DLWP models explicitly built to forecast extremes. These should make use of targeted loss functions and produce robust predictions of all relevant variables at or beyond the limits of their training range. In the next section, we propose a schematic framework on which to build such models. The aim here is to provide a general foundation for such approaches, rather than discussing architectural details. Indeed, several of the architectures adopted by the models in Table 1 and Sect. 2.1 are, in principle, equally suitable for predictions of extreme weather and average weather. The limiting factors are most likely the choice of the optimisation problem and the lack of a specific treatment of the extremes, rather than the architectures themselves.

3.2 A DLWP workflow for extreme weather

A simple way of shifting the focus from the average skill of a deep learning model to its performance in the tails of the distribution is by changing its loss function. Common loss functions, such as the mean absolute error (L1) and the mean-squared error (L2), are minimised by taking the conditional median and mean of the dependent variable, respectively. An alternative loss function is given by the pinball loss, defined as follows (Koenker and Bassett, 1978):

$$\begin{array}{}\text{(1)}& L_{\mathrm{pinball}}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^{N}max(\mathit{\tau }\cdot (y_i-{\widehat{y}}_i),(\mathrm{1}-\mathit{\tau })\cdot ({\widehat{y}}_i-y_i\left)\right),\end{array}$$

where τ is the target quantile, N is the number of training observations, i represents a specific observation, y_i is the actual value of the target variable for that observation, and ${\widehat{y}}_i$ is the forecast generated by the model. This loss function punishes predictions that are further away from the quantile of interest and is minimised by the conditional quantile of the dependent variable.¹ By choosing an extreme quantile of interest, it is possible to study, in a regression setting, how different predictors affect the tails of the distribution. Furthermore, models minimising the pinball loss could be used to set approximate confidence intervals around models maximising the average skill of the prediction.

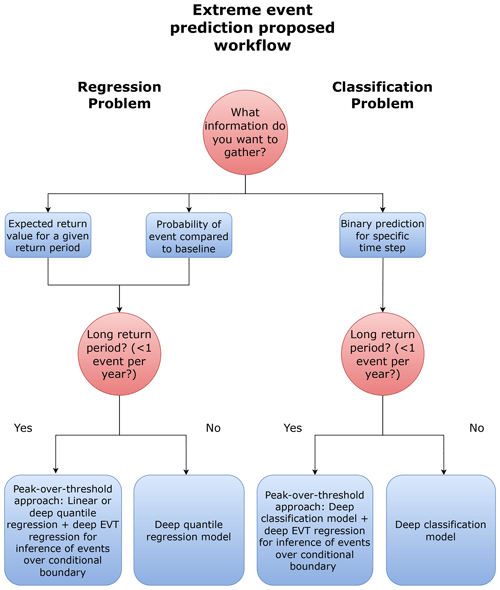
Figure 3 Extreme event prediction model design workflow. The chosen approach should depend on the information one aims to gather and the return period of the extreme events of interest.

Within a deep learning setting, models minimising the pinball loss often go under the name of deep quantile regression or quantile regression neural networks (Taylor, 2000). A limitation of deep quantile regression is that enough observations below and above the quantile of interest need to be available for the model to work properly. This can sometimes be an issue within a DLWP framework, given that the main interest can lie in very extreme quantiles, i.e. seldom-observed extreme events with long return periods.

A solution to this problem has recently been proposed by Pasche and Engelke (2023), who, building upon earlier work by Carreau and Bengio (2007), suggest using a two-step peak-over-threshold approach. First, a quantile-regression-based estimator, such as linear or deep quantile regression, is used to estimate a conditional threshold of interest. Then, the properties of the distribution of the exceedances are modelled with the help of extreme value theory (EVT). Pasche and Engelke (2023) assume that, in accordance with Balkema and De Haan (1974) and Pickands (1975), independent exceedances approximately follow a generalised Pareto distribution, with parameters depending on the value of the regressors. These parameters can then be estimated with the help of a neural network, and the resulting empirical distribution can be used to derive the properties of the distribution of any extreme event of interest, as is commonly done in EVT.

However, even the combination of quantile and EVT-based approaches suffers from a key limitation: it does not provide a deterministic forecast for a given time and place but only return periods or values and a risk ratio of the probability of an event taking place compared to the climatology. In other words, it answers questions such as “Is extreme event `X' more likely to occur than usual on day `Y'?” or “How often does an event of a given severity occur given an initial set of atmospheric conditions?”. It does not answer the question typically associated with deterministic weather forecasts, namely, “Is extreme event `X' going to take place on day `Y' at location `Z'?”.

A possible alternative for cases in which we are interested in answering the latter question, i.e. we want a deterministic forecast of a given extreme event at a specific time and place, is to use a binary classification model. This can, for instance, minimise a binary cross-entropy loss, defined as follows:

$$\begin{array}{}\text{(2)}& L_{\mathrm{bincross}}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{y}_i\cdot \log \left(y_i\right)+(\mathrm{1}-y_i)\cdot \log (\mathrm{1}-y_i).\end{array}$$

By defining the extreme event on the basis of a threshold or a given quantile of the climatology and minimising Eq. (2), we can train a model to estimate the probability of an event of a given magnitude taking place at a specific time and location. The forecasted probability for a specific time and place can then easily be converted into a deterministic forecast by choosing a cutoff probability (e.g. 50 %), where events above that probability are expected to take place and events under that probability are not.

Whenever a heavy class imbalance is present, i.e. the interest lies in very extreme quantiles, training a classification neural network may be challenging, as the model may be prone to reverting to the trivial solution of never predicting an extreme event. In those cases, class weights may help: weights are introduced in Eq. (2) in order to give greater importance to the loss generated by training samples from the minority class, namely, the extremes. In other words, the model is trained to minimise a weighted cross-entropy loss (Eq. 3), defined as follows:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{L}_{\mathrm{weightedbincross}}& ={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N-w_{\mathrm{1}}{y}_i\cdot \log \left(y_i\right)\\ & +w_{\mathrm{0}}(\mathrm{1}-y_i)\cdot \log (\mathrm{1}-y_i),\end{array}\end{array}$$

where w₁ is the weight assigned to observations in the minority class and w₀ is the weight assigned to observations in the majority class.

Even after introducing class weights, this approach, like quantile regression, needs enough observations in each of the two classes for the model to work properly. Thus, it is not suitable in isolation for extremes with a very long return period, appearing no or very few times in the training sample. However, as in the previous case, we can build a two-step peak-over-threshold model that addresses this problem. First, we decide through a classification model whether or not an event above a certain not-too-extreme threshold is going to take place. Then, we model the tails of the distribution with the help of the Pickands–Balkema–De Haan theorem (Balkema and De Haan, 1974; Pickands, 1975), which allows one to make inferences on very extreme cases potentially beyond the model's training range.

The different steps introduced above can be combined in order to obtain forecasts providing a rich set of information. For instance, one may jointly implement a classification-based and a quantile-based deep learning model to obtain time- and location-specific forecasts of an extreme as well as information on its return period. Figure 3 summarises the approaches described in this section in a simple framework that can be used to tailor deep learning models to extreme weather forecasting.

4 Conclusions and recommendations

Accurate prediction of extreme weather events is a central part of a high-quality medium-range weather forecast and is, thus, of great societal and economic relevance (World Meteorological Organization, 2022; Merz et al., 2020). In order for global end-to-end deep learning models to attain widespread operational use, we argue that achieving greater average skill than physics-based numerical weather prediction models is not sufficient. They additionally need to demonstrate skill for extreme weather events.

We identify two key limitations that constrain current state-of-the-art deep learning forecasts of extreme weather. First, current architectures are not optimised to make use of the limited training samples for extreme values. Second, the models are not optimised on extreme event forecasts and make some simplistic assumptions regarding how the forecasting errors are distributed. These issues are compounded by the scant or missing validation of extreme weather forecasts provided by leading global DLWP models.

We argue for the urgency of a DLWP workflow targeted to extreme weather forecasts, whereby deep learning models specifically designed to handle extreme events should complement deep learning models maximising the average skill of the forecast. To enable rapid advances, the implementation of such a workflow should rest on adapting existing deep learning architectures, rather than developing radically new and untested approaches. This should be complemented by placing a greater emphasis on assessing the performance of existing and future models in the tails of the distributions of the forecasted variables (Watson, 2022).

Echoing the above recommendations, in this article, we have proposed a foundational workflow to advance deep learning extreme weather forecasts, in which the method of choice depends on the meteorological question to be answered – whether probabilistic or deterministic – and the return period of the extreme events of interest. The workflow is fully enabled by recent architectural advances in deep learning weather forecast models; thus, we envision it as functional to achieve robust deep learning forecasts of extreme weather in the near future.