GPU-HADVPPM V1.0: a high-efficiency parallel GPU design of the piecewise parabolic method (PPM) for horizontal advection in an air quality model (CAMx V6.10)

With semiconductor technology gradually approaching its physical and thermal limits, graphics processing units (GPUs) are becoming an attractive solution for many scientific applications due to their high performance. This paper presents an application of GPU accelerators in an air quality model. We demonstrate an approach that runs a piecewise parabolic method (PPM) solver of horizontal advection (HADVPPM) for the air quality model CAMx on GPU clusters. Specifically, we first convert the HADVPPM to a new Compute Unified Device Architecture C (CUDA C) code to make it computable on the GPU (GPU-HADVPPM). Then, a series of optimization measures are taken, including reducing the CPU–GPU communication frequency, increasing the data size computation on the GPU, optimizing the GPU memory access, and using thread and block indices to improve the overall computing performance of the CAMx model coupled with GPU-HADVPPM (named the CAMx-CUDA model). Finally, a heterogeneous, hybrid programming paradigm is presented and utilized with GPU-HADVPPM on the GPU clusters with a message passing interface (MPI) and CUDA. The offline experimental results show that running GPU-HADVPPM on one NVIDIA Tesla K40m and an NVIDIA Tesla V100 GPU can achieve up to a 845.4× and 1113.6× acceleration. By implementing a series of optimization schemes, the CAMx-CUDA model results in a 29.0× and 128.4× improvement in computational efficiency by using a GPU accelerator card on a K40m and V100 cluster, respectively. In terms of the single-module computational efficiency of GPU-HADVPPM, it can achieve 1.3× and 18.8× speedup on an NVIDIA Tesla K40m GPU and NVIDIA Tesla V100 GPU, respectively. The multi-GPU acceleration algorithm enables a 4.5× speedup with eight CPU cores and eight GPU accelerators on a V100 cluster.

1 Introduction

Since the introduction of personal computers in the late 1980s, the computer and mobile device industry has created a flourishing worldwide market (Bleichrodt et al., 2012). In recent years, improvements in central processing unit (CPU) performance have been limited by its heat dissipation, and the applicability of Moore's law has flattened. A common trend in high-performance computing today is the utilization of hardware accelerators, which execute codes rich in data parallelism, to form high-performance heterogeneous systems. GPUs are widely used as accelerators due to their high peak performances. In the top 10 supercomputing list released in December 2022 (https://www.top500.org/lists/top500/list/2022/11/, last access: 19 December 2022), there were seven heterogeneous supercomputing platforms built with CPU processors and GPU accelerators, of which the top one, Frontier at the Oak Ridge National Laboratory, uses AMD's third-generation EPYC CPU and AMD's Instinct MI250X GPU, and its computing performance has reached exascale levels (10¹⁸ calculations per second) for the first time (https://www.amd.com/en/press-releases/2022-05-30-world-s-first-exascale-supercomputer-powered-amd-epyc-processors-and-amd, last access: 19 December 2022). Such a powerful computing performance of the heterogeneous system not only injects new vitality into high-performance computing but also generates new solutions for improving the performance of geoscience numerical models.

The GPU has proven successful in weather models such as the Non-Hydrostatic Icosahedral Model (NIM; Govett et al., 2017), Global and Regional Assimilation and Prediction System (GRAPES; Xiao et al., 2022), and Weather Research and Forecasting model (WRF; Huang et al., 2011; Huang et al., 2012; Mielikainen et al., 2012a; Mielikainen et al., 2012b, 2013a, b; Price et al., 2014; Huang et al., 2015); ocean models such as the LASG/IAP Climate System Ocean Model (LICOM; Jiang et al., 2019; P. Wang et al., 2021) and Princeton Ocean Model (POM; Xu et al., 2015); and the earth system model of the Chinese Academy of Sciences (CAS-ESM; Wang et al., 2016; Y. Wang et al., 2021).

Govett et al. (2017) used open accelerator (OpenACC) directives to port the dynamics of NIM to the GPU and achieved a 2.5× acceleration. Additionally, using OpenACC directives, Xiao et al. (2022) ported the PRM (piecewise rational method) scalar advection scheme in GRAPES to the GPU, achieving up to 3.51× faster results than 32 CPU cores. In terms of the most widely used WRF, several parameterization schemes, such as the RRTMG_LW scheme (Price et al., 2014), five-layer thermal diffusion scheme (Huang et al., 2015), Eta Ferrier cloud microphysics scheme (Huang et al., 2012), Goddard short-wave scheme (Mielikainen et al., 2012a), Kessler cloud microphysics scheme (Mielikainen et al., 2013b), SBU-YLIN scheme (Mielikainen et al., 2012b), WMS5 scheme (Huang et al., 2011), and WMS6 scheme (Mielikainen et al., 2013a), have been ported heterogeneously using Compute Unified Device Architecture C (CUDA C) and achieved 37× to 896× acceleration results. LICOM has conducted heterogeneous porting using OpenACC (Jiang et al., 2019) and used heterogeneous-computing interface for portability C (HIP C) technologies and achieved up to a 6.6× and 42× acceleration, respectively (P. Wang et al., 2021). For the Princeton ocean model, Xu et al. (2015) used CUDA C to conduct heterogeneous porting and optimization, and the performance of POM.pgu v1.0 on four GPUs is comparable to that on the 408 standard Intel Xeon X5670 CPU cores. In terms of climate system models, Wang et al. (2016) and Y. Wang et al. (2021) used CUDA Fortran and CUDA C to conduct heterogeneous porting of the RRTMG_SW and RRTMG_LW schemes of the atmospheric component model of the CAS-ESM earth system model and achieved a 38.88× and 77.78× acceleration, respectively.

Programming a GPU accelerator can be a difficult and error-prone process that requires specially designed programming methods. There are three widely used methods for porting programs to GPUs, as described above. The first method uses the OpenACC directive (https://www.openacc.org/, last access: 19 December 2022), which provides a set of high-level directives that enable C/C$++$ and Fortran programmers to utilize accelerators. The second method uses CUDA Fortran. CUDA Fortran is a software compiler that was co-developed by the Portland Group (PGI) and NVIDIA and is a tool chain for building performance-optimized GPU-accelerated Fortran applications targeting the NVIDIA GPU platform (https://developer.nvidia.com/cuda-fortran, last access: 19 December 2022). Using CUDA C involves rewriting the entire program using the standard C programming language and low-level CUDA subroutines (https://developer.nvidia.com/cuda-toolkit, last access: 19 December 2022) to support the NVIDIA GPU accelerator. Compared to the other two technologies, the CUDA C porting scheme is the most complex, but it has the highest computational performance (Mielikainen et al., 2012b; Wahib and Maruyama, 2013; Xu et al., 2015).

Air quality models are critical for understanding how the chemistry and composition of the atmosphere may change throughout the 21st century, as well as for preparing adaptive responses or developing mitigation strategies. Because air quality models need to take into account the complex physico-chemical processes that occur in the atmosphere of anthropogenic and natural emissions, simulations are computationally expensive. Compared to other geoscientific numerical models, few studies have conducted a heterogeneous porting of air quality models. In this study, the CUDA C scheme, implemented in this paper, was used to conduct a hotspot module porting of CAMx to improve the computation efficiency.

2 The CAMx model and experiments

2.1 Model description

The CAMx model is a state-of-the-art air quality model developed by Ramboll Environ (https://www.camx.com/, last access: 19 December 2022). CAMx version 6.10 (CAMx V6.10; ENVIRON, 2014) is chosen in this study; it simulates the emission, dispersion, chemical reaction, and removal of pollutants by marching the Eulerian continuity equation forward in time for each chemical species on a system of nested three-dimensional grids. The Eulerian continuity equation is expressed mathematically in terrain-following height coordinates as Eq. (1):

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial c_i}{\partial t}}& =-{\mathrm{\nabla }}_{\mathrm{H}}\cdot V_{\mathrm{H}}{c}_i+\left[{\displaystyle \frac{\partial \left(c_i\mathit{\eta }\right)}{\partial z}}-c_i{\displaystyle \frac{{\partial }^{\mathrm{2}}h}{\partial z\partial t}}\right]+\mathrm{\nabla }\cdot \mathit{\rho }K\mathrm{\nabla }\left(c_i/\mathit{\rho }\right)\\ & +{\left.{\displaystyle \frac{\partial c_i}{\partial t}}\right|}_{\mathrm{emission}}+{\left.{\displaystyle \frac{\partial c_i}{\partial t}}\right|}_{\mathrm{chemistry}}+{\left.{\displaystyle \frac{\partial c_i}{\partial t}}\right|}_{\mathrm{removal}}\end{array},\text{(2)}& {\displaystyle }{\mathrm{\nabla }}_{\mathrm{H}}\cdot \mathit{\rho }{V}_{\mathrm{H}}={\displaystyle \frac{m^{\mathrm{2}}}{A_{yz}}}{\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{u{A}_{yz}\mathit{\rho }}{m}}\right)+{\displaystyle \frac{m^{\mathrm{2}}}{A_{xz}}}{\displaystyle \frac{\partial }{\partial y}}\left({\displaystyle \frac{v{A}_{xz}\mathit{\rho }}{m}}\right).\end{array}$$

The first term on the right-hand side represents horizontal advection. In numerical methods, the horizontal advection equation (described in Eq. 2) is performed using the area-preserving flux-form advection solver of the piecewise parabolic method (PPM) of Colella and Woodward (1984) as implemented by Odman and Ingram (1996). The PPM horizontal advection solution (HADVPPM) was incorporated into the CAMx model because it provides higher-order accuracy with minimal numerical diffusion.

In the Fortran code implementation of the HADVPPM scheme, the CAMx main program calls the emistrns program, which mainly performs physical processes such as emission, diffusion, advection, and dry/wet deposition of pollutants. Then, the horizontal advection program is invoked by the emistrns program to solve the horizontal advection equation by using the HADVPPM scheme.

2.2 Benchmark performance experiments

The first porting step is to test the performance of the CAMx benchmark version and identify the model's hotspots. On the Intel x86 CPU platform, we launch two processes concurrently to run the CAMx and take advantage of the Intel Trace Analyzer and Collector (ITAC; https://www.intel.com/content/www/us/en/docs/trace-analyzer-collector/get-started-guide/2021-4/overview.html, last access: 19 December 2022) and the Intel VTune Profiler (VTune; https://www.intel.com/content/www/us/en/develop/documentation/vtune-help/top.html, last access: 19 December 2022) performance analysis tools to collect performance information during the CAMx operation.

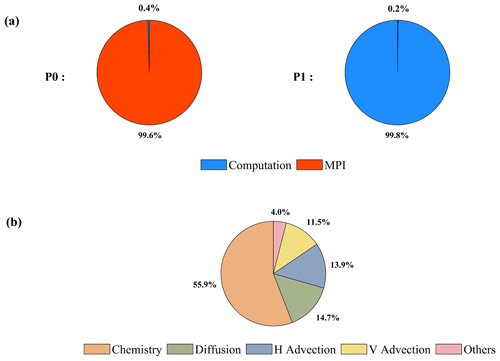
The general message passing interface (MPI) performance can be reported by the ITAC tool, and MPI load balance information, computation, and communication profiling of each process are shown in Fig. 1a. During the running process of the CAMx model, Process 0 (P0) spends 99.6 % of the time on the MPI_Barrier function and only 0.4 % of the time on computation, while Process 1 (P1) spends 99.8 % of its time computing and only 0.2 % of its time receiving messages from P0. It is apparent that the parallel design of the CAMx model adopts the primary/secondary mode, and P0 is responsible for inputting and outputting the data and calling the MPI_Barrier function to synchronize the process, so there is a lot of MPI waiting time. The other processes are responsible for computation.

The VTune tool detects each module's runtime and the most time-consuming functions on P1. As shown in Fig. 1b, the top four time-consuming modules are chemistry, diffusion, horizontal advection, and vertical advection in the CAMx model. In the above four modules, the top five most time-consuming programs are the ebirate, hadvppm, tridiag, diffus, and ebisolv programs, and the total runtime of P1 is 325.1 s. The top one's and top two's most time-consuming programs take 49.4 and 35.6 s, respectively.

By consideration, the hadvppm program was selected to conduct heterogeneous porting for several reasons. First, the advection module is one of the air quality model's compulsory modules and is mainly used to simulate the transport process of air pollutants; additionally it is also a hotspot module detected by the Intel VTune tool. The typical air quality models, CAMx, CMAQ, and NAQPMS, include advection modules and use the exact PPM advection solver. The heterogeneous version developed in this study can be directly applied to the above models. Furthermore, the weather model (e.g. WRF) also contains an advection module, so this study's heterogeneous porting method and experience can be used for reference. Therefore, a GPU acceleration version of the HADVPPM scheme, namely, GPU-HADVPPM, was built to improve the CAMx performance.

Figure 1 The computation performance of the modules in the CAMx model. (a) Computation and communication profiling of P0 and P1. (b) Overhead proportions of P1. The top four most time-consuming modules are chemistry, diffusion, horizontal advection, and vertical advection.

2.3 Porting scheme introduction

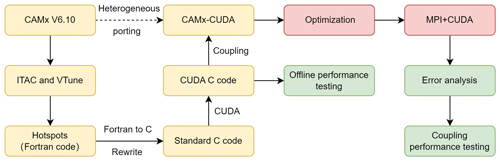
The CAMx model coupled with GPU-HADVPPM (CAMx-CUDA) heterogeneous scheme is shown in Fig. 2. The second time-consuming hadvppm program in the CAMx model was selected to implement heterogeneous porting. To map the hadvppm program to the GPU, the Fortran code was converted to standard C code. Then, the CUDA programming language, which was tailor-made for NVIDIA, was added to convert the standard C code into CUDA C for data-parallel execution on the GPU, as GPU-HADVPPM. It prepared the input data for GPU-HADVPPM by constructing random numbers and tested its offline performance on the GPU platform.

After coupling GPU-HADVPPM to the CAMx model, the advection module code was optimized according to the characteristics of the GPU architecture to improve the overall computational efficiency on the CPU–GPU heterogeneous platform. Then, the multi-CPU core and multi-GPU card acceleration algorithm was adopted to improve the parallel extensibility of heterogeneous computing. Finally, the coupling performance test was implemented after verifying the different CAMx model simulation results.

Figure 2 Heterogeneous porting scheme of the CAMx-CUDA model.

2.4 Hardware components and software environment of the testing system

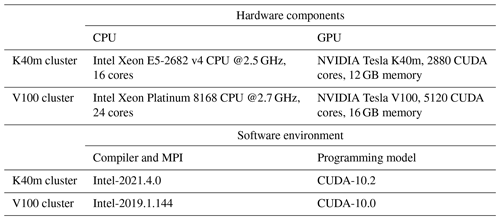
The experiments are conducted on two GPU clusters, K40m and V100. The hardware components and software environment of the two clusters are listed in Table 1. The K40m cluster is equipped with two 2.5 GHz 16-core Intel Xeon E5-2682 v4 CPU processors and one NVIDIA Tesla K40m GPU card on each node. The NVIDIA Tesla K40m GPU has 2880 CUDA cores with 12 GB of memory. The V100 cluster contains two 2.7 GHz 24-core Intel Xeon Platinum 8168 processors and eight NVIDIA Tesla V100 GPU cards with 5120 CUDA cores and 16 GB of memory on each card.

Table 1 Configurations of GPU cluster.

For Fortran and standard C programming, Intel Toolkit (including compiler and MPI library) version 2021.4.0 and version 2019.1.144 are employed for compiling on an Intel Xeon E4-2682 v4 CPU and Intel Xeon Platinum 8168 CPU, respectively. Then, CUDA version 10.2 and version 10.0 are employed on an NVIDIA Tesla K40m GPU and NVIDIA Tesla V100 GPU. CUDA (NVIDIA, 2020) is an extension of the C programming language that offers direct programming of the GPUs. In CUDA programming, a kernel is actually a subroutine that can be executed on the GPU. The underlying code in the kernel is divided into a series of threads, each with a unique “ID” number that simultaneously processes different data through a single-instruction multiple-thread (SIMT) parallel mode. These threads are grouped into equal-sized thread blocks, which are organized into a grid.

3 Porting and optimization of the CAMx advection module on a heterogeneous platform

3.1 Mapping the HADVPPM scheme to the GPU

3.1.1 Manual code translation from Fortran to standard C

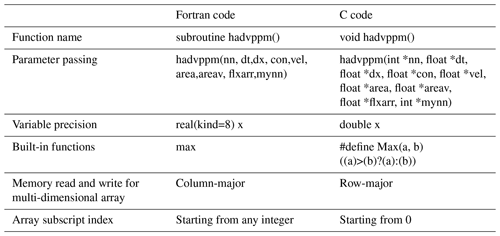
As the CAMx V6.10 code was written in Fortran 90, we rewrote the hadvppm program from Fortran to CUDA C. As an intermediate conversion step, we refactor the original Fortran code using standard C. During the refactoring, some of the considerations, listed in Table 2, are as follows:

1. The subroutine name refactored with standard C must be followed by an underscore identifier, which can only be recognized when Fortran calls.

2. In the Fortran language, the parameters are transferred by a memory address by default. In the case of mixed programming in Fortran and standard C, the parameters transferred by Fortran are processed by the pointer in standard C.

3. Variable precision types defined in standard C must be strictly consistent with those in Fortran.

4. Some built-in functions in Fortran are not available in standard C and need to be defined in the standard C macro definitions.

5. For multi-dimensional arrays, Fortran and standard C follow a column-major and row-major order and in-memory read and write, respectively.

6. Array subscripts in Fortran and standard C are indexed from any integer and 0, respectively.

Table 2 Some considerations during Fortran to C refactoring.

3.1.2 Converting standard C code into CUDA C

After refactoring the Fortran code of the hadvppm program with standard C, CUDA was used to convert the C code into CUDA C to make it computable on the GPU. A standard C program using CUDA extensions distributes a large number of copies of the kernel functions into available multiprocessors and executes them simultaneously on the GPU.

Figure 3 shows the GPU-HADVPPM implementation process. As mentioned in Sect. 2.1, the xyadvec program calls the hadvppm program to solve the horizontal advection function. Since the rewritten CUDA program cannot be called directly by the Fortran program (xyadvec.f), we add an intermediate subroutine (hadvppm.c) as an interface to transfer the parameters and data required for GPU computing from the xyadvec Fortran program to the hadvppm_kernel CUDA C program.

A CUDA program automatically uses numerous threads on the GPU to execute kernel functions. Therefore, the hadvppm_kernel CUDA C program first calculates the number of parallel threads according to the array dimension. Then, the GPU memory is allocated, and the parameters and data are copied from the CPU to the GPU. As the CUDA program launches a large number of parallel threads to execute kernel functions simultaneously, the computation results will be copied from the GPU back to the CPU. Finally, the GPU memory is released, and the data computed on the GPU are returned to the xyadvec program via the hadvppm C program.

Figure 3 The calling and computation process of GPU-HADVPPM on the CPU–GPU heterogeneous platform.

3.2 Coupling and optimization of the GPU-HADVPPM scheme on a single GPU

After the hadvppm program was rewritten with standard C and CUDA, the implementation process of the HADVPPM scheme was loaded from the CPU to the GPU. Then, we coupled GPU-HADVPPM to the CAMx model. For ease of description, we will refer to this original heterogeneous version of CAMx as CAMx-CUDA V1.0. In CAMx-CUDA V1.0, four external loops are nested when the hadvppm C program is called by the xyadvec program. This will result in widespread data transfers from the CPU to the GPU over the peripheral component interconnect express (PCIe) bus within a time step, making the computation of CAMx-CUDA V1.0 inefficient.

Therefore, we optimize the xyadvec Fortran program to significantly reduce the frequency of data transmission between the CPU and GPU, increase the amount of data computation on the GPU, and improve the total computing efficiency of the CAMx on the CPU–GPU heterogeneous platforms. In the original CAMx-CUDA V1.0, four external loops outside the hadvppm C program and several one-dimensional arrays are computed before calling the hadvppm C program. Then, the CPU will frequently launch the GPU and transfer data to it within a time step. When the code optimization is completed, the three- or four-dimensional arrays required for a GPU computation within a time step will be sorted before calling the hadvppm C program, and then the CPU will package and transfer the arrays to the GPU in batches. An example of the xyadvec Fortran program optimization is shown in Fig. S1.

The details of the four different versions are shown in Table 3. In CAMx-CUDA V1.0, the Fortran code of the HADVPPM scheme was rewritten using standard C and CUDA, and the xyadvec program was not optimized. The dimensions of the c1d variable array transmitted to the GPU in the x and y directions are 157 and 145 in this case, respectively. In CAMx-CUDA V1.1 and CAMx-CUDA V1.2, the c1d variable transmitted from the CPU to GPU is expanded to two (approximately 23 000 numbers) and four dimensions (approximately 27.4×10⁶ numbers) by optimizing the xyadvec Fortran program and hadvppm_kernel CUDA C program, respectively.

The order in which the data are accessed in GPU memory affects the computational efficiency of the code. In CAMx-CUDA V1.3 of Table 4, we further optimized the order in which the data are accessed in GPU memory based on the order in which they are stored in memory and eliminated the unnecessary assignment loops that were added due to the difference in memory read order between Fortran and C.

As described in Sect. 2.4, a thread is the basic unit of parallelism in CUDA programming. The thread structure is organized into a three-level hierarchy. The highest level is a grid, which consists of three-dimensional thread blocks. The second level is a block, which also consists of three-dimensional threads. The built-in CUDA variable threadIdx.x determines a unique thread ID number inside a thread block. Similarly, the built-in variables blockIdx.x and blockIdx.y determine which block to execute on, and the size of the block is determined by using the built-in variable blockdim.x. For the two-dimensional horizontal grid points, many threads and blocks can be organized so that each CUDA thread computes the results for different spatial positions simultaneously.

In the original version of the CAMx-CUDA model before version 1.4, the loops for the three-dimensional spatial grid points ($i,j,k$) were replaced by index computations using only the thread index (i= threadIdx.x + blockIdx.x*blockDim.x) to simultaneously compute the grid point in the x or y directions. To take full advantage of the thousands of threads in the GPU, we implement thread and block indices (i= threadIdx.x + blockIdx.x*blockDim.x; j = blockIdx.y) to simultaneously compute all the horizontal grid points (i,j) in CAMx-CUDA V1.4. This is permitted because there are no interactions among the horizontal grid points.

Table 3 The details of different CAMx-CUDA versions during optimization.

3.3 MPI + CUDA acceleration algorithm of CAMx-CUDA on multiple GPUs

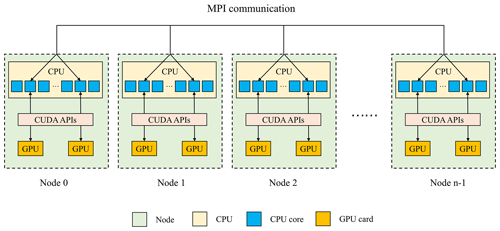
Generally, super-large clusters have thousands of compute nodes. The current CAMx V6.10, implemented by adopting MPI communication technology, typically runs on dozens of compute nodes. Once GPU-HADVPPM is coupled into the CAMx, it also has to run on multiple compute nodes that are equipped with one or more GPUs on each node. To make full use of multicore and multi-GPU supercomputers and further improve the overall computational performance of CAMx-CUDA, we adopt a parallel architecture with an MPI and CUDA (MPI + CUDA) hybrid paradigm; that is, the collaborative computing strategy of multiple CPU cores and multiple GPU cards is adopted during the operation of the CAMx-CUDA model. Adopting this strategy, GPU-HADVPPM can run on multiple GPUs, and the Fortran code of the other modules in the CAMx-CUDA model can run on multiple CPU cores.

As shown in Fig. 4, after the simulated region is subdivided by MPI, a CPU core is responsible for the computation of a subregion. To improve the total computational performance of the CAMx-CUDA model, we further used the NVIDIA CUDA library to obtain the number of GPUs per node and then used the MPI process ID and remainder function to determine the GPU ID to be launched by each node. Finally, we used the NVIDIA CUDA library, cudaSetDevice, to configure a GPU card for each CPU core.

According to the benchmark performance experiments, the parallel design of CAMx adopts the primary/secondary mode, and P0 is responsible for inputting and outputting data. If two processes (P0 and P1) are launched, only the P1 and its configured GPU participate in integration.

Figure 4 An example of parallel architecture with an MPI + CUDA hybrid paradigm on multiple GPUs.

4 Experimental results

The validation and evaluation of porting the HADVPPM scheme from the CPU to the GPU platform were conducted using offline and coupling performance experiments. First, we validated the results between the different CAMx versions, and then the offline performance of GPU-HADVPPM on a single GPU was tested by offline experiments. Finally, coupling performance experiments illustrate its potential in three dimensions with varying chemical regimes. In Sect. 4.2 and 4.4, the CAMx versions of the HADVPPM scheme written in Fortran, standard C, and CUDA C are named F, C, and CUDA C, respectively.

4.1 Experimental setup

The test case is a 48 h simulation covering Beijing, Tianjin, and part of the Hebei Province region. The horizontal resolution is 3 km with 145×157 grid boxes. The model adopted 14 vertical layers. The simulation started at 12:00 UTC on 1 November 2020 and ended at 12:00 UTC on 3 November 2020. The meteorological fields driving the CAMx model were provided by the Weather Research and Forecasting (WRF; Skamarock et al., 2008) model. The Sparse Matrix Operator Kernel Emissions (SMOKE; Houyoux and Vukovich, 1999) version 2.4 model is used to provide gridded emission data for the CAMx model. The emission inventories (Sun et al., 2022) include the regional emissions in East Asia that were obtained from the Transport and Chemical Evolution over the Pacific (TRACE-P; Streets et al., 2003, 2006) project, 30 min (approximately 55.6 km at mid-latitude) spatial resolution Intercontinental Chemical Transport Experiment Phase B (INTEX-B; Zhang et al., 2009), and the updated regional emission inventories in northern China. The physical and chemical numerical methods selected during the CAMx model integration are listed in Table S2.

4.2 Error analysis

The hourly concentrations of different CAMx simulations (Fortran, C, and CUDA C versions) are compared to verify the usefulness of the CUDA C version of CAMx for numerical precision for scientific usage. Here, we chose six major species, i.e. SO₂, O₃, NO₂, CO, H₂O₂, and PSO₄, after 48 h of integration to verify the results. Due to the differences in programming languages and hardware, the simulation results are affected during the porting process. Figures 5 to 7 present the spatial distributions of SO₂, O₃, NO₂, CO, H₂O₂, and PSO₄, as well as the absolute errors (AEs) of their concentrations from different CAMx versions. The species' spatial patterns of the three CAMx versions are visually very similar. Between the Fortran and C versions, especially, the AEs in all the grid boxes are in the range of ±0.01 ppbV (parts per billion by volume; the unit of PSO₄ is µg m⁻³). During the porting process, the primary error comes from converting standard C to CUDA C, and the main reason is related to the hardware difference between the CPU and GPU. Due to the slight difference in data operation and accuracy between the CPU and GPU (NVIDIA, 2023), the concentration variable of the hadvppm program appears to have minimal negative values (approximately $-{\mathrm{10}}^{-\mathrm{4}}$ to $-{\mathrm{10}}^{-\mathrm{9}}$) when integrated on the GPU. To allow the program to continue running, we forcibly replace these negative values with 10⁻⁹. It is because these negative values are replaced by positive values that the simulation results are biased. In general, for SO₂, O₃, NO₂, H₂O₂, and PSO₄, the AEs in the majority of the grid boxes are in the range of ±0.8 ppbV or ±0.8 µg m⁻³ between the standard C and CUDA C versions; for CO, because its background concentration is higher, the AEs of the standard C and CUDA C versions are outside that range, and they fall into the range of −8 and 8 ppbV in some grid boxes and show more obvious AEs than the other species.

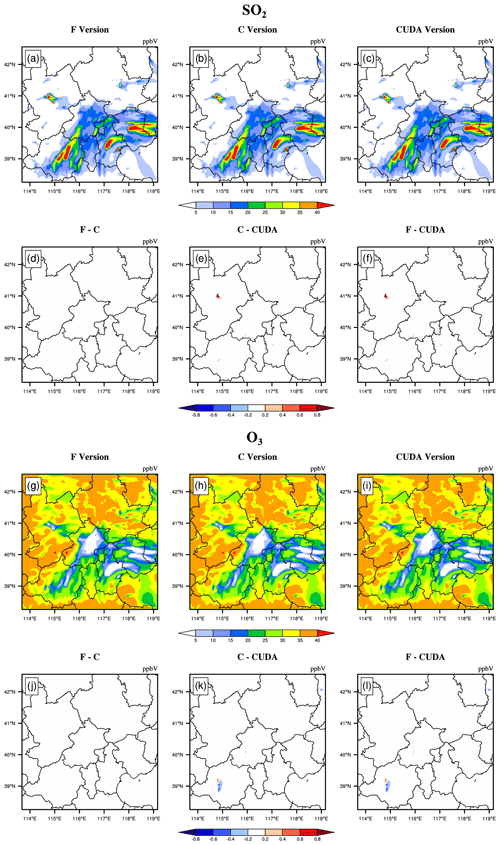
Figure 5 SO₂ and O₃ concentrations outputted by the CAMx model for the Fortran, standard C, and CUDA C versions. Panels (a) and (g) are from the Fortran versions. Panels (b) and (h) are from the standard C versions. Panels (c) and (i) are from the CUDA C versions. Panels (d) and (j) are the output concentration differences in the Fortran and standard C versions. Panels (e) and (k) are the output concentration differences in the standard C and CUDA C versions. Panels (f) and (l) are the output concentration differences in the Fortran and CUDA C versions.

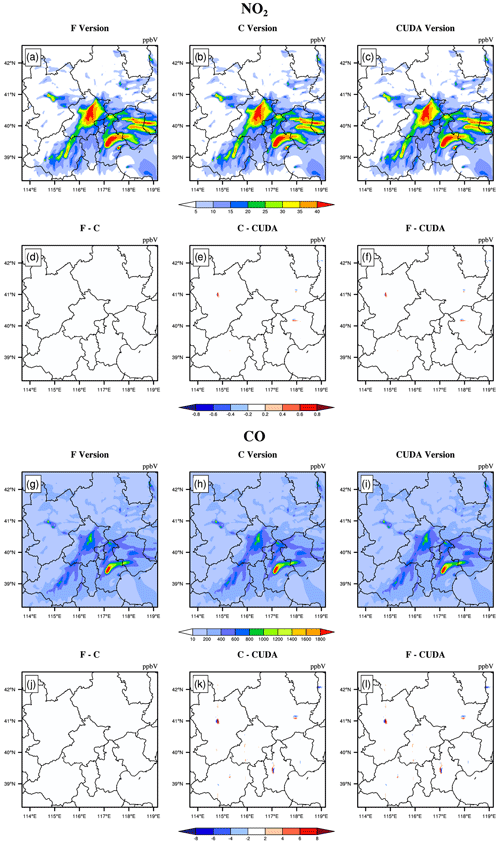
Figure 6 NO₂ and CO concentrations outputted by the CAMx model for the Fortran, standard C, and CUDA C versions. Panels (a) and (g) are from the Fortran versions. Panels (b) and (h) are from the standard C versions. Panels (c) and (i) are from the CUDA C versions. Panels (d) and (j) are the output concentration differences in the Fortran and standard C versions. Panels (e) and (k) are the output concentration differences in the standard C and CUDA C versions. Panels (f) and (l) are the output concentration differences in the Fortran and CUDA C versions.

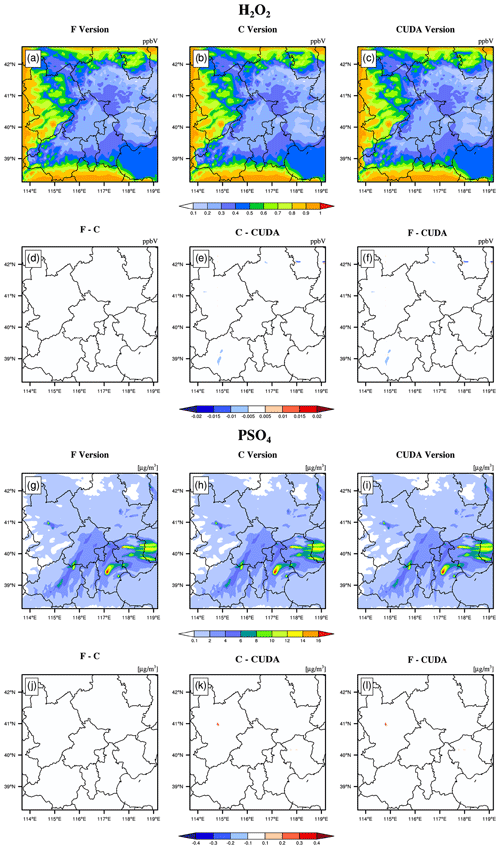
Figure 7 H₂O₂ and PSO₄ concentrations outputted by the CAMx model for the Fortran, standard C, and CUDA C versions. Panels (a) and (g) are from the Fortran versions. Panels (b) and (h) are from the standard C versions. Panels (c) and (i) are from the CUDA C versions. Panels (d) and (j) are the output concentration differences in Fortran and standard C versions. Panels (e) and (k) are the output concentration differences in the standard C and CUDA C versions. Panels (f) and (l) are the output concentration differences in the Fortran and CUDA C versions.

Figure 8 shows the boxplot of the AEs and relative errors (REs) in all the grid boxes for the six species during the porting process. As described above, the AEs and REs introduced by Fortran to the standard C code refactoring process are significantly small, and the primary error comes from converting standard C to CUDA C. Statistically, the average AEs (REs) of SO₂, O₃, NO₂, CO, H₂O₂, and PSO₄ were −0.0009 ppbV (−0.01 %), 0.0004 ppbV (−0.004 %), 0.0005 ppbV (0.008 %), 0.03 ppbV (0.01 %), and $\mathrm{2.1}\times {\mathrm{10}}^{-\mathrm{5}}$ ppbV (−0.01 %) and 0.0002 µg m⁻³ (0.0023 %), respectively, between the Fortran and CUDA C versions. In terms of the time series, the regionally averaged time series of the three versions are almost consistent (as shown in Fig. S2), and the maximum AEs for the above six species are 0.001, 0.005, 0.002, 0.03, and 0.0001 ppbV and 0.0002 µg m⁻³, respectively, between the Fortran and CUDA C versions.

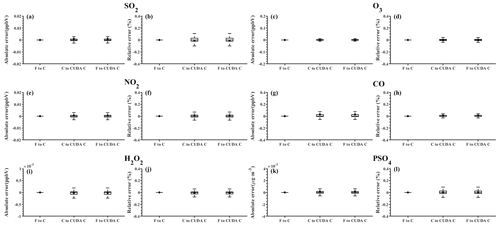
Figure 8 The distributions of absolute errors and relative errors for SO₂, O₃, NO₂, CO, H₂O₂, and PSO₄ in all of the grid boxes after 48 h of integration.

Figure 9 presents the regionally averaged time series and the AEs of SO₂, O₃, NO₂, CO, H₂O₂, and PSO₄. The time series between the different versions is almost consistent, and the maximum AEs for the above six species are 0.001, 0.005, 0.002, 0.03, and 0.0001 ppbV and 0.0002 µg m⁻³, respectively, between the Fortran and CUDA C versions.

It is difficult to verify the scientific applicability of the results from the CUDA C version because the programming language and hardware are different between the Fortran and CUDA C versions. Here, we used the evaluation method of P. Wang et al. (2021) to compute the root mean square errors (RMSEs) of SO₂, O₃, NO₂, CO, H₂O₂, and PSO₄ between the Fortran and CUDA C versions, which are 0.0007, 0.001, 0.0002, 0.0005, and 0.00003 ppbV and 0.0004 µg m⁻³, respectively, much smaller than the spatial variation in the whole region, which is 7.0 ppbV (approximately 0.004 %), 9.7 ppbV (approximately 0.003 %), 7.4 ppbV (approximately 0.003 %), 142.2 ppbV (approximately 0.006 %), and 0.2 ppbV (approximately 0.015 %) and 1.7 µg m⁻³ (approximately 0.004 %). The bias between CUDA C and the Fortran version of the above six species is negligible compared with their own spatial changes, and the results of the CUDA C version are generally acceptable for research purposes.

4.3 Offline performance comparison of GPU-HADVPPM

As described in Sect. 4.2, we validate that the CAMx model result of the CUDA C version is generally acceptable for scientific research. We tested the offline performance of the HADVPPM and GPU-HADVPPM schemes on one CPU core and one GPU card. There are seven variables input into the HADVPPM program, which are nn, dt, dx, con, vel, area, and areav, and their specific meanings are shown in Table S1.

First, we use the random_number function in Fortran to create random single-precision floating-point numbers of different sizes for the above seven variables and then transmit these random numbers to the hadvppm Fortran program and hadvppm_kernel CUDA C program for computation. Finally, we test the offline performance of the HADVPPM and GPU-HADVPPM on the CPU and GPU platforms. During the offline performance experiments, we used two different CPUs and GPUs described in Sect. 2.4, and the experimental results are shown in Fig. 9.

On the CPU platform, the wall time of the hadvppm Fortran program does not change significantly when the data size is less than 1000. With the increase in the data size, its wall time increases linearly. When the data size reaches 10⁷, the wall times of the hadvppm Fortran program on the Intel Xeon E5-2682 v4 and Intel Platinum 8168 CPU platforms are 1737.3 and 1319.0 ms, respectively. On the GPU platform, the reconstructed and extended CUDA C program implements parallel computation of multiple grid points by executing a large number of kernel function copies, so the computational efficiency of the hadvppm_kernel CUDA C code on it is significantly improved. In the size of 10⁷ random numbers, the hadvppm_kernel CUDA C program takes only 12.1 and 1.6 ms to complete the computation on the NVIDIA Tesla K40m GPU and NVIDIA Tesla V100 GPU.

Figure 9b shows the speedup of HADVPPM and GPU-HADVPPM on the CPU platform and GPU platform under different data sizes. When mapping the HADVPPM scheme to the GPU, the computational efficiency under different data sizes is not only significantly improved, but the larger the data size is, the more obvious the acceleration effect of GPU-HADVPPM. For example, in the size of 10⁷ random numbers, GPU-HADVPPM achieved a 1113.6× and 845.4× acceleration on the NVIDIA Tesla V100 GPU compared to the Intel Xeon E5-2682 v4 and Intel Platinum 8168 CPU, respectively. Although the K40m GPU's single-card computing performance is slightly lower than that of the V100 GPU, GPU-HADVPPM can also achieve up to a 143.3× and 108.8× acceleration.

As described in Sect. 3.2, the thread is the most basic GPU unit for parallel computing. Each dimension of the three-dimensional block can contain a maximum number of threads of 1024, 1024, and 64. Each dimension of the three-dimensional grid can contain a maximum number of blocks of 2³¹−1, 65 535, and 65 535. It is theoretically possible to distribute a large number of copies of kernel functions into tens of billions of threads for parallel computing without exceeding the GPU memory. In the offline performance experiments, the GPU achieved up to 10×10⁶ threads of parallel computing, while the CPU could only use serial cyclic computation. Therefore, GPU-HADVPPM achieves a maximum acceleration of approximately 1100× without I/O (input/output). In addition to this study, the GPU-based SBU-YLIN scheme in the WRF model can achieve a 896× acceleration compared to the Fortran implementation running on the CPU (Mielikainen et al., 2012b).

Figure 9 The offline performance of the HADVPPM and GPU-HADVPPM schemes on the CPU and GPU. The unit of the wall times for the offline performance experiments is in milliseconds (ms).

4.4 Coupling performance comparison of GPU-HADVPPM with different GPU configurations

4.4.1 CAMx-CUDA on a single GPU

The offline performance results show that the larger the data size is, the more obvious the acceleration effect of the GPU-HADVPPM scheme. After coupling GPU-HADVPPM to CAMx without changing the advection module algorithm, the overall computational efficiency of the CAMx-CUDA model is extremely low, and it takes approximately 621 min to complete a 1 h integration on the V100 cluster. Therefore, according to the optimization scheme in Sect. 3.2, by optimizing the algorithm of the xyadvec Fortran program, we gradually increase the size of the data transmitted and reduce the data transmission frequency between the CPU and GPU. When the data transmission frequency between the CPU and GPU is reduced to 1 within one time step, we further optimize the GPU memory access order on the GPU card, eliminate unnecessary assignment loops before kernel functions are launched, and use the thread and block indices.

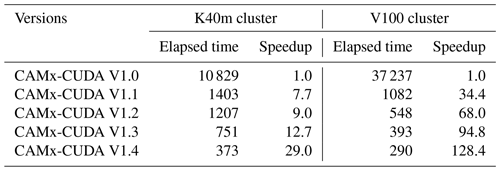
Table 4 lists the total elapsed time for different versions of the CAMx-CUDA model during the optimization, as described in Sect. 3.2. Since the xyadvec program in CAMx-CUDA V1.0 is not optimized, it is extremely computationally inefficient when starting two CPU processes and configuring a GPU card for P1. On the K40m and V100 clusters, it takes 10 829 and 37 237 s, respectively, to complete a 1 h simulation.

By optimizing the algorithm of the xyadvec Fortran program and hadvppm_kernel CUDA C program, the data transmission frequency between the CPU and GPU was decreased, and the overall computing efficiency was improved after GPU-HADVPPM was coupled to the CAMx-CUDA model. In CAMx-CUDA V1.2, the data transmission frequency between CPU–GPU within one time step is reduced to 1; the elapsed time on the two heterogeneous clusters is 1207 and 548 s, respectively; and the speedup is 9.0× and 68.0× compared to CAMx-CUDA V1.0.

The GPU memory access order can directly affect the overall GPU-HADVPPM computational efficiency on the GPU. In CAMx-CUDA V1.3, we optimized the memory access order of the hadvppm_kernel CUDA C program on the GPU and eliminated the unnecessary assignment loops before the kernel functions were launched, which further improved the CAMx-CUDA model's computational efficiency, resulting in 12.7× and 94.8× speedups.

Using thread and block indices to simultaneously compute the horizontal grid points can greatly improve the computational efficiency of GPU-HADVPPM and thus reduce the overall elapsed time of the CAMx-CUDA model. CAMx-CUDA V1.4 further reduces the elapsed time by 378 and 103 s on the K40m cluster and V100 cluster, respectively, compared with CAMx-CUDA V1.3 and achieves up to a 29.0× and 128.4× speedup compared with CAMx-CUDA V1.0.

Table 4 Total elapsed time for different versions of CAMx-CUDA during the optimization. The unit of elapsed time for experiments is in seconds (s).

In terms of the single-module computational efficiency of HADVPPM and GPU-HADVPPM, we further tested the computational performance of the Fortran version of HADVPPM on the CPU, C version of HADVPPM on the CPU, and the CUDA C version of GPU-HADVPPM in CAMx-CUDA V1.4 (GPU-HADVPPM V1.4) on the GPU using system_clock functions in the Fortran language and cudaEvent_t in CUDA programming. The specific results are shown in Fig. 10. On the K40m cluster, it takes 37.7 and 51.4 s to launch the Intel Xeon E5-2682 v4 CPU to run the Fortran and C version HADVPPM, respectively, and the C version is 26.7 % slower than the Fortran version. After the CUDA technology was used to convert the C code into CUDA C, the CUDA C version took 29.6 s to launch an NVIDIA Tesla K40m GPU to run GPU-HADVPPM V1.4, with a 1.3× and 1.7× acceleration. On the V100 cluster, the Fortran, C, and CUDA C versions are computationally more efficient than those on the K40m cluster. It takes 30.1 and 45.2 s to launch the Intel Xeon Platinum 8168 CPU to run the Fortran and C version HADVPPM and 1.6 s to run GPU-HADVPPM V1.4 using an NVIDIA V100 GPU. The computational efficiency of the CUDA C version is 18.8× and 28.3× higher than the Fortran and C versions, respectively.

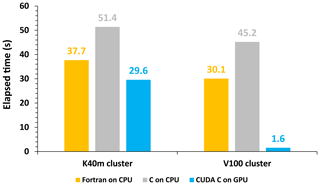
Figure 10 The elapsed time of the Fortran version HADVPPM on the CPU, the C version HADVPPM on the CPU, and the CUDA C version GPU-HADVPPM V1.4 on the GPU. The unit is in seconds (s).

Figure 11 The total elapsed time and speedup of CAMx-CUDA V1.3 and V1.4 on multiple GPUs. The unit of elapsed time for experiments is seconds (s).

4.4.2 CAMx-CUDA on multiple GPUs

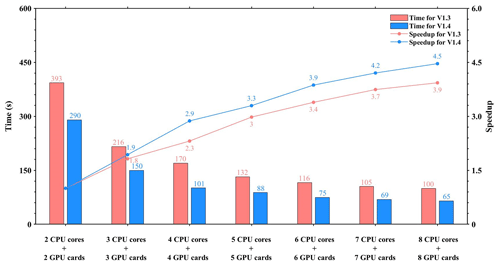
To make full use of the multicore and multi-GPU supercomputers in the heterogeneous cluster, the MPI + CUDA acceleration algorithm was implemented to improve the total computational performance of the CAMx-CUDA model. Two different compile flags were implemented in this study before comparing the computational efficiency of CAMx-CUDA V1.3 and V1.4 on multiple GPUs, namely, -mieee-fp and -fp-model precise. The -mieee-fp compile flag comes from the Makefile of the official CAMx version, which uses the IEEE standard to compare the floating-point numbers. Its computational accuracy is higher, but the efficiency is slower. The -fp-model precise compile flag controls the balance between the precision and efficiency of the floating-point calculations, and it can force the compiler to use the vectorization of some calculations under value safety. The experimental results show that the -fp-model precise compile flag is 41.4 % faster than -mieee-fp, and the AEs of the simulation results are less than ±0.05 ppbV (Fig. S3). Therefore, the -fp-model precise compile flag is implemented when comparing the computational efficiency of CAMx-CUDA V1.3 and V1.4 on multiple GPU cards. Figure 11 shows the total elapsed time and speedup of CAMx-CUDA V1.3 and V1.4 on the V100 cluster. The total elapsed time decreases as the number of CPU cores and GPU cards increases. When starting eight CPU cores and eight GPU cards, the speedup of CAMx-CUDA V1.4 is increased from 3.9× to 4.5× compared with V1.3, and the computational efficiency is increased by 35.0 %.

5 Conclusions and discussion

GPU accelerators are playing an increasingly important role in high-performance computing. In this study, a GPU acceleration version of the PPM solver (GPU-HADVPPM) of horizontal advection for an air quality model was developed, which runs on GPU accelerators using the standard C programming language and CUDA technology. The offline performance results showed that the K40m and V100 GPU can achieve up to a 845.4× and 1113.6× speedup, respectively, and the larger the data input to the GPU, the more obvious the acceleration effect. After coupling GPU-HADVPPM to the CAMx model, a series of optimization measures were taken, including reducing the CPU–GPU communication frequency, increasing the data computation size on the GPU, optimizing the GPU memory access order, and using thread and block indices to improve the overall computing performance of the CAMx-CUDA model. Using a single GPU card, the optimized CAMx-CUDA V1.4 model improved the computing efficiency by 29.0× and 128.4× on the K40m cluster and the V100 cluster, respectively. In terms of the single-module computational efficiency of GPU-HADVPPM, it achieved a 1.3× and 18.8× speedup on an NVIDIA Tesla K40m GPU and NVIDIA Tesla V100 GPU, respectively. To make full use of the multicore and multi-GPU supercomputers and further improve the total computational performance of the CAMx-CUDA model, a parallel architecture with an MPI+CUDA hybrid paradigm was presented. After implementing the acceleration algorithm, the total elapsed time decreased as the number of CPU cores and GPU cards increased, and it achieved up to a 4.5× speedup when launching eight CPU cores and eight GPU cards compared with two CPU cores and two GPU cards.

However, the current approach has some limitations, which are as follows:

1. We currently implement thread and block co-indexing to compute horizontal grid points in parallel. Given the CAMx model three-dimensional grid computing characteristics, in the future, three-dimensional thread and block co-indexing will be considered to compute three-dimensional grid points in parallel.

2. The communication bandwidth of data transfer is one of the main issues restricting the computing performance of the CUDA C codes on the GPUs. This restriction holds true not only for GPU-HADVPPM but also for the WRF module (Mielikainen et al., 2012b, 2013b; Huang et al., 2013). In this study, the data transmission efficiency between the CPU and GPU is improved only by reducing the communication frequency. In the future, more technologies, such as pinned memory (Wang et al., 2016), will be considered to resolve the communication bottleneck between the CPUs and GPUs.

3. To further improve the overall computational efficiency of the CAMx model, the heterogeneous porting scheme proposed in this study will be considered to conduct the heterogeneous porting of other CAMx modules in the future.