A machine learning approach targeting parameter estimation for plant functional type coexistence modeling using ELM-FATES (v2.0)

Tropical forest dynamics play a crucial role in the global carbon, water, and energy cycles. However, realistically simulating the dynamics of competition and coexistence between different plant functional types (PFTs) in tropical forests remains a significant challenge. This study aims to improve the modeling of PFT coexistence in the Functionally Assembled Terrestrial Ecosystem Simulator (FATES), a vegetation demography model implemented in the Energy Exascale Earth System Model (E3SM) land model (ELM), ELM-FATES. Specifically, we explore (1) whether plant trait relationships established from field measurements can constrain ELM-FATES simulations and (2) whether machine learning (ML)-based surrogate models can emulate the complex ELM-FATES model and optimize parameter selections to improve PFT coexistence modeling. We conducted three ensembles of ELM-FATES experiments at a tropical forest site near Manaus, Brazil. By comparing the ensemble experiments without (Exp-CTR) and with (Exp-OBS) consideration of observed trait relationships, we found that accounting for these relationships slightly improves the simulations of water, energy, and carbon variables when compared to observations but degrades the simulation of PFT coexistence. Using ML-based surrogate models trained on Exp-CTR, we optimized the trait parameters in ELM-FATES and conducted another ensemble of experiments (Exp-ML) with these optimized parameters. The proportion of PFT coexistence experiments significantly increased from 21 % in Exp-CTR to 73 % in Exp-ML. After filtering the experiments that allow for PFT coexistence to agree with observations (within 15 % tolerance), 33 % of the Exp-ML experiments were retained, which is a significant improvement compared to the 1.4 % in Exp-CTR. Exp-ML also accurately reproduces the annual means and seasonal variations in water, energy, and carbon fluxes and the field inventory of aboveground biomass. This study represents a reproducible method that utilizes machine learning to identify parameter values that improve model fidelity against observations and PFT coexistence in vegetation demography models for diverse ecosystems. Our study also suggests the need for new mechanisms to enhance the robust simulation of coexisting plants in ELM-FATES and has significant implications for modeling the response and feedbacks of ecosystem dynamics to climate change.

1 Introduction

Tropical ecosystems feature the highest biodiversity on Earth, maintaining more than 75 % of all known species (Mora et al., 2011; Mitchard, 2018). The dynamics of tropical forests are closely related to the regional and global carbon, energy, and water cycles (Bonan, 2008; Piao et al., 2020). Vegetation is expected to face more water stress from vapor pressure deficit increase and soil moisture reduction with global warming (McDowell et al., 2020). Tree mortality rates are accelerating in some tropical regions due to rising atmospheric water stress (Bauman et al., 2022; Hubau et al., 2020; Zuleta et al., 2017). Tropical forests currently make an approximately neutral contribution to the global carbon cycle as a result of a large land use source balanced by sinks in recovering and undisturbed forests, but they may become a carbon source in the future under the threat of climate change and human-induced disturbance (Mitchard, 2018; Gatti et al., 2021). Therefore, both understanding and modeling tropical forest dynamics and related feedbacks have crucial implications for projecting future changes in the global climate system.

Dynamic global vegetation models (DGVMs) are the primary tools to simulate terrestrial ecosystem dynamics of plant functional type distribution, ecosystem composition and functioning, and ecosystem response to and recovery from disturbance (e.g., fire and wind damage) (Longo et al., 2019; Fisher et al., 2018; Foley et al., 1996; Sitch et al., 2003; Cao and Woodward, 1998; Berzaghi et al., 2019; McMahon et al., 2011). Conventional DGVMs represent plant communities using an area-averaged representation of plant functional types (PFTs) in each grid cell. Their relatively simple structures have the advantage of high computational efficiency for use in Earth system models (Fisher et al., 2018; Snell et al., 2014). However, these models do not capture many demographic processes. For example, plants of each represented PFT typically have identical properties (e.g., tree size), which limits the capability of modeling ecosystem dynamics and functioning of canopy gap formation, PFT competition, and disturbance reactions (Feeley et al., 2007; Stark et al., 2012; Hurtt et al., 1998; Moorcroft, 2003; Brister et al., 2020). To address these limitations, researchers have developed a new of generation DGVMs called vegetation demographic models (VDMs), commonly including individual-based models and cohort-based models (Fisher et al., 2018). The individual-based models, also known as forest gap models, explicitly represent vegetation as individual plants and simulate their birth, growth, and death (Fyllas et al., 2014; Christoffersen et al., 2016; Sato et al., 2007; Jonard et al., 2020; Maréchaux and Chave, 2017). These models incorporate the stochasticity and heterogeneity of the plant light environment mechanistically and thereby can typically represent PFT competitive exclusion, succession, and coexistence. However, explicit simulations of individual plants with stochastic processes suffer a substantial computational penalty and limit applicability over large or global scales (Fisher et al., 2018). To capture sufficient ecosystem dynamics and maintain relatively high computational efficiency, “cohort-based” models have been proposed (Haverd et al., 2013; Medvigy et al., 2009; Ma et al., 2022; Moorcroft et al., 2001; Weng et al., 2015; Longo et al., 2019; Martín Belda et al., 2022). In cohort-based approaches, individual plants are grouped together as “cohorts” based on their similar properties, including size, age, and PFT (Fisher et al., 2018). Many cohort-based models have been developed and widely used across regional to global scales. Examples of cohort-based models include the Ecosystem Demography model (ED) (Moorcroft et al., 2001), the Functionally Assembled Terrestrial Ecosystem Simulator (FATES) (Fisher et al., 2018, 2015), and the Geophysical Fluid Dynamics Laboratory (GFDL) Land Model 3 with the Perfect Plasticity Approximation (LM3-PPA) (Weng et al., 2015). In this study, we employ the FATES model, a widely used tool for modeling ecosystem dynamics in multiple ecosystems, including tropical (Holm et al., 2020; Koven et al., 2020; Chitra-Tarak et al., 2021; Cheng et al., 2021), boreal (Lambert et al., 2022), and mixed-conifer forests (Buotte et al., 2021) and forest disturbance (Huang et al., 2020).

Despite ongoing applications, robust simulations of competition and coexistence in cohort-based VDMs remain a major challenge. In niche-based coexistence theory, coexisting species require both convergence in strategy to adapt to the surrounding environment (“environmental filtering”) and divergence in strategy to ensure differentiation in resource requirements (“niche partitioning”) (Kraft et al., 2008; Adler et al., 2013). These same constraints apply to coexisting PFTs as modeled by VDMs. Thus, on the one hand, VDMs need to include mechanisms that capture critical niche dimensions (e.g., spatial and temporal variation in light, water, and nutrients). For example, the multilayer canopy structure in FATES provides vertical light resource differentiation. Another essential aspect is to assign reasonable plant functional traits (i.e., the parameters that define a given plant functional type) to satisfy environmental filtering, ensure niche partitioning, and consequently preserve PFT coexistence. Considering the relatively high computational cost of VDMs and the host land surface models, it is not feasible to directly apply global optimization methods such as shuffled complex evolution (Duan et al., 1992) to calibrate trait-related parameters because this could be a time-consuming and computationally intensive process (Rouholahnejad et al., 2012). Therefore, most previous studies use the filtered ensemble approach to select trait-related parameters involving several steps: (1) generating a parameter ensemble based on reference trait ranges or correlations, (2) conducting ensemble model simulations, and (3) filtering the parameter ensemble by coexistence and other criteria (e.g., observation constraints). For example, Huang et al. (2020) applied FATES implemented in the Community Land Model (CLM; herein CLM-FATES) with two tropical PFTs to study forest dynamics at tropical sites. They performed 70 one-at-a-time experiments before obtaining one reasonable parameter set. Buottte et al. (2021) used CLM-FATES to simulate forest dynamics of pine and incense cedar over the Sierra Nevada of California, and their two stages of experiments (360 plus 72 runs) only yielded four sets of parameters that met the given criteria. The filtered ensemble approach has low efficiency, which hinders VDMs' application to modeling ecosystem dynamics under the changing climate. In addition, trait relationships derived from field measurements are often used to infer parameter selections when simulating coexistence. For example, Longo et al. (2020) used multiple trait relationships derived from various datasets to guide parameter selection for different PFTs in the ED-2.2 model simulations. However, whether the observed trait relationships can efficiently improve PFT coexistence simulation in current VDMs is still unclear. Earlier studies using FATES have also highlighted the importance of reproductive feedbacks in maintaining or prohibiting coexistence (Fisher et al., 2010; Maréchaux and Chave, 2017). Fundamentally, if PFTs have highly contrasting reproductive output, the model tends towards competitive exclusion, and thus discerning areas with at least approximately equal fitness is necessary. While representing a large number of plant functional types may improve the likelihood of coexistence (Koven et al., 2020), this comes at a considerable computational expense.

Machine learning (ML) has facilitated Earth science studies (Shen, 2018; Nearing et al., 2021; Zhu et al., 2022; Pal et al., 2019; Jung et al., 2019), possibly providing a promising approach to improve PFT coexistence modeling in VDMs. ML algorithms have been broadly and successfully employed in recent decades. They can be used as standalone models to predict variables of interest or integrated with process-based models to improve simulations (Xu and Liang, 2021; He et al., 2022; Peatier et al., 2022). Among these applications, ML has shown advantages as a surrogate model for parameter optimization and sensitivity quantification, including its effectiveness and easy application, its ability to implicitly deal with complex nonlinear correlations and high dimensional data, and handle interactions between variables (Sit et al., 2020; Antoniadis et al., 2020; Tsai et al., 2021). One promising approach is to construct ML-based surrogate models using data from initial model simulations to emulate the relationship between inputs (i.e., model parameters) and model outputs (Wang et al., 2014). The computationally inexpensive surrogate model can then be efficiently used for parameter optimization and sensitivity analysis. For example, Dagon et al. (2020) implemented artificial neural networks to emulate the satellite leaf area constrained version of CLM5 (Lawrence et al., 2019) and estimated optimal parameters to improve the global simulation of gross primary production and latent heat flux. Sawada (2020) developed an ML surrogate model to optimize the land surface model parameters and improve soil moisture and vegetation dynamics simulations. Watson-Parris et al. (2021) built a general tool to efficiently emulate Earth system models for uncertainty quantification and model calibration. Although employing ML-based surrogate models to optimize the trait parameters and hence improve the vegetation dynamics modeling in VDMs is promising, this area of research remains under-explored.

This study aims to improve PFT coexistence modeling in VDMs. The cohort-based FATES implemented in the Energy Exascale Earth System Model (E3SM) land model (ELM; Golaz et al., 2019), i.e., ELM-FATES, is taken as our test bed. The ELM land model simulates surface energy fluxes, soil and canopy biophysics, hydrology, and soil biogeochemistry, whereas FATES simulates live vegetation processes, litter dynamics, and fire. We first examine whether trait relationships constructed from field measurements can help improve ELM-FATES simulations. Second, we explore whether ML-based surrogate models can help optimize key trait parameters in ELM-FATES to improve the simulation of PFTs coexistence. Our model experiments are conducted for a tropical rainforest site located in Manaus, Brazil. This paper is organized as follows. Section 2 describes ELM-FATES, summarizes the key functional trait-related parameters, introduces the machine learning algorithms, and explains the overall experimental design. Results are presented in Sect. 3, followed by discussions and conclusions in Sects. 4 and 5, respectively.

2 Methodology

2.1 Study site and data

Our study site is located at kilometer 34 (K34) of the ZF2 road, Manaus, Brazil (latitude: −2.6091^∘ S; longitude: −60.2093^∘ W). The K34 site is an old-growth primary forest with minimal human disturbances (Holm et al., 2020). The annual precipitation is about 2252 mm, and the mean temperature is about 26.68 ^∘C (https://ameriflux.lbl.gov/sites/siteinfo/BR-Ma2, last access: 6 June 2022). The wet season is from November to May, and the dry season is from June to October (Fang et al., 2017). Hourly meteorological forcing (i.e., precipitation, air temperature, relative humidity, wind speed, surface pressure) at the K34 eddy covariance flux tower from 2002 to 2005 was obtained from the LBA-ECO CD-32 Flux Tower Network Data Compilation (Restrepo-Coupe et al., 2021). Observational reference datasets obtained from Holm et al. (2020) include gross primary production (GPP), evapotranspiration (ET), sensible heat flux (SH), Bowen ratio (BW, the ratio between sensible heat and latent heat), and inventory data-based aboveground biomass (AGB). The GPP, ET, SH, and BW observations are monthly climatological averages from 2000 to 2008 (Table S1). The AGB at this site is about 303±2.3 Mg ha⁻¹. These observational data were used to evaluate the ELM-FATES simulations and constrain the ML surrogate models.

2.2 ELM-FATES and parameters

ELM-FATES is used as the model test bed. ELM is the land model of E3SM, which is the host land model of FATES (Golaz et al., 2019; Leung et al., 2020; Holm et al., 2020). FATES is a size- and age-structured vegetation model developed from the Community Land Model with Ecosystem Demography (CLM-ED) (Fisher et al., 2015; Koven et al., 2020). FATES includes two key structural components: ecosystem demography (ED; Moorcroft et al., 2001) and a modified version of perfect plasticity approximation (PPA, Purves et al., 2008). FATES discretizes the simulated landscape into spatially implicit patches representing different disturbance histories of the ecosystem since the last disturbance. Within each patch, the hypothetical population of plants is grouped into cohorts: a cohort consists of a population density of trees with similar size and the same plant functional type. Cohorts are organized, via the PPA concept, into canopy layers, and compete for light based on their canopy vertical positions (e.g., canopy layer vs. understory layer). The understory layer is formed when the canopy area becomes greater than the total ground area, and some fraction of each cohort is “demoted” to the understory as a function of its height. The number of patches and cohorts varies depending on processes, including recruitment, growth, mortality, competition, and disturbance. The modified PPA probabilistically splits cohorts into discrete canopy and understory layers based on a function of their height (Strigul et al., 2008; Fisher et al., 2010). A detailed description of the FATES model can be found in its technical note (Zenodo, https://doi.org/10.5281/zenodo.3517272; FATES Development Team, 2019).

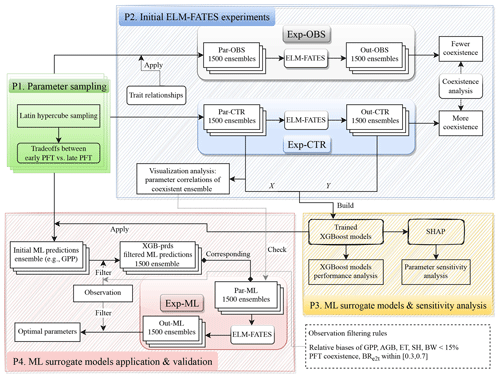
In this study, we configured two PFTs in ELM-FATES, i.e., early successional and late successional broadleaf evergreen tropical trees, which can represent a primary axis of variability in tropical forests (Huang et al., 2020; Reich, 2014; Díaz et al., 2016). There are tradeoffs between the plant traits of these two PFTs. Compared with the late successional PFT, the early successional PFT is more light demanding and fast growing but with lower woody density, shorter leaf and root lifespans, and higher background mortality. To represent the drought impacts on forest dynamics, the early successional PFT is further assumed to be less drought resistant with shallower rooting depth and is hence more easily affected by drought conditions (Oliveira et al., 2021). The corresponding tradeoffs and parameters between these two PFTs are shown in Fig. 1 and Table 1.

Figure 1 Schematic representation of tradeoffs between early and late successional PFTs. Dark red denotes a higher parameter value. The tradeoffs of the top five traits are used to constrain the parameter sampling.

Table 1 Summary of ELM-FATES trait parameters for two PFTs.

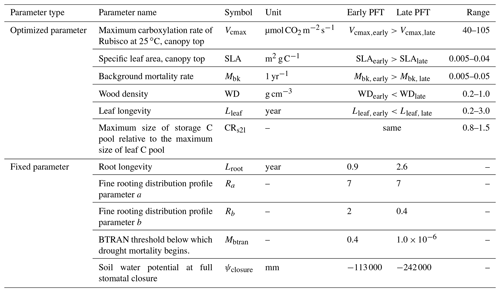
Parameter references (Huang et al., 2020; Koven et al., 2020; Longo et al., 2020; Holm et al., 2020; Cheng et al., 2021; Domingues et al., 2005; Chitra-Tarak et al., 2021; Buotte et al., 2021).
R_a and R_b are parameters that determine the rooting depth and vertical distribution of fine roots.
BTRAN is the plant water stress factor. BTRAN $\in \left[\mathrm{0},\mathrm{1}\right]$, where 0 represents full water stress and 1 represents no water stress.

2.3 Machine learning algorithm

We built ML-based surrogate models to emulate ELM-FATES simulations. To represent the relationships between ELM-FATES parameters and simulations (e.g., AGB), we used eXtreme Gradient Boosting (XGBoost; Chen and Guestrin, 2016), a decision-tree-based ensemble machine learning algorithm. Ensemble learning techniques combine the predictions of multiple independent base models (e.g., decision trees) to produce more accurate predictions, with popular algorithms such as Random Forest (Breiman, 2001) and XGBoost. While Random Forest builds an ensemble of parallel trees using bagging and produces the final prediction by averaging the outputs of all individual trees, XGBoost sequentially trains a set of decision trees using boosting (Friedman, 2001), where each successive tree corrects the mistakes of its predecessors, and the final prediction is obtained by combining the predictions of all trees using a weighted sum. XGBoost not only handles complex nonlinear interactions and collinearity between different features but also provides a parallel implementation that effectively solves a range of data science problems. It has been successfully applied in a variety of fields within Earth and Environmental Sciences, such as urban temperature emulation (Zheng et al., 2021c), wildfire-burned area (Wang et al., 2021), emissions prediction (Wang et al., 2022), flash flood risk assessment (Ma et al., 2022), and aerosol property estimation (Zheng et al., 2021a, b).

2.4 Experimental design

The experimental design flowchart is shown in Fig. 2. Overall, we generated three ensembles of parameter values, i.e., Par-CTR, Par-OBS, and Par-ML, and conducted three ensembles of corresponding ELM-FATES experiments, i.e., Exp-CTR, Exp-OBS, and Exp-ML. Exp-CTR is the control experiment without being constrained by the observed trait relationships. Exp-OBS considered the constraint of the observed trait relationships. Par-ML was generated by machine learning surrogate models, which were trained based on Exp-CTR, and then used to conduct Exp-ML. The detailed experiment procedures are described below.

Figure 2 Overall flowchart of experimental design and associated analysis.

2.4.1 Procedure 1: parameter sampling

The procedure “P1” in Fig. 2 is used to generate an ensemble of parameter values for each experiment ensemble, i.e., Exp-CTR, Exp-OBS, and Exp-ML. First, a number of initial parameter sets (e.g., 5000 sets) were generated using Latin hypercube sampling (LHS; Mckay et al., 2000). Second, the initial parameter sets were filtered by the trait tradeoffs between early and late successional PFTs (Fig. 1). We repeatedly increased the number of initial parameter sets in the first step until 1500 parameter sets were obtained in the second step. Each ELM-FATES experiment starts from bare ground and runs for 350 years to reach an equilibrium state by cycling the meteorological forcing during 2002–2005, and the last 4 years of the simulations were analyzed.

2.4.2 Procedure 2: initial ELM-FATES experiments of Exp-CTR and Exp-OBS

To test whether plant trait relationships established from field measurements can improve the ELM-FATES simulations, we derived three trait relationships based on the tropical studies of Koven et al. (2020) and Longo et al. (2020). Using the digitized data from Fig. 3 in Koven et al. (2020), the background mortality M_bk (see Table 1 for parameter definitions) can be empirically computed from the maximum carboxylation rate V_cmax,

$$\begin{array}{}\text{(1)}& M_{\mathrm{bk}}=\mathrm{0.0082}\times e^{(\mathrm{0.0153}\times V_{\mathrm{cmax}})}.\end{array}$$

Based on the equations in Fig. S18 of Longo et al. (2020), the leaf longevity (L_leaf) and wood density (WD) can be calculated via the specific leaf area (SLA),

$$\begin{array}{}\text{(2)}& {\displaystyle }{L}_{\mathrm{leaf}}=\mathrm{0.0001}\times {\text{SLA}}^{(-\mathrm{2.32})},\text{(3)}& {\displaystyle }\text{WD}=-\mathrm{0.583}\times \ln \left(\text{SLA}\right)-\mathrm{1.6754}.\end{array}$$

These trait relationships were used to generate parameters for Par-OBS.

Two initial sets of experiment ensembles, i.e., Exp-CTR and Exp-OBS (procedure “P2” in Fig. 2), were conducted based on Par-CTR and Par-OBS, respectively. For Par-CTR, 1500 parameter sets were generated from the procedure P1 based on the entire set of 11 parameters, i.e., V_cmax,early, V_cmax,late, SLA_early, SLA_late, M_bk, early, M_bk, late, WD_early, WD_late, L_{leaf, early}, L_leaf, late, and CR_s2l (maximum size of storage C pool relative to the maximum size of leaf C pool, Table 1). For Par-OBS, 1500 parameter sets were generated from the procedure P1 but were only based on five parameters (i.e., V_cmax,early, V_cmax,late, SLA_early,SLA_late, and CR_s2l). The other six parameters (M_bk, early, M_bk, late, WD_early, WD_late, L_{leaf, early}, and L_leaf, late) in Par-OBS were calculated based on the trait relationships defined by Eqs. (1)–(3). Therefore, compared to Par-CTR, the parameters in Par-OBS are constrained by the observed trait relationships. The distributions of these two parameter sets are shown in Fig. S1. V_cmax, SLA, and CR_s2l have similar distributions between Par-CTR and Par-OBS. Compared with Par-CTR, Par-OBS has a narrower distribution of M_bk but broader distributions of WD and L_leaf.

Exp-CTR and Exp-OBS each include 1500 total 350-year ELM-FATES simulations. We averaged the last 4 years of these simulations for analysis, i.e., simulation outputs: Out-CTR and Out-OBS, respectively. To quantify the PFT coexistence, we computed the biomass ratio between early successional PFT and the total biomass, denoted as BR_e2t. For brevity, we denote the ELM-FATES experiments with ${\text{BR}}_{\mathrm{e}\mathrm{2}\mathrm{t}}\in [\mathrm{0.1},\mathrm{0.9}]$ as “coexistence”, ${\text{BR}}_{\mathrm{e}\mathrm{2}\mathrm{t}}\in [\mathrm{0.0},\mathrm{0.1})$ as “late”, and ${\text{BR}}_{\mathrm{e}\mathrm{2}\mathrm{t}}\in (\mathrm{0.9},\mathrm{1.0}]$ as “early”. We calculated BR_e2t based on Out-CTR and Out-OBS and then computed the fraction of coexistence experiments in each ensemble. As we will show in Sect. 3.1, when considering the observed trait relationships, Exp-OBS has a lower fraction of coexistence experiments. Therefore, only Exp-CTR was used for further ML-related analysis. We also performed some analysis of Exp-CTR to explore whether the parameters of the coexistence experiments have correlations with each other (Sect. 3.2).

2.4.3 Procedure 3: ML surrogate models and sensitivity analysis

Based on Exp-CTR, we trained XGBoost models to emulate the ELM-FATES model behavior and analyzed the parameter sensitivity (procedure “P3” in Fig. 2). A total of 16 variables were used as XGBoost model features, including 11 parameters in Par-CTR and 5 parameter differences between early and late successional PFTs. The corresponding ELM-FATES annual average outputs were used as XGBoost model targets. Specifically, six models were built, i.e., XGB_ET, XGB_SH, XGB_BW, XGB_GPP, XGB_AGB, and XGB_BR for predicting ET, SH, BW, GPP, AGB, and BR_e2t, respectively. The ML models were trained, tested, and subsequently utilized to perform the parameter sensitivity analysis, as described in Sect. 2.5.

2.4.4 Procedure 4: ML surrogate models application and validation

The trained XGBoost models were then used to help select ELM-FATES parameters (procedure “P4” in Fig. 2). First, initial parameter sets were generated from procedure P1 based on the entire set of 11 parameters (Table 1, identical to the parameter set used for the generation of Par-CTR). Second, these parameter sets and parameter differences were sent to six XGBoost surrogate models to predict ET, SH, BW, GPP, AGB, and BR_e2t. Third, the predictions were further filtered by two criteria: (1) compared to observations, the relative biases of the predicted ET, SH, BW, GPP, and AGB should be less than 15 %, and (2) the XGBoost model-predicted BR_e2t should be within [0.3, 0.7], which corresponds to the range where the XGB-BR model exhibited relatively better performance (Fig. 5). We repeated these three steps until we obtained 1500 sets of XGBoost model predictions that matched the criteria. Finally, we obtained 1500 sets of XGBoost model predictions and their corresponding 1500 sets of parameters (Par-ML). We also checked whether the selected Par-ML could match the empirical relationships derived from the empirical analysis in procedure P2 (see Sect. 3.2 and 3.5 for details). Following this, the 1500 sets of parameters in Par-ML were sent to ELM-FATES to conduct 350-year runs (i.e., Exp-ML). The last 4 years of the simulations were averaged (i.e., Out-ML) for further analysis. We then filtered Out-ML based on a relative bias of 15 % or less compared to observations and PFT coexistence to identify the optimal experiments and corresponding parameters.

2.5 ML model development and SHAP analysis

The process of building each of the six ML surrogate models is described. Taking BR_e2tas an example, the 1500 pairs of 16 features and the corresponding simulated BR_e2t were randomly split into two groups, with 90 % used for training and the remaining 10 % used for testing. Given that the coexistence experiments only account for 20.6 % in the simulations of Exp-CTR (Sect. 3.1), we used 90 % of the data for training to ensure sufficient coexisting samples were included in the training process. Optimizing the hyperparameters of the XGBoost model is crucial for its performance. To achieve this, we employed the Bayesian optimization method during the training process (Snoek et al., 2012). In addition, to avoid overfitting during hyperparameter optimization, we utilized a 5-fold cross-validation method (Feigl et al., 2021). The mean squared error was used as the objective function to achieve the optimal hyperparameters. The root-mean-squared error (RMSE) and R-squared value (R²) are used to quantify the overall model performance for the training and testing data prediction.

Based on the trained XGBoost models, we subsequently employed a game theory approach called SHapley Additive exPlanations (SHAP; Lundberg and Lee, 2017; Lundberg et al., 2018, 2020) to gain insights into the parameter sensitivity of ELM-FATES. SHAP assumes that features (predictive variables) interact and collaborate in a prediction game, with each feature receiving a payout for its contributions. This approach provides a unified measure of feature importance to explain both individual samples and the entire dataset, which is distinct from intrinsic feature importance methods such as the feature importance in XGBoost (Lundberg and Lee, 2017). This approach has been widely used in various fields, including interpreting a digital soil mapping model (Padarian et al., 2020) and identifying the critical drivers of wildfires (Wang et al., 2021). In this study, we performed SHAP analysis for each XGBoost model and used the SHAP values as a proxy to quantify the relative importance of ELM-FATES parameters.

3 Results

3.1 Comparison between Exp-CTR and Exp-OBS

Constraining the input traits using the observed trait relationships yields slightly better ELM-FATES simulations of water, energy, and carbon variables (Fig. 3a–e). The distributions of the relative biases of ET, SH, BW, and GPP have similar ranges between the two sets of experiments (Fig. 3a–d). Compared with Exp-CTR, the 50th percentiles of relative biases of ET, SH, BW, and GPP for Exp-OBS (with constrained traits) are closer to zero, indicating Exp-OBS is slightly better than Exp-CTR. The distribution of simulated AGB for Exp-OBS is much narrower than Exp-CTR (Fig. 3e), which could be due to the narrower distribution of M_bk (Fig. S1).

Exp-CTR has a much higher fraction of coexisting PFT simulations than Exp-OBS (Fig. 3f and Table S2). Overall, 70.6 % of experiments in Exp-CTR and 94.5 % of experiments in EXP-OBS have simulated BR_e2t that is greater than 0.9. This indicates that both Par-CTR and especially Par-OBS favor the early successional PFT. As for the coexisting experiments with ${\text{BR}}_{\mathrm{e}\mathrm{2}\mathrm{t}}\in [\mathrm{0.1},\mathrm{0.9}]$, Exp-CTR has about 5 times more coexisting experiments (20.6 %) than Exp-OBS (4.1 %). Further filtering the coexisting cases by observations (Table S1), only 21 experiments remain in Exp-CTR, and only 6 experiments remain in Exp-OBS (Table S2). Even though Exp-OBS considered the observed trait relationships, it has fewer coexisting cases within the reasonable observation ranges than Exp-CTR. Therefore, Exp-OBS is not used in our remaining analysis.

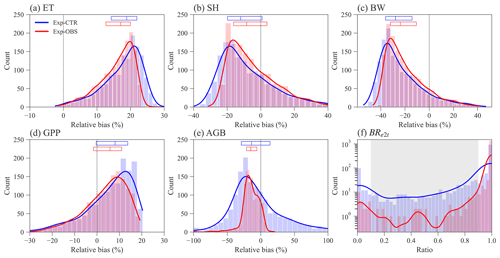
Figure 3 Distribution of ELM-FATES simulations for Exp-CTR and Exp-OBS. The y axis in (f) is logarithmic. Relative bias is equal to $\frac{\text{simulation-observation}}{\text{observation}}\times \mathrm{100}$ (%). In (a)–(e), the top horizontal bars with three vertical lines denote the relative bias at the 25th, 50th, and 75th percentiles, respectively. The grey-shaded area in (f) represents the coexistence biomass ratio between 0.1 and 0.9.

3.2 Parameter analysis of Exp-CTR

We also tested whether simple parameter correlations can be constructed to guide the simulation of PFTs coexistence. No simple parameter correlations can be built to distinguish the coexisting cases from the early and late cases in Exp-CTR (Figs. 4, S2, and S3). Most parameter (or parameter difference) spaces show large overlaps between early, late, and coexisting cases (Figs. S2 and S3). Notably, we empirically built three linear equations based on the boundaries in the parameter spaces for the coexisting cases (Fig. 4). Coexisting cases are primarily located in spaces with ${\text{SLA}}_{\mathrm{late}}>\mathrm{0.35}\times {\text{SLA}}_{\mathrm{early}}+\mathrm{0.003}$ (Fig. 4a and d), $V_{\mathrm{cmax},\mathrm{diff}}<-\mathrm{4800}\times {\text{SLA}}_{\mathrm{diff}}+\mathrm{100}$ (Fig. 4b and e), and ${\text{WD}}_{\mathrm{diff}}>\mathrm{55}\times {\text{SLA}}_{\mathrm{diff}}-\mathrm{1.3}$ (Fig. 4c and f), where $V_{\mathrm{cmax},\mathrm{diff}}=V_{\mathrm{cmax},\mathrm{early}}-V_{\mathrm{cmax},\mathrm{late}}$, and SLA_diff and WD_diff are defined likewise. Within these constrained parameter spaces, the percentage of coexisting cases increases from the original 20.6 % (i.e., 309 out of 1500) to 32.6 % (i.e., 304 out of 932). Therefore, these empirical correlations could help guide ELM-FATES parameter selection for coexisting PFTs. On the other hand, a dominant proportion (i.e., 67.4 % (100 %–32.6 %)) of experiments are still either early or late cases within the constrained parameter spaces and cannot robustly predict PFT coexistence. Moreover, despite further considering the observational constraints (black scatters in Fig. 4; Table S2), the 21 experiments (2.3 %, 21 out of 932) are still sparsely distributed in the parameter space of the coexisting cases, so no simple correlations can be developed based on these simulations. Therefore, simple empirically built relationships between plant traits provide limited benefit to guiding ELM-FATES parameter selection for modeling PFTs coexistence while matching the observations. This finding provides additional motivation for the ML-based approaches.

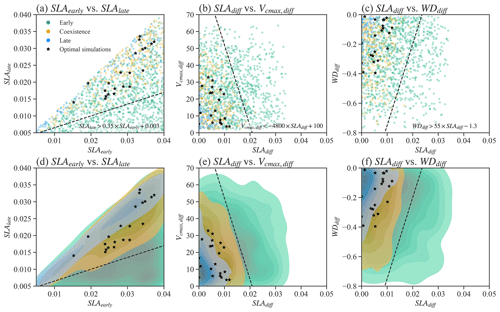
Figure 4 Relationships between selected parameters of Par-CTR. These parameters are presented in three groups, i.e., green color for the late cases with ${\text{BR}}_{\mathrm{e}\mathrm{2}\mathrm{t}}\in [\mathrm{0.0},\mathrm{0.1})$, orange color for the coexisting cases with ${\text{BR}}_{\mathrm{e}\mathrm{2}\mathrm{t}}\in \left[\mathrm{0.1},\mathrm{0.9}\right]$, and blue color for the early cases with ${\text{BR}}_{\mathrm{e}\mathrm{2}\mathrm{t}}\in (\mathrm{0.9},\mathrm{1.0}]$. Black stars represent coexistence cases further filtered by observational constraints. Panels (d)–(f) are the corresponding kernel density estimate plots of the scatter plots shown in (a)–(c). $V_{\mathrm{cmax},\mathrm{diff}}=V_{\mathrm{cmax},\mathrm{early}}-V_{\mathrm{cmax},\mathrm{late}}$. SLA_diff and WD_diff are defined likewise.

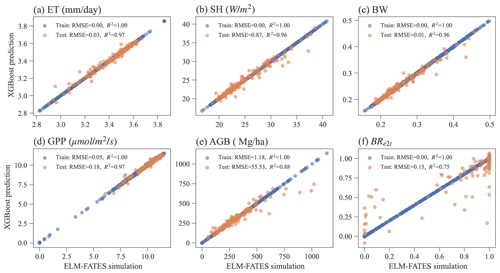
3.3 XGBoost model performance

Overall, the XGBoost surrogate models show good performance in predicting ELM-FATES simulations (Fig. 5). Based on Exp-CTR (i.e., Par-CTR and Out-CTR), six XGBoost models were trained. In training, the RMSEs for the six models are zero or nearly zero, and R²s are close to one. In the testing, four XGBoost models (i.e., XGB_ET, XGB_SH, XGB_BW, XGB_GPP) still show good performance with small RMSE and large R² (>0.95). XGB_AGB shows a little degradation with R² of 0.88. The performance of XGB_BR also shows degradation, with R² decreasing from 1.0 in training to 0.75 in testing. XGB_BR cannot predict the ELM-FATES-simulated BR_e2t of 0 or 1 well when only one PFT survives. This indicates that PFT competition processes in ELM-FATES, which determine BR_e2t and AGB, are highly nonlinear and difficult to emulate even using a state-of-the-art machine learning algorithm.

Figure 5 The performance of XGBoost surrogate models in the training and testing for predicting (a) ET, (b) SH, (c) BW, (d) GPP, (e) AGB, and (f) BR_e2t.

3.4 SHAP parameter importance analysis

Figure 6 shows the feature importance, including parameters and parameter differences, for different XGBoost models. Features (on the y axis) with a higher mean absolute SHAP value (on the x axis) denote a larger contribution to the XGBoost model prediction. The number of most important features is different for predicting ET, SH, BW, and GPP compared to predicting AGB and BR_e2t.

For the XGBoost models that predict ET, SH, BW, and GPP, the top three features have the largest SHAP values compared to the rest (Fig. 6a–d). Notably, these top three features are the same and correspond to the early successional PFT, i.e., V_cmax,early, SLA_early, and L_{leaf, early}. Most ELM-FATES experiments in Exp-CTR used as the training samples for the XGBoost models are early cases. Therefore, the parameters of early successional PFT have dominant contributions in the XGBoost model predictions of overall grid-level fluxes. These three parameters are positively correlated with ET and GPP and negatively correlated with SH and BW (red vs. blue bars in Fig. 6a–d; see Fig. S4 for more details), reflecting the fundamental carbon metabolism of the typically dominant early successional plant.

For the XGBoost surrogate models of AGB and BR_e2t, more than eight features have large SHAP values (Fig. 6e and f). Both early and late successional PFT parameters contribute to predicting the two variables. Compared with the predictions of ET, SH, BW, and GPP with only three major features, predicting AGB and BR_e2t is relatively complex. This is because AGB and particularly BR_e2t are closely related to the PFT competition process in which both the early and late PFT traits are crucial. Especially for BR_e2t, the most important features are the parameter difference between the early and late successional PFTs. For example, SLA_diff is positively correlated to BR_e2t. Therefore, to have coexisting PFTs with ${\text{BR}}_{\mathrm{e}\mathrm{2}\mathrm{t}}\in [\mathrm{0.1},\mathrm{0.9}]$, the SLA of two PFTs should be neither too large nor too small.

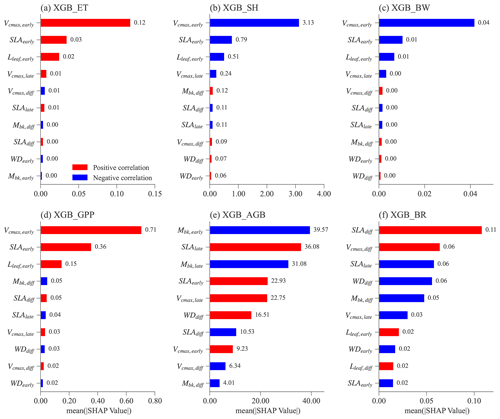
Figure 6 Mean absolute SHAP values for different XGBoost surrogate models for the top 10 most important features. Absolute SHAP values are sorted in decreasing order from top to bottom. For each feature (y axis) in each XGBoost model, the Spearman correlation coefficient is calculated between the feature values and the corresponding SHAP values (Fig. S4). The red color means that a given feature is positively correlated with the predicting variable, whereas blue denotes a negative correlation.

3.5 XGBoost model parameter selection

Using the XGBoost surrogate models, the Par-ML was selected, including 1500 sets of parameters and the corresponding parameter differences between the early and late successional PFTs (Sect. 2.4, procedure P4 in Fig. 2). We examined whether Par-ML matches the empirical relationships shown in Fig. 4 (Sect. 3.2), i.e., ${\text{SLA}}_{\mathrm{late}}>\mathrm{0.35}\times {\text{SLA}}_{\mathrm{early}}+\mathrm{0.003}$, $V_{\mathrm{cmax},\mathrm{diff}}<-\mathrm{4800}\times {\text{SLA}}_{\mathrm{diff}}+\mathrm{100}$, and ${\text{WD}}_{\mathrm{diff}}>\mathrm{55}\times {\text{SLA}}_{\mathrm{diff}}-\mathrm{1.3}$. In total, 99.1 % (1486 out of 1500) of parameter sets are consistent with the empirical relationships, indicating the XGBoost models implicitly learned these simple relationships.

The parameter distributions of Par-ML show different patterns from the early and late parameters of Par-CTR (green vs. blue regions in Fig. 7), but there are large overlaps between the coexistence parameters of Par-CTR and Par-ML (orange vs. green regions, e.g., the third column in Fig. 7). This indicates that the XGBoost surrogate models learned to select parameters around the parameters' space of the coexisting cases. Par-ML also tends to have a smaller parameter difference between the early and late successional PFTs in terms of SLA_diff and V_cmax, diff. However, Par-ML also shows different patterns from the coexisting parameters of Par-CTR, probably because the XGBoost-selected parameters were also constrained by multiple observations and implicitly considered parameter tradeoffs. For example, the V_cmax,early and V_cmax, late of Par-ML are located in narrower ranges than the coexisting parameters of Par-CTR (first two columns in Fig. 7).

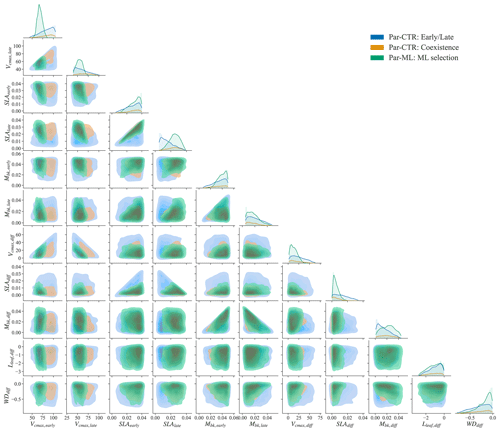
Figure 7 Comparison of parameter or parameter difference in Par-CTR vs. Par-ML for 11 features. The diagonal plots represent each parameter's distribution, and the rest of the subplots are kernel density estimate plots. There are three groups, i.e., blue for the early and late cases of Par-CTR, orange for the coexisting cases of Par-CTR, and green for Par-ML selected by XGBoost models.

3.6 Validation of ML selected parameters

ELM-FATES simulations of Exp-ML based on the ensemble parameters of Par-ML selected by the XGBoost surrogate models can better capture the observations and have more coexisting cases than Exp-CTR (Fig. 8). The median values of simulated variables for Exp-ML are closer to observations with relative biases closer to zero than Exp-CTR (Fig. 8a, blue vs. green boxes). The Exp-ML-simulated variables also have more concentrated distributions than Exp-CTR. Compared to the skewed distribution of BR_e2t in Exp-CTR with a large proportion of early cases, Exp-ML has a more normally distributed BR_e2t (Fig. 8b). Specifically, Exp-ML has about 3.6 times more coexisting cases than Exp-CTR, i.e., 73.1 % (1097 out of 1500) in Exp-ML vs. 20.6 % (309 out of 1500) in Exp-CTR (Table S3). After being further constrained by observations (Table S3), one-third of the experiments (i.e., 495 out of 1500) in Exp-ML remain, and this ratio is 23.6 times more than 1.4 % (21 out of 1500) in Exp-CTR.

The XGBoost surrogate model-predicted variables also match well with those simulated using ELM-FATES in Exp-ML (Fig. 8, orange vs. green boxes), indicating the overall reasonable accuracy for the XGBoost model predictions. Compared to the ELM-FATES results using Par-ML, the XGBoost models show better performance for ET, SH, BW, and GPP but relatively degraded performance for AGB and BR_e2t (Fig. S5). It is consistent with the performance of the XGBoost models' training and testing results (in Sect. 3.3).

Figure 8 Comparison between the ELM-FATES simulations for Exp-CTR and Exp-ML. (a) Relative bias for simulated ET, SH, BW, GPP, and AGB. (b) Simulated BR_e2t. ML prediction represents the selected XGBoost model predictions after filtering with observation and biomass ratio (i.e., the XGB_prds, procedure P4 in Fig. 2).

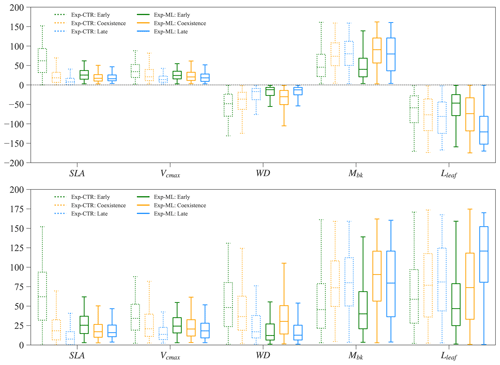
3.7 Parameter tradeoff for coexistence experiments

Parameters of the early and late successional PFTs show tradeoffs for the coexisting experiments. Large relative differences in SLA, V_cmax, and WD (more negative) favor the early successional PFT, while large relative differences in M_bk and L_leaf favor the late successional PFT. Therefore, in Exp-CTR, compared to the early and late cases, the coexisting cases have intermediate relative differences in SLA, V_cmax, WD, M_bk, and L_leaf (dashed boxes in Fig. 9). The coexisting cases in Exp-ML have similar patterns with intermediate relative differences in SLA, V_cmax and L_leaf compared to the early and late cases (solid boxes in Fig. 9). However, M_bk and especially WD show the largest relative difference for the coexisting cases compared to the early and late cases in Exp-ML. These two parameters still show a tradeoff in determining coexisting PFTs because larger WD favors the early PFT, whereas larger M_bk favors the late PFT.

In Exp-ML, the parameter spaces of the coexisting cases show large overlaps with the early and late cases (Fig. S6). There are no simple correlations between these parameters to distinguish the coexisting cases from the early and late cases (also see Sect. 3.2). Although WD_diff of the coexisting cases still overlap with the early and late cases, when WD_diff is less than roughly −0.4 g cm⁻³, only coexisting cases exist (Fig. S6). Nevertheless, this rule (i.e., ${\text{WD}}_{\mathrm{diff}}<-\mathrm{0.4}$) alone cannot ensure PFT coexistence (see Fig. 7).

Figure 9 Parameter relative difference (%) between early successional PFT and late successional PFT for Exp-CTR (box with dashed line) and Exp-ML (box with solid line). Parameter relative difference is calculated, taking SLA as an example, as follows: $\frac{{\text{SLA}}_{\mathrm{early}}-{\text{SLA}}_{\mathrm{late}}}{({\text{SLA}}_{\mathrm{early}}+{\text{SLA}}_{\mathrm{late}})/\mathrm{2}}\times \mathrm{100}$ %.

3.8 Seasonal variation comparison

Figure 10 shows the seasonal variations in ET, SH, BW, and GPP for observations and simulations of the finally selected 495 experiments in Exp-ML with good model performance (Table S3). Overall, the simulated ET shows a similar seasonal variation to ET observation (Fig. 10a), with relatively small ET in the wet season (November–May), high ET in the dry season (June–October), and ET peaks in August. However, compared to the observations, ELM-FATES overestimates ET, especially during the wet season. The simulated SH also shows a similar seasonal variation with the SH observation except in March. ELM-FATES overestimated SH from January to May but underestimated SH from September to December (Fig. 10b). Due to the discrepancy between simulated ET and SH, the model underestimates BW from September to December (Fig. 10c).

The simulated GPP has minor seasonal variability compared to the observed GPP. ELM-FATES overestimates GPP from June–August in the dry season but underestimates GPP over October–December. The lower GPP over June–August indicates that plants may be relatively water stressed or energy limited during these months. However, the large ET observation over the same period implies that this site is unlikely to be water limited or strongly energy limited. The ELM-FATES simulations also display little water stress year-round (Fig. S7). Therefore, there are likely elements of the seasonal cycle (e.g., phenological responses of photosynthetic capacity) that are not yet captured here. Additionally, tower estimates of GPP may also have large uncertainties.

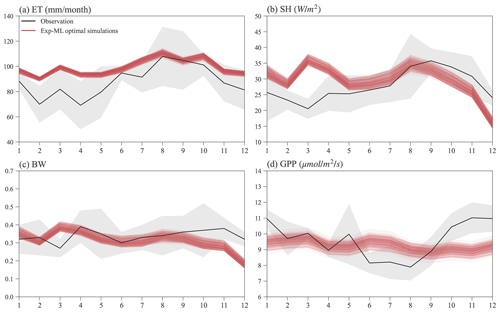
Figure 10 Mean monthly observations and selected optimal ELM-FATES simulations in Exp-ML for (a) ET, (b) SH, (c) BW, and (d) GPP. Each red line represents one experiment simulation (4-year simulation average). The black curves are monthly climatologic averages from 2000 to 2008, and the grey-shaded area represents the interannual variabilities (i.e., mean ± standard deviation).

4 Discussion

4.1 Limited guidance of observed trait relationships for PFT coexistence modeling in FATES

We found degraded PFT coexistence in ELM-FATES simulation when observed trait relationships are considered. More specifically, constrained by observed trait relationships, Exp-OBS has fewer coexisting cases than Exp-CTR, which does not consider the observed trait relationships. The observed trait relationships were derived from site measurements in the species-rich tropical ecosystem where plant coexistence commonly happens (Kraft et al., 2008), which is expected to enhance the PFT coexistence simulations. This inconsistency could be due to several possible reasons. First, ELM-FATES is a typical “trait filtering” model (Fisher et al., 2018), and the realistic simulation of PFT dynamics largely depends on the fidelity with which trait tradeoff surfaces are prescribed in the model (Scheiter et al., 2013). Implicit representation of trait tradeoff in the current ELM-FATES model may not be well balanced, which may differ from the observed trait relationships that lead to coexistence in the real world (at least for the ecosystem at our study site). In particular, there may be correlated tradeoffs that are measured (e.g., with below ground processes, Chitra-Tarak et al., 2021) but not represented in the model. A second reason could be the mismatch between different spatial scales. The observed trait relationships are derived from field measurements across tropical forests over a large region with diverse species and climate. For example, the relationship in Eq. (1) is for plant species in Panama. In contrast, ELM-FATES simulations were conducted at the K34 site scale with specific species composition. Therefore, the large-scale trait relationships may not reflect the small-scale trait relationships. Wright et al. (2005) showed that trait relationships fitted for individual sites varied considerably. Third, the observed trait relationships are based on simplified equations, which may not be able to comprehensively reflect PFT coexistence. For example, although Eq. (2) derived from Longo et al. (2020) can reflect the negative relationship between SLA and L_leaf, the R² of this equation is about 0.49, which may not be accurate enough to represent trait relationships. Additionally, these Eqs. (1)–(3) do not consider the uncertainty in trait covariance. In Koven et al. (2020), the uncertainties between trait covariance were considered when sampling parameters for FATES experiments. Furthermore, machine learning models can also be employed to extract the relationships between plant traits, which can then be incorporated into ELM-FATES and evaluated in future studies.

4.2 Advantages of ML surrogate models on improving PFT coexistence modeling

ELM-FATES simulations driven by parameters selected using the XGBoost models essentially improved PFT coexistence and better captured observations. Compared to the initial Exp-CTR, which was used to train the XGBoost models, the proportion of coexisting PFTs in Exp-ML reaches 73.1 %, 3.6 times more than the 20.6 % in Exp-CTR. Further filtering the coexistence experiments by observations, Exp-ML still has 33.0 % of experiments left with good model performance, 23.6 times that of the 1.4 % of experiments in Exp-CTR with good performance. Our ML-based approach also outperforms the empirical correlations built in Sect. 3.2, which only yield 32.5 % of coexistence experiments, and this reduces to 2.3 % of experiments if further constrained by observation. The large proportion of optimal experiments selected by our ML approach also outperforms previous studies using direct filtering approaches. Buotte et al. (2021) conducted two stages of experiments to select optimal parameters for CLM-FATES modeling with two conifer species; only 0.3 % (1 out of 360) of the cases met the given criteria in the first stage of experiments, which increased to 5.5 % in the second stage of experiments. Huang et al. (2020) conducted CLM-FATES modeling with two tropical PFTs at the Tapajós National Forest sites; only 1 parameter set out of 70 (about 1.4 %) was selected with reasonable fractions of two PFTs and minor errors compared to observations. In addition, the parameter selection procedures of these two studies require some degree of subjective decision making and expert knowledge. On the other hand, our ML-based approach takes a more objective procedure, and little expert knowledge is required except for the initial determination of the parameter reference ranges. Importantly, we believe this approach can be repeatable as, e.g., model developments lead to changes between the parameter values and model predictions of forest structure and function and can be used to define constrained ensemble values that will allow assessment of confidence in model predictions. Even though simulating the coexistence of different plants may not be a big concern for individual-based VDMs, e.g., LPJmL-FIT (Sakschewski et al., 2015, 2016) and TROLL (Maréchaux and Chave, 2017), our approach also could be applied to the selection of key parameters that regulate vegetation dynamics in these models.

Our study also reproduced the observations satisfactorily. Holm et al. (2020) conducted the ELM-FATES simulation with only one PFT considered at the same K34 site. Our study yields better or similar performance in the magnitude of AGB and the magnitude and seasonal variation in GPP, ET, SH, and BW (Table 2 and Fig. 3 in Holm et al., 2020, vs. Figs. 8 and 10 in this study). It should also be noted that the overestimation of simulated energy fluxes (latent heat and SH) from January to May could be associated with the energy-related processes (e.g., energy partition, surface albedo) in ELM-FATES. Other potential reasons could be related to the uncertainties in atmospheric forcing and the common issue of incomplete energy budget closure at eddy covariance towers (Wilson et al., 2002; Foken, 2008; Da Rocha et al., 2009).

Compared to the predictions of GPP, ET, SH, and BW simulated by ELM-FATES, the XGBoost surrogate models show slightly degraded performance in predicting the simulated BR_e2t and AGB (Figs. 5 and S5). Three parameters (V_cmax,early, SLA_early, and L_{leaf, early}) mainly control the predictions of ET, SH, BW, and GPP, while eight features are crucial for predicting AGB and BR_e2t. Even though the XGBoost algorithm has an excellent ability to capture complex nonlinear relationships, it does not predict the PFT-competition-related variables of AGB and BR_e2t well because the physical model cannot robustly predict coexisting PFTs due to the higher dimensionality of predicting PFT composition as compared to other ecosystem variables. Another important point worth mentioning is the small sample size of coexistence cases in Exp-CTR, with only 309 cases having BR_e2t in the range of [0.1, 0.9], while the majority of cases are dominated by either early or late successional PFT. This limited sample size may not provide enough data to train the XGBoost surrogate model sufficiently for predicting BR_e2t within the range of [0.1, 0.9]. Therefore, further studies are still needed to improve the emulation of PFT-competition-related variables. Other approaches that have been applied in VDMs but not specifically for PFT coexistence modeling, for example, the generalized likelihood uncertainty estimation (GLUE) approach (Zhang et al., 2022) and the Bayesian model emulation approach (Fer et al., 2018), could provide alternative ways. Furthermore, we suggest exploring other machine learning algorithms, such as Gaussian processes and neural network algorithms, which may be better suited for capturing nonlinear correlations and learning from sparse data.

Overall, our study presents a reproducible approach that utilizes machine learning to identify parameter values that improve model fidelity against observations and promote coexistence between plant functional types in vegetation demography models across diverse ecosystems. This approach has the potential to enhance the modeling of PFT coexistence in other ecosystems, such as the mixed conifer forests in Sierra Nevada, California (Buotte et al., 2021); Amazon forests subject to selective logging (Huang et al., 2020); and tropical forests with heterogeneous soils and subject to droughts in Panama (Cheng et al., 2021).

4.3 Trait tradeoffs between coexisting PFTs

Trait-related parameters show tradeoffs between early and late successional PFTs for the ELM-FATES-simulated coexisting experiments. The relative differences between the two PFTs in SLA, V_cmax, and WD complementarily coordinate with the relative difference in M_bk and L_leaf and hence avoid competitive exclusion (Fig. 9). These ELM-FATES reflected tradeoffs are consistent with the niche-based species coexistence mechanisms of environmental filtering and niche partitioning (Michalko and Pekár, 2015; Adler et al., 2013). On the one hand, in the coexisting cases, the relative differences between the two PFTs' parameters should not be considerable. For example, a large difference in SLA more likely favors the early cases (dashed green box in Fig. 9). This is related to environmental filtering in which coexisting species require some degree of convergence in strategy to survive and persist under given environmental conditions (Cadotte and Tucker, 2017; Thakur and Wright, 2017). On the other hand, some degree of differences should exist between the two PFTs' parameters in the coexisting cases. This is related to niche partitioning to ensure either differences in resource requirements or differences in tolerance to surrounding conditions (Kraft et al., 2015; Fowler et al., 2013). Phenomenological evidence has shown that functional trait variation promotes coexistence or increases species richness (Uriarte et al., 2010; Angert et al., 2009; Adler et al., 2006; Mason et al., 2012; Ben-Hur et al., 2012).

In our ELM-FATES simulations, the primary axis of competition for resources is light. The tradeoffs between the two PFTs' parameters differentiate their vertical competition in light absorption, which has been shown to strongly control tropical forest community composition (Farrior et al., 2016; Poorter et al., 2003). Even though the early PFT has a shallower rooting depth than the late PFT, there is no critical dry condition during our simulation period (i.e., corresponding to values of the water stress factor (BTRAN) close to 1.0 in Fig. S7). Therefore, competition for water resource access negligibly contributes to PFT coexistence in this study. Previous tropical studies also revealed these coexistence mechanisms. At a tropical forest site in eastern Ecuador, Kraft et al. (2008) found that concurring trees are often less ecologically similar, and both environmental filtering (different topographic habitats of ridgetops vs. valley) and niche differentiation simultaneously contribute to species coexistence. Swenson and Enquist (2009) also found that at small spatial scales in a tropical forest, most traits of coexisting species were under-dispersed, consistent with environmental filtering, while the seed mass and maximum height were over-dispersed, reflecting niche partitioning.

4.4 Limitations and further model development

Some limitations exist in our experiments. Niche partitioning is a critical aspect of promoting species coexistence, which is closely related to spatial heterogeneity, temporal heterogeneity, disturbances (e.g., nature enemy, fire), and resource partitioning (Adler et al., 2013). In our current ELM-FATES simulations, some processes that have been or are being developed in the model are not considered. These processes include nutrient limitation (Holm et al., 2020), fire disturbance (Fisher et al., 2015), subsurface lateral flow (Fang et al., 2022), and plant hydraulics (Chitra-Tarak et al., 2021; Li et al., 2021). Ignoring these processes could limit the potential of niche partitioning among PFTs in our ELM-FATES simulations. Topography has been recognized as an essential spatial heterogeneity factor for tropical forests, but it is not considered in ELM-FATES (Kraft et al., 2008; Costa et al., 2022). For example, Fang et al. (2022) coupled a three-dimensional hydrology model (ParFlow) with ELM-FATES and found that lateral flow plays a prominent role in governing aboveground biomass, and Cheng et al. (2021) also found a critical role for subsurface hydrology on coexistence. As these processes are added to the model, the reproducibility aspects of the XGBoost method to identify PFT combinations that match a broad range of criteria will be particularly important.

Lacking other features or processes could also affect PFT coexistence in the current FATES. For example, plant trait plasticity, the idea that plants can adjust their morphological and/or physiological traits to better adapt to the environment (Nicotra et al., 2010; Bloomfield et al., 2018; McDowell et al., 2022), is also not appropriately considered in FATES. Leaf traits such as V_cmax and SLA do vary vertically through the canopy in FATES via a prescribed relationship described by Lloyd et al. (2010). Liu and Ng (2019) found that the SLA of a desert shrub is significantly correlated with seasonal water availability. Additionally, FATES only considers the inter-PFT variance of functional traits (e.g., different V_cmax for early and late PFTs). However, studies revealed that trait variations commonly exist within and between species (Wright et al., 2005; Engemann et al., 2016; Meng et al., 2015; Dong et al., 2020; Siefert et al., 2015), and these play a vital role in maintaining plant diversity (Violle et al., 2012; Lu et al., 2017). Reproductive features that enhance competitive exclusion tendencies have been illustrated to affect coexistence (Maréchaux and Chave, 2017; Fisher et al., 2018). Hanbury-Brown et al. (2022) discussed the importance of the representation of forest regeneration, including improving parameters and algorithms for reproductive allocation, dispersal, seed survival and germination, environmental filtering in the seedling layer, and tree regeneration strategies adapted to wind, fire, and anthropogenic disturbance regimes. Besides, both growth–survival and stature–recruitment tradeoffs are critical to accurately predict successional patterns in tropical forest structure and competition (see details in Rüger et al., 2020), which should also be better considered in future model development. Furthermore, measured plant traits are increasingly available. For example, the TRY datasets (Kattge et al., 2020) can be used to improve the model process and parameterizations. Future studies into properly and adequately using these datasets to guide VDM parameterizations are advocated.

4.5 Enhancing VDM prediction with machine learning

We provide a brief overview of how machine learning can be applied to improve the modeling of plant dynamics, specifically in the context of vegetation demographic models. Firstly, ML can be used to derive trait parameter values. For instance, in this study, ML could be applied to replace the simple equations to derive the relationships between measured traits (Sect. 4.1). By integrating multiple datasets, including in situ measurements, atmospheric forcing, and remote sensing, ML could derive the spatial patterns and temporal variations in trait parameters for use in large-scale VDM modeling. Secondly, ML can be utilized to optimize parameters by developing surrogate models that emulate the relationships between the parameters and the VDM simulations and using the surrogate models to identify optimal parameter values. This application has demonstrated success in this study and previous studies (e.g., Tsai et al., 2021; Dagon et al., 2020; Watson-Parris et al., 2021). Another benefit of using ML in VDMs is the ability to develop benchmark datasets. For example, studies have successfully employed ML to derive AGB datasets for various ecosystems (Morais et al., 2021; Zhang et al., 2020; Li et al., 2020; da Bispo et al., 2020; Pham et al., 2020). These datasets can serve as benchmarks to evaluate the accuracy of VDM simulations. Lastly, ML can be used to replace semiempirical sub-models with only small theoretical bases in DGVMs (Reichstein et al., 2019). For example, accurately modeling wildfire using process-based wildfire models integrated in DGVMs remains challenging. However, ML-based wildfire models have shown advantages in accuracy and computational efficiency (Rodrigues and de la Riva, 2014; Jain et al., 2020; Sayad et al., 2019) and have the potential to be employed in Earth system models to improve wildfire simulations (e.g., Zhu et al., 2022).

5 Conclusions

In this study, we explored two possible solutions to improve PFT coexistence modeling in a cohort-based model (ELM-FATES): (1) using plant trait relationships established from field measurements and (2) using machine learning surrogate models to optimize trait parameter values. Three ensembles of ELM-FATES experiments were conducted over a tropical forest site at Manaus, Brazil. We found that considering the observed trait relationships (Exp-OBS) slightly improves the simulations of water (ET), energy (SH and BW), and carbon (GPP, AGB) when compared against observations but degrades the simulation of PFT coexistence. Based on Exp-CTR, the ML surrogate models were built to optimize the ELM-FATES parameters by integrating the observations (i.e., ET, SH, BW, GPP, and AGB) and PFT coexistence criteria. Exp-ML, with parameters selected by the ML surrogate models, vastly improves the simulation of PFT coexistence and also better reproduces the annual means and seasonal variations in ET, SH, BW, GPP, and the filed inventory of AGB. This study demonstrates the benefits of using machine learning models to improve the modeling of PFT coexistence in ELM-FATES, with important implications for modeling the response and feedback of ecosystem dynamics to climate change. Our results also suggest that the incorporation of additional mechanisms into ELM-FATES is essential for robust modeling of coexisting PFTs.