Global simulation of dissolved ²³¹Pa and ²³⁰Th in the ocean and the sedimentary ²³¹Pa∕²³⁰Th ratios with the ocean general circulation model COCO ver4.0

Sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios provide clues to estimate the strength of past ocean circulation. For its estimation, understanding the processes controlling the distributions of ²³¹Pa and ²³⁰Th in the ocean is important. However, simulations of dissolved and particulate ²³¹Pa and ²³⁰Th in the modern ocean, recently obtained from the GEOTRACES project, remain challenging. Here we report a model simulation of ²³¹Pa and ²³⁰Th in the global ocean with COCO ver4.0. Starting from the basic water-column reversible scavenging model, we also introduced the bottom scavenging and the dependence of scavenging efficiency on particle concentration. As demonstrated in a previous study, the incorporation of bottom scavenging improves the simulated distribution of dissolved ²³¹Pa and ²³⁰Th in the deep ocean, which has been overestimated in models not considering the bottom scavenging. We further demonstrate that introducing the dependence of scavenging efficiency on particle concentration results in a high concentration of dissolved ²³⁰Th in the Southern Ocean as observed in the GEOTRACES data. Our best simulation can well reproduce not only the oceanic distribution of ²³¹Pa and ²³⁰Th but also the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios. Sensitivity analysis reveals that oceanic advection of ²³¹Pa primarily determines sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios. On the other hand, ²³⁰Th advection and bottom scavenging have an opposite effect to ²³¹Pa advection on the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios, reducing their latitudinal contrast. Our best simulation shows the realistic residence times of ²³¹Pa and ²³⁰Th, but simulation without bottom scavenging and dependence of scavenging efficiency on particle concentration significantly overestimates the residence times for both ²³¹Pa and ²³⁰Th in spite of similar distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios to our best simulation.

1 Introduction

The ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in marine sediments are used for estimating past ocean circulation strength (e.g., Yu et al., 1996; McManus et al., 2004; Gherardi et al., 2009; Böhm et al., 2015; Waelbroeck et al., 2018; Süfke et al., 2020). Alpha decay of ²³⁵U and ²³⁴U produces ²³¹Pa (half-life of ∼32.5 kyr) and ²³⁰Th (half-life of ∼75.2 kyr), respectively, at an approximately constant ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratio of 0.093 in the ocean (Henderson and Anderson, 2003). ²³¹Pa and ²³⁰Th are absorbed onto and desorbed from the surfaces of sinking particles (reversible scavenging; Bacon and Anderson, 1982) and eventually removed from the water column into marine sediments. Differential scavenging efficiencies of ²³¹Pa and ²³⁰Th result in differences in their residence times in the ocean; the residence times of ²³¹Pa and ²³⁰Th were estimated to be 111 and 26 years in Yu et al. (1996), and 130 and 20 years in Henderson and Anderson (2003). The shorter residence time of ²³⁰Th indicates that ²³⁰Th generated from ²³⁴U is removed relatively quickly to marine sediments. On the other hand, the longer residence time of ²³¹Pa indicates that ²³¹Pa produced from ²³⁵U is transported for a longer period by ocean transport. Therefore, the deviation of the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios from the constant production ratio of 0.093 has been used as a proxy for ocean circulation (Yu et al., 1996). For example, the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios from the Bermuda Rise were closer to 0.093 at the Last Glacial Maximum (LGM) than today, possibly suggesting that the Atlantic meridional overturning circulation (AMOC) was weaker at the LGM (McManus et al., 2004; Böhm et al., 2015). To use the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios as a proxy for ocean circulation in a more quantitative manner, modeling about ²³¹Pa and ²³⁰Th is important.

For ²³¹Pa and ²³⁰Th modeling, one needs to take into account the different scavenging efficiencies of different marine particle types (e.g., particulate organic carbon, calcite, and opal) as well as the distribution of these particles (Chase et al., 2002; Edwards et al., 2005). Sinking particles effectively scavenge ²³¹Pa and ²³⁰Th in regions with high particle concentrations. In general, ²³¹Pa has a longer residence time than ²³⁰Th, because sinking particles scavenge ²³⁰Th more efficiently. However, as for opal particles, Chase et al. (2002) argue that opal scavenges ²³¹Pa more effectively than ²³⁰Th. This report is consistent with observational studies that find high ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in the Southern Ocean, where opal sinking flux is high (Rutgers van der Loeff and Berger, 1993; Walter et al., 1997; Chase et al., 2003).

Authors of previous modeling studies have tried to simulate the global distributions of ²³¹Pa and ²³⁰Th by two-dimensional (2D) ocean models (Marchal et al., 2000; Luo et al., 2010) or three-dimensional (3D) ocean models of LSG-OGCM (Henderson et al., 1999), Bern 3D (Siddall et al., 2005; Rempfer et al., 2017), NEMO (Dutay et al., 2009; van Hulten et al., 2018), CESM (Gu and Liu, 2017) and iLOVECLIM (Missiaen et al., 2020a). There are also modeling studies that discuss the relationship between the strength of the AMOC and changes in sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios (Siddall et al., 2005; Lippold et al., 2012; Gu and Liu, 2017; Gu et al., 2020; Missiaen et al., 2020a, b). Siddall et al. (2005) pioneered the 3D simulation of both ²³¹Pa and ²³⁰Th by incorporating reversible scavenging. Their control simulation appropriately reproduced the observed distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios; it showed high sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in regions where the sinking opal particle flux is high. In their control simulation, the concentrations of dissolved ²³¹Pa and ²³⁰Th increased linearly with depth; this pattern agreed broadly with observed features. However, simulated dissolved ²³¹Pa and ²³⁰Th were both higher than observations in the deep ocean. In addition to reversible scavenging by sinking ocean particles, several studies (e.g., Anderson et al., 1983; Roy-Barman, 2009; Okubo et al., 2012) have pointed out the importance of additional scavenging at the seafloor (bottom scavenging) and the continental boundaries (boundary scavenging). The bottom scavenging has not been explicitly included in global 3D ocean models except for Rempfer et al. (2017) which used a simplified 3D ocean model of intermediate complexity similar to that used by Siddall et al. (2005) and reproduced the distributions of dissolved ²³¹Pa and ²³⁰Th more realistically by introducing the bottom scavenging. On the other hand, Henderson et al. (1999) reproduced the distribution of dissolved ²³⁰Th in their ocean general circulation model (OGCM) simulation by changing the efficiency of reversible scavenging depending on particle concentration; this effect has not been directly considered by recent modeling studies but some studies have evaluated the impacts of changes in particle concentration and scavenging efficiency on the distribution of ²³¹Pa and ²³⁰Th (van Hulten et al., 2018; Missiaen et al., 2020a, b). Recently, the GEOTRACES project has led to a dramatic increase in the number of observations of dissolved and particulate ²³¹Pa and ²³⁰Th (Schlitzer et al., 2018). The GEOTRACES database provides an opportunity to test models describing the cycling of these two radioisotopes in the global ocean. In this study, we report our model simulation about the global distribution of ²³¹Pa and ²³⁰Th in the ocean with COCO ver4.0. Starting from the basic water-column reversible scavenging model of Siddall et al. (2005), we also introduced the bottom scavenging and the dependence of scavenging efficiency on particle concentration. Furthermore, we quantitatively discuss the processes that control the global distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios; by performing a series of sensitivity simulations, we discuss how the individual processes (i.e., water-column reversible scavenging, ocean transport, and bottom scavenging) affect the global distribution of dissolved ²³¹Pa and ²³⁰Th and sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios.

2 Materials and methods

2.1 Ocean general circulation model

The OGCM used in this study is COCO version 4.0 (Hasumi, 2006), the ocean component of the coupled ocean-atmosphere general circulation model MIROC version 3.2 (K-1 Model Developers, 2004). The COCO is also used as the ocean part of the MIROC earth system model (Hajima et al., 2020; Ohgaito et al., 2021). The model domain is global, with about 1^∘ horizontal resolution and 43 vertical layers. The vertical resolution varies from 5 m (top) to 250 m (bottom). Surface boundary conditions are given from monthly averages of zonal and meridional components of wind stress, air temperature, specific humidity, net shortwave radiation, downward longwave radiation, freshwater flux, and wind speed. These boundary conditions are taken from the output of a pre-industrial simulation with the MIROC (Kobayashi et al., 2015; Oka et al., 2012). To calculate ²³¹Pa and ²³⁰Th, we perform “offline” tracer simulation using physical fields obtained in advance by the COCO (Oka et al., 2008, 2009). The offline means that the calculation of tracer is separately performed from that of the physical field; since the distributions of ²³¹Pa and ²³⁰Th do not affect the physical fields at all, the results do not depend on whether the model is offline or online. The offline tracer model makes it easier to perform various sensitivity experiments. The tracer model is integrated for 3000 years and tracer fields reach a steady state where changes in ocean tracer inventory almost vanish (less than 10⁻⁵ % per 100 years). We analyze the average of the last 100 years of the integration.

The physical fields used in this study is based on MIROC climate model simulations, and its reproducibility has been discussed and confirmed in a variety of literature (e.g., K-1 Model Developers, 2004; Gregory et al., 2005; Oka et al., 2006; Stouffer et al., 2006). We also note that the physical fields used here are the same as the pre-industrial (PI) simulation reported in Kobayashi et al. (2015) and Kobayashi and Oka (2018). For reference, the Atlantic meridional overturning circulation (AMOC) simulated by the COCO used in this study is shown in Fig. S11.

2.2 Particle fields

Following Siddall et al. (2005), the distribution of biogenic particles (organic carbon, calcite, and opal) is used to evaluate the scavenging of both ²³¹Pa and ²³⁰Th. We define the concentration M of each particle type (g m⁻³) as $M=F/w_{\mathrm{s}}$, where F is the particle flux (g m⁻² yr⁻¹) and w_s is the constant settling velocity (m yr⁻¹). The particle flux is calculated using the export flux from the euphotic zone and an assumed vertical profile of each particle type. The detailed procedure is explained below.

First, the particulate organic carbon (POC) export flux from the euphotic zone is calculated by multiplying the distribution of primary production derived from satellite observations (Behrenfeld and Falkowski, 1997) by the export ratio (Dunne et al., 2005). From POC export flux and $M=F/w_{\mathrm{s}}$, the concentration of POC at the base of the euphotic zone, M_POC(z₀), where z₀ is the depth of the bottom of the euphotic zone, is obtained. After obtaining M_POC(z₀), the POC concentration in the water column is expressed (Marchal et al., 1998) as

$$\begin{array}{}\text{(1)}& M_{\mathrm{POC}}=M_{\mathrm{POC}}\left(z_{\mathrm{0}}\right){\left({\displaystyle \frac{z}{z_{\mathrm{0}}}}\right)}^{-\mathit{\epsilon }},\end{array}$$

where ε is a remineralization exponent for POC.

Next, the calcite and opal export fluxes from the euphotic zone are calculated by multiplying the POC export flux by their rain ratios, which are estimated following formulations of Siddall et al. (2005) and Maier-Reimer (1993); please refer to Eqs. (2)–(5) of Siddall et al. (2005) for detail. The calcite particle concentration is calculated by assuming an exponentially decreasing vertical profile (Henderson et al., 1999; Marchal et al., 2000; Siddall et al., 2005). Thus, we have

$$\begin{array}{}\text{(2)}& M_{{\mathrm{CaCO}}_{\mathrm{3}}}=M_{{\mathrm{CaCO}}_{\mathrm{3}}}\left(z_{\mathrm{0}}\right)\exp \exp \left({\displaystyle \frac{z_{\mathrm{0}}-z}{z_{\mathrm{p}}}}\right),\end{array}$$

where z_p is the calcite penetration depth. While the opal concentration is expressed as an exponentially decreasing vertical profile in some previous studies (e.g., Henderson et al., 1999), we consider opal dissolution to be dependent on temperature, following Siddall et al. (2005), as

$$\begin{array}{}\text{(3a)}& {\displaystyle }{M}_{\mathrm{opal}}=M_{\mathrm{opal}}\left(z_{\mathrm{0}}\right)\exp \left[{\displaystyle \frac{D_{\mathrm{opal}}\cdot (z_{\mathrm{0}}-z)}{w_{\mathrm{s}}}}\right],\text{(3b)}& {\displaystyle }{D}_{\mathrm{opal}}=B\left(T-T_{\mathrm{0}}\right),\end{array}$$

where D_opal (yr⁻¹) is the opal dissolution rate, T₀ is the minimum temperature (^∘C) of seawater in the model, and B is a dissolution constant (^∘C⁻¹ yr⁻¹). Table 1 lists the parameter values used in this study. Figure S10 shows the distribution of particle fluxes in the surface ocean.

Table 1 Parameters of the ²³¹Pa and ²³⁰Th model.

2.3 Reversible scavenging model

We use a tracer model of ²³¹Pa and ²³⁰Th based on Siddall et al. (2005). The dissolved concentration (A_d) and particle concentration (A_p) of ²³¹Pa and ²³⁰Th are calculated from the following equations:

$$\begin{array}{}\text{(4a)}& {\displaystyle \frac{\partial A_{\mathrm{total}}^i}{\partial t}}={\mathit{\beta }}^i-{\mathit{\lambda }}^i{A}_{\mathrm{total}}^i-w_{\mathrm{s}}{\displaystyle \frac{\partial A_{\mathrm{p}}^i}{\partial z}}+\text{Transport},\text{(4b)}& {\displaystyle }{A}_{\mathrm{total}}^i=A_{\mathrm{p}}^i+A_{\mathrm{d}}^i.\end{array}$$

In Eq. (4a), the first term on the right-hand side (βⁱ) represents production from uranium (²³¹Pa from ²³⁵U; ²³⁰Th from ²³⁴U), the second term represents radioactive decay, the third term represents the effect of vertical transport by particle settling, and the fourth term represents ocean transport by advection and diffusion. The superscript i represents the isotope type (²³¹Pa, ²³⁰Th).

By following a reversible scavenging model (Bacon and Anderson, 1982), the relationship between the radionuclide concentration in the dissolved phase (A_d) and particulate phase (A_p) is represented by the partition coefficient ($K_j^i$) as

$$\begin{array}{}\text{(5a)}& {\displaystyle }{A}_{\mathrm{p}}^i={\sum }_j{A}_{j,\mathrm{p}}^i,\text{(5b)}& {\displaystyle }{K}_j^i={\displaystyle \frac{A_{j,\mathrm{p}}^i}{A_{\mathrm{d}}^i\cdot C_j}},\end{array}$$

where subscript j represents the particle type (organic carbon, calcite, opal) and C_j is the dimensionless ratio of particle concentration to the density of seawater. The formulation of the reversible scavenging was also described in Oka et al. (2009, 2021) and readers can obtain its detailed description therein. The partition coefficient depends on the type of particles (Siddall et al., 2005). The partition coefficients of ²³¹Pa and ²³⁰Th for each type of particle have been estimated in previous studies (Luo and Ku, 1999; Chase et al., 2002). Chase et al. (2002) show that opal scavenges ²³¹Pa more efficiently than ²³⁰Th, whereas calcite scavenges ²³⁰Th more efficiently than ²³¹Pa. Here we use partition coefficients following Chase and Anderson (2004), as in other previous modeling studies (Dutay et al., 2009; Gu and Liu, 2017; Siddall et al., 2005; Table 2). The model parameters are summarized in Table 1.

Table 2 Equilibrium partition coefficients in experiments Siddall_EXP and CTRL_EXP.

2.4 One-dimensional reversible scavenging model

In addition to the three-dimensional tracer model based on the OGCM, we use a simple, vertical, one-dimensional model, which was widely used in previous studies (e.g., Bacon and Anderson, 1982), to analyze simulation results in Sect. 4. In the one-dimensional model, we assume a steady state and ignore the effect of ocean transport in Eq. (4a). Furthermore, we do not take the radioactive decay term into account, because it is much smaller than the production term. Under these assumptions, Eq. (4a) becomes

$$\begin{array}{}\text{(6)}& {\mathit{\beta }}^i-w_{\mathrm{s}}{\displaystyle \frac{\partial A_{\mathrm{p}}^i}{\partial z}}=\mathrm{0}.\end{array}$$

In this one-dimensional model, production by uranium radioactive decay (the first term on the left side of Eq. 6) is balanced by vertical transport through particle settling (the second term on the left side of Eq. 6). If we assume that $A_{\mathrm{p}}^i$ is zero at the sea surface (z=0), then Eq. (6) can be solved, leading to

$$\begin{array}{}\text{(7)}& A_{\mathrm{p}}^i={\displaystyle \frac{{\mathit{\beta }}^i}{w_{\mathrm{s}}}}\cdot z.\end{array}$$

Equation (7) shows that the vertical profile of $A_{\mathrm{p}}^i$ is determined from two parameters: βⁱ and w_s. From Eq. (5), we have

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{A}_{\mathrm{p}}^i& ={\sum }_j{A}_{j,\mathrm{p}}^i=\left(K_{{\mathrm{CaCO}}_{\mathrm{3}}}^i\cdot C_{{\mathrm{CaCO}}_{\mathrm{3}}}+K_{\mathrm{opal}}^i\cdot C_{\mathrm{opal}}\right.\\ & \left.+K_{\mathrm{POC}}^i\cdot C_{\mathrm{POC}}\right)\cdot A_{\mathrm{d}}^i\\ & ={\sum }_j(K_j^i\cdot C_j)\cdot A_{\mathrm{d}}^i.\end{array}\end{array}$$

The dissolved concentration can be obtained from Eqs. (7) and (8):

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{A}_{\mathrm{d}}^i& ={\displaystyle \frac{\mathrm{1}}{{\sum }_j(K_j^i\cdot C_j)}}{A}_{\mathrm{p}}^i\\ & ={\displaystyle \frac{\mathrm{1}}{{\sum }_j(K_j^i\cdot C_j)}}{\displaystyle \frac{{\mathit{\beta }}^i}{w_{\mathrm{s}}}}\cdot z.\end{array}\end{array}$$

Equation (9) shows that the vertical profile of $A_{\mathrm{d}}^i$ is determined by the particle settling speed, the partition coefficients, and the concentrations of each particle. By comparing results from the one-dimensional model and the three-dimensional tracer model, we can isolate the influence of ocean transport (i.e., advection, diffusion, and convection) on the simulated distributions of dissolved ²³¹Pa and ²³⁰Th (see Sect. 4; Table 3).

2.5 Experimental design

This study conducts a series of OGCM experiments. First, we perform an experiment named Siddall_EXP using the same parameters and formulations as in Siddall et al. (2005). As stated in the Introduction, Siddall et al. (2005) was a pioneering 3D model for global simulation of both ²³¹Pa and ²³⁰Th. This model is now a relatively old model and the reversible scavenging model introduced in this model is simpler than more recent models. However, this model appropriately reproduced the observed distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios as shown in their Fig. 2 which appears not necessarily inferior to that in more recent models. Therefore, in this study, we start with Siddall_EXP where the most basic reversible scavenging model of Siddall et al. (2005) is introduced.

Second, we perform an experiment named BTM_EXP, in which we additionally take bottom scavenging into account. Following Rempfer et al. (2017), we simply set the deepest model grid layer as the nepheloid layer. The thickness of the nepheloid layer becomes equal to the thickness of the corresponding deepest model grid layer which varies between 5 and 250 m depending on the depth. The intensity of the bottom scavenging depends on two parameters: the partition coefficient (K_bottom) and the concentration (C_bottom) of the bottom particles. Our treatment about C_bottom is the same that in Rempfer et al. (2017); we assume a globally uniform value for C_bottom ($\mathrm{6.0}\times {\mathrm{10}}^{-\mathrm{8}}$ g cm⁻³) which is within the range of $\mathrm{4.0}\times {\mathrm{10}}^{-\mathrm{8}}$ to $\mathrm{1.65}\times {\mathrm{10}}^{-\mathrm{6}}$ g cm⁻³ observed in the benthic nepheloid layers in the North Atlantic (Lam et al., 2015). As for K_bottom, because our formulation of the reversible scavenging is not the same as Rempfer et al. (2017), we needed to find its appropriate parameter value. For this purpose, we perform a number of simulations with different bottom scavenging intensities by changing the value of K_bottom.

Third, we perform a sensitivity experiment named KREF_EXP concerned with the reference partition coefficient (K_ref). In KREF_EXP, in addition to varying the value of the partition coefficient for bottom particles (K_bottom), we also vary the values of the reference partition coefficients (K_ref) from those assumed in Siddall_EXP and BTM_EXP.

Finally, we perform an experiment named PCE_EXP, in which we incorporate the dependence of scavenging efficiency on particle concentration. In PCE_EXP, K_ref is not assumed to be constant but varies according to the following formulation of Henderson et al. (1999):

$$\begin{array}{}\text{(10)}& K_{\mathrm{ref}}={\left({\displaystyle \frac{C_{\mathrm{total}}}{C_{\mathrm{ref}}}}\right)}^{-\mathrm{0.42}}\times {\mathrm{10}}^{\mathrm{7}},\end{array}$$

where C_total [g cm⁻³] is the total concentration of all sinking particles($C_{\mathrm{total}}=C_{{\mathrm{CaCO}}_{\mathrm{3}}}+C_{\mathrm{opal}}+C_{\mathrm{POC}}$) and C_ref [g cm⁻³] is the reference concentration. Note that the value of C_total is differently specified on each grid, whereas C_ref is given as a globally uniform value. Due to the dependence of K_ref on C_total, the scavenging efficiency becomes lower under higher particle concentrations and higher under lower particle concentrations. We conduct several simulations by varying C_ref between 10⁻⁹ and 10⁻⁶ g cm⁻³ (smaller C_ref value leads to stronger scavenging). Although the observed decrease of the partition coefficient with increased bulk particle concentration is not entirely understood (Pavia et al., 2018), we will show that this particle concentration effect becomes important for controlling dissolved ²³⁰Th in some ocean regions.

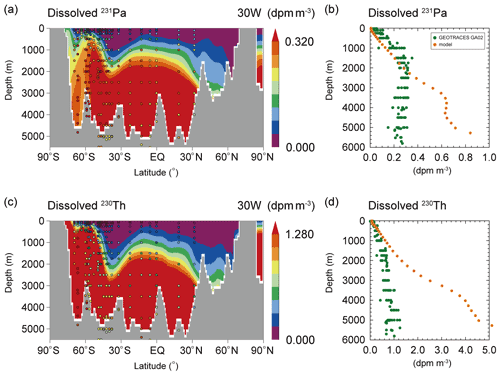
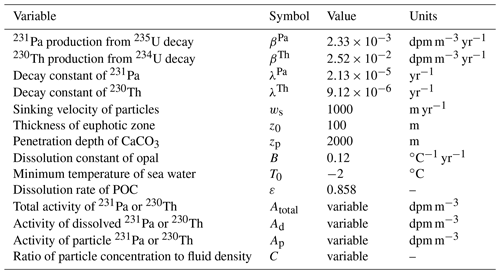
Figure 1 (a) Dissolved ²³¹Pa along 30^∘ W in the Atlantic Ocean and (b) its vertical profile (the latitudinal mean along 30^∘ W in the Atlantic Ocean) in Siddall_EXP. (c, d) Same as (a) and (b) except for ²³⁰Th. The colored circles in (a) and (c) represent data from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The green and orange circles in (b) and (d) represent the GA02 data and simulation results. The unit is dpm m⁻³ (disintegrations per minute per cubic meter).

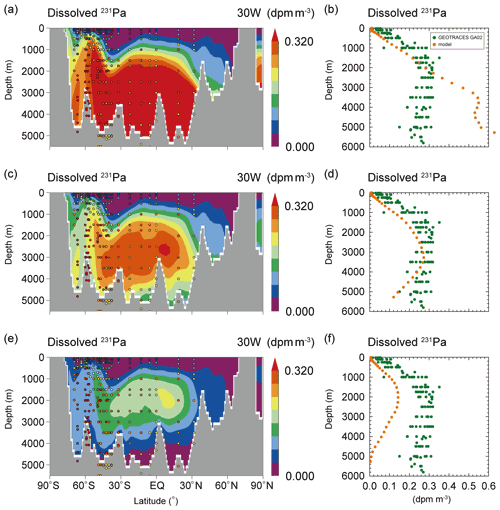
Figure 2 (a, c, e) Dissolved ²³¹Pa along 30^∘ W in the Atlantic Ocean and (b, d, f) its vertical profile (the latitudinal mean along 30^∘ W in the Atlantic Ocean) in BTM EXP. $K_{\mathrm{bottom}}^{\mathrm{Pa}}$ is set to 5.0×10⁴ in (a) and (b), 5.0×10⁵ in (c) and (d), and 5.0×10⁶ in (e) and (f). The colored circles in (a), (c), and (e) represent data from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The green and orange circles in (b), (d), and (f) represent the GA02 data and simulation results.

3 Results

3.1 Dissolved ²³¹Pa and ²³⁰Th along the Atlantic meridional transects

First, we discuss the results of Siddall_EXP, focusing on the meridional distribution of ²³¹Pa and ²³⁰Th in the Atlantic Ocean. Figure 1 shows the dissolved concentrations of ²³¹Pa and ²³⁰Th simulated in Siddall_EXP along the Atlantic 30^∘ W transect, together with GEOTRACES data (see Fig. S1 for the location of observations referenced in this study). We confirm that the distributions of dissolved ²³¹Pa and ²³⁰Th in Siddall_EXP are approximately the same as those reported in Siddall et al. (2005; their Fig. 2). Because ²³¹Pa and ²³⁰Th exchange reversibly with sinking particles and are transported to the deep ocean, the dissolved ²³¹Pa and ²³⁰Th concentrations increase with depth, both in the model simulation and in observations. However, as in Siddall et al. (2005), the model simulation overestimates dissolved ²³¹Pa and ²³⁰Th concentrations at depths greater than 2000 and 1000 m, respectively. For quantitative analysis, we perform a linear regression analysis between the simulation results and observed data from the GEOTRACES GA02 transect; we calculate the root mean square deviation (RMSD), the correlation coefficient (R), and the slope of the linear regression (s) of modeled concentration versus observed concentration, as summarized in Table S1. The linear regression line slope indicates the model's ability to reproduce the observed distribution; it approaches 1.0 when the model simulation realistically reproduces the target distribution (Dutay et al., 2009; Gu and Liu, 2017). For Siddall_EXP, the slope of linear regression line is significantly larger than 1.0 for both ²³¹Pa (s=1.88, R=0.72, and RMSD = 0.15) and ²³⁰Th (s=4.44, R=0.89, and RMSD = 1.31; Table S1). This overestimation in the deep ocean is also found in other previous model simulations (e.g., Dutay et al., 2009; Gu and Liu, 2017; van Hulten et al., 2018).

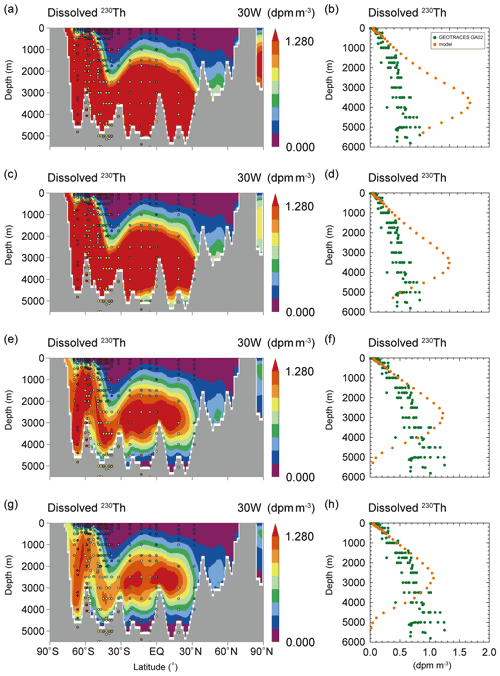
Figure 3 (a, c, e, g) Dissolved²³⁰Th along 30^∘ W in the Atlantic Ocean and (b, d, f, h) its vertical profile (the latitudinal mean along 30^∘ W in the Atlantic Ocean) in BTM_EXP are plotted. $K_{\mathrm{bottom}}^{\mathrm{Th}}$ is set to 5.0×10⁵ in (a) and (b), 1.0×10⁶ in (c) and (d), 5.0×10⁶ in (e) and (f), and 1.0×10⁷ in (g) and (h). The colored circles in (a), (c), (e), and (g) represent data from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The green and orange circles in (b), (d), (f), and (h) represent the GA02 data and simulation results.

Next, to reduce the overestimation of the simulated concentrations in the deep ocean, we additionally incorporate bottom scavenging in benthic nepheloid layers (BTM_EXP). The dissolved ²³¹Pa and ²³⁰Th distributions are shown in Figs. 2 and 3, respectively. As expected, the incorporation of bottom scavenging helps reduce ²³¹Pa and ²³⁰Th concentrations in the deep ocean, improving the model's agreement with the data. As for the distribution of dissolved ²³¹Pa, the model results come relatively close to the GEOTRACES data if $K_{\mathrm{bottom}}^{\mathrm{Pa}}$ is set to 5.0×10⁵ (s=1.04, R=0.90, and RMSD = 0.05; see CTRL_EXP in Table S1; Fig. 2c and d). This result confirmed the importance of the bottom scavenging, which was already reported from a previous global 3D model (Rempfer et al., 2017) and a regional eddy-permitting model (Lerner et al., 2020). On the other hand, it is difficult to reproduce the observed distribution of dissolved ²³⁰Th in BTM_EXP. With $K_{\mathrm{bottom}}^{\mathrm{Th}}=\mathrm{1.0}\times {\mathrm{10}}^{\mathrm{6}}$, the concentrations of ²³⁰Th in bottom waters come close to observed values (Fig. 3c and d), but the concentrations in the deep ocean (from 2000 to 5000 m) remain overestimated. In the case of larger $K_{\mathrm{bottom}}^{\mathrm{Th}}$, the simulated ²³⁰Th concentrations approach observed values in the deep ocean but are significantly lower than observations in bottom waters (e.g., $K_{\mathrm{bottom}}^{\mathrm{Th}}=\mathrm{1.0}\times {\mathrm{10}}^{\mathrm{7}}$ in Fig. 3g and h). These results indicate that modification of Siddall_EXP by considering bottom scavenging alone is not sufficient for accurately simulating ²³⁰Th distribution in our model. As shown in Rempfer et al. (2017) and Lerner et al. (2020), the appropriate selection of scavenging parameter coefficients is required for more realistic simulation. Because our reversible scavenging model (which is the same as Siddall et al., 2005; Sect. 2.3) is not the same as Rempfer et al. (2017) and Lerner et al. (2020), we need to discuss the validity of a scavenging parameter coefficient in our model (i.e., K_ref). In the following experiments (i.e., KREF_EXP and PCE_EXP), we discuss more appropriate treatment about K_ref by focusing solely on ²³⁰Th.

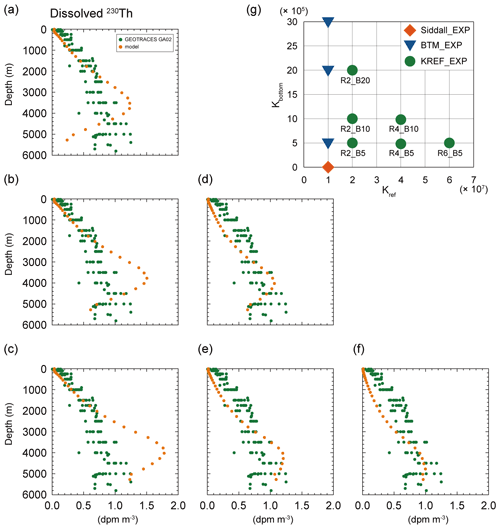
Figure 4 The vertical profile of dissolved ²³⁰Th (the latitudinal mean along 30^∘ W in the Atlantic Ocean) in various simulations of KREF_EXP: (a) R2_B20, (b) R2_B10, (c) R2_B5, (d) R4_B10, (e) R4_B5, and (f) R6_B5. The green and orange circles in (a)–(f) represent the Atlantic GEOTRACES data (GA02; Schlitzer et al., 2018) and simulation results. Panel (g) summarizes the choice of parameters (i.e., $K_{\mathrm{ref}}^{\mathrm{Th}}$ and $K_{\mathrm{bottom}}^{\mathrm{Th}}$) in each simulation.

To reproduce the distribution of ²³⁰Th more realistically, we change the value of the reference partition coefficient ($K_{\mathrm{ref}}^{\mathrm{Th}}$) in addition to $K_{\mathrm{bottom}}^{\mathrm{Th}}$ (KREF_EXP). Figure 4 summarizes the results of KREF_EXP and shows the simulated vertical distributions of dissolved ²³⁰Th for various values of $K_{\mathrm{ref}}^{\mathrm{Th}}$ and $K_{\mathrm{bottom}}^{\mathrm{Th}}$ (see Fig. 4g). Note that, for example, the simulation R2_B5 means that $K_{\mathrm{ref}}^{\mathrm{Th}}$ is set to 2.0×10⁷ and $K_{\mathrm{bottom}}^{\mathrm{Th}}$ to 5.0×10⁵. In the cases where $K_{\mathrm{bottom}}^{\mathrm{Th}}$ is set to 5.0×10⁵ (namely, R2_B5, R4_B5, and R6_B5), the ²³⁰Th concentrations systematically change depending on $K_{\mathrm{ref}}^{\mathrm{Th}}$; as the reversible scavenging on sinking particles becomes stronger (i.e., for larger $K_{\mathrm{ref}}^{\mathrm{Th}}$), the concentrations of dissolved ²³⁰Th become smaller throughout the water column (Fig. 4c, e, and f). As discussed for BTM_EXP, it is also confirmed that the stronger bottom scavenging (i.e., larger $K_{\mathrm{bottom}}^{\mathrm{Th}}$) leads to the lower concentrations near the sea bottom (e.g., see R2_B5, R2_B10, and R2_B20). For some combinations of water-column scavenging and bottom scavenging, simulations (e.g., R6_B5, R4_B5, R4_B10) reasonably reproduce the observed profile of dissolved ²³⁰Th concentration. Among our KREF_EXP simulations, the R6_B5 simulation (Fig. 4f) shows the slope of the linear regression line nearest to 1.0 (s=0.88, R=0.81, and RMSD = 0.20; Table S1) where $K_{\mathrm{ref}}^{\mathrm{Th}}$ is higher ($K_{\mathrm{ref}}^{\mathrm{Th}}=\mathrm{6.0}\times {\mathrm{10}}^{\mathrm{7}}$) than for Siddall_EXP and BTM_EXP ($K_{\mathrm{ref}}^{\mathrm{Th}}=\mathrm{1.0}\times {\mathrm{10}}^{\mathrm{7}}$). In the R6_B5 simulation (Fig. 4f), the vertical profile of dissolved ²³⁰Th is significantly improved from that of Siddall_EXP (Fig. 1d) and BTM_EXP (Fig. 3). We confirmed that the R6_B5 simulation captures the observed features of the Atlantic transects of the GEOTRACES data (Fig. 5a). However, the R6_B5 simulation still underestimates the concentrations of dissolved ²³⁰Th from the surface to intermediate depths (see Fig. 4f). Also, the high concentrations of dissolved ²³⁰Th observed in the Southern Ocean in GEOTRACES data are not well reproduced (Fig. 5a). To address this issue, we performed additional simulations by slightly changing the values of $K_{\mathrm{ref}}^{\mathrm{Th}}$ and $K_{\mathrm{bottom}}^{\mathrm{Th}}$ from the R6_B5 simulation (not shown), but we found that it is difficult to remove the abovementioned deficiencies by merely changing the values of $K_{\mathrm{ref}}^{\mathrm{Th}}$ and $K_{\mathrm{bottom}}^{\mathrm{Th}}$ in KREF_EXP.

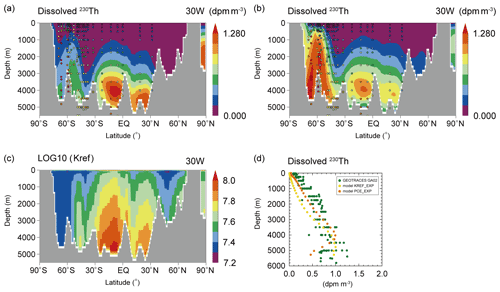
Figure 5 Dissolved ²³⁰Th along 30^∘ W in the Atlantic Ocean in (a) R6_B5 of the KREF_EXP and (b) PCE_EXP. (c) Reference partition coefficient (K_ref) along 30^∘ W in the Atlantic Ocean in PCE_EXP. (d) The vertical profile of dissolved ²³⁰Th (the latitudinal mean along 30^∘ W in the Atlantic Ocean) in R6_B5 of KREF_EXP and PCE_EXP. The colored circles in (a) and (b) represent data from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The green, yellow, and orange circles in (d) represent the GA02 data and KREF_EXP and PCE_EXP simulation results.

Finally, we discuss PCE_EXP, in which the dependence of scavenging efficiency on particle concentration is taken into account, according to Eq. (10). We conduct several simulations by varying the value of the reference concentration (C_ref) between 10⁻⁹ and 10⁻⁶ g cm⁻³. Among these results, we here discuss the case with $C_{\mathrm{ref}}={\mathrm{10}}^{-\mathrm{7}}$ g cm⁻³, which shows the best agreement with observations. Compared to the case in which the dependence of scavenging efficiency on particle concentration is not considered (i.e., R6_B5 simulation of KREF_EXP), PCE_EXP is expected to show smaller (larger) $K_{\mathrm{ref}}^{\mathrm{Th}}$ for the higher (lower) concentration of sinking particles. In Fig. 5, we compare the simulated dissolved ²³⁰Th distribution obtained from PCE_EXP and R6_B5 simulation of KREF_EXP. Owing to the dependence of scavenging efficiency on particle concentration, PCE_EXP reproduces the vertical distribution of dissolved ²³⁰Th slightly better than KREF_EXP (Fig. 5d). The regression analysis also confirms that the agreement with the GEOTRACES data becomes improved in PCE_EXP (s=0.98 and R=0.84; CTRL_EXP in Table S1). It is worthy to note that the distribution in the Southern Ocean is significantly improved in PCE_EXP (Fig. 5b) compared to KREF_EXP (Fig. 5a) as a result of the nonuniform distribution of the reference partition coefficient $K_{\mathrm{ref}}^{\mathrm{Th}}$ (Fig. 5c). In the Southern Ocean, where particle concentration is relatively higher than in other regions (Honjo et al., 2008), the value of $K_{\mathrm{ref}}^{\mathrm{Th}}$ in PCE_EXP is lower than that in the R6_B5 simulation of KREF_EXP ($K_{\mathrm{ref}}^{\mathrm{Th}}=\mathrm{6}\times {\mathrm{10}}^{\mathrm{7}}$; i.e., $K_{\mathrm{ref}}^{\mathrm{Th}}\sim \mathrm{7.8}$) (Fig. 5c). Therefore, the concentration of dissolved ²³⁰Th in PCE_EXP becomes high compared to the KREF_EXP, which leads to a more realistic distribution of dissolved ²³⁰Th in the Southern Ocean. The distributions of ²³⁰Th simulated in previous modeling studies (e.g., Figs. 4 and 5 in Dutay et al., 2009; Fig. 2 in Siddall et al., 2005; Fig. 2 in Gu and Liu, 2017; Fig. 3 in Rempfer et al., 2017; Fig. 12 in van Hulten et al., 2018; Fig. S3 in Missiaen et al., 2020a) are basically similar to our result (Fig. 6b); however, our simulation is the best at reproducing the high concentration in the Southern Ocean. Hereafter, our best simulation (i.e., $K_{\mathrm{bottom}}^{\mathrm{Pa}}=\mathrm{5.0}\times {\mathrm{10}}^{\mathrm{5}}$ case of BTM_EXP for ²³¹Pa and PCE_EXP for ²³⁰Th) is called CTRL_EXP (see Table 2 for parameter values of CTRL_EXP).

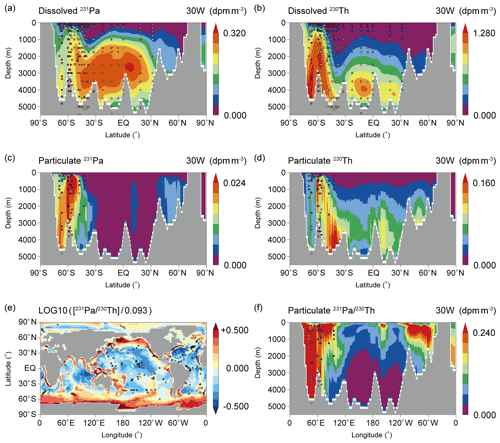
Figure 6 (a) Dissolved ²³¹Pa, (b) dissolved ²³⁰Th, (c) particulate ²³¹Pa, and (d) particulate ²³⁰Th along 30^∘ W in the Atlantic Ocean in CTRL_EXP. (e) Sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios normalized by the production ratio of 0.093 in CTRL_EXP. The colored circles represent observational data. Dissolved and particulate ²³¹Pa and ²³⁰Th data are taken from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The data of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios are taken from the following references (Mangini and Sonntag, 1977; Müller and Mangini, 1980; Anderson et al., 1983; Shimmield et al., 1986; Schmitz et al., 1986; Yang et al., 1986; Shimmield and Price, 1988; Lao et al., 1992; François et al., 1993; Frank et al., 1994; Frank, 1996; Bradtmiller et al., 2014; Luo et al., 2010, and their supplemental data).

3.2 Particulate ²³¹Pa and ²³⁰Th

By conducting a series of experiments described above, this study successfully reproduces the observed distributions of dissolved ²³¹Pa and ²³⁰Th, shown again in Fig. 6a and b, respectively. The model captures the observed tendency that the concentration becomes higher in the high-latitude Southern Ocean, as reported in previous studies (e.g., see Fig. 2 in Siddall et al., 2005). The ratio of ²³¹Pa to ²³⁰Th in the particulate phase in the water column shows low concentrations in the deep ocean, while the ratio becomes high in the northern North Atlantic Ocean and the Southern Ocean (Fig. 6f). This feature is consistent with observational findings and recent modeling studies (e.g., Fig. 2 in Gu and Liu, 2017; Fig. 3 in Rempfer et al., 2017). Although the number of available observations is limited for the particulate phase, it is confirmed that our simulation reasonably reproduces observed distributions for both dissolved and particulate phases.

3.3 Sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios

Our CTRL_EXP also well reproduces the global distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios (Fig. 6e) consistent with the reported observations (Mangini and Sonntag, 1977; Müller and Mangini, 1980; Anderson et al., 1983; Shimmield et al., 1986; Schmitz et al., 1986; Yang et al., 1986; Shimmield and Price, 1988; Lao et al., 1992; François et al., 1993; Frank et al., 1994; Frank, 1996; Bradtmiller et al., 2014; Luo et al., 2010, and their supplemental data). Sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios are high along the margin of the North Pacific and the North Atlantic, as well as in the Southern Ocean, where particle concentrations are high. On the other hand, sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios are low in the low-latitude regions, including subtropical gyres, where particle concentrations are low. These simulated features are consistent with observations (circles in Fig. 6e). Previous modeling studies reported the similar distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios (e.g., Fig. 2 in Siddall et al., 2005; Fig. 11 in Dutay et al., 2009; Fig. 4 in Gu and Liu, 2017; Fig. 10 in van Hulten et al., 2018; Fig. 1 in Missiaen et al., 2020a) and our Siddall_EXP also reasonably reproduced the global distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios (Fig. S4a). However, as shown above, the distributions of dissolved ²³¹Pa and ²³⁰Th in the ocean are significantly different between CTRL_EXP and Siddall_EXP. Thus, each experiment implies a different set of processes controlling the distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios. We will discuss this point later in the next section.

4 Discussion

4.1 Comparison with previous modeling studies

We demonstrated that our CTRL_EXP can reproduce a more realistic distribution of dissolved ²³¹Pa and ²³⁰Th along the Atlantic meridional transects than Siddall_EXP by considering the bottom scavenging and the dependence of scavenging efficiency on particle concentration. Here, we compared our results with previous modeling studies which showed their model results along with Atlantic meridional transects (GEOTRACES GA02 section).

As far as we know, Rempfer et al. (2017) was the only 3D global ocean model which introduces the bottom scavenging, and in our study, we introduced the bottom scavenging into the global OGCM for the first time. Models without the bottom scavenging tend to overestimate the dissolved ²³¹Pa and ²³⁰Th in the deep ocean as in our Siddall_EXP. For example, in Gu and Liu (2017) in which ²³¹Pa and ²³⁰Th tracers are introduced into CESM1.3, their simulated ²³¹Pa and ²³⁰Th concentrations are significantly overestimated in the deep ocean along the GEOTRACES GA02 section (their Fig. 2). In Dutay et al. (2009) in which ²³¹Pa and ²³⁰Th tracers are introduced into NEMO-PISCES, influences of particle size and type on ²³¹Pa and ²³⁰Th are discussed by performing several sensitivity simulations, but all of their simulations overestimate ²³¹Pa and ²³⁰Th concentrations in the deep Atlantic Ocean (their Figs. 4 and 5, respectively). In van Hulten et al. (2018) which was the updated ²³¹Pa and ²³⁰Th simulation with NEMO-PISCES, the model still overestimates ²³¹Pa and ²³⁰Th concentrations in the deep Atlantic Ocean (their Fig. 12), because particles in the nepheloid layers (i.e., bottom scavenging) are not included in their model.

Although the incorporation of bottom scavenging is important for controlling the scavenging efficiency, it is worthy to note that bottom scavenging is not the sole process that controls the scavenging efficiency. Therefore, for example, the model which specified the relatively stronger affinity to the particle can lead to smaller tracer concentration even if the model does not include the bottom scavenging. In fact, in Missiaen et al. (2020a), their simulated ²³¹Pa and ²³⁰Th are underestimated in both the upper and deep oceans (their Fig. S3 in the Supplement) even if the bottom scavenging was not included in their model. This is because their specified scavenging parameters are relatively stronger than the other models (see their Table 2) as a result of their parameter tuning without the bottom scavenging.

In the Re3d_Bt_Bd simulation reported in Rempfer et al. (2017) where the bottom scavenging process is considered, the abovementioned overestimation in the deep ocean was relaxed and their simulated distribution appears similar to our CTRL_EXP. Their study is the first 3D model demonstration about the importance of the bottom scavenging process, which is confirmed again in our study (e.g., from comparison with Siddall_EXP and KREF_EXP). However, their model still tends to somewhat overestimate the dissolved ²³¹Pa compared with GEOTRACES GA02 data (their Fig. 3). Because the formulation of the reversible scavenging and their model parameters are not the same as our CTRL_EXP, we expect that different choice of model parameter values leads to such differences; more specifically, our choice of $K_{\mathrm{ref}}^{\mathrm{Pa}}$ is based on Chase et al. (2002) and Siddall et al. (2005), whereas the scavenging efficiency parameters in Rempfer et al. (2017) are similar to those in Luo et al. (2010) and Marchal et al. (2000). In addition, as for ²³⁰Th, the high concentration in the Southern Ocean is not reproduced in their model, whereas this is reproduced in our CTRL_EXP by considering the dependence of scavenging efficiency on particle concentration. Although the dependence of scavenging efficiency on particle concentration was already introduced in Henderson et al. (1999), our study demonstrates its importance for reproducing high concentrations in the Southern Ocean reported in GEOTRACES GA02 data for the first time.

This study newly introduces a ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ model to the existing global three-dimensional OGCM. Based on the reversible scavenging model, this study well reproduces the distribution of dissolved concentration of ²³¹Pa and ²³⁰Th by considering the bottom scavenging and the dependence of the scavenging efficiency on particle concentration. The importance of bottom scavenging on the dissolved concentration of ²³¹Pa and ²³⁰Th is already discussed in previous studies (Rempfer et al., 2017; Lerner et al., 2020). Therefore, our result should be viewed as a confirmation of these previous results. However, we emphasize that this study provides a new estimate of the contribution of bottom scavenging to the distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios compared to other processes such as advection and water-column scavenging. Rempfer et al. (2017) evaluated the performance of their ²³¹Pa and ²³⁰Th simulations based on the root mean squared deviation normalized by the standard deviation of observations. In our control experiment (CTRL_EXP), the RMSD between the available GEOTRACES data is 0.57 for dissolved ²³¹Pa and 0.51 for dissolved ²³⁰Th. These values lie in the range of values for the “standard” and “optimal” experiments by Rempfer et al. (2017), the latter of which considers both bottom scavenging and boundary scavenging (see Fig. 5 in Rempfer et al., 2017). Lerner et al. (2020) use a regional eddy-permitting ocean circulation model and focus on the western North Atlantic. They also point out that removal in the nepheloid layer significantly impacts the basin-scale distribution of dissolved and particulate phases of ²³¹Pa and ²³⁰Th. In line with these previous studies, our result confirmed the importance of boundary scavenging. Recently, Gardner et al. (2018) reported data on the distribution of particles in benthic nepheloid layers. If such datasets become available for specifying the global distribution of particles in nepheloid layers, the effect of bottom scavenging can be introduced more realistically. It is also expected that additional consideration about boundary scavenging helps to improve our model simulation.

In addition to the bottom scavenging, our study highlights the importance of the dependence of scavenging efficiency on particle concentration. Although the decrease of the partition coefficient with increased bulk particle concentration has been reported from observations, the dependence of scavenging efficiency on particle concentration considered in PCE_EXP is not entirely understood (Honeyman et al., 1988; Henderson et al., 1999; Hayes et al., 2015). Recently, the particle concentration effect on ²³¹Pa and ²³⁰Th partition coefficients in the open ocean along the GEOTRACES GA03 transect has been reported (Hayes et al., 2015; Lerner et al., 2017). Their study suggests that the dependency in the open ocean may deviate from Eq. (10). In discussing the factors responsible for the particle concentration effect, Pavia et al. (2018) point out the possibility that the particle concentration effect is an artifact caused by filtration. Further research is needed to elucidate the mechanisms that control the particle concentration effect.

As pointed out in previous studies (Rempfer et al., 2017; Lerner et al., 2020), the distributions of particle phases of ²³¹Pa and ²³⁰Th are difficult to be reproduced in the model compared with the dissolved phases. Part of the error could be related to the particle fluxes that we give as an empirical distribution based on satellite observations. A ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ modeling study using an ecosystem model that considers six different particles well reproduces the distribution of ²³¹Pa and ²³⁰Th with a simple reversible scavenging model (van Hulten et al., 2018); such detailed treatment of particles might be helpful for more realistic simulation of particulate ²³¹Pa and ²³⁰Th. Furthermore, by examining the response of ²³¹Pa and ²³⁰Th to freshwater forcing into the North Atlantic, Missiaen et al. (2020b) show that changes in biogenic particle fluxes may have caused 30 % of the changes in the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios during the Heinrich stadial 1. Also, in Gu and Liu (2017), the particle change due to freshwater and its impact on sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios is examined. Therefore, the role of particle fields on the distribution of ²³¹Pa and ²³⁰Th, which was not directly investigated in this study, needs to be further discussed in a future study.

4.2 Reproducibility along GEOTRACES GA03 and GP16 transects

So far, we have compared our model results with observations by focusing on the Atlantic meridional GEOTRACES transects (i.e., GA02 and GIPY05). Here, we will compare our CTRL_EXP with other available GEOTRACES transects: GA03 in the subtropical North Atlantic (Hayes et al., 2015) and GP16 in the South Pacific (Pavia et al., 2018).

Figure S5 shows the results of CTRL_EXP along with the GEOTRACES GA03 data. For dissolved ²³¹Pa, the model shows a high concentration around a depth of about 3000 m and higher concentrations on the eastern/southern side of the basin as in observations (Fig. S5a). This feature was also well reproduced in the Re3d_Bt_Bd simulation of Rempfer et al. (2017) as shown in their Fig. 2 but not in other previous models (e.g., Fig. 8 in van Hulten et al., 2018; Fig. 3 in Gu and Liu (2017)). This confirms that the consideration of the bottom scavenging is helpful for improving the model result along the GEOTRACES GA03 section. For dissolved ²³⁰Th, features similar to ²³¹Pa are also found in both the model and observations although the model appears to underestimate north–south or west-east differences (Fig. S5b). For particulate ²³¹Pa and ²³⁰Th, the model tends to simulate high concentration near the sea bottom and the continental margins where the particle concentration becomes high, but such features are not necessarily clear in the GEOTRACES data (Fig. S5c and d). Our model may not sufficiently reproduce the bottom and boundary scavenging associated with terrestrial particles in this region. More sophisticated treatment of bottom and boundary scavenging might be required for addressing these issues.

Figure S6 shows the results of CTRL_EXP along with the GEOTRACES GP16 data. As with the other section data, CTRL_EXP approximately reproduces the distribution of ²³¹Pa and ²³⁰Th. The observational data show a clear signal associated with hydrothermal vents: low concentrations of dissolved ²³¹Pa and ²³⁰Th and high concentrations of particulate ²³¹Pa and ²³⁰Th, which are not simulated in our model. It has been pointed out that trace metals from hydrothermal activities may cause additional removal of ²³¹Pa and ²³⁰Th (Shimmield and Price, 1988; Lopez et al., 2015; Rutgers van der Loeff et al., 2016; German et al., 2016). Along the GEOTRACES GP16 section, ²³¹Pa and ²³⁰Th have been found to decrease with increasing trace metals of iron and manganese supplied from hydrothermal vents (Pavia et al., 2018). Processes related to the hydrothermal vents are not explicitly incorporated in the present ²³¹Pa and ²³⁰Th model simulations; its detailed treatment is beyond the scope of this study but appears necessary for more realistic simulations.

Table 3 Processes considered in additional experiments. A circle means that the process is considered, and a cross means that it is not considered.

4.3 Processes controlling sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios

In this subsection, we discuss the processes controlling the global distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios. For this purpose, we decompose the processes controlling sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios simulated in our best simulation CTRL_EXP into three parts: water-column reversible scavenging, three-dimensional ocean transport, and bottom scavenging. To evaluate how these three processes affect the distribution of ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios, we conduct two additional experiments (see Table 3). The first experiment is 3D_EXP, which is the same as CTRL_EXP except that bottom scavenging is not taken into account (i.e., we set $K_{\mathrm{bottom}}^{\mathrm{Pa}}=K_{\mathrm{bottom}}^{\mathrm{Th}}=\mathrm{0}$ in 3D_EXP). The second is 1D_EXP, which is the one-dimensional reversible scavenging model experiment described in Sect. 2.4. The tracer distribution in 1D_EXP is determined solely by the one-dimensional vertical process of reversible scavenging; the strength of scavenging changes spatially through changes in the partition coefficient ($K_j^i$ of Eq. 9 in Sect. 2.4) that depends on the specified three-dimensional particle concentration (C_j of Eq. 9). By using results of CTRL_EXP, 3D_EXP, and 1D_EXP, we can extract the influence of three processes: the influence of the one-dimensional vertical reversible scavenging is revealed by 1D_EXP, the influence of bottom scavenging is revealed by the difference between CTRL_EXP and 3D_EXP, and the influence of ocean transport is revealed by the difference between 3D_EXP and 1D_EXP. When we focus on sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios, each process described above can be further examined for ²³¹Pa and ²³⁰Th individually. For example, the difference in ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios between CTRL_EXP and 3D_EXP represents the influence of bottom scavenging of both ²³¹Pa and ²³⁰Th, whereas the influence of bottom scavenging of ²³¹Pa alone can also be evaluated from CTRL_EXP and 3D_EXP (i.e., ²³¹Pa(CTRL) $/$ ²³⁰Th(3D) minus ²³¹Pa(3D) $/$ ²³⁰Th(3D)).

In 1D_EXP, the particulate concentration is obtained from Eq. (7); the particulate concentration increases linearly with depth (Fig. S2c and d). The dissolved concentration is calculated from Eq. (9), suggesting that the concentration becomes higher for a lower partition coefficient ($K_j^i$ in Eq. 9) and for a lower particle concentration (C_j in Eq. 9). Mainly due to the dependency on C_j, the dissolved concentration becomes higher (lower) in the area with lower (higher) particle concentration in 1D_EXP. As a result, the dissolved concentration becomes very high in the deeper ocean, where the particle concentration becomes lower for both ²³¹Pa and ²³⁰Th (Fig. S2a and b). It is interesting to point out that the spatial pattern of dissolved ²³¹Pa and ²³⁰Th (Fig. S2a and b) is similar to that of K_ref in PCE_EXP (Fig. 5c), because both are affected by the amount of particle concentration. More importantly, although it is well known from previous studies, we emphasize here that the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in 1D_EXP become uniform everywhere (0.093; Fig. S2e), because, as confirmed from Eq. (7), the ratio of particulate ²³¹Pa to particulate ²³⁰Th amounts everywhere to ${\mathit{\beta }}^{Pa}/{\mathit{\beta }}^{Th}=\mathrm{0.093}$, regardless of geographic location (Fig. S2f).

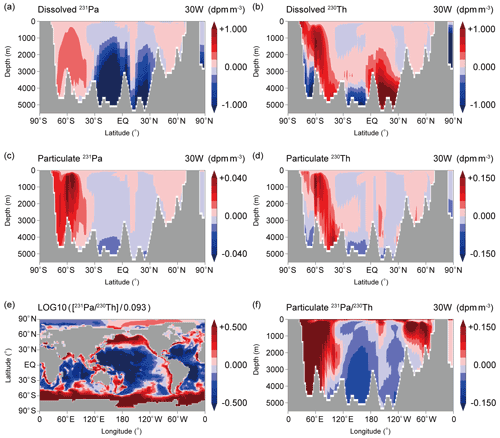
Figure 7 The difference between 3D_EXP and 1D_EXP (i.e., 3D_ EXP minus 1D_EXP, which represents for ocean transport effect) of (a) dissolved ²³¹Pa, (b) dissolved ²³⁰Th, (c) particulate ²³¹Pa, and (d) particulate ²³⁰Th along 30^∘ W in the Atlantic Ocean. (e) The difference between 3D_EXP and 1D_EXP of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios is normalized by the production ratio of 0.093.

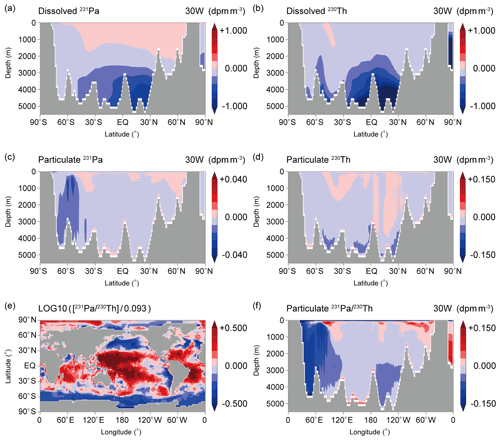
Figure 8 The difference between CTRL_EXP and 3D_EXP (i.e., CTRL_EXP minus 3D_EXP, which represents for bottom scavenging effect) of (a) dissolved ²³¹Pa, (b) dissolved ²³⁰Th, (c) particulate ²³¹Pa, and (d) particulate ²³⁰Th along 30^∘ W in the Atlantic Ocean. (e) The difference between CTRL_EXP and 3D_EXP of the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios is normalized by the production ratio of 0.093.

In 3D_EXP, three-dimensional ocean transport operates, in addition to water-column scavenging considered in 1D_EXP (Fig. S3). As described above, the influence of ocean transport can be evaluated from the difference between 3D_EXP and 1D_EXP (Fig. 7). On the other hand, the influence of bottom scavenging can be obtained from the difference between CTRL_EXP and 3D_EXP (Fig. 8). Note again that since the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in 1D_EXP are globally uniform (${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ = 0.093), their spatial distribution is controlled not by the one-dimensional vertical process but by the ocean transport. Figure 7e and f demonstrate that the ocean transport effect captures the overall features of CTRL_EXP (Fig. 6e and f). On the other hand, bottom scavenging tends to cancel the effects of ocean transport and weaken the spatial contrast of ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios simulated in CTRL_EXP (Fig. 8e and f).

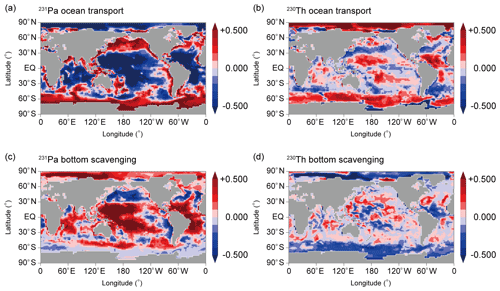
Figure 9 Sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios normalized by the production ratio of 0.093 in CTRL_EXP decomposed into contributions from (a) ocean transport solely from ²³¹Pa (i.e., ²³¹Pa(3D) $/$ ²³⁰Th(1D)), (b) ocean transport solely from ²³⁰Th (i.e., ²³¹Pa(1D) $/$ ²³⁰Th(3D)), (c) bottom scavenging solely from ²³¹Pa (i.e., ²³¹Pa(CTRL) $/$ ²³⁰Th(3D) minus ²³¹Pa(3D) $/$ ²³⁰Th(3D)), and (d) bottom scavenging solely from ²³⁰Th (i.e., ²³¹Pa(3D) $/$ ²³⁰Th(CTRL) minus ²³¹Pa(3D) $/$ ²³⁰Th(3D)).

To evaluate the above processes controlling the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in more detail, we further decompose the ocean transport contribution into those from ²³¹Pa and ²³⁰Th, separately (Fig. 9a for ²³¹Pa and Fig. 9b for ²³⁰Th). Similarly, we further decompose the contribution of bottom scavenging into those for ²³¹Pa and ²³⁰Th (Fig. 9c and d, respectively). In Fig. 9a, we demonstrate that ocean transport solely from ²³¹Pa (i.e., ²³¹Pa(3D) $/$ ²³⁰Th(1D)) can reproduce the overall distribution of the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in CTRL_EXP (Fig. 6e). This result confirms that ocean transport of ²³¹Pa primarily controls the distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios, consistent with previous studies (Yu et al., 1996; Marchal et al., 2000). These previous studies suggest that the distribution of ²³¹Pa mainly determines the global distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios, because the residence time of ²³¹Pa is longer than that of ²³⁰Th.

Here, we further discuss how the ocean transport of ²³¹Pa controls the distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios. Since changes in sedimentary ²³¹Pa correspond to particulate ²³¹Pa changes in the bottom ocean, we focus the ocean transport effect on particulate ²³¹Pa (Fig. 7c). Consistent with Fig. 9a, Fig. 7c indicates that ocean transport acts to decrease (increase) particulate ²³¹Pa in lower (higher) latitudes. We also found that particulate ²³¹Pa changes (Fig. 7c) are similar to those in dissolved ²³¹Pa (Fig. 7a). Because most of ²³¹Pa are in the dissolved phase, the advection of particulate ²³¹Pa itself is very small compared with that of dissolved ²³¹Pa, and ocean transport takes place mainly in the form of dissolved ²³¹Pa. Therefore, it is interpreted that ocean transport first controls the dissolved ²³¹Pa, and then the corresponding changes in particulate ²³¹Pa take place so that the relationship between dissolved and particulate ²³¹Pa (i.e., Eq. 5b) is satisfied. In other words, the changes in particulate ²³¹Pa take place as a result of changes in dissolved ²³¹Pa. Therefore, we need to focus on the processes that control the dissolved ²³¹Pa changes (Fig. 7a). As previously mentioned, in the case of no ocean transport (i.e., 1D_EXP), the dissolved ²³¹Pa concentration near the seabed in lower latitudes becomes very high (Fig. S2a). Ocean transport, which includes both advection and diffusion, reduces high concentrations of dissolved ²³¹Pa in low latitude oceans by transporting dissolved ²³¹Pa from lower latitudes to higher latitudes. As a result of the change in the dissolved ²³¹Pa (Fig. 7a), the changes in particulate ²³¹Pa (Fig. 7c) also take place by satisfying Eq. (5b); this leads to lower sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in lower latitudes and higher ratios in higher latitudes (Fig. 7e and f).

Contrary to ²³¹Pa, the influences of ²³⁰Th transport on sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios have been usually regarded as small because ²³⁰Th is generally assumed to be scavenged very quickly everywhere. However, our results demonstrate that ocean transport of ²³⁰Th also affects the distribution of sediment ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ to some extent. As a matter of fact, ²³⁰Th ocean transport acts in the opposite direction of ²³¹Pa ocean transport, reducing the spatial contrast in sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios (Fig. 9b). However, an exception is found in the Southern Ocean, where the ²³⁰Th ocean transport contributes to higher sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios, in the same way as the ²³¹Pa ocean transport. Because opal scavenges ²³¹Pa more effectively than ²³⁰Th (Chase et al., 2002), ²³¹Pa transported toward the Southern Ocean is expected to be quickly removed there due to the high opal flux. Therefore, previous studies concluded that ocean transport of ²³¹Pa explains high sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in the Southern Ocean. On the other hand, in addition to ocean transport of ²³¹Pa, our results suggest that ocean transport of ²³⁰Th also contributes to the high ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in the Southern Ocean. This result implies that scavenging of ²³⁰Th is not so efficient in the Southern Ocean as previously expected due to the dependence of scavenging efficiency on particle concentration. This interpretation is consistent with the high concentration of dissolved ²³⁰Th in the Southern Ocean (Fig. 6b). Missiaen et al. (2020a) demonstrated that the dissolved ²³⁰Th concentration in the Southern Ocean will increase if the effect of particle scavenging is halved and that most of this effect comes from POC and opal. This implies the scavenging of ²³⁰Th is controlled also by the opal in the Southern Ocean. Together with their and our results, quantification about scavenging of ²³⁰Th by opal in the Southern Ocean may be a key for a more accurate understanding of ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in the global ocean.

Bottom scavenging promotes the removal of both ²³¹Pa and ²³⁰Th near the seafloor and tends to cancel the influence of ocean transport. Namely, the bottom scavenging of ²³¹Pa reduces the contrast among sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios (Fig. 9c), whereas the bottom scavenging of ²³⁰Th increases this contrast (Fig. 9d). Because the influences of bottom scavenging of ²³¹Pa tends to be stronger than that of ²³⁰Th, bottom scavenging overall results in reducing the contrast of ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios (Fig. 8e and f). Precisely speaking, the actual processes of the bottom scavenging effect on the sedimentary ²³¹Pa and ²³⁰Th appear somewhat complicated compared with those of the ocean transport effect. The effect of the bottom scavenging is twofold. First, extra particles in the bottom ocean lead to an increase of sedimentary ²³¹Pa and ²³⁰Th (e.g., positive values near the bottom in low latitudes in Fig. 8c). Second, the bottom scavenging removes ²³¹Pa and ²³⁰Th from the ocean, which reduces the concentration of dissolved ²³¹Pa and ²³⁰Th in the ocean interior (Fig. 8a and b). The changes in dissolved-phase concentration then lead to changes in particulate-phase concentration in a way such that the Eq. (5b) is satisfied. The former leads to higher sedimentary ²³¹Pa and ²³⁰Th, whereas the latter leads to lower sedimentary ²³¹Pa and ²³⁰Th. Our results indicate that the former process becomes more important than the latter in the low latitudes, and the sedimentary ²³¹Pa increases there. In contrast, the latter dominates in the high latitudes, and the sedimentary ²³¹Pa decreases there by the bottom scavenging effect. The effect of bottom scavenging on ²³⁰Th is also basically similar to ²³¹Pa.

4.4 Residence time of ²³¹Pa and ²³⁰Th

Additional insights into the simulated distribution of ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios can be obtained from a comparison of CTRL_EXP with Siddall_EXP which reproduces sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios (Fig. S4a) as realistically as does CTRL_EXP (Fig. 6e). In this subsection, we discuss this point by focusing on the difference in the residence time of ²³¹Pa and ²³⁰Th between CTRL_EXP and Siddall_EXP. Assuming the mass balance of ²³¹Pa and ²³⁰Th are in a steady state, we calculate the residence time of ²³¹Pa and ²³⁰Th from the following formulas:

$$\begin{array}{}\text{(11a)}& {\displaystyle }{\mathit{\tau }}^i={\displaystyle \frac{\int A_{\mathrm{total}}^i\mathrm{d}v}{F_{\mathrm{in}}^i}},\text{(11b)}& {\displaystyle }{F}_{\mathrm{in}}^i=\int {\mathit{\beta }}^i\mathrm{d}v.\end{array}$$

In Eq. (11a) and (11b), the integral domain is global and the parameters are described in Table 1. The residence times of ²³¹Pa and ²³⁰Th are calculated to be 103 and 21 years, respectively, in CTRL_EXP, whereas they are 211 and 89 years, respectively, in Siddall_EXP (Table S2). By incorporating bottom scavenging and modifying the partition coefficient of ²³⁰Th, the modeled residence time in CTRL_EXP comes close to the previous estimate based on data: 111 years for ²³¹Pa and 26 years for ²³⁰Th in Yu et al. (1996) and 130 years for ²³¹Pa and 20 years for ²³⁰Th in Henderson and Anderson (2003). Because the reference partition coefficients for ²³¹Pa of Siddall_EXP and that of CTRL_EXP are the same value (i.e., $K_{\mathrm{ref}}^{\mathrm{Pa}}=\mathrm{1.0}\times {\mathrm{10}}^{\mathrm{7}}$), the influence of ocean transport on ²³¹Pa is identical in both experiments (Fig. 9a). Therefore, the difference in the ²³¹Pa distribution between the model experiments must come from the bottom scavenging, which is included in CTRL_EXP but not in Siddall_EXP. The bottom scavenging reduces the residence time of ²³¹Pa in CTRL_EXP (103 years) compared to Siddall_EXP (211 years). The difference in the ²³⁰Th distribution between CTRL_EXP and Siddall_EXP mainly comes from the difference in reference partition coefficients ($K_{\mathrm{ref}}^{\mathrm{Th}}$). The reference partition coefficient $K_{\mathrm{ref}}^{\mathrm{Th}}$ of CTRL_EXP, which depends on particle concentration, is larger than that of Siddall_EXP ($K_{\mathrm{ref}}^{\mathrm{Th}}=\mathrm{6.0}\times {\mathrm{10}}^{\mathrm{7}}$) in most of the ocean. Therefore, the contribution from the ocean transport of ²³⁰Th becomes larger in Siddall_EXP (Fig. S4b) than in CTRL_EXP (Fig. 6b). Together with additional contribution from the bottom scavenging effect on ²³⁰Th (Fig. 9d), the residence time of ²³⁰Th in CTRL_EXP (21 years) is shorter than that in Siddall_EXP (89 years). Since the residence time is overestimated for both ²³¹Pa and ²³⁰Th in Siddall_EXP compared to CTRL_EXP, the distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in Siddall_EXP ends up similar to that in CTRL_EXP. The residence time in CTRL_EXP is similar to the residence time of their control simulation in Gu and Liu (2017), which does not include the bottom scavenging process. Therefore, total scavenging efficiency in the ocean is more important than the introduction of bottom scavenging to reproduce residence time. Compared with Siddall_EXP based on Siddall et al. (2005), our CTRL_EXP can realistically simulate not only oceanic distribution of ²³¹Pa and ²³⁰Th but also their residence time by introducing the bottom scavenging and the dependence of scavenging efficiency on particulate concentration.

4.5 Remaining issues

Although our model was able to generally reproduce the basin-scale distributions of ²³¹Pa and ²³⁰Th, there are still some mismatches between the model results and observations. For dissolved ²³¹Pa, introducing bottom scavenging helped to reproduce the concentrations seen in the data at depths below 3000 m (Fig. 2). However, the model tends to simulate lower concentration than the observations below 3000 m in Fig. 2c and d, which needs to be improved. The improvement was not possible simply by reducing the bottom scavenging (i.e., specifying smaller $K_{\mathrm{bottom}}^{\mathrm{Pa}}$ than in Fig. 2c and d), therefore more fundamental improvement appears to be required. The dissolved ²³⁰Th simulated in CTRL_EXP (Fig. 5b) also tends to underestimate the observed concentration near the sea bottom. One possibility is that our treatment of the nepheloid layer (i.e., the thickness of the ocean deepest layer) may be too simple and needs to be modified so that the thickness of the nepheloid layer is more realistically specified. The introduction of more realistic bottom scavenging and the consideration of the effects of particles from the continental shelf and hydrothermal vents may also help to improve the model–data agreement for both ²³¹Pa and ²³⁰Th.

In this study, particle fields were not calculated in the model but specified as boundary conditions in our approach where the specified distribution of biological particles is taken from satellite-based estimation. Since the bias of the particle field affects the distribution of ²³¹Pa and ²³⁰Th, our approach has advantages over the other studies where the particles are explicitly simulated in the model. However, satellite-based estimation referenced here may also contain some errors, and understanding about the influence of the particle field on sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios, which was not seriously discussed in this study, is also important as the previous studies pointed out (e.g., Missiaen et al., 2020b; Dutay et al., 2009; van Hulten et al., 2018).

To reconstruct past sedimentation flux, ²³⁰Th normalization was used. Recently, the influence of lithogenic and authigenic ²³⁰Th on ²³⁰Th in sediments was evaluated (Missiaen et al., 2018; Costa et al., 2020). This is not a direct topic of our study, but we need to care about such processes which also affect the ratio of ²³¹Pa and ²³⁰Th obtained from marine sediments. As more observational data and their modeling become available, we expect to make further progress in quantitative understanding of the processes governing ²³¹Pa and ²³⁰Th in the ocean.

5 Summary and concluding remarks

In this study, we performed OGCM experiments that incorporated the bottom scavenging and the dependence of scavenging efficiency on particle concentration together with the water-column reversible scavenging. We quantitatively evaluated the processes that determine the global distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios, which is used as a proxy for the strength of paleo-ocean circulation.

First, we performed an OGCM experiment using the same model settings and parameters as Siddall et al. (2005), which only introduced the water-column reversible scavenging (Siddall_EXP). In Siddall_EXP, the simulated concentrations of ²³¹Pa and ²³⁰Th increase with depth, consistent with data; however, this experiment significantly overestimated the concentrations observed in the deep ocean. By incorporating bottom scavenging in nepheloid layers following Rempfer et al. (2017) (BTM_EXP), we reduced this overestimation and successfully reproduced the vertical profile of dissolved ²³¹Pa. However, this experiment had difficulty in reproducing the observed vertical profile of dissolved ²³⁰Th. Therefore, we modified the parameters associated with the strength of water-column scavenging (i.e., K_ref: the reference partition coefficient for sinking particles) with the consideration of the bottom scavenging (KREF_EXP). When we increased the reference partition coefficient of ²³⁰Th ($K_{\mathrm{ref}}^{\mathrm{Th}}=\mathrm{6.0}\times {\mathrm{10}}^{\mathrm{7}}$) from that used in the Siddall_EXP with the consideration of bottom scavenging ($K_{\mathrm{bottom}}^{\mathrm{Th}}=\mathrm{1.0}\times {\mathrm{10}}^{\mathrm{7}}$), dissolved ²³⁰Th was found to be more realistically simulated, but significant underestimation in the Southern Ocean remained. We found that the underestimation in the Southern Ocean can be improved by introducing dependence of K_ref on particle concentration which was used in Henderson et al. (1999) (PCE_EXP). Although most of the previous ²³¹Pa and ²³⁰Th model results showed significant overestimation in the deep ocean (e.g., Siddall et al., 2005; Dutay et al., 2009; Gu and Liu, 2017; van Hulten et al., 2018), our best OGCM simulation considering the reversible scavenging, bottom scavenging, and the dependence of scavenging efficiency on particle concentration (CTRL_EXP) can reproduce the distributions of dissolved ²³¹Pa and ²³⁰Th consistently with GEOTRACES data, together with the realistic distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios.

We also made a quantitative assessment about the processes that determine the global distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios by decomposing the processes affecting the sediment ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios into three parts: water-column scavenging, ocean transport (advection and diffusion), and bottom scavenging. We confirmed that the global sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in our best model (CTRL_EXP) are primarily determined by ocean transport of ²³¹Pa, as shown in previous studies. Contrary to ²³¹Pa, ocean transport of ²³⁰Th tends to reduce the spatial contrast of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios. However, we found that this is not the case for the Southern Ocean; ²³⁰Th advection increases the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in the Southern Ocean and strengthens the observed high ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios there. This means that not only ²³¹Pa advection but also ²³⁰Th advection contributes to the high ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in the Southern Ocean. This result implies that scavenging of ²³⁰Th is not much efficient in the Southern Ocean as conventionally thought when we consider the dependence of scavenging efficiency on particle concentration. We also show that bottom scavenging works opposite to ocean transport and decreases the spatial contrast of ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios; bottom scavenging promotes the removal of ²³¹Pa near the sea bottom more efficiently than that of ²³⁰Th, and the total effect of bottom scavenging reduces spatial contrasts of the ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios. Our best simulation shows the realistic residence times of ²³¹Pa and ²³⁰Th, but simulation without bottom scavenging and dependence of scavenging efficiency on particle concentration significantly overestimates the residence times for both ²³¹Pa and ²³⁰Th in spite of similar distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios to our best simulation.

The model developed in this study is useful not only for simulating ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios in the present-day ocean but also in different climates such as glacial periods. Our OGCM experiments using the present-day physical fields can clarify the processes governing the global distribution of sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios. A similar analysis using the physical ocean fields during glacial periods may help climate scientists to understand the mechanisms for glacial changes in the sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratio observed in sediment cores. Although simulated sedimentary ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ under glacial times are also discussed in a 2D model (Lippold et al., 2012) and recently in a 3D model (Gu et al., 2020), there is insufficient discussion of the mechanism of change in the three-dimensional distribution. Simulation of ${}^{\mathrm{231}}\mathrm{Pa}{/}^{\mathrm{230}}\mathrm{Th}$ ratios under glacial climates (e.g., Oka et al., 2011; Kobayashi and Oka, 2018) is an exciting avenue of future study.