the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Global simulation of dissolved 231Pa and 230Th in the ocean and the sedimentary 231Pa∕230Th ratios with the ocean general circulation model COCO ver4.0
Yusuke Sasaki
Hidetaka Kobayashi
Akira Oka
Sedimentary ratios provide clues to estimate the strength of past ocean circulation. For its estimation, understanding the processes controlling the distributions of 231Pa and 230Th in the ocean is important. However, simulations of dissolved and particulate 231Pa and 230Th in the modern ocean, recently obtained from the GEOTRACES project, remain challenging. Here we report a model simulation of 231Pa and 230Th in the global ocean with COCO ver4.0. Starting from the basic water-column reversible scavenging model, we also introduced the bottom scavenging and the dependence of scavenging efficiency on particle concentration. As demonstrated in a previous study, the incorporation of bottom scavenging improves the simulated distribution of dissolved 231Pa and 230Th in the deep ocean, which has been overestimated in models not considering the bottom scavenging. We further demonstrate that introducing the dependence of scavenging efficiency on particle concentration results in a high concentration of dissolved 230Th in the Southern Ocean as observed in the GEOTRACES data. Our best simulation can well reproduce not only the oceanic distribution of 231Pa and 230Th but also the sedimentary ratios. Sensitivity analysis reveals that oceanic advection of 231Pa primarily determines sedimentary ratios. On the other hand, 230Th advection and bottom scavenging have an opposite effect to 231Pa advection on the sedimentary ratios, reducing their latitudinal contrast. Our best simulation shows the realistic residence times of 231Pa and 230Th, but simulation without bottom scavenging and dependence of scavenging efficiency on particle concentration significantly overestimates the residence times for both 231Pa and 230Th in spite of similar distribution of sedimentary ratios to our best simulation.
- Article
(3654 KB) - Full-text XML
-
Supplement
(4201 KB) - BibTeX
- EndNote
The ratios in marine sediments are used for estimating past ocean circulation strength (e.g., Yu et al., 1996; McManus et al., 2004; Gherardi et al., 2009; Böhm et al., 2015; Waelbroeck et al., 2018; Süfke et al., 2020). Alpha decay of 235U and 234U produces 231Pa (half-life of ∼32.5 kyr) and 230Th (half-life of ∼75.2 kyr), respectively, at an approximately constant ratio of 0.093 in the ocean (Henderson and Anderson, 2003). 231Pa and 230Th are absorbed onto and desorbed from the surfaces of sinking particles (reversible scavenging; Bacon and Anderson, 1982) and eventually removed from the water column into marine sediments. Differential scavenging efficiencies of 231Pa and 230Th result in differences in their residence times in the ocean; the residence times of 231Pa and 230Th were estimated to be 111 and 26 years in Yu et al. (1996), and 130 and 20 years in Henderson and Anderson (2003). The shorter residence time of 230Th indicates that 230Th generated from 234U is removed relatively quickly to marine sediments. On the other hand, the longer residence time of 231Pa indicates that 231Pa produced from 235U is transported for a longer period by ocean transport. Therefore, the deviation of the sedimentary ratios from the constant production ratio of 0.093 has been used as a proxy for ocean circulation (Yu et al., 1996). For example, the sedimentary ratios from the Bermuda Rise were closer to 0.093 at the Last Glacial Maximum (LGM) than today, possibly suggesting that the Atlantic meridional overturning circulation (AMOC) was weaker at the LGM (McManus et al., 2004; Böhm et al., 2015). To use the sedimentary ratios as a proxy for ocean circulation in a more quantitative manner, modeling about 231Pa and 230Th is important.
For 231Pa and 230Th modeling, one needs to take into account the different scavenging efficiencies of different marine particle types (e.g., particulate organic carbon, calcite, and opal) as well as the distribution of these particles (Chase et al., 2002; Edwards et al., 2005). Sinking particles effectively scavenge 231Pa and 230Th in regions with high particle concentrations. In general, 231Pa has a longer residence time than 230Th, because sinking particles scavenge 230Th more efficiently. However, as for opal particles, Chase et al. (2002) argue that opal scavenges 231Pa more effectively than 230Th. This report is consistent with observational studies that find high ratios in the Southern Ocean, where opal sinking flux is high (Rutgers van der Loeff and Berger, 1993; Walter et al., 1997; Chase et al., 2003).
Authors of previous modeling studies have tried to simulate the global distributions of 231Pa and 230Th by two-dimensional (2D) ocean models (Marchal et al., 2000; Luo et al., 2010) or three-dimensional (3D) ocean models of LSG-OGCM (Henderson et al., 1999), Bern 3D (Siddall et al., 2005; Rempfer et al., 2017), NEMO (Dutay et al., 2009; van Hulten et al., 2018), CESM (Gu and Liu, 2017) and iLOVECLIM (Missiaen et al., 2020a). There are also modeling studies that discuss the relationship between the strength of the AMOC and changes in sedimentary ratios (Siddall et al., 2005; Lippold et al., 2012; Gu and Liu, 2017; Gu et al., 2020; Missiaen et al., 2020a, b). Siddall et al. (2005) pioneered the 3D simulation of both 231Pa and 230Th by incorporating reversible scavenging. Their control simulation appropriately reproduced the observed distribution of sedimentary ratios; it showed high sedimentary ratios in regions where the sinking opal particle flux is high. In their control simulation, the concentrations of dissolved 231Pa and 230Th increased linearly with depth; this pattern agreed broadly with observed features. However, simulated dissolved 231Pa and 230Th were both higher than observations in the deep ocean. In addition to reversible scavenging by sinking ocean particles, several studies (e.g., Anderson et al., 1983; Roy-Barman, 2009; Okubo et al., 2012) have pointed out the importance of additional scavenging at the seafloor (bottom scavenging) and the continental boundaries (boundary scavenging). The bottom scavenging has not been explicitly included in global 3D ocean models except for Rempfer et al. (2017) which used a simplified 3D ocean model of intermediate complexity similar to that used by Siddall et al. (2005) and reproduced the distributions of dissolved 231Pa and 230Th more realistically by introducing the bottom scavenging. On the other hand, Henderson et al. (1999) reproduced the distribution of dissolved 230Th in their ocean general circulation model (OGCM) simulation by changing the efficiency of reversible scavenging depending on particle concentration; this effect has not been directly considered by recent modeling studies but some studies have evaluated the impacts of changes in particle concentration and scavenging efficiency on the distribution of 231Pa and 230Th (van Hulten et al., 2018; Missiaen et al., 2020a, b). Recently, the GEOTRACES project has led to a dramatic increase in the number of observations of dissolved and particulate 231Pa and 230Th (Schlitzer et al., 2018). The GEOTRACES database provides an opportunity to test models describing the cycling of these two radioisotopes in the global ocean. In this study, we report our model simulation about the global distribution of 231Pa and 230Th in the ocean with COCO ver4.0. Starting from the basic water-column reversible scavenging model of Siddall et al. (2005), we also introduced the bottom scavenging and the dependence of scavenging efficiency on particle concentration. Furthermore, we quantitatively discuss the processes that control the global distribution of sedimentary ratios; by performing a series of sensitivity simulations, we discuss how the individual processes (i.e., water-column reversible scavenging, ocean transport, and bottom scavenging) affect the global distribution of dissolved 231Pa and 230Th and sedimentary ratios.
2.1 Ocean general circulation model
The OGCM used in this study is COCO version 4.0 (Hasumi, 2006), the ocean component of the coupled ocean-atmosphere general circulation model MIROC version 3.2 (K-1 Model Developers, 2004). The COCO is also used as the ocean part of the MIROC earth system model (Hajima et al., 2020; Ohgaito et al., 2021). The model domain is global, with about 1∘ horizontal resolution and 43 vertical layers. The vertical resolution varies from 5 m (top) to 250 m (bottom). Surface boundary conditions are given from monthly averages of zonal and meridional components of wind stress, air temperature, specific humidity, net shortwave radiation, downward longwave radiation, freshwater flux, and wind speed. These boundary conditions are taken from the output of a pre-industrial simulation with the MIROC (Kobayashi et al., 2015; Oka et al., 2012). To calculate 231Pa and 230Th, we perform “offline” tracer simulation using physical fields obtained in advance by the COCO (Oka et al., 2008, 2009). The offline means that the calculation of tracer is separately performed from that of the physical field; since the distributions of 231Pa and 230Th do not affect the physical fields at all, the results do not depend on whether the model is offline or online. The offline tracer model makes it easier to perform various sensitivity experiments. The tracer model is integrated for 3000 years and tracer fields reach a steady state where changes in ocean tracer inventory almost vanish (less than 10−5 % per 100 years). We analyze the average of the last 100 years of the integration.
The physical fields used in this study is based on MIROC climate model simulations, and its reproducibility has been discussed and confirmed in a variety of literature (e.g., K-1 Model Developers, 2004; Gregory et al., 2005; Oka et al., 2006; Stouffer et al., 2006). We also note that the physical fields used here are the same as the pre-industrial (PI) simulation reported in Kobayashi et al. (2015) and Kobayashi and Oka (2018). For reference, the Atlantic meridional overturning circulation (AMOC) simulated by the COCO used in this study is shown in Fig. S11.
2.2 Particle fields
Following Siddall et al. (2005), the distribution of biogenic particles (organic carbon, calcite, and opal) is used to evaluate the scavenging of both 231Pa and 230Th. We define the concentration M of each particle type (g m−3) as , where F is the particle flux (g m−2 yr−1) and ws is the constant settling velocity (m yr−1). The particle flux is calculated using the export flux from the euphotic zone and an assumed vertical profile of each particle type. The detailed procedure is explained below.
First, the particulate organic carbon (POC) export flux from the euphotic zone is calculated by multiplying the distribution of primary production derived from satellite observations (Behrenfeld and Falkowski, 1997) by the export ratio (Dunne et al., 2005). From POC export flux and , the concentration of POC at the base of the euphotic zone, MPOC(z0), where z0 is the depth of the bottom of the euphotic zone, is obtained. After obtaining MPOC(z0), the POC concentration in the water column is expressed (Marchal et al., 1998) as
where ε is a remineralization exponent for POC.
Next, the calcite and opal export fluxes from the euphotic zone are calculated by multiplying the POC export flux by their rain ratios, which are estimated following formulations of Siddall et al. (2005) and Maier-Reimer (1993); please refer to Eqs. (2)–(5) of Siddall et al. (2005) for detail. The calcite particle concentration is calculated by assuming an exponentially decreasing vertical profile (Henderson et al., 1999; Marchal et al., 2000; Siddall et al., 2005). Thus, we have
where zp is the calcite penetration depth. While the opal concentration is expressed as an exponentially decreasing vertical profile in some previous studies (e.g., Henderson et al., 1999), we consider opal dissolution to be dependent on temperature, following Siddall et al. (2005), as
where Dopal (yr−1) is the opal dissolution rate, T0 is the minimum temperature (∘C) of seawater in the model, and B is a dissolution constant (∘C−1 yr−1). Table 1 lists the parameter values used in this study. Figure S10 shows the distribution of particle fluxes in the surface ocean.
2.3 Reversible scavenging model
We use a tracer model of 231Pa and 230Th based on Siddall et al. (2005). The dissolved concentration (Ad) and particle concentration (Ap) of 231Pa and 230Th are calculated from the following equations:
In Eq. (4a), the first term on the right-hand side (βi) represents production from uranium (231Pa from 235U; 230Th from 234U), the second term represents radioactive decay, the third term represents the effect of vertical transport by particle settling, and the fourth term represents ocean transport by advection and diffusion. The superscript i represents the isotope type (231Pa, 230Th).
By following a reversible scavenging model (Bacon and Anderson, 1982), the relationship between the radionuclide concentration in the dissolved phase (Ad) and particulate phase (Ap) is represented by the partition coefficient () as
where subscript j represents the particle type (organic carbon, calcite, opal) and Cj is the dimensionless ratio of particle concentration to the density of seawater. The formulation of the reversible scavenging was also described in Oka et al. (2009, 2021) and readers can obtain its detailed description therein. The partition coefficient depends on the type of particles (Siddall et al., 2005). The partition coefficients of 231Pa and 230Th for each type of particle have been estimated in previous studies (Luo and Ku, 1999; Chase et al., 2002). Chase et al. (2002) show that opal scavenges 231Pa more efficiently than 230Th, whereas calcite scavenges 230Th more efficiently than 231Pa. Here we use partition coefficients following Chase and Anderson (2004), as in other previous modeling studies (Dutay et al., 2009; Gu and Liu, 2017; Siddall et al., 2005; Table 2). The model parameters are summarized in Table 1.
2.4 One-dimensional reversible scavenging model
In addition to the three-dimensional tracer model based on the OGCM, we use a simple, vertical, one-dimensional model, which was widely used in previous studies (e.g., Bacon and Anderson, 1982), to analyze simulation results in Sect. 4. In the one-dimensional model, we assume a steady state and ignore the effect of ocean transport in Eq. (4a). Furthermore, we do not take the radioactive decay term into account, because it is much smaller than the production term. Under these assumptions, Eq. (4a) becomes
In this one-dimensional model, production by uranium radioactive decay (the first term on the left side of Eq. 6) is balanced by vertical transport through particle settling (the second term on the left side of Eq. 6). If we assume that is zero at the sea surface (z=0), then Eq. (6) can be solved, leading to
Equation (7) shows that the vertical profile of is determined from two parameters: βi and ws. From Eq. (5), we have
The dissolved concentration can be obtained from Eqs. (7) and (8):
Equation (9) shows that the vertical profile of is determined by the particle settling speed, the partition coefficients, and the concentrations of each particle. By comparing results from the one-dimensional model and the three-dimensional tracer model, we can isolate the influence of ocean transport (i.e., advection, diffusion, and convection) on the simulated distributions of dissolved 231Pa and 230Th (see Sect. 4; Table 3).
2.5 Experimental design
This study conducts a series of OGCM experiments. First, we perform an experiment named Siddall_EXP using the same parameters and formulations as in Siddall et al. (2005). As stated in the Introduction, Siddall et al. (2005) was a pioneering 3D model for global simulation of both 231Pa and 230Th. This model is now a relatively old model and the reversible scavenging model introduced in this model is simpler than more recent models. However, this model appropriately reproduced the observed distribution of sedimentary ratios as shown in their Fig. 2 which appears not necessarily inferior to that in more recent models. Therefore, in this study, we start with Siddall_EXP where the most basic reversible scavenging model of Siddall et al. (2005) is introduced.
Second, we perform an experiment named BTM_EXP, in which we additionally take bottom scavenging into account. Following Rempfer et al. (2017), we simply set the deepest model grid layer as the nepheloid layer. The thickness of the nepheloid layer becomes equal to the thickness of the corresponding deepest model grid layer which varies between 5 and 250 m depending on the depth. The intensity of the bottom scavenging depends on two parameters: the partition coefficient (Kbottom) and the concentration (Cbottom) of the bottom particles. Our treatment about Cbottom is the same that in Rempfer et al. (2017); we assume a globally uniform value for Cbottom ( g cm−3) which is within the range of to g cm−3 observed in the benthic nepheloid layers in the North Atlantic (Lam et al., 2015). As for Kbottom, because our formulation of the reversible scavenging is not the same as Rempfer et al. (2017), we needed to find its appropriate parameter value. For this purpose, we perform a number of simulations with different bottom scavenging intensities by changing the value of Kbottom.
Third, we perform a sensitivity experiment named KREF_EXP concerned with the reference partition coefficient (Kref). In KREF_EXP, in addition to varying the value of the partition coefficient for bottom particles (Kbottom), we also vary the values of the reference partition coefficients (Kref) from those assumed in Siddall_EXP and BTM_EXP.
Finally, we perform an experiment named PCE_EXP, in which we incorporate the dependence of scavenging efficiency on particle concentration. In PCE_EXP, Kref is not assumed to be constant but varies according to the following formulation of Henderson et al. (1999):
where Ctotal [g cm−3] is the total concentration of all sinking particles() and Cref [g cm−3] is the reference concentration. Note that the value of Ctotal is differently specified on each grid, whereas Cref is given as a globally uniform value. Due to the dependence of Kref on Ctotal, the scavenging efficiency becomes lower under higher particle concentrations and higher under lower particle concentrations. We conduct several simulations by varying Cref between 10−9 and 10−6 g cm−3 (smaller Cref value leads to stronger scavenging). Although the observed decrease of the partition coefficient with increased bulk particle concentration is not entirely understood (Pavia et al., 2018), we will show that this particle concentration effect becomes important for controlling dissolved 230Th in some ocean regions.
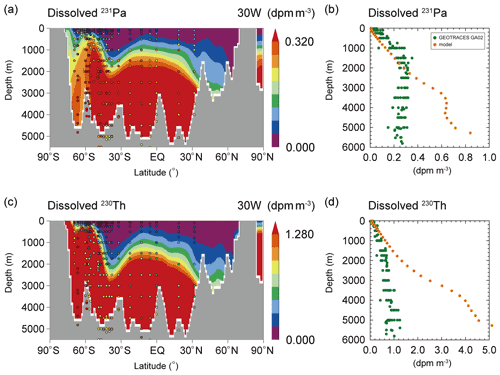
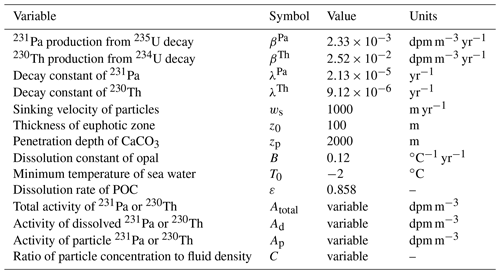
Figure 1(a) Dissolved 231Pa along 30∘ W in the Atlantic Ocean and (b) its vertical profile (the latitudinal mean along 30∘ W in the Atlantic Ocean) in Siddall_EXP. (c, d) Same as (a) and (b) except for 230Th. The colored circles in (a) and (c) represent data from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The green and orange circles in (b) and (d) represent the GA02 data and simulation results. The unit is dpm m−3 (disintegrations per minute per cubic meter).
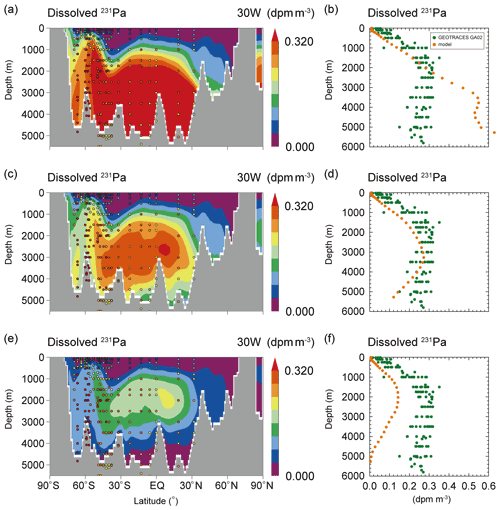
Figure 2(a, c, e) Dissolved 231Pa along 30∘ W in the Atlantic Ocean and (b, d, f) its vertical profile (the latitudinal mean along 30∘ W in the Atlantic Ocean) in BTM EXP. is set to 5.0×104 in (a) and (b), 5.0×105 in (c) and (d), and 5.0×106 in (e) and (f). The colored circles in (a), (c), and (e) represent data from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The green and orange circles in (b), (d), and (f) represent the GA02 data and simulation results.
3.1 Dissolved 231Pa and 230Th along the Atlantic meridional transects
First, we discuss the results of Siddall_EXP, focusing on the meridional distribution of 231Pa and 230Th in the Atlantic Ocean. Figure 1 shows the dissolved concentrations of 231Pa and 230Th simulated in Siddall_EXP along the Atlantic 30∘ W transect, together with GEOTRACES data (see Fig. S1 for the location of observations referenced in this study). We confirm that the distributions of dissolved 231Pa and 230Th in Siddall_EXP are approximately the same as those reported in Siddall et al. (2005; their Fig. 2). Because 231Pa and 230Th exchange reversibly with sinking particles and are transported to the deep ocean, the dissolved 231Pa and 230Th concentrations increase with depth, both in the model simulation and in observations. However, as in Siddall et al. (2005), the model simulation overestimates dissolved 231Pa and 230Th concentrations at depths greater than 2000 and 1000 m, respectively. For quantitative analysis, we perform a linear regression analysis between the simulation results and observed data from the GEOTRACES GA02 transect; we calculate the root mean square deviation (RMSD), the correlation coefficient (R), and the slope of the linear regression (s) of modeled concentration versus observed concentration, as summarized in Table S1. The linear regression line slope indicates the model's ability to reproduce the observed distribution; it approaches 1.0 when the model simulation realistically reproduces the target distribution (Dutay et al., 2009; Gu and Liu, 2017). For Siddall_EXP, the slope of linear regression line is significantly larger than 1.0 for both 231Pa (s=1.88, R=0.72, and RMSD = 0.15) and 230Th (s=4.44, R=0.89, and RMSD = 1.31; Table S1). This overestimation in the deep ocean is also found in other previous model simulations (e.g., Dutay et al., 2009; Gu and Liu, 2017; van Hulten et al., 2018).

Figure 3(a, c, e, g) Dissolved230Th along 30∘ W in the Atlantic Ocean and (b, d, f, h) its vertical profile (the latitudinal mean along 30∘ W in the Atlantic Ocean) in BTM_EXP are plotted. is set to 5.0×105 in (a) and (b), 1.0×106 in (c) and (d), 5.0×106 in (e) and (f), and 1.0×107 in (g) and (h). The colored circles in (a), (c), (e), and (g) represent data from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The green and orange circles in (b), (d), (f), and (h) represent the GA02 data and simulation results.
Next, to reduce the overestimation of the simulated concentrations in the deep ocean, we additionally incorporate bottom scavenging in benthic nepheloid layers (BTM_EXP). The dissolved 231Pa and 230Th distributions are shown in Figs. 2 and 3, respectively. As expected, the incorporation of bottom scavenging helps reduce 231Pa and 230Th concentrations in the deep ocean, improving the model's agreement with the data. As for the distribution of dissolved 231Pa, the model results come relatively close to the GEOTRACES data if is set to 5.0×105 (s=1.04, R=0.90, and RMSD = 0.05; see CTRL_EXP in Table S1; Fig. 2c and d). This result confirmed the importance of the bottom scavenging, which was already reported from a previous global 3D model (Rempfer et al., 2017) and a regional eddy-permitting model (Lerner et al., 2020). On the other hand, it is difficult to reproduce the observed distribution of dissolved 230Th in BTM_EXP. With , the concentrations of 230Th in bottom waters come close to observed values (Fig. 3c and d), but the concentrations in the deep ocean (from 2000 to 5000 m) remain overestimated. In the case of larger , the simulated 230Th concentrations approach observed values in the deep ocean but are significantly lower than observations in bottom waters (e.g., in Fig. 3g and h). These results indicate that modification of Siddall_EXP by considering bottom scavenging alone is not sufficient for accurately simulating 230Th distribution in our model. As shown in Rempfer et al. (2017) and Lerner et al. (2020), the appropriate selection of scavenging parameter coefficients is required for more realistic simulation. Because our reversible scavenging model (which is the same as Siddall et al., 2005; Sect. 2.3) is not the same as Rempfer et al. (2017) and Lerner et al. (2020), we need to discuss the validity of a scavenging parameter coefficient in our model (i.e., Kref). In the following experiments (i.e., KREF_EXP and PCE_EXP), we discuss more appropriate treatment about Kref by focusing solely on 230Th.
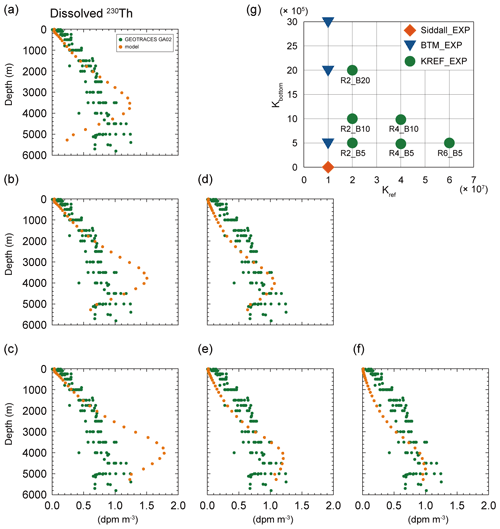
Figure 4The vertical profile of dissolved 230Th (the latitudinal mean along 30∘ W in the Atlantic Ocean) in various simulations of KREF_EXP: (a) R2_B20, (b) R2_B10, (c) R2_B5, (d) R4_B10, (e) R4_B5, and (f) R6_B5. The green and orange circles in (a)–(f) represent the Atlantic GEOTRACES data (GA02; Schlitzer et al., 2018) and simulation results. Panel (g) summarizes the choice of parameters (i.e., and ) in each simulation.
To reproduce the distribution of 230Th more realistically, we change the value of the reference partition coefficient () in addition to (KREF_EXP). Figure 4 summarizes the results of KREF_EXP and shows the simulated vertical distributions of dissolved 230Th for various values of and (see Fig. 4g). Note that, for example, the simulation R2_B5 means that is set to 2.0×107 and to 5.0×105. In the cases where is set to 5.0×105 (namely, R2_B5, R4_B5, and R6_B5), the 230Th concentrations systematically change depending on ; as the reversible scavenging on sinking particles becomes stronger (i.e., for larger ), the concentrations of dissolved 230Th become smaller throughout the water column (Fig. 4c, e, and f). As discussed for BTM_EXP, it is also confirmed that the stronger bottom scavenging (i.e., larger ) leads to the lower concentrations near the sea bottom (e.g., see R2_B5, R2_B10, and R2_B20). For some combinations of water-column scavenging and bottom scavenging, simulations (e.g., R6_B5, R4_B5, R4_B10) reasonably reproduce the observed profile of dissolved 230Th concentration. Among our KREF_EXP simulations, the R6_B5 simulation (Fig. 4f) shows the slope of the linear regression line nearest to 1.0 (s=0.88, R=0.81, and RMSD = 0.20; Table S1) where is higher () than for Siddall_EXP and BTM_EXP (). In the R6_B5 simulation (Fig. 4f), the vertical profile of dissolved 230Th is significantly improved from that of Siddall_EXP (Fig. 1d) and BTM_EXP (Fig. 3). We confirmed that the R6_B5 simulation captures the observed features of the Atlantic transects of the GEOTRACES data (Fig. 5a). However, the R6_B5 simulation still underestimates the concentrations of dissolved 230Th from the surface to intermediate depths (see Fig. 4f). Also, the high concentrations of dissolved 230Th observed in the Southern Ocean in GEOTRACES data are not well reproduced (Fig. 5a). To address this issue, we performed additional simulations by slightly changing the values of and from the R6_B5 simulation (not shown), but we found that it is difficult to remove the abovementioned deficiencies by merely changing the values of and in KREF_EXP.
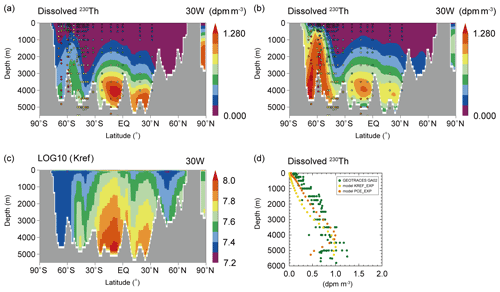
Figure 5Dissolved 230Th along 30∘ W in the Atlantic Ocean in (a) R6_B5 of the KREF_EXP and (b) PCE_EXP. (c) Reference partition coefficient (K_ref) along 30∘ W in the Atlantic Ocean in PCE_EXP. (d) The vertical profile of dissolved 230Th (the latitudinal mean along 30∘ W in the Atlantic Ocean) in R6_B5 of KREF_EXP and PCE_EXP. The colored circles in (a) and (b) represent data from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The green, yellow, and orange circles in (d) represent the GA02 data and KREF_EXP and PCE_EXP simulation results.
Finally, we discuss PCE_EXP, in which the dependence of scavenging efficiency on particle concentration is taken into account, according to Eq. (10). We conduct several simulations by varying the value of the reference concentration (Cref) between 10−9 and 10−6 g cm−3. Among these results, we here discuss the case with g cm−3, which shows the best agreement with observations. Compared to the case in which the dependence of scavenging efficiency on particle concentration is not considered (i.e., R6_B5 simulation of KREF_EXP), PCE_EXP is expected to show smaller (larger) for the higher (lower) concentration of sinking particles. In Fig. 5, we compare the simulated dissolved 230Th distribution obtained from PCE_EXP and R6_B5 simulation of KREF_EXP. Owing to the dependence of scavenging efficiency on particle concentration, PCE_EXP reproduces the vertical distribution of dissolved 230Th slightly better than KREF_EXP (Fig. 5d). The regression analysis also confirms that the agreement with the GEOTRACES data becomes improved in PCE_EXP (s=0.98 and R=0.84; CTRL_EXP in Table S1). It is worthy to note that the distribution in the Southern Ocean is significantly improved in PCE_EXP (Fig. 5b) compared to KREF_EXP (Fig. 5a) as a result of the nonuniform distribution of the reference partition coefficient (Fig. 5c). In the Southern Ocean, where particle concentration is relatively higher than in other regions (Honjo et al., 2008), the value of in PCE_EXP is lower than that in the R6_B5 simulation of KREF_EXP (; i.e., ) (Fig. 5c). Therefore, the concentration of dissolved 230Th in PCE_EXP becomes high compared to the KREF_EXP, which leads to a more realistic distribution of dissolved 230Th in the Southern Ocean. The distributions of 230Th simulated in previous modeling studies (e.g., Figs. 4 and 5 in Dutay et al., 2009; Fig. 2 in Siddall et al., 2005; Fig. 2 in Gu and Liu, 2017; Fig. 3 in Rempfer et al., 2017; Fig. 12 in van Hulten et al., 2018; Fig. S3 in Missiaen et al., 2020a) are basically similar to our result (Fig. 6b); however, our simulation is the best at reproducing the high concentration in the Southern Ocean. Hereafter, our best simulation (i.e., case of BTM_EXP for 231Pa and PCE_EXP for 230Th) is called CTRL_EXP (see Table 2 for parameter values of CTRL_EXP).
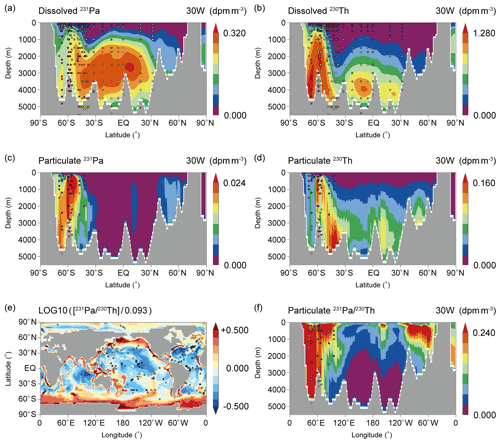
Figure 6(a) Dissolved 231Pa, (b) dissolved 230Th, (c) particulate 231Pa, and (d) particulate 230Th along 30∘ W in the Atlantic Ocean in CTRL_EXP. (e) Sedimentary ratios normalized by the production ratio of 0.093 in CTRL_EXP. The colored circles represent observational data. Dissolved and particulate 231Pa and 230Th data are taken from the Atlantic GEOTRACES data (GA02 and GIPY05; Schlitzer et al., 2018). The data of sedimentary ratios are taken from the following references (Mangini and Sonntag, 1977; Müller and Mangini, 1980; Anderson et al., 1983; Shimmield et al., 1986; Schmitz et al., 1986; Yang et al., 1986; Shimmield and Price, 1988; Lao et al., 1992; François et al., 1993; Frank et al., 1994; Frank, 1996; Bradtmiller et al., 2014; Luo et al., 2010, and their supplemental data).
3.2 Particulate 231Pa and 230Th
By conducting a series of experiments described above, this study successfully reproduces the observed distributions of dissolved 231Pa and 230Th, shown again in Fig. 6a and b, respectively. The model captures the observed tendency that the concentration becomes higher in the high-latitude Southern Ocean, as reported in previous studies (e.g., see Fig. 2 in Siddall et al., 2005). The ratio of 231Pa to 230Th in the particulate phase in the water column shows low concentrations in the deep ocean, while the ratio becomes high in the northern North Atlantic Ocean and the Southern Ocean (Fig. 6f). This feature is consistent with observational findings and recent modeling studies (e.g., Fig. 2 in Gu and Liu, 2017; Fig. 3 in Rempfer et al., 2017). Although the number of available observations is limited for the particulate phase, it is confirmed that our simulation reasonably reproduces observed distributions for both dissolved and particulate phases.
3.3 Sedimentary ratios
Our CTRL_EXP also well reproduces the global distribution of sedimentary ratios (Fig. 6e) consistent with the reported observations (Mangini and Sonntag, 1977; Müller and Mangini, 1980; Anderson et al., 1983; Shimmield et al., 1986; Schmitz et al., 1986; Yang et al., 1986; Shimmield and Price, 1988; Lao et al., 1992; François et al., 1993; Frank et al., 1994; Frank, 1996; Bradtmiller et al., 2014; Luo et al., 2010, and their supplemental data). Sedimentary ratios are high along the margin of the North Pacific and the North Atlantic, as well as in the Southern Ocean, where particle concentrations are high. On the other hand, sedimentary ratios are low in the low-latitude regions, including subtropical gyres, where particle concentrations are low. These simulated features are consistent with observations (circles in Fig. 6e). Previous modeling studies reported the similar distribution of sedimentary ratios (e.g., Fig. 2 in Siddall et al., 2005; Fig. 11 in Dutay et al., 2009; Fig. 4 in Gu and Liu, 2017; Fig. 10 in van Hulten et al., 2018; Fig. 1 in Missiaen et al., 2020a) and our Siddall_EXP also reasonably reproduced the global distribution of sedimentary ratios (Fig. S4a). However, as shown above, the distributions of dissolved 231Pa and 230Th in the ocean are significantly different between CTRL_EXP and Siddall_EXP. Thus, each experiment implies a different set of processes controlling the distribution of sedimentary ratios. We will discuss this point later in the next section.
4.1 Comparison with previous modeling studies
We demonstrated that our CTRL_EXP can reproduce a more realistic distribution of dissolved 231Pa and 230Th along the Atlantic meridional transects than Siddall_EXP by considering the bottom scavenging and the dependence of scavenging efficiency on particle concentration. Here, we compared our results with previous modeling studies which showed their model results along with Atlantic meridional transects (GEOTRACES GA02 section).
As far as we know, Rempfer et al. (2017) was the only 3D global ocean model which introduces the bottom scavenging, and in our study, we introduced the bottom scavenging into the global OGCM for the first time. Models without the bottom scavenging tend to overestimate the dissolved 231Pa and 230Th in the deep ocean as in our Siddall_EXP. For example, in Gu and Liu (2017) in which 231Pa and 230Th tracers are introduced into CESM1.3, their simulated 231Pa and 230Th concentrations are significantly overestimated in the deep ocean along the GEOTRACES GA02 section (their Fig. 2). In Dutay et al. (2009) in which 231Pa and 230Th tracers are introduced into NEMO-PISCES, influences of particle size and type on 231Pa and 230Th are discussed by performing several sensitivity simulations, but all of their simulations overestimate 231Pa and 230Th concentrations in the deep Atlantic Ocean (their Figs. 4 and 5, respectively). In van Hulten et al. (2018) which was the updated 231Pa and 230Th simulation with NEMO-PISCES, the model still overestimates 231Pa and 230Th concentrations in the deep Atlantic Ocean (their Fig. 12), because particles in the nepheloid layers (i.e., bottom scavenging) are not included in their model.
Although the incorporation of bottom scavenging is important for controlling the scavenging efficiency, it is worthy to note that bottom scavenging is not the sole process that controls the scavenging efficiency. Therefore, for example, the model which specified the relatively stronger affinity to the particle can lead to smaller tracer concentration even if the model does not include the bottom scavenging. In fact, in Missiaen et al. (2020a), their simulated 231Pa and 230Th are underestimated in both the upper and deep oceans (their Fig. S3 in the Supplement) even if the bottom scavenging was not included in their model. This is because their specified scavenging parameters are relatively stronger than the other models (see their Table 2) as a result of their parameter tuning without the bottom scavenging.
In the Re3d_Bt_Bd simulation reported in Rempfer et al. (2017) where the bottom scavenging process is considered, the abovementioned overestimation in the deep ocean was relaxed and their simulated distribution appears similar to our CTRL_EXP. Their study is the first 3D model demonstration about the importance of the bottom scavenging process, which is confirmed again in our study (e.g., from comparison with Siddall_EXP and KREF_EXP). However, their model still tends to somewhat overestimate the dissolved 231Pa compared with GEOTRACES GA02 data (their Fig. 3). Because the formulation of the reversible scavenging and their model parameters are not the same as our CTRL_EXP, we expect that different choice of model parameter values leads to such differences; more specifically, our choice of is based on Chase et al. (2002) and Siddall et al. (2005), whereas the scavenging efficiency parameters in Rempfer et al. (2017) are similar to those in Luo et al. (2010) and Marchal et al. (2000). In addition, as for 230Th, the high concentration in the Southern Ocean is not reproduced in their model, whereas this is reproduced in our CTRL_EXP by considering the dependence of scavenging efficiency on particle concentration. Although the dependence of scavenging efficiency on particle concentration was already introduced in Henderson et al. (1999), our study demonstrates its importance for reproducing high concentrations in the Southern Ocean reported in GEOTRACES GA02 data for the first time.
This study newly introduces a model to the existing global three-dimensional OGCM. Based on the reversible scavenging model, this study well reproduces the distribution of dissolved concentration of 231Pa and 230Th by considering the bottom scavenging and the dependence of the scavenging efficiency on particle concentration. The importance of bottom scavenging on the dissolved concentration of 231Pa and 230Th is already discussed in previous studies (Rempfer et al., 2017; Lerner et al., 2020). Therefore, our result should be viewed as a confirmation of these previous results. However, we emphasize that this study provides a new estimate of the contribution of bottom scavenging to the distribution of sedimentary ratios compared to other processes such as advection and water-column scavenging. Rempfer et al. (2017) evaluated the performance of their 231Pa and 230Th simulations based on the root mean squared deviation normalized by the standard deviation of observations. In our control experiment (CTRL_EXP), the RMSD between the available GEOTRACES data is 0.57 for dissolved 231Pa and 0.51 for dissolved 230Th. These values lie in the range of values for the “standard” and “optimal” experiments by Rempfer et al. (2017), the latter of which considers both bottom scavenging and boundary scavenging (see Fig. 5 in Rempfer et al., 2017). Lerner et al. (2020) use a regional eddy-permitting ocean circulation model and focus on the western North Atlantic. They also point out that removal in the nepheloid layer significantly impacts the basin-scale distribution of dissolved and particulate phases of 231Pa and 230Th. In line with these previous studies, our result confirmed the importance of boundary scavenging. Recently, Gardner et al. (2018) reported data on the distribution of particles in benthic nepheloid layers. If such datasets become available for specifying the global distribution of particles in nepheloid layers, the effect of bottom scavenging can be introduced more realistically. It is also expected that additional consideration about boundary scavenging helps to improve our model simulation.
In addition to the bottom scavenging, our study highlights the importance of the dependence of scavenging efficiency on particle concentration. Although the decrease of the partition coefficient with increased bulk particle concentration has been reported from observations, the dependence of scavenging efficiency on particle concentration considered in PCE_EXP is not entirely understood (Honeyman et al., 1988; Henderson et al., 1999; Hayes et al., 2015). Recently, the particle concentration effect on 231Pa and 230Th partition coefficients in the open ocean along the GEOTRACES GA03 transect has been reported (Hayes et al., 2015; Lerner et al., 2017). Their study suggests that the dependency in the open ocean may deviate from Eq. (10). In discussing the factors responsible for the particle concentration effect, Pavia et al. (2018) point out the possibility that the particle concentration effect is an artifact caused by filtration. Further research is needed to elucidate the mechanisms that control the particle concentration effect.
As pointed out in previous studies (Rempfer et al., 2017; Lerner et al., 2020), the distributions of particle phases of 231Pa and 230Th are difficult to be reproduced in the model compared with the dissolved phases. Part of the error could be related to the particle fluxes that we give as an empirical distribution based on satellite observations. A modeling study using an ecosystem model that considers six different particles well reproduces the distribution of 231Pa and 230Th with a simple reversible scavenging model (van Hulten et al., 2018); such detailed treatment of particles might be helpful for more realistic simulation of particulate 231Pa and 230Th. Furthermore, by examining the response of 231Pa and 230Th to freshwater forcing into the North Atlantic, Missiaen et al. (2020b) show that changes in biogenic particle fluxes may have caused 30 % of the changes in the sedimentary ratios during the Heinrich stadial 1. Also, in Gu and Liu (2017), the particle change due to freshwater and its impact on sedimentary ratios is examined. Therefore, the role of particle fields on the distribution of 231Pa and 230Th, which was not directly investigated in this study, needs to be further discussed in a future study.
4.2 Reproducibility along GEOTRACES GA03 and GP16 transects
So far, we have compared our model results with observations by focusing on the Atlantic meridional GEOTRACES transects (i.e., GA02 and GIPY05). Here, we will compare our CTRL_EXP with other available GEOTRACES transects: GA03 in the subtropical North Atlantic (Hayes et al., 2015) and GP16 in the South Pacific (Pavia et al., 2018).
Figure S5 shows the results of CTRL_EXP along with the GEOTRACES GA03 data. For dissolved 231Pa, the model shows a high concentration around a depth of about 3000 m and higher concentrations on the eastern/southern side of the basin as in observations (Fig. S5a). This feature was also well reproduced in the Re3d_Bt_Bd simulation of Rempfer et al. (2017) as shown in their Fig. 2 but not in other previous models (e.g., Fig. 8 in van Hulten et al., 2018; Fig. 3 in Gu and Liu (2017)). This confirms that the consideration of the bottom scavenging is helpful for improving the model result along the GEOTRACES GA03 section. For dissolved 230Th, features similar to 231Pa are also found in both the model and observations although the model appears to underestimate north–south or west-east differences (Fig. S5b). For particulate 231Pa and 230Th, the model tends to simulate high concentration near the sea bottom and the continental margins where the particle concentration becomes high, but such features are not necessarily clear in the GEOTRACES data (Fig. S5c and d). Our model may not sufficiently reproduce the bottom and boundary scavenging associated with terrestrial particles in this region. More sophisticated treatment of bottom and boundary scavenging might be required for addressing these issues.
Figure S6 shows the results of CTRL_EXP along with the GEOTRACES GP16 data. As with the other section data, CTRL_EXP approximately reproduces the distribution of 231Pa and 230Th. The observational data show a clear signal associated with hydrothermal vents: low concentrations of dissolved 231Pa and 230Th and high concentrations of particulate 231Pa and 230Th, which are not simulated in our model. It has been pointed out that trace metals from hydrothermal activities may cause additional removal of 231Pa and 230Th (Shimmield and Price, 1988; Lopez et al., 2015; Rutgers van der Loeff et al., 2016; German et al., 2016). Along the GEOTRACES GP16 section, 231Pa and 230Th have been found to decrease with increasing trace metals of iron and manganese supplied from hydrothermal vents (Pavia et al., 2018). Processes related to the hydrothermal vents are not explicitly incorporated in the present 231Pa and 230Th model simulations; its detailed treatment is beyond the scope of this study but appears necessary for more realistic simulations.
4.3 Processes controlling sedimentary ratios
In this subsection, we discuss the processes controlling the global distribution of sedimentary ratios. For this purpose, we decompose the processes controlling sedimentary ratios simulated in our best simulation CTRL_EXP into three parts: water-column reversible scavenging, three-dimensional ocean transport, and bottom scavenging. To evaluate how these three processes affect the distribution of ratios, we conduct two additional experiments (see Table 3). The first experiment is 3D_EXP, which is the same as CTRL_EXP except that bottom scavenging is not taken into account (i.e., we set in 3D_EXP). The second is 1D_EXP, which is the one-dimensional reversible scavenging model experiment described in Sect. 2.4. The tracer distribution in 1D_EXP is determined solely by the one-dimensional vertical process of reversible scavenging; the strength of scavenging changes spatially through changes in the partition coefficient ( of Eq. 9 in Sect. 2.4) that depends on the specified three-dimensional particle concentration (Cj of Eq. 9). By using results of CTRL_EXP, 3D_EXP, and 1D_EXP, we can extract the influence of three processes: the influence of the one-dimensional vertical reversible scavenging is revealed by 1D_EXP, the influence of bottom scavenging is revealed by the difference between CTRL_EXP and 3D_EXP, and the influence of ocean transport is revealed by the difference between 3D_EXP and 1D_EXP. When we focus on sedimentary ratios, each process described above can be further examined for 231Pa and 230Th individually. For example, the difference in ratios between CTRL_EXP and 3D_EXP represents the influence of bottom scavenging of both 231Pa and 230Th, whereas the influence of bottom scavenging of 231Pa alone can also be evaluated from CTRL_EXP and 3D_EXP (i.e., 231Pa(CTRL) 230Th(3D) minus 231Pa(3D) 230Th(3D)).
In 1D_EXP, the particulate concentration is obtained from Eq. (7); the particulate concentration increases linearly with depth (Fig. S2c and d). The dissolved concentration is calculated from Eq. (9), suggesting that the concentration becomes higher for a lower partition coefficient ( in Eq. 9) and for a lower particle concentration (Cj in Eq. 9). Mainly due to the dependency on Cj, the dissolved concentration becomes higher (lower) in the area with lower (higher) particle concentration in 1D_EXP. As a result, the dissolved concentration becomes very high in the deeper ocean, where the particle concentration becomes lower for both 231Pa and 230Th (Fig. S2a and b). It is interesting to point out that the spatial pattern of dissolved 231Pa and 230Th (Fig. S2a and b) is similar to that of Kref in PCE_EXP (Fig. 5c), because both are affected by the amount of particle concentration. More importantly, although it is well known from previous studies, we emphasize here that the sedimentary ratios in 1D_EXP become uniform everywhere (0.093; Fig. S2e), because, as confirmed from Eq. (7), the ratio of particulate 231Pa to particulate 230Th amounts everywhere to , regardless of geographic location (Fig. S2f).
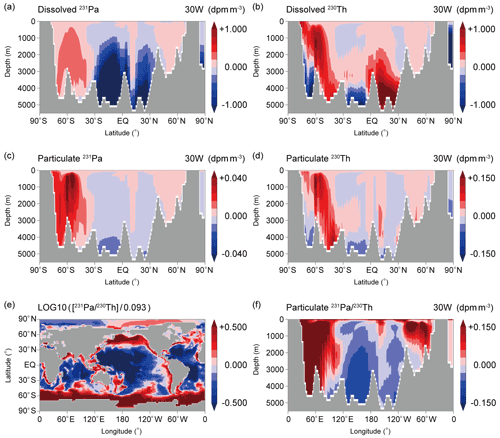
Figure 7The difference between 3D_EXP and 1D_EXP (i.e., 3D_ EXP minus 1D_EXP, which represents for ocean transport effect) of (a) dissolved 231Pa, (b) dissolved 230Th, (c) particulate 231Pa, and (d) particulate 230Th along 30∘ W in the Atlantic Ocean. (e) The difference between 3D_EXP and 1D_EXP of sedimentary ratios is normalized by the production ratio of 0.093.

Figure 8The difference between CTRL_EXP and 3D_EXP (i.e., CTRL_EXP minus 3D_EXP, which represents for bottom scavenging effect) of (a) dissolved 231Pa, (b) dissolved 230Th, (c) particulate 231Pa, and (d) particulate 230Th along 30∘ W in the Atlantic Ocean. (e) The difference between CTRL_EXP and 3D_EXP of the sedimentary ratios is normalized by the production ratio of 0.093.
In 3D_EXP, three-dimensional ocean transport operates, in addition to water-column scavenging considered in 1D_EXP (Fig. S3). As described above, the influence of ocean transport can be evaluated from the difference between 3D_EXP and 1D_EXP (Fig. 7). On the other hand, the influence of bottom scavenging can be obtained from the difference between CTRL_EXP and 3D_EXP (Fig. 8). Note again that since the sedimentary ratios in 1D_EXP are globally uniform ( = 0.093), their spatial distribution is controlled not by the one-dimensional vertical process but by the ocean transport. Figure 7e and f demonstrate that the ocean transport effect captures the overall features of CTRL_EXP (Fig. 6e and f). On the other hand, bottom scavenging tends to cancel the effects of ocean transport and weaken the spatial contrast of ratios simulated in CTRL_EXP (Fig. 8e and f).
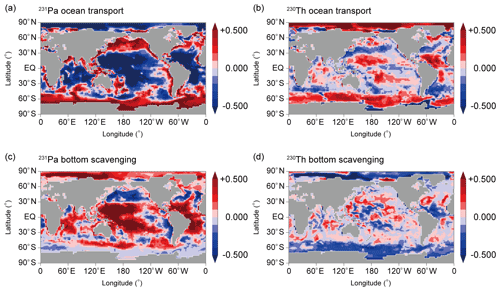
Figure 9Sedimentary ratios normalized by the production ratio of 0.093 in CTRL_EXP decomposed into contributions from (a) ocean transport solely from 231Pa (i.e., 231Pa(3D) 230Th(1D)), (b) ocean transport solely from 230Th (i.e., 231Pa(1D) 230Th(3D)), (c) bottom scavenging solely from 231Pa (i.e., 231Pa(CTRL) 230Th(3D) minus 231Pa(3D) 230Th(3D)), and (d) bottom scavenging solely from 230Th (i.e., 231Pa(3D) 230Th(CTRL) minus 231Pa(3D) 230Th(3D)).
To evaluate the above processes controlling the sedimentary ratios in more detail, we further decompose the ocean transport contribution into those from 231Pa and 230Th, separately (Fig. 9a for 231Pa and Fig. 9b for 230Th). Similarly, we further decompose the contribution of bottom scavenging into those for 231Pa and 230Th (Fig. 9c and d, respectively). In Fig. 9a, we demonstrate that ocean transport solely from 231Pa (i.e., 231Pa(3D) 230Th(1D)) can reproduce the overall distribution of the sedimentary ratios in CTRL_EXP (Fig. 6e). This result confirms that ocean transport of 231Pa primarily controls the distribution of sedimentary ratios, consistent with previous studies (Yu et al., 1996; Marchal et al., 2000). These previous studies suggest that the distribution of 231Pa mainly determines the global distribution of sedimentary ratios, because the residence time of 231Pa is longer than that of 230Th.
Here, we further discuss how the ocean transport of 231Pa controls the distribution of sedimentary ratios. Since changes in sedimentary 231Pa correspond to particulate 231Pa changes in the bottom ocean, we focus the ocean transport effect on particulate 231Pa (Fig. 7c). Consistent with Fig. 9a, Fig. 7c indicates that ocean transport acts to decrease (increase) particulate 231Pa in lower (higher) latitudes. We also found that particulate 231Pa changes (Fig. 7c) are similar to those in dissolved 231Pa (Fig. 7a). Because most of 231Pa are in the dissolved phase, the advection of particulate 231Pa itself is very small compared with that of dissolved 231Pa, and ocean transport takes place mainly in the form of dissolved 231Pa. Therefore, it is interpreted that ocean transport first controls the dissolved 231Pa, and then the corresponding changes in particulate 231Pa take place so that the relationship between dissolved and particulate 231Pa (i.e., Eq. 5b) is satisfied. In other words, the changes in particulate 231Pa take place as a result of changes in dissolved 231Pa. Therefore, we need to focus on the processes that control the dissolved 231Pa changes (Fig. 7a). As previously mentioned, in the case of no ocean transport (i.e., 1D_EXP), the dissolved 231Pa concentration near the seabed in lower latitudes becomes very high (Fig. S2a). Ocean transport, which includes both advection and diffusion, reduces high concentrations of dissolved 231Pa in low latitude oceans by transporting dissolved 231Pa from lower latitudes to higher latitudes. As a result of the change in the dissolved 231Pa (Fig. 7a), the changes in particulate 231Pa (Fig. 7c) also take place by satisfying Eq. (5b); this leads to lower sedimentary ratios in lower latitudes and higher ratios in higher latitudes (Fig. 7e and f).
Contrary to 231Pa, the influences of 230Th transport on sedimentary ratios have been usually regarded as small because 230Th is generally assumed to be scavenged very quickly everywhere. However, our results demonstrate that ocean transport of 230Th also affects the distribution of sediment to some extent. As a matter of fact, 230Th ocean transport acts in the opposite direction of 231Pa ocean transport, reducing the spatial contrast in sedimentary ratios (Fig. 9b). However, an exception is found in the Southern Ocean, where the 230Th ocean transport contributes to higher sedimentary ratios, in the same way as the 231Pa ocean transport. Because opal scavenges 231Pa more effectively than 230Th (Chase et al., 2002), 231Pa transported toward the Southern Ocean is expected to be quickly removed there due to the high opal flux. Therefore, previous studies concluded that ocean transport of 231Pa explains high sedimentary ratios in the Southern Ocean. On the other hand, in addition to ocean transport of 231Pa, our results suggest that ocean transport of 230Th also contributes to the high ratios in the Southern Ocean. This result implies that scavenging of 230Th is not so efficient in the Southern Ocean as previously expected due to the dependence of scavenging efficiency on particle concentration. This interpretation is consistent with the high concentration of dissolved 230Th in the Southern Ocean (Fig. 6b). Missiaen et al. (2020a) demonstrated that the dissolved 230Th concentration in the Southern Ocean will increase if the effect of particle scavenging is halved and that most of this effect comes from POC and opal. This implies the scavenging of 230Th is controlled also by the opal in the Southern Ocean. Together with their and our results, quantification about scavenging of 230Th by opal in the Southern Ocean may be a key for a more accurate understanding of ratios in the global ocean.
Bottom scavenging promotes the removal of both 231Pa and 230Th near the seafloor and tends to cancel the influence of ocean transport. Namely, the bottom scavenging of 231Pa reduces the contrast among sedimentary ratios (Fig. 9c), whereas the bottom scavenging of 230Th increases this contrast (Fig. 9d). Because the influences of bottom scavenging of 231Pa tends to be stronger than that of 230Th, bottom scavenging overall results in reducing the contrast of ratios (Fig. 8e and f). Precisely speaking, the actual processes of the bottom scavenging effect on the sedimentary 231Pa and 230Th appear somewhat complicated compared with those of the ocean transport effect. The effect of the bottom scavenging is twofold. First, extra particles in the bottom ocean lead to an increase of sedimentary 231Pa and 230Th (e.g., positive values near the bottom in low latitudes in Fig. 8c). Second, the bottom scavenging removes 231Pa and 230Th from the ocean, which reduces the concentration of dissolved 231Pa and 230Th in the ocean interior (Fig. 8a and b). The changes in dissolved-phase concentration then lead to changes in particulate-phase concentration in a way such that the Eq. (5b) is satisfied. The former leads to higher sedimentary 231Pa and 230Th, whereas the latter leads to lower sedimentary 231Pa and 230Th. Our results indicate that the former process becomes more important than the latter in the low latitudes, and the sedimentary 231Pa increases there. In contrast, the latter dominates in the high latitudes, and the sedimentary 231Pa decreases there by the bottom scavenging effect. The effect of bottom scavenging on 230Th is also basically similar to 231Pa.
4.4 Residence time of 231Pa and 230Th
Additional insights into the simulated distribution of ratios can be obtained from a comparison of CTRL_EXP with Siddall_EXP which reproduces sedimentary ratios (Fig. S4a) as realistically as does CTRL_EXP (Fig. 6e). In this subsection, we discuss this point by focusing on the difference in the residence time of 231Pa and 230Th between CTRL_EXP and Siddall_EXP. Assuming the mass balance of 231Pa and 230Th are in a steady state, we calculate the residence time of 231Pa and 230Th from the following formulas:
In Eq. (11a) and (11b), the integral domain is global and the parameters are described in Table 1. The residence times of 231Pa and 230Th are calculated to be 103 and 21 years, respectively, in CTRL_EXP, whereas they are 211 and 89 years, respectively, in Siddall_EXP (Table S2). By incorporating bottom scavenging and modifying the partition coefficient of 230Th, the modeled residence time in CTRL_EXP comes close to the previous estimate based on data: 111 years for 231Pa and 26 years for 230Th in Yu et al. (1996) and 130 years for 231Pa and 20 years for 230Th in Henderson and Anderson (2003). Because the reference partition coefficients for 231Pa of Siddall_EXP and that of CTRL_EXP are the same value (i.e., ), the influence of ocean transport on 231Pa is identical in both experiments (Fig. 9a). Therefore, the difference in the 231Pa distribution between the model experiments must come from the bottom scavenging, which is included in CTRL_EXP but not in Siddall_EXP. The bottom scavenging reduces the residence time of 231Pa in CTRL_EXP (103 years) compared to Siddall_EXP (211 years). The difference in the 230Th distribution between CTRL_EXP and Siddall_EXP mainly comes from the difference in reference partition coefficients (). The reference partition coefficient of CTRL_EXP, which depends on particle concentration, is larger than that of Siddall_EXP () in most of the ocean. Therefore, the contribution from the ocean transport of 230Th becomes larger in Siddall_EXP (Fig. S4b) than in CTRL_EXP (Fig. 6b). Together with additional contribution from the bottom scavenging effect on 230Th (Fig. 9d), the residence time of 230Th in CTRL_EXP (21 years) is shorter than that in Siddall_EXP (89 years). Since the residence time is overestimated for both 231Pa and 230Th in Siddall_EXP compared to CTRL_EXP, the distribution of sedimentary ratios in Siddall_EXP ends up similar to that in CTRL_EXP. The residence time in CTRL_EXP is similar to the residence time of their control simulation in Gu and Liu (2017), which does not include the bottom scavenging process. Therefore, total scavenging efficiency in the ocean is more important than the introduction of bottom scavenging to reproduce residence time. Compared with Siddall_EXP based on Siddall et al. (2005), our CTRL_EXP can realistically simulate not only oceanic distribution of 231Pa and 230Th but also their residence time by introducing the bottom scavenging and the dependence of scavenging efficiency on particulate concentration.
4.5 Remaining issues
Although our model was able to generally reproduce the basin-scale distributions of 231Pa and 230Th, there are still some mismatches between the model results and observations. For dissolved 231Pa, introducing bottom scavenging helped to reproduce the concentrations seen in the data at depths below 3000 m (Fig. 2). However, the model tends to simulate lower concentration than the observations below 3000 m in Fig. 2c and d, which needs to be improved. The improvement was not possible simply by reducing the bottom scavenging (i.e., specifying smaller than in Fig. 2c and d), therefore more fundamental improvement appears to be required. The dissolved 230Th simulated in CTRL_EXP (Fig. 5b) also tends to underestimate the observed concentration near the sea bottom. One possibility is that our treatment of the nepheloid layer (i.e., the thickness of the ocean deepest layer) may be too simple and needs to be modified so that the thickness of the nepheloid layer is more realistically specified. The introduction of more realistic bottom scavenging and the consideration of the effects of particles from the continental shelf and hydrothermal vents may also help to improve the model–data agreement for both 231Pa and 230Th.
In this study, particle fields were not calculated in the model but specified as boundary conditions in our approach where the specified distribution of biological particles is taken from satellite-based estimation. Since the bias of the particle field affects the distribution of 231Pa and 230Th, our approach has advantages over the other studies where the particles are explicitly simulated in the model. However, satellite-based estimation referenced here may also contain some errors, and understanding about the influence of the particle field on sedimentary ratios, which was not seriously discussed in this study, is also important as the previous studies pointed out (e.g., Missiaen et al., 2020b; Dutay et al., 2009; van Hulten et al., 2018).
To reconstruct past sedimentation flux, 230Th normalization was used. Recently, the influence of lithogenic and authigenic 230Th on 230Th in sediments was evaluated (Missiaen et al., 2018; Costa et al., 2020). This is not a direct topic of our study, but we need to care about such processes which also affect the ratio of 231Pa and 230Th obtained from marine sediments. As more observational data and their modeling become available, we expect to make further progress in quantitative understanding of the processes governing 231Pa and 230Th in the ocean.
In this study, we performed OGCM experiments that incorporated the bottom scavenging and the dependence of scavenging efficiency on particle concentration together with the water-column reversible scavenging. We quantitatively evaluated the processes that determine the global distribution of sedimentary ratios, which is used as a proxy for the strength of paleo-ocean circulation.
First, we performed an OGCM experiment using the same model settings and parameters as Siddall et al. (2005), which only introduced the water-column reversible scavenging (Siddall_EXP). In Siddall_EXP, the simulated concentrations of 231Pa and 230Th increase with depth, consistent with data; however, this experiment significantly overestimated the concentrations observed in the deep ocean. By incorporating bottom scavenging in nepheloid layers following Rempfer et al. (2017) (BTM_EXP), we reduced this overestimation and successfully reproduced the vertical profile of dissolved 231Pa. However, this experiment had difficulty in reproducing the observed vertical profile of dissolved 230Th. Therefore, we modified the parameters associated with the strength of water-column scavenging (i.e., Kref: the reference partition coefficient for sinking particles) with the consideration of the bottom scavenging (KREF_EXP). When we increased the reference partition coefficient of 230Th () from that used in the Siddall_EXP with the consideration of bottom scavenging (), dissolved 230Th was found to be more realistically simulated, but significant underestimation in the Southern Ocean remained. We found that the underestimation in the Southern Ocean can be improved by introducing dependence of Kref on particle concentration which was used in Henderson et al. (1999) (PCE_EXP). Although most of the previous 231Pa and 230Th model results showed significant overestimation in the deep ocean (e.g., Siddall et al., 2005; Dutay et al., 2009; Gu and Liu, 2017; van Hulten et al., 2018), our best OGCM simulation considering the reversible scavenging, bottom scavenging, and the dependence of scavenging efficiency on particle concentration (CTRL_EXP) can reproduce the distributions of dissolved 231Pa and 230Th consistently with GEOTRACES data, together with the realistic distribution of sedimentary ratios.
We also made a quantitative assessment about the processes that determine the global distribution of sedimentary ratios by decomposing the processes affecting the sediment ratios into three parts: water-column scavenging, ocean transport (advection and diffusion), and bottom scavenging. We confirmed that the global sedimentary ratios in our best model (CTRL_EXP) are primarily determined by ocean transport of 231Pa, as shown in previous studies. Contrary to 231Pa, ocean transport of 230Th tends to reduce the spatial contrast of sedimentary ratios. However, we found that this is not the case for the Southern Ocean; 230Th advection increases the sedimentary ratios in the Southern Ocean and strengthens the observed high ratios there. This means that not only 231Pa advection but also 230Th advection contributes to the high ratios in the Southern Ocean. This result implies that scavenging of 230Th is not much efficient in the Southern Ocean as conventionally thought when we consider the dependence of scavenging efficiency on particle concentration. We also show that bottom scavenging works opposite to ocean transport and decreases the spatial contrast of ratios; bottom scavenging promotes the removal of 231Pa near the sea bottom more efficiently than that of 230Th, and the total effect of bottom scavenging reduces spatial contrasts of the ratios. Our best simulation shows the realistic residence times of 231Pa and 230Th, but simulation without bottom scavenging and dependence of scavenging efficiency on particle concentration significantly overestimates the residence times for both 231Pa and 230Th in spite of similar distribution of sedimentary ratios to our best simulation.
The model developed in this study is useful not only for simulating ratios in the present-day ocean but also in different climates such as glacial periods. Our OGCM experiments using the present-day physical fields can clarify the processes governing the global distribution of sedimentary ratios. A similar analysis using the physical ocean fields during glacial periods may help climate scientists to understand the mechanisms for glacial changes in the sedimentary ratio observed in sediment cores. Although simulated sedimentary under glacial times are also discussed in a 2D model (Lippold et al., 2012) and recently in a 3D model (Gu et al., 2020), there is insufficient discussion of the mechanism of change in the three-dimensional distribution. Simulation of ratios under glacial climates (e.g., Oka et al., 2011; Kobayashi and Oka, 2018) is an exciting avenue of future study.
The model code and data used to produce the results in this study are available at the repository website Zenodo: https://doi.org/10.5281/zenodo.4600287 (Sasaki et al., 2021a) and https://doi.org/10.5281/zenodo.4655883 (Sasaki et al., 2021b), respectively. COCO is an ocean component of MIROC and the code of COCO4 is included as a part of MIROC-ES2L. The source code of MIROC-ES2L can be obtained from https://doi.org/10.5281/zenodo.3893386 (Ohgaito et al., 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-15-2013-2022-supplement.
All the authors contributed to the interpretation of the simulation results. YS performed the numerical simulations. AO designed and supervised the study. YS and HK analyzed the results. YS wrote the first draft, and the final draft was prepared with the inputs from all the co-authors.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors acknowledge many constructive comments from reviewers, which significantly improved the article.
This work was supported by JSPS KAKENHI (grant no. JP19H01963).
This paper was edited by Paul Halloran and reviewed by two anonymous referees.
Anderson, R. F., Bacon, M. P., and Brewer, P. G.: Removal of 230Th and 231Pa from the open ocean, Earth Planet. Sc. Lett., 62, 7–23, https://doi.org/10.1016/0012-821X(83)90067-5, 1983.
Bacon, M. P. and Anderson, R. F.: Distribution of thorium isotopes between dissolved and particulate forms in the deep sea, J. Geophys. Res., 87, 2045, https://doi.org/10.1029/JC087iC03p02045, 1982.
Behrenfeld, M. J. and Falkowski, P. G.: Photosynthetic rates derived from satellite-based chlorophyll concentration, Limnol. Oceanogr., 42, 1–20, https://doi.org/10.4319/lo.1997.42.1.0001, 1997.
Böhm, E., Lippold, J., Gutjahr, M., Frank, M., Blaser, P., Antz, B., Fohlmeister, J., Frank, N., Anderson, M. B., and Deininger, M.: Strong and deep Atlantic meridional overturning circulation during the last glacial cycle, Nature, 517, 73–76, https://doi.org/10.1038/nature14059, 2015.
Bradtmiller, L. I., McManus, J. F., and Robinson, L. F.: evidence for a weakened but persistent Atlantic meridional overturning circulation during Heinrich Stadial 1, Nat. Commun., 5, 5817, https://doi.org/10.1038/ncomms6817, 2014.
Chase, Z. and Anderson, R. F.: Comment on “On the importance of opal, carbonate, and lithogenic clays in scavenging and fractionating 230Th, 231Pa and 10Be in the ocean” by S. Luo and T.-L. Ku, Earth Planet. Sc. Lett., 220, 213–222, https://doi.org/10.1016/S0012-821X(04)00028-7, 2004.
Chase, Z., Anderson, R. F., Fleisher, M. Q., and Kubik, P. W.: The influence of particle composition and particle flux on scavenging of Th, Pa and Be in the ocean, Earth Planet. Sc. Lett., 204, 215–229, https://doi.org/10.1016/S0012-821X(02)00984-6, 2002.
Chase, Z., Anderson, R. F., Fleisher, M. Q., and Kubik, P. W.: Scavenging of 230Th, 231Pa and 10Be in the Southern Ocean (SW Pacific sector): the importance of particle flux, particle composition and advection, Deep-Sea Res. Pt. II, 50, 739–768, https://doi.org/10.1016/S0967-0645(02)00593-3, 2003.
Costa, K. M., Hayes, C. T., Anderson, R. F., Pavia, F. J., Bausch, A., Deng, F., Dutay, J.-C., Geibert, W., Heinze, C., Henderson, G., Hillaire‐Marcel, C., Hoffmann, S., Jaccard, S. L., Jacobel, A. W., Kienast, S. S., Kipp, L., Lerner, P., Lippold, J., Lund, D., Marcantonio, F., McGee, D., McManus, J. F., Mekik, F., Middleton, J. L., Lise Missiaen, L., Not, C., Pichat, S., Robinson, L. F., Rowland, G. H., Roy‐Barman, M., Tagliabue, A., Torfstein, A., Winckler, G., and Zhou, Y.: 230Th normalization: New insights on an essential tool for quantifying sedimentary fluxes in the modern and Quaternary ocean, Paleoceanogr. Paleocl., 35, e2019PA003820, https://doi.org/10.1029/2019PA003820, 2020.
Dunne, J. P., Armstrong, R. A., Gnnadesikan, A., and Sarmiento, J. L.: Empirical and mechanistic models for the particle export ratio, Glob. Biogeochem. Cycles, 19, GB4026, https://doi.org/10.1029/2004GB002390, 2005.
Dutay, J.-C., Lacan, F., Roy-Barman, M., and Bopp, L.: Influence of particle size and type on 231Pa and 230Th simulation with a global coupled biogeochemical-ocean general circulation model: A first approach, Geochem. Geophys. Geosyst., 10, Q01011, https://doi.org/10.1029/2008GC002291, 2009.
Edwards, N. R., Stocker, T. F., Joos, F., Henderson, G. M., Frank, M., Siddall, M., and Müller, S. A.: fractionation by ocean transport, biogenic particle flux and particle type, Earth Planet. Sc. Lett., 237, 135–155, https://doi.org/10.1016/j.epsl.2005.05.031, 2005.
François, R., Bacon, M. P., Altabet, M. A., and Labeyrie, L. D.: Glacial/interglacial changes in sediment rain rate in the SW Indian Sector of subantarctic Waters as recorded by 230Th, 231Pa, U, and δ15N, Paleoceanography, 8, 611–629, https://doi.org/10.1029/93PA00784, 1993.
Frank, M.: Reconstruction of Late Quaternary environmental conditions applying the natural radionuclides 230Th, 10Be, 231Pa and 238U: a study of deep-sea sediments from the eastern sector of the Antarctic Circumpolar Current System, PhD thesis, Alfred Wegener Institute for Polar and Marine Research, 136 pp., 1996.
Frank, M., Eckhardt, J.-D., Eisenhauer, A., Kubik, P. W., Dittrich-Hannen, B., Segl, M., and Mangini, A.: Beryllium 10, thorium 230, and protactinium 231 in Galapagos microplate sediments: Implications of hydrothermal activity and paleoproductivity changes during the last 100,000 years, Paleoceanography, 9, 559–578, https://doi.org/10.1029/94PA01132, 1994.
Gardner, W. D., Mishonov, A. V., and Richardson, M. J.: Decadal Comparisons of Particulate Matter in Repeat Transects in the Atlantic, Pacific, and Indian Ocean Basins, Geophys. Res. Lett., 45, 277–286, https://doi.org/10.1002/2017GL076571, 2018.
German, C. R., Casciotti, K. A., Dutay, J. -C., Heimbürger, L. E., Jenkins, W. J., Measures, C. I., Mills, R. A., Obata, H., Schlitzer, R., Tagliabue, A., Turner, D. R., and Whitby, H.: Hydrothermal impacts on trace element and isotope ocean biogeochemistry, Phil. Trans. R. Soc. A, 374, 20160035, https://doi.org/10.1098/rsta.2016.0035, 2016.
Gherardi, J.-M., Labeyrie, L., Nave, S., François, R., McManus, J. F., and Cortijo, E.: Glacial-interglacial circulation changes inferred from sedimentary record in the North Atlantic region, Paleoceanography, 24, PA2204, https://doi.org/10.1029/2008PA001696, 2009.
Gregory, J. M., Dixon, K. W., Stouffer, R. J., Weaver, A. J., Driesschaert, E., Eby, M., Fichefet, T., Hasumi, H., Hu, A., Jungclaus, J. H., Kamenkovich, I. V., Levermann, A., Montoya, M., Murakami, S., Nawrath, S. Oka, A., Sokolov, A. P., and Thorpe, R. B.: A model intercomparison of changes in the Atlantic thermohaline circulation in response to increasing atmospheric CO2 concentration, Geophys. Res. Lett., 32, 1–5, https://doi.org/10.1029/2005GL023209, 2005.
Gu, S. and Liu, Z.: 231Pa and 230Th in the ocean model of the Community Earth System Model (CESM1.3), Geosci. Model Dev., 10, 4723–4742, https://doi.org/10.5194/gmd-10-4723-2017, 2017.
Gu, S., Liu, Z., Oppo, D. W. Lynch-Stieglitz, J., Jahn, A., Zhang, J., and Wu, L.: Assessing the potential capability of reconstructing glacial Atlantic water masses and AMOC using multiple proxies in CESM, Earth Planet. Sc. Lett., 541, 116294, https://doi.org/10.1016/j.epsl.2020.116294, 2020.
Hajima, T., Watanabe, M., Yamamoto, A., Tatebe, H., Noguchi, M. A., Abe, M., Ohgaito, R., Ito, A., Yamazaki, D., Okajima, H., Ito, A., Takata, K., Ogochi, K., Watanabe, S., and Kawamiya, M.: Development of the MIROC-ES2L Earth system model and the evaluation of biogeochemical processes and feedbacks, Geosci. Model Dev., 13, 2197–2244, https://doi.org/10.5194/gmd-13-2197-2020, 2020.
Hasumi, H.: CCSR Ocean Component Model (COCO) version 4.0, CCSR Rep. 25, 103 pp., Center for Climate System Research, Univ. of Tokyo, 2006.
Hayes, C. T., Anderson, R. F., Fleisher, M. Q., Huang, K.-F., Robinson, L. F., Lu, Y., Cheng, H., Lawrence Edwards, R., and Bradley Moran, S.: 230Th and 231Pa on GEOTRACES GA03, the U.S. GEOTRACES North Atlantic transect, and implications for modern and paleoceanographic chemical fluxes, Deep-Sea Res. Pt. II, 116, 29–41, https://doi.org/10.1016/j.dsr2.2014.07.007, 2015.
Henderson, G. M. and Anderson, R. F.: The U-series Toolbox for Paleoceanography, Rev. Mineral. Geochem., 52, 493–531, https://doi.org/10.2113/0520493, 2003.
Henderson, Gideon M., Heinze, C., Anderson, R. F., and Winguth, A. M. E.: Global distribution of the 230Th flux to ocean sediments constrained by GCM modeling, Deep-Sea Res. Pt. I, 46, 1861–1893, https://doi.org/10.1016/S0967-0637(99)00030-8, 1999.
Honeyman, B. D., Balistrieri, L. S., and Murray, J. W.: Oceanic trace metal scavenging: the importance of particle concentration, Deep-Sea Res. Pt. I, 35, 227–246, https://doi.org/10.1016/0198-0149(88)90038-6, 1988.
Honjo, S., Manganini, S. J., Krishfield, R. A., and François, R.: Particulate organic carbon fluxes to the ocean interior and factors controlling the biological pump: A synthesis of global sediment trap programs since 1983, Prog. Oceanogr., 76, 217–285, https://doi.org/10.1016/j.pocean.2007.11.003, 2008.
K-1 Model Developers: K-1 coupled GCM (MIROC) description, edited by: Hasumi, H., and Emori, S., K-1 Tech. Rep. 1, 34 pp., Center for Climate System Research, Univ. of Tokyo, 2004.
Kobayashi, H. and Oka, A.: Response of atmospheric pCO2 to glacial changes in the Southern Ocean amplified by carbonate compensation, Paleoceanogr. Paleocl., 33, 1206–1229, https://doi.org/10.1029/2018PA003360, 2018.
Kobayashi, H., Abe-Ouchi, A., and Oka, A.: Role of Southern Ocean stratification in glacial atmospheric CO2 reduction evaluated by a three-dimensional ocean general circulation model, Paleoceanography, 30, 1202–1216, https://doi.org/10.1002/2015PA002786, 2015.
Lam, P. J., Ohnemus, D. C., and Auro, M. E.: Size-fractionated major particle composition and concentrations from the US GEOTRACES North Atlantic Zonal Transect, Deep-Sea Res. Pt. II, 116, 303–320, https://doi.org/10.1016/J.DSR2.2014.11.020, 2015.
Lao, Y., Anderson, R. F., Broecker, W. S., Trumbore, S. E., Hofmann, H. J., and Wolfli, W.: Transport and burial rates of 10Be and 231Pa in the Pacific Ocean during the Holocene period, Earth Planet. Sc. Lett., 113, 173–189, https://doi.org/10.1016/0012-821X(92)90218-K, 1992.
Lerner, P., Marchal, O., Lam, P., Buesseler, K., and Charette, M.: Kinetics of thorium and particle cycling along the U.S. GEOTRACES North Atlantic transect, Deep-Sea Res. Pt. I, 125, 106–128, https://doi.org/10.1016/j.dsr.2017.05.003, 2017.
Lerner, P., Marchal, O., Lam, P. J., Gardner, W., Richardson, M. J., and Mishonov, A.: A model study of the relative influences of scavenging and circulation on 230Th and 231Pa in the western North Atlantic, Deep-Sea Res. Pt. I, 155, 103159, https://doi.org/10.1016/j.dsr.2019.103159, 2020.
Lippold, J., Luo, Y., Francois, R., Allen, S. E., Gherardi, J., Pichat, S., Hickey, B., and Schulz, H.: Strength and geometry of the glacial Atlantic Meridional Overturning Circulation, Nat. Geosci., 5, 813–816, https://doi.org/10.1038/NGEO1608, 2012.
Lopez, G. I., Marcantonio, F., Lyle, M., and Lynch-Stieglitz, J.: Dissolved and particulate 230Th–232Th in the Central Equatorial Pacific Ocean: Evidence for far-field transport of the East Pacific Rise hydrothermal plume, Earth Planet. Sc. Lett., 431, 87–95, https://doi.org/10.1016/j.epsl.2015.09.019, 2015.
Luo, S. and Ku, T. L.: Oceanic ratio influenced by particle composition and remineralization, Earth Planet. Sc. Lett., 167, 183–195, https://doi.org/10.1016/S0012-821X(99)00035-7, 1999.
Luo, Y., Francois, R., and Allen, S. E.: Sediment as a recorder of the rate of the Atlantic meridional overturning circulation: insights from a 2-D model, Ocean Sci., 6, 381–400, https://doi.org/10.5194/os-6-381-2010, 2010.
Maier-Reimer, E.: Geochemical cycles in an ocean general circulation model. Preindustrial tracer distributions, Glob. Biogeochem. Cycles, 7, 645–677, https://doi.org/10.1029/93GB01355, 1993.
Mangini, A. and Sonntag, C.: 231Pa dating of deep-sea cores via 227Th counting, Earth Planet. Sc. Lett., 37, 251–256, https://doi.org/10.1016/0012-821X(77)90170-4, 1977.
Marchal, O., Stocker, T. F., and Joos, F.: A latitude-depth, circulation-biogeochemical ocean model for paleoclimate studies. Development and sensitivities, Tellus B, 50, 290–316, https://doi.org/10.3402/tellusb.v50i3.16130, 1998.
Marchal, O., François, R., Stocker, T. F., and Joos, F.: Ocean thermohaline circulation and sedimentary ratio, Paleoceanography, 15, 625–641, https://doi.org/10.1029/2000PA000496, 2000.
Marchal, O., François, R., and Scholten, J.: Contribution of 230Th measurements to the estimation of the abyssal circulation, Deep-Sea Res. Pt. I, 54, 557–585, https://doi.org/10.1016/j.dsr.2007.01.002, 2007.
McManus, J. F., François, R., Gherardl, J. M., Kelgwin, L., and Drown-Leger, S.: Collapse and rapid resumption of Atlantic meridional circulation linked to deglacial climate changes, Nature, 428, 834–837, https://doi.org/10.1038/nature02494, 2004.
Missiaen, L., Pichat, S., Waelbroeck, C., Douville, E., Bordier, L., Dapoigny, A., Thil, F., Foliot, L., and Wacker, L.: Downcore variations of sedimentary detrital () ratio: Implications on the use of 230Thxs and 231Paxs to reconstruct sediment flux and ocean circulation. Geochem. Geophys. Geosyst., 19, 2560–2573, https://doi.org/10.1029/2017GC007410, 2018.
Missiaen, L., Bouttes, N., Roche, D. M., Dutay, J.-C., Quiquet, A., Waelbroeck, C., Pichat, S., and Peterschmitt, J.-Y.: Carbon isotopes and response to forced circulation changes: a model perspective, Clim. Past, 16, 867–883, https://doi.org/10.5194/cp-16-867-2020, 2020a.
Missiaen, L., Menviel, L. C., Meissner, K. J., Roche, D. M., Dutay, J.-C., Bouttes, N., Lhardy, F., Quiquet, A., Pichat, S., and Waelbroeck, C.: Modelling the impact of biogenic particle flux intensity and composition on sedimentary , Quaternary Sci. Rev., 240, 106394, https://doi.org/10.1016/j.quascirev.2020.106394, 2020b.
Müller, P. J. and Mangini, A.: Organic carbon decomposition rates in sediments of the pacific manganese nodule belt dated by 230Th and 231Pa, Earth Planet. Sc. Lett., 51, 94–114, https://doi.org/10.1016/0012-821X(80)90259-9, 1980.
Ohgaito, R., Yamamoto, A., Hajima, T., O'ishi, R., Abe, M., Tatebe, H., Abe-Ouchi, A., and Kawamiya, M.: Core code of MIROC-ES2L, Geoscientific Model Development, Zenodo [code], https://doi.org/10.5281/zenodo.3893386, 2020.
Ohgaito, R., Yamamoto, A., Hajima, T., O'ishi, R., Abe, M., Tatebe, H., Abe-Ouchi, A., and Kawamiya, M.: PMIP4 experiments using MIROC-ES2L Earth system model, Geosci. Model Dev., 14, 1195–1217, https://doi.org/10.5194/gmd-14-1195-2021, 2021.
Oka, A., Hasumi, H, Okada, N., Sakamoto, T. T., and Suzuki, T.: Deep convection seesaw controlled by freshwater transport through the Denmark Strait, Ocean Model., 15, 157–176, https://doi.org/10.1016/j.ocemod.2006.08.004, 2006.
Oka, A., Kato, S., and Hasumi, H.: Evaluating effect of ballast mineral on deep-ocean nutrient concentration by using an ocean general circulation model, Glob. Biogeochem. Cycles, 22, GB3004, https://doi.org/10.1029/2007GB003067, 2008.
Oka, A., Hasumi, H., Obata, H., Gamo, T., and Yamanaka, Y.: Study on vertical profiles of rare earth elements by using an ocean general circulation model, Glob. Biogeochem. Cycles, 23, GB4025, https://doi.org/10.1029/2008GB003353, 2009.
Oka, A., Abe‐Ouchi, A., Chikamoto, M. O., and Ide, T.: Mechanisms controlling export production at the LGM: Effects of changes in oceanic physical fields and atmospheric dust deposition, Global Biogeochem. Cycles, 25, GB2009, https://doi.org/10.1029/2009GB003628, 2011.
Oka, A., Hasumi, H., and Abe-Ouchi, A.: The thermal threshold of the Atlantic meridional overturning circulation and its control by wind stress forcing during glacial climate, Geophys. Res. Lett., 39, https://doi.org/10.1029/2012GL051421, 2012.
Oka, A., Tazoe H., and Obata, H.: Simulation of global distribution of rare earth elements in the ocean using an ocean general circulation model, J. Oceanogr., 77, 413–430, https://doi.org/10.1007/s10872-021-00600-x, 2021.
Okubo, A., Obata, H., Gamo, T., and Yamada, M.: 230Th and 232Th distributions in mid-latitudes of the North Pacific Ocean: Effect of bottom scavenging, Earth Planet. Sc. Lett., 339–340, 139–150, https://doi.org/10.1016/J.EPSL.2012.05.012, 2012.
Pavia, F., Anderson, R., Vivancos, S., Fleisher, M., Lam, P., Lu, Y., Cheng, H., Zhang, P., Lawrence Edwards, R.: Intense hydrothermal scavenging of 230Th and 231Pa in the deep Southeast Pacific, Mar. Chem., 201, 212–228, https://doi.org/10.1016/J.MARCHEM.2017.08.003, 2018.
Rempfer, J., Stocker, T. F., Joos, F., Lippold, J., and Jaccard, S. L.: New insights into cycling of 231Pa and 230Th in the Atlantic Ocean, Earth Planet. Sc. Lett., 468, 27–37, https://doi.org/10.1016/j.epsl.2017.03.027, 2017.
Roy-Barman, M.: Modelling the effect of boundary scavenging on Thorium and Protactinium profiles in the ocean, Biogeosciences, 6, 3091–3107, https://doi.org/10.5194/bg-6-3091-2009, 2009.
Rutgers van der Loeff, M. M. and Berger, G. W.: Scavenging of 230Th and 231Pa near the antarctic polar front in the South Atlantic, Deep-Sea Res. Pt. I, 40, 339–357, https://doi.org/10.1016/0967-0637(93)90007-P, 1993.
Rutgers van der Loeff, M. M., Venchiarutti, C., Stimac, I., van Ooijen, J., Huhn, O., Rohardt, G., and Strass, V.: Meridional circulation across the Antarctic Circumpolar Current serves as a double 231Pa and 230Th trap, Earth Planet. Sc. Lett., 455, 73–84, https://doi.org/10.1016/j.epsl.2016.07.027, 2016.
Sasaki, Y., Kobayashi, H., and Oka, A.: Data for the figures of Sasaki et al. entitled “An investigation into the processes controlling the global distribution of dissolved 231Pa and 230Th in the ocean and the sedimentary ratios by using an ocean general circulation model COCO ver4.0”, Zenodo [data set], https://doi.org/10.5281/zenodo.4600287, 2021a.
Sasaki, Y., Kobayashi, H., and Oka, A.: Code of Sasaki et al. entitled “An investigation into the processes controlling the global distribution of dissolved 231Pa and 230Th in the ocean and the sedimentary ratios by using an ocean general circulation model COCO ver4.0”, Zenodo [code], https://doi.org/10.5281/zenodo.4655883, 2021.
Schlitzer, R., Anderson, R. F., Dodas, E. M., et al.: The GEOTRACES Intermediate Data Product 2017, Chem. Geol., 493, 210–223, https://doi.org/10.1016/j.chemgeo.2018.05.040, 2018.
Schmitz, W., Mangini, A., Stoffers, P., Glasby, G. P., and Plüger, W. L.: Sediment accumulation rates in the southwestern Pacific Basin and Aitutaki Passage, Mar. Geol., 73, 181–190, https://doi.org/10.1016/0025-3227(86)90118-0, 1986.
Shimmield, G. B. and Price, N. B.: The scavenging of U, 230Th and 231Pa during pulsed hydrothermal activity at 20∘ S, East Pacific Rise, Geochim. Cosmochim. Ac., 52, 669–677, https://doi.org/10.1016/0016-7037(88)90329-8, 1988.
Shimmield, G. B., Murray, J. W., Thomson, J., Bacon, M. P., Anderson, R. F., and Price, N. B.: The distribution and behaviour of 230Th and 231Pa at an ocean margin, Baja California, Mexico, Geochim. Cosmochim. Ac., 50, 2499–2507, https://doi.org/10.1016/0016-7037(86)90032-3, 1986.
Siddall, M., Henderson, G. M., Edwards, N. R., Frank, M., Mu, S. A., Stocker, T. F., and Joos, F.: fractionation by ocean transport, biogenic particle flux and particle type, Earth Planet. Sci. Lett., 237, 135–155, https://doi.org/10.1016/j.epsl.2005.05.031, 2005.
Stouffer, R. J., Yin, J., Gregory, J. M., Dixon, K. W., Spelman, M. J., Hurlin, W., Weaver, A. J., Eby, M., Flato, G. M., Hasumi, H., Hu, A., Jungclaus, J. H., Kamenkovich, I. V., Levermann, A., Montoya, M., Murakami, S., Nawrath, S., Oka, A., Peltier, W. R., Robitaille, D. Y., Sokolov, A., Vettoretti, G., and Weber, S. L.: Investigating the Causes of the Response of the Thermohaline Circulation to Past and Future Climate Changes, J. Climate, 19, 1365–1387, https://doi.org/10.1175/JCLI3689.1, 2006.
Süfke, F., Schulz, H., Scheen, J., Szidat, S., Regelous, M., Blaser, P., Pöppelmeier, F., Goepfert, T. J., Stocker, T. F., and Lippold, J.: Inverse response of to variations of the Atlantic meridional overturning circulation in the North Atlantic intermediate water, Geo-Mar. Lett., 40, 75–87, https://doi.org/10.1007/s00367-019-00634-7, 2020.
van Hulten, M., Dutay, J.-C., and Roy-Barman, M.: A global scavenging and circulation ocean model of thorium-230 and protactinium-231 with improved particle dynamics (NEMO–ProThorP 0.1), Geosci. Model Dev., 11, 3537–3556, https://doi.org/10.5194/gmd-11-3537-2018, 2018.
Waelbroeck, C., Pichat, S., Böhm, E., Lougheed, B. C., Faranda, D., Vrac, M., Missiaen, L., Vazquez Riveiros, N., Burckel, P., Lippold, J., Arz, H. W., Dokken, T., Thil, F., and Dapoigny, A.: Relative timing of precipitation and ocean circulation changes in the western equatorial Atlantic over the last 45 kyr, Clim. Past, 14, 1315–1330, https://doi.org/10.5194/cp-14-1315-2018, 2018.
Walter, H. J., Rutgers van der Loeff, M. M., and Hoeltzen, H.: Enhanced scavenging of 231Pa relative to 230Th in the South Atlantic south of the Polar Front: Implications for the use of the ratio as a paleoproductivity proxy, Earth Planet. Sc. Lett., 149, 85–100, https://doi.org/10.1016/s0012-821x(97)00068-x, 1997.
Yang, H.-S., Nozaki, Y., Sakai, H., and Masuda, A.: The distribution of 230Th and 231Pa in the deep-sea surface sediments of the Pacific Ocean, Geochim. Cosmochim. Ac., 50, 81–89, https://doi.org/10.1016/0016-7037(86)90050-5, 1986.
Yu, E.-F., François, R., and Bacon, M. P.: Similar rates of modern and last-glacial ocean thermohaline circulation inferred from radiochemical data, Nature, 379, 689–694, https://doi.org/10.1038/379689a0, 1996.