Building a machine learning surrogate model for wildfire activities within a global Earth system model

Wildfire is an important ecosystem process, influencing land biogeophysical and biogeochemical dynamics and atmospheric composition. Fire-driven loss of vegetation cover, for example, directly modifies the surface energy budget as a consequence of changing albedo, surface roughness, and partitioning of sensible and latent heat fluxes. Carbon dioxide and methane emitted by fires contribute to a positive atmospheric forcing, whereas emissions of carbonaceous aerosols may contribute to surface cooling. Process-based modeling of wildfires in Earth system land models is challenging due to limited understanding of human, climate, and ecosystem controls on fire counts, fire size, and burned area. Integration of mechanistic wildfire models within Earth system models requires careful parameter calibration, which is computationally expensive and subject to equifinality. To explore alternative approaches, we present a deep neural network (DNN) scheme that surrogates the process-based wildfire model with the Energy Exascale Earth System Model (E3SM) interface. The DNN wildfire model accurately simulates observed burned area with over 90 % higher accuracy with a large reduction in parameterization time compared with the current process-based wildfire model. The surrogate wildfire model successfully captured the observed monthly regional burned area during validation period 2011 to 2015 (coefficient of determination, R²=0.93). Since the DNN wildfire model has the same input and output requirements as the E3SM process-based wildfire model, our results demonstrate the applicability of machine learning for high accuracy and efficient large-scale land model development and predictions.

1 Introduction

Wildfires burn ∼500 million hectares of vegetated land surface each year, which significantly modifies the physical properties and biogeochemical cycles of terrestrial ecosystems (Bond-Lamberty et al., 2007; Randerson et al., 2006; Pellegrini et al., 2018; Andela et al., 2017). Living vegetation biomass, surface litter, and coarse woody debris are directly combusted and removed by wildfire (Walker et al., 2019; Harden et al., 2006). It has been suggested that global forest cover would double if fire were eliminated (Bond et al., 2005). Fire has multiple important consequences for the climate system, including directly releasing greenhouse gases (e.g., CO₂, CH₄) (Ross et al., 2013; Kasischke and Bruhwiler, 2002) and aerosols (Jiang et al., 2020); changing land surface albedo and energy budgets (French et al., 2016; Rother and De Sales, 2020) and land–atmosphere exchanges of heat, mass, and momentum (Chambers and Chapin, 2002); limiting plant transpiration and regional water recycling (Holden et al., 2018; Brando et al., 2020); and reshaping forest composition (Mekonnen et al., 2019). In addition, biomass burning emits a large amount of fine particulate matter that contributes to about 30 % of cloud condensation nuclei globally (Day, 2004). Soil organic matter decomposition, nitrogen mineralization, and the richness and diversity of soil fungal communities (Oliver et al., 2015) could also be influenced by wildfire through modifying litter substrate supply and degraded enzymatic activities (Pellegrini et al., 2020; 2018; Bowd et al., 2019; Holden et al., 2018).

Climate change and land use activities have jointly affected fire spatial distribution, frequency, and intensity (Xu et al., 2020; Kelley et al., 2019; Andela et al., 2017) since the pre-industrial era. For example, warmer and drier climate conditions enhance fuel aridity and favor fire occurrence in forest ecosystems where fuels have built up over a period of decades and centuries (Abatzoglou and Williams, 2016; Williams et al., 2019). Even if annual precipitation does not decline, redistribution of precipitation towards extreme wet season rainfall events could contribute to longer dry periods and thus more severe fire activity (Xu et al., 2020). Human activities often shape wildfire activity through regulating patterns of ignition and fire occurrence (e.g., power line ignition) (Keeley and Syphard, 2018) and suppressing wildfire activity by means of land fragmentation, fire management, and livestock grazing (Andela et al., 2017). In California, fire density is highly associated with population density and the distance to the wildland–urban interface (WUI) (Syphard et al., 2007). At the global scale, along gradients of increasing population density, fire frequency initially increases by up to 20 % and then gradually declines in more densely populated areas (Knorr et al., 2014).

Although global wildfire burned area has declined over the recent two decades (Andela et al., 2017), many vulnerable ecosystems and geographic regions have experienced significant increases in wildfire activity (Abatzoglou and Williams, 2016; Walker et al., 2019) resulting in large losses of natural resources and economic assets (Stephenson et al., 2013; Papakosta et al., 2017). In western US forests, wildfire has dramatically increased, costing billions of dollars each year and gaining widespread public attention. This regional wildfire increase is mainly driven by concurrent increases in spring temperature and declining snowpacks (Westerling et al., 2006), mid-summer increases in vapor pressure deficit (Williams et al., 2019), and increases in drought stress during fall (Goss et al., 2020). The enhancement of wet and dry oscillations favors initial vegetation growth and subsequent wildfire activity (Heyerdahl et al., 2002; Saha et al., 2019).

Wildfire models have played an important role in many aspects of wildfire research, including monitoring fire spread (Finney, 1998; Radke et al., 2019), analyzing controllers of wildfire short-term and long-term variability (Kelley et al., 2019), predicting severity of the upcoming fire seasons (Preisler and Westerling, 2007) and climate-scale fire variability (Girardin and Mudelsee, 2008; Yue et al., 2013), and understanding the complex climate–wildfire–ecosystem feedbacks (Clark et al., 2004; Zou et al., 2020; Mekonnen et al., 2019). Two types of wildfire models are widely used: process-based models and data-driven statistical models (Hantson et al., 2016). Process-based wildfire models consider detailed processes related to natural fire ignition (Prentice and Mackerras, 1977), anthropogenic ignition (Venevsky et al., 2002), fire spread and duration (Thonicke et al., 2010), fire suppression (Lenihan and Bachelet, 2015), and fire mass and heat fluxes (Li et al., 2012). Process-based wildfire models have been widely used in dynamic vegetation models and coupled Earth system models (ESMs) with various complexities of parameterization (Li et al., 2019; Rabin et al., 2017). As more and more detailed fire processes are considered and parameterized, structural and parametric uncertainties may increase due to incomplete representation of individual processes and imperfect mathematical formulation (Riley and Thompson, 2017). Historically, data-driven models were often used for fire behavior modeling and aim to track the ignition, spread, duration, and extinction of individual fires (Finney, 1998; Radke et al., 2019) at fine spatial and temporal scales. This group of models are more relevant to operational fire research. While process-based wildfire models in the context of global vegetation models or Earth system land models focuses on the grid-cell aggregated fire burned area dynamics that are more relevant to researches on large-scale patterns and climate scale predictions (Li et al., 2019; Rabin et al., 2017). This study particularly focuses on the second category of wildfire models.

Although explicit processes are simulated, the accuracy of process-based wildfire models are highly dependent on parameterization, which is computationally expensive (Zhu and Zhuang, 2014; Teckentrup et al., 2018; Xu et al., 2021). Data-driven models, however, directly link the driving variables (e.g., climate factors) to the fire activity using simple statistical models or more sophisticated machine learning techniques, ignoring the explicit processes and feedbacks associated with wildfire (Radke et al., 2019; Tonini et al., 2020; Ganapathi Subramanian and Crowley, 2018). Through training and validation, statistical representations of wildfire dynamics are learned by models using principles from machine learning. Data-driven wildfire models are diverse in terms of driving variables and model structure. For example, many current machine learning wildfire models rely on remote oceanic dynamics (e.g., sea surface temperature variability) and atmospheric teleconnections to simulate land surface fire activities (Yu et al., 2020; Chen et al., 2011, 2020). Another group of data-driven wildfire models draws more heavily upon regional climate, plant functional type, and human infrastructure driver variables (Coffield et al., 2019; Sayad et al., 2019).

In this study, we develop a machine learning wildfire model using the process representation of wildfire in the Energy Exascale Earth System Model (E3SM) land model (ELMv1) (Zhu et al., 2019), five observationally inferred burned area products (Andela et al., 2019; Giglio et al., 2018; Lizundia-Loiola et al., 2020, 2018; Van Der Werf et al., 2017), and a deep neural network approach (Goodfellow et al., 2016). We implemented a deep learning model that can better capture the complex and non-linear interactions between controlling factors and wildfire activity. The objectives of this study are to surrogate the wildfire parameterization in ELMv1 with the deep neural network and improve the model-simulated wildfire burned area across various fire regions (Giglio et al., 2013).

2 Methodology

2.1 ELMv1 wildfire model

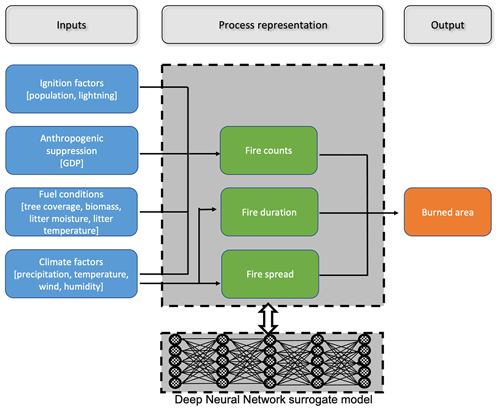
The process-based wildfire model in ELMv1 originates from the Community Land Model (CLM4.5) (Li et al., 2012); we take this wildfire model as the baseline (hereafter referred to as BASE-Fire) without modification on process representation. BASE-Fire combines information regarding ignition, fuel conditions, surface climate, and anthropogenic suppression to simulate total burned area based on the fire counts and spread area of each fire (Fig. 1). The fire count in BASE-Fire is modeled as the sum of anthropogenic ignition and natural ignition, where the latter is proportional to lightning density (Prentice and Mackerras, 1977) and the former is determined by population density (Venevsky et al., 2002). Human activity may also intentionally suppress wildfire occurrence if the fire is detected at an early stage. For example, developed regions with high population density and gross domestic product are less likely to use fire to remove surface biomass. On the other hand, developed regions are more likely to suppress fire given more effective fire management policy and suppression capability. Fire count is also affected by surface fuel availability (aboveground biomass) and fuel combustibility (relative humidity, topsoil temperature, and moisture). The fire spread area in BASE-Fire is modeled as an elliptical-shaped region controlled by wind speed and fuel wetness (Rothermel, 1972) (using topsoil (0–15 cm) moisture as a proxy). The fire duration is set to be one day based on a study that reported the mean global fire persistence of years 2001–2004 (Giglio et al., 2006a). BASE-Fire also does not explicitly consider roads, rivers, and firefighting activity (Arora and Boer, 2005).

Figure 1 Schematic representation of the ELMv1 process-based BASE-Fire model and the components to be surrogated with the deep neural network (DNN) model (dark grey).

2.2 Deep neural network wildfire surrogate model

We developed the new fire model in two steps: (Eq. 1) surrogating BASE-Fire with a deep neural network (DNN) approach and (Eq. 2) improving that surrogate model using five observationally inferred burned area products (Table S1 in the Supplement). First, we surrogated BASE-Fire with a DNN approach (hereafter referred to as DNN-Fire) that uses the same input and output variables as BASE-Fire but treats the explicit intermediate processes (e.g., ignition, fire spread) as latent variables coded by hidden layers in the DNN (Fig. 1). DNN-Fire was developed with five hidden layers and five neurons in each layer for burned area simulation. The DNN approach uses a fully connected feed-forward neural network (Schmidhuber, 2015) that comprises input, hidden, and output layers:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{h}}_{\mathrm{1}}=f_{\mathrm{1}}\left({\mathbf{W}}_{\mathrm{1}}I+b_{\mathrm{1}}\right),\text{(2)}& {\displaystyle }{\mathit{h}}_{\mathrm{2}}=f_{\mathrm{2}}\left({\mathbf{W}}_{\mathrm{2}}{\mathit{h}}_{\mathrm{1}}+b_{\mathrm{2}}\right),\text{(3)}& {\displaystyle }{\mathit{h}}_{\mathrm{3}}=f_{\mathrm{3}}\left({\mathbf{W}}_{\mathrm{3}}{\mathit{h}}_{\mathrm{2}}+b_{\mathrm{3}}\right),\text{(4)}& {\displaystyle }{\mathit{h}}_{\mathrm{4}}=f_{\mathrm{4}}\left({\mathbf{W}}_{\mathrm{4}}{\mathit{h}}_{\mathrm{3}}+b_{\mathrm{4}}\right),\text{(5)}& {\displaystyle }{\mathit{h}}_{\mathrm{5}}=f_{\mathrm{5}}\left({\mathbf{W}}_{\mathrm{5}}{\mathit{h}}_{\mathrm{4}}+b_{\mathrm{5}}\right),\text{(6)}& {\displaystyle }O=f_{\mathrm{6}}\left({\mathbf{W}}_{\mathrm{6}}{\mathit{h}}_{\mathrm{5}}+b_{\mathrm{6}}\right),\end{array}$$

where I denotes the input layer (e.g., climate factors) with 11 neurons, each corresponding to an input variable listed in Table 1. ${\mathit{h}}_{\mathrm{1}},{\mathit{h}}_{\mathrm{2}},{\mathit{h}}_{\mathrm{3}},{\mathit{h}}_{\mathrm{4}}$, and h₅ are five hidden vectors that are calculated with two steps. First is a linear combination of previous layers' input vector (h) and the trainable weight parameter matrix [${\mathbf{W}}_{\mathrm{1}},{\mathbf{W}}_{\mathrm{2}},{\mathbf{W}}_{\mathrm{3}},{\mathbf{W}}_{\mathrm{4}}$, W₅, W₆], considering biases $b_{\mathrm{1}},b_{\mathrm{2}},b_{\mathrm{3}}$, b₄, b₅, and b₆. Then, nonlinear activation functions $f_{\mathrm{1}},f_{\mathrm{2}},f_{\mathrm{3}},f_{\mathrm{4}}$, f₅, and f₆. are applied to the output from the previous step. In this study we used softplus as the activation function (Zheng et al., 2015) that is a non-linear transformation of input signals. O denotes the output layer that summarizes the latent variables from the last hidden layer (h₅) and calculates burned area.

Table 1 Input and output variables of ELMv1 BASE-Fire and surrogate DNN-Fire models.

Second, we improved the surrogate DNN-Fire by fine-tuning the weight parameters using observations (hereafter referred to as DNN-Fire-OBS). Between 2001 and 2010, we initialized DNN-Fire-OBS's weight parameters (${\mathbf{W}}_{\mathrm{1}},{\mathbf{W}}_{\mathrm{2}},{\mathbf{W}}_{\mathrm{3}},{\mathbf{W}}_{\mathrm{4}}$, W₅, and W₆) using results from DNN-Fire; replaced the BASE-Fire burned area by the ensemble mean of five observationally inferred burned area products including GFEDv4s (Van Der Werf et al., 2017), Fire_CCI51 (Lizundia-Loiola et al., 2020), Fire_CCILT11 (Lizundia-Loiola et al., 2018), MODIS MCD64 (Giglio et al., 2018), and Fire_Atlas (Andela et al., 2019) (Table S1 in the Supplement); and adjusted weight parameters until the model best reproduced the observed burned area. This two-step approach will also allow rapid parameterization of the Fire model as new fire data and baseline fire model results become available. DNN-Fire-OBS can be more easily generalized since BASE-Fire provides explicit physical guidance and a larger-than-observation input and output feature space for development of the machine learning fire model. One limitation is the large discrepancy among five burned area products. Tuning DNN-Fire towards the ensemble mean of the five products will potentially compromise the data difference; however, future work is needed to improve the burned area data quality and consistency.

2.3 Model setup and simulation protocol

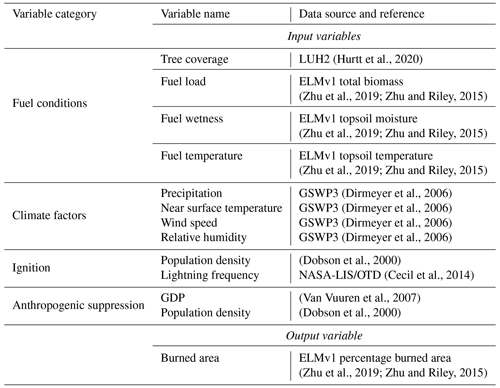
We ran ELMv1 with BASE-Fire at 1.9^∘ by 2.5^∘ spatial resolution (Zhu et al., 2016, 2020) to generate training and testing datasets for the DNN wildfire model. BASE-Fire was first spun up for 600 years with accelerated soil decomposition followed by 200 years regular spinup with regular soil decomposition (Koven et al., 2013). The spinup simulations were forced with constant atmospheric CO₂ concentration (285 ppmv) and 1901–1920 repeated climate forcing from GSWP3 (Global Soil Wetness Project) (Dirmeyer et al., 2006). The purpose of the spinup was to initialize ecosystem carbon pools and stabilize plant and soil carbon and water fluxes. Restarting from the “spun-up” conditions, a transient simulation was then conducted from 1901 to 2015 with GSWP3 transient climate forcing, atmospheric CO₂ concentrations, and nitrogen and phosphorus deposition (Lamarque et al., 2005; Mahowald et al., 2008). Wildfire associated variables were selected for output with a monthly temporal resolution (Table 1).

BASE-Fire output from years 1981 to 2010 were used to train, test, and fine-tune DNN-Fire. We developed 14 region-specific models, corresponding to 14 widely used GFED regions. For each region, all land grid cells (comprising no fire history, infrequent fire, and repeated fire) were concatenated into one data matrix (where rows consist of the number of samples and columns of the number of variables). A total of 80 % of the data matrix was randomly sampled for the training dataset, and the remaining 20 % of the data were reserved for testing. Furthermore, the random sampling was stratified in order to reduce the risk of sampling, e.g., adjacent high fire grid cells. All grid cells were first divided into three “strata”: low burn (0 %–33 % percentile), median burn (33 %–66 % percentile), and high burn (67 %–100 % percentile) grid cells based on the magnitude of the burn. The stratified random sample assured the sampled grid cells for training and testing had the same ratios of low, medium and high burn, thus eliminating the sampling bias from spatial autocorrelation (Wang et al., 2012). In addition to random sampling, we also investigated the impacts of data choice on the model performance, by sampling the testing datasets within specific years (e.g., 2001–2002, 2003–2004, 2005–2006, 2007–2008, 2009–2010), and used the rest of the years for training. We found neglected differences among the models (Fig. S1 in the Supplement) indicating the choice of training/testing data years were not impactful. Therefore, we will discuss the results of the stratified random sampling approach as the major results throughout the paper.

All training and testing datasets were normalized to the range [0, 1] with the following scaler:

$$\begin{array}{}\text{(7)}& \mathit{X}={\displaystyle \frac{\mathit{X}-{\mathit{X}}_{\min }}{{\mathit{X}}_{\max }-{\mathit{X}}_{\min }}},\end{array}$$

where X is the variable vector of interest, and X_min and X_max are minimum and maximum values of X, respectively. During the training stage, we randomly initialized the weighting parameters (Eq. 1–6) and optimized them using the adaptive moment estimation method (Kingma and Ba, 2014), which is a variant of the gradient descent optimization method but considers adaptive learning rate and momentum-like exponentially decaying gradients. The parameter optimization aimed to minimize a mean squared error cost function:

$$\begin{array}{}\text{(8)}& J={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n(y_i^{\mathrm{DNN}}-y_i^{\mathrm{BASE}}{)}^{\mathrm{2}},\end{array}$$

where $y_i^{\mathrm{DNN}}$ and $y_i^{\mathrm{BASE}}$ are DNN-Fire- and BASE-Fire-generated burned area, respectively. i represents a different grid cell. Cost function J summarizes the overall magnitude of the error between the surrogate DNN-Fire and BASE-Fire. We then evaluated model performance using metrics of mean absolute error (Eq. 9), Pearson correlation (Eq. 10), and coefficient of determination (Eq. 11).

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathrm{MAE}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n\left|y_i^{\mathrm{DNN}}-y_i^{\mathrm{BASE}}\right|\text{(10)}& {\displaystyle }p={\displaystyle \frac{\mathrm{covariance}(y^{\mathrm{DNN}},y^{\mathrm{BASE}})}{\mathrm{variance}\left(y^{\mathrm{DNN}}\right)\mathrm{variance}\left(y^{\mathrm{BASE}}\right)}}\text{(11)}& {\displaystyle }{R}^{\mathrm{2}}=\mathrm{1}-{\displaystyle \frac{\sum _{i=\mathrm{1}}^n(y_i^{\mathrm{DNN}}-y_i^{\mathrm{BASE}}{)}^{\mathrm{2}}}{\sum _{i=\mathrm{1}}^n(y_i^{\mathrm{BASE}}-y_{\mathrm{mean}}^{\mathrm{BASE}}{)}^{\mathrm{2}}}}\end{array}$$

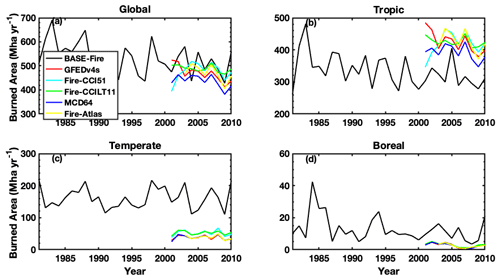
Figure 2 ELMv1 process-based model (BASE-Fire) simulated and five observationally inferred burned area products (Table S1) at (a) global scale in (b) tropical (23.5^∘ S–23.5^∘ N), (c) temperate (23.5– 67.5^∘ N), and (d) boreal (north of 67.5^∘ N) regions.

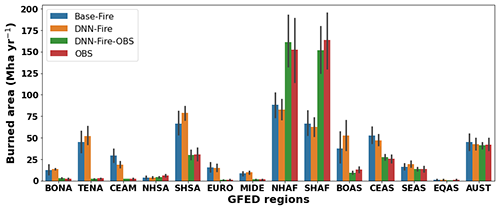
Figure 3 A comparison of wildfire burned area between estimates from the ELMv1 process-based model (BASE-Fire), deep neural network wildfire model (DNN-Fire), deep neural network wildfire model fine-tuned with observed burned area (DNN-Fire-OBS), and observations over 14 GFED fire regions.

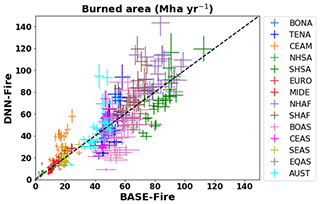
Figure 4 The performance of the deep neural network wildfire model (DNN-Fire), compared with the original ELMv1 process-based wildfire model (BASE-Fire) over 14 GFED regions between years 2001 and 2010.

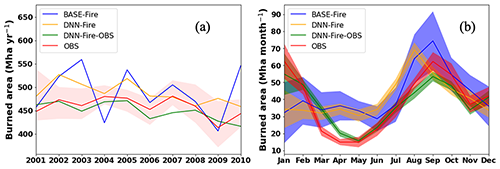
Figure 5 Inter-annual variation of burned area from years 2001 to 2010 (a) and the averaged seasonal cycle (b) of burned area estimated by the ELMv1 process-based wildfire model (BASE-Fire), deep neural network wildfire model (DNN-Fire), deep neural network wildfire model fine-tuned with observations (DNN-Fire-OBS), and observations.

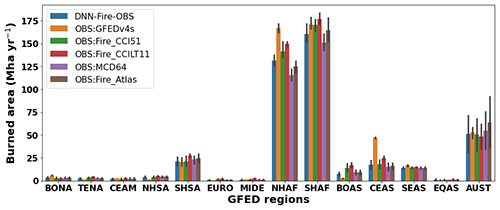
Figure 6 Prognostic simulation of annual wildfire burned area with the deep neural network wildfire model fine-tuned with observations (DNN-Fire-OBS) compared with five burned area products (Table S1) over 2011–2015 for 14 GFED regions.

Figure 7 Prognostic simulation of wildfire burned area (2011–2015) with the deep neural network wildfire model fine-tuned with observations (DNN-Fire-OBS) compared with observations and nine FireMIP models outputs.

3 Results and discussion

3.1 Evaluation of wildfire surrogate model

BASE-Fire performed reasonably well for total global burned area (508±53 Mha yr⁻¹ (millions of hectares per year) between years 2001 and 2010 compared with the observational long-term average of 424–484 Mha yr⁻¹; Fig. 2, Table S1). BASE-Fire also captured the global declining trend of wildfire burned area over this time period, attributed to a decrease in tropical fires (Andela et al., 2017). At the regional scale, however, BASE-Fire underestimated tropical (23.5^∘ S–23.5^∘ N) burned area and overestimated temperate (23.5–67.5^∘ N) and boreal (67.5^∘ N above) burned area (Fig. 2). Large spatial heterogeneity existed for BASE-Fire regional bias. For example, over tropical GFED regions, BASE-Fire overestimated wildfire burned area over Southern Hemisphere South America (SHSA) but underestimated wildfire burned area over both Southern and Northern Hemisphere Africa regions (SHAF and NHAF), despite an overall underestimation over the tropical region (Fig. 3). In contrast, consistent overestimation occurred over all temperate GFED regions. For example, wildfire burning was overestimated by about a factor of 16 (∼1 versus 16 Mha yr⁻¹) over the Europe GFED region (EURO) (Fig. 3). Although there is room to improve BASE-Fire performance, the parameterization would involve large ensemble simulations and computational resources. Instead, we first used BASE-Fire-generated data as training and testing datasets to parameterize DNN-Fire, and then we fine-tuned the DNN-Fire model against observed burned area.

Next we parameterized and compared DNN-Fire with BASE-Fire outputs. Using BASE-Fire-generated $\mathrm{1.9}{}^{\circ }\times \mathrm{2.5}$^∘ resolution datasets of surface fuel conditions (fuel load (vegetation biomass), fuel temperature (topsoil temperature), and fuel wetness (topsoil moisture)) with gridded climate forcing (GSWP3) (Dirmeyer et al., 2006), land use (LUH2 dataset) (Hurtt et al., 2020), and socio-economic (Van Vuuren et al., 2007; Dobson et al., 2000) factors, DNN-Fire captured the spatial pattern of BASE-Fire-predicted wildfire activity (Fig. 4, S2). Across all GFED regions, mean absolute error of DNN-Fire was 4.4 Mha yr⁻¹ (<1 % of total burn area), with median and maximum errors of 1.8 and 13.0 Mha yr⁻¹, respectively (Fig. 3). Equatorial Asia (EQAS), Northern Hemisphere South America (NHSA), Central America (CEAS), and Europe (EURO) regions had the lowest DNN-Fire errors (<1.0 Mha yr⁻¹), while Southern Hemisphere Africa (SHAF), and Boreal Asia (BOAS) had the largest errors (10–13 Mha yr⁻¹). Overall, the correlation coefficient between BASE-Fire and DNN-Fire simulated burned area was 0.91 (p value <0.01), and the coefficient of determination (R²) was 0.79. Across seasons, DNN-Fire also reasonably captured the BASE-Fire peak fire months (June to October), which were dominated by Southern Hemisphere Africa and Southern Hemisphere South America (Fig. 5).

By surrogating BASE-Fire, DNN-Fire is expected to have similar biases and uncertainties. The deficiency of the BASE-Fire model will propagate to DNN-Fire. In our future work we will overcome such limitations by training multiple DNN-Fire models with ensemble simulations of BASE-Fire models that differ in critical parameters and vary in model structures.

3.2 Calibrating the wildfire surrogate model using observations

Although the global pattern was reasonably captured, BASE-Fire had relatively large biases in several GFED regions, as discussed above. Since DNN-Fire was trained and validated only with BASE-Fire-generated inputs (e.g., fuel conditions) and outputs (burned area), we expect that, at best, DNN-Fire would have comparable biases as BASE-Fire. Starting from DNN-Fire, we further calibrated the model weighting parameters to create DNN-Fire-OBS and validated DNN-Fire-OBS performance using observed burned area from five existing burned area products (Table S1) between years 2001 and 2010. The calibration time cost several minutes with an Intel Xeon Phi Processor 7250.

Dramatic improvements were found in most of the 14 regions simulated by DNN-Fire-OBS (Fig. 3). Overall, DNN-Fire-OBS simulated global long-term average burned area was 458 Mha yr⁻¹ (compared with observational average 467 Mha yr⁻¹). Averaged across 14 regions, 73 % reduction of mean absolute error was achieved by DNN-Fire-OBS, compared with the BASE-Fire model. The Pearson correlation coefficient between the DNN-Fire-OBS simulated and observational burned area was 0.98 (p value <0.001) with an R² of 0.97. Bias reduction was disproportionally distributed across the GFED regions (Fig. 3). For example, severely burned regions, including Southern and Northern Hemisphere Africa (SHAF and NHAF) and Southern Hemisphere South America (SHSA) greatly benefited from the tuning, and their regional biases were reduced by 88, 65, and 51 Mha yr⁻¹ (or 88 %, 89 %, 98 % reduction), respectively. Although Temperate North America (TENA) and Europe (EURO) wildfire burned area is relatively small (1–3 Mha yr⁻¹), the impacts of wildfire activity were significant due to their high population densities. DNN-Fire tended to overestimate the burned area in TENA and EURO by 47 and 13 Mha yr⁻¹, while DNN-Fire-OBS significantly reduced biases in both regions to less than 0.3 Mha yr⁻¹ (a 97 %–98 % reduction).

BASE-Fire tended to overestimate inter-annual variability (IAV) and had opposite burned area anomalies between years 2001 and 2005. DNN-Fire dampened BASE-Fire's IAV but systematically overestimated burned area. DNN-Fire-OBS agreed well with the observed IAV between years 2001 and 2010 (Fig. 5a). The seasonal cycle was also improved in DNN-Fire-OBS in terms of reducing BASE-Fire's overestimation of burned area during peak fire seasons (Fig. 5b, S3), although we note that DNN-Fire-OBS is biased high during low fire seasons (March and April).

3.3 Prognostic simulation and limitations

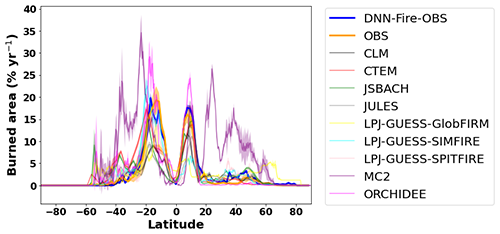
We next evaluated the DNN-Fire-OBS model against observations for the period 2011 to 2015, using data which were not used to train and validate the model. Overall, DNN-Fire-OBS simulated 469–514 Mha yr⁻¹ global burned area, compared with observations of 349–509 Mha yr⁻¹. Note that the large observational ranges were mainly due to the differences among the five burned area products rather than the inter-annual variability (Fig. 6). Regionally, DNN-Fire-OBS overestimated NHAF, SHAF, and SHSA annual burned area by 8, 6, and 2 Mha yr⁻¹, respectively (Fig. 6) compared with the observational mean. Averaged latitudinal distribution of simulated burned area during this period showed that global wildfire activity peaked around 10–15^∘ S and 5–10^∘ N, together accounting for burning 12 %–16 % of the land surface (Fig. 7). These two peaks were dominated by large burned area over Southern (SHAF) and Northern Hemisphere Africa (NHAF) fire regions. Compared with observations, DNN-Fire-OBS simulated reasonable burned area latitudinal distributions (Fig. 7). We also compared the nine FireMIP models (Rabin et al., 2017; Teckentrup et al., 2018) and found diverse latitudinal distribution of burned area. The across-model differences were much larger than the inter-annual variation simulated by each individual model, which indicated large model structural uncertainties. Validation was also conducted for the historical period 1981–2000, when most of the satellite-based burned area data were not available. Compared with charcoal-index-inferred burned area during 1981–2000 (Fig. S4), the DNN-Fire-OBS model reasonably captured the decrease in burned area from ∼530 to 490 Mha yr⁻¹. In summary, DNN-Fire-OBS simulation is reasonably accurate: Eq. (1) improved the simulated wildfire spatial and temporal distributions in ELMv1;Eq. (2) enabled effective and efficient parameterization of fires at regional scale.

This study focuses on design, development, and parameterization of the DNN fire model within the E3SM model interface. In this way the DNN model can be readily coupled in the future and iteratively simulate climate, ecosystem fuel conditions, and fire dynamics. Although no feedbacks exist between biomass and tree cover and burned area under the current offline mode, this study is an important step towards fully coupling E3SM and the DNN-Fire models in the future. We acknowledge several challenges and limitations in our modeling framework. First, the DNN model uncertainty was subject to the accuracy of climate forcings as well as other physical driving variables simulated by the physical wildfire model (ELMv1). For example, in this work ELM simulation of soil temperature, soil moisture, fuel load and so on is subject to the uncertainty of GSWP3 forcings. Furthermore, those simulated variables served as inputs for the DNN model and would result in burned area prediction uncertainty. It was challenging to eliminate the forcing uncertainties in this work, but we could at least evaluate the magnitude of these uncertainties. We ran the DNN-Fire-OBS model with alternative forcings of CRU-JRA, NCEP-DOE2, and CDAS soil moisture from 2001 to 2010 and compared the results with DNN-Fire-OBS driven by default inputs (Fig. S5). The results showed relatively larger uncertainties from climate forcing than that from soil moisture forcing, particularly over the major fire regions (e.g., SHSA, SHAF, and NHAF). For fuel load, although no transient dataset of global living biomass existed yet, we directly compared the ELM model simulated biomass with the global estimate (GEOCARBON ∼455 Pg C). We found that the modeled present-day biomass continuously increased from 425 to 470 Pg C and compared reasonably well with the global benchmark (Fig. S6). Future work will focus on evaluating the uncertainties from dead fuel load and fuel temperature variables.

Second, the original ELMv1 wildfire model has a unified mathematical representation of how fuel, climate, and socio-economic conditions control wildfire burned area (Li et al., 2012). However, training one single DNN wildfire model across the globe will produce a model dominated by grid cells that have a high burned area (e.g., Africa). The performance of the trained DNN model, therefore, will likely have larger biases over the low-fire grid cells, although the globally aggregated burned area could be reasonable. We partly overcame this challenge by applying the widely used 14 GFED fire regions that assume unique and relatively uniform dynamics over each region (Giglio et al., 2006b) and employed a stratified random sampling method for training and testing datasets. Although the regionally specific wildfire model introduces additional complexity, it better represents distinct characteristics of wildfire activity over different climate regimes and biomes (Zou et al., 2019; Zhu and Zhuang, 2013) and allows for future analyses of how the relevant controllers vary across the globe.

Thirdly, the cost function and the training of the DNN model relied on the normality assumption of burned area data. Therefore, the DNN model error might be dominated by highly burned grid cells. A potential solution is to use log transformation on non-normal data or the resultant cost function (Kelley et al., 2021). Finally, our GFED region-based parameterization strategy relied on the combination of climate and biome types, while an alternative parameterization strategy for the DNN-Fire model could be based on plant functional type distributions. Based on our analysis, the plant-functional-type-based DNN-Fire model had similar performance compared with the GFED-based model (Fig. S7, S8). Since the GFED regions were defined by present-day climate and fire regimes, our GFED-based models may not fully capture the changes of future fire dynamics due to longer-timescale climate and fire regime changes.

4 Conclusions

In this study, we first surrogated the baseline ELMv1 wildfire model with a deep neural network (DNN) approach (Pearson correlation coefficient =0.91, p value <0.01, R²=0.79). The development was based on inputs and outputs from the baseline ELMv1 wildfire simulation, which is process-based and reasonably simulates global burned area, although regional biases existed. We then calibrated the neural network weights using the observationally inferred burned area from the years 2001–2010. The final calibrated DNN wildfire model (DNN-Fire-OBS) was shown to be more accurate over the 14 GFED regions. For example, reductions in absolute error over Africa, South America, and Europe were ∼90 %. More importantly, the DNN-Fire-OBS model parameters could be calibrated within minutes, compared with traditional ELMv1 parameterization ensemble simulations that consume a large amount of computational time. The improved DNN-Fire-OBS model also accurately prognosed global and regional burned area in the 5-year period following the training period from 2011 to 2015 (modeled 469–514 Mha yr⁻¹). We conclude that the improved surrogate wildfire model (DNN-Fire-OBS) developed in this study can serve as an effective alternative to the process-based fire model currently used in ELMv1. More broadly, we conclude that machine learning techniques can facilitate Earth system model development, parameterization, and uncertainty reduction with high efficiency and accuracy.