the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The Vertical City Weather Generator (VCWG v1.3.2)
Mohsen Moradi
Benjamin Dyer
Amir Nazem
Manoj K. Nambiar
M. Rafsan Nahian
Bruno Bueno
Chris Mackey
Saeran Vasanthakumar
Negin Nazarian
E. Scott Krayenhoff
Leslie K. Norford
Amir A. Aliabadi
The Vertical City Weather Generator (VCWG) is a computationally efficient urban microclimate model developed to predict temporal and vertical variation of potential temperature, wind speed, specific humidity, and turbulent kinetic energy. It is composed of various sub-models: a rural model, an urban vertical diffusion model, a radiation model, and a building energy model. Forced with weather data from a nearby rural site, the rural model is used to solve for the vertical profiles of potential temperature, specific humidity, and friction velocity at 10 m a.g.l. The rural model also calculates a horizontal pressure gradient. The rural model outputs are applied to a vertical diffusion urban microclimate model that solves vertical transport equations for potential temperature, momentum, specific humidity, and turbulent kinetic energy. The urban vertical diffusion model is also coupled to the radiation and building energy models using two-way interaction. The aerodynamic and thermal effects of urban elements, surface vegetation, and trees are considered. The predictions of the VCWG model are compared to observations of the Basel UrBan Boundary Layer Experiment (BUBBLE) microclimate field campaign for 8 months from December 2001 to July 2002. The model evaluation indicates that the VCWG predicts vertical profiles of meteorological variables in reasonable agreement with the field measurements. The average bias, root mean square error (RMSE), and R2 for potential temperature are 0.25 K, 1.41 K, and 0.82, respectively. The average bias, RMSE, and R2 for wind speed are 0.67 m s−1, 1.06 m s−1, and 0.41, respectively. The average bias, RMSE, and R2 for specific humidity are 0.00057 kg kg−1, 0.0010 kg kg−1, and 0.85, respectively. In addition, the average bias, RMSE, and R2 for the urban heat island (UHI) are 0.36 K, 1.2 K, and 0.35, respectively. Based on the evaluation, the model performance is comparable to the performance of similar models. The performance of the model is further explored to investigate the effects of urban configurations such as plan and frontal area densities, varying levels of vegetation, building energy configuration, radiation configuration, seasonal variations, and different climate zones on the model predictions. The results obtained from the explorations are reasonably consistent with previous studies in the literature, justifying the reliability and computational efficiency of VCWG for operational urban development projects.
- Article
(4165 KB) - Full-text XML
-
Supplement
(566 KB) - BibTeX
- EndNote
Urban areas interact with the atmosphere through various exchange processes of heat, momentum, and mass, which substantially impact human comfort, air quality, and energy consumption. Such complex interactions are observable from the urban canopy layer (UCL) to a few hundred meters within the atmospheric boundary layer (ABL; Britter and Hanna, 2003). Modeling enables a deeper understanding of interactions between urban areas and the atmosphere and can possibly offer solutions toward mitigating adverse effects of urban development on the climate. A brief review of modeling efforts is essential for more accurate model development toward an understanding of urban area–atmosphere interactions.
Mesoscale models incorporating the urban climate were initially aimed to resolve weather features with grid resolutions of at best a few hundred meters horizontally and a few meters vertically, without the functionality to resolve micro-scale three-dimensional flows or to account for atmospheric interactions with specific urban elements such as roads, roofs, and walls (Bornstein, 1975). These models usually consider the effect of built-up areas by introducing an urban aerodynamic roughness length (Grimmond and Oke, 1999) or adding source or sink terms in the momentum (e.g., drag term) and potential temperature (e.g., anthropogenic heat term) equations (Dupont et al., 2004). Therefore, if higher grid resolutions less than 10 m (horizontal and vertical) are desired (Moeng et al., 2007; Wang et al., 2009; Talbot et al., 2012), micro-scale climate models should be deployed. Recently, multi-scale climate models have coupled mesoscale and micro-scale models (Chen et al., 2011; Kochanski et al., 2015; Mauree et al., 2018). Numerous studies have used computational fluid dynamics (CFD) to investigate the urban microclimate while taking into account interactions between the atmosphere and urban elements with full three-dimensional flow analysis (Saneinejad et al., 2012; Blocken, 2015; Nazarian and Kleissl, 2016; Aliabadi et al., 2017; Nazarian et al., 2018). Despite accurate predictions, CFD models are not computationally efficient, particularly for weather forecasting at larger scales and for a long period of time, and they usually do not represent many processes in the real atmosphere such as clouds and precipitation. As an alternative, urban canopy models (UCMs) require understanding of the interactions between the atmosphere and urban elements to parameterize various exchange processes of radiation, momentum, heat, and moisture within and just above the canopy based on experimental data, physical processes from theoretical considerations, three-dimensional simulations, or simplified urban configurations (Masson, 2000; Kusaka et al., 2001; Martilli et al., 2002; Chin et al., 2005; Krayenhoff et al., 2014, 2015; Nazarian and Kleissl, 2016; Aliabadi et al., 2019). These urban canopy models are more computationally efficient than CFD models. They are designed to provide more details on heat storage and radiation exchange, while they employ less detailed flow calculations.
Urban microclimate models must account for a few unique features of the urban environment. Urban obstacles such as trees and buildings substantially contribute to changing flow and turbulence patterns in cities (Kastner-Klein et al., 2004). Difficulties arise when spatially inhomogeneous urban areas create highly three-dimensional wind patterns that result in the difficulty of parameterizations (Roth, 2000; Resler et al., 2017). For example, the surfaces of urban obstacles exert form and skin drag, consequently altering flow direction and producing eddies at different spatiotemporal scales. This can lead to the formation of shear layers at roof level with variable oscillation frequencies (Tseng et al., 2006; Masson et al., 2008; Zajic et al., 2011); all of such phenomena should be properly approximated in parameterizations.
Heat exchanges between indoor and outdoor environments significantly influence the urban microclimate. Various studies have attempted to parametrize heat sources and sinks caused by buildings such as heat fluxes due to infiltration, exfiltration, ventilation, walls, roofs, roads, windows, and building energy systems (e.g., condensers and exhaust stacks) (Kikegawa et al., 2003; Salamanca et al., 2010; Yaghoobian and Kleissl, 2012). Therefore, a building energy model (BEM) is required to be properly integrated into an urban microclimate model to take account of the impact of building energy performance on the urban microclimate (Bueno et al., 2011, 2012b; Gros et al., 2014). This two-way interaction between the urban microclimate and indoor environment can significantly affect the urban heat island (UHI) (K) and energy consumption of buildings (Salamanca et al., 2014).
Urban vegetation can substantially reduce the adverse effects of UHI (K), particularly during heat waves, resulting in improved thermal comfort (Grimmond et al., 1996; Akbari et al., 2001; Armson et al., 2012). Urban trees can potentially provide shade and shelter, therefore changing the energy balance of individual buildings in addition to the entire city (Akbari et al., 2001). A study of the local-scale surface energy balance revealed that the amount of energy dissipated due to the cooling effect of trees is not negligible and should be parameterized properly (Grimmond et al., 1996). In addition, the interaction between urban elements, most importantly trees and buildings, is evident in radiation trapping within the canyon and shading impact of trees (Krayenhoff et al., 2014; Redon et al., 2017; Broadbent et al., 2019). Buildings and trees obstruct the sky with implications for longwave and shortwave radiation fluxes both downward and upward that may create unpredictable diurnal and seasonal changes in UHI (K) (Kleerekoper et al., 2012; Yang and Li, 2015). Also, it has been shown that not only trees but also the fractional vegetation coverage on urban surfaces can alter urban temperatures with implications for UHI (K) (Armson et al., 2012). Trees, depending on their height and abundance relative to buildings, could also exert drag and alter flow patterns within the canopy; however, this effect is not as significant as the drag induced by buildings (Krayenhoff et al., 2015). Such complex interactions must be accounted for in successful urban microclimate models.
1.1 Research gaps
Numerous studies have focused on high-fidelity urban microclimate models with high spatiotemporal flow resolution, capturing important features of the urban microclimate with acceptable accuracy (Gowardhan et al., 2011; Soulhac et al., 2011; Blocken, 2015; Nazarian et al., 2018). Some example CFD models of this kind include Open-source Field Operation And Manipulation (OpenFOAM) (Aliabadi et al., 2017, 2018), the Parallelized Large-Eddy Simulation Model (PALM) (Maronga et al., 2015; Resler et al., 2017), and ENVI-met (Crank et al., 2018). Despite advances, however, high-fidelity models capable of resolving three-dimensional flows at micro-scale are not computationally efficient and are complex to implement for operational applications. As a remedy, lower-dimensional-flow urban microclimate models have been developed with many practical applications in city planning, architecture, and engineering consulting. For example, bulk flow (single-layer) models such as the Urban Weather Generator (UWG) calculate the flow dynamics in one point, usually the center of a hypothetical urban canyon, which is representative of all locations (Mills, 1997; Kusaka et al., 2001; Salamanca et al., 2010; Ryu et al., 2011; Bueno et al., 2012a, 2014). Another bulk flow (single-layer) model is the Canyon Air Temperature (CAT) model, which utilizes standard data from a meteorological station to estimate air temperature in a street canyon (Erell and Williamson, 2006). The Town Energy Balance (TEB) model calculates energy balances for urban surfaces and is forced by meteorological data and incoming solar radiation at the urban site on top of the modeling domain (Masson et al., 2002). The Temperatures of Urban Facets-3D (TUF-3D) model calculates urban surface temperatures with the main focus on three-dimensional radiation exchange, but it adopts bulk flow (single-layer) modeling, and it is forced by meteorological data on top of its domain (Krayenhoff and Voogt, 2007). More recently, TUF-3D was coupled to an Indoor–Outdoor Building Energy Simulator (TUF-3D-IOBES), but this model adopted a bulk flow (single-layer) parameterization (Yaghoobian and Kleissl, 2012). The multi-layer Building Effect Parametrization with Trees (BEP-Tree) model includes variable building heights, the vertical variation of climate variables, and the effects of trees, but it is not linked to a building energy model (Martilli et al., 2002; Krayenhoff, 2014; Krayenhoff et al., 2020). More recently, the BEP model has been coupled to a building energy model (BEP+BEM), but it is forced with meteorological variables from higher altitudes above a city using mesoscale models instead of near-surface meteorological variables measured outside the city (rural areas). An overview of the literature reveals an apparent paucity of independent urban microclimate models that account for spatiotemporal variations of meteorological parameters in the urban environment and consider the effects of trees, building energy, radiation, and the connection to the near-surface rural meteorological conditions measured outside a city, without the need for mesoscale modeling, that are computationally efficient and operationally simple for practical applications.
1.2 Objectives
In this study, we present a new urban microclimate model, called the Vertical City Weather Generator (VCWG), which attempts to overcome some of the limitations mentioned in the previous section. It resolves vertical profiles of climate variables, such as potential temperature, wind, specific humidity, and turbulent kinetic energy in relation to urban design parameters. VCWG also includes a building energy model. It allows parametric investigation of design options with urban climate control at multiple heights, particularly if multistory building design options are considered. This is a significant advantage over bulk flow (single-layer) models such as UWG, which only consider one point for flow dynamics inside a hypothetical canyon (Masson, 2000; Kusaka et al., 2001; Dupont et al., 2004; Krayenhoff and Voogt, 2007; Lee and Park, 2008; Bueno et al., 2012a, 2014). The advantages of VCWG are as follows. (1) It does not need to be coupled to a mesoscale weather model because it functions stand-alone as a microclimate model. (2) Unlike many UCMs that are forced with climate variables above the urban roughness sublayer (e.g., TUF-3D), VCWG is forced with rural climate variables measured at 2 m a.g.l. (temperature and humidity) and 10 m a.g.l. (wind) that are widely accessible and available around the world, making VCWG highly practical for urban design investigations in different climates. Further, unlike UWG, VCWG uses the Monin–Obukhov similarity theory in the rural area to consider effects of thermal stability and aerodynamic, temperature, and specific humidity roughness lengths to establish vertical profiles of potential temperature and specific humidity. (3) VCWG provides urban climate information in one dimension, i.e., resolved vertically, which is advantageous over bulk flow (single-layer) models. (4) VCWG is coupled with the building energy model using two-way interaction. (5) Unlike UWG, VCWG considers the effect of trees in the urban climate by modeling evapotranspiration (latent heat transfer), sensible heat transfer, radiation transfer, drag, and other processes due to trees.
The paper is structured as follows. Section 2 describes the methodology, outlining the components of the VCWG model and their connections: the forcing EnergyPlusTM Weather (EPW) dataset, the rural model (RM), the one-dimensional vertical diffusion model, the building energy model, and the radiation model. This section also describes the location and details of the BUBBLE field campaign used for model evaluation. Section 3 provides the results and discussion. It starts with a detailed evaluation of VCWG by comparing simulation results with those of the BUBBLE field measurements. Then, results from other explorations, including effects of building dimensions, foliage density, building energy configuration, radiation configuration, seasonal variation, and different climate zones on the urban climate, are briefly presented with reference to the Supplement. Finally, Sect. 4 is devoted to conclusions and future work. Additional information about the sub-models and equations used is provided in Appendix A.
2.1 Vertical City Weather Generator (VCWG)
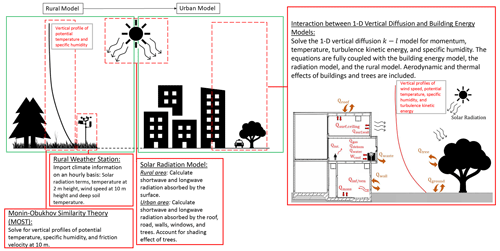
Figure 1 shows the VCWG model schematic. VCWG consists of four integrated sub-models: (1) a rural model (RM) (Sect. 2.1.2) forces meteorological boundary conditions on VCWG based on Monin–Obukhov similarity theory (Paulson, 1970; Businger et al., 1971; Dyer, 1974) and a soil energy balance model (Bueno et al., 2012a, 2014); (2) an urban one-dimensional vertical diffusion model (Sect. 2.1.3) is used for calculation of the vertical profiles of urban microclimate variables including potential temperature, wind speed, specific humidity, and turbulent kinetic energy considering the effect of trees, buildings, and the building energy system (e.g., condensers and exhaust stacks). This model was initially developed by Santiago and Martilli (2010) and Simón-Moral et al. (2017), while it was later ingested into another model called the Building Effect Parametrization with Trees (BEP-Tree) model, considering the effects of trees (Krayenhoff, 2014; Krayenhoff et al., 2015, 2020). (3) A building energy model (BEM; Sect. 2.1.4) is used to determine the waste heat of buildings imposed on the urban environment. This model is a component of the Urban Weather Generator (UWG) model (Bueno et al., 2012a, 2014). (4) A radiation model with vegetation (Sect. 2.1.5) is used to compute the longwave and shortwave heat exchanges between the urban canyon, trees, and the atmosphere and sky. A summary of this model is provided by Meili et al. (2020) and the references within.
The sub-models are integrated to predict vertical variations of urban microclimate variables including potential temperature, wind speed, specific humidity, and turbulent kinetic energy as influenced by aerodynamic and thermal effects of urban elements including longwave and shortwave radiation exchanges, sensible heat fluxes released from urban elements, cooling effect of trees, and the induced drag by urban obstacles. The RM takes into account latitude, longitude, dry bulb temperature, relative humidity, dew point temperature and pressure at 2 m a.g.l., wind speed and direction at 10 m a.g.l., downwelling direct shortwave radiation, downwelling diffuse shortwave radiation, downwelling longwave radiation, and deep soil temperature from an EPW file. For every time step, and forced with the set of weather data, the RM then computes a potential temperature profile, a specific humidity profile, friction velocity, and a horizontal pressure gradient as a function of friction velocity, all of which are forced as boundary conditions to the one-dimensional vertical diffusion model in the urban area. The potential temperature and specific humidity are forced as fixed values on top of the domain for the urban vertical diffusion model in the temperature and specific humidity equations, respectively. The horizontal pressure gradient is forced as a source term for the urban vertical diffusion model in the momentum equation. It must be acknowledged that the model does not consider horizontal advection from the rural area. The model assumes that the rural site is upwind of the urban site and the top of the domain is above the urban boundary layer. While forced by the RM, the urban one-dimensional vertical diffusion model is also coupled with the building energy and radiation models. The three models have feedback interaction. The urban one-dimensional vertical diffusion model calculates the flow quantities at the center of control volumes, which are generated by splitting the urban computational domain into multiple layers within and above the urban canyon (see Fig. 2). The urban domain extends to 3 times the building height that conservatively falls closer to the top of the atmospheric roughness sublayer in the urban area (Santiago and Martilli, 2010; Aliabadi et al., 2017) but within the inertial layer in the rural area, where Monin–Obukhov similarity theory can be applied (Basu and Lacser, 2017). In VCWG, buildings with uniformly distributed height, equal width, and equal spacing from one another represent the urban area. The feedback interaction coupling scheme among the building energy model, radiation model, and the urban one-dimensional vertical diffusion model is designed to update the boundary conditions, surface temperatures, and the source and sink terms in the transport equations in successive time step iterations. More details about the sub-models are provided in the subsequent sections and Appendix A.
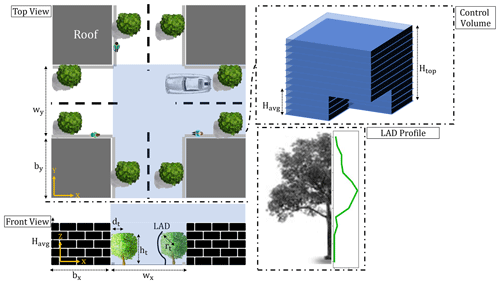
Figure 2Simplified urban area used in VCWG and corresponding layers of control volumes within and above the canyon. The height of the domain is 3 times the average building height. A leaf area density (LAD) (m2 m−3) profile is considered to represent trees.
2.1.1 EnergyPlusTM weather data
Building energy and solar radiation simulations are typically carried out with standardized weather files. EPW files include recent weather data for 2100 locations and are saved in the standard EnergyPlusTM format developed by the US Department of Energy (https://energyplus.net/weather, last access: 10 February 2021). The data are available for most North American cities, European cities, and other regions around the world. The weather data are arranged by the World Meteorological Organization (WMO) based on region and country. An EPW file contains typical hourly-based data for meteorological variables. The meteorological variables are dry bulb temperature, dew point temperature, relative humidity, incoming direct and diffusive shortwave radiation fluxes from the sun and sky, respectively, incoming longwave radiation flux, wind direction, wind speed, sky condition, precipitation (occasionally), deep soil temperature, and general information about field logistics and soil properties. Precipitation data are often missing in the EPW files.
2.1.2 Rural model
In the rural model, the Monin–Obukhov similarity theory (MOST) is used to solve for the vertical profiles of potential temperature, specific humidity, and friction velocity at 10 m a.g.l. using meteorological measurements near the surface. MOST is usually applied to the atmospheric surface layer over flat and homogeneous land to describe the vertical profiles of wind speed, potential temperature, and specific humidity as functions of momentum flux, sensible heat flux, and latent heat flux measured near the surface, respectively. Using MOST the gradient of potential temperature is given by
where (K) is mean potential temperature in the rural area, Qsen,rur (W m−2) is the net rural sensible heat flux, ρ (kg m−3) is air density near the rural surface, Cp () is air specific heat capacity, u* (m s−1) is friction velocity, and κ=0.4 (–) is the von Kármán constant. ΦH (–) is known as the universal dimensionless temperature gradient. This term is estimated for different thermal stability conditions based on experimental data by Businger et al. (1971) and Dyer (1974):
In the dimensionless stability parameter (–), z (m) is the height above ground and L (m) is the Obukhov length given by
It has been observed that there is a monotonic reduction in friction velocity with increasing stratification (Joffre et al., 2001). So, friction velocity in Eq. (1) is estimated from momentum flux generalization (Monin and Obukhov, 1954):
where (m s−1) is the mean horizontal wind speed in the rural area and ΦM (–) is the universal dimensionless wind shear estimated for different thermal stability conditions based on experimental data (Businger et al., 1971; Dyer, 1974).
Friction velocity can be determined by integrating Eq. (4) iteratively over height from the elevation of the rural aerodynamic roughness length (m) to z−drur (m), where z=10 m is the reference height for wind measurement and drur (m) is the zero displacement height. The aerodynamic roughness length and zero displacement height have been rigorously studied and parameterized in the literature as functions of obstacle height hrur (m) and the type of rural area (Raupach et al., 1991; Hanna and Britter, 2002). VCWG permits this specification, but the approximate formulations used in this study are and drur=0.5hrur. This method provides a friction velocity that is corrected for thermal stability effects.
The potential temperature profiles are also obtained by integration of Eq. (1) (Paulson, 1970) over height from the rural roughness length for temperature (m) to z−drur (m), where z (m) is the desired elevation above ground (here the top of the domain). A typical formulation of (m) is often used (Brutsaert, 1982; Garratt, 1994; Järvi et al., 2011; Meili et al., 2020). This formulation is used in the present study.
Given the similarity of heat and mass transfer (sensible and latent heat fluxes), the same universal dimensionless temperature gradient can be used for the universal dimensionless specific humidity gradient, i.e., ΦQ=ΦH (–) (Zeng and Dickinson, 1998). The net rural latent heat flux Qlat,rur (W m−2) can either be directly measured or estimated using the Bowen ratio βrur (–) and the net rural sensible heat flux via (W m−2). So the gradient of the specific humidity can be given by the following expression, employing the latent heat of vaporization Lv (J kg−1), as
which can also be integrated over height to give the vertical profile of specific humidity. This expression should be integrated over height from the rural roughness length for specific humidity (m) to z−drur (m), where z (m) is the desired elevation above ground (here the top of the domain). It is often assumed that (m) (Brutsaert, 1982; Järvi et al., 2011; Meili et al., 2020). This assumption is used in the present study.
Meteorological information obtained from a weather station, including direct and diffuse shortwave radiation, longwave radiation, temperature at 2 m a.g.l., wind speed at 10 m a.g.l., and deep soil temperature, is used to calculate the net rural sensible and latent heat fluxes at the surface via the surface energy balance:
where QS,rur and QL,rur (both in W m−2) are net shortwave and longwave radiation fluxes at the surface (positive with energy flux into the surface), and Qsen,rur, Qlat,rur, and Qgrd (all in W m−2) are net sensible, latent, and ground heat fluxes at the surface (positive with energy flux leaving the surface). Appendix A details the calculation of each term.
The rural model also outputs a horizontal pressure gradient based on the friction velocity calculation that is later used as a source term for the urban one-dimensional vertical diffusion momentum equation. The pressure gradient is parameterized as (), where Htop (m) is the height of the top of the domain (Krayenhoff et al., 2015; Nazarian et al., 2020), here 3 times the average building height.
After calculating potential temperature and specific humidity at the top of the domain by the rural model, these values can be applied as a fixed-value boundary condition at the top of the domain in the urban one-dimensional vertical diffusion model for the potential temperature and specific humidity transport equations.
2.1.3 Urban vertical diffusion model
Numerous studies have attempted to parameterize the interaction between urban elements and the atmosphere in terms of dynamical and thermal effects, from very simple models based on MOST (Stull, 1988) to bulk flow (single-layer) parameterizations (Krayenhoff and Voogt, 2007; Masson, 2000; Kusaka et al., 2001; Bueno et al., 2014) and multilayer models (Hamdi and Masson, 2008; Santiago and Martilli, 2010; Krayenhoff et al., 2015, 2020) with different levels of complexity. Multilayer models usually treat aerodynamic and thermal effects of urban elements as sink or source terms in potential temperature, momentum, specific humidity, and turbulent kinetic energy equations. Parameterization of the exchange processes between urban elements and the atmosphere can be accomplished using either experimental data or CFD simulations (Martilli et al., 2002; Dupont et al., 2004; Kondo et al., 2005; Kono et al., 2010; Lundquist et al., 2010; Santiago and Martilli, 2010; Krayenhoff et al., 2015; Aliabadi et al., 2019). CFD-based parameterizations proposed by Martilli and Santiago (2007), Santiago and Martilli (2010), Krayenhoff et al. (2015), and Nazarian et al. (2020) use results from Reynolds-averaged Navier–Stokes (RANS) or large-eddy simulations (LESs) including effects of trees and buildings. These parameterizations consider the CFD results at different elevations after being temporally and horizontally averaged.
For the one-dimensional vertical diffusion model, any variable such as cross- and along-canyon wind velocities (U and V, respectively; m s−1), potential temperature (Θ; K), and specific humidity (Q; kg kg−1) is presented using Reynolds averaging. The one-dimensional time-averaged momentum equations in the cross- and along-canyon components can be shown as (Santiago and Martilli, 2010; Krayenhoff, 2014; Krayenhoff et al., 2015, 2020; Simón-Moral et al., 2017; Nazarian et al., 2020)
where (Pa) is time-averaged pressure. The terms on the right-hand side of Eqs. (8) and (9) are the vertical gradient of turbulent flux of momentum (I), acceleration due to the large-scale pressure gradient (II), and the sum of pressure, building form, building skin, and vegetation drag terms (III). The parameterization of the latter term is detailed in Appendix A. K theory is used to parameterize the vertical momentum fluxes, i.e., and (the same approach will be used in potential temperature and specific humidity equations), where the diffusion coefficient is calculated using a k–ℓ turbulence model,
where Ck (–) is a constant and ℓk (m) is a length scale optimized using sensitivity analysis based on CFD (Nazarian et al., 2020). Note that the plan area density λp (–) in this study is greater than the limit considered by Nazarian et al. (2020), so we assume that the parameterizations extrapolate to this value of λp (–). More details on Ck (–) and ℓk (m) are provided in Krayenhoff (2014) and Nazarian et al. (2020). The turbulent kinetic energy k (m2s−2) can be calculated using a prognostic equation (Krayenhoff et al., 2015):
where g (m s−2) is acceleration due to gravity and Θ0 (K) is a reference potential temperature. The terms on the right-hand side of Eq. (11) are shear production (I), turbulent transport of kinetic energy parameterized based on K theory (II), buoyant production and dissipation (III), wake production by urban obstacles and trees (IV), and dissipation (V). Parameterizations of the last two terms are presented in more detail in Appendix A and by Krayenhoff (2014). σk (–) is the turbulent Prandtl number for turbulent kinetic energy, which is generally suggested to be σk=1 (–) (Pope, 2000).
To calculate the vertical profile of potential temperature in the urban area, the energy transport equation can be derived as
where Prt (–) is the turbulent Prandtl number, the first term on the right-hand side is the turbulent transport of heat (I), and the heat sink and source terms (II) correspond to sensible heat exchanges with the roof (SΘR), ground (SΘG), walls (SΘW), urban vegetation SΘV, and radiative divergence SΘA (all in K s−1). These terms are detailed in Appendix A and by Krayenhoff (2014). The contribution of waste heat emissions from the building heating ventilation and air conditioning (HVAC) system SΘwaste (K s−1) is parameterized by
where QHVAC (W m−2) is total sensible waste heat released into the urban atmosphere per building footprint area, Fst (–) is the fraction of waste heat released at street level, while the remainder fraction (1−Fst) (–) is released at roof level, and Δz (m) is grid discretization in the vertical direction. Depending on the type of building, waste heat emissions can be partially released at street level and the rest at roof level, which can be adjusted by changing Fst (–) from 0 to 1. For the BUBBLE campaign, it is assumed that all waste heat was released at roof level, which is more typical in most energy-retrofitted mid-rise apartments (Christen and Vogt, 2004; Rotach et al., 2005). The term QHVAC (W m−2) is calculated by the building energy model as
under cooling and heating modes, respectively. In this notation all symbols represent positive quantities unless a negative quantity is emphasized by the negative sign in front of the symbol in the equation. Under cooling mode QHVAC (W m−2) is calculated by adding the cooling demand (Qcool; W m−2), consisting of surface cooling demand, ventilation demand, infiltration (or exfiltration) demand, internal energy demand (lighting, equipment, and occupants), energy consumption of the cooling system (; W m−2; accounting for the coefficient of performance, COP, –), dehumidification demand (Qdehum; W m−2), energy consumption by gas combustion (e.g., cooking) (Qgas; W m−2), and energy consumption for water heating (Qwater; W m−2). Under heating mode, QHVAC (W m−2) is calculated by adding the heating demand (Qheat; W m−2), consisting of surface heating demand, ventilation demand, infiltration (or exfiltration) demand, and internal energy demand (lighting, equipment, and occupants) (divided by thermal efficiency of the heating system, ηheat; –), then subtracting the heating demand and adding the dehumidification demand (Qdehum; W m−2), energy consumption by gas combustion (e.g., cooking) (Qgas; W m−2) and energy consumption for water heating (Qwater; W m−2). To complete the urban one-dimensional vertical diffusion model, the transport equation for specific humidity is
where (kg kg−1) is time-averaged specific humidity. The turbulent transport of specific humidity (I) is parameterized based on K theory, Sct (–) is the turbulent Schmidt number, and the source term SQV () (II) is caused by latent heat from vegetation as detailed in Appendix A and by Krayenhoff (2014).
2.1.4 Building energy model
In this study, the balance equation for convection, conduction, and radiation heat fluxes is applied to all building elements (walls, roof, floor, windows, ceiling, and internal mass) to calculate the indoor air temperature. Then, a sensible heat balance equation, between convective heat fluxes released from indoor surfaces and internal heat gains as well as sensible heat fluxes from the HVAC system and infiltration (or exfiltration), is solved to obtain the time evolution of indoor temperature as
where −V (m3m−2) is indoor volume per building footprint area, Tin (K) is indoor air temperature, and the heat fluxes on the right-hand side are specified in Eqs. (14) and (15). More details on parameterization of the terms in Eq. (17) can be found in Appendix A and Bueno et al. (2012b). In this notation all symbols represent positive quantities; however, in the equation either positive or negative signs should be used to emphasize if a term contributes to indoor temperature increase or decrease, depending on the operation mode (cooling versus heating) and environmental conditions (indoor, outdoor, and surface temperatures).
A similar balance equation can be derived for latent heat to determine the time evolution of the indoor air specific humidity and the dehumidification load Qdehum (W m−2), which is parameterized in Bueno et al. (2012b). Note that energy consumption by gas combustion (e.g., cooking) Qgas and water heating Qwater (both in W m−2) does not influence indoor air temperature or specific humidity, but such energy consumption sources appear in the waste heat equations: Eqs. (14) and (15). These terms are determined from schedules (Bueno et al., 2012b).
The building energy model is a single-zone model with respect to both the indoor and outdoor (urban canopy) environments. That is, only a single temperature is assumed for indoor air, and only a single potential temperature is assumed for outdoor air by integrating the potential temperature profile over height from the street to roof levels. Further, all wall temperatures are assumed to be uniform with height.
2.1.5 Radiation model with vegetation
In VCWG, there are two types of vegetation: ground vegetation cover and trees. The ground vegetation cover fraction is specified by δs (–). Tree vegetation is specified by four parameters: tree height ht (m), tree crown radius rt (m), tree distance from canyon walls dt (m), and leaf area index (LAI) (m2m−2), which is the vertical integral of the leaf area density (LAD) (m2m−3) profile. VCWG considers two trees spaced from the walls of the canyon with distance dt (m). Trees cannot be higher than the building height. Both types of vegetation are specified with the same albedo αV (–) and emissivity εV (–). The VCWG user can change these input parameters for different vegetation structures. The radiation model in VCWG is adapted from the model developed by Meili et al. (2020). The net all-wave radiation flux is the sum of the net shortwave and longwave radiation fluxes:
where S↓, S↑, L↓, and L↑ (all in W m−2) represent the incoming shortwave, outgoing shortwave, incoming longwave, and outgoing longwave radiation fluxes. The incoming shortwave radiation fluxes (direct and diffuse) and the longwave radiation flux from the sky are forced by the EPW file. The absorbed (net) shortwave radiation on surface i is given by
where αi is the albedo of the surface, and and (W m−2) are the direct and diffuse incoming shortwave radiation fluxes to surface i. Here, i can be S, G, V, W, or T for sky, ground, ground vegetation, walls, and trees. The amount of direct shortwave radiation received by each urban surface is calculated considering shade effects according to well-established methodologies for the case with no trees (Masson, 2000; Kusaka et al., 2001; Wang et al., 2018) and with trees (Ryu et al., 2016). Sky view factors are used to determine the amount of diffuse shortwave radiation that reaches a surface from the sky. Infinite reflections of diffuse shortwave radiation are calculated within the urban canyon with the use of view factors for each pair of urban surfaces (Wang, 2010, 2014). The absorbed (net) longwave radiation for each surface is calculated by
where εi (–) is the emissivity of the surface, (1−εi) (–) is the reflectivity of the surface, (W m−2) is the incoming longwave radiation flux, is the Stefan–Boltzmann constant, and Ti (K) is the surface temperature. Infinite reflections of longwave radiation within the urban canyon are considered with the use of reciprocal view factors. These view factors are analytically derived for the case with no trees (Masson, 2000; Lee and Park, 2008; Wang et al., 2013). If trees are present, the view factors are calculated with a simplified two-dimensional Monte Carlo ray-tracing algorithm (Wang, 2014; Frank et al., 2016). More details about the radiation model are provided in Appendix A and by Meili et al. (2020).
2.2 Experimental field campaigns
To evaluate the model, VCWG's predictions are compared to observations from the Basel UrBan Boundary Layer Experiment (BUBBLE) (Christen and Vogt, 2004; Rotach et al., 2005), which was conducted for 8 months from December 2001 to July 2002. The urban microclimate field measurements were conducted in Basel, Switzerland, in a typical quasi two-dimensional urban canyon (47.55∘ N and 7.58∘ E). An EPW file is used to force the VCWG simulations with rural measurements. The rural measurements correspond to a site 7 km southeast of the city (47.53∘ N and 7.67∘ E). The average building height for the urban area is Havg=14.6 m, and the plan area density is λp=0.54 (–). The urban canyon axis is oriented in the northeast–southwest direction with a canyon axis angle of θcan=65∘. The x and y directions are set to be cross- and along-canyon, respectively. The frontal area density is λf=0.37 (–). In BUBBLE, potential temperature was measured at z=3.6, 11.3, 14.7, 17.9, 22.4, and 31.7 m a.g.l.; wind speed was measured at z=2.5, 13.9, 17.5, 21.5, 25.5, and 31.2 m a.g.l.; and relative humidity was measured at z=2.5 and 25.5 m a.g.l. The dataset provides the measurements averaged every 10 min. The model predictions of air temperature, wind speed, and specific humidity are compared to the observations on an hourly basis.
In this section, first the VCWG model results are evaluated against microclimate field measurements. Next, the model performance is explored through various parametric simulations. A uniform Cartesian grid with 2 m vertical resolution is used. The flow is assumed to be pressure-driven with the pressure gradient of (), which is decomposed into the x and y directions based on the wind angle and canyon orientation. This pressure gradient is forced as source terms on momentum Eqs. (8) and (9). The boundary conditions for potential temperature and specific humidity equations (Eqs. 12 and 16) are determined from the rural model (see Fig. 1). Thus, the VCWG is aimed to calculate momentum, temperature, specific humidity, and turbulent kinetic energy exchanges for the center of each cell in the vertical direction based on the boundary conditions obtained from the rural model, the building energy model, and the radiation model.
3.1 Detailed model–observation comparison
3.1.1 Model input variables
The results of the VCWG are compared to the measured data from the BUBBLE campaign. The input parameters representing the urban area are listed in Table 1. The input parameters are inferred from variables, datasets, and simulation codes in the literature that pertain to the BUBBLE campaign and associated models as well as general assumptions found in the literature (Raupach et al., 1991; Garratt, 1994; Hanna and Britter, 2002; Christen and Vogt, 2004; Järvi et al., 2011; Bueno et al., 2012a; Faroux et al., 2013; Ryu et al., 2016; Yang et al., 2017; Meili et al., 2020; Mussetti et al., 2020). In this table, note that the choices of average building height Havg=14.6 (m), street width w=18.2 (m), and the building width to street width ratio (–) provide (–) and (–), which are remarkably close to morphometric variables reported by Christen and Vogt (2004). The simulations are conducted for 8 months from December 2001 to July 2002. Usually the first 24 h of each month are treated as the model spin-up period. For analysis of each month, the simulation time is approximately 1 min; however, it can vary slightly depending on the grid spacing and time step.
Christen and Vogt (2004)Christen and Vogt (2004)Christen and Vogt (2004)Christen and Vogt (2004)Christen and Vogt (2004)Faroux et al. (2013)Yang et al. (2017)Mussetti et al. (2020)Ryu et al. (2016)Ryu et al. (2016)Ryu et al. (2016)Ryu et al. (2016)Christen and Vogt (2004)Bueno et al. (2012a)Bueno et al. (2012a)Ryu et al. (2016)Bueno et al. (2012a)Ryu et al. (2016)Bueno et al. (2012a)Bueno et al. (2012a)Raupach et al. (1991)Bueno et al. (2012a)Garratt (1994)Meili et al. (2020)Järvi et al. (2011)Meili et al. (2020)Hanna and Britter (2002)Christen and Vogt (2004)Bueno et al. (2012a)Bueno et al. (2012a)Christen and Vogt (2004)Table 1List of input parameters used in the VCWG for model evaluation; input variables are extracted from assumptions, datasets, and simulation codes available from Raupach et al. (1991), Garratt (1994), Hanna and Britter (2002), Christen and Vogt (2004), Järvi et al. (2011), Bueno et al. (2012a), Faroux et al. (2013), Ryu et al. (2016), Yang et al. (2017), Meili et al. (2020), and Mussetti et al. (2020).

3.1.2 Potential temperature
To compare VCWG results with measured meteorological variables from the BUBBLE campaign, the bias, root mean square error (RMSE), and coefficient of determination R2 are computed for pairs of model versus observed values every hour for available altitudes and months. This analysis is performed for wind speed, potential temperature, and specific humidity. Figure 3 and Table 2 show scatter plots of the observed versus simulated values of potential temperature and the statistical metrics used for the comparison. Over all altitudes and months, on average, the bias, RMSE, and R2 for potential temperature are 0.25 K, 1.41 K, and 0.82, respectively. These statistics are comparable to what has been reported in the literature for similar models that were compared against observations. For instance, Lauwaet et al. (2016) reported a bias, RMSE, and R2 of 0.76 K, 1.32 K, and 0.88, respectively, near the ground by comparing model and observation values in summer. Meili et al. (2020) reported a bias, RMSE, and R2 of −0.1 K,, 2.2 K,, and 0.98 respectively, near the ground by comparing model and observation values in a full year. Mussetti et al. (2020) reported a bias, RMSE, and R2 of 0.40 K, 1.53 K, and 0.95, respectively, near the ground by comparing model and observation values in summer. Ryu et al. (2016) reported a bias and RMSE of 0.67 and 0.99 K, respectively, near the ground by comparing model and observation values in summer. Bueno et al. (2012a) reported an average bias and RMSE of 0.6 and 0.9 K near the ground for June 2002. For the same month, VCWG predicts a bias, RMSE, and R2 of −0.1,K, 0.72,K, and 0.95 respectively, near the ground. This comparison reveals that the bias and RMSE are improved (reduced) compared to the predecessor UWG model.
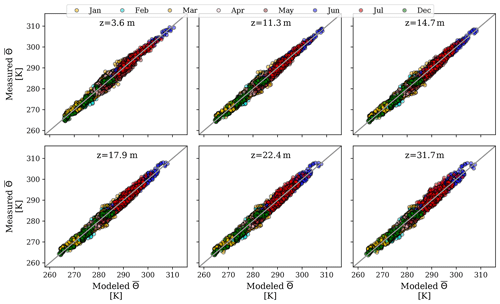
Figure 3Scatter plots of observed (BUBBLE) versus simulated (VCWG) values of potential temperature for different altitudes and months; each data point corresponds to a 1 h comparison between the model and observation.
Table 2Bias (K), RMSE (K), and R2 (–) for VCWG predictions of potential temperature against the BUBBLE observations for different altitudes and months.
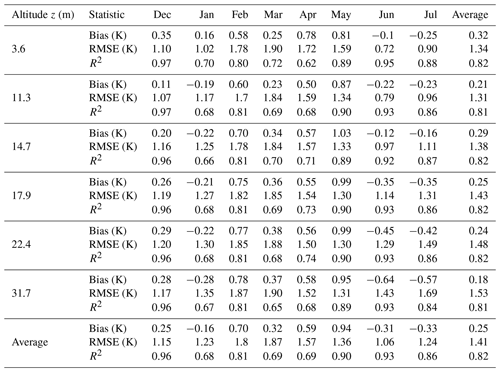
Figure 4 shows the diurnal variation of the observed versus simulated values of potential temperature averaged for every hour of the day for the available months. The diurnal patterns in temperature reveal that the model has similar skill in predicting the potential temperature during all hours at lower elevations (z=3.6 to 14.7 m). This performance is comparable to other models that show a well-captured diurnal variation of potential temperature at low altitudes (Bueno et al., 2012a; Krayenhoff et al., 2020; Meili et al., 2020; Mussetti et al., 2020). However, the diurnal pattern in temperature can deviate between the model and observations at higher elevations (z=17.9 to 31.7 m), especially during midday hours. This can be attributed to more complex flow patterns in the above-roof-level space due to heat advection, horizontal heterogeneity of the urban site, and the above-roof-level shear layer.
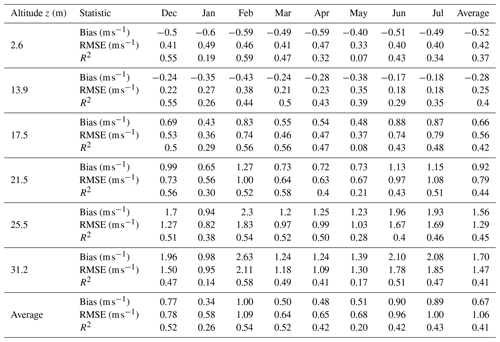
3.1.3 Wind speed
Figure 5 and Table 3 show scatter plots of the observed versus simulated values of wind speed and the statistical metrics used for the comparison. Considering all altitudes and months, the average bias, RMSE, and R2 are 0.67 m s−1, 1.06 m s−1, and 0.41, respectively. Although the comparison reveals a reasonable bias and RMSE, the R2 is lower than values reported for comparisons of potential temperature and specific humidity. This can be explained by the fact that the urban morphology is highly heterogeneous, the measurement of wind is location-specific, and the wind speed and direction can change considerably within each hour. Heterogeneous urban morphology results in great spatial variability of the components of wind velocity vector as a function of wind direction and wind speed (Klein and Clark, 2007; Klein and Galvez, 2015; Afshari and Ramirez, 2021). On the other hand, forced by hourly rural measurements, VCWG assumes a regular urban morphology and predicts the volume-averaged horizontal wind velocity components. So it is expected to obtain lower R2 values. Other models also often report lower R2 values for wind speed compared to potential temperature and specific humidity (Mussetti et al., 2020). Overall, our bias, RMSE, and R2 values are in agreement with values reported in the literature. For instance, Lemonsu et al. (2012) reported a range in bias of −0.16 to 0.56 m s−1. They also reported a range in RMSE of 0.40 to 0.69 m s−1. Mussetti et al. (2020) reported a bias, RMSE, and R2 of 0.61 m s−1, 1.31 m s−1, and 0.70 , respectively.
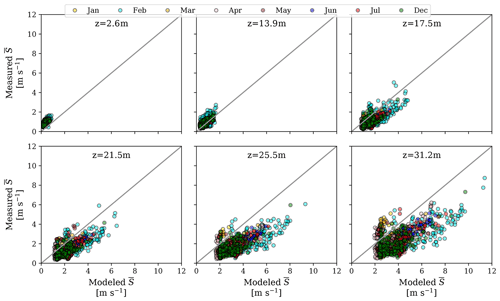
Figure 5Scatter plots of observed (BUBBLE) versus simulated (VCWG) values of wind speed for different altitudes and months; each data point corresponds to a 1 h comparison between the model and observation.
3.1.4 Specific humidity
Figure 6 and Table 4 show scatter plots of the observed versus simulated values of specific humidity and the statistical metrics used for the comparison. Note that specific humidity data were only available in June–July 2002. Over all altitudes and the available months, on average, the bias, RMSE, and R2 for specific humidity are 0.00057 kg kg−1, 0.0010 kg kg−1, and 0.85, respectively. These statistics are comparable to what has been reported in the literature for similar models that were compared against observations. For instance, Mussetti et al. (2020) reported a bias, RMSE, and R2 of −0.00109 kg kg−1, 0.00152 kg kg−1, and 0.74, respectively, above the urban canopy for comparisons of a model and observations in summer. Lemonsu et al. (2012) reported a range in bias of −0.00116 to −0.0005 kg kg−1. They also reported a range in RMSE of 0.00081 to 0.00172 kg kg−1.
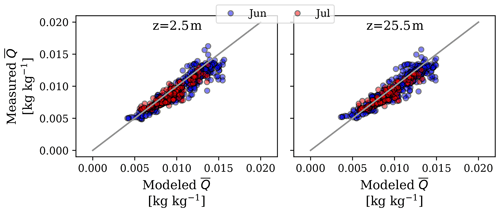
Figure 6Scatter plots of observed (BUBBLE) versus simulated (VCWG) values of specific humidity for different altitudes and months; each data point corresponds to a 1 h comparison between the model and observation.
Table 4Bias (kg kg−1), RMSE (kg kg−1), and R2 (–) for VCWG predictions of specific humidity against the BUBBLE observations for different altitudes and months.
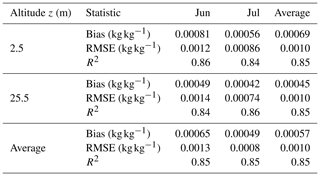
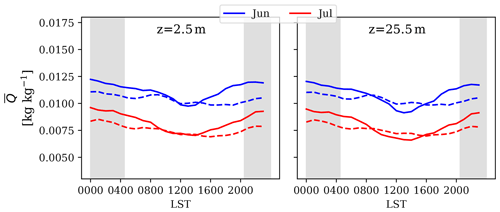
Figure 7 shows the diurnal variation of the observed versus simulated values of specific humidity averaged for every hour of the day for June–July 2002. While the diurnal variation is predicted by the model, some deviations are noted between the model and the observation. The model overpredicts the values at night, while it underpredicts the values during midday, especially at z=25.5 m. This could be due to the assumptions of the rural model to generate the vertical profile of specific humidity. In this model the latent heat flux in the rural area is parameterized as a function of the sensible heat flux and a fixed Bowen ratio. However, the Bowen ratio can vary diurnally (Kalanda et al., 1979). This can result in a slight miscalculation of the latent heat flux and a forcing boundary condition for specific humidity on top of the modeling domain.
3.1.5 Urban heat island (UHI)
To compare VCWG results with measured UHI (K) from the BUBBLE campaign, the bias, RMSE, and R2 are computed for pairs of hourly model versus observed values for the available months. UHI (K) for the observation is computed by considering the difference between the temperature measurements inside the canyon at z=3.6 m and temperatures provided by the EPW dataset. For VCWG, UHI (K) is calculated by considering the difference between the temperature prediction inside the canyon at z=3 m and temperatures provided by the EPW dataset. Figure 8 and Table 5 show the diurnal variation of UHI (for both observations and simulations) and the statistical metrics used for the comparison. On average, the bias, RMSE, and R2 for UHI (K) are 0.36 K, 1.2 K, and 0.35, respectively. VCWG predictions of UHI (K) are more successful for the months of December, January, April, May, June, and July (R2>0.3) than for the months of February and March (R2<0.2). The deviations in predicting UHI (K) may be attributed to several factors. The heterogeneity of the urban environment and placement of urban sensors may result in sensing slightly warmer or colder temperatures than the spatial average due to the spatial variability of temperature (Mussetti et al., 2020). Also, the relative position of the rural site with respect to the urban site, variation of dominant wind directions over different seasons, and horizontal advective transport of heat from the rural area may confound the prediction of UHI. Given that VCWG does not consider all such variations due to simplifying assumptions, it is expected to predict different values of UHI (K) over different seasons in comparison to observations. Nevertheless, overall, the statistics for UHI (K) comparison are in reasonable agreement with those reported by other models. For example, Mussetti et al. (2020) reported bias, RMSE, and R2 values of −1.88 K, 1.66 K, and 0.55, respectively, for near-ground predictions of UHI (K) in the summer.
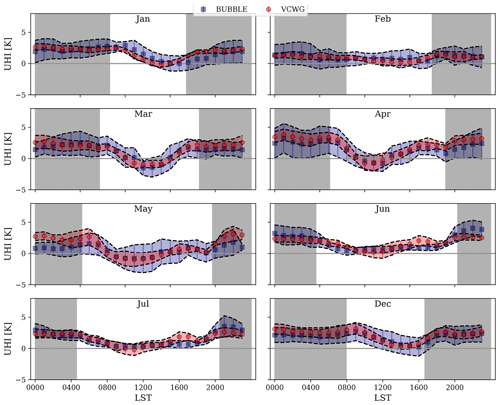
Figure 8Hourly mean and standard deviation (band) of UHI (K) in each month for the observed (BUBBLE) and predicted (VCWG) values; nighttime is indicated by shaded regions. Times are in local standard time (LST).
3.2 Model exploration and comparison with limited UHI observations
In this section we explore the capability of the VCWG model to predict urban climate for investigations of the effects of building dimensions, urban vegetation, building energy configuration, radiation configuration, seasonal variations, and other climates. These results are reported in the Supplement in detail. Here only brief references to the analysis are made. Many explorations consider both nighttime and daytime urban microclimate. First, we investigate how the urban geometry, which is characterized by plan area density λp (–) and frontal area density λf (–), can affect the urban microclimate. An increase in λp from 0.46 to 0.54 (–) is associated with lower air temperatures (due to shading) and reduces wind speed within the urban canyon during daytime (see Fig. S1 in the Supplement). An increase in λf from 0.37 to 0.51 (–) also increases shading effects and consequently reduces daytime temperatures, but it increases nighttime temperatures due to more heat released from urban surfaces that is trapped in the canyon (see Fig. S2 in the Supplement). The cooling effect of urban vegetation is also evaluated by changing the leaf area density (LAD; m2m−3) profiles within the canyon. Increasing the average LAD from 0.1 to 0.2 (m2m−3) shows heat removal from the canyon alongside lower wind speed due to the drag induced by trees (see Fig. S3 in the Supplement). VCWG simulations are also conducted for different building types (a mid-rise apartment and a hospital), cooling system coefficients of performance (–), heating thermal efficiencies ηheat (–), and locations of building waste heat release Fst (–). The results show that a hospital generates more waste heat fluxes associated with cooling and gas consumption, which increase urban temperatures (see Fig. S4 in the Supplement). The analysis of different cooling and heating systems also reveals that less efficient systems (lower COP from 3.13 to 1 (–) and ηheat from 0.8 to 0.4; –) result in more waste heat emission and slightly higher temperatures (see Fig. S5 in the Supplement). It is found that releasing building waste heat at street level contributes to a higher UHI (K), by 1 K, than releasing the waste heat at roof level (see Fig. S6 in the Supplement). This can be due to more effective heat removal from the urban roughness sublayer when the heat is released at roof level. The radiation model is assessed by VCWG simulations for different canyon aspect ratios and axis angles. The radiation fluxes at the road and walls show differences according to canyon aspect ratio and axis angle, while the fluxes at the tree canopy and roof are less sensitive to the canyon aspect ratio and axis angle (see Figs. S7 and S8). The performance of VCWG is assessed over different seasons with simulations for Vancouver for an entire year. It is found that early daytime UHI (K) values are lower than nighttime values, as expected. Also, the greatest UHI (K) values are predicted to occur in August and September (see Fig. S9 in the Supplement). Seasonal variations of the vertical profiles of potential temperature, wind speed, specific humidity, and turbulent kinetic energy reveal that the seasonal variations in potential temperature and specific humidity are higher than those associated with wind speed and turbulent kinetic energy (see Fig. S10 in the Supplement). Finally, the ability of the model to predict UHI (K) in different cities with different climate zones is assessed. The case studies are Buenos Aires, Vancouver, Osaka, and Copenhagen (see Fig. S11 in the Supplement). All exploration results obtained from the VCWG are reasonably consistent with previous observations in the literature.
The Vertical City Weather Generator (VCWG) is an urban microclimate model designed to calculate vertical profiles of meteorological variables including potential temperature, wind speed, specific humidity, and turbulent kinetic energy in an urban area. The VCWG is composed of four sub-models for ingestion of urban parameters and meteorological variables in a rural area (as input and boundary conditions) as well as prediction of the meteorological variables in a nearby urban area, the building energy performance variables, and the shortwave and longwave radiation transfer processes. VCWG combines elements of several previous models developed by Santiago and Martilli (2010), Bueno et al. (2014), Krayenhoff (2014), Krayenhoff et al. (2015), and Meili et al. (2020) to generate a model with the ability to predict vertical profiles of urban meteorological variables forced by rural measurements with two-way coupling to both building energy and radiation models.
To evaluate VCWG, its predictions of potential temperature, wind speed, and specific humidity are compared to observations from the Basel UrBan Boundary Layer Experiment (BUBBLE) microclimate field campaign for 8 months from December 2001 to July 2002 (Christen and Vogt, 2004; Rotach et al., 2005). The model evaluation indicates that the VCWG predicts vertical profiles of meteorological variables in reasonable agreement with field measurements. The average bias, RMSE, and R2 for potential temperature are 0.25 K, 1.41 K, and 0.82, respectively. The average bias, RMSE, and R2 for wind speed are 0.67 m s−1, 1.06 m s−1, and 0.41, respectively. The average bias, RMSE, and R2 for specific humidity are 0.00057 kg kg−1, 0.0010 kg kg−1, and 0.85, respectively. In addition, the average bias, RMSE, and R2 for the urban heat island (UHI) are 0.36 K, 1.2 K, and 0.35, respectively. Based on the evaluations, the model performance is comparable to the performance of similar models. The performance of the model is further explored to investigate the effects of urban configurations such as plan and frontal area densities, varying levels of vegetation, building energy configuration, radiation configuration, seasonal variations, and different climate zones on the model predictions. The exploration results also show acceptable performance in agreement with known urban physical processes and observations.
This study shows that the urban microclimate model VCWG can successfully extend the spatial dimension of preexisting bulk flow (single-layer) urban microclimate models to one dimension in the vertical direction, while it also considers the relationship of the urban microclimate model to the rural meteorological measurements and the building energy conditions. The effect of the key urban elements such as building configuration, building energy systems (e.g., location of condensers and exhaust stacks), surface vegetation, and trees are considered, but there is still opportunity to improve VCWG further. The urban site is simplified as blocks of buildings with symmetric and regular dimensions, which can be more realistically represented if more considerations are taken into account regarding the nonuniform distribution of building dimensions. Also, the building energy model in VCWG is a single-zone model, assuming a uniform temperature with height in both indoor and outdoor environments. This limitation can be overcome by improving the radiation model, urban vertical diffusion model, and building energy model so that wall and indoor temperatures can vary with height, allowing the development of a multi-zone building energy model. In addition, horizontal advection from the rural area can be considered and parameterized in future work. Future studies can also focus on an improvement of the flow-field parameterization or include additional source and sink terms in the transport equations to model horizontal motions, eddies, and flow fluctuations in the urban area, which is realistically very three-dimensional and heterogeneous. Urban hydrology can be added to VCWG in the future to account for precipitation effects. At present, the developed VCWG model can account for the spatial variation of urban microclimate in a computationally efficient manner independent of an auxiliary mesoscale model. This advantage is really important for urban planners, architects, and consulting engineers for operationally fast VCWG simulations.
A1 Surface energy balance in the rural area
In Eq. (7) the net shortwave solar radiation flux absorbed at the surface can be calculated from
where Fveg (–) is the fraction of the rural area covered by vegetation, αrur (–) is overall albedo of the rural area, αV (–) is the albedo of vegetation (here considered to be the same for rural and urban vegetation), and S↓direct and S↓diffuse (W m−2) are the forcing direct and diffuse shortwave radiation fluxes from the EPW file, respectively. The net longwave radiation flux absorbed at the surface can be calculated from
where L↓ (W m−2) is the forcing longwave radiation flux from the EPW file, L↑ (W m−2) is the longwave radiation flux leaving the rural surface at temperature Ts,rur (K), and εrur (–) is rural surface emissivity. The net sensible heat flux is calculated using Louis (1979):
where R (–) is a model constant, RiB (–) is the bulk Richardson number, and Fh (–) is the stability function for sensible heat flux defined by Louis (1979). The net latent heat flux is calculated using the Bowen ratio βrur (–) such that (W m−2). The ground heat flux drives the conduction equation at the uppermost soil layer via Bueno et al. (2012a):
where d (m) is the soil layer thickness, Cv () is volumetric heat capacity of soil, (K) is soil upper layer temperature (the same as soil surface temperature), C () is the soil thermal conductance, and T2 (K) is soil temperature in the second layer underground. In the lowest layer (n) of soil the conduction equation is forced by a deep soil temperature Tdeep (K):
A2 Source and sink term in the 1D model
The pressure and skin drags exerted on the flow in Eqs. (8) and (9) are formulated as follows (Santiago and Martilli, 2010; Krayenhoff, 2014; Krayenhoff et al., 2015, 2020; Simón-Moral et al., 2017; Nazarian et al., 2020):
where term I represents a dispersive pressure variation (form drag) induced by vegetation and building, and term II represents the dispersive viscous dissipation (skin drag) induced by horizontal surfaces. The former can be parameterized as
where BD (m−1) is the sectional building area density, CDBv (–) is the sectional drag coefficient in the presence of trees, LAD (m2m−3) is leaf area density in the canyon, Ω (–) is a clumping factor, CDV (–) is the drag coefficient for tree foliage, and and (m s−1) are wind velocity components in the x and y directions from a previous numerical solution, respectively, which are explicitly assumed to be constants to linearize the system of equations to be solved. The skin drag can be parameterized as follows:
where cd (–) is skin drag coefficient and fm (–) is a function of stability from Louis (1979). The terms related to the wake production Swake and dissipation rate ε (both in m2s−3) in Eq. (11) can be parameterized as
where Ω (–) is a clumping factor, Cε (–) is a model constant, and ℓε,dissip (m) is a dissipation length scale obtained through a sensitivity study using CFD (Nazarian et al., 2020). Note that plan area density λp (–) in this study is greater than the limit considered by Nazarian et al. (2020), so we assume that the parameterizations extrapolate to this value of λp (–). The heat source and sink terms, which are the terms in Eq. (12), caused by the roof (SΘR) and ground (SΘG) (both in K s−1) are calculated based on the study by Louis (1979) and the heat flux from the wall (SΘW; K s−1) is formulated in Martilli et al. (2002). The two other source and sink terms can be parameterized as follows:
where LA (W m−2) is the absorbed flux density of longwave radiation in the canyon, ρabs (kg m−3) is the density of absorbing molecules, kair (m2 kg−1) is their mass extinction cross section, (–) is the fraction of total volume that is outdoor air, gHa () is conductance for heat, cPM () is the molar heat capacity for the air, and (K) is the potential temperature of tree foliage. In the specific humidity equation, Eq. (16), the source and sink term can be calculated using the following equation:
where ΛM (J mol−1) is the molar latent heat of vaporization, Λ (J kg−1) is the latent heat of vaporization, gv () is the average surface and boundary layer conductance for humidity for the whole leaf, s (K−1) is a derivative of saturation vapor pressure with respect to temperature divided by pressure, D (Pa) is the vapor deficit of the atmosphere, and P (Pa) is atmospheric pressure.
A3 Building heat exchanges
The heat fluxes in Eq. (17) can be parameterized as
where hi () is the convective heat transfer coefficient for surface i, and Ai (m2 m−2) is the surface area for surface i per building footprint area. Surface i can correspond to indoor elements such as ceiling, walls, floor, building mass, and windows. Tsi (K) is the temperature of the inner layer of elements, Tin (K) is indoor temperature, Tout (K) is the outdoor temperature averaged over building height, Tsupp (K) is supply temperature, () is the mass flow rate of infiltration (exfiltration) per building footprint area, and () is mass flow rate of ventilated air in the HVAC system per building footprint area.
A4 Radiation model
A summary of details for the radiation model is provided here from Meili et al. (2020). The direct and diffuse shortwave radiation fluxes absorbed by each urban element are computed as functions of urban canyon height, width, tree shape, and albedo. The urban geometry creates shading effects by blocking a portion of the incoming direct solar radiation flux. This flux is further decreased by the sky view factor, which reduces the incoming diffuse solar radiation flux and traps reflected solar rays within the canyon. Two steps are involved to calculate the net shortwave radiation flux: (1a) the direct shortwave radiation flux received by each urban element is calculated as a function of the sun position and shading effects created by buildings and trees; (1b) the diffuse shortwave radiation received by each urban element is computed as a function of the corresponding sky view factor; (2) infinite radiation reflections within the urban canyon are calculated using view factors, and the net shortwave radiation flux for each urban element is then calculated. All urban elements are assumed to be Lambertian with isotropic scattering and reflections. If there are no trees, the view factors are computed analytically. Otherwise, a Monte Carlo ray-tracing algorithm is used. No obstructions are considered for roofs; i.e., trees cannot be taller than buildings. The model computes the net shortwave radiation flux due to both direct and diffuse radiation, allowing to investigate effects of shade and albedo in detail. The energy associated with the shortwave radiation exchange on each urban element is conserved.
For net longwave radiation flux on each urban surface, the difference between the incoming and outgoing longwave radiation fluxes is considered. These fluxes depend on surface temperatures. Infinite reflections of longwave radiation within the urban canyon are considered. Again, no obstructions are considered for roofs; i.e., trees cannot be taller than buildings. The canyon air does not impact the radiation exchange. The energy associated with the longwave radiation exchange on each urban surface is conserved.
For the case of no trees, analytical view factors are calculated using standard equations (Masson, 2000; Lee and Park, 2008; Ryu et al., 2011; Wang et al., 2013), while for trees the method of Ryu et al. (2016) is used. View factors meet three requirements: (1) the self-view factor of a flat surface is zero, (2) energy at the surface is conserved, and (3) view factors are reciprocal. The view factors for the case with trees are calculated using a Monte Carlo ray-tracing algorithm (Wang, 2014; Frank et al., 2016). This algorithm performs a probabilistic sampling of all rays emitted by an urban element. The relative frequency of rays emitted by one element that hit another element is an estimation of the view factor between the two elements. On each element, a large number of randomly distributed emitting points are considered. These view factors are also corrected for the three requirements mentioned above.
The VCWG v1.3.2 is developed at the Atmospheric Innovations Research (AIR) Laboratory at the University of Guelph: http://www.aaa-scientists.com (last access: 10 February 2020). The source code is available under the GPL 3.0 license at https://opensource.org/licenses/GPL-3.0 (last access: October 2020) and can be downloaded from https://www.zenodo.org/ (last access: 10 February 2020; available at: https://doi.org/10.5281/zenodo.4457501; Moradi, 2021).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-14-961-2021-supplement.
MM wrote the paper with significant conceptual input from ESK and AAA as well as critical feedback from all co-authors. BB and LKN developed the base Urban Weather Generator (UWG) program in MATLAB. CM and SV translated UWG from MATLAB to Python. NN and ESK provided their code for the one-dimensional vertical diffusion model for the urban climate that was integrated into VCWG. MM and AAA developed the Vertical City Weather Generator (VCWG) program in Python by integrating various modeling components developed by BB, LKN, CM, SV, ESK, and NN. BD, AN, MKN, and MRN edited the paper.
The authors declare that they have no conflict of interest.
The computational platforms were set up with the assistance of Jeff Madge, Joel Best, and Matthew Kent at the University of Guelph. The authors thank Alberto Martilli at the Centre for Energy, Environment and Technology (CIEMAT) in Madrid, Spain, who developed and shared an earlier version of the one-dimensional vertical diffusion model for the urban climate. The authors thank Naika Meili at the Institute of Environmental Engineering, ETH Zurich, Zurich, Switzerland, who developed and shared an earlier version of the urban radiation model. The authors also thank Andreas Christen at the University of Freiburg (Environmental Meteorology), Freiburg, Germany, who provided the observation data from an extended period of the BUBBLE campaign.
This work was supported by the following: the University of Guelph through the International Graduate Tuition Scholarship (IGTS) for the lead author; the Accelerate program (460847) from Mathematics of Information Technology and Complex Systems (MITACS); the Discovery Grant program (401231) from the Natural Sciences and Engineering Research Council (NSERC) of Canada; the Government of Ontario through the Ontario Centres of Excellence (OCE) under the Alberta–Ontario Innovation Program (AOIP) (053450); and Emission Reduction Alberta (ERA) (053498). OCE is a member of the Ontario Network of Entrepreneurs (ONE).
This research has been supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada (grant no. 401231), the Government of Ontario (grant no. 053450), Emission Reduction Alberta (grant no. 053498), and the Accelerate program (460847) from Mathematics of Information Technology and Complex Systems (MITACS).
This paper was edited by Wolfgang Kurtz and reviewed by four anonymous referees.
Afshari, A. and Ramirez, N.: Improving the accuracy of simplified urban canopy models for arid regions using site-specific prior information, Urban Clim., 35, 100722, https://doi.org/10.1016/j.uclim.2020.100722, 2021. a
Akbari, H., Pomerantz, M., and Taha, H.: Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas, Sol. Energy, 70, 295–310, https://doi.org/10.1016/S0038-092X(00)00089-X, 2001. a, b
Aliabadi, A. A., Krayenhoff, E. S., Nazarian, N., Chew, L. W., Armstrong, P. R., Afshari, A., and Norford, L. K.: Effects of roof-edge roughness on air temperature and pollutant concentration in urban canyons, Bound.-Lay. Meteorol., 164, 249–279, https://doi.org/10.1007/s10546-017-0246-1, 2017. a, b, c
Aliabadi, A. A., Veriotes, N., and Pedro, G.: A Very Large-Eddy Simulation (VLES) model for the investigation of the neutral atmospheric boundary layer, J. Wind Eng. Ind. Aerod., 183, 152–171, https://doi.org/10.1016/j.jweia.2018.10.014, 2018. a
Aliabadi, A. A., Moradi, M., Clement, D., Lubitz, W. D., and Gharabaghi, B.: Flow and temperature dynamics in an urban canyon under a comprehensive set of wind directions, wind speeds, and thermal stability conditions, Environ. Fluid Mech., 19, 81–109, https://doi.org/10.1007/s10652-018-9606-8, 2019. a, b
Armson, D., Stringer, P., and Ennos, A.: The effect of tree shade and grass on surface and globe temperatures in an urban area, Urban For. Urban Green., 11, 245–255, https://doi.org/10.1016/j.ufug.2012.05.002, 2012. a, b
Basu, S. and Lacser, A.: A cautionary note on the use of Monin–Obukhov similarity theory in very high-resolution large-eddy simulations, Bound.-Lay. Meteorol., 163, 351–355, https://doi.org/10.1007/s10546-016-0225-y, 2017. a
Blocken, B.: Computational Fluid Dynamics for urban physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations, Build. Environ., 91, 219–245, https://doi.org/10.1016/j.buildenv.2015.02.015, 2015. a, b
Bornstein, R. D.: The two-dimensional URBMET urban boundary layer model, J. Appl. Meteorol., 14, 1459–1477, https://doi.org/10.1175/1520-0450(1975)014<1459:TTDUUB>2.0.CO;2, 1975. a
Britter, R. E. and Hanna, S. R.: Flow and dispersion in urban areas, Annu. Rev. Fluid Mech., 35, 469–496, https://doi.org/10.1146/annurev.fluid.35.101101.161147, 2003. a
Broadbent, A. M., Coutts, A. M., Nice, K. A., Demuzere, M., Krayenhoff, E. S., Tapper, N. J., and Wouters, H.: The Air-temperature Response to Green/blue-infrastructure Evaluation Tool (TARGET v1.0): an efficient and user-friendly model of city cooling, Geosci. Model Dev., 12, 785–803, https://doi.org/10.5194/gmd-12-785-2019, 2019. a
Brutsaert, W.: Evaporation into the atmosphere, Springer, Dordrecht, https://doi.org/10.1007/978-94-017-1497-6, 1982. a, b
Bueno, B., Norford, L. K., Pigeon, G., and Britter, R.: Combining a detailed building energy model with a physically-based urban canopy model, Bound.-Lay. Meteorol., 140, 471–489, https://doi.org/10.1007/s10546-011-9620-6, 2011. a
Bueno, B., Norford, L. K., Hidalgo, J., and Pigeon, G.: The urban weather generator, J. Build. Perf. Simulat., 6, 269–281, https://doi.org/10.1080/19401493.2012.718797, 2012a. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q
Bueno, B., Pigeon, G., Norford, L. K., Zibouche, K., and Marchadier, C.: Development and evaluation of a building energy model integrated in the TEB scheme, Geosci. Model Dev., 5, 433–448, https://doi.org/10.5194/gmd-5-433-2012, 2012b. a, b, c, d
Bueno, B., Roth, M., Norford, L. K., and Li, R.: Computationally efficient prediction of canopy level urban air temperature at the neighbourhood scale, Urban Clim., 9, 35–53, https://doi.org/10.1016/j.uclim.2014.05.005, 2014. a, b, c, d, e, f
Businger, J. A., Wyngaard, J. C., Izumi, Y., and Bradley, E. F.: Flux-profile relationships in the atmospheric surface layer, J. Atmos. Sci., 28, 181–189, https://doi.org/10.1175/1520-0469(1971)028<0181:FPRITA>2.0.CO;2, 1971. a, b, c
Chen, F., Kusaka, H., Bornstein, R., Ching, J., Grimmond, C. S. B., Grossman-Clarke, S., Loridan, T., Manning, K. W., Martilli, A., Miao, S., Sailor, D., Salamanca, F. P., Taha, H., Tewari, M., Wang, X., Wyszogrodzki, A. A., and Zhang, C.: The integrated WRF/urban modelling system: development, evaluation, and applications to urban environmental problems, Int. J. Climatol., 31, 273–288, https://doi.org/10.1002/joc.2158, 2011. a
Chin, H.-N. S., Leach, M. J., Sugiyama, G. A., Leone Jr, J. M., Walker, H., Nasstrom, J., and Brown, M. J.: Evaluation of an urban canopy parameterization in a mesoscale model using VTMX and URBAN 2000 Data, Mon. Weather Rev., 133, 2043–2068, https://doi.org/10.1175/MWR2962.1, 2005. a
Christen, A. and Vogt, R.: Energy and radiation balance of a central European city, Int. J. Climatol., 24, 1395–1421, https://doi.org/10.1002/joc.1074, 2004. a, b, c, d, e, f, g, h, i, j, k, l, m, n
Crank, P. J., Sailor, D. J., Ban-Weiss, G., and Taleghani, M.: Evaluating the ENVI-met microscale model for suitability in analysis of targeted urban heat mitigation strategies, Urban Clim., 26, 188–197, https://doi.org/10.1016/j.uclim.2018.09.002, 2018. a
Dupont, S., Otte, T. L., and Ching, J. K. S.: Simulation of meteorological fields within and above urban and rural canopies with a mesoscale model, Bound.-Lay. Meteorol., 113, 111–158, https://doi.org/10.1023/B:BOUN.0000037327.19159.ac, 2004. a, b, c
Dyer, A. J.: A review of flux-profile relationships, Bound.-Lay. Meteorol., 7, 363–372, https://doi.org/10.1007/BF00240838, 1974. a, b, c
Erell, E. and Williamson, T.: Simulating air temperature in an urban street canyon in all weather conditions using measured data at a reference meteorological station, Int. J. Climatol., 26, 1671–1694, https://doi.org/10.1002/joc.1328, 2006. a
Faroux, S., Kaptué Tchuenté, A. T., Roujean, J.-L., Masson, V., Martin, E., and Le Moigne, P.: ECOCLIMAP-II/Europe: a twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface, meteorological and climate models, Geosci. Model Dev., 6, 563–582, https://doi.org/10.5194/gmd-6-563-2013, 2013. a, b, c
Frank, A., Heidemann, W., and Spindler, K.: Modeling of the surface-to-surface radiation exchange using a Monte Carlo method, J. Phys. Conf. Ser., 745, 032143, https://doi.org/10.1088/1742-6596/745/3/032143, 2016. a, b
Garratt, J.: The Atmospheric Boundary Layer, Cambridge University Press, London, 1994. a, b, c, d
Gowardhan, A. A., Pardyjak, E. R., Senocak, I., and Brown, M. J.: A CFD-based wind solver for an urban fast response transport and dispersion model, Environ. Fluid Mech., 11, 439–464, https://doi.org/10.1007/s10652-011-9211-6, 2011. a
Grimmond, C. S. B. and Oke, T. R.: Aerodynamic properties of urban areas derived from analysis of surface form, J. Appl. Meteorol., 38, 1262–1292, https://doi.org/10.1175/1520-0450(1999)038<1262:APOUAD>2.0.CO;2, 1999. a
Grimmond, C. S. B., Souch, C., and Hubble, M. D.: Influence of tree cover on summertime surface energy balance fluxes, San Gabriel Valley, Los Angeles, Clim. Res., 6, 45–57, 1996. a, b
Gros, A., Bozonnet, E., and Inard, C.: Cool materials impact at district scale: Coupling building energy and microclimate models, Sustain. Cities Soc., 13, 254–266, https://doi.org/10.1016/j.scs.2014.02.002, 2014. a
Hamdi, R. and Masson, V.: Inclusion of a drag approach in the Town Energy Balance (TEB) Scheme: Offline 1D Evaluation in a Street Canyon, J. Appl. Meteorol. Clim., 47, 2627–2644, https://doi.org/10.1175/2008JAMC1865.1, 2008. a
Hanna, S. R. and Britter, R. E.: Wind flow and vapor cloud dispersion at industrial and urban sites, American Institute of Chemical Engineers, New York, 2002. a, b, c, d
Järvi, L., Grimmond, C. S. B., and Christen, A.: The surface urban energy and water balance scheme (SUEWS): Evaluation in Los Angeles and Vancouver, J. Hydrol., 411, 219–237, https://doi.org/10.1016/j.jhydrol.2011.10.001, 2011. a, b, c, d, e
Joffre, S. M., Kangas, M., Heikinheimo, M., and Kitaigorodskii, S. A.: Variability of the stable and unstable atmospheric boundary-layer height and its scales over a Boreal forest, Bound.-Layer Meteorol., 99, 429–450, https://doi.org/10.1023/A:1018956525605, 2001. a
Kalanda, B. D., Oke, T. R., and Spittlehouse, D. L.: Suburban Energy Balance Estimates for Vancouver, B.C., Using the Bowen Ratio-Energy Balance Approach, J. Appl. Meteorol., 19, 791–802, https://doi.org/10.1175/1520-0450(1980)019<0791:SEBEFV>2.0.CO;2, 1979. a
Kastner-Klein, P., Berkowicz, R., and Britter, R.: The influence of street architecture on flow and dispersion in street canyons, Meteorol. Atmos. Phys, 87, 121–131, https://doi.org/10.1007/s00703-003-0065-4, 2004. a
Kikegawa, Y., Genchi, Y., Yoshikado, H., and Kondo, H.: Development of a numerical simulation system toward comprehensive assessments of urban warming countermeasures including their impacts upon the urban buildings' energy-demands, Appl. Energy, 76, 449–466, https://doi.org/10.1016/S0306-2619(03)00009-6, 2003. a
Kleerekoper, L., van Esch, M., and Salcedo, T. B.: How to make a city climate-proof, addressing the urban heat island effect, Resour. Conserv. Recy., 64, 30–38, https://doi.org/10.1016/j.resconrec.2011.06.004, 2012. a
Klein, P. and Clark, J. V.: Flow variability in a North American downtown street canyon, J. Appl. Meteorol. Clim., 46, 851–877, https://doi.org/10.1175/JAM2494.1, 2007. a
Klein, P. M. and Galvez, J. M.: Flow and turbulence characteristics in a suburban street canyon, Environ. Fluid Mech., 15, 419–438, https://doi.org/10.1007/s10652-014-9352-5, 2015. a
Kochanski, A. K., Pardyjak, E. R., Stoll, R., Gowardhan, A., Brown, M. J., and Steenburgh, W. J.: One-way coupling of the WRF-QUIC urban dispersion modeling system, J. Appl. Meteorol. Clim., 54, 2119–2139, https://doi.org/10.1175/JAMC-D-15-0020.1, 2015. a
Kondo, H., Genchi, Y., Kikegawa, Y., Ohashi, Y., Yoshikado, H., and Komiyama, H.: Development of a multi-layer urban canopy model for the analysis of energy consumption in a big city: structure of the urban canopy model and its basic performance, Bound.-Lay. Meteorol., 116, 395–421, https://doi.org/10.1007/s10546-005-0905-5, 2005. a
Kono, T., Ashie, Y., and Tamura, T.: Mathematical derivation of spatially-averaged momentum equations for an urban canopy model using underlying concepts of the immersed boundary method, Bound.-Lay. Meteorol., 135, 185–207, https://doi.org/10.1007/s10546-010-9475-2, 2010. a
Krayenhoff, E., Christen, A., Martilli, A., and Oke, T.: A multi-layer radiation model for urban neighbourhoods with trees, Bound.-Lay. Meteorol., 151, 139–178, https://doi.org/10.1007/s10546-013-9883-1, 2014. a, b
Krayenhoff, E. S.: A multi-layer urban canopy model for neighbourhoods with trees, PhD thesis, University of British Columbia, Vancouver, Canada, https://doi.org/10.14288/1.0167084, 2014. a, b, c, d, e, f, g, h, i
Krayenhoff, E. S. and Voogt, J. A.: A microscale three-dimensional urban energy balance model for studying surface temperatures, Bound.-Lay. Meteorol., 123, 433–461, https://doi.org/10.1007/s10546-006-9153-6, 2007. a, b, c
Krayenhoff, E. S., Santiago, J.-L., Martilli, A., Christen, A., and Oke, T. R.: Parametrization of drag and turbulence for urban neighbourhoods with trees, Bound.-Lay. Meteorol., 156, 157–189, https://doi.org/10.1007/s10546-015-0028-6, 2015. a, b, c, d, e, f, g, h, i, j, k
Krayenhoff, E. S., Jiang, T., Christen, A., Martilli, A., Oke, T. R., Bailey, B. N., Nazarian, N., Voogt, J. A., Giometto, M. G., Stastny, A., et al.: A multi-layer urban canopy meteorological model with trees (BEP-Tree): Street tree impacts on pedestrian-level climate, Urban Clim., 32, 100590, https://doi.org/10.1016/j.uclim.2020.100590, 2020. a, b, c, d, e, f
Kusaka, H., Kondo, H., Kikegawa, Y., and Kimura, F.: A simple single-layer urban canopy model for atmospheric models: comparison with multi-layer and slab models, Bound.-Lay. Meteorol., 101, 329–358, https://doi.org/10.1023/A:1019207923078, 2001. a, b, c, d, e
Lauwaet, D., De Ridder, K., Saeed, S., Brisson, E., Chatterjee, F., van Lipzig, N., Maiheu, B., and Hooyberghs, H.: Assessing the current and future urban heat island of Brussels, Urban Clim., 15, 1–15, https://doi.org/10.1016/j.uclim.2015.11.008, 2016. a
Lee, S.-H. and Park, S.-U.: A vegetated urban canopy model for meteorological and environmental modelling, Bound.-Lay. Meteorol., 126, 73–102, https://doi.org/10.1007/s10546-007-9221-6, 2008. a, b, c
Lemonsu, A., Masson, V., Shashua-Bar, L., Erell, E., and Pearlmutter, D.: Inclusion of vegetation in the Town Energy Balance model for modelling urban green areas, Geosci. Model Dev., 5, 1377–1393, https://doi.org/10.5194/gmd-5-1377-2012, 2012. a, b
Louis, J.-F.: A parametric model of vertical eddy fluxes in the atmosphere, Bound.-Lay. Meteorol., 17, 187–202, https://doi.org/10.1007/BF00117978, 1979. a, b, c, d
Lundquist, K. A., Chow, F. K., and Lundquist, J. K.: An immersed boundary method for theWeather Research and Forecasting model, Mon. Weather Rev., 138, 796–817, https://doi.org/10.1175/2009MWR2990.1, 2010. a
Maronga, B., Gryschka, M., Heinze, R., Hoffmann, F., Kanani-Sühring, F., Keck, M., Ketelsen, K., Letzel, M. O., Sühring, M., and Raasch, S.: The Parallelized Large-Eddy Simulation Model (PALM) version 4.0 for atmospheric and oceanic flows: model formulation, recent developments, and future perspectives, Geosci. Model Dev., 8, 2515–2551, https://doi.org/10.5194/gmd-8-2515-2015, 2015. a
Martilli, A. and Santiago, J. L.: CFD simulation of airflow over a regular array of cubes. Part II: analysis of spatial average properties, Bound.-Lay. Meteorol., 122, 635–654, https://doi.org/10.1007/s10546-006-9124-y, 2007. a
Martilli, A., Clappier, A., and Rotach, M. W.: An urban surface exchange parameterisation for mesoscale models, Bound.-Lay. Meteorol., 104, 261–304, https://doi.org/10.1023/A:1016099921195, 2002. a, b, c, d
Masson, V.: A physically-based scheme for the urban energy budget in atmospheric models, Bound.-Lay. Meteorol., 94, 357–397, https://doi.org/10.1023/A:1002463829265, 2000. a, b, c, d, e, f
Masson, V., Grimmond, C. S. B., and Oke, T. R.: Evaluation of the Town Energy Balance (TEB) scheme with direct measurements from dry districts in two cities, J. Appl. Meteorol., 41, 1011–1026, https://doi.org/10.1175/1520-0450(2002)041<1011:EOTTEB>2.0.CO;2, 2002. a
Masson, V., Gomes, L., Pigeon, G., Liousse, C., Pont, V., Lagouarde, J. P., Voogt, J., Salmond, J., Oke, T. R., Hidalgo, J., Legain, D., Garrouste, O., Lac, C., Connan, O., Briottet, X., Lachérade, S., and Tulet, P.: The Canopy and Aerosol Particles Interactions in TOlouse Urban Layer (CAPITOUL) experiment, Meterol. Atmos. Phys., 102, 135–157, https://doi.org/10.1007/s00703-008-0289-4, 2008. a
Mauree, D., Blond, N., and Clappier, A.: Multi-scale modeling of the urban meteorology: Integration of a new canopy model in the WRF model, Urban Clim., 26, 60–75, https://doi.org/10.1016/j.uclim.2018.08.002, 2018. a
Meili, N., Manoli, G., Burlando, P., Bou-Zeid, E., Chow, W. T. L., Coutts, A. M., Daly, E., Nice, K. A., Roth, M., Tapper, N. J., Velasco, E., Vivoni, E. R., and Fatichi, S.: An urban ecohydrological model to quantify the effect of vegetation on urban climate and hydrology (UT&C v1.0), Geosci. Model Dev., 13, 335–362, https://doi.org/10.5194/gmd-13-335-2020, 2020. a, b, c, d, e, f, g, h, i, j, k, l, m
Mills, G.: An urban canopy-layer climate model, Theor. Appl. Climatol., 57, 229–244, https://doi.org/10.1007/BF00863615, 1997. a
Moeng, C.-H., Dudhia, J., Klemp, J., and Sullivan, P.: Examining two-way grid nesting for large eddy simulation of the PBL using the WRF model, Mon. Weather Rev., 135, 2295–2311, https://doi.org/10.1175/MWR3406.1, 2007. a
Monin, A. S. and Obukhov, A. M.: Basic regularity in turbulent mixing in the surface layer of the atmosphere, Tr. Akad. Nauk SSSR Geophiz. Inst., 24, 163–187, 1954. a
Moradi, M.: The Vertical City Weather Generator (VCWG) (Version v1.3.2), Zenodo, https://doi.org/10.5281/zenodo.4457501, 2021. a
Mussetti, G., Brunner, D., Henne, S., Allegrini, J., Krayenhoff, E. S., Schubert, S., Feigenwinter, C., Vogt, R., Wicki, A., and Carmeliet, J.: COSMO-BEP-Tree v1.0: a coupled urban climate model with explicit representation of street trees, Geosci. Model Dev., 13, 1685–1710, https://doi.org/10.5194/gmd-13-1685-2020, 2020. a, b, c, d, e, f, g, h, i, j
Nazarian, N. and Kleissl, J.: Realistic solar heating in urban areas: air exchange and street-canyon ventilation, Build. Environ., 95, 75–93, https://doi.org/10.1016/j.buildenv.2015.08.021, 2016. a, b
Nazarian, N., Martilli, A., and Kleissl, J.: Impacts of realistic urban heating, Part I: spatial variability of mean flow, turbulent exchange and pollutant dispersion, Bound.-Lay. Meteorol., 166, 367–393, https://doi.org/10.1007/s10546-017-0311-9, 2018. a, b
Nazarian, N., Krayenhoff, E. S., and Martilli, A.: A one-dimensional model of turbulent flow through “urban” canopies (MLUCM v2.0): updates based on large-eddy simulation, Geosci. Model Dev., 13, 937–953, https://doi.org/10.5194/gmd-13-937-2020, 2020. a, b, c, d, e, f, g, h, i
Paulson, C. A.: The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer, J. Appl. Meteorol., 9, 857–861, https://doi.org/10.1175/1520-0450(1970)009<0857:TMROWS>2.0.CO;2, 1970. a, b
Pope, S. B.: Turbulent flows, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9780511840531, 2000. a
Raupach, M. R., Antonia, R. A., and Rajagopalan, S.: Rough-Wall Turbulent Boundary Layers, Appl. Mech. Rev., 44, 1–25, https://doi.org/10.1115/1.3119492, 1991. a, b, c, d
Redon, E. C., Lemonsu, A., Masson, V., Morille, B., and Musy, M.: Implementation of street trees within the solar radiative exchange parameterization of TEB in SURFEX v8.0, Geosci. Model Dev., 10, 385–411, https://doi.org/10.5194/gmd-10-385-2017, 2017. a
Resler, J., Krč, P., Belda, M., Juruš, P., Benešová, N., Lopata, J., Vlček, O., Damašková, D., Eben, K., Derbek, P., Maronga, B., and Kanani-Sühring, F.: PALM-USM v1.0: A new urban surface model integrated into the PALM large-eddy simulation model, Geosci. Model Dev., 10, 3635–3659, https://doi.org/10.5194/gmd-10-3635-2017, 2017. a, b
Rotach, M. W., Vogt, R., Bernhofer, C., Batchvarova, E., Christen, A., Clappier, A., Feddersen, B., Gryning, S. E., Martucci, G., Mayer, H., Mitev, V., Oke, T. R., Parlow, E., Richner, H., Roth, M., Roulet, Y. A., Ruffieux, D., Salmond, J. A., Schatzmann, M., and Voogt, J. A.: BUBBLE–an Urban boundary layer meteorology project, Theor. Appl. Climatol., 81, 231–261, https://doi.org/10.1007/s00704-004-0117-9, 2005. a, b, c
Roth, M.: Review of atmospheric turbulence over cities, Q. J. Roy. Meteor. Soc., 126, 941–990, https://doi.org/10.1002/qj.49712656409, 2000. a
Ryu, Y.-H., Baik, J.-J., and Lee, S.-H.: A new single-layer urban canopy model for use in mesoscale atmospheric models, J. Appl. Meteorol. Clim., 50, 1773–1794, https://doi.org/10.1175/2011JAMC2665.1, 2011. a, b
Ryu, Y.-H., Bou-Zeid, E., Wang, Z.-H., and Smith, J. A.: Realistic representation of trees in an urban canopy model, Bound.-Lay. Meteorol., 159, 193–220, https://doi.org/10.1007/s10546-015-0120-y, 2016. a, b, c, d, e, f, g, h, i, j, k
Salamanca, F., Krpo, A., Martilli, A., and Clappier, A.: A new building energy model coupled with an urban canopy parameterization for urban climate simulations – part I. formulation, verification, and sensitivity analysis of the model, Theor. Appl. Climatol., 99, 331–344, https://doi.org/10.1007/s00704-009-0142-9, 2010. a, b
Salamanca, F., Georgescu, M., Mahalov, A., Moustaoui, M., and Wang, M.: Anthropogenic heating of the urban environment due to air conditioning, J. Geophys. Res.-Atmos., 119, 5949–5965, https://doi.org/10.1002/2013JD021225, 2014. a
Saneinejad, S., Moonen, P., Defraeye, T., Derome, D., and Carmeliet, J.: Coupled CFD, radiation and porous media transport model for evaluating evaporative cooling in an urban environment, J. Wind. Eng. Ind. Aerodyn., 104-106, 455–463, https://doi.org/10.1016/j.jweia.2012.02.006, 2012. a
Santiago, J. L. and Martilli, A.: A dynamic urban canopy parameterization for mesoscale models based on computational fluid dynamics Reynolds-Averaged Navier-Stokes microscale simulations, Bound.-Lay. Meteorol., 137, 417–439, https://doi.org/10.1007/s10546-010-9538-4, 2010. a, b, c, d, e, f, g, h
Simón-Moral, A., Santiago, J. L., and Martilli, A.: Effects of unstable thermal stratification on vertical fluxes of heat and momentum in urban areas, Bound.-Lay. Meteorol., 163, 103–121, https://doi.org/10.1007/s10546-016-0211-4, 2017. a, b, c
Soulhac, L., Salizzoni, P., Cierco, F.-X., and Perkins, R.: The model SIRANE for atmospheric urban pollutant dispersion; part I, presentation of the model, Atmos. Environ., 45, 7379–7395, https://doi.org/10.1016/j.atmosenv.2011.07.008, 2011. a
Stull, R. B.: An introduction to boundary layer meteorology, Kluwer Academic Publishers, Dordrecht, The Netherlands, https://doi.org/10.1007/978-94-009-3027-8, 1988. a
Talbot, C., Bou-Zeid, E., and Smith, J.: Nested mesoscale large-eddy simulations with WRF: performance in real test cases, J. Hydrometeorol., 13, 1421–1441, https://doi.org/10.1175/JHM-D-11-048.1, 2012. a
Tseng, Y.-H., Meneveau, C., and Parlange, M. B.: Modeling flow around bluff bodies and predicting urban dispersion using large eddy simulation, Environ. Sci. Technol., 40, 2653–2662, https://doi.org/10.1021/es051708m, 2006. a
Wang, C., Wang, Z.-H., and Yang, J.: Cooling effect of urban trees on the built environment of contiguous United States, Earth's Future, 6, 1066–1081, https://doi.org/10.1029/2018EF000891, 2018. a
Wang, H., Skamarock, W. C., and Feingold, G.: Evaluation of scalar advection schemes in the advanced research WRF model using large-eddy simulations of aerosol-cloud interactions, Mon. Weather Rev., 137, 2547–2558, https://doi.org/10.1175/2009MWR2820.1, 2009. a
Wang, Z.-H.: Geometric effect of radiative heat exchange in concave structure with application to heating of steel I-sections in fire, Int. J. Heat Mass Transf., 53, 997–1003, https://doi.org/10.1016/j.ijheatmasstransfer.2009.11.013, 2010. a
Wang, Z.-H.: Monte Carlo simulations of radiative heat exchange in a street canyon with trees, Sol. Energy, 110, 704–713, https://doi.org/10.1016/j.solener.2014.10.012, 2014. a, b, c
Wang, Z.-H., Bou-Zeid, E., and Smith, J. A.: A coupled energy transport and hydrological model for urban canopies evaluated using a wireless sensor network, Q. J. Roy. Meteor. Soc., 139, 1643–1657, https://doi.org/10.1002/qj.2032, 2013. a, b
Yaghoobian, N. and Kleissl, J.: Effect of reflective pavements on building energy use, Urban Clim., 2, 25–42, https://doi.org/10.1016/j.uclim.2012.09.002, 2012. a, b
Yang, H., Yang, X., Heskel, M., Sun, S., and Tang, J.: Seasonal variations of leaf and canopy properties tracked by ground-based NDVI imagery in a temperate forest, Sci. Rep.-UK, 7, 1267, https://doi.org/10.1038/s41598-017-01260-y, 2017. a, b, c
Yang, X. and Li, Y.: The impact of building density and building height heterogeneity on average urban albedo and street surface temperature, Build. Environ., 90, 146–156, https://doi.org/10.1016/j.buildenv.2015.03.037, 2015. a
Zajic, D., Fernando, H. J. S., Calhoun, R., Princevac, M., Brown, M. J., and Pardyjak, E. R.: Flow and turbulence in an urban canyon, J. Appl. Meteorol. Clim., 50, 203–223, https://doi.org/10.1175/2010JAMC2525.1, 2011. a
Zeng, X. and Dickinson, R. E.: Effect of surface sublayer on surface skin temperature and fluxes, J. Climate, 11, 537–550, https://doi.org/10.1175/1520-0442(1998)011<0537:EOSSOS>2.0.CO;2, 1998. a