Lossy compression of Earth system model data based on a hierarchical tensor with Adaptive-HGFDR (v1.0)

Lossy compression has been applied to the data compression of large-scale Earth system model data (ESMD) due to its advantages of a high compression ratio. However, few lossy compression methods consider both global and local multidimensional coupling correlations, which could lead to information loss in data approximation of lossy compression. Here, an adaptive lossy compression method, adaptive hierarchical geospatial field data representation (Adaptive-HGFDR), is developed based on the foundation of a stream compression method for geospatial data called blocked hierarchical geospatial field data representation (Blocked-HGFDR). In addition, the original Blocked-HGFDR method is also improved from the following perspectives. Firstly, the original data are divided into a series of data blocks of a more balanced size to reduce the effect of the dimensional unbalance of ESMD. Following this, based on the mathematical relationship between the compression parameter and compression error in Blocked-HGFDR, the control mechanism is developed to determine the optimal compression parameter for the given compression error. By assigning each data block an independent compression parameter, Adaptive-HGFDR can capture the local variation of multidimensional coupling correlations to improve the approximation accuracy. Experiments are carried out based on the Community Earth System Model (CESM) data. The results show that our method has higher compression ratio and more uniform error distributions compared with ZFP and Blocked-HGFDR. For the compression results among 22 climate variables, Adaptive-HGFDR can achieve good compression performances for most flux variables with significant spatiotemporal heterogeneity and fast changing rate. This study provides a new potential method for the lossy compression of the large-scale Earth system model data.

1 Introduction

Earth system model data (ESMD), which comprehensively characterize the spatiotemporal changes of the Earth system with multiple variables, are presented as multidimensional arrays of floating-point numbers (Kuhn et al., 2016; Simmons et al., 2016). With the rapid development of Earth system models in finer computational grids and growing ensembles of multi-scenario simulation experiments, ESMD have shown an exponential increase in data volume (Nielsen et al., 2017; Sudmanns et al., 2018). The huge data volume brings considerable challenges to the data computation, storage, and analysis on ordinary PCs, which will further limit the research and application of ESMD. Lossy compression, which focuses on saving large amounts of data space by approximating the original data, is considered an alternative solution to meet the challenge of the large data volume (Baker et al., 2016; Nathanael et al., 2013). However, ESMD, as a comprehensive interaction of Earth system variables at different aspects of space, time, and attributes, show significant multidimensional coupling correlations (Runge et al., 2019; Mashhoodi et al., 2019; Shi et al., 2019). The mixture of different coupling correlations then leads to complex structures, such as uneven distribution, spatial nonhomogeneity, and temporal nonstationary, which increase the difficulties in accurately approximating data in lossy compression. Thus, developing a lossy compression method that could adequately explore the multidimensional coupling correlations is an important way to reduce the compression error (Moon et al., 2017).

Predictive and transform methods are two of the most widely used lossy compression approaches in terms of how the data are approximated. Predictive lossy compression predicts the data with parametric functions, and the compression is achieved by typically retaining (and encoding) the residual between the predicted and actual data value. For example, NUMARCK learns emerging distributions of element-wise change ratios and encodes them into an index table to be concisely represented (Zheng et al., 2016). ISABELA applies a preconditioner to seemingly random and noisy data along spatial resolution to achieve an accurate fitting model for the data compression (Lakshminarasimhan et al., 2013). In these methods, the multidimensional ESMD are processed as sequences or series from low dimensions without considering the multidimensional coupling correlations. SZ, one of the most advanced lossy compression methods, features adaptive error-controlled quantization and variable-length encoding to achieve optimized compression (Ziv and Lempel, 2003). In SZ, a set of adjacent quantization bins are used to convert each original floating point data value to an integer along the first dimension of the data based on its prediction error (Di et al., 2019). With a well-designed error control mechanism, SZ can achieve uniform compression error distribution. However, SZ predicts the data point only along the first dimension, and it is not designed to be used along the other dimensions or use a dynamic selection mechanism for the dimension (Tao et al., 2017). This makes data inconsistency a problem for SZ, where the same ESMD with different organization orders can capture different multidimensional coupling correlations and further produce different compressed data.

Transform methods reduce data volume by transforming the original data to another space where the majority of the generated data are small, such that data compression can be achieved by storing a subset of the transform coefficients with a certain loss in terms of the user's required error (Diffenderfer et al., 2019; Andrew et al, 2020). One example is the image-based method, which slices ESMD from different dimensions into separate images and each image is then compressed by feature filtering with wavelet transformation or discrete Fourier transform. As the compression is applied to a single image slice, the coupling correlations among multiple dimensions are not always well utilized. More advanced methods like ZFP split the original data into small blocks with an edge size of four along each dimension and compress each block independently via a floating-point representation with a single common exponent per block, an orthogonal block transform, and embedded encoding (Tao et al., 2018). In ZFP, the multidimensional coupling correlations are integrated by treating all dimensions as a whole through multidimensional blocking. In each block, ZFP converts the high dimensional data into matrices, which flattens the data even further and partially destroys the internal correlations among multiple dimensions. Additionally, with only a single common exponent used in each block, it is inadequate to capture the local variation of the correlations. Thus, the ZFP method is extremely effective in terms of data reduction and accuracy for smooth variables but is unsurprisingly challenged by variables with abrupt value changes and ranges spanning many orders of magnitude, both of which are common in ESMD outputs (Baker et al., 2014).

Most of the current existing lossy compression methods, including predictive and transform lossy compression methods, integrate multidimensional coupling correlations into the process of data approximation as a foundation for mapping multidimensional data into low dimensional vectors or matrices (Wang et al., 2005). Few of these methods directly process multidimensional ESMD as a whole. For instance, current predictive methods usually split the original data into a series of local low dimensional data and then predict local data. In this way, the split data obtained by different split strategies could capture the different coupling correlations, which leads to further inconsistent compressed results for the same data. Transform methods map the original data to the small space by removing the redundant coupling correlations. Most of these methods have already considered the coupling correlations in the global region. However, each local region still utilizes data splitting that destroys the local coupling correlations, which results in a weak compression performance for ESMD with strong local variations. Therefore, constructing a lossy compression method that integrates both global and local coupling correlations from the perspective of multiple dimensions is helpful for improving the performance of lossy compression for ESMD.

Recently, tensor-based decomposition methods, such as canonical polyadic (CP), Tucker, and hierarchical tensor decomposition, have been introduced to the compression of the multidimensional data (Bengua et al., 2016; Jing et al., 2014). Tensor decomposition, which exploits the data features, as well as each mode and the corresponding coupling relationship, by considering the multidimensional data as a whole, can estimate the intrinsic structure of ESMD ignored in the metric model. The core motivation behind tensor-based decomposition is to eliminate the inconsistent, uncertain, and noisy data without destroying the intrinsic multidimensional coupling correlation structures (Kuang et al., 2018; Du et al., 2017). Among these methods, hierarchical tensor decomposition could achieve a higher quality at a larger compression ratio than traditional tensor methods through extracting data features level by level (Wu et al., 2008). Yuan et al. (2015) designed an improved hierarchical tensor method (blocked hierarchical geospatial field data representation, Blocked-HGFDR) to compress geospatial data with a hierarchical tree structure, showing obvious advantages in compression accuracy and compression efficiency. This hierarchical tensor-based method utilizes the multidimensional coupling correlations to approximate the original data by treating all dimensions as a whole, which can largely reduce the information loss in lossy compression. In Blocked-HGFDR, all local data have the same compression parameter, and the global average error is used to control the capture of the global multidimensional coupling correlation. Since ESMD are always spatiotemporally heterogeneous while the coupling correlations are varied in each local region, the same compression parameter applied to local data results in insufficient capturing of local coupling correlation. Although the global average error is relatively small, the obtained results tend to a certain “average” within the local data, which may make the local compression error very large and bring bias into the data approximation.

In this paper, the lossy compression for ESMD is developed based on Blocked-HGFDR. We firstly construct a division strategy that divides the original data into a series of data blocks with relatively balanced dimensions. Following this, the parameter control mechanism is designed to assign each data block an independent compression parameter under the given compression constraint. After that, Blocked-HGFDR is applied to each data block to achieve lossy compression. Experiments on a climate simulation data set with 22 variables are carried out to evaluate the performance and applicability of the methods in ESMD compression. The remainder of this paper is organized as follows. Section 2 introduces the basic ideas for developing an adaptive hierarchical geospatial field data representation (Adaptive-HGFDR) method. Section 3 discusses the block mechanism, the relationship between the compression parameter and compression error, and the fast search algorithm. Section 4 uses the temperature data to verify that the method can obtain an adaptive rank under the accuracy constraint. Section 5 discusses the effectiveness and computational efficiency of the method, as well as the results.

2 Basic idea

The lossy compression of ESMD should comprehensively consider the characteristics of ESMD. Firstly, since ESMD have multiple variables, the compression parameter of an ideal lossy compression should be simple and able to be flexibly adjusted according to the corresponding variables of ESMD. Secondly, since the acceptable error of different variables in ESMD is different, for example, the error of wind speed is very different from that of temperature, an ideal lossy compression should be able to adaptively select compression parameters for the acceptable error range of different variables. Considering that Blocked-HGFDR has a simple compression parameter, it can be used for the lossy compression of ESMD. Thirdly, since many variables of ESMD are spatiotemporally heterogeneous, the corresponding coupling correlations are variable within the local region. Thus, the correlations in both global and local regions should be well integrated in lossy compression to improve approximation accuracy.

In order to adequately integrate the multidimensional coupling correlations and adaptively select the compression parameter in Blocked-HGFDR, there are two issues to be considered. The first issue is the dimensional unbalance of ESMD. For instance, the data accumulated in the temporal dimension are typically longer than that in the spatial dimension for a spatiotemporal series with long observations. Since the tensor decomposition method treats each dimension equally and ignores the dimensional unbalance, it is difficult to accurately approximate data with unbalanced dimensions. Thus, it is better to split the original data into small local data blocks with the more balanced dimension structure and then apply the tensor decomposition to local data individually, which can reduce the approximation bias caused by the dimensional unbalance. The second issue is parameter selection under the given compression constraints. Since the coupling correlations of ESMD vary within local regions, for the given compression constraints, such as the maximum compression error, the compression parameter of different variables or data blocks should be selected flexibly according to the corresponding data characteristic, as to accurately capture the local variation of the coupling correlation and improve the approximation accuracy. Therefore, based on the mathematical relationship between the compression error and the compression parameter in Blocked-HGFDR, a control mechanism that can adjust the compression parameter according to the accuracy demands should be developed.

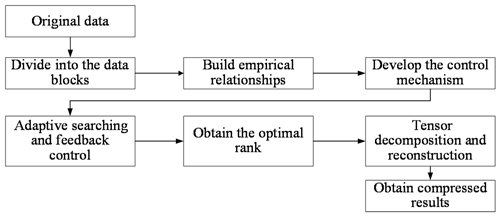
Based on the above considerations, our method, Adaptive-HGFDR, is developed according to the following three procedures (Fig. 1). Procedure 1 is the splitting of the original ESMD into small data blocks. In this procedure, the dimension in which to split the data and the optimal size of the data block are determined by conducting different combinations of data blocking in terms of the dimension and block counts. Procedure 2 consists of conducting the relationship between compression error and compression parameter. In order to obtain a uniform distribution of the compression error for each data block, an empirical relationship between the compression error and the rank value is established, in which the rank value of each data block can be adjusted at any given compression error. Procedure 3 entails adaptive searching for the optimal compression parameter. A binary search method is used to search the optimal compression parameter, which is updated with a parameter control mechanism until the compression error meets the given constraint.

Figure 1 Overall framework of the basic idea.

3 Method

3.1 Block hierarchical tensor compression

ESMD are a multidimensional array. It can be seen as a tensor with the spatiotemporal references and the associated attributes. Without a loss of generality, a three-dimensional tensor can be defined as $Z\in {\mathcal{R}}^{I\times J\times K}$ (Suiker and Chang, 2000), where I, J, and K are values that represent the number of grids along the dimensions of longitude, latitude, and time (or height), respectively. These dimensions are always unbalanced due to the different spatial and temporal resolutions. Thus, the data block is introduced to reduce the impact of dimension unbalance on the data compression.

Definition 1: data block

The spatiotemporal data, $Z\in {\mathcal{R}}^{I\times J\times K}$, can be considered to be composed of a series of local data with the same spatiotemporal reference. Here, local data are defined as a data block as follows:

$$\begin{array}{}\text{(1)}& \text{part}(Z,n)=\mathit{\{}{C}_{\mathrm{1}},C_{\mathrm{2}},\mathrm{\cdots },C_n\mathit{\}}.\end{array}$$

Here, part( ) is the function that divides the original tensor Z into a series of data blocks $\mathit{\{}{C}_i{\mathit{\}}}_{i=\mathrm{1}}^m$, each data block C_i includes local spatial and temporal information, and n is the number of data blocks. Compared with the original data, the dimensions of these data blocks are smaller and more balanced. For the divided data blocks, in order to adequately capture the multidimensional coupling correlation, the key point is how the compression parameter is determined according to the given compression error.

Definition 2: Blocked-HGFDR

Based on the divided data blocks, Yuan et al. (2015) proposed the Blocked-HGFDR method based on the hierarchical tensor compression. In this method, the hierarchical tensor compression is applied to each block, and then the hierarchical tensor compression of each data block is obtained by selecting the prominent feature components and filtering out the residual structure. This method utilizes the hierarchical structure of data features, greatly reducing data redundancy and thereby achieving the efficient compression of the amount of spatiotemporal data (Yuan et al., 2015). The overall compression of Blocked-HGFDR can be formulated as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }\left\{\begin{array}{l}H\left(A\right)=\\ (U_R\otimes U_{R-\mathrm{1}}\otimes \mathrm{\cdots }\otimes U_{\mathrm{1}}){\stackrel{\mathrm{̃}}{B}}_L{\stackrel{\mathrm{̃}}{B}}_{L-\mathrm{1}}\mathrm{\cdots }{\stackrel{\mathrm{̃}}{B}}_{\mathrm{1}}{B}_{\mathrm{12}\mathrm{\cdots }R}+\text{res}\\ {\stackrel{\mathrm{̃}}{B}}_j=B_{p_{L_j}}\otimes \mathrm{\cdots }\otimes B_{p_L}j=\left\{\mathrm{1},\mathrm{2},\mathrm{\dots },L\right\}.\end{array}\right.\end{array}$$

Similar to the prominent components obtained by singular value decomposition (SVD) for two-dimensional data (Yan et al., 2019), the matrix U_R and the sparse transfer tensor B_R are considered to be the rth component of a third-order tensor in each dimension, where R denotes the number of multi-domain features. The residual tensor, res, in Eq. (2) denotes the information not captured by the decomposition model, and $(U_R\otimes U_{R-\mathrm{1}}\otimes \mathrm{\cdots }\otimes U_{\mathrm{1}}){\stackrel{\mathrm{̃}}{B}}_L{\stackrel{\mathrm{̃}}{B}}_{L-\mathrm{1}}\mathrm{\cdots }{\stackrel{\mathrm{̃}}{B}}_{\mathrm{1}}{B}_{\mathrm{12}\mathrm{\cdots }R}$ in Eq. (2) is the reconstructed rth core tensor and feature matrix (Grasedyck, 2010; Song et al., 2013).

3.2 Adaptive selection of parameters and solutions

Considering that the distribution characteristic of each divided data block is different, the key to adequately capturing the multidimensional coupling correlations in Blocked-HGFDR is to adaptively select the compression parameter for local data individually according to the given compression error. So the key step is to construct controlling mechanism based on the relationship between the compression error and compression parameter. Thus, the following terms are defined.

Definition 3: the controlling mechanism

In Blocked-HGFDR, the relationship between the compression error and compression parameter (Rank) is given as $\mathit{\epsilon }=\mathit{\alpha }{\text{Rank}}^{-\mathit{\beta }}$ (Yuan et al., 2015); thus, the controlling mechanism to determine the compression parameter of each data block should be the rank value closest to the given compression error as follows:

$$\begin{array}{}\text{(3)}& \mathit{\epsilon }=\mathit{\alpha }{\text{Rank}}^{-\mathit{\beta }}\le {\mathit{\epsilon }}_{\text{Given}},\end{array}$$

where ε_Given is the given compression error that depends on different application scenarios, and α and β are the coefficients that depend on the structure and complexity of the data, which can be obtained by the simulation experiment for actual data.

In Blocked-HGFDR, the relationship between the compression ratio (φ) and compression parameter (Rank) is given as follows:

$$\begin{array}{}\text{(4)}& \mathit{\phi }={\displaystyle \frac{\text{datasize}}{a{\text{Rank}}^{\mathrm{3}}+b{\text{Rank}}^{\mathrm{2}}+c\text{Rank}+d}}.\end{array}$$

As shown in Eqs. (2), (3), and (4), when the rank decreases in Blocked-HGFDR, the compression ratio and the compression error increase. In Blocked-HGFDR, the rank value of different blocks is fixed, which results in the fluctuation of the compression error in the specific dimension. Since the structure of each block is different, the compression parameter of each data block should be determined independently according to the given compression error. Considering that the actual compression error may not strictly satisfy the given value, the optimal parameter is selected as the minimum rank in which the obtained compression error is close to the given one.

To find the optimal parameter for data block C_i with the above constructed controlling mechanism, a binary search algorithm based on dichotomy is constructed. This means that before adjusting the rank each time, the optimal rank corresponding to the given compression error is constantly broken in half by reducing the selection interval by half of the rank. The algorithm is implemented as follows.

During the whole algorithm, the function EvalErr(C_i,r) is the computing-intensive function that could be the performance bottleneck. If we consider a calculation of EvalErr(C_i,r) as one meta-calculation, the complexity of the traditional traversal method is O(n). When introducing the dichotomy optimization, the complexity can be reduced to O(log n) (Cai et al., 2012).

4 Case study

4.1 Data description and experimental configuration

In this paper, data produced by Community Earth System Model (CESM) are used as the experimental data to evaluate the compression performance of Adaptive-HGFDR; these data can be obtained from the Open Science Data Cloud in NetCDF (network common data form) format (https://doi.org/10.5281/zenodo.3997216). The data set includes air temperature data (T) stored as a $\mathrm{1024}\times \mathrm{512}\times \mathrm{26}$ (latitude × longitude × height) tensor and 22 other variables stored as a $\mathrm{1024}\times \mathrm{512}\times \mathrm{221}$ (latitude × longitude × time) tensor from January 1980 to May 1998. When reading the NetCDF data, a total of 48 GB memory will be occupied. The original data we used are double-precision data, we first process the data into single precision, and then the existing methods (SZ, ZFP, Blocked-HGFDR) and the proposed method are applied to compare the compression performances. Research experiments were performed by the MATLAB R2017a environment on a Windows 10 workstation (HP Compaq Elite 8380 MT) with Intel Core i7-3770 (3.4 GHz) processors and 8 GB of RAM.

The following experiments were performed. (1) In order to transform the original data to data blocks with the balanced dimension, the dimensions of these data blocks are better if they are of the same size. Thus, the optimal counts of data blocks should be determined. For the given compression error, we randomly divide the original data into a series of data blocks with different block counts; Adaptive-HGFDR is then applied to these data blocks, and the corresponding compression ratios are calculated. The optimal block count is achieved at the largest compression ratio. (2) Since ESMD have multiple dimensions and these dimensions may have different organization orders, to verify that the proposed compression method is unrelated with the data organization order, different variables are selected and organized with different orders. Then the advanced prediction method SZ and the proposed method are applied to these reorganized data to realize the lossy compression, and the dimensional distributions of compression errors are used to explore the relevance of the method with the data organization order. (3) To verify the advantages of the proposed method for ESMD, the proposed method was compared with the advanced transform method ZFP and Blocked-HGFDR. (4) To show the applicability and the advantages of the proposed method for data with different characteristics, we select 22 variables in ESMD, and then the proposed method, ZFP, and the Blocked-HGFDR are applied to compare the compression performances. In these experiments, two key indices are used to benchmark the performances: the compression error and compression ratio. The compression error is calculated as follows:

$$\begin{array}{}\text{(5)}& {\displaystyle }\mathit{\epsilon }={\displaystyle \frac{{∥T_{\text{Original}}-T_{\text{Reconstruction}}∥}^{\mathrm{2}}}{{∥T_{\text{Original}}∥}^{\mathrm{2}}}}.\end{array}$$

Here the $\parallel {\parallel }^{\mathrm{2}}$ is the F norm. T_Original is the original tensor data, T_{Reconstruction} is the compressed tensor data.

The compression ratio ϕ is calculated as follows:

$$\begin{array}{}\text{(6)}& \mathit{\varphi }={\displaystyle \frac{D_{\text{original}}}{D_{\text{compression}}}}.\end{array}$$

Here D_original is the memory size of original data before compression and D_compression is the memory size of the compressed reconstructed data.

4.2 Optimal block count selection

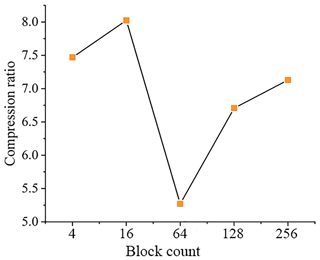
The selection of the optimal block count is carried out using the temperature data (T). Here, block counts with a power of 2 will be the best for use as the near-balanced data blocking. Therefore, a series of block counts of 4, 16, 64, 128, and 256 are generated as the potential block counts. For the compression constraint, 10⁻⁴ is used as an initial given compression error. The relationships between the block count (BC) and the compression ratio are shown in Fig. 2.

Clearly, the highest compression ratio is reached when the block count equals 16 (BC=16). Hence, the optimum block count is 16, and the corresponding block size is $\mathrm{256}\times \mathrm{128}\times \mathrm{26}$. It is interesting to find that the overall compression ratio presents a downward trend with block count in the range 16 and 64. When block count is larger than 64, the data volume of each block becomes smaller, the number of feature components required to achieve the same compression error significantly decreases, and the data volume of each block after compression significantly decreases. Although the number of blocks is increased (BC=128 and BC=256), the significant reduction of local data block volume makes the overall compression ratio show an upward trend. Aside from this, the relationship between the block count and the compression ratio is related to the structure and complexity of the data itself, which is different for the data with different distribution characteristics. For the temperature data (T), the compression ratio reaches a maximum when the block count is equal to 16.

Figure 2 The relationship between the block count and the compression ratio.

Figure 3 shows the original data and the compressed data with different block counts. It can be seen that there is no significant difference between the original data (Fig. 3a) and the compressed data (Fig. 3b–f) and that the distribution characteristics of the compressed data (Fig. 3b–f) are consistent with the original data (Fig. 3a). This may be because the prominent feature components are gradually added to approximate the original data and affect the compression error; no matter how many blocks there are, the proposed method can approach the given compression error by controlling the rank value to provide accurate compression results.

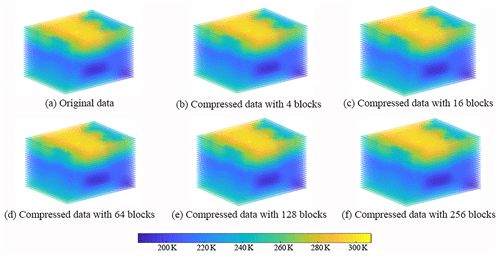
Figure 3 Original data and compressed data with different block counts: (a) the original data, (b) the compressed data when the data count is 4, (c) the compressed data when the data count is 16, (d) the compressed data when the data count is 64, (e) the compressed data when the data count is 128, and (f) the compressed data when the data count is 256.

4.3 Comparison with traditional methods

4.3.1 Comparison with SZ

In order to verify that the proposed compression method is unrelated with the data organization order, we select three variables $\left\{\text{SOLIN, TREFMXAV, FSNTC}\right\}\in {\mathrm{R}}^{\mathrm{1024}\times \mathrm{512}\times \mathrm{221}}$ in ESMD (SOLIN stands for solar insolation, TREFMXAV stands for average of TREFHT daily minimum, and FSNTC stands for clear-sky net solar flux at top of model). For each variable, we organize the data with different orders as follows: $\left\{\mathrm{221}\times \mathrm{512}\times \mathrm{1024},\mathrm{512}\times \mathrm{1024}\times \mathrm{221},\mathrm{1024}\times \mathrm{512}\times \mathrm{221}\right\}$. Following this, the SZ and the proposed method are applied to the data to realize the lossy compression. The error distributions of different compression results in the corresponding dimension are shown in Fig. 4.

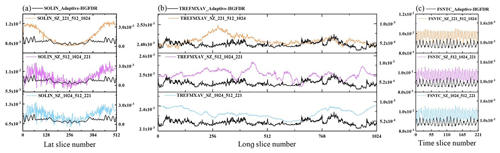
Figure 4 The compression error distribution along different dimensions. (a) The compression error distribution along latitude for SOLIN. (b) The compression error distribution along latitude for TREFMXAV. (c) The compression error distribution along latitude for FSNTC.

Figure 4 shows that the dimensional distribution of the compression error in SZ is quite different when using different organization orders of data. This may be because the SZ predicts the data point only along the first dimension but not along the other dimensions, and thus the compression result varies depending on the order of organization. Since the same ESMD may have the different organization orders, this creates a critical data inconsistency problem of SZ. Because the proposed method processes the multidimensional data as a whole, the error distribution is independent of the data organization order, and thus the dimensional distribution of the error remains consistent.

4.3.2 Comparison with ZFP and Blocked-HGFDR

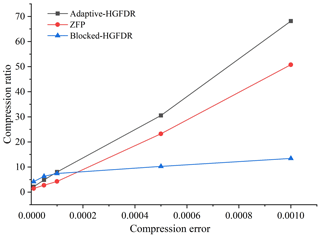
To verify the advantage of the proposed method for ESMD, we compare Adaptive-HGFDR with the Blocked-HGFDR and the ZFP method for the given compression error. Without a loss of generality, the relative compression error ratios are set to 10⁻⁵, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$, 10⁻⁴, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$, and 10⁻³. Here, the block count in the proposed method and the Blocked-HGFDR method are both set to 16, and the rank of Blocked-HGFDR is selected as the average of the adaptive rank in each divided data block. In ZFP, the key parameter is the tolerance. For the compression errors given above, we conduct the simulation experiments with many random tolerances and then find the ideal tolerances; in these cases the corresponding compression errors are close to the given compression errors. Thus, the tolerance parameters are 0.05, 0.3, 0.5, 3.8, and 10. The compression ratios of different compression methods under the conditions of different compression errors are calculated and shown in Fig. 5.

Figure 5 The relationship between the compression error and compression ratio for different methods.

Figure 5 shows that as the compression error ratio grows, the compression ratio of all three methods becomes larger and larger. However, the growth rate of ZFP is much slower than that of Blocked-HGFDR and Adaptive-HGFDR. When the compression error is less than 0.0001, the compression ratio of ZFP is a little higher than that of Adaptive-HGFDR and Blocked-HGFDR. This may be because approximating the original data with high accuracy requires a higher rank, which limits the improvement of compression ratio. When the compression error is 0.001, which is also acceptable for most ESMD applications, the compression ratio of Adaptive-HGFDR increases to 68.16, which means that the compressed data size is 68.16 times smaller than that of the original data. At a compression error of 0.001, the compression ratio of Adaptive-HGFDR, ZFP, and Blocked-HGFDR are 68.16, 13.42, and 50.78, respectively. The compression ratio of Adaptive-HGFDR is 5.07 times and 1.34 times larger than that of ZFP and Blocked-HGFDR, respectively. This may be because that the Adaptive-HGFDR can adaptively adjust the compression parameter (rank value) according to the actual data complexity and thus better capture data features to improve the compression ratio.

We summarize the error distribution along the longitude dimension of each method in Fig. 6. It is clearly seen that the error distributions of both Adaptive-HGFDR and ZFP are nearly uniform among different longitude dimensions. However, the Blocked-HGFDR method shows four significant segments of abrupt changes at different longitude slices. The oscillation characteristics of the three methods are different. For Adaptive-HGFDR, the error distribution is characterized more by low-frequency fluctuations, while ZFP method is characterized more as higher-frequency fluctuations. The Blocked-HGFDR method has very different fluctuation characteristics. For the first 230 longitude slices, the error distribution of Blocked-HGFDR is of high-frequency fluctuations with relatively high frequency, which is similar to ZFP, while in the other three segments it has a low amplitude that has similar fluctuations to that Adaptive-HGFDR. For the comparison of the mean value and standard deviation of the error distribution among the three methods, the Adaptive-HGFDR has much a smaller standard deviation ($\mathrm{6.89}\times {\mathrm{10}}^{-\mathrm{6}}$) compared to ZFP ($\mathrm{2.94}\times {\mathrm{10}}^{-\mathrm{5}}$) and Blocked-HGFDR ($\mathrm{2.80}\times {\mathrm{10}}^{-\mathrm{5}}$). The Blocked-HGFDR method has the smallest mean compression error ($\mathrm{9.35}\times {\mathrm{10}}^{-\mathrm{5}}$), which is slightly lower than Adaptive-HGFDR ($\mathrm{9.83}\times {\mathrm{10}}^{-\mathrm{5}}$), while ZFP has the largest mean compression error ($\mathrm{1.29}\times {\mathrm{10}}^{-\mathrm{4}}$).

Both Blocked-HGFDR and Adaptive-HGFDR show the small differences between the adjacent slices and the big differences among the different local data blocks. Due to the spatiotemporal heterogeneity, the feature distributions of each local ESMD are significantly different, but the feature distributions of adjacent slices have a small difference because of their spatiotemporal similarity. Meanwhile, since the adjacent compressed slice data have similar characteristics, the error fluctuation of these slices is small. In contrast, the structure difference of each compressed local data block is large, and the error fluctuation is also large. In Blocked-HGFDR, the compression parameter of each block is fixed, and the characteristic difference between data in each block is ignored. This weakness is improved in Adaptive-HGFDR by adjusting the compression parameter of each block adaptively according to the compression error to achieve the balanced distribution of error. Although Blocked-HGFDR performs substantially better for several slice numbers, Adaptive-HGFDR shows fewer variations.

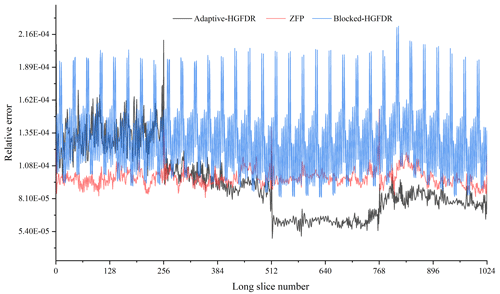
Figure 6 The distributions of compression error along the longitudinal slices (the slice means the partial data that are divided along specific dimensions).

To better reveal the characteristics of the compression error distributions, the distributions of the spatial error for three random spatial pieces (height 2, 8 and 16) are depicted in Fig. 7. From Fig. 7 we can see that the spatial structure of the data is different at different heights and that there are both continuous and abrupt structure changes at different levels. Specifically, the compression error in the Blocked-HGFDR method and the ZFP method fluctuates dramatically, forming multiple peaks and valleys. The error distributions of ZFP suggest that there are high-frequency stripes. There are irregular spatial patterns for Blocked-HGFDR. The Adaptive-HGFDR method is more stable where the error distribution is nearly random.

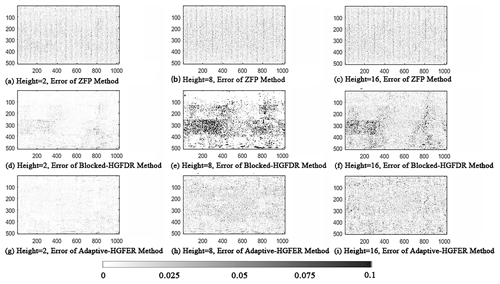
Figure 7 The spatial distribution of compression error of different compression methods: (a) the spatial distribution of compression error with height set to 2 in ZFP, (b) the spatial distribution of compression error with height set to 8 in ZFP, (c) the spatial distribution of compression error with height set to 16 in ZFP, (d) the spatial distribution of compression error with height set to 2 in Blocked-HGFDR, (e) the spatial distribution of compression error with height set to 8 in Blocked-HGFDR, (f) the spatial distribution of compression error with height set to 16 in Blocked-HGFDR, (g) the spatial distribution of compression error with height set to 2 in Adaptive-HGFDR, (h) the spatial distribution of compression error with height set to 8 in Adaptive-HGFDR, and (i) the spatial distribution of compression error with height set to 16 in Adaptive-HGFDR.

4.4 Evaluation with multiple variables

For a comprehensive comparison of the different methods, 22 monthly climate variables were used as the experimental data. Here, we focus on the variables with flux information and fast changing rate. Among these variables, there are variables with weak spatiotemporal heterogeneity, such as the temperature, and variables with strong spatiotemporal heterogeneity, which will help us to better investigate the applicability of the method. The dimensions of the experimental data are $\mathrm{1024}\times \mathrm{512}\times \mathrm{221}$. Here, considering that the compression error and compression performance of each variable can be comparable, the compression error should not be too big or too small for all of the 22 variables, the given error is 0.01, the block size is $\mathrm{256}\times \mathrm{128}\times \mathrm{26}$, and the block count is 144. For the tolerance parameter settings in ZFP, we conduct the simulation experiments with many random tolerances, then find the ideal tolerances in these cases the corresponding compression errors are close to the given compression errors. A detailed description of the variables is shown in Table 1.

Table 1 Descriptions of the 22 climate model data variables.

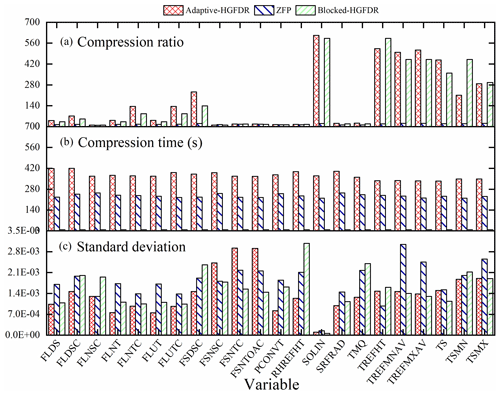
The Adaptive-HGFDR, Blocked-HGFDR, and ZFP methods were applied to the 22 variables. The compression ratio, time, and standard deviation of the slice error were calculated and are shown in Fig. 8. From Fig. 8a it can be seen that compared with the other two methods, the compression ratio of Adaptive-HGFDR is the largest. This may be because Adaptive-HGFDR considers the coupling relationship among the spatial and temporal dimensions and searches for the optimal compression parameter at each data block. This not only makes the number of features required by each data block small but also reduces the effect of data heterogeneity on the compression ratio. Adaptive-HGFDR captures the data features more accurately than the other two methods. The adaptive adjustment of the parameter makes Adaptive-HGFDR yield the uniform error distribution for the multiple variables shown in Fig. 8c. In summary, Adaptive-HGFDR provides good adaptability for ESMD.

Additionally, Fig. 8a also shows that the tensor-based compression methods (Adaptive-HGFDR, Blocked-HGFDR) have high compression ratios for some variables. This may be because during tensor-based compression the relationship between data volume and dimensions is transformed from exponential growth to nearly linear growth by defining the tensor product of tensors, which is essentially the displacement of space by calculating time, and thus the compression ratio is very high. In addition, we can see that with the given compression error the compression rates of different variables are significantly different. It may be because different climate model variables have different distribution features. Generally speaking, for the variables with weak spatiotemporal heterogeneity, a small number of feature components can achieve an accurate approximation that has a high compression rate. However, the variables with strong spatiotemporal heterogeneity may need a large number of feature components that have a low compression rate. Due to the continuous adjustment of compression parameter to search for the optimal rank, Adaptive-HGFDR is the most time-consuming method (Fig. 8b). Despite this, some optimization strategies, such as the spatiotemporal indexes and the unbalanced block split, can help improve the efficiency of Adaptive-HGFDR.

Figure 8 Comparison results of compression ratio, compression time, and standard deviation: (a) the comparison results of compression ratio, (b) the comparison results of compression time, (c) the comparison results of standard deviation.

5 Conclusions

In this study, we propose a lossy compression method, Adaptive-HGFDR, for ESMD based on blocked hierarchical tensor decomposition via integrating multidimensional coupling correlations. In Adaptive-HGFDR, to achieve the lossy compression, ESMD are divided into nearly balanced data blocks, which are then approximated by the hierarchical tensor decomposition. This compression method is applied to all the dimensions of the data blocks, rather than mapping the data into low dimensions, to avoid the destruction of coupling correlations among different dimensions. This also avoids the possible data inconsistency of compression methods like SZ, when the data are extracted and analyzed with different input–output (IO) orders. Thus, this method provides the potential advantage in multidimensional data inspection and exploration. Additionally, the compression parameter is simple and adaptively calculated for each data block independently for a given compression error. Therefore, the compression captures both the global and local variation of the coupling correlations well, which improves the approximation accuracy. The simulated experiments demonstrated that the proposed method has a higher compression ratio and more uniform error distributions than ZFP and Blocked-HGFDR under the same conditions and can support lossy compression of ESMD on ordinary PCs both in terms of memory occupation and compression time. In addition, the comparison results among 22 climate variables show that the proposed method can achieve good compression performance for the variables with significant spatiotemporal heterogeneity and fast changing rate.

The application of the hierarchical tensor in this paper provides several new potential avenues for developing more advanced lossy compression methods. With the hierarchical tensor, both the representation model and computational model can support complex multidimensional computation and analysis (Kressner and Tobler, 2014). For example, commonly used signal analysis methods like singular value decomposition (SVD) and fast Fourier transform (FFT) can achieve efficient stream computing with the hierarchical tensor representation and thus can inherently support efficient on-the-fly computation and analysis. Another interesting topic focusing on the tensor-based compression would be the compression of unstructured data or extremely sparse data (Li et al., 2020). Moreover, comprehensive tensor methods for finding the hierarchical tensor like the partial differential equation (PDE) have also recently been introduced. Thus, it is even possible to integrate some dynamic models of Earth systems directly into the compressed data. With the rapid development of tensor theory and its applications, more and more potential methods for tensor-based spatiotemporal data compression may be provided for modeling and analyzing ESMD.

Multiple dimensionality and heterogeneity are the natural attributes of ESMD. In ESMD, there are various spatiotemporal structures with gradual or sudden change and fast or slow changes, which also illustrates the significant regularity or randomness of the data. From the perspective of the rules of ESMD distribution, constructing the data compression method based on multidimensional coupling correlations may be the key to improving ESMD compression performance in the future. For example, for static or slow-varying variables, a large block and small rank can be used to achieve large compression, while for fast-changing variables a small block and large rank may be needed. The data-coupling correlations obtained by dynamically adjusting the block count and rank not only can be used for data compression but are also helpful for performing data organization and creating compressed storage based on the data characteristics. Additionally, in the large-scale simulation experiment with a long time sequence and multi-mode integration, this characteristic-based data organization and storage of multidimensional ESMD makes it possible to only retain the prominent components in order to achieve efficient comparison of large-scale data, which can help improve the capability of the ESMD application service. For instance, for major natural disasters this multidimensional tensor compression can support progressive transmission with a limited bandwidth by using only the prominent components, which can help to promote the depth and breadth of ESMD applications.