the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
RHEA v1.0: Enabling fully coupled simulations with hydro-geomechanical heterogeneity
José M. Bastías Espejo
Andy Wilkins
Gabriel C. Rau
Philipp Blum
Realistic modelling of tightly coupled hydro-geomechanical processes is relevant for the assessment of many hydrological and geotechnical applications. Such processes occur in geologic formations and are influenced by natural heterogeneity. Current numerical libraries offer capabilities and physics couplings that have proven to be valuable in many geotechnical fields like gas storage, rock fracturing and Earth resources extraction. However, implementation and verification of the full heterogeneity of subsurface properties using high-resolution field data in coupled simulations has not been done before. We develop, verify and document RHEA (Real HEterogeneity App), an open-source, fully coupled, finite-element application capable of including element-resolution hydro-geomechanical properties in coupled simulations. To extend current modelling capabilities of the Multiphysics Object-Oriented Simulation Environment (MOOSE), we added new code that handles spatially distributed data of all hydro-geomechanical properties. We further propose a simple yet powerful workflow to facilitate the incorporation of such data to MOOSE. We then verify RHEA with analytical solutions in one and two dimensions and propose a benchmark semi-analytical problem to verify heterogeneous systems with sharp gradients. Finally, we demonstrate RHEA's capabilities with a comprehensive example including realistic properties. With this we demonstrate that RHEA is a verified open-source application able to include complex geology to perform scalable, fully coupled, hydro-geomechanical simulations. Our work is a valuable tool to assess challenging real-world hydro-geomechanical systems that may include different levels of complexity like heterogeneous geology and sharp gradients produced by contrasting subsurface properties.
- Article
(3829 KB) - Full-text XML
- BibTeX
- EndNote
The complexity of processes occurring in a fluid-saturated deformable porous medium and their importance to a wide range of subsurface applications presents a major challenge for numerical modelling especially when including realistic heterogeneity. Example applications in geo-engineering that inherently require coupling of hydro-geomechanical processes are the interaction between pressure, flow and fracturing of rocks (Atkinson, 2015; Weng, 2015; Berre et al., 2019); land surface subsidence caused by the extraction of Earth resources (Peng, 2020; Ye et al., 2016); underground gas storage (Yang et al., 2016; Tarkowski, 2019); and mass movement (Zaruba and Mencl, 2014; Haque et al., 2016; Gariano and Guzzetti, 2016). Even though the fundamental mathematical description of coupled hydro-geomechanical processes has reached general consensus (Cheng, 2016; Wang, 2017), realistic modelling of such processes requires a precise description of the underground.
Heterogeneity is ubiquitous across scales and strongly affects the mechanical properties as well as the movement of fluids through the subsurface. For instance, the hydraulic conductivity of fractures within a porous rock is often orders of magnitude greater than that of unfractured rock, so that fine spatial discretisation around fractures is needed in certain numerical models, resulting in expensive computational demands (Morris et al., 2006; Eaton, 2006). As a result, the development of coupled hydro-geomechanical models generally requires simplifying or averaging heterogeneity, i.e. homogenising (Blum et al., 2005, 2009). Recent research has identified the need to improve modelling of coupled hydro-geomechanical systems (Lecampion et al., 2018; Grigoli et al., 2017; Birkholzer et al., 2019), and particularly also the importance of introducing high-resolution details to improve the accuracy of numerical simulations (McMillan et al., 2019). However, integrating spatially distributed material properties to numerical tools is not trivial because the shape of geological formations can consist of complex geometries produced by natural processes acting over a long period.
Terzaghi (1923) first described the elastic interactions between a porous medium and a fluid occupying its pore space, and the unidirectional system's dynamic responses to external forces. Biot (1941) later generalised this theory to three dimensions giving rise to the well known theory of consolidation or poroelasticity, also termed Biot theory. Since the 1970s, a large number of numerical libraries have been developed, optimised and applied to a diverse range of poroelastic applications (Bear and Verruijt, 1987; Verruijt, 1995; Cundall and Hart, 1993; Boone and Ingraffea, 1990). Notable is the work of Verruijt (2013), who designed a number of numerical solvers for typical one- and two-dimensional poroelastic problems.
Well known subsurface simulation libraries are concisely reviewed in the following. Since the number of subsurface simulation codes is vast, we only included platforms that are relevant to modelling spatially distributed heterogeneity. For an exhaustive list of codes the reader is referred to White et al. (2018). Current subsurface hydro-geomechanical simulation codes can be classified based on the numerical solution scheme and modelling approach of the coupled physics. For example, sequential coupling solves for the hydraulic and geomechanical variables independently and in sequence. Notable examples are geomechanics models based on TOUGH (Transport Of Unsaturated Groundwater and Heat) (Pruess et al., 1999; Xu et al., 2006; Lei et al., 2015; Lee et al., 2019). These consist of different libraries to solve for coupled thermo-hydro-mechanical (THM) applications relying on the numerical capabilities provided by TOUGH. The libraries differ in their fundamental equations, numerical solution methods and discretisation schemes (Rutqvist, 2017). Although sequential codes allow flexible and efficient code management in conjunction with reasonable computational costs, they tend to perform poorly in tightly coupled processes, since transient interaction between variables may not be computed accurately (Kim et al., 2011; Beck et al., 2020). However, sequential coupling combined with iterative schemes can significantly improve the numerical accuracy. In such implementations, feedback between variables occurs by transferring hydraulic variables to the geomechanics implementation, followed by returning the calculated stress and strain back into the flow problem for the next iteration (Beck et al., 2020). The numerical stability of such iterative methods is discussed by Kim et al. (2011) and Mikelić and Wheeler (2013). Another massively parallel subsurface flow package is PFLORTRAN, an open-source, multi-scale and multi-physics code for subsurface and surface processes (Hammond et al., 2014). PFLORTRAN solves non-isothermal multi-phase flow, reactive transport and geomechanics in a porous medium. It has previously been applied to simulate hydro-geomechanical systems (Lichtner and Karra, 2014).
Another concept is to solve the hydro-geomechanical equations as a fully coupled system (i.e. all equations are solved simultaneously). This is often performed using an implicit time-stepping scheme, which has unconditional numerical stability and high accuracy but is computationally expensive. This approach has proven to be useful in geo-engineering applications (Nghiem et al., 2004; Hein et al., 2016; Pandey et al., 2018). Various fully coupled hydro-geomechanical libraries have been developed and released. Proprietary software such as COMSOL (Holzbecher, 2013) has been used intensively in geomechanical applications, in particular for modelling of coastal aquifers (Zhao et al., 2017). COMSOL can import material data from text files into simulations. However, an automatic interpolation between neighbouring materials is performed automatically and may lead to undesired results. More recently, Pham et al. (2019) included geomechanical and poroelastic capabilities into the proprietary groundwater modelling environment FEFLOW (finite-element flow). MRST is an open-source code developed within the proprietary software MATLAB for fast prototyping of new tools in reservoir modelling (Lie, 2019). While MRST is not a simulator itself, it supports multi-phase flow with THM physics. MRST has been used for hydro-geomechanical problems, such as fracture rocks (Zhao and Jha, 2019) as well as several other subsurface applications (Garipov et al., 2018; Ahmed et al., 2017; Edwards et al., 2017). Notably also, two open-source Python codes have been developed. The first is the FEniCS project (Haagenson et al., 2020; Alnæs et al., 2015), while the second is called Porepy and was specifically developed to simulate THM processes in rock fractures (Keilegavlen et al., 2017, 2021). Despite the fact that Python-based coding offers the advantage of high-level programming within a relatively friendly user interface, these codes are designed to facilitate rapid development of features that cannot be properly represented by standard simulation tools rather than general multiphysics problems. Other fast-prototyping novel codes include Dang and Do (2021), Tran and Jha (2020), Reichenberger (2003), Martin et al. (2005), and Frih et al. (2012).
An additional option is OpenGeoSys (OGS), a well known open-source library to solve multi-phase and fully coupled THM physics (Kolditz et al., 2012). The code is well documented and features several examples in different subsurface areas. Further, different developers are constantly contributing new features to the source code (Graupner et al., 2011; Kosakowski and Watanabe, 2014; Li et al., 2014). Similarly, DuMux is a free, open-source, fully coupled numerical simulator for multi-phase flow and transport in a porous medium, (Flemisch et al., 2011). It is based on the Distributed Unified Numeric Environments (DUNE), a C++-based ecosystem that solves finite-element (FE) models based on PETSc. DuMux is well known for its strong focus on multi-phase flow and transport in a porous medium. Its recent release adds extra features and facilitates physics coupling, such as Navier–Stokes models (Koch et al., 2021). From our experience, however, users without some computational background and experience in programming in C++ or Python as well as using a debugger may require a significant amount of time to take full advantage of the features that OGS and DuMux offer. Furthermore, to our best knowledge we are unaware of a peer-reviewed verification of these codes that includes fully distributed hydraulic and geomechanical heterogeneity.
The multi-physics coupling framework MOOSE (Multiphysics Object Oriented Simulation Environment) (Permann et al., 2020) offers a unique environment where users can couple different physical processes in a modular approach. Within the object-oriented ecosystem of MOOSE, each physical process (or its partial differential equation, PDE) is treated separately as an individual MOOSE object, and coupling is performed by the back-end routines of MOOSE. The MOOSE numerical scheme is based on the FE method. It offers clean and effective numerical PDE solvers as well as mesh capabilities with a uniform approach for each class of problem. This design enables easy comparison and use of different algorithms (for example, to experiment with different Krylov subspace methods, preconditioners, or truncated Newton methods) which are under constant development. MOOSE enables the user to focus on describing the governing equations while the underlying numerical technicalities are taken care of by the system.
We have found that mastering the basic concepts of the MOOSE workflow requires a steep learning curve. However, it requires minimum C++ coding skills, which facilitates the learning experience from users that do not necessarily have a computer science background. Once the basics are mastered the benefits are significant; for example an experienced user can easily modify the source code to add desired features such as multi-scale physics, non-linear material properties, complex boundary conditions or even basic post-processing tools with only a few lines of code.
An example of MOOSE's capabilities in simulating coupled processes in a porous medium was illustrated by Cacace and Jacquey (2017), who developed a MOOSE-based application named GOLEM. It was optimised to model three-dimensional THM processes in fractured rock (Freymark et al., 2019). Another cutting-edge implementation is PorousFlow, an embedded MOOSE library to simulate multi-phase flow and thermal–hydraulic–mechanical–chemical (THMC) processes in a porous medium (Wilkins et al., 2020). PorousFlow has been verified and applied to simulate a number of complex and realistic systems, for example shallow geothermal systems (Birdsell and Saar, 2020), CO2 sequestration (Green et al., 2018) and groundwater modelling with plastic deformation (Herron et al., 2018). However, it has not yet been extended and verified for the simulation of spatial heterogeneity of mechanical parameters. In other words, despite its ability to handle spatially distributed heterogeneity of permeability and porosity, it does not support spatially distributed heterogeneity of mechanical properties such as bulk and Young's moduli. To the best of the authors' knowledge no existing open-source numerical tool is able to integrate full heterogeneity including all hydro-geomechanical parameters representative of complex geologic formations.
The aim of this paper is therefore to develop, verify and illustrate a novel and generic workflow for modelling fully coupled hydro-geomechanical problems allowing the inclusion of hydraulic and geomechanical heterogeneity inherent to realistic geological systems. This was achieved by extending the current capabilities of the native MOOSE physical modules, namely PorousFlow and Tensor Mechanics. We call this workflow RHEA (Real HEterogeneity App). RHEA is based on MOOSE's modular ecosystem and combines the capabilities of PorousFlow and Tensor Mechanics with material objects that are newly developed in our work and provide the novel ability to allocate spatially distributed properties at element resolution in the mesh. By integrating new C++ objects, we modified the underlying MOOSE code within PorousFlow and Tensor Mechanics. To streamline pre-processing efforts arising from this improvement, we developed a Python-based, automated workflow which uses a standard data format to generate input files that are compatible with the material objects in MOOSE format. Finally, we verified the correctness of RHEA with a newly developed, analytical benchmark problems allowing vertical heterogeneity and illustrated its performance using a sophisticated 2D example with distributed hydraulic and mechanical heterogeneity. In this work, we first describe the workflow required to compile a RHEA app, formulate a modelling problem and run a simulation. We then compare RHEA's simulation results with one- and two-dimensional analytical solutions and propose a benchmark semi-analytical solution to validate RHEA's performance when sharp gradients are present. Finally, we apply RHEA to a complicated two-dimensional problem with centimetre-scale heterogeneities demonstrating its capabilities. We anticipate that our work will lay the foundation for accurate numerical modelling of hydro-geomechanical problems allowing full spatial heterogeneity.
Modelling of coupled hydro-geomechanical processes requires solving the equations describing fluid flow in a deformable porous medium. The coupled processes can be described physically in a representative elementary volume (REV) by a balance of fluid, mass and momentum, where local equilibrium of thermodynamics is assumed and macroscopic balance equations are considered to be the governing equations. In this section, the governing equations for hydro-geomechanical processes in a fully saturated porous medium with liquid fluid are presented on the basis of Biot's theory of consolidation. In the pore pressure formulation, the field variables are the liquid-phase pressure pf and the displacement vector u. The material parameters can be spatially variable but remain independent of time. Permeability and elastic parameters are described as tensors, whereas the Biot coefficient is a scalar.
Fluid flow within a deformable and fully saturated porous medium is described by the continuity equation
where α is the Biot coefficient, εkk is the volumetric strain, Qf is a fluid sink or source term, and M is the Biot modulus of the porous medium (the reciprocal of the storage coefficient). In Biot's consolidation theory, the Biot modulus is defined as
where ϕ, Kf and Ks represent the porosity, fluid and solid bulk modulus respectively. As Darcy flow is assumed, the fluid discharge qd can be expressed as a momentum balance of the fluid like
where vf and vs are the fluid and solid matrix velocities respectively, k is the permeability tensor, μf is the dynamic viscosity of the fluid, ρf is the density of the fluid, and g is the gravitational acceleration vector.
The mechanical model is defined via momentum balance in terms of the effective Cauchy stress tensor as
where 𝕀 is the rank-two identity tensor. The mass of fluid per volume of porous medium is expressed as the sum of the phases
where ρs is the solid density. The elastic strain can be expressed in terms of displacements with the relation
The effective stress is related to elastic strains by the generalised Hooke's law:
where ℂijkl is the elastic compliance tensor.
Together, Eqs. (1) to (7) constitute the coupled system that represents hydro-geomechanical systems with linear elastic deformation.
As a derivative of the MOOSE framework, RHEA enables access to a wide array of options to fine tune a simulation. Solver options such as numerical schemes and adaptive time-stepping as well as general PETSc options are available. By default, RHEA uses a first-order fully implicit time integration (backward Euler) for unconditional stability and solves the coupled equations simultaneously (full coupling) (Kavetski et al., 2002; Manzini and Ferraris, 2004; Gaston et al., 2009). RHEA also allows operator splitting to implement loose coupling, i.e. solving the fluid flow while keeping the mechanics fixed, then solving the mechanics while keeping the fluid flow fixed. While this can be executed on separate meshes with different time-stepping schemes; this feature is not explored in the current article (Martineau et al., 2020).
Explicit time integration (with full or loose coupling) and other schemes such as Runge–Kutta are available in MOOSE and RHEA, but stability limits the time-step size, so these are rarely used in the type of subsurface problems handled by RHEA. By default, MOOSE and RHEA use linear Lagrange finite-elements (tetrahedra, hexahedra and prisms for 3D problems, triangles and quads for 2D problems), but higher-order elements may be easily chosen if desired (Hu, 2017).
RHEA does not implement any numerical stabilisation for the fluid equation to eliminate overshoots and undershoots; however, fluid volume is conserved at the element level (Cacace and Jacquey, 2017). Although not explored in this study, RHEA's fluid flow may be extended to multi-phase, multi-component flow with high-precision equations of state, as well as finite-strain elasto-plasticity (Wilkins et al., 2020).
RHEA is an open-source simulation workflow and tool specifically developed to allow fully coupled numerical simulations in a saturated porous medium with spatially distributed heterogeneity in hydraulic and geomechanical properties. We built RHEA as a derivative of MOOSE, the massively parallel and open-source FE simulation environment for coupled multi-physics processes (Gaston et al., 2009; Permann et al., 2020). MOOSE offers virtually unlimited simulation capabilities covering a wide spectrum of applications. This is based on a workflow where the end user does not need to know the details of the FE implementation. To achieve that, MOOSE utilises the libMesh library, a framework capable of manipulating multi-scale, multi-physics, parallel and mesh-adaptive FE simulations (Kirk et al., 2006). While the numerical methods, solvers and routines are executed by PETSc libraries (Balay et al., 2019), MOOSE is designed to allow the user to interact and control these two libraries without having to do any complex programming. Instead, the user frames the problem simply through an input file with unique syntax.
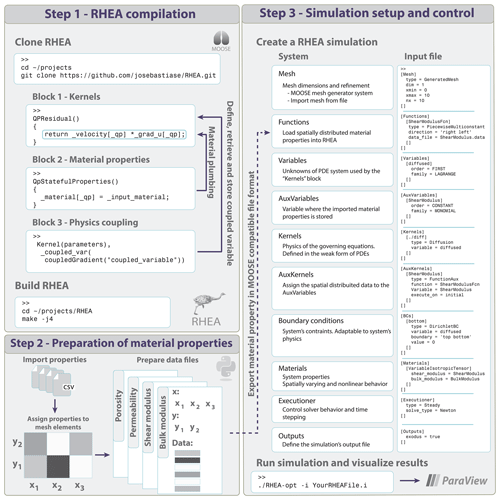
Figure 1Visual illustration of the steps required to create RHEA, generate distributed material properties files and write a simulation script.
We found that learning how to perform numerical simulations based on the MOOSE framework is not a trivial task. Our aim is to further develop modelling capabilities while simplifying the complexity of the problem through an easy-to-follow workflow accompanied by a visual summary. The RHEA workflow can be summarised as follows:
- Step 1 – RHEA compilation:
-
The user creates the RHEA application following the structure outlined in Fig. 1. In other words, the user creates an executable file which is able to model fully coupled hydro-geomechanical systems in a heterogenous medium. We accomplished this through new MOOSE-based materials functions able to allocate data in each element of the mesh based on a pre-generated input file. Furthermore, we integrated the multi-physics of Sect. 2 to RHEA by adding the PorousFlow (Wilkins et al., 2020) and Tensor Mechanics modules that are part of the MOOSE framework. Once RHEA is downloaded, the user can access the necessary files to build RHEA and can even access those files to modify the physics. This procedure is generic for any new MOOSE application. The core components of any MOOSE app such as RHEA are as follows (Fig. 1).
- Block 1 – Kernels:
-
The kernels (or partial differential equation terms) describing the physics are implemented in their weak form (Jacob and Ted, 2007). In the MOOSE ecosystem, PDEs are represented by one simple line of code; this is highlighted with a cyan rectangle in Fig. 1. This straightforward way of describing complex multi-physics constitutes the most powerful feature of MOOSE.
- Block 2 – Material properties:
-
Values, including spatially distributed values, can be prescribed for each of the materials appearing in the kernels.
- Block 3 – Kernel coupling:
-
The user can couple different physics by including different kernels in its model, or by creating new kernels.
This dynamic procedure allows flexible creation of the RHEA application or any MOOSE-based application requiring minimal knowledge of C++ programming skills.
- Step 2 – Preparation of material properties:
-
The spatially distributed data is formatted to the structure required by the RHEA app compiled in Step 1. We implemented this with a custom Python script that imports and formats the original CSV or VTK data set into a RHEA-compatible data structure. Within RHEA, the hydro-geomechanical material properties are field properties, which means that each value in the data set has to be allocated to a respective mesh element. Therefore, when the mesh is generated, the discretisation has to match the number of data points of the data set. That way, each property value is represented within the simulation. Note that if this is not done correctly, RHEA may assign undesired property values. This is because RHEA will automatically linearly interpolate any values provided to the mesh. Thus, if the initial mesh discretisation does not match the user-supplied samples, interpolated values are assigned which could lead to undesired results.
- Step 3 – Simulation setup:
-
To define the numerical model, a RHEA script has to be created in the standard MOOSE syntax. The script consists of an array of systems that describe the mesh, physics, boundary conditions, numerical methods and outputs. A short example along with brief system descriptions is illustrated in Fig. 1. The blocks consist of MOOSE functions that are written and designed in a generic manner and independently of the nature of the problem; this way the blocks can be recycled and reused. The spatially distributed material properties can be imported into the Function system and subsequently be stored in the AuxVariable system to be assigned as material property in the Materials block.
In summary, numerical simulations of hydro-geomechanical problems with spatially distributed material properties can be performed by calling RHEA's executable file (created in Step 1), using the simulation control script (created in Step 3) which contains the necessary instructions, as well as reading in the spatially distributed material properties (created in Step 2).
To test if RHEA accurately solves the differential equations stated in Sect. 2 and if boundary conditions are correctly satisfied, four different tests were developed. The proposed tests use predefined material properties that were imported into RHEA using the workflow presented in Sect. 3. The tests were designed to gradually build up complexity and cover the typical spectrum of consolidation problems. In two of the examples, RHEA's performance in simulations with sharp gradients is tested. First, a one-dimensional consolidation problem where the hydraulic conductivity varies in 4 orders of magnitude between layers and a second two-dimensional example with realistic heterogeneity in which the hydraulic conductivity of the geological facies varies over 6 orders of magnitude.
The first test, the classical Terzaghi's problem, is used as a basic benchmark of the hydro-mechanical coupling in RHEA. In later sections, we illustrate the full potential of RHEA when simulating spatially heterogeneous systems in one and two dimensions. The four verification scenarios are described in the following subsections. All numerical solutions were calculated using an 8-core Intel i7-3770 CPU at 3.40 GHz with 32 GB DDR4 RAM memory, and the results were stored on a hard disk drive.
4.1 Terzaghi's problem
In the one-dimensional consolidation problem, also known as Terzaghi's problem (Terzaghi, 1923), a single load q is applied at t=0 on the top of a fully saturated homogeneous sample with the height L. The system is only drained at the top, where the pressure of the fluid is assumed to be p=0 for t>0. At the moment of loading, t=0, the undrained compressibility of the solid increases the pressure of the sample. For t>0, the system is allowed to drain and the consolidation process begins.
In the absence of sources and sinks, Eq. (1) is reduced to the basic storage equation as
where the product ρf⋅g was written as γf and represents the volumetric weight of the fluid. Equation (3) is used to couple the fluid discharge qd. From Hook's law, assuming one-dimensional deformation, the vertical strain equals the volume change
where mv is the confined compressibility of the porous medium
and Ks and Gs are the bulk and shear moduli of the porous medium respectively. Substituting Eq. (9) into the storage equation (Eq. 8), the general differential equation for one-dimensional consolidation is obtained:
For t>0, the total load q is kept constant and the total stress σzz is also constant. Consequently, Eq. (11) reduces to
Since the system is undrained at t=0, the initial condition can be established from Eq. (11) as
The boundary conditions at the top and bottom of the sample are
and
The analytical solution of the problem is well known and reads as follows (Wang, 2017; Cheng, 2016; Verruijt, 2018):
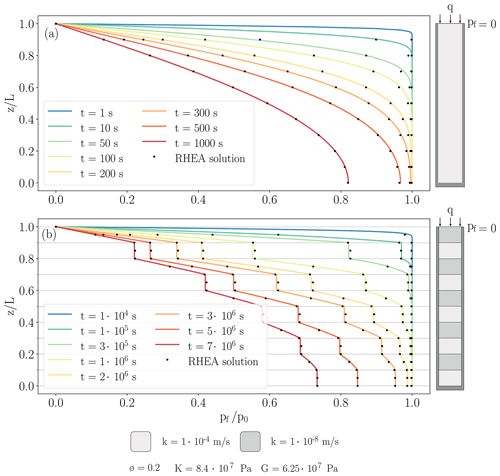
For this example, the height of the sample was set to 100 m, the hydraulic conductivity is m s−1, the porosity is 0.2, the Biot coefficient is 0.9, the bulk modulus is 8.40×107 Pa and the shear modulus is 6.25×107 Pa. The performance and consistency of RHEA on the consolidation problem is shown as pore pressure versus depth profiles at discrete times in Fig. 2a. A comparison of the analytical and RHEA's solution reveals excellent agreement, thereby verifying the numerical solution. The total time for computing 101 time steps was 1.92 s.
4.2 Layered Terzaghi's problem
The objective of this test is to investigate the performance of RHEA when heterogeneity and sharp gradients are present. The consolidation experiment of the previous section is performed on a sample with multiple layers of contrasting properties. For simplicity, porosity and mechanical parameters are assumed to be homogeneous. Since the total load q is constant for t>0, Eq. (11) reduces to Eq. (12) across n layers as follows
which describes the consolidation in each layer. Here, is the depth of the sample, pf,i and ki are the fluid pressure and permeability of the solid in each layer i, respectively. The contact between layers is assumed to be perfect; i.e. the boundary conditions at the layers are represented by equivalent matching fluid pressure as
The sample is drained at the top, whereas the bottom remains undrained
and
The fluid pressure produced by the external load starts to dissipate when t>0, but at different rates depending on the consolidation coefficient of the layer. The height of the sample is 100 m, and 10 layers are equally distributed along the sample with 10 m height. To represent sharp gradients, the selected hydraulic conductivities have a difference of 4 orders of magnitude between layers, m s−1 and m s−1. The high- and low-permeability layers are alternating. The porosity is set to 0.2, the Biot coefficient is 0.9, the bulk modulus is 8.40×107 Pa and the shear modulus is 6.25×107 Pa.
A step-by-step semi-analytical solution of the diffusion problem in a layered sample was derived by Hickson et al. (2009). To solve this problem in RHEA, a mesh of 100 elements was used with a time step of 1×104 s. The total time for computing 701 time steps was 13.8 s. A comparison between the analytical solution and RHEA's numerical simulation is shown in Fig. 2b. In the layers with high hydraulic conductivity, the consolidation process occurs rapidly, leading to faster pore pressure dissipation (vertical pore pressure profile) and therefore also faster water movement. In contrast, the consolidation process is slower in the low-conductivity layers with slower pore pressure dissipation and water movement.
4.3 Plane strain consolidation
To evaluate the performance of RHEA for two-dimensional heterogeneity, a consolidation problem with plane strain is developed. The two-dimensional consolidation caused by a uniform load over a circular homogeneous area can be represented by the storage equation (Eq. 1) in a two-dimensional case as
where ε represents the volumetric strain. Including two equilibrium equations, in terms of total stress, gives
and
The total stress is related to the effective stress through
and
The analytical solution can be found by expressing the equilibrium (Eqs. 22 and 23) in terms of the displacement components ux and uz using Hooke's law as
and
and
Here, the assumed plane strain is the y axis, i.e. uy=0. Replacing Hooke's law in the plane strain (Eqs. 26 to 28) with the effective stress balance (Eqs. 22 and 23) combined with Eqs. (24) and (25) leads to a complete system of equations as
and
where the elastic strain is
The boundary conditions are represented by a constant load in an area of width 2a, applied at t=0. The system is allowed to drain for t>0 as
and
and
When the sample is loaded, a confined pore pressure is generated which starts to drain instantaneously through the borders of the system. A semi-analytical solution in the Fourier domain and Laplace transform for the given equation system and boundary conditions is presented in Verruijt (2013). The height and the width of the sample are 10 m. The load is applied on the surface of the sample between −1 and 1 m. The hydraulic conductivity is m s−1, the porosity is 0.2, the Biot coefficient is 0.9, the bulk modulus is 8.40×107 Pa and the shear modulus is 6.25×107 Pa. To solve this problem, a coarse mesh was defined, and MOOSE's native mesh adaptivity system was employed to automatically generate a finer resolution in areas where the pore pressure gradients are steep. This significantly reduces the computational time when compared with using a fine mesh throughout. The total simulation time was 312.6 s for 101 time steps and 10 000 elements with 20 502 nodes.
The results are illustrated in Fig. 3. Figure 3a shows a cross section of the sample as contour plot. Figure 3b shows a pore pressure profile with depth at the centre of the sample x=0. Excellent agreement between the analytical solution and the simulated solution by RHEA is observed.
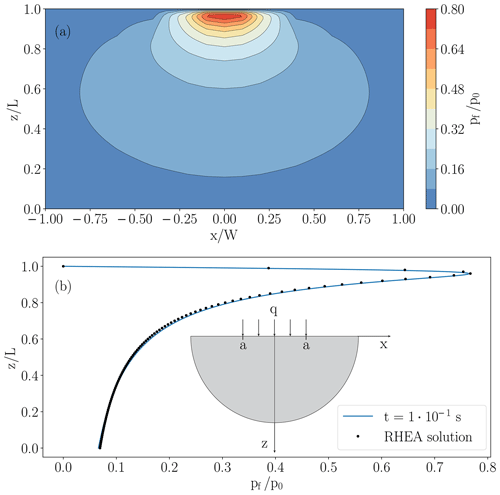
Figure 3The solution of the consolidation problem in plane strain by RHEA is shown in a sample 10 m in width and height. (a) Contour plot of the solution at time s. (b) Comparison of the semi-analytical solution (continuous line) and the RHEA solution (dotted line). The differences in pore pressure between both approaches is due to the assumption of an infinite domain in the analytical solution which is not feasible to replicate the latter with RHEA.
4.4 Modelling realistic geology
The last example aims to study and illustrate the performance of RHEA with a real data set. This example illustrates how to generate input files using the developed workflow and demonstrates the potential of RHEA for simulating increased spatial complexity and sharp gradients. While the Herten analogue is a 3D data set, the example was reduced to two dimensions to facilitate presentation. However, simulations in three dimensions are also possible and can be done using the presented workflow in unmodified form. The 2D consolidation problem was solved with RHEA, integrating the multi-facies realisations and material properties of the Herten analogue (Bayer et al., 2015a). Although the data set does not contain geomechanical subsurface properties, the hydraulic conductivity varies over 6 orders of magnitude, which provides sufficient proof of RHEA's capabilities.
4.4.1 Herten aquifer data set description
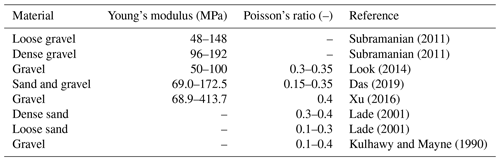
Realistic modelling relies not only on accurate data concerning material parameters, but also on appropriate spatial distribution of such parameters (Houben et al., 2018; Irvine et al., 2015; Kalbus et al., 2009). Typically, distributed material parameters are generated by stochastic random fields based on an a priori statistical distribution (Vanmarcke et al., 1986). Although random fields have proven to be useful, they do not capture the usual continuity of material parameters (Strebelle, 2002). Consequently, the use of high-resolution data, such as “aquifer analogues”, is preferred (Alexander, 1993; Zappa et al., 2006). Aquifer analogues consist of centimetre-resolution data obtained from detailed investigation of geological formations at outcrops. Although aquifer analogues are rare, they have been widely used in different subsurface fields (Höyng et al., 2015; Beaujean et al., 2014; Finkel et al., 2016). The Herten analogue is a well known and rigorously generated 2D outcrop (Bayer et al., 2015a). It consists of a fluvial braided river deposit from the south-east of Germany, which represents one of the most important drinking water resources in central Europe. Its architecture consists of sedimentary facies, and its body of unconsolidated gravel and well sorted sand. The dimensions of the 2D outcrop are 16 m wide by 7 m high, and it features horizontal and vertical data resolution of m for hydraulic conductivity and porosity. Hence, the 2D cross section has a total of 4480 measurements points. The corresponding hydraulic conductivity k ranges from to m s−1, and porosity ϕ from 0.17 to 0.36 (Fig. 4a). To represent spatial distribution of mechanical properties, typical values of bulk and shear moduli for gravel and sand were assumed to be linearly correlated with the porosity of the aquifer: similar trends have been reported in previous studies (Mondol et al., 2008; Hardin and Kalinski, 2005; Hicher, 1996). Representative geomechanical moduli can be found in soil mechanics literature as shown in Table 1. The elastic tensor is assumed to be isotropic in this example; hence elastic moduli are related via (Wang, 2017; Cheng, 2016)
where Es and νs denote the Young's modulus and Poisson's ratio of the solid material respectively. The result is that the bulk moduli vary between 6.70×107 and 1.70×108 Pa, whereas the shear moduli range between 3.0×107 and 3.50×108 Pa, as shown in Fig. 4a. RHEA does not require the mechanical moduli to be related to the hydraulic properties in the way we have described in this particular example.
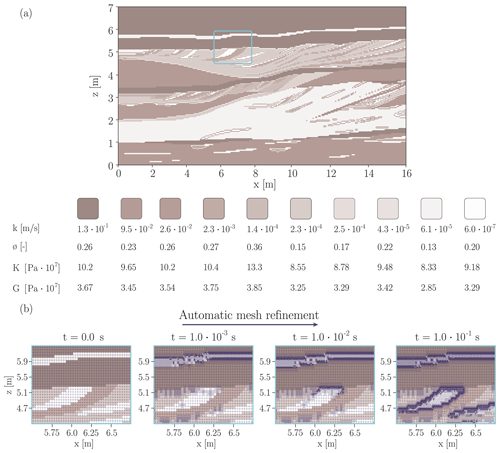
Figure 4Facies architecture and properties of the Herten aquifer analogue. (a) Colour scale of the hydro-geomechanical properties of the aquifer imported to RHEA. (b) Mesh discretisation and its dynamic evolution when the mesh adaptivity system is activated. The time evolution is shown from left to right.
4.4.2 Problem and model description
The two-dimensional consolidation is described by Eqs. (21), (29) and (30). A constant load at the top of the sample is applied at t>0, which generates a confined pore pressure. After that, the system is allowed to drain through the top boundary and is subjected to the normal stress. The sample's bottom and sides are impermeable to the fluid, and subject to roller boundary conditions.
For this simulation, a quadrilateral mesh was generated with the mesh generator system of MOOSE. The mesh has 44 800 elements and 44 940 nodes, which matches the data set resolution. Since the material properties of the data set differs in orders of magnitude, the mesh adaptivity system of MOOSE was used to ensure accurate results. At each time step the 30 % of elements with the highest pore pressure gradient were refined, which reduces the local error at contrasting facies. Hence the mesh is refined in each time step. At the end of the simulation, the number of nodes had grown to 708 548 and the number of elements to 631 615. The total simulation time was 0.49 h for 70 time steps and 44 341 elements with 44 800 nodes.
4.4.3 Simulation results
The pore pressure profiles depicted in Fig. 5 illustrate how the physical heterogeneity of the cross-bedded data set strongly influences the fluid flow through the sample. The effect of the centimetre resolution of the data set can be studied when the initial load is applied at t=0. Since the sample is not yet allowed to drain, confined pore pressure is generated which depends on the geomechanical characteristics of the sand and gravel. In facies where the soil is highly compressible, the generated pore pressure is also relatively high since the total load is shared between the fluid and the soil. In contrast, in facies that have higher elastic moduli values the confined pore pressure is relatively low. This effect is nicely shown in Fig. 5a. At time t>0 the top of the sample is allowed to drain. The effect of the highly permeable units made of poorly sorted and well sorted gravel is shown in Fig. 5b. The top facies of the aquifer consist of a high-permeability soil ( m s−1), which is divided by a thin low-permeability layer ( m s−1); the latter causes contrasting pore pressure profiles. Similar permeability effects have been discussed before (Choo and Lee, 2018; Peng et al., 2017; Kadeethum et al., 2019). The influence of the temporal and spatial scales on the consolidation process is shown in Fig. 5c and d. It can be observed that the process occurs rather quickly and is strongly influenced by the low-permeability facies. This example demonstrates that RHEA can solve complex and realistic heterogenous hydro-geomechanical coupled problems.
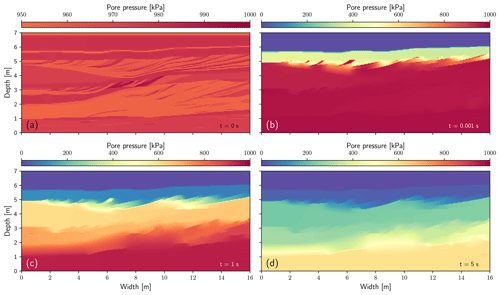
Figure 5Sequence of snapshots of the consolidation process and pore pressure variation in the aquifer with time. (a) Initial condition of the simulation. (b) Snapshot at time s. (c) Snapshot at time 1 s. (d) Snapshot at time 5 s. Note that (a) uses a different colour range to highlight the small variations in pore pressure.
In this paper we develop and verify Real HEterogeneity App (RHEA): a numerical simulation tool that allows fully coupled numerical modelling of hydro-geomechanical systems. Moreover, RHEA can easily include the full heterogeneity of parameters as it occurs in real subsurface systems. RHEA is based on the powerful Multiphysics Object-Oriented Simulation Environment (MOOSE) open-source framework. Furthermore, we provide an easy-to-understand workflow which explains how to compile the application and run a customised numerical simulation. Despite its simplicity, the workflow combines all the technical advantages provided by MOOSE and its well established framework. The latter allows the development and use of state-of-the-art and massively scalable applications backed by the unconditional support of a growing community.
Beyond unlocking the ability to include the full heterogeneity of hydro-geomechanical parameters in simulations, our contribution provides examples to verify future numerical codes. Additionally, a semi-analytical benchmark problem is proposed to verify the performance of numerical code when heterogeneity and sharp gradients are present.
Our example simulations illustrate that the subsurface hydro-geomechanical properties, in particular permeability (or transmissivity), play a key role in the consolidation process. Although this insight is valuable, it can lead to an oversimplification when models assume transmissivity varies heterogeneously while mechanical parameters are assumed to be homogeneous. This approach can lead to biased results in systems where different geologic formations are present. For example, land surface subsidence is a process that can occur due to anthropogenically induced decreases in subsurface pore pressure causing progressive consolidation and slow downward percolation across the layers within the subsurface. This process depends on the spatial distribution of the geomechanical properties, in particular those of clay layers within the subsurface. RHEA could be used to increase our understanding of the spatial and temporal evolution of land surface subsidence. Our newly developed workflow enables such advanced numerical simulations.
RHEA has the potential to advance our understanding of real-world systems that have previously been oversimplified. Further, RHEA offers the integration of high-resolution data sets with sophisticated numerical implementations. Potential numerical instabilities caused by highly heterogeneous systems (i.e. settings with sharp gradients) are handled automatically by combining adaptive meshing capabilities with implicit time stepping. While this work demonstrates RHEA's capabilities for two-dimensional problems, this can easily be extended to three-dimensional simulations. In that case, a three-dimensional mesh that is representative of the spatially distributed hydraulic and geomechanical properties of any available data set can be generated. The tasks follow the data formatting workflow and simulation control as described in Sect. 3.
Our current work focuses on hydro-geomechanical coupling of heterogeneous systems. However, RHEA could potentially be extended to also include thermal processes. While it would allow fully coupled simulations of thermal–hydraulic–mechanical (THM) systems including spatially distributed heterogeneities, verification will require the development of more advanced analytical solutions, a task that is, however, beyond the scope of this contribution.
The code and examples presented in this study are available at a Zenodo repository: https://doi.org/10.5281/zenodo.4767832 (Bastías Espejo and Wilkins, 2021). The continuous development of RHEA code is maintained at the GitHub repository https://github.com/josebastiase/RHEA (last access: 15 October 2021). The Herten analogue data set is available on https://doi.org/10.1594/PANGAEA.844167 (Bayer et al., 2015b).
JMBE developed RHEA and the analytical solutions used for verification, made the figures and tables, and wrote the first manuscript draft. GCR closely supervised JMBE. AW provided JMBE with technical support. PB reviewed the manuscript and provided suggestions.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We would like to thank Mauro Cacace and two anonymous reviewers for their efforts and thoughtful comments that have helped to improve our paper.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. 424795466).
The article processing charges for this open-access publication were covered by the Karlsruhe Institute of Technology (KIT).
This paper was edited by Sergey Gromov and reviewed by Mauro Cacace and two anonymous referees.
Ahmed, E., Jaffré, J., and Roberts, J. E.: A reduced fracture model for two-phase flow with different rock types, Math. Comput. Simulat., 137, 49–70, 2017. a
Alexander, J.: A discussion on the use of analogues for reservoir geology, Geol. Soc. SP, 69, 175–194, 1993. a
Alnæs, M., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M. E., and Wells, G. N.: The FEniCS project version 1.5, Archive of Numerical Software, 3, Heidelberg, Germany, available at: https://journals.ub.uni-heidelberg.de/index.php/ans/article/view/20553 (last access: 13 October 2021), 2015. a
Atkinson, B. K.: Fracture mechanics of rock, Elsevier, London, UK, 2015. a
Balay, S., Abhyankar, S., Adams, M., Brown, J., Brune, P., Buschelman, K., Dalcin, L., Dener, A., Eijkhout, V., and Gropp, W.: PETSc users manual, Argonne National Laboratory, Chicago, USA, available at: https://publications.anl.gov/anlpubs/2016/05/127241.pdf (last access: 13 October 2021), 2019. a
Bastías Espejo, J. and Wilkins, A.: josebastiase/RHEA: RHEA v.1.0 (v1.0.0), Zenodo [code], https://doi.org/10.5281/zenodo.4767832, 2021. a
Bayer, P., Comunian, A., Höyng, D., and Mariethoz, G.: High resolution multi-facies realizations of sedimentary reservoir and aquifer analogs, Scientific data, 2, 1–10, 2015a. a, b
Bayer, P., Comunian, A., Höyng, D., and Mariethoz, G.: Physicochemical properties and 3D geostatistical simulations of the Herten and the Descalvado aquifer analogs, PANGAEA [data set], https://doi.org/10.1594/PANGAEA.844167, 2015b. a
Bear, J. and Verruijt, A.: Modeling groundwater flow and pollution, 2, Springer Science & Business Media, Dordrecht, the Netherlands, 1987. a
Beaujean, J., Lemieux, J.-M., Dassargues, A., Therrien, R., and Brouyère, S.: Physically based groundwater vulnerability assessment using sensitivity analysis methods, Groundwater, 52, 864–874, 2014. a
Beck, M., Rinaldi, A., Flemisch, B., and Class, H.: Accuracy of fully coupled and sequential approaches for modeling hydro-and geomechanical processes, Comput. Geosci., 24, 1707–1723, 2020. a, b
Berre, I., Doster, F., and Keilegavlen, E.: Flow in fractured porous media: A review of conceptual models and discretization approaches, Transport Porous Med., 130, 215–236, 2019. a
Biot, M. A.: General theory of three-dimensional consolidation, J. Appl. Phys., 12, 155–164, 1941. a
Birdsell, D. T. and Saar, M. O.: Modeling ground surface deformation at the Swiss HEATSTORE underground thermal energy storage sites, in: World Geothermal Congress (2020), 24–27 October 2021, online, ETH Zurich, Institute of Geophysics, 2020. a
Birkholzer, J. T., Tsang, C.-F., Bond, A. E., Hudson, J. A., Jing, L., and Stephansson, O.: 25 years of DECOVALEX-Scientific advances and lessons learned from an international research collaboration in coupled subsurface processes, Int. J. Rock Mech. Min., 122, 103995, https://doi.org/10.1016/j.ijrmms.2019.03.015, 2019. a
Blum, P., Mackay, R., Riley, M., and Knight, J.: Performance assessment of a nuclear waste repository: upscaling coupled hydro-mechanical properties for far-field transport analysis, Int. J. Rock Mech. Min., 42, 781–792, 2005. a
Blum, P., Mackay, R., and Riley, M. S.: Stochastic simulations of regional scale advective transport in fractured rock masses using block upscaled hydro-mechanical rock property data, J. Hydrol., 369, 318–325, 2009. a
Boone, T. J. and Ingraffea, A. R.: A numerical procedure for simulation of hydraulically-driven fracture propagation in poroelastic media, Int. J. Numer. Anal. Met., 14, 27–47, 1990. a
Cacace, M. and Jacquey, A. B.: Flexible parallel implicit modelling of coupled thermal–hydraulic–mechanical processes in fractured rocks, Solid Earth, 8, 921–941, 2017. a, b
Cheng, A. H.-D.: Poroelasticity, 27, Springer, Mississippi, USA, 2016. a, b, c
Choo, J. and Lee, S.: Enriched Galerkin finite elements for coupled poromechanics with local mass conservation, Comput. Method. Appl. M., 341, 311–332, 2018. a
Cundall, P. A. and Hart, R. D.: Numerical modeling of discontinua, in: Analysis and design methods, 231–243, Elsevier, Minneapolis, USA, 1993. a
Dang, H.-L. and Do, D.-P.: Finite element implementation of coupled hydro-mechanical modeling of transversely isotropic porous media in DEAL. II, International Journal of Modeling, Simulation, and Scientific Computing, 12, 2150003, https://doi.org/10.1142/S1793962321500033, 2021. a
Das, B. M.: Advanced soil mechanics, Crc Press, London, UK, 2019. a
Eaton, T. T.: On the importance of geological heterogeneity for flow simulation, Sediment. Geol., 184, 187–201, 2006. a
Edwards, R. W., Doster, F., Celia, M. A., and Bandilla, K. W.: Numerical modeling of gas and water flow in shale gas formations with a focus on the fate of hydraulic fracturing fluid, Environ. Sci. Technol., 51, 13779–13787, 2017. a
Finkel, M., Grathwohl, P., and Cirpka, O. A.: A travel time-based approach to model kinetic sorption in highly heterogeneous porous media via reactive hydrofacies, Water Resour. Res., 52, 9390–9411, 2016. a
Flemisch, B., Darcis, M., Erbertseder, K., Faigle, B., Lauser, A., Mosthaf, K., Müthing, S., Nuske, P., Tatomir, A., and Wolff, M.: DuMux: DUNE for multi-{phase, component, scale, physics, …} flow and transport in porous media, Adv. Water Resour., 34, 1102–1112, 2011. a
Freymark, J., Bott, J., Cacace, M., Ziegler, M., and Scheck-Wenderoth, M.: Influence of the main border faults on the 3d hydraulic field of the central Upper Rhine Graben, Geofluids, 2019, 7520714, https://doi.org/10.1155/2019/7520714, 2019. a
Frih, N., Martin, V., Roberts, J. E., and Saâda, A.: Modeling fractures as interfaces with nonmatching grids, Comput. Geosci., 16, 1043–1060, 2012. a
Gariano, S. L. and Guzzetti, F.: Landslides in a changing climate, Earth-Sci. Rev., 162, 227–252, 2016. a
Garipov, T. T., Tomin, P., Rin, R., Voskov, D. V., and Tchelepi, H. A.: Unified thermo-compositional-mechanical framework for reservoir simulation, Comput. Geosci., 22, 1039–1057, 2018. a
Gaston, D., Newman, C., Hansen, G., and Lebrun-Grandie, D.: MOOSE: A parallel computational framework for coupled systems of nonlinear equations, Nucl. Eng. Des., 239, 1768–1778, 2009. a, b
Graupner, B. J., Li, D., and Bauer, S.: The coupled simulator ECLIPSE–OpenGeoSys for the simulation of CO2 storage in saline formations, Energy Proced., 4, 3794–3800, 2011. a
Green, C., Wilkins, A., La Force, T., and Ennis-King, J.: Community code for simulating CO2 storage: Modelling multiphase flow with coupled geomechanics and geochemistry using the open-source multiphysics framework MOOSE, in: 14th Greenhouse Gas Control Technologies Conference, 21–26 October 2018, Melbourne, Australia, 21–26, 2018. a
Grigoli, F., Cesca, S., Priolo, E., Rinaldi, A. P., Clinton, J. F., Stabile, T. A., Dost, B., Fernandez, M. G., Wiemer, S., and Dahm, T.: Current challenges in monitoring, discrimination, and management of induced seismicity related to underground industrial activities: A European perspective, Rev. Geophys., 55, 310–340, 2017. a
Haagenson, R., Rajaram, H., and Allen, J.: A generalized poroelastic model using FEniCS with insights into the Noordbergum effect, Comput. Geosci., 135, 104399, https://doi.org/10.1016/j.cageo.2019.104399, 2020. a
Hammond, G. E., Lichtner, P. C., and Mills, R.: Evaluating the performance of parallel subsurface simulators: An illustrative example with PFLOTRAN, Water Resour. Res., 50, 208–228, 2014. a
Haque, U., Blum, P., Da Silva, P. F., Andersen, P., Pilz, J., Chalov, S. R., Malet, J. P., Mateja, J. A., Andres, N., Poyiadji, E., Lamas, P. C., Zhang, W., Peshevski, I., Pétursson, H. G., Kurt, T., Dobrev, N., Garcia-Davalillo, J. C. G., Halkia, M., Ferri, S., Gaprindashvili, G., Engström, J., and Kelling, D.: Fatal landslides in Europe, Landslides, 13, 1545–1554, 2016. a
Hardin, B. O. and Kalinski, M. E.: Estimating the shear modulus of gravelly soils, J. Geotech. Geoenviron., 131, 867–875, 2005. a
Hein, P., Kolditz, O., Görke, U.-J., Bucher, A., and Shao, H.: A numerical study on the sustainability and efficiency of borehole heat exchanger coupled ground source heat pump systems, Appl. Therm. Eng., 100, 421–433, 2016. a
Herron, N., Peeters, L., Crosbie, R., Marvanek, S., Ramage, A., Rachakonda, P., and Wilkins, A.: Groundwater Numerical Modelling for the Hunter Subregion. Product 2.6.2 for the Hunter Subregion from the Northern Sydney Basin Bioregional Assessment, Australia’s national geoscience agency, Sydney, Australia, 2018. a
Hicher, P.-Y.: Elastic properties of soils, J. Geotech. Eng.-ASCE, 122, 641–648, 1996. a
Hickson, R., Barry, S., and Mercer, G.: Critical times in multilayer diffusion. Part 1: Exact solutions, Int. J. Heat Mass Tran., 52, 5776–5783, 2009. a
Holzbecher, E.: Poroelasticity benchmarking for FEM on analytical solutions, in: Excerpt from the Proceedings of the COMSOL Conference, 5 November 2013, Rotterdam, the Netherlands, 1–7, 2013. a
Houben, G. J., Stoeckl, L., Mariner, K. E., and Choudhury, A. S.: The influence of heterogeneity on coastal groundwater flow-physical and numerical modeling of fringing reefs, dykes and structured conductivity fields, Adv. Water Resour., 113, 155–166, 2018. a
Höyng, D., Prommer, H., Blum, P., Grathwohl, P., and D'Affonseca, F. M.: Evolution of carbon isotope signatures during reactive transport of hydrocarbons in heterogeneous aquifers, J. Contam. Hydrol., 174, 10–27, 2015. a
Hu, R.: A fully-implicit high-order system thermal-hydraulics model for advanced non-LWR safety analyses, Ann. Nucl. Energy, 101, 174–181, 2017. a
Irvine, D. J., Cranswick, R. H., Simmons, C. T., Shanafield, M. A., and Lautz, L. K.: The effect of streambed heterogeneity on groundwater-surface water exchange fluxes inferred from temperature time series, Water Resour. Res., 51, 198–212, 2015. a
Jacob, F. and Ted, B.: A first course in finite elements, Wiley, London, UK, 2007. a
Kadeethum, T., Nick, H., Lee, S., Richardson, C., Salimzadeh, S., and Ballarin, F.: A Novel Enriched Galerkin Method for Modelling Coupled Mechanical Deformation in Heterogeneous Porous Media, in: 53rd US Rock Mechanics/Geomechanics Symposium, 23–26 June 2019, New York, USA, American Rock Mechanics Association, ARMA-2019-0228, 2019. a
Kalbus, E., Schmidt, C., Molson, J. W., Reinstorf, F., and Schirmer, M.: Influence of aquifer and streambed heterogeneity on the distribution of groundwater discharge, Hydrol. Earth Syst. Sci., 13, 69–77, https://doi.org/10.5194/hess-13-69-2009, 2009. a
Kavetski, D., Binning, P., and Sloan, S. W.: Adaptive backward Euler time stepping with truncation error control for numerical modelling of unsaturated fluid flow, Int. J. Numer. Meth. Eng., 53, 1301–1322, 2002. a
Keilegavlen, E., Fumagalli, A., Berge, R., Stefansson, I., and Berre, I.: PorePy: an open-source simulation tool for flow and transport in deformable fractured rocks, arXiv preprint, arXiv:1712.00460, 2017. a
Keilegavlen, E., Berge, R., Fumagalli, A., Starnoni, M., Stefansson, I., Varela, J., and Berre, I.: Porepy: An open-source software for simulation of multiphysics processes in fractured porous media, Comput. Geosci., 25, 243–265, 2021. a
Kim, J., Tchelepi, H. A., and Juanes, R.: Stability and convergence of sequential methods for coupled flow and geomechanics: Fixed-stress and fixed-strain splits, Comput. Method. Appl. M., 200, 1591–1606, 2011. a, b
Kirk, B. S., Peterson, J. W., Stogner, R. H., and Carey, G. F.: libMesh: a C++ library for parallel adaptive mesh refinement/coarsening simulations, Eng. Comput., 22, 237–254, 2006. a
Koch, T., Gläser, D., Weishaupt, K., Ackermann, S., Beck, M., Becker, B., Burbulla, S., Class, H., Coltman, E., Emmaert, S., Fetzer, T., Grüninger, C., Heck, K., Hommel, J., Kury, T., Lipp, M., Mohammadi, F., Scherrer, S., and Flemisch, B.: DuMux 3–an open-source simulator for solving flow and transport problems in porous media with a focus on model coupling, Comput. Math. Appl., 81, 423–443, 2021. a
Kolditz, O., Bauer, S., Bilke, L., Böttcher, N., Delfs, J. O., Fischer, T., Görke, U. J., Kalbacher, T., Kosakowski, G., McDermott, C. I., Park, C. H., Radu, F., Rink, K., Shao, H., Shao, H. B., Sun, F., Sun, Y. Y., Singh, A. K., Taron, J., Walther, M., Wang, W., Watanabe, N., Wu, Y., Xie, M, Xu, W., and Zehner, B.: OpenGeoSys: an open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media, Environ. Earth Sci., 67, 589–599, 2012. a
Kosakowski, G. and Watanabe, N.: OpenGeoSys-Gem: a numerical tool for calculating geochemical and porosity changes in saturated and partially saturated media, Phys. Chem. Earth, 70, 138–149, 2014. a
Kulhawy, F. H. and Mayne, P. W.: Manual on estimating soil properties for foundation design, Tech. Rep., Electric Power Research Inst., Palo Alto, CA (USA); Cornell Univ., Ithaca, NY, USA, 1990. a
Lade, P. V.: Engineering properties of soils and typical correlations, in: Geotechnical and geoenvironmental engineering handbook, 43–67, Springer, Boston, USA, 2001. a, b
Lecampion, B., Bunger, A., and Zhang, X.: Numerical methods for hydraulic fracture propagation: a review of recent trends, J. Nat. Gas Sci. Eng., 49, 66–83, 2018. a
Lee, J., Kim, K.-I., Min, K.-B., and Rutqvist, J.: TOUGH-UDEC: A simulator for coupled multiphase fluid flows, heat transfers and discontinuous deformations in fractured porous media, Comput. Geosci., 126, 120–130, 2019. a
Lei, H., Xu, T., and Jin, G.: TOUGH2Biot–A simulator for coupled thermal–hydrodynamic–mechanical processes in subsurface flow systems: Application to CO2 geological storage and geothermal development, Comput. Geosci., 77, 8–19, 2015. a
Li, D., Bauer, S., Benisch, K., Graupner, B., and Beyer, C.: OpenGeoSys-ChemApp: a coupled simulator for reactive transport in multiphase systems and application to CO2 storage formation in Northern Germany, Acta Geotech., 9, 67–79, 2014. a
Lichtner, P. C. and Karra, S.: Modeling multiscale-multiphase-multicomponent reactive flows in porous media: Application to CO2 sequestration and enhanced geothermal energy using PFLOTRAN, in: Computational Models for CO2 Geo-sequestration & Compressed Air Energy Storage, 121–176, CRC Press, London, UK, 2014. a
Lie, K.-A.: An introduction to reservoir simulation using MATLAB/GNU Octave: User guide for the MATLAB Reservoir Simulation Toolbox (MRST), Cambridge University Press, Cambridge, UK, 2019. a
Look, B. G.: Handbook of geotechnical investigation and design tables, CRC Press, London, UK, 2014. a
Manzini, G. and Ferraris, S.: Mass-conservative finite volume methods on 2-D unstructured grids for the Richards' equation, Adv. Water Resour., 27, 1199–1215, 2004. a
Martin, V., Jaffré, J., and Roberts, J. E.: Modeling fractures and barriers as interfaces for flow in porous media, SIAM J. Sci. Comput., 26, 1667–1691, 2005. a
Martineau, R., Andrs, D., Carlsen, R., Gaston, D., Hansel, J., Kong, F., Lindsay, A., Permann, C., Slaughter, A., and Merzari, E.: Multiphysics for nuclear energy applications using a cohesive computational framework, Nucl. Eng. Des., 367, 110751, https://doi.org/10.1016/j.nucengdes.2020.110751, 2020. a
McMillan, T. C., Rau, G. C., Timms, W. A., and Andersen, M. S.: Utilizing the impact of Earth and atmospheric tides on groundwater systems: A review reveals the future potential, Rev. Geophys., 57, 281–315, 2019. a
Mikelić, A. and Wheeler, M. F.: Convergence of iterative coupling for coupled flow and geomechanics, Comput. Geosci., 17, 455–461, 2013. a
Mondol, N. H., Jahren, J., Bjørlykke, K., and Brevik, I.: Elastic properties of clay minerals, Leading Edge, 27, 758–770, 2008. a
Morris, J. P., Rubin, M., Block, G., and Bonner, M.: Simulations of fracture and fragmentation of geologic materials using combined FEM/DEM analysis, Int. J. Impact Eng., 33, 463–473, 2006. a
Nghiem, L., Sammon, P., Grabenstetter, J., and Ohkuma, H.: Modeling CO2 storage in aquifers with a fully-coupled geochemical EOS compositional simulator, in: SPE/DOE symposium on improved oil recovery, Society of Petroleum Engineers, Oklahoma, USA, 2004. a
Pandey, S., Vishal, V., and Chaudhuri, A.: Geothermal reservoir modeling in a coupled thermo-hydro-mechanical-chemical approach: A review, Earth-Sci. Rev., 185, 1157–1169, 2018. a
Peng, S.: Surface Subsidence Engineering: Theory and Practice, CSIRO PUBLISHING, Morgantown, USA, 2020. a
Peng, X., Zhang, L., Jeng, D., Chen, L., Liao, C., and Yang, H.: Effects of cross-correlated multiple spatially random soil properties on wave-induced oscillatory seabed response, Appl. Ocean Res., 62, 57–69, 2017. a
Permann, C. J., Gaston, D. R., Andrš, D., Carlsen, R. W., Kong, F., Lindsay, A. D., Miller, J. M., Peterson, J. W., Slaughter, A. E., and Stogner, R. H.: MOOSE: Enabling massively parallel multiphysics simulation, SoftwareX, 11, 100430, https://doi.org/10.1016/j.softx.2020.100430, 2020. a, b
Pham, H. T., Rühaak, W., Schuster, V., and Sass, I.: Fully hydro-mechanical coupled Plug-in (SUB+) in FEFLOW for analysis of land subsidence due to groundwater extraction, SoftwareX, 9, 15–19, 2019. a
Pruess, K., Oldenburg, C. M., and Moridis, G.: TOUGH2 user's guide version 2, Tech. Rep., Lawrence Berkeley National Lab.(LBNL), Berkeley, CA, USA, 1999. a
Reichenberger, V.: Numerical simulation of multiphase flow in fractured porous media, PhD thesis, University of Heidelberg, Heidelberg, Germany, 2003. a
Rutqvist, J.: An overview of TOUGH-based geomechanics models, Comput. Geosci., 108, 56–63, 2017. a
Strebelle, S.: Conditional simulation of complex geological structures using multiple-point statistics, Math. Geol., 34, 1–21, 2002. a
Subramanian, N.: Steel structures-Design and practice, Oxford University Press, Oxford, UK, 2011. a, b
Tarkowski, R.: Underground hydrogen storage: Characteristics and prospects, Renew. Sust. Energ. Rev., 105, 86–94, 2019. a
Terzaghi, K.: Die Berechnug der Durchlässigkeit des Tones aus dem Verlauf der hydromechanischen Spannungserscheinungen, Sitzungsber. Akad. Wiss. (Wien), Math.-Naturwiss. Kl., Abt. Iia, 132, 125–138, 1923. a, b
Tran, M. and Jha, B.: Coupling between transport and geomechanics affects spreading and mixing during viscous fingering in deformable aquifers, Adv. Water Resour., 136, 103485, https://doi.org/10.1029/2021WR029584, 2020. a
Vanmarcke, E., Shinozuka, M., Nakagiri, S., Schueller, G., and Grigoriu, M.: Random fields and stochastic finite elements, Struct. Saf., 3, 143–166, 1986. a
Verruijt, A.: Computational geomechanics, 7, Springer Science & Business Media, Delft, the Netherlands, 1995. a
Verruijt, A.: Theory and problems of poroelasticity, Delft University of Technology, Delft, the Netherlands, 71, 2013. a, b
Verruijt, A.: Numerical and analytical solutions of poroelastic problems, Geotechnical Research, 5, 39–50, 2018. a
Wang, H. F.: Theory of linear poroelasticity with applications to geomechanics and hydrogeology, Princeton University Press, Princeton, USA, 2017. a, b, c
Weng, X.: Modeling of complex hydraulic fractures in naturally fractured formation, Journal of Unconventional Oil and Gas Resources, 9, 114–135, 2015. a
White, M., Fu, P., McClure, M., Danko, G., Elsworth, D., Sonnenthal, E., Kelkar, S., and Podgorney, R.: A suite of benchmark and challenge problems for enhanced geothermal systems, Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 4, 79–117, 2018. a
Wilkins, A., Green, C. P., and Ennis-King, J.: PorousFlow: a multiphysics simulation code for coupled problems in porous media, Journal of Open Source Software, 5, 2176, https://doi.org/10.21105/joss.02176, 2020. a, b, c
Xu, L.: Typical values of Young's elastic modulus and Poisson's ratio for pavement materials, technical note, available at: https://edoc.tips/download/typical-values-of-youngs-elastic-modulus-and-edu_pdf (last access: 15 October 2021), 2016. a
Xu, T., Sonnenthal, E., Spycher, N., and Pruess, K.: TOUGHREACT–a simulation program for non-isothermal multiphase reactive geochemical transport in variably saturated geologic media: applications to geothermal injectivity and CO2 geological sequestration, Comput. Geosci., 32, 145–165, 2006. a
Yang, D., Koukouzas, N., Green, M., and Sheng, Y.: Recent development on underground coal gasification and subsequent CO2 storage, J. Energy Inst., 89, 469–484, 2016. a
Ye, S., Xue, Y., Wu, J., Yan, X., and Yu, J.: Progression and mitigation of land subsidence in China, Hydrogeol. J., 24, 685–693, 2016. a
Zappa, G., Bersezio, R., Felletti, F., and Giudici, M.: Modeling heterogeneity of gravel-sand, braided stream, alluvial aquifers at the facies scale, J. Hydrol., 325, 134–153, 2006. a
Zaruba, Q. and Mencl, V.: Landslides and their control, Elsevier, Prague, Czech Republic, 2014. a
Zhao, H., Jeng, D.-S., Liao, C., and Zhu, J.: Three-dimensional modeling of wave-induced residual seabed response around a mono-pile foundation, Coast. Eng., 128, 1–21, 2017. a
Zhao, X. and Jha, B.: Role of well operations and multiphase geomechanics in controlling fault stability during CO2 storage and enhanced oil recovery, J. Geophys. Res.-Sol. Ea., 124, 6359–6375, 2019. a