the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
GP-SWAT (v1.0): a two-level graph-based parallel simulation tool for the SWAT model
Dejian Zhang
Bingqing Lin
Jiefeng Wu
Qiaoying Lin
High-fidelity and large-scale hydrological models are increasingly used to investigate the impacts of human activities and climate change on water availability and quality. However, the detailed representations of real-world systems and processes contained in these models inevitably lead to prohibitively high execution times, ranging from minutes to days. Such models become computationally prohibitive or even infeasible when large iterative model simulations are involved. In this study, we propose a generic two-level (i.e., watershed- and subbasin-level) model parallelization schema to reduce the run time of computationally expensive model applications through a combination of model spatial decomposition and the graph-parallel Pregel algorithm. Taking the Soil and Water Assessment Tool (SWAT) as an example, we implemented a generic tool named GP-SWAT, enabling watershed-level and subbasin-level model parallelization on a Spark computer cluster. We then evaluated GP-SWAT in two sets of experiments to demonstrate the ability of GP-SWAT to accelerate single and iterative model simulations and to run in different environments. In each test set, GP-SWAT was applied for the parallel simulation of four synthetic hydrological models with different input/output (I/O) burdens. The single-model parallelization results showed that GP-SWAT can obtain a 2.3–5.8-times speedup. For multiple simulations with subbasin-level parallelization, GP-SWAT yielded a remarkable speedup of 8.34–27.03 times. In both cases, the speedup ratios increased with an increasing computation burden. The experimental results indicate that GP-SWAT can effectively solve the high-computational-demand problems of the SWAT model. In addition, as a scalable and flexible tool, it can be run in diverse environments, from a commodity computer running the Microsoft Windows operating system to a Spark cluster consisting of a large number of computational nodes. Moreover, it is possible to apply this generic tool to other subbasin-based hydrological models or even acyclic models in other domains to alleviate I/O demands and to optimize model computational performance.
- Article
(3942 KB) - Full-text XML
- BibTeX
- EndNote
With the enhanced availability of high-resolution remote sensing data and long periods of hydrometeorological data, hydrologists are increasingly building high-fidelity hydrological models to investigate water availability (Liang et al., 2020), water quality (Fang et al., 2020), climate change (Cai et al., 2016), and watershed management options (Jayakody et al., 2014; Qi and Altinakar, 2011; Lee et al., 2010). However, these hydrological models, which contain detailed representations of real-world systems and processes, can demand large computational budgets and require prohibitively high execution times, ranging from minutes to days (Razavi et al., 2010). Because modeling practices such as model calibration and uncertainty analysis usually involve thousands of model evaluations or more, they may sometimes become computationally prohibitive or even infeasible (Razavi and Tolson, 2013). Thus, the effective use of computationally expensive simulations remains a challenge for many applications involving a large number of model simulations.
In general, there are four broad types of research methods for alleviating the computational burden associated with computationally expensive model applications: (1) utilizing metamodeling approaches (Chandra et al., 2020; Sun et al., 2015), (2) developing computationally efficient algorithms (Humphrey et al., 2012; Joseph and Guillaume, 2013), (3) opportunistically avoiding model evaluations (Razavi et al., 2010), and (4) utilizing parallel computing technologies and infrastructures (Yang et al., 2020; Huang et al., 2019; Wu et al., 2013, 2014; Zamani et al., 2020). The first, second, and third ideas above share the same goal of reducing computational demand by using lightweight surrogate models, by decreasing the number of model simulations, and by terminating model execution early when the simulation result is poorer than expected, respectively. The fourth idea adopts a different strategy of boosting model application performance by optimizing the efficiency of computational resource utilization.
Among these methods, model parallelization is the most frequently adopted. It has been extensively applied to optimize the efficiency of generic modeling activities, such as model calibration (Zhang et al., 2013; Ercan et al., 2014; Gorgan et al., 2012), sensitivity analysis (Khalid et al., 2016; Hu et al., 2015), uncertainty analysis (Zhang et al., 2016; Wu and Liu, 2012; Zamani et al., 2020) and the identification of beneficial management practices (Liu et al., 2013). For spatially explicit models, it is possible to decompose a large-scale model into multiple smaller models and, in parallel, to simulate the independent smaller models to further improve model performance (hereafter, for simplicity, this spatial-decomposition and simulation method is referred to as the spatial-decomposition method). Through our literature review, we found that the spatial-decomposition method is usually performed through model reconstruction. For example, Wu et al. (2013) improved the performance of the Soil and Water Assessment Tool (SWAT) model by distributing subbasin simulations to different computational cores through the Message Passing Interface (MPI). Wang et al. (2013) developed the temporal–spatial discretization method (TSDM), in which the parallelization degree of subbasins is exploited to the maximum extent by properly organizing the simulation sequences of dependent subbasins. To boost the performance of the fully sequential dependent hydrological model (FSDHM), Liu et al. (2016) adopted the MPI to perform subbasin-level model parallelization in a computer cluster. Based on the MPI and OpenMP frameworks, Zhu et al. (2019) introduced the spatially explicit integrated modeling system (SEIMS) to perform model parallelization in a computer cluster consisting of multiple nodes. However, this parallelization method is relatively complex, as it requires a throughout model reconstruction to enable the parallel simulation of model components, to perform the communication among components that is necessary for integrating the model results, and to deal with issues such as failover and load balance. As a result, a steep learning curve is expected for modelers who are unfamiliar with the model source codes. Although there are some parallel computation frameworks available that can facilitate this method, e.g., the Open MPI and the OpenMP application programming interface (API), it is still a very tedious and time-consuming process.
For acyclic models, it is possible to perform model decomposition without model reconstruction. Taking the SWAT model as an example, a large-scale watershed model involving multiple subbasins can be split into multiple smaller models, each of which consists of only one subbasin (hereafter referred to as subbasin models). The stream flow and chemical loadings from upstream subbasins can be treated as boundary conditions of their downstream subbasins, which can be incorporated as point sources for these downstream subbasins. Through proper organization of the simulation of these models, a result identical to that of the original model can be obtained. In this strategy, upstream subbasin models must be simulated before downstream subbasin models; however, sibling subbasin models can be simulated in parallel to optimize model performance (for detailed information about the implementation of subbasin-level parallelization for the SWAT model, readers should refer to Yalew et al., 2013, and Lin and Zhang, 2021). Therefore, it can gracefully avoid much of the workload (e.g., failover, task management and balancing) that modelers face when consulting the model reconstruction method. Additionally, this aspect results in great opportunities to cooperate with recent advanced information technologies (ITs) and resources. For example, it is possible to loosely couple this spatial-decomposition method and parallel frameworks for processing big data (such as Hadoop, Spark and Flink) to perform model parallelization and alleviate the burden placed on modelers to address low-level programming tasks such as failover as well as task management and balancing. It also provides an economic alternative to deploy these solutions on cloud-based facilities, such as Azure HDInsight, Amazon Web Services Elastic Map Reduce (EMR), and Google Dataproc. Because these parallel frameworks are so universal in the IT industry, many cloud providers currently offer a convenient, on-demand support environment for these frameworks.
In this study, we propose a two-level (watershed- and subbasin-level) model parallelization scheme based on a combination of the graph-parallel Pregel algorithm and model spatial domain decomposition. The objective of this study is to create a simulation-accelerated tool for the SWAT model by adopting both watershed-level and subbasin-level parallelization, without model reconstruction. We hope that this tool will help IT practitioners or modelers improve model performance without requiring specific domain knowledge of the hydrological model. In accordance with this scheme and goal, a graph-parallel simulation tool for SWAT (named GP-SWAT) has been developed using an open-source general-purpose distributed cluster computing framework, Spark. GP-SWAT has been assessed in two sets of experiments to demonstrate its potential to accelerate single and iterative model simulations at different parallelization granularities when implemented on a computer running the Windows operating system (OS) and on a Spark cluster consisting of five computational nodes. Experiment set one was conducted to illustrate that GP-SWAT can be used to perform subbasin-level model parallelization using a multicore computer running Windows OS, while in experiment set two, GP-SWAT was assessed for iterative model runs. For each experiment in the latter set, subbasin- and watershed-level parallelization schemes were employed to execute 1000 model simulations with one to five parallel tasks implemented on each computational node. In each of the test cases, GP-SWAT was evaluated based on four synthetic hydrological models representing different input/output (I/O) burdens.
2.1 Graph representation of hydrological models
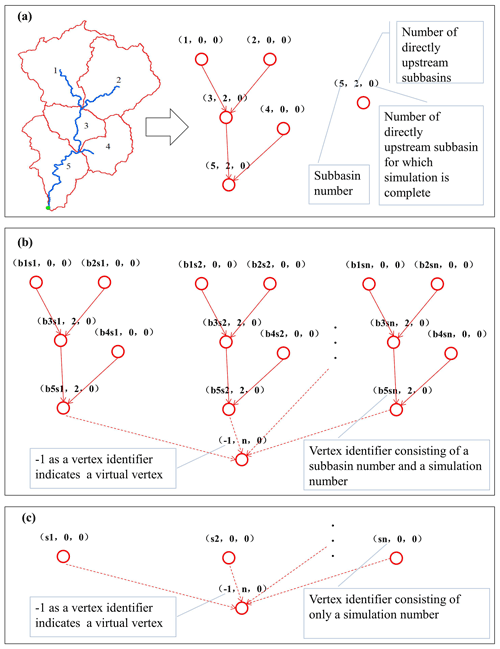
A property graph is a directed graph with properties attached to each vertex and edge. Each vertex is keyed by a unique identifier. Similarly, each edge has corresponding source and destination vertex identifiers. In many domains of the natural and social sciences, relationships of interest can be described by property graphs, such as the relationships in traffic and social networks. Accordingly, many graph algorithms have been devised to simplify and improve the performance on related analytical tasks, including methods for the parallel processing of graph-based data. From this perspective, the relationships between the components of a distributed hydrological model can be described by a dendriform property graph. Figure 1a demonstrates how a simple watershed model can be represented with a property graph. Each subbasin can be represented as a vertex with an identifier and two properties denoting how many subbasins exist directly upstream of the current subbasin (referred to as subNo hereafter) and the number of these directly upstream subbasins for which the simulation process has been completed in the current computation step (referred to as finSubNo hereafter). Each edge denotes an upstream–downstream flow drainage relationship. Modeling routines involving iterative simulations can also be represented in the form of property graphs. In this case, each simulation is represented by a subgraph of the integrated graph, and each outlet vertex of these subgraphs is connected to a virtual vertex to form the integrated graph (Fig. 1b). To uniquely identify a vertex in the integrated graph, the vertex identifier consists of both the subbasin number and the simulation number. In addition, the virtual vertex is identified by a special number (i.e., −1 in our case). Such an integrated property graph representing a modeling routine involving iterative simulation can also be interpreted as a property graph representing a large-scale virtual hydrological model consisting of many identical landscapes (represented by the same model with different parameters) that are connected to a virtual outlet. Moreover, in this case, each vertex can be considered to represent a subbasin model or watershed model, and thus, it is possible to perform model parallelization at the watershed and subbasin levels (Fig. 1c).
2.2 Design and implementation of GP-SWAT
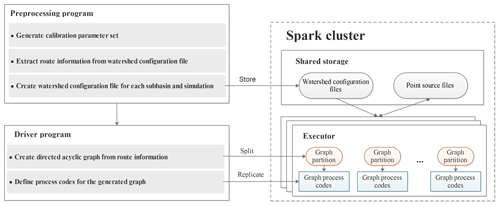
Apache Spark is an open-source general-purpose distributed cluster computing framework that provides distributed task dispatching, scheduling and graph functionalities through an API available in the Java, Python, Scala and R languages. Apache Spark can run in diverse environments, ranging from a single computer (running the Microsoft Windows or Linux OS) to a computer cluster consisting of a large number of computational nodes hosted in an in-house or cloud environment. GP-SWAT is designed to work with the Spark graph API for model-level and subbasin-level parallelization. Figure 2 outlines the main components and required environments of GP-SWAT and their interactions. The required environments include a shared storage environment for sharing model simulation results and other information and a Spark cluster for the parallel simulation of models. In this study, the network file system (NFS) protocol was used as the basis for the shared storage to exchange data among the executors in the computer cluster. GP-SWAT consists of two components: a preprocessing program and a driver program. The preprocessing program is used to generate a calibration parameter set, extract route information from the watershed configuration file (fig.fig) for the SWAT model and create a watershed configuration file for each subbasin model. The second component, the driver program, creates a hydrological model property graph from the route information generated by the preprocessing program and defines how the models are to be simulated in parallel; its output is then replicated to the executors to actually carry out model parallelization.
Figure 3 shows the code of the driver program as implemented in Scala. The code for creating the hydrological model property graph (lines 1–12 in Fig. 3) is straightforward. Vertices and edges are first created based on the route information extracted from the watershed configuration file by the preprocessing program. The property graph for the hydrological model is then created by taking these vertices and edges as function arguments. Model parallelization is performed by means of the graph-parallel Pregel algorithm (lines 14–33 in Fig. 3). The Pregel algorithm is a message-based algorithm. It consists of a series of supersteps in which each vertex receives the sum of its inbound messages from the previous superstep, the vertex properties are updated in accordance with the merged messages, and messages are then sent to neighboring vertices in the next superstep. The Pregel algorithm terminates when there are no messages remaining or the maximum number of iterations defined by the developers has been reached. The Pregel algorithm as implemented in Spark takes two argument lists. The first argument list consists of the initial message, the maximum number of iterations and the edge direction in which to send messages. The second argument list consists of the user-defined functions for receiving messages (receiveMsg program), computing messages (sendMsg program) and combining messages (mergeMsg program). To perform model parallelization with the Pregel algorithm, “0” is specified as the initial message, the maximum number of iterations is assigned to be a very large number (Int.MaxValue) to ensure that the Pregel algorithm will terminate only once no messages remain, and the edge direction is set to “EdgeDirection.Out”, indicating that messages are sent only to downstream neighboring vertices. Three anonymous functions are provided to receive and process messages (lines 16–22 in Fig. 3), generate messages for the next superstep (lines 24–30 in Fig. 3) and merge messages (line 32 in Fig. 3). In the first anonymous function, finSubNo (the second property of a vertex, denoting the number of directly upstream subbasin models for which simulation has been completed) is updated by adding the merged message (denoting the number of directly upstream subbasin models for which simulation had been completed in the previous superstep), and finSubNo is then compared with subNo (denoting the number of subbasins directly upstream of the current subbasin). If finSubNo is equal to subNo (meaning that simulation is complete for all directly upstream subbasins), then the subbasin model represented by the current vertex is executed through an external function that will be discussed later. In the second anonymous function, used to compute the messages for the next superstep, a value of “1” is sent to the downstream neighboring vertex if the current subbasin model has been simulated in the current superstep; otherwise, a value of “0” is sent, indicating that no subbasin model was executed. The third anonymous function simply adds two messages from upstream vertices and returns the result of the addition operation (this function is invoked n−1 times, where n is the number of inbound messages).
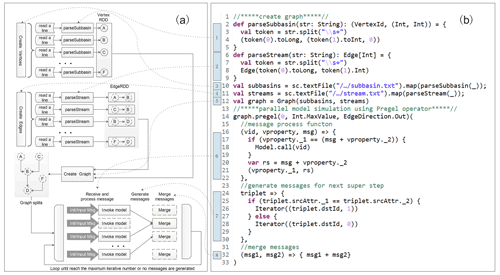
Figure 3Schematic diagram of model parallelization with the Pregel algorithm (a) and code snippet of the driver program (b) (note that imported packages and some signatures have been removed for simplicity).
In Fig. 4, we demonstrate the model parallelization of a simple hydrological model consisting of five subbasins (Fig. 1a) using the Pregel algorithm. In the initial superstep, the receiveMsg program is invoked on all vertices and is passed the default message “0”. As seen from Fig. 4, finSubNo is equal to subNo at vertices 1, 2 and 4; thus, these three subbasin models are executed. Next, the sendMsg program is invoked on all vertices that have inbound messages and downstream neighboring vertices. For vertices 1, 2 and 4, at which subbasin model simulation has been performed, “1” is sent to their downstream neighboring vertices. Because vertex 3 did not execute simulation of its subbasin model, “0” is sent. Finally, at the end of each superstep, the mergeMsg program is invoked on vertices with at least two inbound messages in the next superstep. In the second superstep, the receiveMsg program is invoked on vertices 3 and 5, which have inbound messages. Because finSubNo is equal to subNo only at vertex 3, only the subbasin model associated with this vertex is executed, and sendMsg sends “1” to its downstream neighboring vertex 5. In superstep 3, the receiveMsg program is invoked on vertex 5 and triggers the simulation of its associated subbasin model, as its finSubNo value has reached the number of directly upstream subbasins.
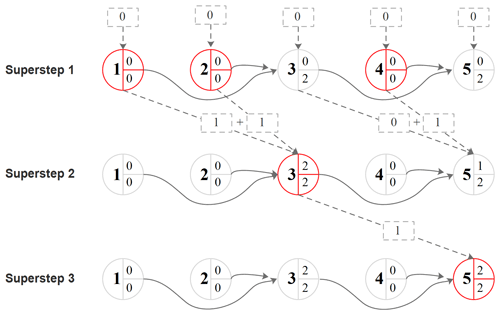
Figure 4Demonstration of the parallel simulation of subbasin models of the example watershed (Fig. 1a) using the Pregel operator of GraphX (the number in the left part of a vertex is the subbasin number, the lower right number denotes how many upstream subbasins are directly connected to the current subbasin, the upper right number indicates the number of directly upstream subbasins for which simulation has been completed, and a red vertex denotes that the corresponding subbasin model is simulated in that superstep).
The function for invoking a model (Model.call in Fig. 3) is implemented in Java to reuse components that have been implemented in previous studies (Zhang et al., 2016). Because the models are designed to be executed in parallel within a computational node and among nodes, we must ensure that a model can be executed only once at a given time. Thus, the first step of model simulation is to find a model that is not occupied; this task is performed through a combination of the synchronous mechanism and static indicators of Java. When a free model is identified, the watershed configuration file is replaced, and the upstream point-source files stored in the NFS shared storage are copied to the model directory. Next, the subbasin model inputs are edited in accordance with the parameter set of the current simulation. Finally, the model is executed, and the model output is copied to the NFS shared storage for later use.
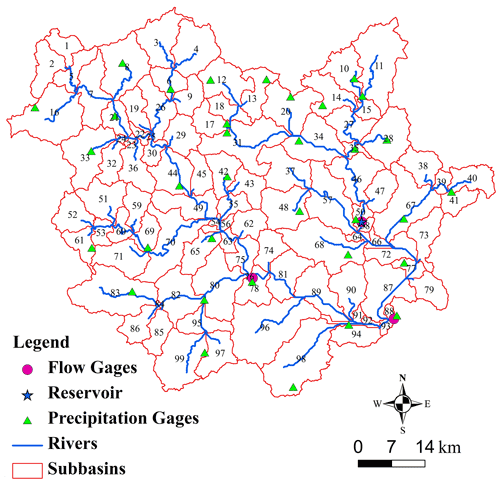
In this study, synthetic hydrological models of the Jinjiang watersheds (Fig. 5) were used to evaluate the performance of GP-SWAT. Jinjiang catchment is located in south-eastern Fujian Province of China. It has a drainage area of 5629 km2, which is occupied predominantly by mountains and rangelands. There are two major river branches within the Jinjiang River, i.e., the east branch and the west branch, which merge into the main stream 2.5 km upstream of the Shilong gauge station. With a typical humid subtropical climate, the area has an annual mean temperature of 20 ∘C and average annual precipitation of 1686 mm.
Four synthetic hydrological models representing different I/O burdens and different levels of river network complexity were used to evaluate the efficiency of GP-SWAT. These synthetic models were built based on the Jinjiang hydrological model (Zhang et al., 2015). These synthetic models were created with a tool implemented in the Java programming language (available at https://github.com/djzhang80/models-and-tools/blob/master/createproject.jar, last access: 25 September 2021). This tool allows users to create synthetic models with any desired hydrological response units (HRUs) per subbasin for performance evaluation but not to create meaningful hydrological models. The Jinjiang hydrological models include 99 subbasins and 1 reservoir. For the various synthetic hydrological models, the number of subbasins, the simulation period and other configuration parameters are the same, but different numbers of HRUs in the subbasins are considered. The synthetic models based on the Jinjiang hydrological model (JJ) with 5, 50, 100 and 150 HRUs per subbasin are denoted by JJ1, JJ2, JJ3 and JJ4, respectively.
Two sets of experiments were established to verify the use cases of GP-SWAT: (1) it can be used to accelerate single model simulations on a multicore computer running Microsoft Windows through subbasin-level parallelization, and (2) it can also be employed to run parallel model simulations on a Spark computer cluster through both model-level and subbasin-level parallelization. In this study, the performance of GP-SWAT was evaluated based on the speedup metric, which is defined as follows:
where n is the total number of simulations for a given job, JET is the total execution time of the job when run in the test environment, ST is the average execution time of one model simulation, and Speedupact measures how much faster a program runs in parallel compared to being run sequentially on a single computer. For subbasin-level parallelization, we also calculated the theoretical speedup, which considers the theoretical speedup that a model can obtain under different test configurations. The theoretical speedup is calculated as follows:
where subnum is the number subbasins of the hydrological model under test, n is the total number of supersteps, i denotes the ith superstep, Counti is the number of subbasin models simulated in the ith superstep, PTnum is the number of parallel tasks performed at an executor, and Ceil is a function that returns the smallest integer value that is greater than or equal to a predetermined parameter value.
Experiment set one was carried out on a workstation with 24 processors operating at a frequency of 2.67 GHz, 24 GB of RAM, and 1 TB of disk storage, running the Windows 2012 Server OS. Spark was configured with one executor, and a maximum of 24 cores were allowed in this executor. The four synthetic hydrological models were used to evaluate subbasin-level parallelization with the number of parallel executor tasks ranging from 1 to 24. Experiment set two was carried out on a Spark cluster consisting of five computational nodes. Each computational node had a quad-core CPU, 8 GB of RAM and 50 GB of disk storage. The CPU frequency was 2.2 GHz, and each node was running 64-bit Linux as the OS. In this Spark cluster, each node could have 1–5 executors, but each executor was allowed to have only one core. Model-level and subbasin-level parallelization of the four synthetic hydrological models was conducted on this Spark cluster with 5, 10, 15, 20 and 25 executors.
4.1 Performance analysis
Spark applications can run either in local mode (nondistributed deployment mode with a single Java Virtual Machine (JVM)) or in cluster mode. When run in local mode, Spark can be deployed on a computer with a Microsoft Windows, Mac, or Linux OS. Experiment set one was designed to verify that GP-SWAT can be used to perform subbasin-level model parallelization using a multicore computer running the Windows OS. Each synthetic model was simulated 10 times with 1–24 cores, and the actual speedup values were calculated using the average execution time. Figure 6a shows the actual and theoretical speedups versus the number of parallel tasks performed in local mode. In general, the actual speedup values increase with increasing model complexity, indicating that subbasin-level parallelization works especially well for complex models. For less complex models, such as JJ1, the best speedup value is 2.3. However, for more complex models, a much better speedup can be obtained. For example, the maximum speedup values obtained for JJ4 is 5.8. It is noted that the actual speedup values surpass the theoretical values for JJ3 and JJ4. The reason for this phenomenon is that the speedup is obtained not only by simulating the model components in parallel but also by alleviating the model's I/O burden. For example, the execution time of the undivided model of JJ4 is 425.02 s, but the execution time of its subbasin model is only 2.35 s. In other words, even if the subbasin models of JJ4 are executed in sequence, this still can lead to a reduction of 192.37 s (425.02–2.35 × 99). This is because the original SWAT model reads all model inputs at once in the initial stages of model execution, which can easily cause I/O saturation and thus prolong the model execution time. The theoretical speedup ratios were calculated against the execution time of the original model. In contrast to the theoretical speedup ratio calculation, the actual speedup ratios were calculated by considering both performance gains from subbasin-level parallelization and I/O alleviation. Figure 6b shows the job execution times of these synthetic models versus the parallel tasks performed on a Windows server. The job execution time includes the times associated with job initiation, task orchestration and model result transfer (system time), and the time pertaining to model execution (model time). The model execution times were calculated by summing the total execution time for each subbasin model, and the system execution times were calculated by subtracting the model execution times from the job execution times. As shown in Fig. 6b, the system execution times were stable for models with different HRUs.
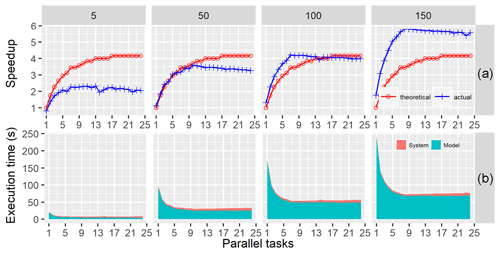
Figure 6Speedups (a) and job execution times (b) for single model simulation on a Windows server versus the number of parallel tasks for the four synthetic hydrological models.
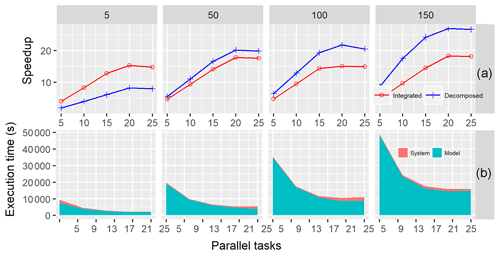
In experiment set two, we evaluated the performance of GP-SWAT for iterative model runs. For each experiment in this set, subbasin- and watershed-level parallelization (hereafter referred to as the decomposed mode and the integrated mode, respectively) were employed to execute 1000 model simulations in the test environment with one to five parallel tasks implemented at each computational node. The speedup values obtained in the integrated mode (red) and in the decomposed mode (blue) are plotted against the number of parallel tasks in Fig. 7a. For a simple synthetic model (i.e., JJ1), the speedups in the integrated mode surpass those in the decomposed model, while for more complex models (models other than JJ1), the speedups in the decomposed mode are better than those in the integrated mode. This is a result of the conflict between the system overheads (including job initiation, task orchestration, and model result transfer) and performance gains associated with subbasin-level parallelization. In general, the speedup gradually increases with up to 20 parallel tasks and then slightly decreases as the number of parallel tasks continues to increase. Similar to the case of single model runs, we also observe that the speedup increases with increasing model complexity for both the decomposed and integrated modes. As discussed before, this phenomenon is caused by the additional performance gains resulting from model decomposition. For example, the maximum speedup for the least complex model is 8.34, while the speedup for JJ4 is 27.03. Figure 7b shows the execution times against the number of parallel tasks. In general, the fraction of system time decreases with increasing parallel tasks, and it increases again when the number of parallel tasks reaches 4 and/or 5. We believe that larger system times with smaller parallel tasks occur because the model execution overheads are relatively small, while in cases with large parallel tasks, the conflict of demanding resources certainly leads to a longer time required to perform task dispatch and secure computational resources.
4.2 Possible usage and guidance
As a two-level parallelization tool, GP-SWAT can be used to reduce the run time of single or iterative model simulations. For modeling routines involving iterative model simulations, such as model calibration, sensitivity and uncertainty analysis, and beneficial management practice (BMP) optimization, users can incorporate GP-SWAT into the corresponding algorithms/tools with proper adaptation to enhance the model simulation performance. Moreover, when GP-SWAT is operating in the decomposed mode (i.e., subbasin-level parallelization), it can be very computationally frugal in some cases. For example, when GP-SWAT is used for BMP optimization or subbasin-scale model calibration, the changes in model input pertain to only a small portion of the model components (e.g., a subbasin or reservoir). In such cases, only the changed and downstream subbasins and reservoirs require new computations during the iterative simulation process, thus greatly reducing the computational complexity through the reuse of the model results for the unchanged subbasins. Compared with the parallelization of iterative model simulations, the parallelization of a single model is of less interest because most model applications involve a large number of simulations. However, we have found that it is essential to accelerate single model simulation when using hydrological models to support applications such as emergency decision-making or flood forecasting in a product environment. Because of its ability to accelerate a single model, we believe that GP-SWAT can be integrated into decision-making and flood forecasting systems to offer quasi-real-time support for decision-making and flood forecasting.
GP-SWAT can be run in either the decomposed mode or the integrated mode. As indicated by the experimental results, the operation mode can exert a great influence on the performance of GP-SWAT. Compared with the integrated mode, the decomposed mode requires more computation time to perform task management and model result transfer; thus, it may not be suitable for lightweight models. On the other hand, the decomposed mode can greatly alleviate the I/O bottleneck for complex models, thereby reducing the computation time. In such a case, the extra time required for task management and model result transfer is negligible. Therefore, we suggest running GP-SWAT in the integrated mode for lightweight models and running it in the decomposed mode otherwise. There is one exception to this suggestion. When conducting iterative simulations of lightweight models, GP-SWAT should run in the decomposed mode if the changes are restricted to a small portion of the downstream subbasins.
4.3 Advantages and limitations
GP-SWAT attempts to accelerate the simulation of a highly computationally intense SWAT model through two-level parallelization using the graph-parallel Pregel algorithm. As a two-level model parallelization tool, it can be used to accelerate single or iterative model simulations, endowing it with a range of possible applications and great flexibility in maximizing performance. In addition, the applicability of a model parallelization tool is also influenced by its running environment. As an open-source tool implemented in Java and Scala, GP-SWAT can be run not only on a commodity computer with a Linux, Unix or Windows OS but also on a Spark cluster with a large number of computational nodes. Moreover, the Spark framework is so universal in the IT industry that many cloud providers currently offer convenient on-demand managed Spark clusters (e.g., Google Dataproc, Amazon Web Services EMR, and Azure HDInsight) with out-of-the-box support for Spark-based applications. Thus, users can easily adapt GP-SWAT to run in these environments, thereby avoiding the technical and financial burdens encountered when building an in-house Spark cluster.
Moreover, the Spark-based implementation of GP-SWAT lends it many advantages that other distributed computation frameworks (e.g., Open MPI) may not have. First, Spark provides many high-level functionalities, such as distributed task dispatching, scheduling, failover management and load balancing, which can greatly reduce the burden on programmers. For example, by means of the failover management functionality, Spark-based programs can gracefully handle partial failures (e.g., partial breakdown of the computational nodes), as the Spark framework can automatically detect failed tasks and then reschedule these tasks on healthy computational nodes. In MPI-based applications, it may be necessary to explicitly manage these issues. Second, the Spark framework is a higher-level parallel computing framework. The SWAT model and Spark need to be coupled only loosely to perform model parallelization. In contrast, to perform model parallelization with MPI, model reconstruction is usually required.
GP-SWAT uses the NFS protocol to exchange data among different computational nodes. While NFS is easy to implement, some problems may be encountered in the case of a large-scale computational cluster. Because NFS employs a master–slave architecture, performance bottlenecks may arise when a large number of nodes are simultaneously attempting to read from or write to the master. Another drawback of GP-SWAT is that it requires additional I/O operations when working in the decomposed mode (i.e., subbasin-level parallelization). For example, the basin-level inputs are replicated to the subbasin models, and point-source files (which contain redundancies with the standard SWAT outputs) are generated and read by the subbasin models. However, this issue can be partially addressed by optimizing the I/O module of SWAT to reduce the redundant output.
In this study, we developed a two-level (i.e., watershed-level and subbasin-level) parallel simulation tool for the SWAT model, called GP-SWAT, based on the graph-parallel Pregel algorithm. The efficiency of GP-SWAT was evaluated through two sets of experiments. Experiment set one was conducted to illustrate that GP-SWAT can be used to perform subbasin-level model parallelization using a multicore computer running the Windows OS. The results show that GP-SWAT can accelerate the single model simulation process, especially for complex models. In experiment set two, GP-SWAT was assessed for iterative model runs. For each experiment in this set, subbasin- and watershed-level parallelization schemes were employed to execute 1000 model simulations in the test environment with one to five parallel tasks implemented at each computational node. Our experimental results show that GP-SWAT can obtain a remarkable performance improvement over traditional SWAT models by leveraging the computational power of a Spark cluster. In addition to performance improvement, GP-SWAT also has some other notable features.
-
It can be employed to perform both individual and iterative model parallelization, endowing it with a range of possible applications and great flexibility in maximizing performance through the selection of a suitable parallelization mode (at the watershed level or the subbasin level).
-
It is a flexible and scalable tool that can run in diverse environments, ranging from a commodity computer with a Microsoft Windows, Mac or Linux OS to a Spark cluster consisting of a large number of computational nodes, either deployed in-house or provided by a third-party cloud service provider.
Further work should also be conducted to improve the performance and extend the usability of our proposed method. In this study, data exchange was performed through the NFS protocol, which can present an I/O bottleneck when a large number of computational nodes are involved. To scale GP-SWAT to a larger computational cluster, a distributed storage system, such as the Hadoop Distributed File System (HDFS) or Redis, should be used to address this potential issue. In addition, the application of the proposed scheme to other environmental models, such as the Hydrologic Simulation Program-FORTRAN (HSPF) model, will be necessary to demonstrate the flexibility and universality of our proposed method.
The model code (GP-SWAT v1.0) is released by MIT under license. Source codes, manual and synthetic models used in this study (https://doi.org/10.5281/zenodo.4270676, Zhang et al., 2021) are available on the Zenodo repository.
The data sets (i.e., the synthetic models) are available along with the source codes of GP-SWAT in the Zenodo repository (https://doi.org/10.5281/zenodo.4270676, Zhang et al., 2021).
QL conceived the study and provided supervision. DZ, BL and JW developed the GP-SWAT and carried out the analysis. DZ, BL and JW prepared the manuscript, with further editing from QL.
The authors declare that they have no conflict of interest.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We appreciate the valuable and constructive comments and suggestions made by the editor, Liangjun Zhu, and the anonymous reviewer.
This research has been supported by the Natural Science Foundation of Fujian Province (grant nos. 2020J01779 and 2021J01660), the Science and Technology Project of Xiamen (grant no. 3502Z20183056), and the Science and Technology Climbing Program of Xiamen University of Technology (grant no. XPDKT19014).
This paper was edited by Wolfgang Kurtz and reviewed by Liangjun Zhu and one anonymous referee.
Cai, X., Yang, Z.-L., Fisher, J. B., Zhang, X., Barlage, M., and Chen, F.: Integration of nitrogen dynamics into the Noah-MP land surface model v1.1 for climate and environmental predictions, Geosci. Model Dev., 9, 1–15, https://doi.org/10.5194/gmd-9-1-2016, 2016.
Chandra, R., Azam, D., Kapoor, A., and Müller, R. D.: Surrogate-assisted Bayesian inversion for landscape and basin evolution models, Geosci. Model Dev., 13, 2959–2979, https://doi.org/10.5194/gmd-13-2959-2020, 2020.
Ercan, M. B., Goodall, J. L., Castronova, A. M., Humphrey, M., and Beekwilder, N.: Calibration of SWAT models using the cloud, Environ. Modell. Softw., 62, 188–196, https://doi.org/10.1016/j.envsoft.2014.09.002, 2014.
Fang, Y., Chen, X., Gomez Velez, J., Zhang, X., Duan, Z., Hammond, G. E., Goldman, A. E., Garayburu-Caruso, V. A., and Graham, E. B.: A multirate mass transfer model to represent the interaction of multicomponent biogeochemical processes between surface water and hyporheic zones (SWAT-MRMT-R 1.0), Geosci. Model Dev., 13, 3553–3569, https://doi.org/10.5194/gmd-13-3553-2020, 2020.
Gorgan, D., Bacu, V., Mihon, D., Rodila, D., Abbaspour, K., and Rouholahnejad, E.: Grid based calibration of SWAT hydrological models, Nat. Hazards Earth Syst. Sci., 12, 2411–2423, https://doi.org/10.5194/nhess-12-2411-2012, 2012.
Hu, Y., Garcia-Cabrejo, O., Cai, X., Valocchi, A. J., and DuPont, B.: Global sensitivity analysis for large-scale socio-hydrological models using Hadoop, Environ. Modell. Softw., 73, 231–243, https://doi.org/10.1016/j.envsoft.2015.08.015, 2015.
Huang, X., Huang, X., Wang, D., Wu, Q., Li, Y., Zhang, S., Chen, Y., Wang, M., Gao, Y., Tang, Q., Chen, Y., Fang, Z., Song, Z., and Yang, G.: OpenArray v1.0: a simple operator library for the decoupling of ocean modeling and parallel computing, Geosci. Model Dev., 12, 4729–4749, https://doi.org/10.5194/gmd-12-4729-2019, 2019.
Humphrey, M., Beekwilder, N., Goodall, J. L., and Ercan, M. B.: Calibration of watershed models using cloud computing, in: Proceedings of the International Conference on E-Science, 2012 IEEE 8th International Conference on E-Science, Chicago, IL, USA, 8–12 October 2012, 1–8, https://doi.org/10.1109/eScience.2012.6404420, 2012.
Jayakody, P., Parajuli, P. B., and Cathcart, T. P.: Impacts of climate variability on water quality with best management practices in sub-tropical climate of USA, Hydrol. Process., 28, 5776–5790, 2014.
Joseph, J. F. and Guillaume, J. H. A.: Using a parallelized MCMC algorithm in R to identify appropriate likelihood functions for SWAT, Environ. Modell. Softw., 46, 292–298, https://doi.org/10.1016/j.envsoft.2013.03.012, 2013.
Khalid, K., Ali, M. F., Rahman, N. F. A., Mispan, M. R., Haron, S. H., Othman, Z., and Bachok, M. F.: Sensitivity Analysis in Watershed Model Using SUFI-2 Algorithm, Procedia Engineer., 162, 441–447, https://doi.org/10.1016/j.proeng.2016.11.086, 2016.
Lee, M., Park, G., Park, M., Park, J., Lee, J., and Kim, S.: Evaluation of non-point source pollution reduction by applying Best Management Practices using a SWAT model and QuickBird high resolution satellite imagery, J. Environ. Sci.-China, 22, 826–833, https://doi.org/10.1016/S1001-0742(09)60184-4, 2010.
Liang, J., Liu, Q., Zhang, H., Li, X. D., Qian, Z., Lei, M. Q., Li, X., Peng, Y. H., Li, S., and Zeng, G. M.: Interactive effects of climate variability and human activities on blue and green water scarcity in rapidly developing watershed, J. Clean. Prod., 265, 121834, https://doi.org/10.1016/j.jclepro.2020.121834, 2020.
Lin, Q. and Zhang, D.: A scalable distributed parallel simulation tool for the SWAT model, Environ. Modell. Softw., 144, 105133, https://doi.org/10.1016/j.envsoft.2021.105133, 2021.
Liu, J., Zhu, A. X., Qin, C.-Z., Wu, H., and Jiang, J.: A two-level parallelization method for distributed hydrological models, Environ. Modell. Softw., 80, 175–184, https://doi.org/10.1016/j.envsoft.2016.02.032, 2016.
Liu, Y., Shen, H., Yang, W., and Yang, J.: Optimization of agricultural BMPs using a parallel computing based multi-objective optimization algorithm, Environmental Resources Research, 1, 39–50, https://doi.org/10.22069/IJERR.2013.1685, 2013.
Qi, H. H. and Altinakar, M. S.: Vegetation Buffer Strips Design Using an Optimization Approach for Non-Point Source Pollutant Control of an Agricultural Watershed, Water Resour. Manag., 25, 565–578, https://doi.org/10.1007/s11269-010-9714-9, 2011.
Razavi, S. and Tolson, B. A.: An efficient framework for hydrologic model calibration on long data periods, Water Resour. Res., 49, 8418–8431, https://doi.org/10.1002/2012wr013442, 2013.
Razavi, S., Tolson, B. A., Matott, L. S., Thomson, N. R., MacLean, A., and Seglenieks, F. R.: Reducing the computational cost of automatic calibration through model preemption, Water Resour. Res., 46, W11523, https://doi.org/10.1029/2009wr008957, 2010.
Sun, A. Y., Miranda, R. M., and Xu, X.: Development of multi-metamodels to support surface water quality management and decision making, Environ. Earth Sci., 73, 423–434, https://doi.org/10.1007/s12665-014-3448-6, 2015.
Wang, H., Fu, X., Wang, Y., and Wang, G.: A High-performance temporal-spatial discretization method for the parallel computing of river basins, Comput. Geosci., 58, 62–68, https://doi.org/10.1016/j.cageo.2013.04.026, 2013.
Wu, Y. and Liu, S.: Automating calibration, sensitivity and uncertainty analysis of complex models using the R package Flexible Modeling Environment (FME): SWAT as an example, Environ. Modell. Softw., 31, 99–109, https://doi.org/10.1016/j.envsoft.2011.11.013, 2012.
Wu, Y., Li, T., Sun, L., and Chen, J.: Parallelization of a hydrological model using the message passing interface, Environ. Modell. Softw., 43, 124–132, https://doi.org/10.1016/j.envsoft.2013.02.002, 2013.
Wu, Y., Liu, S., and Yan, W.: A universal Model-R Coupler to facilitate the use of R functions for model calibration and analysis, Environ. Modell. Softw., 62, 65–69, https://doi.org/10.1016/j.envsoft.2014.08.012, 2014.
Yalew, S., van Griensven, A., Ray, N., Kokoszkiewicz, L., and Betrie, G. D.: Distributed computation of large scale SWAT models on the Grid, Environ. Modell. Softw., 41, 223–230, https://doi.org/10.1016/j.envsoft.2012.08.002, 2013.
Yang, R., Ward, M., and Evans, B.: Parallel I/O in Flexible Modelling System (FMS) and Modular Ocean Model 5 (MOM5), Geosci. Model Dev., 13, 1885–1902, https://doi.org/10.5194/gmd-13-1885-2020, 2020.
Zamani, M., Shrestha, N. K., Akhtar, T., Boston, T., and Daggupati, P.: Advancing model calibration and uncertainty analysis of SWAT models using cloud computing infrastructure: LCC-SWAT, J. Hydroinform., 23, 1–15, https://doi.org/10.2166/hydro.2020.066, 2020.
Zhang, D., Chen, X., Yao, H., and Lin, B.: Improved calibration scheme of SWAT by separating wet and dry seasons, Ecol. Model., 301, 54–61, https://doi.org/10.1016/j.ecolmodel.2015.01.018, 2015.
Zhang, D., Chen, X., Yao, H., and James, A.: Moving SWAT model calibration and uncertainty analysis to an enterprise Hadoop-based cloud, Environ. Modell. Softw., 84, 140–148, https://doi.org/10.1016/j.envsoft.2016.06.024, 2016.
Zhang, D., Lin, B., Wu, J., and Lin, Q.: A graph-parallel simulation tool for SWAT, Zenodo [code], https://doi.org/10.5281/zenodo.4270676, 2021.
Zhang, X., Beeson, P., Link, R., Manowitz, D., Izaurralde, R. C., Sadeghi, A., Thomson, A. M., Sahajpal, R., Srinivasan, R., and Arnold, J. G.: Efficient multi-objective calibration of a computationally intensive hydrologic model with parallel computing software in Python, Environ. Modell. Softw., 46, 208–218, https://doi.org/10.1016/j.envsoft.2013.03.013, 2013.
Zhu, L.-J., Liu, J., Qin, C.-Z., and Zhu, A. X.: A modular and parallelized watershed modeling framework, Environ. Modell. Softw., 122, 104526, https://doi.org/10.1016/j.envsoft.2019.104526, 2019.