the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Exploring deep learning for air pollutant emission estimation
Lin Huang
Song Liu
Zeyuan Yang
Jia Xing
Jia Zhang
Jiang Bian
Siwei Li
Shovan Kumar Sahu
Shuxiao Wang
Tie-Yan Liu
The inaccuracy of anthropogenic emission inventories on a high-resolution scale due to insufficient basic data is one of the major reasons for the deviation between air quality model and observation results. A bottom-up approach, which is a typical emission inventory estimation method, requires a lot of human labor and material resources, whereas a top-down approach focuses on individual pollutants that can be measured directly as well as relying heavily on traditional numerical modeling. Lately, the deep neural network approach has achieved rapid development due to its high efficiency and nonlinear expression ability. In this study, we proposed a novel method to model the dual relationship between an emission inventory and pollution concentrations for emission inventory estimation. Specifically, we utilized a neural-network-based comprehensive chemical transport model (NN-CTM) to explore the complex correlation between emission and air pollution. We further updated the emission inventory based on back-propagating the gradient of the loss function measuring the deviation between NN-CTM and observations from surface monitors. We first mimicked the CTM model with neural networks (NNs) and achieved a relatively good representation of the CTM, with similarity reaching 95 %. To reduce the gap between the CTM and observations, the NN model suggests updated emissions of NOx, NH3, SO2, volatile organic compounds (VOCs) and primary PM2.5 changing, on average, by −1.34 %, −2.65 %, −11.66 %, −19.19 % and 3.51 %, respectively, in China for 2015. Such ratios of NOx and PM2.5 are even higher (∼ 10 %) in regions that suffer from large uncertainties in original emissions, such as Northwest China. The updated emission inventory can improve model performance and make it closer to observations. The mean absolute error for NO2, SO2, O3 and PM2.5 concentrations are reduced significantly (by about 10 %–20 %), indicating the high feasibility of NN-CTM in terms of significantly improving both the accuracy of the emission inventory and the performance of the air quality model.
- Article
(3414 KB) - Full-text XML
- BibTeX
- EndNote
Clean air policies have been implemented by the Chinese government since 2010 and have been effectively reducing pollutant concentrations, such as sulfur dioxide (SO2) and nitrogen oxides (NOx) (Zheng et al., 2018). Nevertheless, China still faces challenges in addressing O3 and PM2.5 pollution. In particular, the level of ozone (O3) in China increased by 1.3 % from 2013 to 2017 (Li, 2019); moreover, concentrations of PM2.5 (particulate matter with an aerodynamic diameter less than 2.5 µm) in most Chinese cities still far exceed the limits (< 10 µg m−3) recommended by the World Health Organization (WHO), leading to frequent heavy-pollution events (Guo et al., 2014; Richter et al., 2005; Vesilind et al., 1988). Such high pollutant concentrations may substantially affect human health given that air pollution has being ranked fifth among global risk factors with respect to mortality (Health Effects Institute, 2019).
A prerequisite for effectively controlling air pollution lies in accurate knowledge of the related emission sources. A well-established emission inventory should summarize the amount of pollutants emitted into the atmosphere from all sources in a specific region and during a specific time span (Health Effects Institute, 2019). A typical bottom-up approach is adopted to develop the emission inventory through investigation of emission sources in the Air Benefit and Cost and Attainment Assessment System Emission Inventory (ABaCAS-EI; Zheng et al., 2019) and the Multi-resolution Emission Inventory (MEIC; He, 2012) developed by Tsinghua University, wherein the activity rate of each source is multiplied by an emission factor (Vallero, 2018). Such technology-oriented bottom-up emission inventories can reflect the types of technology operated in China but are limited with respect to their actual application due to the human labor and material resource requirements, especially in cities where thorough investigation is are difficult to support (Xing et al., 2020b). Furthermore, varied assumptions regarding the activity rate and emission factor from different studies result in large uncertainties (Aardenne and Pulles, 2002). Therefore, the development of a method for efficient, low-cost and sufficiently accurate grid emission information is being considered.
The top-down method, as another typical emission inventory estimation approach, can be used to constrain emission estimations by combining observation results from surface monitors and satellite retrievals. Brioude et al. (2012) estimated the emissions of anthropogenic CO, NOx and CO2 in the Los Angeles Basin using the FLEXible PARTicle dispersion model (FLEXPART) Lagrangian particle dispersion model based on the top-down method. Recently, Yang et al. (2021) linked the bottom-up China Multi-pollutant Abatement Planning and Long-term benefit Evaluation (China-MAPLE), model with the top-down computable general equilibrium (CGE) model to evaluate the comprehensive impacts of deep decarbonization pathways (DDPs) in China. However, most of the previous studies have merely focused on individual pollutants that can be measured directly (Brioude et al., 2012; Xing et al., 2020a; Yang et al., 2021) and have relied on traditional numerical modeling.
On the contrary, neural networks (NNs), as a more efficient tool, can also model complex nonlinear relations in the atmospheric system, thereby converting precursor emissions into ambient concentrations. Due to their end-to-end learning ability, NNs can automatically extract key features of input data and capture the behavior of target data; thus, they have recently been widely used in atmospheric science (Fan et al., 2017; Tao et al., 2019; Wen et al., 2019; Xing et al., 2020a, c). For example, many studies (Fan et al., 2017; Tao et al., 2019; Wen et al., 2019) have combined recurrent NN (RNN) and convolutional NN (CNN) to capture spatial and temporal features in air-pollution-related questions, as RNN is skillful with respect to mining temporal patterns from time series data (Cho et al., 2014; Chung et al., 2014; Hochreiter and Schmidhuber, 1997) and has the ability to handle missing values efficiently (Fan et al., 2017), and CNN exhibits potential with respect to leveraging spatial dependencies (e.g., in meteorological prediction; Krizhevsky et al., 2012). Furthermore, Xing et al. (2020c) applied NN to a response surface model (RSM), thereby significantly enhancing its computational efficiency and demonstrating the utility of deep learning approaches for capturing the nonlinearity of atmospheric chemistry and physics. The application of deep learning improves the efficiency of air quality simulation and can quickly provide data support for the formulation of emission control policies in order to adapt to the dynamic pollution situation and international circumstances. However, the use of deep NN to estimate emission inventories is more complex than traditional machine learning problems because there are no precise emission observations that can be used as supervision for model training.
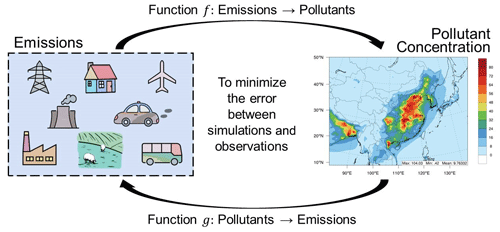
To address all of these issues, we proposed a novel method based on dual learning (He et al., 2016), which leverages the primal-dual structure of artificial intelligence (AI) tasks to obtain informative feedback and regularization signals, thereby enhancing both the learning and inference process. In terms of emission inventory estimation, if we have a precise relationship between the emission inventory and pollution concentrations, we can use the pollution concentrations as a constraint to obtain an accurate emission inventory. In particular, we proposed employing a neural-network-based chemical transport model (NN-CTM) with a delicately designed architecture, which is efficient and differentiable compared with the chemical transport model (CTM). Furthermore, when a well-trained NN-CTM can accurately reflect the direct and indirect physical and chemical reactions between the emission inventory and pollutant concentrations, the emission inventory can be updated by back-propagating the gradient of the error between observed and NN-CTM-predicted pollutant concentrations. Figure 1 shows the framework of this study.
The remainder of this paper is structured as follows: the method used for this study is described in Sect. 2; Sect. 3 uses the emission inventory estimation over China as an example to demonstrate the superiority of our method; in Sect. 4, we make a conclusion and discuss some possible future work.
2.1 Main framework
The task of emission inventory estimation can be naturally formalized into a typical dual learning framework. Concretely, we denote xt as the data of emission volumes and meteorological conditions and yt as the corresponding pollutant concentration at time t. In addition, we denote the mapping function from emission to pollutant concentration as f and that from pollutant concentration to emission as g. As the transformation from emission to pollutant concentration is a continuous process in time, approximately, we have the following equations:
where x[i:j] is defined as for convenience, and y[i:j] represents .
The formulas above are based on two assumptions:
-
The pollutant concentration is only dependent on the emission and meteorological conditions in the past k time steps (e.g., hours or days).
-
There is a bijective relationship between emission and pollutant concentration. This is a necessary prerequisite for the existence of function g.
The first assumption will hold true as long as a sufficiently large k value is set. The second assumption may not be true unless we introduce more external constraints on the emission inventory, as an information loss exists in the emission-to-pollutant concentration process.
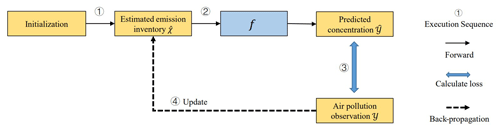
In fact, it is quite difficult to obtain the function g directly without emission observations as supervision. Hence, we employ a dual learning framework to obtain the function g indirectly by leveraging function f. The framework of this process is illustrated in Fig. 2. In particular, the whole process of emission inventory estimation includes the following steps:
-
use the existing emission inventory which is still not accurate enough as the initial emission data ;
-
given , calculate the corresponding predicted pollutant concentration data ;
-
calculate the loss between the observed values of pollutants Y and the predicted pollutant concentrations ;
-
adjust the estimated emission inventory by back-propagating the gradient of the loss based on function f;
-
repeat steps 2–4 until achieving sufficient accuracy for predicted concentration.
Although the CTM system can handle the transition from emission to pollutant concentration, it is not differentiable, which makes it quite hard to update the emission inventory through the back-propagation algorithm in the dual learning framework. In order to establish a differentiable CTM, we propose building a NN-CTM as the system approximation. More details will be described in the following subsections.
2.2 Deep-neural-network-based chemical transition model approximation
The pollutant concentration is usually estimated using a CTM, which employs the emission inventory as input. In the dual learning framework, this input will, in turn, be updated based on observed concentrations via the back-propagation algorithm. This requires the CTM to be differentiable. To this end, we propose using deep neural networks to approximate the CTM system. Concretely, to train this NN-CTM, we apply a supervised learning approach that leverages the training data, whose input is the same as that of CTM and whose corresponding label is the output of CTM. The whole architecture is shown in Fig. 3.
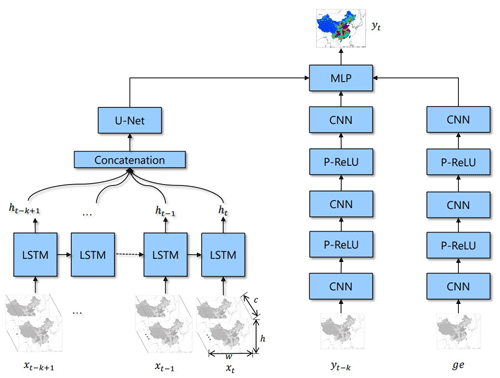
Figure 3NN-CTM structure. c represents channel, which consists of the emission inventory and meteorological data. h and w represent the height and width of input, respectively. ge is geographic information. We employ long short-term memory (LSTM) to capture the temporal information and U-Net to capture the spatial information. CNN represents the convolution network. P-ReLU (He et al., 2015b) is a nonlinear activation function. MLP means multiple layers of perceptrons with threshold activation. The model structure is also named LSTM-U-Net.
The input data for our NN-CTM are similar to that of a CTM, including emission inventory, meteorology and geographical data. The first two are time dependent, whereas the last one, denoted as ge, is static. In the Eulerian grid-based CTM system, for each time step t, the dynamic input data xt is a matrix with the following dimensions: . The concentration is simulated continuously in a continuous time sequence. Unlike CTM, the NN-CTM cannot deal with overly long data sequences. Thus, we only use the data from past k time steps (i.e, ) as input for the pollutant concentration estimation yt. At the same time, we add yt−k as supplementary input data into the network. The output yt of NN-CTM is a matrix with the dimensions , where l is the number of pollutant species concerned.
The NN-CTM consists of three branches: two CNN branches for yt−k and ge, and one long short-term memory (LSTM; Hochreiter and Schmidhuber, 1997) with U-Net (Ronneberger et al., 2015) branch. The CNN branches are used to extract features for yt−k and geographical information. We employ a parametric rectified linear unit (P-RELU; He et al., 2015b) as the nonlinear activation function in these branches to improve model fitting with nearly zero extra computational cost and little overfitting risk. We adopt the architecture of combining LSTM and U-Net based on the understanding of the temporal–spatial relationship in the emission inventory. In the temporal dimension, pollutants are the accumulation of historical emissions. In the spatial dimension, adjacent grids will affect each other because of meteorological and diffusion factors. The LSTM layer is used to aggregate information from time series data . The aggregated sequence of hidden states will be concatenated and entered into the U-Net block. U-Net is a widely adopted pixel-to-pixel model which can effectively utilize neighbor information. In U-Net, the stacking of convolution can get neighbor information with a bigger receptive field (e.g., stacking 5 × 5 convolution and 5 × 5 convolution can get a 9 × 9 convolution), the nonlinear function (P-RELU) is employed to improve model fitting with nearly zero extra computational cost and little overfitting risk, and the batch normalization and dropout are employed to enhance the robustness of the model. We calculate that the receptive field of our model is a 38 × 38 grid. In other words, the predicted pollutant concentration is related to its surrounding 38 × 38 grid's information, which represents the transmission between different grids. Meanwhile, the closer the distance, the greater the contribution. We employ a two-layer U-Net (as shown in Fig. 4) to capture the spatial information between grids.
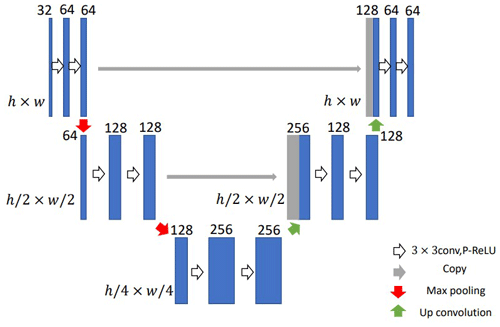
Figure 4U-Net structure (two layers). The model structure yields a u-shaped architecture. 3 × 3 conv is a convolution function (Huang et al., 2016). P-ReLU (Huang et al., 2016) is a nonlinear activation function. Max pooling is a down sample function. Up convolution (Zeiler et al., 2010) is a deconvolution function, which is also named as up sample function.
In the training process, we take (XCTM,YCTM) as the training dataset, where XCTM denotes the input data of the CTM system, and YCTM is the corresponding output. As relative changes in pollutant concentrations are the metric often used by policymakers, we adopt an objective function that measures the relative loss between NN-CTM-predicted and CTM-simulated pollutant concentrations. We denote the output of NN-CTM as , and have
where N is the number of samples, , and , and represents the concentration of the cth pollutant in the grid with location (i,j) in the nth sample. The parameters of NN-CTM will be updated based on the gradients given by gw, and the adaptive moment (Adam) estimation (Kingma and Ba, 2014) is used as the optimizer.
Model robustness
We ensure the robustness of the model from three aspects:
-
model structure – inspired by computer vision tasks, we adopt batch normalization (Ioffe and Szegedy, 2015), dropout (Srivastava et al., 2014), L2 regularization (Zhang et al., 2016) to improve the generalization and robustness;
-
early stop – when we train the NN-CTM, we split the data into training and validation datasets, and we stop the model training when the evaluation in the validation dataset does not improve within 1000 iterations;
-
data augmentation – during training, we employ the noise injection, random rescaling, random rotation method to avoid the overfitting in training dataset.
2.3 Emission inventory estimation based on NN-CTM
Given a well-trained NN-CTM whose approximation accuracy is high enough for predicting pollutant concentrations, the emission inventory can be updated based on the error between the observed and NN-CTM-predicted pollutant concentrations. The observation data will help update the surrounding grids' emission inventory within the receptive field. However, in extreme circumstances, if we have no observation data, our method will not work because we have no more information to adjust the emission inventory. If the observation data are denser, the emission inventory estimation is more accurate because it can consider more observation data.
In particular, we make the relationship between emission and pollutant concentration more robust by fixing the trained LSTM-U-Net model parameter. By training NN-CTM parameter, we then adjust the input emission inventory to minimize the loss between the NN-CTM output and the observations. Such loss can be formally defined as follows:
where represents the observed pollutant concentration (we use an average value in case of multiple observation stations in a grid), and Mi,j is a binary indicator variable indicating whether or not there is site monitoring equipment in grid (i,j). The emission inventory will be updated by back-propagating the gradient ge. The stochastic gradient descent (SGD) method (Bottou, 2010) is used as the optimizer.
Meanwhile, aiming at ensuring the reasonableness and effectiveness of the estimated emission inventory, we set two constraints. The first is that the update rate of the emission inventory must be a maximum of 200 % compared with the prior emission for each grid. Biases exist in meteorological conditions and chemical mechanism, and this determines that we cannot attribute all of the errors to the emission inventory. If the update ratio is very large, the NN-CTM cannot reflect the correlation of the unseen data well. Furthermore, the prior emission is accurate to a certain extent in terms of the spatial and temporal dimensions. The second constraint is that the updated emission inventory must be positive.
In this section, we apply our proposed method to emission inventory estimation in China in 2015. In the following, we will first describe the data and CTM configuration. Subsequently, we will show the experimental results in terms of the accuracy of NN-CTM. We will then conduct further analysis on the prior emission inventory and our emission inventory estimation results.
3.1 Data and CTM configuration
The prior high spatial and temporal resolution emission inventory ABaCAS-EI is based on the bottom-up method, including primary pollutants such as NOx, ammonia (NH3), SO2, volatile organic compounds (VOCs) and primary PM2.5. ABaCAS-EI is a grid-unit-based emission inventory including sources of power, cement, the steel industry and mobile sources. It also takes technical progress and more stringent emission standards into consideration (Zheng et al., 2019). The prior emission inventory is initially used for NN-CTM training and then updated as per the proposed method of dual learning.
Geographical data are a fixed attribute of one grid, like land type, mountains, depressions or elevation, and they are obtained from the Moderate Resolution Imaging Spectroradiometer (MODIS) with a 15 s resolution in this study (Friedl et al., 2002).
Meteorological conditions are simulated from the Weather Research and Forecasting (WRF, version 3.7) model. The WRF configuration includes the Morrison microphysics scheme (Morrison et al., 2009), the RRGM radiation scheme (Mlawer et al., 1998, 1997), the Pleim–Xiu land surface scheme (Pleim and Xiu, 1995; Xiu and Pleim, 2001), the Asymmetric Convective Model, version 2 (ACM2) planetary boundary layer (PBL) physics scheme (Pleim, 2007) and the Kain–Fritsch cumulus cloud parameterization (Kain, 2004), which matches our previous studies (Ghil and Malanotte-Rizzoli, 1991; Wikle, 2003). Data assimilation is adopted in WRF simulations based on observation data for the upper air and surface from the National Centers for Environmental Prediction (NCEP) datasets. The simulated temperature, humidity, wind speed and direction show good agreement with the observations from the National Climatic Data Center (NCDC, https://www.ncdc.noaa.gov/data-access/land-based-station-data/, last access: 26 December 2020) (Ding et al., 2019; Liu et al., 2019; Zhao et al., 2013).
The Community Multiscale Air Quality (CMAQ, version 5.2) model configured with the AERO6 aerosol module (Appel et al., 2013) and the Carbon Bond 6 (CB6) gas-phase chemical mechanism (Sarwar et al., 2008) is chosen as the representative CTM to simulate pollutant concentrations (Appel et al., 2018; Byun, 1999). Hourly observation data for air pollution (including SO2, NO2, O3 and PM2.5), which are used to adjust the emission inventory, are obtained from the China National Environmental Monitoring Centre (http://beijingair.sinaapp.com/, last access: 26 December 2020).
The simulation domain covers mainland China and portions of surrounding countries with a 27 km × 27 km horizontal resolution (with h=182 and w=232) and 14 vertical layers from the ground to 100 hPa. Simulations are performed in January, April, July and October 2015 to represent winter, spring, summer and autumn, respectively. A 5 d simulation spin-up was performed to minimize the effects of initial conditions. Pollutant concentrations are analyzed as monthly averages.
3.2 NN-CTM training and evaluation
Training parameters
The NN-CTM parameters were optimized using the Adam optimizer with a mini-batch size of eight. A learning rate of 0.001 was used. To reduce the risk of over-fitting, we applied weight regularization on all trainable parameters during training and fine-tuning. The NN-CTM was trained for 30 000 epochs.
Metrics
Model performance was evaluated using the mean absolute error (MAE), which is calculated using the following equation:
where N, h, w and l are the number of samples, height, width and the number of observed pollutants in each grid, respectively. Further, , , and .
Evaluation
We examined the performance of NN-CTM to check whether it had learned the relationship between emission and pollutant concentration.
We trained NN-CTM on the data from the first 22 d in January, April, July and October 2015, and we tested it on the remaining successive 8 d of each month. As listed in Table 1, NN-CTM (with LSTM-U-Net) can reproduce the spatial and temporal relation well, with a small MAE of 0.27, 0.17, 1.39 ppbv and 1.46 µg m−3 for NO2, SO2, O3 and PM2.5, respectively, on average for the 4 months. Results suggest that the NN-CTM can reproduce the CTM well within an acceptable bias, and thus it can be used for emission adjustment. Such a bias (< 4 %) is much smaller than that of the simulation compared with the observations, which are normally more than 10 % or even 20 %.
Table 1Evaluation of the NN-CTM simulation in China (mean absolute error between CTM and NN-CTM). LSTM-U-Net is our proposed method. To compare the model performance, we then select another professional deep neural network method – residual network (ResNet; He et al., 2015a).

In order to further verify the superiority of our model architecture, we employed ResNet (He et al., 2015a), another widely adopted deep NN method in image processing. Compared with ResNet, the performance of NN-CTM (with LSTM-U-Net) was superior, with an improved MAE of 0.02, 0.02, 0.10 ppbv and 0.02 µg m−3 for NO2, SO2, O3 and PM2.5, respectively, on average for the 4 months (as listed in Table 1).
3.3 Emission inventory updating and analysis
A well-trained NN-CTM is used to update the emission inventory via back-propagation with the stochastic gradient descent (SGD; Bottou, 2010) optimizer with a mini-batch size of two. The learning rate is 0.1. The optimization of emissions is achieved after 10 000 epochs.
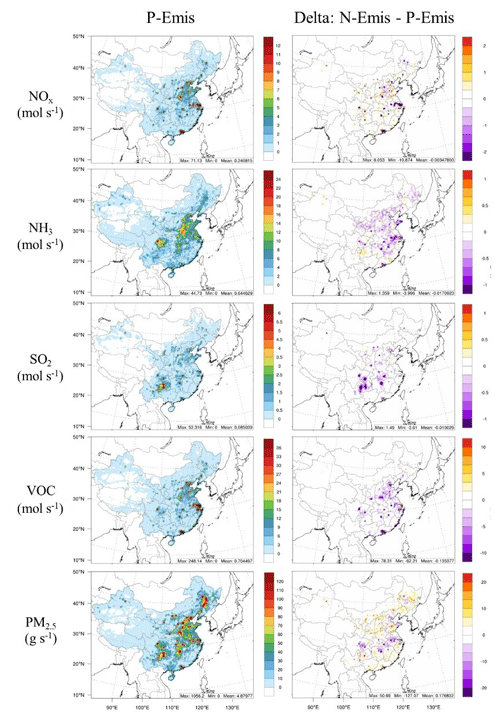
Figure 5Emission rates of NOx, NH3, SO2, VOCs and primary PM2.5 in P-Emis and their changes in N-Emis.
For convenience, we denote the emission inventory from ABaCAS-EI as prior emissions (P-Emis) and the updated emission inventory as NN-emissions (N-Emis), which is constrained by station observations. Compared with P-Emis, N-Emis has adjusted emission rates of NOx, NH3, SO2, VOCs and primary PM2.5 as per the difference between simulated concentrations and the observed values of pollutants in each grid, as shown in Fig. 5. Average emission rates of NH3, SO2 and VOCs in most grids tend to decrease, whereas those of primary PM2.5 tend to increase except for in the Yangtze River Basin, which may be related to the excluded dust emission. Changes in the emission rate of NOx vary a lot by region, and such changes are concentrated in urban areas. The distribution of N-Emis for each grid is consistent with P-Emis, indicating that the deep learning method in this study can identify the distribution of emission sources and focus on the calibration in high-emission areas.
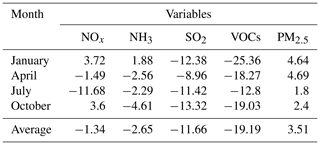
Annual anthropogenic emissions in China for NOx, NH3, SO2, VOCs and primary PM2.5 in P-Emis are 20.44, 10.39, 14.40, 23.05 and 7.19 Mt, respectively (Liu et al., 2020), whereas they changed by −1.34 %, −2.65 %, −11.66 %, −19.19 % and 3.51 %, respectively, in N-Emis.
The sensitivity of change ratios to different seasons varies. Table 2 lists the change ratios of N-Emis compared with P-Emis for the 4 abovementioned months. As for N-Emis, NOx increases in January and October by about 3.5 %–4.0 %, whereas it decreases by more than 10 % in July. The emission of NH3 increases in January, whereas it decreases in the other 3 months with the highest decrease registered in October. The emission of SO2 tends to decrease in all 4 months, with ratios of around 10 %. The emission of VOCs also tends to decrease but with a larger magnitude of about 20 % compared with SO2, which may be related to the overestimation of O3. The emission of primary PM2.5 tends to increase by less than 5 % for the 4 months.
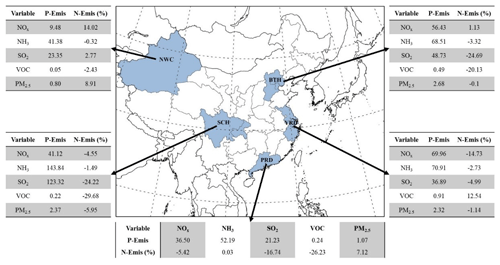
Figure 6Five typical regions of China, the Beijing–Tianjin–Hebei region (denoted as BTH), the Yangtze River Delta (denoted as YRD, covering Jiangsu, Zhejiang and Shanghai), the Pearl River Delta (denoted as PRD, covering Guangdong), the Sichuan Basin (denoted as SCH, covering Sichuan and Chongqing) and Northwest China (denoted as NWC, covering Xinjiang), and their monthly average emissions for 4 months in P-Emis (given in kilotons except for VOCs, which are given in megamoles) and change ratios in N-Emis (given as a percentage).
Such changes in emissions are based on mathematical algorithms and, thus, cannot be explained by physical and chemical processes. The NN method tries to provide a solution to make simulation results of all pollutant species closer to observations by compensating for the errors in the emission inventory. For example, concentrations of PM2.5 obtained using P-Emis are generally lower than the observed level, so the emission of primary PM2.5 will be increased during the adjustment. SO2 tends to be overestimated using P-Emis, so the adjustment tends to decrease. However, because sulfate is an important component of PM2.5, the adjustment of SO2 will be restricted by the underestimation of PM2.5. Concentrations of O3 obtained using P-Emis are generally higher than the observed level, so it tends to reduce the emissions of NOx and VOCs, which are precursors of O3, during the adjustment. It is worth noting that the adjustment range of NOx is much lower than that of VOCs, as only the observed concentration of NO2 is used as a constraint. Such results are consistent with our previous study (Xing et al., 2020a).
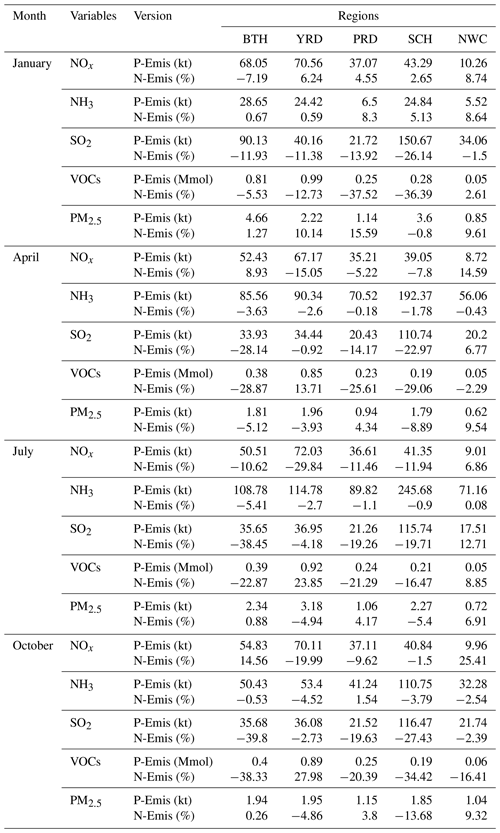
In order to further analyze the change in emissions at a regional level, we calculated the 4-month average emissions of P-Emis and change ratios of N-Emis for five emission species in the Beijing–Tianjin–Hebei region (BTH), the Yangtze River Delta (YRD), the Pearl River Delta (PRD), the Sichuan Basin (SCH) and Northwest China (NWC), as highlighted in Fig. 6. The first four areas were selected because they are the main population clusters, and NWC was selected because there are so few observation sites in this area that the constraints are relatively insufficient.
The adjustment of emission varies greatly by season and region. Seasonal details are listed in Table 3. The 4-month average changes in N-Emis in BTH are the highest for SO2 and VOC emissions, reaching about −20 %, whereas those for NOx, NH3 and primary PM2.5 vary by less than 5 %. In YRD, NOx and VOC emissions record the highest extent of changes with −14.73 % for NOx and 12.54 % for VOCs. The range of changes in other emission species is less than 5 % (all decrease). The emission of primary PM2.5 in PRD increases by about 7 %, which is the largest change ratio among the four urban regions. The emission of NH3 in PRD changes the least compared with other regions. In SCH, the emissions of SO2 and VOCs decrease the most (change ratio) compared with other emission species (> 20 %). The emission of primary PM2.5 in SCH, which decreases by 5.95 %, shows an opposite trend to that in PRD. As for NWC, emissions of NH3 and VOCs show a small decrease (< 5 %), whereas emissions of NOx and primary PM2.5 have a large percentage increase compared with other regions (10 %), specifically indicating the large inaccuracy in the emission inventory in NWC.
3.4 Accuracy improvements of the CTM simulation for pollutants with N-Emis
We use the CTM to evaluate the accuracy of P-Emis and N-Emis. The configuration of CTM remains constant.
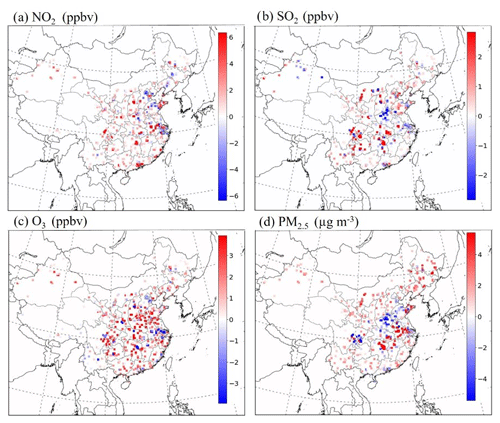
Generally, simulations using P-Emis tend to underestimate the PM2.5 concentrations and overestimate the O3 concentrations in China on average for the 4 months, which is consistent with our previous studies (Ding et al., 2019; Liu et al., 2019). The underestimation of PM2.5 using P-Emis usually appears in northern and southeastern China and sometimes occurs in some provinces of the Yangtze River Basin. The simulations of O3 using P-Emis are generally overestimated at observation sites. Such errors can be narrowed when using N-Emis. We calculated the MAE for each simulation to compare their performance, considering all observation sites. After using adjusted emissions (i.e., N-Emis), the MAE for the NO2, SO2, O3 and PM2.5 concentrations reduced significantly from 7.39 to 5.91 ppbv (20.03 %), 3.64 to 3.22 ppbv (11.54 %), 14.33 to 11.56 ppbv (19.33 %) and 18.94 to 16.67 µg m−3 (11.99 %), respectively, on average for total 612 observation stations (as shown in Fig. 7). Such improvements prove the advantages of using N-Emis compared with P-Emis. Spatial distributions of the comparison between simulations and observations at 612 sites can be found in Fig. 8. The model performance improved for most stations, while a small number of stations reported reduced performance, which shows the link between compound pollutants. For example, stations with larger deviations between PM2.5 simulation results and observations tend to have greatly improved O3 performance and vice versa.
The difference in monthly simulations using N-Emis and P-Emis as input can be utilized to estimate the seasonal impacts of emission changes. Concentrations of O3 and PM2.5 tend to increase in July and decrease in other months on average in China. Concentrations of NO2 and SO2 tend to decrease in the 4 abovementioned months, which is consistent with the direct trend of emission adjustments.
Table 4The 4-month average concentrations of NO2, SO2, O3 and PM2.5 in five typical regions using different emission inventories.
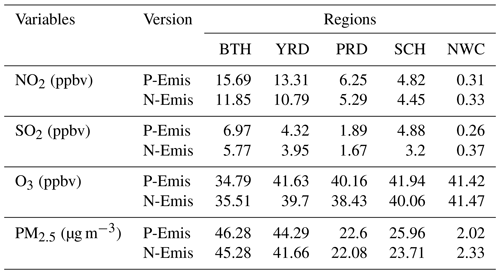
We also calculated the average concentrations of four pollutants in five typical regions to quantify the degree of improvement in pollutant concentrations after adjusting the emission inventory, as listed in Table 4. Changes in the NO2 and SO2 concentrations are consistent with adjustments in emissions but are more sensitive, i.e., a small change (∼ 10 %) in emission results in a larger proportional change (∼ 20 %) in concentration. The reduced SO2 emission is an important reason for the improvement in PM2.5 overestimations in the Yangtze River Basin. PM2.5 concentrations in NWC show the highest increase (15 %) compared with other regions. As the emission inventory in NWC has great potential for improvement (subject to production methods and the acquisition of basic data), the qualitative changes in the PM2.5 concentrations brought about using the NN method seem meaningful. The increase and decrease in NOx and VOC emissions directly control the variance in the O3 concentration. The effect of using N-Emis on the O3 concentration is not obvious, with a change range of less than 5 % in typical regions. Although the adjustment ratio of the emissions of O3 precursors is considerable, the O3 concentration does not change by much. This can be linked to the complex relationship of precursor emissions of NOx and VOCs which might not change simultaneously or in the same direction (e.g., an increase NOx and a decrease in VOCs or vice versa), thereby resulting in only a slight change in the O3 concentration.
In this study, we pioneer the use of machine learning to reformulate the problem of emission inventory estimation. It creates a new perspective that the data-driven approach can be applied to automatically improve the quality of the emission inventory, avoiding manual intervention and empirical error. We proposed a differential neural-network-based chemical transport model (NN-CTM), which achieves a relatively good representation of the CTM. We then employed a back-propagation algorithm to update the emission inventory based on the deviation between observed and NN-CTM-predicted pollutant concentrations. In terms of method, we proposed a novel emission inventory estimation approach based on dual learning that consists of a dual loop: emission-to-pollution and pollution-to-emission. Results indicate that our NN-based method with an adjusted emission inventory performed better than using prior emissions.
Compared with previous studies, our framework employs a dual learning mechanism in which the simulated concentrations are compared to ground observations and the gradient is back-propagated to update the emission inventory in each epoch. Results show that new emissions after the adjustment can improve the model performance with respect to simulating concentrations that are close to observations. The mean absolute error for the NO2, SO2, O3 and PM2.5 concentrations decreased significantly (by 10 % to 20 %). This application uses a constant biogenic emission inventory, so the potential errors in biogenic emissions are also included in the training of anthropogenic emissions.
Our method can be naturally extended to other fundamental problems, such as CO2 and other greenhouse gas emission inventory estimations, and has broad application prospects, such as building a real-time emission monitoring system based on real-time pollutant observation data.
The codes for machine learning are available at https://doi.org/10.5281/zenodo.4607127 (Huang et al., 2021), including the demo case for this study with input data from Ding et al. (2016) and the China National Environmental Monitoring Centre (http://beijingair.sinaapp.com/, last access: 26 December 2020). CMAQv5.2 is an open-source and publicly available model developed by the United States Environmental Protection Agency, which can be downloaded from https://doi.org/10.5281/zenodo.1167892 (US EPA Office of Research and Development, 2017; Appel et al., 2018).
LH and SL conceived the research project; ZY analyzed the data; JX, JZ, JB, SL, SW and TYL provided valuable discussions on research and paper organization; LH, SL, ZY, SKS, JX, JZ and JB wrote the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was completed on the “Explorer 100” cluster system of Tsinghua National Laboratory for Information Science and Technology.
This paper was edited by Samuel Remy and reviewed by two anonymous referees.
This work was supported in part by the National Key R&D Program of China (grant nos. 2016YFC0203306 and 2017YFC0213005), the National Natural Science Foundation of China (grant nos. 41907190 and 51861135102) and the MSRA collaborative research project.
Aardenne, J. V. and Pulles, T.: Uncertainty in emission inventories: What do we mean and how could we assess it?, Thesis Wageningen University, 2002.
Appel, K. W., Pouliot, G. A., Simon, H., Sarwar, G., Pye, H. O. T., Napelenok, S. L., Akhtar, F., and Roselle, S. J.: Evaluation of dust and trace metal estimates from the Community Multiscale Air Quality (CMAQ) model version 5.0, Geosci. Model Dev., 6, 883–899, https://doi.org/10.5194/gmd-6-883-2013, 2013.
Appel, K. W., Napelenok, S., Hogrefe, C., Pouliot, G., Foley, K. M., Roselle, S. J., Pleim, J. E., Bash, J., Pye, H. O. T., and Heath, N.: Overview and Evaluation of the Community Multiscale Air Quality (CMAQ) Modeling System Version 5.2, in: Air Pollution Modeling and its Application XXV, edited by: Mensink, C. and Kallos, G., ITM 2016, Springer Proceedings in Complexity, Springer, Cham, 69–73, https://doi.org/10.1007/978-3-319-57645-9_11, 2018.
Bottou, L.: Large-Scale Machine Learning with Stochastic Gradient Descent, Physica-Verlag HD, 2010.
Brioude, J., Angevine, W. M., Ahmadov, R., Kim, S.-W., Evan, S., McKeen, S. A., Hsie, E.-Y., Frost, G. J., Neuman, J. A., Pollack, I. B., Peischl, J., Ryerson, T. B., Holloway, J., Brown, S. S., Nowak, J. B., Roberts, J. M., Wofsy, S. C., Santoni, G. W., Oda, T., and Trainer, M.: Top-down estimate of surface flux in the Los Angeles Basin using a mesoscale inverse modeling technique: assessing anthropogenic emissions of CO, NOx and CO2 and their impacts, Atmos. Chem. Phys., 13, 3661–3677, https://doi.org/10.5194/acp-13-3661-2013, 2013.
Byun, D.: Science algorithms of the EPA Models-3 community multiscale air quality (CMAQ) modeling system, U.S. Environmental Protection Agency, EPA/600/R-99/030, 1999.
Cho, K., Merrienboer, B. V., Bahdanau, D., and Bengio, Y.: On the Properties of Neural Machine Translation: Encoder-Decoder Approaches, arXiv [preprint], arXiv:1409.1259, 2014.
Chung, J., Gulcehre, C., Cho, K., and Bengio, Y.: Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling, arXiv [preprint], arXiv:1412.3555, 2014.
Ding, D., Xing, J., Wang, S., Liu, K., and Hao, J.: Estimated contributions of emissions controls, meteorological factors, population growth, and changes in baseline mortality to reductions in ambient PM2.5 and PM2.5-related mortality in China, 2013–2017, Environ. Health Persp., 127, 067009, https://doi.org/10.1289/EHP4157, 2019.
Ding, D., Yun, Z., Jang, C., Lin, C. J., Wang, S., Fu, J., and Jian, G.: Evaluation of health benefit using BenMAP-CE with an integrated scheme of model and monitor data during Guangzhou Asian Games, J. Environ., 42, 9–18, 2016.
Fan, J., Li, Q., Hou, J., Feng, X., Karimian, H., and Lin, S.: A Spatiotemporal Prediction Framework for Air Pollution Based on Deep RNN, ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci., IV-4/W2, 15–22, https://doi.org/10.5194/isprs-annals-IV-4-W2-15-2017, 2017.
Friedl, M. A., Mciver, D. K., Hodges, J. C. F., Zhang, X. Y., Muchoney, D., Strahler, A. H., Woodcock, C. E., Gopal, S., Schneider, A., and Cooper, A.: Global land cover mapping from MODIS: algorithms and early results, Remote Sens. Environ., 83, 287–302, 2002.
Ghil, M. and Malanotte-Rizzoli, P.: Data Assimilation in Meteorology and Oceanography, Adv. Geophys., 33, 141–266, 1991.
Guo, S., Hu, M., Zamora, M. L., Peng, J., and Zhang, R.: Elucidating severe urban haze formation in China, P. Natl. Acad. Sci. USA, 111, 17373, https://doi.org/10.1073/pnas.1419604111, 2014.
He, D., Xia, Y., Qin, T., Wang, L., Yu, N., Liu, T.-Y., and Ma, W.-Y.: Dual learning for machine translation, Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 820–828, 2016.
He, K.: Multi-resolution Emission Inventory for China (MEIC): model framework and 1990–2010 anthropogenic emissions, American Geophysical Union, Fall Meeting, A32B-05, 2012.
He, K., Zhang, X., Ren, S., and Sun, J.: Deep Residual Learning for Image Recognition, arXiv [preprint], arXiv:1512.03385, 2015a.
He, K., Zhang, X., Ren, S., and Sun, J.: Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, arXiv [preprint], arXiv:1502.01852, 2015b.
Hochreiter, S. and Schmidhuber, J.: Long Short-Term Memory, Neural Comput., 9, 1735–1780, 1997.
Huang, G., Liu, Z., Laurens, V. D. M., and Weinberger, K. Q.: Densely Connected Convolutional Networks, arXiv [preprint], arXiv:1608.06993, 2016.
Huang, L., Liu, S., Yang, Z., Xing, J., Zhang, J., Bian, J., Li, S., Sahu, S. K., Wang, S., and Liu, T.-Y.: The Inventory Optimization Code for Exploring Deep Learning in Air Pollutant Emission Estimation Scale, Zenodo, https://doi.org/10.5281/zenodo.4607127, 2021.
Health Effects Institute: State of global air 2019, Health Effects Institute, Boston, 2019.
Ioffe, S. and Szegedy, C.: Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, arXiv [preprint], arXiv:1502.03167, 2015.
Kain, J. S.: The Kain–Fritsch convective parameterization: an update, J. Appl. Meteorol., 43, 170–181, 2004.
Kingma, D. and Ba, J.: Adam: A Method for Stochastic Optimization, arXiv [preprint], arXiv:1412.6980, 2014.
Krizhevsky, A., Sutskever, I., and Hinton, G.: ImageNet Classification with Deep Convolutional Neural Networks, Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, December 2012, 1097–1105, 2012.
Li, G.: Report on the completion of environmental conditions and environmental protection targets for 2018, The National People's Congress, available at: http://wx.h2o-china.com/news/290686.html (last access: 26 June 2021), 2019 (in Chinese).
Liu, S., Xing, J., Westervelt, D. M., Liu, S., Ding, D., Fiore, A. M., Kinney, P. L., Zhang, Y., He, M. Z., and Zhang, H.: Role of emission controls in reducing the 2050 climate change penalty for PM2.5 in China, Sci. Total Environ., 765, 144338, https://doi.org/10.1016/j.scitotenv.2020.144338, 2020.
Liu, S., Xing, J., Zhang, H., Ding, D., Zhang, F., Zhao, B., Sahu, S. K., and Wang, S.: Climate-driven trends of biogenic volatile organic compound emissions and their impacts on summertime ozone and secondary organic aerosol in China in the 2050s, Atmos. Environ., 218, 117020, https://doi.org/10.1016/j.atmosenv.2019.117020, 2019.
Mlawer, E., Clough, S., and Kato, S.: Shortwave clear-sky model measurement intercomparison using RRTM, in: Proceedings of the Eighth ARM Science Team Meeting, 23–27, 1998.
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res.-Atmos., 102, 16663–16682, 1997.
Morrison, H., Thompson, G., and Tatarskii, V.: Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one-and two-moment schemes, Mon. Weather Rev., 137, 991–1007, 2009.
Pleim, J. E.: A combined local and nonlocal closure model for the atmospheric boundary layer. Part I: Model description and testing, J. Appl. Meteorol. Climatol., 46, 1383–1395, 2007.
Pleim, J. E. and Xiu, A.: Development and testing of a surface flux and planetary boundary layer model for application in mesoscale models, J. Appl. Meteorol., 34, 16–32, 1995.
Richter, A., Burrows, J. P., Nüss, H., Granier, C., and Niemeier, U.: Increase in nitrogen dioxide over China observed from space, Nature, 437, 129–132, 2005.
Ronneberger, O., Fischer, P., and Brox, T.: U-Net: Convolutional Networks for Biomedical Image Segmentation, arXiv [preprint], arXiv:1505.04597, 2015.
Sarwar, G., Luecken, D., Yarwood, G., Whitten, G. Z., and Carter, W. P. L.: Impact of an Updated Carbon Bond Mechanism on Predictions from the CMAQ Modeling System: Preliminary Assessment, J. Appl. Meteorol. Climatol., 47, 3–14, 2008.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R.: Dropout: A Simple Way to Prevent Neural Networks from Overfitting, J. Mach. Learn. Res., 15, 1929–1958, 2014.
Tao, Q., Liu, F., Li, Y., and Sidorov, D.: Air Pollution Forecasting Using a Deep Learning Model Based on 1D Convnets and Bidirectional GRU, IEEE Access, 7, 76690–76698, 2019.
US EPA Office of Research and Development: CMAQ (Version 5.2), Zenodo, https://doi.org/10.5281/zenodo.1167892, 2017.
Vallero, D.: Translating Diverse Environmental Data into Reliable Information, Elsevier Reference Monographs, 25–41, 2017.
Vesilind, P. A., Peirce, J. J., and Weiner, R. F.: Air Pollution, chap. 18, Elsevier Inc., 1988.
Wen, C., Liu, S., Yao, X., Peng, L., Li, X., Hu, Y., and Chi, T.: A novel spatiotemporal convolutional long short-term neural network for air pollution prediction, Sci. Total Environ., 654, 1091–1099, 2019.
Wikle, C. K.: Atmospheric modeling, data assimilation, and predictability, Technometrics, 47, 521, https://doi.org/10.1198/tech.2005.s326, 2003.
Xing, J., Li, S., Ding, D., Kelly, J. T., and Hao, J.: Data Assimilation of Ambient Concentrations of Multiple Air Pollutants Using an Emission-Concentration Response Modeling Framework, Atmosphere, 11, 1289, https://doi.org/10.3390/atmos11121289, 2020a.
Xing, J., Li, S., Jiang, Y., Wang, S., Ding, D., Dong, Z., Zhu, Y., and Hao, J.: Quantifying the emission changes and associated air quality impacts during the COVID-19 pandemic on the North China Plain: a response modeling study, Atmos. Chem. Phys., 20, 14347–14359, https://doi.org/10.5194/acp-20-14347-2020, 2020b.
Xing, J., Zheng, S., Ding, D., Kelly, J. T., Wang, S., Li, S., Qin, T., Ma, M., Dong, Z., Jang, C., Zhu, Y., Zheng, H., Ren, L., Liu, T.-Y., and Hao, J.: Deep Learning for Prediction of the Air Quality Response to Emission Changes, Environ. Sci. Technol., 54, 8589–8600, 2020c.
Xiu, A. and Pleim, J. E.: Development of a land surface model. Part I: Application in a mesoscale meteorological model, J. Appl. Meteorol., 40, 192–209, 2001.
Yang, X., Pang, J., Teng, F., Gong, R., and Springer, C.: The environmental co-benefit and economic impact of China's low-carbon pathways: Evidence from linking bottom-up and top-down models, Renew. Sustain. Energ. Rev., 136, 110438, https://doi.org/10.1016/j.rser.2020.110438, 2021.
Zeiler, M. D., Krishnan, D., Taylor, G. W., and Fergus, R.: Deconvolutional networks, 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010.
Zhang, C., Be Ngio, S., Hardt, M., Recht, B., and Vinyals, O.: Understanding deep learning requires rethinking generalization, arXiv [preprint], arXiv:1611.03530, 2016.
Zhao, B., Wang, S., Wang, J., Fu, J. S., Liu, T., Xu, J., Fu, X., and Hao, J.: Impact of national NOx and SO2 control policies on particulate matter pollution in China, Atmos. Environ., 77, 453–463, 2013.
Zheng, B., Tong, D., Li, M., Liu, F., Hong, C., Geng, G., Li, H., Li, X., Peng, L., Qi, J., Yan, L., Zhang, Y., Zhao, H., Zheng, Y., He, K., and Zhang, Q.: Trends in China's anthropogenic emissions since 2010 as the consequence of clean air actions, Atmos. Chem. Phys., 18, 14095–14111, https://doi.org/10.5194/acp-18-14095-2018, 2018.
Zheng, H., Zhao, B., Wang, S., Wang, T., Ding, D., Chang, X., Liu, K., Xing, J., Dong, Z., and Aunan, K.: Transition in source contributions of PM2.5 exposure and associated premature mortality in China during 2005–2015, Environ. Int., 132, 105111, https://doi.org/10.1016/j.envint.2019.105111, 2019.