the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A NEMO-based model of Sargassum distribution in the tropical Atlantic: description of the model and sensitivity analysis (NEMO-Sarg1.0)
Rachid Benshila
Léo Berline
Antonin Soulié
Marie-Hélène Radenac
Guillaume Morvan
Frédéric Diaz
Julio Sheinbaum
Cristele Chevalier
Thierry Thibaut
Thomas Changeux
Frédéric Menard
Sarah Berthet
Olivier Aumont
Christian Ethé
Pierre Nabat
Marc Mallet
The tropical Atlantic has been facing a massive proliferation of Sargassum since 2011, with severe environmental and socioeconomic impacts. The development of large-scale modeling of Sargassum transport and physiology is essential to clarify the link between Sargassum distribution and environmental conditions, and to lay the groundwork for a seasonal forecast at the scale of the tropical Atlantic basin. We developed a modeling framework based on the Nucleus for European Modelling of the Ocean (NEMO) ocean model, which integrates transport by currents and waves, and physiology of Sargassum with varying internal nutrients quota, and considers stranding at the coast. The model is initialized from basin-scale satellite observations, and performance was assessed over the year 2017. Model parameters are calibrated through the analysis of a large ensemble of simulations, and the sensitivity to forcing fields like riverine nutrient inputs, atmospheric deposition, and waves is discussed. Overall, results demonstrate the ability of the model to reproduce and forecast the seasonal cycle and large-scale distribution of Sargassum biomass.
- Article
(3934 KB) - Full-text XML
- BibTeX
- EndNote
The massive development of holopelagic Sargassum spp. in the northern tropical Atlantic Ocean from 2011 to the present has caused annual stranding in millions of tons on the coasts of the Lesser Antilles, Central America, Brazil, and western Africa (e.g., Smetacek and Zingone, 2013; Wang and Hu, 2016; Langin, 2018; Wang et al., 2019). The proliferation affects the whole tropical northern Atlantic area, as illustrated by satellite observations for summer 2017 (Fig. 1, Berline et al., 2020).
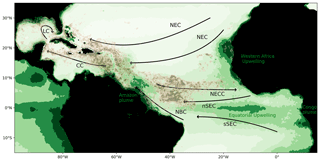
Figure 1Sargassum fractional coverage obtained from MODIS in July–August 2017 (Berline et al., 2020, brown color scale; value between 0.001 % and 0.02 %) and surface chlorophyll distribution in July–August (green color scale; im mg m−3) based on GlobColour MODIS monthly product from 2010 to 2018. Circulation schematic of the surface currents is superimposed: the North Equatorial Current (NEC), the northern and southern branches of the South Equatorial Current (nSEC and sSEC), the North Equatorial Countercurrent (NECC), the North Brazil Current (NBC), the Caribbean Current (CC), and the Loop Current (LC).
Modeling and forecasting the Sargassum proliferation and strandings are essential for designing effective integrated risk management strategies and is a strong and pressing demand from the civil society. This operational challenge concerns both event forecasts (i.e., on a 1-week scale) and long-term forecasts (one to several months). While many efforts have been made for short-term forecasts, initiatives for reliable long-term forecasting are very scarce and face several scientific challenges such as the large uncertainties in Sargassum detection and biomass quantification (Wang et al., 2018; Ody et al., 2019), a lack of knowledge on Sargassum physiology, and last but not least the absence of tools specifically designed to reproduce the large-scale distribution of these macroalgae.
Recent studies suggest that the increasing incidence of Sargassum blooms and their year-to-year variability is multifactorial: it may result from riverine and atmospheric fertilization of the upper ocean, western Africa upwelling variability, vertical exchanges at the mixed-layer base in the region of the Intertropical Convergence Zone (ITCZ), or anomalous transport due to climate variability (Oviatt et al., 2019; Wang et al., 2019; Johns et al., 2020). This highlights the complexity of the phenomenon and the need for a basin-scale and interdisciplinary approach.
In the recent years, modeling effort mainly focused on the transport properties of Sargassum rafts by offshore currents (Wang and Hu, 2017; Brooks et al., 2018; Maréchal et al., 2017; Putman et al., 2018, 2020; Wang et al., 2019; Berline et al., 2020; Beron-Vera and Miron, 2020), with significant advances on the role of inertia in the drift trajectories (Brooks et al., 2019; Beron-Vera and Miron, 2020) and the importance of considering windage to properly resolve the drift of the Sargassum mats (Putman et al., 2020; Berline et al., 2020). To our knowledge, Brooks et al. (2018) were the first to integrate Sargassum physiology along the trajectories and showed that considering growth and mortality improved the modeling of the large-scale distribution of Sargassum. A similar result was obtained in Wang et al. (2019), although they did not consider directly the physiology of the algae but local growth rate based on satellite observations. Indeed, few studies have investigated the biology and ecology of this holopelagic Sargassum species that proliferate in the Atlantic and their response to the variability of environmental parameters (Lapointe, 1995, 1986; Hanisak and Samuel, 1987; Carpenter and Cox, 1974; Hanson, 1977; Howard and Menzies, 1969).
In the present paper, we describe the numerical model we developed to represent the distribution of holopelagic Sargassum. This model relies on an Eulerian approach and integrates both transport and a simplified physiology model of the macroalgae. It is based on the Nucleus for European Modelling of the Ocean (NEMO) modeling system, which is widely used by the research community and European ocean forecasting centers (e.g., Mercator Ocean International, ECMWF), allowing efficient parallelization and interfacing with physical–biogeochemical models. In the following section, we review current knowledge on the ecology of Sargassum. The modeling system is described in Sect. 3. Section 4 shows the performance of the model at seasonal scale and discusses sensitivity of the modeled Sargassum distribution to the forcing fields. Discussion and a summary are given in the final Section.
Pelagic Sargassum species (to date Sargassum natans and S. fluitans) are brown algae (Phaeophyceae) that live at the surface of the ocean, never attached to any substrate. Within these two taxonomic groups, three types of Sargassum that can be distinguished according to morphological features appear to fuel the recent Sargassum inundations in the Caribbean: S. fluitans III, S. natans I, and S. natans VIII (Schell et al., 2015). We still lack knowledge on the distribution of these species, but in recent years, S. fluitans III was predominant in 2017 (Ody et al., 2019) and formed beaching on the Yucatán coast, comprising on average > 60 % of total wet biomass (García-Sánchez et al., 2020), whereas Schell et al. (2015) reported a predominance of S. natans VIII in 2015.
One individual Sargassum fragment can vary in length from just 1 cm to more than 1 m. Under the action of Langmuir cells and ocean currents, Sargassum tends to group together to form large floating rafts on the water surface (e.g., Langmuir, 1938; Zhong et al., 2012). Individuals in these aggregations can be easily dispersed when the dynamical conditions favorable to aggregation cease (Ody et al., 2019). These assemblages spread out horizontally and can reach several tens of kilometers and a few meters' thickness.
Biological and physiological features are species dependent. We know relatively little about the physiology of these Sargassum. Considering biomass, their maximum growth rate is estimated to be around 0.1 d−1 (Lapointe, 1986; Hanisak and Samuel, 1987; Lapointe et al., 2014). The Sargassum growth is sensitive to light and temperature. Carpenter and Cox (1974) suggest light saturation under normal October light conditions in the Sargasso Sea (35 W m−2), while Hanisak and Samuel (1987) found a higher saturation range of ∼ 43–65 W m−2. The temperature dependence in Hanisak and Samuel (1987) for Sargassum natans suggests a broad optimal temperature range of 18–30 ∘C and indicates no growth at 12 ∘C. We lack information on the Sargassum fluitans response to the variability of the environmental parameters.
Lapointe (1986) highlights a growth mainly limited by phosphate availability, while the presence of nitrifying epiphytes (Carpenter, 1972; Michotey et al., 2020) could be a non-negligible source of nitrogen for Sargassum, as could urea and ammonium excreted by fish (Lapointe et al., 2014). It is also likely that Sargassum are able to store some nutrients in their tissues, as do other brown algae (e.g., Hanisak, 1983). This hypothesis is supported by Lapointe (1995), whose measurements revealed variable elemental compositions between individuals sampled in neritic vs. oceanic waters. In addition, no macroherbivores control holopelagic development offshore by grazing (Butler et al., 1983).
Our modeling strategy relies on a physical–biogeochemical model that resolves currents and nutrient variability in the Atlantic. We choose to develop a regional configuration so the model can be tuned to the region specificity and can be used to perform sensitivity tests as discussed in Sect. 4. In addition, our approach is based on a Sargassum model that integrates transport, stranding, and physiology of the macroalgae in the ocean surface layer, forced with surface fields obtained from the physical–biogeochemical model.
The two models share the same horizontal domain and grid, and both are based on the NEMO modeling system version 4.0 (Madec and the NEMO team, 2016). They are not coupled assuming then that Sargassum does not compete with phytoplankton and heterotrophic bacteria for nutrient resources, and that they are not grazed by the herbivore compartments of the biogeochemical model.
3.1 The physical–biogeochemical model TATL025BIO
For the physical component of the simulation, we use the regional NEMO-based configuration described in Hernandez et al. (2016, 2017) and Radenac et al. (2020) that covers the tropical Atlantic between 35∘ S and 35∘ N and from 100∘ W to 15∘ E. The resolution of the horizontal grid is ∘ and there are 75 vertical levels, 24 of which are in the upper 100 m of the ocean. The depth interval ranges from 1 m at the surface to about 10 m at 100 m depth. Interannual atmospheric fluxes of momentum, heat, and freshwater are derived from the DFS5.2 product (Dussin et al., 2016) using bulk formulae from Large and Yeager (2009). Temperature, salinity, currents, and sea level from the Mercator global reanalysis GLORYS2V4 (Storto et al., 2018) are used to force the model at the lateral boundaries. This configuration has proven to properly represent many aspects of the tropical Atlantic dynamics such as the Amazon plume extent (Hernandez et al., 2016), the large-scale circulation (Kounta et al., 2018) or the surface salinity variability (Awo et al., 2018).
The physical model is coupled to the PISCES (Pelagic Interaction Scheme for Carbon and Ecosystem Studies) biogeochemical model (Aumont et al., 2015) that simulates the biological production and the biogeochemical cycles of carbon, nitrogen, phosphorus, silica, and iron. We use the PISCES-Q version with variable stoichiometry described in Kwiatkowski et al. (2018), with an explicit representation of three phytoplankton size classes (picophytoplankton, nanophytoplankton, and microphytoplankton) and two zooplankton compartments (nanozooplankton and mesozooplankton). The model also includes three non-living compartments (dissolved organic matter and small and large sinking particles). The biogeochemical model is initialized and forced at the lateral boundaries with dissolved inorganic carbon, dissolved organic carbon, alkalinity, and iron obtained from stabilized climatological 3-D fields of the global standard configuration ORCA2 (Aumont and Bopp, 2006), and nitrate, phosphate, silicate, and dissolved oxygen from the World Ocean Atlas (WOA; Garcia et al., 2010) observation database. The model is run from 2006 to 2017, and daily physical and biogeochemical fields are extracted to force the Sargassum model.
Particular care has been given to the prescription of the atmospheric and riverine fluxes of nutrients. The river runoffs are based on daily fluxes from the ISBA-CTRIP reanalysis (Decharme et al., 2019), which has proven to accurately reproduce the interannual variability of the large rivers of the basin (e.g., see Giffard et al., 2019, for the Amazon River). The riverine nutrient fluxes concentrations are from the GLOBAL-NEWS2 dataset, corrected with in situ observations from the Amazon basin water resources observatory database (HYBAM, https://hybam.obs-mip.fr/, last access: 1 February 2020) for the Amazon, Orinoco, and Congo rivers. As in Aumont et al. (2015), we consider an atmospheric supply of P, Fe, and Si from dust deposition. Here, these fluxes are forced using monthly dry-plus-wet deposition products (DUDPWTSUM) from the Modern-Era Retrospective analysis for Research and Applications, version 2 (MERRA-2) data available on the NASA Giovanni website (http://disc.sci.gsfc.nasa.gov/giovanni, last access: 3 April 2020). Comparison with in situ observations of dust fluxes in Guyana and in Barbados leads to an excellent match with MERRA2 fluxes (Prospero et al., 2020). A climatological deposit of N is obtained from global climate simulations carried out with the ARPEGE-Climate model (Michou et al., 2020). An interactive aerosol scheme including nitrate and ammonium particles (Drugé et al., 2019) is included in ARPEGE-Climate, allowing us to produce fields of wet and dry deposition of nitrogen, ammonium, and ammonia. Figure 2 illustrates that dust and nitrogen fluxes to the ocean are strong in our region of interest, and most particularly in the ITCZ region where atmospheric convergence may focus the wet fluxes.
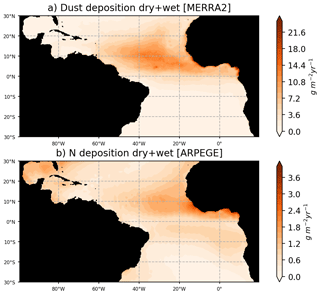
Figure 2Dust fluxes to the ocean from MERRA2 reanalysis for the year 2017 (a) and nitrogen flux to the ocean from ARPEGE simulations averaged over the period 2010–2014. Nitrogen fluxes consider the dry and wet fluxes at the ocean surface of NO3, NH4, and NH3. Dust fluxes consider the total dust dry-plus-wet deposition product (DUDPWTSUM) from MERRA2.
The modeled chlorophyll for the year 2017 is compared with GlobColour satellite estimates of chlorophyll for the same year (Fig. 3a, b). Model NO3 and PO4 concentrations for 2017 are compared with historical in situ measurements (Fig. 3c–f) from the GLODAPV2 database (Olsen et al., 2016). The model reproduces the major chlorophyll structures and in particular the contrast between the oligotrophic subtropical gyre and productive coastal and equatorial upwellings (Fig. 3a, b). As many other models (e.g., see the CMIP6 model evaluation by Séférian et al., 2020), it struggles to reproduce the offshore extent of the large river plumes and Guinea Dome productivity. Moreover, coastal upwellings tend to be too productive offshore or downstream (for the equatorial upwelling). But above all, it represents realistically the chlorophyll distribution in the region of the ITCZ (∼ 0–10∘ N) and in the Caribbean Sea. As observed, nitrate concentrations are high in the upwelling areas (Fig. 3c, d) but weaker than observed off these regions. It is worth noticing that historical observations of surface nitrate concentrations in the tropical band show very heterogeneous and contrasted values between cruises, so the reliability of a nitrate climatology in this area remains uncertain (Fig. 3c). The model reproduces realistically the observed interhemispheric gradient of surface phosphate concentrations even though it likely overestimates areas of high phosphate content (Fig. 3e, f).
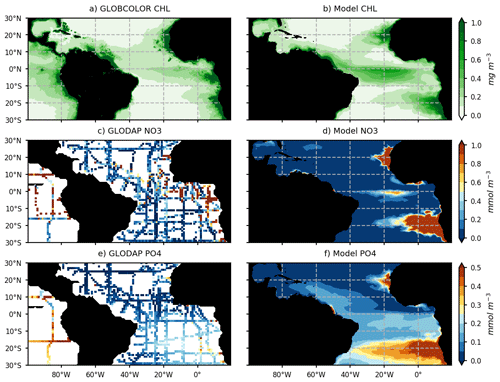
Figure 3Annual mean surface chlorophyll concentrations (mg chl a m−3) from the GlobColour satellite product (a) and model (b) for the year 2017. Spatial distribution of surface NO3 and PO4 concentration (c, e; mmol m−3) from historical cruises of the GLODAPv2_2016 database (https://www.nodc.noaa.gov/ocads/oceans/GLODAPv2/, last access: 1 June 2020) and annual mean surface NO3 and PO4 distribution from the model (d, f).
3.2 The Sargassum model NEMO-Sarg1.0
The Sargassum model relies on the strategy used to represent the distribution of other macroalgae species and their transport by 2-D advection–diffusion equations (e.g., Martins and Marques, 2002; Solidoro et al., 1997; Perrot et al., 2014; Ren et al., 2014; Ménesguen et al., 2006; Bergamasco and Zago, 1999). Here, we also consider sink due to stranding at the coast. Growth is modeled as a function of internal reserves of nutrients, dissolved inorganic nutrients in the external medium, irradiance, and sea temperature. As the eco-phycological features are species dependent, the actual knowledge on the three morphotypes of holopelagic Sargassum does allow us to discriminate between them. Following the formalism given in Ren et al. (2014), the physiological behavior is described from three state variables: the content in carbon (C), nitrogen (N), and phosphorus (P), with local variations reflecting the difference between uptake and loss rates.
where UC, UN and UP are the uptake rates of carbon, nitrogen, and phosphorus, respectively, and ΦC, ΦN, ΦP the loss rates.
The rate of carbon uptake reads as follows: , with μmax the maximum net carbon growth rate, and the four subsequent terms standing for uptake limitation by temperature (T), solar radiation (I), N quota (QN), and P quota (QP), respectively. N and P quotas represent the ratios of nitrogen and phosphorus to carbon in the organism and are computed as and , respectively. The C content (C) can be directly converted to dry biomass considering a mean carbon-to-dry-weight ratio of 27 % (Wang et al., 2018).
The temperature dependence is adapted from Martins and Marques (2002):
with for T≤Topt; for T>Topt. Topt is the optimum temperature at which growth rate is maximum, Tmin is the lower temperature limit below which growth ceases, and Tmax is the upper temperature limit above which growth ceases. Such a function aims at representing a broad optimal temperature range as suggested by experiments in Hanisak and Samuel (1987). The dependence on light is expressed as follows in order to mimic results from Hanisak and Samuel (1987):
We have very little information on the response curve relating the nutrient quota to Sargassum growth but experiments for brown seaweed suggest a hyperbolic relationship (e.g., Hanisak, 1983). So, the dependence on the internal nitrogen and phosphorus pools is computed as a hyperbolic curve controlled by the minimum and maximum cell quotas:
The nitrogen and phosphorus uptake rates depend on the nitrogen (VNmax) and phosphorus (VPmax) maximum uptake velocities, a Monod kinetic that relates uptake to nutrient concentrations in the water, and a function of quota which aims at representing downregulation of the transport system for N and P when approaching the maximum quotas (Lehman et al., 1975):
The carbon loss aims at representing mortality, stranding, and sinking:
The mortality term depends on m the mortality rate, λm a mortality coefficient, and temperature T. We thus represent thallus senescence and bacterial activity as a growing function of temperature (Bendoricchio et al., 1994; Ren et al., 2014).
The stranding is a function of αgrnd which is a rate of Sargassum stranding per unit of time, and δland which is defined as follows:
The sinking rate of Sargassum is estimated as a function of the Langmuir cell length scale HLC and a sinking coefficient mLC. The aim is to reproduce possible Sargassum loss by Langmuir cell, as hypothesized by Johnson and Richardson (1977) or Woodcock (1993) to explain large amounts of Sargassum observed at the sea floor (Schoener and Rowe, 1970; Baker et al., 2018). Following, Axell et al. (2014), we estimate HLC as the depth that a water parcel with kinetic energy can reach on its own by converting its kinetic energy to potential energy. This corresponds to , with us the Stokes drift and N2 the Brunt–Vaisala frequency. We fixed a 100 m depth threshold as Sargassum becomes massively negatively buoyant at these depths (Johnson and Richardson, 1977).
Losses of nitrate and phosphate are function of the loss of biomass and internal N and P quotas:
The transport of C, N, and P is resolved using 2-D advection–diffusion equations discretized on a grid at ∘ resolution with a single vertical layer representing a surface layer of water of 1 m depth. The surface velocities used for the transport account for surface currents, windage effect, and wave transport by Stokes drift:
where (uNEMO,vNEMO) are the horizontal velocity obtained from the physical–biogeochemical model, αwin is a windage coefficient, (u10 m,v10 m) the components of the wind field at 10 m above the sea level, (uStokes,vStokes) the Stokes velocity, and Kh a diffusion coefficient.
3.3 Optimization and sensitivity experiments
The model simulations are performed for the year 2017 because basin-scale Sargassum fractional coverage observations from MODIS were available (Berline et al., 2020), with concurrent observations carried out during two cruises in the tropical Atlantic (Ody et al., 2019).
3.3.1 Initialization and forcing
The simulations are initialized using January Sargassum mean fractional coverage, converted into dry weight biomass considering a surface density of 3.34 kg m−2 and then into carbon content C considering a mean carbon-to-dry-weight ratio of 27 % (Wang et al., 2018). The initial N and P content in Sargassum is derived from the initial C content and N and P quotas computed as the averaged values between their respective minimum values (QNmin, QNmin) and maximum values (QNmax, QNmax). The transport is forced by daily velocities from TATL025BIO simulations (see Sect. 3.1). The windage is forced with 3 h winds from the DFS5.2 dataset (Dussin et al., 2016), which were used to force the physical model. The Stokes drift in the surface layer is computed according to Breivik et al. (2014) and forced with hourly ERA5 Stokes drift product. Daily temperature, available irradiation, and Langmuir depth were also obtained from TATL025BIO. The seawater concentrations in [N] and [P] were obtained from TATL025BIO as the sum of NO3 and NH4 for [N], and PO4 for [P], in the top surface layer.
3.3.2 Ensemble strategy
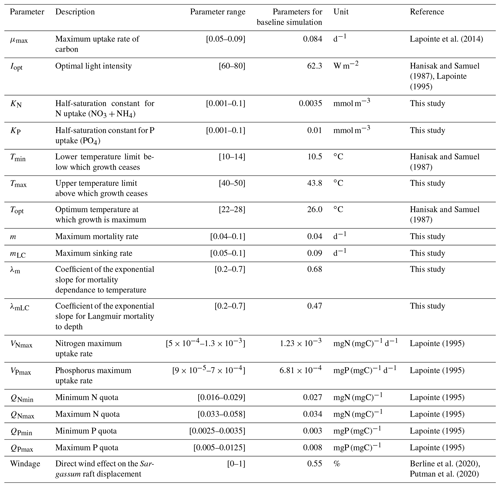
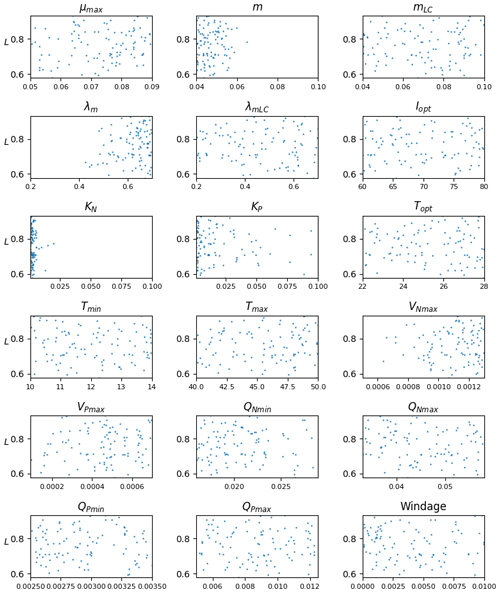
The Sargassum model is controlled by a large number (n=18) of physiological and physical parameters for which large uncertainties exist or most often have not been measured for the Sargassum species considered here. An ensemble approach has been adopted to adjust the set of parameters. We produced 10 000 sets of parameters with uniform distribution obtained from Latin hypercube sampling with multi-dimensional uniformity (Deutsch and Deutsch, 2012). These sets of parameters are generated on ranges of values obtained from the literature, when available (Table 1).
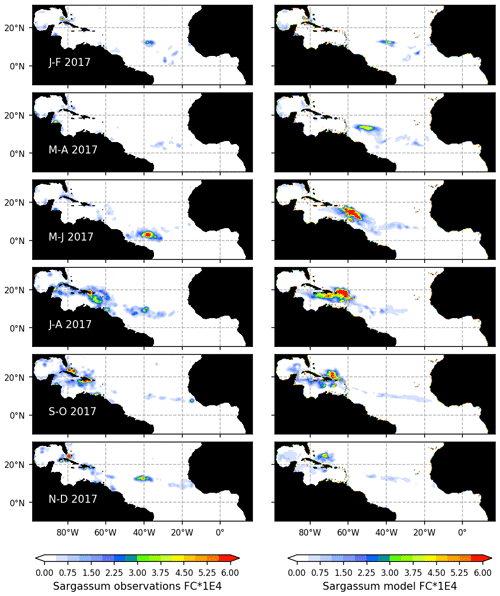
Figure 4Seasonal distribution of Sargassum fractional coverage for the year 2017 from observations (left) and from a selected ensemble of 100 simulations (Ω100) with varying parameters (right).
The range of maximum growth rate is derived from Lapointe et al. (2014) who observed maximum growth rates of Sargassum fluitans and Sargassum natans in neritic waters between 0.03 and 0.09 doubling d−1. The set of parameters for temperature limitation is mainly derived from the results of Hanisak and Samuel (1987). In particular, the Tmax range (40–50 ∘C) is chosen to have a slight decrease of the limitation term at T>Topt as observed in Hanisak and Samuel (1987). The N and P quotas are based on the observations by Lapointe (1995) from which we can estimate that on average ratios vary between 20 and 30 in neritic waters and between 40 and 70 in oceanic waters, while ratios vary between 200 and 500 in neritic waters and 700 and 1000 in oceanic waters. The lower and upper limits for the maximum nitrate uptake rate ([, ] mg N (mg C)−1 d−1) are estimated from measurements by Lapointe (1995). From this study, we estimate maximum carbon uptake rates in neritic water at ∼ 2 mg C (g dry wt)−1 h−1 with ratio of 20 and maximum carbon uptake rates in oceanic water at ∼ 1 mg C (g dry wt)−1 h−1 with ratio of 60. Since the model does not take into account a diurnal cycle of light, the maximum uptake has been divided by 3 in order to have a daily-mean maximum uptake. This ratio of 3 is obtained by comparing instantaneous gross production at full irradiance vs. measured gross production from culturing the Sargassum under natural irradiance in Lapointe et al. (2014). Similarly, the lower and upper limits for the maximum phosphorus uptake rate ( mg N (mg C)−1 d−1) are estimated from measurements by Lapointe (1995), which gives a ratio of 200 in neritic waters and 800 in oceanic waters.
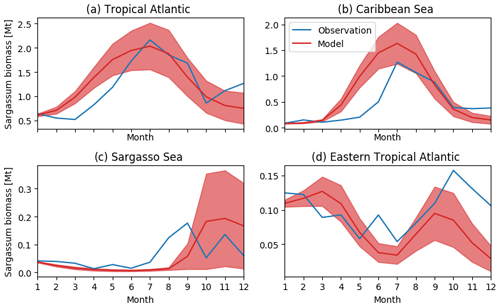
Figure 5Seasonal distribution of Sargassum fractional coverage for the year 2017 from observations (blue) and from a selected ensemble of 100 simulations (Ω100) with varying parameters (mean in red and variance in shaded red) averaged in different areas: (a) tropical Atlantic [0–30∘ N, 98–10∘ W], (b) Caribbean Sea [8–22∘ N, 85–55∘ W], (c) Sargasso Sea [23–30∘ N, 80–50∘ W], and (d) eastern tropical North Atlantic [0–15∘ N, 30∘ W–0∘ E].
3.3.3 Likelihood function
The likelihood function (L) to be minimized is the centered root mean square error between monthly series of observed and modeled Sargassum biomass contained in the tropical North Atlantic Ocean, defined as [0–30∘ N, 98–10∘ W], hereinafter NTAO:
with Nt the number of outputs (12 months in our case), ψm(t) and ψobs(t) the modeled and observed biomass in the NTAO, and the overbars designating the annual average.
The choice of this likelihood function exerts no constraints on the spatial distribution of the Sargassum and does not consider uncertainties in the satellite measurements due to false detection, cloud masking, or Sargassum immersion. But as shown in the following section, such a simple strategy allows us to efficiently select a set of parameters that allow a good representation of the seasonal Sargassum distribution.
3.3.4 Sensitivity analysis
Once a set of values minimizing L was found, one-at-a-time sensitivity experiments were also performed, where only one single parameter is varied by ±10 % in two model runs while the others are fixed (e.g., Ren et al., 2014; Perrot et al., 2014). This allows us to capture the direct contribution from each parameter to the output variance, with parameters varying within an acceptable range. The set of values for the fixed parameters is given in Table 1 and were taken from the simulation with higher L. Following Ren et al. (2014), deviation from the baseline simulation (D) is quantified as
where refers to the simulated biomass in the NTAO from the baseline parameter set at month t, and ψm(i,t) is the simulated biomass with one perturbed parameter i at month t. Two model runs were conducted with ±10 % change to the baseline value.
4.1 Seasonal distribution and sensitivity to model parameters
The observed and model seasonal distributions of Sargassum in 2017 are shown in Fig. 4. Model distribution is obtained from the ensemble mean of the 100 simulations with the lowest L. Hereafter, this ensemble will be referred to as Ω100. Averages over selected areas are shown in Fig. 5. At this stage, it is worth recording that the selection of the ensemble simulations is performed without constraints on the spatial distribution, the only constraint being on the basin-scale seasonal biomass average (L).
Initialized in January, the model reproduces the seasonal distributions of Sargassum fairly closely. It simulates the Sargassum drift toward the Caribbean Sea, with a summer peak of biomass followed by a decrease until the end of the year, although the increase of biomass comes a little too early in February–March. In the Caribbean Sea, the largest abundance of Sargassum in the northern part of the basin near the Greater Antilles compared to the south of the Caribbean is consistent with observations. Despite a bloom that is occurring too early (May–June) near the Lesser Antilles, the modeled seasonal cycle is also consistent with the observations in this area (Fig. 5b). This is encouraging from the perspective of predicting strandings on the Caribbean islands. It also succeeds in maintaining the biomass in the Eastern part of the tropical North Atlantic below the ITCZ (Figs. 4 and 5d). In the Sargasso Sea area (Fig. 5c), simulations and observations consistently show an increase at the end of the year. The model tends to reproduce heavy proliferations in March–June which seem not to be observed. Given current knowledge, it is difficult to determine the causes of such a bias. It could be due to a bias in the nutrient content simulated by PISCES-Q at this period. Moreover, error in the Sargassum initial conditions (January) and in the transport parameterization can lead to this production too far north during March–June. An observation bias cannot be ruled out either since this area is very cloudy and presents very contrasted Sargassum aggregation properties.
The distribution of parameters for the ensemble Ω100 is given in Fig. 6. There is a significant dispersion of most of the parameters, suggesting either low sensitivity to the parameters in question (as discussed below) or interdependency between them. The analysis shows that there are very different sets of parameters, within the prescribed ranges, that lead to similar seasonal biomass distribution (Fig. 5). Having said that, we observe that the mortality parameters m and λm minimizing L are biased toward low and high values, respectively. This highlights the key importance of this mortality function in representing the seasonal distribution. The half-saturation constants (KN and KP) and the maximum uptake rates of nutrients (VNmax and VPmax) are also distributed toward low and high values, respectively, suggesting some sensitivity of the Sargassum distribution to nutrient resources. These parameters are poorly constrained by observations, and such exercise will allow us to refine the optimization ranges for future studies.
The relative mean deviation of the Sargassum seasonal biomass to 10 % variations in model parameters shown in Fig. 7 confirms findings from the analysis of parameter dispersion in Fig. 6. The most influential parameters are the growth rate, the optimal irradiance, mortality dependence on temperature, and parameter controlling the nitrogen uptake VNmax. It also highlights the influence of the minimum N quota (QNmin). There is moderate dependence on temperature which is in good agreement with measurements from Hanisak and Samuel (1987). In agreement with previous Lagrangian studies (Berline et al., 2020; Putman et al., 2020), we find some sensitivity to the windage parameter.
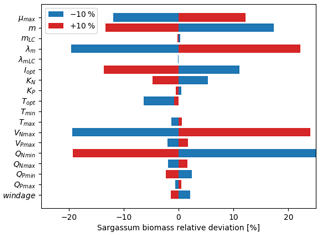
Figure 7Sensitivity analysis to model parameters expressed as the mean relative deviation (%) between the baseline simulation and the simulation in which one parameter was modified by ±10 %. The set of parameters for the baseline simulation is given in Table 1.
The simulated stranding from the ensemble Ω100 is shown in Fig. 8. At the scale of the tropical Atlantic, these strandings sum to 1.05 million tons of dry weight for the whole year. The predicted strandings in the Caribbean, northern Brazil, French Guiana, and Sierra Leone correspond to our current knowledge of Sargassum invasions (Bernard et al., 2019; Louime et al., 2017; Oviatt et al., 2019; Sissini et al., 2017; Oyesiku and Egunyomi, 2014; Smetacek and Zingone, 2013). Nevertheless, there are no available large-scale coastal observations or estimates of stranding to go further in the validation of these simulated strandings.
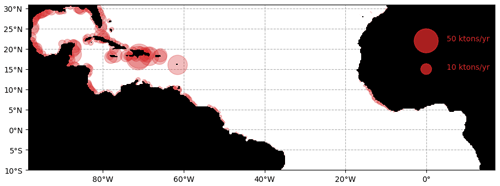
Figure 8Cumulated annual Sargassum wet biomass stranding per area of 25×25 km for the year 2017 obtained from the ensemble Ω100.
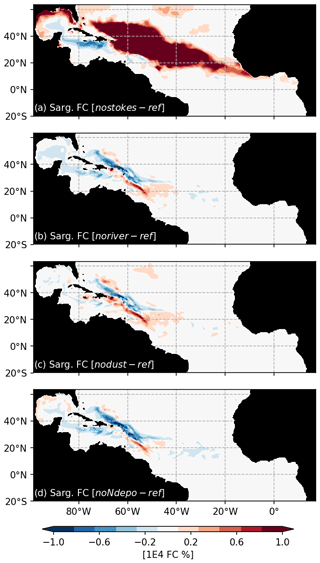
A peculiarity of our modeling strategy is to consider the Stokes drift. The Stokes drift induces a displacement of material parallel to the direction of wave propagation which directly transports the Sargassum. An ensemble of 100 simulations without Stokes drift (“NoStokes”), considering the set of physiological parameters from Ω100, has therefore been conducted. Anomalies of annual Sargassum distribution with respect to Ω100 are shown in Fig. 9a. Sargassum coverage is significantly increased in the central Atlantic but decreases sharply in the Caribbean and the southwestern part of the domain. This highlights the influence of waves, most probably due to the trade winds, in shaping the seasonal distribution, and transporting the algae southward.
4.2 Sensitivity to external nutrient forcing
We now use the Sargassum model to explore how and to which extent continental nutrient sources (riverine nutrient fluxes, dust deposition, atmospheric N deposition) could participate in the proliferation and may shape the seasonal distribution of Sargassum. First, TATL025BIO simulations were run by deactivating the river sources (simulation “noriver”), atmospheric deposition of P, Si, and Fe (simulation “nodust”), or atmospheric deposition of N (simulations “noNdepo”). We choose to distinguish between dust and N deposition because they do not have the same origin and because spatial, seasonal, and long-term variability is not necessarily the same. The simulations were produced from 2006, so the long-term influence of these forcings on the biogeochemical content is considered there. These simulations were then used to force three ensembles of 100 simulations which used the sets of parameters from Ω100.
As expected for the noriver ensemble, the tropical western Atlantic, which is under influence of the Amazon and Orinoco rivers, is experiencing a decrease in nutrient concentrations (Fig. 10b). Nutrients also show a decrease in the equatorial Atlantic. But for other regions, such as the Sargasso Sea or the Guinea Dome, the long-term equilibration results in an increase in nitrogen concentration. The resulting Sargassum coverage shows a negative anomaly in the Caribbean Sea, in the Gulf of Mexico, and in the region of the ITCZ, with an annual mean basin-scale biomass decrease (Fig. 9a). For this ensemble, strandings are decreased from 0.65 to 0.56 Mt (−13 %).
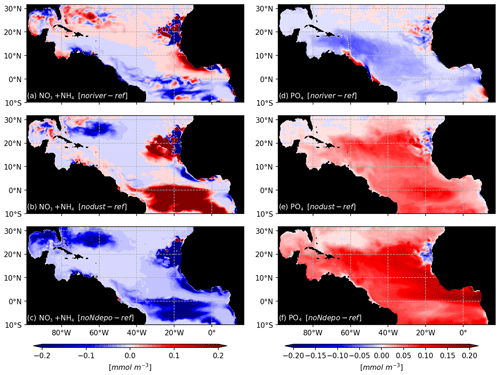
Figure 10Biogeochemical response to sensitivity experiments to river, dust, and N deposition: surface anomalies of NO3+NH4 (a–c) and PO4 (d–f) with respect to the reference TATL025BIO simulation.
The nodust ensemble Sargassum distribution shows a slight positive anomaly over most of the domain (Fig. 9c), particularly in the central Atlantic and off western Africa, with a slight decrease in the Caribbean Sea and the Gulf of Mexico. Cumulative strandings sum to 0.72 Mt, and so, are slightly increased compared to the baseline ensemble (+10 %). This sensitivity can be explained by the large-scale phosphorus increase and regional increases in nitrogen and phosphorus concentrations (Fig. 10) in the biogeochemical simulation. This sensitivity is expected to be produced by the reduced iron concentrations, which limit the phytoplankton growth and thus the nutrient uptake.
The removal of atmospheric nitrogen deposition (noNdepo) leads to a global decrease in surface nitrogen concentration and an increase in surface phosphorus concentrations across the entire domain (Fig. 10). The resulting Sargassum coverage is significantly decreased over the whole domain, and the annual averaged stranding decreases by 1 % (Fig. 9d).
Since 2011, unprecedented massive strandings of the holopelagic Sargassum have been reported on the coasts of the Caribbean Sea, northern Brazil, and western Africa. In this paper, we developed an Eulerian model of Sargassum, which integrates transport, strandings and algal physiology. The Sargassum model is based on the ocean modeling platform NEMO and is forced by the physical and biogeochemical fields of a regional model (TATL025BIO), as well as by the ERA5 wave and wind fields. An ensemble approach has been used to optimize the physiological parameters. The results demonstrate the ability of the model to represent the spatial distribution and seasonal cycle of the Sargassum biomass in the western Atlantic and the Caribbean Sea.
While windage and inertial effects are considered of importance for the drift properties and large-scale advection (Brooks et al., 2019; Berline et al., 2020; Beron-Vera et al., 2020; Putman et al., 2018, 2020), we show here that Stokes drift has also significant impacts on the distribution of the Sargassum and in particular on their entrance in the Caribbean Sea. In addition to the anomalous currents that may be at the origin of the Sargassum bloom in 2011 (Johns et al., 2020), wave drift could also have contributed to the dissemination of the algae toward the equatorial Atlantic in the early 2010s. Wave transport of algae is therefore an important component of Sargassum modeling that has not yet been accounted for in previous modeling efforts (Brooks et al., 2018; Putman et al., 2018; Wang et al., 2019; Johns et al., 2020) and should deserve further attention.
Transport properties may also be impacted by the numerical choices and model resolution. Our model resolution is intermediate (∼ eddy permitting), so we lack some energy at the mesoscale. Since this mesoscale is particularly important for the dynamics in the Caribbean, Gulf of Mexico, or the North Brazil Current area, we would expect more realistic transport properties at higher resolution. But our experience is that ∘ NEMO simulations work well in the region on many aspects of the regional dynamics, such as river plume extent (Hernandez et al., 2016, 2017), large-scale currents (Kounta et al., 2018), biogeochemistry (Radenac et al., 2020), and large-scale salinity distribution (Awo et al., 2018), among others. One reason is that the scales of variability in the tropics are larger than at midlatitudes. This is a posteriori confirmed by the present study since we show that the simulated ocean dynamics are good enough to represent the accumulation of Sargassum in the ITCZ, the advection in the Caribbean through the Antilles, and the episodic shedding of Loop Current eddies in the Gulf of Mexico. We also expect that model resolution is only part of the story regarding the dependence of the transport properties to numerics. Surface transport also depends on the vertical resolution of the model in the mixed layer, the vertical mixing scheme, the degree of coupling of the ocean circulation with the atmosphere or the waves, the wind product used to force the model, etc. In our model, the windage transport coefficient acts as an empirical factor that compensates lacking the explicit simulation of some of these processes and probably helps us to properly simulate a realistic large-scale Sargassum advection. Overall, we definitely need to rely on dedicated Lagrangian studies such as the one performed by Putman et al. (2018), Putman and He (2013), Berline et al. (2020), and Putman et al. (2020) to better constrain our model, and learn about best practices in terms of forcing Sargassum transport.

Figure 11Average N and P uptake by phytoplankton (in mmol m−2 d−1; a and b, respectively) and by Sargassum (in µmol m−2 d−1; c and d, respectively). The N and P uptake by phytoplankton were obtained from the biogeochemical simulation, assuming a constant stoichiometry. The uptake rates were integrated over the model mixed-layer depth for each month of 2017 and averaged over the year. The bottom row shows the Sargassum vs. phytoplankton mean consumption ratio of (e) N and (f) P (in ‰) for the year 2017.
The ability of the model to simulate the large-scale distribution was also used to conduct sensitivity tests on the nutrient forcing from rivers and dust and atmospheric deposition. Here, it is worth remembering that the Sargassum model is not coupled with the biogeochemical model so it is not directly forced by these external inputs of nutrients but through the biogeochemical model. This prevents the representation of some opportunistic utilization of nutrients that could be done by the algae. Moreover, it is worth mentioning that the half-saturation constants obtained from the basin-scale optimization procedure are low (likely because the biogeochemical model tends to have low surface nutrient concentrations in the tropical northern Atlantic). This could limit the sensitivity of the model to high nutrient inputs. With these limitations in mind, we found a 17 % and 21 % decrease in annual Sargassum distribution in the experiments without river nutrient runoff and without atmospheric nitrogen deposition, respectively. This suggest that these forcings alone cannot fuel the total Sargassum biomass. Regarding the nutrient brought by the Amazon, this is in agreement with recent conclusions from Johns et al. (2020) and Jouanno et al. (2021), who suggest that the riverine fertilization of the tropical Atlantic is not at the origin of the phenomenon nor control its year-to-year variability. At this stage, the processes controlling the interannual variability and overall increase of Sargassum remains an open question that will deserve further attention. Application of the numerical tracer method initially proposed by Ménesguen et al. (2006), which tracks nitrogen or phosphorus from any source throughout the biogeochemical network, could help identify the nutrient sources that control the phenomenon without altering the large-scale biogeochemical content.
Several aspects which could be of potential importance for Sargassum growth have not been considered here. First, growth and mortality could depend on the age of the fragments, through colonization by epiphytes. There is a lack of knowledge on these aspects, and mesocosm experiments would be useful to better constrain such dependence in the model, if relevant. Second, we assume that Sargassum does not compete with phytoplankton for resources. The annual mean consumption of N and P in the mixed layer is shown in Fig. 11 for both phytoplankton and Sargassum, obtained from the NEMO-Sarg1.0 and PISCES-Q models, respectively. It reveals that the consumption of N and P by the phytoplankton is 2–3 orders of magnitude larger than the consumption of N and P by the Sargassum. So, at the basin scale, it seems reasonable to consider that Sargassum growth does not affect phytoplankton growth. But at the local scale (scale of a raft or scale of a bay) and particularly with low mixing conditions, Sargassum could compete with phytoplankton for resources. A full coupling of our Sargassum model with PISCES-Q may allow us to address such questions. Third, our results show a strong dependence on the nitrogen uptake parameters. We do not consider possible fixation of atmospheric N through diazotrophic assemblage. Biological nitrogen fixation by diazotrophic macroalgal association has been shown to be important for some Sargassum species (e.g. Sargassum horneri, Raut et al., 2018) and this could also be the case for the holopelagic Sargassum where epibionts N-fixating bacteria have been observed on these species (Carpenter, 1972; Michotey et al., 2020).
Finally, our modeling system succeeds in maintaining some biomass in the tropical central and eastern Atlantic. This pool of Sargassum has been shown to be of key importance in the year-to-year maintenance of the population (Wang et al., 2019). So, we expect the model to be useful to address the question of interannual variations.
The authors wish to pay tribute to Frédéric Diaz, a colleague suddenly deceased, whom we all esteemed for his humanity, his high standards, his dedication to research, and his investment in teaching.
The Sargassum model is built upon the standard NEMO code (release 4.0.1, rev 11533). The reference code can be downloaded from the NEMO website (http://www.nemo-ocean.eu/, last access: 11 September 2019). The NEMO code modified to include the Sargassum physiology and transport is available in the Zenodo archive (Jouanno and Benshila, 2020, https://doi.org/10.5281/zenodo.4275901). Forcing fields for the year 2017 are also included in the Zenodo archive.
JJ and RB developed the model code, with inputs from LB, FD, TC, JS, and CC on the Sargassum modeling strategy. FD, TT, FM, and TC provided insight on the Sargassum physiology. SB, OA, CE, GM, and MHR participated to the physical–biogeochemical model implementation and tuning. LB provided the Sargassum satellite detection product. PN and MM provided fields of atmospheric nitrogen deposition. JJ and AS performed the simulations and analysis. JJ prepared the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study was supported by the “Convention Sargasses” between IRD and the French Ministère de la Transition Écologique, CNRS, ANR project FORESEA (https://sargassum-foresea.cnrs.fr, last access: 28 June 2021), and TOSCA SAREDA-DA project. Supercomputing facilities were provided by GENCI project GEN7298. The authors would also like to thank the two anonymous reviewers for their constructive comments that helped to improve this paper and offered very interesting perspectives on our work and its future development, as well as Sophie Valcke for her editorial work.
This research has been supported by the Agence Nationale de la Recherche (grant no. ANR-19-SARG-0007-01). This work is part of the TRIATLAS European project (South and Tropical Atlantic climate-based marine ecosystem prediction for sustainable management; H2020 grant agreement no. 817578).
This paper was edited by Sophie Valcke and reviewed by two anonymous referees.
Aumont, O. and Bopp, L.: Globalizing results from ocean in- situ iron fertilization experiments, Global Biogeochem. Cy., 20, GB2017, https://doi.org/10.1029/2005GB002591, 2006.
Aumont, O., Ethé, C., Tagliabue, A., Bopp, L., and Gehlen, M.: PISCES-v2: an ocean biogeochemical model for carbon and ecosystem studies, Geosci. Model Dev., 8, 2465–2513, https://doi.org/10.5194/gmd-8-2465-2015, 2015.
Axell, L. B.: Wind-driven internal waves and Langmuir circulations in a numerical ocean model of the southern Baltic Sea, J. Geophys. Res.-Oceans, 107, 3204, https://doi.org/10.1029/2001JC000922, 2002.
Awo F. M., Alory, G., Da-Allada, C., Delcroix, T., Jouanno, J., and Baloïtch, E.: Sea Surface Salinity signature of the tropical Atlantic interannual climatic modes, J. Geophys. Res., 123, 7420–7437, https://doi.org/10.1029/2018JC013837, 2018.
Baker, P., Minzlaff, U., Schoenle, A., Schwabe, E., Hohlfeld, M., Jeuck, A, Brenke, N., Prausse, D., Rothenbeck, M., Brix, S., Frutos, I., Jörger, K. M., Neusser, T. P., Koppelmann, R., Devey, C., Brandt, A., and Arndt, H.: Potential contribution of surface-dwelling Sargassum algae to deep-sea ecosystems in the southern North Atlantic, Deep-Sea Res. Pt. II, 148, 21–34, 2018.
Bendoricchio, G., Coffaro, G., and De Marchi, C.: A trophic model for Ulva rigida in the Lagoon of Venice, Ecol. Model., 75, 485–496, 1994.
Berline, L., Ody, A., Jouanno, J., Chevalier, C., André, J. M., Thibaut, T., and Ménard, F.: Hindcasting the 2017 dispersal of Sargassum algae in the Tropical North Atlantic, Mar. Pollut. Bull., 158, 111431, https://doi.org/10.1016/j.marpolbul.2020.111431, 2020.
Bergamasco, A. and Zago, C.: Exploring the nitrogen cycle and macroalgae dynamics in the lagoon of Venice using a multibox model, Estuar. Coast. Shelf S., 48, 155–175, 1999.
Bernard D., Biabiany, E., Sekkat, N., Chery, R., and Cécé, R.: Massive stranding of pelagic–sargassum seaweeds on the French Antilles coasts: Analysis of observed situations with Operational Mercator global ocean analysis and fore- cast system, 24th Congrès Français de Mécanique, Brest, France, 26–30 August 2019, available at: https://cfm2019.sciencesconf.org/258628/document (last access: 23 September 2020), 2019.
Beron-Vera, F. J. and Miron, P.: A minimal Maxey–Riley model for the drift of Sargassum rafts, J. Fluid Mech., 904, A8, https://doi.org/10.1017/jfm.2020.666, 2020.
Breivik, Ø., Janssen, P. A., and Bidlot, J. R.: Approximate Stokes drift profiles in deep water, J. Phys. Oceanogr., 44, 2433–2445, 2014.
Brooks, M. T., Coles, V. J., Hood, R. R., and Gower, J. F.: Factors controlling the seasonal distribution of pelagic Sargassum, Mar. Ecol.-Prog. Ser., 599, 1–18, 2018.
Brooks, M. T., Coles, V. J., and Coles, W. C.: Inertia influences pelagic sargassum advection and distribution, Geophys. Res. Lett., 46, 2610–2618, 2019.
Butler, J. N., Morris, B. F., Cadwallader, J., and Stoner, A. W.: Studies of Sargassum and the Sargassum community. Bermuda Biological Station Special Publication 22, Hamilton, Bermuda, 307 pp., 1983.
Carpenter, E. J.: Nitrogen fixation by a blue-green epiphyte on pelagic Sargassum, Science, 178, 1207–1209, 1972.
Carpenter, E. J. and Cox, J. L.: Production of pelagic Sargassum and a blue-green epiphyte in the western Sargasso Sea 1, Limnol. Oceanogr., 19, 429–436, 1974.
Decharme, B., Delire, C., Minvielle, M., Colin, J., Vergnes, J. P., Alias, A., Saint-Martin, D., Séférian, R., Sénési, S., and Voldoire, A.: Recent changes in the ISBA-CTRIP land surface system for use in the CNRM-CM6 climate model and in global off-line hydrological applications, J. Adv. Model. Earth Sy., 11, 1207–1252, 2019.
Deutsch, J. L. and Deutsch, C. V.: Latin hypercube sampling with multidimensional uniformity, J. Stat. Plan. Infer., 142, 763–772, 2012.
Drugé, T., Nabat, P., Mallet, M., and Somot, S.: Model simulation of ammonium and nitrate aerosols distribution in the Euro-Mediterranean region and their radiative and climatic effects over 1979–2016, Atmos. Chem. Phys., 19, 3707–3731, https://doi.org/10.5194/acp-19-3707-2019, 2019.
Dussin, R., Barnier, B., and Brodeau, L.: The making of Drakkar forcing set DFS5, DRAKKAR/MyOcean Report 01-04-16, LGGE, Grenoble, France, 2016.
Garcia, H. E., Locarnini, R. A., Boyer, T. P., Antonov, J. I., Zweng, M. M., Baranova, O. K., and Johnson, D. R.: World Ocean Atlas 2009, Volume 4: Nutrients (phosphate, nitrate, silicate), S. Levitus, Ed. NOAA Atlas NESDIS 71, U.S. Government Printing Office, Washington, D.C., 398 pp., 2010.
García-Sánchez, M., Graham, C., Vera, E., Escalante-Mancera, E., Álvarez-Filip, L., and van Tussenbroek, B. I.: Temporal changes in the composition and biomass of beached pelagic Sargassum species in the Mexican Caribbean, Aquat. Bot., 167, 103275, https://doi.org/10.1016/j.aquabot.2020.103275, 2020.
Giffard, P., Llovel, W., Jouanno, J., Morvan, G., and Decharme, B.: Contribution of the Amazon River discharge to regional sea level in the tropical Atlantic Ocean, Water, 11, 2348, https://doi.org/10.3390/w11112348, 2019.
Hanisak, M. D.: The nitrogen relationship of marine macroalgae, in: Nitrogen in the Marine Envinroment, edited by: Carpenter, E. J. and Capone, D. G., Academic Press, New York, 699–730, 1983.
Hanisak, M. D. and Samuel, M. A.: Growth rates in culture of several species of Sargassum from Florida, USA, in: Twelfth International Seaweed Symposium, 399–404, Springer, Dordrecht, 1987.
Hanson, R. B.: Pelagic Sargassum community metabolism: Carbon and nitrogen, J. Exp. Mar. Biol. Ecol., 29, 107–118, 1977.
Hernandez, O., Jouanno, J., and Durand, F.: Do the Amazon and Orinoco river plumes influence tropical cyclone-induced surface cooling, J. Geophys. Res.-Oceans, 121, 2119–2141, 2016.
Hernandez, O., Jouanno, J., Echevin, V., and Aumont, A.: Impacts of chlorophyll concentrations on the Tropical Atlantic Ocean, J. Geophys. Res.-Oceans, 122, 5367–5389, https://doi.org/10.1002/2016JC012330, 2017.
Howard, K. L. and Menzies, R. J.: Distribution and production of Sargassum in the waters off the Carolina coast, Bot. Mar., 12, 244–254, 1969.
Johns, E. M., Lumpkin, R., Putman, N. F., Smith, R. H., Muller-Karger, F., Rueda, D., Hu, C., Wang, M., Brooks, M. T., Gramer, L., and Werner, F. E.: The establishment of a pelagic Sargassum population in the tropical Atlantic: biological consequences of a basin-scale long distance dispersal event, Prog. Oceanogr., 182, 102269, https://doi.org/10.1016/j.pocean.2020.102269, 2020.
Johnson, D. L. and Richardson, P. L.: On the wind-induced sinking of Sargassum, J. Exp. Mar. Biol. Ecol., 28, 255–267, https://doi.org/10.1016/0022-0981(77)90095-8, 1977.
Jouanno J. and Benshila R.: Sargassum distribution model based on the NEMO ocean modelling platform (Version 0.0), Zenodo, https://doi.org/10.5281/zenodo.4275901, 2020.
Jouanno, J., Moquet, J. S., Berline, L., Radenac, M. H., Santini, W., Changeux, T., Thibaut, T., Podlejski, W., Menard, F., Martínez, J.M., Aumont, O., Sheinbaum, J., Filizola, N., and N'Kaya, G. D. M.: Evolution of the riverine nutrient export to the Tropical Atlantic over the last 15 years: is there a link with Sargassum proliferation?, Environ. Res. Lett., 16, 034042, https://doi.org/10.1088/1748-9326/abe11a, 2021.
Kounta, L., Capet, X., Jouanno, J., Kolodziejczyk, N., Sow, B., and Gaye, A. T.: A model perspective on the dynamics of the shadow zone of the eastern tropical North Atlantic – Part 1: the poleward slope currents along West Africa, Ocean Sci., 14, 971–997, https://doi.org/10.5194/os-14-971-2018, 2018.
Kwiatkowski, L., Aumont, O., Bopp, L., and Ciais, P.: The Impact of variable Phytoplankton Stoichiometry on Projections of primary production, food quality, and carbon uptake in the global ocean, Global Biogeochem. Cy., 32, 516–528, 2018.
Langin, K.: Seaweed masses assault Caribbean islands, Science, 360, 1157–1158, 2018.
Langmuir, I.: Surface motion of water induced by wind, Science, 87, 119–123, 1938.
Lapointe, B. E.: Phosphorus-limited photosynthesis and growth of Sargassum natans and Sargassum fluitans (Phaeophyceae) in the western North Atlantic, Deep-Sea Res. Pt. A, 33, 391–399, 1986.
Lapointe, B. E.: A comparison of nutrient-limited productivity in Sargassum natans from neritic vs. oceanic waters of the western North Atlantic Ocean, Limnol. Oceanogr., 40, 625–633, 1995.
Lapointe, B. E., West, L. E., Sutton, T. T., and Hu, C.: Ryther revisited: Nutrient excretions by fishes enhance productivity of pelagic Sargassum in the western North Atlantic Ocean, J. Exp. Mar. Biol. Ecol., 458, 46–56, 2014.
Large, W. G. and Yeager, S.: The global climatology of an interannually varying air-sea flux data set, Clim. Dynam., 33, 341–364, https://doi.org/10.1007/s00382-008-0441-3, 2009.
Lehman, J. T., Botkin, D. B., and Likens, G. E.: The assumptions and rationales of a computer model of phytoplankton population dynamics, Limnol. Oceanogr., 20, 343–364, 1975.
Louime, C., Fortune, J., and Gervais, G.: Sargassum Invasion of Coastal Environments: A Growing Concern, Am. J. Environ. Sci., 13, 58–64, https://doi.org/10.3844/ajessp.2017.58.64, 2017.
Madec, G. and the NEMO team: NEMO ocean engine. Note du Pôle de modélisation, Institut Pierre-Simon Laplace (IPSL), France, Vol. 27, 1288–1619, 2016.
Maréchal, J. P., Hellio, C., and Hu, C.: A simple, fast, and reliable method to predict Sargassum washing ashore in the Lesser Antilles, Remote Sensing Applications: Society and Environment, 5, 54–63, 2017.
Martins, I. and Marques, J. C.: A model for the growth of opportunistic macroalgae (Enteromorpha sp.) in tidal estuaries, Estuar. Coast. Shelf S., 55, 247–257, 2002.
Ménesguen, A., Cugier, P., and Leblond, I.: A new numerical technique for tracking chemical species in a mul-tisource, coastal ecosystem, applied to nitrogen causing Ulva blooms in the Bay of Brest (France), Limnol. Oceanogr., 51, 591–601, 2006.
Michotey, V., Blanfuné, A., Chevalier, C., Garel, M., Diaz, F., Berline, L., and Changeux, T.: In situ observations and modelling revealed environmental factors favouring occurrence of Vibrio in microbiome of the pelagic Sargassum responsible for strandings, Sci. Total Environ., 748, 141216, https://doi.org/10.1016/j.scitotenv.2020.141216, 2020.
Michou, M., Nabat, P., Saint-Martin, D., Bock, J., Decharme, B., Mallet, M., Roehrig, R., Séférian, R., Sénési, S., and Voldoire, A.: Present-day and historical aerosol and ozone characteristics in CNRM CMIP6 simulations, J. Adv. Model Earth Sy., 12, e2019MS001816, https://doi.org/10.1029/2019MS001816, 2020.
Ody, A., Thibaut, T., Berline, L., Changeux, T., André, J.M., Chevalier, C., Blanfuné, A., Blanchot, J., Ruitton, S., StigerPouvreau, V., Connan, S., Grelet, J., Aurelle, D., Guéné, M., Bataille, H., Bachelier, C., Guillemain, D., Schmidt, N., Fauvelle, V., Guasco, S., and Ménard, F.: From in situ to satellite observations of pelagic Sargassum distribution and aggregation in the tropical North Atlantic Ocean, PLoS One 14, 1–29, https://doi.org/10.1371/journal.pone.0222584, 2019.
Olsen, A., Key, R. M., van Heuven, S., Lauvset, S. K., Velo, A., Lin, X., Schirnick, C., Kozyr, A., Tanhua, T., Hoppema, M., Jutterström, S., Steinfeldt, R., Jeansson, E., Ishii, M., Pérez, F. F., and Suzuki, T.: The Global Ocean Data Analysis Project version 2 (GLODAPv2) – an internally consistent data product for the world ocean, Earth Syst. Sci. Data, 8, 297–323, https://doi.org/10.5194/essd-8-297-2016, 2016.
Oviatt, C. A., Huizenga, K., Rogers, C. S., and Miller, W. J.: What nutrient sources support anomalous growth and the recent sargassum mass stranding on Caribbean beaches? A review, Mar. Pollut. Bull., 145, 517–525, 2019.
Oyesiku, O. O. and Egunyomi, A.: Identification and chemical studies of pelagic masses of Sargassum natans (Linnaeus) Gaillon and S. fluitans (Borgessen) Borgesen (brown algae), found offshore in Ondo State, Nigeria, Afr. J. Biotechnol., 13, 1188–1193, https://doi.org/10.5897/AJB2013.12335, 2014.
Perrot, T., Rossi, N., Ménesguen, A., and Dumas, F.: Modelling green macroalgal blooms on the coasts of Brittany, France to enhance water quality management, J. Marine Syst., 132, 38–53, 2014.
Prospero, J. M., Barkley, A. E., Gaston, C. J., Gatineau, A., Campos y Sansano, A., and Panechou, K.: Characterizing and quantifying African dust transport and deposition to South America: Implications for the phosphorus budget in the Amazon Basin, Global Biogeochem. Cy., 34, e2020GB006536, https://doi.org/10.1029/2020GB006536, 2020.
Putman, N. F. and He, R.: Tracking the long-distance dispersal of marine organisms: sensitivity to ocean model resolution, J. Roy. Soc. Interf., 10, p. 20120979, 2013.
Putman, N. F., Goni, G. J., Gramer, L. J., Hu, C., Johns, E. M., Trinanes, J., and Wang, M.: Simulating transport pathways of pelagic Sargassum from the Equatorial Atlantic into the Caribbean Sea, Prog. Oceanogr., 165, 205–214, 2018.
Putman, N. F., Lumpkin, R., Olascoaga, M. J., Trinanes, J., and Goni, G. J.: Improving transport predictions of pelagic Sargassum, J. Exp. Mar. Biol. Ecol., 529, 151398, https://doi.org/10.1016/j.jembe.2020.151398 2020.
Radenac, M.-H., Jouanno, J., Tchamabi, C. C., Awo, M., Bourlès, B., Arnault, S., and Aumont, O.: Physical drivers of the nitrate seasonal variability in the Atlantic cold tongue, Biogeosciences, 17, 529–545, https://doi.org/10.5194/bg-17-529-2020, 2020.
Raut, Y., Morando, M., and Capone, D. G.: Diazotrophic Macroalgal Associations With Living and Decomposing Sargassum, Front. Microbiol., 9, p. 3127, https://doi.org/10.3389/fmicb.2018.03127, 2018.
Ren, J. S., Barr, N. G., Scheuer, K., Schiel, D. R., and Zeldis, J.: A dynamic growth model of macroalgae: application in an estuary recovering from treated wastewater and earthquake-driven eutrophication, Estuar. Coast. Shelf S., 148, 59–69, 2014.
Schell, J. M., Goodwin, D. S., and Siuda, A. N.: Recent Sargassum inundation events in the Caribbean: shipboard observations reveal dominance of a previously rare form, Oceanography, 28, 8–11, 2015.
Schoener, A. and Rowe, G. T.: Pelagic Sargassum and its presence among the deep-sea benthos, Deep-Sea Res., 17, 923–925, https://doi.org/10.1016/0011-7471(70)90010-0, 1970.
Séférian, R., Berthet, S., Yool, A., Palmiéri, J., Bopp, L., Tagliabue, A., Kwiatkowski, L., Aumont, O., Christian, J., Dunne, J., Gehlen, M., Ilyina, T., John, J. G., Li, H., Long, M. C., Luo, J. Y., Nakano, H., Romanou, A., Schwinger, J., Stock, C., Santana-Falcón, Y., Takano, Y., Tjiputra, J., Tsujino, H., Watanabe, M., Wu, T., Wu, F., and Yamamoto, A.: Tracking Improvement in Simulated Marine Biogeochemistry Between CMIP5 and CMIP6, Current Climate Change Reports, 6, 95–119, https://doi.org/10.1007/s40641-020-00160-0, 2020.
Sissini, M. N., de Barros Barreto, M. B. B., Széchy, M. T. M., de Lucena, M. B., Oliveira, M. C., Gower, J., Liu, G., de Oliveira Bastos, E., Milstein, D., Gusmão, F., and Martinelli-Filho, J. E.: The floating Sargassum (Phaeophyceae) of the South Atlantic Ocean–likely scenarios, Phycologia, 56, 321–328, 2017.
Smetacek, V. and Zingone, A.: Green and golden seaweed tides on the rise, Nature, 504, 84–88, 2013.
Solidoro, C., Pecenik, G., Pastres, R., Franco, D., and Dejak, C.: Modelling macroalgae (Ulva rigida) in the Venice lagoon: Model structure identification and first parameters estimation, Ecol. Model., 94, 191–206, 1997.
Storto, A., Masina, S., Simoncelli, S., Iovino, D., Cipollone, A., Drevillon, M., Drillet, Y., von Schuckman, K., Parent, L., Garric, G., Greiner, E., Desportes, C., Zuo, H., Balmaseda, M. A., and Peterson, K. A.: The added value of the multi-system spread information for ocean heat content and steric sea level investigations in the CMEMS GREP ensemble reanalysis product, Clim. Dynam., 53, 287, https://doi.org/10.1007/s00382-018-4585-5, 2018.
Wang, M. and Hu, C.: Mapping and quantifying Sargassum distribution and coverage in the Central Western Atlantic using MODIS observations, Remote Sens. Environ., 183, 350–367, 2016.
Wang, M. and Hu, C.: Predicting Sargassum blooms in the Caribbean Sea from MODIS observations, Geophys. Res. Lett., 44, 3265–3273, 2017.
Wang, M., Hu, C., Cannizzaro, J., English, D., Han, X., Naar, D., Lapointe, B., Brewton, R., and Hernandez, F.: Remote sensing of Sargassum biomass, nutrients, and pigments, Geophys. Res. Lett., 45, 12359–12367, https://doi.org/10.1029/2018GL078858, 2018.
Wang, M., Hu, C., Barnes, B. B., Mitchum, G., Lapointe, B., and Montoya, J. P.: The great Atlantic Sargassum belt, Science, 365, 83–87, 2019.
Woodcock, A. H.: Winds subsurface pelagic Sargassum and Langmuir circulations, J. Exp. Mar. Biol. Ecol., 170, 117–125, https://doi.org/10.1016/0022-0981(93)90132-8, 1993.
Zhong, Y., Bracco, A., and Villareal, T. A.: Pattern formation at the ocean surface: Sargassum distribution and the role of the eddy field, Limnol. Oceanogr., 2, 12–27, 2012.
- Abstract
- Introduction
- Physiological and ecological features of holopelagic Sargassum
- The Sargassum modeling framework
- Results
- Discussion and summary
- In memoriam
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Physiological and ecological features of holopelagic Sargassum
- The Sargassum modeling framework
- Results
- Discussion and summary
- In memoriam
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References