the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Slate: extending Firedrake's domain-specific abstraction to hybridized solvers for geoscience and beyond
Thomas H. Gibson
Lawrence Mitchell
David A. Ham
Colin J. Cotter
Within the finite element community, discontinuous Galerkin (DG) and mixed finite element methods have become increasingly popular in simulating geophysical flows. However, robust and efficient solvers for the resulting saddle point and elliptic systems arising from these discretizations continue to be an ongoing challenge. One possible approach for addressing this issue is to employ a method known as hybridization, where the discrete equations are transformed such that classic static condensation and local post-processing methods can be employed. However, it is challenging to implement hybridization as performant parallel code within complex models whilst maintaining a separation of concerns between applications scientists and software experts. In this paper, we introduce a domain-specific abstraction within the Firedrake finite element library that permits the rapid execution of these hybridization techniques within a code-generating framework. The resulting framework composes naturally with Firedrake's solver environment, allowing for the implementation of hybridization and static condensation as runtime-configurable preconditioners via the Python interface to the Portable, Extensible Toolkit for Scientific Computation (PETSc), petsc4py. We provide examples derived from second-order elliptic problems and geophysical fluid dynamics. In addition, we demonstrate that hybridization shows great promise for improving the performance of solvers for mixed finite element discretizations of equations related to large-scale geophysical flows.
- Article
(3976 KB) - Full-text XML
- BibTeX
- EndNote
The development of simulation software is an increasingly important aspect of modern scientific computing, in the geosciences in particular. Such software requires a vast range of knowledge spanning several disciplines, ranging from applications expertise to mathematical analysis to high-performance computing and low-level code optimization. Software projects developing automatic code generation systems have become quite popular in recent years, as such systems help create a separation of concerns which focuses on a particular complexity independent from the rest. This allows for agile collaboration between computer scientists with hardware and software expertise, computational scientists with numerical algorithm expertise, and domain scientists such as meteorologists, oceanographers and climate scientists. Examples of such projects in the domain of finite element methods include FreeFEM++ (Hecht, 2012), Sundance (Long et al., 2010), the FEniCS Project (Logg et al., 2012a), Feel++ (Prud'Homme et al., 2012), and Firedrake (Rathgeber et al., 2016).
The finite element method (FEM) is a mathematically robust framework for computing numerical solutions of partial differential equations (PDEs) that has become increasingly popular in fluids and solids models across the geosciences, with a formulation that is highly amenable to code generation techniques. A description of the weak formulation of the PDEs, together with appropriate discrete function spaces, is enough to characterize the finite element problem. Both the FEniCS and Firedrake projects employ the Unified Form Language (UFL) (Alnæs et al., 2014) to specify the finite element integral forms and discrete spaces necessary to properly define the finite element problem. UFL is a highly expressive domain-specific language (DSL) embedded in Python, which provides the necessary abstractions for code generation systems.
There are classes of finite element discretizations resulting in discrete systems that can be solved more efficiently by directly manipulating local tensors. For example, the static condensation technique for the reduction of global finite element systems (Guyan, 1965; Irons, 1965) produces smaller globally coupled linear systems by eliminating interior unknowns to arrive at an equation for the degrees of freedom defined on cell interfaces only. This procedure is analogous to the point-wise elimination of variables used in staggered finite difference codes, such as the ENDGame dynamical core (Melvin et al., 2010; Wood et al., 2014) of the UK Meteorological Office (Met Office) but requires the local inversion of finite element systems. For finite element discretizations of coupled PDEs, the hybridization technique provides a mechanism for enabling the static condensation of more complex linear systems. First introduced by Fraeijs de Veubeke (1965) and analyzed further by Brezzi and Fortin (1991), Cockburn et al. (2009a), and Boffi et al. (2013), the hybridization method introduces Lagrange multipliers enforcing certain continuity constraints. Local static condensation can then be applied to the augmented system to produce a reduced equation for the multipliers. Methods of this type are often accompanied by local post-processing techniques, which exploit the approximation properties of the Lagrange multipliers. This enables the manufacturing of fields exhibiting superconvergent phenomena or enhanced conservation properties (Arnold and Brezzi, 1985; Brezzi et al., 1985; Bramble and Xu, 1989; Stenberg, 1991; Cockburn et al., 2009b, 2010b). These procedures require invasive manual intervention during the equation assembly process in intricate numerical code.
In this paper, we provide a simple yet effective high-level abstraction for localized dense linear algebra on systems derived from finite element problems. Using embedded DSL technology, we provide a means to enable the rapid development of hybridization and static condensation techniques within an automatic code generation framework. In other words, the main contribution of this paper is in solving the problem of automatically translating from the mathematics of static condensation and hybridization to compiled code. This automated translation facilitates the separation of concerns between applications scientists and computational/computer scientists and facilitates the automated optimization of compiled code. This framework provides an environment for the development and testing of numerics relevant to the Gung-Ho Project, an initiative by the UK Met Office in designing the next-generation atmospheric dynamical core using mixed finite element methods (Melvin et al., 2019). Our work is implemented in the Firedrake finite element library and the PETSc solver library (Balay et al., 1997, 2019), accessed via the Python interface petsc4py (Dalcin et al., 2011).
The rest of the paper is organized as follows. We introduce common notation used throughout the paper in Sect. 1.1. The embedded DSL, called “Slate”, is introduced in Sect. 2, which allows concise expression of localized linear algebra operations on finite element tensors. We provide some contextual examples for static condensation and hybridization in Sect. 3, including a discussion on post-processing. We then outline in Sect. 4 how, by interpreting static condensation techniques as a preconditioner, we can go further and automate many of the symbolic manipulations necessary for hybridization and static condensation. We first demonstrate our implementation on a manufactured problem derived from a second-order elliptic equation, starting in Sect. 5. The first example compares a hybridizable discontinuous Galerkin (HDG) method with an optimized continuous Galerkin method. Section 5.2 illustrates the composability and relative performance of hybridization for compatible mixed methods applied to a semi-implicit discretization of the nonlinear rotating shallow water equations. Our final example in Sect. 5.3 demonstrates time-step robustness of a hybridizable solver for a compatible finite element discretization of a rotating linear Boussinesq model. Conclusions follow in Sect. 6.
1.1 Notation
We begin by establishing notation used throughout this paper. Let 𝒯h denote a tessellation of Ω⊂ℝn, the computational domain, consisting of polygonal elements K associated with a mesh size parameter h, and the set of facets of 𝒯h. The set of facets interior to the domain Ω is denoted by . Similarly, we denote the set of exterior facets as . For brevity, we denote the finite element integral forms over 𝒯h and any facet set by
where dx and ds denote appropriate integration measures. The operation ⋅ should be interpreted as standard multiplication for scalar functions or a dot product for vector functions.
For any double-valued vector field w on a facet , we define the jump of its normal component across e by
where + and − denote arbitrarily but globally defined sides of the facet. Here, and are the unit normal vectors with respect to the positive and negative sides of the facet e. Whenever the facet domain is clear by the context, we omit the subscripts for brevity and simply write [⋅].
We present an expressive language for dense linear algebra on the elemental matrix systems arising from finite element problems. The language, which we call Slate, provides typical mathematical operations performed on matrices and vectors; hence the input syntax is comparable to high-level linear algebra software such as MATLAB. The Slate language provides basic abstract building blocks which can be used by a specialized compiler for linear algebra to generate low-level code implementations.
Slate is heavily influenced by the Unified Form Language (UFL) (Alnæs et al., 2014; Logg et al., 2012a), a DSL embedded in Python which provides symbolic representations of finite element forms. The expressions can be compiled by a form compiler, which translates UFL into low-level code for the local assembly of a form over the cells and facets of a mesh. In a similar manner, Slate expressions are compiled to low-level code that performs the requested linear algebra element-wise on a mesh.
2.1 An overview of Slate
To clarify conventions and the scope of Slate, we start by establishing our notation for a general finite element form following the convention of Alnæs et al. (2014). We define a real-valued multi-linear form as an operator which maps a list of arguments into ℝ:
where a is linear in each argument vk. The arity of a form is α, an integer denoting the total number of form arguments. In traditional finite element nomenclature (for α≤2), V0 is referred to as the space of test functions and V1 as the space of trial functions. Each Vk are referred to as argument spaces. Forms with arity , or 2 are best interpreted as the more familiar mathematical objects: scalars (0-forms), linear forms or functionals (1-forms), and bilinear forms (2-forms), respectively.
If a given form a is parameterized by one or more coefficients, say , where are coefficient spaces, then we write
From here on, we shall work exclusively with forms that are linear in v and possibly nonlinear in the coefficients c. This is reasonable since nonlinear methods based on Newton iterations produce linear problems via Gâteaux differentiation of a nonlinear form corresponding to a PDE (also known as the form Jacobian). We refer the interested reader to Alnæs et al. (2014, Sect. 2.1.2) for more details. For clarity, we present examples of multi-linear forms of arity , and 2 that frequently appear in finite element discretizations:
In general, a finite element form will consist of integrals over various geometric domains: integration over cells 𝒯h, interior facets ℰh∘, and exterior facets . Therefore, we express a general multi-linear form in terms of integrals over each set of geometric entities:
where denotes a cell integrand on K∈𝒯h, is an integrand on the interior facet e∈ℰh∘, and is an integrand defined on the exterior facet . The form a(c;v) describes a finite element form globally over the entire problem domain.
Here, we will consider the case where the interior facet integrands (c;v) can be decomposed into two independent parts on each interior facet e: one for the positive restriction (+) and the negative restriction (−). That is, for each e∈ℰh∘, we may write . This allows us to express the integral over an interior facet e connecting two adjacent elements, say K+ and K−, as the sum of integrals:
The local contribution of Eq. (10) in each cell K, along with its associated facets , is then
We call Eq. (12) the cell-local contribution of a(c;v), with
To make matters concrete, let us suppose a(c;v) is a bilinear form with arguments . Now let and denote bases for V0 and V1, respectively. Then the global N×M matrix A corresponding to has its entries defined via
By construction, if and only if Φi and Ψj take non-zero values in K. Now we introduce the cell-node map as the mapping from the local node number in K to the global node number i. Suppose there are n and m nodes defining the degrees of freedom for V0 and V1, respectively, in K. Then all non-zero entries of AK,ij arise from integrals involving basis functions with local indices corresponding to the global indices i,j:
These local contributions are collected in the n×m dense matrix AK, which we call the element tensor. The global matrix A is assembled from the collection of element tensors: . For details on the general evaluation of finite element basis functions and multi-linear forms, we refer the reader to Kirby (2004), Kirby and Logg (2006), Logg et al. (2012b), and Homolya et al. (2018). Further details on the global assembly of finite element operators, with a particular focus on code generation, are summarized in the work of Logg and Wells (2010) and Markall et al. (2013).
In standard finite element software packages, the element tensor is mapped entry-wise into a global sparse array using the cell-node map . Within Firedrake, this operation is handled by PyOP2 (Rathgeber et al., 2012) and serves as the main user-facing abstraction for global finite element assembly. For many applications, one may want to produce a new global operator by algebraically manipulating different element tensors. This is relatively invasive in numerical code, as it requires bypassing direct operator assembly to produce the new tensor. This is precisely the scope of Slate.
Like UFL, Slate relies on the grammar of the host-language: Python. The entire Slate language is implemented as a Python module which defines its types (classes) and operations on said types. Together, this forms a high-level language for expressing dense linear algebra on element tensors. The Slate language consists of two primary abstractions for linear algebra:
-
terminal element tensors corresponding to multi-linear integral forms (matrices, vectors, and scalars) or assembled data (for example, coefficient vectors of a finite element function) and
-
expressions consisting of algebraic operations on terminal tensors.
The composition of binary and unary operations on terminal tensors produces a Slate expression. Such expressions can be composed with other Slate objects in arbitrary ways, resulting in concise representations of complex algebraic operations on locally assembled arrays. We summarize all currently supported Slate abstractions here.
2.1.1 Terminal tensors
In Slate, one associates a tensor with data on a cell either by using a multi-linear form, or assembled coefficient data:
-
Tensor(a(c;v))
associates a form, expressed in UFL, with its local element tensorThe form arity α of aK(c;v) determines the rank of the corresponding
Tensor; i.e., scalars, vectors, and matrices are produced from scalars, linear forms, and bilinear forms, respectively.1 The shape of the element tensor is determined by both the number of arguments and total number of degrees of freedom local to the cell. -
AssembledVector(f),
where f is some finite element function. The function f∈V is expressed in terms of the finite element basis of V: . The result is the local coefficient vector of f on K:where is the local node numbering and n is the number of nodes local to the cell K.
2.1.2 Symbolic linear algebra
Slate supports typical binary and unary operations in linear algebra, with a high-level syntax close to mathematics. At the time of this paper, these include the following.
-
A + B, the addition of two equal shaped tensors: AK+BK. -
A∗B, a contraction over the last index ofAand the first index ofB. This is the usual multiplicative operation on matrices, vectors, and scalars: AKBK. -
-A, the additive inverse (negation) of a tensor: −AK. -
A.T, the transpose of a tensor: . -
A.inv, the inverse of a square tensor: . -
A.solve(B, decomposition=``...''), the result, XK, of solving a local linear system AKXK=BK, optionally specifying a factorization strategy. -
A.blocks[indices], whereAis a tensor from a mixed finite element space. This allows for the extraction of sub-blocks, which are indexed by field (slices are allowed). For example, if a matrix A corresponds to the bilinear form , where and are product spaces consisting of finite element spaces , , then the element tensors have the formThe associated submatrix of Eq. (18) with indices , , , is
where , .
Each Tensor object knows all
the information about the underlying UFL form that defines it, such as
form arguments, coefficients, and the underlying finite element space(s)
it operates on. This information is propagated through as unary or
binary transformations are applied. The unary and binary operations
shown here provide the necessary algebraic framework for a
large class of problems, some of which we present in this paper.
In Firedrake, Slate expressions are transformed into low-level code by a linear algebra compiler. The compiler interprets Slate expressions as a syntax tree, where the tree is visited to identify what local arrays need to be assembled and the sequence of array operations. At the time of this work, our compiler generates C++ code, using the templated library Eigen (Guennebaud et al., 2015) for dense linear algebra. The translation from Slate to C++ is fairly straightforward, as all operations supported by Slate have a representation in Eigen.
The compiler pass will generate a single “macro” kernel, which performs the dense linear algebra operations represented in Slate. The resulting code will also include (often multiple) function calls to local assembly kernels generated by TSFC (Two Stage Form Compiler) (Homolya et al., 2018) to assemble all necessary sub-blocks of an element tensor. All code generated by the linear algebra compiler conforms to the application programming interface (API) of the PyOP2 framework, as detailed by Rathgeber et al. (2012, Sect. 3). Figure 1 provides an illustration of the complete tool chain.
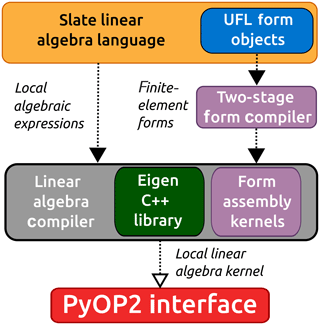
Figure 1The Slate language wraps UFL objects describing the finite element system. The resulting Slate expressions are passed to a specialized linear algebra compiler, which produces a single macro kernel assembling the local contributions and executes the dense linear algebra represented in Slate. The kernels are passed to the Firedrake's PyOP2 interface, which wraps the Slate kernel in a mesh-iteration kernel. Parallel scheduling, code generation, and compilation occurs after the PyOP2 layer.
Most optimization of the resulting dense linear algebra code is handled
directly by Eigen. In the case of unary and binary operations such
as A.inv and A.solve(B), stable default behaviors are applied
by the linear algebra compiler.
For example, A.solve(B) without a specified factorization strategy
will default to using an in-place LU factorization with partial
pivoting. For local matrices smaller than 5×5, the
inverse is translated directly into Eigen's A.inverse(), which
employs stable analytic formulas. For larger matrices, the linear
algebra replaces A.inv with an LU factorization.2
Currently, we only support direct matrix factorizations for solving
local linear systems. However, it would not be difficult to extend Slate
to support more general solution techniques like iterative
methods.
We now present examples and discuss solution methods which require element-wise manipulations of finite element systems and their specification in Slate. We stress here that Slate is not limited to these model problems; rather these examples are chosen for clarity and to demonstrate key features of the Slate language. For our discussion, we use a model elliptic equation defined in a computational domain Ω. Consider the second-order PDE with both Dirichlet and Neumann boundary conditions:
where and κ, are positive-valued coefficients. To obtain a mixed formulation of Eqs. (20)–(22), we introduce the auxiliary velocity variable . We then obtain the first-order system of PDEs:
where .
3.1 Hybridization of mixed methods
To motivate our discussion in this section, we start by recalling the mixed method for Eqs. (23)–(26). Methods of this type seek approximations (uh,ph) in finite-dimensional subspaces , defined by
The space Uh consists of H(div)-conforming piecewise vector polynomials, where choices of U(K) typically include the Raviart–Thomas (RT), Brezzi–Douglas–Marini (BDM), or Brezzi–Douglas–Fortin–Marini (BDFM) elements (Raviart and Thomas, 1977; Nédélec, 1980; Brezzi et al., 1985, 1987). The space Vh is the Lagrange family of discontinuous polynomials. These spaces are of particular interest when simulating geophysical flows, since choosing the right pairing results in stable discretizations with desirable conservation properties and avoids spurious computational modes. We refer the reader to Cotter and Shipton (2012), Cotter and Thuburn (2014), Natale et al. (2016), and Shipton et al. (2018) for a discussion of mixed methods relevant for geophysical fluid dynamics. Two examples of such discretizations are presented in Sect. 5.2.
The mixed formulation of Eqs. (23)–(26) is arrived at by multiplying Eqs. (23)–(24) by test functions and integrating by parts. The resulting finite element problem reads as follows: find satisfying
where Uh,0 is the subspace of Uh with functions whose normal components vanish on ∂ΩN. The discrete system is obtained by first expanding the solutions in terms of the finite element bases:
where and are bases for Uh and Vh, respectively. Here, Ui and Pi are the coefficients to be determined. As per standard Galerkin-based finite element methods, taking w=Ψj, and ϕ=ξj, in Eqs. (29)–(30) produces the following discrete saddle point system:
where , are the coefficient vectors, and
Methods to efficiently invert such systems include H(div)-multigrid (Arnold et al., 2000) (requiring complex overlapping Schwarz smoothers), global Schur complement factorizations (which require an approximation to the inverse of the dense3 elliptic Schur complement ), or auxiliary space multigrid (Hiptmair and Xu, 2007). Here, we focus on a solution approach using a hybridized mixed method (Arnold and Brezzi, 1985; Brezzi and Fortin, 1991; Boffi et al., 2013).
The hybridization technique replaces the original system with a discontinuous variant, decoupling the velocity degrees of freedom between cells. This is done by replacing the discrete solution space for uh with the “broken” space , defined as
The vector finite element space is a subspace of consisting of local H(div) functions, but normal components are no longer required to be continuous on ∂𝒯h. The approximation space for ph remains unchanged.
Next, Lagrange multipliers are introduced as an auxiliary variable in the space Mh, defined only on cell interfaces:
where M(e) denotes a polynomial space defined on each facet. We call Mh the space of approximate traces. Functions in Mh are discontinuous across vertices in two dimensions and vertices or edges in three dimensions.
Deriving the hybridizable mixed system is accomplished through integration by parts over each element K. Testing with and integrating Eq. (23) over the cell K produces
The trace function λh is introduced in the surface integral as an approximation to . An additional constraint equation, called the transmission condition, is added to close the system. The resulting hybridizable formulation reads as follows: find such that
where Mh,0 denotes the space of traces vanishing on ∂ΩD. The transmission condition Eq. (43) enforces both the continuity of across element boundaries as well as the boundary condition on ∂ΩN. If the space of Lagrange multipliers Mh is chosen appropriately, then the broken velocity , albeit sought a priori in a discontinuous space, will coincide with its H(div)-conforming counterpart. Specifically, the formulations in Eqs. (41)–(42) and (29)–(30) are solving equivalent problems if the normal components of w∈Uh lie in the same polynomial space as the trace functions (Arnold and Brezzi, 1985).
The discrete matrix system arising from Eqs. (41)–(43) has the general form
where the discrete system is produced by expanding functions in terms of the finite element bases for , Vh, and Mh like before. Upon initial inspection, it may not appear to be advantageous to replace our original formulation with this augmented equation set; the hybridizable system has substantially more total degrees of freedom. However, Eq. (44) has a considerable advantage over Eq. (32) in the following ways.
-
Since both and Vh are discontinuous spaces, Ud and P are coupled only within the cell. This allows us to simultaneously eliminate both unknowns via local static condensation to produce a significantly smaller global (hybridized) problem for the trace unknowns, Λ:
where and are assembled via the local element tensors:
Note that the inverse of the block matrix in Eqs. (46) and (47) is never evaluated globally; the elimination can be performed locally by performing a sequence of Schur complement reductions within each cell.
-
The matrix S is sparse, symmetric, positive-definite, and spectrally equivalent to the dense Schur complement from Eq. (32) of the original mixed formulation (Gopalakrishnan, 2003; Cockburn et al., 2009a).
-
Once Λ is computed, both Ud and P can be recovered locally in each element. This can be accomplished in a number of ways. One way is to compute PK by solving
followed by solving for :
Similarly, one could rearrange the order in which each variable is reconstructed.
-
If desired, the solutions can be improved further through local post-processing. We highlight two such procedures for Ud and P, respectively, in Sect. 3.3.
Figure 2 displays the corresponding Slate code for assembling the trace system, solving Eq. (45), and recovering the eliminated unknowns. For a complete reference on how to formulate the hybridized mixed system Eqs. (41)–(43) in UFL, we refer the reader to Alnæs et al. (2014). Complete Firedrake code using Slate to solve a hybridizable mixed system is also publicly available in Zenodo/Tabula-Rasa (2019, “Code verification”). We remark that, in the case of this hybridizable system, Eq. (44) contains zero-valued blocks which can simplify the resulting expressions in Eqs. (46)–(47) and (48)–(49). This is not true in general and therefore the expanded form using all sub-blocks of Eq. (44) is presented for completeness.

Figure 2Firedrake code for solving Eq. (44) via static condensation
and local recovery, given UFL expressions a, L for
Eqs. (41)–(43). Arguments of
the mixed space are indexed by 0, 1, and 2, respectively. Lines 8 and 9 are symbolic expressions
for Eqs. (46) and (47), respectively. Any vanishing conditions on the
trace variables should be provided as boundary conditions during operator assembly (line 10). Lines 26 and 28 are expressions
for Eqs. (48) and (49) (using LU). Code generation occurs in lines 10, 11, 30,
and 31. A global linear solver for the reduced system is created and used
in line 15. Configuring the linear solver is done by providing an appropriate Python dictionary of solver options for the PETSc library.
3.2 Hybridization of discontinuous Galerkin methods
The HDG method is a natural extension of discontinuous Galerkin (DG) discretizations. Here, we consider a specific HDG discretization, namely the LDG-H method (Cockburn et al., 2010b). Other forms of HDG that involve local lifting operators can also be implemented in this software framework by the introduction of additional local (i.e., discontinuous) variables into the definition of the local solver.
Deriving the LDG-H formulation follows exactly from standard DG methods. All prognostic variables are sought in the discontinuous spaces . Within a cell K, integration by parts yields
where U(K) and V(K) are vector and scalar polynomial spaces, respectively. Now, we define the numerical fluxes and to be functions of the trial unknowns and a new independent unknown in the trace space Mh:
where λh∈Mh is a function approximating p on ∂𝒯h and τ is a positive stabilization function that may vary on each facet . We further require that λh satisfies the Dirichlet condition for p on ∂ΩD in an L2-projection sense. The full LDG-H formulation reads as follows. Find such that
Equation (56) is the transmission condition, which enforces the continuity of on ∂𝒯h and q. Equation (57) ensures λh satisfies the Dirichlet condition. This ensures that the numerical flux is single-valued on the facets. Hence, the LDG-H method defines a conservative DG method (Cockburn et al., 2010b). Note that the choice of τ has a significant influence on the expected convergence rates of the computed solutions.
The LDG-H method retains the advantages of standard DG methods while also enabling the assembly of reduced linear systems through static condensation. The matrix system arising from Eqs. (54)–(57) has the same general form as the hybridized mixed method in Eq. (44), except all sub-blocks are now populated with non-zero entries due to the coupling of trace functions with both ph and uh. However, all previous properties of the discrete matrix system from Sect. 3.1 still apply. The Slate expressions for the local elimination and reconstruction operations will be identical to those illustrated in Fig. 2. For the interested reader, a unified analysis of hybridization methods (both mixed and DG) for second-order elliptic equations is presented in Cockburn et al. (2009a) and Cockburn (2016).
3.3 Local post-processing
For both mixed (Arnold and Brezzi, 1985; Brezzi et al., 1985; Bramble and Xu, 1989; Stenberg, 1991) and discontinuous Galerkin methods (Cockburn et al., 2010b, 2009b), it is possible to locally post-process solutions to obtain superconvergent approximations (gaining 1 order of accuracy over the unprocessed solution). These methods can be expressed as local solves on each element and are straightforward to implement using Slate. In this section, we present two post-processing techniques: one for scalar fields and another for the vector unknown. The Slate code follows naturally from previous discussions in Sect. 3.1 and 3.2, using the standard set of operations on element tensors summarized in Sect. 2.1.
3.3.1 Post-processing of the scalar solution
Our first example is a modified version of the procedure presented by Stenberg (1991) for enhancing the accuracy of the scalar solution. This was also highlighted within the context of hybridizing eigenproblems by Cockburn et al. (2010a). This post-processing technique can be used for both the hybridizable mixed and LDG-H methods. We proceed by posing the finite element systems cell-wise.
Let 𝒫k(K) denote a polynomial space of degree ≤k on a cell K∈𝒯h. Then for a given pair of computed solutions uh,ph of the hybridized methods, we define the post-processed scalar as the unique solution of the local problem:
where . Here, the space denotes the L2-orthogonal complement of 𝒫l(K). This post-processing method directly uses the definition of the flux uh, the approximation of −κ∇p. In practice, the space may be constructed using an orthogonal hierarchical basis, and solving Eqs. (58)–(59) amounts to inverting a symmetric positive definite system in each cell of the mesh.
At the time of this work, Firedrake does not support the construction of such a finite element basis. However, we can introduce Lagrange multipliers to enforce the orthogonality constraint. The resulting local problem then becomes the following mixed system: find such that
where . The local problems Eqs. (60)–(61) and Eqs. (58)–(59) are equivalent, with the Lagrange multiplier ψ enforcing orthogonality of test functions in 𝒫k+1(K) with functions in 𝒫l(K).
This post-processing method produces a new approximation which superconverges at a rate of k+2 for hybridized mixed methods (Stenberg, 1991; Cockburn et al., 2010a). For the LDG-H method, k+2 superconvergence is achieved when τ=𝒪(1) and τ=𝒪(h), but only k+1 convergence is achieved when (Cockburn et al., 2009b, 2010b). We demonstrate the increased accuracy in computed solutions in Sect. 5.1. An abridged example using Firedrake and Slate to solve the local linear systems is provided in Fig. 3.

Figure 3Example of local post-processing using Firedrake and Slate. Here, we locally solve the mixed system defined in Eqs. (58)–(59). The corresponding symbolic local tensors are defined in lines 9 and 11. The Slate expression for directly inverting the local system is written in line 12. In line 16, a Slate-generated kernel is produced which solves the resulting linear system in each cell. Since we are not interested in the multiplier, we only return the block corresponding to the new pressure field.
3.3.2 Post-processing of the flux
Our second example illustrates a procedure that uses the numerical flux of an HDG discretization for Eqs. (23)–(26). Within the context of the LDG-H method, we can use the numerical trace in Eq. (52) to produce a vector field that is H(div)-conforming. The technique we outline here follows that of Cockburn et al. (2009b).
Let 𝒯h be a mesh consisting of simplices. On each cell K∈𝒯h, we define a new function to be the unique element of the local Raviart–Thomas space satisfying
for all facets e on ∂K, where is the numerical flux defined in Eq. (52). This local problem produces a new velocity with the following properties.
-
converges at the same rate as uh for all choices of τ producing a solvable system for Eqs. (54)–(57). However,
-
. That is, ∘.
-
Additionally, the divergence of convergences at a rate of k+1.
The Firedrake implementation using Slate is similar to the scalar post-processing example (see Fig. 3); the cell-wise linear systems Eqs. (62)–(63) can be expressed in UFL, and therefore the necessary Slate expressions to invert the local systems follows naturally from the set of operations presented in Sect. 2.1. We use the very sensitive parameter dependency in the post-processing methods to validate our software implementation in Zenodo/Tabula-Rasa (2019, “Code-verification”).
Slate enables static condensation approaches to be expressed very concisely. Nonetheless, the application of a particular approach to different variational problems using Slate still requires a certain amount of code repetition. By formulating each form of static condensation as a preconditioner, code can be written once and then applied to any mathematically suitable problem. Rather than writing the static condensation by hand, in many cases, it is sufficient to just select the appropriate, Slate-based, preconditioner.
For context, it is helpful to frame the problem
in the particular context of the solver library: PETSc.
Firedrake uses PETSc as its main solver abstraction
framework and can provide operator-based preconditioners
for solving linear systems as PC objects
expressed in Python via petsc4py (Dalcin et al., 2011).
For a comprehensive overview
on solving linear systems using PETSc, we refer the
interested reader to Balay et al. (2019, Sect. 4).
Suppose we wish to solve a linear system: Ax=b. We can think of (left) preconditioning the system in residual form:
by an operator 𝒫 (which may not necessarily be linear) as a transformation into an equivalent system of the form
Given a current iterate xi the residual at the ith iteration is simply , and 𝒫 acts on the residual to produce an approximation to the error . If 𝒫 is an application of an exact inverse, the residual is converted into an exact (up to numerical roundoff) error.
We will denote the application of a particular Krylov subspace method (KSP)
for the linear system Eq. (64) as
𝒦x(r(A,b)).
Upon preconditioning the system via 𝒫 as
in Eq. (65), we write
If Eq. (66) is solved directly via , then . So Eq. (66) then becomes , producing the exact solution of Eq. (64) in a single iteration of 𝒦. Having established notation, we now present our implementation of static condensation via Slate by defining the appropriate operator, 𝒫.
4.1 Interfacing with PETSc via custom preconditioners
The implementation of preconditioners for the systems considered in this paper requires the manipulation not of assembled matrices but rather their symbolic representation. To do this, we use the preconditioning infrastructure developed by Kirby and Mitchell (2018), which gives preconditioners written in Python access to the symbolic problem description. In Firedrake, this means all derived preconditioners have direct access to the UFL representation of the PDE system. From this mathematical specification, we manipulate this appropriately via Slate and provide operators assembled from Slate expressions to PETSc for further algebraic preconditioning. Using this approach, we have developed a static condensation interface for the hybridization of H(div)×L2 mixed problems and a generic interface for statically condensing finite element systems. The advantage of writing even the latter as a preconditioner is the ability to switch out the solution scheme for the system, even when nested inside a larger set of coupled equations or nonlinear solver (Newton-based methods) at runtime.
4.1.1 A static condensation interface for hybridization
As discussed in Sect. 3.1
and 3.2, one of the main advantages of using a
hybridizable variant of a DG or mixed method is
that such systems permit the use of cell-wise static condensation.
To facilitate this, we provide a PETSc PC static
condensation interface: firedrake.SCPC.
This preconditioner takes the discretized system as
in Eq. (44) and
performs the local elimination and recovery procedures.
Slate expressions are generated from the underlying UFL
problem description.
More precisely, the incoming system has the form
where Xe is the vector of unknowns to be eliminated, Xc
is the vector of unknowns for the condensed field, and Re and Rc
are the incoming right-hand sides. The partitioning in Eq. (67)
is determined by the solver
option: pc_sc_eliminate_fields. Field indices
are provided in the same way one configures solver options to PETSc.
These indices determine which field(s) to statically condense into.
For example, on a three-field problem (with indices 0, 1, and 2),
setting -pc_sc_eliminate_fields 0,1
will configure firedrake.SCPC to cell-wise eliminate
fields 0 and 1; the resulting condensed system is associated with field 2.
The firedrake.SCPC preconditioner can be interpreted
as a Schur complement method for Eq. (67) of the form
where
is the Schur complement operator for the Xc system.
The distinction here from block preconditioners via the
PETSc fieldsplit option (Brown et al., 2012), for example, is
that 𝒫 does not require global actions;
by design can be inverted
locally and S is sparse. As a result, S can be
assembled or applied exactly, up to numerical roundoff,
via Slate-generated kernels.
In practice, the only globally coupled system requiring iterative inversion is S:
where is the condensed right-hand side and 𝒫1 is a preconditioner for S. Once Xc is computed, Xe is reconstructed by inverting the system cell-wise.
By construction, this preconditioner is suitable for both hybridized mixed and HDG discretizations. It can also be used within other contexts, such as the static condensation
of continuous Galerkin discretizations (Guyan, 1965; Irons, 1965) or primal-hybrid methods (Devloo et al., 2018). As with any PETSc preconditioner, solver
options can be specified for inverting S via the appropriate
options prefix (condensed_field).
The resulting KSP for Eq. (69) is
compatible with existing solvers and external
packages provided through the PETSc library. This allows
users to experiment with a direct method and then switch to
a more parallel-efficient iterative solver
without changing the core application code.
4.1.2 Preconditioning mixed methods via hybridization
The preconditioner firedrake.HybridizationPC expands on
the previous one, this time taking an
H(div)×L2 system and automatically
forming the hybridizable problem. This is accomplished through
manipulating the UFL objects representing the discretized
PDE. This includes replacing argument spaces with their
discontinuous counterparts, introducing
test functions on an appropriate trace space, and
providing operators assembled from Slate
expressions in a similar manner as described
in Sect. 4.1.1.
More precisely, let AX=R be the incoming mixed saddle point problem, where , , and U and P are the velocity and scalar unknowns, respectively. Then this preconditioner replaces AX=R with the extended problem:
where Λ are the Lagrange multipliers, , and RP are the right-hand sides for the flux and scalar equations, respectively, and indicates modified matrices and co-vectors with discontinuous functions. Here, are the hybridizable (discontinuous) unknowns to be determined and is the matrix representation of the transmission condition for the hybridizable mixed method (see Eq. 43).
The application of firedrake.HybridizationPC
can be interpreted as the Schur complement reduction of
Eq. (70):
where S is the Schur complement matrix
.
As before, a single global system for Λ can be assembled
cell-wise using Slate-generated kernels.
Configuring the solver for inverting S is done via
the PETSc options prefix: -hybridization.
The recovery of Ud and P happens in the
same manner as firedrake.SCPC.
Since the hybridizable flux solution is constructed in the broken H(div) space , we must project the computed solution into Uh⊂H(div). This can be done cheaply via local facet averaging. The resulting solution is then updated via U←ΠdivUd, where is a projection operator. This ensures that the residual for the original mixed problem is properly evaluated to test for solver convergence. With as in Eq. (71), the preconditioning operator for the original system AX=R then has the form
We note here that assembly of the right-hand side for the Λ system requires special attention. Firstly, when Neumann conditions are present, then Rg is not necessarily 0. Since the hybridization preconditioner has access to the entire Python context (which includes a list of boundary conditions and the spaces in which they are applied), surface integrals on the exterior boundary are added where appropriate and incorporated into the generated Slate expressions. A more subtle issue that requires extra care is the incoming right-hand side tested in the H(div) space Uh.
The situation we are given is that we have RU=RU(w) for w∈Uh but require for . For consistency, we also require for any w∈Uh that
We can construct such an satisfying Eq. (73) in the following way. By construction, we have for each basis function Ψi∈Uh
where , and are basis functions corresponding to the positive and negative restrictions associated with the ith facet node.4 We then define our broken right-hand side via the local definition:
where Ni is the number of cells that the degree of freedom corresponding to Ψi∈Uh is topologically associated with. Using Eq. (74), Eq. (75), and the fact that RU is linear in its argument, we can verify that our construction of satisfies Eq. (73).
We now present results utilizing the Slate DSL and our static condensation preconditioners for a set of test problems. Since we are using the interfaces outlined in Sect. 4, Slate is accessed indirectly and requires no manually written solver code for hybridization or static condensation or local recovery. All parallel results were obtained on a single fully loaded compute node of dual-socket Intel E5-2630v4 (Xeon) processors with 2×10 cores (2 threads per core) running at 2.2GHz. In order to avoid potential memory effects due to the operating system migrating processes between sockets, we pin MPI processes to cores.
The verification of the generated code is performed using parameter-sensitive convergence tests. The study consists of running a variety of discretizations spanning the methods outlined in Sect. 3. Details and numerical results are made public and can be viewed in Zenodo/Tabula-Rasa (2019) (see “Code and data availability”). All results are in full agreement with the theory.
5.1 HDG method for a three-dimensional elliptic equation
In this section, we take a closer look at the LDG-H method for the model elliptic equation (sign-definite Helmholtz):
where f and g are chosen such that the analytic solution is p=exp {sin (πx)sin (πy)sin (πz)}. We use a regular mesh consisting of 6⋅N3 tetrahedral elements (). First, we reformulate Eqs. (76)–(77) as the mixed problem:
We start with linear polynomial approximations, up to cubic, for the LDG-H discretization of Eqs. (78)–(80). Additionally, we compute a post-processed scalar approximation of the HDG solution. This raises the approximation order of the computed solution by an additional degree. In all numerical studies here, we set the HDG parameter τ=1. All results were computed in parallel, utilizing a single compute node (described previously).
A continuous Galerkin (CG) discretization of the primal problem Eqs. (76)–(77) serves as a reference for this experiment. Due to the superconvergence in the post-processed solution for the HDG method, we use CG discretizations of polynomial orders 2, 3, and 4. This takes into account the enhanced accuracy of the HDG solution, despite being initially computed as a lower-order approximation. We therefore expect both methods to produce equally accurate solutions to the model problem.
Our aim here is not to compare the performance of HDG and CG, which has been investigated elsewhere (for example, see Kirby et al., 2012; Yakovlev et al., 2016). Instead, we provide a reference that the reader might be more familiar with in order to evaluate whether our software framework produces a sufficiently performant HDG implementation relative to what might be expected.
To invert the CG system, we use a conjugate gradient solver with Hypre's BoomerAMG implementation of algebraic multigrid (AMG) as a preconditioner (Falgout et al., 2006). For the HDG method, we use the preconditioner described in Sect. 4.1.1 and the same solver setup as the CG method for the trace system. While the trace operator is indeed symmetric and positive-definite, one should keep in mind that conclusions regarding the performance of off-the-shelf AMG packages on the HDG trace system are still relatively unclear. As a result, efforts on developing more efficient multigrid strategies are a topic of ongoing interest (Cockburn et al., 2014; Kronbichler and Wall, 2018).
To avoid over-solving, we iterate to a relative tolerance such that the discretization error is minimal for a given mesh. In other words, the solvers are configured to terminate when there is no further reduction in the L2 error of the computed solution compared with the analytic solution. This means we are not iterating to a fixed solver tolerance across all mesh resolutions. Therefore, we can expect the total number of Krylov iterations (for both the CG and HDG methods) to increase as the mesh resolution becomes finer. The rationale behind this approach is to directly compare the execution time to solve for the best possible approximation to the solution given a fixed resolution.
5.1.1 Error versus execution time
The total execution time is recorded for the CG and HDG solvers, which includes the setup time for the AMG preconditioner, matrix assembly, and the time to solution for the Krylov method. In the HDG case, we include all setup costs, the time spent building the Schur complement for the traces, local recovery of the scalar and flux approximations, and post-processing. The L2 error against execution time and Krylov iterations to reach discretization error for each mesh are summarized in Fig. 4.
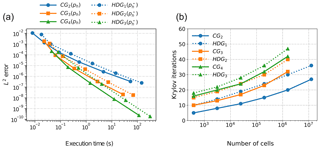
Figure 4Comparison of continuous Galerkin and LDG-H solvers for the model three-dimensional positive-definite Helmholtz equation. Panel (a): a log–log plot showing the error against execution time for the CG and HDG with post-processing (τ=1) methods. Panel (b): a log–linear plot showing Krylov iterations of the AMG-preconditioned conjugate gradient algorithm (to reach discretization error) against number of cells.
The HDG method of order k−1 (HDGk−1) with post-processing, as expected, produces a solution which is as accurate as the CG method of order k (CGk). While the full HDG system is never explicitly assembled, the larger execution time is a result of several factors. The primary factor is that the total number of trace unknowns for the HDG1, HDG2, and HDG3 discretizations is roughly 4, 3, and 2 times larger, respectively, than the corresponding number of CG unknowns. Therefore, each iteration is more expensive. We also observe that the trace system requires more Krylov iterations to reach discretization error, which appears to improve relative to the CG method as the approximation order increases. Further analysis on a multigrid methods for HDG systems is required to draw further conclusions. The main computational bottleneck in HDG methods is the global linear solver. We therefore expect our implementation to be dominated by the cost associated with inverting the trace operator. If one considers just the time-to-solution, the CG method is clearly ahead of the HDG method. However, the superior scaling, local conservation, and stabilization properties of the HDG method make it a particularly appealing choice for fluid dynamics applications (Yakovlev et al., 2016; Kronbichler and Wall, 2018). Therefore, the development of good preconditioning strategies for the HDG method is critical for its competitive use.
5.1.2 Breakdown of solver time
The HDG method requires many more degrees of freedom than CG or primal DG methods. This is largely due to the fact that the HDG method simultaneously approximates the primal solution and its velocity. The global matrix for the traces is significantly larger than the one for the CG system at low polynomial order. The execution time for HDG is then compounded by a more expensive global solve.
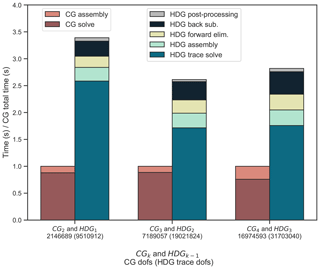
Table 1Breakdown of the raw timings for the HDGk−1 (τ=1) and CGk methods; k=2, 3, and 4. Each method corresponds to a mesh size N=64 on a fully loaded compute node.
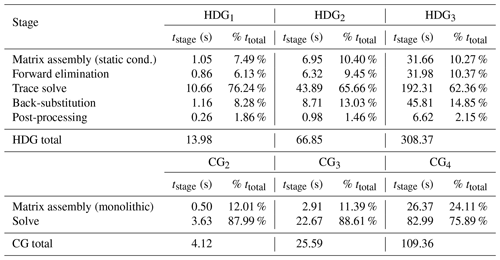
Figure 5 displays a breakdown of total execution times on a simplicial mesh consisting of 1.5 million elements. The execution times have been normalized by the CG total time, showing that the HDG method is roughly 3 times more expensive than the CG method. This is expected given the larger degree-of-freedom count and expensive global solve. The raw numerical breakdown of the HDG and CG solvers are shown in Table 1. We isolate each component of the HDG method contributing to the total execution time. Local operations include static condensation (trace operator assembly), forward elimination (right-hand-side assembly for the trace system), backwards substitution to recover the scalar and velocity unknowns, and local post-processing of the scalar solution. For all k, our HDG implementation is solver-dominated as expected.
Both trace operator and right-hand-side assembly are dominated by the costs of inverting a local square mixed matrix coupling the scalar and velocity unknowns, which is performed directly via an LU factorization. This is also the case for backwards substitution. They should all therefore be of the same magnitude in time spent. We observe that this is the case across all degrees, with times ranging between approximately 6 % and 11 % of total execution time for assembling the condensed system. Back-substitution takes roughly the same time as the static condensation and forward elimination stages (approximately 12 % of execution time on average). Finally, the additional cost of post-processing accrues negligible time (roughly 2 % of execution time across all degrees). This is a small cost for an increase in order of accuracy.
We note that the caching of local tensors does not occur. Each pass to perform the local eliminations and backwards reconstructions rebuilds the local element tensors. It is not clear at this time whether the performance gained from avoiding rebuilding the local operators will offset the memory costs of storing the local matrices. Moreover, in time-dependent problems where the operators may contain state-dependent variables, rebuilding local matrices will be necessary in each time step regardless.
5.2 Hybridizable mixed methods for the shallow water equations
A primary motivator for our interest in hybridizable methods revolves around developing efficient solvers for problems in geophysical flows. In this section, we present some results integrating the nonlinear, rotating shallow water equations on the sphere using test case 5 (flow past an isolated mountain) from Williamson et al. (1992). For our discretization approach, we use the framework of compatible finite elements (Cotter and Shipton, 2012; Cotter and Thuburn, 2014).
The model equations we consider are the vector-invariant rotating nonlinear shallow water system defined on a two-dimensional spherical surface Ω embedded in ℝ3:
where u is the fluid velocity, D is the depth field, f is the Coriolis parameter, g is the acceleration due to gravity, b is the bottom topography, and , with being the unit normal to the surface Ω. After discretizing in time and space using a semi-implicit scheme and Picard linearization, following Natale et al. (2016), we must solve a sequence of the saddle point system at each time step of the form
See Appendix A for a complete description of the entire discretization strategy. The system Eq. (83) is the matrix equation corresponding to the linearized equations in Eqs. (A3)–(A4).
The Picard updates ΔU and ΔD are sought in the mixed finite element spaces Uh⊂H(div) and Vh⊂L2, respectively. Stable mixed finite element pairings correspond to the well-known RT and BDM mixed methods, such as or . These also fall within the set of compatible mixed spaces ideal for geophysical fluid dynamics (Cotter and Shipton, 2012; Natale et al., 2016; Melvin et al., 2019). In particular, the lowest-order RT method (RT1×DG0) on a structured quadrilateral grid (such as the latitude–longitude grid used by many operational dynamical cores) is analogous to the Arakawa C-grid finite difference discretization.
In staggered finite difference models, the standard approach for solving Eq. (83) is to neglect the Coriolis term and eliminate the velocity unknown ΔU to obtain a discrete elliptic equation for ΔD, where smoothers like Richardson iterations or relaxation methods are convergent. This is more problematic in the compatible finite element framework, since A has a dense inverse. Instead, we use the preconditioner described in Sect. 4.1.2 to form the equivalent hybridizable formulation, where both ΔU and ΔD are eliminated locally to produce a sparse elliptic equation for the Lagrange multipliers.
5.2.1 Atmospheric flow over a mountain
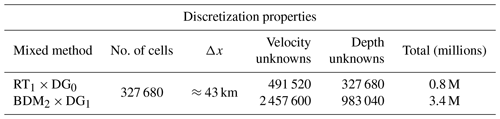
As a test problem, we solve test case 5 of Williamson et al. (1992), on the surface of a sphere with radius R=6371km. We refer the reader to Cotter and Shipton (2012) and Shipton et al. (2018) for a more comprehensive study on mixed finite elements for shallow water systems of this type. We use the mixed finite element pairs (RT1,DG0) (lowest-order RT method) and (BDM2,DG1) (next-to-lowest-order BDM method) for the velocity and depth spaces. A mesh of the sphere is generated from seven refinements of an icosahedron, resulting in a triangulation 𝒯h consisting of 327 680 elements in total. The grid information for both mixed methods is summarized in Table 2.
Table 2The number of unknowns to be determined are summarized for each compatible finite element method. Resolution is the same for both methods.
We run for a total of 25 time steps, with a fixed number of four Picard iterations in each time step. We compare the overall simulation time using two different solver configurations for the implicit linear system. First, we use a flexible variant of the generalized minimal residual method (GMRES) 5 acting on the system Eq. (83) with an approximate Schur complement preconditioner:
where and diag(A) is a diagonal approximation to the velocity mass matrix (plus the addition of a Coriolis matrix). The Schur complement system is inverted via GMRES due to the asymmetry from the Coriolis term, with the inverse of as the preconditioning operator. The sparse approximation is inverted using PETSc's smoothed aggregation multigrid (GAMG). The Krylov method is set to terminate once the preconditioned residual norm is reduced by a factor of 108. A−1 is computed approximately using a single application of incomplete LU (ILU) with zero fill-in.
Next, we use only the application of our hybridization preconditioner (no outer Krylov method), which replaces the original linearized mixed system with its hybridizable equivalent. After hybridization, we have the following extended problem for the Picard updates: find satisfying
Note that the space Mh is chosen such that the trace functions, when restricted to a facet , are in the same polynomial space as . Moreover, it can be shown that the Lagrange multiplier λh is an approximation to the depth unknown ΔtgΔD∕2 restricted to ∂𝒯h.
The resulting three-field problem in Eqs. (85)–(87) produces the following matrix equation:
where is the discontinuous operator coupling and are the problem residuals. An exact Schur complement factorization is performed on Eq. (88), using Slate to generate the local elimination kernels. We use the same set of solver options for the inversion of in Eq. (84) to invert the Lagrange multiplier system. The increments ΔUd and ΔD are recovered locally, using Slate-generated kernels. Once recovery is complete, ΔUd is projected back into the conforming H(div) finite element space via ΔU←ΠdivΔUd. Based on the discussion in Sect. 4.1.2, we apply
Table 3Preconditioner solve times for a 25-step run with Δt=100s. These are cumulative times in each stage of the two preconditioners throughout the entire profile run. We display the average iteration count (rounded to the nearest integer) for both the outer and the inner Krylov solvers. The significant speedup when using hybridization is a direct result of eliminating the outermost solver.
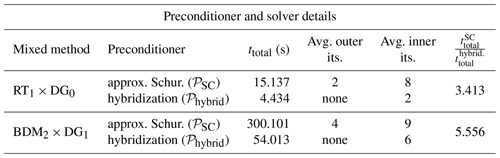
Table 4Breakdown of the cost (average) of a single application of the preconditioned flexible GMRES method and hybridization preconditioner. Hybridization takes approximately the same time per iteration.
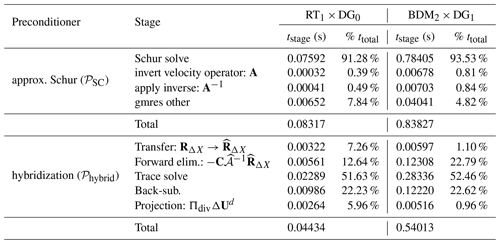
Table 3 displays a summary of our findings. The advantages of a hybridizable method versus a mixed method are more clearly realized in this experiment. When using hybridization, we observe a significant reduction in time spent in the implicit solver compared to the approximate Schur complement approach. This is primarily because we have reduced the number of “outer” iterations to zero; the hybridization preconditioner is performing an exact factorization of the global hybridizable system. This is empirically supported when considering per-application solve times. The values reported in Table 4 show the average cost of a single outer GMRES iteration (which includes the application of 𝒫SC) and a single application of 𝒫hybrid. Hybridization and the approximate Schur complement preconditioner are comparable in terms of average execution time, with hybridization being slightly faster. This further demonstrates that the primary cause for the longer execution time of the latter is directly related to the additional outer iterations induced from using an approximate factorization. In terms of over all time-to-solution, the hybridizable methods are clearly ahead of the original mixed methods.
We also measure the relative reductions in the problem residual of the linear system Eq. (83). Our hybridization preconditioner reduces the residual by a factor of 108 on average, which coincides with the specified relative tolerance for the Krylov method on the trace system. In other words, the reduction in the residual for the trace system translates into an overall reduction in the residual for the mixed system by the same factor.
The test case was run up to day 15 on a coarser resolution (20 480 simplicial cells with Δx≈210km) and a time-step size Δt=500 s. Snapshots of the entire simulation are provided in Fig. 6 using the semi-implicit scheme described in Appendix A. The results we have obtained for days 5, 10, and 15 are comparable to the corresponding results of Nair et al. (2005), Ullrich et al. (2010), and Kang et al. (2020). We refer the reader to Shipton et al. (2018) for further demonstrations of shallow water test cases featuring the use of the hybridization preconditioner described in Sect. 4.1.2.
5.3 Hybridizable methods for a linear Boussinesq model
As a final example, we consider the simplified atmospheric model obtained from a linearization of the compressible Boussinesq equations in a rotating domain:
where u is the fluid velocity, p the pressure, b the buoyancy, Ω the planetary angular rotation vector, c the speed of sound (), and N the buoyancy frequency (). Equations (90)–(92) permit fast-moving acoustic waves driven by perturbations in b. This is the model presented in Skamarock and Klemp (1994), which uses a quadratic equation of state to avoid some of the complications of the full compressible Euler equations (the hybridization of which we shall address in future work). We solve these equations subject to the rigid-lid condition on all boundaries.
Our domain consists of a spherical annulus, with the mesh constructed from a horizontal “base” mesh of the surface of a sphere of radius R, extruded upwards by a height HΩ. The vertical discretization is a structured one-dimensional grid, which facilitates the staggering of thermodynamic variables, such as b. We consider two kinds of meshes: one obtained by extruding an icosahedral sphere mesh and another from a cubed sphere.
Since our mesh has a natural tensor product structure, we construct suitable finite element spaces constructed by taking the tensor product of a horizontal space with a vertical space. To ensure our discretization is “compatible,” we use the one- and two-dimensional finite element de Rham complexes: and . We can then construct the three-dimensional complex: , where
Here, HCurl and HDiv denote operators which ensure that the
correct Piola transformations are applied when mapping from physical to reference
element. We refer the reader to McRae et al. (2016)
for an overview of constructing tensor product finite element spaces in Firedrake.
For the analysis of compatible finite element discretizations and their
relation to the complex Eqs. (93)–(96),
we refer the reader to Natale et al. (2016).
Each discretization used in this section is constructed
from more familiar finite element families, shown in
Table 5.
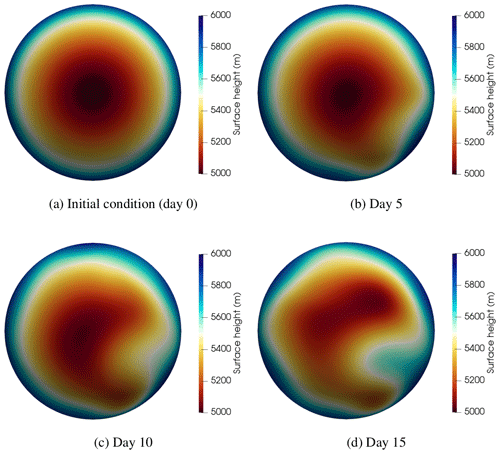
Figure 6Snapshots (view from the northern pole) from the isolated mountain test case. The surface height (m) at days 5, 10, and 15. The snapshots were generated on a mesh with 20 480 simplicial cells, a BDM2×DG1 discretization, and Δt=500 s. The linear system during each Picard cycle was solved using the hybridization preconditioner.
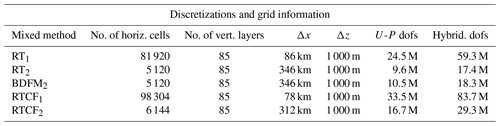
Table 5Vertical and horizontal spaces for the three-dimensional compatible finite element discretization of the linear Boussinesq model. The RTk and BDFMk+1 methods are constructed on triangular prism elements, while the RTCFk method is defined on extruded quadrilateral elements.

5.3.1 Compatible finite element discretization
A compatible finite element discretization of Eqs. (90)–(92) constructs solutions in the following finite element spaces:
where is the subspace of whose functions w satisfy on ∂Ω, , and . Note that is just the scalar version of the vertical velocity space.6 That is, and have the same number of degrees of freedom but differ in how they are pulled back to the reference element.
To obtain the discrete system, we simply multiply Eqs. (90)–(92) by test functions , , and and integrate by parts. We introduce the increments , and set (similarly for δph, p0, δbh, and b0). Using an implicit midpoint rule discretization, we need to solve the following mixed problem at each time step: find , and such that
where the residuals are , , and .
The resulting matrix equations have the form
where , CΩ is the asymmetric matrix associated with the Coriolis term, Mu, Mp, and Mb are mass matrices, D is the weak divergence term, and Q is an operator containing the vertical components of δuh. In the absence of orography, we can use the point-wise expression for the buoyancy,
and eliminate δbh from Eq. (101) by substituting Eq. (102) into Eq. (98). This produces the following mixed velocity–pressure system:
where and are the modified velocity operator and right-hand side, respectively. Note that in our elimination strategy, corresponds to the bilinear form obtained after eliminating the buoyancy at the equation level:
A similar construction holds for . Once Eq. (103) is solved, δbh is reconstructed by solving
Equation (105) can be efficiently inverted using the conjugate gradient method.
5.3.2 Preconditioning the mixed velocity pressure system
The primary difficulty is finding efficient solvers for Eq. (103). This was studied by Mitchell and Müller (2016) within the context of developing a preconditioner which is robust against parameters, like Δt and mesh resolution. However, the implicit treatment of the Coriolis term was not taken into account. We consider two preconditioning strategies.
One strategy proposed by Mitchell and Müller (2016) is to build a preconditioner based on the Schur complement factorization of 𝒜 in Eq. (103):
where is the dense pressure Helmholtz operator. Because we have chosen to include the Coriolis term, the operator H is nonsymmetric and has the form
where is a modified mass matrix. As Δt increases, the contribution of CΩ becomes more prominent in H, making sparse approximations of H more challenging. We shall elaborate on this further below when we present the results of our second solver strategy.
Our preferred strategy solves the hybridizable formulation of the system Eq. (103). Let denote the broken version of and Mh the space of Lagrange multipliers. Then the hybridizable formulation for the velocity–pressure system reads as follows: find , , and λh∈Mh such that
The system Eqs. (108)–(110) is automatically
formed by the Firedrake preconditioner: firedrake.HybridizationPC.
We then locally eliminate the velocity and pressure after hybridization,
producing the following condensed problem:
where denotes matrices or vectors with discontinuous test and trial functions. The nonsymmetric operator H∂ is inverted using a preconditioned generalized conjugate residual (GCR) Krylov method, as suggested in Thomas et al. (2003). For our choice of preconditioner, we follow strategies outlined in Elman et al. (2001) and employ an algebraic multigrid method (V cycle) with GMRES (five iterations) smoothers on the coarse levels. The GMRES smoothers are preconditioned with block ILU on each level. For the finest level, block ILU produces a line smoother (necessary for efficient solution on thin domains) when the trace variable nodes are numbered in vertical lines, as is the case in our Firedrake implementation. On the coarser levels, less is known about the properties of ILU under the AMG coarsening strategies, but as we shall see, we observe performance that suggests ILU is still behaving as a line smoother. More discussion on multigrid for nonsymmetric problems can be found in Bramble et al. (1994, 1988) and Mandel (1986). A gravity wave test using our solution strategy and hybridization preconditioner is illustrated in Fig. 7 for a problem on a condensed Earth (radius scaled down by a factor of 125) and 10 km lid.
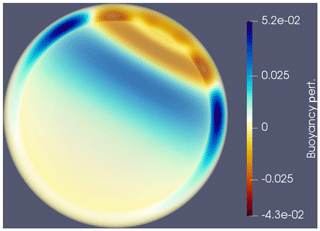
Figure 7Buoyancy perturbation (y−z cross section) at t=3600 s from a simple gravity wave test (Δt=100 s). The initial conditions (in lat–long coordinates) for the velocity are a simple solid-body rotation: u=20eλ, where eλ is the unit vector pointing in the direction of decreasing longitude. A buoyancy anomaly is defined via , where , d=5000 m, is the planet radius, and . The equations are discretized using the lowest-order method RTCF1, with 24 576 quadrilateral cells in the horizontal and 64 extrusion levels. The velocity–pressure system is solved using hybridization.
5.3.3 Robustness against acoustic Courant number with implicit Coriolis
In this final experiment, we repeat a similar study to that presented in Mitchell and Müller (2016). Our setup closely resembles the gravity wave test of Skamarock and Klemp (1994) extended to a spherical annulus. We initialize the velocity in a simple solid-body rotation and introduce a localized buoyancy anomaly. A Coriolis term is introduced as a function of the Cartesian coordinate z and is constant along lines of latitude (f plane): , with angular rotation rate . We fix the resolution of the problem and run the solver over a range of Δt. We measure this by adjusting the horizontal acoustic Courant number , where c is the speed of sound and Δx is the horizontal resolution.
Note that the range of Courant numbers used in this paper exceeds what is typical in operational forecast settings (typically between 𝒪(2)–𝒪(10)). The grid setup mirrors that of actual global weather models; we extrude a spherical mesh of the Earth upwards to a height of 85 km. The setup for the different discretizations (including degrees of freedom for the velocity–pressure and hybridized systems) is presented in Table 6.
Table 6Grid setup and discretizations for the acoustic Courant number study. The total number of degrees of freedom (dofs) for the mixed (velocity and pressure) and hybridizable (velocity, pressure, and trace) discretizations are shown in the last two columns (millions). The vertical resolution is fixed across all discretizations.
It was shown in Mitchell and Müller (2016) that using a sparse approximation of the pressure Schur complement of the form
served as a good preconditioner, leading to a system that was amenable to multigrid methods and resulted in a Courant-number-independent solver. However, when the Coriolis term is included, this is no longer the case: the diagonal approximation becomes worse with increasing λC. To demonstrate this, we solve the gravity wave system on a low-resolution grid (10 km lid, 10 vertical levels, maintaining the same cell aspect ratio as in Table 6) using the Schur complement factorization Eq. (106). LU factorizations are applied to invert both and . Inverting the Schur complement H−1 is done using preconditioned GMRES iterations, and a flexible-GMRES algorithm is used on the full velocity–pressure system. If is a good approximation to H−1, then we should see low iteration counts in the Schur complement solve. Figure 8 shows the results of this study for a range of Courant numbers.
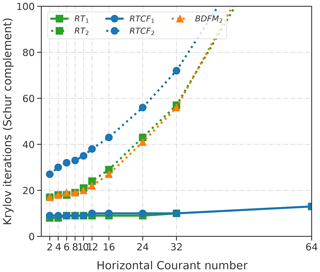
Figure 8Number of Krylov iterations to invert the Helmholtz system using as a preconditioner. The preconditioner is applied using a direct LU factorization within a GMRES method on the entire pressure equation. While the lowest-order methods grow slowly over the Courant number range, the higher-order (by only 1 approximation order) methods quickly degrade and diverge after the critical range λC=𝒪(2)–𝒪(10). At λC>32, the solvers take over 150 iterations.
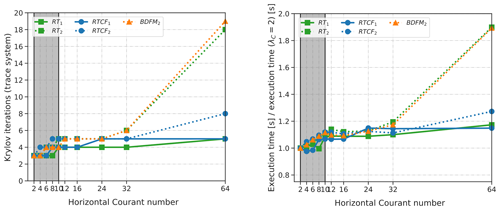
Figure 9Courant number parameter test run on a fully loaded compute node. Both figures display the hybridized solver for each discretization, described in Table 6. Panel (a) displays to total iteration count (preconditioned GCR) to solve the trace system to a relative tolerance of 10−5. Panel (b) displays the relative work of each solver, which takes into account the time required to forward eliminate and locally recover the velocity and pressure.
For the lower-order methods, the number of iterations to invert H grows slowly but remains under control. Increasing the approximation degree by 1 results in degraded performance. As Δt increases, the number of Krylov iterations needed to invert the system to a relative tolerance of 10−5 grows rapidly. It is clear that this sparse approximation is not robust against Courant number. This can be explained by the fact that diagonalizing the velocity operator fails to take into account the effects of the Coriolis term (which appear in off-diagonal positions in the operator). Even if one were to use traditional mass lumping (row-wise sums), the Coriolis effects are effectively canceled out due to asymmetry.
Hybridization avoids this problem entirely: we always construct an exact Schur complement and only have to worry about solving the trace system Eq. (111). We now show that this approach (described in Sect. 5.3.2) is much more robust to changes in Δt. We use the same workstation as for the three-dimensional CG/HDG problem in Sect. 5.1 (executed with a total of 40 MPI processes). Figure 9 shows the parameter test for all the discretizations described in Table 6. We see that, in terms of total number of GCR iterations needed to invert the trace system, hybridization is far more controlled as Courant number increases. They largely remain constant throughout the entire parameter range, only varying by an iteration or two. It is not until after λC>32 that we begin to see a larger jump in the number of GCR iterations. This is expected, since the Coriolis operator causes the problem to become singular for very large Courant numbers. However, unlike with the approximate Schur complement solver, iteration counts are still under control. In particular, each method (lowest and higher order) remains constant throughout the critical range (shaded in gray in Fig. 9).
In Fig. 9b, we display the ratio of execution time and the time-to-solution at the lowest Courant number of 2. We perform this normalization to better compare the lower and higher-order methods (and discretizations on triangular prisms vs. extruded quadrilaterals). The calculation of the ratios includes the time needed to eliminate and reconstruct the hybridized velocity–pressure variables. The fact that the hybridization solver remains close to 1 demonstrates that the entire solution procedure is largely λC-independent until around λC=32. The overall trend is largely the same as the number of Krylov iterations to reach solver convergence. This is due to our hybridization approach being solver dominated, with local operations like forward elimination together with local recovery taking approximately one-third of the total execution time for each method. The percentage breakdown of the hybridization solver is similar to what is already presented in Sect. 5.1.2.
Implicitly treating the Coriolis term has been discussed for semi-implicit discretizations of large-scale geophysical flows (Temperton, 1997; Cullen, 2001; Nechaev and Yaremchuk, 2004). The addition of the Coriolis term presents a particular challenge to the solution finite element discretizations of these equations since it increases the difficulty of finding a good sparse approximation of the nonsymmetric elliptic operator. Hybridization shows promise here, as it allows for the assembly of the elliptic equation that both captures the effects of rotation and results in a sparse linear system.
We have presented Slate, and shown how this language can be used to create concise mathematical representations of localized linear algebra on the tensors corresponding to finite element forms. We have shown how this DSL can be used in tandem with UFL in Firedrake to implement solution approaches making use of automated code generation for static condensation, hybridization, and localized post-processing. Setup and configuration are done at runtime, allowing one to switch in different discretizations at will. In particular, this framework alleviates much of the difficulty in implementing such methods within intricate numerical code and paves the way for future low-level optimizations. In this way, the framework in this paper can be used to help enable the rapid development and exploration of new hybridization and static condensation techniques for a wide class of problems. We remark here that the reduction of global matrices via element-wise algebraic static condensation, as described in Guyan (1965) and Irons (1965) is also possible using Slate, including other more general static condensation procedures outside the context of hybridization.
Our approach to preconditioner design revolves around its composable nature, in that these Slate-based implementations can be seamlessly incorporated into complicated solution schemes. In particular, there is current research in the design of dynamical cores for numerical weather prediction using implementations of hybridization and static condensation with Slate (Bauer and Cotter, 2018; Shipton et al., 2018). The performance of such methods for geophysical flows are a subject of ongoing investigation.
In this paper, we have provided some examples of hybridization procedures for compatible finite element discretizations of geophysical flows. These approaches avoid the difficulty in constructing sparse approximations of dense elliptic operators. Static condensation arising from hybridizable formulations can best be interpreted as producing an exact Schur complement factorization on the global hybridizable system. This eliminates the need for outer iterations from a suitable Krylov method to solve the full mixed system and replaces the original global mixed equations with a condensed elliptic system. More extensive performance benchmarks, which require detailed analysis of the resulting operator systems arising from hybridization, are a necessary next step to determine whether hybridization provides a scalable solution strategy for compatible finite elements in operational settings.
For some tessellation, 𝒯h, our semi-discrete mixed method for Eqs. (81)–(82) seeks approximations satisfying
where indicates that the value of the function should be taken from the upwind side of each facet. The discretization of the velocity advection operator is an extension of the energy-conserving scheme of Natale and Cotter (2017) to the shallow water equations.
The time-stepping scheme follows a Picard iteration semi-implicit approach, where predictive values of the relevant fields are determined via an explicit step of the advection equations and corrective updates are generated by solving an implicit linear system (linearized about a state of rest) for , given by
where H is the mean layer depth and Ru and RD are residual linear forms that vanish when and are solutions to the implicit midpoint rule time discretization of Eqs. (A1)–(A2). The residuals are evaluated using the predictive values of and .
The implicit midpoint rule time discretization of the nonlinear rotating shallow water Eqs. (A1)–(A2) is
where and .
One approach to construct the residual functionals Ru and RD would be to simply define these from Eqs. (A5)–(A6). However, this leads to a small critical time step for the stability of the scheme. To make the numerical scheme more stable, we define residuals as follows. For Ru, we first solve for vh∈Uh such that
where . This is a linear variational problem. Then,
Similarly, for RD we first solve for Eh∈Vh such that
where . This is also a linear problem. Then,
This process can be thought of as iteratively solving for the average velocity and depth that satisfies the implicit midpoint rule discretization. Both Eqs. (A7) and (A9) can be solved separately, since there is no coupling between them. The fields vh and Eh are then used to construct the right-hand side for the implicit linearized system in Eqs. (A3)–(A4). Once the system is solved, the solution (Δuh,ΔDh) is then used to update the iterative values of and according to , having initially chosen .
The contribution in this paper is available through open-source software provided by the Firedrake Project: https://www.firedrakeproject.org/ (last access: 30 January 2020). We cite archives of the exact software versions used to produce the results in this paper. For all components of the Firedrake project used in this paper, see Zenodo/Firedrake (2019). The numerical experiments, full solver configurations, code verification (including local processing), and raw data are available in Zenodo/Tabula-Rasa (2019).
THG is the principal author and developer of the software presented in this paper and main author of the text. Authors LM and DAH assisted and guided the software abstraction as a domain-specific language and edited text. CJC contributed to the formulation of the geophysical fluid dynamics and the design of the numerical experiments and edited text.
David A. Ham is an executive editor of the journal. The other authors declare they have no other competing interests.
The authors would like to acknowledge funding from the Engineering and Physical Sciences Research Council (EPSRC) and the Natural Environment Research Council (NERC). The authors also wish to thank Andrew T. T. McRae for providing thoughtful comments on early drafts of this paper.
This research has been supported by the Engineering and Physical Sciences Research Council (grant nos. EP/M011054/1, EP/L000407/1, and EP/L016613/1) and the Natural Environment Research Council (grant no. NE/K008951/1).
This paper was edited by Simone Marras and reviewed by two anonymous referees.
Alnæs, M. S., Logg, A., Ølgaard, K. B., Rognes, M. E., and Wells, G. N.: Unified form language: A domain-specific language for weak formulations of partial differential equations, ACM Trans. Mathe. Softw. (TOMS), 40, 1–37, 2014. a, b, c, d, e
Arnold, D. N. and Brezzi, F.: Mixed and nonconforming finite element methods: implementation, postprocessing and error estimates, ESAIM: Mathe. Modell. Num. Anal., 19, 7–32, 1985. a, b, c, d
Arnold, D. N., Falk, R. S., and Winther, R.: Multigrid in H(div) and H(curl), Num. Mathe., 85, 197–217, https://doi.org/10.1007/s002110000137, 2000. a
Balay, S., Gropp, W. D., McInnes, L. C., and Smith, B. F.: Efficient management of parallelism in object-oriented numerical software libraries, in: Modern software tools for scientific computing, 163–202, Springer, 1997. a
Balay, S., Abhyankar, S., Adams, M. F., Brown, J., Brune, P., Buschelman, K., Dalcin, L., Eijkhout, V., Gropp, W. D., Karpeyev, D., Kaushik, D., Knepley, M. G., May, D. A., McInnes, L. C., Mills, R. T., Munson, T., Rupp, K., Sanan, P., Smith, B. F., Zampini, S., Zhang, H., and Zhang, H.: PETSc Users Manual, Tech. Rep. ANL-95/11 – Revision 3.11, Argonne National Laboratory, 2019. a, b
Bauer, W. and Cotter, C.: Energy-enstrophy conserving compatible finite element schemes for the rotating shallow water equations with slip boundary conditions, J. Comput. Phys., 373, 171–187, https://doi.org/10.1016/j.jcp.2018.06.071, 2018. a
Boffi, D., Brezzi, F., and Fortin, M.: Mixed finite element methods and applications, vol. 44 of Springer Series in Computational Mathematics, Springer-Verlag New York, 2013. a, b
Bramble, J. H. and Xu, J.: A local post-processing technique for improving the accuracy in mixed finite-element approximations, SIAM J. Num. Anal., 26, 1267–1275, 1989. a, b
Bramble, J. H., Pasciak, J. E., and Xu, J.: The analysis of multigrid algorithms for nonsymmetric and indefinite elliptic problems, Math. Comput., 51, 389–414, 1988. a
Bramble, J. H., Kwak, D. Y., and Pasciak, J. E.: Uniform convergence of multigrid V-cycle iterations for indefinite and nonsymmetric problems, SIAM J. Num. Anal., 31, 1746–1763, 1994. a
Brezzi, F. and Fortin, M.: Mixed and hybrid finite element methods, vol. 15 of Springer Series in Computational Mathematics, Springer-Verlag New York, 1991. a, b
Brezzi, F., Douglas, J., and Marini, L. D.: Two families of mixed finite elements for second order elliptic problems, Num. Mathe., 47, 217–235, 1985. a, b, c
Brezzi, F., Douglas, J., Durán, R., and Fortin, M.: Mixed finite elements for second order elliptic problems in three variables, Num. Mathe., 51, 237–250, 1987. a
Brown, J., Knepley, M. G., May, D. A., McInnes, L. C., and Smith, B.: Composable linear solvers for multiphysics, in: Parallel and Distributed Computing (ISPDC), 2012 11th International Symposium on, 55–62, IEEE, 2012. a
Cockburn, B.: Static condensation, hybridization, and the devising of the HDG methods, in: Building Bridges: Connections and Challenges in Modern Approaches to Numerical Partial Differential Equations, 129–177, Springer, 2016. a
Cockburn, B., Gopalakrishnan, J., and Lazarov, R.: Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems, SIAM J. Num. Anal., 47, 1319–1365, 2009a. a, b, c
Cockburn, B., Guzmán, J., and Wang, H.: Superconvergent discontinuous Galerkin methods for second-order elliptic problems, Mathe. Comput., 78, 1–24, 2009b. a, b, c, d
Cockburn, B., Gopalakrishnan, J., Li, F., Nguyen, N.-C., and Peraire, J.: Hybridization and postprocessing techniques for mixed eigenfunctions, SIAM J. Num. Anal., 48, 857–881, 2010a. a, b
Cockburn, B., Gopalakrishnan, J., and Sayas, F.-J.: A projection-based error analysis of HDG methods, Mathe. Comput., 79, 1351–1367, 2010b. a, b, c, d, e
Cockburn, B., Dubois, O., Gopalakrishnan, J., and Tan, S.: Multigrid for an HDG method, IMA J. Num. Anal., 34, 1386–1425, 2014. a
Cotter, C. J. and Shipton, J.: Mixed finite elements for numerical weather prediction, J. Comput. Phys., 231, 7076–7091, 2012. a, b, c, d
Cotter, C. J. and Thuburn, J.: A finite element exterior calculus framework for the rotating shallow-water equations, J. Comput. Phys., 257, 1506–1526, 2014. a, b
Cullen, M.: Alternative implementations of the semi-Lagrangian semi-implicit schemes in the ECMWF model, Q. J. Roy. Meteorol. Soc., 127, 2787–2802, 2001. a
Dalcin, L. D., Paz, R. R., Kler, P. A., and Cosimo, A.: Parallel distributed computing using python, Adv. Water Resour., 34, 1124–1139, 2011. a, b
Devloo, P., Faria, C., Farias, A., Gomes, S., Loula, A., and Malta, S.: On continuous, discontinuous, mixed, and primal hybrid finite element methods for second-order elliptic problems, Int. J. Num. Method. Eng., 115, 1083–1107, https://doi.org/10.1002/nme.5836, 2018. a
Elman, H. C., Ernst, O. G., and O'leary, D. P.: A multigrid method enhanced by Krylov subspace iteration for discrete Helmholtz equations, SIAM J. Sci. Comput., 23, 1291–1315, 2001. a
Falgout, R. D., Jones, J. E., and Yang, U. M.: The design and implementation of hypre, a library of parallel high performance preconditioners, in: Numerical solution of partial differential equations on parallel computers, 267–294, Springer, 2006. a
Fraeijs de Veubeke, B.: Displacement and equilibrium models in the finite element method, in: Stress Analysis, edited by: Zienkiewicz, O. and Holister, G. S., John Wiley & Sons, reprinted in Internat, J. Numer. Methods Engrg., 52, 287–342, 1965. a
Gopalakrishnan, J.: A Schwarz preconditioner for a hybridized mixed method, Comput. Methods Appl. Math., 3, 116–134, 2003. a
Guennebaud, G., Jacob, B., Avery, P., Bachrach, A., and Barthelemy, S.: Eigen v3, 2010, available at: http://eigen.tuxfamily.org (last access: 7 February 2020), 2015. a
Guyan, R. J.: Reduction of stiffness and mass matrices, AIAA J., 3, 380, 1965. a, b, c
Hecht, F.: New development in FreeFem++, J. Num. Mathe., 20, 251–266, 2012. a
Hiptmair, R. and Xu, J.: Nodal auxiliary space preconditioning in H(curl) and H(div) spaces, SIAM J. Num. Anal., 45, 2483–2509, https://doi.org/10.1137/060660588, 2007. a
Homolya, M., Mitchell, L., Luporini, F., and Ham, D. A.: TSFC: a structure-preserving form compiler, SIAM J. Sci. Comput., 40, C401–C428, https://doi.org/10.1137/17M1130642, 2018. a, b
Irons, B.: Structural eigenvalue problems-elimination of unwanted variables, AIAA J., 3, 961–962, 1965. a, b, c
Kang, S., Giraldo, F. X., and Bui-Thanh, T.: IMEX HDG-DG: A coupled implicit hybridized discontinuous Galerkin and explicit discontinuous Galerkin approach for shallow water systems, J. Comput. Phys., 401, 109010, 2020. a
Kirby, R. C.: Algorithm 839: FIAT, a new paradigm for computing finite element basis functions, ACM Trans. Mathe. Softw. (TOMS), 30, 502–516, 2004. a
Kirby, R. C. and Logg, A.: A compiler for variational forms, ACM Trans. Mathe. Softw. (TOMS), 32, 417–444, 2006. a
Kirby, R. C. and Mitchell, L.: Solver composition across the PDE/linear algebra barrier, SIAM J. Sci. Comput., 40, C76–C98, https://doi.org/10.1137/17M1133208, 2018. a
Kirby, R. M., Sherwin, S. J., and Cockburn, B.: To CG or to HDG: a comparative study, J. Sci. Comput., 51, 183–212, 2012. a
Kronbichler, M. and Wall, W. A.: A performance comparison of continuous and discontinuous Galerkin methods with fast multigrid solvers, SIAM J. Sci. Comput., 40, A3423–A3448, 2018. a, b
Logg, A. and Wells, G. N.: DOLFIN: Automated finite element computing, ACM Trans. Mathe. Softw. (TOMS), 37, 20, 2010. a
Logg, A., Mardal, K.-A., and Wells, G.: Automated solution of differential equations by the finite element method: The FEniCS book, Vol. 84, Springer Science & Business Media, 2012a. a, b
Logg, A., Ølgaard, K. B., Rognes, M. E., and Wells, G. N.: FFC: the FEniCS form compiler, Automated Solution of Differential Equations by the Finite Element Method, 227–238, 2012b. a
Long, K., Kirby, R., and van Bloemen Waanders, B.: Unified embedded parallel finite element computations via software-based Fréchet differentiation, SIAM J. Sci. Comput., 32, 3323–3351, 2010. a
Mandel, J.: Multigrid convergence for nonsymmetric, indefinite variational problems and one smoothing step, Appl. Mathe. Comput., 19, 201–216, 1986. a
Markall, G., Slemmer, A., Ham, D., Kelly, P., Cantwell, C., and Sherwin, S.: Finite element assembly strategies on multi-core and many-core architectures, International J. Num. Method. Fluids, 71, 80–97, 2013. a
McRae, A. T. T., Bercea, G.-T., Mitchell, L., Ham, D. A., and Cotter, C. J.: Automated generation and symbolic manipulation of tensor product finite elements, SIAM J. Sci. Comput., 38, S25–S47, 2016. a
Melvin, T., Dubal, M., Wood, N., Staniforth, A., and Zerroukat, M.: An inherently mass-conserving iterative semi-implicit semi-Lagrangian discretization of the non-hydrostatic vertical-slice equations, Q. J. Roy. Meteorol. Soc. A, 136, 799–814, 2010. a, b
Melvin, T., Benacchio, T., Shipway, B., Wood, N., Thuburn, J., and Cotter, C.: A mixed finite-element, finite-volume, semi-implicit discretization for atmospheric dynamics: Cartesian geometry, Q. J. Roy. Meteorol. Soc., 145, 2835–2853, https://doi.org/10.1002/qj.3501, 2019. a, b
Mitchell, L. and Müller, E. H.: High level implementation of geometric multigrid solvers for finite element problems: Applications in atmospheric modelling, J. Comput. Phys., 327, 1–18, 2016. a, b, c, d
Nair, R. D., Thomas, S. J., and Loft, R. D.: A discontinuous Galerkin global shallow water model, Mon. Weather Rev., 133, 876–888, 2005. a
Natale, A. and Cotter, C. J.: A variational H (div) finite-element discretization approach for perfect incompressible fluids, IMA J. Num. Anal, 38, p. drx033, https://doi.org/10.1093/imanum/drx033, 2017. a
Natale, A., Shipton, J., and Cotter, C. J.: Compatible finite element spaces for geophysical fluid dynamics, Dynam. Stat. Clim. Syst., 1, dzw005, https://doi.org/10.1093/climsys/dzw005, 2016. a, b, c, d
Nechaev, D. and Yaremchuk, M.: On the approximation of the Coriolis terms in C-grid models, Mon. Weather Rev., 132, 2283–2289, 2004. a
Nédélec, J.-C.: Mixed finite elements in ℝ3, Num. Mathe., 35, 315–341, 1980. a
Prud'Homme, C., Chabannes, V., Doyeux, V., Ismail, M., Samake, A., and Pena, G.: Feel++: A computational framework for galerkin methods and advanced numerical methods, in: ESAIM: Proceedings, 38, 429–455, EDP Sciences, 2012. a
Rathgeber, F., Markall, G. R., Mitchell, L., Loriant, N., Ham, D. A., Bertolli, C., and Kelly, P. H. J.: PyOP2: A high-level framework for performance-portable simulations on unstructured meshes, in: High Performance Computing, Networking, Storage and Analysis (SCC), 2012 SC Companion:, 1116–1123, IEEE, 2012. a, b
Rathgeber, F., Ham, D. A., Mitchell, L., Lange, M., Luporini, F., McRae, A. T. T., Bercea, G.-T., Markall, G. R., and Kelly, P. H. J.: Firedrake: automating the finite element method by composing abstractions, ACM Trans. Mathe. Softw. (TOMS), 43, 1–27, 2016. a
Raviart, P.-A. and Thomas, J.-M.: A mixed finite element method for 2-nd order elliptic problems, in: Mathematical aspects of finite element methods, 292–315, Springer, 1977. a
Shipton, J., Gibson, T. H., and Cotter, C. J.: Higher-order compatible finite element schemes for the nonlinear rotating shallow water equations on the sphere, J. Comput. Phys., 375, 1121–1137, 2018. a, b, c, d
Skamarock, W. C. and Klemp, J. B.: Efficiency and accuracy of the Klemp-Wilhelmson time-splitting technique, Mon. Weather Rev., 122, 2623–2630, 1994. a, b
Stenberg, R.: Postprocessing schemes for some mixed finite elements, ESAIM: Mathe. Modell. Num. Anal., 25, 151–167, 1991. a, b, c, d
Temperton, C.: Treatment of the Coriolis terms in semi-Lagrangian spectral models, Atmos.-Ocean, 35, 293–302, 1997. a
Thomas, S. J., Hacker, J. P., Smolarkiewicz, P. K., and Stull, R. B.: Spectral preconditioners for nonhydrostatic atmospheric models, Mon. Weather Rev., 131, 2464–2478, 2003. a
Ullrich, P. A., Jablonowski, C., and Van Leer, B.: High-order finite-volume methods for the shallow-water equations on the sphere, J. Comput. Phys., 229, 6104–6134, 2010. a
Williamson, D. L., Drake, J. B., Hack, J. J., Jakob, R., and Swarztrauber, P. N.: A standard test set for numerical approximations to the shallow water equations in spherical geometry, J. Comput. Phys., 102, 211–224, 1992. a, b
Wood, N., Staniforth, A., White, A., Allen, T., Diamantakis, M., Gross, M., Melvin, T., Smith, C., Vosper, S., Zerroukat, M., et al.: An inherently mass-conserving semi-implicit semi-Lagrangian discretization of the deep-atmosphere global non-hydrostatic equations, Q. J. Roy. Meteorol. Soc., 140, 1505–1520, 2014. a
Yakovlev, S., Moxey, D., Kirby, R. M., and Sherwin, S. J.: To CG or to HDG: a comparative study in 3D, J. Sci. Comput., 67, 192–220, 2016. a, b
Zenodo/Firedrake: Software used in 'Slate: extending Firedrake's domain-specific abstraction to hybridized solvers for geoscience and beyond', Zenodo, https://doi.org/10.5281/zenodo.2587072, 2019. a
Zenodo/Tabula-Rasa: Tabula Rasa: experimentation framework for hybridization and static condensation, Zenodo, https://doi.org/10.5281/zenodo.2616031, 2019. a, b, c, d
Similarly to UFL, Slate is capable of abstractly representing arbitrary rank tensors. However, only rank ≤2 tensors are typically used in most finite element applications, and therefore we currently only generate code for those ranks.
For more details on solving linear equations in Eigen, see https://eigen.tuxfamily.org/dox/group__TutorialLinearAlgebra.html (last access: 3 January 2020).
The Schur complement, while elliptic, is globally dense due to the fact that A has a dense inverse. This is a result of velocities in Uh having continuous normal components across cell interfaces.
These are the two broken parts of Ψi on a particular facet connecting two elements. That is, for two adjacent cells, a basis function in Uh for a particular facet node can be decomposed into two basis functions in defined on their respective sides of the facet.
We use a flexible version of GMRES on the outer system since we use an additional Krylov solver to iteratively invert the Schur complement.
The choice of in Eq. (97) corresponds to a Charney–Phillips vertical staggering of the buoyancy variable, which is the desired approach for the UK Met Office's Unified Model (Melvin et al., 2010). One could also collocate bh with ph (), which corresponds to a Lorenz staggering. This, however, supports a computational mode which is exacerbated by fast-moving waves. We restrict our discussion to the former case.
- Abstract
- Introduction
- A system for localized algebra on finite element tensors
- Examples
- Static condensation as a preconditioner
- Numerical studies
- Conclusions
- Appendix A: Semi-implicit method for the shallow water system
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- A system for localized algebra on finite element tensors
- Examples
- Static condensation as a preconditioner
- Numerical studies
- Conclusions
- Appendix A: Semi-implicit method for the shallow water system
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References