the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
COSIPY v1.3 – an open-source coupled snowpack and ice surface energy and mass balance model
Anselm Arndt
Christoph Schneider
Glacier changes are a vivid example of how environmental systems react to a changing climate. Distributed surface mass balance models, which translate the meteorological conditions on glaciers into local melting rates, help to attribute and detect glacier mass and volume responses to changes in the climate drivers. A well-calibrated model is a suitable test bed for sensitivity, detection, and attribution analyses for many scientific applications and often serves as a tool for quantifying the inherent uncertainties. Here, we present the open-source COupled Snowpack and Ice surface energy and mass balance model in PYthon (COSIPY), which provides a flexible and user-friendly framework for modeling distributed snow and glacier mass changes. The model has a modular structure so that the exchange of routines or parameterizations of physical processes is possible with little effort for the user. The framework consists of a computational kernel, which forms the runtime environment and takes care of the initialization, the input–output routines, and the parallelization, as well as the grid and data structures. This structure offers maximum flexibility without having to worry about the internal numerical flow. The adaptive subsurface scheme allows an efficient and fast calculation of the otherwise computationally demanding fundamental equations. The surface energy balance scheme uses established standard parameterizations for radiation as well as for the energy exchange between atmosphere and surface. The schemes are coupled by solving both surface energy balance and subsurface fluxes iteratively such that consistent surface skin temperature is returned at the interface. COSIPY uses a one-dimensional approach limited to the vertical fluxes of energy and matter but neglects any lateral processes. Accordingly, the model can be easily set up in parallel computational environments for calculating both energy balance and climatic surface mass balance of glacier surfaces based on flexible horizontal grids and with varying temporal resolution. The model is made available on a freely accessible site and can be used for non-profit purposes. Scientists are encouraged to actively participate in the extension and improvement of the model code.
- Article
(3544 KB) - Full-text XML
- BibTeX
- EndNote
Glacier variations are of great interest and relevance in many scientific issues and application such as climate sciences, water resources management, and tourism. In order to identify the climatic drivers for past, current, and future changes, process understanding, observations, and models of glacier mass change need to be combined appropriately. Schemes that relate the surface mass balance of snow and ice bodies to meteorological forcing data have been set up and applied for many decades (e.g., Anderson, 1968; Kraus, 1975; Anderson, 1976; Kuhn, 1979; Male and Granger, 1981; Kuhn, 1987; Siemer, 1988; Morris, 1989, 1991; Munro, 1991). Studies have shown that the synthesis of this information provides a consistent understanding of the relevant mass and energy fluxes at the glacier–atmosphere interface, which in turn provides the necessary physical foundations to translate micrometeorological conditions on glaciers into local melt rates (e.g., Sauter and Galos, 2016; Wagnon et al., 1999; Oerlemans, 2001; Mölg and Hardy, 2004; Obleitner and Lehning, 2004; Van Den Broeke et al., 2006; Reijmer and Hock, 2008; Mölg et al., 2008; Nicholson et al., 2013). Distributed mass balance models combine the local melt information with glacier-wide surface mass change information and thus offer the possibility to attribute and detect glacier mass and volume responses to changes in the climatic forcings (e.g., Klok and Oerlemans, 2002; Hock and Holmgren, 2005; Mölg et al., 2009; Sicart et al., 2011; Cogley et al., 2011). Although the accumulation and redistribution of snow are still deficient (e.g., Sauter et al., 2013), when coupled with atmospheric models, such models have the potential to simulate present and future glacier evolution or to serve as a useful tool for monitoring climatic glacier mass change (Machguth et al., 2006). A well-calibrated model is a suitable platform for sensitivity, detection, and attribution analyses as well as a tool for the quantification of inherent uncertainties (e.g., Mölg et al., 2014; Maussion et al., 2015; Rye et al., 2012; Mölg et al., 2012; Sauter and Obleitner, 2015; Galos et al., 2017; van Pelt et al., 2012; Østby et al., 2017).
Over recent decades, several distributed mass balance models of varying complexity have been developed and successfully applied to different glacier systems and climate regimes. The models range from simple degree-day models (e.g., Radić and Hock, 2006; Schuler et al., 2005) to intermediate models (e.g., Machguth et al., 2009) and complex snow cover and glacier-resolving physical models (e.g., Bartelt and Lehning, 2002; Vionnet et al., 2012; Hock and Holmgren, 2005; Klok and Oerlemans, 2002; Sicart et al., 2011; Weidemann et al., 2018; Huintjes et al., 2015b; Mölg et al., 2009; Michlmayr et al., 2008; van Pelt et al., 2012). The latter model class is usually based on the same fundamental physical principles but differs in the parameterization schemes and implementation techniques. Different research groups have their own in-house solutions which are often extended and modified for specific scientific questions and studies. The fact that often several subversions of the same model exist, with some of them not being freely available, makes it difficult for users to having access to up-to-date software. Ideally, a platform should (i) be continuously maintained, (ii) provide newly developed parameterizations, (iii) compile different model subversions developed for specific research needs, (iv) be easily extensible, and (v) be well documented and readable.
Here, we present an open-source COupled Snowpack and Ice surface energy and mass balance model in PYthon (COSIPY) designed to meet these requirements. The structure is based on the predecessor model COSIMA (COupled Snowpack and Ice surface energy and MAss balance model; Huintjes et al., 2015b). COSIPY provides a lean, flexible, and user-friendly framework for modeling distributed snow and glacier mass changes. The framework consists of a computational core that forms the runtime environment and handles initialization, input–output (IO) routines, parallelization, and the grid and data structures. In most cases, the runtime environment does not require any changes by the user. To increase the user friendliness, additional features are available, such as a restart option for operational applications and automatic comparison between simulation and ablation stakes. These features will be further refined in the future. Physical processes and parameterizations are handled separately by modules. The modules can be easily modified or extended to meet the needs of the end user. This structure provides maximum flexibility without worrying about internal numerical issues. The model is completely based on open-source libraries and is provided on a freely accessible Git repository (https://github.com/cryotools/cosipy, last access: 11 November 2020) for non-profit purpose. Scientists can actively participate in extending and improving the model code. Changes to the code are automatically tested with Travis CI (http://www.travis-ci.org, last access: 11 November 2020) when uploaded to the repository. It is planned to publish updates in regular intervals. To make working with COSIPY easier, a community platform (https://cosipy.slack.com, last access: 11 November 2020) has been set up in addition to a detailed “Read the Docs” documentation (https://cosipy.readthedocs.io/en/latest, last access: 11 November 2020), allowing users and developers to exchange experiences, report bugs, and communicate needs. In this work, we describe the physical basics and parameterizations, and outline the numerical implementation of the COSIPY model (version 1.3) (https://zenodo.org/record/3902191, Sauter and Arndt, 2020a). Section 2 gives an overview of the model concept, followed by the description of the modules (Sect. 3). The model architecture and the input–output are explained in Sect. 4. Section 5 shows different applications of the model. The code availability section documents the code availability and software requirements.
2.1 Fundamental equations
COSIPY is a multi-layered process resolving energy and mass balance model for the simulation of past, current, and future glacier changes. The model is based on the concept of energy and mass conservation. The snow/ice layers are described by the volumetric fraction of ice θi, liquid water content θw, and air porosity θa. Continuity constraints require that
The inherent properties, such as snow density ρs or specific heat of snow cs, follow from the volumetrically weighted properties of the constitutes. For example, snow density is related by
where ρi is the ice density, ρw the water density, and ρa the air density (Bartelt and Lehning, 2002). Exchange processes at the surface, the energy release and consumption through phase changes, control the vertical temperature distribution within the snow and ice layers. The energy balance also includes incoming shortwave radiation absorption and the sublimation or deposition of water vapor. Assuming the vertical temperature profile is given by Ts(z,t), where z is the depth, the energy conservation can be represented by
where θw+cpθa and are the volume-specific bulk heat capacity and bulk thermal conductivity of the snow cover (Bartelt and Lehning, 2002). Alongside the volume-specific heat capacity, COSIPY also offers the option of using empirical form (Huintjes et al., 2015a). The first term on the right-hand side (Qp) is the volumetric energy sink or source by melting and meltwater refreezing. The second term (Qr) is the volumetric energy surplus by the absorption of shortwave radiation (see Eq. 13).
The exchange processes at the snow/ice–atmosphere interface control the surface temperature at an infinitesimal skin layer. From the energy conservation follows
where qsw is the net-shortwave radiation energy, qlw is the net-longwave radiation energy, qsh is the sensible heat flux, qlh is the latent heat flux, and qrr is the heat flux from rain. To solve Eq. (4) for , the fluxes on the right-hand side must be parameterized (see Sect. 3). The parameterization results in a nonlinear equation which is solved iteratively. The left side of Eq. (4) provides the upper Neumann boundary condition (prescribed gradient) for Eq. (3). At the bottom of the domain, the temperature must be specified (Dirichlet boundary condition) by the user. The melting rates in the snow cover and glacier ice are derived diagnostically from the energy conservation by ensuring that the temperature does not exceed the melting point temperature Tm.
Equation (4) is solved using a limited-memory Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm (quasi-Newton method) for bound-constrained minimization (Fletcher, 2000). Equation (3) is then integrated with an implicit second-order central difference scheme (Ferziger and Perić, 2002). The heat sources can warm the snowpack and lead to internal melt processes. In the event that the liquid water content of a layer exceeds its irreducible water content (Coléou and Lesaffre, 1998; Wever et al., 2014),
the excess water is drained into the subsequent layer (bucket approach). The liquid water is passed on until it reaches either a layer of ice or the glacier surface where it is considered to be runoff. For this purpose, a threshold value was introduced which defines the transition from snow to ice. If no such layer exists, water is passed on until it reaches the lower limit of the domain and is then considered as runoff. Meltwater refreezing and subsurface melting during percolation change the volumetric ice and water contents. Subsurface melt occurs when energy fluxes, e.g., penetrating shortwave radiation, warm the layer to physically inconsistent temperatures of Ts>Tm. Since physical constraints require that Ts≤Tm, the energy surplus is used to melt the ice matrix. Melt takes place when Ts>Tm and the liquid water content increases by
where J Kg−1 is the latent heat of fusion (Bartelt and Lehning, 2002). Mass conservation requires that the mass gain of liquid water content equals the mass loss of the volumetric ice content, so that
The latent energy needed by the phase change is
which is an heat sink because Δθi(z,t) is positive at melting. The energy used for melting ensures that Ts(z,t) does not rise above Tm. In the event that θw>0 and Ts<Tm, refreezing can take place. Changes in volumetric fractions and the release of latent energy due to phase changes are treated equally. As the temperature difference must be negative due to the given constraints, it follows from Eqs. (6), (7), and (8) that Qp becomes positive and latent heat release warms the layer.
Many of the quantities and fluxes in Eqs. (3) and (4) are not measured directly and have to be derived via corresponding parameterizations. The next section describes the parameterizations implemented in COSIPY v1.3.
2.2 Discretization and computational mesh
To solve the underlying differential equations, the computing domain must be discretized. Since extreme gradients in temperature, density, and liquid water content can develop in the snowpack, COSIPY uses a dynamic, non-equidistant mesh. The mesh consists of so-called nodes that store the properties of the layers (e.g., temperature, density, and liquid water content) and is continuously adjusted during runtime by a re-meshing algorithm; i.e., the number and height of the individual layers vary with time. Currently, two algorithms are implemented: the first is a logarithmic approach, where the layer thicknesses gradually increase with depth by a constant stretching factor. Thus, layers close to the surface have a higher spatial resolution, which is advantageous for the computation of the energy and mass fluxes at the surface. Re-meshing is performed at each time step. This is a fast method but does not resolve sharp layering transitions, as these are smoothed by the algorithm. This approach is only recommended if a detailed resolution of the snow and ice cover is not required. The other algorithm implemented is an adaptive one that assembles layers according to user-defined criteria. It uses density and temperature thresholds to determine when two successive layers are considered similar and when they are not. When both criteria are met, these layers are merged. Basically, the adaptive algorithm runs in three consecutive steps: (1) adding/removing snow/ice at the surface, (2) adjusting the first layer, (3) updating internal layers.
-
In the first step, it is checked whether snow falls or melts away (note that internal layers can also melt). If snow falls on the glacier surface, it will only remain on the surface if it reaches a user-defined minimum snow thickness. Melt is removed from the first layer and all internal layers. After this step, layers can become very small and the thickness of the first layer no longer corresponds to the user-specified constant thickness. Therefore, it is necessary to re-mesh the layers.
-
In the second step, the top layer is adjusted first. The top layer is re-meshed so that this layer always has the user-defined layer thickness (default value is 0.01 m). The adaptation of the top layers together with internal melting processes can reduce the internal layers to a very low thickness. To avoid thin layers, the layers are merged or split in the third step.
-
In the third step, internal layers are split or merged. For each layer, a check is made to identify layers with a thickness of less than a defined minimum layer thickness. Such thin layers are merged with the layer below. Also if the differences in temperature and density of two subsequent layers are less than a user-defined threshold (similarity criteria), they will be merged. How often a merging/splitting can take place per time step is also defined by the user (correction steps). Unlike CROCUS (Vionnet et al., 2012), internal re-meshing always starts from the surface; i.e., the uppermost layers are adapted first. Depending on how many correction steps are set by the user, it can happen that only the uppermost layers are re-meshed.
When two layers are merged, the liquid water content and the heights of the two layers are added and the new density is calculated from the volumetrically weighted densities of the two layers. To ensure energy conservation, the total energy is determined from the internal energies and converted into the new temperature. Unlike the logarithmic approach, adaptive re-meshing resolves individual layers but slightly increases both computing time and data volume.
3.1 Snowfall and precipitation
When snowfall is given, it is assumed that the data represent the effective accumulation since snowdrift and snow particle sublimation are not explicitly treated in the model. Otherwise, snowfall is derived from the precipitation data using a logistic transfer function. The proportion of solid precipitation smoothly scales between 100 % (0 ∘C) and 0 % (2 ∘C), as suggested by Hantel et al. (2000). The fresh snow density for the conversion into snow depth is a function of air temperature and wind velocity
with the empirical parameters af= 109 kg m−3, bf= 6 kg m−3 K−1, cf= 26 kg m s1∕2, and ρmin=50 kg m−3 (Vionnet et al., 2012). In both cases, fresh snow is only added when the height exceeds a certain user-defined threshold.
3.2 Albedo
The approach suggested by Oerlemans and Knap (1998) parameterizes the evolution of the broadband albedo. The decay of the snow albedo at a specific day depends on the snow age at the surface and is given by
where αs is the fresh snow albedo and αf the firn albedo. The albedo timescale τ* specifies how fast the snow albedo drops from fresh snow to firn. The number of days after the last snowfall is given by parameter s. Besides the temporal change, the overall snowpack thickness impacts the albedo. If the thickness of the snowpack d is thin, the albedo must tend towards the albedo of ice αi. If one introduces a characteristic snow depth scale d* (e-folding), the full albedo can be written as
The model resets the albedo to fresh snow, if the snow accumulation exceeds a certain threshold (default value is 0.01 m) within one time step. This approach neglects sudden short-term jumps in albedo, which can occur when thin fresh snow layers quickly melt away. To account for this effect, the age of the underlying snow is also tracked. If the fresh snow layer melts faster than τ*, the age of the snow cover is reset to the value of the underlying snow (Gurgiser et al., 2013).
3.3 Radiation fluxes
The net-shortwave radiation in the energy-conservation equation Eq. (3) is defined as
where qG is the incoming shortwave radiation, and α the snow/ice albedo. A proportion of qsw can penetrate into the uppermost centimeters of the snow or ice (Bintanja and Van Den Broeke, 1995). The resulting absorbed radiation at depth z is calculated with
where λr is the fraction of absorbed radiation (0.8 for ice; 0.9 for snow) and β the extinction coefficient (2.5 for ice; 17.1 for snow). Physical constraints require that Ts≤Tm so that the energy surplus is used to melt the ice matrix (see Sect. 2).
In the event that the incoming longwave radiation is observed, the net-longwave radiation is obtained by
where εs is the surface emissivity which is set to a constant close or equal to 1. In the absence of , the flux is parameterized by means of air temperature and atmospheric emissivity,
using the Stefan–Boltzmann law. Here, N is the cloud cover fraction, εcl the emissivity of clouds which is set to 0.984 (Klok and Oerlemans, 2002), and εcs the clear-sky emissivity. The latter is given by
where is the water vapor pressure (Klok and Oerlemans, 2002).
3.4 Turbulent fluxes
The turbulent fluxes, qsh and qlh, in Eq. (4) are parameterized based on the flux-gradient similarity which assumes that the fluxes are proportional to the vertical gradient of state parameters. However, since meteorological parameters are only considered from one height in the model, a bulk approach is used whereby the mean property between the measurement height and the surface is considered (e.g., Foken, 2008; Stull, 1988). Assuming that fluxes in the Prandtl layer are constant, dimensionless transport coefficients CH (Stanton number) and CE (Dalton number) can be introduced by vertically integrating the turbulent diffusion coefficients (Foken, 2008; Stull, 1988) so that the turbulent vertical flux densities can be written as
where ρa is the air density (derived from the ideal gas law), cp is the specific heat of air for constant pressure, Lv is the latent heat of vaporization which is replaced by the latent heat of sublimation Ls when T0<Tm, is the wind velocity at height zt, and are the temperature and mixing ratio at height zt (assuming zt=zq), respectively, and q0 is the mixing ratio at the surface where it is assumed that the infinite skin layer is saturated. Unlike the turbulent diffusion coefficients, the bulk coefficients are independent of the wind speed and only depend on the stability of the atmospheric stratification and the roughness of the surface. The aerodynamic roughness length is simply a function of time and increases linearly for snowpacks from fresh snow to firn (Mölg et al., 2012). For glaciers, is set to a constant value. According to the renewal theory for turbulent flow, and are assumed to be 1 and 2 orders of magnitude smaller than , respectively (Smeets and van den Broeke, 2008; Conway and Cullen, 2013).
COSIPY provides two options to correct the flux-profile relationship for non-neutral stratified surface layers, by adding a stability correction using the (1) bulk Richardson number and (2) Monin–Obukhov similarity theory (e.g., Conway and Cullen, 2013; Radić et al., 2017; Stull, 1988; Foken, 2008; Munro, 1989). Using the bulk Richardson number, the dimensionless transport coefficients can be written in the following form:
whereas the stability function
accounts for reduction of the vertical fluxes by thermal stratification and is a function of the Richardson number. The Richardson number
follows from the turbulent kinetic energy equation and relates the generation of turbulence by shear and damping by buoyancy (Stull, 1988). In the stable case (), the function describes the transition from turbulent flow to a quasi-laminar non-turbulent flow and hence reduces the vertical fluxes. Once Rib exceeds the critical value Rib=0.2, turbulence eventually extinguishes, and the vertical exchange is suppressed.
According to the Monin–Obukhov similarity theory, atmospheric stratification can be characterized by the dimensionless parameter
where
is the so-called Obukhov length with u* is the friction velocity and κ (0.41) the von Kármán constant (Stull, 1988; Foken, 2008). The length scale relates dynamic, thermal, and buoyancy processes and is proportional to the height of the dynamic sublayer. The bulk aerodynamic coefficients for momentum CD, heat CH, and moisture CE for non-neutral conditions
can be derived by integrating the universal functions (Businger et al., 1971; Dyer, 1974) where
where , a=16, and b=5 are the stability-dependent correction functions. The computation of the stability functions requires an a priori assumption (Munro, 1989) about L which in turn depends on qsh and the friction velocity
COSIPY uses an iterative approach to resolve the dependency of these variables. At the beginning of the first iteration, u* (Eq. 30) and qsh (Eq. 17) are approximated assuming a neutral stratification (ζ=0). These quantities are then used to calculate L (Eq. 24). In the next iteration, the updated L is then used to correct u* and qsh. The iteration is repeated until either the changes in qsh are less than or a maximum number of 10 iterations is reached. As already shown by other studies, the algorithm usually converges in less than 10 time steps (Munro, 1989).
3.5 Snow densification
Snow settling during metamorphism and compaction under the weight of the overlying snowpack generally increases the snow density over time (Anderson, 1976; Boone, 2004; Essery et al., 2013). The snow density is a key characteristic of the snowpack, which is used by COSIPY to derive important snow properties such as thermal conductivity and liquid water content. Assuming that a rapid settlement of fresh snow occurs simultaneously with slow compaction by the load resisted by the viscosity, the rate of density change of each snow layer becomes
with Ms is the overlying snow mass, s−1, c2= 0.042 K−1, c3= 0.046 m3 kg−1, and the viscosity
where kg m−1 s−1, c4=0.081 K−1, and c5= 0.018 m3 kg−1 (Anderson, 1976; Boone, 2004; Essery et al., 2013).
3.6 Mass changes
The total mass changes may be written as the integral expression
which follows directly from Eq. (2). So any net mass change must be accompanied by changes in ice fraction, liquid water content, and porosity within the snow/ice column of height d. The continuity equation for ice fraction (first term on the right side) may be written as
where the integral on the right side describes the internal mass changes by melt and refreezing, SF the mass gain by snowfall, and qm∕Lf is the mass loss by melt. The last two terms of this equation, qlh∕Ls and qlh∕Lv, are the sublimation/deposition and evaporation/condensation fluxes at the surface, respectively, depending on the sign of qlh and . Melt energy qm is the energy surplus at the surface which is available for melt and follows from Eq. (4). Similarly, we can extend the continuity equation for the liquid water content, which reads as
with the integral on the right side describing the internal mass changes of liquid water by melt and refreezing, Rf the mass gain by liquid precipitation, and Q the runoff at the bottom of the snowpack. COSIPY calculates all terms and writes them to the output file.
Basically, COSIPY consists of a model kernel which is extended by modules. The model kernel forms the underlying model structure and provides the IO routines, takes over the discretization of the computational mesh, parallelizes the simulations, and solves the fundamental mass- and energy-conservation equations (Eqs. 2 and 3). These tasks are independent of the implementations of the parameterization and usually do not require any modification by the end user.
COSIPY is a one-dimensional model that resolves vertical processes at a specific point on the glacier. For spatially distributed simulations, the point model is integrated independently at each point of the glacier domain, neglecting the lateral mass and energy fluxes. The independence of the point models simplifies scaling for larger computer architectures, which led to the COSIPY model architecture being designed for both local workstations and high-performance computing clusters (HPCCs). So far, the model has been successfully tested on Slurm Workload Manager (https://slurm.schedmd.com, last access: 11 November 2020) and Portable Batch System (PBS) job scheduling systems (https://www.pbspro.org, last access: 11 November 2020). Regardless of whether the distributed simulations are integrated on a single-core or multi-core computing environment, the point model sequence is always the same. During initialization, the atmospheric input data are read in, and the mesh is generated. With distributed spatial simulations, the data are distributed across the available cores, and one-dimensional calculations are performed for each grid point.
At the beginning of each time step, it is checked whether snowfall occurs and must be added to the existing snow cover. Subsequently, the computational mesh is re-meshed to ensure numerical stability. Afterwards, the albedo (Eq. 11) and the roughness length are updated. Once these steps have been performed, the heating and melting of snow by penetrating shortwave radiation (Eqs. 13, 6, and 7) is determined and the surface energy fluxes and surface temperature (Eq. 4) are derived. The resulting meltwater, both from surface and subsurface melt, is then percolated through the layers (bucket approach). Next, the heat equation (Eq. 3) is solved after all terms on the right side have been determined.
4.1 Input and output (IO) and initial condition
The model is driven by meteorological data that must be provided in a corresponding NetCDF file (see https://cosipy.readthedocs.io/en/latest/Ressources.html, last access: 11 November 2020). Input parameters include atmospheric pressure, air temperature, cloud cover fraction, relative humidity, incoming shortwave radiation, total precipitation, and wind velocity. Optional snowfall and incoming longwave radiation can be used as forcing parameters. If the snow height (or snow water equivalent) and/or surface temperature are also specified in the input file, these are used as initial conditions. Otherwise, snow depth and surface temperature are assumed to be homogeneous in space at the start of the simulation according to the specifications in the configuration file. In addition to meteorological parameters, COSIPY requires static information such as topographic parameters and a glacier mask. Example workflows for creating and converting static and meteorological data into the required NetCDF input are included in the source code (https://cosipy.readthedocs.io/en/latest/Documentation.html#quick-tutorial, last access: 11 November 2020). Besides the standard output variables, there is also the possibility to store vertical snow profile information, although to save memory we can only recommend this for single-point simulations. To reduce the amount of data, the users can specify which of the output variables will be stored.
5.1 Zhadang glacier, high-mountain Asia
The first example shows the application of COSIPY to the Zhadang glacier, which is located on the northeastern slope of the Nyenchen Tanglha Mountains ( N, E) on the central Tibetan Plateau.
5.1.1 Single-site simulation
For single-site simulation, we use hourly data from May 2009 to June 2012 from an automatic weather station (AWS) on the Zhadang glacier (Huintjes et al., 2015b). The relevant variables air pressure , air temperature , relative humidity RH, incident shortwave radiation qG, snowfall SF, and wind speed were measured by the AWS. Due to the harsh and remote environment, the time series show gaps that were filled with the High Asia Refined Analysis (HAR; Maussion et al., 2014) product. The cloud cover fraction N was provided by ERA5 (Hersbach and Dee, 2016) data. We compare the simulated surface temperature T0 and surface height change ΔH with the AWS measurements. Furthermore, ablation stakes were installed on the glacier to determine the loss of mass at various locations on the glacier. A detailed description of the data, the AWS sensors used, the post-processing procedure, and the discussion can be found in Huintjes et al. (2015b) and Huintjes (2014).
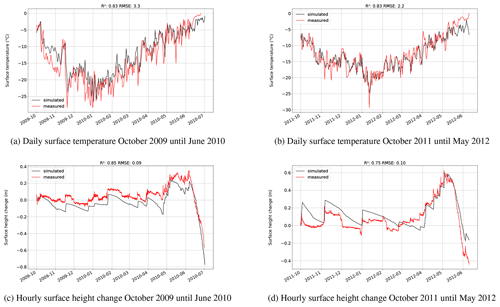
Figure 1Simulated and measured surface temperatures and surface height changes (in both cases, permanent snow cover) at the location of the automatic weather station at the Zhadang glacier.
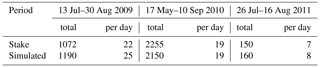
Simulation. Figure 1a and b show the glacier surface temperatures determined from longwave radiation measurements and from COSIPY simulations for two periods where in situ measurements are available. The model represents both the daily variability (R2=0.83, p values <0.001) and the magnitude of the observed surface temperature. The root mean square errors are 3.3 and 2.2 K for the two periods, respectively, and is thus within the typical uncertainty range of longwave radiation measurements. The simulated cumulative mass balance over the entire period from April 2009 to May 2012 is −2.9 m w.e. Figure 1c and d show the simulated and measured ΔH for the two periods (October 2009–June 2010 and October 2011–May 2012) where measurements are available. The daily and seasonal variability is well captured by the model (R2=0.85, p value <0.001 and R2=0.75, p value <0.001), even if snowfall seems to be too low during the first period. Nevertheless, overall, the differences are consistently small with RMSEs of 0.09 and 0.10 m. Table 1 shows the observed and simulated ice ablation for three different periods for which measurements are available. For all three periods, a high degree of agreement is evident, which reveals that the energy fluxes are represented by COSIPY.
5.1.2 Distributed simulation, scalability
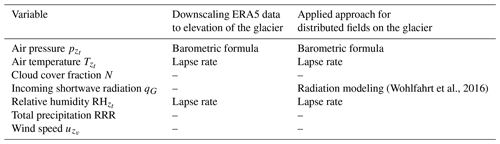
For a distributed glacier-wide run, we drive COSIPY by ERA5 data instead of in situ observations. The ERA5 temperature and humidity data were interpolated across the topography using empirical lapse rates. Atmospheric pressure has been corrected using the barometric formula. The radiation model of Wohlfahrt et al. (2016) was used for the incoming shortwave radiation to account for effects of shadowing, slope and aspect. Total precipitation, cloud cover and horizontal wind velocity were used directly from the closest ERA5 grid point (see Table 2). The computational domain consisted of 1837 grid cells with a spatial resolution of approximately 30 m (1 arcsec) (see Fig. 2).
(Wohlfahrt et al., 2016)Table 2COSIPY forcing variables and applied downscaling approaches for distributed simulation. RRR indicates total precipitation.
Simulation. The glacier-wide cumulative surface mass balance for the decade of 2009 to 2018 is presented in Fig. 2. The simulated annual mass balance for this period is −1.9 m w.e. a−1. The results are in line with the analysis of Qu et al. (2014), who reported negative mass balances of −1.9, −2.0, −0.8, and −2.7 m w.e. for the years 2009 to 2012. Furthermore, COSIPY reproduced the spatial distribution at different locations in the ablation area of the Zhadang glacier (see S1, S2, and S3 in Fig. 2b).
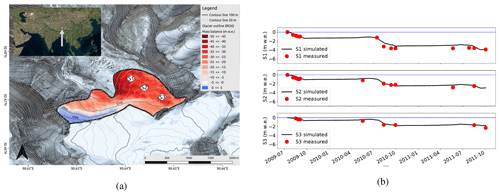
Figure 2Distributed mass balance simulation of the Zhadang glacier. (a) Cumulative climatic mass balance from 2009 to 2018 with 1827 grid points, contour lines (SRTM), glacier outline from the Randolph Glacier Inventory 6.0, and a topographic map from Bing Maps (Microsoft, 2020); (b) comparison of three measurements (ablation stakes) from July 2009 to October 2011 with the simulated cumulative surface mass balance of the corresponding grid point.
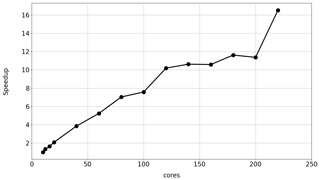
Scalability. A big challenge for large applications is usually the computational cost. To achieve the required performance, models should be scalable on parallel high-performance computing environments. For the model performance analysis, we use a cluster with identical nodes, each consisting of two Intel Xeon(R) E5-2640 v4 CPUs operating at 2.4 GHz and connected via InfiniBand. Each processor has 10 cores, 32 GB memory, and a memory bandwidth of 68.3 GB s−1. To test the performance of the parallelized COSIPY version, we performed a spatial simulation of the Zhadang glacier. We used a 3 arcsec (∼90 m) Shuttle Radar Topography Mission (SRTM) terrain model so that the computational grid consists of 206 points. The performance of the parallel version was then compared to the single-core solution by measuring the required execution time for different core setups (1–220 cores). Figure 3 shows the speedup compared to the single-core version, i.e., the ratio of the original execution time (single core) with the execution time of the corresponding node test (multiple cores). If the model is executed with 20 cores, the speedup is ∼2. With 120 cores, a speedup of ∼10 is reached; i.e., each core has to calculate a maximum of two grid points. A speedup of more than ∼16 is not possible with this system and is achieved with a number of 220 cores (more cores than grid points). The computation time is less than 35 min for a 10-year period (hourly resolution) when using 220 cores. At this point, it should be mentioned that the performance can vary significantly on other HPCC systems and simulation conditions, and should always be checked before submitting larger simulations to the cluster.
5.2 Distributed mass and energy balance simulation and operational application at Hintereisferner in the Austrian Alps
The Hintereisferner (HEF) is a valley glacier located in the Ötztal Alps of Austria (46.79∘ N, 10.74∘ E). The glacier begins high on the flank of the Weißkugel mountain, at approximately 3720 m, and runs down to its terminus at approximately 2460 m. HEF is a prime location for meteorological and glaciological research activities due to its monitoring infrastructure. There is a network of four AWSs and four precipitation gauges operated on, and in the vicinity of, HEF. Since 2016, the University of Innsbruck has also been running a permanent terrestrial laser scanner (TLS) and a 5 m meteorological flux tower. Measurement data are transmitted hourly to a data server. COSIPY is now being used to develop an operational mass balance prediction system for the Hintereisferner. The model is driven by the latest Consortium for Small-scale Modeling (COSMO2) analysis and forecast data (see Fig. 4). With the forecast data, the energy and mass flows on the glacier are predicted for the next 24 h with a horizontal resolution of 30 m. The simulated fields are automatically visualized and provided on a web server. In the future, the TLS measurements will be used to improve the forecast continuously. The system is currently running in test mode but will be available to the public in spring 2021.
In addition to the energy and mass flows at the surface, the snow/ice profiles will be stored. This will allow us to compare the results with snow pits and to test the implementation of different parameterizations.
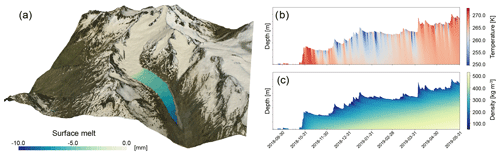
Figure 4Operational application of COSIPY for the Hintereisferner. Panel (a) shows the forecast of surface melt for 22 June 2020 based on COSMO2 data. Panels (b) and (c) show an example of the temperature and density profile for one site on the glacier tongue for the period of September 2018 to June 2019.
5.3 Model intercomparison – Earth System Model–Snow Model Intercomparison Project
Within the Earth System Model–Snow Model Intercomparison Project (ESM-SnowMIP; Krinner et al., 2018), several of snow models were compared to evaluate different snow schemes and to improve the coupling of land surface snow models in Earth system models. Ménard et al. (2019) describes the standardized input and evaluation data. A total of 10 different sites representing mountainous regions (Europe and the western US), boreal forests (Canada), the Arctic (Finland), and urban regions (Japan) for periods between 7 and 20 years (hourly resolution) are provided, including meteorological classification and details on measuring instruments and data processing. These quality-controlled data are freely available on a PANGAEA repository (Ménard and Essery, 2019) and provide the possibility to benchmark new model developments, detect uncertainties, and reduce model errors. Unlike most of the models participating in the intercomparison project, COSIPY is not a pure snow model, but still all necessary forcing variables are available to apply the model to the different test data sets. We downscaled wind speed from 10 to 2 m above ground using the logarithmic wind profile and calculated the relative humidity from the specific humidity using the saturation mixing ratio and water vapor. The simulated albedo, snow water equivalent (SWE), and snow depth were compared with the evaluation data offered on the online repository (https://doi.org/10.1594/PANGAEA.897575, Ménard and Essery, 2019). Surface and soil temperature could not be compared, because no soil scheme is implemented in COSIPY which allows for warm surface and underground temperatures above the melting point. Figure 5 shows the daily long-term mean values of albedo, SWE, and snow depth for two example sites. The albedo parameterization was calibrated to fit the observed values at Col de Porte. With the calibrated albedo parameterization, COSIPY can reproduce the observed long-term snowpack evolution. The results for Sodankylä, Finland (see Fig. 5b), show a slightly lower snowpack compared to the measurements. The COSIPY runs for both sites are in the range of the ESM-SnowMIP ensemble simulations (see Fig. 5; Krinner et al., 2018).
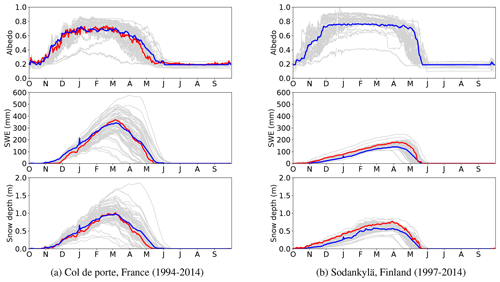
Figure 5Comparison of long-term daily mean COSIPY with ESM-SnowMIP simulations for two sites. COSIPY simulations (blue lines), measurements (red lines), and ESM-SnowMIP (grey lines) simulations of albedo, snow water equivalent (SWE), and snow depth at two sites. Measurements and simulations provided by Krinner et al. (2018).
COSIPY provides a lean, flexible, and user-friendly framework for modeling distributed snow and glacier mass changes. It provides a suitable platform for sensitivity, detection, and attribution analyses as well as a tool for the quantification of inherent uncertainties in mass balance studies. The model has a modular structure and allows the exchange of routines or parameterizations of individual physical processes with little effort. This structure allows the end user to quickly adapt the model to their needs. The open design of COSIPY is well documented, and the modular approach allows joint community-driven further development of the model in the future. In order to increase user friendliness, additional functions are available, such as a restart option for operative applications and an automatic comparison between simulation and ablation data. These functions will be further refined in the future.
The model is written in Python and completely based on open-source libraries. The model, source code, case studies, and code examples for data preprocessing are provided on a freely accessible Git repository (https://github.com/cryotools/cosipy, last access: 11 November 2020) for non-profit purposes. The aim is to set up a community platform where scientists can actively participate in extending and improving the model code. To ensure quality control of the model code, changes to the code are automatically tested with Travis CI (http://www.travis-ci.org, last access: 11 November 2020) when they are uploaded to the repository. It is planned to release updates at regular intervals. To make working with COSIPY easier, a community platform (https://cosipy.slack.com, last access: 11 November 2020) has been set up in addition to the “Read the Docs” documentation (https://cosipy.readthedocs.io/en/latest, last access: 11 November 2020), which allows users and developers to share experiences, report bugs, and communicate needs.
Future improvements of COSIPY are expected by applying the model in different climates and varying topographical settings. Additional processes affecting the climatic mass balance of glaciers such as debris cover and snowdrift can be considered in further developments of the model. In the long run, one of the priorities will be to create a multiphysics environment that allows ensemble runs. In principle, it is already possible to create ensemble simulations with different physical parameterizations and solvers, but COSIPY is not yet an ensemble multiphysics modeling environment. As a vision for the future, it is conceivable to extend COSIPY for automatic ensemble simulations. So far, it is only possible to run COSIPY with different combinations of physical parameterizations or input uncertainties and then evaluate the statistics.
COSIPY is based on the Python 3 language and is provided on a freely accessible Git repository (https://github.com/cryotools/cosipy, Sauter and Arndt, 2020b). COSIPY can be used for non-profit purposes under the GPLv3 license (http://www.gnu.org/licenses/gpl-3.0.html, last access: 10 November 2020). Scientists can actively participate in model development. A documentation with a sample workflow, information about input–output formats, and the code structure is available under “Read the Docs” (https://cosipy.readthedocs.io/en/latest/index.html, Sauter and Arndt, 2020c). As a community platform and user support, we use the groupware Slack (https://cosipy.slack.com, Sauter and Arndt, 2020d). The various official model releases will be registered with a unique DOI on Zenodo (https://doi.org/10.5281/zenodo.2579668, Sauter and Arndt, 2020e). For the results of this publication, version v1.3 (https://doi.org/10.5281/zenodo.3902191, Sauter and Arndt, 2020a) was used. Each commit will be automatically tested with different Python 3 releases on Travis (https://travis-ci.org/cryotools/cosipy, Sauter and Arndt, 2020f). The tested code coverage is tracked on CodeCov (https://codecov.io/github/cryotools/cosipy/, Sauter and Arndt, 2020g). Since we have just started writing the tests, code coverage of 35 % is still low but will be increased in the near future. With the exception of the preprocessor for creating the static file (currently not working on Windows systems), the model should work on any operating system with Python 3 installed. However, support for operating systems other than Linux-based systems is limited because we develop and run COSIPY exclusively on Linux-based systems. COSIPY is built on the following open-source libraries: numpy (van der Walt et al., 2011), scipy (Virtanen et al., 2019), xarray (Hoyer and Hamman, 2017), distribued, dask_jobqueue (Dask Development Team, 2016), and netcdf4 (https://doi.org/10.5281/zenodo.2669496, Whitaker et al., 2019).
TS and CS are the initiators of the model. TS developed the model design and wrote most of the sections on the physical and numerical principles of the model. AA developed parts of the parameterizations and core classes, and applied the model to the Zhadang glacier and the two sites of the ESM-SnowMIP. AA also wrote the sections about the corresponding applications and code availability. TS did the simulations for the Hintereisferner. AA and TS were equally involved in the development of the documentation and maintenance of the community platform (Slack). During the entire development process, all authors discussed the individual steps of model development, the results, and the structure of the manuscript.
The authors declare that they have no conflict of interest.
We would like to thank Eva Huintjes for her dedication to the fieldwork and for her contributions to the earlier versions of the software. Further, we acknowledge the efforts of all researchers and technicians from the involved German institutions and the Institute of Tibetan Plateau Research of the Chinese Academy of Sciences (CAS) for fieldwork at the Zhadang glacier. We specifically acknowledge the contribution of Yang Wei, Yao Tandong, and Kang Shichang in this respect. We gratefully thank Richard Essery and Gerhard Krinner for providing the data of the ensemble simulations for two sites of ESM-SnowMIP. We also wish to thank David Loibl for his contribution in the form of logo, ideas, and discussions regarding programming strategies, and for hosting COSIPY on his platform https://cryo-tools.org/ (last access: 11 November 2020). We would also like to thank Samuel Morin and the anonymous reviewer for their constructive comments and ideas.
We gratefully acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG) with its project “The impact of the dynamic and thermodynamic flow conditions on the spatio-temporal distribution of precipitation in southern Patagonia” (grant no. SA 2339/4-1) and “Snow Cover Dynamics and Mass Balance on Mountain Glaciers” (grant no. SA 2339/7-1). Part of this work and the position of co-author Anselm Arndt was financed through DFG's research grant “Precipitation patterns, snow and glacier response in High Asia and their variability on subdecadal timescales, sub-project: snow cover and glacier energy and mass balance variability” (prime-SG, SCHN 680/13-1). The development of the earlier version of the software and the field data used in this study was financed by the following projects: “Dynamic response of glaciers of the Tibetan Plateau” (Dyn RG TiP; grant nos. SCHN 680/3-1, SCHN 680/3-2, and SCHN 680/3-3) of DFG's Priority Programme 1372 “Tibetan Plateau: Formation–Climate–Ecosystems” (TiP) and the German Federal Ministry of Education and Research's (BMBF) program “Central Asia Monsoon Dynamics and Geo-Ecosystems” (CAME), project “Variability and Trends of Water-Budget Components in Benchmark Catchments of the Tibetan Plateau” (WET; grant no. 03G0804E).
This paper was edited by Heiko Goelzer and reviewed by Samuel Morin and one anonymous referee.
Anderson, E. A.: Development and testing of snow pack energy balance equations, Water Resour. Res., 4, 19–37, https://doi.org/10.1029/WR004i001p00019, 1968. a
Anderson, E. A.: A point energy and mass balance model of a snow cover, Technical Report, National Weather Service (NWS), United States, 1976. a, b, c
Bartelt, P. and Lehning, M.: A physical SNOWPACK model for the Swis avalanche warning: Part I: numerical model, Cold Reg. Sci. Technol., 35, 123–145, https://doi.org/10.1016/S0165-232X(02)00074-5, 2002. a, b, c, d
Bintanja, R. and Van Den Broeke, M. R.: The Surface Energy Balance of Antarctic Snow and Blue Ice, J. Appl. Meteorol., 34, 902–926, https://doi.org/10.1175/1520-0450(1995)034<0902:TSEBOA>2.0.CO;2, 1995. a
Boone, A.: Description du Schema de Neige ISBA-ES (Explicit Snow), Tech. rep., Centre National de Recherches Météorologiques, Météo-France, Toulouse, 2004 (updated in November 2009). a, b
Businger, J. A., Wyngaard, J. C., Izumi, Y., and Bradley, E. F.: Flux-profile relationships in the atmospheric surface layer, J. Atmos. Sci., 28, 181–189, https://doi.org/10.1175/1520-0469(1971)028<0181:FPRITA>2.0.CO;2, 1971. a
Cogley, J. G., Hock, R., Rasmussen, L. A., Arendt, A., Bauder, A., Braithwaite, R. J., Jansson, P., Kaser, G., Möller, M., Nicholson, L., and Zemp, M.: Glossary of glacier mass balance and related terms, International Association of Cryospheric Sciences, IHP-VII Technical Documents in Hydrology No. 86, IACS Contribution No. 2, UNESCO, Paris, https://doi.org/10.5167/uzh-53475, 2011. a
Coléou, C. and Lesaffre, B.: Irreducible water saturation in snow: experimental results in a cold laboratory, Ann. Glaciol., 26, 64–68, https://doi.org/10.3189/1998AoG26-1-64-68, 1998. a
Conway, J. and Cullen, N.: Constraining turbulent heat flux parameterization over a temperate maritime glacier in New Zealand, Ann. Glaciol., 54, 41–51, https://doi.org/10.3189/2013AoG63A604, 2013. a, b
Dask Development Team: Dask: Library for dynamic task scheduling, DASK, available at: https://dask.org (last access: 20 June 2020), 2016. a
Dyer, A. J.: A review of flux-profile relationships, Bound.-Lay. Meteorol., 7, 363–372, https://doi.org/10.1007/BF00240838, 1974. a
Essery, R., Morin, S., Lejeune, Y., and Ménard, C. B.: A comparison of 1701 snow models using observations from an alpine site, Adv. Water Resour., 55, 131–148, https://doi.org/10.1016/j.advwatres.2012.07.013, 2013. a, b
Ferziger, J. H. and Perić, M.: Computational Methods for Fluid Dynamics, Springer Berlin Heidelberg, Berlin, Heidelberg, https://doi.org/10.1007/978-3-642-56026-2, 2002. a
Fletcher, R.: Practical Methods of Optimization, John Wiley & Sons, Chichester, West Sussex England, https://doi.org/10.1002/9781118723203, 2000. a
Foken, T.: Micrometeorology, Springer, Berlin, Heidelberg, https://doi.org/10.1007/978-3-540-74666-9, 2008. a, b, c, d
Galos, S. P., Klug, C., Maussion, F., Covi, F., Nicholson, L., Rieg, L., Gurgiser, W., Mölg, T., and Kaser, G.: Reanalysis of a 10-year record (2004–2013) of seasonal mass balances at Langenferner/Vedretta Lunga, Ortler Alps, Italy, The Cryosphere, 11, 1417–1439, https://doi.org/10.5194/tc-11-1417-2017, 2017. a
Gurgiser, W., Marzeion, B., Nicholson, L., Ortner, M., and Kaser, G.: Modeling energy and mass balance of Shallap Glacier, Peru, The Cryosphere, 7, 1787–1802, https://doi.org/10.5194/tc-7-1787-2013, 2013. a
Hantel, M., Ehrendorfer, M., and Haslinger, A.: Climate sensitivity of snow cover duration in Austria, Int. J. Climatol., 20, 615–640, https://doi.org/10.1002/(SICI)1097-0088(200005)20:6<615::AID-JOC489>3.0.CO;2-0, 2000. a
Hersbach, H. and Dee, D.: ERA5 reanalysis is in production, ECMWF Newsletter, Tech. rep., European Centre for Medium-Range Weather Forecasts, available at: https://www.ecmwf.int/en/newsletter/147/news/era5-reanalysis-production (last access: 11 November 2020), vol. 147, 2016. a
Hock, R. and Holmgren, B.: A distributed surface energy-balance model for complex topography and its application to Storglaciären, Sweden, J. Glaciol., 51, 25–36, https://doi.org/10.3189/172756505781829566, 2005. a, b
Hoyer, S. and Hamman, J. J.: xarray: N-D labeled Arrays and Datasets in Python, Journal of Open Research Software, 5, p. 10, https://doi.org/10.5334/jors.148, 2017. a
Huintjes, E.: Energy and mass balance modelling for glaciers on the Tibetan Plateau – Extension, validation and application of a coupled snow and energy balance model, Ph.D. thesis, Rheinisch-Westfälischen Technischen Hochschule Aachen, Aachen, 2014. a
Huintjes, E., Neckel, N., Hochschild, V., and Schneider, C.: Surface energy and mass balance at Purogangri ice cap, central Tibetan Plateau, 2001–2011, J. Glaciol., 61, 1048–1060, https://doi.org/10.3189/2015JoG15J056, 2015a. a
Huintjes, E., Sauter, T., Schröter, B., Maussion, F., Yang, W., Kropáček, J., Buchroithner, M., Scherer, D., Kang, S., and Schneider, C.: Evaluation of a Coupled Snow and Energy Balance Model for Zhadang Glacier, Tibetan Plateau, Using Glaciological Measurements and Time-Lapse Photography, Arctic, Antarctic, and Alpine Research, 47, 573–590, https://doi.org/10.1657/AAAR0014-073, 2015b. a, b, c, d
Klok, E. and Oerlemans, J.: Model study of the spatial distribution of the energy and mass balance of Morteratschgletscher, Switzerland, J. Glaciol., 48, 505–518, https://doi.org/10.3189/172756502781831133, 2002. a, b, c, d
Kraus, H.: An energy balance model for ablation in mountainous areas, Proceedings of the Moscow Symposium, August 1971; Actes du Colloque de Moscou, août 1971, IAHS-AISH Publ. No. 104, 1975. a
Krinner, G., Derksen, C., Essery, R., Flanner, M., Hagemann, S., Clark, M., Hall, A., Rott, H., Brutel-Vuilmet, C., Kim, H., Ménard, C. B., Mudryk, L., Thackeray, C., Wang, L., Arduini, G., Balsamo, G., Bartlett, P., Boike, J., Boone, A., Chéruy, F., Colin, J., Cuntz, M., Dai, Y., Decharme, B., Derry, J., Ducharne, A., Dutra, E., Fang, X., Fierz, C., Ghattas, J., Gusev, Y., Haverd, V., Kontu, A., Lafaysse, M., Law, R., Lawrence, D., Li, W., Marke, T., Marks, D., Ménégoz, M., Nasonova, O., Nitta, T., Niwano, M., Pomeroy, J., Raleigh, M. S., Schaedler, G., Semenov, V., Smirnova, T. G., Stacke, T., Strasser, U., Svenson, S., Turkov, D., Wang, T., Wever, N., Yuan, H., Zhou, W., and Zhu, D.: ESM-SnowMIP: assessing snow models and quantifying snow-related climate feedbacks, Geosci. Model Dev., 11, 5027–5049, https://doi.org/10.5194/gmd-11-5027-2018, 2018. a, b, c
Kuhn, M.: On the Computation of Heat Transfer Coefficients from Energy-Balance Gradients on a Glacier, J. Glaciol., 22, 263–272, https://doi.org/10.3189/S0022143000014258, 1979. a
Kuhn, M.: Micro-Meteorological Conditions for Snow Melt, J. Glaciol., 33, 24–26, https://doi.org/10.3189/S002214300000530X, 1987. a
Machguth, H., Paul, F., Hoelzle, M., and Haeberli, W.: Distributed glacier mass-balance modelling as an important component of modern multi-level glacier monitoring, Ann. Glaciol., 43, 335–343, https://doi.org/10.3189/172756406781812285, 2006. a
Machguth, H., Paul, F., Kotlarski, S., and Hoelzle, M.: Calculating distributed glacier mass balance for the Swiss Alps from regional climate model output: A methodical description and interpretation of the results, J. Geophys. Res., 114, D19106, https://doi.org/10.1029/2009JD011775, 2009. a
Male, D. H. and Granger, R. J.: Snow surface energy exchange, Water Resour. Res., 17, 609–627, https://doi.org/10.1029/WR017i003p00609, 1981. a
Maussion, F., Scherer, D., Mölg, T., Collier, E., Curio, J., and Finkelnburg, R.: Precipitation Seasonality and Variability over the Tibetan Plateau as Resolved by the High Asia Reanalysis, J. Climate, 27, 1910–1927, https://doi.org/10.1175/JCLI-D-13-00282.1, 2014. a
Maussion, F., Gurgiser, W., Großhauser, M., Kaser, G., and Marzeion, B.: ENSO influence on surface energy and mass balance at Shallap Glacier, Cordillera Blanca, Peru, The Cryosphere, 9, 1663–1683, https://doi.org/10.5194/tc-9-1663-2015, 2015. a
Ménard, C. B. and Essery, R.: ESM-SnowMIP meteorological and evaluation datasets at ten reference sites (in situ and bias corrected reanalysis data), dataset, PANGAEA, https://doi.org/10.1594/PANGAEA.897575, 2019. a, b
Ménard, C. B., Essery, R., Barr, A., Bartlett, P., Derry, J., Dumont, M., Fierz, C., Kim, H., Kontu, A., Lejeune, Y., Marks, D., Niwano, M., Raleigh, M., Wang, L., and Wever, N.: Meteorological and evaluation datasets for snow modelling at 10 reference sites: description of in situ and bias-corrected reanalysis data, Earth Syst. Sci. Data, 11, 865–880, https://doi.org/10.5194/essd-11-865-2019, 2019. a
Michlmayr, G., Lehning, M., Koboltschnig, G., Holzmann, H., Zappa, M., Mott, R., and Schöner, W.: Application of the Alpine 3D model for glacier mass balance and glacier runoff studies at Goldbergkees, Austria, Hydrol. Process, 22, 3941–3949, https://doi.org/10.1002/hyp.7102, 2008. a
Microsoft: Bing Maps, available at: https://www.bing.com/maps/, last access: 10 November 2020. a
Mölg, T. and Hardy, D. R.: Ablation and associated energy balance of a horizontal glacier surface on Kilimanjaro, J. Geophys. Res., 109, D16104, https://doi.org/10.1029/2003JD004338,2004. a
Mölg, T., Cullen, N. J., Hardy, D. R., Kaser, G., and Klok, L.: Mass balance of a slope glacier on Kilimanjaro and its sensitivity to climate, Int. J. Climatol., 28, 881–892, https://doi.org/10.1002/joc.1589, 2008. a
Mölg, T., Cullen, N. J., Hardy, D. R., Winkler, M., and Kaser, G.: Quantifying Climate Change in the Tropical Midtroposphere over East Africa from Glacier Shrinkage on Kilimanjaro, J. Climate, 22, 4162–4181, https://doi.org/10.1175/2009JCLI2954.1, 2009. a, b
Mölg, T., Maussion, F., Yang, W., and Scherer, D.: The footprint of Asian monsoon dynamics in the mass and energy balance of a Tibetan glacier, The Cryosphere, 6, 1445–1461, https://doi.org/10.5194/tc-6-1445-2012, 2012. a, b
Mölg, T., Maussion, F., and Scherer, D.: Mid-latitude westerlies as a driver of glacier variability in monsoonal High Asia, Nat. Clim. Change, 4, 68–73, https://doi.org/10.1038/nclimate2055, 2014. a
Morris, E.: Turbulent transfer over snow and ice, J. Hydrol., 105, 205–223, https://doi.org/10.1016/0022-1694(89)90105-4, 1989. a
Morris, E. M.: Physics-Based Models of Snow, in: Recent Advances in the Modeling of Hydrologic Systems, edited by: Bowles, D. S. and O’Connell, P. E., Springer Netherlands, Dordrecht, 85–112 https://doi.org/10.1007/978-94-011-3480-4_5, 1991. a
Munro, D. S.: Surface Roughness and Bulk Heat Transfer on a Glacier: Comparison with Eddy Correlation, J. Glaciol., 35, 343–348, https://doi.org/10.3189/S0022143000009266, 1989. a, b, c
Munro, D. S.: A surface energy exchange model of glacier melt and net mass balance, Int. J. Climatol., 11, 689–700, https://doi.org/10.1002/joc.3370110610, 1991. a
Nicholson, L. I., Prinz, R., Mölg, T., and Kaser, G.: Micrometeorological conditions and surface mass and energy fluxes on Lewis Glacier, Mt Kenya, in relation to other tropical glaciers, The Cryosphere, 7, 1205–1225, https://doi.org/10.5194/tc-7-1205-2013, 2013. a
Obleitner, F. and Lehning, M.: Measurement and simulation of snow and superimposed ice at the Kongsvegen glacier, Svalbard (Spitzbergen), J. Geophys. Res.-Atmos., 109, D04106, https://doi.org/10.1029/2003JD003945, 2004. a
Oerlemans, J.: Glaciers and climate change, A.A. Balkema Publishers, Lisse; Exton, (PA), 2001. a
Oerlemans, J. and Knap, W. H.: A 1 year record of global radiation and albedo in the ablation zone of Morteratschgletscher, Switzerland, J. Glaciol., 44, 231–238, https://doi.org/10.1017/S0022143000002574, 1998. a
Østby, T. I., Schuler, T. V., Hagen, J. O., Hock, R., Kohler, J., and Reijmer, C. H.: Diagnosing the decline in climatic mass balance of glaciers in Svalbard over 1957–2014, The Cryosphere, 11, 191–215, https://doi.org/10.5194/tc-11-191-2017, 2017. a
Qu, B., Ming, J., Kang, S.-C., Zhang, G.-S., Li, Y.-W., Li, C.-D., Zhao, S.-Y., Ji, Z.-M., and Cao, J.-J.: The decreasing albedo of the Zhadang glacier on western Nyainqentanglha and the role of light-absorbing impurities, Atmos. Chem. Phys., 14, 11117–11128, https://doi.org/10.5194/acp-14-11117-2014, 2014. a
Radić, V. and Hock, R.: Modeling future glacier mass balance and volume changes using ERA-40 reanalysis and climate models: A sensitivity study at Storglaciären, Sweden, J. Geophys. Res.-Earth, 111, F03003, https://doi.org/10.1029/2005JF000440, 2006. a
Radić, V., Menounos, B., Shea, J., Fitzpatrick, N., Tessema, M. A., and Déry, S. J.: Evaluation of different methods to model near-surface turbulent fluxes for a mountain glacier in the Cariboo Mountains, BC, Canada, The Cryosphere, 11, 2897–2918, https://doi.org/10.5194/tc-11-2897-2017, 2017. a
Reijmer, C. H. and Hock, R.: Internal accumulation on Storglaciären, Sweden, in a multi-layer snow model coupled to a distributed energy-and mass-balance model, J. Glaciol., 54, 61–72, https://doi.org/10.3189/002214308784409161, 2008. a
Rye, C. J., Willis, I. C., Arnold, N. S., and Kohler, J.: On the need for automated multiobjective optimization and uncertainty estimation of glacier mass balance models, J. Geophys. Res.-Earth, 117, F02005, https://doi.org/10.1029/2011JF002184, 2012. a
Sauter, T. and Arndt, A.: cryotools/cosipy: COSIPY v1.3 – An open-source coupled snowpack and ice surface energy and mass balance model (Version v1.3), Zenodo, https://doi.org/10.5281/zenodo.3902191, 2020a. a, b
Sauter, T. and Arndt, A.: cryotools/cosipy: COSIPY – An open-source coupled snowpack and ice surface energy and mass balance model, GitHub repository, https://github.com/cryotools/cosipy, last access: 20 June 2020b. a
Sauter, T. and Arndt, A.: COSIPY v1.3 – An open-source coupled snowpack and ice surface energy and mass balance model – Read the Docs documentation, available at: https://cosipy.readthedocs.io/en/latest/index.html, last access: 20 June 2020c. a
Sauter, T. and Arndt, A.: COSIPY v1.3 – An open-source coupled snowpack and ice surface energy and mass balance model – Slack comunity platform for user communication, available at: https://cosipy.slack.com, last access: 20 June 2020d. a
Sauter, T. and Arndt, A.: cryotools/cosipy: COSIPY – An open-source coupled snowpack and ice surface energy and mass balance model – General DOI pointing to the newest release, Zenodo, https://doi.org/10.5281/zenodo.2579668, 2020e. a
Sauter, T. and Arndt, A.: cryotools/cosipy: COSIPY – An open-source coupled snowpack and ice surface energy and mass balance model – Travis CI repository, available at: https://travis-ci.org/cryotools/cosipy, last access: 20 June 2020f. a
Sauter, T. and Arndt, A.: cryotools/cosipy: COSIPY – An open-source coupled snowpack and ice surface energy and mass balance model – CodeCov repository, available at: https://codecov.io/github/cryotools/cosipy/, last access: 20 June 2020g. a
Sauter, T. and Galos, S. P.: Effects of local advection on the spatial sensible heat flux variation on a mountain glacier, The Cryosphere, 10, 2887–2905, https://doi.org/10.5194/tc-10-2887-2016, 2016. a
Sauter, T. and Obleitner, F.: Assessing the uncertainty of glacier mass-balance simulations in the European Arctic based on variance decomposition, Geosci. Model Dev., 8, 3911–3928, https://doi.org/10.5194/gmd-8-3911-2015, 2015. a
Sauter, T., Möller, M., Finkelnburg, R., Grabiec, M., Scherer, D., and Schneider, C.: Snowdrift modelling for the Vestfonna ice cap, north-eastern Svalbard, The Cryosphere, 7, 1287–1301, https://doi.org/10.5194/tc-7-1287-2013, 2013. a
Schuler, T. V., Hock, R., Jackson, M., Elvehøy, H., Braun, M., Brown, I., and Hagen, J.-O.: Distributed mass-balance and climate sensitivity modelling of Engabreen, Norway, Ann. Glaciol., 42, 395–401, https://doi.org/10.3189/172756405781812998, 2005. a
Sicart, J. E., Hock, R., Ribstein, P., Litt, M., and Ramirez, E.: Analysis of seasonal variations in mass balance and meltwater discharge of the tropical Zongo Glacier by application of a distributed energy balance model, J. Geophys. Res., 116, D13105, https://doi.org/10.1029/2010JD015105, 2011. a, b
Siemer, A. H.: Ein eindimensionales Energie-Massenbilanzmodell einer Schneedecke unter Berücksichtigung der Flüssigwassertransmission, Berichte des Institutes für Meteorologie und Klimatologie der Universität Hannover, 34, Universität Hannover, Hannover, 1988. a
Smeets, C. J. P. P. and van den Broeke, M. R.: Temporal and Spatial Variations of the Aerodynamic Roughness Length in the Ablation Zone of the Greenland Ice Sheet, Bound.-Lay. Meteorol., 128, 315–338, https://doi.org/10.1007/s10546-008-9291-0, 2008. a
Stull, R. B.: An Introduction to Boundary Layer Meteorology, Springer Netherlands, Dordrecht, https://doi.org/10.1007/978-94-009-3027-8, 1988. a, b, c, d, e
Van Den Broeke, M., Reijmer, C., Van As, D., and Boot, W.: Daily cycle of the surface energy balance in Antarctica and the influence of clouds, International J. Climatol., 26, 1587–1605, https://doi.org/10.1002/joc.1323, 2006. a
van der Walt, S., Colbert, S. C., and Varoquaux, G.: The NumPy Array: A Structure for Efficient Numerical Computation, Comput. Sci. Eng., 13, 22–30, https://doi.org/10.1109/MCSE.2011.37, 2011. a
van Pelt, W. J. J., Oerlemans, J., Reijmer, C. H., Pohjola, V. A., Pettersson, R., and van Angelen, J. H.: Simulating melt, runoff and refreezing on Nordenskiöldbreen, Svalbard, using a coupled snow and energy balance model, The Cryosphere, 6, 641–659, https://doi.org/10.5194/tc-6-641-2012, 2012. a, b
Vionnet, V., Brun, E., Morin, S., Boone, A., Faroux, S., Le Moigne, P., Martin, E., and Willemet, J.-M.: The detailed snowpack scheme Crocus and its implementation in SURFEX v7.2, Geosci. Model Dev., 5, 773–791, https://doi.org/10.5194/gmd-5-773-2012, 2012. a, b, c
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, I., Feng, Y., Moore, E. W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., and Contributors, S.: SciPy 1.0–Fundamental Algorithms for Scientific Computing in Python, Nature Methods 17, 261, arXiv [preprint], arXiv:1907.10121, 2019. a
Wagnon, P., Ribstein, P., Kaser, G., and Berton, P.: Energy balance and runoff seasonality of a Bolivian glacier, Global Planet. Change, 22, 49–58, https://doi.org/10.1016/S0921-8181(99)00025-9, 1999. a
Weidemann, S. S., Sauter, T., Malz, P., Jaña, R., Arigony-Neto, J., Casassa, G., and Schneider, C.: Glacier Mass Changes of Lake-Terminating Grey and Tyndall Glaciers at the Southern Patagonia Icefield Derived From Geodetic Observations and Energy and Mass Balance Modeling, Front. Earth Sci., 6, 81, https://doi.org/10.3389/feart.2018.00081, 2018. a
Wever, N., Fierz, C., Mitterer, C., Hirashima, H., and Lehning, M.: Solving Richards Equation for snow improves snowpack meltwater runoff estimations in detailed multi-layer snowpack model, The Cryosphere, 8, 257–274, https://doi.org/10.5194/tc-8-257-2014, 2014. a
Whitaker, J., Khrulev, C., Huard, D., Paulik, C., Hoyer, S., and Kinoshita, B. P.: Unidata/netcdf4-python: version 1.5.1.2 release (Version v1.5.1.2rel), Zenodo, https://doi.org/10.5281/zenodo.2669496, 2019. a
Wohlfahrt, G., Hammerle, A., Niedrist, G., Scholz, K., Tomelleri, E., and Zhao, P.: On the energy balance closure and net radiation in complex terrain, Agr. Forest Meteorol., 226–227, 37–49, https://doi.org/10.1016/j.agrformet.2016.05.012, 2016. a, b