Collisional growth in a particle-based cloud microphysical model: insights from column model simulations using LCM1D (v1.0)

Lagrangian cloud models (LCMs) are considered the future of cloud microphysical modelling. Compared to bulk models, however, LCMs are computationally expensive due to the typically high number of simulation particles (SIPs) necessary to represent microphysical processes such as collisional growth of hydrometeors successfully. In this study, the representation of collisional growth is explored in one-dimensional column simulations, allowing for the explicit consideration of sedimentation, complementing the authors' previous study on zero-dimensional collection in a single grid box. Two variants of the Lagrangian probabilistic all-or-nothing (AON) collection algorithm are tested that mainly differ in the assumed spatial distribution of the droplet ensemble: the first variant assumes the droplet ensemble to be well-mixed in a predefined three-dimensional grid box (WM3D), while the second variant considers the (sub-grid) vertical position of the SIPs, reducing the well-mixed assumption to a two-dimensional, horizontal plane (WM2D). Since the number of calculations in AON depends quadratically on the number of SIPs, an established approach is tested that reduces the number of calculations to a linear dependence (so-called linear sampling). All variants are compared to established Eulerian bin model solutions. Generally, all methods approach the same solutions and agree well if the methods are applied with sufficiently high resolution (foremost is the number of SIPs, and to a lesser extent time step and vertical grid spacing). Converging results were found for fairly large time steps, larger than those typically used in the numerical solution of diffusional growth. The dependence on the vertical grid spacing can be reduced if AON-WM2D is applied. The study also shows that AON-WM3D simulations with linear sampling, a common speed-up measure, converge only slightly slower compared to simulations with a quadratic SIP sampling. Hence, AON with linear sampling is the preferred choice when computation time is a limiting factor.

Most importantly, the study highlights that results generally require a smaller number of SIPs per grid box for convergence than previous one-dimensional box simulations indicated. The reason is the ability of sedimenting SIPs to interact with a larger ensemble of particles when they are not restricted to a single grid box. Since sedimentation is considered in most commonly applied three-dimensional models, the results indicate smaller computational requirements for successful simulations, encouraging a wider use of LCMs in the future.

1 Introduction

Clouds are a fundamental part of the global hydrological cycle, responsible for the transport and formation of precipitation. While we expect a global increase in precipitation due to climate change, our knowledge on its spatial distribution, even including decreasing rainfall in some regions of the globe, is still uncertain (Boucher et al., 2013). The formation processes of precipitation are, however, reasonably well understood and contain mechanisms that increase the size of hydrometeors. For liquid clouds, the coalescence of smaller cloud droplets is essential to form precipitating raindrops. In ice clouds, diffusional growth can produce precipitation-sized particles. The aggregation of ice crystals into larger clusters, snowflakes, also occurs frequently. And in mixed-phase clouds, ice crystals accrete supercooled liquid droplets forming graupel or hailstones.

The representation of these microphysical processes in climate models is impelled by the available computational resources, requiring necessary idealisations. Primarily, this is the case for computationally efficient Eulerian bulk models that predict only a small number of statistical moments for each hydrometeor class (e.g. Kessler, 1969; Khairoutdinov and Kogan, 2000; Seifert and Beheng, 2001), with commensurate limitations for the representation of clouds and precipitation. Of course, more detailed cloud microphysics models have also been developed: Eulerian bin models represent cloud droplets on a mass grid that consists of hundreds of bins sampling the droplet size distribution (DSD) (e.g. Berry and Reinhardt, 1974; Tzivion et al., 1987; Bott, 1998; Simmel et al., 2002; Wang et al., 2007). But even these models exhibit limitations and idealisations. For instance, the coalescence of droplets is modelled as a Smoluchowski (1916) process, describing the mean evolution of an infinitely large, well-mixed droplet ensemble. But the underlying Smoluchowski equation (also called the kinetic collection equation or even the stochastic collection equation, although the equation is deterministic) inherently neglects correlations and stochastic fluctuations known to be an integral part of the process chain that leads to precipitation (Gillespie, 1972; Bayewitz et al., 1974; Kostinski and Shaw, 2005; Wang et al., 2006; Alfonso et al., 2008).

In the last decade, Lagrangian cloud models (LCMs) emerged as a valid alternative to bin models (e.g. Andrejczuk et al., 2008; Shima et al., 2009; Sölch and Kärcher, 2010; Riechelmann et al., 2012; Arabas et al., 2015; Naumann and Seifert, 2015; Hoffmann et al., 2019). These models use Lagrangian particles, so-called simulation particles (SIPs) (Sölch and Kärcher, 2010) or super-droplets (Shima et al., 2009), each representing an ensemble of identical real droplets. Collisional growth in LCMs has recently been rigorously evaluated in box model simulations by Unterstrasser et al. (2017) (hereinafter abbreviated as U2017), who compared three algorithms documented in the literature: the remapping algorithm (RMA) by Andrejczuk et al. (2010), the average-impact algorithm (AIM) by Riechelmann et al. (2012), and the all-or-nothing algorithm (AON) concurrently developed by Shima et al. (2009) and Sölch and Kärcher (2010). RMA and AIM are deterministic algorithms and, in theory, approach the Smoluchowski solution of a reference bin model. The actual convergence of the algorithms, however, was found to depend significantly on properties of the SIP ensemble and the chosen kernel. The probabilistic AON indicated much better convergence properties given the simulation outcome is averaged over sufficiently many instances. Furthermore, Dziekan and Pawlowska (2017) showed that AON approximates the stochastically complete master equation including aforementioned correlations and stochastic fluctuations (Gillespie, 1972; Bayewitz et al., 1974). In fact, AON solutions are identical to the master equation solutions (Alfonso and Raga, 2017) when the weighting factors (the number of real droplets represented by a SIP) approach unity. The name AON was introduced in U2017. Note that in the literature, the term super-droplet method (SDM) is not used to refer to the class of particle-based microphysics models in general, but to the particular model introduced in Shima et al. (2009). Hence, AON with linear sampling (this will be explained later) is typically referred to as the SDM method (Shima et al., 2020).

However, many aspects of this relatively young modelling approach in cloud physics have not been tested thoroughly. One important message of our previous box simulations in U2017 was that the representation of collisional growth exhibits considerably more freedom in setting up a simulation than in bin models. Accordingly, in this study, we are going to extend the box simulations of U2017 by analysing collisional growth in a vertical column, including sedimentation, as it has been done in previous studies for Eulerian bulk and bin models (e.g. List et al., 1987; Tzivion et al., 1989; Hu and Srivastava, 1995; Prat and Barros, 2007; Stevens and Seifert, 2008; Seifert, 2008). All simulations will use the AON algorithm since it outperformed RMA and AIM in the box simulations, and we do not expect that this general behaviour is reversed here. The simulations will be compared to established Eulerian bin references. U2017 demonstrated that numerical convergence is harder to achieve for typical liquid cloud kernels (Long, 1974; Hall, 1980) than for a typical aggregation kernel with constant aggregation efficiency. Hence, the present study focuses on cloud droplet coalescence as a benchmarking exercise. But we expect that the results can be generalised for the LCM representation of ice crystal aggregation and the accretion of supercooled droplets. We will use the term collection, comprising coalescence, aggregation and accretion, as we focus on the numerical treatment, which is similar for all these processes, and not on their particular physics.

The paper is structured as follows. First, Sect. 2 will give an overview on the applied models, their foundations and basic set-up. The results are presented in Sect. 3 and divided into highly idealised applications in which the column model emulates a box model (Sect. 3.1), a process-level analysis of the applied algorithms (Sect. 3.2) and finally realistic applications (Sect. 3.3). The paper is concluded in Sect. 4. Table 1 lists frequently used abbreviations. The Appendix presents pure-sedimentation test cases. The Supplement contains additional material and figures (enumerated as S1, S2, and so on).

Unterstrasser et al. (2017)

Table 1 List of frequently used abbreviations.

2 Numerical model and set-up

Two column models, which consider collection and sedimentation, have been implemented; the first one represents a traditional Eulerian bin scheme and the second model uses a particle-based approach. Before we describe both models in some detail, we will write down basic relations, which will help disentangle the effects of particular parameter variations later.

2.1 Basic relations and definitions

We use a column with n_z grid boxes (GBs). Each GB has the volume ΔV and a height of Δz. The total column height is thus

$$\begin{array}{}\text{(1)}& L_z=n_z\times \mathrm{\Delta }z.\end{array}$$

We define that the GB k with $\mathrm{1}\le k\le n_z$ extends from z_k−1 to $z_k:=k\times \mathrm{\Delta }z$; hence the GB with k=1 is the lowest GB. The horizontal area of the column is given by

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }A=\mathrm{\Delta }V/\mathrm{\Delta }z.\end{array}$$

Throughout this study, we implicitly assume that air density ρ_air is constant in time and space.

The droplets are assumed to be spherical with a density of ρ_w=1000 kg m⁻³, and the mass–size relation is simply given by

$$\begin{array}{}\text{(3)}& m={\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathit{\pi }{r}^{\mathrm{3}}{\mathit{\rho }}_{\text{w}}.\end{array}$$

Following Gillespie (1972) and Shima et al. (2009), the probability $P_{ij}^{\mathrm{WM}\mathrm{3}\mathrm{D}}$ that one droplet with mass m_i coalesces with one droplet with mass m_j inside a small volume δV within a short time interval δt is given by

$$\begin{array}{}\text{(4)}& p_{ij}^{\mathrm{WM}\mathrm{3}\mathrm{D}}=K_{ij}\mathit{\delta }t\mathit{\delta }{V}^{-\mathrm{1}},\end{array}$$

where the collection kernel K_ij can be expressed as a function of droplet radii, K(r_i,r_j), or equivalently droplet masses, $\stackrel{\mathrm{̃}}{K}(m_i,m_j)$. We suppose that δt is sufficiently small in order to assure $p_{ij}^{\mathrm{WM}\mathrm{3}\mathrm{D}}\le \mathrm{1}$.

The hydrodynamic collection kernel, driven by differences in the droplet vertical velocity, is given by

$$\begin{array}{}\text{(5)}& K^{\mathrm{WM}\mathrm{3}\mathrm{D}}(r_i,r_j)=E_{\text{c}}(r_i,r_j)\mathit{\pi }(r_i+r_j{)}^{\mathrm{2}}|w_{\mathrm{sed},i}-w_{\mathrm{sed},j}|,\end{array}$$

where w_sed is the size-dependent droplet fall speed and $E_{\text{c}}=E\times E_{\text{coal}}$ is the collection efficiency, which is the product of the collision efficiency E and the coalescence efficiency E_coal. In this study, we use the w_sed parametrisation of Beard (1976) and the tabulated E values of Hall (1980), and the coalescence efficiency E_coal is assumed to be 1. The last assumption is an oversimplification for large droplets with radii ≳ 500 µm, for which E_coal is significantly smaller than 1 (Beard and Ochs III, 1984; Ochs III and Beard, 1984) but does not limit the generality of our findings. For the computation of w_sed, ρ_air=1.225 kg m⁻³ is assumed analogously to Bott (1998) as this enables conclusive comparisons with bin and box model results.

The average number of collisions from ν_i droplets of mass m_i and ν_j droplets of mass m_j (which are assumed to be well-mixed in the volume δV) within time δt is

$$\begin{array}{}\text{(6)}& {\mathit{\nu }}_{\text{coll}}=K_{ij}^{\mathrm{WM}\mathrm{3}\mathrm{D}}{\mathit{\nu }}_i{\mathit{\nu }}_j\mathit{\delta }t\mathit{\delta }{V}^{-\mathrm{1}},\end{array}$$

or equivalently

$$\begin{array}{}\text{(7)}& {\mathit{\nu }}_{\text{coll}}=E_{\text{c}}(r_i,r_j)\mathit{\pi }(r_i+r_j{)}^{\mathrm{2}}|w_{\mathrm{sed},i}-w_{\mathrm{sed},j}|{\mathit{\nu }}_i{\mathit{\nu }}_j\mathit{\delta }{V}^{-\mathrm{1}}\mathit{\delta }t.\end{array}$$

By dividing the above equation by δV, we obtain the common relationship in terms of concentrations, given by $n=\mathit{\nu }/\mathit{\delta }V$,

$$\begin{array}{}\text{(8)}& n_{\text{coll}}=E_{\text{c}}(r_i,r_j)\mathit{\pi }(r_i+r_j{)}^{\mathrm{2}}|w_{\mathrm{sed},i}-w_{\mathrm{sed},j}|n_i{n}_j\mathit{\delta }t.\end{array}$$

Sedimentation and collisional growth are the only processes considered in this study, and any effects of diffusional growth are neglected.

An exponential DSD is used to prescribe the cloud droplets in the beginning

$$\begin{array}{}\text{(9)}& f_{\mathrm{m}}\left(m\right)={\displaystyle \frac{\text{DNC}}{\stackrel{\mathrm{‾}}{m}}}\exp \left(-{\displaystyle \frac{m}{\stackrel{\mathrm{‾}}{m}}}\right).\end{array}$$

As in U2017, Berry (1967) or Wang et al. (2007), we choose by default a mean mass $\stackrel{\mathrm{‾}}{m}=\text{LWC}/\text{DNC}$ that corresponds to a mean droplet radius of r_init=9.3 µm and a droplet number concentration DNC${}_{\text{init}}=\mathrm{2.97}\times {\mathrm{10}}^{\mathrm{8}}$m⁻³ (resulting in a droplet mass concentration of LWC${}_{\text{init}}={\mathrm{10}}^{-\mathrm{3}}$ kg m⁻³).

The function f_m(m) is the number density function with respect to mass. The moments are defined as

$$\begin{array}{}\text{(10)}& {\mathit{\lambda }}_l\left(t\right)=\int m^l{f}_{\mathrm{m}}(m,t)\mathrm{d}m,\end{array}$$

with order l, which gives DNC=λ₀, LWC=λ₁ and Z=λ₂. We will refer to Z as radar reflectivity since the radar reflectivity is proportional to λ₂.

For an exponential DSD, the moments can be expressed analytically as

$$\begin{array}{}\text{(11)}& {\mathit{\lambda }}_{l,\mathrm{anal}}=(l-\mathrm{1})\mathrm{!}\text{DNC}{\stackrel{\mathrm{‾}}{m}}^l.\end{array}$$

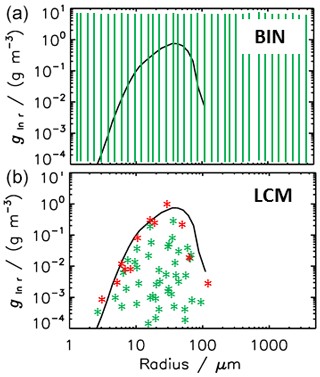
Figure 1 Schematic plot of how a droplet size distribution is discretised in a bin model and represented by a SIP (simulation particle) ensemble in a Lagrangian cloud model (LCM). The red and green stars shows two different realisations of a SIP ensemble.

Using the terminology of Berry (1967), we introduce the mass density function with respect to the logarithm of droplet radius ln r:

$$\begin{array}{}\text{(12)}& g_{\ln \mathrm{r}}\left(r\right)=\mathrm{3}{m}^{\mathrm{2}}{f}_{\mathrm{m}}\left(m\right),\end{array}$$

taking into account the transformation property of distributions (f_y(y)dy=f_x(x(y))dx).

The DSD is usually discretised using exponentially increasing bin sizes. In analogy to U2017, the bin boundaries are defined by the masses

$$\begin{array}{}\text{(13)}& m_{\mathrm{bb},p+\mathrm{1}}=m_{\mathrm{bb},p}{\mathrm{10}}^{\mathrm{1}/\mathit{\kappa }}.\end{array}$$

Note that many other studies use a factor of 2^1∕s for discretisation. The parameters s and κ are related via $s=\mathit{\kappa }{\log }_{\mathrm{10}}\left(\mathrm{2}\right)\approx \mathrm{0.3}\mathit{\kappa }$.

In an LCM, real droplets are represented by simulation particles (SIPs, also called super-droplets). Each SIP has a discrete position (vertical coordinate z_p in our column model applications) and represents ν_p identical real droplets with an individual droplet mass μ_p. The total droplet mass in a SIP is then ν_pμ_p. In conjunction with SIPs, we define that the terms “low” and “high” relate to the SIP vertical position, whereas “small” and “large” relate to the droplet mass μ_p. The number of SIPs in a GB is defined as N_SIP,GB and the total SIP number is given by $N_{\text{SIP,tot}}={\sum }_{k=\mathrm{1}}^{n_z}{N}_{\text{SIP,GB}}\left(k\right)$.

The moments λ_l of order l in a GB are computed via a simple summation:

$$\begin{array}{}\text{(14)}& {\mathit{\lambda }}_{l,\mathrm{SIP}}=\left(\sum _{p=\mathrm{1}}^{N_{\mathrm{SIP},\mathrm{GB}}}{\mathit{\nu }}_p{\mathit{\mu }}_p^l\right)/\phantom{\sum _{pi=\mathrm{0}}^{N_{\mathrm{SIP}}}{\mathit{\nu }}_p{{\mathit{\mu }}_p}^l}\mathrm{\Delta }V,\end{array}$$

Here and in the following, index p refers to any single bin or SIP. If we want to stress that the combination of two SIPs or bins matters, we use indices i and j. Index k is used for altitude and l for the order of the moments by convention.

How does one represent an ensemble of droplets in an Eulerian or Lagrangian cloud model? Their size distribution can be uniquely described in a bin model by simply accounting for each real droplet in its respective bin, where its boundaries are given by the bin model (see illustration in Fig. 1a). In the Lagrangian approach, however, the weighting factor ν_i and the droplet mass μ_i can be chosen independently. Accordingly, there is no unique SIP representation of an ensemble of real droplets; two possible SIP ensemble realisations are illustrated in Fig. 1b.

Various techniques to generate a SIP ensemble in an LCM for a given (analytically prescribed) DSD exist (see Sect. 2.1 in U2017). In this study, we use a SIP initialisation technique (termed “singleSIP-init” in U2017), for which Lagrangian collection algorithms, and in particular AON, achieved the best results in box model tests. In the singleSIP-init, the DSD, more specifically f_m, is discretised in exponentially increasing mass intervals, and a single SIP is generated for each bin (see Sect. 2.1.1 in U2017 for details). The SIP weight is given by

$$\begin{array}{}\text{(15)}& {\mathit{\nu }}_p=f_{\mathrm{m}}\left({\mathit{\mu }}_p\right)\mathrm{\Delta }{m}_{\mathrm{bb},p}\mathrm{\Delta }V,\end{array}$$

where μ_p is chosen randomly from the interval $[m_{\mathrm{bb},p},m_{\mathrm{bb},p+\mathrm{1}})$. The generation of SIPs with ν_p below some threshold is discarded. Due to the probabilistic component, different realisations of SIP ensembles can be created for the same prescribed DSD, and yet the initialisation technique guarantees that the moments λ_l,SIP are close to λ_l,anal. The number of generated SIPs depends on the width of the mass bins and hence on κ, as well as the other parameters of the prescribed DSD. A change of the “system size” ΔV does not change the number of SIPs but simply leads to a rescaling of the SIP weights ν_i. For the exponential DSD given above, around

$$\begin{array}{}\text{(16)}& N_{\text{SIP,GB}}=\mathrm{5}\times \mathit{\kappa }\end{array}$$

SIPs are initialised (the scaling factor depends on the width of DSD and the choice of the lower cut-off threshold). Finally note that if the DSD is prescribed in a specific GB, the position z_p of each SIP in this GB is randomly chosen from $[z_k,z_{k+\mathrm{1}})$. Furthermore, δt and δV of the conceptual model take the values Δt and ΔV in the numerical models.

2.2 Eulerian column model

Eulerian column models have been widely employed in cloud physics, and the present bin implementation is conceptually similar to previous ones (e.g. Prat and Barros, 2007; Stevens and Seifert, 2008; Hu and Srivastava, 1995). We use exponentially increasing bin sizes as defined in Eq. (13). The smallest mass m_bb,0 is chosen to be suitably small (corresponding roughly to a droplet radius of 1 µm), and the grid resolution parameter s sufficiently large (4 by default); i.e. the mass doubles every four bins.

The variable $g_{\ln \mathrm{m}}=\frac{\mathrm{1}}{\mathrm{3}}{g}_{\ln \mathrm{r}}$ will be discretised in mass space and used as a prognostic variable. The droplet mass concentration in each bin p and height k is given by $g_{p,k}\times \mathrm{d}\ln m$ and approximates ${\int }_{m_{\mathrm{bb},p}}^{m_{\mathrm{bb},p+\mathrm{1}}}{g}_{\ln \mathrm{m}}(m,z_k)\mathrm{d}\ln m$. For each GB k, Bott's exponential flux method (Bott, 1998, 2000) is used to solve the Smoluchowski equation. Bott's method is a one-moment scheme and g_ln m is the only prognostic variable. Alternatively, the collection algorithm by Wang et al. (2007) is employed, which additionally employs a prognostic equation for the droplet number concentrations in each bin.

In a second step, the mass concentrations are advected vertically according to the classical advection equation

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{\partial g_{\ln \mathrm{m}}}{\partial t}}=w_{\mathrm{sed}}{\displaystyle \frac{\partial g_{\ln \mathrm{m}}}{\partial z}}.\end{array}$$

For its numerical solution, two different positive definite advection algorithms have been used. The first option is the classical first-order upwind scheme (known for its inherent numerical diffusivity). For w_sed≥0, it is simply given by

$$\begin{array}{}\text{(18)}& g_{p,k}(t+\mathrm{\Delta }t)=g_{p,k}\left(t\right)+{\displaystyle \frac{\mathrm{\Delta }t}{\mathrm{\Delta }z}}{w}_{\mathrm{sed}}\left({\stackrel{\mathrm{‾}}{m}}_{\mathrm{bb},p}\right)\left(g_{p,k+\mathrm{1}}\right(t)-g_{p,k}(t\left)\right).\end{array}$$

The above equation is solved independently for each bin p, where w_sed is evaluated at the arithmetic bin centre ${\stackrel{\mathrm{‾}}{m}}_{\mathrm{bb},p}=\mathrm{0.5}(m_{\mathrm{bb},p+\mathrm{1}}+m_{\mathrm{bb},p})$. ¹ A second option is the popular MPDATA algorithm, which is an iterative solver based on the upwind scheme and yet drastically reduces its diffusivity (Smolarkiewicz, 1984, 2006). By default, the basic MPDATA with two passes is employed as described in Sect. 2.1 of Smolarkiewicz and Margolin (1998).

Irrespective of the chosen advection solver, the prediction of the “new” g_p,k depends on g_p,k and $g_{p,k+\mathrm{1}}$ (i.e. the GB above the one of interest). For the prediction of $g_{p,n_z}$ at the model top, it is necessary to prescribe the value $g_{p,n_z+\mathrm{1}}$, which defines the upper boundary condition (this is detailed in Sect. 2.4).

If the prescribed Δt is too large and the Courant–Friedrichs–Levy (CFL) criterion $\frac{\mathrm{\Delta }t}{\mathrm{\Delta }z}{w}_{\mathrm{sed}}\left({\stackrel{\mathrm{‾}}{m}}_{\mathrm{bb},p}\right)\le r_{\text{CFL}}<\mathrm{1}$ is violated, sub-cycling is introduced. As $w_{\mathrm{sed}}\left({\stackrel{\mathrm{‾}}{m}}_{\mathrm{bb},p}\right)$ does not change over the course of a simulation, the (bin-dependent) number of subcycles n_subc,p is determined in the beginning, such that r_CFL=0.5 holds for the reduced time step $\frac{\mathrm{\Delta }t}{n_{\mathrm{subc},p}}$.

After one call of Bott's algorithm, n_subc,p calls of the selected advection algorithm with reduced time step $\frac{\mathrm{\Delta }t}{n_{\mathrm{subc},p}}$ follow for each bin p.

The moments are computed by

$$\begin{array}{}\text{(19)}& {\mathit{\lambda }}_{l,\mathrm{BIN}}=\sum _{p=\mathrm{1}}^{N_{\mathrm{BIN}}}{g}_{p,k}({\stackrel{\mathrm{̃}}{m}}_{\mathrm{bb},p}{)}^{l-\mathrm{1}}{\displaystyle \frac{\ln \mathrm{2}}{\mathrm{3}s}}\end{array}$$

as given in Eq. (48) of Wang et al. (2007), where ${\stackrel{\mathrm{̃}}{m}}_{\mathrm{bb},p}=m_{\mathrm{bb},p}\times {\mathrm{2}}^{\mathrm{1}/\left(\mathrm{2}s\right)}$ is the geometric bin centre.

2.3 Lagrangian column model

In a Lagrangian model, the inclusion of sedimentation (obeying the transport equation $\text{d}z/\text{d}t=-w_{\mathrm{sed}}$) is straightforward. For each SIP the particle position is updated via

$$\begin{array}{}\text{(20)}& z_p(t+\mathrm{\Delta }t)=z_p\left(t\right)-w_{\mathrm{sed}}\left({\mathit{\mu }}_p\right(t\left)\right)\mathrm{\Delta }t.\end{array}$$

Unlike in Eulerian methods, sedimentation in a Lagrangian approach is independent of the chosen mesh, and the time step is not restricted by numerical reasons. If z_p becomes negative at some point in time, the SIP crossed the lower boundary and is removed.

For the collection process, it assumed that each SIP belongs to a certain GB k obeying $z_{k-\mathrm{1}}\le z_p<z_k$ and that the real droplets of each SIP are well-mixed in the GB volume (WM3D). The collection process is treated with the probabilistic AON algorithm. In the regular version (see Sect. 2.3.1), AON is called for each GB and accounts for all possible collisions among any two SIPs of the same GB. By construction, the information on the vertical position is irrelevant inside the regular AON and is only used in the SIP-to-GB assignment.

In the version with explicit overtakes (WM2D; see Sect. 2.3.2), for any two SIPs (of the whole column) it is checked if the higher SIP (i.e. with larger z_p) overtakes the lower SIP within the current time step. This may have several advantages: First, only 2D well-mixedness in a horizontal plane is assumed and possible size sorting effects within a GB are accounted for. Moreover, in Lagrangian methods the time step is not restricted by the CFL criterion and the largest SIPs may travel through more than one GB. In the classical approach, such a SIP can only collect SIPs from the GB where it was present in the beginning of the time step. In the second approach, collections can also occur across GB boundaries (see Sect. 2.3.2).

In the remainder of this paper, the classical approach is referred to as AON-regular and the new approach as AON-WM2D. Figure 2 sketches how the SIP properties (location, weighting factor, sedimentation speed) are interpreted in either approach. For simplicity, a single GB with one SIP pair is displayed.

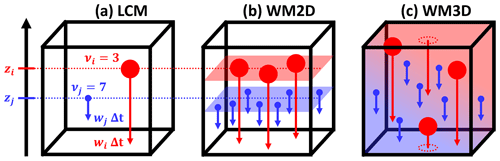
Figure 2 Grid box with a SIP pair in the LCM world (a) and its respective interpretation in the 2D well-mixed (WM2D, b) and 3D well-mixed (WM3D, c) approach of the AON collisional growth algorithm.

AON is probabilistic and an individual realisation does not usually reproduce the mean state as predicted by deterministic methods like Eulerian approaches. The extent of deviations from the mean state is exemplified in Fig. 15 of U2017 for a box model application of AON. Hence, the AON results discussed in the present study are usually ensemble averages over nr_inst=20 realisations.

Pseudo-code of both algorithm implementations is given. For the sake of readability, the pseudo-code examples show easy-to-understand implementations. The actual codes of the algorithms are, however, optimised in terms of computational efficiency. The style conventions for the pseudo-code examples are as follows: commands of the algorithms are written in upright font with keywords in boldface. Comments appear in italic font (explanations are enclosed by brace brackets {}, and headings of code blocks are in boldface).

2.3.1 Regular AON algorithm (AON-regular)

Here we basically repeat the AON description of U2017 (their Sect. 2.5).

Pseudo-code of the regular all-or-nothing (AON) algorithm; style conventions are explained right before Sect. 2.3.1 starts; rand() generates uniformly distributed random numbers $\in [\mathrm{0},\mathrm{1})$. This AON version is called independently for each grid box.

“Figure 3 illustrates how a collection between two SIPs is treated. SIP i is assumed to represent fewer droplets than SIP j, i.e. ν_i<ν_j. Each real droplet in SIP i collects one real droplet from SIP j. Hence, SIP i contains ν_i=4 droplets, now with mass ${\mathit{\mu }}_i+{\mathit{\mu }}_j=\mathrm{15}$. SIP j now contains ${\mathit{\nu }}_j-{\mathit{\nu }}_i=\mathrm{8}-\mathrm{4}=\mathrm{4}$ droplets with mass μ_j=9. Following Eq. (7), only ν_coll=2 pairs of droplets would, however, merge in reality. The idea behind this probabilistic AON is that such a collection event is realised only under certain circumstances in the model, namely such that the expectation values of collection events in the model and in the real world are the same. This is achieved if a collection event occurs with probability

$$\begin{array}{}\text{(21)}& p_{\mathrm{crit}}={\mathit{\nu }}_{\mathrm{coll}}/{\mathit{\nu }}_i\end{array}$$

in the model. Then, the average number of collections in the model,

$$\begin{array}{}\text{(22)}& {\stackrel{\mathrm{‾}}{\mathit{\nu }}}_{\mathrm{coll}}=p_{\mathrm{crit}}{\mathit{\nu }}_i=({\mathit{\nu }}_{\mathrm{coll}}/{\mathit{\nu }}_i){\mathit{\nu }}_i,\end{array}$$

is equal to ν_coll as in the real world. A collection event between two SIPs occurs if p_crit > rand(). The function rand() provides uniformly distributed random numbers $\in [\mathrm{0},\mathrm{1}]$. Noticeably, no operation on a specific SIP pair is performed if p_crit<rand().

The treatment of the special case ${\mathit{\nu }}_{\mathrm{coll}}/{\mathit{\nu }}_i>\mathrm{1}$ needs some clarification. This case is regularly encountered when SIPs with large droplets and small ν_i collect small droplets from a SIP with large ν_j. The large difference in droplet masses μ led to large kernel values and high ν_coll with ${\mathit{\nu }}_i<{\mathit{\nu }}_{\mathrm{coll}}<{\mathit{\nu }}_j$. […] If p_crit>1, we allow multiple collections, as each droplet in SIP i is allowed to collect more than one droplet from SIP j. In total, SIP i collects ν_coll droplets from SIP j and distributes them on ν_i droplets. A total mass of ν_collμ_j is transferred from SIP j to SIP i and the droplet mass in SIPs i becomes ${\mathit{\mu }}_i^{\mathrm{new}}=({\mathit{\nu }}_i{\mathit{\mu }}_i+{\mathit{\nu }}_{\mathrm{coll}}{\mathit{\mu }}_j)/{\mathit{\nu }}_i$. The number of droplets in SIP j is reduced by ν_coll and ${\mathit{\nu }}_j^{\mathrm{new}}={\mathit{\nu }}_j-{\mathit{\nu }}_{\mathrm{coll}}$. Keeping with the example in Fig. 3 and assuming ν_coll=5, each of the ν_i=4 droplets would collect ${\mathit{\nu }}_{\mathrm{coll}}/{\mathit{\nu }}_i=\mathrm{1.25}$ droplets. The properties of SIP i and SIP j are then ν_i=4, μ_i=17.25, ν_j=3 and μ_j=9. […] So far, we explained how a single i–j combination is treated in AON. In every time step, the full algorithm simply checks each i−j combination for a possible collection event. To avoid double counting, only combinations with i<j. Pseudo-code of the algorithm is given in Algorithm (1). The SIP properties are updated on the fly. If a certain SIP is involved in a collection event in the model and changes its properties, all subsequent combinations with this SIP take into account the updated SIP properties. […] For the generation of the random numbers, the well-proven (L'Ecuyer and Simard, 2007) Mersenne Twister algorithm by Matsumoto and Nishimura (1998) is used.”

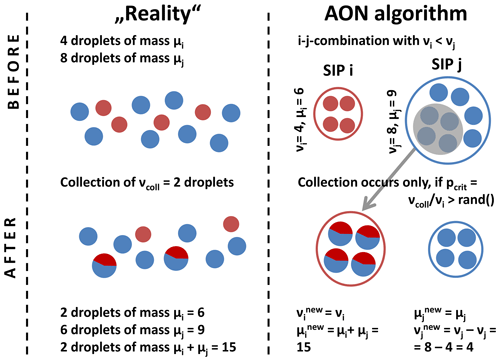
Figure 3 Treatment of a collection between two SIPs in the all-or-nothing (AON) algorithm, partially adopted from Fig. 2 of Unterstrasser et al. (2017).

The AON treatment of collection of droplets within one SIP, as well as the collection of two SIPs with equal weighting factors, is described in U2017. In the simulations presented here these aspects are not relevant and thus omitted.

The current implementation differs in several aspects from the version in Shima et al. (2009). First, they use a linear sampling approach (which will be described in Sect. 2.3.3). Second, the weighting factors are considered to be integer numbers, whereas we use real numbers ν. Integer values are appropriate in discrete test cases of small sample volumes such as the validation test case in Sect. 3 of Dziekan and Pawlowska (2017). For comparing AON with bin model references, usually continuous DSDs are prescribed. Then a SIP ensemble with real-value weighting factors is more appropriate in our opinion. Third, multiple collections (MCs) are differently treated. For $p_{\text{crit}}=({\mathit{\nu }}_{\text{coll}}/{\mathit{\nu }}_i)>\mathrm{1}$, either ⌊p_crit⌋ν_i or ⌈p_crit⌉ν_i droplets of SIP j merge with ν_i droplets of SIP i depending on the probability p_crit−⌊p_crit⌋. This maintains the integer property of the SIP weights. As the latter feature is not required in our approach, we deterministically merge p_critν_i=ν_coll droplets from SIP j with ν_i droplets of SIP i. This is computationally more efficient than the integer-preserving implementation. Test simulations showed that both MC treatments produce similar results.

2.3.2 AON algorithm with explicit use of vertical coordinate (AON-WM2D)

Pseudo-code of the AON-WM2D algorithm; style conventions are explained right before Sect. 2.3.1 starts; rand() generates uniformly distributed random numbers $\in [\mathrm{0},\mathrm{1})$. This AON version is called once for the total column.

We now introduce the AON version based on an idea by Sölch and Kärcher (2010) where the vertical position z_p of the SIPs is explicitly considered. The approach and its implications will be detailed next. Pseudo-code of this AON version (“WM2D”) is given in Algorithm Pseudo-code of the AON-WM2D algorithm; style conventions are explained right before Sect.  starts; rand() generates uniformly distributed random numbers ∈[0,1). This AON version is called once for the total column..

Unlike the classical case where 3D well-mixedness has to be assumed, droplets of a SIP are now assumed to be well-mixed on the x–y plane at z=z_p within the GB (horizontally well-mixed instead of the traditional well-mixed assumption for the entire three-dimensional GB) and represent a “concentration” of $n_{\mathrm{2}D}=\mathit{\nu }/\mathit{\delta }A$ (units L⁻², where L is a length scale). We introduce an adapted kernel definition where the relative velocity term $|w_{\mathrm{sed},i}-w_{\mathrm{sed},j}|$ is dropped from Eq. (5):

$$\begin{array}{}\text{(23)}& K_{ij}^{\mathrm{WM}\mathrm{2}\mathrm{D}}:=E_{\text{c}}(r_i,r_j)\mathit{\pi }(r_i+r_j{)}^{\mathrm{2}}.\end{array}$$

The AON algorithm is split into two steps:

1. Based on the evaluation of the vertical positions z_i and z_j at times t and t+Δt, a check is made to see if SIP i overtakes SIP j within a time step Δt. Given z_i(t)≥z_j(t) (otherwise swap i and j) an overtake takes place in the time interval Δt if $z_i(t+\mathrm{\Delta }t)<z_j(t+\mathrm{\Delta }t)$.

2. In case of such an overtake: compute the average number of droplet collections by

   $$\begin{array}{}\text{(24)}& {\mathit{\nu }}_{\text{coll}}=K_{ij}^{\mathrm{WM}\mathrm{2}\mathrm{D}}{\mathit{\nu }}_i{\mathit{\nu }}_j\mathrm{\Delta }{A}^{-\mathrm{1}}.\end{array}$$

   Analogous to the classical implementation, a collection in the model is performed with a probability ν_coll∕ν_i and SIP i may collect ν_i from SIP j (in this step i and j are chosen such that ν_i<ν_j).

Similarly to the WM3D version, it happens that ν_coll is larger than ν_i, and multiple collections are also considered in AON-WM2D.

Specifically to WM2D, it is also possible that a SIP interacts with other SIPs located in not only one but several GBs. Accordingly, it is not only necessary to check overtakes of other SIPs in the original GB (more specifically, SIPs that lie in the same GB at time t), but also the SIPs that are located underneath, depending on the prescribed time step.

In a Lagrangian model, the time step choice is not numerically restricted by the CFL criterion and in particular the largest collecting drops may fall through several GBs during the time period Δt. Hence, their collections are underrated unless potential overtakes are checked among all N_SIP,tot SIPs of the entire column. Even if the CFL criterion is obeyed, SIPs close to the lower GB boundary will mostly collect SIPs from the GB underneath. Hence, seeking collision candidates only in the present GB is never a good choice.

In a naive implementation, this would dramatically increase the computational costs. In the regular (WM3D) version, n_z calls of AON with $\mathcal{O}\left({N_{\text{SIP,GB}}}^{\mathrm{2}}\right)$ (for simplicity lets assume N_SIP,GB is the same in all GBs) give a total cost of $n_z\times \mathcal{O}\left({N_{\text{SIP,GB}}}^{\mathrm{2}}\right)$. Contrarily, AON-WM2D is called once for all SIPs of the column. Hence the cost is $\mathrm{1}\times \mathcal{O}\left({N_{\text{SIP,tot}}}^{\mathrm{2}}\right)=n_z^{\mathrm{2}}\times \mathcal{O}\left({N_{\text{SIP,GB}}}^{\mathrm{2}}\right)$ and a factor n_z higher than the regular AON version. However, the WM2D version can be sped up by first sorting all SIPs by their position (if sorting is done independently in each GB, the complexity is n_z×𝒪(N_SIP,GBlog (N_SIP,GB))), and second by taking into account that the final position z_i(t+Δt) of the potentially overtaking SIP i must be below the initial position z_j(t) of SIP j. Finding possible candidates for SIP i within the sorted SIP list can be stopped once a SIP j with $z_j\left(t\right)<z_i(t+\mathrm{\Delta }t)$ is encountered (see condition in line 10 of Algorithm Pseudo-code of the AON-WM2D algorithm; style conventions are explained right before Sect.  starts; rand() generates uniformly distributed random numbers ∈[0,1). This AON version is called once for the total column.).

For the smallest SIPs, which often travel only a small distance inside a GB, the list of SIPs that may be overtaken is commensurately small and overtakes have to be checked for a fraction of SIPs of the GB only (that means the actual computational work is smaller than in the regular version). On the other hand, imagine the largest SIPs travel through three GBs – then overtakes have to be tested for roughly 3 times more SIPs than in the regular version. Moreover, testing for overtakes (step 1) is computationally less demanding than calculating the potential collections (step 2). In WM3D we always have the workload of step 2 for all tested combinations, whereas in WM2D only the cheaper step 1 is executed in case of no overtake.

Besides the weaker assumption of 2D well-mixedness, the present approach is actually more intuitive (even though it may first be regarded counter-intuitive by those who are familiar with traditional Eulerian grid-based approaches). Moreover, this approach complies better with the Lagrangian paradigm of a grid-free description (the present approach is independent of n_z and Δz, and yet some horizontal “mixing area” ΔA has to defined, over which the droplets of a SIP are assumed to be dispersed). In the regular AON, the aspect ratios of the grid box do not matter, and only the grid box volume ΔV enters the computations. In WM2D, on the other hand, the value of ΔV is insignificant, and ΔA enters the computations. In a column model with sedimentation, results also depend on Δz as it determines the travel time through a grid box. Note that a variation of Δz can also implicitly change ΔV or ΔA.

For more sophisticated kernels, including for example turbulence enhancement, the present approach may not be adopted easily as the driving mechanism for collisions to occur in the current model is differential sedimentation. Related to this are studies on cylindrical vs. spherical formulations of kernels in Saffman and Turner (1956) and Wang et al. (1998, 2005). A possible route to consider the effects of sub-grid motions on collision in LCMs has recently been presented by Krueger and Kerstein (2018). Their one-dimensional approach is able to represent droplet clustering and turbulence-induced relative droplet velocities in a realistic manner, and its implementation in already applied LCM sub-grid-scale models (e.g. Hoffmann et al., 2019; Hoffmann and Feingold, 2019) is deemed straightforward. However, further research is required on how the limited number of SIPs in current LCM applications may corrupt the correct representation of such processes.

Finally, we briefly summarise the differences between the WM2D and WM3D approach. The standard kernel K^WM3D as given by Eq. (5) has units L³∕T (where L and T are a length scale and timescale, resp.). Multiplying it by concentrations n_i and n_j (units L⁻³), one obtains the rate of a concentration increase in merged droplets ($L^{-\mathrm{3}}/T$) which is finally multiplied by δt (unit T) to obtain n_coll (see Eq. 8). Since SIPs represent droplet concentrations of $n_i={\mathit{\nu }}_i/\mathit{\delta }V$ and $n_j={\mathit{\nu }}_j/\mathit{\delta }V$, Eq. (7) follows. In the WM2D approach, the kernel K^WM2D as given by Eq. (23) has units L². Multiplying it by “2D” concentrations n_2D,i and n_2D,j (units L⁻²) one obtains the collected 2D concentration n_2D,coll (units L⁻²). Since SIPs represent “2D” droplet concentrations of $n_{\mathrm{2}\mathrm{D},i}={\mathit{\nu }}_i/\mathit{\delta }A$ and $n_j={\mathit{\nu }}_{\mathrm{2}\mathrm{D},j}/\mathit{\delta }A$, Eq. (24) follows. A collection can only occur if a larger droplet (or SIP) i overtakes a smaller droplet (or SIP) j. First, z_i>z_j and $w_{\mathrm{sed},i}>w_{\mathrm{sed},j}$ must hold and second the overtake time $\mathrm{\Delta }{t}_{\text{OT}}:=(z_i-z_j)\times (w_{\mathrm{sed},i}-w_{\mathrm{sed},j}{)}^{-\mathrm{1}}$ must fulfil Δt_OT≤δt. One can define the overtake probability p^OT being 0 for Δt_OT>δt and 1 for Δt_OT≤δt, and the “2D” collection probability $p_{ij}^{\mathrm{WM}\mathrm{2}\mathrm{D}}=K_{ij}^{\mathrm{WM}\mathrm{2}\mathrm{D}}\mathit{\delta }{A}^{-\mathrm{1}}$. Simulations in the Supplement demonstrate that the WM2D and WM3D formulations are statistically equivalent; i.e. p^OT×p^WM2D equals p^WM3D, under certain conditions (see Fig. S9).

From a technical point of view, it might be challenging to implement the WM2D version in full 2D/3D cloud models, as one has to keep track of all SIPs in a grid box column. If domain decomposition is used in a vertical direction, collision candidates had to be searched across multiple processors.

2.3.3 Linear sampling version (AON-LinSamp)

The regular AON version can be sped up by introducing a linear sampling technique (LinSamp) as done in Shima et al. (2009) or Dziekan and Pawlowska (2017). ⌊N_SIP∕2⌋ combinations of pairs i−j are randomly picked, where each SIP appears in exactly one pair (if N_SIP is odd, one SIP is ignored). As only a subset of all possible combinations is numerically evaluated, the extent of collisions is underestimated. To compensate for this, the probability p_crit (or equivalently ν_coll) is upscaled by a scaling factor

$$\begin{array}{}\text{(25)}& {\mathit{\gamma }}_{\text{corr}}=N_{\mathrm{SIP}}(N_{\mathrm{SIP}}-\mathrm{1})/(\mathrm{2}\lfloor N_{\mathrm{SIP}}/\mathrm{2}\rfloor )\end{array}$$

to guarantee an expectation value as desired. Clearly, this reduces the computational complexity of the algorithm from $\mathcal{O}\left({N_{\mathrm{SIP}}}^{\mathrm{2}}\right)$ to 𝒪(N_SIP). Multiple collections are more likely than in the regular AON version. The LinSamp version becomes the preferred choice if N_SIP is large.

If ν_coll is larger than both ν_i and ν_j, all AON versions as introduced so far would produce negative weights. In order to prevent this, ν_coll is artificially reduced to ν_j in such a case (let us assume that ν_i<ν_j). The standard procedure would then produce a SIP j with zero weight, which allows the updated SIP i with weight ν_i (the weight ν_i remains unchanged during the update) to be split into two SIPs. We choose a 60 %–40 % partitioning, and the operations are as follows.

$$\begin{array}{}\text{(26a)}& {\displaystyle }{\mathit{\mu }}_j& {\displaystyle }:=({\mathit{\nu }}_i{\mathit{\mu }}_i+{\mathit{\nu }}_j{\mathit{\mu }}_j)/{\mathit{\nu }}_i\text{(26b)}& {\displaystyle }{\mathit{\mu }}_i& {\displaystyle }:={\mathit{\mu }}_j\text{(26c)}& {\displaystyle }{\mathit{\nu }}_j& {\displaystyle }:=\mathrm{0.6}{\mathit{\nu }}_i\text{(26d)}& {\displaystyle }{\mathit{\nu }}_i& {\displaystyle }:=\mathrm{0.4}{\mathit{\nu }}_i\end{array}$$

The Supplement demonstrates that how the limiter is implemented is critical. We thank reviewer Shin-ichiro Shima for pointing us to a better limiter implementation, which has been already described in Shima et al. (2009). There, a 50 %–50 % partitioning was implemented. We avoid this equal splitting as it produces two identical SIPs. In our implementation with floating point weights, SIPs with identical weights are extremely rare and no special care is taken for this. Hence, including an operation that produces identical weights is unfavourable. The dependence of the AON-LinSamp performance on the limiter definition is showcased in the Supplement (Figs. S3–S7, S15 and S16 and Table S1).

Employing a limiter is recommended for all AON versions (even though we never encountered a limiter event in QuadSamp simulations), but it is particularly significant in the LinSamp version due to the upscaling of p_crit. Moreover, note that LinSamp can be reasonably used only in conjunction with AON-WM3D, not AON-WM2D.

In addition to the favourable linear computational complexity, LinSamp can be easily parallelised, in particular on shared-memory multi-processor architectures as used by Arabas et al. (2015) or Dziekan et al. (2019). Once the SIP pairs are determined in the beginning of each time step, each processor treats a subset of SIP pairs. After a collection event, SIP properties are updated on the fly. Note that the need to do updates on the fly precludes simple parallelisation strategies in the quadratic sampling version, where all SIPs are interconnected.

2.4 Boundary condition

At the lower boundary, droplets leave the domain according to their fall speed. Using the LCM, the moment outflow F_l,out is determined by accumulating the contributions ν_p(μ_p)^l of all SIPs p that cross the lower boundary z=0 m. Due to the discreteness of the crossings, instantaneous fluxes are actually averages of the past 200 s. Using the bin model, F_l,out is diagnosed by

$$\begin{array}{}\text{(27)}& F_{l,\mathrm{out}}=\sum _{p=\mathrm{1}}^{N_{\mathrm{BIN}}}{g}_{p,k=\mathrm{1}}\left({\stackrel{\mathrm{̃}}{m}}_{\mathrm{bb},p}{)}^{l-\mathrm{1}}{w}_{\mathrm{sed}}\right({\stackrel{\mathrm{̃}}{m}}_{\mathrm{bb},p}){\displaystyle \frac{\ln \mathrm{10}}{\mathrm{3}\mathit{\kappa }}}.\end{array}$$

At the model top, the simplest condition is to have a zero influx. In this case, the column-integrated droplet mass will decrease once a non-zero flux across the lower boundary occurs. To implement a zero-influx condition in the Eulerian model, the mass concentrations at the ghost cell level n_z+1 are simply set to zero. In the Lagrangian model, a zero influx condition is naturally implemented when no new SIPs are created at the top of the column.

In both models, a non-zero influx at the model top can also be prescribed. One option is to use periodic boundary conditions. In the Lagrangian approach this is done by increasing the altitude z_p of an affected SIP by L_z, once z_p drops below 0. In the Eulerian model, $g_{p,n_z+\mathrm{1}}$ is identified with g_p,1. A second non-zero influx option is a prescribed size distribution that is advected into the domain with its respective fall speed. In the bin model, the prescribed DSD simply defines the $g_{i,n_z+\mathrm{1}}$ values. In the Lagrangian model, new SIPs have to be introduced close to the model top. For this, a new SIP ensemble is drawn from the prescribed DSD at each time step using the SingleSIP-init method. In order to place the SIPs in the column, the greatest distance it would fall from the model top during one time step is considered: $z_{\mathrm{\Delta }}\left(p\right)=w_{\mathrm{sed},p}\times \mathrm{\Delta }t$. In a straightforward implementation, one would create one SIP from each bin with a position z_new,p uniformly drawn from $[L_z,L_z-z_{\mathrm{\Delta }}(p\left)\right)$ and weighting factor ${\mathit{\nu }}_{\text{new,p}}={\mathit{\nu }}_p\times \left(z_{\mathrm{\Delta }}\right(p)/\mathrm{\Delta }z)$. This implementation has, however, several undesirable side effects. For small, slowly falling SIPs z_Δ(p) is much smaller than Δz. Applying this procedure in every time step leads to Δz∕z_Δ(p) SIPs per GB in the end. Hence, we refine this procedure by creating a SIP with probability $p_{\mathrm{init},p}:=z_{\mathrm{\Delta }}\left(p\right)/\mathrm{\Delta }z$, a weighting factor ν_new,p=ν_p and $z_{\text{new,p}}\in [L_z,L_z-z_{\mathrm{\Delta }}(p\left)\right)$. Note that if $p_{\mathrm{init},p}>\mathrm{1}$, then either ⌊p_init,p⌋ or ⌈p_init,p⌉ SIPs are created depending on the probability $p_{\mathrm{init},p}-\lfloor p_{\mathrm{init},p}\rfloor$. This establishes a similar spatial SIP occurrence across the size spectrum with one SIP per GB and bin on average. Moreover, SIP numbers do not scale any longer with Δt.

Table 2 Summary of AON versions.

2.5 Terminology

Before we start discussing the results, we outline the terminology of the various model versions. On a first level, we differentiate between Eulerian (“BIN”) and Lagrangian approaches (“LCM”), which can be both applied in a box (“0D”) or column model (“1D”) framework. By default, BIN uses the MPDATA advection algorithm (clearly only in 1D) and Bott's collection algorithm. Alternatively, MPDATA can be replaced by the first-order upstream scheme (“US1”) and Bott's collection algorithm by Wang's algorithm (“Wang”). The Lagrangian model versions differ only in the way AON is employed. The various model versions are summarised in Table 2. By default, 3D well-mixedness (“WM3D”) is assumed and a quadratic sampling (“QuadSamp”) of the SIP combinations is used. Those simulations are referred to as “regular”. A second type of QuadSamp simulation assumes 2D well-mixedness (“WM2D”). Linear sampling of SIP combinations (“LinSamp”) can be alternatively used for the WM3D version. Accordingly, the terms “regular”, “WM2D” and “LinSamp” each refer to one specific AON version. On the other hand, “QuadSamp” and “WM3D” each denote two AON versions: “QuadSamp” comprises “regular” and “WM2D”, whereas “WM3D” comprises “regular” and “LinSamp”.

By switching off sedimentation in the column model source code (as partially done in Sect. 3.1), box model results are produced in each GB. In order to distinguish the latter simulations from AON box model results in U2017 they are referred to as “noSedi”. In LCM1D-noSedi simulations, the vertical position is not updated from time step to time step. Hence, this implicitly calls for the usage of AON-WM3D, as AON-WM2D relies on checking overtakes based on the vertical SIP positions. Simulations with switched-on sedimentation are the default; for better discrimination from the noSedi case we refer to all such simulations optionally as “full” simulations.

If the space in figure legends is limited, abbreviations “LS” and “nS” are used for “LinSamp” and “noSedi”, respectively.

3 Results

Before we start comparing collisional growth in column model applications, we should first demonstrate that the differences introduced by the different numerical treatment of the sedimentation process are small to negligible. This exercises is deferred to the Appendix.

We find the discrepancies introduced by the different sedimentation treatments small enough as long as the MPDATA advection algorithm is employed in BIN. Hence, all following BIN simulations rely on MPDATA and we can attribute the differences that we may see in the following validation exercises to the different numerical treatment of collisional growth.

3.1 Box model emulation simulations

In this section, we choose a column model set-up that is supposed to produce results that are similar to box model results. For this, we initialise the default DSD in all GBs of the column and use periodic boundary conditions. In LCM1D, different SIP ensemble realisations of this DSD are initialised in each GB.

The deterministic BIN1D model predicts identical DSDs in all GBs, as in each GB the divergence of the sedimentation flux is zero. Hence, for this specific set-up, the BIN1D results attained are identical to those of a corresponding BIN0D model or the data of Wang et al. (2007, see their Tables 3 and 4).

In LCM1D, the combination of homogeneous initial conditions and periodic BCs results in statistically identical results across all GBs. However, the averaged results may not be the same as in LCM0D, as lucky droplets or SIPs (Telford, 1955; Kostinski and Shaw, 2005) can collect other droplets or SIPs not only from a single GB as in LCM0D, but from any GB (depending on how fast they fall), creating potentially larger and/or faster-growing lucky droplets/SIPs than in LCM0D. In other words, the number of SIPs interacting with each other is increased in LCM1D. This, as we will show below, accelerates the convergence of the simulations.

Within the LCM1D model, pure box model results can be obtained by switching off sedimentation (“noSedi”). Without sedimentation, the GBs of the column are not interconnected and the collisional growth process proceeds independently.

All figures related to the box model emulation set-up start their caption with the label “BoxModelEmul set-up”.

By default, we use n_z=50 GBs with Δz=10 m (giving a column height of L_z=500 m), ΔV=1 m³, Δt=10 s and κ=40 throughout Sect. 3.1. The results are averaged over nr_inst=20 independent realisations. Hence, the present AON application can be viewed as a Monte Carlo method.

Moreover, we use the Long kernel (Long, 1974) as default in BoxModelEmul simulations, as U2017 revealed that numerical convergence is harder to reach for the Long kernel than for the Hall kernel or a hydrodynamic kernel with constant aggregation efficiency typically used for cirrus simulations (Sölch and Kärcher, 2010).

3.1.1 Regular AON version

This subsection presents results obtained with the regular AON, i.e. with quadratic sampling of SIP combinations (“QuadSamp”) and 3D well-mixed assumption (WM3D). Sedimentation is switched on unless noted (for better discrimination from the “noSedi” cases, these simulations will be referred to as “full”).

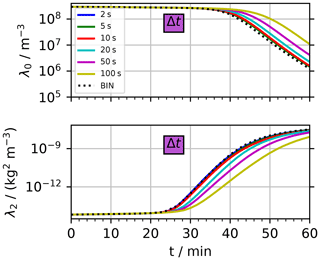
Figure 4 BoxModelEmul set-up: temporal evolution of column-averaged moments λ₀ and λ₂ over 1 h for various time steps Δt (see inserted legend for Δt values) for the regular AON version. All other parameters take the default values as given in the caption of Fig. 5.

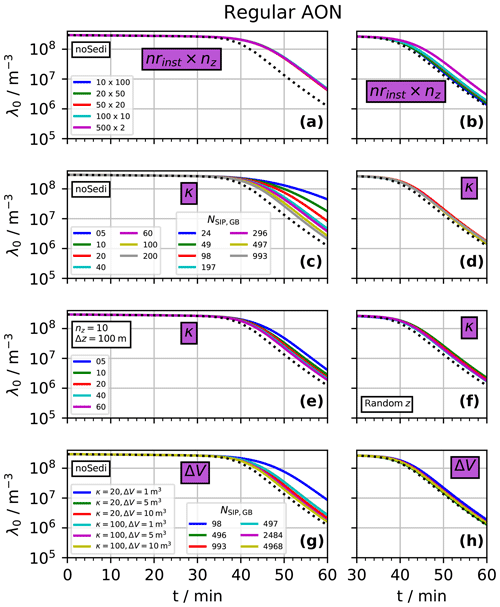
Figure 5 BoxModelEmul set-up: temporal evolution of column-averaged moment λ₀ (i.e. droplet concentration) over 1 h for the regular AON version. The default setting is n_z=50, nr_inst=20, ΔV=1 m³, Δt=10 s, Δz=10 m, κ=40 and $L_z=n_z\times \mathrm{\Delta }z$. The microphysical parameters of the initial exponential droplet size distribution are LWC_init=1 g m⁻³, r_init=9.3 µm and DNC_init=297 cm⁻³ as in many previous studies (Berry, 1967; Wang et al., 2007). The parameter or parameter pair that is varied is added in a purple box to each panel and the legend lists the parameter values for the different colours. If further parameters (besides the varied parameter) take non-default values, it is indicated inside a black rectangle. In any case, the total number of GBs is $n{r}_{\text{inst}}\times n_z=\mathrm{1000}$. By default, sedimentation is switched on. Simulations without sedimentation and independent rain formation in each GB (identical to a box model treatment) are labelled as “noSedi” (appear only in the left column). The panels on the right use a shortened time range.

Figure 4 shows the temporal evolution of column-averaged LCM1D moments λ_l (l=0 and 2) over 1 h for various time steps Δt. The box model data serve as orientation in this and following Figs. 5–7. We find that in terms of λ₀ and λ₂ LCM1D results converge for Δt≤10 s. The noSedi simulations show a similar time step dependence (not shown). Hence, AON works well even for large time steps, a fact that was already shown with the AON box model (see Fig. 18 of U2017).

Next, we discuss the sensitivity to further physical and numerical parameters. Generally, we find faster convergence for higher moments than for λ₀ (not shown). Hence in the following, we confine our analysis to the most “critical” quantity, and Fig. 5 displays the λ₀ evolution for various sensitivity experiments. Even though we analyse the results in some detail, we want to mention that the observed differences are in principle not substantial. In fact, results differ much more due to a different collection kernel or slightly varied initial DSDs (see Sect. 3.1.4). Nevertheless, the analysis will help to understand more deeply how collisional growth works in an LCM with AON. This pronounced effort is justified, as precipitation initiation is still not fully understood and a well-validated Lagrangian approach may lead to new insights (Dziekan and Pawlowska, 2017; Grabowski et al., 2019).

In a first simple step, we vary n_z (see Fig. 5a and b), which changes two aspects of the numerical set-up: the number of GBs over which interactions can occur and the height of the column. This implicitly changes the time it takes for SIPs to fall through the total column and hence changes the ”recycling” timescale L_z∕w_sed. Together with n_z, nr_inst is varied such that n_z×nr_inst is always 1000. Accordingly, all simulation results are averaged over the same number of GBs, and we avoid cases of simulations with smaller n_z producing noisier data.

In the noSedi simulations (panel a), the moment evolution is not affected by varying (n_z, nr_inst). This is trivial, as in any case the average is taken over 1000 independent GBs. At least, these results demonstrate that averaging over that many GBs suffices by far to produce robust averages. In the full simulations (panel b), the λ₀ decrease is more pronounced, and the various set-ups produce nearly identical results (except for the case with n_z=2, which is in between the other full simulations and the noSedi simulations). From this finding alone one may argue that the collisional growth process is more efficient in LCM1D than in LCM0D.

The second row shows a variation of κ which reveals qualitatively different convergence properties of the noSedi simulations (panel c) and the full simulations (panel d). In the noSedi simulations, an increase in κ (and N_SIP; see extra legend for corresponding N_SIP values) leads to a faster decrease in λ₀. Large differences between κ=5 and κ=40 simulations are apparent; above κ=40, an increase in κ leads only to marginal improvements. Also, for the highest κ, the λ₀ values remain above the BIN0D reference. For the smallest κ value, only 24 SIPs are created according to Eq. (16), and interactions among those few computational particles overemphasise the impact of correlations. It is well-known that for small ensembles of real droplets correlations become important (Bayewitz et al., 1974; Wang et al., 2006). Analogously, we introduced correlations in our numerical approach by using too few computational particles. We speculate that this hinders the formation of lucky droplets and fewer droplets get collected (hence λ₀ is larger for smaller κ). Another more technical explanation is that the ν_p distribution of the SIP ensemble is such that the formation of lucky SIPs is not supported. Ideally, there is a reservoir of SIPs with small ν values that can become lucky SIPs. There might be too few SIPs with small ν for small κ.

Contrarily, the full simulations (panel d) give nearly identical results independent of κ. We obtain converged results with as few as 24 SIPs in each GB. Compared to κ=200 with 1000 SIPs, the simulations are a factor of 40² faster. The reason for the much faster convergence in terms of N_SIP,GB is that the GBs are interconnected, which effectively raises the number of potential collision partners. Drops with radii of 100 and 500 µm have fall speeds of around 0.7 and 4 m s⁻¹, respectively. Thus it takes them around 14 and 2.5 s to fall through a Δz=10 m GB and they enter a new GB every time step or every few time steps given Δt=10 s.

How strongly SIPs are interconnected across GBs in LCM1D should also depend on geometrical properties of the column. In the next set-up, we investigate the κ sensitivity in a column with n_z=10 and Δz=100 m instead of n_z=50 and Δz=10 m (panel e). Then, SIP interactions can occur only across 10 GBs, and overall 5 times fewer SIPs are present in the column than for the default case with n_z=50. Moreover, the domain is stretched by increasing Δz to 100 m, which increases the residence time of a SIP in a GB by a factor of 10, additionally slowing down SIP interactions across GBs. Those two changes introduce a weak κ dependence, and yet it is much weaker than in the corresponding noSedi simulations (panel c).

In an even more academic experiment, sedimentation is turned off, but SIPs are randomly redistributed inside the column after each time step (panel f) similar to Schwenkel et al. (2018). Again, we find converged results for small κ values as small as 5 (panel f). This elucidates that convergence is improved once some process exchanges SIPs between GBs, be it for physical reasons like sedimentation or by an artificial operation such as the randomised SIP re-location. We speculate that in full 2D/3D LCM simulations turbulent motions and sedimentation increase the SIP exchange across GBs and hence may additionally increase the performance of AON. The two last simulation series are promising, as they suggest that in a column model (and probably also 2D or 3D models) convergence is potentially reached with fewer SIPs per GB than in a box model. Nevertheless the tests also highlight that convergence with κ depends on many circumstances and convergence tests are a prerequisite to any LCM simulation with AON.

In bin models, the Smoluchowski equation, which is strictly valid only for an infinite volume and hence an infinite number of well-mixed droplets, is solved. Accordingly, only concentrations are prescribed in bin model algorithms. Neither ΔV nor the absolute number of droplets is considered in this approach. At least in the limit of all SIPs having weighting factor ν=1, the AON algorithm solves the master equation (Dziekan and Pawlowska, 2017), which takes into account ΔV, and results may depend on the actual number of involved droplets. Clearly, correlations (which are accounted for in the master equation) are larger in smaller volumes (Bayewitz et al., 1974; Wang et al., 2006; Alfonso and Raga, 2017).

For our SIP-initialisation procedure, N_SIP,GB depends solely on the chosen κ values and is independent of ΔV. By construction, a ΔV variation does not affect at all the simulation results, as all SIP weights are simply rescaled. Indeed, we obtain nearly bit-identical results for a ΔV variation. To explore the ΔV sensitivity in our LCM1D, the SIP-init procedure has to be adapted. In the adapted version the SIP number increases proportionally with ΔV as it would in reality. As computational requirements increase quadratically with N_SIP,GB, the variation of ΔV and N_SIP,GB can be performed only for a small range of ΔV values. ΔV is increased by a factor of 5 or 10. As a base case, we use the simulations with κ=20 and κ=100 and define ΔV:=1 m³. The fourth row shows results for the noSedi (panel g) and the full simulations (panel h). Apparently, the noSedi simulations with larger ΔV converge to the solution we obtained before by using a sufficiently large κ. In full simulations, a ΔV variation has basically no effect. The κ=100, ΔV=10 m³ simulation considered on average collisions between 5000 SIPs in each GB. Yet, the results are basically identical to the case κ=5, ΔV=1 m³ with 24 SIPs in each GB (which runs nearly 40 000 times faster).

In the present simulations, where SIPs with weights ν>1 are used, variations of the numerical parameter κ and the physical parameter ΔV are interconnected and their effects cannot be disentangled. Hence, the AON algorithm can only answer whether correlations matter in systems with a certain number of SIPs. These correlations are not necessarily the correlations one would see in a real system with millions to billions of real droplets. Nevertheless, the last sensitivity series implies that at least in our model system the importance of correlations is likely the same as in a system with N_SIP,GB=24 and with N_SIP,GB≈5000. Assuming that the importance of correlations in a real system with billions of droplets is similar to that of a system with 5000 SIPs, the latter finding demonstrates that LCMs can capture the collisional growth process with astonishingly few SIPs.

The noSedi κ sensitivity series as shown in panel (c) was already presented in Fig. 18 of U2017. There we found that for high enough κ the LCM0D results lie below the BIN0D reference contradictory to the present noSedi simulations. The reason for this inconsistency is a programming bug in the LCM0D-AON version used in U2017. The Hall and Long kernel values are stored in look-up tables and were wrongly accessed (overestimating the actual mass of the involved droplets by 2 %). Hence, the collisional growth process proceeded more rapidly in U2017. Despite this flaw, the main findings of U2017 remain valid. Yet, the more rapid collisional growth of LCM0D-AON in U2017 should clearly not be attributed to conceptual differences of AON and BIN algorithms.

In the discussion of the subsequent sensitivity studies, we refrain from showing time series of λ₀ as done in Fig. 5. Instead we only evaluate λ₀ at t=1 h as this is a suitable metric for the algorithm performance in the BoxModelEmul set-up. Figure 6 comprises Δt and κ sensitivity series of all subsequent BoxModelEmul simulations. The black dotted (horizontal) line depicts the reference BIN result obtained with Wang's algorithm with s=16 and Δt=1 s and was already added in Fig. 5 for orientation.

Figure 6 BoxModelEmul set-up: this figure summarises results of many sensitivity studies for various AON versions and BIN simulations by displaying DNC after 1 h as a function of resolution κ (or analogously s in BIN models) or time step Δt. The default parameter settings are listed in Fig. 5 and the horizontal black dotted curve shows the BIN benchmark reference. For example, the information of Fig. 5c and d is compressed into the two grey curves in panel (a). Panels (a) and (b) additionally show AON simulations with linear sampling (as described in Sect. 2.3.3), unless “reg” in the legend indicates regular AON with quadratic sampling. “nS” is short for “NoSedi”. The second row shows simulations with explicit overtakes and a 2D well-mixed assumption (“WM2D”, as described in Sect. 2.3.2). Again, the regular AON with WM3D serves as reference. In the simulation labelled “WM2D(GB)”, overtakes are considered only between SIPs inside the same GB, whereas “WM2D” checks overtakes in the full column. Panel (e) shows a scenario with (increased) LWC_init=1.5 g m⁻³ and (f) uses the Hall kernel instead of the Long kernel. Note that the y ranges are different in the third row. The fourth row shows BIN results with Bott's and Wang's algorithms. The default parameters are s=4 and Δt=10 s.

3.1.2 AON with linear sampling

This subsection discusses the AON version with linear sampling. Both full simulations and noSedi simulations have been carried out. The first row of Fig. 6 shows sensitivity of λ₀(t=1 h) to κ (a) and Δt (b), respectively. The grey curves repeat the regular AON results (i.e. with quadratic sampling); they show the endpoints of curves shown in Fig. 4 (top) and Fig. 5c and d. We find that the qualitative behaviour does not differ between LinSamp and regular AON.

In the full simulations (solid lines), simulations converge for any κ, whereas for the noSedi simulations (dotted, “nS” in the legend) convergence is reached only for the largest κ values. Using the default time step Δt=10 s, the LinSamp results (orange curves) are slightly further away from the BIN reference (black dots) than the regular results. A second LinSamp series with Δt=1 s (blue) produces better results than the regular AON version with Δt=10 s.

The Δt sensitivity series shown in the right panels of Fig. 6 demonstrates that LinSamp results are slightly worse than the regular results for the default resolution κ=40. Using LinSamp with a finer resolution of κ=100 produces better results than the regular AON with κ=40. In LinSamp simulations with large time steps, limiter cases occur quite often and one may expect that the artificial reduction of collection events strongly deteriorates the model outcome. However, we see that the performance in the high-Δt range drops similarly in the LinSamp and regular AON version.

3.1.3 AON version with explicit overtakes

Next, we will discuss the results of the AON-WM2D version with explicit overtakes. Results are presented in Fig. 6c and d. For the chosen set-up with homogeneous initial conditions and periodic boundary conditions, 3D well-mixedness of the SIPs is expected to be maintained over the course of the simulation. Hence, the AON-WM3D and AON-WM2D version are supposed to produce similar outcomes.

The dotted, green curve in panel (d) shows results for the version where only intra-GB overtakes are considered. Results are far off the benchmark curve; only for the smallest time step of Δt=0.5 s do they become close to the reference. The solid, green curve shows a Δt variation (down to Δt=2 s) for the version where overtakes are considered across the full column. In the present example, it was also necessary to check for overtakes across the periodic boundary. Then, convergence is reached for Δt≤10 s, very similar to the regular (WM3D) version (see grey curve for comparison). Panel (c) shows a slight dependence on κ, and yet the performance of AON-WM2D is almost comparable to that of the regular AON results.

Overall, we can conclude that the feasibility and correct implementation of the WM2D version was demonstrated, with the caveat that overtakes have to be considered in the full column. Checking for overtakes outside of the “own” GB can cause some computational overhead in implementing the WM2D version in higher-dimensional cloud models, which are typically parallelised. If the chosen time step for collection obeys the CFL criterion (as argued in Shima et al., 2020), SIPs can at most travel from one GB to the one right below. Then, potential collision partners can only appear in two different GBs.

As noted in Sect. 2.3.2, the WM2D version can only be used in conjunction with kernels where the differential sedimentation term $|w_{\mathrm{sed},i}-w_{\mathrm{sed},j}|$ is explicitly included and can be dropped. Typically, this is not fulfilled for kernels accounting for turbulence enhancement, in which motions in all spatial directions need to be accounted for. Turbulence in cirrus clouds is often weak. Moreover, cirrus clouds often show a strong layering by ice crystal size, possibly making the 3D well-mixed assumption overly simplistic. Hence, the WM2D version appears to be a reasonable alternative to the regular (WM3D) version. Furthermore, the mixed-phase LCM of Shima et al. (2020) used for the simulation of a cumulonimbus employs a hydrodynamic kernel. Hence, the WM2D version would be applicable in this context as well.

3.1.4 Microphysical and bin model sensitivities

So far, all simulations were initialised with the same initial DSD and the same collection kernel, and the results have always been compared to the same BIN reference simulation.

Accordingly, in this section, we perform simulations with modified LWC_init, r_init and DNC_init. Moreover, we highlight the effect of the employed kernel on the AON performance. And finally, we also present BIN sensitivities (namely, we switch from Bott's algorithm to Wang's algorithm and vary the bin resolution and the time step).

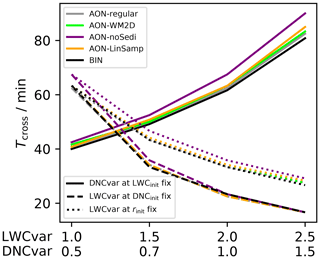
Figure 7 BoxModelEmul set-up: sensitivities to the initial size distribution parameters LWC_init, r_init and DNC_init are summarised by showing T_cross, which is defined as the time when λ₀ drops below 10⁷ m⁻³. LWC_init is varied (the x axis shows the scaling factor LWCvar relative to the default LWC_init) for either fixed DNC_init (dashed lines) or r_init (dotted lines). The solid lines depict a DNC_init variation for fixed LWC_init. Again, the scaling factor DNCvar is depicted on the x axis. Five different model versions, as indicated in the top-left legend, are used: regular AON (reg), AON-WM2D, regular AON with noSedi (“nS”), AON with LinSamp (“LS”) and BIN.

In a first experiment, we increase LWC_init by a factor of 1.5 and repeat the κ sensitivity test; see Fig. 6e. We keep DNC_init fixed and hence the mean radius is $r_{\text{init}}=\mathrm{9.3}\mathrm{\mu }\mathrm{m}\times {\mathrm{1.5}}^{(\mathrm{1}/\mathrm{3})}=\mathrm{10.7}$ µm. Compared to the base case with LWC_init=1 g m⁻³, λ₀ starts to decrease after 20 min (instead of 40 min; see Fig. S10). Eventually, λ₀ decreases below 10⁴ cm⁻³ (instead of 10⁶ cm⁻³). In the full simulations (all solid curves), we again find results nearly independent of κ for all tested AON versions (regular, LinSamp and WM2D). In the noSedi simulations (grey, dotted curve), fewer SIPs are necessary to obtain reasonable results compared to the base case in panel (a).

In a next step, the characteristics of the initial DSD are more systematically varied for fixed κ=40. For such a κ value the noSedi simulation of the base case was considerably off the reference. LWC_init=λ₁(t₀) is varied, for either fixed droplet number or fixed mean radius. The default value is scaled by a factor of 1.5,2.0 or 2.5. Similarly, DNC_init is varied by a factor of 0.5,0.7 or 1.5 keeping LWC_init constant.

A more detailed presentation of simulation results with time series of the mean diameter, λ₀ and λ₂ over 100 min is deferred to the Supplement (see Fig. S11). Here, we focus on a single metric again. We define T_cross as the time, when λ₀ drops below 10⁷ m⁻³. The smaller T_cross, the faster precipitation sets in. Figure 7 shows T_cross for all three sensitivity series (see lower left legend for the various line styles). Simulations with the BIN are contrasted with the regular AON, AON-WM2D, AON-noSedi and AON-LinSamp (see the top-left of the Fig. 7 for the various colours). T_cross and with it precipitation onset changes strongly with LWC_init and DNC_init. Generally, we find a similar behaviour across all tested models. The AON-noSedi version features the largest T_cross values. This is consistent with previous noSedi results in Fig. 5 where the decrease in λ₀ lags behind. All other AON versions match well and are close to the BIN results. Only for the largest DNC_init value does some spread in T_cross exist. Figure S11 shows that BIN predicts in all cases slightly lower droplet numbers similar to what we already observed for the default microphysical initialisation in Fig. 5. Nevertheless, we can confirm the very good agreement of BIN and all full AON simulations.

As a last AON sensitivity study, the default Long kernel is replaced by the Hall kernel. Figure 6f shows the corresponding results. The decrease in λ₀ occurs at a slower rate (the y scale now uses a linear scale). For the full simulations (solid curves), we obtain perfect agreement for any chosen κ value and for all three model versions. Moreover, convergence with κ in the noSedi simulations (dotted curve) is less critical than in the base case (compare with panel a again) and results converge for κ≥40. Time series of λ₀ of all Hall kernel simulations are shown in Fig. S12.

So far, all reference BIN results were obtained with Wang's algorithm, using a time step Δt=1 s and resolution s=16. We conclude the box model emulation section by showing the sensitivities of two BIN versions. For this, we vary the bin resolution s and the time step for the base case with LWC_init=1 g m⁻³ and Long kernel and apply either Bott's or Wang's algorithm. The default time step is Δt=10 s as in the AON simulations and the bin resolution is s=4. Figure 6g–h show results obtained with Bott's and Wang's algorithm, respectively. Again, λ₀ time series of these BIN simulations are shown in Fig. S13.

We find that Bott's algorithm converges for s≥2 (Fig. 6g). Wang's algorithm, on the other hand, does not produce stable results for higher resolutions and Δt=10 s. Thus, the time step had to be reduced (see inserted legend, for the combination of s and Δt). For s≥8 results have converged to the reference. Figure 6h shows the time step dependency for a medium resolution of s=4. While Bott yields stable results for Δt≤100 s, the results only converge for Δt≤20 s. We can even see a slight dependence of λ₀(t=1 h) on Δt. As a side note, this is a clear indication that the BIN reference values used for orientation so far should not be interpreted as absolute reference, and it would be premature to discredit AON results being slightly above the BIN reference.

Wang's algorithm, on the other hand, requires Δt≤10 s for stable results, and convergence is reached for Δt≤5 s. Overall, we can conclude that both algorithms converge to basically the same values, given a sufficiently high s and small Δt is chosen. As Bott's algorithm appears to be more robust than Wang's algorithm, all following BIN simulations are carried out with this algorithm.

Comparing the various collisional growth algorithms, we find that Bott's algorithm has the least requirements in terms of bin resolution and time step as we have converged results for t up to 100 s and s as low as 2. AON simulations may converge for κ=5 (corresponds roughly to s=2) and Δt=10 s if GBs of the column are sufficiently interconnected and averaging over several realisations is done. Wang's algorithm produces correct solutions for s=4 and Δt=5 s, and yet increasing the bin resolution has to be done hand in hand with a reduction of the time step.

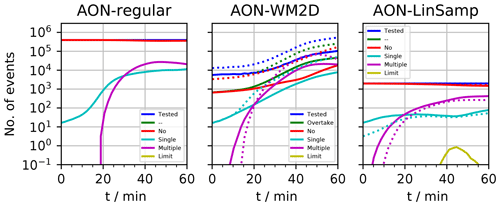
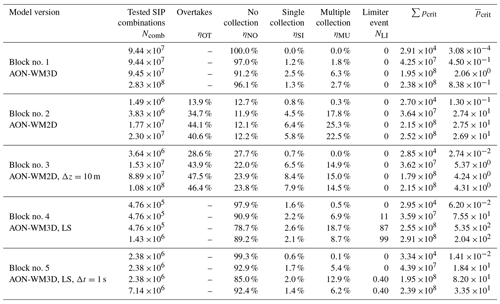
Figure 8 BoxModelEmul set-up: time series of a number of events in the various AON versions. Shown are the number of tested SIP combinations, of overtakes, of no collection, of a single collection and of a multiple collection in every time step. Additionally, the number of limiter cases, where ν_coll had to be artificially reduced, is shown (occurs only in the LinSamp panel). The parameter set-up is given in the text. In the WM2D panel, the dotted lines show the case with Δz=10 m. In the LinSamp panel, the dotted lines show the 1 s simulation. The displayed numbers can be below unity, as averages over 20 instances are shown.

Table 3 BoxModelEmul set-up: a number of events for various AON versions for the parameter set-up given in the text. N_comb is the number of tested SIP combinations and N_LI is the number of limiter cases, where ν_coll had to be artificially reduced. Moreover, η_OT, η_NO, η_SI and η_MU specify the number of overtakes, no collections, single collections and multiple collections divided by N_comb. The two last columns shows summed-up p_crit (summed over all times and SIP combinations and overtakes) and the average p_crit. For each AON simulation, the first three rows show aggregate values over three time periods (0–20, 20–40 and 40–60 min) and the fourth row values for the full time period.

3.2 Algorithm profiling

Now, we turn the attention to an algorithm profiling of the various AON versions.

Figure 8 and Table 3 give an example of how often collections occur in the model. For AON-WM2D, the number of overtakes is also given. The listed numbers give a rough indication of the importance of the various events (overtake, no collection, single collection, multiple collection, limiter), and yet we want to note the caveat that the relative importance changes with a change of the parameter set-up. Here, results are shown for the specific set-up with n_z=20, nr_inst=10, ΔV=1 m³, Δt=5 s, Δz=50 m and κ=40. The figure shows qualitatively the number of occurrences as a function of time, whereas the table gives aggregate values for three 20 min blocks and the total 60 min simulation period. In both WM3D versions (regular and LinSamp), the number of tested SIP combinations N_comb is constant over time. Clearly, the LinSamp value is smaller by a factor of 200 (=N_SIP) and implies a faster execution. For the WM2D version, on the other hand, N_comb increases over time as the DSD gets more mature and larger droplets fall faster. Relative to the regular (WM3D) version, N_comb of WM2D is at any time smaller. In the beginning of the simulation, possible overtakes occur among relatively few SIPs; much fewer on average than there are in a GB; hence the total N_comb is around a factor of 60 smaller (in the first 20 min; 9.44×10⁷ vs. 1.49×10⁶). Even towards the end of the simulation, many SIPs are still small and travel through a small fraction of the GB. Only a few SIPs grow to raindrop size and travel distances of order Δz. The table shows that the total (time-integrated) N_comb is more than a factor of 12 smaller for WM2D than for WM3D (2.30×10⁷ vs. 2.83×10⁸). This demonstrates the numerical efficiency of the current WM2D implementation despite a theoretically unfavourable computational complexity with a factor of n_z higher N_comb compared to the regular WM3D version.

Moreover, the workload per time step is constant in both WM3D versions and determined solely by N_SIP. In the WM2D version, the workload depends additionally on the properties of the DSD and also on Δz. If Δz is reduced by a factor of 5 (see block no. 3 in the table), N_comb roughly increases by the same factor. Similarly, we found a longer execution time of WM2D in the LWCup series than in the base case (not shown).

In the table, the ratios η_NO, η_SI and η_MU specify the number of no collections, single collections and multiple collections divided by N_comb and add up to 100 % for both WM3D versions. In the regular WM3D version, only 1.3 % and 2.7 % of all tested combinations lead to a single or multiple collection. So, for most combinations p_crit is close to zero and makes a collection unlikely. On the other hand, for favourable SIP combinations p_crit can be far above 1 (imagine a SIP combination with ν_i=10⁶, ν_j=10² and ν_coll=10⁴ yielding p_crit=100). This also explains the somewhat surprising fact that the average ${\stackrel{\mathrm{‾}}{p}}_{\text{crit}}$ is close to unity (=0.83; see right-most column). The PDF (probability density function) of all p_crit values is strongly right-skewed (not shown). In the LinSamp case, single and multiple collections occur in 2.1 % and 8.7 % of the tested combinations. Collections are more likely as ${\stackrel{\mathrm{‾}}{p}}_{\text{crit}}$ is larger due to the upscaling. Moreover, ν_coll had to be artificially reduced in N_LI≈100 cases. Note that such limiter cases do not appear in any QuadSamp version (regular and WM2D). In the LinSamp version, N_LI can be cut down by choosing a smaller time step (see fifth block in table). Using Δt=1 s leads to 5 times smaller p_crit values, increases η_NO, and decreases η_SI and η_MU. Limiter cases are now an extremely rare event. For clarification, p_crit of a single SIP combination scales with Δt⁻¹; from this, however, does not follow that the listed ${\stackrel{\mathrm{‾}}{p}}_{\text{crit}}$ values of the two LinSamp simulation differ by a factor of 5, as the DSDs and SIP ensembles and weights evolve differently in the two simulations.

Finally, we focus on the WM2D version (block no. 2). Here, the sum of η_NO, η_SI and η_MU yields η_OT, the number of overtakes divided by N_comb, and not 100 % as before. In the end, around 40 % of all tested SIP combinations undergo an overtake. This quite large fraction comes from the fact that the DSD (or more precisely the size distribution of the SIPs) features a strong bimodal spectrum. So most tested combinations are combinations between a large collector SIP i and a small SIP j with z_i>z_j. These tested SIP combinations fulfil by design $z_i(t+\mathrm{\Delta }t)<z_j\left(t\right)$. For small SIPs j, $z_j(t+\mathrm{\Delta }t)=z_j\left(t\right)-\mathit{ϵ}$ holds. As ϵ is a small distance, it is likely that $z_i(t+\mathrm{\Delta }t)<z_j(t+\mathrm{\Delta }t)$ is fulfilled; i.e. SIP i overtakes SIP j. In more than every second overtake, a multiple collection occurs (i.e. ${\mathit{\eta }}_{\text{MU}}/{\mathit{\eta }}_{\text{OT}}=\mathrm{0.56})$. In one-eighth (one third) of the overtakes a single collection (no collection) happens. So the relative importance of the various events is quite different compared to the regular AON and also ${\stackrel{\mathrm{‾}}{p}}_{\text{crit}}$ is 3 times larger (2.69 vs. 0.83). Note that changing Δz in the WM2D simulation (block no. 3) also affects the relative occurrences of no collection, a single collection and multiple collections. In the WM3D versions, the overall workload is proportional to Δt⁻¹. This is different in the WM2D version. With an increasing time step, droplets travel longer distances. Hence, the number of tested combinations and overtakes per time step increases.

Note that the relative occurrence frequency of p_crit values may depend also on the spectrum of given ν_p values (i.e. on the SIP initialisation method), which is not elaborated here.

Figure S14 demonstrates that all five AON simulations converge and show a basically identical time evolution of λ₀. The analysis here shows that in the end more multiple collections than single collections appeared. Clearly, the occurrence of multiple collections in a simulation does not necessarily deteriorate the simulation results. It is certainly not the case that the time step choice or adaptation must be such that multiple collections barely appear in a simulation. Beyond that, limiter events that occurred in the LinSamp simulation with Δt=10 s did not avert convergence. So even a certain amount of limiter events seems to be acceptable in terms of performance. Figure 6b showed that even for Δt=100 s LinSamp and regular AON produce similarly good results, albeit off from the reference.

Several of the above findings may hold only for the specific set-up used here. To put the findings into a broader context, we next derive scaling relations for basic numerical quantities and, in particular, discuss their sensitivity to the time step and the number of SIPs. For a simplified presentation, we limit ourselves to the regular and LinSamp version and assumed converged simulation results and no limiter events. Moreover, we assume that an increase in N_SIP leads to a uniform decrease in all SIP weights ν_p.

For the following basic quantities we have

$$\begin{array}{}\text{(28)}& {\mathit{\nu }}_p\propto {\displaystyle \frac{\mathrm{1}}{N_{\text{SIP}}}};nt\propto {\displaystyle \frac{\mathrm{1}}{\mathit{\delta }t}};N_{\text{comb}}\propto {N_{\text{SIP}}}^{\mathit{\alpha }};{\mathit{\gamma }}_{\text{corr}}\propto {N_{\text{SIP}}}^{\mathit{\beta }},\end{array}$$

where γ_corr is the correction factor defined in Eq. (25). For QuadSamp α=2, β=0 and for LinSamp α=1, β=1.

Accordingly,

$$\begin{array}{}\text{(29a)}& {\displaystyle }{\mathit{\nu }}_{\text{coll}}& {\displaystyle }\propto {\displaystyle \frac{\mathrm{1}}{{N_{\text{SIP}}}^{\mathrm{2}}}}\times \mathit{\delta }t,\text{(29b)}& {\displaystyle }{\mathit{\nu }}_{\text{sum}}& {\displaystyle }:=\sum ^{nt,N_{\text{comb}}}\left({\mathit{\nu }}_{\text{coll}}{\mathit{\gamma }}_{\text{corr}}\right)\propto {\displaystyle \frac{{N_{\text{SIP}}}^{\mathit{\alpha }+\mathit{\beta }}}{{N_{\text{SIP}}}^{\mathrm{2}}}}=\mathrm{1},\text{ and}\text{(29c)}& {\displaystyle }{\stackrel{\mathrm{‾}}{p}}_{\text{crit}}& {\displaystyle }:={\displaystyle \frac{\mathrm{1}}{N_{\text{comb}}nt}}\sum ^{nt,N_{\text{comb}}}({\mathit{\nu }}_{\text{coll}}/{\mathit{\nu }}_p{\mathit{\gamma }}_{\text{corr}})\propto {N_{\text{SIP}}}^{\mathit{\beta }-\mathrm{1}}\mathit{\delta }t.\end{array}$$

In both versions, ν_sum is independent of N_SIP and δt. Clearly, ν_sum should have the same value (not only the same asymptotic behaviour) across all AON versions in order to obtain consistent results. The average probability ${\stackrel{\mathrm{‾}}{p}}_{\text{crit}}$ scales, not surprisingly, linearly with δt. For QuadSamp, ${\stackrel{\mathrm{‾}}{p}}_{\text{crit}}$ is inversely proportional to N_SIP and an increase in N_SIP decreases the occurrence of multiple collections and limiter events. In the LinSamp case, ${\stackrel{\mathrm{‾}}{p}}_{\text{crit}}$ is independent of N_SIP (as already pointed out by Shima et al., 2009, end of their Sect. 5.1.3) implying that an increase in N_SIP does not decrease the number of multiple collections and limiter events. Nevertheless, an N_SIP increase is also beneficial in LinSamp as it increases the number of trials and reduces the variance of the results.

3.3 Realistic column model simulations

The box model emulation simulations presented in Sect. 3.1 used an academic and unrealistic set-up, not yet exploiting the capabilities of a column model framework. The following two subsections treat realistic set-ups.

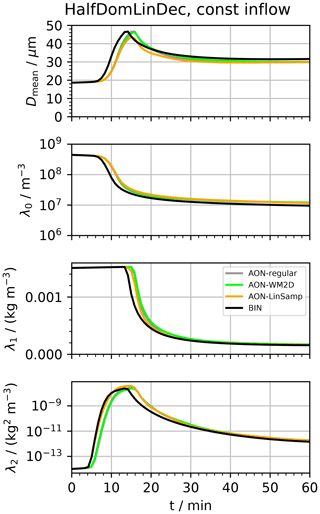
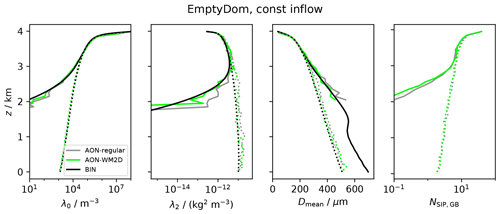
Figure 9 HalfDomLinDec set-up: temporal evolution of D_mean and column-averaged moments λ₀,λ₁ and λ₂ for various model versions (see inserted legend; “LS” is short for linear sampling).

3.3.1 Half domain set-up

We initialise droplets in the upper half of a 4 km column. In each GB the mean radius of the DSD is fixed at the default value r_init=9.3 µm. LWC_init (and with it DNC_init) decreases linearly from 3 g m⁻³ at the model top to zero at z=2 km. At the model top, a constant influx of a DSD with LWC_init=3 g m⁻³ is prescribed, which guarantees a smooth profile over time. Otherwise, a discontinuity would occur at the top-most GB which may cause problems in the BIN model. The further settings are n_z=400, Δz=10 m, Δt=10 s, nr_inst=20, κ=40. All figures related to this set-up start their caption with the label “HalfDomLinDec set-up”.

Figure 9 shows the temporal evolution of the mean diameter and the moments λ₀, λ₁ and λ₂. Due to the influx condition, the total mass increases during the first 10 min, barely visible in the third panel. During this period, however, collisional growth is already efficiently reducing the droplet number. This is accompanied by an increase in the mean diameter and radar reflectivity. Soon after, the first droplets reach the surface, the mass declines rapidly, and the whole column is more or less washed out after 30 min. We find an excellent agreement among the four model versions BIN, AON-regular, AON-WM2D and AON-LinSamp.

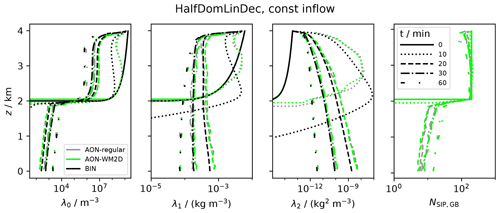
Figure 10 HalfDomLinDec set-up: vertical profiles of moments λ₀, λ₁, λ₂ and N_SIP,GB for various model versions (AON-WM3D, AON-WM2D, BIN; see colour legend in left-most panel) and times (0, 10, 20, 30, 60 min; see line style legend in right-most panel).

Figure 10 shows vertical profiles of DNC, LWC, Z and N_SIP,GB for times t=0, 10, 20, 30 and 60 min. In the upper half, droplet number is roughly homogeneously distributed and decreases over time. In the lower half, droplet number concentrations are several orders of magnitude smaller than in the upper half and increase over time. The profile of the radar reflectivity shows the highest values after 10 min with a pronounced peak in the middle of the domain. Soon after, the Z profiles become smooth and increase monotonically towards the surface. The sedimentation flux also increases towards the surface, and hence λ₂ values decrease over time.

In the upper half, N_SIP,GB is fairly constant over altitude and time with around 200 SIPs. As the LWC is initially highest at the model top, collisional growth is most frequent there. Most likely, SIPs from that layer turn into collector SIPs, meaning they fall through the total column and collect many other SIPs. Consistently, N_SIP,GB decreases over time close to the model top. Yet overall, only a small fraction of the SIPs becomes raindrops eventually (see for example Fig. 4 in U2017) and hence the SIP number is substantially smaller in the lower half. There, each GB is populated by roughly 10 SIPs. Despite this rather small value, convergence in DNC and Z seems to be ubiquitous.

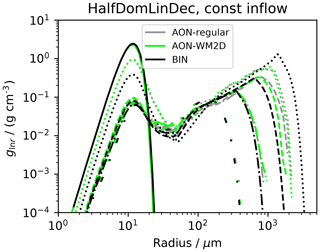
Figure 11 HalfDomLinDec set-up: size distribution g_ln r for various model versions and times as in Fig. 10 (see legends there).

Figure 11 depicts column-averaged DSDs for various points in time. The precipitation mode develops rapidly, and 2 to 3 mm sized drops are produced within 10 min. Those drops soon reach the surface and remove a significant amount of liquid water from the column. Due to this wash-out effect, the raindrops cannot grow that large any longer and the precipitation mode peaks at smaller sizes at later times.

For a cleaner presentation, AON-LinSamp results were not shown in Figs. 10 and 11, but we confirm that these are very similar to those from AON-regular and AON-WM2D.

Overall, the agreement between the four model versions is remarkable given the completely different numerics of the Eulerian and Lagrangian approach.

Next, the vertical resolution Δz is varied in the model versions AON-regular, AON-WM2D and BIN (see Fig. S17). Even though this may look like a trivial sensitivity study, the effect of a Δz variation has different implications in the various models and AON versions. The differences are rather subtle. First, Δz affects the number of GBs n_z and with it the total SIP number N_SIP,tot (as N_SIP,GB is unchanged with the standard SIP-init technique). To eliminate this unwanted numerical side effect in LCM1D, we increase N_SIP,GB proportionally to Δz (analogous to the ΔV sensitivity tests in Sect. 3.1). Second, the advection by sedimentation changes in BIN as the CFL number changes and the subcycling has to be adapted. In LCM1D, the SIP transport by sedimentation is independent of the assumed grid and clearly unaffected by a Δz variation. Third, there is a physical effect as Δz determines the layer depth of the well-mixed volume (effective only in AON-regular and BIN).

It follows that the results of the AON-WM2D version should be independent of Δz. Moreover, the AON-regular version can be used to determine if the size (more specifically the depth) of the well-mixed volume is a crucial parameter. In bin models in general, this sensitivity could not easily be singled out as sedimentation numerics also change with Δz.

Given a constant column height L_z=4 km, Δz takes the values 2, 10, 50 or 100 m and we find λ₀(t) to be independent of Δz (see Fig. S17). As expected, the AON-WM2D simulations are not at all affected by Δz. In particular, the AON-regular simulations are insensitive to a change in Δz and imply that the depth of the well-mixed volume has a negligible impact on the extent of collections in the present set-up. Interestingly, the Δz=10 m simulation uses N_SIP,GB=200 and the Δz=100 m simulation N_SIP,GB=2000. Hence, a factor of 100 more SIP combinations are tested for possible collections in the latter case, yet with no effect on the physical evolution.

Figure 12 EmptyDom set-up: vertical profiles of moments λ₀, λ₂, D_mean and N_SIP,GB for various model versions (see legend). Depicted are the times t=30 and 60 min (solid, dotted).

3.3.2 Empty domain set-up

In this section, the 4 km deep column is initially devoid of droplets and a time-constant influx of a DSD with r_init=16.9 µm and LWC_init=6 g m⁻³ is prescribed. As in the box model emulation set-up, the corresponding DNC_init is 297 cm⁻³. All figures related to this set-up start their caption with the label “EmptyDom set-up”.

Over time the column fills with droplets, a distinct size sorting is established and DSDs at a specific altitude are expected to be rather narrow. Hence, choosing a vertical resolution that is too coarse may result in overestimating collections as the droplets are not supposed to be well-mixed within such deep GBs. In such a case, the AON-WM2D version has a conceptional advantage as it does not assume well-mixedness in the vertical direction. The chosen set-up specifically aims to demonstrate the possible improvement by this. Again, the further parameter settings are n_z=400, Δz=10 m, Δt=10 s, nr_inst=20, κ=40.

Figure 12 shows vertical profiles at t=30 and 60 min for AON-regular, AON-WM2D and BIN. After 30 min the cloud roughly covers the top half of the column. Below z=2 km, fewer than 0.1 SIPs are present in each GB of LCM1D. This implies that only in 1 or 2 out of the 20 realisations do SIPs grow sufficiently large to fall that far. This also explains the jagged λ₂ profiles in the lower part. Below a certain altitude, no SIPs are present at all and hence no mean droplet diameter could be diagnosed. BIN produces non-zero mass and number all the way down to the bottom and allows a smooth D_mean profile to be computed. As the predicted droplet masses and concentrations become vanishingly small, the derived D_mean values in the lower part are, however, meaningless. Anyhow, this small discrepancy between BIN and LCM1D is a transient phenomenon. Once the cloud is fully developed, the profiles match perfectly (see dotted curve for t=60 min). The fact that on average well below 10 SIPs populate GBs in the lower domain half is remarkable. Nevertheless, the LCM1D results seem to be converged. SIPs at those altitudes are large (D_mean>400 µm) and fall fast, which fosters a strong SIP exchange across GBs and is beneficial to convergence (see Sect. 3.1). The AON-LinSamp simulation (not shown) produces again very similar profiles. This is even more remarkable, as on average only 5 SIP pairs are tested for collections per GB in the lower half.

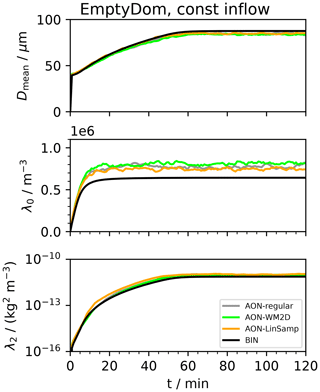
Figure 13 EmptyDom set-up: temporal evolution of D_mean and column-averaged moments λ₀ and λ₂ for various model versions (see legend).

Figure 13 shows the temporal evolution of the mean diameter, column-averaged DNC and Z; here AON-LinSamp curves are added. Within the first 10 min, DNC increases quickly. Soon after, collection becomes effective and DNC reaches a quasi-steady state. The radar reflectivity increases within the first 60 min and then also reaches a quasi-steady state. The only discrepancies between the various models are slightly larger DNC values by all AON versions. The reason for this is elucidated next.

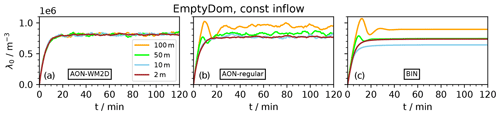
Figure 14 EmptyDom set-up: temporal evolution of column-averaged moments λ₀ and λ₂ for various model versions (AON-WM2D, a; AON-WM3D, b; BIN, c). Each panel shows a variation of the vertical resolution Δz (see legend in the left panel). In LCM simulations, SIP numbers for Δz=100 and 50 m simulations are increased to the level of the Δz=10 m simulation.

Fig. 14 shows the Δz dependence of the DNC evolution in the different models. For Δz=50 and 100 m, the SIP numbers in AON simulations have been upscaled to maintain N_SIP,tot values comparable to the Δz=10 m simulation (as already done in the HalfDom set-up). The Z evolution (see Fig. S19 for a time series) is found to be basically independent of Δz in all three models. For the DNC evolution, we find also no Δz dependence in the WM2D model as intended. However, in AON-regular and BIN models, DNC levels off at different values depending on Δz. This behaviour is most likely caused by an interaction of the unresolved size sorting and the hence larger range of potential collection partners in AON-regular and BIN. Apparently, this results in changes in the rate with which the smallest droplets are collected by larger droplets, as indicated by the substantial effect of this process on DNC, but not on Z.

The Δz dependence persists in AON-LinSamp simulations and in further AON-regular simulations, where we reduced the time step to Δt=1 s or decreased N_SIP,tot (see Fig. S20).

This undesired Δz dependence in BIN and AON-regular seems to showcase the superiority of the AON-WM2D version. However, the Δz dependence does not affect higher moments of the DSD, e.g. Z (as shown in the Supplement) or the accumulated size distribution of all droplets that crossed the lower boundary (Fig. S21). Accordingly, precipitation-related quantities seem to be unaffected by changes in the vertical grid spacing. On the other hand, most of the Δz effect can be attributed to changes in the DNC within the top-most 100–200 m of the column (Fig. 12). Anyhow, based on the presented results, we cannot definitely answer the question of whether using the AON-WM2D approach has in general any practical benefits over the classical 3D well-mixed approaches. Further research in this direction is required.

4 Summary and conclusions

Collection, i.e. the coalescence, accretion and aggregation of hydrometeors, is an important process for the development of precipitation in liquid-, mixed- and ice-phase clouds, respectively. The correct representation of these processes in cloud microphysical models is, therefore, of utmost importance. In this study, we investigated and validated the representation of collection in LCMs, a relatively new approach that uses simulation particles, so-called SIPs or super-droplets, to represent cloud microphysics.

This study is a continuation of U2017, in which we analysed various representations of collisional growth algorithms in LCMs using zero-dimensional box model simulations. Here, this analysis is extended to one-dimensional column simulations that allow the effects of sedimentation to be explicitly considered. This study focuses on the AON algorithm (Shima et al., 2009; Sölch and Kärcher, 2010) that outperformed other collection algorithms, as assessed in our previous study (U2017). Two versions of AON are applied that differ in the assumed distribution of droplets represented by a SIP: in the regular AON version, the droplets are assumed to be well-mixed within a three-dimensional volume (which is typically identical to the GB of the dynamical model coupled to the LCM). In WM2D, the height coordinate of each SIP is used explicitly, and the droplets represented by a SIP are assumed to be well-mixed only within a two-dimensional, horizontal plane. Accordingly, collections are only considered if a SIP overtakes another one during a time step.

Furthermore, two variants of AON-WM3D are tested that differ in the number of SIP combinations that need to be tested during collection. In its simplest form, AON-WM3D depends quadratically on the number of SIPs since every SIP may interact with any other SIP inside a GB (QuadSamp). Additionally, Shima et al. (2009) introduced an approach that depends only linearly on the number of SIPs by appropriately scaling collection probabilities (LinSamp). What we call here AON-LinSamp is also referred to as the SDM (super-droplet method) algorithm in the literature.

All results are compared to established Eulerian bin model results (Bott, 1998; Wang et al., 2007). Accordingly, the capability of Lagrangian and Eulerian approaches to advect a droplet ensemble due to sedimentation is tested first – neglecting the influence of collection. Since numerical diffusion is inherent to any Eulerian advection problem, i.e. also sedimentation, its impact might impede any conclusions drawn from the collection simulations. However, by using an appropriate advection scheme (MPDATA, Smolarkiewicz, 1984), numerical diffusion can be reduced to an acceptable degree in the sense that the present simulations focus on the differences driven by collection numerics.

As a first step and link to U2017 simulations, box model simulations are emulated in the column model. This is done by initialising each GB of the column with the same droplet size distribution and applying cyclic boundary conditions at the surface and the top. By using this framework, we were able to show that sedimentation increases the model convergence rate significantly compared to box model simulations without sedimentation; i.e. fewer SIPs per GB are required in the column model. The reason for this behaviour is that the largest and hence fastest-falling droplets are no longer confined to the same GB and to the same potential collection partners, which increases the ensemble of potential collection partners. A similar observation has been made by Schwenkel et al. (2018), who used randomised motions between individual GBs. Overall, these results indicate that a simulation with only 24 SIPs per GB can yield reasonable results if (i) these SIPs are able to move between GBs and (ii) the SIP weighting factors are ideally chosen in the beginning by using an appropriate SIP initialisation technique.

In general, a remarkably good agreement of the LCM results with the bin reference has been found for all AON versions (regular AON, AON-WM2D and AON-LinSamp). AON-LinSamp results are only slightly worse compared to regular AON simulation of the same time step and SIP number. However, these stronger restrictions on the time step do not at all outweigh the computational benefit gained by the favourable linear computational complexity, making the LinSamp version the preferred choice if computation time is a critical factor. In an operational setting, the QuadSamp approach is a valuable alternative to LinSamp as long as the number of SIPs is not prohibitively high.

We further compared the computational requirements for the WM2D and WM3D implementations of AON. We found that WM2D requires checking for overtakes in the entire column, not only in the GB in which the SIP is located, as is the case for WM3D. However, this seeming disadvantage is turned into an advantage, since only a minority of SIPs overtakes other SIPs. Accordingly, the overall number of calculations necessary for the application of WM2D is reduced compared to WM3D. The physical reason for this effect is the typical bimodal structure of droplet spectra, which consist of only a few large droplets that sediment and collect other droplets efficiently, while the remaining droplets are usually too small to sediment and collect other droplets.

Finally, we applied the various AON versions to two more realistic column cases. While both cases use a prescribed inflow of droplets from the top, the first case is initialised with a linearly increasing liquid water content, and the second case is completely devoid of any initial droplets. Overall, the agreement of AON-regular, AON-WM2D, AON-LinSamp and the bin references is remarkable. Only in the second case, which is designed to be heavily prone to size-sorting, is a dependence on the vertical grid spacing detectable for WM3D and the bin reference, which both assume droplets to be well-mixed within a GB, while the WM2D results are found to be completely independent of the vertical grid spacing.

In all AON variants, simulation results converge for fairly large time steps Δt>10 s. For such high Δt values, the largest droplets routinely travel distances larger than the vertical resolution Δz during one time step (as noted above). Whereas in Eulerian advection this would violate the CFL criterion and cause a numerical break-down, Lagrangian numerics do not fail. In higher-dimensional full microphysical models with diffusional growth included and gradients in moist thermodynamic fields, physical reasons also render it appropriate to apply a time step criterion in the spirit of the CFL condition in Lagrangian approaches. Solving diffusional growth usually sets stricter bounds on Δt (Arnason and Brown, 1971). Moreover, the interplay of diffusional and collisional growth, which was not studied here, may raise the time step requirements of AON for physical reasons. For example Dziekan et al. (2019), using AON with linear sampling in 2D and 3D LCM simulations, found convergence only for a rather small time step of Δt=0.1 s.

All in all, this study has shown that the representation of collisional growth in LCMs using AON successfully reproduces established Eulerian bin results. This ability, of course, depends foremost on the number of SIPs and the applied time step as already indicated in previous zero-dimensional box model studies. Compared to these zero-dimensional studies, the application of an LCM in a column decreases the required number of SIPs significantly. The consequently lower computational costs raise hopes to use LCMs more frequently in large-scale, multidimensional models in the future.

Appendix A: Pure sedimentation test cases

This Appendix presents pure sedimentation test cases that are suited to demonstrating that minor differences are introduced by the different numerical treatment of the sedimentation process. Two simple set-ups with an influx of an exponential DSD with r_init=50 µm are tested. In the first case, the domain is initially empty and fills over time (EmptyDom) as in Sect. 3.3.2. In the second case, the upper half of the domain is filled, with LWC_init and DNC_init decreasing linearly to zero from the domain top to the domain middle (HalfDom) like in Sect. 3.3.1. Figure A1 shows the vertical profiles of normalised zeroth (a and c) and second (b and d) moments for EmptyDom (a and b) and HalfDom (c and d). Because of the lack of numerical diffusion, the solid LCM curves show the exact results, except for the error introduced by discretising the influx DSD with a probabilistic approach. Each panel showcases a convincing agreement between the Eulerian and Lagrangian approach. Only the BIN-US1 solutions are slightly smeared out. The small wiggles in the LCM curves originate from the probabilistic influx condition. Even though the above agreement is favourable, it might be that the advection errors of differently sized droplets compensate each other in the Eulerian approaches. Hence, in a second validation step, the computation of mass profiles is confined to certain droplet size ranges. Figure A2 shows such vertical profiles for EmptyDom. We see that for all four size ranges, the BIN results are smeared out relative to LCM. For the smallest size ranges both BIN versions are equally “bad” (panel a). For the three remaining panels, the MPDATA curves (dashed) are closer to the LCM reference than the US1 curves (dotted). On the other hand, the MPDATA curves in panel (d) show some wiggles. Overall, the agreement between LCM and BIN-MPDATA is good. The discrepancies introduced by the different sedimentation treatment appear to be small enough to warrant a focus on the collisional growth process and its implementations in the main part of the paper.

Figure A1 Pure sedimentation test case: comparison of BIN and LCM (solid) advection. BIN uses either MPDATA (dashed) or first-order upstream scheme (dotted). EmptyDom (a, b) and HalfDom (c, d) set-ups are used with an exponential distribution with r_init=50 µm as influx condition. Displayed are vertical profiles of normalised zeroth and second moment at the indicated points in time.

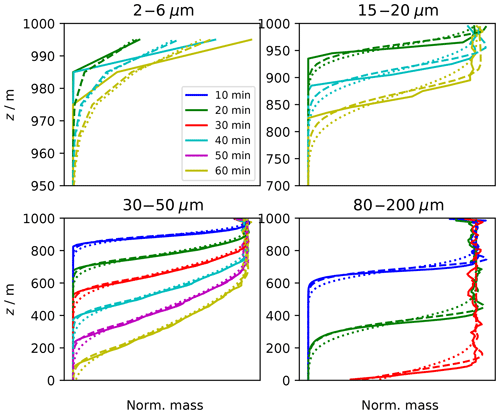
Figure A2 Pure sedimentation test case: comparison of BIN and LCM advection. EmptyDom set-up with an exponential distribution with r_init=50 µm as influx condition. Displayed are vertical profiles of normalised mass within specified size ranges (see the heading of each panel) at the indicated points in time. Note that most panels use different y-axis ranges and do not show all six points in time.

Moreover, we tested the sensitivity to r_CFL and Δt as both parameters in combination determine the local CFL number of each grid box. BIN simulations were carried out for the HalfDomLinDec set-up and with switched-on collisional growth (i.e. the set-up of Sect. 3.3.1). Figure S18 demonstrates that this has no impact on the prediction of the total moments.