An adaptive method for speeding up the numerical integration of chemical mechanisms in atmospheric chemistry models: application to GEOS-Chem version 12.0.0

The major computational bottleneck in atmospheric chemistry models is the numerical integration of the stiff coupled system of kinetic equations describing the chemical evolution of the system as defined by the model chemical mechanism (typically over 100 coupled species). We present an adaptive method to greatly reduce the computational cost of that numerical integration in global 3-D models while maintaining high accuracy. Most of the atmosphere does not in fact require solving for the full chemical complexity of the mechanism, so considerable simplification is possible if one can recognize the dynamic continuum of chemical complexity required across the atmospheric domain. We do this by constructing a limited set of reduced chemical mechanisms (chemical regimes) to cover the range of atmospheric conditions and then pick locally and on the fly which mechanism to use for a given grid box and time step on the basis of computed production and loss rates for individual species. Application to the GEOS-Chem global 3-D model for oxidant–aerosol chemistry in the troposphere and stratosphere (full mechanism of 228 species) is presented. We show that 20 chemical regimes can largely encompass the range of conditions encountered in the model. Results from a 2-year GEOS-Chem simulation shows that our method can reduce the computational cost of chemical integration by 30 %–40 % while maintaining accuracy better than 1 % and with no error growth. Our method retains the full complexity of the original chemical mechanism where it is needed, provides the same model output diagnostics (species production and loss rates, reaction rates) as the full mechanism, and can accommodate changes in the chemical mechanism or in model resolution without having to reconstruct the chemical regimes.

1 Introduction

Accurate representation of atmospheric chemistry is of central importance for air quality and Earth system models (National Research Council, 2016), but it is computationally expensive. The complete Master Chemistry Mechanism (MCM, version 3.3, http://mcm.leeds.ac.uk/MCMv3.3.1/, last access: November 2019) consists of 5832 species and 16 701 reactions. Atmospheric chemistry models use greatly simplified mechanisms, which still include hundreds of species coupled through production and loss pathways and with lifetimes ranging from less than 1 s to many years. Computing the kinetic temporal evolution of such systems involves solving a stiff system of N coupled non-linear ordinary differential equations (ODEs) of the form

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}{n}_i}{\mathrm{d}t}}=P_i\left(\mathit{n}\right)-L_i\left(\mathit{n}\right),\end{array}$$

where $\mathit{n}=(n_{\mathrm{1}},\mathrm{\dots }{n}_K{)}^T$ is the vector of species concentrations, expressed typically as number densities (e.g., molecules per cubic centimeter), and K is the number of species in the mechanism. P_i(n) and L_i(n) are the production and loss rates of species i that depend on the concentrations of other species in the mechanism. Finite-difference solution of the coupled system of ODEs requires an implicit scheme to avoid limitation of the time step by the shortest lifetime in the system (Brasseur and Jacob, 2017). Implicit schemes involve repeated construction and inversion of the Jacobian matrix (K×K) for the system, and this is computationally expensive for large K. But the full coupled chemical mechanism may not be needed everywhere in the model domain. For example, highly reactive volatile organic compounds (VOCs) have little influence far away from their source regions. Here we show that we can obtain a substantial reduction in computational cost in a global 3-D model by adaptively adjusting the ensemble of species that actually need to be solved as a coupled system in a given model grid box. We do so with a general algorithm that is readily applicable to any chemical mechanism or numerical solver.

As the simplest example of an implicit scheme, consider the first-order method which approximates Eq. (1) as

$$\begin{array}{}\text{(2)}& f_i\left(\mathit{n}(t+\mathrm{\Delta }t)\right)=n_i\left(t+\mathrm{\Delta }t\right)-n_i\left(t\right)-s_i\left(\mathit{n}(t+\mathrm{\Delta }t)\right)\mathrm{\Delta }t,\end{array}$$

where Δt is the time step and $s_i\left(\mathit{n}\right(t+\mathrm{\Delta }t\left)\right)=P_i\left(\mathit{n}\right(t+\mathrm{\Delta }t\left)\right)-L_i\left(\mathit{n}\right(t+\mathrm{\Delta }t\left)\right)$ is the net source evaluated at the end of the time step. This defines a vector function $\mathit{f}=(f_{\mathrm{1}},\mathrm{\dots }{f}_K{)}^T$ and an algebraic system $\mathit{f}\left(\mathit{n}\right(t+\mathrm{\Delta }t\left)\right)=\mathrm{0}$ that is solved iteratively by the Newton–Raphson method. The procedure involves iterative calculation and inversion of the K×K Jacobian matrix $\mathbf{J}=\partial \mathit{s}/\partial \mathit{n}$. Most models use higher-order implicit algorithms designed for accuracy and speed, such as the Gear (Gear, 1971; Hindmarsh, 1983) and Rosenbrock (Sandu et al., 1997; Hairer and Wanner, 1991) solvers, but all require iteratively calculating the Jacobian matrix and solving the linear system using a matrix factorization. As a result, the chemical operator that solves for the chemical evolution of species concentrations from Eq. (1) is the most expensive component of atmospheric chemistry models (Eastham et al., 2018), and this computational cost has been a barrier for inclusion of atmospheric chemistry in Earth system models (National Research Council, 2012).

There are various ways to speed up the chemical operator, all involving some loss of accuracy or generality (Brasseur and Jacob, 2017). A general approach is to reduce the dimension of the coupled system of ODEs that needs to be solved implicitly. This can be done by simplifying the chemical mechanism to decrease the number of species (Brown-Steiner et al., 2018; Sportisse and Djouad, 2000) or by isolating long-lived species for which a fast explicit solution scheme is acceptable (Young and Boris, 1977). Jacobson (1995) used different subsets of their full mechanism to simulate the urban atmosphere, the troposphere, and the stratosphere. Machine learning algorithms have been developed to replace the role of the conventional chemical solver; but these methods have only been applied to simple scenarios and are subject to error growth as simulation time progresses (Keller and Evans, 2019).

Santillana et al. (2010) combined these ideas in an adaptive algorithm for 3-D models that determines locally at each time step (“on the fly”) which species in the chemical mechanism need to be solved in the coupled implicit system. This was done by computing the local production (P_i) and loss rates (L_i) for all species at the beginning of the time step. Species with either P_i or L_i above a given threshold were labeled “fast” and solved with an implicit scheme, while the others were labeled “slow” and solved with an explicit scheme. The complexity of the chemical system to be solved was thus adapted to the local environment. Here “fast” and “slow” refer to the rates in the chemical system, not the species lifetime. For example, short-lived VOCs may be considered slow outside of their source regions because they have negligible influence on other species. Whether a species is fast or slow depends on the changing local conditions, hence the need for an adaptive algorithm, The adaptive approach does not prejudge the local environment, unlike in Jacobson (1995), and instead resolves the dynamic continuum of complexity encountered in the atmosphere. Santillana et al. (2010) applied their algorithm to the GEOS-Chem global 3-D Eulerian chemical transport model (Bey et al., 2001). While the computational savings were promising for the chemical integration within each grid box, the need to construct a different system in every single grid box and at every time step canceled out some of the gains and led to only small time savings when compared to the performance of the standard full-chemistry model.

Here we draw from the approach introduced by Santillana et al. (2010) but use a set of pre-defined chemical regimes to take full advantage of the time savings from the adaptive reduction mechanism algorithm. We start with the objective identification of a limited number of chemical regimes that encompass the range of atmospheric conditions encountered in the model. These regimes are defined by the subset of fast species from the full mechanism that need to be considered in the coupled system, and we pre-code the Jacobian matrix and its inverse for each. The model then picks the appropriate chemical regime to be solved locally and on the fly. We show that this approach can achieve large computational savings without significantly compromising accuracy when implemented in GEOS-Chem. Our method can be adapted to any mechanism and model, retains the complexity of the full mechanism where it is needed, and preserves full diagnostic information on chemical evolution (such as reaction rates and production and loss of individual species).

2 Model description

We use the GEOS-Chem 12.0.0 global 3-D model for tropospheric and stratospheric chemistry (https://doi.org/10.5281/zenodo.1343547) as a demonstration for our algorithm. The model is applied here with a horizontal resolution of ${\mathrm{4}}^{\circ }\times {\mathrm{5}}^{\circ }$ and 72 pressure levels extending from the surface to 0.01 hPa. It is driven by MERRA2 assimilated meteorological data from the NASA Global Modeling and Assimilation System (GMAO). The model includes coupled gas-phase and aerosol chemistry as described by Sherwen et al. (2016) and Travis et al. (2016) for the troposphere and Eastham et al. (2014) for the stratosphere. The chemical mechanism has 228 species and 724 reactions. Among these species, 143 are volatile organic compounds (VOCs), 37 are inorganic reactive halogen species, 24 are organic halogen species, and 24 are other inorganic and aerosol species. The chemical reactions are integrated using the Rosenbrock solver (Sandu et al., 1997; Hairer and Wanner, 1991) generated from the Kinetic PreProcessor 2.2.4 (KPP) (Damian et al., 2002) software. The model uses operator splitting between chemistry and transport with a chemistry time step of 20 min (Philip et al., 2016). We use 12 cores with shared memory in the simulations.

The key processes in the KPP chemical operator are as follows. The operator first updates the reaction rate coefficients on the basis of temperature, actinic flux, etc. It then passes these reaction rate coefficients together with initial species concentrations to the Rosenbrock solver, which solves for the temporal evolution of concentrations over the external time step Δt. In the process, the Rosenbrock solver approximates the solution at multiple internal time steps, so it needs to repeatedly recompute the species production and loss rates, construct the corresponding Jacobian matrix, and solve the linear system numerically using a matrix factorization. The bulk of the cost in the overall chemical operator is in the repeated computation of production or loss rates and in solving the linear system using a matrix factorization. Reducing the number of species in the system to be solved can significantly reduce the computational cost.

3 The adaptive algorithm for the chemical operator

Our adaptive algorithm determines locally and on the fly what degree of complexity is needed in the chemical mechanism by diagnosing all species in the full chemical mechanism as either “fast” or “slow”, and choosing among pre-constructed chemical mechanism subsets (“chemical regimes”) which is most appropriate for the local conditions. Here we present (1) the definition of fast and slow species and the different treatments for each and (2) the approach used to pre-construct the chemical regimes.

3.1 Definition of fast and slow species

Following Santillana et al. (2010), we separate atmospheric species as fast or slow based on their production and loss rates in Eq. (1) relative to a threshold δ: fast if either P_i(n)≥δ or L_i(n)≥δ; slow if P_i(n)<δ and L_i(n)<δ. Concentrations of the fast species are integrated as a coupled system with the KPP Rosenbrock solver. Concentrations of slow species are integrated by explicit analytical solution of Eq. (1) assuming first-order loss with effective rate coefficient $k_i=L_i/n_i$:

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle \frac{\mathrm{d}{n}_i}{\mathrm{d}t}}=P_i-k_i{n}_i,\text{(4)}& {\displaystyle }{n}_i\left(t+\mathrm{\Delta }t\right)={\displaystyle \frac{P_i\left(t\right)}{k_i\left(t\right)}}+\left(n_i\left(t\right)-{\displaystyle \frac{P_i\left(t\right)}{k_i\left(t\right)}}\right)e^{-k_i\left(t\right)\mathrm{\Delta }t}.\end{array}$$

Solving for n_i(t+Δt) by Eq. (4) incurs negligible computational cost; therefore, there is considerable advantage in classifying species as slow if this can be done without significant loss in accuracy. We select the threshold δ for species to be classified as fast or slow by numerical testing, as described in Sect. 4, but some basic chemical reasoning is useful. Consider the OH radical, which is a central species in atmospheric chemistry mechanisms. OH has a daytime concentration of the order of 10⁶ molecules cm⁻³ and a lifetime of the order of 1 s, implying production and loss rates of the order of 10⁶ molecules cm⁻³ s⁻¹. Species with production and loss rates that are orders of magnitude lower than 10⁶ molecules cm⁻³ s⁻¹ are therefore unlikely to influence OH or other species in the coupled mechanism, as these are all to some extent related to OH at least in the daytime. So we may expect an appropriate threshold δ to be of the order of 10²–10³ molecules cm⁻³ s⁻¹. Santillana et al. (2010) recommended δ=100 molecules cm⁻³ s⁻¹ in their algorithm.

One issue with the solution for the slow species by Eq. (4) is that it does not strictly conserve mass, because the loss rate for a given species over the time step does not necessarily match the production rate of the product species. This is usually inconsequential, but we found in early testing that it resulted in the total mass of reactive halogen species growing slowly over time in the stratosphere. To avoid this effect, we treat all 37 reactive inorganic halogen species as fast above 10 km altitude. This increases the computation cost of chemical integration by only 4 % relative to letting the algorithm set them as either fast or slow.

3.2 Preselecting the chemical regimes

Instead of building a local chemical mechanism subset at every time step as in Santillana et al. (2010), we greatly improve the computational efficiency by preselecting a limited number (M) of chemical mechanism subsets (chemical regimes) for which we pre-define the Jacobian matrix in KPP. We then determine locally which chemical regime to apply on basis of the ensemble of species classified as fast. This approach reduces the computational overhead of repeatedly allocating and de-allocating memory in the method of Santillana et al. (2010).

Construction of the chemical regimes can be done objectively by searching for a minimum in the computational cost of the chemical operator over the global domain. But some narrowing of the search is necessary. For the 228-species mechanism in GEOS-Chem, there are in principle 2²²⁸−1 possible combinations of species that would form mechanism subsets. The vast majority of those combinations make no chemical sense, but diagnosing this objectively would be computationally unfeasible. Instead, we start by splitting the mechanism species into N different blocks based on similarity of chemical behavior. Then we classify a block as fast if at least one species in the block is fast and slow if all species in the block are slow. The chemical regime is defined as the assemblage of fast blocks.

The partitioning of species into blocks can be optimized by minimizing globally the number of fast species (and hence the computation cost) for a given threshold δ. We use for this purpose a training dataset from a GEOS-Chem simulation for 2013, consisting of the global ensemble of tropospheric and stratospheric grid boxes for the first 10 d of February, May, August, and November sampled every 6 h (160 time steps in total). To reduce the computational cost, we optimize the partitioning of species into blocks for each individual time step, resulting in 160 different partitionings, and we then select the partitioning that yields the lowest cost function when applied to all time steps.

For each grid box j, we diagnose each individual species i as fast or slow following Sect. 3.1. We then diagnose the blocks as fast or slow with the indicator $y_{i,j}=\mathrm{1}$ if the block is fast (at least one species in the block is fast) or $y_{i,j}=\mathrm{0}$ if the block is slow (all species in the block are slow). The fraction Z₁ of all species that needs to be treated as fast over the testing domain is then given by

$$\begin{array}{}\text{(5)}& Z_{\mathrm{1}}={\displaystyle \frac{\mathrm{1}}{\mathrm{\Omega }}}\sum _j\sum _i{y}_{i,j},\end{array}$$

where Ω=195 408 is the total number of grid boxes in the troposphere and stratosphere (195 408 grid boxes, corresponding to the 59 lower levels of the model up to the stratopause) multiplied by the total number of species (228 in our case). We seek the partitioning of species into blocks that will minimize Z₁, and we use for that purpose the simulated annealing algorithm (Kirkpatrick et al., 1983). Starting from an arbitrary partitioning of the 228 species into N blocks, and at each iteration of the algorithm, we randomly move one species from one block to another. If Z₁ decreases, this transition is accepted; if not, the transition is accepted with a probability controlled by a parameter named temperature that decreases gradually as the algorithm proceeds. Among the N blocks, three are allocated to the reactive inorganic halogen species, and N-3 are allocated to the other species. This forced separation of the reactive inorganic halogen species is because the corresponding blocks are imposed to be fast above 10 km altitude (see Sect. 3.1). Throughout this study, we present the results with the lowest cost function after running the optimization multiple times and using different temperature parameters.

Once the blocks have been defined in the above manner, we define the chemical regimes as different assemblages of blocks. This yields 2^N−1 possible chemical regimes. Individual grid boxes in the model domain may correspond to any of these 2^N–1 regimes at any given time depending on which blocks are classified as fast or slow. We need to limit the number of regimes to a much smaller number Mof most useful regimes in order to keep the compilation of the code manageable. In fact, as we will see, the bulk of conditions in the model domain can effectively be represented by just a few regimes. Grid boxes that do not correspond to any of the M regimes need to be matched to one of the M regimes by moving some blocks from slow to fast, which will change the values of the corresponding indicators y_i,j from 0 to 1. We check each of the M regimes and select the one that needs the least number of moves from slow to fast, and this selection can be pre-defined so it does not add extra computational time. We refer to $y_{i,j}^{*}$ as the indicators adjusted by these changes. Thus, the fraction Z₂ of species that needs to be treated as fast over the global domain is given by

$$\begin{array}{}\text{(6)}& {\displaystyle }{Z}_{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{\Omega }}}\left(\sum _{D_{\mathrm{1}}}\sum _i{y}_{i,j}+\sum _{D_{\mathrm{2}}}\sum _i{y}_{i,j}^{\ast }\right),\end{array}$$

where D₁ is the grid boxes that can be represented by the M chemical regimes and D₂ is the grid boxes that are represented by other regimes and must be matched to the M regimes. At the beginning of each time step, we pick the chemical regime to use for each grid box on the basis of computed production and loss rates for individual species. A diagram for this process can be found in Fig. 1.

Figure 1 The diagram for calculating the cost function Z₂.

We tested a range of values from 5 to 20 for the number N of blocks. In this testing we used a threshold δ=100 molecules cm⁻³ s⁻¹ to partition fast and slow species, following Santillana et al. (2010), and a number M=20 of chemical regimes (see next paragraph for choice of M). Figure 2 shows the fraction of fast species in the global domain (Z₂) as a function of N. If N is low such that blocks are large, there is more likelihood that a species in a given block will be fast, causing all species in the block to be treated as fast. If N is high, more blocks will need to be moved from slow to fast in order to match the limited number M of chemical regimes. For M=20 we thus find an optimal value N=12 at which only 40 % of the species need to be treated as fast in the global tropospheric and stratospheric domain.

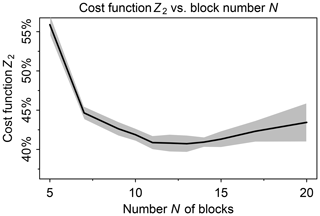
Figure 2 Minimum of cost function Z₂ (global fraction of chemical species treated as fast) as a function of the number N of blocks used to group the species for mechanism reduction. Values were computed using the GEOS-Chem troposphere + stratosphere simulation on the first days of February, April, August, and November 2013, over 24 h and sampled every 6 h. Shaded area shows the standard deviation of the cost function minimum computed for each sample.

Table 1 lists the species of these 12 blocks. Oxidants such as OH, O₃, and NO₂ are important under all circumstances so blocks 8 and 9 are fast in most grid boxes. Non-methane VOC species often have low concentrations outside of the continental boundary layer and very low concentrations in the stratosphere, so the dominant VOC blocks 1–7 are fast in fewer than 40 % of grid boxes. Anthropogenic VOC species (blocks 4 and 5) are found to be fast in the boundary layer and daytime mid-troposphere (Figs. S1–S2 in the Supplement). Biogenic VOC species have shorter lifetimes, so they are found to be fast only in the lower and middle troposphere over land (Figs. S3–S4).

Table 1 Partitioning of GEOS-Chem chemical species into N=12 blocks.^a

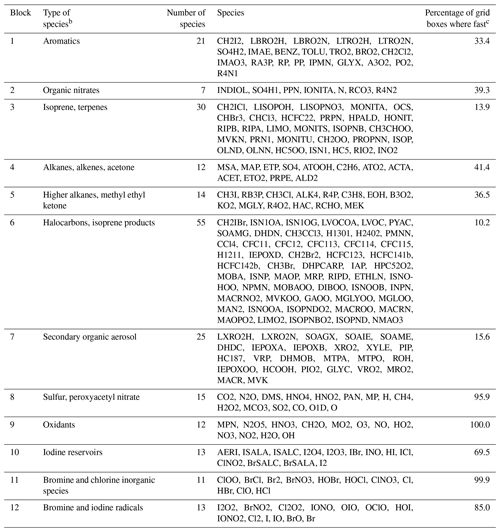
^a The full GEOS-Chem mechanism has 228 species. The full names of these acronyms can be found at http://wiki.seas.harvard.edu/geos-chem/index.php/Species_in_GEOS-Chem (last access: November 2019). Results in columns 2–4 are obtained using data from the first 10 d of February, May, August, and November sampled every 6 h. ^b Qualitative descriptor of the most important species in the block. ^c Global percentage of GEOS-Chem model grid boxes in the troposphere and stratosphere where the block is treated as fast. Values are for 1 August 2013 sampled every 6 h.

This algorithm still has shortcomings. There are some unexpected groupings (such as sulfur species and peroxyacetyl nitrate) and separations (such as HO₂ and H₂O₂). The blocks are constructed by minimizing the number of fast species in the optimization, so species tend to be in the same block as long as they are fast or slow simultaneously. For example, isoprene products and CFCs are both slow in the stratosphere and clean regions, so they may be assigned to the same group (e.g., block 6). In addition, there are still noticeable changes in species groups if we run the simulated annealing algorithm with different initializations and choices of the temperature parameter, even though the optimized blocks can generally separate the oxidants, anthropogenic VOCs, and biogenic VOCs (Table S1 in the Supplement). These two shortcomings may be addressed by introducing regularization terms in the cost function to enforce known species relationships. We will implement this in follow-up work.

We tested different numbers of chemical regimes (M) from 3 to 40 for combining the N=12 blocks and again selected the regimes to minimize the global fraction Z₂ of species to be included in the implicit solver. Z₂ decreases from 65 % to 40 % as M increases from 3 to 20 and flattens at higher values of M (Fig. 3a). This is because 88 % of the grid boxes can be represented by 20 chemical regimes (Fig. 3b). A larger number of blocks (N>12) would extend the improvement to higher values of M, but the size of M is also limited by considerations of code manageability and compilation speed. We use 20 chemical regimes in what follows.

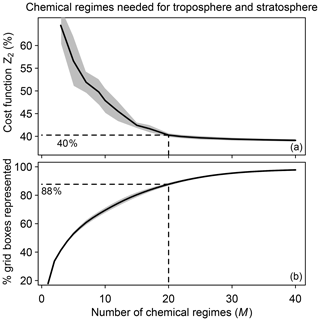
Figure 3 Speedup of the chemical computation as a function of the number M of chemical mechanism subsets (chemical regimes) used in the coupled implicit solver of the GEOS-Chem model for adaptive simulation of the troposphere and stratosphere. (a) Minimum of cost function Z₂ (global fraction of chemical species treated as fast) as a function of the number of chemical regimes. (b) Percentage of model grid boxes that can be represented by the M chemical regimes without adjustment (see Eq. 5 and related text). Dashed lines show the values for M=20. For both panels, results are for the first 10 d of February, May, August, and November sampled every 6 h (shaded area denotes 1 standard deviation of results sampled every 6 h).

Table 2 shows the composition of the 20 chemical regimes as defined by the blocks of Table 1. For 72 % of the grid boxes in the troposphere and stratosphere, we only need to solve for fewer than 50 % of the species as fast. Only 3.6 % of grid boxes need to use the full chemistry mechanism, as defined by the 20th regime.

Table 2 Composition and frequency of the 20 chemical regimes in the adaptive algorithm^a.

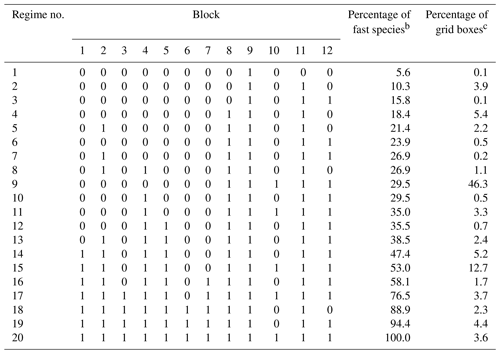
^a The chemical regimes are defined by the ensemble of fast species that need to be treated as a coupled system with an implicit solution in the chemical operator. The species are assembled into blocks as listed in Table 1, and here we identify the blocks treated as fast in the chemical regime (1≡ fast, 0≡ slow). ^b Percentage of the 228 species in the GEOS-Chem chemical mechanism treated as fast in the chemical regime. ^c Global percentage of GEOS-Chem tropospheric and stratospheric grid boxes for which the chemical regime is selected. Values are for 1 August 2013 sampled every 6 h.

Figure 4 shows the distribution of these 20 chemical regimes globally and for different altitudes and the corresponding percentage of fast species that needs to be included in the chemical solver. In continental surface air where VOC emissions are concentrated, we find that over 80 % of species generally need to be included. This percentage is reduced to 20 %–60 % over the ocean and <20 % over Antarctica. At 5 km altitude, we find a distinct boundary between the daytime and nighttime hemisphere; the daytime chemistry is more active, and the percentage of fast species is higher in the daytime (40 %–60 %) than at night (10 %–30 %). At 15 km altitude the extratropics are in the stratosphere, where non-methane VOC chemistry is largely absent, but the model still needs to solve 30 %–40 % species as fast because of the halogens. Deep convection over tropical continents delivers short-lived VOCs and their oxidation products to the upper troposphere, so that a large number of species needs to be treated as fast in the convective outflow where and when it occurs. The importance of deep convective outflow for global atmospheric chemistry has been pointed out in a number of studies (Prather and Jacob, 1997; Bechara et al., 2010; Schroeder et al., 2014) and emphasizes the advantage of reducing the mechanism adaptively on the fly rather than with preset geographic boundaries.

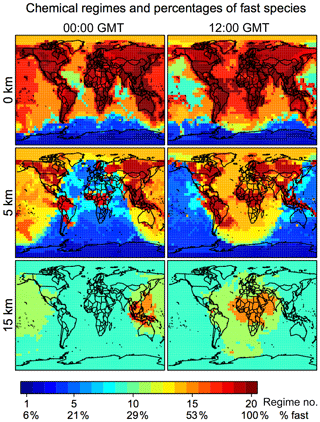
Figure 4 Chemical mechanism complexity needed in different regions of the atmosphere. The figure identifies the chemical regime from Table 2 needed to simulate a given GEOS-Chem grid box on 1 August 2013 at 00:00 and 12:00 GMT. The percentage of the 228 species treated as fast (requiring coupled implicit solution) in that chemical regime is shown on the color bar and more details are in Tables 1 and 2. Results are shown for different altitudes and using a threshold δ of 100 molecules cm⁻³ s⁻¹.

4 Error analysis

Here we quantify the errors in our adaptive reduced mechanism method by comparison with a standard GEOS-Chem simulation for the troposphere and stratosphere (version 12.0.0) including full chemistry (228 species). The comparison is conducted for a 1-month simulation to examine the sensitivity to the rate threshold δ and for a 2-year simulation to evaluate the stability of the method. In both cases, we use the relative root mean square (RRMS) metric as given by Sandu et al. (1997) to characterize the error:

$$\begin{array}{}\text{(7)}& {\mathrm{RRMS}}_i=\sqrt{{\displaystyle \frac{\mathrm{1}}{Q_i}}\sum _{j=\mathrm{1}}^{Q_i}{\left({\displaystyle \frac{n_{i,j}^{\mathrm{reduced}}-n_{i,j}^{\mathrm{full}}}{n_{i,j}^{\mathrm{full}}}}\right)}^{\mathrm{2}}},\end{array}$$

where $n_{i,j}^{\mathrm{reduced}}$ and $n_{i,j}^{\mathrm{full}}$ are the concentrations for species i and grid box j in the reduced and full chemical mechanisms, and the sum is over the Q_i grid boxes where $n_{i,j}^{\mathrm{full}}$ is greater than a threshold a. Here we use $a=\mathrm{1}\times {\mathrm{10}}^{\mathrm{6}}$ molecules cm⁻³ as in Eller et al. (2009) and Santillana et al. (2010).

A critical parameter to select in the algorithm is the rate threshold δ separating fast and slow species on the basis of their production and loss rates. A high threshold decreases the number of fast species and hence speeds up the computation but at the expense of accuracy. We tested different rate thresholds ranging from 10 to 5000 molecules cm⁻³ s⁻¹ in a 1-month GEOS-Chem simulation starting on 1 August 2013. Figure 5 shows the median RRMS error for all species on 1 September and the increased computational performance for different rate thresholds δ. The best range for δ is between 100 and 1000 molecules cm⁻³ s⁻¹, where the median RRMS error is below 1 % and the improvement in computational performance is in the 30 %–40 % range.

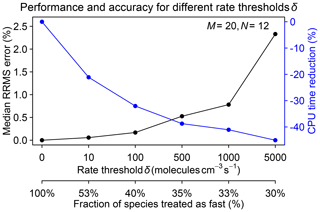
Figure 5 Performance and accuracy of the adaptive chemical mechanism reduction method for different rate thresholds δ (molecules per cubic centimeter per second) to separate fast and slow species. The performance is measured by the reduction in computing processor unit (CPU) time for the chemical operator, and the accuracy is measured by the median relative root mean square (RRMS) error for species concentrations relative to a global GEOS-Chem simulation for the troposphere and stratosphere using the full chemical mechanism (228 species treated as fast). The second x axis gives the global fraction of species that need to be treated as fast depending on the value of δ. The number of blocks (N) is 12 and the number of chemical regimes (M) is 20.

Figure S5 further shows the distribution of RRMS errors over all species for different rate thresholds δ. The 90th percentile RRMS error stays below 5 % if δ≤1000 molecules cm⁻³ s⁻¹ but exceeds 10 % for δ=5000 molecules cm⁻³ s⁻¹. The 99th percentile RRMS error is less than 20 % for δ≤1000 molecules cm⁻³ s⁻¹ but rises to 80 % for δ=5000 molecules cm⁻³ s⁻¹. The largest errors are usually from the tropospheric halogen species (Fig. S6). When near the day–night terminator, the sharp transition of production and loss rates is not properly captured by the first-order explicit equations, resulting in high relative errors.

Figure 6 shows the time evolution over 2 years of simulation of the median RRMS error for all species and also for the selected species OH, ozone, sulfate, and NO₂. The median RRMS for all species is 0.2 %, 0.5 %, and 0.8 % for rate thresholds δ of 100, 500, and 1000 molecules cm⁻³ s⁻¹ respectively. There is no error growth over time. Among the four representative species, the RRMS is highest for NO₂, ranging from 1.0 % to 2.0 % for δ ranging from 100 to 1000 molecules cm⁻³ s⁻¹. For OH, ozone, and sulfate, the RRMSs are below 0.3 % in call cases. Figure 7 displays the spatial distribution of the relative error on the last day of the 2-year simulation, using a rate threshold δ of 500 molecules cm⁻³ s⁻¹ as an example. The relative errors are below 0.5 % everywhere for O₃, OH, and sulfate. The error for NO₂ reaches 1 %–10 % at high latitudes, but this is still well within other systematic sources of errors in estimating NO₂ concentrations (Silvern et al., 2018). Results for rate thresholds δ of 100 and 1000 molecules cm⁻³ s⁻¹ can be found in Figs. S7–8. Running the optimizing algorithm may produce different groupings of species (e.g., Table S1), but they show similar errors.

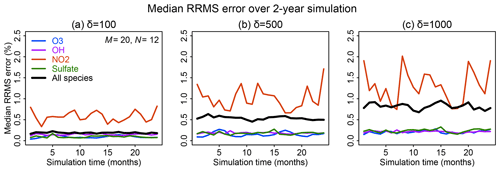
Figure 6 Accuracy of the adaptive reduced chemistry mechanism algorithm over a 2-year GEOS-Chem simulation (see text). The accuracy is measured by the 24 h mean RRMS error on the end day of each month relative to a simulation including the full chemical mechanism. Rate thresholds δ of (a) 100, (b) 500, and (c) 1000 molecules cm⁻³ s⁻¹ are used to partition the fast and slow species in the reduced mechanism. Results are shown for the median RRMS across all 228 species of the full mechanism and more specifically for ozone, OH, NO₂, and sulfate.

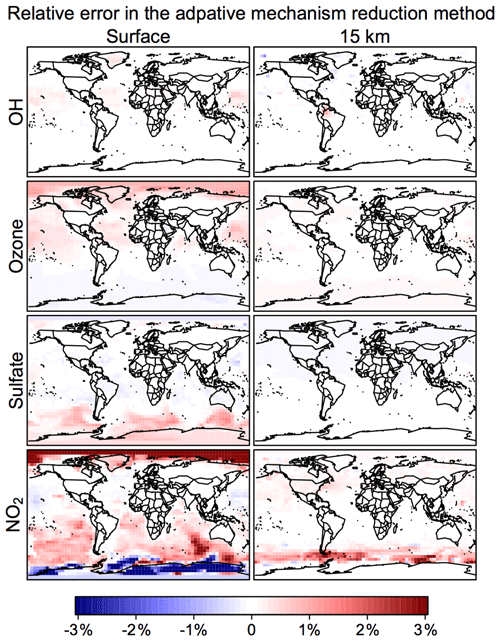
Figure 7 Relative error from the adaptive mechanism reduction method after 2 years of simulation in the GEOS-Chem global 3-D model for tropospheric-stratospheric chemistry. The figure shows relative differences of 24 h average OH, ozone, sulfate, and NO₂ concentrations relative to the full-chemistry simulation on the last day of the 2-year simulation (2013–2014). The relative error for surface NO₂ can be up to ±10 % in polar regions. The calculation uses a rate threshold δ=500 molecules cm⁻³ s⁻¹ to partition the species between fast and slow. The number of blocks (N) is 12 and the number of chemical regimes (M) is 20.

5 Conclusions

We have presented an adaptive method to speed up the temporal integration of chemical mechanisms in global atmospheric chemistry models. This integration (“chemical operator”) involves the implicit solution of a stiff coupled system of ordinary differential equations (ODEs) representing the kinetic evolution of individual species in the mechanism. With typical mechanisms including over 100 coupled species, this chemical integration is the principal computational bottleneck in atmospheric chemistry models and hinders the adoption of detailed atmospheric chemistry in Earth system models.

Our method takes advantage of the fact that different regions of the atmosphere need different levels of detail in the chemical mechanism and that greatly reduced mechanisms can be used in most of the atmosphere. We do this reduction locally and on the fly by choosing from a portfolio of preselected reduced chemical mechanisms (chemical regimes) on the basis of species production and loss rates, distinguishing between “fast” species that need to be in the coupled mechanism and “slow” species that can be solved explicitly. Our method has six advantages over other methods proposed to speed up the chemical computation. (1) It does not sacrifice the complexity of the chemical mechanism where it is needed, while greatly simplifying it over much of the world where it is not. (2) It conserves all of the meaningful diagnostic information of the chemical system, such as production and loss rates of species and families, and individual reaction rates. (3) It can be tailored to achieve the level of simplification that one wishes. (4) It is robust against small mechanistic changes, as these may not alter the choice of chemical regimes or may be accommodated by minor tweaking of the regimes (new species may be assigned to their most appropriate groups on the basis of chemical logic). (5) It is robust against increases in model resolution, where source grid boxes (e.g., urban areas) may simply default to the full mechanism. (6) If an adjoint is available for the full chemical solver, then it can also be used in our method since the software code of the full chemical solver (e.g., KPP) is retained.

We applied the method to the GEOS-Chem global 3-D model for oxidant–aerosol chemistry in the troposphere and stratosphere. The full chemical mechanism in GEOS-Chem has 228 coupled species. We developed an objective numerical method to preselect the reduced chemical regimes on the basis of time slices of full-mechanism model results. We showed that 20 regimes could efficiently cover the range of atmospheric conditions encountered in the model. We then pick appropriate regimes for the chemical operator on the fly by comparing the local production and loss rates of individual model species to a threshold δ. Values of δ in the range 100–1000 molecules cm⁻³ maintain an accuracy better than 1 % relative to a model simulation with the full mechanism and decrease the computational cost of the chemical solver by 32 %–41 %. Comparison testing with a 2-year global GEOS-Chem simulation for the troposphere and stratosphere including the full mechanism shows errors of less than 1 % for critical species and no significant error growth over the 2 years.

The performance tests presented here were for a single-node implementation of GEOS-Chem using 12 CPUs in a shared-memory Open Message Passing (Open-MP) parallel environment. High-performance GEOS-Chem (GCHP) simulations can also be conducted in massively parallel environments with Message Passing Interface (MPI) communication between nodes and domain decomposition across nodes by groups of columns (Eastham et al., 2018). In principle, the chemical operator scales perfectly across nodes because it does not need to exchange information between columns (Long et al., 2015). However, differences in computational costs between columns (due to differences in chemical regimes) could result in load imbalance between nodes, degrading performance. In the current implementation of GCHP, the MPI domain decomposition is by clustered geographical columns in order to minimize the exchange of information across nodes in the advection operator (Eastham et al., 2018). Such a decomposition would penalize our approach since different geographical domains may have different computational loads for chemistry (e.g., oceanic vs. continental regions). This could be corrected by using different MPI domain decompositions for different model operators, and tailoring the domain decomposition for the chemical operator to balance the number of fast species across nodes. Such an approach is used for example in the NCAR Community Earth System Model (CESM) where different domain decompositions are done for advection (clustered geographical regions) and for radiation (number of daytime columns).

Several improvements could be made to our method. (1) The blocks of species used to construct the reduced chemical mechanisms are optimized to minimize the number of fast species but are not always chemically logical, which could be improved by applying prior regularization constraints to the optimization. (2) Optimization in the definition of the reduced mechanisms could take into account not only the number of species but also their lifetimes that affect the stiffness of the system. (3) Separation between fast and slow species could take into account species lifetimes, because species with long lifetimes but high loss rates (such as methane or CO) can be solved explicitly. (4) Mass conservation in the explicit solution could be enforced to enable more species (in particular stratospheric halogens) to be treated explicitly when they play little role in the coupled system. (5) Besides removing the slow species from the implicit chemical operator, we could also remove unimportant reactions, which would reduce the cost in updating the production or loss rates and the Jacobian matrix. These improvements will be the target of future work.