the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
HR3DHG version 1: modeling the spatiotemporal dynamics of mercury in the Augusta Bay (southern Italy)
Giovanni Denaro
Daniela Salvagio Manta
Alessandro Borri
Maria Bonsignore
Davide Valenti
Enza Quinci
Andrea Cucco
Bernardo Spagnolo
Mario Sprovieri
Andrea De Gaetano
The biogeochemical dynamics of Hg, and specifically of its three species Hg0, HgII, and MeHg (elemental, inorganic, and organic, respectively), in the marine coastal area of Augusta Bay (southern Italy) have been explored by the high-resolution 3D Hg (HR3DHG) model, namely an advection–diffusion–reaction model for dissolved mercury in the seawater compartment coupled with a diffusion–reaction model for dissolved mercury in the pore water of sediments in which the desorption process for the sediment total mercury is taken into account. The spatiotemporal variability of the mercury concentration in both seawater ([HgD]) and the first layers of bottom sediments ( and ), as well as the Hg fluxes at the boundaries of the 3D model domain, have been theoretically reproduced, showing acceptable agreement with the experimental data collected in multiple field observations during six different oceanographic cruises. Also, the spatiotemporal dynamics of the total mercury concentration in seawater have been obtained by using both model results and field observations. The mass balance of the total Hg species in seawater has been calculated for the Augusta Harbour, improving previous estimations. The HR3DHG model could be used as an effective tool to predict the spatiotemporal distributions of dissolved and total mercury concentrations, while contributing to better assessing hazards for the environment and therefore for human health in highly polluted areas.
- Article
(7454 KB) - Full-text XML
-
Supplement
(8287 KB) - BibTeX
- EndNote
The investigation of the biogeochemical dynamics of Hg species in the marine environment addresses the need to accurately model sources and pathways of this priority contaminant within and among the different abiotic and biotic compartments of the aquatic ecosystem (Driscoll et al., 2013; Batrakova et al., 2014). Over the last few years some theoretical studies have offered innovative tools to reproduce the mass balance and the dynamics of [Hg] in the marine environment by means of biogeochemical models based on interconnected zero-dimensional boxes representing water or sediment compartments: among these are the River MERLIN-Expo model (Ciffroy, 2015) and the WASP (Water Analysis Simulation Program) model (Melaku Canu et al., 2015; Canu and Rosati, 2017; Rosati et al., 2018). In particular, the River MERLIN-Expo model (Ciffroy, 2015) has been used to reproduce the spatiotemporal distribution of inorganic and organic contaminants in the 1D domain of rivers and to calculate the mass balance for each of them. Although the model is able to describe many of the physical and chemical processes involved in fresh water and sediment, it specifically targets environments characterized by (i) nearly homogeneous water bodies and (ii) limited variations in landscape geometry. The WASP models have been used to simulate the Hg cycle within aquatic ecosystems characterized by well-mixed water layers and homogeneous sediment layers coupled through the boundary conditions at the water–sediment interface (Melaku Canu et al., 2015; Canu and Rosati, 2017; Rosati et al., 2018). In particular, a WASP model applied to a 1D domain and calibrated by using experimental data for dissolved Hg and MeHg allowed us to explore [Hg] dynamics in the Black Sea (Rosati et al., 2018). Similarly, the box model approach has been adopted in a 2D configuration (Melaku Canu et al., 2015; Canu and Rosati, 2017) to calculate Hg mass balance in the coastal areas of the Marano–Grado lagoon (northern Italy), where heterogeneous spatial distributions of Hg species have been observed experimentally. In general, models based on zero-dimensional boxes do not deliver reliable concentration values of contaminants in highly heterogeneous environments unless they provide high spatial resolution and a proper parameterization of the biogeochemical system.
For these reasons, in a recent work (Pakhomova et al., 2018) the biochemistry of Hg in aquatic ecosystems has been studied using a high-resolution (HR) 1D advection–reaction–diffusion model, in which a mercury module has been integrated with the Bottom RedOx Model (BROM) (Yakushev et al., 2017) to reproduce the vertical dynamics of the total dissolved Hg and MeHg in the marine coastal areas of the Étang de Berre lagoon (France) (Pakhomova et al., 2018). However, even this model includes some criticalities in the estimation of mercury dynamics. For example, the temporal variations of mercury benthic fluxes, due to reaction and diffusion processes that involve mercury species present in sediments, are not taken into account in the boundary conditions of this model. On the other hand, sediment chemistry and diffusion were investigated recently by Soerensen et al. (2016), who devised a high-resolution 1D model for Hg species present in water and sediments of the Baltic Sea (Soerensen et al., 2016). In both HR models, however, the strong impact of the horizontal velocity field on the spatiotemporal distribution of [Hg] could not be considered since 1D modeling was used.
In general, the appropriate modeling to reproduce the spatial and temporal variability of Hg species in highly heterogeneous marine ecosystems, such as Augusta Harbour, requires the use of a hydrodynamics model integrated with a biogeochemical model (Zagar et al., 2007, 2014). For this aim, Zagar et al. (2007) introduced a PCFLOW3D model upgraded with the biogeochemical module for simultaneously simulating the velocity field of marine currents, suspended particle transport, and mercury biogeochemical transformations for the whole Mediterranean Sea. The modified PCFLOW3D is a nonstationary 3D model, which consists of four real-time integrated modules: (i) a hydrodynamic module and (ii) transport-dispersion module, both based on the finite-volume method and implemented for obtaining the velocity field of marine currents and the turbulent diffusivities; (iii) a sediment–transport module used to simulate the transport, sedimentation, and resuspension of solid particles; and (iv) a biogeochemical module to reproduce the advection, diffusion, and reaction processes of Hg species. Although the grid used did not guarantee a high spatial resolution, the modified PCFLOW3D model allowed for obtaining, for all the Hg species, theoretical vertical profiles of [Hg] in acceptable agreement with experimental data for most of the Mediterranean Sea (Zagar et al., 2007) and to improve the flux estimations of Hg mass balance for the whole Mediterranean basin (Rajar et al., 2007). By following the same modeling approach of Rajar et al. (2007), over the last decade several authors have used 3D advection–diffusion–reaction models to simulate the spatiotemporal dynamics of [HgD] and [HgT] in oceans, lakes, and estuaries (Zhu et al., 2018). However, the Hg partition mechanisms between the liquid phase and (biotic and abiotic) particulate organic matter (POM) were explicitly included in only a few studies. Among these, Zhang et al. (2014) reproduced the [HgT] in oceans and calculated Hg mass balance by using a 3D ocean tracer model (OFFTRAC) coupled with a general circulation model (GEOS-Chem) (Zhang et al., 2014). Here, the sinking flux of Hg bound to POM was calculated by exploiting remote sensing data for net primary production (NPP) and chlorophyll concentration, which are associated with phytoplankton abundance.
All these approaches do not allow for a fine representation of the spatial variability by approximating the model domain as a set of interconnected boxes or by detailing only in the seawater compartment the spatiotemporal dynamics of the investigated chemical species. For these reasons, we developed a new model to reproduce the spatiotemporal dynamics of [Hg] in polluted marine sites characterized by very high spatial heterogeneity, such as the Augusta Harbour. In the present work we report results obtained using a 3D advection–diffusion–reaction biogeochemical model for three Hg species in seawater (Hg0, HgII, and MeHg) coupled with a diffusion–reaction model for dissolved Hg in the pore water of sediments. The model, named HR3DHG, has been applied to the investigation of mercury dynamics in Augusta Bay (southern Italy; see Fig. 1), specifically in its harbor, a highly polluted coastal site. In this area, a substantial experimental dataset has been collected and improved upon in recent years (Sprovieri et al., 2011; Bagnato et al., 2013; Sprovieri, 2015; Oliveri et al., 2016; Salvagio Manta et al., 2016): oceanographic cruises and data on key physical and chemical parameters from the atmosphere, seawater, and sediments are used to verify and validate the modules of HR3DHG for a reliable and accurate high-resolution investigation of the spatiotemporal dynamics of Hg at highly contaminated coastal marine sites. The HR3DHG model has been designed to predict the biogeochemical behavior of Hg in seawater and sediments, specifically in confined and highly polluted marine coastal areas. It offers the opportunity to explore the effects of both the desorption dynamics of total mercury () in sediments and of diffusion dynamics in pore water in nearly steady conditions. To this aim, in the model we consider both the sediment–pore water distribution coefficients and the desorption rate for the total mercury concentration in the sediment. The former described the ratio between adsorption and desorption rate constants at the steady state without considering perturbations induced by mercury concentration reduction in pore water. The latter reproduced the effects of these perturbations on the solid phase of the sediments.
Moreover, the role played by the spatiotemporal behavior of phytoplankton (La Barbera and Spagnolo, 2002; Fiasconaro et al., 2004; Valenti et al., 2004, 2008; Dutkiewicz et al., 2009; Morozov et al., 2010; Valenti et al., 2012; Denaro et al., 2013a, b, c; Valenti et al., 2015, 2016a, b, c, 2017; Morozov et al., 2019) and the mechanisms responsible for the uptake of Hg within cells (Pickhardt and Fischer, 2007; Radomyski and Ciffroy, 2015; Lee and Fischer, 2017; Williams et al., 2010) are taken into account as specific contributions to the scavenging process and Hg release process by POM, respectively. Also, seasonal oscillations of key environmental variables (velocity of marine currents, amount of precipitation, elemental and inorganic mercury concentration in the atmosphere, etc.) are taken into account.
The main objectives of the HR3DHG model can be synthesized as follows: (i) to accurately reproduce and localize the peaks of [Hg] within the 3D domain; (ii) to estimate the Hg fluxes at domain boundaries; and (iii) to predict the evolution of mercury in the sediment of polluted sites. Moreover, the HR3DHG model offers the possibility to describe the MeHg and HgII partition between the dissolved phase (both seawater and pore water) and the particulate phase (suspended particulate matter and sediment particles). Specifically, in the dissolved phase the model describes the overall behavior of Hg in ionic form and complexed with dissolved organic carbon (DOC). Finally, the HR3DHG model can be a useful tool to predict and prevent the risks for human health in marine areas close to industrial sites affected by Hg pollution extended for very long time intervals.
The paper is organized as follows: a brief overview of the study site is provided in Sect. 2. The HR3DHG model and the model simulation setup are described in Sect. 3, referring to the Supplement for further details. In Sect. 4 the obtained results are reported and compared with experimental data. In Sect. 5 the model and the results are discussed, and, finally, conclusions are drawn in Sect. 6.
The Augusta Bay (Fig. 1) is a semi-closed marine area that occupies a surface of about 30 km2 on the eastern coast of Sicily (southern Italy). The location of one of the most important harbors of the Mediterranean over time since the early 1960s, the Augusta site also hosts several industrial plants, which have adversely affected the whole area with the diffusion of several priority pollutants. In particular, a huge amount of Hg from one of the largest European chlor-alkali plants (Syndial Priolo Gargallo) was discharged into the sea without any treatment until the 1970s, when waste treatment became operational (Bellucci et al., 2012). Although discharge activities were definitively stopped in 2005, the Hg contamination from the chlor-alkali plant remains a critical environmental threat, with extremely high [Hg] in the bottom sediments (ICRAM, 2008; Sprovieri et al., 2011; Oliveri et al., 2016), significant Hg evasion fluxes from sediments to seawater (Salvagio Manta et al., 2016) and to the atmosphere (Bagnato et al., 2013; Sprovieri, 2015), and evident and recently documented risks for the ecosystem (Tomasello et al., 2012; Bonsignore et al., 2013) and for human health (Bianchi et al., 2006; Bonsignore et al., 2015, 2016). The geographical position, together with its geological and oceanographic features, assigns this area a key role in the Hg inventory at Mediterranean scale. The estimate of the Hg export from Augusta Bay to the open sea (0.54 kmol yr−1; Salvagio Manta et al., 2016) corresponds to about 4 % of total input from coastal point and diffuse sources to the Mediterranean Sea (12.5 kmol yr−1; Rajar et al., 2007). A very narrow shelf develops down to 100–130 m with a mean gradient of about 1.0∘ and a next steep slope characterized by a dense net of canyons dropping to the deep Ionian basin (Budillon et al., 2008). The Augusta Harbour covers a surface of 23.5 km2 with two main inlets connecting with the open sea: the Scirocco (300 m wide and 13 m deep) and the Levante inlets (400 m wide and 40 m deep). The bottom is mainly flat with an average depth of 15 m, with the exception of a deeper channel about 30 m deep connecting the inner part of the harbor with the Levante inlet. Water circulation inside the port and the exchanges through the inlets are mainly ruled by the wind and tidal forcing. Tidal fluctuations are generally low, with amplitudes ranging between 10 and 20 cm, and the winds are generally from the northwest and northeast with an average speed of around 3 m s−1 (De Marchis et al., 2014). Water circulation in the outer coastal areas is also mainly affected by wind and tidal forcing and only weakly influenced by the outer baroclinic ocean circulation, which takes place mainly from the shelf break area offshore.
The HR3DHG model has been designed and implemented to reconstruct, at high spatiotemporal resolution, the behavior of [HgT] and [HgD]. The model consists of an advection–diffusion–reaction model for the seawater compartment coupled with a diffusion–reaction sub-model for pore water, in which the dynamics of the desorption of between the solid (sediments) and liquid phase (pore water) are considered.
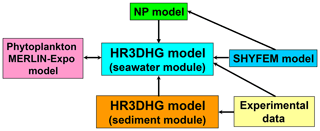
As in the PCFLOW3D model of Zagar et al. (2007), the module of the biogeochemical model for the seawater compartment is integrated with a hydrodynamics module (see Fig. 2). Specifically, SHYFEM (Shallow-water HYdrodynamic Finite-Element Model) is used to calculate the spatiotemporal behavior of the horizontal components of the velocity field in the seawater compartment (Burchard and Petersen, 1999; Umgiesser et al., 2004; Umgiesser, 2009; Umgiesser et al., 2014; Ferrarin et al., 2014; Cucco et al., 2016a, b, 2019), fixing to zero the vertical velocity according to the experimental data (see Sect. S3 of the Supplement for details). In the HR3DHG model, the mercury exchange between the abiotic and biotic compartments is also taken into account. For this purpose, the spatiotemporal behavior of picoeukaryote abundance is reproduced by the Nutrient–Phytoplankton (NP) model (Denaro et al., 2013a, c; Valenti et al., 2015, 2016a, b, 2017) (see Sect. S4 of the Supplement for details). By using the curve of the mean vertical profile obtained by Brunet et al. (2007) the picoeukaryote abundances are converted into the chlorophyll concentration, which allows for the reproduction of the spatiotemporal distribution of NPP. This is used in our model to calculate both the biological rate constants and the sinking flux of Hg adsorbed by POM. The amount of Hg absorbed and released by each picoeukaryote cell in seawater is calculated by using the Phytoplankton MERLIN-Expo model (Ciffroy, 2015; Radomyski and Ciffroy, 2015) (see Sect. S5 of the Supplement for details). The two modules are coupled with the advection–diffusion–reaction sub-model in order to reproduce the spatiotemporal behavior of the load of dissolved Hg released by dead picoeukaryote cells in the seawater compartment (see Fig. 2).

Figure 3Basic scheme used for implementing the HR3DHG model. The scheme describes the transformation processes (k1 – photooxidation, k2 – photoreduction, k3 – biological oxidation, k4 – biological reduction, kPh-de – photodemethylation, kdeme – demethylation, kme – methylation, Kdemeth – demethylation, Kmeth – methylation) and the main transport processes (A – anthropogenic input, AD – atmospheric deposition, B – benthic flux, D – net flux due to particulate deposition and settling, O – net outflow from basin, V – atmospheric evasion), which involve dissolved and particulate-bound Hg species in seawater (, MeHgD, , , MeHgP) and sediments (, MeHgpw, ).
3.1 The advection–diffusion–reaction model for the Hg species in seawater
The dynamics of the [HgD] in the Augusta Bay have been reproduced using an advection–diffusion–reaction model. Specifically, the model equations are solved to identify the behavior of the three main Hg species in seawater, indicated by , , and , which denote the concentrations of each Hg species in the position (x,y,z) within the three-dimensional domain at a specific time t and whose reciprocal interactions are modeled with the reaction terms of the partial differential equations (PDEs). Since the experimental data indicate that the Me2Hg concentration is very low in the Augusta Harbour (Sprovieri, 2015), the behavior of this Hg species is not reproduced in our model. The spatial domain is composed of the sum of several sub-domains (regular parallelepipeds), which cover the bathymetric map of the Augusta Bay (Sprovieri et al., 2011). Specifically, z represents the depth of the barycenter of each sub-domain, localized between the surface (z=0) and the bottom (z=zb), while x and y indicate the distance in meters measured from a reference point (lat. 37∘14.618' N, long. E) located northwest of the town of Augusta.
The model for both compartments is coded in C++ and adopts a finite-volume scheme in explicit form with spatial and temporal discretizations treated separately. The approach followed allows for the combination of various types of discretization procedures for solving the diffusion, advection, and reaction terms. Specifically, the differential equations are solved by performing centered-in-space differencing for the diffusion terms and first-order upwind-biased differencing for the advection terms.
The model domain in seawater is constituted by a mesh of 10 and 18 elements regularly spaced at 454.6 m in both the x and y direction and with a variable number of vertical layers of 5 m depth in the z direction. The mesh covers the whole Augusta Harbour and part of the adjacent coastal area. In Fig. 1 the model domain is shown along with the location of the open boundaries corresponding to the two port inlets. In both compartments (seawater and sediment), a fixed time step of 300 s has been chosen to satisfy the stability conditions and constraints associated with the numerical method adopted (Tveito and Winther, 1998). The stability analysis, performed according to previously published methods (Roache, 1998; Tveito and Winther, 1998; Thi et al., 2005), indicates that the convergence of our algorithm is guaranteed.
The dynamics of the Hg species in seawater are represented through six processes (Zhang et al., 2014; Melaku Canu et al., 2015): (i) photochemical and biological redox transformations (reaction terms); (ii) methylation–demethylation reactions (reaction terms); (iii) movement due to turbulence (diffusion terms); (iv) passive drift due to marine currents (advection terms); (v) organic and inorganic particle scavenging; and (vi) organic particle remineralization.
The photochemical and biological redox transformations between Hg0 and HgII have been described as reaction terms with a first-order kinetic (Batrakova et al., 2014; Zhang et al., 2014; Melaku Canu et al., 2015). In particular, the rate constants of photochemical redox reactions are directly proportional to the shortwave radiation flux at the sea surface attenuated along the water column due to dissolved organic carbon (DOC) and suspended particulate matter (SPM) (Han et al., 2007; Zhang et al., 2014). At the same time, the rate constants of biological redox reactions are proportional to the organic carbon remineralization rate (OCRR), which depends on the net primary production at the sea surface (NPP), surface chlorophyll concentration, and surface atmospheric temperature (Zhang et al., 2014).
The model includes three reaction terms regulated by first-order kinetics, which describe the photodemethylation of MeHg, the methylation of HgII, and the biotic demethylation of MeHg (Batrakova et al., 2014; Melaku Canu et al., 2015). The first is the amount of Hg0 produced by MeHg through photochemical reactions. The second is the amount of MeHg obtained by HgII through biotic and abiotic pathways in seawater. The third is the amount of HgII produced by MeHg through reductive demethylation processes caused by the activity of bacteria in contaminated environments. The rate constants of the three reaction terms are fixed according to previous works (Monperrus et al., 2007b, a; Lehnherr et al., 2011; Batrakova et al., 2014; Melaku Canu et al., 2015).
The PDEs include terms of advection and diffusion for each dimension of the 3D domain. In particular, the diffusion terms reproduce the effects of turbulence on the 3D distribution of HgD through horizontal (Dx and Dy) and vertical (Dz) turbulent diffusivities, which are fixed as constant (see Sect. S1 of the Supplement).
The advection terms describe the effects on the Hg distributions induced by (i) the horizontal velocity components ( and ) of the marine currents along the x and y directions and (ii) the vertical velocity component () along the z direction. The horizontal velocities are calculated using results achieved by applying a hydrodynamic model to the area (Umgiesser et al., 2004; Umgiesser, 2009; Cucco et al., 2016a, 2019) (see Sect. S3 of the Supplement) and change as a function of space and time. The vertical velocity is fixed to zero according to available experimental data.
Moreover, we estimated the dynamics of the dissolved HgII and MeHg species, also considering effects due to (i) adsorption by SPM (scavenging process) and (ii) release by particulate organic matter. The scavenging process for both HgD species is regulated by the sinking flux of particle-bound mercury along the water column (Zhang et al., 2014), which depends on variables calculated by using the NP model. The amount of Hg released by particulate organic matter is primarily estimated through variables defined in the NP model and Phytoplankton MERLIN-Expo model (Valenti et al., 2012; Denaro et al., 2013a, b, c; Valenti et al., 2015, 2016a, b, c, 2017; Radomyski and Ciffroy, 2015) (see Sects. S4 and S5 of the Supplement). Specifically, the NP model provides the spatiotemporal distribution of picoeukaryote abundance, which is used to obtain the chlorophyll concentration and the net primary production through suitable conversion functions (Brunet et al., 2007; Baines et al., 1994) (see Sects. S1 and S4 of the Supplement). These two variables are then exploited to calculate the contribution of the sinking flux for POM-bound Hg within the suspended particulate matter. The Phytoplankton MERLIN-Expo model gives the spatiotemporal dynamics of the HgII and MeHg contents within the picoeukaryote cells (Radomyski and Ciffroy, 2015). These two variables are then used, together with the picoeukaryote abundance, to obtain the amount of HgII and MeHg released by the dead picoeukaryote cells (see Sect. S1.2 and S1.3 of the Supplement).
Thus, the advection–diffusion–reaction model for the Hg species in seawater is defined by the following coupled partial differential equations.
Here, k1, k2, k3, and k4 are the rate constants for the photooxidation of Hg0, the photoreduction of HgII, the biological oxidation of Hg0, and the biological reduction of HgII, respectively (h−1); kPh-de is the rate constant for the photodemethylation of MeHg (h−1); kdeme and kme are the rate constants for the biotic demethylation of MeHg and the methylation of HgII, respectively (h−1); , , and are the direct loads for Hg0, HgII, and MeHg, respectively (); and are the loads of and MeHgD, respectively, released by POM (); and are the sinking fluxes of the SPM-bound mercury for HgII and MeHg, respectively .
The photochemical rate constants (k1 and k2) are directly proportional to the shortwave radiation flux (RAD) at the water–atmosphere interface (Zhang et al., 2014; Soerensen et al., 2010; Qureshi et al., 2010; Batrakova et al., 2014), while the biological rate constants (k3 and k4) are calculated by the organic carbon remineralization rate (OCRR) of the microbial reactions (Zhang et al., 2014) (see Sect. S1 of the Supplement). The kme and kdeme values are fixed according to Lehnherr et al. (2011), while kPh-de is set according to Melaku Canu et al. (2015).
The two sinking fluxes ( and ) are obtained according to previous works (Zhang et al., 2014; Rosati et al., 2018), as follows.
Here, and are the sinking fluxes of POM-bound Hg for HgII and MeHg , respectively; and are the sinking fluxes of silt-bound Hg for HgII and MeHg , respectively; NPP is the net primary production (g C m−2 h−1); the pe ratio is the ratio of particulate organic carbon (POC) export to NPP out of the euphotic zone (dimensionless); z0 is the depth of the euphotic zone (m); kD is the seawater–SPM partition coefficient for HgD (L kg−1); foc is the fraction of suspended particulate matter as organic carbon (dimensionless); vsilt is the silt settling velocity (m h−1); is the partition coefficient of HgII to silt (L kg−1); is the partition coefficient of MeHg to silt (L kg−1); SPIM is the suspended particulate inorganic matter (kg L−1). The NPP is obtained by Baines et al. (1994) using the conversion equation for the chl a concentration (Baines et al., 1994). This is calculated by the picoeukaryote abundance using the conversion curve of Brunet et al. (2007). The pe ratio is calculated by the surface atmospheric temperature measured from remote sensing and the chl a concentration obtained by the NP model (Zhang et al., 2014). The kD value was measured within the Augusta Harbour during the last oceanographic survey, while the spatial distributions of foc and SPIM at the steady state have been reproduced using experimental findings for suspended particulate matter (see Sect. 2.1 of the Supplement). The vsilt, , and values for marine environments with silty SPIM are fixed according to Rosati et al. (2018).
The loads of and MeHgD released by POM are calculated by using the following equations:
where PHgII and PMeHg are the HgII content and MeHg content, respectively, in each cell of picoeukaryotes (µg per cell); b is the picoeukaryote abundance (cells per cubic meter); m is the mortality of picoeukaryotes (h−1); λ is the Hg recycling coefficient for picoeukaryotes (dimensionless). The spatiotemporal dynamics of PHgII and PMeHg are obtained by solving the ODEs of the Phytoplankton MERLIN-Expo model for HgII and MeHg, respectively (Radomyski and Ciffroy, 2015) (see Sect. S5 of the Supplement). The spatiotemporal distribution of b is reproduced by using the NP model (Valenti et al., 2017) (see Sect. S4 of the Supplement). The parameter m is set according to Valenti et al. (2017), while λ is fixed as equal to the nutrient recycling coefficient for picoeukaryotes (Valenti et al., 2015, 2017).
The concentrations [HgD] and [HgT] are calculated as a function of position and time t, as follows:
Here, kD is the seawater–SPM partition coefficient for HgD (only HgII and MeHg) (L kg−1), and SPM is the suspended particulate matter concentration (kg L−1). The partition coefficient kD is set to the value recently experimentally observed in seawater samples collected within the Augusta Bay. The spatial distribution of SPM was set according to the experimental information collected during the oceanographic cruise of October 2017 and is assumed constant for the whole simulation time.
The advection–diffusion–reaction model is completed by a set of ordinary differential equations (ODEs), which describe the mercury fluxes at the boundaries of Augusta Harbour. Specifically, we take the following into account for the three mercury species: (i) the evasion and the deposition of Hg0 at the water–atmosphere interface (Bagnato et al., 2013; Zagar et al., 2007); (ii) the lack of Hg0 diffusion at the water–sediment interface (Ogrinc et al., 2007); (iii) the wet and dry deposition of HgII at the water–atmosphere interface (Rajar et al., 2007; Zagar et al., 2007); (iv) the wet and dry deposition of MeHg at the water–atmosphere interface (Mason et al., 2012); (v) the diffusion of HgII and MeHg at the water–sediment interface; (vi) the constant fixed value of [HgD] out of Augusta Bay (Ionian Sea) (Horvat et al., 2003); and (vii) the exchange of elemental mercury, HgII, and MeHg between the Augusta basin and the Ionian Sea through the two inlets (Salvagio Manta et al., 2016). Since the Augusta Bay is considered a semi-closed basin, the lateral fluxes at the boundaries of the domain are set to zero except for the two inlets (Salvagio Manta et al., 2016). Here, the lateral fluxes depend on the direction of horizontal velocities and therefore change as a function of depth and time (see Sect. S1.1.2 of the Supplement). The boundary conditions for the three mercury species are defined by the following equations.
Here, Hggas-atm is the gaseous elemental mercury (GEM) concentration in the atmosphere (ng m−3); Pr is the amount of precipitation (mm); Δt is the exposition time to precipitation (h); Drydep is the atmospheric dry deposition of HgII (ng m−2 h−1); MTCwater-atm is the gas-phase overall mass transfer coefficient (m h−1); H is the Henry's law constant (dimensionless); is the [Hg0] at the sea surface (µg m−3); is the [HgII] in the atmosphere (ng m−3); is the mass transfer coefficient for HgII at the water–sediment interface (m h−1); is the [HgII] in the pore water of the surface layer (upper 10 cm) of the sediments (µg m−3); is the dissolved [HgII] at the deepest layer of the water column (z=zb) (µg m−3); MTC is the mass transfer coefficient for MeHg at the water–sediment interface (m h−1); MeHgpore water is the [MeHg] in the pore water in the surface layer (upper 10 cm) of the sediments (µg m−3); MeHg is the dissolved [MeHg] in the deepest layer of the water column (z=zb) (µg m−3); , , and MeHgext are the average [Hg0], [HgII], and [MeHg], respectively, reported from the Ionian Sea (µg m−3). The dynamics of the GEM and HgII concentrations in the atmosphere (Hggas-atm and ) are reproduced using the experimental data collected in the Augusta Bay between August 2011 and June 2012 (Bagnato et al., 2013), whereas rainfall is derived from remote sensing (see http://eosweb.larc.nasa.gov, last access: March 2020). The spatiotemporal dynamics of pore water mercury concentrations ( and MeHgpore water) at the sediment surface layer are obtained with the diffusion–reaction model for the sediment compartment, while the mass transfer coefficients (MTC and MTC) at the water–sediment interface are calculated by sediment porosity, the molecular diffusion coefficient, and boundary layer thickness above and below the sediment according to previous works (Covelli et al., 1999; Sørensen et al., 2001; Schulz and Zabel, 2006; Ogrinc et al., 2007; Bryant et al., 2010; Ciffroy, 2015) (see Sect. S1.2.2 and S1.3.2 of the Supplement).
3.1.1 Mass balance of Hg in Augusta Bay
The annual mass balance for the total Hg in the seawater compartment can be estimated using the boundary conditions given in Eqs. (10)–(16), according to the following equation (Sprovieri et al., 2011; Salvagio Manta et al., 2016):
where A is the input of HgD from anthropogenic activities; AD is the atmospheric mercury deposition; B is the mercury flux from sediments to seawater due to diffusion processes; O is the net mercury outflow from the Augusta Harbour to the Ionian Sea; D is the amount of mercury recycled in the Augusta Bay (or the net mercury deposition for settling and burial); V is the GEM evasion from the Augusta Bay to the atmosphere.
By integrating Eqs. (10)–(16), we obtain the terms of the annual mass balance referring to the mercury fluxes exchanged at the interfaces (AD, B, V) and the net mercury outflow from the Augusta Bay to the Ionian Sea (O), while the input of anthropogenic activities (A) is set to zero according to literature sources (Sprovieri et al., 2011; Salvagio Manta et al., 2016).
Finally, we estimate the total amount of mercury recycled (D) from the other terms and compare it with the amount of mercury recycled by scavenging (S). A simple scheme of the fluxes exchanged in the mercury biogeochemical cycle of the Augusta Bay is shown in Fig. 3.
3.2 The diffusion–reaction model for Hg species in pore water
The dynamics of and in the Augusta sediments (average thickness of 1.9 m) have been studied using a diffusion–reaction model. In particular, we investigated the behavior of the two mercury species dissolved in pore water, i.e., HgII () and MeHg (MeHgpore water), which interact with each other directly through the reaction terms of the two PDEs. Moreover, in the model we took into account the variations of mercury concentrations in pore water due to the slow desorption of the fraction bound to particulate sediments. In order to better reproduce the experimental findings, we describe mercury desorption using an exponential equation, which accounts, in the absence of external sources, for the loss of mercury through the desorption mechanism. Since mercury desorption has to depend on its instantaneous concentration, the mechanism is regulated by a first-order kinetic.
The model provides solutions for the spatiotemporal behavior of the mercury concentration for the two species dissolved in pore water, i.e., inorganic mercury () and methyl-mercury (MeHg), and the total mercury concentration in the sediments (). Here, the coordinates (x′, y′, z′) indicate the position within the irregular three-dimensional domain of the sediment compartment. Since the surface sediment slope is very low for the whole basin, the domain is approximated as the sum of several sub-domains shaped as regular parallelepipeds, which reproduce the sediment columns in each position () of the Augusta Bay. Specifically, z′ represents the depth of the barycenter of each sub-domain, localized between the top () and the bottom ( m) of the surface sediment layer, while the other coordinates ( and ) indicate the distance in meters measured from the same reference point used for the seawater compartment.
In the sediment compartment, the PDEs of the model are solved by performing a centered-in-space differencing for the diffusion terms. The sea bottom is discretized in the horizontal plane using the same regular mesh adopted for simulating the dissolved mercury distribution in the seawater compartment (see Fig. 1) with 454.6 m regularly spaced elements. In this case, the vertical discretization is constituted by equally spaced layers of 0.2 m depth, with the exception of the interface layer between the water and sediment, whose depth is set at 0.1 m. This choice has been made in order to best adapt the 3D grid of the model to the scheme used to interpolate available experimental data.
The initial conditions for and are fixed on the basis of experimental findings. As a first step we reproduced the spatial distribution of at time t=0 by interpolating the experimental data collected by ICRAM in 2005 (ICRAM, 2008) (see Sect. S1.2.4 of the Supplement). We then calculated both [HgII] and [MeHg] in pore water using the following equations:
where represents the spatial distribution of [HgT] in the sediments at an initial time (mg kg−1), fMeHg is the fraction of MeHg in the sediments (dimensionless), is the sediment–pore water distribution coefficient for HgII (L kg−1), and is the sediment–pore water distribution coefficient for MeHg (L kg−1).
In pore water, the dynamics of [HgII] and [MeHg] are modeled by considering three chemical–physical processes (Schulz and Zabel, 2006; Melaku Canu et al., 2015; Oliveri et al., 2016): (i) methylation and demethylation (reaction terms); (ii) passive movement due to the Brownian motion of each chemical species (diffusion terms); and (iii) the desorption of mercury bound to sediment particles (desorption term).
The methylation and demethylation processes involved in the dynamics of HgII and MeHg are considered in the model through reaction terms describing first-order kinetics. The rate constants of these reactions are fixed according to previous works (Hines et al., 2012).
The diffusion terms reproduce the effects of Brownian motion on the spatial distribution of in pore water. In particular, the magnitude of the Brownian motion is described by the molecular diffusion coefficients for HgII () and MeHg (), which change in each position of the domain as a function of porosity and tortuosity (see Sect. S1.2.2 and S1.3.2 of the Supplement). The molecular diffusion coefficients are assumed isotropic in all directions and are set as constant functions of time according to previous works (Schulz and Zabel, 2006; Melaku Canu et al., 2015).
The desorption term estimates the increase in and MeHgpore water due to the mercury release from the sediment particles to pore water. The desorption process is regulated by the temporal gradient of (), which changes as a function of position and time (see Sect. S1.2.2 and S1.3.2 of the Supplement).
Thus, the module for the sediment compartment is defined by the following coupled partial differential equations.
Here, Kdemeth is the rate constant for the demethylation of MeHg (h−1); Kmeth is the rate constant for the methylation of HgII (h−1); α is the desorption rate for the bound to the sediment particles (h−1).
As boundary conditions, we assume a null value of mercury flux at the bottom of the sediment column (1.9 m of depth), mainly due to the measured very low porosity, while the vertical gradients of and are set to zero at the water–sediment interface according to field observations. The mercury concentration in sediments is fixed to zero at the lateral boundaries of the 3D domain. The boundary conditions for dissolved and total mercury concentrations in sediments are described by the following equations.
Equations (20)–(26) represent the three-dimensional diffusion–reaction model used to describe and reproduce the spatiotemporal dynamics of [HgII] and [MeHg] in pore water, as well as of in sediments. It should be noted that Eqs. (13)–(14), (20)–(21), and (19), which reproduce the spatiotemporal distributions of the mercury concentrations in both compartments (seawater and sediment), strongly depend on the initial condition for the total mercury concentration observed in the sediments.
3.3 Model and simulation setup
In our model, as initial conditions we assumed a uniformly distributed concentration of HgD and HgT, set to 1.9 ng L−1, corresponding to the experimental detection limit. Specifically, the initial concentration of each Hg species was fixed according to the percentage observed in seawater samples from the Ionian Sea (Horvat et al., 2003) in such a way as to respect the detection limit for total [HgD]. The numerical results were not affected by the chosen initial conditions; indeed, the same spatial distribution of [Hg] at nearly steady state was obtained when initial Hg concentrations higher than the detection limit were fixed.
The model results were obtained by running a single long simulation. To reproduce the spatial mercury distributions at nearly steady state, we integrated the model equations over a time interval ( years) long enough to reach an annual decrease in the mercury concentration of less than 2 %. This percentage value progressively declines for longer time intervals down to an annual decrease of 0.12 % for years.
All environmental parameters and variables used in the model are reported in Tables S1–S3 of the Supplement. Most of the environmental parameters were set to values experimentally observed at sites contaminated by mercury (Horvat et al., 2003; Schulz and Zabel, 2006; Monperrus et al., 2007b, a; Strode et al., 2010; Lehnherr et al., 2011; Melaku Canu et al., 2015; Sprovieri et al., 2011; Salvagio Manta et al., 2016; Sunderland et al., 2006; Zhang et al., 2014; Batrakova et al., 2014), while other parameters, including those most sensitive for the model, were calibrated to correctly reproduce the experimental data collected during the six oceanographic surveys (Sprovieri et al., 2011; ICRAM, 2008; Bagnato et al., 2013; Salvagio Manta et al., 2016; Oliveri et al., 2016). Furthermore, the photochemical and biological rate constants of the redox reactions were calculated using both the outputs of the NP model and the data from remote sensing (see Sect. S1 of the Supplement).
Experimental measurements were carried out during the period between 2005 and 2017 at several stations inside and outside Augusta Harbour (see Fig. 1). The mercury concentration and mercury fluxes were measured both in sediments and seawater (see Tables S6–S10 and S12 of the Supplement). We refer to Bagnato et al. (2013), Salvagio Manta et al. (2016), and Oliveri et al. (2016) for a detailed description of the measured parameters, the related dynamics, and the analytical methods used (ICRAM, 2008; Bagnato et al., 2013; Salvagio Manta et al., 2016; Oliveri et al., 2016). These experimental data were used to identify the most sensitive parameters for the model and to compare them with the theoretical results in order to estimate the model accuracy in reproducing Hg dynamics.
Concerning the calibration procedure, we first focused on the best values of the parameters for the sediment compartment (i.e., sediment–pore water distribution coefficients, desorption rate, and boundary layer thickness above the sediment) in such a way as to optimize the match between theoretical results and experimental observations. Specifically, in Eqs. (20)–(21) the sediment–pore water distribution coefficients were calibrated to guarantee the best theoretical [Hg] in pore water in agreement with the value ranges experimentally observed in a previous work (Oliveri et al., 2016), whereas the fraction of methyl-mercury in sediments for the whole spatial domain was set to that obtained by field observations during the oceanographic survey of October 2017 (see Table S1). In Eq. (22), the desorption rate α was calibrated to obtain the best fit between the theoretical results and experimental observations for [Hg] in pore water. Before calculating the mass transfer coefficients at the water–sediment interface, the boundary layer thickness above the sediment was optimized to better reproduce the spatial distribution of the mercury benthic flux observed experimentally. Unlike the boundary layer thickness above the sediment, the other parameters used to obtain and were not calibrated. In fact, the boundary layer thickness below the sediment was estimated by using the relationship between this parameter and the average velocity of marine currents defined by Sørensen et al. (2001), while the spatial distribution of the sediment porosity within Augusta Harbour was reproduced according to previous works (Covelli et al., 1999; Ogrinc et al., 2007) by exploiting the measurements on the sediment samples performed by ICRAM in 2005. Also, the molecular diffusion coefficient was that reported by Schulz and Zabel (2006).
As a second step, we calibrated model parameters for the seawater compartment (i.e., vertical and horizontal diffusivities) in order to better reproduce the spatiotemporal dynamics of the dissolved mercury concentration. The vertical turbulent diffusivity was calibrated according to experimental data, which indicate weakly mixed water column conditions within the Augusta Bay during the whole year. Specifically, the vertical turbulent diffusivity was set in such a way as to obtain the best match with the experimentally observed dissolved mercury concentration at the surface layer of the water column. The calibrated vertical diffusivity was in good agreement with previously reported values (Denman and Gargett, 1983) under the condition of weakly mixed waters. The horizontal turbulent diffusivity was assumed isotropic in the horizontal water plane (Dx=Dy) and calibrated by considering the values obtained in Massel (1999). In particular, the horizontal turbulent diffusivities were optimized to obtain the best possible match with the observed mercury evasion flux. The calibrated horizontal diffusivities were in accordance with the values estimated by other authors (Massel, 1999) for basins similar in size to those of the Augusta Bay.
In our analysis, no comparison between the calibrated desorption rate and experimental data was possible. However, the other calibrated environmental parameters were in good agreement with those obtained experimentally in the Augusta Bay and at other sites contaminated by mercury (Melaku Canu et al., 2015; Oliveri et al., 2016; Liu et al., 2012; Cossa and Coquery, 2005; Ciffroy, 2015).
Finally, the calibrated model was run by considering the seasonal oscillations of the environmental data (water currents, wind, etc.) provided by hydrodynamic modeling (see Sect. S3 of the Supplement). The model results were validated using the other experimental findings acquired in the Augusta Bay: [MeHgD], [HgD], and [HgT] measured in seawater and all annual Hg fluxes estimated for the mass balance.
In the following the simulation results obtained for the seawater and sediment compartments are described and compared with experimental data.
4.1 Mercury in seawater
The spatial distribution of the three mercury species dissolved in seawater is obtained by solving Eqs. (1)–(17), together with the equation system (20)–(26), for the sediment compartment.
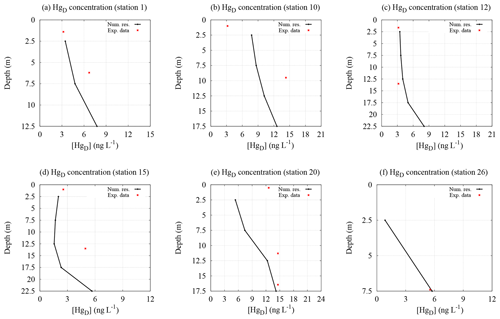
Figure 4Comparison between the experimental data (red points) and the theoretical results (black lines) for the dissolved mercury concentration at six stations in the Augusta Bay. The vertical profiles of [HgD] are obtained by the model for the sites closest to stations 1, 10, 12, and 20 (sampling May 2011), station 15 (sampling June 2012), and station 26 (sampling February 2012).
The theoretical concentrations of the three mercury species dissolved in seawater are reported in Table S5 of the Supplement. Here, we observe that the average concentration ratios among the three mercury species dissolved in seawater (, , and ) are in good agreement with both the experimental and theoretical values reported in recent publications (Zhang et al., 2014; Melaku Canu et al., 2015). Moreover, the theoretical results for the vertical profiles of the mercury concentration show a similar shape for the whole simulated period (2005–2254), while the magnitude of the concentrations in the whole water column decreases slowly as a function of time (see Fig. S1 of the Supplement).
The model results indicate that the dissolved mercury concentration is usually maximal at the seawater–sediment interface (see Fig. 4) where the main sources of HgII and MeHg are localized. These numerical results are in reasonable agreement with the field observations (see Tables S6–S7 of the Supplement). Moreover, taking into account the redox conditions of sediments in the area, we speculate that maxima in MeHg production are confined to the seawater–sediment interface.
Conversely, at some sites of the calculation grid (see Fig. 1) we observe that the peaks of the mercury concentration occur at mid-depth in the water column, possibly due to the distribution of the marine current velocity field within the Augusta basin, which sometimes determines the presence of an [Hg] maximum in the intermediate layers of seawater. In general, in our model the dynamics of the mercury concentration in seawater are strictly connected to the behavior of the benthic mercury fluxes, which decrease slowly as a function of time due to the slow molecular diffusion process of mercury within the pore waters of the sediments.
A quantitative analysis, based on the reduced χ2 test, indicates good agreement between the model results and experimental findings for [MeHg] at stations A3 () and A7 (), while differences can be observed at stations A9 () and A11 (), where the theoretical concentrations appear overestimated at the bottom layer (see Table S6 of the Supplement). This result is probably due to the overestimation of the MeHg benthic fluxes at these two stations.
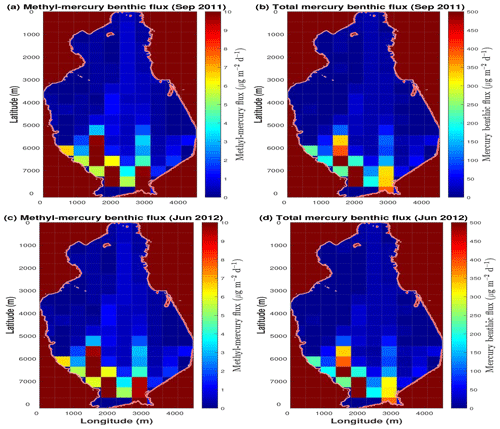
Figure 5Distribution of MeHg and HgD fluxes calculated at the seawater–sediment interface. The maps reproduce the spatial distribution of the benthic flux in the Augusta Bay during the two sampling periods, i.e., 19–21 September 2011 (a, b) and 23–26 June 2012 (c, d).
In our analysis, the spatiotemporal behavior of [HgD] is obtained as the sum of the three dissolved mercury species. On the other hand, the dynamics of the spatial distribution of [HgT] are estimated according to Eq. (9), assuming a linear correlation between the modeled [HgD] and the experimental SPM concentrations. The spatial distributions of [HgD] and [HgT] are reported for May 2011 in Figs. S2–S5 of the Supplement.
The numerical results for [HgD] are in good agreement with the experimental findings for the four investigated periods (see Table S7 of the Supplement). Specifically, the difference between the model result and field observation for [HgD] is less than the experimental error (σ=3.2 ng L−1) in 59 % of sampling points, while it exceeds 2σ in only 17 % of sampling sites. As a conclusion, the comparison between experimental data and theoretical results for [HgD] shows mostly small discrepancies except in some of the most contaminated areas, where concentration hot spots are hard to capture due to the resolution grid used in the present work.
The model results for [HgT] show some discrepancies with experimental data at most of the sites investigated during the first sampling period (May 2011), while in general they evidence acceptable agreement for the other sampling periods (see Table S8 of the Supplement). As a whole, the discrepancy for [HgT] is less than σ in 44 % of cases, while it exceeds 2σ at 32 % of sampling sites. The differences (larger than σ=3.2 ng L−1) can mainly be explained by the significant distance between the sampling sites and the model calculation grid nodes (see Fig. 1). Additionally, we cannot neglect the role played by the theoretical spatial distribution of the SPM concentration (see Eq. 9), which could significantly affect the spatiotemporal dynamics of the total mercury concentration in seawater. In particular, the spatial distribution of SPM concentrations used in the model is probably not appropriate for the first sampling period investigated (May 2011), while it produces good agreement for the other three sampling periods.
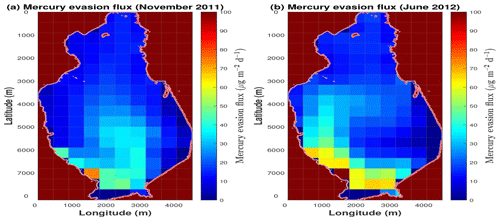
Figure 6Distribution of the Hg0 flux calculated at the seawater–atmosphere interface. The maps reproduce the spatial distribution of the evasion flux in the Augusta Bay during the two sampling periods, i.e., 29–30 November 2011 (a) and 23–25 June 2012 (b).
The theoretical distributions of the benthic mercury fluxes simulated by the model for the two investigated periods (September 2011 and June 2012) are shown in Fig. 5. Here, very high benthic HgII and MeHg fluxes are documented in the southwest sector of Augusta Harbour, where the chlor-alkali plant discharged high amounts of contaminants until the late 1970s. The model also reliably reproduces the high benthic mercury fluxes in the part of the southeast sector close to the inlets of the Augusta Bay. The benthic mercury fluxes are very low in the coastal zones at the north of the basin, while intermediate values have been calculated in the central part of the bay. As a whole, the estimated benthic mercury fluxes are in good agreement with the experimental data collected during the two sampling periods (see Table S9 of the Supplement). It should be noted that the model results suggest that the benthic HgD fluxes are mainly generated by the diffusion process at the seawater–sediment interface and that the amount of HgD release from the resuspended particulate matter is negligible. Moreover, the model results confirm that the spatial heterogeneity of the benthic fluxes observed experimentally is strictly connected to that of the HgT concentration in sediments.
In general, the theoretical distribution of the mercury evasion fluxes is in acceptable agreement with the experimental results for the investigated periods (see Table S10 of the Supplement). Specifically, small discrepancies are observed at most stations (four out of six), while larger difference emerge at stations 3 (November 2011) and 5 (June 2012). From a qualitative point of view, the model results for elemental mercury evasion confirm that a high flux is present in the coastal zones at the southwest of the Augusta Bay (Bagnato et al., 2013), while a reduced evasion flux is observed at the northern sector of the basin (see Fig. 6).
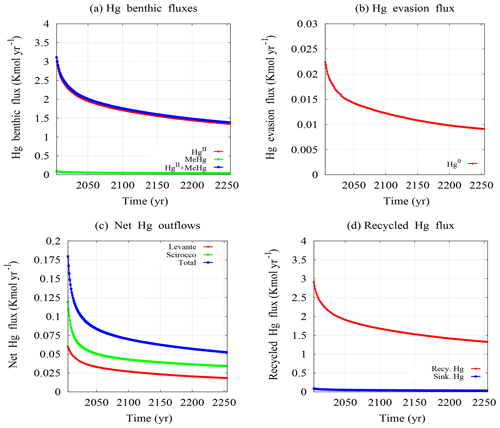
Figure 7Mercury benthic fluxes (a), evasion flux to the atmosphere (b), net outflows at the inlets (c), and recycling fluxes (d).
In this work, we calculate the annual mass balance of the Augusta Bay to study the fate of Hg coming from sediments and to estimate the Hg outflows at the inlets of basin. In Fig. 7, we show the temporal behavior of the annual mercury fluxes used for the mass balance calculation (see also Table S11 of the Supplement). The results of the annual benthic mercury fluxes (B) show that most of the mercury coming up from sediments is in inorganic form (see Fig. 7a), while the benthic MeHg flux appears to be 1 to 2 orders of magnitude lower. The model results are compared with experimental information reported by Salvagio Manta et al. (2016) for three different sampling sites and in two different periods (September 2011 and June 2012). The modeled HgD benthic fluxes (2.65 kmol yr−1 for the year 2011 and 2.61 kmol yr−1 for the year 2012) are significantly larger than those estimated for both sampling periods on the basis of the field observations (1.1 kmol yr−1 in September 2011 and 1.4 kmol yr−1 in June 2012) (Salvagio Manta et al., 2016). This probably depends on the limited number of sampling sites available in the experimental work with a consequent limited capacity to capture reliable estimates of benthic fluxes within a basin, such as Augusta Bay, where the spatial distribution of sediment mercury is highly heterogeneous. Moreover, the higher resolution of the grid used in our model guarantees a better estimation of the annual benthic mercury fluxes once the spatiotemporal integration is performed.
The model results for the dynamics of the annual mercury evasion fluxes are shown in Fig. 7b. The comparison with experimental findings indicates that the mercury evasion fluxes (V) obtained from the model ( kmol yr−1 for the year 2011 and kmol yr−1 for the year 2012) are in good agreement with those estimated by Salvagio Manta et al. (2016) for each year ( kmol yr−1). Conversely, a significant discrepancy is observed between the annual atmospheric mercury deposition (AD) obtained by our model ( kmol yr−1) and that estimated in the experimental work ( kmol yr−1) (Salvagio Manta et al., 2016). This discrepancy is due to the different calculation methods used in the two works. Specifically, in our model the AD is calculated by using both the atmospheric mercury concentrations and the average precipitation measured for all months of the year. In contrast, in Bagnato et al. (2013) the AD is calculated by averaging the experimental data acquired during a time-limited sampling period (from 29 August 2011 to 23 April 2012), namely without considering the period in which the amount of precipitation is very low. In this way, the AD obtained by Bagnato et al. (2013) is much higher than that of our model, even if it is probably overestimated due to the calculation method used. In general, the contribution of AD is negligible in the mercury mass balance of the Augusta Bay. Indeed, the simulations indicate that a strong increase in atmospheric mercury deposition caused by environmental changes (dust fall increase and/or rainfall increase) would not affect the numerical results of our model significantly.
The annual net mercury inflows (A) from rivers and sewerage to the basin are assumed to be negligible, in agreement with field observations. Specifically, the flow rate of the Marcellino River is equal to zero for most of the year, while the inflow from sewerage is low. Moreover, it is fair to speculate that the Hg concentration in fresh waters discharged into the Augusta Bay decreased significantly after the chlor-alkali plant closure.
The dynamics of the annual net mercury outflow (O) at the Levante and Scirocco inlets are described in Fig. 7c. The results encompass both the inflow and outflow of the water mass in each inlet for the whole year and the associated HgT contribution. In Fig. 7c, we show the annual HgT outflow from the Augusta Bay towards the open sea. This has been estimated to be 0.13 kmol yr−1 for the year 2012 and appears significantly lower than the 0.51 kmol yr−1 calculated by Salvagio Manta et al. (2016) for the same year. Our hypothesis to explain this discrepancy is that the previous study does not consider the dynamics of [HgT] at the inlets (the HgT outflow is calculated only on the basis of the mercury concentration measured in February 2012) and that the approach used in the previous paper does not take into account the dynamics of the inflow and outflow of the water mass at the two inlets.
In this work, the annual recycled mercury flux (D) is calculated by subtraction using the mass balance Eq. (18), as was done in previous works on the Augusta Bay (Sprovieri et al., 2011; Salvagio Manta et al., 2016). The model results for the recycled mercury flux are shown in Fig. 7d. Here, the values calculated by our model (2.50 kmol yr−1 for the year 2011 and 2.46 kmol yr−1 for the year 2012) are larger and probably more realistic than those estimated in Salvagio Manta et al. (2016) (0.84 kmol yr−1). Indeed, the former are obtained by considering the seasonal oscillations of all other mercury fluxes during the year, while the latter are calculated without considering the seasonal changes in mercury fluxes (Salvagio Manta et al., 2016).
In order to reproduce the effects induced by the scavenging process on mercury dynamics, our model calculates the annual sinking mercury flux, whose results are shown in Fig. 6d. Here, a significant gap between the recycled flux (2.50 kmol yr−1 for the year 2011) and the sinking flux (0.07 kmol yr−1 for the year 2011) is observed, probably due to the underestimation of the amount of mercury captured by POM (see Eqs. 4–5). More specifically, this behavior could be caused by the underestimation of NPP, which is calculated by using a conversion equation calibrated for oceans (Baines et al., 1994) rather than for coastal zones.
In contrast, very high values of the annual HgT accumulation rate in the surface sediment layer (12.07 kmol yr−1 for the year 2011), with respect to those of the annual recycled flux (2.50 kmol yr−1 for the year 2011), are obtained by our model. This result is caused by the high sedimentation rate (11.7 mm yr−1) estimated experimentally (Sprovieri, 2015; ICRAM, 2008) and used in our calculations for the annual HgT accumulation rate (Covelli et al., 1999). However, the sedimentation rate could be overestimated due to the sampling methods used. In fact, the results obtained by the sediment transport model indicate a low average sedimentation rate for the Augusta Bay.
4.2 Mercury in sediments
The spatiotemporal dynamics of in the sediments of Augusta Bay and the mercury concentration of the two species (HgII and MeHg) dissolved in pore water have been obtained by solving Eqs. (20)–(26). All environmental parameters and variables used for the sediment compartment are reported in Tables S1–S2 of the Supplement.
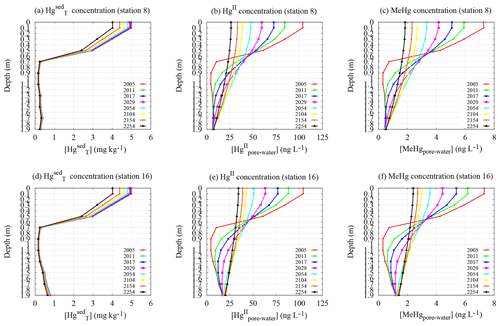
Figure 8Dynamics of the vertical profiles of in sediments (a, d) as well as [HgII] and [MeHg] in pore waters (b, c, e, f) at stations 8 and 16 (sampling May 2011).
In Fig. 8, the vertical profiles of the mercury concentration in the sediments indicate that , , and [MeHgpore water] always reach their maximum value within the surface layer of the sediments (<0.5 m of depth). However, the shape of the vertical profiles for and [MeHgpore water] in pore water changes as a function of time. Also, the magnitude of the concentration peaks decreases over the whole 3D domain during the period studied. In particular, the pore water mercury concentration assumes a nearly uniform distribution along the whole sediment column after several years of model simulation, even if the highest mercury concentrations are always observed in the shallowest layer of the sediments.
The highest and [MeHgpore water] in the sediment surface layer support the high benthic mercury fluxes measured even several years after the chlor-alkali plant closure. Moreover, the results of and [MeHgpore water] also indicate that the benthic mercury fluxes will remain elevated until the beginning of the 23rd century.
Finally, the comparison performed for in pore water indicates good agreement between the theoretical results and the experimental data (see Table S12 of the Supplement).
In this work we introduced the innovative HR3DHG biogeochemical model, which has been verified and validated for all its modules with the rich database acquired for the Augusta Bay. The model is an advection–diffusion–reaction model (Melaku Canu et al., 2015; Yakushev et al., 2017; Pakhomova et al., 2018; Valenti et al., 2017; Dutkiewicz et al., 2009) that reproduces the spatiotemporal dynamics of the mercury concentration in seawater. The advection–diffusion–reaction model was coupled with (i) a diffusion–reaction model, which estimates the mercury concentration in the pore waters of the sediment compartment, and (ii) the equation that reproduces the mechanism responsible for the desorption of the two mercury species from the solid to the liquid phase of the sediments. This “integrated” model, which allows us to give a description of the mercury dynamics at highly polluted marine sites, introduces some novelties in the landscape of the mathematical modeling of spatiotemporal dynamics in a biogeochemical context.
This integrated model also estimates the total amount of mercury present in biological species that occupy the lowest trophic level of the food chain, i.e., phytoplankton populations. For this purpose, we incorporated the Phytoplankton MERLIN-Expo model (Pickhardt and Fischer, 2007; Radomyski and Ciffroy, 2015) to describe the mechanism of mercury uptake in phytoplankton cells. Moreover, we reproduced the spatiotemporal dynamics of phytoplankton communities in seawater using the Nutrient–Phytoplankton model (Dutkiewicz et al., 2009; Morozov et al., 2010; Valenti et al., 2012; Denaro et al., 2013a, b, c; Valenti et al., 2015, 2016a, b, c, 2017; Morozov et al., 2019). This integrated model, together with the Nutrient–Phytoplankton model and the Phytoplankton MERLIN-Expo model, constitutes a new global biogeochemical (HR3DHG) model describing mercury dynamics and their effects on the lowest level of the trophic chain.
The HR3DHG model simultaneously provides the high-resolution spatiotemporal dynamics of [Hg] in seawater and sediment, as well as Hg fluxes at the boundaries of the 3D domain. The former are useful to locate the most polluted areas within the investigated basin. The latter are necessary to obtain the annual mercury mass balance of the basin in the quasi-stationary condition and to predict the mercury outflow towards the open sea, even after a very long time.
For comparison, the different approach used in the WASP models did not allow us to reproduce the dynamics of the mercury concentration distribution at 3D high resolution at polluted sites characterized by elevated spatial heterogeneity. Similar criticalities came out from the study of HR 1D models (Soerensen et al., 2016; Pakhomova et al., 2018), in which the effects of the horizontal velocity field on the mercury dynamics could not be taken into account. Moreover, both the mechanism of the desorption of the total mercury in sediments and the processes involved in dissolved mercury dynamics in pore water were not considered in most advection–diffusion–reaction models, such as the BROM. In general, only a few models (Rajar et al., 2007; Zagar et al., 2007; Canu and Rosati, 2017) were able to make forecasts about the mercury depletion time in the sediment compartment of highly polluted sites, such as Augusta Bay.
Finally, the biogeochemical models introduced in previous works (Soerensen et al., 2016; Pakhomova et al., 2018) provided neither the NPP from the Nutrient–Phytoplankton model (Baines et al., 1994; Brunet et al., 2007; Zhang et al., 2014) nor the load of POM-released HgD obtained using the Phytoplankton MERLIN-Expo model (Pickhardt and Fischer, 2007; Radomyski and Ciffroy, 2015) (see Sect. 3.1).
All the aforementioned aspects are therefore elements of novelty in the context of 3D biogeochemical modeling. The HR3DHG model considers the effects of seasonal changes in the environmental variables on the mercury outflows towards the atmosphere and the open sea.
Application of the HR3DHG model to the case study of Augusta Bay provides crucial information for that environment, helping us to revise our view of the mercury dynamics at the highly contaminated coastal marine sites of the Mediterranean Sea. Firstly, the mass transfer coefficients at the water–sediment interface are highly sensitive to the layer thickness above the sediment. Specifically, for each mercury species in sediments, a small decrease in this parameter causes a great increase in benthic fluxes, with a consequent strong enhancement of the dissolved mercury concentration in seawater.
The model framework for the sediment compartment causes the spatiotemporal dynamics of the benthic mercury flux to strongly depend on the spatial distribution of the sediment porosity and the initial total mercury concentration in the top sediments, which were fixed using the experimental data.
A sensitivity analysis performed on the environmental parameters and variables used in the seawater compartment indicates that the spatiotemporal dynamics of [HgD] primarily depend on the velocity field of the marine currents obtained from the hydrodynamic model (Umgiesser, 2009; Umgiesser et al., 2014; Cucco et al., 2016a, b), even if the role played by the vertical and horizontal diffusivities (Pacanowski and Philander, 1981; Massel, 1999; Denman and Gargett, 1983) cannot be neglected. Specifically, the spatiotemporal behavior of [HgD] changed significantly when alternative velocity fields for the Augusta Bay were used in the biogeochemical module, confirming a feature already observed in previous models (Zagar et al., 2007). Conversely, limited changes in the spatial distribution of [HgD] were observed when different values of the vertical and horizontal diffusivities were set in our model.
The magnitude of the elemental mercury concentration is tightly connected to the values assigned to the rate constants of the photochemical redox reactions, while the role played by the other reaction rates appears negligible for this mercury species.
According to the available experimental data, the theoretical results obtained with the HR3DHG model suggest that the amount of mercury bound to particulate matter is quite high in the seawater compartment (about 47 % of the HgT on average). Because of the exponential decay of [HgT] in sediments, the concentration of the three mercury species dissolved in seawater decreases slowly as a function of time, whereas their concentration ratios remain approximately constant. Specifically, the mean concentrations of mercury are partitioned as 79.0 % of HgII, 18.8 % of elemental mercury, and 2.2 % of MeHg, namely values very similar to those observed experimentally in other contaminated sites (Zhang et al., 2014; Melaku Canu et al., 2015). The same ratio is observed for mercury that outflows from the inlets of Augusta Bay to the open sea. Here, the theoretical results of the HR3DHG model show a progressive decrease in annual mercury outflow from the bay.
On the whole, the mercury dissolved in seawater is derived from sediments through the benthic flux of HgII and MeHg. In particular, these two mercury species are released directly by the sediments, while elemental mercury is generated by redox reactions that involve the other two species. The elemental mercury concentration at the water surface contributes to the mercury evasion flux, even if only a small part of the elemental mercury in the seawater is released in the atmosphere.
Notably, the theoretical results of the HR3DHG model demonstrate the pivotal role played by the recycling process in the mercury mass balance of the Augusta Bay. Estimates for the annual recycled mercury flux indicate that most (94 %) of the mercury released by sediments remains within the Augusta basin, while the mercury outflows at the boundaries of the basin are negligible with respect to the annual benthic mercury fluxes. More specifically, in the quasi-stationary condition, the model results indicate that most of the recycled mercury returns to the sediments where it is reburied, and the amount of mercury absorbed by POM (0.008 kmol yr−1 for the year 2011) and recycled in seawater is negligible. In this last respect, however, it is important to underscore that even a reduced amount of MeHg entering living phytoplankton cells can be very dangerous for the health of human beings due to the bioaccumulation processes that occur throughout the food chain (Williams et al., 2010; Tomasello et al., 2012; Lee and Fischer, 2017).
The theoretical results show that the recycled mercury flux in the Augusta Bay is only partially described by the scavenging process. In particular, an underestimation of the sinking flux for POM-bound mercury is observed when the NPP from the NP model is used in Eqs. (4)–(5). This behavior is probably due to the chl a concentration conversion equation of Baines et al. (1994), which has been calibrated for oceans instead of coastal zones. For this reason, the NPP estimation would need further experimental and theoretical investigations. Moreover, deeper knowledge of the scavenging process, which determines the particulate Hg dynamics, would be necessary from a theoretical point of view to obtain a better estimation of the HgT removed from the water column.
The theoretical results from the HR3DHG model show that, without specific and appropriate recovery actions, the mercury benthic flux could remain high for a very long time, representing a threat for this environment, for its ecosystems, and for human health.
Finally, with its features, the HR3DHG model may represent a useful tool to explore and predict the effects of environmental changes on mercury dynamics for several possible forthcoming scenarios.
A novel biogeochemical integrated model, HR3DHG, has been designed and implemented to reproduce the spatiotemporal dynamics of three species of mercury in the highly contaminated Augusta Bay. The model consistently reproduces the biogeochemical dynamics of mercury fluxes at the boundaries of the 3D domain, which is necessary for an accurate and reliable approximation of the annual mass balance for the whole basin. Direct comparison of model and experimental data suggests a good capacity of HR3DHG to capture the crucial processes dominating the dynamics of Hg species in the different marine compartments and at their interfaces, with reliable estimations of benthic fluxes and evasion towards the atmosphere. The model provides robust information on the recycling of the Hg species in a confined coastal area and can be considered a reliable numerical tool to describe the high-resolution variability of the most important biogeochemical variables driving Hg concentrations. Finally, model results for the Augusta Bay suggest a permanent and relevant long-term (at century scale) mercury benthic flux associated with negative effects for the biota of the investigated marine ecosystem and with significant health risks.
The experimental data used in this study are available and properly referenced in the paper or collected in the tables in the Supplement. The software code files are available on GitHub (https://doi.org/10.5281/zenodo.3384784, Denaro and Borri, 2019) and can be also downloaded from http://biomatlab.iasi.cnr.it/models/hr3dhgv1.zip (last access: 20 March 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-13-2073-2020-supplement.
GD devised the HR3DHG model. GD, AB, and ADG designed the software used to numerically solve the equations of the model. GD and MS jointly wrote the paper. DV and BS supported the HR3DHG model development. AB, DV, BS, and ADG managed the simulations. DSM and MB performed the Hg data collection. DSM developed the sampling strategy. DSM and MB performed the study of Hg biogeochemistry. MS investigated the Hg biogeochemical dynamics. AC investigated the hydrodynamics in Augusta Bay. AC performed the ocean modeling and generated the code of SHYFEM. EQ performed the data statistics and mapping. All authors contributed to reviewing the paper.
The authors declare that they have no conflict of interest.
This research has been supported by the Ministry of University, Research and Education of the Italian government under project “Centro Internazionale di Studi Avanzati su Ambiente, ecosistema e Salute umana – CISAS” (grant no. CUP: B62F15001070005, CIPE n. 105/2015).
This paper was edited by Carlos Sierra and reviewed by Ginevra Rosati and Dusan Zagar.
Bagnato, E., Sprovieri, M., Barra, M., Bitetto, M., Bonsignore, M., Calabrese, S., Di Stefano, V., Oliveri, E., Parello, F., and Mazzola, S.: The sea-air exchange of mercury (Hg) in the marine boundary layer of the Augusta basin (southern Italy): Concentrations and evasion flux, Chemosphere, 93, 2024–2032, https://doi.org/10.1016/j.chemosphere.2013.07.025, 2013. a, b, c, d, e, f, g, h, i, j
Baines, S. B., Pace, M. L., and Karl, D. M.: Why does the relationship between sinking flux and planktonic primary production differ between lakes and oceans?, Limnol. Oceanogr., 39, 213–226, https://doi.org/10.4319/lo.1994.39.2.0213, 1994. a, b, c, d, e, f
Batrakova, N., Travnikov, O., and Rozovskaya, O.: Chemical and physical transformations of mercury in the ocean: a review, Ocean Sci., 10, 1047–1063, https://doi.org/10.5194/os-10-1047-2014, 2014. a, b, c, d, e, f
Bellucci, L. G., Giuliani, S., Romano, S., Albertazzi, S., Mugnai, C., and Frignani, M.: An integrated approach to the assessment of pollutant delivery chronologies to impacted areas: Hg in the Augusta Bay (Italy), Environ. Sci. Technol., 46, 2040–2046, https://doi.org/10.1021/es203054c, 2012. a
Bianchi, F., Dardanoni, G., Linzalone, N., and Pierini, A.: Malformazioni congenite nei nati residenti nel Comune di Gela (Sicilia, Italia), Epidemiol. Prev., 30, 19–26, 2006. a
Bonsignore, M., Manta, D. S., Oliveri, E., Sprovieri, M., Basilone, G., Bonanno, A., Falco, F., Traina, A., and Mazzola, S.: Mercury in fishes from Augusta Bay (southern Italy): risk assessment and health implication, Food Chem. Toxicol., 56, 184–194, https://doi.org/10.1016/j.fct.2013.02.025, 2013. a
Bonsignore, M., Tamburrino, S., Oliveri, E., Marchetti, A., Durante, C., Berni, A., Quinci, E., and Sprovieri, M.: Tracing mercury pathways in Augusta Bay (southern Italy) by total concentration and isotope determination, Environ. Pollut., 205, 178–185, https://doi.org/10.1016/j.envpol.2015.05.033, 2015. a
Bonsignore, M., Andolfi, N., Barra, M., Madeddu, M., Tisano, F., Ingallinella, V., Castorina, M., and Sprovieri, M.: Assessment of mercury exposure in human populations: a status report from Augusta Bay (southern Italy), Environ. Res., 150, 592–599, https://doi.org/10.1016/j.envres.2016.01.016, 2016. a
Brunet, C., Casotti, R., Vantrepotte, V., and Conversano, F.: Vertical variability and diel dynamics of picophytoplankton in the Strait of Sicily, Mediterranean Sea, in summer, Mar. Ecol. Prog. Ser., 346, 15–26, 2007. a, b, c, d
Bryant, L. D., McGinnis, D. F., Lorrai, C., Brand, A., Little, J. C., and Wüest, A.: Evaluating oxygen fluxes using microprofiles from both sides of the sediment–water interface, Limnol. Oceanogr.-Meth., 8, 610–627, https://doi.org/10.4319/lom.2010.8.610, 2010. a
Budillon, F., Ferraro, L., Hopkins, T. S., Iorio, M., Lubritto, C., Sprovieri, M., Bellonia, A., Marzaioli, F., and Tonielli, R.: Effects of intense anthropogenic settlement of coastal areas on seabed and sedimentary systems: a case study from the Augusta Bay (southern Italy), Rend. Online Soc. Geol. Italy, 3, 142–143, 2008. a
Burchard, H. and Petersen, O.: Models of turbulence in the marine environment, A comparative study of two-equation turbulence models, J. Marine Syst., 21, 23–53, https://doi.org/10.1016/S0924-7963(99)00004-4, 1999. a
Canu, D. and Rosati, G.: Long-term scenarios of mercury budgeting and exports for a Mediterranean hot spot (Marano-Grado Lagoon, Adriatic Sea), Estuar. Coast. Shelf S., 198, 518–528, https://doi.org/10.1016/j.ecss.2016.12.005, 2017. a, b, c, d
Ciffroy, P.: The River MERLIN-Expo model, Fun Project 4 – Seventh Framework Programme, 2015. a, b, c, d, e
Cossa, D. and Coquery, M.: The Handbook of Environmental Chemistry, Vol. 5, Part K: The Mediterranean Mercury Anomaly, a Geochemical or a Biologocal Issue, Springer-Verlag Berlin Heidelberg, 177–208, 2005. a
Covelli, S., Faganeli, J., Horvat, M., and Bramati, A.: Porewater Distribution and Benthic Flux Measurements of Mercury and Methylmercury in the Gulf of Trieste (Northern Adriatic Sea), Estuar. Coast. Shelf S., 48, 415–428, https://doi.org/10.1006/ecss.1999.0466, 1999. a, b, c
Cucco, A., Quattrocchi, G., Olita, A., Fazioli, L., Ribotti, A., Sinerchia, M., Tedesco, C., and Sorgente, R.: Hydrodynamic modelling of coastal seas: the role of tidal dynamics in the Messina Strait, Western Mediterranean Sea, Nat. Hazards Earth Syst. Sci., 16, 1553–1569, https://doi.org/10.5194/nhess-16-1553-2016, 2016a. a, b, c
Cucco, A., Quattrocchi, G., Satta, A., Antognarelli, F., De Biasio, F., Cadau, E., Umgiesser, G., and Zecchetto, S.: Predictability of wind-induced sea surface transport in coastal areas, J. Geophys. Res.-Oceans, 121, 5847–5871, https://doi.org/10.1002/2016JC011643, 2016b. a, b
Cucco, A., Quattrocchi, G., and Zecchetto, S.: The role of temporal resolution in modeling the wind induced sea surface transport in coastal seas, J. Marine Syst., 193, 46–58, https://doi.org/10.1016/j.jmarsys.2019.01.004, 2019. a, b
De Marchis, M., Freni, G., and Napoli, E.: Three-dimensional numerical simulations on wind- and tide-induced currents: The case of Augusta Harbour (Italy), Comput. Geosci., 72, 65–75, 2014. a
Denaro, G. and Borri, A.: Spatio-temporal dynamic model of mercury concentration – version 1, Zenodo, https://doi.org/10.5281/zenodo.3384784, 2019. a
Denaro, G., Valenti, D., La Cognata, A., Spagnolo, B., Bonanno, A., Basilone, G., Mazzola, S., Zgozi, S., Aronica, S., and Brunet, C.: Spatio-temporal behaviour of the deep chlorophyll maximum in Mediterranean Sea: Development of a stochastic model for picophytoplankton dynamics, Ecol. Complex., 13, 21–34, https://doi.org/10.1016/j.ecocom.2012.10.002, 2013a. a, b, c, d
Denaro, G., Valenti, D., Spagnolo, B., Basilone, G., Mazzola, S., Zgozi, S., Aronica, S., and Bonanno, A.: Dynamics of two picophytoplankton groups in Mediterranean Sea: Analysis of the Deep Chlorophyll Maximum by a stochastic advection-reaction-diffusion model, PLoS ONE, 8, e66765, https://doi.org/10.1371/journal.pone.0066765, 2013b. a, b, c
Denaro, G., Valenti, D., Spagnolo, B., Bonanno, A., Basilone, G., Mazzola, S., Zgozi, S., and Aronica, S.: Stochastic dynamics of two picophytoplankton populations in a real marine ecosystem, Acta Phys. Pol. B, 44, 977–990, https://doi.org/10.5506/APhysPolB.44.977, 2013c. a, b, c, d
Denman, K. L. and Gargett, A. E.: Time and space scales of vertical mixing and advection of phytoplankton in the upper ocean, Limnol. Oceanogr., 28, 801–815, https://doi.org/10.4319/lo.1983.28.5.0801, 1983. a, b
Driscoll, C. T., Mason, R. P., Chan, H. M., Jacob, D. J., and Pirrone, N.: Mercury as a Global Pollutant: Sources, Pathways, and Effects, Environ. Sci. Technol., 47, 4967–4983, https://doi.org/10.1021/es305071v, 2013. a
Dutkiewicz, S., Follows, M. J., and Bragg, J. G.: Modeling the coupling of ocean ecology and biogeochemistry., Global Biogeochem. Cy., 23, GB4017, https://doi.org/10.1029/2008GB003405, 2009. a, b, c
Ferrarin, C., Bajo, M., Bellafiore, D., Cucco, A., De Pascalis, F., and Ghezzo, M.: Toward homogenization of Mediterranean lagoons and their loss of hydrodiversity, Geophys. Res. Lett., 41, 5935–5941, https://doi.org/10.1002/2014GL060843, 2014. a
Fiasconaro, A., Valenti, D., and Spagnolo, B.: Nonmonotonic Behaviour of Spatiotemporal Pattern Formation in a Noisy Lotka-Volterra System, Acta Phys. Pol. B, 35, 1491–1500, 2004. a
Han, S., Lehman, R. D., Choe, K. Y., and Gill, A.: Chemical and physical speciation of mercury in Offatts Bayou: A seasonally anoxic bayou in Galveston Bay, Limnol. Oceanogr., 52, 1380–1392, https://doi.org/10.4319/lo.2007.52.4.1380, 2007. a
Hines, M. E., Potrait, E. N., Covelli, S., Faganeli, J., Emili, A., Zizek, E., and Horvat, M.: Mercury methylation and demethylation in Hg-contaminated lagoon sediments (Marano and Grado Lagoon, Italy), Estuar. Coast. Shelf S., 113, 85–95, https://doi.org/10.1016/j.ecss.2011.12.021, 2012. a
Horvat, M., Kotnik, J., Logar, M., Fajon, V., Zvoranic, T., and Pirrone, N.: Speciation of mercury in surface and deep-sea waters in the Mediterranean Sea, Atmos. Environ., 37, S93–S108, https://doi.org/10.1016/S1352-2310(03)00249-8, 2003. a, b, c
ICRAM: Progetto preliminare di bonifica dei fondali della rada di Augusta nel sito di interesse nazionale di Priolo e Elaborazione definitiva, BoI-Pr-SI-PR-Rada di Augusta-03.22, 2008. a, b, c, d, e
La Barbera, A. and Spagnolo, B.: Spatio-Temporal Patterns in Population Dynamics, Physica A, 314, 120–124, https://doi.org/10.1016/S0378-4371(02)01173-1, 2002. a
Lee, C. S. and Fischer, N. S.: Bioaccumulation of methylmercury in a marine copepod, Environ. Toxicol. Chem., 36, 1287–1293, https://doi.org/10.1002/etc.3660, 2017. a, b
Lehnherr, I., St. Louis, V. L., Hintelmann, H., and Kirk, J. L.: Methylation of inorganic mercury in polar marine waters, Nat. Geosci., 4, 298–302, https://doi.org/10.1038/ngeo1134, 2011. a, b, c
Liu, G., Cai, J., and O'Driscoll, N.: Environmental Chemistry and Toxycology of Mercury, John Wiley and Sons, Inc., Hoboken, New Jersey, 2012. a
Mason, R. P., Choi, A. L., Fitzgerald, W. F., Hammerschimidt, C. R., Lamborg, C. H., Soerensen, A. L., and Sunderland, E. M.: Mercury biogeochemical cycling in the ocean and policy implications, Environ. Res., 112, 101–117, https://doi.org/10.1016/j.envres.2012.03.013, 2012. a
Massel, S. R.: Fluid Mechanics for Marine Ecologists, Springer-Verlag, Berlin Heidelberg, 1999. a, b, c
Melaku Canu, D., Rosati, G., Solidoro, C., Heimbürger, L., and Acquavita, A.: A comprehensive assessment of the mercury budget in the Marano-Grado Lagoon (Adriatic Sea) using a combined observational modeling approach, Mar. Chem., 177, 742–752, https://doi.org/10.1016/j.marchem.2015.10.013, 2015. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o
Monperrus, M., Tessier, E., Amouroux, D., Leynaert, A., Huonnic, P., and Donard, O. F. X.: Mercury methylation, demethylation and reduction rates in coastal and marine surface waters of the Mediterranean Sea, Mar. Chem., 107, 49–63, https://doi.org/10.1016/j.marchem.2007.01.018, 2007a. a, b
Monperrus, M., Tessier, E., Point, D., Vidimova, K., Amouroux, D., Guyoneaud, R., Leynaert, A., Grall, J., Chauvaud, L., Thouzeau, G., and Donard, O. F. X.: The biogeochemistry of mercury at the sediment-water interface in the Thau Lagoon. 2. Evaluation of mercury methylation potential in both surface sediment and the column, Estuar. Coast. Shelf S., 72, 485–486, https://doi.org/10.1016/j.ecss.2006.11.014, 2007b. a, b
Morozov, A., Arashkevich, E., Nikishina, A., and Solovyev, K.: Nutrient-rich plankton communities stabilized via predator-prey interactions: revisiting the role of vertical heterogeneity, Math. Med. Biol., 28, 185–215, https://doi.org/10.1093/imammb/dqq010, 2010. a, b
Morozov, A., Denaro, G., Spagnolo, B., and Valenti, D.: Revisiting the role of top-down and bottom-up controls in stabilisation of nutrient-rich plankton communities, Commun. Nonlinear Sci., 79, 104885, https://doi.org/10.1016/j.cnsns.2019.104885, 2019. a, b
Ogrinc, N., Monperrus, M., Kotnik, J., Fajon, V., Vidimova, K., Amouroux, D., Kocman, D., Tessier, E., Zizek, S., and Horvat, M.: Distribution of mercury and methylmercury in deep-sea surficial sediments of the Mediterranean Sea, Mar. Chem., 107, 31–48, https://doi.org/10.1016/j.marchem.2007.01.019, 2007. a, b, c
Oliveri, E., Manta, D. S., Bonsignore, M., Cappello, S., Tranchida, G., Bagnato, E., Sabatino, N., Santisi, S., and Sprovieri, M.: Mobility of mercury in contaminated marine sediments: Biogeochemical pathways, Mar. Chem., 186, 1–10, https://doi.org/10.1016/j.marchem.2016.07.002, 2016. a, b, c, d, e, f, g, h
Pacanowski, R. and Philander, S. G. H.: Parameterization of Vertical Mixing in Numerical Models of Tropical Oceans, J. Phys. Oceanogr., 11, 1443–1451, https://doi.org/10.1175/1520-0485(1981)011<1443:POVMIN>2.0.CO;2, 1981. a
Pakhomova, S. V., Yakushev, E. V., Protsenko, E. A., Rigaud, S., Cossa, D., Knoery, J., Couture, R. M., Radakovitch, O., Yakubov, S. K., Krzeminska, D., and Newton, A.: Modeling the Influence of Eutrophication and Redox Conditions on Mercury Cycling at the Sediment-Water Interface in the Berre Lagoon, Front. Mar. Sci., 5, https://doi.org/10.3389/fmars.2018.00291, 2018. a, b, c, d, e
Pickhardt, P. C. and Fischer, N. S.: Accumulation of Inorganic and Methylmercury by Freshwater Phytoplankton in Two Contrasting Water Bodies, Environ. Sci. Technol., 41, 125–131, https://doi.org/10.1021/es060966w, 2007. a, b, c
Qureshi, A., O'Driscoll, N. J., MacLeod, M., Neuhold, Y. M., and Hungerbuhler, K.: Photoreactions of mercury in surface ocean water: gross reaction kinetics and possible pathways, Environ. Sci. Technol., 44, 644–649, https://doi.org/10.1021/es9012728, 2010. a
Radomyski, A. and Ciffroy, P.: The Phytoplankton MERLIN-Expo model, Fun Project 4 – Seventh Framework Programme, 2015. a, b, c, d, e, f, g
Rajar, R., Cetina, M., Horvat, M., and Zagar, D.: Mass balance of mercury in the Mediterranean Sea, Mar. Chem., 107, 89–102, https://doi.org/10.1016/j.marchem.2006.10.001, 2007. a, b, c, d, e
Roache, P. J.: Fundamentals of Computational Fluid Dynamics, Hermosa Publishers, Albuquerque, New Mexico, 1998. a
Rosati, G., Heimbürger, L. E., Melaku Canu, D., Lagane, C., Rijkenberg, M. J. A., Gerringa, L. J. A., Solidoro, C., Gencarelli, C. N., Hedgecock, I. M., De Baar, H. J. W., and Sonke, J. E.: Mercury in the Black Sea: New Insights From Measurements and Numerical Modeling, Global Biogeochem. Cy., 32, 529–550, https://doi.org/10.1002/2017GB005700, 2018. a, b, c, d, e
Salvagio Manta, D., Bonsignore, M., Oliveri, E., Barra, M., Tranchida, G., Giaramita, L., Mazzola, S., and Sprovieri, M.: Fluxes and the mass balance of mercury in Augusta Bay (Sicily, southern Italy), Estuar. Coast. Shelf S., 181, 134–143, https://doi.org/10.1016/j.ecss.2016.08.013, 2016. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s
Schulz, H. D. and Zabel, M.: Marine Geochemistry, Springer – Verlag Berlin Heidelberg, 2006. a, b, c, d, e
Soerensen, A. L., Sunderland, E. M., Holmes, C. D., Jacob, D. J., Yantosca, R. M., Skov, H., Christensen, J. H., Strode, S. A., and Mason, R. P.: An improved global model for air-sea exchange of mercury: High concentrations over the north Atlantic, Environ. Sci. Technol., 44, 8574–8580, https://doi.org/10.1021/es102032g, 2010. a
Soerensen, A. L., Schartup, A. T., Gustafsson, E., Gustafsson, B. G., Undeman, E., and Björn, E.: Eutrophication Increases Phytoplankton Methylmercury Concentrations in a Coastal Sea – A Baltic Sea Case Study, Environ. Sci. Technol., 50, 11787–11796, https://doi.org/10.1021/acs.est.6b02717, 2016. a, b, c, d
Sørensen, P. B., Fauser, P., Carlsen, L., and Vikelsøe, J.: Theoretical evaluation of the sediment/water exchange description in generic compartment models (SimpleBox), NERI Technical Report No.360, 2001. a, b
Sprovieri, M.: Inquinamento ambientale e salute umana, il caso studio della Rada di Augusta, CNR Edizioni, P. Aldo Moro, 7, 00185 Roma, Italia, 2015. a, b, c, d
Sprovieri, M., Oliveri, E., Di Leonardo, R., Romano, E., Ausili, A., Gabellini, M., Barra, M., Tranchida, G., Bellanca, A., Neri, R., Budillon, F., Saggiomo, R., Mazzola, S., and Saggiomo, V.: The key role played by the Augusta basin (southern Italy) in the mercury contamination of the Mediterranean Sea, J. Environ. Monitor., 13, 1753–1760, https://doi.org/10.1039/C0EM00793E, 2011. a, b, c, d, e, f, g, h
Strode, S., Jaeglè, L., and Emerson, S.: Vertical transport of anthropogenic mercury in the ocean, Global Biogeochem. Cy., 24, GB4014, https://doi.org/10.1029/2009GB003728, 2010. a
Sunderland, E. M., Gobas, F. A. P. C., Branfireum, B. A., and Heyes, A.: Environmental controls on the speciation and distribtuion of mercury in coastal sediments, Mar. Chem., 102, 111–123, https://doi.org/10.1016/j.marchem.2005.09.019, 2006. a
Thi, N. N. P., Huisman, J., and Sommeijer, B. P.: Simulation of three-dimensional phytoplankton dynamics: competition in light-limited environments, J. Comput. Appl. Math., 174, 57–77, https://doi.org/10.1016/j.cam.2004.03.023, 2005. a
Tomasello, B., Copat, C., Pulvirenti, V., Ferrito, V., Ferrante, M., Renis, M., Sciacca, S., and Tigano, C.: Biochemical and bioaccumulation approaches for investigating marine pollution using Mediterranean rainbow wrasse, Coris julis (Linneaus 1798), Ecotox. Environ. Safe., 86, 168–175, https://doi.org/10.1016/j.ecoenv.2012.09.012, 2012. a, b
Tveito, A. and Winther, R.: Introduction to Partial Differential Equations: A Computational Approach, Springer-Verlag, New York, 1998. a, b
Umgiesser, G.: SHYFEM, Finite Element Model for Coastal Seas. User Manual, The SHYFEM Group, Georg Umgiesser, ISMAR-CNR, Venezia, Italy, 2009. a, b, c
Umgiesser, G., Canu, D. M., Cucco, A., and Solidoro, C.: A finite element model for the Venice Lagoon. Development, set up, calibration and validation, J. Marine Syst., 51, 123–145, https://doi.org/10.1016/j.jmarsys.2004.05.009, 2004. a, b
Umgiesser, G., Ferrarin, C., Cucco, A., De Pascalis, F., Bellafiore, D., Ghezzo, M., and Bajo, M.: Comparative hydrodynamics of 10 Mediterranean lagoons by means of numerical modeling, J. Geophys. Res.-Oceans, 119, 2212–2226, https://doi.org/10.1002/2013JC009512, 2014. a, b
Valenti, D., Fiasconaro, A., and Spagnolo, B.: Pattern formation and spatial correlation induced by the noise in two competing species, Acta Phys. Pol. B, 35, 1481–1489, 2004. a
Valenti, D., Tranchina, L., Cosentino, C., Brai, M., Caruso, A., and Spagnolo, B.: Environmental Metal Pollution Considered as Noise: Effects on the Spatial Distribution of Benthic Foraminifera in two Coastal Marine Areas of Sicily (Southern Italy), Ecol. Model., 213, 449–462, https://doi.org/10.1016/j.ecolmodel.2008.01.023, 2008. a
Valenti, D., Denaro, G., La Cognata, A., Spagnolo, B., Bonanno, A., Mazzola, S., Zgozi, S., and Aronica, S.: Picophytoplankton dynamics in noisy marine environment, Acta Phys. Pol. B, 43, 1227–1240, https://doi.org/10.5506/APhysPolB.43.1227, 2012. a, b, c
Valenti, D., Denaro, G., Spagnolo, B., Conversano, F., and Brunet, C.: How diffusivity, thermocline and incident light intensity modulate the dynamics of deep chlorphyll maximum in Tyrrhenian Sea, PLoS ONE, 10, e0115468, https://doi.org/10.1371/journal.pone.0115468, 2015. a, b, c, d, e
Valenti, D., Denaro, G., Conversano, F., Brunet, C., Bonanno, A., Basilone, G., Mazzola, S., and Spagnolo, B.: The role of noise on the steady state distributions of phytoplankton populations, J. Stat. Mech., 2016, 054044, https://doi.org/10.1088/1742-5468/2016/05/054044, 2016a. a, b, c, d
Valenti, D., Denaro, G., Spagnolo, B., Mazzola, S., Basilone, G., Conversano, F., Brunet, C., and Bonanno, A.: Stochastic models for phytoplankton dynamics in Mediterranean Sea, Ecol. Complex., 27, 84–103, https://doi.org/10.1016/j.ecocom.2015.06.001, 2016b. a, b, c, d
Valenti, D., Giuffrida, A., Denaro, G., Pizzolato, N., Curcio, L., Mazzola, S., Basilone, G., Bonanno, A., and Spagnolo, B.: Noise Induced Phenomena in the Dynamics of Two Competing Species, Math. Model. Nat. Pheno., 11, 158–174, https://doi.org/10.1051/mmnp/201611510, 2016c. a, b, c
Valenti, D., Denaro, G., Ferreri, R., Genovese, S., Aronica, S., Mazzola, S., Bonanno, A., Basilone, G., and Spagnolo, B.: Spatio-temporal dynamics of a planktonic system and chlorophyll distribution in a 2D spatial domain: matching model and data, Sci. Rep., 7, 220, https://doi.org/10.1038/s41598-017-00112-z, 2017. a, b, c, d, e, f, g, h
Williams, J. J., Dutton, J., Chen, C. Y., and Fischer, N. S.: Metal (As, Cd, Hg, and CH3Hg) bioaccumulation from water and food by the benthic amphypod Leptocheirus Plumulosus, Environ. Toxicol. Chem., 29, 1755–1761, https://doi.org/10.1002/etc.207, 2010. a, b
Yakushev, E. V., Protsenko, E. A., Bruggeman, J., Wallhead, P., Pakhomova, S. V., Yakubov, S. Kh., Bellerby, R. G. J., and Couture, R.-M.: Bottom RedOx Model (BROM v.1.1): a coupled benthic–pelagic model for simulation of water and sediment biogeochemistry, Geosci. Model Dev., 10, 453–482, https://doi.org/10.5194/gmd-10-453-2017, 2017. a, b
Zagar, D., Petkovsek, G., Rajar, R., Sirnik, N., Horvat, M., Voudouri, A., Kallos, G., and Cetina, M.: Modelling of mercury transport and transformations in the water compartment of the Mediterranean Sea, Mar. Chem., 107, 64–88, https://doi.org/10.1016/j.marchem.2007.02.007, 2007. a, b, c, d, e, f, g, h
Zagar, D., Sirnik, N., Cetina, M., Horvat, M., Kotnik, J., Ogrinc, N., Hedgecock, I. M., Cinnirella, S., De Simone, F., Gencarelli, C. N., and Pirrone, N.: Mercury in the Mediterranean. Part 2: processes and mass balance, Environ. Sci. Pollut. R., 21, 4081–4094, https://doi.org/10.1007/s11356-013-2055-5, 2014. a
Zhang, Y., Jaeglé, L., and Thompson, L.: Natural biogeochemical cycle of mercury in a global three-dimensional ocean tracer model, Global Biogeochem. Cy., 28, GB004814, https://doi.org/10.1002/2014GB004814, 2014. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o
Zhu, S., Zhang, Z., and Zagar, D.: Mercury transport and fate models in aquatic systems: A review and synthesis, Sci. Total Environ., 639, 538–549, https://doi.org/10.1016/j.scitotenv.2018.04.397, 2018. a