Accounting for forest age in the tile-based dynamic global vegetation model JSBACH4 (4.20p7; git feature/forests) – a land surface model for the ICON-ESM

Natural and anthropogenic disturbances, in particular forest management, affect forest age structures all around the globe. Forest age structures in turn influence key land surface processes, such as photosynthesis and thus the carbon cycle. Yet, many dynamic global vegetation models (DGVMs), including those used as land surface models (LSMs) in Earth system models (ESMs), do not account for subgrid forest age structures, despite being used to investigate land-use effects on the global carbon budget or simulating biogeochemical responses to climate change. In this paper we present a new scheme to introduce forest age classes in hierarchical tile-based DGVMs combining benefits of recently applied approaches the first being a computationally efficient age-dependent simulation of all relevant processes, such as photosynthesis and respiration, using a restricted number of age classes and the second being the tracking of the exact forest age, which is a prerequisite for any implementation of age-based forest management. This combination is achieved by using the tile hierarchy to track the area fraction for each age on an aggregated plant functional type level, whilst simulating the relevant processes for a set of age classes. We describe how we implemented this scheme in JSBACH4, the LSM of the ICOsahedral Non-hydrostatic Earth system model (ICON-ESM). Subsequently, we compare simulation output to global observation-based products for gross primary production, leaf area index, and above-ground biomass to assess the ability of simulations with and without age classes to reproduce the annual cycle and large-scale spatial patterns of these variables. The comparisons show decreasing differences and increasing computation costs with an increasing number of distinguished age classes. The results demonstrate the benefit of the introduction of age classes, with the optimal number of age classes being a compromise between computation costs and error reduction.

1 Introduction

Land use, particularly forest management, substantially influences the age structure of global forests (Pan et al., 2011; Erb et al., 2017). More than 19 Mkm² of forest area, i.e. about 15 % of global ice-free land, are under some kind of management (Luyssaert et al., 2014), with 65 % being under regular harvest schemes and another 7 % being intensive plantations (Erb et al., 2017). Often, management practices make use of rotation cycles, as is common in shifting cultivation (Boserup, 1966) or even-aged forest management strategies that historically were common in temperate forests and are still the dominant management type in boreal forests (Kuusela, 1994; Puettmann et al., 2015; Kuuluvainen and Gauthier, 2018). Forest age structures are also influenced by other natural or anthropogenically caused disturbances such as fires, windthrows, droughts, pests, and insect outbreaks (e.g. Soja et al., 2006; van Mantgem et al., 2009; Dore et al., 2010; Pan et al., 2011, 2013).

Changes in forest age structure in turn influence biophysical and biogeochemical interactions with the atmosphere, through changes in land surface properties such as albedo and carbon uptake (e.g. Juang et al., 2007; Dore et al., 2010; Sun et al., 2010; Kirschbaum et al., 2011; Pan et al., 2011, 2013; Poorter et al., 2016; Erb et al., 2017). Forest age structure changes can influence the susceptibility to the environment and to environmental changes. It is, for example, hypothesised that the response of forests to increasing atmospheric CO₂ ceases as the forest matures because other resources than CO₂, such as water and nutrients, become growth limiting (Körner, 2006).

It is crucially important to include forest age structures in estimates of the effects of land use on the global scale, primarily (1) due to the aforementioned large extent and substantial effects of forest undergoing changes in age structure; (2) due to the aim of global studies to include forest management effects in addition to anthropogenic land cover changes; and (3) because global studies usually only have a very coarse resolution. One example of such global studies is the estimate of global land-use emissions for the annual global carbon budget (Le Quéré et al., 2018), which is conducted with dynamic global vegetation models (DGVMs). Here, 10 out of the 16 participating DGVMs account for wood harvesting. Other examples are studies estimating biogeochemical and/or biophysical interactions between the land surface and the climate system. Such studies are conducted with Earth system models (ESMs) including their land surface models (LSMs), many of which taking part in the coupled model intercomparison projects (CMIPs). Here, considerations of forest age structure might in particular be important for future scenarios that often include strong land-based mitigation measures, such as forest management and afforestation (e.g. in CMIP6's land use intercomparison project LUMIP; see Lawrence et al., 2016). Global studies, in particular the computationally expensive ESM simulations, inevitably need to be conducted on coarse horizontal resolutions, typically only about 0.5 to 2^∘. Land use will thus usually only happen on fractions of the grid cells, creating the need to represent subgrid forest age structures. The importance of subgrid forest age structures is also underlined by recent studies stressing the role of forest (re-)growth for the historical and future terrestrial carbon uptake (e.g. Kondo et al., 2018; Krause et al., 2018; Yao et al., 2018) and by studies simulating smaller land-use emissions when accounting for secondary forests (e.g. Shevliakova et al., 2009; Yue et al., 2018a). Despite all this evidence, many DGVMs, and particularly also those used as LSMs in ESMs, do not account for subgrid forest age structures (Pongratz et al., 2017).

There are categorically different approaches of how subgrid forest age structures can be implemented in DGVMs, depending on whether these models are individual- and cohort-based or tile-based. In the class of individual- and cohort-based models (referred to as vegetation demographic models in Fisher et al., 2018), subgrid structures are inherently provided. Examples are ED-derivatives (Fisher et al., 2015, 2018), LPJ-Guess (Smith et al., 2001; Bayer et al., 2017), and the SEIB-DGVM (Sato et al., 2007). In the (larger) class of tile-based models (also referred to as area-based in Smith et al., 2001), subgrid structures are not inherently provided. In these models each tile describes an average individual per plant functional type (PFT). Examples of this class of DGVMs are CABLE (Haverd et al., 2018), Class-CTEM (Melton and Arora, 2016), ISAM (Yang et al., 2010), JSBACH (Reick et al., 2013; Mauritsen et al., 2019), LM3 (Shevliakova et al., 2009), LPX-Bern (Stocker et al., 2014b), different versions of ORCHIDEE (Naudts et al., 2015; Yue et al., 2018b), and others. In our study we focus on the second class of DGVMs, as they are more commonly used as LSMs in ESMs. One reason that tile-based models are more commonly used is simply that they have lower computational costs. Another reason is their often historically conditioned top–down development, which facilitates a fully coupled execution within the corresponding ESM.

To expand tile-based DGVMs to represent subgrid forest age structures, two approaches have recently been developed. The more frequently applied approach has been to increase the number of tiles in such a way that a certain number of age classes or structurally similar stands can be distinguished. A pioneer study is found in the paper by Shevliakova et al. (2009), using the model LM3 with a fixed number of in total 12 secondary land tiles for all PFTs and a similarity-based merging of tiles in order to maintain the number of tiles despite further land use or disturbances. Comparably, ORCHIDEE-MICT (Yue et al., 2018b) introduced a fixed number of six tiles per woody PFT, with tile merging upon exceeding predefined woody biomass boundaries. In ORCHIDEE-CAN three tiles per woody PFT with tile merging upon exceeding diameter thresholds have been used, while further within-stand structuring has been applied in each tile by accounting for a user-defined diameter distribution (Naudts et al., 2015). An increase in tiles has also been chosen in ISAM (Yang et al., 2010) and LPX-Bern (Stocker et al., 2014a, b); in these models, however, only one additional tile per PFT has been introduced in order to distinguish primary and secondary vegetation. A common drawback of the hitherto existing implementations is the missing traceability of the actual age of the forests as soon as tiles are merged. Merging of tiles, however, is a necessity when the number of age classes is constrained by computation costs.

The alternative approach for extending the number of tiles to represent subgrid forest age structure in tile-based DGVMs is to keep the information about the forest structure in a separate module. For ORCHIDEE-FM (Bellassen et al., 2010), for example, ORCHIDEE has been coupled to a forest management module (FMM). FMM takes the tile wood increment calculated in ORCHIDEE as input, allocates the increment to tracked individual trees, conducts self-thinning and forest management, and feeds back the leaf area index (LAI), biomass, and litter to the tile. A comparable coupling is described in Haverd et al. (2018), where the DGVM CABLE is coupled to the Population Orders Physiology (POP) module for woody demography and disturbance-mediated landscape heterogeneity (Haverd et al., 2014). POP has a detailed description of the forest structure and simulates the growth of age or size classes of trees competing for soil resources and light. For each forest tile, POP gets the stem net primary production (NPP) from CABLE and returns woody vegetation height, mortality, and sapwood mass. Whilst such a use of a separate module principally enables tracking the exact age of the forest in a grid cell, it has the drawback of using average tile information to compute simulated processes, such as photosynthesis. Age dependencies of these processes can thus not be represented.

In this paper we bridge the two approaches for extending tile-based DGVMs to represent subgrid forest age in the sense that we present a way to trace the actual age of the forests in a grid cell despite following the first approach using a restricted number of additional tiles and thus required merges. The suggested approach is applicable for any tile-based DGVM, provided the tiles are structured in a hierarchical way. We describe the implementation of our approach in the DGVM JSBACH4 and use the new model version to conduct test simulations with different numbers of age classes and age distribution schemes. Subsequently, we compare the different simulation results against observation-based data to investigate the compromise between computation costs and error reduction.

2 Methods

2.1 JSBACH4

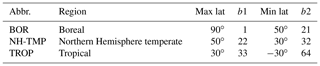
The DGVM JSBACH4 is used as the LSM in the ICON-ESM (Giorgetta et al., 2018). In addition, JSBACH4 is developed with a flexible interface, such that it is also usable within MPI-ESM1.2 (Mauritsen et al., 2019) and as a standalone model driven by climate data. JSBACH4 is a re-implementation of JSBACH3, the original LSM used in MPI-ESM1.2 (Mauritsen et al., 2019), but with a more flexible and extendable structure via a hierarchical representation of tiles (Fig. 1). The implementations described in this paper are based on the current version (4.20p7), which includes most of the processes implemented in JSBACH3, such as land physics, photosynthesis, carbon allocation, and natural disturbances, but is still lacking JSBACH3's representation of anthropogenic land cover change (Reick et al., 2013). Furthermore, the current version does not provide an infrastructure for the horizontal exchange of properties among tiles, such as, for example, the movement of area fractions from one PFT to another.

As an important amendment to the current version (4.20p7), we ported a new JSBACH3 development, which we implemented in a recent independent study (Naudts et al., 2020): while previous JSBACH3 versions assumed a PFT-dependent but constant maximum leaf area index (LAI), that is the LAI value that can maximally be reached at the peak of a season, Naudts et al. (2020) introduced a dependency of the maximum LAI on the available leaf biomass. Such a dependency is a prerequisite for simulating forest regrowth and thus for the introduction of age classes.

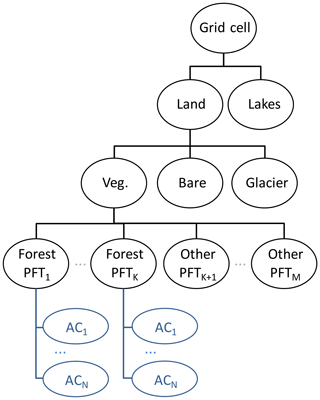
Figure 1 The hierarchical tile structure of JSBACH4. In our study, the default tile structure of JSBACH4 (in black) has been extended by a variable number N of forest age classes (ACs) below each of the K forest plant functional types (PFTs; in blue).

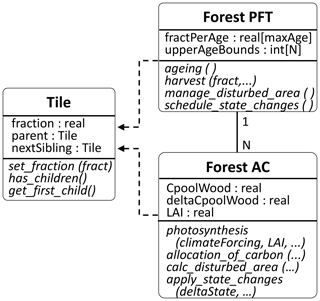
Figure 2 Unified Modelling Language diagram showing the relation between tiles, forest plant functional types (PFTs), and forest age classes (ACs) in JSBACH4–FF, together with a selection of example state variables and functions (in italics). Forest PFTs and ACs are distinct types of tiles, with each PFT having N associated ACs. Each tile hosts certain state variables, for example the grid-cell fraction that it covers, as well as functions, for example to navigate the tile hierarchy. Different types of tiles add further variables and functions. Tiles representing ACs host variables and functions required for processes calculated on the lowest level of the tile hierarchy, such as photosynthesis or carbon allocation. Tiles representing PFTs host variables to maintain meta-information, for example the fractPerAge vector, which contains the fraction covered by each age, i.e. one entry per year up to the maximum tracked age (maxAge). Furthermore, PFTs host functions altering more than one associated AC, for example ageing or harvest.

2.2 JSBACH4–FF

As outlined in the introduction, we aimed for a scheme that allows subgrid forest age structures to be introduced in hierarchical tile-based models in a computationally efficient way, i.e. using a restricted set of age classes, but nevertheless with exact tracing of the age of the forest. For our new JSBACH4 git feature “forests” (JSBACH4–FF) we took advantage of the existing hierarchical tile organisation of JSBACH4, which allows us to introduce different processes and associated state variables on different levels of the tile hierarchy (Fig. 2). Already existing processes which are specific to the development of an age class, such as photosynthesis and carbon allocation, are still executed on the leaves, i.e. now per age class. However, processes related to several age classes, such as natural disturbances and the newly introduced ageing and harvesting processes, are implemented on the PFT level, which we use to manage associated age classes and to maintain meta-information about the forest age structure.

In JSBACH4–FF we introduced a fixed user-defined number N of age classes preset in the configuration file for all forest PFTs (Fig. 1). In addition, an upper age bound per age class AC_K (maxA_K) as well as a total maximum age (maxAge) were introduced, which also have to be predefined. maxAge determines the oldest age up to which the age of an area is tracked, i.e. the length of the fractPerAge vector (Fig. 2). Area fractions with ages exceeding maxAge are not further distinguished and are refereed to as old-grown forest. For a maximum age of 150 years, for example, each forest PFT would contain a vector with a length of 150 to track the exact age of the entire forest area up to 150-year-old forest. Each AC_K covers a certain interval of years [maxA_K−1, maxA_K) (Fig. 3), with the youngest AC (AC₁) always covering the range of year 0 to 1 and the oldest AC_N covering all forest older than maxA_N−1, i.e. [maxA_N−1, ∞), with maxA${}_{N-\mathrm{1}}\le$ maxAge.

In JSBACH4–FF we implemented three processes on the PFT level which can cause shifts of area fractions from one AC to another (Fig. 3), each tracking changes in age fractions in the fractPerAge vector.

Ageing

The newly implemented process of forest “ageing” happens annually: upon ageing each tracked forest fraction gets 1 year older. Yet, a shift from one age class to the next age class only happens for the area of the oldest age (maxA${}_{K-\mathrm{1}}-\mathrm{1}$) of an age class AC_K−1; i.e. only the forest area which upon getting 1 year older exceeds the upper age bound maxA_K−1 of the AC_K−1 needs to be shifted into AC_K. Thanks to the tracking of the age in the fractPerAge vector, the exact area fraction with age maxA${}_{K-\mathrm{1}}-\mathrm{1}$ is known.

Harvest

In the current version, we implemented harvest as a clear-cutting of a certain fraction of an AC, which can happen annually. Harvest causes a shift of the harvested fraction of the affected AC to the youngest AC. Since the exact age of each forest fraction is tracked in the fractPerAge vector, age-based harvest rules can be specified.

Disturbances

Following JSBACH3 (Brovkin et al., 2009) wind and fire disturbances can happen daily in JSBACH4 and are assumed to clear certain area fractions of vegetation. In JSBACH4–FF disturbances were partly re-implemented. While the calculation of the disturbed area is still conducted on each leaf, i.e. on each AC (calc_disturbed_area in Fig. 2), the movement of area between ACs is managed on the PFT level (manage_disturbed_area in Fig. 2). This separation was required since the state variables used to determine the disturbed area, such as available fuel, need to be derived on the lowest layer of the hierarchy. Disturbances are realised as shifts of fractions of affected ACs to the youngest AC (AC₁).

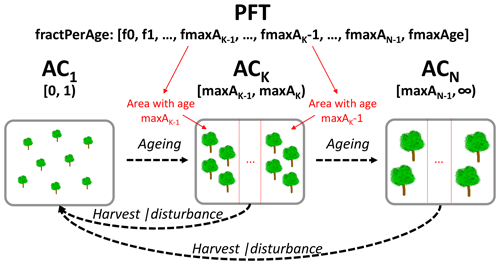
Figure 3 Visualisation of forest age-class (AC) boundaries, the fractPerAge vector, and processes causing shifts from one AC to another in JSBACH–FF. Each AC covers a certain interval of ages. The first AC contains all forest younger than 1 year; an arbitrary AC_K covers [maxA_K−1, maxA_K), i.e. the ages in the right-open interval of the upper age boundary of the previous AC (maxA_K−1) and its own upper age boundary (maxA_K); finally the last class AC_N covers all forest older than and including the upper age boundary of the next younger class (maxA_N−1), with maxA_N−1 being smaller or equal to the total maximum age (maxAge). The information on the area covered by the different ages (indicated in red) is tracked in the fractPerAge vector of the associated forest PFT. Three processes can lead to the movement of area fractions among ACs: ageing leads to the movement of the fraction exceeding the maximum age of an AC; harvest and disturbances lead to the movement of fractions to the first AC.

Since JSBACH4 so far does not provide the infrastructure for the horizontal exchange of properties among tiles (Sect. 2.1), we had to implement such an infrastructure in JSBACH–FF, redistributing area fractions and associated state variables such as the carbon pools or the maximum LAI. This redistribution has been realised in two steps: in the first step, each of the three processes described above determines required redistributions on the PFT level (schedule_state_changes in Fig. 2) according to Eqs. (1) and (2). Here, f_a is the area fraction moved from one AC to another, e.g. upon ageing; V_S is the value of the state variable of the source AC_S and delta_V_S and delta_V_T are the scheduled changes of the state variable on the source AC_S and the target AC_T, respectively.

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }\mathrm{delta}\mathit{\_}{V}_{\mathrm{S}}=\mathrm{delta}\mathit{\_}{V}_{\mathrm{S}}-(V_{\mathrm{S}}\cdot f_{\mathrm{a}})\text{(2)}& {\displaystyle }& {\displaystyle }\mathrm{delta}\mathit{\_}{V}_{\mathrm{T}}=\mathrm{delta}\mathit{\_}{V}_{\mathrm{T}}+(V_{\mathrm{S}}\cdot f_{\mathrm{a}})\end{array}$$

In the second step, the redistributions are applied to the ACs (apply_state_changes in Fig. 2) according to Eq. (3). Here, V_AC represents the affected state variable of the age class AC, delta_V_AC the scheduled change, f_a is the incoming and f_c the current area of the age class AC.

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }{V}_{\mathrm{AC}}^{\prime }={\displaystyle \frac{V_{\mathrm{AC}}\cdot f_{\mathrm{c}}+\mathrm{delta}\mathit{\_}{V}_{\mathrm{AC}}}{(f_{\mathrm{c}}+f_{\mathrm{a}})}}\end{array}$$

2.3 Simulation set-up and measures of model performance

The main purpose of JSBACH is to conduct global applications, often in a mode coupled to an ESM. Therefore, we assess the ability of different set-ups without and with different numbers of age classes to reproduce the annual cycle and large-scale spatial patterns of gross primary production (GPP), forest LAI, and forest above-ground biomass (AGB) by comparing simulated variables against global observation-based products for different seasons and regions. We conducted simulations following a protocol described below (Sect. 2.3.2), with the aim to simulate actual 2010 forest age distributions and forest states. Forest GPP, forest LAI, and forest AGB simulated for 2001 to 2010 were compared to GPP, LAI, and AGB data based on observations using a normalised root mean squared error (NRMSE; Sect. 2.3.5). In addition, we created Taylor diagrams for each variable, season, and region (see Figs S5.5–S5.11 in the Supplement).

2.3.1 Observation-based data

We used 2010 MODIS LAI (Myneni et al., 2002) and GPP data obtained from machine learning methods trained on flux-tower measurements (Tramontana et al., 2016). These LAI and GPP datasets had already been mapped to JSBACH's forest PFTs in a previous study (see Supplement Nyawira et al., 2016). From these datasets seasonal means were calculated and expressed per forest area by dividing them by the sum of the forest cover fractions used for the JSBACH4–FF simulations (Sect. 2.3.2). The AGB per forest area (Avitabile et al., 2016) was downloaded from the GEOCARBON data portal (http://www.bgc-jena.mpg.de/geodb/projects/Data.phd, last access: 19 October 2017) and remapped to T63 using the conservative remapping operator of the climate data operators (CDOs, version 1.9.5). Figures S4.2–S4.4 in the Supplement show maps of the preprocessed observation-based data.

Table 1 Conducted simulations with number of age classes and applied age distribution scheme. The “+1” in the number of age classes refers to the youngest age class, which always covers the years 0 to 1 in JSBACH4–FF.

^a EAS: equal age spacing. ^b IAS: increasing age spacing.

2.3.2 General simulation set-up

We conducted simulations with JSBACH4 (4.20p7) feature/forest in standalone mode hosted within the MPI-ESM environment (see Supplement Sect. S1 for further information). We used JSBACH's default set-up comprising 12 PFTs, of which 4 are of a forest type: tropical evergreen and deciduous forest (TE and TD) and extratropical evergreen and deciduous forest (ETE and ETD). Simulations started in 1860 from scratch, i.e. with empty vegetation carbon stocks, and were run up to 2010. Empty carbon stocks are a simplification used in the absence of global knowledge on the state of the forest in 1860 but have no influence on our results since in simulations with JSBACH4 (4.20p7) LAI, GPP, and AGB only depend on the age since the last clearing event, not on the history before that. The starting date of 1860 was chosen such that it covers at least one full cycle of regrowth, as the oldest age resolved in the simulations matches that of the observation-based data (Poulter et al., 2018). We used T63 resolution (192 longitudes × 96 latitudes; $\mathrm{1.9}{}^{\circ }\times \mathrm{1.9}{}^{\circ }$), a climate forcing based on GSWP3 (Kim et al., 2012), and CO₂ from the collection of greenhouse gas concentrations for CMIP6 (Meinshausen et al., 2017). To obtain forest age distributions comparable to those observed for 2010 (Poulter et al., 2018), harvest was conducted following prescribed maps (Sect. 2.3.4) and natural disturbances were switched off in order to not additionally alter forest age. The simulations were conducted with a static land-use map for 2010, based on TRENDYv4 JSBACH3 output (Le Quéré et al., 2015). The TRENDYv4 JSBACH3 simulation started from a potential vegetation map extrapolated from remote sensing (Pongratz et al., 2008) and was forced by the Land-use Harmonization dataset LUH1 (Hurtt et al., 2011). We conducted simulations with different numbers and distributions of age classes (Sect. 2.3.3). All simulations were conducted on Mistral, the high-performance computing system of the German Climate Computing Center (DKRZ), using an identical number of CPUs.

2.3.3 Simulated number of age classes and age distribution schemes

Table 1 lists the conducted simulations. We used different numbers of age classes and two different age distribution schemes described below. The selected numbers of age classes are arbitrary; however, the finest resolution into 15+1 age classes was motivated by the age map discretisation in Poulter et al. (2018) using 15 age classes that cover 10 years each. In addition to simulations with age classes, we performed one simulation only using PFTs, i.e. without age classes.

The two applied age distribution schemes are defined as follows:

EAS

The equal age-spacing (EAS) distribution scheme spreads the age classes evenly over the age space. For example, a maximum traced age of 150 years distributed evenly over 10+1 age classes (EAS11 in Table 1) results in age classes covering 15 years with the following upper age bounds: 1, 16, 31, 46, …, 136, ∞. This distribution scheme was motivated by the equal spacing applied in the forest age map by Poulter et al. (2018).

IAS

The increasing age-spacing (IAS) distribution scheme uses an increasing age range, i.e. younger age classes cover smaller intervals in the age space than older age classes. The upper age bound of a forest age class K (uLim_K) is defined following Eq. 5.

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }\text{spacing}={\displaystyle \frac{\mathrm{maxAge}}{{\sum }_{i=\mathrm{1}}^{N-\mathrm{1}}i}}\text{(5)}& {\displaystyle }& {\displaystyle }{\text{uLim}}_K=\left\{\begin{array}{ll}\mathrm{1},& \text{if}K=\mathrm{1}\\ \mathrm{\infty },& K=N\\ {\text{uLim}}_{K-\mathrm{1}}+\text{int}(\text{spacing}\cdot K),& \text{else}\end{array}\right.,\end{array}$$

with maxAge being the maximum age and N being the number of age classes. A maximum age of 150 years distributed with IAS over 10+1 age classes (IAS11 in Table 1) results in age classes with the following upper age bounds: 1, 3, 8, 16, 26, 39, 55, 74, 95, 119, ∞2. This second distribution scheme was motivated by the fact that young forests usually have larger incremental changes in most variables than old ones (see, e.g., Amiro et al., 2006; Martínez-Vilalta et al., 2007; Leslie et al., 2018).

Both distribution schemes are applied in a static way, i.e. the age-class boundaries do not change during runtime. Figure 4 shows the division into age classes resulting for the different simulation set-ups for an example grid cell in Canada.

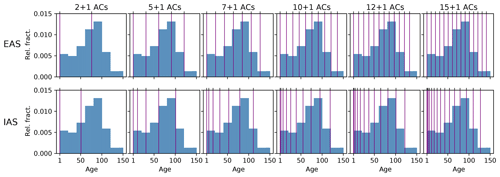
Figure 4 Division into age classes (ACs) for the different simulations listed in Table 1 (EAS: equal age spacing; IAS: increasing age spacing). Purple lines mark the upper age boundary of each age class. The blue bars show the relative fraction for each year resulting for an example cell in Canada (lat 47.5639, long 286.875) in the simulation year 2010. Note that no harvest was conducted in the final simulation year 2010; therefore the smallest age class is empty.

2.3.4 Harvest maps

Harvest maps were derived such that the observed 2010 forest age distribution given by Poulter et al. (2018) is reached in the final simulation year 2010 for simulations using age classes. The observed forest age map of course not only reflects forest harvest, but all processes influencing the age of a forest, i.e. also natural disturbances and anthropogenic land cover change. Because assigning the observed age structure to forest harvesting vs. natural disturbances vs. anthropogenic land cover change would come with uncertainties and is not relevant for our study (as only the affected fraction of an age class matters, independently of the underlying causes), we apply only forest harvest to obtain the observed age distribution.

The map by Poulter et al. (2018) provides a grid with a 0.5^∘ resolution of the global forest age distribution of four forest PFTs: needleleaf evergreen (NE) and needleleaf deciduous (ND), as well as broadleaf evergreen (BE) and broadleaf deciduous (BD). The map uses a discretisation into 15 age classes, covering 10 years each, with the last class containing all area with an age >140 years. In a preprocessing step, the map was remapped to T63 using the conservative remapping operator of the CDOs. Subsequently, the area sums of the two evergreen and the area sums of the two deciduous PFTs from Poulter et al. (2018) were used to derive the age-class maps for JSBACH's evergreen and deciduous PFTs, respectively, following Eq. (6):

$$\begin{array}{}\text{(6)}& \begin{array}{rl}& \mathrm{cf}\mathit{\_}{\mathrm{age}}_i\mathit{\_}{\mathrm{PFT}}_k=(\mathrm{cf}\mathit{\_}{\mathrm{age}}_i\mathit{\_}N+\mathrm{cf}\mathit{\_}{\mathrm{age}}_i\mathit{\_}B)\\ & \cdot {\displaystyle \frac{\mathrm{cf}\mathit{\_}{\mathrm{PFT}}_k}{{\sum }_{i=\mathrm{1}}^{\mathrm{15}}(\mathrm{cf}\mathit{\_}{\mathrm{age}}_i\mathit{\_}N+\mathrm{cf}\mathit{\_}{\mathrm{age}}_i\mathit{\_}B)}}\end{array},\end{array}$$

where i is one of the 15 age classes from Poulter et al. (2018) and k refers to one of the four forest PFTs of JSBACH. N (needleleaf) and B (broadleaf) refer to the PFTs in Poulter et al. (2018), where either both are evergreen (in case PFT_k is evergreen) or both are deciduous PFTs (in case PFT_k is deciduous).

From these age maps, we derived harvest maps for each simulation year such that the simulated age distribution in simulations with age classes conforms with the observed one in 2010, assuming that the fractions given by Poulter et al. (2018) are equally distributed over the 10 years covered by each age class (see Supplement Sect. S2 for more details). In the first (1860) and in the last simulation year (2010) no harvest was conducted.

In different simulation types – with or without age classes – the same harvest maps were used, but different forest management schemes were applied. In simulations with age classes, clear-cutting according to the fractions in the harvest map was taken from the oldest age class. In the simulation without age classes, the PFT simulation, we used the same harvest fractions as in the simulations with age classes, but harvest was applied as done in JSBACH3 (Reick et al., 2013), i.e. by diluting the wood carbon of the harvested PFT tile.

Table 2 Selected regions used for the comparison of simulation results and observation-based data and their latitudinal boundaries and indices.

2.3.5 NRMSE

We calculated the area-weighted root mean squared error (RMSE) according to Eq. (7) based on difference maps between “OBS”, the observation-based data (Sect. 2.3.1), and “SIM”, the results of each simulation (see Table 1). The RMSE was calculated for 2001–2010 simulation output averages, separately for each variable “V” and three selected regions “R”. Each selected region defines a latitudinal band, including all forested land on a subset of the 96 latitudes and the entire 192 longitudes (see Table 2 for the regions, their latitudinal boundaries and the latitude indices b1 and b2). For GPP and LAI the four seasons “S” (DJF, MAM, JJA, SON) were calculated separately. The RMSE for each variable, region, and season was subsequently normalised with the range (max–min) observed for that variable, region, and season (Eq. 8).

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& {\mathrm{RMSE}}_{V,S,R}=\\ & \sqrt{{\displaystyle \frac{\sum _{k=\mathrm{1}}^{\mathrm{192}}\sum _{m=b\mathrm{1}}^{b\mathrm{2}}\left({\displaystyle \begin{array}{c}({\mathrm{OBS}}_{V,S,\mathrm{lon}\left(k\right),\mathrm{lat}\left(m\right)}-{\mathrm{SIM}}_{V,S,\mathrm{lon}\left(k\right),\mathrm{lat}\left(m\right)}{)}^{\mathrm{2}}\\ \cdot \frac{{\mathrm{AREA}}_{\mathrm{lon}\left(k\right),\mathrm{lat}\left(m\right)}}{{\mathrm{AREA}}_R}\end{array}}\right)}{\mathrm{192}\cdot (b\mathrm{2}-b\mathrm{1}+\mathrm{1})}}}\end{array}\end{array}$$

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& {\mathrm{NRMSE}}_{\mathrm{Max}-\mathrm{Min},V,S,R}=\\ & {\displaystyle \frac{{\mathrm{RMSE}}_{V,S,R}}{\mathrm{Max}\left({\mathrm{OBS}}_{V,S,R}\right)-\mathrm{Min}\left({\mathrm{OBS}}_{V,S,R}\right)}}\end{array}\end{array}$$

To more easily assess changes in performance when increasing the number of age classes the different NRMSE_Max−Min values were subsequently aggregated per variable by averaging over the regions (for AGB) and in addition over the seasons (for GPP and LAI), using equal weights.

2.3.6 Computational costs

In addition to determining the NRMSE for different variables, we also determined the computation costs of the different set-ups. We calculated the average CPU time recorded for the simulation years 2001–2010. Whilst absolute computation times are of less interest here, particularly since JSBACH4 is still highly under development and currently does not reach the targeted performance, relative differences among the set-ups depict the costs of the introduction of subgrid forest age structures.

3 Results and discussions

Having forest age classes in JSBACH4–FF facilitates a finer discretisation in each grid cell and is a precondition for any implementation of age-based forest management. The number of age classes in JSBACH4–FF is flexible, and in the following we describe the evaluation of simulation results using different numbers of age classes and age distribution schemes and discuss the compromise between computation costs and error reduction, when selecting a certain number of age classes (Sect. 3.1). Subsequently, we more closely examine differences between an example simulation with a selected number of age classes and a simulation only using PFTs, i.e. without age classes, to investigate the benefits of having age classes in JSBACH4–FF (Sect. 3.2). Finally, we discuss assets and drawbacks of alternative schemes introducing age classes in tile-based DGVMs (Sect. 3.3).

3.1 Evaluation

In this section we use the NRMSE_Max−Min for different regions/seasons as an aggregated measure to compare the different simulation set-ups. A closer examination between a simulation with and without age classes including a spatially explicit comparison follows in Sect. 3.2.

Introducing age classes improves the comparison to observation-based data for nearly all compared variables, regions, and seasons (Fig. 5), with the only notable exception of the AGB in the boreal region, where the PFT simulation was more similar to the observation-based data than the simulations with age classes (Fig. 5c). For most comparisons, the NRMSE_Max−Min indicates a small but distinct improvement over not representing a forest age structure for all simulated numbers of age classes and both age distribution schemes.

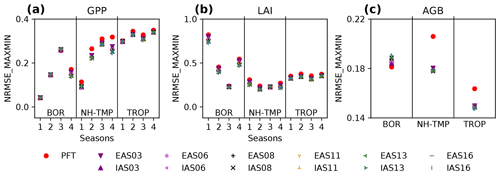
Figure 5 Evaluation of the conducted simulations (Table 1) with observation-based data by means of the normalised root mean squared error (NRMSE_Max−Min, Sect. 2.3.5). Depicted are calculated NRMSE_Max−Min (Sect. 2.3.5) values for each simulation for the gross primary production (GPP; panel a), the leaf area index (LAI; panel b), and the above-ground biomass (AGB; panel c). The NRMSE_Max−Min is calculated as the root mean squared error of observation-based data and simulation results, normalised with the range (max–min) of the according variable for each of the selected regions (Table 2) and for LAI and GPP also for each of the four seasons.

Averaging the NRMSE_Max−Min, giving each region and each season the same weight, results in an NRMSE_Max−Min decreasing with the number of age classes for GPP and LAI (Fig. 6a and b) but saturating for larger numbers of age classes. This shape holds for all regions, with a faster decrease and an earlier saturation for the Northern Hemisphere temperate and tropical regions than for the boreal region (Fig. S3.1a–f). The NRMSE_Max−Min for AGB shows a slowly saturating increase with the number of age classes for the boreal region (Fig. S3.1g) and only small differences among the different numbers of age classes in the Northern Hemisphere temperate and the tropical regions (Fig. S3.1h and i). The observed increase in NRMSE_Max−Min for the boreal AGB is due to an increased underestimation when accounting for more young forest, as is also discussed below (Sect. 3.2). Apart from the boreal AGB comparison, all comparisons show a smaller NRMSE_Max−Min for simulations using the IAS distribution scheme (Figs. 6 and S3.1), i.e. a distribution applying an increasing age space (visualised in Fig. 4). This decrease in NRMSE_Max−Min is due to the finer discretisation of younger age classes which have fast-changing LAI and GPP, which saturates for older age classes (see, e.g., Fig. 7 for LAI). In summary, a finer discretisation, particularly of the younger age classes, is leading to values closer to the observation-based data, even though the benefit of increasing the number of age classes is slowly saturating towards larger numbers of age classes (Fig. 6).

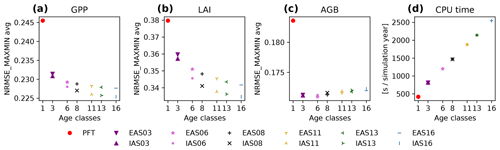
Figure 6 Change in the normalised root mean squared error (NRMSE_Max−Min, Sect. 2.3.5) and in the CPU time when increasing the number of age classes. Panels (a) to (c) show the averaged NRMSE_Max−Min (see also Fig. 5). Averaging has been conducted giving equal weights to all selected regions (Sect. 2.3.5) for AGB (c) and in addition to all four seasons for GPP and LAI (a, b). Figure S3.1 in the Supplement shows the same data separately for each region. Panel (d) shows the computation time required per simulation year averaged over the years 2001–2010.

We performed the averaging of the NRMSE_Max−Min to more easily assess differences among the simulations performed (Table 1). For this, we equally weighted the selected regions because we wanted to equally account for these regions, which strongly differ in simulated PFTs and land–atmosphere interactions. Alternatively, we could have weighted the regions by area, which would have led to an increasing weight of the tropical region and thus to an earlier saturation of the NRMSE_Max−Min with increasing age classes.

Comparisons of required CPU times show a near-linear increase with an increased number of age classes (Fig. 6d) and neither a difference between the two age distribution schemes nor a striking offset as compared to the PFT simulation. A near-linear increase with an increasing number of age classes was expected, since the processes requiring most of the computing time, such as the calculation of photosynthesis, carbon allocation, and respiration, are conducted on the age classes. The absence of a striking offset comparing the PFT simulation with the age-class simulations indicates that the introduced organisational overhead on the PFT level in simulations with age classes, i.e. tracing of the exact forest age and redistributions of area fractions and other state variables among tiles, does not dominate the computation times.

As expected, the optimal number of age classes is a compromise between computation costs and reduction of the error, which is a logical and commonly observed aspect when dealing with discretisation in models (see, e.g., Nabel, 2015; Fisher et al., 2018). In the end, the choice of the number of age classes to be used in a JSBACH4–FF simulation will depend on the application. Simulations comparing different forest management regimes in detail might, for example, aim for a fine discretisation, while more general simulations covering long time spans might tend to aim for fewer age classes. For the remaining parts of this paper, one set-up has been selected as an illustrative example: IAS11 (see Table 1), i.e. the simulation with 10+1 age classes and the age distribution scheme with increasing age space. This set-up is a compromise between the error reduction for GPP and LAI comparisons on the one hand and CPU time on the other. However, the main findings will not depend on the exact number of age classes selected, particularly not as long as they are in the saturation part of the decreasing function regarding GPP and LAI comparisons.

3.2 On the benefit of having age classes

The evaluation with observation-based GPP, LAI, and AGB data showed that simulations with age classes were closer to the observation-based data for nearly all comparisons (Figs. 5 and 6). Spatially explicit comparisons of the results from the PFT simulation and observation-based data (“OBS-PFT” in Figs. S4.2–S4.4, column 2) indicate several areas of underestimation (red) and of overestimation (blue) for all variables. In Fig. 7 we compare results of a JSBACH4–FF simulation with age classes, a simulation only using PFTs, as representative of a DGVM without forest age structures, and the observation-based data of spring (MAM) LAI. The comparison is done for illustrative grid points that were selected to cover areas of both over- and underestimation and to represent different typical land-use histories or forest management regimes, resulting in different age distributions: a grid point with an age distribution matching historically continuous clear-cuttings and some more recent changes in land-use intensity in Germany (Fig. 7a); a grid point with uniform age distribution resulting from a continuous, steady clear-cutting in Finland (Fig. 7b); a grid point with untouched old-grown forest on the one hand and young managed forest on the other hand in India (Fig. 7c); a grid point with intensive harvest or disturbances in the south-east of the US (Fig. 7d); a heavily deforested example in east South America resulting nearly exclusively in young forest (Fig. 7f); a grid cell with recent afforestation in China (Fig. 7e); and a grid cell with predominantly old-grown forests in central Africa (Fig. 7g). In general, the simulation with age classes results in smaller GPP, LAI, and AGB values (Figs. 7 and S4.2–S4.4, column 3), which is expected, since GPP, LAI, and AGB are non-linearly increasing and saturating with age (see, e.g., Fig. 7). Therefore, a harvested age-less forest in the PFT simulation has higher values for these variables than a fraction-weighted average of an age-structured forest in the same grid cell in the simulation with age classes (Fig. 7). Since the simulation with age classes generally results in smaller GPP, LAI, and AGB values, overestimations can be alleviated, causing a decrease in the NRMSE_Max−Min, while underestimations can become more severe, causing an increase in the NRMSE_Max−Min. The comparison of the differences between observation-based data (OBS) and the PFT simulation results on the one hand and OBS and the IAS11 simulation results on the other hand accordingly shows a higher similarity in several areas where the PFT simulation indicated overestimation (areas which are blue in columns 2 and 4 in Figs. S4.2–S4.4) and less similarity in some areas with underestimation (areas which are red in columns 2 and 4 in Figs. S4.2–S4.4). Figure 7 shows several grid-point examples with increased underestimations of spring LAI (Fig. 7a and e), reduced overestimations (panel b and c), and grid points where the previous overestimation is now replaced by a slight underestimation (Fig. 7d and f). Globally, reduced overestimations become particularly visible for LAI in the east of South America, and for several seasons also for example over China, North America, and Europe (Fig. S4.3d, h, i, p). For GPP (Fig. S4.2d, h, i, p) and AGB (Fig. S4d) the pattern is more mixed, with reduced overestimations particularly in the east of North America and China and partly for the east of South America. In addition, there are several areas of under- and overestimation which are very similar in the two simulations (areas coloured in column 2 and white in column 4 in Figs. S4.2–S4.4). These are particularly areas with predominantly old-grown forests, i.e. without a distinct age structure, such as central Africa, the central Amazon, and Siberia, where the PFT and the age-class simulation led to similar results (see, e.g., Fig. 7g). In summary, simulations using age classes led to a decrease in the simulated GPP, LAI, and AGB values due to their non-linear increase with a saturation for older ages. This caused a decrease in the NRMSE_Max−Min in areas where the PFT simulation was biased high and an increase in the NRMSE_Max−Min in areas where the PFT simulation was biased low. Thus, if such a forest age structure would be implemented in a DGVM being predominately biased low, the difference to the observation-based data could increase. In this context, caveats regarding the observation-based data themselves also need to be raised. A known caveat regarding MODIS LAI data is the problem of reflectance saturation in dense canopies making the reflectance insensitive to changes in LAI (Myneni et al., 2002). This problem which is particularly relevant to the tropical region could lead to a general high bias of the model compared to the observation-based data. However, since this problem is more typical for denser, old-grown forests, this high bias would also occur in simulations with age classes. Regarding the GPP data from Tramontana et al. (2016), a recent study by Besnard et al. (2018) criticised that the applied empirical upscaling techniques do not directly consider forest age, making it unclear how well they can capture age-related dynamics. In their study, Besnard et al. (2018) advocate the development of alternative global datasets considering forest age as a predictor.

Importantly, besides the error reduction observed for JSBACH4–FF simulations, the newly implemented forest age structure adds further functionality to JSBACH4–FF. It facilitates keeping the coarse resolution required in ESM simulations while nevertheless capturing some of the sub-grid-scale heterogeneity that is important to better resolve several of the simulated processes. Furthermore, the forest age structure is a precondition for any implementation of forest management regimes while simultaneously accounting for differences in the productivity and the standing stocks. The grid-point examples shown in Fig. 7 highlight the relevance of a distinction of age classes, since they demonstrate the non-linear relationship between LAI and forest age. A similar relationship can be found for AGB and GPP. Consequently, the ability to distinguish age classes enables a more accurate simulation of the biogeochemical consequences of land use and particularly prescribed harvest regimes. For example, harvesting of younger age classes will lead to lower land-use emissions, as also described in other studies (e.g. Shevliakova et al., 2009; Yue et al., 2018a). Similarly, being able to distinguish forest age classes will also affect biophysical land–atmosphere interactions, since younger forests, for example, have lower LAI and higher albedo (e.g. Bright et al., 2013). A constantly thinned age-less forest will therefore always lead to a lower albedo than a young forest regrowing after clear-cutting.

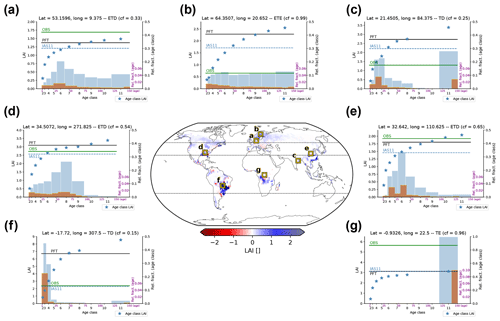
Figure 7 Example grid points comparing 2001–2010 mean spring leaf area index (MAM LAI) from the simulations without (PFT) and with age classes (IAS11) to observation-based data (OBS). The map in the centre shows the difference of differences between the observation-based data and the simulations (abs(OBS-PFT)-abs(OBS-IAS11)); i.e. it shows where the results from the simulation with age classes (IAS11) deviate less (blue) or more (red) from the observation-based data than the PFT simulation results (see also Figs. S4.2–S4.4, column 4). Dashed lines in the map mark the three selected regions (see Table 2). The plots (a)–(g) show the LAI of selected PFTs (ETD: extratropical deciduous; ETE: extratropical evergreen; TD: tropical deciduous; TE: tropical evergreen) as well as their according area fractions per age class and per year at the labelled grid points. Centre latitude, longitude, and grid-cell cover fraction (cf) of the depicted PFT are indicated. The x axis reflects the age from 0–151 (purple) with the age classes (black) indicated at the age centres. The two right y axes represent the bars: depicted are the 2010 area fractions relative to the area of the depicted PFT. Blue bars are per age class (black y axes) and depict the fraction of each age class (i.e. one bar per age class); the yellow framed purple bars depict the fraction of each age (i.e. one bar per year). The left y axis depicts the LAI. Stars mark the simulated LAI per age class and the lines the LAI of the depicted PFT – blue dashed line: IAS11 simulation; black line: PFT simulation; green line: 2010 value from the observation-based data. Note: (1) the age-class LAI is only depicted for age classes having non-zero fractional cover over the whole time span 2001–2010 (this is not the case for the age classes 9 and 10 in panels c, f, and g); (2) age and age-class fractions of classes 2–8 in panel (g) are very small and therefore not visible above the x axis; (3) since we did not apply any harvest in the final simulation year 2010, the first year and accordingly the youngest age class are always empty.

3.3 Limitations and alternative schemes

In the previous sections we compared a JSBACH4–FF simulation when only using PFTs with simulations including forest age classes and discussed associated trade-offs and benefits. In this section we discuss limitations and advantages of the applied and of alternative schemes.

Since JSBACH is a tile-based DGVM, the introduction of an individual- or cohort-based approach as used in some other DGVMs (e.g. Sato et al., 2007; Fisher et al., 2015; Bayer et al., 2017) would be very complex. Regarding forest age structures these models have the essential advantage of naturally providing forest demography (Fisher et al., 2018). Due to their complexity, however, they are less commonly used as fully coupled LSMs for ESMs. Being fully coupled with an ESM, however, is one major aspect and purpose of JSBACH, which historically has been part of the MPI-ESM (Mauritsen et al., 2019) and is now also part of the ICON-ESM (Giorgetta et al., 2018).

For tile-based DGVMs, there is at least one option mentioned in the literature that provides an alternative to simply increasing the number of tiles: the coupling of a separated module dealing with the woody demography (see, e.g., Bellassen et al., 2010; Haverd et al., 2018). On the one hand, this approach shares the advantage with individual- or cohort-based DGVMs that it provides a forest demography and thus principally enables the tracking of forest age. On the other hand, this approach has the important limitation of still calculating key land surface processes at the aggregated tile level; i.e. in this approach, processes such as photosynthesis and respiration, are not computed for separate age classes. This restriction impairs the calculation of biogeochemical and biophysical interactions, due to the non-linearity of forest growth and the associated non-linear relationships of those key processes with forest age (e.g. as depicted for spring LAI in Fig. 7). This limitation can only be avoided by increasing the number of tiles.

Building on the approach of increasing the number of tiles, the scheme suggested in this paper adds an important benefit of the alternative schemes by explicitly tracking forest age. It thereby enables the implementation of age-based forest management schemes that historically were common in temperate forests and are still the dominant management type in boreal forests (Kuusela, 1994; Pan et al., 2011; Puettmann et al., 2015; Kuuluvainen and Gauthier, 2018). Another advantage of the explicit tracking concerns the discretisation error. While the presented approach does require frequent area-weighted merges in order to maintain a limited number of age classes, it only requires shifting the actually affected parts of an age class and not entire age classes or “cohorts”, as was common in previous applications (e.g. Shevliakova et al., 2009; Yue et al., 2018b). Upon ageing, for example, in our approach only those fractions of an age class will be shifted that are actually at the age limits of an age class. An important restriction of the approach presented in this paper is that it is only applicable for a DGVM with a tile hierarchy and would not be applicable for a DGVM with a flat tile organisation, such as JSBACH3, since the different layers of the tile hierarchy are used to introduce different processes. In a DGVM with a flat tile organisation, the PFT level associated with the age classes on the leaf level of the tile hierarchy would be missing, which we use for the management of the forest age classes and for the tracking of the exact forest age.

With regard to previous studies that increased the number of tiles in order to introduce a more detailed representation of the forest state, our evaluation indicates that the number of additional tiles used in previous applications might have been too few. Solely separating primary and secondary forests (e.g. Yang et al., 2010; Stocker et al., 2014a, b) or introducing only a few age classes or cohorts (e.g. Shevliakova et al., 2009; Yue et al., 2018b) might not be sufficient to discretise non-linear relationships with forest age (see, e.g., Fig. 7, and also Fig. 6), at least not on the coarse resolutions that are common in global model studies dealing with human land use (e.g. Le Quéré et al., 2018).

In this paper, we presented two different approaches to distribute the age space onto the available age classes: the equal age distribution scheme EAS, which spreads the age classes evenly, and IAS, a scheme that increases the age space with increasing age. The evaluation indicated the second approach to be superior to the first (Fig. 6), which can be explained by the finer discretisation of younger age classes that more accurately resolves the steep part of the non-linear age-dependent relationship of GPP, LAI, and AGB (see, e.g., Fig. 7). There are, however, other possible age distribution schemes. One could, for example, use smaller age classes for old ages in addition to the smaller age classes used for young ages in the IAS scheme. With such a scheme, one could better cover age-related declines as described in Zaehle et al. (2006) and Bellassen et al. (2010). Another possibility would be to replace the static distribution schemes that are equally applied to all grid cells with a dynamic scheme creating individual distributions for each grid cell. In such a dynamic scheme, age classes could be defined depending on the demand for each grid cell, with merging based on similarity criteria (see, e.g., Shevliakova et al., 2009); i.e. age classes sharing similar values for a selected variable (e.g. GPP) could be merged creating space for new age classes covering an age space with less similar values. Such an approach could potentially further decrease the discretisation error, particularly for cells with only infrequent disturbances or harvest events. A drawback could be an increase in the organisational overhead caused by the similarity tests required for each merging step. However, the additional computational effort is not expected to be very large, considering that currently the organisational overhead seems to be very small (no striking offset as shown in Fig. 6d) and particularly since in the current set-up dynamic merges would only be required once a year.

4 Summary and outlook

In this paper we described a new scheme to introduce forest age structure in a hierarchical tile-based DGVM and presented its implementation in JSBACH4. JSBACH4–FF allows key land surface processes to be simulated in dependence of forest age and, simultaneously, to trace the exact forest age, which is a precondition for any implementation of age-based forest management schemes in JSBACH4–FF.

JSBACH4 itself is still highly under development regarding infrastructure and processes integrated from JSBACH3. In the version used for this paper (4.20p7), the representation of natural and anthropogenic land cover change, in particular, has not yet been ported from JSBACH3. Upon implementation, new processes will have to be integrated with the age structure. In addition, other developments would be desirable: harvest, for example, has so far only been implemented as area clear-cutting, following the implementation of other disturbances in JSBACH3 (see Brovkin et al., 2009). For a representation of different forest management strategies including intermediate thinning before a final felling, an implementation of forest thinning would be required (Otto et al., 2014; Naudts et al., 2015). Anthropogenic thinning could be implemented in JSBACH4–FF by keeping the number of individuals as a state variable for each age class that is manipulated upon thinning, with anthropogenic thinning overruling the already implemented self-thinning.

Despite planned and potential extensions, together with the newly implemented age classes, JSBACH4–FF already now provides a valuable tool to study forest management effects, particularly due to its integration with the ICON-ESM.