the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
P-model v1.0: an optimality-based light use efficiency model for simulating ecosystem gross primary production
Nicholas G. Smith
Sandy P. Harrison
Trevor F. Keenan
David Sandoval
Tyler Davis
I. Colin Prentice
Terrestrial photosynthesis is the basis for vegetation growth and drives the land carbon cycle. Accurately simulating gross primary production (GPP, ecosystem-level apparent photosynthesis) is key for satellite monitoring and Earth system model predictions under climate change. While robust models exist for describing leaf-level photosynthesis, predictions diverge due to uncertain photosynthetic traits and parameters which vary on multiple spatial and temporal scales. Here, we describe and evaluate a GPP (photosynthesis per unit ground area) model, the P-model, that combines the Farquhar–von Caemmerer–Berry model for C3 photosynthesis with an optimality principle for the carbon assimilation–transpiration trade-off, and predicts a multi-day average light use efficiency (LUE) for any climate and C3 vegetation type. The model builds on the theory developed in Prentice et al. (2014) and Wang et al. (2017a) and is extended to include low temperature effects on the intrinsic quantum yield and an empirical soil moisture stress factor. The model is forced with site-level data of the fraction of absorbed photosynthetically active radiation (fAPAR) and meteorological data and is evaluated against GPP estimates from a globally distributed network of ecosystem flux measurements. Although the P-model requires relatively few inputs, the R2 for predicted versus observed GPP based on the full model setup is 0.75 (8 d mean, 126 sites) – similar to comparable satellite-data-driven GPP models but without predefined vegetation-type-specific parameters. The R2 is reduced to 0.70 when not accounting for the reduction in quantum yield at low temperatures and effects of low soil moisture on LUE. The R2 for the P-model-predicted LUE is 0.32 (means by site) and 0.48 (means by vegetation type). Applying this model for global-scale simulations yields a total global GPP of 106–122 Pg C yr−1 (mean of 2001–2011), depending on the fAPAR forcing data. The P-model provides a simple but powerful method for predicting – rather than prescribing – light use efficiency and simulating terrestrial photosynthesis across a wide range of conditions. The model is available as an R package (rpmodel).
- Article
(6714 KB) - Full-text XML
- Companion paper
- BibTeX
- EndNote
Realistic, reliable, and robust estimates of terrestrial photosynthesis are required to understand variations in the carbon cycle, monitor forest and cropland productivity, and predict impacts of global environmental change on ecosystem function (Prentice et al., 2015). Understanding how photosynthetic rates depend on temperature, humidity, solar radiation, CO2, and soil moisture is at the core of this challenge. Process-based dynamic vegetation models (DVMs) and Earth system models (ESMs) in use today almost always use some form of the Farquhar–von Caemmerer–Berry (FvCB) model for C3 photosynthesis (Farquhar et al., 1980; von Caemmerer and Farquhar, 1981), in combination with stomatal conductance (gs) models (Ball et al., 1987; Leuning, 1995; Medlyn et al., 2011) that couple water and carbon fluxes at the leaf surface.
The FvCB model describes the instantaneous saturating relationship between leaf-internal CO2 concentrations (ci) and assimilation (A), and how this relationship depends on absorbed photosynthetically active radiation (APAR). It simulates A as the minimum of a light-limited and a RuBisCO-limited assimilation rate, AJ and AC, respectively:
Although the FvCB model is standard for leaf-scale photosynthesis and its environmental response on timescales of minutes to hours, DVMs and ESMs using FvCB produce divergent results for ecosystem-level fluxes and their response to the environment at longer timescales (Rogers et al., 2017). This is due to assumptions that have to be made about photosynthetic parameters that are not predicted by the FvCB model: stomatal conductance (gs) and the maximum rates of RuBisCO carboxylation (Vcmax) and electron transport (Jmax) for ribulose-1,5-bisphosphate (RuBP) regeneration, which together determine the relationship between ci and A. Common approaches for determining the values of Vcmax and Jmax in DVMs and ESMs are to prescribe fixed values per plant functional type (PFT) and attempt to simulate the distribution of PFTs in space, or to use empirical relationships between leaf N and Vcmax and simulate leaf N internally or prescribe it per PFT (Smith and Dukes, 2013; Rogers, 2014).
While the FvCB model describes a non-linear relationship between instantaneous assimilation and absorbed light, ecosystem production, integrated over weeks to months, scales proportionally with APAR (Monteith, 1972; Medlyn, 1998). This observation underlies the general light use efficiency (LUE) model which describes ecosystem-level photosynthesis (gross primary production; GPP) as the product of APAR and LUE:
where PAR is the incident photosynthetically active radiation and fAPAR is the fraction of PAR that is absorbed by green tissue. The LUE model is the basis for observation-driven GPP models that use fAPAR and PAR based on remote sensing data and combine this with different approaches for simulating LUE (Running et al., 2004; Zhang et al., 2017; Field et al., 1995) and for some forest growth models (Landsberg and Waring, 1997). Other remote-sensing-data-based models (Jiang and Ryu, 2016) apply the FvCB model in combination with vegetation cover and type data and prescribed Vcmax for a set of PFTs.
Here, we describe a model, referred to as the P-model, that unifies the FvCB and LUE models following the theory developed by Prentice et al. (2014) and Wang et al. (2017a). The model assumes an optimality principle that balances the C cost (per unit of assimilation) of maintaining transpiration and carboxylation (Vcmax) capacities. It thus predicts how the ratio of leaf-internal to ambient CO2 () acclimates to the environment, given temperature (T), water vapour pressure deficit (D), atmospheric pressure (p), and ambient CO2 concentration (ca) (Prentice et al., 2014). The P-model also assumes that the photosynthetic machinery tends to coordinate Vcmax and Jmax in order to operate close to the intersection of the light-limited and RuBisCO-limited assimilation rates (coordination hypothesis; Chen et al., 1993; Haxeltine and Prentice, 1996; Maire et al., 2012) under mean daytime environmental conditions. By further assuming equality in the marginal cost and benefit of Jmax, daily-to-monthly average assimilation rates can then be described as fractions of absorbed PAR, i.e. as a LUE model (Eq. 2) (Wang et al., 2017a).
Thus, the P-model embodies an optimality-based theory for predicting the acclimation of leaf-level photosynthesis to its environment and for simulating LUE. In combination with prescribed PAR and remotely sensed fAPAR, it estimates GPP across diverse environmental conditions (Wang et al., 2017a). Its prediction for acclimating photosynthetic parameters reduces the number of prescribed (and temporally fixed) values and avoids the distinction of model parameterisation by vegetation types or biomes (apart from a distinction between the C3 and C4 photosynthetic pathways). The P-model has a further advantage over other data-driven GPP models (Running et al., 2004; Zhang et al., 2017) and empirically upscaled GPP estimates (Jung et al., 2011) in that it accounts for the influence of changing CO2, and that it uses first principles (rather than imposed functions) to represent effects of T, D, and p (Sect. 2). The theory underlying the P-model regarding the water–carbon trade-off has been described by Prentice et al. (2014) and applied by Keenan et al. (2016) to simulate how changes in primary production have driven the terrestrial C sink over past decades, and by Smith et al. (2019) to explain variations in observed Vcmax. Wang et al. (2017a) complemented the theory by including effects of limited electron transport capacity (Jmax) and predicted variations in observed χ across environmental gradients. To resolve model biases under conditions of low soil moisture, Stocker et al. (2019) further applied an empirical stress function to reduce LUE under dry soil conditions.
The purpose of this paper is (i) to provide a full documentation of the model implementation and reference for open-source software (rpmodel R package, available on CRAN); (ii) to provide an evaluation of model-predicted LUE and GPP against GPP derived from eddy covariance flux measurements (FLUXNET 2015 Tier 1 dataset); (iii) to apply this model for global-scale simulations and compare spatial patterns and global totals of simulated GPP with other estimates with global coverage; and (iv) to introduce a robust and pragmatic solution to resolving model bias under dry and cold conditions. With (iv), we do not aim at extending the theoretical basis for the P-model (Prentice et al., 2014; Wang et al., 2017a) but to include environmental controls in the LUE model that serve to make the model applicable as a remote-sensing-data-driven GPP model for a wide range of conditions and vegetation types. The evaluation focuses on different components of variability (spatial, annual, seasonal, daily anomalies) (Sects. 4.6–4.2). We further address uncertainties associated with the fAPAR forcing (Sect. 4.4) and the uncertainties in the evaluation data by using GPP data derived from different flux decomposition methods (Sect. 4.5). The use of continuous GPP measurements, rather than experimentally disturbed measurements, makes it challenging to assess modelled GPP under extreme environmental conditions. We therefore make a further evaluation of simulated GPP during the course of soil moisture drought events (fLUE droughts; Sect. 4.3).
The theory underlying the P-model has been described by Wang et al. (2017a) and the derivation of equations is given therein. It is presented here again for completeness.
2.1 Balancing carbon and water costs
The P-model centres around a prediction for the optimal ratio of leaf-internal to ambient CO2 concentration ci:ca (termed χ) that balances the costs associated with maintaining the transpiration stream and the cost of maintaining a given carboxylation capacity. The optimal balance is achieved when the two marginal costs are equal:
Here, a and b are the respective unit costs. b is assumed to be constant, and a to scale linearly with the temperature-dependent viscosity of water η(T), calculated following Huber et al. (2009). Below, we introduce , with and ∘C). The optimal χ solves the above equation. We use Fick's law (Fick, 1855) to express transpiration and assimilation as a function of stomatal conductance gs:
and
and use the RuBisCO-limited assimilation rate from the FvCB model:
with
where ci is given by caχ. K is the effective Michaelis–Menten coefficient for RuBisCO-limited assimilation (Sect. B3), and Γ∗ is the photorespiratory compensation point in the absence of dark respiration (Sect. B1). The optimal χ can be derived as
with
(See Appendix F1 for intermediate steps.) Because both terms in Eq. (3) are divided by A, the solution is independent of whether the RuBisCO-limited rate AC or the light-limited rate AJ (see below) is followed. With this prediction for χ, we can use the coordination hypothesis (Chen et al., 1993; Haxeltine and Prentice, 1996; Maire et al., 2012) and the light-limited assimilation rate from the FvCB model to write
with
Iabs is the amount of absorbed light and φ0 is the intrinsic quantum yield efficiency. This equation has the form of a LUE model (Eq. 2) in that AJ scales linearly with Iabs. Using Eqs. (9) and (8), m can be expressed directly as
The unit cost ratio β has been estimated by Wang et al. (2017a) to 240 based on global leaf δ13C data and a simplified version of the P-model (assuming and neglecting the Jmax limitation). Here, we re-estimated β to 146 based on the full version of the model using the same global leaf δ13C dataset. This is more strictly consistent with the model formulation implemented here. Equation (12) provides the basis for predicting CO2 assimilation rates in the form of a LUE model (Eq. 2) where LUE is a function of T and p (both affecting Γ∗, K, and η∗; see Sects. B1 and B3), D, and ca.
The prediction of optimal χ has a number of corollaries (see Appendix C). An estimate for stomatal conductance (gs) and the intrinsic water use efficiency (iWUE = A∕gs) directly follow from the optimal water–carbon balance (Eq. 3). By assuming AJ=AC, we can further derive Vcmax, as well as dark respiration (Rd), which is a function of Vcmax (see Sects. C3 and C4).
2.2 Introducing Jmax limitation
Equation (10) assumes that the light response of A is linear up to the coordination point. In reality, rates saturate towards high light levels because the electron transport rate J, necessary for the regeneration of ribulose 1,5-bisphosphate (RuBP), tends towards a maximum Jmax. To account for this effect, Eq. (10) can be modified, following the formulation by Smith (1937), using a non-rectangular hyperbola relationship between AJ and Iabs to allow for the effect of finite Jmax:
In this equation, AJ is no longer linear with respect to Iabs and thus does not have the form of a LUE model. However, Jmax is assumed here to acclimate on longer timescales to Iabs, so that the marginal gain in assimilation A per unit change in Jmax is equal to the unit cost (c) of maintaining Jmax.
The unit cost c is assumed to include the maintenance of light-harvesting complexes and various proteins involved in the electron transport chain. The cost of maintaining a given Jmax is thus assumed to scale linearly with Jmax and that this proportionality is constant (c is constant). By taking the derivative of Eq. (13) with respect to Jmax and rearranging terms (see Appendix F2 for intermediate steps), we obtain the Jmax limitation factor L in Eq. (13) as
with . Note that L is independent of Iabs. Hence, AJ is again a linear function of absorbed light. The cost factor c∗ is estimated from published values of at 25 ∘C. (Kattge and Knorr, 2007) and χ=0.8 (Lloyd and Farquhar, 1994) at (Wang et al., 2017a). The revised LUE model thus becomes
with
Wang et al. (2017a) showed that this formulation of Jmax costs leads to a realistic dependence of the Jmax:Vcmax ratio on growth temperature.
As shown by Smith et al. (2019), an alternative approach can be used to introduce the effects of Jmax limitation, replacing Eq. (13) by the more widely used one-parameter family of saturation curves following Farquhar and Wong (1984). This alternative is described in Appendix F3 and implemented as an optional method in the R package rpmodel.
3.1 The light use efficiency model
A is commonly expressed in mol m−2 s−1. For further model description and evaluation, we refer to ecosystem-scale quantities in mass units of assimilated C and model GPP (g C m−2 d−1) following Eq. (2) with
Here, MC is the molar mass of carbon (12.0107 g mol−1) to convert from molar units to mass units, and PPFD is the photosynthetic photon flux density per square metre, integrated over a day (mol m−2 d−1). fAPAR is unitless and integrates across the canopy, i.e. from fluxes per unit leaf area to fluxes per unit ground area. LUE is in units of g C mol−1. The intrinsic quantum yield parameter φ0 is modelled as temperature dependent, and an additional (unitless) empirical soil moisture stress factor (β(θ)) is included for modelling LUE.
3.1.1 Temperature dependence of the intrinsic quantum yield of photosynthesis
The temperature dependence of the intrinsic quantum yield (φ0(T), mol mol−1) is modelled following the temperature dependence of the maximum quantum yield of photosystem II in light-adapted leaves, determined by Bernacchi et al. (2003) as
where aL is the leaf absorptance, and bL is the fraction of absorbed light that reaches photosystem II. The factor 1∕4 is introduced here as the equation given by Bernacchi et al. (2003) applies to electron transport rather than C assimilation. Here, (aLbL∕4) is treated as a single calibratable parameter (see Sect. 3.3) and is henceforth referred to as . (All calibratable parameters are thereafter indicated by a hat over the symbol.) This temperature dependence was not accounted for in earlier P-model publications (Keenan et al., 2016; Wang et al., 2017a). To test the effect of this temperature dependence on simulated GPP, we conducted alternative simulations, where a constant was calibrated instead (Sect. 3.2). Note that φ0 includes the factor aL for incomplete leaf absorptance, which is commonly quantified separately from the quantum yield efficiency. In other vegetation models, aL is commonly ascribed a value of 0.72–0.88 (Rogers et al., 2017). Values of φ0 used here are accordingly lower than values for the intrinsic quantum yield reported from experimental studies (Long et al., 1993; Singsaas et al., 2001). Furthermore, within-canopy reflection and reabsorption indicate that leaf-level absorptance is not equivalent to canopy-level absorptance; thus, φ0 should be regarded as canopy-scale effective value of intrinsic quantum yield. It is treated here as a calibratable parameter, which may vary according to the fAPAR forcing dataset used.
3.1.2 Soil moisture stress
β(θ) is an empirical soil moisture stress function. We use results by Stocker et al. (2018) to fit this function based on two general patterns. First, the functional form of β(θ) is approximated by a quadratic expression that approaches 1 for soil moisture at a certain threshold θ∗ and held constant at 1 for soil moisture values above this threshold. Here, θ is the plant-available soil water, expressed as a fraction of available water holding capacity, and θ∗ is set to 0.6. The general form is
Second, the sensitivity of β(θ) to extreme soil dryness (θ→0) is related to the mean aridity, quantified as the mean annual ratio of actual over potential evapotranspiration (AET / PET) (Stocker et al., 2018). The decline in β(θ) with drying soils is steep in dry climates and less steep in less dry climates. In Eq. (21), the sensitivity parameter q is defined by the maximum β reduction at low soil moisture , leading to . Note that q has a negative value. β0 is modelled as a linear function of the mean aridity:
and are treated as calibratable parameters.
Soil moisture (θ), AET, and PET are simulated using the SPLASH model (Davis et al., 2017), which treats soil water storage as a single bucket and calculates potential evapotranspiration based on Priestley and Taylor (1972). The only difference with the model version described by Davis et al. (2017) is that we account here for a variable water holding capacity calculated based on soil texture and depth data from SoilGrids (Hengl et al., 2014). A detailed description of the applied empirical functions for calculating plant-available water holding capacity from texture data is given in Appendix D.
3.2 Simulation protocol
3.2.1 Site-scale simulations
We conducted multiple sets of site-scale simulations (Table 1) to investigate the dependence of model performance on alternative model setups (variable/fixed soil moisture and temperature effects), alternative choices of forcing data (fAPAR), and alternative observational target data for calibration (GPP based on different flux decompositions). Parameters (, , and ) were calibrated and evaluated against the appropriate observational data for each set of simulations separately.
The ORG setup is the P-model in its original form, as described in Wang et al. (2017a). It uses a fixed quantum efficiency of photosynthesis ( is calibrated instead of ) and does not account for soil moisture stress (β(θ)=1). Here, the model is forced with fAPAR data based on MODIS FPAR (MCD15A3H), linearly interpolated 4 d values to daily values (see Sect. 3.4.1), and is calibrated against GPP data from FLUXNET 2015 based on the nighttime partitioning method (NT) (see Sect. 3.5.1). The simulation set BRC (“Bernacchi”) is identical to ORG except that is allowed to vary with temperature following Bernacchi et al. (2003) and Eq. (20), and is calibrated. The full P-model setup (FULL) includes the soil moisture stress function described above, and , , and are calibrated simultaneously.
All additional simulations account for both temperature and soil moisture effects. The simulation set FULL_FPARitp also uses MODIS FPAR data for fAPAR but applies a spline to get daily values. This is to evaluate alternative interpolation methods. The simulation set FULL_EVI uses MODIS EVI (MOD13Q1), interpolated to daily from 8 d data, to assess to which the degree the model performance depends on the fAPAR forcing data source. See Sect. 3.4.1 for more information.
All site-scale simulations were calibrated against GPP data (Sect. 3.3), calculated using the nighttime flux decomposition method (Reichstein et al., 2005). Additional simulation sets FULL_DT, FULL_NTsub, and FULL_Ty were used to investigate the dependence of model performance on the choice of observational data used for calibration. We used GPP data based on the nighttime decomposition method (Reichstein et al., 2005) for FULL_NTsub, the daytime decomposition method (Lasslop et al., 2010) for FULL_DT, and an alternative decomposition method, previously used in Wang et al. (2017a), for FULL_Ty. The Ty method estimates a constant monthly background respiration rate fitted to match net ecosystem exchange fluxes of CO2 from measurements assuming a linear or saturating dependence of GPP on PPFD. Calibration and evaluation of FULL_DT, FULL_NTsub, and FULL_Ty are done only for sites and dates where observational data are available for all three datasets (DT, NT, and Ty); hence, there is the distinction between FULL_NTsub and FULL.
3.2.2 Global simulations
Global simulations were conducted for the FULL setup, using the respectively calibrated parameters from the site-scale simulations. All vegetation is assumed to follow the C3 photosynthetic pathway and we do not distinguish between croplands and other vegetation. We conducted two simulations with alternative fAPAR forcing data. These are described in Sect. 3.4.
3.3 Model calibration
Calibration was performed only for the model parameters determining the quantum efficiency of photosynthesis ( or , respectively) and the dependence of the sensitivity of the soil moisture stress function on average aridity (parameters and ). Simulated GPP was calibrated to minimise the root mean square error (RMSE) compared to observed daily GPP (Sect. 3.5). We used generalised simulated annealing from the GenSA R package (Xiang et al., 2013) to calibrate model parameters. This algorithm is particularly suited to find global minima of non-linear objective functions in situations where there can be a large number of local minima. To test the robustness of the calibration and evaluation metrics, we additionally performed out-of-sample calibrations for the FULL setup where the training set included data from all but one site. The test dataset, used to calculate R2 and RMSE, contained only data from the single left-out site.
3.4 Forcing data
Unstressed light use efficiency, m′ in Eq. (19), is simulated using monthly mean values for daytime T and D; temporally constant site-specific elevation (used to calculate atmospheric pressure, scaled from sea-level standard pressure of 101 325 Pa); and annually varying observed atmospheric CO2 (MacFarling Meure et al., 2006), identical across sites. The choice of aggregating to monthly mean values is motivated by the timescale of RuBisCO turnover, which limits the rate at which photosynthetic parameters can acclimate to changing environmental conditions (McNevin et al., 2006).
Predicted monthly LUE (m′) is multiplied by daily varying Iabs, and response functions φ0(T) and β(θ), driven by daily varying temperature and soil moisture. This choice is motivated by the known rapid response in stomatal conductance to drying soils (represented by β(θ)) and the instantaneous temperature response of the quantum yield efficiency (φ0(T)). Simulating GPP as the product of LUE and daily varying PPFD would not be consistent with the non-linear instantaneous response of A to light (Eq. 10) given the acclimation timescale of photosynthesis (Suzuki et al., 2001; Maire et al., 2012). We therefore evaluate simulated GPP averaged over 8 d periods. The choice of appropriate model prediction and evaluation timescales is further discussed in Sect. 5.
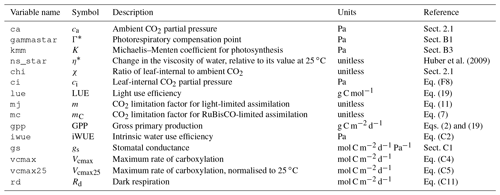
Table 1Model setups. The standard fAPAR data are MODIS FPAR MCD15A3H, where the original data, given at 4 d intervals, are splined to daily values (“spl.”). Alternative greenness forcing data are based on MODIS EVI MOD13Q1, splined from 8 d intervals to daily, and MODIS FPAR MCD15A3H, linearly interpolated (“itpl.”) from 4 d intervals to daily. Standard observational GPP data, used for model calibration and evaluation, are from FLUXNET 2015, based on the nighttime flux decomposition method (“NT” in the table, variable GPP_NT_VUT_REF in FLUXNET 2015). Alternative GPP data used based on the daytime flux decomposition method (“DT” in the table, variable GPP_DT_VUT_REF) and based on an alternative method (Wang et al., 2017a) (“Ty” in the table). For the ORG, BRC, FULL, FULL_FPARitp, and FULL_EVI setups, data used for the model calibration are from all dates where NT data are available. For FULL_DT, FULL_ Ty, and FULL_NTsub setups, calibration data are from all dates where data are available for all three methods (DT, NT, and Ty). Column φ0(T) specifies whether the temperature dependence of intrinsic quantum yield is included. Column β(θ) specifies whether soil moisture stress is included. Columns , , , and provide the calibrated parameter values in each simulation set.
∗ The value represents the fitted LUE, corresponding to (φ0m′MC) in Eq. (19).
3.4.1 fAPAR
For site-scale simulations, we used three alternative datasets as model forcing for fAPAR (MODIS FPAR splined, MODIS FPAR linearly interpolated, and MODIS EVI, splined; see Table 1). MODIS FPAR data are from the MCD15A3H Collection 6 dataset (Myneni et al., 2015), given at a resolution of 500 m and 4 d. The data were filtered to remove data points where clouds were present, values equal to 1.00, and outliers (more than 3 times the interquartile range). Filtered values were replaced by the mean value for the respective day of year. To obtain daily varying Iabs (Eq. 18), two alternatives were explored. For the first (used in all setups except FULL_FPARitp), values were derived using a cubic smoothing spline (function smooth.spline() with parameter spar=0.01 in R; R Core Team, 2016). For the FULL_ FPARitp setup, daily fAPAR values were linearly interpolated to each day. MODIS EVI data are from the MOD13Q1 Collection 6 dataset (Didan, 2015), given at a resolution of 250 m and 8 d. These data were filtered based on the summary quality control flag, removing “cloudy” pixels. Gaps were filled and data were splined to daily values. All fAPAR data were downloaded from the Google Earth Engine using the google_earth_engine_subsets library (Hufkens, 2017).
For global-scale simulations, we used two alternative fAPAR datasets. “MODIS FPAR” is from globally gridded MODIS FPAR data at 0.5∘ resolution derived at the Integrated Climate Data Center (ICDC; https://icdc.cen.uni-hamburg.de/1/daten/land/modis-lai-fpar.html, last access: 5 March 2020), based on the MOD15A2H MODIS Terra leaf area index/FPAR 8 d L4 global 500 m SIN grid V006 dataset (Myneni et al., 2020). For the present application, 8 d data are aggregated (mean) to monthly data. “fAPAR3g” is based on Advanced Very High Resolution Radiometer (AVHRR) Global Inventory Modeling and Mapping Studies (GIMMS) FPAR3g v2 data (Zhu et al., 2013), 15 d, 1/12∘ resolution and aggregated for the present application to 0.5∘ and monthly data. For all global P-model simulations, fAPAR is held constant for each day in respective months. Simulations cover the years 2000–2016. Due to limited temporal coverage, January 2000 data are taken as February 2000 for simulations driven by MODIS FPAR.
3.4.2 Meteorological data
For site-scale simulations, the meteorological forcing data are derived from the FLUXNET 2015 Tier 1 dataset (daily), which provides data from measurements taken and processed along with the CO2 flux measurements. The PPFD (mol m−2 d−1) is derived from shortwave downwelling radiation as , where kEC=2.04 µmol J−1 (Meek et al., 1984), and RSW is incoming shortwave radiation from daily FLUXNET 2015 data (variable name SW_IN_F, given in W m−2). The factor kEC accounts for the energy content of RSW and the fraction of photosynthetically active radiation in total shortwave radiation. Daytime vapour pressure deficit (VPD, or D in Sect. 2) is calculated from half-hourly FLUXNET 2015 data (variable name VPD_F) by averaging over time steps with positive insolation (SW_IN_F). Daytime air temperature is taken directly from the FLUXNET 2015 dataset (variable name T_F_DAY). This is a simplification, as we are not calculating leaf temperature or VPD at the leaf surface, which are more directly relevant for photosynthesis.
For global-scale simulations, we use daily, 0.5∘ meteorological forcing from WATCH-WFDEI (Weedon et al., 2014). We use mean daily 2 m air temperature; daily snow and rainfall; shortwave downwelling radiation converted to mol photons m−2 d−1 by multiplication with kEC; and daily 2 m specific humidity (qair), converted to VPD (D) as described in Appendix E. We used daily minimum and maximum air temperatures for each month from Climate Research Unit (CRU) time series (TS) 4.01 data (Harris et al., 2014) to calculate a respective VPD and use their mean as input to P-model simulations in order to reduce effects of the non-linear dependence of D on T (). All processes that depend on atmospheric pressure use Eq. (B10) and the 0.5∘ resolution elevation map from WATCH-WFDEI (Weedon et al., 2014) to calculate a temporally constant atmospheric pressure for each grid cell.
3.5 Calibration and evaluation data
3.5.1 Data for site-scale simulations
We used data from 59 sites for model calibration and 126 sites for evaluation (Fig. 1 and Table A1). The number of valid daily GPP data points used for the calibration set was 162 158 and 241 084 for the evaluation set. The calibration sites were selected based on the apparent reliability of relationships between CO2 fluxes, co-located greenness data, measured soil moisture, and meteorological variables, emerging from a previous analysis (Stocker et al., 2018). For the evaluation, we used all sites except those classified as croplands or wetlands, and seven sites where C4 vegetation is mentioned in the site description available through the FLUXNET2015 dataset (AU-How, DE-Kli, FR-Gri, IT-BCi, US-Ne1, US-Ne2, and US-Ne3).
GPP predictions by the P-model are compared to GPP estimates from the FLUXNET 2015 Tier 1 dataset (downloaded on 13 November 2016). We used GPP based on the nighttime partitioning method (Reichstein et al., 2005) (GPP_NT_VUT_REF) and removed data for which more than 50 % of the half-hourly data are gap filled and for which the daytime and nighttime partitioning methods (GPP_DT_VUT_REF and GPP_ NT_ VUT_ REF, respectively) are inconsistent, i.e. the upper and lower 2.5 % quantiles of the difference between GPP values quantified by each method. For additional simulation sets, model calibration and evaluation was performed using GPP data based on the daytime partitioning method (GPP_ DT_VUT_REF) (Lasslop et al., 2010) with analogous filtering steps, and GPP data based on an alternative method that fits a constant ecosystem respiration rate as the net ecosystem exchange under conditions where PPFD tends to zero (FULL_Ty; Wang et al., 2017a). For all calibration and evaluation, we removed data points before the “MODIS era” (before 18 February 2000).
3.5.2 Data for global-scale simulations
We compare the simulated spatial distribution of GPP from global-scale simulations against seven different remote-sensing-data-driven GPP estimates with global coverage and two Sun-induced fluorescence (SiF) data products. The global GPP estimates are from the following models: MTE (Jung et al., 2011), FLUXCOM (“RS+METEO” setup) (Tramontana et al., 2016), MODIS GPP (MOD17A2H Collections 55 and 6) (Running et al., 2004; Zhao et al., 2005; Running et al., 2015), BESS (Jiang and Ryu, 2016), BEPS (He et al., 2018; Chen et al., 2016), and VPM (Zhang et al., 2017). A more detailed description of these models and aggregation to a common grid of 0.5∘ and monthly resolution can be found in Luo et al. (2018). For SiF, we use data from Global Ozone Monitoring Experiment-2A (GOME-2A) and GOME-2B, based on v.2 (V27) 740 nm terrestrial chlorophyll fluorescence data from the MetOp-A and MetOp-B satellites (Joiner et al., 2013, 2016). Data were aggregated to monthly and 0.5∘ resolution by mean, as further described in Luo et al. (2018).
3.6 Evaluation methods
We evaluated both simulated LUE and GPP. The P-model (Sect. 2) predicts variations in LUE across sites (space) and months (monthly ), while simulated GPP is affected by the PPFD and fAPAR data used as model forcing (Eq. 19 and Sect. 3.4). Conversely, “observed” LUE is calculated as , and the evaluation is thus also affected by the PPFD and fAPAR data. The evaluation of LUE tests the added explanatory power of the P-model compared to models that rely on fixed prescribed LUE values. Evaluating GPP facilitates the comparison of the model performance to similar models of terrestrial GPP. Model performance for GPP is benchmarked against a null model (NULL), which assumes a temporally constant and spatially uniform LUE. The LUE for the NULL model is fitted to observed GPP using linearly interpolated MODIS FPAR and GPP data from the NT method; see Table 1. Thus, while LUE is constant, the NULL model preserves the spatial and temporal patterns in APAR ().
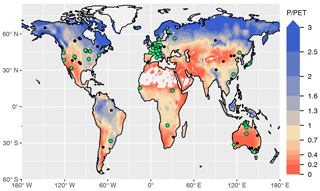
Figure 1Overview of sites selected for model calibration (green dots) and evaluation (black dots). All sites and additional information are listed in Table A1. The colour key of the map represents aridity, quantified as the ratio of precipitation over potential evapotranspiration from Greve et al. (2014).
3.6.1 Components of variability
For LUE, we separately analysed spatial (mean annual values by site) and monthly means only for the FULL setup. For GPP, we analysed spatial, annual, seasonal (mean by day of year), 8 d, and the variability in daily anomalies from the mean seasonal cycle for all setups. The seasonal variability was determined for different Köppen–Geiger climatic zones (see Table 2). Information about the association of sites with climatic zones was extracted from Falge et al. (2017). Evaluations were made only for climatic zones with at least three sites. For each component of variability, we calculated the adjusted coefficient of determination (; hereafter referred to as R2) and the RMSE. Figures showing correlations between simulated and observed values additionally present the mean bias, the slope of the linear regression model, and the number of data points (N).
3.6.2 Drought response
The bias in GPP (modelled minus observed) was calculated for 20 d before and 80 d after the onset of a drought event as identified by Stocker et al. (2018) for 36 sites. Drought events (fLUE droughts) are periods of consecutive days where soil moisture, separated from other drivers using neural networks, reduces LUE below a given threshold. The data specifying the timing and duration of drought events were downloaded from Zenodo (Stocker, 2018). We then rearranged the data to align all drought events at all sites, normalised data to their median value during the 10 d before the onset of droughts (normalisation by subtracting median), and computed quantiles per day, where “day” is defined with respect to the onset of each drought event.
Table 2Description of Köppen–Geiger climate zones and number of sites for which data are available per climate zone and hemisphere. Sites are classified based on Falge et al. (2017) and Beck et al. (2018). Only zones with data from more than three sites are shown.

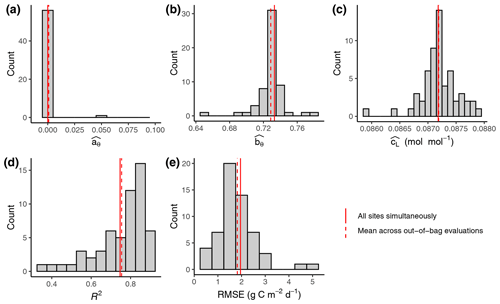
Figure 2Out-of-sample calibration and evaluation results. (a–c) Distribution of parameter values (FULL setup) from calibrations where data from one site were left out for each individual calibration. Parameters and are unitless. (d, e) Distribution of evaluation metrics calculated on data from the left-out site based on simulations with model parameters calibrated on all other sites' data. Solid vertical red lines represent the parameter values calibrated with data from all sites pooled. These are the values reported in Tables 3 and 4 for FULL setup. Dashed red lines represent the mean across values from out-of-bag calibrations and evaluations.
4.1 Calibration results
The calibration of model parameters, done with data from all calibration sites simultaneously, yielded values that closely matched the means across parameter values derived from the out-of-sample calibrations (Fig. 2). This confirms the robustness of the calibration and that the model is not overfitted. Similarly for the evaluation metrics, the R2 and RMSE values reported from evaluations against data from all evaluation sites pooled yielded values that closely match the means across the out-of-sample evaluations (each calculated with data from the single left-out site). This analysis also shows that the distribution of the evaluation metrics is skewed, with evaluations against a few sites indicating relatively poor performance (R2 below 0.5 for ZM-Mon, AR-Vir, and FR-Pue), while the most frequent values indicate very good model performance (evaluations at 21 sites giving R2 values of above 0.8). Because the out-of-sample calibrations are computationally very expensive, we performed this analysis only for one setup (FULL) and report evaluation metrics done with pooled data from all evaluation sites for the remainder of the analysis.
4.2 GPP variability across scales
Tables 3 and 4 provide an overview of model performance (R2 and RMSE) in simulating GPP at different scales. The ORG setup captures 70 % of the variance in observed GPP with data aggregated to 8 d means (33 604 data points). Model performance both with respect to explained variance (R2) and the RMSE is improved by including the effects of temperature on quantum yield efficiency in the BRC model setup (R2=72 %), and by including the effects of soil moisture stress in the FULL model setup (R2=75 %; Fig. 3). Both the BRC and FULL model setups outperform the NULL model.
Table 3R2 of simulated and observed GPP based on different model setups and for different components of variability.

Table 4RMSE of simulated and observed GPP based on different model setups and for different components of variability.
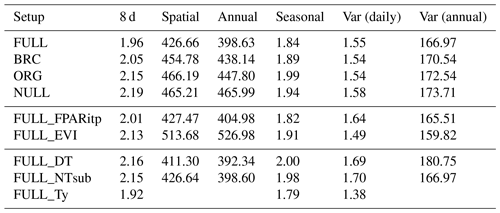
4.2.1 Seasonal variations
Seasonal variations are generally reliably simulated (R2: 0.69–0.73 for P-model setups, and R2: 0.71 for the NULL model; Fig. 4). Also the NULL model captures most of the seasonal variability, especially in climate zones Dfb and Dfc, and Cfb and Cfa. This indicates that seasonal GPP variations are largely driven by seasonal changes in insolation (PPFD) and vegetation greenness (fAPAR). Accounting for temperature effects on the quantum yield efficiency reduces the overestimation of GPP in spring, except in the case of climate zone Dfb. Observed GPP increases are lagged compared to vegetation greenness, with a delay of up to 2 months at some sites. This lag is clearly visible at almost all sites in Dfb. The early-season high bias is largely absent for sites in climate zone Cfb, where observed GPP starts increasing early and the simulations match the observations except at sites CZ-wet, DE-Hai, and FR-Fon, where the start of season is simulated too early.
GPP is overestimated during the dry season in climate zones with a marked dry season (Aw, Bsk, Csa, and Csb) in model setups that do not account for soil moisture stress (ORG, BRC, NULL). The NULL model has the largest bias. High VPD during dry periods reduces simulated LUE and leads to lower GPP values and a smaller bias in all the P-model setups (ORG, BRC, FULL). The empirical soil moisture stress function applied in the FULL setup eliminates the dryness-related bias in zones Aw, Csa, and Csb and substantially reduces this bias for sites in zone Bsk. Observations suggest that GPP declines to values around zero during dry periods at sites in zone Bsk (mostly savannah vegetation and grasslands; see Table A1). The remaining bias in the FULL model, which includes the soil moisture stress function, is related to the fact that prescribed fAPAR remains relatively high and that the soil moisture stress function does not decline to zero.
The ORG and BRC models tend to underestimate peak-season GPP more strongly compared to the FULL model. This is a direct consequence of the calibration which balances errors across all data points. Across-site average peak-season maximum GPP is accurately captured by the FULL model in most zones (Fig. 4), except for an underestimation of GPP in zones Aw, Cfa, and Cfb, and an overestimation in zone Csa. Site-level evaluations suggests no clear relationship between peak-season underestimation and vegetation type in zone Cfb. The overestimation of peak-season GPP in zone Csa is caused by a high bias at sites with evergreen broadleaf vegetation (FR-Pue, IT-Cp2, IT-Cpz); sites with other vegetation types show no consistent peak-season bias.
4.2.2 Spatial and annual variations
The R2 for simulated GPP, aggregated to annual totals, ranges from 0.60 (ORG) to 0.69 (FULL). The NULL model achieves an R2 of 0.58. Most of the explanatory power of the different models for annual total GPP stems from their power in predicting between-site (“spatial”) variations (Fig. 5). The R2 for spatial variations ranges from 0.63 (ORG) to 0.69 (FULL), and 0.65 for the NULL model. In contrast, interannual variations at a site are poorly simulated (R2: 0.05–0.09 for P-model setups, and 0.03 for the NULL model). Interannual variations are generally much smaller than between-site (spatial) variations or seasonal variations. Thus, capturing them is challenging. Interannual GPP variations are generally better simulated at sites where the variability is high and in particular at dry sites.
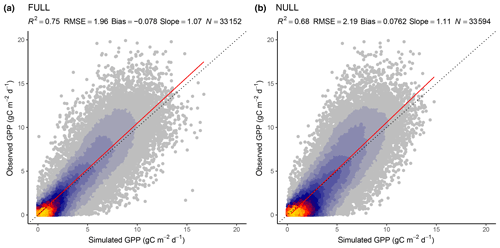
Figure 3Correlation of observed and modelled GPP values of all sites pooled, mean over 8 d periods, for the model setups FULL (a) and NULL (b).
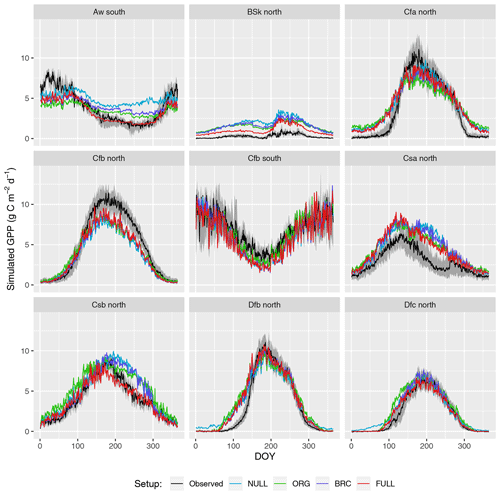
Figure 4Mean seasonal cycle. Observations are given by the black line and grey band, representing the median and 33 %/66 % quantiles of all data (multiple sites and years) pooled by climate zone. Coloured lines represent different model setups. The annotation above each plot specifies the climate zone (see Table 2). Only climate zones are shown here for which data from at least five sites were available.
4.3 Drought response
The P-model setups that do not include the soil moisture stress function (ORG and BRC) systematically overestimate GPP during droughts (Fig. 6). This bias increases sharply at the onset of drought events and continues to increase throughout the drought period. The bias is strongly reduced by applying the empirical soil moisture stress function (Eq. 21) in the FULL model. A small bias remains also in the FULL model. This stems from overestimated values at a few sites (in particular AU-DaP, US-Cop, US-SRG, US-SRM, US-Var, US-Whs, US-Wkg), mostly grasslands and sites in seasonally dry climate zones (Aw, Bsk, and Csa; see Fig. 4), where flux measurements indicate an almost complete shutdown of photosynthetic activity during the dry season. In contrast, the fAPAR data (MODIS FPAR) suggest values substantially greater than zero at these sites during these periods. This suggests either contributions to PAR absorption by photosynthetically inactive tissue, underestimation of LUE sensitivity to dry soils at these sites, or an overestimation of the rooting zone moisture availability by the SPLASH model.
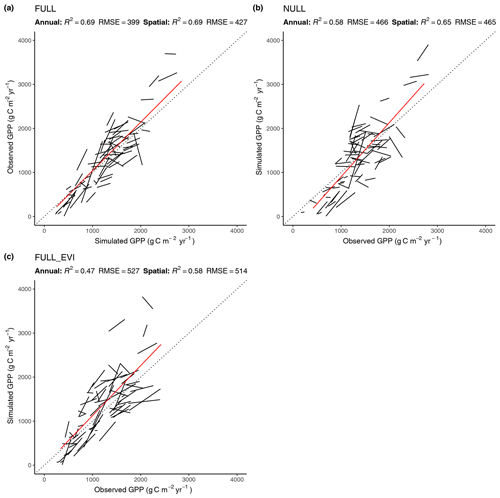
Figure 5Correlation of modelled and observed annual GPP in simulations FULL (a), NULL (b), and FULL_EVI (c). The red lines are based on means across years by site and represent spatial (across-site) variations. Black lines and text are based on annual values, with one line for each site. Lines represent linear regressions. R2 and RMSE statistics for annual values are based on pooled data from all sites. For a perfect fit between modelled and observed annual GPP values, all black lines (representing the linear regression model of annual values for a single site) would lie on the 1:1 line and have a slope of 1. Slopes that deviate substantially from 1, or are even negative, for some sites show poor model performance in capturing interannual variability.

Figure 6Bias in simulated GPP during the course of drought events. Simulated GPP is from a simulation with (FULL) and without (BRC) accounting for soil moisture stress. The timing of drought events is taken from Stocker et al. (2018) and is identified by an apparent soil-moisture-related reduction of observed light use efficiency at 36 FLUXNET sites. The bias is calculated as simulated minus observed GPP. Data from multiple drought events and sites are aligned by the date of drought onset and aggregated across all sites and events (lines for medians; shaded ranges from the 33 % and 66 % quantiles).
4.4 Uncertainty from fAPAR input data
Tests of the sensitivity of model performance to alternative fAPAR forcing datasets show that the difference between splined and linearly interpolated MODIS FPAR is small, with slightly better performance using splined fAPAR data. Model performance is generally better using MODIS FPAR compared to simulations using MODIS EVI. Spatial variations, in particular, are better captured using MODIS FPAR (Fig. 5, R2: 0.69 for the FULL setup) compared to MODIS EVI (R2: 0.58). However, the R2 of interannual variations is 0.15 for MODIS EVI and 0.09 for MODIS FPAR. In terms of biases in climate zones, the overestimation of GPP during the dry period in zone Bsk is larger when using MODIS EVI than when using MODIS FPAR (Fig. 7, right). The positive spring bias in simulated GPP in zone Dfb is present irrespective of the source of the fAPAR forcing (Fig. 7, left), as is the peak-season bias of GPP in zones Bsk, Cfb, and Csb (not shown). Differences between the EVI- and FPAR-forced simulations depend on vegetation type. The EVI-forced simulation tends to be biased low in evergreen needleleaf vegetation and has generally lower values in all evergreen vegetation types compared to the FPAR-forced simulation. However, there is no general difference in model bias between simulations made with the two forcings in other vegetation types.
4.5 GPP target data
The different flux decomposition methods make fundamentally different assumptions regarding the sensitivity of ecosystem respiration to diurnal changes in temperature. This should lead to systematic differences in derived observational GPP values and should affect model–data disagreement.
Model predictions compare better to GPP data based on the flux decomposition method Ty (Wang et al., 2017a) than for GPP data based on the DT and NT methods. For GPP 8 d means, the model achieves an R2 of 0.68 when compared to GPP Ty (FULL_Ty model setup), as opposed to 0.64 and 0.66 compared to the DT and NT methods, respectively (FULL_DT and FULL_NTsub; Table 3, Fig. 8). Spatial and annual correlations are not evaluated for GPP Ty due to missing data. Evaluations presented here rely on dates for which neither the NT, DT, nor Ty methods have missing values and thus contain an equal number of data points. Metrics from the NT evaluation, repeated here, are not identical to the ones above and are referred to as “NTsub” in Tables 3 and 4.
We found a systematic low bias of simulated GPP in the peak-season in the climatic zone Cfb (warm temperate, fully humid, warm summer). However, as shown in Fig. 8, this bias does not seem to be affected by the choice of GPP evaluation data.
4.6 LUE
The FULL version of the P-model captures 32 % of the variability in mean annual LUE across all sites and across the full range of observed mean annual LUE values and vegetation types (Fig. 9). Overall, 48 % of the observed LUE variation within vegetation types is captured by the model through the relationships with climate, without the need to specify parameters for specific vegetation types.
Overall, 31 % of the variability in monthly mean LUE is captured by the model, with data from all sites and years pooled (Fig. 9). The model overestimates monthly LUE values and underestimates LUE at the lowest and highest ends of the LUE range, respectively. The low-end overestimation is reflected by the overestimation of GPP in the spring at winter-cold sites (Sect. 4.2.1) and during soil moisture droughts (Sect. 4.3). The underestimation of high monthly values is not clearly linked to any particular vegetation type.
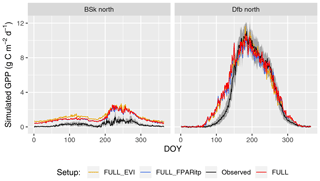
Figure 7Mean seasonal cycle for model setups with different greenness forcing data for two climate zones (Bsk and Dfb, both in the Northern Hemisphere). Observations are given by the black line and grey band, representing the median and 33 %/66 % quantiles by day of year (DOY) of all data (multiple sites and years) pooled by climate zone. Coloured lines represent model setups forced with different greenness data. The annotation above each plot specifies the climate zone (see Table 2). Climate zones shown here are illustrative examples.
4.7 Global GPP
Simulated global total GPP is 106 Pg C yr−1 when using MODIS FPAR and 122 Pg C yr−1 when using fAPAR3g forcing data (mean over the years 2001–2011, FULL setup). The spatial pattern of simulated GPP differs substantially between simulations forced by MODIS FPAR and fAPAR3g (Fig. 10). This is most evident in their latitudinal distribution (Fig. 11). The global spatial pattern of fAPAR3g-based GPP simulated by the P-model generally matches the global distribution of the mean across other remote-sensing-based GPP models and lies within the range of their estimates for the latitudinal distribution. The MODIS FPAR-forced P-model simulation suggests lower values in the tropics that differ from the fAPAR3g-based estimates by a factor of ∼2 around the Equator. The moderate tropical GPP of the MODIS FPAR-based P-model simulation agrees well with the latitudinal distribution of SiF from GOME-2A and GOME-2B.
The performance of the P-model can be compared to results obtained from other remote-sensing-driven GPP models (RS models). In its FULL setup, the P-model achieves an R2 of 0.75 and a RMSE of 1.96 g C m−2 d−1, in simulating 8 d mean GPP and evaluated against GPP data (NT method) from 126 sites. This can be compared to predictions from the VPM model (R2: 0.74, RMSE: 2.08 g C m−2 d−1, 113 sites, 8 d; Zhang et al., 2017) or BESS (R2: 0.67, RMSE: 2.58 g C m−2 d−1, 113 sites, 8 d; Jiang and Ryu, 2016). The performance of the P-model in simulating annual GPP across all 126 sites (R2: 0.69) can be compared to results from MODIS GPP (MOD17A2, R2=0.73, 12 sites; Heinsch et al., 2006; and for the updated version MOD17A2H: R2=0.62, 18 sites; Wang et al., 2017b) or BEPS (R2: 0.81, RMSE: 347 g C m−2 d−1, 124 sites; He et al., 2018). Unfortunately, we cannot present a direct comparison between these models based on data from identical dates and sites. A targeted model intercomparison may address this. While seasonal and spatial variations in GPP are reliably simulated by the P-model, the model's performance in simulating interannual GPP variations is weaker. Similar results regarding relatively poor model performance in explaining interannual variations have been found from previous studies in both empirical (Richardson et al., 2007; Urbanski et al., 2007b) and process model-based (Keenan et al., 2012; Biederman et al., 2016) analyses. This is likely due to lagged effects of climate anomalies expressed through biotic responses (Richardson et al., 2007; Keenan et al., 2012).
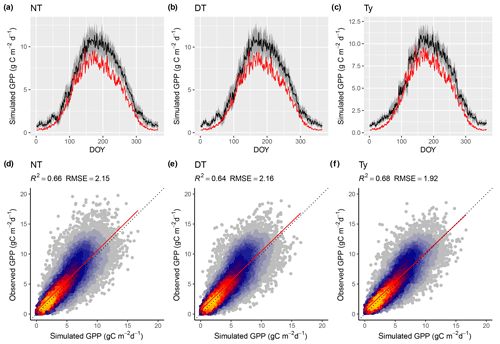
Figure 8Model performance subject to comparison with different flux decomposition methods for GPP. (a–c) Mean seasonal cycle of simulated (red) and observed GPP (black) based on different flux decomposition methods for sites in climate zone Cfb north. The grey band represents the 33 %/66 % quantiles of observed GPP by DOY. (d–f) Correlation of observed and simulated GPP values of all sites pooled, mean over 8 d periods, all sites pooled. “Observed GPP” refers to the different flux decomposition methods: DT for the daytime method (FULL_DT setup), NT for the nighttime method (FULL_NTsub setup), and Ty (FULL_Ty setup) for the method applied for data used in Wang et al. (2017b). Dotted lines in panels (d–f) represent the 1:1 relationship; red lines represent the fitted linear regressions.
The P-model-based estimates of global GPP (106 Pg C yr−1 when using MODIS FPAR and 122 Pg C yr−1 when using fAPAR3g forcing data, mean over 2001–2011, FULL setup) are within the range of other estimates of global GPP (also means over 2001–2011): 133 Pg C yr−1 for MTE (Jung et al., 2011), 130 Pg C yr−1 for FLUXCOM (Tramontana et al., 2016), 112 Pg C yr−1 for MODIS-55 GPP and 105 Pg C yr−1 for MODIS-6 GPP (Running et al., 2004; Zhao et al., 2005), 133 Pg C yr−1 for BESS (Jiang and Ryu, 2016; Ryu et al., 2011), 121 Pg C yr−1 for BEPS (He et al., 2018; Chen et al., 2016), and 135 Pg C yr−1 for VPM (Zhang et al., 2017). The P-model results presented here are based on simulations that embody relatively strong simplifying assumptions. In particular, we assumed all vegetation to follow the C3 photosynthetic pathway and we made no distinction between croplands and other vegetation, although crops are often more productive (Guanter et al., 2014). Due to the short period for which forcing data and outputs from comparable models are available, we did not analyse temporal trends in global GPP here. Analyses not shown here indicate that the introduction of the Jmax cost factor (not included, e.g. in Keenan et al., 2016) increases the sensitivity of modelled GPP to CO2. Further evaluation of model behaviour against data from CO2 manipulation experiments will be necessary before applying the model to simulate CO2-related trends.
The large spread of tropical GPP estimates is striking. The highest estimate among the other GPP models we used for evaluation here – coming from BESS – is more than 50 % higher than MODIS GPP from Collection 6. The fAPAR3g-based P-model tropical GPP estimate falls within the range of other GPP models, while the MODIS FPAR-based estimate is lower than all other models. However, the latter's comparably low tropical GPP agrees well with the latitudinal distribution of SiF (Fig. 11). However, large changes in leaf area index across latitudes, combined with a dependency of the SiF signal on vegetation structure (Zeng et al., 2019) may undermine the validity of SiF as a benchmark for the latitudinal GPP distribution. A lack of evaluation data from eddy covariance measurements in dense tropical forests precludes us from drawing conclusions on the accurateness of these diverging tropical GPP estimates.
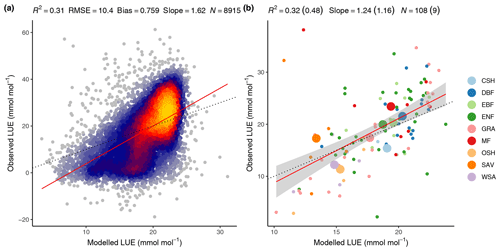
Figure 9Modelled (FULL) versus observed LUE. (a) Mean monthly LUE with data pooled from all sites and available years. (b) Mean annual LUE by site (small dots and colour) and vegetation type (large dots and colour). Model performance metrics are given at the top with numbers in brackets referring to the regression of data aggregated by vegetation types and non-bracketed numbers for data aggregated by sites. Dotted lines represent the 1:1 relationship, red lines represent the fitted linear regression to all data in panel (a) and the fitted linear regression to mean annual LUE by site in panel (b). The grey band in panel (b) represents the 95 % confidence interval of the linear regression. Vegetation types are closed shrubland (CSH); deciduous broadleaf forest (DBF); evergreen broadleaf forest (EBF); evergreen needleleaf forest (ENF); grassland (GRA); mixed deciduous and evergreen needleleaf forest (MF); open shrubland (OSH); savanna ecosystem (SAV); woody savanna (WSA).
With a particular focus on soil moisture effects, Stocker et al. (2019) presented global GPP based on the P-model, corresponding to a setup with the soil moisture stress function but without the temperature dependence of the quantum yield efficiency. They also used a different parameterisation with φ0=0.0579, aθ=0.107, and bθ=0.478 for their intermediate model version. Their estimate for global GPP was around 130 Pg C yr−1 for recent years.
The coefficients of determination (R2) of simulated versus observed values are lower for LUE (0.32 for the spatial correlation in the FULL setup, Fig. 9b) than for GPP (0.69 for the spatial correlation in the FULL setup). This is because GPP variations are strongly driven by variations in absorbed light (PPFD⋅fAPAR), which are observed and used for modelling. In contrast, variations in LUE cannot be observed directly. Using remotely sensed information for estimating LUE variations, e.g. based on SiF (Frankenberg et al., 2018; Li et al., 2018; Ryu et al., 2019) or alternative reflectance indices (Gamon et al., 1992, 2016; Badgley et al., 2017), is an active field of research and the separation of remotely sensed signals into contributions by LUE and absorbed light remains challenging (Porcar-Castell et al., 2014; Ryu et al., 2019). Other remote-sensing-based GPP models rely on vegetation-type-specific model parameters for LUE (Zhang et al., 2017; Running et al., 2004; Jiang and Ryu, 2016). The P-model in its FULL setup explains 48 % of the variations in LUE across sites aggregated to vegetation types without relying on vegetation or biome-type specific parameterisations. In its ORG setup, it explains 12 % of the variations (not shown) and 51 % of the variations when excluding sites classified as “open shrublands”, which tend have a substantially lower LUE than simulated by the P-model (not shown). In spite of this substantial portion of explained variability, the NULL model with its temporally constant and spatially uniform LUE achieves higher R2 values for GPP than the ORG P-model setup at the spatial, annual, and seasonal scales (Table 3). This indicates that the spatial and temporal variations in absorbed light are the main drivers of GPP in LUE-type models and underlines the importance of evaluation against a NULL model benchmark. Taken together, these findings demonstrate that the P-model offers a simple but powerful method for simulating terrestrial GPP using readily available input datasets and a very small number of free (calibratable) parameters. Here, three parameters are calibrated (for the FULL setup). Other model parameters are derived from independent field and laboratory measurements.

Figure 10Global distribution of GPP. Shown are the mean annual values, averaged over the years 2000 to 2016. The GPP shown as “mean of other models” is the average of MTE (Jung et al., 2011), FLUXCOM (`RS+METEO' setup) (Tramontana et al., 2016), MODIS GPP (Collections 55 and 6) (Running et al., 2004; Zhao et al., 2005), BESS (Jiang and Ryu, 2016), BEPS (He et al., 2018; Chen et al., 2016), and VPM (Zhang et al., 2017). P-model results are from simulations with the FULL setup and calibrated parameters as given in Table 1.

Figure 11Latitudinal distribution of GPP and SiF. Values shown (GPP on the left y axis; SiF on the right y axis) are grid cell area-weighted sums along 0.5∘ latitudinal bands.
Accounting for the temperature dependence of the quantum yield efficiency (φ0) clearly improves model predictions. The parameter φ0 is commonly treated as a constant in global vegetation models (Rogers et al., 2017). Our results indicate potential for improving such models' photosynthesis routines by accounting for the temperature dependence of φ0.
φ0 appears as a linear scalar in the LUE model. However, the magnitude of this scalar is uncertain and depends on whether incomplete light absorption by the leaf is included in the definition of φ0 or in fAPAR data. We have used MODIS FPAR and MODIS EVI data to define fAPAR in different model setups. While the two are well correlated, their absolute values differ. Hence, we have calibrated an apparent quantum yield efficiency () to GPP data separately for different fAPAR datasets, thereby implicitly distinguishing what components of light absorption factors are contained in the fAPAR data. The leaf absorptance, aL, which is typically taken to be around 0.8 in global vegetation models (Rogers et al., 2017), is similar to the ratio of fitted values for simulation FULL and FULL_EVI, here calculated as 0.67 (Table 1).
An improvement in model performance is obtained by accounting for soil moisture stress using an empirical function. However, the use of an empirical function masks underlying processes. Furthermore, the use of an empirical function is not consistent with the optimality approach that underlies the P-model. The bias reduction associated with using an empirical soil moisture stress function hints at missing factors in the theoretical approach which rests on an assumed constancy of the unit costs of transpiration (a in Eq. 3). Prentice et al. (2014) provide a definition of a that is explicit in terms of plant hydraulic traits and physical properties that determine water transport along the plant–soil–atmosphere continuum. In particular, , where ΔΨ is the maximum daytime difference in leaf-to-soil water potential and ks is the sapwood area-specific permeability. However, large variations in stomatal conductance are known to occur in response to relatively fast soil dry-downs (timescale of days) (Keenan et al., 2010; Egea et al., 2011; Stocker et al., 2018). This suggests a potential to improve the P-model by allowing the unit cost of transpiration to be a function of rooting-zone moisture availability and by coupling stomatal conductance with the soil water balance.
Observational uncertainty could affect both parameter calibration and model evaluation. Keenan et al. (2019) found a systematic bias in GPP estimates based on the nighttime partitioning method due to inhibition of leaf respiration in the light (Kok, 1949; Wehr et al., 2016), which affects fluxes unevenly throughout the season and across vegetation types. However, we found no clear difference in model–data agreement, nor in fitted parameters, in comparisons of three alternative GPP datasets that use different approaches to decompose net CO2 exchange fluxes from eddy covariance measurements into ecosystem respiration and GPP terms.
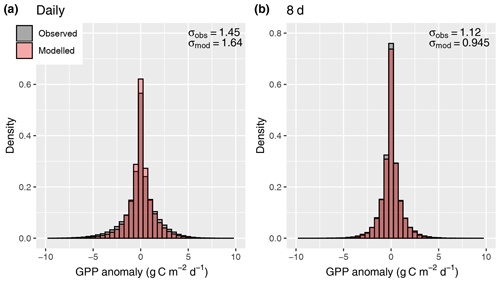
Figure 12Distribution of anomalies from the mean seasonal cycle, evaluated for daily values (a) and 8 d means (b).
We have found a consistent early-season high bias in simulated GPP for numerous sites in regions with deciduous broadleaved vegetation in temperate and cold climates (in particular US-MMS, IT-Col, US-WCr, US-UMd, US-UMB, and US-Ha1), and also in mixed and needleleaf stands (in particular US-Syv, US-NR1, FI-Hyy, CA-Qfo, and CA-Man). The temperature dependence of the intrinsic quantum yield, as introduced in the BRC and FULL setups, did not resolve this bias. Additional analyses (not shown) suggested that this bias is not related to soil temperatures. The P-model, as applied here, uses daily air temperature for simulating temperature stress on the intrinsic quantum yield in the BRC and FULL setups. A reduction in the quantum yield efficiency arises from several mechanisms, including increased non-photochemical quenching, a reduction in chlorophyll, and absorption by screening pigments (Huner et al., 1993; Oquist and Huner, 2003; Ensminger et al., 2004; Adams et al., 2004; Verhoeven, 2014). These adaptations serve to limit oxidative damage under high light and low temperature conditions, where an imbalance between electron supply and demand exists, arising from an imbalance between temperature-insensitive photochemical rates and temperature-sensitive biochemical rates. The reversion of these adaptations and resumption of the intrinsic quantum yield efficiency and photosynthesis requires sustained temperatures above a certain critical threshold (Tanja et al., 2003) and exhibits a delay with respect to instantaneous air temperatures (Pelkonen and Hari, 1980; Mäkelä et al., 2004). Approaches accounting for a delayed resumption of photosynthesis after cold periods offer scope for further improvement of the P-model and may be included in global vegetation and Earth system models where this effect is currently not accounted for (Tanja et al., 2003; Rogers et al., 2017).
There is a positive bias in simulated GPP during the dry season at a number of sites where the vegetation phenology is influenced by drought. The positive bias is related to the combination of using prescribed fAPAR data, which shows substantial absorption by non-green vegetation, and insufficient sensitivity of simulated LUE to soil drying. However, GPP is accurately simulated at other sites affected by seasonally recurring water stress. The modelled sensitivity to dry soils is determined by the soil moisture stress function, which depends on the mean aridity of the site as estimated using a fixed depth soil moisture “bucket”. Accounting for variability in rooting zone depth, which may also be influenced by local topographical factors and access to groundwater (Fan et al., 2013, 2017) may help to minimise model biases in drought-prone areas.
The current implementation of the P-model involves some simplifications in terms of climate drivers by using average daily meteorological conditions, measured above the canopy, as input. Optimality in balancing carbon and water costs for average daily conditions is not necessarily equivalent to optimality in balancing integrated water and carbon costs over the diurnal cycle. Large variations in ambient conditions over a diurnal cycle, combined with a non-linear dependence of costs on these conditions suggest that the approach of taking average daily conditions may be an oversimplification. Nevertheless, prior evaluations have shown robust and accurate predictions of optimal χ across a range conditions (Wang et al., 2017a). Using above-canopy VPD values instead of VPD at the leaf surface for scaling water losses implicitly assumes a perfectly coupled atmospheric boundary layer. Using above-canopy air temperature instead of leaf temperatures introduces a bias when the two become decoupled (Michaletz et al., 2015). The impact of these simplifications may be minor but should be evaluated.
A further simplification is that investment in electron transport capacity (expressed by Jmax) and investments in the carboxylation capacity (expressed by Vcmax) are coordinated so that for conditions with which the model is forced (here, monthly means of daily averages), photosynthesis operates at the co-limitation point of the light- and RuBisCO-limited assimilation rates, and an effective linear relationship between absorbed light and mean assimilation emerges. This assumption follows from the coordination hypothesis, which itself can be understood as an optimality principle (Haxeltine and Prentice, 1996; Maire et al., 2012) and is well supported by observations (Maire et al., 2012). However, this coordination is contingent on the timescale at which photosynthetic acclimation occurs, which is not known precisely (Smith and Dukes, 2013; Way and Yamori, 2014). By simulating χ using monthly mean meteorological variables, we assume a monthly timescale of acclimation. This is probably a conservative estimate (Smith and Dukes, 2017; Veres and Williams III, 1984). Considering the concave relationship of assimilation rates and absorbed light that follows from the FvCB model for a given Jmax, linearly scaling a given monthly LUE term with daily varying absorbed light levels should lead to an overestimation of assimilation rates at high light levels. This overestimation should disappear as the timescale over which light levels are averaged is increased. However, our results do not confirm these expectations (Fig. 12). The fact that the model did not exhibit a systematic error in simulating GPP variations when applied at the daily timescale is probably due to the fact that day-to-day variability in light levels is relatively small compared to the within-day variability and the non-linearity between A and daily varying light levels does not play an important role.
The P-model provides a simple, parameter-sparse but powerful method to predict photosynthetic capacity and light use efficiency across a wide range of climatic conditions and vegetation types. It provides a basis for a terrestrial light use efficiency model driven by remotely sensed vegetation greenness. Using optimality principles for the formulation of the P-model reduces its dependence on uncertain or vegetation-type-specific parameters and enables robust predictions of GPP and its variations through the seasons, between years, and across space. Further work is required to develop a distinct treatment of C4 vegetation for global applications and additional evaluations are needed to examine the P-model's sensitivity to increasing CO2. We have shown that accounting for the effects of low soil moisture and the reduction in the quantum yield efficiency under low temperatures improves model performance. There is potential to include below-ground water limitation effects in the mechanistic optimality framework of the P-model.
The P-model is implemented as an R package (rpmodel) and available through CRAN and Zenodo (Stocker, 2019a). Results shown here correspond to rpmodel version v1.0.4. A documentation of the R package is available under https://stineb.github.io/rpmodel/ (last access: 5 February 2020). Both site-scale and global simulations shown here are done with the Fortran implementation of the P-model within the SOFUN modelling framework (version v1.2.0), available on Zenodo (Stocker, 2019b). Site-scale forcing data ingest and filtering, model calibration, and evaluation were done using the R package rsofun (version v1.0.wrap_sofun), available on Zenodo (Stocker, 2020b). Scripts that implement the workflow (repository eval_pmodel version v2) are available on Zenodo (Stocker, 2020a). Model outputs are available on Zenodo (Stocker, 2019c).
Table A1 provides metadata information and references for each site from the FLUXNET2015 Tier 1 dataset, used for model calibration and evaluation in the present study.
Ulke et al. (2015)Posse et al. (2016)Wohlfahrt et al. (2008)Beringer et al. (2011a)Cleverly et al. (2013)Meyer et al. (2015)Beringer et al. (2016)Beringer et al. (2011b)Hutley et al. (2011)Cernusak et al. (2011)Schroder et al. (2014)Beringer et al. (2016)Prober et al. (2012)Stevens et al. (2011)Bristow et al. (2016)Beringer et al. (2016)Beringer et al. (2016)Beringer et al. (2011c)Cleverly et al. (2016)Leuning et al. (2005)Kilinc et al. (2013)McHugh et al. (2017)Hinko-Najera et al. (2017)Yee et al. (2015)Aubinet et al. (2001)Wick et al. (2005)Dunn et al. (2007)Bergeron et al. (2007)Merbold et al. (2014)Zielis et al. (2014)Imer et al. (2013)Etzold et al. (2011)Ammann et al. (2009)Guan et al. (2006)Shi et al. (2006)Yan et al. (2013)Chen et al. (2009)Kato et al. (2006)Wen et al. (2010)Shao et al. (2017)Acosta et al. (2013)Prescher et al. (2010)Knohl et al. (2003)Lindauer et al. (2014)Post et al. (2015)Grünwald and Bernhofer (2007)Pilegaard et al. (2011)Reverter et al. (2010)Serrano-Ortiz et al. (2011)Suni et al. (2003)Delpierre et al. (2015)Berbigier et al. (2001)Rambal et al. (2004)Bonal et al. (2008)Sabbatini et al. (2016)Sabbatini et al. (2016)Valentini et al. (1996)Fares et al. (2014)Ferréa et al. (2012)Marcolla et al. (2003a)Marcolla et al. (2003b)Marcolla et al. (2011)Papale et al. (2014)Migliavacca et al. (2009)Montagnani et al. (2009)Tedeschi et al. (2006)Hoshika et al. (2017)Chiesi et al. (2005)Galvagno et al. (2013)Matsumoto et al. (2008)Matsumoto et al. (2008)Jacobs et al. (2007)Moors (2012)Kurbatova et al. (2008)Belelli Marchesini et al. (2007)Ardo et al. (2008)Tagesson et al. (2014)Goldstein et al. (2000)Bowling et al. (2010)Zeller and Nikolov (2000)Frank et al. (2014)Urbanski et al. (2007a)Powell et al. (2006)Irvine et al. (2007)Irvine et al. (2008)Ruehr et al. (2012)Dragoni et al. (2011)Monson et al. (2002)Desai et al. (2015)Nakai et al. (2013)Scott et al. (2015a)Scott et al. (2009)Desai et al. (2005)Baldocchi et al. (2010)Gough et al. (2013)Gough et al. (2013)Ma et al. (2007)Cook et al. (2004)Scott et al. (2015b)Noormets et al. (2007)Noormets et al. (2007)Noormets et al. (2007)Noormets et al. (2007)Noormets et al. (2007)Scott et al. (2010)Archibald et al. (2009)Merbold et al. (2009)Table A1Sites used for evaluation. Long. is longitude; negative values indicate west longitude. Lat. is latitude; positive values indicate north latitude. Veg. is vegetation type: deciduous broadleaf forest (DBF); evergreen broadleaf forest (EBF); evergreen needleleaf forest (ENF); grassland (GRA); mixed deciduous and evergreen needleleaf forest (MF); savanna ecosystem (SAV); shrub ecosystem (SHR); wetland (WET). References not available in the metadata provided with the FLUXNET2015 dataset are listed as NA (not available).
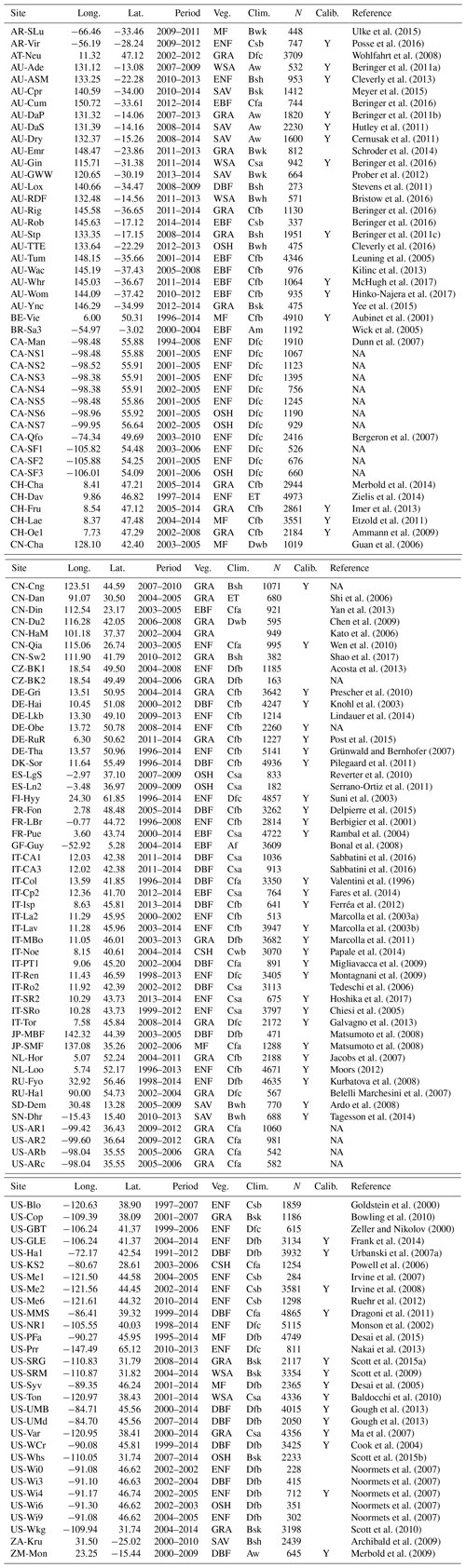
Table A2Fixed parameters. “SC” stands for “at standard conditions” (25 ∘C, 101 325 Pa). “MM coef.” refers to “Michaelis–Menten coefficient”.
B1 Photorespiratory compensation point Γ∗
The temperature- and pressure-dependent photorespiratory compensation point in absence of dark respiration is calculated from its value at standard temperature (T0=25 ∘C) and atmospheric pressure (p0=101 325 Pa), referred to as . It is modified by temperature following an Arrhenius-type temperature response function with activation energy ΔHΓ∗, and is corrected for atmospheric pressure p(z) at elevation z.
Values of ΔHΓ∗ and are taken from Bernacchi et al. (2001). The latter is converted to Pa and standardised to p0 by multiplication with p0 ( µmol mol−1 × 325 Pa =4.332 Pa). ΔHΓ∗ is 37 830 J mol−1. All parameter values are summarised in Table A2. The function p(z) is defined in Sect. B4. Note that TK indicates that the respective temperature value is given in Kelvin and K.
To correct for effects by temperature following the Arrhenius equation with its form , the temperature-correction function fArrh(TK,ΔHa), used in Eq. (B1) and further equations below, is given by
where ΔH is the respective activation energy (e.g. ΔHΓ∗ in Eq. B1), and R is the universal gas constant (8.3145 J mol−1 K−1).
B2 Deriving Γ∗
The temperature and pressure dependency of Γ∗ follows from the temperature dependencies of Kc, Ko, Vc,max, and Vo,max and the pressure dependency of pO2(p):
pO2(p) is the partial pressure of atmospheric oxygen (Pa) and scales linearly with p(z). Kc is the Michaelis–Menten constant for carboxylation (Pa); Ko is the Michaelis–Menten constant for oxygenation (Pa); Vcmax is maximum rate of carboxylation (µmol m−2 s−1); and Vomax is the maximum rate of oxygenation (µmol m−2 s−1). The temperature-dependency equations for these four terms are given in Table 1 of Bernacchi et al. (2001) with respective scaling constants c and activation energies ΔHa as
By substituting the temperature-dependency equations for each term in Eq. (B3) and rearranging terms, Γ∗ can be written as
With pO2(p) at standard atmospheric pressure (101 325 Pa) taken to be 21 000 Pa, and assuming a constant mixing ratio across the troposphere, its pressure dependence can be expressed as
hence,
We can use this to calculate Γ∗ at standard temperature (TK=298.15 K) and pressure (p(z)=101 325 Pa) as Pa.
Note that to convert Eq. (B5) to the form corresponding to the one given by Bernacchi et al. (2001), the partial pressure of oxygen (pO2) has to be assumed at standard conditions. pO2 is approximately 21 000 Pa and with the standard atmospheric pressure of 101 325 Pa, pO2 can be converted from Pascals to parts per million (ppm) as ppm = exp (12.24) ppm. This can be combined with the exponent in Eq. (B5) to . This corresponds to the parameter values determining the temperature dependence of Γ∗ given by Bernacchi et al. (2001) as .
B3 Michaelis–Menten coefficient of photosynthesis
The effective Michaelis–Menten coefficient K (Pa) of RuBisCO-limited photosynthesis (Eq. 6) is determined by the Michaelis–Menten constants for the carboxylation and oxygenation reactions (Farquhar et al., 1980):
where Kc is the Michaelis–Menten constant for CO2 (Pa), Ko is the Michaelis–Menten constant for the carboxylation and oxygenation reaction, respectively, and pO2 is the partial pressure of oxygen (Pa). Kc and Ko follow a temperature dependence, given by the Arrhenius equation analogously to the temperature dependence of Γ∗ (Eq. B1):
Values ΔHKc=79 430 J mol−1, ΔHKo=36 380 J mol−1, Kc25=39.97 Pa, and Ko25=27 480 Pa are taken from Bernacchi et al. (2001) (see also Table A2). The latter two have been converted from µmol mol−1 in Bernacchi et al. (2001) to units of Pa by multiplication with the standard atmosphere (101 325 Pa). Note that Kc25 and Ko25 are rate constants and are independent of atmospheric pressure. Pressure dependence of K is solely in pO2(p) (see Eq. B6).
B4 Atmospheric pressure
The elevation dependence of atmospheric pressure is computed by assuming a linear decrease in temperature with elevation and a mean adiabatic lapse rate (Berberan-Santos et al., 1997):
where z is the elevation above mean sea level (m), g is the gravitational constant (9.80665 m s−2), p0 is the standard atmospheric pressure at 0 m a.s.l. (101 325 Pa), L is the mean adiabatic lapse rate (0.0065 K m−2), Ma is the molecular weight for dry air (0.028963 kg mol−1), and R is the universal gas constant (8.3145 J mol−1 K−1). All parameter values that are held fixed in the model (not calibrated) are summarised in Table A2.
C1 Stomatal conductance
Stomatal conductance gs (mol C Pa−1) follows from the prediction of χ given by Eq. (8) and (from Eq. 5). Stomatal conductance can thus be written as
This has a similar form as the solution for gs derived from a different optimality principle by Medlyn et al. (2011) (their Eq. 11). Differences are that an additional term g0 is missing here and that Γ∗ does not appear in Medlyn et al. (2011). The theory presented by Prentice et al. (2014) provides a theoretical interpretation for the parameter g1 in Medlyn et al. (2011): it is given by ξ (Eq. 9) and can thus be predicted from the environment. However, it is notable that the underlying optimality criterion used by Medlyn et al. (2011), as proposed by Cowan and Farquhar (1977), is one that maintains a constant marginal water cost of carbon gain . It thus describes an instantaneous gs adjustment, e.g. to diurnal variations in D and has been adopted into DVMs and ESMs for respective predictions (with a given Vcmax ). In contrast, the theory presented here and underlying the P-model predicts χ which is jointly controlled by gs and Vcmax. In other words, it predicts a gs that is coordinated with Vcmax and thus acclimates at a similar timescale (which is on the order of days to weeks). This χ can be understood as a “set point” for an average χ with actual χ varying around it at a daily to subdaily timescale.
C2 Intrinsic water use efficiency
The intrinsic water use efficiency (iWUE, in Pa) has been defined as the ratio of assimilation over stomatal conductance (to water) (Beer et al., 2009) as . The factor 1.6 accounts for the difference in diffusivity between CO2 and H2O. Using Fick's law (Eq. 5), this is simply
or, using the prediction of optimal χ given by Eq. (8), this can be expressed as
C3 Maximum carboxylation capacity
With AJ=AC, Vcmax can directly be derived as
ci is given by caχ. The second part of the equation follows from the definitions of m (Eq. 11) and mC (Eq. 7). Normalising Vcmax to standard temperature (25 ∘C) following a modified Arrhenius function based on Kattge and Knorr (2007) gives Vcmax25 as
where HV is the activation energy (71 513 J mol−1), Hd is the deactivation energy (200 000 J mol−1), and ΔS is an entropy term (J mol−1 K−1) calculated using a linear relationship with T from Kattge and Knorr (2007), with a slope of bS=1.07 J mol−1 K−2 and intercept of aS=668.39 J mol−1 K−1:
Note that T is in units of ∘C in the above equation. Equation (C6) describes the instantaneous response to temperature and is not the same as the optimality-driven acclimation to temperature predicted by the P-model.
C4 Dark respiration Rd
Dark respiration at standard temperature Rd25 is calculated as being proportional to Vcmax25:
where b0=0.015 (Atkin et al., 2015). Dark respiration follows a slightly different instantaneous temperature sensitivity than Vcmax following Heskel et al. (2016):
By combining Eqs. (C6), (C8), and (C9), Rd at growth temperature T can directly be calculated from Vcmax as
The soil water balance is solved following the SPLASH model but with the total soil water holding capacity per unit ground area (θWHC, in mm) calculated as a function of the soil texture. Precipitation in the form of rain (Prain) and snow (Psnow) are taken from WATCH-WFDEI (Weedon et al., 2014) and are summed and converted from kg m−2 s−1 to mm d−1 by multiplication of s d−1. To obtain θWHC, we use soil depth to bedrock and texture data from SoilGrids (Hengl et al., 2014), extracted around the FLUXNET sites. We assumed that the plant-available WHC is determined by the WHC down to a maximum depth of 2 m and is limited by the depth to bedrock. The water holding capacity (wWHC, in mm) was defined as the difference in volumetric soil water storage at field capacity (WFC, in m3 m−3) and the permanent wilting point (WPWP, in m3 m−3):
fgravel is the gravel fraction, zbedrock is the depth to bedrock (in mm), and zmax is 2000 mm. The volumetric soil water storage at field capacity and wilting point were derived from texture and organic matter content data through pedotransfer functions, as described by Saxton and Rawls (2006). WFC is calculated as
where
fsand, fclay, fOM are the sand, clay, and organic matter contents in percent by weight. WPWP is calculated as
where
Vapour pressure deficit (D) is calculated from specific humidity (qair) as
with
and
p(z) is atmospheric pressure, taken here as a constant function of elevation z (Sect. B4); wair is the mass mixing ratio of water vapour to dry air (dimensionless) and derived from specific humidity as . Rd and Rv are the specific gas constants of dry air and water vapour, respectively, and are given by R∕Md and R∕Mv, respectively, where R is the universal gas constant (8.314 J mol−1 K−1) and Md (28.963 g mol−1) and Mv (18.02 g mol−1) are the molecular mass of dry air of water vapour, respectively. T is air temperature in ∘C.
F1 Deriving χ
Using Eqs. (4) and (5), the term on the left-hand side of Eq. (3) can thus be written as
Using Eq. (6) and the simplification , the derivative term on the right-hand side of Eq. (3) can be written as
Equation (3) can thus be written as
and solved for χ:
where . The exact solution, without the simplification , and following analogous steps, is
This can also be written as
F2 Deriving the Jmax limitation factor
By taking the derivative of AJ with respect to Jmax , Eq. (14) can be expressed as
This can be rearranged to
For simplification, we can substitute
and
With this, we can write
This can be rearranged to
The right-hand term now corresponds to the Jmax limitation factor L in Eq. (13), and we get Eq. (15).
To sum up, the P-model calculates GPP as
where
and
Iabs is the absorbed light (taken as fAPAR×PPFD, mol m−2), φ0(T) is the temperature-dependent intrinsic quantum yield, β(θ) is the soil moisture stress factor, and MC is the molar mass of carbon (g mol−1).
F3 An alternative method for introducing the Jmax limitation
Section 2.2 introduced the effect of a finite Jmax leading to a saturating relationship between absorbed light and the light-limited assimilation rate, AJ. An alternative method was presented by Smith et al. (2019) and is implemented in rpmodel as an optional method (argument method_jmaxlim = “smith19”). Following their approach, the light-limited assimilation rate is described as
m is the CO2 limitation factor (Eq. 11), and J is a saturating function of absorbed light, approaching Jmax for high light levels, following Farquhar et al. (1980):
θ is a unitless parameter determining the curvature of the response of J to Iabs, here taken as 0.85, based on Smith et al. (2019) and references therein. Equation (F19) can be substituted into Eq. (F18) to yield
from which the smaller root is used to derive AJ. Similar as in the method used by Wang et al. (2017a) and outlined in Sect. 2.2, a proportionality between AJ and Jmax is assumed (; Eq. 14). Taking the derivative of Eq. (F20) with respect to Jmax and setting equal to c leads to
with
Using this, AJ can be written analogously to Eq. (16) but with
and
The cost parameter c was assumed to be non-varying. Under standard conditions of 25 ∘C, 101 325 Pa atmospheric pressure, 1000 Pa vapour pressure deficit, and 360 ppm CO2, at which the ratio of Jmax to Vcmax was assumed to be 2.07 (Smith and Dukes, 2017), c was derived as 0.053 (Smith et al., 2019).
Using the definition of Vcmax from Eq. (C4), m can be replaced by m′ from Eq. (F23) to calculate an “intermediate rate of Vcmax” (Smith et al., 2019) as
rpmodel() function of the rpmodel R package The rpmodel R package provides an implementation of the P-model as described here. The main function is rpmodel(), which returns a list of variables that are mutually consistent within the theory of the P-model (Sect. 2) and based on calculations defined in this paper. References for the returned list of variables are given in Table A3.
BDS designed the study, wrote the model code, conducted the analysis, and wrote the paper. HW developed the model and wrote the initial version of the model description. NGS developed the model and implemented model code. SPH contributed to designing the study and writing the manuscript. TK contributed to the study design, model implementation, and manuscript writing. DS implemented the water holding capacity model. TD wrote an initial version of the model code and model documentation. ICP developed the model and contributed to designing the study.
The authors declare that they have no conflict of interest.
This work contributes to the AXA Chair Programme in Biosphere and Climate Impacts and the Imperial College initiative on Grand Challenges in Ecosystems and the Environment.
This research has been supported by the H2020 Marie Skłodowska-Curie Actions (FIBER grant no. 701329), the Swiss National Science Foundation (grant no. PCEFP2_181115), the Texas Tech University, the Laboratory Directed Research and Development (LDRD) fund under the auspices of DOE (DOE grant), BER Office of Science at Lawrence Berkeley National Laboratory, and the NASA Terrestrial Ecology Program IDS award (award no. NNH17AE86I), the ERC-funded project GC 2.0 (grant no. 694481), and the ERC under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 787203 REALM).
This paper was edited by Jatin Kala and reviewed by two anonymous referees.
Acosta, M., Pavelka, M., Montagnani, L., Kutsch, W., Lindroth, A., Juszczak, R., and Janouš, D.: Soil surface CO2 efflux measurements in Norway spruce forests: Comparison between four different sites across Europe – from boreal to alpine forest, Geoderma, 192, 295–303, https://doi.org/10.1016/j.geoderma.2012.08.027, 2013. a
Adams, W. W., Zarter, C. R., Ebbert, V., and Demmig-Adams, B.: Photoprotective Strategies of Overwintering Evergreens, Biosci., 54, 41–49, 2004. a
Ammann, C., Spirig, C., Leifeld, J., and Neftel, A.: Assessment of the nitrogen and carbon budget of two managed temperate grassland fields, Agr. Ecosyst. Environ., 133, 150–162, https://doi.org/10.1016/j.agee.2009.05.006, 2009. a
Archibald, S. A., Kirton, A., van der Merwe, M. R., Scholes, R. J., Williams, C. A., and Hanan, N.: Drivers of inter-annual variability in Net Ecosystem Exchange in a semi-arid savanna ecosystem, South Africa, Biogeosci., 6, 251–266, https://doi.org/10.5194/bg-6-251-2009, 2009. a
Ardo, J., Molder, M., El-Tahir, B. A., and Elkhidir, H. A. M.: Seasonal variation of carbon fluxes in a sparse savanna in semi arid Sudan, Carb. Bal. Manage., 3, 7, https://doi.org/10.1186/1750-0680-3-7, 2008. a
Atkin, O. K., Bloomfield, K. J., Reich, P. B., Tjoelker, M. G., Asner, G. P., Bonal, D., Bönisch, G., Bradford, M. G., Cernusak, L. A., Cosio, E. G., Creek, D., Crous, K. Y., Domingues, T. F., Dukes, J. S., Egerton, J. J. G., Evans, J. R., Farquhar, G. D., Fyllas, N. M., Gauthier, P. P. G., Gloor, E., Gimeno, T. E., Griffin, K. L., Guerrieri, R., Heskel, M. A., Huntingford, C., Ishida, F. Y., Kattge, J., Lambers, H., Liddell, M. J., Lloyd, J., Lusk, C. H., Martin, R. E., Maksimov, A. P., Maximov, T. C., Malhi, Y., Medlyn, B. E., Meir, P., Mercado, L. M., Mirotchnick, N., Ng, D., Niinemets, U., O'Sullivan, O. S., Phillips, O. L., Poorter, L., Poot, P., Prentice, I. C., Salinas, N., Rowland, L. M., Ryan, M. G., Sitch, S., Slot, M., Smith, N. G., Turnbull, M. H., VanderWel, M. C., Valladares, F., Veneklaas, E. J., Weerasinghe, L. K., Wirth, C., Wright, I. J., Wythers, K. R., Xiang, J., Xiang, S., and Zaragoza-Castells, J.: Global variability in leaf respiration in relation to climate, plant functional types and leaf traits, New Phytol., 206, 614–636, https://doi.org/10.1111/nph.13253, 2015. a
Aubinet, M., Chermanne, B., Vandenhaute, M., Longdoz, B., Yernaux, M., and Laitat, E.: Long term carbon dioxide exchange above a mixed forest in the Belgian Ardennes, Agr. Forest Meteorol., 108, 293–315, https://doi.org/10.1016/s0168-1923(01)00244-1, 2001. a
Badgley, G., Field, C. B., and Berry, J. A.: Canopy near-infrared reflectance and terrestrial photosynthesis, Sci. Adv., 3, e1602244, https://doi.org/10.1126/sciadv.1602244, 2017. a
Baldocchi, D., Chen, Q., Chen, X., Ma, S., Miller, G., Ryu, Y., Xiao, J., Wenk, R., and Battles, J.: The Dynamics of Energy, Water, and Carbon Fluxes in a Blue Oak (Quercus douglasii) Savanna in California, in: Ecosystem Function in Savannas, 135–151, CRC Press, https://doi.org/10.1201/b10275-10, 2010. a
Ball, J. T., Timothy Ball, J., Woodrow, I. E., and Berry, J. A.: A Model Predicting Stomatal Conductance and its Contribution to the Control of Photosynthesis under Different Environmental Conditions, in: Progress in Photosynthesis Research, 221–224, 1987. a
Beck, H. E., Zimmermann, N. E., McVicar, T. R., Vergopolan, N., Berg, A., and Wood, E. F.: Present and future Köppen-Geiger climate classification maps at 1-km resolution, Sci. Data, 5, 180214, https://doi.org/10.1038/sdata.2018.214, 2018. a
Beer, C., Ciais, P., Reichstein, M., Baldocchi, D., Law, B. E., Papale, D., Soussana, J.-F., Ammann, C., Buchmann, N., Frank, D., Gianelle, D., Janssens, I. A., Knohl, A., Köstner, B., Moors, E., Roupsard, O., Verbeeck, H., Vesala, T., Williams, C. A., and Wohlfahrt, G.: Temporal and among-site variability of inherent water use efficiency at the ecosystem level, Global Biogeochem. Cy., 23, GB2018, https://doi.org/10.1029/2008GB003233, 2009. a
Belelli Marchesini, L., Papale, D., Reichstein, M., Vuichard, N., Tchebakova, N., and Valentini, R.: Carbon balance assessment of a natural steppe of southern Siberia by multiple constraint approach, Biogeosciences, 4, 581–595, https://doi.org/10.5194/bg-4-581-2007, 2007. a
Berberan-Santos, M. N., Bodunov, E. N., and Pogliani, L.: On the barometric formula, Am. J. Phys., 65, 404–412, 1997. a
Berbigier, P., Bonnefond, J.-M., and Mellmann, P.: CO2 and water vapour fluxes for 2 years above Euroflux forest site, Agr. Forest Meteorol., 108, 183–197, https://doi.org/10.1016/s0168-1923(01)00240-4, 2001. a
Bergeron, O., Margolis, H. A., Black, T. A., Coursolle, C., Dunn, A. L., Barr, A. G., and Wofsy, S. C.: Comparison of carbon dioxide fluxes over three boreal black spruce forests in Canada, Global Change Biol., 13, 89–107, https://doi.org/10.1111/j.1365-2486.2006.01281.x, 2007. a
Beringer, J., Hacker, J., Hutley, L. B., Leuning, R., Arndt, S. K., Amiri, R., Bannehr, L., Cernusak, L. A., Grover, S., Hensley, C., Hocking, D., Isaac, P., Jamali, H., Kanniah, K., Livesley, S., Neininger, B., U, K. T. P., Sea, W., Straten, D., Tapper, N., Weinmann, R., Wood, S., and Zegelin, S.: SPECIAL–Savanna Patterns of Energy and Carbon Integrated across the Landscape, B. Am. Meteorol. Soc., 92, 1467–1485, https://doi.org/10.1175/2011bams2948.1, 2011a. a
Beringer, J., Hutley, L. B., Hacker, J. M., Neininger, B., and U, K. T. P.: Patterns and processes of carbon, water and energy cycles across northern Australian landscapes: From point to region, Agr. Forest Meteorol., 151, 1409–1416, https://doi.org/10.1016/j.agrformet.2011.05.003, 2011b. a
Beringer, J., Hutley, L. B., Hacker, J. M., Neininger, B., and U, K. T. P.: Patterns and processes of carbon, water and energy cycles across northern Australian landscapes: From point to region, Agr. Forest Meteorol., 151, 1409–1416, https://doi.org/10.1016/j.agrformet.2011.05.003, 2011c. a
Beringer, J., Hutley, L. B., McHugh, I., Arndt, S. K., Campbell, D., Cleugh, H. A., Cleverly, J., Resco de Dios, V., Eamus, D., Evans, B., Ewenz, C., Grace, P., Griebel, A., Haverd, V., Hinko-Najera, N., Huete, A., Isaac, P., Kanniah, K., Leuning, R., Liddell, M. J., Macfarlane, C., Meyer, W., Moore, C., Pendall, E., Phillips, A., Phillips, R. L., Prober, S. M., Restrepo-Coupe, N., Rutledge, S., Schroder, I., Silberstein, R., Southall, P., Yee, M. S., Tapper, N. J., van Gorsel, E., Vote, C., Walker, J., and Wardlaw, T.: An introduction to the Australian and New Zealand flux tower network – OzFlux, Biogeosciences, 13, 5895–5916, https://doi.org/10.5194/bg-13-5895-2016, 2016. a, b, c, d
Bernacchi, C. J., Singsaas, E. L., Pimentel, C., Portis, A. R. J., and Long, S. P.: Improved temperature response functions for models of Rubisco-limited photosynthesis, Plant Cell Environ., 24, 253–259, 2001. a, b, c, d, e, f, g, h, i, j, k, l
Bernacchi, C. J., Pimentel, C., and Long, S. P.: In vivo temperature response functions of parameters required to model RuBP-limited photosynthesis, Plant Cell Environ., 26, 1419–1430, 2003. a, b, c
Biederman, J. A., Scott, R. L., Goulden, M. L., Vargas, R., Litvak, M. E., Kolb, T. E., Yepez, E. A., Oechel, W. C., Blanken, P. D., Bell, T. W., Garatuza-Payan, J., Maurer, G. E., Dore, S., and Burns, S. P.: Terrestrial carbon balance in a drier world: the effects of water availability in southwestern North America, Global Change Biol., 22, 1867–1879, https://doi.org/10.1111/gcb.13222, 2016. a
Bonal, D., Bosc, A., Ponton, S., Goret, J.-Y., Burban, B., Gross, P., Bonnefond, J.-M., Elbers, J., Longdoz, B., Epron, D., Guehl, J.-M., and Granier, A.: Impact of severe dry season on net ecosystem exchange in the Neotropical rainforest of French Guiana, Global Change Biol., 14, 1917–1933, https://doi.org/10.1111/j.1365-2486.2008.01610.x, 2008. a
Bowling, D. R., Bethers-Marchetti, S., Lunch, C. K., Grote, E. E., and Belnap, J.: Carbon, water, and energy fluxes in a semiarid cold desert grassland during and following multiyear drought, J. Geophys. Res., 115, G4, https://doi.org/10.1029/2010jg001322, 2010. a
Bristow, M., Hutley, L. B., Beringer, J., Livesley, S. J., Edwards, A. C., and Arndt, S. K.: Quantifying the relative importance of greenhouse gas emissions from current and future savanna land use change across northern Australia, Biogeosciences, 13, 6285–6303, https://doi.org/10.5194/bg-13-6285-2016, 2016. a
Cernusak, L. A., Hutley, L. B., Beringer, J., Holtum, J. A., and Turner, B. L.: Photosynthetic physiology of eucalypts along a sub-continental rainfall gradient in northern Australia, Agr. Forest Meteorol., 151, 1462–1470, https://doi.org/10.1016/j.agrformet.2011.01.006, 2011. a
Chen, B., Liu, J., Chen, J. M., Croft, H., Gonsamo, A., He, L., and Luo, X.: Assessment of foliage clumping effects on evapotranspiration estimates in forested ecosystems, Agr. Forest Meteorol., 216, 82–92, https://doi.org/10.1016/j.agrformet.2015.09.017, 2016. a, b, c
Chen, J.-L., Reynolds, J. F., Harley, P. C., and Tenhunen, J. D.: Coordination theory of leaf nitrogen distribution in a canopy, Oecologia, 93, 63–69, 1993. a, b
Chen, S., Chen, J., Lin, G., Zhang, W., Miao, H., Wei, L., Huang, J., and Han, X.: Energy balance and partition in Inner Mongolia steppe ecosystems with different land use types, Agr. Forest Meteorol., 149, 1800–1809, https://doi.org/10.1016/j.agrformet.2009.06.009, 2009. a
Chiesi, M., Maselli, F., Bindi, M., Fibbi, L., Cherubini, P., Arlotta, E., Tirone, G., Matteucci, G., and Seufert, G.: Modelling carbon budget of Mediterranean forests using ground and remote sensing measurements, Agr. Forest Meteorol., 135, 22–34, https://doi.org/10.1016/j.agrformet.2005.09.011, 2005. a
Cleverly, J., Boulain, N., Villalobos-Vega, R., Grant, N., Faux, R., Wood, C., Cook, P. G., Yu, Q., Leigh, A., and Eamus, D.: Dynamics of component carbon fluxes in a semi-arid Acacia woodland, central Australia, J. Geophys. Res.-Biogeosci., 118, 1168–1185, https://doi.org/10.1002/jgrg.20101, 2013. a
Cleverly, J., Eamus, D., Van Gorsel, E., Chen, C., Rumman, R., Luo, Q., Coupe, N. R., Li, L., Kljun, N., Faux, R., Yu, Q., and Huete, A.: Productivity and evapotranspiration of two contrasting semiarid ecosystems following the 2011 global carbon land sink anomaly, Agr. Forest Meteorol., 220, 151–159, https://doi.org/10.1016/j.agrformet.2016.01.086, 2016. a
Cook, B. D., Davis, K. J., Wang, W., Desai, A., Berger, B. W., Teclaw, R. M., Martin, J. G., Bolstad, P. V., Bakwin, P. S., Yi, C., and Heilman, W.: Carbon exchange and venting anomalies in an upland deciduous forest in northern Wisconsin, USA, Agr. Forest Meteorol., 126, 271–295, https://doi.org/10.1016/j.agrformet.2004.06.008, 2004. a
Cowan, I. R. and Farquhar, G. D.: Stomatal function in relation to leaf metabolism and environment, Symp. Soc. Exp. Biol., 31, 471–505, 1977. a
Davis, T. W., Prentice, I. C., Stocker, B. D., Thomas, R. T., Whitley, R. J., Wang, H., Evans, B. J., Gallego-Sala, A. V., Sykes, M. T., and Cramer, W.: Simple process-led algorithms for simulating habitats (SPLASH v.1.0): robust indices of radiation, evapotranspiration and plant-available moisture, Geosci. Model Dev., 10, 689–708, https://doi.org/10.5194/gmd-10-689-2017, 2017. a, b
Delpierre, N., Berveiller, D., Granda, E., and Dufrêne, E.: Wood phenology, not carbon input, controls the interannual variability of wood growth in a temperate oak forest, New Phytol., 210, 459–470, https://doi.org/10.1111/nph.13771, 2015. a
Desai, A. R., Bolstad, P. V., Cook, B. D., Davis, K. J., and Carey, E. V.: Comparing net ecosystem exchange of carbon dioxide between an old-growth and mature forest in the upper Midwest, USA, Agr. Forest Meteorol., 128, 33–55, https://doi.org/10.1016/j.agrformet.2004.09.005, 2005. a
Desai, A. R., Xu, K., Tian, H., Weishampel, P., Thom, J., Baumann, D., Andrews, A. E., Cook, B. D., King, J. Y., and Kolka, R.: Landscape-level terrestrial methane flux observed from a very tall tower, Agr. Forest Meteorol., 201, 61–75, https://doi.org/10.1016/j.agrformet.2014.10.017, 2015. a
Didan, K.: MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250 m SIN Grid V006, https://doi.org/10.5067/MODIS/MOD13Q1.006, 2015. a
Dragoni, D., Schmid, H. P., Wayson, C. A., Potter, H., Grimmond, C. S. B., and Randolph, J. C.: Evidence of increased net ecosystem productivity associated with a longer vegetated season in a deciduous forest in south-central Indiana, USA, Global Change Biol., 17, 886–897, https://doi.org/10.1111/j.1365-2486.2010.02281.x, 2011. a
Dunn, A. L., Barford, C. C., Wofsy, S. C., Goulden, M. L., and Daube, B. C.: A long-term record of carbon exchange in a boreal black spruce forest: means, responses to interannual variability, and decadal trends, Global Change Biol., 13, 577–590, https://doi.org/10.1111/j.1365-2486.2006.01221.x, 2007. a
Egea, G., Verhoef, A., and Vidale, P. L.: Towards an improved and more flexible representation of water stress in coupled photosynthesis–stomatal conductance models, Agr. Forest Meteorol., 151, 1370–1384, 2011. a
Ensminger, I., Sveshnikov, D., Campbell, D. A., Funk, C., Jansson, S., Lloyd, J., Shibistova, O., and Öquist, G.: Intermittent low temperatures constrain spring recovery of photosynthesis in boreal Scots pine forests, Global Change Biol., 10, 995–1008, https://doi.org/10.1111/j.1365-2486.2004.00781.x, 2004. a
Etzold, S., Ruehr, N. K., Zweifel, R., Dobbertin, M., Zingg, A., Pluess, P., Häsler, R., Eugster, W., and Buchmann, N.: The Carbon Balance of Two Contrasting Mountain Forest Ecosystems in Switzerland: Similar Annual Trends, but Seasonal Differences, Ecosystems, 14, 1289–1309, https://doi.org/10.1007/s10021-011-9481-3, 2011. a
Falge, E., Aubinet, M., Bakwin, P. S., Baldocchi, D., Berbigier, P., Bernhofer, C., Black, T. A., Ceulemans, R., Davis, K. J., Dolman, A. J., Goldstein, A., Goulden, M. L., Granier, A., Hollinger, D. Y., Jarvis, P. G., Jensen, N., Pilegaard, K., Katul, G., Kyaw Tha Paw, P., Law, B. E., Lindroth, A., Loustau, D., Mahli, Y., Monson, R., Moncrieff, P., Moors, E., Munger, J. W., Meyers, T., Oechel, W., Schulze, E. d., Thorgeirsson, H., Tenhunen, J., Valentini, R., Verma, S. B., Vesala, T., and Wofsy, S. C.: FLUXNET Research Network Site Characteristics, Investigators, and Bibliography, 2016, https://doi.org/10.3334/ornldaac/1530, 2017. a, b
Fan, Y., Li, H., and Miguez-Macho, G.: Global Patterns of Groundwater Table Depth, Science, 339, 940–943, https://doi.org/10.1126/science.1229881, 2013. a
Fan, Y., Miguez-Macho, G., Jobbágy, E. G., Jackson, R. B., and Otero-Casal, C.: Hydrologic regulation of plant rooting depth, P. Natl. Acad. Sci. USA, 114, 10572–10577, https://doi.org/10.1073/pnas.1712381114, 2017. a
Fares, S., Savi, F., Muller, J., Matteucci, G., and Paoletti, E.: Simultaneous measurements of above and below canopy ozone fluxes help partitioning ozone deposition between its various sinks in a Mediterranean Oak Forest, Agr. Forest Meteorol., 198-199, 181–191, https://doi.org/10.1016/j.agrformet.2014.08.014, 2014. a
Farquhar, G. D. and Wong, S. C.: An Empirical Model of Stomatal Conductance, Funct. Plant Biol., 11, 191–210, https://doi.org/10.1071/PP9840191, 1984. a
Farquhar, G. D., von Caemmerer, S., and Berry, J. A.: A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78–90, 1980. a, b, c
Ferréa, C., Zenone, T., Comolli, R., and Seufert, G.: Estimating heterotrophic and autotrophic soil respiration in a semi-natural forest of Lombardy, Italy, Pedobiologia, 55, 285–294, https://doi.org/10.1016/j.pedobi.2012.05.001, 2012. a
Fick, A.: Ueber Diffusion, Ann. Phys., 170, 59–86, https://doi.org/10.1002/andp.18551700105, 1855. a
Field, C. B., Randerson, J. T., and Malmström, C. M.: Global net primary production: Combining ecology and remote sensing, Remote Sens. Environ., 51, 74–88, https://doi.org/10.1016/0034-4257(94)00066-V, 1995. a
Frank, J. M., Massman, W. J., Ewers, B. E., Huckaby, L. S., and Negrón, J. F.: Ecosystem CO2∕H2O fluxes are explained by hydraulically limited gas exchange during tree mortality from spruce bark beetles, J. Geophys. Res.-Biogeosci., 119, 1195–1215, https://doi.org/10.1002/2013jg002597, 2014. a
Frankenberg, C., Köhler, P., Magney, T. S., Geier, S., Lawson, P., Schwochert, M., McDuffie, J., Drewry, D. T., Pavlick, R., and Kuhnert, A.: The Chlorophyll Fluorescence Imaging Spectrometer (CFIS), mapping far red fluorescence from aircraft, Remote Sens. Environ., 217, 523–536, 2018. a
Galvagno, M., Wohlfahrt, G., Cremonese, E., Rossini, M., Colombo, R., Filippa, G., Julitta, T., Manca, G., Siniscalco, C., di Cella, U. M., and Migliavacca, M.: Phenology and carbon dioxide source/sink strength of a subalpine grassland in response to an exceptionally short snow season, Environ. Res. Lett., 8, 025008, https://doi.org/10.1088/1748-9326/8/2/025008, 2013. a
Gamon, J., Peñuelas, J., and Field, C.: A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency, Remote Sens. Environ., 41, 35–44, https://doi.org/10.1016/0034-4257(92)90059-S, 1992. a
Gamon, J. A., Huemmrich, K. F., Wong, C. Y. S., Ensminger, I., Garrity, S., Hollinger, D. Y., Noormets, A., and Peñuelas, J.: A remotely sensed pigment index reveals photosynthetic phenology in evergreen conifers, P. Natl. Acad. Sci. USA, 113, 13087–13092, https://doi.org/10.1073/pnas.1606162113, 2016. a
Goldstein, A., Hultman, N., Fracheboud, J., Bauer, M., Panek, J., Xu, M., Qi, Y., Guenther, A., and Baugh, W.: Effects of climate variability on the carbon dioxide, water, and sensible heat fluxes above a ponderosa pine plantation in the Sierra Nevada (CA), Agr. Forest Meteorol., 101, 113–129, https://doi.org/10.1016/s0168-1923(99)00168-9, 2000. a
Gough, C. M., Hardiman, B. S., Nave, L. E., Bohrer, G., Maurer, K. D., Vogel, C. S., Nadelhoffer, K. J., and Curtis, P. S.: Sustained carbon uptake and storage following moderate disturbance in a Great Lakes forest, Ecol. Appl., 23, 1202–1215, https://doi.org/10.1890/12-1554.1, 2013. a, b
Greve, P., Orlowsky, B., Mueller, B., Sheffield, J., Reichstein, M., and Seneviratne, S. I.: Global assessment of trends in wetting and drying over land, Nat. Geosci, 7, 716–721, https://doi.org/10.1038/ngeo2247, 2014. a
Grünwald, T. and Bernhofer, C.: A decade of carbon, water and energy flux measurements of an old spruce forest at the Anchor Station Tharandt, Tellus B, 59, 387–396, https://doi.org/10.3402/tellusb.v59i3.17000, 2007. a
Guan, D.-X., Wu, J.-B., Zhao, X.-S., Han, S.-J., Yu, G.-R., Sun, X.-M., and Jin, C.-J.: CO2 fluxes over an old, temperate mixed forest in northeastern China, Agr. Forest Meteorol., 137, 138–149, https://doi.org/10.1016/j.agrformet.2006.02.003, 2006. a
Guanter, L., Zhang, Y., Jung, M., Joiner, J., Voigt, M., Berry, J. A., Frankenberg, C., Huete, A. R., Zarco-Tejada, P., Lee, J.-E., Susan Moran, M., Ponce-Campos, G., Beer, C., Camps-Valls, G., Buchmann, N., Gianelle, D., Klumpp, K., Cescatti, A., Baker, J. M., and Griffis, T. J.: Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence, P. Natl. Acad. Sci. USA, 111, E1327–E1333, 2014. a
Harris, I., Jones, P., Osborn, T., and Lister, D.: Updated high-resolution grids of monthly climatic observations – the CRU TS3.10 Dataset, Int. J. Climatol., 34, 623–642, https://doi.org/10.1002/joc.3711, 2014. a
Haxeltine, A. and Prentice, I. C.: A General Model for the Light-Use Efficiency of Primary Production, Funct. Ecol., 10, 551–561, 1996. a, b, c
He, L., Chen, J. M., Gonsamo, A., Luo, X., Wang, R., Liu, Y., and Liu, R.: Changes in the Shadow: The Shifting Role of Shaded Leaves in Global Carbon and Water Cycles Under Climate Change, Geophys. Res. Lett., 45, 5052–5061, https://doi.org/10.1029/2018GL077560, 2018. a, b, c, d
Heinsch, F. A., , Running, S. W., Kimball, J. S., Nemani, R. R., Davis, K. J., Bolstad, P. V., Cook, B. D., Desai, A. R., Ricciuto, D. M., Law, B. E., Oechel, W. C., Wofsy, S. C., Dunn, A. L., Munger, J. W., Baldocchi, D. D., Hollinger, D. Y., Richardson, A. D., Stoy, P. C., Siqueira, M. B. S., Monson, R. K., Burns, S. P., and Flanagan, L. B.: Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations, IEEE Trans. Geosci. Remote Sens., 44, 1908–1925, https://doi.org/10.1109/TGRS.2005.853936, 2006. a
Hengl, T., de Jesus, J. M., MacMillan, R. A., Batjes, N. H., Heuvelink, G. B. M., Ribeiro, E., Samuel-Rosa, A., Kempen, B., Leenaars, J. G. B., Walsh, M. G., and Gonzalez, M. R.: SoilGrids1km–global soil information based on automated mapping, PLoS One, 9, e105992, https://doi.org/10.1371/journal.pone.0105992, 2014. a, b
Heskel, M., O'Sullivan, O., Reich, P., Tjoelker, M., Weerasinghe, L., Penillard, A., Egerton, J., Creek, D., Bloomfield, K., Xiang, J., Sinca, F., Stangl, Z., Martinez-De La Torre, A., Griffin, K., Huntingford, C., Hurry, V., Meir, P., Turnbull, M., and Atkin, O.: Convergence in the temperature response of leaf respiration across biomes and plant functional types, P. Natl. Acad. Sci. USA, 113, 3832–3837, https://doi.org/10.1073/pnas.1520282113, 2016. a
Hinko-Najera, N., Isaac, P., Beringer, J., van Gorsel, E., Ewenz, C., McHugh, I., Exbrayat, J.-F., Livesley, S. J., and Arndt, S. K.: Net ecosystem carbon exchange of a dry temperate eucalypt forest, Biogeosciences, 14, 3781–3800, https://doi.org/10.5194/bg-14-3781-2017, 2017. a
Hoshika, Y., Fares, S., Savi, F., Gruening, C., Goded, I., De Marco, A., Sicard, P., and Paoletti, E.: Stomatal conductance models for ozone risk assessment at canopy level in two Mediterranean evergreen forests, Agr. Forest Meteorol., 234-235, 212–221, https://doi.org/10.1016/j.agrformet.2017.01.005, 2017. a
Huber, M. L., Perkins, R. A., Laesecke, A., Friend, D. G., Sengers, J. V., Assael, M. J., Metaxa, I. N., Vogel, E., Mares̆, R., and Miyagawa, K.: New international formulation for the viscosity of H2O, J. Phys. Chem. Ref. Data, 38, 101–125, 2009. a, b
Hufkens, K.: khufkens/gee_subset: Google Earth Engine subset script and library, https://doi.org/10.5281/zenodo.833789, 2017. a
Huner, N. P., Oquist, G., Hurry, V. M., Krol, M., Falk, S., and Griffith, M.: Photosynthesis, photoinhibition and low temperature acclimation in cold tolerant plants, Photosynth. Res., 37, 19–39, 1993. a
Hutley, L. B., Beringer, J., Isaac, P. R., Hacker, J. M., and Cernusak, L. A.: A sub-continental scale living laboratory: Spatial patterns of savanna vegetation over a rainfall gradient in northern Australia, Agr. Forest Meteorol., 151, 1417–1428, https://doi.org/10.1016/j.agrformet.2011.03.002, 2011. a
Imer, D., Merbold, L., Eugster, W., and Buchmann, N.: Temporal and spatial variations of soil CO2, CH4 and N2O fluxes at three differently managed grasslands, Biogeosciences, 10, 5931–5945, https://doi.org/10.5194/bg-10-5931-2013, 2013. a
Irvine, J., Law, B. E., and Hibbard, K. A.: Postfire carbon pools and fluxes in semiarid ponderosa pine in Central Oregon, Global Change Biol., 13, 1748–1760, https://doi.org/10.1111/j.1365-2486.2007.01368.x, 2007. a
Irvine, J., Law, B. E., Martin, J. G., and Vickers, D.: Interannual variation in soil CO2 efflux and the response of root respiration to climate and canopy gas exchange in mature ponderosa pine, Global Change Biol., 14, 2848–2859, https://doi.org/10.1111/j.1365-2486.2008.01682.x, 2008. a
Jacobs, C. M. J., Jacobs, A. F. G., Bosveld, F. C., Hendriks, D. M. D., Hensen, A., Kroon, P. S., Moors, E. J., Nol, L., Schrier-Uijl, A., and Veenendaal, E. M.: Variability of annual CO2 exchange from Dutch grasslands, Biogeosciences, 4, 803–816, https://doi.org/10.5194/bg-4-803-2007, 2007. a
Jiang, C. and Ryu, Y.: Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS), Remote Sens. Environ., 186, 528–547, 2016. a, b, c, d, e, f
Joiner, J., Guanter, L., Lindstrot, R., Voigt, M., Vasilkov, A. P., Middleton, E. M., Huemmrich, K. F., Yoshida, Y., and Frankenberg, C.: Global monitoring of terrestrial chlorophyll fluorescence from moderate-spectral-resolution near-infrared satellite measurements: methodology, simulations, and application to GOME-2, Atmos. Meas. Tech., 6, 2803–2823, https://doi.org/10.5194/amt-6-2803-2013, 2013. a
Joiner, J., Yoshida, Y., Guanter, L., and Middleton, E. M.: New methods for the retrieval of chlorophyll red fluorescence from hyperspectral satellite instruments: simulations and application to GOME-2 and SCIAMACHY, Atmos. Meas. Tech., 9, 3939–3967, https://doi.org/10.5194/amt-9-3939-2016, 2016. a
Jung, M., Reichstein, M., Margolis, H. A., Cescatti, A., Richardson, A. D., Arain, M. A., Arneth, A., Bernhofer, C., Bonal, D., Chen, J., Gianelle, D., Gobron, N., Kiely, G., Kutsch, W., Lasslop, G., Law, B. E., Lindroth, A., Merbold, L., Montagnani, L., Moors, E. J., Papale, D., Sottocornola, M., Vaccari, F., and Williams, C.: Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations, J. Geophys. Res.-Biogeosci., 116, g00J07, https://doi.org/10.1029/2010JG001566, 2011. a, b, c, d
Kato, T., Tang, Y., Gu, S., Hirota, M., Du, M., Li, Y., and Zhao, X.: Temperature and biomass influences on interannual changes in CO2 exchange in an alpine meadow on the Qinghai-Tibetan Plateau, Global Change Biol., 12, 1285–1298, https://doi.org/10.1111/j.1365-2486.2006.01153.x, 2006. a
Kattge, J. and Knorr, W.: Temperature acclimation in a biochemical model of photosynthesis: a reanalysis of data from 36 species, Plant Cell Environ., 30, 1176–1190, 2007. a, b, c, d, e, f, g
Keenan, T., Sabate, S., and Gracia, C.: Soil water stress and coupled photosynthesis–conductance models: Bridging the gap between conflicting reports on the relative roles of stomatal, mesophyll conductance and biochemical limitations to photosynthesis, Agr. Forest Meteorol., 150, 443–453, 2010. a
Keenan, T., Baker, I., Barr, A., Ciais, P., Davis, K., Dietze, M., Dragoni, D., Gough, C. M., Grant, R., Hollinger, D., Hufkens, K., Poulter, B., McCaughey, H., Raczka, B., Ryu, Y., Schaefer, K., Tian, H., Verbeeck, H., Zhao, M., and Richardson, A. D.: Terrestrial biosphere model performance for inter-annual variability of land-atmosphere CO2 exchange, Global Change Biol., 18, 1971–1987, https://doi.org/10.1111/j.1365-2486.2012.02678.x, 2012. a, b
Keenan, T. F., Prentice, I. C., Canadell, J. G., Williams, C. A., Wang, H., Raupach, M., and Collatz, G. J.: Recent pause in the growth rate of atmospheric CO2 due to enhanced terrestrial carbon uptake, Nat. Commun., 7, 13428, https://doi.org/10.1038/ncomms13428, 2016. a, b, c
Keenan, T. F., Migliavacca, M., Papale, D., Baldocchi, D., Reichstein, M., Torn, M., and Wutzler, T.: Widespread inhibition of daytime ecosystem respiration, Nat. Ecol. Evolut., 3, 407–415, https://doi.org/10.1038/s41559-019-0809-2, 2019. a
Kilinc, M., Beringer, J., Hutley, L. B., Tapper, N. J., and McGuire, D. A.: Carbon and water exchange of the world's tallest angiosperm forest, Agr. Forest Meteorol., 182–183, 215–224, https://doi.org/10.1016/j.agrformet.2013.07.003, 2013. a
Knohl, A., Schulze, E.-D., Kolle, O., and Buchmann, N.: Large carbon uptake by an unmanaged 250-year-old deciduous forest in Central Germany, Agr. Forest Meteorol., 118, 151–167, https://doi.org/10.1016/s0168-1923(03)00115-1, 2003. a
Kok, B.: On the interrelation of respiration and photosynthesis in green plants, Biochim. Biophys. Acta, 3, 625–631, https://doi.org/10.1016/0006-3002(49)90136-5, 1949. a
Kurbatova, J., Li, C., Varlagin, A., Xiao, X., and Vygodskaya, N.: Modeling carbon dynamics in two adjacent spruce forests with different soil conditions in Russia, Biogeosciences, 5, 969–980, https://doi.org/10.5194/bg-5-969-2008, 2008. a
Landsberg, J. J. and Waring, R. H.: A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning, For. Ecol. Manage., 95, 209–228, 1997. a
Lasslop, G., Reichstein, M., Papale, D., Richardson, A., Arneth, A., Barr, A., Stoy, P., and Wohlfahrt, G.: Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: critical issues and global evaluation, Global Change Biol., 16, 187–208, https://doi.org/10.1111/j.1365-2486.2009.02041.x, 2010. a, b
Leuning, R.: A critical appraisal of a combined stomatal-photosynthesis model for C3 plants, Plant Cell Environ., 18, 339–355, 1995. a
Leuning, R., Cleugh, H. A., Zegelin, S. J., and Hughes, D.: Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry savanna in Australia: measurements and comparison with MODIS remote sensing estimates, Agr. Forest Meteorol., 129, 151–173, https://doi.org/10.1016/j.agrformet.2004.12.004, 2005. a
Li, X., Xiao, J., He, B., Altaf Arain, M., Beringer, J., Desai, A. R., Emmel, C., Hollinger, D. Y., Krasnova, A., Mammarella, I., Noe, S. M., Ortiz, P. S., Rey-Sanchez, A. C., Rocha, A. V., and Varlagin, A.: Solar-induced chlorophyll fluorescence is strongly correlated with terrestrial photosynthesis for a wide variety of biomes: First global analysis based on OCO-2 and flux tower observations, Glob. Chang. Biol., 24, 3990–4008, https://doi.org/10.1111/gcb.14297, 2018. a
Lindauer, M., Schmid, H., Grote, R., Mauder, M., Steinbrecher, R., and Wolpert, B.: Net ecosystem exchange over a non-cleared wind-throw-disturbed upland spruce forest–Measurements and simulations, Agr. Forest Meteorol., 197, 219–234, https://doi.org/10.1016/j.agrformet.2014.07.005, 2014. a
Lloyd, J. and Farquhar, G. D.: 13C discrimination during CO2 assimilation by the terrestrial biosphere, Oecologia, 99, 201–215, https://doi.org/10.1007/BF00627732, 1994. a
Long, S. P., Postl, W. F., and Bolhár-Nordenkampf, H. R.: Quantum yields for uptake of carbon dioxide in C3 vascular plants of contrasting habitats and taxonomic groupings, Planta, 189, 226–234, 1993. a
Luo, X., Keenan, T. F., Fisher, J. B., Jiménez-Muñoz, J.-C., Chen, J. M., Jiang, C., Ju, W., Perakalapudi, N.-V., Ryu, Y., and Tadić, J. M.: The impact of the 2015/2016 El Niño on global photosynthesis using satellite remote sensing, Philos. Trans. Roy. Soc. B, 373, 20170409, https://doi.org/10.1098/rstb.2017.0409, 2018. a, b
Ma, S., Baldocchi, D. D., Xu, L., and Hehn, T.: Inter-annual variability in carbon dioxide exchange of an oak/grass savanna and open grassland in California, Agr. Forest Meteorol., 147, 157–171, https://doi.org/10.1016/j.agrformet.2007.07.008, 2007. a
MacFarling Meure, C., Etheridge, D., Trudinger, C., Steele, P., Langenfelds, R., van Ommen, T., Smith, A., and Elkins, J.: Law Dome CO2, CH4 and N2O ice core records extended to 2000 years BP, Geophys. Res. Lett., 33, L14810, https://doi.org/10.1029/2006GL026152, 2006. a
Maire, V., Martre, P., Kattge, J., Gastal, F., Esser, G., Fontaine, S., and Soussana, J.-F.: The coordination of leaf photosynthesis links C and N fluxes in C3 plant species, PLoS One, 7, e38345, https://doi.org/10.1371/journal.pone.0038345, 2012. a, b, c, d, e
Mäkelä, A., Hari, P., Berninger, F., Hänninen, H., and Nikinmaa, E.: Acclimation of photosynthetic capacity in Scots pine to the annual cycle of temperature, Tree Physiol., 24, 369–376, 2004. a
Marcolla, B., Pitacco, A., and Cescatti, A.: Canopy Architecture and Turbulence Structure in a Coniferous Forest, Bound.-Layer Meteorol., 108, 39–59, https://doi.org/10.1023/a:1023027709805, 2003a. a
Marcolla, B., Pitacco, A., and Cescatti, A.: Canopy Architecture and Turbulence Structure in a Coniferous Forest, Bound.-Layer Meteorol., 108, 39–59, https://doi.org/10.1023/a:1023027709805, 2003b. a
Marcolla, B., Cescatti, A., Manca, G., Zorer, R., Cavagna, M., Fiora, A., Gianelle, D., Rodeghiero, M., Sottocornola, M., and Zampedri, R.: Climatic controls and ecosystem responses drive the inter-annual variability of the net ecosystem exchange of an alpine meadow, Agr. Forest Meteorol., 151, 1233–1243, https://doi.org/10.1016/j.agrformet.2011.04.015, 2011. a
Matsumoto, K., Ohta, T., Nakai, T., Kuwada, T., Daikoku, K., Iida, S., Yabuki, H., Kononov, A. V., van der Molen, M. K., Kodama, Y., Maximov, T. C., Dolman, A. J., and Hattori, S.: Energy consumption and evapotranspiration at several boreal and temperate forests in the Far East, Agr. Forest Meteorol., 148, 1978–1989, https://doi.org/10.1016/j.agrformet.2008.09.008, 2008. a, b
McHugh, I. D., Beringer, J., Cunningham, S. C., Baker, P. J., Cavagnaro, T. R., Mac Nally, R., and Thompson, R. M.: Interactions between nocturnal turbulent flux, storage and advection at an “deal” eucalypt woodland site, Biogeosciences, 14, 3027–3050, https://doi.org/10.5194/bg-14-3027-2017, 2017. a
McNevin, D., von Caemmerer, S., and Farquhar, G.: Determining RuBisCO activation kinetics and other rate and equilibrium constants by simultaneous multiple non-linear regression of a kinetic model, J. Exp. Bot., 57, 3883–3900, 2006. a
Medlyn, B. E.: Physiological basis of the light use efficiency model, Tree Physiol., 18, 167–176, 1998. a
Medlyn, B. E., Duursma, R. A., Eamus, D., Ellsworth, D. S., Colin Prentice, I., Barton, C. V. M., Crous, K. Y., de Angelis, P., Freeman, M., and Wingate, L.: Reconciling the optimal and empirical approaches to modelling stomatal conductance, Global Chang. Biol., 17, 2134–2144, 2011. a, b, c, d, e
Meek, D. W., Hatfield, J. L., Howell, T. A., Idso, S. B., and Reginato, R. J.: A Generalized Relationship between Photosynthetically Active Radiation and Solar Radiation1, Agron. J., 76, 939–945, 1984. a
Merbold, L., Ardö, J., Arneth, A., Scholes, R. J., Nouvellon, Y., de Grandcourt, A., Archibald, S., Bonnefond, J. M., Boulain, N., Brueggemann, N., Bruemmer, C., Cappelaere, B., Ceschia, E., El-Khidir, H. A. M., El-Tahir, B. A., Falk, U., Lloyd, J., Kergoat, L., Le Dantec, V., Mougin, E., Muchinda, M., Mukelabai, M. M., Ramier, D., Roupsard, O., Timouk, F., Veenendaal, E. M., and Kutsch, W. L.: Precipitation as driver of carbon fluxes in 11 African ecosystems, Biogeosciences, 6, 1027–1041, https://doi.org/10.5194/bg-6-1027-2009, 2009. a
Merbold, L., Eugster, W., Stieger, J., Zahniser, M., Nelson, D., and Buchmann, N.: Greenhouse gas budget (CO2, CH4 and N2O) of intensively managed grassland following restoration, Global Change Biol., 20, 1913–1928, https://doi.org/10.1111/gcb.12518, 2014. a
Meyer, W. S., Kondrlovà, E., and Koerber, G. R.: Evaporation of perennial semi-arid woodland in southeastern Australia is adapted for irregular but common dry periods, Hydrol. Process., 29, 3714–3726, https://doi.org/10.1002/hyp.10467, 2015. a
Michaletz, S. T., Weiser, M. D., Zhou, J., Kaspari, M., Helliker, B. R., and Enquist, B. J.: Plant Thermoregulation: Energetics, Trait-Environment Interactions, and Carbon Economics, Trends Ecol. Evol., 30, 714–724, 2015. a
Migliavacca, M., Meroni, M., Busetto, L., Colombo, R., Zenone, T., Matteucci, G., Manca, G., and Seufert, G.: Modeling Gross Primary Production of Agro-Forestry Ecosystems by Assimilation of Satellite-Derived Information in a Process-Based Model, Sensors, 9, 922–942, https://doi.org/10.3390/s90200922, 2009. a
Monson, R. K., Turnipseed, A. A., Sparks, J. P., Harley, P. C., Scott-Denton, L. E., Sparks, K., and Huxman, T. E.: Carbon sequestration in a high-elevation, subalpine forest, Global Change Biol., 8, 459–478, https://doi.org/10.1046/j.1365-2486.2002.00480.x, 2002. a
Montagnani, L., Manca, G., Canepa, E., Georgieva, E., Acosta, M., Feigenwinter, C., Janous, D., Kerschbaumer, G., Lindroth, A., Minach, L., Minerbi, S., Mölder, M., Pavelka, M., Seufert, G., Zeri, M., and Ziegler, W.: A new mass conservation approach to the study of CO2 advection in an alpine forest, J. Geophys. Res., 114, D07306, https://doi.org/10.1029/2008jd010650, 2009. a
Monteith, J. L.: Solar Radiation and Productivity in Tropical Ecosystems, J. Appl. Ecol., 9, 747–766, 1972. a
Moors, E.: Water Use of Forests in The Netherlands, Ph.D. thesis, Vrije Universiteit Amsterdam, 2012. a
Myneni, R., Knyazikhin, Y., and Park, T.: MOD15A3H MODIS/Combined Terra+Aqua Leaf Area Index/FPAR Daily L4 Global 500 m SIN Grid V006, Data set, NASA EOSDIS Land Processes DAAC, https://doi.org/10.5067/MODIS/MCD15A3H.006, 2015. a
Myneni, R., Knyazikhin, Y., and Park, T.: MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500 m SIN Grid V006, Data set, NASA EOSDIS Land Processes DAAC, https://doi.org/10.5067/MODIS/MOD15A2H.006, 2020. a
Nakai, T., Kim, Y., Busey, R. C., Suzuki, R., Nagai, S., Kobayashi, H., Park, H., Sugiura, K., and Ito, A.: Characteristics of evapotranspiration from a permafrost black spruce forest in interior Alaska, Polar Sci., 7, 136–148, https://doi.org/10.1016/j.polar.2013.03.003, 2013. a
Noormets, A., Chen, J., and Crow, T. R.: Age-Dependent Changes in Ecosystem Carbon Fluxes in Managed Forests in Northern Wisconsin, USA, Ecosystems, 10, 187–203, https://doi.org/10.1007/s10021-007-9018-y, 2007. a, b, c, d, e
Oquist, G. and Huner, N. P. A.: Photosynthesis of overwintering evergreen plants, Annu. Rev. Plant Biol., 54, 329–355, 2003. a
Papale, D., Migliavacca, M., Cremonese, E., Cescatti, A., Alberti, G., Balzarolo, M., Marchesini, L. B., Canfora, E., Casa, R., Duce, P., Facini, O., Galvagno, M., Genesio, L., Gianelle, D., Magliulo, V., Matteucci, G., Montagnani, L., Petrella, F., Pitacco, A., Seufert, G., Spano, D., Stefani, P., Vaccari, F. P., and Valentini, R.: Carbon, Water and Energy Fluxes of Terrestrial Ecosystems in Italy, in: The Greenhouse Gas Balance of Italy, 11–45, Springer Berlin Heidelberg, https://doi.org/10.1007/978-3-642-32424-6_2, 2014. a
Pelkonen, P. and Hari, P.: The Dependence of the Springtime Recovery of CO2 Uptake in Scots Pine on Temperature and Internal Factors, Flora, 169, 398–404, 1980. a
Pilegaard, K., Ibrom, A., Courtney, M. S., Hummelshøj, P., and Jensen, N. O.: Increasing net CO2 uptake by a Danish beech forest during the period from 1996 to 2009, Agr. Forest Meteorol., 151, 934–946, https://doi.org/10.1016/j.agrformet.2011.02.013, 2011. a
Porcar-Castell, A., Tyystjärvi, E., Atherton, J., van der Tol, C., Flexas, J., Pfündel, E. E., Moreno, J., Frankenberg, C., and Berry, J. A.: Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: mechanisms and challenges, J. Exp. Bot., 65, 4065–4095, 2014. a
Posse, G., Lewczuk, N., Richter, K., and Cristiano, P.: Carbon and water vapor balance in a subtropical pine plantation, iForest – Biogeosci. Forest., 9, 736–742, https://doi.org/10.3832/ifor1815-009, 2016. a
Post, H., Hendricks Franssen, H. J., Graf, A., Schmidt, M., and Vereecken, H.: Uncertainty analysis of eddy covariance CO2 flux measurements for different EC tower distances using an extended two-tower approach, Biogeosciences, 12, 1205–1221, https://doi.org/10.5194/bg-12-1205-2015, 2015. a
Powell, T. L., Bracho, R., Li, J., Dore, S., Hinkle, C. R., and Drake, B. G.: Environmental controls over net ecosystem carbon exchange of scrub oak in central Florida, Agr. Forest Meteorol., 141, 19–34, https://doi.org/10.1016/j.agrformet.2006.09.002, 2006. a
Prentice, I. C., Dong, N., Gleason, S. M., Maire, V., and Wright, I. J.: Balancing the costs of carbon gain and water transport: testing a new theoretical framework for plant functional ecology, Ecol. Lett., 17, 82–91, https://doi.org/10.1111/ele.12211, 2014. a, b, c, d, e, f, g
Prentice, I. C., Liang, X., Medlyn, B. E., and Wang, Y.-P.: Reliable, robust and realistic: the three R's of next-generation land-surface modelling, Atmos. Chem. Phys., 15, 5987–6005, https://doi.org/10.5194/acp-15-5987-2015, 2015. a
Prescher, A.-K., Grünwald, T., and Bernhofer, C.: Land use regulates carbon budgets in eastern Germany: From NEE to NBP, Agr. Forest Meteorol., 150, 1016–1025, https://doi.org/10.1016/j.agrformet.2010.03.008, 2010. a
Priestley, C. H. B. and Taylor, R. J.: On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters, Mon. Weather Rev., 100, 81–92, 1972. a
Prober, S. M., Thiele, K. R., Rundel, P. W., Yates, C. J., Berry, S. L., Byrne, M., Christidis, L., Gosper, C. R., Grierson, P. F., Lemson, K., Lyons, T., Macfarlane, C., O'Connor, M. H., Scott, J. K., Standish, R. J., Stock, W. D., van Etten, E. J., Wardell-Johnson, G. W., and Watson, A.: Facilitating adaptation of biodiversity to climate change: A conceptual framework applied to the world's largest Mediterranean-climate woodland, Clim. Change, 110, 227–248, https://doi.org/10.1007/s10584-011-0092-y, 2012. a
R Core Team: R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/ (last access: 6 March 2020), 2016. a
Rambal, S., Joffre, R., Ourcival, J. M., Cavender-Bares, J., and Rocheteau, A.: The growth respiration component in eddy CO2 flux from a Quercus ilex mediterranean forest, Global Change Biol., 10, 1460–1469, https://doi.org/10.1111/j.1365-2486.2004.00819.x, 2004. a
Reichstein, M., Falge, E., Baldocchi, D., Papale, D., Aubinet, M., Berbigier, P., Bernhofer, C., Buchmann, N., Gilmanov, T., Granier, A., Grunwald, T., Havrankova, K., Ilvesniemi, H., Janous, D., Knohl, A., Laurila, T., Lohila, A., Loustau, D., Matteucci, G., Meyers, T., Miglietta, F., Ourcival, J.-M., Pumpanen, J., Rambal, S., Rotenberg, E., Sanz, M., Tenhunen, J., Seufert, G., Vaccari, F., Vesala, T., Yakir, D., and Valentini, R.: On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm, Global Chang. Biol., 11, 1424–1439, 2005. a, b, c
Reverter, B. R., Sánchez-Cañete, E. P., Resco, V., Serrano-Ortiz, P., Oyonarte, C., and Kowalski, A. S.: Analyzing the major drivers of NEE in a Mediterranean alpine shrubland, Biogeosciences, 7, 2601–2611, https://doi.org/10.5194/bg-7-2601-2010, 2010. a
Richardson, A. D., Hollinger, D. Y., Aber, J. D., Ollinger, S. V., and Braswell, B. H.: Environmental variation is directly responsible for short- but not long-term variation in forest-atmosphere carbon exchange, Global Change Biol., 13, 788–803, https://doi.org/10.1111/j.1365-2486.2007.01330.x, 2007. a, b
Rogers, A.: The use and misuse of Vc,max in Earth System Models, Photosynt. Res., 119, 15–29, https://doi.org/10.1007/s11120-013-9818-1, 2014. a
Rogers, A., Medlyn, B. E., Dukes, J. S., Bonan, G., von Caemmerer, S., Dietze, M. C., Kattge, J., Leakey, A. D. B., Mercado, L. M., Niinemets, U., Prentice, I. C., Serbin, S. P., Sitch, S., Way, D. A., and Zaehle, S.: A roadmap for improving the representation of photosynthesis in Earth system models, New Phytol., 213, 22–42 https://doi.org/10.1111/nph.14283, 2017. a, b, c, d, e
Ruehr, N. K., Martin, J. G., and Law, B. E.: Effects of water availability on carbon and water exchange in a young ponderosa pine forest: Above- and belowground responses, Agr. Forest Meteorol., 164, 136–148, https://doi.org/10.1016/j.agrformet.2012.05.015, 2012. a
Running, S., Mu, Q., and Zhao, M.: MOD17A2H MODIS/Terra Gross Primary Productivity 8-Day L4 Global 500 m SIN Grid V006, Data set, NASA EOSDIS Land Processes DAAC, https://doi.org/10.5067/MODIS/MOD17A2H.006, 2015. a
Running, S. W., Nemani, R. R., Heinsch, F. A., Zhao, M., Reeves, M., and Hashimoto, H.: A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production, BioScience, 54, 547–560, https://doi.org/10.1641/0006-3568(2004)054[0547:ACSMOG]2.0.CO;2, 2004. a, b, c, d, e, f
Ryu, Y., Baldocchi, D. D., Kobayashi, H., van Ingen, C., Li, J., Black, T. A., Beringer, J., van Gorsel, E., Knohl, A., Law, B. E., and Roupsard, O.: Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales, Global Biogeochem. Cy., 25, 4, https://doi.org/10.1029/2011GB004053, 2011. a
Ryu, Y., Berry, J. A., and Baldocchi, D. D.: What is global photosynthesis? History, uncertainties and opportunities, Remote Sens. Environ., 223, 95–114, 2019. a, b
Sabbatini, S., Arriga, N., Bertolini, T., Castaldi, S., Chiti, T., Consalvo, C., Njakou Djomo, S., Gioli, B., Matteucci, G., and Papale, D.: Greenhouse gas balance of cropland conversion to bioenergy poplar short-rotation coppice, Biogeosciences, 13, 95–113, https://doi.org/10.5194/bg-13-95-2016, 2016. a, b
Saxton, K. E. and Rawls, W. J.: Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions, Soil Sci. Soc. Am. J., 70, 1569–1578, 2006. a
Schroder, I., Kuske, T., and Zegelin, S.: Eddy Covariance Dataset for Arcturus (2011–2013), Geoscience Australia, Canberra, Tech. rep., https://doi.org/102.100.100/14249, 2014. a
Scott, R. L., Jenerette, G. D., Potts, D. L., and Huxman, T. E.: Effects of seasonal drought on net carbon dioxide exchange from a woody-plant-encroached semiarid grassland, J. Geophys. Res., 114, G4, https://doi.org/10.1029/2008jg000900, 2009. a
Scott, R. L., Hamerlynck, E. P., Jenerette, G. D., Moran, M. S., and Barron-Gafford, G. A.: Carbon dioxide exchange in a semidesert grassland through drought-induced vegetation change, J. Geophys. Res., 115, G3, https://doi.org/10.1029/2010jg001348, 2010. a
Scott, R. L., Biederman, J. A., Hamerlynck, E. P., and Barron-Gafford, G. A.: The carbon balance pivot point of southwestern U.S. semiarid ecosystems: Insights from the 21st century drought, J. Geophys. Res.-Biogeosci., 120, 2612–2624, https://doi.org/10.1002/2015jg003181, 2015a. a
Scott, R. L., Biederman, J. A., Hamerlynck, E. P., and Barron-Gafford, G. A.: The carbon balance pivot point of southwestern U.S. semiarid ecosystems: Insights from the 21st century drought, J. Geophys. Res.-Biogeosci., 120, 2612–2624, https://doi.org/10.1002/2015jg003181, 2015b. a
Serrano-Ortiz, P., Marañón-Jiménez, S., Reverter, B. R., Sánchez-Cañete, E. P., Castro, J., Zamora, R., and Kowalski, A. S.: Post-fire salvage logging reduces carbon sequestration in Mediterranean coniferous forest, Forest Ecol. Manage., 262, 2287–2296, https://doi.org/10.1016/j.foreco.2011.08.023, 2011. a
Shao, C., Chen, J., Li, L., Dong, G., Han, J., Abraha, M., and John, R.: Grazing effects on surface energy fluxes in a desert steppe on the Mongolian Plateau:, Ecol. Appl., 27, 485–502, https://doi.org/10.1002/eap.1459, 2017. a
Shi, P., Sun, X., Xu, L., Zhang, X., He, Y., Zhang, D., and Yu, G.: Net ecosystem CO2 exchange and controlling factors in a steppe–Kobresia meadow on the Tibetan Plateau, Sci. China Ser. D, 49, 207–218, https://doi.org/10.1007/s11430-006-8207-4, 2006. a
Singsaas, E. L., Ort, D. R., and DeLucia, E. H.: Variation in measured values of photosynthetic quantum yield in ecophysiological studies, Oecologia, 128, 15–23, https://doi.org/10.1007/s004420000624, 2001. a
Smith, E. L.: THE INFLUENCE OF LIGHT AND CARBON DIOXIDE ON PHOTOSYNTHESIS, J. Gen. Physiol., 20, 807–830, 1937. a
Smith, N. G. and Dukes, J. S.: Plant respiration and photosynthesis in global-scale models: incorporating acclimation to temperature and CO2, Glob. Chang. Biol., 19, 45–63, 2013. a, b
Smith, N. G. and Dukes, J. S.: Short-term acclimation to warmer temperatures accelerates leaf carbon exchange processes across plant types, Global Chang. Biol., 23, 4840–4853, 2017. a, b
Smith, N. G., Keenan, T. F., Colin Prentice, I., Wang, H., Wright, I. J., Niinemets, U., Crous, K. Y., Domingues, T. F., Guerrieri, R., Yoko Ishida, F., Kattge, J., Kruger, E. L., Maire, V., Rogers, A., Serbin, S. P., Tarvainen, L., Togashi, H. F., Townsend, P. A., Wang, M., Weerasinghe, L. K., and Zhou, S.-X.: Global photosynthetic capacity is optimized to the environment, Ecol. Lett., 22, 506–517, 2019. a, b, c, d, e, f
Stevens, R. M., Ewenz, C. M., Grigson, G., and Conner, S. M.: Water use by an irrigated almond orchard, Irrig. Sci., 30, 189–200, https://doi.org/10.1007/s00271-011-0270-8, 2011. a
Stocker, B.: fLUE, https://doi.org/10.5281/zenodo.1158524, 2018. a
Stocker, B.: rpmodel: v1.0.4, https://doi.org/10.5281/zenodo.3560169, 2019a. a
Stocker, B.: sofun: v1.2.0, https://doi.org/10.5281/zenodo.3529466, 2019b. a
Stocker, B.: eval_pmodel, https://doi.org/10.5281/zenodo.3632308, 2020a. a
Stocker, B.: rsofun, https://doi.org/10.5281/zenodo.3632328, 2020b. a
Stocker, B. D.: GPP at FLUXNET Tier 1 sites from P-model, https://doi.org/10.5281/zenodo.3559850, 2019c. a
Stocker, B. D., Zscheischler, J., Keenan, T. F., Prentice, I. C., Peñuelas, J., and Seneviratne, S. I.: Quantifying soil moisture impacts on light use efficiency across biomes, New Phytol., 218, 1430–1449, 2018. a, b, c, d, e, f
Stocker, B. D., Zscheischler, J., Keenan, T. F., Prentice, I. C., Seneviratne, S. I., and Peñuelas, J.: Drought impacts on terrestrial primary production underestimated by satellite monitoring, Nat. Geosci., 12, 264–270, https://doi.org/10.1038/s41561-019-0318-6, 2019. a, b
Suni, T., Rinne, J., Reissel, A., Altimir, N., Keronen, P., Rannik, Ü., Maso, M., Kulmala, M., and Vesala, T.: Long-term measurements of surface fluxes above a Scots pine forest in Hyytiälä, southern Finland, Boreal Environ. Res., 4, 287–301, 2003. a
Suzuki, Y., Makino, A., and Mae, T.: Changes in the turnover of Rubisco and levels of mRNAs of rbcL and rbcS in rice leaves from emergence to senescence, Plant Cell Environ., 24, 1353–1360, 2001. a
Tagesson, T., Fensholt, R., Guiro, I., Rasmussen, M. O., Huber, S., Mbow, C., Garcia, M., Horion, S., Sandholt, I., Holm-Rasmussen, B., Göttsche, F. M., Ridler, M.-E., Olén, N., Olsen, J. L., Ehammer, A., Madsen, M., Olesen, F. S., and Ardö, J.: Ecosystem properties of semiarid savanna grassland in West Africa and its relationship with environmental variability, Global Change Biol., 21, 250–264, https://doi.org/10.1111/gcb.12734, 2014. a
Tanja, S., Berninger, F., Vesala, T., Markkanen, T., Hari, P., Mäkelä, A., Ilvesniemi, H., Hänninen, H., Nikinmaa, E., Huttula, T., Laurila, T., Aurela, M., Grelle, A., Lindroth, A., Arneth, A., Shibistova, O., and Lloyd, J.: Air temperature triggers the recovery of evergreen boreal forest photosynthesis in spring, Global Change Biol., 9, 1410–1426, https://doi.org/10.1046/j.1365-2486.2003.00597.x, 2003. a, b
Tedeschi, V., Rey, A., Manca, G., Valentini, R., Jarvis, P. G., and Borghetti, M.: Soil respiration in a Mediterranean oak forest at different developmental stages after coppicing, Global Change Biol., 12, 110–121, https://doi.org/10.1111/j.1365-2486.2005.01081.x, 2006. a
Tramontana, G., Jung, M., Schwalm, C. R., Ichii, K., Camps-Valls, G., Ráduly, B., Reichstein, M., Arain, M. A., Cescatti, A., Kiely, G., Merbold, L., Serrano-Ortiz, P., Sickert, S., Wolf, S., and Papale, D.: Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms, Biogeosciences, 13, 4291–4313, https://doi.org/10.5194/bg-13-4291-2016, 2016. a, b, c
Ulke, A. G., Gattinoni, N. N., and Posse, G.: Analysis and modelling of turbulent fluxes in two different ecosystems in Argentina, International J. Environ. Pollut., 58, 52, https://doi.org/10.1504/ijep.2015.076583, 2015. a
Urbanski, S., Barford, C., Wofsy, S., Kucharik, C., Pyle, E., Budney, J., McKain, K., Fitzjarrald, D., Czikowsky, M., and Munger, J. W.: Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest, J. Geophys. Res., 112, https://doi.org/10.1029/2006jg000293, 2007a. a
Urbanski, S., Barford, C., Wofsy, S., Kucharik, C., Pyle, E., Budney, J., McKain, K., Fitzjarrald, D., Czikowsky, M., and Munger, J. W.: Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest, J. Geophys. Res.-Biogeosci., 112, G2, https://doi.org/10.1029/2006JG000293, 2007b. a
Valentini, R., Angelis, P., Matteucci, G., Monaco, R., Dore, S., and Mucnozza, G. E. S.: Seasonal net carbon dioxide exchange of a beech forest with the atmosphere, Global Change Biol., 2, 199–207, https://doi.org/10.1111/j.1365-2486.1996.tb00072.x, 1996. a
Veres, J. S. and Williams III, G. J.: Time course of photosynthetic temperature acclimation in Carex eleocharis Bailey, Plant Cell Environ., 7, 545–547, 1984. a
Verhoeven, A.: Sustained energy dissipation in winter evergreens, New Phytol., 201, 57–65, 2014. a
von Caemmerer, S. and Farquhar, G. D.: Some relationships between the biochemistry of photosynthesis and the gas exchange of leaves, Planta, 153, 376–387, 1981. a
Wang, H., Prentice, I. C., Keenan, T. F., Davis, T. W., Wright, I. J., Cornwell, W. K., Evans, B. J., and Peng, C.: Towards a universal model for carbon dioxide uptake by plants, Nat. Plants, 3, 734–741, 2017a. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q
Wang, L., Zhu, H., Lin, A., Zou, L., Qin, W., and Du, Q.: Evaluation of the Latest MODIS GPP Products across Multiple Biomes Using Global Eddy Covariance Flux Data, Remote Sensing, 9, 5, https://doi.org/10.3390/rs9050418, 2017b. a, b
Way, D. A. and Yamori, W.: Thermal acclimation of photosynthesis: on the importance of adjusting our definitions and accounting for thermal acclimation of respiration, Photosynth. Res., 119, 89–100, 2014. a
Weedon, G. P., Balsamo, G., Bellouin, N., Gomes, S., Best, M. J., and Viterbo, P.: The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data, Water Resour. Res., 50, 7505–7514, 2014. a, b, c
Wehr, R., Munger, J. W., McManus, J. B., Nelson, D. D., Zahniser, M. S., Davidson, E. A., Wofsy, S. C., and Saleska, S. R.: Seasonality of temperate forest photosynthesis and daytime respiration, Nature, 534, 680–683, https://doi.org/10.1038/nature17966, 2016. a
Wen, X.-F., Wang, H.-M., Wang, J.-L., Yu, G.-R., and Sun, X.-M.: Ecosystem carbon exchanges of a subtropical evergreen coniferous plantation subjected to seasonal drought, 2003–2007, Biogeosciences, 7, 357–369, https://doi.org/10.5194/bg-7-357-2010, 2010. a
Wick, B., Veldkamp, E., de Mello, W. Z., Keller, M., and Crill, P.: Nitrous oxide fluxes and nitrogen cycling along a pasture chronosequence in Central Amazonia, Brazil, Biogeosciences, 2, 175–187, https://doi.org/10.5194/bg-2-175-2005, 2005. a
Wohlfahrt, G., Hammerle, A., Haslwanter, A., Bahn, M., Tappeiner, U., and Cernusca, A.: Seasonal and inter-annual variability of the net ecosystem CO2 exchange of a temperate mountain grassland: Effects of weather and management, J. Geophys. Res., 113, D8, https://doi.org/10.1029/2007jd009286, 2008. a
Xiang, Y., Gubian, S., Suomela, B., and Hoeng, J.: Generalized Simulated Annealing for Efficient Global Optimization: the GenSA Package for R., The R Journal Volume 5/1, June 2013, available at: https://journal.r-project.org/archive/2013/RJ-2013-002/index.html (last access: 6 March 2020), 2013. a
Yan, J., Zhang, Y., Yu, G., Zhou, G., Zhang, L., Li, K., Tan, Z., and Sha, L.: Seasonal and inter-annual variations in net ecosystem exchange of two old-growth forests in southern China, Agr. Forest Meteorol., 182–183, 257–265, https://doi.org/10.1016/j.agrformet.2013.03.002, 2013. a
Yee, M. S., Pauwels, V. R., Daly, E., Beringer, J., Rüdiger, C., McCabe, M. F., and Walker, J. P.: A comparison of optical and microwave scintillometers with eddy covariance derived surface heat fluxes, Agr. Forest Meteorol., 213, 226–239, https://doi.org/10.1016/j.agrformet.2015.07.004, 2015. a
Zeller, K. and Nikolov, N.: Quantifying simultaneous fluxes of ozone, carbon dioxide and water vapor above a subalpine forest ecosystem, Environ. Pollut., 107, 1–20, https://doi.org/10.1016/s0269-7491(99)00156-6, 2000. a
Zeng, Y., Badgley, G., Dechant, B., Ryu, Y., Chen, M., and Berry, J.: A practical approach for estimating the escape ratio of near-infrared solar-induced chlorophyll fluorescence, Remote Sens. Environ., 232, 111209, https://doi.org/10.1016/j.rse.2019.05.028, 2019. a
Zhang, Y., Xiao, X., Wu, X., Zhou, S., Zhang, G., Qin, Y., and Dong, J.: A global moderate resolution dataset of gross primary production of vegetation for 2000–2016, Sci. Data, 4, 170165, https://doi.org/10.1038/sdata.2017.165, 2017. a, b, c, d, e, f, g
Zhao, M., Heinsch, F. A., Nemani, R. R., and Running, S. W.: Improvements of the MODIS terrestrial gross and net primary production global data set, Remote Sens. Environ., 95, 164–176, https://doi.org/10.1016/j.rse.2004.12.011, 2005. a, b, c
Zhu, Z., Bi, J., Pan, Y., Ganguly, S., Anav, A., Xu, L., Samanta, A., Piao, S., Nemani, R. R., and Myneni, R. B.: Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011, Remote Sens., 5, 927–948, https://doi.org/10.3390/rs5020927, 2013. a
Zielis, S., Etzold, S., Zweifel, R., Eugster, W., Haeni, M., and Buchmann, N.: NEP of a Swiss subalpine forest is significantly driven not only by current but also by previous year's weather, Biogeosciences, 11, 1627–1635, https://doi.org/10.5194/bg-11-1627-2014, 2014. a
- Abstract
- Introduction
- Theory
- Methods
- Results
- Discussion
- Conclusions
- Code and data availability
- Appendix A: Site information
- Appendix B: Temperature and pressure dependence of photosynthesis parameters
- Appendix C: Corollary of the χ prediction
- Appendix D: Soil water holding capacity
- Appendix E: Vapour pressure deficit
- Appendix F: Extended theory
-
Appendix G: The
rpmodel()function of the rpmodel R package - Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Theory
- Methods
- Results
- Discussion
- Conclusions
- Code and data availability
- Appendix A: Site information
- Appendix B: Temperature and pressure dependence of photosynthesis parameters
- Appendix C: Corollary of the χ prediction
- Appendix D: Soil water holding capacity
- Appendix E: Vapour pressure deficit
- Appendix F: Extended theory
-
Appendix G: The
rpmodel()function of the rpmodel R package - Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References