Data assimilation of in situ and satellite remote sensing data to 3D hydrodynamic lake models: a case study using Delft3D-FLOW v4.03 and OpenDA v2.4

The understanding of physical dynamics is crucial to provide scientifically credible information on lake ecosystem management. We show how the combination of in situ observations, remote sensing data, and three-dimensional hydrodynamic (3D) numerical simulations is capable of resolving various spatiotemporal scales involved in lake dynamics. This combination is achieved through data assimilation (DA) and uncertainty quantification. In this study, we develop a flexible framework by incorporating DA into 3D hydrodynamic lake models. Using an ensemble Kalman filter, our approach accounts for model and observational uncertainties. We demonstrate the framework by assimilating in situ and satellite remote sensing temperature data into a 3D hydrodynamic model of Lake Geneva. Results show that DA effectively improves model performance over a broad range of spatiotemporal scales and physical processes. Overall, temperature errors have been reduced by 54 %. With a localization scheme, an ensemble size of 20 members is found to be sufficient to derive covariance matrices leading to satisfactory results. The entire framework has been developed with the goal of near-real-time operational systems (e.g., integration into meteolakes.ch).

1 Introduction

The management of aquatic systems is a complex challenge including many stakeholders pursuing sometimes contradictory objectives. This becomes even more complicated in view of climate change, affecting both watershed hydrology and lakes physics. There is thereby an urgent need to provide accurate information on lake hydrodynamics.

Traditionally, perhaps due to the misleading definition of lakes as lentic systems, hydrodynamic studies have focused on the one-dimensional vertical structure of lakes using in situ measurements with limited spatial and temporal coverage (Kiefer et al., 2015). Yet, the lentic definition of lakes is misleading at a short timescale. Dynamical processes such as wind-induced upwellings, rivers discharges, and gyres strongly disrupt the spatial homogeneity of the systems and ultimately affect lake biogeochemistry (MacIntyre and Melack, 1995). Remote sensing observations, as well as one- and three-dimensional hydrodynamic models, have addressed some of the spatial and temporal coverage limitations.

While three-dimensional (3D) hydrodynamic models are important tools capable of simulating multi-scale temporal and spatial 3D lake dynamics, measurements remain essential to properly calibrate and validate models to improve their accuracy. Indeed, model deviations are unavoidable due to uncertainties in processes, forcing, and observations (Lahoz et al., 2010), which have to be taken into account. Remotely sensed observations provide another essential source of information, with improved spatial and temporal resolution. However, this information remains fundamentally 2D. Ultimately, the combination of remote sensing, numerical simulations, and in situ measurements can overcome the large variations of spatiotemporal scales involved in lake dynamics and hence provide an adequate understanding of the system. This combination is achieved by data assimilation (DA).

DA is an effective approach to blend observational data into model simulations (Bannister, 2017; Li et al., 2008). Defined as the process by which the model of an evolving system is corrected by incorporating observations of the real system, DA improves both short-term forecasts and past model reanalysis (Hawley et al., 2006). A fundamental property of DA is to take observation (e.g., instrument accuracy, representativeness) and model (e.g., in processes, forcing, initial conditions) errors into account (Lahoz et al., 2010) and to provide the analysis with corrected errors (Kourzeneva, 2014). Those are crucial elements for parameter inference, monitoring, and forecast reliability.

Multiple methods have been developed for DA, among those the ensemble Kalman filter (EnKF; Evensen, 2003). The EnKF has been successfully applied to numerous applications in oceanography and atmospheric sciences (Eknes and Evensen, 2002; Evensen, 1994; Mao et al., 2009; Natvik and Evensen, 2003). It was found to be an efficient tool for nonlinear problems with high dimensionality (Crow, 2003; Reichle et al., 2002a, b) by computing system error statistics based on system dynamics. But those methods have rarely been applied to lakes, and DA for inland waters is still in its infancy. The different scales involved, and considering the sparse observations in combination with the large heterogeneity found in lake dynamics, limited the direct application of experiments designed for oceans. For instance, Zhang et al. (2007) assimilated current measurements into a two-dimensional circulation model of Lake Michigan, whereby current updates are calculated by kriging interpolation. Yeates et al. (2008) used a pycnocline filter that assimilated thermistor data into a 3D model of a stratified lake to negate numerical diffusion driving model predictions off course. Stroud et al. (2009) assimilated satellite images into a two-dimensional sediment transport model of Lake Michigan using direct insertion and a kriging-based approach, effectively reducing model forecast errors. Later on they used an EnKF and smoother (Stroud et al., 2010) with a similar model and data when a large sediment plume was observed after a major storm event. The results obtained were better relative to standard approaches (a static model and a reduced-rank square root Kalman filter). Finally, Kourzeneva (2014) used an extended Kalman filter (EKF) to assimilate lake surface water temperature into a one-dimensional two-layer freshwater lake model, leading to significant improvements over the free model run. Overall, to our knowledge, this is the first DA experiment that blends both in situ observations and remote sensing data into a three-dimensional hydrodynamic model with high dimensionality.

The aim of this study is to develop a flexible framework, in a Bayesian inference setting, capable of updating and improving model states while taking into account the uncertainty of both the modeled system and observational data. Here, we present a novel DA experiment with an EnKF tailored to lakes and observations using an open-source hydrodynamic model and assimilation platform. This approach uses a new file-based coupling recently developed for OpenDA and Delft3D-FLOW with z-layer support (Baracchini et al., 2019a). Delft3D-FLOW is an open-source three-dimensional hydrodynamic simulation software with numerous successful applications in coastal, river, estuarine, and lake domains. OpenDA is an open-source generic DA environment (El Serafy et al., 2007) used in various calibration and DA experiments (El Serafy et al., 2007; Weerts et al., 2010; Kurniawan et al., 2011), but it has not yet been applied to 3D lake hydrodynamic modeling with DA. Our methodology is tested on the large French–Swiss Lake Geneva with in situ temperature measurements and lake surface water temperature (LSWT) retrieved from satellite data (AVHRR). The choice of testing a first DA of surface temperature on Lake Geneva was motivated by recent studies concluding that data from spaceborne medium-resolution radiometers specifically tailored to Lake Geneva (Oesch et al., 2005) could potentially be assimilated to numerical models (Oesch et al., 2008). Furthermore, Baracchini et al. (2019a) proposed a calibrated model and framework for Lake Geneva, this first step being an absolute requirement for DA. Here, LSWT and in situ data are blended into such a model to expand its monitoring capabilities of physical phenomena. The latter is achieved by considering the stochasticity of the system and an EnKF algorithm to update model results. Environmental research and operational monitoring and forecasting of midsize to large lakes will benefit from this procedure, with noticeable impacts on a broad diversity of societally important issues.

The study is organized as follows: Sect. 2, “Data and methods”, describes the study site, model, tools, and data used. This includes measurement retrieval and the processing chain as well as the quantification of their uncertainty. Although part of the methods, the data assimilation algorithm and its configuration are provided in a different section (Sect. 3) due to their central role in the study. Noise generation, the number of ensembles, and the localization scheme are discussed in this section. Sections 4 and 5 consist of the presentation and discussion of results, respectively. Finally, perspectives and conclusion are given in the final section.

2 Data and methods

Here we describe the various components used in the DA experiment, the challenges associated with high-frequency and high-resolution measurements, modeling datasets, and their error definitions, which previously hampered the application of such systems.

2.1 Study site

Lake Geneva (locally known as Le Léman) is a perialpine lake located between Switzerland and France (46.458^∘ N, 6.528^∘ E) at an altitude of 372 m (Fig. 1). It is the largest freshwater lake in western Europe (surface area and volume of 580 and 89 km³, respectively), with a retention time of 11.4 years. Due to relatively mild winter temperatures and its large depth of 309 m, complete deep convective mixing occurs only every 5 to 10 winters (Schwefel et al., 2016). The lake is composed of two parts: the large eastern basin (Grand Lac), with a maximum depth of 309 m, mean depth of 160 m, and mean width of 10 km in which gyres are frequently observed, and the Petit Lac, the narrow and shallow western basin (maximum depth of 70 m, mean width of 4.5 km). The centers of the two basins are some 30 km apart, which defines the cutoff distance of the EnKF (more details in Sect. 3). The surrounding topography is mountainous, mainly in the southeast, hence affecting the wind circulation above the basin. Lake Geneva is mesotrophic, with strong variation in turbidity and light penetration depth over the year (ranging from 3.6 to 14 m).

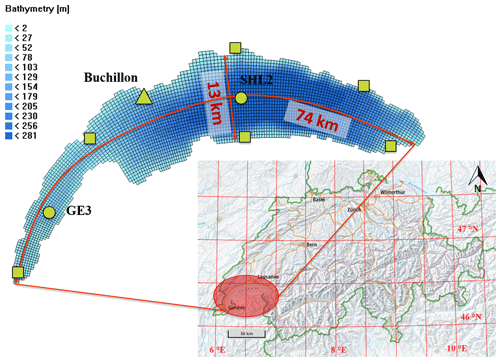
Figure 1 Lake Geneva locations, computational grid, and bathymetry. Circles are in situ measurement sites. The triangle indicates the AVHRR validation station. Squares are selected sampling locations used to generate the wind fields of the COSMO-E products. Basemap source: Federal Office of Topography © Swisstopo.

2.2 Model setup

The primary purpose of a 3D hydrodynamic model is to solve the time-dependent, nonlinear differential equations of the hydrostatic free-surface flows in a computational grid. Various modeling suites have been developed to solve those equations accounting for momentum (Reynolds-averaged Navier–Stokes – RANS) and fluid mass (continuity), as well as heat and mass transfer. The open-source Delft3D-FLOW software is used in this study.

Delft3D-FLOW numerical model

Delft3D-FLOW is an open-source hydrodynamic modeling suite developed by Deltares, Netherlands. Initially designed for coastal regions and estuaries, it has been expanded to rivers and lakes. A detailed model description of the equations and numerical schemes (conjugate gradient solver) can be found in the manual (Deltares, 2015). We stress again that a fundamental prerequisite for any DA experiment is a well-calibrated model. Improper physical parameters could lead to strong discontinuities followed by waves (assimilation shocks), leading to spurious behaviors (Anderson et al., 2000). Assimilated variables could then, for example, go back to their pre-assimilated value. Lake Geneva's model has been extensively studied and calibrated (explicit optimization method by residual minimization) in a previous study (Baracchini et al., 2019a). This model consists of 100 unevenly distributed vertical layers, with thinner layers at the top (from 20 cm at the surface to several meters in the hypolimnion). Due to the steep bathymetry of Lake Geneva, we use the z-coordinate system (layers are horizontal) to avoid strong numerical diffusion and excessive artificial mixing. A computational time step of 2 min is specified for the 450 m horizontal grid size to maintain model stability with the κ-ϵ turbulence closure model. This turbulence closure model accounts for unresolved mixing at sub-grid scales. As initial conditions, the model is initialized (uniformly horizontally) from an in situ temperature profile taken at the deepest location of the lake in January, when the lake is partially mixed. We consider a simulation period of 1 year, thereby covering the entire range of seasonal stratification dynamics.

The dynamics of a lake are mainly driven by interactions with the atmosphere and dissipation at the bed. As boundary forcing, we use MeteoSwiss COSMO-1 reanalysis products from their atmospheric model tailored to the Alpine region. They consist of various meteorological variables on a regular 1.1 km grid with hourly resolution. Seven of those variables are used in this study: solar radiation, wind direction and velocity, relative humidity, cloud cover, pressure, and air temperature.

Lake Geneva is subject to strong variations in turbidity, which affect the stratification mainly in early summer. Monthly time series of Secchi depth observations have therefore been used in the forcing.

Finally, a single deterministic 1-year model run for Lake Geneva without DA requires 3 d of wall-clock computing time on a single Intel Xeon Broadwell core processor.

2.3 Assimilation platform

OpenDA is an open interface standard. It provides access to a set of open-source tools, allowing for the integration of arbitrary numerical models and observations through calibration and data assimilation algorithms. Its goal is to minimize algorithmic development by promoting the exchange of software solutions among researchers and users (Deltares, 2019; http://www.openda.org, last access: 9 March 2020).

An OpenDA interface has recently been developed for the z-layer Delft3D-FLOW using the black-box wrapper (file-based) approach (Baracchini et al., 2019a). This interface has been further expanded for DA in this study. Additions include extended modifications of the Delft3D-FLOW model definition file, model forcing files (on an equidistant grid only) for OpenDA's noise models, and support for localization, which allows users to limit the area of influence of an observation. The entire source code is available on GitHub (https://github.com/OpenDA-Association/OpenDA, last access: 9 March 2020).

2.4 Monitoring data

2.4.1 Role of data accuracy

Key in any DA problem is the observational data and their quality (Madsen, 2003). 3D models require an especially large amount of data to validate their variability. Remote sensing observations are therefore considered together with vertical in situ profiles to constrain the system over the surface and depth. Errors are present in the system through its initial conditions, physical processes, approximations, and forcings (Bárdossy and Singh, 2008). Observations of the true system also require quantifying their uncertainties, as measurements are always an imperfect and incomplete representation (Bertino et al., 2007). This is particularly important as it defines how reliable an observation is and therefore how the model states are corrected. Injecting data with incorrect measurement error distributions into a good model could depreciate its relevance to the point at which assimilation estimates are worse than the non-assimilative solution or the observations. The opposite holds true, and model forecast would still be unreliable.

2.4.2 Lake in situ data

The dataset consists of 31 temperature profiles over the water column at two locations of Lake Geneva (GE3 and SHL2; Fig. 1) sampled during the year 2017. Profiles are collected on a monthly (GE3) to bimonthly (SHL2) basis. Uncertainty of in situ temperature profiles is defined as the maximum value of the instrument precision (0.1 ^∘C) and temporal variability at the measurement location. The reasons for the latter are twofold: first, some in situ profiles did not have their exact collection time recorded; second, this study does not focus on reproducing short-term dynamics such as basin-scale internal waves and thermocline oscillations. The standard deviation of preliminary modeling results is computed over a time window to account for this variability. The temporal variability window is defined by the period of basin-scale internal oscillations (48 h). This procedure allows for the limiting of physical discontinuities created by the EnKF updates from specific physical processes (i.e., internal waves), which are not the focus of this study.

The Buchillon station (Fig. 1), consisting of a mast measuring various atmospheric and hydrodynamic properties in real time, has been used for the validation of AVHRR data as detailed below. Of relevance for this study is a thermistor located at 1 m of water depth, representing the bulk temperature.

2.4.3 AVHRR LSWT

The spaceborne Advanced Very High Resolution Radiometer (AVHRR) sensor has been selected for its high temporal (up to 10 overpasses per day) and moderate spatial (1.1 km in nadir) resolution. We consider it to be the right trade-off for lakes: between the high spatial but low temporal resolution of Landsat 8 (100 m every 2 weeks) and the low spatial but high temporal one of SEVIRI (3 km at the Equator; every 15 min). The access to the AVHRR data was facilitated by a direct downlink and processing chain from the University of Bern. We describe below, and in the Appendix, how AVHRR can be used for DA in lakes.

The AVHRR LSWT retrieval process, with locally adapted split-window coefficients for Lake Geneva, is described in Lieberherr and Wunderle (2018) and Lieberherr et al. (2017). Only pixels with quality levels higher than 3 (Lieberherr and Wunderle, 2018) are considered for the next sections.

An extensive description of the filtering of the data is available in Appendix A. Overall, out of the 3372 AVHRR images of Lake Geneva available for 2017, 124 satisfy the selection criteria (see Appendix A). These data are relatively evenly spread from February to October, with a maximum frequency of one image per 24 h. Very few images are available in January, November, and December due to bad weather conditions or cloud cover. The average lake coverage of those images is about 51 %.

3 Data assimilation

The multiple methods proposed for DA mainly fall into two categories: (i) variational (e.g., 3D-VAR, 4D-VAR) and (ii) sequential methods (e.g., Kalman filtering, particle filtering). For variational methods, the optimization of the model states (or parameters) is based on the minimization of a cost function. Carrassi et al. (2018) have proposed an extensive review of DA assimilation methods and uses in geophysical sciences. Variational methods are popular in meteorological forecasting (Rawlins et al., 2007). However, the computational burden associated with the collection and storage of data can be significant. Moreover, the batch processing of data reduces flexibility and complicates the consideration of time-varying model parameters.

Sequential methods are robust techniques for DA in a broad range of applications. For linear dynamics and measurement processes with Gaussian error statistics, the Kalman filter (Kalman, 1960) is an optimal sequential DA algorithm. However, most processes observed in nature, such as hydrodynamics, are nonlinear. The analytical solution provided by the Kalman filter therefore cannot be derived in order to compute the posterior distribution of simulated variables. To overcome this limitation, variants exist, such as the EKF, which consists of a linearization of the model in the neighborhood of the current estimate of the state vector. This linearization can lead to complicated calculations for systems with high dimensionality, as the integration and propagation of the error covariance result in a significant computational demand (Gillijns et al., 2006). Linearization is done using first-order Taylor expansion, which implies a closure at the second-order moments. For highly nonlinear systems this can result in an improper estimation of the state vector or covariance matrices and can therefore lead to quick divergence and instability (Moradkhani et al., 2005; Nakamura et al., 2006).

In order to cope with nonlinearities and obtain a full representation of the posterior distribution, other statistical methods, such as particle filters, have been developed (Carpenter et al., 1999). The particle filter is a solution following a Darwinian-like process of survival of the fittest. It shares properties with an EnKF in the sense that the particles are the ensemble members. Particle filters do not need any assumption for the state variable distribution (e.g., Gaussian) and can deal with nonlinear observation models as well. The updates are applied on particle weights rather than the state variable, which results in fewer numerical instabilities for process-based models (van Leeuwen, 2009; Liu et al., 2012; Moradkhani et al., 2005). A major drawback is the particle depletion, which requires complex resampling algorithms. Moreover, it is less computationally efficient than the EnKF due to the need for a high number of particles (more particles than EnKF ensembles are often needed, of the order of tens of thousands). Despite its advantages, the use of the particle filter as an assimilation method in oceanography and limnology is limited due to its high computational cost. To address such issues, solutions are undergoing development (Šukys and Kattwinkel, 2018). For its flexibility and affordable computational cost, we further focus on the EnKF.

3.1 Ensemble Kalman filter (EnKF)

The EnKF is an attractive alternative for nonlinear dynamics and systems with high dimensionality. Reichle et al. (2002a) found that the EnKF is more robust than the EKF while being more flexible to obtain system covariances, a core element of the DA problem (Bertino et al., 2007). Indeed, whereas the careful estimation of covariances often required a lot of effort (De Lannoy et al., 2007b), in the EnKF they are derived dynamically from a small ensemble of model trajectories (and therefore take into account the physics of the model), which grasps the essential parts of the error structure (Reichle et al., 2002b). The EnKF only considers a sample of the state variable to represent the processes modeled. The covariance matrix becomes a sampled covariance matrix, and predictive probability density functions of the state vectors are approximated by Monte Carlo simulations (Nakamura et al., 2006). It nonlinearly propagates a finite ensemble of model trajectories instead of using a linearized equation for the error covariance, so no computation of derivatives is required. The EnKF still considers a linear correction procedure and assumes Gaussian distributions of the random variables. When this is not the case, the filter still produces a variance-minimizing solution, though it is not the optimal estimate (Bertino et al., 2007).

We develop below the fundamentals behind the algorithm. We first define the true model state (corresponding to the actual physical state of the lake) vector x of the system at time t as x_t (in our case temperature for the entire 3D model grid), ℳ the nonlinear lake system operator, η the process noise, and u the forcing vector (here meteorological forcing) for a time t. The state propagation equation reads

$$\begin{array}{}\text{(1)}& {\mathit{x}}_t={\mathcal{M}}_t\left({\mathit{x}}_{t-\mathrm{1}},{\mathit{u}}_{t-\mathrm{1}}\right)+{\mathit{\eta }}_{t-\mathrm{1}}.\end{array}$$

In this study, the noise is added in the forcing term u and subsequently dropped in the notation of Eq. (2). The state space vector, noted $\widehat{\mathit{x}}$, is an approximation (done by the hydrodynamic model Delft3D-FLOW) of the true state x. The forecast state (the input information for DA at time t) is defined by ${\widehat{\mathit{x}}}^{\mathrm{f}}$ and the analysis state obtained after DA as ${\widehat{\mathit{x}}}^{\mathrm{a}}$. The model propagation equation now reads

$$\begin{array}{}\text{(2)}& {\widehat{\mathit{x}}}_t^{\mathrm{f}}={\mathcal{M}}_t\left({\widehat{\mathit{x}}}_{t-\mathrm{1}}^{\mathrm{a}},{\mathit{u}}_{t-\mathrm{1}}\right).\end{array}$$

As we do not measure the true state of the system (x), the observation (y) equation is defined by the following, with H an operator relating the system state to the observation and ε is some measurement noise:

$$\begin{array}{}\text{(3)}& {\mathit{y}}_t={\mathbf{H}}_t\left({\mathit{x}}_t\right)+{\mathit{\epsilon }}_t,\end{array}$$

with the observation prediction given by

$$\begin{array}{}\text{(4)}& {\widehat{\mathit{y}}}_t={\mathbf{H}}_t\left({\widehat{\mathit{x}}}_t^{\mathrm{f}}\right).\end{array}$$

Note that in our case, we directly observe what we compute (i.e., surface temperature and profiles at computed grid points), and therefore in this study H is an identity matrix. The resulting data assimilation estimate of the state vector $\left({\widehat{\mathit{x}}}^{\mathrm{a}}\right)$, which will be used in the next cycle as restart condition, is given by

$$\begin{array}{}\text{(5)}& {\widehat{\mathit{x}}}_t^{\mathrm{a}}={\widehat{\mathit{x}}}_t^{\mathrm{f}}+K_t({\mathit{y}}_t-{\widehat{\mathit{y}}}_t).\end{array}$$

That last equation (Eq. 5) is a central concept of DA; it introduces the weighting factor K, also referred to as Kalman gain. The Kalman gain can be viewed as a balance of the model and observation uncertainties, together with the error correlation of all the elements of the state vector. It aims to minimize the error covariance of the state estimate during the analysis time Eq. (5). It is defined as

$$\begin{array}{}\text{(6)}& {\mathbf{K}}_t={\mathbf{P}}_t^{\mathrm{f}}{\mathbf{H}}_t^T{\left({\mathbf{H}}_t{\mathbf{P}}_t^{\mathrm{f}}{\mathbf{H}}_t^T+{\mathbf{R}}_t\right)}^{-\mathrm{1}},\end{array}$$

with R_t the measurement error covariance matrix (in this study we assume no cross-correlation between observation errors, and hence R_t is diagonal and determined from the uncertainty of the measurements; Sect. 2.4) and P^f the a priori state error covariance matrix. Error covariance is a key component of DA. The EnKF is able to compute a time-varying covariance error based on the dynamics of the system. This is a critical property when considering variables with short decorrelation spatiotemporal scales (Kuragano and Kamachi, 2000). In addition to the probability density function of the state (when in the presence of process noise), covariance estimation is achieved considering ensemble members. For an ensemble of forecasts ($j=\mathrm{1},\mathrm{\dots },N$), each subject to a disturbance (e.g., in model processes, forcing, or initial conditions), P is obtained from

$$\begin{array}{}\text{(7)}& {\mathbf{P}}_t^{\mathrm{f}}={\displaystyle \frac{\mathrm{1}}{N-\mathrm{1}}}{\sum }_{j=\mathrm{1}}^N({\mathit{x}}_{t,j}^{\mathrm{f}}-{\overline{\mathit{x}}}_t^{\mathrm{f}})({\mathit{x}}_{t,j}^{\mathrm{f}}-{\overline{\mathit{x}}}_t^{\mathrm{f}}{)}^T.\end{array}$$

From Eq. (7) we can conclude that the error-spreading pattern across the domain is indeed derived from the ensemble members in a systematic way. This is not the case for some variational methods such as 3D-VAR, whereby the statistics are considered isotropic with little variation over time. In the EnKF each ensemble member is then updated individually (based on Eq. 5). The state average over the ensemble provides the a posteriori state estimate. Additionally, in contrast to the extended (or traditional) Kalman filter, there is no need to propagate the state covariance nor to estimate the initial state covariance and model error covariance matrices. The EnKF only uses the first and second moments to construct the probability density functions; it cannot ensure higher-order statistics by opposition to the particle filter (Nakamura et al., 2006).

The EnKF is widely used for large systems with uncertain initial states, and variants are still being developed to leverage its limitations (Hoel et al., 2016). Several authors (Bertino et al., 2007; Evensen, 1994; Verlaan and Heemink, 2001) found better performance for highly nonlinear systems in comparison to the EKF. This approach can accommodate large datasets or missing observations, and it can incorporate correlated nonlinear and error measurement models. Moreover, the ensembles are easy to implement in parallel fashion. Models with high dimensionality are well suited for this type of assimilation, which requires a relatively low number of ensemble members to produce stable and accurate results (detailed in the Results section and Discussion section). We used this algorithm for the results presented in this study.

3.2 System setup

The aim of this section is to detail the various properties of the EnKF and DA setup, which is specific to this study.

3.2.1 Stochasticity and noise

The performance of a DA experiment strongly depends on the characterization of uncertainties (van Velzen and Verlaan, 2007). The hydrodynamics are modeled with deterministic equations. Their initial conditions, in the case of Lake Geneva, play only a limited role in basin-scale dynamics over long periods of time (months, years). Yet, boundary conditions, especially the air–water heat and momentum budgets, still contain large uncertainties that decrease the performance of any theoretically perfectly calibrated model. To overcome this issue, we added stochasticity to the system by including noise in the east (u direction) and north (v direction) components of the wind velocity. These variables, coming from MeteoSwiss COSMO-1 reanalysis products with DA, are known to be the most inaccurate and influential boundary forcing over lakes.

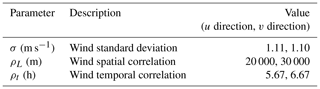
The addition of stochasticity to the deterministic model is done with OpenDA's noise model, which adds spatiotemporally correlated noise to the wind fields. This noise model, distributing the noise based on correlation scales derived from a distance-dependent function decaying to 0, requires three quantities (for both the u and v directions): (i) the wind standard deviation, (ii) the wind spatial correlation scale, and (iii) the temporal correlation scale. They are obtained from an analysis of the COSMO-E (ensemble) products over the entire year of 2017. COSMO-E probabilistic products are derived from 21-ensemble forecasts on a 2.2 km grid and contain information on the variability of the computed atmospheric variables. The wind standard deviation is hence obtained by taking the mean COSMO-E standard deviation of every pixel over the lake for the studied period. The spatiotemporal correlation scales are obtained by computing the cross-correlations of six – fictive – stations around the lake, as shown by Fig. 1. The cross-correlation of a station with itself provides the temporal correlation scale, while the cross-correlation among stations allows for the determination of the spatial correlation scale. Table 1 summarizes the aforementioned noise model parameters.

Table 1 Summary of the noise model parameters.

3.2.2 State variables

OpenDA has recently been updated to support three Delft3D-FLOW state variables (Baracchini et al., 2019a), namely water levels, temperatures, and flow velocities. In this study, only temperatures are updated by the EnKF.

3.2.3 Ensembles

The EnKF operates using a statistical sample of the state of the system. The ensemble size (N) is often determined heuristically and must be a balance between a good representation of the state space and acceptable computation time. The errors in the solution probability distribution function (PDF) will approach zero at the rate $N^{-\mathrm{1}/\mathrm{2}}$ (Evensen, 2003). A preliminary study showed that a satisfying compromise is obtained with 20 ensemble members. The choice for a small number of ensembles is further motivated by future use for operational purposes. More details and an ensemble size assessment are presented in the Results section.

3.2.4 Localization scheme

As mentioned above (Sect. 3.1), the covariance matrix links every domain point with the others. Covariances are derived from the ensemble members. A limitation of a small ensemble size is possible spurious correlations (Evensen, 2009), resulting in artifacts over long distances from the observation location. In such cases, when the model spatial extent is large, a localization scheme has to be applied (an observation usually only influences its near vicinity, and it has limited influence for greater spatial extensions; Stanev et al., 2011). Such a scheme has therefore been implemented in OpenDA, which collaterally also aims to reduce the computational cost of the analysis time. This localization allows users to define a cutoff distance based on a Gaspari–Cohn isotropic distance-based function (decaying to 0 at a defined cutoff distance) to limit the area of influence of an observation. This function ensures a smooth transition between a full and non-update for better model stability. Effectively, this removes long-range spurious correlations by scaling the size of the observation covariance matrix.

In this study, a cutoff distance of 15 km is defined. This distance is based on the spacing of the two in situ stations and the radius of their associated basin gyres (Petit Lac and Grand Lac; Fig. 1). This is further motivated by the fact that such a distance allows users to cover the entire interior of the basin by an update of in situ data. Due to the significant depth of the lake, dynamics at deeper locations are less variable, and hence their correlations at longer distances are easier to estimate. Regarding the LSWT, as it is partly the result of surface heat fluxes, its spatial structure is also expected to be correlated, to some extent, at relatively large spatial scales. Finally, as a result of the coarse vertical resolution of the in situ profiles, we did not define a different localization scheme in the vertical compared to the horizontal direction.

4 Results

In this section, we present both quantitative and qualitative results of the DA experiment. As mentioned in Sect. 2.4, the DA run consisted of the assimilation of 128 AVHRR LSWT datasets and 31 in situ profiles over the entire year of 2017. Mean absolute error (MAE), root mean square error (RMSE), and a Taylor diagram (Taylor, 2001) are used as benchmark indicators. Direct model comparisons with satellite images and in situ profiles are provided to visualize the benefits of the approach for both surface and deepwater dynamics. Implications of the DA for physical phenomena are presented.

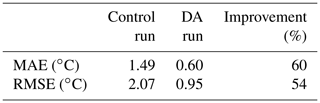
Table 2, providing MAEs and RMSEs before and after DA, indicates significant improvements over the baseline simulation. RMSE and MAE values are reduced by 54 % and 60 %, respectively. The discrepancy between the two indicate some occasional large data–model mismatch, which affects the RMSE more heavily. The Taylor diagram (Fig. 2), displays large improvements in centered root mean square difference (RMSD), correlation, and standard deviation.

Table 2 Summary of the data assimilation performance (MAE and RMSE).

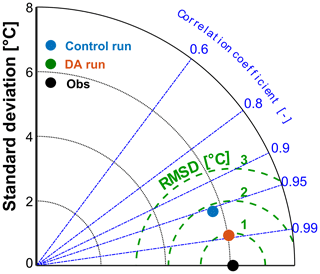
Figure 2 Taylor diagram of Lake Geneva temperature data assimilation. The dots correspond to the observations (black), the control run without DA (blue), and the DA run (red). The radial distance from the observations is the centered root mean square difference; the radial distance from the origin defines the standard deviation, and the azimuthal position is the correlation coefficient.

4.1 Surface assimilation and physical processes

The benefit of DA is shown with four examples in Fig. 3, comparing LSWT from AVHRR measurements with LSWT from the control run model and DA experiment. We first highlight (top panels) the fact that DA assimilation can perform correctly even in the case of missing observations over the lake surface. The state covariance matrix could update the model in areas where no data were available. Model accuracy is thereby improved at the basin scale rather than at observation locations. This is particularly relevant as large lakes are often partly cloudy. The second example demonstrates the potential of DA to correct the state variable – a cold bias in the present case – while maintaining the coherent structure of the complex spatial thermal gradient (Fig. 3, second row). The third example shows gyre-like flow structures. Such rotating structures are difficult to observe from AVHRR LSWT data (third row of Fig. 3), partly due to their limited spatial resolution and weak signature at the surface. However, a gyre created by a NNE wind on 12 August is better visible in the model results (clockwise in the western part of the main basin and counterclockwise in the center). In that case, the DA updated the LSWT while keeping the physical structure and flow spatial coherence of the control run. Finally, the lowest panels in Fig. 3 show how DA improves observations and the future quantification of transient upwelling. While the upwelling in the Petit Lac was partially already caught by the control run, the DA allowed for a much better adjustment of its intensity and extent. Another similar case is presented in Appendix B.

Figure 3 Surface temperature comparison of the AVHRR observations (left column), control run (central column), and DA run (right column) at selected analysis times (four rows) in 2017. The first row highlights the assimilation of sporadic data and the second row of complex surface patterns. The third row is an example for gyre phenomena and the fourth row of an upwelling event.

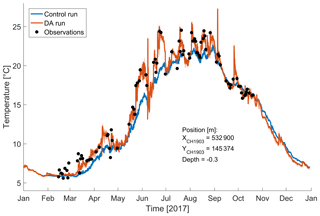
Figure 4 Time series of the LSWT in the center of the lake. The red line corresponds to the mean of the ensemble and the red shaded area to the ensemble spread, while the blue line marks the control run and the black dots the AVHRR observations.

The benefit from DA is also evident when looking at the temporal evolution of LSWT (Figs. 4 and 5). In Figs. 4 and 5, the AVHRR LSWT is again compared at two locations with the simulations with and without DA. The observed strong summer temporal variability with biweekly temperature variations exceeding 5 ^∘C is not well resolved in the control run (Fig. 4); however, it is much better reproduced by applying DA. The warming phase also benefits significantly from the assimilation. The control run surface temperature started to increase in the second part of March, while the warming occurred in early March in the observations and DA. Both models are in good agreement during the cooling phase after August. While few observations were available during this late period, not much improvement is obtained for the baseline, which was already accurate. Overall, every point of the DA run is close to or at least within the ∼1 ^∘C uncertainty of the AVHRR observations (see Sect. 2.4 for more information on uncertainty).

Similar conclusions arise from Fig. 5, which provides a close-up of time series of the summer period in the western basin (Petit Lac). Ensemble spread is smaller during the period of strongest stratification from late July to late August. Overall, the model uncertainty arising from perturbed wind fields reaches 2 ^∘C in the summer, when it is the highest and 1 ^∘C on average. Major upwellings in June and July are caught by both model runs, although the intensity is too weak in the control run. Again, data–model discrepancies and temperature variability are largest from late May to early August. Starting in August, the models with and without DA exhibit similar dynamics, both close to observations.

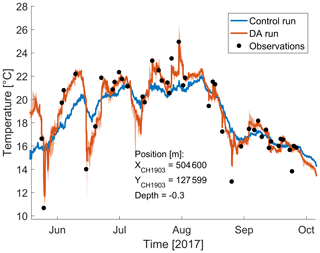
Figure 5 Zoomed time series of LSWT in the center of the western basin (Petit Lac). The red line corresponds to the mean of the ensemble, the red shaded area to the ensemble spread, the blue line to the control run, and the black dots to AVHRR observations.

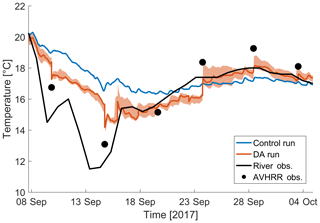
We further compared the upwelling of 15 September with river temperature data with a model surface grid point located 3 km away (Fig. 6). The upwelling has indeed been observed in the lake outflow, dropping from 21 to 12 ^∘C in 6 d. The figure shows that the control run underestimated the upwelling by 5 ^∘C, while the DA run underestimated it by ∼2.5 ^∘C. The AVHRR observation was 1.5 ^∘C warmer than the river temperature. Figure 6 also confirms that the model does not suffer from spurious behavior after an assimilation. Model shocks are not observed and numerical equilibrium is reached in a sub-daily period.

Figure 6 Close-up of the upwelling event in mid-September. River temperature from the lake outlet in Geneva is added as a comparison. The AVHRR data (black dots), control run (blue), and DA run (red) correspond to a surface pixel 3 km from the outflow.

4.2 Deepwater assimilation

We investigated how the vertical structure and subsurface dynamics are affected by the DA. Figure 7 provides a comparison of the DA performance over depth with in situ data instead of AVHRR measurements. Overall, for both stations significant improvements are obtained over the entire water column and throughout the year. Major improvements are observed at the thermocline depth, correctly represented in the DA experiment. Its strong vertical gradient significantly benefited from the assimilation of temperature profiles. The warm bias between 5 and 25 m of depth, resulting in an overestimation of the mixed layer depth in the control run, is effectively eliminated.

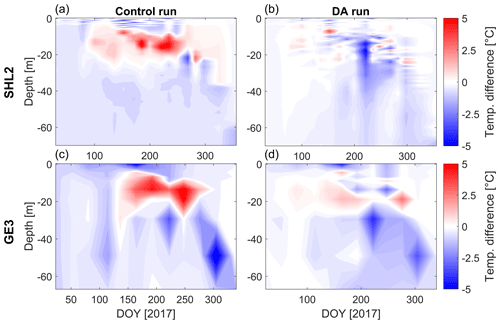
Figure 7 Evolution of the deepwater temperature without and with DA. (a, c) The differences of control runs minus in situ observations; (b, d) the differences of DA runs minus in situ observations. Panels (a–b) correspond to the center of the main basin (SHL2; Fig. 1), and panels (c–d) correspond to Petit Lac (GE3; Fig. 1).

4.3 Ensemble member size

Finally, we evaluated the EnKF ensemble size needed by a convergence analysis. A period of 1.5 months, from June to mid-July with a spin-up time of 2 weeks (without DA), is selected for assessment. This period of weak spring thermal stratification has been selected, as it is the time of the year with the most complex and broadest range of dynamics (Fig. 4).

The results indicate that for an increasing number of ensembles (N) the analysis error decreases. Figure 8 provides RMSEs and MAEs for different ensemble sizes, also differentiating between assimilated data sources. We conclude that major gains are achieved with 10 ensemble members. For in situ data only, 20 ensembles seem to be the sweet spot. Due to the much larger number of AVHRR observations (i.e., one image provides thousands of observations since it covers the entire spatial extent of the computational grid), the red (AVHRR) and black (all measurements) lines are confounded. Finally, assessment of the ensemble spread showed that few gains in second-order moments were found with larger ensemble sizes. Indeed, in the scope of this study, the additional benefits for N>20 are limited. At this stage, the 1 ^∘C uncertainty of the AVHRR LSWT data might become a limiting factor hindering further improvements.

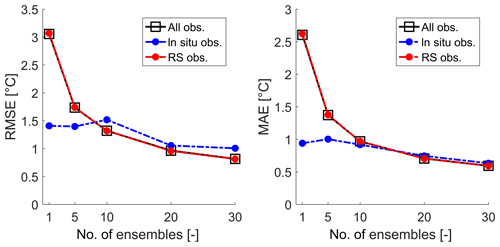
Figure 8 Data assimilation performance as a function of ensemble size. The dashed blue line corresponds to the error with respect to in situ observations only; the red line is the same with respect to LSWT only, and the black squares show the model error with respect to both observation sources.

With a vision towards DA for operational lake forecasting systems and the computational constraints associated with real-time hydrodynamics, we conclude that 20 members provide a satisfactory compromise for the system considered in this study.

5 Discussion

The DA framework has brought significant improvements to the hydrodynamics of Lake Geneva. It demonstrated its effectiveness to improve various model-forecasted mesoscale to large-scale thermal features. The combination of both in situ measurements and remote sensing observations allowed for constraining the 3D thermal structure of the model throughout the water column.

Surface time series (Fig. 4) indicated that spring–early summer observations play a key role in improving the model performance during the warming period (Kourzeneva, 2014). This allows for an adequate modeling of the lake warming, with significant implications expected for water quality models and the typical spring phytoplankton blooms. Later in the year, in late spring and summer, the AVHRR data revealed high-variability temperature dynamics (e.g., upwellings), which are not reproduced by the control run. It is the time when the largest ensemble spread is observed, which indicates that the summer LSWT is sensitive to changes in wind patterns. Additionally, ensemble spread stemming from spatiotemporally correlated noise applied to the wind fields indicates that the model is sensitive to changes in this forcing function. The effects on model outputs are correctly described, and the uncertainty arising from this perturbation ranged from 1 ^∘C on average, with peak values at 2 ^∘C.

A similar conclusion can be drawn for subsurface thermal dynamics. Figure 7 indicates that data–model mismatches in the mixed layer appeared as the lake started to warm and the thermocline formed. Compared to the control run, the DA run exhibited both a more accurate warming phase and vertical temperature gradient during the stratified period.

Overall, the performance of the EnKF has been notable in a broad range of scenarios. Even with complex observational patterns, filter updates were performed with different amplitudes at each spatial location (Fig. 3). Those spatially varying updates are often in agreement with the physical processes governing the hydrodynamics of the lake. Also, in the case of incomplete or sporadic data, the EnKF updates behaved well, and good combinations of data and system dynamics were found. Some authors (De Lannoy et al., 2007b) found that when the update is performed through the covariance propagation (in the case of missing observations), the a posteriori state might not be correct and counteract the updates in the surrounding locations. This behavior has not been observed in the presented hydrodynamics of Lake Geneva. This indicates that the covariance matrices were well estimated from the ensemble members and their physical dynamics. The non-static covariance matrix derived from the EnKF allows for longer-term studies, such as over the entire year, with complex changes in the thermal structure of the water body. Time-varying covariance error estimates for 3D models are complex tasks in DA. Analysis updates were not intense or frequent enough to cause model shocks or solver failure. This would have a minimal impact on the surface layers, since such corrections would not be persistent due to the variable nature of surface layers and sensitivity to atmospheric forcing. However, more issues would arise from model shocks in the deep water, which could trigger movements of large water volumes. Since in situ profiles have a much lower uncertainty than AVHRR observations (<0.1 ^∘C vs. 1 ^∘C; Sect. 2.4), intense state updates are more likely; however, they have not been observed in this study and no model solver failure arose from the EnKF updates. After significant updates, the model generally recovered over a sub-daily period. Increasing the observational frequency (here limited to one satellite observation per day) would increase the likelihood of encountering model shocks, as equilibrium adjustment may not be reached between updates. Higher computational costs also weigh into the data quality–quantity compromise, particularly when considering near-real-time systems. Detailed discussions regarding model error formulation are provided by Akella and Navon (2009) and Daescu and Navon (2013) for variational data assimilation.

5.1 Physical processes

Figure 3 shows that various physical processes, such as upwellings and gyres, are better resolved with the use of EnKF. Upwellings typically occur more prominently at the beginning or end of the season, when stratification is weaker. The better identification of such processes is of prime importance for various water quality aspects (e.g., heat extraction, wastewater discharge, water intakes; Gaudard et al., 2019). Yet the magnitude of such events has rarely been quantified due to difficulties with their large-scale identification. Through the combination of remote sensing observations and 3D hydrodynamic modeling, we open new possibilities for monitoring and predicting such phenomena. In this study we found that upwellings are better reproduced in both intensity and spatial extent. Comparing temperature measurements with a surface model grid point 3 km away from the outflow showed good agreements after DA. An underestimation of the upwelling of 2.5 ^∘C after DA is observed (compared to 5 ^∘C with the control run). Most of this remaining difference can be attributed to the satellite underestimating the event as well (by 1.5 ^∘C, with an uncertainty of 1 ^∘C) and the remoteness and depth (surface) of the pixel compared. For Lake Geneva, this is of particular interest when an upwelling occurs in the western basin (Petit Lac), dropping the outflow temperature for millions of downstream residents. In terms of gyres, those structures are repeatedly observed in Lake Geneva (Bouffard et al., 2018; Kiefer et al., 2015). Because of the Coriolis force, subsequent strong uplifts to down-lifts of the thermocline occur, which structure the lateral dispersion of primary productivity (Soomets et al., 2019).

5.2 Ensemble size

Among the various ensemble sizes assessed for this study (Fig. 8), we found that relatively small ensemble sizes (∼20) are enough to derive suitable time-varying covariances and error-spreading patterns. This is particularly important in the presence of variables with short decorrelation time and spatial scales. Studies indicated that relatively small ensembles fail to accurately estimate the small correlation patterns of remote observations (Houtekamer and Mitchell, 2001). The localization scheme implemented (Sect. 3.1), defining a cutoff radius around each observation, allows users to circumvent this limitation. Houtekamer and Mitchell (2001) found that for an increasing ensemble size, the optimal cutoff value increases as well. Larger ensemble sizes not only restrain the underestimation of ensemble spread and accuracy, but also allow for the use of more remote observations. For DA experiments with limited data, larger ensemble sizes may be a requirement to maximize observational coverage.

5.3 Limitations and perspectives

A main limitation of the EnKF is the Gaussian assumption, which in the case of large data–model mismatches could have led to artifacts and unrealistic a posteriori state values. This has not been observed in this analysis with the provided noise definition and observational stochastic setup. Furthermore, while we did not systematically study the physics after each analysis step, we think the method can still be used for the study of physical processes, provided the user assesses the intensity of those physical discontinuities. Out of the 152 assimilations, only 8 created some numerical instabilities in the model, though they were small enough to prevent solver failure. The existence of an upper limit to the amount of information assimilated was not investigated here, as the aim of this work is to provide an operational system with data assimilation in lakes.

Other difficulties arise in the presence of bias, whereby Kalman filtering performs suboptimal corrections (Dee and Da Silva, 1998), as observations and the model are assumed unbiased. Solutions for dealing with biases in EnKF may become necessary (De Lannoy et al., 2007a). In the present approach, however, occasionally occurring model biases have been effectively handled by the update. The DA model did not drift back to its biased or control run state. We believe that this is a result of the adequate initial parameterization of the model (Baracchini et al., 2019a). This further highlights the crucial importance of accurate model calibration and formulation before applying DA experiments. It is worth noting that the EnKF is able to also provide updates to parameters and forcing conditions, which in some cases may provide more persistent improvements (for example, when time-varying parameters are needed).

This DA experiment is time-consuming from a computational aspect. For example, it took nearly 1 month to compute the present setup on a dual Intel Xeon E5-2697v4 processor with 256 GB of memory, generating close to a terabyte of data. While the analysis time for in situ data has been reasonable (∼1 h), the immense number of observations generated by an AVHRR image (entire coverage of the surface layer of the computational grid) brought the analysis time up to 3 h for a single image. This is largely due to the current lack of multi-core support for the analysis step. A multi-core local analysis has been implemented in the scope of this study for multi-variable (e.g., temperature with water levels and/or flow velocities) assimilations, but gains can further be achieved from a local analysis based on the observation localization scheme.

6 Conclusions

For managerial and scientific purposes, new monitoring and forecasting tools covering wide ranges of spatiotemporal scales are of great interest. The coverage of such scale breadth of inland waters is achieved by combining three information sources, namely (i) in situ measurements, (ii) remote sensing observations, and (iii) model simulations. With data assimilation (DA), optimal combinations can be achieved and valorized.

For several decades, DA has been applied in oceanography and atmospheric sciences, yet its applications in limnology has remained limited. In this study, we developed a flexible framework and tools to blend real-time data into model simulations tailored to lakes. We applied this method to Lake Geneva using large datasets consisting of a three-dimensional hydrodynamic model, AVHRR lake surface water temperature, and in situ profiles over an entire year. Results demonstrated the effectiveness of DA as significant gains were obtained for both the surface and deepwater dynamics over a well-calibrated baseline. We showed that both data types (in situ and remote sensing) are important to constrain the entire spatial extent (horizontal and vertical) of the model. Results also indicate that AVHRR data are a valid remote sensing (RS) data source for DA into lake hydrodynamics, provided that observational error and uncertainties are well defined.

In that regard, the use of an ensemble Kalman filter (EnKF) allowed us to handle non-static covariance estimation, a key element of any DA problem. Additionally, it is able to account for the uncertainties of each data source. Those are essential elements influencing DA performance (Qi et al., 2014). We found that the ensemble size played an important role in reducing model errors. To keep their number limited, a localization scheme has been implemented, hence circumventing the estimation of improper small correlations at large distances (Houtekamer and Mitchell, 2001). In that regard, while the EnKF adds computational cost to the problem, it is capable of dynamically estimating the stochastic model based on the physical properties of the system. This is well encompassed by the paradox defined by Bertino et al. (2007), stating that simple DA methods become complex engineering tasks when the inconsistency between the stochastic and the physical model becomes relevant. Due to the flexibility of the tools developed and used, we that expect this procedure can be transferred to other lake and hydrodynamic models with relatively minor modifications (Baracchini et al., 2019b).

To conclude, this method has been designed with the vision of future near-real-time applications. Implications of DA in the operational context are significant to provide robust and timely short-term forecasts, accurate reanalysis products, and uncertainties for reliable water management. Over the last decades, the number of remote sensing products has grown rapidly; however, they have hardly been used in the operational context in an optimal way (de Rosnay et al., 2013). The timely retrieval and processing of RS products requires interdisciplinary efforts to ensure robustness and the proper error definition of the data, which hinders the development of such operational systems (van Velzen and Verlaan, 2007). In this study, we provided an example of how the entire chain, from the satellite to assimilation into the model, can be performed with limited field infrastructure. More concretely, we expect the findings of this study to be directly applicable to existing lake forecasting platforms, such as the one for Lake Geneva (http://meteolakes.ch, last access: 9 March 2020). Impacts of such an implementation are expected at a scientific, governmental, and public level.

Appendix A: AVHRR validation

Validation

AVHRR data were validated for Lake Geneva by comparing in situ data from the Buchillon station to the remote-sensing-derived skin temperature. Analysis of the data and comparison with both radiometric and in situ observations at Buchillon showed that quality flags are not a sufficient measure to reliably quantify the accuracy of the AVHRR images but to improve the quality, avoiding errors (e.g., cloud-contaminated pixels). Indeed, we observed strong fluctuations of up to ±3 ^∘C between skin and bulk temperature, especially during daytime when a micro-stratification establishes in the surface layer (Gentemann et al., 2003). Skin and bulk temperature becomes similar under windy or convective conditions. Skin-to-bulk corrections were developed in oceanography as a function of the wind intensity (Minnett et al., 2011). Yet, lakes are a much more calm environment and parameterization should also take into account convective processes (Bouffard and Wüest, 2019). Such parameterization is unfortunately lacking for Lake Geneva and we initially selected nighttime to early morning images in which surface convective cooling reduces the skin-to-bulk difference. However, comparison with field data showed that this is still not reliable enough. The discrepancy is indeed strongly linked to day–night cycles, but those are also season-dependent. Therefore, no specific satellite overpass can be selected for the entire computational time (1 year). To determine that images portray an accurate representation of the lake bulk LSWT, the thermistor at 1 m of depth (recording at 1 h intervals) has been used for a direct comparison with the spaceborne AVHRR data. Considering that the Buchillon station is close (80 m) to the shore, its position has been shifted 2 km south to avoid land boundary contamination. Finally, the average of a 3×3 pixel window of the satellite image centered on the south-shifted Buchillon station coordinates is used as a comparison point with the field data. Only images with an absolute deviation with respect to the bulk water lower than 1 ^∘C are retained for further assimilation. The 1 ^∘C threshold will also define the AVHRR observational uncertainty needed for the EnKF. Outlier pixel values colder than 4 ^∘C and warmer than 28 ^∘C are removed. Finally, to avoid assimilating observations at a frequency that is too high (or too close in time), which can result in physical discontinuities and the destruction of model processes (model not reaching equilibrium between assimilations), the maximum frequency of satellite images is limited to one per 24 h. The screened images are then mapped to the computational grid.

This procedure aims to bypass the skin-to-bulk temperature effect, while ensuring the best data quality for assimilation. This procedure assumes horizontal uniformity over the lake area (i.e., atmospheric effects are assumed to be the same over the entire domain) and may be sensitive to local cloud patches.

Appendix B: Additional results

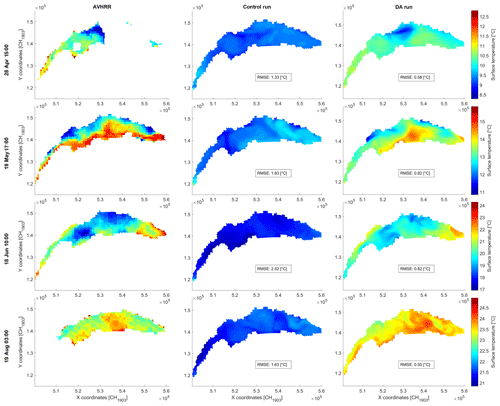
Figure B1 Surface temperature comparison of the AVHRR observations (left column), control run (central column), and DA run (right column) at selected analysis times (four rows) in 2017. The first row highlights the assimilation of sporadic data and the second row of complex surface patterns. The third row is an example of upwelling phenomena and the fourth row of gyre-like structures.