the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A high-resolution biogeochemical model (ROMS 3.4 + bio_Fennel) of the East Australian Current system
Carlos Rocha
Christopher A. Edwards
Moninya Roughan
Paulina Cetina-Heredia
Colette Kerry
Understanding phytoplankton dynamics is critical across a range of topics, spanning from fishery management to climate change mitigation. It is particularly interesting in the East Australian Current (EAC) system, as the region's eddy field strongly conditions nutrient availability and therefore phytoplankton growth. Numerical models provide unparalleled insight into these biogeochemical dynamics. Yet, to date, modelling efforts off southeastern Australia have either targeted case studies (small spatial and temporal scales) or encompassed the whole EAC system but focused on climate change effects at the mesoscale (with a spatial resolution of ). Here we couple a model of the pelagic nitrogen cycle (bio_Fennel) to a 10-year high-resolution (2.5–5 km horizontal) three-dimensional ocean model (ROMS) to resolve both regional and finer-scale biogeochemical processes occurring in the EAC system. We use several statistical metrics to compare the simulated surface chlorophyll to an ocean colour dataset (Copernicus-GlobColour) for the 2003–2011 period and show that the model can reproduce the observed phytoplankton surface patterns with a domain-wide RMSE of approximately 0.2 mg Chl a m−3 and a correlation coefficient of 0.76. This coupled configuration will provide a much-needed framework to examine phytoplankton variability in the EAC system providing insight into important ecosystem dynamics such as regional nutrient supply mechanisms and biogeochemical cycling occurring in EAC eddies.
- Article
(5572 KB) - Full-text XML
- BibTeX
- EndNote
The basic framework for most marine biogeochemical (BGC) models has been in use for the last few decades (e.g. Fasham et al., 1990). These models are highly empirical by nature and attempt to describe non-linear processes such as photosynthesis by phytoplankton, zooplankton grazing, or detrital remineralization through idealized formulations that critically depend on poorly constrained parameters (Doney et al., 2001). Even the most observable parameters, such as phytoplankton growth rates, include substantial uncertainty: laboratory measurements produce considerable scatter around idealized representations, field observations that loosely constrain model parameters are sparse, and analytical or instrumental errors exist. The implementation of observed parameters into models can also introduce error; for instance, the extrapolation of in situ bottle samples to a model grid cell having dimensions of kilometres poses a scalability challenge, and often measurements and models focus on related but different types of information (e.g. measuring pigments but modelling biomass; Matear and Jones, 2011; Jones et al., 2016). In addition, parameter selection is further complicated by temporal and/or spatial variability in parameter values due to natural variability in phytoplankton species or unrepresented ambient conditions. Identification of the best parameters to use in the model usually requires a lengthy process of fine-tuning often carried out manually and occasionally in an automated fashion (e.g. Mattern et al., 2016).
Uncertainty intrinsic to BGC models does not derive from parameter estimation alone but also extends to the choice of equations used to describe the targeted ecosystem (Franks, 2009). These models generally aggregate plankton populations into broadly defined trophic compartments and track the flow of a chemical element, such as nitrogen or carbon, among these compartments. Variations in this model structure, i.e. model complexity, include the use of additional limiting nutrients (such as silicate, phosphate, and iron), the division of the planktonic groups into multiple functional types or size classes, and inclusion of additional state variables such as bacteria or detritus. Model complexity is usually decided based on the targeted ecosystem and/or ecosystem function and has been one of the core topics in BGC modelling; discussed in Anderson (2005) and thoroughly explored in Friedrichs et al. (2007) for example. The selection of a particular model complexity and set of parameters is usually made by evaluating how well they are able to reproduce the available observations of state variables; due to its continuous acquisition and spatial coverage, remotely sensed chlorophyll is the most abundant BGC dataset for marine ecosystem model evaluation. However, the use of this dataset is not without uncertainty of its own. Remotely sensed chlorophyll is not always directly comparable to the simulated chlorophyll fields, as shown in Baird et al. (2016) and confirmed in Jones et al. (2016).
Despite their associated uncertainty, BGC models have proven to be exceptional tools. They are currently applied in research or in support of decision-making. BGC models vary widely in complexity from simple one-dimensional box models to global physical–biogeochemical coupled simulations (Doney et al., 2001). Phytoplankton is the first link in the marine food chain and plays an integral role in marine biogeochemical cycling. Therefore, coupled model configurations that attempt to realistically resolve ocean features and their impact on phytoplankton provide invaluable insight for a diverse range of topics including fisheries (Blanchard et al., 2012), water quality and ecosystem health management (Rombouts et al., 2013), carbon sequestration (Blain et al., 2007), and climate change (Matear et al., 2013). They provide a mechanistic understanding of the targeted ecosystem and allow us to quantify when, where, and how changes in phytoplankton distribution and biomass occur.
The East Australian Current (EAC) is the western boundary current of the South Pacific subtropical gyre. It is formed in the south Coral Sea (15–24∘ S – Ridgway and Dunn, 2003) and dominates the large-scale flow along southeastern Australia to the Tasman Sea (24–40∘ S, Fig. 1a). The EAC advects warm oligotrophic waters poleward, displacing cooler and generally more productive waters, generates mesoscale eddies (Everett et al., 2012), and induces coastal upwelling (Roughan and Middleton, 2004). The EAC typically separates from the coast between 30.7 and 32.4∘ S (Cetina-Heredia et al., 2014) meandering eastward and leaving a dynamic southward-moving eddy field. In the vicinity and to the north of the separation zone, EAC dynamics strongly condition the phytoplankton distribution; while downstream of the separation zone, seasonal effects are more significant drivers of chlorophyll patterns than upwelling or EAC-derived eddies (Everett et al., 2014). The region's ecosystem is generally nitrogen limited (Hassler et al., 2011) and seasonal increases in nitrate supply during austral winter to spring induce phytoplankton blooms that cover a large area, with particularly large amplitudes on the southern part of the region and around Tasmania (41.6∘ S, 146.3∘ E). These blooms are caused by processes that change with latitude, including (a) the contraction of the subtropical gyre over autumn and winter, with the oligotrophic EAC waters replaced by nutrient-rich subantarctic waters, and (b) nutrient replenishment to the euphotic zone caused by the winter deepening of the mixed layer (Condie and Dunn, 2006).
Outside the annual winter-spring bloom period, phytoplankton variability is linked to mesoscale features (Mongin et al., 2011). Pockets of high phytoplankton concentrations south of the EAC separation zone are consistently observed in remote sensing products and bio-physical models of the region (Baird et al., 2006b; Macdonald et al., 2009). These pockets are associated with persistently elevated concentrations of nitrate in the upper 100 m (> 4 µm, CARS – CSIRO Atlas of Regional Seas climatology; Ridgway and Dunn, 2003) caused by separation and upwelling events, which have been shown to deliver 10 times more nutrients to the shelf than river or sewage discharges (Pritchard et al., 2003).
The region's mesoscale eddies are also of special interest. Both cyclonic and anticyclonic eddies are found in large numbers – with an average of 17 eddies on any given day – and affect surface chlorophyll concentrations (Everett et al., 2012). Their contrasting (cyclonic or anticyclonic) dynamical regimes create different biogeochemical environments: cyclonic eddies present low sea-level anomalies, doming isopycnals, and a shoaling nutricline, while anticyclonic eddies are associated with high sea-level anomalies, isopycnal depression, and a deepening nutricline (McGillicuddy, 1998). Cyclonic eddies are usually associated with elevated chlorophyll, while anticyclones present chlorophyll suppression (Everett et al., 2012; Gaube et al., 2014). Eddies close to the shelf may entrain biomass-rich shelf waters which are then transported offshore (Tranter et al., 1986; Everett et al., 2015; Macdonald et al., 2016).
While there have been several efforts to model phytoplankton variability and their mechanisms off southeastern Australia, these have been limited to climate change scenarios at the mesoscale (with a spatial resolution of – Matear et al., 2013) or process studies (e.g. Baird et al., 2006a, b; Macdonald et al., 2009; Laiolo et al., 2016) that did not attempt to analyse the dynamics at a regional scale. Here we have coupled an N2PZD2 BGC model (explained in Sect. 2.2; Fennel et al., 2006) to a three-dimensional regional oceanic circulation model for the EAC system (Kerry et al., 2016) to investigate the BGC dynamics of the region and, for the first time, create a mechanistic understanding of the system dynamics as a whole. The validation effort, presented here, focuses on objective model performance assessments through comparison of surface chlorophyll model output with an extensive satellite dataset (Copernicus-GlobColour 4 km 8-daily product). We also compare the simulated spatial variability in subsurface nutrient concentration (nitrate) to a climatological dataset (CARS – CSIRO Atlas of Regional Seas climatology).
2.1 Physical ocean model
We use the Regional Ocean Modeling System (ROMS, version 3.4) to simulate the circulation of the EAC system for the 2002–2011 period. ROMS is a free-surface, hydrostatic, primitive equation ocean model solved on a curvilinear grid with a terrain-following vertical coordinate system (Shchepetkin and McWilliams, 2005); it has been successfully used in many regional BGC studies (e.g. California Current System – Powell et al., 2006; Fiechter et al., 2018; North Pacific – Kishi et al., 2007; Middle Atlantic Bight – Fennel et al., 2006). We use the 10-year free-running ROMS simulation configured for the EAC region developed by Kerry et al. (2016). While the pertinent details are summarized here, the reader is referred to Kerry et al. (2016) for a thorough description and validation of the EAC hydrodynamic model.
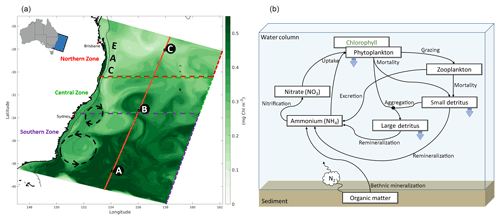
Figure 1(a) Simulated surface chlorophyll (8-day average) from mid-October 2008 illustrates model domain. State capital cities are labelled, and the 200 m isobath is highlighted by a thin black line. The EAC, a cyclonic eddy (clockwise rotation), and an anticyclonic eddy (anti-clockwise rotation) are identified from their signature on the chlorophyll field. The Northern Zone extends from the northern model boundary to 30.5∘ S, the Central Zone from 30.5 to 33.5∘ S, and the Southern Zone from 33.5∘ S to the southern boundary. Illustration of the latitudinal nitrates transect (orange line; see Fig. 6) and profiles (black squares; letters A, B, and C correspond to Fig. 7a, b, and c, respectively). (b) Schematic of the biogeochemical model (adapted from Fennel et al., 2006).
The model domain (Fig. 1a) extends from 25.25 to 41.55∘ S and nearly 1000 km offshore. The northern boundary is chosen at a latitude where the EAC is clearly defined and upstream of the region of elevated eddy variability (Cetina-Heredia et al., 2014). The model has a 5 km () horizontal resolution in the alongshore direction and gradually varies from 2.5 km () resolution over the continental shelf and slope to 6 km () in the open ocean. The model grid is rotated 20∘ clockwise, so that it is oriented predominantly alongshore in the y dimension and cross-shore in the x dimension. We use the vertical stretching scheme of Souza et al. (2014) for the vertical distribution of 30 terrain-following sigma layers which have higher resolution in the upper 500 m to resolve the wind-driven mesoscale circulation and near the bottom for improved resolution of the bottom boundary layer. The bathymetry was obtained from the 50 m multibeam dataset for Australia from Geoscience Australia (Whiteway, 2009), and we use the Mellor and Yamada (1982) level-2.5 second-moment turbulence closure scheme (MY2.5) to parameterize vertical turbulent mixing of momentum and tracers.
The model obtains initial conditions and daily boundary forcing from the Bluelink ReANalysis version 3p5 (BRAN3; Oke et al., 2013). BRAN is a multi-year integration of the Ocean Forecasting Australian Model (OFAM) and the Bluelink Ocean Data Assimilation System (BODAS; Oke et al., 2008). At the open lateral boundaries, the Chapman condition (Chapman, 1985) is applied to the free surface and the Flather condition (Flather, 1976) is applied to the barotropic velocity to ensure that the barotropic energy is effectively transmitted out of the domain. Atmospheric forcing fields from the National Centers for Environmental Prediction (NCEP) reanalysis atmospheric model (Kistler et al., 2001) are applied every 6 h, by computing the surface wind stress and surface net heat and freshwater fluxes using the bulk flux parameterization of Fairall et al. (1996). We run the model with realistic forcing from 2002 to the end of 2011, but allow for a year of model spin-up using the 2003–2011 period (hereafter referred to as the study period) for the analyses.
2.2 Biogeochemical model
We use the BGC model of Fennel et al. (2006), which was initially developed to assess nitrogen cycling in the Middle Atlantic Bight (Fig. 1b; see also Fig. 1 of Fennel et al., 2006). The model simulates two groups of nutrients (nitrate and ammonium), one group of producers (phytoplankton), one group of consumers (zooplankton), and two groups of differently sized detritus in what is usually termed an N2PZD2 model. The model is based on the Fasham et al. (1990) parameterizations with the important addition of phytoplankton chlorophyll (mg Chl m−3) as an estimate of the chlorophyll stored in phytoplankton, considering the effects of acclimation in the carbon to chlorophyll ratio (Geider et al., 1997).
In the Fennel et al. (2006) model, nitrogen available in inorganic nutrients is incorporated into phytoplankton biomass through phytoplankton growth; it is then moved into zooplankton biomass via grazing or into the small and large detrital pools through mortality. Zooplankton mortality also contributes to the detrital pool. Zooplankton losses due to inefficient grazing and detritus are transferred via a decay rate into the ammonium group, which is transformed into nitrate through nitrification processes. Large and small detritus, as well as phytoplankton, have an associated vertical sinking rate.
The model is initialized with seeding populations of 0.01 mmol N m−3 for all state variables except nitrate (NO3), which is derived from the CSIRO Atlas of Regional Seas climatology (CARS, described in Sect. 2.3.2). Interpolated seasonal values of the CARS nitrate climatology are applied daily as boundary forcing and the model is also nudged to CARS nitrate values over the first 10 grid points (approximately 50 km) from the northern, eastern, and southern boundaries. This nudging avoids spurious phytoplankton growth caused by upwelling at the boundaries, identified in previous model runs by a thin lateral zone of high chlorophyll standing stock near the boundaries. The nudging time decreases linearly from 5 to 30 days, from the outermost grid cell of the domain to the interior.
The main parameters used in this configuration are presented in Table 1. The values are all within the common ranges defined in the literature and are comparable to other model configurations in the region (Macdonald, 2013; Matear et al., 2013). Most values are identical to those used by Fennel et al. (2006), with the exceptions of the initial slope of the photosynthesis–irradiance (P–I) curve and half-saturation constants for the uptake of nitrate and ammonium (values in bold in Table 1). These have been modified by fine-tuning the model to best fit the offshore chlorophyll concentrations available through remote sensing (described in Sect. 2.3.1).
Table 1Main biogeochemical model parameters and their range in the literature (Fennel et al., 2006). The values that differ from Fennel et al. (2006) are presented in bold and the original value is presented in brackets.
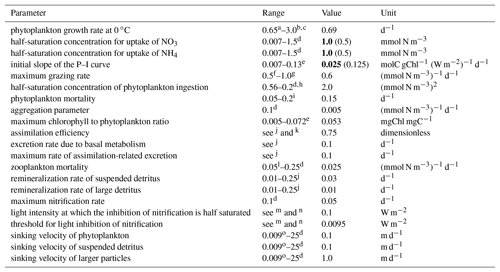
a Taylor (1988). b Andersen et al. (1987). c Note that owing to the temperature dependence for a temperature range from 0 to 20 ∘C the maximum growth rate in our model varies from 0.69 to 2.49 d−1. d Lima and Doney (2004). e Geider et al. (1997). f Wroblewski (1989). g Fasham (1995). h Note that the values were squared to be consistent with the notation of our model. i Taylor et al. (1991). jLeonard et al. (1999). kOschlies and Garcon (1999). lFennel et al. (2001). m Olson (1981). n Note that Olson differentiates between the oxidation of ammonium to nitrite and between nitrite to nitrate. o Moskilde (1996).
Shelf phytoplankton species and community structure are expected to be different from the phytoplankton community found offshore (Armbrecht et al., 2013). For this study, we chose to apply an established, relatively simple, biogeochemical model with only one phytoplankton functional type. In part, this decision reflected the overall emphasis of the physical model on the EAC and vast offshore region; the model has limited ability to resolve critical physical dynamics on the shelf due to model and forcing resolution and omitted freshwater inflow. Our overall focus is on the larger-scale BGC dynamics, their seasonal variability, and local impacts of offshore mesoscale processes. Future modelling efforts will address shelf processes and more complex biogeochemical interactions.
2.3 Observational datasets
2.3.1 Remotely sensed surface chlorophyll
Remotely sensed surface chlorophyll estimates were obtained from the Copernicus Marine Environment Monitoring Service (CMEMS) GlobColour product. This product has a 4 km spatial resolution and is generated by fitting a bio-optical model to the merged set of observed normalized water-leaving radiances from the SeaWiFS, MERIS, MODIS-A, and VIIRS-N sensors (Maritorena and Siegel, 2005). We use 8-daily composite data in order to minimize the data gaps without substantially compromising the time resolution. These data are re-gridded to our model grid through linear interpolation and gap-filled using the DINEOF package (http://modb.oce.ulg.ac.be/mediawiki/index.php/DINEOF, last access: 8 May 2018). DINEOF gap-fills by iteratively decomposing the data field via singular value decomposition (SVD) until a best solution is found. This solution is achieved by comparison with the subset of reference values (non-gaps) and by progressively including more empirical orthogonal functions (EOFs) in the reconstruction of missing values until the minimization of error converges (Alvera-Azcarate et al., 2010).
2.3.2 Climatological nitrate observations
We used the CSIRO Atlas of Regional Seas climatology (CARS; Ridgway and Dunn, 2003) as our source for three-dimensional nitrate fields for initial conditions, boundary forcing, and to assess the model's ability to reproduce the vertical nitrate distribution in the model domain. CARS is a gridded atlas of mean and seasonal ocean water properties obtained from a quality-controlled archive of all available historical subsurface measurements of ocean properties, which covers the full global ocean on a 0.5∘ grid. The nitrate fields, created in June 2011, include the World Ocean Circulation Experiment (WOCE) and World Ocean Database 2009 (WOD09) datasets.
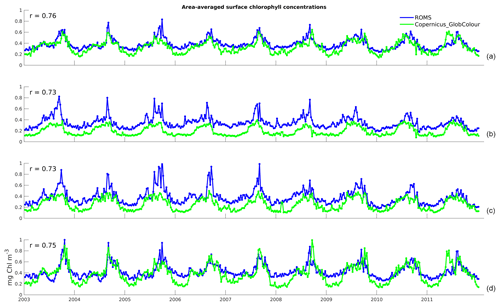
Figure 2Time series of area-averaged surface chlorophyll concentrations for 8-daily data from the model (blue) and satellite observations (green): (a) Full domain; (b) Northern Zone; (c) Central Zone; and (d) Southern Zone. The correlation coefficients of the two time series, r, are shown on the top-left corner of each panel.
2.4 Model evaluation metrics
We use six quantitative metrics to assess model skill (adapted from Stow et al., 2009), where n is the number of satellite chlorophyll observations, Oi is the ith of n observations, Pi is the ith of n model chlorophyll predictions, and and are the satellite observation and model prediction averages, respectively. We calculate these for each surface grid cell of the model in order to generate spatial maps of model skill.
RMSE – the root-mean-squared error:
AE – the average error (bias):
AAE – the average absolute error:
The root-mean-squared error (RMSE), average error (AE), and average absolute error (AAE) measure the size of the discrepancies between model predictions and the observations. So, the closer their value is to zero, the better the match and hence the model accuracy. The AAE is presented to mitigate the fact that values of AE near zero may be created by positive and negative discrepancies cancelling each other.
BAMEF – the bias-adjusted modelling efficiency:
The BAMEF quantifies how well a model simulates the observation compared to the average of the observations (Nash and Sutcliffe, 1970; Loague and Green, 1991), considering the overall bias for each point. Values less than 0 indicate that the observation average would be a better predictor than the model results, 0 indicates that the model predicts individual observations no better than the average of the observations, and a value near 1 indicates a close match between observations and model.
RI – the reliability index:
Pr – the Pearson correlation coefficient:
The RI measures the average factor by which model predictions differ from observations (Leggett and Williams, 1981). Ideally, the RI should be close to 1. An RI of 2.0, for example, indicates that a model predicts the observations within a multiplicative factor of 2. Lastly, the Pearson correlation coefficient (Pr) is a measure of the strength of the linear association between model and observations. It varies between −1 and 1, with negative values indicating that observations and model vary inversely, a value of 0 indicates the model and observation variability is not related, and positive values showing that the model varies with the observations (Stow et al., 2008).
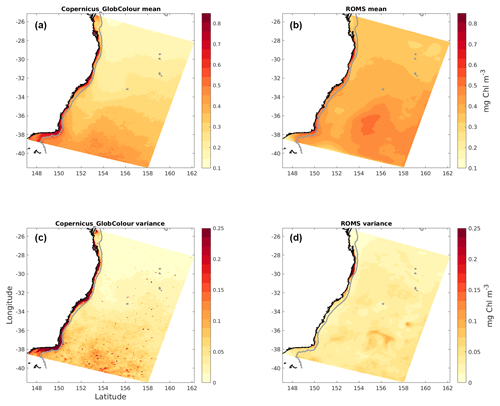
Figure 3Surface chlorophyll mean (a, b) and variance (c, d) for the full study period. Satellite observations (a, c) and model data (b, d).
To assess how well the model is able to represent the main chlorophyll distribution patterns, we determined the dominant orthogonal spatial and temporal signals in the model output and compared them with those of the satellite estimates through an EOF analysis (Bjornsson and Venegas, 1997). We used detrended 8-daily data over the full study period and excluded the points between the coast and shelf break (identified as the 200 m isobath). This exclusion was created because a small number of outliers on the narrow shelf were dominating the first EOF modes in the satellite estimates. Our model is not expected to reproduce these shelf estimates (as discussed in Sect. 2.2), some of which could be spurious data (Sect. 2.3.1).
Here we characterize the model's ability to reproduce the observed surface chlorophyll concentrations for the study period. We focus on temporal and spatial variability, specifically consecutive seasonal cycles and the typical latitudinal gradient. An objective evaluation of model performance is achieved by comparison with satellite-derived surface chlorophyll data using the statistical metrics described in the previous section, and we identify the main spatial and temporal patterns of chlorophyll variability off-shelf. Finally, the vertical distribution of nitrate is validated against CARS climatological values along a latitudinal transect through the model domain and at three different locations.
3.1 Variability of surface chlorophyll concentrations
The time series in Fig. 2a illustrates the domain-averaged surface chlorophyll concentrations of both model (blue) and satellite estimates (green). In addition, we investigate the results for three latitudinal zones based on chlorophyll regimes described by Everett et al. (2014) and identified in Fig. 1a: Northern Zone (NZ) – upstream of the EAC separation zone, from the northern boundary to 30.5∘ S; Central Zone (CZ) – EAC separation zone, 30.5 to 33.5∘ S; and Southern Zone (SZ) – downstream of the separation, 33.5∘ S to the southern boundary. The area-averaged time series for each zone are presented in Fig. 2b, c, and d, respectively. All the spatially averaged chlorophyll concentrations reveal a distinct annual cycle and low interannual variability (Fig. 2). Seasonal variations are largest in SZ, and concentrations are highest in all three zones during spring (spring bloom). The spring bloom signature is emphasized in our area-averaged time series due to the broad spatial coverage of this event.
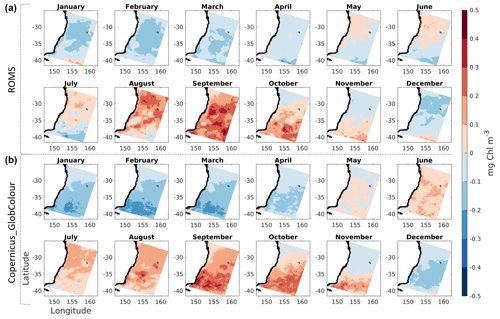
Figure 4Monthly anomalies of chlorophyll concentration from model (a) and from satellite observations (b).
All three zones have a minimum concentration of 0.1 mg Chl m−3 occurring around the end of the austral summer. Both maximum and minimum chlorophyll values are within the bounds of observed concentrations in this region (e.g. Everett et al., 2014; Matear et al., 2013). The model is able to competently reproduce the timing of the main chlorophyll fluctuations, as denoted by the high correlation coefficients between simulated and satellite-derived chlorophyll time series (r of 0.76 for the domain-wide average, 0.73 for NZ and CZ, and 0.75 for SZ). However, the model overestimates chlorophyll by about 0.2 mg Chl m−3 in both NZ and CZ (discussed in Sect. 3.2).
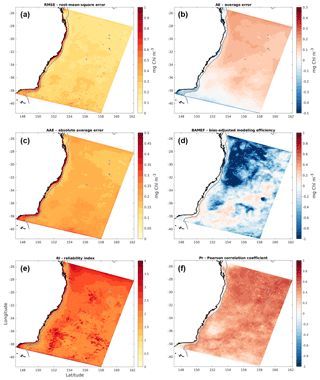
Figure 5Maps of (a) root-mean-square error; (b) average error; (c) absolute average error; (d) bias-adjusted modelling efficiency; (e) reliability index; and (f) Pearson correlation coefficient generated by comparison of simulated 8-daily surface chlorophyll concentrations with 8-daily satellite observations.
Latitudinal gradients in chlorophyll concentration are evident in the temporal mean (Fig. 3). Of special interest is the signature created by the nutrient-poorer EAC waters, which extends from the edge of the continental shelf to about 2∘ of longitude offshore and is characterized by lower-than-average chlorophyll concentrations. Generally, larger mean values and variances are found on the shelf in observations and to a lesser extent in the model. Overall, the patterns shown by model and observations are similar, with the model slightly overestimating surface chlorophyll offshore and underestimating concentrations near the coast.
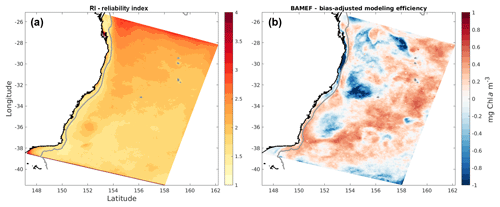
Figure 6Maps of (a) reliability index and (b) bias-adjusted modelling efficiency, generated by comparison of simulated monthly surface chlorophyll concentrations with monthly satellite observations.
Monthly observed chlorophyll anomalies reveal a prevalent seasonal cycle which is well represented in the model (Fig. 4). Over the 10-year period, the months of August and September reveal a slight overestimation of the onset of the spring bloom, as well as a slight northward shift of its pattern when compared to the observations. Nutrient-poor EAC water impacts phytoplankton growth, and associated chlorophyll fields, as visible by negative anomaly values along the northern and central portions of the coast, relative to offshore values at those longitudes, especially throughout the months of October and November. Finally, we note the signature of warm-core eddies, smaller negative anomalies downstream of the EAC separation latitude (near 35∘ S), present in both observed and simulated chlorophyll fields (particularly visible in July and August).
3.2 Skill metrics
To further assess model skill, we solve Eqs. (1)–(6) at each model surface grid cell. The resulting spatial maps are shown in Fig. 5. On average, the model overestimates chlorophyll concentrations offshore, and more so in the north than in the south of the domain (RMSE and AE of ∼0.2 mg chl m−3; Fig. 5a and b). The AAE shows fairly constant errors of about 0.25 mg chl m−3 (Fig. 5c). The fact that the AE near the south is near zero and the AAE is non-zero implies that the error fluctuates about zero, sometimes positive and sometimes negative. This conclusion is supported by the SZ time series (Fig. 2d), which reveals that January and February model overestimation is compensated by short periods of larger-amplitude underestimation at times around the spring bloom.
The high AAE values on the shelf indicate that the model represents phytoplankton less well near the coast, generally underestimating chlorophyll concentrations here, except for the shelf region between 29 and 31∘ S (Fig. 5b). As discussed in Sect. 2.2, our model calibration focused on simulating the chlorophyll concentrations observed offshore; with only one phytoplankton group represented, the model structure itself limits the ability to simultaneously simulate shelf and offshore communities. Moreover, it is known that remote sensing products tend to underestimate open-ocean chlorophyll in the study region due to a weak relationship between the large-sized phytoplankton and remote sensing reflectance (Clementson et al., 1998; Laiolo et al., 2018) and overestimate concentrations near the coast due to the presence of suspended sediments and dissolved organic matter (Moore et al., 2007). Since our model generally underestimates chlorophyll concentrations on the shelf and overestimates them offshore, these remote sensing biases can partly explain the inconsistencies between simulated and observed chlorophyll.
The area usually occupied by EAC waters is characterized by low chlorophyll concentrations and low chlorophyll variability. The model tendency to overestimate chlorophyll concentrations offshore and its variability leads to a negative BAMEF in the EAC-dominated region (Fig. 5d). Moreover, this is the area where the largest average factor by which model chlorophyll differs from satellite observations is found, with an RI of 2.5 to 3 (Fig. 5e). Model data are well correlated with observations, as demonstrated by the correlation coefficient map (Fig. 5f), with higher correlations in the northern zone (∼0.75) and decreasing towards the south (to ∼0.6). The overall higher error variability and lower correlations found in the Southern Zone are likely to stem from the higher eddy activity in the area, in conjunction with generally higher background concentrations (Figs. 2 and 3).
The lower model skill within the EAC revealed by large negative BAMEF and positive RI values results from limited model accuracy capturing high-frequency temporal variability in this region. Inconsistencies at high frequencies likely derive from a combination of physical and biological processes. In a free run such as this, dynamical features like the EAC physical position, mesoscale eddies, and small-scale fronts are generally offset in space and/or time from those in nature. In addition, the modelled N2PZD2 system, with only one phytoplankton and one zooplankton compartments, is an oversimplification of reality. By not capturing the complexity of the natural biological community, it is unable to fully reproduce the observed variability.
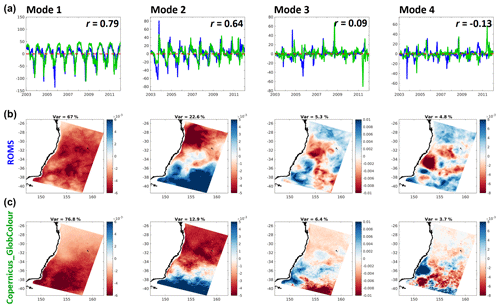
Figure 7Principal components (a: model in blue, satellite observations in green) and spatial structures (b: model; c: satellite observations) of the first four EOF modes of surface chlorophyll variance (left to right). The original units of chlorophyll concentration (mg Chla m−3) are obtained by multiplying the principal components to the corresponding spatial structure. The correlation coefficients of the two principal components, r, are shown on the top-right corner of each top-row panel.
Assessment using these particular metrics reveals the challenge: balancing precision (i.e. how well the model fits each satellite value) with overall accuracy. Even when the main trends and general patterns are well reproduced, small temporal or spatial lags between events registered by satellite and model can lead to large errors in precision. Matching variability on an 8-day timescale is a high bar for a non-data assimilative ocean model. Indeed, when calculated using monthly-averaged information, the BAMEF is considerably more positive overall and particularly in the EAC region, and the RI is much smaller over the entire domain; both metrics reveal considerable model skill on monthly-averaged timescales (Fig. 6). Our model tuning and evaluation emphasized the model's ability to generate average spatial and temporal patterns of chlorophyll, rather than on the absolute values of chlorophyll concentration.
3.3 Dominant spatial and temporal patterns
One way to explore the dominant spatial and temporal patterns of phytoplankton variability is through EOF analysis. The spatial EOF fields describe each component in terms of its dominant spatial structures (Fig. 7 – middle and bottom rows), whereas the principal component's time series give the corresponding temporal weightings for each time step (Fig. 7 – top row). Because this model has been developed to reproduce the general chlorophyll patterns offshore, we exclude shelf (< 200 m isobath) variability. The first four EOF modes explain up to 99.8 % and 99.7 % of the variance in satellite and model data, respectively.
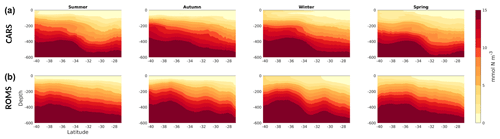
Figure 8Seasonal nitrate transects (mmol N m−3) along a transect through the middle of the domain, South to North (orange line in Fig. 1). (a) CARS climatological values; (b) model.
EOF analysis provides a concise, statistical reduction in the data. As such, there is no guarantee that the statistical modes obtained correspond to dynamical processes or particular features of interest. However, often the modes relate to understandable patterns and forcing timescales that help identify significant underlying dynamics or features, and comparisons between observed and modelled modes are often revealing. That is the case for this analysis, with both model and satellite data showing comparable patterns. Mode 1 captures the spring bloom, peaking to its annual maximum around the beginning of October of each year. The discrepancies on the spatial structures of this mode are better interpreted with the help of Fig. 4, specifically the anomalies for the months of August and September. As mentioned before, these show a northward displacement and slight overestimation of the onset of the spring bloom in the model, which leads to the same differences in the patterns captured by Mode 1. Mode 2 represents meridional variations across the domain and includes the effect of the seasonal propagation and recession of EAC nutrient-depleted waters in latitude. Oligotrophic EAC waters expansively replace nutrient-richer Tasman Sea waters during the austral summer and then recede during the autumn to winter period.
Mode 3 captures diverse mesoscale activity, such as increased productivity along the southern edge of the EAC after it separates from the coast – especially noticeable in the satellite-derived dataset around 35∘ S. Mode 4 contains most of the chlorophyll surface response to smaller scale eddy activity. Model and satellite estimates show a similar distribution in both positive and negative signatures, suggesting that the overall geographic effect of productivity enhancement by cyclonic structures and hindrance by anticyclones is well resolved in the model even though the specific time and location of eddies is not expected to be. As previously mentioned, eddies are more prolific in the southern area, hence the higher density of their signatures there. Of note is an apparent larger (smaller) area occupied by the negative (positive) signatures, which is on par with the difference in the average radius of anticyclones (larger) versus cyclones (smaller).
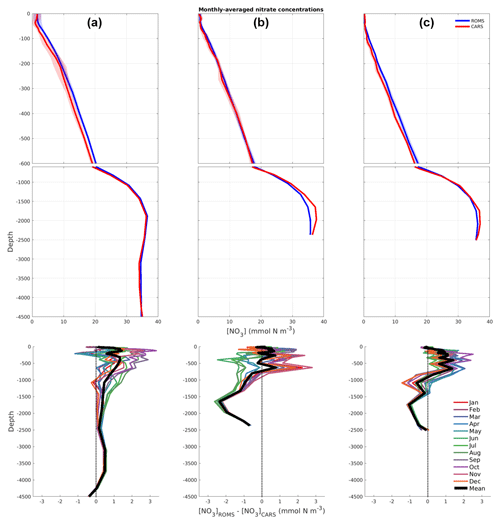
Figure 9Monthly nitrate profiles (mmol N m−3) at three different locations (A, B, and C in Fig. 1). In the top and middle rows, the solid line and the shaded area represent the mean value and the first standard deviation, respectively. These were calculated over the study period (for model data in blue) and climatology (for CARS in red). Bottom row illustrates the difference (ROMS-CARS) for each average month (coloured) and average difference (thick black line).
The principal components of model chlorophyll co-vary with those of satellite estimates with correlation coefficients of 0.79 for Mode 1 and 0.64 for Mode 2. As these modes contain around 90 % of the variance in both model and satellite estimates offshore, these correlations show that the model reproduces the timing of the dominant fluctuations in chlorophyll concentrations over the domain quite well, in agreement with the high correlation coefficients already found for the area-averaged chlorophyll concentration time series. We note that for reasons described above, the small correlation of principal components for the two mesoscale-dominated modes is not surprising for this non-data assimilative model.
3.4 Vertical distribution of nitrate
As a last step in the model validation effort, we investigate how the model represents the vertical distribution of nutrients by comparing the simulated nitrate with climatological values derived from in situ subsurface data (defined in Sect. 2.3.1). Specifically, we extract data along a seasonal transect in the south–north direction across the middle of the domain (Figs. 1a, 9). We have chosen a transect across latitude because of the observed latitudinal gradient in chlorophyll concentrations.
The model represents the distinctive latitudinal gradient in nitrate concentration, showing a poleward shoaling of the nitracline (Fig. 8). In addition, the model reproduces the seasonal cycle well, with the nitracline depth varying ∼50 m upwards (downwards) between winter (summer). The larger variability in the simulated nitrate fields reflects processes that are averaged over in the climatology. Therefore, this high-resolution model allows one to examine the impacts of mesoscale phenomena in the regional ecosystem, which would not be possible using climatological fields alone.
The vertical profiles in Fig. 9 (top) represent the monthly-averaged nitrate values over the full study period for the model, in blue, and from the climatological values of CARS, in red. The shaded areas represent the first standard deviation. The general agreement between the model and data at these locations is remarkably good (never exceeding 2.8 mmol N m−3), indicating that ecosystem processes in the model are not causing substantial drift from initial conditions over the 10-year model run. The southernmost profile (Fig. 9a) shows highest concentrations and greatest variability closer to the surface (larger shaded area), resulting from the combined effect of the established latitudinal gradient and the increased mesoscale activity in this area.
The bottom row of Fig. 9 illustrates the difference in monthly averages (coloured lines) and average difference (black line) between model and observations. This is obtained by subtracting CARS nitrate concentrations to the simulated nitrate fields at the same three locations (A, B, and C) as depicted above. It is worth noting that at these locations the model generally overestimates nitrate concentrations in the upper 800 m, except for the austral winter months (June, July, and August) of the central profile, when it underestimates concentrations by approximately −1.5 mmol N m−3. The central and southernmost profiles are characterized by an inversion from average overestimation to average underestimation at around 1000 m, with the central profile showing the highest average difference of −2.2 mmol N m−3 at 1600 m. The northernmost profile presents the highest overestimation of the upper 250 m, due to a difference of approximately +2.5 mmol N m−3 during the spring months of September, October, and November. This is of particular significance as an overestimation of the nitrate concentrations within the model's euphotic layer, albeit low, may contribute to the slight northern shift of the simulated spring bloom pattern (observed in Sects. 3.1 and 3.3). Further exploring the nutrient dynamics of the region and how these are conditioned by the variability in mixed layer depths, for instance, would be of great interest. However, such a topic is out of the scope of this paper and will be investigated in future work. From a model evaluation approach, the fact that both transect and vertical profiles are comparable to the climatological values allows us to be confident in the model's ability to solve nutrient dynamics with depth.
We have developed a high-resolution (2.5–5 km horizontal) N2PZD2 model of the EAC system and evaluated its performance against satellite-derived estimates of surface chlorophyll and subsurface nutrient data using several skill metrics. The model is able to reproduce the timing and the spatial structure of the dominant patterns of chlorophyll variability and the vertical distribution of nitrate. The validation effort is robust and highlights the high skill of this model in reproducing the observed chlorophyll patterns in the EAC system, deeming it suitable for further dynamical studies. We anticipate this coupled configuration will be an often used framework for exploring how regional oceanic features, and associated biogeochemical dynamics, condition ecosystem response. Such an understanding is critical to a diverse range of research areas, spanning from marine ecology to climate change. It is of particular interest in the EAC system due to the high mesoscale eddy activity observed in the region and because BGC dynamics in the western boundary currents remain an understudied topic.
Model initial conditions and boundary forcing come from the Bluelink ReANalysis version 3p5 (BRAN3; Oke et al., 2013) for all the physical variables and from CSIRO Atlas of Regional Seas climatology (CARS2009: http://www.marine.csiro.au/~dunn/cars2009/, last access: 12 March 2018) for nitrate. Atmospheric forcing is from the National Centers for Environmental Prediction (NCEP) reanalysis atmospheric model (Kistler et al., 2001). Remotely sensed chlorophyll is the Copernicus-GlobColour 8-daily product generated by ACRI-ST, which can be downloaded from the Copernicus Marine Environment Monitoring Service (CMEMS) catalogue. It is available at http://marine.copernicus.eu/services-portfolio/access-to-products/ (last access: 12 March 2018) with ID OCEANCOLOUR_GLO_CHL_L4_REP_OBSERVATIONS_009_082. ROMS is a community open-source model. The most current official versions of the code, including bio_Fennel, are made available at http://www.myroms.org (last access: 10 November 2017). Both physical and BGC model output are saved as daily snapshots and daily averages of three-dimensional fields of ocean physical and biogeochemical properties (sea level, temperature, salinity, velocities, nitrates, ammonium, phytoplankton, chlorophyll, zooplankton, and large and small detritus) for every day over the 10-year simulation period (2002–2011). These data are archived at UNSW Sydney and can be made available for research purposes.
CR, CAE, MR, and PCH designed the experiments and CR carried them out. CK configured the hydrodynamic model and CR and CAE configured the biogeochemical model. CR performed the simulations. CR prepared the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We would like to thank the helpful comments and suggestions of both
reviewers. The contributions of Emlyn Jones were especially in-depth and
thoughtful, leading to added value to this work. This research was supported
by an Australian Research Council linkage project no. LP150100064, and
Discovery Project no. DP140102337 to Moninya Roughan. Carlos Rocha was
supported by a UNSW postgraduate TFS award.
Edited by: Sandra Arndt
Reviewed by: Emlyn Jones and Leonardo Laiolo
Alvera-Azcárate, A., Barth, A., Sirjacobs, D., Lenartz, F., and Beckers, J. M.: Data Interpolating Empirical Orthogonal Functions (DINEOF): a tool for geophysical data analyses, Mediterr. Mar. Sci., 12, 5–11, https://doi.org/10.12681/mms.64, 2010.
Andersen, V., Nival, P., and Harris, R. P.: Modelling of a planktonic ecosystem in an enclosed water column, J. Mar. Biol. Assoc. UK., 67, 407–430, 1987.
Anderson, T. R.: Plankton functional type modelling: running before we can walk?, J. Plankton Res., 27, 1073–1081, https://doi.org/10.1093/plankt/fbi076, 2005.
Armbrecht, L. H., Roughan, M., Rossi, V., Schaeffer, A., Davies, P. L., Waite, A. M., and Armand, L. K.: Phytoplankton composition under contrasting oceanographic conditions: Upwelling and downwelling (Eastern Australia), Cont. Shelf Res., 75, 54–67, https://doi.org/10.1016/j.csr.2013.11.024, 2013.
Baird, M. E., Timko, P. G., Suthers, I. M., and Middleton, J. H.: Coupled physical-biological modelling study of the East Australian Current with idealised wind forcing, Part I: Biological model intercomparison, J. Mar. Syst., 59, 249–270, 2006a.
Baird, M. E., Timko, P. G., Suthers, I. M., and Middleton, J. H.: Coupled physical-biological modelling study of the East Australian Current with idealised wind forcing, Part II: Biological dynamical analysis, J. Mar. Syst., 59, 271–291, 2006b.
Baird, M. E., Cherukuru, N., Jones, E., Margvelashvili, N., Mongin, M., Oubelkheir, K., Ralph, P. J., Rizwi, F., Robson, B. J., Schroeder, T., and Skerratt, J.: Remote sensing reflectance and true colour produced by a coupled hydrodynamic, optical, sediment, biogeochemical model of the Great Barrier Reef, Australia: comparison with satellite data, Environ. Modell. Soft., 78, 79–96, https://doi.org/10.1016/j.envsoft.2015.11.025, 2016.
Bjornsson, H. and Venegas, S. A.: A Manual for EOF and SVD Analyses of Climatic Data, Feb. 1997, 52 pp., CCGCR Report No. 97-1, 1997.
Blain, S., Quéguiner, B., Armand, L., Belviso, S., Bombled, B., Bopp, L., Bowie, A., Brunet, C., Brussaard, C., Carlotti, F., Christaki, U., Corbière, A., Durand, I., Ebersbach, F., Fuda, J., Garcia, N., Gerringa, L., Griffiths, B., Guigue, C., Guillerm, C., Jacquet, S., Jeandel, C., Laan, P., Lefèvre, D., Lo Monaco, C., Malits, A., Mosseri, J., Obernosterer, I., Park, Y., Picheral, M., Pondaven, P., Remenyi, T., Sandroni, V., Sarthou, G., Savoye, N., Scouarnec, L., Souhaut, M., Thuiller, D., Timmermans, K., Trull, T., Uitz, J., van Beek, P., Veldhuis, M., Vincent, D., Viollier, E., Vong, L., and Wagener, T.: Effect of natural iron fertilization on carbon sequestration in the Southern Ocean, Nature, 446, 1070, https://doi.org/10.1038/nature05700, 2007.
Blanchard, J. L., Jennings, S., Holmes, R., Harle, J., Merino, G., Allen, J. I., Holt, J., Dulvy, N. K., and Barange, M.: Potential consequences of climate change for primary production and fish production in large marine ecosystems, Phil. Trans. R. Soc. B, 367, 2979–2989, https://doi.org/10.1098/rstb.2012.0231, 2012.
Cetina-Heredia, P., Roughan, M., Van Sebille, E., and Coleman, M. A.: Long-term trends in the East Australian Current separation latitude and eddy driven transport, J. Geophys. Res.-Oceans, 119, 4351–4366, https://doi.org/10.1002/2014JC010071, 2014.
Chapman, D. C.: Numerical treatment of Cross-Shelf Open Boundaries in a Barotropic Coastal Ocean Model, J. Phys. Oceanogr., 15, 1060–1075, 1985.
Clementson, L. A., Parslow, J. S., Griffiths, F. B., Lyne, V. D., Mackey, D. J., Harris, G. P., McKenzie, D. C., Bonham, P. I., Rathbone, C. E., and Rintoul, S.: Controls on phytoplankton production in the Australasian sector of the subtropical convergence, Deep-Sea Res. Pt. I, 45, 1627–1661, 1998.
Condie, S. and Dunn, J. R.: Seasonal characteristics of the surface mixed layer in the Australasian region: Implications for primary production regimes and biogeography, Mar. Freshwater Res., 57, 569–590, https://doi.org/10.1071/MF06009, 2006.
Doney, S. C., Lima, I., Lindsay, K., Moore, J. K., Dutkiewicz, S., Friedrichs, M. A. M., and Matear, R. J.: Marine biogeochemical modeling: Recent advances and future challenges. Oceanography, 14, 93–107, https://doi.org/10.5670/oceanog.2001.10, 2001.
Everett, J., Baird, M., Oke, P., and Suthers, I.: An avenue of eddies: Quantifying the biophysical properties of mesoscale eddies in the Tasman Sea, Geophys. Res. Lett., 39, L16608, https://doi.org/10.1029/2012GL053091, 2012.
Everett, J., Baird, M., Roughan, M., Suthers, I., and Doblin, M.: Relative impact of seasonal and oceanographic drivers on surface chlorophyll a along a Western Boundary Current, Prog. Oceanogr., 120, 340–351, 2014.
Everett, J., Macdonald, H., Baird, M., Humphries, J., Roughan, M., and Suthers, I. M.: Cyclonic entrainment of preconditioned shelf waters into a frontal eddy, J. Geophys. Res.-Oceans, 120, 677–691, https://doi.org/10.1002/2014JC010301, 2015.
Fairall, C. W., Bradley, E. F., Rogers, D. P., Edson, J. B., and Young, G. S.: Bulk parameterization of air-sea fluxes for tropical oceanglobal atmosphere Coupled-Ocean Atmosphere Response Experiment, J. Geophys. Res., 101, 3747–3764, 1996.
Fasham, M., Ducklow, H., and McKelvie, S.: A nitrogen-based model of plankton dynamics in the oceanic mixed layer, J. Mar. Res., 48, 591–639, 1990.
Fasham, M. J. R.: Variations in the seasonal cycle of biological production in subarctic oceans: A model sensitivity analysis, Deep-Sea Res. Pt. I, 42, 1111–1149, 1995.
Fennel, K., Losch, M., Schroter, J., and Wenzel, M.: Testing a marine ecosystem model: Sensitivity analysis and parameter optimization, J. Mar. Syst., 28, 45–63, 2001.
Fennel, K., Wilkin, J., Levin, J., Moisan, J., O'Reilly, J., and Haidvogel, D.: Nitrogen cycling in the Middle Atlantic Bight: Results from a three-dimensional model and implications for the North Atlantic nitrogen budget, Global Biogeochem. Cy., 20, GB3007, https://doi.org/10.1029/2005GB002456, 2006.
Fiechter, J., Edwards, C. A., and Moore, A. M.: Wind, circulation, and topographic effects on alongshore phytoplankton variability in the California Current, Geophys. Res. Lett., 45, 3238–3245, https://doi.org/10.1002/2017GL076839, 2018.
Flather, R. A.: A tidal model of the northwest European continental shelf, Mem. Soc. R. Sci. Liege, 6, 141–164, 1976.
Franks, P. J. S.: Planktonic ecosystem models: perplexing parameterizations and a failure to fail, J. Plankton Res., 31, 1299–1306, https://doi.org/10.1093/plankt/fbp069, 2009.
Friedrichs, M. A., Dusenberry, J. A., Anderson, L. A., Armstrong, R. A., Chai, F., Christian, J. R., Doney, S. C., Dunne, J., Fujii, M., Hood, R., and McGillicuddy Jr, D. J.: Assessment of skill and portability in regional marine biogeochemical models: Role of multiple planktonic groups, J. Geophys. Res., 112, C08001, https://doi.org/10.1029/2006JC003852, 2007.
Gaube, P., McGillicuddy Jr., D. J., Chelton, D. B., Behrenfeld, M. J., and Strutton, P. G.: Regional variations in the influence of mesoscale eddies on near-surface chlorophyll, J. Geophys. Res.-Oceans, 119, 8195–8220, https://doi.org/10.1002/2014JC010111, 2014.
Geider, R. J., McIntyre, H. L., and Kana, T. M.: Dynamic model of phytoplankton growth and acclimation: Responses of the balanced growth rate and the chlorophyll a: Carbon ratio to light, nutrient-limitation and temperature, Mar. Ecol. Prog. Ser., 148, 187–200, 1997.
Hassler, C., Djajadikarta J., Doblin, M., Everett, J., and Thompson, P.: Characterisation of water masses and phytoplankton nutrient limitation in the East Australian Current separation zone during spring 2008, Deep-Sea Res. Pt. II, 58, 664–677, https://doi.org/10.1016/j.dsr2.2010.06.008, 2011.
Jones, E. M., Baird, M. E., Mongin, M., Parslow, J., Skerratt, J., Lovell, J., Margvelashvili, N., Matear, R. J., Wild-Allen, K., Robson, B., Rizwi, F., Oke, P., King, E., Schroeder, T., Steven, A., and Taylor, J.: Use of remote-sensing reflectance to constrain a data assimilating marine biogeochemical model of the Great Barrier Reef, Biogeosciences, 13, 6441–6469, https://doi.org/10.5194/bg-13-6441-2016, 2016.
Kerry, C., Powell, B., Roughan, M., and Oke, P.: Development and evaluation of a high-resolution reanalysis of the East Australian Current region using the Regional Ocean Modelling System (ROMS 3.4) and Incremental Strong-Constraint 4-Dimensional Variational (IS4D-Var) data assimilation, Geosci. Model Dev., 9, 3779–3801, https://doi.org/10.5194/gmd-9-3779-2016, 2016.
Kishi, M. J., Kashiwai, M., Ware, D. M., Megrey, B. A., Eslinger, D. L., Werner, F. E., Noguchi-Aita, M., Azumaya, T., Fujii, M., Hashimoto, S., Huang, D., Iizumi, H., Ishida, Y., Kang, S., Kantakov, G. A., Kim, H.-C., Komatsu, K., Navrotsky, V. V., Smith, L. S., Tadokoro, K., Tsuda, A., Yamamura, O., Yamanaka, Y., Yokouchi, K., Yoshie, N., Zhang, J., Zuenko, Y. I., and Zvalinsky, V. I.: Nemuro – a lower trophic level model for the North Pacific marine ecosystem, Ecol. Modell., 202, 12–25, 2007.
Kistler, R., Kalnay, E., Collins, W., Saha, S., White, G., Woolen, J., Chelliah, M., Ebisuzaki, W., Kanamitsu, M., Kousky, V., van den Dool, H., Jenne, R., and Fiorino, M.: The NCEP/NCAR 50-Year Reanalysis, B. Am. Meteorol. Soc., 82, 247–268, 2001.
Laiolo, L., McInnes, A. S., Matear, R., and Doblin, M. A.: Key Drivers of Seasonal Plankton Dynamics in Cyclonic and Anticyclonic Eddies off East Australia, Front. Mar. Sci., 3, 155, 2016.
Laiolo, L., Matear, R., Baird, M. E., Soja-Woźniak, M., and Doblin, M. A.: Information content of in situ and remotely sensed chlorophyll-a: Learning from size-structured phytoplankton model, J. Mar. Syst., 183, 1–12, https://doi.org/10.1016/j.jmarsys.2018.03.005, 2018.
Leggett, R. W. and Williams, L. R.: A reliability index for models, Ecol. Modell., 13, 303–312, 1981.
Leonard, C. L., McClain, C. R., Murtugudde, R., Hofmann, E. E., and Harding, L. W.: An iron-based ecosystem model of the central equatorial Pacific, J. Geophys. Res., 104, 1325–1341, 1999.
Lima, I. D. and Doney, S. C.: A three-dimensional, multi-nutrient and size-structured ecosystem model for the North Atlantic, Global Biogeochem. Cy., 18, GB3019, https://doi.org/10.1029/2003GB002146, 2004.
Loague, K. and Green, R. E.: Statistical and graphical methods for evaluating solute transport models: overview and application, J. Contam. Hydrol., 7, 51–73, 1991.
Macdonald, H.: Numerical modelling of mesoscale eddies in the Tasman Sea, PhD Thesis, UNSW Sydney, 2013.
Macdonald, H., Baird, M., and Middleton, J. H.: Effect of wind on continental shelf carbon fluxes off southeast Australia: A numerical model, J. Geophys. Res., 114, C05016, https://doi.org/10.1029/2008JC004946, 2009.
Macdonald, H., Roughan, M., Baird, M., and Wilkin, J.: The formation of a cold-core eddy in the East Australian Current, Cont. Shelf Res., 114, 72–84, https://doi.org/10.1016/j.csr.2016.01.002, 2016.
Maritorena, S. and Siegel, D. A.: Consistent merging of satellite ocean color data sets using a bio-optical model, Remote Sens. Environ., 94, 429–440, https://doi.org/10.1016/j.rse.2004.08.014, 2005.
Matear, R. J. and Jones, E.: Marine Biogeochemical Modelling and Data Assimilation, in: Operational Oceanography in the 21st Century, edited by: Schiller, A. and Brassington, G., Springer, Dordrecht, 2011.
Matear, R. J., Chamberlain, M. A., Sun, C., and Feng, M.: Climate change projection of the Tasman Sea from an Eddy-resolving Ocean Model, J. Geophys. Res.-Oceans, 118, 2961–2976, https://doi.org/10.1002/jgrc.20202, 2013.
Mattern, J., Song, H., Edwards, C. A., Moore, A. M., and Fiechter, J.: Data assimilation of physical and chlorophyll a observations in the California Current System using two biogeochemical models, Ocean Model, 109, 55–71, https://doi.org/10.1016/j.ocemod.2016.12.002, 2016.
McGillicuddy, D. J., Robinson, A. R., Siegel, A. A., Jannasch, H. W., Johnson, R., Dickey, T. D., McNeil, J., Michaels, A. F., and Knap, A. H.: Influence of mesoscale eddies on new production in the Sargasso Sea, Nature, 394, 263–266, 1998.
Mellor, G. L. and Yamada, T.: Development of a turbulence closure model for geophysical fluid problems, Rev. Geophys. Space Ge., 20, 851–875, 1982.
Mongin, M., Matear, R., and Chamberlain, M.: Seasonal and spatial variability of remotely sensed chlorophyll and physical fields in the SAZ-sense region, Deep-Sea Res. Pt. II, 58, 2082–2093, https://doi.org/10.1016/j.dsr2.2011.06.002, 2011.
Moore, T., Matear, R., Marra, J., and Clementson, L.: Phytoplankton variability off the Western Australian Coast: Mesoscale eddies and their role in cross-shelf exchange, Deep-Sea Res. Pt. II, 54, 943–960, 2007.
Moskilde, E.: Topics in Non-Linear Dynamics: Application to Physics, Biology and Economic Systems, World Sci., Hackensack, N. J., 1996.
Nash, J. E. and Sutcliffe, J. V.: River flowforecasting through conceptual models, Part 1 – a discussion of principles, J. Hydrol., 10, 282–290, 1970.
Oke, P., Sakov, P., Cahill, M. L., Dunn, J. R., Fiedler, R., Griffin, D. A., Mansbridge, J. V., Ridgway, K. R., and Schiller, A.: Towards a dynamically balanced eddy-resolving ocean reanalysis: BRAN3, Ocean Modell., 67, 52–70, 2013.
Oke, P. R., Brassington, G. B., Griffin, D. A., and Schiller, A.: The Bluelink ocean data assimilation system (BODAS), Ocean Modell., 21, 46–70, 2008.
Olson, R. J.: Differential photoinhibition of marine nitrifying bacteria: A possible mechanism for the formation of the primary nitrite maximum, J. Mar. Res., 39, 227–238, 1981.
Oschlies, A., and Garcon, V.: An eddy-permitting coupled physical- biological models of the North Atlantic: 1. Sensitivity to advection numerics and mixed layer, Global Biogeochem. Cy., 13, 135–160, 1999.
Powell T. P., Lewis, C. V. W., Curchitser, E. N., Haidvogel, D. B., Hermann, A. J., and Dobbins, E. L.: Results from a three- dimensional, nested biological-physical model of the California Current System and comparisons with statistics from satellite imagery, J. Geophys. Res., 111, C07018, https://doi.org/10.1029/2004JC002506, 2006.
Pritchard, T. R., Lee, R. S., Ajani, P. A., Rendell, P. S., Black, K., and Koop, K.: Phytoplankton responses to nutrient sources in coastal waters off southeastern Australia, Aquat. Ecosyst. Health, 6, 105–117, 2003.
Ridgway, K. R. and Dunn, J. R.: Mesoscale structure of the mean East Australian Current System and its relationship with topography, Prog. Oceanogr., 56, 189–222, https://doi.org/10.1016/S0079-6611(03)00004-1, 2003.
Rombouts, I., Beaugrand, G., Artigas, L. F., Dauvin, J.-C., Gevaert, F., Goberville, E., Kopp, D., Lefebvre, S., Luczak, C., Spilmont, N., Travers-Trolet, M., Villanueva, M. C., and Kirby, R. R.: Evaluating marine ecosystem health: case studies of indicators using direct observations and modelling methods, Ecol. Indic., 24, 353–365, https://doi.org/10.1016/j.ecolind.2012.07.001, 2013.
Roughan, M. and Middleton, J.: On the East Australian Current; Variability, encroachment and upwelling, J. Geophys. Res.-Oceans, 109, C07003, https://doi.org/10.1029/2003JC001833, 2004.
Shchepetkin, A. F. and McWilliams, J. C.: The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model, Ocean Modell., 9, 347–404, 2005.
Souza, J., Powell, B. S., Castillo-Trujillo, A. C., and Flament, P.: The Vorticity Balance of the Ocean Surface in Hawaii from a Regional Reanalysis, J. Phys. Oceanogr., 45, 424–440, 2014.
Stow, C. A., Jolliff, J., McGillicuddy, D. J., Doney, S. C., Allen, J. I., Friedrichs, M. A. M., Rose, K. A., and Wallhead, P.: Skill Assessment for Coupled Biological/Physical Models of Marine Systems, J. Mar. Syst., 76, 4–15, https://doi.org/10.1016/j.jmarsys.2008.03.011, 2009.
Taylor, A. H.: Characteristic properties of models for the vertical distribution of phytoplankton under stratification, Ecol. Modell., 40, 175–199, 1988.
Taylor, A. H., Watson, A. J., Ainsworth, M., Robertson, J. E., and Turner, D. R.: A modelling investigation of the role of phytoplankton in the balance of carbon at the surface of the North Atlantic, Global Biogeochem. Cy., 5, 151–171, 1991.
Tranter, D. J., Carpenter, D. J., and Leech, G. S.: The coastal enrichment effects of the East Australian Current eddy field, Deep-Sea Res., 33, 1705–1728, 1986.
Whiteway, T.: Australian Bathymetry and Topography Grid, Scale 1:5000000, Geoscience Australia, Canberra, 2009.
Wroblewski, J. S.: A model of the spring bloom in the North Atlantic and its impact on ocean optics, Limnol. Oceanogr., 34, 1563–1571, 1989.





