the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The biophysics, ecology, and biogeochemistry of functionally diverse, vertically and horizontally heterogeneous ecosystems: the Ecosystem Demography model, version 2.2 – Part 1: Model description
Ryan G. Knox
David M. Medvigy
Naomi M. Levine
Michael C. Dietze
Yeonjoo Kim
Abigail L. S. Swann
Christine R. Rollinson
Rafael L. Bras
Steven C. Wofsy
Paul R. Moorcroft
Earth system models (ESMs) have been developed to represent the role of terrestrial ecosystems on the energy, water, and carbon cycles. However, many ESMs still lack representation of within-ecosystem heterogeneity and diversity. In this paper, we present the Ecosystem Demography model version 2.2 (ED-2.2). In ED-2.2, the biophysical and physiological processes account for the horizontal and vertical heterogeneity of the ecosystem: the energy, water, and carbon cycles are solved separately for a series of vegetation cohorts (groups of individual plants of similar size and plant functional type) distributed across a series of spatially implicit patches (representing collections of micro-environments that have a similar disturbance history). We define the equations that describe the energy, water, and carbon cycles in terms of total energy, water, and carbon, which simplifies the differential equations and guarantees excellent conservation of these quantities in long-term simulation (< 0.1 % error over 50 years). We also show examples of ED-2.2 simulation results at single sites and across tropical South America. These results demonstrate the model's ability to characterize the variability of ecosystem structure, composition, and functioning both at stand and continental scales. A detailed model evaluation was conducted and is presented in a companion paper (Longo et al., 2019a). Finally, we highlight some of the ongoing model developments designed to improve the model's accuracy and performance and to include processes hitherto not represented in the model.
- Article
(13324 KB) - Full-text XML
- Companion paper
-
Supplement
(4934 KB) - BibTeX
- EndNote
The dynamics of the terrestrial biosphere play an integral role in the Earth's carbon, water, and energy cycles (Betts and Silva Dias, 2010; Santanello Jr et al., 2018; Le Quéré et al., 2018), and consequently, how the Earth's climate system is expected to change over the coming decades due to the increasing levels of atmospheric carbon dioxide arising from anthropogenic activities (IPCC, 2014; Le Quéré et al., 2018). Models for the dynamics of the terrestrial biosphere and its bidirectional interaction with the atmosphere have evolved considerably over the past decades (Levis, 2010; Fisher et al., 2014, 2018). As described by Sellers et al. (1997), the first generation of land surface models (LSMs) was limited to provide boundary conditions to atmospheric models; they only solved a simplified energy and water budget, and accounted for the effects of surface on frictional effects on near-surface winds (e.g., Manabe et al., 1965; Somerville et al., 1974). These models, however, did not account for the active role of vegetation. The second generation of LSMs considered the active role of vegetation and represented the spectral properties of the canopy, the changes in roughness of vegetated surfaces, and the biophysical controls on evaporation and transpiration (Sellers et al., 1997); examples of these models include National Center for Atmospheric Research Biosphere-Atmosphere Transfer Scheme (NCAR/BATS) (Dickinson et al., 1986) and Simple Biosphere model (SiB) (Sellers et al., 1986). The increasing recognition of the role of vegetation in mediating the exchanges of carbon, water, and energy between the land and the atmosphere led to the third generation of LSMs, which incorporated explicit representations of plant photosynthesis and resulting dynamics of terrestrial carbon uptake, turnover, and release within terrestrial ecosystems (Sellers et al., 1997); examples of such models included LSM (Bonan, 1995) and SiB2 (Sellers et al., 1996). While the fluxes of carbon, water, and energy predicted by these models would change in response to changes in their climate forcing, the biophysical and biogeochemical properties of the ecosystem within each climatological grid cell were prescribed and thus did not change over time.
Subsequently, building upon previous work (Prentice et al., 1992; Neilson, 1995; Haxeltine and Prentice, 1996), Foley et al. (1996) adopted an approach to calculate the productivity of a series of plant functional types (PFTs), based on a leaf-level model of photosynthesis. The abundance of each PFT within each grid cell was dynamic, with the abundance changes being determined by the relative productivity of the PFTs. This allowed the fast-timescale exchanges of carbon, water, and energy within the plant canopy to be explicitly linked with the long-term dynamics of the ecosystem. This approach followed the concept of dynamic global vegetation model (DGVM), originally coined by Prentice et al. (1989) to describe this kind of terrestrial biosphere model in which changes in climate could drive changes in ecosystem composition, structure, and functioning. DGVMs, when run coupled to atmospheric models, would then feedback onto climate. The subsequent generation of terrestrial biosphere-based DGVMs (i.e., DGVMs incorporating couple carbon, water, and energy fluxes) such as the Lund–Potsdam–Jena (LPJ) model (Sitch et al., 2003), Community Land Model's Dynamic Global Vegetation Model (CLM-DGVM) (Levis et al., 2004), and Top-down Representation of Interactive Foliage and Flora Including Dynamics Joint UK Land Environment Simulator (TRIFFID/JULES) (Hughes et al., 2004; Clark et al., 2011; Mangeon et al., 2016) have included additional mechanisms such as disturbance through fires and multiple types of mortality.
Analyses have shown that most terrestrial biosphere models are capable of reproducing the current distribution of global biomes (e.g., Sitch et al., 2003; Blyth et al., 2011) and their carbon stocks and fluxes (Piao et al., 2013). However, they diverge markedly in their predictions of how terrestrial ecosystems will respond to future climate change (Friedlingstein et al., 2014). In fully coupled Earth system model simulations, some of these differing predictions arise from divergent predictions about the direction and magnitude of regional climate change. However, offline analyses, in which the models are forced with prescribed climatological forcing, have shown that there is also substantial disagreement between the models about how terrestrial ecosystems will respond to any shift in climate (e.g., Sitch et al., 2008; Zhang et al., 2015). In addition, the transitions between biome types, for example, the transition that occurs between closed-canopy tropical forests and grass- and shrub-dominated savannahs in South America, are generally far more abrupt in typical DGVM results than in observations (Good et al., 2011; Levine et al., 2016).
One important limitation of most DGVMs is that they do not represent within-ecosystem diversity and heterogeneity. The representation of plant functional diversity within terrestrial biosphere models is normally coarse, with broadly defined PFTs defined from a combination of morphological and leaf physiological attributes (Purves and Pacala, 2008). In addition, there is limited variation in the resource conditions (light, water, and nutrient levels) experienced by individual plants within the climatological grid cells of traditional DGVMs. Some models, such as CLM (Oleson et al., 2013), have options to represent a multi-layer plant canopy (e.g., two canopy layers allowing for Sun and shade leaves), and/or differences in rooting depth between PFTs; however, resource conditions are assumed to be horizontally homogeneous, meaning that there is no horizontal spatial variation in resource conditions experienced by individual plants. The lack of significant variability in resource conditions limits the range of environmental niches within the climatological grid cells of terrestrial biosphere and makes the coexistence between PFTs difficult. Consequently, models often predict ecosystems comprised of single homogeneous vegetation types (Moorcroft, 2003, 2006).
Field- and laboratory-based studies conducted over the past 30 years indicate that plant functional diversity significantly affects ecosystem functioning (Loreau and Hector, 2001; Tilman et al., 2014, and references therein), and variations in trait expression are strongly driven by disturbances and local heterogeneity of abiotic factors such as soil characteristics (Bruelheide et al., 2018; Both et al., 2019). In many cases, biodiversity increases ecosystem productivity and ecosystem stability (e.g., Tilman and Downing, 1994; Naeem and Li, 1997; Cardinale et al., 2007; García-Palacios et al., 2018), and biodiversity has also been shown to contribute to enhanced ecosystem functionality in highly stressed environments (e.g., Jucker and Coomes, 2012). Other studies have also established correlations between tropical forest diversity and carbon storage and primary productivity (Cavanaugh et al., 2014; Poorter et al., 2015; Liang et al., 2016; Huang et al., 2018).
In addition to the absence of within-ecosystem diversity in conventional terrestrial biosphere models, plants of each PFT are also assumed to be homogeneous in size, while, in contrast, most terrestrial ecosystems, particularly forests and woodlands, exhibit marked size structure of individuals within plant canopies (Hutchings, 1997). This size-related heterogeneity is important because plant size strongly affects the amount of light, water, and nutrients individual plants within the canopy can access, which, in turn, affects their performance, dynamics, and responses to climatological stress. It also allows representation of the dynamics of pervasive human-driven degradation of forest ecosystems (Lewis et al., 2015; Haddad et al., 2015), which affects carbon stocks and forest structure and composition, which cannot be easily represented in highly aggregated models (Longo and Keller, 2019).
An alternative approach to simulating the dynamics of terrestrial ecosystems has been individual-based vegetation models (Friend et al., 1997; Bugmann, 2001; Sato et al., 2007; Fischer et al., 2016; Maréchaux and Chave, 2017). Also known as forest gap models, due to the importance of canopy gaps for the dynamics of closed canopy forests, these models simulate the birth, growth, and death of individual plants, thereby incorporating diversity and heterogeneity of the plant canopy mechanistically. In forest gap models, the ecosystem properties such as total carbon stocks, and net ecosystem productivity are emergent properties resulting from competition of limiting resources and the differential ability of plants to survive and be productive under a variety of micro-environments (e.g., gaps or the understory of a densely populated patch of old-growth forest).
This approach has two main advantages. First, gap models represent the dynamic changes in the ecosystem structure caused by disturbances such as tree fall, selective logging, and fires. These disturbances create new micro-environments that are significantly different from old-growth vegetation areas and allow plants with different life strategies (for example, shade-intolerants) to coexist in the landscape. Second, because individual trees are represented in the model, the results can be directly compared with field measurements. Gap models have various degrees of complexity, with some models being able to represent the interactions between climate variability and gross primary productivity (Friend et al., 1997; Sato et al., 2007), as well as the impact of climate change in the ecosystem carbon balance (Fischer et al., 2016, and references therein). However, because the birth and death of individuals within a plant canopy are stochastic processes, multiple realizations of given model formulation are required to determine the long-term, large-scale dynamics of these models, which limits their applicability over large regions or global scales and has precluded their use in Earth system modeling studies.
The need to represent heterogeneity in vegetation structure and composition in terrestrial biosphere models, without the computational burden of simulating every tree at regional and global scales, led to the development of cohort-based models (Hurtt et al., 1998; Moorcroft et al., 2001; Fisher et al., 2018). In the cohort-based approach, individual trees are grouped according to their size (e.g., height or diameter at breast height); functional groups, which can be defined along trait axes (e.g., Reich et al., 1997; Wright et al., 2004; Fortunel et al., 2012); and micro-environment conditions (e.g., whether plants are living in a gap, recently burned fragment, or in a patch of old-growth forest). Over the past two decades, several cohort-based models have emerged, including the Ecosystem Demography model (ED; Moorcroft et al., 2001; Hurtt et al., 2002; Albani et al., 2006; Medvigy et al., 2009); the Lund–Potsdam–Jena General Ecosystem Simulator (LPJ-GUESS; Smith et al., 2001; Ahlström et al., 2012; Lindeskog et al., 2013); the Land Model version 3 with perfect plasticity approximation (LM3-PPA; Weng et al., 2015); and the Functionally-Assembled Terrestrial Ecosystem Simulator (FATES; Fisher et al., 2015; Huang et al., 2019). Similar to gap models, these models represent functional diversity and heterogeneity of micro-environments, and consequently the ecosystem's structure, diversity, and functioning emerge from the interactions between plants with different life strategies under different resource availability, albeit at a lesser extent than individual-based models (Fisher et al., 2018).
The Ecosystem Demography model (ED; Moorcroft et al., 2001) is a cohort-based model. Through this approach, it addresses the need to incorporate heterogeneity into models of the long-term, large-scale response of terrestrial ecosystems to changes in climate and other environmental forcings within a deterministic modeling framework. The size- and age-structured partial differential equations that describe the plant community are derived from individual-level properties but are properly scaled to account for the spatially localized nature of interactions within plant canopies. The model was later extended by Hurtt et al. (2002) and Albani et al. (2006) to incorporate multiple forms of disturbance including land clearing, land abandonment, and forest harvesting. An important difference between ED and most DGVMs is that in ED, PFTs are defined not simply based on their biogeographic ranges but also represent diversity in plant life-history strategies within any given ecosystem. These different PFTs represent a suite of physiological, morphological, and life-history traits that mechanistically represent the ways different kinds of plants utilize resources (Fisher et al., 2010).
The original ED model formulation was an offline ecosystem model describing the coupled carbon and water fluxes of a heterogeneous tropical forest ecosystem (Moorcroft et al., 2001). Subsequently, Medvigy et al. (2009) applied a similar approach to develop the Ecosystem Demography model version 2 (ED-2) that describes coupled carbon, water, and energy fluxes of the land surface. Since then, the ED-2 model has been continuously developed to improve several aspects of the model (see Supplement Sect. S1 for further information): (1) the conservation and thermodynamic representation of energy, water, and carbon cycles of the ecosystems; (2) the representation of several components of the energy, water, and carbon cycles, including the canopy radiative transfer, aerodynamic conductances and eddy fluxes, and leaf physiology (photosynthesis); (3) the structure of the code, including efficient data storage, code parallelization, and version control and code availability. ED-2 has been used in many studies including offline simulations (e.g., Medvigy et al., 2009; Antonarakis et al., 2011; Kim et al., 2012; Zhang et al., 2015; Castanho et al., 2016; Levine et al., 2016) and simulations running interactively with a regional atmospheric model (e.g., Knox et al., 2015; Swann et al., 2015).
In this paper, we describe in detail the biophysical, physiological, ecological, and biogeochemical formulation of the most recent version of the ED-2 model (ED-2.2), focusing in particular on the model's formulation of the fast timescale dynamics of the heterogeneous plant canopy that occur at subdaily timescales. While many parameterizations and submodels in ED-2.2 are based on approaches that are also used in other DGVMs, their implementation in ED-2.2 has some critical differences from other ecosystem models and also previous versions of ED. (1) In ED-2.2, the fundamental budget equations use energy and total mass as the main prognostic variables; because we use equations that directly track the time changes of the properties we seek to conserve, we can assess the model conservation of such properties with fewer assumptions. (2) In ED-2.2, all thermodynamic properties are scalable with mass, and the model is constructed such that when individual biomass changes, due to growth and turnover, the thermodynamic properties are also updated to reflect changes in heat and water holding capacity. (3) The water and energy budget equations for vegetation are solved at the individual cohort level and the corresponding equations for environments shared by plants such as soils and canopy air space are solved for each micro-environment in the landscape, and thus ecosystem-scale fluxes are emergent properties of the plant community. This approach allows the model to represent both the horizontal and vertical heterogeneity of environments of the plant communities. It also links the individual's ability to access resources such as light and water and accumulate carbon under a variety of micro-environments, which ultimately drives the long-term dynamics of growth, reproduction, and survivorship.
2.1 The representation of ecosystem heterogeneity in ED-2.2
In ED-2.2 the terrestrial ecosystem within a given region of interest is represented through a hierarchy of structures to capture the physical and biological heterogeneity in the ecosystem's properties (Fig. 1).
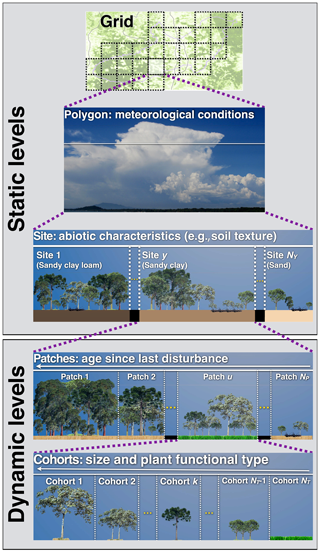
Figure 1Schematic representation of the multiple hierarchical levels in ED-2.2, organized by increasing level of detail from top to bottom. Static levels (grid, polygons, and sites) are assigned during the model initialization and remain constant throughout the simulation. Dynamic levels (patches and cohorts) may change during the simulation according to the dynamics of the ecosystem.
Physical heterogeneity. The domain of interest (grid) is geographically divided into polygons. Within each polygon, the time-varying meteorological forcing above the plant canopy is assumed to be spatially uniform. For example, a single polygon may be used to simulate the dynamics of an ecosystem in the neighborhood of an eddy flux tower, or alternatively, a polygon may represent the lower boundary condition within one horizontal grid cell in an atmospheric model. Each polygon is subdivided into one or more sites that are designed to represent landscape-scale variation in other abiotic properties, such as soil texture, soil depth, elevation, slope, aspect, and topographic moisture index. Each site is defined as a fractional area within the polygon and represents all regions within the polygon that share similar time-invariant physical (abiotic) properties. Both polygons and sites are defined at the beginning of the simulation and are fixed in time, and no geographic information exists below the level of the polygon.
Biotic heterogeneity. Within each site, horizontal, disturbance-related heterogeneity in the ecosystem at any given time t is characterized through a series of patches that are defined by the time elapsed since last disturbance (i.e., age, a) and the type of disturbance that generated them. Like sites, patches are not physically contiguous: each patch represents the collection of canopy gap-sized (∼10 m) areas within the site that have a similar disturbance history, defined in terms of the type of disturbance experienced (represented by subscript q, ; a list of indices is available in Table 1) and time since the disturbance event occurred. The disturbance types accounted for in ED-2.2, and the possible transitions between different disturbance types, are shown in Fig. S1. The collection of gaps within each given site belonging to a polygon follows a probability distribution function α, which can be also thought of as the relative area within a site, that satisfies
Similarly, the plant community population is characterized by the number of plants per unit area (hereafter number density, n) and is further classified according to their PFT, represented by subscript f (; Table 1) and the type of gap (q). The number density distribution depends on the individuals' biomass characteristics (size, C), the age since last disturbance (a), and the time (t), and is expressed as . Size is defined as a vector (units: kgC plant−1) corresponding to biomass of leaves, fine roots, sapwood, heartwood, and non-structural storage (starch and sugars), respectively.
Table 1List of subscripts associated with ED-2.2's hierarchical levels for any variable X. NT is the total number of cohorts, NG is the total number of soil (ground) layers, NS is the total number of temporary surface water/snowpack layers, and NC is the total number of canopy air space layers, currently only used to obtain properties related to canopy conductance. The complete list of subscripts is available in Table S1.

Following Moorcroft et al. (2001), Albani et al. (2006), and Medvigy and Moorcroft (2012), the partial differential equations that describe the dynamics of plant density and probability distribution of patches within each site in the size-and-age structured model are defined as (dependencies omitted in the equations for clarity)
where mf is mortality rate, which may depend on the PFT, size, and the individual carbon balance; gf is the vector of the net growth rates for each carbon pool, which also may depend on the PFT, size, and carbon balance; ∇C⋅ is the divergence operator for the size vector; and is the transition matrix from gaps generated by previous disturbance q′ affected by new disturbance of type q, which may depend on environmental conditions. Boundary conditions are shown in Sect. S2.
Equations (2) and (3) cannot be solved analytically except for the most trivial cases; therefore, the age distribution is discretized into patches (subscript u, ; Table 1) of similar age and same disturbance type, and the population size structure living in any given patch u is discretized into cohorts (subscript k, ; Table 1) of similar size and same PFT (Fig. 1). Unlike polygons and sites, patches and cohorts are dynamic levels: changes in distribution (fractional area) of patches are driven by aging and disturbance rates, whereas changes in the distribution of cohorts in each patch are driven by growth, mortality, and recruitment (Fig. S2).
The environment perceived by each plant (e.g., incident light, temperature, vapor pressure deficit) varies across large scales as a consequence of changes in climate (macro-environment) but also varies at small scales (within the landscape; micro-environment) because of the horizontal and vertical position of each individual relative to other individuals in the plant community (e.g., Bazzaz, 1979) and the position of the local community in landscapes with complex terrains. Both macro- and micro-environmental conditions drive the net primary productivity of each individual, and ultimately determine growth, mortality, and recruitment rates for each individual. Likewise, they can also affect the disturbance rates: for example, during drought conditions (macro-environment), open canopy patches (micro-environment) may experience faster ground desiccation and consequently increase local fire risk. To account for the variability in micro-environments within the landscape and within local plant communities, in ED-2.2 the energy, water, and carbon dioxide cycles are solved separately for each patch, and within each patch, fluxes and storage associated with individual plants are solved for each cohort.
The ED-2.2 model represents processes that have inherently different timescales; therefore, the model also has a hierarchy of time steps, in order to attain maximum computational efficiency (Table 2). Processes associated with the short-term dynamics are presented in this paper. A summary of the phenological processes and those associated with longer-term dynamics is presented in Sects. S3 and S4 (see also Moorcroft et al., 2001; Albani et al., 2006; Medvigy et al., 2009).
Table 2Time steps associated with processes resolved by ED-2.2. The thermodynamic substep is dynamic and it depends on the error evaluation of the integrator, but it cannot be longer than the biophysics step, which is defined by the user. Other steps are fixed as of ED-2.2. Processes marked with an asterisk are presented in the main paper. Other processes are described in Sects. S3 and S4.

2.2 Software requirements and model architecture
Software requirements. The ED-2.2 source code is mainly written in Fortran 90, with a few file management routines written in C. Most input and output files use the Hierarchical Data Format 5 (HDF5) format and libraries (The HDF Group, 2016). In addition, the Message Passing Interface (MPI) is highly recommended for regional simulations and is required for simulations coupled with the Brazilian Improvements on Regional Atmospheric Modeling System (BRAMS) atmospheric model (Knox et al., 2015; Swann et al., 2015; Freitas et al., 2017). The source code can be also compiled with shared memory processing (SMP) libraries, which enable parallel processing of thermodynamics and biophysics steps at the patch level and thus allow shorter simulation time.
Code design and parallel structure. ED-2.2 has been designed to be run in three different configurations: (1) as a stand-alone land surface model over a small list of specified locations (sites); (2) as a stand-alone land surface model distributed over a regional grid; (3) coupled with an atmospheric model distributed over a regional grid (e.g., ED-BRAMS; Knox et al., 2015; Swann et al., 2015). For regional stand-alone grids, the model partitions the grid into spatially contiguous tiles of polygons, which access the initial and boundary conditions and are integrated independently of each other but write the results to a unified output file using collective input/output functions from HDF5. In the case of simulations dynamically coupled with an atmospheric model such as BRAMS, polygons are defined to match each atmospheric grid cell.
Memory allocation. The code uses dynamic allocation of variables and extensive use of pointers to efficiently reduce the amount of data transferred between routines. To reduce the output file size, polygon-, site-, patch-, and cohort-level variables are always written as long vectors, and auxiliary index vectors are used to map variables from higher hierarchical levels to lower hierarchical levels (for example, to which patch a cohort-level variable belongs).
2.3 Model inputs
Every ED-2.2 simulation requires an initial state for forest structure and composition (initial state), a description of soil characteristics (edaphic conditions), and a time-varying list of meteorological drivers (atmospheric conditions).
Initial state. To initialize a plant community from inventory data, one must have either the diameter at breast height of every individual or the stem density of different diameter size classes, along with plant functional type identification and location; in addition, necromass from the litter layer, woody debris, and soil organic carbon are needed. Alternatively, initial conditions can be obtained from airborne lidar measurements (Antonarakis et al., 2011, 2014) or a prescribed near-bare-ground condition may be used for long-term spin up simulations. Previous simulations can be used as initial conditions as well.
Edaphic conditions. The user must also provide soil characteristics such as total soil depth, total number of soil layers, the thickness of each layer, as well as soil texture, color, and the bottom soil boundary condition (bedrock, reduced drainage, free drainage, or permanent water table). This flexibility allows the user to easily adjust the soil characteristics according to their regions of interest. Soil texture can be read from standard data sets (e.g., Global Soil Data Task, 2000; Hengl et al., 2017) or provided directly by the user. Soil layers, soil color, and bottom boundary condition must be provided directly by the user as of ED-2.2. In addition, simulations with multiple sites per polygon also need to provide the fractional areas of each site and the mean soil texture class, soil depth, slope, aspect, elevation, and topographic moisture index of each site.
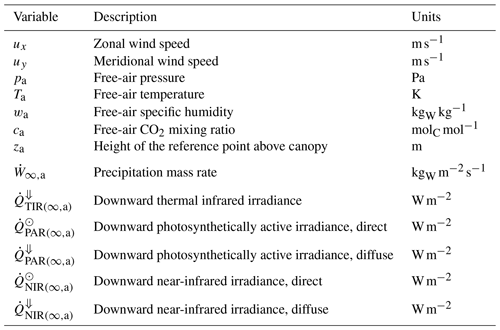
Atmospheric conditions. Meteorological conditions needed to drive ED-2.2 include temperature, specific humidity, CO2 molar fraction, pressure of the air above the canopy, precipitation rate, incoming solar (shortwave) irradiance (radiation flux), and incoming thermal (longwave) irradiance (Table 3) at a reference height that is at least a few meters above the canopy. Subdaily measurements (0.5–6 h) are highly recommended so the model can properly simulate the diurnal cycle and interdiurnal variability. Meteorological drivers can be either at a single location (e.g., eddy covariance towers) or gridded meteorological drivers such as reanalyses (e.g., Dee et al., 2011; Gelaro et al., 2017) or bias-corrected products based on reanalysis (e.g., Sheffield et al., 2006; Weedon et al., 2014). Whenever available, CO2 must be provided at comparable temporal and spatial resolution to other meteorological drivers; otherwise, it is possible to provide spatially homogeneous, time-variant CO2, or constant CO2, although this may increase uncertainties in the model predictions (e.g., Wang et al., 2007). Alternatively, the meteorological forcing (including CO2) may be provided directly by BRAMS (Knox et al., 2015; Swann et al., 2015).
Table 3Atmospheric boundary conditions driving the ED-2.2 model. Variable names and subscripts follow a standard notation throughout the paper (Tables S1 and S2). Flux variables between two thermodynamic systems are defined by a dot and two indices separated by a comma, and they are positive when the net flux goes from the thermodynamic system represented by the first index to the one represented by the second index.
Plant functional types. The user must specify which PFTs are allowed to occur in any given simulation. ED-2.2 has a list of default PFTs, with parameters described in Tables S5–S6. Alternatively, the user can modify the parameters of existing PFTs or define new PFTs through an extensible markup language (XML) file, which is read during the model initialization.
Here, we present the fundamental equations that describe the biogeophysical and biogeochemical cycles. Because the environmental conditions are a function of the local plant community and resources are shared by the individuals, these cycles must be described at the patch level, and the response of the plant community can be aggregated to the polygon level once the cycles are resolved for each patch. In ED-2.2, patches do not exchange enthalpy, water, and carbon dioxide with other patches; thus, patches are treated as independent systems. Throughout this section, we will only refer to the patch and cohort levels, and indices associated with patches, sites, and polygons will be omitted for clarity.
3.1 Definition of the thermodynamic state
Each patch is defined by a thermodynamic envelope (Fig. 2), comprised of multiple thermodynamic systems: each soil layer (total number of layers NG), each temporary surface water or snow layer (total number of layers NS), leaves, and branch wood portion of each cohort (total number of cohorts NT), and the canopy air space. For simplicity, roots are assumed to be in thermal equilibrium with the soil layers and have negligible heat capacity compared to the soil layers. Although patches do not exchange heat and mass with other patches, they are allowed to exchange heat and mass with the free air (i.e., the atmosphere above and outside of the air space control volume we deem as within canopy) and lose water and associated energy through surface and subsurface runoff. We also assume that intensive variables such as pressure and temperature are uniform within each thermodynamic system. Note that free air is not considered a thermodynamic system in ED-2 because the thermodynamic state is determined directly from the boundary conditions and thus external to the model.
Table 4List of state variables solved in ED-2.2. Unless otherwise noted, the reference equation is the ordinary differential equation that defines the rate of change of the thermodynamic state. The list of fluxes that describe the thermodynamic state is presented in Table 5. For a complete list of subscripts and variables used in this paper, refer to Tables S1–S2.
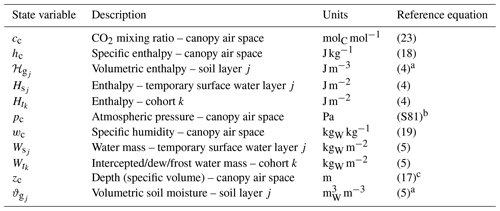
a Budget fluxes are in units of area, and the state variable is updated following the conversion described in Sect. 3.2.1. b Canopy air space pressure is not solved using ordinary differential equations but based on the atmospheric pressure from the meteorological forcing. c Canopy air space depth is determined from vegetation characteristics, not from an ordinary differential equation.
The fundamental equations that describe the system thermodynamics are the first law of thermodynamics in terms of enthalpy H (J m−2), and the mass continuity for incompressible fluids for total water mass W (kgW m−2):
where 𝒱 is the volume of the thermodynamic system and p is the ambient pressure. The components on the right-hand side of Eqs. (4) and (5) depend on the thermodynamic system and will be presented in detail in the following sections. Net heat fluxes () represent changes in enthalpy that are not associated with mass exchange (radiative and sensible heat fluxes), whereas the remaining enthalpy fluxes () correspond to changes in heat capacity due to addition or removal of mass from each thermodynamic system.
The merit of solving the changes in enthalpy over internal energy is that changes in enthalpy are equivalent to the net energy flux when pressure is constant (Eq. 4). Pressure is commonly included in atmospheric measurements, making it easy to track changes in enthalpy not related to energy fluxes. In reality, the only thermodynamic system where the distinction between internal energy and enthalpy matters is the canopy air space. Work associated with thermal expansion of solids and liquids is several orders of magnitude smaller than heat (Dufour and van Mieghem, 1975), and changes in pressure contribute significantly less to enthalpy because the specific volumes of solids and liquids are comparatively small. Likewise, enthalpy fluxes that do not involve gas phase (e.g., canopy dripping and runoff) are nearly indistinguishable from internal energy flux, whereas differences between enthalpy and internal energy fluxes are significant when gas phase is involved (e.g., transpiration and eddy flux). For simplicity, from this point on, we will use the term “enthalpy” whenever internal energy is indistinguishable from enthalpy. The complete list of state variables in ED-2.2 is shown in Table 4.
Variations in enthalpy are more important than their actual values, but they must be consistently defined relative to a pre-determined and known thermodynamic state, at which we define enthalpy to be zero. For any material other than water, enthalpy is defined as zero when the material temperature is 0 K; for water, enthalpy is defined as zero when water is at 0 K and completely frozen. The general definitions of enthalpy and internal energy states used in all thermodynamic systems in ED-2.2 are described in Sect. S5. In ED-2.2, enthalpy is used as the prognostic variable because these are directly and linearly related to the governing ordinary differential equation (Eq. 4). Temperature is diagnostically obtained based on the heat capacity of each thermodynamic system, and the heat capacities of different thermodynamic systems are defined in Sect. S6.
3.2 Heat (), water (), and enthalpy () fluxes
The enthalpy and water cycles for each patch in ED-2.2 are summarized in Fig. 2, and these cycles are solved every thermodynamic substep (ΔtThermo), using a fourth-order Runge–Kutta integrator with dynamic time steps to maintain the error within prescribed tolerance. For all fluxes and variables, we follow the subscript notation described in Table S1, and denote flux variables with a dot and two indices separated by a comma, denoting the systems impacted by the flux. For any variable X that has flux between a system m and a system n, we assume that when the net flux goes from system m to system n, and that . Arrows in Fig. 2 indicate the directions allowed in ED-2.2. The list of fluxes solved in ED-2.2 is provided in Table 5, and a complete list of variables is provided in Table S2. In addition, the values of global constants and global parameters are listed in Tables S3 and S4, respectively, and the default parameters specific for each tropical plant functional type are presented in Tables S5–S6.
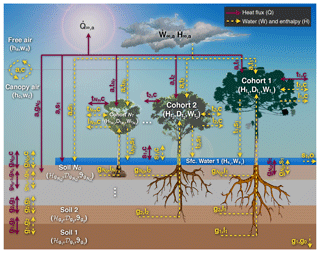
Figure 2Schematic of the fluxes that are solved in ED-2.2 for a single patch (thermodynamic envelope). In this example, the patch has NT cohorts, NG soil layers, and NS=1 temporary surface water. Both NG and the maximum NS are specified by the user; NT is dynamically defined by ED-2.2. Letters near the arrows are the subscripts associated with fluxes, although the flux variables have been omitted here for clarity. Solid red arrows represent heat flux with no exchange of mass, and dashed yellow arrows represent exchange of mass and associated enthalpy. Arrows that point to a single direction represent fluxes that can only go in one (non-negative) direction, and arrows pointing to both directions represent fluxes that can be positive, negative, or zero.
Table 5List of energy, water, and carbon dioxide fluxes that define the thermodynamic state in ED-2.2, along with sections and equations that define them. Fluxes are denoted by a dotted letter, and two subscripts separated with a comma: . Positive fluxes go from thermodynamic system m to thermodynamic system n; negative fluxes go in the opposite direction. Acronyms in the description column: canopy air space (CAS); temporary surface water (TSW). The complete list of subscripts and variables used in this paper is available in Tables S1–S2, and the list of state variables is shown in Table 4.
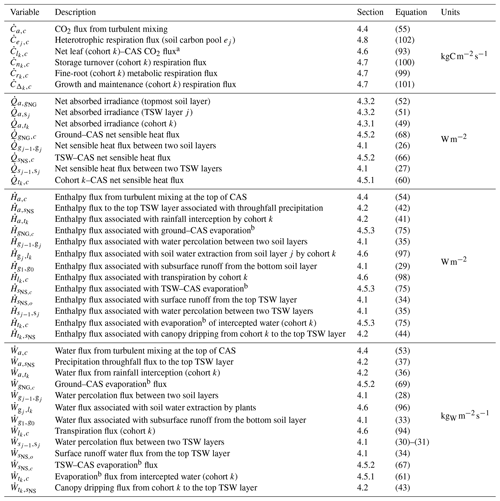
a Net flux between leaf respiration (positive) and gross primary productivity (negative). b When negative, this flux corresponds to dew or frost formation.
3.2.1 Soil
In ED-2.2, the soil characteristics (number of soil layers, thickness of each soil layer and total soil depth, soil texture, soil color) are defined by the user, and assumed constant throughout the simulation. Within each patch, each soil layer (comprised by soil matrix and soil water in each layer) is considered a separate thermodynamic system, with the main size dimension being the layer thickness , with j=1 being the deepest soil layer, and j=NG being the topmost soil layer. Typically, the top layer thickness is set to , which is a compromise between computational efficiency and ability to represent the stronger gradients near the surface, and layers with increasing thickness () are added for the entire rooting zone.
The thermodynamic state is defined in terms of the soil volume: the bulk specific enthalpy (J m−3) and volumetric soil water content (), which can be related to Eqs. (4)–(5) by defining and , where ρℓ is the density of liquid water (Table S3). Soil net fluxes for any layer j are defined as
where is the Kronecker delta for comparing two soil layers gj and (1 if ; 0 otherwise), CAS is the canopy air space, and subscript o denotes the loss through runoff. References in parentheses underneath the terms correspond to the sections in which each term is presented in detail. In the equations above, we assume to be zero (bottom boundary condition in thermal equilibrium) and (; ) to be subsurface runoff fluxes (see Sect. 4.1). In addition, (; ; are equivalent to (; ; ), which are the fluxes between the topmost soil layer and the bottommost temporary surface water layer (see also Sect. 3.2.2).
3.2.2 Temporary surface water (TSW)
Temporary surface water (TSW) exists whenever water falls to the ground, or dew or frost develops on the ground. The layer will be maintained only when the amount of water that reaches the ground exceeds the water holding capacity of the top soil layer (a function of the soil porosity), or when precipitation falls as snow. The maximum number of temporary surface water layers is defined by the user, but the actual number of layers NS and the thickness of each layer depends on the total mass and the water phase, following Walko et al. (2000). When the layer is in liquid phase, only one layer (NS=1) is maintained. If a snowpack develops, the temporary surface water can be divided into several layers (subscript j, with j=1 being the bottommost TSW layer, and j=NS being the topmost TSW layer). Net TSW fluxes are defined as
where is the Kronecker delta for comparing two TSW layers sj and (1 if ; 0 otherwise), CAS is the canopy air space, and subscript o denotes loss from the thermodynamic envelope through runoff. Terms are described in detail in the sections shown underneath each term. Similarly to the soil fluxes (Sect. 3.2.1), we assume that (; ; ) is equivalent to (; ; ), the fluxes between the topmost soil layer and the bottommost TSW layer. When solving Eqs. (9)–(11) for layer , we assume the terms , and to be all zero, as layer NS+1 does not exist.
In the case of liquid TSW, the layer thickness of the single layer is defined as , where ρℓ is the density of liquid water (Table S3). In the case of snowpack development, the snow density and the layer thickness of the TSW are solved as described in Sect. S7. The thickness of each layer of snow () is defined using the same algorithm as LEAF-2 (Walko et al., 2000) and is described in Sect. S7.
3.2.3 Vegetation
In ED-2.2, vegetation is solved as an independent thermodynamic system only if the cohort is sufficiently large. The minimum size is an adjustable parameter and the typical minimum heat capacity solved by ED-2.2 is on the order of and total area index of . Cohorts smaller than this are excluded from all energy and water cycle calculations and assumed to be in thermal equilibrium with canopy air space. The net fluxes of heat, enthalpy, and water for each cohort k that can be resolved are
Each term is described in detail in the sections shown underneath each term on the right-hand side of Eqs. (12)–(14).
3.2.4 Canopy air space (CAS)
The canopy air space is a gas; therefore, extensive properties akin to the other thermodynamic systems are not intuitive because total mass and total volume cannot be directly compared to observations. Therefore, all prognostic and diagnostic variables are solved in the intensive form. Total enthalpy Hc and total water mass Wc of the canopy air space can be written in terms of air density ρc and the equivalent depth of the canopy air space as
where (cm2) and (m) are the basal area and the height of cohort k, respectively; and NT(canopy) is the number of cohorts that are in the canopy, and we assume that cohorts are ordered from tallest to shortest. In the event that the canopy is open, NT(canopy) is the total number of cohorts, and a minimum value of 5 m is imposed when vegetation is absent or too short to prevent numerical instabilities. Because the equivalent canopy depth depends only on the cohort size, is updated at the cohort dynamics step (ΔtCD, Table 2). If we substitute Eqs. (15) and (16) into Eqs. (4) and (5), respectively, and assume that changes in density over short time steps are much smaller than changes in enthalpy or humidity, and then we obtain the following equations for the canopy air space budget:
where
Unlike in the other thermodynamic systems (soil, temporary surface water, and vegetation), the net enthalpy flux of the canopy air space is not exclusively due to associated water flux: the eddy flux between the free air and the canopy air space () includes both water transport and flux associated with mixing of air with different temperatures, and thus enthalpy, between canopy air space and free air.
In addition, we must also track the CAS pressure pc. In ED-2.2, CAS pressure is not solved through a differential equation; instead, pc is updated whenever the meteorological forcing is updated, using the ideal gas law and hydrostatic equilibrium following the method described in Sect. S8. The rate of change of canopy air pressure is then applied in Eq. (18). Likewise, CAS density (ρc) is updated at the end of each thermodynamic step to ensure that the CAS conforms to the ideal gas law.
3.3 Carbon dioxide cycle
In ED-2.2, the carbon dioxide cycle is a subset of the full carbon cycle, which is shown in Fig. 3. The canopy air space is the only thermodynamic system with CO2 storage that is solved by ED-2.2; nonetheless, we assume that the contribution of CO2 to density and heat capacity of the canopy air space is negligible; hence, only the molar CO2 mixing ratio cc (molC mol−1) is traced.
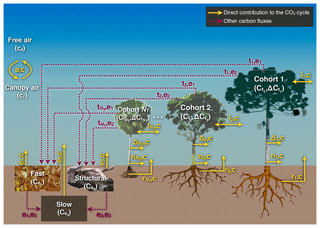
Figure 3Schematic of the patch-level carbon cycle solved in ED-2.2 for a patch containing NT cohorts. Like Fig. 2, letters near the arrows are the subscripts associated with fluxes. Fluxes shown in solid yellow lines are part of the CO2 cycle discussed in this paper, and dashed red lines are part of the carbon cycle but do not directly affect the CO2 flux; these fluxes are summarized in Sects. S3 and S4.
The change in CO2 storage in the canopy air space is determined by the following differential equation:
where ℳd and ℳC are the molar masses of dry air and carbon, respectively, used to convert mass to molar fraction (). The terms on the right-hand side of Eq. (24) are described in detail in the sections displayed underneath each term. The net leaf–CAS flux () for any cohort k is positive when leaf respiration exceeds photosynthetic assimilation. The heterotrophic respiration is based on a simplified implementation of the CENTURY model (Bolker et al., 1998) that combines the decomposition rates from three soil carbon pools, defined by their characteristic lifetime: fast (metabolic litter and microbial; e1), intermediate (structural debris; e2), and slow (humified and passive soil carbon; e3). Note that the soil carbon pools are not directly related to the soil layers used to describe the thermodynamic state (Sect. 3.2.1).
In addition to canopy air space, we also define a virtual cohort pool of carbon corresponding to the accumulated carbon balance (). The accumulated carbon balance links short-term carbon cycle components such as photosynthesis and respiration with long-term dynamics that depend on carbon balance such as such as carbon allocation to growth and reproduction, and mortality (long-term dynamics described in Sect. S3). The accumulated carbon balance is defined by the following equation:
where and are the individual carbon losses caused by leaf shedding and turnover of living tissues that become part of the litter () and structural debris (). The transfer of carbon from plants to the soil carbon pools and between the soil carbon pools does not directly impact the carbon dioxide budget but contributes to the long-term ecosystem carbon stock distribution and carbon balance. These components have been discussed in previous ED and ED-2 publications (Moorcroft et al., 2001; Albani et al., 2006; Medvigy, 2006; Medvigy et al., 2009) and are summarized in Sect. S4.
4.1 Hydrology submodel and ground energy exchange
The ground model encompasses heat, enthalpy, and water fluxes between adjacent layers of soil and temporary surface water, as well as losses of water and enthalpy due to surface runoff and drainage. Fluxes between adjacent layers are positive when they are upwards, and runoff and drainage fluxes are positive or zero.
Sensible heat flux between two adjacent soil or temporary surface water layers j−1 and j is determined from thermal conductivity ΥQ and temperature gradient (Bonan, 2008), with an additional term for temporary surface water to scale the flux when the temporary surface water covers only a fraction fTSW of the ground:
where the operator 〈〉 is the log-linear interpolation from the midpoint height of layers j−1 and j to the height at the interface. The bottom boundary condition of Eq. (26) is . The interface between the top soil layer and the first temporary surface water () is found by applying Eq. (27) with . Soil thermal conductivity depends on soil moisture and texture properties, and the parameterization is described in Sect. S9. Both the fraction of ground covered by the temporary surface water and the thermal conductivity of the temporary surface water are described in Sect. S10.
Soil moisture exchange between layers occurs only if water is in liquid phase. The water flux between soil layers gj−1 and is determined from Darcy's law (Bonan, 2008):
where Ψ is the soil matric potential and ΥΨ is the hydraulic conductivity, both defined after Brooks and Corey (1964), with an additional correction term applied to hydraulic conductivity to reduce conductivity in the event that the soil is partially or completely frozen (Sect. S9). The bottom boundary condition for soil matric potential gradient is .
The term in Eq. (28) is the flux due to gravity, and it is 1 for all layers except the bottom boundary condition, which depends on the subsurface drainage. Subsurface drainage at the bottom boundary depends on the type of drainage and is determined using a slight modification of Eq. (28). Let ð be an angle-like parameter that controls the drainage beneath the deepest soil layer. Because we assume zero gradient in soil matric potential between the deepest soil layer and the boundary condition, the subsurface drainage flux () becomes
Special cases of Eq. (29) are the zero-flow conditions (ð=0) and free drainage ().
For the temporary surface water, water flux between layers through percolation is calculated similarly to LEAF-2 (Walko et al., 2000). Liquid water in excess of 10 % is in principle free to percolate to the layer below, although the maximum percolation of the first surface water layer is limited by the amount of pore space available at the top ground layer:
Surface runoff of liquid water is simulated using a simple extinction function, applied only at the topmost temporary surface water layer:
where tRunoff is a user-defined e-folding decay time, usually on the order of a few minutes to a few hours (Table S4).
In addition to the water fluxes due to subsurface drainage, surface runoff, and the transport of water between layers, we must account for the associated enthalpy fluxes. Enthalpy fluxes due to subsurface drainage and surface runoff are defined based on the water flux and the temperature of the layers where water is lost by applying the definition of enthalpy (Sect. S5):
where qℓ is the specific heat of liquid water (Table S3), and Tℓ0 is defined in Eq. (S53). The enthalpy flux between two adjacent layers is solved similarly, but it must account for the sign of the flux in order to determine the water temperature of the donor layer:
where the subscript xj represents either soil (gj) or temporary surface water (sj).
4.2 Precipitation and vegetation dripping
In ED-2.2, precipitating water from rain and snow increases the water storage of the thermodynamic systems, as rainfall can be intercepted by the canopy or reach the ground. This influx of water also affects the enthalpy storage due to the enthalpy associated with precipitation, although no heat exchange is directly associated with precipitation.
To determine the partitioning of total incoming precipitation () into interception by each cohort () and direct interception by the ground (throughfall, ), we use the fraction of open canopy (𝒪) and the total plant area index of each cohort ():
where is the total plant area index, and being the leaf and wood area indices, both defined from PFT-dependent allometric relations (Sect. S18); is the crown area index of each cohort, also defined in Sect. S18. Throughfall precipitation is always placed on the topmost temporary surface water layer. In the event that no temporary surface water layer exists, a new layer is created, although it may be extinct in the event that all water is able to percolate down to the top soil layer.
Precipitation is a mass flux, but it also has an associated enthalpy flux () that must be partitioned and incorporated into the cohorts and temporary surface water. Similar to the water exchange between soil layers, the enthalpy flux associated with rainfall uses the definition of enthalpy (Sect. S5). Because precipitation temperature is seldom available in meteorological drivers (towers or gridded meteorological forcing data sets), we assume that precipitation temperature is closely associated with the free-air temperature (Ta), and we use Ta to determine whether the precipitation falls as rain, snow, or a mix of both. Importantly, the use of free-air temperature partly accounts for the thermal difference between precipitation temperature and the temperature of intercepted surfaces. Rain is only allowed when Ta is above the water triple point (T3=273.16 K); in this case, the rain temperature is always assumed to be at Ta. Pure snow occurs when the free-air temperature is below T3, and likewise snow temperature is assumed to be Ta. When free-air temperature is only slightly above T3, a mix of rain and snow occurs, with the rain temperature assumed to be Ta and snow temperature assumed to be T3:
where (qi;qℓ) are the specific heats of ice and liquid, respectively, and Tℓ0 is temperature at which supercooled water would have enthalpy equal to zero (Eq. S53). The fraction of precipitation that falls as rain ℓa is based on the Jin et al. (1999) parameterization, slightly modified to make the function continuous:
The enthalpy flux associated with precipitation is then partitioned into canopy interception () and throughfall () using the same scaling factor as in Eqs. (36) and (37):
Leaves and branches can accumulate only a finite amount of water on their surfaces, proportional to their total area. When incoming precipitation rates are too high (or more rarely when dew or frost formation is excessive), any water amount that exceeds the holding capacity is lost to the ground as canopy dripping. Similarly to incoming precipitation, the excess water lost through dripping also has an associated enthalpy that must be taken into account, although dripping has no associated heat flux. The canopy dripping fluxes of water () and the associated enthalpy () are defined such that the leaves and branches lose the excess water within one time step:
where is the liquid fraction of surface water on top of cohort k and is the cohort holding capacity, which is an adjustable parameter (Table S4) but is typically of the order of (Wohlfahrt et al., 2006).
4.3 Radiation model
The radiation budget is solved using a multi-layer version of the two-stream model (Sellers, 1985; Liou, 2002; Medvigy, 2006) applied to three broad spectral bands: photosynthetically active radiation (PAR, wavelengths between 0.4 and 0.7 µm), near-infrared radiation (NIR, wavelengths between 0.7 and 3.0 µm) and thermal infrared radiation (TIR, wavelengths between 3.0 and 15 µm).
4.3.1 Canopy radiation profile
For each spectral band m, the canopy radiation scheme assumes that each cohort corresponds to one layer of vegetation within the canopy, and within each layer the optical and thermal properties are assumed constant. For all bands, the top boundary condition for each band is provided by the meteorological forcing (Table 3). In the cases of PAR (m=1) and NIR (m=2), the downward irradiance is comprised of a beam (direct) and isotropic (diffuse) components, whereas TIR irradiance (m=3) is assumed to be all diffuse. Direct irradiance that is intercepted by the cohorts can be either backscattered or forward-scattered as diffuse radiation, and direct radiation reflected by the ground is assumed to be entirely diffuse.
Following Sellers (1985), the extinction of downward direct irradiance and the two-stream model for hemispheric diffuse irradiance for each of the spectral bands () is given by
where index corresponds to each cohort k or its lower interface (Fig. 4); interface NT+1 is immediately above the tallest cohort; is the downward direct irradiance incident at interface k; ( and ) are the downward and upward (hemispheric) diffuse irradiance incident at interface k; ςmk is the scattering coefficient, and thus (1−ςmk) is the absorptivity; and βmk are the backscattered fraction of scattered direct and diffuse irradiance, respectively; is the effective cumulative plant area index, assumed zero at the top of each layer, and increasing downwards ( is the total for layer k); and are the inverse of the optical depth per unit of effective plant area index for direct and diffuse radiation, respectively; and is the irradiance emitted by a black body at the same temperature as the cohort ().
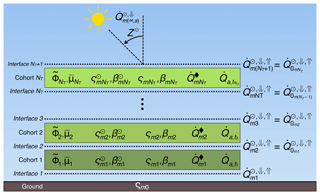
Figure 4Schematic of the radiation module for a patch with NT cohorts, showing the grid arrangement of the irradiance profiles relative to the cohort positions. Index k corresponds to each cohort, or, in the case of , the interface beneath each cohort; m corresponds to each spectral band; are the incoming direct and diffuse irradiance (Table 3); Z⊙ is the Sun's zenith angle; are the downward direct, downward diffuse, and upward diffuse irradiance (Eqs. 45–47); is the effective plant area index (Eq. S100); (ςmk;βmk) are the scattering coefficients and the backscattering fraction for diffuse irradiance (Eqs. S101, S102); are the scattering coefficients and the backscattering fraction for direct irradiance (Eqs. S104–S105); is the black-body irradiance (Eq. 48); and is the net absorbed irradiance (Eq. 49).
Equations (45)–(47) simplify for each spectral band. First, for the TIR (m=3) band, because we assume that all incoming TIR irradiance is diffuse. Likewise, the black-body emission for the PAR (m=1) and NIR (m=2) bands, because thermal emission is negligible at these wavelengths. The black-body emission for the TIR band is defined as
where σSB is the Stefan–Boltzmann constant (Table S3). Note that for emission of TIR radiation (Eqs. 45–47), we assume that emissivity is the same as absorptivity (Kirchhoff's law; Liou, 2002) and hence the (1−ς) term.
The effective plant area index is the total area (leaves and branches) that is corrected to account for that leaves are not uniformly distributed in the layer. It is defined as , where is the PFT-dependent clumping index (Chen and Black, 1992, default values in Tables S5–S6), is the leaf area index, and is the wood area index. is assumed zero at the top of each layer, increasing downwards.
The optical properties of the leaf layers – optical depth and scattering parameters for direct and diffuse radiation for each of the three spectral bands – are assumed constant within each layer. These properties are determined from PFT-dependent characteristics such as mean orientation factor, spectral-band-dependent reflectivity, transmissivity, and emissivity (Sect. S11). Because the properties are constant within each layer, it is possible to analytically solve the full profile of both direct and diffuse radiation using the solver described in Sect. S12.
Once the profiles of , and are determined, we obtain the irradiance that is absorbed by each cohort :
This term is then used in the enthalpy budget of each cohort (Eqs. 4 and 12).
4.3.2 Ground radiation
The ground radiation submodel determines the irradiance emitted by the ground surface and the profile of irradiance through the temporary surface water layers and top soil layer. Note that the ground radiation and the canopy radiation model are interdependent: the incoming radiation at the top ground layer is determined from the canopy radiation model, and the ground scattering coefficient (ςm0; see Sect. S11) is needed for the canopy radiation bottom boundary condition (Sect. S12). However, since the scattering coefficient does not depend on the total incoming radiation, the irradiance profile can be solved for a standardized amount of incoming radiation, and once the downward radiation at the bottom of the canopy has been calculated, the absorbed irradiance for each layer can be scaled appropriately.
Black-body emission from the ground () is calculated as an area-weighted average of the emissivities of exposed soil and temporary surface water:
where (1−ς3g) and (1−ς3s), are, respectively, the thermal-infrared emissivities of the top soil layer and the temporary surface water (Table S4), and fTSW is the fraction of ground covered by temporary surface water. In ED-2.2, the soil and snow scattering coefficients for the TIR band are assumed constant (Table S4), following Walko et al. (2000).
Once the irradiance profile for the canopy is determined from Eqs. (45) to (47), the irradiance absorbed by each temporary surface water layer () is calculated by integrating the transmissivity profile for each layer, starting from the top layer:
where is the inverse of the optical depth of temporary surface water.
The irradiance absorbed by the ground is a combination of irradiance of exposed soil and irradiance that is transmitted through all temporary surface water layers and the net absorption of longwave radiation:
4.4 Surface layer model
The surface layer model determines the fluxes of enthalpy, water, and carbon dioxide between the canopy air space and the free air above. It is based on the Monin–Obukhov similarity theory (Monin and Obukhov, 1954; Foken, 2006), which has been widely used by biosphere–atmosphere models representing a variety of biomes (e.g., Walko et al., 2000; Best et al., 2011; Oleson et al., 2013), although this is often an extrapolation of the theory that was not originally developed for heterogeneous vegetation or tall vegetation (Foken, 2006).
In order to obtain the fluxes, we assume that the eddy diffusivity of buoyancy is the same as the diffusivity of enthalpy, water vapor, and CO2. This assumption allows us to define a single canopy conductance Gc for the three variables, following the algorithm described in Sects. S13 and S14.1. We then obtain the following equations for fluxes between canopy air space and the free atmosphere:
where is the equivalent enthalpy of air at reference height za when the air is adiabatically moved to the top of the canopy air space, using the definition of potential temperature:
where p0 is the reference pressure, ℛ is the universal gas constant, qpd is the specific heat of dry air at constant pressure, and ℳd is the molar mass of dry air (Table S3).
Sensible heat flux between the free atmosphere and canopy air space () can be derived from the definition of enthalpy and enthalpy flux (Eqs. S50 and 54), although it is not directly applied to the energy balance in the canopy air space ( is used instead):
4.5 Heat and water exchange between surfaces and canopy air space
4.5.1 Leaves and branches
Fluxes of sensible heat () and water vapor () between the leaf surface and wood surface and the canopy air space follow the same principle of conductance and gradient that define the eddy fluxes between the free atmosphere and canopy air space (Eqs. 53, 54). Throughout this section, we use subscripts λk and βk to denote leaf and wood boundary layers of cohort k, respectively; the different subscripts are needed to differentiate fluxes coming from the leaves' intercellular space (e.g., transpiration; see also Sect. 4.6). Let (m s−1) and (m s−1) be the conductances of heat and water between the leaf boundary layer of cohort k and the canopy air space, and and be the wood boundary layer counterparts. The surface sensible heat and surface water vapor fluxes are
where () are the leaf surface and branch surface heat and water fluxes by unit of leaf and branch area, respectively; the factors 2 and π in Eq. (60) mean that sensible heat is exchanged on both sides of the leaves and on the longitudinal area of the branches, which are assumed cylindrical. Intercepted water and dew and frost formation is allowed only on one side of the leaves, and an area equivalent to a one-sided flat plate for branches, and therefore only the leaf and wood area indices are used in Eq. (61). Canopy air space temperature, specific humidity, density, and specific heat, leaf temperature, and wood temperature are determined diagnostically. We also assume surface temperature of leaves and branches to be the same as their internal temperatures (i.e., and ). Specific humidity at the leaf surface and branch surface are assumed to be the saturation specific humidity wSat (Sect. S15).
Heat conductance for leaves and branches is based on the convective heat transfer, as described in Sect. S14.2. Further description of the theory can be found in Monteith and Unsworth (2008, Sect. 10.1).
4.5.2 Temporary surface water and soil
Sensible heat and water fluxes between the temporary surface water and soil and the canopy air space are calculated similarly to leaves and branches. Surface conductance GSfc is assumed to be the same for both heat and water, and also the same for soil and temporary surface water:
Specific humidity for temporary surface water is computed exactly as leaves and branches, (Sect. S15). For soils, the specific humidity also accounts for the soil moisture and the sign of the flux, using a method similar to Avissar and Mahrer (1988):
where g is the gravity acceleration, ℳw is the water molar mass, and ℛ is the universal gas constant (Table S3); , , and are the temperature, soil moisture, and soil matric potential of the topmost soil layer, respectively; and ϑFc and ϑRe are the soil moisture at field capacity and the residual soil moisture, respectively. The exponential term in Eq. (70) corresponds to the soil pore relative humidity derived from the Kelvin equation (Philip, 1957), and sg is the soil wetness function, which takes a similar functional form as the relative humidity term from Noilhan and Planton (1989) and the β term from Lee and Pielke (1992). The total resistance between the surface and the canopy air space is a combination of the resistance if the surface was bare, plus the resistance due to the vegetation, as described in Sect. S14.3.
4.5.3 Enthalpy flux due to evaporation and condensation
Dew and frost are formed when water in the canopy air space condenses or freezes on any surface (leaves, branches, or ground); likewise, water that evaporates and ice that sublimates from these surfaces immediately become part of the canopy air space. In terms of energy transfer, two processes occur, the phase change and the mass exchange, and both must be accounted for the enthalpy flux. Phase change depends on the specific latent heat of vaporization (llv) and sublimation (liv), which are linear functions of temperature, based on Eqs. (S48) and (S49):
where llv3 and liv3 are the specific latent heats of vaporization and sublimation at the water triple point (T3), qpv is the specific heat of water vapor at constant pressure, and qi and qℓ are the specific heats of ice and liquid water, respectively (Table S3). The temperature for phase change must be the surface temperature because this is where the phase change occurs. In the most generic case, if a surface x at temperature Tx has a liquid water fraction ℓx, the total enthalpy flux between the surface and canopy air space associated with the water flux Wx,c is
By using the definitions from Eq. (S54), Eq. (74) can be further simplified to
which is consistent with the exchange of pure water vapor and enthalpy between the thermodynamic systems. Equation (75) is used to determine , , and .
4.6 Leaf physiology
In ED-2.2, leaf physiology is modeled following Farquhar et al. (1980) and Collatz et al. (1991) for C3 plants; Collatz et al. (1992) for C4 plants; and the Leuning (1995) model for stomatal conductance. This submodel ultimately determines the net leaf-level CO2 uptake rate of each cohort k (, ), controlled exclusively by the leaf environment, and the corresponding water loss through transpiration (, ).
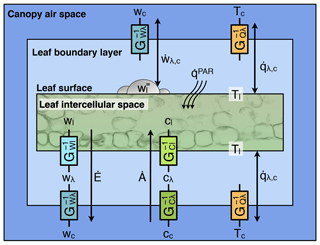
Figure 5Schematic of fluxes between a leaf and the surrounding canopy air space for a hypostomatous plant during the photo period, as represented in ED-2.2. Conductances are represented by the resistances between the different environments (G−1). Leaf-level sensible heat flux (; Eq. 60) and leaf-level vapor flux between intercepted water and canopy air space (; Eq. 61) are also shown for comparison. Cohort index k is omitted from the figure for clarity.
The exchange of water and CO2 between the leaf intercellular space and the canopy air space is mediated by the stomata and the leaf boundary layer, which imposes an additional resistance to fluxes of these substances. For simplicity, we assume that the leaf boundary layer air has low storage capacity, and thus the fluxes of any substance (water or CO2) entering and exiting the boundary layer must be the same. Fluxes of water and carbon between the leaf intercellular space and the canopy air space must overcome both the stomatal resistance and the boundary layer resistance, whereas sensible heat flux and water flux from leaf surface water must overcome the boundary layer resistance only (Fig. 5). When soil moisture is not a limiting factor, the fluxes of CO2 and water can be written as
where
and
and
where and (units m s−1) are the leaf boundary layer and stomatal conductances for element X (either water W or carbon C), respectively; and are the CO2 mixing ratio and the specific humidity of the leaf boundary layer, respectively; and are the CO2 and specific humidity of the leaf intercellular space, respectively; ℳd is the molar mass of dry air; and ρc is the air density. As stated in Eq. (78), we assume the leaf intercellular space to be at water vapor saturation. The leaf boundary layer conductances are obtained following the algorithm shown in Sect. S14.2. The net CO2 assimilation flux and stomatal conductances are described below.
From Farquhar et al. (1980), the net CO2 assimilation flux is defined as
Oxygenation releases 0.5 for every , hence the half multiplier, and it is related to carboxylation by means of the CO2 compensation point Γk (Lambers et al., 2008):
where is the CO2 mixing ratio in the leaf intercellular space. The CO2 compensation point is determined after Collatz et al. (1991, 1992):
where o⊕ is the reference O2 mixing ratio (Table S3), and ϖ represents the ratio between the rates of carboxylase to oxygenase and is a function of temperature. The general form of the function 𝒯 describing the metabolic dependence upon temperature for any variable x (including ϖ) is
where x15 is the value of variable x at temperature T15=288.15 K (15 ∘C), and is the parameter which describes temperature dependence (Table S4).
Because C4 plants have a mechanism to concentrate CO2 near the CO2-fixing enzyme RuBisCO (ribulose-1,5-biphosphate carboxylase oxygenase), photorespiration is nearly nonexistent in C4 plants (Lambers et al., 2008) and hence the assumption that Γk is zero. For C4 plants, the carboxylation rate under ribulose-1,5-biphosphate (RuBP) saturated conditions becomes the maximum capacity of RuBisCO to perform the carboxylase function (). For C3, this rate is unattainable even under RuBP-saturated conditions because carboxylation and oxygenation are mutually inhibitive reactions (Lambers et al., 2008). Therefore, the maximum attainable carboxylation () is expressed by a modified Michaelis–Menten kinetics equation:
where is the effective Michaelis constant, and and are the Michaelis constants for carboxylation and oxygenation, respectively. Both and are dependent on temperature, following Eq. (84) (default parameters in Table S4), whereas follows a modified temperature-dependent function to account for the fast decline of both productivity and respiration at low and high temperatures (Sellers et al., 1996; Moorcroft et al., 2001):
where fCold, fHot, TCold, and THot are PFT-dependent phenomenological parameters to reduce the function value at low and high temperatures (Tables S5–S6).
The original expression for the initial slope of the carboxylation rate under near-zero CO2 () for C4 plants by Collatz et al. (1992) has been modified later (e.g., Foley et al., 1996) to explicitly include ; this is the same expression used in ED-2.2:
where kPEP represents the initial slope of the response curve to increasing CO2; the default value in ED-2.2 (Table S4) is the same value used by Foley et al. (1996).
From the total photosynthetically active irradiance absorbed by the cohort (Eq. 49), we define the photon flux that is absorbed by the leaf ():
where Ein is the average photon-specific energy in the PAR band (0.4–0.7 µm; Table S3). Even though a high fraction of the absorbed irradiance is used to transport electrons needed by the light reactions of photosynthesis (Lambers et al., 2008), only a fraction of the irradiance absorbed by the leaf is absorbed by the chlorophyll; in addition, the number electrons needed by each carboxylation and oxygenation reaction poses an additional restriction to the total carboxylation rate. The product of these three factors is combined into a single scaling factor for total absorbed PAR, the quantum yield (ϵk), which is a PFT-dependent property in ED-2.2 (Tables S5–S6). The maximum carboxylation rate under light limitation is
Carboxylation may also be limited by the export rate of starch and sucrose that is synthesized by triose phosphate, especially when CO2 concentration and irradiance are simultaneously high, at low temperatures, or O2 concentration is low (von Caemmerer, 2000; Lombardozzi et al., 2018). This limitation is not included in ED-2.2.
The leaf respiration term comprises all leaf respiration terms that are not dependent on photosynthesis, and is primarily constituted of mitochondrial respiration; it is currently represented as a function of the maximum carboxylation rate, following Foley et al. (1996):
where fR is a PFT-dependent parameter (Tables S5–S6).
A plant's stomatal conductance is a result of a trade-off between the amount of carbon that leaves uptake and the amount of water that they lose. Leuning (1995) proposed a semi-empirical stomatal conductance expression for water based on these trade-offs:
where is the residual conductance when stomata are closed, Mk is the slope of the stomatal conductance function, and Δwk is an empirical coefficient controlling conductance under severe leaf-level water deficit; , Mk, and Δwk are PFT-dependent parameters (Tables S5–S6). From Cowan and Troughton (1971), stomatal conductance of CO2 is estimated by the ratio fGl between the diffusivities of water and CO2 in the air (Table S4):
Variables , , , ϖk, , , Γk, and are functions of leaf temperature and canopy air space pressure and thus can be determined directly. In contrast, nine variables are unknown for each limitation case, namely the RuBP-saturated (Eq. 85), CO2-limited (Eq. 87), and light-limited (Eq. 89) variables, as well as for the case when the stomata are closed (Eq. 91 for when ): , , , , , , , , and . These are determined numerically for each limiting case, and the value of is taken to be the limiting case that yields the lowest , following the algorithm described in Sect. S16.
The stomatal conductance model by Leuning (1995) (Eq. 91) is regulated by leaf vapor pressure deficit. However, Eqs. (76) and (77) do not account for soil moisture limitation of photosynthesis. To represent this effect, we define a soil-moisture-dependent scaling factor (; Sect. S17) to reduce productivity and transpiration as soil available water decreases. Because stomatal conductance cannot be zero, the scaling factor interpolates between the fully closed case () and the solution without soil moisture limitation (), yielding to the actual fluxes of CO2 (, ) and water (, ):
where þk is 1 if the PFT is hypostomatous or 2 if the PFT is amphistomatous or needleleaf (Tables S5–S6). Alternatively, Xu et al. (2016) implemented a process-based plant hydraulics scheme that solves the soil–stem–leaf water flow in ED-2.2; details of this implementation are available in the above-mentioned paper.
For simplicity, we assume that the water content in the leaf intercellular space and the plant vascular system is constant; therefore, the amount of water lost by the intercellular space through transpiration always matches the amount of water absorbed by roots. Plants may extract water from all layers to which they have access, and the amount of water extracted from each layer is proportional to the available water in the layer relative to the total available water ():
where is defined following Sect. S17 and . The net water flux in the leaf intercellular space due to transpiration is assumed to be zero; however, the associated net energy flux is not: water enters the leaf intercellular space as liquid water at the soil temperature, reaches thermal equilibrium with leaves, and is lost to the canopy air space as water vapor at the leaf temperature. Therefore, the enthalpy flux between the soil layers and the cohort () is calculated in a similar manner to Eq. (35), whereas the enthalpy flux between the leaf intercellular space and the canopy air space () is solved in a similar manner to Eq. (75):
4.7 Non-leaf autotrophic respiration
Respiration from fine roots is defined using a phenomenological function of temperature that has the same functional form as leaf respiration (Moorcroft et al., 2001). Because roots are allowed in multiple layers, and in ED-2.2 roots have a uniform distribution of mass throughout the profile, the total respiration (: ) is the integral of the contribution from each soil layer, weighted by the layer thickness:
where (s−1) is the PFT-dependent factor that describes the relative metabolic activity of fine roots at the reference temperature (15 ∘C) (Tables S5–S6), and 𝒯′ is the same temperature-dependent function from Eq. (86); default parameters are listed in Tables S5–S6.
Plants have two additional respiration terms: a phenomenological term that represents the long-term turnover rate of the accumulated storage pool (), assumed constant (Medvigy et al., 2009), and a term related to the losses associated with the assimilated carbon for growth and maintenance of the living tissues (; Amthor, 1984). The latter term is a function of the plant metabolic rate, which has strong daily variability and hence is a function of the daily carbon balance:
where are the PFT-dependent decay rates associated with storage turnover and consumption for growth, respectively (Tables S5–S6); and (kgC m−2) is the total accumulated carbon from the previous day as defined in Eq. (25). The transport from non-structural storage and the accumulated carbon for maintenance, growth, and storage is summarized in Sect. S3.
4.8 Heterotrophic respiration
Heterotrophic respiration comes from the decomposition of carbon in the three soil/litter carbon pools. For each carbon pool , we determine the maximum carbon loss based on the characteristic decay rate, which corresponds to the typical half-life for metabolic and microbial litter (fast, e1), structural litter (intermediate, e2), and humified and passive soil carbon (slow, e3), determined from Bolker et al. (1998):
where fhe is the fraction of decay that is lost through respiration (Table S4), and by definition must always be 1 (slow soil carbon can only be lost through heterotrophic respiration); is the decay rates at optimal conditions of soil carbon ej, based on Bolker et al. (1998) (Table S4); and are the average temperature and relative soil moisture of the top 0.2 m of soil; the relative soil moisture for each layer is defined as
and and are functions that reduces the decomposition rate due to temperature or soil moisture under non-optimal conditions:
where (;), (;), (;), and (;) are phenomenological parameters to decrease decomposition rates at low and high temperatures, and dry and saturated soils, respectively (Table S4). The decay fraction from fast and structural soil carbon that is not lost through heterotrophic respiration is transported to the slow soil carbon (Sect. S4).
5.1 Conservation of energy, water, and carbon dioxide
The ED-2.2 simulations show a high degree of conservation of the total energy, water, and carbon (Fig. 6). In the example simulation for one patch at Paracou, French Guiana (GYF), a tropical forest site, the accumulated deviation from perfect closure (residual) of the energy budget over 50 years (2 629 800 time steps) was 0.1 % of the total enthalpy storage – sum of enthalpy stored at the canopy air space, cohorts, temporary surface water and soil layers, (Fig. 6a) and 0.002 % of the accumulated losses through eddy flux, the largest cumulative flux of enthalpy. Results for the water budget were even better, with maximum accumulated residuals of 0.04 % of the total water stored in the ED-2.2 thermodynamic systems, or 0.0006 % of the total water input by precipitation (Fig. 6b), and the accumulated residual of carbon was 0.008 % of the total carbon storage or 0.017 % the total accumulated loss through eddy flux. The average absolute residual errors by time step, relative to the total storage, ranged from (carbon) to (energy) and were thus orders of magnitude less than the truncation error of single-precision numbers () and the model tolerance for each time step ().
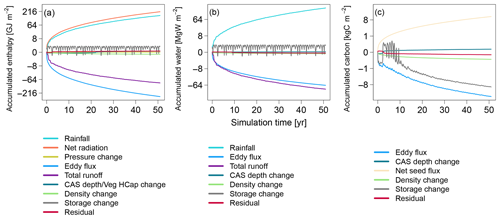
Figure 6Examples of (a) enthalpy, (b) water, and (c) carbon conservation assessment in ED-2.2, for a single-patch simulation at GYF for 50 years. Terms are presented as the cumulative contribution to the change storage. Total storage is the combination of canopy air space, cohorts, and temporary surface water and soil layers in the cases of enthalpy and water, and canopy air space, cohorts, seed bank, and soil carbon pools in the case of carbon. Positive (negative) values mean accumulation (loss) by the combined storage pool over the time. Pressure change accounts for changes in enthalpy when pressure from the meteorological forcing is updated, and density change accounts for changes in mass to ensure the ideal gas law. CAS change and vegetation heat capacity (Veg Hcap) change reflect the addition/subtraction of carbon, water, and enthalpy due to the vegetation dynamics modifying the canopy air space depth and the total heat capacity of the vegetation due to biomass accumulation or loss. Storage change is the net gain or loss of total storage, and the residual corresponds to the deviation from the perfect closure. Note that we present the y axis in cube root scale to improve visualization of the smallest terms.
The conservation of energy and water of ED-2.2 also represents a substantial improvement from previous versions of the model. We carried out additional decade-long simulations with ED-2.2 and two former versions of the model (ED-2.0.12 and ED-2.1) and the most similar configuration possible among versions, and found that cumulative residual of enthalpy relative to eddy flux loss decreased from 15.2 % (ED-2.0.12) or 5.7 % (ED-2.1) to 6.1 % × 10−5 % (ED-2.2) (Fig. S3a–c). Similarly, the cumulative violation of perfect water budget closure, relative to total precipitation input, decreased from 3.4 % (ED-2.0.12) or 1.1 % (ED-2.1) to 1.2 % × 10−4 % (ED-2.2) (Fig. S3d–f).
5.2 Simulated ecosystem heterogeneity
Because ED-2.2 accounts for the vertical distribution of the plant community and the local heterogeneity of ecosystems, it is possible to describe the structural variability of ecosystems using continuous metrics. To illustrate this, we show the results of a 600-year simulation (1400–2002) carried out for tropical South America, starting from near-bare-ground conditions and driven by the Princeton Global Meteorological Forcing (Sheffield et al., 2006, 1969–2008), and with active fires (Sect. S3.4). For the last 100 years, we also prescribed land use changes derived from Hurtt et al. (2006) and Soares-Filho et al. (2006). The distribution of basal area binned by diameter at breast height (DBH) classes shows high variability across the domain and even within biome boundaries (Fig. 7). For example, larger trees (DBH≥50 cm) are nearly absent outside the Amazon biome, with the exception of more humid regions such as the Atlantic forest along the Brazilian coast, western Colombia, and Panama (Fig. 7d,e). In contrast, in seasonally dry areas such as the Brazilian Cerrado, intermediate-sized trees () contribute the most to the basal area (e.g., areas near the Brasília (BSB) site; Fig. 7b, c). Even within the Amazon ecoregion, basal area shows variability in the contribution of trees with different sizes, including the areas outside the arc of deforestation along the southern and eastern edges of the biome (Fig. 7). Similarly, the abundance of different plant functional groups shows great variability across the region, with dominance of grasses and early successional tropical trees in deforested regions and in drier areas in the Brazilian Cerrado, whereas late-successional tropical trees dominate the tropical forests, albeit with lower dominance in parts of central Amazonia (Fig. S4).
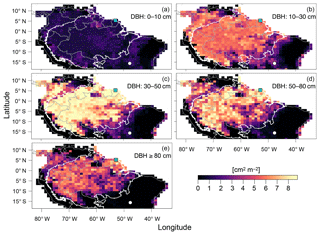
Figure 7Simulated distribution of size-dependent basal area across tropical South America, aggregated for the following diameter at breast height (DBH) bins: (a) 0–10 cm; (b) 10–30 cm; (c) 30–50 cm; (d) 50–80 cm; (e) ≥80 cm. Maps were obtained from the final state of a 6000-year simulation (1400–2002), initialized with near-bare-ground conditions, active fires, and prescribed land use changes between 1900 and 2002. Points indicate the location of the example sites (Fig. 8): (□) Paracou (GYF), a tropical forest site; (◦) Brasília (BSB), a woody savanna site. White contour is the domain of the Amazon biome, and grey contours are the political borders.
The variability of forest structural and functional composition observed in regional simulations emerges from both the competition among cohorts in the local micro-environment and the environmental controls on the disturbance regime. In Fig. 8, we present the impact of different disturbance regimes modulating the predicted ecosystem structure and composition for two sites: Paracou (GYF), a tropical forest region in French Guiana, and Brasília (BSB), a woody savanna site in central Brazil. Both sites were simulated for 500 years using a 40-year meteorological forcing developed from local meteorological observations, following the methodology described in Longo et al. (2018); we allowed fires to occur but for simplicity we did not prescribe land use change. After 500 years of simulation, the structure at the two sites is completely different, with large, late-successional trees dominating the canopy at GYF (Fig. 8a) and open areas with shorter, mostly early successional trees dominating the landscape at BSB (Fig. 8b). For GYF, the structural and functional composition is achieved only after 200 years of simulation, whereas in BSB a dynamic steady state caused by the strong fire regime is achieved in about 100 years (Fig. S5). At both sites, early successional trees dominate the canopy at recently disturbed areas (Fig. 8c, d) with late-successional (GYF) or mid-successional trees (BSB) increasing in size only at the older patches (> 30 years, Fig. 8c, d), and the variation of basal area as a function of age since last disturbance show great similarity at both sites (Fig. 8e). However, the disturbance regimes are markedly different: at GYF, fires never occurred and disturbance was driven exclusively by tree fall (prescribed at 1.11 % year−1), whereas fires substantially increase the disturbance rates at BSB (average fire return interval of 19.3 years). Consequently, old-growth patches (older than 100 years) are nonexistent at BSB and abundant at GYF (Fig. 8f). In addition, the high disturbance regime at BSB meant that large trees and late-successional trees (slow growers) failed to establish but succeeded and maintained a stable population at GYF (Fig. S5).
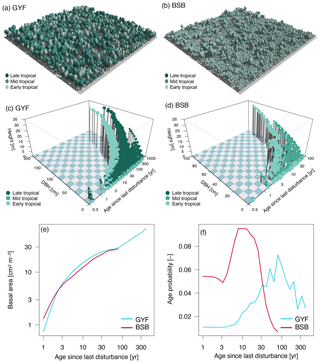
Figure 8Examples of size, age, and functional structure simulated by ED-2.2, after 500 years of simulation using local meteorological forcing and active fires. (a, b) Individual realization of simulated stands for sites (a) Paracou (GYF, tropical forest); (b) Brasília (BSB, woody savanna). The number of individuals shown is proportional to the simulated stem density, the distribution in local communities is proportional to the patch area, the crown size and stem height are proportional to the cohort size, and the crown color indicates the functional group. (c, d) Distribution of cohorts as a function of size (DBH and height) and age since last disturbance (patch age) for sites (c) GYF and (d) BSB. Crown sizes are proportional to the logarithm of the stem density within each patch. (e, f) Patch-specific properties as a function of age since last disturbance (patch age) for sites GYF and BSB after 500 years of simulation: (e) basal area and (f) probability density function of patch age (fractional patch area). See Fig. 7 for the location of both example sites.
The impacts of simulating structurally and functionally diverse ecosystems are also observed in the fluxes of energy, water, carbon, and momentum. For example, in Fig. 9, we show the monthly average fluxes from the last 40 years of simulation at GYF, along with the interannual variability of the fluxes aggregated to the polygon level (hereafter polygon variability; error bars) and the interannual variability of the fluxes accounting for the patch probability (hereafter patch variability; colors in the background). The polygon-level variability can be thought as the variability attributable exclusively to climate variability, whereas the patch variability also incorporates the impact of the structural heterogeneity in the variability. Most highly aggregated (“big-leaf”) models characterize the polygon-level variability but not the patch variability. However, in all cases, the patch variability greatly exceeded the polygon variability, indicating that structural variability is as important as the interannual variability in complex ecosystems. In the case of sensible heat, the polygon variable was between 39 % and 64 % of the patch variability (Fig. 9a). The polygon-to-patch variability ratio was similar for both friction velocity (19 %–39 %) and water fluxes (17 %–44 %) (Fig. 9b, c). In the case of gross primary productivity, the relevance of patch variability was even higher, with the polygon-to-patch variability ratio ranging from 3.7 % during the dry season to 17 % during the wet season (Fig. 9d). Importantly, the broader range of fluxes across patches in the site can be entirely attributed to structural and functional diversity, because all patches were driven by the same meteorological forcing.
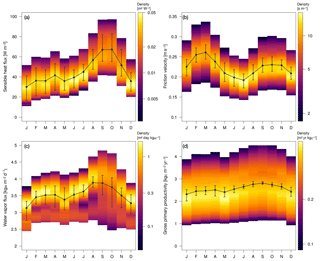
Figure 9Monthly averages and variability of fluxes attributable to meteorological conditions and plant community heterogeneity combined with interannual variability. Results are shown for GYF, a tropical forest site, for (a) sensible heat flux; (b) friction velocity (momentum flux); (c) water vapor flux; and (d) gross primary productivity. The variability was calculated for the last 40 years of a 500-year simulation starting from near-bare ground. Points correspond to the 40-year monthly averages for the entire polygon, line bars correspond to the 2.5 %–97.5 % quantile of monthly averages aggregated at the polygon level (polygon interannual variability), and background colors represent the 40-year probability density function of monthly means for each simulated patch, and scaled by the area of each patch (patch interannual variability). Density function colors outside the 2.5 %–97.5 % quantile interval are not shown. Note that the density function scale is logarithmic. See Fig. 7 for the location of the example site.
6.1 Conservation of biophysical and biogeochemical properties
As demonstrated in Sect. 5.1, it is possible to represent the long-term, large-scale dynamics of heterogeneous and functionally diverse plant canopy, while still accurately conserving the fluxes of carbon, water, and energy fluxes that occur in the ecosystem. ED-2.2 exhibits excellent conservation of energy, water, and carbon dioxide even in multi-decadal scales. After 50 years of simulation, the accumulated residuals from perfect closure never exceeded 0.1 % of the total energy, water, and carbon stored in the pools resolved by the model (Fig. 6), which is significantly less than the error accepted in each time step (1 %).
The model's excellent conservation of these three key properties is possible because the ordinary differential equations are written directly in terms of the variables that we sought to conserve, thus reducing the effects of non-linearities. A key feature that facilitates the model's high level of energy conservation is the use of enthalpy as the primary energy-related state variable within the model. This contrasts with most terrestrial biosphere models, which use temperature as their energy state variable (e.g., Best et al., 2011; Oleson et al., 2013). By using enthalpy, the model can seamlessly incorporate energy storage changes caused by rapid changes in water content and consequently heat capacity. It also reduces errors near phase changes (freezing or melting), when changes in energy may not correspond to changes in temperature. Nonetheless, the residual errors in ED-2.2 are larger than the error of each time step after integrating the model over multiple decades (Fig. 6), which suggests that the errors may have a systematic component that deserves further investigation. The main contribution to the remaining residual errors in carbon, water, and energy fluxes comes from the linearization of the prognostic equations due to changes in density in the canopy air space (Eqs. 18–19; 23). The magnitude of these residuals would likely be further reduced by using the bulk enthalpy, water content, and carbon dioxide content in the canopy air space as the state variables instead of the specific enthalpy, specific humidity, and CO2 mixing ratio.
Unlike most existing terrestrial biosphere models (but see SiB2, e.g., Baker et al., 2003; Vidale and Stöckli, 2005), in ED-2.2, we explicitly include the dynamic storage of energy, water, and carbon dioxide in the canopy air space. Canopy air space storage is particularly important in tall, dense tropical forests; accounting for this storage term, as well as the energy storage of vegetation, allows a more realistic representation of the fluxes between the ecosystem and the air above (see also Haverd et al., 2007). In addition, the separation of the ecosystem fluxes in the model into eddy fluxes and change in canopy air space storage allows a thorough evaluation of the model's ability to represent both the total exchange and the ventilation of water, energy, and carbon in and out of the ecosystem with eddy covariance towers, as shown in the companion paper (Longo et al., 2019a).
6.2 Heterogeneity of ecosystems
It has been long advocated that terrestrial biosphere models must incorporate demographic processes and ecosystem heterogeneity to improve their predictive ability in a changing world (Moorcroft, 2006; Purves and Pacala, 2008; Evans, 2012; Fisher et al., 2018). In ED-2.2, we aggregate individuals and forest communities according to similar characteristics (Fig. 1). For example, individuals are only aggregated into cohorts if they are of similar size, same functional group, and live in comparable micro-environments. Likewise, local plant communities are aggregated only if their disturbance history and their vertical structure are similar. The level of aggregation of ED-2.2 still allows mechanistic representation of ecological processes such as how individuals' access to and competition for resources vary depending on their size, adaptation, and presence of other individuals. This approach allows representing a broad range of structure and composition of ecosystems (Figs. 7, S4), as opposed to simplified biome classification. In this paper, we presented the functional diversity using only the default tropical PFTs, which describe the functional diversity along a single functional trait axis of broadleaf tropical trees. However, the ED-2.2 framework allows users to easily modify the traits and trade-offs of existing PFTs, or include new functional groups; previous studies using ED-2.2 have leveraged this feature of the code to define PFTs according to the research question both in the tropics (e.g., Xu et al., 2016; Trugman et al., 2018; Feng et al., 2018) and in the extratropics (e.g., Raczka et al., 2018; Bogan et al., 2019).
Previous analysis by Levine et al. (2016) has shown that the dynamic, fine-scale heterogeneity and functional diversity of the plant canopy in ED-2.2 is essential for capturing macro-scale patterns in tropical forest properties. Specifically, Levine et al. (2016) found that ED-2.1 was able to characterize the smoother observed transition in tropical forest biomass across a dry-season length gradient in the Amazon, whereas a highly aggregated (big-leaf-like) version of ED-2.1 predicted abrupt shifts in biomass, which is commonly observed in many dynamic global vegetation models (e.g., Good et al., 2011). Results from two related studies have shown that the incorporation of subgrid-scale heterogeneity and diversity within ED-2 also improves its ability to correctly capture the responses of terrestrial ecosystems to environmental perturbation. First, in an assessment of the ability of four terrestrial biosphere models to capture the impact of rainfall changes on biomass in Amazon forests (Powell et al., 2013), ED-2.1 was the only model that captured the timing and average magnitude of aboveground biomass loss that was observed in two experimental drought treatments, while all three big-leaf model formulations predicted minimal impacts of the drought experiment. Second, a recent analysis by Longo et al. (2018) on the impact of recurrent droughts in the Amazon found that drought-induced carbon losses in ED-2.2 arose mostly from the death of canopy trees, a characteristic that is consistent with field and remote-sensing observations of drought impacts in the region (Phillips et al., 2010; Yang et al., 2018).
Importantly, since its inception, the ED model accounts for the disturbance-driven horizontal heterogeneity of ecosystems (Moorcroft et al., 2001). As demonstrated in Moorcroft et al. (2001), the continuous development of tree-fall gaps is fundamental to explaining the long-term trajectory of biomass accumulation in tropical forests; for example, by representing both recently disturbed and old-growth fragments of forests, it is possible to simulate micro-environments where either shade-intolerant plants thrive or slow-growing, shade-tolerant individuals dominate the canopy (Fig. 8a, c). Moreover, ED-2.2 can also represent dynamic and diverse disturbance regimes, which ultimately mediate the regional variation of ecosystem properties. For example, tropical forests and woody savannas may share similarities in local communities with similar age since disturbance (Fig. 8e); however, because fire disturbances frequently affect large areas in the savannas, fragments of old-growth vegetation are nearly absent in these regions (Fig. 8f), which creates an environment dominated mostly by smaller trees (Fig. S5c).
Furthermore, the heterogeneity of ecosystems in ED-2.2 is integrated across all timescales, because we solve the biophysical and biogeochemical cycles for each cohort and each patch separately (Figs. 2–3). While solving the cycles at subgrid scale adds complexity, it also improves the characterization of heterogeneity of available water and energy for plants of different sizes, even within the same polygon: for example, the light profile and soil water availability are not only determined by meteorological conditions but also by the number of individuals, their height and rooting depth, and their traits and trade-offs that determine their ability to extract soil moisture or assimilate carbon. As a result, the variability in ecosystem functioning represented by ED-2.2 is significantly increased relative to the variability that a highly aggregated model based on the average ecosystem structure would be able to capture (Fig. 9).
6.3 Current and future developments
In this paper, we focused on describing the biophysical and biogeochemical core of the ED-2.2 model, and appraising its ability to represent both short-term (intra-annual and interannual) and long-term (decades to century) processes. However, the ED-2.2 community is continuously developing and improving the model. In this section, we summarize some of the recent and ongoing model developments being built on top of the ED-2.2 dynamic core.
Terrestrial biosphere models still show significant uncertainties in representing photosynthesis due to missing processes and inconsistencies in parameter estimations (Rogers et al., 2017). We are currently implementing the carboxylation limitation by the maximum electron transport rate and by the triose phosphate utilization (von Caemmerer, 2000; Lombardozzi et al., 2018), and constrained by observations (Norby et al., 2017), and nitrogen and phosphorus limitation have been recently incorporated (Medvigy et al., 2019). In addition, the model has also been recently updated to mechanistically represent plant hydraulics, and initial results indicate a significant improvement of the model's predictions of water use efficiency and water stress in tropical forests in Central America (Xu et al., 2016). Also, to better represent the dynamics of soil carbon in ED-2.2, we are implementing and optimizing a more detailed version of the CENTURY decomposition model (Bolker et al., 1998).
To improve the representation of surface and soil water dynamics, the model has been coupled with a hydrological routine model that accounts for lateral flux of water as a function of terrain characteristics and simulates river discharge (Pereira et al., 2017; Arias et al., 2018). Moreover, an integrated approach of hydraulic routing based on TOPMODEL (Walko et al., 2000; Beven and Freer, 2001), which allows exchange of water and internal energy exchange between different sites as a function of topographic characteristics, is being implemented in ED-2.2.
The ED-2.2 model framework is designed to simulate functionally diverse ecosystems, but trait values within each functional group are fixed. To account for the observed plasticity in many leaf traits, a new parameterization of leaf trait variation as function of the light level, based on the parameterization by Lloyd et al. (2010) and Xu et al. (2017) is being implemented. In addition, the ED-2.2 model has also been recently updated to represent the light competition and parasite–host relationships between lianas and trees (di Porcia e Brugnera et al., 2019), and it is currently being extended to incorporate plant functional types from different biogeographic regions, such as temperate semi-arid shrublands (Pandit et al., 2018), as well as boreal ecosystems, building on previous works using ED-1 (Ise et al., 2008).
Anthropogenic forest degradation is pervasive throughout the tropics (Lewis et al., 2015). To improve the model's ability to represent damage and recovery from degradation, we are implementing a selective logging module that represents the direct impact of felling of marketable tree stems, and accounts the damage associated with skid trails, roads, and decks, which are modulated by logging intensity and logging techniques (Pereira Jr. et al., 2002; Feldpausch et al., 2005). In addition, the original fire model has been recently improved to account for size- and bark-thickness-dependent survivorship (Trugman et al., 2018), and is being developed to account for natural and anthropogenic drivers of ignition, fire intensity, fire spread, and fire duration, building on existing process-based fire models (Thonicke et al., 2010; Le Page et al., 2015).
The complexity and sophistication of ED-2.2 also creates important scientific challenges. For example, the multiple processes for functionally diverse ecosystems represented by the model also require a large number of parameters, with some of them being highly uncertain given the scarcity of data. To explore the effect of parameter uncertainty on model results and leverage the growing number of observations, the ED-2.2 model has been fully integrated with the Predictive Ecosystem Analyzer (LeBauer et al., 2013; Dietze et al., 2014), a hierarchical Bayesian-based framework that constrains model parameters based on available data and quantifies the uncertainties on model predictions due to parameter uncertainty.
Importantly, the need to incorporate terrestrial ecosystem heterogeneity in Earth system models has been long advocated (e.g., Moorcroft, 2006; Purves et al., 2008; Evans, 2012), but only recently have global models been incorporating ecological mechanisms that allow representing functionally diverse and heterogeneous biomes at global scale without relying on artificial climate envelopes. Two examples are the Geophysical Fluid Dynamics Laboratory (GFDL) Land Model version 3 with perfect plasticity approximation (Weng et al., 2015, LM3-PPA;) and the Functionally Assembled Terrestrial Ecosystem Simulation (FATES; Fisher et al., 2015), which incorporated the patch and cohort structure of ED-2.2 into the Community Land Model (CLM; Oleson et al., 2013) framework.
ED-2.2 represents a significant advance in how to integrate a variety of processes ranging across multiple timescales in heterogeneous landscapes: it retains all the detailed representation of the long-term dynamics of functionally diverse, spatially heterogeneous landscapes and long-term dynamics from the original ED ecosystem model (Moorcroft et al., 2001; Hurtt et al., 2002; Albani et al., 2006) but also solves for the associated energy, water, and CO2 fluxes of plants living in horizontally and vertically stratified micro-environments within the plant canopy, which was initially implemented by Medvigy et al. (2009) (ED-2) by adapting the big-leaf land surface model LEAF-3 (Walko et al., 2000) to the cohort-based structure of ED-2.
The results presented in the model description demonstrated that ED-2.2 has a high degree of conservation of carbon, energy, and water, even over multi-decadal scales (Fig. 6). Importantly, the current formulation of the model allows representation of functional and structural diversity both at local and regional scales (Figs. 7–8; S4–S5), and the effect of the heterogeneity on energy, water, carbon, and momentum fluxes (Fig. 9). In the companion paper, we use data from eddy covariance towers, forest inventory, bottom-up estimates of carbon cycles, and remote-sensing products to assess the strengths and limitations of the current model implementation (Longo et al., 2019a).
This paper focused on the major updates to the energy, water, and carbon cycle within the ED-2.2 framework; the model continues to be actively developed. Some of the further developments include implementing more mechanisms that influence photosynthesis and water cycle, such as plant hydraulics; additional nutrient cycles; expanding the representation of plant functional diversity, including trait plasticity and lianas; and expanding the types of natural and anthropogenic disturbances. ED-2.2 is a collaborative, open-source model that is readily available from its repository, and the scientific community is encouraged to use the model and contribute with new model developments.
The ED-2.2 software and further developments are publicly available. The most up-to-date source code, post-processing R scripts, and an open discussion forum are available on the GitHub repository (The ED-2 Model Development Team, 2014). The code described in this paper, along with a wiki-based technical manual, is stored as a permanent release at https://github.com/mpaiao/ED2/releases/tag/rev-86 (last access: 25 September 2019) and permanently stored at Longo et al. (2019b).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-12-4309-2019-supplement.
ML, RGK, DMM, MCD, YK, RLB, SCW, and PRM designed the ED-2.2 model. ML, RGK, DMM, NML, MCD, YK, ALSS, KZ, CR, and PRM developed the model. ML, RGK, NML, and ALSS carried out the ED-2.2 simulations. ML, RGK, DMM, NML, MCD, YK, ALSS, and PRM wrote the paper.
The authors declare that they have no conflict of interest.
The research was partially carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. We thank the reviewers Ian Baker and Stefan Olin, as well as Miriam Johnston, Luciana Alves, John Kim, and Shawn Serbin for suggestions that improved the manuscript, and Alexander Antonarakis, Fabio Berzaghi, Carl Davidson, Istem Fer, Miriam Johnston, Geraldine Klarenberg, Robert Kooper, Félicien Meunier, Manfredo di Porcia e Brugnera, Afshin Pourmokhtarian, Thomas Powell, Daniel Scott, Shawn Serbin, Alexey Shiklomanov, Anna Trugman, Toni Viskari, and Xiangtao Xu for contributing to the code development. The model simulations were carried out at the Odyssey cluster, supported by the FAS Division of Science, Research Computing Group at Harvard University. Marcos Longo was supported the NASA Postdoctoral Program, administered by Universities Space Research Association under contract with NASA. Abigail L. S. Swann was supported as a Giorgio Ruffolo Fellow in the Sustainability Science Program at Harvard University, for which support from Italy's Ministry for Environment, Land and Sea is gratefully acknowledged.
This research has been supported by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (grant no. 200686/2005-4), the NASA Earth and Space Science Fellowship (grant no. NNX08AU95H), the National Science Foundation, Office of International Science and Engineering (grant no. OISE-0730305), the National Science Foundation (grant no. ATM-0449793), the National Aeronautics and Space Administration (grant no. NNG06GD63G), and the Fundação de Amparo à Pesquisa do Estado de São Paulo (grant no. 2015/07227-6).
This paper was edited by Christoph Müller and reviewed by Ian Baker and Stefan Olin.
Ahlström, A., Schurgers, G., Arneth, A., and Smith, B.: Robustness and uncertainty in terrestrial ecosystem carbon response to CMIP5 climate change projections, Environ. Res. Lett., 7, 044008, https://doi.org/10.1088/1748-9326/7/4/044008, 2012. a
Albani, M., Medvigy, D., Hurtt, G. C., and Moorcroft, P. R.: The contributions of land-use change, CO2 fertilization, and climate variability to the eastern US carbon sink, Glob. Change Biol., 12, 2370–2390, https://doi.org/10.1111/j.1365-2486.2006.01254.x, 2006. a, b, c, d, e, f
Amthor, J. S.: The role of maintenance respiration in plant growth, Plant Cell Environ., 7, 561–569, https://doi.org/10.1111/1365-3040.ep11591833, 1984. a
Antonarakis, A. S., Saatchi, S. S., Chazdon, R. L., and Moorcroft, P. R.: Using Lidar and Radar measurements to constrain predictions of forest ecosystem structure and function, Ecol. Appl., 21, 1120–1137, https://doi.org/10.1890/10-0274.1, 2011. a, b
Antonarakis, A. S., Munger, J. W., and Moorcroft, P. R.: Imaging spectroscopy- and lidar-derived estimates of canopy composition and structure to improve predictions of forest carbon fluxes and ecosystem dynamics, Geophys. Res. Lett., 41, 2535–2542, https://doi.org/10.1002/2013GL058373, 2014. a
Arias, M. E., Lee, E., Farinosi, F., Pereira, F. F., and Moorcroft, P. R.: Decoupling the effects of deforestation and climate variability in the Tapajós river basin in the Brazilian Amazon, Hydrol. Process., 32, 1648–1663, https://doi.org/10.1002/hyp.11517, 2018. a
Avissar, R. and Mahrer, Y.: Mapping frost-sensitive areas with a three-dimensional local-scale numerical model. Part I. Physical and numerical aspects, J. Appl. Meteor., 27, 400–413, https://doi.org/10.1175/1520-0450(1988)027<0400:MFSAWA>2.0.CO;2, 1988. a
Baker, I., Denning, A. S., Hanan, N., Prihodko, L., Uliasz, M., Vidale, P.-L., Davis, K., and Bakwin, P.: Simulated and observed fluxes of sensible and latent heat and CO2 at the WLEF-TV tower using SiB2.5, Glob. Change Biol., 9, 1262–1277, https://doi.org/10.1046/j.1365-2486.2003.00671.x, 2003. a
Bazzaz, F. A.: The physiological ecology of plant succession, Annu. Rev. Ecol. Syst., 10, 351–371, https://doi.org/10.1146/annurev.es.10.110179.002031, 1979. a
Best, M. J., Pryor, M., Clark, D. B., Rooney, G. G., Essery, R. L. H., Ménard, C. B., Edwards, J. M., Hendry, M. A., Porson, A., Gedney, N., Mercado, L. M., Sitch, S., Blyth, E., Boucher, O., Cox, P. M., Grimmond, C. S. B., and Harding, R. J.: The Joint UK Land Environment Simulator (JULES), model description – Part 1: Energy and water fluxes, Geosci. Model Dev., 4, 677–699, https://doi.org/10.5194/gmd-4-677-2011, 2011. a, b
Betts, A. K. and Silva Dias, M. A. F.: Progress in understanding land-surface-atmosphere coupling from LBA research, J. Adv. Model. Earth Syst., 2, 6, https://doi.org/10.3894/JAMES.2010.2.6, 2010. a
Beven, K. and Freer, J.: A dynamic TOPMODEL, Hydrol. Process., 15, 1993–2011, https://doi.org/10.1002/hyp.252, 2001. a
Blyth, E., Clark, D. B., Ellis, R., Huntingford, C., Los, S., Pryor, M., Best, M., and Sitch, S.: A comprehensive set of benchmark tests for a land surface model of simultaneous fluxes of water and carbon at both the global and seasonal scale, Geosci. Model Dev., 4, 255–269, https://doi.org/10.5194/gmd-4-255-2011, 2011. a
Bogan, S. A., Antonarakis, A. S., and Moorcroft, P. R.: Imaging spectrometry-derived estimates of regional ecosystem composition for the Sierra Nevada, California, Remote Sens. Environ., 228, 14–30, https://doi.org/10.1016/j.rse.2019.03.031, 2019. a
Bolker, B. M., Pacala, S. W., and Parton, W. J.: Linear analysis of soil decomposition: insights from the CENTURY model, Ecol. Appl., 8, 425–439, https://doi.org/10.1890/1051-0761(1998)008[0425:LAOSDI]2.0.CO;2, 1998. a, b, c, d
Bonan, G. B.: Land-atmosphere CO2 exchange simulated by a land surface process model coupled to an atmospheric general circulation model, J. Geophys. Res.-Atmos., 100, 2817–2831, https://doi.org/10.1029/94JD02961, 1995. a
Bonan, G. B.: Ecological climatology, Cambridge Univ. Press, Cambridge, UK, 2nd Edn., 2008. a, b
Both, S., Riutta, T., Paine, C. E. T., Elias, D. M. O., Cruz, R. S., Jain, A., Johnson, D., Kritzler, U. H., Kuntz, M., Majalap-Lee, N., Mielke, N., Montoya Pillco, M. X., Ostle, N. J., Arn Teh, Y., Malhi, Y., and Burslem, D. F. R. P.: Logging and soil nutrients independently explain plant trait expression in tropical forests, New Phytol., 221, 1853–1865, https://doi.org/10.1111/nph.15444, 2019. a
Brooks, R. H. and Corey, A. T.: Hydraulic properties of porous media, Hydrology Papers 3, Colorado State University, Fort Collins, USA, 1964. a
Bruelheide, H., Dengler, J., Purschke, O., Lenoir, J., Jiménez-Alfaro, B., Hennekens, S. M., Botta-Dukát, Z., Chytrý, M., Field, R., Jansen, F., Kattge, J., Pillar, V. D., Schrodt, F., Mahecha, M. D., Peet, R. K., Sandel, B., van Bodegom, P., Altman, J., Alvarez-Dávila, E., Arfin Khan, M. A. S., Attorre, F., Aubin, I., Baraloto, C., Barroso, J. G., Bauters, M., Bergmeier, E., Biurrun, I., Bjorkman, A. D., Blonder, B., Čarni, A., Cayuela, L., Černý, T., Cornelissen, J. H. C., Craven, D., Dainese, M., Derroire, G., De Sanctis, M., DÍaz, S., Doležal, J., Farfan-Rios, W., Feldpausch, T. R., Fenton, N. J., Garnier, E., Guerin, G. R., Gutiérrez, A. G., Haider, S., Hattab, T., Henry, G., Hérault, B., Higuchi, P., Hölzel, N., Homeier, J., Jentsch, A., Jürgens, N., Ka̧cki, Z., Karger, D. N., Kessler, M., Kleyer, M., Knollová, I., Korolyuk, A. Y., Kühn, I., Laughlin, D. C., Lens, F., Loos, J., Louault, F., Lyubenova, M. I., Malhi, Y., Marcenò, C., Mencuccini, M., Müller, J. V., Munzinger, J., Myers-Smith, I. H., Neill, D. A., Niinemets, Ü., Orwin, K. H., Ozinga, W. A., Penuelas, J., Pérez-Haase, A., Petřík, P., Phillips, O. L., Pärtel, M., Reich, P. B., Römermann, C., Rodrigues, A. V., Sabatini, F. M., Sardans, J., Schmidt, M., Seidler, G., Silva Espejo, J. E., Silveira, M., Smyth, A., Sporbert, M., Svenning, J.-C., Tang, Z., Thomas, R., Tsiripidis, I., Vassilev, K., Violle, C., Virtanen, R., Weiher, E., Welk, E., Wesche, K., Winter, M., Wirth, C., and Jandt, U.: Global trait–environment relationships of plant communities, Nat. Ecol. Evol., 2, 1906–1917, https://doi.org/10.1038/s41559-018-0699-8, 2018. a
Bugmann, H.: A Review of Forest Gap Models, Clim. Change, 51, 259–305, https://doi.org/10.1023/A:1012525626267, 2001. a
Cardinale, B. J., Wright, J. P., Cadotte, M. W., Carroll, I. T., Hector, A., Srivastava, D. S., Loreau, M., and Weis, J. J.: Impacts of plant diversity on biomass production increase through time because of species complementarity, P. Natl. Acad. Sci. USA, 104, 18123–18128, https://doi.org/10.1073/pnas.0709069104, 2007. a
Castanho, A. D. A., Galbraith, D., Zhang, K., Coe, M. T., Costa, M. H., and Moorcroft, P.: Changing Amazon biomass and the role of atmospheric CO2 concentration, climate and land use, Global Biogeochem. Cy., 30, 18–39, https://doi.org/10.1002/2015GB005135, 2016. a
Cavanaugh, K. C., Gosnell, J. S., Davis, S. L., Ahumada, J., Boundja, P., Clark, D. B., Mugerwa, B., Jansen, P. A., O'Brien, T. G., Rovero, F., Sheil, D., Vasquez, R., and Andelman, S.: Carbon storage in tropical forests correlates with taxonomic diversity and functional dominance on a global scale, Global Ecol. Biogeogr., 23, 563–573, https://doi.org/10.1111/geb.12143, 2014. a
Chen, J. and Black, T.: Foliage area and architecture of plant canopies from sunfleck size distributions, Agr. Forest Meteorol., 60, 249–266, https://doi.org/10.1016/0168-1923(92)90040-B, 1992. a
Clark, D. B., Mercado, L. M., Sitch, S., Jones, C. D., Gedney, N., Best, M. J., Pryor, M., Rooney, G. G., Essery, R. L. H., Blyth, E., Boucher, O., Harding, R. J., Huntingford, C., and Cox, P. M.: The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics, Geosci. Model Dev., 4, 701–722, https://doi.org/10.5194/gmd-4-701-2011, 2011. a
Collatz, G., Ribas-Carbo, M., and Berry, J.: Coupled photosynthesis-stomatal conductance model for leaves of C4 plants, Aust. J. Plant Physiol., 19, 519–538, https://doi.org/10.1071/PP9920519, 1992. a, b, c
Collatz, G. J., Ball, J., Grivet, C., and Berry, J. A.: Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: a model that includes a laminar boundary layer, Agr. Forest Meteorol., 54, 107–136, https://doi.org/10.1016/0168-1923(91)90002-8, 1991. a, b
Cowan, I. and Troughton, J.: The relative role of stomata in transpiration and assimilation, Planta, 97, 325–336, https://doi.org/10.1007/BF00390212, 1971. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
di Porcia e Brugnera, M., Meunier, F., Longo, M., Moorthy, S., De Deurwaerder, H., Schnitzer, S. A., Bonal, D., Faybishenko, B., and Verbeeck, H.: Modelling the impact of liana infestation on the demography and carbon cycle of tropical forests, Global Change Biol., 25, 3767–3780, https://doi.org/10.1111/gcb.14769, 2019. a
Dickinson, R., Henderson-Sellers, A., Kennedy, P., and Wilson, M.: Biosphere-atmosphere transfer scheme (BATS) for the NCAR community climate model, Technical Note NCAR/TN-275+STR, NCAR, Boulder, CO, https://doi.org/10.5065/D6668B58, 1986. a
Dietze, M. C., Serbin, S. P., Davidson, C., Desai, A. R., Feng, X., Kelly, R., Kooper, R., LeBauer, D., Mantooth, J., McHenry, K., and Wang, D.: A quantitative assessment of a terrestrial biosphere model's data needs across North American biomes, J. Geophys. Res.-Biogeosci., 119, 286–300, https://doi.org/10.1002/2013JG002392, 2014. a
Dufour, L. and van Mieghem, J.: Thermodynamique de l'atmosphère, Institut Royal Météorologique de Belgique, Gembloux, Belgium, 2 edn., in French, 1975. a
Evans, M. R.: Modelling ecological systems in a changing world, Philos. Trans. R. Soc. B-Biol. Sci., 367, 181–190, https://doi.org/10.1098/rstb.2011.0172, 2012. a, b
Farquhar, G., von Caemmerer, S., and Berry, J.: A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78–90, https://doi.org/10.1007/BF00386231, 1980. a, b
Feldpausch, T. R., Jirka, S., Passos, C. A. M., Jasper, F., and Riha, S. J.: When big trees fall: Damage and carbon export by reduced impact logging in southern Amazonia, Forest Ecol. Manag., 219, 199–215, https://doi.org/10.1016/j.foreco.2005.09.003, 2005. a
Feng, X., Uriarte, M., González, G., Reed, S., Thompson, J., Zimmerman, J. K., and Murphy, L.: Improving predictions of tropical forest response to climate change through integration of field studies and ecosystem modeling, Global Change Biol., 24, e213–e232, https://doi.org/10.1111/gcb.13863, 2018. a
Fischer, R., Bohn, F., de Paula, M. D., Dislich, C., Groeneveld, J., Gutiérrez, A. G., Kazmierczak, M., Knapp, N., Lehmann, S., Paulick, S., Pütz, S., Rödig, E., Taubert, F., Köhler, P., and Huth, A.: Lessons learned from applying a forest gap model to understand ecosystem and carbon dynamics of complex tropical forests, Ecol. Model., 326, 124–133, https://doi.org/10.1016/j.ecolmodel.2015.11.018, 2016. a, b
Fisher, J. B., Huntzinger, D. N., Schwalm, C. R., and Sitch, S.: Modeling the terrestrial biosphere, Ann. Rev. Environ. Res., 39, 91–123, https://doi.org/10.1146/annurev-environ-012913-093456, 2014. a
Fisher, R., McDowell, N., Purves, D., Moorcroft, P., Sitch, S., Cox, P., Huntingford, C., Meir, P., and Ian Woodward, F.: Assessing uncertainties in a second-generation dynamic vegetation model caused by ecological scale limitations, New Phytol., 187, 666–681, https://doi.org/10.1111/j.1469-8137.2010.03340.x, 2010. a
Fisher, R. A., Muszala, S., Vertenstein, M., Lawrence, P., Xu, C., McDowell, N. G., Knox, R. G., Koven, C., Holm, J., Rogers, B. M., Lawrence, D., and Bonan, G.: Taking off the training wheels: the properties of a dynamic vegetation model without climate envelopes, Geosci. Model Dev., 8, 3593–3619, https://doi.org/10.5194/gmd-8-3593-2015, 2015. a, b
Fisher, R. A., Koven, C. D., Anderegg, W. R. L., Christoffersen, B. O., Dietze, M. C., Farrior, C., Holm, J. A., Hurtt, G., Knox, R. G., Lawrence, P. J., Lichststein, J. W., Longo, M., Matheny, A. M., Medvigy, D., Muller-Landau, H. C., Powell, T. L., Serbin, S. P., Sato, H., Shuman, J., Smith, B., Trugman, A. T., Viskari, T., Verbeeck, H., Weng, E., Xu, C., Xu, X., Zhang, T., and Moorcroft, P.: Vegetation demographics in Earth system models: a review of progress and priorities, Global Change Biol., 24, 35–54, https://doi.org/10.1111/gcb.13910, 2018. a, b, c, d
Foken, T.: 50 years of the Monin–Obukhov similarity theory, Bound.-Lay. Meteorol., 119, 431–447, https://doi.org/10.1007/s10546-006-9048-6, 2006. a, b
Foley, J. A., Prentice, I. C., Ramankutty, N., Levis, S., Pollard, D., Sitch, S., and Haxeltine, A.: An integrated biosphere model of land surface processes, terrestrial carbon balance, and vegetation dynamics, Global Biogeochem. Cy., 10, 603–628, https://doi.org/10.1029/96GB02692, 1996. a, b, c, d
Fortunel, C., Fine, P. V. A., and Baraloto, C.: Leaf, stem and root tissue strategies across 758 Neotropical tree species, Funct. Ecol., 26, 1153–1161, https://doi.org/10.1111/j.1365-2435.2012.02020.x, 2012. a
Freitas, S. R., Panetta, J., Longo, K. M., Rodrigues, L. F., Moreira, D. S., Rosário, N. E., Silva Dias, P. L., Silva Dias, M. A. F., Souza, E. P., Freitas, E. D., Longo, M., Frassoni, A., Fazenda, A. L., Santos e Silva, C. M., Pavani, C. A. B., Eiras, D., França, D. A., Massaru, D., Silva, F. B., Santos, F. C., Pereira, G., Camponogara, G., Ferrada, G. A., Campos Velho, H. F., Menezes, I., Freire, J. L., Alonso, M. F., Gácita, M. S., Zarzur, M., Fonseca, R. M., Lima, R. S., Siqueira, R. A., Braz, R., Tomita, S., Oliveira, V., and Martins, L. D.: The Brazilian developments on the Regional Atmospheric Modeling System (BRAMS 5.2): an integrated environmental model tuned for tropical areas, Geosci. Model Dev., 10, 189–222, https://doi.org/10.5194/gmd-10-189-2017, 2017. a
Friedlingstein, P., Meinshausen, M., Arora, V. K., Jones, C. D., Anav, A., Liddicoat, S. K., and Knutti, R.: Uncertainties in CMIP5 climate projections due to carbon cycle feedbacks, J. Climate, 27, 511–526, https://doi.org/10.1175/JCLI-D-12-00579.1, 2014. a
Friend, A. D., Stevens, A. K., Knox, R. G., and Cannell, M. G. R.: A process-based, terrestrial biosphere model of ecosystem dynamics (Hybrid v3.0), Ecol. Model., 95, 249–287, https://doi.org/10.1016/S0304-3800(96)00034-8, 1997. a, b
García-Palacios, P., Gross, N., Gaitán, J., and Maestre, F. T.: Climate mediates the biodiversity–ecosystem stability relationship globally, P. Natl. Acad. Sci. USA, 115, 8400–8405, https://doi.org/10.1073/pnas.1800425115, 2018. a
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G.-K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern-Era Retrospective Analysis for Research and Applications, version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017. a
Global Soil Data Task: Global Soil Data Products CD-ROM Contents (IGBP-DIS), https://doi.org/10.3334/ORNLDAAC/565, Oak Ridge National Laboratory Distributed Active Archive Center, Oak Ridge, Tennessee, USA, 2000. a
Good, P., Jones, C., Lowe, J., Betts, R., Booth, B., and Huntingford, C.: Quantifying Environmental Drivers of Future Tropical Forest Extent, J. Climate, 24, 1337–1349, https://doi.org/10.1175/2010JCLI3865.1, 2011. a, b
Haddad, N. M., Brudvig, L. A., Clobert, J., Davies, K. F., Gonzalez, A., Holt, R. D., Lovejoy, T. E., Sexton, J. O., Austin, M. P., Collins, C. D., Cook, W. M., Damschen, E. I., Ewers, R. M., Foster, B. L., Jenkins, C. N., King, A. J., Laurance, W. F., Levey, D. J., Margules, C. R., Melbourne, B. A., Nicholls, A. O., Orrock, J. L., Song, D.-X., and Townshend, J. R.: Habitat fragmentation and its lasting impact on Earth's ecosystems, Science Advances, 1, e1500052, https://doi.org/10.1126/sciadv.1500052, 2015. a
Haverd, V., Cuntz, M., Leuning, R., and Keith, H.: Air and biomass heat storage fluxes in a forest canopy: Calculation within a soil vegetation atmosphere transfer model, Agr. Forest Meteorol., 147, 125–139, https://doi.org/10.1016/j.agrformet.2007.07.006, 2007. a
Haxeltine, A. and Prentice, I. C.: BIOME3: An equilibrium terrestrial biosphere model based on ecophysiological constraints, resource availability, and competition among plant functional types, Global Biogeochem. Cy., 10, 693–709, https://doi.org/10.1029/96GB02344, 1996. a
Hengl, T., de Jesus, J. M., Heuvelink, G. B. M., Ruiperez Gonzalez, M., Kilibarda, M., Blagotić, A., Shangguan, W., Wright, M. N., Geng, X., Bauer Marschallinger, B., Guevara, M. A., Vargas, R., MacMillan, R. A., Batjes, N. H., Leenaars, J. G. B., Ribeiro, E., Wheeler, I., Mantel, S., and Kempen, B.: SoilGrids250m: Global gridded soil information based on machine learning, PLoS One, 12, 1–40, https://doi.org/10.1371/journal.pone.0169748, 2017. a
Huang, M., Xu, Y., Longo, M., Keller, M., Knox, R., Koven, C., and Fisher, R.: Assessing impacts of selective logging on water, energy, and carbon budgets and ecosystem dynamics in Amazon forests using the Functionally Assembled Terrestrial Ecosystem Simulator, Biogeosciences Discuss., https://doi.org/10.5194/bg-2019-129, in review, 2019. a
Huang, Y., Chen, Y., Castro-Izaguirre, N., Baruffol, M., Brezzi, M., Lang, A., Li, Y., Härdtle, W., von Oheimb, G., Yang, X., Liu, X., Pei, K., Both, S., Yang, B., Eichenberg, D., Assmann, T., Bauhus, J., Behrens, T., Buscot, F., Chen, X.-Y., Chesters, D., Ding, B.-Y., Durka, W., Erfmeier, A., Fang, J., Fischer, M., Guo, L.-D., Guo, D., Gutknecht, J. L. M., He, J.-S., He, C.-L., Hector, A., Hönig, L., Hu, R.-Y., Klein, A.-M., Kühn, P., Liang, Y., Li, S., Michalski, S., Scherer-Lorenzen, M., Schmidt, K., Scholten, T., Schuldt, A., Shi, X., Tan, M.-Z., Tang, Z., Trogisch, S., Wang, Z., Welk, E., Wirth, C., Wubet, T., Xiang, W., Yu, M., Yu, X.-D., Zhang, J., Zhang, S., Zhang, N., Zhou, H.-Z., Zhu, C.-D., Zhu, L., Bruelheide, H., Ma, K., Niklaus, P. A., and Schmid, B.: Impacts of species richness on productivity in a large-scale subtropical forest experiment, Science, 362, 80–83, https://doi.org/10.1126/science.aat6405, 2018. a
Hughes, J. K., Valdes, P. J., and Betts, R. A.: Dynamical properties of the TRIFFID dynamic global vegetation model, Technical Note HCTN, No. 56, U.K. Met Office Hadley Centre, Exeter, UK, 2004. a
Hurtt, G. C., Moorcroft, P. R., Pacala, S. W., and Levin, S. A.: Terrestrial models and global change: challenges for the future, Global Change Biol., 4, 581–590, https://doi.org/10.1046/j.1365-2486.1998.t01-1-00203.x, 1998. a
Hurtt, G. C., Pacala, S. W., Moorcroft, P. R., Caspersen, J., Shevliakova, E., Houghton, R. A., and Moore, B.: Projecting the future of the U.S. carbon sink, P. Natl. Acad. Sci. USA, 99, 1389–1394, https://doi.org/10.1073/pnas.012249999, 2002. a, b, c
Hurtt, G. C., Frolking, S., Fearon, M. G., Moore, B., Shevliakova, E., Malyshev, S., Pacala, S. W., and Houghton, R. A.: The underpinnings of land-use history: three centuries of global gridded land-use transitions, wood-harvest activity, and resulting secondary lands., Global Change Biol., 12, 1208–1229, https://doi.org/10.1111/j.1365-2486.2006.01150.x, 2006. a
Hutchings, M. J.: The Structure of Plant Populations, chap. 11, 325–358, Wiley-Blackwell, Oxford, U.K., 2nd Edn., https://doi.org/10.1002/9781444313642.ch11, 1997. a
IPCC: Climate change 2014: impacts, adaptation, and vulnerability. Part A: global and sectoral aspects, Cambridge Univ. Press, Cambridge, UK and New York, NY, USA, 2014. a
Ise, T., Dunn, A. L., Wofsy, S. C., and Moorcroft, P. R.: High sensitivity of peat decomposition to climate change through water-table feedback, Nat. Geosci., 1, 763–766, https://doi.org/10.1038/ngeo331, 2008. a
Jin, J., Gao, X., Sorooshian, S., Yang, Z.-L., Bales, R., Dickinson, R. E., Sun, S.-F., and Wu, G.-X.: One-dimensional snow water and energy balance model for vegetated surfaces, Hydrol. Process., 13, 2467–2482, https://doi.org/10.1002/(SICI)1099-1085(199910)13:14/15<2467::AID-HYP861>3.0.CO;2-J, 1999. a
Jucker, T. and Coomes, D. A.: Comment on “Plant Species Richness and Ecosystem Multifunctionality in Global Drylands”, Science, 337, 155, https://doi.org/10.1126/science.1220473, 2012. a
Kim, Y., Knox, R. G., Longo, M., Medvigy, D., Hutyra, L. R., Pyle, E. H., Wofsy, S. C., Bras, R. L., and Moorcroft, P. R.: Seasonal carbon dynamics and water fluxes in an Amazon rainforest, Global Change Biol., 18, 1322–1334, https://doi.org/10.1111/j.1365-2486.2011.02629.x, 2012. a
Knox, R. G., Longo, M., Swann, A. L. S., Zhang, K., Levine, N. M., Moorcroft, P. R., and Bras, R. L.: Hydrometeorological effects of historical land-conversion in an ecosystem-atmosphere model of Northern South America, Hydrol. Earth Syst. Sci., 19, 241–273, https://doi.org/10.5194/hess-19-241-2015, 2015. a, b, c, d
Lambers, H., Chapin III, F. S., and Pons, T. L.: Plant physiological ecology, Springer, New York, USA, 2nd Edn., https://doi.org/10.1007/978-0-387-78341-3, 2008. a, b, c, d
LeBauer, D. S., Wang, D., Richter, K. T., Davidson, C. C., and Dietze, M. C.: Facilitating feedbacks between field measurements and ecosystem models, Ecol. Monogr., 83, 133–154, https://doi.org/10.1890/12-0137.1, 2013. a
Le Page, Y., Morton, D., Bond-Lamberty, B., Pereira, J. M. C., and Hurtt, G.: HESFIRE: a global fire model to explore the role of anthropogenic and weather drivers, Biogeosciences, 12, 887–903, https://doi.org/10.5194/bg-12-887-2015, 2015. a
Le Quéré, C., Andrew, R. M., Friedlingstein, P., Sitch, S., Hauck, J., Pongratz, J., Pickers, P. A., Korsbakken, J. I., Peters, G. P., Canadell, J. G., Arneth, A., Arora, V. K., Barbero, L., Bastos, A., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Doney, S. C., Gkritzalis, T., Goll, D. S., Harris, I., Haverd, V., Hoffman, F. M., Hoppema, M., Houghton, R. A., Hurtt, G., Ilyina, T., Jain, A. K., Johannessen, T., Jones, C. D., Kato, E., Keeling, R. F., Goldewijk, K. K., Landschützer, P., Lefèvre, N., Lienert, S., Liu, Z., Lombardozzi, D., Metzl, N., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., Neill, C., Olsen, A., Ono, T., Patra, P., Peregon, A., Peters, W., Peylin, P., Pfeil, B., Pierrot, D., Poulter, B., Rehder, G., Resplandy, L., Robertson, E., Rocher, M., Rödenbeck, C., Schuster, U., Schwinger, J., Séférian, R., Skjelvan, I., Steinhoff, T., Sutton, A., Tans, P. P., Tian, H., Tilbrook, B., Tubiello, F. N., van der Laan Luijkx, I. T., van der Werf, G. R., Viovy, N., Walker, A. P., Wiltshire, A. J., Wright, R., Zaehle, S., and Zheng, B.: Global carbon budget 2018, Earth Syst. Sci. Data, 10, 2141–2194, https://doi.org/10.5194/essd-10-2141-2018, 2018. a, b
Lee, T. J. and Pielke, R. A.: Estimating the Soil Surface Specific Humidity, J. Appl. Meteor., 31, 480–484, https://doi.org/10.1175/1520-0450(1992)031<0480:ETSSSH>2.0.CO;2, 1992. a
Leuning, R.: A critical appraisal of a combined stomatal-photosynthesis model for C3 plants, Plant Cell Environ., 18, 339–355, https://doi.org/10.1111/j.1365-3040.1995.tb00370.x, 1995. a, b, c
Levine, N. M., Zhang, K., Longo, M., Baccini, A., Phillips, O. L., Lewis, S. L., Alvarez, E., de Andrade, A. C. S., Brienen, R., Erwin, T., Feldpausch, T. R., Mendoza, A. L. M., Vargas, P. N., Prieto, A., Espejo, J. E. S., Malhi, Y., and Moorcroft, P. R.: Ecosystem heterogeneity determines the resilience of the Amazon to climate change, P. Natl. Acad. Sci. USA, 113, 793–797, https://doi.org/10.1073/pnas.1511344112, 2016. a, b, c, d
Levis, S.: Modeling vegetation and land use in models of the Earth System, WIREs Clim. Change, 1, 840–856, https://doi.org/10.1002/wcc.83, 2010. a
Levis, S., Bonan, G., Vertenstein, M., and Oleson, K.: The Community Land Model's Dynamic Global Vegetation Model (CLM-DGVM): Technical description and user's guide, Technical Note NCAR/TN-459+IA, NCAR, Boulder, CO, https://doi.org/10.5065/D6P26W36, 2004. a
Lewis, S. L., Edwards, D. P., and Galbraith, D.: Increasing human dominance of tropical forests, Science, 349, 827–832, https://doi.org/10.1126/science.aaa9932, 2015. a, b
Liang, J., Crowther, T. W., Picard, N., Wiser, S., Zhou, M., Alberti, G., Schulze, E.-D., McGuire, A. D., Bozzato, F., Pretzsch, H., de Miguel, S., Paquette, A., Hérault, B., Scherer-Lorenzen, M., Barrett, C. B., Glick, H. B., Hengeveld, G. M., Nabuurs, G.-J., Pfautsch, S., Viana, H., Vibrans, A. C., Ammer, C., Schall, P., Verbyla, D., Tchebakova, N., Fischer, M., Watson, J. V., Chen, H. Y. H., Lei, X., Schelhaas, M.-J., Lu, H., Gianelle, D., Parfenova, E. I., Salas, C., Lee, E., Lee, B., Kim, H. S., Bruelheide, H., Coomes, D. A., Piotto, D., Sunderland, T., Schmid, B., Gourlet-Fleury, S., Sonké, B., Tavani, R., Zhu, J., Brandl, S., Vayreda, J., Kitahara, F., Searle, E. B., Neldner, V. J., Ngugi, M. R., Baraloto, C., Frizzera, L., Bałazy, R., Oleksyn, J., Zawiła-Niedźwiecki, T., Bouriaud, O., Bussotti, F., Finér, L., Jaroszewicz, B., Jucker, T., Valladares, F., Jagodzinski, A. M., Peri, P. L., Gonmadje, C., Marthy, W., O'Brien, T., Martin, E. H., Marshall, A. R., Rovero, F., Bitariho, R., Niklaus, P. A., Alvarez-Loayza, P., Chamuya, N., Valencia, R., Mortier, F., Wortel, V., Engone-Obiang, N. L., Ferreira, L. V., Odeke, D. E., Vasquez, R. M., Lewis, S. L., and Reich, P. B.: Positive biodiversity-productivity relationship predominant in global forests, Science, 354, aaf8957, https://doi.org/10.1126/science.aaf8957, 2016. a
Lindeskog, M., Arneth, A., Bondeau, A., Waha, K., Seaquist, J., Olin, S., and Smith, B.: Implications of accounting for land use in simulations of ecosystem carbon cycling in Africa, Earth Syst. Dynam., 4, 385–407, https://doi.org/10.5194/esd-4-385-2013, 2013. a
Liou, K. N.: An introduction to atmospheric radiation, vol. 84 of International Geophysics Series, Academic Press, San Diego, CA, USA, 2nd Edn., 2002. a, b
Lloyd, J., Patiño, S., Paiva, R. Q., Nardoto, G. B., Quesada, C. A., Santos, A. J. B., Baker, T. R., Brand, W. A., Hilke, I., Gielmann, H., Raessler, M., Luizão, F. J., Martinelli, L. A., and Mercado, L. M.: Optimisation of photosynthetic carbon gain and within-canopy gradients of associated foliar traits for Amazon forest trees, Biogeosciences, 7, 1833–1859, https://doi.org/10.5194/bg-7-1833-2010, 2010. a
Lombardozzi, D. L., Smith, N. G., Cheng, S. J., Dukes, J. S., Sharkey, T. D., Rogers, A., Fisher, R., and Bonan, G. B.: Triose phosphate limitation in photosynthesis models reduces leaf photosynthesis and global terrestrial carbon storage, Environ. Res. Lett., 13, 074025, https://doi.org/10.1088/1748-9326/aacf68, 2018. a, b
Longo, M. and Keller, M.: Not the same old(-growth) forest, New Phytol., 221, 1672–1675, https://doi.org/10.1111/nph.15636, 2019. a
Longo, M., Knox, R. G., Levine, N. M., Alves, L. F., Bonal, D., Camargo, P. B., Fitzjarrald, D. R., Hayek, M. N., Restrepo-Coupe, N., Saleska, S. R., da Silva, R., Stark, S. C., Tapajós, R. P., Wiedemann, K. T., Zhang, K., Wofsy, S. C., and Moorcroft, P. R.: Ecosystem heterogeneity and diversity mitigate Amazon forest resilience to frequent extreme droughts, New Phytol., 219, 914–931, https://doi.org/10.1111/nph.15185, 2018. a, b
Longo, M., Knox, R. G., Levine, N. M., Swann, A. L. S., Medvigy, D. M., Dietze, M. C., Kim, Y., Zhang, K., Bonal, D., Burban, B., Camargo, P. B., Hayek, M. N., Saleska, S. R., da Silva, R., Bras, R. L., Wofsy, S. C., and Moorcroft, P. R.: The biophysics, ecology, and biogeochemistry of functionally diverse, vertically and horizontally heterogeneous ecosystems: the Ecosystem Demography model, version 2.2 – Part 2: Model evaluation for tropical South America, Geosci. Model Dev., 12, 4347–4374, https://doi.org/10.5194/gmd-12-4347-2019, 2019a. a, b, c
Longo, M., Knox, R. G., Medvigy, D. M., Levine, N. M., Dietze, M. C., Swann, A. L. S., Zhang, K., Rollinson, C. R., di Porcia e Brugnera, M., Scott, D., Serbin, S. P., Kooper, R., Pourmokhtarian, A., Shiklomanov, A., Viskari, T., and Moorcroft, P.: Ecosystem Demography Model, version 2.2 (ED-2.2) (Version rev-86), https://doi.org/10.5281/zenodo.3365659, Zenodo, 2019b. a
Loreau, M. and Hector, A.: Partitioning selection and complementarity in biodiversity experiments, Nature, 412, 72–76, https://doi.org/10.1038/35083573, 2001. a
Manabe, S., Smagorinsky, J., and Strickler, R. F.: Simulated climatology of a general circulation model with a hydrologic cycle, Mon. Weather Rev., 93, 769–798, https://doi.org/10.1175/1520-0493(1965)093<0769:SCOAGC>2.3.CO;2, 1965. a
Mangeon, S., Voulgarakis, A., Gilham, R., Harper, A., Sitch, S., and Folberth, G.: INFERNO: a fire and emissions scheme for the UK Met Office's Unified Model, Geosci. Model Dev., 9, 2685–2700, https://doi.org/10.5194/gmd-9-2685-2016, 2016. a
Maréchaux, I. and Chave, J.: An individual-based forest model to jointly simulate carbon and tree diversity in Amazonia: description and applications, Ecol. Monogr., 87, 632–664, https://doi.org/10.1002/ecm.1271, 2017. a
Medvigy, D. and Moorcroft, P. R.: Predicting ecosystem dynamics at regional scales: an evaluation of a terrestrial biosphere model for the forests of northeastern North America, Philos. Trans. R. Soc. B-Biol. Sci., 367, 222–235, https://doi.org/10.1098/rstb.2011.0253, 2012. a
Medvigy, D., Wang, G., Zhu, Q., Riley, W. J., Trierweiler, A. M., Waring, B. G., Xu, X., and Powers, J. S.: Observed variation in soil properties can drive large variation in modeled forest functioning and composition during tropical forest secondary succession, New Phytol., 223, 1820–1833, https://doi.org/10.1111/nph.15848, 2019. a
Medvigy, D. M.: The state of the regional carbon cycle: results from a constrained coupled ecosystem-atmosphere model, Ph.D. dissertation, Harvard University, Cambridge, MA, 2006. a, b
Medvigy, D. M., Wofsy, S. C., Munger, J. W., Hollinger, D. Y., and Moorcroft, P. R.: Mechanistic scaling of ecosystem function and dynamics in space and time: Ecosystem Demography model version 2, J. Geophys. Res.-Biogeosci., 114, G01002, https://doi.org/10.1029/2008JG000812, 2009. a, b, c, d, e, f, g
Monin, A. S. and Obukhov, A. M.: Osnovnye zakonomernosti turbulentnogo pere- meshivanija v prizemnom sloe atmosfery (Basic laws of turbulent mixing in the atmosphere near the ground), Trudy Geofiz. Inst. AN SSSR, 24, 163–187, 1954 (in Russian). a
Monteith, J. L. and Unsworth, M. H.: Principles of environmental physics, Academic Press, London, 3rd Edn., 418 pp., 2008. a
Moorcroft, P. R.: Recent advances in ecosystem-atmosphere interactions: an ecological perspective, Proc. R. Soc. Lond. B-Biol. Sci., 270, 1215–1227, https://doi.org/10.1098/rspb.2002.2251, 2003. a
Moorcroft, P. R.: How close are we to a predictive science of the biosphere?, Trends Ecol. Evol., 21, 400–407, https://doi.org/10.1016/j.tree.2006.04.009, 2006. a, b, c
Moorcroft, P. R., Hurtt, G. C., and Pacala, S. W.: A method for scaling vegetation dynamics: The Ecosystem Demography model (ED), Ecol. Monogr., 71, 557–586, https://doi.org/10.1890/0012-9615(2001)071[0557:AMFSVD]2.0.CO;2, 2001. a, b, c, d, e, f, g, h, i, j, k, l
Naeem, S. and Li, S.: Biodiversity enhances ecosystem reliability, Nature, 390, 507–509, https://doi.org/10.1038/37348, 1997. a
Neilson, R. P.: A Model for Predicting Continental-Scale Vegetation Distribution and Water Balance, Ecol. Appl., 5, 362–385, https://doi.org/10.2307/1942028, 1995. a
Noilhan, J. and Planton, S.: A Simple Parameterization of Land Surface Processes for Meteorological Models, Mon. Weather Rev., 117, 536–549, https://doi.org/10.1175/1520-0493(1989)117<0536:ASPOLS>2.0.CO;2, 1989. a
Norby, R. J., Gu, L., Haworth, I. C., Jensen, A. M., Turner, B. L., Walker, A. P., Warren, J. M., Weston, D. J., Xu, C., and Winter, K.: Informing models through empirical relationships between foliar phosphorus, nitrogen and photosynthesis across diverse woody species in tropical forests of Panama, New Phytol., 215, 1425–1437, https://doi.org/10.1111/nph.14319, 2017. a
Oleson, K. W., Lawrence, D. M., Bonan, G. B., Drewniak, B., Huang, M., Koven, C. D., Levis, S., Li, F., Riley, W. J., Subin, Z. M., Swenson, S. C., Thornton, P. E., Bozbiyik, A., Fisher, R., Heald, C. L., Kluzek, E., Lamarque, J.-F., Lawrence, P. J., Leung, L. R., Lipscomb, W., Muszala, S., Ricciuto, D. M., Sacks, W., Sun, Y., Tang, J., and Yang, Z.-L.: Technical description of version 4.5 of the Community Land Model (CLM), Technical Report NCAR/TN-503+STR, NCAR, Boulder, CO, https://doi.org/10.5065/D6RR1W7M, 420pp., 2013. a, b, c, d
Pandit, K., Dashti, H., Glenn, N. F., Flores, A. N., Maguire, K. C., Shinneman, D. J., Flerchinger, G. N., and Fellows, A. W.: Optimizing shrub parameters to estimate gross primary production of the sagebrush ecosystem using the Ecosystem Demography (EDv2.2) model, Geosci. Model Dev. Discuss., https://doi.org/10.5194/gmd-2018-264, in review, 2018. a
Pereira, F. F., Farinosi, F., Arias, M. E., Lee, E., Briscoe, J., and Moorcroft, P. R.: Technical note: A hydrological routing scheme for the Ecosystem Demography model (ED2+R) tested in the Tapajós River basin in the Brazilian Amazon, Hydrol. Earth Syst. Sci., 21, 4629–4648, https://doi.org/10.5194/hess-21-4629-2017, 2017. a
Pereira Jr., R., Zweede, J., Asner, G. P., and Keller, M.: Forest canopy damage and recovery in reduced-impact and conventional selective logging in eastern Para, Brazil, Forest Ecol. Manag., 168, 77–89, https://doi.org/10.1016/S0378-1127(01)00732-0, 2002. a
Philip, J. R.: Evaporation, and moisture and heat fields in the soil, J. Meteor., 14, 354–366, https://doi.org/10.1175/1520-0469(1957)014<0354:EAMAHF>2.0.CO;2, 1957. a
Phillips, O. L., van der Heijden, G., Lewis, S. L., López-González, G., Aragão, L. E. O. C., Lloyd, J., Malhi, Y., Monteagudo, A., Almeida, S., Alvarez Dávila, E., Amaral, I., Andelman, S., Andrade, A., Arroyo, L., Aymard, G., Baker, T. R., Blanc, L., Bonal, D., Alves de Oliveira, A. C., Chao, K.-J., Dávila Cardozo, N., da Costa, L., Feldpausch, T. R., Fisher, J. B., Fyllas, N. M., Freitas, M. A., Galbraith, D., Gloor, E., Higuchi, N., Honorio, E., Jiménez, E., Keeling, H., Killeen, T. J., Lovett, J. C., Meir, P., Mendoza, C., Morel, A., Núñez Vargas, P., Patiño, S., Peh, K. S.-H., Peña Cruz, A., Prieto, A., Quesada, C. A., Ramírez, F., Ramírez, H., Rudas, A., Salamão, R., Schwarz, M., Silva, J., Silveira, M., Slik, J. W. F., Sonké, B., Thomas, A. S., Stropp, J., Taplin, J. R. D., Vásquez, R., and Vilanova, E.: Drought-mortality relationships for tropical forests, New Phytol., 187, 631–646, https://doi.org/10.1111/j.1469-8137.2010.03359.x, 2010. a
Piao, S., Sitch, S., Ciais, P., Friedlingstein, P., Peylin, P., Wang, X., Ahlström, A., Anav, A., Canadell, J. G., Cong, N., Huntingford, C., Jung, M., Levis, S., Levy, P. E., Li, J., Lin, X., Lomas, M. R., Lu, M., Luo, Y., Ma, Y., Myneni, R. B., Poulter, B., Sun, Z., Wang, T., Viovy, N., Zaehle, S., and Zeng, N.: Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends, Global Change Biol., 19, 2117–2132, https://doi.org/10.1111/gcb.12187, 2013. a
Poorter, L., van der Sande, M. T., Thompson, J., Arets, E. J. M. M., Alarcón, A., Álvarez-Sánchez, J., Ascarrunz, N., Balvanera, P., Barajas-Guzmán, G., Boit, A., Bongers, F., Carvalho, F. A., Casanoves, F., Cornejo-Tenorio, G., Costa, F. R. C., de Castilho, C. V., Duivenvoorden, J. F., Dutrieux, L. P., Enquist, B. J., Fernández-Méndez, F., Finegan, B., Gormley, L. H. L., Healey, J. R., Hoosbeek, M. R., Ibarra-Manríquez, G., Junqueira, A. B., Levis, C., Licona, J. C., Lisboa, L. S., Magnusson, W. E., Martínez-Ramos, M., Martínez-Yrizar, A., Martorano, L. G., Maskell, L. C., Mazzei, L., Meave, J. A., Mora, F., Muñoz, R., Nytch, C., Pansonato, M. P., Parr, T. W., Paz, H., Pérez-García, E. A., Rentería, L. Y., Rodríguez-Velázquez, J., Rozendaal, D. M. A., Ruschel, A. R., Sakschewski, B., Salgado-Negret, B., Schietti, J., Simões, M., Sinclair, F. L., Souza, P. F., Souza, F. C., Stropp, J., ter Steege, H., Swenson, N. G., Thonicke, K., Toledo, M., Uriarte, M., van der Hout, P., Walker, P., Zamora, N., and Peña-Claros, M.: Diversity enhances carbon storage in tropical forests, Global Ecol. Biogeogr., 24, 1314–1328, https://doi.org/10.1111/geb.12364, 2015. a
Powell, T. L., Galbraith, D. R., Christoffersen, B. O., Harper, A., Imbuzeiro, H. M. A., Rowland, L., Almeida, S., Brando, P. M., da Costa, A. C. L., Costa, M. H., Levine, N. M., Malhi, Y., Saleska, S. R., Sotta, E., Williams, M., Meir, P., and Moorcroft, P. R.: Confronting model predictions of carbon fluxes with measurements of Amazon forests subjected to experimental drought, New Phytol., 200, 350–365, https://doi.org/10.1111/nph.12390, 2013. a
Prentice, I. C., Webb, R. S., Ter-Mikhaelian, M. T., Solomon, A. M., Smith, T. M., Pitovranov, S. E., Nikolov, N. T., Minin, A. A., Leemans, R., Lavorel, S., Korzukhin, M. D., Hrabovszky, J. P., Helmisaari, H. O., Harrison, S. P., Emanuel, W. R., and Bonan, G. B.: Developing a global vegetation dynamics model: Results of an IIASA summer workshop, Research Report RR-89-7, International Institute for Applied Systems Analysis, Laxenburg, Austria, available at: http://pure.iiasa.ac.at/3223 (last access: 25 September 2019), 1989. a
Prentice, I. C., Cramer, W., Harrison, S. P., Leemans, R., Monserud, R. A., and Solomon, A. M.: A Global Biome Model Based on Plant Physiology and Dominance, Soil Properties and Climate, J. Biogeogr., 19, 117–134, https://doi.org/10.2307/2845499, 1992. a
Purves, D. and Pacala, S.: Predictive Models of Forest Dynamics, Science, 320, 1452–1453, https://doi.org/10.1126/science.1155359, 2008. a, b
Purves, D. W., Lichstein, J. W., Strigul, N., and Pacala, S. W.: Predicting and understanding forest dynamics using a simple tractable model, P. Natl. Acad. Sci. USA, 105, 17018–17022, https://doi.org/10.1073/pnas.0807754105, 2008. a
Raczka, B., Dietze, M. C., Serbin, S. P., and Davis, K. J.: What limits predictive certainty of long-term carbon uptake?, J. Geophys. Res.-Biogeosci., 123, 3570–3588, https://doi.org/10.1029/2018JG004504, 2018. a
Reich, P. B., Walters, M. B., and Ellsworth, D. S.: From tropics to tundra: Global convergence in plant functioning, P. Natl. Acad. Sci. USA, 94, 13730–13734, https://doi.org/10.1073/pnas.94.25.13730, 1997. a
Rogers, A., Medlyn, B. E., Dukes, J. S., Bonan, G., von Caemmerer, S., Dietze, M. C., Kattge, J., Leakey, A. D. B., Mercado, L. M., Niinemets, U., Prentice, I. C., Serbin, S. P., Sitch, S., Way, D. A., and Zaehle, S.: A roadmap for improving the representation of photosynthesis in Earth system models, New Phytol., 213, 22–42, https://doi.org/10.1111/nph.14283, 2017. a
Santanello Jr, J. A., Dirmeyer, P. A., Ferguson, C. R., Findell, K. L., Tawfik, A. B., Berg, A., Ek, M., Gentine, P., Guillod, B. P., van Heerwaarden, C., Roundy, J., and Wulfmeyer, V.: Land–atmosphere interactions: the LoCo perspective, B. Am. Meteorol. Soc., 99, 1253–1272, https://doi.org/10.1175/BAMS-D-17-0001.1, 2018. a
Sato, H., Itoh, A., and Kohyama, T.: SEIB–DGVM: A new Dynamic Global Vegetation Model using a spatially explicit individual-based approach, Ecol. Model., 200, 279–307, https://doi.org/10.1016/j.ecolmodel.2006.09.006, 2007. a, b
Sellers, P. J.: Canopy reflectance, photosynthesis and transpiration, Int. J. Remote Sens., 6, 1335–1372, https://doi.org/10.1080/01431168508948283, 1985. a, b
Sellers, P. J., Mintz, Y., Sud, Y. C., and Dalcher, A.: A Simple Biosphere model (SIB) for use within general circulation models, J. Atmos. Sci., 43, 505–531, https://doi.org/10.1175/1520-0469(1986)043<0505:ASBMFU>2.0.CO;2, 1986. a
Sellers, P. J., Randall, D. A., Collatz, G. J., Berry, J. A., Field, C. B., Dazlich, D. A., Zhang, C., Collelo, G. D., and Bounoua, L.: A revised land surface parameterization (SiB2) for atmospheric GCMs. Part I: model formulation, J. Climate, 9, 676–705, https://doi.org/10.1175/1520-0442(1996)009<0676:ARLSPF>2.0.CO;2, 1996. a, b
Sellers, P. J., Dickinson, R. E., Randall, D. A., Betts, A. K., Hall, F. G., Berry, J. A., Collatz, G. J., Denning, A. S., Mooney, H. A., Nobre, C. A., Sato, N., Field, C. B., and Henderson-Sellers, A.: Modeling the exchanges of energy, water, and carbon between continents and the atmosphere, Science, 275, 502–509, https://doi.org/10.1126/science.275.5299.502, 1997. a, b, c
Sheffield, J., Goteti, G., and Wood, E. F.: Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling, J. Climate, 19, 3088–3111, https://doi.org/10.1175/JCLI3790.1, 2006. a, b
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J. O., Levis, S., Lucht, W., Sykes, M. T., Thonicke, K., and Venevsky, S.: Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model, Global Change Biol., 9, 161–185, https://doi.org/10.1046/j.1365-2486.2003.00569.x, 2003. a, b
Sitch, S., Huntingford, C., Gedney, N., Levy, P. E., Lomas, M., Piao, S. L., Betts, R., Ciais, P., Cox, P., Friedlingstein, P., Jones, C. D., Prentice, I. C., and Woodward, F. I.: Evaluation of the terrestrial carbon cycle, future plant geography and climate-carbon cycle feedbacks using five Dynamic Global Vegetation Models (DGVMs), Global Change Biol., 14, 2015–2039, https://doi.org/10.1111/j.1365-2486.2008.01626.x, 2008. a
Smith, B., Prentice, I. C., and Sykes, M. T.: Representation of vegetation dynamics in the modelling of terrestrial ecosystems: comparing two contrasting approaches within European climate space, Global Ecol. Biogeogr., 10, 621–637, https://doi.org/10.1046/j.1466-822X.2001.t01-1-00256.x, 2001. a
Soares-Filho, B. S., Nepstad, D. C., Curran, L. M., Cerqueira, G. C., Garcia, R. A., Ramos, C. A., Voll, E., McDonald, A., Lefebvre, P., and Schlesinger, P.: Modelling conservation in the Amazon basin, Nature, 440, 520–523, https://doi.org/10.1038/nature04389, 2006. a
Somerville, R., Stone, P., Halem, M., Hansen, J., Hogan, J., Druyan, L., Russell, G., Lacis, A., Quirk, W., and Tenenbaum, J.: The GISS model of the global atmosphere, J. Atmos. Sci., 31, 84–117, https://doi.org/10.1175/1520-0469(1974)031<0084:TGMOTG>2.0.CO;2, 1974. a
Swann, A. L. S., Longo, M., Knox, R. G., Lee, E., and Moorcroft, P. R.: Future deforestation in the Amazon and consequences for South American climate, Agr. Forest Meteorol., 214–215, 12–24, https://doi.org/10.1016/j.agrformet.2015.07.006, 2015. a, b, c, d
The ED-2 model development team: Ecosystem Demography model (ED-2) code repository, available at: https://github.com/EDmodel/ED2 (last access: 25 September 2019), 2014.
The HDF Group: Hierarchical data format, version 5, available at: http://www.hdfgroup.org/HDF5/ (last access: 25 September 2019), 2016. a
Thonicke, K., Spessa, A., Prentice, I. C., Harrison, S. P., Dong, L., and Carmona-Moreno, C.: The influence of vegetation, fire spread and fire behaviour on biomass burning and trace gas emissions: results from a process-based model, Biogeosciences, 7, 1991–2011, https://doi.org/10.5194/bg-7-1991-2010, 2010. a
Tilman, D. and Downing, John, A.: Biodiversity and stability in grasslands, Nature, 367, 363–365, https://doi.org/10.1038/367363a0, 1994. a
Tilman, D., Isbell, F., and Cowles, J. M.: Biodiversity and ecosystem functioning, Ann. Rev. Ecol. Evol. Syst., 45, 471–493, https://doi.org/10.1146/annurev-ecolsys-120213-091917, 2014. a
Trugman, A. T., Medvigy, D., Hoffmann, W. A., and Pellegrini, A. F. A.: Sensitivity of woody carbon stocks to bark investment strategy in Neotropical savannas and forests, Biogeosciences, 15, 233–243, https://doi.org/10.5194/bg-15-233-2018, 2018. a, b
Vidale, P. L. and Stöckli, R.: Prognostic canopy air space solutions for land surface exchanges, Theor. Appl. Climatol., 80, 245–257, https://doi.org/10.1007/s00704-004-0103-2, 2005. a
von Caemmerer, S.: Biochemical models of leaf photosynthesis, no. 2 in Techniques in Plant Sciences, CSIRO Publishing, Collingwood, VIC, Australia, https://doi.org/10.1006/anbo.2000.1296, 2000. a, b
Walko, R. L., Band, L. E., Baron, J., Kittel, T. G. F., Lammers, R., Lee, T. J., Ojima, D., Pielke, R. A., Taylor, C., Tague, C., Tremback, C. J., and Vidale, P. L.: Coupled atmosphere–biophysics–hydrology models for environmental modeling, J. Appl. Meteor., 39, 931–944, https://doi.org/10.1175/1520-0450(2000)039<0931:CABHMF>2.0.CO;2, 2000. a, b, c, d, e, f, g
Wang, J.-W., Denning, A. S., Lu, L., Baker, I. T., Corbin, K. D., and Davis, K. J.: Observations and simulations of synoptic, regional, and local variations in atmospheric CO2, J. Geophys. Res.-Atmos., 112, D04108, https://doi.org/10.1029/2006JD007410, 2007. a
Weedon, G. P., Balsamo, G., Bellouin, N., Gomes, S., Best, M. J., and Viterbo, P.: The WFDEI meteorological forcing data set: WATCH forcing data methodology applied to ERA-Interim reanalysis data, Water Resour. Res., 50, 7505–7514, https://doi.org/10.1002/2014WR015638, 2014. a
Weng, E. S., Malyshev, S., Lichstein, J. W., Farrior, C. E., Dybzinski, R., Zhang, T., Shevliakova, E., and Pacala, S. W.: Scaling from individual trees to forests in an Earth system modeling framework using a mathematically tractable model of height-structured competition, Biogeosciences, 12, 2655–2694, https://doi.org/10.5194/bg-12-2655-2015, 2015. a, b
Wohlfahrt, G., Bianchi, K., and Cernusca, A.: Leaf and stem maximum water storage capacity of herbaceous plants in a mountain meadow, J. Hydrol., 319, 383–390, https://doi.org/10.1016/j.jhydrol.2005.06.036, 2006. a
Wright, I. J., Reich, P. B., Westoby, M., Ackerly, D. D., Baruch, Z., Bongers, F., Cavender-Bares, J., Chapin, T., Cornelissen, J. H. C., Diemer, M., Flexas, J., Garnier, E., Groom, P. K., Gulias, J., Hikosaka, K., Lamont, B. B., Lee, T., Lee, W., Lusk, C., Midgley, J. J., Navas, M.-L., Niinemets, U., Oleksyn, J., Osada, N., Poorter, H., Poot, P., Prior, L., Pyankov, V. I., Roumet, C., Thomas, S. C., Tjoelker, M. G., Veneklaas, E. J., and Villar, R.: The worldwide leaf economics spectrum, Nature, 428, 821–827, https://doi.org/10.1038/nature02403, 2004. a
Xu, X., Medvigy, D., Powers, J. S., Becknell, J. M., and Guan, K.: Diversity in plant hydraulic traits explains seasonal and inter-annual variations of vegetation dynamics in seasonally dry tropical forests, New Phytol., 212, 80–95, https://doi.org/10.1111/nph.14009, 2016. a, b, c
Xu, X., Medvigy, D., Wright, S. J., Kitajima, K., Wu, J., Albert, L. P., Martins, G. A., Saleska, S. R., and Pacala, S. W.: Variations of leaf longevity in tropical moist forests predicted by a trait-driven carbon optimality model, Ecol. Lett., 20, 1097–1106, https://doi.org/10.1111/ele.12804, 2017. a
Yang, Y., Saatchi, S. S., Xu, L., Yu, Y., Choi, S., Phillips, N., Kennedy, R., Keller, M., Knyazikhin, Y., and Myneni, R. B.: Post-drought decline of the Amazon carbon sink, Nat. Comm., 9, 3172, https://doi.org/10.1038/s41467-018-05668-6, 2018. a
Zhang, K., Castanho, A. D. D. A., Galbraith, D. R., Moghim, S., Levine, N., Bras, R. L., Coe, M., Costa, M. H., Malhi, Y., Longo, M., Knox, R. G., McKnight, S., Wang, J., and Moorcroft, P. R.: The fate of Amazonian ecosystems over the coming century arising from changes in climate, atmospheric CO2 and land-use, Global Change Biol., 21, 2569–2587, https://doi.org/10.1111/gcb.12903, 2015. a, b
- Abstract
- Introduction
- Model overview
- Overview of enthalpy, water, and carbon dioxide cycles
- Submodels and parameterizations of terms of the general equations
- Results
- Discussion
- Conclusions
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Model overview
- Overview of enthalpy, water, and carbon dioxide cycles
- Submodels and parameterizations of terms of the general equations
- Results
- Discussion
- Conclusions
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement





